code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
# Health news recommendation system using multi-level topic modeling.
- Here we use the news dataset for development of recommendation system.
- We apply topic modeling at multiple level for this.
- Topic modelling help to build differet topic and among them we choose the health topic.
- But the problem is to choose the correct number of topic which give more syncronised results of health data.
### Importing the 'News dataset' for topic modelling.
```
import pandas as pd
data=pd.read_csv('abcnews-date-text.csv',error_bad_lines=False)
data_text = data[['headline_text']]
data_text['index'] = data_text.index
documents = data_text
print(len(documents))
print(documents[:5])
```
# Data preprocessing
## Different process we do here like as Tokenization ,lemetization and stemming the data
- we wanted to convert the data to their normal form for example 'stolen' would converted to steal
### Here nltk is used for removing different language rather than english (Hindi and urdu like that word would be removed)
- In preprocessing actually we remove all the punctuation marks , exclamatory marks and commas
```
import gensim
from gensim.utils import simple_preprocess
from gensim.parsing.preprocessing import STOPWORDS
from nltk.stem import WordNetLemmatizer, SnowballStemmer
from nltk.stem.porter import *
import numpy as np
np.random.seed(2018)
import nltk
nltk.download('wordnet')
```
# Lemmatization
## Lemmatization is used for gouping of word that's contains the same meaning(synonyms,antonyms)
# Tokenization
## Tokenization is used for keeps the word having meaningfull meaning
- This is used for removal of word like if,the ,a,an that word doesn't make any sense in Topic
# Stemming
## Stemming is used for convert the word into their root form
```
def lemmatize_stemming(text):
return WordNetLemmatizer().lemmatize(text, pos='v')
def preprocess(text):
result = []
for token in gensim.utils.simple_preprocess(text):
if token not in gensim.parsing.preprocessing.STOPWORDS and len(token) > 3:
result.append(lemmatize_stemming(token))
return result
```
# preview data after preprocessing
- How the data will look like
```
# Select a document to preview after preprocessing
doc_sample = documents[documents['index'] == 4310].values[0][0]
print('original document: ')
words = []
for word in doc_sample.split(' '):
words.append(word)
print(words)
print('\n\n tokenized and lemmatized document: ')
print(preprocess(doc_sample))
processed_docs = documents['headline_text'].map(preprocess)
processed_docs[:10]
```
### Dictionary is formed for
```
dictionary = gensim.corpora.Dictionary(processed_docs)
count = 0
for k, v in dictionary.iteritems():
print(k, v)
count += 1
if count > 10:
break
```
## filtering the number of word taken for building the corpus.
```
dictionary.filter_extremes(no_below=15, no_above=0.5, keep_n=100000)
bow_corpus = [dictionary.doc2bow(doc) for doc in processed_docs]
bow_corpus[4310]
```
## Saving the model by using the 'pickle'
```
import pickle
pickle.dump(bow_corpus, open('bow_corpus.pkl', 'wb'))
dictionary.save('dictionary.gensim')
bow_doc_4310 = bow_corpus[4310]
for i in range(len(bow_doc_4310)):
print("Word {} (\"{}\") appears {} time.".format(bow_doc_4310[i][0],
dictionary[bow_doc_4310[i][0]],
bow_doc_4310[i][1]))
from gensim import corpora, models
tfidf = models.TfidfModel(bow_corpus)
corpus_tfidf = tfidf[bow_corpus]
from pprint import pprint
for doc in corpus_tfidf:
pprint(doc)
break
lda_model = gensim.models.LdaMulticore(bow_corpus, num_topics=2, id2word=dictionary, passes=2, workers=2)
lda_model.save('model2.gensim')
for idx, topic in lda_model.print_topics(-1):
print('Topic: {} \nWords: {}'.format(idx, topic))
processed_docs[4310]
```
### Running the model on unseen documents
```
unseen_document = 'How a Pentagon de to help him identity crisis for Google'
bow_vector = dictionary.doc2bow(preprocess(unseen_document))
for index, score in sorted(lda_model[bow_vector], key=lambda tup: -1*tup[1]):
print("Score: {}\t Topic: {}".format(score, lda_model.print_topic(index, 10)))
dictionary = gensim.corpora.Dictionary.load('dictionary.gensim')
corpus = pickle.load(open('bow_corpus.pkl', 'rb'))
lda = gensim.models.ldamodel.LdaModel.load('model2.gensim')
```
### Analyse the result by using the pyLDAvis
```
import pyLDAvis.gensim
lda_display = pyLDAvis.gensim.prepare(lda, corpus, dictionary, sort_topics=False)
pyLDAvis.display(lda_display)
```
## As we see the above results, 2 topic is not give the syncronized result/topic related to health.so, we try it with 5 topic.
|
github_jupyter
|
import pandas as pd
data=pd.read_csv('abcnews-date-text.csv',error_bad_lines=False)
data_text = data[['headline_text']]
data_text['index'] = data_text.index
documents = data_text
print(len(documents))
print(documents[:5])
import gensim
from gensim.utils import simple_preprocess
from gensim.parsing.preprocessing import STOPWORDS
from nltk.stem import WordNetLemmatizer, SnowballStemmer
from nltk.stem.porter import *
import numpy as np
np.random.seed(2018)
import nltk
nltk.download('wordnet')
def lemmatize_stemming(text):
return WordNetLemmatizer().lemmatize(text, pos='v')
def preprocess(text):
result = []
for token in gensim.utils.simple_preprocess(text):
if token not in gensim.parsing.preprocessing.STOPWORDS and len(token) > 3:
result.append(lemmatize_stemming(token))
return result
# Select a document to preview after preprocessing
doc_sample = documents[documents['index'] == 4310].values[0][0]
print('original document: ')
words = []
for word in doc_sample.split(' '):
words.append(word)
print(words)
print('\n\n tokenized and lemmatized document: ')
print(preprocess(doc_sample))
processed_docs = documents['headline_text'].map(preprocess)
processed_docs[:10]
dictionary = gensim.corpora.Dictionary(processed_docs)
count = 0
for k, v in dictionary.iteritems():
print(k, v)
count += 1
if count > 10:
break
dictionary.filter_extremes(no_below=15, no_above=0.5, keep_n=100000)
bow_corpus = [dictionary.doc2bow(doc) for doc in processed_docs]
bow_corpus[4310]
import pickle
pickle.dump(bow_corpus, open('bow_corpus.pkl', 'wb'))
dictionary.save('dictionary.gensim')
bow_doc_4310 = bow_corpus[4310]
for i in range(len(bow_doc_4310)):
print("Word {} (\"{}\") appears {} time.".format(bow_doc_4310[i][0],
dictionary[bow_doc_4310[i][0]],
bow_doc_4310[i][1]))
from gensim import corpora, models
tfidf = models.TfidfModel(bow_corpus)
corpus_tfidf = tfidf[bow_corpus]
from pprint import pprint
for doc in corpus_tfidf:
pprint(doc)
break
lda_model = gensim.models.LdaMulticore(bow_corpus, num_topics=2, id2word=dictionary, passes=2, workers=2)
lda_model.save('model2.gensim')
for idx, topic in lda_model.print_topics(-1):
print('Topic: {} \nWords: {}'.format(idx, topic))
processed_docs[4310]
unseen_document = 'How a Pentagon de to help him identity crisis for Google'
bow_vector = dictionary.doc2bow(preprocess(unseen_document))
for index, score in sorted(lda_model[bow_vector], key=lambda tup: -1*tup[1]):
print("Score: {}\t Topic: {}".format(score, lda_model.print_topic(index, 10)))
dictionary = gensim.corpora.Dictionary.load('dictionary.gensim')
corpus = pickle.load(open('bow_corpus.pkl', 'rb'))
lda = gensim.models.ldamodel.LdaModel.load('model2.gensim')
import pyLDAvis.gensim
lda_display = pyLDAvis.gensim.prepare(lda, corpus, dictionary, sort_topics=False)
pyLDAvis.display(lda_display)
| 0.198841 | 0.884139 |
# 03 Simulating an experiment
Currently liionpack only supports constant current experiments but it is our intention to implement the full PyBaMM experiment functionality in due course. Let's get started by importing the packages.
```
import liionpack as lp
import pybamm
import numpy as np
import matplotlib.pyplot as plt
```
Set up the circuit
```
# Generate the netlist
netlist = lp.setup_circuit(Np=4, Ns=1, Rb=1.5e-3, Rc=1e-2, Ri=5e-2, V=4.0, I=5.0)
lp.draw_circuit(netlist, scale_factor=0.5, cpt_size=1.0, dpi=300, node_spacing=2.5)
```
Set up the output variables and heat transfer coefficients and battery parameters.
```
output_variables = [
'X-averaged total heating [W.m-3]',
'Volume-averaged cell temperature [K]',
'X-averaged negative particle surface concentration [mol.m-3]',
'X-averaged positive particle surface concentration [mol.m-3]',
]
# Heat transfer coefficients
htc = np.ones(4) * 10
# PyBaMM parameters
chemistry = pybamm.parameter_sets.Chen2020
parameter_values = pybamm.ParameterValues(chemistry=chemistry)
```
Now define the experiment as a constant current discharge for 1000 seconds followed by a rest of 1000 seconds followed by a constant current charge of 1000 seconds, repeated three times with a 10 second period. The period in PyBaMM determines the output data reporting period but here it also determines the global time step. This means that when solving the problem the local currents are held fixed for a period of 10 seconds and then a the new cell internal resistances and open circuit voltages are used to solve the circuit and new currents are determined by the global balance.
```
# Cycling experiment
experiment = pybamm.Experiment(
[
(
"Discharge at 5 A for 1000 s or until 3.3 V",
"Rest for 1000 s",
"Charge at 5 A for 1000 s or until 4.1 V",
"Rest for 1000 s",
)
]
* 3, period="10 s"
)
```
Now we have out experiment we can take a look at the steps involved
```
experiment.operating_conditions
```
Currently, this is the only information used by liionpack and voltage limits are ignored. There is also some additional checks that take place behind the scenes. The current must be specified in [A] and not in [C] and the time for each step must be an integer multiple of the period.
```
# Cycling experiment
bad_exp_1 = pybamm.Experiment(
[
(
"Discharge at 5 C for 1000 s",
)
]
* 3, period="10 s"
)
bad_exp_2 = pybamm.Experiment(
[
(
"Discharge at 5 A for 999 s",
)
]
* 3, period="10 s"
)
```
These bad experiments will be acceptable to PyBaMM and there is no error thrown but the liionpack solver will not like them. We can check what the protocol looks like using the `generate_protocol_from_experiment` function, and this will return a list of currents that are applied at each timestep.
```
protocol = lp.generate_protocol_from_experiment(experiment)
plt.figure()
plt.plot(protocol)
plt.xlabel("Time [s]")
plt.ylabel("Current [A]");
```
And we can see that the others throw errors.
```
bad_proto_1 = lp.generate_protocol_from_experiment(bad_exp_1)
bad_proto_2 = lp.generate_protocol_from_experiment(bad_exp_2)
```
Let's solve the problem and view the results
```
# Solve pack
output = lp.solve(netlist=netlist,
parameter_values=parameter_values,
experiment=experiment,
output_variables=output_variables,
htc=htc)
lp.plot_pack(output)
```
|
github_jupyter
|
import liionpack as lp
import pybamm
import numpy as np
import matplotlib.pyplot as plt
# Generate the netlist
netlist = lp.setup_circuit(Np=4, Ns=1, Rb=1.5e-3, Rc=1e-2, Ri=5e-2, V=4.0, I=5.0)
lp.draw_circuit(netlist, scale_factor=0.5, cpt_size=1.0, dpi=300, node_spacing=2.5)
output_variables = [
'X-averaged total heating [W.m-3]',
'Volume-averaged cell temperature [K]',
'X-averaged negative particle surface concentration [mol.m-3]',
'X-averaged positive particle surface concentration [mol.m-3]',
]
# Heat transfer coefficients
htc = np.ones(4) * 10
# PyBaMM parameters
chemistry = pybamm.parameter_sets.Chen2020
parameter_values = pybamm.ParameterValues(chemistry=chemistry)
# Cycling experiment
experiment = pybamm.Experiment(
[
(
"Discharge at 5 A for 1000 s or until 3.3 V",
"Rest for 1000 s",
"Charge at 5 A for 1000 s or until 4.1 V",
"Rest for 1000 s",
)
]
* 3, period="10 s"
)
experiment.operating_conditions
# Cycling experiment
bad_exp_1 = pybamm.Experiment(
[
(
"Discharge at 5 C for 1000 s",
)
]
* 3, period="10 s"
)
bad_exp_2 = pybamm.Experiment(
[
(
"Discharge at 5 A for 999 s",
)
]
* 3, period="10 s"
)
protocol = lp.generate_protocol_from_experiment(experiment)
plt.figure()
plt.plot(protocol)
plt.xlabel("Time [s]")
plt.ylabel("Current [A]");
bad_proto_1 = lp.generate_protocol_from_experiment(bad_exp_1)
bad_proto_2 = lp.generate_protocol_from_experiment(bad_exp_2)
# Solve pack
output = lp.solve(netlist=netlist,
parameter_values=parameter_values,
experiment=experiment,
output_variables=output_variables,
htc=htc)
lp.plot_pack(output)
| 0.505859 | 0.9633 |
```
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from gap_statistic import OptimalK
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
```
## Construct the OptimalK class using the joblib backend
### Supported backends are:
- joblib
- multiprocessing (python builtin)
- None (use single core)
```
optimalK = OptimalK(parallel_backend='rust')
optimalK
```
## Create test data, with 3 cluster centers and call optimalK with a list of clusters to fit to.
```
X, y = make_blobs(n_samples=int(1e5), n_features=2, centers=3, random_state=25)
print('Data shape: ', X.shape)
n_clusters = optimalK(X, cluster_array=np.arange(1, 15))
print('Optimal clusters: ', n_clusters)
```
## A DataFrame of gap values with each passed cluster count is now available
```
optimalK.gap_df.head()
```
## Plot the n_clusters against their gap values.
```
plt.plot(optimalK.gap_df.n_clusters, optimalK.gap_df.gap_value, linewidth=3)
plt.scatter(optimalK.gap_df[optimalK.gap_df.n_clusters == n_clusters].n_clusters,
optimalK.gap_df[optimalK.gap_df.n_clusters == n_clusters].gap_value, s=250, c='r')
plt.grid(True)
plt.xlabel('Cluster Count')
plt.ylabel('Gap Value')
plt.title('Gap Values by Cluster Count')
plt.show()
```
## `optimalK()` returns n_clusters, we can use that to fit the final KMeans model...
```
# Now that we have the optimal clusters, n, we build our own KMeans model...
km = KMeans(n_clusters)
km.fit(X)
df = pd.DataFrame(X, columns=['x','y'])
df['label'] = km.labels_
colors = plt.cm.Spectral(np.linspace(0, 1, len(df.label.unique())))
for color, label in zip(colors, df.label.unique()):
tempdf = df[df.label == label]
plt.scatter(tempdf.x, tempdf.y, c=color)
plt.scatter(km.cluster_centers_[:,0], km.cluster_centers_[:, 1], c='r', s=500, alpha=0.7, )
plt.grid(True)
plt.show()
```
### Notes:
Please be aware that, as the image above hints to, number of clusters can be subjective. This is merely meant to provide a suggestion to the number of clusters in your data; the true amount can vary depending upon your specific objective. The clusters here can be interpreted as three, but also clearly just two. Also due to random initialization, the suggested n_clusters could also vary.
---
### Use your own clustering algorithm! (Added in v1.6.0)
As the default implementation is KMeans, but Gap Statistic allows using any clusting algorithm, you can define your own in the following example:
---
#### First, define a function which takes `X` and `k`, it _must_ return a tuple of the centroid locations, and the labels assigned to `X`
```
# We'll wrap the `MeanShift` algorithm from sklearn
from sklearn.cluster import MeanShift
def special_clustering_func(X, k):
"""
Special clustering function which uses the MeanShift
model from sklearn.
These user defined functions *must* take the X and a k
and can take an arbitrary number of other kwargs, which can
be pass with `clusterer_kwargs` when initializing OptimalK
"""
# Here you can do whatever clustering algorithm you heart desires,
# but we'll do a simple wrap of the MeanShift model in sklearn.
m = MeanShift()
m.fit(X)
# Return the location of each cluster center,
# and the labels for each point.
return m.cluster_centers_, m.predict(X)
# Make some data
X, y = make_blobs(n_samples=50, n_features=2, centers=3, random_state=25)
# Define the OptimalK instance, but pass in our own clustering function
optimalk = OptimalK(clusterer=special_clustering_func)
# Use the callable instance as normal.
n_clusters = optimalk(X, n_refs=3, cluster_array=range(1, 4))
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from gap_statistic import OptimalK
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
optimalK = OptimalK(parallel_backend='rust')
optimalK
X, y = make_blobs(n_samples=int(1e5), n_features=2, centers=3, random_state=25)
print('Data shape: ', X.shape)
n_clusters = optimalK(X, cluster_array=np.arange(1, 15))
print('Optimal clusters: ', n_clusters)
optimalK.gap_df.head()
plt.plot(optimalK.gap_df.n_clusters, optimalK.gap_df.gap_value, linewidth=3)
plt.scatter(optimalK.gap_df[optimalK.gap_df.n_clusters == n_clusters].n_clusters,
optimalK.gap_df[optimalK.gap_df.n_clusters == n_clusters].gap_value, s=250, c='r')
plt.grid(True)
plt.xlabel('Cluster Count')
plt.ylabel('Gap Value')
plt.title('Gap Values by Cluster Count')
plt.show()
# Now that we have the optimal clusters, n, we build our own KMeans model...
km = KMeans(n_clusters)
km.fit(X)
df = pd.DataFrame(X, columns=['x','y'])
df['label'] = km.labels_
colors = plt.cm.Spectral(np.linspace(0, 1, len(df.label.unique())))
for color, label in zip(colors, df.label.unique()):
tempdf = df[df.label == label]
plt.scatter(tempdf.x, tempdf.y, c=color)
plt.scatter(km.cluster_centers_[:,0], km.cluster_centers_[:, 1], c='r', s=500, alpha=0.7, )
plt.grid(True)
plt.show()
# We'll wrap the `MeanShift` algorithm from sklearn
from sklearn.cluster import MeanShift
def special_clustering_func(X, k):
"""
Special clustering function which uses the MeanShift
model from sklearn.
These user defined functions *must* take the X and a k
and can take an arbitrary number of other kwargs, which can
be pass with `clusterer_kwargs` when initializing OptimalK
"""
# Here you can do whatever clustering algorithm you heart desires,
# but we'll do a simple wrap of the MeanShift model in sklearn.
m = MeanShift()
m.fit(X)
# Return the location of each cluster center,
# and the labels for each point.
return m.cluster_centers_, m.predict(X)
# Make some data
X, y = make_blobs(n_samples=50, n_features=2, centers=3, random_state=25)
# Define the OptimalK instance, but pass in our own clustering function
optimalk = OptimalK(clusterer=special_clustering_func)
# Use the callable instance as normal.
n_clusters = optimalk(X, n_refs=3, cluster_array=range(1, 4))
| 0.851891 | 0.940626 |
<center>
<img src="https://gitlab.com/ibm/skills-network/courses/placeholder101/-/raw/master/labs/module%201/images/IDSNlogo.png" width="300" alt="cognitiveclass.ai logo" />
</center>
# **SpaceX Falcon 9 first stage Landing Prediction**
# Lab 1: Collecting the data
Estimated time needed: **45** minutes
In this capstone, we will predict if the Falcon 9 first stage will land successfully. SpaceX advertises Falcon 9 rocket launches on its website with a cost of 62 million dollars; other providers cost upward of 165 million dollars each, much of the savings is because SpaceX can reuse the first stage. Therefore if we can determine if the first stage will land, we can determine the cost of a launch. This information can be used if an alternate company wants to bid against SpaceX for a rocket launch. In this lab, you will collect and make sure the data is in the correct format from an API. The following is an example of a successful and launch.

Several examples of an unsuccessful landing are shown here:

Most unsuccessful landings are planned. Space X performs a controlled landing in the oceans.
## Objectives
In this lab, you will make a get request to the SpaceX API. You will also do some basic data wrangling and formating.
* Request to the SpaceX API
* Clean the requested data
***
## Import Libraries and Define Auxiliary Functions
We will import the following libraries into the lab
```
# Requests allows us to make HTTP requests which we will use to get data from an API
import requests
# Pandas is a software library written for the Python programming language for data manipulation and analysis.
import pandas as pd
# NumPy is a library for the Python programming language, adding support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays
import numpy as np
# Datetime is a library that allows us to represent dates
import datetime
# Setting this option will print all collumns of a dataframe
pd.set_option('display.max_columns', None)
# Setting this option will print all of the data in a feature
pd.set_option('display.max_colwidth', None)
print('done')
```
Below we will define a series of helper functions that will help us use the API to extract information using identification numbers in the launch data.
From the <code>rocket</code> column we would like to learn the booster name.
```
# Takes the dataset and uses the rocket column to call the API and append the data to the list
def getBoosterVersion(data):
for x in data['rocket']:
response = requests.get("https://api.spacexdata.com/v4/rockets/"+str(x)).json()
BoosterVersion.append(response['name'])
```
From the <code>launchpad</code> we would like to know the name of the launch site being used, the logitude, and the latitude.
```
# Takes the dataset and uses the launchpad column to call the API and append the data to the list
def getLaunchSite(data):
for x in data['launchpad']:
response = requests.get("https://api.spacexdata.com/v4/launchpads/"+str(x)).json()
Longitude.append(response['longitude'])
Latitude.append(response['latitude'])
LaunchSite.append(response['name'])
```
From the <code>payload</code> we would like to learn the mass of the payload and the orbit that it is going to.
```
# Takes the dataset and uses the payloads column to call the API and append the data to the lists
def getPayloadData(data):
for load in data['payloads']:
response = requests.get("https://api.spacexdata.com/v4/payloads/"+load).json()
PayloadMass.append(response['mass_kg'])
Orbit.append(response['orbit'])
```
From <code>cores</code> we would like to learn the outcome of the landing, the type of the landing, number of flights with that core, whether gridfins were used, wheter the core is reused, wheter legs were used, the landing pad used, the block of the core which is a number used to seperate version of cores, the number of times this specific core has been reused, and the serial of the core.
```
# Takes the dataset and uses the cores column to call the API and append the data to the lists
def getCoreData(data):
for core in data['cores']:
if core['core'] != None:
response = requests.get("https://api.spacexdata.com/v4/cores/"+core['core']).json()
Block.append(response['block'])
ReusedCount.append(response['reuse_count'])
Serial.append(response['serial'])
else:
Block.append(None)
ReusedCount.append(None)
Serial.append(None)
Outcome.append(str(core['landing_success'])+' '+str(core['landing_type']))
Flights.append(core['flight'])
GridFins.append(core['gridfins'])
Reused.append(core['reused'])
Legs.append(core['legs'])
LandingPad.append(core['landpad'])
```
Now let's start requesting rocket launch data from SpaceX API with the following URL:
```
spacex_url="https://api.spacexdata.com/v4/launches/past"
response = requests.get(spacex_url)
```
Check the content of the response
```
print(response.content)
```
You should see the response contains massive information about SpaceX launches. Next, let's try to discover some more relevant information for this project.
### Task 1: Request and parse the SpaceX launch data using the GET request
To make the requested JSON results more consistent, we will use the following static response object for this project:
```
static_json_url='https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/API_call_spacex_api.json'
```
We should see that the request was successfull with the 200 status response code
```
response.status_code
```
Now we decode the response content as a Json using <code>.json()</code> and turn it into a Pandas dataframe using <code>.json_normalize()</code>
```
# Use json_normalize meethod to convert the json result into a dataframe
data = pd.json_normalize(response.json())
```
Using the dataframe <code>data</code> print the first 5 rows
```
# Get the head of the dataframe
data.head()
```
You will notice that a lot of the data are IDs. For example the rocket column has no information about the rocket just an identification number.
We will now use the API again to get information about the launches using the IDs given for each launch. Specifically we will be using columns <code>rocket</code>, <code>payloads</code>, <code>launchpad</code>, and <code>cores</code>.
```
# Lets take a subset of our dataframe keeping only the features we want and the flight number, and date_utc.
data = data[['rocket', 'payloads', 'launchpad', 'cores', 'flight_number', 'date_utc']]
# We will remove rows with multiple cores because those are falcon rockets with 2 extra rocket boosters and rows that have multiple payloads in a single rocket.
data = data[data['cores'].map(len)==1]
data = data[data['payloads'].map(len)==1]
# Since payloads and cores are lists of size 1 we will also extract the single value in the list and replace the feature.
data['cores'] = data['cores'].map(lambda x : x[0])
data['payloads'] = data['payloads'].map(lambda x : x[0])
# We also want to convert the date_utc to a datetime datatype and then extracting the date leaving the time
data['date'] = pd.to_datetime(data['date_utc']).dt.date
# Using the date we will restrict the dates of the launches
data = data[data['date'] <= datetime.date(2020, 11, 13)]
data.head()
```
* From the <code>rocket</code> we would like to learn the booster name
* From the <code>payload</code> we would like to learn the mass of the payload and the orbit that it is going to
* From the <code>launchpad</code> we would like to know the name of the launch site being used, the longitude, and the latitude.
* From <code>cores</code> we would like to learn the outcome of the landing, the type of the landing, number of flights with that core, whether gridfins were used, whether the core is reused, whether legs were used, the landing pad used, the block of the core which is a number used to seperate version of cores, the number of times this specific core has been reused, and the serial of the core.
The data from these requests will be stored in lists and will be used to create a new dataframe.
```
#Global variables
BoosterVersion = []
PayloadMass = []
Orbit = []
LaunchSite = []
Outcome = []
Flights = []
GridFins = []
Reused = []
Legs = []
LandingPad = []
Block = []
ReusedCount = []
Serial = []
Longitude = []
Latitude = []
```
These functions will apply the outputs globally to the above variables. Let's take a looks at <code>BoosterVersion</code> variable. Before we apply <code>getBoosterVersion</code> the list is empty:
```
BoosterVersion
```
Now, let's apply <code> getBoosterVersion</code> function method to get the booster version
```
# Call getBoosterVersion
getBoosterVersion(data)
```
the list has now been update
```
BoosterVersion[0:5]
```
we can apply the rest of the functions here:
```
# Call getLaunchSite
getLaunchSite(data)
# Call getPayloadData
getPayloadData(data)
# Call getCoreData
getCoreData(data)
```
Finally lets construct our dataset using the data we have obtained. We we combine the columns into a dictionary.
```
launch_dict = {'FlightNumber': list(data['flight_number']),
'Date': list(data['date']),
'BoosterVersion':BoosterVersion,
'PayloadMass':PayloadMass,
'Orbit':Orbit,
'LaunchSite':LaunchSite,
'Outcome':Outcome,
'Flights':Flights,
'GridFins':GridFins,
'Reused':Reused,
'Legs':Legs,
'LandingPad':LandingPad,
'Block':Block,
'ReusedCount':ReusedCount,
'Serial':Serial,
'Longitude': Longitude,
'Latitude': Latitude}
```
Then, we need to create a Pandas data frame from the dictionary launch_dict.
```
# Create a data from launch_dict
df = pd.DataFrame(launch_dict)
```
Show the summary of the dataframe
```
# Show the head of the dataframe
df.head()
```
### Task 2: Filter the dataframe to only include `Falcon 9` launches
Finally we will remove the Falcon 1 launches keeping only the Falcon 9 launches. Filter the data dataframe using the <code>BoosterVersion</code> column to only keep the Falcon 9 launches. Save the filtered data to a new dataframe called <code>data_falcon9</code>.
```
# Hint data['BoosterVersion']!='Falcon 1'
data_falcon9 = df[df['BoosterVersion']!='Falcon 1']
data_falcon9.head()
```
Now that we have removed some values we should reset the FlgihtNumber column
```
data_falcon9.loc[:,'FlightNumber'] = list(range(1, data_falcon9.shape[0]+1))
data_falcon9
```
## Data Wrangling
We can see below that some of the rows are missing values in our dataset.
```
data_falcon9.isnull().sum()
```
Before we can continue we must deal with these missing values. The <code>LandingPad</code> column will retain None values to represent when landing pads were not used.
### Task 3: Dealing with Missing Values
Calculate below the mean for the <code>PayloadMass</code> using the <code>.mean()</code>. Then use the mean and the <code>.replace()</code> function to replace `np.nan` values in the data with the mean you calculated.
```
# Calculate the mean value of PayloadMass column
mean = data_falcon9["PayloadMass"].mean()
# Replace the np.nan values with its mean value
data_falcon9['PayloadMass'].replace(np.nan, mean)
data_falcon9
data_falcon9.isnull().sum()
```
You should see the number of missing values of the <code>PayLoadMass</code> change to zero.
Now we should have no missing values in our dataset except for in <code>LandingPad</code>.
We can now export it to a <b>CSV</b> for the next section,but to make the answers consistent, in the next lab we will provide data in a pre-selected date range.
<code>data_falcon9.to_csv('dataset_part\_1.csv', index=False)</code>
## Authors
<a href="https://www.linkedin.com/in/joseph-s-50398b136/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDS0321ENSkillsNetwork26802033-2021-01-01">Joseph Santarcangelo</a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
## Change Log
| Date (YYYY-MM-DD) | Version | Changed By | Change Description |
| ----------------- | ------- | ---------- | ----------------------------------- |
| 2020-09-20 | 1.1 | Joseph | get result each time you run |
| 2020-09-20 | 1.1 | Azim | Created Part 1 Lab using SpaceX API |
| 2020-09-20 | 1.0 | Joseph | Modified Multiple Areas |
Copyright © 2021 IBM Corporation. All rights reserved.
|
github_jupyter
|
# Requests allows us to make HTTP requests which we will use to get data from an API
import requests
# Pandas is a software library written for the Python programming language for data manipulation and analysis.
import pandas as pd
# NumPy is a library for the Python programming language, adding support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays
import numpy as np
# Datetime is a library that allows us to represent dates
import datetime
# Setting this option will print all collumns of a dataframe
pd.set_option('display.max_columns', None)
# Setting this option will print all of the data in a feature
pd.set_option('display.max_colwidth', None)
print('done')
# Takes the dataset and uses the rocket column to call the API and append the data to the list
def getBoosterVersion(data):
for x in data['rocket']:
response = requests.get("https://api.spacexdata.com/v4/rockets/"+str(x)).json()
BoosterVersion.append(response['name'])
# Takes the dataset and uses the launchpad column to call the API and append the data to the list
def getLaunchSite(data):
for x in data['launchpad']:
response = requests.get("https://api.spacexdata.com/v4/launchpads/"+str(x)).json()
Longitude.append(response['longitude'])
Latitude.append(response['latitude'])
LaunchSite.append(response['name'])
# Takes the dataset and uses the payloads column to call the API and append the data to the lists
def getPayloadData(data):
for load in data['payloads']:
response = requests.get("https://api.spacexdata.com/v4/payloads/"+load).json()
PayloadMass.append(response['mass_kg'])
Orbit.append(response['orbit'])
# Takes the dataset and uses the cores column to call the API and append the data to the lists
def getCoreData(data):
for core in data['cores']:
if core['core'] != None:
response = requests.get("https://api.spacexdata.com/v4/cores/"+core['core']).json()
Block.append(response['block'])
ReusedCount.append(response['reuse_count'])
Serial.append(response['serial'])
else:
Block.append(None)
ReusedCount.append(None)
Serial.append(None)
Outcome.append(str(core['landing_success'])+' '+str(core['landing_type']))
Flights.append(core['flight'])
GridFins.append(core['gridfins'])
Reused.append(core['reused'])
Legs.append(core['legs'])
LandingPad.append(core['landpad'])
spacex_url="https://api.spacexdata.com/v4/launches/past"
response = requests.get(spacex_url)
print(response.content)
static_json_url='https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/API_call_spacex_api.json'
response.status_code
# Use json_normalize meethod to convert the json result into a dataframe
data = pd.json_normalize(response.json())
# Get the head of the dataframe
data.head()
# Lets take a subset of our dataframe keeping only the features we want and the flight number, and date_utc.
data = data[['rocket', 'payloads', 'launchpad', 'cores', 'flight_number', 'date_utc']]
# We will remove rows with multiple cores because those are falcon rockets with 2 extra rocket boosters and rows that have multiple payloads in a single rocket.
data = data[data['cores'].map(len)==1]
data = data[data['payloads'].map(len)==1]
# Since payloads and cores are lists of size 1 we will also extract the single value in the list and replace the feature.
data['cores'] = data['cores'].map(lambda x : x[0])
data['payloads'] = data['payloads'].map(lambda x : x[0])
# We also want to convert the date_utc to a datetime datatype and then extracting the date leaving the time
data['date'] = pd.to_datetime(data['date_utc']).dt.date
# Using the date we will restrict the dates of the launches
data = data[data['date'] <= datetime.date(2020, 11, 13)]
data.head()
#Global variables
BoosterVersion = []
PayloadMass = []
Orbit = []
LaunchSite = []
Outcome = []
Flights = []
GridFins = []
Reused = []
Legs = []
LandingPad = []
Block = []
ReusedCount = []
Serial = []
Longitude = []
Latitude = []
BoosterVersion
# Call getBoosterVersion
getBoosterVersion(data)
BoosterVersion[0:5]
# Call getLaunchSite
getLaunchSite(data)
# Call getPayloadData
getPayloadData(data)
# Call getCoreData
getCoreData(data)
launch_dict = {'FlightNumber': list(data['flight_number']),
'Date': list(data['date']),
'BoosterVersion':BoosterVersion,
'PayloadMass':PayloadMass,
'Orbit':Orbit,
'LaunchSite':LaunchSite,
'Outcome':Outcome,
'Flights':Flights,
'GridFins':GridFins,
'Reused':Reused,
'Legs':Legs,
'LandingPad':LandingPad,
'Block':Block,
'ReusedCount':ReusedCount,
'Serial':Serial,
'Longitude': Longitude,
'Latitude': Latitude}
# Create a data from launch_dict
df = pd.DataFrame(launch_dict)
# Show the head of the dataframe
df.head()
# Hint data['BoosterVersion']!='Falcon 1'
data_falcon9 = df[df['BoosterVersion']!='Falcon 1']
data_falcon9.head()
data_falcon9.loc[:,'FlightNumber'] = list(range(1, data_falcon9.shape[0]+1))
data_falcon9
data_falcon9.isnull().sum()
# Calculate the mean value of PayloadMass column
mean = data_falcon9["PayloadMass"].mean()
# Replace the np.nan values with its mean value
data_falcon9['PayloadMass'].replace(np.nan, mean)
data_falcon9
data_falcon9.isnull().sum()
| 0.506836 | 0.991084 |
**K-Means Clustering in Python with scikit-learn**
The training set contains several records about the passengers of Titanic (hence the name of the dataset). It has 12 features capturing information about passenger_class, port_of_Embarkation, passenger_fare etc. The dataset's label is survival which denotes the survivial status of a particular passenger. Your task is to cluster the records into two i.e. the ones who survived and the ones who did not.
Drop the 'survival' column from the dataset and make it unlabeled. It's the task of K-Means to cluster the records of the datasets if they survived or not.
you will need the following Python packages: pandas, NumPy, scikit-learn, Seaborn and Matplotlib.
```
"""
================================
Kmeans
================================
*************************************************************************************
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!! /!\ DOES NOT WORK /!\ !!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
*************************************************************************************
Sample usage of Kmeans clustering.
This notebook is all about finding the best tuning with the Kmeans model,
for predicting activities types in function of acceleration measurements.
It will plot the decision boundaries for each class.
"""
print(__doc__)
# Import statements
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import MinMaxScaler
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# Import data into a dataframe
CSV_PATH = '../data/cleaned_data/full_with_act_1_transitory_regimes_cleaned.csv'
X = pd.read_csv(CSV_PATH,header=None,delimiter=',',usecols=[1, 2, 3, 4]).astype(int)
X.head()
# Create train and test datasets as dataframes
import random
from sklearn.model_selection import train_test_split
train, test = train_test_split(X,test_size=0.3,random_state=3) # random seed set to a fix value
# Check whether data is well imported
print("***** Train_Set *****")
print(train.head())
print("\n")
print("***** Test_Set *****")
print(test.head())
# Initial statistics of both the train and test DataFrames using pandas' describe() method.
print(train.columns.values)
print("***** Train_Set *****")
print(train.describe())
print("\n")
print("***** Test_Set *****")
print(test.describe())
# Analyze missing values in the datasets
# where are they ?
# For the train set
train.isna().head()
# For the test set
test.isna().head()
# Their numbers
print("*****In the train set*****")
print(train.isna().sum())
print("\n")
print("*****In the test set*****")
print(test.isna().sum())
# Missing values imputation
# Fill missing values with mean column values in the train set
train.fillna(train.mean(), inplace=True)
# Fill missing values with mean column values in the test set
test.fillna(test.mean(), inplace=True)
# Check if that's ok
print(train.isna().sum())
# Still missing values for categorical variables
train[[1,2,3]]
# Check mean accelerations in (x, y, z) according to activity type
train[[1,2,3,4]].groupby([4], as_index=False).mean().sort_values(by=4, ascending=False)
# Check standard deviation accelerations in (x, y, z) according to activity type
train[[1,2,3,4]].groupby([4], as_index=False).std().sort_values(by=4, ascending=False)
# By Pclass
for k in range(1,4):
train[[k, 4]].groupby([4], as_index=False).mean().sort_values(by=k, ascending=False)
print(train)
# Some Graphics
g = sns.FacetGrid(train, col=4)
for k in range(0,4):
g.map(plt.hist, k, bins=20)
grid = sns.FacetGrid(train, col='Survived', row='Pclass', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend()
```
# Preprocessing data set for kmeans
```
train.info()
# You can see that Name, Sex, Ticket, Cabin, Embarked are not numerical
# We drop all of them except Sex that we convert to numerical
DD = train.drop(['Name','Ticket', 'Cabin','Embarked','PassengerId'], axis=1)
DD2 = test.drop(['Name','Ticket', 'Cabin','Embarked','PassengerId'], axis=1)
labelEncoder = LabelEncoder()
labelEncoder.fit(DD['Sex'])
labelEncoder.fit(DD2['Sex'])
DD['Sex'] = labelEncoder.transform(DD['Sex'])
DD2['Sex'] = labelEncoder.transform(DD2['Sex'])
# You can first drop the Survival column from the data with the drop() function.
X = np.array(DD.drop(['Survived'], 1).astype(float))
y = np.array(DD['Survived'])
print(X.shape)
import seaborn as sns
sns.pairplot(pd.DataFrame(X))
km = KMeans(n_clusters=2)
# You want cluster the passenger records into 2and check if they correspond to Survived or Not survived
km.fit(X)
print(km.labels_)
```
**TODO**
You can compare kmeans labelling with the survival status
* Look at the confusion matrix using confusion_matrix() from sklearn.metrics
* You can compute the adjusted_rand_score() from sklearn.metrics.cluster import
* Does scaling affect the result ? use a scaling approach like MinMaxScaler()
|
github_jupyter
|
"""
================================
Kmeans
================================
*************************************************************************************
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!! /!\ DOES NOT WORK /!\ !!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
*************************************************************************************
Sample usage of Kmeans clustering.
This notebook is all about finding the best tuning with the Kmeans model,
for predicting activities types in function of acceleration measurements.
It will plot the decision boundaries for each class.
"""
print(__doc__)
# Import statements
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import MinMaxScaler
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# Import data into a dataframe
CSV_PATH = '../data/cleaned_data/full_with_act_1_transitory_regimes_cleaned.csv'
X = pd.read_csv(CSV_PATH,header=None,delimiter=',',usecols=[1, 2, 3, 4]).astype(int)
X.head()
# Create train and test datasets as dataframes
import random
from sklearn.model_selection import train_test_split
train, test = train_test_split(X,test_size=0.3,random_state=3) # random seed set to a fix value
# Check whether data is well imported
print("***** Train_Set *****")
print(train.head())
print("\n")
print("***** Test_Set *****")
print(test.head())
# Initial statistics of both the train and test DataFrames using pandas' describe() method.
print(train.columns.values)
print("***** Train_Set *****")
print(train.describe())
print("\n")
print("***** Test_Set *****")
print(test.describe())
# Analyze missing values in the datasets
# where are they ?
# For the train set
train.isna().head()
# For the test set
test.isna().head()
# Their numbers
print("*****In the train set*****")
print(train.isna().sum())
print("\n")
print("*****In the test set*****")
print(test.isna().sum())
# Missing values imputation
# Fill missing values with mean column values in the train set
train.fillna(train.mean(), inplace=True)
# Fill missing values with mean column values in the test set
test.fillna(test.mean(), inplace=True)
# Check if that's ok
print(train.isna().sum())
# Still missing values for categorical variables
train[[1,2,3]]
# Check mean accelerations in (x, y, z) according to activity type
train[[1,2,3,4]].groupby([4], as_index=False).mean().sort_values(by=4, ascending=False)
# Check standard deviation accelerations in (x, y, z) according to activity type
train[[1,2,3,4]].groupby([4], as_index=False).std().sort_values(by=4, ascending=False)
# By Pclass
for k in range(1,4):
train[[k, 4]].groupby([4], as_index=False).mean().sort_values(by=k, ascending=False)
print(train)
# Some Graphics
g = sns.FacetGrid(train, col=4)
for k in range(0,4):
g.map(plt.hist, k, bins=20)
grid = sns.FacetGrid(train, col='Survived', row='Pclass', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend()
train.info()
# You can see that Name, Sex, Ticket, Cabin, Embarked are not numerical
# We drop all of them except Sex that we convert to numerical
DD = train.drop(['Name','Ticket', 'Cabin','Embarked','PassengerId'], axis=1)
DD2 = test.drop(['Name','Ticket', 'Cabin','Embarked','PassengerId'], axis=1)
labelEncoder = LabelEncoder()
labelEncoder.fit(DD['Sex'])
labelEncoder.fit(DD2['Sex'])
DD['Sex'] = labelEncoder.transform(DD['Sex'])
DD2['Sex'] = labelEncoder.transform(DD2['Sex'])
# You can first drop the Survival column from the data with the drop() function.
X = np.array(DD.drop(['Survived'], 1).astype(float))
y = np.array(DD['Survived'])
print(X.shape)
import seaborn as sns
sns.pairplot(pd.DataFrame(X))
km = KMeans(n_clusters=2)
# You want cluster the passenger records into 2and check if they correspond to Survived or Not survived
km.fit(X)
print(km.labels_)
| 0.665302 | 0.936343 |
#1. Install Dependencies
First install the libraries needed to execute recipes, this only needs to be done once, then click play.
```
!pip install git+https://github.com/google/starthinker
```
#2. Get Cloud Project ID
To run this recipe [requires a Google Cloud Project](https://github.com/google/starthinker/blob/master/tutorials/cloud_project.md), this only needs to be done once, then click play.
```
CLOUD_PROJECT = 'PASTE PROJECT ID HERE'
print("Cloud Project Set To: %s" % CLOUD_PROJECT)
```
#3. Get Client Credentials
To read and write to various endpoints requires [downloading client credentials](https://github.com/google/starthinker/blob/master/tutorials/cloud_client_installed.md), this only needs to be done once, then click play.
```
CLIENT_CREDENTIALS = 'PASTE CREDENTIALS HERE'
print("Client Credentials Set To: %s" % CLIENT_CREDENTIALS)
```
#4. Enter Trends Places To Sheets Via Values Parameters
Move using hard coded WOEID values.
1. Provide <a href='https://apps.twitter.com/' target='_blank'>Twitter credentials</a>.
1. Provide a comma delimited list of WOEIDs.
1. Specify Sheet url and tab to write API call results to.
1. Writes: WOEID, Name, Url, Promoted_Content, Query, Tweet_Volume
1. Note Twitter API is rate limited to 15 requests per 15 minutes. So keep WOEID lists short.
Modify the values below for your use case, can be done multiple times, then click play.
```
FIELDS = {
'auth_write': 'service', # Credentials used for writing data.
'secret': '',
'key': '',
'places_dataset': '',
'places_query': '',
'places_legacy': False,
'destination_sheet': '',
'destination_tab': '',
}
print("Parameters Set To: %s" % FIELDS)
```
#5. Execute Trends Places To Sheets Via Values
This does NOT need to be modified unles you are changing the recipe, click play.
```
from starthinker.util.project import project
from starthinker.script.parse import json_set_fields
USER_CREDENTIALS = '/content/user.json'
TASKS = [
{
'twitter': {
'auth': 'user',
'secret': {'field': {'name': 'secret','kind': 'string','order': 1,'default': ''}},
'key': {'field': {'name': 'key','kind': 'string','order': 2,'default': ''}},
'trends': {
'places': {
'single_cell': True,
'bigquery': {
'dataset': {'field': {'name': 'places_dataset','kind': 'string','order': 3,'default': ''}},
'query': {'field': {'name': 'places_query','kind': 'string','order': 4,'default': ''}},
'legacy': {'field': {'name': 'places_legacy','kind': 'boolean','order': 5,'default': False}}
}
}
},
'out': {
'sheets': {
'sheet': {'field': {'name': 'destination_sheet','kind': 'string','order': 6,'default': ''}},
'tab': {'field': {'name': 'destination_tab','kind': 'string','order': 7,'default': ''}},
'range': 'A1'
}
}
}
}
]
json_set_fields(TASKS, FIELDS)
project.initialize(_recipe={ 'tasks':TASKS }, _project=CLOUD_PROJECT, _user=USER_CREDENTIALS, _client=CLIENT_CREDENTIALS, _verbose=True, _force=True)
project.execute(_force=True)
```
|
github_jupyter
|
!pip install git+https://github.com/google/starthinker
CLOUD_PROJECT = 'PASTE PROJECT ID HERE'
print("Cloud Project Set To: %s" % CLOUD_PROJECT)
CLIENT_CREDENTIALS = 'PASTE CREDENTIALS HERE'
print("Client Credentials Set To: %s" % CLIENT_CREDENTIALS)
FIELDS = {
'auth_write': 'service', # Credentials used for writing data.
'secret': '',
'key': '',
'places_dataset': '',
'places_query': '',
'places_legacy': False,
'destination_sheet': '',
'destination_tab': '',
}
print("Parameters Set To: %s" % FIELDS)
from starthinker.util.project import project
from starthinker.script.parse import json_set_fields
USER_CREDENTIALS = '/content/user.json'
TASKS = [
{
'twitter': {
'auth': 'user',
'secret': {'field': {'name': 'secret','kind': 'string','order': 1,'default': ''}},
'key': {'field': {'name': 'key','kind': 'string','order': 2,'default': ''}},
'trends': {
'places': {
'single_cell': True,
'bigquery': {
'dataset': {'field': {'name': 'places_dataset','kind': 'string','order': 3,'default': ''}},
'query': {'field': {'name': 'places_query','kind': 'string','order': 4,'default': ''}},
'legacy': {'field': {'name': 'places_legacy','kind': 'boolean','order': 5,'default': False}}
}
}
},
'out': {
'sheets': {
'sheet': {'field': {'name': 'destination_sheet','kind': 'string','order': 6,'default': ''}},
'tab': {'field': {'name': 'destination_tab','kind': 'string','order': 7,'default': ''}},
'range': 'A1'
}
}
}
}
]
json_set_fields(TASKS, FIELDS)
project.initialize(_recipe={ 'tasks':TASKS }, _project=CLOUD_PROJECT, _user=USER_CREDENTIALS, _client=CLIENT_CREDENTIALS, _verbose=True, _force=True)
project.execute(_force=True)
| 0.268174 | 0.725576 |
# HW1 Data Curation
## Step1: Data Acquistion
Using wikipedia API, The Pageviews API provides data for desktop, mobile -web, and mobile-app from July 2015- Sep 2017, and the legacy Pagecounts API provides traffic data for desktop and mobile from January 2008 to July 2016
At first, import the package we need:
```
import json
import requests
import matplotlib.pyplot as plt
import datetime
import numpy as np
import pandas as pd
```
Next, I need get the data for desktop, mobile-web, and mobile-app on page views from 2015-07-01 to 2016-09-30. I set a endpoint and changing the parameter for different access.
```
# endpoint with parameters
endpoint = 'https://wikimedia.org/api/rest_v1/metrics/pageviews/aggregate/{project}/{access}/{agent}/{granularity}/{start}/{end}'
headers={'User-Agent' : 'https://github.com/runlaizeng', 'From' : 'runlaiz@uw.edu'}
#access for desktop
params = {'project' : 'en.wikipedia.org',
'access' : 'desktop',
'agent' : 'user',
'granularity' : 'monthly',
'start' : '2015070100',
'end' : '2017093000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pageviews_desktop_201507-201709.json','w') as f:
json.dump(response,f)
#access for mobile-app
params = {'project' : 'en.wikipedia.org',
'access' : 'mobile-app',
'agent' : 'user',
'granularity' : 'monthly',
'start' : '2015070100',
'end' : '2017093000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pageviews_mobile-app_201507-201709.json','w') as f:
json.dump(response,f)
#access for mobile-web
params = {'project' : 'en.wikipedia.org',
'access' : 'mobile-web',
'agent' : 'user',
'granularity' : 'monthly',
'start' : '2015070100',
'end' : '2017093000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pageviews_mobile-web_201507-201709.json','w') as f:
json.dump(response,f)
```
Now, we change the end point for pagecounts to get desktop and mobile views from 2008-01-01 to 2016-07-30
```
#change endpoint for pagecounts with parameters
endpoint = 'https://wikimedia.org/api/rest_v1/metrics/legacy/pagecounts/aggregate/{project}/{access-site}/{granularity}/{start}/{end}'
#get data for desktop
params = {'project' : 'en.wikipedia',
'access-site' : 'desktop-site',
'granularity' : 'monthly',
'start' : '2008010100',
'end' : '2016073000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pagecounts_desktop-site_200801-201607.json','w') as f:
json.dump(response,f)
# get data for mobile
params = {'project' : 'en.wikipedia.org',
'access-site' : 'mobile-site',
'granularity' : 'monthly',
'start' : '2008010100',
'end' : '2016073000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pagecounts_mobile-site_200801-201607.json','w') as f:
json.dump(response,f)
```
## Step 2: Data Processing
We need to do somt proccessing on these json file data inorder to analysis. I conbine monthly mobile-app and monthly mobile-web to total mobile for pageviews.
First, read the json file sepreatedly
```
#read json files
with open('pageviews_desktop_201507-201709.json','r') as f:
data_1 = json.load(f)
with open('pageviews_mobile-app_201507-201709.json','r') as f:
data_2 = json.load(f)
with open('pageviews_mobile-web_201507-201709.json','r') as f:
data_3= json.load(f)
with open('pagecounts_desktop-site_200801-201607.json','r') as f:
data_4 = json.load(f)
with open('pagecounts_mobile-site_200801-201607.json','r') as f:
data_5 = json.load(f)
#load json in datapfram
df_1 = pd.DataFrame(data_1['items'])
df_2 = pd.DataFrame(data_2['items'])
df_3 = pd.DataFrame(data_3['items'])
df_4 = pd.DataFrame(data_4['items'])
df_5 = pd.DataFrame(data_5['items'])
```
### (1) pageview_mobile_views
```
#combine web and app views and create pageview_mobile_views df
pageview_mobile_views = pd.concat([df_2['timestamp'],df_2['views']+df_3['views']], axis=1, join='inner')
pageview_mobile_views.columns = ["Date", "pageview_mobile_views"]
pageview_mobile_views[:5]
```
### (2) pageview_desktop_views
```
# create pageview_mobile_views df
pageview_desktop_views = pd.concat([df_1['timestamp'],df_1['views']], axis=1, join='inner')
pageview_desktop_views.columns = ["Date","pageview_desktop_views"]
pageview_desktop_views[:5]
```
### (3) pageview_all_views
```
#combine to total view and create df
pageview_all_views = pd.concat([df_1['timestamp'],pageview_mobile_views['pageview_mobile_views']+pageview_desktop_views['pageview_desktop_views']], axis=1, join='inner')
pageview_all_views.columns = ["Date", "pageview_all_views"]
pageview_all_views[:5]
```
### (4) pagecount_desktop_views
```
#create df for pagecount_desktop
pagecount_desktop_views = pd.concat([df_4['timestamp'],df_4['count']], axis=1, join='inner')
pagecount_desktop_views.columns = ["Date","pagecount_desktop_views"]
pagecount_desktop_views[:5]
```
### (5) pagecount_mobile_views
```
#Create df for pagecount_mobile_views
pagecount_mobile_views = pd.concat([df_5['timestamp'],df_5['count']], axis=1, join='inner')
pagecount_mobile_views.columns = ["Date","pagecount_mobile_views"]
pagecount_mobile_views[:5]
```
### (6)pagecount_all_views
```
#left join desktop df and mobile df
df_merge=df_4.merge(df_5, how='left', on='timestamp')
df_merge['count_y'].fillna(0,inplace=True)
#adding views togather and create df for pagecount_all_views
pagecount_all_views = pd.concat([df_merge['timestamp'],df_merge['count_x']+df_merge['count_y']], axis=1, join='inner')
pagecount_all_views.columns = ['Date','pagecount_all_views']
pagecount_all_views[:5]
```
### (7)mege dataframes
```
#split date to year and month as requirment
result = pagecount_all_views.merge(pagecount_desktop_views,how='left', on='Date').merge(pagecount_mobile_views,how='left', on='Date').merge(pageview_all_views,how='outer', on='Date').merge(pageview_desktop_views,how='left', on='Date').merge(pageview_mobile_views,how='left', on='Date')
result.fillna(0,inplace=True)
year = result['Date'].str[0:4]
month = result['Date'].str[4:6]
result.insert(loc=0,column='year',value=year)
result.insert(loc=1,column='month',value=month)
del result['Date']
#convert views to integer
result.pagecount_all_views = result.pagecount_all_views.astype(int)
result.pagecount_desktop_views= result.pagecount_desktop_views.astype(int)
result.pagecount_mobile_views = result.pagecount_mobile_views.astype(int)
result.pageview_all_views = result.pageview_all_views.astype(int)
result.pageview_mobile_views = result.pageview_mobile_views.astype(int)
result.pageview_desktop_views = result.pageview_desktop_views.astype(int)
result[:5]
```
### (8) output
```
#save it as csv file
result.to_csv('en-wikipedia_traffic_200801-201709.csv', sep=',')
```
## Step3 : Analysis
In order to analyze pageviews on English Wikipedia, I made a graph to show the desktop, mobile and total views.
```
result = result.replace(0,np.nan)
fig, ax = plt.subplots()
date = pd.to_datetime(result.year + result.month, format = '%Y%m')
ax.plot(date, result['pagecount_mobile_views'], color = 'blue', linestyle = '--', alpha=0.7)
ax.plot(date, result['pagecount_desktop_views'], color = 'red', linestyle = '--', alpha=0.7)
ax.plot(date, result['pagecount_all_views'], color = 'green', linestyle = '--', alpha=0.7)
ax.plot(date, result['pageview_all_views'], color = 'green', alpha=0.7)
ax.plot(date, result['pageview_mobile_views'], color = 'blue', alpha=0.7)
ax.plot(date, result['pageview_desktop_views'], color = 'red', alpha=0.7)
fig.set_size_inches(13, 8)
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, prop={'size': 20}, borderaxespad=0.)
fig.suptitle('Views on English Wikipedia', fontsize=30)
ax.set_xlabel('Year')
ax.set_ylabel('Views')
plt.show()
```
Conclusion: from the visualization above, we could say that desktop views are hihger than mobile views forom the comparsion. Also, there are two peak points for all views, the first occured on oct 2010, and the second occured on oct 2013.
|
github_jupyter
|
import json
import requests
import matplotlib.pyplot as plt
import datetime
import numpy as np
import pandas as pd
# endpoint with parameters
endpoint = 'https://wikimedia.org/api/rest_v1/metrics/pageviews/aggregate/{project}/{access}/{agent}/{granularity}/{start}/{end}'
headers={'User-Agent' : 'https://github.com/runlaizeng', 'From' : 'runlaiz@uw.edu'}
#access for desktop
params = {'project' : 'en.wikipedia.org',
'access' : 'desktop',
'agent' : 'user',
'granularity' : 'monthly',
'start' : '2015070100',
'end' : '2017093000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pageviews_desktop_201507-201709.json','w') as f:
json.dump(response,f)
#access for mobile-app
params = {'project' : 'en.wikipedia.org',
'access' : 'mobile-app',
'agent' : 'user',
'granularity' : 'monthly',
'start' : '2015070100',
'end' : '2017093000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pageviews_mobile-app_201507-201709.json','w') as f:
json.dump(response,f)
#access for mobile-web
params = {'project' : 'en.wikipedia.org',
'access' : 'mobile-web',
'agent' : 'user',
'granularity' : 'monthly',
'start' : '2015070100',
'end' : '2017093000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pageviews_mobile-web_201507-201709.json','w') as f:
json.dump(response,f)
#change endpoint for pagecounts with parameters
endpoint = 'https://wikimedia.org/api/rest_v1/metrics/legacy/pagecounts/aggregate/{project}/{access-site}/{granularity}/{start}/{end}'
#get data for desktop
params = {'project' : 'en.wikipedia',
'access-site' : 'desktop-site',
'granularity' : 'monthly',
'start' : '2008010100',
'end' : '2016073000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pagecounts_desktop-site_200801-201607.json','w') as f:
json.dump(response,f)
# get data for mobile
params = {'project' : 'en.wikipedia.org',
'access-site' : 'mobile-site',
'granularity' : 'monthly',
'start' : '2008010100',
'end' : '2016073000'#use the first day of the following month to ensure a full month of data is collected
}
api_call = requests.get(endpoint.format(**params))
response = api_call.json()
with open('pagecounts_mobile-site_200801-201607.json','w') as f:
json.dump(response,f)
#read json files
with open('pageviews_desktop_201507-201709.json','r') as f:
data_1 = json.load(f)
with open('pageviews_mobile-app_201507-201709.json','r') as f:
data_2 = json.load(f)
with open('pageviews_mobile-web_201507-201709.json','r') as f:
data_3= json.load(f)
with open('pagecounts_desktop-site_200801-201607.json','r') as f:
data_4 = json.load(f)
with open('pagecounts_mobile-site_200801-201607.json','r') as f:
data_5 = json.load(f)
#load json in datapfram
df_1 = pd.DataFrame(data_1['items'])
df_2 = pd.DataFrame(data_2['items'])
df_3 = pd.DataFrame(data_3['items'])
df_4 = pd.DataFrame(data_4['items'])
df_5 = pd.DataFrame(data_5['items'])
#combine web and app views and create pageview_mobile_views df
pageview_mobile_views = pd.concat([df_2['timestamp'],df_2['views']+df_3['views']], axis=1, join='inner')
pageview_mobile_views.columns = ["Date", "pageview_mobile_views"]
pageview_mobile_views[:5]
# create pageview_mobile_views df
pageview_desktop_views = pd.concat([df_1['timestamp'],df_1['views']], axis=1, join='inner')
pageview_desktop_views.columns = ["Date","pageview_desktop_views"]
pageview_desktop_views[:5]
#combine to total view and create df
pageview_all_views = pd.concat([df_1['timestamp'],pageview_mobile_views['pageview_mobile_views']+pageview_desktop_views['pageview_desktop_views']], axis=1, join='inner')
pageview_all_views.columns = ["Date", "pageview_all_views"]
pageview_all_views[:5]
#create df for pagecount_desktop
pagecount_desktop_views = pd.concat([df_4['timestamp'],df_4['count']], axis=1, join='inner')
pagecount_desktop_views.columns = ["Date","pagecount_desktop_views"]
pagecount_desktop_views[:5]
#Create df for pagecount_mobile_views
pagecount_mobile_views = pd.concat([df_5['timestamp'],df_5['count']], axis=1, join='inner')
pagecount_mobile_views.columns = ["Date","pagecount_mobile_views"]
pagecount_mobile_views[:5]
#left join desktop df and mobile df
df_merge=df_4.merge(df_5, how='left', on='timestamp')
df_merge['count_y'].fillna(0,inplace=True)
#adding views togather and create df for pagecount_all_views
pagecount_all_views = pd.concat([df_merge['timestamp'],df_merge['count_x']+df_merge['count_y']], axis=1, join='inner')
pagecount_all_views.columns = ['Date','pagecount_all_views']
pagecount_all_views[:5]
#split date to year and month as requirment
result = pagecount_all_views.merge(pagecount_desktop_views,how='left', on='Date').merge(pagecount_mobile_views,how='left', on='Date').merge(pageview_all_views,how='outer', on='Date').merge(pageview_desktop_views,how='left', on='Date').merge(pageview_mobile_views,how='left', on='Date')
result.fillna(0,inplace=True)
year = result['Date'].str[0:4]
month = result['Date'].str[4:6]
result.insert(loc=0,column='year',value=year)
result.insert(loc=1,column='month',value=month)
del result['Date']
#convert views to integer
result.pagecount_all_views = result.pagecount_all_views.astype(int)
result.pagecount_desktop_views= result.pagecount_desktop_views.astype(int)
result.pagecount_mobile_views = result.pagecount_mobile_views.astype(int)
result.pageview_all_views = result.pageview_all_views.astype(int)
result.pageview_mobile_views = result.pageview_mobile_views.astype(int)
result.pageview_desktop_views = result.pageview_desktop_views.astype(int)
result[:5]
#save it as csv file
result.to_csv('en-wikipedia_traffic_200801-201709.csv', sep=',')
result = result.replace(0,np.nan)
fig, ax = plt.subplots()
date = pd.to_datetime(result.year + result.month, format = '%Y%m')
ax.plot(date, result['pagecount_mobile_views'], color = 'blue', linestyle = '--', alpha=0.7)
ax.plot(date, result['pagecount_desktop_views'], color = 'red', linestyle = '--', alpha=0.7)
ax.plot(date, result['pagecount_all_views'], color = 'green', linestyle = '--', alpha=0.7)
ax.plot(date, result['pageview_all_views'], color = 'green', alpha=0.7)
ax.plot(date, result['pageview_mobile_views'], color = 'blue', alpha=0.7)
ax.plot(date, result['pageview_desktop_views'], color = 'red', alpha=0.7)
fig.set_size_inches(13, 8)
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, prop={'size': 20}, borderaxespad=0.)
fig.suptitle('Views on English Wikipedia', fontsize=30)
ax.set_xlabel('Year')
ax.set_ylabel('Views')
plt.show()
| 0.331985 | 0.728338 |
<img src="./intro_images/MIE.PNG" width="100%" align="left" />
<table style="float:right;">
<tr>
<td>
<div style="text-align: right"><a href="https://alandavies.netlify.com" target="_blank">Dr Alan Davies</a></div>
<div style="text-align: right">Senior Lecturer Health Data Science</div>
<div style="text-align: right">University of Manchester</div>
</td>
<td>
<img src="./intro_images/alan.PNG" width="30%" />
</td>
</tr>
</table>
# 11.0 Beyond notebooks
****
#### About this Notebook
This notebook introduces Integrated Development Environments (IDEs) that are used to manage larger Python projects. We also look at some of the other uses of Python (e.g. for data science and analysis).
<div class="alert alert-block alert-warning"><b>Learning Objectives:</b>
<br/> At the end of this notebook you will be able to:
- Investigate key features of Integrated Development Environments (IDEs)
- Explore some of the other uses of Python
</div>
<a id="top"></a>
<b>Table of contents</b><br>
11.1 [Integrated development environments](#ide)
11.2 [Python for data science](#ds)
11.3 [Data visualization](#dataviz)
So far we have used Python in the context of <code>Jupyter</code> notebooks. Notebooks are often used in research to report findings as an interactive means of presenting results with text and other resources. This is also good practice for reproducible research where the data and analysis can be displayed together for other researchers to examine and use. Although widely used for teaching and research, notebooks are less useful for building complete software systems. For this sort of work programmers would usually use an <code>IDE</code> (Integrated Development Environment). One that comes for free with the <code>Anaconda</code> Python distribution is called <code>Spyder</code>, another widely used free IDE for Python is <code>PyCharm</code>. There are many more available. These can handle multiple files and provide a wealth of other tools to help with coding tasks.
<a id="ide"></a>
#### 11.1 Integrated development environments
<img src="./intro_images/spyder.PNG" width="100%" />
The image above shows the Spyder IDE. IDE's provide several useful features. These usually include a file/function explorer to work on and switch between multiple files in a project. A main code editing window or windows. In the case of Spyder a variable explorer showing the contents of variables and a console for viewing output or trying out bits of code.
<img src="./intro_images/pycharm.PNG" width="100%" />
The image above shows the PyCharm IDE. With the file/project navigation panel on the left and two code windows. IDEs also allow for tasks like <code>debugging</code> where you can step through code executing it line by line or watch the contents of variables to determine where errors may be occurring.
For large projects, programmers will use an IDE to manage the various resources of a project (images, source code files, etc.) To see some of the features of an IDE play the video below to see some of the basic features.
<video controls src="./intro_images/IDE.mp4" width="100%" />
<div class="alert alert-block alert-info">
<b>Task 1:</b>
<br>
Download one of the IDEs mentioned and view the getting started guide. Have a go with the various settings and features. You can usually adjust the colours, font size, add line numbers etc. Aim to become familiar with the various features of the IDE as they can be very useful and powerful. You may also prefer watching a video on how to use them on YouTube.
</div>
<a id="ds"></a>
#### 11.2 Python for data science
<div class="alert alert-danger">
<b>Note:</b> This section of the notebook is just for additional information to see some of the extra functionality of Python. It is not essential for you to learn this.
</div>
One structure for holding data used often in data science is the <code>data frame</code>. One can think of a data frame in a similar way to that of spreadsheet. It is made up of rows and columns. The columns are typically features (data fields) and the rows are records. The <code>pandas</code> module has functionality for creating and manipulating data frames. In the example below we make a data frame containing data about 3 peoples names, ages and blood pressure readings.
```
import pandas as pd
data = [['Paul Smith', 52, "128/70"], ['Nick Bandera', 18, "130/60"], ['Julie Miller', 31, "142/72"]]
my_df = pd.DataFrame(data, columns = ["Name", "Age", "BP"])
print(my_df)
```
For a nicer output just use the data frame name:
```
my_df
```
<div class="alert alert-success">
<b>Note:</b> In reality data scientists will often load data from other sources, such as CSV (Comma Separated Value) files into data frames so they can perform analysis with the data, rather than making their own data frames like we do here.
</div>
We can also look at the columns with the inbuilt functionality.
```
my_df.columns
```
And select data using the name of the column
```
my_df["BP"]
my_df["BP"][2]
```
We can also use the <code>describe</code> function to get some basic statistical information out of the data as well. Here we see the count, average, standard deviation, min and max values and quartiles.
```
my_df["Age"].describe()
```
<a id="dataviz"></a>
#### 11.3 Data visualization
We can also create visualizations of data using the <code>matplotlib</code> module (among others). The first line is a special command that allows us to render the plot inline on the notebook and can be ignored (unless you are using a notebook). Here we create a <code>boxplot</code> of the <code>Age</code> data that you can compare to the textual output produced with the <code>describe()</code> function.
```
%matplotlib inline
import matplotlib.pyplot as plt
fig1, ax1 = plt.subplots()
ax1.boxplot(my_df["Age"]);
```
There are many different types of plot that you can use in Python. Some of the popular libraries include <code>matplotlib</code>, <code>seaborn</code>, <code>ploty</code> and <code>ggplot</code> based on the R (statistical programming languages) library of the same name to name just a few. You can check out some examples on the <a href="https://matplotlib.org/gallery.html#" target="_blank">matplotlib gallery</a>.
<div class="alert alert-success">
<b>Note:</b> You can also adapt some of these visualisations to create your own. Here is a blog post I wrote in towards data science on <a href="https://towardsdatascience.com/creating-the-ecology-classic-kite-diagram-in-python-46989e1310ad" target="_blank">Creating the ecology classic 'Kite diagram' in Python</a>. Where I recreate the ecology Kite diagram in Python by using the matplotlib library.
</div>
Here is another example, this time of a <code>bar chart</code> showing the name plotted against the age. This time we have include axis labels.
```
plt.rcdefaults()
fig, ax = plt.subplots()
ax.barh(my_df["Name"], my_df["Age"], align='center',color='blue')
ax.set_ylabel('Patient name')
ax.set_xlabel('Age (years)')
```
Let's add some more information. A column of heart rates.
```
my_df["HR"] = [101, 68, 80]
my_df
```
<div class="alert alert-block alert-info">
<b>Task 2:</b>
<br>
Look up how to create a <code>scatterplot</code> and plot <code>Age</code> on the x-axis against <code>HR</code> on the y-axis
</div>
```
plt.scatter(my_df["Age"], my_df["HR"], alpha=0.5)
plt.title("Scatter plot of age and heart rate")
plt.xlabel("Age (years)")
plt.ylabel("Heart rate (beats per minute)")
plt.show()
```
<div class="alert alert-success">
<b>Note:</b> We can also develop graphical front ends (Graphical User Interfaces - GUI's) in Python to make our programs easier to use and more attractive. We can do this by creating web front ends (for example using the Python <code>Flask</code> library) or by using packages like <code>PyQt5</code> for a specific operating system. If you want to see an example of this, check out this blog post I wrote on <a href="https://towardsdatascience.com/transcribing-interview-data-from-video-to-text-with-python-5cdb6689eea1" target="_blank">Transcribing interview data from video to text with Python</a> which features building a GUI in Python using the QT Designer tool.
</div>
<div class="alert alert-warning">
<b>Conclusion</b>
</div>
This is just a small sample of the sort of things you can use Python for. If you have a sound understanding of the topics covered to this point, you can build on them to use Python in different ways. Data science tasks are just one such application. Python can be used to build complete software systems, including hosting web pages, accessing databases and other files (not covered in this short intro) and carrying out data analysis. Hopefully this short introduction to programming using Python has provided a broad background on which you can go on to develop your skills. Many of the concepts explained here are present in many other modern programming languages (even if their syntax is different). Programming is a skill that requires practice and trial and error. The more you do it, the better you will get, rather like playing a musical instrument. So...
```
"practice " * 3
```
### Notebook details
<br>
<i>Notebook created by <strong>Dr. Alan Davies</strong>.
<br>
© Alan Davies 2021
## Notes:
|
github_jupyter
|
import pandas as pd
data = [['Paul Smith', 52, "128/70"], ['Nick Bandera', 18, "130/60"], ['Julie Miller', 31, "142/72"]]
my_df = pd.DataFrame(data, columns = ["Name", "Age", "BP"])
print(my_df)
my_df
my_df.columns
my_df["BP"]
my_df["BP"][2]
my_df["Age"].describe()
%matplotlib inline
import matplotlib.pyplot as plt
fig1, ax1 = plt.subplots()
ax1.boxplot(my_df["Age"]);
plt.rcdefaults()
fig, ax = plt.subplots()
ax.barh(my_df["Name"], my_df["Age"], align='center',color='blue')
ax.set_ylabel('Patient name')
ax.set_xlabel('Age (years)')
my_df["HR"] = [101, 68, 80]
my_df
plt.scatter(my_df["Age"], my_df["HR"], alpha=0.5)
plt.title("Scatter plot of age and heart rate")
plt.xlabel("Age (years)")
plt.ylabel("Heart rate (beats per minute)")
plt.show()
"practice " * 3
| 0.348645 | 0.988222 |
```
import numpy as np
import matplotlib.pyplot as plt
import scipy
from sklearn.model_selection import ParameterGrid
from sklearn.manifold import Isomap
import time
from tqdm import tqdm
import librosa
from librosa import cqt
from librosa.core import amplitude_to_db
from librosa.display import specshow
import os
import glob
data_dir= '/Users/sripathisridhar/googleDrive/projects/helix/helix2019_data/SOL'
file_paths= sorted(glob.glob(os.path.join(data_dir, '**', '*.wav')))
file_names= []
for file_path in file_paths:
file_names.append(os.path.basename(file_path))
hop_size= 512
q= 24
features_dict= {}
feature_key= ''
for file_path in tqdm(file_paths, disable=False):
# Read audio files
waveform, sample_rate= librosa.load(file_path, sr=None)
# Compute CQTs
cqt_complex= cqt(y= waveform,
sr= sample_rate,
hop_length= hop_size,
bins_per_octave= q,
n_bins= q*7,
sparsity=1e-6,
)
scalogram= np.abs(cqt_complex)**2
# Find frame with maximum RMS value
rms= librosa.feature.rms(y= waveform,
hop_length= hop_size,
)
rms_argmax= np.argmax(rms)
feature= scalogram[:,rms_argmax]
# Stack in dict
file_name= os.path.basename(file_path)
feature_key= f'{file_name}'
features_dict[feature_key]= feature
grid = {
'Q': [24],
'k': [3],
'comp': ['none','cuberoot'],
'instr': ['all'],
'dyn': ['all']
}
settings = list(ParameterGrid(grid))
for setting in settings:
if setting["instr"] == 'all':
setting['instr'] = ''
if setting['dyn'] == 'all':
setting['dyn'] = ''
```
## Fig 5a: Linear loudness mapping
```
batch_str= []
q= 0
CQT_OCTAVES= 7
features_keys= list(features_dict.keys())
setting= settings[0]
q= setting['Q']
# Batch process and store in a folder
batch_str= [setting['instr'], setting['dyn']]
# print(batch_str)
batch_features= []
for feature_key in features_keys:
# Get features that match setting
if all(x in feature_key for x in batch_str):
batch_features.append(features_dict[feature_key])
batch_features= np.stack(batch_features, axis=1)
# print(batch_features.shape)
# Isomap parameters
hop_size= 512
compression= setting['comp']
if compression== 'none':
features= batch_features
elif compression== 'cuberoot':
features= np.power(batch_features, 1/3.0)
n_neighbors= setting['k']
n_dimensions= 3
n_octaves= 3
# Prune feature matrix
bin_low = np.where((np.std(features, axis=1) / np.std(features)) > 0.1)[0][0] + q
bin_high = bin_low + n_octaves*q
X = features[bin_low:bin_high, :]
# Z-score Standardization- improves contrast in correlation matrix
mus = np.mean(X, axis=1)
sigmas = np.std(X, axis=1)
X_std = (X - mus[:, np.newaxis]) / (1e-6 + sigmas[:, np.newaxis]) # 1e-6 to avoid runtime division by zero
# Pearson correlation matrix
rho_std = np.dot(X_std, X_std.T) / X_std.shape[1]
# Isomap embedding
isomap= Isomap(n_components= n_dimensions, n_neighbors= n_neighbors)
coords = isomap.fit_transform(rho_std)
# Get note value
freqs= librosa.cqt_frequencies(q*CQT_OCTAVES, fmin=librosa.note_to_hz('C1'), bins_per_octave=q) #librosa CQT default fmin is C1
chroma_list= librosa.core.hz_to_note(freqs[bin_low:bin_high])
notes=[]
reps= q//12
for chroma in chroma_list:
for i in range(reps):
notes.append(chroma)
curr_fig= plt.figure(figsize=(5.5, 2.75))
ax= curr_fig.add_subplot(121)
ax.axis('off')
import colorcet as cc
subsampled_color_ids = np.floor(np.linspace(0, 256, q, endpoint=False)).astype('int')
color_list= [cc.cyclic_mygbm_30_95_c78[i] for i in subsampled_color_ids]
# Plot embedding with color
for i in range(coords.shape[0]):
plt.scatter(coords[i, 0], coords[i, 1], color= color_list[i%q], s=30.0)
plt.plot(coords[:, 0], coords[:, 1], color='black', linewidth=0.2)
# Plot Pearson correlation matrix
rho_frequencies = freqs[bin_low:bin_high]
freq_ticklabels = ['A2', 'A3', 'A4']
freq_ticks = librosa.core.note_to_hz(freq_ticklabels)
tick_bins = []
tick_labels= []
for i,freq_tick in enumerate(freq_ticks):
tick_bin = np.argmin(np.abs(rho_frequencies-freq_tick))
tick_bins.append(tick_bin)
tick_labels.append(freq_ticklabels[i])
plt.figure(figsize=(2.5,2.5))
plt.imshow(np.abs(rho_std), cmap='magma_r')
plt.xticks(tick_bins)
plt.gca().set_xticklabels(freq_ticklabels)
# plt.xlabel('Log-frequency (octaves)')
plt.yticks(tick_bins)
plt.gca().set_yticklabels(freq_ticklabels)
# plt.ylabel('Log-frequency (octaves)')
plt.gca().invert_yaxis()
plt.clim(0, 1)
```
## Fig 5b: Cube-root loudness mapping
```
batch_str= []
q= 0
CQT_OCTAVES= 7
features_keys= list(features_dict.keys())
setting= settings[1]
q= setting['Q']
# Batch process and store in a folder
batch_str= [setting['instr'], setting['dyn']]
# print(batch_str)
batch_features= []
for feature_key in features_keys:
# Get features that match setting
if all(x in feature_key for x in batch_str):
batch_features.append(features_dict[feature_key])
batch_features= np.stack(batch_features, axis=1)
# print(batch_features.shape)
# Isomap parameters
hop_size= 512
compression= setting['comp']
if compression== 'none':
features= batch_features
elif compression== 'cuberoot':
features= np.power(batch_features, 1/3.0)
n_neighbors= setting['k']
n_dimensions= 3
n_octaves= 3
# Prune feature matrix
bin_low = np.where((np.std(features, axis=1) / np.std(features)) > 0.1)[0][0] + q
bin_high = bin_low + n_octaves*q
X = features[bin_low:bin_high, :]
# Z-score Standardization- improves contrast in correlation matrix
mus = np.mean(X, axis=1)
sigmas = np.std(X, axis=1)
X_std = (X - mus[:, np.newaxis]) / (1e-6 + sigmas[:, np.newaxis]) # 1e-6 to avoid runtime division by zero
# Pearson correlation matrix
rho_std = np.dot(X_std, X_std.T) / X_std.shape[1]
# Isomap embedding
isomap= Isomap(n_components= n_dimensions, n_neighbors= n_neighbors)
coords = isomap.fit_transform(rho_std)
# Get note value
freqs= librosa.cqt_frequencies(q*CQT_OCTAVES, fmin=librosa.note_to_hz('C1'), bins_per_octave=q) #librosa CQT default fmin is C1
chroma_list= librosa.core.hz_to_note(freqs[bin_low:bin_high])
notes=[]
reps= q//12
for chroma in chroma_list:
for i in range(reps):
notes.append(chroma)
curr_fig= plt.figure(figsize=(5.5, 2.75))
ax= curr_fig.add_subplot(121)
ax.axis('off')
import colorcet as cc
subsampled_color_ids = np.floor(np.linspace(0, 256, q, endpoint=False)).astype('int')
color_list= [cc.cyclic_mygbm_30_95_c78[i] for i in subsampled_color_ids]
# Plot embedding with color
for i in range(coords.shape[0]):
plt.scatter(coords[i, 0], coords[i, 1], color= color_list[i%q], s=30.0)
plt.plot(coords[:, 0], coords[:, 1], color='black', linewidth=0.2)
# Plot Pearson correlation matrix
rho_frequencies = freqs[bin_low:bin_high]
freq_ticklabels = ['A2', 'A3', 'A4']
freq_ticks = librosa.core.note_to_hz(freq_ticklabels)
tick_bins = []
tick_labels= []
for i,freq_tick in enumerate(freq_ticks):
tick_bin = np.argmin(np.abs(rho_frequencies-freq_tick))
tick_bins.append(tick_bin)
tick_labels.append(freq_ticklabels[i])
plt.figure(figsize=(2.5,2.5))
plt.imshow(np.abs(rho_std), cmap='magma_r')
plt.xticks(tick_bins)
plt.gca().set_xticklabels(freq_ticklabels)
# plt.xlabel('Log-frequency (octaves)')
plt.yticks(tick_bins)
plt.gca().set_yticklabels(freq_ticklabels)
# plt.ylabel('Log-frequency (octaves)')
plt.gca().invert_yaxis()
plt.clim(0, 1)
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import scipy
from sklearn.model_selection import ParameterGrid
from sklearn.manifold import Isomap
import time
from tqdm import tqdm
import librosa
from librosa import cqt
from librosa.core import amplitude_to_db
from librosa.display import specshow
import os
import glob
data_dir= '/Users/sripathisridhar/googleDrive/projects/helix/helix2019_data/SOL'
file_paths= sorted(glob.glob(os.path.join(data_dir, '**', '*.wav')))
file_names= []
for file_path in file_paths:
file_names.append(os.path.basename(file_path))
hop_size= 512
q= 24
features_dict= {}
feature_key= ''
for file_path in tqdm(file_paths, disable=False):
# Read audio files
waveform, sample_rate= librosa.load(file_path, sr=None)
# Compute CQTs
cqt_complex= cqt(y= waveform,
sr= sample_rate,
hop_length= hop_size,
bins_per_octave= q,
n_bins= q*7,
sparsity=1e-6,
)
scalogram= np.abs(cqt_complex)**2
# Find frame with maximum RMS value
rms= librosa.feature.rms(y= waveform,
hop_length= hop_size,
)
rms_argmax= np.argmax(rms)
feature= scalogram[:,rms_argmax]
# Stack in dict
file_name= os.path.basename(file_path)
feature_key= f'{file_name}'
features_dict[feature_key]= feature
grid = {
'Q': [24],
'k': [3],
'comp': ['none','cuberoot'],
'instr': ['all'],
'dyn': ['all']
}
settings = list(ParameterGrid(grid))
for setting in settings:
if setting["instr"] == 'all':
setting['instr'] = ''
if setting['dyn'] == 'all':
setting['dyn'] = ''
batch_str= []
q= 0
CQT_OCTAVES= 7
features_keys= list(features_dict.keys())
setting= settings[0]
q= setting['Q']
# Batch process and store in a folder
batch_str= [setting['instr'], setting['dyn']]
# print(batch_str)
batch_features= []
for feature_key in features_keys:
# Get features that match setting
if all(x in feature_key for x in batch_str):
batch_features.append(features_dict[feature_key])
batch_features= np.stack(batch_features, axis=1)
# print(batch_features.shape)
# Isomap parameters
hop_size= 512
compression= setting['comp']
if compression== 'none':
features= batch_features
elif compression== 'cuberoot':
features= np.power(batch_features, 1/3.0)
n_neighbors= setting['k']
n_dimensions= 3
n_octaves= 3
# Prune feature matrix
bin_low = np.where((np.std(features, axis=1) / np.std(features)) > 0.1)[0][0] + q
bin_high = bin_low + n_octaves*q
X = features[bin_low:bin_high, :]
# Z-score Standardization- improves contrast in correlation matrix
mus = np.mean(X, axis=1)
sigmas = np.std(X, axis=1)
X_std = (X - mus[:, np.newaxis]) / (1e-6 + sigmas[:, np.newaxis]) # 1e-6 to avoid runtime division by zero
# Pearson correlation matrix
rho_std = np.dot(X_std, X_std.T) / X_std.shape[1]
# Isomap embedding
isomap= Isomap(n_components= n_dimensions, n_neighbors= n_neighbors)
coords = isomap.fit_transform(rho_std)
# Get note value
freqs= librosa.cqt_frequencies(q*CQT_OCTAVES, fmin=librosa.note_to_hz('C1'), bins_per_octave=q) #librosa CQT default fmin is C1
chroma_list= librosa.core.hz_to_note(freqs[bin_low:bin_high])
notes=[]
reps= q//12
for chroma in chroma_list:
for i in range(reps):
notes.append(chroma)
curr_fig= plt.figure(figsize=(5.5, 2.75))
ax= curr_fig.add_subplot(121)
ax.axis('off')
import colorcet as cc
subsampled_color_ids = np.floor(np.linspace(0, 256, q, endpoint=False)).astype('int')
color_list= [cc.cyclic_mygbm_30_95_c78[i] for i in subsampled_color_ids]
# Plot embedding with color
for i in range(coords.shape[0]):
plt.scatter(coords[i, 0], coords[i, 1], color= color_list[i%q], s=30.0)
plt.plot(coords[:, 0], coords[:, 1], color='black', linewidth=0.2)
# Plot Pearson correlation matrix
rho_frequencies = freqs[bin_low:bin_high]
freq_ticklabels = ['A2', 'A3', 'A4']
freq_ticks = librosa.core.note_to_hz(freq_ticklabels)
tick_bins = []
tick_labels= []
for i,freq_tick in enumerate(freq_ticks):
tick_bin = np.argmin(np.abs(rho_frequencies-freq_tick))
tick_bins.append(tick_bin)
tick_labels.append(freq_ticklabels[i])
plt.figure(figsize=(2.5,2.5))
plt.imshow(np.abs(rho_std), cmap='magma_r')
plt.xticks(tick_bins)
plt.gca().set_xticklabels(freq_ticklabels)
# plt.xlabel('Log-frequency (octaves)')
plt.yticks(tick_bins)
plt.gca().set_yticklabels(freq_ticklabels)
# plt.ylabel('Log-frequency (octaves)')
plt.gca().invert_yaxis()
plt.clim(0, 1)
batch_str= []
q= 0
CQT_OCTAVES= 7
features_keys= list(features_dict.keys())
setting= settings[1]
q= setting['Q']
# Batch process and store in a folder
batch_str= [setting['instr'], setting['dyn']]
# print(batch_str)
batch_features= []
for feature_key in features_keys:
# Get features that match setting
if all(x in feature_key for x in batch_str):
batch_features.append(features_dict[feature_key])
batch_features= np.stack(batch_features, axis=1)
# print(batch_features.shape)
# Isomap parameters
hop_size= 512
compression= setting['comp']
if compression== 'none':
features= batch_features
elif compression== 'cuberoot':
features= np.power(batch_features, 1/3.0)
n_neighbors= setting['k']
n_dimensions= 3
n_octaves= 3
# Prune feature matrix
bin_low = np.where((np.std(features, axis=1) / np.std(features)) > 0.1)[0][0] + q
bin_high = bin_low + n_octaves*q
X = features[bin_low:bin_high, :]
# Z-score Standardization- improves contrast in correlation matrix
mus = np.mean(X, axis=1)
sigmas = np.std(X, axis=1)
X_std = (X - mus[:, np.newaxis]) / (1e-6 + sigmas[:, np.newaxis]) # 1e-6 to avoid runtime division by zero
# Pearson correlation matrix
rho_std = np.dot(X_std, X_std.T) / X_std.shape[1]
# Isomap embedding
isomap= Isomap(n_components= n_dimensions, n_neighbors= n_neighbors)
coords = isomap.fit_transform(rho_std)
# Get note value
freqs= librosa.cqt_frequencies(q*CQT_OCTAVES, fmin=librosa.note_to_hz('C1'), bins_per_octave=q) #librosa CQT default fmin is C1
chroma_list= librosa.core.hz_to_note(freqs[bin_low:bin_high])
notes=[]
reps= q//12
for chroma in chroma_list:
for i in range(reps):
notes.append(chroma)
curr_fig= plt.figure(figsize=(5.5, 2.75))
ax= curr_fig.add_subplot(121)
ax.axis('off')
import colorcet as cc
subsampled_color_ids = np.floor(np.linspace(0, 256, q, endpoint=False)).astype('int')
color_list= [cc.cyclic_mygbm_30_95_c78[i] for i in subsampled_color_ids]
# Plot embedding with color
for i in range(coords.shape[0]):
plt.scatter(coords[i, 0], coords[i, 1], color= color_list[i%q], s=30.0)
plt.plot(coords[:, 0], coords[:, 1], color='black', linewidth=0.2)
# Plot Pearson correlation matrix
rho_frequencies = freqs[bin_low:bin_high]
freq_ticklabels = ['A2', 'A3', 'A4']
freq_ticks = librosa.core.note_to_hz(freq_ticklabels)
tick_bins = []
tick_labels= []
for i,freq_tick in enumerate(freq_ticks):
tick_bin = np.argmin(np.abs(rho_frequencies-freq_tick))
tick_bins.append(tick_bin)
tick_labels.append(freq_ticklabels[i])
plt.figure(figsize=(2.5,2.5))
plt.imshow(np.abs(rho_std), cmap='magma_r')
plt.xticks(tick_bins)
plt.gca().set_xticklabels(freq_ticklabels)
# plt.xlabel('Log-frequency (octaves)')
plt.yticks(tick_bins)
plt.gca().set_yticklabels(freq_ticklabels)
# plt.ylabel('Log-frequency (octaves)')
plt.gca().invert_yaxis()
plt.clim(0, 1)
| 0.496338 | 0.612484 |
```
# Given a list slice it into a 3 equal chunks and revert each list
sampleList = [11, 45, 8, 23, 14, 12, 78, 45, 89]
length = len(sampleList)
chunkSize = int(length/3)
start = 0
end = chunkSize
for i in range(1, 4, 1):
indexes = slice(start, end, 1)
listChunk = sampleList[indexes]
mylist = [i for i in listChunk]
print("After reversing it ", mylist)
start = end
if(i != 2):
end +=chunkSize
else:
end += length - chunkSize
# write a program to calculate exponents of an input
input = 9
exponent = 2
final = pow(input, exponent)
print(f'Exponent Value is:{final}')
# write a program to multiply two Matrix
# 3x3 matrix
X = [[12,7,3],
[4 ,5,6],
[7 ,8,9]]
# 3x4 matrix
Y = [[5,8,1,2],
[6,7,3,0],
[4,5,9,1]]
# result is 3x4
result = [[0,0,0,0],
[0,0,0,0],
[0,0,0,0]]
# iterate through rows of X
for i in range(len(X)):
# iterate through columns of Y
for j in range(len(Y[0])):
# iterate through rows of Y
for k in range(len(Y)):
result[i][j] += X[i][k] * Y[k][j]
print(f"Final Result is{result}")
# write a program to find and print the remainder of two number
num1 = 12
num2 = 10
ratio = num1 % num2
print(f'remainder:{ratio}')
# reverse a number in Python
number = 1367891
revs_number = 0
while (number > 0):
remainder = number % 10
revs_number = (revs_number * 10) + remainder
number = number // 10
print("The reverse number is : {}".format(revs_number))
# Python program to compute sum of digits in number
def sumDigits(no):
return 0 if no == 0 else int(no % 10) + sumDigits(int(no / 10))
n = 1234511
print(sumDigits(n))
# Find the middle element of a random number list
my_list = [4,3,2,9,10,44,1]
print("mid value is ",my_list[int(len(my_list)/2)])
# Sort the list in ascending order
my_list = [4,3,2,9,10,44,1]
my_list.sort()
print(f"Ascending Order list:,{my_list}")
# Sort the list in descending order
my_list = [4,3,2,9,10,44,1]
my_list.sort(reverse=True)
print(f"Descending Order list:,{my_list}")
# Concatenation of two List
my_list1 = [4,3,2,9,10,44,1]
my_list2 = [5,6,2,8,15,14,12]
print(f"Sum of two list:,{my_list1+my_list2}")
# Removes the item at the given index from the list and returns the removed item
my_list1 = [4,3,2,9,10,44,1,9,12]
index = 4
print(f"Sum of two list:,{my_list1.pop(index)}")
# Adding Element to a List
animals = ['cat', 'dog', 'rabbit']
animals.append('guinea pig')
print('Updated animals list: ', animals)
# Returns the number of times the specified element appears in the list
vowels = ['a', 'e', 'i', 'o', 'i', 'u']
count = vowels.count('i')
print('The count of i is:', count)
# Count Tuple Elements Inside List
random = ['a', ('a', 'b'), ('a', 'b'), [3, 4]]
count = random.count(('a', 'b'))
print("The count of ('a', 'b') is:", count)
# Removes all items from the list
list = [{1, 2}, ('a'), ['1.1', '2.2']]
list.clear()
print('List:', list)
# access first characters in a string
word = "Hello World"
letter=word[0]
print(f"First Charecter in String:{letter}")
# access Last characters in a string
word = "Hello World"
letter=word[-1]
print(f"First Charecter in String:{letter}")
# Generate a list by list comprehension
list = [x for x in range(10)]
print(f"List Generated by list comprehension:{list}")
# Set the values in the new list to upper case
list = "AMITKAYAL"
newlist = [x.upper() for x in list]
print(f"New list to upper case:{newlist}")
# Sort the string list alphabetically
thislist = ["orange", "mango", "kiwi", "pineapple", "banana"]
thislist.sort()
print(f"Sorted List:{thislist}")
# Join Two Sets
set1 = {"a", "b" , "c"}
set2 = {1, 2, 3}
set3 = set2.union(set1)
print(f"Joined Set:{set3}")
# keep only the items that are present in both sets
x = {"apple", "banana", "cherry"}
y = {"google", "microsoft", "apple"}
x.intersection_update(y)
print(f"Duplicate Value in Two set:{x}")
# Keep All items from List But NOT the Duplicates
x = {"apple", "banana", "cherry"}
y = {"google", "microsoft", "apple"}
x.symmetric_difference_update(y)
print(f"Duplicate Value in Two set:{x}")
# Create and print a dictionary
thisdict = {
"brand": "Ford",
"model": "Mustang",
"year": 1964
}
print(f"Sample Dictionary:{thisdict}")
# Calculate the length of dictionary
thisdict = {
"brand": "Ford",
"model": "Mustang",
"year": 1964
}
print(f"Length of Dictionary:{len(thisdict)}")
# Evaluate a string and a number
print(bool("Hello"))
print(bool(15))
# Calculate length of a string
word = "Hello World"
print(f"Length of string: {len(word)}")
# Count the number of spaces in a sring
s = "Count, the number of spaces"
lenx = s.count(' ')
print(f"number of spaces in sring: {lenx}")
# Split Strings
word = "Hello World"
ksplit = word.split(' ')
print(f"Splited Strings: {ksplit}")
# Prints ten dots
ten = "." * 10
print(f"Ten dots: {ten}")
# Replacing a string with another string
word = "Hello World"
replace = "Bye"
input = "Hello"
after_replace = word.replace(input, replace)
print(f"String ater replacement: {after_replace}")
#removes leading characters
word = " xyz "
lstrip = word.lstrip()
print(f"String ater removal of leading characters:{lstrip}")
#removes trailing characters
word = " xyz "
rstrip = word.rstrip()
print(f"String ater removal of trailing characters:{rstrip}")
# check if all char are alphanumeric
word = "Hello World"
check = word.isalnum()
print(f"All char are alphanumeric?:{check}")
# check if all char in the string are alphabetic
word = "Hello World"
check = word.isalpha()
print(f"All char are alphabetic?:{check}")
# test if string contains digits
word = "Hello World"
check = word.isdigit()
print(f"String contains digits?:{check}")
# Test if string contains upper case
word = "Hello World"
check = word.isupper()
print(f"String contains upper case?:{check}")
# Test if string starts with H
word = "Hello World"
check = word.startswith('H')
print(f"String starts with H?:{check}")
# Returns an integer value for the given character
str = "A"
val = ord(str)
print(f"Integer value for the given character?:{val}")
# Fibonacci series up to 100
n = 100
result = []
a, b = 0 , 1
while b < n:
result. append( b)
a, b = b, a + b
final = result
print(f"Fibonacci series up to 100:{final}")
# Counting total Digits in a string
str1 = "abc4234AFde"
digitCount = 0
for i in range(0,len(str1)):
char = str1[i]
if(char.isdigit()):
digitCount += 1
print('Number of digits: ',digitCount)
# Counting total alphanumeric in a string
str1 = "abc4234AFde"
digitCount = 0
for i in range(0,len(str1)):
char = str1[i]
if(char.isalpha()):
digitCount += 1
print('Number of alphanumeric: ',digitCount)
# Counting total Upper Case in a string
str1 = "abc4234AFde"
digitCount = 0
for i in range(0,len(str1)):
char = str1[i]
if(char.upper()):
digitCount += 1
print('Number total Upper Case: ',digitCount)
# Counting total lower Case in a string
str1 = "abc4234AFdeaa"
digitCount = 0
for i in range(0,len(str1)):
char = str1[i]
if(char.lower()):
digitCount += 1
print('Number total lower Case: ',digitCount)
# Bubble sort in python
list1 = [1, 5, 3, 4]
for i in range(len(list1)-1):
for j in range(i+1,len(list1)):
if(list1[i] > list1[j]):
temp = list1[i]
list1[i] = list1[j]
list1[j] = temp
print("Bubble Sorted list: ",list1)
# Compute the product of every pair of numbers from two lists
list1 = [1, 2, 3]
list2 = [5, 6, 7]
final = [a*b for a in list1 for b in list2]
print(f"Product of every pair of numbers from two lists:{final}")
# Calculate the sum of every pair of numbers from two lists
list1 = [1, 2, 3]
list2 = [5, 6, 7]
final = [a+b for a in list1 for b in list2]
print(f"sum of every pair of numbers from two lists:{final}")
# Calculate the pair-wise product of two lists
list1 = [1, 2, 3]
list2 = [5, 6, 7]
final = [list1[i]*list2[i] for i in range(len(list1))]
print(f"pair-wise product of two lists:{final}")
# Remove the last element from the stack
s = [1,2,3,4]
print(f"last element from the stack:{s.pop()}")
# Insert a number at the beginning of the queue
q = [1,2,3,4]
q.insert(0,5)
print(f"Revised List:{q}")
# Addition of two vector
v1 = [1,2,3]
v2 = [1,2,3]
s1 = [0,0,0]
for i in range(len(v1)):
s1[i] = v1[i] + v2[i]
print(f"New Vector:{s1}")
# # Merge of two dictionary
# x = {"key1": "value1 from x", "key2": "value2 from x"}
# y = {"key2": "value2 from y", "key3": "value3 from y"}
# z = x | y
# print(f"Merged Dictionary:{z}")
# Replace negative prices with 0 and leave the positive values unchanged in a list
original_prices = [1.25, -9.45, 10.22, 3.78, -5.92, 1.16]
prices = [i if i > 0 else 0 for i in original_prices]
print(f"Final List:{prices}")
# Convert dictionary to JSON
import json
person_dict = {'name': 'Bob',
'age': 12,
'children': None
}
person_json = json.dumps(person_dict)
print(person_json)
# Writing JSON to a file
import json
person_dict = {"name": "Bob",
"languages": ["English", "Fench"],
"married": True,
"age": 32
}
with open('person.txt', 'w') as json_file:
json.dump(person_dict, json_file)
# Pretty print JSON
import json
person_string = '{"name": "Bob", "languages": "English", "numbers": [2, 1.6, null]}'
person_dict = json.loads(person_string)
print(json.dumps(person_dict, indent = 4, sort_keys=True))
# Converting JSON to CSV
import json
import csv
employee_data = '{"employee_details":[{"employee_name": "James", "email": "james@gmail.com", "job_profile": "Sr. Developer"},{"employee_name": "Smith", "email": "Smith@gmail.com", "job_profile": "Project Lead"}]}'
employee_parsed = json.loads(employee_data)
emp_data = employee_parsed['employee_details']
employ_data = open('/tmp/EmployData.csv', 'w')
csvwriter = csv.writer(employ_data)
for emp in emp_data:
if count == 0:
header = emp.keys()
csvwriter.writerow(header)
count += 1
csvwriter.writerow(emp.values())
employ_data.close()
# Check if the key exists or not in JSON
import json
studentJson ="""{
"id": 1,
"name": "john wick",
"class": 8,
"percentage": 75,
"email": "jhon@pynative.com"
}"""
print("Checking if percentage key exists in JSON")
student = json.loads(studentJson)
if "percentage" in student:
print("Key exist in JSON data")
print(student["name"], "marks is: ", student["percentage"])
else:
print("Key doesn't exist in JSON data")
# Check if there is a value for a key in JSON
import json
studentJson ="""{
"id": 1,
"name": "john wick",
"class": null,
"percentage": 75,
"email": "jhon@pynative.com"
}"""
student = json.loads(studentJson)
if not (student.get('email') is None):
print("value is present for given JSON key")
print(student.get('email'))
else:
print("value is not present for given JSON key")
# Sort JSON keys in Python and write it into a file
import json
sampleJson = {"id" : 1, "name" : "value2", "age" : 29}
with open("sampleJson.json", "w") as write_file:
json.dump(sampleJson, write_file, indent=4, sort_keys=True)
print("Done writing JSON data into a file")
# Given a Python list. Turn every item of a list into its square
aList = [1, 2, 3, 4, 5, 6, 7]
aList = [x * x for x in aList]
print(aList)
# Remove empty strings from the list of strings
list1 = ["Mike", "", "Emma", "Kelly", "", "Brad"]
resList = [i for i in (filter(None, list1))]
print(resList)
# Write a program which will achieve given a Python list, remove all occurrence of an input from the list
list1 = [5, 20, 15, 20, 25, 50, 20]
def removeValue(sampleList, val):
return [value for value in sampleList if value != val]
resList = removeValue(list1, 20)
print(resList)
# Generate 3 random integers between 100 and 999 which is divisible by 5
import random
print("Generating 3 random integer number between 100 and 999 divisible by 5")
for num in range(3):
print(random.randrange(100, 999, 5), end=', ')
# Pick a random character from a given String
import random
name = 'pynative'
char = random.choice(name)
print("random char is ", char)
# Generate random String of length 5
import random
import string
def randomString(stringLength):
"""Generate a random string of 5 charcters"""
letters = string.ascii_letters
return ''.join(random.choice(letters) for i in range(stringLength))
print ("Random String is ", randomString(5) )
# Generate a random date between given start and end dates
import random
import time
def getRandomDate(startDate, endDate ):
print("Printing random date between", startDate, " and ", endDate)
randomGenerator = random.random()
dateFormat = '%m/%d/%Y'
startTime = time.mktime(time.strptime(startDate, dateFormat))
endTime = time.mktime(time.strptime(endDate, dateFormat))
randomTime = startTime + randomGenerator * (endTime - startTime)
randomDate = time.strftime(dateFormat, time.localtime(randomTime))
return randomDate
print ("Random Date = ", getRandomDate("1/1/2016", "12/12/2018"))
# Write a program which will create a new string by appending s2 in the middle of s1 given two strings, s1 and s2
def appendMiddle(s1, s2):
middleIndex = int(len(s1) /2)
middleThree = s1[:middleIndex:]+ s2 +s1[middleIndex:]
print("After appending new string in middle", middleThree)
appendMiddle("Ault", "Kelly")
# Arrange string characters such that lowercase letters should come first
str1 = "PyNaTive"
lower = []
upper = []
for char in str1:
if char.islower():
lower.append(char)
else:
upper.append(char)
sorted_string = ''.join(lower + upper)
print(sorted_string)
# Given a string, return the sum and average of the digits that appear in the string, ignoring all other characters
import re
inputStr = "English = 78 Science = 83 Math = 68 History = 65"
markList = [int(num) for num in re.findall(r'\b\d+\b', inputStr)]
totalMarks = 0
for mark in markList:
totalMarks+=mark
percentage = totalMarks/len(markList)
print("Total Marks is:", totalMarks, "Percentage is ", percentage)
# Given an input string, count occurrences of all characters within a string
str1 = "Apple"
countDict = dict()
for char in str1:
count = str1.count(char)
countDict[char]=count
print(countDict)
# Reverse a given string
str1 = "PYnative"
print("Original String is:", str1)
str1 = str1[::-1]
print("Reversed String is:", str1)
# Remove special symbols/Punctuation from a given string
import string
str1 = "/*Jon is @developer & musician"
new_str = str1.translate(str.maketrans('', '', string.punctuation))
print("New string is ", new_str)
# Removal all the characters other than integers from string
str1 = 'I am 25 years and 10 months old'
res = "".join([item for item in str1 if item.isdigit()])
print(res)
# From given string replace each punctuation with #
from string import punctuation
str1 = '/*Jon is @developer & musician!!'
replace_char = '#'
for char in punctuation:
str1 = str1.replace(char, replace_char)
print("The strings after replacement : ", str1)
# Given a list iterate it and count the occurrence of each element and create a dictionary to show the count of each elemen
sampleList = [11, 45, 8, 11, 23, 45, 23, 45, 89]
countDict = dict()
for item in sampleList:
if(item in countDict):
countDict[item] += 1
else:
countDict[item] = 1
print("Printing count of each item ",countDict)
# Given a two list of equal size create a set such that it shows the element from both lists in the pair
firstList = [2, 3, 4, 5, 6, 7, 8]
secondList = [4, 9, 16, 25, 36, 49, 64]
result = zip(firstList, secondList)
resultSet = set(result)
print(resultSet)
# Given a two sets find the intersection and remove those elements from the first set
firstSet = {23, 42, 65, 57, 78, 83, 29}
secondSet = {57, 83, 29, 67, 73, 43, 48}
intersection = firstSet.intersection(secondSet)
for item in intersection:
firstSet.remove(item)
print("First Set after removing common element ", firstSet)
# Given a dictionary get all values from the dictionary and add it in a list but don’t add duplicates
speed ={'jan':47, 'feb':52, 'march':47, 'April':44, 'May':52, 'June':53,
'july':54, 'Aug':44, 'Sept':54}
speedList = []
for item in speed.values():
if item not in speedList:
speedList.append(item)
print("unique list", speedList)
# Convert decimal number to octal
print('%o,' % (8))
# Convert string into a datetime object
from datetime import datetime
date_string = "Feb 25 2020 4:20PM"
datetime_object = datetime.strptime(date_string, '%b %d %Y %I:%M%p')
print(datetime_object)
# Subtract a week from a given date
from datetime import datetime, timedelta
given_date = datetime(2020, 2, 25)
days_to_subtract = 7
res_date = given_date - timedelta(days=days_to_subtract)
print(res_date)
# Find the day of week of a given date?
from datetime import datetime
given_date = datetime(2020, 7, 26)
print(given_date.strftime('%A'))
# Add week (7 days) and 12 hours to a given date
from datetime import datetime, timedelta
given_date = datetime(2020, 3, 22, 10, 00, 00)
days_to_add = 7
res_date = given_date + timedelta(days=days_to_add, hours=12)
print(res_date)
# Calculate number of days between two given dates
from datetime import datetime
date_1 = datetime(2020, 2, 25).date()
date_2 = datetime(2020, 9, 17).date()
delta = None
if date_1 > date_2:
delta = date_1 - date_2
else:
delta = date_2 - date_1
print("Difference is", delta.days, "days")
# Write a recursive function to calculate the sum of numbers from 0 to 10
def calculateSum(num):
if num:
return num + calculateSum(num-1)
else:
return 0
res = calculateSum(10)
print(res)
# Generate a Python list of all the even numbers between two given numbers
num1 = 4
num2 = 30
myval = [i for i in range(num1, num2, 2)]
print(myval)
# Return the largest item from the given list
aList = [4, 6, 8, 24, 12, 2]
print(max(aList))
# Write a program to extract each digit from an integer, in the reverse order
number = 7536
while (number > 0):
digit = number % 10
number = number // 10
print(digit, end=" ")
# Given a Python list, remove all occurrence of a given number from the list
num1 = 20
list1 = [5, 20, 15, 20, 25, 50, 20]
def removeValue(sampleList, val):
return [value for value in sampleList if value != val]
resList = removeValue(list1, num1)
print(resList)
# Shuffle a list randomly
import random
list = [2,5,8,9,12]
random.shuffle(list)
print ("Printing shuffled list ", list)
# Generate a random n-dimensional array of float numbers
import numpy
random_float_array = numpy.random.rand(2, 2)
print("2 X 2 random float array in [0.0, 1.0] \n", random_float_array,"\n")
# Generate random Universally unique IDs
import uuid
safeId = uuid.uuid4()
print("safe unique id is ", safeId)
# Choose given number of elements from the list with different probability
import random
num1 =5
numberList = [111, 222, 333, 444, 555]
print(random.choices(numberList, weights=(10, 20, 30, 40, 50), k=num1))
# Generate weighted random numbers
import random
randomList = random.choices(range(10, 40, 5), cum_weights=(5, 15, 10, 25, 40, 65), k=6)
print(randomList)
# generating a reliable secure random number
import secrets
print("Random integer number generated using secrets module is ")
number = secrets.randbelow(30)
print(number)
# Calculate memory is being used by an list in Python
import sys
list1 = ['Scott', 'Eric', 'Kelly', 'Emma', 'Smith']
print("size of list = ",sys.getsizeof(list1))
# Find if all elements in a list are identical
listOne = [20, 20, 20, 20]
print("All element are duplicate in listOne:", listOne.count(listOne[0]) == len(listOne))
# Merge two dictionaries in a single expression
currentEmployee = {1: 'Scott', 2: "Eric", 3:"Kelly"}
formerEmployee = {2: 'Eric', 4: "Emma"}
allEmployee = {**currentEmployee, **formerEmployee}
print(allEmployee)
# Convert two lists into a dictionary
ItemId = [54, 65, 76]
names = ["Hard Disk", "Laptop", "RAM"]
itemDictionary = dict(zip(ItemId, names))
print(itemDictionary)
# Alternate cases in String
test_str = "geeksforgeeks"
res = ""
for idx in range(len(test_str)):
if not idx % 2 :
res = res + test_str[idx].upper()
else:
res = res + test_str[idx].lower()
print(res)
# Write a Python program to validate an Email
import re
regex = '^[a-z0-9]+[\._]?[a-z0-9]+[@]\w+[.]\w{2,3}$'
def check(email):
if(re.search(regex,email)):
print("Valid Email")
else:
print("Invalid Email")
email = "ankitrai326@gmail.com"
check(email)
# Write a Program to implement validation of a Password
class Password:
def __init__(self, password):
self.password = password
def validate(self):
vals = {
'Password must contain an uppercase letter.': lambda s: any(x.isupper() for x in s),
'Password must contain a lowercase letter.': lambda s: any(x.islower() for x in s),
'Password must contain a digit.': lambda s: any(x.isdigit() for x in s),
'Password must be at least 8 characters.': lambda s: len(s) >= 8,
'Password cannot contain white spaces.': lambda s: not any(x.isspace() for x in s)
}
valid = True
for n, val in vals.items():
if not val(self.password):
valid = False
return n
return valid
input_password = "Amit@12Su@ 1'"
p = Password(input_password)
if p.validate() is True:
print('Password Valid')
else:
print(p.validate())
```
|
github_jupyter
|
# Given a list slice it into a 3 equal chunks and revert each list
sampleList = [11, 45, 8, 23, 14, 12, 78, 45, 89]
length = len(sampleList)
chunkSize = int(length/3)
start = 0
end = chunkSize
for i in range(1, 4, 1):
indexes = slice(start, end, 1)
listChunk = sampleList[indexes]
mylist = [i for i in listChunk]
print("After reversing it ", mylist)
start = end
if(i != 2):
end +=chunkSize
else:
end += length - chunkSize
# write a program to calculate exponents of an input
input = 9
exponent = 2
final = pow(input, exponent)
print(f'Exponent Value is:{final}')
# write a program to multiply two Matrix
# 3x3 matrix
X = [[12,7,3],
[4 ,5,6],
[7 ,8,9]]
# 3x4 matrix
Y = [[5,8,1,2],
[6,7,3,0],
[4,5,9,1]]
# result is 3x4
result = [[0,0,0,0],
[0,0,0,0],
[0,0,0,0]]
# iterate through rows of X
for i in range(len(X)):
# iterate through columns of Y
for j in range(len(Y[0])):
# iterate through rows of Y
for k in range(len(Y)):
result[i][j] += X[i][k] * Y[k][j]
print(f"Final Result is{result}")
# write a program to find and print the remainder of two number
num1 = 12
num2 = 10
ratio = num1 % num2
print(f'remainder:{ratio}')
# reverse a number in Python
number = 1367891
revs_number = 0
while (number > 0):
remainder = number % 10
revs_number = (revs_number * 10) + remainder
number = number // 10
print("The reverse number is : {}".format(revs_number))
# Python program to compute sum of digits in number
def sumDigits(no):
return 0 if no == 0 else int(no % 10) + sumDigits(int(no / 10))
n = 1234511
print(sumDigits(n))
# Find the middle element of a random number list
my_list = [4,3,2,9,10,44,1]
print("mid value is ",my_list[int(len(my_list)/2)])
# Sort the list in ascending order
my_list = [4,3,2,9,10,44,1]
my_list.sort()
print(f"Ascending Order list:,{my_list}")
# Sort the list in descending order
my_list = [4,3,2,9,10,44,1]
my_list.sort(reverse=True)
print(f"Descending Order list:,{my_list}")
# Concatenation of two List
my_list1 = [4,3,2,9,10,44,1]
my_list2 = [5,6,2,8,15,14,12]
print(f"Sum of two list:,{my_list1+my_list2}")
# Removes the item at the given index from the list and returns the removed item
my_list1 = [4,3,2,9,10,44,1,9,12]
index = 4
print(f"Sum of two list:,{my_list1.pop(index)}")
# Adding Element to a List
animals = ['cat', 'dog', 'rabbit']
animals.append('guinea pig')
print('Updated animals list: ', animals)
# Returns the number of times the specified element appears in the list
vowels = ['a', 'e', 'i', 'o', 'i', 'u']
count = vowels.count('i')
print('The count of i is:', count)
# Count Tuple Elements Inside List
random = ['a', ('a', 'b'), ('a', 'b'), [3, 4]]
count = random.count(('a', 'b'))
print("The count of ('a', 'b') is:", count)
# Removes all items from the list
list = [{1, 2}, ('a'), ['1.1', '2.2']]
list.clear()
print('List:', list)
# access first characters in a string
word = "Hello World"
letter=word[0]
print(f"First Charecter in String:{letter}")
# access Last characters in a string
word = "Hello World"
letter=word[-1]
print(f"First Charecter in String:{letter}")
# Generate a list by list comprehension
list = [x for x in range(10)]
print(f"List Generated by list comprehension:{list}")
# Set the values in the new list to upper case
list = "AMITKAYAL"
newlist = [x.upper() for x in list]
print(f"New list to upper case:{newlist}")
# Sort the string list alphabetically
thislist = ["orange", "mango", "kiwi", "pineapple", "banana"]
thislist.sort()
print(f"Sorted List:{thislist}")
# Join Two Sets
set1 = {"a", "b" , "c"}
set2 = {1, 2, 3}
set3 = set2.union(set1)
print(f"Joined Set:{set3}")
# keep only the items that are present in both sets
x = {"apple", "banana", "cherry"}
y = {"google", "microsoft", "apple"}
x.intersection_update(y)
print(f"Duplicate Value in Two set:{x}")
# Keep All items from List But NOT the Duplicates
x = {"apple", "banana", "cherry"}
y = {"google", "microsoft", "apple"}
x.symmetric_difference_update(y)
print(f"Duplicate Value in Two set:{x}")
# Create and print a dictionary
thisdict = {
"brand": "Ford",
"model": "Mustang",
"year": 1964
}
print(f"Sample Dictionary:{thisdict}")
# Calculate the length of dictionary
thisdict = {
"brand": "Ford",
"model": "Mustang",
"year": 1964
}
print(f"Length of Dictionary:{len(thisdict)}")
# Evaluate a string and a number
print(bool("Hello"))
print(bool(15))
# Calculate length of a string
word = "Hello World"
print(f"Length of string: {len(word)}")
# Count the number of spaces in a sring
s = "Count, the number of spaces"
lenx = s.count(' ')
print(f"number of spaces in sring: {lenx}")
# Split Strings
word = "Hello World"
ksplit = word.split(' ')
print(f"Splited Strings: {ksplit}")
# Prints ten dots
ten = "." * 10
print(f"Ten dots: {ten}")
# Replacing a string with another string
word = "Hello World"
replace = "Bye"
input = "Hello"
after_replace = word.replace(input, replace)
print(f"String ater replacement: {after_replace}")
#removes leading characters
word = " xyz "
lstrip = word.lstrip()
print(f"String ater removal of leading characters:{lstrip}")
#removes trailing characters
word = " xyz "
rstrip = word.rstrip()
print(f"String ater removal of trailing characters:{rstrip}")
# check if all char are alphanumeric
word = "Hello World"
check = word.isalnum()
print(f"All char are alphanumeric?:{check}")
# check if all char in the string are alphabetic
word = "Hello World"
check = word.isalpha()
print(f"All char are alphabetic?:{check}")
# test if string contains digits
word = "Hello World"
check = word.isdigit()
print(f"String contains digits?:{check}")
# Test if string contains upper case
word = "Hello World"
check = word.isupper()
print(f"String contains upper case?:{check}")
# Test if string starts with H
word = "Hello World"
check = word.startswith('H')
print(f"String starts with H?:{check}")
# Returns an integer value for the given character
str = "A"
val = ord(str)
print(f"Integer value for the given character?:{val}")
# Fibonacci series up to 100
n = 100
result = []
a, b = 0 , 1
while b < n:
result. append( b)
a, b = b, a + b
final = result
print(f"Fibonacci series up to 100:{final}")
# Counting total Digits in a string
str1 = "abc4234AFde"
digitCount = 0
for i in range(0,len(str1)):
char = str1[i]
if(char.isdigit()):
digitCount += 1
print('Number of digits: ',digitCount)
# Counting total alphanumeric in a string
str1 = "abc4234AFde"
digitCount = 0
for i in range(0,len(str1)):
char = str1[i]
if(char.isalpha()):
digitCount += 1
print('Number of alphanumeric: ',digitCount)
# Counting total Upper Case in a string
str1 = "abc4234AFde"
digitCount = 0
for i in range(0,len(str1)):
char = str1[i]
if(char.upper()):
digitCount += 1
print('Number total Upper Case: ',digitCount)
# Counting total lower Case in a string
str1 = "abc4234AFdeaa"
digitCount = 0
for i in range(0,len(str1)):
char = str1[i]
if(char.lower()):
digitCount += 1
print('Number total lower Case: ',digitCount)
# Bubble sort in python
list1 = [1, 5, 3, 4]
for i in range(len(list1)-1):
for j in range(i+1,len(list1)):
if(list1[i] > list1[j]):
temp = list1[i]
list1[i] = list1[j]
list1[j] = temp
print("Bubble Sorted list: ",list1)
# Compute the product of every pair of numbers from two lists
list1 = [1, 2, 3]
list2 = [5, 6, 7]
final = [a*b for a in list1 for b in list2]
print(f"Product of every pair of numbers from two lists:{final}")
# Calculate the sum of every pair of numbers from two lists
list1 = [1, 2, 3]
list2 = [5, 6, 7]
final = [a+b for a in list1 for b in list2]
print(f"sum of every pair of numbers from two lists:{final}")
# Calculate the pair-wise product of two lists
list1 = [1, 2, 3]
list2 = [5, 6, 7]
final = [list1[i]*list2[i] for i in range(len(list1))]
print(f"pair-wise product of two lists:{final}")
# Remove the last element from the stack
s = [1,2,3,4]
print(f"last element from the stack:{s.pop()}")
# Insert a number at the beginning of the queue
q = [1,2,3,4]
q.insert(0,5)
print(f"Revised List:{q}")
# Addition of two vector
v1 = [1,2,3]
v2 = [1,2,3]
s1 = [0,0,0]
for i in range(len(v1)):
s1[i] = v1[i] + v2[i]
print(f"New Vector:{s1}")
# # Merge of two dictionary
# x = {"key1": "value1 from x", "key2": "value2 from x"}
# y = {"key2": "value2 from y", "key3": "value3 from y"}
# z = x | y
# print(f"Merged Dictionary:{z}")
# Replace negative prices with 0 and leave the positive values unchanged in a list
original_prices = [1.25, -9.45, 10.22, 3.78, -5.92, 1.16]
prices = [i if i > 0 else 0 for i in original_prices]
print(f"Final List:{prices}")
# Convert dictionary to JSON
import json
person_dict = {'name': 'Bob',
'age': 12,
'children': None
}
person_json = json.dumps(person_dict)
print(person_json)
# Writing JSON to a file
import json
person_dict = {"name": "Bob",
"languages": ["English", "Fench"],
"married": True,
"age": 32
}
with open('person.txt', 'w') as json_file:
json.dump(person_dict, json_file)
# Pretty print JSON
import json
person_string = '{"name": "Bob", "languages": "English", "numbers": [2, 1.6, null]}'
person_dict = json.loads(person_string)
print(json.dumps(person_dict, indent = 4, sort_keys=True))
# Converting JSON to CSV
import json
import csv
employee_data = '{"employee_details":[{"employee_name": "James", "email": "james@gmail.com", "job_profile": "Sr. Developer"},{"employee_name": "Smith", "email": "Smith@gmail.com", "job_profile": "Project Lead"}]}'
employee_parsed = json.loads(employee_data)
emp_data = employee_parsed['employee_details']
employ_data = open('/tmp/EmployData.csv', 'w')
csvwriter = csv.writer(employ_data)
for emp in emp_data:
if count == 0:
header = emp.keys()
csvwriter.writerow(header)
count += 1
csvwriter.writerow(emp.values())
employ_data.close()
# Check if the key exists or not in JSON
import json
studentJson ="""{
"id": 1,
"name": "john wick",
"class": 8,
"percentage": 75,
"email": "jhon@pynative.com"
}"""
print("Checking if percentage key exists in JSON")
student = json.loads(studentJson)
if "percentage" in student:
print("Key exist in JSON data")
print(student["name"], "marks is: ", student["percentage"])
else:
print("Key doesn't exist in JSON data")
# Check if there is a value for a key in JSON
import json
studentJson ="""{
"id": 1,
"name": "john wick",
"class": null,
"percentage": 75,
"email": "jhon@pynative.com"
}"""
student = json.loads(studentJson)
if not (student.get('email') is None):
print("value is present for given JSON key")
print(student.get('email'))
else:
print("value is not present for given JSON key")
# Sort JSON keys in Python and write it into a file
import json
sampleJson = {"id" : 1, "name" : "value2", "age" : 29}
with open("sampleJson.json", "w") as write_file:
json.dump(sampleJson, write_file, indent=4, sort_keys=True)
print("Done writing JSON data into a file")
# Given a Python list. Turn every item of a list into its square
aList = [1, 2, 3, 4, 5, 6, 7]
aList = [x * x for x in aList]
print(aList)
# Remove empty strings from the list of strings
list1 = ["Mike", "", "Emma", "Kelly", "", "Brad"]
resList = [i for i in (filter(None, list1))]
print(resList)
# Write a program which will achieve given a Python list, remove all occurrence of an input from the list
list1 = [5, 20, 15, 20, 25, 50, 20]
def removeValue(sampleList, val):
return [value for value in sampleList if value != val]
resList = removeValue(list1, 20)
print(resList)
# Generate 3 random integers between 100 and 999 which is divisible by 5
import random
print("Generating 3 random integer number between 100 and 999 divisible by 5")
for num in range(3):
print(random.randrange(100, 999, 5), end=', ')
# Pick a random character from a given String
import random
name = 'pynative'
char = random.choice(name)
print("random char is ", char)
# Generate random String of length 5
import random
import string
def randomString(stringLength):
"""Generate a random string of 5 charcters"""
letters = string.ascii_letters
return ''.join(random.choice(letters) for i in range(stringLength))
print ("Random String is ", randomString(5) )
# Generate a random date between given start and end dates
import random
import time
def getRandomDate(startDate, endDate ):
print("Printing random date between", startDate, " and ", endDate)
randomGenerator = random.random()
dateFormat = '%m/%d/%Y'
startTime = time.mktime(time.strptime(startDate, dateFormat))
endTime = time.mktime(time.strptime(endDate, dateFormat))
randomTime = startTime + randomGenerator * (endTime - startTime)
randomDate = time.strftime(dateFormat, time.localtime(randomTime))
return randomDate
print ("Random Date = ", getRandomDate("1/1/2016", "12/12/2018"))
# Write a program which will create a new string by appending s2 in the middle of s1 given two strings, s1 and s2
def appendMiddle(s1, s2):
middleIndex = int(len(s1) /2)
middleThree = s1[:middleIndex:]+ s2 +s1[middleIndex:]
print("After appending new string in middle", middleThree)
appendMiddle("Ault", "Kelly")
# Arrange string characters such that lowercase letters should come first
str1 = "PyNaTive"
lower = []
upper = []
for char in str1:
if char.islower():
lower.append(char)
else:
upper.append(char)
sorted_string = ''.join(lower + upper)
print(sorted_string)
# Given a string, return the sum and average of the digits that appear in the string, ignoring all other characters
import re
inputStr = "English = 78 Science = 83 Math = 68 History = 65"
markList = [int(num) for num in re.findall(r'\b\d+\b', inputStr)]
totalMarks = 0
for mark in markList:
totalMarks+=mark
percentage = totalMarks/len(markList)
print("Total Marks is:", totalMarks, "Percentage is ", percentage)
# Given an input string, count occurrences of all characters within a string
str1 = "Apple"
countDict = dict()
for char in str1:
count = str1.count(char)
countDict[char]=count
print(countDict)
# Reverse a given string
str1 = "PYnative"
print("Original String is:", str1)
str1 = str1[::-1]
print("Reversed String is:", str1)
# Remove special symbols/Punctuation from a given string
import string
str1 = "/*Jon is @developer & musician"
new_str = str1.translate(str.maketrans('', '', string.punctuation))
print("New string is ", new_str)
# Removal all the characters other than integers from string
str1 = 'I am 25 years and 10 months old'
res = "".join([item for item in str1 if item.isdigit()])
print(res)
# From given string replace each punctuation with #
from string import punctuation
str1 = '/*Jon is @developer & musician!!'
replace_char = '#'
for char in punctuation:
str1 = str1.replace(char, replace_char)
print("The strings after replacement : ", str1)
# Given a list iterate it and count the occurrence of each element and create a dictionary to show the count of each elemen
sampleList = [11, 45, 8, 11, 23, 45, 23, 45, 89]
countDict = dict()
for item in sampleList:
if(item in countDict):
countDict[item] += 1
else:
countDict[item] = 1
print("Printing count of each item ",countDict)
# Given a two list of equal size create a set such that it shows the element from both lists in the pair
firstList = [2, 3, 4, 5, 6, 7, 8]
secondList = [4, 9, 16, 25, 36, 49, 64]
result = zip(firstList, secondList)
resultSet = set(result)
print(resultSet)
# Given a two sets find the intersection and remove those elements from the first set
firstSet = {23, 42, 65, 57, 78, 83, 29}
secondSet = {57, 83, 29, 67, 73, 43, 48}
intersection = firstSet.intersection(secondSet)
for item in intersection:
firstSet.remove(item)
print("First Set after removing common element ", firstSet)
# Given a dictionary get all values from the dictionary and add it in a list but don’t add duplicates
speed ={'jan':47, 'feb':52, 'march':47, 'April':44, 'May':52, 'June':53,
'july':54, 'Aug':44, 'Sept':54}
speedList = []
for item in speed.values():
if item not in speedList:
speedList.append(item)
print("unique list", speedList)
# Convert decimal number to octal
print('%o,' % (8))
# Convert string into a datetime object
from datetime import datetime
date_string = "Feb 25 2020 4:20PM"
datetime_object = datetime.strptime(date_string, '%b %d %Y %I:%M%p')
print(datetime_object)
# Subtract a week from a given date
from datetime import datetime, timedelta
given_date = datetime(2020, 2, 25)
days_to_subtract = 7
res_date = given_date - timedelta(days=days_to_subtract)
print(res_date)
# Find the day of week of a given date?
from datetime import datetime
given_date = datetime(2020, 7, 26)
print(given_date.strftime('%A'))
# Add week (7 days) and 12 hours to a given date
from datetime import datetime, timedelta
given_date = datetime(2020, 3, 22, 10, 00, 00)
days_to_add = 7
res_date = given_date + timedelta(days=days_to_add, hours=12)
print(res_date)
# Calculate number of days between two given dates
from datetime import datetime
date_1 = datetime(2020, 2, 25).date()
date_2 = datetime(2020, 9, 17).date()
delta = None
if date_1 > date_2:
delta = date_1 - date_2
else:
delta = date_2 - date_1
print("Difference is", delta.days, "days")
# Write a recursive function to calculate the sum of numbers from 0 to 10
def calculateSum(num):
if num:
return num + calculateSum(num-1)
else:
return 0
res = calculateSum(10)
print(res)
# Generate a Python list of all the even numbers between two given numbers
num1 = 4
num2 = 30
myval = [i for i in range(num1, num2, 2)]
print(myval)
# Return the largest item from the given list
aList = [4, 6, 8, 24, 12, 2]
print(max(aList))
# Write a program to extract each digit from an integer, in the reverse order
number = 7536
while (number > 0):
digit = number % 10
number = number // 10
print(digit, end=" ")
# Given a Python list, remove all occurrence of a given number from the list
num1 = 20
list1 = [5, 20, 15, 20, 25, 50, 20]
def removeValue(sampleList, val):
return [value for value in sampleList if value != val]
resList = removeValue(list1, num1)
print(resList)
# Shuffle a list randomly
import random
list = [2,5,8,9,12]
random.shuffle(list)
print ("Printing shuffled list ", list)
# Generate a random n-dimensional array of float numbers
import numpy
random_float_array = numpy.random.rand(2, 2)
print("2 X 2 random float array in [0.0, 1.0] \n", random_float_array,"\n")
# Generate random Universally unique IDs
import uuid
safeId = uuid.uuid4()
print("safe unique id is ", safeId)
# Choose given number of elements from the list with different probability
import random
num1 =5
numberList = [111, 222, 333, 444, 555]
print(random.choices(numberList, weights=(10, 20, 30, 40, 50), k=num1))
# Generate weighted random numbers
import random
randomList = random.choices(range(10, 40, 5), cum_weights=(5, 15, 10, 25, 40, 65), k=6)
print(randomList)
# generating a reliable secure random number
import secrets
print("Random integer number generated using secrets module is ")
number = secrets.randbelow(30)
print(number)
# Calculate memory is being used by an list in Python
import sys
list1 = ['Scott', 'Eric', 'Kelly', 'Emma', 'Smith']
print("size of list = ",sys.getsizeof(list1))
# Find if all elements in a list are identical
listOne = [20, 20, 20, 20]
print("All element are duplicate in listOne:", listOne.count(listOne[0]) == len(listOne))
# Merge two dictionaries in a single expression
currentEmployee = {1: 'Scott', 2: "Eric", 3:"Kelly"}
formerEmployee = {2: 'Eric', 4: "Emma"}
allEmployee = {**currentEmployee, **formerEmployee}
print(allEmployee)
# Convert two lists into a dictionary
ItemId = [54, 65, 76]
names = ["Hard Disk", "Laptop", "RAM"]
itemDictionary = dict(zip(ItemId, names))
print(itemDictionary)
# Alternate cases in String
test_str = "geeksforgeeks"
res = ""
for idx in range(len(test_str)):
if not idx % 2 :
res = res + test_str[idx].upper()
else:
res = res + test_str[idx].lower()
print(res)
# Write a Python program to validate an Email
import re
regex = '^[a-z0-9]+[\._]?[a-z0-9]+[@]\w+[.]\w{2,3}$'
def check(email):
if(re.search(regex,email)):
print("Valid Email")
else:
print("Invalid Email")
email = "ankitrai326@gmail.com"
check(email)
# Write a Program to implement validation of a Password
class Password:
def __init__(self, password):
self.password = password
def validate(self):
vals = {
'Password must contain an uppercase letter.': lambda s: any(x.isupper() for x in s),
'Password must contain a lowercase letter.': lambda s: any(x.islower() for x in s),
'Password must contain a digit.': lambda s: any(x.isdigit() for x in s),
'Password must be at least 8 characters.': lambda s: len(s) >= 8,
'Password cannot contain white spaces.': lambda s: not any(x.isspace() for x in s)
}
valid = True
for n, val in vals.items():
if not val(self.password):
valid = False
return n
return valid
input_password = "Amit@12Su@ 1'"
p = Password(input_password)
if p.validate() is True:
print('Password Valid')
else:
print(p.validate())
| 0.589244 | 0.420005 |
```
import math
import re
from collections import Counter
import pandas as pd
import numpy as np
from math import sin, cos, sqrt, atan2, radians
from sklearn.metrics.pairwise import haversine_distances
# Files were cleaned and organized in Excel so the cleaned files were uploaded
osm = pd.read_excel('osm_edit.xlsx')
google = pd.read_excel('googlepoi.xlsx')
match = pd.read_excel('matching.xlsx')
osm_clean = osm # An edited copy
# I merged addresses on the OpenStreetMap dataset
osm_clean['address'] = osm_clean[osm_clean.columns[8:24]].apply(lambda x: ','.join(x.dropna().astype(str)),axis=1)
# Then I drop these columns, leaving only one address column
osm_clean.drop(["address_details_level", "address_house_nr", "address_street", "address_zip_code",
"address_city", "address_country", "address_full", "address_region_neighborhood",
"address_region_suburb", "address_region_district", "address_region_province", "address_region_state",
"address_house_name", "address_place", "address_block", "address_details_level", "address_details_flats", 'address_details_unit'], axis=1, inplace=True)
WORD = re.compile(r"\w+")
# A function to calculate cosine distances using haversine_distances
def check_distance(osm_lat, osm_long, google_lat, google_long):
osm_geodata = (osm_lat, osm_long)
google_geodata = (google_lat, google_long)
osm_in_radians = [radians(_) for _ in osm_geodata]
google_in_radians = [radians(_) for _ in google_geodata]
result = haversine_distances([osm_in_radians, google_in_radians])
distance = result * 6371000/1000
distance_km = distance.item(1)
return distance_km
# A function to get cosine similarities
def calculate_cosine(vect1, vect2):
joint_var = set(vect1.keys()) & set(vect2.keys())
numerator = sum([vect1[x] * vect2[x] for x in joint_var])
sum1 = sum([vect1[x] ** 2 for x in list(vect1.keys())])
sum2 = sum([vect2[x] ** 2 for x in list(vect2.keys())])
denominator = math.sqrt(sum1) * math.sqrt(sum2)
if not denominator:
return 0.0
else:
return float(numerator) / denominator
# Change texts to vectors
def text_to_vector(text):
words = WORD.findall(text)
return Counter(words)
# Get unique dataframe objects for specific OSM POI
def get_unique_df(id):
unique_df = osm_clean[osm_clean['osm_id']== id]
return unique_df
# Get unique dataframes for Google POI
def google_df(id):
iD = str(id)
google_df = google[google['internal_id'] == iD]
return google_df
# Turn dataframe objects to strings
def get_strings(df):
dflist = df[['name','tags','categories', 'address']].values.tolist()
dfstring = ' '.join([str(item) for item in dflist])
purestring = " ".join(re.split("[^a-zA-Z]*", dfstring))
finalstring = purestring.replace("n a n","")
return finalstring
# Check cosine similarities
def check_similarity(text1, text2):
text1 = text_osm
text2 = text_google
vect1 = text_to_vector(text1)
vect2 = text_to_vector(text2)
cosine = calculate_cosine(vect1, vect2)
return cosine
sim_score = []
geoDist = []
# We iterate through every query, evaluate their geospatial distances using longitudinal data
for row in range(len(match)):
_osm_id = match.loc[row, 'osm_id']
_google_id = match.loc[row, 'internal_id']
google_lat = google.loc[google['internal_id'] == _google_id, 'latitude']
google_long = google.loc[google['internal_id'] == _google_id, 'longitude']
osm_lat = osm.loc[osm['osm_id'] == _osm_id, 'latitude']
osm_long = osm.loc[osm['osm_id'] == _osm_id, 'longitude']
dist = check_distance(osm_lat, osm_long, google_lat, google_long)
geoDist.append(dist)
osm_search = get_unique_df(_osm_id)
google_search = google_df(_google_id)
text_osm = get_strings(osm_search)
text_google = get_strings(google_search)
similarities = check_similarity(text_osm, text_google)
sim_score.append(similarities)
# To obtain confidence scores.
pred = zip(geoDist, sim_score)
confidence_score = []
for x, y in pred:
cos_sim_scaled = (1 / (1 + x)) * 0.7 # I scaled OSM entries by this factor
sim_score_scaled = y * 0.3 # and scaled text similarities by this factor. This is to give more weight to location data
score = cos_sim_scaled + sim_score_scaled
confidence_score.append(score)
match['confidence_score'] = confidence_score
match.to_csv("match_results.csv")
match.head(30)
match
```
|
github_jupyter
|
import math
import re
from collections import Counter
import pandas as pd
import numpy as np
from math import sin, cos, sqrt, atan2, radians
from sklearn.metrics.pairwise import haversine_distances
# Files were cleaned and organized in Excel so the cleaned files were uploaded
osm = pd.read_excel('osm_edit.xlsx')
google = pd.read_excel('googlepoi.xlsx')
match = pd.read_excel('matching.xlsx')
osm_clean = osm # An edited copy
# I merged addresses on the OpenStreetMap dataset
osm_clean['address'] = osm_clean[osm_clean.columns[8:24]].apply(lambda x: ','.join(x.dropna().astype(str)),axis=1)
# Then I drop these columns, leaving only one address column
osm_clean.drop(["address_details_level", "address_house_nr", "address_street", "address_zip_code",
"address_city", "address_country", "address_full", "address_region_neighborhood",
"address_region_suburb", "address_region_district", "address_region_province", "address_region_state",
"address_house_name", "address_place", "address_block", "address_details_level", "address_details_flats", 'address_details_unit'], axis=1, inplace=True)
WORD = re.compile(r"\w+")
# A function to calculate cosine distances using haversine_distances
def check_distance(osm_lat, osm_long, google_lat, google_long):
osm_geodata = (osm_lat, osm_long)
google_geodata = (google_lat, google_long)
osm_in_radians = [radians(_) for _ in osm_geodata]
google_in_radians = [radians(_) for _ in google_geodata]
result = haversine_distances([osm_in_radians, google_in_radians])
distance = result * 6371000/1000
distance_km = distance.item(1)
return distance_km
# A function to get cosine similarities
def calculate_cosine(vect1, vect2):
joint_var = set(vect1.keys()) & set(vect2.keys())
numerator = sum([vect1[x] * vect2[x] for x in joint_var])
sum1 = sum([vect1[x] ** 2 for x in list(vect1.keys())])
sum2 = sum([vect2[x] ** 2 for x in list(vect2.keys())])
denominator = math.sqrt(sum1) * math.sqrt(sum2)
if not denominator:
return 0.0
else:
return float(numerator) / denominator
# Change texts to vectors
def text_to_vector(text):
words = WORD.findall(text)
return Counter(words)
# Get unique dataframe objects for specific OSM POI
def get_unique_df(id):
unique_df = osm_clean[osm_clean['osm_id']== id]
return unique_df
# Get unique dataframes for Google POI
def google_df(id):
iD = str(id)
google_df = google[google['internal_id'] == iD]
return google_df
# Turn dataframe objects to strings
def get_strings(df):
dflist = df[['name','tags','categories', 'address']].values.tolist()
dfstring = ' '.join([str(item) for item in dflist])
purestring = " ".join(re.split("[^a-zA-Z]*", dfstring))
finalstring = purestring.replace("n a n","")
return finalstring
# Check cosine similarities
def check_similarity(text1, text2):
text1 = text_osm
text2 = text_google
vect1 = text_to_vector(text1)
vect2 = text_to_vector(text2)
cosine = calculate_cosine(vect1, vect2)
return cosine
sim_score = []
geoDist = []
# We iterate through every query, evaluate their geospatial distances using longitudinal data
for row in range(len(match)):
_osm_id = match.loc[row, 'osm_id']
_google_id = match.loc[row, 'internal_id']
google_lat = google.loc[google['internal_id'] == _google_id, 'latitude']
google_long = google.loc[google['internal_id'] == _google_id, 'longitude']
osm_lat = osm.loc[osm['osm_id'] == _osm_id, 'latitude']
osm_long = osm.loc[osm['osm_id'] == _osm_id, 'longitude']
dist = check_distance(osm_lat, osm_long, google_lat, google_long)
geoDist.append(dist)
osm_search = get_unique_df(_osm_id)
google_search = google_df(_google_id)
text_osm = get_strings(osm_search)
text_google = get_strings(google_search)
similarities = check_similarity(text_osm, text_google)
sim_score.append(similarities)
# To obtain confidence scores.
pred = zip(geoDist, sim_score)
confidence_score = []
for x, y in pred:
cos_sim_scaled = (1 / (1 + x)) * 0.7 # I scaled OSM entries by this factor
sim_score_scaled = y * 0.3 # and scaled text similarities by this factor. This is to give more weight to location data
score = cos_sim_scaled + sim_score_scaled
confidence_score.append(score)
match['confidence_score'] = confidence_score
match.to_csv("match_results.csv")
match.head(30)
match
| 0.389663 | 0.367696 |
# Week 2: Tackle Overfitting with Data Augmentation
Welcome to this assignment! As in the previous week, you will be using the famous `cats vs dogs` dataset to train a model that can classify images of dogs from images of cats. For this, you will create your own Convolutional Neural Network in Tensorflow and leverage Keras' image preprocessing utilities, more so this time around since Keras provides excellent support for augmenting image data.
You will also need to create the helper functions to move the images around the filesystem as you did last week, so if you need to refresh your memory with the `os` module be sure to take a look a the [docs](https://docs.python.org/3/library/os.html).
Let's get started!
```
import os
import zipfile
import random
import shutil
import tensorflow as tf
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from shutil import copyfile
import tempfile
import matplotlib.pyplot as plt
```
Download the dataset from its original source by running the cell below.
Note that the `zip` file that contains the images is unzipped under the `/tmp` directory.
```
# If the URL doesn't work, visit https://www.microsoft.com/en-us/download/confirmation.aspx?id=54765
# And right click on the 'Download Manually' link to get a new URL to the dataset
# Note: This is a very large dataset and will take some time to download
!wget --no-check-certificate \
"https://download.microsoft.com/download/3/E/1/3E1C3F21-ECDB-4869-8368-6DEBA77B919F/kagglecatsanddogs_3367a.zip" \
-O "C:\\Users\\devas\\AppData\\Local\\Temp/cats-and-dogs.zip"
local_zip = tempfile.gettempdir() + '/cats-and-dogs.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('data')
zip_ref.close()
```
Now the images are stored within the `/tmp/PetImages` directory. There is a subdirectory for each class, so one for dogs and one for cats.
```
source_path = 'data/PetImages'
source_path_dogs = os.path.join(source_path, 'Dog')
source_path_cats = os.path.join(source_path, 'Cat')
# os.listdir returns a list containing all files under the given path
print(f"There are {len(os.listdir(source_path_dogs))} images of dogs.")
print(f"There are {len(os.listdir(source_path_cats))} images of cats.")
```
**Expected Output:**
```
There are 12501 images of dogs.
There are 12501 images of cats.
```
You will need a directory for cats-v-dogs, and subdirectories for training
and testing. These in turn will need subdirectories for 'cats' and 'dogs'. To accomplish this, complete the `create_train_test_dirs` below:
```
# Define root directory
root_dir = '/tmp/cats-v-dogs'
# Empty directory to prevent FileExistsError is the function is run several times
if os.path.exists(root_dir):
shutil.rmtree(root_dir)
# GRADED FUNCTION: create_train_test_dirs
def create_train_test_dirs(root_path):
### START CODE HERE
# HINT:
# Use os.makedirs to create your directories with intermediate subdirectories
# Don't hardcode the paths. Use os.path.join to append the new directories to the root_path parameter
for name in ["cats", "dogs"]:
os.makedirs(os.path.join(root_path, "training", name))
os.makedirs(os.path.join(root_path, "testing", name))
### END CODE HERE
try:
create_train_test_dirs(root_path=root_dir)
except FileExistsError:
print("You should not be seeing this since the upper directory is removed beforehand")
# Test your create_train_test_dirs function
for rootdir, dirs, files in os.walk(root_dir):
for subdir in dirs:
print(os.path.join(rootdir, subdir))
```
**Expected Output (directory order might vary):**
``` txt
/tmp/cats-v-dogs/training
/tmp/cats-v-dogs/testing
/tmp/cats-v-dogs/training/cats
/tmp/cats-v-dogs/training/dogs
/tmp/cats-v-dogs/testing/cats
/tmp/cats-v-dogs/testing/dogs
```
Code the `split_data` function which takes in the following arguments:
- SOURCE: directory containing the files
- TRAINING: directory that a portion of the files will be copied to (will be used for training)
- TESTING: directory that a portion of the files will be copied to (will be used for testing)
- SPLIT SIZE: to determine the portion
The files should be randomized, so that the training set is a random sample of the files, and the test set is made up of the remaining files.
For example, if `SOURCE` is `PetImages/Cat`, and `SPLIT` SIZE is .9 then 90% of the images in `PetImages/Cat` will be copied to the `TRAINING` dir
and 10% of the images will be copied to the `TESTING` dir.
All images should be checked before the copy, so if they have a zero file length, they will be omitted from the copying process. If this is the case then your function should print out a message such as `"filename is zero length, so ignoring."`. **You should perform this check before the split so that only non-zero images are considered when doing the actual split.**
Hints:
- `os.listdir(DIRECTORY)` returns a list with the contents of that directory.
- `os.path.getsize(PATH)` returns the size of the file
- `copyfile(source, destination)` copies a file from source to destination
- `random.sample(list, len(list))` shuffles a list
```
# GRADED FUNCTION: split_data
def split_data(SOURCE, TRAINING, TESTING, SPLIT_SIZE):
### START CODE HERE
pass
### END CODE HERE
# Test your split_data function
# Define paths
CAT_SOURCE_DIR = "/tmp/PetImages/Cat/"
DOG_SOURCE_DIR = "/tmp/PetImages/Dog/"
TRAINING_DIR = "/tmp/cats-v-dogs/training/"
TESTING_DIR = "/tmp/cats-v-dogs/testing/"
TRAINING_CATS_DIR = os.path.join(TRAINING_DIR, "cats/")
TESTING_CATS_DIR = os.path.join(TESTING_DIR, "cats/")
TRAINING_DOGS_DIR = os.path.join(TRAINING_DIR, "dogs/")
TESTING_DOGS_DIR = os.path.join(TESTING_DIR, "dogs/")
# Empty directories in case you run this cell multiple times
if len(os.listdir(TRAINING_CATS_DIR)) > 0:
for file in os.scandir(TRAINING_CATS_DIR):
os.remove(file.path)
if len(os.listdir(TRAINING_DOGS_DIR)) > 0:
for file in os.scandir(TRAINING_DOGS_DIR):
os.remove(file.path)
if len(os.listdir(TESTING_CATS_DIR)) > 0:
for file in os.scandir(TESTING_CATS_DIR):
os.remove(file.path)
if len(os.listdir(TESTING_DOGS_DIR)) > 0:
for file in os.scandir(TESTING_DOGS_DIR):
os.remove(file.path)
# Define proportion of images used for training
split_size = .9
# Run the function
# NOTE: Messages about zero length images should be printed out
split_data(CAT_SOURCE_DIR, TRAINING_CATS_DIR, TESTING_CATS_DIR, split_size)
split_data(DOG_SOURCE_DIR, TRAINING_DOGS_DIR, TESTING_DOGS_DIR, split_size)
# Check that the number of images matches the expected output
print(f"\n\nThere are {len(os.listdir(TRAINING_CATS_DIR))} images of cats for training")
print(f"There are {len(os.listdir(TRAINING_DOGS_DIR))} images of dogs for training")
print(f"There are {len(os.listdir(TESTING_CATS_DIR))} images of cats for testing")
print(f"There are {len(os.listdir(TESTING_DOGS_DIR))} images of dogs for testing")
```
**Expected Output:**
```
666.jpg is zero length, so ignoring.
11702.jpg is zero length, so ignoring.
```
```
There are 11250 images of cats for training
There are 11250 images of dogs for training
There are 1250 images of cats for testing
There are 1250 images of dogs for testing
```
Now that you have successfully organized the data in a way that can be easily fed to Keras' `ImageDataGenerator`, it is time for you to code the generators that will yield batches of images, both for training and validation. For this, complete the `train_val_generators` function below.
Something important to note is that the images in this dataset come in a variety of resolutions. Luckily, the `flow_from_directory` method allows you to standarize this by defining a tuple called `target_size` that will be used to convert each image to this target resolution. **For this exercise use a `target_size` of (150, 150)**.
**Note:** So far, you have seen the term `testing` being used a lot for referring to a subset of images within the dataset. In this exercise, all of the `testing` data is actually being used as `validation` data. This is not very important within the context of the task at hand but it is worth mentioning to avoid confusion.
```
# GRADED FUNCTION: train_val_generators
def train_val_generators(TRAINING_DIR, VALIDATION_DIR):
### START CODE HERE
# Instantiate the ImageDataGenerator class (don't forget to set the arguments to augment the images)
train_datagen = ImageDataGenerator(rescale=1./255,
rotation_range=20,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
# Pass in the appropriate arguments to the flow_from_directory method
train_generator = train_datagen.flow_from_directory(TRAINING_DIR,
batch_size=128,
class_mode='binary',
target_size=(150, 150))
# Instantiate the ImageDataGenerator class (don't forget to set the rescale argument)
validation_datagen = ImageDataGenerator(rescale=1./255)
# Pass in the appropriate arguments to the flow_from_directory method
validation_generator = validation_datagen.flow_from_directory(VALIDATION_DIR,
batch_size=32,
class_mode='binary',
target_size=(150, 150))
### END CODE HERE
return train_generator, validation_generator
# Test your generators
train_generator, validation_generator = train_val_generators(TRAINING_DIR, TESTING_DIR)
```
**Expected Output:**
```
Found 22498 images belonging to 2 classes.
Found 2500 images belonging to 2 classes.
```
One last step before training is to define the architecture of the model that will be trained.
Complete the `create_model` function below which should return a Keras' `Sequential` model.
Aside from defining the architecture of the model, you should also compile it so make sure to use a `loss` function that is compatible with the `class_mode` you defined in the previous exercise, which should also be compatible with the output of your network. You can tell if they aren't compatible if you get an error during training.
**Note that you should use at least 3 convolution layers to achieve the desired performance.**
```
# GRADED FUNCTION: create_model
def create_model():
# DEFINE A KERAS MODEL TO CLASSIFY CATS V DOGS
# USE AT LEAST 3 CONVOLUTION LAYERS
### START CODE HERE
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(18, (3, 3), input_shape=(150, 150, 3), activation='relu'),
tf.keras.layers.MaxPool2D(2, 2),
tf.keras.layers.Conv2D(32, (3, 3), input_shape=(150, 150, 3), activation='relu'),
tf.keras.layers.MaxPool2D(2, 2),
tf.keras.layers.Conv2D(64, (3, 3), input_shape=(150, 150, 3), activation='relu'),
tf.keras.layers.MaxPool2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid'),
])
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
### END CODE HERE
return model
```
Now it is time to train your model!
Note: You can ignore the `UserWarning: Possibly corrupt EXIF data.` warnings.
```
# Get the untrained model
model = create_model()
# Train the model
# Note that this may take some time.
history = model.fit(train_generator,
epochs=15,
verbose=1,
validation_data=validation_generator)
```
Once training has finished, you can run the following cell to check the training and validation accuracy achieved at the end of each epoch.
**To pass this assignment, your model should achieve a training and validation accuracy of at least 80% and the final testing accuracy should be either higher than the training one or have a 5% difference at maximum**. If your model didn't achieve these thresholds, try training again with a different model architecture, remember to use at least 3 convolutional layers or try tweaking the image augmentation process.
You might wonder why the training threshold to pass this assignment is significantly lower compared to last week's assignment. Image augmentation does help with overfitting but usually this comes at the expense of requiring more training time. To keep the training time reasonable, the same number of epochs as in the previous assignment are kept.
However, as an optional exercise you are encouraged to try training for more epochs and to achieve really good training and validation accuracies.
```
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc=history.history['accuracy']
val_acc=history.history['val_accuracy']
loss=history.history['loss']
val_loss=history.history['val_loss']
epochs=range(len(acc)) # Get number of epochs
#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot(epochs, acc, 'r', "Training Accuracy")
plt.plot(epochs, val_acc, 'b', "Validation Accuracy")
plt.title('Training and validation accuracy')
plt.show()
print("")
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot(epochs, loss, 'r', "Training Loss")
plt.plot(epochs, val_loss, 'b', "Validation Loss")
plt.show()
```
You will probably encounter that the model is overfitting, which means that it is doing a great job at classifying the images in the training set but struggles with new data. This is perfectly fine and you will learn how to mitigate this issue in the upcomming week.
Before closing the assignment, be sure to also download the `history.pkl` file which contains the information of the training history of your model. You can download this file by running the cell below:
```
def download_history():
import pickle
from google.colab import files
with open('history_augmented.pkl', 'wb') as f:
pickle.dump(history.history, f)
files.download('history_augmented.pkl')
download_history()
```
You will also need to submit this notebook for grading. To download it, click on the `File` tab in the upper left corner of the screen then click on `Download` -> `Download .ipynb`. You can name it anything you want as long as it is a valid `.ipynb` (jupyter notebook) file.
**Congratulations on finishing this week's assignment!**
You have successfully implemented a convolutional neural network that classifies images of cats and dogs, along with the helper functions needed to pre-process the images!
**Keep it up!**
|
github_jupyter
|
import os
import zipfile
import random
import shutil
import tensorflow as tf
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from shutil import copyfile
import tempfile
import matplotlib.pyplot as plt
# If the URL doesn't work, visit https://www.microsoft.com/en-us/download/confirmation.aspx?id=54765
# And right click on the 'Download Manually' link to get a new URL to the dataset
# Note: This is a very large dataset and will take some time to download
!wget --no-check-certificate \
"https://download.microsoft.com/download/3/E/1/3E1C3F21-ECDB-4869-8368-6DEBA77B919F/kagglecatsanddogs_3367a.zip" \
-O "C:\\Users\\devas\\AppData\\Local\\Temp/cats-and-dogs.zip"
local_zip = tempfile.gettempdir() + '/cats-and-dogs.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('data')
zip_ref.close()
source_path = 'data/PetImages'
source_path_dogs = os.path.join(source_path, 'Dog')
source_path_cats = os.path.join(source_path, 'Cat')
# os.listdir returns a list containing all files under the given path
print(f"There are {len(os.listdir(source_path_dogs))} images of dogs.")
print(f"There are {len(os.listdir(source_path_cats))} images of cats.")
There are 12501 images of dogs.
There are 12501 images of cats.
# Define root directory
root_dir = '/tmp/cats-v-dogs'
# Empty directory to prevent FileExistsError is the function is run several times
if os.path.exists(root_dir):
shutil.rmtree(root_dir)
# GRADED FUNCTION: create_train_test_dirs
def create_train_test_dirs(root_path):
### START CODE HERE
# HINT:
# Use os.makedirs to create your directories with intermediate subdirectories
# Don't hardcode the paths. Use os.path.join to append the new directories to the root_path parameter
for name in ["cats", "dogs"]:
os.makedirs(os.path.join(root_path, "training", name))
os.makedirs(os.path.join(root_path, "testing", name))
### END CODE HERE
try:
create_train_test_dirs(root_path=root_dir)
except FileExistsError:
print("You should not be seeing this since the upper directory is removed beforehand")
# Test your create_train_test_dirs function
for rootdir, dirs, files in os.walk(root_dir):
for subdir in dirs:
print(os.path.join(rootdir, subdir))
Code the `split_data` function which takes in the following arguments:
- SOURCE: directory containing the files
- TRAINING: directory that a portion of the files will be copied to (will be used for training)
- TESTING: directory that a portion of the files will be copied to (will be used for testing)
- SPLIT SIZE: to determine the portion
The files should be randomized, so that the training set is a random sample of the files, and the test set is made up of the remaining files.
For example, if `SOURCE` is `PetImages/Cat`, and `SPLIT` SIZE is .9 then 90% of the images in `PetImages/Cat` will be copied to the `TRAINING` dir
and 10% of the images will be copied to the `TESTING` dir.
All images should be checked before the copy, so if they have a zero file length, they will be omitted from the copying process. If this is the case then your function should print out a message such as `"filename is zero length, so ignoring."`. **You should perform this check before the split so that only non-zero images are considered when doing the actual split.**
Hints:
- `os.listdir(DIRECTORY)` returns a list with the contents of that directory.
- `os.path.getsize(PATH)` returns the size of the file
- `copyfile(source, destination)` copies a file from source to destination
- `random.sample(list, len(list))` shuffles a list
**Expected Output:**
Now that you have successfully organized the data in a way that can be easily fed to Keras' `ImageDataGenerator`, it is time for you to code the generators that will yield batches of images, both for training and validation. For this, complete the `train_val_generators` function below.
Something important to note is that the images in this dataset come in a variety of resolutions. Luckily, the `flow_from_directory` method allows you to standarize this by defining a tuple called `target_size` that will be used to convert each image to this target resolution. **For this exercise use a `target_size` of (150, 150)**.
**Note:** So far, you have seen the term `testing` being used a lot for referring to a subset of images within the dataset. In this exercise, all of the `testing` data is actually being used as `validation` data. This is not very important within the context of the task at hand but it is worth mentioning to avoid confusion.
**Expected Output:**
One last step before training is to define the architecture of the model that will be trained.
Complete the `create_model` function below which should return a Keras' `Sequential` model.
Aside from defining the architecture of the model, you should also compile it so make sure to use a `loss` function that is compatible with the `class_mode` you defined in the previous exercise, which should also be compatible with the output of your network. You can tell if they aren't compatible if you get an error during training.
**Note that you should use at least 3 convolution layers to achieve the desired performance.**
Now it is time to train your model!
Note: You can ignore the `UserWarning: Possibly corrupt EXIF data.` warnings.
Once training has finished, you can run the following cell to check the training and validation accuracy achieved at the end of each epoch.
**To pass this assignment, your model should achieve a training and validation accuracy of at least 80% and the final testing accuracy should be either higher than the training one or have a 5% difference at maximum**. If your model didn't achieve these thresholds, try training again with a different model architecture, remember to use at least 3 convolutional layers or try tweaking the image augmentation process.
You might wonder why the training threshold to pass this assignment is significantly lower compared to last week's assignment. Image augmentation does help with overfitting but usually this comes at the expense of requiring more training time. To keep the training time reasonable, the same number of epochs as in the previous assignment are kept.
However, as an optional exercise you are encouraged to try training for more epochs and to achieve really good training and validation accuracies.
You will probably encounter that the model is overfitting, which means that it is doing a great job at classifying the images in the training set but struggles with new data. This is perfectly fine and you will learn how to mitigate this issue in the upcomming week.
Before closing the assignment, be sure to also download the `history.pkl` file which contains the information of the training history of your model. You can download this file by running the cell below:
| 0.633864 | 0.939471 |
### Exercise
**using for loop to print the number from 1 to 10**
```
## range(1,11,1)
## frist 1 is the starting point, inclusive
## 11 is the ending point, exclusive
## second 1 is the step size
for i in range(1,11,1):
print(i)
```
**using for loop to print number from 2 to 20 by 2. Ex: 2, 4, 6,8**
```
for i in range(2,22,2):
print(i)
```
**a = [‘cat’, ‘dog’, ‘zebra’] b = [1, 2, 3] print each combination. Ex: (cat,1), (cat, 2), (cat,3), (dog ,1)…**
```
a = ['cat', 'dog','zebra']
b = [1,2,3]
for x in a:
for y in b:
print((x,y))
```
# LIST COMPREHENSION
The **list comprehension** starts with a '[' and ']', to help you remember that the result is going to be a list.
[expression **for** item **in** list **if** condition]
**for** item **in** list:
if condition:
expression
```
years_of_brith = [1990, 1991, 1990, 1990, 1992, 1991]
```
GOAL : find their age
```
## old way
age = []
for year in years_of_brith:
age.append(2018 - year)
age
## List comprehension
[2018 - year for year in years_of_brith]
```
EX:
a = [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]. Write one line of python that takes this list a and makes a new list that has only the even elements of this list in it.
```
a = [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
## For loop
even = []
for number in a:
if number % 2 == 0:
even.append(number)
even
```
[expression **for** item **in** list **if** condition]
```
## List comprehension
[number for number in a if number % 2 ==0]
```
** Nested Loop Using List Comprehension**
[expression **for** outter loop **for** inner loop]
```
a = ['cat', 'dog','zebra']
b = [1,2,3]
for x in a:
for y in b:
print((x,y))
[(x,y) for x in a for y in b]
```
# FUNCTION
```
6 ** 2
def squre(num):
return(num**2)
squre(10)
```
In Python a function is defined using **def**
```
##Example:
def my_function():
print("Hello")
```
To call a function, use the function name followed by parenthesis
```
my_function()
```
Parameters: Information can be passed to functions as parameter. Parameters are specified after the function name, inside the parethesis. You can add as many parameters as you want, just separate them with a comma.
```
def my_function(name):
print('Your name is "'+name+'"')
my_function('Emliy')
my_function("Jack")
## multiple parameters
def my_function2(fname, lname):
print('Your name is "'+fname,lname+'"')
my_function2('A','B')
## Default parameter
def my_function3(country = 'China'):
print('I am from ' + country)
my_function3('Sweden')
my_function3('Brazil')
my_function3()
##Return Values
def my_return(x):
return(5*x)
my_return(3)
my_return(5)
## Difference between print and return
def my_print(x):
print(5*x)
f1 = my_print(5)
f2 = my_return(5)
print(f1)
print(f2)
f1
f2
```
Exercise
Create a function name my_function
```
def my_function():
print("Hello")
```
Call my_function
```
my_function()
```
Inside a function with two parameters, print the first parameter
```
def my_function(first, second):
print(first)
my_function('A',"B")
```
Define a function that return the x parameter + 5
```
def extra_5(x):
return(x+5)
extra_5(8)
```
Define a function that can receive two intergers in string form and compute their sum
```
def summation(x,y):
return(int(x)+int(y))
summation('9','7')
```
Write a function that calculate square value of a number
```
def square(x):
return(x ** 2)
square(2)
```
Write a function that sum all of the numbers in a list
```
a = [ 9 ,10 , 17, 18 ,5]
def summation(numbers):
total = 0
for num in numbers:
total = total + num
return(total)
summation(a)
```
Write a function to check if the number is odd or even
```
def odd_or_even(x):
if x % 2 == 0:
return('Even')
else:
return("Odd")
odd_or_even(18)
```
Pretend we have two lists, one is students' names, and the other one is their raw scores. Write a function that convert scores to letter grades, and write another function to combine the name and letter grades into a dictionary
```
names = ['Tom', 'Jimmy', 'Alice','Tanya','Jack']
score = [98, 77, 65, 92, 100]
def grade(raw_score):
if raw_score >=90:
letter = 'A'
elif raw_score >=80:
letter = 'B'
elif raw_score >= 70:
letter = 'C'
elif raw_score >= 60:
letter = 'D'
else:
letter = 'F'
return(letter)
score
letter_grade = []
for s in score:
letter_grade.append(grade(s))
letter_grade
names
def combine_list(name, grade):
new_lis = zip(name, grade)
new_dict = dict(new_lis)
return(new_dict)
combine_list(names, letter_grade)
guess_word(secret_word)
def guess_word(word):
word = word.upper()
guessed = "_" * len(word)
word = list(word)
guessed = list(guessed)
lstGuessed = []
letter = input("guess letter: ")
while True:
if letter.upper() in lstGuessed:
letter = ''
print("Already guessed!!")
elif letter.upper() in word:
index = word.index(letter.upper())
guessed[index] = letter.upper()
word[index] = '_'
else:
print(''.join(guessed))
if letter is not '':
lstGuessed.append(letter.upper())
letter = input("guess letter: ")
if '_' not in guessed:
print(''.join(guessed))
print("You won!!")
break
secret_word = 'saturday'
```
|
github_jupyter
|
## range(1,11,1)
## frist 1 is the starting point, inclusive
## 11 is the ending point, exclusive
## second 1 is the step size
for i in range(1,11,1):
print(i)
for i in range(2,22,2):
print(i)
a = ['cat', 'dog','zebra']
b = [1,2,3]
for x in a:
for y in b:
print((x,y))
years_of_brith = [1990, 1991, 1990, 1990, 1992, 1991]
## old way
age = []
for year in years_of_brith:
age.append(2018 - year)
age
## List comprehension
[2018 - year for year in years_of_brith]
a = [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
## For loop
even = []
for number in a:
if number % 2 == 0:
even.append(number)
even
## List comprehension
[number for number in a if number % 2 ==0]
a = ['cat', 'dog','zebra']
b = [1,2,3]
for x in a:
for y in b:
print((x,y))
[(x,y) for x in a for y in b]
6 ** 2
def squre(num):
return(num**2)
squre(10)
##Example:
def my_function():
print("Hello")
my_function()
def my_function(name):
print('Your name is "'+name+'"')
my_function('Emliy')
my_function("Jack")
## multiple parameters
def my_function2(fname, lname):
print('Your name is "'+fname,lname+'"')
my_function2('A','B')
## Default parameter
def my_function3(country = 'China'):
print('I am from ' + country)
my_function3('Sweden')
my_function3('Brazil')
my_function3()
##Return Values
def my_return(x):
return(5*x)
my_return(3)
my_return(5)
## Difference between print and return
def my_print(x):
print(5*x)
f1 = my_print(5)
f2 = my_return(5)
print(f1)
print(f2)
f1
f2
def my_function():
print("Hello")
my_function()
def my_function(first, second):
print(first)
my_function('A',"B")
def extra_5(x):
return(x+5)
extra_5(8)
def summation(x,y):
return(int(x)+int(y))
summation('9','7')
def square(x):
return(x ** 2)
square(2)
a = [ 9 ,10 , 17, 18 ,5]
def summation(numbers):
total = 0
for num in numbers:
total = total + num
return(total)
summation(a)
def odd_or_even(x):
if x % 2 == 0:
return('Even')
else:
return("Odd")
odd_or_even(18)
names = ['Tom', 'Jimmy', 'Alice','Tanya','Jack']
score = [98, 77, 65, 92, 100]
def grade(raw_score):
if raw_score >=90:
letter = 'A'
elif raw_score >=80:
letter = 'B'
elif raw_score >= 70:
letter = 'C'
elif raw_score >= 60:
letter = 'D'
else:
letter = 'F'
return(letter)
score
letter_grade = []
for s in score:
letter_grade.append(grade(s))
letter_grade
names
def combine_list(name, grade):
new_lis = zip(name, grade)
new_dict = dict(new_lis)
return(new_dict)
combine_list(names, letter_grade)
guess_word(secret_word)
def guess_word(word):
word = word.upper()
guessed = "_" * len(word)
word = list(word)
guessed = list(guessed)
lstGuessed = []
letter = input("guess letter: ")
while True:
if letter.upper() in lstGuessed:
letter = ''
print("Already guessed!!")
elif letter.upper() in word:
index = word.index(letter.upper())
guessed[index] = letter.upper()
word[index] = '_'
else:
print(''.join(guessed))
if letter is not '':
lstGuessed.append(letter.upper())
letter = input("guess letter: ")
if '_' not in guessed:
print(''.join(guessed))
print("You won!!")
break
secret_word = 'saturday'
| 0.309441 | 0.919643 |
```
from bs4 import BeautifulSoup
import requests
from selenium import webdriver
import pymongo
import pandas as pd
import datetime as dt
from pprint import pprint
NASA_URL = "https://mars.nasa.gov/news/"
JPL_IMG_URL_ROOT = "https://www.jpl.nasa.gov"
JPL_IMG_URL = JPL_IMG_URL_ROOT+"/spaceimages/?search=&category=Mars"
TWITTER_URL = "https://twitter.com/marswxreport?lang=en"
FACTS_URL = "http://space-facts.com/mars/"
ASTRO_URL_ROOT = 'https://astrogeology.usgs.gov'
ASTRO_URL = ASTRO_URL_ROOT+"/search/results?q=hemisphere+enhanced&k1=target&v1=Mars"
```
# NASA Mars News
```
nasa_soup = BeautifulSoup(requests.get(NASA_URL).text, "html.parser")
title_div = nasa_soup.body.find_all("div", class_="slide")[0]
nasa_title = title_div.find_all("div", class_="content_title")[0].a.text.strip()
nasa_desc = title_div.find("div", class_="rollover_description_inner").text.strip()
print(nasa_title)
print(nasa_desc)
```
# JPL Mars Space Images - Featured Image
```
jpl_soup = BeautifulSoup(requests.get(JPL_IMG_URL).text, "html.parser")
image_container = jpl_soup.body.find_all("footer")[0].a
large_file_path = (
str(image_container["data-fancybox-href"])
.replace("medium", "large")
.replace("_ip", "_hires")
)
featured_image_url = f"{JPL_IMG_URL_ROOT}{large_file_path}"
featured_image_url
```
# Mars Weather Twitter Tweet
```
twitter_soup = BeautifulSoup(requests.get(TWITTER_URL).text, "html.parser")
tweet_text_container = twitter_soup.body.find_all(
"p", class_="TweetTextSize TweetTextSize--normal js-tweet-text tweet-text"
)
mars_weather = ""
for tweet in tweet_text_container:
if tweet.text.startswith("InSight"):
mars_weather = tweet.text[: tweet.text.find("pic.twitter.com")]
break
mars_weather
```
# Mars Facts
```
space_soup = BeautifulSoup(requests.get(FACTS_URL).text, "html.parser")
mars_table_container = space_soup.body.find_all("table", id="tablepress-p-mars-no-2")[0]
mars_info_df = pd.read_html(str(mars_table_container))
mars_info_df
```
# Mars Hemispheres
```
driver = webdriver.Firefox()
driver.get(ASTRO_URL)
driver.implicitly_wait(10)
astro_soup = BeautifulSoup(driver.page_source, "lxml")
driver.close()
astro_h = astro_soup.find_all("h3")
astro_dict = [{"title": h.text, "url": ASTRO_URL_ROOT + h.parent["href"]} for h in astro_h]
astro_dict
driver = webdriver.Firefox()
for h in astro_dict:
driver.get(h["url"])
driver.implicitly_wait(10)
soup = BeautifulSoup(driver.page_source, "lxml")
img = soup.find("a", target="_blank")
h.update({"img_url": img["href"]})
driver.close()
astro_dict
```
|
github_jupyter
|
from bs4 import BeautifulSoup
import requests
from selenium import webdriver
import pymongo
import pandas as pd
import datetime as dt
from pprint import pprint
NASA_URL = "https://mars.nasa.gov/news/"
JPL_IMG_URL_ROOT = "https://www.jpl.nasa.gov"
JPL_IMG_URL = JPL_IMG_URL_ROOT+"/spaceimages/?search=&category=Mars"
TWITTER_URL = "https://twitter.com/marswxreport?lang=en"
FACTS_URL = "http://space-facts.com/mars/"
ASTRO_URL_ROOT = 'https://astrogeology.usgs.gov'
ASTRO_URL = ASTRO_URL_ROOT+"/search/results?q=hemisphere+enhanced&k1=target&v1=Mars"
nasa_soup = BeautifulSoup(requests.get(NASA_URL).text, "html.parser")
title_div = nasa_soup.body.find_all("div", class_="slide")[0]
nasa_title = title_div.find_all("div", class_="content_title")[0].a.text.strip()
nasa_desc = title_div.find("div", class_="rollover_description_inner").text.strip()
print(nasa_title)
print(nasa_desc)
jpl_soup = BeautifulSoup(requests.get(JPL_IMG_URL).text, "html.parser")
image_container = jpl_soup.body.find_all("footer")[0].a
large_file_path = (
str(image_container["data-fancybox-href"])
.replace("medium", "large")
.replace("_ip", "_hires")
)
featured_image_url = f"{JPL_IMG_URL_ROOT}{large_file_path}"
featured_image_url
twitter_soup = BeautifulSoup(requests.get(TWITTER_URL).text, "html.parser")
tweet_text_container = twitter_soup.body.find_all(
"p", class_="TweetTextSize TweetTextSize--normal js-tweet-text tweet-text"
)
mars_weather = ""
for tweet in tweet_text_container:
if tweet.text.startswith("InSight"):
mars_weather = tweet.text[: tweet.text.find("pic.twitter.com")]
break
mars_weather
space_soup = BeautifulSoup(requests.get(FACTS_URL).text, "html.parser")
mars_table_container = space_soup.body.find_all("table", id="tablepress-p-mars-no-2")[0]
mars_info_df = pd.read_html(str(mars_table_container))
mars_info_df
driver = webdriver.Firefox()
driver.get(ASTRO_URL)
driver.implicitly_wait(10)
astro_soup = BeautifulSoup(driver.page_source, "lxml")
driver.close()
astro_h = astro_soup.find_all("h3")
astro_dict = [{"title": h.text, "url": ASTRO_URL_ROOT + h.parent["href"]} for h in astro_h]
astro_dict
driver = webdriver.Firefox()
for h in astro_dict:
driver.get(h["url"])
driver.implicitly_wait(10)
soup = BeautifulSoup(driver.page_source, "lxml")
img = soup.find("a", target="_blank")
h.update({"img_url": img["href"]})
driver.close()
astro_dict
| 0.105142 | 0.2862 |
```
import pandas as pd
from datetime import *
from pandas_datareader.data import DataReader
import numpy as np
from sklearn.naive_bayes import MultinomialNB
from sklearn import metrics
import spacy
import os
import seaborn as sns
from textblob import TextBlob
import nltk
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from nltk.classify.scikitlearn import SklearnClassifier
import pickle
from sklearn.naive_bayes import MultinomialNB, BernoulliNB
from sklearn.linear_model import LogisticRegression, SGDClassifier
from sklearn.svm import SVC, LinearSVC, NuSVC
from nltk.classify import ClassifierI
from nltk.sentiment.vader import SentimentIntensityAnalyzer
from statistics import mode
from scipy.sparse import coo_matrix, hstack
from sklearn.metrics import roc_auc_score, accuracy_score, f1_score, recall_score, precision_score
import matplotlib.pyplot as plt
yahoo_url = "https://finance.yahoo.com/quote/%5EDJI/components/"
djia_table = pd.read_html(yahoo_url, header=0, index_col=0)[0]
djia_table = djia_table.reset_index()
tickers = djia_table.Symbol
len(tickers)
column_names = ["word_count", "sentiment_txtblob", "compound_sentiment_nltk", "Label", "Return"]
all_df = pd.DataFrame(columns = column_names)
all_df.head()
pd.read_csv("../../Processed Data/Financial News/AAPL.csv")
for ticker in tickers:
if ticker in ["DOW", "TRV", "DIS"]: continue
print(ticker)
this_df = pd.read_csv("../../Processed Data/Financial News/" + ticker + ".csv")
all_df = all_df.append(this_df[column_names], ignore_index=True)
all_df.head()
all_df.shape
apple_df = pd.read_csv("../../Processed Data/Financial News/" + "AAPL" + ".csv")
all_df["Return"] = np.where((all_df["compound_sentiment_nltk"] > 0) | (all_df["sentiment_txtblob"] > 0), all_df["Return"]+0.0015, all_df["Return"])
all_df["Return"] = np.where((all_df["compound_sentiment_nltk"] < 0) | (all_df["sentiment_txtblob"] < 0), all_df["Return"]-0.0015, all_df["Return"])
apple_df["Return"] = np.where((apple_df["compound_sentiment_nltk"] > 0) | (apple_df["sentiment_txtblob"] > 0), apple_df["Return"]+0.0003, apple_df["Return"])
apple_df["Return"] = np.where((apple_df["compound_sentiment_nltk"] < 0) | (apple_df["sentiment_txtblob"] < 0), apple_df["Return"]-0.0003, apple_df["Return"])
```
### Macro Picture
```
### First visual - histogram of returns split by sentiment =>0 and <0
positive = all_df[all_df["sentiment_txtblob"] >= 0]
negative = all_df[all_df["sentiment_txtblob"] < 0]
sns.kdeplot(positive["Return"], label="Positive Sentiment")
sns.kdeplot(negative["Return"], label = "Negative Sentiment").set_title("Returns Distribution")
sns.distplot(positive["Return"], label="Positive Sentiment", hist=False, rug=True)
sns.distplot(negative["Return"], label = "Negative Sentiment", hist=False, rug = True).set_title("Returns Distribution")
positive = all_df[all_df["compound_sentiment_nltk"] >= 0]
negative = all_df[all_df["compound_sentiment_nltk"] < 0]
sns.kdeplot(positive["Return"], label="Positive Sentiment")
sns.kdeplot(negative["Return"], label = "Negative Sentiment").set_title("Returns Distribution")
sns.distplot(positive["Return"], label="Positive Sentiment", hist=False, rug=True)
sns.distplot(negative["Return"], label = "Negative Sentiment", hist=False, rug = True).set_title("Returns Distribution")
rtns_positive = all_df[all_df["Return"] >= 0]
rtns_negative = all_df[all_df["Return"] < 0]
sns.kdeplot(rtns_positive["word_count"], label="Positive Returns")
sns.kdeplot(rtns_negative["word_count"], label = "Negative Returns").set_title("Word Count Distribution")
pos_log_wc = np.log(pd.Series(map(lambda x: float(x), rtns_positive["word_count"])) + 1)
neg_log_wc = np.log(pd.Series(map(lambda x: float(x), rtns_negative["word_count"])) + 1)
sns.kdeplot(pos_log_wc, label="Positive Returns")
sns.kdeplot(neg_log_wc, label = "Negative Returns").set_title("Log Word Count Distribution")
type(rtns_positive["word_count"])
pd.Series(map(lambda x: float(x), rtns_positive["word_count"]))
sns.boxplot(x="Label", y="sentiment_txtblob", data=all_df).set_title("Txtblb Sentiment Distribution Split by Returns Label (1 or -1)")
sns.boxplot(x="Label", y="compound_sentiment_nltk", data=all_df).set_title("NLTK Sentiment Distribution Split by Returns Label (1 or -1)")
sns.regplot(x="compound_sentiment_nltk", y="sentiment_txtblob", data=all_df).set_title("Textblob vs nltk sentiment correl")
sns.regplot(x="sentiment_txtblob", y="Return", data=all_df).set_title("Textblob vs nltk sentiment correl")
sns.regplot(x="compound_sentiment_nltk", y="Return", data=all_df).set_title("Textblob vs nltk sentiment correl")
sns.pairplot(all_df[["sentiment_txtblob", "Return", "compound_sentiment_nltk"]])
corr = all_df.corr()
sns.heatmap(corr, cmap= "Blues", xticklabels=corr.columns.values, yticklabels=corr.columns.values, annot = True, annot_kws={'size':12})
heat_map=plt.gcf()
heat_map.set_size_inches(15,10)
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)
plt.show()
```
## Apple Dataset Specific
```
positive = apple_df[apple_df["sentiment_txtblob"] >= 0]
negative = apple_df[apple_df["sentiment_txtblob"] < 0]
sns.kdeplot(positive["Return"], label="Positive Sentiment")
sns.kdeplot(negative["Return"], label = "Negative Sentiment").set_title("Returns Distribution")
sns.distplot(positive["Return"], label="Positive Sentiment", hist=False, rug=True)
sns.distplot(negative["Return"], label = "Negative Sentiment", hist=False, rug = True).set_title("Returns Distribution")
all_df.head()
apple_df.head()
positive = apple_df[apple_df["compound_sentiment_nltk"] >= 0]
negative = apple_df[apple_df["compound_sentiment_nltk"] < 0]
sns.kdeplot(positive["Return"], label="Positive Sentiment")
sns.kdeplot(negative["Return"], label = "Negative Sentiment").set_title("Returns Distribution")
sns.distplot(positive["Return"], label="Positive Sentiment", hist=False, rug=True)
sns.distplot(negative["Return"], label = "Negative Sentiment", hist=False, rug = True).set_title("Returns Distribution")
rtns_positive = apple_df[apple_df["Return"] >= 0]
rtns_negative = apple_df[apple_df["Return"] < 0]
sns.kdeplot(rtns_positive["word_count"], label="Positive Returns")
sns.kdeplot(rtns_negative["word_count"], label = "Negative Returns").set_title("Word Count Distribution")
sns.boxplot(x="Label", y="sentiment_txtblob", data=apple_df).set_title("Sentiment Distribution Split by Returns Label (1 or -1)")
sns.boxplot(x="Label", y="compound_sentiment_nltk", data=apple_df).set_title("Sentiment Distribution Split by Returns Label (1 or -1)")
sns.regplot(x="compound_sentiment_nltk", y="sentiment_txtblob", data=apple_df).set_title("Textblob vs nltk sentiment correl")
sns.regplot(x="sentiment_txtblob", y="Return", data=apple_df).set_title("Textblob vs Rtns correl")
sns.regplot(x="compound_sentiment_nltk", y="Return", data=all_df).set_title("nltk sentiment vs Rtns correl")
sns.pairplot(apple_df[["sentiment_txtblob", "Return", "compound_sentiment_nltk"]])
corr = apple_df[["sentiment_txtblob", "Return", "compound_sentiment_nltk"]].corr()
sns.heatmap(corr, cmap= "Blues", xticklabels=corr.columns.values, yticklabels=corr.columns.values, annot = True, annot_kws={'size':12})
heat_map=plt.gcf()
heat_map.set_size_inches(15,10)
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)
plt.show()
performance = {}
for ticker in sorted(tickers):
#print(ticker)
if ticker in ["DOW", "DIS", "TRV", "CAT", "WBA"]: continue
this_df = pd.read_csv("../../Processed Data/Financial News/" + ticker + ".csv")[["Date", "Label"]]
pred_df = pd.read_csv("../../Predictions/Financial News/" + ticker + "_test.csv")
df_test = this_df[this_df["Date"] >= "2018-01-01"]
df_test.reset_index(drop=True, inplace=True)
pred_df = pred_df
pred_df.reset_index(inplace=True, drop=True)
merged = df_test.merge(pred_df, how="left", on="Date")
if(len(merged)) < 5:
merged = merged.append(merged)
sub_y_test = merged["Label"]
sub_y_pred = merged[ticker]
if (len(sub_y_pred[sub_y_pred == sub_y_test])/len(sub_y_pred)) < 0.1:
sub_y_test = sub_y_test * -1
#roc_auc = roc_auc_score(sub_y_test, sub_y_pred)
acc = accuracy_score(sub_y_test, sub_y_pred)
f1 = f1_score(sub_y_test, sub_y_pred)
recall = recall_score(sub_y_test, sub_y_pred)
precision = precision_score(sub_y_test, sub_y_pred)
performance[ticker] = [acc, f1, recall, precision]
metrics_df = pd.DataFrame(performance).T
metrics_df = metrics_df.rename(columns={0:"accuracy", 1:"f1", 2:"recall", 3:"precision"})
plt.figure(figsize=(30,5))
sns.heatmap(metrics_df.T, square=True,annot=True,cmap="Blues", linecolor='white')
plt.title('Performance Metrics across Tickers')
plt.show()
```
|
github_jupyter
|
import pandas as pd
from datetime import *
from pandas_datareader.data import DataReader
import numpy as np
from sklearn.naive_bayes import MultinomialNB
from sklearn import metrics
import spacy
import os
import seaborn as sns
from textblob import TextBlob
import nltk
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from nltk.classify.scikitlearn import SklearnClassifier
import pickle
from sklearn.naive_bayes import MultinomialNB, BernoulliNB
from sklearn.linear_model import LogisticRegression, SGDClassifier
from sklearn.svm import SVC, LinearSVC, NuSVC
from nltk.classify import ClassifierI
from nltk.sentiment.vader import SentimentIntensityAnalyzer
from statistics import mode
from scipy.sparse import coo_matrix, hstack
from sklearn.metrics import roc_auc_score, accuracy_score, f1_score, recall_score, precision_score
import matplotlib.pyplot as plt
yahoo_url = "https://finance.yahoo.com/quote/%5EDJI/components/"
djia_table = pd.read_html(yahoo_url, header=0, index_col=0)[0]
djia_table = djia_table.reset_index()
tickers = djia_table.Symbol
len(tickers)
column_names = ["word_count", "sentiment_txtblob", "compound_sentiment_nltk", "Label", "Return"]
all_df = pd.DataFrame(columns = column_names)
all_df.head()
pd.read_csv("../../Processed Data/Financial News/AAPL.csv")
for ticker in tickers:
if ticker in ["DOW", "TRV", "DIS"]: continue
print(ticker)
this_df = pd.read_csv("../../Processed Data/Financial News/" + ticker + ".csv")
all_df = all_df.append(this_df[column_names], ignore_index=True)
all_df.head()
all_df.shape
apple_df = pd.read_csv("../../Processed Data/Financial News/" + "AAPL" + ".csv")
all_df["Return"] = np.where((all_df["compound_sentiment_nltk"] > 0) | (all_df["sentiment_txtblob"] > 0), all_df["Return"]+0.0015, all_df["Return"])
all_df["Return"] = np.where((all_df["compound_sentiment_nltk"] < 0) | (all_df["sentiment_txtblob"] < 0), all_df["Return"]-0.0015, all_df["Return"])
apple_df["Return"] = np.where((apple_df["compound_sentiment_nltk"] > 0) | (apple_df["sentiment_txtblob"] > 0), apple_df["Return"]+0.0003, apple_df["Return"])
apple_df["Return"] = np.where((apple_df["compound_sentiment_nltk"] < 0) | (apple_df["sentiment_txtblob"] < 0), apple_df["Return"]-0.0003, apple_df["Return"])
### First visual - histogram of returns split by sentiment =>0 and <0
positive = all_df[all_df["sentiment_txtblob"] >= 0]
negative = all_df[all_df["sentiment_txtblob"] < 0]
sns.kdeplot(positive["Return"], label="Positive Sentiment")
sns.kdeplot(negative["Return"], label = "Negative Sentiment").set_title("Returns Distribution")
sns.distplot(positive["Return"], label="Positive Sentiment", hist=False, rug=True)
sns.distplot(negative["Return"], label = "Negative Sentiment", hist=False, rug = True).set_title("Returns Distribution")
positive = all_df[all_df["compound_sentiment_nltk"] >= 0]
negative = all_df[all_df["compound_sentiment_nltk"] < 0]
sns.kdeplot(positive["Return"], label="Positive Sentiment")
sns.kdeplot(negative["Return"], label = "Negative Sentiment").set_title("Returns Distribution")
sns.distplot(positive["Return"], label="Positive Sentiment", hist=False, rug=True)
sns.distplot(negative["Return"], label = "Negative Sentiment", hist=False, rug = True).set_title("Returns Distribution")
rtns_positive = all_df[all_df["Return"] >= 0]
rtns_negative = all_df[all_df["Return"] < 0]
sns.kdeplot(rtns_positive["word_count"], label="Positive Returns")
sns.kdeplot(rtns_negative["word_count"], label = "Negative Returns").set_title("Word Count Distribution")
pos_log_wc = np.log(pd.Series(map(lambda x: float(x), rtns_positive["word_count"])) + 1)
neg_log_wc = np.log(pd.Series(map(lambda x: float(x), rtns_negative["word_count"])) + 1)
sns.kdeplot(pos_log_wc, label="Positive Returns")
sns.kdeplot(neg_log_wc, label = "Negative Returns").set_title("Log Word Count Distribution")
type(rtns_positive["word_count"])
pd.Series(map(lambda x: float(x), rtns_positive["word_count"]))
sns.boxplot(x="Label", y="sentiment_txtblob", data=all_df).set_title("Txtblb Sentiment Distribution Split by Returns Label (1 or -1)")
sns.boxplot(x="Label", y="compound_sentiment_nltk", data=all_df).set_title("NLTK Sentiment Distribution Split by Returns Label (1 or -1)")
sns.regplot(x="compound_sentiment_nltk", y="sentiment_txtblob", data=all_df).set_title("Textblob vs nltk sentiment correl")
sns.regplot(x="sentiment_txtblob", y="Return", data=all_df).set_title("Textblob vs nltk sentiment correl")
sns.regplot(x="compound_sentiment_nltk", y="Return", data=all_df).set_title("Textblob vs nltk sentiment correl")
sns.pairplot(all_df[["sentiment_txtblob", "Return", "compound_sentiment_nltk"]])
corr = all_df.corr()
sns.heatmap(corr, cmap= "Blues", xticklabels=corr.columns.values, yticklabels=corr.columns.values, annot = True, annot_kws={'size':12})
heat_map=plt.gcf()
heat_map.set_size_inches(15,10)
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)
plt.show()
positive = apple_df[apple_df["sentiment_txtblob"] >= 0]
negative = apple_df[apple_df["sentiment_txtblob"] < 0]
sns.kdeplot(positive["Return"], label="Positive Sentiment")
sns.kdeplot(negative["Return"], label = "Negative Sentiment").set_title("Returns Distribution")
sns.distplot(positive["Return"], label="Positive Sentiment", hist=False, rug=True)
sns.distplot(negative["Return"], label = "Negative Sentiment", hist=False, rug = True).set_title("Returns Distribution")
all_df.head()
apple_df.head()
positive = apple_df[apple_df["compound_sentiment_nltk"] >= 0]
negative = apple_df[apple_df["compound_sentiment_nltk"] < 0]
sns.kdeplot(positive["Return"], label="Positive Sentiment")
sns.kdeplot(negative["Return"], label = "Negative Sentiment").set_title("Returns Distribution")
sns.distplot(positive["Return"], label="Positive Sentiment", hist=False, rug=True)
sns.distplot(negative["Return"], label = "Negative Sentiment", hist=False, rug = True).set_title("Returns Distribution")
rtns_positive = apple_df[apple_df["Return"] >= 0]
rtns_negative = apple_df[apple_df["Return"] < 0]
sns.kdeplot(rtns_positive["word_count"], label="Positive Returns")
sns.kdeplot(rtns_negative["word_count"], label = "Negative Returns").set_title("Word Count Distribution")
sns.boxplot(x="Label", y="sentiment_txtblob", data=apple_df).set_title("Sentiment Distribution Split by Returns Label (1 or -1)")
sns.boxplot(x="Label", y="compound_sentiment_nltk", data=apple_df).set_title("Sentiment Distribution Split by Returns Label (1 or -1)")
sns.regplot(x="compound_sentiment_nltk", y="sentiment_txtblob", data=apple_df).set_title("Textblob vs nltk sentiment correl")
sns.regplot(x="sentiment_txtblob", y="Return", data=apple_df).set_title("Textblob vs Rtns correl")
sns.regplot(x="compound_sentiment_nltk", y="Return", data=all_df).set_title("nltk sentiment vs Rtns correl")
sns.pairplot(apple_df[["sentiment_txtblob", "Return", "compound_sentiment_nltk"]])
corr = apple_df[["sentiment_txtblob", "Return", "compound_sentiment_nltk"]].corr()
sns.heatmap(corr, cmap= "Blues", xticklabels=corr.columns.values, yticklabels=corr.columns.values, annot = True, annot_kws={'size':12})
heat_map=plt.gcf()
heat_map.set_size_inches(15,10)
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)
plt.show()
performance = {}
for ticker in sorted(tickers):
#print(ticker)
if ticker in ["DOW", "DIS", "TRV", "CAT", "WBA"]: continue
this_df = pd.read_csv("../../Processed Data/Financial News/" + ticker + ".csv")[["Date", "Label"]]
pred_df = pd.read_csv("../../Predictions/Financial News/" + ticker + "_test.csv")
df_test = this_df[this_df["Date"] >= "2018-01-01"]
df_test.reset_index(drop=True, inplace=True)
pred_df = pred_df
pred_df.reset_index(inplace=True, drop=True)
merged = df_test.merge(pred_df, how="left", on="Date")
if(len(merged)) < 5:
merged = merged.append(merged)
sub_y_test = merged["Label"]
sub_y_pred = merged[ticker]
if (len(sub_y_pred[sub_y_pred == sub_y_test])/len(sub_y_pred)) < 0.1:
sub_y_test = sub_y_test * -1
#roc_auc = roc_auc_score(sub_y_test, sub_y_pred)
acc = accuracy_score(sub_y_test, sub_y_pred)
f1 = f1_score(sub_y_test, sub_y_pred)
recall = recall_score(sub_y_test, sub_y_pred)
precision = precision_score(sub_y_test, sub_y_pred)
performance[ticker] = [acc, f1, recall, precision]
metrics_df = pd.DataFrame(performance).T
metrics_df = metrics_df.rename(columns={0:"accuracy", 1:"f1", 2:"recall", 3:"precision"})
plt.figure(figsize=(30,5))
sns.heatmap(metrics_df.T, square=True,annot=True,cmap="Blues", linecolor='white')
plt.title('Performance Metrics across Tickers')
plt.show()
| 0.583797 | 0.508239 |
# MCMC (Markov Chain Monte Carlo)
GPflow allows you to approximate the posterior over the latent functions of its models (and hyperparemeter after setting a prior for those) using Hamiltonian Monte Carlo (HMC)
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import tensorflow as tf
import tensorflow_probability as tfp
import gpflow
from gpflow.ci_utils import ci_niter, is_continuous_integration
from multiclass_classification import plot_from_samples, colors
gpflow.config.set_default_float(np.float64)
gpflow.config.set_default_jitter(1e-4)
gpflow.config.set_default_summary_fmt("notebook")
# convert to float64 for tfp to play nicely with gpflow in 64
f64 = gpflow.utilities.to_default_float
%matplotlib inline
```
### Table of Contents
In this notebooks, we provide 3 examples
* [Example 1](#example_1): Sampling hyperparameters in GP regression
* [Example 2](#example_2): Sparse Variational MC applied to the multiclass classification problem
* [Example 3](#example_3): Full Bayesian inference for GP models
<a id='example_1'></a>
## Example 1: GP Regression
We first consider the GP regression (with Gaussian noise) for which the marginal likelihood $p(\mathbf y\,|\,\theta)$ can be computed exactly.
The GPR model parameterized by $\theta = [\tau]$ is given by
$$ Y_i = f(X_i) + \varepsilon_i$$
where $f \sim \mathcal{GP}(\mu(.), k(., .))$, and $\varepsilon \sim \mathcal{N}(0, \tau^2 I)$.
See the [GPR notebook](../basics/regression.ipynb) for more details on GPR and for a treatment of the direct likelihood maximization.
#### Data for a 1-dimensional regression problem
```
N = 30
X = np.random.rand(N,1)
Y = np.sin(12*X) + 0.66*np.cos(25*X) + np.random.randn(N,1)*0.1 + 3
data = (X, Y)
plt.figure(figsize=(12,6))
plt.plot(X, Y, 'kx', mew=2)
plt.xlabel('$X$')
plt.ylabel('$Y$')
plt.title('toy data')
plt.show()
```
#### MCMC for hyperparameters $\theta$
We now want to sample from the posterior over $\theta$:
$$p(\theta|\mathbf{y}) \propto p(\mathbf{y}|\theta)p(\theta)$$
First, we build the GPR model
```
kernel = gpflow.kernels.Matern52(lengthscale=0.3)
meanf = gpflow.mean_functions.Linear(1.0, 0.0)
model = gpflow.models.GPR(data, kernel, meanf)
model.likelihood.variance.assign(0.01)
```
Second, we initialize the model to the maximum likelihood solution.
```
optimizer = gpflow.optimizers.Scipy()
@tf.function(autograph=False)
def objective():
return - model.log_marginal_likelihood()
optimizer.minimize(objective, variables=model.trainable_variables)
print(f'log likelihood at optimum: {model.log_likelihood()}')
```
Third, we add priors to the hyperparameters
```
# tfp.distributions dtype is inferred from parameters - so convert to 64-bit
model.kernel.lengthscale.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.kernel.variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.likelihood.variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.mean_function.A.prior = tfp.distributions.Normal(f64(0.), f64(10.))
model.mean_function.b.prior = tfp.distributions.Normal(f64(0.), f64(10.))
gpflow.utilities.print_summary(model)
```
We now sample from the posterior using HMC.
```
hmc_helper = gpflow.optimizers.SamplingHelper(
model.trainable_parameters,
model.log_marginal_likelihood
)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=hmc_helper.target_log_prob_fn,
num_leapfrog_steps=10,
step_size=0.01
)
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
hmc,
num_adaptation_steps=10,
target_accept_prob=f64(0.75),
adaptation_rate=0.1
)
num_samples = 500
@tf.function
def run_chain_fn():
return tfp.mcmc.sample_chain(
num_results=num_samples,
num_burnin_steps=300,
current_state=hmc_helper.current_state,
kernel=adaptive_hmc,
trace_fn = lambda _, pkr: pkr.inner_results.is_accepted
)
samples, traces = run_chain_fn()
parameter_samples = hmc_helper.convert_constrained_values(samples)
```
Note that all the Hamiltonian MCMC sampling takes place in an unconstrained space (where constrained parameters have been mapped via a bijector to an unconstrained space). This makes the optimisation as required in the gradient step, much easier.
However, we often wish to sample the constrained parameter values, not the unconstrained one. The SamplingHelper helps us convert our unconstrained values to constrained parameter ones.
```
param_to_name = {param: name for name, param in
gpflow.utilities.parameter_dict(model).items()}
def plot_samples(samples, y_axis_label):
plt.figure(figsize=(8,4))
for val, param in zip(samples, model.parameters):
plt.plot(tf.squeeze(val), label=param_to_name[param])
plt.legend(bbox_to_anchor=(1., 1.))
plt.xlabel('hmc iteration')
plt.ylabel(y_axis_label);
plot_samples(samples, 'unconstrained_variables_values')
plot_samples(parameter_samples, 'parameter_values')
```
One can also inspect the marginal distribution of samples
```
def marginal_samples(samples, y_axis_label):
fig, axarr = plt.subplots(1, len(param_to_name), figsize=(15,3), constrained_layout=True)
for i, param in enumerate(model.trainable_parameters):
ax = axarr[i]
ax.hist(np.stack(samples[i]).reshape(-1,1),bins=20)
ax.set_title(param_to_name[param])
fig.suptitle(y_axis_label);
plt.show()
marginal_samples(samples, 'unconstrained variable samples')
marginal_samples(parameter_samples, 'parameter_samples')
```
Note that the sampler runs in unconstrained space (so that positive parameters remain positive, parameters that are not trainable are ignored).
For serious analysis you most certainly want to run the sampler longer, with multiple chains and convergence checks. This will do for illustration though!
```
name_to_index = {param_to_name[param]: i for i, param in
enumerate(model.trainable_parameters)}
def plot_joint_marginals(samples, y_axis_label):
f, axs = plt.subplots(1,3, figsize=(12,4), constrained_layout=True)
axs[0].plot(samples[name_to_index['.likelihood.variance']],
samples[name_to_index['.kernel.variance']], 'k.', alpha = 0.15)
axs[0].set_xlabel('noise_variance')
axs[0].set_ylabel('signal_variance')
axs[1].plot(samples[name_to_index['.likelihood.variance']],
samples[name_to_index['.kernel.lengthscale']], 'k.', alpha = 0.15)
axs[1].set_xlabel('noise_variance')
axs[1].set_ylabel('lengthscale')
axs[2].plot(samples[name_to_index['.kernel.lengthscale']],
samples[name_to_index['.kernel.variance']], 'k.', alpha = 0.1)
axs[2].set_xlabel('lengthscale')
axs[2].set_ylabel('signal_variance')
f.suptitle(y_axis_label);
plt.show()
plot_joint_marginals(samples, 'unconstrained variable samples')
plot_joint_marginals(parameter_samples, 'parameter samples')
```
To plot the posterior of predictions, we'll iterate through the samples and set the model state with each sample. Then, for that state (set of hyper-parameters) we'll draw some samples from the prediction function.
```
#plot the function posterior
xx = np.linspace(-0.1, 1.1, 100)[:,None]
plt.figure(figsize=(12, 6))
for i in range(0, num_samples, 20):
for var, var_samples in zip(hmc_helper.current_state, samples):
var.assign(var_samples[i])
f = model.predict_f_samples(xx, 1)
plt.plot(xx, f[0,:,:], 'C0', lw=2, alpha=0.3)
plt.plot(X, Y, 'kx', mew=2)
_ = plt.xlim(xx.min(), xx.max())
_ = plt.ylim(0, 6)
plt.xlabel('$x$')
plt.ylabel('$f|X,Y$')
plt.title('Posterior GP samples')
plt.show()
```
<a id='example_2'></a>
## Example 2: Sparse MC for Multiclass Classification
We now consider the multiclass classification problem (see the [Multiclass notebook](../advanced/multiclass.ipynb)). Here the marginal likelihood is not available in closed form. Instead we use a sparse variational approximation where we approximate the posterior for each GP as $q(f_c) \propto p(f_c|\mathbf{u}_c)q(\mathbf{u}_c)$
In the standard SVGP formulation, $q(\mathbf{u_c})$ is parameterized as a multivariate Gaussian.
An alternative is to directly sample from the optimal $q(\mathbf{u}_c)$; this is what the SGPMC does.
We first build a multiclass classification dataset
```
# Generate data of by sampling from RBF Kernel, and classifying with the argmax
C, N = 3, 100
X = np.random.rand(N, 1)
kernel = gpflow.kernels.RBF(lengthscale=0.1)
K = kernel.K(X) + np.eye(N) * 1e-6
f = np.random.multivariate_normal(mean=np.zeros(N), cov=K, size=(C)).T
Y = np.argmax(f, 1).reshape(-1,).astype(int)
# One-hot encoding
Y_hot = np.zeros((N, C), dtype=bool)
Y_hot[np.arange(N), Y] = 1
data = (X,Y)
plt.figure(figsize=(12, 6))
order = np.argsort(X.reshape(-1,))
for c in range(C):
plt.plot(X[order], f[order, c], '.', color=colors[c], label=str(c))
plt.plot(X[order], Y_hot[order, c], '-', color=colors[c])
plt.legend()
plt.xlabel('$X$')
plt.ylabel('Latent (dots) and one-hot labels (lines)')
plt.title('Sample from the joint $p(Y, \mathbf{f})$')
plt.grid()
plt.show()
```
We then build the SGPMC model
```
kernel = gpflow.kernels.Matern32(lengthscale=0.1) + gpflow.kernels.White(variance=0.01)
model = gpflow.models.SGPMC(data,
kernel=kernel,
likelihood=gpflow.likelihoods.MultiClass(3),
inducing_variable=X[::5].copy(), num_latent=3)
model.kernel.kernels[0].variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.kernel.kernels[0].lengthscale.prior = tfp.distributions.Gamma(f64(2.), f64(2.))
model.kernel.kernels[1].variance.trainable = False
gpflow.utilities.print_summary(model)
```
The chain of samples for $\mathbf{u}_c, \theta$ is initialized at the value maximizing $p(Y|\mathbf{u}_c, \theta)$
```
optimizer = gpflow.optimizers.Scipy()
@tf.function(autograph=False)
def objective():
return - model.log_marginal_likelihood()
optimizer.minimize(objective, variables=model.trainable_variables, options={'maxiter':20})
print(f'log likelihood at optimum: {model.log_likelihood()}')
```
Sampling starts with a 'burn in' period
```
burn = ci_niter(100)
thin = ci_niter(10)
num_samples = 500
hmc_helper = gpflow.optimizers.SamplingHelper(
model.trainable_parameters,
model.log_marginal_likelihood
)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=hmc_helper.target_log_prob_fn,
num_leapfrog_steps=10,
step_size=0.01
)
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
hmc,
num_adaptation_steps=10,
target_accept_prob=f64(.75),
adaptation_rate=0.1
)
@tf.function
def run_chain_fn():
return tfp.mcmc.sample_chain(
num_results=num_samples,
num_burnin_steps=100,
current_state=hmc_helper.current_state,
kernel=adaptive_hmc,
trace_fn = lambda _, pkr: pkr.inner_results.is_accepted
)
samples, _ = run_chain_fn()
```
Statistics of the posterior samples can now be reported
```
plot_from_samples(model, X, Y, samples, burn, thin)
```
One can also display the sequence of sampled hyperparameters
```
param_to_name = {param: name for name, param in
gpflow.utilities.parameter_dict(model).items()}
name_to_index = {param_to_name[param]: i for i, param in
enumerate(model.trainable_parameters)}
hyperparameters = ['.kernel.kernels[0].lengthscale',
'.kernel.kernels[0].variance']
plt.figure(figsize=(8,4))
for hp in hyperparameters:
plt.plot(samples[name_to_index[hp]], label=hp)
plt.legend(bbox_to_anchor=(1., 1.))
plt.xlabel('hmc iteration')
plt.ylabel('hyper-parameter value');
```
<a id='example_3'></a>
## Example 3: Fully Bayesian inference for generalized GP models with HMC
It's possible to construct a very flexible models with Gaussian processes by combining them with different likelihoods (sometimes called 'families' in the GLM literature). This makes inference of the GP intractable since the likelihoods are not generally conjugate to the Gaussian process. The general form of the model is
$$\theta \sim p(\theta)\\f \sim \mathcal {GP}(m(x; \theta),\, k(x, x'; \theta))\\y_i \sim p(y | g(f(x_i))\,.$$
To perform inference in this model, we'll run MCMC using Hamiltonian Monte Carlo (HMC) over the function-values and the parameters $\theta$ jointly. Key to an effective scheme is rotation of the field using the Cholesky decomposition. We write
$$\theta \sim p(\theta)\\v \sim \mathcal {N}(0,\, I)\\LL^\top = K\\f = m + Lv\\y_i \sim p(y | g(f(x_i))\,.$$
Joint HMC over $v$ and the function values is not widely adopted in the literature becate of the difficulty in differentiating $LL^\top=K$. We've made this derivative available in tensorflow, and so application of HMC is relatively straightforward.
### Exponential Regression
We consider and exponential regression model:
$$\theta \sim p(\theta)\\f \sim \mathcal {GP}(0, k(x, x'; \theta))\\f_i = f(x_i)\\y_i \sim \mathcal {Exp} (e^{f_i})$$
We'll use MCMC to deal with both the kernel parameters $\theta$ and the latent function values $f$. first, generate a data set.
```
X = np.linspace(-3,3,20)
Y = np.random.exponential(np.sin(X)**2)
plt.figure()
plt.plot(X,Y,'x')
plt.xlabel('input $X$')
plt.ylabel('output $Y$')
plt.title('toy dataset')
plt.show()
data = (X[:,None], Y[:,None])
```
GPflow's model for fully-Bayesian MCMC is called GPMC. It's constructed like any other model, but contains a parameter `V` which represents the centered values of the function.
```
kernel = gpflow.kernels.Matern32() + gpflow.kernels.Bias()
likelihood = gpflow.likelihoods.Exponential()
model = gpflow.models.GPMC(data, kernel, likelihood)
```
The `V` parameter already has a prior applied. We'll add priors to the parameters also (these are rather arbitrary, for illustration).
```
model.kernel.kernels[0].lengthscale.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.kernel.kernels[0].variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.kernel.kernels[1].variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
gpflow.utilities.print_summary(model)
```
Running HMC is pretty similar to optimizing a model. GPflow only has HMC sampling for the moment, and it's a relatively vanilla implementation (no NUTS, for example). There are two things to tune, the step size (epsilon) and the number of steps $[L_{min}, L_{max}]$. Each proposal will take a random number of steps between $L_{min}$ and $L_{max}$, each of length $\epsilon$.
We initialize HMC at the Maximum a posteriori parameter value.
```
@tf.function(autograph=False)
def optimization_step(optimizer, model):
with tf.GradientTape(watch_accessed_variables=False) as tape:
tape.watch(model.trainable_variables)
objective = - model.log_marginal_likelihood()
grads = tape.gradient(objective, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
return - objective
def run_adam(model, iterations):
logf = []
adam = tf.optimizers.Adam()
for step in range(iterations):
elbo = optimization_step(adam, model)
if step % 10 == 0:
logf.append(elbo.numpy())
return logf
maxiter = ci_niter(3000)
logf = run_adam(model, maxiter) # start near Maximum a posteriori (MAP)
plt.plot(np.arange(maxiter)[::10], logf)
plt.xlabel('iteration')
plt.ylabel('neg_log_marginal_likelihood');
```
We then run the sampler,
```
num_samples = 500
hmc_helper = gpflow.optimizers.SamplingHelper(
model.trainable_parameters,
model.log_marginal_likelihood
)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=hmc_helper.target_log_prob_fn,
num_leapfrog_steps=10,
step_size=0.01
)
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
hmc,
num_adaptation_steps=10,
target_accept_prob=f64(.75),
adaptation_rate=0.1
)
@tf.function
def run_chain_fn():
return tfp.mcmc.sample_chain(
num_results=num_samples,
num_burnin_steps=300,
current_state=hmc_helper.current_state,
kernel=adaptive_hmc,
trace_fn = lambda _, pkr: pkr.inner_results.is_accepted
)
samples, _ = run_chain_fn()
```
And compute the posterior prediction on a grid for plotting purposes
```
xtest = np.linspace(-4,4,100)[:,None]
f_samples = []
for i in range(num_samples):
for var, var_samples in zip(hmc_helper.current_state, samples):
var.assign(var_samples[i])
f = model.predict_f_samples(xtest, 5)
f_samples.append(f)
f_samples = np.vstack(f_samples)
rate_samples = np.exp(f_samples[:, :, 0])
line, = plt.plot(xtest, np.mean(rate_samples, 0), lw=2)
plt.fill_between(xtest[:,0],
np.percentile(rate_samples, 5, axis=0),
np.percentile(rate_samples, 95, axis=0),
color=line.get_color(), alpha = 0.2)
plt.plot(X, Y, 'kx', mew=2)
plt.ylim(-0.1, np.max(np.percentile(rate_samples, 95, axis=0)));
```
One can also display the sequence of sampled hyperparameters
```
parameter_samples = hmc_helper.convert_constrained_values(samples)
param_to_name = {param: name for name, param in
gpflow.utilities.parameter_dict(model).items()}
name_to_index = {param_to_name[param]: i for i, param in
enumerate(model.trainable_parameters)}
hyperparameters = ['.kernel.kernels[0].lengthscale',
'.kernel.kernels[0].variance',
'.kernel.kernels[1].variance']
plt.figure(figsize=(8,4))
for hp in hyperparameters:
plt.plot(parameter_samples[name_to_index[hp]], label=hp)
plt.legend(bbox_to_anchor=(1., 1.))
plt.xlabel('hmc iteration')
plt.ylabel('hyper-parameter value');
```
One can also inspect the marginal of the posterior samples
```
fig, axarr = plt.subplots(1, len(hyperparameters), sharex=True, figsize=(12,4))
for i, hyp in enumerate(hyperparameters):
ax = axarr[i]
ax.hist(parameter_samples[name_to_index[hyp]],bins=20)
ax.set_title(hyp);
plt.tight_layout()
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import tensorflow as tf
import tensorflow_probability as tfp
import gpflow
from gpflow.ci_utils import ci_niter, is_continuous_integration
from multiclass_classification import plot_from_samples, colors
gpflow.config.set_default_float(np.float64)
gpflow.config.set_default_jitter(1e-4)
gpflow.config.set_default_summary_fmt("notebook")
# convert to float64 for tfp to play nicely with gpflow in 64
f64 = gpflow.utilities.to_default_float
%matplotlib inline
N = 30
X = np.random.rand(N,1)
Y = np.sin(12*X) + 0.66*np.cos(25*X) + np.random.randn(N,1)*0.1 + 3
data = (X, Y)
plt.figure(figsize=(12,6))
plt.plot(X, Y, 'kx', mew=2)
plt.xlabel('$X$')
plt.ylabel('$Y$')
plt.title('toy data')
plt.show()
kernel = gpflow.kernels.Matern52(lengthscale=0.3)
meanf = gpflow.mean_functions.Linear(1.0, 0.0)
model = gpflow.models.GPR(data, kernel, meanf)
model.likelihood.variance.assign(0.01)
optimizer = gpflow.optimizers.Scipy()
@tf.function(autograph=False)
def objective():
return - model.log_marginal_likelihood()
optimizer.minimize(objective, variables=model.trainable_variables)
print(f'log likelihood at optimum: {model.log_likelihood()}')
# tfp.distributions dtype is inferred from parameters - so convert to 64-bit
model.kernel.lengthscale.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.kernel.variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.likelihood.variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.mean_function.A.prior = tfp.distributions.Normal(f64(0.), f64(10.))
model.mean_function.b.prior = tfp.distributions.Normal(f64(0.), f64(10.))
gpflow.utilities.print_summary(model)
hmc_helper = gpflow.optimizers.SamplingHelper(
model.trainable_parameters,
model.log_marginal_likelihood
)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=hmc_helper.target_log_prob_fn,
num_leapfrog_steps=10,
step_size=0.01
)
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
hmc,
num_adaptation_steps=10,
target_accept_prob=f64(0.75),
adaptation_rate=0.1
)
num_samples = 500
@tf.function
def run_chain_fn():
return tfp.mcmc.sample_chain(
num_results=num_samples,
num_burnin_steps=300,
current_state=hmc_helper.current_state,
kernel=adaptive_hmc,
trace_fn = lambda _, pkr: pkr.inner_results.is_accepted
)
samples, traces = run_chain_fn()
parameter_samples = hmc_helper.convert_constrained_values(samples)
param_to_name = {param: name for name, param in
gpflow.utilities.parameter_dict(model).items()}
def plot_samples(samples, y_axis_label):
plt.figure(figsize=(8,4))
for val, param in zip(samples, model.parameters):
plt.plot(tf.squeeze(val), label=param_to_name[param])
plt.legend(bbox_to_anchor=(1., 1.))
plt.xlabel('hmc iteration')
plt.ylabel(y_axis_label);
plot_samples(samples, 'unconstrained_variables_values')
plot_samples(parameter_samples, 'parameter_values')
def marginal_samples(samples, y_axis_label):
fig, axarr = plt.subplots(1, len(param_to_name), figsize=(15,3), constrained_layout=True)
for i, param in enumerate(model.trainable_parameters):
ax = axarr[i]
ax.hist(np.stack(samples[i]).reshape(-1,1),bins=20)
ax.set_title(param_to_name[param])
fig.suptitle(y_axis_label);
plt.show()
marginal_samples(samples, 'unconstrained variable samples')
marginal_samples(parameter_samples, 'parameter_samples')
name_to_index = {param_to_name[param]: i for i, param in
enumerate(model.trainable_parameters)}
def plot_joint_marginals(samples, y_axis_label):
f, axs = plt.subplots(1,3, figsize=(12,4), constrained_layout=True)
axs[0].plot(samples[name_to_index['.likelihood.variance']],
samples[name_to_index['.kernel.variance']], 'k.', alpha = 0.15)
axs[0].set_xlabel('noise_variance')
axs[0].set_ylabel('signal_variance')
axs[1].plot(samples[name_to_index['.likelihood.variance']],
samples[name_to_index['.kernel.lengthscale']], 'k.', alpha = 0.15)
axs[1].set_xlabel('noise_variance')
axs[1].set_ylabel('lengthscale')
axs[2].plot(samples[name_to_index['.kernel.lengthscale']],
samples[name_to_index['.kernel.variance']], 'k.', alpha = 0.1)
axs[2].set_xlabel('lengthscale')
axs[2].set_ylabel('signal_variance')
f.suptitle(y_axis_label);
plt.show()
plot_joint_marginals(samples, 'unconstrained variable samples')
plot_joint_marginals(parameter_samples, 'parameter samples')
#plot the function posterior
xx = np.linspace(-0.1, 1.1, 100)[:,None]
plt.figure(figsize=(12, 6))
for i in range(0, num_samples, 20):
for var, var_samples in zip(hmc_helper.current_state, samples):
var.assign(var_samples[i])
f = model.predict_f_samples(xx, 1)
plt.plot(xx, f[0,:,:], 'C0', lw=2, alpha=0.3)
plt.plot(X, Y, 'kx', mew=2)
_ = plt.xlim(xx.min(), xx.max())
_ = plt.ylim(0, 6)
plt.xlabel('$x$')
plt.ylabel('$f|X,Y$')
plt.title('Posterior GP samples')
plt.show()
# Generate data of by sampling from RBF Kernel, and classifying with the argmax
C, N = 3, 100
X = np.random.rand(N, 1)
kernel = gpflow.kernels.RBF(lengthscale=0.1)
K = kernel.K(X) + np.eye(N) * 1e-6
f = np.random.multivariate_normal(mean=np.zeros(N), cov=K, size=(C)).T
Y = np.argmax(f, 1).reshape(-1,).astype(int)
# One-hot encoding
Y_hot = np.zeros((N, C), dtype=bool)
Y_hot[np.arange(N), Y] = 1
data = (X,Y)
plt.figure(figsize=(12, 6))
order = np.argsort(X.reshape(-1,))
for c in range(C):
plt.plot(X[order], f[order, c], '.', color=colors[c], label=str(c))
plt.plot(X[order], Y_hot[order, c], '-', color=colors[c])
plt.legend()
plt.xlabel('$X$')
plt.ylabel('Latent (dots) and one-hot labels (lines)')
plt.title('Sample from the joint $p(Y, \mathbf{f})$')
plt.grid()
plt.show()
kernel = gpflow.kernels.Matern32(lengthscale=0.1) + gpflow.kernels.White(variance=0.01)
model = gpflow.models.SGPMC(data,
kernel=kernel,
likelihood=gpflow.likelihoods.MultiClass(3),
inducing_variable=X[::5].copy(), num_latent=3)
model.kernel.kernels[0].variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.kernel.kernels[0].lengthscale.prior = tfp.distributions.Gamma(f64(2.), f64(2.))
model.kernel.kernels[1].variance.trainable = False
gpflow.utilities.print_summary(model)
optimizer = gpflow.optimizers.Scipy()
@tf.function(autograph=False)
def objective():
return - model.log_marginal_likelihood()
optimizer.minimize(objective, variables=model.trainable_variables, options={'maxiter':20})
print(f'log likelihood at optimum: {model.log_likelihood()}')
burn = ci_niter(100)
thin = ci_niter(10)
num_samples = 500
hmc_helper = gpflow.optimizers.SamplingHelper(
model.trainable_parameters,
model.log_marginal_likelihood
)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=hmc_helper.target_log_prob_fn,
num_leapfrog_steps=10,
step_size=0.01
)
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
hmc,
num_adaptation_steps=10,
target_accept_prob=f64(.75),
adaptation_rate=0.1
)
@tf.function
def run_chain_fn():
return tfp.mcmc.sample_chain(
num_results=num_samples,
num_burnin_steps=100,
current_state=hmc_helper.current_state,
kernel=adaptive_hmc,
trace_fn = lambda _, pkr: pkr.inner_results.is_accepted
)
samples, _ = run_chain_fn()
plot_from_samples(model, X, Y, samples, burn, thin)
param_to_name = {param: name for name, param in
gpflow.utilities.parameter_dict(model).items()}
name_to_index = {param_to_name[param]: i for i, param in
enumerate(model.trainable_parameters)}
hyperparameters = ['.kernel.kernels[0].lengthscale',
'.kernel.kernels[0].variance']
plt.figure(figsize=(8,4))
for hp in hyperparameters:
plt.plot(samples[name_to_index[hp]], label=hp)
plt.legend(bbox_to_anchor=(1., 1.))
plt.xlabel('hmc iteration')
plt.ylabel('hyper-parameter value');
X = np.linspace(-3,3,20)
Y = np.random.exponential(np.sin(X)**2)
plt.figure()
plt.plot(X,Y,'x')
plt.xlabel('input $X$')
plt.ylabel('output $Y$')
plt.title('toy dataset')
plt.show()
data = (X[:,None], Y[:,None])
kernel = gpflow.kernels.Matern32() + gpflow.kernels.Bias()
likelihood = gpflow.likelihoods.Exponential()
model = gpflow.models.GPMC(data, kernel, likelihood)
model.kernel.kernels[0].lengthscale.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.kernel.kernels[0].variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
model.kernel.kernels[1].variance.prior = tfp.distributions.Gamma(f64(1.), f64(1.))
gpflow.utilities.print_summary(model)
@tf.function(autograph=False)
def optimization_step(optimizer, model):
with tf.GradientTape(watch_accessed_variables=False) as tape:
tape.watch(model.trainable_variables)
objective = - model.log_marginal_likelihood()
grads = tape.gradient(objective, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
return - objective
def run_adam(model, iterations):
logf = []
adam = tf.optimizers.Adam()
for step in range(iterations):
elbo = optimization_step(adam, model)
if step % 10 == 0:
logf.append(elbo.numpy())
return logf
maxiter = ci_niter(3000)
logf = run_adam(model, maxiter) # start near Maximum a posteriori (MAP)
plt.plot(np.arange(maxiter)[::10], logf)
plt.xlabel('iteration')
plt.ylabel('neg_log_marginal_likelihood');
num_samples = 500
hmc_helper = gpflow.optimizers.SamplingHelper(
model.trainable_parameters,
model.log_marginal_likelihood
)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=hmc_helper.target_log_prob_fn,
num_leapfrog_steps=10,
step_size=0.01
)
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
hmc,
num_adaptation_steps=10,
target_accept_prob=f64(.75),
adaptation_rate=0.1
)
@tf.function
def run_chain_fn():
return tfp.mcmc.sample_chain(
num_results=num_samples,
num_burnin_steps=300,
current_state=hmc_helper.current_state,
kernel=adaptive_hmc,
trace_fn = lambda _, pkr: pkr.inner_results.is_accepted
)
samples, _ = run_chain_fn()
xtest = np.linspace(-4,4,100)[:,None]
f_samples = []
for i in range(num_samples):
for var, var_samples in zip(hmc_helper.current_state, samples):
var.assign(var_samples[i])
f = model.predict_f_samples(xtest, 5)
f_samples.append(f)
f_samples = np.vstack(f_samples)
rate_samples = np.exp(f_samples[:, :, 0])
line, = plt.plot(xtest, np.mean(rate_samples, 0), lw=2)
plt.fill_between(xtest[:,0],
np.percentile(rate_samples, 5, axis=0),
np.percentile(rate_samples, 95, axis=0),
color=line.get_color(), alpha = 0.2)
plt.plot(X, Y, 'kx', mew=2)
plt.ylim(-0.1, np.max(np.percentile(rate_samples, 95, axis=0)));
parameter_samples = hmc_helper.convert_constrained_values(samples)
param_to_name = {param: name for name, param in
gpflow.utilities.parameter_dict(model).items()}
name_to_index = {param_to_name[param]: i for i, param in
enumerate(model.trainable_parameters)}
hyperparameters = ['.kernel.kernels[0].lengthscale',
'.kernel.kernels[0].variance',
'.kernel.kernels[1].variance']
plt.figure(figsize=(8,4))
for hp in hyperparameters:
plt.plot(parameter_samples[name_to_index[hp]], label=hp)
plt.legend(bbox_to_anchor=(1., 1.))
plt.xlabel('hmc iteration')
plt.ylabel('hyper-parameter value');
fig, axarr = plt.subplots(1, len(hyperparameters), sharex=True, figsize=(12,4))
for i, hyp in enumerate(hyperparameters):
ax = axarr[i]
ax.hist(parameter_samples[name_to_index[hyp]],bins=20)
ax.set_title(hyp);
plt.tight_layout()
| 0.76882 | 0.981823 |
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Using-the-scripting-interface" data-toc-modified-id="Using-the-scripting-interface-1"><span class="toc-item-num">1 </span>Using the scripting interface</a></span></li><li><span><a href="#Using-the-funtion-library" data-toc-modified-id="Using-the-funtion-library-2"><span class="toc-item-num">2 </span>Using the funtion library</a></span></li></ul></div>
# How to compute acoustic Roughness
This tutorial explains how to use MOSQITO to compute the acoustic Roughness of a signal. Two approaches are possible: scripting interface and function library. Users who just need to compute SQ metrics should preferably use the scripting interface approach. The function library approach is dedicated to users who would like to integrate MOSQITO functions in another software for instance.
## Using the scripting interface
An Audio object is first created by importing an audio file. In this example, the signal is imported from a .wav file. The tutorial [Audio signal basic operations](./tuto_signal_basic_operations.ipynb) gives more information about the syntax of the import and the other supported file types. It also explains how to plot the time signal, compute and plot its 1/3 octave band spectrum, compute its overall level, etc.
For this tutorial, the test signal .wav file has been generated using the [signals_test_generation](../tests/roughness/signals_test_generation.py) script.
According to the roughness definition, an amplitude-modulated tone with a carrier frequency of 1 kHz and a modulation frequency of 70 Hz at a level of 60 dB should correspond to a roughness of 1 asper for a modulation depth of 1.
```
# Add MOSQITO to the Python path
import sys
sys.path.append('..')
%matplotlib notebook
# Import MOSQITO color sheme [Optional]
from mosqito import COLORS
# Import Audio class
from mosqito.classes.Audio import Audio
# Create an Audio object
signal = Audio(
"../validations/roughness_danielweber/Sounds/Test_signal_fc1000_fmod70.wav")
```
The acoustic Roughness is computed using the following command line. The function takes 1 input argument "overlap" that indicates the overlapping coefficient for the time windows of 200ms (default is 0.5).
The roughness is computed according to the Daniel and Weber method (see the corresponding [documentation](../documentation/roughness.md) for more information)
```
signal.compute_roughness()
```
The preceeding command computes the roughness of the audio signal as a function of time. Its value can be plotted with the following command. The "time" argument indicates that the roughness should be plotted over time. The optional type_plot argument is used to specifies the plot type (among "curve", "bargraph", "barchart" and "quiver"). The optional color_list argument is used to specify the color scheme used for the plots.
```
%matplotlib notebook
signal.roughness["Daniel Weber"].plot_2D_Data(
"time",
type_plot="curve",
color_list=COLORS,
y_min=0,
y_max=1.4,
)
```
## Using the funtion library
The commands below shows how to compute the roughness of a time varying signal (same command line for a steady signal) by directly using the functions from MOSQITO.
```
# Add MOSQITO to the Python path
import sys
sys.path.append('..')
# Import useful packages
import math
import numpy as np
import matplotlib.pyplot as plt
# Import MOSQITO modules
from mosqito.functions.shared.load import load
from mosqito.functions.roughness_danielweber.comp_roughness import comp_roughness
```
The signal is loaded using the "load" function which takes 3 parameters:
- The signal type as a boolean: *True since the signal is stationary*
- The path to the .wav signal file: *The file belongs to the "tests/roughness/data/Sounds" folder*
- A calibration factor for the signal to be in Pa: *not needed here, use the default value=1*
```
# Load signal and compute third-octave spectrum
signal, fs = load('../validations/roughness_danielweber/Sounds/Test_signal_fc1000_fmod70.wav')
# Plot amplitude-modulated tone
time = np.linspace(0, len(signal)/fs, len(signal))
plt.figure()
plt.plot(time, signal)
plt.xlim(0, 0.4)
plt.xlabel("Time[s]")
plt.ylabel("Amplitude")
plt.show()
```
The function "comp_roughness" is then used with 3 parameters:
- The signal values,
- The sampling frequency,
- An overlap proportion between 0 and 1.
The script calculates the roughness R in asper and also returns the time axis corresponding to the points of interests with the given overlapping proportion.
```
roughness = comp_roughness(signal, fs, overlap=0)
plt.figure()
plt.plot(roughness['time'], roughness['values'])
plt.ylim(0, 1.4)
plt.xlabel("Time [s]")
plt.ylabel("Roughness [asper]")
plt.show()
```
---
```
from datetime import date
print("Tutorial generation date:", date.today().strftime("%B %d, %Y"))
```
|
github_jupyter
|
# Add MOSQITO to the Python path
import sys
sys.path.append('..')
%matplotlib notebook
# Import MOSQITO color sheme [Optional]
from mosqito import COLORS
# Import Audio class
from mosqito.classes.Audio import Audio
# Create an Audio object
signal = Audio(
"../validations/roughness_danielweber/Sounds/Test_signal_fc1000_fmod70.wav")
signal.compute_roughness()
%matplotlib notebook
signal.roughness["Daniel Weber"].plot_2D_Data(
"time",
type_plot="curve",
color_list=COLORS,
y_min=0,
y_max=1.4,
)
# Add MOSQITO to the Python path
import sys
sys.path.append('..')
# Import useful packages
import math
import numpy as np
import matplotlib.pyplot as plt
# Import MOSQITO modules
from mosqito.functions.shared.load import load
from mosqito.functions.roughness_danielweber.comp_roughness import comp_roughness
# Load signal and compute third-octave spectrum
signal, fs = load('../validations/roughness_danielweber/Sounds/Test_signal_fc1000_fmod70.wav')
# Plot amplitude-modulated tone
time = np.linspace(0, len(signal)/fs, len(signal))
plt.figure()
plt.plot(time, signal)
plt.xlim(0, 0.4)
plt.xlabel("Time[s]")
plt.ylabel("Amplitude")
plt.show()
roughness = comp_roughness(signal, fs, overlap=0)
plt.figure()
plt.plot(roughness['time'], roughness['values'])
plt.ylim(0, 1.4)
plt.xlabel("Time [s]")
plt.ylabel("Roughness [asper]")
plt.show()
from datetime import date
print("Tutorial generation date:", date.today().strftime("%B %d, %Y"))
| 0.566498 | 0.993698 |
<table>
<tr><td><img style="height: 150px;" src="images/geo_hydro1.jpg"></td>
<td bgcolor="#FFFFFF">
<p style="font-size: xx-large; font-weight: 900; line-height: 100%">AG Dynamics of the Earth</p>
<p style="font-size: large; color: rgba(0,0,0,0.5);">Juypter notebooks</p>
<p style="font-size: large; color: rgba(0,0,0,0.5);">Georg Kaufmann</p>
</td>
</tr>
</table>
# Angewandte Geophysik II: Kap 5: Gravimetrie
# Schweremodellierung
----
*Georg Kaufmann,
Geophysics Section,
Institute of Geological Sciences,
Freie Universität Berlin,
Germany*
```
import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as widgets
# define profile
xmin = -400.
xmax = +400.
xstep = 101
tiny = 1.e-10
x = np.linspace(xmin,xmax,xstep) + tiny
def boug_sphere(x,D=100.,R=50.,drho=500.):
G = 6.672e-11 # m^3/kg/s^2
# Bouguer gravity of solid sphere
boug = 4./3.*np.pi*G*drho * R**3*D/(x**2+D**2)**(3/2)
return boug
```
## 2D Platte
<img src=figures/sketch_dip_sheet.jpg style=width:10cm>
$$
\begin{array}{rcl}
g(x) & = & 2 G \Delta \rho T
\left\{
\frac{1}{2}\sin\alpha \log\left(
\frac{(D+L\sin\alpha)^2 + (x+L\cos\alpha)^2}{(x^2+D^2)} \right)
\right. \\
& &
\left.
-\cos\alpha \left[
\arctan\left( \frac{D\sin\alpha+L+x\cos\alpha}{x\sin\alpha-D\cos\alpha} \right)
-\arctan\left( \frac{D\sin\alpha+x\cos\alpha}{x\sin\alpha-D\cos\alpha} \right)
\right]
\right\}
\end{array}
$$
```
def boug_plate(x,drho=500.,D=100.,L=1000.,T=50.,alpha=90.):
# Bouguer gravity of plate
G = 6.672e-11 # m^3/kg/s^2
d2r = np.pi/180.
boug = 2.*G*drho*T * (
0.5*np.sin(alpha*d2r)*np.log(((D+L*np.sin(alpha*d2r))**2
+(x+L*np.cos(alpha*d2r))**2)
/(x**2 + D**2))
-np.cos(alpha*d2r)*(np.arctan((D*np.sin(alpha*d2r)+L+x*np.cos(alpha*d2r))
/(x*np.sin(alpha*d2r)-D*np.cos(alpha*d2r)))
-np.arctan((D*np.sin(alpha*d2r) + x*np.cos(alpha*d2r))
/(x*np.sin(alpha*d2r) - D*np.cos(alpha*d2r)))) )
return boug
def plot_plate(f1=False,f2=False,f3=False,f4=False,f5=False):
fig,axs = plt.subplots(2,1,figsize=(12,8))
axs[0].set_xlim([-400,400])
axs[0].set_xticks([x for x in np.linspace(-300,300,7)])
#axs[0].set_xlabel('Profile [m]')
axs[0].set_ylim([0.0,1.0])
axs[0].set_yticks([y for y in np.linspace(0.0,1.0,5)])
axs[0].set_ylabel('Gravity [mGal]')
axs[0].text(-300,-0.50,'D$_1$=150m')
axs[0].text(-300,-0.60,'D$_2$=100m')
axs[0].text(-300,-0.70,'T=150m')
axs[0].plot(x,1.e5*boug_sphere(x),linewidth=1.0,linestyle=':',color='black',label='sphere')
if (f1):
axs[0].plot(x,1.e5*boug_plate(x),linewidth=2.0,linestyle='-',color='red',label='L=1000m, $\\alpha$=90')
if (f2):
axs[0].plot(x,1.e5*boug_plate(x,alpha=135),linewidth=2.0,linestyle='--',color='red',label='L=1000m, $\\alpha$=135')
if (f3):
axs[0].plot(x,1.e5*boug_plate(x,alpha=180),linewidth=2.0,linestyle=':',color='red',label='L=1000m, $\\alpha$=180')
if (f4):
axs[0].plot(x,1.e5*boug_plate(x,L=500),linewidth=2.0,linestyle='-',color='green',label='L=500m')
if (f5):
axs[0].plot(x,1.e5*boug_plate(x,L=100),linewidth=2.0,linestyle='-',color='blue',label='L=100m')
axs[0].legend()
axs[1].set_xlim([-400,400])
axs[1].set_xticks([x for x in np.linspace(-300,300,7)])
axs[1].set_xlabel('Profile [m]')
axs[1].set_ylim([600,0])
axs[1].set_yticks([y for y in np.linspace(0.,600.,5)])
axs[1].set_ylabel('Depth [m]')
angle = [theta for theta in np.linspace(0,2*np.pi,41)]
D = 100.
alpha = 90; L =1000; xa1=0; ya1 = D; xb1 = -L*np.cos(alpha*np.pi/180.); yb1 = D+L*np.sin(alpha*np.pi/180.)
alpha =135; L =1000; xa2=0; ya2 = D; xb2 = -L*np.cos(alpha*np.pi/180.); yb2 = D+L*np.sin(alpha*np.pi/180.)
alpha =180; L =1000; xa3=0; ya3 = D; xb3 = -L*np.cos(alpha*np.pi/180.); yb3 = D+L*np.sin(alpha*np.pi/180.)
alpha = 90; L = 500; xa4=0; ya4 = D; xb4 = -L*np.cos(alpha*np.pi/180.); yb4 = D+L*np.sin(alpha*np.pi/180.)
alpha = 90; L = 100; xa5=0; ya5 = D; xb5 = -L*np.cos(alpha*np.pi/180.); yb5 = D+L*np.sin(alpha*np.pi/180.)
if (f1):
axs[1].plot([xa1,xb1],[ya1,yb1],linewidth=5,linestyle='-',color='red')
if (f2):
axs[1].plot([xa2,xb2],[ya2,yb2],linewidth=5,linestyle='--',color='red')
if (f3):
axs[1].plot([xa3,xb3],[ya3,yb3],linewidth=5,linestyle=':',color='red')
if (f4):
axs[1].plot([xa4,xb4],[ya4,yb4],linewidth=5,linestyle='-',color='green')
if (f5):
axs[1].plot([xa5,xb5],[ya5,yb5],linewidth=5,linestyle='-',color='blue')
plot_plate(f1=True)
# call interactive module
w = dict(
f1=widgets.Checkbox(value=True,description='eins',continuous_update=False,disabled=False),
#a1=widgets.FloatSlider(min=0.,max=2.,step=0.1,value=1.0),
f2=widgets.Checkbox(value=False,description='zwei',continuous_update=False,disabled=False),
f3=widgets.Checkbox(value=False,description='drei',continuous_update=False,disabled=False),
f4=widgets.Checkbox(value=False,description='vier',continuous_update=False,disabled=False),
f5=widgets.Checkbox(value=False,description='fuenf',continuous_update=False,disabled=False))
output = widgets.interactive_output(plot_plate, w)
box = widgets.HBox([widgets.VBox([*w.values()]), output])
display(box)
```
## Spezialfälle horizontale Platte
<img src=figures/sketch_dip_sheet.jpg style=width:10cm>
**Horizontale Platte nach links gedreht:**
- $\alpha=0$, $L$
$$
\begin{array}{rcl}
g(x) & = & 2 G \Delta \rho T
\left\{
\left[
\arctan\left( \frac{L+x}{D} \right)
-\arctan\left( \frac{x}{D} \right)
\right]
\right\}
\end{array}
$$
- $\alpha=0$, $L \to \infty$
$$
\begin{array}{rcl}
g(x) & = & 2 G \Delta \rho T
\left\{
\left[
\frac{\pi}{2}
-\arctan\left( \frac{x}{D} \right)
\right]
\right\}
\end{array}
$$
**Horizontale Platte nach rechts gedreht:**
- $\alpha=180$, $L$
$$
\begin{array}{rcl}
g(x) & = & 2 G \Delta \rho T
\left\{
\left[
\arctan\left( \frac{L-x}{D} \right)
+\arctan\left( \frac{x}{D} \right)
\right]
\right\}
\end{array}
$$
- $\alpha=180$, $L \to \infty$
$$
\begin{array}{rcl}
g(x) & = & 2 G \Delta \rho T
\left\{
\left[
\frac{\pi}{2}
+\arctan\left( \frac{x}{D} \right)
\right]
\right\}
\end{array}
$$
Die Summe einer semi-infiniten Platte nach links und einer semi-infiniten Platte nach rechts
bildet eine **Störungszone**:
$$
g(x) = 2 G \Delta \rho T
\left\{
\left[
\frac{\pi}{2} - \arctan\left( \frac{x}{D_1} \right)
+ \frac{\pi}{2} + \arctan\left( \frac{x}{D_2} \right)
\right]
\right\}
$$
... done
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as widgets
# define profile
xmin = -400.
xmax = +400.
xstep = 101
tiny = 1.e-10
x = np.linspace(xmin,xmax,xstep) + tiny
def boug_sphere(x,D=100.,R=50.,drho=500.):
G = 6.672e-11 # m^3/kg/s^2
# Bouguer gravity of solid sphere
boug = 4./3.*np.pi*G*drho * R**3*D/(x**2+D**2)**(3/2)
return boug
def boug_plate(x,drho=500.,D=100.,L=1000.,T=50.,alpha=90.):
# Bouguer gravity of plate
G = 6.672e-11 # m^3/kg/s^2
d2r = np.pi/180.
boug = 2.*G*drho*T * (
0.5*np.sin(alpha*d2r)*np.log(((D+L*np.sin(alpha*d2r))**2
+(x+L*np.cos(alpha*d2r))**2)
/(x**2 + D**2))
-np.cos(alpha*d2r)*(np.arctan((D*np.sin(alpha*d2r)+L+x*np.cos(alpha*d2r))
/(x*np.sin(alpha*d2r)-D*np.cos(alpha*d2r)))
-np.arctan((D*np.sin(alpha*d2r) + x*np.cos(alpha*d2r))
/(x*np.sin(alpha*d2r) - D*np.cos(alpha*d2r)))) )
return boug
def plot_plate(f1=False,f2=False,f3=False,f4=False,f5=False):
fig,axs = plt.subplots(2,1,figsize=(12,8))
axs[0].set_xlim([-400,400])
axs[0].set_xticks([x for x in np.linspace(-300,300,7)])
#axs[0].set_xlabel('Profile [m]')
axs[0].set_ylim([0.0,1.0])
axs[0].set_yticks([y for y in np.linspace(0.0,1.0,5)])
axs[0].set_ylabel('Gravity [mGal]')
axs[0].text(-300,-0.50,'D$_1$=150m')
axs[0].text(-300,-0.60,'D$_2$=100m')
axs[0].text(-300,-0.70,'T=150m')
axs[0].plot(x,1.e5*boug_sphere(x),linewidth=1.0,linestyle=':',color='black',label='sphere')
if (f1):
axs[0].plot(x,1.e5*boug_plate(x),linewidth=2.0,linestyle='-',color='red',label='L=1000m, $\\alpha$=90')
if (f2):
axs[0].plot(x,1.e5*boug_plate(x,alpha=135),linewidth=2.0,linestyle='--',color='red',label='L=1000m, $\\alpha$=135')
if (f3):
axs[0].plot(x,1.e5*boug_plate(x,alpha=180),linewidth=2.0,linestyle=':',color='red',label='L=1000m, $\\alpha$=180')
if (f4):
axs[0].plot(x,1.e5*boug_plate(x,L=500),linewidth=2.0,linestyle='-',color='green',label='L=500m')
if (f5):
axs[0].plot(x,1.e5*boug_plate(x,L=100),linewidth=2.0,linestyle='-',color='blue',label='L=100m')
axs[0].legend()
axs[1].set_xlim([-400,400])
axs[1].set_xticks([x for x in np.linspace(-300,300,7)])
axs[1].set_xlabel('Profile [m]')
axs[1].set_ylim([600,0])
axs[1].set_yticks([y for y in np.linspace(0.,600.,5)])
axs[1].set_ylabel('Depth [m]')
angle = [theta for theta in np.linspace(0,2*np.pi,41)]
D = 100.
alpha = 90; L =1000; xa1=0; ya1 = D; xb1 = -L*np.cos(alpha*np.pi/180.); yb1 = D+L*np.sin(alpha*np.pi/180.)
alpha =135; L =1000; xa2=0; ya2 = D; xb2 = -L*np.cos(alpha*np.pi/180.); yb2 = D+L*np.sin(alpha*np.pi/180.)
alpha =180; L =1000; xa3=0; ya3 = D; xb3 = -L*np.cos(alpha*np.pi/180.); yb3 = D+L*np.sin(alpha*np.pi/180.)
alpha = 90; L = 500; xa4=0; ya4 = D; xb4 = -L*np.cos(alpha*np.pi/180.); yb4 = D+L*np.sin(alpha*np.pi/180.)
alpha = 90; L = 100; xa5=0; ya5 = D; xb5 = -L*np.cos(alpha*np.pi/180.); yb5 = D+L*np.sin(alpha*np.pi/180.)
if (f1):
axs[1].plot([xa1,xb1],[ya1,yb1],linewidth=5,linestyle='-',color='red')
if (f2):
axs[1].plot([xa2,xb2],[ya2,yb2],linewidth=5,linestyle='--',color='red')
if (f3):
axs[1].plot([xa3,xb3],[ya3,yb3],linewidth=5,linestyle=':',color='red')
if (f4):
axs[1].plot([xa4,xb4],[ya4,yb4],linewidth=5,linestyle='-',color='green')
if (f5):
axs[1].plot([xa5,xb5],[ya5,yb5],linewidth=5,linestyle='-',color='blue')
plot_plate(f1=True)
# call interactive module
w = dict(
f1=widgets.Checkbox(value=True,description='eins',continuous_update=False,disabled=False),
#a1=widgets.FloatSlider(min=0.,max=2.,step=0.1,value=1.0),
f2=widgets.Checkbox(value=False,description='zwei',continuous_update=False,disabled=False),
f3=widgets.Checkbox(value=False,description='drei',continuous_update=False,disabled=False),
f4=widgets.Checkbox(value=False,description='vier',continuous_update=False,disabled=False),
f5=widgets.Checkbox(value=False,description='fuenf',continuous_update=False,disabled=False))
output = widgets.interactive_output(plot_plate, w)
box = widgets.HBox([widgets.VBox([*w.values()]), output])
display(box)
| 0.366476 | 0.881258 |
# Matrix Factorization for Recommender Systems - Part 1
**Table of contents of this tutorial series on matrix factorization for recommender systems:**
- [Part 1 - Traditional Matrix Factorization methods for Recommender Systems](https://MaxHalford.github.io/examples/matrix-factorization-for-recommender-systems-part-1)
- [Part 2 - Factorization Machines and Field-aware Factorization Machines](https://MaxHalford.github.io/examples/matrix-factorization-for-recommender-systems-part-2)
- [Part 3 - Large scale learning and better predictive power with multiple pass learning](https://MaxHalford.github.io/examples/matrix-factorization-for-recommender-systems-part-3)
## Introduction
A [recommender system](https://en.wikipedia.org/wiki/Recommender_system) is a software tool designed to generate and suggest items or entities to the users. Popular large scale examples include:
- Amazon (suggesting products)
- Facebook (suggesting posts in users' news feeds)
- Spotify (suggesting music)
Social recommendation from graph (mostly used by social networks) are not covered in `creme`. We focus on the general case, item recommendation. This problem can be represented with the user-item matrix:
$$
\normalsize
\begin{matrix}
& \begin{matrix} _1 & _\cdots & _\cdots & _\cdots & _I \end{matrix} \\
\begin{matrix} _1 \\ _\vdots \\ _\vdots \\ _\vdots \\ _U \end{matrix} &
\begin{bmatrix}
{\color{Red} ?} & 2 & \cdots & {\color{Red} ?} & {\color{Red} ?} \\
{\color{Red} ?} & {\color{Red} ?} & \cdots & {\color{Red} ?} & 4.5 \\
\vdots & \ddots & \ddots & \ddots & \vdots \\
3 & {\color{Red} ?} & \cdots & {\color{Red} ?} & {\color{Red} ?} \\
{\color{Red} ?} & {\color{Red} ?} & \cdots & 5 & {\color{Red} ?}
\end{bmatrix}
\end{matrix}
$$
Where $U$ and $I$ are the number of user and item of the system, respectively. A matrix entry represents a user's preference for an item, it can be a rating, a like or dislike, etc. Because of the huge number of users and items compared to the number of observed entries, those matrices are very sparsed (usually less than 1% filled).
[Matrix Factorization (MF)](https://en.wikipedia.org/wiki/Matrix_factorization_(recommender_systems)) is a class of [collaborative filtering](https://en.wikipedia.org/wiki/Collaborative_filtering) algorithms derived from [Singular Value Decomposition (SVD)](https://en.wikipedia.org/wiki/Singular_value_decomposition). MF strength lies in its capacity to able to model high cardinality categorical variables interactions. This subfield boomed during the famous [Netflix Prize](https://en.wikipedia.org/wiki/Netflix_Prize) contest in 2006, when numerous novel variants has been invented and became popular thanks to their attractive accuracy and scalability.
MF approach seeks to fill the user-item matrix considering the problem as a [matrix completion](https://en.wikipedia.org/wiki/Matrix_completion) one. MF core idea assume a latent model learning its own representation of the users and the items in a lower latent dimensional space by factorizing the observed parts of the matrix.
A factorized user or item is represented as a vector $\mathbf{v}_u$ or $\mathbf{v}_i$ composed of $k$ latent factors, with $k << U, I$. Those learnt latent variables represent, for an item the various aspects describing it, and for a user its interests in terms of those aspects. The model then assume a user's choice or fondness is composed of a sum of preferences about the various aspects of the concerned item. This sum being the dot product between the latent vectors of a given user-item pair:
$$
\normalsize
\langle \mathbf{v}_u, \mathbf{v}_i \rangle = \sum_{f=1}^{k} \mathbf{v}_{u, f} \cdot \mathbf{v}_{i, f}
$$
MF models weights are learnt in an online fashion, often with stochastic gradient descent as it provides relatively fast running time and good accuracy. There is a great and widely popular library named [surprise](http://surpriselib.com/) that implements MF models (and others) but in contrast with `creme` doesn't follow a pure online philosophy (all the data have to be loaded in memory and the API doesn't allow you to update your model with new data).
**Notes:**
- In recent years, proposed deep learning techniques for recommendation tasks claim state of the art results. However, [recent work](https://arxiv.org/abs/1907.06902) (August 2019) showed that those promises can't be taken for granted and traditional MF methods are still relevant today.
- For more information about how the business value of recommender systems is measured and why they are one of the main success stories of machine learning, see the following [literature survey](https://arxiv.org/abs/1908.08328) (December 2019).
## Let's start
In this tutorial, we are going to explore MF algorithms available in `creme` and test them on a movie recommendation problem with the MovieLens 100K dataset. This latter is a collection of movie ratings (from 1 to 5) that includes various information about both the items and the users. We can access it from the [creme.datasets](https://MaxHalford.github.io/api-reference/overview/#datasets) module:
```
import json
from creme import datasets
for x, y in datasets.MovieLens100K():
print(f'x = {json.dumps(x, indent=4)}\ny = {y}')
break
```
Let's define a routine to evaluate our different models on MovieLens 100K. Mean Absolute Error and Root Mean Squared Error will be our metrics printed alongside model's computation time and memory usage:
```
from creme import metrics
from creme.evaluate import progressive_val_score
def evaluate(model):
X_y = datasets.MovieLens100K()
metric = metrics.MAE() + metrics.RMSE()
_ = progressive_val_score(X_y, model, metric, print_every=25_000, show_time=True, show_memory=True)
```
## Naive prediction
It's good practice in machine learning to start with a naive baseline and then iterate from simple things to complex ones observing progress incrementally. Let's start by predicing the target running mean as a first shot:
```
from creme import stats
mean = stats.Mean()
metric = metrics.MAE() + metrics.RMSE()
for i, x_y in enumerate(datasets.MovieLens100K(), start=1):
_, y = x_y
metric.update(y, mean.get())
mean.update(y)
if not i % 25_000:
print(f'[{i:,d}] {metric}')
```
## Baseline model
Now we can do machine learning and explore available models in [creme.reco](https://MaxHalford.github.io/api-reference/overview/#reco) module starting with the baseline model. It extends our naive prediction by adding to the global running mean two bias terms characterizing the user and the item discrepancy from the general tendency. The model equation is defined as:
$$
\normalsize
\hat{y}(x) = \bar{y} + bu_{u} + bi_{i}
$$
This baseline model can be viewed as a linear regression where the intercept is replaced by the target running mean with the users and the items one hot encoded.
All machine learning models in `creme` expect dicts as input with feature names as keys and feature values as values. Specifically, models from `creme.reco` expect a `'user'` and an `'item'` entries without any type constraint on their values (i.e. can be strings or numbers), e.g.:
```python
x = {
'user': 'Guido',
'item': "Monty Python's Flying Circus"
}
```
Other entries, if exist, are simply ignored. This is quite usefull as we don't need to spend time and storage doing one hot encoding.
```
from creme import meta
from creme import optim
from creme import reco
baseline_params = {
'optimizer': optim.SGD(0.025),
'l2': 0.,
'initializer': optim.initializers.Zeros()
}
model = meta.PredClipper(
regressor=reco.Baseline(**baseline_params),
y_min=1,
y_max=5
)
evaluate(model)
```
We won two tenth of MAE compared to our naive prediction (0.7546 vs 0.9421) meaning that significant information has been learnt by the model.
## Funk Matrix Factorization (FunkMF)
It's the pure form of matrix factorization consisting of only learning the users and items latent representations as discussed in introduction. Simon Funk popularized its [stochastic gradient descent optimization](https://sifter.org/simon/journal/20061211.html) in 2006 during the Netflix Prize. The model equation is defined as:
$$
\normalsize
\hat{y}(x) = \langle \mathbf{v}_u, \mathbf{v}_i \rangle
$$
**Note:** FunkMF is sometimes refered as [Probabilistic Matrix Factorization](https://papers.nips.cc/paper/3208-probabilistic-matrix-factorization.pdf) which is an extended probabilistic version.
```
funk_mf_params = {
'n_factors': 10,
'optimizer': optim.SGD(0.05),
'l2': 0.1,
'initializer': optim.initializers.Normal(mu=0., sigma=0.1, seed=73)
}
model = meta.PredClipper(
regressor=reco.FunkMF(**funk_mf_params),
y_min=1,
y_max=5
)
evaluate(model)
```
Results are equivalent to our naive prediction (0.9448 vs 0.9421). By only focusing on the users preferences and the items characteristics, the model is limited in his ability to capture different views of the problem. Despite its poor performance alone, this algorithm is quite usefull combined in other models or when we need to build dense representations for other tasks.
## Biased Matrix Factorization (BiasedMF)
It's the combination of the Baseline model and FunkMF. The model equation is defined as:
$$
\normalsize
\hat{y}(x) = \bar{y} + bu_{u} + bi_{i} + \langle \mathbf{v}_u, \mathbf{v}_i \rangle
$$
**Note:** *Biased Matrix Factorization* name is used by some people but some others refer to it by *SVD* or *Funk SVD*. It's the case of Yehuda Koren and Robert Bell in [Recommender Systems Handbook](https://www.cse.iitk.ac.in/users/nsrivast/HCC/Recommender_systems_handbook.pdf) (Chapter 5 *Advances in Collaborative Filtering*) and of `surprise` library. Nevertheless, *SVD* could be confused with the original *Singular Value Decomposition* from which it's derived from, and *Funk SVD* could also be misleading because of the biased part of the model equation which doesn't come from Simon Funk's work. For those reasons, we chose to side with *Biased Matrix Factorization* which fits more naturally to it.
```
biased_mf_params = {
'n_factors': 10,
'bias_optimizer': optim.SGD(0.025),
'latent_optimizer': optim.SGD(0.05),
'weight_initializer': optim.initializers.Zeros(),
'latent_initializer': optim.initializers.Normal(mu=0., sigma=0.1, seed=73),
'l2_bias': 0.,
'l2_latent': 0.
}
model = meta.PredClipper(
regressor=reco.BiasedMF(**biased_mf_params),
y_min=1,
y_max=5
)
evaluate(model)
```
Results improved (0.7485 vs 0.7546) demonstrating that users and items latent representations bring additional information.
To conclude this first tutorial about factorization models, let's review the important parameters to tune when dealing with this family of methods:
- `n_factors`: the number of latent factors. The more you set, the more items aspects and users preferences you are going to learn. Too many will cause overfitting, `l2` regularization could help.
- `*_optimizer`: the optimizers. Classic stochastic gradient descent performs well, finding the good learning rate will make the difference.
- `initializer`: the latent weights initialization. Latent vectors have to be initialized with non-constant values. We generally sample them from a zero-mean normal distribution with small standard deviation.
|
github_jupyter
|
import json
from creme import datasets
for x, y in datasets.MovieLens100K():
print(f'x = {json.dumps(x, indent=4)}\ny = {y}')
break
from creme import metrics
from creme.evaluate import progressive_val_score
def evaluate(model):
X_y = datasets.MovieLens100K()
metric = metrics.MAE() + metrics.RMSE()
_ = progressive_val_score(X_y, model, metric, print_every=25_000, show_time=True, show_memory=True)
from creme import stats
mean = stats.Mean()
metric = metrics.MAE() + metrics.RMSE()
for i, x_y in enumerate(datasets.MovieLens100K(), start=1):
_, y = x_y
metric.update(y, mean.get())
mean.update(y)
if not i % 25_000:
print(f'[{i:,d}] {metric}')
x = {
'user': 'Guido',
'item': "Monty Python's Flying Circus"
}
from creme import meta
from creme import optim
from creme import reco
baseline_params = {
'optimizer': optim.SGD(0.025),
'l2': 0.,
'initializer': optim.initializers.Zeros()
}
model = meta.PredClipper(
regressor=reco.Baseline(**baseline_params),
y_min=1,
y_max=5
)
evaluate(model)
funk_mf_params = {
'n_factors': 10,
'optimizer': optim.SGD(0.05),
'l2': 0.1,
'initializer': optim.initializers.Normal(mu=0., sigma=0.1, seed=73)
}
model = meta.PredClipper(
regressor=reco.FunkMF(**funk_mf_params),
y_min=1,
y_max=5
)
evaluate(model)
biased_mf_params = {
'n_factors': 10,
'bias_optimizer': optim.SGD(0.025),
'latent_optimizer': optim.SGD(0.05),
'weight_initializer': optim.initializers.Zeros(),
'latent_initializer': optim.initializers.Normal(mu=0., sigma=0.1, seed=73),
'l2_bias': 0.,
'l2_latent': 0.
}
model = meta.PredClipper(
regressor=reco.BiasedMF(**biased_mf_params),
y_min=1,
y_max=5
)
evaluate(model)
| 0.571288 | 0.991788 |
# Part 8 - Federated Learning on MNIST using a CNN
## Upgrade to Federated Learning in 10 Lines of PyTorch + PySyft
### Context
Federated Learning is a very exciting and upsurging Machine Learning technique that aims at building systems that learn on decentralized data. The idea is that the data remains in the hands of its producer (which is also known as the _worker_), which helps improving privacy and ownership, and the model is shared between workers. One immediate application is for example to predict the next word on your mobile phone when you write text: you don't want the data used for training — i.e. your text messages — to be sent to a central server.
The rise of Federated Learning is therefore tightly connected to the spread of data privacy awareness, and the GDPR in EU which enforces data protection since May 2018 has acted as a catalyst. To anticipate on regulation, large actors like Apple or Google have started investing massively in this technology, especially to protect the mobile users' privacy, but they have not made their tools available. At OpenMined, we believe that anyone willing to conduct a Machine Learning project should be able to implement privacy preserving tools with very little effort. We have built tools for encrypting data in a single line [as mentioned in our blog post](https://blog.openmined.org/training-cnns-using-spdz/) and we now release our Federated Learning framework which leverage the new PyTorch 1.0 version to provide an intuitive interface to building secure and scalable models.
In this tutorial, we'll use directly [the canonical example of training a CNN on MNIST using PyTorch](https://github.com/pytorch/examples/blob/master/mnist/main.py) and show how simple it is to implement Federated Learning with it using our [PySyft library](https://github.com/OpenMined/PySyft/). We will go through each part of the example and underline the code which is changed.
You can also find this material in [our blogpost](https://blog.openmined.org/upgrade-to-federated-learning-in-10-lines).
Authors:
- Théo Ryffel - GitHub: [@LaRiffle](https://github.com/LaRiffle)
**Ok, let's get started!**
### Imports and model specifications
First we make the official imports
```
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
```
And than those specific to PySyft. In particular we define remote workers `alice` and `bob`.
```
import syft as sy # <-- NEW: import the Pysyft library
hook = sy.TorchHook(torch) # <-- NEW: hook PyTorch ie add extra functionalities to support Federated Learning
bob = sy.VirtualWorker(hook, id="bob") # <-- NEW: define remote worker bob
alice = sy.VirtualWorker(hook, id="alice") # <-- NEW: and alice
```
We define the setting of the learning task
```
class Arguments():
def __init__(self):
self.batch_size = 64
self.test_batch_size = 1000
self.epochs = 10
self.lr = 0.01
self.momentum = 0.5
self.no_cuda = False
self.seed = 1
self.log_interval = 30
self.save_model = False
args = Arguments()
use_cuda = not args.no_cuda and torch.cuda.is_available()
torch.manual_seed(args.seed)
device = torch.device("cuda" if use_cuda else "cpu")
kwargs = {'num_workers': 1, 'pin_memory': True} if use_cuda else {}
```
### Data loading and sending to workers
We first load the data and transform the training Dataset into a Federated Dataset split across the workers using the `.federate` method. This federated dataset is now given to a Federated DataLoader. The test dataset remains unchanged.
```
federated_train_loader = sy.FederatedDataLoader( # <-- this is now a FederatedDataLoader
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
.federate((bob, alice)), # <-- NEW: we distribute the dataset across all the workers, it's now a FederatedDataset
batch_size=args.batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=args.test_batch_size, shuffle=True, **kwargs)
logging.warning(f"The following options are no\n jsoos")
```
### CNN specification
Here we use exactly the same CNN as in the official example.
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 20, 5, 1)
self.conv2 = nn.Conv2d(20, 50, 5, 1)
self.fc1 = nn.Linear(4*4*50, 500)
self.fc2 = nn.Linear(500, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2, 2)
x = x.view(-1, 4*4*50)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return F.log_softmax(x, dim=1)
```
### Define the train and test functions
For the train function, because the data batches are distributed across `alice` and `bob`, you need to send the model to the right location for each batch. Then, you perform all the operations remotely with the same syntax like you're doing local PyTorch. When you're done, you get back the model updated and the loss to look for improvement.
```
def train(args, model, device, federated_train_loader, optimizer, epoch):
model.train()
for batch_idx, (data, target) in enumerate(federated_train_loader): # <-- now it is a distributed dataset
model.send(data.location) # <-- NEW: send the model to the right location
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
model.get() # <-- NEW: get the model back
if batch_idx % args.log_interval == 0:
loss = loss.get() # <-- NEW: get the loss back
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * args.batch_size, len(federated_train_loader) * args.batch_size,
100. * batch_idx / len(federated_train_loader), loss.item()))
```
The test function does not change!
```
def test(args, model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
```
### Launch the training !
```
%%time
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=args.lr) # TODO momentum is not supported at the moment
for epoch in range(1, args.epochs + 1):
train(args, model, device, federated_train_loader, optimizer, epoch)
test(args, model, device, test_loader)
if (args.save_model):
torch.save(model.state_dict(), "mnist_cnn.pt")
```
Et voilà! Here you are, you have trained a model on remote data using Federated Learning!
## One Last Thing
I know there's a question you're dying to ask: **how long does it takes to do Federated Learning compared to normal PyTorch?**
The computation time is actually **less than twice the time** used for normal PyTorch execution! More precisely, it takes 1.9 times longer, which is very little compared to the features we were able to add.
## Conclusion
As you observe, we modified 10 lines of code to upgrade the official Pytorch example on MNIST to a real Federated Learning setting!
Of course, there are dozen of improvements we could think of. We would like the computation to operate in parallel on the workers and to perform federated averaging, to update the central model every `n` batches only, to reduce the number of messages we use to communicate between workers, etc. These are features we're working on to make Federated Learning ready for a production environment and we'll write about them as soon as they are released!
You should now be able to do Federated Learning by yourself! If you enjoyed this and would like to join the movement toward privacy preserving, decentralized ownership of AI and the AI supply chain (data), you can do so in the following ways!
### Star PySyft on GitHub
The easiest way to help our community is just by starring the repositories! This helps raise awareness of the cool tools we're building.
- [Star PySyft](https://github.com/OpenMined/PySyft)
### Pick our tutorials on GitHub!
We made really nice tutorials to get a better understanding of what Federated and Privacy-Preserving Learning should look like and how we are building the bricks for this to happen.
- [Checkout the PySyft tutorials](https://github.com/OpenMined/PySyft/tree/master/examples/tutorials)
### Join our Slack!
The best way to keep up to date on the latest advancements is to join our community!
- [Join slack.openmined.org](http://slack.openmined.org)
### Join a Code Project!
The best way to contribute to our community is to become a code contributor! If you want to start "one off" mini-projects, you can go to PySyft GitHub Issues page and search for issues marked `Good First Issue`.
- [Good First Issue Tickets](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
### Donate
If you don't have time to contribute to our codebase, but would still like to lend support, you can also become a Backer on our Open Collective. All donations go toward our web hosting and other community expenses such as hackathons and meetups!
- [Donate through OpenMined's Open Collective Page](https://opencollective.com/openmined)
|
github_jupyter
|
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import syft as sy # <-- NEW: import the Pysyft library
hook = sy.TorchHook(torch) # <-- NEW: hook PyTorch ie add extra functionalities to support Federated Learning
bob = sy.VirtualWorker(hook, id="bob") # <-- NEW: define remote worker bob
alice = sy.VirtualWorker(hook, id="alice") # <-- NEW: and alice
class Arguments():
def __init__(self):
self.batch_size = 64
self.test_batch_size = 1000
self.epochs = 10
self.lr = 0.01
self.momentum = 0.5
self.no_cuda = False
self.seed = 1
self.log_interval = 30
self.save_model = False
args = Arguments()
use_cuda = not args.no_cuda and torch.cuda.is_available()
torch.manual_seed(args.seed)
device = torch.device("cuda" if use_cuda else "cpu")
kwargs = {'num_workers': 1, 'pin_memory': True} if use_cuda else {}
federated_train_loader = sy.FederatedDataLoader( # <-- this is now a FederatedDataLoader
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
.federate((bob, alice)), # <-- NEW: we distribute the dataset across all the workers, it's now a FederatedDataset
batch_size=args.batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=args.test_batch_size, shuffle=True, **kwargs)
logging.warning(f"The following options are no\n jsoos")
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 20, 5, 1)
self.conv2 = nn.Conv2d(20, 50, 5, 1)
self.fc1 = nn.Linear(4*4*50, 500)
self.fc2 = nn.Linear(500, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2, 2)
x = x.view(-1, 4*4*50)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return F.log_softmax(x, dim=1)
def train(args, model, device, federated_train_loader, optimizer, epoch):
model.train()
for batch_idx, (data, target) in enumerate(federated_train_loader): # <-- now it is a distributed dataset
model.send(data.location) # <-- NEW: send the model to the right location
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
model.get() # <-- NEW: get the model back
if batch_idx % args.log_interval == 0:
loss = loss.get() # <-- NEW: get the loss back
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * args.batch_size, len(federated_train_loader) * args.batch_size,
100. * batch_idx / len(federated_train_loader), loss.item()))
def test(args, model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
%%time
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=args.lr) # TODO momentum is not supported at the moment
for epoch in range(1, args.epochs + 1):
train(args, model, device, federated_train_loader, optimizer, epoch)
test(args, model, device, test_loader)
if (args.save_model):
torch.save(model.state_dict(), "mnist_cnn.pt")
| 0.900805 | 0.989938 |
# Plot correspondences in registration
## Imports and magics
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as ipyw
import matplotlib.animation as animation
from mpl_toolkits.axes_grid1 import make_axes_locatable
from scipy.io import loadmat
from IPython.display import HTML
from otimage import imagerep, io
from otimage.utils import plot_maxproj
from otimage.imagereg import ot_registration, gw_registration
```
## Load Zimmer data
```
# Frame index
t1 = 15
t2 = 45
# Load two successive frames from dataset
img_path = '/home/mn2822/Desktop/WormOT/data/zimmer/raw/mCherry_v00065-00115.hdf5'
with io.ZimmerReader(img_path) as reader:
img_1 = reader.get_frame(t1)
img_2 = reader.get_frame(t2)
# Load MP components
mp_path = '/home/mn2822/Desktop/WormOT/data/zimmer/mp_components/mp_0000_0050.mat'
with io.MPReader(mp_path) as reader:
mp_1 = reader.get_frame(t1)
mp_2 = reader.get_frame(t2)
# Reconstruct images from MPs
rec_1 = imagerep.reconstruct_mp_image(mp_1)
rec_2 = imagerep.reconstruct_mp_image(mp_2)
plt.figure(figsize=(10, 10))
plt.subplot(221)
plot_maxproj(img_1)
plt.title(f'frame: {t1}')
plt.axis('off')
plt.subplot(222)
plot_maxproj(img_2)
plt.title(f'frame: {t2}')
plt.axis('off');
plt.subplot(223)
plot_maxproj(rec_1)
plt.title('MP recon')
plt.axis('off')
plt.subplot(224)
plot_maxproj(rec_2)
plt.title('MP recon')
plt.axis('off');
```
## Compute registration for images
```
degree = 2
n_iter = 50
model, debug = gw_registration(mp_2, mp_1, degree=degree, n_iter=n_iter)
print('beta (est):')
print(model.beta)
```
## Compute pullback with identified MP component
```
# Transform MP points for second image using mapping
pb_pts = model.predict(mp_2.pts).astype(int)
# Reconstruct image from transformed points
mp_pb = imagerep.ImageMP(pb_pts, mp_2.wts, mp_2.cov, mp_2.img_shape)
rec_pb = imagerep.reconstruct_mp_image(mp_pb)
```
## Plot pullback and MP components
```
plt.figure(figsize=(15, 15))
plt.subplot(131)
plot_maxproj(rec_1)
plt.title(f'frame: {t1}')
plt.subplot(132)
plot_maxproj(rec_2)
plt.title(f'frame: {t2}')
plt.subplot(133)
plot_maxproj(rec_pb)
plt.title(f'frame: {t2} (pullback)');
def plot_mp(idx):
c_pt = mp_2.pts[idx]
c_pb = mp_pb.pts[idx]
fig, (ax_1, ax_2, ax_3) = plt.subplots(1, 3, figsize=(15, 15))
plot_maxproj(rec_1, ax_1)
ax_1.set_title(f'frame: {t1}')
plot_maxproj(rec_2, ax_2)
ax_2.plot(c_pt[0], c_pt[1], color='red', marker='*')
ax_2.set_title(f'frame: {t2}')
plot_maxproj(rec_pb, ax_3)
ax_3.plot(c_pb[0], c_pb[1], color='red', marker='*')
ax_3.set_title(f'frame: {t2} (pullback)');
ipyw.interact(
plot_mp,
idx=ipyw.IntSlider(
min=0, max=mp_1.pts.shape[0], step=1,
continuous_update=False, description='MP:'
)
);
```
## Notes
### Correspondence accuracy
(all registrations were run with `n_iter=50`
#### OT registration, quadratic model
- Ran on frames 3 and 4, and correspondence was accurate
- Ran on frames 3 and 10, and correspondence was not accurate
- Example indices where MPs are poorly matched: 5, 7, 8, 15, 17, 19, 25, 28
#### OT registration, cubic model
- Ran on frames 3 and 10, and correspondence was not accurate, but might be better than quadratic model
- Example indices where MPs are poorly matched: 2, 3, 8, 10, 13, 31, 33
#### GW registration, quadratic model
- Ran on frames 3 and 4, and correspondence was accurate
- Ran on frames 3 and 10, and correspondence was accurate
- Ran on frames 15 and 45, and correspondence was accurate (this is crazy -- frames are extremely different)
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as ipyw
import matplotlib.animation as animation
from mpl_toolkits.axes_grid1 import make_axes_locatable
from scipy.io import loadmat
from IPython.display import HTML
from otimage import imagerep, io
from otimage.utils import plot_maxproj
from otimage.imagereg import ot_registration, gw_registration
# Frame index
t1 = 15
t2 = 45
# Load two successive frames from dataset
img_path = '/home/mn2822/Desktop/WormOT/data/zimmer/raw/mCherry_v00065-00115.hdf5'
with io.ZimmerReader(img_path) as reader:
img_1 = reader.get_frame(t1)
img_2 = reader.get_frame(t2)
# Load MP components
mp_path = '/home/mn2822/Desktop/WormOT/data/zimmer/mp_components/mp_0000_0050.mat'
with io.MPReader(mp_path) as reader:
mp_1 = reader.get_frame(t1)
mp_2 = reader.get_frame(t2)
# Reconstruct images from MPs
rec_1 = imagerep.reconstruct_mp_image(mp_1)
rec_2 = imagerep.reconstruct_mp_image(mp_2)
plt.figure(figsize=(10, 10))
plt.subplot(221)
plot_maxproj(img_1)
plt.title(f'frame: {t1}')
plt.axis('off')
plt.subplot(222)
plot_maxproj(img_2)
plt.title(f'frame: {t2}')
plt.axis('off');
plt.subplot(223)
plot_maxproj(rec_1)
plt.title('MP recon')
plt.axis('off')
plt.subplot(224)
plot_maxproj(rec_2)
plt.title('MP recon')
plt.axis('off');
degree = 2
n_iter = 50
model, debug = gw_registration(mp_2, mp_1, degree=degree, n_iter=n_iter)
print('beta (est):')
print(model.beta)
# Transform MP points for second image using mapping
pb_pts = model.predict(mp_2.pts).astype(int)
# Reconstruct image from transformed points
mp_pb = imagerep.ImageMP(pb_pts, mp_2.wts, mp_2.cov, mp_2.img_shape)
rec_pb = imagerep.reconstruct_mp_image(mp_pb)
plt.figure(figsize=(15, 15))
plt.subplot(131)
plot_maxproj(rec_1)
plt.title(f'frame: {t1}')
plt.subplot(132)
plot_maxproj(rec_2)
plt.title(f'frame: {t2}')
plt.subplot(133)
plot_maxproj(rec_pb)
plt.title(f'frame: {t2} (pullback)');
def plot_mp(idx):
c_pt = mp_2.pts[idx]
c_pb = mp_pb.pts[idx]
fig, (ax_1, ax_2, ax_3) = plt.subplots(1, 3, figsize=(15, 15))
plot_maxproj(rec_1, ax_1)
ax_1.set_title(f'frame: {t1}')
plot_maxproj(rec_2, ax_2)
ax_2.plot(c_pt[0], c_pt[1], color='red', marker='*')
ax_2.set_title(f'frame: {t2}')
plot_maxproj(rec_pb, ax_3)
ax_3.plot(c_pb[0], c_pb[1], color='red', marker='*')
ax_3.set_title(f'frame: {t2} (pullback)');
ipyw.interact(
plot_mp,
idx=ipyw.IntSlider(
min=0, max=mp_1.pts.shape[0], step=1,
continuous_update=False, description='MP:'
)
);
| 0.719088 | 0.887351 |

# Programación funcional
En programación hay varios tipos de lenguajes. Como vimos en Notebooks anteriores, **Python es un lenguaje de programación orientado a objetos**. No obstante, es bastante versatil y **admite** otras funcionalidades propias de otros lenguajes, como es la **programación funcional**. En este Notebook verás qué utilidad tiene este tipo de programación, y cómo usarla en Python.
1. [Programacion funcional](#1.-Programacion-funcional)
2. [Funcion lambda](#2.-Funcion-lambda)
3. [Map](#3.-Map)
4. [Reduce](#4.-Reduce)
5. [Filter](#5.-Filter)
6. [Timeit](#6.-Timeit)
7. [Programacion funcional en Pandas](#7.-Programacion-funcional-en-Pandas)
8. [Resumen](#8.-Resumen)
## 1. Programacion funcional
Dependiendo del problema que queramos resolver, utilizaremos un tipo de lenguaje de programación u otro. Veamos la diferencia entre un lenguaje de programación orientado a objetos y uno funcional:
* **Programación Orientada a Objetos (OOP)**: sería el caso de Python. En este caso se encapsulan todos los elementos del programa en objetos, que son de cierto tipo, **tienen un estado**, atributos y funcionalidades. Lenguajes orientados a objetos son Java, Python, JavaScript, Ruby... entre otros.
* **Programación Funcional**: El programa se divide en un conjunto de funciones. Por tanto, es un entrada/salida continuo, ya que las funciones tienen un *input*, realizan operaciones, y después un *output*. Son lenguajes que ofrecen un buen rendimiento pero difíciles de desarrollar ya que hay que acudir mucho a la recursividad. Algunos de los lenguajes más usados son [Clojure](https://clojure.org) o [Scala](https://www.scala-lang.org).
Por tanto, ¿Python que es? ¿Es orientado a objetos...? ¿Es funcinal? **Python es orientado a objetos, pero además cuenta con ciertas funciones *built-in* propias de la programación funcional**, como `map` o `filter`, lo que nos va a aportar nuevas maneras de solventar problemas en nuestro programa, además de mejoras en rendimiento.
Como ves, Python nos va a permitir usar todas sus funcionalidades propias como lenguaje orientado a objetos que es, y además la posibilidad de combinarlas con otro tipo de programación, como es la funcional.
¿Cómo podemos iterar sobre una lista y calcular la suma de sus elementos?
```
lista = [1,2,3,4,5]
suma = 0
for i in lista:
suma += i
suma
#a = a + b a += b
#a = a - b a -= b
#a = a * b a *= b
#a = a / b a /= b
#a = a % b a %= b
```
Aparte de la función *built-in* de Python `sum()`, tenemos también la opción de la recursividad, con la que no usamos bucles, y únicamente realizamos operaciones mediante funciones.
```
lista = [1,2,3]
def suma_fun(lista):
if len(lista) == 0:
return 0
return lista[0] + suma_fun(lista[1:])
suma_fun(lista)
#La ventaja de esta aproximación es que no se usan variables para almacenar los resultados intermedios
```
1 + [2, 3]<br>
2 + [3]<br>
3 + [ ]<br>
6
La principal diferecia radica en **el estado**. En el caso del `for` tenemos un programa que va cambiando su estado, debido a las diferentes variables que toman `suma` e `i`. Sin embargo, en el segundo ejemplo no hay estados. Son funciones que llaman a otras, tienen un *input* y un *output*. Lo veremos más en detalle en el Notebook.
## 2. Funcion lambda
Recuerda cómo era la sintaxis para crear funciones:
```Python
def nombre_funcion(argumentos):
cosas de la funcion
return output
```
Una función tiene un nombre, unos parámetros de entrada, operaciones dentro y un output. En este apartado se presenta una nueva manera más ágil de crear funciones, gracias a la sentencia `lambda`. Con `lambda` podrás crear funciones sencillas y de una única expresión.
Las funciones `lambda` **son anónimas**, no tienen un nombre que las identifique, simplemente se ejecuta el código de la función que declaremos.
La sintaxis de una función `lambda` es:
```Python
lambda argumentos: expresion
```
Veamos un ejemplo
```
# Declaramos funcion
def suma(x, y):
return x + y
# Guardamos en variable
# En Pythontutor se ve como se crea una referencia desde suma_var al objeto suma(x, y) en memoria
suma_var = suma
#Si llamramos a la función con paréntesis se ejecutaría y almacenaría el resultado en una variable
#suma_var = suma(1, 2)
# Vemos el tipo
print(type(suma_var))
# Usamos la funcion
suma_var(1, 2)
```
Como ves, las funciones son un objeto más, que podemos asignar a una variable. Veamos ahora cómo traducimos esto a una función `lambda`
```
lambda x, y : x + y
# Si la asignamos a una variable
suma_lambda = lambda x, y : x + y
suma_lambda(5, 7)
```
Las funciones `lambda` no se usan solas, sino que son argumentos de funciones de más alto nivel, es decir, funciones cuyos parámetros de entrada son otras funciones, como `map`, `reduce` o `filter`.
Las `lambdas` también pueden ser una buena manera de escribir código más entendible. Veamos un ejemplo en el que trabajamos con coordenadas.
```
estaciones = ((40.4440297, -3.6956047), (40.4585318, -3.684715))
inicio = lambda x: x[0]
fin = lambda x: x[1]
print(inicio(estaciones))
print(fin(estaciones))
lat = lambda x: x[0]
lon = lambda x: x[1]
print(lat(inicio(estaciones)))
print(lon(inicio(estaciones)))
#Se podrían usar las funciones inicio, fin originales
print(inicio(inicio(estaciones)))
print(fin(inicio(estaciones)))
```
<table align="left">
<tr><td width="80"><img src="./img/ejercicio.png" style="width:auto;height:auto"></td>
<td style="text-align:left">
<h3>Trabajando con lambda</h3>
<ol>
<li>Crea una función lambda con tres argumentos, y que multiplique los tres </li>
<li>Crea otra función lambda con un único argumento y que calcule la raíz cuadrada del mismo.</li>
</ol>
</td></tr>
</table>
```
multi3 = lambda x,y,z : x * y * z
cuadrado = lambda x : x ** x
print(multi3(1,2,3))
print(cuadrado(2))
# 3 ** 2 --> al cuadrado
# 3 ** (1/2) --> raiz cuadrada de 3
# 3 ** 0.5 --> raiz cuadrada de 3
# 4 ** (1/3) --> raiz cúbica de 4
# 4 ** -2 --> 1 / (4 ** 2)
# 4 ** -3 --> 1 / (4 ** 3)
# 4 ** (2/3) --> 4 ** (2 * 1/3) --> raiz cúbica de (4 ** 2)
import math
raiz = lambda x : math.sqrt(x)
raiz(25)
```
## 3. Map
Se trata de una función *built-in* que tiene dos argumentos. Unos es una función, y el otro un iterable, que puede ser una lista, tupla, string... **Lo que hace es aplicarle la función a cada uno de los argumentos del iterable**. Mapea cada valor del iterable, le aplica una operación, y crea un nuevo iterable al que le ha aplicado dicha operación.
Su sintaxis es:
```Python
map(funcion, iterable)
```
Se trata de una manera de sustituir la funcionalidad de los bucles. Muy útil cuando queramos aplicar operaciones a una lista entera.
```
my_list = [1,5,4,6,11]
#my_list + 2 NO
new_list = map(lambda x : x + 2, my_list)
print(new_list)
print(type(new_list))
print(list(new_list))
```
Fíjate que la función `map` devuelve un *map object*, que no es más que un iterable, convertible fácilmente a una lista. Como ves, de momento aplicaremos una función `lambda` con una única expresión, pero más adelante verás cómo puedes aplicarle tus propias funciones más complejas.
Veamos otro ejemplo con operaciones diferentes
```
my_list = (True, False, True, True)
new_list = map(lambda x: not x, my_list)
print(list(new_list))
```
`map` trabaja con iterables, por lo que también será posible aplicarle un `map` a un string.
```
my_list = ("AAA", "BBB", "CCC")
modif_tupla1 = map(lambda x : 'W-' + x, my_list)
print(tuple(modif_tupla1))
modif_tupla2 = map(lambda x : 'W-'.join(x), my_list)
print(tuple(modif_tupla2))
modif_tupla3 = map(lambda x : x.join('W-'), my_list)
print(tuple(modif_tupla3))
```
Puedes incluso separar la función `lambda`, para posteriormente usarla en otros lugares.
```
my_list = ("AAA", "BBB", "CCC")
```
**Incluso podrás aplicar tus propias funciones**. Imagina la versatilidad que te da esto. Dentro de cada función podrás realizar el cálculo que quieras, y ese calculo se le aplicará a cada elemento de tu iterable.
```
my_list = ("AAA", "BBB", "CCC")
def aniade_w(x):
return "W-" + x
new_list = map(aniade_w, my_list)
print(tuple(new_list))
```
`map` también trabaja con funciones con varios argumentos, lo único que hay que hacer es añadirle un argumento más al `map`. Y esto es aplicable a *n* argumentos. Podría darse el caso en el que alguno de los iterables tenga menores dimensiones que el resto. Si ocurre eso, se aplicará el `map` hasta el iterable con la mínima longitud.
```
circle_areas = [3.56773, 5.57668, 4.00914, 56.24241, 9.01344, 32.00013]
decimales = range(1,7)
print("range no devuleve una lista sino un rango !!!")
print(type(decimales))
print(list(decimales))
# round(numero decimal, cantidad de decimales)
result = map(round, circle_areas, decimales)
print(list(result))
```
<table align="left">
<tr><td width="80"><img src="./img/ejercicio.png" style="width:auto;height:auto"></td>
<td style="text-align:left">
<h3>Trabajando con map</h3>
<ol>
<li>Añádele "W-"a todas las claves del diccionario</li>
<li>Convierte todos los elementos de la tupla en enteros</li>
</ol>
</td></tr>
</table>
```
my_dict = {"a": 1, "b": 2, "c": 3}
my_list = ('1', '5', '4', '6', '8', '11', '3', '12')
print(f'1)')
new_dict_for = {}
for k,v in my_dict.items():
new_dict_for['W-' + k] = v
print(new_dict_for)
print("\nAl iterar sobre un diccionario se itera sobre las claves\nHay que combinar keys y values para crear una tupla de tuplas")
new_dict_map = map(lambda x, y : ('W-' + x, y), my_dict.keys(), my_dict.values())
print(dict(new_dict_map))
print(f'\n2)')
convert_tupla = map(lambda x : int(float(x)) ,my_list)
print(tuple(convert_tupla))
```
## 4. Reduce
La función `reduce` no es *built-in* como tal, sino que está incorporada en el paquete de `functools`. Su nombre ya nos da alguna pista sobre lo que hace, **es una manera de agregar los datos**. Tiene esta sintaxis:
```Python
reduce(funcion, iterable[, initial]))
```
`reduce`, al igual que `map`, tiene dos argumentos. Uno de ellos es el iterable que vayamos a usar, y el otro es la lógica que le queramos aplicar al `reduce`. La función que se le aplica al reduce tiene dos argumentos, que son los dos primeros elementos del iterable. Tiene un tercer argumento que es opcional, y nos permite iniciar la operación con un valor. Lo veremos luego en un ejemplo.
Si te fijas, `map` aplica la operación definida en la función a todos los elementos, devolviendo la misma lista, pero con los elementos transformados, mientras que **`reduce`, agrega todos los datos de la lista**.
```
from functools import reduce
lista = [1,3,5,6,2]
resultado = reduce(lambda x, y : x+y, lista)
print(resultado)
```
`reduce` hay que entendero como si fuese una función recursiva. La función de dentro tiene dos argumentos que son los dos primeros elementos del iterable, y después al resultado de la suma de ambos, se le aplica la misma operación sobre el tercer elemento, y así hasta que acaba el iterable.
```
lista = [1,3,5,6,2]
```
Realmente el `reduce` lleva un tercer argumento llamado `initializer`. Por defecto es `None`, pero si lo cambiamos, cuando llamemos a la función, su primer argumento será ese `initializer`. Por ejemplo, si estamos sumando toda una colección sería como si el primer elemento de la colección fuese el `initializer`.
```
lista_strings = ["Hola ", " me", " llamo", " Ralph"]
resultado = reduce(lambda x, y : x.strip(' ') + ' ' + y.strip(' '), lista_strings, 'Cadena resultado:')
print(resultado)
```
<table align="left">
<tr><td width="80"><img src="./img/ejercicio.png" style="width:auto;height:auto"></td>
<td style="text-align:left">
<h3>Trabajando con reduce</h3>
Utiliza reduce para calcular el producto de todos los elementos de la siguiente tupla
</td></tr>
</table>
```
lista = (2,5,4)
resultado = reduce(lambda x, y : x*y, lista)
print(resultado)
```
## 5. Filter
Con esta función *built-in* podremos **filtrar elementos de un iterable**. `filter` tiene la siguiente sintaxis:
```Python
filter(funcion, iterable)
```
Como ves, funciona muy parecido a map. La diferencia es que ahora la función que se le aplica tiene una salida estilo `True`/`False` **(lo que se conoce como máscara)**. Y con ese `True`/`False` se filtra el iterable, respetando sus posiciones. Por ejemplo
```Python
lista1 = [-1, 10, 23, -5, -10]
```
Si filtras los números positivos, te queda un array del tipo:
```Python
lista_bools = [False, True, True, False, False]
```
Y eso es lo que se le aplica a la lista, conservando únicamente los `True`:
```Python
lista_resultado = [10, 23]
```
A diferencia de `map`, **en `filter` sólo se usa un iterable**. Además, recuerda que en el argumento de la función, no sólo podrás usar `lambda`s, sino que podrás aplicar tus propias funciones. Ahora bien, ten en cuenta que **el output de esas funciones tiene que ser un `True`/`False`**.
Veamos un ejemplo
```
lista = [ 1 , 3, 5, 6, 2]
filtrado = filter(lambda x : x >= 5 ,lista)
print(type(filtrado))
print(list(filtrado))
```
O implementando nuestra propia función
```
lista = [ 1 , 3, 5, 6, 2]
def mas_cinco(x):
if x >= 5:
return True
return False
filtrado = filter(mas_cinco ,lista)
print(type(filtrado))
print(list(filtrado))
```
Como ves, estas son otras formas más rápidas y elegantes de aplicar operaciones sobre colecciones.
<table align="left">
<tr><td width="80"><img src="./img/ejercicio.png" style="width:auto;height:auto"></td>
<td style="text-align:left">
<h3>Trabajando con filter</h3>
Utiliza filter para conseguir quedarte únicamente con los floats de la siguiente tupla.
</td></tr>
</table>
```
mis_nums = (1, 4., 10., 25, 67)
filtrado1 = filter(lambda x : type(x) == float ,mis_nums)
print(list(filtrado1))
filtrado2 = filter(lambda x : isinstance(x, float) ,mis_nums)
print(list(filtrado2))
```
## 6. Timeit
Para el bootcamp, y en general si vas a realizar una analítica descriptiva de datos, no suele ser crítico el rendimiento en tu programa. Imagina que has desarrollado un clasificador de movimientos bancarios tipo *Fintonic*. Estos algoritmos suelen ser muy pesados ya que hay que buscar en muchos strings y hacer varias comprobaciones. Aun así, has conseguido que te clasifique cada movimiento en 0,5 segundos. Que está muy bien. El problema es cuando un cliente tiene 1000 movimientos en una cuenta y tienes que clasificarlos todos aplicando tu clasificador mediante un bucle. El programa se te dispara a 250 segundos -> 4 minutos aprox, que estará el cliente esperando a que tu clasificador acabe... muchísimo. Con programación funcional mejora mucho la cosa ya que no hay que iterar.
Por tanto, **cuando trabajes con muchos datos, ten en mente este tipo de funciones (`map`, `reduce`, `filter`) ya que la mejora en rendimiento es más que considerable.**
```
num_elementos = 100000
lista = list(range(num_elementos))
%%timeit
lista_output = []
for i in lista:
lista_output.append(i + 5)
%%timeit
lista_output = map(lambda x: x + 5, lista)
```
Como ves, pasamos de milisegundos a nanosegundos.
## 7. Programacion funcional en Pandas
La programación funcional resulta muy útil cuando queremos aplicar operaciones a cada elemento de una columna. Para ello utilizamos la función de pandas `apply`.
Imaginemos que tenemos un DataFrame de temperaturas
```
import pandas as pd
weather = pd.DataFrame({"temperatura": [20, 15, 34, 4, 1, 25, 21, 29, 40]})
weather
```
Si quiero calcular una nueva variable que me indique si estoy en verano o invierno, aplicamos una función personalizada mediante `apply`. Para ello primero me defino la función
```
def season(temp):
if temp < 5:
return "Invierno"
elif temp > 30:
return "Verano"
else:
return "Otra"
#Añadimos una columna al DataFrame weather
weather["season"] = weather["temperatura"].apply(season)
weather
```
Es posible también aplicar una función lambda
```
weather["mas temperatura"] = weather["temperatura"].apply(lambda x : x + 5)
weather
#Añadimos una columna al DataFrame weather
weather["mas season"] = weather["temperatura"].apply(lambda x : "Invierno" if x < 5 else ("Verano" if x > 30 else "Otra"))
weather
```
## 8. Resumen
Como habrás podido comprobar en este Notebook, y en lo vimos en recursividad, esta manera de programar es bastante diferente. Ya no entendemos el programa como un conjunto de variables o estados, sino como una serie de `input`/`output`. Lo bueno que tiene **Python es que combina la programación orientada a objetos con la programación funcional**, lo que le otorga una gran potencia.
```
# Funciones lambda
suma_lambda = lambda x, y: x + y
print(suma_lambda(5, 7))
# Funcion map
my_list = [1, 5, 4, 6, 8, 11, 3, 12]
new_list = map(lambda x: x + 2 , my_list)
print(list(new_list))
# Funcion reduce
from functools import reduce
lista = [ 1 , 3, 5, 6, 2]
print(reduce(lambda a,b : a+b, lista))
# Filter
lista = [ 1 , 3, 5, 6, 2]
filtrado = filter(lambda x: x >= 5, lista)
print(list(filtrado))
```
|
github_jupyter
|
lista = [1,2,3,4,5]
suma = 0
for i in lista:
suma += i
suma
#a = a + b a += b
#a = a - b a -= b
#a = a * b a *= b
#a = a / b a /= b
#a = a % b a %= b
lista = [1,2,3]
def suma_fun(lista):
if len(lista) == 0:
return 0
return lista[0] + suma_fun(lista[1:])
suma_fun(lista)
#La ventaja de esta aproximación es que no se usan variables para almacenar los resultados intermedios
def nombre_funcion(argumentos):
cosas de la funcion
return output
lambda argumentos: expresion
# Declaramos funcion
def suma(x, y):
return x + y
# Guardamos en variable
# En Pythontutor se ve como se crea una referencia desde suma_var al objeto suma(x, y) en memoria
suma_var = suma
#Si llamramos a la función con paréntesis se ejecutaría y almacenaría el resultado en una variable
#suma_var = suma(1, 2)
# Vemos el tipo
print(type(suma_var))
# Usamos la funcion
suma_var(1, 2)
lambda x, y : x + y
# Si la asignamos a una variable
suma_lambda = lambda x, y : x + y
suma_lambda(5, 7)
estaciones = ((40.4440297, -3.6956047), (40.4585318, -3.684715))
inicio = lambda x: x[0]
fin = lambda x: x[1]
print(inicio(estaciones))
print(fin(estaciones))
lat = lambda x: x[0]
lon = lambda x: x[1]
print(lat(inicio(estaciones)))
print(lon(inicio(estaciones)))
#Se podrían usar las funciones inicio, fin originales
print(inicio(inicio(estaciones)))
print(fin(inicio(estaciones)))
multi3 = lambda x,y,z : x * y * z
cuadrado = lambda x : x ** x
print(multi3(1,2,3))
print(cuadrado(2))
# 3 ** 2 --> al cuadrado
# 3 ** (1/2) --> raiz cuadrada de 3
# 3 ** 0.5 --> raiz cuadrada de 3
# 4 ** (1/3) --> raiz cúbica de 4
# 4 ** -2 --> 1 / (4 ** 2)
# 4 ** -3 --> 1 / (4 ** 3)
# 4 ** (2/3) --> 4 ** (2 * 1/3) --> raiz cúbica de (4 ** 2)
import math
raiz = lambda x : math.sqrt(x)
raiz(25)
map(funcion, iterable)
my_list = [1,5,4,6,11]
#my_list + 2 NO
new_list = map(lambda x : x + 2, my_list)
print(new_list)
print(type(new_list))
print(list(new_list))
my_list = (True, False, True, True)
new_list = map(lambda x: not x, my_list)
print(list(new_list))
my_list = ("AAA", "BBB", "CCC")
modif_tupla1 = map(lambda x : 'W-' + x, my_list)
print(tuple(modif_tupla1))
modif_tupla2 = map(lambda x : 'W-'.join(x), my_list)
print(tuple(modif_tupla2))
modif_tupla3 = map(lambda x : x.join('W-'), my_list)
print(tuple(modif_tupla3))
my_list = ("AAA", "BBB", "CCC")
my_list = ("AAA", "BBB", "CCC")
def aniade_w(x):
return "W-" + x
new_list = map(aniade_w, my_list)
print(tuple(new_list))
circle_areas = [3.56773, 5.57668, 4.00914, 56.24241, 9.01344, 32.00013]
decimales = range(1,7)
print("range no devuleve una lista sino un rango !!!")
print(type(decimales))
print(list(decimales))
# round(numero decimal, cantidad de decimales)
result = map(round, circle_areas, decimales)
print(list(result))
my_dict = {"a": 1, "b": 2, "c": 3}
my_list = ('1', '5', '4', '6', '8', '11', '3', '12')
print(f'1)')
new_dict_for = {}
for k,v in my_dict.items():
new_dict_for['W-' + k] = v
print(new_dict_for)
print("\nAl iterar sobre un diccionario se itera sobre las claves\nHay que combinar keys y values para crear una tupla de tuplas")
new_dict_map = map(lambda x, y : ('W-' + x, y), my_dict.keys(), my_dict.values())
print(dict(new_dict_map))
print(f'\n2)')
convert_tupla = map(lambda x : int(float(x)) ,my_list)
print(tuple(convert_tupla))
reduce(funcion, iterable[, initial]))
from functools import reduce
lista = [1,3,5,6,2]
resultado = reduce(lambda x, y : x+y, lista)
print(resultado)
lista = [1,3,5,6,2]
lista_strings = ["Hola ", " me", " llamo", " Ralph"]
resultado = reduce(lambda x, y : x.strip(' ') + ' ' + y.strip(' '), lista_strings, 'Cadena resultado:')
print(resultado)
lista = (2,5,4)
resultado = reduce(lambda x, y : x*y, lista)
print(resultado)
filter(funcion, iterable)
lista1 = [-1, 10, 23, -5, -10]
lista_bools = [False, True, True, False, False]
lista_resultado = [10, 23]
lista = [ 1 , 3, 5, 6, 2]
filtrado = filter(lambda x : x >= 5 ,lista)
print(type(filtrado))
print(list(filtrado))
lista = [ 1 , 3, 5, 6, 2]
def mas_cinco(x):
if x >= 5:
return True
return False
filtrado = filter(mas_cinco ,lista)
print(type(filtrado))
print(list(filtrado))
mis_nums = (1, 4., 10., 25, 67)
filtrado1 = filter(lambda x : type(x) == float ,mis_nums)
print(list(filtrado1))
filtrado2 = filter(lambda x : isinstance(x, float) ,mis_nums)
print(list(filtrado2))
num_elementos = 100000
lista = list(range(num_elementos))
%%timeit
lista_output = []
for i in lista:
lista_output.append(i + 5)
%%timeit
lista_output = map(lambda x: x + 5, lista)
import pandas as pd
weather = pd.DataFrame({"temperatura": [20, 15, 34, 4, 1, 25, 21, 29, 40]})
weather
def season(temp):
if temp < 5:
return "Invierno"
elif temp > 30:
return "Verano"
else:
return "Otra"
#Añadimos una columna al DataFrame weather
weather["season"] = weather["temperatura"].apply(season)
weather
weather["mas temperatura"] = weather["temperatura"].apply(lambda x : x + 5)
weather
#Añadimos una columna al DataFrame weather
weather["mas season"] = weather["temperatura"].apply(lambda x : "Invierno" if x < 5 else ("Verano" if x > 30 else "Otra"))
weather
# Funciones lambda
suma_lambda = lambda x, y: x + y
print(suma_lambda(5, 7))
# Funcion map
my_list = [1, 5, 4, 6, 8, 11, 3, 12]
new_list = map(lambda x: x + 2 , my_list)
print(list(new_list))
# Funcion reduce
from functools import reduce
lista = [ 1 , 3, 5, 6, 2]
print(reduce(lambda a,b : a+b, lista))
# Filter
lista = [ 1 , 3, 5, 6, 2]
filtrado = filter(lambda x: x >= 5, lista)
print(list(filtrado))
| 0.146881 | 0.991263 |
# CSCI E7 Introduction to Programming with Python
## Lecture 01 Jupyter Notebook
Fall 2021 (c) Jeff Parker
## How to Run a Jupyter Notebook
Method 01: Use the Anaconda Navigator to launch a notebook
- Launch the Navigator, navigate to the directory with the notebook you wish to run and click on the notebook
Method 02: Use the command line
The command line is discussed in Appendix A: Command Line Crash Course of **Learn Python The Hard Way**
https://learnpythonthehardway.org/book/appendixa.html
At the command line, change directory (cd) to the directory with the notebook you want to run, and type
```
python
jupyter notebook
```
## Check Python Version
We will be using version 3.8 or later.
```
## Run this cell
import sys # Import the library sys (short for system)
print(sys.version) # Print the version
```
You want to see 3.8 or later; Here is what I saw today:
```python
3.8.8 (default, Apr 13 2021, 12:59:45)
[Clang 10.0.0 ]
```
When I run this on a machine that hasn't been updated, I see something like this:
```python
3.5.6 |Anaconda custom (64-bit)| (default, Aug 26 2018, 16:30:03)
[GCC 4.2.1 Compatible Clang 4.0.1 (tags/RELEASE_401/final)]
```
### You may have multiple versions of Python installed.
### Your PATH variable determines which one you see first, or if you see one at all.
## How to check your Path
The PATH variable is discussed in Appendix 1 of **Python The Hardway**
https://learnpythonthehardway.org/book/appendix-a-cli/ex2.html
### *We use ! to send a line to the Operating System (OS)*
```
## Look at the path on a Windows System
! PATH
## Look at the path on a Unix System
! echo $PATH
```
## If you path does not include the directory where python is installed,
reboot the system and check again. If the path has not changed, you will need to augment your path. Check your system's documentation.
### If you already have an Anaconda distribution, you can update it at the command line
```python
conda update conda
conda update anaconda
conda update python
```
## *Stop and think: Do you have Python 3.8 or later?*
Run the first cell on your machine to see
If not, plan to upgrade your system. I hope to be on 3.9 this Fall.
# First steps in Python
## We can print a 'text string'
```
print('Hello, World!')
```
## We can create variables of various types
```
greeting = "Hola!"
n = 17
pi = 3.141592653589793
print(greeting)
print(n)
print(pi)
```
## What happens when we reassign a variable?
Try to predict what will happen in each cell
You won't always be right, but having skin in the game helps you learn.
```
message = 'And now for something'
message = "completely different"
print(message)
```
## Initialize two variables
```
a = 'hot'
b = 'cold'
print(a,b)
```
## Now exchange their values
Predict what will be printed
```
a = b
print(a, b)
b = a
print(a, b)
```
### *Can you explain what happened?*
## Proper way to swap two elements
```
a = 'hot'
b = 'cold'
print(a, b)
## Introduce a third variable
c = b
b = a
a = c
print(a, b)
```
### *We will learn a more Pythonic way to exchange two values*
## Variable Names in Python
We discuss picking good variable names in Modules/Resources/Documenting Your Work
- A variable name must start with a letter or the underscore character _.
- A variable name cannot start with a number.
- A variable name can only contain letters, digits and underscores (A-z, 0-9, and _ )
## Why are the following variable names invalid?
```
76trombones = 'big parade'
```
### Learn to inspect error statements: what do they tell us?
```python
File "<ipython-input-12-ee59a172c534>", line 1
76trombones = 'big parade'
^
SyntaxError: invalid syntax
```
### This is a Syntax Error
Digits are legal, but they cannot be the first character of a variable name.
```
trombones76 = 'big parade'
print(trombones76)
```
## What is wrong with these?
```
more@ = 1000000
class = 'Advanced Zymurgy'
```
### "Beware of any variable that appears in green." - Joe Pallin
```
import keyword
## Print the list of keywords
print(keyword.kwlist)
## Print the tenth keyword
print(keyword.kwlist[9])
```
## Comments help reader follow your thinking, or confuse them.
## *The choice is yours*
```
a = 10 # The '#' sign starts a comment
b = 3 # The number of faces of Eve in the 1957 feature film
```
## Python can perform aritmetic
```
a = 10
b = 3
print('a + b = ', a + b) # Add
print('a * b = ', a * b) # Multiply
print('a / b = ', a / b) # Division
print('a // b = ', a // b) # Integer division
print('a % b = ', a % b) # Remainder
print('a ** b = ', a ** b) # Exponentiation
```
## We can create (very) big numbers
```
a = 123
b = 456
print(a ** b)
```
### *Most computer languages would not support this*
## Stop and Think
Which are valid variable names?
```python
+four+
-score-
_seven_
```
Are the variables names 'roger' and 'Roger' the same or different?
Prove you are right with short program fragments in the cell below
```
print('roger'=='Roger')
```
## *To create new cells to play with, use '+' box in notebook header*
# Python strings
A string can hold a sequence of characters.
In Python 3, strings can hold Unicode.
```
a = 'one'
print(a)
b = 'two'
print(b)
c = "\U0001f638"
print(c)
```
## We can add strings and we can multiply a string by an integer
Predict what each cell will produce
```
print(a + b)
print(a*2)
print(c*12)
```
## Two ways to define strings: single or double quotes
```
a = 'one'
b = "two"
s = a + b
print(s)
```
## Having two ways allows us to embed quotes
```
quote = 'He said "Bravo!"'
print(quote)
quote = "I don't know."
print(quote)
```
## What does this do?
```
print('Hello, World!")
```
## *What kind of error?*
## Fix it...
```
print("Hello, World!")
```
## String Indexing
Allows us to access a single character
```
s = 'onetwo'
print(s)
print(s[1] + s[0])
```
## Assignment
```
s[0] = 't'
print(s)
```
## *This is not a syntax error: the syntax works on a list*
```python
s[0] = 't'
```
Python cannot tell if this is an error until it runs it and sees what variable s holds
```
# Create a Python list and store reference in s
s = ['a', 'b', 'c']
s[0] = 't' # We can assign a value into a List object
print(s)
s = 'abc'
s[0] = 't' # Syntax is the same
print(s)
```
## This is a run-time error
## *Strings are immutable* - that is, you can't change them
### *Python cannot tell it is an error until we run it*
## Strings have a Length
```
s = 'pepper'
print(s, len(s))
```
## What does this print?
```
print(s[6])
```
## Another Run Time error
We don't know until run time how long string is
## How to access the last item
```
print(s, len(s))
print(s[5])
print(s[6 - 1])
```
## Python provides syntax to access the last item
You don't need to know the length of the string to use this form
```
print(s[-1])
```
## We can use other negative indices
```
print(s[-3])
```
# Different types of Whitespace
### https://www.petefreitag.com/cheatsheets/ascii-codes/
```
print("->", ' ', "<-") # Space
print("->", '\t', "<-") # Tab
print("->", '\n', "<-") # Newline
print("->", '\r', "<-") # Carriage Return
```
https://www.youtube.com/watch?v=ed5NZI0T5ZQ
## Each type of whitespace in practice
```
print("Hello, Sam") # Space
print("Hello,\tSam") # Tab
print("Hello,\nSam") # Newline
print("Hello,\rSam") # Carriage Return
```
# String Methods
### We have used the function len()
### Let's look at *methods* that detect upper and lower case
### Syntax is
```python
object.method_name ( parameters )
```
## Naming Convention for methods that return a Boolean:
#### isAttribute()
```python
isalpha(), islower(), isupper()
```
```
s = 'onetwo'
print(s.islower())
s = 'OneTwo'
print(s.islower())
s = 'OneTwo'
print(s.isUpper())
s = 'OneTwo'
print(s.isupper())
s = "SAD!"
print(s.isupper())
s = 'groovy'
print(s.iscopacetic(s))
```
## Convert to Lower Case
### Convention for methods returning variant of an object: 'verb'
```
s = "SAD!"
s = s.lower()
print(s)
```
## lower() vs islower()
### islower() is a question - is you lower?
### lower() is an imperative verb - "Convert to lower case!"
# Searching for a substring with method find()
Let's look for the letter 'e'
```
s = 'onetwo'
print(s.find('e'))
```
## Highlight position of letter
```
## Find 't'
s = 'onetwo'
print(s)
print(' '*s.find('t') + '^')
```
```python
print(' '*s.find('t') + '^')
```
### Break this down
Find the position of t
```python
s.find('t')
```
Produce that many spaces
```python
' '*s.find('t')
```
Add a '^' as a marker in the final spot
```python
' '*s.find('t') + '^'
```
Print the whole mishpocha
```python
print(' '*s.find('t') + '^')
```
```
## Find 'x'
s = "Quick Red Fox"
print(s)
print(' '*s.find('x') + '^')
## Find 'z'
print(s)
print(' '*s.find('z') + '^')
```
## OK. That's didn't work.
```
s.find('z')
```
## *find() returns -1 when it doesn't find the substring*
## Let's look at the Documentation
To become self sufficient in any computer language, you will need to learn to read the documentation.
This isn't easy at first
Search for find() here:
https://docs.python.org/3/library/stdtypes.html
```python
str.find(sub[, start[, end]])
Return the lowest index in the string where substring sub is found within the slice s[start:end]. Optional arguments start and end are interpreted as in slice notation.
Return -1 if sub is not found.
```
Let's break this down, Start with the first line, which tells you how to call find()
```python
str.find(sub[, start[, end]])
```
Method find() takes one required parameter, sub, and two optional parameters, start and end.
Legal calls are:
```python
str.find('x') # Find x in the string
str.find('x', 10) # Find x in the string starting at 10
str.find('x', 10, 20) # Find x in the string from 10 to 19
```
And notice the final line:
```python
Return -1 if sub is not found.
```
```
## We can also check documentation right in notebook
s.find?
## Or we can call help()
help(s.find)
## Note that we can't lookup a string method without a string instance
help(find)
```
## *We will soon see where this information is stored*
## String Slice
Often we want a substing. Python defines "Slice notation" for this
```
s = 'onetwo'
print(s)
print(s[0:2])
print(s[4:6])
```

I am displaying Slice.jpg, a file in the subdirectory img.
To view this image on your system, you will need to download the jpg and place it in a subdirectory called img.
Alas, this is how we share figures in notebooks.
```
print(s[:2]) # Up to, but not including, s[2]
print(s[4:]) # s[4] and beyond
print(s[:]) # Everything
print(s[::2]) # Skip by 2
```
## Slice Conventions
While the conventions used to define a slice may seem odd, they are quite logical.
Here is Edsger Dijkstra discussing the convention, years before Python
https://www.cs.utexas.edu/users/EWD/ewd08xx/EWD831.PDF
## Slice is Forgiving
```
s = 'Short String'
len(s)
s[12]
s[10:20]
s[100:200]
```
## *Slice is Forgiving*
## Stop and Think
1) What do these slices produce?
```python
s = 'onetwo'
print(s[::3]) # ???
print(s[3::2]) # ???
```
2) Investigate the Documentation: What does rfind() do in general?
```python
print(s.rfind('pattern'))
```
See https://docs.python.org/3/library/stdtypes.html or use help() or '?'
3) Use the first optional parameter to string method find() and write an expression that
finds the first copy of a symbol in the back half of a string
```python
text = 'xx marks the x spot x'
substring = 'x'
```
Your expression should yield 13, not 0, 1, or 20
# Three types of errors
```
## Syntax error - will not run
s = 'onetwo"
## Runtime error - runs, but produces an error
s = 'onetwo'
s[1] = 't'
## Semantic Error - runs to completion, but produces the wrong output
a = 'one '
c = 'two '
b = 'three '
s = a + b + c
print(s)
```
## Stop and think
What type of error is this?
```python
print(1/0)
```
What type of error is this?
```python
s = 'cheese'
print(s[100])
```
# Python Libraries - https://pymotw.com/3/
## The Batteries included. For handing dates:
```
print(datetime.date.today()) # What day is it today?
```
## *What kind of error is this?*
```python
------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-1-389e1c27fe18> in <module>
----> 1 print(datetime.date.today()) # What day is it today?
NameError: name 'datetime' is not defined
```
## datetime is not part of core Python
## We need to import the library
Let's explain the steps.
```
# Import the datetime library
import datetime
print(datetime.date.today()) # What day is it today?
print(datetime.date(2021, 9, 4))
```
My datetime library is found in the Python file datetime.py
### /Users/jparker/opt/anaconda3/lib/python3.8/datetime.py
Yours will be in a simlar spot relative to your anaconda3 directory.
You can take a look at the file now: you will be make some sense of it soon
```
! head -n 10 /Users/jparker/opt/anaconda3/lib/python3.8/datetime.py
```
## We can access the attributes of a date
```
import datetime
print(datetime.date.today().year)
print(datetime.date.today().month)
print(datetime.date.today().day)
```
## Stop and Think
datetime.py defines a constant MAXYEAR. What is the value assigned to MAXYEAR?
# For next week
Download the PyCharm IDE and play with it.
www.jetbrains.com/pycharm/download/
I will show you how to create a program in PyCharm next week.
In two weeks we will look at the PyCharm Debugger.
# Wow, That's Fantastic!
### *A regular feature: a look beyond what we know now.*
I won't try to explain everything in the WTF section
```
import this
```
## Stop and Think
Find the library this.py and take a peek. It is short: under 30 lines, but it isn't clear what it does. In fact, it is deliberately confusing: we say that the code is obfuscated.
```python
Ornhgvshy vf orggre guna htyl.
```
We'll be able to decode this in a month.
# Questions?
## Ask on Piazza
How is the pace? To fast? Too slow?
|
github_jupyter
|
python
jupyter notebook
## Run this cell
import sys # Import the library sys (short for system)
print(sys.version) # Print the version
3.8.8 (default, Apr 13 2021, 12:59:45)
[Clang 10.0.0 ]
3.5.6 |Anaconda custom (64-bit)| (default, Aug 26 2018, 16:30:03)
[GCC 4.2.1 Compatible Clang 4.0.1 (tags/RELEASE_401/final)]
## Look at the path on a Windows System
! PATH
## Look at the path on a Unix System
! echo $PATH
conda update conda
conda update anaconda
conda update python
print('Hello, World!')
greeting = "Hola!"
n = 17
pi = 3.141592653589793
print(greeting)
print(n)
print(pi)
message = 'And now for something'
message = "completely different"
print(message)
a = 'hot'
b = 'cold'
print(a,b)
a = b
print(a, b)
b = a
print(a, b)
a = 'hot'
b = 'cold'
print(a, b)
## Introduce a third variable
c = b
b = a
a = c
print(a, b)
76trombones = 'big parade'
File "<ipython-input-12-ee59a172c534>", line 1
76trombones = 'big parade'
^
SyntaxError: invalid syntax
trombones76 = 'big parade'
print(trombones76)
more@ = 1000000
class = 'Advanced Zymurgy'
import keyword
## Print the list of keywords
print(keyword.kwlist)
## Print the tenth keyword
print(keyword.kwlist[9])
a = 10 # The '#' sign starts a comment
b = 3 # The number of faces of Eve in the 1957 feature film
a = 10
b = 3
print('a + b = ', a + b) # Add
print('a * b = ', a * b) # Multiply
print('a / b = ', a / b) # Division
print('a // b = ', a // b) # Integer division
print('a % b = ', a % b) # Remainder
print('a ** b = ', a ** b) # Exponentiation
a = 123
b = 456
print(a ** b)
+four+
-score-
_seven_
print('roger'=='Roger')
a = 'one'
print(a)
b = 'two'
print(b)
c = "\U0001f638"
print(c)
print(a + b)
print(a*2)
print(c*12)
a = 'one'
b = "two"
s = a + b
print(s)
quote = 'He said "Bravo!"'
print(quote)
quote = "I don't know."
print(quote)
print('Hello, World!")
print("Hello, World!")
s = 'onetwo'
print(s)
print(s[1] + s[0])
s[0] = 't'
print(s)
s[0] = 't'
# Create a Python list and store reference in s
s = ['a', 'b', 'c']
s[0] = 't' # We can assign a value into a List object
print(s)
s = 'abc'
s[0] = 't' # Syntax is the same
print(s)
s = 'pepper'
print(s, len(s))
print(s[6])
print(s, len(s))
print(s[5])
print(s[6 - 1])
print(s[-1])
print(s[-3])
print("->", ' ', "<-") # Space
print("->", '\t', "<-") # Tab
print("->", '\n', "<-") # Newline
print("->", '\r', "<-") # Carriage Return
print("Hello, Sam") # Space
print("Hello,\tSam") # Tab
print("Hello,\nSam") # Newline
print("Hello,\rSam") # Carriage Return
object.method_name ( parameters )
isalpha(), islower(), isupper()
s = 'onetwo'
print(s.islower())
s = 'OneTwo'
print(s.islower())
s = 'OneTwo'
print(s.isUpper())
s = 'OneTwo'
print(s.isupper())
s = "SAD!"
print(s.isupper())
s = 'groovy'
print(s.iscopacetic(s))
s = "SAD!"
s = s.lower()
print(s)
s = 'onetwo'
print(s.find('e'))
## Find 't'
s = 'onetwo'
print(s)
print(' '*s.find('t') + '^')
print(' '*s.find('t') + '^')
s.find('t')
' '*s.find('t')
' '*s.find('t') + '^'
print(' '*s.find('t') + '^')
## Find 'x'
s = "Quick Red Fox"
print(s)
print(' '*s.find('x') + '^')
## Find 'z'
print(s)
print(' '*s.find('z') + '^')
s.find('z')
str.find(sub[, start[, end]])
Return the lowest index in the string where substring sub is found within the slice s[start:end]. Optional arguments start and end are interpreted as in slice notation.
Return -1 if sub is not found.
str.find(sub[, start[, end]])
str.find('x') # Find x in the string
str.find('x', 10) # Find x in the string starting at 10
str.find('x', 10, 20) # Find x in the string from 10 to 19
Return -1 if sub is not found.
## We can also check documentation right in notebook
s.find?
## Or we can call help()
help(s.find)
## Note that we can't lookup a string method without a string instance
help(find)
s = 'onetwo'
print(s)
print(s[0:2])
print(s[4:6])
print(s[:2]) # Up to, but not including, s[2]
print(s[4:]) # s[4] and beyond
print(s[:]) # Everything
print(s[::2]) # Skip by 2
s = 'Short String'
len(s)
s[12]
s[10:20]
s[100:200]
s = 'onetwo'
print(s[::3]) # ???
print(s[3::2]) # ???
See https://docs.python.org/3/library/stdtypes.html or use help() or '?'
3) Use the first optional parameter to string method find() and write an expression that
finds the first copy of a symbol in the back half of a string
Your expression should yield 13, not 0, 1, or 20
# Three types of errors
## Stop and think
What type of error is this?
What type of error is this?
# Python Libraries - https://pymotw.com/3/
## The Batteries included. For handing dates:
## *What kind of error is this?*
## datetime is not part of core Python
## We need to import the library
Let's explain the steps.
My datetime library is found in the Python file datetime.py
### /Users/jparker/opt/anaconda3/lib/python3.8/datetime.py
Yours will be in a simlar spot relative to your anaconda3 directory.
You can take a look at the file now: you will be make some sense of it soon
## We can access the attributes of a date
## Stop and Think
datetime.py defines a constant MAXYEAR. What is the value assigned to MAXYEAR?
# For next week
Download the PyCharm IDE and play with it.
www.jetbrains.com/pycharm/download/
I will show you how to create a program in PyCharm next week.
In two weeks we will look at the PyCharm Debugger.
# Wow, That's Fantastic!
### *A regular feature: a look beyond what we know now.*
I won't try to explain everything in the WTF section
## Stop and Think
Find the library this.py and take a peek. It is short: under 30 lines, but it isn't clear what it does. In fact, it is deliberately confusing: we say that the code is obfuscated.
| 0.331012 | 0.921499 |
# Logging
(back to the overview [offline](../Main.ipynb),[online](https://nbviewer.jupyter.org/github/QCoDeS/Qcodes/tree/master/docs/examples/Main.ipynb))
[read on nbviewer](https://nbviewer.jupyter.org/github/QCoDeS/Qcodes/tree/master/docs/examples/logging/logging_example.ipynb)
## TL;DR
* There is a QCoDeS logging module: `qcodes.utils.logger`
* Call `logger.start_all_logging` at the start of every script/session to make sure all log messages get stored to the `.qcodes/logs` folder in your home directory.
* For debugging purposes you can log messages of an individual instrument (and see the VISA dialog).
* You can obtain all logging messages in a `pandas.DataFrame` for further analysis.
## Contents
- [Introduction](#Introduction)
- [Set up logging in QCoDeS](#Set-up-logging-in-QCoDeS)
- [QCoDeS default handlers](#QCoDeS-default-handlers)
- [IPython command history](#IPython-command-history)
- [Temporarily elevating the logging level](#Temporarily-elevating-the-logging-level)
- [Filtering log messages by instrument](#Filtering-log-messages-by-instrument)
- [Capturing Pandas.DataFrame](#Capturing-Pandas.DataFrame)
## Introduction
Python offers an excellent logging framework that is widely used in QCoDeS. As a user you might be interested in reading the log messages that are generated by QCoDeS for debugging and also profiling purposes.
All log records(=messages+meta data) are created using a python `logging.logger` object. In QCoDeS there is a logger for every module with the same name as the module itself, i.e. you can use `logging.getLogger('qcodes.instrument.base')` for getting the logger of the QCoDeS `Instrument`. From the dots in the names of the loggers a hierarchy is define, at the top of which is the so called *root logger* that catches all messages.
The log records created in a logger are processed by the *handlers* that have been attached to this specific *logger*.
The handlers can for example be used to output the log messages into different locations, like the console or a log file.
Every logger, handler and log record has an associated level. The default levels are: `CRITICAL` `ERROR`, `WARNING`, `INFO`, `DEBUG`. The levels determine how messages are passed: A logger passes only records that exceeds its minimal passing level to its handlers and the handlers in turn only output those messages that exceed their minimal passing level.
For a more detailed description of Python logging refer to the [official manual](https://docs.python.org/3.6/library/logging.html#module-logging) (This is all well summed up [in this chart](https://docs.python.org/3.6/howto/logging.html#logging-flow))
## Instrument communication loggers
Not all the used loggers in QCoDeS follow the previously presented rule of naming the logger after the module. For instruments there are the following loggers:
- **qcodes.instrument.base.com**:
This logger logs all the communication of the `Instrument` and its descendants with the actual physical instruments e.g. the messages generated by the `write` and `query` calls.
- **qcodes.instrument.base.com.visa**:
This is a sublogger that logs all the communication related messages of the `VisaInstrument` and its descendants.
## Set up logging in QCoDeS
At the beginning of every experiment script file you should include the following lines:
```
from qcodes.logger import start_all_logging
start_all_logging()
```
The call to `start_all_logging` does two things:
1. Create handlers to output logging messages from the root logger to the console and to a log file.
2. Enable logging of the ipython commands into a separate log file.
### QCoDeS default handlers
The effect of the console handler can be seen in the two printed lines with a red background below the previous code cell. Every line corresponds to a log record. The fields of the records are separated by `¦` and have the following meaning:
0. time stamp
1. logger name, here the module name
2. record log level
3. name of the function that created the log message
4. line at which the message has been issued
5. actual log message
The same format is used for the file handler. By default QCoDeS logs to the file `<user directory>/.qcodes/logs/qcodes.log`. To avoid endlessly long files, the files roll over at midnight and get the date appended to their name where `qcodes.log` without date always gives you the log messages of the same day.
To configure the levels you want to log/handle, you need to edit the `qcodesrc.json` file in you home directory. The default values are:
```
"logger":{
"console_level": "WARNING",
"file_level": "INFO",
"logger_levels":{
"pyvisa": "INFO"
}
```
While `console_level` and `file_level` describe the levels of the two default handlers described previously, `logger_levels` is a dictionary that can be used to limit the messages passed on by module level loggers. This means with these defaults, the pyvisa module will not log messages on a `DEBUG` level. Therefore setting the `console_level` to `DEBUG` will not show the pyvisa debug messages (you certainly don't want to see them as they log every single character that is passed to an instrument with an individual message). On the other hand setting the console level to warning will still suppress pyvisa info messages.
### IPython command history
The output above that follows these logging messages comes from IPython. It tells us that all issued IPython commands will be logged to a file. The file lives in the same log directory as the python logs and is called `command_history.log`. It will not roll over.
To change the command history logging directory you will need to call `start_command_history_logger` with the new path as an argument.
## Temporarily elevating the logging level
Sometimes you might wish to catch e.g. all debug messages for a few lines of code. You can do this simply by:
```
import logging
import qcodes.logger as logger
log = logging.getLogger('example_logger')
log.debug('This message will not be visible as the logging level is set to `DEBUG`')
with logger.console_level(logging.DEBUG):
log.debug('This message is visible as the logging level is temporarily elevated to `DEBUG`')
log.debug('The level is back to what it used to be')
```
For other handlers than the console handler you can do the same thing using the `handler_level` context manager.
## Filtering log messages by instrument
A very common use case for logging in qcodes is to analyze the communication with a VISA instrument. For this purpose the logger module provides a context manager to filter the logging messages by instrument.
Generally one could of course simply attach a handler to the logger of `qcodes.instrument_drivers.Vendor.Type` but this would not show the messages that are generated by the visa communication in `qcodes.instrument.visa`. Additionally with the approach implemented here one can not only filter messages for a given type of instrument but also of a specific instance.
To demonstrate this consider the following mock up of the AMI430 Magnet controller that consists of individual visa instruments for each axis, here with the names `x`, `y` and `z`:
```
from qcodes.instrument.ip_to_visa import AMI430_VISA
from qcodes.instrument_drivers.american_magnetics.AMI430 import AMI430_3D, AMI430Warning
import qcodes.instrument.sims as sims
visalib = sims.__file__.replace('__init__.py', 'AMI430.yaml@sim')
mag_x = AMI430_VISA('x', address='GPIB::1::INSTR', visalib=visalib,
terminator='\n', port=1)
mag_y = AMI430_VISA('y', address='GPIB::2::INSTR', visalib=visalib,
terminator='\n', port=1)
mag_z = AMI430_VISA('z', address='GPIB::3::INSTR', visalib=visalib,
terminator='\n', port=1)
import numpy as np
field_limit = [
lambda x, y, z: x == 0 and y == 0 and z < 3,
lambda x, y, z: np.linalg.norm([x, y, z]) < 2
]
driver = AMI430_3D("AMI430-3D", mag_x, mag_y, mag_z, field_limit)
```
In the above messages you can see the prefix `[<instrument_name>(<instrument_type>)]`. To analyze the visa communication one can use `filter_instrument`:
```
driver.cartesian((0, 0, 0))
with logger.console_level('DEBUG'):
with logger.filter_instrument(mag_x):
driver.cartesian((0, 0, 1))
```
The output on the console shows as expected only messages from the `x` instrument. For multiple instruments pass a sequence of instruments to `filter_instrument`:
```
driver.cartesian((0, 0, 0))
with logger.console_level('DEBUG'):
with logger.filter_instrument((mag_x, mag_y)):
driver.cartesian((0, 0, 1))
```
## Capturing Pandas.DataFrame
To process the logs, especially with the timestamps the [pandas module](https://pandas.pydata.org/) is highly suited. With `logger.log_to_dataframe` or `logger.logfile_to_dataframe` you can convert a log(file) to a pandas `DataFrame`. See this ([online](https://nbviewer.jupyter.org/github/QCoDeS/Qcodes/tree/master/docs/examples/logging/logfile_parsing.ipynb), [offline](logfile_parsing.ipynb)) notebook for an example.
You can also use a context manager to capture the logs directly into a `DataFrame`
```
from qcodes.logger.log_analysis import capture_dataframe
with logger.console_level(logging.WARN):
driver.cartesian((0, 0, 0))
with capture_dataframe(level='DEBUG') as (handler, get_dataframe):
driver.cartesian((0, 0, 1))
df = get_dataframe()
driver.cartesian((0, 0, 2))
df2 = get_dataframe() # this is the cummulative log
df
df2
```
You can of course combine the context managers like this:
```
with logger.console_level(logging.WARN):
driver.cartesian((0, 0, 0))
with capture_dataframe(level='DEBUG') as (handler, get_dataframe):
with logger.filter_instrument(mag_x, handler=handler):
driver.cartesian((0, 0, 1))
df = get_dataframe()
df
```
For an analysis of the timestamps please also refer to the log analysis example notebook ([online](https://nbviewer.jupyter.org/github/QCoDeS/Qcodes/tree/master/docs/examples/logging/logfile_parsing.ipynb), [offline](logfile_parsing.ipynb)).
|
github_jupyter
|
from qcodes.logger import start_all_logging
start_all_logging()
"logger":{
"console_level": "WARNING",
"file_level": "INFO",
"logger_levels":{
"pyvisa": "INFO"
}
import logging
import qcodes.logger as logger
log = logging.getLogger('example_logger')
log.debug('This message will not be visible as the logging level is set to `DEBUG`')
with logger.console_level(logging.DEBUG):
log.debug('This message is visible as the logging level is temporarily elevated to `DEBUG`')
log.debug('The level is back to what it used to be')
from qcodes.instrument.ip_to_visa import AMI430_VISA
from qcodes.instrument_drivers.american_magnetics.AMI430 import AMI430_3D, AMI430Warning
import qcodes.instrument.sims as sims
visalib = sims.__file__.replace('__init__.py', 'AMI430.yaml@sim')
mag_x = AMI430_VISA('x', address='GPIB::1::INSTR', visalib=visalib,
terminator='\n', port=1)
mag_y = AMI430_VISA('y', address='GPIB::2::INSTR', visalib=visalib,
terminator='\n', port=1)
mag_z = AMI430_VISA('z', address='GPIB::3::INSTR', visalib=visalib,
terminator='\n', port=1)
import numpy as np
field_limit = [
lambda x, y, z: x == 0 and y == 0 and z < 3,
lambda x, y, z: np.linalg.norm([x, y, z]) < 2
]
driver = AMI430_3D("AMI430-3D", mag_x, mag_y, mag_z, field_limit)
driver.cartesian((0, 0, 0))
with logger.console_level('DEBUG'):
with logger.filter_instrument(mag_x):
driver.cartesian((0, 0, 1))
driver.cartesian((0, 0, 0))
with logger.console_level('DEBUG'):
with logger.filter_instrument((mag_x, mag_y)):
driver.cartesian((0, 0, 1))
from qcodes.logger.log_analysis import capture_dataframe
with logger.console_level(logging.WARN):
driver.cartesian((0, 0, 0))
with capture_dataframe(level='DEBUG') as (handler, get_dataframe):
driver.cartesian((0, 0, 1))
df = get_dataframe()
driver.cartesian((0, 0, 2))
df2 = get_dataframe() # this is the cummulative log
df
df2
with logger.console_level(logging.WARN):
driver.cartesian((0, 0, 0))
with capture_dataframe(level='DEBUG') as (handler, get_dataframe):
with logger.filter_instrument(mag_x, handler=handler):
driver.cartesian((0, 0, 1))
df = get_dataframe()
df
| 0.361728 | 0.881053 |
# Solving combinatorial optimization problems using QAOA
This example based on [this Qiskit tutorial notebook](https://qiskit.org/textbook/ch-applications/qaoa.html) runs the same general example of the Quantum Approximate Optimization Algorithm (QAOA) in PyQrack.
```
import networkx as nx
import matplotlib.pyplot as plt
import networkx as nx
G = nx.Graph()
G.add_nodes_from([0, 1, 2, 3])
G.add_edges_from([(0, 1), (1, 2), (2, 3), (3, 0)])
nx.draw(G, with_labels=True, alpha=0.8, node_size=500)
from collections import Counter
from pyqrack import QrackSimulator, Pauli
def maxcut_obj(x, G):
"""
Given a (bitstring-equivalent) integer as a solution,
this function returns the number of edges shared
between the two partitions of the graph.
Args:
x: str
solution bitstring
G: networkx graph
Returns:
obj: float
Objective
"""
obj = 0
for i, j in G.edges():
if ((x >> i) & 1) != ((x >> j) & 1):
obj -= 1
return obj
def compute_expectation(counts, G):
"""
Computes expectation value based on measurement results
Args:
counts: dict
key as integer, val as count
G: networkx graph
Returns:
avg: float
expectation value
"""
avg = 0
sum_count = 0
for bitstring, count in counts.items():
obj = maxcut_obj(bitstring, G)
avg += obj * count
sum_count += count
return avg/sum_count
def run_qaoa_circ(G, theta, shots):
"""
Creates a parametrized qaoa circuit
Args:
G: networkx graph
theta: list
unitary parameters
Returns:
collections.Counter of measurement results
"""
nqubits = len(G.nodes())
p = len(theta)//2 # number of alternating unitaries
qc = QrackSimulator(nqubits)
beta = theta[:p]
gamma = theta[p:]
# initial_state
for i in range(0, nqubits):
qc.h(i)
for irep in range(0, p):
# problem unitary
for pair in list(G.edges()):
qc.mcx([pair[0]], pair[1])
qc.r(Pauli.PauliZ, 2 * gamma[irep], pair[1])
qc.mcx([pair[0]], pair[1])
# mixer unitary
for i in range(0, nqubits):
qc.r(Pauli.PauliX, 2 * beta[irep], i)
return Counter(qc.measure_shots(range(0, nqubits), shots))
# Finally we write a function that executes the circuit on the chosen backend
def get_expectation(G, p, shots=512):
"""
Runs parametrized circuit
Args:
G: networkx graph
p: int,
Number of repetitions of unitaries
"""
def execute_circ(theta):
counts = run_qaoa_circ(G, theta, shots)
return compute_expectation(counts, G)
return execute_circ
from scipy.optimize import minimize
expectation = get_expectation(G, p=1)
res = minimize(expectation,
[1.0, 1.0],
method='COBYLA')
res
counts = run_qaoa_circ(G, res.x, 512)
counts.most_common()
```
|
github_jupyter
|
import networkx as nx
import matplotlib.pyplot as plt
import networkx as nx
G = nx.Graph()
G.add_nodes_from([0, 1, 2, 3])
G.add_edges_from([(0, 1), (1, 2), (2, 3), (3, 0)])
nx.draw(G, with_labels=True, alpha=0.8, node_size=500)
from collections import Counter
from pyqrack import QrackSimulator, Pauli
def maxcut_obj(x, G):
"""
Given a (bitstring-equivalent) integer as a solution,
this function returns the number of edges shared
between the two partitions of the graph.
Args:
x: str
solution bitstring
G: networkx graph
Returns:
obj: float
Objective
"""
obj = 0
for i, j in G.edges():
if ((x >> i) & 1) != ((x >> j) & 1):
obj -= 1
return obj
def compute_expectation(counts, G):
"""
Computes expectation value based on measurement results
Args:
counts: dict
key as integer, val as count
G: networkx graph
Returns:
avg: float
expectation value
"""
avg = 0
sum_count = 0
for bitstring, count in counts.items():
obj = maxcut_obj(bitstring, G)
avg += obj * count
sum_count += count
return avg/sum_count
def run_qaoa_circ(G, theta, shots):
"""
Creates a parametrized qaoa circuit
Args:
G: networkx graph
theta: list
unitary parameters
Returns:
collections.Counter of measurement results
"""
nqubits = len(G.nodes())
p = len(theta)//2 # number of alternating unitaries
qc = QrackSimulator(nqubits)
beta = theta[:p]
gamma = theta[p:]
# initial_state
for i in range(0, nqubits):
qc.h(i)
for irep in range(0, p):
# problem unitary
for pair in list(G.edges()):
qc.mcx([pair[0]], pair[1])
qc.r(Pauli.PauliZ, 2 * gamma[irep], pair[1])
qc.mcx([pair[0]], pair[1])
# mixer unitary
for i in range(0, nqubits):
qc.r(Pauli.PauliX, 2 * beta[irep], i)
return Counter(qc.measure_shots(range(0, nqubits), shots))
# Finally we write a function that executes the circuit on the chosen backend
def get_expectation(G, p, shots=512):
"""
Runs parametrized circuit
Args:
G: networkx graph
p: int,
Number of repetitions of unitaries
"""
def execute_circ(theta):
counts = run_qaoa_circ(G, theta, shots)
return compute_expectation(counts, G)
return execute_circ
from scipy.optimize import minimize
expectation = get_expectation(G, p=1)
res = minimize(expectation,
[1.0, 1.0],
method='COBYLA')
res
counts = run_qaoa_circ(G, res.x, 512)
counts.most_common()
| 0.863679 | 0.9852 |
# CNNs
In this notebook you will learn how to build Convolutional Neural Networks (CNNs) for image processing.
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/ageron/tf2_course/blob/master/05_cnns.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
</table>
## Imports
```
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import sklearn
import sys
import tensorflow as tf
from tensorflow import keras
import time
print("python", sys.version)
for module in mpl, np, pd, sklearn, tf, keras:
print(module.__name__, module.__version__)
assert sys.version_info >= (3, 5) # Python ≥3.5 required
assert tf.__version__ >= "2.0" # TensorFlow ≥2.0 required
```

## Exercise 1 – Simple CNN
### 1.1)
Load CIFAR10 using `keras.datasets.cifar10.load_data()`, and split it into a training set (45,000 images), a validation set (5,000 images) and a test set (10,000 images). Make sure the pixel values range from 0 to 1. Visualize a few images using `plt.imshow()`.
```
classes = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
```
### 1.2)
Build and train a baseline model with a few dense layers, and plot the learning curves. Use the model's `summary()` method to count the number of parameters in this model.
**Tip**:
* Recall that to plot the learning curves, you can simply create a Pandas `DataFrame` with the `history.history` dict, then call its `plot()` method.
### 1.3)
Build and train a Convolutional Neural Network using a "classical" architecture: N * (Conv2D → Conv2D → Pool2D) → Flatten → Dense → Dense. Before you print the `summary()`, try to manually calculate the number of parameters in your model's architecture, as well as the shape of the inputs and outputs of each layer. Next, plot the learning curves and compare the performance with the previous model.
### 1.4)
Looking at the learning curves, you can see that the model is overfitting. Add a Batch Normalization layer after each convolutional layer. Compare the model's performance and learning curves with the previous model.
**Tip**: there is no need for an activation function just before the pooling layers.

## Exercise 1 – Solution
### 1.1)
Load CIFAR10 using `keras.datasets.cifar10.load_data()`, and split it into a training set (45,000 images), a validation set (5,000 images) and a test set (10,000 images). Make sure the pixel values range from 0 to 1. Visualize a few images using `plt.imshow()`.
```
classes = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.cifar10.load_data()
X_train = X_train_full[:-5000] / 255
y_train = y_train_full[:-5000]
X_valid = X_train_full[-5000:] / 255
y_valid = y_train_full[-5000:]
X_test = X_test / 255
plt.figure(figsize=(10, 7))
n_rows, n_cols = 10, 15
for row in range(n_rows):
for col in range(n_cols):
i = row * n_cols + col
plt.subplot(n_rows, n_cols, i + 1)
plt.axis("off")
plt.imshow(X_train[i])
```
Let's print the classes of the images in the first row:
```
for i in range(n_cols):
print(classes[y_train[i][0]], end=" ")
```
### 1.2)
Build and train a baseline model with a few dense layers, and plot the learning curves. Use the model's `summary()` method to count the number of parameters in this model.
**Tip**:
* Recall that to plot the learning curves, you can simply create a Pandas `DataFrame` with the `history.history` dict, then call its `plot()` method.
```
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[32, 32, 3]),
keras.layers.Dense(64, activation="selu"),
keras.layers.Dense(64, activation="selu"),
keras.layers.Dense(64, activation="selu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
model.summary()
```
### 1.3)
Build and train a Convolutional Neural Network using a "classical" architecture: N * (Conv2D → Conv2D → Pool2D) → Flatten → Dense → Dense. Before you print the `summary()`, try to manually calculate the number of parameters in your model's architecture, as well as the shape of the inputs and outputs of each layer. Next, plot the learning curves and compare the performance with the previous model.
```
model = keras.models.Sequential([
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu", input_shape=[32, 32, 3]),
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu"),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Conv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.Conv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Flatten(),
keras.layers.Dense(128, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
# Number of params in a convolutional layer =
# (kernel_width * kernel_height * channels_in + 1 for bias) * channels_out
(
(3 * 3 * 3 + 1) * 32 # in: 32x32x3 out: 32x32x32 Conv2D
+ (3 * 3 * 32 + 1) * 32 # in: 32x32x32 out: 32x32x32 Conv2D
+ 0 # in: 32x32x32 out: 16x16x32 MaxPool2D
+ (3 * 3 * 32 + 1) * 64 # in: 16x16x32 out: 16x16x64 Conv2D
+ (3 * 3 * 64 + 1) * 64 # in: 16x16x64 out: 16x16x64 Conv2D
+ 0 # in: 16x16x64 out: 8x8x64 MaxPool2D
+ 0 # in: 8x8x64 out: 4096 Flatten
+ (4096 + 1) * 128 # in: 4096 out: 128 Dense
+ (128 + 1) * 10 # in: 128 out: 10 Dense
)
```
Let's check:
```
model.summary()
```
### 1.4)
Looking at the learning curves, you can see that the model is overfitting. Add a Batch Normalization layer after each convolutional layer. Compare the model's performance and learning curves with the previous model.
**Tip**: there is no need for an activation function just before the pooling layers.
```
model = keras.models.Sequential([
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu", input_shape=[32, 32, 3]),
keras.layers.BatchNormalization(),
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Conv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Conv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Flatten(),
keras.layers.Dense(128, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
```

## Exercise 2 – Separable Convolutions
### 2.1)
Replace the `Conv2D` layers with `SeparableConv2D` layers (except the first one), fit your model and compare its performance and learning curves with the previous model.
### 2.2)
Try to estimate the number of parameters in your network, then check your result with `model.summary()`.
**Tip**: the batch normalization layer adds two parameters for each feature map (the scale and bias).

## Exercise 2 – Solution
### 2.1)
Replace the `Conv2D` layers with `SeparableConv2D` layers (except the first one), fit your model and compare its performance and learning curves with the previous model.
```
model = keras.models.Sequential([
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu", input_shape=[32, 32, 3]),
keras.layers.BatchNormalization(),
keras.layers.SeparableConv2D(filters=32, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.SeparableConv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.SeparableConv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Flatten(),
keras.layers.Dense(128, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
```
### 2.2)
Try to estimate the number of parameters in your network, then check your result with `model.summary()`.
**Tip**: the batch normalization layer adds two parameters for each feature map (the scale and bias).
```
# Number of params in a depthwise separable 2D convolution layer =
# kernel_width * kernel_height * channels_in + (channels_in + 1 for bias) * channels_out
(
(3 * 3 * 3 + 1) * 32 # in: 32x32x3 out: 32x32x32 Conv2D
+ 32 * 2 # in: 32x32x32 out: 32x32x32 BN
+ 3 * 3 * 32 + (32 + 1) * 32 # in: 32x32x32 out: 32x32x32 SeparableConv2D
+ 32 * 2 # in: 32x32x32 out: 32x32x32 BN
+ 0 # in: 32x32x32 out: 16x16x32 MaxPool2D
+ 3 * 3 * 32 + (32 + 1) * 64 # in: 16x16x32 out: 16x16x64 SeparableConv2D
+ 64 * 2 # in: 16x16x64 out: 16x16x64 BN
+ 3 * 3 * 64 + (64 + 1) * 64 # in: 16x16x64 out: 16x16x64 SeparableConv2D
+ 64 * 2 # in: 16x16x64 out: 16x16x64 BN
+ 0 # in: 16x16x64 out: 8x8x64 MaxPool2D
+ 0 # in: 8x8x64 out: 4096 Flatten
+ (4096 + 1) * 128 # in: 4096 out: 128 Dense
+ (128 + 1) * 10 # in: 128 out: 10 Dense
)
```
Let's check:
```
model.summary()
```

## Exercise 3 – Pretrained CNNs
### 3.1)
Using `tf.keras.utils.get_file()`, download the image `fig.jpg` from https://github.com/ageron/tf2_course/raw/master/images/fig.jpg, then load it using `keras.preprocessing.image.load_img()` followed by `keras.preprocessing.image.img_to_array()`. You also load the `ostrich.jpg` image if you want, from the same folder. You should set `target_size=(299, 299)` when calling `load_img()`, as this is the shape that the Xception network expects.
### 3.2)
Create a batch containing the image(s) you just loaded, and preprocess this batch using `keras.applications.xception.preprocess_input()`. Verify that the features now vary from -1 to 1: this is what the Xception network expects.
### 3.3)
Create an instance of the Xception model (`keras.applications.xception.Xception`) and use its `predict()` method to classify the images in the batch. You can use `keras.applications.resnet50.decode_predictions()` to convert the output matrix into a list of top-N predictions (with their corresponding class labels).

## Exercise 3 – Solution
### 3.1)
Using `keras.preprocessing.image.load_img()` followed by `keras.preprocessing.image.img_to_array()`, load one or more images (e.g., `fig.jpg` or `ostrich.jpg` in the `images` folder). You should set `target_size=(299, 299)` when calling `load_img()`, as this is the shape that the Xception network expects.
```
img_fig_path = keras.utils.get_file(
"fig.jpg",
"https://github.com/ageron/tf2_course/raw/master/images/fig.jpg")
img_fig = keras.preprocessing.image.load_img(img_fig_path, target_size=(299, 299))
img_fig = keras.preprocessing.image.img_to_array(img_fig)
plt.imshow(img_fig / 255)
plt.axis("off")
plt.show()
img_fig.shape
img_ostrich_path = keras.utils.get_file(
"ostrich.jpg",
"https://github.com/ageron/tf2_course/raw/master/images/ostrich.jpg")
img_ostrich = keras.preprocessing.image.load_img(img_ostrich_path, target_size=(299, 299))
img_ostrich = keras.preprocessing.image.img_to_array(img_ostrich)
plt.imshow(img_ostrich / 255)
plt.axis("off")
plt.show()
img_ostrich.shape
```
### 3.2)
Create a batch containing the image(s) you just loaded, and preprocess this batch using `keras.applications.xception.preprocess_input()`. Verify that the features now vary from -1 to 1: this is what the Xception network expects.
```
X_batch = np.array([img_fig, img_ostrich])
X_preproc = keras.applications.xception.preprocess_input(X_batch)
X_preproc.min(), X_preproc.max()
```
### 3.3)
Create an instance of the Xception model (`keras.applications.xception.Xception`) and use its `predict()` method to classify the images in the batch. You can use `keras.applications.resnet50.decode_predictions()` to convert the output matrix into a list of top-N predictions (with their corresponding class labels).
```
model = keras.applications.xception.Xception()
Y_proba = model.predict(X_preproc)
Y_proba.shape
np.argmax(Y_proba, axis=1)
decoded_predictions = keras.applications.resnet50.decode_predictions(Y_proba)
for preds in decoded_predictions:
for wordnet_id, name, proba in preds:
print("{} ({}): {:.1f}%".format(name, wordnet_id, 100 * proba))
print()
```

## Exercise 4 – Data Augmentation and Transfer Learning
In this exercise you will reuse a pretrained Xception model to build a flower classifier.
First, let's download the dataset:
```
import tensorflow as tf
from tensorflow import keras
import os
flowers_url = "http://download.tensorflow.org/example_images/flower_photos.tgz"
flowers_path = keras.utils.get_file("flowers.tgz", flowers_url, extract=True)
flowers_dir = os.path.join(os.path.dirname(flowers_path), "flower_photos")
for root, subdirs, files in os.walk(flowers_dir):
print(root)
for filename in files[:3]:
print(" ", filename)
if len(files) > 3:
print(" ...")
```
### 4.1)
Build a `keras.preprocessing.image.ImageDataGenerator` that will preprocess the images and do some data augmentation (the [documentation](https://keras.io/preprocessing/image/) contains useful examples):
* It should at least perform horizontal flips and keep 10% of the data for validation, but you may also make it perform a bit of rotation, rescaling, etc.
* Also make sure to apply the Xception preprocessing function (using the `preprocessing_function` argument).
* Call this generator's `flow_from_directory()` method to get an iterator that will load and preprocess the flower photos from the `flower_photos` directory, setting the target size to (299, 299) and `subset` to `"training"`.
* Call this method again with the same parameters except `subset="validation"` to get a second iterator for validation.
* Get the next batch from the validation iterator and display the first image from the batch.
### 4.2)
Now let's build the model:
* Create a new `Xception` model, but this time set `include_top=False` to get the model without the top layer. **Tip**: you will need to access its `input` and `output` properties.
* Make all its layers non-trainable.
* Using the functional API, add a `GlobalAveragePooling2D` layer (feeding it the Xception model's output), and add a `Dense` layer with 5 neurons and the Softmax activation function.
* Compile the model. **Tip**: don't forget to add the `"accuracy"` metric.
* Fit your model using `fit_generator()`, passing it the training and validation iterators (and setting `steps_per_epoch` and `validation_steps` appropriately).

## Exercise 4 – Solution
### 4.1)
Build a `keras.preprocessing.image.ImageDataGenerator` that will preprocess the images and do some data augmentation (the [documentation](https://keras.io/preprocessing/image/) contains useful examples):
* It should at least perform horizontal flips and keep 10% of the data for validation, but you may also make it perform a bit of rotation, rescaling, etc.
* Also make sure to apply the Xception preprocessing function (using the `preprocessing_function` argument).
* Call this generator's `flow_from_directory()` method to get an iterator that will load and preprocess the flower photos from the `flower_photos` directory, setting the target size to (299, 299) and `subset` to `"training"`.
* Call this method again with the same parameters except `subset="validation"` to get a second iterator for validation.
* Get the next batch from the validation iterator and display the first image from the batch.
```
datagen = keras.preprocessing.image.ImageDataGenerator(
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
validation_split=0.1,
preprocessing_function=keras.applications.xception.preprocess_input)
train_generator = datagen.flow_from_directory(
flowers_dir,
target_size=(299, 299),
batch_size=32,
subset="training")
valid_generator = datagen.flow_from_directory(
flowers_dir,
target_size=(299, 299),
batch_size=32,
subset="validation")
X_batch, y_batch = next(valid_generator)
plt.imshow((X_batch[0] + 1)/2)
plt.axis("off")
plt.show()
```
### 4.2)
Now let's build the model:
* Create a new `Xception` model, but this time set `include_top=False` to get the model without the top layer. **Tip**: you will need to access its `input` and `output` properties.
* Make all its layers non-trainable.
* Using the functional API, add a `GlobalAveragePooling2D` layer (feeding it the Xception model's output), and add a `Dense` layer with 5 neurons and the Softmax activation function.
* Compile the model. **Tip**: don't forget to add the `"accuracy"` metric.
* Fit your model using `fit_generator()`, passing it the training and validation iterators (and setting `steps_per_epoch` and `validation_steps` appropriately).
```
n_classes = 5
base_model = keras.applications.xception.Xception(include_top=False)
for layer in base_model.layers:
layer.trainable = False
global_pool = keras.layers.GlobalAveragePooling2D()(base_model.output)
predictions = keras.layers.Dense(n_classes, activation='softmax')(global_pool)
model = keras.models.Model(base_model.input, predictions)
model.compile(loss="categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit_generator(
train_generator,
steps_per_epoch=3306 // 32,
epochs=50,
validation_data=valid_generator,
validation_steps=364 // 32)
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
```

## Object Detection Project
The Google [Street View House Numbers](http://ufldl.stanford.edu/housenumbers/) (SVHN) dataset contains pictures of digits in all shapes and colors, taken by the Google Street View cars. The goal is to classify and locate all the digits in large images.
* Train a Fully Convolutional Network on the 32x32 images.
* Use this FCN to build a digit detector in the large images.
|
github_jupyter
|
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import sklearn
import sys
import tensorflow as tf
from tensorflow import keras
import time
print("python", sys.version)
for module in mpl, np, pd, sklearn, tf, keras:
print(module.__name__, module.__version__)
assert sys.version_info >= (3, 5) # Python ≥3.5 required
assert tf.__version__ >= "2.0" # TensorFlow ≥2.0 required
classes = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
classes = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.cifar10.load_data()
X_train = X_train_full[:-5000] / 255
y_train = y_train_full[:-5000]
X_valid = X_train_full[-5000:] / 255
y_valid = y_train_full[-5000:]
X_test = X_test / 255
plt.figure(figsize=(10, 7))
n_rows, n_cols = 10, 15
for row in range(n_rows):
for col in range(n_cols):
i = row * n_cols + col
plt.subplot(n_rows, n_cols, i + 1)
plt.axis("off")
plt.imshow(X_train[i])
for i in range(n_cols):
print(classes[y_train[i][0]], end=" ")
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[32, 32, 3]),
keras.layers.Dense(64, activation="selu"),
keras.layers.Dense(64, activation="selu"),
keras.layers.Dense(64, activation="selu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
model.summary()
model = keras.models.Sequential([
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu", input_shape=[32, 32, 3]),
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu"),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Conv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.Conv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Flatten(),
keras.layers.Dense(128, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
# Number of params in a convolutional layer =
# (kernel_width * kernel_height * channels_in + 1 for bias) * channels_out
(
(3 * 3 * 3 + 1) * 32 # in: 32x32x3 out: 32x32x32 Conv2D
+ (3 * 3 * 32 + 1) * 32 # in: 32x32x32 out: 32x32x32 Conv2D
+ 0 # in: 32x32x32 out: 16x16x32 MaxPool2D
+ (3 * 3 * 32 + 1) * 64 # in: 16x16x32 out: 16x16x64 Conv2D
+ (3 * 3 * 64 + 1) * 64 # in: 16x16x64 out: 16x16x64 Conv2D
+ 0 # in: 16x16x64 out: 8x8x64 MaxPool2D
+ 0 # in: 8x8x64 out: 4096 Flatten
+ (4096 + 1) * 128 # in: 4096 out: 128 Dense
+ (128 + 1) * 10 # in: 128 out: 10 Dense
)
model.summary()
model = keras.models.Sequential([
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu", input_shape=[32, 32, 3]),
keras.layers.BatchNormalization(),
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Conv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Conv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Flatten(),
keras.layers.Dense(128, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
model = keras.models.Sequential([
keras.layers.Conv2D(filters=32, kernel_size=3, padding="same", activation="relu", input_shape=[32, 32, 3]),
keras.layers.BatchNormalization(),
keras.layers.SeparableConv2D(filters=32, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.SeparableConv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.SeparableConv2D(filters=64, kernel_size=3, padding="same", activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Flatten(),
keras.layers.Dense(128, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
# Number of params in a depthwise separable 2D convolution layer =
# kernel_width * kernel_height * channels_in + (channels_in + 1 for bias) * channels_out
(
(3 * 3 * 3 + 1) * 32 # in: 32x32x3 out: 32x32x32 Conv2D
+ 32 * 2 # in: 32x32x32 out: 32x32x32 BN
+ 3 * 3 * 32 + (32 + 1) * 32 # in: 32x32x32 out: 32x32x32 SeparableConv2D
+ 32 * 2 # in: 32x32x32 out: 32x32x32 BN
+ 0 # in: 32x32x32 out: 16x16x32 MaxPool2D
+ 3 * 3 * 32 + (32 + 1) * 64 # in: 16x16x32 out: 16x16x64 SeparableConv2D
+ 64 * 2 # in: 16x16x64 out: 16x16x64 BN
+ 3 * 3 * 64 + (64 + 1) * 64 # in: 16x16x64 out: 16x16x64 SeparableConv2D
+ 64 * 2 # in: 16x16x64 out: 16x16x64 BN
+ 0 # in: 16x16x64 out: 8x8x64 MaxPool2D
+ 0 # in: 8x8x64 out: 4096 Flatten
+ (4096 + 1) * 128 # in: 4096 out: 128 Dense
+ (128 + 1) * 10 # in: 128 out: 10 Dense
)
model.summary()
img_fig_path = keras.utils.get_file(
"fig.jpg",
"https://github.com/ageron/tf2_course/raw/master/images/fig.jpg")
img_fig = keras.preprocessing.image.load_img(img_fig_path, target_size=(299, 299))
img_fig = keras.preprocessing.image.img_to_array(img_fig)
plt.imshow(img_fig / 255)
plt.axis("off")
plt.show()
img_fig.shape
img_ostrich_path = keras.utils.get_file(
"ostrich.jpg",
"https://github.com/ageron/tf2_course/raw/master/images/ostrich.jpg")
img_ostrich = keras.preprocessing.image.load_img(img_ostrich_path, target_size=(299, 299))
img_ostrich = keras.preprocessing.image.img_to_array(img_ostrich)
plt.imshow(img_ostrich / 255)
plt.axis("off")
plt.show()
img_ostrich.shape
X_batch = np.array([img_fig, img_ostrich])
X_preproc = keras.applications.xception.preprocess_input(X_batch)
X_preproc.min(), X_preproc.max()
model = keras.applications.xception.Xception()
Y_proba = model.predict(X_preproc)
Y_proba.shape
np.argmax(Y_proba, axis=1)
decoded_predictions = keras.applications.resnet50.decode_predictions(Y_proba)
for preds in decoded_predictions:
for wordnet_id, name, proba in preds:
print("{} ({}): {:.1f}%".format(name, wordnet_id, 100 * proba))
print()
import tensorflow as tf
from tensorflow import keras
import os
flowers_url = "http://download.tensorflow.org/example_images/flower_photos.tgz"
flowers_path = keras.utils.get_file("flowers.tgz", flowers_url, extract=True)
flowers_dir = os.path.join(os.path.dirname(flowers_path), "flower_photos")
for root, subdirs, files in os.walk(flowers_dir):
print(root)
for filename in files[:3]:
print(" ", filename)
if len(files) > 3:
print(" ...")
datagen = keras.preprocessing.image.ImageDataGenerator(
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
validation_split=0.1,
preprocessing_function=keras.applications.xception.preprocess_input)
train_generator = datagen.flow_from_directory(
flowers_dir,
target_size=(299, 299),
batch_size=32,
subset="training")
valid_generator = datagen.flow_from_directory(
flowers_dir,
target_size=(299, 299),
batch_size=32,
subset="validation")
X_batch, y_batch = next(valid_generator)
plt.imshow((X_batch[0] + 1)/2)
plt.axis("off")
plt.show()
n_classes = 5
base_model = keras.applications.xception.Xception(include_top=False)
for layer in base_model.layers:
layer.trainable = False
global_pool = keras.layers.GlobalAveragePooling2D()(base_model.output)
predictions = keras.layers.Dense(n_classes, activation='softmax')(global_pool)
model = keras.models.Model(base_model.input, predictions)
model.compile(loss="categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit_generator(
train_generator,
steps_per_epoch=3306 // 32,
epochs=50,
validation_data=valid_generator,
validation_steps=364 // 32)
pd.DataFrame(history.history).plot()
plt.axis([0, 19, 0, 1])
plt.show()
| 0.694821 | 0.992654 |
# second part of spark activity
```
import pyspark
sc = pyspark.SparkContext('local[*]')
```
read the data from the (ml-100k/u.data) file :
```
textFile = sc.textFile("../data/raw/Datasets/ml-100k/u.data")
#data Split
rdd = textFile.map(lambda line: line.split("\t"))
# explore user rating
print("User ratings (user id, item id, rating, timestamp)"+format(rdd.first()))
```
now i will convert the rating data into float and integer, and explore them again:
```
converted_rdd = rdd.map(lambda fields: (int(float(fields[0])), float(fields[2]), int(float(fields[1]))))
# Print user rating after convert
print("Numerical user ratings (user id, rating, item id):" + format(converted_rdd.first()))
```
create a pair RDD:
```
paired_rdd = converted_rdd.map(lambda fields: (fields[0], (fields[1], fields[2])))
print("Pair RDD (user id, (rating, item id))" + format(paired_rdd.first()))
```
sum of rating, and the number of rated movies for each user
```
aggregated_rdd = paired_rdd.aggregateByKey((0.0, 0.0),\
lambda acc, val: (val[0] + acc[0], acc[1] + 1),\
lambda acc1, acc2: (acc1[0]+acc2[0], acc1[1]+acc2[1]))
print("Agregate user ratings and movies ((user id, (rating sum, number of movies)):"
+ format(aggregated_rdd.takeOrdered(5, lambda x: x[0])))
```
average of ratings by movie for each user
```
avg_rdd = aggregated_rdd.mapValues(lambda x:(x[0]/x[1]))
print("average ratings of user((user id, rating sum/number of movies):"
+ format(avg_rdd.takeOrdered(5, lambda x: x[0])))
```
the received rating of each movie
```
movies_rating = paired_rdd.map(lambda x : (x[1][1], 1)).reduceByKey(lambda a,b: a+b)
print("Movie number of ratings (movie id, ratings number):"
+ format(movies_rating.take(5)))
```
number of movies which have a higher than average rating
```
high_rating_movies = paired_rdd.map(lambda x : (x[1][1], x[1][0])).filter(lambda x : x[1] >= 4.0)\
.map(lambda x : (x[0], 1)).reduceByKey(lambda a,b: a+b)
print("High Rating Movies:"
+ format(high_rating_movies.takeOrdered(5, lambda x: x[0])))
```
Top 5 the Last 5 rated movies
```
print("Top 5 Rated movies:"
+ format(movies_rating.takeOrdered(5, lambda x: -x[1])))
print("Last 5 Rated movies:"
+ format(movies_rating.takeOrdered(5, lambda x: x[1])))
```
Join the two movie_counts and high_rating_movies datasets using a leftOuterJoin
```
def generate_ratio(x, y):
try:
return float(x)/float(y)
except:
return 0 #x or y are None
join_movies = movies_rating.leftOuterJoin(high_rating_movies)
print("Join the two movie_counts and high_rating_movies datasets using a leftOuterJoin:"
+ format(join_movies.take(5)))
print("Movie with id = 314:"
+ format(join_movies.filter(lambda x : x[0] == 314).collect()))
print("Top higher rates movie (movie id, (high ratings number/ ratings number):"
+ format(join_movies.mapValues(lambda x : (generate_ratio(x[1], x[0])))\
.takeOrdered(10, lambda x: -x[1])))
```
|
github_jupyter
|
import pyspark
sc = pyspark.SparkContext('local[*]')
textFile = sc.textFile("../data/raw/Datasets/ml-100k/u.data")
#data Split
rdd = textFile.map(lambda line: line.split("\t"))
# explore user rating
print("User ratings (user id, item id, rating, timestamp)"+format(rdd.first()))
converted_rdd = rdd.map(lambda fields: (int(float(fields[0])), float(fields[2]), int(float(fields[1]))))
# Print user rating after convert
print("Numerical user ratings (user id, rating, item id):" + format(converted_rdd.first()))
paired_rdd = converted_rdd.map(lambda fields: (fields[0], (fields[1], fields[2])))
print("Pair RDD (user id, (rating, item id))" + format(paired_rdd.first()))
aggregated_rdd = paired_rdd.aggregateByKey((0.0, 0.0),\
lambda acc, val: (val[0] + acc[0], acc[1] + 1),\
lambda acc1, acc2: (acc1[0]+acc2[0], acc1[1]+acc2[1]))
print("Agregate user ratings and movies ((user id, (rating sum, number of movies)):"
+ format(aggregated_rdd.takeOrdered(5, lambda x: x[0])))
avg_rdd = aggregated_rdd.mapValues(lambda x:(x[0]/x[1]))
print("average ratings of user((user id, rating sum/number of movies):"
+ format(avg_rdd.takeOrdered(5, lambda x: x[0])))
movies_rating = paired_rdd.map(lambda x : (x[1][1], 1)).reduceByKey(lambda a,b: a+b)
print("Movie number of ratings (movie id, ratings number):"
+ format(movies_rating.take(5)))
high_rating_movies = paired_rdd.map(lambda x : (x[1][1], x[1][0])).filter(lambda x : x[1] >= 4.0)\
.map(lambda x : (x[0], 1)).reduceByKey(lambda a,b: a+b)
print("High Rating Movies:"
+ format(high_rating_movies.takeOrdered(5, lambda x: x[0])))
print("Top 5 Rated movies:"
+ format(movies_rating.takeOrdered(5, lambda x: -x[1])))
print("Last 5 Rated movies:"
+ format(movies_rating.takeOrdered(5, lambda x: x[1])))
def generate_ratio(x, y):
try:
return float(x)/float(y)
except:
return 0 #x or y are None
join_movies = movies_rating.leftOuterJoin(high_rating_movies)
print("Join the two movie_counts and high_rating_movies datasets using a leftOuterJoin:"
+ format(join_movies.take(5)))
print("Movie with id = 314:"
+ format(join_movies.filter(lambda x : x[0] == 314).collect()))
print("Top higher rates movie (movie id, (high ratings number/ ratings number):"
+ format(join_movies.mapValues(lambda x : (generate_ratio(x[1], x[0])))\
.takeOrdered(10, lambda x: -x[1])))
| 0.287168 | 0.932699 |
## Dependencies
```
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
class RectifiedAdam(tf.keras.optimizers.Optimizer):
"""Variant of the Adam optimizer whose adaptive learning rate is rectified
so as to have a consistent variance.
It implements the Rectified Adam (a.k.a. RAdam) proposed by
Liyuan Liu et al. in [On The Variance Of The Adaptive Learning Rate
And Beyond](https://arxiv.org/pdf/1908.03265v1.pdf).
Example of usage:
```python
opt = tfa.optimizers.RectifiedAdam(lr=1e-3)
```
Note: `amsgrad` is not described in the original paper. Use it with
caution.
RAdam is not a placement of the heuristic warmup, the settings should be
kept if warmup has already been employed and tuned in the baseline method.
You can enable warmup by setting `total_steps` and `warmup_proportion`:
```python
opt = tfa.optimizers.RectifiedAdam(
lr=1e-3,
total_steps=10000,
warmup_proportion=0.1,
min_lr=1e-5,
)
```
In the above example, the learning rate will increase linearly
from 0 to `lr` in 1000 steps, then decrease linearly from `lr` to `min_lr`
in 9000 steps.
Lookahead, proposed by Michael R. Zhang et.al in the paper
[Lookahead Optimizer: k steps forward, 1 step back]
(https://arxiv.org/abs/1907.08610v1), can be integrated with RAdam,
which is announced by Less Wright and the new combined optimizer can also
be called "Ranger". The mechanism can be enabled by using the lookahead
wrapper. For example:
```python
radam = tfa.optimizers.RectifiedAdam()
ranger = tfa.optimizers.Lookahead(radam, sync_period=6, slow_step_size=0.5)
```
"""
def __init__(self,
learning_rate=0.001,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-7,
weight_decay=0.,
amsgrad=False,
sma_threshold=5.0,
total_steps=0,
warmup_proportion=0.1,
min_lr=0.,
name='RectifiedAdam',
**kwargs):
r"""Construct a new RAdam optimizer.
Args:
learning_rate: A `Tensor` or a floating point value. or a schedule
that is a `tf.keras.optimizers.schedules.LearningRateSchedule`
The learning rate.
beta_1: A float value or a constant float tensor.
The exponential decay rate for the 1st moment estimates.
beta_2: A float value or a constant float tensor.
The exponential decay rate for the 2nd moment estimates.
epsilon: A small constant for numerical stability.
weight_decay: A floating point value. Weight decay for each param.
amsgrad: boolean. Whether to apply AMSGrad variant of this
algorithm from the paper "On the Convergence of Adam and
beyond".
sma_threshold. A float value.
The threshold for simple mean average.
total_steps: An integer. Total number of training steps.
Enable warmup by setting a positive value.
warmup_proportion: A floating point value.
The proportion of increasing steps.
min_lr: A floating point value. Minimum learning rate after warmup.
name: Optional name for the operations created when applying
gradients. Defaults to "RectifiedAdam".
**kwargs: keyword arguments. Allowed to be {`clipnorm`,
`clipvalue`, `lr`, `decay`}. `clipnorm` is clip gradients
by norm; `clipvalue` is clip gradients by value, `decay` is
included for backward compatibility to allow time inverse
decay of learning rate. `lr` is included for backward
compatibility, recommended to use `learning_rate` instead.
"""
super(RectifiedAdam, self).__init__(name, **kwargs)
self._set_hyper('learning_rate', kwargs.get('lr', learning_rate))
self._set_hyper('beta_1', beta_1)
self._set_hyper('beta_2', beta_2)
self._set_hyper('decay', self._initial_decay)
self._set_hyper('weight_decay', weight_decay)
self._set_hyper('sma_threshold', sma_threshold)
self._set_hyper('total_steps', float(total_steps))
self._set_hyper('warmup_proportion', warmup_proportion)
self._set_hyper('min_lr', min_lr)
self.epsilon = epsilon or tf.keras.backend.epsilon()
self.amsgrad = amsgrad
self._initial_weight_decay = weight_decay
self._initial_total_steps = total_steps
def _create_slots(self, var_list):
for var in var_list:
self.add_slot(var, 'm')
for var in var_list:
self.add_slot(var, 'v')
if self.amsgrad:
for var in var_list:
self.add_slot(var, 'vhat')
def set_weights(self, weights):
params = self.weights
num_vars = int((len(params) - 1) / 2)
if len(weights) == 3 * num_vars + 1:
weights = weights[:len(params)]
super(RectifiedAdam, self).set_weights(weights)
def _resource_apply_dense(self, grad, var):
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype)
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
beta_1_t = self._get_hyper('beta_1', var_dtype)
beta_2_t = self._get_hyper('beta_2', var_dtype)
epsilon_t = tf.convert_to_tensor(self.epsilon, var_dtype)
local_step = tf.cast(self.iterations + 1, var_dtype)
beta_1_power = tf.pow(beta_1_t, local_step)
beta_2_power = tf.pow(beta_2_t, local_step)
if self._initial_total_steps > 0:
total_steps = self._get_hyper('total_steps', var_dtype)
warmup_steps = total_steps *\
self._get_hyper('warmup_proportion', var_dtype)
min_lr = self._get_hyper('min_lr', var_dtype)
decay_steps = tf.maximum(total_steps - warmup_steps, 1)
decay_rate = (min_lr - lr_t) / decay_steps
lr_t = tf.where(
local_step <= warmup_steps,
lr_t * (local_step / warmup_steps),
lr_t + decay_rate * tf.minimum(local_step - warmup_steps,
decay_steps),
)
sma_inf = 2.0 / (1.0 - beta_2_t) - 1.0
sma_t = sma_inf - 2.0 * local_step * beta_2_power / (
1.0 - beta_2_power)
m_t = m.assign(
beta_1_t * m + (1.0 - beta_1_t) * grad,
use_locking=self._use_locking)
m_corr_t = m_t / (1.0 - beta_1_power)
v_t = v.assign(
beta_2_t * v + (1.0 - beta_2_t) * tf.square(grad),
use_locking=self._use_locking)
if self.amsgrad:
vhat = self.get_slot(var, 'vhat')
vhat_t = vhat.assign(
tf.maximum(vhat, v_t), use_locking=self._use_locking)
v_corr_t = tf.sqrt(vhat_t / (1.0 - beta_2_power))
else:
vhat_t = None
v_corr_t = tf.sqrt(v_t / (1.0 - beta_2_power))
r_t = tf.sqrt((sma_t - 4.0) / (sma_inf - 4.0) * (sma_t - 2.0) /
(sma_inf - 2.0) * sma_inf / sma_t)
sma_threshold = self._get_hyper('sma_threshold', var_dtype)
var_t = tf.where(sma_t >= sma_threshold,
r_t * m_corr_t / (v_corr_t + epsilon_t), m_corr_t)
if self._initial_weight_decay > 0.0:
var_t += self._get_hyper('weight_decay', var_dtype) * var
var_update = var.assign_sub(
lr_t * var_t, use_locking=self._use_locking)
updates = [var_update, m_t, v_t]
if self.amsgrad:
updates.append(vhat_t)
return tf.group(*updates)
def _resource_apply_sparse(self, grad, var, indices):
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype)
beta_1_t = self._get_hyper('beta_1', var_dtype)
beta_2_t = self._get_hyper('beta_2', var_dtype)
epsilon_t = tf.convert_to_tensor(self.epsilon, var_dtype)
local_step = tf.cast(self.iterations + 1, var_dtype)
beta_1_power = tf.pow(beta_1_t, local_step)
beta_2_power = tf.pow(beta_2_t, local_step)
if self._initial_total_steps > 0:
total_steps = self._get_hyper('total_steps', var_dtype)
warmup_steps = total_steps *\
self._get_hyper('warmup_proportion', var_dtype)
min_lr = self._get_hyper('min_lr', var_dtype)
decay_steps = tf.maximum(total_steps - warmup_steps, 1)
decay_rate = (min_lr - lr_t) / decay_steps
lr_t = tf.where(
local_step <= warmup_steps,
lr_t * (local_step / warmup_steps),
lr_t + decay_rate * tf.minimum(local_step - warmup_steps,
decay_steps),
)
sma_inf = 2.0 / (1.0 - beta_2_t) - 1.0
sma_t = sma_inf - 2.0 * local_step * beta_2_power / (
1.0 - beta_2_power)
m = self.get_slot(var, 'm')
m_scaled_g_values = grad * (1 - beta_1_t)
m_t = m.assign(m * beta_1_t, use_locking=self._use_locking)
with tf.control_dependencies([m_t]):
m_t = self._resource_scatter_add(m, indices, m_scaled_g_values)
m_corr_t = m_t / (1.0 - beta_1_power)
v = self.get_slot(var, 'v')
v_scaled_g_values = (grad * grad) * (1 - beta_2_t)
v_t = v.assign(v * beta_2_t, use_locking=self._use_locking)
with tf.control_dependencies([v_t]):
v_t = self._resource_scatter_add(v, indices, v_scaled_g_values)
if self.amsgrad:
vhat = self.get_slot(var, 'vhat')
vhat_t = vhat.assign(
tf.maximum(vhat, v_t), use_locking=self._use_locking)
v_corr_t = tf.sqrt(vhat_t / (1.0 - beta_2_power))
else:
vhat_t = None
v_corr_t = tf.sqrt(v_t / (1.0 - beta_2_power))
r_t = tf.sqrt((sma_t - 4.0) / (sma_inf - 4.0) * (sma_t - 2.0) /
(sma_inf - 2.0) * sma_inf / sma_t)
sma_threshold = self._get_hyper('sma_threshold', var_dtype)
var_t = tf.where(sma_t >= sma_threshold,
r_t * m_corr_t / (v_corr_t + epsilon_t), m_corr_t)
if self._initial_weight_decay > 0.0:
var_t += self._get_hyper('weight_decay', var_dtype) * var
with tf.control_dependencies([var_t]):
var_update = self._resource_scatter_add(
var, indices, tf.gather(-lr_t * var_t, indices))
updates = [var_update, m_t, v_t]
if self.amsgrad:
updates.append(vhat_t)
return tf.group(*updates)
def get_config(self):
config = super(RectifiedAdam, self).get_config()
config.update({
'learning_rate':
self._serialize_hyperparameter('learning_rate'),
'beta_1':
self._serialize_hyperparameter('beta_1'),
'beta_2':
self._serialize_hyperparameter('beta_2'),
'decay':
self._serialize_hyperparameter('decay'),
'weight_decay':
self._serialize_hyperparameter('weight_decay'),
'sma_threshold':
self._serialize_hyperparameter('sma_threshold'),
'epsilon':
self.epsilon,
'amsgrad':
self.amsgrad,
'total_steps':
self._serialize_hyperparameter('total_steps'),
'warmup_proportion':
self._serialize_hyperparameter('warmup_proportion'),
'min_lr':
self._serialize_hyperparameter('min_lr'),
})
return config
```
# Load data
```
database_base_path = '/kaggle/input/tweet-dataset-split-roberta-base-96/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# Unzip files
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_1.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_2.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_3.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_4.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_5.tar.gz
```
# Model parameters
```
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
"MAX_LEN": 96,
"BATCH_SIZE": 32,
"EPOCHS": 5,
"LEARNING_RATE": 3e-5,
"ES_PATIENCE": 1,
"question_size": 4,
"N_FOLDS": 3,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
```
# Model
```
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
sequence_output = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
last_state = sequence_output[0]
x_start = layers.Dropout(0.1)(last_state)
x_start = layers.Conv1D(128, 2, padding='same')(x_start)
x_start = layers.LeakyReLU()(x_start)
x_start = layers.Conv1D(64, 2, padding='same')(x_start)
x_start = layers.Dense(1)(x_start)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('sigmoid', name='y_start')(x_start)
x_end = layers.Dropout(0.1)(last_state)
x_end = layers.Conv1D(128, 2, padding='same')(x_end)
x_end = layers.LeakyReLU()(x_end)
x_end = layers.Conv1D(64, 2, padding='same')(x_end)
x_end = layers.Dense(1)(x_end)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('sigmoid', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
optimizer = RectifiedAdam(lr=config['LEARNING_RATE'],
total_steps=(len(k_fold[k_fold['fold_1'] == 'train']) // config['BATCH_SIZE']) * config['EPOCHS'],
warmup_proportion=0.1,
min_lr=1e-7)
model.compile(optimizer, loss={'y_start': losses.BinaryCrossentropy(),
'y_end': losses.BinaryCrossentropy()},
metrics={'y_start': metrics.BinaryAccuracy(),
'y_end': metrics.BinaryAccuracy()})
return model
```
# Tokenizer
```
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
```
# Train
```
history_list = []
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
### Delete data dir
shutil.rmtree(base_data_path)
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=True, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
history = model.fit(list(x_train), list(y_train),
validation_data=(list(x_valid), list(y_valid)),
batch_size=config['BATCH_SIZE'],
callbacks=[checkpoint, es],
epochs=config['EPOCHS'],
verbose=2).history
history_list.append(history)
# Make predictions
train_preds = model.predict(list(x_train))
valid_preds = model.predict(list(x_valid))
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold['end_fold_%d' % (n_fold)] = k_fold['end_fold_%d' % (n_fold)].astype(int)
k_fold['start_fold_%d' % (n_fold)] = k_fold['start_fold_%d' % (n_fold)].astype(int)
k_fold['end_fold_%d' % (n_fold)].clip(0, k_fold['text_len'], inplace=True)
k_fold['start_fold_%d' % (n_fold)].clip(0, k_fold['end_fold_%d' % (n_fold)], inplace=True)
k_fold['prediction_fold_%d' % (n_fold)] = k_fold.apply(lambda x: decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], config['question_size'], tokenizer), axis=1)
k_fold['prediction_fold_%d' % (n_fold)].fillna(k_fold["text"], inplace=True)
k_fold['jaccard_fold_%d' % (n_fold)] = k_fold.apply(lambda x: jaccard(x['selected_text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
```
# Model loss graph
```
sns.set(style="whitegrid")
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
```
# Model evaluation
```
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Visualize predictions
```
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
```
|
github_jupyter
|
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
class RectifiedAdam(tf.keras.optimizers.Optimizer):
"""Variant of the Adam optimizer whose adaptive learning rate is rectified
so as to have a consistent variance.
It implements the Rectified Adam (a.k.a. RAdam) proposed by
Liyuan Liu et al. in [On The Variance Of The Adaptive Learning Rate
And Beyond](https://arxiv.org/pdf/1908.03265v1.pdf).
Example of usage:
```python
opt = tfa.optimizers.RectifiedAdam(lr=1e-3)
```
Note: `amsgrad` is not described in the original paper. Use it with
caution.
RAdam is not a placement of the heuristic warmup, the settings should be
kept if warmup has already been employed and tuned in the baseline method.
You can enable warmup by setting `total_steps` and `warmup_proportion`:
```python
opt = tfa.optimizers.RectifiedAdam(
lr=1e-3,
total_steps=10000,
warmup_proportion=0.1,
min_lr=1e-5,
)
```
In the above example, the learning rate will increase linearly
from 0 to `lr` in 1000 steps, then decrease linearly from `lr` to `min_lr`
in 9000 steps.
Lookahead, proposed by Michael R. Zhang et.al in the paper
[Lookahead Optimizer: k steps forward, 1 step back]
(https://arxiv.org/abs/1907.08610v1), can be integrated with RAdam,
which is announced by Less Wright and the new combined optimizer can also
be called "Ranger". The mechanism can be enabled by using the lookahead
wrapper. For example:
```python
radam = tfa.optimizers.RectifiedAdam()
ranger = tfa.optimizers.Lookahead(radam, sync_period=6, slow_step_size=0.5)
```
"""
def __init__(self,
learning_rate=0.001,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-7,
weight_decay=0.,
amsgrad=False,
sma_threshold=5.0,
total_steps=0,
warmup_proportion=0.1,
min_lr=0.,
name='RectifiedAdam',
**kwargs):
r"""Construct a new RAdam optimizer.
Args:
learning_rate: A `Tensor` or a floating point value. or a schedule
that is a `tf.keras.optimizers.schedules.LearningRateSchedule`
The learning rate.
beta_1: A float value or a constant float tensor.
The exponential decay rate for the 1st moment estimates.
beta_2: A float value or a constant float tensor.
The exponential decay rate for the 2nd moment estimates.
epsilon: A small constant for numerical stability.
weight_decay: A floating point value. Weight decay for each param.
amsgrad: boolean. Whether to apply AMSGrad variant of this
algorithm from the paper "On the Convergence of Adam and
beyond".
sma_threshold. A float value.
The threshold for simple mean average.
total_steps: An integer. Total number of training steps.
Enable warmup by setting a positive value.
warmup_proportion: A floating point value.
The proportion of increasing steps.
min_lr: A floating point value. Minimum learning rate after warmup.
name: Optional name for the operations created when applying
gradients. Defaults to "RectifiedAdam".
**kwargs: keyword arguments. Allowed to be {`clipnorm`,
`clipvalue`, `lr`, `decay`}. `clipnorm` is clip gradients
by norm; `clipvalue` is clip gradients by value, `decay` is
included for backward compatibility to allow time inverse
decay of learning rate. `lr` is included for backward
compatibility, recommended to use `learning_rate` instead.
"""
super(RectifiedAdam, self).__init__(name, **kwargs)
self._set_hyper('learning_rate', kwargs.get('lr', learning_rate))
self._set_hyper('beta_1', beta_1)
self._set_hyper('beta_2', beta_2)
self._set_hyper('decay', self._initial_decay)
self._set_hyper('weight_decay', weight_decay)
self._set_hyper('sma_threshold', sma_threshold)
self._set_hyper('total_steps', float(total_steps))
self._set_hyper('warmup_proportion', warmup_proportion)
self._set_hyper('min_lr', min_lr)
self.epsilon = epsilon or tf.keras.backend.epsilon()
self.amsgrad = amsgrad
self._initial_weight_decay = weight_decay
self._initial_total_steps = total_steps
def _create_slots(self, var_list):
for var in var_list:
self.add_slot(var, 'm')
for var in var_list:
self.add_slot(var, 'v')
if self.amsgrad:
for var in var_list:
self.add_slot(var, 'vhat')
def set_weights(self, weights):
params = self.weights
num_vars = int((len(params) - 1) / 2)
if len(weights) == 3 * num_vars + 1:
weights = weights[:len(params)]
super(RectifiedAdam, self).set_weights(weights)
def _resource_apply_dense(self, grad, var):
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype)
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
beta_1_t = self._get_hyper('beta_1', var_dtype)
beta_2_t = self._get_hyper('beta_2', var_dtype)
epsilon_t = tf.convert_to_tensor(self.epsilon, var_dtype)
local_step = tf.cast(self.iterations + 1, var_dtype)
beta_1_power = tf.pow(beta_1_t, local_step)
beta_2_power = tf.pow(beta_2_t, local_step)
if self._initial_total_steps > 0:
total_steps = self._get_hyper('total_steps', var_dtype)
warmup_steps = total_steps *\
self._get_hyper('warmup_proportion', var_dtype)
min_lr = self._get_hyper('min_lr', var_dtype)
decay_steps = tf.maximum(total_steps - warmup_steps, 1)
decay_rate = (min_lr - lr_t) / decay_steps
lr_t = tf.where(
local_step <= warmup_steps,
lr_t * (local_step / warmup_steps),
lr_t + decay_rate * tf.minimum(local_step - warmup_steps,
decay_steps),
)
sma_inf = 2.0 / (1.0 - beta_2_t) - 1.0
sma_t = sma_inf - 2.0 * local_step * beta_2_power / (
1.0 - beta_2_power)
m_t = m.assign(
beta_1_t * m + (1.0 - beta_1_t) * grad,
use_locking=self._use_locking)
m_corr_t = m_t / (1.0 - beta_1_power)
v_t = v.assign(
beta_2_t * v + (1.0 - beta_2_t) * tf.square(grad),
use_locking=self._use_locking)
if self.amsgrad:
vhat = self.get_slot(var, 'vhat')
vhat_t = vhat.assign(
tf.maximum(vhat, v_t), use_locking=self._use_locking)
v_corr_t = tf.sqrt(vhat_t / (1.0 - beta_2_power))
else:
vhat_t = None
v_corr_t = tf.sqrt(v_t / (1.0 - beta_2_power))
r_t = tf.sqrt((sma_t - 4.0) / (sma_inf - 4.0) * (sma_t - 2.0) /
(sma_inf - 2.0) * sma_inf / sma_t)
sma_threshold = self._get_hyper('sma_threshold', var_dtype)
var_t = tf.where(sma_t >= sma_threshold,
r_t * m_corr_t / (v_corr_t + epsilon_t), m_corr_t)
if self._initial_weight_decay > 0.0:
var_t += self._get_hyper('weight_decay', var_dtype) * var
var_update = var.assign_sub(
lr_t * var_t, use_locking=self._use_locking)
updates = [var_update, m_t, v_t]
if self.amsgrad:
updates.append(vhat_t)
return tf.group(*updates)
def _resource_apply_sparse(self, grad, var, indices):
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype)
beta_1_t = self._get_hyper('beta_1', var_dtype)
beta_2_t = self._get_hyper('beta_2', var_dtype)
epsilon_t = tf.convert_to_tensor(self.epsilon, var_dtype)
local_step = tf.cast(self.iterations + 1, var_dtype)
beta_1_power = tf.pow(beta_1_t, local_step)
beta_2_power = tf.pow(beta_2_t, local_step)
if self._initial_total_steps > 0:
total_steps = self._get_hyper('total_steps', var_dtype)
warmup_steps = total_steps *\
self._get_hyper('warmup_proportion', var_dtype)
min_lr = self._get_hyper('min_lr', var_dtype)
decay_steps = tf.maximum(total_steps - warmup_steps, 1)
decay_rate = (min_lr - lr_t) / decay_steps
lr_t = tf.where(
local_step <= warmup_steps,
lr_t * (local_step / warmup_steps),
lr_t + decay_rate * tf.minimum(local_step - warmup_steps,
decay_steps),
)
sma_inf = 2.0 / (1.0 - beta_2_t) - 1.0
sma_t = sma_inf - 2.0 * local_step * beta_2_power / (
1.0 - beta_2_power)
m = self.get_slot(var, 'm')
m_scaled_g_values = grad * (1 - beta_1_t)
m_t = m.assign(m * beta_1_t, use_locking=self._use_locking)
with tf.control_dependencies([m_t]):
m_t = self._resource_scatter_add(m, indices, m_scaled_g_values)
m_corr_t = m_t / (1.0 - beta_1_power)
v = self.get_slot(var, 'v')
v_scaled_g_values = (grad * grad) * (1 - beta_2_t)
v_t = v.assign(v * beta_2_t, use_locking=self._use_locking)
with tf.control_dependencies([v_t]):
v_t = self._resource_scatter_add(v, indices, v_scaled_g_values)
if self.amsgrad:
vhat = self.get_slot(var, 'vhat')
vhat_t = vhat.assign(
tf.maximum(vhat, v_t), use_locking=self._use_locking)
v_corr_t = tf.sqrt(vhat_t / (1.0 - beta_2_power))
else:
vhat_t = None
v_corr_t = tf.sqrt(v_t / (1.0 - beta_2_power))
r_t = tf.sqrt((sma_t - 4.0) / (sma_inf - 4.0) * (sma_t - 2.0) /
(sma_inf - 2.0) * sma_inf / sma_t)
sma_threshold = self._get_hyper('sma_threshold', var_dtype)
var_t = tf.where(sma_t >= sma_threshold,
r_t * m_corr_t / (v_corr_t + epsilon_t), m_corr_t)
if self._initial_weight_decay > 0.0:
var_t += self._get_hyper('weight_decay', var_dtype) * var
with tf.control_dependencies([var_t]):
var_update = self._resource_scatter_add(
var, indices, tf.gather(-lr_t * var_t, indices))
updates = [var_update, m_t, v_t]
if self.amsgrad:
updates.append(vhat_t)
return tf.group(*updates)
def get_config(self):
config = super(RectifiedAdam, self).get_config()
config.update({
'learning_rate':
self._serialize_hyperparameter('learning_rate'),
'beta_1':
self._serialize_hyperparameter('beta_1'),
'beta_2':
self._serialize_hyperparameter('beta_2'),
'decay':
self._serialize_hyperparameter('decay'),
'weight_decay':
self._serialize_hyperparameter('weight_decay'),
'sma_threshold':
self._serialize_hyperparameter('sma_threshold'),
'epsilon':
self.epsilon,
'amsgrad':
self.amsgrad,
'total_steps':
self._serialize_hyperparameter('total_steps'),
'warmup_proportion':
self._serialize_hyperparameter('warmup_proportion'),
'min_lr':
self._serialize_hyperparameter('min_lr'),
})
return config
database_base_path = '/kaggle/input/tweet-dataset-split-roberta-base-96/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# Unzip files
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_1.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_2.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_3.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_4.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_5.tar.gz
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
"MAX_LEN": 96,
"BATCH_SIZE": 32,
"EPOCHS": 5,
"LEARNING_RATE": 3e-5,
"ES_PATIENCE": 1,
"question_size": 4,
"N_FOLDS": 3,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
sequence_output = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
last_state = sequence_output[0]
x_start = layers.Dropout(0.1)(last_state)
x_start = layers.Conv1D(128, 2, padding='same')(x_start)
x_start = layers.LeakyReLU()(x_start)
x_start = layers.Conv1D(64, 2, padding='same')(x_start)
x_start = layers.Dense(1)(x_start)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('sigmoid', name='y_start')(x_start)
x_end = layers.Dropout(0.1)(last_state)
x_end = layers.Conv1D(128, 2, padding='same')(x_end)
x_end = layers.LeakyReLU()(x_end)
x_end = layers.Conv1D(64, 2, padding='same')(x_end)
x_end = layers.Dense(1)(x_end)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('sigmoid', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
optimizer = RectifiedAdam(lr=config['LEARNING_RATE'],
total_steps=(len(k_fold[k_fold['fold_1'] == 'train']) // config['BATCH_SIZE']) * config['EPOCHS'],
warmup_proportion=0.1,
min_lr=1e-7)
model.compile(optimizer, loss={'y_start': losses.BinaryCrossentropy(),
'y_end': losses.BinaryCrossentropy()},
metrics={'y_start': metrics.BinaryAccuracy(),
'y_end': metrics.BinaryAccuracy()})
return model
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
history_list = []
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
### Delete data dir
shutil.rmtree(base_data_path)
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=True, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
history = model.fit(list(x_train), list(y_train),
validation_data=(list(x_valid), list(y_valid)),
batch_size=config['BATCH_SIZE'],
callbacks=[checkpoint, es],
epochs=config['EPOCHS'],
verbose=2).history
history_list.append(history)
# Make predictions
train_preds = model.predict(list(x_train))
valid_preds = model.predict(list(x_valid))
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold['end_fold_%d' % (n_fold)] = k_fold['end_fold_%d' % (n_fold)].astype(int)
k_fold['start_fold_%d' % (n_fold)] = k_fold['start_fold_%d' % (n_fold)].astype(int)
k_fold['end_fold_%d' % (n_fold)].clip(0, k_fold['text_len'], inplace=True)
k_fold['start_fold_%d' % (n_fold)].clip(0, k_fold['end_fold_%d' % (n_fold)], inplace=True)
k_fold['prediction_fold_%d' % (n_fold)] = k_fold.apply(lambda x: decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], config['question_size'], tokenizer), axis=1)
k_fold['prediction_fold_%d' % (n_fold)].fillna(k_fold["text"], inplace=True)
k_fold['jaccard_fold_%d' % (n_fold)] = k_fold.apply(lambda x: jaccard(x['selected_text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
sns.set(style="whitegrid")
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
| 0.921915 | 0.697403 |
<img src="data/img/np_basics_2_logo.png" height=300px width=650px>
```
import numpy as np
```
To revise what we have learnt till now, let's look at the following example
# Diffusion using random walks
The following example has been adapted from [scipylectures.org](https://scipy-lectures.org/intro/numpy/operations.html#basic-reductions).
We will model the diffussion of a particle in a one dimensional gird using a random walk. The particle starts at the origin at $t=0$ and at each time step jumps right or left with equal probability. A step towards left is denoted by a displacement of `-1` units and a step towards right is `+1` units.
<img src="data/img/random_walk_1.png" height=100 width=450>
**We want to find the typical distance (in units of grid points) from the origin of a random walker after `t` left or right jumps**
To achieve this, we will generate a random trajectory for a walker. We will then generate a lot of such walks (lets call them *stories*) and check their statistical properties to find a pattern.
The simulation will be done using NumPy array computing tricks: we are going to create a 2D array with the *stories* along one axis and time along another.
<img src="data/img/random_walk_schema_1.png" height=300px width=300px>
```
n_stories = 10000 # number of stories i.e the maximum number of independent walks
t_max = 200 # time during which we follow the walker
```
We will create the array of steps taken by the walkers shown in the above schema using the function `np.random.choice()`. The first argument will be a list of values from which the numbers will be chosen i.e. `[-1,1]`. The second argument will be a tuple denoting the shape of the array to be created.
```
steps = np.random.choice() # COMPLETE THIS LINE OF CODE
```
We find the *displacement* from the origin for each of the walker as a function of time by calculating the cumulative sum of the steps **along the time axis** using `np.cumsum()`.
<img src="data/img/random_walk_schema_2.png" height=300px width=300px>
```
displacements = np.cumsum() # COMPLETE THIS LINE OF CODE
```
We now find the root mean squared displacement as a function of time by calculating the statistic along the axis of the *stories*. You can use the `np.sqrt()`, `np.mean` and `**` functions and operations.
```
# COMPLETE THESE THREE LINES OF CODE
sq_displacement = #squared displacement
mean_sq_disp = #mean squared displacement along the story axis
rms_disp = # root mean squared displacement
```
Let's now plot our results. We generate an array containing the time steps and plot the RMS displacement versus the time steps. We also plot a $\sqrt{t}$ in the same plot.
```
# generate the time axis
t = # COMPLETE THIS LINE OF CODE
import matplotlib.pyplot as plt
plt.figure(figsize=(12,8))
plt.scatter(t, rms_disp, label = "Simulation", marker="x", c="C0")
plt.plot(t, np.sqrt(t), label = r"$t$", c="C1", lw=2)
plt.legend()
plt.xlabel(r"$t$", fontsize=20)
plt.ylabel(r"$\sqrt{\langle (\delta x)^2 \rangle}$", fontsize=20)
```
We find a well-known result in physics: the RMS distance grows as the square root of the time!
To get a feel of how efficiently we did all the above calculations on such a huge number of elements, let us time the code used to do all the calculations. Paste the all code to do the calculations (except plotting) in the cell below:
```
%%timeit
# PASTE THE CODE HERE
```
For comparison we will do a very simple calculation on the same number of elements using native Python. I hope this helps you to appreciate vectorized calculations!
```
%%timeit
vals = [i for i in range(n_stories*t_max)]
new_vals = [i+1 for i in vals]
```
# Fancy Indexing
### Boolean arrays and logical operations
Just like `int` and `float` the elements of a NumPy array can also be boolean values i.e. `True` or `False`. These arrays may be created as a result of element wise comparison between two arrays.
```
a1 = np.array([1, 2, 3, 4])
b1 = np.array([4, 2, 2, 4])
a1 == b1
a1 > b1
```
**NOTE:** if we want to check whether two arrays are identical to each other, we can use the function `np.array_equal()`
Element wise logical operations can be done using built in functions
```
a2 = np.array([True, True, False, False])
b2 = np.array([True, True, False, False])
np.logical_or(a2, b2)
```
**NOTE:** In addition to the predefined functions shown above the binary operators `&`, `|` and `~` can also be used to determine the element wise logical AND, OR and NOT.
When performing `sum()` on boolean arrays, the `True` values are treated as 1 and `False` as zero.
```
a2.sum()
```
### Indexing with boolean arrays
If instead of using integers we index arrays with other boolean arrays of same (or compatible) shape, the returned array will be composed of elements of the original array for which the corresponding boolean index was True. For example
```
a1
a1[[True, False, False, True]]
```
We may have an array of data where negative values indicate some kind of error. We can use a boolean *mask* to select array elements which satisfy our criteria
```
x = np.array([1.2, 2.8, 3.5, -999, 2.7, 4.8, -999])
mask = (x > 0)
mask
x[mask]
```
Generally it is done in a single step
```
x[x>0]
```
We can also set specific values for array elements which satisfy our criteria
```
x[x<0] = np.nan
x
```
**NOTE:** `np.nan` is a special data object (of type `float`) which is used to denote invalid or missing values. NumPy is built to gracefully handle invalid or missing data points as long as they are marked with `NaN` (Not a Number). This is the recommended way of doing this instead of the more traditional way of denoting missing data with absurd numbers. For convenience, NumPy has a host of such special constants defined which are listed [here](https://numpy.org/doc/stable/reference/constants.html?highlight=constants).
### `np.where()`: Turning a mask into indices
```
x = np.arange(10).reshape((2, 5))
x
```
The `np.where` function returns the locations of the elements where the given condition is `True`
```
np.where(x < 3)
```
**NOTE:** Instead of returning just the locations of elements `np.where` can also return elements from one of two arrays based on the condition. You can find details [here](https://numpy.org/doc/stable/reference/generated/numpy.where.html?highlight=where#numpy.where)
### Indexing with other sequences
We can also index elements of arrays using other arrays whose elements denote the indices of the elements to be selected.
```
x = np.arange(16).reshape((4, 4))
x
x[range(4), range(4)]
```
The image below from [scipylectures.org](https://scipy-lectures.org/intro/numpy/array_object.html#fancy-indexing) summarizes fancy indexing.
<img src="data/img/np_fancy_indexing.png" height=300px width=650px>
### Classifying the pretty pictures
Another `.npy` file (`data/sdss_morpho.npy`) has been provided which contains morphological classification of the galaxies we dealt with in the previous notebook. The galaxy is *spheroidal* if the value of the corresponding element is `0` and *discy* if the value is `1`. First read the two data files (images and morphologies) into NumPy arrays.
```
# COMPLETE THESE TWO LINES OF CODE
img =
morpho =
```
How many of the given galaxies are spheroids?
```
morpho[] #COMPLETE THIS LINE OF CODE
```
Using boolean indexing, select only the images of spheroidal galaxies
```
spheroid_img = #COMPLETE THIS LINE OF CODE
```
Flag all the pixels which have negative values by replacing them with `np.nan`.
```
spheroid_img[] = #COMPLETE THIS LINE OF CODE
```
Now plot the $r$ wavelength band of all these spheroids in a similar way to the last notebook.
```
# COMPLETE THESE TWO LINES OF CODE
for i in range(): #loop over the number of spheroid
plt.imshow(np.tanh(spheroid[]) , cmap="gray") #select the correct galaxy and wavelength band
```
# Array shape manipulation
NumPy lets us rearrange the elements in an array and reshape them into other forms.
### Flattening
We can unpack the elements of a multidimensional array into a 1D array using the `array.ravel()` method.
```
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a.shape)
print(a.ravel())
```
Create the transpose of the above array and flatten it to see how the method works on arrays of different shapes.
```
a_transpose = # COMPLETE THIS LINE OF CODE
print(a_transpose)
a_transpose.ravel()
```
### Dimension adding
Indexing with the np.newaxis object allows us to add an axis to an array
```
z = np.array([1, 2, 3])
print(z)
print(z.shape)
z[:, np.newaxis]
```
### Reshaping
The shape of an array can be modified, as long as the total number of elements is unchanged. Here we use reshape put the flattened array back to its original shape.
```
b = a.ravel()
b = b.reshape((2, 3))
b
```
Create a 2$\times$4 matrix with elements starting from 0 and increasing by 1 using `array.reshape()`
```
.reshape() # COMPLETE THIS LINE OF CODE
```
**NOTE:** The reshape operation (also slicing and many other NumPy operations) creates a *view* of the original array. This is just an efficient way of accessing array data.
**When modifying the view, the original array is modified as well:**
```
arr = np.arange(8) # Create an array
arr2 = arr.reshape(2, 4) #Reshape the array (this creates a view)
arr[0] = 1000 # change an element of the first array
arr
arr2
```
# Broadcasting
As we have seen basic operations on NumPy arrays (addition, etc.) are elementwise. Operations between two arrays work when the arrays are of same size. **However** It is also possible to do operations (i.e. `+`, `-`, `*`, `/`) between arrays of different sizes if NumPy can transform these arrays so that they all have the same size, this conversion is called *broadcasting*. The process can be illustrated using this image from [scipy-lectures.org](https://scipy-lectures.org/intro/numpy/operations.html#broadcasting).
<img src="data/img/np_broadcasting.png" height=300px width=800px>
We can check the above by seeing that this works
```
arr1 = np.ones((2, 3))
arr2 = np.ones((2, 1))
arr1 + arr2
```
While this does not
```
arr1 = np.ones((2, 3))
arr2 = np.ones(2)
arr1 + arr2
```
Now try this:
`A = [[1 2 3 4]
[5 6 7 8]]`
Use `np.arange` and `np.reshape` to create the array `A`.
The array is defined as `B = [1 2]`
Use broadcasting to add B to each column of A to create the final array
`A + B = [[2 3 4 5]
[7 8 9 10]`
```
A = # COMPLETE THIS LINE OF CODE
B = np.array([1,2])
A + B # COMPLETE THIS LINE OF CODE
```
### Scaling a dataset
As a first step of many kinds of data analysis, we scale the data my subtracting the mean and dividing by the standard deviation. We will perform such an operation efficiently with the help of Broadcasting. First lets create our simulated dataset.
```
X = np.random.normal([5,10,15],[2,3,4], (10000, 3))
X.shape
```
Our simulated data set `X` has measurements of 3 properties for 10000 different objects. Their respective distributions (Gaussians with different means and variances) are plotted below. The aim is to scale the data set so that it has zero mean and unit standard deviation.
```
plt.figure(figsize=(12,7))
plt.hist(X[:,0], bins=50, histtype="step", label="Property 1")
plt.hist(X[:,1], bins=50, histtype="step", label="Property 2")
plt.hist(X[:,2], bins=50, histtype="step", label="Property 3")
plt.legend()
```
Find the mean (`np.mean()`) and the standard deviation (`np.std()`) for each of the property
```
X_mean = #COMPLETE THESE TWO LINES OF CODE
X_std =
```
Computed the scaled dataset by subtracting the mean and dividing by the standard deviation corresponding to each property
```
X_scaled = #COMPLETE THIS LINE OF CODE
```
We can verify the operation by seeing the distributions.
```
plt.figure(figsize=(12,7))
plt.hist(X[:,0], bins=50, histtype="step", label="Scaled property 1")
plt.hist(X[:,1], bins=50, histtype="step", label="Scaled property 2")
plt.hist(X[:,2], bins=50, histtype="step", label="Scaled property 3")
plt.legend()
```
# Summary
I hope by now you appreciate how efficiently (both in terms of run time and number of lines of code written) we can perform operations on multi-dimensional arrays using NumPy.
**If there are three main lessons to be learnt from this tutorial, they should be:**
- vectorize (eliminate loops!)
- vectorize (eliminate loops!)
- vectorize (eliminate loops!)
# Acknowledments
This tutorial is heavily derived from the following sources. It is recommended to check them out for a comprehensive coverage of topics.
- [scipy-lectures](https://scipy-lectures.org/)
- [The Python Data Science Handbook](https://jakevdp.github.io/PythonDataScienceHandbook/)
- [2016 Python Bootcamp for UW Astronomy and Physics](https://github.com/bmorris3/2014_fall_ASTR599)
- [Numpy Documentation](https://numpy.org/doc/stable/)
|
github_jupyter
|
import numpy as np
n_stories = 10000 # number of stories i.e the maximum number of independent walks
t_max = 200 # time during which we follow the walker
steps = np.random.choice() # COMPLETE THIS LINE OF CODE
displacements = np.cumsum() # COMPLETE THIS LINE OF CODE
# COMPLETE THESE THREE LINES OF CODE
sq_displacement = #squared displacement
mean_sq_disp = #mean squared displacement along the story axis
rms_disp = # root mean squared displacement
# generate the time axis
t = # COMPLETE THIS LINE OF CODE
import matplotlib.pyplot as plt
plt.figure(figsize=(12,8))
plt.scatter(t, rms_disp, label = "Simulation", marker="x", c="C0")
plt.plot(t, np.sqrt(t), label = r"$t$", c="C1", lw=2)
plt.legend()
plt.xlabel(r"$t$", fontsize=20)
plt.ylabel(r"$\sqrt{\langle (\delta x)^2 \rangle}$", fontsize=20)
%%timeit
# PASTE THE CODE HERE
%%timeit
vals = [i for i in range(n_stories*t_max)]
new_vals = [i+1 for i in vals]
a1 = np.array([1, 2, 3, 4])
b1 = np.array([4, 2, 2, 4])
a1 == b1
a1 > b1
a2 = np.array([True, True, False, False])
b2 = np.array([True, True, False, False])
np.logical_or(a2, b2)
a2.sum()
a1
a1[[True, False, False, True]]
x = np.array([1.2, 2.8, 3.5, -999, 2.7, 4.8, -999])
mask = (x > 0)
mask
x[mask]
x[x>0]
x[x<0] = np.nan
x
x = np.arange(10).reshape((2, 5))
x
np.where(x < 3)
x = np.arange(16).reshape((4, 4))
x
x[range(4), range(4)]
# COMPLETE THESE TWO LINES OF CODE
img =
morpho =
morpho[] #COMPLETE THIS LINE OF CODE
spheroid_img = #COMPLETE THIS LINE OF CODE
spheroid_img[] = #COMPLETE THIS LINE OF CODE
# COMPLETE THESE TWO LINES OF CODE
for i in range(): #loop over the number of spheroid
plt.imshow(np.tanh(spheroid[]) , cmap="gray") #select the correct galaxy and wavelength band
a = np.array([[1, 2, 3], [4, 5, 6]])
print(a.shape)
print(a.ravel())
a_transpose = # COMPLETE THIS LINE OF CODE
print(a_transpose)
a_transpose.ravel()
z = np.array([1, 2, 3])
print(z)
print(z.shape)
z[:, np.newaxis]
b = a.ravel()
b = b.reshape((2, 3))
b
.reshape() # COMPLETE THIS LINE OF CODE
arr = np.arange(8) # Create an array
arr2 = arr.reshape(2, 4) #Reshape the array (this creates a view)
arr[0] = 1000 # change an element of the first array
arr
arr2
arr1 = np.ones((2, 3))
arr2 = np.ones((2, 1))
arr1 + arr2
arr1 = np.ones((2, 3))
arr2 = np.ones(2)
arr1 + arr2
A = # COMPLETE THIS LINE OF CODE
B = np.array([1,2])
A + B # COMPLETE THIS LINE OF CODE
X = np.random.normal([5,10,15],[2,3,4], (10000, 3))
X.shape
plt.figure(figsize=(12,7))
plt.hist(X[:,0], bins=50, histtype="step", label="Property 1")
plt.hist(X[:,1], bins=50, histtype="step", label="Property 2")
plt.hist(X[:,2], bins=50, histtype="step", label="Property 3")
plt.legend()
X_mean = #COMPLETE THESE TWO LINES OF CODE
X_std =
X_scaled = #COMPLETE THIS LINE OF CODE
plt.figure(figsize=(12,7))
plt.hist(X[:,0], bins=50, histtype="step", label="Scaled property 1")
plt.hist(X[:,1], bins=50, histtype="step", label="Scaled property 2")
plt.hist(X[:,2], bins=50, histtype="step", label="Scaled property 3")
plt.legend()
| 0.493164 | 0.993022 |
<img src="../images/aeropython_logo.png" alt="AeroPython" style="width: 300px;"/>
# Resolución de Ecuaciones Diferenciales Ordinarias
_¿Te acuerdas de todos esos esquemas numéricos para integrar ecuaciones diferenciales ordinarias? Es bueno saber que existen y qué peculiaridades tiene cada uno, pero en este curso no queremos implementar esos esquemas: queremos resolver las ecuaciones. Los problemas de evolución están por todas partes en ingeniería y son de los más divertidos de programar._
Para integrar EDOs vamos a usar la función `odeint` del paquete `integrate`, que permite integrar sistemas del tipo:
$$ \frac{d\mathbf{y}}{dt}=\mathbf{f}\left(\mathbf{y},t\right)$$
con condiciones iniciales $\mathbf{y}(\mathbf{0}) = \mathbf{y_0}$.
<div class="alert alert-error">**¡Importante!**: La función del sistema recibe como primer argumento $\mathbf{y}$ (un array) y como segundo argumento el instante $t$ (un escalar). Esta convención va exactamente al revés que en MATLAB y si se hace al revés obtendremos errores o, lo que es peor, resultados incorrectos.</div>
Vamos a integrar primero una EDO elemental, cuya solución ya conocemos:
$$y' + y = 0$$
$$f(y, t) = \frac{dy}{dt} = -y$$
Condiciones iniciales:
Integramos y representamos la solución:
Pero, ¿cómo se han seleccionado los puntos en los que se calcula la solución? El solver los ha calculado por nosotros. Si queremos tener control sobre estos puntos, podemos pasar de manera explícita el vector de tiempos:
Probemos a pintar las dos soluciones anteriores, una encima de la otra:
Podemos observar que a pesar de que en la primera se han usado muchos menos puntos, aquellos en los que se ha calculado la solución coinciden con el segundo resultado. Esto se debe a que, en realidad, el solver siempre da los pasos que considere necesarios para calcular la solución, pero sólo guarda los que nosotros le indicamos. Esto lo podemos ver del siguiente modo:
De hecho podemos usar la salida densa para obtener la solución en un punto cualquiera:
### EDOs de orden superior
Tendremos que acordarnos ahora de cómo reducir las ecuaciones de orden. De nuevo, vamos a probar con un ejemplo académico:
$$y + y'' = 0$$
$$\mathbf{y} \leftarrow \pmatrix{y \\ y'}$$
$$\mathbf{f}(\mathbf{y}) = \frac{d\mathbf{y}}{dt} = \pmatrix{y \\ y'}' = \pmatrix{y' \\ y''} = \pmatrix{y' \\ -y}$$
## Para ampliar
En nuestra edición anterior del curso de AeroPython puedes ver una aplicación muy interesante de lo que hemos visto hasta ahora al **salto de Felix Baumgartner**. ¡Aquí lo tienes!
http://nbviewer.ipython.org/github/AeroPython/Curso_AeroPython/blob/v1.0/Notebooks/Clase6b_Finale.ipynb
$$\displaystyle m \frac{d^2 y}{d t^2} = -m g + D$$
---
<br/>
#### <h4 align="right">¡Síguenos en Twitter!
<br/>
###### <a href="https://twitter.com/AeroPython" class="twitter-follow-button" data-show-count="false">Follow @AeroPython</a> <script>!function(d,s,id){var js,fjs=d.getElementsByTagName(s)[0],p=/^http:/.test(d.location)?'http':'https';if(!d.getElementById(id)){js=d.createElement(s);js.id=id;js.src=p+'://platform.twitter.com/widgets.js';fjs.parentNode.insertBefore(js,fjs);}}(document, 'script', 'twitter-wjs');</script>
<br/>
###### Este notebook ha sido realizado por: Juan Luis Cano, y Álex Sáez
<br/>
##### <a rel="license" href="http://creativecommons.org/licenses/by/4.0/deed.es"><img alt="Licencia Creative Commons" style="border-width:0" src="http://i.creativecommons.org/l/by/4.0/88x31.png" /></a><br /><span xmlns:dct="http://purl.org/dc/terms/" property="dct:title">Curso AeroPython</span> por <span xmlns:cc="http://creativecommons.org/ns#" property="cc:attributionName">Juan Luis Cano Rodriguez y Alejandro Sáez Mollejo</span> se distribuye bajo una <a rel="license" href="http://creativecommons.org/licenses/by/4.0/deed.es">Licencia Creative Commons Atribución 4.0 Internacional</a>.
---
_Las siguientes celdas contienen configuración del Notebook_
_Para visualizar y utlizar los enlaces a Twitter el notebook debe ejecutarse como [seguro](http://ipython.org/ipython-doc/dev/notebook/security.html)_
File > Trusted Notebook
```
# Esta celda da el estilo al notebook
from IPython.core.display import HTML
css_file = '../styles/aeropython.css'
HTML(open(css_file, "r").read())
```
|
github_jupyter
|
# Esta celda da el estilo al notebook
from IPython.core.display import HTML
css_file = '../styles/aeropython.css'
HTML(open(css_file, "r").read())
| 0.317109 | 0.962285 |
# Model evaluation using cross-validation
In this notebook, we will still use only numerical features.
We will discuss the practical aspects of assessing the generalization
performance of our model via **cross-validation** instead of a single
train-test split.
## Data preparation
First, let's load the full adult census dataset.
```
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
```
We will now drop the target from the data we will use to train our
predictive model.
```
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=target_name)
```
Then, we select only the numerical columns, as seen in the previous
notebook.
```
numerical_columns = ["age", "capital-gain", "capital-loss", "hours-per-week"]
data_numeric = data[numerical_columns]
```
We can now create a model using the `make_pipeline` tool to chain the
preprocessing and the estimator in every iteration of the cross-validation.
```
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
model = make_pipeline(StandardScaler(), LogisticRegression())
```
## The need for cross-validation
In the previous notebook, we split the original data into a training set and a
testing set. The score of a model will in general depend on the way we make
such a split. One downside of doing a single split is that it does not give
any information about this variability. Another downside, in a setting where
the amount of data is small, is that the data available for training and
testing will be even smaller after splitting.
Instead, we can use cross-validation. Cross-validation consists of repeating
the procedure such that the training and testing sets are different each time.
Generalization performance metrics are collected for each repetition and then
aggregated. As a result we can assess the variability of our measure of the
model's generalization performance.
Note that there exists several cross-validation strategies, each of them
defines how to repeat the `fit`/`score` procedure. In this section, we will
use the K-fold strategy: the entire dataset is split into `K` partitions. The
`fit`/`score` procedure is repeated `K` times where at each iteration `K - 1`
partitions are used to fit the model and `1` partition is used to score. The
figure below illustrates this K-fold strategy.

<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">This figure shows the particular case of <strong>K-fold</strong> cross-validation strategy.
For each cross-validation split, the procedure trains a clone of model on all the red
samples and evaluate the score of the model on the blue samples.
As mentioned earlier, there is a variety of different cross-validation
strategies. Some of these aspects will be covered in more detail in future notebooks.</p>
</div>
Cross-validation is therefore computationally intensive because it requires
training several models instead of one.
In scikit-learn, the function `cross_validate` allows to do cross-validation
and you need to pass it the model, the data, and the target. Since there
exists several cross-validation strategies, `cross_validate` takes a parameter
`cv` which defines the splitting strategy.
```
%%time
from sklearn.model_selection import cross_validate
model = make_pipeline(StandardScaler(), LogisticRegression())
cv_result = cross_validate(model, data_numeric, target, cv=5)
cv_result
```
The output of `cross_validate` is a Python dictionary, which by default
contains three entries:
- (i) the time to train the model on the training data for each fold,
- (ii) the time to predict with the model on the testing data for each fold,
- (iii) the default score on the testing data for each fold.
Setting `cv=5` created 5 distinct splits to get 5 variations for the training
and testing sets. Each training set is used to fit one model which is then
scored on the matching test set. The default strategy when setting `cv=int` is
the K-fold cross-validation where `K` corresponds to the (integer) number of
splits. Setting `cv=5` or `cv=10` is a common practice, as it is a good
trade-off between computation time and stability of the estimated variability.
Note that by default the `cross_validate` function discards the `K` models
that were trained on the different overlapping subset of the dataset. The goal
of cross-validation is not to train a model, but rather to estimate
approximately the generalization performance of a model that would have been
trained to the full training set, along with an estimate of the variability
(uncertainty on the generalization accuracy).
You can pass additional parameters to
[`sklearn.model_selection.cross_validate`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_validate.html)
to collect additional information, such as the training scores of the models
obtained on each round or even return the models themselves instead of
discarding them. These features will be covered in a future notebook.
Let's extract the scores computed on the test fold of each cross-validation
round from the `cv_result` dictionary and compute the mean accuracy and the
variation of the accuracy across folds.
```
scores = cv_result["test_score"]
print(
"The mean cross-validation accuracy is: "
f"{scores.mean():.3f} +/- {scores.std():.3f}"
)
```
Note that by computing the standard-deviation of the cross-validation scores,
we can estimate the uncertainty of our model generalization performance. This
is the main advantage of cross-validation and can be crucial in practice, for
example when comparing different models to figure out whether one is better
than the other or whether our measures of the generalization performance of each
model are within the error bars of one-another.
In this particular case, only the first 2 decimals seem to be trustworthy. If
you go up in this notebook, you can check that the performance we get with
cross-validation is compatible with the one from a single train-test split.
In this notebook we assessed the generalization performance of our model via
**cross-validation**.
|
github_jupyter
|
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=target_name)
numerical_columns = ["age", "capital-gain", "capital-loss", "hours-per-week"]
data_numeric = data[numerical_columns]
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
model = make_pipeline(StandardScaler(), LogisticRegression())
%%time
from sklearn.model_selection import cross_validate
model = make_pipeline(StandardScaler(), LogisticRegression())
cv_result = cross_validate(model, data_numeric, target, cv=5)
cv_result
scores = cv_result["test_score"]
print(
"The mean cross-validation accuracy is: "
f"{scores.mean():.3f} +/- {scores.std():.3f}"
)
| 0.571767 | 0.99395 |
# What, Why and How to Use ECDFS
by John DeJesus
This is the notebook for the [ECDF Youtube Tutorial](https://www.youtube.com/watch?v=fCllDyW9Nn4&t=1s). You may read this on its own or follow along with the video.
## By the end of the tutorial you will be able to:
* Understand what an ecdf is.
* Implement an ecdf with python code.
* Interpret an ecdf
An **Empirical Cumulative Distribution Function** is a step function used to show the distribution of data. It can answer what percentage of the data is under a specific value.
```
# Load Libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
# Load the data from data.world
avocado = pd.read_csv('https://query.data.world/s/qou5hvocejsu4qt4qb2xlndg5ntzbm')
# Preview the data
avocado.head()
# check the info
avocado.info()
# Since there is a year column let's see how many years are there.
avocado.Year.unique()
```
### Why use ecdfs over histograms?
Histogram can show the distribution of your data also. However you can be tricked by histograms depending on the number of bins you used. See the example below
```
# Looking at the price data as a histogram with 5 bins
plt.hist(avocado.AveragePrice, bins = 5 )
plt.title('Average Price Hist with 5 Bins')
plt.xlabel('Average Price')
plt.ylabel('Count')
plt.show()
# Looking at the price data as a histogram with 25 bins.
plt.hist(avocado.AveragePrice, bins = 25)
plt.title('Average Price Hist with 25 Bins')
plt.xlabel('Average Price')
plt.ylabel('Count')
plt.show()
# Looking at the price data as a histogram with 50 bins.
plt.hist(avocado.AveragePrice, bins = 50)
plt.title('Average Price Hist with 50 Bins')
plt.xlabel('Average Price')
plt.ylabel('Count')
plt.show()
```
Now all of a sudden our data is bimodal with 25 bins instead of unimodal with 5 bins. The bimodal peaks show more when we increase the number of bins.
```
# Creating our ecdf function
def ecdf(data):
"""
This function creates the x and y axis for a ecdf
plot given the data as input.
"""
xaxis = np.sort(data)
yaxis = np.arange(1,len(data)+1)/len(data)
return xaxis, yaxis
# Creating the xaxis and yaxis for our ecdf on price
x,y = ecdf(avocado['AveragePrice'])
# Plotting our ecdf
plt.plot(x,y,linestyle='none',marker='.')
plt.title('ECDF of Average Avocado Prices')
plt.xlabel('Price per Unit')
plt.ylabel('Percentage')
plt.margins(0.02)
plt.show()
```
### Recall the normal distribution and how to read it.

Gaussian Distribution. Image from etfhq.com
```
# Create a function for computing and plotting the ECDF with default parameters
def plot_ecdf(data,title = "ECDF Plot", xlabel = 'Data Values', ylabel = 'Percentage'):
"""
Function to plot ecdf taking a column of data as input.
"""
xaxis = np.sort(data)
yaxis = np.arange(1, len(data)+1)/len(data)
plt.plot(xaxis,yaxis,linestyle='none',marker='.')
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.margins(0.02)
# Creating the same plot with our ecdf function
plot_ecdf(avocado['AveragePrice'])
plt.show()
```
### Information we can get from our ECDF
1. 20% of the avocados had a price of about 1 dollar or less.
2. About 90% of the avocados had a price of 2 dollars or less
```
# plotting multiple may be difficult to read.
# set a variable for years
years = avocado.Year.unique()
# plot all years of the
for year in years:
plot_ecdf(avocado['AveragePrice'][avocado.Year == year])
plt.legend(labels=years)
plt.show()
# Sometimes less is more
plot_ecdf(avocado['AveragePrice'][avocado.Year == 2017])
plot_ecdf(avocado['AveragePrice'][avocado.Year == 2018])
plt.legend(labels=years[-2:])
plt.show()
```
### Info we can obtain from our ECDF
1. Average Prices of avocados overall were less in 2018 versus 2017.
2. The maximum average price of avocados was less than 2.50 in 2018.
3. The minimum average price of avocadoes was less in 2017 versus 2018.
# Practice Exercises
* Plot an ecdf using the other numeric columns in this data set.
* Plot the ecdfs of a numeric column with conditions.
* Plot ecdfs of your own data.
* Practice interpreting the charts.
# Summary
* ECDFs are used to show the distribution of your data.
* The advantage over histograms is that they are immune to binning bias.
* You can read them similarily to a normal distribution.
# Thanks for watching/reading! Let me know if you found this helpful.
* [Video Tutorial](https://www.youtube.com/watch?v=fCllDyW9Nn4&t=1s)
* [GitHub](http://github.com/johndeJesus22)
* [Twitter](https://twitter.com/johnnydata22)
* [LinkedIn](https://www.linkedin.com/in/jdejesus22/)
|
github_jupyter
|
# Load Libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
# Load the data from data.world
avocado = pd.read_csv('https://query.data.world/s/qou5hvocejsu4qt4qb2xlndg5ntzbm')
# Preview the data
avocado.head()
# check the info
avocado.info()
# Since there is a year column let's see how many years are there.
avocado.Year.unique()
# Looking at the price data as a histogram with 5 bins
plt.hist(avocado.AveragePrice, bins = 5 )
plt.title('Average Price Hist with 5 Bins')
plt.xlabel('Average Price')
plt.ylabel('Count')
plt.show()
# Looking at the price data as a histogram with 25 bins.
plt.hist(avocado.AveragePrice, bins = 25)
plt.title('Average Price Hist with 25 Bins')
plt.xlabel('Average Price')
plt.ylabel('Count')
plt.show()
# Looking at the price data as a histogram with 50 bins.
plt.hist(avocado.AveragePrice, bins = 50)
plt.title('Average Price Hist with 50 Bins')
plt.xlabel('Average Price')
plt.ylabel('Count')
plt.show()
# Creating our ecdf function
def ecdf(data):
"""
This function creates the x and y axis for a ecdf
plot given the data as input.
"""
xaxis = np.sort(data)
yaxis = np.arange(1,len(data)+1)/len(data)
return xaxis, yaxis
# Creating the xaxis and yaxis for our ecdf on price
x,y = ecdf(avocado['AveragePrice'])
# Plotting our ecdf
plt.plot(x,y,linestyle='none',marker='.')
plt.title('ECDF of Average Avocado Prices')
plt.xlabel('Price per Unit')
plt.ylabel('Percentage')
plt.margins(0.02)
plt.show()
# Create a function for computing and plotting the ECDF with default parameters
def plot_ecdf(data,title = "ECDF Plot", xlabel = 'Data Values', ylabel = 'Percentage'):
"""
Function to plot ecdf taking a column of data as input.
"""
xaxis = np.sort(data)
yaxis = np.arange(1, len(data)+1)/len(data)
plt.plot(xaxis,yaxis,linestyle='none',marker='.')
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.margins(0.02)
# Creating the same plot with our ecdf function
plot_ecdf(avocado['AveragePrice'])
plt.show()
# plotting multiple may be difficult to read.
# set a variable for years
years = avocado.Year.unique()
# plot all years of the
for year in years:
plot_ecdf(avocado['AveragePrice'][avocado.Year == year])
plt.legend(labels=years)
plt.show()
# Sometimes less is more
plot_ecdf(avocado['AveragePrice'][avocado.Year == 2017])
plot_ecdf(avocado['AveragePrice'][avocado.Year == 2018])
plt.legend(labels=years[-2:])
plt.show()
| 0.84489 | 0.985691 |
```
Start Location - Lat & Long
Destination - Lat & long
Time of job
1. Start from HQ
2. Calculate all time duration between all possible pairs using google matrix api and select the shortest duration as next checkpoint
3. Update startpoint as the next checkpoint
4. Repeat steps until no more job/threhold reached (latest working hour or number ofjobs)
import requests
import json
import googlemaps
def get_dist_duration(origin,destination):
#Enter your source and destination city
originPoint = origin
destinationPoint= destination
#Place your google map API_KEY to a variable
apiKey = 'AIzaSyDj5Vg9hZLlb78EtvVsmXeMONDajrzl32c'
#Store google maps api url in a variable
gmaps = googlemaps.Client(key=apiKey)
results = gmaps.distance_matrix(originPoint,destinationPoint)
return results
response = requests.get("http://54.254.210.52:8080/api/v1/jobs/")
if response.status_code == 200:
mock_data = []
data = response.json()
for datum in data:
mock_data.append(datum['end_address'])
else:
mock_data = ['MOE HQ (Buona Vista), 1 N Buona Vista Dr','JTC Launchpad, 73A Ayer Rajah Crescent', 'National University Hospital, 5 Lower Kent Ridge Rd,']
def get_optimal_path(job_list): #job list = list of available jobs to consider containing jobs with (lat,long, time)
hq = 'ACS Barker Road'
start_pt = hq
destination = ''
trip_path = [start_pt]
total_time = 0
temp_duration = 0
time_left = 7 * 60 * 60
# get distance duration between hq and all possible points
while len(job_list) > 0:
for data in job_list:
results = get_dist_duration(start_pt,data)
duration = results['rows'][0]['elements'][0]['duration']['value']
if temp_duration == 0:
temp_duration = duration
destination = data
else:
if duration < temp_duration:
temp_duration = duration
destination = data
start_pt = destination
total_time += temp_duration
time_left -= temp_duration
#condition to stop, when trip back to HQ less than time_left
hq_timeback = get_dist_duration(start_pt,hq)['rows'][0]['elements'][0]['duration']['value']
if time_left < hq_timeback:
break
else:
trip_path.append(destination)
job_list.pop(job_list.index((destination)))
temp_duration = 0
hq_timeback = get_dist_duration(start_pt,hq)['rows'][0]['elements'][0]['duration']['value']
total_time += hq_timeback
trip_path.append(hq)
return(trip_path, total_time)
# hq = 'acs barker road'
# results = get_dist_duration(hq,'National University Hospital, 5 Lower Kent Ridge Rd')
# print(results)
# print(results['rows'][0]['elements'][0]['duration']['value'])
print(get_optimal_path(mock_data))
```
|
github_jupyter
|
Start Location - Lat & Long
Destination - Lat & long
Time of job
1. Start from HQ
2. Calculate all time duration between all possible pairs using google matrix api and select the shortest duration as next checkpoint
3. Update startpoint as the next checkpoint
4. Repeat steps until no more job/threhold reached (latest working hour or number ofjobs)
import requests
import json
import googlemaps
def get_dist_duration(origin,destination):
#Enter your source and destination city
originPoint = origin
destinationPoint= destination
#Place your google map API_KEY to a variable
apiKey = 'AIzaSyDj5Vg9hZLlb78EtvVsmXeMONDajrzl32c'
#Store google maps api url in a variable
gmaps = googlemaps.Client(key=apiKey)
results = gmaps.distance_matrix(originPoint,destinationPoint)
return results
response = requests.get("http://54.254.210.52:8080/api/v1/jobs/")
if response.status_code == 200:
mock_data = []
data = response.json()
for datum in data:
mock_data.append(datum['end_address'])
else:
mock_data = ['MOE HQ (Buona Vista), 1 N Buona Vista Dr','JTC Launchpad, 73A Ayer Rajah Crescent', 'National University Hospital, 5 Lower Kent Ridge Rd,']
def get_optimal_path(job_list): #job list = list of available jobs to consider containing jobs with (lat,long, time)
hq = 'ACS Barker Road'
start_pt = hq
destination = ''
trip_path = [start_pt]
total_time = 0
temp_duration = 0
time_left = 7 * 60 * 60
# get distance duration between hq and all possible points
while len(job_list) > 0:
for data in job_list:
results = get_dist_duration(start_pt,data)
duration = results['rows'][0]['elements'][0]['duration']['value']
if temp_duration == 0:
temp_duration = duration
destination = data
else:
if duration < temp_duration:
temp_duration = duration
destination = data
start_pt = destination
total_time += temp_duration
time_left -= temp_duration
#condition to stop, when trip back to HQ less than time_left
hq_timeback = get_dist_duration(start_pt,hq)['rows'][0]['elements'][0]['duration']['value']
if time_left < hq_timeback:
break
else:
trip_path.append(destination)
job_list.pop(job_list.index((destination)))
temp_duration = 0
hq_timeback = get_dist_duration(start_pt,hq)['rows'][0]['elements'][0]['duration']['value']
total_time += hq_timeback
trip_path.append(hq)
return(trip_path, total_time)
# hq = 'acs barker road'
# results = get_dist_duration(hq,'National University Hospital, 5 Lower Kent Ridge Rd')
# print(results)
# print(results['rows'][0]['elements'][0]['duration']['value'])
print(get_optimal_path(mock_data))
| 0.2763 | 0.444263 |
<!-- dom:TITLE: Computational Physics Lectures: Numerical integration, from Newton-Cotes quadrature to Gaussian quadrature -->
# Computational Physics Lectures: Numerical integration, from Newton-Cotes quadrature to Gaussian quadrature
<!-- dom:AUTHOR: Morten Hjorth-Jensen at Department of Physics, University of Oslo & Department of Physics and Astronomy and National Superconducting Cyclotron Laboratory, Michigan State University -->
<!-- Author: -->
**Morten Hjorth-Jensen**, Department of Physics, University of Oslo and Department of Physics and Astronomy and National Superconducting Cyclotron Laboratory, Michigan State University
Date: **Aug 23, 2017**
Copyright 1999-2017, Morten Hjorth-Jensen. Released under CC Attribution-NonCommercial 4.0 license
## Numerical Integration
Here we will discuss some of the classical methods for integrating a function. The methods we discuss are
1. Equal step methods like the trapezoidal, rectangular and Simpson's rule, parts of what are called Newton-Cotes quadrature methods.
2. Integration approaches based on Gaussian quadrature.
The latter are more suitable
for the case where the abscissas are not equally spaced.
We emphasize methods for evaluating few-dimensional (typically up to four dimensions) integrals. Multi-dimensional integrals will be discussed in connection with Monte Carlo methods.
## Newton-Cotes Quadrature or equal-step methods
The integral
<!-- Equation labels as ordinary links -->
<div id="eq:integraldef"></div>
$$
\begin{equation}
I=\int_a^bf(x) dx
\label{eq:integraldef} \tag{1}
\end{equation}
$$
has a very simple meaning. The integral is the
area enscribed by the function $f(x)$ starting from $x=a$ to $x=b$. It is subdivided in several smaller areas whose evaluation is to be approximated by different techniques. The areas under the curve can for example be approximated by rectangular boxes or trapezoids.
<!-- !split -->
## Basic philosophy of equal-step methods
In considering equal step methods, our basic approach is that of approximating
a function $f(x)$ with a polynomial of at most
degree $N-1$, given $N$ integration points. If our polynomial is of degree $1$,
the function will be approximated with $f(x)\approx a_0+a_1x$.
<!-- !split -->
## Simple algorithm for equal step methods
The algorithm for these integration methods is rather simple, and the number of approximations perhaps unlimited!
* Choose a step size $h=(b-a)/N$ where $N$ is the number of steps and $a$ and $b$ the lower and upper limits of integration.
* With a given step length we rewrite the integral as
$$
\int_a^bf(x) dx= \int_a^{a+h}f(x)dx + \int_{a+h}^{a+2h}f(x)dx+\dots \int_{b-h}^{b}f(x)dx.
$$
* The strategy then is to find a reliable polynomial approximation for $f(x)$ in the various intervals. Choosing a given approximation for $f(x)$, we obtain a specific approximation to the integral.
* With this approximation to $f(x)$ we perform the integration by computing the integrals over all subintervals.
<!-- !split -->
## Simple algorithm for equal step methods
One possible strategy then is to find a reliable polynomial expansion for $f(x)$ in the smaller
subintervals. Consider for example evaluating
$$
\int_a^{a+2h}f(x)dx,
$$
which we rewrite as
<!-- Equation labels as ordinary links -->
<div id="eq:hhint"></div>
$$
\begin{equation}
\int_a^{a+2h}f(x)dx=
\int_{x_0-h}^{x_0+h}f(x)dx.
\label{eq:hhint} \tag{2}
\end{equation}
$$
We have chosen a midpoint $x_0$ and have defined $x_0=a+h$.
<!-- !split -->
## Lagrange's interpolation formula
Using Lagrange's interpolation formula
$$
P_N(x)=\sum_{i=0}^{N}\prod_{k\ne i} \frac{x-x_k}{x_i-x_k}y_i,
$$
we could attempt to approximate the function $f(x)$ with a first-order polynomial in $x$ in the two
sub-intervals $x\in[x_0-h,x_0]$ and $x\in[x_0,x_0+h]$. A first order polynomial means simply that
we have for say the interval $x\in[x_0,x_0+h]$
$$
f(x)\approx P_1(x)=\frac{x-x_0}{(x_0+h)-x_0}f(x_0+h)+\frac{x-(x_0+h)}{x_0-(x_0+h)}f(x_0),
$$
and for the interval $x\in[x_0-h,x_0]$
$$
f(x)\approx P_1(x)=\frac{x-(x_0-h)}{x_0-(x_0-h)}f(x_0)+\frac{x-x_0}{(x_0-h)-x_0}f(x_0-h).
$$
<!-- !split -->
## Polynomial approximation
Having performed this subdivision and polynomial approximation,
one from $x_0-h$ to $x_0$ and the other from $x_0$ to $x_0+h$,
$$
\int_a^{a+2h}f(x)dx=\int_{x_0-h}^{x_0}f(x)dx+\int_{x_0}^{x_0+h}f(x)dx,
$$
we can easily calculate for example the second integral as
$$
\int_{x_0}^{x_0+h}f(x)dx\approx \int_{x_0}^{x_0+h}\left(\frac{x-x_0}{(x_0+h)-x_0}f(x_0+h)+\frac{x-(x_0+h)}{x_0-(x_0+h)}f(x_0)\right)dx.
$$
<!-- !split -->
## Simplifying the integral
This integral can be simplified to
$$
\int_{x_0}^{x_0+h}f(x)dx\approx \int_{x_0}^{x_0+h}\left(\frac{x-x_0}{h}f(x_0+h)-\frac{x-(x_0+h)}{h}f(x_0)\right)dx,
$$
resulting in
$$
\int_{x_0}^{x_0+h}f(x)dx=\frac{h}{2}\left(f(x_0+h) + f(x_0)\right)+O(h^3).
$$
Here we added the error made in approximating our integral
with a polynomial of degree $1$.
<!-- !split -->
## The trapezoidal rule
The other integral gives
$$
\int_{x_0-h}^{x_0}f(x)dx=\frac{h}{2}\left(f(x_0) + f(x_0-h)\right)+O(h^3),
$$
and adding up we obtain
<!-- Equation labels as ordinary links -->
<div id="eq:trapez"></div>
$$
\begin{equation}
\int_{x_0-h}^{x_0+h}f(x)dx=\frac{h}{2}\left(f(x_0+h) + 2f(x_0) + f(x_0-h)\right)+O(h^3),
\label{eq:trapez} \tag{3}
\end{equation}
$$
which is the well-known trapezoidal rule. Concerning the error in the approximation made,
$O(h^3)=O((b-a)^3/N^3)$, you should note
that this is the local error. Since we are splitting the integral from
$a$ to $b$ in $N$ pieces, we will have to perform approximately $N$
such operations.
<!-- !split -->
## Global error
This means that the *global error* goes like $\approx O(h^2)$.
The trapezoidal reads then
<!-- Equation labels as ordinary links -->
<div id="eq:trapez1"></div>
$$
\begin{equation}
I=\int_a^bf(x) dx=h\left(f(a)/2 + f(a+h) +f(a+2h)+
\dots +f(b-h)+ f_{b}/2\right),
\label{eq:trapez1} \tag{4}
\end{equation}
$$
with a global error which goes like $O(h^2)$.
Hereafter we use the shorthand notations $f_{-h}=f(x_0-h)$, $f_{0}=f(x_0)$
and $f_{h}=f(x_0+h)$.
<!-- !split -->
## Error in the trapezoidal rule
The correct mathematical expression for the local error for the trapezoidal rule is
$$
\int_a^bf(x)dx -\frac{b-a}{2}\left[f(a)+f(b)\right]=-\frac{h^3}{12}f^{(2)}(\xi),
$$
and the global error reads
$$
\int_a^bf(x)dx -T_h(f)=-\frac{b-a}{12}h^2f^{(2)}(\xi),
$$
where $T_h$ is the trapezoidal result and $\xi \in [a,b]$.
<!-- !split -->
## Algorithm for the trapezoidal rule
The trapezoidal rule is easy to implement numerically
through the following simple algorithm
* Choose the number of mesh points and fix the step length.
* calculate $f(a)$ and $f(b)$ and multiply with $h/2$.
* Perform a loop over $n=1$ to $n-1$ ($f(a)$ and $f(b)$ are known) and sum up the terms $f(a+h) +f(a+2h)+f(a+3h)+\dots +f(b-h)$. Each step in the loop corresponds to a given value $a+nh$.
* Multiply the final result by $h$ and add $hf(a)/2$ and $hf(b)/2$.
<!-- !split -->
## Code example
A simple function which implements this algorithm is as follows
double TrapezoidalRule(double a, double b, int n, double (*func)(double))
{
double TrapezSum;
double fa, fb, x, step;
int j;
step=(b-a)/((double) n);
fa=(*func)(a)/2. ;
fb=(*func)(b)/2. ;
TrapezSum=0.;
for (j=1; j <= n-1; j++){
x=j*step+a;
TrapezSum+=(*func)(x);
}
TrapezSum=(TrapezSum+fb+fa)*step;
return TrapezSum;
} // end TrapezoidalRule
The function returns a new value for the specific integral through the variable **TrapezSum**.
<!-- !split -->
## Transfer of function names
There is one new feature to note here, namely
the transfer of a user defined function called **func** in the
definition
void TrapezoidalRule(double a, double b, int n, double *TrapezSum, double (*func)(double) )
What happens here is that we are transferring a pointer to the name
of a user defined function, which has as input a double precision variable and returns
a double precision number. The function **TrapezoidalRule** is called as
TrapezoidalRule(a, b, n, &MyFunction )
in the calling function. We note that **a**, **b** and **n** are called by value,
while **TrapezSum** and the user defined function **MyFunction**
are called by reference.
## Going back to Python, why?
**Symbolic calculations and numerical calculations in one code!**
Python offers an extremely versatile programming environment, allowing for
the inclusion of analytical studies in a numerical program. Here we show an
example code with the **trapezoidal rule** using **SymPy** to evaluate an integral and compute the absolute error
with respect to the numerically evaluated one of the integral
$4\int_0^1 dx/(1+x^2) = \pi$:
```
from math import *
from sympy import *
def Trapez(a,b,f,n):
h = (b-a)/float(n)
s = 0
x = a
for i in range(1,n,1):
x = x+h
s = s+ f(x)
s = 0.5*(f(a)+f(b)) +s
return h*s
# function to compute pi
def function(x):
return 4.0/(1+x*x)
a = 0.0; b = 1.0; n = 100
result = Trapez(a,b,function,n)
print("Trapezoidal rule=", result)
# define x as a symbol to be used by sympy
x = Symbol('x')
exact = integrate(function(x), (x, 0.0, 1.0))
print("Sympy integration=", exact)
# Find relative error
print("Relative error", abs((exact-result)/exact))
```
## Error analysis
The following extended version of the trapezoidal rule allows you to plot the relative error by comparing with the exact result. By increasing to $10^8$ points one arrives at a region where numerical errors start to accumulate.
```
%matplotlib inline
from math import log10
import numpy as np
from sympy import Symbol, integrate
import matplotlib.pyplot as plt
# function for the trapezoidal rule
def Trapez(a,b,f,n):
h = (b-a)/float(n)
s = 0
x = a
for i in range(1,n,1):
x = x+h
s = s+ f(x)
s = 0.5*(f(a)+f(b)) +s
return h*s
# function to compute pi
def function(x):
return 4.0/(1+x*x)
# define integration limits
a = 0.0; b = 1.0;
# find result from sympy
# define x as a symbol to be used by sympy
x = Symbol('x')
exact = integrate(function(x), (x, a, b))
# set up the arrays for plotting the relative error
n = np.zeros(9); y = np.zeros(9);
# find the relative error as function of integration points
for i in range(1, 8, 1):
npts = 10**i
result = Trapez(a,b,function,npts)
RelativeError = abs((exact-result)/exact)
n[i] = log10(npts); y[i] = log10(RelativeError);
plt.plot(n,y, 'ro')
plt.xlabel('n')
plt.ylabel('Relative error')
plt.show()
```
## Integrating numerical mathematics with calculus
The last example shows the potential of combining numerical algorithms with
symbolic calculations, allowing us thereby to
* Validate and verify our algorithms.
* Including concepts like unit testing, one has the possibility to test and validate several or all parts of the code.
* Validation and verification are then included *naturally*.
* The above example allows you to test the mathematical error of the algorithm for the trapezoidal rule by changing the number of integration points. You get trained from day one to think error analysis.
<!-- !split -->
## The rectangle method
Another very simple approach is the so-called midpoint or rectangle method.
In this case the integration area is split in a given number of rectangles with length $h$ and height given by the mid-point value of the function. This gives the following simple rule for approximating an integral
<!-- Equation labels as ordinary links -->
<div id="eq:rectangle"></div>
$$
\begin{equation}
I=\int_a^bf(x) dx \approx h\sum_{i=1}^N f(x_{i-1/2}),
\label{eq:rectangle} \tag{5}
\end{equation}
$$
where $f(x_{i-1/2})$ is the midpoint value of $f$ for a given rectangle. We will discuss its truncation
error below. It is easy to implement this algorithm, as shown here
double RectangleRule(double a, double b, int n, double (*func)(double))
{
double RectangleSum;
double fa, fb, x, step;
int j;
step=(b-a)/((double) n);
RectangleSum=0.;
for (j = 0; j <= n; j++){
x = (j+0.5)*step+; // midpoint of a given rectangle
RectangleSum+=(*func)(x); // add value of function.
}
RectangleSum *= step; // multiply with step length.
return RectangleSum;
} // end RectangleRule
<!-- !split -->
## Truncation error for the rectangular rule
The correct mathematical expression for the local error for the rectangular rule $R_i(h)$ for element $i$ is
$$
\int_{-h}^hf(x)dx - R_i(h)=-\frac{h^3}{24}f^{(2)}(\xi),
$$
and the global error reads
$$
\int_a^bf(x)dx -R_h(f)=-\frac{b-a}{24}h^2f^{(2)}(\xi),
$$
where $R_h$ is the result obtained with rectangular rule and $\xi \in [a,b]$.
<!-- !split -->
## Second-order polynomial
Instead of using the above first-order polynomials
approximations for $f$, we attempt at using a second-order polynomials.
In this case we need three points in order to define a second-order
polynomial approximation
$$
f(x) \approx P_2(x)=a_0+a_1x+a_2x^2.
$$
Using again Lagrange's interpolation formula we have
$$
P_2(x)=\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}y_2+
\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}y_1+
\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}y_0.
$$
Inserting this formula in the integral of Eq. ([eq:hhint](#eq:hhint)) we obtain
$$
\int_{-h}^{+h}f(x)dx=\frac{h}{3}\left(f_h + 4f_0 + f_{-h}\right)+O(h^5),
$$
which is Simpson's rule.
<!-- !split -->
## Simpson's rule
Note that the improved accuracy in the evaluation of
the derivatives gives a better error approximation, $O(h^5)$ vs.\ $O(h^3)$ .
But this is again the *local error approximation*.
Using Simpson's rule we can easily compute
the integral of Eq. ([eq:integraldef](#eq:integraldef)) to be
<!-- Equation labels as ordinary links -->
<div id="eq:simpson"></div>
$$
\begin{equation}
I=\int_a^bf(x) dx=\frac{h}{3}\left(f(a) + 4f(a+h) +2f(a+2h)+
\dots +4f(b-h)+ f_{b}\right),
\label{eq:simpson} \tag{6}
\end{equation}
$$
with a global error which goes like $O(h^4)$.
<!-- !split -->
## Mathematical expressions for the truncation error
More formal expressions for the local and global errors are for the local error
$$
\int_a^bf(x)dx -\frac{b-a}{6}\left[f(a)+4f((a+b)/2)+f(b)\right]=-\frac{h^5}{90}f^{(4)}(\xi),
$$
and for the global error
$$
\int_a^bf(x)dx -S_h(f)=-\frac{b-a}{180}h^4f^{(4)}(\xi).
$$
with $\xi\in[a,b]$ and $S_h$ the results obtained with Simpson's method.
<!-- !split -->
## Algorithm for Simpson's rule
The method
can easily be implemented numerically through the following simple algorithm
* Choose the number of mesh points and fix the step.
* calculate $f(a)$ and $f(b)$
* Perform a loop over $n=1$ to $n-1$ ($f(a)$ and $f(b)$ are known) and sum up the terms $4f(a+h) +2f(a+2h)+4f(a+3h)+\dots +4f(b-h)$. Each step in the loop corresponds to a given value $a+nh$. Odd values of $n$ give $4$ as factor while even values yield $2$ as factor.
* Multiply the final result by $\frac{h}{3}$.
<!-- !split -->
## Summary for equal-step methods
In more general terms, what we have done here is to approximate a given function $f(x)$ with a polynomial
of a certain degree. One can show that
given $n+1$ distinct points $x_0,\dots, x_n\in[a,b]$ and $n+1$ values $y_0,\dots,y_n$ there exists a
unique polynomial $P_n(x)$ with the property
$$
P_n(x_j) = y_j\hspace{0.5cm} j=0,\dots,n
$$
<!-- !split -->
## Lagrange's polynomial
In the Lagrange representation the interpolating polynomial is given by
$$
P_n = \sum_{k=0}^nl_ky_k,
$$
with the Lagrange factors
$$
l_k(x) = \prod_{\begin{array}{c}i=0 \\ i\ne k\end{array}}^n\frac{x-x_i}{x_k-x_i}\hspace{0.2cm} k=0,\dots,n.
$$
<!-- !split -->
## Polynomial approximation
If we for example set $n=1$, we obtain
$$
P_1(x) = y_0\frac{x-x_1}{x_0-x_1}+y_1\frac{x-x_0}{x_1-x_0}=\frac{y_1-y_0}{x_1-x_0}x-\frac{y_1x_0+y_0x_1}{x_1-x_0},
$$
which we recognize as the equation for a straight line.
The polynomial interpolatory quadrature of order $n$ with equidistant quadrature points $x_k=a+kh$
and step $h=(b-a)/n$ is called the Newton-Cotes quadrature formula of order $n$.
## Gaussian Quadrature
The methods we have presented hitherto are tailored to problems where the
mesh points $x_i$ are equidistantly spaced, $x_i$ differing from $x_{i+1}$ by the step $h$.
The basic idea behind all integration methods is to approximate the integral
$$
I=\int_a^bf(x)dx \approx \sum_{i=1}^N\omega_if(x_i),
$$
where $\omega$ and $x$ are the weights and the chosen mesh points, respectively.
In our previous discussion, these mesh points were fixed at the beginning, by choosing
a given number of points $N$. The weigths $\omega$ resulted then from the integration
method we applied. Simpson's rule, see Eq. ([eq:simpson](#eq:simpson)) would give
$$
\omega : \left\{h/3,4h/3,2h/3,4h/3,\dots,4h/3,h/3\right\},
$$
for the weights, while the trapezoidal rule resulted in
$$
\omega : \left\{h/2,h,h,\dots,h,h/2\right\}.
$$
## Gaussian Quadrature, main idea
In general, an integration formula which is based on a Taylor series using $N$ points,
will integrate exactly a polynomial $P$ of degree $N-1$. That is, the $N$ weights
$\omega_n$ can be chosen to satisfy $N$ linear equations, see chapter 3 of Ref.\ [3].
A greater precision for a given amount of numerical work can be achieved
if we are willing to give up the requirement of equally spaced integration points.
In Gaussian quadrature (hereafter GQ), both the mesh points and the weights are to
be determined. The points will not be equally spaced.
The theory behind GQ is to obtain an arbitrary weight $\omega$ through the use of
so-called orthogonal polynomials. These polynomials are orthogonal in some
interval say e.g., [-1,1]. Our points $x_i$ are chosen in some optimal sense subject
only to the constraint that they should lie in this interval. Together with the weights
we have then $2N$ ($N$ the number of points) parameters at our disposal.
## Gaussian Quadrature
Even though the integrand is not smooth, we could render it smooth by extracting
from it the weight function of an orthogonal polynomial, i.e.,
we are rewriting
<!-- Equation labels as ordinary links -->
<div id="eq:generalint"></div>
$$
\begin{equation}
I= \int_a^b f(x)dx =\int_a^b W(x)g(x)dx \approx \sum_{i=1}^N\omega_ig(x_i),
\label{eq:generalint} \tag{7}
\end{equation}
$$
where $g$ is smooth and $W$ is the weight function, which is to be associated with a given
orthogonal polynomial. Note that with a given weight function we end up evaluating the integrand
for the function $g(x_i)$.
## Gaussian Quadrature, weight function
The weight function $W$ is non-negative in the integration interval
$x\in [a,b]$ such that
for any $n \ge 0$, the integral $\int_a^b |x|^n W(x) dx$ is integrable. The naming
weight function arises from the fact that it may be used to give more emphasis
to one part of the interval than another.
A quadrature formula
<!-- Equation labels as ordinary links -->
<div id="_auto1"></div>
$$
\begin{equation}
\int_a^b W(x)f(x)dx \approx \sum_{i=1}^N\omega_if(x_i),
\label{_auto1} \tag{8}
\end{equation}
$$
with $N$ distinct quadrature points (mesh points) is a called a Gaussian quadrature
formula if it integrates all polynomials $p\in P_{2N-1}$ exactly, that is
<!-- Equation labels as ordinary links -->
<div id="_auto2"></div>
$$
\begin{equation}
\int_a^bW(x)p(x)dx =\sum_{i=1}^N\omega_ip(x_i),
\label{_auto2} \tag{9}
\end{equation}
$$
It is assumed that $W(x)$ is continuous and positive and that the integral
$$
\int_a^bW(x)dx
$$
exists. Note that the replacement of $f\rightarrow Wg$ is normally a better approximation
due to the fact that we may isolate possible singularities of $W$ and its
derivatives at the endpoints of the interval.
## Gaussian Quadrature weights and integration points
The quadrature weights or just weights (not to be confused with the weight function)
are positive and the sequence of Gaussian quadrature formulae is convergent
if the sequence $Q_N$ of quadrature formulae
$$
Q_N(f)\rightarrow Q(f)=\int_a^bf(x)dx,
$$
in the limit $N\rightarrow \infty$.
## Gaussian Quadrature
Then we say that the sequence
$$
Q_N(f) = \sum_{i=1}^N\omega_i^{(N)}f(x_i^{(N)}),
$$
is convergent for all polynomials $p$, that is
$$
Q_N(p) = Q(p)
$$
if there exits a constant $C$ such that
$$
\sum_{i=1}^N|\omega_i^{(N)}| \le C,
$$
for all $N$ which are natural numbers.
## Error in Gaussian Quadrature
The error for the Gaussian quadrature formulae of order $N$ is given
by
$$
\int_a^bW(x)f(x)dx-\sum_{k=1}^Nw_kf(x_k)=\frac{f^{2N}(\xi)}{(2N)!}\int_a^bW(x)[q_{N}(x)]^2dx
$$
where $q_{N}$ is the chosen orthogonal polynomial and $\xi$ is a number in the interval $[a,b]$.
We have assumed that $f\in C^{2N}[a,b]$, viz. the space of all real or complex $2N$ times continuously
differentiable functions.
## Important polynomials in Gaussian Quadrature
In science there are several important orthogonal polynomials which arise
from the solution of differential equations. Well-known examples are the
Legendre, Hermite, Laguerre and Chebyshev polynomials. They have the following weight functions
<table border="1">
<thead>
<tr><th align="center"> Weight function </th> <th align="center"> Interval </th> <th align="center">Polynomial</th> </tr>
</thead>
<tbody>
<tr><td align="right"> $W(x)=1$ </td> <td align="right"> $x\in [-1,1]$ </td> <td align="right"> Legendre </td> </tr>
<tr><td align="right"> $W(x)=e^{-x^2}$ </td> <td align="right"> $-\infty \le x \le \infty$ </td> <td align="right"> Hermite </td> </tr>
<tr><td align="right"> $W(x)=x^{\alpha}e^{-x}$ </td> <td align="right"> $0 \le x \le \infty$ </td> <td align="right"> Laguerre </td> </tr>
<tr><td align="right"> $W(x)=1/(\sqrt{1-x^2})$ </td> <td align="right"> $-1 \le x \le 1$ </td> <td align="right"> Chebyshev </td> </tr>
</tbody>
</table>
The importance of the use of orthogonal polynomials in the evaluation
of integrals can be summarized as follows.
## Gaussian Quadrature, win-win situation
Methods based on Taylor series using $N$ points will integrate exactly a polynomial $P$ of degree $N-1$. If a function $f(x)$ can be approximated with a polynomial of degree $N-1$
$$
f(x)\approx P_{N-1}(x),
$$
with $N$ mesh points we should be able to integrate exactly the polynomial $P_{N-1}$.
Gaussian quadrature methods promise more than this. We can get a better polynomial approximation with order greater than $N$ to $f(x)$ and still get away with only $N$ mesh points. More precisely, we approximate
$$
f(x) \approx P_{2N-1}(x),
$$
and with only $N$ mesh points these methods promise that
$$
\int f(x)dx \approx \int P_{2N-1}(x)dx=\sum_{i=0}^{N-1} P_{2N-1}(x_i)\omega_i,
$$
## Gaussian Quadrature, determining mesh points and weights
The reason why we can represent a function $f(x)$ with a polynomial of degree
$2N-1$ is due to the fact that we have $2N$ equations, $N$ for the mesh points and $N$
for the weights.
*The mesh points are the zeros of the chosen orthogonal polynomial* of
order $N$, and the weights are determined from the inverse of a matrix.
An orthogonal polynomials of degree $N$ defined in an interval $[a,b]$
has precisely $N$ distinct zeros on the open interval $(a,b)$.
Before we detail how to obtain mesh points and weights with orthogonal
polynomials, let us revisit some features of orthogonal polynomials
by specializing to Legendre polynomials. In the text below, we reserve
hereafter the labelling
$L_N$ for a Legendre polynomial of order $N$, while $P_N$ is an arbitrary polynomial
of order $N$.
These polynomials form then the basis for the Gauss-Legendre method.
## Orthogonal polynomials, Legendre
The Legendre polynomials are the solutions of an important
differential equation in Science, namely
$$
C(1-x^2)P-m_l^2P+(1-x^2)\frac{d}{dx}\left((1-x^2)\frac{dP}{dx}\right)=0.
$$
Here $C$ is a constant. For $m_l=0$ we obtain the Legendre polynomials
as solutions, whereas $m_l \ne 0$ yields the so-called associated Legendre
polynomials. This differential equation arises in for example the solution
of the angular dependence of Schroedinger's
equation with spherically symmetric potentials such as
the Coulomb potential.
## Orthogonal polynomials, Legendre
The corresponding polynomials $P$ are
$$
L_k(x)=\frac{1}{2^kk!}\frac{d^k}{dx^k}(x^2-1)^k \hspace{1cm} k=0,1,2,\dots,
$$
which, up to a factor, are the Legendre polynomials $L_k$.
The latter fulfil the orthogonality relation
<!-- Equation labels as ordinary links -->
<div id="eq:ortholeg"></div>
$$
\begin{equation}
\int_{-1}^1L_i(x)L_j(x)dx=\frac{2}{2i+1}\delta_{ij},
\label{eq:ortholeg} \tag{10}
\end{equation}
$$
and the recursion relation
<!-- Equation labels as ordinary links -->
<div id="eq:legrecur"></div>
$$
\begin{equation}
(j+1)L_{j+1}(x)+jL_{j-1}(x)-(2j+1)xL_j(x)=0.
\label{eq:legrecur} \tag{11}
\end{equation}
$$
## Orthogonal polynomials, Legendre
It is common to choose the normalization condition
$$
L_N(1)=1.
$$
With these equations we can determine a Legendre polynomial of arbitrary order
with input polynomials of order $N-1$ and $N-2$.
As an example, consider the determination of $L_0$, $L_1$ and $L_2$.
We have that
$$
L_0(x) = c,
$$
with $c$ a constant. Using the normalization equation $L_0(1)=1$
we get that
$$
L_0(x) = 1.
$$
## Orthogonal polynomials, Legendre
For $L_1(x)$ we have the general expression
$$
L_1(x) = a+bx,
$$
and using the orthogonality relation
$$
\int_{-1}^1L_0(x)L_1(x)dx=0,
$$
we obtain $a=0$ and with the condition $L_1(1)=1$, we obtain $b=1$, yielding
$$
L_1(x) = x.
$$
## Orthogonal polynomials, Legendre
We can proceed in a similar fashion in order to determine
the coefficients of $L_2$
$$
L_2(x) = a+bx+cx^2,
$$
using the orthogonality relations
$$
\int_{-1}^1L_0(x)L_2(x)dx=0,
$$
and
$$
\int_{-1}^1L_1(x)L_2(x)dx=0,
$$
and the condition
$L_2(1)=1$ we would get
<!-- Equation labels as ordinary links -->
<div id="eq:l2"></div>
$$
\begin{equation}
L_2(x) = \frac{1}{2}\left(3x^2-1\right).
\label{eq:l2} \tag{12}
\end{equation}
$$
## Orthogonal polynomials, Legendre
We note that we have three equations to determine the three coefficients
$a$, $b$ and $c$.
Alternatively, we could have
employed the recursion relation of Eq. ([eq:legrecur](#eq:legrecur)), resulting in
$$
2L_2(x)=3xL_1(x)-L_0,
$$
which leads to Eq. ([eq:l2](#eq:l2)).
## Orthogonal polynomials, Legendre
The orthogonality relation above is important in our discussion
on how to obtain the weights and mesh points. Suppose we have an arbitrary
polynomial $Q_{N-1}$ of order $N-1$ and a Legendre polynomial $L_N(x)$ of
order $N$. We could represent $Q_{N-1}$
by the Legendre polynomials through
<!-- Equation labels as ordinary links -->
<div id="eq:legexpansion"></div>
$$
\begin{equation}
Q_{N-1}(x)=\sum_{k=0}^{N-1}\alpha_kL_{k}(x),
\label{eq:legexpansion} \tag{13}
\end{equation}
$$
where $\alpha_k$'s are constants.
Using the orthogonality relation of Eq. ([eq:ortholeg](#eq:ortholeg)) we see that
<!-- Equation labels as ordinary links -->
<div id="eq:ortholeg2"></div>
$$
\begin{equation}
\int_{-1}^1L_N(x)Q_{N-1}(x)dx=\sum_{k=0}^{N-1} \int_{-1}^1L_N(x) \alpha_kL_{k}(x)dx=0.
\label{eq:ortholeg2} \tag{14}
\end{equation}
$$
We will use this result in our construction of mesh points and weights
in the next subsection.
## Orthogonal polynomials, Legendre
In summary, the first few Legendre polynomials are
6
1
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
6
2
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
6
3
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
$$
L_3(x) = (5x^3-3x)/2,
$$
and
$$
L_4(x) = (35x^4-30x^2+3)/8.
$$
## Orthogonal polynomials, simple code for Legendre polynomials
The following simple function implements the above recursion relation
of Eq. ([eq:legrecur](#eq:legrecur)).
for computing Legendre polynomials of order $N$.
// This function computes the Legendre polynomial of degree N
double Legendre( int n, double x)
{
double r, s, t;
int m;
r = 0; s = 1.;
// Use recursion relation to generate p1 and p2
for (m=0; m < n; m++ )
{
t = r; r = s;
s = (2*m+1)*x*r - m*t;
s /= (m+1);
} // end of do loop
return s;
} // end of function Legendre
The variable $s$ represents $L_{j+1}(x)$, while $r$ holds
$L_j(x)$ and $t$ the value $L_{j-1}(x)$.
## Integration points and weights with orthogonal polynomials
To understand how the weights and the mesh points are generated, we define first
a polynomial of degree $2N-1$ (since we have $2N$ variables at hand, the mesh points
and weights for $N$ points). This polynomial can be represented through polynomial
division by
$$
P_{2N-1}(x)=L_N(x)P_{N-1}(x)+Q_{N-1}(x),
$$
where $P_{N-1}(x)$ and $Q_{N-1}(x)$ are some polynomials of degree $N-1$ or less.
The function $L_N(x)$ is a Legendre polynomial of order $N$.
Recall that we wanted to approximate an arbitrary function $f(x)$ with a
polynomial $P_{2N-1}$ in order to evaluate
$$
\int_{-1}^1f(x)dx\approx \int_{-1}^1P_{2N-1}(x)dx.
$$
## Integration points and weights with orthogonal polynomials
We can use Eq. ([eq:ortholeg2](#eq:ortholeg2))
to rewrite the above integral as
$$
\int_{-1}^1P_{2N-1}(x)dx=\int_{-1}^1(L_N(x)P_{N-1}(x)+Q_{N-1}(x))dx=\int_{-1}^1Q_{N-1}(x)dx,
$$
due to the orthogonality properties of the Legendre polynomials. We see that it suffices
to evaluate the integral over $\int_{-1}^1Q_{N-1}(x)dx$ in order to evaluate
$\int_{-1}^1P_{2N-1}(x)dx$. In addition, at the points $x_k$ where $L_N$ is zero, we have
$$
P_{2N-1}(x_k)=Q_{N-1}(x_k)\hspace{1cm} k=0,1,\dots, N-1,
$$
and we see that through these $N$ points we can fully define $Q_{N-1}(x)$ and thereby the
integral. Note that we have chosen to let the numbering of the points run from $0$ to $N-1$.
The reason for this choice is that we wish to have the same numbering as the order of a
polynomial of degree $N-1$. This numbering will be useful below when we introduce the matrix
elements which define the integration weights $w_i$.
## Integration points and weights with orthogonal polynomials
We develope then $Q_{N-1}(x)$ in terms of Legendre polynomials,
as done in Eq. ([eq:legexpansion](#eq:legexpansion)),
<!-- Equation labels as ordinary links -->
<div id="eq:lsum1"></div>
$$
\begin{equation}
Q_{N-1}(x)=\sum_{i=0}^{N-1}\alpha_iL_i(x).
\label{eq:lsum1} \tag{15}
\end{equation}
$$
Using the orthogonality property of the Legendre polynomials we have
$$
\int_{-1}^1Q_{N-1}(x)dx=\sum_{i=0}^{N-1}\alpha_i\int_{-1}^1L_0(x)L_i(x)dx=2\alpha_0,
$$
where we have just inserted $L_0(x)=1$!
## Integration points and weights with orthogonal polynomials
Instead of an integration problem we need now to define the coefficient $\alpha_0$.
Since we know the values of $Q_{N-1}$ at the zeros of $L_N$, we may rewrite
Eq. ([eq:lsum1](#eq:lsum1)) as
<!-- Equation labels as ordinary links -->
<div id="eq:lsum2"></div>
$$
\begin{equation}
Q_{N-1}(x_k)=\sum_{i=0}^{N-1}\alpha_iL_i(x_k)=\sum_{i=0}^{N-1}\alpha_iL_{ik} \hspace{1cm} k=0,1,\dots, N-1.
\label{eq:lsum2} \tag{16}
\end{equation}
$$
Since the Legendre polynomials are linearly independent of each other, none
of the columns in the matrix $L_{ik}$ are linear combinations of the others.
## Integration points and weights with orthogonal polynomials
This means that the matrix $L_{ik}$ has an inverse with the properties
$$
\hat{L}^{-1}\hat{L} = \hat{I}.
$$
Multiplying both sides of Eq. ([eq:lsum2](#eq:lsum2)) with $\sum_{j=0}^{N-1}L_{ji}^{-1}$ results in
<!-- Equation labels as ordinary links -->
<div id="eq:lsum3"></div>
$$
\begin{equation}
\sum_{i=0}^{N-1}(L^{-1})_{ki}Q_{N-1}(x_i)=\alpha_k.
\label{eq:lsum3} \tag{17}
\end{equation}
$$
## Integration points and weights with orthogonal polynomials
We can derive this result in an alternative way by defining the vectors
$$
\hat{x}_k=\left(\begin{array} {c} x_0\\
x_1\\
.\\
.\\
x_{N-1}\end{array}\right) \hspace{0.5cm}
\hat{\alpha}=\left(\begin{array} {c} \alpha_0\\
\alpha_1\\
.\\
.\\
\alpha_{N-1}\end{array}\right),
$$
and the matrix
$$
\hat{L}=\left(\begin{array} {cccc} L_0(x_0) & L_1(x_0) &\dots &L_{N-1}(x_0)\\
L_0(x_1) & L_1(x_1) &\dots &L_{N-1}(x_1)\\
\dots & \dots &\dots &\dots\\
L_0(x_{N-1}) & L_1(x_{N-1}) &\dots &L_{N-1}(x_{N-1})
\end{array}\right).
$$
## Integration points and weights with orthogonal polynomials
We have then
$$
Q_{N-1}(\hat{x}_k) = \hat{L}\hat{\alpha},
$$
yielding (if $\hat{L}$ has an inverse)
$$
\hat{L}^{-1}Q_{N-1}(\hat{x}_k) = \hat{\alpha},
$$
which is Eq. ([eq:lsum3](#eq:lsum3)).
## Integration points and weights with orthogonal polynomials
Using the above results and the fact that
$$
\int_{-1}^1P_{2N-1}(x)dx=\int_{-1}^1Q_{N-1}(x)dx,
$$
we get
$$
\int_{-1}^1P_{2N-1}(x)dx=\int_{-1}^1Q_{N-1}(x)dx=2\alpha_0=
2\sum_{i=0}^{N-1}(L^{-1})_{0i}P_{2N-1}(x_i).
$$
## Integration points and weights with orthogonal polynomials
If we identify the weights with $2(L^{-1})_{0i}$, where the points $x_i$ are
the zeros of $L_N$, we have an integration formula of the type
$$
\int_{-1}^1P_{2N-1}(x)dx=\sum_{i=0}^{N-1}\omega_iP_{2N-1}(x_i)
$$
and if our function $f(x)$ can be approximated by a polynomial $P$ of degree
$2N-1$, we have finally that
$$
\int_{-1}^1f(x)dx\approx \int_{-1}^1P_{2N-1}(x)dx=\sum_{i=0}^{N-1}\omega_iP_{2N-1}(x_i) .
$$
In summary, the mesh points $x_i$ are defined by the zeros of an orthogonal polynomial of degree $N$, that is
$L_N$, while the weights are
given by $2(L^{-1})_{0i}$.
## Application to the case $N=2$
Let us apply the above formal results to the case $N=2$.
This means that we can approximate a function $f(x)$ with a
polynomial $P_3(x)$ of order $2N-1=3$.
The mesh points are the zeros of $L_2(x)=1/2(3x^2-1)$.
These points are $x_0=-1/\sqrt{3}$ and $x_1=1/\sqrt{3}$.
Specializing Eq. ([eq:lsum2](#eq:lsum2))
$$
Q_{N-1}(x_k)=\sum_{i=0}^{N-1}\alpha_iL_i(x_k) \hspace{1cm} k=0,1,\dots, N-1.
$$
to $N=2$ yields
$$
Q_1(x_0)=\alpha_0-\alpha_1\frac{1}{\sqrt{3}},
$$
and
$$
Q_1(x_1)=\alpha_0+\alpha_1\frac{1}{\sqrt{3}},
$$
since $L_0(x=\pm 1/\sqrt{3})=1$ and $L_1(x=\pm 1/\sqrt{3})=\pm 1/\sqrt{3}$.
## Application to the case $N=2$
The matrix $L_{ik}$ defined in Eq. ([eq:lsum2](#eq:lsum2)) is then
$$
\hat{L}=\left(\begin{array} {cc} 1 & -\frac{1}{\sqrt{3}}\\
1 & \frac{1}{\sqrt{3}}\end{array}\right),
$$
with an inverse given by
$$
\hat{L}^{-1}=\frac{\sqrt{3}}{2}\left(\begin{array} {cc} \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}}\\
-1 & 1\end{array}\right).
$$
The weights are given by the matrix elements $2(L_{0k})^{-1}$. We have thence
$\omega_0=1$ and $\omega_1=1$.
## Application to the case $N=2$
Obviously, there is no problem in changing the numbering of the matrix elements $i,k=0,1,2,\dots,N-1$ to
$i,k=1,2,\dots,N$. We have chosen to start from zero, since we deal with polynomials of degree $N-1$.
Summarizing, for Legendre polynomials with $N=2$ we have
weights
$$
\omega : \left\{1,1\right\},
$$
and mesh points
$$
x : \left\{-\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\right\}.
$$
## Application to the case $N=2$
If we wish to integrate
$$
\int_{-1}^1f(x)dx,
$$
with $f(x)=x^2$, we approximate
$$
I=\int_{-1}^1x^2dx \approx \sum_{i=0}^{N-1}\omega_ix_i^2.
$$
## Application to the case $N=2$
The exact answer is $2/3$. Using $N=2$ with the above two weights
and mesh points we get
$$
I=\int_{-1}^1x^2dx =\sum_{i=0}^{1}\omega_ix_i^2=\frac{1}{3}+\frac{1}{3}=\frac{2}{3},
$$
the exact answer!
If we were to emply the trapezoidal rule we would get
$$
I=\int_{-1}^1x^2dx =\frac{b-a}{2}\left((a)^2+(b)^2\right)/2=
\frac{1-(-1)}{2}\left((-1)^2+(1)^2\right)/2=1!
$$
With just two points we can calculate exactly the integral for a second-order
polynomial since our methods approximates the exact function with higher
order polynomial.
How many points do you need with the trapezoidal rule in order to achieve a
similar accuracy?
## General integration intervals for Gauss-Legendre
Note that the Gauss-Legendre method is not limited
to an interval [-1,1], since we can always through a change of variable
$$
t=\frac{b-a}{2}x+\frac{b+a}{2},
$$
rewrite the integral for an interval [a,b]
$$
\int_a^bf(t)dt=\frac{b-a}{2}\int_{-1}^1f\left(\frac{(b-a)x}{2}+\frac{b+a}{2}\right)dx.
$$
## Mapping integration points and weights
If we have an integral on the form
$$
\int_0^{\infty}f(t)dt,
$$
we can choose new mesh points and weights by using the mapping
$$
\tilde{x}_i=tan\left\{\frac{\pi}{4}(1+x_i)\right\},
$$
and
$$
\tilde{\omega}_i= \frac{\pi}{4}\frac{\omega_i}{cos^2\left(\frac{\pi}{4}(1+x_i)\right)},
$$
where $x_i$ and $\omega_i$ are the original mesh points and weights in the
interval $[-1,1]$, while $\tilde{x}_i$ and $\tilde{\omega}_i$ are the new
mesh points and weights for the interval $[0,\infty)$.
## Mapping integration points and weights
To see that this is correct by inserting the
the value of $x_i=-1$ (the lower end of the interval $[-1,1]$)
into the expression for $\tilde{x}_i$. That gives $\tilde{x}_i=0$,
the lower end of the interval $[0,\infty)$. For
$x_i=1$, we obtain $\tilde{x}_i=\infty$. To check that the new
weights are correct, recall that the weights should correspond to the
derivative of the mesh points. Try to convince yourself that the
above expression fulfills this condition.
## Other orthogonal polynomials, Laguerre polynomials
If we are able to rewrite our integral of Eq. ([eq:generalint](#eq:generalint)) with a
weight function $W(x)=x^{\alpha}e^{-x}$ with integration limits
$[0,\infty)$, we could then use the Laguerre polynomials.
The polynomials form then the basis for the Gauss-Laguerre method which can be applied
to integrals of the form
$$
I=\int_0^{\infty}f(x)dx =\int_0^{\infty}x^{\alpha}e^{-x}g(x)dx.
$$
## Other orthogonal polynomials, Laguerre polynomials
These polynomials arise from the solution of the differential
equation
$$
\left(\frac{d^2 }{dx^2}-\frac{d }{dx}+\frac{\lambda}{x}-\frac{l(l+1)}{x^2}\right){\cal L}(x)=0,
$$
where $l$ is an integer $l\ge 0$ and $\lambda$ a constant. This equation
arises for example from the solution of the radial Schr\"odinger equation with
a centrally symmetric potential such as the Coulomb potential.
## Other orthogonal polynomials, Laguerre polynomials
The first few polynomials are
1
0
1
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
1
0
2
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
1
0
3
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
$$
{\cal L}_3(x)=6-18x+9x^2-x^3,
$$
and
$$
{\cal L}_4(x)=x^4-16x^3+72x^2-96x+24.
$$
## Other orthogonal polynomials, Laguerre polynomials
They fulfil the orthogonality relation
$$
\int_{0}^{\infty}e^{-x}{\cal L}_n(x)^2dx=1,
$$
and the recursion relation
$$
(n+1){\cal L}_{n+1}(x)=(2n+1-x){\cal L}_{n}(x)-n{\cal L}_{n-1}(x).
$$
## Other orthogonal polynomials, Hermite polynomials
In a similar way, for an integral which goes like
$$
I=\int_{-\infty}^{\infty}f(x)dx =\int_{-\infty}^{\infty}e^{-x^2}g(x)dx.
$$
we could use the Hermite polynomials in order to extract weights and mesh points.
The Hermite polynomials are the solutions of the following differential
equation
<!-- Equation labels as ordinary links -->
<div id="eq:hermite"></div>
$$
\begin{equation}
\frac{d^2H(x)}{dx^2}-2x\frac{dH(x)}{dx}+
(\lambda-1)H(x)=0.
\label{eq:hermite} \tag{18}
\end{equation}
$$
## Other orthogonal polynomials, Hermite polynomials
A typical example is again the solution of Schrodinger's
equation, but this time with a harmonic oscillator potential.
The first few polynomials are
1
1
0
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
1
1
1
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
1
1
2
<
<
<
!
!
M
A
T
H
_
B
L
O
C
K
$$
H_3(x)=8x^3-12,
$$
and
$$
H_4(x)=16x^4-48x^2+12.
$$
They fulfil the orthogonality relation
$$
\int_{-\infty}^{\infty}e^{-x^2}H_n(x)^2dx=2^nn!\sqrt{\pi},
$$
and the recursion relation
$$
H_{n+1}(x)=2xH_{n}(x)-2nH_{n-1}(x).
$$
<!-- !split -->
## Demonstration of Gaussian Quadrature
Let us here compare three methods for integrating, namely the trapezoidal rule,
Simpson's method and the Gauss-Legendre approach.
We choose two functions to integrate:
$$
\int_1^{100}\frac{\exp{(-x)}}{x}dx,
$$
and
$$
\int_{0}^{3}\frac{1}{2+x^2}dx.
$$
<!-- !split -->
## Demonstration of Gaussian Quadrature, simple program
A program example which uses the trapezoidal rule, Simpson's rule
and the Gauss-Legendre method is included here.
#include <iostream>
#include "lib.h"
using namespace std;
// Here we define various functions called by the main program
// this function defines the function to integrate
double int_function(double x);
// Main function begins here
int main()
{
int n;
double a, b;
cout << "Read in the number of integration points" << endl;
cin >> n;
cout << "Read in integration limits" << endl;
cin >> a >> b;
// reserve space in memory for vectors containing the mesh points
// weights and function values for the use of the gauss-legendre
// method
double *x = new double [n];
double *w = new double [n];
// set up the mesh points and weights
gauss_legendre(a, b,x,w, n);
// evaluate the integral with the Gauss-Legendre method
// Note that we initialize the sum
double int_gauss = 0.;
for ( int i = 0; i < n; i++){
int_gauss+=w[i]*int_function(x[i]);
}
// final output
cout << "Trapez-rule = " << trapezoidal_rule(a, b,n, int_function)
<< endl;
cout << "Simpson's rule = " << simpson(a, b,n, int_function)
<< endl;
cout << "Gaussian quad = " << int_gauss << endl;
delete [] x;
delete [] w;
return 0;
} // end of main program
// this function defines the function to integrate
double int_function(double x)
{
double value = 4./(1.+x*x);
return value;
} // end of function to evaluate
<!-- !split -->
## Demonstration of Gaussian Quadrature
To be noted in this program is that we can transfer the name of a given function to integrate.
In the table here we show the results for the first integral using various
mesh points,.
<table border="1">
<thead>
<tr><th align="center">$N$ </th> <th align="center"> Trapez </th> <th align="center">Simpson </th> <th align="center">Gauss-Legendre</th> </tr>
</thead>
<tbody>
<tr><td align="right"> 10 </td> <td align="left"> 1.821020 </td> <td align="left"> 1.214025 </td> <td align="left"> 0.1460448 </td> </tr>
<tr><td align="right"> 20 </td> <td align="left"> 0.912678 </td> <td align="left"> 0.609897 </td> <td align="left"> 0.2178091 </td> </tr>
<tr><td align="right"> 40 </td> <td align="left"> 0.478456 </td> <td align="left"> 0.333714 </td> <td align="left"> 0.2193834 </td> </tr>
<tr><td align="right"> 100 </td> <td align="left"> 0.273724 </td> <td align="left"> 0.231290 </td> <td align="left"> 0.2193839 </td> </tr>
<tr><td align="right"> 1000 </td> <td align="left"> 0.219984 </td> <td align="left"> 0.219387 </td> <td align="left"> 0.2193839 </td> </tr>
</tbody>
</table>
We note here that, since the area over where we integrate is rather large and the integrand
goes slowly to zero for large values of $x$, both the trapezoidal rule and Simpson's method
need quite many points in order to approach the Gauss-Legendre method.
This integrand demonstrates clearly the strength of the Gauss-Legendre method
(and other GQ methods as well), viz., few points
are needed in order to achieve a very high precision.
<!-- !split -->
## Demonstration of Gaussian Quadrature
The second table however shows that for smaller integration intervals, both the trapezoidal rule
and Simpson's method compare well with the results obtained with the Gauss-Legendre
approach.
<table border="1">
<thead>
<tr><th align="center">$N$ </th> <th align="center"> Trapez </th> <th align="center">Simpson </th> <th align="center">Gauss-Legendre</th> </tr>
</thead>
<tbody>
<tr><td align="right"> 10 </td> <td align="left"> 0.798861 </td> <td align="left"> 0.799231 </td> <td align="left"> 0.799233 </td> </tr>
<tr><td align="right"> 20 </td> <td align="left"> 0.799140 </td> <td align="left"> 0.799233 </td> <td align="left"> 0.799233 </td> </tr>
<tr><td align="right"> 40 </td> <td align="left"> 0.799209 </td> <td align="left"> 0.799233 </td> <td align="left"> 0.799233 </td> </tr>
<tr><td align="right"> 100 </td> <td align="left"> 0.799229 </td> <td align="left"> 0.799233 </td> <td align="left"> 0.799233 </td> </tr>
<tr><td align="right"> 1000 </td> <td align="left"> 0.799233 </td> <td align="left"> 0.799233 </td> <td align="left"> 0.799233 </td> </tr>
</tbody>
</table>
## Comparing methods and using symbolic Python
The following python code allows you to run interactively either in a browser or using ipython notebook. It compares the trapezoidal rule and Gaussian quadrature with the exact result from symbolic python **SYMPY** up to 1000 integration points for the integral
$$
I = 2 = \int_0^{\infty} x^2 \exp{-x} dx.
$$
For the trapezoidal rule the results will vary strongly depending on how the infinity limit is approximated. Try to run the code below for different finite approximations to $\infty$.
```
from math import exp
import numpy as np
from sympy import Symbol, integrate, exp, oo
# function for the trapezoidal rule
def TrapezoidalRule(a,b,f,n):
h = (b-a)/float(n)
s = 0
x = a
for i in range(1,n,1):
x = x+h
s = s+ f(x)
s = 0.5*(f(a)+f(b)) +s
return h*s
# function for the Gaussian quadrature with Laguerre polynomials
def GaussLaguerreRule(n):
s = 0
xgauleg, wgauleg = np.polynomial.laguerre.laggauss(n)
for i in range(1,n,1):
s = s+ xgauleg[i]*xgauleg[i]*wgauleg[i]
return s
# function to compute
def function(x):
return x*x*exp(-x)
# Integration limits for the Trapezoidal rule
a = 0.0; b = 10000.0
# define x as a symbol to be used by sympy
x = Symbol('x')
# find result from sympy
exact = integrate(function(x), (x, a, oo))
# set up the arrays for plotting the relative error
n = np.zeros(40); Trapez = np.zeros(4); LagGauss = np.zeros(4);
# find the relative error as function of integration points
for i in range(1, 3, 1):
npts = 10**i
n[i] = npts
Trapez[i] = abs((TrapezoidalRule(a,b,function,npts)-exact)/exact)
LagGauss[i] = abs((GaussLaguerreRule(npts)-exact)/exact)
print ("Integration points=", n[1], n[2])
print ("Trapezoidal relative error=", Trapez[1], Trapez[2])
print ("LagGuass relative error=", LagGauss[1], LagGauss[2])
```
## Treatment of Singular Integrals
So-called principal value (PV) integrals are often employed in physics,
from Green's functions for scattering to dispersion relations.
Dispersion relations are often related to measurable quantities
and provide important consistency checks in atomic, nuclear and
particle physics.
A PV integral is defined as
$$
I(x)={\cal P}\int_a^bdt\frac{f(t)}{t-x}=\lim_{\epsilon\rightarrow 0^+}
\left[\int_a^{x-\epsilon}dt\frac{f(t)}{t-x}+\int_{x+\epsilon}^bdt\frac{f(t)}{t-x}\right],
$$
and
arises in applications
of Cauchy's residue theorem when the pole $x$ lies
on the real axis within the interval of integration $[a,b]$. Here ${\cal P}$ stands for the principal value. *An important assumption is that the function $f(t)$ is continuous
on the interval of integration*.
## Treatment of Singular Integrals
In case $f(t)$ is a closed form expression or it has an analytic continuation
in the complex plane, it may be possible to obtain an expression on closed
form for the above integral.
However, the situation which we are often confronted with is that
$f(t)$ is only known at some points $t_i$ with corresponding
values $f(t_i)$. In order to obtain $I(x)$ we need to resort to a
numerical evaluation.
To evaluate such an integral, let us first rewrite it as
$$
{\cal P}\int_a^bdt\frac{f(t)}{t-x}=
\int_a^{x-\Delta}dt\frac{f(t)}{t-x}+\int_{x+\Delta}^bdt\frac{f(t)}{t-x}+
{\cal P}\int_{x-\Delta}^{x+\Delta}dt\frac{f(t)}{t-x},
$$
where we have isolated the principal value part in the last integral.
## Treatment of Singular Integrals, change of variables
Defining a new variable $u=t-x$, we can rewrite the principal value
integral as
<!-- Equation labels as ordinary links -->
<div id="eq:deltaint"></div>
$$
\begin{equation}
I_{\Delta}(x)={\cal P}\int_{-\Delta}^{+\Delta}du\frac{f(u+x)}{u}.
\label{eq:deltaint} \tag{19}
\end{equation}
$$
One possibility is to Taylor expand $f(u+x)$ around $u=0$, and compute
derivatives to a certain order as we did for the Trapezoidal rule or
Simpson's rule.
Since all terms with even powers of $u$ in the Taylor expansion dissapear,
we have that
$$
I_{\Delta}(x)\approx \sum_{n=0}^{N_{max}}f^{(2n+1)}(x)
\frac{\Delta^{2n+1}}{(2n+1)(2n+1)!}.
$$
## Treatment of Singular Integrals, higher-order derivatives
To evaluate higher-order derivatives may be both time
consuming and delicate from a numerical point of view, since
there is always the risk of loosing precision when calculating
derivatives numerically. Unless we have an analytic expression
for $f(u+x)$ and can evaluate the derivatives in a closed form,
the above approach is not the preferred one.
Rather, we show here how to use the Gauss-Legendre method
to compute Eq. ([eq:deltaint](#eq:deltaint)).
Let us first introduce a new variable $s=u/\Delta$ and rewrite
Eq. ([eq:deltaint](#eq:deltaint)) as
<!-- Equation labels as ordinary links -->
<div id="eq:deltaint2"></div>
$$
\begin{equation}
I_{\Delta}(x)={\cal P}\int_{-1}^{+1}ds\frac{f(\Delta s+x)}{s}.
\label{eq:deltaint2} \tag{20}
\end{equation}
$$
## Treatment of Singular Integrals
The integration limits are now from $-1$ to $1$, as for the Legendre
polynomials.
The principal value in Eq. ([eq:deltaint2](#eq:deltaint2)) is however rather tricky
to evaluate numerically, mainly since computers have limited
precision. We will here use a subtraction trick often used
when dealing with singular integrals in numerical calculations.
We introduce first the calculus relation
$$
\int_{-1}^{+1} \frac{ds}{s} =0.
$$
It means that the curve $1/(s)$ has equal and opposite
areas on both sides of the singular point $s=0$.
## Treatment of Singular Integrals
If we then note that $f(x)$ is just a constant, we have also
$$
f(x)\int_{-1}^{+1} \frac{ds}{s}=\int_{-1}^{+1}f(x) \frac{ds}{s} =0.
$$
Subtracting this equation from
Eq. ([eq:deltaint2](#eq:deltaint2)) yields
<!-- Equation labels as ordinary links -->
<div id="eq:deltaint3"></div>
$$
\begin{equation}
I_{\Delta}(x)={\cal P}\int_{-1}^{+1}ds\frac{f(\Delta s+x)}{s}=\int_{-1}^{+1}ds\frac{f(\Delta s+x)-f(x)}{s},
\label{eq:deltaint3} \tag{21}
\end{equation}
$$
and the integrand is no longer singular since we have that
$\lim_{s \rightarrow 0} (f(s+x) -f(x))=0$ and for the particular case
$s=0$ the integrand
is now finite.
## Treatment of Singular Integrals
Eq. ([eq:deltaint3](#eq:deltaint3)) is now rewritten using the Gauss-Legendre
method resulting in
<!-- Equation labels as ordinary links -->
<div id="eq:deltaint4"></div>
$$
\begin{equation}
\int_{-1}^{+1}ds\frac{f(\Delta s+x)-f(x)}{s}=\sum_{i=1}^{N}\omega_i\frac{f(\Delta s_i+x)-f(x)}{s_i},
\label{eq:deltaint4} \tag{22}
\end{equation}
$$
where $s_i$ are the mesh points ($N$ in total) and $\omega_i$ are the weights.
In the selection of mesh points for a PV integral, it is important
to use an even number of points, since an odd number of mesh
points always picks $s_i=0$ as one of the mesh points. The sum in
Eq. ([eq:deltaint4](#eq:deltaint4)) will then diverge.
## Treatment of Singular Integrals
Let us apply this method to the integral
<!-- Equation labels as ordinary links -->
<div id="eq:deltaint5"></div>
$$
\begin{equation}
I(x)={\cal P}\int_{-1}^{+1}dt\frac{e^t}{t}.
\label{eq:deltaint5} \tag{23}
\end{equation}
$$
The integrand diverges at $x=t=0$. We
rewrite it using Eq. ([eq:deltaint3](#eq:deltaint3)) as
<!-- Equation labels as ordinary links -->
<div id="eq:deltaint6"></div>
$$
\begin{equation}
{\cal P}\int_{-1}^{+1}dt\frac{e^t}{t}=\int_{-1}^{+1}\frac{e^t-1}{t},
\label{eq:deltaint6} \tag{24}
\end{equation}
$$
since $e^x=e^0=1$. With Eq. ([eq:deltaint4](#eq:deltaint4)) we have then
<!-- Equation labels as ordinary links -->
<div id="eq:deltaint7"></div>
$$
\begin{equation}
\int_{-1}^{+1}\frac{e^t-1}{t}\approx \sum_{i=1}^{N}\omega_i\frac{e^{t_i}-1}{t_i}.
\label{eq:deltaint7} \tag{25}
\end{equation}
$$
## Treatment of Singular Integrals
The exact results is $2.11450175075....$. With just two mesh points we recall
from the previous subsection that $\omega_1=\omega_2=1$ and that the mesh points are the zeros of $L_2(x)$, namely $x_1=-1/\sqrt{3}$ and
$x_2=1/\sqrt{3}$. Setting $N=2$ and inserting these values in the last
equation gives
$$
I_2(x=0)=\sqrt{3}\left(e^{1/\sqrt{3}}-e^{-1/\sqrt{3}}\right)=2.1129772845.
$$
With six mesh points we get even the exact result to the tenth digit
$$
I_6(x=0)=2.11450175075!
$$
## Treatment of Singular Integrals
We can repeat the above subtraction trick for more complicated
integrands.
First we modify the integration limits to $\pm \infty$ and use the fact
that
$$
\int_{-\infty}^{\infty} \frac{dk}{k-k_0}=
\int_{-\infty}^{0} \frac{dk}{k-k_0}+
\int_{0}^{\infty} \frac{dk}{k-k_0} =0.
$$
A change of variable $u=-k$ in the integral with limits from $-\infty$ to $0$ gives
$$
\int_{-\infty}^{\infty} \frac{dk}{k-k_0}=
\int_{\infty}^{0} \frac{-du}{-u-k_0}+
\int_{0}^{\infty} \frac{dk}{k-k_0}= \int_{0}^{\infty} \frac{dk}{-k-k_0}+
\int_{0}^{\infty} \frac{dk}{k-k_0}=0.
$$
## Treatment of Singular Integrals
It means that the curve $1/(k-k_0)$ has equal and opposite
areas on both sides of the singular point $k_0$. If we break
the integral into one over positive $k$ and one over
negative $k$, a change of variable $k\rightarrow -k$
allows us to rewrite the last equation as
$$
\int_{0}^{\infty} \frac{dk}{k^2-k_0^2} =0.
$$
## Treatment of Singular Integrals
We can use this to express a principal values integral
as
<!-- Equation labels as ordinary links -->
<div id="eq:trick_pintegral"></div>
$$
\begin{equation}
{\cal P}\int_{0}^{\infty} \frac{f(k)dk}{k^2-k_0^2} =
\int_{0}^{\infty} \frac{(f(k)-f(k_0))dk}{k^2-k_0^2},
\label{eq:trick_pintegral} \tag{26}
\end{equation}
$$
where the right-hand side is no longer singular at
$k=k_0$, it is proportional to the derivative $df/dk$,
and can be evaluated numerically as any other integral.
Such a trick is often used when evaluating integral equations.
## Example of a multidimensional integral
Here we show an example of a multidimensional integral which appears in quantum mechanical calculations.
The ansatz for the wave function for two electrons is given by the product of two
$1s$ wave functions as
$$
\Psi({\bf r}_1,{\bf r}_2) = \exp{-(\alpha (r_1+r_2))}.
$$
The integral we need to solve is the quantum mechanical expectation value of the correlation
energy between two electrons, namely
$$
I = \int_{-\infty}^{\infty} d{\bf r}_1d{\bf r}_2 \exp{-2(\alpha (r_1+r_2))}\frac{1}{|{\bf r}_1-{\bf r}_2|}.
$$
The integral has an exact solution $5\pi^2/16 = 0.19277$.
## Parts of code and brute force Gauss-Legendre quadrature
If we use Gaussian quadrature with Legendre polynomials (without rewriting the integral), we have
double *x = new double [N];
double *w = new double [N];
// set up the mesh points and weights
GaussLegendrePoints(a,b,x,w, N);
// evaluate the integral with the Gauss-Legendre method
// Note that we initialize the sum
double int_gauss = 0.;
// six-double loops
for (int i=0;i<N;i++){
for (int j = 0;j<N;j++){
for (int k = 0;k<N;k++){
for (int l = 0;l<N;l++){
for (int m = 0;m<N;m++){
for (int n = 0;n<N;n++){
int_gauss+=w[i]*w[j]*w[k]*w[l]*w[m]*w[n]
*int_function(x[i],x[j],x[k],x[l],x[m],x[n]);
}}}}}
}
## The function to integrate, code example
// this function defines the function to integrate
double int_function(double x1, double y1, double z1, double x2, double y2, double z2)
{
double alpha = 2.;
// evaluate the different terms of the exponential
double exp1=-2*alpha*sqrt(x1*x1+y1*y1+z1*z1);
double exp2=-2*alpha*sqrt(x2*x2+y2*y2+z2*z2);
double deno=sqrt(pow((x1-x2),2)+pow((y1-y2),2)+pow((z1-z2),2));
return exp(exp1+exp2)/deno;
} // end of function to evaluate
## Laguerre polynomials
Using Legendre polynomials for the Gaussian quadrature is not very efficient. There are several reasons for this:
* You can easily end up in situations where the integrand diverges
* The limits $\pm \infty$ have to be approximated with a finite number
It is very useful here to change to spherical coordinates
$$
d{\bf r}_1d{\bf r}_2 = r_1^2dr_1 r_2^2dr_2 dcos(\theta_1)dcos(\theta_2)d\phi_1d\phi_2,
$$
and
$$
\frac{1}{r_{12}}= \frac{1}{\sqrt{r_1^2+r_2^2-2r_1r_2cos(\beta)}}
$$
with
$$
\cos(\beta) = \cos(\theta_1)\cos(\theta_2)+\sin(\theta_1)\sin(\theta_2)\cos(\phi_1-\phi_2))
$$
## Laguerre polynomials, the new integrand
This means that our integral becomes
$$
I=\int_0^{\infty} r_1^2dr_1 \int_0^{\infty}r_2^2dr_2 \int_0^{\pi}dcos(\theta_1)\int_0^{\pi}dcos(\theta_2)\int_0^{2\pi}d\phi_1\int_0^{2\pi}d\phi_2 \frac{\exp{-2\alpha (r_1+r_2)}}{r_{12}}
$$
where we have defined
$$
\frac{1}{r_{12}}= \frac{1}{\sqrt{r_1^2+r_2^2-2r_1r_2cos(\beta)}}
$$
with
$$
\cos(\beta) = \cos(\theta_1)\cos(\theta_2)+\sin(\theta_1)\sin(\theta_2)\cos(\phi_1-\phi_2))
$$
## Laguerre polynomials, new integration rule: Gauss-Laguerre
Our integral is now given by
$$
I=\int_0^{\infty} r_1^2dr_1 \int_0^{\infty}r_2^2dr_2 \int_0^{\pi}dcos(\theta_1)\int_0^{\pi}dcos(\theta_2)\int_0^{2\pi}d\phi_1\int_0^{2\pi}d\phi_2 \frac{\exp{-2\alpha (r_1+r_2)}}{r_{12}}
$$
For the angles we need to perform the integrations over $\theta_i\in [0,\pi]$ and $\phi_i \in [0,2\pi]$. However, for the radial part we can now either use
* Gauss-Legendre wth an appropriate mapping or
* Gauss-Laguerre taking properly care of the integrands involving the $r_i^2 \exp{-(2\alpha r_i)}$ terms.
## Results with $N=20$ with Gauss-Legendre
<table border="1">
<thead>
<tr><th align="center">$r_{\mathrm{max}}$</th> <th align="center"> Integral </th> <th align="center"> Error </th> </tr>
</thead>
<tbody>
<tr><td align="center"> 1.00 </td> <td align="center"> 0.161419805 </td> <td align="center"> 0.0313459063 </td> </tr>
<tr><td align="center"> 1.50 </td> <td align="center"> 0.180468967 </td> <td align="center"> 0.012296744 </td> </tr>
<tr><td align="center"> 2.00 </td> <td align="center"> 0.177065182 </td> <td align="center"> 0.0157005292 </td> </tr>
<tr><td align="center"> 2.50 </td> <td align="center"> 0.167970694 </td> <td align="center"> 0.0247950165 </td> </tr>
<tr><td align="center"> 3.00 </td> <td align="center"> 0.156139391 </td> <td align="center"> 0.0366263199 </td> </tr>
</tbody>
</table>
## Results for $r_{\mathrm{max}}=2$ with Gauss-Legendre
<table border="1">
<thead>
<tr><th align="center">$N$</th> <th align="center"> Integral </th> <th align="center"> Error </th> </tr>
</thead>
<tbody>
<tr><td align="center"> 10 </td> <td align="center"> 0.129834248 </td> <td align="center"> 0.0629314631 </td> </tr>
<tr><td align="center"> 16 </td> <td align="center"> 0.167860437 </td> <td align="center"> 0.0249052742 </td> </tr>
<tr><td align="center"> 20 </td> <td align="center"> 0.177065182 </td> <td align="center"> 0.0157005292 </td> </tr>
<tr><td align="center"> 26 </td> <td align="center"> 0.183543237 </td> <td align="center"> 0.00922247353 </td> </tr>
<tr><td align="center"> 30 </td> <td align="center"> 0.185795624 </td> <td align="center"> 0.00697008738 </td> </tr>
</tbody>
</table>
## Results with Gauss-Laguerre
<table border="1">
<thead>
<tr><th align="center">$N$</th> <th align="center"> Integral </th> <th align="center"> Error </th> </tr>
</thead>
<tbody>
<tr><td align="center"> 10 </td> <td align="center"> 0.186457345 </td> <td align="center"> 0.00630836601 </td> </tr>
<tr><td align="center"> 16 </td> <td align="center"> 0.190113364 </td> <td align="center"> 0.00265234708 </td> </tr>
<tr><td align="center"> 20 </td> <td align="center"> 0.19108178 </td> <td align="center"> 0.00168393093 </td> </tr>
<tr><td align="center"> 26 </td> <td align="center"> 0.191831828 </td> <td align="center"> 0.000933882594 </td> </tr>
<tr><td align="center"> 30 </td> <td align="center"> 0.192113712 </td> <td align="center"> 0.000651999339 </td> </tr>
</tbody>
</table>
The code that was used to generate these results can be found under the [program link](https://github.com/CompPhysics/ComputationalPhysics/blob/master/doc/Programs/LecturePrograms/programs/NumericalIntegration/cpp/program2.cpp).
|
github_jupyter
|
from math import *
from sympy import *
def Trapez(a,b,f,n):
h = (b-a)/float(n)
s = 0
x = a
for i in range(1,n,1):
x = x+h
s = s+ f(x)
s = 0.5*(f(a)+f(b)) +s
return h*s
# function to compute pi
def function(x):
return 4.0/(1+x*x)
a = 0.0; b = 1.0; n = 100
result = Trapez(a,b,function,n)
print("Trapezoidal rule=", result)
# define x as a symbol to be used by sympy
x = Symbol('x')
exact = integrate(function(x), (x, 0.0, 1.0))
print("Sympy integration=", exact)
# Find relative error
print("Relative error", abs((exact-result)/exact))
%matplotlib inline
from math import log10
import numpy as np
from sympy import Symbol, integrate
import matplotlib.pyplot as plt
# function for the trapezoidal rule
def Trapez(a,b,f,n):
h = (b-a)/float(n)
s = 0
x = a
for i in range(1,n,1):
x = x+h
s = s+ f(x)
s = 0.5*(f(a)+f(b)) +s
return h*s
# function to compute pi
def function(x):
return 4.0/(1+x*x)
# define integration limits
a = 0.0; b = 1.0;
# find result from sympy
# define x as a symbol to be used by sympy
x = Symbol('x')
exact = integrate(function(x), (x, a, b))
# set up the arrays for plotting the relative error
n = np.zeros(9); y = np.zeros(9);
# find the relative error as function of integration points
for i in range(1, 8, 1):
npts = 10**i
result = Trapez(a,b,function,npts)
RelativeError = abs((exact-result)/exact)
n[i] = log10(npts); y[i] = log10(RelativeError);
plt.plot(n,y, 'ro')
plt.xlabel('n')
plt.ylabel('Relative error')
plt.show()
from math import exp
import numpy as np
from sympy import Symbol, integrate, exp, oo
# function for the trapezoidal rule
def TrapezoidalRule(a,b,f,n):
h = (b-a)/float(n)
s = 0
x = a
for i in range(1,n,1):
x = x+h
s = s+ f(x)
s = 0.5*(f(a)+f(b)) +s
return h*s
# function for the Gaussian quadrature with Laguerre polynomials
def GaussLaguerreRule(n):
s = 0
xgauleg, wgauleg = np.polynomial.laguerre.laggauss(n)
for i in range(1,n,1):
s = s+ xgauleg[i]*xgauleg[i]*wgauleg[i]
return s
# function to compute
def function(x):
return x*x*exp(-x)
# Integration limits for the Trapezoidal rule
a = 0.0; b = 10000.0
# define x as a symbol to be used by sympy
x = Symbol('x')
# find result from sympy
exact = integrate(function(x), (x, a, oo))
# set up the arrays for plotting the relative error
n = np.zeros(40); Trapez = np.zeros(4); LagGauss = np.zeros(4);
# find the relative error as function of integration points
for i in range(1, 3, 1):
npts = 10**i
n[i] = npts
Trapez[i] = abs((TrapezoidalRule(a,b,function,npts)-exact)/exact)
LagGauss[i] = abs((GaussLaguerreRule(npts)-exact)/exact)
print ("Integration points=", n[1], n[2])
print ("Trapezoidal relative error=", Trapez[1], Trapez[2])
print ("LagGuass relative error=", LagGauss[1], LagGauss[2])
| 0.550124 | 0.877844 |
<a href="https://colab.research.google.com/github/murlokito/Miscellanea/blob/python_dev/Copy_of_101_Tensorflow_e_Keras.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# TensorFlow
Um simples exemplo de apresentar uma mensagem.
Estamos a criar um simples grafo com uma constante.
```
import tensorflow as tf
'''O resultado do construtor representa a "Constant op" '''
hello = tf.constant("Hello, TensorFlow!")
'''Iniciar a sessão'''
sess = tf.Session()
'''Executar o grafo'''
print(sess.run(hello))
```
### Extra
#### Shape?
```
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
```
#### Porquê o b' antes do texto
O resultado do grafo de sessão é do tipo 'bytestring' dai o resultado impresso ter o prefixo "b'"
```
# Extra:
# O resultado do grafo de sessão é do tipo 'bytestring' dai o resultado impresso
# tem o prefixo "b'"
print(sess.run(hello).decode())
```
#### Está o GPU a correr?
Não : ''
Sim : ''/device:GPU:0''
```
tf.test.gpu_device_name()
```
#### Ver Bibliotecas instaladas
```
!pip list
```
## Regressão Linear
Y = W * X + b
---
Y = W1X1 + W2X2 + ... + WnXn + b
```
# Parametros do Modelo
W = tf.Variable([3.0], name="weight")
b = tf.Variable([-2.0], name="bias")
# Inputs do Modelo
# Data de treino
X = tf.placeholder(tf.float32)
# y
Y = tf.placeholder(tf.float32)
# Definição do Modelo
predictions = M*X + b
# loss function. Aqui fazemos o quadrado do erro ( mse )
loss = tf.reduce_sum(tf.square(predictions-Y))
# Operação de Treino (op trainning)
train = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
# train data e Sessão
x = [1.1,2.0,3.5,4.8]
y = [2.0,3.4,4.2,5.1]
sess.run(tf.global_variables_initializer())
for train_step in range(2000):
sess.run(train,{X:x,Y:y})
# Resultado
weight, bias, loss = sess.run([W, b, loss], {X:x, Y:y})
print("W: %s b: %s loss: %s"%(weight,bias,loss))
```
# Keras
É uma API de alto nível para construir e treinar modelos 'deep learning'. É usado para criar de forma rápida modelos avançados para pesquisa e producão, focado em três pontos:
* Fácil de usar
> Keras tem uma simples, consistente interface optimizada para os casos mais comuns. Fornece uma resposta limpa dos erros do utilizador
* Modular
> Os modelos de Keras são criados por blocos configuraveis com poucas restrições
* Fácil de extender
> Criar blocos personalizados basta usar as várias 'layers', 'loss functions' que existem para criar modelos de estado de arte
[[Keras Website]](https://www.tensorflow.org/guide/keras)
### Keras vs tf.Keras
Keras em 2017 tornou-se uma componente oficial no Tensorflow indicado como 'tf.keras'. Estando todas as mesmas funcionlidades integradas, não sendo necessário incluir umas outra linguagem. [anuncio](https://www.fast.ai/2017/01/03/keras/)
Keras tem o conceito de "backend", onde o backend poder ser: Tensorflow, CNTK ou Theano. Uma linguagem 3 frameworks
[tf.keras](https://www.tensorflow.org/api_docs/python/tf/keras) consegue correr qualquer código compativel mas tenham em mente que:
* Que a versão de ```tf.keras``` mais recente de Tensorflow pode não ser exactamente a mesma que a do PyPi, verificar sempre a compatibilidade por ```tf.keras.version```
* Quando se for a gravar os pesos de um modelo, tf.keras vai por omissão para ```checkpoint format```. Passar o formato 'h5' com ```save_format='h5'``` para usar HDF5
```
import tensorflow as tf
from tensorflow.keras import layers
print(tf.VERSION)
print(tf.keras.__version__)
```
## Um simples modelo
### Tensorflow
```
x = tf.placeholder(tf.float32, [1, 64])
model = tf.layers.dense(x, 64, tf.nn.relu)
model = tf.layers.dense(model, 64, tf.nn.relu)
model = tf.layers.dense(model, 10, tf.nn.softmax)
model
```
### Keras
```
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='relu', input_shape= (1,64) ),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.summary()
```
### Regressão Linear com Keras
1 - Importação das bibliotecas
```
import tensorflow as tf
import pandas as pd
import numpy as np
import random
random.seed(42)
```
2 - Variáveis
```
# Média, desvio padrão, e dimensão do dataset
mu, sigma, size = 0, 4, 100
# Inclinação/slope (m) e onde corta com o eixo y-intercept (b)
m, b = 2, 10
```
3 - Geração dados sintéticos
```
x = np.random.uniform(0,10, size)
df = pd.DataFrame({'x':x})
df['y_perfect'] = df['x'].apply(lambda x: m*x+b)
df['noise'] = np.random.normal(mu, sigma, size=(size,))
df['y'] = df['y_perfect'] + df['noise']
```
4 - Criar o modelo
```
model = tf.keras.Sequential([
tf.keras.layers.Dense(1, activation='linear', input_shape=(1,))
])
```
5 - Compilar o Modelo
```
model.compile(loss='mse', optimizer='adam')
```
6 - Treinar o modelo
```
history = model.fit(x=df['x'], y=df['y'], validation_split=0.2, batch_size=1, epochs=100)
```
7 - Resultado dos pesos
```
predicted_m = model.get_weights()[0][0][0]
predicted_b = model.get_weights()[1][0]
print("m={0:.2f} b={1:.2f}".format(predicted_m, predicted_b))
```
8 - Previsão
```
df['y_predicted'] = df['x'].apply(lambda x: predicted_m*x + predicted_b)
```
9 - Visualização dos Resultados
```
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
plt.plot(df['x'], df['y_perfect'], c='blue')
plt.scatter(df['x'], df['y_perfect'], c='blue')
plt.plot(df['x'], df['y_predicted'], c='red')
plt.scatter(df['x'], df['y'], c='green')
plt.ylabel('y')
plt.xlabel('x')
plt.show()
```
|
github_jupyter
|
import tensorflow as tf
'''O resultado do construtor representa a "Constant op" '''
hello = tf.constant("Hello, TensorFlow!")
'''Iniciar a sessão'''
sess = tf.Session()
'''Executar o grafo'''
print(sess.run(hello))
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
# Extra:
# O resultado do grafo de sessão é do tipo 'bytestring' dai o resultado impresso
# tem o prefixo "b'"
print(sess.run(hello).decode())
tf.test.gpu_device_name()
!pip list
# Parametros do Modelo
W = tf.Variable([3.0], name="weight")
b = tf.Variable([-2.0], name="bias")
# Inputs do Modelo
# Data de treino
X = tf.placeholder(tf.float32)
# y
Y = tf.placeholder(tf.float32)
# Definição do Modelo
predictions = M*X + b
# loss function. Aqui fazemos o quadrado do erro ( mse )
loss = tf.reduce_sum(tf.square(predictions-Y))
# Operação de Treino (op trainning)
train = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
# train data e Sessão
x = [1.1,2.0,3.5,4.8]
y = [2.0,3.4,4.2,5.1]
sess.run(tf.global_variables_initializer())
for train_step in range(2000):
sess.run(train,{X:x,Y:y})
# Resultado
weight, bias, loss = sess.run([W, b, loss], {X:x, Y:y})
print("W: %s b: %s loss: %s"%(weight,bias,loss))
* Quando se for a gravar os pesos de um modelo, tf.keras vai por omissão para ```checkpoint format```. Passar o formato 'h5' com ```save_format='h5'``` para usar HDF5
## Um simples modelo
### Tensorflow
### Keras
### Regressão Linear com Keras
1 - Importação das bibliotecas
2 - Variáveis
3 - Geração dados sintéticos
4 - Criar o modelo
5 - Compilar o Modelo
6 - Treinar o modelo
7 - Resultado dos pesos
8 - Previsão
9 - Visualização dos Resultados
| 0.614857 | 0.97658 |
```
username_1 = input("Enter Name user 1: ")
username_2 = input("Enter Name user 2 : ")
username_3 = input("Enter Name user 3: ")
username_4 = input("Enter Name user 4: ")
username_5 = input("Enter Name user 5: ")
password_for_user1 = input("Create password u1: ")
password_for_user2 = input("Create password u2: ")
password_for_user3 = input("Create password u3: ")
password_for_user4 = input("Create password u4: ")
password_for_user5 = input("Create password u5: ")
balacne_1 = int(input())
balacne_2 = int(input())
balacne_3 = int(input())
balacne_4 = int(input())
balacne_5 = int(input())
def Account_check():
print('Welcome to Sample bank program!!\n')
while True:
u,p = login()
if u == key1['name'] and p == key1['passw'] or u == key2['name'] and p == key2['passw'] or u == key3['name'] and p == key3['passw'] or u == key4['name'] and p == key4['passw'] or u == key5['name'] and p == key5['passw']:
print(f'Welcome {u} Have a good banking with us !!')
return u,p
else:
print('\nSorry username not found!!')
G = input('Do you wana try again ? Y/N: ')
if G.lower() in ('y','yes'):
login_form = True
else:
print('Thanks for Banking!!')
login_form = False
break
def login():
print('Login with your user name and password\n')
username = input("Your user name :")
password = input("Password :")
return username,password
key1 = {'name':username_1, 'passw':password_for_user1,'Bal_amount':balacne_1}
key2 = {'name':username_2, 'passw':password_for_user2,'Bal_amount':balacne_2}
key3 = {'name':username_3, 'passw':password_for_user3,'Bal_amount':balacne_3}
key4 = {'name':username_4, 'passw':password_for_user4,'Bal_amount':balacne_4}
key5 = {'name':username_5, 'passw':password_for_user5,'Bal_amount':balacne_5}
def Banking_menu(u1):
#Account details.name == name ---> Balance(amount),Options for Banking
print("""\n THIS IS THE MAIN PAGE OF THE SIMPLE BANK PROGRAM \n
PLease Choose any option that Listed below :\n
_______________________________________________
1.Balance Check
2.Withdraw
3.Deposit
4.Transfer
5.Exit
________________________________________________
""")
choice = True
while choice:
try:
option = int(input("Pick a Choice! 1-5 :"))
except ValueError:
print("Please enter a valid digit!!")
else:
if option not in range(1,6):
print('Enter a valid number !')
elif option == 5:
print("Logging Out!! Please wait.....")
print('Thanks for Banking!!')
choice = False
break
else:
print('Choice Accepted.. Loading..!')
Choice_1 = Choice_affect(option)
def Choice_affect(option_value):
if option_value == 1:
balance = balance_full()
elif option_value == 2:
withdrw = withdrawl_Full()
elif option_value == 3:
deposit_fun = Deposit_Full()
else:
Transfer_fun = Transfer_full(u1)
def balance_full():
def balce_check1():
if u1 == key1['name']:
b1 = key1['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b1}")
def balce_check2():
if u1 == key2['name']:
b2 = key2['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b2}")
def balce_check3():
if u1 == key3['name']:
b3 = key3['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b3}")
def balce_check4():
if u1 == key4['name']:
b4 = key4['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b4}")
def balce_check5():
if u1 == key5['name']:
b5 = key5['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b5}")
balce_check1()
balce_check2()
balce_check3()
balce_check4()
balce_check5()
def withdrawl_Full():
#Making each withdrw for every user
def withdraw1():
#note key value match should be important
if u1 == key1['name']:
b1 = key1['Bal_amount']
#making a loop for insufficient balance
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b1)<Amount:
print('Insufficent Balance !!')
else:
key1['Bal_amount'] = int(b1) - Amount
print(f'Please take the amount {Amount}')
b1 = key1['Bal_amount']
print(f'Balance amount is {b1}')
break
def withdraw2():
if u1 == key2['name']:
b2 = key2['Bal_amount']
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b2)<Amount:
print('Insufficent Balance !!')
else:
key2['Bal_amount'] = int(b2) - Amount
print(f'Please take the amount {Amount}')
b2 = key2['Bal_amount']
print(f'Balance amount is {b2}')
break
def withdraw3():
if u1 == key3['name']:
b3 = key3['Bal_amount']
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b3)<Amount:
print('Insufficent Balance !!')
else:
key3['Bal_amount'] = int(b3) - Amount
print(f'Please take the amount {Amount}')
b3 = key3['Bal_amount']
print(f'Balance amount is {b3}')
break
def withdraw4():
if u1 == key4['name']:
b1 = key4['Bal_amount']
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b4)<Amount:
print('Insufficent Balance !!')
else:
key4['Bal_amount'] = int(b4) - Amount
print(f'Please take the amount {Amount}')
b4 = key1['Bal_amount']
print(f'Balance amount is {b4}')
break
def withdraw5():
if u1 == key5['name']:
b5 = key5['Bal_amount']
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b5)<Amount:
print('Insufficent Balance !!')
else:
key5['Bal_amount'] = int(b5) - Amount
print(f'Please take the amount {Amount}')
b5 = key5['Bal_amount']
print(f'Balance amount is {b5}')
break
withdraw1()
withdraw2()
withdraw3()
withdraw4()
withdraw5()
def Deposit_Full():
def deposit_U1():
if u1 == key1['name']:
d1 = key1['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key1['Bal_amount'] = int(d1) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d1} ')
d1 = key1['Bal_amount']
print(f'Current Balance is {d1}')
break
def deposit_U2():
if u1 == key2['name']:
d2 = key2['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key2['Bal_amount'] = int(d2) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d2} ')
d2 = key2['Bal_amount']
print(f'Current Balance is {d2}')
break
def deposit_U3():
if u1 == key3['name']:
d3 = key3['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key3['Bal_amount'] = int(d3) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d3} ')
d3 = key3['Bal_amount']
print(f'Current Balance is {d3}')
break
def deposit_U4():
if u1 == key4['name']:
d4 = key4['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key4['Bal_amount'] = int(d4) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d4} ')
d4 = key4['Bal_amount']
print(f'Current Balance is {d4}')
break
def deposit_U5():
if u1 == key5['name']:
d2 = key5['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key5['Bal_amount'] = int(d5) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d5}')
d5 = key5['Bal_amount']
print(f'Currrent Balance is {d5}')
break
deposit_U1()
deposit_U2()
deposit_U3()
deposit_U4()
deposit_U5()
def Transfer_nn(TUD,u1,T1,Amount):
print(f'your account has {T1} balance')
def tansfer_amount1(T1):
TUN1 = key1['name']
TUNA1 = key1['Bal_amount']
print(f' Amount Transfer to {TUN1} !')
key1['Bal_amount'] = int(TUNA1) + Amount
print("Amount Transfered successfully!!")
TUNA1 = key1['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN1,TUNA1,u1,T1,Amount
def tansfer_amount2(T1):
TUN2 = key2['name']
TUNA2 = key2['Bal_amount']
print(f'Enter Transfer amount to {TUN2} !')
key2['Bal_amount'] = int(TUNA2) + Amount
print("Amount Transfered successfully!!")
TUNA2 = key2['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN2,TUNA2,u1,T1,Amount
def tansfer_amount3(T1):
TUN3 = key3['name']
TUNA3 = key3['Bal_amount']
print(f'Enter Transfer amount to {TUN3} !')
key3['Bal_amount'] = int(TUNA3) + Amount
print("Amount Transfered successfully!!")
TUNA3 = key3['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN3,TUNA3,u1,T1,Amount
def tansfer_amount4(T1):
TUN4 = key4['name']
TUNA4 = key4['Bal_amount']
print(f'Enter Transfer amount to {TUN4} !')
key4['Bal_amount'] = int(TUNA4) + Amount
print("Amount Transfered successfully!!")
TUNA4 = key4['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN4,TUNA4,u1,T1,Amount
def tansfer_amount5(T1):
TUN5 = key5['name']
TUNA5 = key5['Bal_amount']
print(f'Enter Transfer amount to {TUN5} !')
key5['Bal_amount'] = int(TUNA5) + Amount
print("Amount Transfered successfully!!")
TUNA5 = key5['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN5,TUNA5,u1,T1,Amount
if TUD == key1['name']:
TUN1,TUNA1,u1,T1,Amount_get = tansfer_amount1(T1)
return Amount_get
elif TUD == key2['name']:
TUN2,TUNA2,u1,T1,Amount_get = tansfer_amount2(T1)
return Amount_get
elif TUD == key3['name']:
TUN3,TUNA3,u1,T1,Amount_get = tansfer_amount3(T1)
return Amount_get
elif TUD == key4['name']:
TUN4,TUNA4,u1,T1,Amount_get = tansfer_amount4(T1)
return Amount_get
elif TUD == key5['name']:
TUN4,TUNA4,u1,T1,Amount_get = tansfer_amount5(T1)
return Amount_get
else:
print('NONE')
def Transfer_full(u1):
def transfer_1():
T1 = key1['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key1['Bal_amount'] = int(T1) - Amount
T1 = key1['Bal_amount']
break
return TUD,u1,T1,Amount
def transfer_2():
T1 = key2['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key2['Bal_amount'] = int(T1) - Amount
T1 = key2['Bal_amount']
break
return TUD,u1,T1,Amount
def transfer_3():
T1 = key3['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key3['Bal_amount'] = int(T1) - Amount
T1 = key3['Bal_amount']
break
return TUD,u1,T1,Amount
def transfer_4():
T1 = key4['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key4['Bal_amount'] = int(T1) - Amount
T1 = key4['Bal_amount']
break
return TUD,u1,T1,Amount
def transfer_5():
T1 = key5['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key5['Bal_amount'] = int(T1) - Amount
T1 = key5['Bal_amount']
break
return TUD,u1,T1,Amount
if u1 == key1['name']:
TUD,u1,T1,Amount = transfer_1()
elif u1 == key2['name']:
TUD,u1,T1,Amount = transfer_2()
elif u1 == key3['name']:
TUD,u1,T1,Amount = transfer_3()
elif u1 == key4['name']:
TUD,u1,T1,Amount = transfer_4()
elif u1 == key5['name']:
TUD,u1,T1,Amount = transfer_5()
else:
print('NONE FOUND!!')
Result = Transfer_nn(TUD,u1,T1,Amount)
u1,p1 = Account_check()
b = Banking_menu(u1)
u1,p1 = Account_check()
Banking_menu(u1)
key1
key2
key3
key4
key5
```
|
github_jupyter
|
username_1 = input("Enter Name user 1: ")
username_2 = input("Enter Name user 2 : ")
username_3 = input("Enter Name user 3: ")
username_4 = input("Enter Name user 4: ")
username_5 = input("Enter Name user 5: ")
password_for_user1 = input("Create password u1: ")
password_for_user2 = input("Create password u2: ")
password_for_user3 = input("Create password u3: ")
password_for_user4 = input("Create password u4: ")
password_for_user5 = input("Create password u5: ")
balacne_1 = int(input())
balacne_2 = int(input())
balacne_3 = int(input())
balacne_4 = int(input())
balacne_5 = int(input())
def Account_check():
print('Welcome to Sample bank program!!\n')
while True:
u,p = login()
if u == key1['name'] and p == key1['passw'] or u == key2['name'] and p == key2['passw'] or u == key3['name'] and p == key3['passw'] or u == key4['name'] and p == key4['passw'] or u == key5['name'] and p == key5['passw']:
print(f'Welcome {u} Have a good banking with us !!')
return u,p
else:
print('\nSorry username not found!!')
G = input('Do you wana try again ? Y/N: ')
if G.lower() in ('y','yes'):
login_form = True
else:
print('Thanks for Banking!!')
login_form = False
break
def login():
print('Login with your user name and password\n')
username = input("Your user name :")
password = input("Password :")
return username,password
key1 = {'name':username_1, 'passw':password_for_user1,'Bal_amount':balacne_1}
key2 = {'name':username_2, 'passw':password_for_user2,'Bal_amount':balacne_2}
key3 = {'name':username_3, 'passw':password_for_user3,'Bal_amount':balacne_3}
key4 = {'name':username_4, 'passw':password_for_user4,'Bal_amount':balacne_4}
key5 = {'name':username_5, 'passw':password_for_user5,'Bal_amount':balacne_5}
def Banking_menu(u1):
#Account details.name == name ---> Balance(amount),Options for Banking
print("""\n THIS IS THE MAIN PAGE OF THE SIMPLE BANK PROGRAM \n
PLease Choose any option that Listed below :\n
_______________________________________________
1.Balance Check
2.Withdraw
3.Deposit
4.Transfer
5.Exit
________________________________________________
""")
choice = True
while choice:
try:
option = int(input("Pick a Choice! 1-5 :"))
except ValueError:
print("Please enter a valid digit!!")
else:
if option not in range(1,6):
print('Enter a valid number !')
elif option == 5:
print("Logging Out!! Please wait.....")
print('Thanks for Banking!!')
choice = False
break
else:
print('Choice Accepted.. Loading..!')
Choice_1 = Choice_affect(option)
def Choice_affect(option_value):
if option_value == 1:
balance = balance_full()
elif option_value == 2:
withdrw = withdrawl_Full()
elif option_value == 3:
deposit_fun = Deposit_Full()
else:
Transfer_fun = Transfer_full(u1)
def balance_full():
def balce_check1():
if u1 == key1['name']:
b1 = key1['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b1}")
def balce_check2():
if u1 == key2['name']:
b2 = key2['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b2}")
def balce_check3():
if u1 == key3['name']:
b3 = key3['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b3}")
def balce_check4():
if u1 == key4['name']:
b4 = key4['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b4}")
def balce_check5():
if u1 == key5['name']:
b5 = key5['Bal_amount']
print(f"User {u1}'s Current Balance is ---> {b5}")
balce_check1()
balce_check2()
balce_check3()
balce_check4()
balce_check5()
def withdrawl_Full():
#Making each withdrw for every user
def withdraw1():
#note key value match should be important
if u1 == key1['name']:
b1 = key1['Bal_amount']
#making a loop for insufficient balance
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b1)<Amount:
print('Insufficent Balance !!')
else:
key1['Bal_amount'] = int(b1) - Amount
print(f'Please take the amount {Amount}')
b1 = key1['Bal_amount']
print(f'Balance amount is {b1}')
break
def withdraw2():
if u1 == key2['name']:
b2 = key2['Bal_amount']
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b2)<Amount:
print('Insufficent Balance !!')
else:
key2['Bal_amount'] = int(b2) - Amount
print(f'Please take the amount {Amount}')
b2 = key2['Bal_amount']
print(f'Balance amount is {b2}')
break
def withdraw3():
if u1 == key3['name']:
b3 = key3['Bal_amount']
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b3)<Amount:
print('Insufficent Balance !!')
else:
key3['Bal_amount'] = int(b3) - Amount
print(f'Please take the amount {Amount}')
b3 = key3['Bal_amount']
print(f'Balance amount is {b3}')
break
def withdraw4():
if u1 == key4['name']:
b1 = key4['Bal_amount']
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b4)<Amount:
print('Insufficent Balance !!')
else:
key4['Bal_amount'] = int(b4) - Amount
print(f'Please take the amount {Amount}')
b4 = key1['Bal_amount']
print(f'Balance amount is {b4}')
break
def withdraw5():
if u1 == key5['name']:
b5 = key5['Bal_amount']
while True:
try:
Amount = int(input("Enter amount to be taken : "))
except ValueError:
print('sorry enter no.of amount:')
else:
if int(b5)<Amount:
print('Insufficent Balance !!')
else:
key5['Bal_amount'] = int(b5) - Amount
print(f'Please take the amount {Amount}')
b5 = key5['Bal_amount']
print(f'Balance amount is {b5}')
break
withdraw1()
withdraw2()
withdraw3()
withdraw4()
withdraw5()
def Deposit_Full():
def deposit_U1():
if u1 == key1['name']:
d1 = key1['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key1['Bal_amount'] = int(d1) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d1} ')
d1 = key1['Bal_amount']
print(f'Current Balance is {d1}')
break
def deposit_U2():
if u1 == key2['name']:
d2 = key2['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key2['Bal_amount'] = int(d2) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d2} ')
d2 = key2['Bal_amount']
print(f'Current Balance is {d2}')
break
def deposit_U3():
if u1 == key3['name']:
d3 = key3['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key3['Bal_amount'] = int(d3) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d3} ')
d3 = key3['Bal_amount']
print(f'Current Balance is {d3}')
break
def deposit_U4():
if u1 == key4['name']:
d4 = key4['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key4['Bal_amount'] = int(d4) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d4} ')
d4 = key4['Bal_amount']
print(f'Current Balance is {d4}')
break
def deposit_U5():
if u1 == key5['name']:
d2 = key5['Bal_amount']
print('How much do u wana deposit :\n')
while True:
amountdep = int(input('Enter the Amount :'))
key5['Bal_amount'] = int(d5) + amountdep
print(f'Amount addedd!!! to your account ,Old Balance {d5}')
d5 = key5['Bal_amount']
print(f'Currrent Balance is {d5}')
break
deposit_U1()
deposit_U2()
deposit_U3()
deposit_U4()
deposit_U5()
def Transfer_nn(TUD,u1,T1,Amount):
print(f'your account has {T1} balance')
def tansfer_amount1(T1):
TUN1 = key1['name']
TUNA1 = key1['Bal_amount']
print(f' Amount Transfer to {TUN1} !')
key1['Bal_amount'] = int(TUNA1) + Amount
print("Amount Transfered successfully!!")
TUNA1 = key1['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN1,TUNA1,u1,T1,Amount
def tansfer_amount2(T1):
TUN2 = key2['name']
TUNA2 = key2['Bal_amount']
print(f'Enter Transfer amount to {TUN2} !')
key2['Bal_amount'] = int(TUNA2) + Amount
print("Amount Transfered successfully!!")
TUNA2 = key2['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN2,TUNA2,u1,T1,Amount
def tansfer_amount3(T1):
TUN3 = key3['name']
TUNA3 = key3['Bal_amount']
print(f'Enter Transfer amount to {TUN3} !')
key3['Bal_amount'] = int(TUNA3) + Amount
print("Amount Transfered successfully!!")
TUNA3 = key3['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN3,TUNA3,u1,T1,Amount
def tansfer_amount4(T1):
TUN4 = key4['name']
TUNA4 = key4['Bal_amount']
print(f'Enter Transfer amount to {TUN4} !')
key4['Bal_amount'] = int(TUNA4) + Amount
print("Amount Transfered successfully!!")
TUNA4 = key4['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN4,TUNA4,u1,T1,Amount
def tansfer_amount5(T1):
TUN5 = key5['name']
TUNA5 = key5['Bal_amount']
print(f'Enter Transfer amount to {TUN5} !')
key5['Bal_amount'] = int(TUNA5) + Amount
print("Amount Transfered successfully!!")
TUNA5 = key5['Bal_amount']
print(f'Current balance of {u1} is {T1}')
return TUN5,TUNA5,u1,T1,Amount
if TUD == key1['name']:
TUN1,TUNA1,u1,T1,Amount_get = tansfer_amount1(T1)
return Amount_get
elif TUD == key2['name']:
TUN2,TUNA2,u1,T1,Amount_get = tansfer_amount2(T1)
return Amount_get
elif TUD == key3['name']:
TUN3,TUNA3,u1,T1,Amount_get = tansfer_amount3(T1)
return Amount_get
elif TUD == key4['name']:
TUN4,TUNA4,u1,T1,Amount_get = tansfer_amount4(T1)
return Amount_get
elif TUD == key5['name']:
TUN4,TUNA4,u1,T1,Amount_get = tansfer_amount5(T1)
return Amount_get
else:
print('NONE')
def Transfer_full(u1):
def transfer_1():
T1 = key1['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key1['Bal_amount'] = int(T1) - Amount
T1 = key1['Bal_amount']
break
return TUD,u1,T1,Amount
def transfer_2():
T1 = key2['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key2['Bal_amount'] = int(T1) - Amount
T1 = key2['Bal_amount']
break
return TUD,u1,T1,Amount
def transfer_3():
T1 = key3['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key3['Bal_amount'] = int(T1) - Amount
T1 = key3['Bal_amount']
break
return TUD,u1,T1,Amount
def transfer_4():
T1 = key4['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key4['Bal_amount'] = int(T1) - Amount
T1 = key4['Bal_amount']
break
return TUD,u1,T1,Amount
def transfer_5():
T1 = key5['Bal_amount']
print(f'\n Welcome {u1}')
print("""\nWlcome to transfer Window !
Please, Check the details about the receiver Correctly...
NOTE : Once the process is done it cannot be Changed!!!
""")
while True:
TUD = input('Enter the Receiver ID : ')
try:
Amount = int(input('Amount : '))
except ValueError:
print('Please enter only respective values!')
else:
if T1 < Amount :
print('Insufficient Balance !\n')
print('Try again!!!')
else:
key5['Bal_amount'] = int(T1) - Amount
T1 = key5['Bal_amount']
break
return TUD,u1,T1,Amount
if u1 == key1['name']:
TUD,u1,T1,Amount = transfer_1()
elif u1 == key2['name']:
TUD,u1,T1,Amount = transfer_2()
elif u1 == key3['name']:
TUD,u1,T1,Amount = transfer_3()
elif u1 == key4['name']:
TUD,u1,T1,Amount = transfer_4()
elif u1 == key5['name']:
TUD,u1,T1,Amount = transfer_5()
else:
print('NONE FOUND!!')
Result = Transfer_nn(TUD,u1,T1,Amount)
u1,p1 = Account_check()
b = Banking_menu(u1)
u1,p1 = Account_check()
Banking_menu(u1)
key1
key2
key3
key4
key5
| 0.053663 | 0.242654 |
# RST design for a DC-motor
From HW3 2017 spring semester
## Plant model
Zero-order-hold sampling of the DC-motor with transfer function
$$ G(s) = \frac{1}{s(2s+1)} $$
gives a discrete-time system with pulse transfer function
\begin{equation}
G_d(z) = \frac{B(z)}{A(z)}= \frac{2\big(\frac{h}{2}-1+\mathrm{e}^{-\frac{h}{2}}\big)z + 2\big(1-\mathrm{e}^{-\frac{h}{2}}-\frac{h}{2}\mathrm{e}^{-\frac{h}{2}}\big)}{(z-1)\big(z-\mathrm{e}^{-\frac{h}{2}}\big)}.
\end{equation}
```
import numpy as np
import sympy as sy
from sympy.utilities.codegen import codegen
import control.matlab as cm
import re
import matplotlib.pyplot as plt
from scipy import signal
z = sy.symbols('z', real=False)
r1,s0,s1 = sy.symbols('r1,s0,s1', real=True)
hh = sy.symbols('h', real=True, positive=True)
Bp = 2*(0.5*hh - 1 + sy.exp(-0.5*hh))*z + 2*(1-sy.exp(-0.5*hh) - 0.5*hh*sy.exp(-0.5*hh))
Ap = (z-sy.exp(-0.5*hh))*(z-1)
print(Bp)
print(Ap)
```
## Determine sampling period and desired closed loop poles
In a continuous-time description of the desired closed-loop system we want the system to have two dominating poles at
$$ -5 \pm i5. $$
In addition to the two dominating poles, we want a third pole at
$$ a=-20 $$
to be able to control the response to disturbances. Determine a suitable sampling period $h$, and determine the poles (and characteristic polynomial) of the desired discrete-time closed-loop system.
### Solution
Since we have dominating complex-conjugated poles, the sampling period should be such that
$$ h\omega_n = 0.1 -- 0.6. $$
Choose $$h = \frac{0.3}{\omega_n} = \frac{0.3}{\sqrt{5^2+5^2}} = \frac{0.3}{5\sqrt{2}} \approx 0.04. $$
We get the discrete-time poles
\begin{align*}
p_{d_1} &= \exp{0.04(-5+i5)} = \exp(-0.2) \exp(i0.2) = 0.81\big(\cos(0.21) + i\sin(0.21)\big) \approx 0.80 + i0.16\\
p_{d_2} &= p_{d_1}^* = 0.80 - i0.16\\
p_{d_3} &= \exp(ah) = \exp(-20\cdot 0.04) = 0.45.
\end{align*}
```
Ap = sy.simplify(Ap.subs(hh, 0.04))
Bp = sy.simplify(Bp.subs(hh, 0.04))
print(Bp)
print(Ap)
```
## Design a 2-DoF controller
Assume a structure of the controller as given in figure \ref{fig:2dof}. The controller is given by
$$ R(q)u = -S(q)y + T(q)u_c. $$
With the plant-model
$$ A(q)y = B(q)u$$
we get the following difference equation for the closed-loop system
$$ \big( A(q)R(q) + B(q)S(q) \big) y = B(q)T(q) u_c. $$
Assume a suitable order (as low as possible) of the controller polynomials $R(q)$ and $S(q)$ and solve the diophantine equation
$$ A(q)R(q) + B(q)S(q) = Ac(q) $$
for $R$ and $S$.
Solve the equations for arbitrary $a$: Use a symbol $a$ in your calculations so that you can easily recalculate your controller for a different value of $a$.
```
z = sy.symbols('z', real=False)
r1,s0,s1,aa = sy.symbols('r1,s0,s1,aa', real=True)
Ac = z**2 - z*(0.8*2) + (0.8**2 + 0.16**2)
Ao = z-aa
Acl = Ac*Ao
Rp = z+r1
Sp = s0*z + s1
RHS = sy.simplify(sy.expand(Acl))
diopheq =sy.poly(Ap*Rp+Bp*Sp-Acl, z)
dioph = diopheq.all_coeffs()
print(sy.latex(sy.poly(RHS, z)))
print(dioph)
print(Acl)
print(Ap*Rp)
print(Ac)
print(Ap*Rp)
print(sy.poly(sy.simplify(sy.expand(Ap*Rp + Bp*Sp)), z))
sol = sy.solve(dioph, (r1,s0,s1))
print (-np.exp(-20*0.04) + 0.38)
print (- 0.98 + 0.6656)
print (1.6*np.exp(-20*0.04) - 0.98 + 0.6656)
print (-0.6656*np.exp(-20*0.04))
sol[r1].subs(aa, np.exp(-20*0.04))
print('r_1 = %f' % sol[r1].subs(aa, np.exp(-20*0.04)))
print('s_0 = %f' % sol[s0].subs(aa, np.exp(-20*0.04)))
print('s_1 = %f' % sol[s1].subs(aa, np.exp(-20*0.04)))
t0 = Ac.evalf(subs={z:1})/Bp.evalf(subs={z:1,})
print('t_0 = %f' % t0)
R = Rp.subs(sol)
S = Sp.subs(sol)
T = t0*Ao
Hc = T*Bp/(Ac*Ao)
Hcc = t0*0.8/Ac
sy.pretty_print(sy.expand(Hc))
sy.pretty_print(sy.expand(Hcc))
sy.pretty_print(Hc.evalf(subs={z:1}))
sy.pretty_print(sy.simplify(Ap*R + Bp*S))
0 + 2*1j
sy.Poly((Ac*Ao).subs(aa, -0.2), z).all_coeffs()
def my_bode(num, den, h=1.0):
n = len(den)-1
m = len(num)-1
w = np.linspace(0.01, np.pi, 400);
z = np.exp(1j*w);
dd = den[-1]
nd = num[-1]
for i in range(n):
dd += den[i]*np.power(z, n-i)
for i in range(m):
nd += num[i]*np.power(z, m-i)
return nd/dd,w
def bodeplots(a, aa, Ap, R, Ac, Ao):
numS = sy.list2numpy(sy.Poly((Ap*R).subs(aa, a), z).all_coeffs(),
dtype=np.float64)
numT = sy.list2numpy(sy.Poly((Bp*S).subs(aa, a), z).all_coeffs(),
dtype=np.float64)
den = sy.list2numpy(sy.Poly((Ac*Ao).subs(aa, a), z).all_coeffs(),
dtype=np.float64)
qS, wS = my_bode(numS, den)
qT, wT = my_bode(numT, den)
plt.figure()
plt.loglog(wS, np.abs(qS))
plt.loglog(wT, np.abs(qT))
plt.ylim((0.001, 10))
plt.legend(('Ss', 'Tt'))
#cm.bode([Ss, Tt])
bodeplots(-0.009, aa, Ap, R, Ac, Ao)
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from functools import partial
interact(bodeplots, a=(0.0, 1.0), aa=fixed(aa), Ap=fixed(Ap), R=fixed(R), Ac=fixed(Ac),
Ao=fixed(Ao))
# Reorganize solution expression for matlab code generation
sol_expr = ('RST_DC_lab', [Bp.all_coeffs()[0], Bp.all_coeffs()[1],
Ap.all_coeffs()[1], Ap.all_coeffs()[2],
sol[r1], sol[s0], sol[s1], A2p.subs(z, 1)/Bp.subs(z,1), h,np.exp(h*po1) ])
# Export to matlab code
[(m_name, m_code)] = codegen(sol_expr, 'octave')
m_code = m_code.replace("out1", "b0").replace("out2", "b1").replace("out3", "a1").replace("out4", "a2")
m_code = m_code.replace("out5", "r1").replace("out6", "s0").replace("out7", "s1").replace("out8", "t0")
m_code = m_code.replace("out9", "h").replace("out10", "obsPole")
m_code = m_code.replace("function ", "% function ")
m_code = m_code.replace("end", "")
print m_code
with open("/home/kjartan/Dropbox/undervisning/tec/MR2007/labs/dc_rst_design.m", "w") as text_file:
text_file.write(m_code)
cm.step?
G = Km * cm.tf([1], [tau, 1, 0])
Gd = Km * cm.tf([tau*(hpt-1+np.exp(-hpt)), tau*(1-(1+hpt)*np.exp(-hpt))], [1, -(1+np.exp(-hpt)), np.exp(-hpt)], h)
Gd2 = cm.c2d(G, h)
print Gd
print Gd2
print A2p
print A2p.evalf(subs={z:1})
print Bp
print Bp.evalf(subs={z:1})
0.3/(5*np.sqrt(2))
np.exp(-0.21)*np.sin(0.21)
np.exp(0.03*(-14))
0.746*41.8
```
|
github_jupyter
|
import numpy as np
import sympy as sy
from sympy.utilities.codegen import codegen
import control.matlab as cm
import re
import matplotlib.pyplot as plt
from scipy import signal
z = sy.symbols('z', real=False)
r1,s0,s1 = sy.symbols('r1,s0,s1', real=True)
hh = sy.symbols('h', real=True, positive=True)
Bp = 2*(0.5*hh - 1 + sy.exp(-0.5*hh))*z + 2*(1-sy.exp(-0.5*hh) - 0.5*hh*sy.exp(-0.5*hh))
Ap = (z-sy.exp(-0.5*hh))*(z-1)
print(Bp)
print(Ap)
Ap = sy.simplify(Ap.subs(hh, 0.04))
Bp = sy.simplify(Bp.subs(hh, 0.04))
print(Bp)
print(Ap)
z = sy.symbols('z', real=False)
r1,s0,s1,aa = sy.symbols('r1,s0,s1,aa', real=True)
Ac = z**2 - z*(0.8*2) + (0.8**2 + 0.16**2)
Ao = z-aa
Acl = Ac*Ao
Rp = z+r1
Sp = s0*z + s1
RHS = sy.simplify(sy.expand(Acl))
diopheq =sy.poly(Ap*Rp+Bp*Sp-Acl, z)
dioph = diopheq.all_coeffs()
print(sy.latex(sy.poly(RHS, z)))
print(dioph)
print(Acl)
print(Ap*Rp)
print(Ac)
print(Ap*Rp)
print(sy.poly(sy.simplify(sy.expand(Ap*Rp + Bp*Sp)), z))
sol = sy.solve(dioph, (r1,s0,s1))
print (-np.exp(-20*0.04) + 0.38)
print (- 0.98 + 0.6656)
print (1.6*np.exp(-20*0.04) - 0.98 + 0.6656)
print (-0.6656*np.exp(-20*0.04))
sol[r1].subs(aa, np.exp(-20*0.04))
print('r_1 = %f' % sol[r1].subs(aa, np.exp(-20*0.04)))
print('s_0 = %f' % sol[s0].subs(aa, np.exp(-20*0.04)))
print('s_1 = %f' % sol[s1].subs(aa, np.exp(-20*0.04)))
t0 = Ac.evalf(subs={z:1})/Bp.evalf(subs={z:1,})
print('t_0 = %f' % t0)
R = Rp.subs(sol)
S = Sp.subs(sol)
T = t0*Ao
Hc = T*Bp/(Ac*Ao)
Hcc = t0*0.8/Ac
sy.pretty_print(sy.expand(Hc))
sy.pretty_print(sy.expand(Hcc))
sy.pretty_print(Hc.evalf(subs={z:1}))
sy.pretty_print(sy.simplify(Ap*R + Bp*S))
0 + 2*1j
sy.Poly((Ac*Ao).subs(aa, -0.2), z).all_coeffs()
def my_bode(num, den, h=1.0):
n = len(den)-1
m = len(num)-1
w = np.linspace(0.01, np.pi, 400);
z = np.exp(1j*w);
dd = den[-1]
nd = num[-1]
for i in range(n):
dd += den[i]*np.power(z, n-i)
for i in range(m):
nd += num[i]*np.power(z, m-i)
return nd/dd,w
def bodeplots(a, aa, Ap, R, Ac, Ao):
numS = sy.list2numpy(sy.Poly((Ap*R).subs(aa, a), z).all_coeffs(),
dtype=np.float64)
numT = sy.list2numpy(sy.Poly((Bp*S).subs(aa, a), z).all_coeffs(),
dtype=np.float64)
den = sy.list2numpy(sy.Poly((Ac*Ao).subs(aa, a), z).all_coeffs(),
dtype=np.float64)
qS, wS = my_bode(numS, den)
qT, wT = my_bode(numT, den)
plt.figure()
plt.loglog(wS, np.abs(qS))
plt.loglog(wT, np.abs(qT))
plt.ylim((0.001, 10))
plt.legend(('Ss', 'Tt'))
#cm.bode([Ss, Tt])
bodeplots(-0.009, aa, Ap, R, Ac, Ao)
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from functools import partial
interact(bodeplots, a=(0.0, 1.0), aa=fixed(aa), Ap=fixed(Ap), R=fixed(R), Ac=fixed(Ac),
Ao=fixed(Ao))
# Reorganize solution expression for matlab code generation
sol_expr = ('RST_DC_lab', [Bp.all_coeffs()[0], Bp.all_coeffs()[1],
Ap.all_coeffs()[1], Ap.all_coeffs()[2],
sol[r1], sol[s0], sol[s1], A2p.subs(z, 1)/Bp.subs(z,1), h,np.exp(h*po1) ])
# Export to matlab code
[(m_name, m_code)] = codegen(sol_expr, 'octave')
m_code = m_code.replace("out1", "b0").replace("out2", "b1").replace("out3", "a1").replace("out4", "a2")
m_code = m_code.replace("out5", "r1").replace("out6", "s0").replace("out7", "s1").replace("out8", "t0")
m_code = m_code.replace("out9", "h").replace("out10", "obsPole")
m_code = m_code.replace("function ", "% function ")
m_code = m_code.replace("end", "")
print m_code
with open("/home/kjartan/Dropbox/undervisning/tec/MR2007/labs/dc_rst_design.m", "w") as text_file:
text_file.write(m_code)
cm.step?
G = Km * cm.tf([1], [tau, 1, 0])
Gd = Km * cm.tf([tau*(hpt-1+np.exp(-hpt)), tau*(1-(1+hpt)*np.exp(-hpt))], [1, -(1+np.exp(-hpt)), np.exp(-hpt)], h)
Gd2 = cm.c2d(G, h)
print Gd
print Gd2
print A2p
print A2p.evalf(subs={z:1})
print Bp
print Bp.evalf(subs={z:1})
0.3/(5*np.sqrt(2))
np.exp(-0.21)*np.sin(0.21)
np.exp(0.03*(-14))
0.746*41.8
| 0.276984 | 0.984017 |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from sklearn import linear_model
import scipy.stats as stats
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
pd.set_option("display.precision", 4)
```
### 1 Conceptual issues for LTCM
1. Describe LTCM’s investment strategy in less than 100 words.
<span style="color:#00008B">**Solution:** Many reasonable things to put here. Should identify their reliance on relative value and convergence trades. Should also mention their opportunistic trading as they spot dislocations due to institutional demands. (For example, liquidity needs.)
</span>
2. What are LTCM’s biggest advantages over its competitors?
<span style="color:#00008B">**Solution:**
Several advantages.</span>
<span style="color:#00008B">
• Efficient financing. LTCM got very favorable terms on all financing—sometimes even zero haircut! Typically had small, if any, outlay.</span>
<span style="color:#00008B">
• Fund size. Have market power even in the large market of institutional wholesale.</span>
<span style="color:#00008B">
• Liquidity. LTCM has in place many mechanisms to ensure liquidity.</span>
<span style="color:#00008B">
• Long-term horizon. In financing and assessing trades, LTCM takes a relatively long-term view.</span>
<span style="color:#00008B">
• Hedged. LTCM avoids taking too much default risk or explicit directional bets.</span>
<span style="color:#00008B">
Then again, LTCM went bust in Aug. 1998, so maybe these advantages were not as strong as it
seemed!
</span>
3. The case discusses four types of funding risk facing LTCM:
• collateral haircuts
• repo maturity
• equity redemption
• loan access
The case discusses specific ways in which LTCM manages each of these risks. Briefly discuss
them.
<span style="color:#00008B">**Solution:**
The case discusses steps LTCM took to manage four types of funding risks.</span>
<span style="color:#00008B">
1. Collateral haircuts. For most trades, LTCM obtains 100% financing on a fully collateralized
basis. Furthermore, LTCM stress tests the haircuts across its asset classes.</span>
<span style="color:#00008B">
2. Repo. LTCM goes against the norm by entering into relatively long-maturity repo. While much of it is overnight, LTCM uses contracts that typically have maturity of 6-12 months. Furthermore, LTCM manages their aggregate repo maturity.</span>
<span style="color:#00008B">
3. Equity redemption. The firm is highly levered, so equity funding risk is especially important. LTCM restricts redemptions of equity year by year. The restriction is particularly strong in that unredeemed money is re-locked.
They also spread the redemption windows across the year to ensure there is never a possi- bility of immediate withdrawal of a large portion of equity.</span>
<span style="color:#00008B">
4. For debt funding, LTCM negotiated a revolving loan that has no Material Adverse Change clause. Thus, the availability of debt funding is not so highly correlated with fund performance.
</span>
4. LTCM is largely in the business of selling liquidity and volatility. Describe how LTCM accounts for liquidity risk in their quantitative measurements.
<span style="color:#00008B">**Solution:** LTCM attempts to account for liquidity risk quantitatively by adjusting security correlations. For short-term horizons, LTCM assumes positive correlation between all trade cat- egories. Even if their net exposure to a strategy flips sides, they still assume positive correlation to the new net position.
Given the efforts of LTCM to hedge out obvious market risks, there are many strategies which would seem to have zero correlation. However, LTCM feels that liquidity concerns can cause the effective trading to be positively correlated.
</span>
5. Is leverage risk currently a concern for LTCM?
<span style="color:#00008B">**Solution:** It would seem that leverage is not particularly dangerous at the moment. The fund’s volatility is relatively low, its VaR is relatively low, nor is it particularly high relative to the rest of the industry.
Moreover, the firm actively manages its funding risk which theoretically means it should be able to handle the natural risks of high leverage.
At the time of the case, the firm is trying to determine whether to further increase leverage. Subsequently, at the end of 1997 the fund returned about a third of its 7.5 billion equity capital to investors.
Of course, less than a year later, the fund blew up, but from the time of the case it’s hard to see the leverage risk.
</span>
6. Many strategies of LTCM rely on converging spreads. LTCM feels that these are almost win/win situations because of the fact that if the spread converges, they make money. If it diverges, the trade becomes even more attractive, as convergence is still expected at a future date. What is the risk in these convergence trades?
<span style="color:#00008B">**Solution:** About a year after the time of the case, the fund loses most of its value due to non-converging trades. So clearly there is some risk!
Positions are subject to liquidity risk. If market liquidity dries up or the markets become segmented, the divergent spreads can persist for a long time. This indeed happens later to LTCM. The trades that get them in trouble ultimately pay off, but not before LTCM blows up.
LTCM believes it can exit these convergence trades if they become too unprofitable. However, a stop-loss order is not the same as a put option. If the price jumps discontinuously through the stop-loss, then it is ineffective. Or a market may be paralyzed/illiquid when trying to execute the stop-loss. A put option does not need to worry about price impact, whereas a stop-loss does. Finally, a stop-loss ensures that an investor sells as soon as a security price hits a worst-case scenario, ensuring unfavorable market timing.
</span>
### 2 LTCM Risk Decomposition
```
ltcm = pd.read_excel('ltcm_exhibits_data.xlsx', sheet_name = "Sheet1").set_index('Date')
ltcm.head()
rf = pd.read_excel('gmo_analysis_data.xlsx', sheet_name = 3).set_index('Date')['1994-03-31':'1998-07-31']
rf.head()
spy = pd.read_excel('gmo_analysis_data.xlsx', sheet_name = 2).set_index('Date')['1994-03-31':'1998-07-31']
ltcm = ltcm.join(spy['SPY'])
ltcm.head()
ex_ltcm = ltcm.subtract(rf['US3M'],axis = 'rows')
ex_ltcm.head()
def summary_stats(df, annual_fac):
ss_df = (df.mean() * annual_fac).to_frame('Mean')
ss_df['Vol'] = df.std() * np.sqrt(annual_fac)
ss_df['Sharpe'] = ss_df['Mean'] / ss_df['Vol']
#ss_df['VaR'] = df.quantile(0.05)
return ss_df.T
def tail_risk_report(data, q):
df = data.copy()
df.index = data.index.date
report = pd.DataFrame(columns = df.columns)
report.loc['Skewness'] = df.skew()
report.loc['Excess Kurtosis'] = df.kurtosis()
report.loc['VaR'] = df.quantile(q)
return report
```
1. Summary stats.
(a) For both the gross and net series of LTCM excess returns, report the mean, volatility, and
Sharpe ratios. (Annualize them.)
(b) Report the skewness, kurtosis, and (historic) VaR(.05).
(c) Comment on how these stats compare to SPY and other assets we have seen. How much
do they differ between gross and net?
<span style="color:#00008B">**Solution:**
The return performances of both gross and net are very similar to those of SPY, but gross and net returns have more tail risk than SPY. Compared with other assets such as the FF-factors or hedge fund series we've seen so far, the Sharpe ratios of LTCM are much higher.
The gross return has higher mean, slightly higher volatility, and higher Sharpe ratio than the net return. The gross return also has less negative skewness, less excess kurtosis, and smaller VaR than the net return. All these stats show that gross return looks more attractive than the net return.
</span>
```
# 1
summary_stats(ex_ltcm,12)
tail_risk_report(ex_ltcm,0.05)
```
2. Using the series of net LTCM excess returns, denoted $\tilde{r}^{LTCM}$, estimate the following regression:
(a) Report $\alpha$ and $\beta_m$. Report the $R_2$ stat.
(b) From this regression, does LTCM appear to be a “closet indexer”?
<span style="color:#00008B">**Solution:**
LTCM is definitely not a closet indexer - at least with respect to the market index. The market factor explains only 0.019 of the fund’s return variation. Furthermore, the response to the market is quite small on average as the market beta is only 0.1371.
</span>
(c) From the regression, does LTCM appear to deliver excess returns beyond the risk premium
we expect from market exposure?
<span style="color:#00008B">**Solution:**
Yes. LTCM has market exposure of $\beta_m=0.1371$. If this were the only channel of delivering risk premium, then LTCM would have a tiny risk premium. However, the summary stats show it has a relatively large mean excess return - much larger than 0.1371 multiplied by the market risk premium.
More simply, one could note that LTCM and the market are both traded securities, yet LTCM delivers mean excess return beyond the market given that it has positive $\alpha$ of 0.011 per month.
</span>
```
lhs = ex_ltcm['Net return']
rhs = sm.add_constant(ex_ltcm['SPY'])
res = sm.OLS(lhs, rhs, missing='drop').fit()
single_report = res.params.to_frame('Single')
single_report.loc['R_squared','Single'] = res.rsquared
single_report
```
3. Let’s check for non-linear market exposure. Run the following regression on LTCM’s net excess returns:
(a) Report $\beta_1$, $\beta_2$, and the $R_2$ stat.
(b) Does the quadratic market factor do much to increase the overall LTCM variation explained by the market?
<span style="color:#00008B">**Solution:**
Yes. The $R_2$ goes from .0190 to .0243. Still, the quadratic market model leaves much of LTCM unexplained.
</span>
(c) From the regression evidence, does LTCM’s market exposure behave as if it is long market options or short market options?
<span style="color:#00008B">**Solution:**
The negative quadratic beta tells us that LTCM’s return is, on average, concave in the market return. That is, LTCM is less than proportionally up with the market and more than proportionally down when the market is down. This is the type of exposure LTCM would get by selling put options and call options on the market.
</span>
(d) Should we describe LTCM as being positively or negatively exposed to market volatility?
<span style="color:#00008B">**Solution:**
LTCM is hurt by market volatility given that the quadratic term implies low LTCM returns when the market is particularly high or low.
</span>
```
# 3
X = pd.DataFrame(columns = ['SPY','SPY Squared'],index = ex_ltcm.index)
X['SPY'] = ex_ltcm['SPY']
X['SPY Squared'] = ex_ltcm['SPY']**2
lhs = ex_ltcm['Net return']
rhs = sm.add_constant(X)
res = sm.OLS(lhs, rhs, missing='drop').fit()
quad_report = res.params.to_frame('Quadratic')
quad_report['P-values'] = res.pvalues
quad_report.loc['R_squared','Quadratic'] = res.rsquared
quad_report
```
4. Let’s try to pinpoint the nature of LTCM’s nonlinear exposure. Does it come more from exposure to up-markets or down-markets? Run the following regression on LTCM’s net excess returns:
(a) Report $\beta$, $\beta_u$, $\beta_d$, and the $R_2$ stat.
(b) Is LTCM long or short the call-like factor? And the put-like factor?
<span style="color:#00008B">**Solution:**
LTCM is short a call option as seen by the negative estimate of $\beta_u$. LTCM also has a positive $\beta_d$ which would appear to give it a long put exposure.
</span>
(c) Which factor moves LTCM more, the call-like factor, or the put-like factor?
<span style="color:#00008B">**Solution:**
The put-like factor influences LTCM more as the magnitude of $\beta_u$ is less than 1 and the magnitude of $\beta_d$ is greater than 1.
</span>
(d) In the previous problem, you commented on whether LTCM is positively or negatively exposed to market volatility. Using this current regression, does this volatility exposure come more from being long the market’s upside? Short the market’s downside? Something else?
<span style="color:#00008B">**Solution:**
This regression shows that LTCM is neither levered to the downside nor exposed upside of the market, which agrees with the previous comment.
</span>
```
# 4
k1 = 0.03
k2 = -0.03
X = pd.DataFrame(columns = ['call','put'],index = ex_ltcm.index)
X['call'] = (ex_ltcm['SPY'] - k1).clip(lower = 0)
X['put'] = (k2 - ex_ltcm['SPY']).clip(lower = 0)
X['SPY'] = ex_ltcm['SPY']
lhs = ex_ltcm['Net return']
rhs = sm.add_constant(X)
res = sm.OLS(lhs, rhs, missing='drop').fit()
option_report = res.params.to_frame('Option')
option_report['P-values'] = res.pvalues
option_report.loc['R_squared','Option'] = res.rsquared
option_report
```
### 3 The FX Carry Trade
```
rf_rates = pd.read_excel('fx_carry_data.xlsx', sheet_name = 1)
rf_rates = rf_rates.set_index('DATE')
log_rf_rates = np.log(1+rf_rates)
log_rf_rates
fx_rates = pd.read_excel('fx_carry_data.xlsx', sheet_name = 2)
fx_rates = fx_rates.set_index('DATE')
log_fx_rates = np.log(fx_rates)
log_fx_rates
sub_rf = log_rf_rates.iloc[:,1:]
sub_rf.columns = log_fx_rates.columns
sub_rf
```
1. The Static Carry Trade
Report the following stats, (based on the excess log returns.) Annualize them.
(a) mean
(b) volatility
(c) Sharpe ratio
```
# 1
ex_carry = (log_fx_rates - log_fx_rates.shift(1) + sub_rf).subtract(log_rf_rates['USD3M'],axis = 'rows')
summary_stats(ex_carry,12)
```
2. Implications for UIP:
(a) Do any of these stats contradict the (log version) of Uncovered Interest Parity (UIP)?
<span style="color:#00008B">**Solution:**
According to UIP, currency appreciation will counterbalance rate differentials, on average. Thus, the mean excess returns would all be zero, as well as the Sharpe ratios.
However, currency appreciation would not necessarily counterbalance rate differentials for any given month—just on average. Thus, non-zero volatility, skewness, and kurtosis do not contradict UIP.
</span>
(b) A long position in which foreign currency offered the best Sharpe ratio over the sample?
<span style="color:#00008B">**Solution:**
The Sharpe ratio is largest for holding GBP.
</span>
(c) Are there any foreign currencies for which a long position earned a negative excess return (in USD) over the sample?
<span style="color:#00008B">**Solution:**
Over the sample, holding EUR, CHF, and JPY will give a negative excess return.
</span>
3. Predicting FX
(a) Make a table with 6 columns—each corresponding to a different currency regression. Report the regression estimates $\alpha_i$ and $\beta_i$ in the first two rows. Report the $R_2$ stat in the third row.
(b) Suppose the foreign risk-free rate increases relative to the US rate.
i. For which foreign currencies would we predict a relative strengthening of the USD in the following period?
<span style="color:#00008B">**Solution:**
JPY has positive regression slopes. Thus, when the currency has relatively large riskless rates relative to the USD, we predict relatively more USD appreciation.
</span>
ii. For which currencies would we predict relative weakening of the USD in the following period?
<span style="color:#00008B">**Solution:**
GBP, EUR, and CHF have negative regression slopes. Thus, when the currency has relatively large riskless rates relative to the USD, we predict relatively more USD depreciation.
</span>
iii. This FX predictability is strongest in the case of which foreign currency?
<span style="color:#00008B">**Solution:**
According to the $R_2$ stats, the predictability of FX rates is much stronger for CHF and EUR relative to the other four currencies. Even so, FX predictability is relatively small—there is a lot of variation in FX rates unexplained by interest rate differentials.
</span>
```
# 3
Y = log_fx_rates - log_fx_rates.shift(1)
X = - sub_rf.subtract(log_rf_rates['USD3M'],axis = 'rows')
ols_report = pd.DataFrame(index=log_fx_rates.columns)
for col in log_fx_rates.columns:
lhs = Y[col]
rhs = sm.add_constant(X[col])
res = sm.OLS(lhs, rhs, missing='drop').fit()
ols_report.loc[col, 'alpha'] = res.params['const'] * 12
ols_report.loc[col, 'beta'] = res.params[col]
ols_report.loc[col, 'R_squared'] = res.rsquared
ols_report.T
```
4. The Dynamic Carry Trade
(a) Use your regression estimates from Problem 3 along with the formula above to calculate the fraction of months for which the estimated FX risk premium positive.
(b) Which currencies most consistently have a positive FX risk premium? And for which
currencies does the FX risk premium most often go negative?
<span style="color:#00008B">**Solution:**
The table indicates the fraction of months for which the dynamic carry trade would have recommended a long position in the foreign currency (against the USD.) Note that for the CHF, the interest rate differentials were favorable enough that the dynamic strategy would have gone long this currency in every month.
For JPY, on the other hand, the strategy would not have long at all.
</span>
(c) Explain how we could use these conditional risk premia to improve the static carry trade returns calculated in Problem 1.
<span style="color:#00008B">**Solution:**
We can use these conditional risk premia to help us decide whether and when to enter the carry trade.
</span>
```
# 4
estimate_fx = (ols_report['beta'] - 1) * X + ols_report['alpha']
freq_report = pd.DataFrame(index=log_fx_rates.columns)
for col in log_fx_rates.columns:
freq_report.loc[col,'Frequency of positive weight'] = (estimate_fx[col] > 0).sum() / len(estimate_fx)
freq_report.T
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from sklearn import linear_model
import scipy.stats as stats
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
pd.set_option("display.precision", 4)
ltcm = pd.read_excel('ltcm_exhibits_data.xlsx', sheet_name = "Sheet1").set_index('Date')
ltcm.head()
rf = pd.read_excel('gmo_analysis_data.xlsx', sheet_name = 3).set_index('Date')['1994-03-31':'1998-07-31']
rf.head()
spy = pd.read_excel('gmo_analysis_data.xlsx', sheet_name = 2).set_index('Date')['1994-03-31':'1998-07-31']
ltcm = ltcm.join(spy['SPY'])
ltcm.head()
ex_ltcm = ltcm.subtract(rf['US3M'],axis = 'rows')
ex_ltcm.head()
def summary_stats(df, annual_fac):
ss_df = (df.mean() * annual_fac).to_frame('Mean')
ss_df['Vol'] = df.std() * np.sqrt(annual_fac)
ss_df['Sharpe'] = ss_df['Mean'] / ss_df['Vol']
#ss_df['VaR'] = df.quantile(0.05)
return ss_df.T
def tail_risk_report(data, q):
df = data.copy()
df.index = data.index.date
report = pd.DataFrame(columns = df.columns)
report.loc['Skewness'] = df.skew()
report.loc['Excess Kurtosis'] = df.kurtosis()
report.loc['VaR'] = df.quantile(q)
return report
# 1
summary_stats(ex_ltcm,12)
tail_risk_report(ex_ltcm,0.05)
lhs = ex_ltcm['Net return']
rhs = sm.add_constant(ex_ltcm['SPY'])
res = sm.OLS(lhs, rhs, missing='drop').fit()
single_report = res.params.to_frame('Single')
single_report.loc['R_squared','Single'] = res.rsquared
single_report
# 3
X = pd.DataFrame(columns = ['SPY','SPY Squared'],index = ex_ltcm.index)
X['SPY'] = ex_ltcm['SPY']
X['SPY Squared'] = ex_ltcm['SPY']**2
lhs = ex_ltcm['Net return']
rhs = sm.add_constant(X)
res = sm.OLS(lhs, rhs, missing='drop').fit()
quad_report = res.params.to_frame('Quadratic')
quad_report['P-values'] = res.pvalues
quad_report.loc['R_squared','Quadratic'] = res.rsquared
quad_report
# 4
k1 = 0.03
k2 = -0.03
X = pd.DataFrame(columns = ['call','put'],index = ex_ltcm.index)
X['call'] = (ex_ltcm['SPY'] - k1).clip(lower = 0)
X['put'] = (k2 - ex_ltcm['SPY']).clip(lower = 0)
X['SPY'] = ex_ltcm['SPY']
lhs = ex_ltcm['Net return']
rhs = sm.add_constant(X)
res = sm.OLS(lhs, rhs, missing='drop').fit()
option_report = res.params.to_frame('Option')
option_report['P-values'] = res.pvalues
option_report.loc['R_squared','Option'] = res.rsquared
option_report
rf_rates = pd.read_excel('fx_carry_data.xlsx', sheet_name = 1)
rf_rates = rf_rates.set_index('DATE')
log_rf_rates = np.log(1+rf_rates)
log_rf_rates
fx_rates = pd.read_excel('fx_carry_data.xlsx', sheet_name = 2)
fx_rates = fx_rates.set_index('DATE')
log_fx_rates = np.log(fx_rates)
log_fx_rates
sub_rf = log_rf_rates.iloc[:,1:]
sub_rf.columns = log_fx_rates.columns
sub_rf
# 1
ex_carry = (log_fx_rates - log_fx_rates.shift(1) + sub_rf).subtract(log_rf_rates['USD3M'],axis = 'rows')
summary_stats(ex_carry,12)
# 3
Y = log_fx_rates - log_fx_rates.shift(1)
X = - sub_rf.subtract(log_rf_rates['USD3M'],axis = 'rows')
ols_report = pd.DataFrame(index=log_fx_rates.columns)
for col in log_fx_rates.columns:
lhs = Y[col]
rhs = sm.add_constant(X[col])
res = sm.OLS(lhs, rhs, missing='drop').fit()
ols_report.loc[col, 'alpha'] = res.params['const'] * 12
ols_report.loc[col, 'beta'] = res.params[col]
ols_report.loc[col, 'R_squared'] = res.rsquared
ols_report.T
# 4
estimate_fx = (ols_report['beta'] - 1) * X + ols_report['alpha']
freq_report = pd.DataFrame(index=log_fx_rates.columns)
for col in log_fx_rates.columns:
freq_report.loc[col,'Frequency of positive weight'] = (estimate_fx[col] > 0).sum() / len(estimate_fx)
freq_report.T
| 0.470493 | 0.870267 |
# Access PODAAC AWS cloud data examples tutorial
- Funding: Interagency Implementation and Advanced Concepts Team [IMPACT](https://earthdata.nasa.gov/esds/impact) for the Earth Science Data Systems (ESDS) program and AWS Public Dataset Program
### Credits: Tutorial development
* [Dr. Chelle Gentemann](mailto:gentemann@faralloninstitute.org) - [Twitter](https://twitter.com/ChelleGentemann) - Farallon Institute
* [Dr. Ryan Abernathey](mailto:rpa@ldeo.columbia.edu) - [Twitter](https://twitter.com/rabernat) - LDEO
Credits: Tutorial review and comments.
* [Dr. Ed Armstrong](mailto:edward.m.armstrong@jpl.nasa.gov) - JPL PODAAC
### Data proximate computing: These are BIG datasets that you can analyze on the cloud without downloading the data.
### Here we will demonstrate some ways to access the:
- AWS MUR sea surface temperatures
### To run this notebook
Code is in the cells that have <span style="color: blue;">In [ ]:</span> to the left of the cell and have a colored background
To run the code:
- option 1) click anywhere in the cell, then hold shift and press Enter
- option 2) click on the Run button at the top of the page in the dashboard
### First start by importing libraries
```
import warnings
# filter some warning messages
warnings.filterwarnings("ignore")
import xarray as xr
import fsspec
from matplotlib import pyplot as plt
import numpy as np
import cartopy
import cartopy.crs as ccrs
import intake
import dask
xr.set_options(display_style="html") #display dataset nicely
%matplotlib inline
plt.rcParams['figure.figsize'] = 12, 6
%config InlineBackend.figure_format = 'retina'
```
### Start a cluster, a group of computers that will work together.
(A cluster is the key to big data analysis on on Cloud.)
- This will set up a [dask kubernetes](https://docs.dask.org/en/latest/setup/kubernetes.html) cluster for your analysis and give you a path that you can paste into the top of the Dask dashboard to visualize parts of your cluster.
- You don't need to paste the link below into the Dask dashboard for this to work, but it will help you visualize progress.
- Try 20 workers to start (during the tutorial) but you can increase to speed things up later
```
from dask_gateway import Gateway
from dask.distributed import Client
gateway = Gateway()
cluster = gateway.new_cluster()
cluster.adapt(minimum=1, maximum=20)
client = Client(cluster)
cluster
```
** ☝️ Don’t forget to click the link above or copy it to the Dask dashboard on the left to view the scheduler dashboard! **
## [MUR SST](https://podaac.jpl.nasa.gov/Multi-scale_Ultra-high_Resolution_MUR-SST) [AWS Public dataset program](https://registry.opendata.aws/mur/)
### Access the MUR SST which is in an s3 bucket.
### This Pangeo binder is running on Google Cloud and data access will be slower than running it on AWS.

This code is an example of how to read from a s3 bucket.
Right now (2/16/2020) this takes ~1min on AWS and ~2 min on google cloud, there are two issues here and we are working to solve both.
1. In our Zarr datastore the time coodinate is chunked. We should have this fixed by 3/1/2020.
1. Some shortcomings in the s3fs and zarr formats have been identified. To work on these, git issues were raised to the developers [here](https://github.com/dask/s3fs/issues/285) and [here](https://github.com/zarr-developers/zarr-python/issues/536)
```
%%time
file_location = 's3://mur-sst/zarr'
ds_sst = xr.open_zarr(fsspec.get_mapper(file_location, anon=True),consolidated=True)
ds_sst
```
### Read entire 10 years of data at 1 point.
Select the ``analysed_sst`` variable over a specific time period, `lat`, and `lon` and load the data into memory.
```
%%time
sst_timeseries = ds_sst['analysed_sst'].sel(time=slice('2010-01-01','2020-01-01'),
lat=47,
lon=-145
).load()
sst_timeseries.plot()
```
### The anomaly is more interesting...
Use [.groupby](http://xarray.pydata.org/en/stable/generated/xarray.DataArray.groupby.html#xarray-dataarray-groupby) method to calculate the climatology and [.resample](http://xarray.pydata.org/en/stable/generated/xarray.Dataset.resample.html#xarray-dataset-resample) method to then average it into 1-month bins
```
sst_climatology = sst_timeseries.groupby('time.dayofyear').mean()
sst_anomaly = sst_timeseries.groupby('time.dayofyear')-sst_climatology
sst_anomaly_monthly = sst_anomaly.resample(time='1MS').mean()
#plot the data
sst_anomaly.plot()
sst_anomaly_monthly.plot()
plt.axhline(linewidth=2,color='k')
```
## Close the cluster
```
client.close()
cluster.close()
```
|
github_jupyter
|
import warnings
# filter some warning messages
warnings.filterwarnings("ignore")
import xarray as xr
import fsspec
from matplotlib import pyplot as plt
import numpy as np
import cartopy
import cartopy.crs as ccrs
import intake
import dask
xr.set_options(display_style="html") #display dataset nicely
%matplotlib inline
plt.rcParams['figure.figsize'] = 12, 6
%config InlineBackend.figure_format = 'retina'
from dask_gateway import Gateway
from dask.distributed import Client
gateway = Gateway()
cluster = gateway.new_cluster()
cluster.adapt(minimum=1, maximum=20)
client = Client(cluster)
cluster
%%time
file_location = 's3://mur-sst/zarr'
ds_sst = xr.open_zarr(fsspec.get_mapper(file_location, anon=True),consolidated=True)
ds_sst
%%time
sst_timeseries = ds_sst['analysed_sst'].sel(time=slice('2010-01-01','2020-01-01'),
lat=47,
lon=-145
).load()
sst_timeseries.plot()
sst_climatology = sst_timeseries.groupby('time.dayofyear').mean()
sst_anomaly = sst_timeseries.groupby('time.dayofyear')-sst_climatology
sst_anomaly_monthly = sst_anomaly.resample(time='1MS').mean()
#plot the data
sst_anomaly.plot()
sst_anomaly_monthly.plot()
plt.axhline(linewidth=2,color='k')
client.close()
cluster.close()
| 0.320928 | 0.983359 |
<img src="../../../images/qiskit_header.png" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" align="middle">
# Qiskit Aer: Noise Transformation
The latest version of this notebook is available on https://github.com/Qiskit/qiskit-tutorials.
## Introduction
This notebook shows how to use the Qiskit Aer `noise.utils.approximate_quantum_error` and `noise.utils. approximate_noise_model` to transform quantum noise channels into a different, more suitable, noise channel.
Our guiding example is Clifford simulation. A Clifford simulator can efficiently simulate quantum computations which include gates only from a limited, non-universal set of gates (the Clifford gates). Not all quantum noises can be added to such simulations; hence, we aim to find a "close" noise channel which can be simulated in a Clifford simulator.
We begin by importing the transformation functions.
```
from qiskit.providers.aer.noise.utils import approximate_quantum_error
from qiskit.providers.aer.noise.utils import approximate_noise_model
```
The name "approximate" suggests that this functions generate the closest (in the Hilbert-Schmidt metric) error possible to the given one.
We demonstrate the approximation using several standard error channels defined in Qiskit.
```
from qiskit.providers.aer.noise.errors.standard_errors import amplitude_damping_error
from qiskit.providers.aer.noise.errors.standard_errors import reset_error
from qiskit.providers.aer.noise.errors.standard_errors import pauli_error
import numpy as np
```
## Overview
A 1-qubit quantum channel is a function $\mathcal{C}:\mathbb{C}^{2\times2}\to\mathbb{C}^{2\times2}$ mapping density operators to density operators (to ensure the image is a density operator $\mathcal{C}$ is required to be completely positive and trace preserving, **CTCP**).
Given quantum channels $\mathcal{E}_{1},\dots,\mathcal{E}_{r}$, and probabilities $p_1, p_2, \dots, p_r$ such that $0\le p_i \le 1$ and $p_1+\dots +p_r = 1$, a new quantum channel $\mathcal{C}_\mathcal{E}$ can be constructed such that $\mathcal{C}_\mathcal{E}(\rho)$ has the effect of choosing the channel $\mathcal{E}_i$ with probability $p_i$ and applying it to $\rho$.
The noise transformation module solves the following optimization problem: Given a channel $\mathcal{C}$ ("goal") and a list of channels $\mathcal{E}_{1},\dots,\mathcal{E}_{r}$, find the probabilities $p_1, p_2, \dots, p_r$ minimizing $D(\mathcal{C}, \mathcal{C}_\mathcal{E})$ according to some distance metric $D$ (the Hilbert-Schmidt metric is currently used).
To ensure the approximation is honest, in the sense that the approximate error channel serves as an "upper bound" for the actual error channel, we add the additional honesty constraint
$$\text{F}(I,\mathcal{C})\ge F(I,\mathcal{C}_\mathcal{E})$$
Where $\text{F}$ is a fidelity measure and $I$ is the identity channel.
## Example: Approximating amplitude damping noise with reset noise.
**Amplitude damping** noise is described by a single parameter $0\le \gamma \le 1$ and given by the Kraus operators:
$$\left(\begin{array}{cc}
1 & 0\\
0 & \sqrt{1-\gamma}
\end{array}\right),\left(\begin{array}{cc}
0 & \sqrt{\gamma}\\
0 & 0
\end{array}\right)$$
**Reset** error is described by probabilities $0\le p, q\le 1$ such that $p+q\le 1$ and given by the Kraus operators:
$$\left(\begin{array}{cc}
\sqrt{p} & 0\\
0 & 0
\end{array}\right),\left(\begin{array}{cc}
0 & \sqrt{p}\\
0 & 0
\end{array}\right),\left(\begin{array}{cc}
0 & 0\\
\sqrt{q} & 0
\end{array}\right),\left(\begin{array}{cc}
0 & 0\\
0 & \sqrt{q}
\end{array}\right)$$
This can be thought of as "resetting" the quantum state of the affected qubit to $\left|0\right\rangle$ with probability $p$, to $\left|1\right\rangle$ with probability $q$, and do nothing with probability $1-(p+q)$.
It is not too difficult to determine analytically the best values of $p,q$ to approximate a-$\gamma$ amplitude damping channel, see the details __[here](https://arxiv.org/abs/1207.0046)__. The best approximation is
$$p=\frac{1}{2}\left(1+\gamma-\sqrt{1-\gamma}\right), q=0$$
```
gamma = 0.23
error = amplitude_damping_error(gamma)
results = approximate_quantum_error(error, operator_string="reset")
```
We only needed the above code to perform the actual approximation.
```
print(results)
p = (1 + gamma - np.sqrt(1 - gamma)) / 2
q = 0
print("")
print("Expected results:")
print("P(0) = {}".format(1-(p+q)))
print("P(1) = {}".format(p))
print("P(2) = {}".format(q))
```
We got the results predicted analytically.
## Different input types
The approximation function is given two inputs: The error channel to approximate, and a set of error channels that can be used in constructing the approximation.
The **error channel** to approximate can be given as any input that can be converted to the `QuantumError` object.
As an example, we explicitly construct the Kraus matrices of amplitude damping and pass to the same approximation function as before:
```
gamma = 0.23
K0 = np.array([[1,0],[0,np.sqrt(1-gamma)]])
K1 = np.array([[0,np.sqrt(gamma)],[0,0]])
results = approximate_quantum_error((K0, K1), operator_string="reset")
print(results)
```
The **error operators** that are used to construct the approximating channel can be either given as a list, a dictionary or a string indicating hard-coded channels.
Any channel can be either a list of Kraus operators, or 'QuantumError' objects.
The identity channel does not need to be passed directly; it is always implicitly used.
As an example, we approximate amplitude damping using an explicit Kraus representation for reset noises:
```
reset_to_0 = [np.array([[1,0],[0,0]]), np.array([[0,1],[0,0]])]
reset_to_1 = [np.array([[0,0],[1,0]]), np.array([[0,0],[0,1]])]
reset_kraus = (reset_to_0, reset_to_1)
gamma = 0.23
error = amplitude_damping_error(gamma)
results = approximate_quantum_error(error, operator_list=reset_kraus)
print(results)
```
Note the difference in the output channel: The probabilities are the same, but the input Kraus operators were converted to general Kraus channels, which cannot be used in a Clifford simulator. Hence, it is always better to pass a `QuantumError` object instead of the Kraus matrices, when possible.
|
github_jupyter
|
from qiskit.providers.aer.noise.utils import approximate_quantum_error
from qiskit.providers.aer.noise.utils import approximate_noise_model
from qiskit.providers.aer.noise.errors.standard_errors import amplitude_damping_error
from qiskit.providers.aer.noise.errors.standard_errors import reset_error
from qiskit.providers.aer.noise.errors.standard_errors import pauli_error
import numpy as np
gamma = 0.23
error = amplitude_damping_error(gamma)
results = approximate_quantum_error(error, operator_string="reset")
print(results)
p = (1 + gamma - np.sqrt(1 - gamma)) / 2
q = 0
print("")
print("Expected results:")
print("P(0) = {}".format(1-(p+q)))
print("P(1) = {}".format(p))
print("P(2) = {}".format(q))
gamma = 0.23
K0 = np.array([[1,0],[0,np.sqrt(1-gamma)]])
K1 = np.array([[0,np.sqrt(gamma)],[0,0]])
results = approximate_quantum_error((K0, K1), operator_string="reset")
print(results)
reset_to_0 = [np.array([[1,0],[0,0]]), np.array([[0,1],[0,0]])]
reset_to_1 = [np.array([[0,0],[1,0]]), np.array([[0,0],[0,1]])]
reset_kraus = (reset_to_0, reset_to_1)
gamma = 0.23
error = amplitude_damping_error(gamma)
results = approximate_quantum_error(error, operator_list=reset_kraus)
print(results)
| 0.658857 | 0.992697 |
```
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
from sympy import *
init_printing()
import sys
sys.path.append('../')
import uPVT.PVT_correlations as PVT
```
## Объемный коэффициент нефти
### Корреляция при давлении выше давления насыщения
Корреляция для объемного коэффициента нефти при давлении выше давления насыщения в некоторых источниках указывается, что она принадлежит Стендингу, в некоторых Vasquez & Beggs. На самом деле это не корреляция, так как природа ее происхождения не статистическая, а вполне себе физическое уравнение.
$$ b_o = b_{ob} \cdot \exp(c_o(p_b - p)) $$
где:
$ b_o $ - объемный коэффициент нефти при давлении p, м3/м3
$ b_{ob} $ - объемный коэффициент нефти при давлении насыщения, м3/м3
$ c_o $ - сжимаемость нефти, 1/МПа
$ p $ - давление, МПа
$ p_b $ - давление насыщения, МПа
```
# Уравнение для объемного коэффициента нефти реализовано
# в виде функции unf_fvf_VB_m3m3_above в модуле PVT_correlations.
# Подробные данные по функции включая исходный код приведены ниже
PVT.unf_fvf_VB_m3m3_above??
# параметры определяющие диапазоны значений для построения графиков
p_set=np.arange(8,11,0.25)
co_set=np.arange(1 * 10 ** (-3),4 * 10 ** (-3),10 ** (-3))
bob = 1.2
pb = 8
# функция для автоматизации построения графиков по давлению насыщения
def prep_plot(func,p_set,co_set,pb,bob,plot_title,plot_xlab,plot_ylab):
for co in co_set:
b_o_set=[]
for p in p_set:
b_o_set.append(func(bob,co,pb,p))
plt.plot(p_set, b_o_set, label='co ={}'.format(co))
plt.title(plot_title)
plt.ylabel(plot_ylab, color = 'black')
plt.xlabel(plot_xlab, color = 'black')
plt.legend()
# код для построения графиков
plt.figure(figsize=(15,8))
f = PVT.unf_fvf_VB_m3m3_above
prep_plot(f,p_set,co_set,pb,bob,
'Объемный коэффициент нефти от давления (выше давления насыщения)',
'$P, MPa$',
'$b_o, м^3/м^3$')
# рисуем все
plt.grid()
plt.show()
```
### Корреляция Маккейна при давлении меньше или равном давлению насыщения
Уравнение выводится из материального баланса и не является корреляцией.
$$ b_o = \left( \frac{ \rho_{STO} + 0.01357 R_s \gamma_g}{\rho_{or}}\right) $$
где:
$ b_o $ - объемный коэффициент нефти при давлении p, м3/м3
$ \rho_{STO} $ - плотность дегазированной нефти, фунт/фт3 (кг/м3)
$ R_s $ - газосодержание при давлении p, фт3/баррель (м3/м3)
$ \gamma_g $ - плотность газа относительно воздуха
$ \rho_{or} $ - плотность пластовой нефти, фунт/фт3 (кг/м3)
#### Внутри функции уже реализован перевод величин, единицы измерения в скобках - входные параметры в функцию
```
# Уравнение для объемного коэффициента нефти реализовано
# в виде функции unf_fvf_Mccain_m3m3_below в модуле PVT_correlations.
# Подробные данные по функции включая исходный код приведены ниже
PVT.unf_fvf_Mccain_m3m3_below??
# параметры определяющие диапазоны значений для построения графиков
rs_set=np.arange(0,300,25)
rho_set=np.arange(600,850,50)
rho_sto = 800
gamma_gas = 0.8
# функция для автоматизации построения графиков по давлению насыщения
def prep_plot(func,rs_set,rho_set,gamma_gas,rho_sto,plot_title,plot_xlab,plot_ylab):
for rho in rho_set:
b_o_set=[]
for rs in rs_set:
b_o_set.append(func(rho_sto,rs,rho,gamma_gas))
plt.plot(rs_set, b_o_set, label='rho ={}'.format(rho))
plt.title(plot_title)
plt.ylabel(plot_ylab, color = 'black')
plt.xlabel(plot_xlab, color = 'black')
plt.legend()
# код для построения графиков
plt.figure(figsize=(15,8))
f = PVT.unf_fvf_Mccain_m3m3_below
prep_plot(f,rs_set,rho_set,gamma_gas,rho_sto,
'Объемный коэффициент нефти от давления (ниже давления насыщения)',
'$Rs, м^3/м^3$',
'$b_o, м^3/м^3$')
# рисуем все
plt.grid()
plt.show()
```
Этот график вообще говоря неверный,он построен для понимания, потому что при разном Rs будет разная плотность и график будет нелинейным.
|
github_jupyter
|
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
from sympy import *
init_printing()
import sys
sys.path.append('../')
import uPVT.PVT_correlations as PVT
# Уравнение для объемного коэффициента нефти реализовано
# в виде функции unf_fvf_VB_m3m3_above в модуле PVT_correlations.
# Подробные данные по функции включая исходный код приведены ниже
PVT.unf_fvf_VB_m3m3_above??
# параметры определяющие диапазоны значений для построения графиков
p_set=np.arange(8,11,0.25)
co_set=np.arange(1 * 10 ** (-3),4 * 10 ** (-3),10 ** (-3))
bob = 1.2
pb = 8
# функция для автоматизации построения графиков по давлению насыщения
def prep_plot(func,p_set,co_set,pb,bob,plot_title,plot_xlab,plot_ylab):
for co in co_set:
b_o_set=[]
for p in p_set:
b_o_set.append(func(bob,co,pb,p))
plt.plot(p_set, b_o_set, label='co ={}'.format(co))
plt.title(plot_title)
plt.ylabel(plot_ylab, color = 'black')
plt.xlabel(plot_xlab, color = 'black')
plt.legend()
# код для построения графиков
plt.figure(figsize=(15,8))
f = PVT.unf_fvf_VB_m3m3_above
prep_plot(f,p_set,co_set,pb,bob,
'Объемный коэффициент нефти от давления (выше давления насыщения)',
'$P, MPa$',
'$b_o, м^3/м^3$')
# рисуем все
plt.grid()
plt.show()
# Уравнение для объемного коэффициента нефти реализовано
# в виде функции unf_fvf_Mccain_m3m3_below в модуле PVT_correlations.
# Подробные данные по функции включая исходный код приведены ниже
PVT.unf_fvf_Mccain_m3m3_below??
# параметры определяющие диапазоны значений для построения графиков
rs_set=np.arange(0,300,25)
rho_set=np.arange(600,850,50)
rho_sto = 800
gamma_gas = 0.8
# функция для автоматизации построения графиков по давлению насыщения
def prep_plot(func,rs_set,rho_set,gamma_gas,rho_sto,plot_title,plot_xlab,plot_ylab):
for rho in rho_set:
b_o_set=[]
for rs in rs_set:
b_o_set.append(func(rho_sto,rs,rho,gamma_gas))
plt.plot(rs_set, b_o_set, label='rho ={}'.format(rho))
plt.title(plot_title)
plt.ylabel(plot_ylab, color = 'black')
plt.xlabel(plot_xlab, color = 'black')
plt.legend()
# код для построения графиков
plt.figure(figsize=(15,8))
f = PVT.unf_fvf_Mccain_m3m3_below
prep_plot(f,rs_set,rho_set,gamma_gas,rho_sto,
'Объемный коэффициент нефти от давления (ниже давления насыщения)',
'$Rs, м^3/м^3$',
'$b_o, м^3/м^3$')
# рисуем все
plt.grid()
plt.show()
| 0.184253 | 0.880181 |
```
import pickle
import pandas as pd
import os
from skimage.io import imread
from torch.utils.data import Dataset, DataLoader
import matplotlib.pyplot as plt
import torch
from PIL import Image, ImageDraw
import numpy as np
from torchvision import transforms
image_dim = 224
def show_sample(sample):
"""
Displays a sample as they come out of the trainloader.
"""
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.suptitle(sample['caption'], size=20)
ax1.imshow(sample['full_image'].permute(1,2,0))
ax2.imshow(sample['masked_image'].permute(1,2,0))
plt.show()
class COCODataset(Dataset):
def __init__(self, annotations, datadir, transform=None):
"""
Dataset of obfuscated coco images, with captions.
annotations: load from pickle, akshay's processed annotations
datadir: Preprocessed data. Contains /originals and /masked
tranforms: function to be run on each sample
"""
self.datadir = datadir
self.transform = transform
self.annotations = annotations
self.filenames = os.listdir(datadir)
# Since every 5 samples is the same image, we have a one image cache.
# TODO this may get fucky with shuffle? we can find out later.
self.last_image = None
self.last_index = None
def __len__(self):
return len(self.filenames) * 5
def __getitem__(self, idx):
"""
Gets images from the dataset.
Each image has 5 replicas, with different captions and sections
Returns: dictionary with blanked out ['image'] and ['caption']
image: FloatTensor
caption: string (may later be a list)
"""
# Load image or retrieve from cache
image_filename = self.filenames[idx // 5]
image_id = int(image_filename.split(".")[0])
if self.last_index is not None and idx // 5 == self.last_index // 5:
full_image = self.last_image
else:
image_filepath = os.path.join(self.datadir, image_filename)
full_image = Image.open(image_filepath)
self.last_image = full_image
self.last_index = idx
full_image = full_image.convert("RGB") # The occasional 1 channel grayscale image is in there.
full_image = full_image.resize((image_dim, image_dim))
# Fetch annotation, mask out area
anno = self.annotations[image_id][idx % 5]
masked_image = full_image.copy()
draw = ImageDraw.Draw(masked_image)
draw.rectangle([(anno['coord_start'][0], anno['coord_start'][1]), (anno['coord_end'][0], anno['coord_end'][1])], fill="black")
sample = {'masked_image': masked_image, 'caption': anno['caption'], 'full_image': full_image, 'image_id':image_id}
if self.transform:
sample = self.transform(sample)
return sample
%%time
annos = pd.read_pickle("../annotations_train2017.pickle")
# Recommended resnet transforms.
normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
# TODO change masking logic to accomodate this
#resnet_transform = transforms.Compose([transforms.Resize(256), transforms.CenterCrop(224), normalize, transforms.ToTensor()])
#resnet_transform = transforms.Compose([transforms.Resize((image_dim,image_dim)), transforms.ToTensor(), normalize])
resnet_transform = transforms.Compose([transforms.ToTensor(), normalize])
def basic_transform_sample(sample):
"""
A "default" transformer. Applies recommended resnet transforms.
"""
sample['masked_image'] = resnet_transform(sample['masked_image'])
sample['full_image'] = resnet_transform(sample['full_image'])
return sample
dataset_train = COCODataset(annos, "../data/train2017", transform=basic_transform_sample)
%%time
show_sample(dataset_train[0])
trainloader = DataLoader(dataset_train, batch_size=10, shuffle=False, num_workers=2) # VERY important to make sure num_workers > 0.
# Simple Benchmarking Code
import time
count = 0
times = np.asarray([])
for b in trainloader:
count += 1
if count % 10 == 0:
times = np.append(times, time.time())
if count == 500:
break
print("Mean per 10 batches (seconds):", np.diff(times).mean())
print("STD:", np.diff(times).std())
```
|
github_jupyter
|
import pickle
import pandas as pd
import os
from skimage.io import imread
from torch.utils.data import Dataset, DataLoader
import matplotlib.pyplot as plt
import torch
from PIL import Image, ImageDraw
import numpy as np
from torchvision import transforms
image_dim = 224
def show_sample(sample):
"""
Displays a sample as they come out of the trainloader.
"""
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.suptitle(sample['caption'], size=20)
ax1.imshow(sample['full_image'].permute(1,2,0))
ax2.imshow(sample['masked_image'].permute(1,2,0))
plt.show()
class COCODataset(Dataset):
def __init__(self, annotations, datadir, transform=None):
"""
Dataset of obfuscated coco images, with captions.
annotations: load from pickle, akshay's processed annotations
datadir: Preprocessed data. Contains /originals and /masked
tranforms: function to be run on each sample
"""
self.datadir = datadir
self.transform = transform
self.annotations = annotations
self.filenames = os.listdir(datadir)
# Since every 5 samples is the same image, we have a one image cache.
# TODO this may get fucky with shuffle? we can find out later.
self.last_image = None
self.last_index = None
def __len__(self):
return len(self.filenames) * 5
def __getitem__(self, idx):
"""
Gets images from the dataset.
Each image has 5 replicas, with different captions and sections
Returns: dictionary with blanked out ['image'] and ['caption']
image: FloatTensor
caption: string (may later be a list)
"""
# Load image or retrieve from cache
image_filename = self.filenames[idx // 5]
image_id = int(image_filename.split(".")[0])
if self.last_index is not None and idx // 5 == self.last_index // 5:
full_image = self.last_image
else:
image_filepath = os.path.join(self.datadir, image_filename)
full_image = Image.open(image_filepath)
self.last_image = full_image
self.last_index = idx
full_image = full_image.convert("RGB") # The occasional 1 channel grayscale image is in there.
full_image = full_image.resize((image_dim, image_dim))
# Fetch annotation, mask out area
anno = self.annotations[image_id][idx % 5]
masked_image = full_image.copy()
draw = ImageDraw.Draw(masked_image)
draw.rectangle([(anno['coord_start'][0], anno['coord_start'][1]), (anno['coord_end'][0], anno['coord_end'][1])], fill="black")
sample = {'masked_image': masked_image, 'caption': anno['caption'], 'full_image': full_image, 'image_id':image_id}
if self.transform:
sample = self.transform(sample)
return sample
%%time
annos = pd.read_pickle("../annotations_train2017.pickle")
# Recommended resnet transforms.
normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
# TODO change masking logic to accomodate this
#resnet_transform = transforms.Compose([transforms.Resize(256), transforms.CenterCrop(224), normalize, transforms.ToTensor()])
#resnet_transform = transforms.Compose([transforms.Resize((image_dim,image_dim)), transforms.ToTensor(), normalize])
resnet_transform = transforms.Compose([transforms.ToTensor(), normalize])
def basic_transform_sample(sample):
"""
A "default" transformer. Applies recommended resnet transforms.
"""
sample['masked_image'] = resnet_transform(sample['masked_image'])
sample['full_image'] = resnet_transform(sample['full_image'])
return sample
dataset_train = COCODataset(annos, "../data/train2017", transform=basic_transform_sample)
%%time
show_sample(dataset_train[0])
trainloader = DataLoader(dataset_train, batch_size=10, shuffle=False, num_workers=2) # VERY important to make sure num_workers > 0.
# Simple Benchmarking Code
import time
count = 0
times = np.asarray([])
for b in trainloader:
count += 1
if count % 10 == 0:
times = np.append(times, time.time())
if count == 500:
break
print("Mean per 10 batches (seconds):", np.diff(times).mean())
print("STD:", np.diff(times).std())
| 0.616243 | 0.677351 |
<a href="https://colab.research.google.com/github/frostshoxx/google-colab/blob/main/Welcome_To_Colaboratory.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<p><img alt="Colaboratory logo" height="45px" src="/img/colab_favicon.ico" align="left" hspace="10px" vspace="0px"></p>
<h1>What is Colaboratory?</h1>
Colaboratory, or "Colab" for short, allows you to write and execute Python in your browser, with
- Zero configuration required
- Free access to GPUs
- Easy sharing
Whether you're a **student**, a **data scientist** or an **AI researcher**, Colab can make your work easier. Watch [Introduction to Colab](https://www.youtube.com/watch?v=inN8seMm7UI) to learn more, or just get started below!
## **Getting started**
The document you are reading is not a static web page, but an interactive environment called a **Colab notebook** that lets you write and execute code.
For example, here is a **code cell** with a short Python script that computes a value, stores it in a variable, and prints the result:
```
seconds_in_a_day = 24 * 60 * 60
seconds_in_a_day
```
To execute the code in the above cell, select it with a click and then either press the play button to the left of the code, or use the keyboard shortcut "Command/Ctrl+Enter". To edit the code, just click the cell and start editing.
Variables that you define in one cell can later be used in other cells:
```
seconds_in_a_week = 7 * seconds_in_a_day
seconds_in_a_week
```
Colab notebooks allow you to combine **executable code** and **rich text** in a single document, along with **images**, **HTML**, **LaTeX** and more. When you create your own Colab notebooks, they are stored in your Google Drive account. You can easily share your Colab notebooks with co-workers or friends, allowing them to comment on your notebooks or even edit them. To learn more, see [Overview of Colab](/notebooks/basic_features_overview.ipynb). To create a new Colab notebook you can use the File menu above, or use the following link: [create a new Colab notebook](http://colab.research.google.com#create=true).
Colab notebooks are Jupyter notebooks that are hosted by Colab. To learn more about the Jupyter project, see [jupyter.org](https://www.jupyter.org).
## Data science
With Colab you can harness the full power of popular Python libraries to analyze and visualize data. The code cell below uses **numpy** to generate some random data, and uses **matplotlib** to visualize it. To edit the code, just click the cell and start editing.
```
import numpy as np
from matplotlib import pyplot as plt
ys = 200 + np.random.randn(100)
x = [x for x in range(len(ys))]
plt.plot(x, ys, '-')
plt.fill_between(x, ys, 195, where=(ys > 195), facecolor='g', alpha=0.6)
plt.title("Sample Visualization")
plt.show()
```
You can import your own data into Colab notebooks from your Google Drive account, including from spreadsheets, as well as from Github and many other sources. To learn more about importing data, and how Colab can be used for data science, see the links below under [Working with Data](#working-with-data).
## Machine learning
With Colab you can import an image dataset, train an image classifier on it, and evaluate the model, all in just [a few lines of code](https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/quickstart/beginner.ipynb). Colab notebooks execute code on Google's cloud servers, meaning you can leverage the power of Google hardware, including [GPUs and TPUs](#using-accelerated-hardware), regardless of the power of your machine. All you need is a browser.
Colab is used extensively in the machine learning community with applications including:
- Getting started with TensorFlow
- Developing and training neural networks
- Experimenting with TPUs
- Disseminating AI research
- Creating tutorials
To see sample Colab notebooks that demonstrate machine learning applications, see the [machine learning examples](#machine-learning-examples) below.
## More Resources
### Working with Notebooks in Colab
- [Overview of Colaboratory](/notebooks/basic_features_overview.ipynb)
- [Guide to Markdown](/notebooks/markdown_guide.ipynb)
- [Importing libraries and installing dependencies](/notebooks/snippets/importing_libraries.ipynb)
- [Saving and loading notebooks in GitHub](https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb)
- [Interactive forms](/notebooks/forms.ipynb)
- [Interactive widgets](/notebooks/widgets.ipynb)
- <img src="/img/new.png" height="20px" align="left" hspace="4px" alt="New"></img>
[TensorFlow 2 in Colab](/notebooks/tensorflow_version.ipynb)
<a name="working-with-data"></a>
### Working with Data
- [Loading data: Drive, Sheets, and Google Cloud Storage](/notebooks/io.ipynb)
- [Charts: visualizing data](/notebooks/charts.ipynb)
- [Getting started with BigQuery](/notebooks/bigquery.ipynb)
### Machine Learning Crash Course
These are a few of the notebooks from Google's online Machine Learning course. See the [full course website](https://developers.google.com/machine-learning/crash-course/) for more.
- [Intro to Pandas DataFrame](https://colab.research.google.com/github/google/eng-edu/blob/main/ml/cc/exercises/pandas_dataframe_ultraquick_tutorial.ipynb)
- [Linear regression with tf.keras using synthetic data](https://colab.research.google.com/github/google/eng-edu/blob/main/ml/cc/exercises/linear_regression_with_synthetic_data.ipynb)
<a name="using-accelerated-hardware"></a>
### Using Accelerated Hardware
- [TensorFlow with GPUs](/notebooks/gpu.ipynb)
- [TensorFlow with TPUs](/notebooks/tpu.ipynb)
<a name="machine-learning-examples"></a>
## Machine Learning Examples
To see end-to-end examples of the interactive machine learning analyses that Colaboratory makes possible, check out these tutorials using models from [TensorFlow Hub](https://tfhub.dev).
A few featured examples:
- [Retraining an Image Classifier](https://tensorflow.org/hub/tutorials/tf2_image_retraining): Build a Keras model on top of a pre-trained image classifier to distinguish flowers.
- [Text Classification](https://tensorflow.org/hub/tutorials/tf2_text_classification): Classify IMDB movie reviews as either *positive* or *negative*.
- [Style Transfer](https://tensorflow.org/hub/tutorials/tf2_arbitrary_image_stylization): Use deep learning to transfer style between images.
- [Multilingual Universal Sentence Encoder Q&A](https://tensorflow.org/hub/tutorials/retrieval_with_tf_hub_universal_encoder_qa): Use a machine learning model to answer questions from the SQuAD dataset.
- [Video Interpolation](https://tensorflow.org/hub/tutorials/tweening_conv3d): Predict what happened in a video between the first and the last frame.
|
github_jupyter
|
seconds_in_a_day = 24 * 60 * 60
seconds_in_a_day
seconds_in_a_week = 7 * seconds_in_a_day
seconds_in_a_week
import numpy as np
from matplotlib import pyplot as plt
ys = 200 + np.random.randn(100)
x = [x for x in range(len(ys))]
plt.plot(x, ys, '-')
plt.fill_between(x, ys, 195, where=(ys > 195), facecolor='g', alpha=0.6)
plt.title("Sample Visualization")
plt.show()
| 0.45302 | 0.984752 |
<img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# Plotly - Create Leaderboard
<a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/Plotly/Plotly_Create_Leaderboard.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
**Tags:** #plotly #chart #horizontalbar #dataviz #snippet
**Author:** [Florent Ravenel](https://www.linkedin.com/in/ACoAABCNSioBW3YZHc2lBHVG0E_TXYWitQkmwog/)
Learn more on the Plotly doc : https://plotly.com/python/horizontal-bar-charts/
## Input
### Import libraries
```
import plotly.express as px
import pandas as pd
```
### Variables
```
title = "Leaderboard"
# Output paths
output_image = f"{title}.png"
output_html = f"{title}.html"
```
## Model
### Get data model
```
data = [
{"LABEL": "A", "VALUE": 88},
{"LABEL": "B", "VALUE": 12},
{"LABEL": "C", "VALUE": 43},
{"LABEL": "D", "VALUE": 43},
{"LABEL": "E", "VALUE": 2},
{"LABEL": "F", "VALUE": 87},
{"LABEL": "G", "VALUE": 67},
{"LABEL": "H", "VALUE": 111},
{"LABEL": "I", "VALUE": 24},
{"LABEL": "J", "VALUE": 123},
]
df = pd.DataFrame(data)
df = df.sort_values(by=["VALUE"], ascending=True) #Order will be reversed in plot
df
```
### Create the plot
```
def create_barchart(df, label, value):
last_value = '{:,.0f}'.format(df[value].sum())
fig = px.bar(df,
y=label,
x=value,
orientation='h',
text=value)
fig.update_layout(
title=f"<b>Ranking by label</b><br><span style='font-size: 13px;'>Total value: {last_value}</span>",
title_font=dict(family="Arial", size=18, color="black"),
legend_title="Packs",
legend_title_font=dict(family="Arial", size=11, color="black"),
legend_font=dict(family="Arial", size=10, color="black"),
font=dict(family="Arial", size=12, color="black"),
plot_bgcolor="#ffffff",
width=1200,
height=800,
xaxis_title=None,
xaxis_showticklabels=False,
yaxis_title=None,
margin_pad=10,
margin_t=100,
)
# Display fig
config = {'displayModeBar': False}
fig.show(config=config)
return fig
fig = create_barchart(df, "LABEL", "VALUE")
```
## Output
### Export in PNG and HTML
```
fig.write_image(output_image, width=1200)
fig.write_html(output_html)
```
### Generate shareable assets
```
link_image = naas.asset.add(output_image)
link_html = naas.asset.add(output_html, {"inline":True})
#-> Uncomment the line below to remove your assets
# naas.asset.delete(output_image)
# naas.asset.delete(output_html)
```
|
github_jupyter
|
import plotly.express as px
import pandas as pd
title = "Leaderboard"
# Output paths
output_image = f"{title}.png"
output_html = f"{title}.html"
data = [
{"LABEL": "A", "VALUE": 88},
{"LABEL": "B", "VALUE": 12},
{"LABEL": "C", "VALUE": 43},
{"LABEL": "D", "VALUE": 43},
{"LABEL": "E", "VALUE": 2},
{"LABEL": "F", "VALUE": 87},
{"LABEL": "G", "VALUE": 67},
{"LABEL": "H", "VALUE": 111},
{"LABEL": "I", "VALUE": 24},
{"LABEL": "J", "VALUE": 123},
]
df = pd.DataFrame(data)
df = df.sort_values(by=["VALUE"], ascending=True) #Order will be reversed in plot
df
def create_barchart(df, label, value):
last_value = '{:,.0f}'.format(df[value].sum())
fig = px.bar(df,
y=label,
x=value,
orientation='h',
text=value)
fig.update_layout(
title=f"<b>Ranking by label</b><br><span style='font-size: 13px;'>Total value: {last_value}</span>",
title_font=dict(family="Arial", size=18, color="black"),
legend_title="Packs",
legend_title_font=dict(family="Arial", size=11, color="black"),
legend_font=dict(family="Arial", size=10, color="black"),
font=dict(family="Arial", size=12, color="black"),
plot_bgcolor="#ffffff",
width=1200,
height=800,
xaxis_title=None,
xaxis_showticklabels=False,
yaxis_title=None,
margin_pad=10,
margin_t=100,
)
# Display fig
config = {'displayModeBar': False}
fig.show(config=config)
return fig
fig = create_barchart(df, "LABEL", "VALUE")
fig.write_image(output_image, width=1200)
fig.write_html(output_html)
link_image = naas.asset.add(output_image)
link_html = naas.asset.add(output_html, {"inline":True})
#-> Uncomment the line below to remove your assets
# naas.asset.delete(output_image)
# naas.asset.delete(output_html)
| 0.582729 | 0.89167 |

[](https://colab.research.google.com/github/JohnSnowLabs/nlu/blob/master/examples/collab/Text_Pre_Processing_and_Cleaning/NLU_Normalizer_example.ipynb)
# Normalziing with NLU
The Normalizer cleans text data from dirty characters, lowercases it by default and removes punctuation.
### Removes all dirty characters and from text following a regex pattern.
- Dirty characters are things like !@#$%^&*()?>< etc..
- Useful for reducing dimension/variance of your data since fewer symbols will occur
- Useful for cleaning tweets
- Matches slangs
- Language independent
- You can use a regex pattern to specify which tokens will *not* be removed.
I.e the pattern [a-z] matches all characters from a,b,c... to x,y,z. It will throw
```
pipe['normalizer'].setCleanupPatterns('[a-z]')
```
# 1. Install Java and NLU
```
import os
! apt-get update -qq > /dev/null
# Install java
! apt-get install -y openjdk-8-jdk-headless -qq > /dev/null
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ["PATH"] = os.environ["JAVA_HOME"] + "/bin:" + os.environ["PATH"]
! pip install nlu > /dev/null
```
## 2. Load Model and normalize sample string
```
import nlu
nlu.load('norm').predict('@CKL_IT says: that #normalizers are pretty useful to clean #structured_strings in #NLU like tweets')
```
## 2. Configure the normalizer with custom parameters
Use the pipe.print_info() to see all configurable parameters and infos about them for every NLU component in the pipeline pipeline.
Even tough only 'norm' is loaded, many NLU component dependencies are automatically loaded into the pipeline and also configurable.
By default the normalizer will set all tokens to lower case.
Lets change that
```
pipe = nlu.load('norm')
pipe.predict('LOWERCASE BY DEFAULT')
```
### 2.1 Print all parameters for all NLU components in the pipeline
```
pipe.print_info()
```
### 2.2 Configure the Normalizer not to lowercase text
```
pipe['normalizer'].setLowercase(True)
pipe.predict('LOWERCASE BY DEFAULT')
```
### 2.3Configure normalizer to remove strings based on regex pattern.
Lets remove all occurences of the lowercase letters x to z with the pattern [x-z].
```
# Configure the Normalizer
pipe['normalizer'].setCleanupPatterns(['[x-z]'])
pipe.predict('From the x to the y to the z')
```
#### NOTE: The regex pattern is applied **BEFORE** lowercasing.
This is why the X,Y,Z tokens are kept i nthe following example
```
# Configure the Normalizer
pipe['normalizer'].setCleanupPatterns(['[x-z]'])
pipe.predict('From the X to the Y to the Z')
```
# 3. Get one row per normalized token by setting outputlevel to token.
This lets us compare what the original token was and what it was normalized to.
```
pipe.predict('From the X to the Y to the Z', output_level='token')
```
|
github_jupyter
|
pipe['normalizer'].setCleanupPatterns('[a-z]')
import os
! apt-get update -qq > /dev/null
# Install java
! apt-get install -y openjdk-8-jdk-headless -qq > /dev/null
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ["PATH"] = os.environ["JAVA_HOME"] + "/bin:" + os.environ["PATH"]
! pip install nlu > /dev/null
import nlu
nlu.load('norm').predict('@CKL_IT says: that #normalizers are pretty useful to clean #structured_strings in #NLU like tweets')
pipe = nlu.load('norm')
pipe.predict('LOWERCASE BY DEFAULT')
pipe.print_info()
pipe['normalizer'].setLowercase(True)
pipe.predict('LOWERCASE BY DEFAULT')
# Configure the Normalizer
pipe['normalizer'].setCleanupPatterns(['[x-z]'])
pipe.predict('From the x to the y to the z')
# Configure the Normalizer
pipe['normalizer'].setCleanupPatterns(['[x-z]'])
pipe.predict('From the X to the Y to the Z')
pipe.predict('From the X to the Y to the Z', output_level='token')
| 0.267313 | 0.923523 |
# Sequence to Sequence Learning
:label:`sec_seq2seq`
As we have seen in :numref:`sec_machine_translation`,
in machine translation
both the input and output are a variable-length sequence.
To address this type of problem,
we have designed a general encoder-decoder architecture
in :numref:`sec_encoder-decoder`.
In this section,
we will
use two RNNs to design
the encoder and the decoder of
this architecture
and apply it to *sequence to sequence* learning
for machine translation
:cite:`Sutskever.Vinyals.Le.2014,Cho.Van-Merrienboer.Gulcehre.ea.2014`.
Following the design principle
of the encoder-decoder architecture,
the RNN encoder can
take a variable-length sequence as the input and transforms it into a fixed-shape hidden state.
In other words,
information of the input (source) sequence
is *encoded* in the hidden state of the RNN encoder.
To generate the output sequence token by token,
a separate RNN decoder
can predict the next token based on
what tokens have been seen (such as in language modeling) or generated,
together with the encoded information of the input sequence.
:numref:`fig_seq2seq` illustrates
how to use two RNNs
for sequence to sequence learning
in machine translation.

:label:`fig_seq2seq`
In :numref:`fig_seq2seq`,
the special "<eos>" token
marks the end of the sequence.
The model can stop making predictions
once this token is generated.
At the initial time step of the RNN decoder,
there are two special design decisions.
First, the special beginning-of-sequence "<bos>" token is an input.
Second,
the final hidden state of the RNN encoder is used
to initiate the hidden state of the decoder.
In designs such as :cite:`Sutskever.Vinyals.Le.2014`,
this is exactly
how the encoded input sequence information
is fed into the decoder for generating the output (target) sequence.
In some other designs such as :cite:`Cho.Van-Merrienboer.Gulcehre.ea.2014`,
the final hidden state of the encoder
is also fed into the decoder as
part of the inputs
at every time step as shown in :numref:`fig_seq2seq`.
Similar to the training of language models in
:numref:`sec_language_model`,
we can allow the labels to be the original output sequence,
shifted by one token:
"<bos>", "Ils", "regardent", "." $\rightarrow$
"Ils", "regardent", ".", "<eos>".
In the following,
we will explain the design of :numref:`fig_seq2seq`
in greater detail.
We will train this model for machine translation
on the English-French dataset as introduced in
:numref:`sec_machine_translation`.
```
import collections
import math
from mxnet import autograd, gluon, init, np, npx
from mxnet.gluon import nn, rnn
from d2l import mxnet as d2l
npx.set_np()
```
## Encoder
Technically speaking,
the encoder transforms an input sequence of variable length into a fixed-shape *context variable* $\mathbf{c}$, and encodes the input sequence information in this context variable.
As depicted in :numref:`fig_seq2seq`,
we can use an RNN to design the encoder.
Let us consider a sequence example (batch size: 1).
Suppose that
the input sequence is $x_1, \ldots, x_T$, such that $x_t$ is the $t^{\mathrm{th}}$ token in the input text sequence.
At time step $t$, the RNN transforms
the input feature vector $\mathbf{x}_t$ for $x_t$
and the hidden state $\mathbf{h} _{t-1}$ from the previous time step
into the current hidden state $\mathbf{h}_t$.
We can use a function $f$ to express the transformation of the RNN's recurrent layer:
$$\mathbf{h}_t = f(\mathbf{x}_t, \mathbf{h}_{t-1}). $$
In general,
the encoder transforms the hidden states at
all the time steps
into the context variable through a customized function $q$:
$$\mathbf{c} = q(\mathbf{h}_1, \ldots, \mathbf{h}_T).$$
For example, when choosing $q(\mathbf{h}_1, \ldots, \mathbf{h}_T) = \mathbf{h}_T$ such as in :numref:`fig_seq2seq`,
the context variable is just the hidden state $\mathbf{h}_T$
of the input sequence at the final time step.
So far we have used a unidirectional RNN
to design the encoder,
where
a hidden state only depends on
the input subsequence at and before the time step of the hidden state.
We can also construct encoders using bidirectional RNNs. In this case, a hidden state depends on
the subsequence before and after the time step (including the input at the current time step), which encodes the information of the entire sequence.
Now let us implement the RNN encoder.
Note that we use an *embedding layer*
to obtain the feature vector for each token in the input sequence.
The weight
of an embedding layer
is a matrix
whose number of rows equals to the size of the input vocabulary (`vocab_size`)
and number of columns equals to the feature vector's dimension (`embed_size`).
For any input token index $i$,
the embedding layer
fetches the $i^{\mathrm{th}}$ row (starting from 0) of the weight matrix
to return its feature vector.
Besides,
here we choose a multilayer GRU to
implement the encoder.
```
#@save
class Seq2SeqEncoder(d2l.Encoder):
"""The RNN encoder for sequence to sequence learning."""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqEncoder, self).__init__(**kwargs)
# Embedding layer
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = rnn.GRU(num_hiddens, num_layers, dropout=dropout)
def forward(self, X, *args):
# The output `X` shape: (`batch_size`, `num_steps`, `embed_size`)
X = self.embedding(X)
# In RNN models, the first axis corresponds to time steps
X = X.swapaxes(0, 1)
state = self.rnn.begin_state(batch_size=X.shape[1], ctx=X.ctx)
output, state = self.rnn(X, state)
# `output` shape: (`num_steps`, `batch_size`, `num_hiddens`)
# `state[0]` shape: (`num_layers`, `batch_size`, `num_hiddens`)
return output, state
```
The returned variables of recurrent layers
have been explained in :numref:`sec_rnn-concise`.
Let us still use a concrete example
to illustrate the above encoder implementation.
Below
we instantiate a two-layer GRU encoder
whose number of hidden units is 16.
Given
a minibatch of sequence inputs `X`
(batch size: 4, number of time steps: 7),
the hidden states of the last layer
at all the time steps
(`output` return by the encoder's recurrent layers)
are a tensor
of shape
(number of time steps, batch size, number of hidden units).
```
encoder = Seq2SeqEncoder(vocab_size=10, embed_size=8, num_hiddens=16,
num_layers=2)
encoder.initialize()
X = np.zeros((4, 7))
output, state = encoder(X)
output.shape
```
Since a GRU is employed here,
the shape of the multilayer hidden states
at the final time step
is
(number of hidden layers, batch size, number of hidden units).
If an LSTM is used,
memory cell information will also be contained in `state`.
```
len(state), state[0].shape
```
## Decoder
:label:`sec_seq2seq_decoder`
As we just mentioned,
the context variable $\mathbf{c}$ of the encoder's output encodes the entire input sequence $x_1, \ldots, x_T$. Given the output sequence $y_1, y_2, \ldots, y_{T'}$ from the training dataset,
for each time step $t'$
(the symbol differs from the time step $t$ of input sequences or encoders),
the probability of the decoder output $y_{t'}$
is conditional
on the previous output subsequence
$y_1, \ldots, y_{t'-1}$ and
the context variable $\mathbf{c}$, i.e., $P(y_{t'} \mid y_1, \ldots, y_{t'-1}, \mathbf{c})$.
To model this conditional probability on sequences,
we can use another RNN as the decoder.
At any time step $t^\prime$ on the output sequence,
the RNN takes the output $y_{t^\prime-1}$ from the previous time step
and the context variable $\mathbf{c}$ as its input,
then transforms
them and
the previous hidden state $\mathbf{s}_{t^\prime-1}$
into the
hidden state $\mathbf{s}_{t^\prime}$ at the current time step.
As a result, we can use a function $g$ to express the transformation of the decoder's hidden layer:
$$\mathbf{s}_{t^\prime} = g(y_{t^\prime-1}, \mathbf{c}, \mathbf{s}_{t^\prime-1}).$$
:eqlabel:`eq_seq2seq_s_t`
After obtaining the hidden state of the decoder,
we can use an output layer and the softmax operation to compute the conditional probability distribution
$P(y_{t^\prime} \mid y_1, \ldots, y_{t^\prime-1}, \mathbf{c})$ for the output at time step $t^\prime$.
Following :numref:`fig_seq2seq`,
when implementing the decoder as follows,
we directly use the hidden state at the final time step
of the encoder
to initialize the hidden state of the decoder.
This requires that the RNN encoder and the RNN decoder have the same number of layers and hidden units.
To further incorporate the encoded input sequence information,
the context variable is concatenated
with the decoder input at all the time steps.
To predict the probability distribution of the output token,
a fully-connected layer is used to transform
the hidden state at the final layer of the RNN decoder.
```
class Seq2SeqDecoder(d2l.Decoder):
"""The RNN decoder for sequence to sequence learning."""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqDecoder, self).__init__(**kwargs)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = rnn.GRU(num_hiddens, num_layers, dropout=dropout)
self.dense = nn.Dense(vocab_size, flatten=False)
def init_state(self, enc_outputs, *args):
return enc_outputs[1]
def forward(self, X, state):
# The output `X` shape: (`num_steps`, `batch_size`, `embed_size`)
X = self.embedding(X).swapaxes(0, 1)
# `context` shape: (`batch_size`, `num_hiddens`)
context = state[0][-1]
# Broadcast `context` so it has the same `num_steps` as `X`
context = np.broadcast_to(
context, (X.shape[0], context.shape[0], context.shape[1]))
X_and_context = np.concatenate((X, context), 2)
output, state = self.rnn(X_and_context, state)
output = self.dense(output).swapaxes(0, 1)
# `output` shape: (`batch_size`, `num_steps`, `vocab_size`)
# `state[0]` shape: (`num_layers`, `batch_size`, `num_hiddens`)
return output, state
```
To illustrate the implemented decoder,
below we instantiate it with the same hyperparameters from the aforementioned encoder.
As we can see, the output shape of the decoder becomes (batch size, number of time steps, vocabulary size),
where the last dimension of the tensor stores the predicted token distribution.
```
decoder = Seq2SeqDecoder(vocab_size=10, embed_size=8, num_hiddens=16,
num_layers=2)
decoder.initialize()
state = decoder.init_state(encoder(X))
output, state = decoder(X, state)
output.shape, len(state), state[0].shape
```
To summarize,
the layers in the above RNN encoder-decoder model are illustrated in :numref:`fig_seq2seq_details`.

:label:`fig_seq2seq_details`
## Loss Function
At each time step, the decoder
predicts a probability distribution for the output tokens.
Similar to language modeling,
we can apply softmax to obtain the distribution
and calculate the cross-entropy loss for optimization.
Recall :numref:`sec_machine_translation`
that the special padding tokens
are appended to the end of sequences
so sequences of varying lengths
can be efficiently loaded
in minibatches of the same shape.
However,
prediction of padding tokens
should be excluded from loss calculations.
To this end,
we can use the following
`sequence_mask` function
to mask irrelevant entries with zero values
so later
multiplication of any irrelevant prediction
with zero equals to zero.
For example,
if the valid length of two sequences
excluding padding tokens
are one and two, respectively,
the remaining entries after
the first one
and the first two entries are cleared to zeros.
```
X = np.array([[1, 2, 3], [4, 5, 6]])
npx.sequence_mask(X, np.array([1, 2]), True, axis=1)
```
We can also mask all the entries across the last
few axes.
If you like, you may even specify
to replace such entries with a non-zero value.
```
X = np.ones((2, 3, 4))
npx.sequence_mask(X, np.array([1, 2]), True, value=-1, axis=1)
```
Now we can extend the softmax cross-entropy loss
to allow the masking of irrelevant predictions.
Initially,
masks for all the predicted tokens are set to one.
Once the valid length is given,
the mask corresponding to any padding token
will be cleared to zero.
In the end,
the loss for all the tokens
will be multipled by the mask to filter out
irrelevant predictions of padding tokens in the loss.
```
#@save
class MaskedSoftmaxCELoss(gluon.loss.SoftmaxCELoss):
"""The softmax cross-entropy loss with masks."""
# `pred` shape: (`batch_size`, `num_steps`, `vocab_size`)
# `label` shape: (`batch_size`, `num_steps`)
# `valid_len` shape: (`batch_size`,)
def forward(self, pred, label, valid_len):
# `weights` shape: (`batch_size`, `num_steps`, 1)
weights = np.expand_dims(np.ones_like(label), axis=-1)
weights = npx.sequence_mask(weights, valid_len, True, axis=1)
return super(MaskedSoftmaxCELoss, self).forward(pred, label, weights)
```
For a sanity check, we can create three identical sequences.
Then we can
specify that the valid lengths of these sequences
are 4, 2, and 0, respectively.
As a result,
the loss of the first sequence
should be twice as large as that of the second sequence,
while the third sequence should have a zero loss.
```
loss = MaskedSoftmaxCELoss()
loss(np.ones((3, 4, 10)), np.ones((3, 4)), np.array([4, 2, 0]))
```
## Training
:label:`sec_seq2seq_training`
In the following training loop,
we concatenate the special beginning-of-sequence token
and the original output sequence excluding the final token as
the input to the decoder, as shown in :numref:`fig_seq2seq`.
This is called *teacher forcing* because
the original output sequence (token labels) is fed into the decoder.
Alternatively,
we could also feed the *predicted* token
from the previous time step
as the current input to the decoder.
```
#@save
def train_seq2seq(net, data_iter, lr, num_epochs, tgt_vocab, device):
"""Train a model for sequence to sequence."""
net.initialize(init.Xavier(), force_reinit=True, ctx=device)
trainer = gluon.Trainer(net.collect_params(), 'adam',
{'learning_rate': lr})
loss = MaskedSoftmaxCELoss()
animator = d2l.Animator(xlabel='epoch', ylabel='loss',
xlim=[10, num_epochs])
for epoch in range(num_epochs):
timer = d2l.Timer()
metric = d2l.Accumulator(2) # Sum of training loss, no. of tokens
for batch in data_iter:
X, X_valid_len, Y, Y_valid_len = [
x.as_in_ctx(device) for x in batch]
bos = np.array([tgt_vocab['<bos>']] * Y.shape[0],
ctx=device).reshape(-1, 1)
dec_input = np.concatenate([bos, Y[:, :-1]], 1) # Teacher forcing
with autograd.record():
Y_hat, _ = net(X, dec_input, X_valid_len)
l = loss(Y_hat, Y, Y_valid_len)
l.backward()
d2l.grad_clipping(net, 1)
num_tokens = Y_valid_len.sum()
trainer.step(num_tokens)
metric.add(l.sum(), num_tokens)
if (epoch + 1) % 10 == 0:
animator.add(epoch + 1, (metric[0] / metric[1],))
print(f'loss {metric[0] / metric[1]:.3f}, {metric[1] / timer.stop():.1f} '
f'tokens/sec on {str(device)}')
```
Now we can create and train an RNN encoder-decoder model
for sequence to sequence learning on the machine translation dataset.
```
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 300, d2l.try_gpu()
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = Seq2SeqEncoder(len(src_vocab), embed_size, num_hiddens, num_layers,
dropout)
decoder = Seq2SeqDecoder(len(tgt_vocab), embed_size, num_hiddens, num_layers,
dropout)
net = d2l.EncoderDecoder(encoder, decoder)
train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
```
## Prediction
To predict the output sequence
token by token,
at each decoder time step
the predicted token from the previous
time step is fed into the decoder as an input.
Similar to training,
at the initial time step
the beginning-of-sequence ("<bos>") token
is fed into the decoder.
This prediction process
is illustrated in :numref:`fig_seq2seq_predict`.
When the end-of-sequence ("<eos>") token is predicted,
the prediction of the output sequence is complete.

:label:`fig_seq2seq_predict`
We will introduce different
strategies for sequence generation in
:numref:`sec_beam-search`.
```
#@save
def predict_seq2seq(net, src_sentence, src_vocab, tgt_vocab, num_steps,
device, save_attention_weights=False):
"""Predict for sequence to sequence."""
src_tokens = src_vocab[src_sentence.lower().split(' ')] + [
src_vocab['<eos>']]
enc_valid_len = np.array([len(src_tokens)], ctx=device)
src_tokens = d2l.truncate_pad(src_tokens, num_steps, src_vocab['<pad>'])
# Add the batch axis
enc_X = np.expand_dims(np.array(src_tokens, ctx=device), axis=0)
enc_outputs = net.encoder(enc_X, enc_valid_len)
dec_state = net.decoder.init_state(enc_outputs, enc_valid_len)
# Add the batch axis
dec_X = np.expand_dims(np.array([tgt_vocab['<bos>']], ctx=device), axis=0)
output_seq, attention_weight_seq = [], []
for _ in range(num_steps):
Y, dec_state = net.decoder(dec_X, dec_state)
# We use the token with the highest prediction likelihood as the input
# of the decoder at the next time step
dec_X = Y.argmax(axis=2)
pred = dec_X.squeeze(axis=0).astype('int32').item()
# Save attention weights (to be covered later)
if save_attention_weights:
attention_weight_seq.append(net.decoder.attention_weights)
# Once the end-of-sequence token is predicted, the generation of the
# output sequence is complete
if pred == tgt_vocab['<eos>']:
break
output_seq.append(pred)
return ' '.join(tgt_vocab.to_tokens(output_seq)), attention_weight_seq
```
## Evaluation of Predicted Sequences
We can evaluate a predicted sequence
by comparing it with the
label sequence (the ground-truth).
BLEU (Bilingual Evaluation Understudy),
though originally proposed for evaluating
machine translation results :cite:`Papineni.Roukos.Ward.ea.2002`,
has been extensively used in measuring
the quality of output sequences for different applications.
In principle, for any $n$-grams in the predicted sequence,
BLEU evaluates whether this $n$-grams appears
in the label sequence.
Denote by $p_n$
the precision of $n$-grams,
which is
the ratio of
the number of matched $n$-grams in
the predicted and label sequences
to
the number of $n$-grams in the predicted sequence.
To explain,
given a label sequence $A$, $B$, $C$, $D$, $E$, $F$,
and a predicted sequence $A$, $B$, $B$, $C$, $D$,
we have $p_1 = 4/5$, $p_2 = 3/4$, $p_3 = 1/3$, and $p_4 = 0$.
Besides,
let $\mathrm{len}_{\text{label}}$ and $\mathrm{len}_{\text{pred}}$
be
the numbers of tokens in the label sequence and the predicted sequence, respectively.
Then, BLEU is defined as
$$ \exp\left(\min\left(0, 1 - \frac{\mathrm{len}_{\text{label}}}{\mathrm{len}_{\text{pred}}}\right)\right) \prod_{n=1}^k p_n^{1/2^n},$$
:eqlabel:`eq_bleu`
where $k$ is the longest $n$-grams for matching.
Based on the definition of BLEU in :eqref:`eq_bleu`,
whenever the predicted sequence is the same as the label sequence, BLEU is 1.
Moreover,
since matching longer $n$-grams is more difficult,
BLEU assigns a greater weight
to a longer $n$-gram precision.
Specifically, when $p_n$ is fixed,
$p_n^{1/2^n}$ increases as $n$ grows (the original paper uses $p_n^{1/n}$).
Furthermore,
since
predicting shorter sequences
tends to obtain a higher $p_n$ value,
the coefficient before the multiplication term in :eqref:`eq_bleu`
penalizes shorter predicted sequences.
For example, when $k=2$,
given the label sequence $A$, $B$, $C$, $D$, $E$, $F$ and the predicted sequence $A$, $B$,
although $p_1 = p_2 = 1$, the penalty factor $\exp(1-6/2) \approx 0.14$ lowers the BLEU.
We implement the BLEU measure as follows.
```
def bleu(pred_seq, label_seq, k): #@save
"""Compute the BLEU."""
pred_tokens, label_tokens = pred_seq.split(' '), label_seq.split(' ')
len_pred, len_label = len(pred_tokens), len(label_tokens)
score = math.exp(min(0, 1 - len_label / len_pred))
for n in range(1, k + 1):
num_matches, label_subs = 0, collections.defaultdict(int)
for i in range(len_label - n + 1):
label_subs[''.join(label_tokens[i:i + n])] += 1
for i in range(len_pred - n + 1):
if label_subs[''.join(pred_tokens[i:i + n])] > 0:
num_matches += 1
label_subs[''.join(pred_tokens[i:i + n])] -= 1
score *= math.pow(num_matches / (len_pred - n + 1), math.pow(0.5, n))
return score
```
In the end,
we use the trained RNN encoder-decoder
to translate a few English sentences into French
and compute the BLEU of the results.
```
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, attention_weight_seq = predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device)
print(f'{eng} => {translation}, bleu {bleu(translation, fra, k=2):.3f}')
```
## Summary
* Following the design of the encoder-decoder architecture, we can use two RNNs to design a model for sequence to sequence learning.
* When implementing the encoder and the decoder, we can use multilayer RNNs.
* We can use masks to filter out irrelevant computations, such as when calculating the loss.
* In encoder-decoder training, the teacher forcing approach feeds original output sequences (in contrast to predictions) into the decoder.
* BLEU is a popular measure for evaluating output sequences by matching $n$-grams between the predicted sequence and the label sequence.
## Exercises
1. Can you adjust the hyperparameters to improve the translation results?
1. Rerun the experiment without using masks in the loss calculation. What results do you observe? Why?
1. If the encoder and the decoder differ in the number of layers or the number of hidden units, how can we initialize the hidden state of the decoder?
1. In training, replace teacher forcing with feeding the prediction at the previous time step into the decoder. How does this influence the performance?
1. Rerun the experiment by replacing GRU with LSTM.
1. Are there any other ways to design the output layer of the decoder?
[Discussions](https://discuss.d2l.ai/t/345)
|
github_jupyter
|
import collections
import math
from mxnet import autograd, gluon, init, np, npx
from mxnet.gluon import nn, rnn
from d2l import mxnet as d2l
npx.set_np()
#@save
class Seq2SeqEncoder(d2l.Encoder):
"""The RNN encoder for sequence to sequence learning."""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqEncoder, self).__init__(**kwargs)
# Embedding layer
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = rnn.GRU(num_hiddens, num_layers, dropout=dropout)
def forward(self, X, *args):
# The output `X` shape: (`batch_size`, `num_steps`, `embed_size`)
X = self.embedding(X)
# In RNN models, the first axis corresponds to time steps
X = X.swapaxes(0, 1)
state = self.rnn.begin_state(batch_size=X.shape[1], ctx=X.ctx)
output, state = self.rnn(X, state)
# `output` shape: (`num_steps`, `batch_size`, `num_hiddens`)
# `state[0]` shape: (`num_layers`, `batch_size`, `num_hiddens`)
return output, state
encoder = Seq2SeqEncoder(vocab_size=10, embed_size=8, num_hiddens=16,
num_layers=2)
encoder.initialize()
X = np.zeros((4, 7))
output, state = encoder(X)
output.shape
len(state), state[0].shape
class Seq2SeqDecoder(d2l.Decoder):
"""The RNN decoder for sequence to sequence learning."""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqDecoder, self).__init__(**kwargs)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = rnn.GRU(num_hiddens, num_layers, dropout=dropout)
self.dense = nn.Dense(vocab_size, flatten=False)
def init_state(self, enc_outputs, *args):
return enc_outputs[1]
def forward(self, X, state):
# The output `X` shape: (`num_steps`, `batch_size`, `embed_size`)
X = self.embedding(X).swapaxes(0, 1)
# `context` shape: (`batch_size`, `num_hiddens`)
context = state[0][-1]
# Broadcast `context` so it has the same `num_steps` as `X`
context = np.broadcast_to(
context, (X.shape[0], context.shape[0], context.shape[1]))
X_and_context = np.concatenate((X, context), 2)
output, state = self.rnn(X_and_context, state)
output = self.dense(output).swapaxes(0, 1)
# `output` shape: (`batch_size`, `num_steps`, `vocab_size`)
# `state[0]` shape: (`num_layers`, `batch_size`, `num_hiddens`)
return output, state
decoder = Seq2SeqDecoder(vocab_size=10, embed_size=8, num_hiddens=16,
num_layers=2)
decoder.initialize()
state = decoder.init_state(encoder(X))
output, state = decoder(X, state)
output.shape, len(state), state[0].shape
X = np.array([[1, 2, 3], [4, 5, 6]])
npx.sequence_mask(X, np.array([1, 2]), True, axis=1)
X = np.ones((2, 3, 4))
npx.sequence_mask(X, np.array([1, 2]), True, value=-1, axis=1)
#@save
class MaskedSoftmaxCELoss(gluon.loss.SoftmaxCELoss):
"""The softmax cross-entropy loss with masks."""
# `pred` shape: (`batch_size`, `num_steps`, `vocab_size`)
# `label` shape: (`batch_size`, `num_steps`)
# `valid_len` shape: (`batch_size`,)
def forward(self, pred, label, valid_len):
# `weights` shape: (`batch_size`, `num_steps`, 1)
weights = np.expand_dims(np.ones_like(label), axis=-1)
weights = npx.sequence_mask(weights, valid_len, True, axis=1)
return super(MaskedSoftmaxCELoss, self).forward(pred, label, weights)
loss = MaskedSoftmaxCELoss()
loss(np.ones((3, 4, 10)), np.ones((3, 4)), np.array([4, 2, 0]))
#@save
def train_seq2seq(net, data_iter, lr, num_epochs, tgt_vocab, device):
"""Train a model for sequence to sequence."""
net.initialize(init.Xavier(), force_reinit=True, ctx=device)
trainer = gluon.Trainer(net.collect_params(), 'adam',
{'learning_rate': lr})
loss = MaskedSoftmaxCELoss()
animator = d2l.Animator(xlabel='epoch', ylabel='loss',
xlim=[10, num_epochs])
for epoch in range(num_epochs):
timer = d2l.Timer()
metric = d2l.Accumulator(2) # Sum of training loss, no. of tokens
for batch in data_iter:
X, X_valid_len, Y, Y_valid_len = [
x.as_in_ctx(device) for x in batch]
bos = np.array([tgt_vocab['<bos>']] * Y.shape[0],
ctx=device).reshape(-1, 1)
dec_input = np.concatenate([bos, Y[:, :-1]], 1) # Teacher forcing
with autograd.record():
Y_hat, _ = net(X, dec_input, X_valid_len)
l = loss(Y_hat, Y, Y_valid_len)
l.backward()
d2l.grad_clipping(net, 1)
num_tokens = Y_valid_len.sum()
trainer.step(num_tokens)
metric.add(l.sum(), num_tokens)
if (epoch + 1) % 10 == 0:
animator.add(epoch + 1, (metric[0] / metric[1],))
print(f'loss {metric[0] / metric[1]:.3f}, {metric[1] / timer.stop():.1f} '
f'tokens/sec on {str(device)}')
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 300, d2l.try_gpu()
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = Seq2SeqEncoder(len(src_vocab), embed_size, num_hiddens, num_layers,
dropout)
decoder = Seq2SeqDecoder(len(tgt_vocab), embed_size, num_hiddens, num_layers,
dropout)
net = d2l.EncoderDecoder(encoder, decoder)
train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
#@save
def predict_seq2seq(net, src_sentence, src_vocab, tgt_vocab, num_steps,
device, save_attention_weights=False):
"""Predict for sequence to sequence."""
src_tokens = src_vocab[src_sentence.lower().split(' ')] + [
src_vocab['<eos>']]
enc_valid_len = np.array([len(src_tokens)], ctx=device)
src_tokens = d2l.truncate_pad(src_tokens, num_steps, src_vocab['<pad>'])
# Add the batch axis
enc_X = np.expand_dims(np.array(src_tokens, ctx=device), axis=0)
enc_outputs = net.encoder(enc_X, enc_valid_len)
dec_state = net.decoder.init_state(enc_outputs, enc_valid_len)
# Add the batch axis
dec_X = np.expand_dims(np.array([tgt_vocab['<bos>']], ctx=device), axis=0)
output_seq, attention_weight_seq = [], []
for _ in range(num_steps):
Y, dec_state = net.decoder(dec_X, dec_state)
# We use the token with the highest prediction likelihood as the input
# of the decoder at the next time step
dec_X = Y.argmax(axis=2)
pred = dec_X.squeeze(axis=0).astype('int32').item()
# Save attention weights (to be covered later)
if save_attention_weights:
attention_weight_seq.append(net.decoder.attention_weights)
# Once the end-of-sequence token is predicted, the generation of the
# output sequence is complete
if pred == tgt_vocab['<eos>']:
break
output_seq.append(pred)
return ' '.join(tgt_vocab.to_tokens(output_seq)), attention_weight_seq
def bleu(pred_seq, label_seq, k): #@save
"""Compute the BLEU."""
pred_tokens, label_tokens = pred_seq.split(' '), label_seq.split(' ')
len_pred, len_label = len(pred_tokens), len(label_tokens)
score = math.exp(min(0, 1 - len_label / len_pred))
for n in range(1, k + 1):
num_matches, label_subs = 0, collections.defaultdict(int)
for i in range(len_label - n + 1):
label_subs[''.join(label_tokens[i:i + n])] += 1
for i in range(len_pred - n + 1):
if label_subs[''.join(pred_tokens[i:i + n])] > 0:
num_matches += 1
label_subs[''.join(pred_tokens[i:i + n])] -= 1
score *= math.pow(num_matches / (len_pred - n + 1), math.pow(0.5, n))
return score
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, attention_weight_seq = predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device)
print(f'{eng} => {translation}, bleu {bleu(translation, fra, k=2):.3f}')
| 0.837554 | 0.993294 |
# Numpy Basics
NumPy bietet einen N-dimensionalen Array-Typ, den ndarray, der eine Sammlung von „Elementen“ des *gleichen* Typs beschreibt.
Die Elemente können unter Verwendung von beispielsweise N ganzen Zahlen indiziert werden.
Alle ndarrays sind homogen: Jedes Element nimmt einen gleich großen Speicherblock ein, und alle Blöcke werden genau gleich interpretiert.
Ein aus einem Array extrahiertes Element, z. B. durch Indizierung, wird durch ein Python-Objekt dargestellt, dessen Typ einer der in NumPy erstellten skalaren Array-Typen ist.
<p align="center">
<img src="https://numpy.org/doc/stable/_images/threefundamental.png">
</p>
## NumPy Array Attributes
```
import numpy as np
np.random.seed(0)
# Hilfsfunktion array
def array_info(array: np.ndarray) -> None:
print(f"ndim = dimension: {array.ndim}")
print(f"shape = größe: {array.shape}")
print(f"size = anzahl Elemente: {array.size}")
print(f"dtype = datentyp: {array.dtype}")
print(f"values = wert: \n{array}\n")
```
## Array Indexing and Slicing
Array-Indizierung bezieht sich auf jede Verwendung der eckigen Klammern ([]) zum Indexieren von Array-Werten. Es gibt viele Optionen für die Indexierung, die der numpy-Indexierung eine große Macht verleihen.
Die meisten der folgenden Beispiele zeigen die Verwendung der Indizierung beim Verweisen auf Daten in einem Array. Die Beispiele funktionieren genauso gut, wenn Sie einem Array zuweisen.
Beachten Sie, dass Slices von Arrays nicht die internen Array-Daten kopieren, sondern nur neue Ansichten der Originaldaten erzeugen.

<p align="center">
<img src="https://numpy.org/doc/stable/_images/np_indexing.png">
</p>
<p align="center">
<img src="https://numpy.org/doc/stable/_images/np_matrix_indexing.png">
</p>
```
data = np.array([[1, 2], [3, 4], [5, 6]])
array_info(data)
print(data[:3])
print(data[1:])
print(data[1:2])
print(data[::-1])
print(data[0, :])
print(data[0])
print(data[:, 0])
mean = [0, 0]
cov = [[1, 2],
[2, 5]]
data = np.random.multivariate_normal(mean=mean, cov=cov, size=10)
print(data)
print(data.shape)
rand_idxs = np.random.randint(low=0, high=data.shape[0], size=3)
print(rand_idxs)
x_subsample = data[rand_idxs, :]
print(x_subsample)
x_subsample = data[rand_idxs]
print(x_subsample)
```
## Subarrays are views
```
print(data)
x_sub_array = data[:2, :2]
array_info(x_sub_array)
x_sub_array[0, 0] = -1
array_info(x_sub_array)
array_info(data)
```
## Creating copies of arrays
```
x_copy = data[:2, :2].copy()
array_info(x_copy)
x_copy[0, 0] = 42
array_info(x_copy)
array_info(data)
```
## Reshaping of Arrays
<p align="center">
<img src="https://numpy.org/doc/stable/_images/np_reshape.png">
</p>
```
a = np.arange(start=1, stop=10)
array_info(a)
grid = np.reshape(a, newshape=(3, 3))
array_info(grid)
data = np.array([1, 2, 3])
array_info(data)
data = np.reshape(data, newshape=(1, 3))
array_info(data)
array_info(data)
data = data[np.newaxis, :]
array_info(data)
array_info(data)
data = data.reshape((3, 1))
array_info(data)
array_info(data)
data = data.ravel()
array_info(data)
data = data.reshape((3, 1))
array_info(data)
data = data.flatten()
array_info(data)
```
### “Automatic” Reshaping
```
a = np.arange(30)
array_info(a)
b = a.reshape((2, -1, 3))
array_info(b)
```
## Changing the Dtype
| Numpy type | C type | Description |
|-|-|-|
| numpy.int8 | int8_t | Byte (-128 to 127) |
| numpy.int16 | int16_t | Integer (-32768 to 32767) |
| numpy.int32 | int32_t | Integer (-2147483648 to 2147483647) |
| numpy.int64 | int64_t | Integer (-9223372036854775808 to 9223372036854775807) |
| numpy.uint8 | uint8_t | Unsigned integer (0 to 255) |
| numpy.uint16 | uint16_t | Unsigned integer (0 to 65535) |
| numpy.uint32 | uint32_t | Unsigned integer (0 to 4294967295) |
| numpy.uint64 | uint64_t | Unsigned integer (0 to 18446744073709551615) |
| numpy.intp | intptr_t | Integer used for indexing, typically the same as ssize_t |
| numpy.uintp | uintptr_t | Integer large enough to hold a pointer |
| numpy.float32 | float | |
| numpy.float64 | double | Note that this matches the precision of the builtin python float. |
| numpy.complex64 | float complex | Complex number, represented by two 32-bit floats. |
| numpy.complex128 | double complex | Note that this matches the precision of the builtin python complex. |
```
data = np.float32([-1.0, 2.0, 3.0])
array_info(data)
data = np.array([-1.0, 2.0, 3.0], dtype=np.float32)
y = data.astype(np.int8)
array_info(y)
z = np.uint16(data)
array_info(z)
```
## Concatenation of arrays
```
# aneinanderhängen
data = np.array([1, 2, 3])
y = np.array([3, 2, 1])
result = np.concatenate([data, y])
array_info(result)
grid = np.array([[1, 2, 3],
[4, 5, 6]])
array_info(grid)
result = np.concatenate([grid, grid])
array_info(result)
result = np.concatenate([grid, grid], axis=0)
array_info(result)
result = np.concatenate([grid, grid], axis=1)
array_info(result)
data = np.array([1, 2, 3])
grid = np.array([[4, 5, 6],
[7, 8, 9]])
result = np.vstack([data, grid])
array_info(result)
y = np.array([[-1], [-1]])
result = np.hstack([grid, y])
array_info(result)
```
|
github_jupyter
|
import numpy as np
np.random.seed(0)
# Hilfsfunktion array
def array_info(array: np.ndarray) -> None:
print(f"ndim = dimension: {array.ndim}")
print(f"shape = größe: {array.shape}")
print(f"size = anzahl Elemente: {array.size}")
print(f"dtype = datentyp: {array.dtype}")
print(f"values = wert: \n{array}\n")
data = np.array([[1, 2], [3, 4], [5, 6]])
array_info(data)
print(data[:3])
print(data[1:])
print(data[1:2])
print(data[::-1])
print(data[0, :])
print(data[0])
print(data[:, 0])
mean = [0, 0]
cov = [[1, 2],
[2, 5]]
data = np.random.multivariate_normal(mean=mean, cov=cov, size=10)
print(data)
print(data.shape)
rand_idxs = np.random.randint(low=0, high=data.shape[0], size=3)
print(rand_idxs)
x_subsample = data[rand_idxs, :]
print(x_subsample)
x_subsample = data[rand_idxs]
print(x_subsample)
print(data)
x_sub_array = data[:2, :2]
array_info(x_sub_array)
x_sub_array[0, 0] = -1
array_info(x_sub_array)
array_info(data)
x_copy = data[:2, :2].copy()
array_info(x_copy)
x_copy[0, 0] = 42
array_info(x_copy)
array_info(data)
a = np.arange(start=1, stop=10)
array_info(a)
grid = np.reshape(a, newshape=(3, 3))
array_info(grid)
data = np.array([1, 2, 3])
array_info(data)
data = np.reshape(data, newshape=(1, 3))
array_info(data)
array_info(data)
data = data[np.newaxis, :]
array_info(data)
array_info(data)
data = data.reshape((3, 1))
array_info(data)
array_info(data)
data = data.ravel()
array_info(data)
data = data.reshape((3, 1))
array_info(data)
data = data.flatten()
array_info(data)
a = np.arange(30)
array_info(a)
b = a.reshape((2, -1, 3))
array_info(b)
data = np.float32([-1.0, 2.0, 3.0])
array_info(data)
data = np.array([-1.0, 2.0, 3.0], dtype=np.float32)
y = data.astype(np.int8)
array_info(y)
z = np.uint16(data)
array_info(z)
# aneinanderhängen
data = np.array([1, 2, 3])
y = np.array([3, 2, 1])
result = np.concatenate([data, y])
array_info(result)
grid = np.array([[1, 2, 3],
[4, 5, 6]])
array_info(grid)
result = np.concatenate([grid, grid])
array_info(result)
result = np.concatenate([grid, grid], axis=0)
array_info(result)
result = np.concatenate([grid, grid], axis=1)
array_info(result)
data = np.array([1, 2, 3])
grid = np.array([[4, 5, 6],
[7, 8, 9]])
result = np.vstack([data, grid])
array_info(result)
y = np.array([[-1], [-1]])
result = np.hstack([grid, y])
array_info(result)
| 0.309858 | 0.935346 |
<p><img alt="DataOwl" width=150 src="http://gwsolutions.cl/Images/dataowl.png", align="left", hspace=0, vspace=5></p>
<h1 align="center">Numpy y Pandas</h1>
<h4 align="center">Arreglos y Dataframes</h4>
<pre><div align="center"> La idea de este notebook es que sirva para iniciarse en el preprocesamiento de datos.</div>
<div align="right"> En términos de código y estructura, este notebook esta basado en el BootCamp
<a href="https://github.com/Shekhar-rv/Python-for-Data-Science-and-Machine-Learning-Bootcamp">Python for Data Science and Machine Learning</a>.
.</div></pre>
## ¿Qué es Numpy?
<p><img alt="Numpy" width=70 src="https://user-images.githubusercontent.com/50221806/81123350-b7c5bb00-8ee7-11ea-9bfc-88f676c80315.png", align="right", hspace=0, vspace=5></p>
NumPy es una extensión de Python, que le agrega mayor soporte para vectores y matrices, constituyendo una biblioteca de funciones matemáticas de alto nivel para operar con esos vectores o matrices.
Para instalar la librería puede hacerse a través del comando **pip** o el comando **conda** en la consola de comandos:
```cmd
conda install numpy
pip install numpy
```
```
# Importando la librería
import numpy as np
```
Numpy nos permite crear y trabajar con vectores (llamados arreglos) y matrices de forma simple, y se enfoca principalmente en añadir funciones matematicas, a diferencia de las listas que son estructuras de mayor complejidad. Existen varias maneras de construir un arreglo, entre ellas la más sencilla es realizarlo a partir de una lista, no obstante, podemos hacerlo a partir de una matriz o de comandos predefinidos.
```
# Creando arreglo a partir de una lista
my_list = [1,2,3,4,5]
my_array = np.array(my_list)
my_array
# Creando arreglo a partir de una lista de listas
my_list_of_lists = [ [1,2,3] , [4,5,6] , [7,8,9] ]
my_array_2 = np.array(my_list_of_lists)
my_array_2
# Definiendo un array ordenado (Función arange)
arr = np.arange(1,11)
arr
# Definiendo un array de ceros (Función zeros)
arr_0 = np.zeros(10)
arr_0
# Definiendo un array de unos (Función ones)
arr_1 = np.ones(10)
arr_1
# Definiendo un arreglo equiespaciado
arr = np.linspace(0,1,15)
arr
# Definiendo la matriz identidad
arr = np.eye(4)
arr
```
Además de la creación de arreglos, existen además maneras de indexar y operaciones alrededor de los arreglos, no obstante no porfundizaremos en ellos ya que hoy en día esta librería no se utiliza en demasía, por lo que pasaremos a Pandas.
## ¿Qué es Pandas?
<p><img alt="Pandas" width=150 src="https://zhihuicao.files.wordpress.com/2016/05/pandas.png?w=399", align="right", hspace=0, vspace=5></p>
Pandas es una biblioteca de software escrita como extensión de NumPy para manipulación y análisis de datos para el lenguaje de programación Python. En particular, ofrece estructuras de datos y operaciones para manipular tablas numéricas y series temporales.
Para instalar la librería puede hacerse a través del comando **pip** o el comando **conda** en la consola de comandos:
```cmd
conda install pandas
pip install pandas
```
```
#Importando la librería
import pandas as pd
```
<h3>Secciones</h3>
<div class="alert alert-danger" role="alert">
<ol>
<li><a href="#section1"> Series</a></li>
<li><a href="#section2"> DataFrames </a></li>
<li><a href="#section3"> Datos faltantes (Missing Data) </a></li>
<li><a href="#section4"> Agrupaciones (Groupby)</a></li>
<li><a href="#section5"> Fusiones (Merge), Uniones (Join) y Concatenaciones</a></li>
</ol>
</div>
<hr>
<a id="section1"></a>
<h3>1. Series</h3>
<hr>
El primer tipo de datos principal que aprenderemos para los pandas es el tipo de datos **Serie**. Importemos Pandas y exploremos el objeto Serie.
<p><img alt="Dataframe" width=150 src="https://miro.medium.com/max/1284/1*iI8ltITQlsrX7Mc6E-OKKg.png", align="center", hspace=0, vspace=5></p>
Una serie es muy similar a un arreglo de NumPy (de hecho, está construida sobre el objeto de arreglo de NumPy). Lo que diferencia el arreglo de una Serie es que una Serie puede tener etiquetas de eje, lo que significa que puede ser indexada por una etiqueta, en lugar de solo una ubicación numérica. Tampoco necesita contener datos numéricos, puede contener cualquier objeto Python arbitrario.
Una serie puede ser creada a partir de un arreglo, de una lista o de un diccionario.
```
# Creando una serie
labels = ['a','b','c']
my_list = [10,20,30]
arr = np.array([10,20,30])
d = { 'a' : 10 , 'b' : 20 , 'c' : 30 }
Serie = pd.Series( d )
Serie
```
Los índices se utilizan de la misma manera que en las listas, diccionarios o arreglos:
```
# Llamando un elemento de la serie
Serie[ ['b','c'] ]
```
Cuando operamos dos series tenemos que tener cuidado, ya que estas se operan a partir de las etiquetas, no de la posición que utilizen en esta:
```
# Operación simple entre series
ser_1 = pd.Series([1,2,3,4],index = ['USA', 'Germany','USSR', 'Japan'])
ser_2 = pd.Series([1,2,5,4],index = ['USA', 'Germany','Italy', 'Japan'])
ser_1+ser_2
```
<a id="section2"></a>
<h3>2. Dataframe</h3>
<hr>
Los DataFrames son el caballo de batalla de los pandas y están directamente inspirados en el lenguaje de programación R. Podemos pensar en un DataFrame como una matriz, donde cada columna es una serie.
<p><img alt="Dataframe" width=450 src="https://vrzkj25a871bpq7t1ugcgmn9-wpengine.netdna-ssl.com/wp-content/uploads/2022/01/pandas-dataframe-integer-location.png", align="center", hspace=0, vspace=5></p>
Las columnas nos representan variables y las filas los datos, algunas veces indexados.
```
# Creando nuestro primer dataframe
arr = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
df_1 = pd.DataFrame( data = arr )
df_2 = pd.DataFrame( data = arr , index = ["d_1","d_2","d_3"] , columns = ["V_1","V_2","V_3","V_4"])
df_2
```
#### Leyendo y guardando ficheros
No solo podemos crear dataframes a partir de objetos creados en Python, además podemos leer datos de nuestra propia base datos o de un directorio externo.
```
# Leyendo un archivo .csv
df_covid19 = pd.read_csv("cases_country.csv")
df_covid19
# Leyendo archivo desde url
df_covid19_url = pd.read_csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv")
df_covid19_url
# Guardando un archivo localmente
df_covid19_url.to_csv("df_covid19.csv" , index="False")
```
#### Selección por columnas
Como ahora estamos trabajando con matrices, podemos querer seleccionar tanto por variables (Columnas) como por datos (Filas), por lo cual existen distintas formas de indexación, la primera a ver será la indexación por columnas.
Si indexamos 1 columna, entonces obtenemos una serie por resultado, pero si indexamos una lista de columnas obtenemos un dataframe
```
# Seleccionando 1 columna
df_covid19["Country_Region"]
# Seleccionando 4 columnas
df = df_covid19[ ["Country_Region","Confirmed","Deaths","Recovered"] ]
df
```
#### Trabajando con variables
* Para generar una nueva variable (columna) basta con crearla como si estuvieramos seleccionandola, y asignarle su valor.
* Para eliminar una variable se utiliza la función **.drop( )**
* Podemos indexar condiciones para establecer condiciones sobre las variables
```
# Creando una nueva variable
df["Active"] = df["Confirmed"]-df["Deaths"]-df["Recovered"]
# Eliminando la variable
df = df.drop("Active" , axis = 1)
df
# Condicionando variables
df_high_deaths = df[ df["Deaths"]>10000 ]
df_high_deaths
```
#### Indexación por filas
Para comenzar, podemos establecer que una de nuestras columnas sea el indice para nuestro dataframe, para esto utilizamos la funcion **.set_index( )**
```
# Escogiendo un índice
df = df.set_index("Country_Region")
df
```
Para escoger 1 o 2 datos, utilizamos la función **.loc[ ]**.
```
# Escogiendo datos particulares
df.loc[ ["Argentina","Chile"] ]
```
<a id="section3"></a>
<h3>3. Datos faltantes (Missing Data)</h3>
<hr>
Generalmente los datos vienen con valores faltantes en algunas de sus columnas, y esto puede traernos problema a la hora de trabajar y establecer criterios de decisión con la información que obtenemos de estos.
Debemos saber que hacer con la data que falta y cuándo hacerlo, para así no tener problemas a la hora de establecer un modelo, o obtener insights.
Hay 3 formas usuales de trabajar con datos faltantes:
1. La primera es simplemente eliminar las filas con datos faltantes, y evitarse el riesgo de asignar mal un valor. El problema que esto podría traer es que estamos omitiendo información relevante de nuestra muestra.
2. La segunda es rellenar con algun valor determinado, ya sea la media, mediana u otro que nosotros consideremos. Aquí podríamos estar centralizando demasiado nuestros datos, y cuando las desviaciones son altas este método no es muy efectivo.
3. Otro método consiste en utilizar modelos para tratar de predecir o remplanzar los datos faltantes, aunque esto podría tomarnos mucho tiempo y recursos.
<p><img alt="Multiple_Imputation" width=450 src="https://media.springernature.com/lw785/springer-static/image/chp%3A10.1007%2F978-3-319-43742-2_13/MediaObjects/339333_1_En_13_Fig3_HTML.gif", align="center", hspace=0, vspace=5></p>
En Python las funciones que nos ayudan a esto son **.dropna( )** para eliminar y la función **.fillna( )** para rellenar.
```
# Consideramos este dataframe
df = pd.DataFrame({'v_1':[1,2,np.nan],
'v_2':[5,np.nan,np.nan],
'v_3':[1,2,3]})
df
# Eliminando filas con NA
df.dropna()
# Eliminando columnas con NA
df.dropna(axis=1)
# Eliminando filas que tengan mas de n datos faltantes
n = 2
df.dropna( thresh=n , axis = 1)
# Esto se puede replicar para columnas con axis=1 en los argumentos
# Llenando con el promedio
for i in df.columns:
df[i] = df[i].fillna( value = df[i].mean() )
df
```
<a id="section4"></a>
<h3>4. Agrupaciones (Groupby)</h3>
<hr>
Para agrupar los datos en varios dataframes utilizando valores que se repitan en alguna de sus variables, utilizamos la funcion **.groupby( )**
```
# Agrupamos el conjunto por paises
df = df_covid19_url.dropna()
countrys = df.groupby("Country/Region")
countrys
```
Cuando ya tenemos agrupados los datos por alguna variable podemos hacer diversas operaciones, entre ellas estan
* Suma con la funcion **.sum( )**
* Calcular el promedio con **.mean( )**
* Calcular mínimo y máximo con **.max( )** y **.min( )** respectivamente.
* Contar cuantos datos hay con **.count( )**
* Realizar estadística descriptiva con **.describe( )**
Ademas con la función **.get_group( )** podemos obtener un dataframe específico.
```
# Hacemos una suma sobre los grupos
countrys.count()
# Podemos obtener el dataframe de un elemento en particular
countrys.get_group("Australia").describe()
df.columns
```
<a id="section5"></a>
<h3>5. Fusiones (Merges), Uniones (Joins) y Concatenaciones</h3>
<hr>
Las siguientes operaciones que veremos entre dataframes nos permiten realizar uniones de algún tipo con 2 dataframes.
#### Join
Entre las tres operaciones de DataFrame, **join()** es la más sencilla y la que menos control nos da sobre la unión. Combina todas las columnas existentes en dos tablas, y las columnas en común las renombrara con un *lsuffix* y un *rsuffix* definidos.
Existen a su ves varios tipos de join, los cuales se deben definir en los argumentos de la función con un argumento *how*.
<p><img alt="Join" width=750 src="https://miro.medium.com/max/1400/1*-I_1qa5TIiB5eNYxnodfAA.png", align="center", hspace=0, vspace=5></p>
```Python
df.join(self, how='left', lsuffix='', rsuffix='')
```
```
# Definimos los dataframes para el join()
df_1 = pd.DataFrame({'A': ['A0', 'A1', 'A2'],
'B': ['B0', 'B1', 'B2']},
index=['K0', 'K1', 'K2'])
df_2 = pd.DataFrame({'B': ['B0', 'B1', 'B2'],
'C': ['C0', 'C2', 'C3'],
'D': ['D0', 'D2', 'D3']},
index=['K0', 'K2', 'K3'])
# Visualizamos el primer Dataframe
df_1
# Visualizamos el segundo Dataframe
df_2
# Realizamos el join()
df_join = df_1.join(df_2, how='outer', lsuffix='_1', rsuffix='_2')
df_join
```
#### Merge
Similar al join, el **merge()** también combina todas las columnas de dos tablas, con las columnas comunes renombradas con los sufijos definidos. Sin embargo, el merge proporciona tres formas de control flexible sobre la alineación en filas:
1. La primera forma es usar *on = COLUMN NAME*, aquí la columna dada debe ser la columna común en ambas tablas.
2. La segunda forma es usar *left_on = COLUMN NAME* y *right_on = COLUMN NAME*, y permite alinear las dos tablas usando dos columnas diferentes.
3. La tercera forma es usar *left_index = True* y *right_index = True*, y las dos tablas están alineadas en función de su índice.
```Python
pd.merge(left, right, how='inner', on=None, left_on=None, right_on=None,
left_index=False, right_index=False, suffixes=('_x', '_y'))
```
#### Concatenation
A diferencia del join() y del merge(), que por defecto operan en columnas, **concat()** puede realizar tambien operaciones de union para filas. El argumento en este caso es una lista con dataframes.
.
* *Axis = 1*
<p><img alt="Join" width=450 src="https://miro.medium.com/max/1400/1*LoUq8uZrbg_tO3t4tqZfqg.png", align="center", hspace=0, vspace=5></p>
* *Axis = 0*
<p><img alt="Join" width=450 src="https://miro.medium.com/max/1400/1*bQ3Bl6_N_V4er6XZxVxIZA.png", align="center", hspace=0, vspace=5></p>
```Python
pd.concat(objs, axis=0, join='outer', join_axes=None, ignore_index=False, keys=None)
```
#### ¡Motivense a seguir probando distintas combinaciones en los argumentos de las funciones!
**Guía de Uniones:** <a href="https://pandas.pydata.org/pandas-docs/stable/user_guide/merging.html">Click aquí</a>
|
github_jupyter
|
conda install numpy
pip install numpy
# Importando la librería
import numpy as np
# Creando arreglo a partir de una lista
my_list = [1,2,3,4,5]
my_array = np.array(my_list)
my_array
# Creando arreglo a partir de una lista de listas
my_list_of_lists = [ [1,2,3] , [4,5,6] , [7,8,9] ]
my_array_2 = np.array(my_list_of_lists)
my_array_2
# Definiendo un array ordenado (Función arange)
arr = np.arange(1,11)
arr
# Definiendo un array de ceros (Función zeros)
arr_0 = np.zeros(10)
arr_0
# Definiendo un array de unos (Función ones)
arr_1 = np.ones(10)
arr_1
# Definiendo un arreglo equiespaciado
arr = np.linspace(0,1,15)
arr
# Definiendo la matriz identidad
arr = np.eye(4)
arr
conda install pandas
pip install pandas
#Importando la librería
import pandas as pd
# Creando una serie
labels = ['a','b','c']
my_list = [10,20,30]
arr = np.array([10,20,30])
d = { 'a' : 10 , 'b' : 20 , 'c' : 30 }
Serie = pd.Series( d )
Serie
# Llamando un elemento de la serie
Serie[ ['b','c'] ]
# Operación simple entre series
ser_1 = pd.Series([1,2,3,4],index = ['USA', 'Germany','USSR', 'Japan'])
ser_2 = pd.Series([1,2,5,4],index = ['USA', 'Germany','Italy', 'Japan'])
ser_1+ser_2
# Creando nuestro primer dataframe
arr = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
df_1 = pd.DataFrame( data = arr )
df_2 = pd.DataFrame( data = arr , index = ["d_1","d_2","d_3"] , columns = ["V_1","V_2","V_3","V_4"])
df_2
# Leyendo un archivo .csv
df_covid19 = pd.read_csv("cases_country.csv")
df_covid19
# Leyendo archivo desde url
df_covid19_url = pd.read_csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv")
df_covid19_url
# Guardando un archivo localmente
df_covid19_url.to_csv("df_covid19.csv" , index="False")
# Seleccionando 1 columna
df_covid19["Country_Region"]
# Seleccionando 4 columnas
df = df_covid19[ ["Country_Region","Confirmed","Deaths","Recovered"] ]
df
# Creando una nueva variable
df["Active"] = df["Confirmed"]-df["Deaths"]-df["Recovered"]
# Eliminando la variable
df = df.drop("Active" , axis = 1)
df
# Condicionando variables
df_high_deaths = df[ df["Deaths"]>10000 ]
df_high_deaths
# Escogiendo un índice
df = df.set_index("Country_Region")
df
# Escogiendo datos particulares
df.loc[ ["Argentina","Chile"] ]
# Consideramos este dataframe
df = pd.DataFrame({'v_1':[1,2,np.nan],
'v_2':[5,np.nan,np.nan],
'v_3':[1,2,3]})
df
# Eliminando filas con NA
df.dropna()
# Eliminando columnas con NA
df.dropna(axis=1)
# Eliminando filas que tengan mas de n datos faltantes
n = 2
df.dropna( thresh=n , axis = 1)
# Esto se puede replicar para columnas con axis=1 en los argumentos
# Llenando con el promedio
for i in df.columns:
df[i] = df[i].fillna( value = df[i].mean() )
df
# Agrupamos el conjunto por paises
df = df_covid19_url.dropna()
countrys = df.groupby("Country/Region")
countrys
# Hacemos una suma sobre los grupos
countrys.count()
# Podemos obtener el dataframe de un elemento en particular
countrys.get_group("Australia").describe()
df.columns
df.join(self, how='left', lsuffix='', rsuffix='')
# Definimos los dataframes para el join()
df_1 = pd.DataFrame({'A': ['A0', 'A1', 'A2'],
'B': ['B0', 'B1', 'B2']},
index=['K0', 'K1', 'K2'])
df_2 = pd.DataFrame({'B': ['B0', 'B1', 'B2'],
'C': ['C0', 'C2', 'C3'],
'D': ['D0', 'D2', 'D3']},
index=['K0', 'K2', 'K3'])
# Visualizamos el primer Dataframe
df_1
# Visualizamos el segundo Dataframe
df_2
# Realizamos el join()
df_join = df_1.join(df_2, how='outer', lsuffix='_1', rsuffix='_2')
df_join
pd.merge(left, right, how='inner', on=None, left_on=None, right_on=None,
left_index=False, right_index=False, suffixes=('_x', '_y'))
```
#### Concatenation
A diferencia del join() y del merge(), que por defecto operan en columnas, **concat()** puede realizar tambien operaciones de union para filas. El argumento en este caso es una lista con dataframes.
.
* *Axis = 1*
<p><img alt="Join" width=450 src="https://miro.medium.com/max/1400/1*LoUq8uZrbg_tO3t4tqZfqg.png", align="center", hspace=0, vspace=5></p>
* *Axis = 0*
<p><img alt="Join" width=450 src="https://miro.medium.com/max/1400/1*bQ3Bl6_N_V4er6XZxVxIZA.png", align="center", hspace=0, vspace=5></p>
| 0.38549 | 0.965996 |
# Collaborative filtering on the MovieLense Dataset
## Learning Objectives
1. Know how to explore the data using BigQuery
2. Know how to use the model to make recommendations for a user
3. Know how to use the model to recommend an item to a group of users
###### This notebook is based on part of Chapter 9 of [BigQuery: The Definitive Guide](https://www.oreilly.com/library/view/google-bigquery-the/9781492044451/ "http://shop.oreilly.com/product/0636920207399.do") by Lakshmanan and Tigani.
### MovieLens dataset
To illustrate recommender systems in action, let’s use the MovieLens dataset. This is a dataset of movie reviews released by GroupLens, a research lab in the Department of Computer Science and Engineering at the University of Minnesota, through funding by the US National Science Foundation.
Download the data and load it as a BigQuery table using:
```
import os
import tensorflow as tf
PROJECT = "qwiklabs-gcp-00-eeb852ce8ccb" # REPLACE WITH YOUR PROJECT ID
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["TFVERSION"] = '2.1'
%%bash
rm -r bqml_data
mkdir bqml_data
cd bqml_data
curl -O 'http://files.grouplens.org/datasets/movielens/ml-20m.zip'
unzip ml-20m.zip
yes | bq rm -r $PROJECT:movielens
bq --location=US mk --dataset \
--description 'Movie Recommendations' \
$PROJECT:movielens
bq --location=US load --source_format=CSV \
--autodetect movielens.ratings ml-20m/ratings.csv
bq --location=US load --source_format=CSV \
--autodetect movielens.movies_raw ml-20m/movies.csv
```
## Exploring the data
Two tables should now be available in <a href="https://console.cloud.google.com/bigquery">BigQuery</a>.
Collaborative filtering provides a way to generate product recommendations for users, or user targeting for products. The starting point is a table, <b>movielens.ratings</b>, with three columns: a user id, an item id, and the rating that the user gave the product. This table can be sparse -- users don’t have to rate all products. Then, based on just the ratings, the technique finds similar users and similar products and determines the rating that a user would give an unseen product. Then, we can recommend the products with the highest predicted ratings to users, or target products at users with the highest predicted ratings.
```
%%bigquery --project $PROJECT
SELECT *
FROM movielens.ratings
LIMIT 10
```
A quick exploratory query yields that the dataset consists of over 138 thousand users, nearly 27 thousand movies, and a little more than 20 million ratings, confirming that the data has been loaded successfully.
```
%%bigquery --project $PROJECT
SELECT
COUNT(DISTINCT userId) numUsers,
COUNT(DISTINCT movieId) numMovies,
COUNT(*) totalRatings
FROM movielens.ratings
```
On examining the first few movies using the query following query, we can see that the genres column is a formatted string:
```
%%bigquery --project $PROJECT
SELECT *
FROM movielens.movies_raw
WHERE movieId < 5
```
We can parse the genres into an array and rewrite the table as follows:
```
%%bigquery --project $PROJECT
CREATE OR REPLACE TABLE movielens.movies AS
SELECT * REPLACE(SPLIT(genres, "|") AS genres)
FROM movielens.movies_raw
%%bigquery --project $PROJECT
SELECT *
FROM movielens.movies
WHERE movieId < 5
```
## Matrix factorization
Matrix factorization is a collaborative filtering technique that relies on factorizing the ratings matrix into two vectors called the user factors and the item factors. The user factors is a low-dimensional representation of a user_id and the item factors similarly represents an item_id.
```
%%bigquery --project $PROJECT
SELECT *
-- Note: remove cloud-training-demos if you are using your own model:
FROM ML.TRAINING_INFO(MODEL `cloud-training-demos.movielens.recommender`)
```
What did you get? Our model took an hour to train, and the training loss starts out extremely bad and gets driven down to near-zero over next the four iterations:
<table>
<tr>
<th>Iteration</th>
<th>Training Data Loss</th>
<th>Evaluation Data Loss</th>
<th>Duration (seconds)</th>
</tr>
<tr>
<td>4</td>
<td>0.5734</td>
<td>172.4057</td>
<td>180.99</td>
</tr>
<tr>
<td>3</td>
<td>0.5826</td>
<td>187.2103</td>
<td>1,040.06</td>
</tr>
<tr>
<td>2</td>
<td>0.6531</td>
<td>4,758.2944</td>
<td>219.46</td>
</tr>
<tr>
<td>1</td>
<td>1.9776</td>
<td>6,297.2573</td>
<td>1,093.76</td>
</tr>
<tr>
<td>0</td>
<td>63,287,833,220.5795</td>
<td>168,995,333.0464</td>
<td>1,091.21</td>
</tr>
</table>
However, the evaluation data loss is quite high, and much higher than the training data loss. This indicates that overfitting is happening, and so we need to add some regularization. Let’s do that next. Note the added l2_reg=0.2:
```
%%bigquery --project $PROJECT
SELECT *
-- Note: remove cloud-training-demos if you are using your own model:
FROM ML.TRAINING_INFO(MODEL `cloud-training-demos.movielens.recommender_l2`)
```
Now, we get faster convergence (three iterations instead of five), and a lot less overfitting. Here are our results:
<table>
<tr>
<th>Iteration</th>
<th>Training Data Loss</th>
<th>Evaluation Data Loss</th>
<th>Duration (seconds)</th>
</tr>
<tr>
<td>2</td>
<td>0.6509</td>
<td>1.4596</td>
<td>198.17</td>
</tr>
<tr>
<td>1</td>
<td>1.9829</td>
<td>33,814.3017</td>
<td>1,066.06</td>
</tr>
<tr>
<td>0</td>
<td>481,434,346,060.7928</td>
<td>2,156,993,687.7928</td>
<td>1,024.59</td>
</tr>
</table>
By default, BigQuery sets the number of factors to be the log2 of the number of rows. In our case, since we have 20 million rows in the table, the number of factors would have been chosen to be 24. As with the number of clusters in K-Means clustering, this is a reasonable default but it is often worth experimenting with a number about 50% higher (36) and a number that is about a third lower (16):
```
%%bigquery --project $PROJECT
SELECT *
-- Note: remove cloud-training-demos if you are using your own model:
FROM ML.TRAINING_INFO(MODEL `cloud-training-demos.movielens.recommender_16`)
```
When we did that, we discovered that the evaluation loss was lower (0.97) with num_factors=16 than with num_factors=36 (1.67) or num_factors=24 (1.45). We could continue experimenting, but we are likely to see diminishing returns with further experimentation.
## Making recommendations
With the trained model, we can now provide recommendations. For example, let’s find the best comedy movies to recommend to the user whose userId is 903. In the query below, we are calling ML.PREDICT passing in the trained recommendation model and providing a set of movieId and userId to carry out the predictions on. In this case, it’s just one userId (903), but all movies whose genre includes Comedy.
```
%%bigquery --project $PROJECT
SELECT * FROM
ML.PREDICT(MODEL `cloud-training-demos.movielens.recommender_16`, (
SELECT
movieId, title, 903 AS userId
FROM movielens.movies, UNNEST(genres) g
WHERE g = 'Comedy'
))
ORDER BY predicted_rating DESC
LIMIT 5
```
## Filtering out already rated movies
Of course, this includes movies the user has already seen and rated in the past. Let’s remove them.
**TODO 1**: Make a prediction for user 903 that does not include already seen movies.
```
%%bigquery --project $PROJECT
SELECT * FROM
ML.PREDICT(MODEL `cloud-training-demos.movielens.recommender_16`, (
WITH seen AS (
SELECT ARRAY_AGG(movieId) AS movies
FROM movielens.ratings
WHERE userId = 903
)
SELECT
movieId, title, 903 AS userId
FROM movielens.movies, UNNEST(genres) g, seen
WHERE g = 'Comedy' AND movieId NOT IN UNNEST(seen.movies)
))
ORDER BY predicted_rating DESC
LIMIT 5
```
For this user, this happens to yield the same set of movies -- the top predicted ratings didn’t include any of the movies the user has already seen.
## Customer targeting
In the previous section, we looked at how to identify the top-rated movies for a specific user. Sometimes, we have a product and have to find the customers who are likely to appreciate it. Suppose, for example, we wish to get more reviews for movieId = 96481 (American Mullet) which has only one rating and we wish to send coupons to the 5 users who are likely to rate it the highest.
**TODO 2**: Find the top five users who will likely enjoy *American Mullet (2001)*
```
%%bigquery --project $PROJECT
SELECT * FROM
ML.PREDICT(MODEL `cloud-training-demos.movielens.recommender_16`, (
WITH allUsers AS (
SELECT DISTINCT userId
FROM movielens.ratings
)
SELECT
96481 AS movieId,
(SELECT title FROM movielens.movies WHERE movieId=96481) title,
userId
FROM
allUsers
))
ORDER BY predicted_rating DESC
LIMIT 5
```
### Batch predictions for all users and movies
What if we wish to carry out predictions for every user and movie combination? Instead of having to pull distinct users and movies as in the previous query, a convenience function is provided to carry out batch predictions for all movieId and userId encountered during training. A limit is applied here, otherwise, all user-movie predictions will be returned and will crash the notebook.
```
%%bigquery --project $PROJECT
SELECT *
FROM ML.RECOMMEND(MODEL `cloud-training-demos.movielens.recommender_16`)
LIMIT 10
```
As seen in a section above, it is possible to filter out movies the user has already seen and rated in the past. The reason already seen movies aren’t filtered out by default is that there are situations (think of restaurant recommendations, for example) where it is perfectly expected that we would need to recommend restaurants the user has liked in the past.
Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
|
github_jupyter
|
import os
import tensorflow as tf
PROJECT = "qwiklabs-gcp-00-eeb852ce8ccb" # REPLACE WITH YOUR PROJECT ID
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["TFVERSION"] = '2.1'
%%bash
rm -r bqml_data
mkdir bqml_data
cd bqml_data
curl -O 'http://files.grouplens.org/datasets/movielens/ml-20m.zip'
unzip ml-20m.zip
yes | bq rm -r $PROJECT:movielens
bq --location=US mk --dataset \
--description 'Movie Recommendations' \
$PROJECT:movielens
bq --location=US load --source_format=CSV \
--autodetect movielens.ratings ml-20m/ratings.csv
bq --location=US load --source_format=CSV \
--autodetect movielens.movies_raw ml-20m/movies.csv
%%bigquery --project $PROJECT
SELECT *
FROM movielens.ratings
LIMIT 10
%%bigquery --project $PROJECT
SELECT
COUNT(DISTINCT userId) numUsers,
COUNT(DISTINCT movieId) numMovies,
COUNT(*) totalRatings
FROM movielens.ratings
%%bigquery --project $PROJECT
SELECT *
FROM movielens.movies_raw
WHERE movieId < 5
%%bigquery --project $PROJECT
CREATE OR REPLACE TABLE movielens.movies AS
SELECT * REPLACE(SPLIT(genres, "|") AS genres)
FROM movielens.movies_raw
%%bigquery --project $PROJECT
SELECT *
FROM movielens.movies
WHERE movieId < 5
%%bigquery --project $PROJECT
SELECT *
-- Note: remove cloud-training-demos if you are using your own model:
FROM ML.TRAINING_INFO(MODEL `cloud-training-demos.movielens.recommender`)
%%bigquery --project $PROJECT
SELECT *
-- Note: remove cloud-training-demos if you are using your own model:
FROM ML.TRAINING_INFO(MODEL `cloud-training-demos.movielens.recommender_l2`)
%%bigquery --project $PROJECT
SELECT *
-- Note: remove cloud-training-demos if you are using your own model:
FROM ML.TRAINING_INFO(MODEL `cloud-training-demos.movielens.recommender_16`)
%%bigquery --project $PROJECT
SELECT * FROM
ML.PREDICT(MODEL `cloud-training-demos.movielens.recommender_16`, (
SELECT
movieId, title, 903 AS userId
FROM movielens.movies, UNNEST(genres) g
WHERE g = 'Comedy'
))
ORDER BY predicted_rating DESC
LIMIT 5
%%bigquery --project $PROJECT
SELECT * FROM
ML.PREDICT(MODEL `cloud-training-demos.movielens.recommender_16`, (
WITH seen AS (
SELECT ARRAY_AGG(movieId) AS movies
FROM movielens.ratings
WHERE userId = 903
)
SELECT
movieId, title, 903 AS userId
FROM movielens.movies, UNNEST(genres) g, seen
WHERE g = 'Comedy' AND movieId NOT IN UNNEST(seen.movies)
))
ORDER BY predicted_rating DESC
LIMIT 5
%%bigquery --project $PROJECT
SELECT * FROM
ML.PREDICT(MODEL `cloud-training-demos.movielens.recommender_16`, (
WITH allUsers AS (
SELECT DISTINCT userId
FROM movielens.ratings
)
SELECT
96481 AS movieId,
(SELECT title FROM movielens.movies WHERE movieId=96481) title,
userId
FROM
allUsers
))
ORDER BY predicted_rating DESC
LIMIT 5
%%bigquery --project $PROJECT
SELECT *
FROM ML.RECOMMEND(MODEL `cloud-training-demos.movielens.recommender_16`)
LIMIT 10
| 0.232049 | 0.985271 |
# Gridded Datasets
```
import xarray as xr
import numpy as np
import holoviews as hv
from holoviews import opts
hv.extension('matplotlib')
opts.defaults(opts.Scatter3D(color='Value', cmap='fire', edgecolor='black', s=50))
```
In the [Tabular Data](./08-Tabular_Datasets.ipynb) guide we covered how to work with columnar data in HoloViews. Apart from tabular or column based data there is another data format that is particularly common in the science and engineering contexts, namely multi-dimensional arrays. The gridded data interfaces allow working with grid-based datasets directly.
Grid-based datasets have two types of dimensions:
* they have coordinate or key dimensions, which describe the sampling of each dimension in the value arrays
* they have value dimensions which describe the quantity of the multi-dimensional value arrays
There are many different types of gridded datasets, which each approximate or measure a surface or space at discretely specified coordinates. In HoloViews, gridded datasets are typically one of three possible types: Regular rectilinear grids, irregular rectilinear grids, and curvilinear grids. Regular rectilinear grids can be defined by 1D coordinate arrays specifying the spacing along each dimension, while the other types require grid coordinates with the same dimensionality as the underlying value arrays, specifying the full n-dimensional coordinates of the corresponding array value. HoloViews provides many different elements supporting regularly spaced rectilinear grids, but currently only QuadMesh supports irregularly spaced rectilinear and curvilinear grids.
The difference between uniform, rectilinear and curvilinear grids is best illustrated by the figure below:
<figure>
<img src="http://earthsystemmodeling.org/docs/release/ESMF_8_1_1/ESMC_crefdoc/img11.png" alt="grid-types">
<figcaption>Types of logically rectangular grid tiles. Red circles show the values needed to specify grid coordinates for each type. Reproduced from <a href="http://earthsystemmodeling.org/docs/release/ESMF_8_1_1/ESMC_crefdoc/node5.html">ESMF documentation</a></figcaption>
</figure>
In this section we will first discuss how to work with the simpler rectilinear grids and then describe how to define a curvilinear grid with 2D coordinate arrays.
## Declaring gridded data
All Elements that support a ColumnInterface also support the GridInterface. The simplest example of a multi-dimensional (or more precisely 2D) gridded dataset is an image, which has implicit or explicit x-coordinates, y-coordinates and an array representing the values for each combination of these coordinates. Let us start by declaring an Image with explicit x- and y-coordinates:
```
img = hv.Image((range(10), range(5), np.random.rand(5, 10)), datatype=['grid'])
img
```
In the above example we defined that there would be 10 samples along the x-axis, 5 samples along the y-axis and then defined a random ``5x10`` array, matching those dimensions. This follows the NumPy (row, column) indexing convention. When passing a tuple HoloViews will use the first gridded data interface, which stores the coordinates and value arrays as a dictionary mapping the dimension name to a NumPy array representing the data:
```
img.data
```
However HoloViews also ships with an interface for ``xarray`` and the [GeoViews](https://geoviews.org) library ships with an interface for ``iris`` objects, which are two common libraries for working with multi-dimensional datasets:
```
arr_img = img.clone(datatype=['image'])
print(type(arr_img.data))
try:
xr_img = img.clone(datatype=['xarray'])
print(type(xr_img.data))
except:
print('xarray interface could not be imported.')
```
In the case of an Image HoloViews also has a simple image representation which stores the data as a single array and converts the x- and y-coordinates to a set of bounds:
```
print("Array type: %s with bounds %s" % (type(arr_img.data), arr_img.bounds))
```
To summarize the constructor accepts a number of formats where the value arrays should always match the shape of the coordinate arrays:
1. A simple np.ndarray along with (l, b, r, t) bounds
2. A tuple of the coordinate and value arrays
3. A dictionary of the coordinate and value arrays indexed by their dimension names
3. XArray DataArray or XArray Dataset
4. An Iris cube
# Working with a multi-dimensional dataset
A gridded Dataset may have as many dimensions as desired, however individual Element types only support data of a certain dimensionality. Therefore we usually declare a ``Dataset`` to hold our multi-dimensional data and take it from there.
```
dataset3d = hv.Dataset((range(3), range(5), range(7), np.random.randn(7, 5, 3)),
['x', 'y', 'z'], 'Value')
dataset3d
```
This is because even a 3D multi-dimensional array represents volumetric data which we can display easily only if it contains few samples. In this simple case we can get an overview of what this data looks like by casting it to a ``Scatter3D`` Element (which will help us visualize the operations we are applying to the data:
```
hv.Scatter3D(dataset3d)
```
### Indexing
In order to explore the dataset we therefore often want to define a lower dimensional slice into the array and then convert the dataset:
```
dataset3d.select(x=1).to(hv.Image, ['y', 'z']) + hv.Scatter3D(dataset3d.select(x=1))
```
### Groupby
Another common method to apply to our data is to facet or animate the data using ``groupby`` operations. HoloViews provides a convenient interface to apply ``groupby`` operations and select which dimensions to visualize.
```
(dataset3d.to(hv.Image, ['y', 'z'], 'Value', ['x']) +
hv.HoloMap({x: hv.Scatter3D(dataset3d.select(x=x)) for x in range(3)}, kdims='x'))
```
### Aggregating
Another common operation is to aggregate the data with a function thereby reducing a dimension. You can either ``aggregate`` the data by passing the dimensions to aggregate or ``reduce`` a specific dimension. Both have the same function:
```
hv.Image(dataset3d.aggregate(['x', 'y'], np.mean)) + hv.Image(dataset3d.reduce(z=np.mean))
```
By aggregating the data we can reduce it to any number of dimensions we want. We can for example compute the spread of values for each z-coordinate and plot it using a ``Spread`` and ``Curve`` Element. We simply aggregate by that dimension and pass the aggregation functions we want to apply:
```
hv.Spread(dataset3d.aggregate('z', np.mean, np.std)) * hv.Curve(dataset3d.aggregate('z', np.mean))
```
It is also possible to generate lower-dimensional views into the dataset which can be useful to summarize the statistics of the data along a particular dimension. A simple example is a box-whisker of the ``Value`` for each x-coordinate. Using the ``.to`` conversion interface we declare that we want a ``BoxWhisker`` Element indexed by the ``x`` dimension showing the ``Value`` dimension. Additionally we have to ensure to set ``groupby`` to an empty list because by default the interface will group over any remaining dimension.
```
dataset3d.to(hv.BoxWhisker, 'x', 'Value', groupby=[])
```
Similarly we can generate a ``Distribution`` Element showing the ``Value`` dimension, group by the 'x' dimension and then overlay the distributions, giving us another statistical summary of the data:
```
dataset3d.to(hv.Distribution, 'Value', [], groupby='x').overlay()
```
## Categorical dimensions
The key dimensions of the multi-dimensional arrays do not have to represent continuous values, we can display datasets with categorical variables as a ``HeatMap`` Element:
```
heatmap = hv.HeatMap((['A', 'B', 'C'], ['a', 'b', 'c', 'd', 'e'], np.random.rand(5, 3)))
heatmap + hv.Table(heatmap)
```
## Non-uniform rectilinear grids
As discussed above, there are two main types of grids handled by HoloViews. So far, we have mainly dealt with uniform, rectilinear grids, but we can use the ``QuadMesh`` element to work with non-uniform rectilinear grids and curvilinear grids.
In order to define a non-uniform, rectilinear grid we can declare explicit irregularly spaced x- and y-coordinates. In the example below we specify the x/y-coordinate bin edges of the grid as arrays of shape ``M+1`` and ``N+1`` and a value array (``zs``) of shape ``NxM``:
```
n = 8 # Number of bins in each direction
xs = np.logspace(1, 3, n)
ys = np.linspace(1, 10, n)
zs = np.arange((n-1)**2).reshape(n-1, n-1)
print('Shape of x-coordinates:', xs.shape)
print('Shape of y-coordinates:', ys.shape)
print('Shape of value array:', zs.shape)
hv.QuadMesh((xs, ys, zs))
```
## Curvilinear grids
To define a curvilinear grid the x/y-coordinates of the grid should be defined as 2D arrays of shape ``NxM`` or ``N+1xM+1``, i.e. either as the bin centers or the bin edges of each 2D bin.
```
n=20
coords = np.linspace(-1.5,1.5,n)
X,Y = np.meshgrid(coords, coords);
Qx = np.cos(Y) - np.cos(X)
Qy = np.sin(Y) + np.sin(X)
Z = np.sqrt(X**2 + Y**2)
print('Shape of x-coordinates:', Qx.shape)
print('Shape of y-coordinates:', Qy.shape)
print('Shape of value array:', Z.shape)
qmesh = hv.QuadMesh((Qx, Qy, Z))
qmesh
```
## Working with xarray data types
As demonstrated previously, `Dataset` comes with support for the `xarray` library, which offers a powerful way to work with multi-dimensional, regularly spaced data. In this example, we'll load an example dataset, turn it into a HoloViews `Dataset` and visualize it. First, let's have a look at the xarray dataset's contents:
```
xr_ds = xr.tutorial.open_dataset("air_temperature").load()
xr_ds
```
It is trivial to turn this xarray Dataset into a Holoviews `Dataset` (the same also works for DataArray):
```
hv_ds = hv.Dataset(xr_ds)[:, :, "2013-01-01"]
print(hv_ds)
```
We have used the usual slice notation in order to select one single day in the rather large dataset. Finally, let's visualize the dataset by converting it to a `HoloMap` of `Images` using the `to()` method. We need to specify which of the dataset's key dimensions will be consumed by the images (in this case "lat" and "lon"), where the remaing key dimensions will be associated with the HoloMap (here: "time"). We'll use the slice notation again to clip the longitude.
```
airtemp = hv_ds.to(hv.Image, kdims=["lon", "lat"], dynamic=False)
airtemp[:, 220:320, :].opts(colorbar=True, fig_size=200)
```
Here, we have explicitly specified the default behaviour `dynamic=False`, which returns a HoloMap. Note, that this approach immediately converts all available data to images, which will take up a lot of RAM for large datasets. For these situations, use `dynamic=True` to generate a [DynamicMap](./07-Live_Data.ipynb) instead. Additionally, [xarray features dask support](http://xarray.pydata.org/en/stable/dask.html), which is helpful when dealing with large amounts of data.
It is also possible to render curvilinear grids with xarray, and here we will load one such example. The dataset below defines a curvilinear grid of air temperatures varying over time. The curvilinear grid can be identified by the fact that the ``xc`` and ``yc`` coordinates are defined as two-dimensional arrays:
```
rasm = xr.tutorial.open_dataset("rasm").load()
rasm.coords
```
To simplify the example we will select a single timepoint and add explicit coordinates for the x and y dimensions:
```
rasm = rasm.isel(time=0, x=slice(0, 200)).assign_coords(x=np.arange(200), y=np.arange(205))
rasm.coords
```
Now that we have defined both rectilinear and curvilinear coordinates we can visualize the difference between the two by explicitly defining which set of coordinates to use:
```
hv.QuadMesh(rasm, ['x', 'y']) + hv.QuadMesh(rasm, ['xc', 'yc'])
```
Additional examples of visualizing xarrays in the context of geographical data can be found in the GeoViews documentation: [Gridded Datasets I](http://geoviews.org/user_guide/Gridded_Datasets_I.html) and
[Gridded Datasets II](http://geoviews.org/user_guide/Gridded_Datasets_II.html). These guides also contain useful information on the interaction between xarray data structures and HoloViews Datasets in general.
# API
## Accessing the data
In order to be able to work with data in different formats Holoviews defines a general interface to access the data. The dimension_values method allows returning underlying arrays.
#### Key dimensions (coordinates)
By default ``dimension_values`` will return the expanded columnar format of the data:
```
heatmap.dimension_values('x')
```
To access just the unique coordinates along a dimension simply supply the ``expanded=False`` keyword:
```
heatmap.dimension_values('x', expanded=False)
```
Finally we can also get a non-flattened, expanded coordinate array returning a coordinate array of the same shape as the value arrays
```
heatmap.dimension_values('x', flat=False)
```
#### Value dimensions
When accessing a value dimension the method will similarly return a flat view of the data:
```
heatmap.dimension_values('z')
```
We can pass the ``flat=False`` argument to access the multi-dimensional array:
```
heatmap.dimension_values('z', flat=False)
```
|
github_jupyter
|
import xarray as xr
import numpy as np
import holoviews as hv
from holoviews import opts
hv.extension('matplotlib')
opts.defaults(opts.Scatter3D(color='Value', cmap='fire', edgecolor='black', s=50))
img = hv.Image((range(10), range(5), np.random.rand(5, 10)), datatype=['grid'])
img
img.data
arr_img = img.clone(datatype=['image'])
print(type(arr_img.data))
try:
xr_img = img.clone(datatype=['xarray'])
print(type(xr_img.data))
except:
print('xarray interface could not be imported.')
print("Array type: %s with bounds %s" % (type(arr_img.data), arr_img.bounds))
dataset3d = hv.Dataset((range(3), range(5), range(7), np.random.randn(7, 5, 3)),
['x', 'y', 'z'], 'Value')
dataset3d
hv.Scatter3D(dataset3d)
dataset3d.select(x=1).to(hv.Image, ['y', 'z']) + hv.Scatter3D(dataset3d.select(x=1))
(dataset3d.to(hv.Image, ['y', 'z'], 'Value', ['x']) +
hv.HoloMap({x: hv.Scatter3D(dataset3d.select(x=x)) for x in range(3)}, kdims='x'))
hv.Image(dataset3d.aggregate(['x', 'y'], np.mean)) + hv.Image(dataset3d.reduce(z=np.mean))
hv.Spread(dataset3d.aggregate('z', np.mean, np.std)) * hv.Curve(dataset3d.aggregate('z', np.mean))
dataset3d.to(hv.BoxWhisker, 'x', 'Value', groupby=[])
dataset3d.to(hv.Distribution, 'Value', [], groupby='x').overlay()
heatmap = hv.HeatMap((['A', 'B', 'C'], ['a', 'b', 'c', 'd', 'e'], np.random.rand(5, 3)))
heatmap + hv.Table(heatmap)
n = 8 # Number of bins in each direction
xs = np.logspace(1, 3, n)
ys = np.linspace(1, 10, n)
zs = np.arange((n-1)**2).reshape(n-1, n-1)
print('Shape of x-coordinates:', xs.shape)
print('Shape of y-coordinates:', ys.shape)
print('Shape of value array:', zs.shape)
hv.QuadMesh((xs, ys, zs))
n=20
coords = np.linspace(-1.5,1.5,n)
X,Y = np.meshgrid(coords, coords);
Qx = np.cos(Y) - np.cos(X)
Qy = np.sin(Y) + np.sin(X)
Z = np.sqrt(X**2 + Y**2)
print('Shape of x-coordinates:', Qx.shape)
print('Shape of y-coordinates:', Qy.shape)
print('Shape of value array:', Z.shape)
qmesh = hv.QuadMesh((Qx, Qy, Z))
qmesh
xr_ds = xr.tutorial.open_dataset("air_temperature").load()
xr_ds
hv_ds = hv.Dataset(xr_ds)[:, :, "2013-01-01"]
print(hv_ds)
airtemp = hv_ds.to(hv.Image, kdims=["lon", "lat"], dynamic=False)
airtemp[:, 220:320, :].opts(colorbar=True, fig_size=200)
rasm = xr.tutorial.open_dataset("rasm").load()
rasm.coords
rasm = rasm.isel(time=0, x=slice(0, 200)).assign_coords(x=np.arange(200), y=np.arange(205))
rasm.coords
hv.QuadMesh(rasm, ['x', 'y']) + hv.QuadMesh(rasm, ['xc', 'yc'])
heatmap.dimension_values('x')
heatmap.dimension_values('x', expanded=False)
heatmap.dimension_values('x', flat=False)
heatmap.dimension_values('z')
heatmap.dimension_values('z', flat=False)
| 0.338077 | 0.991891 |
## FOR GOOGLE COLAB USERS
```
#!apt-get install openjdk-8-jdk-headless -qq > /dev/null
!wget -q http://archive.apache.org/dist/spark/spark-2.4.2/spark-2.4.2-bin-hadoop2.7.tgz
!tar xf spark-2.4.2-bin-hadoop2.7.tgzdf!pip install -q findspark
!java -version
import os
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-1.11.0-openjdk-amd64/"
os.environ["SPARK_HOME"] = "/content/spark-2.4.2-bin-hadoop2.7"
import findspark
findspark.init()
from pyspark.sql import SparkSession
spark = SparkSession.builder.master("local[*]").getOrCreate()
```
### Chamada da biblioteca
```
from pyspark.sql import SparkSession
import pyspark.sql.functions as F
from pyspark.sql.types import StringType
from pyspark.sql.types import IntegerType
```
### Inicializando o Sessão do Spark -
##### Para usuários jupyter desktop
```
spark = SparkSession.builder \
.appName("Tutorial PySpark SQL") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
```
### Lendo dataframe com spark DataFrame
```
df = spark.read.csv('DNPBA2017.csv', header=True)
```
### Identificando a estrutura da base
```
df.printSchema()
```
### Quantificando os registros da base
```
df.count()
```
### Quantificando municipios distintos
```
df.select('CODMUNRES').distinct().count()
```
### Retornando sexo e data de nascimento dos nascidos
```
df.select('SEXO', 'DTNASC').show()
```
### Retornando sexo e data de nascimento da 3 crianças mais velhas da base
```
df.select('SEXO', 'DTNASC').orderBy('DTNASC').take(3)
df.select('SEXO', 'DTNASC').orderBy('DTNASC').show(3)
```
### Retornando so o primeiro registo entre as crianças mais velhas
```
df.select('SEXO', 'DTNASC').orderBy('DTNASC').first()
```
### Contar os nascimentos que ocorreram em 01 de 01 de 2017
```
df.filter(F.col('DTNASC') == '01012017').count()
```
### Retornando os nascimentos que ocorreram em Julho
```
df.select('DTNASC', F.when(F.substring(F.col('DTNASC'), 2,4) == '07', 1).otherwise(0)).show()
```
### Criando coluna com o mês de nascimento
```
df = df.withColumn('MESNASC', F.substring(F.col('DTNASC'), 3,2))
```
### Criando coluna através de alias
```
df.select(F.substring(F.col('DTNASC'), 3, 2).alias('mes'), 'DTNASC').show()
```
### Criando e usando minha primeira UDF
#### Note que User Defined Functions precisam ser registradas para funcionar.
#### UDFs podem ser usadas em transformações "withColum" ou "select"
```
def mesnasc(col):
return col[2:4]
udf_mesnasc = F.udf(mesnasc, StringType())
df = df.withColumn('MESNASC_2', udf_mesnasc(F.col('DTNASC')))
df.printSchema()
df.select('MESNASC', 'MESNASC_2').limit(10).toPandas()
```
### Agrupando os dados em função do mês de nascimento
```
df.groupBy('MESNASC').count().orderBy('MESNASC').show()
```
### Usando o agrupamento para conhecer a proporção de nascidos por mês
```
tot = df.count()
df.groupBy('MESNASC').count().orderBy('MESNASC').withColumn('%', F.col('count')/tot*100).show()
```
### Buscando ou contando registros cujo valor do atributo inicia, termina ou está entre...
```
df.filter(F.col('CODMUNRES').startswith("29")).count()
df.filter(F.col('CODMUNRES').startswith("29")).select('CODMUNRES').show()
df.filter(F.col('CODMUNRES').endswith("2740")).count()
df.filter(F.col('CODMUNRES').endswith("2740")).select('CODMUNRES').show()
df.filter(F.col('PESO').between('0110', '6710' )).count()
```
### Descrevendo uma variável
```
df.describe('PESO').show()
```
### Contando valores "NA"
```
df.filter(F.col('PESO')=='NA').count()
```
### Contando valores Nulos
```
df.filter(F.col('PESO').isNull()).count()
```
### Buscando valores "NA" em "PESO" e criando uma coluna nova para guardar os resultados
#### As demais linhas são para validar os resultados
```
df = df.withColumn('NOVO_PESO', F.when(F.col('PESO') == 'NA', None).otherwise(F.col('PESO')))
df.filter(F.col('PESO')=='NA').select('PESO', 'NOVO_PESO').show()
df.filter(F.col('PESO')!='NA').select('PESO', 'NOVO_PESO').show()
```
### Renomeando Coluna
```
df = df.withColumnRenamed('NOVO_PESO', 'PESO_PP') #PESO PRE PROCESSADO
```
### Descrevendo coluna nova
```
df.describe('PESO_PP').show()
```
# PARTE 2: ROTEIRO PARA LINKAGE
### Lendo e visualizando as bases
```
datasetA = spark.read.csv('dataset_a_v3.csv', header=True, sep=';')
datasetB = spark.read.csv('dataset_b_v3.csv', header=True, sep=';')
print datasetA.count()
print datasetB.count()
datasetA.limit(5).show()
datasetB.limit(5).show()
```
### Criando colunas com codigos foneticos
```
import jellyfish
def criaMetaphone(col):
return jellyfish.metaphone(col)
udf_criaMetaphone = F.udf(criaMetaphone, StringType())
datasetA = datasetA.withColumn('phonetic_nome_a', udf_criaMetaphone(F.col('nome_a')))
datasetA = datasetA.withColumn('phonetic_mae_a', udf_criaMetaphone(F.col('mae_a')))
datasetB = datasetB.withColumn('phonetic_nome_b', udf_criaMetaphone(F.col('nome_b')))
datasetB = datasetB.withColumn('phonetic_mae_b', udf_criaMetaphone(F.col('mae_b')))
datasetA.limit(3).show()
datasetB.limit(3).show()
```
### Criando coluna com último nome
```
def criaUltimoNome(col):
return col.split(' ')[-1]
udf_criaUltimoNome = F.udf(criaUltimoNome, StringType())
datasetA = datasetA.withColumn('ultimo_nome_a', udf_criaUltimoNome(F.col('nome_a')))
datasetB = datasetB.withColumn('ultimo_nome_b', udf_criaUltimoNome(F.col('nome_b')))
datasetA.limit(3).show()
datasetB.limit(3).show()
```
### Separando atributos para linkage
```
datasetA = datasetA.select(['cod_a', 'dn_a',
'sexo_a', 'cidade_a',
'primeiro_nome_a', 'ultimo_nome_a',
'phonetic_nome_a', 'phonetic_mae_a'])
datasetB = datasetB.select(['cod_b', 'dn_b',
'sexo_b', 'cidade_b',
'primeiro_nome_b', 'ultimo_nome_b',
'phonetic_nome_b', 'phonetic_mae_b'])
```
### Criando dataset de comparação
```
dataset_linkage = datasetA.crossJoin(datasetB)
dataset_linkage.count()
dataset_linkage.limit(5).show()
```
### Criando função de comparação
```
def compare(cod_a, dn_a, sexo_a, cidade_a, primeiro_nome_a, ultimo_nome_a, phonetic_nome_a, phonetic_mae_a,
cod_b, dn_b, sexo_b, cidade_b, primeiro_nome_b, ultimo_nome_b, phonetic_nome_b, phonetic_mae_b):
sim = 0
# Comparando atributos nominais
sim_nominais = jellyfish.jaro_winkler(unicode(primeiro_nome_a), unicode(primeiro_nome_b))
sim_nominais += jellyfish.jaro_winkler(unicode(ultimo_nome_a), unicode(ultimo_nome_b))
sim_nominais += jellyfish.jaro_winkler(unicode(phonetic_nome_a), unicode(phonetic_nome_b))
sim_nominais += jellyfish.jaro_winkler(unicode(phonetic_mae_a), unicode(phonetic_mae_b))
# Comparando categorias
# Note que Hamming é uma distancia, então para saber a similiarade, precisamos
# encontrar o complemento da medida.
sim_cat = 1 - (jellyfish.hamming_distance(unicode(sexo_a), unicode(sexo_b)))
sim_cat += 1 - (jellyfish.hamming_distance(unicode(dn_a), unicode(sexo_b)))
sim_cat += 1 - (jellyfish.hamming_distance(unicode(cidade_a), unicode(cidade_b)))
# Media aritmetica simples
sim = str(abs(float(sim_nominais + sim_cat)/7))
return sim
udf_compare = F.udf(compare, StringType())
```
### Rodando comparação
```
result_linkage = dataset_linkage.withColumn('similaridade', udf_compare(F.col('cod_a'), F.col('dn_a'), F.col('sexo_a'), F.col('cidade_a'), F.col('primeiro_nome_a'), F.col('ultimo_nome_a'), F.col('phonetic_nome_a'), F.col('phonetic_mae_a'),
F.col('cod_b'), F.col('dn_b'), F.col('sexo_b'), F.col('cidade_b'), F.col('primeiro_nome_b'), F.col('ultimo_nome_b'), F.col('phonetic_nome_b'), F.col('phonetic_mae_b')))
result_linkage.select(['cod_a', 'cod_b', 'similaridade']).show()
```
## DESAFIOS
##### Desafio 1: Deduplique a base de linkage para encontrar os melhores resultados para cada registro do datasetB
##### Desafio 2: Separe a data em três colunas diferentes (dia, mês e ano) e reimplemente a função 'compare' para que a distancia de hamming participe do calculo da similaridade
##### Desafio 3: Quais os atributos mais importantes a serem comparados? Ao invés de uma média aritmética simples, implemente uma média aritmética ponderada dando pesos diferentes para cada atributos.
##### Desafio 4: Explore novas similaridades. Faça uso de diferentes medidas para identidficar as que melhor se encaixam nesse par de datasets. ##### Desafio 5: Leia um pouco sobre penalidades, um decréscimo que se dá à similaridade quando um valor nulo participa da comparação.
##### Desafio 6: Leia um pouco sobre avaliação de acurácia e faça uma planilha tabulando os resultados de sensibilidade, especificidade e precisão para todos os seus experimentos.
##### Desafio 7: Tem como melhorar essa implementação? Tente otimizar essa implementação usando os conceitos discutidos em sala.
|
github_jupyter
|
#!apt-get install openjdk-8-jdk-headless -qq > /dev/null
!wget -q http://archive.apache.org/dist/spark/spark-2.4.2/spark-2.4.2-bin-hadoop2.7.tgz
!tar xf spark-2.4.2-bin-hadoop2.7.tgzdf!pip install -q findspark
!java -version
import os
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-1.11.0-openjdk-amd64/"
os.environ["SPARK_HOME"] = "/content/spark-2.4.2-bin-hadoop2.7"
import findspark
findspark.init()
from pyspark.sql import SparkSession
spark = SparkSession.builder.master("local[*]").getOrCreate()
from pyspark.sql import SparkSession
import pyspark.sql.functions as F
from pyspark.sql.types import StringType
from pyspark.sql.types import IntegerType
spark = SparkSession.builder \
.appName("Tutorial PySpark SQL") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
df = spark.read.csv('DNPBA2017.csv', header=True)
df.printSchema()
df.count()
df.select('CODMUNRES').distinct().count()
df.select('SEXO', 'DTNASC').show()
df.select('SEXO', 'DTNASC').orderBy('DTNASC').take(3)
df.select('SEXO', 'DTNASC').orderBy('DTNASC').show(3)
df.select('SEXO', 'DTNASC').orderBy('DTNASC').first()
df.filter(F.col('DTNASC') == '01012017').count()
df.select('DTNASC', F.when(F.substring(F.col('DTNASC'), 2,4) == '07', 1).otherwise(0)).show()
df = df.withColumn('MESNASC', F.substring(F.col('DTNASC'), 3,2))
df.select(F.substring(F.col('DTNASC'), 3, 2).alias('mes'), 'DTNASC').show()
def mesnasc(col):
return col[2:4]
udf_mesnasc = F.udf(mesnasc, StringType())
df = df.withColumn('MESNASC_2', udf_mesnasc(F.col('DTNASC')))
df.printSchema()
df.select('MESNASC', 'MESNASC_2').limit(10).toPandas()
df.groupBy('MESNASC').count().orderBy('MESNASC').show()
tot = df.count()
df.groupBy('MESNASC').count().orderBy('MESNASC').withColumn('%', F.col('count')/tot*100).show()
df.filter(F.col('CODMUNRES').startswith("29")).count()
df.filter(F.col('CODMUNRES').startswith("29")).select('CODMUNRES').show()
df.filter(F.col('CODMUNRES').endswith("2740")).count()
df.filter(F.col('CODMUNRES').endswith("2740")).select('CODMUNRES').show()
df.filter(F.col('PESO').between('0110', '6710' )).count()
df.describe('PESO').show()
df.filter(F.col('PESO')=='NA').count()
df.filter(F.col('PESO').isNull()).count()
df = df.withColumn('NOVO_PESO', F.when(F.col('PESO') == 'NA', None).otherwise(F.col('PESO')))
df.filter(F.col('PESO')=='NA').select('PESO', 'NOVO_PESO').show()
df.filter(F.col('PESO')!='NA').select('PESO', 'NOVO_PESO').show()
df = df.withColumnRenamed('NOVO_PESO', 'PESO_PP') #PESO PRE PROCESSADO
df.describe('PESO_PP').show()
datasetA = spark.read.csv('dataset_a_v3.csv', header=True, sep=';')
datasetB = spark.read.csv('dataset_b_v3.csv', header=True, sep=';')
print datasetA.count()
print datasetB.count()
datasetA.limit(5).show()
datasetB.limit(5).show()
import jellyfish
def criaMetaphone(col):
return jellyfish.metaphone(col)
udf_criaMetaphone = F.udf(criaMetaphone, StringType())
datasetA = datasetA.withColumn('phonetic_nome_a', udf_criaMetaphone(F.col('nome_a')))
datasetA = datasetA.withColumn('phonetic_mae_a', udf_criaMetaphone(F.col('mae_a')))
datasetB = datasetB.withColumn('phonetic_nome_b', udf_criaMetaphone(F.col('nome_b')))
datasetB = datasetB.withColumn('phonetic_mae_b', udf_criaMetaphone(F.col('mae_b')))
datasetA.limit(3).show()
datasetB.limit(3).show()
def criaUltimoNome(col):
return col.split(' ')[-1]
udf_criaUltimoNome = F.udf(criaUltimoNome, StringType())
datasetA = datasetA.withColumn('ultimo_nome_a', udf_criaUltimoNome(F.col('nome_a')))
datasetB = datasetB.withColumn('ultimo_nome_b', udf_criaUltimoNome(F.col('nome_b')))
datasetA.limit(3).show()
datasetB.limit(3).show()
datasetA = datasetA.select(['cod_a', 'dn_a',
'sexo_a', 'cidade_a',
'primeiro_nome_a', 'ultimo_nome_a',
'phonetic_nome_a', 'phonetic_mae_a'])
datasetB = datasetB.select(['cod_b', 'dn_b',
'sexo_b', 'cidade_b',
'primeiro_nome_b', 'ultimo_nome_b',
'phonetic_nome_b', 'phonetic_mae_b'])
dataset_linkage = datasetA.crossJoin(datasetB)
dataset_linkage.count()
dataset_linkage.limit(5).show()
def compare(cod_a, dn_a, sexo_a, cidade_a, primeiro_nome_a, ultimo_nome_a, phonetic_nome_a, phonetic_mae_a,
cod_b, dn_b, sexo_b, cidade_b, primeiro_nome_b, ultimo_nome_b, phonetic_nome_b, phonetic_mae_b):
sim = 0
# Comparando atributos nominais
sim_nominais = jellyfish.jaro_winkler(unicode(primeiro_nome_a), unicode(primeiro_nome_b))
sim_nominais += jellyfish.jaro_winkler(unicode(ultimo_nome_a), unicode(ultimo_nome_b))
sim_nominais += jellyfish.jaro_winkler(unicode(phonetic_nome_a), unicode(phonetic_nome_b))
sim_nominais += jellyfish.jaro_winkler(unicode(phonetic_mae_a), unicode(phonetic_mae_b))
# Comparando categorias
# Note que Hamming é uma distancia, então para saber a similiarade, precisamos
# encontrar o complemento da medida.
sim_cat = 1 - (jellyfish.hamming_distance(unicode(sexo_a), unicode(sexo_b)))
sim_cat += 1 - (jellyfish.hamming_distance(unicode(dn_a), unicode(sexo_b)))
sim_cat += 1 - (jellyfish.hamming_distance(unicode(cidade_a), unicode(cidade_b)))
# Media aritmetica simples
sim = str(abs(float(sim_nominais + sim_cat)/7))
return sim
udf_compare = F.udf(compare, StringType())
result_linkage = dataset_linkage.withColumn('similaridade', udf_compare(F.col('cod_a'), F.col('dn_a'), F.col('sexo_a'), F.col('cidade_a'), F.col('primeiro_nome_a'), F.col('ultimo_nome_a'), F.col('phonetic_nome_a'), F.col('phonetic_mae_a'),
F.col('cod_b'), F.col('dn_b'), F.col('sexo_b'), F.col('cidade_b'), F.col('primeiro_nome_b'), F.col('ultimo_nome_b'), F.col('phonetic_nome_b'), F.col('phonetic_mae_b')))
result_linkage.select(['cod_a', 'cod_b', 'similaridade']).show()
| 0.411111 | 0.708931 |
# Prediction of Mutation Effect
<b><i class="fa fa-folder-o" area-hidden="true" style="color:#1976D2"> </i> File Location</b><br>
<p style="background:#F5F5F5; text-indent: 1em;">
<code style="background:#F5F5F5; color:#404040; font-weight:bold">C:\Users\ibrah\Desktop\TUSEB_Study\Prediction_of_Mutation_Effects\Machine_Learning\ML_7</code>
</p>
<b><i class="far fa-file" area-hidden="true" style="color:#1976D2"> </i> File Name</b>
<p style="background:#F5F5F5; text-indent: 1em;">
<code style="background:#F5F5F5; color:#404040; font-weight:bold">01_Single_protein_single_position.ipynb</code>
</p>
<b><i class="far fa-calendar-alt" area-hidden="true" style="color:#1976D2"> </i> Last Edited</b>
<p style="background:#F5F5F5; text-indent: 1em;">
<code style="background:#F5F5F5; color:#404040; font-weight:bold">July 9th, 2021</code>
</p>
<div class="alert alert-block" style="background-color: #F5F5F5; border: 1px solid; padding: 10px; border-color: #E0E0E0">
<b><i class="fa fa-compass" aria-hidden="true" style="color:#404040"></i></b> <b style="color: #404040">Purpose </b> <br>
<div>
- [x] $\textit{mutation effect label}$ prediction using Random Forest algorithm.
- [x] Classification will be $\textit{Disrupting vs (No effect + Increasing)}$.
> $\textit{Disrupting} → 0$\
> $\textit{No effect + Increasing} → 1$\
> $\textit{Decreasing} → \textit{ignored}$
- [x] Evaluate the performane of the model.
- [x] Training set will be consisting of one type of gene.\
I have tried with 5 features. Results are not that good.
**Dependent files:**
* Training (mutations) data:
- *training_data_M1.txt*
## Setup
```
# Common imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
import sys
import seaborn as sns
from IPython.display import display
# To make this notebook's output stable across runs
# np.random.seed(42)
# PATHS
PROJECT_COMMON_FILE_DIR = "../ML_common_files/"
MUTATIONS_PATH = "training_data_M1.txt"
def print_annotation(s):
print(f"\n{s}\n{'-' * len(s)}")
def get_file_path(filename):
return os.path.join(PROJECT_COMMON_FILE_DIR, filename)
```
## Reading the Datasets
### 1. Training Data: Mutations
```
# Read Training Data
mutations = pd.read_csv(get_file_path(MUTATIONS_PATH), sep='\t')
# Size of dataframe
print_annotation(f"Size of dataframe: {mutations.shape}")
# First 5 entries
mutations.head()
```
## Data Cleaning
### Select column names
```
selected_columns = ['Mutation_Effect_Label', 'UniProt_ID', 'Mutation', 'Interactor_UniProt_ID']\
+ ['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']
```
### Reduce Columns
#### Train (Mutations) Data
```
# Declare train data using selected column names
train_data = mutations[selected_columns].copy()
# Size of dataframe
print_annotation(f"Size of dataframe: {train_data.shape}")
# First 5 entries
train_data.head()
# Dropping the duplicates
train_data.drop_duplicates(keep="first", inplace=True)
```
Ensuring that there is no duplicated row.
```
train_data[train_data.duplicated()].empty # True, duplicate is empty
train_data.shape
```
## Data Preprocessing
* [x] Not all selected columns are interpreted as numeric, so coerce them to numeric.
### Mutation Effect Label Binning
Mutation Effect label binning is only applied to train_data.
* [x] Apply Label binning.
> $\textit{Disruptive} → 0$\
> $\textit{No effect + Increasing} → 1$\
> $\textit{Decreasing} → \textit{ignored}$
```
def display_label_counts(data_param):
"""
Display a dataframe that contains label categories and their counts.
"""
label_counts = pd.DataFrame(data_param["Mutation_Effect_Label"].value_counts())
label_counts.reset_index(inplace=True)
label_counts.columns = ["Mutation_Effect_Label", "Counts"]
label_counts.rename(index={0: 'Disrupting', 1: 'Increasing + No Effect'}, inplace=True)
display(label_counts)
def display_labels(data_param):
"""
Display a dataframe that contains label categories.
"""
label_counts = pd.DataFrame(data_param["Mutation_Effect_Label"].value_counts().index)
label_counts.columns = ["Mutation_Effect_Label"]
display(label_counts)
```
For $\textit{mutation effect label}$ we have following categories:
```
# Displaying possible label categories.
display_labels(train_data)
```
Applying binning operation on $\textit{mutation effect label}$ column in $\textit{mutations}$ data with described rule below \
- $\textit{Disrupting} → 0$\
- $\textit{No effect + Increasing} → 1$\
- $\textit{Decreasing} → \textit{dropped}$\
- $\textit{Causing} → \textit{dropped}$\
yields following data frame:
```
labels_to_bins = {
"mutation disrupting(MI:0573)": 0,
"mutation decreasing(MI:0119)": "IGNORED",
"mutation disrupting strength(MI:1128)": 0,
"mutation decreasing strength(MI:1133)": "IGNORED",
"mutation with no effect(MI:2226)": 1,
"disrupting": 0,
"mutation increasing(MI:0382)": 1,
"mutation increasing strength(MI:1132)": 1,
"mutation decreasing rate(MI:1130)": "IGNORED",
"mutation disrupting rate(MI:1129)": 0,
"mutation causing(MI:2227)": "IGNORED",
"mutation increasing rate(MI:1131)": 1}
replace_map = {"Mutation_Effect_Label": labels_to_bins}
# Size of dataframe before binning.
print_annotation(f"Size of dataframe before binning: {train_data.shape}")
# Modifications will be done on train_data_binned.
train_data_binned = train_data.copy()
# Replace the labels as described above.
train_data_binned.replace(replace_map, inplace=True)
# Drop the entries with "IGNORED": 'mutation cusing' in this case.
train_data_binned = train_data_binned[train_data_binned["Mutation_Effect_Label"] != "IGNORED"]
# Reset index of the dataframe to avoid any possible errors
train_data_binned.reset_index(drop=True, inplace=True)
# Size of dataframe after binning.
print_annotation(f"Size of dataframe after binning: {train_data_binned.shape}")
# First 5 rows of binned data.
train_data_binned.head()
```
Confirming replacement of values are properly done. $\textit{Mutation_Effect_Label}$ only contains of $0$ or $1$.
```
train_data_binned["Mutation_Effect_Label"].value_counts()
```
### Type Coercion
Some columns have been interpreted as `object` type, eventhough they are actually numeric.
```
# Train (mutations) data
set(train_data_binned.dtypes)
```
These non-numeric interpereted columns will be coerced. $\textit{NaN}$ values will be converted to $0$.
```
# Get column names where its type is *not* int or float, i.e. whose type is object.
coerce_numeric_cols = set([cname for cname in train_data_binned.columns if train_data_binned[cname].dtype not in ['int64', 'float64']])
# + [cname for cname in target_brca_data.columns if target_brca_data[cname].dtype not in ['int64', 'float64']]) # \
# + [cname for cname in target_coad_data.columns if target_coad_data[cname].dtype not in ['int64', 'float64']]\
# + [cname for cname in target_ov_data.columns if target_ov_data[cname].dtype not in ['int64', 'float64']])
# Remove target variable from the list
coerce_numeric_cols = coerce_numeric_cols - {"Mutation_Effect_Label", "UniProt_ID", "Mutation", "Interactor_UniProt_ID"}
for cname in coerce_numeric_cols:
train_data_binned[cname] = pd.to_numeric(train_data_binned[cname], errors='coerce')
# target_brca_data[cname] = pd.to_numeric(target_brca_data[cname], errors='coerce')
# target_coad_data[cname] = pd.to_numeric(target_coad_data[cname], errors='coerce')
# target_ov_data[cname] = pd.to_numeric(target_ov_data[cname], errors='coerce')
train_data_binned.fillna(0, inplace=True)
# target_brca_data.fillna(0, inplace=True)
# target_coad_data.fillna(0, inplace=True)
# target_ov_data.fillna(0, inplace=True)
```
Now all columns are interpreted as numeric type, except "_UniProt_ID_", "_Mutation_", "_Interactor_UniProt_ID_"
```
# Train (mutations) data
set(train_data_binned.dtypes)
train_data_binned.dtypes
```
### Processed train data and Label Counts
```
def visualize_label_counts(data_param, label_name_param="Mutation_Effect_Label"):
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
ax = sns.barplot(x=data_param[label_name_param].value_counts().index,
y=data_param[label_name_param].value_counts(),
palette="ch:s=-.2,r=.6")
ax.set_title('Disrupting vs Increasing & No Effect') # ch:s=-.2,r=.6, ocean
ax.set_ylabel('Value counts')
ax.set_xticklabels(['Distrupting', 'Increasing + No Effect']);
```
From now on, training data is refered as `data_processed`.
```
# Declaing `data_processed`.
data_processed = train_data_binned.copy()
# Size of processed data.
print_annotation(f"Size of processed data: {data_processed.shape}")
# First 5 rows of binned data.
data_processed.head()
visualize_label_counts(data_processed)
display_label_counts(data_processed)
```
## Data Creation with Unique Proteins
Here, we desire training data to have one occurance of each protein in `UniProt_ID` column.
```
# Get the unique proteins from `UniProt_ID` column.
unique_proteins = list(data_processed['UniProt_ID'].unique())
# Number of unique_proteins
print('Number of `unique_proteins`:', len(unique_proteins))
# First five proteins
print(unique_proteins[:5])
```
There are $164$ unique proteins in `UniProt_ID` column. Now, we will re-construct the training data where it will have $164$ rows, i.e. one row for each unique protein. In the case where multiple row option possible, we randomly select one.
```
sampled_row_dataframes = []
for unique_protein in unique_proteins:
sampled_row_dataframes.append(data_processed[data_processed['UniProt_ID'] == unique_protein].sample())
# Merge row dataframes into single dataframe, stack rows on top of each other.
sampled_train_data = pd.concat(sampled_row_dataframes)
# Reset index of the dataframe to avoid any possible errors
sampled_train_data.reset_index(drop=True, inplace=True)
# Dimensions of dataframe
print_annotation(f"Dimensions of sampled_dataframe: {sampled_train_data.shape}")
# First five entries
sampled_train_data.head()
visualize_label_counts(sampled_train_data)
display_label_counts(sampled_train_data)
```
## Prepare the Train Data for Machine Learning Algorithms
Remove "_UniProt_ID_", "_Mutation_", "_Interactor_UniProt_ID_" columns, since they are not feature columns.
```
sampled_train_data = sampled_train_data.drop(["UniProt_ID", "Mutation", "Interactor_UniProt_ID"], axis='columns')
```
### Shuffle the data
```
# Shuffle the rows in data_prepared:
data_prepared = sampled_train_data.sample(frac=1, random_state=96).reset_index(drop=True).copy()
```
### Train and Validation variables
Splitting `data_prepared` into training set and validation set using random splitting:
```
from sklearn.model_selection import train_test_split
random_train_set, random_valid_set = train_test_split(
data_prepared, test_size=0.2, random_state=42)
print(random_train_set.shape, random_valid_set.shape)
random_train_set.head()
```
Splitting `train_data` into training set and validation set using stratified random splitting, we get something like (with `random_state=42` in shuffle):
```python
>>> train_index
array([513, 676, 164, 520, 23], dtype=int64)
```
**Note:** Due to the shuffling, it may change when different `random_state` is provided in shuffling.
StratifiedShuffleSplit and StratifiedKFold returns the *different* permutation of numbers. The following cell contains `n_splits=1`, meaning that it is used for generation of a sequence of numbers in a random order.
```
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, valid_index in split.split(data_prepared, data_prepared["Mutation_Effect_Label"]):
strat_train_set = data_prepared.iloc[train_index]
strat_valid_set = data_prepared.iloc[valid_index]
train_index[:5]
strat_train_set.head()
strat_train_set.shape, strat_valid_set.shape
def label_proportions(data_param):
return data_param["Mutation_Effect_Label"].value_counts() / len(data_param)
compare_props = pd.DataFrame({
"Overall": label_proportions(data_prepared),
"Stratified": label_proportions(strat_valid_set),
"Random": label_proportions(random_valid_set)
}).sort_index()
compare_props["Rand. %error"] = 100 * compare_props["Random"] / compare_props["Overall"] - 100
compare_props["Strat. %error"] = 100 * compare_props["Stratified"] / compare_props["Overall"] - 100
compare_props.rename(index={0: 'Disruptive', 1: 'Increasing + No Effect'}, inplace=True)
compare_props
```
Splitting data randomly results in representativeness error, therefore, `strat_train_set` and `strat_valid_set` can be used.
### Declare `X_train`, `y_train`, `X_valid`, `y_valid`
```
# All data, i.e. data_prepared
X = data_prepared.drop(["Mutation_Effect_Label"], axis="columns")
y = data_prepared["Mutation_Effect_Label"].copy()
# Stratified version
X_train = strat_train_set.drop(["Mutation_Effect_Label"], axis="columns")
y_train = strat_train_set["Mutation_Effect_Label"].copy()
X_valid = strat_valid_set.drop(["Mutation_Effect_Label"], axis="columns")
y_valid = strat_valid_set["Mutation_Effect_Label"].copy()
# Printing their shapes
print(X_train.shape, y_train.shape)
print(X_valid.shape, y_valid.shape)
# Randomized version
X_train_random = random_train_set.drop(["Mutation_Effect_Label"], axis="columns")
y_train_random = random_train_set["Mutation_Effect_Label"].copy()
X_valid_random = random_valid_set.drop(["Mutation_Effect_Label"], axis="columns")
y_valid_random = random_valid_set["Mutation_Effect_Label"].copy()
# Printing their shapes
print(X_train.shape, y_train.shape)
print(X_valid.shape, y_valid.shape)
```
# Machine Learning Utils
```
# Imports
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import cross_val_predict
from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import accuracy_score
from sklearn.metrics import balanced_accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import classification_report
from itertools import combinations
import seaborn as sns
def cross_validation_options(cv_option_param, n_jobs_param=-1):
"""
A helper function that returns (my) desired cv_option and n_jobs.
"""
# Options for cross-validation cv= parameter.
if isinstance(cv_option_param, int):
cv_option_param = cv_option_param
elif cv_option_param == "skf_5":
cv_option_param = StratifiedKFold(shuffle=True, n_splits=5)
elif cv_option_param == "skf_10":
cv_option_param = StratifiedKFold(shuffle=True, n_splits=10)
elif cv_option_param == "kf_5":
cv_option_param = KFold(shuffle=True, n_splits=5)
elif cv_option_param == "kf_10":
cv_option_param = KFold(shuffle=True, n_splits=10)
else:
raise ValueError("cv_option value error!")
# Option for j_jobs:
n_jobs_param = -1
return cv_option_param, n_jobs_param
```
# Classification: Initial Insights
```
attributes = list(X.columns)
# Plotting feature importance in barplot
def plot_feature_importances(feature_importances):
feature_imp_series = pd.Series(feature_importances,
index = attributes).sort_values(ascending=False)
plt.figure(figsize=(5, 20))
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
sns.barplot(x=feature_imp_series, y=feature_imp_series.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances')
plt.show()
# Plotting top n feature importance in barplot
def plot_top_feature_importances(feature_importances, top_n=10, figsize=None):
feature_imp_series = pd.Series(feature_importances,
index = attributes).sort_values(ascending=False)
figsize = (5 , top_n//3) if not figsize else (5, 5)
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
feature_imp_series_top_n = feature_imp_series[:top_n]
plt.figure(figsize=figsize)
sns.barplot(x=feature_imp_series_top_n, y=feature_imp_series_top_n.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances (top {})'.format(top_n))
plt.show()
```
### Initial Scoring
```
# Initial scoring: X_train, y_train with prediction of X_valid
forest_clf_inital = RandomForestClassifier(random_state=42)
forest_clf_inital.fit(X_train, y_train)
forest_predictions = forest_clf_inital.predict(X_valid)
print("Balanced accuracy score : {:.4f}".format(balanced_accuracy_score(y_valid, forest_predictions)))
print("Accuracy score\t\t: {:.4f}".format(accuracy_score(y_valid, forest_predictions)))
```
### Initial Feature Importance
```
attributes = list(X.columns)
# plot_feature_importances(forest_clf_inital.feature_importances_)
plot_top_feature_importances(forest_clf_inital.feature_importances_, top_n=10,
figsize=(5,5))
forest_clf_inital.feature_importances_
```
# Classification
## Initial Insights
```
# Imports
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import balanced_accuracy_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import balanced_accuracy_score
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold
feature_columns = list(data_prepared.columns)[1:]
# Plotting feature importance in barplot
def plot_feature_importances(feature_importances):
attributes = feature_columns
feature_imp_series = pd.Series(feature_importances,
index = attributes).sort_values(ascending=False)
plt.figure(figsize=(5, 20))
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
sns.barplot(x=feature_imp_series, y=feature_imp_series.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances')
plt.show()
# Plotting top n feature importance in barplot
def plot_top_feature_importances(feature_importances, top_n=10, figsize=None):
attributes = feature_columns
feature_imp_series = pd.Series(feature_importances,
index = attributes).sort_values(ascending=False)
figsize = (5 , top_n//3) if not figsize else (5, 5)
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
feature_imp_series_top_n = feature_imp_series[:top_n]
plt.figure(figsize=figsize)
sns.barplot(x=feature_imp_series_top_n, y=feature_imp_series_top_n.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances (top {})'.format(top_n))
plt.show()
# Initial scoring: X_train, y_train with prediction of X_valid
forest_clf_inital = RandomForestClassifier(random_state=42)
forest_clf_inital.fit(X_train, y_train)
forest_predictions = forest_clf_inital.predict(X_valid)
print("Balanced accuracy score : {:.4f}".format(balanced_accuracy_score(y_valid, forest_predictions)))
print("Accuracy score\t\t: {:.4f}".format(accuracy_score(y_valid, forest_predictions)))
def evaluate_cross_val(X_train_param, y_train_param, cv_option_param):
# Cross Validation options
cv_option, n_jobs = cross_validation_options(cv_option_param, -1)
# Model
forest_clf = RandomForestClassifier(random_state=42)
# Cross-validation Accuracy and Balanced Accuracy Scores
forest_scores_bas = cross_val_score(forest_clf,
X_train_param, y_train_param,
cv=cv_option, scoring="balanced_accuracy", n_jobs=n_jobs)
forest_scores_as = cross_val_score(forest_clf,
X_train_param, y_train_param,
cv=cv_option, scoring="accuracy", n_jobs=n_jobs)
# Print scores and averages
print("Balanced accuracy score AVG : {:.4f}".format(forest_scores_bas.mean()))
# print(forest_scores_bas)
print("Accuracy score AVG : {:.4f}".format(forest_scores_as.mean()))
# print(forest_scores_as)
evaluate_cross_val(X, y, "skf_10")
evaluate_cross_val(X, y, "skf_10")
evaluate_cross_val(X, y, "skf_10")
evaluate_cross_val(X_train, y_train, "skf_5")
evaluate_cross_val(X, y, "skf_10")
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import classification_report
import seaborn as sns
def cross_val_confusion_matrix_via(model_param, X_train_param, y_train_param,
return_report=False):
skf = StratifiedKFold(shuffle=True, n_splits=10)
y_pred_temp = cross_val_predict(model_param, X_train_param, y_train_param, cv=skf)
label_names = ["Disrupting", "NoEffect+Increasing"]
sns.heatmap(confusion_matrix(y_train_param, y_pred_temp), annot=True, fmt="d", xticklabels=label_names, yticklabels=label_names)
plt.title(r'$\mathbf{Confusion\ Matrix}$', fontsize=16, fontweight='bold')
plt.ylabel('Actual', fontsize=16, fontweight='bold')
plt.xlabel('Predicted', fontsize=16, fontweight='bold')
plt.show()
if return_report:
print(classification_report(y_train_param, y_pred_temp, target_names=label_names))
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X, y, return_report=True)
```
## Exhoustively Selected Features
```
# X_mfs = X[['EL2_score', 'Provean_score', 'Matrix_score', 'Final_ddG']]
# X_Alignment_score = X[['Alignment_score']]
# X_Provean_score = X[['Provean_score']]
# X_selected_11 = X[['Template_sequence_identity', 'Alignment_score', 'Interactor_template_sequence_identity', 'Interactor_alignment_score', 'Final_ddG', 'ProtBert_score', 'ProteinSolver_score', 'EL2_score', 'Model/DOPE_score', 'Provean_score', 'Matrix_score']]
# # 3
# X_selected_exhaustive_3_1 = X[['Template_sequence_identity', 'Alignment_score', 'Provean_score']]
# X_selected_exhaustive_3_2 = X[['Template_sequence_identity', 'Provean_score', 'Matrix_score']]
# # 4
# X_selected_exhaustive_4_1 = X[['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Matrix_score']]
# X_selected_exhaustive_4_2 = X[['Template_sequence_identity', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
# X_selected_exhaustive_4_3 = X[['Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
# # 5
# X_selected_exhaustive_5 = X[['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
# X_benchmark_feature_names_dataframes =\
# [("X_Alignment_score", X_Alignment_score),
# ("X_Provean_score", X_Provean_score),
# ("X_selected_11", X_selected_11),
# ("X_selected_exhaustive_3_1", X_selected_exhaustive_3_1),
# ("X_selected_exhaustive_3_2", X_selected_exhaustive_3_2),
# ("X_selected_exhaustive_4_1", X_selected_exhaustive_4_1),
# ("X_selected_exhaustive_4_2", X_selected_exhaustive_4_2),
# ("X_selected_exhaustive_4_3", X_selected_exhaustive_4_3),
# ("X_selected_exhaustive_5", X_selected_exhaustive_5),
# ("X_mfs", X_mfs),
# ('X', X)]
X_benchmark_feature_names_dataframes = [("X", X)]
```
## Evaluation Metrics
```
from sklearn.model_selection import RepeatedStratifiedKFold
def cross_val_score_feature_comparison(X_param, y_param, scoring_param):
return(round(cross_val_score(RandomForestClassifier(),
X_param, y_param,
cv=RepeatedStratifiedKFold(n_splits=10, n_repeats=10),
scoring=scoring_param, n_jobs=-1).mean(), 4))
```
In calculation of scores, cross-validation is repeated 10 times, which yields a total of 100 folds.
### Scores
#### F1 score
```
# Testing F1 score
f1_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "f1")
f1_scores_comparison.append(scores)
print("{: <28}: {}".format(X_item_name, scores))
```
#### balanced_accuracy score
```
# Testing balanced_accuracy score
balanced_acc_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "balanced_accuracy")
balanced_acc_scores_comparison.append(scores)
print("{: <28}: {}".format(X_item_name, scores))
```
#### accuracy score
```
# Testing accuracy score
acc_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "accuracy")
acc_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
```
#### f1-macro score
```
# Testing f1-macro score
f1_macro_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "f1_macro")
f1_macro_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
```
#### f1-micro score
```
# Testing f1-micro score
f1_micro_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "f1_micro")
f1_micro_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
```
#### precision score
```
# Testing precision score
precision_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "precision")
precision_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
```
#### recall score
```
# Testing recall score
recall_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "recall")
recall_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
```
#### roc auc
```
# Testing roc auc score
roc_auc_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "roc_auc")
roc_auc_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
```
#### precision_macro
```
# Testing precision_macro score
precision_macro_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "precision_macro")
precision_macro_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
```
#### precision_micro
```
# Testing precision_micro score
precision_micro_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "precision_micro")
precision_micro_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
```
### Scores Table
```
scoring_metrics_table =\
pd.DataFrame({
"F1": f1_scores_comparison,
"Balanced Acc": balanced_acc_scores_comparison,
"Accuracy": acc_scores_comparison,
"F1 Macro": f1_macro_scores_comparison,
"F1 Micro": f1_micro_scores_comparison,
"Precision": precision_scores_comparison,
"Recall": recall_scores_comparison,
"ROC_AUC": roc_auc_scores_comparison,
"Precision Macro": precision_macro_scores_comparison,
"Precision Micro": precision_micro_scores_comparison,
}, index=[e[0] for e in X_benchmark_feature_names_dataframes])
scoring_metrics_table
# Copy for pasting Excel sheet.
scoring_metrics_table.to_clipboard()
```
#### Matthews Corr Coeff (Additional)
```
from sklearn.metrics import matthews_corrcoef
def benchmark_matthews_corrcoef(X_train_param, y_train_param,
X_valid_param, y_valid_param):
"""
Evaluate matthews corrcoef of given input on RandomForestClassifier.
"""
clf = RandomForestClassifier()
clf.fit(X_train_param, y_train_param)
preds = clf.predict(X_valid_param)
print("MCC: {:.4f}".format(matthews_corrcoef(y_valid_param, preds)))
X_train_Alignment_score = X_train[['Alignment_score']]
X_train_Provean_score = X_train[['Provean_score']]
X_train_selected_11 = X_train[['Template_sequence_identity', 'Alignment_score', 'Interactor_template_sequence_identity', 'Interactor_alignment_score', 'Final_ddG', 'ProtBert_score', 'ProteinSolver_score', 'EL2_score', 'Model/DOPE_score', 'Provean_score', 'Matrix_score']]
X_train_selected_exhaustive_3_1 = X_train[['Template_sequence_identity', 'Alignment_score', 'Provean_score']]
X_train_selected_exhaustive_5 = X_train[['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
X_valid_Alignment_score = X_valid[['Alignment_score']]
X_valid_Provean_score = X_valid[['Provean_score']]
X_valid_selected_11 = X_valid[['Template_sequence_identity', 'Alignment_score', 'Interactor_template_sequence_identity', 'Interactor_alignment_score', 'Final_ddG', 'ProtBert_score', 'ProteinSolver_score', 'EL2_score', 'Model/DOPE_score', 'Provean_score', 'Matrix_score']]
X_valid_selected_exhaustive_3_1 = X_valid[['Template_sequence_identity', 'Alignment_score', 'Provean_score']]
X_valid_selected_exhaustive_5 = X_valid[['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
benchmark_matthews_corrcoef(X_train, y_train, X_valid, y_valid)
benchmark_matthews_corrcoef(X_train_Provean_score, y_train, X_valid_Provean_score, y_valid)
benchmark_matthews_corrcoef(X_train_selected_11, y_train, X_valid_selected_11, y_valid)
benchmark_matthews_corrcoef(X_train_selected_exhaustive_3_1, y_train,
X_valid_selected_exhaustive_3_1, y_valid)
benchmark_matthews_corrcoef(X_train_selected_exhaustive_5, y_train,
X_valid_selected_exhaustive_5, y_valid)
```
### Confusion Matrices
```
# X_Provean_score
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X_Provean_score, y, return_report=True)
# X_selected_exhaustive_5
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X_selected_exhaustive_5, y)
# X_selected_exhaustive_3_1
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X_selected_exhaustive_3_1, y, return_report=True)
# X
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X, y)
```
### Cross Val Scores
```
evaluate_cross_val(X, y, "skf_5")
evaluate_cross_val(X, y, "skf_10")
evaluate_cross_val(X_selected_exhaustive_3_1, y, "skf_10")
evaluate_cross_val(X_selected_exhaustive_5, y, "skf_10")
evaluate_cross_val(X, y, "skf_10")
```
# Fine Tuning
```
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import RandomizedSearchCV
def plot_top_feature_importances_final(feature_importances, attributes_param, top_n=10, figsize=None):
feature_imp_series = pd.Series(feature_importances,
index = attributes_param).sort_values(ascending=False)
figsize = (5 , top_n//3) if not figsize else (5, 5)
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
feature_imp_series_top_n = feature_imp_series[:top_n]
plt.figure(figsize=figsize)
sns.barplot(x=feature_imp_series_top_n, y=feature_imp_series_top_n.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances (top {})'.format(top_n))
plt.show()
param_grid_randomized = {'bootstrap': [True, False],
'max_depth': [10, 20, 30, 40, 50, 60, 70, 80, 90, 100],
'max_features': ['auto', 'sqrt'],
'n_estimators': [200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000]}
forest_clf = RandomForestClassifier()
# forest_clf = RandomForestClassifier(random_state=42)
randomized_search = RandomizedSearchCV(forest_clf, param_grid_randomized, n_iter=10,
# random_state=42,
cv=RepeatedStratifiedKFold(n_splits=10, n_repeats=1, random_state=42),
scoring='balanced_accuracy',
return_train_score=True, n_jobs=-1, verbose=2)
randomized_search.fit(X_train_selected_exhaustive_5, y_train)
randomized_search.best_params_
randomized_search.best_score_
final_model = randomized_search.best_estimator_
final_model
```
# Final Evalution
**Default Model with `X_train_selected_exhaustive_3_5`**
```
# Final scoring comparison: X_train_selected_exhaustive_5, y_train with prediction of X_valid_selected_exhaustive_5
forest_clf = RandomForestClassifier(random_state=42)
forest_clf.fit(X_train_selected_exhaustive_5, y_train)
forest_predictions = forest_clf.predict(X_valid_selected_exhaustive_5)
plot_confusion_matrix(forest_clf, X_valid_selected_exhaustive_5, y_valid)
plt.show()
print("Balanced accuracy score : {:.4f}".format(balanced_accuracy_score(y_valid, forest_predictions)))
print("Accuracy score\t\t: {:.4f}".format(accuracy_score(y_valid, forest_predictions)))
```
**Hyper-param Tuned Model with `X_train_selected_exhaustive_5`**
```
# Final scoring comparison: X_train_selected_exhaustive_5, y_train with prediction of X_valid_selected_exhaustive_5
forest_clf = randomized_search.best_estimator_
forest_clf.fit(X_train_selected_exhaustive_5, y_train)
forest_predictions = forest_clf.predict(X_valid_selected_exhaustive_5)
plot_confusion_matrix(forest_clf, X_valid_selected_exhaustive_5, y_valid)
plt.show()
print("Balanced accuracy score : {:.4f}".format(balanced_accuracy_score(y_valid, forest_predictions)))
print("Accuracy score\t\t: {:.4f}".format(accuracy_score(y_valid, forest_predictions)))
```
```
def evaluate_cross_val_avg_via(model_param, X_train_param, y_train_param,
plot_param=True, repeation_param=10):
# Options for cross-validation cv= parameter.
cv_option, n_jobs = cross_validation_options("skf_10", -1)
repeation=repeation_param
forest_scores_bas, forest_scores_as = [], []
for i in range(repeation):
# Cross-validation Accuracy and Balanced Accuracy Scores
forest_scores_bas.append(cross_val_score(model_param,
X_train_param, y_train_param,
cv=cv_option,
scoring="balanced_accuracy", n_jobs=n_jobs))
forest_scores_as.append(cross_val_score(model_param,
X_train_param, y_train_param,
cv=cv_option,
scoring="accuracy", n_jobs=n_jobs))
# # Print scores and averages
# print("Balanced accuracy score AVG : {:.4f}".format(forest_scores_bas[i].mean()))
# print("Accuracy score AVG : {:.4f}".format(forest_scores_as[i].mean()))
if plot_param:
plt.plot(range(1, len(forest_scores_as) + 1), np.array(forest_scores_as).mean(axis=1), "+", color='#265191', alpha=0.5, label="Accuracy_Scores")
plt.plot(range(1, len(forest_scores_bas) + 1), np.array(forest_scores_bas).mean(axis=1), ".", color='#9F2945', alpha=0.5, label="Balanced_Accuracy_Scores")
plt.ylim(0.70, 1)
plt.xticks(range(1, 11))
plt.legend()
plt.xlabel("Repetitions")
plt.ylabel("Scores AVG")
plt.title("Accuracy and Balanced Accuracy AVG Scores per Repetition")
plt.show();
evaluate_cross_val_avg_via(randomized_search.best_estimator_, X_Provean_score, y)
evaluate_cross_val_avg_via(randomized_search.best_estimator_, X, y)
evaluate_cross_val_avg_via(randomized_search.best_estimator_, X_selected_exhaustive_3_1, y)
evaluate_cross_val_avg_via(randomized_search.best_estimator_, X_selected_exhaustive_5, y)
evaluate_cross_val_avg_via(RandomForestClassifier(), X_selected_exhaustive_3_1, y)
evaluate_cross_val_avg_via(RandomForestClassifier(), X_selected_exhaustive_5, y)
```
## Final Models
# **CHECK HERE???** **CHECK HERE???** **CHECK HERE???** **CHECK HERE???** **CHECK HERE???**
**Model I: ???**
```
final_model_randomized = randomized_search.best_estimator_
balanced_accuracy_score(y_valid, final_model_randomized.predict(X_valid_selected_exhaustive_5))
```
**Model II: *RandomForestClassifier* fitted with whole train data**
```
final_model_forest = RandomForestClassifier(random_state=42)
final_model_forest.fit(X_selected_exhaustive_5, y)
```
## Final Features and Importances
```
def plot_top_feature_importances_final_2(feature_importances, attributes_param):
attributes = feature_columns
feature_imp_series = pd.Series(feature_importances,
index = attributes_param).sort_values(ascending=False)
plt.figure(figsize=(5, 3))
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
sns.barplot(x=feature_imp_series, y=feature_imp_series.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importances')
plt.ylabel('Features')
plt.title('Feature Importances of Selected Features')
plt.show()
plot_top_feature_importances_final_2(randomized_search.best_estimator_.feature_importances_, X_selected_exhaustive_5.columns)
```
|
github_jupyter
|
# Common imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
import sys
import seaborn as sns
from IPython.display import display
# To make this notebook's output stable across runs
# np.random.seed(42)
# PATHS
PROJECT_COMMON_FILE_DIR = "../ML_common_files/"
MUTATIONS_PATH = "training_data_M1.txt"
def print_annotation(s):
print(f"\n{s}\n{'-' * len(s)}")
def get_file_path(filename):
return os.path.join(PROJECT_COMMON_FILE_DIR, filename)
# Read Training Data
mutations = pd.read_csv(get_file_path(MUTATIONS_PATH), sep='\t')
# Size of dataframe
print_annotation(f"Size of dataframe: {mutations.shape}")
# First 5 entries
mutations.head()
selected_columns = ['Mutation_Effect_Label', 'UniProt_ID', 'Mutation', 'Interactor_UniProt_ID']\
+ ['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']
# Declare train data using selected column names
train_data = mutations[selected_columns].copy()
# Size of dataframe
print_annotation(f"Size of dataframe: {train_data.shape}")
# First 5 entries
train_data.head()
# Dropping the duplicates
train_data.drop_duplicates(keep="first", inplace=True)
train_data[train_data.duplicated()].empty # True, duplicate is empty
train_data.shape
def display_label_counts(data_param):
"""
Display a dataframe that contains label categories and their counts.
"""
label_counts = pd.DataFrame(data_param["Mutation_Effect_Label"].value_counts())
label_counts.reset_index(inplace=True)
label_counts.columns = ["Mutation_Effect_Label", "Counts"]
label_counts.rename(index={0: 'Disrupting', 1: 'Increasing + No Effect'}, inplace=True)
display(label_counts)
def display_labels(data_param):
"""
Display a dataframe that contains label categories.
"""
label_counts = pd.DataFrame(data_param["Mutation_Effect_Label"].value_counts().index)
label_counts.columns = ["Mutation_Effect_Label"]
display(label_counts)
# Displaying possible label categories.
display_labels(train_data)
labels_to_bins = {
"mutation disrupting(MI:0573)": 0,
"mutation decreasing(MI:0119)": "IGNORED",
"mutation disrupting strength(MI:1128)": 0,
"mutation decreasing strength(MI:1133)": "IGNORED",
"mutation with no effect(MI:2226)": 1,
"disrupting": 0,
"mutation increasing(MI:0382)": 1,
"mutation increasing strength(MI:1132)": 1,
"mutation decreasing rate(MI:1130)": "IGNORED",
"mutation disrupting rate(MI:1129)": 0,
"mutation causing(MI:2227)": "IGNORED",
"mutation increasing rate(MI:1131)": 1}
replace_map = {"Mutation_Effect_Label": labels_to_bins}
# Size of dataframe before binning.
print_annotation(f"Size of dataframe before binning: {train_data.shape}")
# Modifications will be done on train_data_binned.
train_data_binned = train_data.copy()
# Replace the labels as described above.
train_data_binned.replace(replace_map, inplace=True)
# Drop the entries with "IGNORED": 'mutation cusing' in this case.
train_data_binned = train_data_binned[train_data_binned["Mutation_Effect_Label"] != "IGNORED"]
# Reset index of the dataframe to avoid any possible errors
train_data_binned.reset_index(drop=True, inplace=True)
# Size of dataframe after binning.
print_annotation(f"Size of dataframe after binning: {train_data_binned.shape}")
# First 5 rows of binned data.
train_data_binned.head()
train_data_binned["Mutation_Effect_Label"].value_counts()
# Train (mutations) data
set(train_data_binned.dtypes)
# Get column names where its type is *not* int or float, i.e. whose type is object.
coerce_numeric_cols = set([cname for cname in train_data_binned.columns if train_data_binned[cname].dtype not in ['int64', 'float64']])
# + [cname for cname in target_brca_data.columns if target_brca_data[cname].dtype not in ['int64', 'float64']]) # \
# + [cname for cname in target_coad_data.columns if target_coad_data[cname].dtype not in ['int64', 'float64']]\
# + [cname for cname in target_ov_data.columns if target_ov_data[cname].dtype not in ['int64', 'float64']])
# Remove target variable from the list
coerce_numeric_cols = coerce_numeric_cols - {"Mutation_Effect_Label", "UniProt_ID", "Mutation", "Interactor_UniProt_ID"}
for cname in coerce_numeric_cols:
train_data_binned[cname] = pd.to_numeric(train_data_binned[cname], errors='coerce')
# target_brca_data[cname] = pd.to_numeric(target_brca_data[cname], errors='coerce')
# target_coad_data[cname] = pd.to_numeric(target_coad_data[cname], errors='coerce')
# target_ov_data[cname] = pd.to_numeric(target_ov_data[cname], errors='coerce')
train_data_binned.fillna(0, inplace=True)
# target_brca_data.fillna(0, inplace=True)
# target_coad_data.fillna(0, inplace=True)
# target_ov_data.fillna(0, inplace=True)
# Train (mutations) data
set(train_data_binned.dtypes)
train_data_binned.dtypes
def visualize_label_counts(data_param, label_name_param="Mutation_Effect_Label"):
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
ax = sns.barplot(x=data_param[label_name_param].value_counts().index,
y=data_param[label_name_param].value_counts(),
palette="ch:s=-.2,r=.6")
ax.set_title('Disrupting vs Increasing & No Effect') # ch:s=-.2,r=.6, ocean
ax.set_ylabel('Value counts')
ax.set_xticklabels(['Distrupting', 'Increasing + No Effect']);
# Declaing `data_processed`.
data_processed = train_data_binned.copy()
# Size of processed data.
print_annotation(f"Size of processed data: {data_processed.shape}")
# First 5 rows of binned data.
data_processed.head()
visualize_label_counts(data_processed)
display_label_counts(data_processed)
# Get the unique proteins from `UniProt_ID` column.
unique_proteins = list(data_processed['UniProt_ID'].unique())
# Number of unique_proteins
print('Number of `unique_proteins`:', len(unique_proteins))
# First five proteins
print(unique_proteins[:5])
sampled_row_dataframes = []
for unique_protein in unique_proteins:
sampled_row_dataframes.append(data_processed[data_processed['UniProt_ID'] == unique_protein].sample())
# Merge row dataframes into single dataframe, stack rows on top of each other.
sampled_train_data = pd.concat(sampled_row_dataframes)
# Reset index of the dataframe to avoid any possible errors
sampled_train_data.reset_index(drop=True, inplace=True)
# Dimensions of dataframe
print_annotation(f"Dimensions of sampled_dataframe: {sampled_train_data.shape}")
# First five entries
sampled_train_data.head()
visualize_label_counts(sampled_train_data)
display_label_counts(sampled_train_data)
sampled_train_data = sampled_train_data.drop(["UniProt_ID", "Mutation", "Interactor_UniProt_ID"], axis='columns')
# Shuffle the rows in data_prepared:
data_prepared = sampled_train_data.sample(frac=1, random_state=96).reset_index(drop=True).copy()
from sklearn.model_selection import train_test_split
random_train_set, random_valid_set = train_test_split(
data_prepared, test_size=0.2, random_state=42)
print(random_train_set.shape, random_valid_set.shape)
random_train_set.head()
>>> train_index
array([513, 676, 164, 520, 23], dtype=int64)
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, valid_index in split.split(data_prepared, data_prepared["Mutation_Effect_Label"]):
strat_train_set = data_prepared.iloc[train_index]
strat_valid_set = data_prepared.iloc[valid_index]
train_index[:5]
strat_train_set.head()
strat_train_set.shape, strat_valid_set.shape
def label_proportions(data_param):
return data_param["Mutation_Effect_Label"].value_counts() / len(data_param)
compare_props = pd.DataFrame({
"Overall": label_proportions(data_prepared),
"Stratified": label_proportions(strat_valid_set),
"Random": label_proportions(random_valid_set)
}).sort_index()
compare_props["Rand. %error"] = 100 * compare_props["Random"] / compare_props["Overall"] - 100
compare_props["Strat. %error"] = 100 * compare_props["Stratified"] / compare_props["Overall"] - 100
compare_props.rename(index={0: 'Disruptive', 1: 'Increasing + No Effect'}, inplace=True)
compare_props
# All data, i.e. data_prepared
X = data_prepared.drop(["Mutation_Effect_Label"], axis="columns")
y = data_prepared["Mutation_Effect_Label"].copy()
# Stratified version
X_train = strat_train_set.drop(["Mutation_Effect_Label"], axis="columns")
y_train = strat_train_set["Mutation_Effect_Label"].copy()
X_valid = strat_valid_set.drop(["Mutation_Effect_Label"], axis="columns")
y_valid = strat_valid_set["Mutation_Effect_Label"].copy()
# Printing their shapes
print(X_train.shape, y_train.shape)
print(X_valid.shape, y_valid.shape)
# Randomized version
X_train_random = random_train_set.drop(["Mutation_Effect_Label"], axis="columns")
y_train_random = random_train_set["Mutation_Effect_Label"].copy()
X_valid_random = random_valid_set.drop(["Mutation_Effect_Label"], axis="columns")
y_valid_random = random_valid_set["Mutation_Effect_Label"].copy()
# Printing their shapes
print(X_train.shape, y_train.shape)
print(X_valid.shape, y_valid.shape)
# Imports
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import cross_val_predict
from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import accuracy_score
from sklearn.metrics import balanced_accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import classification_report
from itertools import combinations
import seaborn as sns
def cross_validation_options(cv_option_param, n_jobs_param=-1):
"""
A helper function that returns (my) desired cv_option and n_jobs.
"""
# Options for cross-validation cv= parameter.
if isinstance(cv_option_param, int):
cv_option_param = cv_option_param
elif cv_option_param == "skf_5":
cv_option_param = StratifiedKFold(shuffle=True, n_splits=5)
elif cv_option_param == "skf_10":
cv_option_param = StratifiedKFold(shuffle=True, n_splits=10)
elif cv_option_param == "kf_5":
cv_option_param = KFold(shuffle=True, n_splits=5)
elif cv_option_param == "kf_10":
cv_option_param = KFold(shuffle=True, n_splits=10)
else:
raise ValueError("cv_option value error!")
# Option for j_jobs:
n_jobs_param = -1
return cv_option_param, n_jobs_param
attributes = list(X.columns)
# Plotting feature importance in barplot
def plot_feature_importances(feature_importances):
feature_imp_series = pd.Series(feature_importances,
index = attributes).sort_values(ascending=False)
plt.figure(figsize=(5, 20))
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
sns.barplot(x=feature_imp_series, y=feature_imp_series.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances')
plt.show()
# Plotting top n feature importance in barplot
def plot_top_feature_importances(feature_importances, top_n=10, figsize=None):
feature_imp_series = pd.Series(feature_importances,
index = attributes).sort_values(ascending=False)
figsize = (5 , top_n//3) if not figsize else (5, 5)
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
feature_imp_series_top_n = feature_imp_series[:top_n]
plt.figure(figsize=figsize)
sns.barplot(x=feature_imp_series_top_n, y=feature_imp_series_top_n.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances (top {})'.format(top_n))
plt.show()
# Initial scoring: X_train, y_train with prediction of X_valid
forest_clf_inital = RandomForestClassifier(random_state=42)
forest_clf_inital.fit(X_train, y_train)
forest_predictions = forest_clf_inital.predict(X_valid)
print("Balanced accuracy score : {:.4f}".format(balanced_accuracy_score(y_valid, forest_predictions)))
print("Accuracy score\t\t: {:.4f}".format(accuracy_score(y_valid, forest_predictions)))
attributes = list(X.columns)
# plot_feature_importances(forest_clf_inital.feature_importances_)
plot_top_feature_importances(forest_clf_inital.feature_importances_, top_n=10,
figsize=(5,5))
forest_clf_inital.feature_importances_
# Imports
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import balanced_accuracy_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import balanced_accuracy_score
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold
feature_columns = list(data_prepared.columns)[1:]
# Plotting feature importance in barplot
def plot_feature_importances(feature_importances):
attributes = feature_columns
feature_imp_series = pd.Series(feature_importances,
index = attributes).sort_values(ascending=False)
plt.figure(figsize=(5, 20))
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
sns.barplot(x=feature_imp_series, y=feature_imp_series.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances')
plt.show()
# Plotting top n feature importance in barplot
def plot_top_feature_importances(feature_importances, top_n=10, figsize=None):
attributes = feature_columns
feature_imp_series = pd.Series(feature_importances,
index = attributes).sort_values(ascending=False)
figsize = (5 , top_n//3) if not figsize else (5, 5)
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
feature_imp_series_top_n = feature_imp_series[:top_n]
plt.figure(figsize=figsize)
sns.barplot(x=feature_imp_series_top_n, y=feature_imp_series_top_n.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances (top {})'.format(top_n))
plt.show()
# Initial scoring: X_train, y_train with prediction of X_valid
forest_clf_inital = RandomForestClassifier(random_state=42)
forest_clf_inital.fit(X_train, y_train)
forest_predictions = forest_clf_inital.predict(X_valid)
print("Balanced accuracy score : {:.4f}".format(balanced_accuracy_score(y_valid, forest_predictions)))
print("Accuracy score\t\t: {:.4f}".format(accuracy_score(y_valid, forest_predictions)))
def evaluate_cross_val(X_train_param, y_train_param, cv_option_param):
# Cross Validation options
cv_option, n_jobs = cross_validation_options(cv_option_param, -1)
# Model
forest_clf = RandomForestClassifier(random_state=42)
# Cross-validation Accuracy and Balanced Accuracy Scores
forest_scores_bas = cross_val_score(forest_clf,
X_train_param, y_train_param,
cv=cv_option, scoring="balanced_accuracy", n_jobs=n_jobs)
forest_scores_as = cross_val_score(forest_clf,
X_train_param, y_train_param,
cv=cv_option, scoring="accuracy", n_jobs=n_jobs)
# Print scores and averages
print("Balanced accuracy score AVG : {:.4f}".format(forest_scores_bas.mean()))
# print(forest_scores_bas)
print("Accuracy score AVG : {:.4f}".format(forest_scores_as.mean()))
# print(forest_scores_as)
evaluate_cross_val(X, y, "skf_10")
evaluate_cross_val(X, y, "skf_10")
evaluate_cross_val(X, y, "skf_10")
evaluate_cross_val(X_train, y_train, "skf_5")
evaluate_cross_val(X, y, "skf_10")
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import classification_report
import seaborn as sns
def cross_val_confusion_matrix_via(model_param, X_train_param, y_train_param,
return_report=False):
skf = StratifiedKFold(shuffle=True, n_splits=10)
y_pred_temp = cross_val_predict(model_param, X_train_param, y_train_param, cv=skf)
label_names = ["Disrupting", "NoEffect+Increasing"]
sns.heatmap(confusion_matrix(y_train_param, y_pred_temp), annot=True, fmt="d", xticklabels=label_names, yticklabels=label_names)
plt.title(r'$\mathbf{Confusion\ Matrix}$', fontsize=16, fontweight='bold')
plt.ylabel('Actual', fontsize=16, fontweight='bold')
plt.xlabel('Predicted', fontsize=16, fontweight='bold')
plt.show()
if return_report:
print(classification_report(y_train_param, y_pred_temp, target_names=label_names))
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X, y, return_report=True)
# X_mfs = X[['EL2_score', 'Provean_score', 'Matrix_score', 'Final_ddG']]
# X_Alignment_score = X[['Alignment_score']]
# X_Provean_score = X[['Provean_score']]
# X_selected_11 = X[['Template_sequence_identity', 'Alignment_score', 'Interactor_template_sequence_identity', 'Interactor_alignment_score', 'Final_ddG', 'ProtBert_score', 'ProteinSolver_score', 'EL2_score', 'Model/DOPE_score', 'Provean_score', 'Matrix_score']]
# # 3
# X_selected_exhaustive_3_1 = X[['Template_sequence_identity', 'Alignment_score', 'Provean_score']]
# X_selected_exhaustive_3_2 = X[['Template_sequence_identity', 'Provean_score', 'Matrix_score']]
# # 4
# X_selected_exhaustive_4_1 = X[['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Matrix_score']]
# X_selected_exhaustive_4_2 = X[['Template_sequence_identity', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
# X_selected_exhaustive_4_3 = X[['Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
# # 5
# X_selected_exhaustive_5 = X[['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
# X_benchmark_feature_names_dataframes =\
# [("X_Alignment_score", X_Alignment_score),
# ("X_Provean_score", X_Provean_score),
# ("X_selected_11", X_selected_11),
# ("X_selected_exhaustive_3_1", X_selected_exhaustive_3_1),
# ("X_selected_exhaustive_3_2", X_selected_exhaustive_3_2),
# ("X_selected_exhaustive_4_1", X_selected_exhaustive_4_1),
# ("X_selected_exhaustive_4_2", X_selected_exhaustive_4_2),
# ("X_selected_exhaustive_4_3", X_selected_exhaustive_4_3),
# ("X_selected_exhaustive_5", X_selected_exhaustive_5),
# ("X_mfs", X_mfs),
# ('X', X)]
X_benchmark_feature_names_dataframes = [("X", X)]
from sklearn.model_selection import RepeatedStratifiedKFold
def cross_val_score_feature_comparison(X_param, y_param, scoring_param):
return(round(cross_val_score(RandomForestClassifier(),
X_param, y_param,
cv=RepeatedStratifiedKFold(n_splits=10, n_repeats=10),
scoring=scoring_param, n_jobs=-1).mean(), 4))
# Testing F1 score
f1_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "f1")
f1_scores_comparison.append(scores)
print("{: <28}: {}".format(X_item_name, scores))
# Testing balanced_accuracy score
balanced_acc_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "balanced_accuracy")
balanced_acc_scores_comparison.append(scores)
print("{: <28}: {}".format(X_item_name, scores))
# Testing accuracy score
acc_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "accuracy")
acc_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
# Testing f1-macro score
f1_macro_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "f1_macro")
f1_macro_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
# Testing f1-micro score
f1_micro_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "f1_micro")
f1_micro_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
# Testing precision score
precision_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "precision")
precision_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
# Testing recall score
recall_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "recall")
recall_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
# Testing roc auc score
roc_auc_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "roc_auc")
roc_auc_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
# Testing precision_macro score
precision_macro_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "precision_macro")
precision_macro_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
# Testing precision_micro score
precision_micro_scores_comparison = []
for X_item_name, X_item in X_benchmark_feature_names_dataframes:
scores = cross_val_score_feature_comparison(X_item, y, "precision_micro")
precision_micro_scores_comparison.append(scores)
print("{: <25}: {}".format(X_item_name, scores))
scoring_metrics_table =\
pd.DataFrame({
"F1": f1_scores_comparison,
"Balanced Acc": balanced_acc_scores_comparison,
"Accuracy": acc_scores_comparison,
"F1 Macro": f1_macro_scores_comparison,
"F1 Micro": f1_micro_scores_comparison,
"Precision": precision_scores_comparison,
"Recall": recall_scores_comparison,
"ROC_AUC": roc_auc_scores_comparison,
"Precision Macro": precision_macro_scores_comparison,
"Precision Micro": precision_micro_scores_comparison,
}, index=[e[0] for e in X_benchmark_feature_names_dataframes])
scoring_metrics_table
# Copy for pasting Excel sheet.
scoring_metrics_table.to_clipboard()
from sklearn.metrics import matthews_corrcoef
def benchmark_matthews_corrcoef(X_train_param, y_train_param,
X_valid_param, y_valid_param):
"""
Evaluate matthews corrcoef of given input on RandomForestClassifier.
"""
clf = RandomForestClassifier()
clf.fit(X_train_param, y_train_param)
preds = clf.predict(X_valid_param)
print("MCC: {:.4f}".format(matthews_corrcoef(y_valid_param, preds)))
X_train_Alignment_score = X_train[['Alignment_score']]
X_train_Provean_score = X_train[['Provean_score']]
X_train_selected_11 = X_train[['Template_sequence_identity', 'Alignment_score', 'Interactor_template_sequence_identity', 'Interactor_alignment_score', 'Final_ddG', 'ProtBert_score', 'ProteinSolver_score', 'EL2_score', 'Model/DOPE_score', 'Provean_score', 'Matrix_score']]
X_train_selected_exhaustive_3_1 = X_train[['Template_sequence_identity', 'Alignment_score', 'Provean_score']]
X_train_selected_exhaustive_5 = X_train[['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
X_valid_Alignment_score = X_valid[['Alignment_score']]
X_valid_Provean_score = X_valid[['Provean_score']]
X_valid_selected_11 = X_valid[['Template_sequence_identity', 'Alignment_score', 'Interactor_template_sequence_identity', 'Interactor_alignment_score', 'Final_ddG', 'ProtBert_score', 'ProteinSolver_score', 'EL2_score', 'Model/DOPE_score', 'Provean_score', 'Matrix_score']]
X_valid_selected_exhaustive_3_1 = X_valid[['Template_sequence_identity', 'Alignment_score', 'Provean_score']]
X_valid_selected_exhaustive_5 = X_valid[['Template_sequence_identity', 'Alignment_score', 'ProtBert_score', 'Provean_score', 'Matrix_score']]
benchmark_matthews_corrcoef(X_train, y_train, X_valid, y_valid)
benchmark_matthews_corrcoef(X_train_Provean_score, y_train, X_valid_Provean_score, y_valid)
benchmark_matthews_corrcoef(X_train_selected_11, y_train, X_valid_selected_11, y_valid)
benchmark_matthews_corrcoef(X_train_selected_exhaustive_3_1, y_train,
X_valid_selected_exhaustive_3_1, y_valid)
benchmark_matthews_corrcoef(X_train_selected_exhaustive_5, y_train,
X_valid_selected_exhaustive_5, y_valid)
# X_Provean_score
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X_Provean_score, y, return_report=True)
# X_selected_exhaustive_5
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X_selected_exhaustive_5, y)
# X_selected_exhaustive_3_1
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X_selected_exhaustive_3_1, y, return_report=True)
# X
cross_val_confusion_matrix_via(RandomForestClassifier(random_state=42),
X, y)
evaluate_cross_val(X, y, "skf_5")
evaluate_cross_val(X, y, "skf_10")
evaluate_cross_val(X_selected_exhaustive_3_1, y, "skf_10")
evaluate_cross_val(X_selected_exhaustive_5, y, "skf_10")
evaluate_cross_val(X, y, "skf_10")
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import RandomizedSearchCV
def plot_top_feature_importances_final(feature_importances, attributes_param, top_n=10, figsize=None):
feature_imp_series = pd.Series(feature_importances,
index = attributes_param).sort_values(ascending=False)
figsize = (5 , top_n//3) if not figsize else (5, 5)
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
feature_imp_series_top_n = feature_imp_series[:top_n]
plt.figure(figsize=figsize)
sns.barplot(x=feature_imp_series_top_n, y=feature_imp_series_top_n.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importance Scores')
plt.ylabel('Variables')
plt.title('Feature Importances (top {})'.format(top_n))
plt.show()
param_grid_randomized = {'bootstrap': [True, False],
'max_depth': [10, 20, 30, 40, 50, 60, 70, 80, 90, 100],
'max_features': ['auto', 'sqrt'],
'n_estimators': [200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000]}
forest_clf = RandomForestClassifier()
# forest_clf = RandomForestClassifier(random_state=42)
randomized_search = RandomizedSearchCV(forest_clf, param_grid_randomized, n_iter=10,
# random_state=42,
cv=RepeatedStratifiedKFold(n_splits=10, n_repeats=1, random_state=42),
scoring='balanced_accuracy',
return_train_score=True, n_jobs=-1, verbose=2)
randomized_search.fit(X_train_selected_exhaustive_5, y_train)
randomized_search.best_params_
randomized_search.best_score_
final_model = randomized_search.best_estimator_
final_model
# Final scoring comparison: X_train_selected_exhaustive_5, y_train with prediction of X_valid_selected_exhaustive_5
forest_clf = RandomForestClassifier(random_state=42)
forest_clf.fit(X_train_selected_exhaustive_5, y_train)
forest_predictions = forest_clf.predict(X_valid_selected_exhaustive_5)
plot_confusion_matrix(forest_clf, X_valid_selected_exhaustive_5, y_valid)
plt.show()
print("Balanced accuracy score : {:.4f}".format(balanced_accuracy_score(y_valid, forest_predictions)))
print("Accuracy score\t\t: {:.4f}".format(accuracy_score(y_valid, forest_predictions)))
# Final scoring comparison: X_train_selected_exhaustive_5, y_train with prediction of X_valid_selected_exhaustive_5
forest_clf = randomized_search.best_estimator_
forest_clf.fit(X_train_selected_exhaustive_5, y_train)
forest_predictions = forest_clf.predict(X_valid_selected_exhaustive_5)
plot_confusion_matrix(forest_clf, X_valid_selected_exhaustive_5, y_valid)
plt.show()
print("Balanced accuracy score : {:.4f}".format(balanced_accuracy_score(y_valid, forest_predictions)))
print("Accuracy score\t\t: {:.4f}".format(accuracy_score(y_valid, forest_predictions)))
def evaluate_cross_val_avg_via(model_param, X_train_param, y_train_param,
plot_param=True, repeation_param=10):
# Options for cross-validation cv= parameter.
cv_option, n_jobs = cross_validation_options("skf_10", -1)
repeation=repeation_param
forest_scores_bas, forest_scores_as = [], []
for i in range(repeation):
# Cross-validation Accuracy and Balanced Accuracy Scores
forest_scores_bas.append(cross_val_score(model_param,
X_train_param, y_train_param,
cv=cv_option,
scoring="balanced_accuracy", n_jobs=n_jobs))
forest_scores_as.append(cross_val_score(model_param,
X_train_param, y_train_param,
cv=cv_option,
scoring="accuracy", n_jobs=n_jobs))
# # Print scores and averages
# print("Balanced accuracy score AVG : {:.4f}".format(forest_scores_bas[i].mean()))
# print("Accuracy score AVG : {:.4f}".format(forest_scores_as[i].mean()))
if plot_param:
plt.plot(range(1, len(forest_scores_as) + 1), np.array(forest_scores_as).mean(axis=1), "+", color='#265191', alpha=0.5, label="Accuracy_Scores")
plt.plot(range(1, len(forest_scores_bas) + 1), np.array(forest_scores_bas).mean(axis=1), ".", color='#9F2945', alpha=0.5, label="Balanced_Accuracy_Scores")
plt.ylim(0.70, 1)
plt.xticks(range(1, 11))
plt.legend()
plt.xlabel("Repetitions")
plt.ylabel("Scores AVG")
plt.title("Accuracy and Balanced Accuracy AVG Scores per Repetition")
plt.show();
evaluate_cross_val_avg_via(randomized_search.best_estimator_, X_Provean_score, y)
evaluate_cross_val_avg_via(randomized_search.best_estimator_, X, y)
evaluate_cross_val_avg_via(randomized_search.best_estimator_, X_selected_exhaustive_3_1, y)
evaluate_cross_val_avg_via(randomized_search.best_estimator_, X_selected_exhaustive_5, y)
evaluate_cross_val_avg_via(RandomForestClassifier(), X_selected_exhaustive_3_1, y)
evaluate_cross_val_avg_via(RandomForestClassifier(), X_selected_exhaustive_5, y)
final_model_randomized = randomized_search.best_estimator_
balanced_accuracy_score(y_valid, final_model_randomized.predict(X_valid_selected_exhaustive_5))
final_model_forest = RandomForestClassifier(random_state=42)
final_model_forest.fit(X_selected_exhaustive_5, y)
def plot_top_feature_importances_final_2(feature_importances, attributes_param):
attributes = feature_columns
feature_imp_series = pd.Series(feature_importances,
index = attributes_param).sort_values(ascending=False)
plt.figure(figsize=(5, 3))
sns.set(style="white", font_scale=1.15) # white, dark, whitegrid, darkgrid, ticks
sns.barplot(x=feature_imp_series, y=feature_imp_series.index, palette="ch:s=-.2,r=.6")
plt.xlabel('Feature Importances')
plt.ylabel('Features')
plt.title('Feature Importances of Selected Features')
plt.show()
plot_top_feature_importances_final_2(randomized_search.best_estimator_.feature_importances_, X_selected_exhaustive_5.columns)
| 0.470737 | 0.855489 |
# Closing the loop with a PD controller
We have seen in the previous notebook how to do a simple control loop that read sensors and applied torque commands. However, we did not use the sensor measurements to compute the torque commands.
Now we would like to do our first closed-loop controller. We will design a simple Proportional-Derivative (PD) position controller. The goal of the controller is to compute a command that will move the joints of the robot to a desired position.
Assume that we want the first joint, with measurement position $\theta$, to move to the desired position $\theta_{des}$. The idea is to apply a command proportional to the error between the measured and desired position (the P in PD controller). The error is
$$\textrm{error} = (\theta_{des} - \theta)$$ and
the controller will be $\tau = P \cdot \textrm{error} = P (\theta_{des} - \theta)$ where $P$ is a constant.
However, when using only a term proportional to the position, the controller will tend to create oscillations and get easily unstable (you can try!). It is then a good idea to add a term proportional to the time derivative of the error (the D term).
The time derivative of the error is
$$\frac{d}{dt}\textrm{error} = \frac{d}{dt}(\theta_{des} - \theta) = \dot{\theta}_{des} - \dot{\theta}$$
So a PD controller takes the general form
$\tau = P (\theta_{des} - \theta) + D (\dot{\theta}_{des} - \dot{\theta})$
where $P$ and $D$ are positive numbers called the **PD gains**
Intuitively it applies a command that tries to follow at the same time a desired position and a desired velocity (which dampens fast oscillations).
When we want to be in a static position, $\dot{\theta}_{des}$ will be 0, but if we want to follow a trajectory $\theta_{des}(t)$ which varies over time, the derivative $\dot{\theta}_{des}(t)$ will not be 0 anymore.
```
#setup nice plotting
%matplotlib widget
# we import useful libraries
import time
import numpy as np
import matplotlib as mp
import matplotlib.pyplot as plt
# we import the helper class / we will use a similar class to work with the real robot
from nyu_finger_simulator import NYUFingerSimulator
# we can now create a robot simulation
robot = NYUFingerSimulator()
# here is an example of a simple PD controller
# we reset the simulation
robot.reset_state([0.,0.,0.])
# we simulate for 5 seconds
run_time = 5.
num_steps = int(run_time/robot.dt)
# the PD gains
P = np.array([0.5, .5, .5])
D = np.array([0.01, 0.01, 0.01])
# the desired position
q_des = np.array([0.,0.,np.pi/2.])
dq_des = np.zeros_like(q_des) # the desired velocity here is 0
# we store information
measured_positions = np.zeros([num_steps,3])
measured_velocities = np.zeros_like(measured_positions)
desired_torques = np.zeros_like(measured_positions)
time = np.zeros_like(measured_positions)
for i in range(num_steps):
# get the current time
time[i] = robot.dt * i
# we get the position and velocities of the joints
q, dq = robot.get_state()
measured_positions[i,:] = q
measured_velocities[i,:] = dq
error = q_des - q # the position error for all the joints (it's a 3D vector)
d_error = dq_des-dq # the velocity error for all the joints
# we compute the desired torques as a PD controller
joint_torques = P * error + D * d_error
desired_torques[i,:] = joint_torques
# we send them to the robot and do one simulation step
robot.send_joint_torque(joint_torques)
robot.step()
# we plot the measured position and velocities of all the joints
# and add the desired values
time = np.linspace(0., run_time, num=num_steps)
plt.figure(figsize=[6, 12])
for i in range(3):
plt.subplot(3,1,i+1)
plt.plot(time, measured_positions[:,i])
plt.plot(time, np.ones_like(time)*q_des[i],'--')
plt.ylabel(robot.joint_names[i] + ' [rad]')
plt.xlabel('Time[s]')
plt.title('joint positions')
plt.figure(figsize=[6, 12])
for i in range(3):
plt.subplot(3,1,i+1)
plt.plot(time, measured_velocities[:,i])
plt.plot(time, np.ones_like(time)*dq_des[i],'--')
plt.ylabel(robot.joint_names[i] + ' [rad/s]')
plt.xlabel('Time[s]')
plt.title('joint velocities')
```
## Questions:
(submit a pdf with detailed answers to these questions, including the plots through NYUClasses)
1. Describe qualitatively what you observe when you increase/decrease P and D.
2. Tune the P and D gains to have a good tracking of the positions $[0,0,\frac{\pi}{2}]$ without any oscillations. The P and D gains need not be the same for different joints. What gains did you find? Plot the position and velocities of each joints as a function of time with these gains. (starting from the original initial robot configuration).
3. Use the PD controller to do the following task: keep the position of the first two joints fixed and follows the following position trajectory for the last joint $0.8 \sin(\pi t)$. Plot the results (positions and velocities as a function of time for all joints). Simulate for at least 10 seconds.
4. Change the joint trajectories to get the robot to draw a circle in the air with its fingertip.
|
github_jupyter
|
#setup nice plotting
%matplotlib widget
# we import useful libraries
import time
import numpy as np
import matplotlib as mp
import matplotlib.pyplot as plt
# we import the helper class / we will use a similar class to work with the real robot
from nyu_finger_simulator import NYUFingerSimulator
# we can now create a robot simulation
robot = NYUFingerSimulator()
# here is an example of a simple PD controller
# we reset the simulation
robot.reset_state([0.,0.,0.])
# we simulate for 5 seconds
run_time = 5.
num_steps = int(run_time/robot.dt)
# the PD gains
P = np.array([0.5, .5, .5])
D = np.array([0.01, 0.01, 0.01])
# the desired position
q_des = np.array([0.,0.,np.pi/2.])
dq_des = np.zeros_like(q_des) # the desired velocity here is 0
# we store information
measured_positions = np.zeros([num_steps,3])
measured_velocities = np.zeros_like(measured_positions)
desired_torques = np.zeros_like(measured_positions)
time = np.zeros_like(measured_positions)
for i in range(num_steps):
# get the current time
time[i] = robot.dt * i
# we get the position and velocities of the joints
q, dq = robot.get_state()
measured_positions[i,:] = q
measured_velocities[i,:] = dq
error = q_des - q # the position error for all the joints (it's a 3D vector)
d_error = dq_des-dq # the velocity error for all the joints
# we compute the desired torques as a PD controller
joint_torques = P * error + D * d_error
desired_torques[i,:] = joint_torques
# we send them to the robot and do one simulation step
robot.send_joint_torque(joint_torques)
robot.step()
# we plot the measured position and velocities of all the joints
# and add the desired values
time = np.linspace(0., run_time, num=num_steps)
plt.figure(figsize=[6, 12])
for i in range(3):
plt.subplot(3,1,i+1)
plt.plot(time, measured_positions[:,i])
plt.plot(time, np.ones_like(time)*q_des[i],'--')
plt.ylabel(robot.joint_names[i] + ' [rad]')
plt.xlabel('Time[s]')
plt.title('joint positions')
plt.figure(figsize=[6, 12])
for i in range(3):
plt.subplot(3,1,i+1)
plt.plot(time, measured_velocities[:,i])
plt.plot(time, np.ones_like(time)*dq_des[i],'--')
plt.ylabel(robot.joint_names[i] + ' [rad/s]')
plt.xlabel('Time[s]')
plt.title('joint velocities')
| 0.630799 | 0.992809 |
# CoderDojo - Obrázkové Džitsu 2
## Zpracování obrazu (image processing)
Tyto notebooky ukážou, jak je možné programovat obrázky.
# Kam se podělo štěňátko?
Neboj. Zobrazíme štěňátko (stejně jako v minulém notebooku)...
```
import numpy as np
from IPython.core.display import display
from PIL import Image
# Reading the image
img=Image.open('../images/puppy.png')
display(img)
```
### A trochu ho vylepšíme! Ale všechno popořadě
Velikost obrázku zjistíme pomocí atributu `img.size`:
```
img.size
```
První číslo je šířka, druhé výška. Odhadneš, jakými čísly je ohraničený pejskův obličej? Zkus změnit čísla u proměnných `top`, `left`, `bottom`, `right`. Metoda `crop()` udělá výřez.
```
left = 230
bottom = 550
top = 240
right = 530
face = img.crop((left, top, right, bottom))
display(face)
```
Minulé džitsu se týkalo barev. Tohle štěňátko je ale smutně černobílé.
### Nabarvíme štěňátko na červeno!
Šedou barvu dostaneme, když jsou hodnoty pixelu všechny stejné (když jsou všechny minimální, dostaneme černou, když jsou všechny maximální, dostaneme bílou). Všechny pixely v obrázku tedy mají trojici stejných čísel. Z minulého džitsu víme, že první v trojici je červená, nastavíme tedy první člen na maximum a ostatní necháme.
Pozor, minule jsme pracovali s `matplotlib`, kde se hodnoty RGB nastavují jako čísla od 0 do 1. Tentokrát ale používáme (pohodlnější) modul `pillow`, kde se nastavují hodnoty od 0 do 255, to znamená, že každý pixel může mít 256 různých hodnot na každém barevném kanále.
```
red_face = np.array(face)
red_face[...,0]=255
display(Image.fromarray(red_face))
```
### Chudák pes!
Zkus ještě jiné barvy. Toho dosáhneš změnou nuly v tomto řádku
`red_face[...,0] = 255`
na jiné číslo. Protože je barva popsána třemi čísly (R, G a B), můžeš místo nuly dosadit jedničku nebo dvojku.
Hodnotám pod čísly 0, 1 a 2 se také někdy říká barevné kanály (color channels), takže máme červený kanál, zelený a modrý.
Když do kódu napíšeš dva řádky
`red_face[...,0] = 255`
`red_face[...,1] = 255`,
změníš dvě barvy ze tří.
Zkus všechny kombinace (0 a 1, 0 a 2, 1 a 2).<br>
Co když změníš všechny?<br>
```
red_face = np.array(face)
red_face[...,0]=255
red_face[...,1]=255
display(Image.fromarray(red_face))
```
Jak to funguje? Pejsek se přebarví, pokud změníme jeden nebo dva barevné kanály (např. hodnoty pro R a B) na určité pevně dané číslo. Pokud takto změníme všechny tři kanály dostaneme barevný čtverec. Informace o tom, že na obrázku byl pejsek, se ztratí.
Výzva: co se stane, když místo 255 dáš jiné číslo?
### Gratuluju! Máš splněno druhé džitsu ze zpracování obrazu. Umíš vyříznout pixely z obrázku a měnit jejich barevné kanály.
:)
|
github_jupyter
|
import numpy as np
from IPython.core.display import display
from PIL import Image
# Reading the image
img=Image.open('../images/puppy.png')
display(img)
img.size
left = 230
bottom = 550
top = 240
right = 530
face = img.crop((left, top, right, bottom))
display(face)
red_face = np.array(face)
red_face[...,0]=255
display(Image.fromarray(red_face))
red_face = np.array(face)
red_face[...,0]=255
red_face[...,1]=255
display(Image.fromarray(red_face))
| 0.338733 | 0.925701 |
Thanks to Tim and others for the basics of this Jupyter notebook
see also https://medium.com/@ts1829/policy-gradient-reinforcement-learning-in-pytorch-df1383ea0baf
and https://gist.github.com/tamlyn/a9d2b3990f9dab0f82d1dfc1588c876a
# Implementing Policy Gradients on CartPole with PyTorch
```
import gym
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from tqdm import tqdm, trange
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.autograd import Variable
%matplotlib inline
env = gym.make('CartPole-v1')
#env = gym.make('MountainCar-v0')
env.seed(1)
_ = torch.manual_seed(1) #suppress stdout
```
## Policy Gradients
A policy gradient attempts to train an agent without explicitly mapping the value for every state-action pair in an environment by taking small steps and updating the policy based on the reward associated with that step. The agent can receive a reward immediately for an action or the agent can receive the award at a later time such as the end of the episode.
We’ll designate the policy function our agent is trying to learn as $\pi_\theta(a,s)$, where $\theta$ is the parameter vector, $s$ is a particular state, and $a$ is an action.
We'll apply a technique called Monte-Carlo Policy Gradient which means we will have the agent run through an entire episode and then update our policy based on the rewards obtained.
## Model Construction
### Create Neural Network Model
We will use a simple feed forward neural network with one hidden layer of 128 neurons and a dropout of 0.6. We'll use Adam as our optimizer and a learning rate of 0.01. Using dropout will significantly improve the performance of our policy. I encourage you to compare results with and without dropout and experiment with other hyper-parameter values.
```
#Hyperparameters
learning_rate = 1e-2
gamma = 0.99
class Policy(nn.Module):
def __init__(self):
super(Policy, self).__init__()
state_space = env.observation_space.shape[0]
action_space = env.action_space.n
num_hidden = 128
self.l1 = nn.Linear(state_space, num_hidden, bias=False)
self.dropout = nn.Dropout(0.5)
self.l2 = nn.Linear(num_hidden, action_space, bias=False)
self.reward_history = []
self.reset()
def reset(self):
self.episode_actions = torch.Tensor([])
self.episode_rewards = []
def forward(self, x):
x = F.relu(self.dropout(self.l1(x)))
x = F.softmax(self.l2(x), dim=-1)
return x
```
### Select Action
The select_action function chooses an action based on our policy probability distribution using the PyTorch distributions package. Our policy returns a probability for each possible action in our action space (move left or move right) as an array of length two such as [0.7, 0.3]. We then choose an action based on these probabilities, record our history, and return our action.
```
def predict(state):
state = torch.from_numpy(state).type(torch.FloatTensor)
action_probs = policy(state)
distribution = torch.distributions.Categorical(action_probs)
action = distribution.sample()
# Add log probability of our chosen action to our history
policy.episode_actions = torch.cat([policy.episode_actions, distribution.log_prob(action).reshape(1)])
return action
```
### Reward $v_t$
We update our policy by taking a sample of the action value function $Q^{\pi_\theta} (s_t,a_t)$ by playing through episodes of the game. $Q^{\pi_\theta} (s_t,a_t)$ is defined as the expected return by taking action $a$ in state $s$ following policy $\pi$.
We know that for every step the simulation continues we receive a reward of 1. We can use this to calculate the policy gradient at each time step, where $r$ is the reward for a particular state-action pair. Rather than using the instantaneous reward, $r$, we instead use a long term reward $ v_{t} $ where $v_t$ is the discounted sum of all future rewards for the length of the episode. In this way, the **longer** the episode runs into the future, the **greater** the reward for a particular state-action pair in the present. $v_{t}$ is then,
$$ v_{t} = \sum_{k=0}^{N} \gamma^{k}r_{t+k} $$
where $\gamma$ is the discount factor (0.99). For example, if an episode lasts 5 steps, the reward for each step will be [4.90, 3.94, 2.97, 1.99, 1].
Next we scale our reward vector by substracting the mean from each element and scaling to unit variance by dividing by the standard deviation. This practice is common for machine learning applications and the same operation as Scikit Learn's __[StandardScaler](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html)__. It also has the effect of compensating for future uncertainty.
## Update Policy
After each episode we apply Monte-Carlo Policy Gradient to improve our policy according to the equation:
$$\Delta\theta_t = \alpha\nabla_\theta \, \log \pi_\theta (s_t,a_t)v_t $$
We will then feed our policy history multiplied by our rewards to our optimizer and update the weights of our neural network using stochastic gradent *ascent*. This should increase the likelihood of actions that got our agent a larger reward.
```
def update_policy():
R = 0
rewards = []
# backtracking rewards-to-go and calculate returns
for r in policy.episode_rewards[::-1]:
R = r + gamma * R
rewards.insert(0, R)
# Scale rewards
rewards = torch.FloatTensor(rewards)
rewards = (rewards - rewards.mean()) / (rewards.std() + np.finfo(np.float32).eps)
# Calculate loss
loss = (torch.sum(torch.mul(policy.episode_actions, rewards).mul(-1), -1))
# Update network weights
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Save and intialize episode history counters
policy.reward_history.append(np.sum(policy.episode_rewards))
policy.reset()
```
### Training
This is our main policy training loop. For each step in a training episode, we choose an action, take a step through the environment, and record the resulting new state and reward. We call update_policy() at the end of each episode to feed the episode history to our neural network and improve our policy.
```
def train(episodes):
episode_rewards = []
for episode in range(episodes):
state = env.reset()
for time in range(1000):
action = predict(state)
state, reward, done, _ = env.step(action.item())
policy.episode_rewards.append(reward)
if done:
break
episode_rewards.append(np.sum(policy.episode_rewards))
mean_episode_reward = np.mean(episode_rewards[-100:])
if episode % 50 == 0:
print(episode, "episodes finished (with average sum of rewards: {:.2f})".format(mean_episode_reward))
if mean_episode_reward > env.spec.reward_threshold:
print("===============================")
print("Solved after", episode, "episodes.")
print("Running average:", mean_episode_reward)
break
update_policy()
```
## Run Model
```
policy = Policy()
optimizer = optim.Adam(policy.parameters(), lr=learning_rate)
train(episodes=500)
```
Usually, the policy solves the environment prior to reaching 600 episodes for Cartpole-v1 (473 episodes with an average of 477.71) and around 300 episodes for Cartpole-v0 (298 episodes with an average of 195.81).
For the requirements of the environment see also how they get registered in gym:
```
register(
id='CartPole-v0',
entry_point='gym.envs.classic_control:CartPoleEnv',
max_episode_steps=200,
reward_threshold=195.0,
)
register(
id='CartPole-v1',
entry_point='gym.envs.classic_control:CartPoleEnv',
max_episode_steps=500,
reward_threshold=475.0,
)
```
### Plot Results
```
sns.set(style="darkgrid")
ax = sns.lineplot(style="event", hue="event", data=pd.Series(policy.reward_history), dashes=False, ci="sd")
ax.set_title('Episode Length')
ax.set_xlabel('Episode')
ax.set_ylabel('Episode Length')
plt.show()
mean = pd.Series(policy.reward_history).rolling(50).mean()
std = pd.Series(policy.reward_history).rolling(50).std()
sns.set(style="darkgrid")
ax = sns.lineplot(style="event", hue="event", data=mean, dashes=False, ci="sd")
ax.fill_between(range(len(policy.reward_history)), mean-std, mean+std, color='red', alpha=0.2)
plt.show()
```
|
github_jupyter
|
import gym
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from tqdm import tqdm, trange
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.autograd import Variable
%matplotlib inline
env = gym.make('CartPole-v1')
#env = gym.make('MountainCar-v0')
env.seed(1)
_ = torch.manual_seed(1) #suppress stdout
#Hyperparameters
learning_rate = 1e-2
gamma = 0.99
class Policy(nn.Module):
def __init__(self):
super(Policy, self).__init__()
state_space = env.observation_space.shape[0]
action_space = env.action_space.n
num_hidden = 128
self.l1 = nn.Linear(state_space, num_hidden, bias=False)
self.dropout = nn.Dropout(0.5)
self.l2 = nn.Linear(num_hidden, action_space, bias=False)
self.reward_history = []
self.reset()
def reset(self):
self.episode_actions = torch.Tensor([])
self.episode_rewards = []
def forward(self, x):
x = F.relu(self.dropout(self.l1(x)))
x = F.softmax(self.l2(x), dim=-1)
return x
def predict(state):
state = torch.from_numpy(state).type(torch.FloatTensor)
action_probs = policy(state)
distribution = torch.distributions.Categorical(action_probs)
action = distribution.sample()
# Add log probability of our chosen action to our history
policy.episode_actions = torch.cat([policy.episode_actions, distribution.log_prob(action).reshape(1)])
return action
def update_policy():
R = 0
rewards = []
# backtracking rewards-to-go and calculate returns
for r in policy.episode_rewards[::-1]:
R = r + gamma * R
rewards.insert(0, R)
# Scale rewards
rewards = torch.FloatTensor(rewards)
rewards = (rewards - rewards.mean()) / (rewards.std() + np.finfo(np.float32).eps)
# Calculate loss
loss = (torch.sum(torch.mul(policy.episode_actions, rewards).mul(-1), -1))
# Update network weights
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Save and intialize episode history counters
policy.reward_history.append(np.sum(policy.episode_rewards))
policy.reset()
def train(episodes):
episode_rewards = []
for episode in range(episodes):
state = env.reset()
for time in range(1000):
action = predict(state)
state, reward, done, _ = env.step(action.item())
policy.episode_rewards.append(reward)
if done:
break
episode_rewards.append(np.sum(policy.episode_rewards))
mean_episode_reward = np.mean(episode_rewards[-100:])
if episode % 50 == 0:
print(episode, "episodes finished (with average sum of rewards: {:.2f})".format(mean_episode_reward))
if mean_episode_reward > env.spec.reward_threshold:
print("===============================")
print("Solved after", episode, "episodes.")
print("Running average:", mean_episode_reward)
break
update_policy()
policy = Policy()
optimizer = optim.Adam(policy.parameters(), lr=learning_rate)
train(episodes=500)
register(
id='CartPole-v0',
entry_point='gym.envs.classic_control:CartPoleEnv',
max_episode_steps=200,
reward_threshold=195.0,
)
register(
id='CartPole-v1',
entry_point='gym.envs.classic_control:CartPoleEnv',
max_episode_steps=500,
reward_threshold=475.0,
)
sns.set(style="darkgrid")
ax = sns.lineplot(style="event", hue="event", data=pd.Series(policy.reward_history), dashes=False, ci="sd")
ax.set_title('Episode Length')
ax.set_xlabel('Episode')
ax.set_ylabel('Episode Length')
plt.show()
mean = pd.Series(policy.reward_history).rolling(50).mean()
std = pd.Series(policy.reward_history).rolling(50).std()
sns.set(style="darkgrid")
ax = sns.lineplot(style="event", hue="event", data=mean, dashes=False, ci="sd")
ax.fill_between(range(len(policy.reward_history)), mean-std, mean+std, color='red', alpha=0.2)
plt.show()
| 0.874854 | 0.968201 |
# Introduction à xarray
`xarray` est une librarie Python conçue pour faciliter les manipulations de données sur grille. xarray peut lire différents formats de fichiers, dont netCDF et grib. Il existe beaucoup de matériel de formation sur xarray, et on ne présente ici qu'un très, très bref aperçu.
Pour une présentation plus en profondeur, consultez http://xarray.pydata.org
```
import xarray as xr
```
```
%matplotlib inline
```
## Ouvrir un fichier
```
ds = xr.open_dataset('../../../tests/testdata/CRCM5/tasmax_bby_198406_se.nc')
ds
```
dimension coordinates are one dimensional coordinates with a name equal to their sole dimension (marked by * when printing a dataset or data array).
## On accède aux dimensions par leur nom
Dans la plupart des interfaces netCDF, on manipule un cube de données en n-dimensions, et on doit se référer aux attributs pour savoir quel est l'indice de la dimension time, lat lon. Si vous voulez accéder aux éléments du premier time step, il faut d'abord savoir si la dimension du temps et la première, deuxième ou troisième.
On peut faire la même chose avec `xarray`:
```
ds.tasmax[0]
```
Mais on peut aussi accéder aux données par le nom de leur dimension via leur indice par la méhode `isel`:
```
ds.tasmax.isel(time=0)
```
où la valeur de la coordonnée par la méthode `sel`:
```
ds.tasmax.sel(time='1984-06-01')
```
## Faire un graphique ne demande pas tellement d'efforts
```
ds.tasmax.sel(time='1984-06-01').plot(figsize=(10,8), aspect='equal')
```
## On peut sélectionner plusieurs dimensions à la fois
Le méthode `sel` permet d'aller chercher les valeurs pour une coordonnée précise, une plage de coordonnées, ou même par plus proche voisin. Toutes ces sélections peuvent être mélangées dans n'importe quel ordre.
```
ds.tasmax.sel(time='1984-06-03', rlat=slice(-10, 15), rlon=slice(10, 35)).plot()
```
Ou aller chercher les valeurs de la coordonnées la plus proche:
```
ds.tasmax.sel(rlat=34, method='nearest', tolerance=1).isel(time=0)
```
## Les opérations se font aussi selon les dimensions
Comme pour la sélection, les opérations sont effectuées le long de dimensions nommées explicitement.
```
# Le max pour tous les pas de temps
ds.tasmax.max(dim='time')
# Le max pour chaque pas de temps
ds.tasmax.max(dim=('rlon', 'rlat'))
```
## Les calendriers non-standards sont supportés
L'exemple plus haut utilise un calendrier `365_day`, automatiquement reconnu.
## Le rééchantillonnage est trop facile
On peut agréger une série à n'importe quelle échelle temporelle, peu importe que le calendrier soit standard ou pas. La méthode `resample` prend un paramètre de fréquence (`freq`) et retourne des groupes sur lesquels ont peut appliquer des opérateurs.
```
g = ds.tasmax.resample(time='3D')
g.groups
g.mean()
#g.mean().plot.line(marker='o')
```
## On peut faire facilement des vraies cartes projetées
```
from matplotlib import pyplot as plt
import cartopy.crs as ccrs
# On crée la projection permettant d'interpréter les données brutes
rp = ccrs.RotatedPole(pole_longitude=ds.rotated_pole.grid_north_pole_longitude,
pole_latitude=ds.rotated_pole.grid_north_pole_latitude,
central_rotated_longitude=ds.rotated_pole.north_pole_grid_longitude)
# On crée la figure et ses axes. L'axe 1 utilise la projection native, et l'axe 2 une projection stéréographique.
fig = plt.figure(figsize=(18,7))
ax1 = plt.subplot(121, projection=rp)
ax2 = plt.subplot(122, projection=ccrs.Stereographic(central_longitude=-100, central_latitude=45))
# On calcule la valeur à cartographier
x = ds.tasmax.mean(dim='time')
# Notez le paramètre "transform"
x.plot(ax=ax1, transform=rp, cbar_kwargs={'shrink': 0.8})
x.plot(ax=ax2, transform=rp, cbar_kwargs={'shrink': 0.8})
ax1.set_title('Rotated pole projection')
ax2.set_title('Stereographic projection')
ax1.coastlines()
ax2.coastlines()
plt.close()
fig
```
|
github_jupyter
|
import xarray as xr
%matplotlib inline
ds = xr.open_dataset('../../../tests/testdata/CRCM5/tasmax_bby_198406_se.nc')
ds
ds.tasmax[0]
ds.tasmax.isel(time=0)
ds.tasmax.sel(time='1984-06-01')
ds.tasmax.sel(time='1984-06-01').plot(figsize=(10,8), aspect='equal')
ds.tasmax.sel(time='1984-06-03', rlat=slice(-10, 15), rlon=slice(10, 35)).plot()
ds.tasmax.sel(rlat=34, method='nearest', tolerance=1).isel(time=0)
# Le max pour tous les pas de temps
ds.tasmax.max(dim='time')
# Le max pour chaque pas de temps
ds.tasmax.max(dim=('rlon', 'rlat'))
g = ds.tasmax.resample(time='3D')
g.groups
g.mean()
#g.mean().plot.line(marker='o')
from matplotlib import pyplot as plt
import cartopy.crs as ccrs
# On crée la projection permettant d'interpréter les données brutes
rp = ccrs.RotatedPole(pole_longitude=ds.rotated_pole.grid_north_pole_longitude,
pole_latitude=ds.rotated_pole.grid_north_pole_latitude,
central_rotated_longitude=ds.rotated_pole.north_pole_grid_longitude)
# On crée la figure et ses axes. L'axe 1 utilise la projection native, et l'axe 2 une projection stéréographique.
fig = plt.figure(figsize=(18,7))
ax1 = plt.subplot(121, projection=rp)
ax2 = plt.subplot(122, projection=ccrs.Stereographic(central_longitude=-100, central_latitude=45))
# On calcule la valeur à cartographier
x = ds.tasmax.mean(dim='time')
# Notez le paramètre "transform"
x.plot(ax=ax1, transform=rp, cbar_kwargs={'shrink': 0.8})
x.plot(ax=ax2, transform=rp, cbar_kwargs={'shrink': 0.8})
ax1.set_title('Rotated pole projection')
ax2.set_title('Stereographic projection')
ax1.coastlines()
ax2.coastlines()
plt.close()
fig
| 0.417984 | 0.986992 |
<a href="https://colab.research.google.com/github/https-deeplearning-ai/tensorflow-1-public/blob/master/C3/W2/ungraded_labs/C3_W2_Lab_1_imdb.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Ungraded Lab: Training a binary classifier with the IMDB Reviews Dataset
In this lab, you will be building a sentiment classification model to distinguish between positive and negative movie reviews. You will train it on the [IMDB Reviews](http://ai.stanford.edu/~amaas/data/sentiment/) dataset and visualize the word embeddings generated after training.
Let's get started!
## Download the Dataset
First, you will need to fetch the dataset you will be working on. This is hosted via [Tensorflow Datasets](https://www.tensorflow.org/datasets), a collection of prepared datasets for machine learning. If you're running this notebook on your local machine, make sure to have the [`tensorflow-datasets`](https://pypi.org/project/tensorflow-datasets/) package installed before importing it. You can install it via `pip` as shown in the commented cell below.
```
# Install this package if running on your local machine
!pip install -q tensorflow-datasets
```
The [`tfds.load`](https://www.tensorflow.org/datasets/api_docs/python/tfds/load) method downloads the dataset into your working directory. You can set the `with_info` parameter to `True` if you want to see the description of the dataset. The `as_supervised` parameter, on the other hand, is set to load the data as `(input, label)` pairs.
```
import tensorflow_datasets as tfds
# Load the IMDB Reviews dataset
imdb, info = tfds.load("imdb_reviews", with_info=True, as_supervised=True)
# Print information about the dataset
print(info)
```
As you can see in the output above, there is a total of 100,000 examples in the dataset and it is split into `train`, `test` and `unsupervised` sets. For this lab, you will only use `train` and `test` sets because you will need labeled examples to train your model.
## Split the dataset
If you try printing the `imdb` dataset that you downloaded earlier, you will see that it contains the dictionary that points to [`tf.data.Dataset`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset) objects. You will explore more of this class and its API in Course 4 of this specialization. For now, you can just think of it as a collection of examples.
```
# Print the contents of the dataset you downloaded
print(imdb)
```
You can preview the raw format of a few examples by using the [`take()`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#take) method and iterating over it as shown below:
```
# Take 2 training examples and print its contents
for example in imdb['train'].take(2):
print(example)
```
You can see that each example is a 2-element tuple of tensors containing the text first, then the label (shown in the `numpy()` property). The next cell below will take all the `train` and `test` sentences and labels into separate lists so you can preprocess the text and feed it to the model later.
```
import numpy as np
# Get the train and test sets
train_data, test_data = imdb['train'], imdb['test']
# Initialize sentences and labels lists
training_sentences = []
training_labels = []
testing_sentences = []
testing_labels = []
# Loop over all training examples and save the sentences and labels
for s,l in train_data:
training_sentences.append(s.numpy().decode('utf8'))
training_labels.append(l.numpy())
# Loop over all test examples and save the sentences and labels
for s,l in test_data:
testing_sentences.append(s.numpy().decode('utf8'))
testing_labels.append(l.numpy())
# Convert labels lists to numpy array
training_labels_final = np.array(training_labels)
testing_labels_final = np.array(testing_labels)
```
## Generate Padded Sequences
Now you can do the text preprocessing steps you've learned last week. You will tokenize the sentences and pad them to a uniform length. We've separated the parameters into its own code cell below so it will be easy for you to tweak it later if you want.
```
# Parameters
vocab_size = 10000
max_length = 120
embedding_dim = 16
trunc_type='post'
oov_tok = "<OOV>"
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
# Initialize the Tokenizer class
tokenizer = Tokenizer(num_words = vocab_size, oov_token=oov_tok)
# Generate the word index dictionary for the training sentences
tokenizer.fit_on_texts(training_sentences)
word_index = tokenizer.word_index
# Generate and pad the training sequences
sequences = tokenizer.texts_to_sequences(training_sentences)
padded = pad_sequences(sequences,maxlen=max_length, truncating=trunc_type)
# Generate and pad the test sequences
testing_sequences = tokenizer.texts_to_sequences(testing_sentences)
testing_padded = pad_sequences(testing_sequences,maxlen=max_length)
```
## Build and Compile the Model
With the data already preprocessed, you can proceed to building your sentiment classification model. The input will be an [`Embedding`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Embedding) layer. The main idea here is to represent each word in your vocabulary with vectors. These vectors have trainable weights so as your neural network learns, words that are most likely to appear in a positive tweet will converge towards similar weights. Similarly, words in negative tweets will be clustered more closely together. You can read more about word embeddings [here](https://www.tensorflow.org/text/guide/word_embeddings).
After the `Embedding` layer, you will flatten its output and feed it into a `Dense` layer. You will explore other architectures for these hidden layers in the next labs.
The output layer would be a single neuron with a sigmoid activation to distinguish between the 2 classes. As is typical with binary classifiers, you will use the `binary_crossentropy` as your loss function while training.
```
import tensorflow as tf
# Build the model
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(6, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
# Setup the training parameters
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
# Print the model summary
model.summary()
```
## Train the Model
Next, of course, is to train your model. With the current settings, you will get near perfect training accuracy after just 5 epochs but the validation accuracy will plateau at around 83%. See if you can still improve this by adjusting some of the parameters earlier (e.g. the `vocab_size`, number of `Dense` neurons, number of epochs, etc.).
```
num_epochs = 10
# Train the model
model.fit(padded, training_labels_final, epochs=num_epochs, validation_data=(testing_padded, testing_labels_final))
```
## Visualize Word Embeddings
After training, you can visualize the trained weights in the `Embedding` layer to see words that are clustered together. The [Tensorflow Embedding Projector](https://projector.tensorflow.org/) is able to reduce the 16-dimension vectors you defined earlier into fewer components so it can be plotted in the projector. First, you will need to get these weights and you can do that with the cell below:
```
# Get the embedding layer from the model (i.e. first layer)
embedding_layer = model.layers[0]
# Get the weights of the embedding layer
embedding_weights = embedding_layer.get_weights()[0]
# Print the shape. Expected is (vocab_size, embedding_dim)
print(embedding_weights.shape)
```
You will need to generate two files:
* `vecs.tsv` - contains the vector weights of each word in the vocabulary
* `meta.tsv` - contains the words in the vocabulary
For this, it is useful to have `reverse_word_index` dictionary so you can quickly lookup a word based on a given index. For example, `reverse_word_index[1]` will return your OOV token because it is always at index = 1. Fortunately, the `Tokenizer` class already provides this dictionary through its `index_word` property. Yes, as the name implies, it is the reverse of the `word_index` property which you used earlier!
```
# Get the index-word dictionary
reverse_word_index = tokenizer.index_word
```
Now you can start the loop to generate the files. You will loop `vocab_size-1` times, skipping the `0` key because it is just for the padding.
```
import io
# Open writeable files
out_v = io.open('vecs.tsv', 'w', encoding='utf-8')
out_m = io.open('meta.tsv', 'w', encoding='utf-8')
# Initialize the loop. Start counting at `1` because `0` is just for the padding
for word_num in range(1, vocab_size):
# Get the word associated at the current index
word_name = reverse_word_index[word_num]
# Get the embedding weights associated with the current index
word_embedding = embedding_weights[word_num]
# Write the word name
out_m.write(word_name + "\n")
# Write the word embedding
out_v.write('\t'.join([str(x) for x in word_embedding]) + "\n")
# Close the files
out_v.close()
out_m.close()
```
When running this on Colab, you can run the code below to download the files. Otherwise, you can see the files in your current working directory and download it manually.
```
# Import files utilities in Colab
try:
from google.colab import files
except ImportError:
pass
# Download the files
else:
files.download('vecs.tsv')
files.download('meta.tsv')
```
Now you can go to the [Tensorflow Embedding Projector](https://projector.tensorflow.org/) and load the two files you downloaded to see the visualization. You can search for words like `worst` and `fantastic` and see the other words closely located to these.
## Wrap Up
In this lab, you were able build a simple sentiment classification model and train it on preprocessed text data. In the next lessons, you will revisit the Sarcasm Dataset you used in Week 1 and build a model to train on it.
|
github_jupyter
|
# Install this package if running on your local machine
!pip install -q tensorflow-datasets
import tensorflow_datasets as tfds
# Load the IMDB Reviews dataset
imdb, info = tfds.load("imdb_reviews", with_info=True, as_supervised=True)
# Print information about the dataset
print(info)
# Print the contents of the dataset you downloaded
print(imdb)
# Take 2 training examples and print its contents
for example in imdb['train'].take(2):
print(example)
import numpy as np
# Get the train and test sets
train_data, test_data = imdb['train'], imdb['test']
# Initialize sentences and labels lists
training_sentences = []
training_labels = []
testing_sentences = []
testing_labels = []
# Loop over all training examples and save the sentences and labels
for s,l in train_data:
training_sentences.append(s.numpy().decode('utf8'))
training_labels.append(l.numpy())
# Loop over all test examples and save the sentences and labels
for s,l in test_data:
testing_sentences.append(s.numpy().decode('utf8'))
testing_labels.append(l.numpy())
# Convert labels lists to numpy array
training_labels_final = np.array(training_labels)
testing_labels_final = np.array(testing_labels)
# Parameters
vocab_size = 10000
max_length = 120
embedding_dim = 16
trunc_type='post'
oov_tok = "<OOV>"
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
# Initialize the Tokenizer class
tokenizer = Tokenizer(num_words = vocab_size, oov_token=oov_tok)
# Generate the word index dictionary for the training sentences
tokenizer.fit_on_texts(training_sentences)
word_index = tokenizer.word_index
# Generate and pad the training sequences
sequences = tokenizer.texts_to_sequences(training_sentences)
padded = pad_sequences(sequences,maxlen=max_length, truncating=trunc_type)
# Generate and pad the test sequences
testing_sequences = tokenizer.texts_to_sequences(testing_sentences)
testing_padded = pad_sequences(testing_sequences,maxlen=max_length)
import tensorflow as tf
# Build the model
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(6, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
# Setup the training parameters
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
# Print the model summary
model.summary()
num_epochs = 10
# Train the model
model.fit(padded, training_labels_final, epochs=num_epochs, validation_data=(testing_padded, testing_labels_final))
# Get the embedding layer from the model (i.e. first layer)
embedding_layer = model.layers[0]
# Get the weights of the embedding layer
embedding_weights = embedding_layer.get_weights()[0]
# Print the shape. Expected is (vocab_size, embedding_dim)
print(embedding_weights.shape)
# Get the index-word dictionary
reverse_word_index = tokenizer.index_word
import io
# Open writeable files
out_v = io.open('vecs.tsv', 'w', encoding='utf-8')
out_m = io.open('meta.tsv', 'w', encoding='utf-8')
# Initialize the loop. Start counting at `1` because `0` is just for the padding
for word_num in range(1, vocab_size):
# Get the word associated at the current index
word_name = reverse_word_index[word_num]
# Get the embedding weights associated with the current index
word_embedding = embedding_weights[word_num]
# Write the word name
out_m.write(word_name + "\n")
# Write the word embedding
out_v.write('\t'.join([str(x) for x in word_embedding]) + "\n")
# Close the files
out_v.close()
out_m.close()
# Import files utilities in Colab
try:
from google.colab import files
except ImportError:
pass
# Download the files
else:
files.download('vecs.tsv')
files.download('meta.tsv')
| 0.88839 | 0.992415 |
<font face="Verdana, cursive, sans-serif" >
<H1><center>Map Visualization with leaflets.js and mapbox.js</center></H1>
<font face="Verdana, cursive, sans-serif" >
<p>This notebook explains how to overlay data on a geo shape file. There 2 parts in this program. The first part explains how to add new attributes from a csv file to a shape-json file. The second part explain how the pre-coded javascript works</p>
<b>Self-paced Learning Resources</b>
<ul>
<li><a href="https://www.youtube.com/watch?v=SCAqyPfwzcU">Complete leaflets tutorial</a></li>
<li><a href="http://leafletjs.com/examples/choropleth/">Leaflet.js - Interactive Choropleth</a></li>
<li><a href="https://www.mapbox.com/help/tutorials/">Mapbox turorials</a></li>
<li><a href="https://www.mapbox.com/api-documentation/#maps">Mapbox style</a></li>
<li><a href="https://github.com/codeforamerica/click_that_hood/tree/master/public/data">Country Polygon Files</a></li>
</ul>
<font face="Verdana, cursive, sans-serif" >
<br>
<H2>Part 1 : Merge GeoJson with external Data </H2>
<br>
<img src="./image/part1.png" >
<font face="Verdana, cursive, sans-serif" >
<h3>Importing packages</h3>
The json package is used for processing json format files in python
https://docs.python.org/2/library/json.html
```
import pandas as pd
import numpy as np
import json
```
<font face="Verdana, cursive, sans-serif" >
<h3>Define input / output files</h3>
```
data_csvfile = './data/ext_province_th.csv'
shape_jsonfile = './data/thailand.json'
output_js = './data/th_geo.js'
```
<font face="Verdana, cursive, sans-serif" >
<h3>Depends on the csv file, carefully identify the key needed to use for merging</h3>
<p>
<img src="./image/th_key.png" >
Note that the key values should be: <b>cleaned, upcased and no spaces</b>
```
#this is the key column to merge btw the shape file and the external data
key='provinces'
```
<font face="Verdana, cursive, sans-serif" >
<h3>Read and pre-process the csv data</h3>
<p>Please note that the csv data used in this program a a mockup data</p>
```
data_csv = pd.read_csv(data_csvfile)
data_csv.fillna(0,inplace=True)
data_csv.head()
# Pre-processing (convert numeric to same serializable format )
for col in data_csv.columns:
if data_csv[col].dtype == 'int64':
data_csv[col] = data_csv[col].astype(np.float64)
```
<font face="Verdana, cursive, sans-serif" >
<h3>Read and pre-process the shape file</h3>
<p>Depends on the shape file, carefully identify the features-names needed to use for processing and merging
<p>
<img src="./image/th_shapejson.png" >
```
with open(shape_jsonfile, "r") as jsonFile:
data_shapejson = json.load(jsonFile)
#grab all nodes, put it in a dictionary for later processing
geo_map = {}
for f in data_shapejson['features']:
k = f['properties']['name']
v = k.replace(" ","").upper()
geo_map[k] = v
# It is good to check the number of nodes that we have, for Thailand, it should be 77 because we have 77 provinces
print(len(geo_map))
```
<font face="Verdana, cursive, sans-serif" >
<h3>For each item in csv, add a new node 'info' at the corresponding key</h3>
```
for f in data_shapejson['features']:
info = {}
name = f['properties']['name']
info['name'] = name
if not name in geo_map.keys():
continue
value_df = data_csv[data_csv[key]==geo_map[name]].reset_index(drop=True)
for col in [x for x in data_csv.columns.values if x not in [key]]:
info[col] = value_df[col].values[0]
f['info'] = info
print(data_shapejson['features'][0]['properties']['name'])
print(data_shapejson['features'][0]['info']['total_pop'])
print(data_shapejson['features'][0]['info']['avg_income'])
print(data_shapejson['features'][0]['info']['mkt_penlt'])
```
<font face="Verdana, cursive, sans-serif" >
<h3>Save data+shape json into a javascript file</h3>
<p><code>var locationId</code> is needed for leaflets.js, hence we are going to assigned the whole json body into this variable and save it into a javascript file
```
tmp = json.dumps(data_shapejson)
output_var = 'var locationId = [' + tmp + ']'
print("writing js to {}".format(output_js))
with open(output_js, 'w') as the_file:
the_file.write(output_var)
```
<font face="Verdana, cursive, sans-serif" >
<br>
<H2>Part 2 : Leaflets.js Configuration </H2>
<p></p>
An html is provided; of which all actions has been implemented in <code>script/setup_past_1.js</code> and <code>script/setup_part_2.js</code>
<br><code>MapViz - Thailand.html</code>
<img src="./image/mapviz_th.png" >
<p></p>
This section shows how all javascripts are imported
<img src="./image/import_html.png" >
<p></p>
This section shows how to add new attributes in the dropdown lists and how to add more color themes
<img src="./image/color_scale.png" >
Note that, the scales of each themes are calculated dynamically based on the input <code>max,min</code>
<br>Should you need to add more themes, please edit <code>script/setup_past_1.js</code>
<p></p>
To modify the top right title and to configurate which data to show on the top right section
<img src="./image/hover.png" >
<img src="./image/show_hover.png" >
<p></p>
To modify popup onclick icon and onclick polygon
<img src="./image/popup.png" >
<p></p>
Finally, this shows how the geojson data get loaded into the html
<img src="./image/locationId.png" >
|
github_jupyter
|
import pandas as pd
import numpy as np
import json
data_csvfile = './data/ext_province_th.csv'
shape_jsonfile = './data/thailand.json'
output_js = './data/th_geo.js'
#this is the key column to merge btw the shape file and the external data
key='provinces'
data_csv = pd.read_csv(data_csvfile)
data_csv.fillna(0,inplace=True)
data_csv.head()
# Pre-processing (convert numeric to same serializable format )
for col in data_csv.columns:
if data_csv[col].dtype == 'int64':
data_csv[col] = data_csv[col].astype(np.float64)
with open(shape_jsonfile, "r") as jsonFile:
data_shapejson = json.load(jsonFile)
#grab all nodes, put it in a dictionary for later processing
geo_map = {}
for f in data_shapejson['features']:
k = f['properties']['name']
v = k.replace(" ","").upper()
geo_map[k] = v
# It is good to check the number of nodes that we have, for Thailand, it should be 77 because we have 77 provinces
print(len(geo_map))
for f in data_shapejson['features']:
info = {}
name = f['properties']['name']
info['name'] = name
if not name in geo_map.keys():
continue
value_df = data_csv[data_csv[key]==geo_map[name]].reset_index(drop=True)
for col in [x for x in data_csv.columns.values if x not in [key]]:
info[col] = value_df[col].values[0]
f['info'] = info
print(data_shapejson['features'][0]['properties']['name'])
print(data_shapejson['features'][0]['info']['total_pop'])
print(data_shapejson['features'][0]['info']['avg_income'])
print(data_shapejson['features'][0]['info']['mkt_penlt'])
tmp = json.dumps(data_shapejson)
output_var = 'var locationId = [' + tmp + ']'
print("writing js to {}".format(output_js))
with open(output_js, 'w') as the_file:
the_file.write(output_var)
| 0.130604 | 0.8474 |
# Basic Qiskit Syntax
### Installation
Qiskit is a package in Python for doing everything you'll ever need with quantum computing.
If you don't have it already, you need to install it. Once it is installed, you need to import it.
There are generally two steps to installing Qiskit. The first one is to install Anaconda, a python package that comes with almost all dependencies that you will ever need. Once you've done this, Qiskit can then be installed by running the command
```
pip install qiskit
```
in your terminal. For detailed installation instructions, refer to [the documentation page here](https://qiskit.org/documentation/install.html).
**Note: The rest of this section is intended for people who already know the fundamental concepts of quantum computing.** It can be used by readers who wish to skip straight to the later chapters in which those concepts are put to use. All other readers should read the [Introduction to Python and Jupyter notebooks](../ch-prerequisites/python-and-jupyter-notebooks.html), and then move on directly to the start of [Chapter 1](../ch-states/introduction.html).
### Quantum circuits
```
from qiskit import *
# For Jupyter Notebooks:
%config InlineBackend.figure_format = 'svg' # Makes the images look nice
```
The object at the heart of Qiskit is the quantum circuit. Here's how we create one, which we will call `qc`
```
qc = QuantumCircuit()
```
This circuit is currently completely empty, with no qubits and no outputs.
### Quantum registers
To make the circuit less trivial, we need to define a register of qubits. This is done using a `QuantumRegister` object. For example, let's define a register consisting of two qubits and call it `qr`.
```
qr = QuantumRegister(2,'qreg')
```
Giving it a name like `'qreg'` is optional.
Now we can add it to the circuit using the `add_register` method, and see that it has been added by checking the `qregs` variable of the circuit object. This guide uses [Jupyter Notebooks](https://jupyter.org/). In Jupter Notebooks, the output of the last line of a cell is displayed below the cell:
```
qc.add_register( qr )
qc.qregs
```
Now our circuit has some qubits, we can use another attribute of the circuit to see what it looks like: `draw()` .
```
qc.draw(output='mpl')
```
Our qubits are ready to begin their journey, but are currently just sitting there in state $\left|0\right\rangle$.
#### Applying Gates
To make something happen, we need to add gates. For example, let's try out `h()`.
```
qc.h()
```
Here we got an error, because we didn't tell the operation which qubit it should act on. The two qubits in our register `qr` can be individually addressed as `qr[0]` and `qr[1]`.
```
qc.h(qr[0])
```
Ignore the output in the above. When the last line of a cell has no `=`, Jupyter notebooks like to print out what is there. In this case, it's telling us that there is a Hadamard as defined by Qiskit. To suppress this output, we could use a `;`.
We can also add a controlled-NOT using `cx`. This requires two arguments: control qubit, and then target qubit.
```
qc.cx(qr[0], qr[1]);
```
Now our circuit has more to show
```
qc.draw(output='mpl')
```
### Statevector simulator
We are now at the stage that we can actually look at an output from the circuit. Specifically, we will use the 'statevector simulator' to see what is happening to the state vector of the two qubits.
To get this simulator ready to go, we use the following line.
```
vector_sim = Aer.get_backend('statevector_simulator')
```
In Qiskit, we use *backend* to refer to the things on which quantum programs actually run (simulators or real quantum devices). To set up a job for a backend, we need to set up the corresponding backend object.
The simulator we want is defined in the part of qiskit known as `Aer`. By giving the name of the simulator we want to the `get_backend()` method of Aer, we get the backend object we need. In this case, the name is `'statevector_simulator'`.
A list of all possible simulators in Aer can be found using
```
Aer.backends()
```
All of these simulators are 'local', meaning that they run on the machine on which Qiskit is installed. Using them on your own machine can be done without signing up to the IBMQ user agreement.
Running the simulation is done by Qiskit's `execute` command, which needs to be provided with the circuit to be run and the 'backend' to run it on (in this case, a simulator).
```
job = execute(qc, vector_sim)
```
This creates an object that handles the job, which here has been called `job`. All we need from this is to extract the result. Specifically, we want the state vector.
```
ket = job.result().get_statevector()
for amplitude in ket:
print(amplitude)
```
This is the vector for a Bell state $\left( \left|00\right\rangle + \left|11\right\rangle \right)/\sqrt{2}$, which is what we'd expect given the circuit.
While we have a nicely defined state vector, we can show another feature of Qiskit: it is possible to initialize a circuit with an arbitrary pure state.
```
new_qc = QuantumCircuit(qr)
new_qc.initialize(ket, qr)
```
### Classical registers and the qasm simulator
In the above simulation, we got out a statevector. That's not what we'd get from a real quantum computer. For that we need measurement. And to handle measurement we need to define where the results will go. This is done with a `ClassicalRegister`. Let's define a two bit classical register, in order to measure both of our two qubits.
```
cr = ClassicalRegister(2,'creg')
qc.add_register(cr)
```
Now we can use the `measure` method of the quantum circuit. This requires two arguments: the qubit being measured, and the bit where the result is written.
Let's measure both qubits, and write their results in different bits.
```
qc.measure(qr[0],cr[0])
qc.measure(qr[1],cr[1])
qc.draw(output='mpl')
```
Now we can run this on a local simulator whose effect is to emulate a real quantum device. For this we need to add another input to the `execute` function, `shots`, which determines how many times we run the circuit to take statistics. If you don't provide any `shots` value, you get the default of 1024.
```
emulator = Aer.get_backend('qasm_simulator')
job = execute( qc, emulator, shots=8192 )
```
The result is essentially a histogram in the form of a Python dictionary. We can use `print` to display this for us.
```
hist = job.result().get_counts()
print(hist)
```
We can even get Qiskit to plot it as a histogram.
```
from qiskit.visualization import plot_histogram
plot_histogram(hist)
```
For compatible backends we can also ask for and get the ordered list of results.
```
job = execute(qc, emulator, shots=10, memory=True)
samples = job.result().get_memory()
print(samples)
```
Note that the bits are labelled from right to left. So `cr[0]` is the one to the furthest right, and so on. As an example of this, here's an 8 qubit circuit with a Pauli $X$ on only the qubit numbered `7`, which has its output stored to the bit numbered `7`.
```
qubit = QuantumRegister(8)
bit = ClassicalRegister(8)
circuit = QuantumCircuit(qubit,bit)
circuit.x(qubit[7])
circuit.measure(qubit,bit) # this is a way to do all the qc.measure(qr8[j],cr8[j]) at once
execute(circuit, emulator, shots=8192).result().get_counts()
```
The `1` appears at the left.
This numbering reflects the role of the bits when they represent an integer.
$$ b_{n-1} ~ b_{n-2} ~ \ldots ~ b_1 ~ b_0 = \sum_j ~ b_j ~ 2^j $$
So the string we get in our result is the binary for $2^7$ because it has a `1` for the bit numbered `7`.
### Simplified notation
Multiple quantum and classical registers can be added to a circuit. However, if we need no more than one of each, we can use a simplified notation.
For example, consider the following.
```
qc = QuantumCircuit(3)
```
The single argument to `QuantumCircuit` is interpreted as the number of qubits we want. So this circuit is one that has a single quantum register consisting of three qubits, and no classical register.
When adding gates, we can then refer to the three qubits simply by their index: 0, 1 or 2. For example, here's a Hadamard on qubit 1.
```
qc.h(1)
qc.draw(output='mpl')
```
To define a circuit with both quantum and classical registers, we can supply two arguments to `QuantumCircuit`. The first will be interpreted as the number of qubits, and the second will be the number of bits. For example, here's a two qubit circuit for which we'll take a single bit of output.
```
qc = QuantumCircuit(2,1)
```
To see this in action, here is a simple circuit. Note that, when making a measurement, we also refer to the bits in the classical register by index.
```
qc.h(0)
qc.cx(0,1)
qc.measure(1,0)
qc.draw(output='mpl')
```
### Creating custom gates
As we've seen, it is possible to combine different circuits to make bigger ones. We can also use a more sophisticated version of this to make custom gates. For example, here is a circuit that implements a `cx` between qubits 0 and 2, using qubit 1 to mediate the process.
```
sub_circuit = QuantumCircuit(3, name='toggle_cx')
sub_circuit.cx(0,1)
sub_circuit.cx(1,2)
sub_circuit.cx(0,1)
sub_circuit.cx(1,2)
sub_circuit.draw(output='mpl')
```
We can now turn this into a gate
```
toggle_cx = sub_circuit.to_instruction()
```
and then insert it into other circuits using any set of qubits we choose
```
qr = QuantumRegister(4)
new_qc = QuantumCircuit(qr)
new_qc.append(toggle_cx, [qr[1],qr[2],qr[3]])
new_qc.draw(output='mpl')
```
### Accessing on real quantum hardware
Backend objects can also be set up using the `IBMQ` package. The use of these requires us to [sign with an IBMQ account](https://qiskit.org/documentation/install.html#access-ibm-q-systems). Assuming the credentials are already loaded onto your computer, you sign in with
```
IBMQ.load_account()
```
Now let's see what additional backends we have available.
```
provider = IBMQ.get_provider(hub='ibm-q')
provider.backends()
```
Here there is one simulator, but the rest are prototype quantum devices.
We can see what they are up to with the `status()` method.
```
for backend in provider.backends():
print(backend.status())
```
Let's get the backend object for the largest public device.
```
real_device = provider.get_backend('ibmq_16_melbourne')
```
We can use this to run a job on the device in exactly the same way as for the emulator.
We can also extract some of its properties.
```
properties = real_device.properties()
coupling_map = real_device.configuration().coupling_map
```
From this we can construct a noise model to mimic the noise on the device (we will discuss noise models further later in the textbook).
```
from qiskit.providers.aer.noise import NoiseModel
noise_model = NoiseModel.from_backend(properties)
```
And then run the job on the emulator, with it reproducing all these features of the real device. Here's an example with a circuit that should output `'10'` in the noiseless case.
```
qc = QuantumCircuit(2,2)
qc.x(1)
qc.measure(0,0)
qc.measure(1,1)
job = execute(qc, emulator, shots=1024, noise_model=noise_model,
coupling_map=coupling_map,
basis_gates=noise_model.basis_gates)
job.result().get_counts()
```
Now the very basics have been covered, let's learn more about what qubits and quantum circuits are all about.
```
import qiskit
qiskit.__qiskit_version__
```
|
github_jupyter
|
pip install qiskit
from qiskit import *
# For Jupyter Notebooks:
%config InlineBackend.figure_format = 'svg' # Makes the images look nice
qc = QuantumCircuit()
qr = QuantumRegister(2,'qreg')
qc.add_register( qr )
qc.qregs
qc.draw(output='mpl')
qc.h()
qc.h(qr[0])
qc.cx(qr[0], qr[1]);
qc.draw(output='mpl')
vector_sim = Aer.get_backend('statevector_simulator')
Aer.backends()
job = execute(qc, vector_sim)
ket = job.result().get_statevector()
for amplitude in ket:
print(amplitude)
new_qc = QuantumCircuit(qr)
new_qc.initialize(ket, qr)
cr = ClassicalRegister(2,'creg')
qc.add_register(cr)
qc.measure(qr[0],cr[0])
qc.measure(qr[1],cr[1])
qc.draw(output='mpl')
emulator = Aer.get_backend('qasm_simulator')
job = execute( qc, emulator, shots=8192 )
hist = job.result().get_counts()
print(hist)
from qiskit.visualization import plot_histogram
plot_histogram(hist)
job = execute(qc, emulator, shots=10, memory=True)
samples = job.result().get_memory()
print(samples)
qubit = QuantumRegister(8)
bit = ClassicalRegister(8)
circuit = QuantumCircuit(qubit,bit)
circuit.x(qubit[7])
circuit.measure(qubit,bit) # this is a way to do all the qc.measure(qr8[j],cr8[j]) at once
execute(circuit, emulator, shots=8192).result().get_counts()
qc = QuantumCircuit(3)
qc.h(1)
qc.draw(output='mpl')
qc = QuantumCircuit(2,1)
qc.h(0)
qc.cx(0,1)
qc.measure(1,0)
qc.draw(output='mpl')
sub_circuit = QuantumCircuit(3, name='toggle_cx')
sub_circuit.cx(0,1)
sub_circuit.cx(1,2)
sub_circuit.cx(0,1)
sub_circuit.cx(1,2)
sub_circuit.draw(output='mpl')
toggle_cx = sub_circuit.to_instruction()
qr = QuantumRegister(4)
new_qc = QuantumCircuit(qr)
new_qc.append(toggle_cx, [qr[1],qr[2],qr[3]])
new_qc.draw(output='mpl')
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
provider.backends()
for backend in provider.backends():
print(backend.status())
real_device = provider.get_backend('ibmq_16_melbourne')
properties = real_device.properties()
coupling_map = real_device.configuration().coupling_map
from qiskit.providers.aer.noise import NoiseModel
noise_model = NoiseModel.from_backend(properties)
qc = QuantumCircuit(2,2)
qc.x(1)
qc.measure(0,0)
qc.measure(1,1)
job = execute(qc, emulator, shots=1024, noise_model=noise_model,
coupling_map=coupling_map,
basis_gates=noise_model.basis_gates)
job.result().get_counts()
import qiskit
qiskit.__qiskit_version__
| 0.554953 | 0.991178 |
# autodiffpy Package Demo
```
!pip install update autodiffpy==1.2.8
# Import packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as graph
import autodiffpy.autodiffmod as ad
import autodiffpy.autodiff_math as admath
```
### Part 1: Standard automatic differentiation with elementary operations
```
# Create autodiff instances
x = ad.autodiff(name='x', val=[1.0, 2.0], der=[1.0, 1.0])
y = ad.autodiff(name='y', val=[-5.0, -3.0], der=[2.0, 1.0])
z = ad.autodiff(name='z', val=[0.5, -4.0], der=[1.0, 1.0])
# Examine each instance
print(x)
print("")
print(y)
print("")
print(z)
# Calculate various functions
f1 = (x/y)**2
f2 = x*z - 3 - y + z
f3 = (x**2)**z
# Examine each function
print(f1)
print("")
print(f2)
print("")
print(f3)
# Generate jacobian for just two variables
print(f2.jacobian(order=['x', 'y']))
```
### Part 2: Standard automatic differentiation with mathematical operations
```
# Create autodiff instances again
x = ad.autodiff(name='x', val=[1.0, 2.0], der=[1.0, 1.0])
y = ad.autodiff(name='y', val=[-5.0, -3.0], der=[1.0, 1.0])
z = ad.autodiff(name='z', val=[0.5, -4.0], der=[1.0, 1.0])
# Examine each instance again
print(x)
print("")
print(y)
print("")
print(z)
# Calculate various functions
f1 = admath.sinh(admath.cosh(x*np.pi/2.0))
f2 = admath.log(admath.exp(-y/z))
f3 = admath.sqrt(x**2 + z**2)
# Examine each function
print(f1)
print("")
print(f2)
print("")
print(f3)
```
### Part 3: Exploring derivatives calculated through automatic differentiation
```
# Create new autodiff instances
numpoints = 100
xval = np.linspace(0, 5*np.pi, numpoints)
x1 = ad.autodiff(name='x1', val=xval, der=np.ones(numpoints))
x2 = ad.autodiff(name='x2', val=xval, der=np.ones(numpoints))
# Create a function
f1 = 4*admath.sin(x1/2) + 2*admath.cos(x2*3)
# Graph first function and its derivative
graph.plot(xval, f1.val, color='black', linewidth=3, linestyle='-', label='Sine + Cosine')
graph.plot(xval, f1.der['x1'], color='blue', linewidth=3, linestyle='--', label='x1 Derivative')
graph.plot(xval, f1.der['x2'], color='red', linewidth=3, linestyle='--', label='x2 Derivative')
graph.xlabel('Inputs')
graph.ylabel('Outputs')
graph.title('Sine + Cosine and its Derivative')
graph.legend(loc='best')
graph.show()
# Create new autodiff instances
numpoints = 100
y = ad.autodiff(name='y', val=np.linspace(0, 10, numpoints), der=np.ones(numpoints))
# Create a function
f2 = (2*((y - 5)**2) + 3*y - 5)
# Graph second function and its derivative
graph.plot(y.val, f2.val, color='black', linewidth=3, linestyle='-', label='Quadratic')
graph.plot(y.val, f2.der['y'], color='blue', linewidth=3, linestyle='--', label='Derivative')
graph.xlabel('Inputs')
graph.ylabel('Outputs')
graph.title('Quadratic and its Derivative')
graph.legend(loc='best')
graph.show()
```
### Part 4: Gradient descent with MAE loss on noisy linear data
```
# Read in and process data file (will be used later in this demo)
data = pd.read_csv("demo.csv") # Demo data
X_data = data.drop('y', axis = 1) # Input x-data
Y_true = data['y'] # Actual y-values
# Create initial weights for the data
w = ad.autodiff('w', [1 for i in X_data.columns.values]) # Initialize weights to all ones
f1 = w*X_data # Functional form
# Run MAE-loss gradient descent
g = ad.gradient_descent(f1, Y_true, loss='MAE', beta=0.001, max_iter=5000, tol=1E-5)
# Print characteristics of this gradient descent
print("Initial loss:", g["loss_array"][0])
print("Final loss:", g["loss_array"][-1])
print(f"Final weights: {g['w'].val}")
# Graph the loss as a function of iterations
xgrid = np.linspace(1, g['num_iter']+1, g["num_iter"])
graph.plot(xgrid, g['loss_array'])
graph.title('MAE Loss vs. Iteration for Linear Noisy Data')
graph.xlabel('Iteration')
graph.ylabel('Loss')
graph.show()
```
### Part 5: Gradient descent with MSE loss on noisy logistic data
```
# Create initial weights for the data
w = ad.autodiff('w', [1 for i in X_data.columns.values]) # Initialize weights to all ones
f2 = admath.logistic(w*X_data)
# Run MSE-loss gradient descent
g = ad.gradient_descent(f2, Y_true, loss='MSE', beta=0.005, max_iter=5000, tol=1E-5)
# Print characteristics of this gradient descent
print("Initial loss:", g["loss_array"][0])
print("Final loss:", g["loss_array"][-1])
print(f"Final weights: {g['w'].val}")
# Graph the loss as a function of iterations
xgrid = np.linspace(1, g['num_iter']+1, g["num_iter"])
graph.plot(xgrid, g['loss_array'])
graph.title('MSE Loss vs. Iteration for Logistic Noisy Data')
graph.xlabel('Iteration')
graph.ylabel('Loss')
graph.show()
```
|
github_jupyter
|
!pip install update autodiffpy==1.2.8
# Import packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as graph
import autodiffpy.autodiffmod as ad
import autodiffpy.autodiff_math as admath
# Create autodiff instances
x = ad.autodiff(name='x', val=[1.0, 2.0], der=[1.0, 1.0])
y = ad.autodiff(name='y', val=[-5.0, -3.0], der=[2.0, 1.0])
z = ad.autodiff(name='z', val=[0.5, -4.0], der=[1.0, 1.0])
# Examine each instance
print(x)
print("")
print(y)
print("")
print(z)
# Calculate various functions
f1 = (x/y)**2
f2 = x*z - 3 - y + z
f3 = (x**2)**z
# Examine each function
print(f1)
print("")
print(f2)
print("")
print(f3)
# Generate jacobian for just two variables
print(f2.jacobian(order=['x', 'y']))
# Create autodiff instances again
x = ad.autodiff(name='x', val=[1.0, 2.0], der=[1.0, 1.0])
y = ad.autodiff(name='y', val=[-5.0, -3.0], der=[1.0, 1.0])
z = ad.autodiff(name='z', val=[0.5, -4.0], der=[1.0, 1.0])
# Examine each instance again
print(x)
print("")
print(y)
print("")
print(z)
# Calculate various functions
f1 = admath.sinh(admath.cosh(x*np.pi/2.0))
f2 = admath.log(admath.exp(-y/z))
f3 = admath.sqrt(x**2 + z**2)
# Examine each function
print(f1)
print("")
print(f2)
print("")
print(f3)
# Create new autodiff instances
numpoints = 100
xval = np.linspace(0, 5*np.pi, numpoints)
x1 = ad.autodiff(name='x1', val=xval, der=np.ones(numpoints))
x2 = ad.autodiff(name='x2', val=xval, der=np.ones(numpoints))
# Create a function
f1 = 4*admath.sin(x1/2) + 2*admath.cos(x2*3)
# Graph first function and its derivative
graph.plot(xval, f1.val, color='black', linewidth=3, linestyle='-', label='Sine + Cosine')
graph.plot(xval, f1.der['x1'], color='blue', linewidth=3, linestyle='--', label='x1 Derivative')
graph.plot(xval, f1.der['x2'], color='red', linewidth=3, linestyle='--', label='x2 Derivative')
graph.xlabel('Inputs')
graph.ylabel('Outputs')
graph.title('Sine + Cosine and its Derivative')
graph.legend(loc='best')
graph.show()
# Create new autodiff instances
numpoints = 100
y = ad.autodiff(name='y', val=np.linspace(0, 10, numpoints), der=np.ones(numpoints))
# Create a function
f2 = (2*((y - 5)**2) + 3*y - 5)
# Graph second function and its derivative
graph.plot(y.val, f2.val, color='black', linewidth=3, linestyle='-', label='Quadratic')
graph.plot(y.val, f2.der['y'], color='blue', linewidth=3, linestyle='--', label='Derivative')
graph.xlabel('Inputs')
graph.ylabel('Outputs')
graph.title('Quadratic and its Derivative')
graph.legend(loc='best')
graph.show()
# Read in and process data file (will be used later in this demo)
data = pd.read_csv("demo.csv") # Demo data
X_data = data.drop('y', axis = 1) # Input x-data
Y_true = data['y'] # Actual y-values
# Create initial weights for the data
w = ad.autodiff('w', [1 for i in X_data.columns.values]) # Initialize weights to all ones
f1 = w*X_data # Functional form
# Run MAE-loss gradient descent
g = ad.gradient_descent(f1, Y_true, loss='MAE', beta=0.001, max_iter=5000, tol=1E-5)
# Print characteristics of this gradient descent
print("Initial loss:", g["loss_array"][0])
print("Final loss:", g["loss_array"][-1])
print(f"Final weights: {g['w'].val}")
# Graph the loss as a function of iterations
xgrid = np.linspace(1, g['num_iter']+1, g["num_iter"])
graph.plot(xgrid, g['loss_array'])
graph.title('MAE Loss vs. Iteration for Linear Noisy Data')
graph.xlabel('Iteration')
graph.ylabel('Loss')
graph.show()
# Create initial weights for the data
w = ad.autodiff('w', [1 for i in X_data.columns.values]) # Initialize weights to all ones
f2 = admath.logistic(w*X_data)
# Run MSE-loss gradient descent
g = ad.gradient_descent(f2, Y_true, loss='MSE', beta=0.005, max_iter=5000, tol=1E-5)
# Print characteristics of this gradient descent
print("Initial loss:", g["loss_array"][0])
print("Final loss:", g["loss_array"][-1])
print(f"Final weights: {g['w'].val}")
# Graph the loss as a function of iterations
xgrid = np.linspace(1, g['num_iter']+1, g["num_iter"])
graph.plot(xgrid, g['loss_array'])
graph.title('MSE Loss vs. Iteration for Logistic Noisy Data')
graph.xlabel('Iteration')
graph.ylabel('Loss')
graph.show()
| 0.591723 | 0.842475 |
# Inflearn 파이썬 중급 - 클래스 & 메소드 심화(3-1, 3-2)
- toc: false
- badges: false
- comments: true
- author: Jay Sung
- categories: [ ___ A. ENGINEERING __________ > PYTHON 인프런 강의]
- - -
```
# 클래스 선언
class Car(object):
'''
Car Class
Author : Me
Date : 2019.11.08
Description : Class, Static, Instance Method
'''
# Class Variable
price_per_raise = 1.0
def __init__(self, company, details):
self._company = company
self._details = details
def __str__(self):
return 'str : {} - {}'.format(self._company, self._details)
def __repr__(self):
return 'repr : {} - {}'.format(self._company, self._details)
# Instance Method
# self : 객체의 고유한 속성 값 사용
def detail_info(self):
print('Current Id : {}'.format(id(self)))
print('Car Detail Info : {} {}'.format(self._company, self._details.get('price')))
# Instance Method
def get_price(self):
return 'Before Car Price -> company : {}, price : {}'.format(self._company, self._details.get('price'))
# Instance Method
def get_price_culc(self):
return 'After Car Price -> company : {}, price : {}'.format(self._company, self._details.get('price') * Car.price_per_raise)
# Class Method
@classmethod # decorator
def raise_price(cls, per): # 클래스메소드는 self 대신 cls를 받는다.
if per <= 1:
print('Please Enter 1 or More')
return
cls.price_per_raise = per
print('Succeed! price increased.')
# Static Method
@staticmethod
def is_bmw(inst): # 아무것도 인수로 받지 않는다.. 그러나 필요성에 대해서는 의문
if inst._company == 'Bmw':
return 'OK! This car is {}.'.format(inst._company)
return 'Sorry. This car is not Bmw.'
# 자동차 인스턴스
car1 = Car('Bmw', {'color' : 'Black', 'horsepower': 270, 'price': 5000})
car2 = Car('Audi', {'color' : 'Silver', 'horsepower': 300, 'price': 6000})
# 전체정보
car1.detail_info()
car2.detail_info()
# 가격 정보(인상 전)
print(car1.get_price())
print(car2.get_price())
# 가격 인상(클래스 메소드 미사용)
Car.price_per_raise = 1.2
# 가격 정보(인상 후)
print(car1.get_price_culc())
print(car2.get_price_culc())
print()
# 가격 인상(클래스 메소드 사용)
Car.raise_price(1.6)
# 가격 정보(인상 후 : 클래스메소드)
print(car1.get_price_culc())
print(car2.get_price_culc())
print()
# Bmw 여부(스테이틱 메소드 미사용)
def is_bmw(inst):
if inst._company == 'Bmw':
return 'OK! This car is {}.'.format(inst._company)
return 'Sorry. This car is not Bmw.'
# 별도의 메소드 작성 후 호출
print(is_bmw(car1))
print(is_bmw(car2))
# Bmw 여부(스테이틱 메소드 사용)
print('Static : ', Car.is_bmw(car1))
print('Static : ', Car.is_bmw(car2))
print()
print('Static : ', car1.is_bmw(car1))
print('Static : ', car2.is_bmw(car2))
```
|
github_jupyter
|
# 클래스 선언
class Car(object):
'''
Car Class
Author : Me
Date : 2019.11.08
Description : Class, Static, Instance Method
'''
# Class Variable
price_per_raise = 1.0
def __init__(self, company, details):
self._company = company
self._details = details
def __str__(self):
return 'str : {} - {}'.format(self._company, self._details)
def __repr__(self):
return 'repr : {} - {}'.format(self._company, self._details)
# Instance Method
# self : 객체의 고유한 속성 값 사용
def detail_info(self):
print('Current Id : {}'.format(id(self)))
print('Car Detail Info : {} {}'.format(self._company, self._details.get('price')))
# Instance Method
def get_price(self):
return 'Before Car Price -> company : {}, price : {}'.format(self._company, self._details.get('price'))
# Instance Method
def get_price_culc(self):
return 'After Car Price -> company : {}, price : {}'.format(self._company, self._details.get('price') * Car.price_per_raise)
# Class Method
@classmethod # decorator
def raise_price(cls, per): # 클래스메소드는 self 대신 cls를 받는다.
if per <= 1:
print('Please Enter 1 or More')
return
cls.price_per_raise = per
print('Succeed! price increased.')
# Static Method
@staticmethod
def is_bmw(inst): # 아무것도 인수로 받지 않는다.. 그러나 필요성에 대해서는 의문
if inst._company == 'Bmw':
return 'OK! This car is {}.'.format(inst._company)
return 'Sorry. This car is not Bmw.'
# 자동차 인스턴스
car1 = Car('Bmw', {'color' : 'Black', 'horsepower': 270, 'price': 5000})
car2 = Car('Audi', {'color' : 'Silver', 'horsepower': 300, 'price': 6000})
# 전체정보
car1.detail_info()
car2.detail_info()
# 가격 정보(인상 전)
print(car1.get_price())
print(car2.get_price())
# 가격 인상(클래스 메소드 미사용)
Car.price_per_raise = 1.2
# 가격 정보(인상 후)
print(car1.get_price_culc())
print(car2.get_price_culc())
print()
# 가격 인상(클래스 메소드 사용)
Car.raise_price(1.6)
# 가격 정보(인상 후 : 클래스메소드)
print(car1.get_price_culc())
print(car2.get_price_culc())
print()
# Bmw 여부(스테이틱 메소드 미사용)
def is_bmw(inst):
if inst._company == 'Bmw':
return 'OK! This car is {}.'.format(inst._company)
return 'Sorry. This car is not Bmw.'
# 별도의 메소드 작성 후 호출
print(is_bmw(car1))
print(is_bmw(car2))
# Bmw 여부(스테이틱 메소드 사용)
print('Static : ', Car.is_bmw(car1))
print('Static : ', Car.is_bmw(car2))
print()
print('Static : ', car1.is_bmw(car1))
print('Static : ', car2.is_bmw(car2))
| 0.354657 | 0.747731 |
# Chapter 4 Tutorial
In this tutorial, we use Twitter data to create and explore directed networks of social interactions.
Contents:
* Preface: Twitter API access
1. Authenticating with Twitter's API
2. Twitter API basics
3. Using Twitter's search API to get tweets of interest
4. Creating social network graphs
5. Twitter retweet network
6. Twitter mention network
# Preface: Twitter API access
In order to get Twitter data using their API, one must first have a Twitter App. In Twitter parlance, an "app" is just a pair of API keys, ostensibly used for a particular purpose; this doesn't mean that we are creating an application to run on mobile or desktop computers. Unfortunately, creating a Twitter App requires access to Twitter's developer platform, which requires an application process with Twitter. Instructors and students have three basic options on how to proceed for this tutorial.
**Team member app:** In the first of these options, the instructor
applies for and obtains organizational access to the developer platform following [Twitter's Playbook for Educators](https://developer.twitter.com/en/docs/basics/developer-portal/guides/twitter-for-education).
Then the instructor invites students as team members. Each student subsequently creates their own Twitter App for use with this tutorial.
The downside to this option is that the application for organizational access is somewhat involved and approval takes significant time. In addition, this reqires an additional step of students accepting their invitations to the team, which currently requires each student's Twitter account to have email notifications enabled. As the Twitter-official recommendation, we expect this workflow to improve over time.
**Shared course app:** In this workflow, the instructor
[applies for and obtains access](https://developer.twitter.com/en/apply-for-access)
to the developer platform, creates a single app for classroom use, then shares the app keys with the students. Since more than one user can authenticate with an app, this is enough to get a classroom of students access to Twitter's APIs. The downside here is security: with all students sharing a single app, the potential exists for a single student's actions to get the app's access revoked, negatively affecting the rest of the class. This is the recommended workflow for someone using these materials for small classes or self-study where the extra steps in the organizational workflow are unnecessary.
**No app:** Due to the approval process for Twitter API access taking a significant amount of time, we have provided a file containing Twitter data that can be used for this tutorial. Of course this is less exciting than getting real data on a topic of your choice, but this backup is better than nothing. The file `science_tweets.json` is located in the `datasets` directory and can be loaded like this:
import json
search_tweets = json.load(open('../datasets/science_tweets.json'))
In this case, you could skip the first section on authentication and read sections 2-4 without running the code. By replacing the code in 5.1 and 6.1 with the above snippet, the code in those sections can then be edited and executed.
# 1. Authenticating with Twitter's API
Twitter uses OAuth in order to allow third-party apps to access data on your behalf without requiring your Twitter login credentials -- note that none of the code in this notebook asks for your Twitter screen name or password.
The OAuth "dance" can be intimidating when you first use it, but it provides a far more secure way for software to make requests on your behalf than providing your username and password.
We'll make use of the
[Twython](https://twython.readthedocs.io/en/latest/usage/starting_out.html#authentication)
package to help us with authentication and querying Twitter's APIs.
```
from twython import Twython
```
For this tutorial, we'll be using a developer workflow where we assume you have access to an app's API key and secret. The app could be a team mamber app or a shared course app, as explained above.
## 1.1 Enter app info and get auth URL
In order to authenticate with Twitter, we'll provide the app details and ask for a one-time authorization URL to authenticate your user with this app.
Copy and paste the API key and secret from your Twitter app into the first two lines below.
Executing the cell should then print out a clickable URL. This link is unique and will work **exactly** once. Visit this URL, log into Twitter, and then copy the verifier pin that is given to you so as to paste it in the next step.
```
API_KEY = 'xxxxxxxxxxxx'
API_SECRET_KEY = 'xxxxxxxxxxxxxxxxxxxxxxxxx'
twitter = Twython(API_KEY, API_SECRET_KEY)
authentication_tokens = twitter.get_authentication_tokens()
print(authentication_tokens['auth_url'])
```
## 1.2 Authorize app using verifier PIN
That verifier PIN goes into the next cell. This will be different every time you run these steps. The `authentication_tokens` include temporary tokens that go with this verifier PIN; by submitting these together, we show Twitter that we are who we say we are.
```
# Replace the verifier with the pin number obtained with your web browser in the previous step
VERIFIER = '0000000'
twitter = Twython(API_KEY, API_SECRET_KEY,
authentication_tokens['oauth_token'],
authentication_tokens['oauth_token_secret'])
authorized_tokens = twitter.get_authorized_tokens(VERIFIER)
```
Note: If you are using your own team member app, you could alternatively obtain a permanent token pair (OAuth access token and secret) directly from the [Twitter app dashboard](https://developer.twitter.com/en/apps).
## 1.3 Use authorized tokens
Now we have a permanent token pair that we can use to make authenticated calls to the Twitter API. We'll create a new Twython object using these authenticated keys and verify the credentials of the logged-in user.
```
twitter = Twython(API_KEY, API_SECRET_KEY,
authorized_tokens['oauth_token'],
authorized_tokens['oauth_token_secret'])
twitter.verify_credentials()
```
If the previous cell ran without error and printed out a dict corresponding to a
[Twitter User](https://developer.twitter.com/en/docs/tweets/data-dictionary/overview/user-object),
then you're good. The authorized token pair is like a username/password and should be protected as such.
# 2. Twitter API basics
In this tutorial, we'll be dealing with two different types of data, Users and Tweets.
## 2.1 User objects
We've already seen one
[User Object](https://developer.twitter.com/en/docs/tweets/data-dictionary/overview/user-object),
the one corresponding to the logged-in user, via the call to `verify_credentials()` above. We can also fetch data for an arbitrary user:
```
user = twitter.show_user(screen_name='OSoMe_IU')
user
```
This dictionary of user data contains several items of note. First, the screen name of the user, while obvious in this case, is very useful later:
```
user['screen_name']
```
The user data also contains information such as the number of followers, friends (other users followerd by this user), and tweets (called `'statuses'` in the API):
```
print("""
Twitter user @{screen_name}
has {followers_count} followers,
follows {friends_count} users,
and has tweeted {statuses_count} times.
""".format(**user))
```
## 2.2 Tweet Objects
The second type of data of which we will make use is the
[Tweet Object](https://developer.twitter.com/en/docs/tweets/data-dictionary/overview/tweet-object).
A user object actually contains the user's most recent tweet:
```
most_recent_tweet = user['status']
most_recent_tweet
```
Tweet objects contain several interesting data and metadata, but the most basic are the `'text'` and `'entities'`. The `'text'` is what you expect it to be: the text of the tweet:
```
most_recent_tweet['text']
```
The `'entities'` field contains several tokens of interest already extracted from the tweet such as hashtags, URLs, images, and mentions of other users:
```
most_recent_tweet['entities']
```
In particular, we'll make use of the `'user_mentions'` later:
```
most_recent_tweet['entities']['user_mentions']
```
# 3. Using Twitter's search API to get tweets of interest
Twitter's
[Search API](https://developer.twitter.com/en/docs/tweets/search/api-reference/get-search-tweets.html)
allows you to fetch recent tweets according to a query of keywords, URLs, hashtags, user mentions, etc.
## 3.1 Get tweets matching a hashtag
We'll make use of the ability to search by hashtags:
```
search_response = twitter.search(q='#science', count=100)
```
While the search API response is a dictionary, the `'statuses'` field contains the list of
[Tweet Objects](https://developer.twitter.com/en/docs/tweets/data-dictionary/overview/tweet-object)
we're after.
```
search_tweets = search_response['statuses']
tweet = search_tweets[0]
tweet
```
Note that each tweet obtained from this API contains a `'user'` field -- this is a User Object for the user who created the tweet.
```
tweet['user']
```
## 3.2 Using a cursor to get more than 100 tweets from a search
We can only fetch up to 100 tweets at a time from a single search API call:
```
# even with count=1000, we still get at most 100 tweets
search_response = twitter.search(q='#science', count=1000)
len(search_response['statuses'])
```
In order to get more tweets from a search, we can make use of a cursor:
```
import itertools
NUM_TWEETS_TO_FETCH = 1000
cursor = twitter.cursor(twitter.search, q='#science', count=100, result_type='mixed')
search_tweets = list(itertools.islice(cursor, NUM_TWEETS_TO_FETCH))
len(search_tweets)
type(cursor)
```
Note the following:
* The cursor object is a
[generator](https://docs.python.org/3/tutorial/classes.html#generators),
a type of iterator that "lazily" generates items. We use Python's `itertools.islice` in order to get up to a set number of items from this generator. The second argument passed to `islice` is the max number of tweets we want to fetch from the user.
* Even though we want to get more than 100 tweets here, we provide the `count=100` argument. This tells the cursor to fetch the maximum number of tweets with each API call.
* As documented in [Twitter's Search API documentation](https://developer.twitter.com/en/docs/tweets/search/api-reference/get-search-tweets.html), specifying `result_type='mixed'` provides a mix of recent and popular tweets matching the query. If one desires a more "random" sample, you can specify `result_type='recent'`, but Twitter may provide fewer tweets than desired.
* We provide the API function name as the first argument followed by the function's arguments. It's tempting but **incorrect** to do the following:
cursor = twitter.cursor(twitter.get_user_timeline(screen_name='osome_iu', count=200))
## 3.3 API method rate limits
Each API method has a *rate limit* imposed by Twitter, a limit on the number of function calls per 15-minute window. We can check on the rate limit status for this endpoint:
```
twitter.get_application_rate_limit_status()['resources']['search']
```
These limits apply to the number of API *calls*, as opposed to the number of *items* fetched. This is why, when creating a cursor, we specify `count=` to fetch the maximum number of items per API call.
# 4. Creating social network graphs
In the remaining sections of this tutorial, we're going to use NetworkX to create social networks from Twitter data. The examples are going to have users as nodes, so at a very basic level, we're going to do something like the following:
```
import networkx as nx
D = nx.DiGraph()
publisher = twitter.show_user(screen_name='CambridgeUP')
author = twitter.show_user(screen_name='osome_iu')
D.add_edge(publisher['screen_name'], author['screen_name'], weight=1)
list(D.edges(data=True))
```
Note that NetworkX will let us use the full user dictionaries as the node names, e.g. `D.add_edge(publisher, author)`. However, it is inconvenient to work with such a graph. More preferable is to use `screen_name` or `id` as the node names, and then use
[node attributes](https://networkx.github.io/documentation/stable/tutorial.html#node-attributes)
for the user profile data if desired.
# 5. Twitter retweet network
One fundamental interaction in the Twitter ecosystem is the "retweet" -- rebroadcasting another user's tweet to your followers. A tweet object returned by the API is a retweet if it includes a `'retweeted_status'`. We're going to fetch tweets matching a hashtag and create a retweet network of the conversation.
## 5.1 Get some tweets
```
import itertools
NUM_TWEETS_TO_FETCH = 1000
cursor = twitter.cursor(twitter.search, q='#science', count=100, result_type='mixed')
search_tweets = list(itertools.islice(cursor, NUM_TWEETS_TO_FETCH))
len(search_tweets)
```
## 5.2 Filter retweets
Of the tweets we fetched, a subset will be retweets. Let's create a new list of just the retweets:
```
retweets = []
for tweet in search_tweets:
if 'retweeted_status' in tweet:
retweets.append(tweet)
len(retweets)
```
## 5.3 Create DiGraph
Each tweet in this list of retweets represents an edge in our network. We're going to draw these edges in the direction of information flow: from the retweeted user to the retweeter, the user doing the retweeting. Since a user can retweet another user more than once, we want this graph to be weighted, with the number of retweets as the weight.
```
import networkx as nx
D = nx.DiGraph()
for retweet in retweets:
retweeted_status = retweet['retweeted_status']
retweeted_sn = retweeted_status['user']['screen_name']
retweeter_sn = retweet['user']['screen_name']
# Edge direction: retweeted_sn -> retweeter_sn
if D.has_edge(retweeted_sn, retweeter_sn):
D.edges[retweeted_sn, retweeter_sn]['weight'] += 1
else:
D.add_edge(retweeted_sn, retweeter_sn, weight=1)
```
The edge addition logic here is to increase the edge weight by 1 if the edge exists, or else create the edge with weight 1 if it does not exist.
When writing code such as this that refers multiple times to the same directed edge, make sure to be consistent with the edge direction.
## 5.4 Analyze graph
Now that we have this graph, let's ask some questions about it.
### Most retweeted user
Since the edges are in the direction of information flow, out-degree gives us the number of other users retweeting a given user. We can get the user with highest out-degree using the built-in `max` function:
```
max(D.nodes, key=D.out_degree)
```
but we can get more context and information from the "top N" users:
```
from operator import itemgetter
sorted(D.out_degree(), key=itemgetter(1), reverse=True)[:5]
```
In this piece of code, we take advantage of the fact that `D.out_degree()` returns a sequence of `(name, degree)` 2-tuples; specifying `key=itemgetter(1)` tells the `sorted` function to sort these 2-tuples by their value at index 1. Giving `reverse=True` tells the `sorted` function that we want this in descending order, and the `[:5]` at the end slices the first 5 items from the resulting list.
However, this is a weighted graph! By default, `out_degree()` ignores the edge weights. We can get out-strength by telling the `out_degree()` function to take into account the edge weight:
```
sorted(D.out_degree(weight='weight'), key=itemgetter(1), reverse=True)[:5]
```
In some cases these two results will be the same, namely if none of these users has been retweeted multiple times by the same user. Depending on your use case, you may or may not wish to take the weights into account.
### Anomaly detection
One type of social media manipulation involves accounts that create very little original content, instead "spamming" retweets of any and all content in a particular conversation. Can we detect any users doing significantly more retweeting than others? Let's look at the top N retweeters:
```
sorted(D.in_degree(weight='weight'), key=itemgetter(1), reverse=True)[:5]
```
### Connectivity
We can ask if the tweets obtained by the search represent one large conversation or many small conversations; broadly speaking, each weakly-connected component represents a conversation.
```
nx.is_weakly_connected(D)
nx.number_weakly_connected_components(D)
```
### Drawing
We can try to draw this graph with the nodes sized by their out-strength:
```
node_sizes = [D.out_degree(n, weight='weight') * 50 for n in D.nodes]
%matplotlib inline
nx.draw(D, node_size=node_sizes)
```
Note that in this simplistic drawing, nodes with zero out-strength are not drawn on the diagram because their size is 0. This suits us fine; only the users who have been retweeted are drawn here.
# 6. Twitter mention network
Another Twitter interaction between users occurs when one user mentions another in a tweet by their @screen_name. As an example, consider the following hypothetical tweet from @osome_iu:
> Check out the new research from @IUSICE and @USC_ISI https://...
From this tweet we would create two edges:
('osome_iu', 'IUSICE')
('osome_iu', 'USC_ISI')
It's up to us which direction we draw these edges, but we should be consistent. In this example, we will draw edges in the direction of attention flow: @osome_iu is giving attention to @IUSICE and @USC_ISI.
## 6.1 Get some tweets
```
import itertools
NUM_TWEETS_TO_FETCH = 1000
cursor = twitter.cursor(twitter.search, q='#science', count=100, result_type='mixed')
search_tweets = list(itertools.islice(cursor, NUM_TWEETS_TO_FETCH))
len(search_tweets)
```
## 6.2 Create DiGraph
It's not necessary to first filter out tweets containing user mentions due to a feature of
[Tweet Objects](https://developer.twitter.com/en/docs/tweets/data-dictionary/overview/tweet-object):
every tweet has
[Entities](https://developer.twitter.com/en/docs/tweets/data-dictionary/overview/entities-object#entitiesobject)
which always contains a `'user_mentions'` list, even if that list is empty. Since a tweet may mention more than one user, we need a nested for-loop.
```
import networkx as nx
D = nx.DiGraph()
for tweet in search_tweets:
tweet_sn = tweet['user']['screen_name']
for user_mention in tweet['entities']['user_mentions']:
mentioned_sn = user_mention['screen_name']
my_edge = (tweet_sn, mentioned_sn)
if D.has_edge(*my_edge):
D.edges[my_edge]['weight'] += 1
else:
D.add_edge(*my_edge, weight=1)
```
## 6.3 Analyze graph
Now that we have this graph, let's ask some questions about it.
### Most popular users
Since these edges are in the direction of attention flow, in-degree gives us the number of other users mentioning a given user. We can get the user with highest in-degree using the built-in `max` function:
```
max(D.nodes, key=D.in_degree)
```
but we can get more context and information from the "top N" users:
```
from operator import itemgetter
sorted(D.in_degree(), key=itemgetter(1), reverse=True)[:5]
```
By specifying `weight='weight'` we can instead get the top 5 users by in-strength instead of in-degree:
```
sorted(D.in_degree(weight='weight'), key=itemgetter(1), reverse=True)[:5]
```
In some cases these two results will be the same, namely if none of these users has been mentioned multiple times by the same user. Depending on your use case, you may or may not wish to take the weights into account.
### Conversation drivers
A user mentioning many others in a conversation may be "driving" the conversation and trying to include others in the dialogue. It could also be spam. Let's see who is doing the most mentioning here:
```
sorted(D.out_degree(weight='weight'), key=itemgetter(1), reverse=True)[:5]
```
### Connectivity
We can ask if the tweets obtained by the search represent one large conversation or many small conversations; broadly speaking, each weakly-connected component represents a conversation.
```
nx.is_weakly_connected(D)
nx.number_weakly_connected_components(D)
```
### Drawing
We can try to draw this graph with the nodes sized by their in-strength:
```
node_sizes = [D.in_degree(n, weight='weight') * 50 for n in D.nodes]
%matplotlib inline
nx.draw(D, node_size=node_sizes)
```
Note that in this simplistic drawing, nodes with zero in-strength are not drawn on the diagram because their size is 0. This suits us fine; only the users who have been mentioned are drawn here.
|
github_jupyter
|
from twython import Twython
API_KEY = 'xxxxxxxxxxxx'
API_SECRET_KEY = 'xxxxxxxxxxxxxxxxxxxxxxxxx'
twitter = Twython(API_KEY, API_SECRET_KEY)
authentication_tokens = twitter.get_authentication_tokens()
print(authentication_tokens['auth_url'])
# Replace the verifier with the pin number obtained with your web browser in the previous step
VERIFIER = '0000000'
twitter = Twython(API_KEY, API_SECRET_KEY,
authentication_tokens['oauth_token'],
authentication_tokens['oauth_token_secret'])
authorized_tokens = twitter.get_authorized_tokens(VERIFIER)
twitter = Twython(API_KEY, API_SECRET_KEY,
authorized_tokens['oauth_token'],
authorized_tokens['oauth_token_secret'])
twitter.verify_credentials()
user = twitter.show_user(screen_name='OSoMe_IU')
user
user['screen_name']
print("""
Twitter user @{screen_name}
has {followers_count} followers,
follows {friends_count} users,
and has tweeted {statuses_count} times.
""".format(**user))
most_recent_tweet = user['status']
most_recent_tweet
most_recent_tweet['text']
most_recent_tweet['entities']
most_recent_tweet['entities']['user_mentions']
search_response = twitter.search(q='#science', count=100)
search_tweets = search_response['statuses']
tweet = search_tweets[0]
tweet
tweet['user']
# even with count=1000, we still get at most 100 tweets
search_response = twitter.search(q='#science', count=1000)
len(search_response['statuses'])
import itertools
NUM_TWEETS_TO_FETCH = 1000
cursor = twitter.cursor(twitter.search, q='#science', count=100, result_type='mixed')
search_tweets = list(itertools.islice(cursor, NUM_TWEETS_TO_FETCH))
len(search_tweets)
type(cursor)
twitter.get_application_rate_limit_status()['resources']['search']
import networkx as nx
D = nx.DiGraph()
publisher = twitter.show_user(screen_name='CambridgeUP')
author = twitter.show_user(screen_name='osome_iu')
D.add_edge(publisher['screen_name'], author['screen_name'], weight=1)
list(D.edges(data=True))
import itertools
NUM_TWEETS_TO_FETCH = 1000
cursor = twitter.cursor(twitter.search, q='#science', count=100, result_type='mixed')
search_tweets = list(itertools.islice(cursor, NUM_TWEETS_TO_FETCH))
len(search_tweets)
retweets = []
for tweet in search_tweets:
if 'retweeted_status' in tweet:
retweets.append(tweet)
len(retweets)
import networkx as nx
D = nx.DiGraph()
for retweet in retweets:
retweeted_status = retweet['retweeted_status']
retweeted_sn = retweeted_status['user']['screen_name']
retweeter_sn = retweet['user']['screen_name']
# Edge direction: retweeted_sn -> retweeter_sn
if D.has_edge(retweeted_sn, retweeter_sn):
D.edges[retweeted_sn, retweeter_sn]['weight'] += 1
else:
D.add_edge(retweeted_sn, retweeter_sn, weight=1)
max(D.nodes, key=D.out_degree)
from operator import itemgetter
sorted(D.out_degree(), key=itemgetter(1), reverse=True)[:5]
sorted(D.out_degree(weight='weight'), key=itemgetter(1), reverse=True)[:5]
sorted(D.in_degree(weight='weight'), key=itemgetter(1), reverse=True)[:5]
nx.is_weakly_connected(D)
nx.number_weakly_connected_components(D)
node_sizes = [D.out_degree(n, weight='weight') * 50 for n in D.nodes]
%matplotlib inline
nx.draw(D, node_size=node_sizes)
import itertools
NUM_TWEETS_TO_FETCH = 1000
cursor = twitter.cursor(twitter.search, q='#science', count=100, result_type='mixed')
search_tweets = list(itertools.islice(cursor, NUM_TWEETS_TO_FETCH))
len(search_tweets)
import networkx as nx
D = nx.DiGraph()
for tweet in search_tweets:
tweet_sn = tweet['user']['screen_name']
for user_mention in tweet['entities']['user_mentions']:
mentioned_sn = user_mention['screen_name']
my_edge = (tweet_sn, mentioned_sn)
if D.has_edge(*my_edge):
D.edges[my_edge]['weight'] += 1
else:
D.add_edge(*my_edge, weight=1)
max(D.nodes, key=D.in_degree)
from operator import itemgetter
sorted(D.in_degree(), key=itemgetter(1), reverse=True)[:5]
sorted(D.in_degree(weight='weight'), key=itemgetter(1), reverse=True)[:5]
sorted(D.out_degree(weight='weight'), key=itemgetter(1), reverse=True)[:5]
nx.is_weakly_connected(D)
nx.number_weakly_connected_components(D)
node_sizes = [D.in_degree(n, weight='weight') * 50 for n in D.nodes]
%matplotlib inline
nx.draw(D, node_size=node_sizes)
| 0.321993 | 0.966474 |
# Setup
```
from src.data.make_dataset import DataCreator
from src.features.preprocess import create_dataframe, DataPreprocessor, noising
from src.models.model_setup import gmmhmm, IwrGaussianHMMModel
from src.models.model_selection import Noiser, GridSearch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import colorednoise as cn
import librosa
import IPython
np.random.seed(7)
```
# Data Preparation
We will create DataCreator instance to simulate our dataset with 2400 observations (200 in each class + 400 in test set). <br>
Note: In case of converting .mp3 to .wav files, which is done with generate_observation method, you may need ffmpeg added to your local PATH.
```
dc = DataCreator()
dc.generate_observations(200)
```
We can inspect the length of each audio file in seconds.
```
# sr = 22050
# dc.max_len / sr
# > 1.2384580498866213
```
# Preprocessing
From created files we make data frames for train and test set. Furthermore, we create mapper which is dictionary mapping id labels to class names.
```
train_df, test_df, mapper = create_dataframe(how_many=200)
train_df.head()
```
Then we create DataProcesor instances to preprocess data sets, specifically calculate mfcc coefficients for each time window.
```
train_dp = DataPreprocessor(train_df)
X_train, y_train = train_dp.mfcc(12, S=0.045, R=0.05)
test_dp = DataPreprocessor(test_df)
X_test, y_test = test_dp.mfcc(12, S=0.045, R=0.05)
X_train.shape
X_test.shape
```
# Modelling
Creating exemplary model instance and checking how does it perform.
```
model = IwrGaussianHMMModel(n_states=6, n_iter=20)
model.fit(X_train, y_train)
```
We obtain 95% on train set and
```
model.score(X_train, y_train)
model.score(X_test, y_test)
```
# Noising
In thesis we will check how Gaussian HMM models performs on data with noise. We introduce 5 types of noise used in simulations.
## White noise
```
y = cn.powerlaw_psd_gaussian(0, 3000)
plt.plot(y)
plt.show()
```
## Pink noise
- gaussian noise for beta =1
```
s = cn.powerlaw_psd_gaussian(1, 3000)
plt.plot(s)
plt.show()
```
## Szum browna
- gaussian noise for beta = 2
```
s = cn.powerlaw_psd_gaussian(2, 3000)
plt.plot(s)
plt.show()
```
## Niebieski szum
- gaussian noise for beta =-2
```
y = cn.powerlaw_psd_gaussian(-2, 3000)
plt.plot(y)
plt.show()
```
## Fioletowy szum
- gaussian noise for beta =-1
```
y = cn.powerlaw_psd_gaussian(-1, 3000)
plt.plot(y)
plt.show()
```
## Code
We will import random sample end check how it will be noised with our method.
```
y, sr = librosa.load(r'data\train\yes\yes_93.wav')
plt.plot(y)
plt.show()
plt.plot(noising(y, 0, 0))
plt.show()
plt.plot(noising(y, 1, 0))
plt.show()
```
We can also check how does the difference between clean signal and noised sound.
```
IPython.display.Audio(data=y, rate=sr)
IPython.display.Audio(data=noising(y, 0, 0), rate=sr)
```
# Results
## Choosing model params
We will seek the most optimal model by searching the whole param net using k=5 fold stratified cross validation.
```
params = {'n_samples':[20, 100, 200],
'n_mfcc':[13],
'hop_wins':[0.01, 0.03, 0.05],
'len_wins':[0.025, 0.04],
'n_iters':[15, 30, 50],
'n_hiddens':[4, 6, 12]}
gs = GridSearch(random_state=7)
results = gs.grid_search_model(params, k=5)
# results.to_csv(r'results\result_choose_model_params.csv')
```
## Adding randomness
We may also check how changing random parameters during data creation may affect the change in results.
```
params = {
'random_horizontal_shift': [0.1, 0.25, 0.4],
'random_vertical_scaling': [0.5, 1, 10],
'n_iter' : [15, 30, 50],
'n_hiddens': [5, 6, 7]
}
gs = GridSearch(random_state=7)
results = gs.grid_search_randomness(params)
# results.to_csv(r'results\result_randomness.csv')
```
## Noising
Now after selecting proper model we can analyze how well can it predict noised test data
```
params = {
'beta': [-2, -1, 0, 1, 2],
'SNR': [-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
'n_iters' : [15],
'n_hiddens': [6]
}
noise_gs = Noiser(random_state=7)
results = noise_gs.noise_hmm_results(params)
# results.to_csv(r'results\result_noise.csv')
```
## Noise to noise
We provide a method to stabilize results across bunch of different noises with different signal-noise ratio. We search for model trained on specific noise genre data which is most often better than base model.
```
params = {
'beta': [-2, -1, 0, 1, 2],
'SNR': [-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
'chosen_snr': [5, 6, 7, 8, 9],
'n_iters' : [15],
'n_hiddens': [6]
}
noise_gs = Noiser(random_state=7)
best, cost = noise_gs.best_noise_on_noise_grid_search(params)
```
We may observe how many times after applying our method the results are better than base model. As we can see, for beta=-2 and snr=9, accuracy most often is better than base model.
```
cost
best
# cost.to_csv(r'results\cost_search_noise_on_noise.csv')
```
We performed simulations and selected best results via them. The next stage is visualization and inference from our solutions. Everything is conducted in visualization.ipynb file.
|
github_jupyter
|
from src.data.make_dataset import DataCreator
from src.features.preprocess import create_dataframe, DataPreprocessor, noising
from src.models.model_setup import gmmhmm, IwrGaussianHMMModel
from src.models.model_selection import Noiser, GridSearch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import colorednoise as cn
import librosa
import IPython
np.random.seed(7)
dc = DataCreator()
dc.generate_observations(200)
# sr = 22050
# dc.max_len / sr
# > 1.2384580498866213
train_df, test_df, mapper = create_dataframe(how_many=200)
train_df.head()
train_dp = DataPreprocessor(train_df)
X_train, y_train = train_dp.mfcc(12, S=0.045, R=0.05)
test_dp = DataPreprocessor(test_df)
X_test, y_test = test_dp.mfcc(12, S=0.045, R=0.05)
X_train.shape
X_test.shape
model = IwrGaussianHMMModel(n_states=6, n_iter=20)
model.fit(X_train, y_train)
model.score(X_train, y_train)
model.score(X_test, y_test)
y = cn.powerlaw_psd_gaussian(0, 3000)
plt.plot(y)
plt.show()
s = cn.powerlaw_psd_gaussian(1, 3000)
plt.plot(s)
plt.show()
s = cn.powerlaw_psd_gaussian(2, 3000)
plt.plot(s)
plt.show()
y = cn.powerlaw_psd_gaussian(-2, 3000)
plt.plot(y)
plt.show()
y = cn.powerlaw_psd_gaussian(-1, 3000)
plt.plot(y)
plt.show()
y, sr = librosa.load(r'data\train\yes\yes_93.wav')
plt.plot(y)
plt.show()
plt.plot(noising(y, 0, 0))
plt.show()
plt.plot(noising(y, 1, 0))
plt.show()
IPython.display.Audio(data=y, rate=sr)
IPython.display.Audio(data=noising(y, 0, 0), rate=sr)
params = {'n_samples':[20, 100, 200],
'n_mfcc':[13],
'hop_wins':[0.01, 0.03, 0.05],
'len_wins':[0.025, 0.04],
'n_iters':[15, 30, 50],
'n_hiddens':[4, 6, 12]}
gs = GridSearch(random_state=7)
results = gs.grid_search_model(params, k=5)
# results.to_csv(r'results\result_choose_model_params.csv')
params = {
'random_horizontal_shift': [0.1, 0.25, 0.4],
'random_vertical_scaling': [0.5, 1, 10],
'n_iter' : [15, 30, 50],
'n_hiddens': [5, 6, 7]
}
gs = GridSearch(random_state=7)
results = gs.grid_search_randomness(params)
# results.to_csv(r'results\result_randomness.csv')
params = {
'beta': [-2, -1, 0, 1, 2],
'SNR': [-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
'n_iters' : [15],
'n_hiddens': [6]
}
noise_gs = Noiser(random_state=7)
results = noise_gs.noise_hmm_results(params)
# results.to_csv(r'results\result_noise.csv')
params = {
'beta': [-2, -1, 0, 1, 2],
'SNR': [-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
'chosen_snr': [5, 6, 7, 8, 9],
'n_iters' : [15],
'n_hiddens': [6]
}
noise_gs = Noiser(random_state=7)
best, cost = noise_gs.best_noise_on_noise_grid_search(params)
cost
best
# cost.to_csv(r'results\cost_search_noise_on_noise.csv')
| 0.494385 | 0.951142 |
# Lab 2 - Convolutional Neural Networks and TensorFlow Graphs
In this second lab session, you will build and train a shallow convolutaional neural network for recognising objects using the [CIFAR-10 dataset](https://www.cs.toronto.edu/~kriz/cifar.html). CIFAR-10 has 10 object classes, 60,000 examples with 6,000 examples per class.
[](https://www.cs.toronto.edu/~kriz/cifar.html)
### Objectives:
1. Build your first convolutional model using TensorFlow 1.2 for recognising objects using the CIFAR-10 dataset.
2. Train your model on BC4 and visualize the training process
3. Evaluate your model.
# 1. TensorFlow - Graphs and Sessions
## 1.1 TensorFlow-1.2
TensorFlow was originally developed by the Google Brain team as an internal machine learning tool and was open-sourced under the Apache 2.0 License in November 2015. Since then, it has become a popular choice among researchers and companies due to its balanced trade-off between flexibility (required in research) and production-worthiness (required in industry). Additionally, it's well documented and maintained, backed by a large community (> 10,000 commits and > 3000 TF-related repos in one year).
### Graphs and sessions
TensorFlow does all its computation in graphs (creators referred to them as **dataflow graphs**), [Danijar Hafner's website](https://danijar.com/what-is-a-tensorflow-session/) and [TensorFlow's documentation](https://www.tensorflow.org/programmers_guide/graphs) contains more details about the concept of computational graphs and their advantages, in this Lab we will focus only on how to build and excecute them.
The **graph** will define the variables and computation. It doesn’t compute anything nor does it hold any values, it just defines the operations that we want to be performed.
The excecution of the graph, referred as a **session**, allocates resources, feeds the data, computes the operations and holds the values of intermediate results and variables. The figure below shows how the data flows from the *input readers* through the *opertations* such as convolutions and activations, then the *gradients* are computed and error is *backpropagated* to the *weight* and *bias variables*.
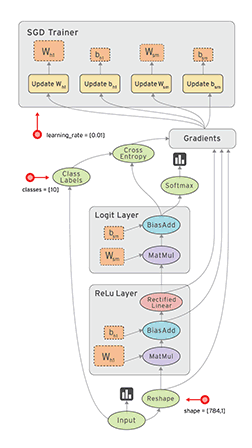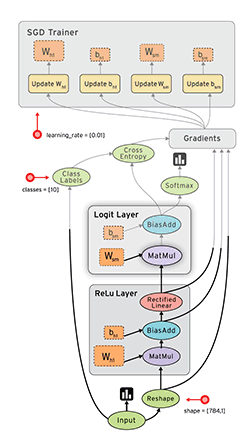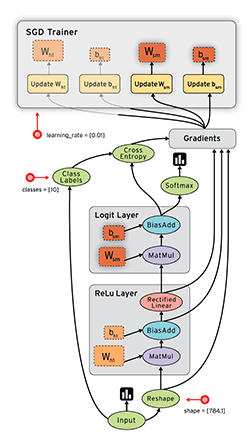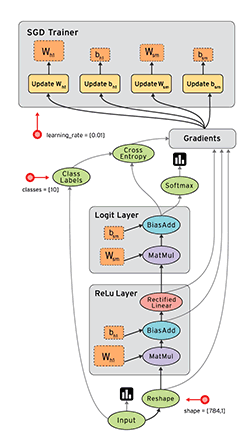
**We encourage to use single graphs and single session** for your models in this course.
## 1.2 Downloading Relevant Files
* First, visit the [GitHub labsheet repository](https://github.com/COMSM0018-Applied-Deep-Learning/labsheets)
* Clone the repository `git clone "https://github.com/COMSM0018-Applied-Deep-Learning/labsheets.git"`
* Copy both `CIFAR10`, `Lab_2_CNNs` into a new folder which we will refer to as `/path_to_files/`
* Using Jupyter notebook, open the file `Lab_2_CNNs/simple_train_cifar.py`
## 1.3 Building your first Model
Next, we will describe the code in the ```simple_train_cifar.py``` file for implementing a CNN for recognising objects on the [CIFAR10](https://www.cs.toronto.edu/~kriz/cifar.html) dataset. Your first CNN will be formed of two *convolutional layers* and two *fully connected layers* with the following sizes and hyperparameters:
* Filter 5 x 5, with stride 1 and padding [`'SAME'`](https://stackoverflow.com/questions/37674306/what-is-the-difference-between-same-and-valid-padding-in-tf-nn-max-pool-of-t) for convolutions
* Kernel 2 x 2 , with stride 2 and padding [`'SAME'`](https://stackoverflow.com/questions/37674306/what-is-the-difference-between-same-and-valid-padding-in-tf-nn-max-pool-of-t) for max pooling
* 1024 Neurons for the fully connected layer
* ReLU activation functions for both convolutional layers, and fully connected layers
* Weight and bias initialization using random values from a truncated normal distribution with $\sigma= 0.1$ and $\mu=0$
### Imports
Here you can see the provided code stub with all relevant imports
```
# %load -r 12:35 simple_train_cifar.py
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import sys
import os
import tensorflow as tf
sys.path.append(os.path.join(os.path.dirname(__file__), '..', 'CIFAR10'))
import cifar10 as cf
FLAGS = tf.app.flags.FLAGS
tf.app.flags.DEFINE_string('data-dir', os.getcwd() + '/dataset/',
'Directory where the dataset will be stored and checkpoint.')
tf.app.flags.DEFINE_integer('max-steps', 1000,
'Number of mini-batches to train on.')
tf.app.flags.DEFINE_integer('log-frequency', 100,
'Number of steps between logging results to the console and saving summaries')
tf.app.flags.DEFINE_integer('save-model', 1000,
'Number of steps between model saves')
```
### Hyperparameters
We also defined all variables required for training globally, including batch size, learning rate, as well as the dataset's information including input size (img_height, img_channels) and the number of classes.
`train_dir` refers to the location of the training files in the dataset
```
# %load -r 36:48 simple_train_cifar.py
# Optimisation hyperparameters
tf.app.flags.DEFINE_integer('batch-size', 128, 'Number of examples per mini-batch')
tf.app.flags.DEFINE_float('learning-rate', 1e-4, 'The learning rate for our training.')
tf.app.flags.DEFINE_integer('img-width', 32, 'Image width')
tf.app.flags.DEFINE_integer('img-height', 32, 'Image height')
tf.app.flags.DEFINE_integer('img-channels', 3, 'Image channels')
tf.app.flags.DEFINE_integer('num-classes', 10, 'Number of classes')
tf.app.flags.DEFINE_string('train-dir',
'{cwd}/logs/exp_bs_{bs}_lr_{lr}'.format(cwd=os.getcwd(),
bs=FLAGS.batch_size,
lr=FLAGS.learning_rate),
'Directory where to write event logs and checkpoint.')
```
### Weight and Bias Variables
Next we also defined functions that will create weight and bias variables of given shapes, and the correct truncated normal distribution initialisation:
```
def weight_variable(shape):
'''weight_variable generates a weight variable of a given shape.'''
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial, name='weights')
def bias_variable(shape):
'''bias_variable generates a bias variable of a given shape.'''
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial, name='biases')
```
### Defining Input Size
Note in the file, the input size is defined as 32X32X3, reflecting 3 colour channels - R,G,B

You can check this in the code:
```
x = tf.placeholder(tf.float32, [None, FLAGS.img_width * FLAGS.img_height * FLAGS.img_channels])
```
### Convolutional and Pooling Layers
In your file, you will find the definition of the first convolutional filter shown here []

```
with tf.variable_scope('Conv_1'):
W_conv1 = weight_variable([5, 5, FLAGS.img_channels, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(tf.nn.conv2d(x_image, W_conv1, strides=[1, 1, 1, 1], padding='SAME',
name='convolution') + b_conv1)
```
Followed by the definition of a max-pooling layer:

```
# Pooling layer - downsamples by 2X.
h_pool1 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME', name='pooling')
```
### Build the rest of your CNN (Your Code)
**NOW** Introduce the next convolutional layer, and label it as `Conv_2` based on the following figure

**THEN** follow it by the same max-pooling, again using 2x2 kernel as before

**NOW** reshape the output of your max pooling to be one dimensional

**NOW** remind yourself from the last lab how to introduce fully connected layers, with RELU as your activation function as follows

**FINALLY** Add another fully connected layer of the same size and define the output accordingly. The number of classes in CIFAR-10 is defined in the flag: FLAGS.num_classes

All the above should be defined with the function `def deepnn(x):`
We can now declare our main function, which uses a tensoflow session that initialises the CNN we defined, and allows us to check that all the conections and data feeding are in the right place through [TensorBoard](https://www.tensorflow.org/get_started/summaries_and_tensorboard).
### Optimisation and Gradient Descent
**Now** that we have a CNN we want to actually train it! Time to include a loss function. We're using the standard cross entropy loss between the logits and the labels from the ground truth. Replace the code *in main*
```
# Define your loss function - softmax_cross_entropy
cross_entropy = 0
```
with
```
with tf.variable_scope('x_entropy'):
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y_conv))
```
**NOW** replace the code with the right optimiser and the test accuracy
```
# Define your AdamOptimiser, using FLAGS.learning_rate to minimise the loss function
# calculate the prediction and the accuracy
correct_prediction = 0
accuracy = 0
```
We find the main training loop inside of the main function inside the tensorflow session. We run the loop 10,000 times however we only bother printing out the training information every 100 steps. Note we do not have to write any derivatives explicitely due to TensorFlow's [automatic differentiation](http://www.columbia.edu/~ahd2125/post/2015/12/5/).
```
for step in range(FLAGS.max_steps):
# Training: Backpropagation using train set
(trainImages, trainLabels) = cifar.getTrainBatch()
(testImages, testLabels) = cifar.getTestBatch()
```
We have defined everything your TF model needs to be trained, so we only need to include some code for visualising the training progess and saving checkpoints.
**NOW** uncomment ALL lines in your code that start with **`##`**, making sure you correctly defined the `optimiser`.
Study the code as follows:
### Summaries and Tensorboard
Tensorboard allows for the visualisation of training and testing statistics in addition to a graphical output of the CNN that was trained. To do this we can run tensorboard on Blue Crystal and, via the use of port forwarding, view the results on the lab machines.
First, we need to indicate what we want to be save on the summaries, for now we will save some images that are feed in to model, the loss and accuracy for every batch.
**Important** study the code to ensure you understand what summaries it writes to the tensorboard.
#### Saving checkpoints
Lastly, we include a saver for saving checkpoints so you can use them as a backup of your training and later for evaluation of your model.
Through the flags, we have set the the code to save the model every 1000 steps.
```
# %load -r 186:189 simple_train_cifar.py
# Save the model checkpoint periodically.
if step % FLAGS.save_model == 0 or (step + 1) == FLAGS.max_steps:
checkpoint_path = os.path.join(FLAGS.train_dir + '_train', 'model.ckpt')
```
### Validating and evaluating results
Finally, below we show how to use the CIFAR-10's *test set*, in order to see how well the model performs for classifing unseen examples. In this Lab sessions will use the test set primarly for hyperparameters selection. Bare in mind that for this task, usually a subsampling of the training set (commonly detoned as *validation set*) is used for this task. Using validation and test sets helps to identify cases of under and overfitting, as well as for benchmarking the performance among different algorithms.
```
# Testing
# resetting the internal batch indexes
cifar.reset()
evaluatedImages = 0
test_accuracy = 0
nRuns = 0
while evaluatedImages != cifar.nTestSamples:
# don't loop back when we reach the end of the test set
(testImages, testLabels) = cifar.getTestBatch(allowSmallerBatches=True)
test_accuracy_temp, _ = sess.run([accuracy, test_summary], feed_dict={x: testImages, y_: testLabels})
nRuns = nRuns + 1
test_accuracy = test_accuracy + test_accuracy_temp
evaluatedImages = evaluatedImages + testLabels.shape[0]
test_accuracy = test_accuracy / nRuns
```
## 1.4 Complete File
We now have a complete file for defining a CNN, training, validation and checkpoints. We will next move onto training the model using Blue Crystal 4
## 2 Blue Crystal Phase 4
BlueCrystal Phase 4 (BC4) is the latest update on the University's High Performance Computing (HPC) machine. It includes 32 GPU-accelerated nodes, each of them with two NVIDIA Tesla P100 GPU accelerators and also a visualization node equipped with NVIDIA GRID GPUs; what matters to us are the Tesla P100 GPU accelerators that we will use for training your Deep Learing algorithms.
Further information on BC4 and the support we have for it are available at: https://www.acrc.bris.ac.uk/acrc/phase4.htm
**NOTE**: You may try to debug and run programs on your own machine, but sadly we are unable to offer assistance for installing and/or set-up of the dependencies on personal machines.
There are two *modes* for using BC4: *Interactive* and *Batch*. We will use *Interactive* as much as possible during lab sessions, since it allows the immediate excution of your program and you can see outputs directy on the terminal window (great for debugging); while the *Batch* method queues your job and generates files related with the excecution of your file. You will use *Batch* as part of CW2, so we will revisit that later.
## 2.1 Copying Lab-1 files between your machine and BC4
You need to copy the provided folders `CIFAR10` and `Lab_1_intro` (which contains `simple_train_cifar.py`, `submit_job.sh`, `tensorboard_params.sh`, `go_interactive.sh`) to your account in BC4. For copying individual files from your machine to your home directory on BC4 use the next example with go_interactive.sh:
For copying individual files from your machine to your home directory on BC4 use the next example with `go_interactive.sh`:
```bash
scp /path_to_files/Lab_1_intro/go_interactive.sh <your_UoB_ID>@bc4login.acrc.bris.ac.uk:
```
or all files at once by using:
```bash
scp -r /path_to_files/* <your_UoB_ID>@bc4login.acrc.bris.ac.uk:
```
For copying back files from BC4 to your machine use the command ```scp``` from a terminal on your machine, you can copy individual files, as well as directories:
```bash
scp <your_UoB_ID>@bc4login.acrc.bris.ac.uk:/path_on_bc4/foo.foo /path_in_your_machine/
```
Alternatively, you may wish to use SSHFS to mount a directory on BC4 to a directory using:
```bash
mkdir -p ~/bc4 && sshfs <your_UOB_ID>@bc4login.acrc.bris.ac.uk:/dir_on_bc4/ ~/bc4
```
## 2.2 Logging in, running scripts and managing your directory
Replicate the next steps for logging-in BC4.
### **Logging in**
The connection to BC4 is done via SSH, thus open a **new** Terminal window and type:
```bash
ssh <your_UoB_ID>@bc4login.acrc.bris.ac.uk
```
You should see something like this in your home directory:
```
CIFAR10
|----------cifar10.py
Lab_2_CNNs
|----------simple_train_cifar.py
|----------submit_job.sh
|----------tensorboard_params.sh
|----------go_interactive.sh```
**NOTE: If you cannot see the file structure above, you have not copied the files correctly**
## 2.3 Training your first CNN.
**It's finally here, the moment you've been waiting for!**
Follow the next steps for running the training script:
1. Using the blue crystal ssh login change to the lab 2 directory:
```cd Lab_2_CNNs/```
2. make all .sh files executables by using the command `chmod`:
```chmod +x go_interactive.sh submit_job.sh tensorboard_params.sh```
3. Switch to interactive mode, and note the change of the gpu login to a reserved gpu:
```./go_interactive.sh ```
4. Run the following script. It will pop up two values: `ipnport=XXXXX` and `ipnip=XX.XXX.X.X.`
```./tensorboard_params.sh```
**Write them down since we will use them for using TensorBoard.**
5. Train the model using the command:
```bash
python simple_train_cifar.py &
tensorboard --logdir=logs/ --port=<ipnport>
```
where `ipnport` comes from the previous step. It might take a minute or two before you start seeing the accuracy on the validation batch at every step
## 2.4 Visualising and Monitoring Your Training
1. Open a **new Terminal window** on your machine and type:
``` ssh <USER_NAME>@bc4login.acrc.bris.ac.uk -L 6006:<ipnip>:<ipnport>```</mark>
where `ipnip` and `ipnport` comes from step 2 in **2.3**.
2. Open your web browser (Use Chrome; Firefox currently has issues with tensorboard) and open the port 6006 (http://localhost:6006). This should open TensorBoard, and you can navigate through the summaries that we included.
3. Go to the **GRAPH** tab and navigate to your CNN, identifying the two convolutional layers `CONV_1`, `CONV_2`, and their hyperparameters as well as the two fully-connected layers `FC_1` and `FC_2`
4. Go to the **SCALARS** tab
5. Tick the box *Show data download links*
6. Click on **Loss**
7. Download the csv file `run_exp_bs_128_lr_0.0001_train,tag_Loss.csv`
** Keep the csv file for your portfolio of Lab_1 **
By using TensorBoard you can monitor the training process. In the following labs you will perform experiments by varying hyperparemeters such as learning rate, batch size, epochs, etc.
## 2.6 Saving your trained model
You should copy your log files back from BC4, and save them for your first lab portfolio
```bash
scp -r <your_UoB_ID>@bc4login.acrc.bris.ac.uk:/Lab_2_CNNs/logs /path_in_your_machine/
```
Both your directory `logs/` and your `csv` file should be submitted as part of your Lab_2 portfolio (see [**section 5**](#5.-Preparing-Lab_2-Portfolio)).
# 3. Training your Second CNN
It is now time to train your own modification to the CNN above.
Choose one hyperparameter to change in your built CNN. You might add/remove layers, change layer sizes, ...
** Discuss your choice with a TA **
1. Duplicate and rename your file ```simple_train_cifar.py``` into ```second_train_cifar.py```
2. Change the code to reflect **your chosen hyperparameter change**
3. Copy ```second_train_cifar.py``` to BC4 as you've done previously
4. Train the model using the following command.
```bash
python second_train_cifar.py &
tensorboard --logdir=logs_second/ --port=<ipnport>
```
**NOTE: the change in the logs directory**
5. Load your tensorboard to read from the *new logs* directory
6. Save *logs_second* folder and the new *csv* back to your machine
# 4. Closing all sessions
Once the training has finished, **close all sessions** by typing `exit`. You need to do this twice for an **interactive session.**
**Please make sure closing your session in order to release the gpu node.**
# 5. Preparing Lab_2 Portfolio
You should by now have the following files, which you can zip under the name `Lab_1_<username>.zip`
**From your logs, include only the TensorBoard summaries and remove the checkpoints (model.ckpt-* files)**
```
Lab_2_<username>.zip
|----------logs\
|----------exp_bs_128_lr_0.0001_train
|----------events.out.tfevents.xxxxxxxxxx.gpuxx.bc4.acrc.priv
|----------exp_bs_128_lr_0.0001_validate
|----------events.out.tfevents.xxxxxxxxxx.gpuxx.bc4.acrc.priv
|----------run_exp_bs_128_lr_0.0001_train,tag_Loss.csv
|----------logs_second\
|----------<your second training>_train
|----------events.out.tfevents.xxxxxxxxxx.gpuxx.bc4.acrc.priv
|----------<your second training>_validate
|----------events.out.tfevents.xxxxxxxxxx.gpuxx.bc4.acrc.priv
|----------<your second training.csv>
```
Store this zip safely. You will be asked to upload all your labs' portfolio to ** SAFE during Week 9 ** - check SAFE for deadline details.
# NOTE: Using the batch method
During the course it may occur that very few GPUs are available due maintenance, other people using them, unforseen events, etc. making it not possible to use the *Interactive Session* previously described. Should this happen you will have to use the *batch method*. To do this establish a connection to BC4 as described before. Open the file "submit_job.sh" using emacs, vim or your favourite CLI text editor, and **modify line #10** to include your email (Blue Crystal will send you notifications about the jobs you're submitting) and **modify line #14** for the filename you are running. Now, run the next command for submitting a job to the BC4 queueing system:
```sbatch submit_job.sh```
And you should see a generated files (`hostname_<job_number>.err` and `hostname_<job_number>.out`) that shows the outputs after running your python script.
In the `hostname_<job_number>.out` you should see output that you normally see on the terminal window when using the interactive mode, `hostname_<job_number>.err` shows the output that occurred during the runing of script that exited with a non-zero exit status.
**NOW** try your batch mode to get used to it for upcoming labs, and primarily for your group project
|
github_jupyter
|
# %load -r 12:35 simple_train_cifar.py
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import sys
import os
import tensorflow as tf
sys.path.append(os.path.join(os.path.dirname(__file__), '..', 'CIFAR10'))
import cifar10 as cf
FLAGS = tf.app.flags.FLAGS
tf.app.flags.DEFINE_string('data-dir', os.getcwd() + '/dataset/',
'Directory where the dataset will be stored and checkpoint.')
tf.app.flags.DEFINE_integer('max-steps', 1000,
'Number of mini-batches to train on.')
tf.app.flags.DEFINE_integer('log-frequency', 100,
'Number of steps between logging results to the console and saving summaries')
tf.app.flags.DEFINE_integer('save-model', 1000,
'Number of steps between model saves')
# %load -r 36:48 simple_train_cifar.py
# Optimisation hyperparameters
tf.app.flags.DEFINE_integer('batch-size', 128, 'Number of examples per mini-batch')
tf.app.flags.DEFINE_float('learning-rate', 1e-4, 'The learning rate for our training.')
tf.app.flags.DEFINE_integer('img-width', 32, 'Image width')
tf.app.flags.DEFINE_integer('img-height', 32, 'Image height')
tf.app.flags.DEFINE_integer('img-channels', 3, 'Image channels')
tf.app.flags.DEFINE_integer('num-classes', 10, 'Number of classes')
tf.app.flags.DEFINE_string('train-dir',
'{cwd}/logs/exp_bs_{bs}_lr_{lr}'.format(cwd=os.getcwd(),
bs=FLAGS.batch_size,
lr=FLAGS.learning_rate),
'Directory where to write event logs and checkpoint.')
def weight_variable(shape):
'''weight_variable generates a weight variable of a given shape.'''
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial, name='weights')
def bias_variable(shape):
'''bias_variable generates a bias variable of a given shape.'''
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial, name='biases')
x = tf.placeholder(tf.float32, [None, FLAGS.img_width * FLAGS.img_height * FLAGS.img_channels])
with tf.variable_scope('Conv_1'):
W_conv1 = weight_variable([5, 5, FLAGS.img_channels, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(tf.nn.conv2d(x_image, W_conv1, strides=[1, 1, 1, 1], padding='SAME',
name='convolution') + b_conv1)
# Pooling layer - downsamples by 2X.
h_pool1 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME', name='pooling')
# Define your loss function - softmax_cross_entropy
cross_entropy = 0
with tf.variable_scope('x_entropy'):
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y_conv))
# Define your AdamOptimiser, using FLAGS.learning_rate to minimise the loss function
# calculate the prediction and the accuracy
correct_prediction = 0
accuracy = 0
for step in range(FLAGS.max_steps):
# Training: Backpropagation using train set
(trainImages, trainLabels) = cifar.getTrainBatch()
(testImages, testLabels) = cifar.getTestBatch()
# %load -r 186:189 simple_train_cifar.py
# Save the model checkpoint periodically.
if step % FLAGS.save_model == 0 or (step + 1) == FLAGS.max_steps:
checkpoint_path = os.path.join(FLAGS.train_dir + '_train', 'model.ckpt')
# Testing
# resetting the internal batch indexes
cifar.reset()
evaluatedImages = 0
test_accuracy = 0
nRuns = 0
while evaluatedImages != cifar.nTestSamples:
# don't loop back when we reach the end of the test set
(testImages, testLabels) = cifar.getTestBatch(allowSmallerBatches=True)
test_accuracy_temp, _ = sess.run([accuracy, test_summary], feed_dict={x: testImages, y_: testLabels})
nRuns = nRuns + 1
test_accuracy = test_accuracy + test_accuracy_temp
evaluatedImages = evaluatedImages + testLabels.shape[0]
test_accuracy = test_accuracy / nRuns
scp /path_to_files/Lab_1_intro/go_interactive.sh <your_UoB_ID>@bc4login.acrc.bris.ac.uk:
scp -r /path_to_files/* <your_UoB_ID>@bc4login.acrc.bris.ac.uk:
scp <your_UoB_ID>@bc4login.acrc.bris.ac.uk:/path_on_bc4/foo.foo /path_in_your_machine/
mkdir -p ~/bc4 && sshfs <your_UOB_ID>@bc4login.acrc.bris.ac.uk:/dir_on_bc4/ ~/bc4
ssh <your_UoB_ID>@bc4login.acrc.bris.ac.uk
CIFAR10
|----------cifar10.py
Lab_2_CNNs
|----------simple_train_cifar.py
|----------submit_job.sh
|----------tensorboard_params.sh
|----------go_interactive.sh```
**NOTE: If you cannot see the file structure above, you have not copied the files correctly**
## 2.3 Training your first CNN.
**It's finally here, the moment you've been waiting for!**
Follow the next steps for running the training script:
1. Using the blue crystal ssh login change to the lab 2 directory:
```cd Lab_2_CNNs/```
2. make all .sh files executables by using the command `chmod`:
```chmod +x go_interactive.sh submit_job.sh tensorboard_params.sh```
3. Switch to interactive mode, and note the change of the gpu login to a reserved gpu:
```./go_interactive.sh ```
4. Run the following script. It will pop up two values: `ipnport=XXXXX` and `ipnip=XX.XXX.X.X.`
```./tensorboard_params.sh```
**Write them down since we will use them for using TensorBoard.**
5. Train the model using the command:
```bash
python simple_train_cifar.py &
tensorboard --logdir=logs/ --port=<ipnport>
```
where `ipnport` comes from the previous step. It might take a minute or two before you start seeing the accuracy on the validation batch at every step
## 2.4 Visualising and Monitoring Your Training
1. Open a **new Terminal window** on your machine and type:
``` ssh <USER_NAME>@bc4login.acrc.bris.ac.uk -L 6006:<ipnip>:<ipnport>```</mark>
where `ipnip` and `ipnport` comes from step 2 in **2.3**.
2. Open your web browser (Use Chrome; Firefox currently has issues with tensorboard) and open the port 6006 (http://localhost:6006). This should open TensorBoard, and you can navigate through the summaries that we included.
3. Go to the **GRAPH** tab and navigate to your CNN, identifying the two convolutional layers `CONV_1`, `CONV_2`, and their hyperparameters as well as the two fully-connected layers `FC_1` and `FC_2`
4. Go to the **SCALARS** tab
5. Tick the box *Show data download links*
6. Click on **Loss**
7. Download the csv file `run_exp_bs_128_lr_0.0001_train,tag_Loss.csv`
** Keep the csv file for your portfolio of Lab_1 **
By using TensorBoard you can monitor the training process. In the following labs you will perform experiments by varying hyperparemeters such as learning rate, batch size, epochs, etc.
## 2.6 Saving your trained model
You should copy your log files back from BC4, and save them for your first lab portfolio
Both your directory `logs/` and your `csv` file should be submitted as part of your Lab_2 portfolio (see [**section 5**](#5.-Preparing-Lab_2-Portfolio)).
# 3. Training your Second CNN
It is now time to train your own modification to the CNN above.
Choose one hyperparameter to change in your built CNN. You might add/remove layers, change layer sizes, ...
** Discuss your choice with a TA **
1. Duplicate and rename your file ```simple_train_cifar.py``` into ```second_train_cifar.py```
2. Change the code to reflect **your chosen hyperparameter change**
3. Copy ```second_train_cifar.py``` to BC4 as you've done previously
4. Train the model using the following command.
```bash
python second_train_cifar.py &
tensorboard --logdir=logs_second/ --port=<ipnport>
```
**NOTE: the change in the logs directory**
5. Load your tensorboard to read from the *new logs* directory
6. Save *logs_second* folder and the new *csv* back to your machine
# 4. Closing all sessions
Once the training has finished, **close all sessions** by typing `exit`. You need to do this twice for an **interactive session.**
**Please make sure closing your session in order to release the gpu node.**
# 5. Preparing Lab_2 Portfolio
You should by now have the following files, which you can zip under the name `Lab_1_<username>.zip`
**From your logs, include only the TensorBoard summaries and remove the checkpoints (model.ckpt-* files)**
```
Lab_2_<username>.zip
|----------logs\
|----------exp_bs_128_lr_0.0001_train
|----------events.out.tfevents.xxxxxxxxxx.gpuxx.bc4.acrc.priv
|----------exp_bs_128_lr_0.0001_validate
|----------events.out.tfevents.xxxxxxxxxx.gpuxx.bc4.acrc.priv
|----------run_exp_bs_128_lr_0.0001_train,tag_Loss.csv
|----------logs_second\
|----------<your second training>_train
|----------events.out.tfevents.xxxxxxxxxx.gpuxx.bc4.acrc.priv
|----------<your second training>_validate
|----------events.out.tfevents.xxxxxxxxxx.gpuxx.bc4.acrc.priv
|----------<your second training.csv>
```
Store this zip safely. You will be asked to upload all your labs' portfolio to ** SAFE during Week 9 ** - check SAFE for deadline details.
# NOTE: Using the batch method
During the course it may occur that very few GPUs are available due maintenance, other people using them, unforseen events, etc. making it not possible to use the *Interactive Session* previously described. Should this happen you will have to use the *batch method*. To do this establish a connection to BC4 as described before. Open the file "submit_job.sh" using emacs, vim or your favourite CLI text editor, and **modify line #10** to include your email (Blue Crystal will send you notifications about the jobs you're submitting) and **modify line #14** for the filename you are running. Now, run the next command for submitting a job to the BC4 queueing system:
| 0.73077 | 0.986416 |
# Working with graphical user interfaces
## Example: Long Author List formatting tool
We will create a graphical user interface (GUI) from the tkinter module and use it to interact with a pandas array.
### Input data:
Here is a list of authors and affiliations from a recent paper.
I use a semicolon separated text format to accommodate commas and other special characters in the affiliations strings. I am sure there is something more appropriate, but I want to be flexible to quickly modify in a text editor.
Input: lal_data2.txt with one author per row and up to 5 affiliations
<First>;<Last>;<Email>;<Group1>;<Group2>;<Group3>;<Group4>;<Group5>
Example: Heiko;Goelzer;h.goelzer@uu.nl;IMAU,UU;ULB;nil;nil;nil
Use 'nil','nan','0' or '-' to fill unused affiliations
And here is an example file to work with:
```
f = open('lal_data2.txt')
inputdata = f.read()
f.close()
print(inputdata)
```
Let's read this to a pandas array to use high level features, like sorting.
```
import pandas as pd
import numpy as np
# Read input data from file
df = pd.read_csv('lal_data2.txt', sep=';', header=None ,names=np.array(['FirstName', 'LastName', 'Email', 'Group1','Group2','Group3','Group4','Group5']))
print(df.size)
print(df.shape[0])
print(df)
```
### The listbox:
Here we set up a reorderable listbox view, which will hold the author names.
This listbox has a couple of methods to manipulate it's content: drag-and-drop reordering, sorting, deleting.
In the second part a number of different parsing options are defined.
```
import tkinter as tk;
# Listbox for ordering
class ReorderableListbox(tk.Listbox):
""" A Tkinter listbox with drag & drop reordering of lines """
def __init__(self, master, **kw):
kw['selectmode'] = tk.EXTENDED
tk.Listbox.__init__(self, master, kw)
self.bind('<Button-1>', self.setCurrent)
self.bind('<Control-1>', self.toggleSelection)
self.bind('<B1-Motion>', self.shiftSelection)
self.bind('<Leave>', self.onLeave)
self.bind('<Enter>', self.onEnter)
self.selectionClicked = False
self.left = False
self.unlockShifting()
self.ctrlClicked = False
def orderChangedEventHandler(self):
pass
def onLeave(self, event):
# prevents changing selection when dragging
# already selected items beyond the edge of the listbox
if self.selectionClicked:
self.left = True
return 'break'
def onEnter(self, event):
#TODO
self.left = False
def setCurrent(self, event):
self.ctrlClicked = False
i = self.nearest(event.y)
self.selectionClicked = self.selection_includes(i)
if (self.selectionClicked):
return 'break'
def toggleSelection(self, event):
self.ctrlClicked = True
def moveElement(self, source, target):
if not self.ctrlClicked:
element = self.get(source)
self.delete(source)
self.insert(target, element)
def unlockShifting(self):
self.shifting = False
def lockShifting(self):
# prevent moving processes from disturbing each other
# and prevent scrolling too fast
# when dragged to the top/bottom of visible area
self.shifting = True
def shiftSelection(self, event):
if self.ctrlClicked:
return
selection = self.curselection()
if not self.selectionClicked or len(selection) == 0:
return
selectionRange = range(min(selection), max(selection))
currentIndex = self.nearest(event.y)
if self.shifting:
return 'break'
lineHeight = 12
bottomY = self.winfo_height()
if event.y >= bottomY - lineHeight:
self.lockShifting()
self.see(self.nearest(bottomY - lineHeight) + 1)
self.master.after(500, self.unlockShifting)
if event.y <= lineHeight:
self.lockShifting()
self.see(self.nearest(lineHeight) - 1)
self.master.after(500, self.unlockShifting)
if currentIndex < min(selection):
self.lockShifting()
notInSelectionIndex = 0
for i in selectionRange[::-1]:
if not self.selection_includes(i):
self.moveElement(i, max(selection)-notInSelectionIndex)
notInSelectionIndex += 1
currentIndex = min(selection)-1
self.moveElement(currentIndex, currentIndex + len(selection))
self.orderChangedEventHandler()
elif currentIndex > max(selection):
self.lockShifting()
notInSelectionIndex = 0
for i in selectionRange:
if not self.selection_includes(i):
self.moveElement(i, min(selection)+notInSelectionIndex)
notInSelectionIndex += 1
currentIndex = max(selection)+1
self.moveElement(currentIndex, currentIndex - len(selection))
self.orderChangedEventHandler()
self.unlockShifting()
return 'break'
def deleteSelection(self):
# delete selected items
if len(self.curselection()) == 0:
return
self.delete(min(self.curselection()),max(self.curselection()))
def sortAll(self):
# sort all items alphabetically
temp_list = list(self.get(0, tk.END))
temp_list.sort(key=str.lower)
# delete contents of present listbox
self.delete(0, tk.END)
# load listbox with sorted data
for item in temp_list:
self.insert(tk.END, item)
def sortSelection(self):
# sort selected items alphabetically
if len(self.curselection()) == 0:
return
mmax = max(self.curselection())
mmin = min(self.curselection())
temp_list = list(self.get(mmin,mmax))
#print(temp_list)
# Sort reverse because pushed back in reverse order
temp_list.sort(key=str.lower,reverse=True)
# delete contents of present listbox
self.delete(mmin,mmax)
# load listbox with sorted data
for item in temp_list:
self.insert(mmin, item)
#### Different saving and parsing options
def save(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
matche = (df["Email"].isin([items[2]]))
dfout = dfout.append(df[matchf & matchl])
dfout.to_csv('lal_inout2.txt', sep=';', header=None, index=None)
print("File saved!")
def parse_word(self,df):
# parse current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
grp = dfout[["Group1","Group2","Group3","Group4","Group5"]]
unique_groups = []
group_ids = []
k = 0
# collect unique groups and indices
for i in range(0,dfout.shape[0]):
groups = []
# loop through max 5 groups
for j in range(0,5):
# Exclude some common dummy place holders
if (grp.iloc[i,j] not in ['nil','nan','0','-']):
if (grp.iloc[i,j] not in unique_groups):
unique_groups.append(grp.iloc[i,j])
k = k + 1
groups.append(k)
else:
ix = unique_groups.index(grp.iloc[i,j])+1
groups.append(ix)
# Add author group ids
group_ids.append(groups)
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_word.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print(first.iloc[i].strip(), end =" ", file=text_file)
print(last.iloc[i].strip(), end ="", file=text_file)
for j in range(0,len(group_ids[i])):
if j < len(group_ids[i])-1:
print(str(group_ids[i][j]), end =",", file=text_file)
else:
print(str(group_ids[i][j]), end ="", file=text_file)
#print(" ", end ="", file=text_file)
if (i < dfout.shape[0]-1):
# comma and space before next name
print(", ", end ="", file=text_file)
# Add some space between names and affiliations
print("\n\n", file=text_file)
# Write out affiliations
for i in range(0,len(unique_groups)):
print("(", end ="", file=text_file)
print(str(i+1), end ="", file=text_file)
print(")", end =" ", file=text_file)
print(unique_groups[i], end ="\n", file=text_file)
print("File lal_parsed_word.txt written")
# Parse tex \author and \affil
def parse_tex(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
grp = dfout[["Group1","Group2","Group3","Group4","Group5"]]
unique_groups = []
group_ids = []
k = 0
# collect unique groups and indices
for i in range(0,dfout.shape[0]):
groups = []
# loop through max 5 groups
for j in range(0,5):
# Exclude some common dummy place holders
if (grp.iloc[i,j] not in ['nil','nan','0','-']):
if (grp.iloc[i,j] not in unique_groups):
unique_groups.append(grp.iloc[i,j])
k = k + 1
groups.append(k)
else:
ix = unique_groups.index(grp.iloc[i,j])+1
groups.append(ix)
# Add author group ids
group_ids.append(groups)
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_tex.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print("\\Author[", end ="", file=text_file)
for j in range(0,len(group_ids[i])):
if j < len(group_ids[i])-1:
print(str(group_ids[i][j]), end =",", file=text_file)
else:
print(str(group_ids[i][j]), end ="]", file=text_file)
print("{", end ="", file=text_file)
print(first.iloc[i].strip(), end ="", file=text_file)
print("}{", end ="", file=text_file)
print(last.iloc[i].strip(), end ="", file=text_file)
print("}", end ="\n", file=text_file)
# Add some space between names and affiliations
print("\n", file=text_file)
# Write out affiliations
for i in range(0,len(unique_groups)):
print("\\affil", end ="", file=text_file)
print("[", end ="", file=text_file)
print(str(i+1), end ="", file=text_file)
print("]", end ="", file=text_file)
print("{", end ="", file=text_file)
print(unique_groups[i], end ="}\n", file=text_file)
print("File lal_parsed_tex.txt written")
# Parse simple list of names
def parse_list(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_list.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print(first.iloc[i].strip(), end =" ", file=text_file)
print(last.iloc[i].strip(), end ="", file=text_file)
print("", file=text_file)
print("File lal_parsed_list.txt written!")
# Parse list of names and emails
def parse_email(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
email = dfout["Email"]
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_email.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print(first.iloc[i].strip(), end =" ", file=text_file)
print(last.iloc[i].strip(), end =" ", file=text_file)
print("<", end ="", file=text_file)
print(email.iloc[i].strip(), end ="", file=text_file)
print(">", end ="", file=text_file)
print("", file=text_file)
print("File lal_parsed_email.txt written!")
# Parse sorted list of names
def parse_sorted(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# sort all items alphabetically
temp_list.sort(key=str.lower)
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_sorted.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print(first.iloc[i].strip(), end =" ", file=text_file)
print(last.iloc[i].strip(), end ="", file=text_file)
print("", file=text_file)
print("File lal_parsed_sorted.txt written!")
# Define what files should be parsed
def parse_all(self,df):
self.parse_word(df)
self.parse_tex(df)
self.parse_list(df)
self.parse_email(df)
self.parse_sorted(df)
print("All files parsed!")
```
### The graphical user interface:
Here we set up the tkinter GUI.
First we create a reorderable listbox view and populates it with our author information.
```
# GUI to sort names
root = tk.Tk()
root.geometry("200x800")
root.title("LongAuthorList")
root.attributes("-topmost", True)
listbox = ReorderableListbox(root)
for i in range(0,df.shape[0]):
listbox.insert(tk.END, df.at[i,'LastName'] + ',' + df.at[i,'FirstName'] +
',' + str(i) )
listbox.pack(fill=tk.BOTH, expand=True)
```
Add a couple of buttons that connect to methods of the list view.
```
# Add a delete button
db = tk.Button(root, text="Delete", height=2,
command=lambda listbox=listbox: listbox.deleteSelection())
db.pack(fill=tk.BOTH, expand=False)
# Add button to sort all entries
sortallb = tk.Button(root, text="Sort All", height=2, command = lambda: listbox.sortAll())
sortallb.pack(fill=tk.BOTH, expand=False)
# Add button to sort the selection
sortb = tk.Button(root, text="Sort Selection", height=2, command = lambda: listbox.sortSelection())
sortb.pack(fill=tk.BOTH, expand=False)
# Add a save button
saveb = tk.Button(root, text="Save", height=2, command = lambda: listbox.save(df))
saveb.pack(fill=tk.BOTH, expand=False)
# Add a parse button
parseb = tk.Button(root, text="Parse", height=2, command = lambda: listbox.parse_all(df))
parseb.pack(fill=tk.BOTH, expand=False)
```
### Fire it up:
```
# Run the main tool
root.mainloop()
```
### Output:
Output: lal_inout2.txt
After saving the modified listing, this file can be used as input the next time.
```
f = open('lal_inout2.txt')
outputdata = f.read()
f.close()
print(outputdata)
```
### Parsed:
Parsed: lal_parsed_*.txt
Text parsed in different formats e.g. to be inserted in a manuscript.
```
f = open('lal_parsed_word.txt')
worddata = f.read()
f.close()
print(worddata)
f = open('lal_parsed_tex.txt')
texdata = f.read()
f.close()
print(texdata)
f = open('lal_parsed_email.txt')
emaildata = f.read()
f.close()
print(emaildata)
```
## Additional information
Graphical User Interfaces with Tk
https://docs.python.org/3/library/tk.html
Some basic Tk examples
https://likegeeks.com/python-gui-examples-tkinter-tutorial/
Other GUI frameworks
- PyQT https://wiki.python.org/moin/PyQt/Tutorials
- Kivy https://kivy.org/#home
|
github_jupyter
|
f = open('lal_data2.txt')
inputdata = f.read()
f.close()
print(inputdata)
import pandas as pd
import numpy as np
# Read input data from file
df = pd.read_csv('lal_data2.txt', sep=';', header=None ,names=np.array(['FirstName', 'LastName', 'Email', 'Group1','Group2','Group3','Group4','Group5']))
print(df.size)
print(df.shape[0])
print(df)
import tkinter as tk;
# Listbox for ordering
class ReorderableListbox(tk.Listbox):
""" A Tkinter listbox with drag & drop reordering of lines """
def __init__(self, master, **kw):
kw['selectmode'] = tk.EXTENDED
tk.Listbox.__init__(self, master, kw)
self.bind('<Button-1>', self.setCurrent)
self.bind('<Control-1>', self.toggleSelection)
self.bind('<B1-Motion>', self.shiftSelection)
self.bind('<Leave>', self.onLeave)
self.bind('<Enter>', self.onEnter)
self.selectionClicked = False
self.left = False
self.unlockShifting()
self.ctrlClicked = False
def orderChangedEventHandler(self):
pass
def onLeave(self, event):
# prevents changing selection when dragging
# already selected items beyond the edge of the listbox
if self.selectionClicked:
self.left = True
return 'break'
def onEnter(self, event):
#TODO
self.left = False
def setCurrent(self, event):
self.ctrlClicked = False
i = self.nearest(event.y)
self.selectionClicked = self.selection_includes(i)
if (self.selectionClicked):
return 'break'
def toggleSelection(self, event):
self.ctrlClicked = True
def moveElement(self, source, target):
if not self.ctrlClicked:
element = self.get(source)
self.delete(source)
self.insert(target, element)
def unlockShifting(self):
self.shifting = False
def lockShifting(self):
# prevent moving processes from disturbing each other
# and prevent scrolling too fast
# when dragged to the top/bottom of visible area
self.shifting = True
def shiftSelection(self, event):
if self.ctrlClicked:
return
selection = self.curselection()
if not self.selectionClicked or len(selection) == 0:
return
selectionRange = range(min(selection), max(selection))
currentIndex = self.nearest(event.y)
if self.shifting:
return 'break'
lineHeight = 12
bottomY = self.winfo_height()
if event.y >= bottomY - lineHeight:
self.lockShifting()
self.see(self.nearest(bottomY - lineHeight) + 1)
self.master.after(500, self.unlockShifting)
if event.y <= lineHeight:
self.lockShifting()
self.see(self.nearest(lineHeight) - 1)
self.master.after(500, self.unlockShifting)
if currentIndex < min(selection):
self.lockShifting()
notInSelectionIndex = 0
for i in selectionRange[::-1]:
if not self.selection_includes(i):
self.moveElement(i, max(selection)-notInSelectionIndex)
notInSelectionIndex += 1
currentIndex = min(selection)-1
self.moveElement(currentIndex, currentIndex + len(selection))
self.orderChangedEventHandler()
elif currentIndex > max(selection):
self.lockShifting()
notInSelectionIndex = 0
for i in selectionRange:
if not self.selection_includes(i):
self.moveElement(i, min(selection)+notInSelectionIndex)
notInSelectionIndex += 1
currentIndex = max(selection)+1
self.moveElement(currentIndex, currentIndex - len(selection))
self.orderChangedEventHandler()
self.unlockShifting()
return 'break'
def deleteSelection(self):
# delete selected items
if len(self.curselection()) == 0:
return
self.delete(min(self.curselection()),max(self.curselection()))
def sortAll(self):
# sort all items alphabetically
temp_list = list(self.get(0, tk.END))
temp_list.sort(key=str.lower)
# delete contents of present listbox
self.delete(0, tk.END)
# load listbox with sorted data
for item in temp_list:
self.insert(tk.END, item)
def sortSelection(self):
# sort selected items alphabetically
if len(self.curselection()) == 0:
return
mmax = max(self.curselection())
mmin = min(self.curselection())
temp_list = list(self.get(mmin,mmax))
#print(temp_list)
# Sort reverse because pushed back in reverse order
temp_list.sort(key=str.lower,reverse=True)
# delete contents of present listbox
self.delete(mmin,mmax)
# load listbox with sorted data
for item in temp_list:
self.insert(mmin, item)
#### Different saving and parsing options
def save(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
matche = (df["Email"].isin([items[2]]))
dfout = dfout.append(df[matchf & matchl])
dfout.to_csv('lal_inout2.txt', sep=';', header=None, index=None)
print("File saved!")
def parse_word(self,df):
# parse current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
grp = dfout[["Group1","Group2","Group3","Group4","Group5"]]
unique_groups = []
group_ids = []
k = 0
# collect unique groups and indices
for i in range(0,dfout.shape[0]):
groups = []
# loop through max 5 groups
for j in range(0,5):
# Exclude some common dummy place holders
if (grp.iloc[i,j] not in ['nil','nan','0','-']):
if (grp.iloc[i,j] not in unique_groups):
unique_groups.append(grp.iloc[i,j])
k = k + 1
groups.append(k)
else:
ix = unique_groups.index(grp.iloc[i,j])+1
groups.append(ix)
# Add author group ids
group_ids.append(groups)
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_word.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print(first.iloc[i].strip(), end =" ", file=text_file)
print(last.iloc[i].strip(), end ="", file=text_file)
for j in range(0,len(group_ids[i])):
if j < len(group_ids[i])-1:
print(str(group_ids[i][j]), end =",", file=text_file)
else:
print(str(group_ids[i][j]), end ="", file=text_file)
#print(" ", end ="", file=text_file)
if (i < dfout.shape[0]-1):
# comma and space before next name
print(", ", end ="", file=text_file)
# Add some space between names and affiliations
print("\n\n", file=text_file)
# Write out affiliations
for i in range(0,len(unique_groups)):
print("(", end ="", file=text_file)
print(str(i+1), end ="", file=text_file)
print(")", end =" ", file=text_file)
print(unique_groups[i], end ="\n", file=text_file)
print("File lal_parsed_word.txt written")
# Parse tex \author and \affil
def parse_tex(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
grp = dfout[["Group1","Group2","Group3","Group4","Group5"]]
unique_groups = []
group_ids = []
k = 0
# collect unique groups and indices
for i in range(0,dfout.shape[0]):
groups = []
# loop through max 5 groups
for j in range(0,5):
# Exclude some common dummy place holders
if (grp.iloc[i,j] not in ['nil','nan','0','-']):
if (grp.iloc[i,j] not in unique_groups):
unique_groups.append(grp.iloc[i,j])
k = k + 1
groups.append(k)
else:
ix = unique_groups.index(grp.iloc[i,j])+1
groups.append(ix)
# Add author group ids
group_ids.append(groups)
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_tex.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print("\\Author[", end ="", file=text_file)
for j in range(0,len(group_ids[i])):
if j < len(group_ids[i])-1:
print(str(group_ids[i][j]), end =",", file=text_file)
else:
print(str(group_ids[i][j]), end ="]", file=text_file)
print("{", end ="", file=text_file)
print(first.iloc[i].strip(), end ="", file=text_file)
print("}{", end ="", file=text_file)
print(last.iloc[i].strip(), end ="", file=text_file)
print("}", end ="\n", file=text_file)
# Add some space between names and affiliations
print("\n", file=text_file)
# Write out affiliations
for i in range(0,len(unique_groups)):
print("\\affil", end ="", file=text_file)
print("[", end ="", file=text_file)
print(str(i+1), end ="", file=text_file)
print("]", end ="", file=text_file)
print("{", end ="", file=text_file)
print(unique_groups[i], end ="}\n", file=text_file)
print("File lal_parsed_tex.txt written")
# Parse simple list of names
def parse_list(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_list.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print(first.iloc[i].strip(), end =" ", file=text_file)
print(last.iloc[i].strip(), end ="", file=text_file)
print("", file=text_file)
print("File lal_parsed_list.txt written!")
# Parse list of names and emails
def parse_email(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
email = dfout["Email"]
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_email.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print(first.iloc[i].strip(), end =" ", file=text_file)
print(last.iloc[i].strip(), end =" ", file=text_file)
print("<", end ="", file=text_file)
print(email.iloc[i].strip(), end ="", file=text_file)
print(">", end ="", file=text_file)
print("", file=text_file)
print("File lal_parsed_email.txt written!")
# Parse sorted list of names
def parse_sorted(self,df):
# save current list
temp_list = list(self.get(0, tk.END))
# sort all items alphabetically
temp_list.sort(key=str.lower)
# create output df
dfout = pd.DataFrame()
for item in temp_list:
items = item.split(",")
matchl = (df["LastName"].isin([items[0]]))
matchf = (df["FirstName"].isin([items[1]]))
dfout = dfout.append(df[matchf & matchl])
# parse
first = dfout["FirstName"]
last = dfout["LastName"]
#print(group_ids)
#print(unique_groups)
# Compose text
with open("lal_parsed_sorted.txt", "w") as text_file:
# write out names
for i in range(0,dfout.shape[0]):
print(first.iloc[i].strip(), end =" ", file=text_file)
print(last.iloc[i].strip(), end ="", file=text_file)
print("", file=text_file)
print("File lal_parsed_sorted.txt written!")
# Define what files should be parsed
def parse_all(self,df):
self.parse_word(df)
self.parse_tex(df)
self.parse_list(df)
self.parse_email(df)
self.parse_sorted(df)
print("All files parsed!")
# GUI to sort names
root = tk.Tk()
root.geometry("200x800")
root.title("LongAuthorList")
root.attributes("-topmost", True)
listbox = ReorderableListbox(root)
for i in range(0,df.shape[0]):
listbox.insert(tk.END, df.at[i,'LastName'] + ',' + df.at[i,'FirstName'] +
',' + str(i) )
listbox.pack(fill=tk.BOTH, expand=True)
# Add a delete button
db = tk.Button(root, text="Delete", height=2,
command=lambda listbox=listbox: listbox.deleteSelection())
db.pack(fill=tk.BOTH, expand=False)
# Add button to sort all entries
sortallb = tk.Button(root, text="Sort All", height=2, command = lambda: listbox.sortAll())
sortallb.pack(fill=tk.BOTH, expand=False)
# Add button to sort the selection
sortb = tk.Button(root, text="Sort Selection", height=2, command = lambda: listbox.sortSelection())
sortb.pack(fill=tk.BOTH, expand=False)
# Add a save button
saveb = tk.Button(root, text="Save", height=2, command = lambda: listbox.save(df))
saveb.pack(fill=tk.BOTH, expand=False)
# Add a parse button
parseb = tk.Button(root, text="Parse", height=2, command = lambda: listbox.parse_all(df))
parseb.pack(fill=tk.BOTH, expand=False)
# Run the main tool
root.mainloop()
f = open('lal_inout2.txt')
outputdata = f.read()
f.close()
print(outputdata)
f = open('lal_parsed_word.txt')
worddata = f.read()
f.close()
print(worddata)
f = open('lal_parsed_tex.txt')
texdata = f.read()
f.close()
print(texdata)
f = open('lal_parsed_email.txt')
emaildata = f.read()
f.close()
print(emaildata)
| 0.130424 | 0.795181 |
# Group Assignment
Group Members
1. PGCBAA02B002 Akshara Sivakumar
2. PGCBAA02B012 Badari narayan k
3. PGCBAA02B042 Nitin parihar
4. PGCBAA02B051 Rahul Bhowmick
5. PGCBAA02B062 Sayan Choudhury
6. PGCBAA02B072 Suraj Kumar
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pickle
import math
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
import statsmodels.formula.api as smf
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from math import sqrt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
from sklearn import metrics
import numpy as np
from sklearn.linear_model import Ridge
import warnings
warnings.filterwarnings('ignore')
auto=pd.read_csv("../Data/Auto.csv",sep=',')
auto.head()
auto.tail()
```
There are 397 rows and 9 columns in the dataset.
```
auto.shape
```
There are only 392 non null records in horsepower out of 397 total number of rows.
```
auto.info()
auto.describe()
```
Finding out if there are any missing values in the dataset
```
auto.isna().sum()
```
There are 5 missing values in horsepower. Removing the missing value from the dataset.
```
for column in ['horsepower']:
auto[column] = pd.to_numeric(auto[column], errors = 'coerce')
auto[auto['horsepower'].isna()]
auto.dropna(axis = 0,inplace = True)
```
Range of numbers in each column: Check if the column values within the dataset are in the same magnitude
```
for i in auto.columns:
print(" Range of {} min {}, max {}" .format(i, min(auto[i]), max(auto[i])))
```
# Univariate Analysis
Plotting a count plot to see the count of cylinder
```
sns.countplot(auto.cylinders,data=auto,palette = "rainbow")
plt.show()
```
From the above plot we can visualize that there are maximum number of 4 cylinder vehicles. Around 98% of the vehicles are either of 4, 6, 8 cylinders and only small percent of vehicles are either of 3 and 5 cylinders.
```
sns.countplot(auto.cylinders,data=auto,hue = auto.origin)
plt.show()
```
From the above plot, we can say that only American vehicles have more number of cylinders.
```
sns.displot(data=auto, x='weight', kind='hist',
height=6, aspect=2,bins=10,hue = auto.origin,palette = "dark")
```
Japanese and European vehicles are mostly light weighted while American vehicles are heavy weighted.
```
sns.displot(data=auto, x='displacement', kind='hist',
height=6, aspect=2,bins=10,hue = auto.origin,palette = "dark")
```
Japanese and european vehicles has lower displacement while american vehicles have higher displacement.
```
sns.displot(data=auto, x='mpg', kind='hist',
height=6, aspect=2,bins=10,hue = auto.origin,palette = "dark")
sns.displot(data=auto, x='horsepower', kind='hist',
height=6, aspect=2,bins=10,hue = auto.origin,palette = "dark")
```
Japanese and European vehicles have lower horsepower while American vehicles have higher horsepower.
```
sns.countplot(auto.origin,palette = "rainbow")
plt.show()
```
Most of the vehicles are from Amaerica as compared to the other two regions.
```
auto[auto['horsepower']>=200]
plot = sns.lmplot('horsepower','mpg',data=auto,hue='origin',palette = "rainbow")
plt.show()
auto[(auto['horsepower']>125) & (auto['mpg']>30)]
```
There is one outlier from japan and the vehicle is datsun 280-zx.
```
auto[(auto['horsepower']<80) & (auto['mpg']>40)]
horsepower = auto['horsepower']
mpg = auto['mpg']
HorsepowermpgCorr = horsepower.corr(mpg)
print(HorsepowermpgCorr)
```
The above lineplot shows a negative correlation between horsepower and mpg. The above records are some of the outliers in which the increase in horsepower have increased it's mpg.
```
horsepower = auto['horsepower']
cylinder = auto['cylinders']
HorsepowerCylinderCorr = horsepower.corr(cylinder)
print(HorsepowerCylinderCorr)
```
There is a strong correlation between horsepower and cylinder. each cylinder is connected to a crankshaft. The crankshaft delivers the energy created by the combustion process to the transmission and ultimately to the wheels that drive the vehicle. Generally speaking, the more cylinders an engine has the more horsepower and torque an engine makes.
```
mpg = auto['mpg']
mpgCylindersCorr = mpg.corr(cylinder)
print(mpgCylindersCorr)
```
There is a strong negative correlation between mpg and cylinder.
As a general rule, the smaller the engine, the more efficient it's use of fuel is.
```
sns.countplot(auto['year'],palette = "rainbow")
plt.show()
```
Maximum number of vehicles are of the year 1973 and minumum number of the year 1974.
```
sns.countplot(auto.origin,palette = "rainbow")
plt.show()
```
America is a major manufacturer and most of the vehicles are American origin.
```
auto['horsepower'] = pd.to_numeric(auto['horsepower'])
sns.distplot(auto['horsepower'])
plt.show()
```
Horsepower rates the engine performance of cars.
From the above plot we can see the distribution of the horsepower of the vehicles.
We can visualize that most of the vehicles have around 75-110 horsepower and only few vehicles have horsepoer above 200.
```
sns.distplot(auto.displacement,rug=False)
plt.show()
```
Engine displacement is the swept volume of all the pistons inside the cylinders of a reciprocating engine in a single movement from top dead centre (TDC) to bottom dead centre (BDC).
# Multivariate Analysis
```
sns.boxplot(y='mpg',x='cylinders',data=auto,palette = "rainbow")
plt.show()
```
We can easily visualize that the mileage per gallon (mpg) of 4 cylinder vehicles is maximum and we also saw that most of the vehicles are 4 cylinder.
From the above result we can carry out the inference that for most of the people mileage(mpg) is one of the major factor while buying a vehicle.
```
sns.boxplot(y='horsepower',x='cylinders',data=auto,palette = "rainbow")
plt.show()
```
Even number cylinder vehicles are having a better horsepower. Most of the vehicles are 4 cylindered and the horsepower of these vehicles are not very high. We can say that horsepower of vehicles are mostly considered by Americans while buying a car.
```
sns.boxplot(y='mpg',x='horsepower',data=auto,palette = "rainbow")
plt.show()
sns.boxplot(y='mpg',x='year',data=auto,palette = "rainbow")
plt.show()
```
With every year and with the newer models of the vehicles mileage per gallon (mpg) also increases.
# Regression
```
sns.set()
sns.pairplot(auto, size = 2.0,hue ='origin')
plt.show()
```
Converting the categorical variable origin into numerical variable to perform regression.
```
# creating a dict file
origin = {'American': 1,'European': 2, 'Japanese': 3}
# traversing through dataframe
# Gender column and writing
# values where key matches
auto.origin = [origin[item] for item in auto.origin]
print(auto)
model = smf.ols(formula = 'mpg ~ horsepower + origin + weight' , data = auto)
result = model.fit()
print(result.summary())
```
The above model explains 71.9% of data with 392 observations. Our Prob (F-statistic) is much smaller than alpha 0.01 and so we can reject our null hypothesis. The p statistics are very low so we can say that we have good coefficients. There is a positive relationship between origin and mpg. There is a negative relationship between horsepower and mpg and weight and mpg. More the horsepower and weight of a vehicle, lesser the mpg would be. Since the p-value of the independent variables Horsepower, Origin and Weight is very close to 0, we can be extremely confident that there is a significant linear relationship between Horsepower,weight,origin with mpg.
LINEAR EQUATION
MPG = 41.2173 + 1.3486(origin) -0.0530(horsepower) -0.0048(weight)
For every additional unit of horsepower added to the vehicle is going to bring the mpg down by 0.0530 units. For every additional unit of weight added to the vehicle is going to bring the mpg down by 0.0048 units.
Using a trial and error with the given dataset to predict a model which best describes the MPG.
```
factors = ['horsepower','weight','origin','cylinders','displacement','acceleration']
X = pd.DataFrame(auto[factors].copy())
y = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x = StandardScaler().fit_transform(X)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3,random_state=324)
model = LinearRegression()
model.fit(x_train, y_train)
print("The coefficients are : "+str(model.coef_))
print("The Intercept is : " +str(model.intercept_))
print("The score of this model is : " + str(model.score(x_train, y_train)))
predictions = model.predict(x_test)
print(predictions)
print(model.score(x_train, y_train))
plt.scatter(y_test, predictions)
from sklearn import metrics
metrics.mean_absolute_error(y_test, predictions)
```
The above model is constructed with horsepower, weight, origin, cylinder, displacement and acceleration as independent variables. The model has an absolute error of 2.82.
Constructing another model excluding the acceleration.
```
factors1 = ['horsepower','weight','origin','cylinders','displacement']
X1 = pd.DataFrame(auto[factors1].copy())
y1 = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x1 = StandardScaler().fit_transform(X1)
x_train1, x_test1, y_train1, y_test1 = train_test_split(x1, y1, test_size = 0.3,random_state=324)
model1 = LinearRegression()
model1.fit(x_train1, y_train1)
print("The coefficients are : "+str(model1.coef_))
print("The Intercept is : " +str(model1.intercept_))
print("The score of this model is : " + str(model1.score(x_train1, y_train1)))
predictions1 = model1.predict(x_test1)
metrics.mean_absolute_error(y_test1, predictions1)
```
The absolute error of the above model is slightly higher than the previous model and hence we can infer that this isn't an ideal model
Constructing another model excluding acceleration and displacement.
```
factors2 = ['horsepower','weight','origin','cylinders']
X2 = pd.DataFrame(auto[factors2].copy())
y2 = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x2 = StandardScaler().fit_transform(X2)
x_train2, x_test2, y_train2, y_test2 = train_test_split(x2, y2, test_size = 0.3,random_state=324)
model2 = LinearRegression()
model2.fit(x_train2, y_train2)
print("The coefficients are : "+str(model2.coef_))
print("The Intercept is : " +str(model2.intercept_))
print("The score of this model is : " + str(model2.score(x_train2 ,y_train2)))
predictions2 = model2.predict(x_test2)
metrics.mean_absolute_error(y_test2, predictions2)
```
The absolute error from the above module is comparitively lower compared to the other models.
Constructing another model excluding weight, acceleration and displacement
```
factors3 = ['horsepower','origin','cylinders']
X3 = pd.DataFrame(auto[factors3].copy())
y3 = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x3 = StandardScaler().fit_transform(X3)
x_train3, x_test3, y_train3, y_test3 = train_test_split(x3, y3, test_size = 0.3,random_state=324)
model3 = LinearRegression()
model3.fit(x_train3, y_train3)
print("The coefficients are : "+str(model3.coef_))
print("The Intercept is : " +str(model3.intercept_))
print("The score of this model is : " + str(model3.score(x_train3 ,y_train3)))
predictions3 = model3.predict(x_test3)
metrics.mean_absolute_error(y_test3, predictions3)
```
The absolute error of the above model is highest of all and hence cannot be considered as a good model.
Constructing another model excluding cylinder, acceleration and displacement.
```
factors4 = ['horsepower','origin','weight']
X4 = pd.DataFrame(auto[factors4].copy())
y4 = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x4 = StandardScaler().fit_transform(X4)
x_train4, x_test4, y_train4, y_test4 = train_test_split(x4, y4, test_size = 0.3,random_state=324)
model4 = LinearRegression()
model4.fit(x_train4, y_train4)
print("The coefficients are : "+str(model4.coef_))
print("The Intercept is : " +str(model4.intercept_))
print("The score of this model is : " + str(model4.score(x_train4 ,y_train4)))
predictions4 = model4.predict(x_test4)
metrics.mean_absolute_error(y_test4, predictions4)
```
Out of all the models, model2 constructed with horsepower, weight, origin and cylinder as independent variables has the lowest absolute error of 2.816. Hence,this model can be considered the best model of all.
Linear Equation
MPG = 23.35 -1.85 (horsepower) -4.34 (weight) +0.79(origin) -0.095(cylinders)
There is a negative correlation between horsepower and mpg. As the horsepower increases by 1 unit, Mpg decreases by 1.85 units. There is a negative correlation between mpg and weight. As the weight increases by 1 unit , Mpg decreases by 4.34 units.
Plotting the predicted model 2.
```
plt.scatter(y_test2, predictions2)
```
As you can see, our predicted values are very close to the actual values for the observations in the data set. A perfectly straight diagonal line in this scatterplot would indicate that our model perfectly predicted the y-array values.
Another way to visually assess the performance of our model is to plot its residuals, which are the difference between the actual y-array values and the predicted y-array values.
```
plt.hist(y_test2 - predictions2)
```
This is a histogram of the residuals from our machine learning model.
You may notice that the residuals from our machine learning model appear to be normally distributed. This is a very good sign!
It indicates that we have selected an appropriate model type to make predictions from our data set.
```
from sklearn.linear_model import Ridge
rng = np.random.RandomState(0)
rdg = Ridge(alpha = 0.5)
rdg.fit(x2, y2)
rdg.score(x2,y2)
```
The output shows that the above Ridge Regression model gave the score of around 71 percent.
# Conclusion
1. Maximum number of vehicles are manufactured with 4 cylinders. Most of the vehicles have even number of cylinders. This might be because of Balance and packaging. An engine typically wants to be in the smallest possible physical package and inherently balanced for low vibration, and for the most part even number of cylinders do that better than odd numbers in the desired configuration, albeit subject to debate. American vehciles mostly have more number of cylinders and they do not manufacture vehicles with odd number of cylinders.
2. American vehicles are predominantly of heavy weight while Japanese and European vehciles are light weighted. This might be because American vehicles use heavy caliber of displacement which is around more of high horsepower V8 Engine & have to add in safety features as well like bumpers and side impact beams.
3. Engine displacement is the measure of the cylinder volume swept by all of the pistons of a piston engine, excluding the combustion chambers. And hence, American vehicles have higher displacement.
4. Horsepower and mpg are negatively correlated and hence the Japanese and European vehicles have higher mpg while American vehicles have higher horsepower.
5. 4 cylinder vehicles has the highest mpg. Hence it is observed that for most of the people mileage(mpg) is one of the major factor while buying a vehicle.
6. Our predictive model says that a vehicle's origin, weight, horsepower and number of cylinders affect the Miles Per Gallon of a vehicle.
# Recommendations
Miles Per Gallon is a key factor while buying a car. There is an increase in the demand of vehicles with higher mpg every year. However, there is still a market for vehicles with higher horsepower in the American region.
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pickle
import math
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
import statsmodels.formula.api as smf
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from math import sqrt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
from sklearn import metrics
import numpy as np
from sklearn.linear_model import Ridge
import warnings
warnings.filterwarnings('ignore')
auto=pd.read_csv("../Data/Auto.csv",sep=',')
auto.head()
auto.tail()
auto.shape
auto.info()
auto.describe()
auto.isna().sum()
for column in ['horsepower']:
auto[column] = pd.to_numeric(auto[column], errors = 'coerce')
auto[auto['horsepower'].isna()]
auto.dropna(axis = 0,inplace = True)
for i in auto.columns:
print(" Range of {} min {}, max {}" .format(i, min(auto[i]), max(auto[i])))
sns.countplot(auto.cylinders,data=auto,palette = "rainbow")
plt.show()
sns.countplot(auto.cylinders,data=auto,hue = auto.origin)
plt.show()
sns.displot(data=auto, x='weight', kind='hist',
height=6, aspect=2,bins=10,hue = auto.origin,palette = "dark")
sns.displot(data=auto, x='displacement', kind='hist',
height=6, aspect=2,bins=10,hue = auto.origin,palette = "dark")
sns.displot(data=auto, x='mpg', kind='hist',
height=6, aspect=2,bins=10,hue = auto.origin,palette = "dark")
sns.displot(data=auto, x='horsepower', kind='hist',
height=6, aspect=2,bins=10,hue = auto.origin,palette = "dark")
sns.countplot(auto.origin,palette = "rainbow")
plt.show()
auto[auto['horsepower']>=200]
plot = sns.lmplot('horsepower','mpg',data=auto,hue='origin',palette = "rainbow")
plt.show()
auto[(auto['horsepower']>125) & (auto['mpg']>30)]
auto[(auto['horsepower']<80) & (auto['mpg']>40)]
horsepower = auto['horsepower']
mpg = auto['mpg']
HorsepowermpgCorr = horsepower.corr(mpg)
print(HorsepowermpgCorr)
horsepower = auto['horsepower']
cylinder = auto['cylinders']
HorsepowerCylinderCorr = horsepower.corr(cylinder)
print(HorsepowerCylinderCorr)
mpg = auto['mpg']
mpgCylindersCorr = mpg.corr(cylinder)
print(mpgCylindersCorr)
sns.countplot(auto['year'],palette = "rainbow")
plt.show()
sns.countplot(auto.origin,palette = "rainbow")
plt.show()
auto['horsepower'] = pd.to_numeric(auto['horsepower'])
sns.distplot(auto['horsepower'])
plt.show()
sns.distplot(auto.displacement,rug=False)
plt.show()
sns.boxplot(y='mpg',x='cylinders',data=auto,palette = "rainbow")
plt.show()
sns.boxplot(y='horsepower',x='cylinders',data=auto,palette = "rainbow")
plt.show()
sns.boxplot(y='mpg',x='horsepower',data=auto,palette = "rainbow")
plt.show()
sns.boxplot(y='mpg',x='year',data=auto,palette = "rainbow")
plt.show()
sns.set()
sns.pairplot(auto, size = 2.0,hue ='origin')
plt.show()
# creating a dict file
origin = {'American': 1,'European': 2, 'Japanese': 3}
# traversing through dataframe
# Gender column and writing
# values where key matches
auto.origin = [origin[item] for item in auto.origin]
print(auto)
model = smf.ols(formula = 'mpg ~ horsepower + origin + weight' , data = auto)
result = model.fit()
print(result.summary())
factors = ['horsepower','weight','origin','cylinders','displacement','acceleration']
X = pd.DataFrame(auto[factors].copy())
y = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x = StandardScaler().fit_transform(X)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3,random_state=324)
model = LinearRegression()
model.fit(x_train, y_train)
print("The coefficients are : "+str(model.coef_))
print("The Intercept is : " +str(model.intercept_))
print("The score of this model is : " + str(model.score(x_train, y_train)))
predictions = model.predict(x_test)
print(predictions)
print(model.score(x_train, y_train))
plt.scatter(y_test, predictions)
from sklearn import metrics
metrics.mean_absolute_error(y_test, predictions)
factors1 = ['horsepower','weight','origin','cylinders','displacement']
X1 = pd.DataFrame(auto[factors1].copy())
y1 = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x1 = StandardScaler().fit_transform(X1)
x_train1, x_test1, y_train1, y_test1 = train_test_split(x1, y1, test_size = 0.3,random_state=324)
model1 = LinearRegression()
model1.fit(x_train1, y_train1)
print("The coefficients are : "+str(model1.coef_))
print("The Intercept is : " +str(model1.intercept_))
print("The score of this model is : " + str(model1.score(x_train1, y_train1)))
predictions1 = model1.predict(x_test1)
metrics.mean_absolute_error(y_test1, predictions1)
factors2 = ['horsepower','weight','origin','cylinders']
X2 = pd.DataFrame(auto[factors2].copy())
y2 = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x2 = StandardScaler().fit_transform(X2)
x_train2, x_test2, y_train2, y_test2 = train_test_split(x2, y2, test_size = 0.3,random_state=324)
model2 = LinearRegression()
model2.fit(x_train2, y_train2)
print("The coefficients are : "+str(model2.coef_))
print("The Intercept is : " +str(model2.intercept_))
print("The score of this model is : " + str(model2.score(x_train2 ,y_train2)))
predictions2 = model2.predict(x_test2)
metrics.mean_absolute_error(y_test2, predictions2)
factors3 = ['horsepower','origin','cylinders']
X3 = pd.DataFrame(auto[factors3].copy())
y3 = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x3 = StandardScaler().fit_transform(X3)
x_train3, x_test3, y_train3, y_test3 = train_test_split(x3, y3, test_size = 0.3,random_state=324)
model3 = LinearRegression()
model3.fit(x_train3, y_train3)
print("The coefficients are : "+str(model3.coef_))
print("The Intercept is : " +str(model3.intercept_))
print("The score of this model is : " + str(model3.score(x_train3 ,y_train3)))
predictions3 = model3.predict(x_test3)
metrics.mean_absolute_error(y_test3, predictions3)
factors4 = ['horsepower','origin','weight']
X4 = pd.DataFrame(auto[factors4].copy())
y4 = auto['mpg'].copy()
#Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data
x4 = StandardScaler().fit_transform(X4)
x_train4, x_test4, y_train4, y_test4 = train_test_split(x4, y4, test_size = 0.3,random_state=324)
model4 = LinearRegression()
model4.fit(x_train4, y_train4)
print("The coefficients are : "+str(model4.coef_))
print("The Intercept is : " +str(model4.intercept_))
print("The score of this model is : " + str(model4.score(x_train4 ,y_train4)))
predictions4 = model4.predict(x_test4)
metrics.mean_absolute_error(y_test4, predictions4)
plt.scatter(y_test2, predictions2)
plt.hist(y_test2 - predictions2)
from sklearn.linear_model import Ridge
rng = np.random.RandomState(0)
rdg = Ridge(alpha = 0.5)
rdg.fit(x2, y2)
rdg.score(x2,y2)
| 0.479016 | 0.933309 |
# Parts-of-Speech Tagging - Working with tags and Numpy
In this lecture notebook you will create a matrix using some tag information and then modify it using different approaches.
This will serve as hands-on experience working with Numpy and as an introduction to some elements used for POS tagging.
```
import numpy as np
import pandas as pd
```
### Some information on tags
For this notebook you will be using a toy example including only three tags (or states). In a real world application there are many more tags which can be found [here](https://www.ling.upenn.edu/courses/Fall_2003/ling001/penn_treebank_pos.html).
```
# Define tags for Adverb, Noun and To (the preposition) , respectively
tags = ['RB', 'NN', 'TO']
```
In this week's assignment you will construct some dictionaries that provide useful information of the tags and words you will be working with.
One of these dictionaries is the `transition_counts` which counts the number of times a particular tag happened next to another. The keys of this dictionary have the form `(previous_tag, tag)` and the values are the frequency of occurrences.
Another one is the `emission_counts` dictionary which will count the number of times a particular pair of `(tag, word)` appeared in the training dataset.
In general think of `transition` when working with tags only and of `emission` when working with tags and words.
In this notebook you will be looking at the first one:
```
# Define 'transition_counts' dictionary
# Note: values are the same as the ones in the assignment
transition_counts = {
('NN', 'NN'): 16241,
('RB', 'RB'): 2263,
('TO', 'TO'): 2,
('NN', 'TO'): 5256,
('RB', 'TO'): 855,
('TO', 'NN'): 734,
('NN', 'RB'): 2431,
('RB', 'NN'): 358,
('TO', 'RB'): 200
}
```
Notice that there are 9 combinations of the 3 tags used. Each tag can appear after the same tag so you should include those as well.
### Using Numpy for matrix creation
Now you will create a matrix that includes these frequencies using Numpy arrays:
```
# Store the number of tags in the 'num_tags' variable
num_tags = len(tags)
# Initialize a 3X3 numpy array with zeros
transition_matrix = np.zeros((num_tags, num_tags))
# Print matrix
transition_matrix
```
Visually you can see the matrix has the correct dimensions. Don't forget you can check this too using the `shape` attribute:
```
# Print shape of the matrix
transition_matrix.shape
```
Before filling this matrix with the values of the `transition_counts` dictionary you should sort the tags so that their placement in the matrix is consistent:
```
# Create sorted version of the tag's list
sorted_tags = sorted(tags)
# Print sorted list
sorted_tags
```
To fill this matrix with the correct values you can use a `double for loop`. You could also use `itertools.product` to one line this double loop:
```
# Loop rows
for i in range(num_tags):
# Loop columns
for j in range(num_tags):
# Define tag pair
tag_tuple = (sorted_tags[i], sorted_tags[j])
# Get frequency from transition_counts dict and assign to (i, j) position in the matrix
transition_matrix[i, j] = transition_counts.get(tag_tuple)
# Print matrix
transition_matrix
```
Looks like this worked fine. However the matrix can be hard to read as `Numpy` is more about efficiency, rather than presenting values in a pretty format.
For this you can use a `Pandas DataFrame`. In particular, a function that takes the matrix as input and prints out a pretty version of it will be very useful:
```
# Define 'print_matrix' function
def print_matrix(matrix):
print(pd.DataFrame(matrix, index=sorted_tags, columns=sorted_tags))
```
Notice that the tags are not a parameter of the function. This is because the `sorted_tags` list will not change in the rest of the notebook so it is safe to use the variable previously declared. To test this function simply run:
```
# Print the 'transition_matrix' by calling the 'print_matrix' function
print_matrix(transition_matrix)
```
That is a lot better, isn't it?
As you may have already deducted this matrix is not symmetrical.
### Working with Numpy for matrix manipulation
Now that you got the matrix set up it is time to see how a matrix can be manipulated after being created.
`Numpy` allows vectorized operations which means that operations that would normally include looping over the matrix can be done in a simpler manner. This is consistent with treating numpy arrays as matrices since you get support for common matrix operations. You can do matrix multiplication, scalar multiplication, vector addition and many more!
For instance try scaling each value in the matrix by a factor of $\frac{1}{10}$. Normally you would loop over each value in the matrix, updating them accordingly. But in Numpy this is as easy as dividing the whole matrix by 10:
```
# Scale transition matrix
transition_matrix = transition_matrix/10
# Print scaled matrix
print_matrix(transition_matrix)
```
Another trickier example is to normalize each row so that each value is equal to $\frac{value}{sum \,of \,row}$.
This can be easily done with vectorization. First you will compute the sum of each row:
```
# Compute sum of row for each row
rows_sum = transition_matrix.sum(axis=1, keepdims=True)
# Print sum of rows
rows_sum
```
Notice that the `sum()` method was used. This method does exactly what its name implies. Since the sum of the rows was desired the axis was set to `1`. In Numpy `axis=1` refers to the columns so the sum is done by summing each column of a particular row, for each row.
Also the `keepdims` parameter was set to `True` so the resulting array had shape `(3, 1)` rather than `(3,)`. This was done so that the axes were consistent with the desired operation.
When working with Numpy, always remember to check the shape of the arrays you are working with, many unexpected errors happen because of axes not being consistent. The `shape` attribute is your friend for these cases.
```
# Normalize transition matrix
transition_matrix = transition_matrix / rows_sum
# Print normalized matrix
print_matrix(transition_matrix)
```
Notice that the normalization that was carried out forces the sum of each row to be equal to `1`. You can easily check this by running the `sum` method on the resulting matrix:
```
transition_matrix.sum(axis=1, keepdims=True)
```
For a final example you are asked to modify each value of the diagonal of the matrix so that they are equal to the `log` of the sum of the current row plus the current value. When doing mathematical operations like this one don't forget to import the `math` module.
This can be done using a standard `for loop` or `vectorization`. You'll see both in action:
```
import math
# Copy transition matrix for for-loop example
t_matrix_for = np.copy(transition_matrix)
# Copy transition matrix for numpy functions example
t_matrix_np = np.copy(transition_matrix)
```
#### Using a for-loop
```
# Loop values in the diagonal
for i in range(num_tags):
t_matrix_for[i, i] = t_matrix_for[i, i] + math.log(rows_sum[i])
# Print matrix
print_matrix(t_matrix_for)
```
#### Using vectorization
```
# Save diagonal in a numpy array
d = np.diag(t_matrix_np)
# Print shape of diagonal
d.shape
```
You can save the diagonal in a numpy array using Numpy's `diag()` function. Notice that this array has shape `(3,)` so it is inconsistent with the dimensions of the `rows_sum` array which are `(3, 1)`. You'll have to reshape before moving forward. For this you can use Numpy's `reshape()` function, specifying the desired shape in a tuple:
```
# Reshape diagonal numpy array
d = np.reshape(d, (3,1))
# Print shape of diagonal
d.shape
```
Now that the diagonal has the correct shape you can do the vectorized operation by applying the `math.log()` function to the `rows_sum` array and adding the diagonal.
To apply a function to each element of a numpy array use Numpy's `vectorize()` function providing the desired function as a parameter. This function returns a vectorized function that accepts a numpy array as a parameter.
To update the original matrix you can use Numpy's `fill_diagonal()` function.
```
# Perform the vectorized operation
d = d + np.vectorize(math.log)(rows_sum)
# Use numpy's 'fill_diagonal' function to update the diagonal
np.fill_diagonal(t_matrix_np, d)
# Print the matrix
print_matrix(t_matrix_np)
```
To perform a sanity check that both methods yield the same result you can compare both matrices. Notice that this operation is also vectorized so you will get the equality check for each element in both matrices:
```
# Check for equality
t_matrix_for == t_matrix_np
```
**Congratulations on finishing this lecture notebook!** Now you should be more familiar with some elements used by a POS tagger such as the `transition_counts` dictionary and with working with Numpy.
**Keep it up!**
|
github_jupyter
|
import numpy as np
import pandas as pd
# Define tags for Adverb, Noun and To (the preposition) , respectively
tags = ['RB', 'NN', 'TO']
# Define 'transition_counts' dictionary
# Note: values are the same as the ones in the assignment
transition_counts = {
('NN', 'NN'): 16241,
('RB', 'RB'): 2263,
('TO', 'TO'): 2,
('NN', 'TO'): 5256,
('RB', 'TO'): 855,
('TO', 'NN'): 734,
('NN', 'RB'): 2431,
('RB', 'NN'): 358,
('TO', 'RB'): 200
}
# Store the number of tags in the 'num_tags' variable
num_tags = len(tags)
# Initialize a 3X3 numpy array with zeros
transition_matrix = np.zeros((num_tags, num_tags))
# Print matrix
transition_matrix
# Print shape of the matrix
transition_matrix.shape
# Create sorted version of the tag's list
sorted_tags = sorted(tags)
# Print sorted list
sorted_tags
# Loop rows
for i in range(num_tags):
# Loop columns
for j in range(num_tags):
# Define tag pair
tag_tuple = (sorted_tags[i], sorted_tags[j])
# Get frequency from transition_counts dict and assign to (i, j) position in the matrix
transition_matrix[i, j] = transition_counts.get(tag_tuple)
# Print matrix
transition_matrix
# Define 'print_matrix' function
def print_matrix(matrix):
print(pd.DataFrame(matrix, index=sorted_tags, columns=sorted_tags))
# Print the 'transition_matrix' by calling the 'print_matrix' function
print_matrix(transition_matrix)
# Scale transition matrix
transition_matrix = transition_matrix/10
# Print scaled matrix
print_matrix(transition_matrix)
# Compute sum of row for each row
rows_sum = transition_matrix.sum(axis=1, keepdims=True)
# Print sum of rows
rows_sum
# Normalize transition matrix
transition_matrix = transition_matrix / rows_sum
# Print normalized matrix
print_matrix(transition_matrix)
transition_matrix.sum(axis=1, keepdims=True)
import math
# Copy transition matrix for for-loop example
t_matrix_for = np.copy(transition_matrix)
# Copy transition matrix for numpy functions example
t_matrix_np = np.copy(transition_matrix)
# Loop values in the diagonal
for i in range(num_tags):
t_matrix_for[i, i] = t_matrix_for[i, i] + math.log(rows_sum[i])
# Print matrix
print_matrix(t_matrix_for)
# Save diagonal in a numpy array
d = np.diag(t_matrix_np)
# Print shape of diagonal
d.shape
# Reshape diagonal numpy array
d = np.reshape(d, (3,1))
# Print shape of diagonal
d.shape
# Perform the vectorized operation
d = d + np.vectorize(math.log)(rows_sum)
# Use numpy's 'fill_diagonal' function to update the diagonal
np.fill_diagonal(t_matrix_np, d)
# Print the matrix
print_matrix(t_matrix_np)
# Check for equality
t_matrix_for == t_matrix_np
| 0.616474 | 0.989622 |
```
import librosa
import librosa.display
import matplotlib.pyplot as plt
import IPython.display as ipd
import numpy as np
import scipy.signal as signal
```
# Sawtooth Oscillator
```
def sawtooth_osc(f0, dur, sr):
# sr: sampling rate
# dur: duration
# f0: fundamental frequency
phase_inc = 2/(sr/f0)
phase = 0
x = np.zeros(int(sr*dur))
for n in range(len(x)):
phase = phase + phase_inc
if (phase > 1):
phase = phase - 2
x[n] = phase
return x
sr = 44100
f0 = 220
dur = 1
x_saw = sawtooth_osc(f0, dur, sr)
plt.figure(figsize=(10, 5))
n= np.arange(400)
plt.plot(n/sr, x_saw[:400])
plt.grid(True)
plt.xlabel('sec')
ipd.Audio(x_saw, rate=sr)
```
# Sqaure Oscillator
```
def square_osc(f0, dur, sr):
# sr: sampling rate
# dur: duration
# f0: fundamental frequency
phase_inc = 2/(sr/f0)
phase = 0
x = np.zeros(int(sr*dur))
for n in range(len(x)):
phase = phase + phase_inc
if (phase > 1):
phase = phase - 2
if phase > 0:
x[n] = 0.9
else:
x[n] = -0.9
return x
sr = 44100
f0 = 220
dur = 1
x_sqr = square_osc(f0, dur, sr)
plt.figure(figsize=(10, 5))
n= np.arange(400)
plt.plot(n/sr, x_sqr[:400])
plt.grid(True)
plt.xlabel('sec')
ipd.Audio(x_sqr, rate=sr)
```
# Resonant Lowpass Filter
```
def res_lowpass(x, cutoff_freq, Q):
# x: input signal
# cutoff_freq: cut-off frquency, Hz
# Q: resonance, a small positive value (e.g. 0.001)to +inf
# bi-quad lowpass filter
theta = 2*np.pi*cutoff_freq/sr
alpha = np.sin(theta)/2/Q
b = [(1-np.cos(theta)), +2*(1-np.cos(theta)), (1-np.cos(theta))]
a = [(1+alpha), -2*np.cos(theta), (1-alpha)]
# apply the filter
y = signal.lfilter(b,a,x)
return y
cutoff_freq = 2000
Q = 0.5
x_saw_low = res_lowpass(x_saw, cutoff_freq, Q)
plt.figure(figsize=(10, 5))
n= np.arange(200)
plt.plot(n/sr, x_saw_low[:200])
plt.grid(True)
plt.xlabel('sec')
ipd.Audio(x_saw_low, rate=sr)
```
# Adding Amp Envelope (ADSR)
```
def amp_envelop(note_dur, attack_time, decay_time, sustain_level, release_time, sr):
env_attack = np.linspace(0,1,int(attack_time*sr))
env_decay = np.logspace(np.log10(1),np.log10(sustain_level),int(decay_time*sr))
env_sustain = np.linspace(sustain_level,sustain_level,int((note_dur-attack_time-decay_time)*sr))
env_release = np.logspace(np.log10(sustain_level),np.log10(0.001),int(release_time*sr))
amp_env = np.append(env_attack, env_decay)
amp_env = np.append(amp_env, env_sustain)
amp_env = np.append(amp_env, env_release)
return amp_env
sr = 44100
f0 = 261
cutoff_freq = 2000
Q = 1
note_dur = 0.4 # time intervial betwen note-on and note-off
attack_time = 0.01 # second
decay_time = 0.2 # second
sustain_level = 0.6 # the relative level of the peak level
release_time = 0.2 # second, after the note-off
# osc--> filter --> amp_envelop
x_note = square_osc(f0, note_dur+release_time, sr)
x_note = res_lowpass(x_note, cutoff_freq, Q)
amp_env = amp_envelop(note_dur, attack_time, decay_time, sustain_level, release_time, sr)
x_note = amp_env*x_note[:len(amp_env)]
n= np.arange(len(x_note))
plt.plot(n/sr, x_note)
plt.grid(True)
plt.xlabel('sec')
ipd.Audio(x_note, rate=sr)
```
|
github_jupyter
|
import librosa
import librosa.display
import matplotlib.pyplot as plt
import IPython.display as ipd
import numpy as np
import scipy.signal as signal
def sawtooth_osc(f0, dur, sr):
# sr: sampling rate
# dur: duration
# f0: fundamental frequency
phase_inc = 2/(sr/f0)
phase = 0
x = np.zeros(int(sr*dur))
for n in range(len(x)):
phase = phase + phase_inc
if (phase > 1):
phase = phase - 2
x[n] = phase
return x
sr = 44100
f0 = 220
dur = 1
x_saw = sawtooth_osc(f0, dur, sr)
plt.figure(figsize=(10, 5))
n= np.arange(400)
plt.plot(n/sr, x_saw[:400])
plt.grid(True)
plt.xlabel('sec')
ipd.Audio(x_saw, rate=sr)
def square_osc(f0, dur, sr):
# sr: sampling rate
# dur: duration
# f0: fundamental frequency
phase_inc = 2/(sr/f0)
phase = 0
x = np.zeros(int(sr*dur))
for n in range(len(x)):
phase = phase + phase_inc
if (phase > 1):
phase = phase - 2
if phase > 0:
x[n] = 0.9
else:
x[n] = -0.9
return x
sr = 44100
f0 = 220
dur = 1
x_sqr = square_osc(f0, dur, sr)
plt.figure(figsize=(10, 5))
n= np.arange(400)
plt.plot(n/sr, x_sqr[:400])
plt.grid(True)
plt.xlabel('sec')
ipd.Audio(x_sqr, rate=sr)
def res_lowpass(x, cutoff_freq, Q):
# x: input signal
# cutoff_freq: cut-off frquency, Hz
# Q: resonance, a small positive value (e.g. 0.001)to +inf
# bi-quad lowpass filter
theta = 2*np.pi*cutoff_freq/sr
alpha = np.sin(theta)/2/Q
b = [(1-np.cos(theta)), +2*(1-np.cos(theta)), (1-np.cos(theta))]
a = [(1+alpha), -2*np.cos(theta), (1-alpha)]
# apply the filter
y = signal.lfilter(b,a,x)
return y
cutoff_freq = 2000
Q = 0.5
x_saw_low = res_lowpass(x_saw, cutoff_freq, Q)
plt.figure(figsize=(10, 5))
n= np.arange(200)
plt.plot(n/sr, x_saw_low[:200])
plt.grid(True)
plt.xlabel('sec')
ipd.Audio(x_saw_low, rate=sr)
def amp_envelop(note_dur, attack_time, decay_time, sustain_level, release_time, sr):
env_attack = np.linspace(0,1,int(attack_time*sr))
env_decay = np.logspace(np.log10(1),np.log10(sustain_level),int(decay_time*sr))
env_sustain = np.linspace(sustain_level,sustain_level,int((note_dur-attack_time-decay_time)*sr))
env_release = np.logspace(np.log10(sustain_level),np.log10(0.001),int(release_time*sr))
amp_env = np.append(env_attack, env_decay)
amp_env = np.append(amp_env, env_sustain)
amp_env = np.append(amp_env, env_release)
return amp_env
sr = 44100
f0 = 261
cutoff_freq = 2000
Q = 1
note_dur = 0.4 # time intervial betwen note-on and note-off
attack_time = 0.01 # second
decay_time = 0.2 # second
sustain_level = 0.6 # the relative level of the peak level
release_time = 0.2 # second, after the note-off
# osc--> filter --> amp_envelop
x_note = square_osc(f0, note_dur+release_time, sr)
x_note = res_lowpass(x_note, cutoff_freq, Q)
amp_env = amp_envelop(note_dur, attack_time, decay_time, sustain_level, release_time, sr)
x_note = amp_env*x_note[:len(amp_env)]
n= np.arange(len(x_note))
plt.plot(n/sr, x_note)
plt.grid(True)
plt.xlabel('sec')
ipd.Audio(x_note, rate=sr)
| 0.391871 | 0.839142 |
# Classical ON/OFF Analysis: Exclusion regions and generating RBM maps
We've seen how to run a standard ON/OFF analysis from scratch for the most simple case. But what if we have a more complex region that requires excluding other sources, or bright stars? This tutorial will walk through how to define exclusion regions and apply them during the data preparation phase. It will also show how to use those exclusions to generate an RBM significance map.
```
# Import the standard modules
import gammalib
import ctools
import cscripts
# Import matplotlib for visualization
%matplotlib inline
import matplotlib.pyplot as plt
```
## Defining the input exclusion map
The primary input for defining the regions for exclusions is a skymap. If a bin in the skymap has a non-zero value then any events that fall in that bin will be excluded from analysis.
In addition to the Crab itself, we'll use the three typical stars in the field of view:
* Zeta Tauri (84.4112, 21.1426)
* O Tauri (81.9087, 21.937)
* 121 Tauri (83.863, 24.0396)
**Note:** ncluding the Crab in our exclusion map has no effect on our fit (`ctlike`) since the source region is excluded by default. However, as we'll see later, it does have an impact when we try to generate an RBM map.
```
# Define the crab position
srcname = 'Crab'
ra = 83.633
dec = 22.0145
# Define exclusion regions (ra, dec, radius)
regions = gammalib.GSkyRegions()
regions.append(gammalib.GSkyRegionCircle(84.4112, 21.1426, 0.3)) # Zeta Tauri
regions.append(gammalib.GSkyRegionCircle(81.9087, 21.9370, 0.3)) # O Tauri
regions.append(gammalib.GSkyRegionCircle(83.8630, 24.0396, 0.3)) # 121 Tauri
excl_reg_stars = 'resources/exclmap_stars.reg'
regions.save(excl_reg_stars)
# Add the Crab
regions.append(gammalib.GSkyRegionCircle(ra, dec, 0.4)) # Crab Nebula
excl_reg_all = 'resources/exclmap_all.reg'
regions.save(excl_reg_all)
# Create a skymap
binsz = 0.02
exclmap = gammalib.GSkyMap('CAR', 'CEL', ra, dec, -binsz, binsz, 400, 400)
# Set pixels to be excluded
for indx in range(exclmap.npix()):
dir = exclmap.inx2dir(indx) # Get the position of the bin
if regions.contains(dir): # Check if the bin contains this exclusion
exclmap[indx] += 1.0
# Save the exclusion map
exclmap_file = 'resources/exclmap.fits'
exclmap.save(exclmap_file, True)
```
Visualizing the the exclusion map:
```
#module used to stretch the color palette
import matplotlib.colors as colors
# Scale the plot size
default_fs = plt.rcParamsDefault['figure.figsize']
plt.rcParams['figure.figsize'] = [2.0*v for v in default_fs]
# Define a function because we're going to be generating alot of these
def plot_skymap(skymap, ztitle, title='', norm=None):
nx = skymap.nx()/2
ny = skymap.ny()/2
plt.imshow(skymap.array(),origin='lower',
extent=[ra+binsz*nx,ra-binsz*nx,dec-binsz*ny,dec+binsz*ny],
norm=norm, cmap=plt.get_cmap('jet')) # square root scale
plt.xlabel('R.A. (deg)')
plt.ylabel('Dec (deg)')
plt.title(title)
plt.colorbar().set_label(ztitle)
plot_skymap(exclmap, ztitle='Is Excluded?')
```
## Running the analysis
As we did before, the first step is to prepare the data for analysis using `csphagen`. This time, however, we will also pass in the exclusion map
```
# Define the observation file generated in the previous tutorials
obsfile = 'resources/obs_selected.xml'
# Setup the csphagen script
phagen = cscripts.csphagen()
phagen['inobs'] = obsfile
phagen['inexclusion'] = exclmap_file # The name of the exclusion map
phagen['outobs'] = 'resources/obs_onoff_unstacked_excl.xml'
phagen['outmodel'] = 'resources/onoff_unstacked_excl_model.xml'
phagen['prefix'] = 'resources/onoff_unstacked_excl'
phagen['inmodel'] = 'NONE' # assume that the source is pointlike
phagen['ebinalg'] = 'LOG' # Method for defining energy bins
phagen['emin'] = 0.1 # Minimum energy (TeV)
phagen['emax'] = 30.0 # Maximum energy (TeV)
phagen['enumbins'] = 20 # Number of energy bins
phagen['coordsys'] = 'CEL' # Coord. system for analysis
phagen['ra'] = 83.633 # RA of ON region center
phagen['dec'] = 22.0145 # Dec of ON region center
phagen['rad'] = 0.1 # Radius of ON region (degrees)
phagen['bkgmethod'] = 'REFLECTED' # Reflected region analysis
phagen['use_model_bkg'] = False # No model for the background
phagen['maxoffset'] = 1.6 # Maximum source offset for data file to be considered
phagen['stack'] = False # Dont stack the data
phagen.execute()
# Rename the source model
phagen.obs().models()['Dummy'].name(srcname)
phagen.obs().models()[srcname].tscalc(True)
# Make the Crab a log-parabola model
pref = 3.4e-17
index = -2.4
pivot = gammalib.GEnergy(1.0, 'TeV')
curv = -0.15
spectrum = gammalib.GModelSpectralLogParabola(pref, index, pivot, curv)
# Set the Crab spectrum
phagen.obs().models()[srcname].spectral(spectrum)
# Likelihood
like = ctools.ctlike(phagen.obs())
like['outmodel'] = 'resources/crab_onoff_unstacked_excl.xml'
like.execute()
# Print the results of the fit
print(like.opt())
print(like.obs().models())
```
## RBM significance map
Let's try to generate a ring-background residual-counts map from the data. Note that we're only using two observations, so it will probably look pretty terrible.
To generate the map we will use `ctskymap` again, but this time we'll set the background subtraction method to 'RING'
```
# Run ctskymap
skymap = ctools.ctskymap()
skymap['inobs'] = obsfile
skymap['outmap'] = 'resources/skymap_wExcl.fits'
skymap['emin'] = 0.16
skymap['emax'] = 30.0
skymap['nxpix'] = 200
skymap['nypix'] = 200
skymap['binsz'] = 0.02
skymap['coordsys'] = 'CEL'
skymap['proj'] = 'CAR' # Cartesian projection
skymap['xref'] = ra
skymap['yref'] = dec
skymap['usefft'] = False
skymap['bkgsubtract'] = 'RING'
skymap['roiradius'] = 0.1
skymap['inradius'] = 0.6
skymap['outradius'] = 0.8
skymap.execute()
# Visualize the map
plot_skymap(skymap.skymap(), ztitle='Counts', norm=colors.PowerNorm(gamma=0.5))
accmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[ACCEPTANCE]') # Acceptance
bkgmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[BACKGROUND]') # OFF counts
# Visualize the map
ax1 = plt.subplot(1,2,1)
plot_skymap(accmap, ztitle='Acceptance', title='Acceptance')
ax2 = plt.subplot(1,2,2)
plot_skymap(bkgmap, ztitle='Background counts', title='OFF Counts', norm=colors.PowerNorm(gamma=0.5))
plt.tight_layout()
```
As expected, there's a deficit ring around the Crab. Why? Because we didn't exclude the Crab! So let's apply the exclusion map that we defined above.
```
# Clear the old map and define exclusions
skymap.exclusion_map(gammalib.GSkyRegionMap(exclmap))
skymap.execute()
# Visualize the map
plot_skymap(skymap.skymap(), ztitle='Counts', norm=colors.PowerNorm(gamma=0.5))
```
That looks much better!
**IMPORTANT NOTE:** You should keep in mind that this is not a TRUE RBM map. There is no accounting for the changing background sensitivity, so the difference in the area between the ring and source region is the only correction applied to the estimate of OFF counts in the ON region. It is possible to add a background IRF column to the data, which would then be used for weighting pixels in the OFF region. However, the observations we're using don't have that information, so it is ignored when generating the above maps.
We can visualize the generated acceptance map and background maps in the following way
```
accmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[ACCEPTANCE]')
bkgmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[BACKGROUND]')
# Visualize the map
ax1 = plt.subplot(1,2,1)
plot_skymap(accmap, ztitle='Acceptance', title='Acceptance')
ax2 = plt.subplot(1,2,2)
plot_skymap(bkgmap, ztitle='Background counts', title='OFF Counts')
plt.tight_layout()
```
As expected the acceptance is flat over the entire field of view.
`ctskymap` also computes a significance map if background subtraction is requested. As of v1.6.0 there is no way to directly access this map from ctskymap, but it is saved in the output skymap file under the 'SIGNIFICANCE' header keyword. We can load this in the following way:
```
sigmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[SIGNIFICANCE]')
plot_skymap(sigmap, ztitle='Significance')
plt.clim(-5,5)
ax = plt.gca()
# Add exclusion regions
from matplotlib.patches import Circle
for reg in regions:
circle = Circle((reg.centre().ra_deg(), reg.centre().dec_deg()), reg.radius(),
fill=False, color='blue')
ax.add_patch(circle)
```
There is also a python script that is capable of generating the significance distributions. Let's take a look and apply this script to our significance map.
```
# Load the module
import os, sys
sys.path.append(os.environ['CTOOLS']+'/share/examples/python/')
from show_significance_distribution import plot_significance_distribution
# Plot the full distribution
plot_significance_distribution(skymap['outmap'].filename(), 100, -5, 10,
'', '', 'No Exclusions', '')
```
Notice the very large peak at 0 because we are not excluding all of the bins where we have no data. There are two ways around this:
1. **Zoom in on the region we actually care about:** This is fairly easy, just rerun ctskymap with fewer bins in x,y.
2. **Pass 'inclusion' regions to the significance generator:** For this, we need to generate a list of regions based on the field of view of all our observations
```
# Create a regions container
obs_regions = gammalib.GSkyRegions()
# Loop over all obser
for obs in gammalib.GObservations(obsfile):
roi = obs.roi()
reg = gammalib.GSkyRegionCircle(roi.centre().dir(), roi.radius())
obs_regions.append(reg)
obs_reg_file = 'resources/obs_reg.reg'
obs_regions.save(obs_reg_file)
```
Now we can pass this as the list of 'inclusion' regions
```
# Plot the full distribution
plot_significance_distribution(skymap['outmap'].filename(), 100, -5, 10,
obs_reg_file, '', 'No Exclusions', '')
```
We can also pass the exclusion region files that we defined above to exclude specific regions around stars and the source.
```
# Plot the full distribution without stars
plot_significance_distribution(skymap['outmap'].filename(), 100, -5, 10,
obs_reg_file, excl_reg_stars, 'Star Exclusions', '')
plot_significance_distribution(skymap['outmap'].filename(), 100, -5, 10,
obs_reg_file, excl_reg_all, 'Source & Star Exclusions', '')
```
|
github_jupyter
|
# Import the standard modules
import gammalib
import ctools
import cscripts
# Import matplotlib for visualization
%matplotlib inline
import matplotlib.pyplot as plt
# Define the crab position
srcname = 'Crab'
ra = 83.633
dec = 22.0145
# Define exclusion regions (ra, dec, radius)
regions = gammalib.GSkyRegions()
regions.append(gammalib.GSkyRegionCircle(84.4112, 21.1426, 0.3)) # Zeta Tauri
regions.append(gammalib.GSkyRegionCircle(81.9087, 21.9370, 0.3)) # O Tauri
regions.append(gammalib.GSkyRegionCircle(83.8630, 24.0396, 0.3)) # 121 Tauri
excl_reg_stars = 'resources/exclmap_stars.reg'
regions.save(excl_reg_stars)
# Add the Crab
regions.append(gammalib.GSkyRegionCircle(ra, dec, 0.4)) # Crab Nebula
excl_reg_all = 'resources/exclmap_all.reg'
regions.save(excl_reg_all)
# Create a skymap
binsz = 0.02
exclmap = gammalib.GSkyMap('CAR', 'CEL', ra, dec, -binsz, binsz, 400, 400)
# Set pixels to be excluded
for indx in range(exclmap.npix()):
dir = exclmap.inx2dir(indx) # Get the position of the bin
if regions.contains(dir): # Check if the bin contains this exclusion
exclmap[indx] += 1.0
# Save the exclusion map
exclmap_file = 'resources/exclmap.fits'
exclmap.save(exclmap_file, True)
#module used to stretch the color palette
import matplotlib.colors as colors
# Scale the plot size
default_fs = plt.rcParamsDefault['figure.figsize']
plt.rcParams['figure.figsize'] = [2.0*v for v in default_fs]
# Define a function because we're going to be generating alot of these
def plot_skymap(skymap, ztitle, title='', norm=None):
nx = skymap.nx()/2
ny = skymap.ny()/2
plt.imshow(skymap.array(),origin='lower',
extent=[ra+binsz*nx,ra-binsz*nx,dec-binsz*ny,dec+binsz*ny],
norm=norm, cmap=plt.get_cmap('jet')) # square root scale
plt.xlabel('R.A. (deg)')
plt.ylabel('Dec (deg)')
plt.title(title)
plt.colorbar().set_label(ztitle)
plot_skymap(exclmap, ztitle='Is Excluded?')
# Define the observation file generated in the previous tutorials
obsfile = 'resources/obs_selected.xml'
# Setup the csphagen script
phagen = cscripts.csphagen()
phagen['inobs'] = obsfile
phagen['inexclusion'] = exclmap_file # The name of the exclusion map
phagen['outobs'] = 'resources/obs_onoff_unstacked_excl.xml'
phagen['outmodel'] = 'resources/onoff_unstacked_excl_model.xml'
phagen['prefix'] = 'resources/onoff_unstacked_excl'
phagen['inmodel'] = 'NONE' # assume that the source is pointlike
phagen['ebinalg'] = 'LOG' # Method for defining energy bins
phagen['emin'] = 0.1 # Minimum energy (TeV)
phagen['emax'] = 30.0 # Maximum energy (TeV)
phagen['enumbins'] = 20 # Number of energy bins
phagen['coordsys'] = 'CEL' # Coord. system for analysis
phagen['ra'] = 83.633 # RA of ON region center
phagen['dec'] = 22.0145 # Dec of ON region center
phagen['rad'] = 0.1 # Radius of ON region (degrees)
phagen['bkgmethod'] = 'REFLECTED' # Reflected region analysis
phagen['use_model_bkg'] = False # No model for the background
phagen['maxoffset'] = 1.6 # Maximum source offset for data file to be considered
phagen['stack'] = False # Dont stack the data
phagen.execute()
# Rename the source model
phagen.obs().models()['Dummy'].name(srcname)
phagen.obs().models()[srcname].tscalc(True)
# Make the Crab a log-parabola model
pref = 3.4e-17
index = -2.4
pivot = gammalib.GEnergy(1.0, 'TeV')
curv = -0.15
spectrum = gammalib.GModelSpectralLogParabola(pref, index, pivot, curv)
# Set the Crab spectrum
phagen.obs().models()[srcname].spectral(spectrum)
# Likelihood
like = ctools.ctlike(phagen.obs())
like['outmodel'] = 'resources/crab_onoff_unstacked_excl.xml'
like.execute()
# Print the results of the fit
print(like.opt())
print(like.obs().models())
# Run ctskymap
skymap = ctools.ctskymap()
skymap['inobs'] = obsfile
skymap['outmap'] = 'resources/skymap_wExcl.fits'
skymap['emin'] = 0.16
skymap['emax'] = 30.0
skymap['nxpix'] = 200
skymap['nypix'] = 200
skymap['binsz'] = 0.02
skymap['coordsys'] = 'CEL'
skymap['proj'] = 'CAR' # Cartesian projection
skymap['xref'] = ra
skymap['yref'] = dec
skymap['usefft'] = False
skymap['bkgsubtract'] = 'RING'
skymap['roiradius'] = 0.1
skymap['inradius'] = 0.6
skymap['outradius'] = 0.8
skymap.execute()
# Visualize the map
plot_skymap(skymap.skymap(), ztitle='Counts', norm=colors.PowerNorm(gamma=0.5))
accmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[ACCEPTANCE]') # Acceptance
bkgmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[BACKGROUND]') # OFF counts
# Visualize the map
ax1 = plt.subplot(1,2,1)
plot_skymap(accmap, ztitle='Acceptance', title='Acceptance')
ax2 = plt.subplot(1,2,2)
plot_skymap(bkgmap, ztitle='Background counts', title='OFF Counts', norm=colors.PowerNorm(gamma=0.5))
plt.tight_layout()
# Clear the old map and define exclusions
skymap.exclusion_map(gammalib.GSkyRegionMap(exclmap))
skymap.execute()
# Visualize the map
plot_skymap(skymap.skymap(), ztitle='Counts', norm=colors.PowerNorm(gamma=0.5))
accmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[ACCEPTANCE]')
bkgmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[BACKGROUND]')
# Visualize the map
ax1 = plt.subplot(1,2,1)
plot_skymap(accmap, ztitle='Acceptance', title='Acceptance')
ax2 = plt.subplot(1,2,2)
plot_skymap(bkgmap, ztitle='Background counts', title='OFF Counts')
plt.tight_layout()
sigmap = gammalib.GSkyMap(skymap['outmap'].filename()+'[SIGNIFICANCE]')
plot_skymap(sigmap, ztitle='Significance')
plt.clim(-5,5)
ax = plt.gca()
# Add exclusion regions
from matplotlib.patches import Circle
for reg in regions:
circle = Circle((reg.centre().ra_deg(), reg.centre().dec_deg()), reg.radius(),
fill=False, color='blue')
ax.add_patch(circle)
# Load the module
import os, sys
sys.path.append(os.environ['CTOOLS']+'/share/examples/python/')
from show_significance_distribution import plot_significance_distribution
# Plot the full distribution
plot_significance_distribution(skymap['outmap'].filename(), 100, -5, 10,
'', '', 'No Exclusions', '')
# Create a regions container
obs_regions = gammalib.GSkyRegions()
# Loop over all obser
for obs in gammalib.GObservations(obsfile):
roi = obs.roi()
reg = gammalib.GSkyRegionCircle(roi.centre().dir(), roi.radius())
obs_regions.append(reg)
obs_reg_file = 'resources/obs_reg.reg'
obs_regions.save(obs_reg_file)
# Plot the full distribution
plot_significance_distribution(skymap['outmap'].filename(), 100, -5, 10,
obs_reg_file, '', 'No Exclusions', '')
# Plot the full distribution without stars
plot_significance_distribution(skymap['outmap'].filename(), 100, -5, 10,
obs_reg_file, excl_reg_stars, 'Star Exclusions', '')
plot_significance_distribution(skymap['outmap'].filename(), 100, -5, 10,
obs_reg_file, excl_reg_all, 'Source & Star Exclusions', '')
| 0.535098 | 0.923936 |
# 5. Model the Solution
### Preprocessing to get the tidy dataframe
```
# Import the library we need, which is Pandas and Matplotlib
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Set some parameters to get good visuals - style to ggplot and size to 15,10
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (15, 10)
# Read the csv file of Monthwise Quantity and Price csv file we have.
df = pd.read_csv('MonthWiseMarketArrivals_clean.csv')
# Changing the date column to a Time Interval columnn
df.date = pd.DatetimeIndex(df.date)
# Change the index to the date column
df.index = pd.PeriodIndex(df.date, freq='M')
# Sort the data frame by date
df = df.sort_values(by = "date")
df.head()
```
## Question 3: How is Price and Quantity related for Onion in Bangalore?
```
dfBang = df[df.city == 'BANGALORE']
dfBang.head()
dfBang.plot(kind = "scatter", x = "quantity", y = "priceMod", s = 100)
dfBang.plot(kind = "scatter", x = "quantity", y = "priceMod", s = 100, alpha = 0.7, xlim = [0,2000000])
```
### PRINCIPLE: Correlation
Correlation refers to any of a broad class of statistical relationships involving dependence, though in common usage it most often refers to the extent to which two variables have a linear relationship with each other.

```
dfBang.corr()
pd.set_option('precision', 2)
dfBang.corr()
from pandas.tools.plotting import scatter_matrix
scatter_matrix(dfBang, figsize=(15, 15), diagonal='kde', s = 50)
```
### PRINCIPLE: Linear Regression
```
import statsmodels.api as sm
x = dfBang.quantity
y = dfBang.priceMod
lm = sm.OLS(y, x).fit()
lm.summary()
```
### PRINCIPLE: Visualizing linear relationships
```
# Import seaborn library for more funcitionality
import seaborn as sns
# We can try and fit a linear line to the data to see if there is a relaltionship
sns.regplot(x="quantity", y="priceMod", data=dfBang);
sns.jointplot(x="quantity", y="priceMod", data=dfBang, kind="reg");
```
## Question 4: Can we forecast the price of Onion in Bangalore?
### TIme Series Modelling
However, we have our data at constant time intervals of every month. Therefore we can analyze this data to determine the long term trend so as to forecast the future or perform some other form of analysis.
- Instead of using linear regression model where observations are independent, our observations are really time-dependent and we should use that.
- Second, we need to account for both a trend component and seasonality component in the time series data to better improve our forecast
```
# Set some parameters to get good visuals - style to ggplot and size to 15,10
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (15, 10)
dfBang.index = pd.DatetimeIndex(dfBang.date)
dfBang.head()
# Let us create a time series variable for priceMin
ts = dfBang.priceMin
ts.plot()
# We take the log transform to reduce the impact of high values
ts_log = np.log(ts)
ts_log.plot()
# One approach to remove the trend and seasonality impact is to take the difference between each observation
ts_log_diff = ts_log - ts_log.shift()
ts_log_diff.plot()
ts_log.plot()
# For smoothing the values we can use
# 12 month Moving Averages
ts_log_diff_ma = pd.rolling_mean(ts_log_diff, window = 12)
# Simple Exponential Smoothing
ts_log_diff_exp = pd.ewma(ts_log_diff, halflife=24)
ts_log_diff_ma.plot()
ts_log_diff_exp.plot()
ts_log_diff.plot()
```
Now we can fit an ARIMA model on this (Explaining ARIMA is out of scope of this workshop)
```
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(ts_log, order=(0, 1, 2))
results_MA = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_MA.fittedvalues, color='blue')
```
|
github_jupyter
|
# Import the library we need, which is Pandas and Matplotlib
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Set some parameters to get good visuals - style to ggplot and size to 15,10
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (15, 10)
# Read the csv file of Monthwise Quantity and Price csv file we have.
df = pd.read_csv('MonthWiseMarketArrivals_clean.csv')
# Changing the date column to a Time Interval columnn
df.date = pd.DatetimeIndex(df.date)
# Change the index to the date column
df.index = pd.PeriodIndex(df.date, freq='M')
# Sort the data frame by date
df = df.sort_values(by = "date")
df.head()
dfBang = df[df.city == 'BANGALORE']
dfBang.head()
dfBang.plot(kind = "scatter", x = "quantity", y = "priceMod", s = 100)
dfBang.plot(kind = "scatter", x = "quantity", y = "priceMod", s = 100, alpha = 0.7, xlim = [0,2000000])
dfBang.corr()
pd.set_option('precision', 2)
dfBang.corr()
from pandas.tools.plotting import scatter_matrix
scatter_matrix(dfBang, figsize=(15, 15), diagonal='kde', s = 50)
import statsmodels.api as sm
x = dfBang.quantity
y = dfBang.priceMod
lm = sm.OLS(y, x).fit()
lm.summary()
# Import seaborn library for more funcitionality
import seaborn as sns
# We can try and fit a linear line to the data to see if there is a relaltionship
sns.regplot(x="quantity", y="priceMod", data=dfBang);
sns.jointplot(x="quantity", y="priceMod", data=dfBang, kind="reg");
# Set some parameters to get good visuals - style to ggplot and size to 15,10
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (15, 10)
dfBang.index = pd.DatetimeIndex(dfBang.date)
dfBang.head()
# Let us create a time series variable for priceMin
ts = dfBang.priceMin
ts.plot()
# We take the log transform to reduce the impact of high values
ts_log = np.log(ts)
ts_log.plot()
# One approach to remove the trend and seasonality impact is to take the difference between each observation
ts_log_diff = ts_log - ts_log.shift()
ts_log_diff.plot()
ts_log.plot()
# For smoothing the values we can use
# 12 month Moving Averages
ts_log_diff_ma = pd.rolling_mean(ts_log_diff, window = 12)
# Simple Exponential Smoothing
ts_log_diff_exp = pd.ewma(ts_log_diff, halflife=24)
ts_log_diff_ma.plot()
ts_log_diff_exp.plot()
ts_log_diff.plot()
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(ts_log, order=(0, 1, 2))
results_MA = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_MA.fittedvalues, color='blue')
| 0.665737 | 0.984185 |
### Note
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import pandas as pd
import os
# File to Load (Remember to Change These)
file_to_load = os.path.join(".", "Resources", "purchase_data.csv")
# Read Purchasing File and store into Pandas data frame
purchase_data = pd.read_csv(file_to_load)
purchase_data
#purchase_data.dtypes
#Might need to convert some rows to different data types....************************
```
## Player Count
* Display the total number of players
```
#Total players:
total_players = purchase_data["SN"].count() #counts total in column
print(total_players)
#Unique players plus their count:
count_unique_players_df = len(purchase_data["SN"].unique())#returns count of times a unique item
print(count_unique_players_df)
#Didn't Work:
#unique_players_df = purchase_data["SN"].nunique() #creates list of unique items
#print(unique_players)
#unique_players_df = purchase_data["SN"].value_counts() #returns count of times a unique item is displayed in column
#print(unique_players_df)
#DONE***************************
```
## Purchasing Analysis (Total)
* Run basic calculations to obtain number of unique items, average price, etc.
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
```
#Number of Unique Items:
count_unique_items_df = len(purchase_data["Item ID"].unique())#returns count of times a unique item
print(count_unique_items_df)
#Average Price:
average_price = purchase_data["Price"].mean()
print(average_price)
#Number of Purchases:
count_purchases = len(purchase_data["Purchase ID"].unique())#returns count of times a unique item
print(count_purchases)
#Total Revenue:
total_revenue = purchase_data["Price"].sum()
print(total_revenue)
#Data Frame:
purchasing_analysis = pd.DataFrame(count_unique_items_df)
print(purchasing_analysis)#purchasing_analysis = pd.DataFrame("Number of Unique Items": count_unique_items_df, "Average Price": average_price, "Number of Purchases": count_purchases, "Total Revenue": total_revenue)
#print(purchasing_analysis)
#Formatting:
# First convert columns to float then Format to go to two decimal places, include a dollar sign, and use comma notation
#purchasing_analysis["Average Price"] = purchasing_analysis["Average Price"].astype(float).map(
# "${:,.2f}".format)
#purchasing_analysis["Total Revenue"] = purchasing_analysis["Total Revenue"].astype(float).map(
# "${:,.2f}".format)
#purchasing_analysis
```
## Gender Demographics
* Percentage and Count of Male Players
* Percentage and Count of Female Players
* Percentage and Count of Other / Non-Disclosed
```
#Limit Data for information needed for Analysis:
limited_df = purchase_data.loc[:, ["SN", "Gender"]]
print(limited_df)
#find unique
#unique_players_df = limited_df["SN"].unique()
#print(unique_players_df)
#idk = unique_players_df['SN'].value_counts()
#print(idk)
limited_df['SN'].value_counts()
#limited_df.describe()
#calc total: Total Count
#calc percent: Percentage of Players
#format:
#purchasing_analysis["Total Revenue"] = purchasing_analysis["Total Revenue"].astype(float).map(
# "${:,.2f}".format)
#df
#Male, Female, Other / Non-Disclosed
```
## Purchasing Analysis (Gender)
* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. by gender
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
```
purchase_data.loc[:, ["Gender", "Purchase ID", "Price"]].head()
#Per Gender Find:
#ted_group = ted_df.groupby("View Group")
#Purchase Count
#Avg Price
#Total Purchase Value
#Avg Total Purchase per Person
#DF
#Format
#Display summary data frame
```
## Age Demographics
* Establish bins for ages
* Categorize the existing players using the age bins. Hint: use pd.cut()
* Calculate the numbers and percentages by age group
* Create a summary data frame to hold the results
* Optional: round the percentage column to two decimal points
* Display Age Demographics Table
## Purchasing Analysis (Age)
* Bin the purchase_data data frame by age
* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. in the table below
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
## Top Spenders
* Run basic calculations to obtain the results in the table below
* Create a summary data frame to hold the results
* Sort the total purchase value column in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the summary data frame
## Most Popular Items
* Retrieve the Item ID, Item Name, and Item Price columns
* Group by Item ID and Item Name. Perform calculations to obtain purchase count, average item price, and total purchase value
* Create a summary data frame to hold the results
* Sort the purchase count column in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the summary data frame
## Most Profitable Items
* Sort the above table by total purchase value in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the data frame
|
github_jupyter
|
# Dependencies and Setup
import pandas as pd
import os
# File to Load (Remember to Change These)
file_to_load = os.path.join(".", "Resources", "purchase_data.csv")
# Read Purchasing File and store into Pandas data frame
purchase_data = pd.read_csv(file_to_load)
purchase_data
#purchase_data.dtypes
#Might need to convert some rows to different data types....************************
#Total players:
total_players = purchase_data["SN"].count() #counts total in column
print(total_players)
#Unique players plus their count:
count_unique_players_df = len(purchase_data["SN"].unique())#returns count of times a unique item
print(count_unique_players_df)
#Didn't Work:
#unique_players_df = purchase_data["SN"].nunique() #creates list of unique items
#print(unique_players)
#unique_players_df = purchase_data["SN"].value_counts() #returns count of times a unique item is displayed in column
#print(unique_players_df)
#DONE***************************
#Number of Unique Items:
count_unique_items_df = len(purchase_data["Item ID"].unique())#returns count of times a unique item
print(count_unique_items_df)
#Average Price:
average_price = purchase_data["Price"].mean()
print(average_price)
#Number of Purchases:
count_purchases = len(purchase_data["Purchase ID"].unique())#returns count of times a unique item
print(count_purchases)
#Total Revenue:
total_revenue = purchase_data["Price"].sum()
print(total_revenue)
#Data Frame:
purchasing_analysis = pd.DataFrame(count_unique_items_df)
print(purchasing_analysis)#purchasing_analysis = pd.DataFrame("Number of Unique Items": count_unique_items_df, "Average Price": average_price, "Number of Purchases": count_purchases, "Total Revenue": total_revenue)
#print(purchasing_analysis)
#Formatting:
# First convert columns to float then Format to go to two decimal places, include a dollar sign, and use comma notation
#purchasing_analysis["Average Price"] = purchasing_analysis["Average Price"].astype(float).map(
# "${:,.2f}".format)
#purchasing_analysis["Total Revenue"] = purchasing_analysis["Total Revenue"].astype(float).map(
# "${:,.2f}".format)
#purchasing_analysis
#Limit Data for information needed for Analysis:
limited_df = purchase_data.loc[:, ["SN", "Gender"]]
print(limited_df)
#find unique
#unique_players_df = limited_df["SN"].unique()
#print(unique_players_df)
#idk = unique_players_df['SN'].value_counts()
#print(idk)
limited_df['SN'].value_counts()
#limited_df.describe()
#calc total: Total Count
#calc percent: Percentage of Players
#format:
#purchasing_analysis["Total Revenue"] = purchasing_analysis["Total Revenue"].astype(float).map(
# "${:,.2f}".format)
#df
#Male, Female, Other / Non-Disclosed
purchase_data.loc[:, ["Gender", "Purchase ID", "Price"]].head()
#Per Gender Find:
#ted_group = ted_df.groupby("View Group")
#Purchase Count
#Avg Price
#Total Purchase Value
#Avg Total Purchase per Person
#DF
#Format
#Display summary data frame
| 0.296552 | 0.77437 |
# Multi-annotator Pool-based Active Learning - Getting Started
This notebook gives an introduction for dealing with multiple annotators using `skactiveml`.
```
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from skactiveml.classifier import ParzenWindowClassifier
from skactiveml.pool import ProbabilisticAL
from skactiveml.pool.multiannotator import SingleAnnotatorWrapper
from skactiveml.utils import MISSING_LABEL, majority_vote
from skactiveml.visualization import plot_decision_boundary, plot_annotator_utilities
FONTSIZE = 20
MARKER_SIZE = 100
```
Suppose we have the following problem. We have 100 two-dimensional samples belonging to one of two classes. To generate the example problem, we use the `make_blobs` function by `sklearn`.
```
n_samples = 100
X, y_true = make_blobs(
n_samples=n_samples, centers=6, random_state=0
)
bound = [[min(X[:, 0]), min(X[:, 1])], [max(X[:, 0]), max(X[:, 1])]]
y_true %= 2
fig, ax = plt.subplots(1, 1)
ax.scatter(X[:, 0], X[:, 1], c=y_true, s=MARKER_SIZE)
ax.set_title("omniscient annotator", fontsize=FONTSIZE)
fig.tight_layout()
plt.show()
```
Further, suppose we have 5 annotators to label the samples. The annotators have different accuracies for labeling the samples.
```
rng = np.random.default_rng(seed=0)
n_annotators = 5
y_annot = np.zeros(shape=(n_samples, n_annotators), dtype=int)
for i, p in enumerate(np.linspace(0.0, 0.5, num=n_annotators)):
y_noise = rng.binomial(1, p, n_samples)
y_annot[:, i] = y_noise ^ y_true
fig, axes = plt.subplots(1, n_annotators, figsize=(20, 5))
for a in range(n_annotators):
is_true = y_annot[:, a] == y_true
axes[a].scatter(X[is_true, 0], X[is_true, 1], c=y_annot[is_true, a], s=MARKER_SIZE)
axes[a].scatter(X[~is_true, 0], X[~is_true, 1], c=y_annot[~is_true, a], marker='x', s=MARKER_SIZE)
axes[a].set_title(f'annotator {a}', fontsize=FONTSIZE)
fig.tight_layout()
plt.show()
```
We want to label these samples using a Parzen window classifier. We query the samples using uncertainty sampling, and the annotators at random using the `SingleAnnotWrapper`. To achieve this, we first pass the Parzen window classifier as an argument to the single annotator query strategy `ProbabilisticAL`. Then we pass the single annotator query strategy as an argument to the wrapper, also specifying the number of annotators.
```
clf = ParzenWindowClassifier(
classes=np.unique(y_true),
metric="rbf",
metric_dict={"gamma": 0.1},
class_prior=0.001,
random_state=0,
)
sa_qs = ProbabilisticAL(random_state=0, prior=0.001)
ma_qs = SingleAnnotatorWrapper(sa_qs, random_state=0)
```
We loop through the process of querying samples and annotators over a total of 20 cycles. Each iteration, we query three annotators for one sample, setting the
batch size and the number of annotators per sample to three. We set the candidate annotators for each sample to be those, who have not already labeled the given sample.
Further we fit our classifier using the majority votes of the queried labels. The results are displayed after the 5th, the 14th, and the 20th cycle.
The assigned utilities of the query strategy for labeling a sample annotator pair are displayed by the saturation of the green color in the plot.
```
# function to be able to index via an array of indices
idx = lambda A: (A[:, 0], A[:, 1])
n_cycle = 20
# the already observed labels for each sample and annotator
y = np.full(shape=(n_samples, n_annotators), fill_value=MISSING_LABEL)
clf.fit(X, majority_vote(y))
for c in range(n_cycle):
# the needed query parameters for the wrapped single annotator query strategy
query_params_dict = {"clf": clf}
query_idx = ma_qs.query(
X,
y,
batch_size=3,
n_annotators_per_sample=3,
query_params_dict=query_params_dict,
)
y[idx(query_idx)] = y_annot[idx(query_idx)]
clf.fit(X, majority_vote(y, random_state=0))
if c in [4, 13, 19]:
ma_qs_arg_dict = {"query_params_dict": query_params_dict}
fig, axes = plt.subplots(1, n_annotators, figsize=(20, 5))
axes = plot_annotator_utilities(ma_qs, X=X, y=y, query_params_dict={'clf': clf}, axes=axes, feature_bound=bound)
for a in range(n_annotators):
plot_decision_boundary(clf, ax=axes[a], feature_bound=bound)
is_true = y_annot[:, a] == y_true
axes[a].scatter(X[is_true, 0], X[is_true, 1], c=y_annot[is_true, a], s=MARKER_SIZE)
axes[a].scatter(X[~is_true, 0], X[~is_true, 1], c=y_annot[~is_true, a], marker='x', s=MARKER_SIZE)
axes[a].set_title(f'annotator {a}', fontsize=FONTSIZE)
fig.tight_layout()
plt.show()
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from skactiveml.classifier import ParzenWindowClassifier
from skactiveml.pool import ProbabilisticAL
from skactiveml.pool.multiannotator import SingleAnnotatorWrapper
from skactiveml.utils import MISSING_LABEL, majority_vote
from skactiveml.visualization import plot_decision_boundary, plot_annotator_utilities
FONTSIZE = 20
MARKER_SIZE = 100
n_samples = 100
X, y_true = make_blobs(
n_samples=n_samples, centers=6, random_state=0
)
bound = [[min(X[:, 0]), min(X[:, 1])], [max(X[:, 0]), max(X[:, 1])]]
y_true %= 2
fig, ax = plt.subplots(1, 1)
ax.scatter(X[:, 0], X[:, 1], c=y_true, s=MARKER_SIZE)
ax.set_title("omniscient annotator", fontsize=FONTSIZE)
fig.tight_layout()
plt.show()
rng = np.random.default_rng(seed=0)
n_annotators = 5
y_annot = np.zeros(shape=(n_samples, n_annotators), dtype=int)
for i, p in enumerate(np.linspace(0.0, 0.5, num=n_annotators)):
y_noise = rng.binomial(1, p, n_samples)
y_annot[:, i] = y_noise ^ y_true
fig, axes = plt.subplots(1, n_annotators, figsize=(20, 5))
for a in range(n_annotators):
is_true = y_annot[:, a] == y_true
axes[a].scatter(X[is_true, 0], X[is_true, 1], c=y_annot[is_true, a], s=MARKER_SIZE)
axes[a].scatter(X[~is_true, 0], X[~is_true, 1], c=y_annot[~is_true, a], marker='x', s=MARKER_SIZE)
axes[a].set_title(f'annotator {a}', fontsize=FONTSIZE)
fig.tight_layout()
plt.show()
clf = ParzenWindowClassifier(
classes=np.unique(y_true),
metric="rbf",
metric_dict={"gamma": 0.1},
class_prior=0.001,
random_state=0,
)
sa_qs = ProbabilisticAL(random_state=0, prior=0.001)
ma_qs = SingleAnnotatorWrapper(sa_qs, random_state=0)
# function to be able to index via an array of indices
idx = lambda A: (A[:, 0], A[:, 1])
n_cycle = 20
# the already observed labels for each sample and annotator
y = np.full(shape=(n_samples, n_annotators), fill_value=MISSING_LABEL)
clf.fit(X, majority_vote(y))
for c in range(n_cycle):
# the needed query parameters for the wrapped single annotator query strategy
query_params_dict = {"clf": clf}
query_idx = ma_qs.query(
X,
y,
batch_size=3,
n_annotators_per_sample=3,
query_params_dict=query_params_dict,
)
y[idx(query_idx)] = y_annot[idx(query_idx)]
clf.fit(X, majority_vote(y, random_state=0))
if c in [4, 13, 19]:
ma_qs_arg_dict = {"query_params_dict": query_params_dict}
fig, axes = plt.subplots(1, n_annotators, figsize=(20, 5))
axes = plot_annotator_utilities(ma_qs, X=X, y=y, query_params_dict={'clf': clf}, axes=axes, feature_bound=bound)
for a in range(n_annotators):
plot_decision_boundary(clf, ax=axes[a], feature_bound=bound)
is_true = y_annot[:, a] == y_true
axes[a].scatter(X[is_true, 0], X[is_true, 1], c=y_annot[is_true, a], s=MARKER_SIZE)
axes[a].scatter(X[~is_true, 0], X[~is_true, 1], c=y_annot[~is_true, a], marker='x', s=MARKER_SIZE)
axes[a].set_title(f'annotator {a}', fontsize=FONTSIZE)
fig.tight_layout()
plt.show()
| 0.618665 | 0.956431 |
```
import os
import webbrowser
import requests
from bs4 import BeautifulSoup
import pandas as pd
import geocoder
from geopy.geocoders import Nominatim
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as colors
import sklearn
from sklearn.cluster import KMeans
import folium
import numpy as np
import matplotlib.pyplot as plt
from selenium import webdriver
import time
from fuzzywuzzy import fuzz
def get_new_york_data():
"""
This method is to collect New York City data with Borough, Neighborhood, Latitude and Longitude.
Will return a pandas dataframe
"""
NY_DATASET = "https://cocl.us/new_york_dataset"
resp = requests.get(NY_DATASET).json()
features = resp['features']
column_names = ['Borough', 'Neighborhood', 'Latitude', 'Longitude']
new_york_data = pd.DataFrame(columns=column_names)
for data in features:
borough = data['properties']['borough']
neighborhood_name = data['properties']['name']
neighborhood_latlon = data['geometry']['coordinates']
neighborhood_lat = neighborhood_latlon[1]
neighborhood_lon = neighborhood_latlon[0]
new_york_data = new_york_data.append({'Borough': borough,
'Neighborhood': neighborhood_name,
'Latitude': neighborhood_lat,
'Longitude': neighborhood_lon}, ignore_index=True)
return new_york_data
ny_df = get_new_york_data()
ny_df.head()
def get_population_per_neighbourhood(read_from_csv=False):
"""
It will first fetch the borugh and neighborhood table from wikipedia. Then go to each link of the neighborhoods in the table. Finally, it will create a dataframe cotaining Borough, Neighborhood and Population. It has a functionality to store the data in csv format, and it is possible to read this data from csv to reduce time consuming operations later.
"""
if not read_from_csv:
WIKI_LINK = "https://en.wikipedia.org/wiki/Neighborhoods_in_New_York_City"
ROOT_WIKI_LINK = "https://en.wikipedia.org"
page = requests.get(WIKI_LINK)
soup = BeautifulSoup(page.text, 'html.parser')
population_list = []
for table_row in soup.select("table.wikitable tr"):
cells = table_row.findAll('td')
if len(cells) > 0:
borough = cells[0].text.strip().replace(
'\xa0', ' ').split(' ')[0]
population = int(cells[3].text.strip().replace(',', ''))
for item in cells[4].findAll('a'):
neighborhood = item.text
neighbourhood_page = requests.get(
ROOT_WIKI_LINK+item['href'])
soup = BeautifulSoup(
neighbourhood_page.text, 'html.parser')
table = soup.select("table.infobox tr")
should_record = False
for row in table:
head = row.find('th')
body = row.find('td')
if head and 'population' in head.text.lower():
should_record = True
continue
if should_record:
try:
population_list.append(
[borough, neighborhood, int(body.text.replace(',', ''))])
except:
pass
should_record = False
df = pd.DataFrame(population_list, columns=[
"Borough", "Neighborhood", "Population"])
df.to_csv('population.csv')
else:
df = pd.read_csv('population.csv')
df = df.sort_values(by=['Borough'])
df = df.drop_duplicates(subset='Neighborhood', keep='last')
return df
nyc_population_df = get_population_per_neighbourhood()
nyc_population_df.head()
# Combine NYC Geo data with Population data
ny_df.set_index('Neighborhood')
nyc_population_df.set_index('Neighborhood')
nyc_df = pd.merge(ny_df, nyc_population_df, how="inner", on=["Borough", "Neighborhood"])
nyc_df.head()
# Let us see some bar charts of this data
def show_bar_chart(df, group, field, title, x_label, y_label, calculation="sum"):
"""
A generic function to render bar charts
"""
plt.figure(figsize=(9, 5), dpi=100)
plt.title(title)
plt.xlabel(x_label, fontsize=15)
plt.ylabel(y_label, fontsize=15)
if calculation == "sum":
df.groupby(group)[field].sum().plot(kind='bar')
if calculation == "count":
df.groupby(group)[field].count().plot(kind='bar')
plt.legend()
plt.show()
show_bar_chart(nyc_df, group="Borough", field="Population", title="Population per Borough", x_label="Borough", y_label="Population")
show_bar_chart(nyc_df, group="Borough", field="Neighborhood", title="Neighborhoods per Borough", x_label="Borough", y_label="Neighborhood", calculation="count")
# Now, let us fetch hospital information for each Neighborhood
def get_hospital_data(lat, lng, borough, neighborhood):
"""
We are going to utilize foursquare API to fetch hospital data. It will take latitude, longitude and return hospital information.
"""
radius = 1000
LIMIT = 100
VERSION = '20200328'
FS_CLIENT_ID = "A5S2CJNU43XNBJEADGVEDLOR024ZP5BC5KZY2E1F0WT0DZEI"
FS_CLIENT_SECRET = "GIPWZSDNB1GYTVSRWTFV2E2JZBHBDYCORNL3MVRVDUOWQADI"
FS_HOSPITAL_KEY = "4bf58dd8d48988d196941735"
url = 'https://api.foursquare.com/v2/venues/search?&client_id={}&client_secret={}&v={}&ll={},{}&radius={}&limit={}&categoryId={}'.format(
FS_CLIENT_ID,
FS_CLIENT_SECRET,
VERSION,
lat,
lng,
radius,
LIMIT,
FS_HOSPITAL_KEY)
response = requests.get(url)
if not response.status_code == 200:
print("ERROR", response.status_code, response.content)
return None
results = response.json()
venue_data = results["response"]["venues"]
venue_details = []
for row in venue_data:
try:
venue_id = row['id']
venue_name = row['name']
lat = row["location"]["lat"]
lng = row["location"]["lng"]
venue_details.append(
[venue_id, venue_name, lat, lng, borough, neighborhood])
except KeyError:
pass
column_names = ['ID', 'Name', 'Latitude',
'Longitude', "Borough", "Neighborhood"]
df = pd.DataFrame(venue_details, columns=column_names)
return df
# Let us also write another function to utilize the nyc_df to get hospital data
def get_hospital_per_neighborhood_borough(df):
"""
It will utilize NYC_DF and get hospital per neighborhood.
"""
column_names = ['ID', 'Name', 'Latitude',
'Longitude', "Borough", "Neighborhood"]
data = []
for i, row in df.iterrows():
h_df = get_hospital_data(
row["Latitude"], row["Longitude"], row["Borough"], row["Neighborhood"])
if h_df is not None:
for x, hrow in h_df.iterrows():
data.append([hrow[column] for column in column_names])
n_df = pd.DataFrame(data, columns=column_names)
n_df.to_csv('hospital_per_boro_nei.csv')
return n_df
# Now let us use the above function
hospital_df = get_hospital_per_neighborhood_borough(nyc_df)
hospital_df.head()
# Now let us fetch hospital bed data from NYS Health Profile
def get_bed_per_hospital():
"""
We are going to fetch data NYS Health Profile. A selenium based scrapper will be used as it is a dynamic site. A fixed list of IDs have been used for fetching data. These IDs are collected manualy from the website. They represent the NYC hospitals.
"""
ROOT_URL = "https://profiles.health.ny.gov/hospital/printview/{}"
NYM_NYC = [
103016, 106804, 102908, 103035, 102934, 1256608, 105117, 103009, 102974, 103006, 103041, 105086, 103056, 103086, 102973,
102970, 102950, 103074, 103008, 103007, 102985, 103012, 106809, 102937, 103068, 102944, 102995, 106803, 102916, 105109,
102914, 102960, 103038, 106810, 106811, 102961, 102940, 102933, 103078, 254693, 103065, 103021, 103080, 103033, 102919,
105116, 106825, 103084, 103087, 102989, 102929, 106817, 106819, 103073, 103085, 103025
] # New York Metro: New York City Hospitals' IDs
NYM_LI = [
102999, 103062, 102928, 103002, 102980, 103077, 103049, 103011, 102918, 102965, 102994, 102966, 103069, 1189331, 102926,
103088, 103045, 103000, 103070, 105137, 103082, 102954, 103072
] # New York Metro: Long Iceland Hospitals' IDs
BRONX = [
102908, 106804, 105117, 102973, 102950, 106809, 102937, 103068, 102944, 103078, 103087
] # New York Metro: Bronx Hospitals' IDs
QUEENS = [
102974, 103006, 102912, 103074, 103008, 105109, 102933, 103033, 103084
] # New York Metro: Queens Hospitals' IDs
HOSPITALS = list(set(NYM_LI + NYM_NYC + BRONX + QUEENS))
print('Total hospitals', len(HOSPITALS))
hospital_data = []
for val in HOSPITALS:
print("Processing hospital id", val)
url = ROOT_URL.format(val)
browser = webdriver.Safari()
try:
browser.get(url)
time.sleep(10)
html = browser.page_source
soup = BeautifulSoup(html, 'html.parser')
hospital_name = soup.find('h2').text
table = soup.select("table", id="number-of-beds")[0]
rows = table.findAll('tr')
hospital_name = soup.find('h2').text.strip()
icu_beds = 0
for row in rows:
tds = row.findAll('td')
should_record = False
for td in tds:
if "intensive care beds" == td.text.lower():
should_record = True
continue
if should_record:
icu_beds = td.text
bed_number = rows[-1].findAll('td')[-1].text
print(hospital_name, bed_number, icu_beds)
hospital_data.append([hospital_name, bed_number, icu_beds])
except Exception as e:
print(e)
browser.quit()
df = pd.DataFrame(
hospital_data, columns=[
"Hospital Name", "Bed Number", "ICU Bed Number"
]
)
df = df.drop_duplicates(subset='Hospital Name', keep='last')
df.to_csv('hospital_beds.csv')
return df
# Let us get the hospital bed data
hospital_bed_df = get_bed_per_hospital()
hospital_bed_df.head()
# Now let us combine hospital ber neighborhood data with hospital bed data
def combine_hospital_beds_with_boro_neighborhood(hospital_df, hospital_boro_nei_df):
# Uses fuzzywuzzy to match hospital name from Foursquare to NYS
data = []
column_names = ["Hospital Name", "Bed Number", "ICU Bed Number"]
boro_neig_column_names = ["Borough", "Neighborhood"]
for i, row in hospital_df.iterrows():
data_per_hospital = None
max_ratio = 0
for x, hrow in hospital_boro_nei_df.iterrows():
ratio = fuzz.token_sort_ratio(row["Hospital Name"], hrow["Name"])
if ratio > max_ratio:
max_ratio = ratio
data_per_hospital = [
row[column] for column in column_names] + \
[hrow[column] for column in boro_neig_column_names
]
if data_per_hospital:
data.append(data_per_hospital)
df = pd.DataFrame(data, columns=column_names+boro_neig_column_names)
df.to_csv('cleaned_hospital_data.csv')
return df
h_df = combine_hospital_beds_with_boro_neighborhood(hospital_bed_df, hospital_df)
h_df.head()
# Now let us clean up the hospital. We will combine total bed count and icu bed count per borough and neighbourhood
h_df.dtypes
h_df = h_df.astype({'Bed Number': 'int32', 'ICU Bed Number': 'int32'})
# Let us clean up the data by combining total bed count and icu bed count per neighborhood and borough
h_df = h_df.groupby(
["Neighborhood", "Borough"]
).agg(
{
"Bed Number": "sum",
"ICU Bed Number": "sum"
}
)
h_df.head()
# Cool. Now let us see how this data looks in bar chart
show_bar_chart(h_df, group="Borough", field="Bed Number", title="Bed Count per Borough", x_label="Borough", y_label="Bed Count", calculation="sum")
show_bar_chart(h_df, group="Borough", field="ICU Bed Number", title="ICU Bed Count per Borough", x_label="Borough", y_label="ICU Bed Count", calculation="sum")
# We can see that Manhattan has most hospital beds
# Now let us combine the nyc_data with h_data
df = pd.merge(h_df, nyc_df, how="inner", on=["Borough", "Neighborhood"])
df.head()
# We will add bed per 100 people data with the dataframe
def get_bed_per_hunderd_person(row, field="Bed Number"):
"""
Will return bed per hundered data. field can be beds or icu beds
"""
return row[field] * 100 / row["Population"]
df["ICU Bed Per Hundred People"] = df.apply(
lambda row: get_bed_per_hunderd_person(row, field="ICU Bed Number"), axis=1)
df["Bed Per Hundred People"] = df.apply(
lambda row: get_bed_per_hunderd_person(row), axis=1)
df.head()
# Cleaning data for k-means
df_clusters = df.drop(['Borough', 'Neighborhood', 'Latitude', 'Longitude', 'ICU Bed Number', 'Bed Number'],axis = 1)
# Now we are going to use k-means clustering to partition data in k partitions
# We are going to use elbow method to find the optimum number of cluster
def plot_kmeans(dataset):
obs = dataset.copy()
silhouette_score_values = list()
number_of_clusters = range(3, 30)
for i in number_of_clusters:
classifier = KMeans(i, init='k-means++', n_init=10,
max_iter=300, tol=0.0001, random_state=10)
classifier.fit(obs)
labels = classifier.predict(obs)
silhouette_score_values.append(sklearn.metrics.silhouette_score(
obs, labels, metric='euclidean', random_state=0))
plt.plot(number_of_clusters, silhouette_score_values)
plt.title("Silhouette score values vs Numbers of Clusters ")
plt.show()
optimum_number_of_components = number_of_clusters[silhouette_score_values.index(
max(silhouette_score_values))]
print("Optimal number of components is:")
print(optimum_number_of_components)
# Normalizing data
df_clusters = sklearn.preprocessing.StandardScaler().fit_transform(df_clusters)
df_clusters
# Performing k-means clustering
plot_kmeans(df_clusters)
# We get the optimum number of k is 3
kclusters = 3
# run k-means clustering
kmeans = KMeans(n_clusters=kclusters, random_state=0).fit(df_clusters)
# check cluster labels generated for each row in the dataframe
kmeans.labels_[0:24]
# Combining cluster data with dataframe
df.insert(0, 'Cluster Labels', kmeans.labels_)
df.head()
# Now, it is time to create maps representing our clusters. The first map is illustrating the clusters where the radius of the Circle marker is proportional to Bed Countof 100 people in each borough.
def get_geo_location(address):
"""
This function will return lattitude and longitude of an given address
"""
geolocator = Nominatim(user_agent="ny_explorer")
location = geolocator.geocode(address)
if location:
latitude = location.latitude
longitude = location.longitude
return [latitude, longitude]
return [None, None]
def save_map(m, filepath='map.html'):
m.save(filepath)
def render_map_clusters(df, df_clusters, bpp_df=df_clusters[:, 1],kclusters=3, m_boost=5, add_boost=5):
"""
This function will render map for dataframe using folium
"""
map_clusters = folium.Map(
location=get_geo_location("New York"), zoom_start=11)
colours = ['red', 'black', 'blue']
x = np.arange(kclusters)
ys = [i + x + (i*x)**2 for i in range(kclusters)]
colors_array = cm.rainbow(np.linspace(0, 1, len(ys)))
rainbow = [colors.rgb2hex(i) for i in colors_array]
markers_colors = []
for lat, lon, poi, nei, cluster, bed_per_people in zip(df['Latitude'], df['Longitude'], df['Borough'], df["Neighborhood"], df['Cluster Labels'], bpp_df):
label = folium.Popup(
' Cluster ' + str(cluster)+': ' + str(poi) + "-" + str(nei),
parse_html=True
)
folium.CircleMarker(
[lat, lon],
radius=bed_per_people*m_boost+add_boost,
popup=label,
color=colours[cluster],
fill=True,
fill_color=colours[cluster],
fill_opacity=0.7).add_to(map_clusters)
return map_clusters
# Now let us render the map
map_clusters = render_map_clusters(df, df_clusters)
map_clusters
save_map(map_clusters)
# Now let us render the map for bed per 100 people
map_clusters = render_map_clusters(df, df_clusters,df['Bed Per Hundred People'],m_boost=1,add_boost=5)
map_clusters
save_map(map_clusters, 'bed_per_hundred.html')
# Now let us render the map for ICU bed per 100 people
map_clusters = render_map_clusters(df, df_clusters,df['ICU Bed Per Hundred People'],m_boost=2,add_boost=5)
map_clusters
save_map(map_clusters, 'icu_bed_per_hundred.html')
# Now we are going to use scatter plot
y_kmeans = kmeans.predict(df_clusters)
plt.scatter(df_clusters[:, 0], df_clusters[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5)
plt.xlabel('Population')
plt.ylabel('Bed per 100 people')
plt.show()
# Scatter plot for ICU bed per person
y_kmeans = kmeans.predict(df_clusters)
plt.scatter(df_clusters[:, 0], df_clusters[:, 2], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 2], c='black', s=200, alpha=0.5);
plt.xlabel('Population')
plt.ylabel('Bed per 100 people')
plt.show()
# One outlier here is manhattun
# Now let us check the df per cluster
df[(df['Cluster Labels'] == 0)]
df[(df['Cluster Labels'] == 1)]
df[(df['Cluster Labels'] == 2)]
# Let us see neighborhoods which does not have any hospitals
excluded_df = pd.merge(nyc_df, df, how='outer', indicator=True, on=["Borough", "Neighborhood"])
excluded_df = excluded_df.loc[excluded_df._merge == 'left_only', ["Borough", "Neighborhood"]]
excluded_df.head(10)
# Let us see the length of df with/without hospital information
print("Neighborhood without hospital count:", len(excluded_df.index))
print("Neighborhood with hospital count:", len(df.index))
# Full report can be found here: https://ruddra.com/posts/project-battle-of-capstones/
```
|
github_jupyter
|
import os
import webbrowser
import requests
from bs4 import BeautifulSoup
import pandas as pd
import geocoder
from geopy.geocoders import Nominatim
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as colors
import sklearn
from sklearn.cluster import KMeans
import folium
import numpy as np
import matplotlib.pyplot as plt
from selenium import webdriver
import time
from fuzzywuzzy import fuzz
def get_new_york_data():
"""
This method is to collect New York City data with Borough, Neighborhood, Latitude and Longitude.
Will return a pandas dataframe
"""
NY_DATASET = "https://cocl.us/new_york_dataset"
resp = requests.get(NY_DATASET).json()
features = resp['features']
column_names = ['Borough', 'Neighborhood', 'Latitude', 'Longitude']
new_york_data = pd.DataFrame(columns=column_names)
for data in features:
borough = data['properties']['borough']
neighborhood_name = data['properties']['name']
neighborhood_latlon = data['geometry']['coordinates']
neighborhood_lat = neighborhood_latlon[1]
neighborhood_lon = neighborhood_latlon[0]
new_york_data = new_york_data.append({'Borough': borough,
'Neighborhood': neighborhood_name,
'Latitude': neighborhood_lat,
'Longitude': neighborhood_lon}, ignore_index=True)
return new_york_data
ny_df = get_new_york_data()
ny_df.head()
def get_population_per_neighbourhood(read_from_csv=False):
"""
It will first fetch the borugh and neighborhood table from wikipedia. Then go to each link of the neighborhoods in the table. Finally, it will create a dataframe cotaining Borough, Neighborhood and Population. It has a functionality to store the data in csv format, and it is possible to read this data from csv to reduce time consuming operations later.
"""
if not read_from_csv:
WIKI_LINK = "https://en.wikipedia.org/wiki/Neighborhoods_in_New_York_City"
ROOT_WIKI_LINK = "https://en.wikipedia.org"
page = requests.get(WIKI_LINK)
soup = BeautifulSoup(page.text, 'html.parser')
population_list = []
for table_row in soup.select("table.wikitable tr"):
cells = table_row.findAll('td')
if len(cells) > 0:
borough = cells[0].text.strip().replace(
'\xa0', ' ').split(' ')[0]
population = int(cells[3].text.strip().replace(',', ''))
for item in cells[4].findAll('a'):
neighborhood = item.text
neighbourhood_page = requests.get(
ROOT_WIKI_LINK+item['href'])
soup = BeautifulSoup(
neighbourhood_page.text, 'html.parser')
table = soup.select("table.infobox tr")
should_record = False
for row in table:
head = row.find('th')
body = row.find('td')
if head and 'population' in head.text.lower():
should_record = True
continue
if should_record:
try:
population_list.append(
[borough, neighborhood, int(body.text.replace(',', ''))])
except:
pass
should_record = False
df = pd.DataFrame(population_list, columns=[
"Borough", "Neighborhood", "Population"])
df.to_csv('population.csv')
else:
df = pd.read_csv('population.csv')
df = df.sort_values(by=['Borough'])
df = df.drop_duplicates(subset='Neighborhood', keep='last')
return df
nyc_population_df = get_population_per_neighbourhood()
nyc_population_df.head()
# Combine NYC Geo data with Population data
ny_df.set_index('Neighborhood')
nyc_population_df.set_index('Neighborhood')
nyc_df = pd.merge(ny_df, nyc_population_df, how="inner", on=["Borough", "Neighborhood"])
nyc_df.head()
# Let us see some bar charts of this data
def show_bar_chart(df, group, field, title, x_label, y_label, calculation="sum"):
"""
A generic function to render bar charts
"""
plt.figure(figsize=(9, 5), dpi=100)
plt.title(title)
plt.xlabel(x_label, fontsize=15)
plt.ylabel(y_label, fontsize=15)
if calculation == "sum":
df.groupby(group)[field].sum().plot(kind='bar')
if calculation == "count":
df.groupby(group)[field].count().plot(kind='bar')
plt.legend()
plt.show()
show_bar_chart(nyc_df, group="Borough", field="Population", title="Population per Borough", x_label="Borough", y_label="Population")
show_bar_chart(nyc_df, group="Borough", field="Neighborhood", title="Neighborhoods per Borough", x_label="Borough", y_label="Neighborhood", calculation="count")
# Now, let us fetch hospital information for each Neighborhood
def get_hospital_data(lat, lng, borough, neighborhood):
"""
We are going to utilize foursquare API to fetch hospital data. It will take latitude, longitude and return hospital information.
"""
radius = 1000
LIMIT = 100
VERSION = '20200328'
FS_CLIENT_ID = "A5S2CJNU43XNBJEADGVEDLOR024ZP5BC5KZY2E1F0WT0DZEI"
FS_CLIENT_SECRET = "GIPWZSDNB1GYTVSRWTFV2E2JZBHBDYCORNL3MVRVDUOWQADI"
FS_HOSPITAL_KEY = "4bf58dd8d48988d196941735"
url = 'https://api.foursquare.com/v2/venues/search?&client_id={}&client_secret={}&v={}&ll={},{}&radius={}&limit={}&categoryId={}'.format(
FS_CLIENT_ID,
FS_CLIENT_SECRET,
VERSION,
lat,
lng,
radius,
LIMIT,
FS_HOSPITAL_KEY)
response = requests.get(url)
if not response.status_code == 200:
print("ERROR", response.status_code, response.content)
return None
results = response.json()
venue_data = results["response"]["venues"]
venue_details = []
for row in venue_data:
try:
venue_id = row['id']
venue_name = row['name']
lat = row["location"]["lat"]
lng = row["location"]["lng"]
venue_details.append(
[venue_id, venue_name, lat, lng, borough, neighborhood])
except KeyError:
pass
column_names = ['ID', 'Name', 'Latitude',
'Longitude', "Borough", "Neighborhood"]
df = pd.DataFrame(venue_details, columns=column_names)
return df
# Let us also write another function to utilize the nyc_df to get hospital data
def get_hospital_per_neighborhood_borough(df):
"""
It will utilize NYC_DF and get hospital per neighborhood.
"""
column_names = ['ID', 'Name', 'Latitude',
'Longitude', "Borough", "Neighborhood"]
data = []
for i, row in df.iterrows():
h_df = get_hospital_data(
row["Latitude"], row["Longitude"], row["Borough"], row["Neighborhood"])
if h_df is not None:
for x, hrow in h_df.iterrows():
data.append([hrow[column] for column in column_names])
n_df = pd.DataFrame(data, columns=column_names)
n_df.to_csv('hospital_per_boro_nei.csv')
return n_df
# Now let us use the above function
hospital_df = get_hospital_per_neighborhood_borough(nyc_df)
hospital_df.head()
# Now let us fetch hospital bed data from NYS Health Profile
def get_bed_per_hospital():
"""
We are going to fetch data NYS Health Profile. A selenium based scrapper will be used as it is a dynamic site. A fixed list of IDs have been used for fetching data. These IDs are collected manualy from the website. They represent the NYC hospitals.
"""
ROOT_URL = "https://profiles.health.ny.gov/hospital/printview/{}"
NYM_NYC = [
103016, 106804, 102908, 103035, 102934, 1256608, 105117, 103009, 102974, 103006, 103041, 105086, 103056, 103086, 102973,
102970, 102950, 103074, 103008, 103007, 102985, 103012, 106809, 102937, 103068, 102944, 102995, 106803, 102916, 105109,
102914, 102960, 103038, 106810, 106811, 102961, 102940, 102933, 103078, 254693, 103065, 103021, 103080, 103033, 102919,
105116, 106825, 103084, 103087, 102989, 102929, 106817, 106819, 103073, 103085, 103025
] # New York Metro: New York City Hospitals' IDs
NYM_LI = [
102999, 103062, 102928, 103002, 102980, 103077, 103049, 103011, 102918, 102965, 102994, 102966, 103069, 1189331, 102926,
103088, 103045, 103000, 103070, 105137, 103082, 102954, 103072
] # New York Metro: Long Iceland Hospitals' IDs
BRONX = [
102908, 106804, 105117, 102973, 102950, 106809, 102937, 103068, 102944, 103078, 103087
] # New York Metro: Bronx Hospitals' IDs
QUEENS = [
102974, 103006, 102912, 103074, 103008, 105109, 102933, 103033, 103084
] # New York Metro: Queens Hospitals' IDs
HOSPITALS = list(set(NYM_LI + NYM_NYC + BRONX + QUEENS))
print('Total hospitals', len(HOSPITALS))
hospital_data = []
for val in HOSPITALS:
print("Processing hospital id", val)
url = ROOT_URL.format(val)
browser = webdriver.Safari()
try:
browser.get(url)
time.sleep(10)
html = browser.page_source
soup = BeautifulSoup(html, 'html.parser')
hospital_name = soup.find('h2').text
table = soup.select("table", id="number-of-beds")[0]
rows = table.findAll('tr')
hospital_name = soup.find('h2').text.strip()
icu_beds = 0
for row in rows:
tds = row.findAll('td')
should_record = False
for td in tds:
if "intensive care beds" == td.text.lower():
should_record = True
continue
if should_record:
icu_beds = td.text
bed_number = rows[-1].findAll('td')[-1].text
print(hospital_name, bed_number, icu_beds)
hospital_data.append([hospital_name, bed_number, icu_beds])
except Exception as e:
print(e)
browser.quit()
df = pd.DataFrame(
hospital_data, columns=[
"Hospital Name", "Bed Number", "ICU Bed Number"
]
)
df = df.drop_duplicates(subset='Hospital Name', keep='last')
df.to_csv('hospital_beds.csv')
return df
# Let us get the hospital bed data
hospital_bed_df = get_bed_per_hospital()
hospital_bed_df.head()
# Now let us combine hospital ber neighborhood data with hospital bed data
def combine_hospital_beds_with_boro_neighborhood(hospital_df, hospital_boro_nei_df):
# Uses fuzzywuzzy to match hospital name from Foursquare to NYS
data = []
column_names = ["Hospital Name", "Bed Number", "ICU Bed Number"]
boro_neig_column_names = ["Borough", "Neighborhood"]
for i, row in hospital_df.iterrows():
data_per_hospital = None
max_ratio = 0
for x, hrow in hospital_boro_nei_df.iterrows():
ratio = fuzz.token_sort_ratio(row["Hospital Name"], hrow["Name"])
if ratio > max_ratio:
max_ratio = ratio
data_per_hospital = [
row[column] for column in column_names] + \
[hrow[column] for column in boro_neig_column_names
]
if data_per_hospital:
data.append(data_per_hospital)
df = pd.DataFrame(data, columns=column_names+boro_neig_column_names)
df.to_csv('cleaned_hospital_data.csv')
return df
h_df = combine_hospital_beds_with_boro_neighborhood(hospital_bed_df, hospital_df)
h_df.head()
# Now let us clean up the hospital. We will combine total bed count and icu bed count per borough and neighbourhood
h_df.dtypes
h_df = h_df.astype({'Bed Number': 'int32', 'ICU Bed Number': 'int32'})
# Let us clean up the data by combining total bed count and icu bed count per neighborhood and borough
h_df = h_df.groupby(
["Neighborhood", "Borough"]
).agg(
{
"Bed Number": "sum",
"ICU Bed Number": "sum"
}
)
h_df.head()
# Cool. Now let us see how this data looks in bar chart
show_bar_chart(h_df, group="Borough", field="Bed Number", title="Bed Count per Borough", x_label="Borough", y_label="Bed Count", calculation="sum")
show_bar_chart(h_df, group="Borough", field="ICU Bed Number", title="ICU Bed Count per Borough", x_label="Borough", y_label="ICU Bed Count", calculation="sum")
# We can see that Manhattan has most hospital beds
# Now let us combine the nyc_data with h_data
df = pd.merge(h_df, nyc_df, how="inner", on=["Borough", "Neighborhood"])
df.head()
# We will add bed per 100 people data with the dataframe
def get_bed_per_hunderd_person(row, field="Bed Number"):
"""
Will return bed per hundered data. field can be beds or icu beds
"""
return row[field] * 100 / row["Population"]
df["ICU Bed Per Hundred People"] = df.apply(
lambda row: get_bed_per_hunderd_person(row, field="ICU Bed Number"), axis=1)
df["Bed Per Hundred People"] = df.apply(
lambda row: get_bed_per_hunderd_person(row), axis=1)
df.head()
# Cleaning data for k-means
df_clusters = df.drop(['Borough', 'Neighborhood', 'Latitude', 'Longitude', 'ICU Bed Number', 'Bed Number'],axis = 1)
# Now we are going to use k-means clustering to partition data in k partitions
# We are going to use elbow method to find the optimum number of cluster
def plot_kmeans(dataset):
obs = dataset.copy()
silhouette_score_values = list()
number_of_clusters = range(3, 30)
for i in number_of_clusters:
classifier = KMeans(i, init='k-means++', n_init=10,
max_iter=300, tol=0.0001, random_state=10)
classifier.fit(obs)
labels = classifier.predict(obs)
silhouette_score_values.append(sklearn.metrics.silhouette_score(
obs, labels, metric='euclidean', random_state=0))
plt.plot(number_of_clusters, silhouette_score_values)
plt.title("Silhouette score values vs Numbers of Clusters ")
plt.show()
optimum_number_of_components = number_of_clusters[silhouette_score_values.index(
max(silhouette_score_values))]
print("Optimal number of components is:")
print(optimum_number_of_components)
# Normalizing data
df_clusters = sklearn.preprocessing.StandardScaler().fit_transform(df_clusters)
df_clusters
# Performing k-means clustering
plot_kmeans(df_clusters)
# We get the optimum number of k is 3
kclusters = 3
# run k-means clustering
kmeans = KMeans(n_clusters=kclusters, random_state=0).fit(df_clusters)
# check cluster labels generated for each row in the dataframe
kmeans.labels_[0:24]
# Combining cluster data with dataframe
df.insert(0, 'Cluster Labels', kmeans.labels_)
df.head()
# Now, it is time to create maps representing our clusters. The first map is illustrating the clusters where the radius of the Circle marker is proportional to Bed Countof 100 people in each borough.
def get_geo_location(address):
"""
This function will return lattitude and longitude of an given address
"""
geolocator = Nominatim(user_agent="ny_explorer")
location = geolocator.geocode(address)
if location:
latitude = location.latitude
longitude = location.longitude
return [latitude, longitude]
return [None, None]
def save_map(m, filepath='map.html'):
m.save(filepath)
def render_map_clusters(df, df_clusters, bpp_df=df_clusters[:, 1],kclusters=3, m_boost=5, add_boost=5):
"""
This function will render map for dataframe using folium
"""
map_clusters = folium.Map(
location=get_geo_location("New York"), zoom_start=11)
colours = ['red', 'black', 'blue']
x = np.arange(kclusters)
ys = [i + x + (i*x)**2 for i in range(kclusters)]
colors_array = cm.rainbow(np.linspace(0, 1, len(ys)))
rainbow = [colors.rgb2hex(i) for i in colors_array]
markers_colors = []
for lat, lon, poi, nei, cluster, bed_per_people in zip(df['Latitude'], df['Longitude'], df['Borough'], df["Neighborhood"], df['Cluster Labels'], bpp_df):
label = folium.Popup(
' Cluster ' + str(cluster)+': ' + str(poi) + "-" + str(nei),
parse_html=True
)
folium.CircleMarker(
[lat, lon],
radius=bed_per_people*m_boost+add_boost,
popup=label,
color=colours[cluster],
fill=True,
fill_color=colours[cluster],
fill_opacity=0.7).add_to(map_clusters)
return map_clusters
# Now let us render the map
map_clusters = render_map_clusters(df, df_clusters)
map_clusters
save_map(map_clusters)
# Now let us render the map for bed per 100 people
map_clusters = render_map_clusters(df, df_clusters,df['Bed Per Hundred People'],m_boost=1,add_boost=5)
map_clusters
save_map(map_clusters, 'bed_per_hundred.html')
# Now let us render the map for ICU bed per 100 people
map_clusters = render_map_clusters(df, df_clusters,df['ICU Bed Per Hundred People'],m_boost=2,add_boost=5)
map_clusters
save_map(map_clusters, 'icu_bed_per_hundred.html')
# Now we are going to use scatter plot
y_kmeans = kmeans.predict(df_clusters)
plt.scatter(df_clusters[:, 0], df_clusters[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5)
plt.xlabel('Population')
plt.ylabel('Bed per 100 people')
plt.show()
# Scatter plot for ICU bed per person
y_kmeans = kmeans.predict(df_clusters)
plt.scatter(df_clusters[:, 0], df_clusters[:, 2], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 2], c='black', s=200, alpha=0.5);
plt.xlabel('Population')
plt.ylabel('Bed per 100 people')
plt.show()
# One outlier here is manhattun
# Now let us check the df per cluster
df[(df['Cluster Labels'] == 0)]
df[(df['Cluster Labels'] == 1)]
df[(df['Cluster Labels'] == 2)]
# Let us see neighborhoods which does not have any hospitals
excluded_df = pd.merge(nyc_df, df, how='outer', indicator=True, on=["Borough", "Neighborhood"])
excluded_df = excluded_df.loc[excluded_df._merge == 'left_only', ["Borough", "Neighborhood"]]
excluded_df.head(10)
# Let us see the length of df with/without hospital information
print("Neighborhood without hospital count:", len(excluded_df.index))
print("Neighborhood with hospital count:", len(df.index))
# Full report can be found here: https://ruddra.com/posts/project-battle-of-capstones/
| 0.50293 | 0.420719 |
# Excercises Electric Machinery Fundamentals
## Chapter 1
## Problem 1-8
```
%pylab inline
%precision 4
from scipy import constants as c # we like to use some constants
```
### Description
A core with three legs is shown in Figure P1-5 below:
<img src="figs/FigC_P1-5.jpg" width="70%">
Its depth is 5 cm, and there are 100 turns on the leftmost
leg. The relative permeability of the core can be assumed to be 2000 and constant.
* What flux exists in each of the three legs of the core?
* What is the flux density in each of the legs?
Assume a 5% increase in the effective area of the air gap due to fringing effects.
```
mu_r = 2000
mu = mu_r * c.mu_0
```
### SOLUTION
This core can be divided up into four regions. Let:
* $\mathcal{R}_1$ be the reluctance of the left-hand portion of the core,
* $\mathcal{R}_2$ be the reluctance of the center leg of the core,
* $\mathcal{R}_3$ be the reluctance of the center airgap, and
* $\mathcal{R}_4$ be the reluctance of the right-hand portion of the core.
If we assume that the mean path length of the flux is in the center of each leg of the core, and if we ignore spreading at the corners of the core, then the path lengths are:
```
l1 = 1.08 # [m]
l2 = 0.34 # [m]
l3 = 0.0005 # [m]
l4 = 1.08 # [m]
```
* The reluctances of the regions in core are: $\mathcal{R}_\text{CORE} = \frac{l}{\mu_0 \mu_r A}$,
* The reluctances of the regions in the air gaps are: $\mathcal{R}_\text{GAP} = \frac{l}{\mu_0 A }$.
The areas can be calculated as:
```
A1 = 0.09 * 0.05 # [m²]
A2 = 0.15 * 0.05 # [m²]
A3 = 0.15 * 0.05 * 1.05 # [m²] 5% fringing
A4 = 0.09 * 0.05 # [m²]
```
And the reluctances are hence:
```
R1 = l1 / (mu * A1) # At /Wb = At/Vs
R2 = l2 / (mu * A2) # At /Wb = At/Vs
R3 = l3 / (c.mu_0 * A3) # At /Wb = At/Vs
R4 = l4 / (mu * A4) # At /Wb = At/Vs
print('R1 = {:.1f} kAt/Wb'.format(R1/1000) )
print('R2 = {:.1f} kAt/Wb'.format(R2/1000) )
print('R3 = {:.1f} kAt/Wb'.format(R3/1000) )
print('R4 = {:.1f} kAt/Wb'.format(R4/1000) )
```
Then the total reluctance of the core is $\mathcal{R}_\text{TOT} = \mathcal{R}_1 + \frac{(\mathcal{R}_2 + \mathcal{R}_3)\mathcal{R}_4}{\mathcal{R}_2 + \mathcal{R}_3 + \mathcal{R}_4}$.
```
Rtot = R1 + ((R2 + R3) * R4) / (R2 + R3 + R4)
print('Rtot = {:.1f} kAt/Wb'.format(Rtot/1000))
```
and the magnetomotive force is $\mathcal{F} = \mathcal{N} \mathcal{I}$:
```
N = 100 # t given in description
I = 2.0 # A given in description
F = N * I
```
**The total flux in the core $\phi_\text{TOT}$ is equal to the flux in the left leg $\phi_\text{left} = \frac{\mathcal{F}}{\mathcal{R}_\text{TOT}}$ , which is:**
```
phi_left = F / Rtot
print('phi_left = {:.3f} mWb'.format(phi_left*1000))
```
The fluxes in the center and right legs can be found by the "flux divider rule", which is analogous to the current divider rule.
**Thus the flux in the left leg $\phi_\text{center} = \frac{ \mathcal{R}_4}{\mathcal{R}_2 + \mathcal{R}_3 + \mathcal{R}_4}\phi_\text{TOT}$ is:**
```
phi_center = R4 / (R2 + R3 + R4) * phi_left
print('phi_center = {:.3f} mWb'.format(phi_center*1000))
```
**The flux in the right leg $\phi_\text{right} = \frac{\mathcal{R}_2 + \mathcal{R}_3}{\mathcal{R}_2 + \mathcal{R}_3 + \mathcal{R}_4}\phi_\text{TOT}$ is:**
```
phi_right = (R2 + R3) / (R2 + R3 + R4) * phi_left
print('phi_right = {:.3f} mWb'.format(phi_right*1000))
```
**The flux densities $B = \frac{\phi}{A}$ are:**
```
B_left = phi_left / A1
B_center = phi_center / A2
B_right = phi_right / A4
print('B_left = {:.3f} T'.format(B_left))
print('B_center = {:.3f} T'.format(B_center))
print('B_right = {:.3f} T'.format(B_right))
```
|
github_jupyter
|
%pylab inline
%precision 4
from scipy import constants as c # we like to use some constants
mu_r = 2000
mu = mu_r * c.mu_0
l1 = 1.08 # [m]
l2 = 0.34 # [m]
l3 = 0.0005 # [m]
l4 = 1.08 # [m]
A1 = 0.09 * 0.05 # [m²]
A2 = 0.15 * 0.05 # [m²]
A3 = 0.15 * 0.05 * 1.05 # [m²] 5% fringing
A4 = 0.09 * 0.05 # [m²]
R1 = l1 / (mu * A1) # At /Wb = At/Vs
R2 = l2 / (mu * A2) # At /Wb = At/Vs
R3 = l3 / (c.mu_0 * A3) # At /Wb = At/Vs
R4 = l4 / (mu * A4) # At /Wb = At/Vs
print('R1 = {:.1f} kAt/Wb'.format(R1/1000) )
print('R2 = {:.1f} kAt/Wb'.format(R2/1000) )
print('R3 = {:.1f} kAt/Wb'.format(R3/1000) )
print('R4 = {:.1f} kAt/Wb'.format(R4/1000) )
Rtot = R1 + ((R2 + R3) * R4) / (R2 + R3 + R4)
print('Rtot = {:.1f} kAt/Wb'.format(Rtot/1000))
N = 100 # t given in description
I = 2.0 # A given in description
F = N * I
phi_left = F / Rtot
print('phi_left = {:.3f} mWb'.format(phi_left*1000))
phi_center = R4 / (R2 + R3 + R4) * phi_left
print('phi_center = {:.3f} mWb'.format(phi_center*1000))
phi_right = (R2 + R3) / (R2 + R3 + R4) * phi_left
print('phi_right = {:.3f} mWb'.format(phi_right*1000))
B_left = phi_left / A1
B_center = phi_center / A2
B_right = phi_right / A4
print('B_left = {:.3f} T'.format(B_left))
print('B_center = {:.3f} T'.format(B_center))
print('B_right = {:.3f} T'.format(B_right))
| 0.432543 | 0.989741 |
### Example 1. Element-wise arithmetic operations on 1-D arrays
```
import numpy as np
# We create two rank 1 ndarrays
x = np.array([1,2,3,4])
y = np.array([5.5,6.5,7.5,8.5])
# We print x
print()
print('x = ', x)
# We print y
print()
print('y = ', y)
print()
# We perfrom basic element-wise operations using arithmetic symbols and functions
print('x + y = ', x + y)
print('add(x,y) = ', np.add(x,y))
print()
print('x - y = ', x - y)
print('subtract(x,y) = ', np.subtract(x,y))
print()
print('x * y = ', x * y)
print('multiply(x,y) = ', np.multiply(x,y))
print()
print('x / y = ', x / y)
print('divide(x,y) = ', np.divide(x,y))
```
### Example 2. Element-wise arithmetic operations on a 2-D array (Same shape)
```
# We create two rank 2 ndarrays
X = np.array([1,2,3,4]).reshape(2,2)
Y = np.array([5.5,6.5,7.5,8.5]).reshape(2,2)
# We print X
print()
print('X = \n', X)
# We print Y
print()
print('Y = \n', Y)
print()
# We perform basic element-wise operations using arithmetic symbols and functions
print('X + Y = \n', X + Y)
print()
print('add(X,Y) = \n', np.add(X,Y))
print()
print('X - Y = \n', X - Y)
print()
print('subtract(X,Y) = \n', np.subtract(X,Y))
print()
print('X * Y = \n', X * Y)
print()
print('multiply(X,Y) = \n', np.multiply(X,Y))
print()
print('X / Y = \n', X / Y)
print()
print('divide(X,Y) = \n', np.divide(X,Y))
```
### Example 3. Additional mathematical functions
```
# We create a rank 1 ndarray
x = np.array([1,2,3,4])
# We print x
print()
print('x = ', x)
# We apply different mathematical functions to all elements of x
print()
print('EXP(x) =', np.exp(x))
print()
print('SQRT(x) =',np.sqrt(x))
print()
print('POW(x,2) =',np.power(x,2)) # We raise all elements to the power of 2
```
### Example 4. Statistical functions
```
# We create a 2 x 2 ndarray
X = np.array([[1,2], [3,4]])
# We print x
print()
print('X = \n', X)
print()
print('Average of all elements in X:', X.mean())
print('Average of all elements in the columns of X:', X.mean(axis=0))
print('Average of all elements in the rows of X:', X.mean(axis=1))
print()
print('Sum of all elements in X:', X.sum())
print('Sum of all elements in the columns of X:', X.sum(axis=0))
print('Sum of all elements in the rows of X:', X.sum(axis=1))
print()
print('Standard Deviation of all elements in X:', X.std())
print('Standard Deviation of all elements in the columns of X:', X.std(axis=0))
print('Standard Deviation of all elements in the rows of X:', X.std(axis=1))
print()
print('Median of all elements in X:', np.median(X))
print('Median of all elements in the columns of X:', np.median(X,axis=0))
print('Median of all elements in the rows of X:', np.median(X,axis=1))
print()
print('Maximum value of all elements in X:', X.max())
print('Maximum value of all elements in the columns of X:', X.max(axis=0))
print('Maximum value of all elements in the rows of X:', X.max(axis=1))
print()
print('Minimum value of all elements in X:', X.min())
print('Minimum value of all elements in the columns of X:', X.min(axis=0))
print('Minimum value of all elements in the rows of X:', X.min(axis=1))
```
### Example 5. Change value of all elements of an array
```
# We create a 2 x 2 ndarray
X = np.array([[1,2], [3,4]])
# We print x
print()
print('X = \n', X)
print()
print('3 * X = \n', 3 * X)
print()
print('3 + X = \n', 3 + X)
print()
print('X - 3 = \n', X - 3)
print()
print('X / 3 = \n', X / 3)
```
### Example 6. Arithmetic operations on a 2-D arrays (Compatible shape)
```
# We create a rank 1 ndarray
x = np.array([1,2,3])
# We create a 3 x 3 ndarray
Y = np.array([[1,2,3],[4,5,6],[7,8,9]])
# We create a 3 x 1 ndarray
Z = np.array([1,2,3]).reshape(3,1)
# We print x
print()
print('x = ', x)
print()
# We print Y
print()
print('Y = \n', Y)
print()
# We print Z
print()
print('Z = \n', Z)
print()
print('x + Y = \n', x + Y)
print()
print('Z + Y = \n',Z + Y)
```
|
github_jupyter
|
import numpy as np
# We create two rank 1 ndarrays
x = np.array([1,2,3,4])
y = np.array([5.5,6.5,7.5,8.5])
# We print x
print()
print('x = ', x)
# We print y
print()
print('y = ', y)
print()
# We perfrom basic element-wise operations using arithmetic symbols and functions
print('x + y = ', x + y)
print('add(x,y) = ', np.add(x,y))
print()
print('x - y = ', x - y)
print('subtract(x,y) = ', np.subtract(x,y))
print()
print('x * y = ', x * y)
print('multiply(x,y) = ', np.multiply(x,y))
print()
print('x / y = ', x / y)
print('divide(x,y) = ', np.divide(x,y))
# We create two rank 2 ndarrays
X = np.array([1,2,3,4]).reshape(2,2)
Y = np.array([5.5,6.5,7.5,8.5]).reshape(2,2)
# We print X
print()
print('X = \n', X)
# We print Y
print()
print('Y = \n', Y)
print()
# We perform basic element-wise operations using arithmetic symbols and functions
print('X + Y = \n', X + Y)
print()
print('add(X,Y) = \n', np.add(X,Y))
print()
print('X - Y = \n', X - Y)
print()
print('subtract(X,Y) = \n', np.subtract(X,Y))
print()
print('X * Y = \n', X * Y)
print()
print('multiply(X,Y) = \n', np.multiply(X,Y))
print()
print('X / Y = \n', X / Y)
print()
print('divide(X,Y) = \n', np.divide(X,Y))
# We create a rank 1 ndarray
x = np.array([1,2,3,4])
# We print x
print()
print('x = ', x)
# We apply different mathematical functions to all elements of x
print()
print('EXP(x) =', np.exp(x))
print()
print('SQRT(x) =',np.sqrt(x))
print()
print('POW(x,2) =',np.power(x,2)) # We raise all elements to the power of 2
# We create a 2 x 2 ndarray
X = np.array([[1,2], [3,4]])
# We print x
print()
print('X = \n', X)
print()
print('Average of all elements in X:', X.mean())
print('Average of all elements in the columns of X:', X.mean(axis=0))
print('Average of all elements in the rows of X:', X.mean(axis=1))
print()
print('Sum of all elements in X:', X.sum())
print('Sum of all elements in the columns of X:', X.sum(axis=0))
print('Sum of all elements in the rows of X:', X.sum(axis=1))
print()
print('Standard Deviation of all elements in X:', X.std())
print('Standard Deviation of all elements in the columns of X:', X.std(axis=0))
print('Standard Deviation of all elements in the rows of X:', X.std(axis=1))
print()
print('Median of all elements in X:', np.median(X))
print('Median of all elements in the columns of X:', np.median(X,axis=0))
print('Median of all elements in the rows of X:', np.median(X,axis=1))
print()
print('Maximum value of all elements in X:', X.max())
print('Maximum value of all elements in the columns of X:', X.max(axis=0))
print('Maximum value of all elements in the rows of X:', X.max(axis=1))
print()
print('Minimum value of all elements in X:', X.min())
print('Minimum value of all elements in the columns of X:', X.min(axis=0))
print('Minimum value of all elements in the rows of X:', X.min(axis=1))
# We create a 2 x 2 ndarray
X = np.array([[1,2], [3,4]])
# We print x
print()
print('X = \n', X)
print()
print('3 * X = \n', 3 * X)
print()
print('3 + X = \n', 3 + X)
print()
print('X - 3 = \n', X - 3)
print()
print('X / 3 = \n', X / 3)
# We create a rank 1 ndarray
x = np.array([1,2,3])
# We create a 3 x 3 ndarray
Y = np.array([[1,2,3],[4,5,6],[7,8,9]])
# We create a 3 x 1 ndarray
Z = np.array([1,2,3]).reshape(3,1)
# We print x
print()
print('x = ', x)
print()
# We print Y
print()
print('Y = \n', Y)
print()
# We print Z
print()
print('Z = \n', Z)
print()
print('x + Y = \n', x + Y)
print()
print('Z + Y = \n',Z + Y)
| 0.321141 | 0.911613 |
# 融合各个模型结果
```
import os
import random
import time
import copy
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from tqdm import tqdm
tqdm.pandas()
import matplotlib.pyplot as plt
from sklearn.model_selection import KFold,StratifiedKFold
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.utils.rnn import pack_padded_sequence, pack_sequence, pad_packed_sequence, pad_sequence
from torch.utils.data import DataLoader, Dataset, SequentialSampler
DEVICE = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
%load_ext autoreload
%autoreload 2
torch.__version__
# set random seeds to keep the results identical
def setup_seed(seed):
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
np.random.seed(seed)
random.seed(seed)
torch.backends.cudnn.deterministic = True
GLOBAL_SEED = 2020
setup_seed(GLOBAL_SEED)
data_path = './processed_data/'
res_path = './result/'
save_path = './processed_result'
if not os.path.exists(save_path):
os.makedirs(save_path)
```
## 读取数据
```
df = pd.read_pickle(os.path.join(data_path, 'processed_data_numerical.pkl'))
df['age'] = df['age'] - 1
df['gender'] = df['gender'] - 1
os.listdir(res_path)
def load_res(name):
res = np.load(os.path.join(res_path, name))
X_train = res[:3000000, :12]
y_train = res[:3000000, 12:]
X_test = res[3000000:, :12]
return X_train, y_train, X_test
X_train_list = []
y_train_list = []
X_test_list = []
select_res = [
'lstm_v10_300size_win30_10folds_1.4648.npy',
'lstm_v11_128_128_10folds_1.4646.npy',
'lstm_v6_300size_win20_5folds_1.4642.npy',
'lstm_v7_300size_win30_5folds_1.4642.npy',
'lstm_v8_300size_win40_5folds_1.4638.npy',
'lstm_v9_300size_win50_5folds_1.4642.npy',
'lstm_v1_300size_win10_5folds_1.4634.npy',
'lstm_v2_300size_win10_dropout_5folds_1.4644.npy',
'lstm_v3_300size_win100_5folds_1.4624.npy',
'lstm_v4_128_128_5folds_1.4629.npy',
'lstm_v5_512size_win10_5folds_1.4624.npy',
'attention_lstm_v1_128_128_5folds_1.4613.npy']
for name in select_res:
X_train, y_train, X_test = load_res(name)
X_train_list.append(X_train)
y_train_list.append(y_train)
X_test_list.append(X_test)
X_train = np.stack(X_train_list)
y_train = y_train_list[0]
X_test = np.stack(X_test_list)
y_pred_age = X_test.mean(axis=0)[:, :10].argmax(axis=1)
y_pred_gender = X_test.mean(axis=0)[:, 10:].argmax(axis=1)
df_submit = df.iloc[3000000:, -2:].rename({'age': 'predicted_age', 'gender':'predicted_gender'}, axis=1)
df_submit['predicted_age'] = y_pred_age + 1
df_submit['predicted_gender'] = y_pred_gender + 1
df_submit.to_csv(os.path.join(res_path, "submission.csv"))
df_submit
```
|
github_jupyter
|
import os
import random
import time
import copy
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from tqdm import tqdm
tqdm.pandas()
import matplotlib.pyplot as plt
from sklearn.model_selection import KFold,StratifiedKFold
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.utils.rnn import pack_padded_sequence, pack_sequence, pad_packed_sequence, pad_sequence
from torch.utils.data import DataLoader, Dataset, SequentialSampler
DEVICE = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
%load_ext autoreload
%autoreload 2
torch.__version__
# set random seeds to keep the results identical
def setup_seed(seed):
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
np.random.seed(seed)
random.seed(seed)
torch.backends.cudnn.deterministic = True
GLOBAL_SEED = 2020
setup_seed(GLOBAL_SEED)
data_path = './processed_data/'
res_path = './result/'
save_path = './processed_result'
if not os.path.exists(save_path):
os.makedirs(save_path)
df = pd.read_pickle(os.path.join(data_path, 'processed_data_numerical.pkl'))
df['age'] = df['age'] - 1
df['gender'] = df['gender'] - 1
os.listdir(res_path)
def load_res(name):
res = np.load(os.path.join(res_path, name))
X_train = res[:3000000, :12]
y_train = res[:3000000, 12:]
X_test = res[3000000:, :12]
return X_train, y_train, X_test
X_train_list = []
y_train_list = []
X_test_list = []
select_res = [
'lstm_v10_300size_win30_10folds_1.4648.npy',
'lstm_v11_128_128_10folds_1.4646.npy',
'lstm_v6_300size_win20_5folds_1.4642.npy',
'lstm_v7_300size_win30_5folds_1.4642.npy',
'lstm_v8_300size_win40_5folds_1.4638.npy',
'lstm_v9_300size_win50_5folds_1.4642.npy',
'lstm_v1_300size_win10_5folds_1.4634.npy',
'lstm_v2_300size_win10_dropout_5folds_1.4644.npy',
'lstm_v3_300size_win100_5folds_1.4624.npy',
'lstm_v4_128_128_5folds_1.4629.npy',
'lstm_v5_512size_win10_5folds_1.4624.npy',
'attention_lstm_v1_128_128_5folds_1.4613.npy']
for name in select_res:
X_train, y_train, X_test = load_res(name)
X_train_list.append(X_train)
y_train_list.append(y_train)
X_test_list.append(X_test)
X_train = np.stack(X_train_list)
y_train = y_train_list[0]
X_test = np.stack(X_test_list)
y_pred_age = X_test.mean(axis=0)[:, :10].argmax(axis=1)
y_pred_gender = X_test.mean(axis=0)[:, 10:].argmax(axis=1)
df_submit = df.iloc[3000000:, -2:].rename({'age': 'predicted_age', 'gender':'predicted_gender'}, axis=1)
df_submit['predicted_age'] = y_pred_age + 1
df_submit['predicted_gender'] = y_pred_gender + 1
df_submit.to_csv(os.path.join(res_path, "submission.csv"))
df_submit
| 0.521471 | 0.562777 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split, KFold, StratifiedShuffleSplit
from sklearn.preprocessing import KBinsDiscretizer, RobustScaler, LabelEncoder
from sklearn.metrics import roc_auc_score, roc_curve
from xgboost import XGBClassifier
from catboost import CatBoostClassifier
from lightgbm import LGBMClassifier
from tqdm.notebook import tqdm ,tnrange
train = pd.read_csv("data/train.csv")
test = pd.read_csv("data/test.csv")
# Python Method 1 : Displays Data Information :
# Need to convert float64 to int for Catboost Classifier
def display_data_information(data, data_types, dataframe_name):
print(" Information of ",dataframe_name,": Rows = ",data.shape[0],"| Columns = ",data.shape[1],"\n")
data.info()
print("\n")
for VARIABLE in data_types :
data_type = data.select_dtypes(include=[ VARIABLE ]).dtypes
if len(data_type) > 0 :
print(str(len(data_type))+" "+VARIABLE+" Features\n"+str(data_type)+"\n" )
# Display Data Information of "train" :
data_types = ["float32","float64","int32","int64","object","category","datetime64[ns]"]
display_data_information(train, data_types, "train")
display_data_information(test, data_types, "test")
def display_head_tail(data, head_rows, tail_rows):
display("Data Head & Tail :")
display(data.head(head_rows).append(data.tail(tail_rows)))
display_head_tail(train, 5, 5)
display_head_tail(test, 5, 5)
# Python Method 3 : Displays Data Description using Statistics :
def display_data_description(data, numeric_data_types, categorical_data_types):
print("Data Description :")
display(data.describe( include = numeric_data_types))
print("")
display(data.describe( include = categorical_data_types))
# Display Data Description of "train" :
data_types = ["float32","float64","int32","int64","object","category","datetime64[ns]"]
display_data_description(train, data_types[0:4], data_types[4:7])
# Python Method 4 : Removes Data Duplicates while Retaining the First one - Similar to SQL DISTINCT :
def remove_duplicate(data):
print("BEFORE REMOVING DUPLICATES - No. of Rows = ",data.shape[0])
data.drop_duplicates(keep="first", inplace=True)
print("AFTER REMOVING DUPLICATES - No. of Rows = ",data.shape[0])
return data
remove_duplicate(train)
# Python Method 5 : Fills or Imputes Missing values with Various Methods :
def fill_missing_values(data, fill_value, fill_types, columns, dataframe_name):
print("Missing Values BEFORE REMOVAL in ",dataframe_name," data")
display(data.isnull().sum())
for column in columns :
# Fill Missing Values with Specific Value :
if "Value_Fill" in fill_types :
data[ column ] = data[ column ].fillna(fill_value)
# print("Value_Fill")
# Fill Missing Values with Forward Fill (Previous Row Value as Current Row in Table) :
if "Forward_Fill" in fill_types :
data[ column ] = data[ column ].ffill(axis = 0)
# print("Forward_Fill")
# Fill Missing Values with Backward Fill (Next Row Value as Current Row in Table) :
if "Backward_Fill" in fill_types :
data[ column ] = data[ column ].bfill(axis = 0)
# print("Backward_Fill")
print("Missing Values AFTER REMOVAL in ",dataframe_name," data")
display(data.isnull().sum())
return data
fill_types = [ "Forward_Fill"]
fill_value = 0
# Fills or Imputes Missing values in "Registration_Date" Column with "Forward_Fill" Method in "train" :
train = fill_missing_values(train, fill_value, fill_types, ["Gender"],"train")
# Fills or Imputes Missing values in "Registration_Date" Column with "Forward_Fill" Method in "train" :
test = fill_missing_values(test, fill_value, fill_types, ["Gender"],"test")
# No Missing Values !!!
# Python Method 6 : Displays Unique Values in Each Column of the Dataframe(Table) :
def display_unique(data):
for column in data.columns :
print("No of Unique Values in "+column+" Column are : "+str(data[column].nunique()))
# print("Actual Unique Values in "+column+" Column are : "+str(data[column].sort_values(ascending=True,na_position='last').unique() ))
# print("NULL Values :")
# print(data[ column ].isnull().sum())
print("Value Counts :")
print(data[column].value_counts())
print("")
# Displays Unique Values in Each Column of "train" :
# Check "train" data for Values of each Column - Long Form :
display_unique(train)
for i in train:
print(f"column {i} unique values {train[i].unique()}")
train['source'] = 'train'
test['source'] = 'test'
data = pd.concat([train, test])
vehicle_age = {'< 1 Year':0, '1-2 Year':1, '> 2 Years':2}
data['Vehicle_Age'] = data['Vehicle_Age'].map(vehicle_age)
gender = {'Male':1, 'Female':0}
data['Gender'] = data['Gender'].map(gender)
vehicle_damage = {'Yes':1, 'No':0}
data['Vehicle_Damage'] = data['Vehicle_Damage'].map(vehicle_damage)
data
# New Aggregated Features
data['Vehicle_Age_Region_per_Damage'] = data.groupby(['Region_Code', 'Vehicle_Age'])['Vehicle_Damage'].transform('sum')
data['Term'] = data['Vintage']/365
data['Vehicle_Region_Policy_Damage'] = data.groupby(['Region_Code', 'Policy_Sales_Channel'])['Vehicle_Damage'].transform('sum')
data.loc[(data['Vehicle_Age'] == 2) & (data['Vehicle_Damage'] == 1), 'Old_Vehicle'] = 1
data.loc[(data['Vehicle_Age'] != 2) & (data['Vehicle_Damage'] == 0), 'Old_Vehicle'] = 0
data['Annual_Premium'] = np.log(data['Annual_Premium'])
data
final_train = data.loc[data['source'] == 'train']
final_test = data.loc[data['source'] == 'test']
y = final_train['Response']
X = final_train.drop(columns=['id', 'Response', 'source'])
id_test = final_test['id']
final_test = final_test.drop(columns=['id', 'Response', 'source'])
final_test
def feature_importance(model, X_train):
fI = model.feature_importances_
print(fI)
names = X_train.columns.values
ticks = [i for i in range(len(names))]
plt.bar(ticks, fI)
plt.xticks(ticks, names,rotation = 90)
plt.show()
# XGBoost Classifier
probs = np.zeros(shape=(len(final_test)))
scores = []
avg_loss = []
X_train, y_train = X, y
seeds = [1]
for seed in tnrange(len(seeds)):
print(' ')
print('#'*100)
print('Seed', seeds[seed])
sf = StratifiedShuffleSplit(n_splits=4, test_size=0.3, random_state=seed)
for i, (idxT, idxV) in enumerate(sf.split(X_train, y_train)):
print('Fold', i)
print('Rows of Train= ', len(idxT), 'Rows of Holdout = ', len(idxV))
clf = XGBClassifier(n_estimators=1000,
max_depth=6,
learning_rate=0.05,
subsample=0.9,
colsample_bytree=0.35,
objective='binary:logistic',
random_state=1)
preds = clf.fit(X_train.iloc[idxT], y_train.iloc[idxT],
eval_set=[(X_train.iloc[idxV], y_train.iloc[idxV])],
verbose=100, eval_metric=['auc', 'logloss'],
early_stopping_rounds=40)
probs_oof = clf.predict_proba(X_train.iloc[idxV])[:,1]
probs += clf.predict_proba(final_test)[:,1]
roc = roc_auc_score(y_train.iloc[idxV], probs_oof)
scores.append(roc)
avg_loss.append(clf.best_score)
print("ROC_AUC= ", roc)
print('#'*100)
if i==0:
feature_importance(clf,X_train)
print("Loss= {0:0.5f}, {1:0.5f}".format(np.array(avg_loss).mean(), np.array(avg_loss).std()))
print('%.6f (%.6f)' % (np.array(scores).mean(), np.array(scores).std()))
sample = pd.read_csv("data/sample.csv")
sample['Response'] = probs/4
sample.to_csv('submission.csv',index =False)
import joblib
xgb_model = open("xgb_model.pkl", "wb")
joblib.dump(clf, xgb_model)
xgb_model.close()
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split, KFold, StratifiedShuffleSplit
from sklearn.preprocessing import KBinsDiscretizer, RobustScaler, LabelEncoder
from sklearn.metrics import roc_auc_score, roc_curve
from xgboost import XGBClassifier
from catboost import CatBoostClassifier
from lightgbm import LGBMClassifier
from tqdm.notebook import tqdm ,tnrange
train = pd.read_csv("data/train.csv")
test = pd.read_csv("data/test.csv")
# Python Method 1 : Displays Data Information :
# Need to convert float64 to int for Catboost Classifier
def display_data_information(data, data_types, dataframe_name):
print(" Information of ",dataframe_name,": Rows = ",data.shape[0],"| Columns = ",data.shape[1],"\n")
data.info()
print("\n")
for VARIABLE in data_types :
data_type = data.select_dtypes(include=[ VARIABLE ]).dtypes
if len(data_type) > 0 :
print(str(len(data_type))+" "+VARIABLE+" Features\n"+str(data_type)+"\n" )
# Display Data Information of "train" :
data_types = ["float32","float64","int32","int64","object","category","datetime64[ns]"]
display_data_information(train, data_types, "train")
display_data_information(test, data_types, "test")
def display_head_tail(data, head_rows, tail_rows):
display("Data Head & Tail :")
display(data.head(head_rows).append(data.tail(tail_rows)))
display_head_tail(train, 5, 5)
display_head_tail(test, 5, 5)
# Python Method 3 : Displays Data Description using Statistics :
def display_data_description(data, numeric_data_types, categorical_data_types):
print("Data Description :")
display(data.describe( include = numeric_data_types))
print("")
display(data.describe( include = categorical_data_types))
# Display Data Description of "train" :
data_types = ["float32","float64","int32","int64","object","category","datetime64[ns]"]
display_data_description(train, data_types[0:4], data_types[4:7])
# Python Method 4 : Removes Data Duplicates while Retaining the First one - Similar to SQL DISTINCT :
def remove_duplicate(data):
print("BEFORE REMOVING DUPLICATES - No. of Rows = ",data.shape[0])
data.drop_duplicates(keep="first", inplace=True)
print("AFTER REMOVING DUPLICATES - No. of Rows = ",data.shape[0])
return data
remove_duplicate(train)
# Python Method 5 : Fills or Imputes Missing values with Various Methods :
def fill_missing_values(data, fill_value, fill_types, columns, dataframe_name):
print("Missing Values BEFORE REMOVAL in ",dataframe_name," data")
display(data.isnull().sum())
for column in columns :
# Fill Missing Values with Specific Value :
if "Value_Fill" in fill_types :
data[ column ] = data[ column ].fillna(fill_value)
# print("Value_Fill")
# Fill Missing Values with Forward Fill (Previous Row Value as Current Row in Table) :
if "Forward_Fill" in fill_types :
data[ column ] = data[ column ].ffill(axis = 0)
# print("Forward_Fill")
# Fill Missing Values with Backward Fill (Next Row Value as Current Row in Table) :
if "Backward_Fill" in fill_types :
data[ column ] = data[ column ].bfill(axis = 0)
# print("Backward_Fill")
print("Missing Values AFTER REMOVAL in ",dataframe_name," data")
display(data.isnull().sum())
return data
fill_types = [ "Forward_Fill"]
fill_value = 0
# Fills or Imputes Missing values in "Registration_Date" Column with "Forward_Fill" Method in "train" :
train = fill_missing_values(train, fill_value, fill_types, ["Gender"],"train")
# Fills or Imputes Missing values in "Registration_Date" Column with "Forward_Fill" Method in "train" :
test = fill_missing_values(test, fill_value, fill_types, ["Gender"],"test")
# No Missing Values !!!
# Python Method 6 : Displays Unique Values in Each Column of the Dataframe(Table) :
def display_unique(data):
for column in data.columns :
print("No of Unique Values in "+column+" Column are : "+str(data[column].nunique()))
# print("Actual Unique Values in "+column+" Column are : "+str(data[column].sort_values(ascending=True,na_position='last').unique() ))
# print("NULL Values :")
# print(data[ column ].isnull().sum())
print("Value Counts :")
print(data[column].value_counts())
print("")
# Displays Unique Values in Each Column of "train" :
# Check "train" data for Values of each Column - Long Form :
display_unique(train)
for i in train:
print(f"column {i} unique values {train[i].unique()}")
train['source'] = 'train'
test['source'] = 'test'
data = pd.concat([train, test])
vehicle_age = {'< 1 Year':0, '1-2 Year':1, '> 2 Years':2}
data['Vehicle_Age'] = data['Vehicle_Age'].map(vehicle_age)
gender = {'Male':1, 'Female':0}
data['Gender'] = data['Gender'].map(gender)
vehicle_damage = {'Yes':1, 'No':0}
data['Vehicle_Damage'] = data['Vehicle_Damage'].map(vehicle_damage)
data
# New Aggregated Features
data['Vehicle_Age_Region_per_Damage'] = data.groupby(['Region_Code', 'Vehicle_Age'])['Vehicle_Damage'].transform('sum')
data['Term'] = data['Vintage']/365
data['Vehicle_Region_Policy_Damage'] = data.groupby(['Region_Code', 'Policy_Sales_Channel'])['Vehicle_Damage'].transform('sum')
data.loc[(data['Vehicle_Age'] == 2) & (data['Vehicle_Damage'] == 1), 'Old_Vehicle'] = 1
data.loc[(data['Vehicle_Age'] != 2) & (data['Vehicle_Damage'] == 0), 'Old_Vehicle'] = 0
data['Annual_Premium'] = np.log(data['Annual_Premium'])
data
final_train = data.loc[data['source'] == 'train']
final_test = data.loc[data['source'] == 'test']
y = final_train['Response']
X = final_train.drop(columns=['id', 'Response', 'source'])
id_test = final_test['id']
final_test = final_test.drop(columns=['id', 'Response', 'source'])
final_test
def feature_importance(model, X_train):
fI = model.feature_importances_
print(fI)
names = X_train.columns.values
ticks = [i for i in range(len(names))]
plt.bar(ticks, fI)
plt.xticks(ticks, names,rotation = 90)
plt.show()
# XGBoost Classifier
probs = np.zeros(shape=(len(final_test)))
scores = []
avg_loss = []
X_train, y_train = X, y
seeds = [1]
for seed in tnrange(len(seeds)):
print(' ')
print('#'*100)
print('Seed', seeds[seed])
sf = StratifiedShuffleSplit(n_splits=4, test_size=0.3, random_state=seed)
for i, (idxT, idxV) in enumerate(sf.split(X_train, y_train)):
print('Fold', i)
print('Rows of Train= ', len(idxT), 'Rows of Holdout = ', len(idxV))
clf = XGBClassifier(n_estimators=1000,
max_depth=6,
learning_rate=0.05,
subsample=0.9,
colsample_bytree=0.35,
objective='binary:logistic',
random_state=1)
preds = clf.fit(X_train.iloc[idxT], y_train.iloc[idxT],
eval_set=[(X_train.iloc[idxV], y_train.iloc[idxV])],
verbose=100, eval_metric=['auc', 'logloss'],
early_stopping_rounds=40)
probs_oof = clf.predict_proba(X_train.iloc[idxV])[:,1]
probs += clf.predict_proba(final_test)[:,1]
roc = roc_auc_score(y_train.iloc[idxV], probs_oof)
scores.append(roc)
avg_loss.append(clf.best_score)
print("ROC_AUC= ", roc)
print('#'*100)
if i==0:
feature_importance(clf,X_train)
print("Loss= {0:0.5f}, {1:0.5f}".format(np.array(avg_loss).mean(), np.array(avg_loss).std()))
print('%.6f (%.6f)' % (np.array(scores).mean(), np.array(scores).std()))
sample = pd.read_csv("data/sample.csv")
sample['Response'] = probs/4
sample.to_csv('submission.csv',index =False)
import joblib
xgb_model = open("xgb_model.pkl", "wb")
joblib.dump(clf, xgb_model)
xgb_model.close()
| 0.365343 | 0.410461 |
```
%load_ext autoreload
%autoreload 2
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%env CUDA_VISIBLE_DEVICES=3
from avgn.utils.paths import DATA_DIR, most_recent_subdirectory, ensure_dir
from avgn.tensorflow.data import _parse_function
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tqdm.autonotebook import tqdm
%matplotlib inline
from IPython import display
import pandas as pd
# the nightly build of tensorflow_probability is required as of the time of writing this
import tensorflow_probability as tfp
ds = tfp.distributions
print(tf.__version__, tfp.__version__)
TRAIN_SIZE=101726
BATCH_SIZE=128
TEST_SIZE=10000
DIMS = (128, 128, 1)
N_TRAIN_BATCHES =int((TRAIN_SIZE-TEST_SIZE)/BATCH_SIZE)
N_TEST_BATCHES = int(TEST_SIZE/BATCH_SIZE)
TRAIN_BUF = 1000
TEST_BUF = 1000
record_loc = DATA_DIR / 'tfrecords' / "starling.tfrecords"
# read the dataset
raw_dataset = tf.data.TFRecordDataset([record_loc.as_posix()])
data_types = {
"spectrogram": tf.uint8,
"index": tf.int64,
"indv": tf.string,
}
# parse each data type to the raw dataset
dataset = raw_dataset.map(lambda x: _parse_function(x, data_types=data_types))
spec, index, indv = next(iter(dataset))
plt.matshow(spec.numpy().reshape(128,128))
test_dataset = dataset.take(TEST_SIZE).shuffle(TRAIN_BUF).batch(BATCH_SIZE)
train_dataset = dataset.skip(TEST_SIZE).take(TRAIN_SIZE-TEST_SIZE).shuffle(TEST_BUF).batch(BATCH_SIZE)
N_Z = 128
encoder = [
tf.keras.layers.InputLayer(input_shape=DIMS),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2D(
filters=128, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2D(
filters=256, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2D(
filters=256, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=N_Z*2),
]
decoder = [
tf.keras.layers.Dense(units=4 * 4 * 256, activation=tf.nn.leaky_relu),
tf.keras.layers.Reshape(target_shape=(4, 4, 256)),
tf.keras.layers.Conv2DTranspose(
filters=256, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=256, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=128, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=(1, 1), padding="SAME"
),
]
from avgn.tensorflow.VAE2 import VAE, plot_reconstruction
# the optimizer for the model
optimizer = tf.keras.optimizers.Adam(1e-4)
# train the model
model = VAE(
enc = encoder,
dec = decoder,
optimizer = optimizer,
beta = 1.0
)
# exampled data for plotting results
example_data = next(iter(test_dataset))
example_data = (
tf.cast(tf.reshape(example_data[0], [BATCH_SIZE] + list(DIMS)), tf.float32)
/ 255
)
x= example_data
x_recon = model.reconstruct(x)
np.max(x_recon)
test = x * tf.math.log(1e-5 + x_recon) + (1 - x) * tf.math.log(1e-5 + 1 - x_recon)
np.max(test)
np.max(x_recon)
model.compute_loss(example_data)
# a pandas dataframe to save the loss information to
losses = pd.DataFrame(columns = ['recon_loss', 'latent_loss'])
N_TRAIN_BATCHES = 100
N_TEST_BATCHES = 15
n_epochs = 500
epoch = 0
def plot_losses(losses):
cols = list(losses.columns)
fig, axs = plt.subplots(ncols = len(cols), figsize= (len(cols)*4, 4))
for ci, col in enumerate(cols):
if len(cols) == 1:
ax = axs
else:
ax = axs.flatten()[ci]
ax.loglog(losses[col].values)
ax.set_title(col)
plt.show()
for epoch in range(epoch, n_epochs):
# train
for batch, train_x in tqdm(
zip(range(N_TRAIN_BATCHES), train_dataset), total=N_TRAIN_BATCHES
):
x = tf.cast(tf.reshape(train_x[0], [BATCH_SIZE] + list(DIMS)), tf.float32) / 255
model.train_net(x)
# test on holdout
loss = []
for batch, test_x in tqdm(
zip(range(N_TEST_BATCHES), test_dataset), total=N_TEST_BATCHES
):
x = tf.cast(tf.reshape(test_x[0], [BATCH_SIZE] + list(DIMS)), tf.float32) / 255
loss.append(model.compute_loss(x))
losses.loc[len(losses)] = np.mean(loss, axis=0)
# plot results
display.clear_output()
print(
"Epoch: {} | recon_loss: {} | latent_loss: {}".format(
epoch, losses.recon_loss.values[-1], losses.latent_loss.values[-1]
)
)
plot_reconstruction(model, example_data, N_Z=N_Z)
plot_losses(losses)
fig, ax = plt.subplots()
z = tf.split(model.enc(example_data), num_or_size_splits=2, axis=1)[0].numpy()
ax.hist(z.flatten(), bins = 50);
plt.show()
```
### Save model
```
DATASET_ID = 'european_starling_gentner_segmented'
network_type = 'VAE'
save_loc = DATA_DIR / 'models' / network_type / (DATASET_ID + '_128')
ensure_dir(save_loc)
# Save the entire model to a HDF5 file.
# The '.h5' extension indicates that the model shuold be saved to HDF5.
model.save_weights((save_loc / (str(epoch).zfill(4))).as_posix())
# Recreate the exact same model, including its weights and the optimizer
#new_model = tf.keras.models.load_model('my_model.h5')
```
### J Diagram
```
from avgn.visualization.projections import scatter_spec
from avgn.utils.general import save_fig
from avgn.utils.paths import FIGURE_DIR, ensure_dir
ensure_dir(FIGURE_DIR / 'networks' / 'starling128')
gen_func = model.decode
interp_len = 5
dset_iter = iter(dataset)
x1 = np.reshape(next(dset_iter)[0] / 255, (1,128,128,1))
x2 = np.reshape(next(dset_iter)[0] / 255, (1,128,128,1))
x3 = np.reshape(next(dset_iter)[0] / 255, (1,128,128,1))
exdat = np.vstack([x1, x2, x3])
fig, axs = plt.subplots(ncols=3, figsize=(15,5))
axs[0].matshow(np.squeeze(x1), origin='lower')
axs[1].matshow(np.squeeze(x2), origin='lower')
axs[2].matshow(np.squeeze(x3), origin='lower')
(pt1, pt2, pt3), _ = model.encode(exdat)
xr1, xr2, xr3 = model.decode(np.vstack([pt1, pt2, pt3]), apply_sigmoid=True)
fig, axs = plt.subplots(ncols=3, figsize=(15,5))
axs[0].matshow(np.squeeze(xr1.numpy()), origin='lower')
axs[1].matshow(np.squeeze(xr2.numpy()), origin='lower')
axs[2].matshow(np.squeeze(xr3.numpy()), origin='lower')
#pt1x,pt2x,pt3x =gen_func(tf.stack([pt1,pt2,pt3]))
#get proportions
z_list = []
for ci, C in enumerate(np.linspace(0, 1, interp_len)):
for bi, B in enumerate(np.linspace(0, 1, interp_len)):
A = 1 - C - B
z_list.append(
C * pt1 +
B * pt2 +
A * pt3
)
z_list = np.vstack(z_list)
# get X
x_list = gen_func(z_list, apply_sigmoid=True).numpy()
# make diagram
Jdiagram = np.ones((x_list.shape[1]*(interp_len), x_list.shape[2]*(interp_len+2), x_list.shape[3]))
np.shape(Jdiagram)
#populate
i = 0
for ci, C in enumerate(np.linspace(0, 1, interp_len)):
for bi, B in enumerate(np.linspace(0, 1, interp_len)):
Jdiagram[(interp_len -1 - bi)*x_list.shape[1]:((interp_len - bi))*x_list.shape[1], (ci+1)*x_list.shape[2]:(ci+2)*x_list.shape[2], :] = x_list[i]
i+=1
Jdiagram[(interp_len - 1)*x_list.shape[1]: (interp_len)*x_list.shape[1],
:x_list.shape[2], :] = x3
Jdiagram[(interp_len - 1)*x_list.shape[1]: (interp_len)*x_list.shape[1],
(interp_len +1)*x_list.shape[2]: (interp_len+2)*x_list.shape[2] , :] = x1
Jdiagram[: x_list.shape[1],
:x_list.shape[2], :] = x2
fig, ax = plt.subplots(figsize=(10,10))
ax.matshow(np.squeeze(Jdiagram), vmin = 0, cmap=plt.cm.afmhot, origin = 'lower')
ax.axis('off')
save_fig(FIGURE_DIR / 'networks' / 'starling128'/ ('VAE_JDiagram_128'), dpi=300, save_jpg=True)
#model.beta = 1
fig, ax = plt.subplots()
z = tf.split(model.enc(example_data), num_or_size_splits=2, axis=1)[0].numpy()
ax.hist(z.flatten(), bins = 50);
np.shape(z)
xmax, ymax = np.max(z[:,:2], axis=0)
xmin, ymin = np.min(z[:,:2], axis=0)
print(xmax, ymax, xmin, ymin)
plot_reconstruction(model, example_data, N_Z)
RECON = model.reconstruct(example_data)
np.max(RECON.numpy().flatten())
# sample from grid
nx = ny =10
meshgrid = np.meshgrid(np.linspace(-3, 3, nx), np.linspace(-3, 3, ny))
meshgrid = np.array(meshgrid).reshape(2, nx*ny).T
x_grid = model.decode(meshgrid)
x_grid = x_grid.numpy().reshape(nx, ny, 28,28, 1)
# fill canvas
canvas = np.zeros((nx*28, ny*28))
for xi in range(nx):
for yi in range(ny):
canvas[xi*28:xi*28+28, yi*28:yi*28+28] = x_grid[xi, yi,:,:,:].squeeze()
fig, ax = plt.subplots(figsize=(10,10))
ax.matshow(canvas, cmap=plt.cm.Greys)
ax.axis('off')
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%env CUDA_VISIBLE_DEVICES=3
from avgn.utils.paths import DATA_DIR, most_recent_subdirectory, ensure_dir
from avgn.tensorflow.data import _parse_function
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tqdm.autonotebook import tqdm
%matplotlib inline
from IPython import display
import pandas as pd
# the nightly build of tensorflow_probability is required as of the time of writing this
import tensorflow_probability as tfp
ds = tfp.distributions
print(tf.__version__, tfp.__version__)
TRAIN_SIZE=101726
BATCH_SIZE=128
TEST_SIZE=10000
DIMS = (128, 128, 1)
N_TRAIN_BATCHES =int((TRAIN_SIZE-TEST_SIZE)/BATCH_SIZE)
N_TEST_BATCHES = int(TEST_SIZE/BATCH_SIZE)
TRAIN_BUF = 1000
TEST_BUF = 1000
record_loc = DATA_DIR / 'tfrecords' / "starling.tfrecords"
# read the dataset
raw_dataset = tf.data.TFRecordDataset([record_loc.as_posix()])
data_types = {
"spectrogram": tf.uint8,
"index": tf.int64,
"indv": tf.string,
}
# parse each data type to the raw dataset
dataset = raw_dataset.map(lambda x: _parse_function(x, data_types=data_types))
spec, index, indv = next(iter(dataset))
plt.matshow(spec.numpy().reshape(128,128))
test_dataset = dataset.take(TEST_SIZE).shuffle(TRAIN_BUF).batch(BATCH_SIZE)
train_dataset = dataset.skip(TEST_SIZE).take(TRAIN_SIZE-TEST_SIZE).shuffle(TEST_BUF).batch(BATCH_SIZE)
N_Z = 128
encoder = [
tf.keras.layers.InputLayer(input_shape=DIMS),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2D(
filters=128, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2D(
filters=256, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2D(
filters=256, kernel_size=3, strides=(2, 2), activation=tf.nn.leaky_relu
),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=N_Z*2),
]
decoder = [
tf.keras.layers.Dense(units=4 * 4 * 256, activation=tf.nn.leaky_relu),
tf.keras.layers.Reshape(target_shape=(4, 4, 256)),
tf.keras.layers.Conv2DTranspose(
filters=256, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=256, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=128, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=(2, 2), padding="SAME", activation=tf.nn.leaky_relu
),
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=(1, 1), padding="SAME"
),
]
from avgn.tensorflow.VAE2 import VAE, plot_reconstruction
# the optimizer for the model
optimizer = tf.keras.optimizers.Adam(1e-4)
# train the model
model = VAE(
enc = encoder,
dec = decoder,
optimizer = optimizer,
beta = 1.0
)
# exampled data for plotting results
example_data = next(iter(test_dataset))
example_data = (
tf.cast(tf.reshape(example_data[0], [BATCH_SIZE] + list(DIMS)), tf.float32)
/ 255
)
x= example_data
x_recon = model.reconstruct(x)
np.max(x_recon)
test = x * tf.math.log(1e-5 + x_recon) + (1 - x) * tf.math.log(1e-5 + 1 - x_recon)
np.max(test)
np.max(x_recon)
model.compute_loss(example_data)
# a pandas dataframe to save the loss information to
losses = pd.DataFrame(columns = ['recon_loss', 'latent_loss'])
N_TRAIN_BATCHES = 100
N_TEST_BATCHES = 15
n_epochs = 500
epoch = 0
def plot_losses(losses):
cols = list(losses.columns)
fig, axs = plt.subplots(ncols = len(cols), figsize= (len(cols)*4, 4))
for ci, col in enumerate(cols):
if len(cols) == 1:
ax = axs
else:
ax = axs.flatten()[ci]
ax.loglog(losses[col].values)
ax.set_title(col)
plt.show()
for epoch in range(epoch, n_epochs):
# train
for batch, train_x in tqdm(
zip(range(N_TRAIN_BATCHES), train_dataset), total=N_TRAIN_BATCHES
):
x = tf.cast(tf.reshape(train_x[0], [BATCH_SIZE] + list(DIMS)), tf.float32) / 255
model.train_net(x)
# test on holdout
loss = []
for batch, test_x in tqdm(
zip(range(N_TEST_BATCHES), test_dataset), total=N_TEST_BATCHES
):
x = tf.cast(tf.reshape(test_x[0], [BATCH_SIZE] + list(DIMS)), tf.float32) / 255
loss.append(model.compute_loss(x))
losses.loc[len(losses)] = np.mean(loss, axis=0)
# plot results
display.clear_output()
print(
"Epoch: {} | recon_loss: {} | latent_loss: {}".format(
epoch, losses.recon_loss.values[-1], losses.latent_loss.values[-1]
)
)
plot_reconstruction(model, example_data, N_Z=N_Z)
plot_losses(losses)
fig, ax = plt.subplots()
z = tf.split(model.enc(example_data), num_or_size_splits=2, axis=1)[0].numpy()
ax.hist(z.flatten(), bins = 50);
plt.show()
DATASET_ID = 'european_starling_gentner_segmented'
network_type = 'VAE'
save_loc = DATA_DIR / 'models' / network_type / (DATASET_ID + '_128')
ensure_dir(save_loc)
# Save the entire model to a HDF5 file.
# The '.h5' extension indicates that the model shuold be saved to HDF5.
model.save_weights((save_loc / (str(epoch).zfill(4))).as_posix())
# Recreate the exact same model, including its weights and the optimizer
#new_model = tf.keras.models.load_model('my_model.h5')
from avgn.visualization.projections import scatter_spec
from avgn.utils.general import save_fig
from avgn.utils.paths import FIGURE_DIR, ensure_dir
ensure_dir(FIGURE_DIR / 'networks' / 'starling128')
gen_func = model.decode
interp_len = 5
dset_iter = iter(dataset)
x1 = np.reshape(next(dset_iter)[0] / 255, (1,128,128,1))
x2 = np.reshape(next(dset_iter)[0] / 255, (1,128,128,1))
x3 = np.reshape(next(dset_iter)[0] / 255, (1,128,128,1))
exdat = np.vstack([x1, x2, x3])
fig, axs = plt.subplots(ncols=3, figsize=(15,5))
axs[0].matshow(np.squeeze(x1), origin='lower')
axs[1].matshow(np.squeeze(x2), origin='lower')
axs[2].matshow(np.squeeze(x3), origin='lower')
(pt1, pt2, pt3), _ = model.encode(exdat)
xr1, xr2, xr3 = model.decode(np.vstack([pt1, pt2, pt3]), apply_sigmoid=True)
fig, axs = plt.subplots(ncols=3, figsize=(15,5))
axs[0].matshow(np.squeeze(xr1.numpy()), origin='lower')
axs[1].matshow(np.squeeze(xr2.numpy()), origin='lower')
axs[2].matshow(np.squeeze(xr3.numpy()), origin='lower')
#pt1x,pt2x,pt3x =gen_func(tf.stack([pt1,pt2,pt3]))
#get proportions
z_list = []
for ci, C in enumerate(np.linspace(0, 1, interp_len)):
for bi, B in enumerate(np.linspace(0, 1, interp_len)):
A = 1 - C - B
z_list.append(
C * pt1 +
B * pt2 +
A * pt3
)
z_list = np.vstack(z_list)
# get X
x_list = gen_func(z_list, apply_sigmoid=True).numpy()
# make diagram
Jdiagram = np.ones((x_list.shape[1]*(interp_len), x_list.shape[2]*(interp_len+2), x_list.shape[3]))
np.shape(Jdiagram)
#populate
i = 0
for ci, C in enumerate(np.linspace(0, 1, interp_len)):
for bi, B in enumerate(np.linspace(0, 1, interp_len)):
Jdiagram[(interp_len -1 - bi)*x_list.shape[1]:((interp_len - bi))*x_list.shape[1], (ci+1)*x_list.shape[2]:(ci+2)*x_list.shape[2], :] = x_list[i]
i+=1
Jdiagram[(interp_len - 1)*x_list.shape[1]: (interp_len)*x_list.shape[1],
:x_list.shape[2], :] = x3
Jdiagram[(interp_len - 1)*x_list.shape[1]: (interp_len)*x_list.shape[1],
(interp_len +1)*x_list.shape[2]: (interp_len+2)*x_list.shape[2] , :] = x1
Jdiagram[: x_list.shape[1],
:x_list.shape[2], :] = x2
fig, ax = plt.subplots(figsize=(10,10))
ax.matshow(np.squeeze(Jdiagram), vmin = 0, cmap=plt.cm.afmhot, origin = 'lower')
ax.axis('off')
save_fig(FIGURE_DIR / 'networks' / 'starling128'/ ('VAE_JDiagram_128'), dpi=300, save_jpg=True)
#model.beta = 1
fig, ax = plt.subplots()
z = tf.split(model.enc(example_data), num_or_size_splits=2, axis=1)[0].numpy()
ax.hist(z.flatten(), bins = 50);
np.shape(z)
xmax, ymax = np.max(z[:,:2], axis=0)
xmin, ymin = np.min(z[:,:2], axis=0)
print(xmax, ymax, xmin, ymin)
plot_reconstruction(model, example_data, N_Z)
RECON = model.reconstruct(example_data)
np.max(RECON.numpy().flatten())
# sample from grid
nx = ny =10
meshgrid = np.meshgrid(np.linspace(-3, 3, nx), np.linspace(-3, 3, ny))
meshgrid = np.array(meshgrid).reshape(2, nx*ny).T
x_grid = model.decode(meshgrid)
x_grid = x_grid.numpy().reshape(nx, ny, 28,28, 1)
# fill canvas
canvas = np.zeros((nx*28, ny*28))
for xi in range(nx):
for yi in range(ny):
canvas[xi*28:xi*28+28, yi*28:yi*28+28] = x_grid[xi, yi,:,:,:].squeeze()
fig, ax = plt.subplots(figsize=(10,10))
ax.matshow(canvas, cmap=plt.cm.Greys)
ax.axis('off')
| 0.724481 | 0.572065 |
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
import os
print(os.listdir("../input"))
# Any results you write to the current directory are saved as output.
```
**MNIST Digits - Classification Using SVM****
**Objective**
We will develop a model using Support Vector Machine which should correctly classify the handwritten digits from 0-9 based on the pixel values given as features. Thus, this is a 10-class classification problem.
**Data Description**
For this problem, we use the MNIST data which is a large database of handwritten digits. The 'pixel values' of each digit (image) comprise the features, and the actual number between 0-9 is the label.
Since each image is of 28 x 28 pixels, and each pixel forms a feature, there are 784 features. MNIST digit recognition is a well-studied problem in the ML community, and people have trained numerous models (Neural Networks, SVMs, boosted trees etc.) achieving error rates as low as 0.23% (i.e. accuracy = 99.77%, with a convolutional neural network).
Before the popularity of neural networks, though, models such as SVMs and boosted trees were the state-of-the-art in such problems.
We'll first explore the dataset a bit, prepare it (scale etc.) and then experiment with linear and non-linear SVMs with various hyperparameters.
We'll divide the analysis into the following parts:
**Data understanding and cleaning
Data preparation for model building
Building an SVM model - hyperparameter tuning, model evaluation etc.**
**Data Understanding**
Let's first load the data and understand the attributes meanings, shape of the dataset etc.
```
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import validation_curve
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
import matplotlib.pyplot as plt
import seaborn as sns
train_data = pd.read_csv("../input/train.csv") #reading the csv files using pandas
test_data = pd.read_csv("../input/test.csv")
train_data.shape # print the dimension or shape of train data
test_data.shape # print the dimension or shape of test data
train_data.head() # printing first five columns of train_data
```
test_data.shape # print the dimension or shape of test data
```
test_data.head() # printing first five columns of test_data
# there are no missing values in the dataset
train_data.isnull().sum().head(10)
test_data.isnull().sum().head(10)
test_data.describe()
train_data.describe()
# about the dataset
# dimensions
print("Dimensions: ",test_data.shape, "\n")
# data types
print(test_data.info())
# head
test_data.head()
# about the dataset
# dimensions
print("Dimensions: ",train_data.shape, "\n")
# data types
print(train_data.info())
# head
train_data.head()
print(train_data.columns)
print(test_data.columns)
order = list(np.sort(train_data['label'].unique()))
print(order)
## Visualizing the number of class and counts in the datasets
sns.countplot(train_data["label"])
## Visualizing the number of class and counts in the datasets
plt.plot(figure = (16,10))
g = sns.countplot( train_data["label"], palette = 'icefire')
plt.title('NUmber of digit classes')
train_data.label.astype('category').value_counts()
# Plotting some samples as well as converting into matrix
four = train_data.iloc[3, 1:]
four.shape
four = four.values.reshape(28,28)
plt.imshow(four, cmap='gray')
plt.title("Digit 4")
seven = train_data.iloc[6, 1:]
seven.shape
seven = seven.values.reshape(28, 28)
plt.imshow(seven, cmap='gray')
plt.title("Digit 7")
```
********Data Preparation**
Let's conduct some data preparation steps before modeling. Firstly, let's see if it is important to rescale the features, since they may have varying ranges.
```
# average feature values
round(train_data.drop('label', axis=1).mean(), 2)
```
In this case, the average values do not vary a lot (e.g. having a diff of an order of magnitude). Nevertheless, it is better to rescale them.
```
## Separating the X and Y variable
y = train_data['label']
## Dropping the variable 'label' from X variable
X = train_data.drop(columns = 'label')
## Printing the size of data
print(train_data.shape)
## Normalization
X = X/255.0
test_data = test_data/255.0
print("X:", X.shape)
print("test_data:", test_data.shape)
# scaling the features
from sklearn.preprocessing import scale
X_scaled = scale(X)
# train test split
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size = 0.3, train_size = 0.2 ,random_state = 10)
```
******Model Building**
Let's fist build two basic models - linear and non-linear with default hyperparameters, and compare the accuracies.
```
# linear model
model_linear = SVC(kernel='linear')
model_linear.fit(X_train, y_train)
# predict
y_pred = model_linear.predict(X_test)
# confusion matrix and accuracy
from sklearn import metrics
from sklearn.metrics import confusion_matrix
# accuracy
print("accuracy:", metrics.accuracy_score(y_true=y_test, y_pred=y_pred), "\n")
# cm
print(metrics.confusion_matrix(y_true=y_test, y_pred=y_pred))
```
The linear model gives approx. 91% accuracy. Let's look at a sufficiently non-linear model with randomly chosen hyperparameters.
```
# non-linear model
# using rbf kernel, C=1, default value of gamma
# model
non_linear_model = SVC(kernel='rbf')
# fit
non_linear_model.fit(X_train, y_train)
# predict
y_pred = non_linear_model.predict(X_test)
# confusion matrix and accuracy
# accuracy
print("accuracy:", metrics.accuracy_score(y_true=y_test, y_pred=y_pred), "\n")
# cm
print(metrics.confusion_matrix(y_true=y_test, y_pred=y_pred))
```
The non-linear model gives approx. 93% accuracy. Thus, going forward, let's choose hyperparameters corresponding to non-linear models
**Grid Search: Hyperparameter Tuning**
Let's now tune the model to find the optimal values of C and gamma corresponding to an RBF kernel. We'll use 5-fold cross validation.
```
# creating a KFold object with 5 splits
folds = KFold(n_splits = 5, shuffle = True, random_state = 10)
# specify range of hyperparameters
# Set the parameters by cross-validation
hyper_params = [ {'gamma': [1e-2, 1e-3, 1e-4],
'C': [5,10]}]
# specify model
model = SVC(kernel="rbf")
# set up GridSearchCV()
model_cv = GridSearchCV(estimator = model,
param_grid = hyper_params,
scoring= 'accuracy',
cv = folds,
verbose = 1,
return_train_score=True)
# fit the model
model_cv.fit(X_train, y_train)
# cv results
cv_results = pd.DataFrame(model_cv.cv_results_)
cv_results
# converting C to numeric type for plotting on x-axis
cv_results['param_C'] = cv_results['param_C'].astype('int')
# # plotting
plt.figure(figsize=(16,8))
# subplot 1/3
plt.subplot(131)
gamma_01 = cv_results[cv_results['param_gamma']==0.01]
plt.plot(gamma_01["param_C"], gamma_01["mean_test_score"])
plt.plot(gamma_01["param_C"], gamma_01["mean_train_score"])
plt.xlabel('C')
plt.ylabel('Accuracy')
plt.title("Gamma=0.01")
plt.ylim([0.60, 1])
plt.legend(['test accuracy', 'train accuracy'], loc='upper left')
plt.xscale('log')
# subplot 2/3
plt.subplot(132)
gamma_001 = cv_results[cv_results['param_gamma']==0.001]
plt.plot(gamma_001["param_C"], gamma_001["mean_test_score"])
plt.plot(gamma_001["param_C"], gamma_001["mean_train_score"])
plt.xlabel('C')
plt.ylabel('Accuracy')
plt.title("Gamma=0.001")
plt.ylim([0.60, 1])
plt.legend(['test accuracy', 'train accuracy'], loc='upper left')
plt.xscale('log')
# subplot 3/3
plt.subplot(133)
gamma_0001 = cv_results[cv_results['param_gamma']==0.0001]
plt.plot(gamma_0001["param_C"], gamma_0001["mean_test_score"])
plt.plot(gamma_0001["param_C"], gamma_0001["mean_train_score"])
plt.xlabel('C')
plt.ylabel('Accuracy')
plt.title("Gamma=0.0001")
plt.ylim([0.60, 1])
plt.legend(['test accuracy', 'train accuracy'], loc='upper left')
plt.xscale('log')
```
From the plot above, we can observe that (from higher to lower gamma / left to right):
At very high gamma (0.01), the model is achieving 100% accuracy on the training data, though the test score is quite low (<80%). Thus, the model is overfitting.
At gamma=0.001, the training and test scores are comparable at around C=1, though the model starts to overfit at higher values of C
At gamma=0.0001, the model does not overfit till C=10 but starts showing signs at C=100. Also, the training and test scores are slightly lower than at gamma=0.001.
Thus, it seems that the best combination is gamma=0.001 and C=15 (the plot in the middle), which gives the highest test accuracy (~94%) while avoiding overfitting.
Let's now build the final model and see the performance on test data.
Let's now choose the best hyperparameters.
```
# printing the optimal accuracy score and hyperparameters
best_score = model_cv.best_score_
best_hyperparams = model_cv.best_params_
print("The best test score is {0} corresponding to hyperparameters {1}".format(best_score, best_hyperparams))
```
**Building and Evaluating the Final Model**
Let's now build and evaluate the final model, i.e. the model with highest test accuracy.
```
# model with optimal hyperparameters
# model
model = SVC(C=10, gamma=0.001, kernel="rbf")
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# metrics
print("accuracy", metrics.accuracy_score(y_test, y_pred), "\n")
print(metrics.confusion_matrix(y_test, y_pred), "\n")
```
Conclusion
The accuracy achieved using a non-linear kernel (~0.94) is mush higher than that of a linear one (~0.91). We can conclude that the problem is highly non-linear in nature.
|
github_jupyter
|
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
import os
print(os.listdir("../input"))
# Any results you write to the current directory are saved as output.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import validation_curve
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
import matplotlib.pyplot as plt
import seaborn as sns
train_data = pd.read_csv("../input/train.csv") #reading the csv files using pandas
test_data = pd.read_csv("../input/test.csv")
train_data.shape # print the dimension or shape of train data
test_data.shape # print the dimension or shape of test data
train_data.head() # printing first five columns of train_data
test_data.head() # printing first five columns of test_data
# there are no missing values in the dataset
train_data.isnull().sum().head(10)
test_data.isnull().sum().head(10)
test_data.describe()
train_data.describe()
# about the dataset
# dimensions
print("Dimensions: ",test_data.shape, "\n")
# data types
print(test_data.info())
# head
test_data.head()
# about the dataset
# dimensions
print("Dimensions: ",train_data.shape, "\n")
# data types
print(train_data.info())
# head
train_data.head()
print(train_data.columns)
print(test_data.columns)
order = list(np.sort(train_data['label'].unique()))
print(order)
## Visualizing the number of class and counts in the datasets
sns.countplot(train_data["label"])
## Visualizing the number of class and counts in the datasets
plt.plot(figure = (16,10))
g = sns.countplot( train_data["label"], palette = 'icefire')
plt.title('NUmber of digit classes')
train_data.label.astype('category').value_counts()
# Plotting some samples as well as converting into matrix
four = train_data.iloc[3, 1:]
four.shape
four = four.values.reshape(28,28)
plt.imshow(four, cmap='gray')
plt.title("Digit 4")
seven = train_data.iloc[6, 1:]
seven.shape
seven = seven.values.reshape(28, 28)
plt.imshow(seven, cmap='gray')
plt.title("Digit 7")
# average feature values
round(train_data.drop('label', axis=1).mean(), 2)
## Separating the X and Y variable
y = train_data['label']
## Dropping the variable 'label' from X variable
X = train_data.drop(columns = 'label')
## Printing the size of data
print(train_data.shape)
## Normalization
X = X/255.0
test_data = test_data/255.0
print("X:", X.shape)
print("test_data:", test_data.shape)
# scaling the features
from sklearn.preprocessing import scale
X_scaled = scale(X)
# train test split
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size = 0.3, train_size = 0.2 ,random_state = 10)
# linear model
model_linear = SVC(kernel='linear')
model_linear.fit(X_train, y_train)
# predict
y_pred = model_linear.predict(X_test)
# confusion matrix and accuracy
from sklearn import metrics
from sklearn.metrics import confusion_matrix
# accuracy
print("accuracy:", metrics.accuracy_score(y_true=y_test, y_pred=y_pred), "\n")
# cm
print(metrics.confusion_matrix(y_true=y_test, y_pred=y_pred))
# non-linear model
# using rbf kernel, C=1, default value of gamma
# model
non_linear_model = SVC(kernel='rbf')
# fit
non_linear_model.fit(X_train, y_train)
# predict
y_pred = non_linear_model.predict(X_test)
# confusion matrix and accuracy
# accuracy
print("accuracy:", metrics.accuracy_score(y_true=y_test, y_pred=y_pred), "\n")
# cm
print(metrics.confusion_matrix(y_true=y_test, y_pred=y_pred))
# creating a KFold object with 5 splits
folds = KFold(n_splits = 5, shuffle = True, random_state = 10)
# specify range of hyperparameters
# Set the parameters by cross-validation
hyper_params = [ {'gamma': [1e-2, 1e-3, 1e-4],
'C': [5,10]}]
# specify model
model = SVC(kernel="rbf")
# set up GridSearchCV()
model_cv = GridSearchCV(estimator = model,
param_grid = hyper_params,
scoring= 'accuracy',
cv = folds,
verbose = 1,
return_train_score=True)
# fit the model
model_cv.fit(X_train, y_train)
# cv results
cv_results = pd.DataFrame(model_cv.cv_results_)
cv_results
# converting C to numeric type for plotting on x-axis
cv_results['param_C'] = cv_results['param_C'].astype('int')
# # plotting
plt.figure(figsize=(16,8))
# subplot 1/3
plt.subplot(131)
gamma_01 = cv_results[cv_results['param_gamma']==0.01]
plt.plot(gamma_01["param_C"], gamma_01["mean_test_score"])
plt.plot(gamma_01["param_C"], gamma_01["mean_train_score"])
plt.xlabel('C')
plt.ylabel('Accuracy')
plt.title("Gamma=0.01")
plt.ylim([0.60, 1])
plt.legend(['test accuracy', 'train accuracy'], loc='upper left')
plt.xscale('log')
# subplot 2/3
plt.subplot(132)
gamma_001 = cv_results[cv_results['param_gamma']==0.001]
plt.plot(gamma_001["param_C"], gamma_001["mean_test_score"])
plt.plot(gamma_001["param_C"], gamma_001["mean_train_score"])
plt.xlabel('C')
plt.ylabel('Accuracy')
plt.title("Gamma=0.001")
plt.ylim([0.60, 1])
plt.legend(['test accuracy', 'train accuracy'], loc='upper left')
plt.xscale('log')
# subplot 3/3
plt.subplot(133)
gamma_0001 = cv_results[cv_results['param_gamma']==0.0001]
plt.plot(gamma_0001["param_C"], gamma_0001["mean_test_score"])
plt.plot(gamma_0001["param_C"], gamma_0001["mean_train_score"])
plt.xlabel('C')
plt.ylabel('Accuracy')
plt.title("Gamma=0.0001")
plt.ylim([0.60, 1])
plt.legend(['test accuracy', 'train accuracy'], loc='upper left')
plt.xscale('log')
# printing the optimal accuracy score and hyperparameters
best_score = model_cv.best_score_
best_hyperparams = model_cv.best_params_
print("The best test score is {0} corresponding to hyperparameters {1}".format(best_score, best_hyperparams))
# model with optimal hyperparameters
# model
model = SVC(C=10, gamma=0.001, kernel="rbf")
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# metrics
print("accuracy", metrics.accuracy_score(y_test, y_pred), "\n")
print(metrics.confusion_matrix(y_test, y_pred), "\n")
| 0.720467 | 0.924347 |
**Importing Libraries**
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn import decomposition
marketplace = pd.read_csv('marketplace.csv')
marketplace.head()
```
**1. Berapa banyak observasi yang ada dalam dataset? dan kolom mana yang tidak memiliki nilai duplikat/nilai unik?**
```
marketplace.shape
dup = marketplace.duplicated()
print(dup.sum())
marketplace[dup]
```
*tidak ada data yang duplikat*
```
marketplace.nunique()
```
*sebelumnya telah diketahui bahwa ada data sebanyak 26014, namun jumlah product_id hanya 12120. Dengan kata lain masih ada beberapa data yang sama.*
```
marketplace[marketplace.duplicated(subset = 'product_id', keep = False)].sort_values('product_id')
```
**2. Periksa tipe data dalam dataset. Lakukan beberapa perubahan tipe data jika ada tipe data yang salah.**
```
marketplace.dtypes
marketplace.info()
```
**3. Apakah ada nilai dalam variabel yang nol? yang mana jika ada beberapa variabel null pada dataset tersebut, silahkan isi nilainya dengan 0.**
```
marketplace.isnull().sum()
from sklearn.impute import SimpleImputer
from scipy.stats import mode
marketplace['merchant_code'] = marketplace['merchant_code'].fillna(marketplace['merchant_code'].mean())
marketplace.isnull().sum()
marketplace['merchant_code'] = marketplace['merchant_code'].astype('int')
marketplace.dtypes
```
**4. Apa jenis produk kategori yang dijual dalam kumpuan data?**
```
marketplace['product_type'].unique()
```
**5. Jenis produk apa yang termasuk dalam 3 produk teratas dalam penjualan?**
```
marketplace.groupby('product_type')['total_sold'].sum().sort_values(ascending=False).head(3)
```
**6. Berdasarkan produk teratas pertama. Berapa harga rata-rata dan seberapa bervariasinya harga jual? dan menampilkan visualisasi distribusi harga dengan histogram.**
```
produk_teratas = marketplace[marketplace['product_type'] == 'Samsung Galaxy A10s']
produk_teratas
#Harga Rata-rata
rata_rata = produk_teratas['price'].mean()
print('Harga rata-rata produk teratas : ', rata_rata)
#Visualisasi Distribusi Harga dengan Histogram
plt.figure(figsize=(8,4))
sns.distplot(marketplace['price'], bins=40)
```
**7. Filter dataset hanya dengan 'Samsung Galaxy A10s' dan temukan 3 kota pedagang terlaris. Tunjukkan dengan beberapa bloxpot distribusi harga antara kota pedagang 3 teratas itu!**
```
filter = marketplace[marketplace['product_type'] == 'Samsung Galaxy A10s']
filter.groupby('merchant_city')['total_sold'].mean().sort_values(ascending=False).head(3)
#Boxplot Distribusi Harga antara Kota Pedagang 3 Teratas
kota = ['Kota Tangerang', 'Kab. Bantul', 'Kota Administrasi Jakarta Pusat']
filter_kota = marketplace[marketplace['merchant_city'].isin(kota)]
plt.figure(figsize=(15,15))
boxplot = sns.boxplot(x='merchant_city', y='total_sold', data=filter_kota)
print(boxplot)
```
**8. Ujilah perbedaan total_sold produk Samsung Galaxy A10s dengan Xiaomi Redmi 6A menggunakan t-sample test**
```
from scipy.stats import ttest_ind
samsung = marketplace[marketplace["product_type"] == "Samsung Galaxy A10s"]["total_sold"]
xiaomi = marketplace[marketplace["product_type"] == "Xiaomi Redmi 6A"]["total_sold"]
#Rata-rata penjualan dari Samsung dan Xiaomi
samsung_mean = np.mean(samsung)
xiaomi_mean = np.mean(xiaomi)
print("Rata-rata penjualan Samsung galaxy A10s : ", samsung_mean)
print("Rata-rata penjualan Xiaomi Redmi 6A : ", xiaomi_mean)
#Selisih Penjualan Samsung dan Xiaomi
selisih = samsung_mean - xiaomi_mean
print("Selisih penjualan : ",selisih)
```
1. Banyak observasi yang ada dalam dataset adalah 26014 baris dan 16 kolom
2. 3 Produk teratas dalam penjualan ialah Samsung galaxy A10s, Xiaomi Redmi 6A, dan Realmi 6
3. Rata-rata harga teratas dari produk Samsung GalaxyA10s adalah 1622650.8446327683 dengan Persebaran distribusi harga condong ke kiri dan memiliki ekor di kanan.
4. 3 Kota dengan penjualan produk Samsung Galaxy A10s terbanyak yaitu Kota Tangerang, kab. Bantul, dan Kota Administrasi Jakarta Pusat
5. Setelah diuji perbedaan total_sold antara produk Samsung Galaxy A10s dengan Xiaomi Redmi 6A menggunakan t-sample test dapat dilihat bahwa selisih rata-rata yang sekitar 50. Maka bisa disimpulkan bahwa total_sold produk Samsung Galaxy A10s tidak sama dengan total_sold produk Xiaomi Redmi 6A
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn import decomposition
marketplace = pd.read_csv('marketplace.csv')
marketplace.head()
marketplace.shape
dup = marketplace.duplicated()
print(dup.sum())
marketplace[dup]
marketplace.nunique()
marketplace[marketplace.duplicated(subset = 'product_id', keep = False)].sort_values('product_id')
marketplace.dtypes
marketplace.info()
marketplace.isnull().sum()
from sklearn.impute import SimpleImputer
from scipy.stats import mode
marketplace['merchant_code'] = marketplace['merchant_code'].fillna(marketplace['merchant_code'].mean())
marketplace.isnull().sum()
marketplace['merchant_code'] = marketplace['merchant_code'].astype('int')
marketplace.dtypes
marketplace['product_type'].unique()
marketplace.groupby('product_type')['total_sold'].sum().sort_values(ascending=False).head(3)
produk_teratas = marketplace[marketplace['product_type'] == 'Samsung Galaxy A10s']
produk_teratas
#Harga Rata-rata
rata_rata = produk_teratas['price'].mean()
print('Harga rata-rata produk teratas : ', rata_rata)
#Visualisasi Distribusi Harga dengan Histogram
plt.figure(figsize=(8,4))
sns.distplot(marketplace['price'], bins=40)
filter = marketplace[marketplace['product_type'] == 'Samsung Galaxy A10s']
filter.groupby('merchant_city')['total_sold'].mean().sort_values(ascending=False).head(3)
#Boxplot Distribusi Harga antara Kota Pedagang 3 Teratas
kota = ['Kota Tangerang', 'Kab. Bantul', 'Kota Administrasi Jakarta Pusat']
filter_kota = marketplace[marketplace['merchant_city'].isin(kota)]
plt.figure(figsize=(15,15))
boxplot = sns.boxplot(x='merchant_city', y='total_sold', data=filter_kota)
print(boxplot)
from scipy.stats import ttest_ind
samsung = marketplace[marketplace["product_type"] == "Samsung Galaxy A10s"]["total_sold"]
xiaomi = marketplace[marketplace["product_type"] == "Xiaomi Redmi 6A"]["total_sold"]
#Rata-rata penjualan dari Samsung dan Xiaomi
samsung_mean = np.mean(samsung)
xiaomi_mean = np.mean(xiaomi)
print("Rata-rata penjualan Samsung galaxy A10s : ", samsung_mean)
print("Rata-rata penjualan Xiaomi Redmi 6A : ", xiaomi_mean)
#Selisih Penjualan Samsung dan Xiaomi
selisih = samsung_mean - xiaomi_mean
print("Selisih penjualan : ",selisih)
| 0.385375 | 0.804713 |
```
!export | grep $LANG
# -*- coding: utf-8 -*-
# Copyright (C) 2018.02.09 kyung seok jeong <humanist96@koscom.co.kr>
from __future__ import absolute_import, unicode_literals
from natto import MeCab
import pandas as pd
import collections
import re
import datrie
import string
def load_stopword(fpath):
"""
Return the trie object of stopword dictionary
- input : stopword file path
- output : trie instance
"""
_escape_pattern = ['\n']
try:
trie=datrie.Trie(ranges=[(u'\u0000', u'\uFFFF')])
with open(fpath, "rb", 0) as f:
for word in f.readlines():
word=word.decode("utf-8").rstrip()
trie[word] = True
except Exception as e:
print("[load_storpwod] messages of error :", e)
return ''
return trie
def is_stopword(morpheme, trie):
"""
Returns the presence or absence of stopword in stopword dictionary.
- input : morpheme string, trie instance
- output : boolean (Ture, False)
"""
if morpheme in trie:
return True
return False
def run_ma(text, stop_path='', nBest=1):
"""
Returns the dataframe of all Information of morpheme analyzer.
- input : string, {stopword file path}, {nbest number}
- output : dataframe
"""
options=r'-F%m,%f[0],%f[1],%f[2],%f[3],%f[4],%f[5],%f[6],%f[7]\n'
options+=" -N"+str(nBest)
stopword_flag=False
if stop_path != '':
stopword_flag=True
try:
_me=MeCab(options)
_df = pd.DataFrame(None, columns=['surface', 'tag', 'meaning_class', 'final_consonant',
'reading', 'type', 'first_tag', 'final_tag','expression'])
if stopword_flag:
trie=load_stopword(stop_path)
i=0
for term_str in str(_me.parse(text)).split('\n'):
term_list = re.split(',', term_str)
if stopword_flag == True and is_stopword(term_list[0], trie):
continue
if len(term_list) < 2:
continue
_df.loc[i]=term_list
i+=1
except Exception as e:
print("[run_ma] messages of error : ", e)
return _me, _df
me, df=run_ma("빅데이터 커뮤니티는 너무 어려운것 같다", "./stopword.txt")
print(me)
print(df)
help(run_ma)
print(df)
def get_all_morph(df):
"""
Returns all morphemes and Part-of-Speech.
- input : dataframe
- output : string
"""
ret=''
for index, row in df.iterrows():
if row['type'] == 'Inflect' or row['type'] == 'Compound':
tag=row['expression']
ret+=tag.replace('+',' ').replace("/*", '')+" "
else:
tag=row['tag']
ret+=row['surface']+"/"+tag+" "
ret=ret.rstrip()
ret=ret+"\n"
return(ret)
get_all_morph(df)
print(df)
def get_noun_morph(df, option='N'):
"""
Returns noun morphemes and Part-of-Speech.
- input : dataframe, {option : compound noun decomposition flag, default : N}
- output : string
"""
_noun_type = ['NNG', 'NNP']
ret=''
for index, row in df.iterrows():
if row['tag'] in _noun_type:
if row['type'] == 'Compound' and option != 'N':
tag=row['expression']
ret+=tag.replace('+',' ').replace("/*", '')+" "
else:
ret+=row['surface']+"/"+row['tag']+" "
ret=ret.rstrip()
ret=ret+"\n"
return(ret)
get_noun_morph(df)
def get_noun_term_freq(df, option='N'):
"""
Returns noun morphemes and freqeuncy
- input : dataframe, {option : compound noun decomposition flag, default : N}
- output : list of tuples(morpheme, frequency)
"""
_noun_type = ['NNG', 'NNP']
_terms = []
for index, row in df.iterrows():
if row['tag'] in _noun_type:
if row['type'] == 'Compound' and option != 'N':
tag=row['expression']
_terms.extend(re.split(' ', tag.replace('+',' ').replace("/*", '')))
else:
_terms.append(row['surface'])
return sorted(collections.Counter(_terms).items(), key=lambda x: x[1], reverse=True)
get_noun_term_freq(df)
```
|
github_jupyter
|
!export | grep $LANG
# -*- coding: utf-8 -*-
# Copyright (C) 2018.02.09 kyung seok jeong <humanist96@koscom.co.kr>
from __future__ import absolute_import, unicode_literals
from natto import MeCab
import pandas as pd
import collections
import re
import datrie
import string
def load_stopword(fpath):
"""
Return the trie object of stopword dictionary
- input : stopword file path
- output : trie instance
"""
_escape_pattern = ['\n']
try:
trie=datrie.Trie(ranges=[(u'\u0000', u'\uFFFF')])
with open(fpath, "rb", 0) as f:
for word in f.readlines():
word=word.decode("utf-8").rstrip()
trie[word] = True
except Exception as e:
print("[load_storpwod] messages of error :", e)
return ''
return trie
def is_stopword(morpheme, trie):
"""
Returns the presence or absence of stopword in stopword dictionary.
- input : morpheme string, trie instance
- output : boolean (Ture, False)
"""
if morpheme in trie:
return True
return False
def run_ma(text, stop_path='', nBest=1):
"""
Returns the dataframe of all Information of morpheme analyzer.
- input : string, {stopword file path}, {nbest number}
- output : dataframe
"""
options=r'-F%m,%f[0],%f[1],%f[2],%f[3],%f[4],%f[5],%f[6],%f[7]\n'
options+=" -N"+str(nBest)
stopword_flag=False
if stop_path != '':
stopword_flag=True
try:
_me=MeCab(options)
_df = pd.DataFrame(None, columns=['surface', 'tag', 'meaning_class', 'final_consonant',
'reading', 'type', 'first_tag', 'final_tag','expression'])
if stopword_flag:
trie=load_stopword(stop_path)
i=0
for term_str in str(_me.parse(text)).split('\n'):
term_list = re.split(',', term_str)
if stopword_flag == True and is_stopword(term_list[0], trie):
continue
if len(term_list) < 2:
continue
_df.loc[i]=term_list
i+=1
except Exception as e:
print("[run_ma] messages of error : ", e)
return _me, _df
me, df=run_ma("빅데이터 커뮤니티는 너무 어려운것 같다", "./stopword.txt")
print(me)
print(df)
help(run_ma)
print(df)
def get_all_morph(df):
"""
Returns all morphemes and Part-of-Speech.
- input : dataframe
- output : string
"""
ret=''
for index, row in df.iterrows():
if row['type'] == 'Inflect' or row['type'] == 'Compound':
tag=row['expression']
ret+=tag.replace('+',' ').replace("/*", '')+" "
else:
tag=row['tag']
ret+=row['surface']+"/"+tag+" "
ret=ret.rstrip()
ret=ret+"\n"
return(ret)
get_all_morph(df)
print(df)
def get_noun_morph(df, option='N'):
"""
Returns noun morphemes and Part-of-Speech.
- input : dataframe, {option : compound noun decomposition flag, default : N}
- output : string
"""
_noun_type = ['NNG', 'NNP']
ret=''
for index, row in df.iterrows():
if row['tag'] in _noun_type:
if row['type'] == 'Compound' and option != 'N':
tag=row['expression']
ret+=tag.replace('+',' ').replace("/*", '')+" "
else:
ret+=row['surface']+"/"+row['tag']+" "
ret=ret.rstrip()
ret=ret+"\n"
return(ret)
get_noun_morph(df)
def get_noun_term_freq(df, option='N'):
"""
Returns noun morphemes and freqeuncy
- input : dataframe, {option : compound noun decomposition flag, default : N}
- output : list of tuples(morpheme, frequency)
"""
_noun_type = ['NNG', 'NNP']
_terms = []
for index, row in df.iterrows():
if row['tag'] in _noun_type:
if row['type'] == 'Compound' and option != 'N':
tag=row['expression']
_terms.extend(re.split(' ', tag.replace('+',' ').replace("/*", '')))
else:
_terms.append(row['surface'])
return sorted(collections.Counter(_terms).items(), key=lambda x: x[1], reverse=True)
get_noun_term_freq(df)
| 0.30767 | 0.242923 |
# Getting Started with RAiDER
**Author**: Jeremy Maurer, David Bekaert, Simran Sangha, Yang Lei - Jet Propulsion Laboratory, California Institute of Technology
This notebook provides an overview of how to get started using the RAiDER package for estimating tropospheric RADAR delays, and other functionality included in the **raiderDelay.py** program. We give an example of how to download and process delays using the ERA-5 weather model for the Los Angeles region.
In this notebook, we will demonstrate how to:
- Use the raiderDelay.py command-line utility to download and process tropospheric delays
- Generate Zenith Delays over the Los Angeles region
- Generate Zenith Delays for a set of GNSS stations over the Los Angeles region
The notebook will take approximately 15 minutes to run all the way through aside from the data download step.
<div class="alert alert-warning">
The initial setup (<b>Prep A</b> section) should be run at the start of the notebook. The overview sections do not need to be run in order.
</div>
<div class="alert alert-danger">
<b>Potential Errors:</b>
- Pandas 1.2.0 or greater is required for some of the the plotting examples.
- GDAL uses "HDF5" driver instead of "netCDF/Network Common Data Format." Verify GDAL version >= 3.
- RAiDER needs to be installed to run this notebook
</div>
<div class="alert alert-info">
<b>Terminology:</b>
- *Acquisition*: A single image acquired by a satellite at a particular time
- *AOI*: Area of interest: the lat/lon area (in RAiDER a square region) containing your query points
- *Interferogram*: An unwrapped image containing the surface displacement accumulated between two acquisitions.
- *SLC*: Single-look complex image. A complex single-band raster that contains a single focused RADAR frame from a SAR satellite. For Sentinel-1, SLCs are Level-1 products.
- *Weather model*: A reanalysis weather product defining temperature, pressure, and humidity on a regular grid in some coordinate system (e.g., at regular lat/lon intervals in the standard EPSG:4326 reference frame).
- *Delay*: The apparent displacement in an interferogram that occurs solely due to changes in weather conditions between two acquisitions.
</div>
## Table of Contents
[**Overview of the raiderDelay.py program**](#overview)
[1. Details of the user input options](#user-input)
[- DateList](#date_arg)
[- Time](#time_arg)
[- Area of Interest](#aoi_arg)
[- Line-of-sight information](#los_arg)
[- Height information](#height_arg)
[- Weather Model Type](#weather_model_arg)
[- Other Runtime Parameters](#runtime_arg)
[**Example Calculations**](#examples)
[1. Downloading the weather model data using a bounding box](#bounding_box_example)
[2. Compute Zenith Delays using a bounding box](#bounding_box_ztd)
[3. Compute Zenith Delays using a list of GNSS stations](#station_list_example)
[4. Visualizing Zenith Delays for a list of GNSS stations](#station_list_visualization)
[5. Compute Slant Delays using ISCE raster files](#raster_example)
## Prep: Initial setup of the notebook
Please run the cell below prior to running the rest of the notebook to ensure RAiDER is installed and set your working directory. You can change the relevant directories as desired for your system.
```
import os
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
## Defining the home and data directories
tutorial_home_dir = os.path.abspath(os.getcwd())
work_dir = os.path.abspath(os.getcwd())
print("Tutorial directory: ", tutorial_home_dir)
print("Work directory: ", work_dir)
# Verifying if RAiDER is installed correctly
try:
import RAiDER
except:
raise Exception('RAiDER is missing from your PYTHONPATH')
os.chdir(work_dir)
```
## Overview of the raiderDelay.py program
<a id='overview'></a>
**`raiderDelay.py`** is a command-line program written in Python that allows for easy downloading and processing of tropospheric weather delays for InSAR correction or comparison with GNSS tropospheric delays.
We can explore the options by looking at the help menu for the program.
```
# Running raiderDelay.py -h will print the help menu
!raiderDelay.py -h
```
## Details of the user input options
<a id='user-input'></a>
RAiDER is quite flexible in terms of the input arguments it allows.
### 1. Date or date list (**`--date DATE1 [DATE2 DATESTEP]`**)
<a id='date_arg'></a>
This argument is required unless pre-downloaded weather model files are directly specified. (see the [`--files`](#weather_model_arg) argument below).
The date(s) passed can be either:
1) a single date, specified in psuedo-ISO 8601 format: 20180101, 2018-01-01, etc.
2) a space-deliminated pair of dates, in which case all the dates between the pair listed will be downloaded and processed. E.g., '20180101 20190101'
3) a space-delimited pair of dates plus an interval in days, to specify the date interval to download. E.g., '20180101 20190101 12'
### 2. Time of day (**`--time TIME`**)
<a id='time_arg'></a>
This argument is also required unless pre-downloaded weather model files are explicitly passed. Specify the time of day to download and process in psuedo-ISO 8601 format:
1) T020000
2) T02:00:00.000
3) T0200
4) 12:00:00
5) 120000
etc.
### 3. Area of Interest (AOI) arguments
<a id='aoi_arg'></a>
RAiDER requires one of three different options as inputs for the AOI: 1) a bounding box, in which case the weather model grid nodes are used for x/y locations, 2) a station file, which should be a .csv containing at minimum the columns "Lat" and "Lon," and 3) ISCE-style latitude and longitude grid files in radar coordinates. Only one option should be used, and the arguments can be passed as described below.
#### Bounding Box (**`--bbox S N W E`**)
- A list of four numbers describing a bounding box
- Format is South North West East
- Values can be integers or decimals.
- A buffer will automatically be added to compensate for rays at the edge of the bounding box
- Example: ```--bbox 41 42 -78 -77```
#### Latitude / Longitude files (**`--latlon LAT LONG`**)
- Format is ```--latlon <latitude file> <longitude file>```.
- Files in gridded radar coordinates; i.e. 2-D files containing the latitude and longitude of each pixel
- Example: ```--latlon lat.rdr lon.rdr```
#### Station file (**`--station_file STATION_FILE`**)
- A comma-delimited file with at least the columns "Lat" and "Lon"
- An example is a file containing a list of GNSS stations with location info
- If the heights of the stations are known, the height column should have the name "Hgt_m" and give ellipsoidal heights in meters. If heights are not known, RAiDER will download a DEM for the region encompassing the station locations to get the height info.
- Example: ```--station_file stations.csv```
### 4. Line-of-sight Information
<a id='los_arg'></a>
This option is used to specify line-of-sight information.
The line-of-sight is used to calculate the true rays from the ground pixel to the top of the troposphere, along of the line-of-sight to the sensor platform. One of the following two optional arguments may be specified; otherwise, RAiDER will compute the zenith delay (ZTD).
In the future we will also incorporate the conventional slant delay calculation.
#### RADAR Line-of-sight file in ISCE format (**`--lineofsight LOS`**)
- A two-band GDAL-readable raster file containing the look vector components for the sensor, of the same size as the radar/SLC images
- Band 1 should be incidence angle in degrees from vertical
- Band 2 should be heading in degrees clockwise from north
- Example: ```--lineofsight los.rdr```
#### State vector file (**`--statevectors SV`**)
- An ISCE-derived XML file, shelve file, text file, or ESA orbit file containing state vectors specifying the orbit of the sensor.
- Example: ```--statevectors orbit.xml```
### 5. Height information
<a id='height_arg'></a>
Ellipsoidal heights are needed to compute absolute delays. These can come from a DEM or simply by specifying fixed height levels. By default, RAiDER will download a DEM. A user can also specify an existing DEM or a set of specified height levels. For the latter, RAiDER will produce a 3D cube of delays, where the xy information is specified by the AOI arguments and the z-levels are specified directly.
#### DEM (**`--dem DEM`**)
- The DEM over the area of interest can be specified explicitly, or it will be downloaded on-the-fly. RAiDER will check the default location for a DEM (./geom), so if you download the DEM once it will not be downloaded again.
#### Height levels (**`--heightlvs HEIGHTLVS`**)
- This option specifies a list of heights, for which the delay will be calculated. The result is a full 3-D cube of delays at the specified lat/lon grid and height levels.
### 6. Weather Model Information
<a id='weather_model_arg'></a>
#### Weather model (**`--model {ERA5,ERA5T,ERAI,MERRA2,WRF,HRRR,GMAO,HDF5,HRES,NCMR}`**)
- Specifies the type of weather model to use
- Allowed models currently include ERA5, ERA5T, ERAI, MERRA2, HRRR, GMAO, HRES, and NCMR
- Must be included in the ALLOWED_MODELS list in allowed.py and have a reader module defined
- New weather models can be included following the template given in template.py
#### Files (**`--files FILES`**)
- A file containing the weather model data that can be processed using a defined reader
- An example usage is to re-process a file previously downloaded
#### Weather file directory (**`--weatherFiles WMLOC`**)
- Specifies the directory location of/to write weather model files
- Default is ./weather_files
### 7. Runtime parameters
<a id='runtime_arg'></a>
#### Reference integration height (**`--zref ZREF`**)
- Integration height to use when computing the total delay.
- Default is 15 km.
#### Parallel Computation flag (**`--parallel`**)
- Specifies the number of CPUs to use for parallel calculations
- Default is 1 (one) for serial processing
#### Output file format (**`--outformat OUTFORMAT`**)
- GDAL-compatible raster image format
- Default is ENVI
- For other types of inputs (bounding box, station list) this argument is not used
#### Output file directory (**`--out OUT`**)
- This specifies the location of the output files.
- Default is the current directory
#### Download the weather model only (**`--download_only`**)
- Download the weather model only and do nothing else.
#### Run in verbose mode (**`-v/--verbose`**)
- Runs the code in verbose mode.
## Examples using RAiDER
<a id='runtime_arg'></a>
In this section we will demostrate some of the basic capabilities of RAiDER, using a region in southern California shown below.
The study area is around Los Angles, chosen to be a a square box 10 x 10 deg centered on 34 deg latitude, -118 deg longitude. (See the optical image below.)
![Optical Image at Los Angeles]()
<img src="img/optical.png" width="300" height="150">
### Downloading the weather model data using a bounding box
<a id='bounding_box_example'></a>
RAiDER uses weather model data from third parties to calculate weather model delays. We can use the --download_only option to download the data without doing any processing. For this excercise we will use the weather model available from the __[Global Model Assimilation Office](https://gmao.gsfc.nasa.gov/weather_prediction/)__ at NASA.
You can also try the ERA-5 model from the __[European Medium-range Weather Forecast](https://www.ecmwf.int/)__ if you have access to ECMWF weather models, simply change "GMAO" to "ERA5".
```
# Try downloading the data
!raiderDelay.py --date 20200103 --time 00:00:00 -b 29 39 -123 -113 --model GMAO --download_only -v
```
The weather model data is accessed through different APIs depending on the model. GMAO and MERRA-2 are both directly accessed using the OpenDAP interface, while ECMWF models have a custom API. RAiDER automatically uses the appropriate API for the weather model that you specify. Each model has a custom reader defined that is used to access the API and manipulate it to a consistent set of variables.
By default the weather model files are stored in a subfolder of the local directory called "weather_files." You can change this using the `--weatherFiles` option described above.
```
# We can look at the downloaded file
!ls weather_files/
```
The downloaded weather model is a NETCDF file, so it can be viewed and manipulated using GDAL or any NETCDF utility or package.
```
# GDAL provides an API to access the variables and attributes of the file
!gdalinfo weather_files/GMAO_2020_01_03_T00_00_00.nc
```
Notice the file contains (usually) four variables, including height, pressure, temperature, and humidity. In some cases, pressure is not explicitly stored; instead the variables are provided at fixed pressure levels, or an intermediate variable like geopotential is provided.
Notice that no information is printed about the projection or size of the variables. These variables can be queried using GDAL individually to show the projection and shape information.
```
!cd weather_files
!gdalinfo NETCDF:"weather_files/GMAO_2020_01_03_T00_00_00.nc":QV
!cd ..
```
Once the weather model file has been downloaded, you can compute delays for the same area without re-downloading. RAiDER will check your input query points against the extents of the downloaded file and proceed with processing if the weather model file includes a large enough area. If not, then it will ask you to delete the existing file so that it can download a new one.
```
# If we try to run the same datetime but a larger bounding box, we get a message asking us to delete the existing file
!raiderDelay.py --date 20200103 --time 00:00:00 -b 25 45 -123 -113 --model GMAO
```
### Compute Zenith Delays for a bounding box
<a id='bounding_box_ztd'></a>
If you only specify a bounding box as your AOI, RAiDER will compute the Zenith delay at the locations of the native grid nodes of the weather model itself. Because our bounding box is the same as before, RAiDER will skip the download step and directly process the delays.
RAiDER will warn you that it is using the existing weather model file, which is specific to a 1) date, 2) time, 3) model, and 4) AOI.
```
!ls weather_files/
```
Since we've already downloaded the file and we're using the native grid nodes as our query points, the processing happens fairly quickly.
<div class="alert alert-danger">
<b>Note:</b>
Different weather models have different resolutions. GMAO has about a 50 km horizontal grid node spacing, while HRRR for example has a 3-km horizontal grid node spacing. As a result, some weather models will be much faster to process than others. </div>
```
# passing the original bounding
!raiderDelay.py --date 20200103 --time 00:00:00 -b 29 39 -123 -113 --model GMAO
```
Once the delays have been processed, there are several files that get created. One is a set of plots that are for sanity checking the weather model data. These are .pdf files and show the weather model variables at two different heights and a profile at a central point. These plots are mainly used to ensure that custom weather models are getting processed correctly (see __[Defining Custom Weather Models](../Defining_Custom_Weather_Models/Defining_custom_Weather_Models_in_RAiDER.ipynb)__ for more details).
```
!ls *.pdf
```
In addition, there are log files that get printed out. These can be especially helpful when troubleshooting or debugging. The "debug.log" file records all of the same information that gets printed to the console, while the "error.log" file records warnings and error messages, including tracebacks. These files are appended to instead of being overwritten, so the output of several calls to raiderDelay.py will be saved.
```
!ls *.log
!head debug.log
!head error.log
```
Notice that there are flags ("INFO", "WARNING", etc.) that alert you to the type of message that is being saved.
Finally, we have the processed delay files. These are of two types:
1) A NETCDF file containing a modified version of the weather model that has been processed and regularized
2) Depending on the type of input query points, there may be a separate final delay file
```
!ls -lt weather_files/
```
In the case of a bounding box input, there is no additional file written; the delays are stored in the processed weather model file.
As before, we can use GDAL to examine the processed NETCDF file.
```
!gdalinfo weather_files/GMAO_2020_01_03_T00_00_00_29N_40N_125W_113W.nc
```
Notice that there are several new variables in comparison with the original weather model data, including lats/lons and two new variables "wet" and "hydro;" these are the wet and hydrostatic refractivities (point-wise delays) that are calculated using the equation:
$$ N_{\text{hydro}} = k_1 \frac{P}{T} $$
$$ N_{\text{wet}} = k_2 \frac{e}{T} + k_3 \frac{e}{T^2} $$
These are integrated in the z-direction to produce the "wet_total" and "hydro_total" variables, which are the integrated (i.e. total) delays:
$$ \text{ZTD}_{\text{wet}} = 10^{-6} \int_{z = h}^{z_{ref}} N_{\text{wet}}(z) \hspace{3pt} dz $$
$$ \text{ZTD}_{\text{hydro}} = 10^{-6} \int_{z = h}^{z_{ref}} N_{\text{hydro}}(z) \hspace{3pt} dz $$
When passing a station list or raster files containing query points, RAiDER will generate separate files containing the wet and hydrostatic total delays in the main directory.
Although not explicit in variable descriptions above, a further difference between the original and processed weather model data is that it is all in a uniform cube; i.e. the grid heights are the same across the entire area of interest. In contrast, the native weather models typically use some other fixed variable such as pressure levels.
### Compute Zenith delays using a GNSS station list
<a id='station_list_example'></a>
When using a GNSS station list, the program by default will create a bounding box around the list of points.
For demonstration purposes, we will use an example list of stations from
the L.A. area so that we don't have to download another weather model file.
The station file **must be comma-delimited, and must contain at the minimum column names "Lat" and "Lon."** By default, RAiDER will download a DEM to get the height information for the list of stations; if the heights are specified in a column named "Hgt_m" RAiDER will use those and this will save some processing time.
```
!raiderDelay.py --date 20200103 --time 00:00:00 --station_file data/sample_gnss_list.csv --model GMAO
```
We can compare the files in weather_files to see what has been added:
```
!ls -lt weather_files/
```
We now have a new file in the base directory, which has been copied from the original station list file and to which has been added some new variables.
```
!ls *.csv
!head GMAO_Delay_20200103T000000_Zmax15000.0.csv
```
You can see that the new .csv file contains the original station data, but with the addition of the wet, hydrostatic, and total delays, all in meters.
### Visualizing Zenith delays for a list of GNSS stations
<a id='station_list_visualization'></a>
Once we have the delays in the .csv file, we can use Pandas to view and manipulate the data
```
delays = pd.read_csv('GMAO_Delay_20200103T000000_Zmax15000.0.csv')
delays.head()
delays.plot.scatter(x='Hgt_m',y='totalDelay', marker='.', xlabel = 'Height (m)', ylabel='Total Delay (m)')
```
We can also plot the total (absolute) delays in space.
```
delays.plot.scatter(x='Lon',y='Lat', marker='.', c='totalDelay')
```
### Compute Slant Delays with ISCE raster files
<a id='raster_example'></a>
```
# To be completed
```
|
github_jupyter
|
import os
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
## Defining the home and data directories
tutorial_home_dir = os.path.abspath(os.getcwd())
work_dir = os.path.abspath(os.getcwd())
print("Tutorial directory: ", tutorial_home_dir)
print("Work directory: ", work_dir)
# Verifying if RAiDER is installed correctly
try:
import RAiDER
except:
raise Exception('RAiDER is missing from your PYTHONPATH')
os.chdir(work_dir)
# Running raiderDelay.py -h will print the help menu
!raiderDelay.py -h
#### Latitude / Longitude files (**`--latlon LAT LONG`**)
- Format is ```--latlon <latitude file> <longitude file>```.
- Files in gridded radar coordinates; i.e. 2-D files containing the latitude and longitude of each pixel
- Example: ```--latlon lat.rdr lon.rdr```
#### Station file (**`--station_file STATION_FILE`**)
- A comma-delimited file with at least the columns "Lat" and "Lon"
- An example is a file containing a list of GNSS stations with location info
- If the heights of the stations are known, the height column should have the name "Hgt_m" and give ellipsoidal heights in meters. If heights are not known, RAiDER will download a DEM for the region encompassing the station locations to get the height info.
- Example: ```--station_file stations.csv```
### 4. Line-of-sight Information
<a id='los_arg'></a>
This option is used to specify line-of-sight information.
The line-of-sight is used to calculate the true rays from the ground pixel to the top of the troposphere, along of the line-of-sight to the sensor platform. One of the following two optional arguments may be specified; otherwise, RAiDER will compute the zenith delay (ZTD).
In the future we will also incorporate the conventional slant delay calculation.
#### RADAR Line-of-sight file in ISCE format (**`--lineofsight LOS`**)
- A two-band GDAL-readable raster file containing the look vector components for the sensor, of the same size as the radar/SLC images
- Band 1 should be incidence angle in degrees from vertical
- Band 2 should be heading in degrees clockwise from north
- Example: ```--lineofsight los.rdr```
#### State vector file (**`--statevectors SV`**)
- An ISCE-derived XML file, shelve file, text file, or ESA orbit file containing state vectors specifying the orbit of the sensor.
- Example: ```--statevectors orbit.xml```
### 5. Height information
<a id='height_arg'></a>
Ellipsoidal heights are needed to compute absolute delays. These can come from a DEM or simply by specifying fixed height levels. By default, RAiDER will download a DEM. A user can also specify an existing DEM or a set of specified height levels. For the latter, RAiDER will produce a 3D cube of delays, where the xy information is specified by the AOI arguments and the z-levels are specified directly.
#### DEM (**`--dem DEM`**)
- The DEM over the area of interest can be specified explicitly, or it will be downloaded on-the-fly. RAiDER will check the default location for a DEM (./geom), so if you download the DEM once it will not be downloaded again.
#### Height levels (**`--heightlvs HEIGHTLVS`**)
- This option specifies a list of heights, for which the delay will be calculated. The result is a full 3-D cube of delays at the specified lat/lon grid and height levels.
### 6. Weather Model Information
<a id='weather_model_arg'></a>
#### Weather model (**`--model {ERA5,ERA5T,ERAI,MERRA2,WRF,HRRR,GMAO,HDF5,HRES,NCMR}`**)
- Specifies the type of weather model to use
- Allowed models currently include ERA5, ERA5T, ERAI, MERRA2, HRRR, GMAO, HRES, and NCMR
- Must be included in the ALLOWED_MODELS list in allowed.py and have a reader module defined
- New weather models can be included following the template given in template.py
#### Files (**`--files FILES`**)
- A file containing the weather model data that can be processed using a defined reader
- An example usage is to re-process a file previously downloaded
#### Weather file directory (**`--weatherFiles WMLOC`**)
- Specifies the directory location of/to write weather model files
- Default is ./weather_files
### 7. Runtime parameters
<a id='runtime_arg'></a>
#### Reference integration height (**`--zref ZREF`**)
- Integration height to use when computing the total delay.
- Default is 15 km.
#### Parallel Computation flag (**`--parallel`**)
- Specifies the number of CPUs to use for parallel calculations
- Default is 1 (one) for serial processing
#### Output file format (**`--outformat OUTFORMAT`**)
- GDAL-compatible raster image format
- Default is ENVI
- For other types of inputs (bounding box, station list) this argument is not used
#### Output file directory (**`--out OUT`**)
- This specifies the location of the output files.
- Default is the current directory
#### Download the weather model only (**`--download_only`**)
- Download the weather model only and do nothing else.
#### Run in verbose mode (**`-v/--verbose`**)
- Runs the code in verbose mode.
## Examples using RAiDER
<a id='runtime_arg'></a>
In this section we will demostrate some of the basic capabilities of RAiDER, using a region in southern California shown below.
The study area is around Los Angles, chosen to be a a square box 10 x 10 deg centered on 34 deg latitude, -118 deg longitude. (See the optical image below.)
![Optical Image at Los Angeles]()
<img src="img/optical.png" width="300" height="150">
### Downloading the weather model data using a bounding box
<a id='bounding_box_example'></a>
RAiDER uses weather model data from third parties to calculate weather model delays. We can use the --download_only option to download the data without doing any processing. For this excercise we will use the weather model available from the __[Global Model Assimilation Office](https://gmao.gsfc.nasa.gov/weather_prediction/)__ at NASA.
You can also try the ERA-5 model from the __[European Medium-range Weather Forecast](https://www.ecmwf.int/)__ if you have access to ECMWF weather models, simply change "GMAO" to "ERA5".
The weather model data is accessed through different APIs depending on the model. GMAO and MERRA-2 are both directly accessed using the OpenDAP interface, while ECMWF models have a custom API. RAiDER automatically uses the appropriate API for the weather model that you specify. Each model has a custom reader defined that is used to access the API and manipulate it to a consistent set of variables.
By default the weather model files are stored in a subfolder of the local directory called "weather_files." You can change this using the `--weatherFiles` option described above.
The downloaded weather model is a NETCDF file, so it can be viewed and manipulated using GDAL or any NETCDF utility or package.
Notice the file contains (usually) four variables, including height, pressure, temperature, and humidity. In some cases, pressure is not explicitly stored; instead the variables are provided at fixed pressure levels, or an intermediate variable like geopotential is provided.
Notice that no information is printed about the projection or size of the variables. These variables can be queried using GDAL individually to show the projection and shape information.
Once the weather model file has been downloaded, you can compute delays for the same area without re-downloading. RAiDER will check your input query points against the extents of the downloaded file and proceed with processing if the weather model file includes a large enough area. If not, then it will ask you to delete the existing file so that it can download a new one.
### Compute Zenith Delays for a bounding box
<a id='bounding_box_ztd'></a>
If you only specify a bounding box as your AOI, RAiDER will compute the Zenith delay at the locations of the native grid nodes of the weather model itself. Because our bounding box is the same as before, RAiDER will skip the download step and directly process the delays.
RAiDER will warn you that it is using the existing weather model file, which is specific to a 1) date, 2) time, 3) model, and 4) AOI.
Since we've already downloaded the file and we're using the native grid nodes as our query points, the processing happens fairly quickly.
<div class="alert alert-danger">
<b>Note:</b>
Different weather models have different resolutions. GMAO has about a 50 km horizontal grid node spacing, while HRRR for example has a 3-km horizontal grid node spacing. As a result, some weather models will be much faster to process than others. </div>
Once the delays have been processed, there are several files that get created. One is a set of plots that are for sanity checking the weather model data. These are .pdf files and show the weather model variables at two different heights and a profile at a central point. These plots are mainly used to ensure that custom weather models are getting processed correctly (see __[Defining Custom Weather Models](../Defining_Custom_Weather_Models/Defining_custom_Weather_Models_in_RAiDER.ipynb)__ for more details).
In addition, there are log files that get printed out. These can be especially helpful when troubleshooting or debugging. The "debug.log" file records all of the same information that gets printed to the console, while the "error.log" file records warnings and error messages, including tracebacks. These files are appended to instead of being overwritten, so the output of several calls to raiderDelay.py will be saved.
Notice that there are flags ("INFO", "WARNING", etc.) that alert you to the type of message that is being saved.
Finally, we have the processed delay files. These are of two types:
1) A NETCDF file containing a modified version of the weather model that has been processed and regularized
2) Depending on the type of input query points, there may be a separate final delay file
In the case of a bounding box input, there is no additional file written; the delays are stored in the processed weather model file.
As before, we can use GDAL to examine the processed NETCDF file.
Notice that there are several new variables in comparison with the original weather model data, including lats/lons and two new variables "wet" and "hydro;" these are the wet and hydrostatic refractivities (point-wise delays) that are calculated using the equation:
$$ N_{\text{hydro}} = k_1 \frac{P}{T} $$
$$ N_{\text{wet}} = k_2 \frac{e}{T} + k_3 \frac{e}{T^2} $$
These are integrated in the z-direction to produce the "wet_total" and "hydro_total" variables, which are the integrated (i.e. total) delays:
$$ \text{ZTD}_{\text{wet}} = 10^{-6} \int_{z = h}^{z_{ref}} N_{\text{wet}}(z) \hspace{3pt} dz $$
$$ \text{ZTD}_{\text{hydro}} = 10^{-6} \int_{z = h}^{z_{ref}} N_{\text{hydro}}(z) \hspace{3pt} dz $$
When passing a station list or raster files containing query points, RAiDER will generate separate files containing the wet and hydrostatic total delays in the main directory.
Although not explicit in variable descriptions above, a further difference between the original and processed weather model data is that it is all in a uniform cube; i.e. the grid heights are the same across the entire area of interest. In contrast, the native weather models typically use some other fixed variable such as pressure levels.
### Compute Zenith delays using a GNSS station list
<a id='station_list_example'></a>
When using a GNSS station list, the program by default will create a bounding box around the list of points.
For demonstration purposes, we will use an example list of stations from
the L.A. area so that we don't have to download another weather model file.
The station file **must be comma-delimited, and must contain at the minimum column names "Lat" and "Lon."** By default, RAiDER will download a DEM to get the height information for the list of stations; if the heights are specified in a column named "Hgt_m" RAiDER will use those and this will save some processing time.
We can compare the files in weather_files to see what has been added:
We now have a new file in the base directory, which has been copied from the original station list file and to which has been added some new variables.
You can see that the new .csv file contains the original station data, but with the addition of the wet, hydrostatic, and total delays, all in meters.
### Visualizing Zenith delays for a list of GNSS stations
<a id='station_list_visualization'></a>
Once we have the delays in the .csv file, we can use Pandas to view and manipulate the data
We can also plot the total (absolute) delays in space.
### Compute Slant Delays with ISCE raster files
<a id='raster_example'></a>
| 0.799951 | 0.959611 |
# Quick start, sudoku example
If you want to run this on your local machine, make sure to install CPMpy first:
pip3 install cpmpy
## Loading the libraries
```
# load the libraries
import numpy as np
from cpmpy import *
```
## A sudoku puzzle
Sudoku is a logic-based number puzzle, played on a partially filled 9x9 grid. The goal is to find the unique solution by filling in the empty grid cells with numbers from 1 to 9 in such a way that each row, each column and each of the nine 3x3 subgrids contain all the numbers from 1 to 9 once and only once.
We now define an example 9x9 puzzle, with some grid cells given and some empty:
```
e = 0 # value for empty cells
given = np.array([
[e, e, e, 2, e, 5, e, e, e],
[e, 9, e, e, e, e, 7, 3, e],
[e, e, 2, e, e, 9, e, 6, e],
[2, e, e, e, e, e, 4, e, 9],
[e, e, e, e, 7, e, e, e, e],
[6, e, 9, e, e, e, e, e, 1],
[e, 8, e, 4, e, e, 1, e, e],
[e, 6, 3, e, e, e, e, 8, e],
[e, e, e, 6, e, 8, e, e, e]])
```
Note how we use `e` to represent the empty cells, where `e` is a standard python variable that we gave value `0`, e.g. the cells with a `0` value are the ones we seek.
## Variables and domains
Let's have a look at the problem description again:
* The goal is to find the unique solution by filling in the empty grid cells with numbers from 1 to 9
We will model this with Integer Decision Variables with a value of at least 1 and at most 9, arranged in a matrix just like the given puzzle:
```
# Variables
puzzle = intvar(1, 9, shape=given.shape, name="puzzle")
```
## Modeling the constraints
* each row,
* each column and
* each of the nine 3x3 subgrids contain all the numbers from 1 to 9 once and only once.
We will use the `AllDifferent()` global constraint for this.
```
# we create a model with the row/column constraints
model = Model(
# Constraints on rows and columns
[AllDifferent(row) for row in puzzle],
[AllDifferent(col) for col in puzzle.T], # numpy's Transpose
)
# we extend it with the block constraints
# Constraints on blocks
for i in range(0,9, 3):
for j in range(0,9, 3):
model += AllDifferent(puzzle[i:i+3, j:j+3]) # python's indexing
# Constraints on values (cells that are not empty)
model += (puzzle[given!=e] == given[given!=e]) # numpy's indexing
```
The last constraint ensures that grid cells that are not empty (e.g. `given != e`) receive their given value.
## Solving
With the data, variables and constraints set, we can now combine these in a CP model, and use a solver to solve it:
```
# Solve and print
if model.solve():
print(puzzle.value())
else:
print("No solution found")
```
More examples can be found in the `examples/` folder.
Have fun!
|
github_jupyter
|
# load the libraries
import numpy as np
from cpmpy import *
e = 0 # value for empty cells
given = np.array([
[e, e, e, 2, e, 5, e, e, e],
[e, 9, e, e, e, e, 7, 3, e],
[e, e, 2, e, e, 9, e, 6, e],
[2, e, e, e, e, e, 4, e, 9],
[e, e, e, e, 7, e, e, e, e],
[6, e, 9, e, e, e, e, e, 1],
[e, 8, e, 4, e, e, 1, e, e],
[e, 6, 3, e, e, e, e, 8, e],
[e, e, e, 6, e, 8, e, e, e]])
# Variables
puzzle = intvar(1, 9, shape=given.shape, name="puzzle")
# we create a model with the row/column constraints
model = Model(
# Constraints on rows and columns
[AllDifferent(row) for row in puzzle],
[AllDifferent(col) for col in puzzle.T], # numpy's Transpose
)
# we extend it with the block constraints
# Constraints on blocks
for i in range(0,9, 3):
for j in range(0,9, 3):
model += AllDifferent(puzzle[i:i+3, j:j+3]) # python's indexing
# Constraints on values (cells that are not empty)
model += (puzzle[given!=e] == given[given!=e]) # numpy's indexing
# Solve and print
if model.solve():
print(puzzle.value())
else:
print("No solution found")
| 0.293 | 0.965119 |
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.gridspec as gs
import anatools.data as data
import anatools.analysis as ana
ana.start()
```
Generate a list of datasets for each sample
----
```
basedir = "/home/gcorreia/cernbox/HEP_Project/CMS_HHDM/OUTPUT/Test"
list_basedir = os.listdir(basedir)
TreeName = 'selection'
period = '17'
yearTag = period + "_files"
samples = {
'Signal_1000_100': [i for i in list_basedir if 'Signal_1000_100' in i and yearTag in i],
'Signal_1000_400': [i for i in list_basedir if 'Signal_1000_400' in i and yearTag in i],
'Signal_400_100': [i for i in list_basedir if 'Signal_400_100' in i and yearTag in i],
'Signal_500_100': [i for i in list_basedir if 'Signal_500_100' in i and yearTag in i],
'Signal_500_200': [i for i in list_basedir if 'Signal_500_200' in i and yearTag in i],
'Signal_600_100': [i for i in list_basedir if 'Signal_600_100' in i and yearTag in i],
'Signal_800_200': [i for i in list_basedir if 'Signal_800_200' in i and yearTag in i],
#'DYJetsToLL_M-10to50': [i for i in list_basedir if 'DYJetsToLL_M-10to50' in i and yearTag in i],
'DYJetsToLL_M-50': [i for i in list_basedir if 'DYJetsToLL_M-50' in i and yearTag in i],
#'DYJetsToLL_M-50_HT-70to100': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-70to100' in i and yearTag in i],
'DYJetsToLL_M-50_HT-100to200': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-100to200' in i and yearTag in i],
'DYJetsToLL_M-50_HT-200to400': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-200to400' in i and yearTag in i],
'DYJetsToLL_M-50_HT-400to600': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-400to600' in i and yearTag in i],
'DYJetsToLL_M-50_HT-600to800': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-600to800' in i and yearTag in i],
'DYJetsToLL_M-50_HT-800to1200': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-800to1200' in i and yearTag in i],
'DYJetsToLL_M-50_HT-1200to2500':[i for i in list_basedir if 'DYJetsToLL_M-50_HT-1200to2500' in i and yearTag in i],
'DYJetsToLL_M-50_HT-2500toInf': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-2500toInf' in i and yearTag in i],
'TTTo2L2Nu': [i for i in list_basedir if 'TTTo2L2Nu' in i and yearTag in i],
'TTToSemiLeptonic': [i for i in list_basedir if 'TTToSemiLeptonic' in i and yearTag in i],
'ST_tW_top': [i for i in list_basedir if 'ST_tW_top' in i and yearTag in i],
'ST_tW_antitop': [i for i in list_basedir if 'ST_tW_antitop' in i and yearTag in i],
#'ST_t-channel_top': [i for i in list_basedir if 'ST_t-channel_top' in i and yearTag in i],
#'ST_t-channel_antitop': [i for i in list_basedir if 'ST_t-channel_antitop' in i and yearTag in i],
#'ST_s-channel': [i for i in list_basedir if 'ST_s-channel' in i and yearTag in i],
'ZZ': [i for i in list_basedir if 'ZZ' == i.split("_")[0] and yearTag in i],
'WZ': [i for i in list_basedir if 'WZ' == i.split("_")[0] and yearTag in i],
'WW': [i for i in list_basedir if 'WW' == i.split("_")[0] and yearTag in i],
'WZZ': [i for i in list_basedir if 'WZZ' in i and yearTag in i],
'WWZ': [i for i in list_basedir if 'WWZ' in i and yearTag in i],
'ZZZ': [i for i in list_basedir if 'ZZZ' in i and yearTag in i],
'WWW': [i for i in list_basedir if 'WWW' in i and yearTag in i],
#'TTZToQQ': [i for i in list_basedir if 'TTZToQQ' in i and yearTag in i],
#'TTZToNuNu': [i for i in list_basedir if 'TTZToNuNu' in i and yearTag in i],
#'TWZToLL_thad_Wlept': [i for i in list_basedir if 'TWZToLL_thad_Wlept' in i and yearTag in i],
#'TWZToLL_tlept_Whad': [i for i in list_basedir if 'TWZToLL_tlept_Whad' in i and yearTag in i],
#'TWZToLL_tlept_Wlept': [i for i in list_basedir if 'TWZToLL_tlept_Wlept' in i and yearTag in i],
#'WGToLNuG': [i for i in list_basedir if 'WGToLNuG' in i and yearTag in i],
'ZGToLLG': [i for i in list_basedir if 'ZGToLLG' in i and yearTag in i],
#'WJetsToLNu': [i for i in list_basedir if 'WJetsToLNu' in i and yearTag in i],
'TTGJets': [i for i in list_basedir if 'TTGJets' in i and yearTag in i],
'TTGamma': [i for i in list_basedir if 'TTGamma' in i and yearTag in i],
#'TTWZ': [i for i in list_basedir if 'TTWZ' in i and yearTag in i],
#'TTZZ': [i for i in list_basedir if 'TTZZ' in i and yearTag in i],
'Data_B': [i for i in list_basedir if 'Data' in i and '_B_' in i and yearTag in i],
'Data_C': [i for i in list_basedir if 'Data' in i and '_C_' in i and yearTag in i],
'Data_D': [i for i in list_basedir if 'Data' in i and '_D_' in i and yearTag in i],
'Data_E': [i for i in list_basedir if 'Data' in i and '_E_' in i and yearTag in i],
'Data_F': [i for i in list_basedir if 'Data' in i and '_F_' in i and yearTag in i],
}
```
Check jobs integrity
----
```
Integrity_Jobs, Error_OldJobs, Error_Output = data.check_integrity(basedir, period, samples)
Integrity_Jobs = pd.DataFrame(Integrity_Jobs)
display(Integrity_Jobs)
print("")
print("====================================================================================================")
print("List of jobs that are not part of the jobs submitted: (remove them!)")
print(*Error_OldJobs, sep=' ')
print("====================================================================================================")
print("")
print("====================================================================================================")
print("List of jobs with error in the output:")
print(*Error_Output, sep=' ')
print("====================================================================================================")
print("")
```
Generate cutflow and files
----
```
data.generate_cutflow(basedir, period, samples)
data.generate_files(basedir, period, samples, format="parquet")
```
|
github_jupyter
|
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.gridspec as gs
import anatools.data as data
import anatools.analysis as ana
ana.start()
basedir = "/home/gcorreia/cernbox/HEP_Project/CMS_HHDM/OUTPUT/Test"
list_basedir = os.listdir(basedir)
TreeName = 'selection'
period = '17'
yearTag = period + "_files"
samples = {
'Signal_1000_100': [i for i in list_basedir if 'Signal_1000_100' in i and yearTag in i],
'Signal_1000_400': [i for i in list_basedir if 'Signal_1000_400' in i and yearTag in i],
'Signal_400_100': [i for i in list_basedir if 'Signal_400_100' in i and yearTag in i],
'Signal_500_100': [i for i in list_basedir if 'Signal_500_100' in i and yearTag in i],
'Signal_500_200': [i for i in list_basedir if 'Signal_500_200' in i and yearTag in i],
'Signal_600_100': [i for i in list_basedir if 'Signal_600_100' in i and yearTag in i],
'Signal_800_200': [i for i in list_basedir if 'Signal_800_200' in i and yearTag in i],
#'DYJetsToLL_M-10to50': [i for i in list_basedir if 'DYJetsToLL_M-10to50' in i and yearTag in i],
'DYJetsToLL_M-50': [i for i in list_basedir if 'DYJetsToLL_M-50' in i and yearTag in i],
#'DYJetsToLL_M-50_HT-70to100': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-70to100' in i and yearTag in i],
'DYJetsToLL_M-50_HT-100to200': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-100to200' in i and yearTag in i],
'DYJetsToLL_M-50_HT-200to400': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-200to400' in i and yearTag in i],
'DYJetsToLL_M-50_HT-400to600': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-400to600' in i and yearTag in i],
'DYJetsToLL_M-50_HT-600to800': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-600to800' in i and yearTag in i],
'DYJetsToLL_M-50_HT-800to1200': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-800to1200' in i and yearTag in i],
'DYJetsToLL_M-50_HT-1200to2500':[i for i in list_basedir if 'DYJetsToLL_M-50_HT-1200to2500' in i and yearTag in i],
'DYJetsToLL_M-50_HT-2500toInf': [i for i in list_basedir if 'DYJetsToLL_M-50_HT-2500toInf' in i and yearTag in i],
'TTTo2L2Nu': [i for i in list_basedir if 'TTTo2L2Nu' in i and yearTag in i],
'TTToSemiLeptonic': [i for i in list_basedir if 'TTToSemiLeptonic' in i and yearTag in i],
'ST_tW_top': [i for i in list_basedir if 'ST_tW_top' in i and yearTag in i],
'ST_tW_antitop': [i for i in list_basedir if 'ST_tW_antitop' in i and yearTag in i],
#'ST_t-channel_top': [i for i in list_basedir if 'ST_t-channel_top' in i and yearTag in i],
#'ST_t-channel_antitop': [i for i in list_basedir if 'ST_t-channel_antitop' in i and yearTag in i],
#'ST_s-channel': [i for i in list_basedir if 'ST_s-channel' in i and yearTag in i],
'ZZ': [i for i in list_basedir if 'ZZ' == i.split("_")[0] and yearTag in i],
'WZ': [i for i in list_basedir if 'WZ' == i.split("_")[0] and yearTag in i],
'WW': [i for i in list_basedir if 'WW' == i.split("_")[0] and yearTag in i],
'WZZ': [i for i in list_basedir if 'WZZ' in i and yearTag in i],
'WWZ': [i for i in list_basedir if 'WWZ' in i and yearTag in i],
'ZZZ': [i for i in list_basedir if 'ZZZ' in i and yearTag in i],
'WWW': [i for i in list_basedir if 'WWW' in i and yearTag in i],
#'TTZToQQ': [i for i in list_basedir if 'TTZToQQ' in i and yearTag in i],
#'TTZToNuNu': [i for i in list_basedir if 'TTZToNuNu' in i and yearTag in i],
#'TWZToLL_thad_Wlept': [i for i in list_basedir if 'TWZToLL_thad_Wlept' in i and yearTag in i],
#'TWZToLL_tlept_Whad': [i for i in list_basedir if 'TWZToLL_tlept_Whad' in i and yearTag in i],
#'TWZToLL_tlept_Wlept': [i for i in list_basedir if 'TWZToLL_tlept_Wlept' in i and yearTag in i],
#'WGToLNuG': [i for i in list_basedir if 'WGToLNuG' in i and yearTag in i],
'ZGToLLG': [i for i in list_basedir if 'ZGToLLG' in i and yearTag in i],
#'WJetsToLNu': [i for i in list_basedir if 'WJetsToLNu' in i and yearTag in i],
'TTGJets': [i for i in list_basedir if 'TTGJets' in i and yearTag in i],
'TTGamma': [i for i in list_basedir if 'TTGamma' in i and yearTag in i],
#'TTWZ': [i for i in list_basedir if 'TTWZ' in i and yearTag in i],
#'TTZZ': [i for i in list_basedir if 'TTZZ' in i and yearTag in i],
'Data_B': [i for i in list_basedir if 'Data' in i and '_B_' in i and yearTag in i],
'Data_C': [i for i in list_basedir if 'Data' in i and '_C_' in i and yearTag in i],
'Data_D': [i for i in list_basedir if 'Data' in i and '_D_' in i and yearTag in i],
'Data_E': [i for i in list_basedir if 'Data' in i and '_E_' in i and yearTag in i],
'Data_F': [i for i in list_basedir if 'Data' in i and '_F_' in i and yearTag in i],
}
Integrity_Jobs, Error_OldJobs, Error_Output = data.check_integrity(basedir, period, samples)
Integrity_Jobs = pd.DataFrame(Integrity_Jobs)
display(Integrity_Jobs)
print("")
print("====================================================================================================")
print("List of jobs that are not part of the jobs submitted: (remove them!)")
print(*Error_OldJobs, sep=' ')
print("====================================================================================================")
print("")
print("====================================================================================================")
print("List of jobs with error in the output:")
print(*Error_Output, sep=' ')
print("====================================================================================================")
print("")
data.generate_cutflow(basedir, period, samples)
data.generate_files(basedir, period, samples, format="parquet")
| 0.099399 | 0.6766 |
# Usage of Taylor Series
1. **Theoretical applications:** Often when we try to understand a too complex function, using Taylor series enables us to turn it into a polynomial that we can work with directly.
2. **Numerical applications:** Some functions like $e^x$ or $\cos(x)$ are difficult for machines to compute. They can store tables of values at a fixed precision (and this is often done), but it still leaves open questions like “What is the 1000-th digit of cos(1)?” Taylor series are often helpful to answer such questions.
# 泰勒(Taylor)中值定理 1 (佩亚诺(Peano)余项)
**[定理]** 如果函数$f(x)$在$x_0$处具有$n$阶导数, 那么存在$x_0$的一个领域,对于该领域内的任一$x$, 有:
\begin{equation}
f(x) = p_n(x) + R_n(x)
\label{eq:taylor_1}
\end{equation}
其中:
\begin{equation} \begin{aligned}
n次泰勒多项式: p_n(x) &= f(x_0) + f^{'}(x_0)(x-x_0) + \frac{f^{``}(x_0)}{2!}(x-x_0)^2 + \ldots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\
佩亚诺(Peano)余项: R_n(x) &= O((x-x_0)^n)
\end{aligned}\end{equation}
\begin{proof} Assume R_n(x) = f(x) - p_n(x), then
\begin{align}
R_n(x_0) = R^{'}_n(x_0) = R^{''}_n(x_0) = \ldots = R^{(n)}_n(x_0) = 0
\end{align}
\end{proof}
# 泰勒(Taylor)中值定理 2 (拉格朗日(Lagrange)余项)
**[定理]** 如果函数$f(x)$在$x_0$的某个邻域$U(x_0)$具有$n+1$阶导数,对于任一$x \in U(x_0)$, 有:
\begin{equation}
f(x) = p_n(x) + R_n(x)
\label{eq:taylor_2}
\end{equation}
其中:
\begin{equation} \begin{aligned}
多项式: p_n(x) &= f(x_0) + f^{'}(x_0)(x-x_0) + \frac{f^{``}(x_0)}{2!}(x-x_0)^2 + \ldots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\
拉格朗日余项: R_n(x) &= \frac{f^{n+1}(\xi)}{(n+1)!}(x-x_0)^{n + 1}
\end{aligned}\end{equation}
这里$\xi$是$x_0$与$x$之间的某一个值。
当$n=0$时, 泰勒公式变成拉格朗日中值公式:
\begin{equation}
f(x) = f(x_0) + f^{'}(x_0)(x-x_0) \; (\xi在x_0与x之间)
\end{equation}
在Taylor公式(\ref{eq:taylor_2})中, 是以多项式$p_n(x)$近似表达函数$f(x)$, 其误差为$|R_n(x)|$. 如果对于某一个固定的n, 当$x\in U(x_0)$时, $f^{(n+1)}(x) \leq M$, 那么有估计式:
\begin{equation}
|R_n(x)| = |\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}| \leq |\frac{M}{(n+1)!}(x-x_0)^{n+1}|
\label{eq:taylor_diff}
\end{equation}
# 麦克劳林(Maclaurin)公式
在Taylor公式(\ref{eq:taylor_1})中, 如果取$x_0=0$, 那么带有**佩亚诺余项**的麦克劳林(Maclaurin)公式:
\begin{equation}
f(x) = f(0) + f^{'}(0)(x) + \frac{f^{``}(0)}{2!}(x)^2 + \ldots + \frac{f^{(n)}(0)}{n!}(x)^n + O(x^n)
\label{eq:mac_taylor_0}
\end{equation}
在Taylor公式(\ref{eq:taylor_2})中, 如果取$x_0=0$, 那么$\xi \in (0, x)$, 因此$\xi=\theta x$ where $0<\theta<1$, 从而Taylor公式(\ref{eq:taylor_2})变成较简单的形式,即所谓带有**拉格朗日余项**的麦克劳林(Maclaurin)公式:
\begin{equation}
f(x) = f(0) + f^{'}(0)(x) + \frac{f^{``}(0)}{2!}(x)^2 + \ldots + \frac{f^{(n)}(0)}{n!}(x)^n + \frac{f^{(n+1)}(\theta x)}{(n+1)!}x^{n+1} \; where \; 0<\theta<1
\label{eq:lag_taylor_0}
\end{equation}
由公式\ref{eq:mac_taylor_0}或是\ref{eq:lag_taylor_0}, 可得近似公式:
\begin{equation}
f(x) = f(0) + f^{'}(0)(x) + \frac{f^{``}(0)}{2!}(x)^2 + \ldots + \frac{f^{(n)}(0)}{n!}(x)^n
\end{equation}
误差估计公式\ref{eq:taylor_diff}相应地变成
\begin{equation}
|R_n(x)| = \leq |\frac{M}{(n+1)!}(x)^{n+1}|
\label{eq:taylor_diff_updated}
\end{equation}
# Example
## 写出函数$f(x) = e^x$的带有拉格朗日余项的n阶麦克劳林公式
\begin{equation}\begin{aligned}
f^{'}(x) = f^{''}(x) = \ldots = f^{n}(x) = e^x \\
f^{'}(0) = f^{''}(0) = \ldots = f^{n}(0) = 1 \\
e^x = 1 + x + \frac{x^2}{2!} + \ldots + \frac{x^n}{n!} + \frac{e^{\theta x}}{(n+1)!} x^{n+1}
\end{aligned}\end{equation}
# 多元函数的泰勒(Taylor)展开式
## 一元函数在点$x_0$处的泰勒展开式为:
\begin{align}
\begin{split}
f(x) = {}& f(x_0) \;+ \frac{f^{'}(x_0)}{1!}(x-x_0) \;+ \frac{f^{''}(x_0)}{2!}(x-x_0)^2 \;+ & o^n
\end{split}\\
\end{align}
## 二元函数在点$x_0 = (x^1_0,x^2_0)$处的泰勒展开式为:
\begin{align}
\begin{split}
f(x^1, x^2) ={}& f(x^1_0, x^2_0) \;+ \\
& \frac{f^{'}_{x^1}(x^1_0, x^2_0)}{1!}(x^1-x^1_0) + \frac{f^{'}_{x^2}(x^1_0, x^2_0)}{1!}(x^2-x^2_0)\;+\\
& \frac{f^{''}_{x^1x^1}(x^1_0, x^2_0)}{2!}(x^1-x^1_0)^2 + \frac{f^{''}_{x^1x^2}(x^1_0, x^2_0)}{2!}(x^1-x^1_0)(x^2-x^2_0)\;+ \frac{f^{''}_{x^2x^1}(x^1_0, x^2_0)}{2!}(x^1-x^1_0)(x^2-x^2_0) + \frac{f^{''}_{x^2x^2}(x^1_0, x^2_0)}{2!}(x^2-x^2_0)^2\;+\\
& o^n
\end{split}\\
\end{align}
上面可能还有些抽象,下面给出二元函数泰勒展开的具体推导帮助理,用偏导函数表达:
\begin{align}
\begin{split}
f(x^1, x^2) = {}& f(x^1_0, x^2_0) \;+ \\
& \frac{\frac{\partial f}{\partial x^1}|_{x_0}}{1!}(x^1-x^1_0) + \frac{\frac{\partial f}{\partial x^2}|_{x_0}}{1!}(x^2-x^2_0)\;+\\
& \frac{\frac{\partial^2 f}{\partial x^1 \partial x^1}|_{x_0}}{2!}(x^1-x^1_0)^2 + \frac{\frac{\partial^2 f}{\partial x^1 \partial x^2}|_{x_0}}{2!}(x^1-x^1_0)(x^2-x^2_0)\;+ \frac{\frac{\partial^2 f}{\partial x^1 \partial x^1}|_{x_0}}{2!}(x^1-x^1_0)(x^2-x^2_0) + \frac{\frac{\partial^2 f}{\partial x^2 \partial x^2}|_{x_0}}{2!}(x^2-x^2_0)^2\;+ o^n \\
= {}& f(x^1_0, x^2_0) \;+ \\
& \frac{1}{1!}[\frac{\partial f}{\partial x^1}|_{x_0}(x^1-x^1_0) + \frac{\partial f}{\partial x^2}|_{x_0}(x^2-x^2_0)]\;+\\
& \frac{1}{2!}[ \frac{\partial^2 f}{\partial x^1 \partial x^1}|_{x_0}(x^1-x^1_0)^2 + 2\frac{\partial^2 f}{\partial x^1 \partial x^2}|_{x_0}(x^1-x^1_0)(x^2-x^2_0) + \frac{\partial^2 f}{\partial x^2 \partial x^2}|_{x_0}(x^2-x^2_0)^2\ ]\;+ o^n \\
= {}& f(x^1_0, x^2_0) \;+ \frac{1}{1!}\begin{pmatrix} \frac{\partial f}{\partial x^1} & \frac{\partial f}{\partial x^2} \end{pmatrix}_{x_0} \times \begin{pmatrix} x-x^1_0 \\ x-x^2_0 \end{pmatrix} + \frac{1}{2!} \times \begin{pmatrix} x-x^1_0 & x-x^2_0 \end{pmatrix} \times \begin{pmatrix} \frac{\partial^2 f}{\partial x^1 \partial x^1} & \frac{\partial^2 f}{\partial x^1 \partial x^2} \\ \frac{\partial^2 f}{\partial x^1 \partial x^2} & \frac{\partial^2 f}{\partial x^2 \partial x^2} \end{pmatrix}_{x_0} \times \begin{pmatrix} x-x^1_0 \\ x-x^2_0 \end{pmatrix} \;+ o^n
\end{split}
\end{align}
**把多变量情形下($x_0 = (x^1_0, x^2_0, \ldots, x^n_0)$)的aylor二阶的形式**
\begin{align}
f(x) = f(x_0) + [\nabla f(x_0)]^T(x-x_0) + \frac{1}{2!}[x-x_0]^T H^2(x_0) [x-x_0] + o^n
\end{align}
其中:
\begin{align}
H(x_0) = \begin{bmatrix}
\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_n}}\\
\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_n}}\\
\vdots & \vdots & \ddots &\vdots\\
\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_n}}\\
\end{bmatrix}
\end{align}
## 多元函数(n)在点$x_0 = (x^1_0, x^2_0, \ldots, x^n_0)$处的二阶泰勒展开式为:
\begin{align}
\begin{split}
f(x^1, x^2, \ldots, x^n) = {}& f(x^1_0, x^2_0, \ldots, x^n_0) \;+ \\
& \sum_{i=1}^{n}\frac{f^{'}_{x^i}(x^1_0, x^2_0, \ldots, x^n_0)}{1!}(x^i - x^i_0)\;+\\
& \sum_{i=1}^{n}\sum_{j=1}^{n}\frac{f^{''}_{x^ix^j}(x^1_0, x^2_0, \ldots, x^n_0)}{2!}(x^i - x^i_0)(x^j - x^j_0)\;+\\
& o^n
\end{split}\\
\end{align}
\begin{align}
\end{align}
## 多元函数(n)在点$x_0 = (x^1_0, x^2_0, \ldots, x^n_0)$处的二阶泰勒展开式为(矩阵的形式)
\begin{align}
f(x) = f(x_0) + [\nabla f(x_0)]^T(x-x_0) + \frac{1}{2!}[x-x_0]^T H(x_0) [x-x_0] + o^n
\end{align}
其中黑塞矩阵(Hessian Matrix, $H(x_0)$)为
\begin{align}
H(x_0) = \begin{bmatrix}
\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_n}}\\
\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_n}}\\
\vdots & \vdots & \ddots &\vdots\\
\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_n}}\\
\end{bmatrix}
\end{align}
# 黑塞矩阵(Hessian Matrix)
其中黑塞矩阵(Hessian Matrix, $H(x_0)$)是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。黑塞矩阵常用于牛顿法解决优化问题,利用黑塞矩阵可判定多元函数的极值问题。在工程实际问题的优化设计中,所列的目标函数往往很复杂,为了使问题简化,常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵. 对于一个多元函数$f(x^1, x^2, \ldots, x^n)$, 如果函数$f$的二阶偏导数,由定义$f$的黑塞矩阵为:
\begin{align}
H_{i,j}(x) = D_iD_jf(x)
\end{align}
其中$D_i$表示对第$i$个变量微分算子, $x=(x^1, x^2, \ldots, x^n)$. 那么, $f$的黑塞矩阵为
\begin{align}
H(x_0) = \begin{bmatrix}
\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_n}}\\
\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_n}}\\
\vdots & \vdots & \ddots &\vdots\\
\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_n}}\\
\end{bmatrix}
\end{align}
\begin{align}
f(x) = f(x_0) + [\nabla f(x_0)]^T(x-x_0) + \frac{1}{2!}[x-x_0]^T H(x_0) [x-x_0] + o^n
\end{align}
**对称性**
如果函数$f$在$D$区域内二阶连续可导, 那么$f$黑塞矩阵$H(f)$在D内对称矩阵。 原因是:如果函数$f$的二阶偏导连续,则二阶偏导数的求导顺序没有区别, 即:
\begin{equation}
\frac{\partial}{\partial x}(\frac{\partial f}{\partial y}) = \frac{\partial}{\partial y}(\frac{\partial f}{\partial x})
\end{equation}
则对于矩阵$H(f)$, 则$H_{i,j}(f) = H_{j,i}(f)$, 所以$H(f)$为对称矩阵。
\begin{equation}
\frac{d^2 f}{dx_i dx_j} = \frac{d^2 f}{dx_j dx_i}
\end{equation}
This follows by considering first perturbing a function in the direction of $x_i$, and then perturbing it in $x_j$ and then comparing the result of that with what happens if we perturb first $x_j$ and then $x_i$, with the knowledge that both of these orders lead to the same final change in the output of f.
**多元函数极值的判定**
如果实值多元函数$f(x^1, x^2, \ldots, x^n)$二阶连续可导,并且在临界点$M(x_i)$(其中$i=1,2,\ldots,n$, 并且$x_i$已知)处梯度(一阶导数)等于0, 即$\nabla f(M) = 0$, $M$为驻点。 仅通过一阶导数无法判断临界点$M$处是极大值或是极小值。
记$f$在$M$点处的黑塞矩阵$H(M)$, 由于$f$在$M$点连续,所以$H(M)$是一个$n \times n$的对称矩阵。对于$M(M)$,有如下结论:
1. 如果$H(M)$是正定矩阵, 则临界点$M$处是一个局部的极小值
2. 如果$H(M)$是负定矩阵, 则临界点$M$处是一个局部的极大值
3. 如果$H(M)$是不定矩阵, 则临界点$M$处不是极值
Hessian Matrix,它有着广泛的应用,如在牛顿方法、求极值以及边缘检测、消除边缘响应等方面的应用,图像处理里,可以抽取图像特征,在金融里可以用来作量化分析。
1. [用Hessian矩阵提出图片的关键特征](https://blog.csdn.net/jia20003/article/details/16874237)
2. [用Hessian矩阵进行量化分析](http://ookiddy.iteye.com/blog/2204127)
3. [边缘检测以及边缘响应消除](https://blog.csdn.net/lwzkiller/article/details/55050275)
既然检测到的对应点确认为边缘点,那么我们就有理由消除这个边缘点,所以边缘检测与边缘响应消除的应用是一回事。边缘到底有什么特征呢?如下图所示,一个二维平面上的一条直线,图像的特征具体可以描述为:沿着直线方向,亮度变化极小,垂直于直线方向,亮度由暗变亮,再由亮变暗,沿着这个方向,亮度变化很大。我们可以将边缘图像分布特征与二次型函数图形进行类比,是不是发现很相似,我们可以找到两个方向,一个方向图像梯度变化最慢,另一个方向图像梯度变化最快。那么图像中的边缘特征就与二次型函数的图像对应起来了,其实二次型函数中的hessian矩阵,也是通过对二次型函数进行二阶偏导得到的(可以自己求偏导测试下),这就是我们为什么可以使用hessian矩阵来对边缘进行检测以及进行边缘响应消除,我想大家应该明白其中的缘由了。还是那句话,数学模型其实就是一种反映图像特征的模型。
所以Hessian matrix实际上就是多变量情形下的二阶导数,他描述了各方向上灰度梯度变化,这句话应该很好理解了吧。我们在使用对应点的hessian矩阵求取的特征向量以及对应的特征值,较大特征值所对应的特征向量是垂直于直线的,较小特征值对应的特征向量是沿着直线方向的。对于SIFT算法中的边缘响应的消除可以根据hessian矩阵进行判定。
## Example of f(x_1, x_2)
Suppose that $y = f(x_1, x_2) = a + b_1x_1 + b_2x_2 + c_{11}x^2_1 + c_{12}x_1x_2 + c_{22}x^2_2$
\begin{equation}
f(0, 0) = 0 \\
\nabla f(0, 0) = \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} \\
Hf(0, 0) = \begin{bmatrix} 2c_{11} & c_{12} \\ c_{12} & 2c_{22} \end{bmatrix}
\end{equation}
we can get our original polynomial back by saying
\begin{align}
f(x) = f(x_0) + [\nabla f(x_0)]^T(x-x_0) + \frac{1}{2!}[x-x_0]^T H(x_0) [x-x_0] + o^n
\end{align}
|
github_jupyter
|
# Usage of Taylor Series
1. **Theoretical applications:** Often when we try to understand a too complex function, using Taylor series enables us to turn it into a polynomial that we can work with directly.
2. **Numerical applications:** Some functions like $e^x$ or $\cos(x)$ are difficult for machines to compute. They can store tables of values at a fixed precision (and this is often done), but it still leaves open questions like “What is the 1000-th digit of cos(1)?” Taylor series are often helpful to answer such questions.
# 泰勒(Taylor)中值定理 1 (佩亚诺(Peano)余项)
**[定理]** 如果函数$f(x)$在$x_0$处具有$n$阶导数, 那么存在$x_0$的一个领域,对于该领域内的任一$x$, 有:
\begin{equation}
f(x) = p_n(x) + R_n(x)
\label{eq:taylor_1}
\end{equation}
其中:
\begin{equation} \begin{aligned}
n次泰勒多项式: p_n(x) &= f(x_0) + f^{'}(x_0)(x-x_0) + \frac{f^{``}(x_0)}{2!}(x-x_0)^2 + \ldots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\
佩亚诺(Peano)余项: R_n(x) &= O((x-x_0)^n)
\end{aligned}\end{equation}
\begin{proof} Assume R_n(x) = f(x) - p_n(x), then
\begin{align}
R_n(x_0) = R^{'}_n(x_0) = R^{''}_n(x_0) = \ldots = R^{(n)}_n(x_0) = 0
\end{align}
\end{proof}
# 泰勒(Taylor)中值定理 2 (拉格朗日(Lagrange)余项)
**[定理]** 如果函数$f(x)$在$x_0$的某个邻域$U(x_0)$具有$n+1$阶导数,对于任一$x \in U(x_0)$, 有:
\begin{equation}
f(x) = p_n(x) + R_n(x)
\label{eq:taylor_2}
\end{equation}
其中:
\begin{equation} \begin{aligned}
多项式: p_n(x) &= f(x_0) + f^{'}(x_0)(x-x_0) + \frac{f^{``}(x_0)}{2!}(x-x_0)^2 + \ldots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\
拉格朗日余项: R_n(x) &= \frac{f^{n+1}(\xi)}{(n+1)!}(x-x_0)^{n + 1}
\end{aligned}\end{equation}
这里$\xi$是$x_0$与$x$之间的某一个值。
当$n=0$时, 泰勒公式变成拉格朗日中值公式:
\begin{equation}
f(x) = f(x_0) + f^{'}(x_0)(x-x_0) \; (\xi在x_0与x之间)
\end{equation}
在Taylor公式(\ref{eq:taylor_2})中, 是以多项式$p_n(x)$近似表达函数$f(x)$, 其误差为$|R_n(x)|$. 如果对于某一个固定的n, 当$x\in U(x_0)$时, $f^{(n+1)}(x) \leq M$, 那么有估计式:
\begin{equation}
|R_n(x)| = |\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}| \leq |\frac{M}{(n+1)!}(x-x_0)^{n+1}|
\label{eq:taylor_diff}
\end{equation}
# 麦克劳林(Maclaurin)公式
在Taylor公式(\ref{eq:taylor_1})中, 如果取$x_0=0$, 那么带有**佩亚诺余项**的麦克劳林(Maclaurin)公式:
\begin{equation}
f(x) = f(0) + f^{'}(0)(x) + \frac{f^{``}(0)}{2!}(x)^2 + \ldots + \frac{f^{(n)}(0)}{n!}(x)^n + O(x^n)
\label{eq:mac_taylor_0}
\end{equation}
在Taylor公式(\ref{eq:taylor_2})中, 如果取$x_0=0$, 那么$\xi \in (0, x)$, 因此$\xi=\theta x$ where $0<\theta<1$, 从而Taylor公式(\ref{eq:taylor_2})变成较简单的形式,即所谓带有**拉格朗日余项**的麦克劳林(Maclaurin)公式:
\begin{equation}
f(x) = f(0) + f^{'}(0)(x) + \frac{f^{``}(0)}{2!}(x)^2 + \ldots + \frac{f^{(n)}(0)}{n!}(x)^n + \frac{f^{(n+1)}(\theta x)}{(n+1)!}x^{n+1} \; where \; 0<\theta<1
\label{eq:lag_taylor_0}
\end{equation}
由公式\ref{eq:mac_taylor_0}或是\ref{eq:lag_taylor_0}, 可得近似公式:
\begin{equation}
f(x) = f(0) + f^{'}(0)(x) + \frac{f^{``}(0)}{2!}(x)^2 + \ldots + \frac{f^{(n)}(0)}{n!}(x)^n
\end{equation}
误差估计公式\ref{eq:taylor_diff}相应地变成
\begin{equation}
|R_n(x)| = \leq |\frac{M}{(n+1)!}(x)^{n+1}|
\label{eq:taylor_diff_updated}
\end{equation}
# Example
## 写出函数$f(x) = e^x$的带有拉格朗日余项的n阶麦克劳林公式
\begin{equation}\begin{aligned}
f^{'}(x) = f^{''}(x) = \ldots = f^{n}(x) = e^x \\
f^{'}(0) = f^{''}(0) = \ldots = f^{n}(0) = 1 \\
e^x = 1 + x + \frac{x^2}{2!} + \ldots + \frac{x^n}{n!} + \frac{e^{\theta x}}{(n+1)!} x^{n+1}
\end{aligned}\end{equation}
# 多元函数的泰勒(Taylor)展开式
## 一元函数在点$x_0$处的泰勒展开式为:
\begin{align}
\begin{split}
f(x) = {}& f(x_0) \;+ \frac{f^{'}(x_0)}{1!}(x-x_0) \;+ \frac{f^{''}(x_0)}{2!}(x-x_0)^2 \;+ & o^n
\end{split}\\
\end{align}
## 二元函数在点$x_0 = (x^1_0,x^2_0)$处的泰勒展开式为:
\begin{align}
\begin{split}
f(x^1, x^2) ={}& f(x^1_0, x^2_0) \;+ \\
& \frac{f^{'}_{x^1}(x^1_0, x^2_0)}{1!}(x^1-x^1_0) + \frac{f^{'}_{x^2}(x^1_0, x^2_0)}{1!}(x^2-x^2_0)\;+\\
& \frac{f^{''}_{x^1x^1}(x^1_0, x^2_0)}{2!}(x^1-x^1_0)^2 + \frac{f^{''}_{x^1x^2}(x^1_0, x^2_0)}{2!}(x^1-x^1_0)(x^2-x^2_0)\;+ \frac{f^{''}_{x^2x^1}(x^1_0, x^2_0)}{2!}(x^1-x^1_0)(x^2-x^2_0) + \frac{f^{''}_{x^2x^2}(x^1_0, x^2_0)}{2!}(x^2-x^2_0)^2\;+\\
& o^n
\end{split}\\
\end{align}
上面可能还有些抽象,下面给出二元函数泰勒展开的具体推导帮助理,用偏导函数表达:
\begin{align}
\begin{split}
f(x^1, x^2) = {}& f(x^1_0, x^2_0) \;+ \\
& \frac{\frac{\partial f}{\partial x^1}|_{x_0}}{1!}(x^1-x^1_0) + \frac{\frac{\partial f}{\partial x^2}|_{x_0}}{1!}(x^2-x^2_0)\;+\\
& \frac{\frac{\partial^2 f}{\partial x^1 \partial x^1}|_{x_0}}{2!}(x^1-x^1_0)^2 + \frac{\frac{\partial^2 f}{\partial x^1 \partial x^2}|_{x_0}}{2!}(x^1-x^1_0)(x^2-x^2_0)\;+ \frac{\frac{\partial^2 f}{\partial x^1 \partial x^1}|_{x_0}}{2!}(x^1-x^1_0)(x^2-x^2_0) + \frac{\frac{\partial^2 f}{\partial x^2 \partial x^2}|_{x_0}}{2!}(x^2-x^2_0)^2\;+ o^n \\
= {}& f(x^1_0, x^2_0) \;+ \\
& \frac{1}{1!}[\frac{\partial f}{\partial x^1}|_{x_0}(x^1-x^1_0) + \frac{\partial f}{\partial x^2}|_{x_0}(x^2-x^2_0)]\;+\\
& \frac{1}{2!}[ \frac{\partial^2 f}{\partial x^1 \partial x^1}|_{x_0}(x^1-x^1_0)^2 + 2\frac{\partial^2 f}{\partial x^1 \partial x^2}|_{x_0}(x^1-x^1_0)(x^2-x^2_0) + \frac{\partial^2 f}{\partial x^2 \partial x^2}|_{x_0}(x^2-x^2_0)^2\ ]\;+ o^n \\
= {}& f(x^1_0, x^2_0) \;+ \frac{1}{1!}\begin{pmatrix} \frac{\partial f}{\partial x^1} & \frac{\partial f}{\partial x^2} \end{pmatrix}_{x_0} \times \begin{pmatrix} x-x^1_0 \\ x-x^2_0 \end{pmatrix} + \frac{1}{2!} \times \begin{pmatrix} x-x^1_0 & x-x^2_0 \end{pmatrix} \times \begin{pmatrix} \frac{\partial^2 f}{\partial x^1 \partial x^1} & \frac{\partial^2 f}{\partial x^1 \partial x^2} \\ \frac{\partial^2 f}{\partial x^1 \partial x^2} & \frac{\partial^2 f}{\partial x^2 \partial x^2} \end{pmatrix}_{x_0} \times \begin{pmatrix} x-x^1_0 \\ x-x^2_0 \end{pmatrix} \;+ o^n
\end{split}
\end{align}
**把多变量情形下($x_0 = (x^1_0, x^2_0, \ldots, x^n_0)$)的aylor二阶的形式**
\begin{align}
f(x) = f(x_0) + [\nabla f(x_0)]^T(x-x_0) + \frac{1}{2!}[x-x_0]^T H^2(x_0) [x-x_0] + o^n
\end{align}
其中:
\begin{align}
H(x_0) = \begin{bmatrix}
\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_n}}\\
\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_n}}\\
\vdots & \vdots & \ddots &\vdots\\
\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_n}}\\
\end{bmatrix}
\end{align}
## 多元函数(n)在点$x_0 = (x^1_0, x^2_0, \ldots, x^n_0)$处的二阶泰勒展开式为:
\begin{align}
\begin{split}
f(x^1, x^2, \ldots, x^n) = {}& f(x^1_0, x^2_0, \ldots, x^n_0) \;+ \\
& \sum_{i=1}^{n}\frac{f^{'}_{x^i}(x^1_0, x^2_0, \ldots, x^n_0)}{1!}(x^i - x^i_0)\;+\\
& \sum_{i=1}^{n}\sum_{j=1}^{n}\frac{f^{''}_{x^ix^j}(x^1_0, x^2_0, \ldots, x^n_0)}{2!}(x^i - x^i_0)(x^j - x^j_0)\;+\\
& o^n
\end{split}\\
\end{align}
\begin{align}
\end{align}
## 多元函数(n)在点$x_0 = (x^1_0, x^2_0, \ldots, x^n_0)$处的二阶泰勒展开式为(矩阵的形式)
\begin{align}
f(x) = f(x_0) + [\nabla f(x_0)]^T(x-x_0) + \frac{1}{2!}[x-x_0]^T H(x_0) [x-x_0] + o^n
\end{align}
其中黑塞矩阵(Hessian Matrix, $H(x_0)$)为
\begin{align}
H(x_0) = \begin{bmatrix}
\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_n}}\\
\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_n}}\\
\vdots & \vdots & \ddots &\vdots\\
\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_n}}\\
\end{bmatrix}
\end{align}
# 黑塞矩阵(Hessian Matrix)
其中黑塞矩阵(Hessian Matrix, $H(x_0)$)是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。黑塞矩阵常用于牛顿法解决优化问题,利用黑塞矩阵可判定多元函数的极值问题。在工程实际问题的优化设计中,所列的目标函数往往很复杂,为了使问题简化,常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵. 对于一个多元函数$f(x^1, x^2, \ldots, x^n)$, 如果函数$f$的二阶偏导数,由定义$f$的黑塞矩阵为:
\begin{align}
H_{i,j}(x) = D_iD_jf(x)
\end{align}
其中$D_i$表示对第$i$个变量微分算子, $x=(x^1, x^2, \ldots, x^n)$. 那么, $f$的黑塞矩阵为
\begin{align}
H(x_0) = \begin{bmatrix}
\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_1}\partial_{x_n}}\\
\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_2}\partial_{x_n}}\\
\vdots & \vdots & \ddots &\vdots\\
\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_1}} & \frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_2}} & \ldots &\frac{\partial^2f(x_0)}{\partial_{x_n}\partial_{x_n}}\\
\end{bmatrix}
\end{align}
\begin{align}
f(x) = f(x_0) + [\nabla f(x_0)]^T(x-x_0) + \frac{1}{2!}[x-x_0]^T H(x_0) [x-x_0] + o^n
\end{align}
**对称性**
如果函数$f$在$D$区域内二阶连续可导, 那么$f$黑塞矩阵$H(f)$在D内对称矩阵。 原因是:如果函数$f$的二阶偏导连续,则二阶偏导数的求导顺序没有区别, 即:
\begin{equation}
\frac{\partial}{\partial x}(\frac{\partial f}{\partial y}) = \frac{\partial}{\partial y}(\frac{\partial f}{\partial x})
\end{equation}
则对于矩阵$H(f)$, 则$H_{i,j}(f) = H_{j,i}(f)$, 所以$H(f)$为对称矩阵。
\begin{equation}
\frac{d^2 f}{dx_i dx_j} = \frac{d^2 f}{dx_j dx_i}
\end{equation}
This follows by considering first perturbing a function in the direction of $x_i$, and then perturbing it in $x_j$ and then comparing the result of that with what happens if we perturb first $x_j$ and then $x_i$, with the knowledge that both of these orders lead to the same final change in the output of f.
**多元函数极值的判定**
如果实值多元函数$f(x^1, x^2, \ldots, x^n)$二阶连续可导,并且在临界点$M(x_i)$(其中$i=1,2,\ldots,n$, 并且$x_i$已知)处梯度(一阶导数)等于0, 即$\nabla f(M) = 0$, $M$为驻点。 仅通过一阶导数无法判断临界点$M$处是极大值或是极小值。
记$f$在$M$点处的黑塞矩阵$H(M)$, 由于$f$在$M$点连续,所以$H(M)$是一个$n \times n$的对称矩阵。对于$M(M)$,有如下结论:
1. 如果$H(M)$是正定矩阵, 则临界点$M$处是一个局部的极小值
2. 如果$H(M)$是负定矩阵, 则临界点$M$处是一个局部的极大值
3. 如果$H(M)$是不定矩阵, 则临界点$M$处不是极值
Hessian Matrix,它有着广泛的应用,如在牛顿方法、求极值以及边缘检测、消除边缘响应等方面的应用,图像处理里,可以抽取图像特征,在金融里可以用来作量化分析。
1. [用Hessian矩阵提出图片的关键特征](https://blog.csdn.net/jia20003/article/details/16874237)
2. [用Hessian矩阵进行量化分析](http://ookiddy.iteye.com/blog/2204127)
3. [边缘检测以及边缘响应消除](https://blog.csdn.net/lwzkiller/article/details/55050275)
既然检测到的对应点确认为边缘点,那么我们就有理由消除这个边缘点,所以边缘检测与边缘响应消除的应用是一回事。边缘到底有什么特征呢?如下图所示,一个二维平面上的一条直线,图像的特征具体可以描述为:沿着直线方向,亮度变化极小,垂直于直线方向,亮度由暗变亮,再由亮变暗,沿着这个方向,亮度变化很大。我们可以将边缘图像分布特征与二次型函数图形进行类比,是不是发现很相似,我们可以找到两个方向,一个方向图像梯度变化最慢,另一个方向图像梯度变化最快。那么图像中的边缘特征就与二次型函数的图像对应起来了,其实二次型函数中的hessian矩阵,也是通过对二次型函数进行二阶偏导得到的(可以自己求偏导测试下),这就是我们为什么可以使用hessian矩阵来对边缘进行检测以及进行边缘响应消除,我想大家应该明白其中的缘由了。还是那句话,数学模型其实就是一种反映图像特征的模型。
所以Hessian matrix实际上就是多变量情形下的二阶导数,他描述了各方向上灰度梯度变化,这句话应该很好理解了吧。我们在使用对应点的hessian矩阵求取的特征向量以及对应的特征值,较大特征值所对应的特征向量是垂直于直线的,较小特征值对应的特征向量是沿着直线方向的。对于SIFT算法中的边缘响应的消除可以根据hessian矩阵进行判定。
## Example of f(x_1, x_2)
Suppose that $y = f(x_1, x_2) = a + b_1x_1 + b_2x_2 + c_{11}x^2_1 + c_{12}x_1x_2 + c_{22}x^2_2$
\begin{equation}
f(0, 0) = 0 \\
\nabla f(0, 0) = \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} \\
Hf(0, 0) = \begin{bmatrix} 2c_{11} & c_{12} \\ c_{12} & 2c_{22} \end{bmatrix}
\end{equation}
we can get our original polynomial back by saying
\begin{align}
f(x) = f(x_0) + [\nabla f(x_0)]^T(x-x_0) + \frac{1}{2!}[x-x_0]^T H(x_0) [x-x_0] + o^n
\end{align}
| 0.595022 | 0.943971 |
<a href="https://colab.research.google.com/github/Mimansa-Negi/PYTHON1/blob/main/Untitled2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
QUEUE-SIMPLE
```
class Queue:
def __init__(self):
self.queue=[]
def enqueue(self,item):
return self.queue.append(item)
def dequeue(self):
if len(self.queue)<1:
return None
return self.queue.pop(0)
def display(self):
print(self.queue)
def size(self):
return len(self.queue)
q=Queue()
q.enqueue(90)
q.enqueue(89)
q.enqueue(88)
q.display()
q.dequeue()
q.display()
```
CIRCULAR QUEUE:
```
class MyCirQueue:
def __init__(self,k):
self.k=k
self.queue=[None]*k
self.head=self.tail=-1
def enqueue(self,item):
if(self.tail+1)%self.k==self.head:
print("The queue is full")
elif(self.head==-1):
self.head=0
self.tail=0
self.queue[self.tail]=item
else:
self.tail=(self.tail+1)%self.k
self.queue[self.tail]=item
def dequeue(self):
if(self.head==-1):
print("queue is empty")
elif(self.head==self.tail):
temp=self.queue[self.head]
self.head=-1
self.tail=-1
return temp
else:
temp=self.queue[self.head]
self.head=(self.head+1)%self.k
return temp
def display(self):
if(self.head==-1):
print("nothing to display")
elif(self.tail>=self.head):
for i in range(self.head,self.tail+1):
print(self.queue[i],end=" ")
print()
else:
for i in range(self.head,self.k):
print(self.queue[i],end=" ")
for i in range(0,self.tail+1):
print(self.queue[i],end=" ")
print()
q=MyCirQueue(6)
q.enqueue(1)
q.enqueue(2)
q.enqueue(89)
q.enqueue(90)
q.enqueue(91)
q.enqueue(92)
q.display()
q.dequeue()
q.display()
```
STACK
```
def create_stack():
stack=[]
return stack
def check_empty(stack):
return len(stack)==0
def push(stack,item):
stack.append(item)
print(item)
def pop(stack):
if (check_empty(stack)):
return "stackisempty"
return stack.pop()
stack=create_stack()
push(stack,str(1))
push(stack,str(2))
```
CREATING A DOUBLE LINKED LIST
```
class Node:
def __init__(self,data):
self.data=data
self.prev=None
self.next=None
class DLL:
def __init__(self):
self.head=None
def display(self):
if self.head is None:
print("empty")
else:
temp=self.head
while temp:
print(temp.data,"-->",end="")
temp=temp.next
l=DLL()
l.display()
n1=Node(10)
l.head=n1
n2=Node(20)
n2.prev=n1
n1.next=n2
n3=Node(30)
n3.prev=n2
n2.next=n3
l.display()
```
DOUBLE LINKED LIST INSERTION
```
class Node:
def __init__(self,data):
self.data=data
self.prev=None
self.next=None
class DLL:
def __init__(self):
self.head=None
def display(self):
if self.head is None:
print("empty")
else:
temp=self.head
while temp:
print(temp.data,"-->",end="")
temp=temp.next
def insert_beginning(self,data):
n=Node(5)
temp=self.head
temp.prev=n
n.next=temp
self.head=n
l=DLL()
l.display()
n1=Node(10)
l.head=n1
n2=Node(20)
n2.prev=n1
n1.next=n2
n3=Node(30)
n3.prev=n2
n2.next=n3
l.display()
l.insert_beginning(20)
l.display
```
INSERTION AND DELETION OPERATIONS ON DOUBLED LINKED LIST
```
class Node:
def __init__(self,data):
self.data=data
self.head=None
self.next=None
class DLL:
def display(self):
if self.head is None:
print("Empty list")
else:
temp=self.head
while temp:
print(temp.data,"-->",end=" ")
temp=temp.next
def insert_At_Beg(self,data):
n=Node(5)
temp=self.head
temp.prev=n
n.next=temp
self.head=n
def insert_At_last(self,data):
n=Node(78)
temp=self.head
while temp.next is not None:
temp=temp.next
temp.next=n
n.prev=temp
def insert_At_pos(self,pos):
n=Node(31)
temp=self.head
for i in range(1,pos-1):
temp=temp.next
n.prev=temp
n.next=temp.next
temp.next.prev=n
temp.next=n
def del_At_begg(self):
temp=self.head
self.head=temp.next
temp.next=None
self.head.prev=None
def del_At_last(self):
temp=self.head.next
before=self.head
while temp.next is not None:
temp=temp.next
before=before.next
before.next=None
temp.prev=None
def del_At_pos(self,pos):
temp=self.head.next
before=self.head
for i in range(1,pos-1):
temp=temp.next
before=before.next
before.next=temp.next
temp.next.prev=before
temp.prev=None
temp.next=None
l=DLL()
n1=Node(19)
l.head=n1
n2=Node(67)
n1.next=n2
n2.prev=n1
n3=Node(30)
n2.next=n3
n3.prev=n2
l.insert_At_pos(2)
l.insert_At_pos(3)
l.del_At_begg()
l.del_At_pos(2)
l.display()
```
|
github_jupyter
|
class Queue:
def __init__(self):
self.queue=[]
def enqueue(self,item):
return self.queue.append(item)
def dequeue(self):
if len(self.queue)<1:
return None
return self.queue.pop(0)
def display(self):
print(self.queue)
def size(self):
return len(self.queue)
q=Queue()
q.enqueue(90)
q.enqueue(89)
q.enqueue(88)
q.display()
q.dequeue()
q.display()
class MyCirQueue:
def __init__(self,k):
self.k=k
self.queue=[None]*k
self.head=self.tail=-1
def enqueue(self,item):
if(self.tail+1)%self.k==self.head:
print("The queue is full")
elif(self.head==-1):
self.head=0
self.tail=0
self.queue[self.tail]=item
else:
self.tail=(self.tail+1)%self.k
self.queue[self.tail]=item
def dequeue(self):
if(self.head==-1):
print("queue is empty")
elif(self.head==self.tail):
temp=self.queue[self.head]
self.head=-1
self.tail=-1
return temp
else:
temp=self.queue[self.head]
self.head=(self.head+1)%self.k
return temp
def display(self):
if(self.head==-1):
print("nothing to display")
elif(self.tail>=self.head):
for i in range(self.head,self.tail+1):
print(self.queue[i],end=" ")
print()
else:
for i in range(self.head,self.k):
print(self.queue[i],end=" ")
for i in range(0,self.tail+1):
print(self.queue[i],end=" ")
print()
q=MyCirQueue(6)
q.enqueue(1)
q.enqueue(2)
q.enqueue(89)
q.enqueue(90)
q.enqueue(91)
q.enqueue(92)
q.display()
q.dequeue()
q.display()
def create_stack():
stack=[]
return stack
def check_empty(stack):
return len(stack)==0
def push(stack,item):
stack.append(item)
print(item)
def pop(stack):
if (check_empty(stack)):
return "stackisempty"
return stack.pop()
stack=create_stack()
push(stack,str(1))
push(stack,str(2))
class Node:
def __init__(self,data):
self.data=data
self.prev=None
self.next=None
class DLL:
def __init__(self):
self.head=None
def display(self):
if self.head is None:
print("empty")
else:
temp=self.head
while temp:
print(temp.data,"-->",end="")
temp=temp.next
l=DLL()
l.display()
n1=Node(10)
l.head=n1
n2=Node(20)
n2.prev=n1
n1.next=n2
n3=Node(30)
n3.prev=n2
n2.next=n3
l.display()
class Node:
def __init__(self,data):
self.data=data
self.prev=None
self.next=None
class DLL:
def __init__(self):
self.head=None
def display(self):
if self.head is None:
print("empty")
else:
temp=self.head
while temp:
print(temp.data,"-->",end="")
temp=temp.next
def insert_beginning(self,data):
n=Node(5)
temp=self.head
temp.prev=n
n.next=temp
self.head=n
l=DLL()
l.display()
n1=Node(10)
l.head=n1
n2=Node(20)
n2.prev=n1
n1.next=n2
n3=Node(30)
n3.prev=n2
n2.next=n3
l.display()
l.insert_beginning(20)
l.display
class Node:
def __init__(self,data):
self.data=data
self.head=None
self.next=None
class DLL:
def display(self):
if self.head is None:
print("Empty list")
else:
temp=self.head
while temp:
print(temp.data,"-->",end=" ")
temp=temp.next
def insert_At_Beg(self,data):
n=Node(5)
temp=self.head
temp.prev=n
n.next=temp
self.head=n
def insert_At_last(self,data):
n=Node(78)
temp=self.head
while temp.next is not None:
temp=temp.next
temp.next=n
n.prev=temp
def insert_At_pos(self,pos):
n=Node(31)
temp=self.head
for i in range(1,pos-1):
temp=temp.next
n.prev=temp
n.next=temp.next
temp.next.prev=n
temp.next=n
def del_At_begg(self):
temp=self.head
self.head=temp.next
temp.next=None
self.head.prev=None
def del_At_last(self):
temp=self.head.next
before=self.head
while temp.next is not None:
temp=temp.next
before=before.next
before.next=None
temp.prev=None
def del_At_pos(self,pos):
temp=self.head.next
before=self.head
for i in range(1,pos-1):
temp=temp.next
before=before.next
before.next=temp.next
temp.next.prev=before
temp.prev=None
temp.next=None
l=DLL()
n1=Node(19)
l.head=n1
n2=Node(67)
n1.next=n2
n2.prev=n1
n3=Node(30)
n2.next=n3
n3.prev=n2
l.insert_At_pos(2)
l.insert_At_pos(3)
l.del_At_begg()
l.del_At_pos(2)
l.display()
| 0.21264 | 0.670399 |
# Lesson 1 Practice: NumPy Part 1
Use this notebook to follow along with the lesson in the corresponding lesson notebook: [L01-Numpy_Part1-Lesson.ipynb](./L01-Numpy_Part1-Lesson.ipynb).
## Instructions
Follow along with the teaching material in the lesson. Throughout the tutorial sections labeled as "Tasks" are interspersed and indicated with the icon: . You should follow the instructions provided in these sections by performing them in the practice notebook. When the tutorial is completed you can turn in the final practice notebook. For each task, use the cell below it to write and test your code. You may add additional cells for any task as needed or desired.
## Task 1a: Setup
In the practice notebook, import the following packages:
+ `numpy` as `np`
```
import numpy as np
```
## Task 2a: Creating Arrays
In the practice notebook, perform the following.
- Create a 1-dimensional numpy array and print it.
- Create a 2-dimensional numpy array and print it.
- Create a 3-dimensional numpy array and print it.
```
one_D_array = np.array([1, 2, 3, 4])
print(one_D_array)
two_D_array = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(two_D_array)
three_D_array = np.array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[1, 2, 3, 4], [9, 10, 11, 12]]])
print(three_D_array)
```
## Task 3a: Accessing Array Attributes
In the practice notebook, perform the following.
- Create a NumPy array.
- Write code that prints these attributes (one per line): `ndim`, `shape`, `size`, `dtype`, `itemsize`, `data`, `nbytes`.
- Add a comment line, before each line describing what value the attribute returns.
```
two_D_array = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(two_D_array.ndim)
print(two_D_array.shape)
print(two_D_array.size)
print(two_D_array.dtype)
print(two_D_array.itemsize)
print(two_D_array.data)
print(two_D_array.nbytes)
```
## Task 4a: Initializing Arrays
In the practice notebook, perform the following.
+ Create an initialized array by using these functions: `ones`, `zeros`, `empty`, `full`, `arange`, `linspace` and `random.random`. Be sure to follow each array creation with a call to `print()` to display your newly created arrays.
+ Add a comment above each function call describing what is being done.
```
ones = np.ones((2, 4))
print(ones)
zeros =np.zeros((2, 4))
print(zeros)
empty = np.empty((3, 3))
print(empty)
full = np.full((3, 3), 3)
print(full)
arange = np.arange(0, 10, 2)
print(arange)
linspace = np.linspace(1.0, 10.0, num = 6)
print(linspace)
random = np.random.random()
print(random)
random2 = np.random.random((2, 2))
print(random2)
```
## Task 5a: Broadcasting Arrays
In the practice notebook, perform the following.
+ Create two arrays of differing sizes but compatible with broadcasting.
+ Perform addition, multiplication and subtraction.
+ Create two additional arrays of differing size that do not meet the rules for broadcasting and try a mathematical operation.
```
array1 = np.full((3, 4), 3)
array2 = np.random.random((2, 1, 4))
print(array1 + array2)
print(array1 - array2)
print(array1 * array2)
array3 = np.random.random((2, 1, 3))
print(array1 + array3)
```
## Task 6a: Math/Stats Aggregate Functions
In the practice notebook, perform the following.
+ Create three to five arrays
+ Experiment with each of the aggregation functions: `sum`, `minimum`, `maximum`, `cumsum`, `mean`, `np.corrcoef`, `np.std`, `np.var`.
+ For each function call, add a comment line above it that describes what it does.
```
```
array1 = np.full((3, 4), 3)
array2 = np.random.random((2, 1, 4))
array3 = np.random.random((2, 3))
print(np.sum(array1))
print(np.sum(array1, axis = 0))
print(np.minimum(array1, array2))
print(np.maximum(array1, array2))
print(np.cumsum(array1))
print(np.mean(array2))
print(np.mean(array2, axis = 1))
print(np.corrcoef([1 ,5, 3, 2], [4, 3, 7 ,9]))
print(np.std(array3, axis =0))
print(np.std(array3))
print(np.var(array3, axis =0))
```
## Task 6b: Logical Aggregate Functions
In the practice notebook, perform the following.
+ Create two arrays containing boolean values.
+ Experiment with each of the aggregation functions: `logical_and`, `logical_or`, `logical_not`.
+ For each function call, add a comment line above it that describes what it does.
```
```
arrayA = [True, True, False, True]
arrayB = [False, True, True, False]
print(np.logical_and(arrayA, arrayB))
print(np.logical_or(arrayA, arrayB))
print(np.logical_not(arrayA))
```
|
github_jupyter
|
import numpy as np
one_D_array = np.array([1, 2, 3, 4])
print(one_D_array)
two_D_array = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(two_D_array)
three_D_array = np.array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[1, 2, 3, 4], [9, 10, 11, 12]]])
print(three_D_array)
two_D_array = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(two_D_array.ndim)
print(two_D_array.shape)
print(two_D_array.size)
print(two_D_array.dtype)
print(two_D_array.itemsize)
print(two_D_array.data)
print(two_D_array.nbytes)
ones = np.ones((2, 4))
print(ones)
zeros =np.zeros((2, 4))
print(zeros)
empty = np.empty((3, 3))
print(empty)
full = np.full((3, 3), 3)
print(full)
arange = np.arange(0, 10, 2)
print(arange)
linspace = np.linspace(1.0, 10.0, num = 6)
print(linspace)
random = np.random.random()
print(random)
random2 = np.random.random((2, 2))
print(random2)
array1 = np.full((3, 4), 3)
array2 = np.random.random((2, 1, 4))
print(array1 + array2)
print(array1 - array2)
print(array1 * array2)
array3 = np.random.random((2, 1, 3))
print(array1 + array3)
## Task 6b: Logical Aggregate Functions
In the practice notebook, perform the following.
+ Create two arrays containing boolean values.
+ Experiment with each of the aggregation functions: `logical_and`, `logical_or`, `logical_not`.
+ For each function call, add a comment line above it that describes what it does.
arrayA = [True, True, False, True]
arrayB = [False, True, True, False]
print(np.logical_and(arrayA, arrayB))
print(np.logical_or(arrayA, arrayB))
print(np.logical_not(arrayA))
| 0.358016 | 0.990216 |
# Megaman: Manifold Learning for Millions of Points
This notebook gives a brief example of using manifold learning to discover hidden structure within a dataset.
We use the [``megaman``](http://mmp2.github.io/megaman/) package, which implements efficient methods for large manifold learning applications.
```
%matplotlib inline
import matplotlib.pyplot as plt
```
## The Data
Here we will explore a dataset that is available within the megaman package, using the ``generate_megaman_manifold()`` function:
```
from megaman.datasets import generate_megaman_manifold
X, color = generate_megaman_manifold(sampling=3, random_state=42)
print(X.shape)
```
The data consists of nearly 7000 points in eight dimensions.
If we look at pairs of dimensions, we can see that there is some sort of regular structure within the data:
```
def pairwise_grid(X, labels=None):
N = X.shape[1]
if labels is None:
labels = ['X{0}'.format(i) for i in range(N)]
fig, ax = plt.subplots(N, N, figsize=(8, 8),
sharex='col', sharey='row')
for i in range(N):
for j in range(N):
ax[j, i].scatter(X[:, i], X[:, j], c=color, lw=0.5)
if j == N - 1:
ax[j, i].set_xlabel(labels[i])
if i == 0:
ax[j, i].set_ylabel(labels[j])
pairwise_grid(X[:, :4])
```
It is obvious that there is some meaningful structure in this data, but it is difficult to determine from these pairwise coordinate exactly what this structure means.
## Linear Projections: PCA
One common approach to visualizing higher-dimensional data is to use [Principal Component Analysis](), which finds an optimal **linear** projection of the data that maximizes variance captured by each successive component.
We can do this in a few lines using the scikit-learn PCA implementation.
Here we will compute the first four principal components and plot their pairwise relationships:
```
from sklearn.decomposition import PCA
X_pca = PCA(4).fit_transform(X)
pairwise_grid(X_pca)
```
The result shows some intriguing structure in the data: some of the component pairs show a grid-like distribution, while other component pairs show an evidently nonlinear – but univariate – sequence of points.
When there is evidence of nonlinear relationships within a dataset, a manifold method can sometimes be useful in extracting the intrinsic structure.
## Manifold Learning
Let's explore a *manifold learning* approach to visualizing this data.
Manifold Learning is a class of algorithms that finds *non-linear* low-dimensional projections of high-dimensional data, while maximizing some local metric that seeks to preserve relevant structure in the data.
The details of this local metric vary from algorithm to algorithm, and this results in slightly different views of the underlying data.
Here is an example of using the ``megaman`` package to perform a flavor of manifold learning called *Local Tangent Space Alignment*:
```
from megaman.embedding import LTSA
from megaman.geometry import Geometry
geom = Geometry(adjacency_kwds=dict(n_neighbors=6))
model = LTSA(geom=geom, eigen_solver='arpack', random_state=6)
X_ltsa = model.fit_transform(X)
print(X_ltsa.shape)
```
The result is a two-dimensional representation of the original 7000 points.
To see what comes out, we can plot the 2D LTSA-projected embedding of these points:
```
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(X_ltsa[:, 1], X_ltsa[:, 0], c=color, s=20, lw=0.1)
ax.axis([-0.025, 0.025, 0.025, -0.025])
```
Finally, we see what this data was: it was a simple 2D grid of points, contorted in a nonlinear manner into an eight-dimensional embedded space.
The manifold learning algorithm was able to see through this obscuration of the data, and pull out the input: a pose of the main character from the original [Nintendo Mega Man game](https://en.wikipedia.org/wiki/Mega_Man_%28video_game%29).
This is certainly a contrived example, but it shows the power of the manifold learning approach.
Manifold learning has also been shown to be useful in visualizing much more realistic datasets as well.
I invite you to read through our [paper describing the megaman package](http://arxiv.org/abs/1603.02763) for more information and references.
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
from megaman.datasets import generate_megaman_manifold
X, color = generate_megaman_manifold(sampling=3, random_state=42)
print(X.shape)
def pairwise_grid(X, labels=None):
N = X.shape[1]
if labels is None:
labels = ['X{0}'.format(i) for i in range(N)]
fig, ax = plt.subplots(N, N, figsize=(8, 8),
sharex='col', sharey='row')
for i in range(N):
for j in range(N):
ax[j, i].scatter(X[:, i], X[:, j], c=color, lw=0.5)
if j == N - 1:
ax[j, i].set_xlabel(labels[i])
if i == 0:
ax[j, i].set_ylabel(labels[j])
pairwise_grid(X[:, :4])
from sklearn.decomposition import PCA
X_pca = PCA(4).fit_transform(X)
pairwise_grid(X_pca)
from megaman.embedding import LTSA
from megaman.geometry import Geometry
geom = Geometry(adjacency_kwds=dict(n_neighbors=6))
model = LTSA(geom=geom, eigen_solver='arpack', random_state=6)
X_ltsa = model.fit_transform(X)
print(X_ltsa.shape)
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(X_ltsa[:, 1], X_ltsa[:, 0], c=color, s=20, lw=0.1)
ax.axis([-0.025, 0.025, 0.025, -0.025])
| 0.516352 | 0.992334 |
#### Libraries
```
%load_ext autoreload
%autoreload 2
import discrimination
import numpy as np
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.layers import Embedding, Dense, Activation, Flatten, Dropout
from keras.models import Sequential
from keras import regularizers
import itertools
import pickle
import random
import re
import os
```
---
### Split texts into sentences, combine in two groups, and tokenize
---
```
# Load texts
nsex_txts = pickle.load(open("pickles/texts_diary.p", "rb"))
nsex_txts.extend(pickle.load(open("pickles/texts_mydiary.p", "rb")))
sex_txts = pickle.load(open("pickles/texts_everydaysexism.p", "rb"))
# Split each text into a list of sentences
nsex_temp = discrimination.texts.sentences_split(nsex_txts)
sex_temp = discrimination.texts.sentences_split(sex_txts)
# Combine all lists in one
nsex_sentences = []
for item in nsex_temp:
for sentence in item:
nsex_sentences.append(sentence)
sex_sentences = []
for item in sex_temp:
for sentence in item:
sex_sentences.append(sentence)
# Tokenize sentences and remove stop-words
sex_tokens = discrimination.texts.tokenize(sex_sentences)
nsex_tokens = discrimination.texts.tokenize(nsex_sentences)
# Spell-check tokens. This actually takes some time (not too much) so there's a timer every 20.000 tokens checked.
sex_tokens = discrimination.texts.spellcheck_tokens(sex_tokens)
nsex_tokens = discrimination.texts.spellcheck_tokens(nsex_tokens)
# Remove stop-words a second time, in case some stopwords where misspelled.
sex_tokens = discrimination.texts.remove_stopwords(sex_tokens)
nsex_tokens = discrimination.texts.remove_stopwords(nsex_tokens)
for
print(len(sex_tokens),"sexist sentences\tokens and",len(nsex_tokens),"non-sexist sentences\tokens.")
# Save
pickle.dump(nsex_tokens, open("pickles4/nsex_tokens.p", "wb"))
pickle.dump(sex_tokens, open("pickles4/sex_tokens.p", "wb"))
pickle.dump(sex_sentences, open("pickles4/sex_sentences.p", "wb"))
pickle.dump(nsex_sentences, open("pickles4/nsex_sentences.p", "wb"))
```
---
### Convert tokens back to text. Label the old texts. Save.
---
```
# Load
sex_tokens = pickle.load(open("pickles4/sex_tokens.p", "rb"))
nsex_tokens = pickle.load(open("pickles4/nsex_tokens.p", "rb"))
# Remove tokens with less than 3 words.
temp = []
for token in sex_tokens:
if len(token) >= 3:
temp.append(token)
sex_tokens = temp.copy()
temp.clear()
for token in nsex_tokens:
if len(token) >= 3:
temp.append(token)
nsex_tokens = temp.copy()
# Randomly keep only as many non-sexist tokens as sexist ones.
nsex_tokens = random.sample(nsex_tokens, len(sex_tokens))
# Convert tokens back to text for Keras to be happy
keras_sentences = []
for token in itertools.chain(sex_tokens, nsex_tokens):
sentence = " ".join(token)
keras_sentences.append(sentence)
# Create labels
keras_labels = np.zeros(len(keras_sentences))
keras_labels[:len(sex_tokens)] = 1
# Save
pickle.dump(keras_sentences, open("pickles4/keras_sentences.p", "wb"))
pickle.dump(keras_labels, open("pickles4/keras_labels.p", "wb"))
```
___
### NN preparation
___
```
# Load
keras_sentences = pickle.load(open("pickles4/keras_sentences.p", "rb"))
keras_labels = pickle.load(open("pickles4/keras_labels.p", "rb"))
# Tokenizing - Sequencing
tokenizer = Tokenizer(lower = False)
tokenizer.fit_on_texts(keras_sentences)
sequences = tokenizer.texts_to_sequences(keras_sentences)
word_index = tokenizer.word_index
# Create and shuffle data and labels
data = pad_sequences(sequences, maxlen=50)
keras_labels = np.zeros(len(keras_sentences))
keras_labels[:len(sex_tokens)] = 1
labels = np.asarray(keras_labels)
indices = np.arange(data.shape[0])
np.random.shuffle(indices)
data = data[indices]
labels = labels[indices]
# Split 80-20
nb_validation_samples = int(0.2 * data.shape[0])
x_train = data[:-nb_validation_samples]
y_train = labels[:-nb_validation_samples]
x_val = data[-nb_validation_samples:]
y_val = labels[-nb_validation_samples:]
# Parse the GloVe word embeddings
glove_dir = "glove/"
embeddings_index = {}
f = open(os.path.join(glove_dir, "glove.42B.300d.txt"))
for line in f:
values = line.split()
word = values[0]
coefs = np.asarray(values[1:], dtype="float32")
embeddings_index[word] = coefs
f.close()
# Create the embedding matrix
embedding_matrix = np.zeros((len(word_index) + 1, 300))
for word, i in word_index.items():
embedding_vector = embeddings_index.get(word)
if embedding_vector is not None:
# words not found in embedding index will be all-zeros.
embedding_matrix[i] = embedding_vector
# Delete the embeddings index as it's no longer needed.
del embeddings_index
# Create the embedding layer
embedding_layer = Embedding(len(word_index) + 1, 300, input_length=50,
weights=[embedding_matrix],
trainable=False)
```
---
### NN setup and compilation
---
```
# Setup
model = Sequential()
model.add(embedding_layer)
model.add(Flatten())
# model.add(Dropout(0.1))
model.add(Dense(128, activation="relu", kernel_regularizer = regularizers.l2(0.001)))
model.add(Dense(16, activation="relu", kernel_regularizer = regularizers.l2(0.001)))
model.add(Dense(1, activation="sigmoid"))
model.summary()
# Compilation
model.compile(optimizer = "Adam",
loss = "binary_crossentropy",
metrics = ["acc"])
history = model.fit(x_train, y_train,
epochs = 10,
batch_size = 512,
validation_data = (x_val, y_val))
# Save model weights
model.save_weights("pickles4/model4.h5")
# Predictions
predictions = model.predict(data)
# Save
pickle.dump(predictions, open("pickles4/predictions.p", "wb"))
# Load labels and predictions
keras_labels = pickle.load(open("pickles4/keras_labels.p", "rb"))
predictions = pickle.load(open("pickles4/predictions.p", "rb"))
# Create a predicted labels list
labels_predicted = []
for prediction in predictions:
labels_predicted.append( round(prediction[0]) )
# Calculate the confusion matrix
from sklearn.metrics import confusion_matrix, precision_score, recall_score, accuracy_score
CF = confusion_matrix(keras_labels, labels_predicted)
#"Disentangle" the matrix
TN = round((CF[0,0] / sum(CF[0,:])) * 100, 1)
FN = round((CF[0,1] / sum(CF[0,:])) * 100, 1)
TP = round((CF[1,1] / sum(CF[1,:])) * 100, 1)
FP = round((CF[1,0] / sum(CF[1,:])) * 100, 1)
GTN = round((CF[0,0] / (sum(CF[0,:]) + sum(CF[1,:]))) * 100, 1)
GFN = round((CF[0,1] / (sum(CF[0,:]) + sum(CF[1,:]))) * 100, 1)
GTP = round((CF[1,1] / (sum(CF[0,:]) + sum(CF[1,:]))) * 100, 1)
GFP = round((CF[1,0] / (sum(CF[0,:]) + sum(CF[1,:]))) * 100, 1)
# Print the results
print("True positives account for "+str(TP)+"% or "+str(GTP)+"% of the total (sexist texts labelled as sexist).")
print("True negatives account for "+str(TN)+"% or "+str(GTN)+"% of the total (non-sexist texts labelled as non-sexist).")
print("False positives account for "+str(FP)+"% or "+str(GFP)+"% of the total (sexist texts labelled as non-sexist).")
print("False negatives account for "+str(FN)+"% or "+str(GFN)+"% of the total (non-sexist texts labelled as sexist).")
```
## Test the model!
```
# Test the network
test = ['''I don't have an issue with anything except women.''']
# Convert the test phrase to lowercase, tokenize, spellcheck, remove stopwords.
test = discrimination.texts.lowercase(test)
test = discrimination.texts.tokenize(test)
test = discrimination.texts.spellcheck_tokens(test)
test = discrimination.texts.remove_stopwords(test)
# Convert the token back to text, sequence it, pad it, feed it into the model.
text = ""
for item in test:
for word in item:
text += word + " "
test_sequence = tokenizer.texts_to_sequences([text])
x_test = pad_sequences(test_sequence, maxlen=50)
model.load_weights("pickles4/model4.h5")
# Make the output look pretty... because it deserves it.
str(round(model.predict(x_test)[0,0]*100,0))[:-2] + "% sexist"
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
import discrimination
import numpy as np
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.layers import Embedding, Dense, Activation, Flatten, Dropout
from keras.models import Sequential
from keras import regularizers
import itertools
import pickle
import random
import re
import os
# Load texts
nsex_txts = pickle.load(open("pickles/texts_diary.p", "rb"))
nsex_txts.extend(pickle.load(open("pickles/texts_mydiary.p", "rb")))
sex_txts = pickle.load(open("pickles/texts_everydaysexism.p", "rb"))
# Split each text into a list of sentences
nsex_temp = discrimination.texts.sentences_split(nsex_txts)
sex_temp = discrimination.texts.sentences_split(sex_txts)
# Combine all lists in one
nsex_sentences = []
for item in nsex_temp:
for sentence in item:
nsex_sentences.append(sentence)
sex_sentences = []
for item in sex_temp:
for sentence in item:
sex_sentences.append(sentence)
# Tokenize sentences and remove stop-words
sex_tokens = discrimination.texts.tokenize(sex_sentences)
nsex_tokens = discrimination.texts.tokenize(nsex_sentences)
# Spell-check tokens. This actually takes some time (not too much) so there's a timer every 20.000 tokens checked.
sex_tokens = discrimination.texts.spellcheck_tokens(sex_tokens)
nsex_tokens = discrimination.texts.spellcheck_tokens(nsex_tokens)
# Remove stop-words a second time, in case some stopwords where misspelled.
sex_tokens = discrimination.texts.remove_stopwords(sex_tokens)
nsex_tokens = discrimination.texts.remove_stopwords(nsex_tokens)
for
print(len(sex_tokens),"sexist sentences\tokens and",len(nsex_tokens),"non-sexist sentences\tokens.")
# Save
pickle.dump(nsex_tokens, open("pickles4/nsex_tokens.p", "wb"))
pickle.dump(sex_tokens, open("pickles4/sex_tokens.p", "wb"))
pickle.dump(sex_sentences, open("pickles4/sex_sentences.p", "wb"))
pickle.dump(nsex_sentences, open("pickles4/nsex_sentences.p", "wb"))
# Load
sex_tokens = pickle.load(open("pickles4/sex_tokens.p", "rb"))
nsex_tokens = pickle.load(open("pickles4/nsex_tokens.p", "rb"))
# Remove tokens with less than 3 words.
temp = []
for token in sex_tokens:
if len(token) >= 3:
temp.append(token)
sex_tokens = temp.copy()
temp.clear()
for token in nsex_tokens:
if len(token) >= 3:
temp.append(token)
nsex_tokens = temp.copy()
# Randomly keep only as many non-sexist tokens as sexist ones.
nsex_tokens = random.sample(nsex_tokens, len(sex_tokens))
# Convert tokens back to text for Keras to be happy
keras_sentences = []
for token in itertools.chain(sex_tokens, nsex_tokens):
sentence = " ".join(token)
keras_sentences.append(sentence)
# Create labels
keras_labels = np.zeros(len(keras_sentences))
keras_labels[:len(sex_tokens)] = 1
# Save
pickle.dump(keras_sentences, open("pickles4/keras_sentences.p", "wb"))
pickle.dump(keras_labels, open("pickles4/keras_labels.p", "wb"))
# Load
keras_sentences = pickle.load(open("pickles4/keras_sentences.p", "rb"))
keras_labels = pickle.load(open("pickles4/keras_labels.p", "rb"))
# Tokenizing - Sequencing
tokenizer = Tokenizer(lower = False)
tokenizer.fit_on_texts(keras_sentences)
sequences = tokenizer.texts_to_sequences(keras_sentences)
word_index = tokenizer.word_index
# Create and shuffle data and labels
data = pad_sequences(sequences, maxlen=50)
keras_labels = np.zeros(len(keras_sentences))
keras_labels[:len(sex_tokens)] = 1
labels = np.asarray(keras_labels)
indices = np.arange(data.shape[0])
np.random.shuffle(indices)
data = data[indices]
labels = labels[indices]
# Split 80-20
nb_validation_samples = int(0.2 * data.shape[0])
x_train = data[:-nb_validation_samples]
y_train = labels[:-nb_validation_samples]
x_val = data[-nb_validation_samples:]
y_val = labels[-nb_validation_samples:]
# Parse the GloVe word embeddings
glove_dir = "glove/"
embeddings_index = {}
f = open(os.path.join(glove_dir, "glove.42B.300d.txt"))
for line in f:
values = line.split()
word = values[0]
coefs = np.asarray(values[1:], dtype="float32")
embeddings_index[word] = coefs
f.close()
# Create the embedding matrix
embedding_matrix = np.zeros((len(word_index) + 1, 300))
for word, i in word_index.items():
embedding_vector = embeddings_index.get(word)
if embedding_vector is not None:
# words not found in embedding index will be all-zeros.
embedding_matrix[i] = embedding_vector
# Delete the embeddings index as it's no longer needed.
del embeddings_index
# Create the embedding layer
embedding_layer = Embedding(len(word_index) + 1, 300, input_length=50,
weights=[embedding_matrix],
trainable=False)
# Setup
model = Sequential()
model.add(embedding_layer)
model.add(Flatten())
# model.add(Dropout(0.1))
model.add(Dense(128, activation="relu", kernel_regularizer = regularizers.l2(0.001)))
model.add(Dense(16, activation="relu", kernel_regularizer = regularizers.l2(0.001)))
model.add(Dense(1, activation="sigmoid"))
model.summary()
# Compilation
model.compile(optimizer = "Adam",
loss = "binary_crossentropy",
metrics = ["acc"])
history = model.fit(x_train, y_train,
epochs = 10,
batch_size = 512,
validation_data = (x_val, y_val))
# Save model weights
model.save_weights("pickles4/model4.h5")
# Predictions
predictions = model.predict(data)
# Save
pickle.dump(predictions, open("pickles4/predictions.p", "wb"))
# Load labels and predictions
keras_labels = pickle.load(open("pickles4/keras_labels.p", "rb"))
predictions = pickle.load(open("pickles4/predictions.p", "rb"))
# Create a predicted labels list
labels_predicted = []
for prediction in predictions:
labels_predicted.append( round(prediction[0]) )
# Calculate the confusion matrix
from sklearn.metrics import confusion_matrix, precision_score, recall_score, accuracy_score
CF = confusion_matrix(keras_labels, labels_predicted)
#"Disentangle" the matrix
TN = round((CF[0,0] / sum(CF[0,:])) * 100, 1)
FN = round((CF[0,1] / sum(CF[0,:])) * 100, 1)
TP = round((CF[1,1] / sum(CF[1,:])) * 100, 1)
FP = round((CF[1,0] / sum(CF[1,:])) * 100, 1)
GTN = round((CF[0,0] / (sum(CF[0,:]) + sum(CF[1,:]))) * 100, 1)
GFN = round((CF[0,1] / (sum(CF[0,:]) + sum(CF[1,:]))) * 100, 1)
GTP = round((CF[1,1] / (sum(CF[0,:]) + sum(CF[1,:]))) * 100, 1)
GFP = round((CF[1,0] / (sum(CF[0,:]) + sum(CF[1,:]))) * 100, 1)
# Print the results
print("True positives account for "+str(TP)+"% or "+str(GTP)+"% of the total (sexist texts labelled as sexist).")
print("True negatives account for "+str(TN)+"% or "+str(GTN)+"% of the total (non-sexist texts labelled as non-sexist).")
print("False positives account for "+str(FP)+"% or "+str(GFP)+"% of the total (sexist texts labelled as non-sexist).")
print("False negatives account for "+str(FN)+"% or "+str(GFN)+"% of the total (non-sexist texts labelled as sexist).")
# Test the network
test = ['''I don't have an issue with anything except women.''']
# Convert the test phrase to lowercase, tokenize, spellcheck, remove stopwords.
test = discrimination.texts.lowercase(test)
test = discrimination.texts.tokenize(test)
test = discrimination.texts.spellcheck_tokens(test)
test = discrimination.texts.remove_stopwords(test)
# Convert the token back to text, sequence it, pad it, feed it into the model.
text = ""
for item in test:
for word in item:
text += word + " "
test_sequence = tokenizer.texts_to_sequences([text])
x_test = pad_sequences(test_sequence, maxlen=50)
model.load_weights("pickles4/model4.h5")
# Make the output look pretty... because it deserves it.
str(round(model.predict(x_test)[0,0]*100,0))[:-2] + "% sexist"
| 0.72526 | 0.692395 |
# A basic training loop
This notebook builds upone the work of the [previous notebook](001a_nn_basics.ipynb) in which we created a simlple training loop (including calculating the loss on a validation set) and then a 3-layer CNN using PyTorch's Sequential class.
Here, we will
## From the last notebook...
```
#export
import pickle, gzip, torch, math, numpy as np, torch.nn.functional as F
from pathlib import Path
from IPython.core.debugger import set_trace
from torch import nn, optim
#export
from torch.utils.data import TensorDataset, DataLoader, Dataset
from dataclasses import dataclass
from typing import Any, Collection, Callable
from functools import partial, reduce
```
The data was downloaded in section 1.1 of the [previous notebook](001a_nn_basics.ipynb) so make sure you have run that code before you continue.
```
DATA_PATH = Path('data')
PATH = DATA_PATH/'mnist'
with gzip.open(PATH/'mnist.pkl.gz', 'rb') as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding='latin-1')
x_train,y_train,x_valid,y_valid = map(torch.tensor, (x_train,y_train,x_valid,y_valid))
```
After creating our training and validation sets, we print out the min and max to get a sense for the range of feature values. It is always a good idea to inspect your data. In the case of the MNIST dataset, the x-values for each training example correspond to pixel values that, range from 0 to ~1.
```
x_train.min(),x_train.max()
torch.tensor(x_train)
```
`bs` stands for batch size and `lr` stands for learning rate. [Here is a reference](https://github.com/fastai/fastai_v1/blob/master/docs/abbr.md) for these and other abbreviations used as variable names. The fast.ai library differs from PEP 8 and instead follows conventions developed around the [APL](https://en.wikipedia.org/wiki/APL_\(programming_language\)) / [J](https://en.wikipedia.org/wiki/J_\(programming_language\)) / [K](https://en.wikipedia.org/wiki/K_\(programming_language\)) programming languages (all of which are centered around multi-dimensional arrays), which are more concise and closer to math notation. [Here is a more detailed explanation](https://github.com/fastai/fastai/blob/master/docs/style.md) of the fast.ai style guide.
```
bs=64
epochs = 2
lr=0.2
```
PyTorch's [TensorDataset](https://pytorch.org/docs/stable/_modules/torch/utils/data/dataset.html#TensorDataset) is a Dataset wrapping tensors. It gives us a way to iterate, index, and slice along the first dimension of a tensor. This will make it easier to access both the independent and dependent variables in the same line as we train.
```
train_ds = TensorDataset(x_train, y_train)
valid_ds = TensorDataset(x_valid, y_valid)
```
We are using the same `loss_batch`, `fit`, and `Lambda` as were defined in the previous notebook:
```
#export
def loss_batch(model, xb, yb, loss_fn, opt=None):
loss = loss_fn(model(xb), yb)
if opt is not None:
loss.backward()
opt.step()
opt.zero_grad()
return loss.item(), len(xb)
def fit(epochs, model, loss_fn, opt, train_dl, valid_dl):
for epoch in range(epochs):
model.train()
for xb,yb in train_dl: loss_batch(model, xb, yb, loss_fn, opt)
model.eval()
with torch.no_grad():
losses,nums = zip(*[loss_batch(model, xb, yb, loss_fn)
for xb,yb in valid_dl])
val_loss = np.sum(np.multiply(losses,nums)) / np.sum(nums)
print(epoch, val_loss)
#export
class Lambda(nn.Module):
def __init__(self, func):
super().__init__()
self.func=func
def forward(self, x): return self.func(x)
```
## Simplify nn.Sequential layers
As a reminder, our 3-layer CNN from the previous notebook was defined:
```
model = nn.Sequential(
Lambda(lambda x: x.view(-1,1,28,28)),
nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.AvgPool2d(4),
Lambda(lambda x: x.view(x.size(0),-1))
)
```
Let's refactor this a bit to make it more readable, and to make the components more reusable:
```
#export
def ResizeBatch(*size): return Lambda(lambda x: x.view((-1,)+size))
def Flatten(): return Lambda(lambda x: x.view((x.size(0), -1)))
def PoolFlatten(): return nn.Sequential(nn.AdaptiveAvgPool2d(1), Flatten())
```
Using our newly defined `ResizeBatch`, `Flatten`, and `PoolFlatten`, we can instead now define the same networks as:
```
model = nn.Sequential(
ResizeBatch(1,28,28),
nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1), nn.ReLU(),
PoolFlatten()
)
```
Note that we will nearly always use small kernels of size 3 due to the reasons presented in section 2.3 in [this paper](https://arxiv.org/pdf/1409.1556.pdf) (a few small kernels achieve a receptive field of the same dimension as one bigger kernel while at the same time achieving increased discriminative power and using fewer parameters).
We will use the same `get_data method` as defined in the previous notebook:
```
def get_data(train_ds, valid_ds, bs):
return (DataLoader(train_ds, batch_size=bs, shuffle=True),
DataLoader(valid_ds, batch_size=bs*2))
train_dl,valid_dl = get_data(train_ds, valid_ds, bs)
```
**Set loss function**
[Here](https://rdipietro.github.io/friendly-intro-to-cross-entropy-loss/) is tutorial explaining why cross entropy is a resonable loss function for classifciation tasks.
```
loss_fn = F.cross_entropy
```
**Set optimizer**
We stick with stochastic gradient descent without momentum as our optimizer. This is a basic optimizer and it is [easy to understand](http://ruder.io/optimizing-gradient-descent/index.html#stochasticgradientdescent). We will move into better optimizers as we go forward.
```
opt = optim.SGD(model.parameters(), lr=lr)
```
**Test our loss function**
We try out our loss function on one batch of X features and y targets to make sure it's working correctly.
```
loss_fn(model(x_valid[0:bs]), y_valid[0:bs])
```
**Fit**
Everything looks ready, we call the fit function we developed earlier for two epochs to confirm that the model learns.
```
fit(epochs, model, loss_fn, opt, train_dl, valid_dl)
```
## Transformations
We are going to refactor some of the data transformations out of the network and into a pipeline that is applied to the data being fed into the Dataloders.
This is more flexible, simplifies the model, and will be useful later when we want to apply additional transformations for things like data augmentation.
**Define transformations**
In this example our only transformation will be *mnist2image*. This is a utility function to reshape our features into 28x28 arrays.
X is a batch of features where the first dimension is the number of samples in the batch and the remaining dimensions define the shape of the training example. y is the target variable to be learned, in this case it an integer representing one of 10 image classes.
With MNIST data, the X features start out as a 1x784 vector and we want to convert the features to 1x28x28 images (see line 62). This helper function does that for an entire batch of features.
```
def mnist2image(b): return b.view(1,28,28)
#export
@dataclass
class DatasetTfm(Dataset):
ds: Dataset
tfm: Callable = None
def __len__(self): return len(self.ds)
def __getitem__(self,idx):
x,y = self.ds[idx]
if self.tfm is not None: x = self.tfm(x)
return x,y
train_tds = DatasetTfm(train_ds, mnist2image)
valid_tds = DatasetTfm(valid_ds, mnist2image)
def get_data(train_ds, valid_ds, bs):
return (DataLoader(train_ds, bs, shuffle=True),
DataLoader(valid_ds, bs*2, shuffle=False))
train_dl,valid_dl = get_data(train_tds, valid_tds, bs)
```
We make some checks to make sure that *mnist2image* is working correctly:
1. The input and output shapes are as expected
2. The input and output data (features) are the same
```
x,y = next(iter(valid_dl))
valid_ds[0][0].shape, x[0].shape
torch.allclose(valid_ds[0][0], x[0].view(-1))
```
## Refactor network
**Define layer types and loop over them**
When use a layer type more than once in a contiguous fashion (one after the other), it makes sense to define a function for that layer type and then use that function to build our model function.
That is what we do here with *conv2_relu* with which we avoid the three subsequent lines of code in line 12 (this saving becomes more significant in deeper networks).
```
#export
def conv2_relu(nif, nof, ks, stride):
return nn.Sequential(nn.Conv2d(nif, nof, ks, stride, padding=ks//2), nn.ReLU())
def simple_cnn(actns, kernel_szs, strides):
layers = [conv2_relu(actns[i], actns[i+1], kernel_szs[i], stride=strides[i])
for i in range(len(strides))]
layers.append(PoolFlatten())
return nn.Sequential(*layers)
def get_model():
model = simple_cnn([1,16,16,10], [3,3,3], [2,2,2])
return model, optim.SGD(model.parameters(), lr=lr)
model,opt = get_model()
fit(epochs, model, loss_fn, opt, train_dl, valid_dl)
```
## CUDA
**Run in GPU and add progress bar**
To run our Pytorch networks in the GPU we have to specify it in the code. This is done by setting *torch.device('cuda')*. We will also add a progress bar to keep track of the progress during training. This we acomplish with the *tqdm_notebook* module of the [tqdm](https://github.com/tqdm/tqdm) package.
We integrate both these features into a custom Dataloader which we build on top of the Pytorch Dataloader.
```
#export
from tqdm import tqdm, tqdm_notebook, trange, tnrange
from ipykernel.kernelapp import IPKernelApp
def in_notebook(): return IPKernelApp.initialized()
def to_device(device, b): return [o.to(device) for o in b]
default_device = torch.device('cuda')
if in_notebook():
tqdm = tqdm_notebook
trange = tnrange
@dataclass
class DeviceDataLoader():
dl: DataLoader
device: torch.device
progress_func:Callable=None
def __len__(self): return len(self.dl)
def __iter__(self):
self.gen = (to_device(self.device,o) for o in self.dl)
if self.progress_func is not None:
self.gen = self.progress_func(self.gen, total=len(self.dl), leave=False)
return iter(self.gen)
@classmethod
def create(cls, *args, device=default_device, progress_func=tqdm, **kwargs):
return cls(DataLoader(*args, **kwargs), device=device, progress_func=progress_func)
def get_data(train_ds, valid_ds, bs):
return (DeviceDataLoader.create(train_ds, bs, shuffle=True),
DeviceDataLoader.create(valid_ds, bs*2, shuffle=False))
train_dl,valid_dl = get_data(train_tds, valid_tds, bs)
def get_model():
model = simple_cnn([1,16,16,10], [3,3,3], [2,2,2]).to(default_device)
return model, optim.SGD(model.parameters(), lr=lr)
model,opt = get_model()
fit(epochs, model, loss_fn, opt, train_dl, valid_dl)
```
## Learner
**Define learner**
Finally, we are missing a learner class to close the gap between our loaded data and our model. The learner class will recieve our loaded data (after transformations) and the model and we will be able to call fit on it to start the training phase.
Note that we must define another fit function to track the progress of our training with the progress bar we included in the Dataloader.
```
#export
def fit(epochs, model, loss_fn, opt, train_dl, valid_dl):
for epoch in tnrange(epochs):
model.train()
for xb,yb in train_dl:
loss,_ = loss_batch(model, xb, yb, loss_fn, opt)
if train_dl.progress_func is not None: train_dl.gen.set_postfix_str(loss)
model.eval()
with torch.no_grad():
losses,nums = zip(*[loss_batch(model, xb, yb, loss_fn)
for xb,yb in valid_dl])
val_loss = np.sum(np.multiply(losses,nums)) / np.sum(nums)
print(epoch, val_loss)
#export
class DataBunch():
def __init__(self, train_ds, valid_ds, bs=64, device=None, train_tfm=None, valid_tfm=None):
self.device = default_device if device is None else device
self.train_dl = DeviceDataLoader.create(DatasetTfm(train_ds,train_tfm), bs, shuffle=True)
self.valid_dl = DeviceDataLoader.create(DatasetTfm(valid_ds, valid_tfm), bs*2, shuffle=False)
class Learner():
def __init__(self, data, model):
self.data,self.model = data,model.to(data.device)
def fit(self, epochs, lr, opt_fn=optim.SGD):
opt = opt_fn(self.model.parameters(), lr=lr)
loss_fn = F.cross_entropy
fit(epochs, self.model, loss_fn, opt, self.data.train_dl, self.data.valid_dl)
data = DataBunch(train_ds, valid_ds, bs, train_tfm=mnist2image, valid_tfm=mnist2image)
model = simple_cnn([1,16,16,10], [3,3,3], [2,2,2])
learner = Learner(data, model)
opt_fn = partial(optim.SGD, momentum=0.9)
learner.fit(4, lr/5, opt_fn=opt_fn)
learner = Learner(data, simple_cnn([1,16,16,10], [3,3,3], [2,2,2]))
learner.fit(1, lr/5, opt_fn=opt_fn)
learner.fit(2, lr, opt_fn=opt_fn)
learner.fit(1, lr/5, opt_fn=opt_fn)
# TODO: metrics
```
|
github_jupyter
|
#export
import pickle, gzip, torch, math, numpy as np, torch.nn.functional as F
from pathlib import Path
from IPython.core.debugger import set_trace
from torch import nn, optim
#export
from torch.utils.data import TensorDataset, DataLoader, Dataset
from dataclasses import dataclass
from typing import Any, Collection, Callable
from functools import partial, reduce
DATA_PATH = Path('data')
PATH = DATA_PATH/'mnist'
with gzip.open(PATH/'mnist.pkl.gz', 'rb') as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding='latin-1')
x_train,y_train,x_valid,y_valid = map(torch.tensor, (x_train,y_train,x_valid,y_valid))
x_train.min(),x_train.max()
torch.tensor(x_train)
bs=64
epochs = 2
lr=0.2
train_ds = TensorDataset(x_train, y_train)
valid_ds = TensorDataset(x_valid, y_valid)
#export
def loss_batch(model, xb, yb, loss_fn, opt=None):
loss = loss_fn(model(xb), yb)
if opt is not None:
loss.backward()
opt.step()
opt.zero_grad()
return loss.item(), len(xb)
def fit(epochs, model, loss_fn, opt, train_dl, valid_dl):
for epoch in range(epochs):
model.train()
for xb,yb in train_dl: loss_batch(model, xb, yb, loss_fn, opt)
model.eval()
with torch.no_grad():
losses,nums = zip(*[loss_batch(model, xb, yb, loss_fn)
for xb,yb in valid_dl])
val_loss = np.sum(np.multiply(losses,nums)) / np.sum(nums)
print(epoch, val_loss)
#export
class Lambda(nn.Module):
def __init__(self, func):
super().__init__()
self.func=func
def forward(self, x): return self.func(x)
model = nn.Sequential(
Lambda(lambda x: x.view(-1,1,28,28)),
nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.AvgPool2d(4),
Lambda(lambda x: x.view(x.size(0),-1))
)
#export
def ResizeBatch(*size): return Lambda(lambda x: x.view((-1,)+size))
def Flatten(): return Lambda(lambda x: x.view((x.size(0), -1)))
def PoolFlatten(): return nn.Sequential(nn.AdaptiveAvgPool2d(1), Flatten())
model = nn.Sequential(
ResizeBatch(1,28,28),
nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1), nn.ReLU(),
nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1), nn.ReLU(),
PoolFlatten()
)
def get_data(train_ds, valid_ds, bs):
return (DataLoader(train_ds, batch_size=bs, shuffle=True),
DataLoader(valid_ds, batch_size=bs*2))
train_dl,valid_dl = get_data(train_ds, valid_ds, bs)
loss_fn = F.cross_entropy
opt = optim.SGD(model.parameters(), lr=lr)
loss_fn(model(x_valid[0:bs]), y_valid[0:bs])
fit(epochs, model, loss_fn, opt, train_dl, valid_dl)
def mnist2image(b): return b.view(1,28,28)
#export
@dataclass
class DatasetTfm(Dataset):
ds: Dataset
tfm: Callable = None
def __len__(self): return len(self.ds)
def __getitem__(self,idx):
x,y = self.ds[idx]
if self.tfm is not None: x = self.tfm(x)
return x,y
train_tds = DatasetTfm(train_ds, mnist2image)
valid_tds = DatasetTfm(valid_ds, mnist2image)
def get_data(train_ds, valid_ds, bs):
return (DataLoader(train_ds, bs, shuffle=True),
DataLoader(valid_ds, bs*2, shuffle=False))
train_dl,valid_dl = get_data(train_tds, valid_tds, bs)
x,y = next(iter(valid_dl))
valid_ds[0][0].shape, x[0].shape
torch.allclose(valid_ds[0][0], x[0].view(-1))
#export
def conv2_relu(nif, nof, ks, stride):
return nn.Sequential(nn.Conv2d(nif, nof, ks, stride, padding=ks//2), nn.ReLU())
def simple_cnn(actns, kernel_szs, strides):
layers = [conv2_relu(actns[i], actns[i+1], kernel_szs[i], stride=strides[i])
for i in range(len(strides))]
layers.append(PoolFlatten())
return nn.Sequential(*layers)
def get_model():
model = simple_cnn([1,16,16,10], [3,3,3], [2,2,2])
return model, optim.SGD(model.parameters(), lr=lr)
model,opt = get_model()
fit(epochs, model, loss_fn, opt, train_dl, valid_dl)
#export
from tqdm import tqdm, tqdm_notebook, trange, tnrange
from ipykernel.kernelapp import IPKernelApp
def in_notebook(): return IPKernelApp.initialized()
def to_device(device, b): return [o.to(device) for o in b]
default_device = torch.device('cuda')
if in_notebook():
tqdm = tqdm_notebook
trange = tnrange
@dataclass
class DeviceDataLoader():
dl: DataLoader
device: torch.device
progress_func:Callable=None
def __len__(self): return len(self.dl)
def __iter__(self):
self.gen = (to_device(self.device,o) for o in self.dl)
if self.progress_func is not None:
self.gen = self.progress_func(self.gen, total=len(self.dl), leave=False)
return iter(self.gen)
@classmethod
def create(cls, *args, device=default_device, progress_func=tqdm, **kwargs):
return cls(DataLoader(*args, **kwargs), device=device, progress_func=progress_func)
def get_data(train_ds, valid_ds, bs):
return (DeviceDataLoader.create(train_ds, bs, shuffle=True),
DeviceDataLoader.create(valid_ds, bs*2, shuffle=False))
train_dl,valid_dl = get_data(train_tds, valid_tds, bs)
def get_model():
model = simple_cnn([1,16,16,10], [3,3,3], [2,2,2]).to(default_device)
return model, optim.SGD(model.parameters(), lr=lr)
model,opt = get_model()
fit(epochs, model, loss_fn, opt, train_dl, valid_dl)
#export
def fit(epochs, model, loss_fn, opt, train_dl, valid_dl):
for epoch in tnrange(epochs):
model.train()
for xb,yb in train_dl:
loss,_ = loss_batch(model, xb, yb, loss_fn, opt)
if train_dl.progress_func is not None: train_dl.gen.set_postfix_str(loss)
model.eval()
with torch.no_grad():
losses,nums = zip(*[loss_batch(model, xb, yb, loss_fn)
for xb,yb in valid_dl])
val_loss = np.sum(np.multiply(losses,nums)) / np.sum(nums)
print(epoch, val_loss)
#export
class DataBunch():
def __init__(self, train_ds, valid_ds, bs=64, device=None, train_tfm=None, valid_tfm=None):
self.device = default_device if device is None else device
self.train_dl = DeviceDataLoader.create(DatasetTfm(train_ds,train_tfm), bs, shuffle=True)
self.valid_dl = DeviceDataLoader.create(DatasetTfm(valid_ds, valid_tfm), bs*2, shuffle=False)
class Learner():
def __init__(self, data, model):
self.data,self.model = data,model.to(data.device)
def fit(self, epochs, lr, opt_fn=optim.SGD):
opt = opt_fn(self.model.parameters(), lr=lr)
loss_fn = F.cross_entropy
fit(epochs, self.model, loss_fn, opt, self.data.train_dl, self.data.valid_dl)
data = DataBunch(train_ds, valid_ds, bs, train_tfm=mnist2image, valid_tfm=mnist2image)
model = simple_cnn([1,16,16,10], [3,3,3], [2,2,2])
learner = Learner(data, model)
opt_fn = partial(optim.SGD, momentum=0.9)
learner.fit(4, lr/5, opt_fn=opt_fn)
learner = Learner(data, simple_cnn([1,16,16,10], [3,3,3], [2,2,2]))
learner.fit(1, lr/5, opt_fn=opt_fn)
learner.fit(2, lr, opt_fn=opt_fn)
learner.fit(1, lr/5, opt_fn=opt_fn)
# TODO: metrics
| 0.901576 | 0.988928 |
# VERIFICATION AND VALIDATION - EXERCISES
# Preliminaries
```
IS_COLAB = True
if IS_COLAB:
!pip install -q tellurium
!pip install -q SBMLLint
pass
```
## Imports
```
# Python packages used in this section
import os
import matplotlib.pyplot as plt
import numpy as np
import urllib.request # use this library to download file from GitHub
from SBMLLint.tools.sbmllint import lint
import tellurium as te
# Constants
ENDTIME = 10
NUMPOINT = 10*ENDTIME
def getSharedCodes(moduleName):
"""
Obtains common codes from the github repository.
Parameters
----------
moduleName: str
name of the python module in the src directory
"""
if IS_COLAB:
url = "https://github.com/sys-bio/network-modeling-summer-school-2021/raw/main/src/%s.py" % moduleName
local_python = "python.py"
_, _ = urllib.request.urlretrieve(url=url, filename=local_python)
else:
local_python = "../../src/%s.py" % moduleName
with open(local_python, "r") as fd:
codeStr = "".join(fd.readlines())
print(codeStr)
exec(codeStr, globals())
# Acquire codes
getSharedCodes("util")
# TESTS
assert(isinstance(LINEAR_PATHWAY_DF, pd.DataFrame))
```
## Constants
### Wolf model
```
print(WOLF_MODEL)
rr = te.loada(WOLF_MODEL)
rr.plot(rr.simulate())
```
### Global constants
```
# Constants used in the section
MOLECULES = ["Glucose", "fructose_1_6_bisphosphate", "glyceraldehyde_3_phosphate", "glycerate_3_phosphate",
"pyruvate", "Acetyladehyde", "External_acetaldehyde", "ATP", "ADP", "NAD", "NADH"]
ENDTIME = 5
NUMPOINT = 100*ENDTIME
ROADRUNNER = te.loada(WOLF_MODEL)
```
# Exercise 1: Mass Balance Errors
1. Use SBMLLint to find mass check for mass balance errors in the Wolf model.
1. Reaction ``J9`` implies that ``ATP`` and ``ADP`` have the same mass, which is clearly false since they differ
by an inorganic phosphate.
Revise the Wolf model to explicitly include
inorganic phosphate and check your revised model
with SBMLLint.
Do you get the same dynamics with the revised model
as with the original Wolf model?
## (1) Check for mass balance
We begin by checking if the Wolf model has any stoichiometric inconsistencies.
First, we create the antimony model as a string.
```
_ = lint(WOLF_MODEL, mass_balance_check="games")
```
## (2) Revise the Wolf model to include inorganic phosphate
```
REVISED_WOLF_MODEL = """
species $External_glucose in compartment_, $ethanol in compartment_, $Glycerol in compartment_;
species $Sink in compartment_;
// Reactions:
J0: $External_glucose => Glucose; J0_inputFlux;
// **Added P to products
J1: Glucose + 2 ATP => fructose_1_6_bisphosphate + 2 ADP + 2 P; J1_k1*Glucose*ATP*(1/(1 + (ATP/J1_Ki)^J1_n));
J2: fructose_1_6_bisphosphate => glyceraldehyde_3_phosphate + glyceraldehyde_3_phosphate; J2_k*fructose_1_6_bisphosphate;
J3: glyceraldehyde_3_phosphate + NADH => NAD + $Glycerol; J3_k*glyceraldehyde_3_phosphate*NADH;
// **Added P to reactants and kinetics
J4: glyceraldehyde_3_phosphate + ADP + P + NAD => ATP + glycerate_3_phosphate + NADH; (J4_kg*J4_kp*glyceraldehyde_3_phosphate*NAD*ADP*P - J4_ka*J4_kk*glycerate_3_phosphate*ATP*NADH)/(J4_ka*NADH + J4_kp*ADP);
// **Added P to reactants and kinetics
J5: glycerate_3_phosphate + ADP + P => ATP + pyruvate; J5_k*glycerate_3_phosphate*ADP*P;
J6: pyruvate => Acetyladehyde; J6_k*pyruvate;
J7: Acetyladehyde + NADH => NAD + $ethanol; J7_k*Acetyladehyde*NADH;
J8: Acetyladehyde => External_acetaldehyde; J8_k1*Acetyladehyde - J8_k2*External_acetaldehyde;
// **Added P to products
J9: ATP => ADP + P; J9_k*ATP;
J10: External_acetaldehyde => $Sink; J10_k*External_acetaldehyde;
// Species initializations:
Glucose = 0;
fructose_1_6_bisphosphate = 0;
glyceraldehyde_3_phosphate = 0;
glycerate_3_phosphate = 0;
pyruvate = 0;
Acetyladehyde = 0;
External_acetaldehyde = 0;
ATP = 3;
P = 1.7; # added inorganic phosphate
ADP = 1;
NAD = 0.5;
NADH = 0.5;
External_glucose = 0;
ethanol = 0;
Glycerol = 0;
Sink = 0;
// Compartment initializations:
compartment_ = 1;
// Variable initializations:
J0_inputFlux = 50;
J1_k1 = 550;
J1_Ki = 1;
J1_n = 4;
J2_k = 9.8;
J3_k = 85.7;
J4_kg = 323.8;
J4_kp = 76411.1;
J4_ka = 57823.1;
J4_kk = 23.7;
J5_k = 80;
J6_k = 9.7;
J7_k = 2000;
J8_k1 = 375;
J8_k2 = 375;
J9_k = 28;
J10_k = 80;
// Other declarations:
const compartment_, J0_inputFlux, J1_k1, J1_Ki, J1_n, J2_k, J3_k;
const J4_kg, J4_kp, J4_ka, J4_kk, J5_k, J6_k, J7_k, J8_k1, J8_k2;
const J9_k, J10_k;
"""
# Make sure that the model works
rr = te.loada(REVISED_WOLF_MODEL)
rr.simulate()
rr.plot(figsize=(14, 10))
_ = lint(REVISED_WOLF_MODEL, mass_balance_check="games")
```
There dynamics are not the same as with the original Wolf model since the interpretations and values of some kinetics constants are different because of the inclusion of ``P`` in ``J4`` and ``J5``.
# Exercise 2: Dynamic Tests
This exercise uses the Wolf model of glycolytic oscillations.
1. What is the relationship between the concentrations of
glucose, furctose_1_6_bisphosphate, and pyruvate after the initial transients.
Does this relationship always hold?
1. Propose a test that checks for that the order of the concentrations at steady state of glucose, furctose_1_6_bisphosphate, and pyruvate.
Hint: Implement a function that checks that one vector
is greater than a second vector after a specified index.
1. Another characteristic of the Wolf model is the presence of oscillations at the same frequency.
Describe in words how you would implement a test to
checks for the presence of these oscillations.
## (1) Relationships between concentrations
After the initial transient, the concentration of
pyruvate is almost always larger than the concentration of furctose_1_6_bisphosphate which is almost always larger than glucose.
The ordinal relationship holds a large fraction of the time but not *all* of the time.
The plots below show this.
```
rr = te.loada(WOLF_MODEL)
data = rr.simulate(0, 5, 200)
import pandas as pd
wolfDF = pd.DataFrame(data)
wolfDF.columns = data.colnames
wolfDF
fig, ax = plt.subplots(1)
ax.plot(wolfDF["time"], wolfDF["[Glucose]"])
ax.plot(wolfDF["time"], wolfDF["[fructose_1_6_bisphosphate]"])
ax.plot(wolfDF["time"], wolfDF["[pyruvate]"])
ax.legend(["Glucose", "fructose_1_6_bisphosphate", "pyruvate"])
```
## (2) Test for relative size of concentrations
```
def isLarger(ser1, ser2, fractionTrue=1.0, startIdx=0):
"""
Checks that arr1[startIdx:] > arr2[startIdx:]
Parameters
----------
ser1: pd.Series
ser2: pd.Series
fractionTrue: float in [0, 1]
startIdx: int
Returns
-------
bool
"""
numTrue = sum(ser1.loc[startIdx:] > ser2.loc[startIdx:])
result = 1.0*numTrue / (len(ser1) - startIdx)
return result >= fractionTrue
# TESTS
ser1 = pd.Series(range(10))
ser2 = pd.Series(range(-10, 0))
assert(isLarger(ser1, ser2))
assert(not isLarger(ser2, ser1))
assert(not isLarger(ser1, ser2, fractionTrue=1.1)) # Test fractionTrue
import unittest
# Performs unittests on wolf model
# Define a class in which the tests will run
class TestWolfModel(unittest.TestCase):
def setUp(self):
self.df = wolfDF
self.startIdx = 50
def testPyruvateGlucose(self):
self.assertTrue(isLarger(self.df["[pyruvate]"],
# self.df["fructose_1_6_bisphosphate"],
self.df["[Glucose]"],
startIdx=self.startIdx,
fractionTrue=1.0))
def testFructoseGlucose(self):
self.assertTrue(isLarger(self.df["[fructose_1_6_bisphosphate]"],
self.df["[Glucose]"],
fractionTrue=0.95,
startIdx=self.startIdx))
def testPyruvateFructose(self):
self.assertTrue(isLarger(self.df["[pyruvate]"],
self.df["[fructose_1_6_bisphosphate]"],
startIdx=self.startIdx,
fractionTrue=0.95))
suite = unittest.TestLoader().loadTestsFromTestCase(TestWolfModel)
_ = unittest.TextTestRunner().run(suite)
```
## (3) Frequency Tests
After the initial transient of about 2 sec, concentrations oscillate. One way to characterize oscillations is by using the fourier transform. To construct tests, we could implement the function ``getFft`` that calculates the fast fourier transform
(FFT) for a chemical species, and a second function, ``isOscillate``, that checks to calls ``getFft`` to determine if oscillations of the expected frequency are present.
|
github_jupyter
|
IS_COLAB = True
if IS_COLAB:
!pip install -q tellurium
!pip install -q SBMLLint
pass
# Python packages used in this section
import os
import matplotlib.pyplot as plt
import numpy as np
import urllib.request # use this library to download file from GitHub
from SBMLLint.tools.sbmllint import lint
import tellurium as te
# Constants
ENDTIME = 10
NUMPOINT = 10*ENDTIME
def getSharedCodes(moduleName):
"""
Obtains common codes from the github repository.
Parameters
----------
moduleName: str
name of the python module in the src directory
"""
if IS_COLAB:
url = "https://github.com/sys-bio/network-modeling-summer-school-2021/raw/main/src/%s.py" % moduleName
local_python = "python.py"
_, _ = urllib.request.urlretrieve(url=url, filename=local_python)
else:
local_python = "../../src/%s.py" % moduleName
with open(local_python, "r") as fd:
codeStr = "".join(fd.readlines())
print(codeStr)
exec(codeStr, globals())
# Acquire codes
getSharedCodes("util")
# TESTS
assert(isinstance(LINEAR_PATHWAY_DF, pd.DataFrame))
print(WOLF_MODEL)
rr = te.loada(WOLF_MODEL)
rr.plot(rr.simulate())
# Constants used in the section
MOLECULES = ["Glucose", "fructose_1_6_bisphosphate", "glyceraldehyde_3_phosphate", "glycerate_3_phosphate",
"pyruvate", "Acetyladehyde", "External_acetaldehyde", "ATP", "ADP", "NAD", "NADH"]
ENDTIME = 5
NUMPOINT = 100*ENDTIME
ROADRUNNER = te.loada(WOLF_MODEL)
_ = lint(WOLF_MODEL, mass_balance_check="games")
REVISED_WOLF_MODEL = """
species $External_glucose in compartment_, $ethanol in compartment_, $Glycerol in compartment_;
species $Sink in compartment_;
// Reactions:
J0: $External_glucose => Glucose; J0_inputFlux;
// **Added P to products
J1: Glucose + 2 ATP => fructose_1_6_bisphosphate + 2 ADP + 2 P; J1_k1*Glucose*ATP*(1/(1 + (ATP/J1_Ki)^J1_n));
J2: fructose_1_6_bisphosphate => glyceraldehyde_3_phosphate + glyceraldehyde_3_phosphate; J2_k*fructose_1_6_bisphosphate;
J3: glyceraldehyde_3_phosphate + NADH => NAD + $Glycerol; J3_k*glyceraldehyde_3_phosphate*NADH;
// **Added P to reactants and kinetics
J4: glyceraldehyde_3_phosphate + ADP + P + NAD => ATP + glycerate_3_phosphate + NADH; (J4_kg*J4_kp*glyceraldehyde_3_phosphate*NAD*ADP*P - J4_ka*J4_kk*glycerate_3_phosphate*ATP*NADH)/(J4_ka*NADH + J4_kp*ADP);
// **Added P to reactants and kinetics
J5: glycerate_3_phosphate + ADP + P => ATP + pyruvate; J5_k*glycerate_3_phosphate*ADP*P;
J6: pyruvate => Acetyladehyde; J6_k*pyruvate;
J7: Acetyladehyde + NADH => NAD + $ethanol; J7_k*Acetyladehyde*NADH;
J8: Acetyladehyde => External_acetaldehyde; J8_k1*Acetyladehyde - J8_k2*External_acetaldehyde;
// **Added P to products
J9: ATP => ADP + P; J9_k*ATP;
J10: External_acetaldehyde => $Sink; J10_k*External_acetaldehyde;
// Species initializations:
Glucose = 0;
fructose_1_6_bisphosphate = 0;
glyceraldehyde_3_phosphate = 0;
glycerate_3_phosphate = 0;
pyruvate = 0;
Acetyladehyde = 0;
External_acetaldehyde = 0;
ATP = 3;
P = 1.7; # added inorganic phosphate
ADP = 1;
NAD = 0.5;
NADH = 0.5;
External_glucose = 0;
ethanol = 0;
Glycerol = 0;
Sink = 0;
// Compartment initializations:
compartment_ = 1;
// Variable initializations:
J0_inputFlux = 50;
J1_k1 = 550;
J1_Ki = 1;
J1_n = 4;
J2_k = 9.8;
J3_k = 85.7;
J4_kg = 323.8;
J4_kp = 76411.1;
J4_ka = 57823.1;
J4_kk = 23.7;
J5_k = 80;
J6_k = 9.7;
J7_k = 2000;
J8_k1 = 375;
J8_k2 = 375;
J9_k = 28;
J10_k = 80;
// Other declarations:
const compartment_, J0_inputFlux, J1_k1, J1_Ki, J1_n, J2_k, J3_k;
const J4_kg, J4_kp, J4_ka, J4_kk, J5_k, J6_k, J7_k, J8_k1, J8_k2;
const J9_k, J10_k;
"""
# Make sure that the model works
rr = te.loada(REVISED_WOLF_MODEL)
rr.simulate()
rr.plot(figsize=(14, 10))
_ = lint(REVISED_WOLF_MODEL, mass_balance_check="games")
rr = te.loada(WOLF_MODEL)
data = rr.simulate(0, 5, 200)
import pandas as pd
wolfDF = pd.DataFrame(data)
wolfDF.columns = data.colnames
wolfDF
fig, ax = plt.subplots(1)
ax.plot(wolfDF["time"], wolfDF["[Glucose]"])
ax.plot(wolfDF["time"], wolfDF["[fructose_1_6_bisphosphate]"])
ax.plot(wolfDF["time"], wolfDF["[pyruvate]"])
ax.legend(["Glucose", "fructose_1_6_bisphosphate", "pyruvate"])
def isLarger(ser1, ser2, fractionTrue=1.0, startIdx=0):
"""
Checks that arr1[startIdx:] > arr2[startIdx:]
Parameters
----------
ser1: pd.Series
ser2: pd.Series
fractionTrue: float in [0, 1]
startIdx: int
Returns
-------
bool
"""
numTrue = sum(ser1.loc[startIdx:] > ser2.loc[startIdx:])
result = 1.0*numTrue / (len(ser1) - startIdx)
return result >= fractionTrue
# TESTS
ser1 = pd.Series(range(10))
ser2 = pd.Series(range(-10, 0))
assert(isLarger(ser1, ser2))
assert(not isLarger(ser2, ser1))
assert(not isLarger(ser1, ser2, fractionTrue=1.1)) # Test fractionTrue
import unittest
# Performs unittests on wolf model
# Define a class in which the tests will run
class TestWolfModel(unittest.TestCase):
def setUp(self):
self.df = wolfDF
self.startIdx = 50
def testPyruvateGlucose(self):
self.assertTrue(isLarger(self.df["[pyruvate]"],
# self.df["fructose_1_6_bisphosphate"],
self.df["[Glucose]"],
startIdx=self.startIdx,
fractionTrue=1.0))
def testFructoseGlucose(self):
self.assertTrue(isLarger(self.df["[fructose_1_6_bisphosphate]"],
self.df["[Glucose]"],
fractionTrue=0.95,
startIdx=self.startIdx))
def testPyruvateFructose(self):
self.assertTrue(isLarger(self.df["[pyruvate]"],
self.df["[fructose_1_6_bisphosphate]"],
startIdx=self.startIdx,
fractionTrue=0.95))
suite = unittest.TestLoader().loadTestsFromTestCase(TestWolfModel)
_ = unittest.TextTestRunner().run(suite)
| 0.546012 | 0.688508 |
# Image classification workflow with distributed training
The following example demonstrates an end to end data science workflow for building an an image classifier <br>
The model is trained on an images dataset of cats and dogs. Then the model is deployed as a function in a serving layer <br>
Users can send http request with an image of cats/dogs image and get a respond back that identify whether it is a cat or a dog
This typical data science workflow comprises of the following:
* Download anb label the dataset
* Training a model on the images dataset
* Deploy a function with the new model in a serving layer
* Testing the function
Key technologies:
* Tensorflow-Keras for training the model
* Horovod for running a distributed training
* MLRun (open source library for tracking experiments https://github.com/mlrun/mlrun) for building the functions and tracking experiments
* Nuclio function for creating a funciton that runs the model in a serving layer
This demo is based on the following:<br>
* https://github.com/tensorflow/docs/tree/master/site/en/tutorials
* https://www.kaggle.com/uysimty/keras-cnn-dog-or-cat-classification/log
```
# nuclio: ignore
import nuclio
```
## Helper functions for downloading and labeling images
In the code below we have two functions:
1. open_archive - Get and extract a zip file that contains cats and dog images. users need to pass the source URL and the target directory which is stored in Iguazio data layer
2. categories_map_builder - labeling the dataset based on the file name. the functions creates a pandas dataframe with the filename and category (i.e. cat & dog)
Note that sometime after running pip install you need to restart the jupyer kernel
#### Function config and code
```
import os
import zipfile
import json
import shutil
from glob import glob
from tempfile import mktemp
import pandas as pd
import numpy as np
from mlrun import DataItem
def _extract_category(filename):
return os.path.basename(filename).split('.')[0]
def _extract_detatset(i, per_class):
return 'train' if i <= per_class else 'validation'
# download the image archive
def open_archive(context,
archive_url: DataItem,
target_path,
refresh=False,
train_size=0.8):
"""Open a file/object archive into a target directory
Currently supports zip and tar.gz
:param context: function execution context
:param archive_url: url of archive file
:param target_path: file system path to store extracted files
:param key: key of archive contents in artifact store
:param test_size: set the train dataset size out of total dataset
"""
os.makedirs(target_path, exist_ok=True)
# get the archive as a local file (download if needed)
archive_url = archive_url.local()
context.logger.info('Extracting zip')
extraction_path = os.path.join(target_path, 'tmp')
zip_ref = zipfile.ZipFile(archive_url, 'r')
zip_ref.extractall(extraction_path)
# get all files paths
filenames = [file for file in glob(extraction_path + '/*/*') if file.endswith('.jpg')]
# extract classes and classes ratio
file_classes = [_extract_category(file) for file in filenames]
classes, class_counts = np.unique(file_classes, return_counts=True)
files = {c: [] for c in classes}
for label, file in zip(file_classes, filenames):
files[label].append(file)
# Infer training dataset absolute size
num_files = len(filenames)
num_train = int(np.ceil(num_files * train_size))
num_samples_per_class = int(np.ceil(num_train / len(classes)))
# create dirs for train and validation
for category in classes:
train_dir = os.path.join(target_path, "train", category)
validation_dir = os.path.join(target_path, "validation", category)
os.makedirs(train_dir, exist_ok=True)
os.makedirs(validation_dir, exist_ok=True)
# move files and clean directory
for label, filenames in files.items():
for i, file in enumerate(filenames):
shutil.move(file, os.path.join(target_path, _extract_detatset(i, num_samples_per_class), label, os.path.basename(file)))
shutil.rmtree(extraction_path)
# log
context.logger.info(f'extracted archive to {target_path}')
context.logger.info(f'Dataset container the classes {classes}')
context.log_artifact('content', target_path=target_path)
# nuclio: end-code
```
### mlconfig
Set the MLRun database location and the base directory
```
from os import environ, path
from mlrun import mlconf
mlconf.dbpath = mlconf.dbpath or 'http://mlrun-api:8080'
mlconf.artifact_path = mlconf.artifact_path or f'{environ["HOME"]}/artifacts'
# set tensorflow version (v1 or v2)
tf_ver = 'v2'
# specify paths and artifacts target location
code_dir = path.join(path.abspath('./'), 'src-tf' + tf_ver) # Where our source code files are saved
images_path = path.join(mlconf.artifact_path, 'images')
code_dir, images_path
project_name='cat-and-dog-servers'
```
### Test locally, Download and extract image archive
The dataset is taken from the Iguazio-sample bucket in S3 <br>
>Note that this step is captured in the MLRun database. <br>
We create a new local function with our inline code from above.
We then define a `NewTask` with the `open_archive` function handler and the needed parameters and run it.
```
# download images from s3 using the local `open_archive` function
from mlrun import NewTask, run_local
open_archive_task = NewTask(name='download',
handler=open_archive,
params={'target_path': os.path.abspath('./images')},
inputs={'archive_url': 'http://iguazio-sample-data.s3.amazonaws.com/catsndogs.zip'})
download_run = run_local(open_archive_task,
project=project_name)
```
# Complete Data-Science Pipeline with MLRun and Kubeflow
We are using a library called MLRun for running the functions and storing the experiments meta data in the MLRun database <br>
Users can query the database to view all the experiments along with their associated meta data <br>
- Get data
- Create categories map
- Train horovod model on the cluster
- Deploy model
## Create a multi-stage project (ingest, label, train, deploy model)
Projects are used to package multiple functions, workflows, and artifacts. We usually store project code and definitions in a Git archive.
The following code creates a new project in a local dir and initialize git tracking on that
```
from mlrun import new_project, code_to_function
project_dir = './'
hvdproj = new_project(project_name, project_dir)
```
#### Add our `utils` function to the project
We convert our inline (notebook) code to a function object and register that under our project
```
utils = code_to_function(kind='job',
name='utils',
image='mlrun/mlrun')
hvdproj.set_function(utils)
```
### Define a new function for distributed Training with TensorFlow, Keras and Horovod
Here we use the same structure as before to deploy our **[cats vs. dogs tensorflow model training file](horovod-training.py)** to run on the defined horovod cluster in a distributed manner.
1. Define the input parameters for the training function.
2. Set the function's `kind='mpijob'` to let MLRun know to apply the job to the MPI CRD and create the requested horovod cluster.
3. Set the number of workers for the horovod cluster to use by setting `trainer.spec.replicas = 4` (default is 1 replica).
#### To run training using GPUs
To provide GPU support for our workers we need to edit the following:
1. Set the function image to a CUDA enabled image (Required) with GPU versions of the frameworks (if needed - TF 1.x gpu version for example)
2. Set the number of GPUs **each worker** will receive by setting `trainer.gpus(1)` (default is 0 GPUs).
> You can change `use_gpu` to `True` to enable GPU support with 1 gpu/worker
> Please verify that the `HOROVOD_FILE` path is available from the cluster (Local path and Mounted path may vary)
```
from mlrun import new_function
import os
# Set `use_gpu` to True to run the function using a GPU
use_gpu = True
image = lambda gpu: 'mlrun/ml-models-gpu' if gpu else 'mlrun/ml-models'
# Set basic function parameters
HOROVOD_FILE = os.path.join(code_dir, 'horovod-training.py')
trainer = new_function(name='trainer',
kind='mpijob',
command=HOROVOD_FILE)
trainer.spec.replicas = 2
# Pick image by wanted TF version
if tf_ver == 'v1':
trainer.spec.image = f'{image(use_gpu)}:{mlconf.version}-py36'
else:
trainer.spec.image = image(use_gpu)
# Add GPUs to workers?
if use_gpu:
trainer.gpus(1)
hvdproj.set_function(trainer)
```
#### Add a serving function from the functions hub (marketplace)
```
if tf_ver == 'v1':
hvdproj.set_function('hub://tf1_serving', 'serving')
else:
hvdproj.set_function('hub://tf2_serving', 'serving')
```
#### Register the source images directory as a project artifact (can be accessed by name)
```
hvdproj.log_artifact(
'images',
target_path='http://iguazio-sample-data.s3.amazonaws.com/catsndogs.zip',
artifact_path=mlconf.artifact_path)
#print(hvdproj.to_yaml())
```
#### Define and save a pipeline
The following workflow definition will be written into a file, it describes an execution graph (DAG) and how functions are conncted to form an end to end pipline.
* Download the images
* Label the images (Cats & Dogs)
* Train the model using distributed TensorFlow (Horovod)
* Deploy the model into a serverless function
```
%%writefile workflow.py
from kfp import dsl
from mlrun import mount_v3io
funcs = {}
def init_functions(functions: dict, project=None, secrets=None):
'''
This function will run before running the project.
It allows us to add our specific system configurations to the functions
like mounts or secrets if needed.
In this case we will add Iguazio's user mount to our functions using the
`mount_v3io()` function to automatically set the mount with the needed
variables taken from the environment.
* mount_v3io can be replaced with mlrun.platforms.mount_pvc() for
non-iguazio mount
@param functions: <function_name: function_yaml> dict of functions in the
workflow
@param project: project object
@param secrets: secrets required for the functions for s3 connections and
such
'''
for f in functions.values():
f.apply(mount_v3io()) # On Iguazio (Auto-mount /User)
# f.apply(mlrun.platforms.mount_pvc()) # Non-Iguazio mount
functions['serving'].set_env('MODEL_CLASS', 'TFModel')
functions['serving'].set_env('IMAGE_HEIGHT', '224')
functions['serving'].set_env('IMAGE_WIDTH', '224')
functions['serving'].set_env('ENABLE_EXPLAINER', 'False')
functions['serving'].spec.min_replicas = 1
@dsl.pipeline(
name='Image classification demo',
description='Train an Image Classification TF Algorithm using MLRun'
)
def kfpipeline(
image_archive='store:///images',
images_dir='/User/artifacts/images',
checkpoints_dir='/User/artifacts/models/checkpoints',
model_name='cat_vs_dog_tfv1',
epochs=2):
# step 1: download and prep images
open_archive = funcs['utils'].as_step(name='download',
handler='open_archive',
params={'target_path': images_dir},
inputs={'archive_url': image_archive},
outputs=['content'])
# step 2: train the model
train_dir = str(open_archive.outputs['content']) + '/train'
val_dir = str(open_archive.outputs['content']) + '/validation'
train = funcs['trainer'].as_step(name='train',
params={'epochs': epochs,
'checkpoints_dir': checkpoints_dir,
'model_dir' : 'tfmodels',
'train_path' : train_dir,
'val_path' : val_dir,
'batch_size' : 32},
outputs=['model'])
# deploy the model using nuclio functions
deploy = funcs['serving'].deploy_step(models={model_name: train.outputs['model']})
hvdproj.set_workflow('main', 'workflow.py', embed=True)
hvdproj.save()
```
<a id='run-pipeline'></a>
## Run a pipeline workflow
You can check the **[workflow.py](src/workflow.py)** file to see how functions objects are initialized and used (by name) inside the workflow.
The `workflow.py` file has two parts, initialize the function objects and define pipeline dsl (connect the function inputs and outputs).
> Note the pipeline can include CI steps like building container images and deploying models.
### Run
use the `run` method to execute a workflow, you can provide alternative arguments and specify the default target for workflow artifacts.<br>
The workflow ID is returned and can be used to track the progress or you can use the hyperlinks
> Note: The same command can be issued through CLI commands:<br>
`mlrun project my-proj/ -r main -p "v3io:///users/admin/mlrun/kfp/{{workflow.uid}}/"`
The dirty flag allow us to run a project with uncommited changes (when the notebook is in the same git dir it will always be dirty)
```
artifact_path = path.abspath('./pipe/{{workflow.uid}}')
run_id = hvdproj.run(
'main',
arguments={'model_name': 'cat_vs_dog_tf' + tf_ver,
'images_dir': artifact_path + '/images'},
artifact_path=artifact_path,
dirty=True, watch=True)
```
## Test the serving function
After the function has been deployed we can test it as a regular REST Endpoint using `requests`.
```
import requests
from PIL import Image
from io import BytesIO
import matplotlib.pyplot as plt
```
### Define test params
```
# Testing event
cat_image_url = 'https://s3.amazonaws.com/iguazio-sample-data/images/catanddog/cat.102.jpg'
response = requests.get(cat_image_url)
cat_image = response.content
img = Image.open(BytesIO(cat_image))
print('Test image:')
plt.imshow(img)
```
### Test The Serving Function (with Image URL)
```
addr = 'http://nuclio-{}-{}:8080'.format(hvdproj.name, hvdproj.func('serving').metadata.name)
headers = {'Content-type': 'image/jpeg'}
url = addr + f'/cat_vs_dog_tf{tf_ver}/predict'
response = requests.post(url=url,
data=json.dumps({'data_url': cat_image_url}),
headers=headers)
print(response.content.decode('utf-8'))
%%timeit
requests.post(url=url,
data=json.dumps({'data_url': cat_image_url}),
headers=headers)
```
### Test The Serving Function (with Jpeg Image)
```
headers = {'Content-type': 'image/jpeg'}
response = requests.post(url=url,
data=cat_image,
headers=headers)
print(response.content.decode('utf-8'))
%%timeit
requests.post(url=url,
data=cat_image,
headers=headers)
```
**[back to top](#top)**
|
github_jupyter
|
# nuclio: ignore
import nuclio
import os
import zipfile
import json
import shutil
from glob import glob
from tempfile import mktemp
import pandas as pd
import numpy as np
from mlrun import DataItem
def _extract_category(filename):
return os.path.basename(filename).split('.')[0]
def _extract_detatset(i, per_class):
return 'train' if i <= per_class else 'validation'
# download the image archive
def open_archive(context,
archive_url: DataItem,
target_path,
refresh=False,
train_size=0.8):
"""Open a file/object archive into a target directory
Currently supports zip and tar.gz
:param context: function execution context
:param archive_url: url of archive file
:param target_path: file system path to store extracted files
:param key: key of archive contents in artifact store
:param test_size: set the train dataset size out of total dataset
"""
os.makedirs(target_path, exist_ok=True)
# get the archive as a local file (download if needed)
archive_url = archive_url.local()
context.logger.info('Extracting zip')
extraction_path = os.path.join(target_path, 'tmp')
zip_ref = zipfile.ZipFile(archive_url, 'r')
zip_ref.extractall(extraction_path)
# get all files paths
filenames = [file for file in glob(extraction_path + '/*/*') if file.endswith('.jpg')]
# extract classes and classes ratio
file_classes = [_extract_category(file) for file in filenames]
classes, class_counts = np.unique(file_classes, return_counts=True)
files = {c: [] for c in classes}
for label, file in zip(file_classes, filenames):
files[label].append(file)
# Infer training dataset absolute size
num_files = len(filenames)
num_train = int(np.ceil(num_files * train_size))
num_samples_per_class = int(np.ceil(num_train / len(classes)))
# create dirs for train and validation
for category in classes:
train_dir = os.path.join(target_path, "train", category)
validation_dir = os.path.join(target_path, "validation", category)
os.makedirs(train_dir, exist_ok=True)
os.makedirs(validation_dir, exist_ok=True)
# move files and clean directory
for label, filenames in files.items():
for i, file in enumerate(filenames):
shutil.move(file, os.path.join(target_path, _extract_detatset(i, num_samples_per_class), label, os.path.basename(file)))
shutil.rmtree(extraction_path)
# log
context.logger.info(f'extracted archive to {target_path}')
context.logger.info(f'Dataset container the classes {classes}')
context.log_artifact('content', target_path=target_path)
# nuclio: end-code
from os import environ, path
from mlrun import mlconf
mlconf.dbpath = mlconf.dbpath or 'http://mlrun-api:8080'
mlconf.artifact_path = mlconf.artifact_path or f'{environ["HOME"]}/artifacts'
# set tensorflow version (v1 or v2)
tf_ver = 'v2'
# specify paths and artifacts target location
code_dir = path.join(path.abspath('./'), 'src-tf' + tf_ver) # Where our source code files are saved
images_path = path.join(mlconf.artifact_path, 'images')
code_dir, images_path
project_name='cat-and-dog-servers'
# download images from s3 using the local `open_archive` function
from mlrun import NewTask, run_local
open_archive_task = NewTask(name='download',
handler=open_archive,
params={'target_path': os.path.abspath('./images')},
inputs={'archive_url': 'http://iguazio-sample-data.s3.amazonaws.com/catsndogs.zip'})
download_run = run_local(open_archive_task,
project=project_name)
from mlrun import new_project, code_to_function
project_dir = './'
hvdproj = new_project(project_name, project_dir)
utils = code_to_function(kind='job',
name='utils',
image='mlrun/mlrun')
hvdproj.set_function(utils)
from mlrun import new_function
import os
# Set `use_gpu` to True to run the function using a GPU
use_gpu = True
image = lambda gpu: 'mlrun/ml-models-gpu' if gpu else 'mlrun/ml-models'
# Set basic function parameters
HOROVOD_FILE = os.path.join(code_dir, 'horovod-training.py')
trainer = new_function(name='trainer',
kind='mpijob',
command=HOROVOD_FILE)
trainer.spec.replicas = 2
# Pick image by wanted TF version
if tf_ver == 'v1':
trainer.spec.image = f'{image(use_gpu)}:{mlconf.version}-py36'
else:
trainer.spec.image = image(use_gpu)
# Add GPUs to workers?
if use_gpu:
trainer.gpus(1)
hvdproj.set_function(trainer)
if tf_ver == 'v1':
hvdproj.set_function('hub://tf1_serving', 'serving')
else:
hvdproj.set_function('hub://tf2_serving', 'serving')
hvdproj.log_artifact(
'images',
target_path='http://iguazio-sample-data.s3.amazonaws.com/catsndogs.zip',
artifact_path=mlconf.artifact_path)
#print(hvdproj.to_yaml())
%%writefile workflow.py
from kfp import dsl
from mlrun import mount_v3io
funcs = {}
def init_functions(functions: dict, project=None, secrets=None):
'''
This function will run before running the project.
It allows us to add our specific system configurations to the functions
like mounts or secrets if needed.
In this case we will add Iguazio's user mount to our functions using the
`mount_v3io()` function to automatically set the mount with the needed
variables taken from the environment.
* mount_v3io can be replaced with mlrun.platforms.mount_pvc() for
non-iguazio mount
@param functions: <function_name: function_yaml> dict of functions in the
workflow
@param project: project object
@param secrets: secrets required for the functions for s3 connections and
such
'''
for f in functions.values():
f.apply(mount_v3io()) # On Iguazio (Auto-mount /User)
# f.apply(mlrun.platforms.mount_pvc()) # Non-Iguazio mount
functions['serving'].set_env('MODEL_CLASS', 'TFModel')
functions['serving'].set_env('IMAGE_HEIGHT', '224')
functions['serving'].set_env('IMAGE_WIDTH', '224')
functions['serving'].set_env('ENABLE_EXPLAINER', 'False')
functions['serving'].spec.min_replicas = 1
@dsl.pipeline(
name='Image classification demo',
description='Train an Image Classification TF Algorithm using MLRun'
)
def kfpipeline(
image_archive='store:///images',
images_dir='/User/artifacts/images',
checkpoints_dir='/User/artifacts/models/checkpoints',
model_name='cat_vs_dog_tfv1',
epochs=2):
# step 1: download and prep images
open_archive = funcs['utils'].as_step(name='download',
handler='open_archive',
params={'target_path': images_dir},
inputs={'archive_url': image_archive},
outputs=['content'])
# step 2: train the model
train_dir = str(open_archive.outputs['content']) + '/train'
val_dir = str(open_archive.outputs['content']) + '/validation'
train = funcs['trainer'].as_step(name='train',
params={'epochs': epochs,
'checkpoints_dir': checkpoints_dir,
'model_dir' : 'tfmodels',
'train_path' : train_dir,
'val_path' : val_dir,
'batch_size' : 32},
outputs=['model'])
# deploy the model using nuclio functions
deploy = funcs['serving'].deploy_step(models={model_name: train.outputs['model']})
hvdproj.set_workflow('main', 'workflow.py', embed=True)
hvdproj.save()
artifact_path = path.abspath('./pipe/{{workflow.uid}}')
run_id = hvdproj.run(
'main',
arguments={'model_name': 'cat_vs_dog_tf' + tf_ver,
'images_dir': artifact_path + '/images'},
artifact_path=artifact_path,
dirty=True, watch=True)
import requests
from PIL import Image
from io import BytesIO
import matplotlib.pyplot as plt
# Testing event
cat_image_url = 'https://s3.amazonaws.com/iguazio-sample-data/images/catanddog/cat.102.jpg'
response = requests.get(cat_image_url)
cat_image = response.content
img = Image.open(BytesIO(cat_image))
print('Test image:')
plt.imshow(img)
addr = 'http://nuclio-{}-{}:8080'.format(hvdproj.name, hvdproj.func('serving').metadata.name)
headers = {'Content-type': 'image/jpeg'}
url = addr + f'/cat_vs_dog_tf{tf_ver}/predict'
response = requests.post(url=url,
data=json.dumps({'data_url': cat_image_url}),
headers=headers)
print(response.content.decode('utf-8'))
%%timeit
requests.post(url=url,
data=json.dumps({'data_url': cat_image_url}),
headers=headers)
headers = {'Content-type': 'image/jpeg'}
response = requests.post(url=url,
data=cat_image,
headers=headers)
print(response.content.decode('utf-8'))
%%timeit
requests.post(url=url,
data=cat_image,
headers=headers)
| 0.494141 | 0.969353 |
# Ex 1.1
## Part 1
$\langle r \rangle = \int_0^1 r dr = 1/2$. <font color="red">Make a picture of the estimation of $\langle r \rangle$ and its uncertainty (which corresponds to Standard Deviation of the mean for the estimation of $\langle r \rangle$) with a large number of *throws* $M$ (e.g. $M\ge 10^4$) as a function of the number of blocks, $N$</font> (see below: Computing statistical uncertainties).
```
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pyplot import figure
from time import time
start = time()
M=10000 #number of throws
N=100 #number of blocks
L=int(M/N) #number of throws per block
x = np.arange(N)
x*=L
f = np.loadtxt("averages.txt", skiprows=1)
figure(figsize=(7,5), dpi=100)
plt.errorbar(x,f[:,0],yerr=f[:,1])
plt.axhline(0.5, color='red', label='1/2')
plt.legend(loc="upper right")
plt.xlabel("# throw")
plt.ylabel("<r>")
plt.grid(True)
plt.show()
```
Results are as expected: the cumulative average tends to stabilize around $\frac 1 2$, and the error decreases with it.
## Part 2
$\sigma^2 = \int_0^1 (r-1/2)^2 dr = 1/12$. <font color="red">Make a picture of the estimation of $\sigma^2$ and its uncertainty (which corresponds to Standard Deviation of the mean for the estimation of $\langle (r-1/2)^2 \rangle$) with a large number of *throws* $M$ (e.g. $M\ge 10^4$) as a function of the number of blocks, $N$</font> (see below: Computing statistical uncertainties).
```
f1 = np.loadtxt("errors.txt", skiprows=1)
figure(figsize=(7,5), dpi=100)
plt.errorbar(x,f1[:,0],yerr=f1[:,1])
plt.axhline(1/12, color='red', label="1/12")
plt.legend(loc="upper right")
plt.xlabel("# throw")
plt.ylabel("<σ²>")
plt.grid(True)
plt.show()
```
The average of the errors stabilizes around $\frac 1 {12}$ and it's deviation decreases with it, as expected.
## Parte 3
Divide $[0,1]$ into $M$ identical sub-intervals and implement the $\chi^2$ test. Obviously, the number of expected events observed in each sub-interval after $n$ *throws*, according to a uniform distribution, is $np = n\times 1/M= n/M$. Fix $M=10^2$ and use for $n$ the first $10^4$ pseudo-random numbers, then the successive $10^4$ pseudo-random numbers, and so on ... 100 times. <font color="red">Plot $\chi^2_j$ for $j=1, ..., 100$</font>. In this case the chi-square statistic is:
$$\chi^2 = \sum_{i=1}^M \frac{\left( n_i - n/M \right)^2}{n/M}$$
We should expect on average that $(n_i - n/M)^2 \simeq n/M$ and thus $\chi^2 \simeq 100$, i.e. the number of sub-intervals.
A larger value of $\chi^2$ indicates that the hypothesis ($n_i$ are drawn from a uniform distribution) is rather unlikely.
```
figure(figsize=(7,5), dpi=100)
f2=np.loadtxt("ki.txt")
x2=np.arange(100)
x2+=1
plt.axhline(100, color='red')
plt.scatter(x2,f2[:,0])
plt.xlabel("# cycles")
plt.ylabel("χ²")
plt.grid(True)
plt.show()
figure(figsize=(7,5), dpi=100)
plt.errorbar(x2,f2[:,1],yerr=f2[:,2])
plt.axhline(100, color='red', label="χ²=100")
plt.legend(loc="upper right")
plt.xlabel("# cycles")
plt.ylabel("<χ²>")
plt.grid(True)
plt.show()
print("χ²:", np.average(f2[:,0]))
if(np.average(f2) < 150):
print("The χ² is considered passed: the values generated reflect to a good degree a true uniform distribution.")
else:
print("The generated values do not agree with a uniform distribution.")
end = time()
print("Total computing time:", int((end-start)*100)/100., "sec.")
```
|
github_jupyter
|
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pyplot import figure
from time import time
start = time()
M=10000 #number of throws
N=100 #number of blocks
L=int(M/N) #number of throws per block
x = np.arange(N)
x*=L
f = np.loadtxt("averages.txt", skiprows=1)
figure(figsize=(7,5), dpi=100)
plt.errorbar(x,f[:,0],yerr=f[:,1])
plt.axhline(0.5, color='red', label='1/2')
plt.legend(loc="upper right")
plt.xlabel("# throw")
plt.ylabel("<r>")
plt.grid(True)
plt.show()
f1 = np.loadtxt("errors.txt", skiprows=1)
figure(figsize=(7,5), dpi=100)
plt.errorbar(x,f1[:,0],yerr=f1[:,1])
plt.axhline(1/12, color='red', label="1/12")
plt.legend(loc="upper right")
plt.xlabel("# throw")
plt.ylabel("<σ²>")
plt.grid(True)
plt.show()
figure(figsize=(7,5), dpi=100)
f2=np.loadtxt("ki.txt")
x2=np.arange(100)
x2+=1
plt.axhline(100, color='red')
plt.scatter(x2,f2[:,0])
plt.xlabel("# cycles")
plt.ylabel("χ²")
plt.grid(True)
plt.show()
figure(figsize=(7,5), dpi=100)
plt.errorbar(x2,f2[:,1],yerr=f2[:,2])
plt.axhline(100, color='red', label="χ²=100")
plt.legend(loc="upper right")
plt.xlabel("# cycles")
plt.ylabel("<χ²>")
plt.grid(True)
plt.show()
print("χ²:", np.average(f2[:,0]))
if(np.average(f2) < 150):
print("The χ² is considered passed: the values generated reflect to a good degree a true uniform distribution.")
else:
print("The generated values do not agree with a uniform distribution.")
end = time()
print("Total computing time:", int((end-start)*100)/100., "sec.")
| 0.324235 | 0.987616 |
```
import os
import argparse
import logging
import time
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
!pip install torchvision
import torchvision.datasets as datasets
import torchvision.transforms as transforms
# parser = argparse.ArgumentParser()
# parser.add_argument('--network', type=str, choices=['resnet', 'odenet'], default='odenet')
# parser.add_argument('--tol', type=float, default=1e-3)
# parser.add_argument('--adjoint', type=eval, default=False, choices=[True, False])
# parser.add_argument('--downsampling-method', type=str, default='conv', choices=['conv', 'res'])
# parser.add_argument('--nepochs', type=int, default=160)
# parser.add_argument('--data_aug', type=eval, default=True, choices=[True, False])
# parser.add_argument('--lr', type=float, default=0.1)
# parser.add_argument('--batch_size', type=int, default=128)
# parser.add_argument('--test_batch_size', type=int, default=1000)
# parser.add_argument('--save', type=str, default='./experiment1')
# parser.add_argument('--debug', action='store_true')
# parser.add_argument('--gpu', type=int, default=0)
# args = parser.parse_args()
class Args:
network = 'odenet' # choices=['resnet', 'odenet']
tol = 1e-3
downsampling_method = 'conv' # choices=['conv', 'res'] ESTO NO VEO QUE SE USE EN NINGUN LADO
batch_size = 128
lr = 0.1
nepochs = 160
data_aug = True
test_batch_size = 1000
save = './experiment1'
degub = False
gpu = True
adjoint = False
args=Args()
if args.adjoint:
from torchdiffeq import odeint_adjoint as odeint
else:
from torchdiffeq import odeint
def conv3x3(in_planes, out_planes, stride=1):
"""3x3 convolution with padding"""
return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride, padding=1, bias=False)
def conv1x1(in_planes, out_planes, stride=1):
"""1x1 convolution"""
return nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=stride, bias=False)
def norm(dim):
return nn.GroupNorm(min(32, dim), dim)
class ResBlock(nn.Module):
expansion = 1
def __init__(self, inplanes, planes, stride=1, downsample=None):
super(ResBlock, self).__init__()
self.norm1 = norm(inplanes)
self.relu = nn.ReLU(inplace=True)
self.downsample = downsample
self.conv1 = conv3x3(inplanes, planes, stride)
self.norm2 = norm(planes)
self.conv2 = conv3x3(planes, planes)
def forward(self, x):
shortcut = x
out = self.relu(self.norm1(x))
if self.downsample is not None:
shortcut = self.downsample(out)
out = self.conv1(out)
out = self.norm2(out)
out = self.relu(out)
out = self.conv2(out)
return out + shortcut
class ConcatConv2d(nn.Module):
def __init__(self, dim_in, dim_out, ksize=3, stride=1, padding=0, dilation=1, groups=1, bias=True, transpose=False):
super(ConcatConv2d, self).__init__()
module = nn.ConvTranspose2d if transpose else nn.Conv2d
self._layer = module(
dim_in + 1, dim_out, kernel_size=ksize, stride=stride, padding=padding, dilation=dilation, groups=groups,
bias=bias
)
def forward(self, t, x):
tt = torch.ones_like(x[:, :1, :, :]) * t
ttx = torch.cat([tt, x], 1)
return self._layer(ttx)
class ODEfunc(nn.Module):
def __init__(self, dim):
super(ODEfunc, self).__init__()
self.norm1 = norm(dim)
self.relu = nn.ReLU(inplace=True)
self.conv1 = ConcatConv2d(dim, dim, 3, 1, 1)
self.norm2 = norm(dim)
self.conv2 = ConcatConv2d(dim, dim, 3, 1, 1)
self.norm3 = norm(dim)
self.nfe = 0
def forward(self, t, x):
self.nfe += 1
out = self.norm1(x)
out = self.relu(out)
out = self.conv1(t, out)
out = self.norm2(out)
out = self.relu(out)
out = self.conv2(t, out)
out = self.norm3(out)
return out
class ODEBlock(nn.Module):
def __init__(self, odefunc):
super(ODEBlock, self).__init__()
self.odefunc = odefunc
self.integration_time = torch.tensor([0, 1]).float()
def forward(self, x):
self.integration_time = self.integration_time.type_as(x)
out = odeint(self.odefunc, x, self.integration_time, rtol=args.tol, atol=args.tol)
return out[1]
@property
def nfe(self):
return self.odefunc.nfe
@nfe.setter
def nfe(self, value):
self.odefunc.nfe = value
class Flatten(nn.Module):
def __init__(self):
super(Flatten, self).__init__()
def forward(self, x):
shape = torch.prod(torch.tensor(x.shape[1:])).item()
return x.view(-1, shape)
class RunningAverageMeter(object):
"""Computes and stores the average and current value"""
def __init__(self, momentum=0.99):
self.momentum = momentum
self.reset()
def reset(self):
self.val = None
self.avg = 0
def update(self, val):
if self.val is None:
self.avg = val
else:
self.avg = self.avg * self.momentum + val * (1 - self.momentum)
self.val = val
def get_mnist_loaders(data_aug=False, batch_size=128, test_batch_size=1000, perc=1.0):
if data_aug:
transform_train = transforms.Compose([
transforms.RandomCrop(28, padding=4),
transforms.ToTensor(),
])
else:
transform_train = transforms.Compose([
transforms.ToTensor(),
])
transform_test = transforms.Compose([
transforms.ToTensor(),
])
train_loader = DataLoader(
datasets.MNIST(root='.data/mnist', train=True, download=True, transform=transform_train), batch_size=batch_size,
shuffle=True, num_workers=2, drop_last=True
)
train_eval_loader = DataLoader(
datasets.MNIST(root='.data/mnist', train=True, download=True, transform=transform_test),
batch_size=test_batch_size, shuffle=False, num_workers=2, drop_last=True
)
test_loader = DataLoader(
datasets.MNIST(root='.data/mnist', train=False, download=True, transform=transform_test),
batch_size=test_batch_size, shuffle=False, num_workers=2, drop_last=True
)
return train_loader, test_loader, train_eval_loader
def inf_generator(iterable):
"""Allows training with DataLoaders in a single infinite loop:
for i, (x, y) in enumerate(inf_generator(train_loader)):
"""
iterator = iterable.__iter__()
while True:
try:
yield iterator.__next__()
except StopIteration:
iterator = iterable.__iter__()
def learning_rate_with_decay(batch_size, batch_denom, batches_per_epoch, boundary_epochs, decay_rates):
initial_learning_rate = args.lr * batch_size / batch_denom
boundaries = [int(batches_per_epoch * epoch) for epoch in boundary_epochs]
vals = [initial_learning_rate * decay for decay in decay_rates]
def learning_rate_fn(itr):
lt = [itr < b for b in boundaries] + [True]
i = np.argmax(lt)
return vals[i]
return learning_rate_fn
def one_hot(x, K):
return np.array(x[:, None] == np.arange(K)[None, :], dtype=int)
def accuracy(model, dataset_loader):
total_correct = 0
for x, y in dataset_loader:
x = x.to(device)
y = one_hot(np.array(y.numpy()), 10)
target_class = np.argmax(y, axis=1)
predicted_class = np.argmax(model(x).cpu().detach().numpy(), axis=1)
total_correct += np.sum(predicted_class == target_class)
return total_correct / len(dataset_loader.dataset)
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
def makedirs(dirname):
if not os.path.exists(dirname):
os.makedirs(dirname)
def get_logger(logpath, filepath, package_files=[], displaying=True, saving=True, debug=False):
logger = logging.getLogger()
if debug:
level = logging.DEBUG
else:
level = logging.INFO
logger.setLevel(level)
if saving:
info_file_handler = logging.FileHandler(logpath, mode="a")
info_file_handler.setLevel(level)
logger.addHandler(info_file_handler)
if displaying:
console_handler = logging.StreamHandler()
console_handler.setLevel(level)
logger.addHandler(console_handler)
logger.info(filepath)
with open(filepath, "r") as f:
logger.info(f.read())
for f in package_files:
logger.info(f)
with open(f, "r") as package_f:
logger.info(package_f.read())
return logger
if __name__ == '__main__':
makedirs(args.save)
# logger = get_logger(logpath=os.path.join(args.save, 'logs'), filepath=os.path.abspath(__file__))
# logger.info(args)
device = torch.device('cuda:' + str(args.gpu) if torch.cuda.is_available() else 'cpu')
is_odenet = args.network == 'odenet'
if args.downsampling_method == 'conv':
downsampling_layers = [
nn.Conv2d(1, 64, 3, 1),
norm(64),
nn.ReLU(inplace=True),
nn.Conv2d(64, 64, 4, 2, 1),
norm(64),
nn.ReLU(inplace=True),
nn.Conv2d(64, 64, 4, 2, 1),
]
elif args.downsampling_method == 'res':
downsampling_layers = [
nn.Conv2d(1, 64, 3, 1),
ResBlock(64, 64, stride=2, downsample=conv1x1(64, 64, 2)),
ResBlock(64, 64, stride=2, downsample=conv1x1(64, 64, 2)),
]
feature_layers = [ODEBlock(ODEfunc(64))] if is_odenet else [ResBlock(64, 64) for _ in range(6)]
fc_layers = [norm(64), nn.ReLU(inplace=True), nn.AdaptiveAvgPool2d((1, 1)), Flatten(), nn.Linear(64, 10)]
model = nn.Sequential(*downsampling_layers, *feature_layers, *fc_layers).to(device)
# logger.info(model)
# logger.info('Number of parameters: {}'.format(count_parameters(model)))
criterion = nn.CrossEntropyLoss().to(device)
train_loader, test_loader, train_eval_loader = get_mnist_loaders(
args.data_aug, args.batch_size, args.test_batch_size
)
data_gen = inf_generator(train_loader)
batches_per_epoch = len(train_loader)
lr_fn = learning_rate_with_decay(
args.batch_size, batch_denom=128, batches_per_epoch=batches_per_epoch, boundary_epochs=[60, 100, 140],
decay_rates=[1, 0.1, 0.01, 0.001]
)
optimizer = torch.optim.SGD(model.parameters(), lr=args.lr, momentum=0.9)
best_acc = 0
batch_time_meter = RunningAverageMeter()
f_nfe_meter = RunningAverageMeter()
b_nfe_meter = RunningAverageMeter()
end = time.time()
for itr in range(args.nepochs * batches_per_epoch):
for param_group in optimizer.param_groups:
param_group['lr'] = lr_fn(itr)
optimizer.zero_grad()
x, y = data_gen.__next__()
x = x.to(device)
y = y.to(device)
logits = model(x)
loss = criterion(logits, y)
if is_odenet:
nfe_forward = feature_layers[0].nfe
feature_layers[0].nfe = 0
loss.backward()
optimizer.step()
if is_odenet:
nfe_backward = feature_layers[0].nfe
feature_layers[0].nfe = 0
batch_time_meter.update(time.time() - end)
if is_odenet:
f_nfe_meter.update(nfe_forward)
b_nfe_meter.update(nfe_backward)
end = time.time()
if itr % batches_per_epoch == 0:
with torch.no_grad():
train_acc = accuracy(model, train_eval_loader)
val_acc = accuracy(model, test_loader)
if val_acc > best_acc:
torch.save({'state_dict': model.state_dict(), 'args': args}, os.path.join(args.save, 'model.pth'))
best_acc = val_acc
logger.info(
"Epoch {:04d} | Time {:.3f} ({:.3f}) | NFE-F {:.1f} | NFE-B {:.1f} | "
"Train Acc {:.4f} | Test Acc {:.4f}".format(
itr // batches_per_epoch, batch_time_meter.val, batch_time_meter.avg, f_nfe_meter.avg,
b_nfe_meter.avg, train_acc, val_acc
)
)
```
|
github_jupyter
|
import os
import argparse
import logging
import time
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
!pip install torchvision
import torchvision.datasets as datasets
import torchvision.transforms as transforms
# parser = argparse.ArgumentParser()
# parser.add_argument('--network', type=str, choices=['resnet', 'odenet'], default='odenet')
# parser.add_argument('--tol', type=float, default=1e-3)
# parser.add_argument('--adjoint', type=eval, default=False, choices=[True, False])
# parser.add_argument('--downsampling-method', type=str, default='conv', choices=['conv', 'res'])
# parser.add_argument('--nepochs', type=int, default=160)
# parser.add_argument('--data_aug', type=eval, default=True, choices=[True, False])
# parser.add_argument('--lr', type=float, default=0.1)
# parser.add_argument('--batch_size', type=int, default=128)
# parser.add_argument('--test_batch_size', type=int, default=1000)
# parser.add_argument('--save', type=str, default='./experiment1')
# parser.add_argument('--debug', action='store_true')
# parser.add_argument('--gpu', type=int, default=0)
# args = parser.parse_args()
class Args:
network = 'odenet' # choices=['resnet', 'odenet']
tol = 1e-3
downsampling_method = 'conv' # choices=['conv', 'res'] ESTO NO VEO QUE SE USE EN NINGUN LADO
batch_size = 128
lr = 0.1
nepochs = 160
data_aug = True
test_batch_size = 1000
save = './experiment1'
degub = False
gpu = True
adjoint = False
args=Args()
if args.adjoint:
from torchdiffeq import odeint_adjoint as odeint
else:
from torchdiffeq import odeint
def conv3x3(in_planes, out_planes, stride=1):
"""3x3 convolution with padding"""
return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride, padding=1, bias=False)
def conv1x1(in_planes, out_planes, stride=1):
"""1x1 convolution"""
return nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=stride, bias=False)
def norm(dim):
return nn.GroupNorm(min(32, dim), dim)
class ResBlock(nn.Module):
expansion = 1
def __init__(self, inplanes, planes, stride=1, downsample=None):
super(ResBlock, self).__init__()
self.norm1 = norm(inplanes)
self.relu = nn.ReLU(inplace=True)
self.downsample = downsample
self.conv1 = conv3x3(inplanes, planes, stride)
self.norm2 = norm(planes)
self.conv2 = conv3x3(planes, planes)
def forward(self, x):
shortcut = x
out = self.relu(self.norm1(x))
if self.downsample is not None:
shortcut = self.downsample(out)
out = self.conv1(out)
out = self.norm2(out)
out = self.relu(out)
out = self.conv2(out)
return out + shortcut
class ConcatConv2d(nn.Module):
def __init__(self, dim_in, dim_out, ksize=3, stride=1, padding=0, dilation=1, groups=1, bias=True, transpose=False):
super(ConcatConv2d, self).__init__()
module = nn.ConvTranspose2d if transpose else nn.Conv2d
self._layer = module(
dim_in + 1, dim_out, kernel_size=ksize, stride=stride, padding=padding, dilation=dilation, groups=groups,
bias=bias
)
def forward(self, t, x):
tt = torch.ones_like(x[:, :1, :, :]) * t
ttx = torch.cat([tt, x], 1)
return self._layer(ttx)
class ODEfunc(nn.Module):
def __init__(self, dim):
super(ODEfunc, self).__init__()
self.norm1 = norm(dim)
self.relu = nn.ReLU(inplace=True)
self.conv1 = ConcatConv2d(dim, dim, 3, 1, 1)
self.norm2 = norm(dim)
self.conv2 = ConcatConv2d(dim, dim, 3, 1, 1)
self.norm3 = norm(dim)
self.nfe = 0
def forward(self, t, x):
self.nfe += 1
out = self.norm1(x)
out = self.relu(out)
out = self.conv1(t, out)
out = self.norm2(out)
out = self.relu(out)
out = self.conv2(t, out)
out = self.norm3(out)
return out
class ODEBlock(nn.Module):
def __init__(self, odefunc):
super(ODEBlock, self).__init__()
self.odefunc = odefunc
self.integration_time = torch.tensor([0, 1]).float()
def forward(self, x):
self.integration_time = self.integration_time.type_as(x)
out = odeint(self.odefunc, x, self.integration_time, rtol=args.tol, atol=args.tol)
return out[1]
@property
def nfe(self):
return self.odefunc.nfe
@nfe.setter
def nfe(self, value):
self.odefunc.nfe = value
class Flatten(nn.Module):
def __init__(self):
super(Flatten, self).__init__()
def forward(self, x):
shape = torch.prod(torch.tensor(x.shape[1:])).item()
return x.view(-1, shape)
class RunningAverageMeter(object):
"""Computes and stores the average and current value"""
def __init__(self, momentum=0.99):
self.momentum = momentum
self.reset()
def reset(self):
self.val = None
self.avg = 0
def update(self, val):
if self.val is None:
self.avg = val
else:
self.avg = self.avg * self.momentum + val * (1 - self.momentum)
self.val = val
def get_mnist_loaders(data_aug=False, batch_size=128, test_batch_size=1000, perc=1.0):
if data_aug:
transform_train = transforms.Compose([
transforms.RandomCrop(28, padding=4),
transforms.ToTensor(),
])
else:
transform_train = transforms.Compose([
transforms.ToTensor(),
])
transform_test = transforms.Compose([
transforms.ToTensor(),
])
train_loader = DataLoader(
datasets.MNIST(root='.data/mnist', train=True, download=True, transform=transform_train), batch_size=batch_size,
shuffle=True, num_workers=2, drop_last=True
)
train_eval_loader = DataLoader(
datasets.MNIST(root='.data/mnist', train=True, download=True, transform=transform_test),
batch_size=test_batch_size, shuffle=False, num_workers=2, drop_last=True
)
test_loader = DataLoader(
datasets.MNIST(root='.data/mnist', train=False, download=True, transform=transform_test),
batch_size=test_batch_size, shuffle=False, num_workers=2, drop_last=True
)
return train_loader, test_loader, train_eval_loader
def inf_generator(iterable):
"""Allows training with DataLoaders in a single infinite loop:
for i, (x, y) in enumerate(inf_generator(train_loader)):
"""
iterator = iterable.__iter__()
while True:
try:
yield iterator.__next__()
except StopIteration:
iterator = iterable.__iter__()
def learning_rate_with_decay(batch_size, batch_denom, batches_per_epoch, boundary_epochs, decay_rates):
initial_learning_rate = args.lr * batch_size / batch_denom
boundaries = [int(batches_per_epoch * epoch) for epoch in boundary_epochs]
vals = [initial_learning_rate * decay for decay in decay_rates]
def learning_rate_fn(itr):
lt = [itr < b for b in boundaries] + [True]
i = np.argmax(lt)
return vals[i]
return learning_rate_fn
def one_hot(x, K):
return np.array(x[:, None] == np.arange(K)[None, :], dtype=int)
def accuracy(model, dataset_loader):
total_correct = 0
for x, y in dataset_loader:
x = x.to(device)
y = one_hot(np.array(y.numpy()), 10)
target_class = np.argmax(y, axis=1)
predicted_class = np.argmax(model(x).cpu().detach().numpy(), axis=1)
total_correct += np.sum(predicted_class == target_class)
return total_correct / len(dataset_loader.dataset)
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
def makedirs(dirname):
if not os.path.exists(dirname):
os.makedirs(dirname)
def get_logger(logpath, filepath, package_files=[], displaying=True, saving=True, debug=False):
logger = logging.getLogger()
if debug:
level = logging.DEBUG
else:
level = logging.INFO
logger.setLevel(level)
if saving:
info_file_handler = logging.FileHandler(logpath, mode="a")
info_file_handler.setLevel(level)
logger.addHandler(info_file_handler)
if displaying:
console_handler = logging.StreamHandler()
console_handler.setLevel(level)
logger.addHandler(console_handler)
logger.info(filepath)
with open(filepath, "r") as f:
logger.info(f.read())
for f in package_files:
logger.info(f)
with open(f, "r") as package_f:
logger.info(package_f.read())
return logger
if __name__ == '__main__':
makedirs(args.save)
# logger = get_logger(logpath=os.path.join(args.save, 'logs'), filepath=os.path.abspath(__file__))
# logger.info(args)
device = torch.device('cuda:' + str(args.gpu) if torch.cuda.is_available() else 'cpu')
is_odenet = args.network == 'odenet'
if args.downsampling_method == 'conv':
downsampling_layers = [
nn.Conv2d(1, 64, 3, 1),
norm(64),
nn.ReLU(inplace=True),
nn.Conv2d(64, 64, 4, 2, 1),
norm(64),
nn.ReLU(inplace=True),
nn.Conv2d(64, 64, 4, 2, 1),
]
elif args.downsampling_method == 'res':
downsampling_layers = [
nn.Conv2d(1, 64, 3, 1),
ResBlock(64, 64, stride=2, downsample=conv1x1(64, 64, 2)),
ResBlock(64, 64, stride=2, downsample=conv1x1(64, 64, 2)),
]
feature_layers = [ODEBlock(ODEfunc(64))] if is_odenet else [ResBlock(64, 64) for _ in range(6)]
fc_layers = [norm(64), nn.ReLU(inplace=True), nn.AdaptiveAvgPool2d((1, 1)), Flatten(), nn.Linear(64, 10)]
model = nn.Sequential(*downsampling_layers, *feature_layers, *fc_layers).to(device)
# logger.info(model)
# logger.info('Number of parameters: {}'.format(count_parameters(model)))
criterion = nn.CrossEntropyLoss().to(device)
train_loader, test_loader, train_eval_loader = get_mnist_loaders(
args.data_aug, args.batch_size, args.test_batch_size
)
data_gen = inf_generator(train_loader)
batches_per_epoch = len(train_loader)
lr_fn = learning_rate_with_decay(
args.batch_size, batch_denom=128, batches_per_epoch=batches_per_epoch, boundary_epochs=[60, 100, 140],
decay_rates=[1, 0.1, 0.01, 0.001]
)
optimizer = torch.optim.SGD(model.parameters(), lr=args.lr, momentum=0.9)
best_acc = 0
batch_time_meter = RunningAverageMeter()
f_nfe_meter = RunningAverageMeter()
b_nfe_meter = RunningAverageMeter()
end = time.time()
for itr in range(args.nepochs * batches_per_epoch):
for param_group in optimizer.param_groups:
param_group['lr'] = lr_fn(itr)
optimizer.zero_grad()
x, y = data_gen.__next__()
x = x.to(device)
y = y.to(device)
logits = model(x)
loss = criterion(logits, y)
if is_odenet:
nfe_forward = feature_layers[0].nfe
feature_layers[0].nfe = 0
loss.backward()
optimizer.step()
if is_odenet:
nfe_backward = feature_layers[0].nfe
feature_layers[0].nfe = 0
batch_time_meter.update(time.time() - end)
if is_odenet:
f_nfe_meter.update(nfe_forward)
b_nfe_meter.update(nfe_backward)
end = time.time()
if itr % batches_per_epoch == 0:
with torch.no_grad():
train_acc = accuracy(model, train_eval_loader)
val_acc = accuracy(model, test_loader)
if val_acc > best_acc:
torch.save({'state_dict': model.state_dict(), 'args': args}, os.path.join(args.save, 'model.pth'))
best_acc = val_acc
logger.info(
"Epoch {:04d} | Time {:.3f} ({:.3f}) | NFE-F {:.1f} | NFE-B {:.1f} | "
"Train Acc {:.4f} | Test Acc {:.4f}".format(
itr // batches_per_epoch, batch_time_meter.val, batch_time_meter.avg, f_nfe_meter.avg,
b_nfe_meter.avg, train_acc, val_acc
)
)
| 0.887893 | 0.317638 |
# CHAPTER 21 - Deep Learning
### George Tzanetakis, University of Victoria
## WORKPLAN
The section number is based on the 4th edition of the AIMA textbook and is the suggested
reading for this week. Each list entry provides just the additional sections. For example the Expected reading include the sections listed under Basic as well as the sections listed under Expected. Some additional readings are suggested for Advanced.
1. Basic: Sections **21.1**, **21.2**, , and **Summary**
2. Expected: Same as Basic plus **21.3**
3. Advanced: All the chapter including bibligraphical and historical notes
# Deep Learning
Understanding deep learing starts from the simple feed-forward netowrk with input layer, hidden layers, and output layer. Each node/unit in a layer is collected with weights to every node in the next layer. The resulting weighted sum is then processed by a nonlinear activition function to produce output. So one can think of the entire network as a sequence of applying vector-matrix multiplication followed by non-linar activations.
We can add +1 to the input so that total weighted sum can be non-zero even when all the output of the previous layer/inputs of the current layer are all zero.
\begin{equation}
a_j = g_j(\mathbf{w}^T \mathbf{x})
\end{equation}
where $\mathbf(w)$ is the vector of weights leading into unit $j$, and $\mathbf x$ is the vector of inputs to unit $j$.
Activation is non-linear otherwise any composition of units would still represent a linear function. The nonlinearity is what allows sufficiently large networks of units to represent arbitrary functions.
There are different activation functions:
1. Logistic or sigmoid
\begin{equation}
\sigma(x) = 1 / (1 + e^{-x})
\end{equation}
2. Rectified linear unit
\begin{equation}
ReLU(x) = max(0,x)
\end{equation}
3. Softplus
\begin{equation}
softplus(x) = log(1 + e^{x})
\end{equation}
4. tanh
Vector form of network:
\begin{equation}
h_w(\mathbf x) = g^{2}(\mathbf{W}^{2}g^{1}(\mathbf W^{(1)}\mathbf x))
\end{equation}
For supervised learning training we can use **gradient descent** i.e calculate of the gradient of the loss function with respect to the weights, and then adjust the weights along the gradient direction to reduce the loss.
Example loss function where $y$ is the ground truth value and $\hat y$ is the output prediction of the network.
\begin{equation}
Loss(h_{w}) = (y-\hat y)^2
\end{equation}
The idea is that for each training sample (or mini-batch of samples) we can calcuate the gradient with respect to the loss function and propagate the error backwards from the output layer through the hidden layers, and eventually to the input layer. This algorithm is called **back propagtion**.
## Input encoding
Boolean attributes are typically encoded as $0$ for False and $1$ for True. Numeric attributes whether integer
or real-valued are typically used as is or sometimes mapped onto a log-scale. Networks used with images have array-like internal structures that aim to reflect the semantics of adjacency of pixels. Categorial values are usually encoded with **one-hot-encoding** to avoid numerical adjacency issues.
## Output layers and loss functions
In most deep learning applications, it is more common to interpret the output value $\mathbf{\hat y}$ as probabilities and to use the **negative log likelihood** as the loss function.
\begin{equation}
\mathbf{w^*} = \underset{w}{\operatorname{argmin}} - \sum_{j=1}^{N} logP_w(\mathbf{y_j}|\mathbf{x_j})
\end{equation}
Without going into details this is called the cross-entropy loss in Deep Learning literature.
For binary classification problems a **sigmoid output** layer will do what we want and output
probabilities. For multiclass problems we can use a **softmax** layer which outputs a vector of non-negative
numbers that sum up to 1. For regression problems we can use a linear output layer without any activation function. This corresponds to doing a classical linear regression at the output layer after the multiple non-linear transforms.
## Hidden Layers
From 1985-2010 internal nodes typically used sigmoid and tanh activation functions almost exclusively. From around 20210 onwards the ReLU and softplus become more popular, partly because they are believed to avoid the problem of vanishing gradients. Experiments suggest that deep and narrow networks learn better than shallow and wide given a fixed total number of weights.
There is little understanding at the moment as to why some structures seem to work better than others for some particular problem.
```
import torch
import torchvision
import torchvision.transforms as transforms
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
batch_size = 4
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
import matplotlib.pyplot as plt
import numpy as np
# functions to show an image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(batch_size)))
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = torch.flatten(x, 1) # flatten all dimensions except batch
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs; data is a list of [inputs, labels]
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
PATH = './cifar_net.pth'
torch.save(net.state_dict(), PATH)
net = Net()
net.load_state_dict(torch.load(PATH))
outputs = net(images)
_, predicted = torch.max(outputs, 1)
print(outputs)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
for j in range(4)))
import torch
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
Q = 3*a**3 - b**2
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)
print(9*a**2)
print(a.grad)
```
## Differentiation using computers
1. Symbolic differentiation: Automatic manipulation of mathematical expressions to get derivatives
* Input and output are mathematical expressions
* Used in Mathematica, Maple, Sympy, etc.
2. Numeric differentiation: Approximating derivatives by finite differences:
\begin{equation}
\frac{\partial f(x_1, \dots, x_N}{\partial x_i)} = \frac{f(x_1, \dots, x_i+h, \dots, x_N)}{2h}
\end{equation}
∂xi
f(x1, . . . , xN) = lim
h→0
f(x1, . . . , xi + h, . . . , xN) − f(x1, . . . , xi − h, . . . , xN)
2h
• Automatic differentiation (AD): A method to get exact derivatives
efficiently, by storing information as you go forward that you can reuse
as you go backwards
• Takes code that computes a function and returns code that computes the
derivative of that function.
• “The goal isn’t to obtain closed-form solutions, but to be able to write a
program that efficiently computes the derivatives.”
• Autograd, Torch Autograd
```
import autograd.numpy as np
from autograd import elementwise_grad as egrad
import matplotlib.pyplot as plt
x = np.linspace(-31.4,31.4, 256)
sinc = lambda x: np.sin(x) / x
plt.figure(figsize=(12,7))
plt.title("sinc function and derivatives", fontsize=24)
my_fn = sinc
for ii in range(5):
plt.plot(x, my_fn(x), lw=3, label="d{} sinc(x)/dx{}".format(ii,ii))
plt.legend(fontsize=18)
plt.axis([-32, 32, -0.50, 1.2])
my_fn = egrad(my_fn)
```
## Differentiable programming
The idea of computing using building blocks that can be differentiated orinated in Deep Learning but has found applications in other areas. For example it is possible to model chains of digital signal processing effects
using differentiable DSP.
## Convolutional neural networks
In order to preserve local adjacency information, the first hidden layer should receive input from only a small, local region of the image. In addition, we would like approximate **spatial invariance** at small to moderate scales - i.e an edge or an eye should look the same if it appears in a different, small region of the image.
Constraining the $l$ weights connecting a local region to a unit in the hidden layer to be the same for each hidden unit (i.e $w_{1,i}, \dots w_{l,i}$ should be the same as $w_{1,j}, \dots, w_{l, j}$ for hidden unit $i$ and $j$. A pattern of weights that is replicated across multiple local regions is called a **kernel** and the process of applying the **kernel** to the pixels of an image is called **convolution**. Note that in DSP this is called cross-correlation and convolution means something else.
Let's illustrate **convolution** with an example in 1D. Consider the sequence $5,6,6,2,5,6,5$ and the **kernel**
$+1,-1,+1$. This kernel will detect (produce higher values) when there is a "dark" pixel. The result of applying
the kernel at the first position of the sequence will be: $5-6+6 = 5$. The kernel is then moved by **stride** pixels. For example if the **stride** is two the next output value will be $6-2+5=9$. If the stride is one the next output value will be $6-6+2=2$.
Convolution is a linear operation and therefore we can propagate gradients through it, just like we did with fully connected networks.
CNNs were inspired originally by models of the visual cortex proposed in neuroscience. In those models, the **receptive field** of a neuron is the portion of the sensory input that can affect that neuron's activation.
```
# Example of 1D convolution with kernel size 3 and stride 2
a = np.array([[+1,-1,+1,0,0,0,0],[0,0,+1,-1,+1,0,0], [0,0,0,0,+1,-1,+1]])
b = np.array([[5,6,6,2,5,6,5]])
c = np.matmul(a,b.T)
print(a)
print(b.T)
print('=')
print(c)
```
## Pooling layer
A **pooling** layer in a neural network summarizes a set of adjacent units from the preceding layer with a single value. **Average-pooling** computes the average value of its $l$ inputs. Average pooling facilitates multiscale recognition. It also reduces the number of weights required in subsequent layers, leading to lower computational cost and prossibly faster learning. **Max pooling** computes the maximum value of its $l$ inputs. Max-pooling acts as a kind of logical disjunction, saying that a feature exists somewhere in the unit's receptive field.
In a image classification network the final layer of the network will be a softmax with $c$ output units. The early layers of the CNN are image-sized, so somewhere in between there must be significant reductions in layer size. Convolutional layers and pooling layers with stride larger than 1 all serve to reduce a layer size.
### Tensors
Multi-dimensional arrays of any dimension - they keep track of the "shape" of the data as it progress through layers of the network. Describing the CNN in terms of tensors and tensor operators, a deep learning package can generate compiled code that is highly optimized for the underlying computational substrate.
Support we are traying on $256 \times 256$ RGB images with a minibatch size of $64$. The input will be a 4-dimensional tensor of size $256 \times 256 \times 3 \times 64$. The we applyu 96 kernel of size $5 \times 5 \times 3$ with a stride of $2$ in both $x$ and $y$ dimensions. This gives as an output tensor of size
$128 \times 128 \times 96 \times 64$. Such a tensor is called a **feature map** - note no dedicated color
channels but color information has been incorporated if the learning algorithm finds it useful for the final
predictions of the network.
Graphical Processing units (GPUs) are specialized hardware for graphics operations that can be used
to perform tensor operations. Tensor processing units (TPUs) are specialized hardware for computing tensor
operations that optimize for speed and throughput rather than high numerical precision.
### Residual networks
## Learning Algorithms
Standard gradient descent with $\alpha$ learning rate. The loss L is defined with respect to the entire training set.
\begin{equation}
\mathbf{w} \leftarrow \mathbf{w} - \alpha \nabla_{w} L(\mathbf w)
\end{equation}
Stochastic Gradient Descent (SGD), the loss $L$ is defined with respect to a minibatch of $m$ examples chosen randomly at each step.
Empirical considerations:
1. Small-mini batch size helps escape small local minima and computational cost of each weight update is a small constant, independent of training set size.
2. The gradient contribution of each training example in the SGD minibatch can be computed independently, the minibatch size is often chosen so as to take maximum advantage of hardware parallelism in GPUs or TPUs.
3. Learning rate needs to decrease over time. Choosing the right schedule is usually a matter of trial and error.
4. Care must be taken to mitigate numerical instabilities that may arise due to overflow, underflow, and rounding error.
Process of learning stops when there are diminishing returns.
### Batch normalization
### Generalization
Approaches to improving generalization in deep learning include:
1. Choosing the right architecture, varying number of layers, connectivity, and types of nodes
2. Penalizing large weights
3. Randomly perturing the values passing through the network during training
4. Data augmentation
Deeper (and narrow) networks tend to do better than shallow and wide networks for the same number of weights.
Deep learning works well with high-dimensional data such as images, video, speech. They have to a large extent
replaced preprocessing approaches that extracted features that prevailed prior to 2010.
**Weight decay** encourages weights to become small in some ways enforcing **reguralization** i.e limiting the complexity of the model.
**Dropout**
At each step of training, dropout applies one step of back-propagation learning to a new version of the network that is created by deactivating a randomly chosen subset of the units.
1. Introduce noise that provides robustness
2. Approximation of large ensemble of thinned networks
3. Paying attention to all features of the example rather than focusing on just a few
Usually makes it harder to fit the training set, it is usually necessary to use a larger model and to train it for more iterations.
**Data augmentation**
Provide multiple version of the same input (for example for images: add noise, crop, rotate, scale) to increase the size of the training data and the robustness to the various transformations applied.
### Graduate student descent
Incremental exploratory work carried out by graduate students to figure out which architectures
work best for which problems.
## Recurrent neural networks
Recurrent neural networks (RNNs) are distinct from feedforward networks in that they allow cycles in the computational graph. Each cycle has a delay i.e units may take as input a value computed from their own output at an earlier steop in the computation. This allows the RNN to have internal state or **memory**.
## Unsupervised learning and transfer learning
Unsupervised learning:
1. Representation learning
2. Generative modeling
Joint model $P_w(\mathbf x,\mathbf z)$, where $\mathbf z$ is a set of latent, unobserved variables that represent the content of the data $\mathbf x$ in some way.
A learned probability model achieves both representation learning (it has constructed meaningful $z$ vectors from the raw $\mathbf x$ vectors) and generative modelingL if we integrate $\mathbf z$ out of $P_{w}(\mathbf x,\mathbf z)$ we obtain $P_{w}(\mathbf x)$.
1. Probabilistic PCA
2. Autoencoders
3. Deep autoregressive models
4. Generative adversarial networks
5. Unsupervised translation
6. Transfer learning and multitask learning
|
github_jupyter
|
import torch
import torchvision
import torchvision.transforms as transforms
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
batch_size = 4
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
import matplotlib.pyplot as plt
import numpy as np
# functions to show an image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(batch_size)))
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = torch.flatten(x, 1) # flatten all dimensions except batch
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs; data is a list of [inputs, labels]
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
PATH = './cifar_net.pth'
torch.save(net.state_dict(), PATH)
net = Net()
net.load_state_dict(torch.load(PATH))
outputs = net(images)
_, predicted = torch.max(outputs, 1)
print(outputs)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
for j in range(4)))
import torch
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
Q = 3*a**3 - b**2
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)
print(9*a**2)
print(a.grad)
import autograd.numpy as np
from autograd import elementwise_grad as egrad
import matplotlib.pyplot as plt
x = np.linspace(-31.4,31.4, 256)
sinc = lambda x: np.sin(x) / x
plt.figure(figsize=(12,7))
plt.title("sinc function and derivatives", fontsize=24)
my_fn = sinc
for ii in range(5):
plt.plot(x, my_fn(x), lw=3, label="d{} sinc(x)/dx{}".format(ii,ii))
plt.legend(fontsize=18)
plt.axis([-32, 32, -0.50, 1.2])
my_fn = egrad(my_fn)
# Example of 1D convolution with kernel size 3 and stride 2
a = np.array([[+1,-1,+1,0,0,0,0],[0,0,+1,-1,+1,0,0], [0,0,0,0,+1,-1,+1]])
b = np.array([[5,6,6,2,5,6,5]])
c = np.matmul(a,b.T)
print(a)
print(b.T)
print('=')
print(c)
| 0.854399 | 0.991263 |
# DDPG algorithm implemented for single reacher continuous control environment
This notebook contains an implementation of the **DDPG** algorithm for solving the Unity's Reacher environment. Please follow the instructions to reproduce the results.
In order to solve the environment, [DDPG](https://arxiv.org/abs/1509.02971) (Deep Deterministic Policy Gradient) algorithm has been used. It is an **actor-critic model-free algorithm** based on the [DPG](http://proceedings.mlr.press/v32/silver14.pdf) (Deterministic Policy Gradient) algorithm that can operate over **continuous action spaces**. The algorithm is defined as follows.
$$\nabla_{\theta^\mu}J = \mathop{\mathbb{E}}_{s_t \sim p^\beta} [\nabla_a Q(s,a|\theta^Q)|_{s=s_t, a=\mu(s_t)} \nabla_{\theta_\mu} \mu(s|\theta^\mu)|_{s=s_t}]$$
$$L(\theta^Q) = \mathop{\mathbb{E}}_{s \sim p^\beta, a_t \sim \beta, r_t \sim E}[(Q(s_t, a_t|\mu^Q)-y_t)^2]$$
where $y_t = r(s_t, a_t) + \gamma Q(s_{t+1}, \mu(s_{t+1})|_{\theta^Q})$, $\theta^Q$ are the parameters of the critic, $\theta^mu$ are the parameters of the actor, $E$ represents the environment, $\beta$ is the behavior policy and $\mu$ is the learned policy.

```
# Adjusts the python path to the root of the repository. This must be run only once
%cd ..
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import clear_output
from unityagents import UnityEnvironment
from src.agents import *
from src.rl_utilities import *
%matplotlib inline
```
## Instantiate the environment
The code below initializes the Unity environment and extracts the main features of it. To set it up, please, follow the instructions below.
1. Download the environment from one of the links below. You need only select the environment that matches your operating system:
- Linux: [click here](https://s3-us-west-1.amazonaws.com/udacity-drlnd/P2/Reacher/one_agent/Reacher_Linux.zip)
- MacOSX: [click here](https://s3-us-west-1.amazonaws.com/udacity-drlnd/P2/Reacher/one_agent/Reacher.app.zip)
- Windows (32-bit): [click here](https://s3-us-west-1.amazonaws.com/udacity-drlnd/P2/Reacher/one_agent/Reacher_Windows_x86.zip)
- Windows (64-bit): [click here](https://s3-us-west-1.amazonaws.com/udacity-drlnd/P2/Reacher/one_agent/Reacher_Windows_x86_64.zip)
(_For Windows users_) Check out [this link](https://support.microsoft.com/en-us/help/827218/how-to-determine-whether-a-computer-is-running-a-32-bit-version-or-64) if you need help with determining if your computer is running a 32-bit version or 64-bit version of the Windows operating system.
(_For AWS_) If you'd like to train the agent on AWS (and have not [enabled a virtual screen](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Training-on-Amazon-Web-Service.md)), then please use [this link](https://s3-us-west-1.amazonaws.com/udacity-drlnd/P1/Banana/Banana_Linux_NoVis.zip) to obtain the environment.
2. Place the file in the DRLND GitHub repository, in the `envs` folder, and unzip (or decompress) the file.
```
env_path = "<path to the single reacher environment>"
env = UnityEnvironment(env_path)
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
env_info = env.reset(train_mode=True)[brain_name]
num_agents = len(env_info.agents)
action_size = brain.vector_action_space_size
state = env_info.vector_observations
state_size = state.shape[1]
```
## Define the model parameters
```
batch_size = 128 # Size of the batch to train the neural networks
n_episodes = 1000 # Number of episodes to run when training the agent
n_batches_train = 1 # Number of times to train for each time step
exp_replay_buffer_size = int(2e5) # Experience replay buffer size
epsilon_decay = 0.9925 # Decay of the exploration constant
epsilon = 1 # Initial value of the exploration constant
epsilon_final = 0.1 # Final value of the exploration constant
plot_every_n = 10 # Period to update the rewards chart
save_every_n = 100 # Period to save the model if an improvement has been found
tau = 0.001 # Parameter that controls how fast the local networks update the target networks
gamma = 0.99 # Discount factor
```
## Initialize the agent
```
agent = DDPGAgent(CriticArchitecture, ActorArchitecture, state_size=state_size, action_size=action_size,
tau=tau, gamma=gamma, batch_size=batch_size, replay_size = exp_replay_buffer_size,
n_batches_train=n_batches_train, random_seed=655321)
scores = []
epsilons = []
max_score = 0
```
## Run the training process
The following code runs the training process, reports the cumulative reward and saves the models weights
```
for episode in range(n_episodes):
epsilons.append(epsilon)
epsilon = epsilon_decay * epsilon + (1-epsilon_decay) * epsilon_final
env_info = env.reset(train_mode=True)[brain_name]
agent.reset()
state = env_info.vector_observations
score = 0
done = [False]
c = 0
while not any(done):
# take random action
action = agent.act(state, epsilon=epsilon)
env_info = env.step(action)[brain_name]
next_state = env_info.vector_observations
reward = env_info.rewards
done = env_info.local_done
agent.step(state, action, reward, next_state, done)
state = next_state
score += np.mean(reward)
c += 1
scores.append(score)
if (episode+1) % plot_every_n == 0:
clear_output(True)
plt.figure(figsize=(15, 6))
plt.subplot(1,2,1)
plot_smoothed_return(scores)
plt.subplot(1,2,2)
plt.grid()
plt.plot(epsilons)
plt.xlabel("# of episodes")
plt.ylabel("Epsilon")
plt.show()
if (episode + 1) % save_every_n == 0:
if max_score < np.mean(scores[-100:]):
torch.save(agent.critic_local.state_dict(), 'checkpoint_critic_local.pth')
torch.save(agent.critic_target.state_dict(), 'checkpoint_critic_target.pth')
torch.save(agent.actor_local.state_dict(), 'checkpoint_actor_local.pth')
torch.save(agent.actor_target.state_dict(), 'checkpoint_actor_target.pth')
max_score = np.mean(scores[-100:])
```
## Load and test the model
```
agent = DDPGAgent(CriticArchitecture, ActorArchitecture, state_size=state_size, action_size=action_size,
tau=0.001, epsilon=0.01, gamma=0.99, batch_size=batch_size, replay_size = exp_replay_buffer_size,
n_batches_train=n_batches_train, random_seed=655321)
agent.critic_local.load_state_dict(torch.load('checkpoint_critic_local.pth'))
agent.critic_target.load_state_dict(torch.load('checkpoint_critic_target.pth'))
agent.actor_local.load_state_dict(torch.load('checkpoint_actor_local.pth'))
agent.actor_target.load_state_dict(torch.load('checkpoint_actor_target.pth'))
env_info = env.reset(train_mode=False)[brain_name]
state = env_info.vector_observations
done = False
c=0
agent.reset()
score=0
while not done:
# take random action
action = agent.act(state, epsilon=0)
env_info = env.step(action)[brain_name]
next_state = env_info.vector_observations
reward = env_info.rewards[0]
done = env_info.local_done[0]
score +=reward
c += 1
state = next_state
```
|
github_jupyter
|
# Adjusts the python path to the root of the repository. This must be run only once
%cd ..
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import clear_output
from unityagents import UnityEnvironment
from src.agents import *
from src.rl_utilities import *
%matplotlib inline
env_path = "<path to the single reacher environment>"
env = UnityEnvironment(env_path)
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
env_info = env.reset(train_mode=True)[brain_name]
num_agents = len(env_info.agents)
action_size = brain.vector_action_space_size
state = env_info.vector_observations
state_size = state.shape[1]
batch_size = 128 # Size of the batch to train the neural networks
n_episodes = 1000 # Number of episodes to run when training the agent
n_batches_train = 1 # Number of times to train for each time step
exp_replay_buffer_size = int(2e5) # Experience replay buffer size
epsilon_decay = 0.9925 # Decay of the exploration constant
epsilon = 1 # Initial value of the exploration constant
epsilon_final = 0.1 # Final value of the exploration constant
plot_every_n = 10 # Period to update the rewards chart
save_every_n = 100 # Period to save the model if an improvement has been found
tau = 0.001 # Parameter that controls how fast the local networks update the target networks
gamma = 0.99 # Discount factor
agent = DDPGAgent(CriticArchitecture, ActorArchitecture, state_size=state_size, action_size=action_size,
tau=tau, gamma=gamma, batch_size=batch_size, replay_size = exp_replay_buffer_size,
n_batches_train=n_batches_train, random_seed=655321)
scores = []
epsilons = []
max_score = 0
for episode in range(n_episodes):
epsilons.append(epsilon)
epsilon = epsilon_decay * epsilon + (1-epsilon_decay) * epsilon_final
env_info = env.reset(train_mode=True)[brain_name]
agent.reset()
state = env_info.vector_observations
score = 0
done = [False]
c = 0
while not any(done):
# take random action
action = agent.act(state, epsilon=epsilon)
env_info = env.step(action)[brain_name]
next_state = env_info.vector_observations
reward = env_info.rewards
done = env_info.local_done
agent.step(state, action, reward, next_state, done)
state = next_state
score += np.mean(reward)
c += 1
scores.append(score)
if (episode+1) % plot_every_n == 0:
clear_output(True)
plt.figure(figsize=(15, 6))
plt.subplot(1,2,1)
plot_smoothed_return(scores)
plt.subplot(1,2,2)
plt.grid()
plt.plot(epsilons)
plt.xlabel("# of episodes")
plt.ylabel("Epsilon")
plt.show()
if (episode + 1) % save_every_n == 0:
if max_score < np.mean(scores[-100:]):
torch.save(agent.critic_local.state_dict(), 'checkpoint_critic_local.pth')
torch.save(agent.critic_target.state_dict(), 'checkpoint_critic_target.pth')
torch.save(agent.actor_local.state_dict(), 'checkpoint_actor_local.pth')
torch.save(agent.actor_target.state_dict(), 'checkpoint_actor_target.pth')
max_score = np.mean(scores[-100:])
agent = DDPGAgent(CriticArchitecture, ActorArchitecture, state_size=state_size, action_size=action_size,
tau=0.001, epsilon=0.01, gamma=0.99, batch_size=batch_size, replay_size = exp_replay_buffer_size,
n_batches_train=n_batches_train, random_seed=655321)
agent.critic_local.load_state_dict(torch.load('checkpoint_critic_local.pth'))
agent.critic_target.load_state_dict(torch.load('checkpoint_critic_target.pth'))
agent.actor_local.load_state_dict(torch.load('checkpoint_actor_local.pth'))
agent.actor_target.load_state_dict(torch.load('checkpoint_actor_target.pth'))
env_info = env.reset(train_mode=False)[brain_name]
state = env_info.vector_observations
done = False
c=0
agent.reset()
score=0
while not done:
# take random action
action = agent.act(state, epsilon=0)
env_info = env.step(action)[brain_name]
next_state = env_info.vector_observations
reward = env_info.rewards[0]
done = env_info.local_done[0]
score +=reward
c += 1
state = next_state
| 0.505127 | 0.986879 |
### Phase 1: Part 6: Combine all clean_data files from the various sources and create a Master data file for reading proficiency
```
import pandas
pandas.__version__
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
cd /Users/dansa/Documents/GitHub/Phase1/Data/CCD
ccd_master = pandas.read_csv("Clean_ccd_master.csv")
ccd_master['NCESSCH'] = ccd_master['NCESSCH'].apply(lambda x: '{0:0>12}'.format(x))
ccd_master.head()
ccd_master.shape
cd /Users/dansa/Documents/GitHub/Phase1/Data/CRDC
crdc_master_read = pandas.read_csv("Clean_crdc_master_read.csv")
crdc_master_read['NCESSCH'] = crdc_master_read['NCESSCH'].apply(lambda x: '{0:0>12}'.format(x))
crdc_master_read.head()
crdc_master_read.shape
cd /Users/dansa/Documents/GitHub/Phase1/Data/EDGE
edge = pandas.read_csv("Clean_EDGE.csv")
edge['NCESSCH'] = edge['NCESSCH'].apply(lambda x: '{0:0>12}'.format(x))
edge.head()
edge.shape
cd /Users/dansa/Documents/GitHub/Phase1/Data/EDFacts
Eng_prof = pandas.read_csv("edfacts_eng_merged_ccd.csv")
Eng_prof['NCESSCH'] = Eng_prof['NCESSCH'].apply(lambda x: '{0:0>12}'.format(x))
Eng_prof.head()
Eng_prof.shape
```
### Merge ccd and crdc file
```
merged_ccd_crdc = pandas.merge(left=ccd_master,right=crdc_master_read, how='left', left_on='NCESSCH', right_on='NCESSCH')
merged_ccd_crdc.shape
merged_ccd_crdc.columns
#merged_ccd_crdc.head().T
```
### Merge ccd_crdc file with edge file
```
merged_ccd_crdc_edge = pandas.merge(left=merged_ccd_crdc,right=edge, how='left', left_on='NCESSCH', right_on='NCESSCH')
merged_ccd_crdc_edge.shape
merged_ccd_crdc_edge.columns
#merged_ccd_crdc_edge.head().T
```
### Merge ccd_crdc_edge file with edfacts file
```
merged_ccd_crdc_edge_engProf = pandas.merge(left=merged_ccd_crdc_edge,right=Eng_prof, how='left', left_on='NCESSCH', right_on='NCESSCH')
merged_ccd_crdc_edge_engProf.shape
merged_ccd_crdc_edge_engProf.columns
```
#### Drop duplicate columns
```
merged_ccd_crdc_edge_engProf.drop([col for col in merged_ccd_crdc_edge_engProf.columns if col.endswith('_y')],axis=1,inplace=True)
merged_ccd_crdc_edge_engProf.shape
merged_ccd_crdc_edge_engProf.columns
```
#### Resorting columns
```
master_reading=merged_ccd_crdc_edge_engProf[['SCHOOL_YEAR_x', 'ST_x','NAME', 'NCESSCH', 'LEVEL', 'SCH_TYPE_TEXT_x', 'SCH_TYPE_x',
'TITLEI_STATUS', 'TITLEI_STATUS_TEXT', 'TEACHERS',
'FARMS_COUNT', 'Special_ed_schl_new','Magnet_schl_new', 'Charter_Schl_new', 'Alternate_schl_new',
'Total_enroll_students',
'SCH_FTETEACH_TOT', 'SCH_FTETEACH_CERT','SCH_FTETEACH_NOTCERT', 'FTE_teachers_count', 'SalaryforTeachers',
'Total_SAT_ACT_students',
'SCH_IBENR_IND_new', 'Total_IB_students',
'SCH_APENR_IND_new', 'SCH_APCOURSES', 'SCH_APOTHENR_IND_new','Total_AP_other_students', 'Total_students_tookAP',
'Income_Poverty_ratio', 'IPR_SE',
'ALL_RLA00NUMVALID_1718','ALL_RLA00PCTPROF_1718_new']]
master_reading.shape
master_reading.head()
sns.heatmap(master_reading.isnull(),yticklabels=False,cbar=True,cmap='viridis')
```
#### Dropping rows with null values
```
null_columns=master_reading.columns[master_reading.isnull().any()]
master_reading[null_columns].isnull().sum()
master_reading_new = master_reading.dropna(axis = 0, how ='any')
print("Old data frame length:", len(master_reading))
print("New data frame length:", len(master_reading_new))
print("Number of rows with at least 1 NA value: ",
(len(master_reading)-len(master_reading_new)))
sns.heatmap(master_reading_new.isnull(),yticklabels=False,cbar=True,cmap='viridis')
master_reading_new.describe()
master_reading_new.shape
master_reading_new.to_csv (r'/Users/dansa/Documents/GitHub/Phase1/Data/MASTER/Master_reading.csv', index = False, header=True)
```
|
github_jupyter
|
import pandas
pandas.__version__
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
cd /Users/dansa/Documents/GitHub/Phase1/Data/CCD
ccd_master = pandas.read_csv("Clean_ccd_master.csv")
ccd_master['NCESSCH'] = ccd_master['NCESSCH'].apply(lambda x: '{0:0>12}'.format(x))
ccd_master.head()
ccd_master.shape
cd /Users/dansa/Documents/GitHub/Phase1/Data/CRDC
crdc_master_read = pandas.read_csv("Clean_crdc_master_read.csv")
crdc_master_read['NCESSCH'] = crdc_master_read['NCESSCH'].apply(lambda x: '{0:0>12}'.format(x))
crdc_master_read.head()
crdc_master_read.shape
cd /Users/dansa/Documents/GitHub/Phase1/Data/EDGE
edge = pandas.read_csv("Clean_EDGE.csv")
edge['NCESSCH'] = edge['NCESSCH'].apply(lambda x: '{0:0>12}'.format(x))
edge.head()
edge.shape
cd /Users/dansa/Documents/GitHub/Phase1/Data/EDFacts
Eng_prof = pandas.read_csv("edfacts_eng_merged_ccd.csv")
Eng_prof['NCESSCH'] = Eng_prof['NCESSCH'].apply(lambda x: '{0:0>12}'.format(x))
Eng_prof.head()
Eng_prof.shape
merged_ccd_crdc = pandas.merge(left=ccd_master,right=crdc_master_read, how='left', left_on='NCESSCH', right_on='NCESSCH')
merged_ccd_crdc.shape
merged_ccd_crdc.columns
#merged_ccd_crdc.head().T
merged_ccd_crdc_edge = pandas.merge(left=merged_ccd_crdc,right=edge, how='left', left_on='NCESSCH', right_on='NCESSCH')
merged_ccd_crdc_edge.shape
merged_ccd_crdc_edge.columns
#merged_ccd_crdc_edge.head().T
merged_ccd_crdc_edge_engProf = pandas.merge(left=merged_ccd_crdc_edge,right=Eng_prof, how='left', left_on='NCESSCH', right_on='NCESSCH')
merged_ccd_crdc_edge_engProf.shape
merged_ccd_crdc_edge_engProf.columns
merged_ccd_crdc_edge_engProf.drop([col for col in merged_ccd_crdc_edge_engProf.columns if col.endswith('_y')],axis=1,inplace=True)
merged_ccd_crdc_edge_engProf.shape
merged_ccd_crdc_edge_engProf.columns
master_reading=merged_ccd_crdc_edge_engProf[['SCHOOL_YEAR_x', 'ST_x','NAME', 'NCESSCH', 'LEVEL', 'SCH_TYPE_TEXT_x', 'SCH_TYPE_x',
'TITLEI_STATUS', 'TITLEI_STATUS_TEXT', 'TEACHERS',
'FARMS_COUNT', 'Special_ed_schl_new','Magnet_schl_new', 'Charter_Schl_new', 'Alternate_schl_new',
'Total_enroll_students',
'SCH_FTETEACH_TOT', 'SCH_FTETEACH_CERT','SCH_FTETEACH_NOTCERT', 'FTE_teachers_count', 'SalaryforTeachers',
'Total_SAT_ACT_students',
'SCH_IBENR_IND_new', 'Total_IB_students',
'SCH_APENR_IND_new', 'SCH_APCOURSES', 'SCH_APOTHENR_IND_new','Total_AP_other_students', 'Total_students_tookAP',
'Income_Poverty_ratio', 'IPR_SE',
'ALL_RLA00NUMVALID_1718','ALL_RLA00PCTPROF_1718_new']]
master_reading.shape
master_reading.head()
sns.heatmap(master_reading.isnull(),yticklabels=False,cbar=True,cmap='viridis')
null_columns=master_reading.columns[master_reading.isnull().any()]
master_reading[null_columns].isnull().sum()
master_reading_new = master_reading.dropna(axis = 0, how ='any')
print("Old data frame length:", len(master_reading))
print("New data frame length:", len(master_reading_new))
print("Number of rows with at least 1 NA value: ",
(len(master_reading)-len(master_reading_new)))
sns.heatmap(master_reading_new.isnull(),yticklabels=False,cbar=True,cmap='viridis')
master_reading_new.describe()
master_reading_new.shape
master_reading_new.to_csv (r'/Users/dansa/Documents/GitHub/Phase1/Data/MASTER/Master_reading.csv', index = False, header=True)
| 0.139748 | 0.645427 |
# COVID-19 Data Visualization & Prediction
This notebook explores the impact/spread of COVID-19 in Canada. Intentions were to provide some visualizations of time-series data, forecast the total number of cases/recoveries/deaths in Canada, and to predict the number of days a patient will spend recovering in the hospital (using the DS4C dataset).
<p>Resources that were used in this notebook:</p>
1. <a href="https://www.kaggle.com/kimjihoo/coronavirusdataset" target="_blank">DS4C Kaggle Korea Dataset</a><br/>
2. <a href="https://github.com/CSSEGISandData/COVID-19" target="_blank">John Hopkins University Dataset</a><br/>
3. <a href="https://github.com/quantummind/caltech_covid_19_modeling" target="_blank">CalTech CS156b Dataset Collection</a>
### Import libs
```
import math
import os
import shutil
import stat
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from datetime import date, datetime
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.linear_model import LinearRegression, BayesianRidge
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import PolynomialFeatures
from sklearn import svm
from git import Repo
from subprocess import call
%matplotlib inline
```
### Data preprocessing steps
Updating the dataset on a daily basis using a simple script that will clone the dataset repo and update our local contents.
```
# Remove hidden folders and its contents
def on_rm_error(func, p, exc_info):
os.chmod(p, stat.S_IWRITE)
os.unlink(p)
ppath = "\COVID19"
path = "./COVID19"
if os.path.isdir(path):
if len(os.listdir(path)) == 0:
print("Empty")
# Loop through entire project dir
for fn in os.listdir(path):
fp = os.path.join(path, fn)
try:
if os.path.isfile(fp) or os.path.islink(fp):
os.unlink(fp)
elif os.path.isdir(fp):
shutil.rmtree(fp, ignore_errors=True)
except Exception as e:
print("Failed to remove %s" % fp)
ggit = os.listdir(path)[0]
if ggit.endswith("git"):
tmp = os.path.join(path, ggit)
while True:
call(['attrib', '-H', tmp])
break
shutil.rmtree(tmp, onerror=on_rm_error)
#print(os.listdir(path))
shutil.rmtree(ppath, ignore_errors=True)
Repo.clone_from("https://github.com/CSSEGISandData/COVID-19.git", "./COVID19")
```
<p>Read and store all the datasets into a dataframe</p>
```
c_ts = pd.read_csv("./COVID19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv")
r_ts = pd.read_csv("./COVID19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv")
d_ts = pd.read_csv("./COVID19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv")
```
Convert the time-series dates into the numbers of days since the initial recordings. This will make it easier for the regression model for forecasting.
```
dates = c_ts.columns[4:]
days_since = [day for day in range(len(dates))]
canada_confirmed = []
canada_recovered = []
canada_deaths = []
canada_confirmed_cases = c_ts[c_ts["Country/Region"] == "Canada"]
canada_recovered_cases = r_ts[r_ts["Country/Region"] == "Canada"]
canada_death_cases = d_ts[d_ts["Country/Region"] == "Canada"]
for date in dates:
canada_confirmed.append(canada_confirmed_cases[date].sum())
canada_recovered.append(canada_recovered_cases[date].sum())
canada_deaths.append(canada_death_cases[date].sum())
```
Here, we're going to make a separate dataframe that will contain all the data for Canada (confirmed, recovery, deaths) from all the provinces/territories.
```
cc = {"days_since_Jan22": days_since, "cases_in_canada": canada_confirmed}
c_df = pd.DataFrame(data=cc)
c_df["recovered_in_canada"] = canada_recovered
c_df["deaths_in_canada"] = canada_deaths
```
Visualizing the three categories that will be forecasting for future predictions.
```
fig, axs = plt.subplots(ncols=3, figsize=(17,5))
sns.lineplot(x="days_since_Jan22", y="cases_in_canada", data=c_df, ax=axs[0]).set_title("Confirmed Cases in Canada")
sns.lineplot(x="days_since_Jan22", y="recovered_in_canada", data=c_df, ax=axs[1]).set_title("Total Recoveries in Canada")
sns.lineplot(x="days_since_Jan22", y="deaths_in_canada", data=c_df, ax=axs[2]).set_title("Total Deaths in Canada")
plt.show()
```
Our goal is to be able to predict numbers with a reasonable accuracy by 14 days in advanced. Here, we're updating our existing count with the additional 2 weeks.
```
days_to_predict = 14
days_since = np.array(days_since).reshape(-1,1)
future_days_since = np.array([day for day in range(len(dates)+days_to_predict)]).reshape(-1,1)
# Separating data into train/test
y = np.array(c_df["cases_in_canada"].ravel()).reshape(-1,1)
X_train_confirmed, X_test_confirmed, y_train_confirmed, y_test_confirmed = train_test_split(
days_since, y, test_size=0.2, shuffle=False)
y_death = np.array(c_df["deaths_in_canada"].ravel()).reshape(-1,1)
X_train_death, X_test_death, y_train_death, y_test_death = train_test_split(days_since,
y_death, test_size=0.2, shuffle=False)
y_recover = np.array(c_df["recovered_in_canada"].ravel()).reshape(-1,1)
X_train_recover, X_test_recover, y_train_recover, y_test_recover = train_test_split(days_since, y_recover,
test_size=0.2, shuffle=False)
```
## Building the Linear Regression Model
### Without polynomial preprocessing
I realized that inputting the data as is after doing slight preprocessing was not enough. The graphs, RMSE, and R^2 score explains itself. Generally, my goal was to aim for a R^2 score > 50% and a RSME that was below the midpoint of the max/min of the features that we are using.
```
reg = LinearRegression()
reg.fit(X_train_confirmed, y_train_confirmed)
y_confirm_pred = reg.predict(X_test_confirmed)
reg.fit(X_train_recover, y_train_recover)
y_recover_pred = reg.predict(X_test_recover)
reg.fit(X_train_death, y_train_death)
y_death_pred = reg.predict(X_test_death)
fig = plt.gcf()
fig.set_size_inches(17, 5)
plt.subplot(1,3,1)
plt.plot(y_confirm_pred, label="Confirmed cases preds")
plt.plot(y_test_confirmed, label="Confirmed cases ground truth")
plt.legend()
plt.subplot(1,3,2)
plt.plot(y_recover_pred, label="Recovered total preds")
plt.plot(y_test_recover, label="Recovered total ground truth")
plt.legend()
plt.subplot(1,3,3)
plt.plot(y_death_pred, label="Total deaths preds")
plt.plot(y_test_death, label="Total deaths ground truth")
plt.legend()
plt.show()
```
We'll be reusing the RSME and R2-score functions quite a bit, so I'll just short-hand some of the math functions
```
def rsme(ground_truth, preds):
return math.sqrt(mean_squared_error(ground_truth, preds))
def r2(ground_truth, preds):
return r2_score(ground_truth, preds)
```
We can see that all our predictions didn't meet the criteria that we described earlier. All the time it was below the requirements that we have set (RSME < midpoint and R2 > 50%)
```
nopoly_results = {
"Name": ["Total confirmed", "Total recovered", "Total deaths"],
"Min": [y_test_confirmed.min(), y_test_recover.min(), y_test_death.min()],
"Max": [y_test_confirmed.max(), y_test_recover.max(), y_test_death.max()],
"RSME": [rsme(y_test_confirmed, y_confirm_pred), rsme(y_test_recover, y_recover_pred), rsme(y_test_death, y_death_pred)],
"r^2": [r2(y_test_confirmed, y_confirm_pred), r2(y_test_recover, y_recover_pred), r2(y_test_death, y_death_pred)]
}
nopoly_results_df = pd.DataFrame(nopoly_results)
print(nopoly_results_df)
```
### Rebuilding our linear regression model
This is why I explored the Polynomial Features function available, where I played around with the degrees to find a good match visually, RSME/R2-wise.
```
poly_lin = PolynomialFeatures(3)
poly_X_train_confirmed = poly_lin.fit_transform(np.array(X_train_confirmed).reshape(-1,1))
poly_X_test_confirmed = poly_lin.fit_transform(np.array(X_test_confirmed).reshape(-1,1))
poly_future_days_since = poly_lin.fit_transform(np.array(future_days_since).reshape(-1,1))
poly_death = PolynomialFeatures(4)
poly_X_train_death = poly_death.fit_transform(np.array(X_train_death).reshape(-1,1))
poly_X_test_death = poly_death.fit_transform(np.array(X_test_death).reshape(-1,1))
poly_recover = PolynomialFeatures(3)
poly_X_train_recover = poly_recover.fit_transform(np.array(X_train_recover).reshape(-1,1))
poly_X_test_recover = poly_recover.fit_transform(np.array(X_test_recover).reshape(-1,1))
```
New linear regression model after applying polynomial preprocessing
```
poly_reg = LinearRegression()
poly_reg.fit(poly_X_train_confirmed, y_train_confirmed)
y_lin_confirm = poly_reg.predict(poly_X_test_confirmed)
poly_reg.fit(poly_X_train_death, y_train_death)
y_lin_death = poly_reg.predict(poly_X_test_death)
poly_reg.fit(poly_X_train_recover, y_train_recover)
y_lin_recover = poly_reg.predict(poly_X_test_recover)
```
The model does pretty good at forecasting the total recovered and deaths by meeting the criteria for RSME and R2. However, the model has trouble with forecasting the total confirmed cases. Another conclusion that can be made is that for the total recovery and deaths that the model may be underfitting.
```
poly_results = {
"Name": ["Total confirmed", "Total recovered", "Total deaths"],
"Min": [y_test_confirmed.min(), y_test_recover.min(), y_test_death.min()],
"Max": [y_test_confirmed.max(), y_test_recover.max(), y_test_death.max()],
"RSME": [rsme(y_test_confirmed, y_lin_confirm), rsme(y_test_recover, y_lin_recover), rsme(y_test_death, y_lin_death)],
"r^2": [r2(y_test_confirmed, y_lin_confirm), r2(y_test_recover, y_lin_recover), r2(y_test_death, y_lin_death)]
}
poly_results_df = pd.DataFrame(poly_results)
print(poly_results_df)
fig = plt.gcf()
fig.set_size_inches(17, 5)
plt.subplot(1,3,1)
plt.plot(y_lin_confirm, label="Confirmed cases preds")
plt.plot(y_test_confirmed, label="Confirmed cases ground truth")
plt.legend()
plt.subplot(1,3,2)
plt.plot(y_lin_recover, label="Total Recovered preds")
plt.plot(y_test_recover, label="Total Recovered ground truth")
plt.legend()
plt.subplot(1,3,3)
plt.plot(y_lin_death, label="Total Deaths preds")
plt.plot(y_test_death, label="Total Deaths ground truth")
plt.legend()
plt.show()
```
### Visualizing correlations
We can compare how the recovery/death relation plays out for the next 2 weeks, as well as the recovery/confirmed relation.
```
fig = plt.gcf()
fig.set_size_inches(17, 5)
plt.subplot(1,2,1)
plt.plot(y_lin_recover, label="Forecasted recovery")
plt.plot(y_lin_confirm, label="Forecasted confirmed")
plt.legend()
plt.subplot(1,2,2)
plt.plot(y_lin_recover, label="Forecasted recovery")
plt.plot(y_lin_death, label="Forecasted death")
plt.legend()
plt.show()
```
# Forecasting the average recovery period
I also wanted to be able to predict the average number of days that a patient will spend in a hospital before recovering from COVID-19. These predictions are for Korea, however, I will be comparing the ratios between doctors:patients, patients:hospital beds, etc.
## Data preprocessing
```
p_info = pd.read_csv("./korea_dataset/PatientInfo.csv")
# Saving this for future functions (if needed)
infected_by = p_info["infected_by"].ravel()
contact_number = p_info["contact_number"].ravel()
deceased_date = p_info["deceased_date"].ravel()
patient_id = p_info["patient_id"].ravel()
```
Converting categorical values to numerical values. This will make it easier for the model to make predictions.
```
d_disease = {"TRUE": 0, "FALSE": 1}
d_gender = {"male": 0, "female": 1, "n/a": 2}
d_state = {"released": 0, "isolated": 1, "deceased": 2}
```
The next 8 cells are dedicated towards handling NaN values. I realized that a lot of the CSV file was sparse data, which meant that I had to handle the values in a particular manner. Also, a lot of the features were categorical, and also didn't have many correlations, which we will see later with the Pearson Correlation.
```
# Fill NaN values with the dict above
p_info["disease"].fillna("FALSE", inplace=True)
p_info["disease"] = p_info["disease"].map(d_disease)
# There was a bug that didn't fill all NaN values, so this dbl checks and fills it manually, O(n) search
for count, disease in enumerate(p_info["disease"], 0):
if math.isnan(disease):
p_info.at[count, "disease"] = "1.0"
p_info["sex"].fillna("n/a", inplace=True)
p_info["sex"] = p_info["sex"].map(d_gender)
p_info["state"] = p_info["state"].map(d_state)
# Converts string date to a number since Jan. 1
def nth_day(d, format="%m/%d/%y"):
d = pd.to_datetime(d, format=format)
day = pd.Timestamp(year=d.year, month=1, day=1)
return int((d-day).days + 1)
for count, cd in enumerate(p_info["confirmed_date"], 0):
p_info.at[count, "confirmed_date"] = int(nth_day(str(cd)))
p_info["released_date"].fillna(date.today().strftime("%m/%d/%y"))
for count, rd in enumerate(p_info["released_date"], 0):
try:
p_info.at[count, "released_date"] = int(nth_day(str(rd)))
except:
# If it encounters a NaN value - same issue above where it didn't fill all NaN values
p_info.at[count, "released_date"] = int(nth_day(str(date.today().strftime("%m/%d/%y"))))
```
Looking through the <a href="https://www.kaggle.com/kimjihoo/coronavirusdataset#PatientInfo.csv" target="_blank">original CSV</a>, there was over 20+ cities and 100+ provinces. I'm too lazy to type and format all of them, so I just made a script that'll do that for me.
```
d_infection_case = {}
d_city = {}
d_province = {}
d_country = {}
infection_case_counter = 0
city_counter = 0
province_counter = 0
country_counter = 0
p_info["infection_case"].fillna("etc", inplace=True)
p_info["city"].fillna("etc", inplace=True)
p_info["country"].fillna("etc", inplace=True)
for case in p_info["infection_case"]:
if case not in d_infection_case:
d_infection_case[str(case)] = infection_case_counter
infection_case_counter += 1
# TODO: Modify - add props. -gu, -gun, -si with regex
for city in p_info["city"]:
if city not in d_city:
d_city[str(city)] = city_counter
city_counter += 1
# TODO: Modify - add props. Special City / Metropolitan City / Province(-do) with regex
for province in p_info["province"]:
if province not in d_province:
d_province[str(province)] = province_counter
province_counter += 1
for country in p_info["country"]:
if country not in d_country:
d_country[str(country)] = country_counter
country_counter += 1
p_info["infection_case"] = p_info["infection_case"].map(d_infection_case)
p_info["city"] = p_info["city"].map(d_city)
p_info["province"] = p_info["province"].map(d_province)
p_info["country"] = p_info["country"].map(d_country)
```
This block of code handles the NaN values for the birth year and age. Majority of these values were filled except for a few, which made it reasonable to fill the NaN values with the mean. Another approach would be the value from KNN. This is just a script that goes through to check if 1 or both cells are empty for that patient and fills it with the according mean.
```
year = date.today().year
# 0 - indicates nan
p_info["age"].fillna(0, inplace=True)
p_info["birth_year"].fillna(0, inplace=True)
for count, age in enumerate(p_info["age"], 0):
birth = p_info["birth_year"][count]
if age == 0 and birth == 0:
continue
elif age != 0 and birth == 0:
# No birth date recorded
age = age[:-1]
born = int(year-int(age))
p_info.at[count, "birth_year"] = born
else:
n_age = int(year-int(birth))
p_info.at[count, "age"] = n_age
c_info = p_info[p_info["age"] != 0]
c_info = p_info[p_info["birth_year"] != 0]
print(c_info.head())
a_avg = int(c_info["age"].values.mean())
b_avg = int(c_info["birth_year"].values.mean())
for count, age in enumerate(p_info["age"], 0):
birth = p_info["birth_year"][count]
if age == 0 and birth == 0:
p_info.at[count, "age"] = str(a_avg)
p_info.at[count, "birth_year"] = str(b_avg)
```
This is the Pearson correlation mentioned earlier. Darker cells indicate a stronger correlation with its pair, vise versa. I noticed that a lot on this matrix had weak correlation, which is why I dropped all the columns in the next cell.
```
plt.figure(figsize=(12,10))
cor = p_info.corr()
sns.heatmap(cor, annot=True, cmap=plt.cm.Reds)
plt.show()
# Used for train/test
y = p_info["released_date"].ravel()
X_train_korea, X_test_korea, y_train_korea, y_test_korea = train_test_split(p_info, y, test_size=0.25, random_state=1)
# Based on Pearson correlation that we drop the columns that don't have a factor in our target.
p_info.drop("global_num", axis=1, inplace=True)
p_info.drop("infection_order", axis=1, inplace=True)
p_info.drop("symptom_onset_date", axis=1, inplace=True)
p_info.drop("infected_by", axis=1, inplace=True)
p_info.drop("contact_number", axis=1, inplace=True)
p_info.drop("deceased_date", axis=1, inplace=True)
p_info.drop("patient_id", axis=1, inplace=True)
p_info.drop("released_date", axis=1, inplace=True)
p_info.drop("birth_year", axis=1, inplace=True)
p_info.drop("disease", axis=1, inplace=True)
```
## Building our recovery regression
```
korea_reg = LinearRegression()
korea_reg.fit(X_train_korea, y_train_korea)
korea_lin_pred = korea_reg.predict(X_test_korea)
```
Based on the guidelines that we set earlier, we can see that our R2 score is valid, however, an argument can be made that our model is underfitting with the RSME below the min value of the feature we're trying to measure.
```
print("Min: ", y_test_korea.min())
print("Max: ", y_test_korea.max())
print("RMSE: ", math.sqrt(mean_squared_error(y_test_korea, korea_lin_pred)))
print("r^2: ", r2_score(y_test_korea, korea_lin_pred))
print(korea_lin_pred)
```
### How realistic is it?
This section explores weather or not the recovery time predictions for Korea will be feasible to use for predicting Canada's recovery period.
```
hospital_df = pd.read_csv("./caltech_covid_19_modeling/data/international/health/hospital-beds-per-1000-people.csv")
phys_df = pd.read_csv("./caltech_covid_19_modeling/data/international/health/physicians-per-1000-people.csv")
# Keywords
hospital_beds = "Hospital beds (per 1,000 people) (per 1,000 people)"
physicians = "Physicians (per 1,000 people) (per 1,000 people)"
# Hospital bed ratios (2010)
c_hospital_ratio = hospital_df[hospital_beds][531]
sk_hospital_ratio = hospital_df[hospital_beds][2983]
print("Canada Hospital Beds:1000 people -> %s" % c_hospital_ratio)
print("South Korea Hospital Beds:1000 people -> %s" % sk_hospital_ratio)
# Physicians ratios (2015)
c_phys_ratio = phys_df[physicians][717]
sk_phys_ratio = phys_df[physicians][3604]
print("Canada Physician:1000 people -> %s" % c_phys_ratio)
print("South Korea Physician:1000 people -> %s" % sk_phys_ratio)
c_hos_df = hospital_df[hospital_df["Entity"] == "Canada"]
sk_hos_df = hospital_df[hospital_df["Entity"] == "South Korea"]
c_phys_df = phys_df[phys_df["Entity"] == "Canada"]
sk_phys_df = phys_df[phys_df["Entity"] == "South Korea"]
```
Visualizing and comparing the trends between the two ratios over time. An inference about the quality of the healthcare can be concluded and how well Canada & South Korea react to changing demographics. As the population increases in the past decade, trends show that the number of beds per 1000 people decreases significantly, whereas South Korea's healthcare system adapts this change. Just from the graph itself, both countries seem to keep up with the demand of physicians. As well, the <a href="https://github.com/quantummind/caltech_covid_19_modeling/blob/master/data/international/demographics/median-age.csv" target="_blank">median age</a> between both countries are fairly similar, (Canada is 41.4 years and South Korea is 43.3 years) which gives us a slightly better understanding of the demographics.
The South Korean regression model is accurate to an extent until many other factors are applied that were not accounted for (average household income, do they pay health insurance, smoking, death-related causes, other societal factors, etc.)
*Note: These inferences are only concluded from the datasets that were used in this notebook.
```
fig = plt.gcf()
fig.set_size_inches(17, 5)
fig.suptitle("Hospital Bed Distribution && Physician Distribution", fontsize=12)
plt.subplot(1,2,1)
plt.plot(c_hos_df["Year"], c_hos_df[hospital_beds], label="Canada")
plt.plot(sk_hos_df["Year"], sk_hos_df[hospital_beds], label="South Korea")
plt.legend()
plt.subplot(1,2,2)
plt.plot(c_phys_df["Year"], c_phys_df[physicians], label="Canada")
plt.plot(sk_phys_df["Year"], sk_phys_df[physicians], label="South Korea")
plt.legend()
plt.show()
```
|
github_jupyter
|
import math
import os
import shutil
import stat
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from datetime import date, datetime
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.linear_model import LinearRegression, BayesianRidge
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import PolynomialFeatures
from sklearn import svm
from git import Repo
from subprocess import call
%matplotlib inline
# Remove hidden folders and its contents
def on_rm_error(func, p, exc_info):
os.chmod(p, stat.S_IWRITE)
os.unlink(p)
ppath = "\COVID19"
path = "./COVID19"
if os.path.isdir(path):
if len(os.listdir(path)) == 0:
print("Empty")
# Loop through entire project dir
for fn in os.listdir(path):
fp = os.path.join(path, fn)
try:
if os.path.isfile(fp) or os.path.islink(fp):
os.unlink(fp)
elif os.path.isdir(fp):
shutil.rmtree(fp, ignore_errors=True)
except Exception as e:
print("Failed to remove %s" % fp)
ggit = os.listdir(path)[0]
if ggit.endswith("git"):
tmp = os.path.join(path, ggit)
while True:
call(['attrib', '-H', tmp])
break
shutil.rmtree(tmp, onerror=on_rm_error)
#print(os.listdir(path))
shutil.rmtree(ppath, ignore_errors=True)
Repo.clone_from("https://github.com/CSSEGISandData/COVID-19.git", "./COVID19")
c_ts = pd.read_csv("./COVID19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv")
r_ts = pd.read_csv("./COVID19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv")
d_ts = pd.read_csv("./COVID19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv")
dates = c_ts.columns[4:]
days_since = [day for day in range(len(dates))]
canada_confirmed = []
canada_recovered = []
canada_deaths = []
canada_confirmed_cases = c_ts[c_ts["Country/Region"] == "Canada"]
canada_recovered_cases = r_ts[r_ts["Country/Region"] == "Canada"]
canada_death_cases = d_ts[d_ts["Country/Region"] == "Canada"]
for date in dates:
canada_confirmed.append(canada_confirmed_cases[date].sum())
canada_recovered.append(canada_recovered_cases[date].sum())
canada_deaths.append(canada_death_cases[date].sum())
cc = {"days_since_Jan22": days_since, "cases_in_canada": canada_confirmed}
c_df = pd.DataFrame(data=cc)
c_df["recovered_in_canada"] = canada_recovered
c_df["deaths_in_canada"] = canada_deaths
fig, axs = plt.subplots(ncols=3, figsize=(17,5))
sns.lineplot(x="days_since_Jan22", y="cases_in_canada", data=c_df, ax=axs[0]).set_title("Confirmed Cases in Canada")
sns.lineplot(x="days_since_Jan22", y="recovered_in_canada", data=c_df, ax=axs[1]).set_title("Total Recoveries in Canada")
sns.lineplot(x="days_since_Jan22", y="deaths_in_canada", data=c_df, ax=axs[2]).set_title("Total Deaths in Canada")
plt.show()
days_to_predict = 14
days_since = np.array(days_since).reshape(-1,1)
future_days_since = np.array([day for day in range(len(dates)+days_to_predict)]).reshape(-1,1)
# Separating data into train/test
y = np.array(c_df["cases_in_canada"].ravel()).reshape(-1,1)
X_train_confirmed, X_test_confirmed, y_train_confirmed, y_test_confirmed = train_test_split(
days_since, y, test_size=0.2, shuffle=False)
y_death = np.array(c_df["deaths_in_canada"].ravel()).reshape(-1,1)
X_train_death, X_test_death, y_train_death, y_test_death = train_test_split(days_since,
y_death, test_size=0.2, shuffle=False)
y_recover = np.array(c_df["recovered_in_canada"].ravel()).reshape(-1,1)
X_train_recover, X_test_recover, y_train_recover, y_test_recover = train_test_split(days_since, y_recover,
test_size=0.2, shuffle=False)
reg = LinearRegression()
reg.fit(X_train_confirmed, y_train_confirmed)
y_confirm_pred = reg.predict(X_test_confirmed)
reg.fit(X_train_recover, y_train_recover)
y_recover_pred = reg.predict(X_test_recover)
reg.fit(X_train_death, y_train_death)
y_death_pred = reg.predict(X_test_death)
fig = plt.gcf()
fig.set_size_inches(17, 5)
plt.subplot(1,3,1)
plt.plot(y_confirm_pred, label="Confirmed cases preds")
plt.plot(y_test_confirmed, label="Confirmed cases ground truth")
plt.legend()
plt.subplot(1,3,2)
plt.plot(y_recover_pred, label="Recovered total preds")
plt.plot(y_test_recover, label="Recovered total ground truth")
plt.legend()
plt.subplot(1,3,3)
plt.plot(y_death_pred, label="Total deaths preds")
plt.plot(y_test_death, label="Total deaths ground truth")
plt.legend()
plt.show()
def rsme(ground_truth, preds):
return math.sqrt(mean_squared_error(ground_truth, preds))
def r2(ground_truth, preds):
return r2_score(ground_truth, preds)
nopoly_results = {
"Name": ["Total confirmed", "Total recovered", "Total deaths"],
"Min": [y_test_confirmed.min(), y_test_recover.min(), y_test_death.min()],
"Max": [y_test_confirmed.max(), y_test_recover.max(), y_test_death.max()],
"RSME": [rsme(y_test_confirmed, y_confirm_pred), rsme(y_test_recover, y_recover_pred), rsme(y_test_death, y_death_pred)],
"r^2": [r2(y_test_confirmed, y_confirm_pred), r2(y_test_recover, y_recover_pred), r2(y_test_death, y_death_pred)]
}
nopoly_results_df = pd.DataFrame(nopoly_results)
print(nopoly_results_df)
poly_lin = PolynomialFeatures(3)
poly_X_train_confirmed = poly_lin.fit_transform(np.array(X_train_confirmed).reshape(-1,1))
poly_X_test_confirmed = poly_lin.fit_transform(np.array(X_test_confirmed).reshape(-1,1))
poly_future_days_since = poly_lin.fit_transform(np.array(future_days_since).reshape(-1,1))
poly_death = PolynomialFeatures(4)
poly_X_train_death = poly_death.fit_transform(np.array(X_train_death).reshape(-1,1))
poly_X_test_death = poly_death.fit_transform(np.array(X_test_death).reshape(-1,1))
poly_recover = PolynomialFeatures(3)
poly_X_train_recover = poly_recover.fit_transform(np.array(X_train_recover).reshape(-1,1))
poly_X_test_recover = poly_recover.fit_transform(np.array(X_test_recover).reshape(-1,1))
poly_reg = LinearRegression()
poly_reg.fit(poly_X_train_confirmed, y_train_confirmed)
y_lin_confirm = poly_reg.predict(poly_X_test_confirmed)
poly_reg.fit(poly_X_train_death, y_train_death)
y_lin_death = poly_reg.predict(poly_X_test_death)
poly_reg.fit(poly_X_train_recover, y_train_recover)
y_lin_recover = poly_reg.predict(poly_X_test_recover)
poly_results = {
"Name": ["Total confirmed", "Total recovered", "Total deaths"],
"Min": [y_test_confirmed.min(), y_test_recover.min(), y_test_death.min()],
"Max": [y_test_confirmed.max(), y_test_recover.max(), y_test_death.max()],
"RSME": [rsme(y_test_confirmed, y_lin_confirm), rsme(y_test_recover, y_lin_recover), rsme(y_test_death, y_lin_death)],
"r^2": [r2(y_test_confirmed, y_lin_confirm), r2(y_test_recover, y_lin_recover), r2(y_test_death, y_lin_death)]
}
poly_results_df = pd.DataFrame(poly_results)
print(poly_results_df)
fig = plt.gcf()
fig.set_size_inches(17, 5)
plt.subplot(1,3,1)
plt.plot(y_lin_confirm, label="Confirmed cases preds")
plt.plot(y_test_confirmed, label="Confirmed cases ground truth")
plt.legend()
plt.subplot(1,3,2)
plt.plot(y_lin_recover, label="Total Recovered preds")
plt.plot(y_test_recover, label="Total Recovered ground truth")
plt.legend()
plt.subplot(1,3,3)
plt.plot(y_lin_death, label="Total Deaths preds")
plt.plot(y_test_death, label="Total Deaths ground truth")
plt.legend()
plt.show()
fig = plt.gcf()
fig.set_size_inches(17, 5)
plt.subplot(1,2,1)
plt.plot(y_lin_recover, label="Forecasted recovery")
plt.plot(y_lin_confirm, label="Forecasted confirmed")
plt.legend()
plt.subplot(1,2,2)
plt.plot(y_lin_recover, label="Forecasted recovery")
plt.plot(y_lin_death, label="Forecasted death")
plt.legend()
plt.show()
p_info = pd.read_csv("./korea_dataset/PatientInfo.csv")
# Saving this for future functions (if needed)
infected_by = p_info["infected_by"].ravel()
contact_number = p_info["contact_number"].ravel()
deceased_date = p_info["deceased_date"].ravel()
patient_id = p_info["patient_id"].ravel()
d_disease = {"TRUE": 0, "FALSE": 1}
d_gender = {"male": 0, "female": 1, "n/a": 2}
d_state = {"released": 0, "isolated": 1, "deceased": 2}
# Fill NaN values with the dict above
p_info["disease"].fillna("FALSE", inplace=True)
p_info["disease"] = p_info["disease"].map(d_disease)
# There was a bug that didn't fill all NaN values, so this dbl checks and fills it manually, O(n) search
for count, disease in enumerate(p_info["disease"], 0):
if math.isnan(disease):
p_info.at[count, "disease"] = "1.0"
p_info["sex"].fillna("n/a", inplace=True)
p_info["sex"] = p_info["sex"].map(d_gender)
p_info["state"] = p_info["state"].map(d_state)
# Converts string date to a number since Jan. 1
def nth_day(d, format="%m/%d/%y"):
d = pd.to_datetime(d, format=format)
day = pd.Timestamp(year=d.year, month=1, day=1)
return int((d-day).days + 1)
for count, cd in enumerate(p_info["confirmed_date"], 0):
p_info.at[count, "confirmed_date"] = int(nth_day(str(cd)))
p_info["released_date"].fillna(date.today().strftime("%m/%d/%y"))
for count, rd in enumerate(p_info["released_date"], 0):
try:
p_info.at[count, "released_date"] = int(nth_day(str(rd)))
except:
# If it encounters a NaN value - same issue above where it didn't fill all NaN values
p_info.at[count, "released_date"] = int(nth_day(str(date.today().strftime("%m/%d/%y"))))
d_infection_case = {}
d_city = {}
d_province = {}
d_country = {}
infection_case_counter = 0
city_counter = 0
province_counter = 0
country_counter = 0
p_info["infection_case"].fillna("etc", inplace=True)
p_info["city"].fillna("etc", inplace=True)
p_info["country"].fillna("etc", inplace=True)
for case in p_info["infection_case"]:
if case not in d_infection_case:
d_infection_case[str(case)] = infection_case_counter
infection_case_counter += 1
# TODO: Modify - add props. -gu, -gun, -si with regex
for city in p_info["city"]:
if city not in d_city:
d_city[str(city)] = city_counter
city_counter += 1
# TODO: Modify - add props. Special City / Metropolitan City / Province(-do) with regex
for province in p_info["province"]:
if province not in d_province:
d_province[str(province)] = province_counter
province_counter += 1
for country in p_info["country"]:
if country not in d_country:
d_country[str(country)] = country_counter
country_counter += 1
p_info["infection_case"] = p_info["infection_case"].map(d_infection_case)
p_info["city"] = p_info["city"].map(d_city)
p_info["province"] = p_info["province"].map(d_province)
p_info["country"] = p_info["country"].map(d_country)
year = date.today().year
# 0 - indicates nan
p_info["age"].fillna(0, inplace=True)
p_info["birth_year"].fillna(0, inplace=True)
for count, age in enumerate(p_info["age"], 0):
birth = p_info["birth_year"][count]
if age == 0 and birth == 0:
continue
elif age != 0 and birth == 0:
# No birth date recorded
age = age[:-1]
born = int(year-int(age))
p_info.at[count, "birth_year"] = born
else:
n_age = int(year-int(birth))
p_info.at[count, "age"] = n_age
c_info = p_info[p_info["age"] != 0]
c_info = p_info[p_info["birth_year"] != 0]
print(c_info.head())
a_avg = int(c_info["age"].values.mean())
b_avg = int(c_info["birth_year"].values.mean())
for count, age in enumerate(p_info["age"], 0):
birth = p_info["birth_year"][count]
if age == 0 and birth == 0:
p_info.at[count, "age"] = str(a_avg)
p_info.at[count, "birth_year"] = str(b_avg)
plt.figure(figsize=(12,10))
cor = p_info.corr()
sns.heatmap(cor, annot=True, cmap=plt.cm.Reds)
plt.show()
# Used for train/test
y = p_info["released_date"].ravel()
X_train_korea, X_test_korea, y_train_korea, y_test_korea = train_test_split(p_info, y, test_size=0.25, random_state=1)
# Based on Pearson correlation that we drop the columns that don't have a factor in our target.
p_info.drop("global_num", axis=1, inplace=True)
p_info.drop("infection_order", axis=1, inplace=True)
p_info.drop("symptom_onset_date", axis=1, inplace=True)
p_info.drop("infected_by", axis=1, inplace=True)
p_info.drop("contact_number", axis=1, inplace=True)
p_info.drop("deceased_date", axis=1, inplace=True)
p_info.drop("patient_id", axis=1, inplace=True)
p_info.drop("released_date", axis=1, inplace=True)
p_info.drop("birth_year", axis=1, inplace=True)
p_info.drop("disease", axis=1, inplace=True)
korea_reg = LinearRegression()
korea_reg.fit(X_train_korea, y_train_korea)
korea_lin_pred = korea_reg.predict(X_test_korea)
print("Min: ", y_test_korea.min())
print("Max: ", y_test_korea.max())
print("RMSE: ", math.sqrt(mean_squared_error(y_test_korea, korea_lin_pred)))
print("r^2: ", r2_score(y_test_korea, korea_lin_pred))
print(korea_lin_pred)
hospital_df = pd.read_csv("./caltech_covid_19_modeling/data/international/health/hospital-beds-per-1000-people.csv")
phys_df = pd.read_csv("./caltech_covid_19_modeling/data/international/health/physicians-per-1000-people.csv")
# Keywords
hospital_beds = "Hospital beds (per 1,000 people) (per 1,000 people)"
physicians = "Physicians (per 1,000 people) (per 1,000 people)"
# Hospital bed ratios (2010)
c_hospital_ratio = hospital_df[hospital_beds][531]
sk_hospital_ratio = hospital_df[hospital_beds][2983]
print("Canada Hospital Beds:1000 people -> %s" % c_hospital_ratio)
print("South Korea Hospital Beds:1000 people -> %s" % sk_hospital_ratio)
# Physicians ratios (2015)
c_phys_ratio = phys_df[physicians][717]
sk_phys_ratio = phys_df[physicians][3604]
print("Canada Physician:1000 people -> %s" % c_phys_ratio)
print("South Korea Physician:1000 people -> %s" % sk_phys_ratio)
c_hos_df = hospital_df[hospital_df["Entity"] == "Canada"]
sk_hos_df = hospital_df[hospital_df["Entity"] == "South Korea"]
c_phys_df = phys_df[phys_df["Entity"] == "Canada"]
sk_phys_df = phys_df[phys_df["Entity"] == "South Korea"]
fig = plt.gcf()
fig.set_size_inches(17, 5)
fig.suptitle("Hospital Bed Distribution && Physician Distribution", fontsize=12)
plt.subplot(1,2,1)
plt.plot(c_hos_df["Year"], c_hos_df[hospital_beds], label="Canada")
plt.plot(sk_hos_df["Year"], sk_hos_df[hospital_beds], label="South Korea")
plt.legend()
plt.subplot(1,2,2)
plt.plot(c_phys_df["Year"], c_phys_df[physicians], label="Canada")
plt.plot(sk_phys_df["Year"], sk_phys_df[physicians], label="South Korea")
plt.legend()
plt.show()
| 0.334372 | 0.933552 |
# How to perform aperture photometry with custom apertures
We have discussed in [previous tutorials](http://lightkurve.keplerscience.org/tutorials/1.03-what-are-lightcurves.html) how Simple Aperture Photometry works. We choose a set of pixels in the image and sum those to produce a single flux value. We do this for every image as a function of time to produce a light curve.
The [Kepler Data Pipeline](https://github.com/nasa/kepler-pipeline) produces an aperture, which is used by default by lightkurve. However, there are some cases where you might want to produce your own aperture. The field may be crowded, or you may wish to change the aperture size to change the relative contribution of the background. We can do this simply with lightkurve.
First, let's load a target pixel file. Let's choose [KIC 6679295](https://exoplanetarchive.ipac.caltech.edu/cgi-bin/DisplayOverview/nph-DisplayOverview?objname=KOI-2862.01&type=KEPLER_CANDIDATE). This is a Kepler planet canidate. We'll use the `from_archive` function to download every target pixel file available for each quarter of this data set.
```
%%capture
from lightkurve import KeplerTargetPixelFile
import matplotlib.pyplot as plt
%matplotlib inline
kic = '6679295'
#List to hold our TPFs
tpfs = []
for q in range(1,18):
#Note some quarters are missing, so we'll use Python's try/except to avoid crashing
try:
tpfs.append(KeplerTargetPixelFile.from_archive(kic, quarter=q))
except:
continue
```
We've now created a list of `KeplerTargetPixelFiles`, where each item is a different quarter. We're going to be able to combine these just like in the [stitching tutorial]().
```
tpfs
```
Let's take a look at just one of those target pixel files.
```
#Build the light curve
pipeline_lc = tpfs[0].to_lightcurve().flatten()
for tpf in tpfs:
pipeline_lc = pipeline_lc.append(tpf.to_lightcurve().flatten())
#Clean the light curve
pipeline_lc = pipeline_lc.remove_nans().remove_outliers()
```
Above we have created the light curve from the target pixel files, stitched them all together in the same way as in the [stitching tutorial] using lightkurves `append` function. To recap the steps we:
* Convert to a `KeplerLightCurve` object with `to_lightcurve()`
* Remove NaNs with `remove_nans()`
* Remove long term trends with `flatten()`
* Remove outliers with simple sigma clipping using `remove_outliers()`
The period for this planet candidate is 24.57537 days. Let's plot it up and take a look.
```
pipeline_lc.fold(period=24.57537, phase=-0.133).bin().plot();
plt.xlim(-0.015,0.015)
plt.ylim(0.998,1.0015)
```
Looks like a great candidate. However, we might just want to check on the pixels. Let's plot one of the target pixel files.
```
tpf.plot(frame=100, aperture_mask=tpf.pipeline_mask, mask_color='red')
```
The Kepler Pipeline aperture is in red. It looks like there is a nearby contaminate star! We might want to check that the signal is not really coming from the bright, nearby contaminant, rather than our target star. Let's use the top right corner four pixels as our new mask.
```
import numpy as np
aper = np.zeros(tpf.shape[1:])
aper[-2:, 0:2] = 1
tpf.plot(aperture_mask=aper, mask_color='red')
```
The new mask covers the bright star. Now we can iterate through the target pixel files and build the light curve in the same way as before, but this time
```
#Build the NEW aperture, and the light curve
aper = np.zeros(tpfs[0].shape[1:])
aper[-2:, 0:2] = 1
user_lc = tpfs[0].to_lightcurve(aperture_mask=aper.astype(bool)).flatten()
for tpf in tpfs:
aper = np.zeros(tpf.shape[1:])
aper[-2:, 0:2]=1
user_lc = user_lc.append(tpf.to_lightcurve(aperture_mask=aper.astype(bool)).flatten())
#Clean the light curve
user_lc = user_lc.remove_nans().remove_outliers()
```
Now we have our new light curve we can plot it up again and find out if there is still a planet signal.
```
user_lc.fold(period=24.57537, phase=-0.133).bin().plot();
plt.xlim(-0.015,0.015)
plt.ylim(0.998,1.0015)
```
Looks like the planet signal is only in the target star and doesn't belong to the contaminant. This is just one of many checks you might want to perform to validate your planet candidates!
|
github_jupyter
|
%%capture
from lightkurve import KeplerTargetPixelFile
import matplotlib.pyplot as plt
%matplotlib inline
kic = '6679295'
#List to hold our TPFs
tpfs = []
for q in range(1,18):
#Note some quarters are missing, so we'll use Python's try/except to avoid crashing
try:
tpfs.append(KeplerTargetPixelFile.from_archive(kic, quarter=q))
except:
continue
tpfs
#Build the light curve
pipeline_lc = tpfs[0].to_lightcurve().flatten()
for tpf in tpfs:
pipeline_lc = pipeline_lc.append(tpf.to_lightcurve().flatten())
#Clean the light curve
pipeline_lc = pipeline_lc.remove_nans().remove_outliers()
pipeline_lc.fold(period=24.57537, phase=-0.133).bin().plot();
plt.xlim(-0.015,0.015)
plt.ylim(0.998,1.0015)
tpf.plot(frame=100, aperture_mask=tpf.pipeline_mask, mask_color='red')
import numpy as np
aper = np.zeros(tpf.shape[1:])
aper[-2:, 0:2] = 1
tpf.plot(aperture_mask=aper, mask_color='red')
#Build the NEW aperture, and the light curve
aper = np.zeros(tpfs[0].shape[1:])
aper[-2:, 0:2] = 1
user_lc = tpfs[0].to_lightcurve(aperture_mask=aper.astype(bool)).flatten()
for tpf in tpfs:
aper = np.zeros(tpf.shape[1:])
aper[-2:, 0:2]=1
user_lc = user_lc.append(tpf.to_lightcurve(aperture_mask=aper.astype(bool)).flatten())
#Clean the light curve
user_lc = user_lc.remove_nans().remove_outliers()
user_lc.fold(period=24.57537, phase=-0.133).bin().plot();
plt.xlim(-0.015,0.015)
plt.ylim(0.998,1.0015)
| 0.393618 | 0.989692 |
```
import cv2
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
#img = cv2.imread('Lid UP cropped plus.png')
#b, g, r = cv2.split(img)
#rgb_img = cv2.merge([r, g, b])
#rgb_img = cv2.medianBlur(rgb_img, 9)
#gimg = cv2.cvtColor(rgb_img, cv2.COLOR_RGB2GRAY)
#thresh = cv2.adaptiveThreshold(gimg, 165,
# cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
# cv2.THRESH_BINARY_INV,11,2)
#th, im_th = cv2.threshold(gimg, 165, 255, cv2.THRESH_BINARY_INV)
#im_floodfill = im_th.copy()
#h, w = im_th.shape[:2]
#mask = np.zeros((h + 2, w + 2), np.uint8)
#cv2.floodFill(im_floodfill, mask, (0, 0), 255)
#im_floodfill_inv = cv2.bitwise_not(floodfill)
#im_out = im_th | im_floodfill_inv
#plt.figure()
#plt.imshow(im_th, cmap='gray', interpolation='none')
#plt.figure()
#plt.imshow(im_floodfill, cmap='gray', interpolation='none')
#plt.figure()
#plt.imshow(im_floodfill_inv, cmap='gray', interpolation='none')
#plt.figure()
#plt.imshow(im_out, cmap='gray')
img = cv2.imread('Lid UP cropped plus.png')
b, g, r = cv2.split(img)
rgb_img = cv2.merge([r, g, b])
plt.figure()
plt.imshow(rgb_img)
rgb_img = cv2.medianBlur(rgb_img, 9)
rgb_img = cv2.meaBlur(rgb_img, 9)
plt.figure()
plt.imshow(rgb_img)
gimg = cv2.cvtColor(rgb_img, cv2.COLOR_RGB2GRAY)
thresh = cv2.adaptiveThreshold(gimg, 165,
cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
cv2.THRESH_BINARY_INV,11,2)
#th, im_th = cv2.threshold(gimg, 165, 255, cv2.THRESH_BINARY_INV)
im2, contours, hierarchy = cv2.findContours(thresh,
cv2.RETR_TREE,
cv2.CHAIN_APPROX_SIMPLE)
copy = rgb_img.copy()
cv2.drawContours(rgb_img, contours, -1, (0, 255, 0), 3)
print(len(contours))
plt.figure()
plt.imshow(thresh, cmap='gray')
plt.figure()
plt.imshow(rgb_img)
fig1 = plt.figure()
fig2 = plt.figure()
63
copy_gimg = np.asarray(gimg)
dst = np.zeros(shape=(len(gimg), len(gimg[0])))
b = cv2.normalize(copy_gimg, dst, alpha=140, beta=150,
norm_type=cv2.NORM_MINMAX,
dtype=cv2.CV_32F)
ax = fig1.add_subplot(121)
ax.imshow(gimg, cmap='gray')
ax = fig1.add_subplot(122)
ax.imshow(b, cmap='gray')
plt.show()
print np.max(gimg), np.min(gimg)
circles = cv2.HoughCircles(thresh, cv2.HOUGH_GRADIENT,
1, 20,
param1=50, param2=30,
minRadius=30, maxRadius=100)
circles = np.uint16(np.around(circles))
for i in circles[0, :]:
cv2.circle(rgb_img, (i[0], i[1]), i[2], (0, 255, 0), 2)
cv2.circle(rgb_img, (i[0], i[1]), 2, (0, 0, 255), 3)
plt.imshow(rgb_img)
```
|
github_jupyter
|
import cv2
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
#img = cv2.imread('Lid UP cropped plus.png')
#b, g, r = cv2.split(img)
#rgb_img = cv2.merge([r, g, b])
#rgb_img = cv2.medianBlur(rgb_img, 9)
#gimg = cv2.cvtColor(rgb_img, cv2.COLOR_RGB2GRAY)
#thresh = cv2.adaptiveThreshold(gimg, 165,
# cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
# cv2.THRESH_BINARY_INV,11,2)
#th, im_th = cv2.threshold(gimg, 165, 255, cv2.THRESH_BINARY_INV)
#im_floodfill = im_th.copy()
#h, w = im_th.shape[:2]
#mask = np.zeros((h + 2, w + 2), np.uint8)
#cv2.floodFill(im_floodfill, mask, (0, 0), 255)
#im_floodfill_inv = cv2.bitwise_not(floodfill)
#im_out = im_th | im_floodfill_inv
#plt.figure()
#plt.imshow(im_th, cmap='gray', interpolation='none')
#plt.figure()
#plt.imshow(im_floodfill, cmap='gray', interpolation='none')
#plt.figure()
#plt.imshow(im_floodfill_inv, cmap='gray', interpolation='none')
#plt.figure()
#plt.imshow(im_out, cmap='gray')
img = cv2.imread('Lid UP cropped plus.png')
b, g, r = cv2.split(img)
rgb_img = cv2.merge([r, g, b])
plt.figure()
plt.imshow(rgb_img)
rgb_img = cv2.medianBlur(rgb_img, 9)
rgb_img = cv2.meaBlur(rgb_img, 9)
plt.figure()
plt.imshow(rgb_img)
gimg = cv2.cvtColor(rgb_img, cv2.COLOR_RGB2GRAY)
thresh = cv2.adaptiveThreshold(gimg, 165,
cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
cv2.THRESH_BINARY_INV,11,2)
#th, im_th = cv2.threshold(gimg, 165, 255, cv2.THRESH_BINARY_INV)
im2, contours, hierarchy = cv2.findContours(thresh,
cv2.RETR_TREE,
cv2.CHAIN_APPROX_SIMPLE)
copy = rgb_img.copy()
cv2.drawContours(rgb_img, contours, -1, (0, 255, 0), 3)
print(len(contours))
plt.figure()
plt.imshow(thresh, cmap='gray')
plt.figure()
plt.imshow(rgb_img)
fig1 = plt.figure()
fig2 = plt.figure()
63
copy_gimg = np.asarray(gimg)
dst = np.zeros(shape=(len(gimg), len(gimg[0])))
b = cv2.normalize(copy_gimg, dst, alpha=140, beta=150,
norm_type=cv2.NORM_MINMAX,
dtype=cv2.CV_32F)
ax = fig1.add_subplot(121)
ax.imshow(gimg, cmap='gray')
ax = fig1.add_subplot(122)
ax.imshow(b, cmap='gray')
plt.show()
print np.max(gimg), np.min(gimg)
circles = cv2.HoughCircles(thresh, cv2.HOUGH_GRADIENT,
1, 20,
param1=50, param2=30,
minRadius=30, maxRadius=100)
circles = np.uint16(np.around(circles))
for i in circles[0, :]:
cv2.circle(rgb_img, (i[0], i[1]), i[2], (0, 255, 0), 2)
cv2.circle(rgb_img, (i[0], i[1]), 2, (0, 0, 255), 3)
plt.imshow(rgb_img)
| 0.310799 | 0.329297 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.