code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
<img src="http://sct.inf.utfsm.cl/wp-content/uploads/2020/04/logo_di.png" style="width:60%">
<center>
<h1>ILI285/INF285 Computación Científica </h1>
<h1>Pauta Pregunta de "Newton + Gradiente Conjugado" - COP3</h1>
</center>
Necesitamos ajustar un conjunto de datos $D=\{(x_1,y_1),(x_2,y_2), \dots, (x_n, y_n)\}$, con una Spline cúbica de un intervalo, es decir, $S(x)=a+bx+cx^2+dx^3$. Para esto requerimos minimizar la función $F(a,b,c,d)=\displaystyle \sum_{i=1}^n (y_i- S(x_i))^4=\sum_{i=1}^n (y_i-a-bx_i-cx_i^2-dx_i^3)^4$. Esto significa que debemos obtener:
\begin{equation}
\begin{split}
\frac{\partial F}{\partial a} &= \sum_{i=1}^n -4(y_i-a-bx_i-cx_i^2-dx_i^3)^3 = 0 \\
\frac{\partial F}{\partial b} &= \sum_{i=1}^n -4x_i(y_i-a-bx_i-cx_i^2-dx_i^3)^3 = 0 \\
\frac{\partial F}{\partial c} &= \sum_{i=1}^n -4x_i^2(y_i-a-bx_i-cx_i^2-dx_i^3)^3 = 0 \\
\frac{\partial F}{\partial d} &= \sum_{i=1}^n -4x_i^3(y_i-a-bx_i-cx_i^2-dx_i^3)^3 = 0 \\
\end{split}
\end{equation}
Notar que simplificando la expresión anterior y definiendo $\mathbf{z}=(a,b,c,d)$ podemos llevar el resultado anterior al problema $\mathbf{G}(\mathbf{z})=\mathbf{0}$, donde $\mathbf{G}(\mathbf{z})$ se define como:
\begin{equation}
\mathbf{G}(\mathbf{z}) =
\begin{bmatrix}
\displaystyle \sum_{i=1}^n(y_i-a-bx_i-cx_i^2-dx_i^3)^3 \\
\displaystyle \sum_{i=1}^nx_i(y_i-a-bx_i-cx_i^2-dx_i^3)^3 \\
\displaystyle \sum_{i=1}^nx_i^2(y_i-a-bx_i-cx_i^2-dx_i^3)^3 \\
\displaystyle \sum_{i=1}^nx_i^3(y_i-a-bx_i-cx_i^2-dx_i^3)^3
\end{bmatrix} =
\begin{bmatrix}
0 \\ 0 \\ 0 \\ 0
\end{bmatrix}.
\end{equation}
Para obtener el $\mathbf{z}=(a,b,c,d)$ que minimiza $F$, modificaremos el método de Newton utilizando *Gradiente Conjugado* y así resolver el sistema de ecuaciones lineales que aparece en cada iteración. Si bien no sabemos de antemano si $J(\mathbf{z})$ es simétrica y definida positiva, $J(\mathbf{z})^TJ(\mathbf{z})$ si lo es, por lo que el nuevo sistema que se resuelve dentro del método de Newton es:
\begin{equation}
J(\mathbf{z}_i)^TJ(\mathbf{z}_i) \Delta \mathbf{z}_i= -J(\mathbf{z}_i)^T\mathbf{G}(\mathbf{z}_i).
\end{equation}
¿Cuál es el valor del parámetro $p\in\{a, b, c, d\}$ luego de $k\in\{2,3,4\}$ iteraciones del método de Newton?
Considere como *initial guess* el vector nulo tanto para el método del *Gradiente Conjugado* como para el *Método de Newton*. Además utilice como $10^{-10}$ como tolerancia para el método del *Gradiente Conjugado*.
# Solución propuesta
```
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
import ipywidgets as widgets
```
## Implementación Gradiente Conjugado
```
def conjugateGradient(A, b, x_0=None, n=None, tol=1e-10):
if n == None:
n = b.shape[-1]
X = np.zeros((n + 1, b.shape[0]))
R = np.zeros_like(X)
D = np.zeros_like(X)
if x_0 is not None:
X[0] = x_0
R[0] = b - np.dot(A, X[0])
D[0] = R[0]
for k in range(n):
a_k = np.dot(D[k], R[k]) / np.dot(D[k], np.dot(A, D[k]))
X[k+1] = X[k] + a_k * D[k]
R[k+1] = b - np.dot(A, X[k+1])
b_k = np.dot(D[k], np.dot(A, R[k+1])) / np.dot(D[k], np.dot(A, D[k]))
D[k+1] = R[k+1] - b_k * D[k]
if np.linalg.norm(R[k+1]) < tol:
X = X[:k+2]
R = R[:k+2]
D = D[:k+2]
break
return X[-1]#, R, D
```
## Implementación Newton en $\mathbb{R}^n$
```
def newtonRn(F, J, x_0, n, tol=1e-10):
x = np.zeros((n + 1, x_0.shape[0]))
x[0] = x_0
for k in range(n):
JT = J(x[k]).T
JTJ = np.dot(JT, J(x[k]))
JTF = np.dot(JT, F(x[k]))
w = conjugateGradient(JTJ, -JTF)
x[k+1] = x[k] + w
if np.linalg.norm(F(x[k+1])) < tol:
x = x[:k+2]
break
return x
```
## Spline cúbica
```
S = lambda a, b, c, d, x: a + b * x + c * x ** 2 + d * x ** 3
```
## Cálculo del Jacobiano de $\mathbf{G}(\mathbf{z})$
La matriz Jacobiana asociada a este problema se define como:
\begin{equation}
\scriptsize
J(\mathbf{z})=
\begin{bmatrix}
\displaystyle -3\sum_{i=1}^n(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^2(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^3(y_i-a-bx_i-cx_i^2-dx_i^3)^2 \\
\displaystyle -3\sum_{i=1}^nx_i(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^2(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^3(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^4(y_i-a-bx_i-cx_i^2-dx_i^3)^2 \\
\displaystyle -3\sum_{i=1}^nx_i^2(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^3(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^4(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^5(y_i-a-bx_i-cx_i^2-dx_i^3)^2 \\
\displaystyle -3\sum_{i=1}^nx_i^3(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^4(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^5(y_i-a-bx_i-cx_i^2-dx_i^3)^2 &
\displaystyle -3\sum_{i=1}^nx_i^6(y_i-a-bx_i-cx_i^2-dx_i^3)^2 \\
\end{bmatrix}
\end{equation}
Función para construir $\mathbf{G}(\mathbf{z})$ y $J(\mathbf{z})$.
```
def buildGJ(x_i, y_i):
g1 = lambda z: np.sum((y_i - S(*z, x_i)) ** 3)
g2 = lambda z: np.sum(x_i * (y_i - S(*z, x_i)) ** 3)
g3 = lambda z: np.sum(x_i ** 2 * (y_i - S(*z, x_i)) ** 3)
g4 = lambda z: np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 3)
G = lambda z: np.array([g1(z), g2(z), g3(z), g4(z)])
J = lambda z: -3 * np.array([
[np.sum((y_i - S(*z, x_i)) ** 2),
np.sum(x_i * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 2 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 2)],
[np.sum(x_i * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 2 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 4 * (y_i - S(*z, x_i)) ** 2)],
[np.sum(x_i ** 2 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 4 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 5 * (y_i - S(*z, x_i)) ** 2)],
[np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 4 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 5 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 6 * (y_i - S(*z, x_i)) ** 2)]
])
return G, J
```
# Respuestas
Función para obtener los parámetros de $S$ dado un dataset.
```
def solution(x_i, y_i, k, GJ, n_par):
x_0 = np.zeros(n_par)
G, J = GJ(x_i, y_i)
p = newtonRn(G, J, x_0, k, tol=1e-10)
return p[-1]
```
### Lectura de datos
```
DIR = 'data/'
# NPY
dataset_npy_1 = np.load(DIR + '1.npy')
dataset_npy_2 = np.load(DIR + '2.npy')
dataset_npy_3 = np.load(DIR + '3.npy')
y_npy_1 = dataset_npy_1[:, 1]
y_npy_2 = dataset_npy_2[:, 1]
y_npy_3 = dataset_npy_3[:, 1]
# CSV
dataset_csv_1 = np.loadtxt(DIR + '1.csv', delimiter=',')
dataset_csv_2 = np.loadtxt(DIR + '2.csv', delimiter=',')
dataset_csv_3 = np.loadtxt(DIR + '3.csv', delimiter=',')
y_csv_1 = dataset_csv_1[:, 1]
y_csv_2 = dataset_csv_2[:, 1]
y_csv_3 = dataset_csv_3[:, 1]
# TXT
dataset_txt_1 = np.loadtxt(DIR + '1.txt', delimiter=',')
dataset_txt_2 = np.loadtxt(DIR + '2.txt', delimiter=',')
dataset_txt_3 = np.loadtxt(DIR + '3.txt', delimiter=',')
y_txt_1 = dataset_txt_1[:, 1]
y_txt_2 = dataset_txt_2[:, 1]
y_txt_3 = dataset_txt_3[:, 1]
```
Selección de datos. Salvo el archivo ```2.npy```, todos los otros dataset son iguales solo cambia el formato del archivo.
```
n = 100
x_a, x_b = -1, 1
x_i = np.linspace(x_a, x_b, n)
y_i1 = dataset_npy_1[:, 1] # 1.{npy, csv, txt}
y_i2 = dataset_npy_2[:, 1] # 2.npy
y_i22 = dataset_csv_2[:, 1] # 2.{csv, txt}
y_i3 = dataset_npy_3[:, 1] # 3.{npy, csv, txt}
```
Combinaciones de parámetros.
```
K = [2, 3, 4] # Number of iterations
IP = [0, 1, 2, 3] # Parameter index
PL = ["a", "b", "c", "d"] # Parameter name
D = [y_i1, y_i2, y_i22, y_i3] # Dataset
Dn = ['1.{npy, csv, txt}', '2.npy', '2.{csv, txt}', '3.{npy, csv, txt}'] # Dataset name
def experiment(i, p, k):
par = solution(x_i, D[i], k, buildGJ, 4)
print("k: %d, parametro: %s, valor: %f" % (k, PL[p], par[p]))
interact(experiment,
i=widgets.Dropdown(
options=[('1.{npy, csv, txt}', 0), ('2.npy', 1), ('2.{csv, txt}', 2), ('3.{npy, csv, txt}', 3)],
value=0,
description='Dataset:'
),
p=widgets.Dropdown(
options=[("a", 0), ("b", 1), ("c", 2), ("d", 3)],
value=0,
description='Parámetro:'
),
k=K
)
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
import ipywidgets as widgets
def conjugateGradient(A, b, x_0=None, n=None, tol=1e-10):
if n == None:
n = b.shape[-1]
X = np.zeros((n + 1, b.shape[0]))
R = np.zeros_like(X)
D = np.zeros_like(X)
if x_0 is not None:
X[0] = x_0
R[0] = b - np.dot(A, X[0])
D[0] = R[0]
for k in range(n):
a_k = np.dot(D[k], R[k]) / np.dot(D[k], np.dot(A, D[k]))
X[k+1] = X[k] + a_k * D[k]
R[k+1] = b - np.dot(A, X[k+1])
b_k = np.dot(D[k], np.dot(A, R[k+1])) / np.dot(D[k], np.dot(A, D[k]))
D[k+1] = R[k+1] - b_k * D[k]
if np.linalg.norm(R[k+1]) < tol:
X = X[:k+2]
R = R[:k+2]
D = D[:k+2]
break
return X[-1]#, R, D
def newtonRn(F, J, x_0, n, tol=1e-10):
x = np.zeros((n + 1, x_0.shape[0]))
x[0] = x_0
for k in range(n):
JT = J(x[k]).T
JTJ = np.dot(JT, J(x[k]))
JTF = np.dot(JT, F(x[k]))
w = conjugateGradient(JTJ, -JTF)
x[k+1] = x[k] + w
if np.linalg.norm(F(x[k+1])) < tol:
x = x[:k+2]
break
return x
S = lambda a, b, c, d, x: a + b * x + c * x ** 2 + d * x ** 3
def buildGJ(x_i, y_i):
g1 = lambda z: np.sum((y_i - S(*z, x_i)) ** 3)
g2 = lambda z: np.sum(x_i * (y_i - S(*z, x_i)) ** 3)
g3 = lambda z: np.sum(x_i ** 2 * (y_i - S(*z, x_i)) ** 3)
g4 = lambda z: np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 3)
G = lambda z: np.array([g1(z), g2(z), g3(z), g4(z)])
J = lambda z: -3 * np.array([
[np.sum((y_i - S(*z, x_i)) ** 2),
np.sum(x_i * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 2 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 2)],
[np.sum(x_i * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 2 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 4 * (y_i - S(*z, x_i)) ** 2)],
[np.sum(x_i ** 2 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 4 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 5 * (y_i - S(*z, x_i)) ** 2)],
[np.sum(x_i ** 3 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 4 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 5 * (y_i - S(*z, x_i)) ** 2),
np.sum(x_i ** 6 * (y_i - S(*z, x_i)) ** 2)]
])
return G, J
def solution(x_i, y_i, k, GJ, n_par):
x_0 = np.zeros(n_par)
G, J = GJ(x_i, y_i)
p = newtonRn(G, J, x_0, k, tol=1e-10)
return p[-1]
DIR = 'data/'
# NPY
dataset_npy_1 = np.load(DIR + '1.npy')
dataset_npy_2 = np.load(DIR + '2.npy')
dataset_npy_3 = np.load(DIR + '3.npy')
y_npy_1 = dataset_npy_1[:, 1]
y_npy_2 = dataset_npy_2[:, 1]
y_npy_3 = dataset_npy_3[:, 1]
# CSV
dataset_csv_1 = np.loadtxt(DIR + '1.csv', delimiter=',')
dataset_csv_2 = np.loadtxt(DIR + '2.csv', delimiter=',')
dataset_csv_3 = np.loadtxt(DIR + '3.csv', delimiter=',')
y_csv_1 = dataset_csv_1[:, 1]
y_csv_2 = dataset_csv_2[:, 1]
y_csv_3 = dataset_csv_3[:, 1]
# TXT
dataset_txt_1 = np.loadtxt(DIR + '1.txt', delimiter=',')
dataset_txt_2 = np.loadtxt(DIR + '2.txt', delimiter=',')
dataset_txt_3 = np.loadtxt(DIR + '3.txt', delimiter=',')
y_txt_1 = dataset_txt_1[:, 1]
y_txt_2 = dataset_txt_2[:, 1]
y_txt_3 = dataset_txt_3[:, 1]
n = 100
x_a, x_b = -1, 1
x_i = np.linspace(x_a, x_b, n)
y_i1 = dataset_npy_1[:, 1] # 1.{npy, csv, txt}
y_i2 = dataset_npy_2[:, 1] # 2.npy
y_i22 = dataset_csv_2[:, 1] # 2.{csv, txt}
y_i3 = dataset_npy_3[:, 1] # 3.{npy, csv, txt}
K = [2, 3, 4] # Number of iterations
IP = [0, 1, 2, 3] # Parameter index
PL = ["a", "b", "c", "d"] # Parameter name
D = [y_i1, y_i2, y_i22, y_i3] # Dataset
Dn = ['1.{npy, csv, txt}', '2.npy', '2.{csv, txt}', '3.{npy, csv, txt}'] # Dataset name
def experiment(i, p, k):
par = solution(x_i, D[i], k, buildGJ, 4)
print("k: %d, parametro: %s, valor: %f" % (k, PL[p], par[p]))
interact(experiment,
i=widgets.Dropdown(
options=[('1.{npy, csv, txt}', 0), ('2.npy', 1), ('2.{csv, txt}', 2), ('3.{npy, csv, txt}', 3)],
value=0,
description='Dataset:'
),
p=widgets.Dropdown(
options=[("a", 0), ("b", 1), ("c", 2), ("d", 3)],
value=0,
description='Parámetro:'
),
k=K
)
| 0.328529 | 0.959875 |
```
import torch
from torch.autograd import Variable
import warnings
from torch import nn
from collections import OrderedDict
import os
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore")
```
# Generator Check
```
# fix this stuff below. visualize generator output and filters for conv
def load_netG(path, isize, nz, nc, ngf, n_extra_layers):
assert isize % 16 == 0, "isize has to be a multiple of 16"
cngf, tisize = ngf//2, 4
while tisize != isize:
cngf = cngf * 2
tisize = tisize * 2
main = nn.Sequential()
# input is Z, going into a convolution
main.add_module('initial:{0}-{1}:convt'.format(nz, cngf),
nn.ConvTranspose2d(nz, cngf, 4, 1, 0, bias=False))
main.add_module('initial:{0}:batchnorm'.format(cngf),
nn.BatchNorm2d(cngf))
main.add_module('initial:{0}:relu'.format(cngf),
nn.ReLU(True))
csize, cndf = 4, cngf
while csize < isize//2:
main.add_module('pyramid:{0}-{1}:convt'.format(cngf, cngf//2),
nn.ConvTranspose2d(cngf, cngf//2, 4, 2, 1, bias=False))
main.add_module('pyramid:{0}:batchnorm'.format(cngf//2),
nn.BatchNorm2d(cngf//2))
main.add_module('pyramid:{0}:relu'.format(cngf//2),
nn.ReLU(True))
cngf = cngf // 2
csize = csize * 2
# Extra layers
for t in range(n_extra_layers):
main.add_module('extra-layers-{0}:{1}:conv'.format(t, cngf),
nn.Conv2d(cngf, cngf, 3, 1, 1, bias=False))
main.add_module('extra-layers-{0}:{1}:batchnorm'.format(t, cngf),
nn.BatchNorm2d(cngf))
main.add_module('extra-layers-{0}:{1}:relu'.format(t, cngf),
nn.ReLU(True))
main.add_module('final:{0}-{1}:convt'.format(cngf, nc),
nn.ConvTranspose2d(cngf, nc, 4, 2, 1, bias=False))
main.add_module('final:{0}:tanh'.format(nc),
nn.Tanh())
state_dict = torch.load(path, map_location=torch.device('cpu'))
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[5:] # remove `main.`
new_state_dict[name] = v
main.load_state_dict(new_state_dict, strict=False)
return main
def load_netG_mlp(path, isize, nz, nc, ngf):
main = nn.Sequential(
# Z goes into a linear of size: ngf
nn.Linear(nz, ngf),
nn.ReLU(True),
nn.Linear(ngf, ngf),
nn.ReLU(True),
nn.Linear(ngf, ngf),
nn.ReLU(True),
nn.Linear(ngf, nc * isize * isize),
)
state_dict = torch.load(path, map_location=torch.device('cpu'))
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[5:] # remove `main.`
new_state_dict[name] = v
main.load_state_dict(new_state_dict, strict=False)
return main
path = './loss_curves/netG_5k.pth'
netG_5k = load_netG(path, isize=32, nz=100, nc=1, ngf=64, n_extra_layers=0)
path = './loss_curves/netG_5k_mlp.pth'
netG_5k_mlp = load_netG_mlp(path, isize=25, nz=100, nc=1, ngf=640)
batchSize = 27
nz = 100
noise = torch.FloatTensor(batchSize, 1, 25, 25)
noise.resize_(batchSize, nz, 1, 1).normal_(0, 1)
noisev = Variable(noise, volatile = True)
fake_5k = Variable(netG_5k(noisev).data)
```
## Individual Rows
```
# netG_5k samples
torch.round(fake_5k[3,0,3,3:].data).numpy()[:-4]
torch.round(fake_5k[4,0,3,3:].data).numpy()[:-4]
torch.round(fake_5k[5,0,3,3:].data).numpy()[:-4]
torch.round(fake_5k[6,0,3,3:].data).numpy()[:-4]
torch.round(fake_5k[7,0,6,3:].data).numpy()[:-4]
torch.round(fake_5k[12,0,4,3:].data).numpy()[:-4]
```
## Visualizing fake samples
```
num_rows = 6
num_cols = 5
isize = 32
fig, axs = plt.subplots(num_rows, num_cols, figsize = (15, 15))
for i, axscol in enumerate(axs):
for j, ax in enumerate(axscol):
ax.imshow(fake_5k[j + num_cols * i].data.numpy().reshape((isize, isize)), interpolation = 'bilinear')
```
# Critic Evaluation of HMs
```
def load_netD(path, isize, nc, ndf, n_extra_layers):
assert isize % 16 == 0, "isize has to be a multiple of 16"
main = nn.Sequential()
# input is nc x isize x isize
main.add_module('initial:{0}-{1}:conv'.format(nc, ndf),
nn.Conv2d(nc, ndf, 4, 2, 1, bias=False))
main.add_module('initial:{0}:relu'.format(ndf),
nn.LeakyReLU(0.2, inplace=True))
csize, cndf = isize / 2, ndf
# Extra layers
for t in range(n_extra_layers):
main.add_module('extra-layers-{0}:{1}:conv'.format(t, cndf),
nn.Conv2d(cndf, cndf, 3, 1, 1, bias=False))
main.add_module('extra-layers-{0}:{1}:batchnorm'.format(t, cndf),
nn.BatchNorm2d(cndf))
main.add_module('extra-layers-{0}:{1}:relu'.format(t, cndf),
nn.LeakyReLU(0.2, inplace=True))
while csize > 4:
in_feat = cndf
out_feat = cndf * 2
main.add_module('pyramid:{0}-{1}:conv'.format(in_feat, out_feat),
nn.Conv2d(in_feat, out_feat, 4, 2, 1, bias=False))
main.add_module('pyramid:{0}:batchnorm'.format(out_feat),
nn.BatchNorm2d(out_feat))
main.add_module('pyramid:{0}:relu'.format(out_feat),
nn.LeakyReLU(0.2, inplace=True))
cndf = cndf * 2
csize = csize / 2
# state size. K x 4 x 4
main.add_module('final:{0}-{1}:conv'.format(cndf, 1),
nn.Conv2d(cndf, 1, 4, 1, 0, bias=False))
state_dict = torch.load(path, map_location=torch.device('cpu'))
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[5:] # remove `module.`
new_state_dict[name] = v
main.load_state_dict(new_state_dict, strict=False)
return main
def load_netD_mlp(path, isize, nc, ndf):
main = nn.Sequential(
# Z goes into a linear of size: ndf
nn.Linear(nc * isize * isize, ndf),
nn.ReLU(True),
nn.Linear(ndf, ndf),
nn.ReLU(True),
nn.Linear(ndf, ndf),
nn.ReLU(True),
nn.Linear(ndf, 1),
)
state_dict = torch.load(path, map_location=torch.device('cpu'))
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[5:] # remove `module.`
new_state_dict[name] = v
main.load_state_dict(new_state_dict, strict=False)
return main
def reshape_mlp_input(input_sample):
return input_sample.view(input_sample.size(0),
input_sample.size(1) * input_sample.size(2) * input_sample.size(3))
path = './loss_curves/netD_50k_mlp_40df.pth'
netD_mlp = load_netD_mlp(path, isize=25, nc=1, ndf=40)
path = './loss_curves/netD_50k.pth'
netD = load_netD(path, isize=32, nc=1, ndf=64, n_extra_layers=0)
import data as data
from data.BehavioralDataset import BehavioralDataset
from data.BehavioralHmSamples import BehavioralHmSamples
dataset_dcgan = BehavioralDataset(isCnnData=True, isScoring=False)
dataset_mlp = BehavioralDataset(isCnnData=False, isScoring=False)
fake_samples_m1_dcgan = BehavioralHmSamples(modelNum=1, isCnnData=True, isScoring=False)
fake_samples_m1_mlp = BehavioralHmSamples(modelNum=1, isCnnData=False, isScoring=False)
fake_samples_m2_dcgan = BehavioralHmSamples(modelNum=2, isCnnData=True, isScoring=False)
fake_samples_m2_mlp = BehavioralHmSamples(modelNum=2, isCnnData=False, isScoring=False)
fake_samples_m3_dcgan = BehavioralHmSamples(modelNum=3, isCnnData=True, isScoring=False)
fake_samples_m4_dcgan = BehavioralHmSamples(modelNum=4, isCnnData=True, isScoring=False)
fake_samples_m5_dcgan = BehavioralHmSamples(modelNum=5, isCnnData=True, isScoring=False)
# read in real samples
dataloader_dcgan = torch.utils.data.DataLoader(dataset_dcgan, batch_size=30, shuffle=True, num_workers=2)
dataloader_mlp = torch.utils.data.DataLoader(dataset_mlp, batch_size=30, shuffle=True, num_workers=2)
data_iter_dcgan = iter(dataloader_dcgan)
data_iter_mlp = iter(dataloader_mlp)
data = data_iter_mlp.next()
data_samples, _ = data
# must balance out proportion of reals to fakes
fake_datasets_dcgan = [dataset_dcgan, dataset_dcgan, fake_samples_m1_dcgan, fake_samples_m2_dcgan]
fake_datasets_mlp = [dataset_mlp, dataset_mlp, fake_samples_m1_mlp, fake_samples_m2_mlp]
all_scores_dcgan = []
input = torch.FloatTensor(30, 1, 32, 32)
for dataset in fake_datasets_dcgan:
dataloader = torch.utils.data.DataLoader(dataset, batch_size=30, shuffle=True, num_workers=2)
data_iter = iter(dataloader)
data = data_iter.next()
fake_samples, _ = data
input.resize_as_(fake_samples).copy_(fake_samples)
inputv = Variable(input)
critic_scores = netD(inputv)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(30,1))
# make random noise
batchSize = 30
isize = 32
noise = torch.FloatTensor(batchSize, 1, isize, isize)
noise.resize_(batchSize, 1, isize, isize).normal_(0, 1)
noisev = Variable(noise, volatile = True)
critic_scores = netD(noisev)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(30,1))
# make striped random noise arrays
samples = []
for i in range(batchSize):
next_row = np.array(np.random.normal(size=32))
next_sample = [next_row for i in range(32)]
next_sample = np.vstack(next_sample)
samples.append(next_sample)
noise = np.dstack(samples).reshape(30, 1, 32, 32)
noisev = Variable(torch.from_numpy(noise))
critic_scores = netD(noisev.float())
all_scores_dcgan.append(critic_scores.data.numpy().reshape(30,1))
# perform platt scaling on scores
def classify(all_scores, num_fake_datasets):
'''
perform platt scaling on scores
all_scores is a list of scores by datase
'''
all_scores = tuple(all_scores)
scores = np.vstack(all_scores)
true_labels = np.vstack((np.ones((30 * num_fake_datasets,1)), np.zeros((30 * num_fake_datasets,1))))
clf = LogisticRegression().fit(scores, true_labels)
pred_labels = clf.predict(scores)
print(pred_labels)
pass_as_real = []
for i in range(num_fake_datasets*2):
pass_as_real.append(np.sum(pred_labels[30 * i:30 * (i+1),]==np.ones((1,30))))
return pass_as_real
pass_as_real = classify(all_scores_dcgan, 2)
print('----------------')
print('Pass As Real Samples')
print('Real Dataset: ', pass_as_real[0])
print('Real Dataset Again: ', pass_as_real[1])
print('Model 1: ', pass_as_real[2])
print('Model 2: ', pass_as_real[3])
np.hstack((all_scores_dcgan[0], all_scores_dcgan[2], all_scores_dcgan[3]))
all_scores_mlp = []
input = torch.FloatTensor(30, 1, 25, 25)
for dataset in fake_datasets_mlp:
dataloader = torch.utils.data.DataLoader(dataset, batch_size=30, shuffle=True, num_workers=2)
data_iter = iter(dataloader)
data = data_iter.next()
fake_samples, _ = data
input.resize_as_(fake_samples).copy_(fake_samples)
inputv = Variable(input)
critic_scores = netD_mlp(reshape_mlp_input(inputv))
all_scores_mlp.append(critic_scores.data.numpy().reshape(30,1))
pass_as_real = classify(all_scores_mlp, 2)
print('----------------')
print('Pass As Real Samples')
print('Real Dataset: ', pass_as_real[0])
print('Real Dataset Again: ', pass_as_real[1])
print('Model 1: ', pass_as_real[2])
print('Model 2: ', pass_as_real[3])
np.hstack((all_scores_mlp[0], all_scores_mlp[1], all_scores_mlp[2]))
```
## With Random Arrays and Random Striped Arrays
```
# must balance out proportion of reals to fakes
fake_datasets_dcgan = [dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, fake_samples_m1_dcgan, fake_samples_m2_dcgan, fake_samples_m3_dcgan, fake_samples_m4_dcgan, fake_samples_m5_dcgan]
fake_datasets_mlp = [dataset_mlp, dataset_mlp, dataset_mlp, dataset_mlp, dataset_mlp, fake_samples_m1_mlp, fake_samples_m2_mlp]
all_scores_dcgan = []
batchSize = 27
input = torch.FloatTensor(batchSize, 1, 32, 32)
for dataset in fake_datasets_dcgan:
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batchSize, shuffle=True, num_workers=2)
data_iter = iter(dataloader)
data = data_iter.next()
fake_samples, _ = data
input.resize_as_(fake_samples).copy_(fake_samples)
inputv = Variable(input)
critic_scores = netD(inputv)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(batchSize,1))
# make random noise
isize = 32
noise = torch.FloatTensor(batchSize, 1, isize, isize)
noise.resize_(batchSize, 1, isize, isize).normal_(0, 1)
noisev = Variable(noise, volatile = True)
critic_scores = netD(noisev)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(batchSize,1))
# make striped random noise arrays
samples = []
for i in range(batchSize):
next_row = np.array(np.random.normal(size=32))
next_sample = [next_row for i in range(32)]
next_sample = np.vstack(next_sample)
samples.append(next_sample)
noise = np.dstack(samples).reshape(batchSize, 1, 32, 32)
noisev = Variable(torch.from_numpy(noise))
critic_scores = netD(noisev.float())
all_scores_dcgan.append(critic_scores.data.numpy().reshape(batchSize,1))
# add fake samples from DCGAN generator
input.resize_as_(fake_5k).copy_(fake_5k)
inputv = Variable(input)
critic_scores = netD(inputv)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(batchSize,1))
pass_as_real = classify(all_scores_dcgan, 4)
print('----------------')
print('Pass As Real Samples')
print('Real Dataset: ', pass_as_real[0])
print('Completely Random Array: ', pass_as_real[6])
print('Random Striped Array: ', pass_as_real[7])
print('Model 1: ', pass_as_real[4])
print('Model 2: ', pass_as_real[5])
len(all_scores_dcgan)
vals = all_scores_dcgan[1].reshape(1,batchSize).tolist()[0]
num_sample_sets = len(all_scores_dcgan)
for i in range(num_sample_sets//2, num_sample_sets):
#print(i)
vals = vals + all_scores_dcgan[i].reshape(1,batchSize).tolist()[0]
labels_names = ['Real', 'Model 1', 'Model 2', 'Model 3', 'Model 4', 'Model 5', 'Completely Random', 'Random Striped', 'Generator Samples']
labels = []
for name in labels_names:
labels = labels + [name] * batchSize
scores_df = pd.DataFrame(list(zip(vals, labels)), columns=['Critic Score', 'Sample Type'])
vals = all_scores_dcgan[0].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[8].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[9].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[10].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[15].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[15].reshape(1,batchSize).tolist()[0]
labels = ['Real'] * batchSize + ['Model 1'] * batchSize + ['Model 2'] * batchSize + ['Completely Random'] * batchSize + ['Random Striped'] * batchSize
scores_df = pd.DataFrame(list(zip(vals, labels)), columns=['Critic Score', 'Sample Type'])
ax = sns.boxplot(x="Critic Score", y="Sample Type", data=scores_df)
ax.set_title('DCGAN Critic')
all_scores_mlp = []
input = torch.FloatTensor(30, 1, 25, 25)
for dataset in fake_datasets_mlp:
dataloader = torch.utils.data.DataLoader(dataset, batch_size=30, shuffle=True, num_workers=2)
data_iter = iter(dataloader)
data = data_iter.next()
fake_samples, _ = data
input.resize_as_(fake_samples).copy_(fake_samples)
inputv = Variable(input)
critic_scores = netD_mlp(reshape_mlp_input(inputv))
all_scores_mlp.append(critic_scores.data.numpy().reshape(30,1))
# make random noise
batchSize = 30
isize = 25
noise = torch.FloatTensor(batchSize, 1, isize, isize)
noise.resize_(batchSize, 1, isize, isize).normal_(0, 1)
noisev = Variable(noise, volatile = True)
critic_scores = netD_mlp(reshape_mlp_input(noisev))
all_scores_mlp.append(critic_scores.data.numpy().reshape(30,1))
# make striped random noise arrays
samples = []
for i in range(batchSize):
next_row = np.array(np.random.normal(size=isize))
next_sample = [next_row for i in range(isize)]
next_sample = np.vstack(next_sample)
samples.append(next_sample)
noise = np.dstack(samples).reshape(30, 1, isize, isize)
noisev = Variable(torch.from_numpy(noise))
critic_scores = netD_mlp(reshape_mlp_input(noisev.float()))
all_scores_mlp.append(critic_scores.data.numpy().reshape(30,1))
pass_as_real = classify(all_scores_mlp, 4)
print('----------------')
print('Pass As Real Samples')
print('Real Dataset: ', pass_as_real[0])
print('Completely Random Array: ', pass_as_real[6])
print('Random Striped Array: ', pass_as_real[7])
print('Model 1: ', pass_as_real[4])
print('Model 2: ', pass_as_real[5])
vals = all_scores_mlp[0].reshape(1,30).tolist()[0] + all_scores_mlp[4].reshape(1,30).tolist()[0] + all_scores_mlp[5].reshape(1,30).tolist()[0] + all_scores_mlp[6].reshape(1,30).tolist()[0] + all_scores_mlp[7].reshape(1,30).tolist()[0]
labels = ['Real'] * 30 + ['Model 1'] * 30 + ['Model 2'] * 30 + ['Completely Random'] * 30 + ['Random Striped'] * 30
scores_df = pd.DataFrame(list(zip(vals, labels)), columns=['Critic Score', 'Sample Type'])
ax = sns.boxplot(x="Critic Score", y="Sample Type", data=scores_df)
ax.set_title('MLP Critic')
```
## Visualize Conv Filters
```
netD[0].weight.shape
netD
num_rows = 8
num_cols = 8
isize = 4
fig, axs = plt.subplots(num_rows, num_cols, figsize = (15, 15))
for i, axscol in enumerate(axs):
for j, ax in enumerate(axscol):
ax.imshow(netD[0].weight[j + num_cols * i].detach().numpy().reshape((isize, isize)), cmap=plt.cm.coolwarm)
```
|
github_jupyter
|
import torch
from torch.autograd import Variable
import warnings
from torch import nn
from collections import OrderedDict
import os
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
warnings.filterwarnings("ignore")
# fix this stuff below. visualize generator output and filters for conv
def load_netG(path, isize, nz, nc, ngf, n_extra_layers):
assert isize % 16 == 0, "isize has to be a multiple of 16"
cngf, tisize = ngf//2, 4
while tisize != isize:
cngf = cngf * 2
tisize = tisize * 2
main = nn.Sequential()
# input is Z, going into a convolution
main.add_module('initial:{0}-{1}:convt'.format(nz, cngf),
nn.ConvTranspose2d(nz, cngf, 4, 1, 0, bias=False))
main.add_module('initial:{0}:batchnorm'.format(cngf),
nn.BatchNorm2d(cngf))
main.add_module('initial:{0}:relu'.format(cngf),
nn.ReLU(True))
csize, cndf = 4, cngf
while csize < isize//2:
main.add_module('pyramid:{0}-{1}:convt'.format(cngf, cngf//2),
nn.ConvTranspose2d(cngf, cngf//2, 4, 2, 1, bias=False))
main.add_module('pyramid:{0}:batchnorm'.format(cngf//2),
nn.BatchNorm2d(cngf//2))
main.add_module('pyramid:{0}:relu'.format(cngf//2),
nn.ReLU(True))
cngf = cngf // 2
csize = csize * 2
# Extra layers
for t in range(n_extra_layers):
main.add_module('extra-layers-{0}:{1}:conv'.format(t, cngf),
nn.Conv2d(cngf, cngf, 3, 1, 1, bias=False))
main.add_module('extra-layers-{0}:{1}:batchnorm'.format(t, cngf),
nn.BatchNorm2d(cngf))
main.add_module('extra-layers-{0}:{1}:relu'.format(t, cngf),
nn.ReLU(True))
main.add_module('final:{0}-{1}:convt'.format(cngf, nc),
nn.ConvTranspose2d(cngf, nc, 4, 2, 1, bias=False))
main.add_module('final:{0}:tanh'.format(nc),
nn.Tanh())
state_dict = torch.load(path, map_location=torch.device('cpu'))
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[5:] # remove `main.`
new_state_dict[name] = v
main.load_state_dict(new_state_dict, strict=False)
return main
def load_netG_mlp(path, isize, nz, nc, ngf):
main = nn.Sequential(
# Z goes into a linear of size: ngf
nn.Linear(nz, ngf),
nn.ReLU(True),
nn.Linear(ngf, ngf),
nn.ReLU(True),
nn.Linear(ngf, ngf),
nn.ReLU(True),
nn.Linear(ngf, nc * isize * isize),
)
state_dict = torch.load(path, map_location=torch.device('cpu'))
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[5:] # remove `main.`
new_state_dict[name] = v
main.load_state_dict(new_state_dict, strict=False)
return main
path = './loss_curves/netG_5k.pth'
netG_5k = load_netG(path, isize=32, nz=100, nc=1, ngf=64, n_extra_layers=0)
path = './loss_curves/netG_5k_mlp.pth'
netG_5k_mlp = load_netG_mlp(path, isize=25, nz=100, nc=1, ngf=640)
batchSize = 27
nz = 100
noise = torch.FloatTensor(batchSize, 1, 25, 25)
noise.resize_(batchSize, nz, 1, 1).normal_(0, 1)
noisev = Variable(noise, volatile = True)
fake_5k = Variable(netG_5k(noisev).data)
# netG_5k samples
torch.round(fake_5k[3,0,3,3:].data).numpy()[:-4]
torch.round(fake_5k[4,0,3,3:].data).numpy()[:-4]
torch.round(fake_5k[5,0,3,3:].data).numpy()[:-4]
torch.round(fake_5k[6,0,3,3:].data).numpy()[:-4]
torch.round(fake_5k[7,0,6,3:].data).numpy()[:-4]
torch.round(fake_5k[12,0,4,3:].data).numpy()[:-4]
num_rows = 6
num_cols = 5
isize = 32
fig, axs = plt.subplots(num_rows, num_cols, figsize = (15, 15))
for i, axscol in enumerate(axs):
for j, ax in enumerate(axscol):
ax.imshow(fake_5k[j + num_cols * i].data.numpy().reshape((isize, isize)), interpolation = 'bilinear')
def load_netD(path, isize, nc, ndf, n_extra_layers):
assert isize % 16 == 0, "isize has to be a multiple of 16"
main = nn.Sequential()
# input is nc x isize x isize
main.add_module('initial:{0}-{1}:conv'.format(nc, ndf),
nn.Conv2d(nc, ndf, 4, 2, 1, bias=False))
main.add_module('initial:{0}:relu'.format(ndf),
nn.LeakyReLU(0.2, inplace=True))
csize, cndf = isize / 2, ndf
# Extra layers
for t in range(n_extra_layers):
main.add_module('extra-layers-{0}:{1}:conv'.format(t, cndf),
nn.Conv2d(cndf, cndf, 3, 1, 1, bias=False))
main.add_module('extra-layers-{0}:{1}:batchnorm'.format(t, cndf),
nn.BatchNorm2d(cndf))
main.add_module('extra-layers-{0}:{1}:relu'.format(t, cndf),
nn.LeakyReLU(0.2, inplace=True))
while csize > 4:
in_feat = cndf
out_feat = cndf * 2
main.add_module('pyramid:{0}-{1}:conv'.format(in_feat, out_feat),
nn.Conv2d(in_feat, out_feat, 4, 2, 1, bias=False))
main.add_module('pyramid:{0}:batchnorm'.format(out_feat),
nn.BatchNorm2d(out_feat))
main.add_module('pyramid:{0}:relu'.format(out_feat),
nn.LeakyReLU(0.2, inplace=True))
cndf = cndf * 2
csize = csize / 2
# state size. K x 4 x 4
main.add_module('final:{0}-{1}:conv'.format(cndf, 1),
nn.Conv2d(cndf, 1, 4, 1, 0, bias=False))
state_dict = torch.load(path, map_location=torch.device('cpu'))
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[5:] # remove `module.`
new_state_dict[name] = v
main.load_state_dict(new_state_dict, strict=False)
return main
def load_netD_mlp(path, isize, nc, ndf):
main = nn.Sequential(
# Z goes into a linear of size: ndf
nn.Linear(nc * isize * isize, ndf),
nn.ReLU(True),
nn.Linear(ndf, ndf),
nn.ReLU(True),
nn.Linear(ndf, ndf),
nn.ReLU(True),
nn.Linear(ndf, 1),
)
state_dict = torch.load(path, map_location=torch.device('cpu'))
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[5:] # remove `module.`
new_state_dict[name] = v
main.load_state_dict(new_state_dict, strict=False)
return main
def reshape_mlp_input(input_sample):
return input_sample.view(input_sample.size(0),
input_sample.size(1) * input_sample.size(2) * input_sample.size(3))
path = './loss_curves/netD_50k_mlp_40df.pth'
netD_mlp = load_netD_mlp(path, isize=25, nc=1, ndf=40)
path = './loss_curves/netD_50k.pth'
netD = load_netD(path, isize=32, nc=1, ndf=64, n_extra_layers=0)
import data as data
from data.BehavioralDataset import BehavioralDataset
from data.BehavioralHmSamples import BehavioralHmSamples
dataset_dcgan = BehavioralDataset(isCnnData=True, isScoring=False)
dataset_mlp = BehavioralDataset(isCnnData=False, isScoring=False)
fake_samples_m1_dcgan = BehavioralHmSamples(modelNum=1, isCnnData=True, isScoring=False)
fake_samples_m1_mlp = BehavioralHmSamples(modelNum=1, isCnnData=False, isScoring=False)
fake_samples_m2_dcgan = BehavioralHmSamples(modelNum=2, isCnnData=True, isScoring=False)
fake_samples_m2_mlp = BehavioralHmSamples(modelNum=2, isCnnData=False, isScoring=False)
fake_samples_m3_dcgan = BehavioralHmSamples(modelNum=3, isCnnData=True, isScoring=False)
fake_samples_m4_dcgan = BehavioralHmSamples(modelNum=4, isCnnData=True, isScoring=False)
fake_samples_m5_dcgan = BehavioralHmSamples(modelNum=5, isCnnData=True, isScoring=False)
# read in real samples
dataloader_dcgan = torch.utils.data.DataLoader(dataset_dcgan, batch_size=30, shuffle=True, num_workers=2)
dataloader_mlp = torch.utils.data.DataLoader(dataset_mlp, batch_size=30, shuffle=True, num_workers=2)
data_iter_dcgan = iter(dataloader_dcgan)
data_iter_mlp = iter(dataloader_mlp)
data = data_iter_mlp.next()
data_samples, _ = data
# must balance out proportion of reals to fakes
fake_datasets_dcgan = [dataset_dcgan, dataset_dcgan, fake_samples_m1_dcgan, fake_samples_m2_dcgan]
fake_datasets_mlp = [dataset_mlp, dataset_mlp, fake_samples_m1_mlp, fake_samples_m2_mlp]
all_scores_dcgan = []
input = torch.FloatTensor(30, 1, 32, 32)
for dataset in fake_datasets_dcgan:
dataloader = torch.utils.data.DataLoader(dataset, batch_size=30, shuffle=True, num_workers=2)
data_iter = iter(dataloader)
data = data_iter.next()
fake_samples, _ = data
input.resize_as_(fake_samples).copy_(fake_samples)
inputv = Variable(input)
critic_scores = netD(inputv)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(30,1))
# make random noise
batchSize = 30
isize = 32
noise = torch.FloatTensor(batchSize, 1, isize, isize)
noise.resize_(batchSize, 1, isize, isize).normal_(0, 1)
noisev = Variable(noise, volatile = True)
critic_scores = netD(noisev)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(30,1))
# make striped random noise arrays
samples = []
for i in range(batchSize):
next_row = np.array(np.random.normal(size=32))
next_sample = [next_row for i in range(32)]
next_sample = np.vstack(next_sample)
samples.append(next_sample)
noise = np.dstack(samples).reshape(30, 1, 32, 32)
noisev = Variable(torch.from_numpy(noise))
critic_scores = netD(noisev.float())
all_scores_dcgan.append(critic_scores.data.numpy().reshape(30,1))
# perform platt scaling on scores
def classify(all_scores, num_fake_datasets):
'''
perform platt scaling on scores
all_scores is a list of scores by datase
'''
all_scores = tuple(all_scores)
scores = np.vstack(all_scores)
true_labels = np.vstack((np.ones((30 * num_fake_datasets,1)), np.zeros((30 * num_fake_datasets,1))))
clf = LogisticRegression().fit(scores, true_labels)
pred_labels = clf.predict(scores)
print(pred_labels)
pass_as_real = []
for i in range(num_fake_datasets*2):
pass_as_real.append(np.sum(pred_labels[30 * i:30 * (i+1),]==np.ones((1,30))))
return pass_as_real
pass_as_real = classify(all_scores_dcgan, 2)
print('----------------')
print('Pass As Real Samples')
print('Real Dataset: ', pass_as_real[0])
print('Real Dataset Again: ', pass_as_real[1])
print('Model 1: ', pass_as_real[2])
print('Model 2: ', pass_as_real[3])
np.hstack((all_scores_dcgan[0], all_scores_dcgan[2], all_scores_dcgan[3]))
all_scores_mlp = []
input = torch.FloatTensor(30, 1, 25, 25)
for dataset in fake_datasets_mlp:
dataloader = torch.utils.data.DataLoader(dataset, batch_size=30, shuffle=True, num_workers=2)
data_iter = iter(dataloader)
data = data_iter.next()
fake_samples, _ = data
input.resize_as_(fake_samples).copy_(fake_samples)
inputv = Variable(input)
critic_scores = netD_mlp(reshape_mlp_input(inputv))
all_scores_mlp.append(critic_scores.data.numpy().reshape(30,1))
pass_as_real = classify(all_scores_mlp, 2)
print('----------------')
print('Pass As Real Samples')
print('Real Dataset: ', pass_as_real[0])
print('Real Dataset Again: ', pass_as_real[1])
print('Model 1: ', pass_as_real[2])
print('Model 2: ', pass_as_real[3])
np.hstack((all_scores_mlp[0], all_scores_mlp[1], all_scores_mlp[2]))
# must balance out proportion of reals to fakes
fake_datasets_dcgan = [dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, dataset_dcgan, fake_samples_m1_dcgan, fake_samples_m2_dcgan, fake_samples_m3_dcgan, fake_samples_m4_dcgan, fake_samples_m5_dcgan]
fake_datasets_mlp = [dataset_mlp, dataset_mlp, dataset_mlp, dataset_mlp, dataset_mlp, fake_samples_m1_mlp, fake_samples_m2_mlp]
all_scores_dcgan = []
batchSize = 27
input = torch.FloatTensor(batchSize, 1, 32, 32)
for dataset in fake_datasets_dcgan:
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batchSize, shuffle=True, num_workers=2)
data_iter = iter(dataloader)
data = data_iter.next()
fake_samples, _ = data
input.resize_as_(fake_samples).copy_(fake_samples)
inputv = Variable(input)
critic_scores = netD(inputv)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(batchSize,1))
# make random noise
isize = 32
noise = torch.FloatTensor(batchSize, 1, isize, isize)
noise.resize_(batchSize, 1, isize, isize).normal_(0, 1)
noisev = Variable(noise, volatile = True)
critic_scores = netD(noisev)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(batchSize,1))
# make striped random noise arrays
samples = []
for i in range(batchSize):
next_row = np.array(np.random.normal(size=32))
next_sample = [next_row for i in range(32)]
next_sample = np.vstack(next_sample)
samples.append(next_sample)
noise = np.dstack(samples).reshape(batchSize, 1, 32, 32)
noisev = Variable(torch.from_numpy(noise))
critic_scores = netD(noisev.float())
all_scores_dcgan.append(critic_scores.data.numpy().reshape(batchSize,1))
# add fake samples from DCGAN generator
input.resize_as_(fake_5k).copy_(fake_5k)
inputv = Variable(input)
critic_scores = netD(inputv)
all_scores_dcgan.append(critic_scores.data.numpy().reshape(batchSize,1))
pass_as_real = classify(all_scores_dcgan, 4)
print('----------------')
print('Pass As Real Samples')
print('Real Dataset: ', pass_as_real[0])
print('Completely Random Array: ', pass_as_real[6])
print('Random Striped Array: ', pass_as_real[7])
print('Model 1: ', pass_as_real[4])
print('Model 2: ', pass_as_real[5])
len(all_scores_dcgan)
vals = all_scores_dcgan[1].reshape(1,batchSize).tolist()[0]
num_sample_sets = len(all_scores_dcgan)
for i in range(num_sample_sets//2, num_sample_sets):
#print(i)
vals = vals + all_scores_dcgan[i].reshape(1,batchSize).tolist()[0]
labels_names = ['Real', 'Model 1', 'Model 2', 'Model 3', 'Model 4', 'Model 5', 'Completely Random', 'Random Striped', 'Generator Samples']
labels = []
for name in labels_names:
labels = labels + [name] * batchSize
scores_df = pd.DataFrame(list(zip(vals, labels)), columns=['Critic Score', 'Sample Type'])
vals = all_scores_dcgan[0].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[8].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[9].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[10].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[15].reshape(1,batchSize).tolist()[0] + all_scores_dcgan[15].reshape(1,batchSize).tolist()[0]
labels = ['Real'] * batchSize + ['Model 1'] * batchSize + ['Model 2'] * batchSize + ['Completely Random'] * batchSize + ['Random Striped'] * batchSize
scores_df = pd.DataFrame(list(zip(vals, labels)), columns=['Critic Score', 'Sample Type'])
ax = sns.boxplot(x="Critic Score", y="Sample Type", data=scores_df)
ax.set_title('DCGAN Critic')
all_scores_mlp = []
input = torch.FloatTensor(30, 1, 25, 25)
for dataset in fake_datasets_mlp:
dataloader = torch.utils.data.DataLoader(dataset, batch_size=30, shuffle=True, num_workers=2)
data_iter = iter(dataloader)
data = data_iter.next()
fake_samples, _ = data
input.resize_as_(fake_samples).copy_(fake_samples)
inputv = Variable(input)
critic_scores = netD_mlp(reshape_mlp_input(inputv))
all_scores_mlp.append(critic_scores.data.numpy().reshape(30,1))
# make random noise
batchSize = 30
isize = 25
noise = torch.FloatTensor(batchSize, 1, isize, isize)
noise.resize_(batchSize, 1, isize, isize).normal_(0, 1)
noisev = Variable(noise, volatile = True)
critic_scores = netD_mlp(reshape_mlp_input(noisev))
all_scores_mlp.append(critic_scores.data.numpy().reshape(30,1))
# make striped random noise arrays
samples = []
for i in range(batchSize):
next_row = np.array(np.random.normal(size=isize))
next_sample = [next_row for i in range(isize)]
next_sample = np.vstack(next_sample)
samples.append(next_sample)
noise = np.dstack(samples).reshape(30, 1, isize, isize)
noisev = Variable(torch.from_numpy(noise))
critic_scores = netD_mlp(reshape_mlp_input(noisev.float()))
all_scores_mlp.append(critic_scores.data.numpy().reshape(30,1))
pass_as_real = classify(all_scores_mlp, 4)
print('----------------')
print('Pass As Real Samples')
print('Real Dataset: ', pass_as_real[0])
print('Completely Random Array: ', pass_as_real[6])
print('Random Striped Array: ', pass_as_real[7])
print('Model 1: ', pass_as_real[4])
print('Model 2: ', pass_as_real[5])
vals = all_scores_mlp[0].reshape(1,30).tolist()[0] + all_scores_mlp[4].reshape(1,30).tolist()[0] + all_scores_mlp[5].reshape(1,30).tolist()[0] + all_scores_mlp[6].reshape(1,30).tolist()[0] + all_scores_mlp[7].reshape(1,30).tolist()[0]
labels = ['Real'] * 30 + ['Model 1'] * 30 + ['Model 2'] * 30 + ['Completely Random'] * 30 + ['Random Striped'] * 30
scores_df = pd.DataFrame(list(zip(vals, labels)), columns=['Critic Score', 'Sample Type'])
ax = sns.boxplot(x="Critic Score", y="Sample Type", data=scores_df)
ax.set_title('MLP Critic')
netD[0].weight.shape
netD
num_rows = 8
num_cols = 8
isize = 4
fig, axs = plt.subplots(num_rows, num_cols, figsize = (15, 15))
for i, axscol in enumerate(axs):
for j, ax in enumerate(axscol):
ax.imshow(netD[0].weight[j + num_cols * i].detach().numpy().reshape((isize, isize)), cmap=plt.cm.coolwarm)
| 0.77827 | 0.722062 |
<img src="img/logo.png"/>
<h1 style="margin: 0; padding: 0;"><center>Club de Programación e Inteligencia Artificial</center></h1>
<center><i>Una inciativa de los estudiantes y egresados del Programa de Ingeniería de Sistemas de la Universidad del Magdalena</i></center>
<br/><br/>
<center> <strong> === </strong> </center>
<h2><center>Temas de Interés</center></h2>
* ** Competencias integrales en pensamiento algoritmico: **
Consideramos que una base fundamental de la Ingeniería de Sistemas es la programación. Sin embargo, esta debe llevarse a cabo con un enfoque algoritmico que permita analizar los problemas y seleccionar la mejor herramienta para cada uno.
* **Python y Matlab: **
Python y Matlab han demostrado ser dos de los lenguajes de programación más potentes de la actualidad. Su popularidad en la escena científica ha llevado a la creación de centenares de paquetes para la resolución de problemas en diversos ámbitos.
* ** Inteligencia Artificial: **
Los algoritmos inteligentes forman parte de nuestro día a día y permiten resolver multitud de problemas que de otra forma serían imposibles de atacar.
<h2><center>Metodología</center></h2>
* ** Clases presenciales (2 horas a la semana): **
*Como parte de las actividades del club se incluyen clases presenciales en las que se planea abordar los temas clave de Algoritmos y avanzar hasta llegar a Inteligencia Artificial. Estas clases se dictarán haciendo uso de materiales interactivos preparados en Jupyter Notebook, con el objetivo de facilitar la integración de los aspectos teóricos y prácticos.*
* ** Talleres colaborativos (2 horas a la semana): **
*En estos talleres se tiene la intención de formar grupos en los que cada miembro del club pueda proponer su idea de trabajo y desarrollarla con la ayuda de sus compañeros. El objetivo de estas actividades es permitir a los estudiantes que tengan intereses particulares trabajar en equipo, lo que a su vez genera insumos adicionales para las futuras clases del club.*
* ** Semillero de investigación e innovación: **
*Como parte de las actividades del Club, se pretende dar el espacio a que sus miembros planteen ideas no solo como parte de los talleres colaborativos sino también como posibles proyectos de investigación e innovación. De esta forma, los alumnos podrán recibir asesorías sobre cómo orientar sus ideas y tener el respaldo del Club a la hora de presentarlas ante las dependencias pertinentes, así como en los eventos que organiza la Universidad. *
* ** Espacios de discusión y repositorios en línea: **
*Se pretende administrar grupos de discusión en redes sociales, como Facebook, donde los miembros del club puedan publicar dudas, proponer ideas y compartir materiales. Asímismo, todos los materiales serán publicados en un repositorio de GitHub al que la comunidad universitaria tendrá total acceso.*
<h2><center>Temas Centrales</center></h2>
Son los temas que forman el núcleo del club, y que serán tratados de forma consistente en las clases presenciales.
* **Desarrollo de competencias integrales en pensamiento algoritmico I:**
* Variables y tipos de datos.
* Operaciones de entrada y visualización de datos.
* Operaciones matemáticas.
* Estructuras de datos I: listas, arreglos.
* Programación estructurada: condiciones, ciclos.
* Programación recursiva.
* Lectura y escritura de archivos de texto plano.
* Interpretación de problemas, aplicación de soluciones algoritmicas I.
* **Repaso de matemática básica para ingeniería de sistemas: **
* Conceptos básicos de funciones.
* Lógica booleana.
* Teoría de conjuntos.
* Algebra lineal básica.
* **Desarrollo de competencias integrales en pensamiento algoritmico II:**
* Funciones.
* Operaciones con conjuntos.
* Funciones anónimas o lambda.
* Mapeo, filtros y reducción.
* Estructuras de datos II: Pilas, colas, arboles.
* Introducción a la complejidad computacional.
* Algoritmos de ordenamiento.
* Interpretación de problemas, aplicación de soluciones algoritmicas II.
* **Inteligencia Artificial: Problemas de búsqueda **
* Algoritmos de búsqueda.
* Algoritmos de búsqueda con heurística.
* Algoritmos de búsqueda con componente aleatorio.
* Algoritmos de búsqueda biológicamente inspirados.
* **Técnicas avanzadas para el diseño de algoritmos: **
* Introducción a la programación competitiva.
* Complejidad computacional.
* Algoritmos vóraces y búsqueda exhaustiva.
* Divide y vencerás.
* Programación dinámica.
* Grafos.
* **Inteligencia Artificial: Aprendizaje de Máquinas I **
* Repaso: probabilidad.
* La línea base: aproximaciones ingenuas.
* Datos númericos y categóricos.
* Los distintos problemas del aprendizaje de máquina.
* One-R.
* K-Vecinos cercanos.
* Regresión lineal.
* **Inteligencia Artificial: Aprendizaje de Máquinas II **
* Preprocesamiento de datos.
* Validación de modelos.
* Regresión logística.
* Inferencia bayesiana.
* Recomendación a priori.
* K-Means.
* Árboles y bósques de clasificación.
* **Inteligencia Artificial: Aprendizaje de Máquinas III **
* Máquinas de vector de soporte.
* Redes neuronales artificiales.
* Deep learning.
<h2><center>Temas Adicionales</center></h2>
Son temas para los que se pretende preparar material con base en los talleres colaborativos, y que pueden
ser integrados en las temáticas núcleo dependiendo del interés de los miembros del grupo.
* ** Aplicaciones específicas: **
* Formateo de texto con la librería estándar de Python <sup>1</sup>.
* Manipulación de cadenas de texto con la librería estándar de Python <sup>1</sup>.
* Lectura y manipulación de archivos de distintos formatos con la librería estándar de Python <sup>1</sup>.
* Expresiones regulares para la manipulación de cadenas de texto <sup>3</sup>.
* Vectorización de diferentes estructuras de datos <sup>1,</sup><sup>2</sup>.
* Computación matemática con Numpy <sup>1</sup> y librería estándar de Matlab <sup>2</sup>.
* La librería Pandas para manejo de conjuntos de datos <sup>1</sup>.
* Graficación con matplotlib y seaborn para Python<sup>1</sup>, librería estándar de Matlab <sup>2</sup>.
<small> 1: Contenidos dictados en Python. </small><br/>
<small> 2: Contenidos dictados en Matlab. </small><br/>
<small> 3: Contenidos de índole general. </small>
* ** Cálculo y estadística desde la perspectiva de la Ingeniería de Sistemas: **
* Derivadas.
* Regla de la cadena.
* Gradientes.
* Probabilidad.
* Estadística.
* Análisis Numérico.
* Señales.
* Transformadas.
* ** Procesamiento de Señales I: Audio: **
* Captura de audio.
* Análisis en Frecuencias.
* Operaciones Matemáticas.
* Diseño y aplicación de filtros.
* ** Procesamiento de Señales II: Imágenes: **
* Lectura y representación de Imágenes.
* Pixelamiento de una imagen.
* Operaciones sobre una imagen.
* Captura de Imágenes.
* Detección de bordes de una imagen.
* Conteo y etiquetado de objetos.
* Reconocimiento Óptico de Caracteres.
* Procesamiento digital de video.
<h2><center>Software Requerido</center></h2>
* Python
* Parte de los sistemas operativos macOS y Linux.
* Python Software Foundation (https://www.python.org)
* Enthought Canopy (https://www.enthought.com)
* Anaconda (https://www.continuum.io)
* Jupyter Notebook
* Método dinamico para la creación y aprendizaje de programacion con Python.
* Matlab
* Software matématico de gran potencial para la solución de problemas complejos.
<h2><center>Hardware Requerido</center></h2>
Debido al énfasis teoricopráctico del Club, no es posible llevar a cabo las actividades sin los espacios adecuados. La mayoria de estudiantes del programa no tienen acceso a equipos necesarios para las actividades. Por esta razón se solicitará a la dirección de programa acceso a la sala de Sistemas Operativos, el cual es el único laboratorio del programa con el sistema operativo linux en sus equipos.
|
github_jupyter
|
<img src="img/logo.png"/>
<h1 style="margin: 0; padding: 0;"><center>Club de Programación e Inteligencia Artificial</center></h1>
<center><i>Una inciativa de los estudiantes y egresados del Programa de Ingeniería de Sistemas de la Universidad del Magdalena</i></center>
<br/><br/>
<center> <strong> === </strong> </center>
<h2><center>Temas de Interés</center></h2>
* ** Competencias integrales en pensamiento algoritmico: **
Consideramos que una base fundamental de la Ingeniería de Sistemas es la programación. Sin embargo, esta debe llevarse a cabo con un enfoque algoritmico que permita analizar los problemas y seleccionar la mejor herramienta para cada uno.
* **Python y Matlab: **
Python y Matlab han demostrado ser dos de los lenguajes de programación más potentes de la actualidad. Su popularidad en la escena científica ha llevado a la creación de centenares de paquetes para la resolución de problemas en diversos ámbitos.
* ** Inteligencia Artificial: **
Los algoritmos inteligentes forman parte de nuestro día a día y permiten resolver multitud de problemas que de otra forma serían imposibles de atacar.
<h2><center>Metodología</center></h2>
* ** Clases presenciales (2 horas a la semana): **
*Como parte de las actividades del club se incluyen clases presenciales en las que se planea abordar los temas clave de Algoritmos y avanzar hasta llegar a Inteligencia Artificial. Estas clases se dictarán haciendo uso de materiales interactivos preparados en Jupyter Notebook, con el objetivo de facilitar la integración de los aspectos teóricos y prácticos.*
* ** Talleres colaborativos (2 horas a la semana): **
*En estos talleres se tiene la intención de formar grupos en los que cada miembro del club pueda proponer su idea de trabajo y desarrollarla con la ayuda de sus compañeros. El objetivo de estas actividades es permitir a los estudiantes que tengan intereses particulares trabajar en equipo, lo que a su vez genera insumos adicionales para las futuras clases del club.*
* ** Semillero de investigación e innovación: **
*Como parte de las actividades del Club, se pretende dar el espacio a que sus miembros planteen ideas no solo como parte de los talleres colaborativos sino también como posibles proyectos de investigación e innovación. De esta forma, los alumnos podrán recibir asesorías sobre cómo orientar sus ideas y tener el respaldo del Club a la hora de presentarlas ante las dependencias pertinentes, así como en los eventos que organiza la Universidad. *
* ** Espacios de discusión y repositorios en línea: **
*Se pretende administrar grupos de discusión en redes sociales, como Facebook, donde los miembros del club puedan publicar dudas, proponer ideas y compartir materiales. Asímismo, todos los materiales serán publicados en un repositorio de GitHub al que la comunidad universitaria tendrá total acceso.*
<h2><center>Temas Centrales</center></h2>
Son los temas que forman el núcleo del club, y que serán tratados de forma consistente en las clases presenciales.
* **Desarrollo de competencias integrales en pensamiento algoritmico I:**
* Variables y tipos de datos.
* Operaciones de entrada y visualización de datos.
* Operaciones matemáticas.
* Estructuras de datos I: listas, arreglos.
* Programación estructurada: condiciones, ciclos.
* Programación recursiva.
* Lectura y escritura de archivos de texto plano.
* Interpretación de problemas, aplicación de soluciones algoritmicas I.
* **Repaso de matemática básica para ingeniería de sistemas: **
* Conceptos básicos de funciones.
* Lógica booleana.
* Teoría de conjuntos.
* Algebra lineal básica.
* **Desarrollo de competencias integrales en pensamiento algoritmico II:**
* Funciones.
* Operaciones con conjuntos.
* Funciones anónimas o lambda.
* Mapeo, filtros y reducción.
* Estructuras de datos II: Pilas, colas, arboles.
* Introducción a la complejidad computacional.
* Algoritmos de ordenamiento.
* Interpretación de problemas, aplicación de soluciones algoritmicas II.
* **Inteligencia Artificial: Problemas de búsqueda **
* Algoritmos de búsqueda.
* Algoritmos de búsqueda con heurística.
* Algoritmos de búsqueda con componente aleatorio.
* Algoritmos de búsqueda biológicamente inspirados.
* **Técnicas avanzadas para el diseño de algoritmos: **
* Introducción a la programación competitiva.
* Complejidad computacional.
* Algoritmos vóraces y búsqueda exhaustiva.
* Divide y vencerás.
* Programación dinámica.
* Grafos.
* **Inteligencia Artificial: Aprendizaje de Máquinas I **
* Repaso: probabilidad.
* La línea base: aproximaciones ingenuas.
* Datos númericos y categóricos.
* Los distintos problemas del aprendizaje de máquina.
* One-R.
* K-Vecinos cercanos.
* Regresión lineal.
* **Inteligencia Artificial: Aprendizaje de Máquinas II **
* Preprocesamiento de datos.
* Validación de modelos.
* Regresión logística.
* Inferencia bayesiana.
* Recomendación a priori.
* K-Means.
* Árboles y bósques de clasificación.
* **Inteligencia Artificial: Aprendizaje de Máquinas III **
* Máquinas de vector de soporte.
* Redes neuronales artificiales.
* Deep learning.
<h2><center>Temas Adicionales</center></h2>
Son temas para los que se pretende preparar material con base en los talleres colaborativos, y que pueden
ser integrados en las temáticas núcleo dependiendo del interés de los miembros del grupo.
* ** Aplicaciones específicas: **
* Formateo de texto con la librería estándar de Python <sup>1</sup>.
* Manipulación de cadenas de texto con la librería estándar de Python <sup>1</sup>.
* Lectura y manipulación de archivos de distintos formatos con la librería estándar de Python <sup>1</sup>.
* Expresiones regulares para la manipulación de cadenas de texto <sup>3</sup>.
* Vectorización de diferentes estructuras de datos <sup>1,</sup><sup>2</sup>.
* Computación matemática con Numpy <sup>1</sup> y librería estándar de Matlab <sup>2</sup>.
* La librería Pandas para manejo de conjuntos de datos <sup>1</sup>.
* Graficación con matplotlib y seaborn para Python<sup>1</sup>, librería estándar de Matlab <sup>2</sup>.
<small> 1: Contenidos dictados en Python. </small><br/>
<small> 2: Contenidos dictados en Matlab. </small><br/>
<small> 3: Contenidos de índole general. </small>
* ** Cálculo y estadística desde la perspectiva de la Ingeniería de Sistemas: **
* Derivadas.
* Regla de la cadena.
* Gradientes.
* Probabilidad.
* Estadística.
* Análisis Numérico.
* Señales.
* Transformadas.
* ** Procesamiento de Señales I: Audio: **
* Captura de audio.
* Análisis en Frecuencias.
* Operaciones Matemáticas.
* Diseño y aplicación de filtros.
* ** Procesamiento de Señales II: Imágenes: **
* Lectura y representación de Imágenes.
* Pixelamiento de una imagen.
* Operaciones sobre una imagen.
* Captura de Imágenes.
* Detección de bordes de una imagen.
* Conteo y etiquetado de objetos.
* Reconocimiento Óptico de Caracteres.
* Procesamiento digital de video.
<h2><center>Software Requerido</center></h2>
* Python
* Parte de los sistemas operativos macOS y Linux.
* Python Software Foundation (https://www.python.org)
* Enthought Canopy (https://www.enthought.com)
* Anaconda (https://www.continuum.io)
* Jupyter Notebook
* Método dinamico para la creación y aprendizaje de programacion con Python.
* Matlab
* Software matématico de gran potencial para la solución de problemas complejos.
<h2><center>Hardware Requerido</center></h2>
Debido al énfasis teoricopráctico del Club, no es posible llevar a cabo las actividades sin los espacios adecuados. La mayoria de estudiantes del programa no tienen acceso a equipos necesarios para las actividades. Por esta razón se solicitará a la dirección de programa acceso a la sala de Sistemas Operativos, el cual es el único laboratorio del programa con el sistema operativo linux en sus equipos.
| 0.387459 | 0.955775 |
# Simple Wine Quality Classifier on Wine Quality Dataset
```
# Import important libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Statistical Visualization
import seaborn as sns
# Classification or Regression imports
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.svm import SVC
#Model Selection Specific
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
# Preprocessing
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
%matplotlib inline
```
# Load Dataset
```
df = pd.read_csv('../data/winequality-red.csv', delimiter=';')
```
# Analyze Train Dataset
```
df.head()
df.shape
df.info()
df.describe()
```
# Correlation map between features
```
f,ax = plt.subplots(figsize=(18, 18))
sns.heatmap(df.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax)
# Quality vs Sulphates barplot
sns.barplot(x = 'quality', y = 'sulphates', data = df )
# Quality vs volatile acidity barplot
sns.barplot(x = 'quality', y = 'volatile acidity', data = df )
# Quality vs Alcohol barplot
sns.barplot(x = 'quality', y = 'alcohol', data = df )
```
### Count number of instances for each quality
```
df['quality'].value_counts()
```
# Categorize Quality label
```
df_cat = df.copy()
bins = (df_cat['quality'].min(),6.5,df_cat['quality'].max())
group_names = ['bad','good']
categories = pd.cut(df_cat['quality'], bins, labels = group_names)
df_cat['quality'] = categories
df_cat['quality'].value_counts()
```
### Barplots after categorigation
```
sns.barplot(x='quality', y='alcohol',data=df_cat)
sns.barplot(x='quality', y='volatile acidity',data=df_cat)
```
# Create Features and Label Splits
```
X= df_cat.drop(['quality'], axis=1)
y = df_cat['quality']
# y.head()
df_cat.info()
```
### Encoding dependent variable - Quality
```
# bad = 0, good = 1
y = y.cat.codes
df_cat.head()
```
# Train Test Split
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
print(X_train.shape, X_test.shape)
```
# Feature Scaling to X_train and X_test to classify better.
```
fsc = StandardScaler()
X_train = fsc.fit_transform(X_train)
X_test = fsc.transform(X_test)
models = []
models.append(("Logistic Regression:", LogisticRegression()))
models.append(("K-Nearest Neighbour:", KNeighborsClassifier(n_neighbors=3)))
models.append(("Decision Tree Classifier:", DecisionTreeClassifier()))
models.append(("Random Forest Classifier:", RandomForestClassifier(n_estimators=32)))
models.append(("MLP:", MLPClassifier(hidden_layer_sizes=(45,30,15),solver='sgd',learning_rate_init=0.01,max_iter=500)))
models.append(("GradientBoostingClassifier:", GradientBoostingClassifier()))
models.append(("SVC:", SVC(kernel = 'rbf', random_state = 0)))
print('Models appended...')
def run_models():
results = []
names = []
for name,model in models:
cv_result = cross_val_score(model, X_train, y_train.values.ravel(), cv = 5, scoring = "accuracy")
names.append(name)
results.append(cv_result)
for i in range(len(names)):
print(names[i],results[i].mean()*100)
```
# Function to run the Models with Cross Validation
```
run_models()
```
### In this very simple Classifier without any preprocessing Random Forest has been performing the best with **90.93** % accuracy.
# Grid search for best model and parameters
```
models_gs = {
'K-Nearest Neighbour': KNeighborsClassifier(),
'Decision Tree Classifier': DecisionTreeClassifier(),
'RandomForestClassifier': RandomForestClassifier(),
'GradientBoostingClassifier': GradientBoostingClassifier(),
'SVC': SVC()
}
params_gs = {
'K-Nearest Neighbour': {'n_neighbors':[3, 5, 8]},
'Decision Tree Classifier': {'max_depth': [8, 16, 32]},
'RandomForestClassifier': { 'n_estimators': [16, 32, 64, 128] },
'GradientBoostingClassifier': { 'n_estimators': [64, 128, 256, 512], 'learning_rate': [0.05, 0.1, 0.3, 0.9] },
'SVC': [
# {'kernel': ['linear'], 'C': [1, 10, 100, 1000]},
{'kernel': ['rbf'], 'C': [1, 10, 100, 1000], 'gamma': [0.1, 0.3, 0.7, 0.9, 1.0]},
]
}
def run_models_with_GS(models_gs, params_gs):
results = []
for model in models_gs:
grid_search = GridSearchCV(estimator = models_gs[model],
param_grid = params_gs[model],
scoring = 'accuracy',
cv = 5, n_jobs = 6)
grid_search.fit(X_train, y_train)
best_accuracy = grid_search.best_score_
best_parameters = grid_search.best_params_
#here is the best accuracy
results.append(( model, best_accuracy, best_parameters ))
return results
results = run_models_with_GS(models_gs, params_gs)
for model, accuracy, params in results:
print(model, accuracy * 100, params)
```
### Best Results
- K-Nearest Neighbour **87.6465989054** {'n_neighbors': 8}
- Decision Tree Classifier **87.4902267396** {'max_depth': 8}
- RandomForestClassifier **91.2431587177** {'n_estimators': 128}
- GradientBoostingClassifier **90.2267396403** {'learning_rate': 0.1, 'n_estimators': 128}
- SVC **89.9139953088** {'C': 1, 'gamma': 0.7, 'kernel': 'rbf'}
|
github_jupyter
|
# Import important libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Statistical Visualization
import seaborn as sns
# Classification or Regression imports
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.svm import SVC
#Model Selection Specific
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
# Preprocessing
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
%matplotlib inline
df = pd.read_csv('../data/winequality-red.csv', delimiter=';')
df.head()
df.shape
df.info()
df.describe()
f,ax = plt.subplots(figsize=(18, 18))
sns.heatmap(df.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax)
# Quality vs Sulphates barplot
sns.barplot(x = 'quality', y = 'sulphates', data = df )
# Quality vs volatile acidity barplot
sns.barplot(x = 'quality', y = 'volatile acidity', data = df )
# Quality vs Alcohol barplot
sns.barplot(x = 'quality', y = 'alcohol', data = df )
df['quality'].value_counts()
df_cat = df.copy()
bins = (df_cat['quality'].min(),6.5,df_cat['quality'].max())
group_names = ['bad','good']
categories = pd.cut(df_cat['quality'], bins, labels = group_names)
df_cat['quality'] = categories
df_cat['quality'].value_counts()
sns.barplot(x='quality', y='alcohol',data=df_cat)
sns.barplot(x='quality', y='volatile acidity',data=df_cat)
X= df_cat.drop(['quality'], axis=1)
y = df_cat['quality']
# y.head()
df_cat.info()
# bad = 0, good = 1
y = y.cat.codes
df_cat.head()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
print(X_train.shape, X_test.shape)
fsc = StandardScaler()
X_train = fsc.fit_transform(X_train)
X_test = fsc.transform(X_test)
models = []
models.append(("Logistic Regression:", LogisticRegression()))
models.append(("K-Nearest Neighbour:", KNeighborsClassifier(n_neighbors=3)))
models.append(("Decision Tree Classifier:", DecisionTreeClassifier()))
models.append(("Random Forest Classifier:", RandomForestClassifier(n_estimators=32)))
models.append(("MLP:", MLPClassifier(hidden_layer_sizes=(45,30,15),solver='sgd',learning_rate_init=0.01,max_iter=500)))
models.append(("GradientBoostingClassifier:", GradientBoostingClassifier()))
models.append(("SVC:", SVC(kernel = 'rbf', random_state = 0)))
print('Models appended...')
def run_models():
results = []
names = []
for name,model in models:
cv_result = cross_val_score(model, X_train, y_train.values.ravel(), cv = 5, scoring = "accuracy")
names.append(name)
results.append(cv_result)
for i in range(len(names)):
print(names[i],results[i].mean()*100)
run_models()
models_gs = {
'K-Nearest Neighbour': KNeighborsClassifier(),
'Decision Tree Classifier': DecisionTreeClassifier(),
'RandomForestClassifier': RandomForestClassifier(),
'GradientBoostingClassifier': GradientBoostingClassifier(),
'SVC': SVC()
}
params_gs = {
'K-Nearest Neighbour': {'n_neighbors':[3, 5, 8]},
'Decision Tree Classifier': {'max_depth': [8, 16, 32]},
'RandomForestClassifier': { 'n_estimators': [16, 32, 64, 128] },
'GradientBoostingClassifier': { 'n_estimators': [64, 128, 256, 512], 'learning_rate': [0.05, 0.1, 0.3, 0.9] },
'SVC': [
# {'kernel': ['linear'], 'C': [1, 10, 100, 1000]},
{'kernel': ['rbf'], 'C': [1, 10, 100, 1000], 'gamma': [0.1, 0.3, 0.7, 0.9, 1.0]},
]
}
def run_models_with_GS(models_gs, params_gs):
results = []
for model in models_gs:
grid_search = GridSearchCV(estimator = models_gs[model],
param_grid = params_gs[model],
scoring = 'accuracy',
cv = 5, n_jobs = 6)
grid_search.fit(X_train, y_train)
best_accuracy = grid_search.best_score_
best_parameters = grid_search.best_params_
#here is the best accuracy
results.append(( model, best_accuracy, best_parameters ))
return results
results = run_models_with_GS(models_gs, params_gs)
for model, accuracy, params in results:
print(model, accuracy * 100, params)
| 0.520253 | 0.903337 |
# Precipitation
```
import pandas as pd
data = pd.read_csv('Petersburg Station Weather Data.csv', delimiter=',')
data
import matplotlib.pyplot as plt
len(data)
precipitation = data['PRECIPITATION']
import numpy as np
days=np.arange(365)
days
fig, ax1 = plt.subplots(1, 1)
ax1.plot(days, precipitation, 'b-', label='Petersburg')
ax1.set_title('Precipitation')
ax1.set_xlabel('Time [days]')
ax1.set_ylabel('Precipitation [mm]')
ax1.set_xlim([0, 365])
ax1.set_ylim([0, 400])
ax1.legend(numpoints=1, loc=2)
plt.tight_layout()
plt.show()
accumulated_precipitation = data['PRECIPITATION']
accumulated_precipitation = np.array(accumulated_precipitation)
drops = []
drop_index = []
for i in range(len(accumulated_precipitation)-1):
if accumulated_precipitation[i+1] < accumulated_precipitation[i]:
drops.append(accumulated_precipitation[i])
drop_index.append(i)
drops
drop_index
for j in range(len(drops)):
for i in range(drop_index[j]+1,len(accumulated_precipitation)):
accumulated_precipitation[i] = accumulated_precipitation[i]+drops[j]
fig, ax1 = plt.subplots(1, 1)
ax1.plot(days, accumulated_precipitation, 'b-', label='Petersburg')
ax1.set_title('Precipitation')
ax1.set_xlabel('Time [days]')
ax1.set_ylabel('Precipitation [mm]')
ax1.set_xlim([0, 365])
ax1.legend(numpoints=1, loc=2)
plt.tight_layout()
plt.show()
precipitation = [[] for i in range(len(accumulated_precipitation))]
for i in range(len(accumulated_precipitation)-1,-1,-1):
precipitation[i] = accumulated_precipitation[i] - accumulated_precipitation[i-1]
precipitation[0] = 2
fig, ax1 = plt.subplots(1, 1)
ax1.plot(days, precipitation, 'b-', label='Petersburg')
ax1.set_title('Precipitation')
ax1.set_xlabel('Time [days]')
ax1.set_ylabel('Precipitation [mm]')
ax1.set_xlim([0, 365])
ax1.set_ylim([0, 15])
ax1.legend(numpoints=1, loc=2)
plt.tight_layout()
plt.show()
bins = np.linspace(0, 15, 7)
distribution, bins = np.histogram(precipitation, bins)
bins
distribution
dtype = [('Number of Days','float32')]
values = np.array(distribution, dtype=dtype)
index = [str(i*2.5)+'-'+str((i+1)*2.5)+'mm' for i in range(0, len(values))]
df = pd.DataFrame(values, index=index)
values
df
df['Precipitation'] = index
df
from matplotlib import cm
f = plt.figure(figsize=(6,6))
plt.axes().set_aspect('equal')
cs = cm.Greens(np.arange(6)/6.)
wedges, tn = plt.pie(df['Number of Days'], labels=df['Precipitation'], colors = cs)
plt.title('Precipitation')
f.savefig('Precipitation_PieChart.png', format='png', dpi=300, bbox_inches='tight')
plt.show()
f = plt.figure(figsize=(8,6))
ind = np.arange(len(df))
width = 0.6
rects = plt.axes().barh(ind, df['Number of Days'], width, color='lightgreen')
plt.xlabel('Number of Days')
plt.title('Precipitation')
plt.yticks(ind)
plt.axes().set_yticklabels(df['Precipitation'], va='bottom')
f.savefig('Precipitation_BarChart.png', format='png', dpi=300, bbox_inches='tight')
plt.show()
```
|
github_jupyter
|
import pandas as pd
data = pd.read_csv('Petersburg Station Weather Data.csv', delimiter=',')
data
import matplotlib.pyplot as plt
len(data)
precipitation = data['PRECIPITATION']
import numpy as np
days=np.arange(365)
days
fig, ax1 = plt.subplots(1, 1)
ax1.plot(days, precipitation, 'b-', label='Petersburg')
ax1.set_title('Precipitation')
ax1.set_xlabel('Time [days]')
ax1.set_ylabel('Precipitation [mm]')
ax1.set_xlim([0, 365])
ax1.set_ylim([0, 400])
ax1.legend(numpoints=1, loc=2)
plt.tight_layout()
plt.show()
accumulated_precipitation = data['PRECIPITATION']
accumulated_precipitation = np.array(accumulated_precipitation)
drops = []
drop_index = []
for i in range(len(accumulated_precipitation)-1):
if accumulated_precipitation[i+1] < accumulated_precipitation[i]:
drops.append(accumulated_precipitation[i])
drop_index.append(i)
drops
drop_index
for j in range(len(drops)):
for i in range(drop_index[j]+1,len(accumulated_precipitation)):
accumulated_precipitation[i] = accumulated_precipitation[i]+drops[j]
fig, ax1 = plt.subplots(1, 1)
ax1.plot(days, accumulated_precipitation, 'b-', label='Petersburg')
ax1.set_title('Precipitation')
ax1.set_xlabel('Time [days]')
ax1.set_ylabel('Precipitation [mm]')
ax1.set_xlim([0, 365])
ax1.legend(numpoints=1, loc=2)
plt.tight_layout()
plt.show()
precipitation = [[] for i in range(len(accumulated_precipitation))]
for i in range(len(accumulated_precipitation)-1,-1,-1):
precipitation[i] = accumulated_precipitation[i] - accumulated_precipitation[i-1]
precipitation[0] = 2
fig, ax1 = plt.subplots(1, 1)
ax1.plot(days, precipitation, 'b-', label='Petersburg')
ax1.set_title('Precipitation')
ax1.set_xlabel('Time [days]')
ax1.set_ylabel('Precipitation [mm]')
ax1.set_xlim([0, 365])
ax1.set_ylim([0, 15])
ax1.legend(numpoints=1, loc=2)
plt.tight_layout()
plt.show()
bins = np.linspace(0, 15, 7)
distribution, bins = np.histogram(precipitation, bins)
bins
distribution
dtype = [('Number of Days','float32')]
values = np.array(distribution, dtype=dtype)
index = [str(i*2.5)+'-'+str((i+1)*2.5)+'mm' for i in range(0, len(values))]
df = pd.DataFrame(values, index=index)
values
df
df['Precipitation'] = index
df
from matplotlib import cm
f = plt.figure(figsize=(6,6))
plt.axes().set_aspect('equal')
cs = cm.Greens(np.arange(6)/6.)
wedges, tn = plt.pie(df['Number of Days'], labels=df['Precipitation'], colors = cs)
plt.title('Precipitation')
f.savefig('Precipitation_PieChart.png', format='png', dpi=300, bbox_inches='tight')
plt.show()
f = plt.figure(figsize=(8,6))
ind = np.arange(len(df))
width = 0.6
rects = plt.axes().barh(ind, df['Number of Days'], width, color='lightgreen')
plt.xlabel('Number of Days')
plt.title('Precipitation')
plt.yticks(ind)
plt.axes().set_yticklabels(df['Precipitation'], va='bottom')
f.savefig('Precipitation_BarChart.png', format='png', dpi=300, bbox_inches='tight')
plt.show()
| 0.296451 | 0.840979 |
# Accelerating Maestro's Reactions with OpenACC
**Step 1: Markup all subroutines, functions**
To call a subroutine from code running on the GPU, you must compile a version for the GPU. With OpenACC, this is done with the `routine` directive. Our integrator makes use of many linear algebra packages which Maestro has a local copy of. One of the first tasks was to mark these up as sequential routines. For example,
```fortran
subroutine dgesl (a,lda,n,ipvt,b,job)
!$acc routine seq
!$acc routine(daxpy) seq
!$acc routine(vddot) seq
integer lda,n,ipvt(*),job
double precision a(lda,n),b(*)
!
! dgesl solves the double precision system
! a * x = b or trans(a) * x = b
! using the factors computed by dgeco or dgefa.
! ...
end subroutine
```
Notice that we also tell the compiler that routines `daxpy` and `vddot` have a GPU version. This is required because we do not access these routines through a module but instead link them directly.
Thirty routines were marked up in this way:
```
# %load oac_routines.txt
Microphysics/screening/screen.f90-subroutine screenz (t,d,z1,z2,a1,a2,ymass,aion,zion,nion,scfac, dscfacdt)
Microphysics/screening/screen.f90: !$acc routine seq
--
Util/LINPACK/dgesl.f- subroutine dgesl (a,lda,n,ipvt,b,job)
Util/LINPACK/dgesl.f:!$acc routine seq
Util/LINPACK/dgesl.f:!$acc routine(daxpy) seq
Util/LINPACK/dgesl.f:!$acc routine(vddot) seq
--
Util/LINPACK/dgefa.f- subroutine dgefa (a,lda,n,ipvt,info)
Util/LINPACK/dgefa.f:!$acc routine seq
Util/LINPACK/dgefa.f:!$acc routine(idamax) seq
Util/LINPACK/dgefa.f:!$acc routine(dscal) seq
Util/LINPACK/dgefa.f:!$acc routine(daxpy) seq
--
Util/BLAS/idamax.f- INTEGER FUNCTION IDAMAX(N,DX,INCX)
Util/BLAS/idamax.f:!$acc routine seq
--
Util/BLAS/vddot.f- double precision function vddot (n,dx,incx,dy,incy)
Util/BLAS/vddot.f:!$acc routine seq
--
Util/BLAS/dscal.f- SUBROUTINE DSCAL(N,DA,DX,INCX)
Util/BLAS/dscal.f:!$acc routine seq
--
Util/BLAS/daxpy.f- SUBROUTINE DAXPY(N,DA,DX,INCX,DY,INCY)
Util/BLAS/daxpy.f:!$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_advance(ts, neq, npt, y0, t0, y1, t1, dt0, reset, reuse, ierr, initial_call)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_update(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_predict(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_solve(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine(dgefa) seq
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine(dgesl) seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_check(ts, retry, err)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_correct(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_adjust(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_reset(ts, y0, dt, reuse)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine rescale_timestep(ts, eta_in, force)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine decrease_order(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine increase_order(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function alpha0(k) result(a0)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function alphahat0(k, h) result(a0)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function xi_star_inv(k, h) result(xii)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function xi_j(h, j) result(xi)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine ewts(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function norm(y, ewt) result(r)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine eye_r(A)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- recursive function factorial(n) result(r)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine eoshift_local(arr, sh, shifted_arr)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function minloc(arr) result(ret)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90- subroutine f_rhs_vec(neq, npt, y, t, yd, upar)
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90: !$acc routine seq
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90: !$acc routine(screenz) seq
--
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90- subroutine jac_vec(neq, npt, y, t, pd, upar)
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90: !$acc routine seq
--
```
**Step 2: Markup a computationally expensive loop over hydro cells**
One of the balances one must attempt to strike with GPU coding is you must give it *a lot* of computation to keep it busy. Though they're not like conventional cores, the GPUs in Titan (Kepler K20x) have 2688 CUDA cores. To keep all of these busy, you want to get as much of your code onto the GPU as possible. Of course you want a computationally intensive portion of code, but you also must put enough of the code onto the GPU that you do not lose all performance gains to data transfer costs.
The strategy I've taken for the moment is to markup all routines as sequential and to markup a huge loop over hydro cells that calls the initial sequential routine `bdf_advance`. The markup looks like this:
```fortran
!$acc parallel loop gang vector present(dens, temp, eos_cp, eos_dhdX, &
!$acc Xin, Xout, rho_omegadot, rho_Hnuc, ebin, ts) &
!$acc private(ierr, y, y0, y1) reduction(+:ierr_tot)
do i = 1, npt
! ...
call bdf_advance(ts(i), NEQ, bdf_npt, y0, t0, y1, t1, &
DT0, RESET, REUSE, ierr, .true.)
! ...
end do
```
Here we tell the compiler we want this loop to be run in parallel on the GPU. The `gang` and `vector` options represent the heirarchy of parallelism we want to use on the GPU. To understand this, it's helpful to take a look at the card:

Here's a zoom-in on an SMX unit:

There is a rough correlation between the heirarchy of parallelism on the hardware and that exposed in the OpenACC standard. My understanding is it's not necessarily rigidly followed by compilers if they think they can be clever, but it's helpful for thinking about how your code is being run.
`gang` parallelism is across SMX units, of which the K20x's have 14 active. For initial development, I do not recommend trying to think of what's called `worker` parallelism. This is parallelism over the warp schedulers in an SMX. Rather, initially I prefer to focus on `vector` parallelism, which is parallelism over the CUDA cores in an SMX if you *don't* use `worker` parallelism and over the CUDA cores in a warp if you do. Thus, in the loop I showed above, we parallelize over the SMX's and the CUDA cores within each SMX by giving the loop directive `gang` and `vector` options.
Note that our directive also includes data statements `present` and `private`:
```fortran
!$acc parallel loop gang vector present(dens, temp, eos_cp, eos_dhdX, &
!$acc Xin, Xout, rho_omegadot, rho_Hnuc, ebin, ts) &
!$acc private(ierr, y, y0, y1) reduction(+:ierr_tot)
do i = 1, npt
! ...
call bdf_advance(ts(i), NEQ, bdf_npt, y0, t0, y1, t1, &
DT0, RESET, REUSE, ierr, .true.)
! ...
end do
```
`present` tells the compiler that the listed data is already present on the GPU, while `private` tells the compiler that each thread on the GPU should have its own copy of the listed data. We also see a `reduction`, which will sum up the value of `ierr` from all cores and return the summed up value to the host/CPU.
**Step 3: Get the data to the GPU**
GPU's do not have access to the CPU/host's memory (e.g. the RAM and cache memory that all of your computer's cores have access to). Thus, we must explicitly put any data we need into the GPU's memory. This is acheived with `data` directives in OpenACC.
Often in our codes, and other production science codes, we make use of data in modules. This global data can be put on the GPU with the `declare` directive. Here's an example of this from my work accelerating the reactions:
```fortran
module network
use bl_types
implicit none
! ...
real(kind=dp_t), save :: aion(nspec), zion(nspec), ebin(nspec)
!$acc declare create(aion(:), zion(:), ebin(:))
! ...
contains
subroutine network_init()
! ...
aion(ic12_) = 12.0_dp_t
aion(io16_) = 16.0_dp_t
aion(img24_) = 24.0_dp_t
zion(ic12_) = 6.0_dp_t
zion(io16_) = 8.0_dp_t
zion(img24_) = 12.0_dp_t
ebin(ic12_) = -7.4103097e18_dp_t ! 92.16294 MeV
ebin(io16_) = -7.6959672e18_dp_t ! 127.62093 MeV
ebin(img24_) = -7.9704080e18_dp_t ! 198.2579 MeV
!$acc update device(aion(:), zion(:), ebin(:))
! ...
end subroutine network_init
! ...
end module network
```
Here we had a module array that we need on the GPU. A combination of a `declare create` and `update device` directives makes sure this data is accessible on the GPU and contains the same data as the host. Note that this ability to use global data is relatively new, introduced in the OpenACC 2.0 standard.
A major difficulty in working with GPUs is dealing with user-defined types (similar to `struct`s in C, and to a lesser extent classes in object-oriented languages). It is exceptionally good software engineering practice to make use of such types and they're plentiful in BoxLib/Maestro. However, types that include dynamic memory (in Fortran, this means types that have the `alloctable` or `pointer` attribute) are currently poorly handled by compiler implementations of OpenACC. There are plans in the next major update of the standard, 3.0, to incorporate deep copy functionality that should rid us of many of the these difficulties. For now, howerver, we must manually deep copy non-trivial user-defined types.
In this case, our integrator uses a timestepper type called `bdf_ts`. Our loop over hydro cells includes an array of these types `ts(:)`. Before getting to this loop, I deep copy each over to the GPU. It looks like this:
```fortran
!$acc enter data create(ts)
do i = 1, npt
! we need the specific heat at constant pressure and dhdX |_p. Take
! T, rho, Xin as input
eos_state%rho = dens(i)
eos_state%T = temp(i)
eos_state%xn(:) = Xin(:,i)
call eos(eos_input_rt, eos_state, .false.)
eos_cp(i) = eos_state%cp
eos_dhdX(:,i) = eos_state%dhdX(:)
! Build the bdf_ts time-stepper object
call bdf_ts_build(ts(i), NEQ, bdf_npt, rtol, atol, MAX_ORDER, upar)
!Now we update all non-dynamic data members, meaning those that aren't
!allocatables, pointers, etc. They can be arrays as long as they're
!static. To make my previous note more concrete, if we did something
!like `update device(ts(i))` it would overwrite the device's pointer
!address with that of the host, according to PGI/NVIDIA consults.
!Updating individual members avoids this.
!$acc update device( &
!$acc ts(i)%neq, &
!$acc ts(i)%npt, &
!$acc ts(i)%max_order, &
!$acc ts(i)%max_steps, &
!$acc ts(i)%max_iters, &
!$acc ts(i)%verbose, &
!$acc ts(i)%dt_min, &
!$acc ts(i)%eta_min, &
!$acc ts(i)%eta_max, &
!$acc ts(i)%eta_thresh, &
!$acc ts(i)%max_j_age, &
!$acc ts(i)%max_p_age, &
!$acc ts(i)%debug, &
!$acc ts(i)%dump_unit, &
!$acc ts(i)%t, &
!$acc ts(i)%t1, &
!$acc ts(i)%dt, &
!$acc ts(i)%dt_nwt, &
!$acc ts(i)%k, &
!$acc ts(i)%n, &
!$acc ts(i)%j_age, &
!$acc ts(i)%p_age, &
!$acc ts(i)%k_age, &
!$acc ts(i)%tq, &
!$acc ts(i)%tq2save, &
!$acc ts(i)%temp_data, &
!$acc ts(i)%refactor, &
!$acc ts(i)%nfe, &
!$acc ts(i)%nje, &
!$acc ts(i)%nlu, &
!$acc ts(i)%nit, &
!$acc ts(i)%nse, &
!$acc ts(i)%ncse, &
!$acc ts(i)%ncit, &
!$acc ts(i)%ncdtmin)
!Now it's time to deal with dynamic data. At the moment, they only
!exist as pointers on the device. For PGI at least, doing a copyin on
!dynamic data serves to create, allocate, and then attach each dynamic
!data member to the corresponding pointer in ts(i).
!$acc enter data copyin( &
!$acc ts(i)%rtol, &
!$acc ts(i)%atol, &
!$acc ts(i)%J, &
!$acc ts(i)%P, &
!$acc ts(i)%z(:,:,0:), &
!$acc ts(i)%z0(:,:,0:), &
!$acc ts(i)%h(0:), &
!$acc ts(i)%l(0:), &
!$acc ts(i)%shift(0:), &
!$acc ts(i)%upar, &
!$acc ts(i)%y, &
!$acc ts(i)%yd, &
!$acc ts(i)%rhs, &
!$acc ts(i)%e, &
!$acc ts(i)%e1, &
!$acc ts(i)%ewt, &
!$acc ts(i)%b, &
!$acc ts(i)%ipvt, &
!$acc ts(i)%A(0:,0:))
end do
```
Here I make use of the `enter data` directive, which allows you to put data on the GPU in one part of your code and close that data out in another. First, I create the array of `bdf_ts` types, `ts(:)`. I then build these object on the host and update the static data while doings a `copyin` for the dynamic data. For PGI, this `copyin` serves to 1) create, 2) allocate, and 3) attach each dynamic data member to the appropriate type on the GPU.
Later, there's an analgous loop in which I retrieve any data I might need on the host and destroy all of the data on the GPU.
We've seen how I get global data and a non-trivial derived type onto the GPU. Finally, before my loop I have a data statement that gets other needed variables onto the GPU:
```fortran
!$acc data &
!$acc copyin(dens(:), temp(:), eos_cp(:), eos_dhdX(:,:), Xin(:,:)) &
!$acc copyout(Xout(:,:), rho_omegadot(:,:), rho_Hnuc(:))
```
I `copyin` data that need only be read on the GPU and not returned to the host. I `copyout` data needed on the host for subsequent computation. Note that in practice you need only do this for non-scalar data like arrays. By default, scalar data used in an OpenACC compute region will be copied over and readily available.
**Hidden Step 0/4: Rewrite your code to satisfy GPU restrictions**
GPUs are not CPUs. A CPU core is very sophisticated and able to handle complex code flows. GPU cores are plentiful, but dumb. What this means is that although I would love to tell you the three-step narrative I laid out above is sufficient for getting your code running on GPUs, I can't. Were you to execute this series of steps your code almost certainly wouldn't compile. So either before (step 0) or, more realistically, after (step 4) you must modify your code so that any portion that needs to run on the GPU doesn't violate GPU restrictions. Briefly, the primary restrictions I had to rewrite to avoid are:
* No `allocate` statements on the GPU
* This includes implicit ones! In practice, this means you should avoid statements that implicitly require a temporary variable which the compiler will be allocating behind the scenes. So, no this:
```fortran
ts%l = ts%l + eoshift_local(ts%l, -1) / xi_j(ts%h, j)
```
* Generally, I've found that using Fortran's concise array notation on GPUs leads to errors. I replace all instances of it with explicit loops.
* subroutines or functions cannot be passed as arguments to GPU routines
* Many intrinsic functions may not be available on the GPU (e.g. `sum`, `eoshift`, `max`, etc). Some are, some aren't. If code is giving you trouble and it contains an intrinsic, that's likely the problem.
* No I/O! You can't `print *, 'Hey, I am on a GPU'`
|
github_jupyter
|
subroutine dgesl (a,lda,n,ipvt,b,job)
!$acc routine seq
!$acc routine(daxpy) seq
!$acc routine(vddot) seq
integer lda,n,ipvt(*),job
double precision a(lda,n),b(*)
!
! dgesl solves the double precision system
! a * x = b or trans(a) * x = b
! using the factors computed by dgeco or dgefa.
! ...
end subroutine
# %load oac_routines.txt
Microphysics/screening/screen.f90-subroutine screenz (t,d,z1,z2,a1,a2,ymass,aion,zion,nion,scfac, dscfacdt)
Microphysics/screening/screen.f90: !$acc routine seq
--
Util/LINPACK/dgesl.f- subroutine dgesl (a,lda,n,ipvt,b,job)
Util/LINPACK/dgesl.f:!$acc routine seq
Util/LINPACK/dgesl.f:!$acc routine(daxpy) seq
Util/LINPACK/dgesl.f:!$acc routine(vddot) seq
--
Util/LINPACK/dgefa.f- subroutine dgefa (a,lda,n,ipvt,info)
Util/LINPACK/dgefa.f:!$acc routine seq
Util/LINPACK/dgefa.f:!$acc routine(idamax) seq
Util/LINPACK/dgefa.f:!$acc routine(dscal) seq
Util/LINPACK/dgefa.f:!$acc routine(daxpy) seq
--
Util/BLAS/idamax.f- INTEGER FUNCTION IDAMAX(N,DX,INCX)
Util/BLAS/idamax.f:!$acc routine seq
--
Util/BLAS/vddot.f- double precision function vddot (n,dx,incx,dy,incy)
Util/BLAS/vddot.f:!$acc routine seq
--
Util/BLAS/dscal.f- SUBROUTINE DSCAL(N,DA,DX,INCX)
Util/BLAS/dscal.f:!$acc routine seq
--
Util/BLAS/daxpy.f- SUBROUTINE DAXPY(N,DA,DX,INCX,DY,INCY)
Util/BLAS/daxpy.f:!$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_advance(ts, neq, npt, y0, t0, y1, t1, dt0, reset, reuse, ierr, initial_call)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_update(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_predict(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_solve(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine(dgefa) seq
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine(dgesl) seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_check(ts, retry, err)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_correct(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_adjust(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine bdf_reset(ts, y0, dt, reuse)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine rescale_timestep(ts, eta_in, force)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine decrease_order(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine increase_order(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function alpha0(k) result(a0)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function alphahat0(k, h) result(a0)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function xi_star_inv(k, h) result(xii)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function xi_j(h, j) result(xi)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine ewts(ts)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function norm(y, ewt) result(r)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine eye_r(A)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- recursive function factorial(n) result(r)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- subroutine eoshift_local(arr, sh, shifted_arr)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90- function minloc(arr) result(ret)
Util/VBDF/dev/oac_vbdf/test_react/bdf.f90: !$acc routine seq
--
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90- subroutine f_rhs_vec(neq, npt, y, t, yd, upar)
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90: !$acc routine seq
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90: !$acc routine(screenz) seq
--
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90- subroutine jac_vec(neq, npt, y, t, pd, upar)
Util/VBDF/dev/oac_vbdf/ignition_simple_bdf/f_rhs.f90: !$acc routine seq
--
!$acc parallel loop gang vector present(dens, temp, eos_cp, eos_dhdX, &
!$acc Xin, Xout, rho_omegadot, rho_Hnuc, ebin, ts) &
!$acc private(ierr, y, y0, y1) reduction(+:ierr_tot)
do i = 1, npt
! ...
call bdf_advance(ts(i), NEQ, bdf_npt, y0, t0, y1, t1, &
DT0, RESET, REUSE, ierr, .true.)
! ...
end do
!$acc parallel loop gang vector present(dens, temp, eos_cp, eos_dhdX, &
!$acc Xin, Xout, rho_omegadot, rho_Hnuc, ebin, ts) &
!$acc private(ierr, y, y0, y1) reduction(+:ierr_tot)
do i = 1, npt
! ...
call bdf_advance(ts(i), NEQ, bdf_npt, y0, t0, y1, t1, &
DT0, RESET, REUSE, ierr, .true.)
! ...
end do
module network
use bl_types
implicit none
! ...
real(kind=dp_t), save :: aion(nspec), zion(nspec), ebin(nspec)
!$acc declare create(aion(:), zion(:), ebin(:))
! ...
contains
subroutine network_init()
! ...
aion(ic12_) = 12.0_dp_t
aion(io16_) = 16.0_dp_t
aion(img24_) = 24.0_dp_t
zion(ic12_) = 6.0_dp_t
zion(io16_) = 8.0_dp_t
zion(img24_) = 12.0_dp_t
ebin(ic12_) = -7.4103097e18_dp_t ! 92.16294 MeV
ebin(io16_) = -7.6959672e18_dp_t ! 127.62093 MeV
ebin(img24_) = -7.9704080e18_dp_t ! 198.2579 MeV
!$acc update device(aion(:), zion(:), ebin(:))
! ...
end subroutine network_init
! ...
end module network
!$acc enter data create(ts)
do i = 1, npt
! we need the specific heat at constant pressure and dhdX |_p. Take
! T, rho, Xin as input
eos_state%rho = dens(i)
eos_state%T = temp(i)
eos_state%xn(:) = Xin(:,i)
call eos(eos_input_rt, eos_state, .false.)
eos_cp(i) = eos_state%cp
eos_dhdX(:,i) = eos_state%dhdX(:)
! Build the bdf_ts time-stepper object
call bdf_ts_build(ts(i), NEQ, bdf_npt, rtol, atol, MAX_ORDER, upar)
!Now we update all non-dynamic data members, meaning those that aren't
!allocatables, pointers, etc. They can be arrays as long as they're
!static. To make my previous note more concrete, if we did something
!like `update device(ts(i))` it would overwrite the device's pointer
!address with that of the host, according to PGI/NVIDIA consults.
!Updating individual members avoids this.
!$acc update device( &
!$acc ts(i)%neq, &
!$acc ts(i)%npt, &
!$acc ts(i)%max_order, &
!$acc ts(i)%max_steps, &
!$acc ts(i)%max_iters, &
!$acc ts(i)%verbose, &
!$acc ts(i)%dt_min, &
!$acc ts(i)%eta_min, &
!$acc ts(i)%eta_max, &
!$acc ts(i)%eta_thresh, &
!$acc ts(i)%max_j_age, &
!$acc ts(i)%max_p_age, &
!$acc ts(i)%debug, &
!$acc ts(i)%dump_unit, &
!$acc ts(i)%t, &
!$acc ts(i)%t1, &
!$acc ts(i)%dt, &
!$acc ts(i)%dt_nwt, &
!$acc ts(i)%k, &
!$acc ts(i)%n, &
!$acc ts(i)%j_age, &
!$acc ts(i)%p_age, &
!$acc ts(i)%k_age, &
!$acc ts(i)%tq, &
!$acc ts(i)%tq2save, &
!$acc ts(i)%temp_data, &
!$acc ts(i)%refactor, &
!$acc ts(i)%nfe, &
!$acc ts(i)%nje, &
!$acc ts(i)%nlu, &
!$acc ts(i)%nit, &
!$acc ts(i)%nse, &
!$acc ts(i)%ncse, &
!$acc ts(i)%ncit, &
!$acc ts(i)%ncdtmin)
!Now it's time to deal with dynamic data. At the moment, they only
!exist as pointers on the device. For PGI at least, doing a copyin on
!dynamic data serves to create, allocate, and then attach each dynamic
!data member to the corresponding pointer in ts(i).
!$acc enter data copyin( &
!$acc ts(i)%rtol, &
!$acc ts(i)%atol, &
!$acc ts(i)%J, &
!$acc ts(i)%P, &
!$acc ts(i)%z(:,:,0:), &
!$acc ts(i)%z0(:,:,0:), &
!$acc ts(i)%h(0:), &
!$acc ts(i)%l(0:), &
!$acc ts(i)%shift(0:), &
!$acc ts(i)%upar, &
!$acc ts(i)%y, &
!$acc ts(i)%yd, &
!$acc ts(i)%rhs, &
!$acc ts(i)%e, &
!$acc ts(i)%e1, &
!$acc ts(i)%ewt, &
!$acc ts(i)%b, &
!$acc ts(i)%ipvt, &
!$acc ts(i)%A(0:,0:))
end do
!$acc data &
!$acc copyin(dens(:), temp(:), eos_cp(:), eos_dhdX(:,:), Xin(:,:)) &
!$acc copyout(Xout(:,:), rho_omegadot(:,:), rho_Hnuc(:))
ts%l = ts%l + eoshift_local(ts%l, -1) / xi_j(ts%h, j)
| 0.310694 | 0.636636 |
```
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
#label_path = 'evaluation(_855)완성.txt'
#label_path = 'evaluation(_3000).txt'
label_path = 'evaluation_완성본.txt'
vehicleList = []
estimationList = []
answerList = []
allList = []
same = 0
opposite= 0
with open(label_path, encoding='utf-8') as f:
lines = f.readlines()
del lines[:1] # exclude the title of elements
for ii, line in enumerate(lines):
label = line.strip().split(' ')
allList.append(label)
vehicleList.append(ii+1)
a = float(label[-2])
estimationList.append(float(label[-2]))
answerList.append(float(label[-1]))
if label[1]=='same':
same+=1
else:
opposite +=1
print(f"same direction vehicle:{same}")
print(f"opposite direction vehicle:{opposite}")
#print(vehicleList)
#print(estimationList)
#print(answerList)
for ii, a in enumerate(estimationList):
if estimationList[ii]-answerList[ii] < -1:
print(ii)
print(estimationList[ii])
estimationArray = np.array(estimationList)
answerArray = np.array(answerList)
newArray = answerArray - estimationArray
newList = list(newArray)
print(np.mean(newArray))
plt.plot(vehicleList, estimationList, 'r',
vehicleList, answerList, 'y')
#plt.plot(newList)
plt.xlabel('#Vehicle')
plt.ylabel("Lateral Distance")
plt.show()
# Mean absolute error
from sklearn.metrics import mean_absolute_error as mae
from sklearn.metrics import mean_squared_error as mse
from math import sqrt
absolute_error = mae(answerArray, estimationArray)
square_error = mse(answerArray, estimationArray)
print("Mean absolute error: " + str(absolute_error))
print("Mean squared error: " + str(square_error))
print("Root mean squared error: " + str(sqrt(square_error)))
# Standard Error
from scipy.stats import sem
print("Standard Deviation of sample is % s "% (sem(answerArray - estimationArray)))
# Sort
def myFunc(e):
return float(e[2])
allList.sort(key=myFunc)
# 0<=aGroup<20 / 20<=bGroup<40 / 40<=cGroup
aGroup = []
aVehicle = []
a_estimationList = []
a_answerList = []
bGroup = []
bVehicle = []
b_estimationList = []
b_answerList = []
cGroup = []
cVehicle = []
c_estimationList = []
c_answerList = []
for i in allList:
if float(i[2])>= 0 and float(i[2])<20:
aGroup.append(i)
elif float(i[2])>= 20 and float(i[2])<40:
bGroup.append(i)
else:
cGroup.append(i)
for ii, a in enumerate(aGroup):
aVehicle.append(ii+1)
a_estimationList.append(float(a[-2]))
a_answerList.append(float(a[-1]))
for ii, a in enumerate(bGroup):
bVehicle.append(ii+1)
b_estimationList.append(float(a[-2]))
b_answerList.append(float(a[-1]))
for ii, a in enumerate(cGroup):
cVehicle.append(ii+1)
c_estimationList.append(float(a[-2]))
c_answerList.append(float(a[-1]))
a_estimationArray = np.array(a_estimationList)
a_answerArray = np.array(a_answerList)
anewArray = a_answerArray-a_estimationArray
anewList = list(anewArray)
b_estimationArray = np.array(b_estimationList)
b_answerArray = np.array(b_answerList)
bnewArray = b_answerArray-b_estimationArray
bnewList = list(bnewArray)
c_estimationArray = np.array(c_estimationList)
c_answerArray = np.array(c_answerList)
cnewArray = c_answerArray-c_estimationArray
cnewList = list(cnewArray)
print(len(aVehicle))
print(len(bVehicle))
print(len(cVehicle))
# Mean absolute error
from sklearn.metrics import mean_absolute_error as mae
from sklearn.metrics import mean_squared_error as mse
a_absolute_error = mae(a_answerArray, a_estimationArray)
a_square_error = mse(a_answerArray, a_estimationArray)
print("A Group's Mean absolute error: " + str(a_absolute_error))
print("A Group's Mean squared error: " + str(a_square_error))
# Standard Error
from scipy.stats import sem
print("A Group's Standard Deviation of sample is % s "% (sem(a_answerArray - a_estimationArray)))
# ---------- B Group
b_absolute_error = mae(b_answerArray, b_estimationArray)
b_square_error = mse(b_answerArray, b_estimationArray)
print("B Group's Mean absolute error: " + str(b_absolute_error))
print("B Group's Mean squared error: " + str(b_square_error))
print("B Group's Standard Deviation of sample is % s "% (sem(b_answerArray - b_estimationArray)))
# ---------- C Group
c_absolute_error = mae(c_answerArray, c_estimationArray)
c_square_error = mse(c_answerArray, c_estimationArray)
print("C Group's Mean absolute error: " + str(c_absolute_error))
print("C Group's Mean squared error: " + str(c_square_error))
print("C Group's Standard Deviation of sample is % s "% (sem(c_answerArray - c_estimationArray)))
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-4, 30)
plt.plot(aVehicle, a_estimationList, label = 'Algorithm', color='r')
plt.plot(aVehicle, a_answerList, label = 'Ground Truth', color='y', )
plt.legend(loc='upper right', ncol=2)
#plt.plot(aVehicle, a_estimationList, 'r',
# aVehicle, a_answerList, 'y')
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance")
plt.show()
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-4, 30)
plt.plot(bVehicle, b_estimationList, label = 'Algorithm', color='r')
plt.plot(bVehicle, b_answerList, label = 'Ground Truth', color='y', )
plt.legend(loc='upper right', ncol=2)
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance")
plt.show()
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-4, 30)
plt.plot(cVehicle, c_estimationList, label = 'Algorithm', color='r')
plt.plot(cVehicle, c_answerList, label = 'Ground Truth', color='y', )
plt.legend(loc='upper right', ncol=2)
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance")
plt.show()
# Error Graph Plotting
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-3, 3)
plt.plot(aVehicle, anewList, label = 'Algorithm', color='r')
plt.plot(aVehicle, [0]*len(aVehicle), label = 'Ground Truth', color='y', )
plt.legend(loc='best', ncol=2)
#plt.plot(aVehicle, a_estimationList, 'r',
# aVehicle, a_answerList, 'y')
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance Error")
plt.show()
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-3, 3)
plt.plot(bVehicle, bnewList, label = 'Algorithm', color='r')
plt.plot(bVehicle, [0]*len(bVehicle), label = 'Ground Truth', color='y', )
plt.legend(loc='best', ncol=2)
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance Error")
plt.show()
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-3, 3)
plt.plot(cVehicle, cnewList, label = 'Algorithm', color='r')
plt.plot(cVehicle, [0]*len(cVehicle), label = 'Ground Truth', color='y', )
plt.legend(loc='best', ncol=2)
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance Error")
plt.show()
```
|
github_jupyter
|
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
#label_path = 'evaluation(_855)완성.txt'
#label_path = 'evaluation(_3000).txt'
label_path = 'evaluation_완성본.txt'
vehicleList = []
estimationList = []
answerList = []
allList = []
same = 0
opposite= 0
with open(label_path, encoding='utf-8') as f:
lines = f.readlines()
del lines[:1] # exclude the title of elements
for ii, line in enumerate(lines):
label = line.strip().split(' ')
allList.append(label)
vehicleList.append(ii+1)
a = float(label[-2])
estimationList.append(float(label[-2]))
answerList.append(float(label[-1]))
if label[1]=='same':
same+=1
else:
opposite +=1
print(f"same direction vehicle:{same}")
print(f"opposite direction vehicle:{opposite}")
#print(vehicleList)
#print(estimationList)
#print(answerList)
for ii, a in enumerate(estimationList):
if estimationList[ii]-answerList[ii] < -1:
print(ii)
print(estimationList[ii])
estimationArray = np.array(estimationList)
answerArray = np.array(answerList)
newArray = answerArray - estimationArray
newList = list(newArray)
print(np.mean(newArray))
plt.plot(vehicleList, estimationList, 'r',
vehicleList, answerList, 'y')
#plt.plot(newList)
plt.xlabel('#Vehicle')
plt.ylabel("Lateral Distance")
plt.show()
# Mean absolute error
from sklearn.metrics import mean_absolute_error as mae
from sklearn.metrics import mean_squared_error as mse
from math import sqrt
absolute_error = mae(answerArray, estimationArray)
square_error = mse(answerArray, estimationArray)
print("Mean absolute error: " + str(absolute_error))
print("Mean squared error: " + str(square_error))
print("Root mean squared error: " + str(sqrt(square_error)))
# Standard Error
from scipy.stats import sem
print("Standard Deviation of sample is % s "% (sem(answerArray - estimationArray)))
# Sort
def myFunc(e):
return float(e[2])
allList.sort(key=myFunc)
# 0<=aGroup<20 / 20<=bGroup<40 / 40<=cGroup
aGroup = []
aVehicle = []
a_estimationList = []
a_answerList = []
bGroup = []
bVehicle = []
b_estimationList = []
b_answerList = []
cGroup = []
cVehicle = []
c_estimationList = []
c_answerList = []
for i in allList:
if float(i[2])>= 0 and float(i[2])<20:
aGroup.append(i)
elif float(i[2])>= 20 and float(i[2])<40:
bGroup.append(i)
else:
cGroup.append(i)
for ii, a in enumerate(aGroup):
aVehicle.append(ii+1)
a_estimationList.append(float(a[-2]))
a_answerList.append(float(a[-1]))
for ii, a in enumerate(bGroup):
bVehicle.append(ii+1)
b_estimationList.append(float(a[-2]))
b_answerList.append(float(a[-1]))
for ii, a in enumerate(cGroup):
cVehicle.append(ii+1)
c_estimationList.append(float(a[-2]))
c_answerList.append(float(a[-1]))
a_estimationArray = np.array(a_estimationList)
a_answerArray = np.array(a_answerList)
anewArray = a_answerArray-a_estimationArray
anewList = list(anewArray)
b_estimationArray = np.array(b_estimationList)
b_answerArray = np.array(b_answerList)
bnewArray = b_answerArray-b_estimationArray
bnewList = list(bnewArray)
c_estimationArray = np.array(c_estimationList)
c_answerArray = np.array(c_answerList)
cnewArray = c_answerArray-c_estimationArray
cnewList = list(cnewArray)
print(len(aVehicle))
print(len(bVehicle))
print(len(cVehicle))
# Mean absolute error
from sklearn.metrics import mean_absolute_error as mae
from sklearn.metrics import mean_squared_error as mse
a_absolute_error = mae(a_answerArray, a_estimationArray)
a_square_error = mse(a_answerArray, a_estimationArray)
print("A Group's Mean absolute error: " + str(a_absolute_error))
print("A Group's Mean squared error: " + str(a_square_error))
# Standard Error
from scipy.stats import sem
print("A Group's Standard Deviation of sample is % s "% (sem(a_answerArray - a_estimationArray)))
# ---------- B Group
b_absolute_error = mae(b_answerArray, b_estimationArray)
b_square_error = mse(b_answerArray, b_estimationArray)
print("B Group's Mean absolute error: " + str(b_absolute_error))
print("B Group's Mean squared error: " + str(b_square_error))
print("B Group's Standard Deviation of sample is % s "% (sem(b_answerArray - b_estimationArray)))
# ---------- C Group
c_absolute_error = mae(c_answerArray, c_estimationArray)
c_square_error = mse(c_answerArray, c_estimationArray)
print("C Group's Mean absolute error: " + str(c_absolute_error))
print("C Group's Mean squared error: " + str(c_square_error))
print("C Group's Standard Deviation of sample is % s "% (sem(c_answerArray - c_estimationArray)))
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-4, 30)
plt.plot(aVehicle, a_estimationList, label = 'Algorithm', color='r')
plt.plot(aVehicle, a_answerList, label = 'Ground Truth', color='y', )
plt.legend(loc='upper right', ncol=2)
#plt.plot(aVehicle, a_estimationList, 'r',
# aVehicle, a_answerList, 'y')
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance")
plt.show()
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-4, 30)
plt.plot(bVehicle, b_estimationList, label = 'Algorithm', color='r')
plt.plot(bVehicle, b_answerList, label = 'Ground Truth', color='y', )
plt.legend(loc='upper right', ncol=2)
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance")
plt.show()
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-4, 30)
plt.plot(cVehicle, c_estimationList, label = 'Algorithm', color='r')
plt.plot(cVehicle, c_answerList, label = 'Ground Truth', color='y', )
plt.legend(loc='upper right', ncol=2)
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance")
plt.show()
# Error Graph Plotting
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-3, 3)
plt.plot(aVehicle, anewList, label = 'Algorithm', color='r')
plt.plot(aVehicle, [0]*len(aVehicle), label = 'Ground Truth', color='y', )
plt.legend(loc='best', ncol=2)
#plt.plot(aVehicle, a_estimationList, 'r',
# aVehicle, a_answerList, 'y')
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance Error")
plt.show()
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-3, 3)
plt.plot(bVehicle, bnewList, label = 'Algorithm', color='r')
plt.plot(bVehicle, [0]*len(bVehicle), label = 'Ground Truth', color='y', )
plt.legend(loc='best', ncol=2)
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance Error")
plt.show()
fig, ax = plt.subplots()
#ax.set_xlim(-10, 10)
ax.set_ylim(-3, 3)
plt.plot(cVehicle, cnewList, label = 'Algorithm', color='r')
plt.plot(cVehicle, [0]*len(cVehicle), label = 'Ground Truth', color='y', )
plt.legend(loc='best', ncol=2)
plt.xlabel('Vehicle#')
plt.ylabel("Lateral Distance Error")
plt.show()
| 0.490724 | 0.454654 |
```
from google.colab import drive
drive.mount('/content/drive')
cd /content/drive/MyDrive/ML-LaDECO/LaDECO
import numpy as np
print('Project MLaDECO')
print('Author: Viswambhar Yasa')
print('Software version: 0.1')
from sklearn.preprocessing import MinMaxScaler, StandardScaler
import tensorflow as tf
from tensorflow.keras import models
from thermograms.Utilities import Utilities
from ml_training.dataset_generation.fourier_transformation import fourier_transformation
from ml_training.dataset_generation.principal_componant_analysis import principal_componant_analysis
from utilites.segmentation_colormap_anno import segmentation_colormap_anno
from utilites.tolerance_maks_gen import tolerance_predicted_mask
import matplotlib.pyplot as plt
root_path = r'utilites/datasets'
data_file_name = r'material_thickness_1000W.hdf5'
thermal_class = Utilities()
thermal_data,experiment_list=thermal_class.open_file(root_path, data_file_name,True)
experiment_name=r'2021-12-07-Materialstudie-5.2-40µmS1013-1000W-10s'
experimental_data=thermal_data[experiment_name]
experiment_thickness=[]
for experiment in experiment_list.values():
index=0
thickness=0
while True:
index = experiment.find("µm",index+1)
if index==-1:
break
thickness+=int(experiment[index-2:index])*0.001
print(experiment,':',thickness)
experiment_thickness.append(thickness)
experiment_thickness[4]=0.04
experiment_thickness[12]=0.08
number_of_classes=15
bins=np.linspace(0.001,0.1,number_of_classes+1)
bins
plt.hist(experiment_thickness, bins)
plt.xlabel('thickness classes (mm)')
plt.ylabel('Number of datasets')
plt.grid()
count, _ = np.histogram(experiment_thickness, bins)
decades = np.arange(1910, 2020, 10)
colors = ['aqua', 'red', 'gold', 'royalblue', 'darkorange', 'green', 'purple', 'cyan', 'yellow', 'lime']
plt.figure(figsize=(12,6))
plt.hist(experiment_thickness, bins, edgecolor='red',
linewidth=2)
plt.xlabel('Thickness Classes (mm)')
plt.ylabel('Number of datasets')
plt.xticks(bins);
plt.grid()
i=0
for x,y in zip(bins,count):
plt.text(x+0.0025, y+0.2, i, fontsize=10)
i+=1
plt.savefig(r"/content/thickness_bins.png",dpi=100,bbox_inches='tight')
thickness_classes=np.digitize(experiment_thickness,bins)
thickness_classes
import tensorflow as tf
EOF=principal_componant_analysis(np.array(experimental_data))
plt.imshow(np.squeeze(EOF))
plt.colorbar()
input_data,ref_st_index,ref_end_index=fourier_transformation(experimental_data)
from ml_training.dataset_generation.data_preprocessing import thickness_data_preprocessing
x_train_ds=thickness_data_preprocessing(thermal_data,experiment_list)
y_train_ds=tf.one_hot(thickness_classes,number_of_classes)
x_train_ds.shape,y_train_ds.shape
from therml.ml_models import Thickness_estimation
thickness_nn=Thickness_estimation()
thickness_model_GRU=thickness_nn.thickness_model(type='GRU')
thickness_model_GRU.compile(optimizer=tf.keras.optimizers.Adam(),loss=tf.losses.categorical_crossentropy,
metrics=['accuracy'])
from sklearn.utils import class_weight
weights=class_weight.compute_class_weight(class_weight='balanced',classes=np.unique(thickness_classes),y=thickness_classes)
inbalanced_weight=dict(zip(np.unique(thickness_classes),weights))
inbalanced_weight
for i in range(number_of_classes):
if i in inbalanced_weight:
continue
else:
inbalanced_weight[i]=0.0
inbalanced_weight
stopping_criteria=tf.keras.callbacks.EarlyStopping(monitor='accuracy', baseline=0.90, patience=5)
model_history=thickness_model_GRU.fit(x_train_ds,y_train_ds,epochs=500,class_weight=inbalanced_weight,shuffle=True,batch_size=8
)
model_para=model_history.history
model_para=model_history.history
path=r'trained_models\GRU\model_history\\'
filename="PSP.pkl"
file_path=path+filename
import pickle
# define dictionary
# create a binary pickle file
f = open(file_path,"wb")
# write the python object (dict) to pickle file
pickle.dump(model_para,f)
# close file
f.close()
thickness_model_GRU.evaluate(x_train_ds,y_train_ds)
y_predicted=thickness_model_GRU.predict_on_batch(x_train_ds)
thickness_classes,np.argmax(y_predicted,axis=1)
x_train_ds.shape
thickness_classes
y_pred=np.argmax(y_predicted,axis=1)
plt.figure(figsize=(8,4))
plt.plot(np.squeeze(x_train_ds[1,:,:]),label="Materialstudie-5.2-40µmS1013 : class-"+str(thickness_classes[1]),linewidth=2)
plt.plot(np.squeeze(x_train_ds[4,:,:]),label="Materialstudie-7.2-EW38-505_40 µmS1013: class-"+str(thickness_classes[4]),linewidth=2)
plt.plot(np.squeeze(x_train_ds[-4,:,:]),label="Materialstudie-8.6-40µmS1013_40µm_S9005_schwarz: class-"+str(thickness_classes[-4]),linewidth=2)
plt.plot(np.squeeze(x_train_ds[-1,:,:]),label="Materialstudie-S1-Silikatischer_Beton: class-"+str(thickness_classes[-1]),linewidth=2)
plt.legend()
plt.text(201,np.squeeze(x_train_ds[1,:,-1]),'prediction: '+str(y_pred[1]),color='tab:blue')
plt.text(201,np.squeeze(x_train_ds[4,:,-1]),'prediction: '+str(y_pred[4]),color='tab:orange')
plt.text(201,np.squeeze(x_train_ds[-4,:,-1]),'prediction: '+str(y_pred[-4]),color='tab:green')
plt.text(201,np.squeeze(x_train_ds[-1,:,-1]),'prediction: '+str(y_pred[-1]),color='tab:red')
plt.xlabel('Time(frames)')
plt.ylabel('contrast')
plt.grid()
plt.xlim(0,240)
#plt.savefig("/content/thermal_coating_thickness_1.png",dpi=100,bbox_inches='tight',transparent=True)
model_save_path=r'trained_models\GRU\\'
model_name=r'GRU.h5'
model_path=model_save_path+model_name
thickness_model_GRU.save(model_path,overwrite=False)
j=1
pr=np.expand_dims(x_train_ds[j,:,:],axis=0)
thickness=thickness_model_GRU.predict(pr)
index=np.argmax(thickness)
index,experiment_thickness[j]
j=6
pr=np.expand_dims(x_train_ds[j,:,:],axis=0)
thickness=thickness_model_GRU.predict(pr)
index=np.argmax(thickness)
index,experiment_thickness[j]
root_path = r'utilites/datasets'
data_file_name = r'material_thickness_1000W_5s.hdf5'
a = Utilities()
thermal_test_data,experiment_test_list=a.open_file(root_path, data_file_name,True)
#experiment = '2021-05-11 - Variantenvergleich - VarioTherm Halogenlampe - Winkel 45°'
experiment_name=r'2021-12-07-Materialstudie-5.2-40µmS1013-1000W-5s'
experimental_data=thermal_test_data[experiment_name]
x_test_ds=thickness_data_preprocessing(thermal_test_data,experiment_test_list)
experiment_test_thickness=[]
for experiment in experiment_test_list.values():
index=0
thickness=0
while True:
index = experiment.find("µm",index+1)
if index==-1:
break
thickness+=int(experiment[index-2:index])*0.001
print(experiment,':',thickness)
experiment_test_thickness.append(thickness)
thickness_classes=np.digitize(experiment_test_thickness,bins)
y_test_ds=tf.one_hot(thickness_classes,number_of_classes)
thickness_model_GRU.evaluate(x_test_ds,y_test_ds)
thickness_model_GRU.evaluate(x_test_ds,y_test_ds)
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/drive')
cd /content/drive/MyDrive/ML-LaDECO/LaDECO
import numpy as np
print('Project MLaDECO')
print('Author: Viswambhar Yasa')
print('Software version: 0.1')
from sklearn.preprocessing import MinMaxScaler, StandardScaler
import tensorflow as tf
from tensorflow.keras import models
from thermograms.Utilities import Utilities
from ml_training.dataset_generation.fourier_transformation import fourier_transformation
from ml_training.dataset_generation.principal_componant_analysis import principal_componant_analysis
from utilites.segmentation_colormap_anno import segmentation_colormap_anno
from utilites.tolerance_maks_gen import tolerance_predicted_mask
import matplotlib.pyplot as plt
root_path = r'utilites/datasets'
data_file_name = r'material_thickness_1000W.hdf5'
thermal_class = Utilities()
thermal_data,experiment_list=thermal_class.open_file(root_path, data_file_name,True)
experiment_name=r'2021-12-07-Materialstudie-5.2-40µmS1013-1000W-10s'
experimental_data=thermal_data[experiment_name]
experiment_thickness=[]
for experiment in experiment_list.values():
index=0
thickness=0
while True:
index = experiment.find("µm",index+1)
if index==-1:
break
thickness+=int(experiment[index-2:index])*0.001
print(experiment,':',thickness)
experiment_thickness.append(thickness)
experiment_thickness[4]=0.04
experiment_thickness[12]=0.08
number_of_classes=15
bins=np.linspace(0.001,0.1,number_of_classes+1)
bins
plt.hist(experiment_thickness, bins)
plt.xlabel('thickness classes (mm)')
plt.ylabel('Number of datasets')
plt.grid()
count, _ = np.histogram(experiment_thickness, bins)
decades = np.arange(1910, 2020, 10)
colors = ['aqua', 'red', 'gold', 'royalblue', 'darkorange', 'green', 'purple', 'cyan', 'yellow', 'lime']
plt.figure(figsize=(12,6))
plt.hist(experiment_thickness, bins, edgecolor='red',
linewidth=2)
plt.xlabel('Thickness Classes (mm)')
plt.ylabel('Number of datasets')
plt.xticks(bins);
plt.grid()
i=0
for x,y in zip(bins,count):
plt.text(x+0.0025, y+0.2, i, fontsize=10)
i+=1
plt.savefig(r"/content/thickness_bins.png",dpi=100,bbox_inches='tight')
thickness_classes=np.digitize(experiment_thickness,bins)
thickness_classes
import tensorflow as tf
EOF=principal_componant_analysis(np.array(experimental_data))
plt.imshow(np.squeeze(EOF))
plt.colorbar()
input_data,ref_st_index,ref_end_index=fourier_transformation(experimental_data)
from ml_training.dataset_generation.data_preprocessing import thickness_data_preprocessing
x_train_ds=thickness_data_preprocessing(thermal_data,experiment_list)
y_train_ds=tf.one_hot(thickness_classes,number_of_classes)
x_train_ds.shape,y_train_ds.shape
from therml.ml_models import Thickness_estimation
thickness_nn=Thickness_estimation()
thickness_model_GRU=thickness_nn.thickness_model(type='GRU')
thickness_model_GRU.compile(optimizer=tf.keras.optimizers.Adam(),loss=tf.losses.categorical_crossentropy,
metrics=['accuracy'])
from sklearn.utils import class_weight
weights=class_weight.compute_class_weight(class_weight='balanced',classes=np.unique(thickness_classes),y=thickness_classes)
inbalanced_weight=dict(zip(np.unique(thickness_classes),weights))
inbalanced_weight
for i in range(number_of_classes):
if i in inbalanced_weight:
continue
else:
inbalanced_weight[i]=0.0
inbalanced_weight
stopping_criteria=tf.keras.callbacks.EarlyStopping(monitor='accuracy', baseline=0.90, patience=5)
model_history=thickness_model_GRU.fit(x_train_ds,y_train_ds,epochs=500,class_weight=inbalanced_weight,shuffle=True,batch_size=8
)
model_para=model_history.history
model_para=model_history.history
path=r'trained_models\GRU\model_history\\'
filename="PSP.pkl"
file_path=path+filename
import pickle
# define dictionary
# create a binary pickle file
f = open(file_path,"wb")
# write the python object (dict) to pickle file
pickle.dump(model_para,f)
# close file
f.close()
thickness_model_GRU.evaluate(x_train_ds,y_train_ds)
y_predicted=thickness_model_GRU.predict_on_batch(x_train_ds)
thickness_classes,np.argmax(y_predicted,axis=1)
x_train_ds.shape
thickness_classes
y_pred=np.argmax(y_predicted,axis=1)
plt.figure(figsize=(8,4))
plt.plot(np.squeeze(x_train_ds[1,:,:]),label="Materialstudie-5.2-40µmS1013 : class-"+str(thickness_classes[1]),linewidth=2)
plt.plot(np.squeeze(x_train_ds[4,:,:]),label="Materialstudie-7.2-EW38-505_40 µmS1013: class-"+str(thickness_classes[4]),linewidth=2)
plt.plot(np.squeeze(x_train_ds[-4,:,:]),label="Materialstudie-8.6-40µmS1013_40µm_S9005_schwarz: class-"+str(thickness_classes[-4]),linewidth=2)
plt.plot(np.squeeze(x_train_ds[-1,:,:]),label="Materialstudie-S1-Silikatischer_Beton: class-"+str(thickness_classes[-1]),linewidth=2)
plt.legend()
plt.text(201,np.squeeze(x_train_ds[1,:,-1]),'prediction: '+str(y_pred[1]),color='tab:blue')
plt.text(201,np.squeeze(x_train_ds[4,:,-1]),'prediction: '+str(y_pred[4]),color='tab:orange')
plt.text(201,np.squeeze(x_train_ds[-4,:,-1]),'prediction: '+str(y_pred[-4]),color='tab:green')
plt.text(201,np.squeeze(x_train_ds[-1,:,-1]),'prediction: '+str(y_pred[-1]),color='tab:red')
plt.xlabel('Time(frames)')
plt.ylabel('contrast')
plt.grid()
plt.xlim(0,240)
#plt.savefig("/content/thermal_coating_thickness_1.png",dpi=100,bbox_inches='tight',transparent=True)
model_save_path=r'trained_models\GRU\\'
model_name=r'GRU.h5'
model_path=model_save_path+model_name
thickness_model_GRU.save(model_path,overwrite=False)
j=1
pr=np.expand_dims(x_train_ds[j,:,:],axis=0)
thickness=thickness_model_GRU.predict(pr)
index=np.argmax(thickness)
index,experiment_thickness[j]
j=6
pr=np.expand_dims(x_train_ds[j,:,:],axis=0)
thickness=thickness_model_GRU.predict(pr)
index=np.argmax(thickness)
index,experiment_thickness[j]
root_path = r'utilites/datasets'
data_file_name = r'material_thickness_1000W_5s.hdf5'
a = Utilities()
thermal_test_data,experiment_test_list=a.open_file(root_path, data_file_name,True)
#experiment = '2021-05-11 - Variantenvergleich - VarioTherm Halogenlampe - Winkel 45°'
experiment_name=r'2021-12-07-Materialstudie-5.2-40µmS1013-1000W-5s'
experimental_data=thermal_test_data[experiment_name]
x_test_ds=thickness_data_preprocessing(thermal_test_data,experiment_test_list)
experiment_test_thickness=[]
for experiment in experiment_test_list.values():
index=0
thickness=0
while True:
index = experiment.find("µm",index+1)
if index==-1:
break
thickness+=int(experiment[index-2:index])*0.001
print(experiment,':',thickness)
experiment_test_thickness.append(thickness)
thickness_classes=np.digitize(experiment_test_thickness,bins)
y_test_ds=tf.one_hot(thickness_classes,number_of_classes)
thickness_model_GRU.evaluate(x_test_ds,y_test_ds)
thickness_model_GRU.evaluate(x_test_ds,y_test_ds)
| 0.410402 | 0.274961 |
<img src="https://raw.githubusercontent.com/Qiskit/qiskit-tutorials/master/images/qiskit-heading.png" width="500 px" align="center">
# _*Qiskit Aqua: Experimenting with Traveling Salesman problem with variational quantum eigensolver*_
This notebook is based on an official notebook by Qiskit team, available at https://github.com/qiskit/qiskit-tutorial under the [Apache License 2.0](https://github.com/Qiskit/qiskit-tutorial/blob/master/LICENSE) license.
The original notebook was developed by Antonio Mezzacapo<sup>[1]</sup>, Jay Gambetta<sup>[1]</sup>, Kristan Temme<sup>[1]</sup>, Ramis Movassagh<sup>[1]</sup>, Albert Frisch<sup>[1]</sup>, Takashi Imamichi<sup>[1]</sup>, Giacomo Nannicni<sup>[1]</sup>, Richard Chen<sup>[1]</sup>, Marco Pistoia<sup>[1]</sup>, Stephen Wood<sup>[1]</sup>(<sup>[1]</sup>IBMQ)
Your **TASK** is to execute every step of this notebook while learning to use qiskit-aqua and also how to leverage general problem modeling into know problems that qiskit-aqua can solve, namely the [Travelling salesman problem](https://en.wikipedia.org/wiki/Travelling_salesman_problem).
## Introduction
Many problems in quantitative fields such as finance and engineering are optimization problems. Optimization problems lay at the core of complex decision-making and definition of strategies.
Optimization (or combinatorial optimization) means searching for an optimal solution in a finite or countably infinite set of potential solutions. Optimality is defined with respect to some criterion function, which is to be minimized or maximized. This is typically called cost function or objective function.
**Typical optimization problems**
Minimization: cost, distance, length of a traversal, weight, processing time, material, energy consumption, number of objects
Maximization: profit, value, output, return, yield, utility, efficiency, capacity, number of objects
We consider here max-cut problem of practical interest in many fields, and show how they can mapped on quantum computers.
### Weighted Max-Cut
Max-Cut is an NP-complete problem, with applications in clustering, network science, and statistical physics. To grasp how practical applications are mapped into given Max-Cut instances, consider a system of many people that can interact and influence each other. Individuals can be represented by vertices of a graph, and their interactions seen as pairwise connections between vertices of the graph, or edges. With this representation in mind, it is easy to model typical marketing problems. For example, suppose that it is assumed that individuals will influence each other's buying decisions, and knowledge is given about how strong they will influence each other. The influence can be modeled by weights assigned on each edge of the graph. It is possible then to predict the outcome of a marketing strategy in which products are offered for free to some individuals, and then ask which is the optimal subset of individuals that should get the free products, in order to maximize revenues.
The formal definition of this problem is the following:
Consider an $n$-node undirected graph *G = (V, E)* where *|V| = n* with edge weights $w_{ij}>0$, $w_{ij}=w_{ji}$, for $(i, j)\in E$. A cut is defined as a partition of the original set V into two subsets. The cost function to be optimized is in this case the sum of weights of edges connecting points in the two different subsets, *crossing* the cut. By assigning $x_i=0$ or $x_i=1$ to each node $i$, one tries to maximize the global profit function (here and in the following summations run over indices 0,1,...n-1)
$$\tilde{C}(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j).$$
In our simple marketing model, $w_{ij}$ represents the probability that the person $j$ will buy a product after $i$ gets a free one. Note that the weights $w_{ij}$ can in principle be greater than $1$, corresponding to the case where the individual $j$ will buy more than one product. Maximizing the total buying probability corresponds to maximizing the total future revenues. In the case where the profit probability will be greater than the cost of the initial free samples, the strategy is a convenient one. An extension to this model has the nodes themselves carry weights, which can be regarded, in our marketing model, as the likelihood that a person granted with a free sample of the product will buy it again in the future. With this additional information in our model, the objective function to maximize becomes
$$C(\textbf{x}) = \sum_{i,j} w_{ij} x_i (1-x_j)+\sum_i w_i x_i. $$
In order to find a solution to this problem on a quantum computer, one needs first to map it to an Ising Hamiltonian. This can be done with the assignment $x_i\rightarrow (1-Z_i)/2$, where $Z_i$ is the Pauli Z operator that has eigenvalues $\pm 1$. Doing this we find that
$$C(\textbf{Z}) = \sum_{i,j} \frac{w_{ij}}{4} (1-Z_i)(1+Z_j) + \sum_i \frac{w_i}{2} (1-Z_i) = -\frac{1}{2}\left( \sum_{i<j} w_{ij} Z_i Z_j +\sum_i w_i Z_i\right)+\mathrm{const},$$
where const = $\sum_{i<j}w_{ij}/2+\sum_i w_i/2 $. In other terms, the weighted Max-Cut problem is equivalent to minimizing the Ising Hamiltonian
$$ H = \sum_i w_i Z_i + \sum_{i<j} w_{ij} Z_iZ_j.$$
Aqua can generate the Ising Hamiltonian for the first profit function $\tilde{C}$.
### Approximate Universal Quantum Computing for Optimization Problems
There has been a considerable amount of interest in recent times about the use of quantum computers to find a solution to combinatorial problems. It is important to say that, given the classical nature of combinatorial problems, exponential speedup in using quantum computers compared to the best classical algorithms is not guaranteed. However, due to the nature and importance of the target problems, it is worth investigating heuristic approaches on a quantum computer that could indeed speed up some problem instances. Here we demonstrate an approach that is based on the Quantum Approximate Optimization Algorithm by Farhi, Goldstone, and Gutman (2014). We frame the algorithm in the context of *approximate quantum computing*, given its heuristic nature.
The Algorithm works as follows:
1. Choose the $w_i$ and $w_{ij}$ in the target Ising problem. In principle, even higher powers of Z are allowed.
2. Choose the depth of the quantum circuit $m$. Note that the depth can be modified adaptively.
3. Choose a set of controls $\theta$ and make a trial function $|\psi(\boldsymbol\theta)\rangle$, built using a quantum circuit made of C-Phase gates and single-qubit Y rotations, parameterized by the components of $\boldsymbol\theta$.
4. Evaluate $C(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)~|H|~\psi(\boldsymbol\theta)\rangle = \sum_i w_i \langle\psi(\boldsymbol\theta)~|Z_i|~\psi(\boldsymbol\theta)\rangle+ \sum_{i<j} w_{ij} \langle\psi(\boldsymbol\theta)~|Z_iZ_j|~\psi(\boldsymbol\theta)\rangle$ by sampling the outcome of the circuit in the Z-basis and adding the expectation values of the individual Ising terms together. In general, different control points around $\boldsymbol\theta$ have to be estimated, depending on the classical optimizer chosen.
5. Use a classical optimizer to choose a new set of controls.
6. Continue until $C(\boldsymbol\theta)$ reaches a minimum, close enough to the solution $\boldsymbol\theta^*$.
7. Use the last $\boldsymbol\theta$ to generate a final set of samples from the distribution $|\langle z_i~|\psi(\boldsymbol\theta)\rangle|^2\;\forall i$ to obtain the answer.
It is our belief the difficulty of finding good heuristic algorithms will come down to the choice of an appropriate trial wavefunction. For example, one could consider a trial function whose entanglement best aligns with the target problem, or simply make the amount of entanglement a variable. In this tutorial, we will consider a simple trial function of the form
$$|\psi(\theta)\rangle = [U_\mathrm{single}(\boldsymbol\theta) U_\mathrm{entangler}]^m |+\rangle$$
where $U_\mathrm{entangler}$ is a collection of C-Phase gates (fully entangling gates), and $U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})$, where $n$ is the number of qubits and $m$ is the depth of the quantum circuit. The motivation for this choice is that for these classical problems this choice allows us to search over the space of quantum states that have only real coefficients, still exploiting the entanglement to potentially converge faster to the solution.
One advantage of using this sampling method compared to adiabatic approaches is that the target Ising Hamiltonian does not have to be implemented directly on hardware, allowing this algorithm not to be limited to the connectivity of the device. Furthermore, higher-order terms in the cost function, such as $Z_iZ_jZ_k$, can also be sampled efficiently, whereas in adiabatic or annealing approaches they are generally impractical to deal with.
References:
- A. Lucas, Frontiers in Physics 2, 5 (2014)
- E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028 (2014)
- D. Wecker, M. B. Hastings, M. Troyer Phys. Rev. A 94, 022309 (2016)
- E. Farhi, J. Goldstone, S. Gutmann, H. Neven e-print arXiv 1703.06199 (2017)
```
# useful additional packages
import matplotlib.pyplot as plt
import matplotlib.axes as axes
%matplotlib inline
import numpy as np
import networkx as nx
from qiskit.tools.visualization import plot_histogram
from qiskit.aqua import Operator, run_algorithm, get_algorithm_instance
from qiskit.aqua.input import get_input_instance
from qiskit.aqua.translators.ising import max_cut, tsp
# setup aqua logging
import logging
from qiskit.aqua._logging import set_logging_config, build_logging_config
# set_logging_config(build_logging_config(logging.DEBUG)) # choose INFO, DEBUG to see the log
# ignoring deprecation errors on matplotlib
import warnings
import matplotlib.cbook
warnings.filterwarnings("ignore",category=matplotlib.cbook.mplDeprecation)
```
### [Optional] Setup token to run the experiment on a real device
If you would like to run the experiement on a real device, you need to setup your account first.
Note: If you do not store your token yet, use `IBMQ.save_accounts()` to store it first.
```
from qiskit import IBMQ
IBMQ.load_account()
```
## Traveling Salesman Problem
In addition to being a notorious NP-complete problem that has drawn the attention of computer scientists and mathematicians for over two centuries, the Traveling Salesman Problem (TSP) has important bearings on finance and marketing, as its name suggests. Colloquially speaking, the traveling salesman is a person that goes from city to city to sell merchandise. The objective in this case is to find the shortest path that would enable the salesman to visit all the cities and return to its hometown, i.e. the city where he started traveling. By doing this, the salesman gets to maximize potential sales in the least amount of time.
The problem derives its importance from its "hardness" and ubiquitous equivalence to other relevant combinatorial optimization problems that arise in practice.
The mathematical formulation with some early analysis was proposed by W.R. Hamilton in the early 19th century. Mathematically the problem is, as in the case of Max-Cut, best abstracted in terms of graphs. The TSP on the nodes of a graph asks for the shortest *Hamiltonian cycle* that can be taken through each of the nodes. A Hamilton cycle is a closed path that uses every vertex of a graph once. The general solution is unknown and an algorithm that finds it efficiently (e.g., in polynomial time) is not expected to exist.
Find the shortest Hamiltonian cycle in a graph $G=(V,E)$ with $n=|V|$ nodes and distances, $w_{ij}$ (distance from vertex $i$ to vertex $j$). A Hamiltonian cycle is described by $N^2$ variables $x_{i,p}$, where $i$ represents the node and $p$ represents its order in a prospective cycle. The decision variable takes the value 1 if the solution occurs at node $i$ at time order $p$. We require that every node can only appear once in the cycle, and for each time a node has to occur. This amounts to the two constraints (here and in the following, whenever not specified, the summands run over 0,1,...N-1)
$$\sum_{i} x_{i,p} = 1 ~~\forall p$$
$$\sum_{p} x_{i,p} = 1 ~~\forall i.$$
For nodes in our prospective ordering, if $x_{i,p}$ and $x_{j,p+1}$ are both 1, then there should be an energy penalty if $(i,j) \notin E$ (not connected in the graph). The form of this penalty is
$$\sum_{i,j\notin E}\sum_{p} x_{i,p}x_{j,p+1}>0,$$
where it is assumed the boundary condition of the Hamiltonian cycle $(p=N)\equiv (p=0)$. However, here it will be assumed a fully connected graph and not include this term. The distance that needs to be minimized is
$$C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}.$$
Putting this all together in a single objective function to be minimized, we get the following:
$$C(\textbf{x})=\sum_{i,j}w_{ij}\sum_{p} x_{i,p}x_{j,p+1}+ A\sum_p\left(1- \sum_i x_{i,p}\right)^2+A\sum_i\left(1- \sum_p x_{i,p}\right)^2,$$
where $A$ is a free parameter. One needs to ensure that $A$ is large enough so that these constraints are respected. One way to do this is to choose $A$ such that $A > \mathrm{max}(w_{ij})$.
Once again, it is easy to map the problem in this form to a quantum computer, and the solution will be found by minimizing a Ising Hamiltonian.
```
# Generating a graph of 3 nodes
n = 3
num_qubits = n ** 2
ins = tsp.random_tsp(n)
G = nx.Graph()
G.add_nodes_from(np.arange(0, n, 1))
colors = ['r' for node in G.nodes()]
pos = {k: v for k, v in enumerate(ins.coord)}
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G, node_color=colors, node_size=600, alpha=.8, ax=default_axes, pos=pos)
print('distance\n', ins.w)
```
### Brute force approach
```
from itertools import permutations
def brute_force_tsp(w, N):
a=list(permutations(range(1,N)))
last_best_distance = 1e10
for i in a:
distance = 0
pre_j = 0
for j in i:
distance = distance + w[j,pre_j]
pre_j = j
distance = distance + w[pre_j,0]
order = (0,) + i
if distance < last_best_distance:
best_order = order
last_best_distance = distance
print('order = ' + str(order) + ' Distance = ' + str(distance))
return last_best_distance, best_order
best_distance, best_order = brute_force_tsp(ins.w, ins.dim)
print('Best order from brute force = ' + str(best_order) + ' with total distance = ' + str(best_distance))
def draw_tsp_solution(G, order, colors, pos):
G2 = G.copy()
n = len(order)
for i in range(n):
j = (i + 1) % n
G2.add_edge(order[i], order[j])
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G2, node_color=colors, node_size=600, alpha=.8, ax=default_axes, pos=pos)
draw_tsp_solution(G, best_order, colors, pos)
```
### Mapping to the Ising problem
```
qubitOp, offset = tsp.get_tsp_qubitops(ins)
algo_input = get_input_instance('EnergyInput')
algo_input.qubit_op = qubitOp
```
### Checking that the full Hamiltonian gives the right cost
```
#Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
algorithm_cfg = {
'name': 'ExactEigensolver',
}
params = {
'problem': {'name': 'ising'},
'algorithm': algorithm_cfg
}
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
```
### Running it on quantum computer
We run the optimization routine using a feedback loop with a quantum computer that uses trial functions built with Y single-qubit rotations, $U_\mathrm{single}(\theta) = \prod_{i=1}^n Y(\theta_{i})$, and entangler steps $U_\mathrm{entangler}$.
```
algorithm_cfg = {
'name': 'VQE',
'operator_mode': 'matrix'
}
optimizer_cfg = {
'name': 'SPSA',
'max_trials': 300
}
var_form_cfg = {
'name': 'RY',
'depth': 5,
'entanglement': 'linear'
}
params = {
'problem': {'name': 'ising', 'random_seed': 10598},
'algorithm': algorithm_cfg,
'optimizer': optimizer_cfg,
'variational_form': var_form_cfg,
'backend': {'name': 'statevector_simulator'}
}
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
print('time:', result['eval_time'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
# run quantum algorithm with shots
params['algorithm']['operator_mode'] = 'grouped_paulis'
params['backend']['name'] = 'qasm_simulator'
params['backend']['shots'] = 1024
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
print('time:', result['eval_time'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
plot_histogram(result['eigvecs'][0])
draw_tsp_solution(G, z, colors, pos)
```
|
github_jupyter
|
# useful additional packages
import matplotlib.pyplot as plt
import matplotlib.axes as axes
%matplotlib inline
import numpy as np
import networkx as nx
from qiskit.tools.visualization import plot_histogram
from qiskit.aqua import Operator, run_algorithm, get_algorithm_instance
from qiskit.aqua.input import get_input_instance
from qiskit.aqua.translators.ising import max_cut, tsp
# setup aqua logging
import logging
from qiskit.aqua._logging import set_logging_config, build_logging_config
# set_logging_config(build_logging_config(logging.DEBUG)) # choose INFO, DEBUG to see the log
# ignoring deprecation errors on matplotlib
import warnings
import matplotlib.cbook
warnings.filterwarnings("ignore",category=matplotlib.cbook.mplDeprecation)
from qiskit import IBMQ
IBMQ.load_account()
# Generating a graph of 3 nodes
n = 3
num_qubits = n ** 2
ins = tsp.random_tsp(n)
G = nx.Graph()
G.add_nodes_from(np.arange(0, n, 1))
colors = ['r' for node in G.nodes()]
pos = {k: v for k, v in enumerate(ins.coord)}
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G, node_color=colors, node_size=600, alpha=.8, ax=default_axes, pos=pos)
print('distance\n', ins.w)
from itertools import permutations
def brute_force_tsp(w, N):
a=list(permutations(range(1,N)))
last_best_distance = 1e10
for i in a:
distance = 0
pre_j = 0
for j in i:
distance = distance + w[j,pre_j]
pre_j = j
distance = distance + w[pre_j,0]
order = (0,) + i
if distance < last_best_distance:
best_order = order
last_best_distance = distance
print('order = ' + str(order) + ' Distance = ' + str(distance))
return last_best_distance, best_order
best_distance, best_order = brute_force_tsp(ins.w, ins.dim)
print('Best order from brute force = ' + str(best_order) + ' with total distance = ' + str(best_distance))
def draw_tsp_solution(G, order, colors, pos):
G2 = G.copy()
n = len(order)
for i in range(n):
j = (i + 1) % n
G2.add_edge(order[i], order[j])
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G2, node_color=colors, node_size=600, alpha=.8, ax=default_axes, pos=pos)
draw_tsp_solution(G, best_order, colors, pos)
qubitOp, offset = tsp.get_tsp_qubitops(ins)
algo_input = get_input_instance('EnergyInput')
algo_input.qubit_op = qubitOp
#Making the Hamiltonian in its full form and getting the lowest eigenvalue and eigenvector
algorithm_cfg = {
'name': 'ExactEigensolver',
}
params = {
'problem': {'name': 'ising'},
'algorithm': algorithm_cfg
}
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
algorithm_cfg = {
'name': 'VQE',
'operator_mode': 'matrix'
}
optimizer_cfg = {
'name': 'SPSA',
'max_trials': 300
}
var_form_cfg = {
'name': 'RY',
'depth': 5,
'entanglement': 'linear'
}
params = {
'problem': {'name': 'ising', 'random_seed': 10598},
'algorithm': algorithm_cfg,
'optimizer': optimizer_cfg,
'variational_form': var_form_cfg,
'backend': {'name': 'statevector_simulator'}
}
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
print('time:', result['eval_time'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos)
# run quantum algorithm with shots
params['algorithm']['operator_mode'] = 'grouped_paulis'
params['backend']['name'] = 'qasm_simulator'
params['backend']['shots'] = 1024
result = run_algorithm(params,algo_input)
print('energy:', result['energy'])
print('time:', result['eval_time'])
#print('tsp objective:', result['energy'] + offset)
x = tsp.sample_most_likely(result['eigvecs'][0])
print('feasible:', tsp.tsp_feasible(x))
z = tsp.get_tsp_solution(x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
plot_histogram(result['eigvecs'][0])
draw_tsp_solution(G, z, colors, pos)
| 0.373533 | 0.995719 |
# Graph Convolutions For Tox21
In this notebook, we will explore the use of TensorGraph to create graph convolutional models with DeepChem. In particular, we will build a graph convolutional network on the Tox21 dataset.
Let's start with some basic imports.
```
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import numpy as np
import tensorflow as tf
import deepchem as dc
from deepchem.models.tensorgraph.models.graph_models import GraphConvTensorGraph
```
Now, let's use MoleculeNet to load the Tox21 dataset. We need to make sure to process the data in a way that graph convolutional networks can use For that, we make sure to set the featurizer option to 'GraphConv'. The MoleculeNet call will return a training set, an validation set, and a test set for us to use. The call also returns `transformers`, a list of data transformations that were applied to preprocess the dataset. (Most deep networks are quite finicky and require a set of data transformations to ensure that training proceeds stably.)
```
# Load Tox21 dataset
tox21_tasks, tox21_datasets, transformers = dc.molnet.load_tox21(featurizer='GraphConv')
train_dataset, valid_dataset, test_dataset = tox21_datasets
```
Let's now train a graph convolutional network on this dataset. DeepChem has the class `GraphConvTensorGraph` that wraps a standard graph convolutional architecture underneath the hood for user convenience. Let's instantiate an object of this class and train it on our dataset.
```
model = GraphConvTensorGraph(
len(tox21_tasks), batch_size=50, mode='classification')
# Set nb_epoch=10 for better results.
model.fit(train_dataset, nb_epoch=1)
```
Let's try to evaluate the performance of the model we've trained. For this, we need to define a metric, a measure of model performance. `dc.metrics` holds a collection of metrics already. For this dataset, it is standard to use the ROC-AUC score, the area under the receiver operating characteristic curve (which measures the tradeoff between precision and recall). Luckily, the ROC-AUC score is already available in DeepChem.
To measure the performance of the model under this metric, we can use the convenience function `model.evaluate()`.
```
metric = dc.metrics.Metric(
dc.metrics.roc_auc_score, np.mean, mode="classification")
print("Evaluating model")
train_scores = model.evaluate(train_dataset, [metric], transformers)
print("Training ROC-AUC Score: %f" % train_scores["mean-roc_auc_score"])
valid_scores = model.evaluate(valid_dataset, [metric], transformers)
print("Validation ROC-AUC Score: %f" % valid_scores["mean-roc_auc_score"])
```
What's going on under the hood? Could we build `GraphConvTensorGraph` ourselves? Of course! The first step is to create a `TensorGraph` object. This object will hold the "computational graph" that defines the computation that a graph convolutional network will perform.
```
from deepchem.models.tensorgraph.tensor_graph import TensorGraph
tg = TensorGraph(use_queue=False)
```
Let's now define the inputs to our model. Conceptually, graph convolutions just requires a the structure of the molecule in question and a vector of features for every atom that describes the local chemical environment. However in practice, due to TensorFlow's limitations as a general programming environment, we have to have some auxiliary information as well preprocessed.
`atom_features` holds a feature vector of length 75 for each atom. The other feature inputs are required to support minibatching in TensorFlow. `degree_slice` is an indexing convenience that makes it easy to locate atoms from all molecules with a given degree. `membership` determines the membership of atoms in molecules (atom `i` belongs to molecule `membership[i]`). `deg_adjs` is a list that contains adjacency lists grouped by atom degree For more details, check out the [code](https://github.com/deepchem/deepchem/blob/master/deepchem/feat/mol_graphs.py).
To define feature inputs in `TensorGraph`, we use the `Feature` layer. Conceptually, a `TensorGraph` is a mathematical graph composed of layer objects. `Features` layers have to be the root nodes of the graph since they consitute inputs.
```
from deepchem.models.tensorgraph.layers import Feature
atom_features = Feature(shape=(None, 75))
degree_slice = Feature(shape=(None, 2), dtype=tf.int32)
membership = Feature(shape=(None,), dtype=tf.int32)
deg_adjs = []
for i in range(0, 10 + 1):
deg_adj = Feature(shape=(None, i + 1), dtype=tf.int32)
deg_adjs.append(deg_adj)
```
Let's now implement the body of the graph convolutional network. `TensorGraph` has a number of layers that encode various graph operations. Namely, the `GraphConv`, `GraphPool` and `GraphGather` layers. We will also apply standard neural network layers such as `Dense` and `BatchNorm`.
The layers we're adding effect a "feature transformation" that will create one vector for each molecule.
```
from deepchem.models.tensorgraph.layers import Dense, GraphConv, BatchNorm
from deepchem.models.tensorgraph.layers import GraphPool, GraphGather
batch_size = 50
gc1 = GraphConv(
64,
activation_fn=tf.nn.relu,
in_layers=[atom_features, degree_slice, membership] + deg_adjs)
batch_norm1 = BatchNorm(in_layers=[gc1])
gp1 = GraphPool(in_layers=[batch_norm1, degree_slice, membership] + deg_adjs)
gc2 = GraphConv(
64,
activation_fn=tf.nn.relu,
in_layers=[gp1, degree_slice, membership] + deg_adjs)
batch_norm2 = BatchNorm(in_layers=[gc2])
gp2 = GraphPool(in_layers=[batch_norm2, degree_slice, membership] + deg_adjs)
dense = Dense(out_channels=128, activation_fn=tf.nn.relu, in_layers=[gp2])
batch_norm3 = BatchNorm(in_layers=[dense])
readout = GraphGather(
batch_size=batch_size,
activation_fn=tf.nn.tanh,
in_layers=[batch_norm3, degree_slice, membership] + deg_adjs)
```
Let's now make predictions from the `TensorGraph` model. Tox21 is a multitask dataset. That is, there are 12 different datasets grouped together, which share many common molecules, but with different outputs for each. As a result, we have to add a separate output layer for each task. We will use a `for` loop over the `tox21_tasks` list to make this happen. We need to add labels for each
We also have to define a loss for the model which tells the network the objective to minimize during training.
We have to tell `TensorGraph` which layers are outputs with `TensorGraph.add_output(layer)`. Similarly, we tell the network its loss with `TensorGraph.set_loss(loss)`.
```
from deepchem.models.tensorgraph.layers import Dense, SoftMax, \
SoftMaxCrossEntropy, WeightedError, Concat
from deepchem.models.tensorgraph.layers import Label, Weights
costs = []
labels = []
for task in range(len(tox21_tasks)):
classification = Dense(
out_channels=2, activation_fn=None, in_layers=[readout])
softmax = SoftMax(in_layers=[classification])
tg.add_output(softmax)
label = Label(shape=(None, 2))
labels.append(label)
cost = SoftMaxCrossEntropy(in_layers=[label, classification])
costs.append(cost)
all_cost = Concat(in_layers=costs, axis=1)
weights = Weights(shape=(None, len(tox21_tasks)))
loss = WeightedError(in_layers=[all_cost, weights])
tg.set_loss(loss)
```
Now that we've successfully defined our graph convolutional model in `TensorGraph`, we need to train it. We can call `fit()`, but we need to make sure that each minibatch of data populates all four `Feature` objects that we've created. For this, we need to create a Python generator that given a batch of data generates a dictionary whose keys are the `Feature` layers and whose values are Numpy arrays we'd like to use for this step of training.
```
from deepchem.metrics import to_one_hot
from deepchem.feat.mol_graphs import ConvMol
def data_generator(dataset, epochs=1, predict=False, pad_batches=True):
for epoch in range(epochs):
if not predict:
print('Starting epoch %i' % epoch)
for ind, (X_b, y_b, w_b, ids_b) in enumerate(
dataset.iterbatches(
batch_size, pad_batches=True, deterministic=True)):
d = {}
for index, label in enumerate(labels):
d[label] = to_one_hot(y_b[:, index])
d[weights] = w_b
multiConvMol = ConvMol.agglomerate_mols(X_b)
d[atom_features] = multiConvMol.get_atom_features()
d[degree_slice] = multiConvMol.deg_slice
d[membership] = multiConvMol.membership
for i in range(1, len(multiConvMol.get_deg_adjacency_lists())):
d[deg_adjs[i - 1]] = multiConvMol.get_deg_adjacency_lists()[i]
yield d
```
Now, we can train the model using `TensorGraph.fit_generator(generator)` which will use the generator we've defined to train the model.
```
# Epochs set to 1 to render tutorials online.
# Set epochs=10 for better results.
tg.fit_generator(data_generator(train_dataset, epochs=1))
```
Now that we have trained our graph convolutional method, let's evaluate its performance. We again have to use our defined generator to evaluate model performance.
```
metric = dc.metrics.Metric(
dc.metrics.roc_auc_score, np.mean, mode="classification")
print("Evaluating model")
train_scores = tg.evaluate_generator(data_generator(train_dataset, predict=True),
[metric], labels=labels, weights=[weights])
print("Training ROC-AUC Score: %f" % train_scores["mean-roc_auc_score"])
valid_scores = tg.evaluate_generator(data_generator(valid_dataset, predict=True),
[metric], labels=labels, weights=[weights])
print("Valid ROC-AUC Score: %f" % valid_scores["mean-roc_auc_score"])
```
Success! The model we've constructed behaves nearly identically to `GraphConvTensorGraph`. If you're looking to build your own custom models, you can follow the example we've provided here to do so. We hope to see exciting constructions from your end soon!
|
github_jupyter
|
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import numpy as np
import tensorflow as tf
import deepchem as dc
from deepchem.models.tensorgraph.models.graph_models import GraphConvTensorGraph
# Load Tox21 dataset
tox21_tasks, tox21_datasets, transformers = dc.molnet.load_tox21(featurizer='GraphConv')
train_dataset, valid_dataset, test_dataset = tox21_datasets
model = GraphConvTensorGraph(
len(tox21_tasks), batch_size=50, mode='classification')
# Set nb_epoch=10 for better results.
model.fit(train_dataset, nb_epoch=1)
metric = dc.metrics.Metric(
dc.metrics.roc_auc_score, np.mean, mode="classification")
print("Evaluating model")
train_scores = model.evaluate(train_dataset, [metric], transformers)
print("Training ROC-AUC Score: %f" % train_scores["mean-roc_auc_score"])
valid_scores = model.evaluate(valid_dataset, [metric], transformers)
print("Validation ROC-AUC Score: %f" % valid_scores["mean-roc_auc_score"])
from deepchem.models.tensorgraph.tensor_graph import TensorGraph
tg = TensorGraph(use_queue=False)
from deepchem.models.tensorgraph.layers import Feature
atom_features = Feature(shape=(None, 75))
degree_slice = Feature(shape=(None, 2), dtype=tf.int32)
membership = Feature(shape=(None,), dtype=tf.int32)
deg_adjs = []
for i in range(0, 10 + 1):
deg_adj = Feature(shape=(None, i + 1), dtype=tf.int32)
deg_adjs.append(deg_adj)
from deepchem.models.tensorgraph.layers import Dense, GraphConv, BatchNorm
from deepchem.models.tensorgraph.layers import GraphPool, GraphGather
batch_size = 50
gc1 = GraphConv(
64,
activation_fn=tf.nn.relu,
in_layers=[atom_features, degree_slice, membership] + deg_adjs)
batch_norm1 = BatchNorm(in_layers=[gc1])
gp1 = GraphPool(in_layers=[batch_norm1, degree_slice, membership] + deg_adjs)
gc2 = GraphConv(
64,
activation_fn=tf.nn.relu,
in_layers=[gp1, degree_slice, membership] + deg_adjs)
batch_norm2 = BatchNorm(in_layers=[gc2])
gp2 = GraphPool(in_layers=[batch_norm2, degree_slice, membership] + deg_adjs)
dense = Dense(out_channels=128, activation_fn=tf.nn.relu, in_layers=[gp2])
batch_norm3 = BatchNorm(in_layers=[dense])
readout = GraphGather(
batch_size=batch_size,
activation_fn=tf.nn.tanh,
in_layers=[batch_norm3, degree_slice, membership] + deg_adjs)
from deepchem.models.tensorgraph.layers import Dense, SoftMax, \
SoftMaxCrossEntropy, WeightedError, Concat
from deepchem.models.tensorgraph.layers import Label, Weights
costs = []
labels = []
for task in range(len(tox21_tasks)):
classification = Dense(
out_channels=2, activation_fn=None, in_layers=[readout])
softmax = SoftMax(in_layers=[classification])
tg.add_output(softmax)
label = Label(shape=(None, 2))
labels.append(label)
cost = SoftMaxCrossEntropy(in_layers=[label, classification])
costs.append(cost)
all_cost = Concat(in_layers=costs, axis=1)
weights = Weights(shape=(None, len(tox21_tasks)))
loss = WeightedError(in_layers=[all_cost, weights])
tg.set_loss(loss)
from deepchem.metrics import to_one_hot
from deepchem.feat.mol_graphs import ConvMol
def data_generator(dataset, epochs=1, predict=False, pad_batches=True):
for epoch in range(epochs):
if not predict:
print('Starting epoch %i' % epoch)
for ind, (X_b, y_b, w_b, ids_b) in enumerate(
dataset.iterbatches(
batch_size, pad_batches=True, deterministic=True)):
d = {}
for index, label in enumerate(labels):
d[label] = to_one_hot(y_b[:, index])
d[weights] = w_b
multiConvMol = ConvMol.agglomerate_mols(X_b)
d[atom_features] = multiConvMol.get_atom_features()
d[degree_slice] = multiConvMol.deg_slice
d[membership] = multiConvMol.membership
for i in range(1, len(multiConvMol.get_deg_adjacency_lists())):
d[deg_adjs[i - 1]] = multiConvMol.get_deg_adjacency_lists()[i]
yield d
# Epochs set to 1 to render tutorials online.
# Set epochs=10 for better results.
tg.fit_generator(data_generator(train_dataset, epochs=1))
metric = dc.metrics.Metric(
dc.metrics.roc_auc_score, np.mean, mode="classification")
print("Evaluating model")
train_scores = tg.evaluate_generator(data_generator(train_dataset, predict=True),
[metric], labels=labels, weights=[weights])
print("Training ROC-AUC Score: %f" % train_scores["mean-roc_auc_score"])
valid_scores = tg.evaluate_generator(data_generator(valid_dataset, predict=True),
[metric], labels=labels, weights=[weights])
print("Valid ROC-AUC Score: %f" % valid_scores["mean-roc_auc_score"])
| 0.863435 | 0.990092 |
# Create a Batch Inferencing Service
Imagine a health clinic takes patient measurements all day, saving the details for each patient in a separate file. Then overnight, the diabetes prediction model can be used to process all of the day's patient data as a batch, generating predictions that will be waiting the following morning so that the clinic can follow up with patients who are predicted to be at risk of diabetes. With Azure Machine Learning, you can accomplish this by creating a *batch inferencing pipeline*; and that's what you'll implement in this exercise.
## Connect to your workspace
To get started, connect to your workspace.
> **Note**: If you haven't already established an authenticated session with your Azure subscription, you'll be prompted to authenticate by clicking a link, entering an authentication code, and signing into Azure.
```
import azureml.core
from azureml.core import Workspace
# Load the workspace from the saved config file
ws = Workspace.from_config()
print('Ready to use Azure ML {} to work with {}'.format(azureml.core.VERSION, ws.name))
```
## Train and register a model
Now let's train and register a model to deploy in a batch inferencing pipeline.
```
from azureml.core import Experiment
from azureml.core import Model
import pandas as pd
import numpy as np
import joblib
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
# Create an Azure ML experiment in your workspace
experiment = Experiment(workspace=ws, name='mslearn-train-diabetes')
run = experiment.start_logging()
print("Starting experiment:", experiment.name)
# load the diabetes dataset
print("Loading Data...")
diabetes = pd.read_csv('data/diabetes.csv')
# Separate features and labels
X, y = diabetes[['Pregnancies','PlasmaGlucose','DiastolicBloodPressure','TricepsThickness','SerumInsulin','BMI','DiabetesPedigree','Age']].values, diabetes['Diabetic'].values
# Split data into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=0)
# Train a decision tree model
print('Training a decision tree model')
model = DecisionTreeClassifier().fit(X_train, y_train)
# calculate accuracy
y_hat = model.predict(X_test)
acc = np.average(y_hat == y_test)
print('Accuracy:', acc)
run.log('Accuracy', np.float(acc))
# calculate AUC
y_scores = model.predict_proba(X_test)
auc = roc_auc_score(y_test,y_scores[:,1])
print('AUC: ' + str(auc))
run.log('AUC', np.float(auc))
# Save the trained model
model_file = 'diabetes_model.pkl'
joblib.dump(value=model, filename=model_file)
run.upload_file(name = 'outputs/' + model_file, path_or_stream = './' + model_file)
# Complete the run
run.complete()
# Register the model
run.register_model(model_path='outputs/diabetes_model.pkl', model_name='diabetes_model',
tags={'Training context':'Inline Training'},
properties={'AUC': run.get_metrics()['AUC'], 'Accuracy': run.get_metrics()['Accuracy']})
print('Model trained and registered.')
```
## Generate and upload batch data
Since we don't actually have a fully staffed clinic with patients from whom to get new data for this exercise, you'll generate a random sample from our diabetes CSV file, upload that data to a datastore in the Azure Machine Learning workspace, and register a dataset for it.
```
from azureml.core import Datastore, Dataset
import pandas as pd
import os
# Set default data store
ws.set_default_datastore('workspaceblobstore')
default_ds = ws.get_default_datastore()
# Enumerate all datastores, indicating which is the default
for ds_name in ws.datastores:
print(ds_name, "- Default =", ds_name == default_ds.name)
# Load the diabetes data
diabetes = pd.read_csv('data/diabetes2.csv')
# Get a 100-item sample of the feature columns (not the diabetic label)
sample = diabetes[['Pregnancies','PlasmaGlucose','DiastolicBloodPressure','TricepsThickness','SerumInsulin','BMI','DiabetesPedigree','Age']].sample(n=100).values
# Create a folder
batch_folder = './batch-data'
os.makedirs(batch_folder, exist_ok=True)
print("Folder created!")
# Save each sample as a separate file
print("Saving files...")
for i in range(100):
fname = str(i+1) + '.csv'
sample[i].tofile(os.path.join(batch_folder, fname), sep=",")
print("files saved!")
# Upload the files to the default datastore
print("Uploading files to datastore...")
default_ds = ws.get_default_datastore()
default_ds.upload(src_dir="batch-data", target_path="batch-data", overwrite=True, show_progress=True)
# Register a dataset for the input data
batch_data_set = Dataset.File.from_files(path=(default_ds, 'batch-data/'), validate=False)
try:
batch_data_set = batch_data_set.register(workspace=ws,
name='batch-data',
description='batch data',
create_new_version=True)
except Exception as ex:
print(ex)
print("Done!")
```
## Create compute
We'll need a compute context for the pipeline, so we'll use the following code to specify an Azure Machine Learning compute cluster (it will be created if it doesn't already exist).
> **Important**: Change *your-compute-cluster* to the name of your compute cluster in the code below before running it! Cluster names must be globally unique names between 2 to 16 characters in length. Valid characters are letters, digits, and the - character.
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
cluster_name = "your-compute-cluster"
try:
# Check for existing compute target
inference_cluster = ComputeTarget(workspace=ws, name=cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
# If it doesn't already exist, create it
try:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_DS11_V2', max_nodes=2)
inference_cluster = ComputeTarget.create(ws, cluster_name, compute_config)
inference_cluster.wait_for_completion(show_output=True)
except Exception as ex:
print(ex)
```
## Create a pipeline for batch inferencing
Now we're ready to define the pipeline we'll use for batch inferencing. Our pipeline will need Python code to perform the batch inferencing, so let's create a folder where we can keep all the files used by the pipeline:
```
import os
# Create a folder for the experiment files
experiment_folder = 'batch_pipeline'
os.makedirs(experiment_folder, exist_ok=True)
print(experiment_folder)
```
Now we'll create a Python script to do the actual work, and save it in the pipeline folder:
```
%%writefile $experiment_folder/batch_diabetes.py
import os
import numpy as np
from azureml.core import Model
import joblib
def init():
# Runs when the pipeline step is initialized
global model
# load the model
model_path = Model.get_model_path('diabetes_model')
model = joblib.load(model_path)
def run(mini_batch):
# This runs for each batch
resultList = []
# process each file in the batch
for f in mini_batch:
# Read the comma-delimited data into an array
data = np.genfromtxt(f, delimiter=',')
# Reshape into a 2-dimensional array for prediction (model expects multiple items)
prediction = model.predict(data.reshape(1, -1))
# Append prediction to results
resultList.append("{}: {}".format(os.path.basename(f), prediction[0]))
return resultList
```
Next we'll define a run context that includes the dependencies required by the script
```
from azureml.core import Environment
from azureml.core.runconfig import DEFAULT_CPU_IMAGE
from azureml.core.runconfig import CondaDependencies
# Add dependencies required by the model
# For scikit-learn models, you need scikit-learn
# For parallel pipeline steps, you need azureml-core and azureml-dataprep[fuse]
cd = CondaDependencies.create(conda_packages=['scikit-learn','pip'],
pip_packages=['azureml-defaults','azureml-core','azureml-dataprep[fuse]'])
batch_env = Environment(name='batch_environment')
batch_env.python.conda_dependencies = cd
batch_env.docker.enabled = True
batch_env.docker.base_image = DEFAULT_CPU_IMAGE
print('Configuration ready.')
```
You're going to use a pipeline to run the batch prediction script, generate predictions from the input data, and save the results as a text file in the output folder. To do this, you can use a **ParallelRunStep**, which enables the batch data to be processed in parallel and the results collated in a single output file named *parallel_run_step.txt*.
```
from azureml.pipeline.steps import ParallelRunConfig, ParallelRunStep
from azureml.pipeline.core import PipelineData
default_ds = ws.get_default_datastore()
output_dir = PipelineData(name='inferences',
datastore=default_ds,
output_path_on_compute='diabetes/results')
parallel_run_config = ParallelRunConfig(
source_directory=experiment_folder,
entry_script="batch_diabetes.py",
mini_batch_size="5",
error_threshold=10,
output_action="append_row",
environment=batch_env,
compute_target=inference_cluster,
node_count=2)
parallelrun_step = ParallelRunStep(
name='batch-score-diabetes',
parallel_run_config=parallel_run_config,
inputs=[batch_data_set.as_named_input('diabetes_batch')],
output=output_dir,
arguments=[],
allow_reuse=True
)
print('Steps defined')
```
Now it's time to put the step into a pipeline, and run it.
> **Note**: This may take some time!
```
from azureml.core import Experiment
from azureml.pipeline.core import Pipeline
pipeline = Pipeline(workspace=ws, steps=[parallelrun_step])
pipeline_run = Experiment(ws, 'mslearn-diabetes-batch').submit(pipeline)
pipeline_run.wait_for_completion(show_output=True)
```
When the pipeline has finished running, the resulting predictions will have been saved in the outputs of the experiment associated with the first (and only) step in the pipeline. You can retrieve it as follows:
```
import pandas as pd
import shutil
# Remove the local results folder if left over from a previous run
shutil.rmtree('diabetes-results', ignore_errors=True)
# Get the run for the first step and download its output
prediction_run = next(pipeline_run.get_children())
prediction_output = prediction_run.get_output_data('inferences')
prediction_output.download(local_path='diabetes-results')
# Traverse the folder hierarchy and find the results file
for root, dirs, files in os.walk('diabetes-results'):
for file in files:
if file.endswith('parallel_run_step.txt'):
result_file = os.path.join(root,file)
# cleanup output format
df = pd.read_csv(result_file, delimiter=":", header=None)
df.columns = ["File", "Prediction"]
# Display the first 20 results
df.head(20)
```
## Publish the Pipeline and use its REST Interface
Now that you have a working pipeline for batch inferencing, you can publish it and use a REST endpoint to run it from an application.
```
published_pipeline = pipeline_run.publish_pipeline(
name='diabetes-batch-pipeline', description='Batch scoring of diabetes data', version='1.0')
published_pipeline
```
Note that the published pipeline has an endpoint, which you can see in the Azure portal. You can also find it as a property of the published pipeline object:
```
rest_endpoint = published_pipeline.endpoint
print(rest_endpoint)
```
To use the endpoint, client applications need to make a REST call over HTTP. This request must be authenticated, so an authorization header is required. To test this out, we'll use the authorization header from your current connection to your Azure workspace, which you can get using the following code:
> **Note**: A real application would require a service principal with which to be authenticated.
```
from azureml.core.authentication import InteractiveLoginAuthentication
interactive_auth = InteractiveLoginAuthentication()
auth_header = interactive_auth.get_authentication_header()
print('Authentication header ready.')
```
Now we're ready to call the REST interface. The pipeline runs asynchronously, so we'll get an identifier back, which we can use to track the pipeline experiment as it runs:
```
import requests
rest_endpoint = published_pipeline.endpoint
response = requests.post(rest_endpoint,
headers=auth_header,
json={"ExperimentName": "mslearn-diabetes-batch"})
run_id = response.json()["Id"]
run_id
```
Since we have the run ID, we can use the **RunDetails** widget to view the experiment as it runs:
```
from azureml.pipeline.core.run import PipelineRun
from azureml.widgets import RunDetails
published_pipeline_run = PipelineRun(ws.experiments['mslearn-diabetes-batch'], run_id)
# Block until the run completes
published_pipeline_run.wait_for_completion(show_output=True)
```
Wait for the pipeline run to complete, and then run the following cell to see the results.
As before, the results are in the output of the first pipeline step:
```
import pandas as pd
import shutil
# Remove the local results folder if left over from a previous run
shutil.rmtree('diabetes-results', ignore_errors=True)
# Get the run for the first step and download its output
prediction_run = next(pipeline_run.get_children())
prediction_output = prediction_run.get_output_data('inferences')
prediction_output.download(local_path='diabetes-results')
# Traverse the folder hierarchy and find the results file
for root, dirs, files in os.walk('diabetes-results'):
for file in files:
if file.endswith('parallel_run_step.txt'):
result_file = os.path.join(root,file)
# cleanup output format
df = pd.read_csv(result_file, delimiter=":", header=None)
df.columns = ["File", "Prediction"]
# Display the first 20 results
df.head(20)
```
Now you have a pipeline that can be used to batch process daily patient data.
**More Information**: For more details about using pipelines for batch inferencing, see the [How to Run Batch Predictions](https://docs.microsoft.com/azure/machine-learning/how-to-run-batch-predictions) in the Azure Machine Learning documentation.
|
github_jupyter
|
import azureml.core
from azureml.core import Workspace
# Load the workspace from the saved config file
ws = Workspace.from_config()
print('Ready to use Azure ML {} to work with {}'.format(azureml.core.VERSION, ws.name))
from azureml.core import Experiment
from azureml.core import Model
import pandas as pd
import numpy as np
import joblib
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
# Create an Azure ML experiment in your workspace
experiment = Experiment(workspace=ws, name='mslearn-train-diabetes')
run = experiment.start_logging()
print("Starting experiment:", experiment.name)
# load the diabetes dataset
print("Loading Data...")
diabetes = pd.read_csv('data/diabetes.csv')
# Separate features and labels
X, y = diabetes[['Pregnancies','PlasmaGlucose','DiastolicBloodPressure','TricepsThickness','SerumInsulin','BMI','DiabetesPedigree','Age']].values, diabetes['Diabetic'].values
# Split data into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=0)
# Train a decision tree model
print('Training a decision tree model')
model = DecisionTreeClassifier().fit(X_train, y_train)
# calculate accuracy
y_hat = model.predict(X_test)
acc = np.average(y_hat == y_test)
print('Accuracy:', acc)
run.log('Accuracy', np.float(acc))
# calculate AUC
y_scores = model.predict_proba(X_test)
auc = roc_auc_score(y_test,y_scores[:,1])
print('AUC: ' + str(auc))
run.log('AUC', np.float(auc))
# Save the trained model
model_file = 'diabetes_model.pkl'
joblib.dump(value=model, filename=model_file)
run.upload_file(name = 'outputs/' + model_file, path_or_stream = './' + model_file)
# Complete the run
run.complete()
# Register the model
run.register_model(model_path='outputs/diabetes_model.pkl', model_name='diabetes_model',
tags={'Training context':'Inline Training'},
properties={'AUC': run.get_metrics()['AUC'], 'Accuracy': run.get_metrics()['Accuracy']})
print('Model trained and registered.')
from azureml.core import Datastore, Dataset
import pandas as pd
import os
# Set default data store
ws.set_default_datastore('workspaceblobstore')
default_ds = ws.get_default_datastore()
# Enumerate all datastores, indicating which is the default
for ds_name in ws.datastores:
print(ds_name, "- Default =", ds_name == default_ds.name)
# Load the diabetes data
diabetes = pd.read_csv('data/diabetes2.csv')
# Get a 100-item sample of the feature columns (not the diabetic label)
sample = diabetes[['Pregnancies','PlasmaGlucose','DiastolicBloodPressure','TricepsThickness','SerumInsulin','BMI','DiabetesPedigree','Age']].sample(n=100).values
# Create a folder
batch_folder = './batch-data'
os.makedirs(batch_folder, exist_ok=True)
print("Folder created!")
# Save each sample as a separate file
print("Saving files...")
for i in range(100):
fname = str(i+1) + '.csv'
sample[i].tofile(os.path.join(batch_folder, fname), sep=",")
print("files saved!")
# Upload the files to the default datastore
print("Uploading files to datastore...")
default_ds = ws.get_default_datastore()
default_ds.upload(src_dir="batch-data", target_path="batch-data", overwrite=True, show_progress=True)
# Register a dataset for the input data
batch_data_set = Dataset.File.from_files(path=(default_ds, 'batch-data/'), validate=False)
try:
batch_data_set = batch_data_set.register(workspace=ws,
name='batch-data',
description='batch data',
create_new_version=True)
except Exception as ex:
print(ex)
print("Done!")
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
cluster_name = "your-compute-cluster"
try:
# Check for existing compute target
inference_cluster = ComputeTarget(workspace=ws, name=cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
# If it doesn't already exist, create it
try:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_DS11_V2', max_nodes=2)
inference_cluster = ComputeTarget.create(ws, cluster_name, compute_config)
inference_cluster.wait_for_completion(show_output=True)
except Exception as ex:
print(ex)
import os
# Create a folder for the experiment files
experiment_folder = 'batch_pipeline'
os.makedirs(experiment_folder, exist_ok=True)
print(experiment_folder)
%%writefile $experiment_folder/batch_diabetes.py
import os
import numpy as np
from azureml.core import Model
import joblib
def init():
# Runs when the pipeline step is initialized
global model
# load the model
model_path = Model.get_model_path('diabetes_model')
model = joblib.load(model_path)
def run(mini_batch):
# This runs for each batch
resultList = []
# process each file in the batch
for f in mini_batch:
# Read the comma-delimited data into an array
data = np.genfromtxt(f, delimiter=',')
# Reshape into a 2-dimensional array for prediction (model expects multiple items)
prediction = model.predict(data.reshape(1, -1))
# Append prediction to results
resultList.append("{}: {}".format(os.path.basename(f), prediction[0]))
return resultList
from azureml.core import Environment
from azureml.core.runconfig import DEFAULT_CPU_IMAGE
from azureml.core.runconfig import CondaDependencies
# Add dependencies required by the model
# For scikit-learn models, you need scikit-learn
# For parallel pipeline steps, you need azureml-core and azureml-dataprep[fuse]
cd = CondaDependencies.create(conda_packages=['scikit-learn','pip'],
pip_packages=['azureml-defaults','azureml-core','azureml-dataprep[fuse]'])
batch_env = Environment(name='batch_environment')
batch_env.python.conda_dependencies = cd
batch_env.docker.enabled = True
batch_env.docker.base_image = DEFAULT_CPU_IMAGE
print('Configuration ready.')
from azureml.pipeline.steps import ParallelRunConfig, ParallelRunStep
from azureml.pipeline.core import PipelineData
default_ds = ws.get_default_datastore()
output_dir = PipelineData(name='inferences',
datastore=default_ds,
output_path_on_compute='diabetes/results')
parallel_run_config = ParallelRunConfig(
source_directory=experiment_folder,
entry_script="batch_diabetes.py",
mini_batch_size="5",
error_threshold=10,
output_action="append_row",
environment=batch_env,
compute_target=inference_cluster,
node_count=2)
parallelrun_step = ParallelRunStep(
name='batch-score-diabetes',
parallel_run_config=parallel_run_config,
inputs=[batch_data_set.as_named_input('diabetes_batch')],
output=output_dir,
arguments=[],
allow_reuse=True
)
print('Steps defined')
from azureml.core import Experiment
from azureml.pipeline.core import Pipeline
pipeline = Pipeline(workspace=ws, steps=[parallelrun_step])
pipeline_run = Experiment(ws, 'mslearn-diabetes-batch').submit(pipeline)
pipeline_run.wait_for_completion(show_output=True)
import pandas as pd
import shutil
# Remove the local results folder if left over from a previous run
shutil.rmtree('diabetes-results', ignore_errors=True)
# Get the run for the first step and download its output
prediction_run = next(pipeline_run.get_children())
prediction_output = prediction_run.get_output_data('inferences')
prediction_output.download(local_path='diabetes-results')
# Traverse the folder hierarchy and find the results file
for root, dirs, files in os.walk('diabetes-results'):
for file in files:
if file.endswith('parallel_run_step.txt'):
result_file = os.path.join(root,file)
# cleanup output format
df = pd.read_csv(result_file, delimiter=":", header=None)
df.columns = ["File", "Prediction"]
# Display the first 20 results
df.head(20)
published_pipeline = pipeline_run.publish_pipeline(
name='diabetes-batch-pipeline', description='Batch scoring of diabetes data', version='1.0')
published_pipeline
rest_endpoint = published_pipeline.endpoint
print(rest_endpoint)
from azureml.core.authentication import InteractiveLoginAuthentication
interactive_auth = InteractiveLoginAuthentication()
auth_header = interactive_auth.get_authentication_header()
print('Authentication header ready.')
import requests
rest_endpoint = published_pipeline.endpoint
response = requests.post(rest_endpoint,
headers=auth_header,
json={"ExperimentName": "mslearn-diabetes-batch"})
run_id = response.json()["Id"]
run_id
from azureml.pipeline.core.run import PipelineRun
from azureml.widgets import RunDetails
published_pipeline_run = PipelineRun(ws.experiments['mslearn-diabetes-batch'], run_id)
# Block until the run completes
published_pipeline_run.wait_for_completion(show_output=True)
import pandas as pd
import shutil
# Remove the local results folder if left over from a previous run
shutil.rmtree('diabetes-results', ignore_errors=True)
# Get the run for the first step and download its output
prediction_run = next(pipeline_run.get_children())
prediction_output = prediction_run.get_output_data('inferences')
prediction_output.download(local_path='diabetes-results')
# Traverse the folder hierarchy and find the results file
for root, dirs, files in os.walk('diabetes-results'):
for file in files:
if file.endswith('parallel_run_step.txt'):
result_file = os.path.join(root,file)
# cleanup output format
df = pd.read_csv(result_file, delimiter=":", header=None)
df.columns = ["File", "Prediction"]
# Display the first 20 results
df.head(20)
| 0.718989 | 0.934873 |
<a href="https://colab.research.google.com/github/annadymanus/IR-project/blob/main/model_metrics.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Evaluation of Models
Metrics:
- Mean Reciprocal Rank at k
- (normalized) Discounted Cumulative Gain
- Pairwise Accuracy
## 1. Import libs and read files
```
from google.colab import drive
drive.mount('/content/drive')
!pip install pickle5
import pickle5 as pickle
import pandas as pd
gold_standard_path = '/content/drive/Shareddrives/IRProject/validation/2019qrels-docs.txt'
gold_standard = pd.read_csv(
gold_standard_path,
sep=' ',
names=[
'queryid',
'Q0',
'docid',
'rating',
],
)
models_base_path = '/content/drive/Shareddrives/IRProject/model_predictions'
def format_model_predictions(raw_model_predictions):
formatted_results = {}
for queryid in raw_model_predictions.keys():
formatted_results[queryid] = []
for docid in raw_model_predictions[queryid].keys():
score = raw_model_predictions[queryid][docid][0][0]
formatted_results[queryid].append((docid, score))
return formatted_results
# Baseline
with open(f'{models_base_path}/cosine_similarity.pickle', 'rb') as file:
model_cosine_similarity_raw = pickle.load(file)
model_cosine_similarity = format_model_predictions(model_cosine_similarity_raw)
# Pointwise
with open(f'{models_base_path}/tf_idf_pointwise_preds.pickle', 'rb') as file:
model_tf_idf = pickle.load(file)
with open(f'{models_base_path}/tf_idf_pointwise_scoring_preds.pickle', 'rb') as file:
model_tf_idf_scoring = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_pointwise_preds.pickle', 'rb') as file:
model_bart_tokenized = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_word_pointwise_preds.pickle', 'rb') as file:
model_bart_tokenized_word = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_pointwise_scoring_preds.pickle', 'rb') as file:
model_bart_tokenized_scoring = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_pointwise_word_scoring_preds.pickle', 'rb') as file:
model_bart_tokenized_word_scoring = pickle.load(file)
with open(f'{models_base_path}/non_cont_word_emb_pointwise_preds.pickle', 'rb') as file:
model_non_cont_word_emb = pickle.load(file)
with open(f'{models_base_path}/non_cont_word_emb_pointwise_scoring_preds.pickle', 'rb') as file:
model_non_cont_word_emb_scoring = pickle.load(file)
# Pairwise
with open(f'{models_base_path}/tf_idf_pairwise_preds.pickle', 'rb') as file:
model_tf_idf_pairwise = pickle.load(file)
with open(f'{models_base_path}/tf_idf_pairwise_scoring_preds.pickle', 'rb') as file:
model_tf_idf_pairwise_scoring = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_pairwise_preds.pickle', 'rb') as file:
model_bart_tokenized_pairwise = pickle.load(file)
with open(f'{models_base_path}/non_cont_word_emb_pairwise_preds.pickle', 'rb') as file:
model_non_cont_word_emb_pairwise = pickle.load(file)
with open(f'{models_base_path}/non_cont_word_emb_pairwise_scoring_preds.pickle', 'rb') as file:
model_non_cont_word_emb_pairwise_scoring = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_word_pairwise_preds.pickle', 'rb') as file:
model_bart_tokenized_word_pairwise = pickle.load(file)
```
## 2. Evaluation functions
```
def rank_k_documents(query_results, k=None):
"""
Rank the results of a query based on its descending model score,
remove duplicates, and (optionally) cut at max length k.
Args:
query_results (list): List of tuples (docid, score) for a
certain queryid.
k (int): optional cutpoint of the results, where metrics should
be evaluated.
Returns:
list[str]: ranked list of docids, with max length k (if defined).
"""
ranked_results = sorted(query_results, key=lambda tup: tup[1], reverse=True)
ranked_docids = [result[0] for result in ranked_results]
ranked_docids = list(dict.fromkeys(ranked_docids)) # remove duplicates
if isinstance(k, int):
if len(ranked_docids) > k:
ranked_docids = ranked_docids[0:k]
return ranked_docids
# Example: top 10 documents for query 156493
rank_k_documents(model_tf_idf['156493'], 10)
def get_rating_queryid_docid(queryid, docid: str, gold_standard):
"""
Search for the gold standard rating given for a specific pair of
`queryid` and `docid`.
Args:
queryid: ID of the query, in either string or integer format.
docid (str): string with the ID of the document.
gold_standard (pandas.DataFrame): DataFrame with true relevant docids
for each query.
Returns:
int: Pair's rating (0-3).
"""
rating = gold_standard[
(gold_standard['queryid']==int(queryid))
& (gold_standard['docid']==str(docid))
]['rating'].values[0]
return rating if rating > 0 else 0
# Example: Rating of (queryid=156493, docid=D685712)
get_rating_queryid_docid(156493, 'D685712', gold_standard)
def get_list_of_relevances(queryid, model_predictions, gold_standard, k=None):
"""
Rank the results of a `queryid` and replace `docids` by their relevance
rating for the query.
Args:
queryid: ID of the query, in either string or integer format.
model_predictions (dict): Dict of queryids and their lists of
documents retrieved by the model. Each key should by the queryid
in string format, and its value should be a list of tuples
(docid, score), not necessarily ordered.
gold_standard (pandas.DataFrame): DataFrame with true relevant docids
for each query.
k (int): optional cutpoint of the results, where metrics should
be evaluated.
Returns:
list[int]: list of documents' ratings for the query, ordered by
the relevance score given by the model.
"""
list_of_relevances = []
for docid in rank_k_documents(model_predictions[str(queryid)], k):
list_of_relevances.append(
get_rating_queryid_docid(queryid, docid, gold_standard)
)
return list_of_relevances
# Example: actual relevance of each of the first 10 results for queryid 156493
get_list_of_relevances(156493, model_tf_idf, gold_standard, 10)
def get_reciprocal_rank(list_of_relevances, relevance_threshold=1):
"""
Get inverse of the position (reciprocal rank) of the first relevant
document in the `list_of_relevances`, based on a relevance threshold.
Args:
list_of_relevances (list[int]): list of documents' ratings for
the query, ordered by the relevance score given by the model.
relevance_threshold (int): Miminum rating considered relevant.
Returns:
float: Reciprocal rank of the list.
"""
reciprocal_rank = 0.0
for position, relevance in enumerate(list_of_relevances):
if relevance >= relevance_threshold:
reciprocal_rank = 1/(position+1.0)
break
return reciprocal_rank
# Example 1: RR for queryid 156493, with relevance threshold = 1:
print(get_reciprocal_rank(
get_list_of_relevances(
156493,
model_tf_idf,
gold_standard,
10,
),
1,
))
# Example 1: RR for the same query, but with relevance threshold = 2:
print(get_reciprocal_rank(
get_list_of_relevances(
156493,
model_tf_idf,
gold_standard,
10,
),
2,
))
import math
def calculate_dcg(list_of_relevances:list):
"""
Calculate Discounted Cumulative Gain for a given list of relevances.
Args:
list_of_relevances (list[int]): list of documents' ratings for
the query, ordered by the relevance score given by the model.
Returns:
float: Discounted Cumulative Gain of the list.
"""
if isinstance(list_of_relevances, list):
if len(list_of_relevances)==0:
return 0
else:
dcg = []
for position, relevance in enumerate(list_of_relevances):
dcg.append(relevance / math.log2(position+2))
return sum(dcg)
def get_ideal_dcg(queryid, gold_standard):
"""
Calculate Ideal (Maximal) Discounted Cumulative Gain for a `queryid`, given
the gold standard ratings.
Args:
queryid: ID of the query, in either string or integer format.
gold_standard (pandas.DataFrame): DataFrame with true relevant docids
for each query.
Returns:
float: Discounted Cumulative Gain of the list.
"""
ideal_list_of_relevances = gold_standard[
gold_standard['queryid']==int(queryid)
].sort_values(
by='rating',
ascending=False,
)['rating'].tolist()
return calculate_dcg(ideal_list_of_relevances)
# Example: DCG of an imperfect list of ratings divided by ideal DCG of same list
calculate_dcg([0, 2, 4, 0, 1]) / calculate_dcg([4, 2, 1, 0, 0])
def get_pairwise_accuracy(list_of_relevances:list):
"""
Calculate pairwise accuracy of a given list of relevances.
Args:
list_of_relevances (list[int]): list of documents' ratings for
the query, ordered by the relevance score given by the model.
Returns:
float: pairwise accuracy of the list.
"""
hits_list = []
miss_list = []
for position, relevance in enumerate(list_of_relevances):
hits = len([1 for result in list_of_relevances[position:] if relevance > result])
miss = len([1 for result in list_of_relevances[position:] if relevance < result])
hits_list.append(hits)
miss_list.append(miss)
overall_hits = sum(hits_list)
overall_miss = sum(miss_list)
return overall_hits / (overall_hits + overall_miss)
get_pairwise_accuracy([0, 2, 4, 0, 1])
def get_query_dcg_rr_at_k(
queryid,
model_predictions,
gold_standard,
k=10,
relevance_threshold=2
):
"""
Calculate Reciprocal Rank at k, DCG, nDCG and pairwise accuracy for a
certain queryid, by comparing its results with gold_standard.
Args:
queryid: Query ID to be evaluated.
model_predictions (dict): Dict of queryids and their lists of
documents retrieved by the model. Each key should by the queryid
in string format, and its value should be a list of tuples
(docid, score), not necessarily ordered.
gold_standard (pandas.DataFrame): DataFrame with true relevant docids
for each query.
k (int): cutpoint of the results, where Reciprocal Rank should be
evaluated. Defaults to 10.
relevance_threshold (int): Miminum rating considered relevant for
Reciprocal Rank. Defaults to 2.
Returns:
tuple[float, float, float, float]: Tuple (reciprocal rank at k,
DCG, nDCG, pairwise accuracy) for the given queryid.
"""
# RR
list_of_k_relevances = get_list_of_relevances(
queryid,
model_predictions,
gold_standard,
k
)
rr = get_reciprocal_rank(
list_of_k_relevances,
relevance_threshold
)
# nDCG
list_of_relevances = get_list_of_relevances(
queryid,
model_predictions,
gold_standard,
)
dcg = calculate_dcg(list_of_relevances)
idcg = get_ideal_dcg(queryid, gold_standard)
ndcg = dcg / idcg if idcg > 0 else 0
# Pairwise Accuracy
pairwise_acc = get_pairwise_accuracy(list_of_relevances)
return rr, dcg, ndcg, pairwise_acc
# Example: metrics for query 156493, with default k and relevance threshold
get_query_dcg_rr_at_k(156493, model_tf_idf, gold_standard)
def get_model_metrics_per_query_at_k(
model_predictions,
gold_standard,
k=10,
relevance_threshold=2
):
"""
Calculate Mean Reciprocal Rank at k, DCG, nDCG and pairwise accuracy for
all queryids in dict model_predictions.
Args:
model_predictions (dict): Dict of queryids and their lists of
documents retrieved by the model. Each key should by the queryid
in string format, and its value should be a list of tuples
(docid, score). Lists don't need to be ordered.
k (int): cutpoint of the results, where Reciprocal Rank should be
evaluated. Defaults to 10.
relevance_threshold (int): Miminum rating considered relevant for
Mean Reciprocal Rank. Defaults to 2.
Returns:
list[dict]: List of records (queryid, MRR at k, DCG, nDCG,
pairwise accuracy) for all queryids in model_predictions.
"""
query_metrics = []
for queryid in model_predictions.keys():
rr, dcg, ndcg, pairwise_acc = get_query_dcg_rr_at_k(
queryid,
model_predictions,
gold_standard,
k,
relevance_threshold
)
query_metrics.append({
'queryid': queryid,
f'MRR_at_{k}': rr,
'DCG': dcg,
'nDCG': ndcg,
'pairwise_acc': pairwise_acc,
})
return query_metrics
pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf,
gold_standard,
)
)
```
## 3. Evaluate each model
### Baseline
```
metrics_model_cosine_similarity = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_cosine_similarity,
gold_standard,
)
)
metrics_model_cosine_similarity.drop(columns=['queryid']).mean()
```
### Pointwise
```
metrics_model_tf_idf = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf,
gold_standard,
)
)
metrics_model_tf_idf.drop(columns=['queryid']).mean()
metrics_model_tf_idf_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf_scoring,
gold_standard,
)
)
metrics_model_tf_idf_scoring.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized,
gold_standard,
)
)
metrics_model_bart_tokenized.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_scoring,
gold_standard,
)
)
metrics_model_bart_tokenized_scoring.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_word = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_word,
gold_standard,
)
)
metrics_model_bart_tokenized_word.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_word_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_word_scoring,
gold_standard,
)
)
metrics_model_bart_tokenized_word_scoring.drop(columns=['queryid']).mean()
metrics_model_non_cont_word_emb = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_non_cont_word_emb,
gold_standard,
)
)
metrics_model_non_cont_word_emb.drop(columns=['queryid']).mean()
metrics_model_non_cont_word_emb_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_non_cont_word_emb_scoring,
gold_standard,
)
)
metrics_model_non_cont_word_emb_scoring.drop(columns=['queryid']).mean()
```
### Pairwise
```
metrics_model_tf_idf_pairwise = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf_pairwise,
gold_standard,
)
)
metrics_model_tf_idf_pairwise.drop(columns=['queryid']).mean()
metrics_model_tf_idf_pairwise_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf_pairwise_scoring,
gold_standard,
)
)
metrics_model_tf_idf_pairwise_scoring.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_pairwise = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_pairwise,
gold_standard,
)
)
metrics_model_bart_tokenized_pairwise.drop(columns=['queryid']).mean()
metrics_model_non_cont_word_emb_pairwise = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_non_cont_word_emb_pairwise,
gold_standard,
)
)
metrics_model_non_cont_word_emb_pairwise.drop(columns=['queryid']).mean()
metrics_model_non_cont_word_emb_pairwise_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_non_cont_word_emb_pairwise_scoring,
gold_standard,
)
)
metrics_model_non_cont_word_emb_pairwise_scoring.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_word_pairwise = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_word_pairwise,
gold_standard,
)
)
metrics_model_bart_tokenized_word_pairwise.drop(columns=['queryid']).mean()
```
## 4. Compare all models
```
pd.concat(
[
# Baseline
metrics_model_cosine_similarity.drop(columns=['queryid']).mean(),
# Pointwise
metrics_model_tf_idf.drop(columns=['queryid']).mean(),
metrics_model_tf_idf_scoring.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_scoring.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_word.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_word_scoring.drop(columns=['queryid']).mean(),
metrics_model_non_cont_word_emb.drop(columns=['queryid']).mean(),
metrics_model_non_cont_word_emb_scoring.drop(columns=['queryid']).mean(),
# Pairwise
metrics_model_tf_idf_pairwise.drop(columns=['queryid']).mean(),
metrics_model_tf_idf_pairwise_scoring.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_pairwise.drop(columns=['queryid']).mean(),
metrics_model_non_cont_word_emb_pairwise.drop(columns=['queryid']).mean(),
metrics_model_non_cont_word_emb_pairwise_scoring.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_word_pairwise.drop(columns=['queryid']).mean()
],
axis=1,
names=['a', 'b', 'c', 'd', 'e', 'f']
).T.rename(index={
0: 'Cosine Similarity',
1: 'Tf-Idf',
2: 'Tf-Idf Scoring',
3: 'Bart Doc Embedding',
4: 'Bart Doc Embedding Scoring',
5: 'Bart Word Embedding',
6: 'Bart Word Embedding Scoring',
7: 'GloVe',
8: 'GloVe Scoring',
9: 'Tf-Idf Pairwise',
10: 'Tf-Idf Pairwise Scoring',
11: 'Bart Doc Embedding Pairwise',
12: 'GloVe Pairwise',
13: 'GloVe Pairwise Scoring',
14: 'Bart Word Embedding Pairwise'
}).sort_values(by='nDCG', ascending=False)
```
## 5. Investigate easy and hard queries
### Hard queries, according to baseline
```
queries_df = pd.read_csv(
'/content/drive/Shareddrives/IRProject/msmarco-test2019-queries.tsv',
sep='\t',
names=[
'queryid',
'query',
],
)
queries_df.info()
metrics_model_cosine_similarity.sort_values(by='nDCG').head(3)
metrics_model_non_cont_word_emb.sort_values(by='nDCG').head(3)
hard_queries = [855410, 287683, 1115776]
queries_df[queries_df['queryid'].isin(hard_queries)]
```
### Easy queries, according to baseline
```
metrics_model_cosine_similarity.sort_values(by='nDCG').tail(3)
queries_df[queries_df['queryid'].isin([47923, 489204, 1114819])]
metrics_model_non_cont_word_emb.sort_values(by='nDCG').tail(3)
queries_df[queries_df['queryid'].isin([183378, 1106007, 1114819])]
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/drive')
!pip install pickle5
import pickle5 as pickle
import pandas as pd
gold_standard_path = '/content/drive/Shareddrives/IRProject/validation/2019qrels-docs.txt'
gold_standard = pd.read_csv(
gold_standard_path,
sep=' ',
names=[
'queryid',
'Q0',
'docid',
'rating',
],
)
models_base_path = '/content/drive/Shareddrives/IRProject/model_predictions'
def format_model_predictions(raw_model_predictions):
formatted_results = {}
for queryid in raw_model_predictions.keys():
formatted_results[queryid] = []
for docid in raw_model_predictions[queryid].keys():
score = raw_model_predictions[queryid][docid][0][0]
formatted_results[queryid].append((docid, score))
return formatted_results
# Baseline
with open(f'{models_base_path}/cosine_similarity.pickle', 'rb') as file:
model_cosine_similarity_raw = pickle.load(file)
model_cosine_similarity = format_model_predictions(model_cosine_similarity_raw)
# Pointwise
with open(f'{models_base_path}/tf_idf_pointwise_preds.pickle', 'rb') as file:
model_tf_idf = pickle.load(file)
with open(f'{models_base_path}/tf_idf_pointwise_scoring_preds.pickle', 'rb') as file:
model_tf_idf_scoring = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_pointwise_preds.pickle', 'rb') as file:
model_bart_tokenized = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_word_pointwise_preds.pickle', 'rb') as file:
model_bart_tokenized_word = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_pointwise_scoring_preds.pickle', 'rb') as file:
model_bart_tokenized_scoring = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_pointwise_word_scoring_preds.pickle', 'rb') as file:
model_bart_tokenized_word_scoring = pickle.load(file)
with open(f'{models_base_path}/non_cont_word_emb_pointwise_preds.pickle', 'rb') as file:
model_non_cont_word_emb = pickle.load(file)
with open(f'{models_base_path}/non_cont_word_emb_pointwise_scoring_preds.pickle', 'rb') as file:
model_non_cont_word_emb_scoring = pickle.load(file)
# Pairwise
with open(f'{models_base_path}/tf_idf_pairwise_preds.pickle', 'rb') as file:
model_tf_idf_pairwise = pickle.load(file)
with open(f'{models_base_path}/tf_idf_pairwise_scoring_preds.pickle', 'rb') as file:
model_tf_idf_pairwise_scoring = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_pairwise_preds.pickle', 'rb') as file:
model_bart_tokenized_pairwise = pickle.load(file)
with open(f'{models_base_path}/non_cont_word_emb_pairwise_preds.pickle', 'rb') as file:
model_non_cont_word_emb_pairwise = pickle.load(file)
with open(f'{models_base_path}/non_cont_word_emb_pairwise_scoring_preds.pickle', 'rb') as file:
model_non_cont_word_emb_pairwise_scoring = pickle.load(file)
with open(f'{models_base_path}/bart_tokenized_word_pairwise_preds.pickle', 'rb') as file:
model_bart_tokenized_word_pairwise = pickle.load(file)
def rank_k_documents(query_results, k=None):
"""
Rank the results of a query based on its descending model score,
remove duplicates, and (optionally) cut at max length k.
Args:
query_results (list): List of tuples (docid, score) for a
certain queryid.
k (int): optional cutpoint of the results, where metrics should
be evaluated.
Returns:
list[str]: ranked list of docids, with max length k (if defined).
"""
ranked_results = sorted(query_results, key=lambda tup: tup[1], reverse=True)
ranked_docids = [result[0] for result in ranked_results]
ranked_docids = list(dict.fromkeys(ranked_docids)) # remove duplicates
if isinstance(k, int):
if len(ranked_docids) > k:
ranked_docids = ranked_docids[0:k]
return ranked_docids
# Example: top 10 documents for query 156493
rank_k_documents(model_tf_idf['156493'], 10)
def get_rating_queryid_docid(queryid, docid: str, gold_standard):
"""
Search for the gold standard rating given for a specific pair of
`queryid` and `docid`.
Args:
queryid: ID of the query, in either string or integer format.
docid (str): string with the ID of the document.
gold_standard (pandas.DataFrame): DataFrame with true relevant docids
for each query.
Returns:
int: Pair's rating (0-3).
"""
rating = gold_standard[
(gold_standard['queryid']==int(queryid))
& (gold_standard['docid']==str(docid))
]['rating'].values[0]
return rating if rating > 0 else 0
# Example: Rating of (queryid=156493, docid=D685712)
get_rating_queryid_docid(156493, 'D685712', gold_standard)
def get_list_of_relevances(queryid, model_predictions, gold_standard, k=None):
"""
Rank the results of a `queryid` and replace `docids` by their relevance
rating for the query.
Args:
queryid: ID of the query, in either string or integer format.
model_predictions (dict): Dict of queryids and their lists of
documents retrieved by the model. Each key should by the queryid
in string format, and its value should be a list of tuples
(docid, score), not necessarily ordered.
gold_standard (pandas.DataFrame): DataFrame with true relevant docids
for each query.
k (int): optional cutpoint of the results, where metrics should
be evaluated.
Returns:
list[int]: list of documents' ratings for the query, ordered by
the relevance score given by the model.
"""
list_of_relevances = []
for docid in rank_k_documents(model_predictions[str(queryid)], k):
list_of_relevances.append(
get_rating_queryid_docid(queryid, docid, gold_standard)
)
return list_of_relevances
# Example: actual relevance of each of the first 10 results for queryid 156493
get_list_of_relevances(156493, model_tf_idf, gold_standard, 10)
def get_reciprocal_rank(list_of_relevances, relevance_threshold=1):
"""
Get inverse of the position (reciprocal rank) of the first relevant
document in the `list_of_relevances`, based on a relevance threshold.
Args:
list_of_relevances (list[int]): list of documents' ratings for
the query, ordered by the relevance score given by the model.
relevance_threshold (int): Miminum rating considered relevant.
Returns:
float: Reciprocal rank of the list.
"""
reciprocal_rank = 0.0
for position, relevance in enumerate(list_of_relevances):
if relevance >= relevance_threshold:
reciprocal_rank = 1/(position+1.0)
break
return reciprocal_rank
# Example 1: RR for queryid 156493, with relevance threshold = 1:
print(get_reciprocal_rank(
get_list_of_relevances(
156493,
model_tf_idf,
gold_standard,
10,
),
1,
))
# Example 1: RR for the same query, but with relevance threshold = 2:
print(get_reciprocal_rank(
get_list_of_relevances(
156493,
model_tf_idf,
gold_standard,
10,
),
2,
))
import math
def calculate_dcg(list_of_relevances:list):
"""
Calculate Discounted Cumulative Gain for a given list of relevances.
Args:
list_of_relevances (list[int]): list of documents' ratings for
the query, ordered by the relevance score given by the model.
Returns:
float: Discounted Cumulative Gain of the list.
"""
if isinstance(list_of_relevances, list):
if len(list_of_relevances)==0:
return 0
else:
dcg = []
for position, relevance in enumerate(list_of_relevances):
dcg.append(relevance / math.log2(position+2))
return sum(dcg)
def get_ideal_dcg(queryid, gold_standard):
"""
Calculate Ideal (Maximal) Discounted Cumulative Gain for a `queryid`, given
the gold standard ratings.
Args:
queryid: ID of the query, in either string or integer format.
gold_standard (pandas.DataFrame): DataFrame with true relevant docids
for each query.
Returns:
float: Discounted Cumulative Gain of the list.
"""
ideal_list_of_relevances = gold_standard[
gold_standard['queryid']==int(queryid)
].sort_values(
by='rating',
ascending=False,
)['rating'].tolist()
return calculate_dcg(ideal_list_of_relevances)
# Example: DCG of an imperfect list of ratings divided by ideal DCG of same list
calculate_dcg([0, 2, 4, 0, 1]) / calculate_dcg([4, 2, 1, 0, 0])
def get_pairwise_accuracy(list_of_relevances:list):
"""
Calculate pairwise accuracy of a given list of relevances.
Args:
list_of_relevances (list[int]): list of documents' ratings for
the query, ordered by the relevance score given by the model.
Returns:
float: pairwise accuracy of the list.
"""
hits_list = []
miss_list = []
for position, relevance in enumerate(list_of_relevances):
hits = len([1 for result in list_of_relevances[position:] if relevance > result])
miss = len([1 for result in list_of_relevances[position:] if relevance < result])
hits_list.append(hits)
miss_list.append(miss)
overall_hits = sum(hits_list)
overall_miss = sum(miss_list)
return overall_hits / (overall_hits + overall_miss)
get_pairwise_accuracy([0, 2, 4, 0, 1])
def get_query_dcg_rr_at_k(
queryid,
model_predictions,
gold_standard,
k=10,
relevance_threshold=2
):
"""
Calculate Reciprocal Rank at k, DCG, nDCG and pairwise accuracy for a
certain queryid, by comparing its results with gold_standard.
Args:
queryid: Query ID to be evaluated.
model_predictions (dict): Dict of queryids and their lists of
documents retrieved by the model. Each key should by the queryid
in string format, and its value should be a list of tuples
(docid, score), not necessarily ordered.
gold_standard (pandas.DataFrame): DataFrame with true relevant docids
for each query.
k (int): cutpoint of the results, where Reciprocal Rank should be
evaluated. Defaults to 10.
relevance_threshold (int): Miminum rating considered relevant for
Reciprocal Rank. Defaults to 2.
Returns:
tuple[float, float, float, float]: Tuple (reciprocal rank at k,
DCG, nDCG, pairwise accuracy) for the given queryid.
"""
# RR
list_of_k_relevances = get_list_of_relevances(
queryid,
model_predictions,
gold_standard,
k
)
rr = get_reciprocal_rank(
list_of_k_relevances,
relevance_threshold
)
# nDCG
list_of_relevances = get_list_of_relevances(
queryid,
model_predictions,
gold_standard,
)
dcg = calculate_dcg(list_of_relevances)
idcg = get_ideal_dcg(queryid, gold_standard)
ndcg = dcg / idcg if idcg > 0 else 0
# Pairwise Accuracy
pairwise_acc = get_pairwise_accuracy(list_of_relevances)
return rr, dcg, ndcg, pairwise_acc
# Example: metrics for query 156493, with default k and relevance threshold
get_query_dcg_rr_at_k(156493, model_tf_idf, gold_standard)
def get_model_metrics_per_query_at_k(
model_predictions,
gold_standard,
k=10,
relevance_threshold=2
):
"""
Calculate Mean Reciprocal Rank at k, DCG, nDCG and pairwise accuracy for
all queryids in dict model_predictions.
Args:
model_predictions (dict): Dict of queryids and their lists of
documents retrieved by the model. Each key should by the queryid
in string format, and its value should be a list of tuples
(docid, score). Lists don't need to be ordered.
k (int): cutpoint of the results, where Reciprocal Rank should be
evaluated. Defaults to 10.
relevance_threshold (int): Miminum rating considered relevant for
Mean Reciprocal Rank. Defaults to 2.
Returns:
list[dict]: List of records (queryid, MRR at k, DCG, nDCG,
pairwise accuracy) for all queryids in model_predictions.
"""
query_metrics = []
for queryid in model_predictions.keys():
rr, dcg, ndcg, pairwise_acc = get_query_dcg_rr_at_k(
queryid,
model_predictions,
gold_standard,
k,
relevance_threshold
)
query_metrics.append({
'queryid': queryid,
f'MRR_at_{k}': rr,
'DCG': dcg,
'nDCG': ndcg,
'pairwise_acc': pairwise_acc,
})
return query_metrics
pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf,
gold_standard,
)
)
metrics_model_cosine_similarity = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_cosine_similarity,
gold_standard,
)
)
metrics_model_cosine_similarity.drop(columns=['queryid']).mean()
metrics_model_tf_idf = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf,
gold_standard,
)
)
metrics_model_tf_idf.drop(columns=['queryid']).mean()
metrics_model_tf_idf_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf_scoring,
gold_standard,
)
)
metrics_model_tf_idf_scoring.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized,
gold_standard,
)
)
metrics_model_bart_tokenized.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_scoring,
gold_standard,
)
)
metrics_model_bart_tokenized_scoring.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_word = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_word,
gold_standard,
)
)
metrics_model_bart_tokenized_word.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_word_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_word_scoring,
gold_standard,
)
)
metrics_model_bart_tokenized_word_scoring.drop(columns=['queryid']).mean()
metrics_model_non_cont_word_emb = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_non_cont_word_emb,
gold_standard,
)
)
metrics_model_non_cont_word_emb.drop(columns=['queryid']).mean()
metrics_model_non_cont_word_emb_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_non_cont_word_emb_scoring,
gold_standard,
)
)
metrics_model_non_cont_word_emb_scoring.drop(columns=['queryid']).mean()
metrics_model_tf_idf_pairwise = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf_pairwise,
gold_standard,
)
)
metrics_model_tf_idf_pairwise.drop(columns=['queryid']).mean()
metrics_model_tf_idf_pairwise_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_tf_idf_pairwise_scoring,
gold_standard,
)
)
metrics_model_tf_idf_pairwise_scoring.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_pairwise = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_pairwise,
gold_standard,
)
)
metrics_model_bart_tokenized_pairwise.drop(columns=['queryid']).mean()
metrics_model_non_cont_word_emb_pairwise = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_non_cont_word_emb_pairwise,
gold_standard,
)
)
metrics_model_non_cont_word_emb_pairwise.drop(columns=['queryid']).mean()
metrics_model_non_cont_word_emb_pairwise_scoring = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_non_cont_word_emb_pairwise_scoring,
gold_standard,
)
)
metrics_model_non_cont_word_emb_pairwise_scoring.drop(columns=['queryid']).mean()
metrics_model_bart_tokenized_word_pairwise = pd.DataFrame(
get_model_metrics_per_query_at_k(
model_bart_tokenized_word_pairwise,
gold_standard,
)
)
metrics_model_bart_tokenized_word_pairwise.drop(columns=['queryid']).mean()
pd.concat(
[
# Baseline
metrics_model_cosine_similarity.drop(columns=['queryid']).mean(),
# Pointwise
metrics_model_tf_idf.drop(columns=['queryid']).mean(),
metrics_model_tf_idf_scoring.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_scoring.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_word.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_word_scoring.drop(columns=['queryid']).mean(),
metrics_model_non_cont_word_emb.drop(columns=['queryid']).mean(),
metrics_model_non_cont_word_emb_scoring.drop(columns=['queryid']).mean(),
# Pairwise
metrics_model_tf_idf_pairwise.drop(columns=['queryid']).mean(),
metrics_model_tf_idf_pairwise_scoring.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_pairwise.drop(columns=['queryid']).mean(),
metrics_model_non_cont_word_emb_pairwise.drop(columns=['queryid']).mean(),
metrics_model_non_cont_word_emb_pairwise_scoring.drop(columns=['queryid']).mean(),
metrics_model_bart_tokenized_word_pairwise.drop(columns=['queryid']).mean()
],
axis=1,
names=['a', 'b', 'c', 'd', 'e', 'f']
).T.rename(index={
0: 'Cosine Similarity',
1: 'Tf-Idf',
2: 'Tf-Idf Scoring',
3: 'Bart Doc Embedding',
4: 'Bart Doc Embedding Scoring',
5: 'Bart Word Embedding',
6: 'Bart Word Embedding Scoring',
7: 'GloVe',
8: 'GloVe Scoring',
9: 'Tf-Idf Pairwise',
10: 'Tf-Idf Pairwise Scoring',
11: 'Bart Doc Embedding Pairwise',
12: 'GloVe Pairwise',
13: 'GloVe Pairwise Scoring',
14: 'Bart Word Embedding Pairwise'
}).sort_values(by='nDCG', ascending=False)
queries_df = pd.read_csv(
'/content/drive/Shareddrives/IRProject/msmarco-test2019-queries.tsv',
sep='\t',
names=[
'queryid',
'query',
],
)
queries_df.info()
metrics_model_cosine_similarity.sort_values(by='nDCG').head(3)
metrics_model_non_cont_word_emb.sort_values(by='nDCG').head(3)
hard_queries = [855410, 287683, 1115776]
queries_df[queries_df['queryid'].isin(hard_queries)]
metrics_model_cosine_similarity.sort_values(by='nDCG').tail(3)
queries_df[queries_df['queryid'].isin([47923, 489204, 1114819])]
metrics_model_non_cont_word_emb.sort_values(by='nDCG').tail(3)
queries_df[queries_df['queryid'].isin([183378, 1106007, 1114819])]
| 0.650134 | 0.608449 |
# Spherical Harmonics
In this notebook we try to reproduce the eigenfunctions of the Laplacian on the 2D sphere embedded in $\mathbb{R}^3$. The eigenfunctions are the spherical harmonics $Y_l^m(\theta, \phi)$.
```
import numpy as np
from pydiffmap import diffusion_map as dm
from scipy.sparse import csr_matrix
np.random.seed(100)
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
```
## generate data on a Sphere
we sample longitude and latitude uniformly and then transform to $\mathbb{R}^3$ using geographical coordinates (latidude is measured from the equator).
```
m = 10000
Phi = 2*np.pi*np.random.rand(m) - np.pi
Theta = np.pi*np.random.rand(m) - 0.5*np.pi
X = np.cos(Theta)*np.cos(Phi)
Y = np.cos(Theta)*np.sin(Phi)
Z = np.sin(Theta)
data = np.array([X, Y, Z]).transpose()
```
## run diffusion maps
Now we initialize the diffusion map object and fit it to the dataset. We set n_evecs = 4, and since we want to unbias with respect to the non-uniform sampling density we set alpha = 1.0. The epsilon parameter controls the scale and is set here by hand. The k parameter controls the neighbour lists, a smaller k will increase performance but decrease accuracy.
```
eps = 0.01
mydmap = dm.DiffusionMap.from_sklearn(n_evecs=4, epsilon=eps, alpha=1.0, k=400)
mydmap.fit_transform(data)
test_evals = -4./eps*(mydmap.evals - 1)
print(test_evals)
```
The true eigenfunctions here are spherical harmonics $Y_l^m(\theta, \phi)$ and the true eigenvalues are $\lambda_l = l(l+1)$. The eigenfunction corresponding to $l=0$ is the constant function, which we ommit. Since $l=1$ has multiplicity three, this gives the benchmark eigenvalues [2, 2, 2, 6].
```
real_evals = np.array([2, 2, 2, 6])
test_evals = -4./eps*(mydmap.evals - 1)
eval_error = np.abs(test_evals-real_evals)/real_evals
print(test_evals)
print(eval_error)
```
## visualisation
With pydiffmap's visualization toolbox, we can get a quick look at the embedding produced by the first two diffusion coordinates and the data colored by the first eigenfunction.
```
from pydiffmap.visualization import embedding_plot, data_plot
embedding_plot(mydmap, dim=3, scatter_kwargs = {'c': mydmap.dmap[:,0], 'cmap': 'Spectral'})
plt.show()
data_plot(mydmap, dim=3, scatter_kwargs = {'cmap': 'Spectral'})
plt.show()
```
## Rotating the dataset
There is rotational symmetry in this dataset. To remove it, we define the 'north pole' to be the point where the first diffusion coordinate attains its maximum value.
```
northpole = np.argmax(mydmap.dmap[:,0])
north = data[northpole,:]
phi_n = Phi[northpole]
theta_n = Theta[northpole]
R = np.array([[np.sin(theta_n)*np.cos(phi_n), np.sin(theta_n)*np.sin(phi_n), -np.cos(theta_n)],
[-np.sin(phi_n), np.cos(phi_n), 0],
[np.cos(theta_n)*np.cos(phi_n), np.cos(theta_n)*np.sin(phi_n), np.sin(theta_n)]])
data_rotated = np.dot(R,data.transpose())
data_rotated.shape
```
Now that the dataset is rotated, we can check how well the first diffusion coordinate approximates the first spherical harmonic $Y_1^1(\theta, \phi) = \sin(\theta) = Z$.
```
print('Correlation between \phi and \psi_1')
print(np.corrcoef(mydmap.dmap[:,0], data_rotated[2,:]))
plt.figure(figsize=(16,6))
ax = plt.subplot(121)
ax.scatter(data_rotated[2,:], mydmap.dmap[:,0])
ax.set_title('First DC against $Z$')
ax.set_xlabel(r'$Z$')
ax.set_ylabel(r'$\psi_1$')
ax.axis('tight')
ax2 = plt.subplot(122,projection='3d')
ax2.scatter(data_rotated[0,:],data_rotated[1,:],data_rotated[2,:], c=mydmap.dmap[:,0], cmap=plt.cm.Spectral)
#ax2.view_init(75, 10)
ax2.set_title('sphere dataset rotated, color according to $\psi_1$')
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')
plt.show()
```
|
github_jupyter
|
import numpy as np
from pydiffmap import diffusion_map as dm
from scipy.sparse import csr_matrix
np.random.seed(100)
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
m = 10000
Phi = 2*np.pi*np.random.rand(m) - np.pi
Theta = np.pi*np.random.rand(m) - 0.5*np.pi
X = np.cos(Theta)*np.cos(Phi)
Y = np.cos(Theta)*np.sin(Phi)
Z = np.sin(Theta)
data = np.array([X, Y, Z]).transpose()
eps = 0.01
mydmap = dm.DiffusionMap.from_sklearn(n_evecs=4, epsilon=eps, alpha=1.0, k=400)
mydmap.fit_transform(data)
test_evals = -4./eps*(mydmap.evals - 1)
print(test_evals)
real_evals = np.array([2, 2, 2, 6])
test_evals = -4./eps*(mydmap.evals - 1)
eval_error = np.abs(test_evals-real_evals)/real_evals
print(test_evals)
print(eval_error)
from pydiffmap.visualization import embedding_plot, data_plot
embedding_plot(mydmap, dim=3, scatter_kwargs = {'c': mydmap.dmap[:,0], 'cmap': 'Spectral'})
plt.show()
data_plot(mydmap, dim=3, scatter_kwargs = {'cmap': 'Spectral'})
plt.show()
northpole = np.argmax(mydmap.dmap[:,0])
north = data[northpole,:]
phi_n = Phi[northpole]
theta_n = Theta[northpole]
R = np.array([[np.sin(theta_n)*np.cos(phi_n), np.sin(theta_n)*np.sin(phi_n), -np.cos(theta_n)],
[-np.sin(phi_n), np.cos(phi_n), 0],
[np.cos(theta_n)*np.cos(phi_n), np.cos(theta_n)*np.sin(phi_n), np.sin(theta_n)]])
data_rotated = np.dot(R,data.transpose())
data_rotated.shape
print('Correlation between \phi and \psi_1')
print(np.corrcoef(mydmap.dmap[:,0], data_rotated[2,:]))
plt.figure(figsize=(16,6))
ax = plt.subplot(121)
ax.scatter(data_rotated[2,:], mydmap.dmap[:,0])
ax.set_title('First DC against $Z$')
ax.set_xlabel(r'$Z$')
ax.set_ylabel(r'$\psi_1$')
ax.axis('tight')
ax2 = plt.subplot(122,projection='3d')
ax2.scatter(data_rotated[0,:],data_rotated[1,:],data_rotated[2,:], c=mydmap.dmap[:,0], cmap=plt.cm.Spectral)
#ax2.view_init(75, 10)
ax2.set_title('sphere dataset rotated, color according to $\psi_1$')
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')
plt.show()
| 0.654895 | 0.988657 |
# NuSVR with RobustScaler & Power Transformer
This Code template is for regression analysis using a Nu-Support Vector Regressor(NuSVR) based on the Support Vector Machine algorithm with PowerTransformer as Feature Transformation Technique and RobustScaler for Feature Scaling in a pipeline.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import RobustScaler, PowerTransformer
from sklearn.model_selection import train_test_split
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
file_path= ""
```
List of features which are required for model training .
```
features =[]
```
Target feature for prediction.
```
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
Y=NullClearner(Y)
X=EncodeX(X)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
X_train,X_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
```
### Model
Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection.
A Support Vector Machine is a discriminative classifier formally defined by a separating hyperplane. In other terms, for a given known/labelled data points, the SVM outputs an appropriate hyperplane that classifies the inputted new cases based on the hyperplane. In 2-Dimensional space, this hyperplane is a line separating a plane into two segments where each class or group occupied on either side.
Here we will use NuSVR, the NuSVR implementation is based on libsvm. Similar to NuSVC, for regression, uses a parameter nu to control the number of support vectors. However, unlike NuSVC, where nu replaces C, here nu replaces the parameter epsilon of epsilon-SVR.
#### Model Tuning Parameters
1. nu : float, default=0.5
> An upper bound on the fraction of training errors and a lower bound of the fraction of support vectors. Should be in the interval (0, 1]. By default 0.5 will be taken.
2. C : float, default=1.0
> Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive. The penalty is a squared l2 penalty.
3. kernel : {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}, default=’rbf’
> Specifies the kernel type to be used in the algorithm. It must be one of ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ or a callable. If none is given, ‘rbf’ will be used. If a callable is given it is used to pre-compute the kernel matrix from data matrices; that matrix should be an array of shape (n_samples, n_samples).
4. gamma : {‘scale’, ‘auto’} or float, default=’scale’
> Gamma is a hyperparameter that we have to set before the training model. Gamma decides how much curvature we want in a decision boundary.
5. degree : int, default=3
> Degree of the polynomial kernel function (‘poly’). Ignored by all other kernels.Using degree 1 is similar to using a linear kernel. Also, increasing degree parameter leads to higher training times.
#### Rescaling technique
RobustScaler scales features using statistics that are robust to outliers.
This Scaler removes the median and scales the data according to the quantile range (defaults to IQR: Interquartile Range). The IQR is the range between the 1st quartile (25th quantile) and the 3rd quartile (75th quantile).
Centering and scaling happen independently on each feature by computing the relevant statistics on the samples in the training set. Median and interquartile range are then stored to be used on later data using the transform method.
##### For more information on RobustScaler [ click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.RobustScaler.html)
#### Feature Transformation
PowerTransformer applies a power transform featurewise to make data more Gaussian-like.
Power transforms are a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. This is useful for modeling issues related to heteroscedasticity (non-constant variance), or other situations where normality is desired.
##### For more information on PowerTransformer [ click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PowerTransformer.html#rf3e1504535de-2)
```
model=make_pipeline(RobustScaler(),PowerTransformer(),NuSVR())
model.fit(X_train,y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
> **score**: The **score** function returns the coefficient of determination <code>R<sup>2</sup></code> of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(X_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a scatter plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
n=len(X_test) if len(X_test)<20 else 20
plt.figure(figsize=(14,10))
plt.plot(range(n),y_test[0:n], color = "green")
plt.plot(range(n),model.predict(X_test[0:n]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator: Saharsh Laud , Github: [Profile](https://github.com/SaharshLaud)
|
github_jupyter
|
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import RobustScaler, PowerTransformer
from sklearn.model_selection import train_test_split
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
file_path= ""
features =[]
target=''
df=pd.read_csv(file_path)
df.head()
X=df[features]
Y=df[target]
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
Y=NullClearner(Y)
X=EncodeX(X)
X.head()
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
X_train,X_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
model=make_pipeline(RobustScaler(),PowerTransformer(),NuSVR())
model.fit(X_train,y_train)
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
y_pred=model.predict(X_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
n=len(X_test) if len(X_test)<20 else 20
plt.figure(figsize=(14,10))
plt.plot(range(n),y_test[0:n], color = "green")
plt.plot(range(n),model.predict(X_test[0:n]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
| 0.337422 | 0.987592 |
```
"iwf-competition-analysis-visualizations"
# # A function to concate all of the above .csv files into one file
# file_name = "Olympic-Weightlifting-total-results-1980-2016"
# wf.datatable_cleanup.concat_csv(file_name)
import os
from glob import glob
import pandas as pd
import webscraping_functions as wf
country_codes = pd.read_html("https://www.iban.com/country-codes")[0]
country_codes.head()
phoebe = pd.read_html("https://www.iban.com/country-codes")[0].values.tolist()
phoebe
if "China" in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index("China")
code = country_codes["Alpha-3 code"][index]
print(code)
else:
print("1")
%pwd
import os
from glob import glob
import pandas as pd
import webscraping_functions as wf
%pwd
file_name = "IWF-OLY-weightlifting-total-results-combined"
os.chdir("C:\\Users\\jacqu\\Desktop\\Github Portfolio\\olympic-weightlifting-results\\")
file_name = "Olympic-Weightlifting-total-results-1980-2016"
os.chdir("C:\\Users\\jacqu\\Desktop\\Github Portfolio\\olympic-weightlifting-results\\competition-results\\olympic-weightlifting-results-1980-2016")
file_pattern = ".csv"
file_rename = file_name + file_pattern
list_of_files = [file for file in glob("*{}".format(file_pattern))]
# Combine all files in the list into a dataframe
dataframe_csv = pd.concat([pd.read_csv(file, engine="python") for file in list_of_files])
# Export the dataframe to csv
dataframe_csv.to_csv(file_rename, index=False, encoding='utf-8')
list_of_files
file_name = "IWF-championships-total-results-1996-2019"
os.chdir("C:\\Users\\jacqu\\Desktop\\Github Portfolio\\olympic-weightlifting-results\iwf-championships-weightclass-results-1996-2019")
file_pattern = ".csv"
file_rename = file_name + file_pattern
list_of_files = [file for file in glob("*{}".format(file_pattern))]
# Combine all files in the list into a dataframe
dataframe_csv = pd.concat([pd.read_csv(file, engine="python") for file in list_of_files])
# Export the dataframe to csv
dataframe_csv.to_csv(file_rename, index=False, encoding='utf-8')
list_of_files
concat
import pdb; pdb.set_trace()
from datetime import datetime
import pandas as pd
from pandas import Series, DataFrame
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
%matplotlib inline
# #plt.show()
if website_url[79:82] == "Men":
gender = "M"
return gender
elif website_url[79:84] == "Women":
gender = "W"
return gender
elif website_url[82:85] == "Men":
gender = "M"
return gender
elif website_url[82:87] == "Women":
gender = "W"
return gender
len("https://en.wikipedia.org/wiki/1997_World_Weightlifting_Championships_%E2%80%93_")
len("https://en.wikipedia.org/wiki/1997_World_Weightlifting_Championships_%E2%80%93_Men%27s_54_kg")
len("https://en.wikipedia.org/wiki/1997_World_Weightlifting_Championships_%E2%80%93_Women%27s_46_kg")
len("https://en.wikipedia.org/wiki/Weightlifting_at_the_2008_Summer_Olympics_%E2%80%93_Women%27s_53_kg")
len("https://en.wikipedia.org/wiki/Weightlifting_at_the_2008_Summer_Olympics_%E2%80%93_")
len("https://en.wikipedia.org/wiki/Weightlifting_at_the_2004_Summer_Olympics_%E2%80%93_Men%27s_77_kg")
len("https://en.wikipedia.org/wiki/Weightlifting_at_the_2004_Summer_Olympics_%E2%80%93_")
# def results_table(website_url):
# try:
year = wf.datatable_cleanup.insert_year(website_url)
gender = wf.datatable_cleanup.insert_gender(website_url)
url_header = wf.WikiParser.get_h1_text(website_url)
header_name = "Results"
snatch_cols = ["Snatch 1 (kg)", "Snatch 2 (kg)", "Snatch 3 (kg)"]
clean_cols = ["C/J 1 (kg)", "C/J 2 (kg)", "C/J 3 (kg)"]
df = wf.WikiParser.results_to_dataframe(website_url, header_name)
wf.ResultsCleanup.column_row_cleanup(df)
wf.ResultsCleanup.data_cleanup(df)
wf.ResultsCleanup.lift_rankings(df, snatch_cols, "Max Snatch", "Snatch Rank")
wf.ResultsCleanup.lift_rankings(df, clean_cols, "Max C/J", "C/J Rank")
df.insert(0,"Year", year)
df.insert(1, "Gender", gender)
file_name = url_header + ".csv"
df.to_csv(file_name)
# return file_name
# except:
# return "Error"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_2012_Summer_Olympics_%E2%80%93_Men%27s_69_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1980_Summer_Olympics_%E2%80%93_Men%27s_60_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_2016_Summer_Olympics_%E2%80%93_Men%27s_69_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_2016_Summer_Olympics_%E2%80%93_Women%27s_75_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1992_Summer_Olympics_%E2%80%93_Men%27s_56_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_2000_Summer_Olympics_%E2%80%93_Men%27s_105_kg"
wesbite_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1996_Summer_Olympics_%E2%80%93_Men%27s_76_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1996_Summer_Olympics_%E2%80%93_Men%27s_99_kg"
header_name = "Results"
results_dataframe = wf.WikiParser.results_to_dataframe(website_url, header_name)
results_dataframe.head()
check_group(results_dataframe)
check_bodyweight(results_dataframe)
check_nation(results_dataframe)
check_max_lift(results_dataframe)
check_rank(results_dataframe)
column_names = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Max Snatch, Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), Max C/J, C/J Rank, Total").split(", ")
results_dataframe.columns = column_names
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
def check_group(results_dataframe):
try:
if not "Group\n" in results_dataframe.iloc[0].values:
results_dataframe.insert(2, "Group", "A")
return results_dataframe
else:
return results_dataframe
except:
pass
def check_bodyweight(results_dataframe):
try:
if (not "Bodyweight\n" or not "Body weight\n") in results_dataframe.iloc[0].values:
results_dataframe.insert(3, "Body Weight (kg)", "NaN")
return results_dataframe
else:
return results_dataframe
except:
pass
def check_nation(results_dataframe):
try:
if not "Nation\n" in results_dataframe.iloc[0].values:
new_cols = results_dataframe[1].str.split("(", 1, expand=True)
results_dataframe[1] = new_cols[0]
results_dataframe.insert(2, "Nationality", new_cols[1])
results_dataframe["Nationality"] = results_dataframe["Nationality"].str.rstrip(")")
return results_dataframe
else:
return results_dataframe
except:
pass
def check_max_lift(results_dataframe):
try:
if not "Result\n" in results_dataframe.iloc[1].values:
results_dataframe.insert(8, "Max Snatch", 0)
results_dataframe.insert(13, "Max C/J", 0)
return results_dataframe
else:
return results_dataframe
except:
pass
def check_rank(results_dataframe):
try:
if not "Rank\n" in results_dataframe.iloc[1].values:
results_dataframe.insert(9, "Snatch Rank", 0)
results_dataframe.insert(14, "C/J Rank", 0)
return results_dataframe
else:
results_dataframe["Snatch Rank"] = results_dataframe[9]
results_dataframe["C/J Rank"] = results_dataframe[14]
results_dataframe.drop(columns=[8, 14], inplace = True)
return results_dataframe
except:
pass
def check_group(results_dataframe):
try:
if not "Group\n" in results_dataframe.iloc[0].values:
results_dataframe.insert(2, "Group", "A")
return results_dataframe
else:
pass
except:
pass
def check_bodyweight(results_dataframe):
try:
if (not "Bodyweight\n" or not "Body weight\n") in results_dataframe.iloc[0].values:
results_dataframe.insert(3, "Body Weight (kg)", "NaN")
return results_dataframe
else:
pass
except:
pass
def check_nation(results_dataframe):
try:
if not "Nation\n" in results_dataframe.iloc[0].values:
new_cols = results_dataframe[1].str.split("(", 1, expand=True)
results_dataframe[1] = new_cols[0]
results_dataframe.insert(2, "Nationality", new_cols[1])
results_dataframe["Nationality"] = results_dataframe["Nationality"].str.rstrip(")")
return results_dataframe
else:
pass
except:
pass
def check_max_lift(results_dataframe):
try:
if not "Result\n" in results_dataframe.iloc[1].values:
results_dataframe.insert(8, "Max Snatch", 0)
results_dataframe.insert(13, "Max C/J", 0)
return results_dataframe
else:
pass
except:
pass
def check_rank(results_dataframe):
try:
if not "Rank\n" in results_dataframe.iloc[1].values:
results_dataframe.insert(9, "Snatch Rank", 0)
results_dataframe.insert(14, "C/J Rank", 0)
return results_dataframe
else:
results_dataframe["Snatch Rank"] = results_dataframe[8]
results_dataframe["C/J Rank"] = results_dataframe[14]
results_dataframe.drop([8, 14], inplace = True)
return results_dataframe
except:
pass
wf.CheckFunctions.check_group(results_dataframe)
wf.CheckFunctions.check_bodyweight(results_dataframe)
wf.CheckFunctions.check_nation(results_dataframe)
wf.CheckFunctions.check_max_lift(results_dataframe)
wf.CheckFunctions.check_rank(results_dataframe)
column_names = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Max Snatch, Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), Max C/J, C/J Rank, Total").split(", ")
results_dataframe.columns = column_names
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
wf.CheckFunctions.check_group(results_dataframe)
wf.CheckFunctions.check_bodyweight(results_dataframe)
wf.CheckFunctions.check_nation(results_dataframe)
wf.CheckFunctions.check_result(results_dataframe)
column_names = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Max Snatch, Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), Max C/J, C/J Rank, Total").split(", ")
results_dataframe.columns = column_names
# Insert Max Snatch and Max C/J
results_dataframe.insert(7, "Max Snatch", 0)
results_dataframe.insert(12, "Max C/J", 0)
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
# Need to check for body weight, group, nation, and result data in table
if not "Group\n" in results_dataframe.iloc[0].values:
results_dataframe.insert(2, "Group", "A")
elif not ("Bodyweight\n" or "Body weight\n") in results_dataframe.iloc[0].values:
results_dataframe.insert(3, "Body Weight (kg)", "NaN")
elif not "Nation\n" in results_dataframe.iloc[0].values:
new_cols = results_dataframe["Athlete Name"].str.split("(", 1, expand=True)
results_dataframe["Athlete Name"] = new_cols[0]
results_dataframe.insert(2, "Nationality", new_cols[1])
results_dataframe["Nationality"] = results_dataframe["Nationality"].str.rstrip(")")
elif not "Result\n" in results_dataframe.iloc[0].values:
results_dataframe.insert(6, "Snatch Rank", 0)
results_dataframe.inser(10, "C/J Rank", 0)
column_names = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names
# Insert Max Snatch and Max C/J
results_dataframe.insert(7, "Max Snatch", 0)
results_dataframe.insert(12, "Max C/J", 0)
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
# Need to check for body weight, group data, and nation in table
if "Group\n" and ("Bodyweight\n" or "Body weight\n") and "Nation\n" in results_dataframe.iloc[0].values:
column_names4 = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names4
else:
if ("Bodyweight\n" or "Body weight") and not "Group\n" in results_dataframe.iloc[0].values:
column_names1 = (
"Comp Rank, Athlete Name, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names1
results_dataframe.insert(2, "Group", "A")
elif "Group\n" and not ("Bodyweight\n" or "Body weight") in results_dataframe.iloc[0].values:
column_names2 = (
"Comp Rank, Athlete Name, Group, "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names2
results_dataframe.insert(3, "Body Weight (kg)", "NaN")
elif "Group\n" and ("Bodyweight\n" or "Body weight") in results_dataframe.iloc[0].values:
column_names3 = (
"Comp Rank, Athlete Name, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names3
new_cols = results_dataframe["Athlete Name"].str.split("(", 1, expand=True)
results_dataframe["Athlete Name"] = new_cols[0]
results_dataframe.insert(2, "Nationality", new_cols[1])
results_dataframe["Nationality"] = results_dataframe["Nationality"].str.rstrip(")")
# Insert Max Snatch and Max C/J
results_dataframe.insert(8, "Max Snatch", 0)
results_dataframe.insert(13, "Max C/J", 0)
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
website_url1 = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1980_Summer_Olympics"
website_url2 = "https://en.wikipedia.org/wiki/1996_World_Weightlifting_Championships"
website_url1[51:55]
website_url2[30:34]
blue = "https://en.wikipedia.org/wiki/"
len(blue)
green = "https://en.wikipedia.org/wiki/Weightlifting"
len(green)
red = "https://en.wikipedia.org/wiki/Weightlifting_at_the_"
len(red)
yellow = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1980"
len(yellow)
def check(website_url):
if website_url[30:43] == "Weightlifting":
year = website_url1[51:55]
print("olympic")
else:
year = website_url2[30:34]
print("iwf")
check(website_url1)
check(website_url2)
# Setting custom color palette from hex color codes
"""
Hexcodes and Color Names
"#B38867", # Coffee
"#283655", # Blueberry
"#69983D", # Green Apple
"#D50000", # Guardsman Red
"#A57298", # Boquet
"#FFAA00", # Web Orange/Goldenrod
"#F18D93", # Pink Tulip
"#F0810F", # Tangerine
"#66A5AD", # Ocean
"""
color_names = "coffee, blueberry, green, red, boquet, goldenrod, pink tulip, tangerine, ocean".split(", ")
hexcodes = "#B38867 #283655 #69983D #D50000 #A57298 #FFAA00 #F18D93 #F0810F #66A5AD".split()
colors_codes = list(zip(color_names, hexcodes))
exercise_names = "Deadlift BackSquat OverheadSquat FrontSquat BenchPress ShoulderPress SnatchPress Snatch Clean&Jerk".split()
color_map= dict(zip(exercise_names, colors_codes))
color_df = pd.DataFrame.from_dict(color_map, orient="index", columns=["Color Name", "Hexcode"])
color_df
colors = color_df["Hexcode"].tolist()
palette = sns.set_palette(sns.color_palette(colors))
sns.set_context("paper")
df = pd.read_csv("workout_data_database.csv")
df.head()
df.drop(columns =["Unnamed: 0"], inplace = True)
df.head()
workout_data_list = df.values.tolist()
workout_data_list[0:5]
# This changes the "%Y-%m-%d %H:%M:%S" string format in the list to datetime format "%Y-%m-%d %H:%M:%S"
# to be able to use seaborn graphs below.
for i in range(len(workout_data_list)):
try:
temp = datetime.strptime(workout_data_list[i][4], "%Y-%m-%d %H:%M:%S")
temp.strftime("%Y-%m-%d %H:%M:%S")
workout_data_list[i][4] = temp
except:
pass
workout_data = pd.DataFrame(workout_data_list)
workout_data.head()
workout_data.columns = "exercise, sets, reps, weight_lbs, datetime, duration_minutes".split(", ")
workout_data.head()
# A dataframe for total count of workouts for each exercise
workout_count = workout_data[["exercise", "datetime"]]
workout_count.head()
# Plot for total count of workouts for each exercise
plt.figure(figsize = (12,9))
sns.set_context("paper", font_scale = 2)
graph = sns.swarmplot(
x="exercise",
y="datetime",
data=workout_count,
palette=colors,
order=exercise_names
)
graph.set_xticklabels(graph.get_xticklabels(), rotation = 30)
graph.yaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.yaxis.set_major_formatter(mdates.DateFormatter("%b %d, %y"))
graph.set(
title="Workout Count per Exercise",
xlabel="Exercise",
ylabel="Date"
)
plt.savefig("Workout Count per Exercise.png")
# A dataframe for max weight by each exercise.
exercise_max = workout_data[["exercise", "weight_lbs"]].groupby("exercise").max()
exercise_max["exercise"] = exercise_max.index
exercise_max
# Plot of max weight for each exercise
plt.figure(figsize = (12,9))
sns.set_context("paper", font_scale = 2)
graph = sns.barplot(
x="exercise",
y="weight_lbs",
data=exercise_max,
order=exercise_names
)
graph.set_xticklabels(graph.get_xticklabels(), rotation = 30)
graph.set(
title="Max Lifts per Exercise",
xlabel="Exercise",
ylabel="Weight (lbs)",
yticks=np.arange(0, 300, 25)
)
plt.savefig("Max Lifts per Exercise.png")
# A dataframe for total intensity(total weight lifted) for each exercise
total_intensity = workout_data[["exercise", "weight_lbs"]].groupby("exercise").sum()
total_intensity["exercise"] = total_intensity.index
total_intensity
# Plot of total intensity for each exercise
plt.figure(figsize = (12,9))
sns.set_context("paper", font_scale = 2)
graph = sns.barplot(
x="exercise",
y="weight_lbs",
data=total_intensity,
order=exercise_names
)
graph.set_xticklabels(graph.get_xticklabels(), rotation=30)
graph.set(
title="Total Intensity",
xlabel="Exercise",
ylabel="Total Weight Lifted (lbs)",
yticks=np.arange(0, 8000, 500)
)
plt.savefig("Total Intensity.png")
# A dataframe for total volume for each exercise
total_reps = workout_data["sets"]*workout_data["reps"]
workout_data["total volume"] = total_reps
total_volume = workout_data[["exercise", "total volume"]].groupby("exercise").sum()
total_volume["exercise"] = total_volume.index
total_volume
# Plot for total volume for each exercise
plt.figure(figsize = (12,9))
sns.set_context("paper", font_scale = 2)
graph = sns.barplot(
x="exercise",
y="total volume",
data=total_volume,
order=exercise_names
)
graph.set_xticklabels(graph.get_xticklabels(), rotation = 30)
graph.set(
title="Total Volume per Exercise",
xlabel="Exercise",
ylabel="Total Reps",
yticks=np.arange(0, 1200, 100)
)
plt.savefig("Total Volume.png")
squats_intensity = workout_data[
["exercise", "datetime", "weight_lbs"]
].loc[
(workout_data["exercise"] == "BackSquat") |
(workout_data["exercise"] == "OverheadSquat") |
(workout_data["exercise"] == "FrontSquat")
]
squats_intensity.head()
squats_volume = workout_data[
["exercise", "datetime", "total volume"]
].loc[
(workout_data["exercise"] == "BackSquat") |
(workout_data["exercise"] == "OverheadSquat") |
(workout_data["exercise"] == "FrontSquat")
]
squats_volume.head()
presses_intensity = workout_data[
["exercise", "datetime", "weight_lbs"]
].loc[(workout_data["exercise"] == "BenchPress") |
(workout_data["exercise"] == "ShoulderPress")]
presses_intensity.head()
presses_volume = workout_data[
["exercise", "datetime", "total volume"]
].loc[(workout_data["exercise"] == "BenchPress") |
(workout_data["exercise"] == "ShoulderPress")
]
presses_volume.head()
oly_lifts_intensity = workout_data[
["exercise", "datetime", "weight_lbs"]
].loc[
(workout_data["exercise"] == "Clean&Jerk") |
(workout_data["exercise"] == "Snatch")
]
oly_lifts_intensity.head()
oly_lifts_volume = workout_data[
["exercise", "datetime", "total volume"]
].loc[(workout_data["exercise"] == "Clean&Jerk") |
(workout_data["exercise"] == "Snatch")
]
oly_lifts_volume.head()
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="weight_lbs",
data=squats_intensity,
palette=colors[1:4],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(squats_intensity["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Squats Intensity vs. Time",
xlabel="Time",
ylabel="Weight (lbs)",
yticks=np.arange(0, 250, 25)
)
plt.legend(
title="Exercise",
loc="upper right",
labels=squats_intensity["exercise"].unique()
)
plt.savefig("Squats Intensity.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="total volume",
data=squats_volume,
palette=colors[1:4],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(squats_volume["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Squats Volume vs. Time",
xlabel="Time",
ylabel="Total Reps per Session",
yticks=np.arange(0, 55, 5)
)
plt.legend(
title="Exercise",
loc="upper left",
labels=squats_volume["exercise"].unique()
)
plt.savefig("Squats Volume.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="weight_lbs",
data=presses_intensity,
palette=colors[4:6],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(presses_intensity["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Presses Intensity vs. Time",
xlabel="Time",
ylabel="Weight (lbs)",
yticks=np.arange(0, 200, 25)
)
plt.legend(
title="Exercise",
loc="upper right",
labels=presses_intensity["exercise"].unique()
)
plt.savefig("Presses Intensity.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="total volume",
data=presses_volume,
palette=colors[4:6],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(presses_volume["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Presses Volume vs. Time",
xlabel="Time",
ylabel="Total Reps per Session",
yticks=np.arange(0, 55, 5)
)
plt.legend(
title="Exercise",
loc="upper left",
labels=presses_volume["exercise"].unique()
)
plt.savefig("Presses Volume.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="weight_lbs",
data=oly_lifts_intensity,
palette=colors[7:9],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(oly_lifts_intensity["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Olympic Lifts Intensity vs. Time",
xlabel="Time",
ylabel="Weight (lbs)",
yticks=np.arange(0, 150, 25)
)
plt.legend(
title="Exercise",
loc="upper right",
labels=oly_lifts_intensity["exercise"].unique()
)
plt.savefig("Olympic Lifts Intensity.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="total volume",
data=oly_lifts_volume,
palette=colors[7:9],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(oly_lifts_volume["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Olympic Lifts Volume vs. Time",
xlabel="Time",
ylabel="Total Reps per Session",
yticks=np.arange(0, 30, 3)
)
plt.legend(
title="Exercise",
loc="upper right",
labels=oly_lifts_volume["exercise"].unique()
)
plt.savefig("Olympic Lifts Volume.png")
""" Analytics Below """
# Shoulder Press Volume to Deadlift Volme Percent Ratio
dl = total_volume.loc["Deadlift"][0]
sp = total_volume.loc["ShoulderPress"][0]
round(sp/dl*100, 2)
# Deadlift Max to Shoulder Press Max Percent Ratio
dl = exercise_max.loc["Deadlift"][0]
sp = exercise_max.loc["ShoulderPress"][0]
round(dl/sp*100, 2)
# Squats Total Volume to Presses Total Volume Percent Ratio
sq = squats_volume["total volume"].sum()
pr = presses_volume["total volume"].sum()
round(sq/pr*100, 2)
# Squts Total Intensity to Presses Total Intensity Percent Ratio
sq = squats_intensity["weight_lbs"].sum()
pr = presses_intensity["weight_lbs"].sum()
round(sq/pr*100, 2)
# Snatch Total Volume to Clean&Jerk Total Volume Percent Ratio
cj = total_volume.loc["Clean&Jerk"][0]
sn = total_volume.loc["Snatch"][0]
round(sn/cj*100, 2)
# Snatch Total Intensity to Clean&Jerk Total Intensity Percent Ratio
cj = total_intensity.loc["Clean&Jerk"][0]
sn = total_intensity.loc["Snatch"][0]
round(sn/cj*100, 2)
# Front Squat Max to Back Squat Max Percent Ratio
fs = exercise_max.loc["FrontSquat"][0]
bs = exercise_max.loc["BackSquat"][0]
round(fs/bs*100, 2)
# Average duration of workouts out of 111 workouts with non-null data in duration_minutes
len(workout_data["duration_minutes"].loc[workout_data["duration_minutes"] != -1]) # No. workouts with non-null duration
avg_duration = workout_data["duration_minutes"].loc[workout_data["duration_minutes"] != -1].mean()
round(avg_duration, 2)
# Average number of sets in workouts
avg_sets = workout_data["sets"].mean()
round(avg_sets, 2)
# Average number of reps in workouts
avg_reps = workout_data["reps"].mean()
round(avg_reps, 2)
# Average weight lifted in workouts
avg_weight = workout_data["weight_lbs"].mean()
round(avg_weight, 2)
```
|
github_jupyter
|
"iwf-competition-analysis-visualizations"
# # A function to concate all of the above .csv files into one file
# file_name = "Olympic-Weightlifting-total-results-1980-2016"
# wf.datatable_cleanup.concat_csv(file_name)
import os
from glob import glob
import pandas as pd
import webscraping_functions as wf
country_codes = pd.read_html("https://www.iban.com/country-codes")[0]
country_codes.head()
phoebe = pd.read_html("https://www.iban.com/country-codes")[0].values.tolist()
phoebe
if "China" in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index("China")
code = country_codes["Alpha-3 code"][index]
print(code)
else:
print("1")
%pwd
import os
from glob import glob
import pandas as pd
import webscraping_functions as wf
%pwd
file_name = "IWF-OLY-weightlifting-total-results-combined"
os.chdir("C:\\Users\\jacqu\\Desktop\\Github Portfolio\\olympic-weightlifting-results\\")
file_name = "Olympic-Weightlifting-total-results-1980-2016"
os.chdir("C:\\Users\\jacqu\\Desktop\\Github Portfolio\\olympic-weightlifting-results\\competition-results\\olympic-weightlifting-results-1980-2016")
file_pattern = ".csv"
file_rename = file_name + file_pattern
list_of_files = [file for file in glob("*{}".format(file_pattern))]
# Combine all files in the list into a dataframe
dataframe_csv = pd.concat([pd.read_csv(file, engine="python") for file in list_of_files])
# Export the dataframe to csv
dataframe_csv.to_csv(file_rename, index=False, encoding='utf-8')
list_of_files
file_name = "IWF-championships-total-results-1996-2019"
os.chdir("C:\\Users\\jacqu\\Desktop\\Github Portfolio\\olympic-weightlifting-results\iwf-championships-weightclass-results-1996-2019")
file_pattern = ".csv"
file_rename = file_name + file_pattern
list_of_files = [file for file in glob("*{}".format(file_pattern))]
# Combine all files in the list into a dataframe
dataframe_csv = pd.concat([pd.read_csv(file, engine="python") for file in list_of_files])
# Export the dataframe to csv
dataframe_csv.to_csv(file_rename, index=False, encoding='utf-8')
list_of_files
concat
import pdb; pdb.set_trace()
from datetime import datetime
import pandas as pd
from pandas import Series, DataFrame
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
%matplotlib inline
# #plt.show()
if website_url[79:82] == "Men":
gender = "M"
return gender
elif website_url[79:84] == "Women":
gender = "W"
return gender
elif website_url[82:85] == "Men":
gender = "M"
return gender
elif website_url[82:87] == "Women":
gender = "W"
return gender
len("https://en.wikipedia.org/wiki/1997_World_Weightlifting_Championships_%E2%80%93_")
len("https://en.wikipedia.org/wiki/1997_World_Weightlifting_Championships_%E2%80%93_Men%27s_54_kg")
len("https://en.wikipedia.org/wiki/1997_World_Weightlifting_Championships_%E2%80%93_Women%27s_46_kg")
len("https://en.wikipedia.org/wiki/Weightlifting_at_the_2008_Summer_Olympics_%E2%80%93_Women%27s_53_kg")
len("https://en.wikipedia.org/wiki/Weightlifting_at_the_2008_Summer_Olympics_%E2%80%93_")
len("https://en.wikipedia.org/wiki/Weightlifting_at_the_2004_Summer_Olympics_%E2%80%93_Men%27s_77_kg")
len("https://en.wikipedia.org/wiki/Weightlifting_at_the_2004_Summer_Olympics_%E2%80%93_")
# def results_table(website_url):
# try:
year = wf.datatable_cleanup.insert_year(website_url)
gender = wf.datatable_cleanup.insert_gender(website_url)
url_header = wf.WikiParser.get_h1_text(website_url)
header_name = "Results"
snatch_cols = ["Snatch 1 (kg)", "Snatch 2 (kg)", "Snatch 3 (kg)"]
clean_cols = ["C/J 1 (kg)", "C/J 2 (kg)", "C/J 3 (kg)"]
df = wf.WikiParser.results_to_dataframe(website_url, header_name)
wf.ResultsCleanup.column_row_cleanup(df)
wf.ResultsCleanup.data_cleanup(df)
wf.ResultsCleanup.lift_rankings(df, snatch_cols, "Max Snatch", "Snatch Rank")
wf.ResultsCleanup.lift_rankings(df, clean_cols, "Max C/J", "C/J Rank")
df.insert(0,"Year", year)
df.insert(1, "Gender", gender)
file_name = url_header + ".csv"
df.to_csv(file_name)
# return file_name
# except:
# return "Error"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_2012_Summer_Olympics_%E2%80%93_Men%27s_69_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1980_Summer_Olympics_%E2%80%93_Men%27s_60_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_2016_Summer_Olympics_%E2%80%93_Men%27s_69_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_2016_Summer_Olympics_%E2%80%93_Women%27s_75_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1992_Summer_Olympics_%E2%80%93_Men%27s_56_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_2000_Summer_Olympics_%E2%80%93_Men%27s_105_kg"
wesbite_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1996_Summer_Olympics_%E2%80%93_Men%27s_76_kg"
website_url = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1996_Summer_Olympics_%E2%80%93_Men%27s_99_kg"
header_name = "Results"
results_dataframe = wf.WikiParser.results_to_dataframe(website_url, header_name)
results_dataframe.head()
check_group(results_dataframe)
check_bodyweight(results_dataframe)
check_nation(results_dataframe)
check_max_lift(results_dataframe)
check_rank(results_dataframe)
column_names = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Max Snatch, Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), Max C/J, C/J Rank, Total").split(", ")
results_dataframe.columns = column_names
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
def check_group(results_dataframe):
try:
if not "Group\n" in results_dataframe.iloc[0].values:
results_dataframe.insert(2, "Group", "A")
return results_dataframe
else:
return results_dataframe
except:
pass
def check_bodyweight(results_dataframe):
try:
if (not "Bodyweight\n" or not "Body weight\n") in results_dataframe.iloc[0].values:
results_dataframe.insert(3, "Body Weight (kg)", "NaN")
return results_dataframe
else:
return results_dataframe
except:
pass
def check_nation(results_dataframe):
try:
if not "Nation\n" in results_dataframe.iloc[0].values:
new_cols = results_dataframe[1].str.split("(", 1, expand=True)
results_dataframe[1] = new_cols[0]
results_dataframe.insert(2, "Nationality", new_cols[1])
results_dataframe["Nationality"] = results_dataframe["Nationality"].str.rstrip(")")
return results_dataframe
else:
return results_dataframe
except:
pass
def check_max_lift(results_dataframe):
try:
if not "Result\n" in results_dataframe.iloc[1].values:
results_dataframe.insert(8, "Max Snatch", 0)
results_dataframe.insert(13, "Max C/J", 0)
return results_dataframe
else:
return results_dataframe
except:
pass
def check_rank(results_dataframe):
try:
if not "Rank\n" in results_dataframe.iloc[1].values:
results_dataframe.insert(9, "Snatch Rank", 0)
results_dataframe.insert(14, "C/J Rank", 0)
return results_dataframe
else:
results_dataframe["Snatch Rank"] = results_dataframe[9]
results_dataframe["C/J Rank"] = results_dataframe[14]
results_dataframe.drop(columns=[8, 14], inplace = True)
return results_dataframe
except:
pass
def check_group(results_dataframe):
try:
if not "Group\n" in results_dataframe.iloc[0].values:
results_dataframe.insert(2, "Group", "A")
return results_dataframe
else:
pass
except:
pass
def check_bodyweight(results_dataframe):
try:
if (not "Bodyweight\n" or not "Body weight\n") in results_dataframe.iloc[0].values:
results_dataframe.insert(3, "Body Weight (kg)", "NaN")
return results_dataframe
else:
pass
except:
pass
def check_nation(results_dataframe):
try:
if not "Nation\n" in results_dataframe.iloc[0].values:
new_cols = results_dataframe[1].str.split("(", 1, expand=True)
results_dataframe[1] = new_cols[0]
results_dataframe.insert(2, "Nationality", new_cols[1])
results_dataframe["Nationality"] = results_dataframe["Nationality"].str.rstrip(")")
return results_dataframe
else:
pass
except:
pass
def check_max_lift(results_dataframe):
try:
if not "Result\n" in results_dataframe.iloc[1].values:
results_dataframe.insert(8, "Max Snatch", 0)
results_dataframe.insert(13, "Max C/J", 0)
return results_dataframe
else:
pass
except:
pass
def check_rank(results_dataframe):
try:
if not "Rank\n" in results_dataframe.iloc[1].values:
results_dataframe.insert(9, "Snatch Rank", 0)
results_dataframe.insert(14, "C/J Rank", 0)
return results_dataframe
else:
results_dataframe["Snatch Rank"] = results_dataframe[8]
results_dataframe["C/J Rank"] = results_dataframe[14]
results_dataframe.drop([8, 14], inplace = True)
return results_dataframe
except:
pass
wf.CheckFunctions.check_group(results_dataframe)
wf.CheckFunctions.check_bodyweight(results_dataframe)
wf.CheckFunctions.check_nation(results_dataframe)
wf.CheckFunctions.check_max_lift(results_dataframe)
wf.CheckFunctions.check_rank(results_dataframe)
column_names = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Max Snatch, Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), Max C/J, C/J Rank, Total").split(", ")
results_dataframe.columns = column_names
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
wf.CheckFunctions.check_group(results_dataframe)
wf.CheckFunctions.check_bodyweight(results_dataframe)
wf.CheckFunctions.check_nation(results_dataframe)
wf.CheckFunctions.check_result(results_dataframe)
column_names = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Max Snatch, Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), Max C/J, C/J Rank, Total").split(", ")
results_dataframe.columns = column_names
# Insert Max Snatch and Max C/J
results_dataframe.insert(7, "Max Snatch", 0)
results_dataframe.insert(12, "Max C/J", 0)
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
# Need to check for body weight, group, nation, and result data in table
if not "Group\n" in results_dataframe.iloc[0].values:
results_dataframe.insert(2, "Group", "A")
elif not ("Bodyweight\n" or "Body weight\n") in results_dataframe.iloc[0].values:
results_dataframe.insert(3, "Body Weight (kg)", "NaN")
elif not "Nation\n" in results_dataframe.iloc[0].values:
new_cols = results_dataframe["Athlete Name"].str.split("(", 1, expand=True)
results_dataframe["Athlete Name"] = new_cols[0]
results_dataframe.insert(2, "Nationality", new_cols[1])
results_dataframe["Nationality"] = results_dataframe["Nationality"].str.rstrip(")")
elif not "Result\n" in results_dataframe.iloc[0].values:
results_dataframe.insert(6, "Snatch Rank", 0)
results_dataframe.inser(10, "C/J Rank", 0)
column_names = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names
# Insert Max Snatch and Max C/J
results_dataframe.insert(7, "Max Snatch", 0)
results_dataframe.insert(12, "Max C/J", 0)
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
# Need to check for body weight, group data, and nation in table
if "Group\n" and ("Bodyweight\n" or "Body weight\n") and "Nation\n" in results_dataframe.iloc[0].values:
column_names4 = (
"Comp Rank, Athlete Name, Nationality, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names4
else:
if ("Bodyweight\n" or "Body weight") and not "Group\n" in results_dataframe.iloc[0].values:
column_names1 = (
"Comp Rank, Athlete Name, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names1
results_dataframe.insert(2, "Group", "A")
elif "Group\n" and not ("Bodyweight\n" or "Body weight") in results_dataframe.iloc[0].values:
column_names2 = (
"Comp Rank, Athlete Name, Group, "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names2
results_dataframe.insert(3, "Body Weight (kg)", "NaN")
elif "Group\n" and ("Bodyweight\n" or "Body weight") in results_dataframe.iloc[0].values:
column_names3 = (
"Comp Rank, Athlete Name, Group, Body Weight (kg), "
"Snatch 1 (kg), Snatch 2 (kg), Snatch 3 (kg), Snatch Rank, "
"C/J 1 (kg), C/J 2 (kg), C/J 3 (kg), C/J Rank, Total").split(", ")
results_dataframe.columns = column_names3
new_cols = results_dataframe["Athlete Name"].str.split("(", 1, expand=True)
results_dataframe["Athlete Name"] = new_cols[0]
results_dataframe.insert(2, "Nationality", new_cols[1])
results_dataframe["Nationality"] = results_dataframe["Nationality"].str.rstrip(")")
# Insert Max Snatch and Max C/J
results_dataframe.insert(8, "Max Snatch", 0)
results_dataframe.insert(13, "Max C/J", 0)
results_dataframe.drop([0,1], inplace=True)
results_dataframe.reset_index(inplace=True)
results_dataframe.drop("index", axis=1, inplace=True)
# Change country name to country code for consistency
for country in results_dataframe["Nationality"].values.tolist():
if country in country_codes["Country"].values.tolist():
index = country_codes["Country"].values.tolist().index(country)
code = country_codes["Alpha-3 code"][index]
results_dataframe["Nationality"][index] = code
else:
pass
results_dataframe.head()
website_url1 = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1980_Summer_Olympics"
website_url2 = "https://en.wikipedia.org/wiki/1996_World_Weightlifting_Championships"
website_url1[51:55]
website_url2[30:34]
blue = "https://en.wikipedia.org/wiki/"
len(blue)
green = "https://en.wikipedia.org/wiki/Weightlifting"
len(green)
red = "https://en.wikipedia.org/wiki/Weightlifting_at_the_"
len(red)
yellow = "https://en.wikipedia.org/wiki/Weightlifting_at_the_1980"
len(yellow)
def check(website_url):
if website_url[30:43] == "Weightlifting":
year = website_url1[51:55]
print("olympic")
else:
year = website_url2[30:34]
print("iwf")
check(website_url1)
check(website_url2)
# Setting custom color palette from hex color codes
"""
Hexcodes and Color Names
"#B38867", # Coffee
"#283655", # Blueberry
"#69983D", # Green Apple
"#D50000", # Guardsman Red
"#A57298", # Boquet
"#FFAA00", # Web Orange/Goldenrod
"#F18D93", # Pink Tulip
"#F0810F", # Tangerine
"#66A5AD", # Ocean
"""
color_names = "coffee, blueberry, green, red, boquet, goldenrod, pink tulip, tangerine, ocean".split(", ")
hexcodes = "#B38867 #283655 #69983D #D50000 #A57298 #FFAA00 #F18D93 #F0810F #66A5AD".split()
colors_codes = list(zip(color_names, hexcodes))
exercise_names = "Deadlift BackSquat OverheadSquat FrontSquat BenchPress ShoulderPress SnatchPress Snatch Clean&Jerk".split()
color_map= dict(zip(exercise_names, colors_codes))
color_df = pd.DataFrame.from_dict(color_map, orient="index", columns=["Color Name", "Hexcode"])
color_df
colors = color_df["Hexcode"].tolist()
palette = sns.set_palette(sns.color_palette(colors))
sns.set_context("paper")
df = pd.read_csv("workout_data_database.csv")
df.head()
df.drop(columns =["Unnamed: 0"], inplace = True)
df.head()
workout_data_list = df.values.tolist()
workout_data_list[0:5]
# This changes the "%Y-%m-%d %H:%M:%S" string format in the list to datetime format "%Y-%m-%d %H:%M:%S"
# to be able to use seaborn graphs below.
for i in range(len(workout_data_list)):
try:
temp = datetime.strptime(workout_data_list[i][4], "%Y-%m-%d %H:%M:%S")
temp.strftime("%Y-%m-%d %H:%M:%S")
workout_data_list[i][4] = temp
except:
pass
workout_data = pd.DataFrame(workout_data_list)
workout_data.head()
workout_data.columns = "exercise, sets, reps, weight_lbs, datetime, duration_minutes".split(", ")
workout_data.head()
# A dataframe for total count of workouts for each exercise
workout_count = workout_data[["exercise", "datetime"]]
workout_count.head()
# Plot for total count of workouts for each exercise
plt.figure(figsize = (12,9))
sns.set_context("paper", font_scale = 2)
graph = sns.swarmplot(
x="exercise",
y="datetime",
data=workout_count,
palette=colors,
order=exercise_names
)
graph.set_xticklabels(graph.get_xticklabels(), rotation = 30)
graph.yaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.yaxis.set_major_formatter(mdates.DateFormatter("%b %d, %y"))
graph.set(
title="Workout Count per Exercise",
xlabel="Exercise",
ylabel="Date"
)
plt.savefig("Workout Count per Exercise.png")
# A dataframe for max weight by each exercise.
exercise_max = workout_data[["exercise", "weight_lbs"]].groupby("exercise").max()
exercise_max["exercise"] = exercise_max.index
exercise_max
# Plot of max weight for each exercise
plt.figure(figsize = (12,9))
sns.set_context("paper", font_scale = 2)
graph = sns.barplot(
x="exercise",
y="weight_lbs",
data=exercise_max,
order=exercise_names
)
graph.set_xticklabels(graph.get_xticklabels(), rotation = 30)
graph.set(
title="Max Lifts per Exercise",
xlabel="Exercise",
ylabel="Weight (lbs)",
yticks=np.arange(0, 300, 25)
)
plt.savefig("Max Lifts per Exercise.png")
# A dataframe for total intensity(total weight lifted) for each exercise
total_intensity = workout_data[["exercise", "weight_lbs"]].groupby("exercise").sum()
total_intensity["exercise"] = total_intensity.index
total_intensity
# Plot of total intensity for each exercise
plt.figure(figsize = (12,9))
sns.set_context("paper", font_scale = 2)
graph = sns.barplot(
x="exercise",
y="weight_lbs",
data=total_intensity,
order=exercise_names
)
graph.set_xticklabels(graph.get_xticklabels(), rotation=30)
graph.set(
title="Total Intensity",
xlabel="Exercise",
ylabel="Total Weight Lifted (lbs)",
yticks=np.arange(0, 8000, 500)
)
plt.savefig("Total Intensity.png")
# A dataframe for total volume for each exercise
total_reps = workout_data["sets"]*workout_data["reps"]
workout_data["total volume"] = total_reps
total_volume = workout_data[["exercise", "total volume"]].groupby("exercise").sum()
total_volume["exercise"] = total_volume.index
total_volume
# Plot for total volume for each exercise
plt.figure(figsize = (12,9))
sns.set_context("paper", font_scale = 2)
graph = sns.barplot(
x="exercise",
y="total volume",
data=total_volume,
order=exercise_names
)
graph.set_xticklabels(graph.get_xticklabels(), rotation = 30)
graph.set(
title="Total Volume per Exercise",
xlabel="Exercise",
ylabel="Total Reps",
yticks=np.arange(0, 1200, 100)
)
plt.savefig("Total Volume.png")
squats_intensity = workout_data[
["exercise", "datetime", "weight_lbs"]
].loc[
(workout_data["exercise"] == "BackSquat") |
(workout_data["exercise"] == "OverheadSquat") |
(workout_data["exercise"] == "FrontSquat")
]
squats_intensity.head()
squats_volume = workout_data[
["exercise", "datetime", "total volume"]
].loc[
(workout_data["exercise"] == "BackSquat") |
(workout_data["exercise"] == "OverheadSquat") |
(workout_data["exercise"] == "FrontSquat")
]
squats_volume.head()
presses_intensity = workout_data[
["exercise", "datetime", "weight_lbs"]
].loc[(workout_data["exercise"] == "BenchPress") |
(workout_data["exercise"] == "ShoulderPress")]
presses_intensity.head()
presses_volume = workout_data[
["exercise", "datetime", "total volume"]
].loc[(workout_data["exercise"] == "BenchPress") |
(workout_data["exercise"] == "ShoulderPress")
]
presses_volume.head()
oly_lifts_intensity = workout_data[
["exercise", "datetime", "weight_lbs"]
].loc[
(workout_data["exercise"] == "Clean&Jerk") |
(workout_data["exercise"] == "Snatch")
]
oly_lifts_intensity.head()
oly_lifts_volume = workout_data[
["exercise", "datetime", "total volume"]
].loc[(workout_data["exercise"] == "Clean&Jerk") |
(workout_data["exercise"] == "Snatch")
]
oly_lifts_volume.head()
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="weight_lbs",
data=squats_intensity,
palette=colors[1:4],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(squats_intensity["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Squats Intensity vs. Time",
xlabel="Time",
ylabel="Weight (lbs)",
yticks=np.arange(0, 250, 25)
)
plt.legend(
title="Exercise",
loc="upper right",
labels=squats_intensity["exercise"].unique()
)
plt.savefig("Squats Intensity.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="total volume",
data=squats_volume,
palette=colors[1:4],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(squats_volume["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Squats Volume vs. Time",
xlabel="Time",
ylabel="Total Reps per Session",
yticks=np.arange(0, 55, 5)
)
plt.legend(
title="Exercise",
loc="upper left",
labels=squats_volume["exercise"].unique()
)
plt.savefig("Squats Volume.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="weight_lbs",
data=presses_intensity,
palette=colors[4:6],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(presses_intensity["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Presses Intensity vs. Time",
xlabel="Time",
ylabel="Weight (lbs)",
yticks=np.arange(0, 200, 25)
)
plt.legend(
title="Exercise",
loc="upper right",
labels=presses_intensity["exercise"].unique()
)
plt.savefig("Presses Intensity.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="total volume",
data=presses_volume,
palette=colors[4:6],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(presses_volume["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Presses Volume vs. Time",
xlabel="Time",
ylabel="Total Reps per Session",
yticks=np.arange(0, 55, 5)
)
plt.legend(
title="Exercise",
loc="upper left",
labels=presses_volume["exercise"].unique()
)
plt.savefig("Presses Volume.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="weight_lbs",
data=oly_lifts_intensity,
palette=colors[7:9],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(oly_lifts_intensity["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Olympic Lifts Intensity vs. Time",
xlabel="Time",
ylabel="Weight (lbs)",
yticks=np.arange(0, 150, 25)
)
plt.legend(
title="Exercise",
loc="upper right",
labels=oly_lifts_intensity["exercise"].unique()
)
plt.savefig("Olympic Lifts Intensity.png")
# Plot comparison for intensity for squats.
plt.figure(figsize = (16,9))
sns.set_context("paper", font_scale = 2)
graph = sns.lineplot(
x="datetime",
y="total volume",
data=oly_lifts_volume,
palette=colors[7:9],
hue="exercise",
linewidth=3
)
graph.set_xticklabels(oly_lifts_volume["datetime"].values, rotation = 30)
graph.xaxis.set_major_locator(mdates.WeekdayLocator(interval=5))
graph.xaxis.set_major_formatter(mdates.DateFormatter("%m/%d/%y"))
graph.set(
title="Olympic Lifts Volume vs. Time",
xlabel="Time",
ylabel="Total Reps per Session",
yticks=np.arange(0, 30, 3)
)
plt.legend(
title="Exercise",
loc="upper right",
labels=oly_lifts_volume["exercise"].unique()
)
plt.savefig("Olympic Lifts Volume.png")
""" Analytics Below """
# Shoulder Press Volume to Deadlift Volme Percent Ratio
dl = total_volume.loc["Deadlift"][0]
sp = total_volume.loc["ShoulderPress"][0]
round(sp/dl*100, 2)
# Deadlift Max to Shoulder Press Max Percent Ratio
dl = exercise_max.loc["Deadlift"][0]
sp = exercise_max.loc["ShoulderPress"][0]
round(dl/sp*100, 2)
# Squats Total Volume to Presses Total Volume Percent Ratio
sq = squats_volume["total volume"].sum()
pr = presses_volume["total volume"].sum()
round(sq/pr*100, 2)
# Squts Total Intensity to Presses Total Intensity Percent Ratio
sq = squats_intensity["weight_lbs"].sum()
pr = presses_intensity["weight_lbs"].sum()
round(sq/pr*100, 2)
# Snatch Total Volume to Clean&Jerk Total Volume Percent Ratio
cj = total_volume.loc["Clean&Jerk"][0]
sn = total_volume.loc["Snatch"][0]
round(sn/cj*100, 2)
# Snatch Total Intensity to Clean&Jerk Total Intensity Percent Ratio
cj = total_intensity.loc["Clean&Jerk"][0]
sn = total_intensity.loc["Snatch"][0]
round(sn/cj*100, 2)
# Front Squat Max to Back Squat Max Percent Ratio
fs = exercise_max.loc["FrontSquat"][0]
bs = exercise_max.loc["BackSquat"][0]
round(fs/bs*100, 2)
# Average duration of workouts out of 111 workouts with non-null data in duration_minutes
len(workout_data["duration_minutes"].loc[workout_data["duration_minutes"] != -1]) # No. workouts with non-null duration
avg_duration = workout_data["duration_minutes"].loc[workout_data["duration_minutes"] != -1].mean()
round(avg_duration, 2)
# Average number of sets in workouts
avg_sets = workout_data["sets"].mean()
round(avg_sets, 2)
# Average number of reps in workouts
avg_reps = workout_data["reps"].mean()
round(avg_reps, 2)
# Average weight lifted in workouts
avg_weight = workout_data["weight_lbs"].mean()
round(avg_weight, 2)
| 0.309024 | 0.247413 |
```
%matplotlib notebook
# Import modules
import os
import math
import numpy as np
import matplotlib.pyplot
from pyne import serpent
from pyne import nucname
ace_lib_path = '/home/andrei2/serpent/xsdata/jeff312'
acelib = "sss_jeff312.xsdata"
#dep = serpent.parse_dep('../second_case/flux/TMSRPu_dep.m', make_mats=False)
dep = serpent.parse_dep('../third_case/flux/TMSRTRU_dep.m', make_mats=False)
#res = serpent.parse_res('../serpent/60-years-analysis/TMSR_res.m')
#res2 = serpent.parse_res('/home/andrei2/Desktop/git/msr-neutronics/depletion/online_1200days_Pa_less_Th/less_Th_rate/core_res.m')
target_iso = 'U233'
plot_title = 'Pa outflow 1.25E-10, U-233 inflow 3.5E-9, Th 9E-9\n'
days = dep['DAYS'] # Time array parsed from *_dep.m file
bu = dep['MAT_fuel_BURNUP'] # Time array parsed from *_dep.m file
time_step = np.diff(days) # Depletion time step evaluation
names = dep['NAMES'][0].split() # Names of isotopes parsed from *_dep.m file
#keff_analytical = res['ANA_KEFF'] # K-eff parsing from dictionary
#keff_analytical2 = res2['ANA_KEFF']
#kinf_dict = res['ABS_KINF'] # K-inf parsing from dictionary
#kinf_dict2 = res2['ABS_KINF']
#bu = res['BURNUP'] # Burnup parsing from dictionary
#keff_a = keff_analytical[:,0] # K-eff value
#keff_error = keff_analytical[:,1] # K-eff standart deviation
#kinf = kinf_dict[:,0]
#burnup = bu[:,0]
EOC = np.amax(days) # End of cycle (simulation time length)
#total_mass_list = dep['TOT_MASS']
adens_fuel = dep['MAT_fuel_ADENS'] # atomic density for each isotope in material 'fuel'
mdens_fuel = dep['MAT_fuel_MDENS'] # mass density for each isotope in material 'fuel'
vol_fuel = dep['MAT_fuel_VOLUME'] # total volume of material 'fuel'
density_fuel = mdens_fuel[-1,:] # total mass density for material 'fuel'
print(dep.keys()) #prints keys
def get_library_isotopes():
""" Returns the isotopes in the cross section library
Parameters:
-----------
Returns:
--------
iso_array: array
array of isotopes in cross section library:
"""
lib_isos = []
# check if environment variable is set
if os.environ.get('SERPENT_DATA') is not None:
path = os.environ['SERPENT_DATA']
else:
path = ace_lib_path
acelib_path = path +"/sss_jeff312.xsdata"
with open(acelib_path, 'r') as f:
metaflag = 0
lines = f.readlines()
for line in lines:
iso = (line.split()[1]).split('.')[0]
metaflag = line.split()[4]
zzaaa = line.split()[3]
if metaflag == '1':
iso = iso.replace(iso, zzaaa)
iso = str(iso) + str(metaflag)
lib_isos.append(iso)
return np.array(lib_isos)
#print (days)
print (days[21])
#print (bu)
#print(dep['iLOST'])
#print(adens_fuel[223-1])
#print(mdens_fuel[223-1])
print(nucname.serpent(952421))
#print(mdens_fuel[-1,:])
moment = -1
lib_isotopes = get_library_isotopes()
matf = open('mat_comp', 'w')
matf.write('mat fuel -%7.9E tmp 900 vol %7.5E\n' % (density_fuel[moment],
vol_fuel[moment]))
for key, value in dep.items():
if key[0]=='i':
if key[1:] not in lib_isotopes:
matf.write('%15s -%7.9E\n' % (key[1:], mdens_fuel[value-1,moment]))
elif key[1:] in lib_isotopes:
matf.write('%11s.09c -%7.9E\n' % (nucname.serpent(key[1:]), mdens_fuel[value-1,moment]))
else:
raise ValueError('Wrong isotope name')
#print (mdens_fuel[value-2, 0])
matf.close()
```
|
github_jupyter
|
%matplotlib notebook
# Import modules
import os
import math
import numpy as np
import matplotlib.pyplot
from pyne import serpent
from pyne import nucname
ace_lib_path = '/home/andrei2/serpent/xsdata/jeff312'
acelib = "sss_jeff312.xsdata"
#dep = serpent.parse_dep('../second_case/flux/TMSRPu_dep.m', make_mats=False)
dep = serpent.parse_dep('../third_case/flux/TMSRTRU_dep.m', make_mats=False)
#res = serpent.parse_res('../serpent/60-years-analysis/TMSR_res.m')
#res2 = serpent.parse_res('/home/andrei2/Desktop/git/msr-neutronics/depletion/online_1200days_Pa_less_Th/less_Th_rate/core_res.m')
target_iso = 'U233'
plot_title = 'Pa outflow 1.25E-10, U-233 inflow 3.5E-9, Th 9E-9\n'
days = dep['DAYS'] # Time array parsed from *_dep.m file
bu = dep['MAT_fuel_BURNUP'] # Time array parsed from *_dep.m file
time_step = np.diff(days) # Depletion time step evaluation
names = dep['NAMES'][0].split() # Names of isotopes parsed from *_dep.m file
#keff_analytical = res['ANA_KEFF'] # K-eff parsing from dictionary
#keff_analytical2 = res2['ANA_KEFF']
#kinf_dict = res['ABS_KINF'] # K-inf parsing from dictionary
#kinf_dict2 = res2['ABS_KINF']
#bu = res['BURNUP'] # Burnup parsing from dictionary
#keff_a = keff_analytical[:,0] # K-eff value
#keff_error = keff_analytical[:,1] # K-eff standart deviation
#kinf = kinf_dict[:,0]
#burnup = bu[:,0]
EOC = np.amax(days) # End of cycle (simulation time length)
#total_mass_list = dep['TOT_MASS']
adens_fuel = dep['MAT_fuel_ADENS'] # atomic density for each isotope in material 'fuel'
mdens_fuel = dep['MAT_fuel_MDENS'] # mass density for each isotope in material 'fuel'
vol_fuel = dep['MAT_fuel_VOLUME'] # total volume of material 'fuel'
density_fuel = mdens_fuel[-1,:] # total mass density for material 'fuel'
print(dep.keys()) #prints keys
def get_library_isotopes():
""" Returns the isotopes in the cross section library
Parameters:
-----------
Returns:
--------
iso_array: array
array of isotopes in cross section library:
"""
lib_isos = []
# check if environment variable is set
if os.environ.get('SERPENT_DATA') is not None:
path = os.environ['SERPENT_DATA']
else:
path = ace_lib_path
acelib_path = path +"/sss_jeff312.xsdata"
with open(acelib_path, 'r') as f:
metaflag = 0
lines = f.readlines()
for line in lines:
iso = (line.split()[1]).split('.')[0]
metaflag = line.split()[4]
zzaaa = line.split()[3]
if metaflag == '1':
iso = iso.replace(iso, zzaaa)
iso = str(iso) + str(metaflag)
lib_isos.append(iso)
return np.array(lib_isos)
#print (days)
print (days[21])
#print (bu)
#print(dep['iLOST'])
#print(adens_fuel[223-1])
#print(mdens_fuel[223-1])
print(nucname.serpent(952421))
#print(mdens_fuel[-1,:])
moment = -1
lib_isotopes = get_library_isotopes()
matf = open('mat_comp', 'w')
matf.write('mat fuel -%7.9E tmp 900 vol %7.5E\n' % (density_fuel[moment],
vol_fuel[moment]))
for key, value in dep.items():
if key[0]=='i':
if key[1:] not in lib_isotopes:
matf.write('%15s -%7.9E\n' % (key[1:], mdens_fuel[value-1,moment]))
elif key[1:] in lib_isotopes:
matf.write('%11s.09c -%7.9E\n' % (nucname.serpent(key[1:]), mdens_fuel[value-1,moment]))
else:
raise ValueError('Wrong isotope name')
#print (mdens_fuel[value-2, 0])
matf.close()
| 0.245175 | 0.227319 |
## 2. Nonstationary Bandit
The k-armed bandit problem in 'simple_bandit.ipynb) was stationary in that the expected reward for taking an action did not change with time (i.e. the mean and variance was fixed). In some problems, it is possible that the expected reward changes with time. Such problems are said to be nonstationary
From the incremental update rule,
\begin{align}
Q_{n+1} & = Q_n + \alpha[R_n - Q_n] \\
& = \alpha R_n + (1 - \alpha)Q_n \\
& = \alpha R_n + (1 - \alpha)\left[\alpha R_{n-1} + (1-\alpha)Q_{n-1} \right] \\
& = \alpha R_n + (1 - \alpha)\alpha R_{n-1} + (1-\alpha)^2Q_{n-1} \\
& = \alpha R_n + (1 - \alpha)\alpha R_{n-1} + (1-\alpha)^2\alpha R_{n-2} + ... + (1-\alpha)^{n-1}\alpha R_1 + (1-\alpha)^n Q_1 \\
& = (1-\alpha)^n Q_1 + \sum_{i=1}^n \alpha(1-\alpha)^{n-i} R_i
\end{align}
This is called a **weighted average**. Note that the weight given to a previous reward decays exponentially as the number of intervening rewards increases. $\alpha$ is called the step-size parameter. How do we set $\alpha$? In some cases, it is conveneint to vary it with time. Let $\alpha_n(a)$ denote the step-size parameter used to process the reward received after the nth selection of action a. In the sample average method, $\alpha_n(a) = \frac{1}{n}$. Another often used variant is the constant step-size parameter, $\alpha_n(a) = \alpha$.
Below we investigate the effect of $\alpha$ on the performance of an agent in a nonstationary k-armed bandit problem.
#### Exercise 2.3 $^1$
Design and conduct an experiment to demonstrate the difficulties that sample-average methods have for nonstationary problems. Use a modified version of the 10-armed testbed in which all the $q_*(a)$ start out equal and then take independent random walks. Prepare plots like Figure 2.2 for an action-value method using sample averages, incrementally computed by $\alpha = \frac{1}{n}$, and another action-value method using a constant step-size parameter, $\alpha = 0.1$. Use $\epsilon = 0.1$ and if necessary, runs longer than 1000 steps
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def sample_average_step_size(N, i):
"""
:param N: N[i] is the no. of times action i has been executed
:param i: The index of the selected action
"""
return 1.0 / N[i]
def constant_step_size(N, i):
return 0.1
def get_reward(true_values, a):
"""
Returns the reward for selecting action a.
Reward is selected around true_values[a] with unit variance (as in problem description)
:param true_values: true_values[i] is the expected reward for action i
:param a: index of action to return reward for
"""
reward = np.random.normal(true_values[a], size=1)[0]
return reward
def random_walk(true_values):
"""
Updates each expected reward by random amounts to imitate a nonstationary reward
:param true_values: true_values[i] is the expected reward for action i
"""
true_values += np.random.uniform(-1.0, 1.0, true_values.shape)
# We get rid of the sample_average() method and modify k_armed_bandit as follows:
def k_armed_bandit(k, epsilon, iterations, step_fn):
"""
Performs a single run of the k-armed bandit experiment
:param k: the number of arms
:param epsilon: Value of epsilon for epoch-greedy action selection
:param iterations: number of steps in a single run
:param step_fn: step-size function
"""
# Equal action values at start
true_values = np.ones(k) * np.random.uniform(-1.0, 1.0)
# Estimates of action values
Q = np.zeros(k)
# N[i] is the no. of times action i has been taken
N = np.zeros(k)
# Store the rewards received for this experiment
rewards = []
# Track how often the optimal action was selected
optimal = []
for _ in range(iterations):
prob = np.random.rand(1)
if prob > epsilon:
# Greedy (exploit current knowledge)
a = np.random.choice(np.flatnonzero(Q == Q.max()))
else:
# Explore (take random action)
a = np.random.randint(0, k)
reward = get_reward(true_values, a)
# Update statistics for executed action
N[a] += 1
Q[a] += step_fn(N, a) * (reward - Q[a])
rewards.append(reward)
optimal.append(1 if a == true_values.argmax() else 0)
# Update the rewards after each step
random_walk(true_values)
return rewards, optimal
def experiment(k, epsilon, iters, epochs, step_fn):
"""
Runs the k-armed bandit experiment
:param k: the number of arms
:param epsilon: the value of epsilon for epoch-greedy action selection
:param iters: the number of steps in a single run
:param epochs: the number of runs to execute
:param step_fn: the step-size function
"""
rewards = []
optimal = []
for i in range(epochs):
r, o = k_armed_bandit(k, epsilon, iters, step_fn)
rewards.append(r)
optimal.append(o)
print('Experiment with \u03b5 = {} completed.'.format(epsilon))
# Compute the mean reward for each iteration
r_means = np.mean(rewards, axis=0)
o_means = np.mean(optimal, axis=0)
return r_means, o_means
k = 10
epsilon = 0.1
iters = 5000
runs = 2000
# Experiment with sample-average step-size and constant step-size
r_exp1, o_exp1 = experiment(k, epsilon, iters, runs, sample_average_step_size)
r_exp2, o_exp2 = experiment(k, epsilon, iters, runs, constant_step_size)
x = range(iters)
plt.plot(x, r_exp1, label='sample average step-size')
plt.plot(x, r_exp2, label='constant step-size')
plt.xlabel('Steps')
plt.ylabel('Average reward')
plt.legend()
plt.show()
plt.plot(x, o_exp1, label='sample average step-size')
plt.plot(x, o_exp2, label='constant step-size')
plt.xlabel('Steps')
plt.ylabel('% Optimal action')
plt.legend()
plt.show()
```
The results show that indeed, the sample average method suffers when used in a nonstationary environment. As n increases, the update to Q[a] decreases and so our estimates suffer leading to poor results.
## References
1. Richard S. Sutton, Andrew G. Barto (1998). Reinforcement Learning: An Introduction. MIT Press.
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def sample_average_step_size(N, i):
"""
:param N: N[i] is the no. of times action i has been executed
:param i: The index of the selected action
"""
return 1.0 / N[i]
def constant_step_size(N, i):
return 0.1
def get_reward(true_values, a):
"""
Returns the reward for selecting action a.
Reward is selected around true_values[a] with unit variance (as in problem description)
:param true_values: true_values[i] is the expected reward for action i
:param a: index of action to return reward for
"""
reward = np.random.normal(true_values[a], size=1)[0]
return reward
def random_walk(true_values):
"""
Updates each expected reward by random amounts to imitate a nonstationary reward
:param true_values: true_values[i] is the expected reward for action i
"""
true_values += np.random.uniform(-1.0, 1.0, true_values.shape)
# We get rid of the sample_average() method and modify k_armed_bandit as follows:
def k_armed_bandit(k, epsilon, iterations, step_fn):
"""
Performs a single run of the k-armed bandit experiment
:param k: the number of arms
:param epsilon: Value of epsilon for epoch-greedy action selection
:param iterations: number of steps in a single run
:param step_fn: step-size function
"""
# Equal action values at start
true_values = np.ones(k) * np.random.uniform(-1.0, 1.0)
# Estimates of action values
Q = np.zeros(k)
# N[i] is the no. of times action i has been taken
N = np.zeros(k)
# Store the rewards received for this experiment
rewards = []
# Track how often the optimal action was selected
optimal = []
for _ in range(iterations):
prob = np.random.rand(1)
if prob > epsilon:
# Greedy (exploit current knowledge)
a = np.random.choice(np.flatnonzero(Q == Q.max()))
else:
# Explore (take random action)
a = np.random.randint(0, k)
reward = get_reward(true_values, a)
# Update statistics for executed action
N[a] += 1
Q[a] += step_fn(N, a) * (reward - Q[a])
rewards.append(reward)
optimal.append(1 if a == true_values.argmax() else 0)
# Update the rewards after each step
random_walk(true_values)
return rewards, optimal
def experiment(k, epsilon, iters, epochs, step_fn):
"""
Runs the k-armed bandit experiment
:param k: the number of arms
:param epsilon: the value of epsilon for epoch-greedy action selection
:param iters: the number of steps in a single run
:param epochs: the number of runs to execute
:param step_fn: the step-size function
"""
rewards = []
optimal = []
for i in range(epochs):
r, o = k_armed_bandit(k, epsilon, iters, step_fn)
rewards.append(r)
optimal.append(o)
print('Experiment with \u03b5 = {} completed.'.format(epsilon))
# Compute the mean reward for each iteration
r_means = np.mean(rewards, axis=0)
o_means = np.mean(optimal, axis=0)
return r_means, o_means
k = 10
epsilon = 0.1
iters = 5000
runs = 2000
# Experiment with sample-average step-size and constant step-size
r_exp1, o_exp1 = experiment(k, epsilon, iters, runs, sample_average_step_size)
r_exp2, o_exp2 = experiment(k, epsilon, iters, runs, constant_step_size)
x = range(iters)
plt.plot(x, r_exp1, label='sample average step-size')
plt.plot(x, r_exp2, label='constant step-size')
plt.xlabel('Steps')
plt.ylabel('Average reward')
plt.legend()
plt.show()
plt.plot(x, o_exp1, label='sample average step-size')
plt.plot(x, o_exp2, label='constant step-size')
plt.xlabel('Steps')
plt.ylabel('% Optimal action')
plt.legend()
plt.show()
| 0.854247 | 0.985243 |
### Deliverable 1: Preprocessing the Data for a Neural Network
```
# Import main dependencies
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler,OneHotEncoder
import pandas as pd
import tensorflow as tf
# Import checkpoint dependencies
import os
from tensorflow.keras.callbacks import ModelCheckpoint
# Import and read the charity_data.csv.
application_df = pd.read_csv("resources/charity_data.csv")
application_df.head()
application_df.dtypes
# Drop the non-beneficial ID columns, 'EIN' and 'NAME'.
application_df = application_df.drop(columns=['EIN', 'NAME'])
# Determine the number of unique values in each column.
application_cat = application_df.dtypes[application_df.dtypes == "object"].index.tolist()
application_df[application_cat].nunique()
# Look at APPLICATION_TYPE value counts for binning
app_type_val_counts = application_df.APPLICATION_TYPE.value_counts()
app_type_val_counts
# Visualize the value counts of APPLICATION_TYPE
app_type_val_counts.plot.density()
# Determine which values to replace if counts are less than ...?
replace_app_type = list(app_type_val_counts[app_type_val_counts<1000].index)
# Replace in dataframe
for app in replace_app_type:
application_df.APPLICATION_TYPE = application_df.APPLICATION_TYPE.replace(app,"Other")
# Check to make sure binning was successful
application_df.APPLICATION_TYPE.value_counts()
# Look at CLASSIFICATION value counts for binning
classification_val_counts = application_df.CLASSIFICATION.value_counts()
classification_val_counts.head(10)
# Visualize the value counts of CLASSIFICATION
classification_val_counts.plot.density()
# Determine which values to replace if counts are less than ..?
replace_class = list(classification_val_counts[classification_val_counts<1000].index)
# Replace in dataframe
for cls in replace_class:
application_df.CLASSIFICATION = application_df.CLASSIFICATION.replace(cls,"Other")
# Check to make sure binning was successful
application_df.CLASSIFICATION.value_counts()
# Look at INCOME_AMT value counts for binning
income_amt_val_cnts = application_df.INCOME_AMT.value_counts()
income_amt_val_cnts
# Determine which values to replace if counts are less than ..?
replace_incomes = list(income_amt_val_cnts[income_amt_val_cnts<500].index)
# Replace in dataframe
for incomes in replace_incomes:
application_df.INCOME_AMT = application_df.INCOME_AMT.replace(incomes,"5M+")
# Check to make sure binning was successful
application_df.INCOME_AMT.value_counts()
application_df.ASK_AMT.describe()
# Generate our categorical variable lists
application_catags = application_df.dtypes[application_df.dtypes == "object"].index.tolist()
application_df[application_catags].nunique()
# Create a OneHotEncoder instance
enc = OneHotEncoder(sparse=False)
# Fit and transform the OneHotEncoder using the categorical variable list
encode_df = pd.DataFrame(enc.fit_transform(application_df[application_catags]))
# Add the encoded variable names to the dataframe
encode_df.columns = enc.get_feature_names(application_catags)
encode_df.head()
# Merge one-hot encoded features and drop the originals
application_df = application_df.merge(encode_df,left_index=True, right_index=True)
application_df = application_df.drop(application_catags,1)
application_df.head()
application_df.columns
# Split our preprocessed data into our features and target arrays
y = application_df["IS_SUCCESSFUL"].values
X = application_df.drop(["IS_SUCCESSFUL","SPECIAL_CONSIDERATIONS_N"],1).values
# Split the preprocessed data into a training and testing dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=78)
# Create a StandardScaler instances
scaler = StandardScaler()
# Fit the StandardScaler
X_scaler = scaler.fit(X_train)
# Scale the data
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
```
### Deliverable 2: Compile, Train and Evaluate the Model
```
# Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
number_input_features = len(X_train_scaled[0])
hidden_nodes_layer1 = 80
hidden_nodes_layer2 = 50
hidden_nodes_layer3 = 40
nn=tf.keras.models.Sequential()
# First hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer1,
input_dim=number_input_features,
activation='tanh'))
# Second hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer2,
activation="tanh"))
# Third hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer3,
activation="tanh"))
# Output layer
nn.add(tf.keras.layers.Dense(units=1,
activation="sigmoid"))
# Check the structure of the model
nn.summary()
# Compile the model
nn.compile(loss="binary_crossentropy",
optimizer="nadam",
metrics=["accuracy"])
# Train the model
fit_model = nn.fit(X_train_scaled,
y_train,epochs=300)
# Define the checkpoint path and filenames
os.makedirs("checkpoints_optimization02/",exist_ok=True)
checkpoint_path = "checkpoints_optimization02/weights.{epoch:02d}.hdf5"
# Evaluate the model using the test data
model_loss, model_accuracy = nn.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Compile the model
nn.compile(loss="binary_crossentropy",
optimizer="nadam",
metrics=["accuracy"])
# Create a callback that saves the model's weights every 5 epochs
cp_callback = ModelCheckpoint(filepath=checkpoint_path,
verbose=1,
save_weights_only=True,
save_freq='epoch')
# Train the model
fit_model = nn.fit(X_train_scaled,
y_train,
epochs=100,
callbacks=[cp_callback])
# Evaluate the model using the test data
model_loss, model_accuracy = nn.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Export model to HDF5 file
nn.save('AlphabetSoupCharity_Optimization02.h5')
```
|
github_jupyter
|
# Import main dependencies
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler,OneHotEncoder
import pandas as pd
import tensorflow as tf
# Import checkpoint dependencies
import os
from tensorflow.keras.callbacks import ModelCheckpoint
# Import and read the charity_data.csv.
application_df = pd.read_csv("resources/charity_data.csv")
application_df.head()
application_df.dtypes
# Drop the non-beneficial ID columns, 'EIN' and 'NAME'.
application_df = application_df.drop(columns=['EIN', 'NAME'])
# Determine the number of unique values in each column.
application_cat = application_df.dtypes[application_df.dtypes == "object"].index.tolist()
application_df[application_cat].nunique()
# Look at APPLICATION_TYPE value counts for binning
app_type_val_counts = application_df.APPLICATION_TYPE.value_counts()
app_type_val_counts
# Visualize the value counts of APPLICATION_TYPE
app_type_val_counts.plot.density()
# Determine which values to replace if counts are less than ...?
replace_app_type = list(app_type_val_counts[app_type_val_counts<1000].index)
# Replace in dataframe
for app in replace_app_type:
application_df.APPLICATION_TYPE = application_df.APPLICATION_TYPE.replace(app,"Other")
# Check to make sure binning was successful
application_df.APPLICATION_TYPE.value_counts()
# Look at CLASSIFICATION value counts for binning
classification_val_counts = application_df.CLASSIFICATION.value_counts()
classification_val_counts.head(10)
# Visualize the value counts of CLASSIFICATION
classification_val_counts.plot.density()
# Determine which values to replace if counts are less than ..?
replace_class = list(classification_val_counts[classification_val_counts<1000].index)
# Replace in dataframe
for cls in replace_class:
application_df.CLASSIFICATION = application_df.CLASSIFICATION.replace(cls,"Other")
# Check to make sure binning was successful
application_df.CLASSIFICATION.value_counts()
# Look at INCOME_AMT value counts for binning
income_amt_val_cnts = application_df.INCOME_AMT.value_counts()
income_amt_val_cnts
# Determine which values to replace if counts are less than ..?
replace_incomes = list(income_amt_val_cnts[income_amt_val_cnts<500].index)
# Replace in dataframe
for incomes in replace_incomes:
application_df.INCOME_AMT = application_df.INCOME_AMT.replace(incomes,"5M+")
# Check to make sure binning was successful
application_df.INCOME_AMT.value_counts()
application_df.ASK_AMT.describe()
# Generate our categorical variable lists
application_catags = application_df.dtypes[application_df.dtypes == "object"].index.tolist()
application_df[application_catags].nunique()
# Create a OneHotEncoder instance
enc = OneHotEncoder(sparse=False)
# Fit and transform the OneHotEncoder using the categorical variable list
encode_df = pd.DataFrame(enc.fit_transform(application_df[application_catags]))
# Add the encoded variable names to the dataframe
encode_df.columns = enc.get_feature_names(application_catags)
encode_df.head()
# Merge one-hot encoded features and drop the originals
application_df = application_df.merge(encode_df,left_index=True, right_index=True)
application_df = application_df.drop(application_catags,1)
application_df.head()
application_df.columns
# Split our preprocessed data into our features and target arrays
y = application_df["IS_SUCCESSFUL"].values
X = application_df.drop(["IS_SUCCESSFUL","SPECIAL_CONSIDERATIONS_N"],1).values
# Split the preprocessed data into a training and testing dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=78)
# Create a StandardScaler instances
scaler = StandardScaler()
# Fit the StandardScaler
X_scaler = scaler.fit(X_train)
# Scale the data
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
# Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
number_input_features = len(X_train_scaled[0])
hidden_nodes_layer1 = 80
hidden_nodes_layer2 = 50
hidden_nodes_layer3 = 40
nn=tf.keras.models.Sequential()
# First hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer1,
input_dim=number_input_features,
activation='tanh'))
# Second hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer2,
activation="tanh"))
# Third hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer3,
activation="tanh"))
# Output layer
nn.add(tf.keras.layers.Dense(units=1,
activation="sigmoid"))
# Check the structure of the model
nn.summary()
# Compile the model
nn.compile(loss="binary_crossentropy",
optimizer="nadam",
metrics=["accuracy"])
# Train the model
fit_model = nn.fit(X_train_scaled,
y_train,epochs=300)
# Define the checkpoint path and filenames
os.makedirs("checkpoints_optimization02/",exist_ok=True)
checkpoint_path = "checkpoints_optimization02/weights.{epoch:02d}.hdf5"
# Evaluate the model using the test data
model_loss, model_accuracy = nn.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Compile the model
nn.compile(loss="binary_crossentropy",
optimizer="nadam",
metrics=["accuracy"])
# Create a callback that saves the model's weights every 5 epochs
cp_callback = ModelCheckpoint(filepath=checkpoint_path,
verbose=1,
save_weights_only=True,
save_freq='epoch')
# Train the model
fit_model = nn.fit(X_train_scaled,
y_train,
epochs=100,
callbacks=[cp_callback])
# Evaluate the model using the test data
model_loss, model_accuracy = nn.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Export model to HDF5 file
nn.save('AlphabetSoupCharity_Optimization02.h5')
| 0.867176 | 0.811303 |
# Processing gene expression of 10k PBMCs
This is the first chapter of the multimodal single-cell gene expression and chromatin accessibility analysis. In this notebook, scRNA-seq data processing is described, largely following [this scanpy notebook](https://scanpy-tutorials.readthedocs.io/en/latest/pbmc3k.html) on processing and clustering PBMCs.
One major distinction is using Pearson residuals to normalise and scale counts (see [Lause et al., 2020](https://www.biorxiv.org/content/10.1101/2020.12.01.405886v1) and the respective [repository](https://github.com/berenslab/umi-normalization)).
## Download data
Download the data that we will use for this series of notebooks. [The data is available here](https://support.10xgenomics.com/single-cell-multiome-atac-gex/datasets/1.0.0/pbmc_granulocyte_sorted_10k).
For the tutorial, we will use the filtered feature barcode matrix (HDF5).
```
# This is the directory where those files are downloaded to
data_dir = "data"
```
## Load libraries and data
Import libraries:
```
import numpy as np
import pandas as pd
import scanpy as sc
import anndata as ad
import muon as mu
%%time
rna = sc.read_10x_h5(f"{data_dir}/filtered_feature_bc_matrix.h5")
rna.var_names_make_unique()
rna
```
## Preprocessing
### QC
Perform some quality control. For now, we will filter out cells that do not pass QC.
```
rna.var['mt'] = rna.var_names.str.startswith('MT-') # annotate the group of mitochondrial genes as 'mt'
sc.pp.calculate_qc_metrics(rna, qc_vars=['mt'], percent_top=None, log1p=False, inplace=True)
mu.pl.histogram(rna, ['n_genes_by_counts', 'total_counts', 'pct_counts_mt'])
```
Filter genes which expression is not detected:
```
mu.pp.filter_var(rna, 'n_cells_by_counts', lambda x: x >= 3)
```
Filter cells:
```
mu.pp.filter_obs(rna, 'n_genes_by_counts', lambda x: (x >= 200) & (x < 5000))
mu.pp.filter_obs(rna, 'total_counts', lambda x: x < 15000)
mu.pp.filter_obs(rna, 'pct_counts_mt', lambda x: x < 20)
```
Let's see how the data looks after filtering:
```
mu.pl.histogram(rna, ['n_genes_by_counts', 'total_counts', 'pct_counts_mt'])
```
### Normalisation and scaling
We'll save original counts in the `'counts'` layer:
```
rna.layers['counts'] = rna.X.copy()
```
We'll save log-normalised counts in the `'lognorm'` layer:
```
sc.pp.normalize_total(rna, target_sum=1e4)
sc.pp.log1p(rna)
rna.layers['lognorm'] = rna.X.copy()
```
Restore original counts for the following normalisation:
```
rna.X = rna.layers['counts'].copy()
def normalize_residuals(adata, inplace: bool = True, clip: bool = True, theta: int = 100):
"""
Compute analytical residuals for NB model with a fixed theta.
Potentially clip outlier residuals to sqrt(N).
Adapted from Lause et al., 2020.
"""
n, d = adata.shape
# Calculate sums
# np.asarray() ensures they are ndarrays and not matrices
counts_sum0 = np.asarray(np.sum(adata.X, axis=0).reshape(-1, d))
counts_sum1 = np.asarray(np.sum(adata.X, axis=1).reshape(n, -1))
counts_sum = np.asarray(np.sum(adata.X))
# Calculate residuals
mu = counts_sum1 @ counts_sum0 / counts_sum
z = np.array((adata.X - mu) / np.sqrt(mu + mu**2/theta))
# Clip values
if clip:
z[z > np.sqrt(n)] = np.sqrt(n)
z[z < -np.sqrt(n)] = -np.sqrt(n)
if not inplace:
adata = adata.copy()
adata.X = z
return None if inplace else adata
```
We'll normalise the data so that we get Pearson residuals to work with.
```
%%time
normalize_residuals(rna)
```
## Analysis
Having filtered low-quality cells, normalised and scaled the counts matrix, we can run PCA, compute cell neighbourhood graph, and perform clustering to define cell types.
### PCA and neighbourhood graph
Here we run PCA on all of the genes having omitted the feature selection step.
```
%%time
sc.tl.pca(rna, svd_solver='arpack')
```
To visualise the result, we will use some markers for (large-scale) cell populations we expect to see such as T cells and NK cells (CD2), B cells (CD79A), and KLF4 (monocytes).
```
sc.pl.pca(rna, color=['CD2', 'CD79A', 'KLF4', 'IRF8'])
```
Use log-normalised coutns for visualisation purposes:
```
sc.pl.pca(rna, color=['CD2', 'CD79A', 'KLF4', 'IRF8'], layer='lognorm')
```
The first principal component (PC1) is separating myeloid (monocytes) and lymphoid (T, B, NK) cells while B cells-related features seem to drive the second one. Also we see plasmocytoid dendritic cells (marked by IRF8) being close to B cells along the PC2.
```
sc.pl.pca_variance_ratio(rna, log=True)
```
Now we can compute a neighbourhood graph for cells:
```
sc.pp.neighbors(rna, n_neighbors=10, n_pcs=20)
```
### Non-linear dimensionality reduction and clustering
With the neighbourhood graph computed, we can now perform clustering. We will use `leiden` clustering as an example.
```
sc.tl.leiden(rna, resolution=.4)
```
To visualise the results, we'll first generate a 2D latent space with cells that we can colour according to their cluster assignment.
```
sc.tl.umap(rna, spread=1., min_dist=.2, random_state=11)
sc.pl.umap(rna, color="leiden", legend_loc="on data")
```
We can define finer cell types for clusters 4 and 5.
```
sc.tl.leiden(rna, restrict_to=('leiden', ['4']), key_added='leiden2', resolution=.15)
sc.tl.leiden(rna, restrict_to=('leiden2', ['5']), key_added='leiden2', resolution=.1)
sc.pl.umap(rna, color="leiden2", legend_loc='on data')
```
### Marker genes and celltypes
```
sc.tl.rank_genes_groups(rna, 'leiden2', method='t-test_overestim_var')
result = rna.uns['rank_genes_groups']
groups = result['names'].dtype.names
pd.set_option('display.max_columns', 50)
pd.DataFrame(
{group + '_' + key[:1]: result[key][group]
for group in groups for key in ['names', 'pvals']}).head(10)
```
Exploring the data we notice clusters 8, 13, and 5,2 seem to be composed of cells bearing markers for different cell lineages so likely to be noise (e.g. doublets). Cluster 6 has higher ribosomal gene expression when compared to other clusters. Cluster 10 seem to consist of proliferating cells, cluster 14 — of stressed cells.
We will remove cells from these clusters before assigning cell types names to clusters.
```
mu.pp.filter_obs(rna, "leiden2", lambda x: ~x.isin(["8", "13", "5,2", "6", "14", "10"]))
new_cluster_names = {
"1": "CD4+ memory T", "2": "CD4+ naïve T", "3": "CD8+ naïve T",
"4,0": "CD8+ cytotoxic effector T", "4,1": "CD8+ transitional effector T", "4,2": "MAIT", "9": "NK",
"5,1": "naïve B", "5,0": "memory B", "5,3": "plasma B",
"0": "classical mono", "7": "non-classical mono",
"11": "mDC", "12": "pDC",
}
rna.obs['celltype'] = rna.obs.leiden2.astype("str").values
rna.obs.celltype = rna.obs.celltype.astype("category")
rna.obs.celltype = rna.obs.celltype.cat.rename_categories(new_cluster_names)
```
We will also re-order categories for the next plots:
```
rna.obs.celltype.cat.reorder_categories([
'CD4+ naïve T', 'CD4+ memory T',
'CD8+ naïve T', 'MAIT',
'CD8+ cytotoxic effector T', 'CD8+ transitional effector T', 'NK',
'naïve B', 'memory B', 'plasma B',
'classical mono', 'non-classical mono',
'mDC', 'pDC'], inplace=True)
```
... and take colours from a palette:
```
import matplotlib
import matplotlib.pyplot as plt
cmap = plt.get_cmap('rainbow')
colors = cmap(np.linspace(0, 1, len(rna.obs.celltype.cat.categories)))
rna.uns["celltype_colors"] = list(map(matplotlib.colors.to_hex, colors))
sc.pl.umap(rna, color="celltype", legend_loc="on data")
```
Finally, we'll visualise some marker genes across cell types.
```
marker_genes = [
'IL7R', 'TRAC', 'GATA3', # CD4+ T
'LEF1', 'FHIT', 'RORA', 'ITGB1', # naïve/memory
'CD8A', 'CD8B', 'CD248', 'CCL5', # CD8+ T
'GZMH', 'GZMK', # cytotoxic/transitional effector T cells
'KLRB1', 'SLC4A10', # MAIT
'IL32', # T/NK
'GNLY', 'NKG7', # NK
'CD79A', 'MS4A1', 'IGHD', 'IGHM', 'IL4R', 'TNFRSF13C', # B
'JCHAIN', # plasma
'KLF4', 'LYZ', 'S100A8', 'ITGAM', 'CD14', # mono
'DPYD', 'ITGAM', # classical/intermediate/non-classical mono
'FCGR3A', 'MS4A7', 'CST3', # non-classical mono
'CLEC10A', 'IRF8', 'TCF4' # DC
]
sc.pl.dotplot(rna, marker_genes, groupby='celltype', vmax=10)
```
## Saving data on disk
```
rna.write("data/pbmc10k_rna.h5ad")
```
|
github_jupyter
|
# This is the directory where those files are downloaded to
data_dir = "data"
import numpy as np
import pandas as pd
import scanpy as sc
import anndata as ad
import muon as mu
%%time
rna = sc.read_10x_h5(f"{data_dir}/filtered_feature_bc_matrix.h5")
rna.var_names_make_unique()
rna
rna.var['mt'] = rna.var_names.str.startswith('MT-') # annotate the group of mitochondrial genes as 'mt'
sc.pp.calculate_qc_metrics(rna, qc_vars=['mt'], percent_top=None, log1p=False, inplace=True)
mu.pl.histogram(rna, ['n_genes_by_counts', 'total_counts', 'pct_counts_mt'])
mu.pp.filter_var(rna, 'n_cells_by_counts', lambda x: x >= 3)
mu.pp.filter_obs(rna, 'n_genes_by_counts', lambda x: (x >= 200) & (x < 5000))
mu.pp.filter_obs(rna, 'total_counts', lambda x: x < 15000)
mu.pp.filter_obs(rna, 'pct_counts_mt', lambda x: x < 20)
mu.pl.histogram(rna, ['n_genes_by_counts', 'total_counts', 'pct_counts_mt'])
rna.layers['counts'] = rna.X.copy()
sc.pp.normalize_total(rna, target_sum=1e4)
sc.pp.log1p(rna)
rna.layers['lognorm'] = rna.X.copy()
rna.X = rna.layers['counts'].copy()
def normalize_residuals(adata, inplace: bool = True, clip: bool = True, theta: int = 100):
"""
Compute analytical residuals for NB model with a fixed theta.
Potentially clip outlier residuals to sqrt(N).
Adapted from Lause et al., 2020.
"""
n, d = adata.shape
# Calculate sums
# np.asarray() ensures they are ndarrays and not matrices
counts_sum0 = np.asarray(np.sum(adata.X, axis=0).reshape(-1, d))
counts_sum1 = np.asarray(np.sum(adata.X, axis=1).reshape(n, -1))
counts_sum = np.asarray(np.sum(adata.X))
# Calculate residuals
mu = counts_sum1 @ counts_sum0 / counts_sum
z = np.array((adata.X - mu) / np.sqrt(mu + mu**2/theta))
# Clip values
if clip:
z[z > np.sqrt(n)] = np.sqrt(n)
z[z < -np.sqrt(n)] = -np.sqrt(n)
if not inplace:
adata = adata.copy()
adata.X = z
return None if inplace else adata
%%time
normalize_residuals(rna)
%%time
sc.tl.pca(rna, svd_solver='arpack')
sc.pl.pca(rna, color=['CD2', 'CD79A', 'KLF4', 'IRF8'])
sc.pl.pca(rna, color=['CD2', 'CD79A', 'KLF4', 'IRF8'], layer='lognorm')
sc.pl.pca_variance_ratio(rna, log=True)
sc.pp.neighbors(rna, n_neighbors=10, n_pcs=20)
sc.tl.leiden(rna, resolution=.4)
sc.tl.umap(rna, spread=1., min_dist=.2, random_state=11)
sc.pl.umap(rna, color="leiden", legend_loc="on data")
sc.tl.leiden(rna, restrict_to=('leiden', ['4']), key_added='leiden2', resolution=.15)
sc.tl.leiden(rna, restrict_to=('leiden2', ['5']), key_added='leiden2', resolution=.1)
sc.pl.umap(rna, color="leiden2", legend_loc='on data')
sc.tl.rank_genes_groups(rna, 'leiden2', method='t-test_overestim_var')
result = rna.uns['rank_genes_groups']
groups = result['names'].dtype.names
pd.set_option('display.max_columns', 50)
pd.DataFrame(
{group + '_' + key[:1]: result[key][group]
for group in groups for key in ['names', 'pvals']}).head(10)
mu.pp.filter_obs(rna, "leiden2", lambda x: ~x.isin(["8", "13", "5,2", "6", "14", "10"]))
new_cluster_names = {
"1": "CD4+ memory T", "2": "CD4+ naïve T", "3": "CD8+ naïve T",
"4,0": "CD8+ cytotoxic effector T", "4,1": "CD8+ transitional effector T", "4,2": "MAIT", "9": "NK",
"5,1": "naïve B", "5,0": "memory B", "5,3": "plasma B",
"0": "classical mono", "7": "non-classical mono",
"11": "mDC", "12": "pDC",
}
rna.obs['celltype'] = rna.obs.leiden2.astype("str").values
rna.obs.celltype = rna.obs.celltype.astype("category")
rna.obs.celltype = rna.obs.celltype.cat.rename_categories(new_cluster_names)
rna.obs.celltype.cat.reorder_categories([
'CD4+ naïve T', 'CD4+ memory T',
'CD8+ naïve T', 'MAIT',
'CD8+ cytotoxic effector T', 'CD8+ transitional effector T', 'NK',
'naïve B', 'memory B', 'plasma B',
'classical mono', 'non-classical mono',
'mDC', 'pDC'], inplace=True)
import matplotlib
import matplotlib.pyplot as plt
cmap = plt.get_cmap('rainbow')
colors = cmap(np.linspace(0, 1, len(rna.obs.celltype.cat.categories)))
rna.uns["celltype_colors"] = list(map(matplotlib.colors.to_hex, colors))
sc.pl.umap(rna, color="celltype", legend_loc="on data")
marker_genes = [
'IL7R', 'TRAC', 'GATA3', # CD4+ T
'LEF1', 'FHIT', 'RORA', 'ITGB1', # naïve/memory
'CD8A', 'CD8B', 'CD248', 'CCL5', # CD8+ T
'GZMH', 'GZMK', # cytotoxic/transitional effector T cells
'KLRB1', 'SLC4A10', # MAIT
'IL32', # T/NK
'GNLY', 'NKG7', # NK
'CD79A', 'MS4A1', 'IGHD', 'IGHM', 'IL4R', 'TNFRSF13C', # B
'JCHAIN', # plasma
'KLF4', 'LYZ', 'S100A8', 'ITGAM', 'CD14', # mono
'DPYD', 'ITGAM', # classical/intermediate/non-classical mono
'FCGR3A', 'MS4A7', 'CST3', # non-classical mono
'CLEC10A', 'IRF8', 'TCF4' # DC
]
sc.pl.dotplot(rna, marker_genes, groupby='celltype', vmax=10)
rna.write("data/pbmc10k_rna.h5ad")
| 0.592431 | 0.981257 |
### import required libraries
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
```
### Load the dataset
```
features_desc = {
'CRIM': 'per capita crime rate by town',
'ZN': 'proportion of residential land zoned for lots over 25,000 sq.ft.',
'INDUS': 'proportion of non-retail business acres per town',
'CHAS': 'Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)',
'NOX': 'nitric oxides concentration (parts per 10 million)',
'RM': 'average number of rooms per dwelling',
'AGE': 'proportion of owner-occupied units built prior to 1940',
'DIS': 'weighted distances to five Boston employment centres',
'RAD': 'index of accessibility to radial highways',
'TAX': 'full-value property-tax rate per $10,000',
'PTRATIO': 'pupil-teacher ratio by town',
'B': '1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town',
'LSTAT': '% lower status of the population',
'PRICE': "Median value of owner-occupied homes in $1000's"
}
boston = pd.read_csv('housing.csv', delimiter='\s+')
```
### Data analysis
```
boston.head()
boston.shape
# how many nan we have in this dataset
boston.isna().sum()
```
* There is nor null values, good news for us!
```
boston.describe()
# check the correlation between the columns
correlation = boston.corr()
# this is pearson correlation: we have both positive and negative correlations
correlation
```
* Understanding this table using colors would be much easier?
```
plt.figure(figsize=(10, 8))
sns.heatmap(
correlation,
square=True,
annot=True,
center=0.0,
fmt='.1f',
cmap='RdBu', # divergence
linewidths=1.0
);
```
* There is a strong negative correlation between **LSTAT** and **PRICE**
```
features_desc['LSTAT']
features_desc['ZN']
features_desc['RM']
```
## Train models:
1. A simple linear regression
2. Ridge
3. Lasso
4. KNNRegressor
```
# Let's train a model on the all 13 features
X = boston.drop('PRICE', axis=1)
y = boston.PRICE
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=12)
len(X_train), len(X_test)
```
### Train a simple linear regression (Least Sqaure)
```
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
linreg.fit(X_train, y_train)
linreg_y_pred = linreg.predict(X_test)
from sklearn import metrics
metrics.mean_squared_error(y_test, linreg_y_pred)
```
### Train Ridge
```
from sklearn.linear_model import Ridge
rdg = Ridge()
rdg.fit(X_train, y_train)
rdg_y_pred = rdg.predict(X_test)
metrics.mean_squared_error(y_test, rdg_y_pred)
```
#### Compare Ridge and LS
```
pd.DataFrame(
{'Least Square': linreg.coef_, 'Ridge': rdg.coef_},
index=boston.columns.drop('PRICE')
)
```
### What are the five most important features from Lasso's standpoint
```
from sklearn.linear_model import Lasso
MAX_FEATURES: int = 5
rsss = []
l1_values_n_features = {}
l1_values = np.linspace(1, 20, num=25)
for l1_penalty in l1_values:
lasso = Lasso(alpha=l1_penalty, max_iter=10**5)
lasso.fit(X_train, y_train)
l1_values_n_features[l1_penalty] = len(lasso.feature_names_in_[lasso.coef_.nonzero()])
only_max_features = [l1_penalty for l1_penalty, n_features in l1_values_n_features.items() if n_features == MAX_FEATURES]
# find the maximum and minimum alpha that produces a lasso with MAX_FEATURES
max_l1_penalty: float = max(only_max_features)
min_l1_penalty: float = min(only_max_features)
rsss: list[float] = []
l1_penalty_values = np.linspace(min_l1_penalty, max_l1_penalty, num=8)
for l1_penalty in l1_penalty_values:
lasso = Lasso(alpha=l1_penalty, max_iter=10**5)
scores = cross_val_score(lasso, X, y, cv=5, scoring='neg_mean_squared_error')
scores = -scores
rsss.append(scores.mean())
best_l1_penalty = l1_penalty_values[np.argmin(rsss)]
print(f'Best l1_penatly that produces a model with {MAX_FEATURES} is {best_l1_penalty}')
lasso = Lasso(alpha=best_l1_penalty)
lasso.fit(X_train, y_train)
print("Five most important features:", ", ".join(lasso.feature_names_in_[lasso.coef_.nonzero()]))
```
### Train a KNN Regressor
```
from sklearn.neighbors import KNeighborsRegressor
knn = KNeighborsRegressor(n_neighbors=5, weights='distance', )
knn.fit(X_train, y_train)
knn_y_pred = knn.predict(X_test)
metrics.mean_squared_error(y_test, knn_y_pred)
```
## Compare all models
```
pd.DataFrame({'Actual Price': y_test, 'LS Prediction': linreg_y_pred, 'Ridge Prediction': rdg_y_pred, 'KNN': knn_y_pred})
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
features_desc = {
'CRIM': 'per capita crime rate by town',
'ZN': 'proportion of residential land zoned for lots over 25,000 sq.ft.',
'INDUS': 'proportion of non-retail business acres per town',
'CHAS': 'Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)',
'NOX': 'nitric oxides concentration (parts per 10 million)',
'RM': 'average number of rooms per dwelling',
'AGE': 'proportion of owner-occupied units built prior to 1940',
'DIS': 'weighted distances to five Boston employment centres',
'RAD': 'index of accessibility to radial highways',
'TAX': 'full-value property-tax rate per $10,000',
'PTRATIO': 'pupil-teacher ratio by town',
'B': '1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town',
'LSTAT': '% lower status of the population',
'PRICE': "Median value of owner-occupied homes in $1000's"
}
boston = pd.read_csv('housing.csv', delimiter='\s+')
boston.head()
boston.shape
# how many nan we have in this dataset
boston.isna().sum()
boston.describe()
# check the correlation between the columns
correlation = boston.corr()
# this is pearson correlation: we have both positive and negative correlations
correlation
plt.figure(figsize=(10, 8))
sns.heatmap(
correlation,
square=True,
annot=True,
center=0.0,
fmt='.1f',
cmap='RdBu', # divergence
linewidths=1.0
);
features_desc['LSTAT']
features_desc['ZN']
features_desc['RM']
# Let's train a model on the all 13 features
X = boston.drop('PRICE', axis=1)
y = boston.PRICE
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=12)
len(X_train), len(X_test)
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
linreg.fit(X_train, y_train)
linreg_y_pred = linreg.predict(X_test)
from sklearn import metrics
metrics.mean_squared_error(y_test, linreg_y_pred)
from sklearn.linear_model import Ridge
rdg = Ridge()
rdg.fit(X_train, y_train)
rdg_y_pred = rdg.predict(X_test)
metrics.mean_squared_error(y_test, rdg_y_pred)
pd.DataFrame(
{'Least Square': linreg.coef_, 'Ridge': rdg.coef_},
index=boston.columns.drop('PRICE')
)
from sklearn.linear_model import Lasso
MAX_FEATURES: int = 5
rsss = []
l1_values_n_features = {}
l1_values = np.linspace(1, 20, num=25)
for l1_penalty in l1_values:
lasso = Lasso(alpha=l1_penalty, max_iter=10**5)
lasso.fit(X_train, y_train)
l1_values_n_features[l1_penalty] = len(lasso.feature_names_in_[lasso.coef_.nonzero()])
only_max_features = [l1_penalty for l1_penalty, n_features in l1_values_n_features.items() if n_features == MAX_FEATURES]
# find the maximum and minimum alpha that produces a lasso with MAX_FEATURES
max_l1_penalty: float = max(only_max_features)
min_l1_penalty: float = min(only_max_features)
rsss: list[float] = []
l1_penalty_values = np.linspace(min_l1_penalty, max_l1_penalty, num=8)
for l1_penalty in l1_penalty_values:
lasso = Lasso(alpha=l1_penalty, max_iter=10**5)
scores = cross_val_score(lasso, X, y, cv=5, scoring='neg_mean_squared_error')
scores = -scores
rsss.append(scores.mean())
best_l1_penalty = l1_penalty_values[np.argmin(rsss)]
print(f'Best l1_penatly that produces a model with {MAX_FEATURES} is {best_l1_penalty}')
lasso = Lasso(alpha=best_l1_penalty)
lasso.fit(X_train, y_train)
print("Five most important features:", ", ".join(lasso.feature_names_in_[lasso.coef_.nonzero()]))
from sklearn.neighbors import KNeighborsRegressor
knn = KNeighborsRegressor(n_neighbors=5, weights='distance', )
knn.fit(X_train, y_train)
knn_y_pred = knn.predict(X_test)
metrics.mean_squared_error(y_test, knn_y_pred)
pd.DataFrame({'Actual Price': y_test, 'LS Prediction': linreg_y_pred, 'Ridge Prediction': rdg_y_pred, 'KNN': knn_y_pred})
| 0.719778 | 0.90882 |
# FINN - End-to-End Flow
-----------------------------------------------------------------
In this notebook, we will show how to take a simple, binarized, fully-connected network trained on the MNIST data set and take it all the way down to a customized bitfile running on a PYNQ board.
This notebook is quite lengthy, and some of the cells (involving Vivado synthesis) may take up to an hour to finish running. To let you save and resume your progress, we will save the intermediate ONNX models that are generated in the various steps to disk, so that you can jump back directly to where you left off.
## Overview
The FINN compiler comes with many *transformations* that modify the ONNX representation of the network according to certain patterns. This notebook will demonstrate a *possible* sequence of such transformations to take a particular trained network all the way down to hardware, as shown in the figure below.

The white fields show the state of the network representation in the respective step. The colored fields represent the transformations that are applied to the network to achieve a certain result. The diagram is divided into 5 sections represented by a different color, each of it includes several flow steps. The flow starts in top left corner with Brevitas export (green section), followed by the preparation of the network (blue section) for the Vivado HLS synthesis and Vivado IPI stitching (orange section), and finally building a PYNQ overlay bitfile and testing it on a PYNQ board (yellow section).
There is an additional section for functional verification (red section) on the right side of the diagram, which we will not cover in this notebook. For details please take a look in the verification notebook which you can find [here](tfc_end2end_verification.ipynb)
This Jupyter notebook is organized based on the sections described above. We will use the following helper functions, `showSrc` to show source code of FINN library calls and `showInNetron` to show the ONNX model at the current transformation step. The Netron displays are interactive, but they only work when running the notebook actively and not on GitHub (i.e. if you are viewing this on GitHub you'll only see blank squares).
```
from finn.util.visualization import showSrc, showInNetron
from finn.util.basic import make_build_dir
build_dir = "/workspace/finn"
```
## Outline
-------------
1. [Brevitas export](#brev_exp)
2. [Network preparation](#nw_prep)
3. [Hardware build](#vivado)
4. [PYNQ deployment](#hw_test)
## 1. Brevitas export <a id='brev_exp'></a>
FINN expects an ONNX model as input. This can be a model trained with [Brevitas](https://github.com/Xilinx/brevitas). Brevitas is a PyTorch library for quantization-aware training and the FINN Docker image comes with several [example Brevitas networks](https://github.com/Xilinx/brevitas/tree/master/brevitas_examples/bnn_pynq). To show the FINN end-to-end flow, we'll use the TFC-w1a1 model as example network.
First a few things have to be imported. Then the model can be loaded with the pretrained weights.
```
import onnx
from finn.util.test import get_test_model_trained
import brevitas.onnx as bo
tfc = get_test_model_trained("TFC", 1, 1)
bo.export_finn_onnx(tfc, (1, 1, 28, 28), build_dir+"/tfc_w1_a1.onnx")
```
The model was now exported, loaded with the pretrained weights and saved under the name "lfc_w1_a1.onnx".
To visualize the exported model, Netron can be used. Netron is a visualizer for neural networks and allows interactive investigation of network properties. For example, you can click on the individual nodes and view the properties.
```
showInNetron(build_dir+"/tfc_w1_a1.onnx")
```
Now that we have the model in .onnx format, we can work with it using FINN. For that FINN `ModelWrapper` is used. It is a wrapper around the ONNX model which provides several helper functions to make it easier to work with the model.
```
from finn.core.modelwrapper import ModelWrapper
model = ModelWrapper(build_dir+"/tfc_w1_a1.onnx")
```
Now the model is prepared and could be simulated using Python. How this works is described in the Jupyter notebook about verification and can be found [here](tfc_end2end_verification.ipynb#simpy).
The model can now also be processed in different ways. The principle of FINN are analysis and transformation passes, which can be applied to the model. An analysis pass extracts specific information about the model and returns it to the user in the form of a dictionary. A transformation pass changes the model and returns the changed model back to the FINN flow.
Since the goal in this notebook is to process the model to such an extent that a bitstream can be generated from it, the focus is on the transformations that are necessary for this. In the next section these are discussed in more detail.
## 2. Network preparation <a id='nw_prep'></a>
* [FINN-style Dataflow Architectures](#dataflow_arch)
* [Tidy-up transformations](#basic_trafo)
* [Streamlining](#streamline)
* [Conversion to HLS layers](#hls_layers)
* [Creating a Dataflow Partition](#dataflow_partition)
* [Folding and Datawidth Converter, FIFO and TLastMarker Insertion](#folding)
In this section, we will put the network through a series of transformations that puts it in a form that can be stitched together to form a FINN-style dataflow architecture, yielding a high-performance, high-efficiency FPGA accelerator.
### FINN-style Dataflow Architectures <a id='dataflow_arch'></a>
We start with a quick recap of FINN-style dataflow architectures. The key idea in such architectures is to parallelize across layers as well as within layers by dedicating a proportionate amount of compute resources to each layer, as illustrated in the figure below taken from the [FINN-R paper](https://arxiv.org/pdf/1809.04570.pdf):

In practice, the compute arrays are instantiated by function calls to optimized Vivado HLS building blocks from the [finn-hlslib](https://github.com/Xilinx/finn-hlslib) library. As these function calls can only handle certain patterns/cases, we need to transform the network into an appropriate form so that we can replace network layers with these function calls, which is the goal of the network preparation process.
### Tidy-up transformations <a id='basic_trafo'></a>
This section deals with some basic transformations, which are applied to the model like a kind of "tidy-up" to make it easier to be processed. They do not appear in the diagram above, but they are applied in many steps in the FINN flow to postprocess the model after a transformation and/or to prepare it for the next transformation.
These transformations are:
* GiveUniqueNodeNames
* GiveReadableTensorNames
* InferShapes
* InferDataTypes
* FoldConstants
* RemoveStaticGraphInputs
In the first two transformations (`GiveUniqueNodeNames`, `GiveReadableTensorNames`) the nodes in the graph are first given unique (by enumeration) names, then the tensors are given human-readable names (based on the node names). The following two transformations (`InferShapes`, `InferDataTypes`) derive the shapes and data types of the tensors from the model properties and set them in the `ValueInfo` of the model. These transformations can almost always be applied without negative effects and do not affect the structure of the graph, ensuring that all the information needed is available.
The next listed transformation is `FoldConstants`, which performs constant folding. It identifies a node with constant inputs and determines its output. The result is then set as constant-only inputs for the following node and the old node is removed. Although this transformation changes the structure of the model, it is a transformation that is usually always desired and can be applied to any model. And finally, we have `RemoveStaticGraphInputs` to remove any top-level graph inputs that already have ONNX initializers associated with them.
These transformations can be imported and applied as follows.
```
from finn.transformation.general import GiveReadableTensorNames, GiveUniqueNodeNames, RemoveStaticGraphInputs
from finn.transformation.infer_shapes import InferShapes
from finn.transformation.infer_datatypes import InferDataTypes
from finn.transformation.fold_constants import FoldConstants
model = model.transform(InferShapes())
model = model.transform(FoldConstants())
model = model.transform(GiveUniqueNodeNames())
model = model.transform(GiveReadableTensorNames())
model = model.transform(InferDataTypes())
model = model.transform(RemoveStaticGraphInputs())
model.save(build_dir+"/tfc_w1_a1_tidy.onnx")
```
The result of these transformations can be viewed with netron after the model has been saved again. By clicking on the individual nodes, it can now be seen, for example, that each node has been given a name. Also the whole upper area could be folded, so that now the first node is "Reshape".
```
showInNetron(build_dir+"/tfc_w1_a1_tidy.onnx")
```
### Adding Pre- and Postprocessing <a id='prepost'></a>
In many cases, it's common to apply some preprocessing to the raw data in a machine learning framework prior to training. For image classification networks, this may include conversion of raw 8-bit RGB values into floating point values between 0 and 1. Similarly, at the output of the network some postprocessing may be performed during deployment, such as extracting the indices of the classifications with the largest value (top-K indices).
In FINN, we can bake some of these pre/postprocessing operatings into the graph, and in some cases these can be highly beneficial for performance by allowing our accelerator to directly consume raw data instead of going through CPU preprocessing.
We'll demonstrate this for our small image classification network as follows. Brevitas preprocesses BNN-PYNQ network inputs with `torchvision.transforms.ToTensor()` [prior to training](https://github.com/Xilinx/brevitas/blob/master/brevitas_examples/bnn_pynq/trainer.py#L85), which converts 8-bit RGB values into floats between 0 and 1 by dividing the input by 255. We can achieve the same effect in FINN by exporting a single-node ONNX graph for division by 255 (which already exists as `finn.util.pytorch.ToTensor` and merging this with our original model. Finally, we're going to mark our input tensor as 8-bit to let FINN know which level of precision to use.
```
from finn.util.pytorch import ToTensor
from finn.transformation.merge_onnx_models import MergeONNXModels
from finn.core.datatype import DataType
model = ModelWrapper(build_dir+"/tfc_w1_a1_tidy.onnx")
global_inp_name = model.graph.input[0].name
ishape = model.get_tensor_shape(global_inp_name)
# preprocessing: torchvision's ToTensor divides uint8 inputs by 255
totensor_pyt = ToTensor()
chkpt_preproc_name = build_dir+"/tfc_w1_a1_preproc.onnx"
bo.export_finn_onnx(totensor_pyt, ishape, chkpt_preproc_name)
# join preprocessing and core model
pre_model = ModelWrapper(chkpt_preproc_name)
model = model.transform(MergeONNXModels(pre_model))
# add input quantization annotation: UINT8 for all BNN-PYNQ models
global_inp_name = model.graph.input[0].name
model.set_tensor_datatype(global_inp_name, DataType.UINT8)
model.save(build_dir+"/tfc_w1_a1_with_preproc.onnx")
showInNetron(build_dir+"/tfc_w1_a1_with_preproc.onnx")
```
You can observe two changes in the graph above: a `Div` node has appeared in the beginning to perform the input preprocessing, and the `global_in` tensor now has a quantization annotation to mark it as an unsigned 8-bit value.
For the postprocessing we'll insert a TopK node for k=1 at the end of our graph. This will extract the index (class number) for the largest-valued output.
```
from finn.transformation.insert_topk import InsertTopK
# postprocessing: insert Top-1 node at the end
model = model.transform(InsertTopK(k=1))
chkpt_name = build_dir+"/tfc_w1_a1_pre_post.onnx"
# tidy-up again
model = model.transform(InferShapes())
model = model.transform(FoldConstants())
model = model.transform(GiveUniqueNodeNames())
model = model.transform(GiveReadableTensorNames())
model = model.transform(InferDataTypes())
model = model.transform(RemoveStaticGraphInputs())
model.save(chkpt_name)
showInNetron(build_dir+"/tfc_w1_a1_pre_post.onnx")
```
Notice the`TopK` node that has appeared at the end of the network. With our pre- and postprocessing in place, we can move on to the next step in the flow, which is streamlining.
### Streamlining <a id='streamline'></a>
Streamlining is a transformation containing several sub-transformations. The goal of streamlining is to eliminate floating point operations by moving them around, then collapsing them into one operation and in the last step transform them into multi-thresholding nodes. For more information on the theoretical background of this, see [this paper](https://arxiv.org/pdf/1709.04060).
Let's have a look at which sub-transformations `Streamline` consists of:
```
from finn.transformation.streamline import Streamline
showSrc(Streamline)
```
As can be seen, several transformations are involved in the streamlining transformation. There are move and collapse transformations. In the last step the operations are transformed into multithresholds. The involved transformations can be viewed in detail [here](https://github.com/Xilinx/finn/tree/master/src/finn/transformation/streamline). After each transformation, three of the tidy-up transformations (`GiveUniqueNodeNames`, `GiveReadableTensorNames` and `InferDataTypes`) are applied to the model.
After streamlining the network looks as follows:
```
from finn.transformation.streamline.reorder import MoveScalarLinearPastInvariants
import finn.transformation.streamline.absorb as absorb
model = ModelWrapper(build_dir+"/tfc_w1_a1_pre_post.onnx")
# move initial Mul (from preproc) past the Reshape
model = model.transform(MoveScalarLinearPastInvariants())
# streamline
model = model.transform(Streamline())
model.save(build_dir+"/tfc_w1_a1_streamlined.onnx")
showInNetron(build_dir+"/tfc_w1_a1_streamlined.onnx")
```
You can see that the network has become simplified considerably compared to the previous step -- a lot of nodes have disappeared between the `MatMul` layers, and the `Sign` nodes have been replaced with `MultiThreshold` nodes instead.
**The current implementation of streamlining is highly network-specific and may not work for your network if its topology is very different than the example network here. We hope to rectify this in future releases.**
Our example network is a quantized network with 1-bit bipolar (-1, +1 values) precision, and we want FINN to implement them as XNOR-popcount operations [as described in the original FINN paper](https://arxiv.org/pdf/1612.07119). For this reason, after streamlining, the resulting bipolar matrix multiplications are converted into xnorpopcount operations. This transformation produces operations that are again collapsed and converted into thresholds. This procedure is shown below.
```
from finn.transformation.bipolar_to_xnor import ConvertBipolarMatMulToXnorPopcount
from finn.transformation.streamline.round_thresholds import RoundAndClipThresholds
from finn.transformation.infer_data_layouts import InferDataLayouts
from finn.transformation.general import RemoveUnusedTensors
model = model.transform(ConvertBipolarMatMulToXnorPopcount())
model = model.transform(absorb.AbsorbAddIntoMultiThreshold())
model = model.transform(absorb.AbsorbMulIntoMultiThreshold())
# absorb final add-mul nodes into TopK
model = model.transform(absorb.AbsorbScalarMulAddIntoTopK())
model = model.transform(RoundAndClipThresholds())
# bit of tidy-up
model = model.transform(InferDataLayouts())
model = model.transform(RemoveUnusedTensors())
model.save(build_dir+"/tfc_w1a1_ready_for_hls_conversion.onnx")
showInNetron(build_dir+"/tfc_w1a1_ready_for_hls_conversion.onnx")
```
Observe the pairs of `XnorPopcountmatMul` and `MultiThreshold` layers following each other -- this is the particular pattern that the next step will be looking for in order to convert them to HLS layers.
### Conversion to HLS layers <a id='hls_layers'></a>
Converts the nodes to HLS layers that correspond to the functions in [finn-hls library](https://finn-hlslib.readthedocs.io/en/latest/). In our case this transformation converts pairs of binary XnorPopcountMatMul layers to StreamingFCLayer_Batch layers. Any immediately following MultiThreshold layers will also be absorbed into the MVTU.
Below is the code for the transformation and the network is visualized using netron to create the new structure with `StreamingFCLayer_Batch` nodes, which will correspond to a function call from the [finn-hlslib](https://finn-hlslib.readthedocs.io/en/latest/library/fclayer.html#_CPPv4I_j_j_j_j000_i_i000E22StreamingFCLayer_BatchvRN3hls6streamI7ap_uintI9InStreamWEEERN3hls6streamI7ap_uintI10OutStreamWEEERK2TWRK2TAKjRK1R) library.
**Note:** The transformation `to_hls.InferBinaryStreamingFCLayer` gets the string "decoupled" as argument, this indicates the `mem_mode` for the weights. In FINN there are different options to set the way the weights are stored and accessed. For details please have a look on the [FINN readthedocs website](https://finn.readthedocs.io/) under Internals.
```
import finn.transformation.fpgadataflow.convert_to_hls_layers as to_hls
model = ModelWrapper(build_dir+"/tfc_w1a1_ready_for_hls_conversion.onnx")
model = model.transform(to_hls.InferBinaryStreamingFCLayer("decoupled"))
# TopK to LabelSelect
model = model.transform(to_hls.InferLabelSelectLayer())
# input quantization (if any) to standalone thresholding
model = model.transform(to_hls.InferThresholdingLayer())
model.save(build_dir+"/tfc_w1_a1_hls_layers.onnx")
showInNetron(build_dir+"/tfc_w1_a1_hls_layers.onnx")
```
Each StreamingFCLayer_Batch node has two attributes that specify the degree of folding, PE and SIMD. In all nodes the values for these attributes are set as default to 1, which would correspond to a maximum folding (time multiplexing) and thus minimum performance. We will shortly cover how these can be adjusted, but first we want to separate the HLS layers from the non-HLS layers in this network.
### Creating a Dataflow Partition <a id='dataflow_partition'></a>
In the graph above, you can see that there is a mixture of FINN HLS layers (StreamingFCLayer_Batch) with regular ONNX layers (Reshape, Mul, Add). To create a bitstream, FINN needs a model with only HLS layers. In order to achieve this, we will use the `CreateDataflowPartition` transformation to create a "dataflow partition" in this graph, separating out the HLS layers into another model, and replacing them with a placeholder layer called StreamingDataflowPartition:
```
from finn.transformation.fpgadataflow.create_dataflow_partition import CreateDataflowPartition
model = ModelWrapper(build_dir+"/tfc_w1_a1_hls_layers.onnx")
parent_model = model.transform(CreateDataflowPartition())
parent_model.save(build_dir+"/tfc_w1_a1_dataflow_parent.onnx")
showInNetron(build_dir+"/tfc_w1_a1_dataflow_parent.onnx")
```
We can see that the StreamingFCLayer instances have all been replaced with a single `StreamingDataflowPartition`, which has an attribute `model` that points to the extracted, HLS dataflow-only graph:
```
from finn.custom_op.registry import getCustomOp
sdp_node = parent_model.get_nodes_by_op_type("StreamingDataflowPartition")[0]
sdp_node = getCustomOp(sdp_node)
dataflow_model_filename = sdp_node.get_nodeattr("model")
showInNetron(dataflow_model_filename)
```
We can see all the extracted `StreamingFCLayer` instances have been moved to the child (dataflow) model. We will load the child model with `ModelWrapper` and continue working on it.
```
model = ModelWrapper(dataflow_model_filename)
```
### Folding: Adjusting the Parallelism <a id='folding'></a>
*Folding* in FINN describes how much a layer is time-multiplexed in terms of execution resources. There are several *folding factors* for each layer, controlled by the PE (parallelization over outputs) and SIMD (parallelization over inputs) parameters as described by the original [FINN paper](https://arxiv.org/pdf/1612.07119). The higher the PE and SIMD values are set, the faster the generated accelerator will run, and the more FPGA resources it will consume.
Since the folding parameters are node attributes, they can be easily accessed and changed using a helper function of the `ModelWrapper`. But first we take a closer look at one of the nodes that implement a StreamingFCLayer_Batch operation. This is where the Netron visualization helps us, in the above diagram we can see that the first four nodes are StreamingFCLayer_Batch. So as an example we extract the first node.
We can use the higher-level [HLSCustomOp](https://github.com/Xilinx/finn/blob/master/src/finn/custom_op/fpgadataflow/__init__.py) wrappers for this node. These wrappers provide easy access to specific properties of these nodes, such as the folding factors (PE and SIMD). Let's have a look at which node attributes are defined by the CustomOp wrapper, and adjust the SIMD and PE attributes.
```
fc0 = model.graph.node[0]
fc0w = getCustomOp(fc0)
print("CustomOp wrapper is of class " + fc0w.__class__.__name__)
fc0w.get_nodeattr_types()
```
We can see that the PE and SIMD are listed as node attributes, as well as the depths of the FIFOs that will be inserted between consecutive layers, and all can be adjusted using `set_nodeattr` subject to certain constraints.
**In this notebook we are setting the folding factors and FIFO depths manually, but in a future version we will support determining the folding factors given an FPGA resource budget according to the analytical model from the [FINN-R paper](https://arxiv.org/pdf/1809.04570).**
```
fc_layers = model.get_nodes_by_op_type("StreamingFCLayer_Batch")
# (PE, SIMD, in_fifo_depth, out_fifo_depth, ramstyle) for each layer
config = [
(16, 49, 16, 64, "block"),
(8, 8, 64, 64, "auto"),
(8, 8, 64, 64, "auto"),
(10, 8, 64, 10, "distributed"),
]
for fcl, (pe, simd, ififo, ofifo, ramstyle) in zip(fc_layers, config):
fcl_inst = getCustomOp(fcl)
fcl_inst.set_nodeattr("PE", pe)
fcl_inst.set_nodeattr("SIMD", simd)
fcl_inst.set_nodeattr("inFIFODepth", ififo)
fcl_inst.set_nodeattr("outFIFODepth", ofifo)
fcl_inst.set_nodeattr("ram_style", ramstyle)
# set parallelism for input quantizer to be same as first layer's SIMD
inp_qnt_node = model.get_nodes_by_op_type("Thresholding_Batch")[0]
inp_qnt = getCustomOp(inp_qnt_node)
inp_qnt.set_nodeattr("PE", 49)
```
We are setting PE and SIMD so that each layer has a total folding of 16.
Besides PE and SIMD three other node attributes are set. `ram_style` specifies how the weights are to be stored (BRAM, LUTRAM, and so on). It can be selected explicitly or with the option `auto` you can let Vivado decide.
`inFIFODepth` and `outFIFODepth` specifies the FIFO depths that is needed by the node from the surrounding FIFOs. These attributes are used in the transformation 'InsertFIFO' to insert the appropriate FIFOs between the nodes, which will be automatically called as part of the hardware build process.
In previous versions of FINN we had to call transformations to insert data width converters, FIFOs and `TLastMarker` manually at this step. This is no longer needed, as all this is taken care of by the `ZynqBuild` or `VitisBuild` transformations.
```
model.save(build_dir+"/tfc_w1_a1_set_folding_factors.onnx")
showInNetron(build_dir+"/tfc_w1_a1_set_folding_factors.onnx")
```
This completes the network preparation and the network can be passed on to the next block *Vivado HLS and IPI*, which is described below.
## 3. Hardware Build <a id='vivado'></a>
We're finally ready to start generating hardware from our network. Depending on whether you want to target a Zynq or Alveo platform, FINN offers two transformations to build the accelerator, integrate into an appropriate shell and build a bitfile. These are `ZynqBuild` and `VitisBuild` for Zynq and Alveo, respectively. In this notebook we'll demonstrate the `ZynqBuild` as these boards are more common and it's much faster to complete bitfile generation for the smaller FPGAs found on them.
As we will be dealing with FPGA synthesis tools in these tasks, we'll define two helper variables that describe the Xilinx FPGA part name and the PYNQ board name that we are targeting.
```
# print the names of the supported PYNQ boards
from finn.util.basic import pynq_part_map
print(pynq_part_map.keys())
# change this if you have a different PYNQ board, see list above
pynq_board = "Pynq-Z1"
fpga_part = pynq_part_map[pynq_board]
target_clk_ns = 10
```
In previous versions of FINN, we had to manually go through several steps to generate HLS code, stitch IP, create a PYNQ project and run synthesis. All these steps are now performed by the `ZynqBuild` transform (or the `VitisBuild` transform for Alveo). **As this involves calling HLS synthesis and Vivado synthesis, this transformation will run for some time (up to half an hour depending on your PC).**
```
from finn.transformation.fpgadataflow.make_zynq_proj import ZynqBuild
model = ModelWrapper(build_dir+"/tfc_w1_a1_set_folding_factors.onnx")
model = model.transform(ZynqBuild(platform = pynq_board, period_ns = target_clk_ns))
model.save(build_dir + "/tfc_w1_a1_post_synthesis.onnx")
```
### Examining the generated outputs <a id='gen_outputs'></a>
Let's start by viewing the post-synthesis model in Netron:
```
showInNetron(build_dir + "/tfc_w1_a1_post_synthesis.onnx")
```
We can see that our sequence of HLS layers has been replaced with `StreamingDataflowPartition`s, each of which point to a different ONNX file. You can open a Netron session for each of them to view their contents. Here, the first and last partitions contain only an `IODMA` node, which was inserted automatically to move data between DRAM and the accelerator. Let's take a closer look at the middle partition, which contains all our layers:
```
model = ModelWrapper(build_dir + "/tfc_w1_a1_post_synthesis.onnx")
sdp_node_middle = getCustomOp(model.graph.node[1])
postsynth_layers = sdp_node_middle.get_nodeattr("model")
showInNetron(postsynth_layers)
```
We can see that `StreamingFIFO` and `StreamingDataWidthConverter` instances have been automatically inserted into the graph prior to hardware build. Transformations like `ZynqBuild` use the `metadata_props` of the model to put in additional metadata information relevant to the results of the transformation. Let's examine the metadata for the current graph containing all layers:
```
model = ModelWrapper(postsynth_layers)
model.model.metadata_props
```
Here we see that a Vivado project was built to create what we call the `stitched IP`, where all the IP blocks implementing various layers will be stitched together. You can view this stitched block design in Vivado, or [here](StreamingDataflowPartition_1.pdf) as an exported PDF.
Moving back to the top-level model, recall that `ZynqBuild` will create a Vivado project and synthesize it, so it will be creating metadata entries related to the paths and files that were created:
```
model = ModelWrapper(build_dir + "/tfc_w1_a1_post_synthesis.onnx")
model.model.metadata_props
```
Here, we can see the directories that were created for the PYNQ driver (`pynq_driver_dir`) and the Vivado synthesis project (`vivado_pynq_proj`), as well as the locations of the bitfile, hardware handoff file and synthesis report.
```
! ls {model.get_metadata_prop("vivado_pynq_proj")}
```
Feel free to examine the generated Vivado project to get a feel for how the system-level integration is performed for the FINN-generated "stitched IP", which appears as `StreamingDataflowPartition_1` in the top-level block design -- you can see it as a block diagram exported to PDF [here](top.pdf).
## 4. PYNQ deployment <a id='hw_test'></a>
* [Deployment and Remote Execution](#deploy)
* [Validation on PYNQ Board](#validation)
* [Throughput Test on PYNQ Board](#throughput)
We are almost done preparing our hardware design. We'll now put it in a form suitable for use as a PYNQ overlay, synthesize and deploy it.
### Deployment and Remote Execution <a id='deploy'></a>
We'll now use the `DeployToPYNQ` transformation to create a deployment folder with the bitfile and driver file(s), and copy that to the PYNQ board. You can change the default IP address, username, password and target folder for the PYNQ below.
**Make sure you've [set up the SSH keys for your PYNQ board](https://finn-dev.readthedocs.io/en/latest/getting_started.html#pynq-board-first-time-setup) before executing this step.**
```
import os
# set up the following values according to your own environment
# FINN will use ssh to deploy and run the generated accelerator
ip = os.getenv("PYNQ_IP", "192.168.2.99")
username = os.getenv("PYNQ_USERNAME", "xilinx")
password = os.getenv("PYNQ_PASSWORD", "xilinx")
port = os.getenv("PYNQ_PORT", 22)
target_dir = os.getenv("PYNQ_TARGET_DIR", "/home/xilinx/finn_tfc_end2end_example")
# set up ssh options to only allow publickey authentication
options = "-o PreferredAuthentications=publickey -o PasswordAuthentication=no"
# test access to PYNQ board
! ssh {options} {username}@{ip} -p {port} cat /var/run/motd.dynamic
from finn.transformation.fpgadataflow.make_deployment import DeployToPYNQ
model = model.transform(DeployToPYNQ(ip, port, username, password, target_dir))
model.save(build_dir + "/tfc_w1_a1_pynq_deploy.onnx")
```
Let's verify that the remote access credentials is saved in the model metadata, and that the deployment folder has been successfully copied to the board:
```
model.model.metadata_props
target_dir_pynq = target_dir + "/" + model.get_metadata_prop("pynq_deployment_dir").split("/")[-1]
target_dir_pynq
! ssh {options} {username}@{ip} -p {port} 'ls -l {target_dir_pynq}'
```
We only have two more steps to be able to remotely execute the deployed bitfile with some test data from the MNIST dataset. Let's load up some test data that comes bundled with FINN.
```
from pkgutil import get_data
import onnx.numpy_helper as nph
import matplotlib.pyplot as plt
raw_i = get_data("finn.data", "onnx/mnist-conv/test_data_set_0/input_0.pb")
x = nph.to_array(onnx.load_tensor_from_string(raw_i))
plt.imshow(x.reshape(28,28), cmap='gray')
model = ModelWrapper(build_dir + "/tfc_w1_a1_pynq_deploy.onnx")
iname = model.graph.input[0].name
oname = parent_model.graph.output[0].name
ishape = model.get_tensor_shape(iname)
print("Expected network input shape is " + str(ishape))
```
Finally, we can call `execute_onnx` on the graph, which will internally call remote execution with the bitfile, grab the results and return a numpy array. You may recall that one "reshape" node was left out of the StreamingDataflowPartition. We'll do that manually with a numpy function call when passing in the input, but everything else in the network ended up inside the StreamingDataflowPartition so that's all we need to do.
```
import numpy as np
from finn.core.onnx_exec import execute_onnx
input_dict = {iname: x.reshape(ishape)}
ret = execute_onnx(model, input_dict)
ret[oname]
```
We see that the network correctly predicts this as a digit 2.
### Validating the Accuracy on a PYNQ Board <a id='validation'></a>
All the command line prompts here are meant to be executed with `sudo` on the PYNQ board, so we'll use a workaround (`echo password | sudo -S command`) to get that working from this notebook running on the host computer.
**Ensure that your PYNQ board has a working internet connecting for the next steps, since some there is some downloading involved.**
To validate the accuracy, we first need to install the [`dataset-loading`](https://github.com/fbcotter/dataset_loading) Python package to the PYNQ board. This will give us a convenient way of downloading and accessing the MNIST dataset.
Command to execute on PYNQ:
```sudo pip3 install git+https://github.com/fbcotter/dataset_loading.git@0.0.4#egg=dataset_loading```
```
! ssh {options} -t {username}@{ip} -p {port} 'echo {password} | sudo -S pip3 install git+https://github.com/fbcotter/dataset_loading.git@0.0.4#egg=dataset_loading'
```
We can now use the `validate.py` script that was generated together with the driver to measure top-1 accuracy on the MNIST dataset.
Command to execute on PYNQ:
`python3.6 validate.py --dataset mnist --batchsize 1000`
```
! ssh {options} -t {username}@{ip} -p {port} 'cd {target_dir_pynq}; echo {password} | sudo -S python3.6 validate.py --dataset mnist --batchsize 1000'
```
We see that the final top-1 accuracy is 92.96%, which is very close to the 93.17% reported on the [BNN-PYNQ accuracy table in Brevitas](https://github.com/Xilinx/brevitas/tree/master/brevitas_examples/bnn_pynq).
### Throughput Test on PYNQ Board <a id='throughput'></a>
In addition to the functional verification, FINN also offers the possibility to measure the network performance directly on the PYNQ board. This can be done using the core function `throughput_test`. In the next section we import the function and execute it.
First we extract the `remote_exec_model` again and pass it to the function. The function returns the metrics of the network as dictionary.
```
from finn.core.throughput_test import throughput_test_remote
model = ModelWrapper(build_dir + "/tfc_w1_a1_pynq_deploy.onnx")
res = throughput_test_remote(model, 10000)
print("Network metrics:")
for key in res:
print(str(key) + ": " + str(res[key]))
```
Together with the values for folding we can evaluate the performance of our accelerator. Each layer has a total folding factor of 64 and because the network is fully pipelined, it follows: `II = 64`. II is the initiation interval and indicates how many cycles are needed for one input to be processed.
```
II = 64
# frequency in MHz
f_MHz = 100
# expected throughput in MFPS
expected_throughput = f_MHz / II
# measured throughput (FPS) from throughput test, converted to MFPS
measured_throughput = res["throughput[images/s]"] * 0.000001
# peformance
print("We reach approximately " + str(round((measured_throughput / expected_throughput)*100)) + "% of the ideal performance.")
```
The measured values were recorded with a batch size of 10000 and at a frequency of 100 MHz. We will be improving the efficiency of the generated accelerator examples in the coming FINN releases.
|
github_jupyter
|
from finn.util.visualization import showSrc, showInNetron
from finn.util.basic import make_build_dir
build_dir = "/workspace/finn"
import onnx
from finn.util.test import get_test_model_trained
import brevitas.onnx as bo
tfc = get_test_model_trained("TFC", 1, 1)
bo.export_finn_onnx(tfc, (1, 1, 28, 28), build_dir+"/tfc_w1_a1.onnx")
showInNetron(build_dir+"/tfc_w1_a1.onnx")
from finn.core.modelwrapper import ModelWrapper
model = ModelWrapper(build_dir+"/tfc_w1_a1.onnx")
from finn.transformation.general import GiveReadableTensorNames, GiveUniqueNodeNames, RemoveStaticGraphInputs
from finn.transformation.infer_shapes import InferShapes
from finn.transformation.infer_datatypes import InferDataTypes
from finn.transformation.fold_constants import FoldConstants
model = model.transform(InferShapes())
model = model.transform(FoldConstants())
model = model.transform(GiveUniqueNodeNames())
model = model.transform(GiveReadableTensorNames())
model = model.transform(InferDataTypes())
model = model.transform(RemoveStaticGraphInputs())
model.save(build_dir+"/tfc_w1_a1_tidy.onnx")
showInNetron(build_dir+"/tfc_w1_a1_tidy.onnx")
from finn.util.pytorch import ToTensor
from finn.transformation.merge_onnx_models import MergeONNXModels
from finn.core.datatype import DataType
model = ModelWrapper(build_dir+"/tfc_w1_a1_tidy.onnx")
global_inp_name = model.graph.input[0].name
ishape = model.get_tensor_shape(global_inp_name)
# preprocessing: torchvision's ToTensor divides uint8 inputs by 255
totensor_pyt = ToTensor()
chkpt_preproc_name = build_dir+"/tfc_w1_a1_preproc.onnx"
bo.export_finn_onnx(totensor_pyt, ishape, chkpt_preproc_name)
# join preprocessing and core model
pre_model = ModelWrapper(chkpt_preproc_name)
model = model.transform(MergeONNXModels(pre_model))
# add input quantization annotation: UINT8 for all BNN-PYNQ models
global_inp_name = model.graph.input[0].name
model.set_tensor_datatype(global_inp_name, DataType.UINT8)
model.save(build_dir+"/tfc_w1_a1_with_preproc.onnx")
showInNetron(build_dir+"/tfc_w1_a1_with_preproc.onnx")
from finn.transformation.insert_topk import InsertTopK
# postprocessing: insert Top-1 node at the end
model = model.transform(InsertTopK(k=1))
chkpt_name = build_dir+"/tfc_w1_a1_pre_post.onnx"
# tidy-up again
model = model.transform(InferShapes())
model = model.transform(FoldConstants())
model = model.transform(GiveUniqueNodeNames())
model = model.transform(GiveReadableTensorNames())
model = model.transform(InferDataTypes())
model = model.transform(RemoveStaticGraphInputs())
model.save(chkpt_name)
showInNetron(build_dir+"/tfc_w1_a1_pre_post.onnx")
from finn.transformation.streamline import Streamline
showSrc(Streamline)
from finn.transformation.streamline.reorder import MoveScalarLinearPastInvariants
import finn.transformation.streamline.absorb as absorb
model = ModelWrapper(build_dir+"/tfc_w1_a1_pre_post.onnx")
# move initial Mul (from preproc) past the Reshape
model = model.transform(MoveScalarLinearPastInvariants())
# streamline
model = model.transform(Streamline())
model.save(build_dir+"/tfc_w1_a1_streamlined.onnx")
showInNetron(build_dir+"/tfc_w1_a1_streamlined.onnx")
from finn.transformation.bipolar_to_xnor import ConvertBipolarMatMulToXnorPopcount
from finn.transformation.streamline.round_thresholds import RoundAndClipThresholds
from finn.transformation.infer_data_layouts import InferDataLayouts
from finn.transformation.general import RemoveUnusedTensors
model = model.transform(ConvertBipolarMatMulToXnorPopcount())
model = model.transform(absorb.AbsorbAddIntoMultiThreshold())
model = model.transform(absorb.AbsorbMulIntoMultiThreshold())
# absorb final add-mul nodes into TopK
model = model.transform(absorb.AbsorbScalarMulAddIntoTopK())
model = model.transform(RoundAndClipThresholds())
# bit of tidy-up
model = model.transform(InferDataLayouts())
model = model.transform(RemoveUnusedTensors())
model.save(build_dir+"/tfc_w1a1_ready_for_hls_conversion.onnx")
showInNetron(build_dir+"/tfc_w1a1_ready_for_hls_conversion.onnx")
import finn.transformation.fpgadataflow.convert_to_hls_layers as to_hls
model = ModelWrapper(build_dir+"/tfc_w1a1_ready_for_hls_conversion.onnx")
model = model.transform(to_hls.InferBinaryStreamingFCLayer("decoupled"))
# TopK to LabelSelect
model = model.transform(to_hls.InferLabelSelectLayer())
# input quantization (if any) to standalone thresholding
model = model.transform(to_hls.InferThresholdingLayer())
model.save(build_dir+"/tfc_w1_a1_hls_layers.onnx")
showInNetron(build_dir+"/tfc_w1_a1_hls_layers.onnx")
from finn.transformation.fpgadataflow.create_dataflow_partition import CreateDataflowPartition
model = ModelWrapper(build_dir+"/tfc_w1_a1_hls_layers.onnx")
parent_model = model.transform(CreateDataflowPartition())
parent_model.save(build_dir+"/tfc_w1_a1_dataflow_parent.onnx")
showInNetron(build_dir+"/tfc_w1_a1_dataflow_parent.onnx")
from finn.custom_op.registry import getCustomOp
sdp_node = parent_model.get_nodes_by_op_type("StreamingDataflowPartition")[0]
sdp_node = getCustomOp(sdp_node)
dataflow_model_filename = sdp_node.get_nodeattr("model")
showInNetron(dataflow_model_filename)
model = ModelWrapper(dataflow_model_filename)
fc0 = model.graph.node[0]
fc0w = getCustomOp(fc0)
print("CustomOp wrapper is of class " + fc0w.__class__.__name__)
fc0w.get_nodeattr_types()
fc_layers = model.get_nodes_by_op_type("StreamingFCLayer_Batch")
# (PE, SIMD, in_fifo_depth, out_fifo_depth, ramstyle) for each layer
config = [
(16, 49, 16, 64, "block"),
(8, 8, 64, 64, "auto"),
(8, 8, 64, 64, "auto"),
(10, 8, 64, 10, "distributed"),
]
for fcl, (pe, simd, ififo, ofifo, ramstyle) in zip(fc_layers, config):
fcl_inst = getCustomOp(fcl)
fcl_inst.set_nodeattr("PE", pe)
fcl_inst.set_nodeattr("SIMD", simd)
fcl_inst.set_nodeattr("inFIFODepth", ififo)
fcl_inst.set_nodeattr("outFIFODepth", ofifo)
fcl_inst.set_nodeattr("ram_style", ramstyle)
# set parallelism for input quantizer to be same as first layer's SIMD
inp_qnt_node = model.get_nodes_by_op_type("Thresholding_Batch")[0]
inp_qnt = getCustomOp(inp_qnt_node)
inp_qnt.set_nodeattr("PE", 49)
model.save(build_dir+"/tfc_w1_a1_set_folding_factors.onnx")
showInNetron(build_dir+"/tfc_w1_a1_set_folding_factors.onnx")
# print the names of the supported PYNQ boards
from finn.util.basic import pynq_part_map
print(pynq_part_map.keys())
# change this if you have a different PYNQ board, see list above
pynq_board = "Pynq-Z1"
fpga_part = pynq_part_map[pynq_board]
target_clk_ns = 10
from finn.transformation.fpgadataflow.make_zynq_proj import ZynqBuild
model = ModelWrapper(build_dir+"/tfc_w1_a1_set_folding_factors.onnx")
model = model.transform(ZynqBuild(platform = pynq_board, period_ns = target_clk_ns))
model.save(build_dir + "/tfc_w1_a1_post_synthesis.onnx")
showInNetron(build_dir + "/tfc_w1_a1_post_synthesis.onnx")
model = ModelWrapper(build_dir + "/tfc_w1_a1_post_synthesis.onnx")
sdp_node_middle = getCustomOp(model.graph.node[1])
postsynth_layers = sdp_node_middle.get_nodeattr("model")
showInNetron(postsynth_layers)
model = ModelWrapper(postsynth_layers)
model.model.metadata_props
model = ModelWrapper(build_dir + "/tfc_w1_a1_post_synthesis.onnx")
model.model.metadata_props
! ls {model.get_metadata_prop("vivado_pynq_proj")}
import os
# set up the following values according to your own environment
# FINN will use ssh to deploy and run the generated accelerator
ip = os.getenv("PYNQ_IP", "192.168.2.99")
username = os.getenv("PYNQ_USERNAME", "xilinx")
password = os.getenv("PYNQ_PASSWORD", "xilinx")
port = os.getenv("PYNQ_PORT", 22)
target_dir = os.getenv("PYNQ_TARGET_DIR", "/home/xilinx/finn_tfc_end2end_example")
# set up ssh options to only allow publickey authentication
options = "-o PreferredAuthentications=publickey -o PasswordAuthentication=no"
# test access to PYNQ board
! ssh {options} {username}@{ip} -p {port} cat /var/run/motd.dynamic
from finn.transformation.fpgadataflow.make_deployment import DeployToPYNQ
model = model.transform(DeployToPYNQ(ip, port, username, password, target_dir))
model.save(build_dir + "/tfc_w1_a1_pynq_deploy.onnx")
model.model.metadata_props
target_dir_pynq = target_dir + "/" + model.get_metadata_prop("pynq_deployment_dir").split("/")[-1]
target_dir_pynq
! ssh {options} {username}@{ip} -p {port} 'ls -l {target_dir_pynq}'
from pkgutil import get_data
import onnx.numpy_helper as nph
import matplotlib.pyplot as plt
raw_i = get_data("finn.data", "onnx/mnist-conv/test_data_set_0/input_0.pb")
x = nph.to_array(onnx.load_tensor_from_string(raw_i))
plt.imshow(x.reshape(28,28), cmap='gray')
model = ModelWrapper(build_dir + "/tfc_w1_a1_pynq_deploy.onnx")
iname = model.graph.input[0].name
oname = parent_model.graph.output[0].name
ishape = model.get_tensor_shape(iname)
print("Expected network input shape is " + str(ishape))
import numpy as np
from finn.core.onnx_exec import execute_onnx
input_dict = {iname: x.reshape(ishape)}
ret = execute_onnx(model, input_dict)
ret[oname]
We can now use the `validate.py` script that was generated together with the driver to measure top-1 accuracy on the MNIST dataset.
Command to execute on PYNQ:
`python3.6 validate.py --dataset mnist --batchsize 1000`
We see that the final top-1 accuracy is 92.96%, which is very close to the 93.17% reported on the [BNN-PYNQ accuracy table in Brevitas](https://github.com/Xilinx/brevitas/tree/master/brevitas_examples/bnn_pynq).
### Throughput Test on PYNQ Board <a id='throughput'></a>
In addition to the functional verification, FINN also offers the possibility to measure the network performance directly on the PYNQ board. This can be done using the core function `throughput_test`. In the next section we import the function and execute it.
First we extract the `remote_exec_model` again and pass it to the function. The function returns the metrics of the network as dictionary.
Together with the values for folding we can evaluate the performance of our accelerator. Each layer has a total folding factor of 64 and because the network is fully pipelined, it follows: `II = 64`. II is the initiation interval and indicates how many cycles are needed for one input to be processed.
| 0.294316 | 0.991788 |
请点击[此处](https://ai.baidu.com/docs#/AIStudio_Project_Notebook/a38e5576)查看本环境基本用法. <br>
Please click [here ](https://ai.baidu.com/docs#/AIStudio_Project_Notebook/a38e5576) for more detailed instructions.
# 一、项目背景介绍
## 1. 项目背景及意义
近几年来,在我国交通运输网络快速发展的环境背景下,全国汽车保有量出现井喷式的增长。随着道路车辆越来越多,人们越来越重视道路交通中的行驶安全。当下自动辅助驾驶已成为智能化交通的研究热点,在智能化的交通背景下交通标志识别系统是自动辅助驾驶重要的一部分。在现实环境道路上进行自动驾驶,意味着采用的交通标志识别系统必须能够快速准确的捕捉到交通标志。然而实际道路的环境因素非常复杂,如何准确、高效地识别交通标志,是交通标志识别系统研究的重点。
## 2. 国内外研究现状
### 2.1 国外研究现状
国外对交通标志的研究起步较早,且发展速度非常迅速。早在上世纪80年代,日本就开始了相应的研究工作。从90年代开始许多欧洲国家也加入到了相应的研究。在理论方面国外对交通标志的检测从理论基础和可行性分析方面已做了大量研究。其中主要采用基于颜色和形状的方法对交通标志进行分割提取和形状分析。1987年,日本率先开启了智能交通系统研究的大门,主要采用阈值分割、模版匹配等一系列经典的方法对限速标志进行识别,所需时间约为0.516秒,但未给出具体的检测识别准确率。1992年,法国的Saint-Blancard对带红色的标志进行研究,采用红色滤波器边缘及闭合曲线方法获取目标。其针对小规模样本进行实验,平均识别率高达94.9%。1993年,美国开发了ADIS系统,它的明军分辨率为75%,但尚不能用于检测。1994年,意大利热那亚大学的Piccioli等人根据交通标志不同的几何形状进行检测,该方法对不同形状的标志检测准确率不同,三角形标志可达92%,圆形可达94%左右。1998年起,意大利帕尔马大学采用颜色分割、形状约束、径向基函数RBF分类器进行检测识别,准确率可达90%以上。
进入21世纪,随着图像处理技术和计算机视觉理论的不断发展,交通标志检测的方法变的多样化,无论是实效性还是准确性都有所提高。2004年,澳大利亚的Nick Barnes自动化研究所和瑞典的Gareth Loy实验室合作研发了一套交通标志识别系统,识别率可达95%,但仍难以满足实时性要求。2007年,Won等人引入人类视觉选择注意力机制进行交通标志检测,该方法趋于完美,识别率也高达94.52%。但该方法仍有一些局限性。
应用方面,交通标志检测的最终目标是在实际的智能车辆导航系统中得到广泛的应用。如今,许多科技发达的西方国家这方面有了很大的成就,而且已经有不少技术开始投入使用。
### 2.2 国内研究现状
国内对于智能研究系统的起步较晚,在交通标志检测方面的研究较少,目前仍处于探索性研究阶段,虽已在研究模型实验车,但尚未形成完整的实际应用系统。
理论方面,1998年蒋刚毅等人利用数学形态学方法、骨架函数为特征的模版匹配对警告标志进行检测,初步实现了位移不变性和鲁棒性。随后许多研究机构和大学也进行了研究,并在理论方面已取得了一定的成果。有学者将多种方法进行结合来提高检测效率,如浙江大学的何耀平等人将Adaboost算法与支持向量机融合用于交通标志的识别中。除此之外,基于视觉显著性的方法也逐渐被国内学者使用,如尹涛采用自顶向下和自底向上相结合的视觉视觉显著性检测算法实现了交通标志检测定位,但是这种方法计算速度较慢,难以完成实施检测。
应用方面,随着科技的发展和人类生活水平的提高,我国对智能汽车的投入越来越多,同时交通标志的识别系统也受到了广大学者的关注,近几年也取得了一批重要的科技成果。
# 二、数据介绍
本项目采用[中国交通标志](https://aistudio.baidu.com/aistudio/datasetdetail/107275/0)数据集进行算法设计和测试。
## 1. 图片数据
该数据集源自中国交通标志识别数据库。里加数据科学俱乐部成员已经探索了它,以便对卷积神经网络进行一些培训。
数据集由 58 个类别的 5998 张交通标志图像组成。每个图像都是单个交通标志的放大视图。(例如,限速 5 公里/小时)

## 2. 注释文档
注释提供图像属性(文件名、宽度、高度)以及图像和类别中的交通标志坐标。
注释说明:
annotations.csv:
* file_name:包含交通标志的图像的文件名
* width:图片宽度
* height:图片高度
* x1:边界矩形左上角X坐标
* y1:边界矩形左上角Y坐标
* x2:边界矩形右下角X坐标
* y2:边界矩形右下角Y坐标
* category:交通标志类别
*(随机图片展示在本节最后代码框)*
```
# 解压交通标志数据集及预训练参数
# 交通标志数据集
!cd data/data107275 && unzip -oq archive\(5\).zip
# 预训练参数
!cd data/data6487 && unzip -oq ResNet50_pretrained.zip
# 简单处理数据
# 生产两者的标签文件以及所有图片的RGB得均值与均方差
import codecs
import os
import random
import shutil
import pandas as pd
import numpy as np
import cv2
import glob
from PIL import Image
def get_mean_std(image_path_list):
print('Total images:', len(image_path_list))
max_val, min_val = np.zeros(3), np.ones(3) * 255
mean, std = np.zeros(3), np.zeros(3)
for image_path in image_path_list:
image = cv2.imread(image_path)
for c in range(3):
mean[c] += image[:, :, c].mean()
std[c] += image[:, :, c].std()
max_val[c] = max(max_val[c], image[:, :, c].max())
min_val[c] = min(min_val[c], image[:, :, c].min())
mean /= len(image_path_list)
std /= len(image_path_list)
mean /= max_val - min_val
std /= max_val - min_val
return mean, std
mean,std=get_mean_std(glob.glob('data/data107275/images/*.png'))
print('mean={} std={}'.format(mean,std))
df = pd.read_csv('data/data107275/annotations.csv')
df = df.drop_duplicates(subset='file_name', keep='last', inplace=False).reset_index(drop=True) # 删除注释中重复值
print(df.shape)
for path in range(1+df['category'].max()):
if not os.path.exists('data/data107275/images/'+str(path)):
os.makedirs('data/data107275/images/'+str(path))
for i in range(df.shape[0]):
shutil.move('data/data107275/images/'+str(df['file_name'][i]), 'data/data107275/images/'+str(df['category'][i]))
# 对本地数据做一些预处理,主要用于随机分组,一部分用于训练,一部分用于验证。
import codecs
import os
import random
import shutil
import pandas as pd
from PIL import Image
train_ratio = 4.0 / 5
all_file_dir = 'data/data107275/images/'
class_list = [c for c in os.listdir(all_file_dir) if os.path.isdir(os.path.join(all_file_dir, c)) and not c.endswith('Set') and not c.startswith('.')]
class_list.sort()
print(class_list)
train_image_dir = os.path.join(all_file_dir, "trainImageSet")
if not os.path.exists(train_image_dir):
os.makedirs(train_image_dir)
eval_image_dir = os.path.join(all_file_dir, "evalImageSet")
if not os.path.exists(eval_image_dir):
os.makedirs(eval_image_dir)
train_file = codecs.open(os.path.join(all_file_dir, "train.txt"), 'w')
eval_file = codecs.open(os.path.join(all_file_dir, "eval.txt"), 'w')
def picCrop(image_path):
img_info=df.loc[df['file_name']==image_path.split('/')[-1]]
box=(img_info['x1'],img_info['y1'],img_info['x2'],img_info['y2'])
region = img.crop(box)
region.save(image_path)
df = pd.read_csv('data/data107275/annotations.csv')
df = df.drop_duplicates(subset='file_name', keep='last', inplace=False).reset_index(drop=True) # 删除注释中重复值
with codecs.open(os.path.join(all_file_dir, "label_list.txt"), "w") as label_list:
for class_dir in class_list:
label_list.write("{0}\t{1}\n".format(class_dir, class_dir))
image_path_pre = os.path.join(all_file_dir, class_dir)
for file in os.listdir(image_path_pre):
try:
img = Image.open(os.path.join(image_path_pre, file))
if random.uniform(0, 1) <= train_ratio:
# picCrop(os.path.join(image_path_pre, file))
shutil.copyfile(os.path.join(image_path_pre, file), os.path.join(train_image_dir, file))
train_file.write("{0}\t{1}\n".format(os.path.join(train_image_dir, file), class_dir))
else:
# picCrop(os.path.join(image_path_pre, file))
shutil.copyfile(os.path.join(image_path_pre, file), os.path.join(eval_image_dir, file))
eval_file.write("{0}\t{1}\n".format(os.path.join(eval_image_dir, file), class_dir))
except Exception as e:
pass
# 存在一些文件打不开,此处需要稍作清洗
train_file.close()
eval_file.close()
# 随机展示数据集中的图片
from PIL import Image
import random
import matplotlib.pyplot as plt
img_path='./data/data107275/images/trainImageSet/'
for root, dirs, files in os.walk(img_path, topdown=False):
img_path_list = files
img=Image.open(img_path+img_path_list[random.randint(0,len(img_path_list))])
plt.imshow(img)
plt.axis('off')
plt.show()
```
# 三、模型介绍
ResNet(Residual Network)是2015年ImageNet图像分类、图像物体定位和图像物体检测比赛的冠军。针对随着网络训练加深导致准确度下降的问题,ResNet提出了残差学习方法来减轻训练深层网络的困难。在已有设计思路(BN, 小卷积核,全卷积网络)的基础上,引入了残差模块。每个残差模块包含两条路径,其中一条路径是输入特征的直连通路,另一条路径对该特征做两到三次卷积操作得到该特征的残差,最后再将两条路径上的特征相加。
残差模块如图1所示,左边是基本模块连接方式,由两个输出通道数相同的3x3卷积组成。右边是瓶颈模块(Bottleneck)连接方式,之所以称为瓶颈,是因为上面的1x1卷积用来降维(图示例即256->64),下面的1x1卷积用来升维(图示例即64->256),这样中间3x3卷积的输入和输出通道数都较小(图示例即64->64)。

图1. 残差模块
图2展示了50、101、152层网络连接示意图,使用的是瓶颈模块。这三个模型的区别在于每组中残差模块的重复次数不同(见图右上角)。ResNet训练收敛较快,成功的训练了上百乃至近千层的卷积神经网络。

图2. 基于ImageNet的ResNet模型
ResNet解读博客https://blog.csdn.net/lanran2/article/details/79057994
想写好一个好的精品项目,项目的内容必须包含理论内容和实践相互结合,该部分主要是理论部分,向大家介绍一下你的模型原理等内容。
```
# ResNet 模型网络结构
class ResNet(object):
"""
resnet的网络结构类
"""
def __init__(self, layers=50):
"""
resnet的网络构造函数
:param layers: 网络层数
"""
self.layers = layers
def name(self):
"""
获取网络结构名字
:return:
"""
return 'resnet'
def net(self, input, class_dim=1000):
"""
构建网络结构
:param input: 输入图片
:param class_dim: 分类类别
:return:
"""
layers = self.layers
supported_layers = [50, 101, 152]
assert layers in supported_layers, \
"supported layers are {} but input layer is {}".format(supported_layers, layers)
if layers == 50:
depth = [3, 4, 6, 3]
elif layers == 101:
depth = [3, 4, 23, 3]
elif layers == 152:
depth = [3, 8, 36, 3]
num_filters = [64, 128, 256, 512]
conv = self.conv_bn_layer(
input=input,
num_filters=64,
filter_size=7,
stride=2,
act='relu',
name="conv1")
conv = fluid.layers.pool2d(
input=conv,
pool_size=3,
pool_stride=2,
pool_padding=1,
pool_type='max')
for block in range(len(depth)):
for i in range(depth[block]):
if layers in [101, 152] and block == 2:
if i == 0:
conv_name = "res" + str(block + 2) + "a"
else:
conv_name = "res" + str(block + 2) + "b" + str(i)
else:
conv_name = "res" + str(block + 2) + chr(97 + i)
conv = self.bottleneck_block(
input=conv,
num_filters=num_filters[block],
stride=2 if i == 0 and block != 0 else 1,
name=conv_name)
pool = fluid.layers.pool2d(input=conv, pool_size=7, pool_type='avg', global_pooling=True)
stdv = 1.0 / math.sqrt(pool.shape[1] * 1.0)
out = fluid.layers.fc(input=pool,
size=class_dim,
act='softmax',
param_attr=fluid.param_attr.ParamAttr(initializer=Uniform(-stdv, stdv)))
return out
def conv_bn_layer(self,
input,
num_filters,
filter_size,
stride=1,
groups=1,
act=None,
name=None):
"""
便捷型卷积结构,包含了batch_normal处理
:param input: 输入图片
:param num_filters: 卷积核个数
:param filter_size: 卷积核大小
:param stride: 平移
:param groups: 分组
:param act: 激活函数
:param name: 卷积层名字
:return:
"""
conv = fluid.layers.conv2d(
input=input,
num_filters=num_filters,
filter_size=filter_size,
stride=stride,
padding=(filter_size - 1) // 2,
groups=groups,
act=None,
param_attr=ParamAttr(name=name + "_weights"),
bias_attr=False,
name=name + '.conv2d.output.1')
if name == "conv1":
bn_name = "bn_" + name
else:
bn_name = "bn" + name[3:]
return fluid.layers.batch_norm(
input=conv,
act=act,
name=bn_name + '.output.1',
param_attr=ParamAttr(name=bn_name + '_scale'),
bias_attr=ParamAttr(bn_name + '_offset'),
moving_mean_name=bn_name + '_mean',
moving_variance_name=bn_name + '_variance', )
def shortcut(self, input, ch_out, stride, name):
"""
转换结构,转换输入和输出一致,方便最后的短链接结构
:param input:
:param ch_out:
:param stride:
:param name:
:return:
"""
ch_in = input.shape[1]
if ch_in != ch_out or stride != 1:
return self.conv_bn_layer(input, ch_out, 1, stride, name=name)
else:
return input
def bottleneck_block(self, input, num_filters, stride, name):
"""
resnet的短路链接结构中的一种,采用压缩方式先降维,卷积后再升维
利用转换结构将输入变成瓶颈卷积一样的尺寸,最后将两者按照位相加,完成短路链接
:param input:
:param num_filters:
:param stride:
:param name:
:return:
"""
conv0 = self.conv_bn_layer(
input=input,
num_filters=num_filters,
filter_size=1,
act='relu',
name=name + "_branch2a")
conv1 = self.conv_bn_layer(
input=conv0,
num_filters=num_filters,
filter_size=3,
stride=stride,
act='relu',
name=name + "_branch2b")
conv2 = self.conv_bn_layer(
input=conv1,
num_filters=num_filters * 4,
filter_size=1,
act=None,
name=name + "_branch2c")
short = self.shortcut(
input, num_filters * 4, stride, name=name + "_branch1")
return fluid.layers.elementwise_add(
x=short, y=conv2, act='relu', name=name + ".add.output.5")
```
# 四、模型训练
该部分主要是实践部分,也是相对来说话费时间最长的一部分,该部分主要展示模型训练的内容,同时向大家讲解模型参数的设置
## 1.训练配置
* 训练轮数
* 每批次训练图片数量
* 是否使用GPU训练
* 学习率调整
* 训练图片尺寸
```
"""
训练常用视觉基础网络,用于分类任务
需要将训练图片,类别文件 label_list.txt 放置在同一个文件夹下
程序会先读取 train.txt 文件获取类别数和图片数量
"""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os
import numpy as np
import time
import math
import paddle
import paddle.fluid as fluid
import codecs
import logging
from paddle.fluid.initializer import MSRA
from paddle.fluid.initializer import Uniform
from paddle.fluid.param_attr import ParamAttr
from PIL import Image
from PIL import ImageEnhance
train_parameters = {
"input_size": [3, 224, 224],
"class_dim": -1, # 分类数,会在初始化自定义 reader 的时候获得
"image_count": -1, # 训练图片数量,会在初始化自定义 reader 的时候获得
"label_dict": {},
"data_dir": "data/data107275/images/", # 训练数据存储地址
"train_file_list": "train.txt",
"label_file": "label_list.txt",
"save_freeze_dir": "./freeze-model",
"save_persistable_dir": "./persistable-params",
"continue_train": True, # 是否接着上一次保存的参数接着训练,优先级高于预训练模型
"pretrained": True, # 是否使用预训练的模型
"pretrained_dir": "data/data6487/ResNet50_pretrained",
"mode": "train",
"num_epochs": 100,
"train_batch_size": 128,
"mean_rgb": mean, # 常用图片的三通道均值,通常来说需要先对训练数据做统计,此处仅取中间值
"use_gpu": True,
"image_enhance_strategy": { # 图像增强相关策略
"need_distort": True, # 是否启用图像颜色增强
"need_rotate": True, # 是否需要增加随机角度
"need_crop": True, # 是否要增加裁剪
"need_flip": True, # 是否要增加水平随机翻转
"hue_prob": 0.5,
"hue_delta": 18,
"contrast_prob": 0.5,
"contrast_delta": 0.5,
"saturation_prob": 0.5,
"saturation_delta": 0.5,
"brightness_prob": 0.5,
"brightness_delta": 0.125
},
"early_stop": {
"sample_frequency": 50,
"successive_limit": 10,
"good_acc1": 0.90
},
"rsm_strategy": {
"learning_rate": 0.002,
"lr_epochs": [100, 200, 400, 800, 1200, 2000, 3000],
"lr_decay": [1, 0.5, 0.25, 0.1, 0.05, 0.01, 0.005, 0.002]
},
"momentum_strategy": {
"learning_rate": 0.002,
"lr_epochs": [100, 200, 400, 800, 1200, 2000, 3000],
"lr_decay": [1, 0.5, 0.25, 0.1, 0.05, 0.01, 0.005, 0.002]
},
"sgd_strategy": {
"learning_rate": 0.002,
"lr_epochs": [100, 200, 400, 800, 1200, 2000, 3000],
"lr_decay": [1, 0.5, 0.25, 0.1, 0.05, 0.01, 0.005, 0.002]
},
"adam_strategy": {
"learning_rate": 0.002
}
}
def init_train_parameters():
"""
初始化训练参数,主要是初始化图片数量,类别数
:return:
"""
train_file_list = os.path.join(train_parameters['data_dir'], train_parameters['train_file_list'])
label_list = os.path.join(train_parameters['data_dir'], train_parameters['label_file'])
index = 0
print(label_list)
print(train_file_list)
with codecs.open(label_list, encoding='utf-8') as flist:
lines = [line.strip() for line in flist]
for line in lines:
parts = line.strip().split()
train_parameters['label_dict'][parts[1]] = int(parts[0])
index += 1
train_parameters['class_dim'] = index
with codecs.open(train_file_list, encoding='utf-8') as flist:
lines = [line.strip() for line in flist]
train_parameters['image_count'] = len(lines)
```
## 2. 日志输出配置
输出模型训练每阶段的日志信息
```
def init_log_config():
"""
初始化日志相关配置
:return:
"""
global logger
logger = logging.getLogger()
logger.setLevel(logging.INFO)
log_path = os.path.join(os.getcwd(), 'logs')
if not os.path.exists(log_path):
os.makedirs(log_path)
log_name = os.path.join(log_path, 'train.log')
sh = logging.StreamHandler()
fh = logging.FileHandler(log_name, mode='w')
fh.setLevel(logging.DEBUG)
formatter = logging.Formatter("%(asctime)s - %(filename)s[line:%(lineno)d] - %(levelname)s: %(message)s")
fh.setFormatter(formatter)
sh.setFormatter(formatter)
logger.addHandler(sh)
logger.addHandler(fh)
```
## 3. 图像增强
* 图片尺寸归一
* 随机裁剪
* 随机选装角度
* 随机调整亮度
* 随机调整对比度
* 随机调整饱和度
* 随机调整色度
```
def resize_img(img, target_size):
"""
强制缩放图片
:param img:
:param target_size:
:return:
"""
target_size = input_size
img = img.resize((target_size[1], target_size[2]), Image.BILINEAR)
return img
def random_crop(img, scale=[0.08, 1.0], ratio=[3. / 4., 4. / 3.]):
aspect_ratio = math.sqrt(np.random.uniform(*ratio))
w = 1. * aspect_ratio
h = 1. / aspect_ratio
bound = min((float(img.size[0]) / img.size[1]) / (w**2),
(float(img.size[1]) / img.size[0]) / (h**2))
scale_max = min(scale[1], bound)
scale_min = min(scale[0], bound)
target_area = img.size[0] * img.size[1] * np.random.uniform(scale_min,
scale_max)
target_size = math.sqrt(target_area)
w = int(target_size * w)
h = int(target_size * h)
i = np.random.randint(0, img.size[0] - w + 1)
j = np.random.randint(0, img.size[1] - h + 1)
img = img.crop((i, j, i + w, j + h))
img = img.resize((train_parameters['input_size'][1], train_parameters['input_size'][2]), Image.BILINEAR)
return img
def rotate_image(img):
"""
图像增强,增加随机旋转角度
"""
angle = np.random.randint(-14, 15)
img = img.rotate(angle)
return img
def random_brightness(img):
"""
图像增强,亮度调整
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
if prob < train_parameters['image_enhance_strategy']['brightness_prob']:
brightness_delta = train_parameters['image_enhance_strategy']['brightness_delta']
delta = np.random.uniform(-brightness_delta, brightness_delta) + 1
img = ImageEnhance.Brightness(img).enhance(delta)
return img
def random_contrast(img):
"""
图像增强,对比度调整
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
if prob < train_parameters['image_enhance_strategy']['contrast_prob']:
contrast_delta = train_parameters['image_enhance_strategy']['contrast_delta']
delta = np.random.uniform(-contrast_delta, contrast_delta) + 1
img = ImageEnhance.Contrast(img).enhance(delta)
return img
def random_saturation(img):
"""
图像增强,饱和度调整
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
if prob < train_parameters['image_enhance_strategy']['saturation_prob']:
saturation_delta = train_parameters['image_enhance_strategy']['saturation_delta']
delta = np.random.uniform(-saturation_delta, saturation_delta) + 1
img = ImageEnhance.Color(img).enhance(delta)
return img
def random_hue(img):
"""
图像增强,色度调整
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
if prob < train_parameters['image_enhance_strategy']['hue_prob']:
hue_delta = train_parameters['image_enhance_strategy']['hue_delta']
delta = np.random.uniform(-hue_delta, hue_delta)
img_hsv = np.array(img.convert('HSV'))
img_hsv[:, :, 0] = img_hsv[:, :, 0] + delta
img = Image.fromarray(img_hsv, mode='HSV').convert('RGB')
return img
def distort_color(img):
"""
概率的图像增强
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
# Apply different distort order
if prob < 0.35:
img = random_brightness(img)
img = random_contrast(img)
img = random_saturation(img)
img = random_hue(img)
elif prob < 0.7:
img = random_brightness(img)
img = random_saturation(img)
img = random_hue(img)
img = random_contrast(img)
return img
```
## 4. 自定义数据读取器
读取图片数据进行训练及测试
```
def custom_image_reader(file_list, data_dir, mode):
"""
自定义用户图片读取器,先初始化图片种类,数量
:param file_list:
:param data_dir:
:param mode:
:return:
"""
with codecs.open(file_list) as flist:
lines = [line.strip() for line in flist]
def reader():
np.random.shuffle(lines)
for line in lines:
if mode == 'train' or mode == 'val':
img_path, label = line.split()
img = Image.open(img_path)
try:
if img.mode != 'RGB':
img = img.convert('RGB')
if train_parameters['image_enhance_strategy']['need_distort'] == True:
img = distort_color(img)
if train_parameters['image_enhance_strategy']['need_rotate'] == True:
img = rotate_image(img)
if train_parameters['image_enhance_strategy']['need_crop'] == True:
img = random_crop(img, train_parameters['input_size'])
if train_parameters['image_enhance_strategy']['need_flip'] == True:
mirror = int(np.random.uniform(0, 2))
if mirror == 1:
img = img.transpose(Image.FLIP_LEFT_RIGHT)
# HWC--->CHW && normalized
img = np.array(img).astype('float32')
img -= train_parameters['mean_rgb']
img = img.transpose((2, 0, 1)) # HWC to CHW
img *= 0.007843 # 像素值归一化
yield img, int(label)
except Exception as e:
pass # 以防某些图片读取处理出错,加异常处理
elif mode == 'test':
img_path = os.path.join(data_dir, line)
img = Image.open(img_path)
if img.mode != 'RGB':
img = img.convert('RGB')
img = resize_img(img, train_parameters['input_size'])
# HWC--->CHW && normalized
img = np.array(img).astype('float32')
img -= train_parameters['mean_rgb']
img = img.transpose((2, 0, 1)) # HWC to CHW
img *= 0.007843 # 像素值归一化
yield img
return reader
```
## 5. 不同类型优化器定义
定义不同的优化器方便模型训练调用
* Monmentum
* RMS
* SGD
* ADAM
```
def optimizer_momentum_setting():
"""
阶梯型的学习率适合比较大规模的训练数据
"""
learning_strategy = train_parameters['momentum_strategy']
batch_size = train_parameters["train_batch_size"]
iters = train_parameters["image_count"] // batch_size
lr = learning_strategy['learning_rate']
boundaries = [i * iters for i in learning_strategy["lr_epochs"]]
values = [i * lr for i in learning_strategy["lr_decay"]]
learning_rate = fluid.layers.piecewise_decay(boundaries, values)
optimizer = fluid.optimizer.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9)
return optimizer
def optimizer_rms_setting():
"""
阶梯型的学习率适合比较大规模的训练数据
"""
batch_size = train_parameters["train_batch_size"]
iters = train_parameters["image_count"] // batch_size
learning_strategy = train_parameters['rsm_strategy']
lr = learning_strategy['learning_rate']
boundaries = [i * iters for i in learning_strategy["lr_epochs"]]
values = [i * lr for i in learning_strategy["lr_decay"]]
optimizer = fluid.optimizer.RMSProp(
learning_rate=fluid.layers.piecewise_decay(boundaries, values))
return optimizer
def optimizer_sgd_setting():
"""
loss下降相对较慢,但是最终效果不错,阶梯型的学习率适合比较大规模的训练数据
"""
learning_strategy = train_parameters['sgd_strategy']
batch_size = train_parameters["train_batch_size"]
iters = train_parameters["image_count"] // batch_size
lr = learning_strategy['learning_rate']
boundaries = [i * iters for i in learning_strategy["lr_epochs"]]
values = [i * lr for i in learning_strategy["lr_decay"]]
learning_rate = fluid.layers.piecewise_decay(boundaries, values)
optimizer = fluid.optimizer.SGD(learning_rate=learning_rate)
return optimizer
def optimizer_adam_setting():
"""
能够比较快速的降低 loss,但是相对后期乏力
"""
learning_strategy = train_parameters['adam_strategy']
learning_rate = learning_strategy['learning_rate']
optimizer = fluid.optimizer.Adam(learning_rate=learning_rate)
return optimizer
```
## 6. 模型数据加载及训练
```
from visualdl import LogWriter
def load_params(exe, program):
if train_parameters['continue_train'] and os.path.exists(train_parameters['save_persistable_dir']):
logger.info('load params from retrain model')
fluid.io.load_persistables(executor=exe,
dirname=train_parameters['save_persistable_dir'],
main_program=program)
elif train_parameters['pretrained'] and os.path.exists(train_parameters['pretrained_dir']):
logger.info('load params from pretrained model')
def if_exist(var):
return os.path.exists(os.path.join(train_parameters['pretrained_dir'], var.name))
fluid.io.load_vars(exe, train_parameters['pretrained_dir'], main_program=program,
predicate=if_exist)
def train():
with LogWriter(logdir="./log/scalar_test/train") as writer:
pass
train_prog = fluid.Program()
train_startup = fluid.Program()
logger.info("create prog success")
logger.info("train config: %s", str(train_parameters))
logger.info("build input custom reader and data feeder")
file_list = os.path.join(train_parameters['data_dir'], "train.txt")
mode = train_parameters['mode']
batch_reader = paddle.batch(custom_image_reader(file_list, train_parameters['data_dir'], mode),
batch_size=train_parameters['train_batch_size'],
drop_last=True)
place = fluid.CUDAPlace(0) if train_parameters['use_gpu'] else fluid.CPUPlace()
# 定义输入数据的占位符
img = fluid.layers.data(name='img', shape=train_parameters['input_size'], dtype='float32')
label = fluid.layers.data(name='label', shape=[1], dtype='int64')
feeder = fluid.DataFeeder(feed_list=[img, label], place=place)
# 选取不同的网络
logger.info("build newwork")
model = ResNet()
out = model.net(input=img, class_dim=train_parameters['class_dim'])
cost = fluid.layers.cross_entropy(out, label)
avg_cost = fluid.layers.mean(x=cost)
acc_top1 = fluid.layers.accuracy(input=out, label=label, k=1)
# 选取不同的优化器
# optimizer = optimizer_rms_setting()
# optimizer = optimizer_momentum_setting()
optimizer = optimizer_sgd_setting()
# optimizer = optimizer_adam_setting()
optimizer.minimize(avg_cost)
exe = fluid.Executor(place)
main_program = fluid.default_main_program()
exe.run(fluid.default_startup_program())
train_fetch_list = [avg_cost.name, acc_top1.name, out.name]
load_params(exe, main_program)
# 训练循环主体
stop_strategy = train_parameters['early_stop']
successive_limit = stop_strategy['successive_limit']
sample_freq = stop_strategy['sample_frequency']
good_acc1 = stop_strategy['good_acc1']
successive_count = 0
stop_train = False
total_batch_count = 0
for pass_id in range(train_parameters["num_epochs"]):
logger.info("current pass: %d, start read image", pass_id)
batch_id = 0
for step_id, data in enumerate(batch_reader()):
t1 = time.time()
loss, acc1, pred_ot = exe.run(main_program,
feed=feeder.feed(data),
fetch_list=train_fetch_list)
t2 = time.time()
batch_id += 1
total_batch_count += 1
period = t2 - t1
loss = np.mean(np.array(loss))
acc1 = np.mean(np.array(acc1))
writer.add_scalar(tag="acc", step=total_batch_count, value=acc1)
writer.add_scalar(tag="loss", step=total_batch_count, value=loss)
if batch_id % 10 == 0:
logger.info("Pass {0}, trainbatch {1}, loss {2}, acc1 {3}, time {4}".format(pass_id, batch_id, loss, acc1,
"%2.2f sec" % period))
# 简单的提前停止策略,认为连续达到某个准确率就可以停止了
if acc1 >= good_acc1:
successive_count += 1
logger.info("current acc1 {0} meets good {1}, successive count {2}".format(acc1, good_acc1, successive_count))
fluid.io.save_inference_model(dirname=train_parameters['save_freeze_dir'],
feeded_var_names=['img'],
target_vars=[out],
main_program=main_program,
executor=exe)
if successive_count >= successive_limit:
logger.info("end training")
stop_train = True
break
else:
successive_count = 0
# 通用的保存策略,减小意外停止的损失
if total_batch_count % sample_freq == 0:
logger.info("temp save {0} batch train result, current acc1 {1}".format(total_batch_count, acc1))
fluid.io.save_persistables(dirname=train_parameters['save_persistable_dir'],
main_program=main_program,
executor=exe)
if stop_train:
break
logger.info("training till last epcho, end training")
fluid.io.save_persistables(dirname=train_parameters['save_persistable_dir'],
main_program=main_program,
executor=exe)
fluid.io.save_inference_model(dirname=train_parameters['save_freeze_dir'],
feeded_var_names=['img'],
target_vars=[out],
main_program=main_program,
executor=exe)
if __name__ == '__main__':
init_log_config()
init_train_parameters()
train()
```
* 训练过程中,训练集精确度变化图

* 训练过程中,loss值变化图

训练结束后,模型对训练集数据识别最高精确度为96.09%。
# 五、模型评估
该部分主要是对训练好的模型进行评估,可以是用验证集进行评估,或者是直接预测结果。评估结果和预测结果尽量展示出来,增加吸引力。
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os
import numpy as np
import random
import time
import codecs
import sys
import functools
import math
import pandas as pd
import paddle
import paddle.fluid as fluid
from paddle.fluid import core
from paddle.fluid.param_attr import ParamAttr
from PIL import Image, ImageEnhance
import matplotlib.pyplot as plt
target_size = [3, 224, 224]
mean_rgb = mean
data_dir = "data/data107275/images/"
eval_file = "eval.txt"
use_gpu = True
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
exe = fluid.Executor(place)
save_freeze_dir = "./freeze-model"
[inference_program, feed_target_names, fetch_targets] = fluid.io.load_inference_model(dirname=save_freeze_dir, executor=exe)
# print(fetch_targets)
def crop_image(img, target_size):
width, height = img.size
w_start = (width - target_size[2]) / 2
h_start = (height - target_size[1]) / 2
w_end = w_start + target_size[2]
h_end = h_start + target_size[1]
img = img.crop((w_start, h_start, w_end, h_end))
return img
def resize_img(img, target_size):
ret = img.resize((target_size[1], target_size[2]), Image.BILINEAR)
return ret
def read_image(img_path):
img = Image.open(img_path)
if img.mode != 'RGB':
img = img.convert('RGB')
img = crop_image(img, target_size)
img = np.array(img).astype('float32')
img -= mean_rgb
img = img.transpose((2, 0, 1)) # HWC to CHW
img *= 0.007843
img = img[np.newaxis,:]
return img
def infer(image_path):
tensor_img = read_image(image_path)
label = exe.run(inference_program, feed={feed_target_names[0]: tensor_img}, fetch_list=fetch_targets)
return np.argmax(label)
def eval_all():
eval_file_path = os.path.join(data_dir, eval_file)
total_count = 0
right_count = 0
with codecs.open(eval_file_path, encoding='utf-8') as flist:
lines = [line.strip() for line in flist]
t1 = time.time()
for line in lines:
total_count += 1
parts = line.strip().split()
result = infer(parts[0])
if str(result) == parts[1]:
right_count += 1
period = time.time() - t1
print("total eval count:{0} cost time:{1} predict accuracy:{2}".format(total_count, "%2.2f sec" % period, right_count / total_count))
def showOnePic():
pic_file_path_list = os.path.join(data_dir, eval_file)
df=pd.read_csv(pic_file_path_list, sep='\t', header=None)
# 子图1
random_idx = np.random.randint(0,df.shape[0])
pic_file_path = df[0][random_idx]
img = Image.open(pic_file_path)
true_label = df[1][random_idx]
pred_label = infer(pic_file_path)
plt.subplot(221)
plt.imshow(img)
plt.title('True Label:{}\n Predict Label:{}'.format(true_label,pred_label))
plt.axis('off')
# 子图2
random_idx = np.random.randint(0,df.shape[0])
pic_file_path = df[0][random_idx]
img = Image.open(pic_file_path)
true_label = df[1][random_idx]
pred_label = infer(pic_file_path)
plt.subplot(222)
plt.imshow(img)
plt.title('True Label:{}\n Predict Label:{}'.format(true_label,pred_label))
plt.axis('off')
# 子图3
random_idx = np.random.randint(0,df.shape[0])
pic_file_path = df[0][random_idx]
img = Image.open(pic_file_path)
true_label = df[1][random_idx]
pred_label = infer(pic_file_path)
plt.subplot(223)
plt.imshow(img)
plt.title('True Label:{}\n Predict Label:{}'.format(true_label,pred_label))
plt.axis('off')
# 子图4
random_idx = np.random.randint(0,df.shape[0])
pic_file_path = df[0][random_idx]
img = Image.open(pic_file_path)
true_label = df[1][random_idx]
pred_label = infer(pic_file_path)
plt.subplot(224)
plt.imshow(img)
plt.title('True Label:{}\n Predict Label:{}'.format(true_label,pred_label))
plt.axis('off')
plt.tight_layout()
plt.show()
if __name__ == '__main__':
eval_all()
showOnePic()
```
# 六、总结与升华
本项目是依靠[中国交通标志](https://aistudio.baidu.com/aistudio/datasetdetail/107275/0)数据集进行Resnet网络算法学习和测试。该项目在反复优化调参,处理图像数据后最终在训练集中最大识别精度为96.09%,在测试集中识别精度已达到68.98%,存在模型过拟合的情况。该项目虽不及现在研究领域上其他优秀算法,但在经过这段时间我自己的努力后达到这样的精确度,我比较满意。
该项目在配置调参中我也发现了一些问题并有一些初步的想法。
比如在图像预处理阶段中,虽已尝试通过图片尺寸归一、随机裁剪、随机选装角度、随机调整亮度、随机调整对比度等方式将训练样本扩大,但仍有一些图片预处理方法仍未尝试,以后工作中可以增加新的图片预处理继续增加训练样本,这样可能会些许提高训练后模型的识别精确度。
关于选择神经网络模型,本项目采用的是比较成熟Resnet,现在在图像研究中热点时transformer模型,今后在有一定神经网络基础后,可以尝试使用transformer模型进行训练,对比各网络优势并结合其优点,尝试得到更好的神经网络模型。
对于Resnet的优化问题,可以结合现如相关方向研究热点,结合进化算法、注意力机制等,优化Resnet网络,提高模型精度。
# 七、个人总结
本人AI萌新一枚,现居重庆,在AI相关的算法知识还有很多东西要去学习吸收。欢迎各位大佬带我学习。
# 提交链接
aistudio链接:https://aistudio.baidu.com/aistudio/projectdetail/3529700?contributionType=1
github链接:
gitee链接:
|
github_jupyter
|
# 解压交通标志数据集及预训练参数
# 交通标志数据集
!cd data/data107275 && unzip -oq archive\(5\).zip
# 预训练参数
!cd data/data6487 && unzip -oq ResNet50_pretrained.zip
# 简单处理数据
# 生产两者的标签文件以及所有图片的RGB得均值与均方差
import codecs
import os
import random
import shutil
import pandas as pd
import numpy as np
import cv2
import glob
from PIL import Image
def get_mean_std(image_path_list):
print('Total images:', len(image_path_list))
max_val, min_val = np.zeros(3), np.ones(3) * 255
mean, std = np.zeros(3), np.zeros(3)
for image_path in image_path_list:
image = cv2.imread(image_path)
for c in range(3):
mean[c] += image[:, :, c].mean()
std[c] += image[:, :, c].std()
max_val[c] = max(max_val[c], image[:, :, c].max())
min_val[c] = min(min_val[c], image[:, :, c].min())
mean /= len(image_path_list)
std /= len(image_path_list)
mean /= max_val - min_val
std /= max_val - min_val
return mean, std
mean,std=get_mean_std(glob.glob('data/data107275/images/*.png'))
print('mean={} std={}'.format(mean,std))
df = pd.read_csv('data/data107275/annotations.csv')
df = df.drop_duplicates(subset='file_name', keep='last', inplace=False).reset_index(drop=True) # 删除注释中重复值
print(df.shape)
for path in range(1+df['category'].max()):
if not os.path.exists('data/data107275/images/'+str(path)):
os.makedirs('data/data107275/images/'+str(path))
for i in range(df.shape[0]):
shutil.move('data/data107275/images/'+str(df['file_name'][i]), 'data/data107275/images/'+str(df['category'][i]))
# 对本地数据做一些预处理,主要用于随机分组,一部分用于训练,一部分用于验证。
import codecs
import os
import random
import shutil
import pandas as pd
from PIL import Image
train_ratio = 4.0 / 5
all_file_dir = 'data/data107275/images/'
class_list = [c for c in os.listdir(all_file_dir) if os.path.isdir(os.path.join(all_file_dir, c)) and not c.endswith('Set') and not c.startswith('.')]
class_list.sort()
print(class_list)
train_image_dir = os.path.join(all_file_dir, "trainImageSet")
if not os.path.exists(train_image_dir):
os.makedirs(train_image_dir)
eval_image_dir = os.path.join(all_file_dir, "evalImageSet")
if not os.path.exists(eval_image_dir):
os.makedirs(eval_image_dir)
train_file = codecs.open(os.path.join(all_file_dir, "train.txt"), 'w')
eval_file = codecs.open(os.path.join(all_file_dir, "eval.txt"), 'w')
def picCrop(image_path):
img_info=df.loc[df['file_name']==image_path.split('/')[-1]]
box=(img_info['x1'],img_info['y1'],img_info['x2'],img_info['y2'])
region = img.crop(box)
region.save(image_path)
df = pd.read_csv('data/data107275/annotations.csv')
df = df.drop_duplicates(subset='file_name', keep='last', inplace=False).reset_index(drop=True) # 删除注释中重复值
with codecs.open(os.path.join(all_file_dir, "label_list.txt"), "w") as label_list:
for class_dir in class_list:
label_list.write("{0}\t{1}\n".format(class_dir, class_dir))
image_path_pre = os.path.join(all_file_dir, class_dir)
for file in os.listdir(image_path_pre):
try:
img = Image.open(os.path.join(image_path_pre, file))
if random.uniform(0, 1) <= train_ratio:
# picCrop(os.path.join(image_path_pre, file))
shutil.copyfile(os.path.join(image_path_pre, file), os.path.join(train_image_dir, file))
train_file.write("{0}\t{1}\n".format(os.path.join(train_image_dir, file), class_dir))
else:
# picCrop(os.path.join(image_path_pre, file))
shutil.copyfile(os.path.join(image_path_pre, file), os.path.join(eval_image_dir, file))
eval_file.write("{0}\t{1}\n".format(os.path.join(eval_image_dir, file), class_dir))
except Exception as e:
pass
# 存在一些文件打不开,此处需要稍作清洗
train_file.close()
eval_file.close()
# 随机展示数据集中的图片
from PIL import Image
import random
import matplotlib.pyplot as plt
img_path='./data/data107275/images/trainImageSet/'
for root, dirs, files in os.walk(img_path, topdown=False):
img_path_list = files
img=Image.open(img_path+img_path_list[random.randint(0,len(img_path_list))])
plt.imshow(img)
plt.axis('off')
plt.show()
# ResNet 模型网络结构
class ResNet(object):
"""
resnet的网络结构类
"""
def __init__(self, layers=50):
"""
resnet的网络构造函数
:param layers: 网络层数
"""
self.layers = layers
def name(self):
"""
获取网络结构名字
:return:
"""
return 'resnet'
def net(self, input, class_dim=1000):
"""
构建网络结构
:param input: 输入图片
:param class_dim: 分类类别
:return:
"""
layers = self.layers
supported_layers = [50, 101, 152]
assert layers in supported_layers, \
"supported layers are {} but input layer is {}".format(supported_layers, layers)
if layers == 50:
depth = [3, 4, 6, 3]
elif layers == 101:
depth = [3, 4, 23, 3]
elif layers == 152:
depth = [3, 8, 36, 3]
num_filters = [64, 128, 256, 512]
conv = self.conv_bn_layer(
input=input,
num_filters=64,
filter_size=7,
stride=2,
act='relu',
name="conv1")
conv = fluid.layers.pool2d(
input=conv,
pool_size=3,
pool_stride=2,
pool_padding=1,
pool_type='max')
for block in range(len(depth)):
for i in range(depth[block]):
if layers in [101, 152] and block == 2:
if i == 0:
conv_name = "res" + str(block + 2) + "a"
else:
conv_name = "res" + str(block + 2) + "b" + str(i)
else:
conv_name = "res" + str(block + 2) + chr(97 + i)
conv = self.bottleneck_block(
input=conv,
num_filters=num_filters[block],
stride=2 if i == 0 and block != 0 else 1,
name=conv_name)
pool = fluid.layers.pool2d(input=conv, pool_size=7, pool_type='avg', global_pooling=True)
stdv = 1.0 / math.sqrt(pool.shape[1] * 1.0)
out = fluid.layers.fc(input=pool,
size=class_dim,
act='softmax',
param_attr=fluid.param_attr.ParamAttr(initializer=Uniform(-stdv, stdv)))
return out
def conv_bn_layer(self,
input,
num_filters,
filter_size,
stride=1,
groups=1,
act=None,
name=None):
"""
便捷型卷积结构,包含了batch_normal处理
:param input: 输入图片
:param num_filters: 卷积核个数
:param filter_size: 卷积核大小
:param stride: 平移
:param groups: 分组
:param act: 激活函数
:param name: 卷积层名字
:return:
"""
conv = fluid.layers.conv2d(
input=input,
num_filters=num_filters,
filter_size=filter_size,
stride=stride,
padding=(filter_size - 1) // 2,
groups=groups,
act=None,
param_attr=ParamAttr(name=name + "_weights"),
bias_attr=False,
name=name + '.conv2d.output.1')
if name == "conv1":
bn_name = "bn_" + name
else:
bn_name = "bn" + name[3:]
return fluid.layers.batch_norm(
input=conv,
act=act,
name=bn_name + '.output.1',
param_attr=ParamAttr(name=bn_name + '_scale'),
bias_attr=ParamAttr(bn_name + '_offset'),
moving_mean_name=bn_name + '_mean',
moving_variance_name=bn_name + '_variance', )
def shortcut(self, input, ch_out, stride, name):
"""
转换结构,转换输入和输出一致,方便最后的短链接结构
:param input:
:param ch_out:
:param stride:
:param name:
:return:
"""
ch_in = input.shape[1]
if ch_in != ch_out or stride != 1:
return self.conv_bn_layer(input, ch_out, 1, stride, name=name)
else:
return input
def bottleneck_block(self, input, num_filters, stride, name):
"""
resnet的短路链接结构中的一种,采用压缩方式先降维,卷积后再升维
利用转换结构将输入变成瓶颈卷积一样的尺寸,最后将两者按照位相加,完成短路链接
:param input:
:param num_filters:
:param stride:
:param name:
:return:
"""
conv0 = self.conv_bn_layer(
input=input,
num_filters=num_filters,
filter_size=1,
act='relu',
name=name + "_branch2a")
conv1 = self.conv_bn_layer(
input=conv0,
num_filters=num_filters,
filter_size=3,
stride=stride,
act='relu',
name=name + "_branch2b")
conv2 = self.conv_bn_layer(
input=conv1,
num_filters=num_filters * 4,
filter_size=1,
act=None,
name=name + "_branch2c")
short = self.shortcut(
input, num_filters * 4, stride, name=name + "_branch1")
return fluid.layers.elementwise_add(
x=short, y=conv2, act='relu', name=name + ".add.output.5")
"""
训练常用视觉基础网络,用于分类任务
需要将训练图片,类别文件 label_list.txt 放置在同一个文件夹下
程序会先读取 train.txt 文件获取类别数和图片数量
"""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os
import numpy as np
import time
import math
import paddle
import paddle.fluid as fluid
import codecs
import logging
from paddle.fluid.initializer import MSRA
from paddle.fluid.initializer import Uniform
from paddle.fluid.param_attr import ParamAttr
from PIL import Image
from PIL import ImageEnhance
train_parameters = {
"input_size": [3, 224, 224],
"class_dim": -1, # 分类数,会在初始化自定义 reader 的时候获得
"image_count": -1, # 训练图片数量,会在初始化自定义 reader 的时候获得
"label_dict": {},
"data_dir": "data/data107275/images/", # 训练数据存储地址
"train_file_list": "train.txt",
"label_file": "label_list.txt",
"save_freeze_dir": "./freeze-model",
"save_persistable_dir": "./persistable-params",
"continue_train": True, # 是否接着上一次保存的参数接着训练,优先级高于预训练模型
"pretrained": True, # 是否使用预训练的模型
"pretrained_dir": "data/data6487/ResNet50_pretrained",
"mode": "train",
"num_epochs": 100,
"train_batch_size": 128,
"mean_rgb": mean, # 常用图片的三通道均值,通常来说需要先对训练数据做统计,此处仅取中间值
"use_gpu": True,
"image_enhance_strategy": { # 图像增强相关策略
"need_distort": True, # 是否启用图像颜色增强
"need_rotate": True, # 是否需要增加随机角度
"need_crop": True, # 是否要增加裁剪
"need_flip": True, # 是否要增加水平随机翻转
"hue_prob": 0.5,
"hue_delta": 18,
"contrast_prob": 0.5,
"contrast_delta": 0.5,
"saturation_prob": 0.5,
"saturation_delta": 0.5,
"brightness_prob": 0.5,
"brightness_delta": 0.125
},
"early_stop": {
"sample_frequency": 50,
"successive_limit": 10,
"good_acc1": 0.90
},
"rsm_strategy": {
"learning_rate": 0.002,
"lr_epochs": [100, 200, 400, 800, 1200, 2000, 3000],
"lr_decay": [1, 0.5, 0.25, 0.1, 0.05, 0.01, 0.005, 0.002]
},
"momentum_strategy": {
"learning_rate": 0.002,
"lr_epochs": [100, 200, 400, 800, 1200, 2000, 3000],
"lr_decay": [1, 0.5, 0.25, 0.1, 0.05, 0.01, 0.005, 0.002]
},
"sgd_strategy": {
"learning_rate": 0.002,
"lr_epochs": [100, 200, 400, 800, 1200, 2000, 3000],
"lr_decay": [1, 0.5, 0.25, 0.1, 0.05, 0.01, 0.005, 0.002]
},
"adam_strategy": {
"learning_rate": 0.002
}
}
def init_train_parameters():
"""
初始化训练参数,主要是初始化图片数量,类别数
:return:
"""
train_file_list = os.path.join(train_parameters['data_dir'], train_parameters['train_file_list'])
label_list = os.path.join(train_parameters['data_dir'], train_parameters['label_file'])
index = 0
print(label_list)
print(train_file_list)
with codecs.open(label_list, encoding='utf-8') as flist:
lines = [line.strip() for line in flist]
for line in lines:
parts = line.strip().split()
train_parameters['label_dict'][parts[1]] = int(parts[0])
index += 1
train_parameters['class_dim'] = index
with codecs.open(train_file_list, encoding='utf-8') as flist:
lines = [line.strip() for line in flist]
train_parameters['image_count'] = len(lines)
def init_log_config():
"""
初始化日志相关配置
:return:
"""
global logger
logger = logging.getLogger()
logger.setLevel(logging.INFO)
log_path = os.path.join(os.getcwd(), 'logs')
if not os.path.exists(log_path):
os.makedirs(log_path)
log_name = os.path.join(log_path, 'train.log')
sh = logging.StreamHandler()
fh = logging.FileHandler(log_name, mode='w')
fh.setLevel(logging.DEBUG)
formatter = logging.Formatter("%(asctime)s - %(filename)s[line:%(lineno)d] - %(levelname)s: %(message)s")
fh.setFormatter(formatter)
sh.setFormatter(formatter)
logger.addHandler(sh)
logger.addHandler(fh)
def resize_img(img, target_size):
"""
强制缩放图片
:param img:
:param target_size:
:return:
"""
target_size = input_size
img = img.resize((target_size[1], target_size[2]), Image.BILINEAR)
return img
def random_crop(img, scale=[0.08, 1.0], ratio=[3. / 4., 4. / 3.]):
aspect_ratio = math.sqrt(np.random.uniform(*ratio))
w = 1. * aspect_ratio
h = 1. / aspect_ratio
bound = min((float(img.size[0]) / img.size[1]) / (w**2),
(float(img.size[1]) / img.size[0]) / (h**2))
scale_max = min(scale[1], bound)
scale_min = min(scale[0], bound)
target_area = img.size[0] * img.size[1] * np.random.uniform(scale_min,
scale_max)
target_size = math.sqrt(target_area)
w = int(target_size * w)
h = int(target_size * h)
i = np.random.randint(0, img.size[0] - w + 1)
j = np.random.randint(0, img.size[1] - h + 1)
img = img.crop((i, j, i + w, j + h))
img = img.resize((train_parameters['input_size'][1], train_parameters['input_size'][2]), Image.BILINEAR)
return img
def rotate_image(img):
"""
图像增强,增加随机旋转角度
"""
angle = np.random.randint(-14, 15)
img = img.rotate(angle)
return img
def random_brightness(img):
"""
图像增强,亮度调整
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
if prob < train_parameters['image_enhance_strategy']['brightness_prob']:
brightness_delta = train_parameters['image_enhance_strategy']['brightness_delta']
delta = np.random.uniform(-brightness_delta, brightness_delta) + 1
img = ImageEnhance.Brightness(img).enhance(delta)
return img
def random_contrast(img):
"""
图像增强,对比度调整
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
if prob < train_parameters['image_enhance_strategy']['contrast_prob']:
contrast_delta = train_parameters['image_enhance_strategy']['contrast_delta']
delta = np.random.uniform(-contrast_delta, contrast_delta) + 1
img = ImageEnhance.Contrast(img).enhance(delta)
return img
def random_saturation(img):
"""
图像增强,饱和度调整
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
if prob < train_parameters['image_enhance_strategy']['saturation_prob']:
saturation_delta = train_parameters['image_enhance_strategy']['saturation_delta']
delta = np.random.uniform(-saturation_delta, saturation_delta) + 1
img = ImageEnhance.Color(img).enhance(delta)
return img
def random_hue(img):
"""
图像增强,色度调整
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
if prob < train_parameters['image_enhance_strategy']['hue_prob']:
hue_delta = train_parameters['image_enhance_strategy']['hue_delta']
delta = np.random.uniform(-hue_delta, hue_delta)
img_hsv = np.array(img.convert('HSV'))
img_hsv[:, :, 0] = img_hsv[:, :, 0] + delta
img = Image.fromarray(img_hsv, mode='HSV').convert('RGB')
return img
def distort_color(img):
"""
概率的图像增强
:param img:
:return:
"""
prob = np.random.uniform(0, 1)
# Apply different distort order
if prob < 0.35:
img = random_brightness(img)
img = random_contrast(img)
img = random_saturation(img)
img = random_hue(img)
elif prob < 0.7:
img = random_brightness(img)
img = random_saturation(img)
img = random_hue(img)
img = random_contrast(img)
return img
def custom_image_reader(file_list, data_dir, mode):
"""
自定义用户图片读取器,先初始化图片种类,数量
:param file_list:
:param data_dir:
:param mode:
:return:
"""
with codecs.open(file_list) as flist:
lines = [line.strip() for line in flist]
def reader():
np.random.shuffle(lines)
for line in lines:
if mode == 'train' or mode == 'val':
img_path, label = line.split()
img = Image.open(img_path)
try:
if img.mode != 'RGB':
img = img.convert('RGB')
if train_parameters['image_enhance_strategy']['need_distort'] == True:
img = distort_color(img)
if train_parameters['image_enhance_strategy']['need_rotate'] == True:
img = rotate_image(img)
if train_parameters['image_enhance_strategy']['need_crop'] == True:
img = random_crop(img, train_parameters['input_size'])
if train_parameters['image_enhance_strategy']['need_flip'] == True:
mirror = int(np.random.uniform(0, 2))
if mirror == 1:
img = img.transpose(Image.FLIP_LEFT_RIGHT)
# HWC--->CHW && normalized
img = np.array(img).astype('float32')
img -= train_parameters['mean_rgb']
img = img.transpose((2, 0, 1)) # HWC to CHW
img *= 0.007843 # 像素值归一化
yield img, int(label)
except Exception as e:
pass # 以防某些图片读取处理出错,加异常处理
elif mode == 'test':
img_path = os.path.join(data_dir, line)
img = Image.open(img_path)
if img.mode != 'RGB':
img = img.convert('RGB')
img = resize_img(img, train_parameters['input_size'])
# HWC--->CHW && normalized
img = np.array(img).astype('float32')
img -= train_parameters['mean_rgb']
img = img.transpose((2, 0, 1)) # HWC to CHW
img *= 0.007843 # 像素值归一化
yield img
return reader
def optimizer_momentum_setting():
"""
阶梯型的学习率适合比较大规模的训练数据
"""
learning_strategy = train_parameters['momentum_strategy']
batch_size = train_parameters["train_batch_size"]
iters = train_parameters["image_count"] // batch_size
lr = learning_strategy['learning_rate']
boundaries = [i * iters for i in learning_strategy["lr_epochs"]]
values = [i * lr for i in learning_strategy["lr_decay"]]
learning_rate = fluid.layers.piecewise_decay(boundaries, values)
optimizer = fluid.optimizer.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9)
return optimizer
def optimizer_rms_setting():
"""
阶梯型的学习率适合比较大规模的训练数据
"""
batch_size = train_parameters["train_batch_size"]
iters = train_parameters["image_count"] // batch_size
learning_strategy = train_parameters['rsm_strategy']
lr = learning_strategy['learning_rate']
boundaries = [i * iters for i in learning_strategy["lr_epochs"]]
values = [i * lr for i in learning_strategy["lr_decay"]]
optimizer = fluid.optimizer.RMSProp(
learning_rate=fluid.layers.piecewise_decay(boundaries, values))
return optimizer
def optimizer_sgd_setting():
"""
loss下降相对较慢,但是最终效果不错,阶梯型的学习率适合比较大规模的训练数据
"""
learning_strategy = train_parameters['sgd_strategy']
batch_size = train_parameters["train_batch_size"]
iters = train_parameters["image_count"] // batch_size
lr = learning_strategy['learning_rate']
boundaries = [i * iters for i in learning_strategy["lr_epochs"]]
values = [i * lr for i in learning_strategy["lr_decay"]]
learning_rate = fluid.layers.piecewise_decay(boundaries, values)
optimizer = fluid.optimizer.SGD(learning_rate=learning_rate)
return optimizer
def optimizer_adam_setting():
"""
能够比较快速的降低 loss,但是相对后期乏力
"""
learning_strategy = train_parameters['adam_strategy']
learning_rate = learning_strategy['learning_rate']
optimizer = fluid.optimizer.Adam(learning_rate=learning_rate)
return optimizer
from visualdl import LogWriter
def load_params(exe, program):
if train_parameters['continue_train'] and os.path.exists(train_parameters['save_persistable_dir']):
logger.info('load params from retrain model')
fluid.io.load_persistables(executor=exe,
dirname=train_parameters['save_persistable_dir'],
main_program=program)
elif train_parameters['pretrained'] and os.path.exists(train_parameters['pretrained_dir']):
logger.info('load params from pretrained model')
def if_exist(var):
return os.path.exists(os.path.join(train_parameters['pretrained_dir'], var.name))
fluid.io.load_vars(exe, train_parameters['pretrained_dir'], main_program=program,
predicate=if_exist)
def train():
with LogWriter(logdir="./log/scalar_test/train") as writer:
pass
train_prog = fluid.Program()
train_startup = fluid.Program()
logger.info("create prog success")
logger.info("train config: %s", str(train_parameters))
logger.info("build input custom reader and data feeder")
file_list = os.path.join(train_parameters['data_dir'], "train.txt")
mode = train_parameters['mode']
batch_reader = paddle.batch(custom_image_reader(file_list, train_parameters['data_dir'], mode),
batch_size=train_parameters['train_batch_size'],
drop_last=True)
place = fluid.CUDAPlace(0) if train_parameters['use_gpu'] else fluid.CPUPlace()
# 定义输入数据的占位符
img = fluid.layers.data(name='img', shape=train_parameters['input_size'], dtype='float32')
label = fluid.layers.data(name='label', shape=[1], dtype='int64')
feeder = fluid.DataFeeder(feed_list=[img, label], place=place)
# 选取不同的网络
logger.info("build newwork")
model = ResNet()
out = model.net(input=img, class_dim=train_parameters['class_dim'])
cost = fluid.layers.cross_entropy(out, label)
avg_cost = fluid.layers.mean(x=cost)
acc_top1 = fluid.layers.accuracy(input=out, label=label, k=1)
# 选取不同的优化器
# optimizer = optimizer_rms_setting()
# optimizer = optimizer_momentum_setting()
optimizer = optimizer_sgd_setting()
# optimizer = optimizer_adam_setting()
optimizer.minimize(avg_cost)
exe = fluid.Executor(place)
main_program = fluid.default_main_program()
exe.run(fluid.default_startup_program())
train_fetch_list = [avg_cost.name, acc_top1.name, out.name]
load_params(exe, main_program)
# 训练循环主体
stop_strategy = train_parameters['early_stop']
successive_limit = stop_strategy['successive_limit']
sample_freq = stop_strategy['sample_frequency']
good_acc1 = stop_strategy['good_acc1']
successive_count = 0
stop_train = False
total_batch_count = 0
for pass_id in range(train_parameters["num_epochs"]):
logger.info("current pass: %d, start read image", pass_id)
batch_id = 0
for step_id, data in enumerate(batch_reader()):
t1 = time.time()
loss, acc1, pred_ot = exe.run(main_program,
feed=feeder.feed(data),
fetch_list=train_fetch_list)
t2 = time.time()
batch_id += 1
total_batch_count += 1
period = t2 - t1
loss = np.mean(np.array(loss))
acc1 = np.mean(np.array(acc1))
writer.add_scalar(tag="acc", step=total_batch_count, value=acc1)
writer.add_scalar(tag="loss", step=total_batch_count, value=loss)
if batch_id % 10 == 0:
logger.info("Pass {0}, trainbatch {1}, loss {2}, acc1 {3}, time {4}".format(pass_id, batch_id, loss, acc1,
"%2.2f sec" % period))
# 简单的提前停止策略,认为连续达到某个准确率就可以停止了
if acc1 >= good_acc1:
successive_count += 1
logger.info("current acc1 {0} meets good {1}, successive count {2}".format(acc1, good_acc1, successive_count))
fluid.io.save_inference_model(dirname=train_parameters['save_freeze_dir'],
feeded_var_names=['img'],
target_vars=[out],
main_program=main_program,
executor=exe)
if successive_count >= successive_limit:
logger.info("end training")
stop_train = True
break
else:
successive_count = 0
# 通用的保存策略,减小意外停止的损失
if total_batch_count % sample_freq == 0:
logger.info("temp save {0} batch train result, current acc1 {1}".format(total_batch_count, acc1))
fluid.io.save_persistables(dirname=train_parameters['save_persistable_dir'],
main_program=main_program,
executor=exe)
if stop_train:
break
logger.info("training till last epcho, end training")
fluid.io.save_persistables(dirname=train_parameters['save_persistable_dir'],
main_program=main_program,
executor=exe)
fluid.io.save_inference_model(dirname=train_parameters['save_freeze_dir'],
feeded_var_names=['img'],
target_vars=[out],
main_program=main_program,
executor=exe)
if __name__ == '__main__':
init_log_config()
init_train_parameters()
train()
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os
import numpy as np
import random
import time
import codecs
import sys
import functools
import math
import pandas as pd
import paddle
import paddle.fluid as fluid
from paddle.fluid import core
from paddle.fluid.param_attr import ParamAttr
from PIL import Image, ImageEnhance
import matplotlib.pyplot as plt
target_size = [3, 224, 224]
mean_rgb = mean
data_dir = "data/data107275/images/"
eval_file = "eval.txt"
use_gpu = True
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
exe = fluid.Executor(place)
save_freeze_dir = "./freeze-model"
[inference_program, feed_target_names, fetch_targets] = fluid.io.load_inference_model(dirname=save_freeze_dir, executor=exe)
# print(fetch_targets)
def crop_image(img, target_size):
width, height = img.size
w_start = (width - target_size[2]) / 2
h_start = (height - target_size[1]) / 2
w_end = w_start + target_size[2]
h_end = h_start + target_size[1]
img = img.crop((w_start, h_start, w_end, h_end))
return img
def resize_img(img, target_size):
ret = img.resize((target_size[1], target_size[2]), Image.BILINEAR)
return ret
def read_image(img_path):
img = Image.open(img_path)
if img.mode != 'RGB':
img = img.convert('RGB')
img = crop_image(img, target_size)
img = np.array(img).astype('float32')
img -= mean_rgb
img = img.transpose((2, 0, 1)) # HWC to CHW
img *= 0.007843
img = img[np.newaxis,:]
return img
def infer(image_path):
tensor_img = read_image(image_path)
label = exe.run(inference_program, feed={feed_target_names[0]: tensor_img}, fetch_list=fetch_targets)
return np.argmax(label)
def eval_all():
eval_file_path = os.path.join(data_dir, eval_file)
total_count = 0
right_count = 0
with codecs.open(eval_file_path, encoding='utf-8') as flist:
lines = [line.strip() for line in flist]
t1 = time.time()
for line in lines:
total_count += 1
parts = line.strip().split()
result = infer(parts[0])
if str(result) == parts[1]:
right_count += 1
period = time.time() - t1
print("total eval count:{0} cost time:{1} predict accuracy:{2}".format(total_count, "%2.2f sec" % period, right_count / total_count))
def showOnePic():
pic_file_path_list = os.path.join(data_dir, eval_file)
df=pd.read_csv(pic_file_path_list, sep='\t', header=None)
# 子图1
random_idx = np.random.randint(0,df.shape[0])
pic_file_path = df[0][random_idx]
img = Image.open(pic_file_path)
true_label = df[1][random_idx]
pred_label = infer(pic_file_path)
plt.subplot(221)
plt.imshow(img)
plt.title('True Label:{}\n Predict Label:{}'.format(true_label,pred_label))
plt.axis('off')
# 子图2
random_idx = np.random.randint(0,df.shape[0])
pic_file_path = df[0][random_idx]
img = Image.open(pic_file_path)
true_label = df[1][random_idx]
pred_label = infer(pic_file_path)
plt.subplot(222)
plt.imshow(img)
plt.title('True Label:{}\n Predict Label:{}'.format(true_label,pred_label))
plt.axis('off')
# 子图3
random_idx = np.random.randint(0,df.shape[0])
pic_file_path = df[0][random_idx]
img = Image.open(pic_file_path)
true_label = df[1][random_idx]
pred_label = infer(pic_file_path)
plt.subplot(223)
plt.imshow(img)
plt.title('True Label:{}\n Predict Label:{}'.format(true_label,pred_label))
plt.axis('off')
# 子图4
random_idx = np.random.randint(0,df.shape[0])
pic_file_path = df[0][random_idx]
img = Image.open(pic_file_path)
true_label = df[1][random_idx]
pred_label = infer(pic_file_path)
plt.subplot(224)
plt.imshow(img)
plt.title('True Label:{}\n Predict Label:{}'.format(true_label,pred_label))
plt.axis('off')
plt.tight_layout()
plt.show()
if __name__ == '__main__':
eval_all()
showOnePic()
| 0.263884 | 0.650065 |
<a href="https://colab.research.google.com/github/rubyvanrooyen/radio-astronomy-for-beginners/blob/master/FFTconcepts/Fourier_Transform_in_Practice.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# The Fourier Transform in Python
```
import numpy as np
import matplotlib.pylab as plt
```
To understand how the Fourier Transform extract frequency components from a signal, we will create a function which we will Fourier transform.
We will construct a simple signal by adding together two cosine functions with different periods and amplitudes. You can play with this later and create your own function.
```
# create an array of x-axis values, from 0 to 1000, with step size of 1
delta_n = 1.0
n_array = np.arange(0, 1000., delta_n)
# create two cos functions with specified periods and amplitudes
P1 = 100.
A1 = 1.0
fn1 = A1*np.cos(2.*np.pi*n_array/P1)
P2 = 50.
A2 = 0.5
fn2 = A2*np.cos(2.*np.pi*n_array/P2)
# add the functions to form our array x to Fourier transform
x_array = fn1 + fn2
# print the periods and frequencies of the two components of our x array
print('Periods: ', P1, ' ', P2)
print('Frequencies: ', 1./P1, ' ', 1./P2)
# plot our contructed (x array) signals
plt.figure(facecolor='white')
plt.plot(n_array, x_array)
plt.xlabel('time')
plt.ylabel('f(t)')
plt.title('Contructed signal showing two frequency components')
plt.show()
```
## Discrete Fourier Transform (DFT)
Now we want to take the Fourier transform of our x array.
Lets remind ourselves of the definition of the Discrete Fourier Transform:
$$X(k) = \sum_{n=0}^{N-1} x(n) e^{-i 2 \pi n \frac{k}{N} }$$
where:
* $x(n)$ is the $n$th sample for the time-domain function (the DFT input).
* $N$ is the total number of samples.
* $X(k)$ is the output of the DFT for values of $k$ ranging from $-(N/2-1)$ to $N/2$.
* The integer values k correspond to frequencies $k/N$.
```
N = len(n_array)
k_array = np.arange(-(N/2.0-1.0), N/2.0, 1.0)
X = np.zeros(len(k_array), dtype=np.complex)
# iterate over the fourier-space variable k
for k_indx, k in enumerate(k_array):
# iterate over the original-space variable n
for n_indx, n in enumerate(n_array):
arg = x_array[n_indx]*np.exp(-1.j*2.0*np.pi*k*n/N)
X[k_indx] = X[k_indx] + arg
# the frequency components of the FT are complex values
# create plot
f, ax = plt.subplots(nrows=1,ncols=2,
figsize=[13,3],
facecolor='white')
ax[0].plot(k_array/N, X.real,'o-')
ax[0].set_xlabel('Frequency')
ax[0].set_ylabel('Real')
ax[0].set_title('Real part of component complex values')
ax[1].plot(k_array/N, X.imag,'o-')
ax[1].set_xlabel('Frequency')
ax[1].set_ylabel('Imag')
ax[1].set_title('Imaginary part of complex components')
plt.show()
```
The frequency components returned by the Fourier Transform are complex numbers.
Because we constructed the signal we are deconstructing, we know that the signal's frequencies are all real valued, thus the imaginary components of the FT should be very small in value.
Lets take a closer look at the real plot on the left
```
plt.figure(facecolor='white')
plt.stem(k_array/N, X.real, use_line_collection=True)
plt.xlabel('Frequency')
plt.ylabel('Amplitude')
plt.xlim(0, 0.05)
plt.ylim(-10, 510)
plt.show()
```
So we are seeing the Fourier Transform components of the two cos functions comprising our signal, at the frequencies we set them to: f1 and f2.
Some questions to think about:
* Why are the amplitudes different to the amplitudes A1 and A2 that we used to create the function?
* Why are there four spikes in the original unzoomed Fourier transform plot?
```
```
|
github_jupyter
|
import numpy as np
import matplotlib.pylab as plt
# create an array of x-axis values, from 0 to 1000, with step size of 1
delta_n = 1.0
n_array = np.arange(0, 1000., delta_n)
# create two cos functions with specified periods and amplitudes
P1 = 100.
A1 = 1.0
fn1 = A1*np.cos(2.*np.pi*n_array/P1)
P2 = 50.
A2 = 0.5
fn2 = A2*np.cos(2.*np.pi*n_array/P2)
# add the functions to form our array x to Fourier transform
x_array = fn1 + fn2
# print the periods and frequencies of the two components of our x array
print('Periods: ', P1, ' ', P2)
print('Frequencies: ', 1./P1, ' ', 1./P2)
# plot our contructed (x array) signals
plt.figure(facecolor='white')
plt.plot(n_array, x_array)
plt.xlabel('time')
plt.ylabel('f(t)')
plt.title('Contructed signal showing two frequency components')
plt.show()
N = len(n_array)
k_array = np.arange(-(N/2.0-1.0), N/2.0, 1.0)
X = np.zeros(len(k_array), dtype=np.complex)
# iterate over the fourier-space variable k
for k_indx, k in enumerate(k_array):
# iterate over the original-space variable n
for n_indx, n in enumerate(n_array):
arg = x_array[n_indx]*np.exp(-1.j*2.0*np.pi*k*n/N)
X[k_indx] = X[k_indx] + arg
# the frequency components of the FT are complex values
# create plot
f, ax = plt.subplots(nrows=1,ncols=2,
figsize=[13,3],
facecolor='white')
ax[0].plot(k_array/N, X.real,'o-')
ax[0].set_xlabel('Frequency')
ax[0].set_ylabel('Real')
ax[0].set_title('Real part of component complex values')
ax[1].plot(k_array/N, X.imag,'o-')
ax[1].set_xlabel('Frequency')
ax[1].set_ylabel('Imag')
ax[1].set_title('Imaginary part of complex components')
plt.show()
plt.figure(facecolor='white')
plt.stem(k_array/N, X.real, use_line_collection=True)
plt.xlabel('Frequency')
plt.ylabel('Amplitude')
plt.xlim(0, 0.05)
plt.ylim(-10, 510)
plt.show()
| 0.385143 | 0.990301 |
```
%matplotlib inline
from tabula import read_pdf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def extract_data():
data_columns = ['Campus',
'Name',
'Job Title',
'FTE',
'Annual Base Pay']
df_read = read_pdf('data/usnh_salary_book_2018.pdf',
pages='all',
pandas_options={'header': None})
df_read.columns = data_columns
print('Data dimension:', df_read.shape)
df_read.to_csv('data/usnh_salary_book_2018_extracted.csv', index=False)
return df_read
def salaries_individuals(roster):
roster_joined = '|'.join(roster).lower()
salaries = df.loc[df['Name'].str.lower().str.contains(roster_joined)].sort_values(by='Annual Base Pay', ascending=False)
display(salaries)
return salaries
```
Read data:
```
# df = extract_data()
df = pd.read_csv('data/usnh_salary_book_2018_extracted.csv')
display(df)
df.info()
```
Do some **preprocessing**!
```
df['Annual Base Pay'] = df['Annual Base Pay'].apply(lambda x: x.lstrip('$').replace(',', ''))
df['Annual Base Pay'] = df['Annual Base Pay'].astype(float)
```
The most frequent job title:
```
df.groupby(by='Job Title').count().sort_values(['Campus'], ascending=False)
plt.figure()
df.groupby(by='Job Title').count()['Campus'].plot(kind='pie')
plt.show()
```
The **highest salary** among **the New Hampshire universities**:
```
max_salary = df['Annual Base Pay'].max()
max_salary_idx = df['Annual Base Pay'].idxmax()
display(df.iloc[max_salary_idx])
```
The top 20 highest and lowest salaries:
```
salaries_sorted = df.sort_values(by=['Annual Base Pay'], ascending=False)
highest_salaries = salaries_sorted.iloc[0:20]
lowest_salaries = salaries_sorted.iloc[-20:]
print('Highest salaries:')
display(highest_salaries)
print('Lowest salaries:')
display(lowest_salaries)
```
Some stats
```
print('Average Salary:')
display(df['Annual Base Pay'].mean())
print('Mode:')
display(df['Annual Base Pay'].mode())
print('Median:')
display(df['Annual Base Pay'].median())
```
-------
Top 20 and bottom 20 Professors' salaries:
```
prof_salaries = df.loc[df['Job Title'].str.lower().str.contains('professor')].sort_values(by='Annual Base Pay', ascending=False)
prof_top20 = prof_salaries.iloc[0:20].reset_index()
prof_bottom20 = prof_salaries.iloc[-20:].reset_index()
display(prof_top20)
display(prof_bottom20)
cs_names = ['Hatcher', 'Ruml',
'Bartos', 'Petrik', 'Varki', 'Charpentier',
'Dietz', 'Begum', 'Xu, Dongpeng' 'Weiner, James', 'Valcourt, Scott',
'Narayan', 'Magnusson', 'Hausner', 'Graf, Ken', 'Gildersleeve',
'Coleman, Betsy', 'Bochert', 'Plumlee', 'Lemon',
'Kibler', 'Kitterman', 'Desmarais']
cs_salaries = salaries_individuals(cs_names)
oiss_names = ['Webber, Elizabeth', 'Chiarantona']
oiss_salaries = salaries_individuals(oiss_names)
temp_names = ['Lyon, Mark', 'Macmanes']
temp_salaries = salaries_individuals(temp_names)
```
--------
Find the name you're looking for:
```
desired = salaries_individuals(['kun'])
```
|
github_jupyter
|
%matplotlib inline
from tabula import read_pdf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def extract_data():
data_columns = ['Campus',
'Name',
'Job Title',
'FTE',
'Annual Base Pay']
df_read = read_pdf('data/usnh_salary_book_2018.pdf',
pages='all',
pandas_options={'header': None})
df_read.columns = data_columns
print('Data dimension:', df_read.shape)
df_read.to_csv('data/usnh_salary_book_2018_extracted.csv', index=False)
return df_read
def salaries_individuals(roster):
roster_joined = '|'.join(roster).lower()
salaries = df.loc[df['Name'].str.lower().str.contains(roster_joined)].sort_values(by='Annual Base Pay', ascending=False)
display(salaries)
return salaries
# df = extract_data()
df = pd.read_csv('data/usnh_salary_book_2018_extracted.csv')
display(df)
df.info()
df['Annual Base Pay'] = df['Annual Base Pay'].apply(lambda x: x.lstrip('$').replace(',', ''))
df['Annual Base Pay'] = df['Annual Base Pay'].astype(float)
df.groupby(by='Job Title').count().sort_values(['Campus'], ascending=False)
plt.figure()
df.groupby(by='Job Title').count()['Campus'].plot(kind='pie')
plt.show()
max_salary = df['Annual Base Pay'].max()
max_salary_idx = df['Annual Base Pay'].idxmax()
display(df.iloc[max_salary_idx])
salaries_sorted = df.sort_values(by=['Annual Base Pay'], ascending=False)
highest_salaries = salaries_sorted.iloc[0:20]
lowest_salaries = salaries_sorted.iloc[-20:]
print('Highest salaries:')
display(highest_salaries)
print('Lowest salaries:')
display(lowest_salaries)
print('Average Salary:')
display(df['Annual Base Pay'].mean())
print('Mode:')
display(df['Annual Base Pay'].mode())
print('Median:')
display(df['Annual Base Pay'].median())
prof_salaries = df.loc[df['Job Title'].str.lower().str.contains('professor')].sort_values(by='Annual Base Pay', ascending=False)
prof_top20 = prof_salaries.iloc[0:20].reset_index()
prof_bottom20 = prof_salaries.iloc[-20:].reset_index()
display(prof_top20)
display(prof_bottom20)
cs_names = ['Hatcher', 'Ruml',
'Bartos', 'Petrik', 'Varki', 'Charpentier',
'Dietz', 'Begum', 'Xu, Dongpeng' 'Weiner, James', 'Valcourt, Scott',
'Narayan', 'Magnusson', 'Hausner', 'Graf, Ken', 'Gildersleeve',
'Coleman, Betsy', 'Bochert', 'Plumlee', 'Lemon',
'Kibler', 'Kitterman', 'Desmarais']
cs_salaries = salaries_individuals(cs_names)
oiss_names = ['Webber, Elizabeth', 'Chiarantona']
oiss_salaries = salaries_individuals(oiss_names)
temp_names = ['Lyon, Mark', 'Macmanes']
temp_salaries = salaries_individuals(temp_names)
desired = salaries_individuals(['kun'])
| 0.274838 | 0.783616 |
#### Importing the relevant libraries
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import seaborn as sns
# We can override the default matplotlib styles with those of Seaborn
sns.set()## Importing the relevant libraries
# Load the data from a .csv
raw_ratings_data = pd.read_csv(os.path.join(os.path.pardir,'data','raw','ratings.csv'))
raw_movies_data = pd.read_csv(os.path.join(os.path.pardir,'data','raw','movies.csv'))
raw_ratings_data.head(5)
raw_movies_data.head()
```
##### Since the movieId columns are the same we can merge these datasets on this column.
```
df = pd.merge(raw_ratings_data, raw_movies_data, on='movieId')
df.head()
```
###### Brief description of the dataset
```
df.describe()
df.info()
```
## Lets inspect the data
> Let’s now create a dataframe with the average rating for each movie and the number of ratings. We are going to use these ratings to calculate the correlation between the movies later. Correlation is a statistical measure that indicates the extent to which two or more variables fluctuate together. Movies that have a high correlation coefficient are the movies that are most similar to each other. In our case we shall use the Pearson correlation coefficient. This number will lie between -1 and 1. 1 indicates a positive linear correlation while -1 indicates a negative correlation. 0 indicates no linear correlation. Therefore movies with a zero correlation are not similar at all. In order to create this dataframe we use pandas groupby functionality. We group the dataset by the title column and compute its mean to obtain the average rating for each movie.
```
ratings_df = pd.DataFrame(df.groupby('title')['rating'].mean())
ratings_df.head()
```
>Next we would like to see the number of ratings for each movie. We do this by creating a `number_of_ratings` column. This is important so that we can see the relationship between the average rating of a movie and the number of ratings the movie got. It is very possible that a 5 star movie was rated by just one person. It is therefore statistically incorrect to classify that movie has a 5 star movie. We will therefore need to set a threshold for the minimum number of ratings as we build the recommender system.
```
ratings_df['number_of_ratings'] = df.groupby('title')['rating'].count()
ratings_df.head()
```
##### Plot histogram
```
ratings_df['rating'].hist(bins=50);
# We can see that most of the movies are rated between 2.5 and 4
ratings_df['genres'] = df.groupby('title')['rating'].count()
ratings_df['genres'].hist(bins=50);
ratings_df['number_of_ratings'].hist(bins=60);
# it is clear that most movies have few ratings. Movies with most ratings are those that are most famous.
# Let’s now check the relationship between the rating of a movie and the number of ratings.
sns.jointplot(x='rating', y='number_of_ratings', data=ratings_df);
```
> From the diagram we can see that their is a positive relationship between the average rating of a movie and the number of ratings. The graph indicates that the more the ratings a movie gets the higher the average rating it gets. This is important to note especially when choosing the threshold for the number of ratings per movie.
***
> Let’s now move on swiftly and create a simple item based recommender system. In order to do this we need to convert our dataset into a matrix with the movie titles as the columns, the user_id as the index and the ratings as the values. By doing this we shall get a dataframe with the columns as the movie titles and the rows as the user ids. Each column represents all the ratings of a movie by all users. The rating appear as NAN where a user didn't rate a certain movie. We shall use this matrix to compute the correlation between the ratings of a single movie and the rest of the movies in the matrix. We use pandas pivot_table utility to create the movie matrix.
```
movie_matrix = df.pivot_table(index='userId', columns='title', values='rating')
movie_matrix
```
> Next let’s look at the most rated movies and choose two of them to work with in this simple recommender system. We use pandas sort_values utility and set ascending to false in order to arrange the movies from the most rated.
```
ratings_df.sort_values('number_of_ratings', ascending=False).head(10)
```
> Let’s assume that a user has watched Air Force One (1997) and Contact (1997). We would like like to recommend movies to this user based on this watching history. The goal is to look for movies that are similar to Contact (1997) and Air Force One (1997 which we shall recommend to this user. We can achieve this by computing the correlation between these two movies’ ratings and the ratings of the rest of the movies in the dataset. The first step is to create a dataframe with the ratings of these movies from our movie_matrix.
```
AFO_user_rating = movie_matrix['Air Force One (1997)']
contact_user_rating = movie_matrix['Contact (1997)']
```
> In order to compute the correlation between two dataframes we use pandas corwith functionality. Corrwith computes the pairwise correlation of rows or columns of two dataframe objects. Let's use this functionality to get the correlation between each movie's rating and the ratings of the Air Force One movie.
```
similar_to_air_force_one=movie_matrix.corrwith(AFO_user_rating)
```
>We can see that the correlation between Air Force One movie and Til There Was You (1997) is 0.867. This indicates a very strong similarity between these two movies.
```
similar_to_air_force_one.head()
```
> Let’s move on and compute the correlation between Contact (1997) ratings and the rest of the movies ratings. The procedure is the same as the one used above.
```
similar_to_contact = movie_matrix.corrwith(contact_user_rating)
```
>We realize from the computation that there is a very strong correlation (of 0.904) between Contact (1997) and Til There Was You (1997).
similar_to_contact.head()
```
similar_to_contact.head()
```
> As noticed earlier our matrix had very many missing values since not all the movies were rated by all the users. We therefore drop those null values and transform correlation results into dataframes to make the results look more appealing.
```
# similar_to_contact
corr_contact = pd.DataFrame(similar_to_contact, columns=['Correlation'])
corr_contact.dropna(inplace=True)
corr_contact.head()
# similar_to_contact
corr_AFO = pd.DataFrame(similar_to_air_force_one, columns=['correlation'])
corr_AFO.dropna(inplace=True)
corr_AFO.head()
```
> These two dataframes above show us the movies that are most similar to Contact (1997) and Air Force One (1997) movies respectively. However we have a challenge in that some of the movies have very few ratings and may end up being recommended simply because one or two people gave them a 5 star rating. We can fix this by setting a threshold for the number of ratings. From the histogram earlier we saw a sharp decline in number of ratings from 100. We shall therefore set this as the threshold, however this is a number you can play around with until you get a suitable option. In order to do this we need to join the two dataframes with the number_of_ratings column in the ratings dataframe.
```
corr_AFO = corr_AFO.join(ratings_df['number_of_ratings'])
corr_AFO .head()
corr_contact = corr_contact.join(ratings_df['number_of_ratings'])
corr_contact.head()
```
> We shall now obtain the movies that are most similar to Air Force One (1997) by limiting them to movies that have at least 100 reviews. We then sort them by the correlation column and view the first 10.
```
corr_AFO[corr_AFO['number_of_ratings'] > 100].sort_values(by='correlation', ascending=False).head(10)
```
> We notice that Air Force One (1997) has a high correlation with Clear and Present Danger (1994), with a correlation of 0.69883. Clearly by changing the threshold for the number of reviews we get different results from the previous way of doing it. Limiting the number of rating gives us better results and we can confidently recommend the above movies to someone who has watched Air Force One (1997).
Now let’s do the same for Contact (1997) movie and see the movies that are most correlated to it.
```
corr_contact[corr_contact['number_of_ratings'] > 100].sort_values(by='Correlation', ascending=False).head(10)
```
> The most similar movie to Contact (1997) is Sleepless in Seattle (1993) with a correlation coefficient of 0.689602 with 106 ratings. So if somebody liked Contact (1997) we can recommend the above movies to them.
> Obviously this is a very simple way of building recommender system and is no where close to industry standards.
How to improve the recommendation system
This system can be improved by building a Memory-Based Collaborative Filtering based system. In this case we’d divide the data into a training set and a test set. We’d then use techniques such as cosine similarity to compute the similarity between the movies. An alternative is to build a Model-based Collaborative Filtering system. This is based on matrix factorization. Matrix factorization is good at dealing with scalability and sparsity than the former. You can then evaluate your model using techniques such as Root Mean Squared Error(RMSE).
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import seaborn as sns
# We can override the default matplotlib styles with those of Seaborn
sns.set()## Importing the relevant libraries
# Load the data from a .csv
raw_ratings_data = pd.read_csv(os.path.join(os.path.pardir,'data','raw','ratings.csv'))
raw_movies_data = pd.read_csv(os.path.join(os.path.pardir,'data','raw','movies.csv'))
raw_ratings_data.head(5)
raw_movies_data.head()
df = pd.merge(raw_ratings_data, raw_movies_data, on='movieId')
df.head()
df.describe()
df.info()
ratings_df = pd.DataFrame(df.groupby('title')['rating'].mean())
ratings_df.head()
ratings_df['number_of_ratings'] = df.groupby('title')['rating'].count()
ratings_df.head()
ratings_df['rating'].hist(bins=50);
# We can see that most of the movies are rated between 2.5 and 4
ratings_df['genres'] = df.groupby('title')['rating'].count()
ratings_df['genres'].hist(bins=50);
ratings_df['number_of_ratings'].hist(bins=60);
# it is clear that most movies have few ratings. Movies with most ratings are those that are most famous.
# Let’s now check the relationship between the rating of a movie and the number of ratings.
sns.jointplot(x='rating', y='number_of_ratings', data=ratings_df);
movie_matrix = df.pivot_table(index='userId', columns='title', values='rating')
movie_matrix
ratings_df.sort_values('number_of_ratings', ascending=False).head(10)
AFO_user_rating = movie_matrix['Air Force One (1997)']
contact_user_rating = movie_matrix['Contact (1997)']
similar_to_air_force_one=movie_matrix.corrwith(AFO_user_rating)
similar_to_air_force_one.head()
similar_to_contact = movie_matrix.corrwith(contact_user_rating)
similar_to_contact.head()
# similar_to_contact
corr_contact = pd.DataFrame(similar_to_contact, columns=['Correlation'])
corr_contact.dropna(inplace=True)
corr_contact.head()
# similar_to_contact
corr_AFO = pd.DataFrame(similar_to_air_force_one, columns=['correlation'])
corr_AFO.dropna(inplace=True)
corr_AFO.head()
corr_AFO = corr_AFO.join(ratings_df['number_of_ratings'])
corr_AFO .head()
corr_contact = corr_contact.join(ratings_df['number_of_ratings'])
corr_contact.head()
corr_AFO[corr_AFO['number_of_ratings'] > 100].sort_values(by='correlation', ascending=False).head(10)
corr_contact[corr_contact['number_of_ratings'] > 100].sort_values(by='Correlation', ascending=False).head(10)
| 0.512205 | 0.927953 |
```
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV, train_test_split, cross_val_score
from sklearn.preprocessing import MinMaxScaler
from sklearn.datasets import load_breast_cancer
```
# PCA - Principal Component Analysis
When dealing with text we looked at the truncated SVD algorithm that could reduce the massive datasets generated from encoding text down to a subset of features.
PCA is a similar concept, we can take high dimension feature sets and reduce them down to a subset of features used for prediction. PCA is a very common method for dimensionality reduction.
## PCA Concepts
PCA reduces dimensionality by breaking down the variance in the data into its "principal components", then keeping only those components that do the best job in explaining said variance. We can understand this well with an example, in 2D. We'll create something that looks like an example from simple linear regression type of data - we have a bunch of points, each point is located by its X and Y values.
```
#make some random numbers
plt.rcParams['figure.figsize'] = 12,6
fig, ax = plt.subplots(1, 2)
X = np.dot(np.random.rand(2, 2), np.random.randn(2, 200)).T
sns.regplot(data=X, x=X[:,0], y=X[:,1], ci=0, ax=ax[0])
ax[0].set_ylabel('Y')
ax[0].set_xlabel('X')
tmpPCA = PCA(2)
tmpData = tmpPCA.fit_transform(X)
sns.regplot(data=tmpData, x=tmpData[:,0], y=tmpData[:,1], ci=0, ax=ax[1])
ax[1].set_ylabel('PC 2')
ax[1].set_xlabel('PC 1')
plt.show()
```
## Principal Components
In normal analysis, each of these points is defined by their X and Y values:
<ul>
<li> X - how far left and right the point is.
<li> Y - how far up and down the point is.
</ul>
Together these points explain all of the position data of the points.
Once we look at PCA, we can also think of these points being defined by two components:
<ul>
<li> Along the regression line. The majority of the variance in Y is explained by the position along this line.
<li> Perpindicular to the regression line. Some smaller part of the variance in Y is explained by how "far off" it is from the regession line.
</ul>
In essence, we can explain the position of our points mostly by examining where it is along the regression line (component 1), along with a little info on how far off it is from that line. These two components can explain our data - "A" amount "up and down" the line, along with "B" amount "off the line". This also explains the position of the points, but does so with different values than X and Y.
If we look at the plot of the PCA components, PC1 (plotted as X) has a wide range, or lots of variance. PC2 (plotted as Y) has a small range, or a small amount of variance.
#### Animated Example
See: https://setosa.io/ev/principal-component-analysis/
### PCA and Eigenvectors
The components generated by the PCA are called eigenvectors. We don't need to worry about much of the math, but this PCA can be calculated by hand with some linear math. We can skip that, computers are good at math.
## PCA and Dimensionality Reduction
Once we've established the components, reducing the dimensions of our feature set is simple - just reduce the components that matter least to 0. In our example, we'd ignore the "off the line" component that is responsible for only a little bit of the position of our points, and keep the "up the line" component that explains the majority of the position of our points.
In the XY system, both X and Y are very important in specifying where a point is, X somewhat more important than Y. In our component system, the "up the line" component provides the majority of the information on our points, with the "off the line" component only adding a little bit of info. This is the key to the dimensionality reduction - if we feature selected away the Y value, we would lose substantial information on the location of the points. If we PCA-away the "off the line" component, we only lose a small amount of information! So we can describe this data "pretty well" with only 1/2 the number of features if we describe the data with the components over the original features. When dealing with large numbers of features, this can allow us to reduce them down to a much smaller number of components, without missing out on too much information describing the real data.
The true benefit of PCA is if there are a lot of features. We can do something like the example here to grab the "best" components, drop the rest, and have a smaller feature set with a comparable level of accuracy.
#### Colinearity and Multi-colinearity
One of the other benefits of PCA is that it reduces colinearity between features. The components that PCA generates are orthogonal of each other - the colinearity is reduced to effectively 0.
## Dimension Reduction in Multiple Dimensions
This 2D example is simple to picture. The same concept applies when we have data with lots of dimensions. We can break the data down into components, remove the least impactful, and end up with a feature set that captures most of the variance in our target with fewer inputs.
### Example with Real Data
This dataset is one of the sklearn samples, containing measurements from people with and without breast cancer. The classification of cancer/no cancer is the target.
```
def sklearn_to_df(sklearn_dataset):
df = pd.DataFrame(sklearn_dataset.data, columns=sklearn_dataset.feature_names)
df['target'] = pd.Series(sklearn_dataset.target)
return df
df = sklearn_to_df(load_breast_cancer())
y1 = df["target"]
X1 = df.drop(columns="target")
df.head()
```
#### Pre PCA Test
We can run a test to approximate the accuracy without doing PCA. We don't want accuracy to drop too much after the PCA process. This is our baseline.
```
pre_model = LogisticRegression()
pre_scale = MinMaxScaler()
pre_pipe = Pipeline([("scale", pre_scale), ("model", pre_model)])
print("Estimated Initial Accuracy:", np.mean(cross_val_score(pre_pipe, X1, y1)))
```
### Original Dimensionality and Correlation
One classfication target, along with 30 features. We can look for correlation between those features.
```
# Check Original Correlation
plt.rcParams['figure.figsize'] = 15,5
sns.heatmap(X1.corr(), cmap="BuPu")
# Calculate VIF for Multicolinearity
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(X1.values, i) for i in range(X1.shape[1])]
vif["features"] = X1.columns
vif.sort_values("VIF Factor", ascending=False).head(10)
```
#### Colinearity Results
Looks like there is a lot of correlation going on. The heatmap shows many values that are pretty correlated, and the VIF shows some really high values. Recall, values for a VIF over about 10 are really large.
For the model, we'll be sure to use a logistic regression, that is very impacted by the colinearity.
Feel free to play with the number of components and observe results.
```
#Check accuracy
X_train1, X_test1, y_train1, y_test1 = train_test_split(X1, y1)
can_pca = PCA()
can_model = LogisticRegression()
can_steps = [
("scale", MinMaxScaler()),
("pca", can_pca),
("can_model", can_model)
]
can_pipe = Pipeline(steps=can_steps)
can_params = {
"pca__n_components":[15]
}
clf1 = GridSearchCV(estimator=can_pipe, param_grid=can_params, cv=5, n_jobs=-1)
clf1.fit(X_train1, y_train1.ravel())
print(clf1.score(X_test1, y_test1))
best1 = clf1.best_estimator_
print(best1)
```
#### Results - We Have Accuracy!
Accuracy looks pretty good, even though we've reduced the number of features. How is the information on our target (the variance) distributed amongst our components?
```
# Get PCA Info
comps1 = best1.named_steps['pca'].components_
ev1 = best1.named_steps['pca'].explained_variance_ratio_
plt.rcParams['figure.figsize'] = 6,6
plt.plot(np.cumsum(ev1))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
```
#### What is in the PCA Components?
We can also reconstruct the importance of the contributions of the different features to the components.
```
labels = []
for i in range(len(comps1)):
label = "PC-"+str(i)
labels.append(label)
PCA1_res_comps = pd.DataFrame(comps1,columns=X1.columns, index = labels)
PCA1_res_comps.head()
```
#### Results of PCA
PCA allows us to reduce down the original 30 feature set to a much smaller number, while still making accurate predictions. In this case, it looks like we can get about 90% of the explained varaiance in the data by using around 6 or so components. Yay, that's cool!
### PCA and Feature Selection
PCA is not a feature selection technique. PCA does do a similar thing to feature selection in reducing the size of our feature set that goes into a model, but it is technically different.
Feature selection removes features. PCA removes components, that are created from features, but that are not, themselves, features. In PCA, the features are being transformed for the components to be created, and each component includes portions of multiple features - for example, in the scatter plot above, both the "up the line" and "off the line" components contain parts of the X and Y features. If we drop the "off the line" feature when doing PCA we aren't really eliminating any features - we still need X and Y to calculate each of our components. In the breast cancer example, each of those features still contributes to the components, but the actual predictors are far reduced.
## Working Example
Predict if people have diabetes (Outcome) using PCA to help.
```
df = pd.read_csv("data/diabetes.csv")
df.head()
#Get data
```
#### Plot Component Importance
We can plot the effectiveness with different numbers of components.
```
# Plot the variance by component
```
## PCA with Images - Big Dimensions!
One common example of something with a large feature set is images - even our simple set of handwritten numbers had 784 features for each digit. Generating models from all 70,000 of those simple images could take forever, and those are about the most simple images we can imagine!
Reducing the dimensions of very large images can be highly beneficial, especially if we can keep the useful bits that we need to do identification.
### Faces, PCA, and You
This dataset is a more complex set of images than the digits we used previously. It is a set of a bunch of faces of past world leaders, our goal being to make a model that will recognize each person from their picture.
```
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=60)
print(faces.target_names)
print(faces.images.shape)
```
### Starting Dimensions and PCA Dimensions
We start with ~1350 images, each 62 x 47 pixels, color depth of 1 - resulting in a feature set that is around 3000 columns wide.
We can fit the data to a PCA transformation, and chop the feature set down to a much smaller number of components.
```
# Generate PCA and inversed face-sets
pca150 = PCA(150).fit(faces.data)
components150 = pca150.transform(faces.data)
projected150 = pca150.inverse_transform(components150)
pca15 = PCA(15).fit(faces.data)
components15 = pca15.transform(faces.data)
projected15 = pca15.inverse_transform(components15)
```
### Picture Some Pictures
We can look at what the pictures look like in their original state, and after the PCA process has reduced their dimensions by various amounts.
```
# Plot faces and PCA faces
fig, ax = plt.subplots(3, 12, figsize=(12, 6),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(12):
ax[0,i].imshow(faces.data[i].reshape(62, 47), cmap='bone')
ax[1,i].imshow(projected150[i].reshape(62, 47), cmap='bone')
ax[2,i].imshow(projected15[i].reshape(62, 47), cmap='bone')
ax[0, 0].set_ylabel('Original')
ax[1, 0].set_ylabel('150-dim')
ax[2, 0].set_ylabel('15-dim')
```
### Amount of Variance Captured in Components
We can look at our PCA'd data and see that while the images are much less clear and defined, they are pretty similar on the whole! We can probably still do a good job of IDing the people, even though we have roughly 1/20 (or 1/200) the number of features as we started with. Cool. Even with the 15 component set, the images are still somewhat able to be recognized.
The PCA allows us to call up the details on how much of the variance was captured in each component. The first few contain lots of the useful info, once we reach 20 components we have about ~75% or so of the original varaince.
```
plt.plot(np.cumsum(pca150.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
```
### Scree Plot and Number of Components
One question we're left with is how many components should we keep? This answer varies, common suggestions are enough to capture somewhere around 80% to 95% of the explained variance. These metrics are somewhat arbitrary - testing different numbers of components will likely make sense in many cases.
One method to choose the number of features is a scree plot. This is a plot that shows the contribution of each component. The scree plot shows the same information as the graph above, but formatted differently. The idea of a scree plot is to find the "elbow", or where the plot levels out. This flattening point is approximately where you should cut off the number of components - the idea being that you capture all the components that make a substantial difference, and let the ones that make a small difference go.
Personally, I think the cumulative plot above is easier to view, but scree plots are pretty common.
```
#Scree Plot
PC_values = np.arange(pca150.n_components_) + 1
plt.plot(PC_values, pca150.explained_variance_ratio_, 'o-', linewidth=2, color='blue')
plt.title('Scree Plot')
plt.xlabel('Principal Component')
plt.ylabel('Variance Explained')
plt.show()
```
### Predictions with PCA
We can try to make some predictions and see what the results are with PCA'd data. We'll use a multinomial HP to tell our regression to directly predict multiple classes with our friend the softmax.
```
#Get data
y = faces.target
X = faces.data
X_train, X_test, y_train, y_test = train_test_split(X, y)
#Model and grid search of components.
scaler = MinMaxScaler()
logistic = LogisticRegression(max_iter=10000, tol=0.1, multi_class="multinomial")
pca_dia = PCA()
pipe = Pipeline(steps=[("scaler", scaler), ("pca", pca_dia), ("logistic", logistic)])
param_grid = {
"pca__n_components": [130]
}
grid = GridSearchCV(pipe, param_grid, n_jobs=-1)
grid.fit(X_train, y_train.ravel())
print("Best parameter (CV score=%0.3f):" % grid.best_score_)
print(grid.best_params_)
print("Test Score:", grid.score(X_test, y_test))
```
## Kernel PCA
Similarly to support vector machines, we can use a kernel transformation to make PCA better suit data with non-linear relationships. The concept is the same as with the SVMs - we can provide a kernel that does a transformation, then the linear algebra of PCA can be executed on the transformed data.
The implementation is very simple - we replace PCA with KernelPCA, and provide the kernel we want to use.
We can see if a different kernel is better than the original... Try with a grid search of the different kernels other than linear. Also, for the polynomial kernel, try with multiple values in the grid search. Documentation is: https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.KernelPCA.html
```
# Use Kernel PCA
from sklearn.decomposition import KernelPCA
```
## Sparse PCA
Sparse PCA is another implementation of PCA that includes L1 regularization - resulting in some of the values being regularized down to 0. The end result of this is that you end up with a subset of the features being used to construct the components. The others are feature selected out just like Lasso rregression.
We can redo the table of component details from the previous breast cancer example.
```
from sklearn.decomposition import SparsePCA
sPCA = SparsePCA(15)
sparse = sPCA.fit_transform(X1)
comps3 = sPCA.components_
labels = []
for i in range(len(comps3)):
label = "PC-"+str(i)
labels.append(label)
PCA3_res_comps = pd.DataFrame(comps3, columns=X1.columns, index = labels)
PCA3_res_comps.head()
PCA3_res_comps.describe().T.sort_values("mean")
```
|
github_jupyter
|
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV, train_test_split, cross_val_score
from sklearn.preprocessing import MinMaxScaler
from sklearn.datasets import load_breast_cancer
#make some random numbers
plt.rcParams['figure.figsize'] = 12,6
fig, ax = plt.subplots(1, 2)
X = np.dot(np.random.rand(2, 2), np.random.randn(2, 200)).T
sns.regplot(data=X, x=X[:,0], y=X[:,1], ci=0, ax=ax[0])
ax[0].set_ylabel('Y')
ax[0].set_xlabel('X')
tmpPCA = PCA(2)
tmpData = tmpPCA.fit_transform(X)
sns.regplot(data=tmpData, x=tmpData[:,0], y=tmpData[:,1], ci=0, ax=ax[1])
ax[1].set_ylabel('PC 2')
ax[1].set_xlabel('PC 1')
plt.show()
def sklearn_to_df(sklearn_dataset):
df = pd.DataFrame(sklearn_dataset.data, columns=sklearn_dataset.feature_names)
df['target'] = pd.Series(sklearn_dataset.target)
return df
df = sklearn_to_df(load_breast_cancer())
y1 = df["target"]
X1 = df.drop(columns="target")
df.head()
pre_model = LogisticRegression()
pre_scale = MinMaxScaler()
pre_pipe = Pipeline([("scale", pre_scale), ("model", pre_model)])
print("Estimated Initial Accuracy:", np.mean(cross_val_score(pre_pipe, X1, y1)))
# Check Original Correlation
plt.rcParams['figure.figsize'] = 15,5
sns.heatmap(X1.corr(), cmap="BuPu")
# Calculate VIF for Multicolinearity
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(X1.values, i) for i in range(X1.shape[1])]
vif["features"] = X1.columns
vif.sort_values("VIF Factor", ascending=False).head(10)
#Check accuracy
X_train1, X_test1, y_train1, y_test1 = train_test_split(X1, y1)
can_pca = PCA()
can_model = LogisticRegression()
can_steps = [
("scale", MinMaxScaler()),
("pca", can_pca),
("can_model", can_model)
]
can_pipe = Pipeline(steps=can_steps)
can_params = {
"pca__n_components":[15]
}
clf1 = GridSearchCV(estimator=can_pipe, param_grid=can_params, cv=5, n_jobs=-1)
clf1.fit(X_train1, y_train1.ravel())
print(clf1.score(X_test1, y_test1))
best1 = clf1.best_estimator_
print(best1)
# Get PCA Info
comps1 = best1.named_steps['pca'].components_
ev1 = best1.named_steps['pca'].explained_variance_ratio_
plt.rcParams['figure.figsize'] = 6,6
plt.plot(np.cumsum(ev1))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
labels = []
for i in range(len(comps1)):
label = "PC-"+str(i)
labels.append(label)
PCA1_res_comps = pd.DataFrame(comps1,columns=X1.columns, index = labels)
PCA1_res_comps.head()
df = pd.read_csv("data/diabetes.csv")
df.head()
#Get data
# Plot the variance by component
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=60)
print(faces.target_names)
print(faces.images.shape)
# Generate PCA and inversed face-sets
pca150 = PCA(150).fit(faces.data)
components150 = pca150.transform(faces.data)
projected150 = pca150.inverse_transform(components150)
pca15 = PCA(15).fit(faces.data)
components15 = pca15.transform(faces.data)
projected15 = pca15.inverse_transform(components15)
# Plot faces and PCA faces
fig, ax = plt.subplots(3, 12, figsize=(12, 6),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(12):
ax[0,i].imshow(faces.data[i].reshape(62, 47), cmap='bone')
ax[1,i].imshow(projected150[i].reshape(62, 47), cmap='bone')
ax[2,i].imshow(projected15[i].reshape(62, 47), cmap='bone')
ax[0, 0].set_ylabel('Original')
ax[1, 0].set_ylabel('150-dim')
ax[2, 0].set_ylabel('15-dim')
plt.plot(np.cumsum(pca150.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
#Scree Plot
PC_values = np.arange(pca150.n_components_) + 1
plt.plot(PC_values, pca150.explained_variance_ratio_, 'o-', linewidth=2, color='blue')
plt.title('Scree Plot')
plt.xlabel('Principal Component')
plt.ylabel('Variance Explained')
plt.show()
#Get data
y = faces.target
X = faces.data
X_train, X_test, y_train, y_test = train_test_split(X, y)
#Model and grid search of components.
scaler = MinMaxScaler()
logistic = LogisticRegression(max_iter=10000, tol=0.1, multi_class="multinomial")
pca_dia = PCA()
pipe = Pipeline(steps=[("scaler", scaler), ("pca", pca_dia), ("logistic", logistic)])
param_grid = {
"pca__n_components": [130]
}
grid = GridSearchCV(pipe, param_grid, n_jobs=-1)
grid.fit(X_train, y_train.ravel())
print("Best parameter (CV score=%0.3f):" % grid.best_score_)
print(grid.best_params_)
print("Test Score:", grid.score(X_test, y_test))
# Use Kernel PCA
from sklearn.decomposition import KernelPCA
from sklearn.decomposition import SparsePCA
sPCA = SparsePCA(15)
sparse = sPCA.fit_transform(X1)
comps3 = sPCA.components_
labels = []
for i in range(len(comps3)):
label = "PC-"+str(i)
labels.append(label)
PCA3_res_comps = pd.DataFrame(comps3, columns=X1.columns, index = labels)
PCA3_res_comps.head()
PCA3_res_comps.describe().T.sort_values("mean")
| 0.761538 | 0.955277 |
<a href="https://colab.research.google.com/github/Phantom-Ren/PR_TH/blob/master/SVM.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<center>
# 模式识别·第二次作业·支持向量机(SVM)
#### 纪泽西 17375338
#### Last Modified:14th,March,2020
</center>
<table align="center">
<td align="center"><a target="_blank" href="https://colab.research.google.com/github/Phantom-Ren/PR_TH/blob/master/SVM.ipynb">
<img src="http://introtodeeplearning.com/images/colab/colab.png?v2.0" style="padding-bottom:5px;" /><br>Run in Google Colab</a></td>
</table>
## Part1: 导入库文件及数据集
#### 如需在其他环境运行需改变数据集所在路径
```
%tensorflow_version 2.x
import tensorflow as tf
import sklearn
import numpy as np
import matplotlib.pyplot as plt
import os
import scipy.io as sio
from sklearn import svm
path="/content/drive/My Drive/Pattern Recognition/Dataset"
os.chdir(path)
os.listdir(path)
```
## Part2:数据预处理
```
train_images=sio.loadmat("train_images.mat")
test_images=sio.loadmat("test_images.mat")
train_labels=sio.loadmat("train_labels.mat")
test_labels=sio.loadmat("test_labels.mat")
def trans(a):
a1=a.swapaxes(0,2)
a2=a1.swapaxes(1,2)
return a2
train_dataset_np=np.array(train_images.pop('train_images'))
train_dataset_np=trans(train_dataset_np)
train_labels_np=np.array(train_labels.pop('train_labels1'))
train_labels_np=train_labels_np.reshape(60000)
test_dataset_np=np.array(test_images.pop('test_images'))
test_dataset_np=trans(test_dataset_np)
test_labels_np=np.array(test_labels.pop('test_labels1'))
test_labels_np=test_labels_np.reshape(10000)
```
### 显示预处理后数据集格式及例举数据
```
print(train_dataset_np.shape,train_dataset_np.size,train_dataset_np.ndim)
print(train_labels_np.shape,train_labels_np.size,train_labels_np.ndim)
print(test_dataset_np.shape,test_dataset_np.size,test_dataset_np.ndim)
print(test_labels_np.shape,test_labels_np.size,test_labels_np.ndim)
for i in range(0,2):
plt.imshow(test_dataset_np[i,:,:])
plt.xlabel(test_labels_np[i])
plt.colorbar()
plt.show()
plt.imshow(train_dataset_np[i,:,:])
plt.xlabel(train_labels_np[i])
plt.colorbar()
plt.show()
```
### 将数据限幅至[-1,1]
```
train_dataset_svm=train_dataset_np.reshape([60000,784])
test_dataset_svm=test_dataset_np.reshape([10000,784])
from sklearn.preprocessing import MinMaxScaler
scaling = MinMaxScaler(feature_range=(-1, 1)).fit(train_dataset_svm)
train_dataset_svm = scaling.transform(train_dataset_svm)
test_dataset_svm = scaling.transform(test_dataset_svm)
print(train_dataset_svm.shape,train_dataset_svm.size,train_dataset_svm.ndim)
print(test_dataset_svm.shape,test_dataset_svm.size,test_dataset_svm.ndim)
```
### 再次看一看结果
```
plt.plot(train_dataset_svm[1,:])
plt.show()
plt.imshow(train_dataset_svm[1,:].reshape([28,28]))
plt.show()
```
## Part3:模型建立
### 使用SKlearn快速建立模型
```
clf = svm.SVC(max_iter=1500)
clf
```
#### 由于样本中元素相对较多,使用SVM方法计算量大,故将最大迭代次数限制到1500,以限制运行时间
### 模型训练
```
from time import *
begin_time=time()
cv_performance = sklearn.model_selection.cross_val_score(clf, train_dataset_svm,train_labels_np, cv=5)
test_performance = clf.fit(train_dataset_svm,train_labels_np).score(test_dataset_svm,test_labels_np)
print ('Cross-validation accuracy score: %0.3f, test accuracy score: %0.3f' % (np.mean(cv_performance),test_performance))
end_time=time()
final=end_time-begin_time
print('Time Usage:',final)
```
Cross-validation accuracy score: 0.977,
test accuracy score: 0.979
Time Usage: 3502.80228972435(58min)
#### 可见由于元素过多,svm优化速度较慢。
## Part4:建立预测模型
```
y_pred = clf.predict(test_dataset_svm)
```
### 显示对第一个样本的预测
```
print(y_pred[0],test_labels_np[0])
```
### 定义函数形象化预测
```
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array, true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = predictions_array
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} ({})".format( predicted_label,
true_label),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array, true_label[i]
plt.grid(False)
plt.xticks(range(10))
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = predictions_array
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
```
### 展现预测情况
```
# Plot the first X test images, their predicted labels, and the true labels.
# Color correct predictions in blue and incorrect predictions in red.
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, y_pred[i], test_labels_np, test_dataset_np)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, y_pred[i], test_labels_np)
plt.tight_layout()
plt.show()
```
|
github_jupyter
|
%tensorflow_version 2.x
import tensorflow as tf
import sklearn
import numpy as np
import matplotlib.pyplot as plt
import os
import scipy.io as sio
from sklearn import svm
path="/content/drive/My Drive/Pattern Recognition/Dataset"
os.chdir(path)
os.listdir(path)
train_images=sio.loadmat("train_images.mat")
test_images=sio.loadmat("test_images.mat")
train_labels=sio.loadmat("train_labels.mat")
test_labels=sio.loadmat("test_labels.mat")
def trans(a):
a1=a.swapaxes(0,2)
a2=a1.swapaxes(1,2)
return a2
train_dataset_np=np.array(train_images.pop('train_images'))
train_dataset_np=trans(train_dataset_np)
train_labels_np=np.array(train_labels.pop('train_labels1'))
train_labels_np=train_labels_np.reshape(60000)
test_dataset_np=np.array(test_images.pop('test_images'))
test_dataset_np=trans(test_dataset_np)
test_labels_np=np.array(test_labels.pop('test_labels1'))
test_labels_np=test_labels_np.reshape(10000)
print(train_dataset_np.shape,train_dataset_np.size,train_dataset_np.ndim)
print(train_labels_np.shape,train_labels_np.size,train_labels_np.ndim)
print(test_dataset_np.shape,test_dataset_np.size,test_dataset_np.ndim)
print(test_labels_np.shape,test_labels_np.size,test_labels_np.ndim)
for i in range(0,2):
plt.imshow(test_dataset_np[i,:,:])
plt.xlabel(test_labels_np[i])
plt.colorbar()
plt.show()
plt.imshow(train_dataset_np[i,:,:])
plt.xlabel(train_labels_np[i])
plt.colorbar()
plt.show()
train_dataset_svm=train_dataset_np.reshape([60000,784])
test_dataset_svm=test_dataset_np.reshape([10000,784])
from sklearn.preprocessing import MinMaxScaler
scaling = MinMaxScaler(feature_range=(-1, 1)).fit(train_dataset_svm)
train_dataset_svm = scaling.transform(train_dataset_svm)
test_dataset_svm = scaling.transform(test_dataset_svm)
print(train_dataset_svm.shape,train_dataset_svm.size,train_dataset_svm.ndim)
print(test_dataset_svm.shape,test_dataset_svm.size,test_dataset_svm.ndim)
plt.plot(train_dataset_svm[1,:])
plt.show()
plt.imshow(train_dataset_svm[1,:].reshape([28,28]))
plt.show()
clf = svm.SVC(max_iter=1500)
clf
from time import *
begin_time=time()
cv_performance = sklearn.model_selection.cross_val_score(clf, train_dataset_svm,train_labels_np, cv=5)
test_performance = clf.fit(train_dataset_svm,train_labels_np).score(test_dataset_svm,test_labels_np)
print ('Cross-validation accuracy score: %0.3f, test accuracy score: %0.3f' % (np.mean(cv_performance),test_performance))
end_time=time()
final=end_time-begin_time
print('Time Usage:',final)
y_pred = clf.predict(test_dataset_svm)
print(y_pred[0],test_labels_np[0])
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array, true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = predictions_array
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} ({})".format( predicted_label,
true_label),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array, true_label[i]
plt.grid(False)
plt.xticks(range(10))
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = predictions_array
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
# Plot the first X test images, their predicted labels, and the true labels.
# Color correct predictions in blue and incorrect predictions in red.
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, y_pred[i], test_labels_np, test_dataset_np)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, y_pred[i], test_labels_np)
plt.tight_layout()
plt.show()
| 0.759493 | 0.946151 |
```
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.mixture import GaussianMixture
from data import resample_nba_data as re
from data import clean_nba_data as cl
from data import clean_and_split_nba_data as clean
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import StandardScaler
import xgboost as xgb
from models import plot_validation_curve as vc
from models import eval_model as evm
from joblib import dump
import joblib
from yellowbrick.cluster import KElbowVisualizer
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
from sklearn.inspection import permutation_importance
from mlxtend.evaluate import feature_importance_permutation
from sklearn.inspection import plot_partial_dependence
df=pd.read_csv('../data/processed/Train_Stg1_Output.csv')
df.shape, df.columns
x_data, x_train, x_val, x_test, y_data , y_train, y_val, y_test = clean.clean_and_split_nba_data(df)
x_data.head()
x_train.head()
x_test.head()
x_val.head()
default_xg = xgb.XGBClassifier(random_state=8, verbosity=1,use_label_encoder=False,objective ='binary:logistic',eval_metric='auc')
evm.eval_model(default_xg,x_train,y_train,x_val,y_val)
evm.get_performance(default_xg, x_test, y_test, "Test", True)
feat_imp = default_xg.get_booster().get_score(importance_type="gain")
xgb.plot_importance(feat_imp, max_num_features=20)
feat_imp
r = permutation_importance(
default_xg, x_train, y_train,
n_repeats=30,
random_state=8
)
feature_cols=x_train.columns
for i in r.importances_mean.argsort()[::-1]:
print(f"{x_train.columns[i]}: {r.importances_mean[i]:.5f}")
feature_cols=x_train.columns
k=0
for i in r.importances_mean.argsort()[::-1]:
if k<=15:
feature_name=x_train.columns[i]
feature_index = feature_cols.get_loc(feature_name)
print('feature_name',feature_name,'feature_index',feature_index)
plot_partial_dependence(default_xg, x_train, features=[feature_index],target=y_train)
k=k+1
```
# Future Insights
Looking at these numbers give me a lot of future potential to tune the numbers further
- calculate the all rebound rates
- investigte the Turnovers a bit more
```
dump(default_xg, '../models/sp_wk3_Stg2_Final_model.joblib')
```
|
github_jupyter
|
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.mixture import GaussianMixture
from data import resample_nba_data as re
from data import clean_nba_data as cl
from data import clean_and_split_nba_data as clean
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import StandardScaler
import xgboost as xgb
from models import plot_validation_curve as vc
from models import eval_model as evm
from joblib import dump
import joblib
from yellowbrick.cluster import KElbowVisualizer
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
from sklearn.inspection import permutation_importance
from mlxtend.evaluate import feature_importance_permutation
from sklearn.inspection import plot_partial_dependence
df=pd.read_csv('../data/processed/Train_Stg1_Output.csv')
df.shape, df.columns
x_data, x_train, x_val, x_test, y_data , y_train, y_val, y_test = clean.clean_and_split_nba_data(df)
x_data.head()
x_train.head()
x_test.head()
x_val.head()
default_xg = xgb.XGBClassifier(random_state=8, verbosity=1,use_label_encoder=False,objective ='binary:logistic',eval_metric='auc')
evm.eval_model(default_xg,x_train,y_train,x_val,y_val)
evm.get_performance(default_xg, x_test, y_test, "Test", True)
feat_imp = default_xg.get_booster().get_score(importance_type="gain")
xgb.plot_importance(feat_imp, max_num_features=20)
feat_imp
r = permutation_importance(
default_xg, x_train, y_train,
n_repeats=30,
random_state=8
)
feature_cols=x_train.columns
for i in r.importances_mean.argsort()[::-1]:
print(f"{x_train.columns[i]}: {r.importances_mean[i]:.5f}")
feature_cols=x_train.columns
k=0
for i in r.importances_mean.argsort()[::-1]:
if k<=15:
feature_name=x_train.columns[i]
feature_index = feature_cols.get_loc(feature_name)
print('feature_name',feature_name,'feature_index',feature_index)
plot_partial_dependence(default_xg, x_train, features=[feature_index],target=y_train)
k=k+1
dump(default_xg, '../models/sp_wk3_Stg2_Final_model.joblib')
| 0.241668 | 0.330363 |
```
import azureml.core
from azureml.core import Workspace
from azureml.core.webservice import Webservice
from azureml.core.authentication import AzureCliAuthentication
import requests
import json
#Provide the Subscription ID of your existing Azure subscription
subscription_id = "..." # <- needs to be the subscription with the Quick-Starts resource group
#Provide values for the existing Resource Group
resource_group = "MLOps" # <- replace XXXXX with your unique identifier
#Provide the Workspace Name and Azure Region of the Azure Machine Learning Workspace
workspace_name = "MLOpsDemo" # <- replace XXXXX with your unique identifier
workspace_region = "westeurope" # <- region of your Quick-Starts resource group
#Provide the name of the webservice
webservice_name = "compliance-classifier-service" # <- the name used by Azure DevOps pipeline
webservice_url = "..." # <- the url created as a result of publication
webservice_key = "..." # <- the api key generated as a result of publication
# By using the exist_ok param, if the worskpace already exists you get a reference to the existing workspace
# allowing you to re-run this cell multiple times as desired (which is fairly common in notebooks).
ws = Workspace.create(
name = workspace_name,
subscription_id = subscription_id,
resource_group = resource_group,
location = workspace_region,
exist_ok = True)
ws.write_config()
print('Workspace configuration succeeded')
```
### Call the deployed model
Since telemetry is not yet activated, no information will be recorded as a result of this call.
**Note**: These calls are just used to demonstrate the telemetry functionality. We don't care here about the inputs and outputs of the deployed model.
```
# This is dummy data, just to test the call
test_data = [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 8, 2, 5, 6, 4, 3, 1, 34]]
headers = {'Content-Type':'application/json', 'Authorization':('Bearer '+ webservice_key)}
response = requests.post(webservice_url, json.dumps(test_data), headers=headers)
print('Predictions')
print(response.text)
```
### Activate telemetry
We are going to activate telemetry on the deployed model. Then we will make another call which will end up being logged by both Application Insights and data collection.
```
web_service = Webservice(ws, webservice_name)
web_service.update(enable_app_insights=True, collect_model_data=True)
```
Make a few calls that will be collected.
```
headers = {'Content-Type':'application/json', 'Authorization':('Bearer '+ webservice_key)}
response = requests.post(webservice_url, json.dumps(test_data), headers=headers)
print('Predictions')
print(response.text)
response = requests.post(webservice_url, json.dumps(test_data), headers=headers)
print('Predictions')
print(response.text)
response = requests.post(webservice_url, json.dumps(test_data), headers=headers)
print('Predictions')
print(response.text)
```
|
github_jupyter
|
import azureml.core
from azureml.core import Workspace
from azureml.core.webservice import Webservice
from azureml.core.authentication import AzureCliAuthentication
import requests
import json
#Provide the Subscription ID of your existing Azure subscription
subscription_id = "..." # <- needs to be the subscription with the Quick-Starts resource group
#Provide values for the existing Resource Group
resource_group = "MLOps" # <- replace XXXXX with your unique identifier
#Provide the Workspace Name and Azure Region of the Azure Machine Learning Workspace
workspace_name = "MLOpsDemo" # <- replace XXXXX with your unique identifier
workspace_region = "westeurope" # <- region of your Quick-Starts resource group
#Provide the name of the webservice
webservice_name = "compliance-classifier-service" # <- the name used by Azure DevOps pipeline
webservice_url = "..." # <- the url created as a result of publication
webservice_key = "..." # <- the api key generated as a result of publication
# By using the exist_ok param, if the worskpace already exists you get a reference to the existing workspace
# allowing you to re-run this cell multiple times as desired (which is fairly common in notebooks).
ws = Workspace.create(
name = workspace_name,
subscription_id = subscription_id,
resource_group = resource_group,
location = workspace_region,
exist_ok = True)
ws.write_config()
print('Workspace configuration succeeded')
# This is dummy data, just to test the call
test_data = [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 8, 2, 5, 6, 4, 3, 1, 34]]
headers = {'Content-Type':'application/json', 'Authorization':('Bearer '+ webservice_key)}
response = requests.post(webservice_url, json.dumps(test_data), headers=headers)
print('Predictions')
print(response.text)
web_service = Webservice(ws, webservice_name)
web_service.update(enable_app_insights=True, collect_model_data=True)
headers = {'Content-Type':'application/json', 'Authorization':('Bearer '+ webservice_key)}
response = requests.post(webservice_url, json.dumps(test_data), headers=headers)
print('Predictions')
print(response.text)
response = requests.post(webservice_url, json.dumps(test_data), headers=headers)
print('Predictions')
print(response.text)
response = requests.post(webservice_url, json.dumps(test_data), headers=headers)
print('Predictions')
print(response.text)
| 0.468061 | 0.669524 |
# Neural Machine Translation
* I will build a Neural Machine Translation (NMT) model to translate human-readable dates ("25th of June, 2009") into machine-readable dates ("2009-06-25").
* I will do this using an attention model, one of the most sophisticated sequence-to-sequence models.
Let's load all the packages I will need for this project.
```
from keras.layers import Bidirectional, Concatenate, Permute, Dot, Input, LSTM, Multiply
from keras.layers import RepeatVector, Dense, Activation, Lambda
from keras.optimizers import Adam
from keras.utils import to_categorical
from keras.models import load_model, Model
import keras.backend as K
import numpy as np
from faker import Faker
import random
from tqdm import tqdm
from babel.dates import format_date
from nmt_utils import *
import matplotlib.pyplot as plt
%matplotlib inline
```
## 1 - Translating human readable dates into machine readable dates
* The model I will build here could be used to translate from one language to another, such as translating from English to Hindi.
* However, language translation requires massive datasets and usually takes days of training on GPUs.
* To give one a place to experiment with these models without using massive datasets, I will perform a simpler "date translation" task.
* The network will input a date written in a variety of possible formats (*e.g. "the 29th of August 1958", "03/30/1968", "24 JUNE 1987"*)
* The network will translate them into standardized, machine readable dates (*e.g. "1958-08-29", "1968-03-30", "1987-06-24"*).
* I will have the network learn to output dates in the common machine-readable format YYYY-MM-DD.
<!--
Take a look at [nmt_utils.py](./nmt_utils.py) to see all the formatting. Count and figure out how the formats work, you will need this knowledge later. !-->
### 1.1 - Dataset
I will train the model on a dataset of 10,000 human readable dates and their equivalent, standardized, machine readable dates. Let's run the following cells to load the dataset and print some examples.
```
m = 10000
dataset, human_vocab, machine_vocab, inv_machine_vocab = load_dataset(m)
dataset[:10]
```
I've loaded:
- `dataset`: a list of tuples of (human readable date, machine readable date).
- `human_vocab`: a python dictionary mapping all characters used in the human readable dates to an integer-valued index.
- `machine_vocab`: a python dictionary mapping all characters used in machine readable dates to an integer-valued index.
- **Note**: These indices are not necessarily consistent with `human_vocab`.
- `inv_machine_vocab`: the inverse dictionary of `machine_vocab`, mapping from indices back to characters.
Let's preprocess the data and map the raw text data into the index values.
- I will set Tx=30
- I assume Tx is the maximum length of the human readable date.
- If I get a longer input, I would have to truncate it.
- I will set Ty=10
- "YYYY-MM-DD" is 10 characters long.
```
Tx = 30
Ty = 10
X, Y, Xoh, Yoh = preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty)
print("X.shape:", X.shape)
print("Y.shape:", Y.shape)
print("Xoh.shape:", Xoh.shape)
print("Yoh.shape:", Yoh.shape)
```
I now have:
- `X`: a processed version of the human readable dates in the training set.
- Each character in X is replaced by an index (integer) mapped to the character using `human_vocab`.
- Each date is padded to ensure a length of $T_x$ using a special character (< pad >).
- `X.shape = (m, Tx)` where m is the number of training examples in a batch.
- `Y`: a processed version of the machine readable dates in the training set.
- Each character is replaced by the index (integer) it is mapped to in `machine_vocab`.
- `Y.shape = (m, Ty)`.
- `Xoh`: one-hot version of `X`
- Each index in `X` is converted to the one-hot representation (if the index is 2, the one-hot version has the index position 2 set to 1, and the remaining positions are 0.
- `Xoh.shape = (m, Tx, len(human_vocab))`
- `Yoh`: one-hot version of `Y`
- Each index in `Y` is converted to the one-hot representation.
- `Yoh.shape = (m, Tx, len(machine_vocab))`.
- `len(machine_vocab) = 11` since there are 10 numeric digits (0 to 9) and the `-` symbol.
* Let's also look at some examples of preprocessed training examples.
* Feel free to play with `index` in the cell below to navigate the dataset and see how source/target dates are preprocessed.
```
index = 0
print("Source date:", dataset[index][0])
print("Target date:", dataset[index][1])
print()
print("Source after preprocessing (indices):", X[index])
print("Target after preprocessing (indices):", Y[index])
print()
print("Source after preprocessing (one-hot):", Xoh[index])
print("Target after preprocessing (one-hot):", Yoh[index])
```
## 2 - Neural machine translation with attention
* If I had to translate a book's paragraph from French to English, I would not read the whole paragraph, then close the book and translate.
* Even during the translation process, I would read/re-read and focus on the parts of the French paragraph corresponding to the parts of the English I am writing down.
* The attention mechanism tells a Neural Machine Translation model where it should pay attention to at any step.
### 2.1 - Attention mechanism
In this part, I will implement the attention mechanism presented in the literature.
* Here is a figure to remind us how the model works.
* The diagram on the left shows the attention model.
* The diagram on the right shows what one "attention" step does to calculate the attention variables $\alpha^{\langle t, t' \rangle}$.
* The attention variables $\alpha^{\langle t, t' \rangle}$ are used to compute the context variable $context^{\langle t \rangle}$ for each timestep in the output ($t=1, \ldots, T_y$).
<table>
<td>
<img src="images/attn_model.png" style="width:500;height:500px;"> <br>
</td>
<td>
<img src="images/attn_mechanism.png" style="width:500;height:500px;"> <br>
</td>
</table>
<caption><center> **Figure 1**: Neural machine translation with attention</center></caption>
Here are some properties of the model that one may notice:
#### Pre-attention and Post-attention LSTMs on both sides of the attention mechanism
- There are two separate LSTMs in this model (see diagram on the left): pre-attention and post-attention LSTMs.
- *Pre-attention* Bi-LSTM is the one at the bottom of the picture is a Bi-directional LSTM and comes *before* the attention mechanism.
- The attention mechanism is shown in the middle of the left-hand diagram.
- The pre-attention Bi-LSTM goes through $T_x$ time steps
- *Post-attention* LSTM: at the top of the diagram comes *after* the attention mechanism.
- The post-attention LSTM goes through $T_y$ time steps.
- The post-attention LSTM passes the hidden state $s^{\langle t \rangle}$ and cell state $c^{\langle t \rangle}$ from one time step to the next.
#### An LSTM has both a hidden state and cell state
* We can use only a basic RNN for the post-attention sequence model
* This means that the state captured by the RNN was outputting only the hidden state $s^{\langle t\rangle}$.
* In this project, we are using an LSTM instead of a basic RNN.
* So the LSTM has both the hidden state $s^{\langle t\rangle}$ and the cell state $c^{\langle t\rangle}$.
#### Each time step does not use predictions from the previous time step
* Unlike previous text generation examples earlier in the course, in this model, the post-attention LSTM at time $t$ does not take the previous time step's prediction $y^{\langle t-1 \rangle}$ as input.
* The post-attention LSTM at time 't' only takes the hidden state $s^{\langle t\rangle}$ and cell state $c^{\langle t\rangle}$ as input.
* I have designed the model this way because unlike language generation (where adjacent characters are highly correlated) there isn't as strong a dependency between the previous character and the next character in a YYYY-MM-DD date.
#### Concatenation of hidden states from the forward and backward pre-attention LSTMs
- $\overrightarrow{a}^{\langle t \rangle}$: hidden state of the forward-direction, pre-attention LSTM.
- $\overleftarrow{a}^{\langle t \rangle}$: hidden state of the backward-direction, pre-attention LSTM.
- $a^{\langle t \rangle} = [\overrightarrow{a}^{\langle t \rangle}, \overleftarrow{a}^{\langle t \rangle}]$: the concatenation of the activations of both the forward-direction $\overrightarrow{a}^{\langle t \rangle}$ and backward-directions $\overleftarrow{a}^{\langle t \rangle}$ of the pre-attention Bi-LSTM.
#### Computing "energies" $e^{\langle t, t' \rangle}$ as a function of $s^{\langle t-1 \rangle}$ and $a^{\langle t' \rangle}$
- In "Attention Model", the definition of "e" as a function of $s^{\langle t-1 \rangle}$ and $a^{\langle t \rangle}$.
- "e" is called the "energies" variable.
- $s^{\langle t-1 \rangle}$ is the hidden state of the post-attention LSTM
- $a^{\langle t' \rangle}$ is the hidden state of the pre-attention LSTM.
- $s^{\langle t-1 \rangle}$ and $a^{\langle t \rangle}$ are fed into a simple neural network, which learns the function to output $e^{\langle t, t' \rangle}$.
- $e^{\langle t, t' \rangle}$ is then used when computing the attention $a^{\langle t, t' \rangle}$ that $y^{\langle t \rangle}$ should pay to $a^{\langle t' \rangle}$.
- The diagram on the right of figure 1 uses a `RepeatVector` node to copy $s^{\langle t-1 \rangle}$'s value $T_x$ times.
- Then it uses `Concatenation` to concatenate $s^{\langle t-1 \rangle}$ and $a^{\langle t \rangle}$.
- The concatenation of $s^{\langle t-1 \rangle}$ and $a^{\langle t \rangle}$ is fed into a "Dense" layer, which computes $e^{\langle t, t' \rangle}$.
- $e^{\langle t, t' \rangle}$ is then passed through a softmax to compute $\alpha^{\langle t, t' \rangle}$.
- Note that the diagram doesn't explicitly show variable $e^{\langle t, t' \rangle}$, but $e^{\langle t, t' \rangle}$ is above the Dense layer and below the Softmax layer in the diagram in the right half of figure 1.
- I'll explain how to use `RepeatVector` and `Concatenation` in Keras below.
### Implementation Details
Let's implement this neural translator. I will start by implementing two functions: `one_step_attention()` and `model()`.
#### one_step_attention
* The inputs to the one_step_attention at time step $t$ are:
- $[a^{<1>},a^{<2>}, ..., a^{<T_x>}]$: all hidden states of the pre-attention Bi-LSTM.
- $s^{<t-1>}$: the previous hidden state of the post-attention LSTM
* one_step_attention computes:
- $[\alpha^{<t,1>},\alpha^{<t,2>}, ..., \alpha^{<t,T_x>}]$: the attention weights
- $context^{ \langle t \rangle }$: the context vector:
$$context^{<t>} = \sum_{t' = 1}^{T_x} \alpha^{<t,t'>}a^{<t'>}\tag{1}$$
##### Clarifying 'context' and 'c'
- The context is usually denoted $c^{\langle t \rangle}$
- In the project, we are calling the context $context^{\langle t \rangle}$.
- This is to avoid confusion with the post-attention LSTM's internal memory cell variable, which is also denoted $c^{\langle t \rangle}$.
#### Implement `one_step_attention`
**Implement `one_step_attention()`.**
* The function `model()` will call the layers in `one_step_attention()` $T_y$ using a for-loop.
* It is important that all $T_y$ copies have the same weights.
* It should not reinitialize the weights every time.
* In other words, all $T_y$ steps should have shared weights.
* Here's how I can implement layers with shareable weights in Keras:
1. Define the layer objects in a variable scope that is outside of the `one_step_attention` function. For example, defining the objects as global variables would work.
- Note that defining these variables inside the scope of the function `model` would technically work, since `model` will then call the `one_step_attention` function. For the purposes of making grading and troubleshooting easier, we are defining these as global variables.
2. Call these objects when propagating the input.
* I have defined the layers as global variables.
* Please run the following cells to create them.
* Please check the Keras documentation to learn more about these layers. The layers are functions. Below are examples of how to call these functions.
* [RepeatVector()](https://keras.io/layers/core/#repeatvector)
```Python
var_repeated = repeat_layer(var1)
```
* [Concatenate()](https://keras.io/layers/merge/#concatenate)
```Python
concatenated_vars = concatenate_layer([var1,var2,var3])
```
* [Dense()](https://keras.io/layers/core/#dense)
```Python
var_out = dense_layer(var_in)
```
* [Activation()](https://keras.io/layers/core/#activation)
```Python
activation = activation_layer(var_in)
```
* [Dot()](https://keras.io/layers/merge/#dot)
```Python
dot_product = dot_layer([var1,var2])
```
```
# Defined shared layers as global variables
repeator = RepeatVector(Tx)
concatenator = Concatenate(axis=-1)
densor1 = Dense(10, activation = "tanh")
densor2 = Dense(1, activation = "relu")
activator = Activation(softmax, name='attention_weights') # We are using a custom softmax(axis = 1) loaded in this notebook
dotor = Dot(axes = 1)
# one_step_attention
def one_step_attention(a, s_prev):
"""
Performs one step of attention: Outputs a context vector computed as a dot product of the attention weights
"alphas" and the hidden states "a" of the Bi-LSTM.
Arguments:
a -- hidden state output of the Bi-LSTM, numpy-array of shape (m, Tx, 2*n_a)
s_prev -- previous hidden state of the (post-attention) LSTM, numpy-array of shape (m, n_s)
Returns:
context -- context vector, input of the next (post-attention) LSTM cell
"""
# Use repeator to repeat s_prev to be of shape (m, Tx, n_s) so that I can concatenate it with all hidden states "a"
s_prev = repeator(s_prev)
# Use concatenator to concatenate a and s_prev on the last axis
concat = concatenator([a, s_prev])
# Use densor1 to propagate concat through a small fully-connected neural network to compute the "intermediate energies" variable e.
e = densor1(concat)
# Use densor2 to propagate e through a small fully-connected neural network to compute the "energies" variable energies.
energies = densor2(e)
# Use "activator" on "energies" to compute the attention weights "alphas"
alphas = activator(energies)
# Use dotor together with "alphas" and "a" to compute the context vector to be given to the next (post-attention) LSTM-cell
context = dotor([alphas, a])
return context
```
I will be able to check the expected output of `one_step_attention()` after I've coded the `model()` function.
#### model
* `model` first runs the input through a Bi-LSTM to get $[a^{<1>},a^{<2>}, ..., a^{<T_x>}]$.
* Then, `model` calls `one_step_attention()` $T_y$ times using a `for` loop. At each iteration of this loop:
- It gives the computed context vector $context^{<t>}$ to the post-attention LSTM.
- It runs the output of the post-attention LSTM through a dense layer with softmax activation.
- The softmax generates a prediction $\hat{y}^{<t>}$.
**Exercise**: Implement `model()` as explained in figure 1 and the text above. Again, I have defined global layers that will share weights to be used in `model()`.
```
n_a = 32 # number of units for the pre-attention, bi-directional LSTM's hidden state 'a'
n_s = 64 # number of units for the post-attention LSTM's hidden state "s"
# Please note, this is the post attention LSTM cell.
# please do not modify this global variable.
post_activation_LSTM_cell = LSTM(n_s, return_state = True) # post-attention LSTM
output_layer = Dense(len(machine_vocab), activation=softmax)
```
Now I can use these layers $T_y$ times in a `for` loop to generate the outputs, and their parameters will not be reinitialized. I will have to carry out the following steps:
1. Propagate the input `X` into a bi-directional LSTM.
* [Bidirectional](https://keras.io/layers/wrappers/#bidirectional)
* [LSTM](https://keras.io/layers/recurrent/#lstm)
* Remember that we want the LSTM to return a full sequence instead of just the last hidden state.
Sample code:
```Python
sequence_of_hidden_states = Bidirectional(LSTM(units=..., return_sequences=...))(the_input_X)
```
2. Iterate for $t = 0, \cdots, T_y-1$:
1. Call `one_step_attention()`, passing in the sequence of hidden states $[a^{\langle 1 \rangle},a^{\langle 2 \rangle}, ..., a^{ \langle T_x \rangle}]$ from the pre-attention bi-directional LSTM, and the previous hidden state $s^{<t-1>}$ from the post-attention LSTM to calculate the context vector $context^{<t>}$.
2. Give $context^{<t>}$ to the post-attention LSTM cell.
- Remember to pass in the previous hidden-state $s^{\langle t-1\rangle}$ and cell-states $c^{\langle t-1\rangle}$ of this LSTM
* This outputs the new hidden state $s^{<t>}$ and the new cell state $c^{<t>}$.
Sample code:
```Python
next_hidden_state, _ , next_cell_state =
post_activation_LSTM_cell(inputs=..., initial_state=[prev_hidden_state, prev_cell_state])
```
Please note that the layer is actually the "post attention LSTM cell". Please do not modify the naming of this global variable.
3. Apply a dense, softmax layer to $s^{<t>}$, get the output.
Sample code:
```Python
output = output_layer(inputs=...)
```
4. Save the output by adding it to the list of outputs.
3. Create the Keras model instance.
* It should have three inputs:
* `X`, the one-hot encoded inputs to the model, of shape ($T_{x}, humanVocabSize)$
* $s^{\langle 0 \rangle}$, the initial hidden state of the post-attention LSTM
* $c^{\langle 0 \rangle}$), the initial cell state of the post-attention LSTM
* The output is the list of outputs.
Sample code
```Python
model = Model(inputs=[...,...,...], outputs=...)
```
```
# model
def model(Tx, Ty, n_a, n_s, human_vocab_size, machine_vocab_size):
"""
Arguments:
Tx -- length of the input sequence
Ty -- length of the output sequence
n_a -- hidden state size of the Bi-LSTM
n_s -- hidden state size of the post-attention LSTM
human_vocab_size -- size of the python dictionary "human_vocab"
machine_vocab_size -- size of the python dictionary "machine_vocab"
Returns:
model -- Keras model instance
"""
# Define the inputs of your model with a shape (Tx,)
# Define s0 (initial hidden state) and c0 (initial cell state)
# for the decoder LSTM with shape (n_s,)
X = Input(shape=(Tx, human_vocab_size))
s0 = Input(shape=(n_s,), name='s0')
c0 = Input(shape=(n_s,), name='c0')
s = s0
c = c0
# Initialize empty list of outputs
outputs = []
# Step 1: Define your pre-attention Bi-LSTM.
a = Bidirectional(LSTM(units = n_a, return_sequences = True))(X)
# Step 2: Iterate for Ty steps
for t in range(Ty):
# Step 2.A: Perform one step of the attention mechanism to get back the context vector at step t
context = one_step_attention(a, s)
# Step 2.B: Apply the post-attention LSTM cell to the "context" vector.
# Don't forget to pass: initial_state = [hidden state, cell state]
s, _, c = post_activation_LSTM_cell(inputs= context, initial_state=[s, c])
# Step 2.C: Apply Dense layer to the hidden state output of the post-attention LSTM
out = output_layer(inputs = s)
# Step 2.D: Append "out" to the "outputs" list
outputs.append(out)
# Step 3: Create model instance taking three inputs and returning the list of outputs.
model = Model(inputs = [X, s0,c0], outputs = outputs)
return model
```
Run the following cell to create the model.
```
model = model(Tx, Ty, n_a, n_s, len(human_vocab), len(machine_vocab))
```
#### Troubleshooting Note
* If you are getting repeated errors after an initially incorrect implementation of "model", but believe that you have corrected the error, you may still see error messages when building your model.
* A solution is to save and restart your kernel (or shutdown then restart your notebook), and re-run the cells.
Let's get a summary of the model to check if it matches the expected output.
```
model.summary()
```
**Expected Output**:
Here is the summary you should see
<table>
<tr>
<td>
**Total params:**
</td>
<td>
52,960
</td>
</tr>
<tr>
<td>
**Trainable params:**
</td>
<td>
52,960
</td>
</tr>
<tr>
<td>
**Non-trainable params:**
</td>
<td>
0
</td>
</tr>
<tr>
<td>
**bidirectional_1's output shape **
</td>
<td>
(None, 30, 64)
</td>
</tr>
<tr>
<td>
**repeat_vector_1's output shape **
</td>
<td>
(None, 30, 64)
</td>
</tr>
<tr>
<td>
**concatenate_1's output shape **
</td>
<td>
(None, 30, 128)
</td>
</tr>
<tr>
<td>
**attention_weights's output shape **
</td>
<td>
(None, 30, 1)
</td>
</tr>
<tr>
<td>
**dot_1's output shape **
</td>
<td>
(None, 1, 64)
</td>
</tr>
<tr>
<td>
**dense_3's output shape **
</td>
<td>
(None, 11)
</td>
</tr>
</table>
#### Compile the model
* After creating the model in Keras, I need to compile it and define the loss function, optimizer and metrics I want to use.
* Loss function: 'categorical_crossentropy'.
* Optimizer: [Adam](https://keras.io/optimizers/#adam) [optimizer](https://keras.io/optimizers/#usage-of-optimizers)
- learning rate = 0.005
- $\beta_1 = 0.9$
- $\beta_2 = 0.999$
- decay = 0.01
* metric: 'accuracy'
Sample code
```Python
optimizer = Adam(lr=..., beta_1=..., beta_2=..., decay=...)
model.compile(optimizer=..., loss=..., metrics=[...])
```
```
opt = Adam(lr = 0.005, beta_1 = 0.9, beta_2 = 0.999, decay = 0.01)
model.compile(optimizer = opt, loss= 'categorical_crossentropy', metrics = ['accuracy'])
```
#### Define inputs and outputs, and fit the model
The last step is to define all the inputs and outputs to fit the model:
- I have input X of shape $(m = 10000, T_x = 30)$ containing the training examples.
- I need to create `s0` and `c0` to initialize the `post_attention_LSTM_cell` with zeros.
- Given the `model()` I coded, I need the "outputs" to be a list of 10 elements of shape (m, T_y).
- The list `outputs[i][0], ..., outputs[i][Ty]` represents the true labels (characters) corresponding to the $i^{th}$ training example (`X[i]`).
- `outputs[i][j]` is the true label of the $j^{th}$ character in the $i^{th}$ training example.
```
s0 = np.zeros((m, n_s))
c0 = np.zeros((m, n_s))
outputs = list(Yoh.swapaxes(0,1))
```
Let's now fit the model and run it for one epoch.
```
model.fit([Xoh, s0, c0], outputs, epochs=1, batch_size=100)
```
While training I can see the loss as well as the accuracy on each of the 10 positions of the output. The table below gives me an example of what the accuracies could be if the batch had 2 examples:
<img src="images/table.png" style="width:700;height:200px;"> <br>
<caption><center>Thus, `dense_2_acc_8: 0.89` means that I am predicting the 7th character of the output correctly 89% of the time in the current batch of data. </center></caption>
I have run this model for longer, and saved the weights. Run the next cell to load our weights. (By training a model for several minutes, I should be able to obtain a model of similar accuracy, but loading our model will save me time.)
```
model.load_weights('models/model.h5')
```
I can now see the results on new examples.
```
EXAMPLES = ['3 May 1979', '5 April 09', '21th of August 2016', 'Tue 10 Jul 2007', 'Saturday May 9 2018', 'March 3 2001', 'March 3rd 2001', '1 March 2001']
for example in EXAMPLES:
source = string_to_int(example, Tx, human_vocab)
source = np.array(list(map(lambda x: to_categorical(x, num_classes=len(human_vocab)), source))).swapaxes(0,1)
prediction = model.predict([source, s0, c0])
prediction = np.argmax(prediction, axis = -1)
output = [inv_machine_vocab[int(i)] for i in prediction]
print("source:", example)
print("output:", ''.join(output),"\n")
```
I can also change these examples to test with my own examples. The next part will give you a better sense of what the attention mechanism is doing--i.e., what part of the input the network is paying attention to when generating a particular output character.
## 3 - Visualizing Attention (Optional)
Since the problem has a fixed output length of 10, it is also possible to carry out this task using 10 different softmax units to generate the 10 characters of the output. But one advantage of the attention model is that each part of the output (such as the month) knows it needs to depend only on a small part of the input (the characters in the input giving the month). I can visualize what each part of the output is looking at which part of the input.
Consider the task of translating "Saturday 9 May 2018" to "2018-05-09". If I visualize the computed $\alpha^{\langle t, t' \rangle}$ I get this:
<img src="date_attention.png" style="width:600;height:300px;"> <br>
<caption><center> **Figure 8**: Full Attention Map</center></caption>
Notice how the output ignores the "Saturday" portion of the input. None of the output timesteps are paying much attention to that portion of the input. We also see that 9 has been translated as 09 and May has been correctly translated into 05, with the output paying attention to the parts of the input it needs to to make the translation. The year mostly requires it to pay attention to the input's "18" in order to generate "2018."
### 3.1 - Getting the attention weights from the network
Lets now visualize the attention values in my network. I'll propagate an example through the network, then visualize the values of $\alpha^{\langle t, t' \rangle}$.
To figure out where the attention values are located, let's start by printing a summary of the model .
```
model.summary()
```
Navigate through the output of `model.summary()` above. I can see that the layer named `attention_weights` outputs the `alphas` of shape (m, 30, 1) before `dot_2` computes the context vector for every time step $t = 0, \ldots, T_y-1$. Let's get the attention weights from this layer.
The function `attention_map()` pulls out the attention values from my model and plots them.
```
attention_map = plot_attention_map(model, human_vocab, inv_machine_vocab, "Tuesday 09 Oct 1993", num = 7, n_s = 64);
```
On the generated plot I can observe the values of the attention weights for each character of the predicted output. Examine this plot and check that the places where the network is paying attention makes sense to you.
In the date translation application, you will observe that most of the time attention helps predict the year, and doesn't have much impact on predicting the day or month.
### Conclusion!
I have come to the end of this project.
## Here's what I should remember
- Machine translation models can be used to map from one sequence to another. They are useful not just for translating human languages (like French->English) but also for tasks like date format translation.
- An attention mechanism allows a network to focus on the most relevant parts of the input when producing a specific part of the output.
- A network using an attention mechanism can translate from inputs of length $T_x$ to outputs of length $T_y$, where $T_x$ and $T_y$ can be different.
- I can visualize attention weights $\alpha^{\langle t,t' \rangle}$ to see what the network is paying attention to while generating each output.
I am now able to implement an attention model and use it to learn complex mappings from one sequence to another.
|
github_jupyter
|
from keras.layers import Bidirectional, Concatenate, Permute, Dot, Input, LSTM, Multiply
from keras.layers import RepeatVector, Dense, Activation, Lambda
from keras.optimizers import Adam
from keras.utils import to_categorical
from keras.models import load_model, Model
import keras.backend as K
import numpy as np
from faker import Faker
import random
from tqdm import tqdm
from babel.dates import format_date
from nmt_utils import *
import matplotlib.pyplot as plt
%matplotlib inline
m = 10000
dataset, human_vocab, machine_vocab, inv_machine_vocab = load_dataset(m)
dataset[:10]
Tx = 30
Ty = 10
X, Y, Xoh, Yoh = preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty)
print("X.shape:", X.shape)
print("Y.shape:", Y.shape)
print("Xoh.shape:", Xoh.shape)
print("Yoh.shape:", Yoh.shape)
index = 0
print("Source date:", dataset[index][0])
print("Target date:", dataset[index][1])
print()
print("Source after preprocessing (indices):", X[index])
print("Target after preprocessing (indices):", Y[index])
print()
print("Source after preprocessing (one-hot):", Xoh[index])
print("Target after preprocessing (one-hot):", Yoh[index])
var_repeated = repeat_layer(var1)
concatenated_vars = concatenate_layer([var1,var2,var3])
var_out = dense_layer(var_in)
activation = activation_layer(var_in)
dot_product = dot_layer([var1,var2])
# Defined shared layers as global variables
repeator = RepeatVector(Tx)
concatenator = Concatenate(axis=-1)
densor1 = Dense(10, activation = "tanh")
densor2 = Dense(1, activation = "relu")
activator = Activation(softmax, name='attention_weights') # We are using a custom softmax(axis = 1) loaded in this notebook
dotor = Dot(axes = 1)
# one_step_attention
def one_step_attention(a, s_prev):
"""
Performs one step of attention: Outputs a context vector computed as a dot product of the attention weights
"alphas" and the hidden states "a" of the Bi-LSTM.
Arguments:
a -- hidden state output of the Bi-LSTM, numpy-array of shape (m, Tx, 2*n_a)
s_prev -- previous hidden state of the (post-attention) LSTM, numpy-array of shape (m, n_s)
Returns:
context -- context vector, input of the next (post-attention) LSTM cell
"""
# Use repeator to repeat s_prev to be of shape (m, Tx, n_s) so that I can concatenate it with all hidden states "a"
s_prev = repeator(s_prev)
# Use concatenator to concatenate a and s_prev on the last axis
concat = concatenator([a, s_prev])
# Use densor1 to propagate concat through a small fully-connected neural network to compute the "intermediate energies" variable e.
e = densor1(concat)
# Use densor2 to propagate e through a small fully-connected neural network to compute the "energies" variable energies.
energies = densor2(e)
# Use "activator" on "energies" to compute the attention weights "alphas"
alphas = activator(energies)
# Use dotor together with "alphas" and "a" to compute the context vector to be given to the next (post-attention) LSTM-cell
context = dotor([alphas, a])
return context
n_a = 32 # number of units for the pre-attention, bi-directional LSTM's hidden state 'a'
n_s = 64 # number of units for the post-attention LSTM's hidden state "s"
# Please note, this is the post attention LSTM cell.
# please do not modify this global variable.
post_activation_LSTM_cell = LSTM(n_s, return_state = True) # post-attention LSTM
output_layer = Dense(len(machine_vocab), activation=softmax)
sequence_of_hidden_states = Bidirectional(LSTM(units=..., return_sequences=...))(the_input_X)
next_hidden_state, _ , next_cell_state =
post_activation_LSTM_cell(inputs=..., initial_state=[prev_hidden_state, prev_cell_state])
```
Please note that the layer is actually the "post attention LSTM cell". Please do not modify the naming of this global variable.
3. Apply a dense, softmax layer to $s^{<t>}$, get the output.
Sample code:
```Python
output = output_layer(inputs=...)
```
4. Save the output by adding it to the list of outputs.
3. Create the Keras model instance.
* It should have three inputs:
* `X`, the one-hot encoded inputs to the model, of shape ($T_{x}, humanVocabSize)$
* $s^{\langle 0 \rangle}$, the initial hidden state of the post-attention LSTM
* $c^{\langle 0 \rangle}$), the initial cell state of the post-attention LSTM
* The output is the list of outputs.
Sample code
```Python
model = Model(inputs=[...,...,...], outputs=...)
```
Run the following cell to create the model.
#### Troubleshooting Note
* If you are getting repeated errors after an initially incorrect implementation of "model", but believe that you have corrected the error, you may still see error messages when building your model.
* A solution is to save and restart your kernel (or shutdown then restart your notebook), and re-run the cells.
Let's get a summary of the model to check if it matches the expected output.
**Expected Output**:
Here is the summary you should see
<table>
<tr>
<td>
**Total params:**
</td>
<td>
52,960
</td>
</tr>
<tr>
<td>
**Trainable params:**
</td>
<td>
52,960
</td>
</tr>
<tr>
<td>
**Non-trainable params:**
</td>
<td>
0
</td>
</tr>
<tr>
<td>
**bidirectional_1's output shape **
</td>
<td>
(None, 30, 64)
</td>
</tr>
<tr>
<td>
**repeat_vector_1's output shape **
</td>
<td>
(None, 30, 64)
</td>
</tr>
<tr>
<td>
**concatenate_1's output shape **
</td>
<td>
(None, 30, 128)
</td>
</tr>
<tr>
<td>
**attention_weights's output shape **
</td>
<td>
(None, 30, 1)
</td>
</tr>
<tr>
<td>
**dot_1's output shape **
</td>
<td>
(None, 1, 64)
</td>
</tr>
<tr>
<td>
**dense_3's output shape **
</td>
<td>
(None, 11)
</td>
</tr>
</table>
#### Compile the model
* After creating the model in Keras, I need to compile it and define the loss function, optimizer and metrics I want to use.
* Loss function: 'categorical_crossentropy'.
* Optimizer: [Adam](https://keras.io/optimizers/#adam) [optimizer](https://keras.io/optimizers/#usage-of-optimizers)
- learning rate = 0.005
- $\beta_1 = 0.9$
- $\beta_2 = 0.999$
- decay = 0.01
* metric: 'accuracy'
Sample code
#### Define inputs and outputs, and fit the model
The last step is to define all the inputs and outputs to fit the model:
- I have input X of shape $(m = 10000, T_x = 30)$ containing the training examples.
- I need to create `s0` and `c0` to initialize the `post_attention_LSTM_cell` with zeros.
- Given the `model()` I coded, I need the "outputs" to be a list of 10 elements of shape (m, T_y).
- The list `outputs[i][0], ..., outputs[i][Ty]` represents the true labels (characters) corresponding to the $i^{th}$ training example (`X[i]`).
- `outputs[i][j]` is the true label of the $j^{th}$ character in the $i^{th}$ training example.
Let's now fit the model and run it for one epoch.
While training I can see the loss as well as the accuracy on each of the 10 positions of the output. The table below gives me an example of what the accuracies could be if the batch had 2 examples:
<img src="images/table.png" style="width:700;height:200px;"> <br>
<caption><center>Thus, `dense_2_acc_8: 0.89` means that I am predicting the 7th character of the output correctly 89% of the time in the current batch of data. </center></caption>
I have run this model for longer, and saved the weights. Run the next cell to load our weights. (By training a model for several minutes, I should be able to obtain a model of similar accuracy, but loading our model will save me time.)
I can now see the results on new examples.
I can also change these examples to test with my own examples. The next part will give you a better sense of what the attention mechanism is doing--i.e., what part of the input the network is paying attention to when generating a particular output character.
## 3 - Visualizing Attention (Optional)
Since the problem has a fixed output length of 10, it is also possible to carry out this task using 10 different softmax units to generate the 10 characters of the output. But one advantage of the attention model is that each part of the output (such as the month) knows it needs to depend only on a small part of the input (the characters in the input giving the month). I can visualize what each part of the output is looking at which part of the input.
Consider the task of translating "Saturday 9 May 2018" to "2018-05-09". If I visualize the computed $\alpha^{\langle t, t' \rangle}$ I get this:
<img src="date_attention.png" style="width:600;height:300px;"> <br>
<caption><center> **Figure 8**: Full Attention Map</center></caption>
Notice how the output ignores the "Saturday" portion of the input. None of the output timesteps are paying much attention to that portion of the input. We also see that 9 has been translated as 09 and May has been correctly translated into 05, with the output paying attention to the parts of the input it needs to to make the translation. The year mostly requires it to pay attention to the input's "18" in order to generate "2018."
### 3.1 - Getting the attention weights from the network
Lets now visualize the attention values in my network. I'll propagate an example through the network, then visualize the values of $\alpha^{\langle t, t' \rangle}$.
To figure out where the attention values are located, let's start by printing a summary of the model .
Navigate through the output of `model.summary()` above. I can see that the layer named `attention_weights` outputs the `alphas` of shape (m, 30, 1) before `dot_2` computes the context vector for every time step $t = 0, \ldots, T_y-1$. Let's get the attention weights from this layer.
The function `attention_map()` pulls out the attention values from my model and plots them.
| 0.843057 | 0.944995 |
# 12 시계열 데이터
시계열 데이터는 데이터 분석 분야에서 중요하게 다루는 데이터 중 하나입니다. 우리가 지금까지 다룬 날씨 관측 데이터, 에볼라 전염병으로 인한 사망자 수 관측 데이터, 빌보드 차트 데이터에는 모두 시계열 데이터가 포함되어 있었죠. 즉, 일정 시간 간격으로 어떤 값을 기록한 데이터에서는 시계열 데이터가 매우 중요합니다. 따라서 데이터를 자유자재로 다룰 줄 알아야 유능한 데이터 분석가라고 할 수 있습니다. 그러면 시계열 데이터란 무엇인지 알아볼까요?
## 12-1 datetime 오브젝트
## 12-2 사례별 시계열 데이터 계산하기
# 12-1 datetime 오브젝트
datetime 라이브러리는 날짜와 시간을 처리하는 등의 다양한 기능을 제공하는 파이썬 라이브러리입니다. datetime 라이브러리에는 날자를 처리하는 date 오브젝트, 시간을 처리하는 time 오브젝트, 날짜와 시간을 모두 처리하는 datetime 오브젝트가 포함되어 있습니다. 앞으로 3개의 오브젝트를 명확히 구분하기 위해 영무을 그대로 살려 date, time, datetime 오브젝트라고 부르겠습니다.
#### datetime 오브젝트 사용하기
#### 1.
datetime 오브젝트를 사용하기 위해 datetime 라이브러리를 불러옵니다.
```
from datetime import datetime
```
#### 2.
now, today 메서드를 사용하면 다음과 같이 현재 시간을 출력할 수 있습니다.
```
now1 = datetime.now()
print(now1)
now2 = datetime.today()
print(now2)
```
#### 3.
다음은 datetime 오브젝트를 생성할 때 시간을 직접 입력하여 인자로 전달한 것입니다. 각 변수를 출력하여 확인해 보면 입력한 시간을 바탕으로 datetime 오브젝트가 생성괸 것을 알 수 있습니다
```
t1 = datetime.now()
t2 = datetime(1970, 1, 1)
t3 = datetime(1970, 12, 12, 13, 24, 34)
print(t1)
print(t2)
print(t3)
```
#### 4.
datetime 오브젝트를 사용하는 이유 중 하나는 시간 계산을 할 수 있다는 점입니다. 다음은 두 datetime 오브젝트의 차이를 구한 것입니다.
```
diff1 = t1 - t2
print(diff1)
print(type(diff1))
diff2 = t2 - t1
print(diff2)
print(type(diff2))
```
#### datetime 오브젝트로 변환하기 - to_datetime 메서드
경우에 따라서는 시계열 데이터를 문자열로 저장해야 할 때도 있습니다. 하지만 문자열은 시간 계산을 할 수 없기 때문에 datetime 오브젝트로 변환해 주어야 합니다. 이번에는 to_datetime 메서드를 사용하여 문자열을 datetime 오브젝트로 변환하는 방법에 대해 알아보겠습니다.
#### 문자열을 datetime 오브젝트로 변환하기
#### 1.
먼저 ebola 데이터 집합을 불러옵니다.
```
import pandas as pd
import os
ebola = pd.read_csv('./data/country_timeseries.csv')
```
#### 2.
ebola 데이터프레임을 보면 문자열로 저장된 Date 열이 있는 것을 알 수 있습니다.
```
print(ebola.info())
```
#### 3.
to_datetime 메서드를 사용하면 Date 열의 자료형을 datetime 오브젝트로 변환할 수 있습니다. 다음과 같이 to_datetime 메서드를 사용하여 Date열의 자료형을 datetime 오브젝트로 변환한 다음 ebola 데이터프레임에 새로운 열로 추가합니다.
```
ebola['date_dt'] = pd.to_datetime(ebola['Date'])
print(ebola.info())
```
#### 4.
to_datetime 메서드를 좀 더 자세히 알아볼까요? 시간 형식 지정자(%d, %m, %y)와 기호(|,-)를 적절히 조합하여 format 인자에 전달하면 그 형식에 맞게 정리된 datetime 오브젝트를 얻을 수 있습니다. 다음 실습을 참고하여 format 인자의 사용법을 꼭 익혀두세요.
```
test_df1 = pd.DataFrame({'order_day':['01/01/15', '02/01/15', '03/01/15']})
test_df1['date_dt1'] = pd.to_datetime(test_df1['order_day'], format = '%d/%m/%y')
test_df1['date_dt2'] = pd.to_datetime(test_df1['order_day'], format = '%m/%d/%y')
test_df1['date_dt3'] = pd.to_datetime(test_df1['order_day'], format = '%y/%m/%d')
print(test_df1)
test_df2 = pd.DataFrame({'order_day':['01-01-15', '02-01-15', '03-01-15']})
test_df2['date_dt'] = pd.to_datetime(test_df2['order_day'], format='%d-%m-%y')
print(test_df2)
```
#### 시간 형식 지정자
다음은 시간 형식 지정자를 정리한 표입니다. 이 장의 실습에서 종종 사용하므로 한 번 읽고 넘어가기 바랍니다.
- %a : 요일출력
- %A : 요일출력(긴 이름)
- %w : 요일 출력(숫자, 0부터 일요일)
- %d : 날짜 출력 (2자리표시)
- %b : 월 출력
- %B : 월 출력 (긴 이름)
- %m : 월 출력 (숫자)
- %y : 년 출력(2자리로 표시)
- %Y : 년 출력(4자리로 표시)
- %H : 시간출력(24시간)
- %l : 시간출력(12시간)
- %p : AM 또는 PM 출력
- %M : 분 출력(2자리로 표시)
- %S : 초 출력(2자리로 표시)
- %f : 마이크로초 출력
- %z : UTC 차이 출력
- %Z : 기준 지역 이름 출력
- %j : 올해의 지난 일 수 출력
- %U : 올해의 지난 주 수 출력
- %c : 날짜와 시간 출력
- %x : 날자 출력
- %X : 시간 출력
- %G : 년 출력
- %u : 요일 출력
- %V : 올해의 지난 주 수 출력(ISO 8601 형식)
#### datetime 오브젝트로 변환하기 - read_csv 메서드
앞에서는 to_datetime 메서드를 사용하여 문자열로 저장되어 있는 Date 열을 datetime 오브젝트로 변환했습니다. 하지만 datetime 오브젝트로 변환하려는 열을 지정하여 데이터 집합을 불러오는 것이 더 간단합니다. 다음 실습을 통해 알아보겠습니다.
#### datetime 오브젝트로 변환하려는 열을 지정하여 데이터 집합 불러오기
#### 1.
다음은 read_csv 메서드의 parse_dates 인자에 datetime 오브젝트로 변환하고자 하는 열의 이름을 전달하여 데이터 집합을 불러온 것입니다. 결과를 보면 Date 열이 문자열이 아니라 datetime 오브젝트라는 것을 확인할 수 있습니다.
```
ebola1 = pd.read_csv('./data/country_timeseries.csv', parse_dates = ['Date'])
print(ebola1.info())
```
#### datetime 오브젝트에서 날짜 정보 추출하기
datetime 오브젝트에는 년,월,일과 같은 날짜 정보를 따로 저장하고 있는 속성이 이미 준비되어 있습니다. 다음 실습을 통해 datetime 오브젝트에서 날짜 정보를 하나씩 추출해 보겠습니다.
#### datetime 오브젝트에서 날짜 정보 추출하기
#### 1.
다음은 문자열로 저장된 날짜를 시리즈에 담아 datetime 오브젝트로 변환한 것입니다.
```
date_series = pd.Series(['2018-05-16', '2018-05-17', '2018-05-18'])
d1 = pd.to_datetime(date_series)
print(d1)
```
#### 2.
datetime 오브젝트(d1)의 year,month,day 속성을 이용하면 년,월,일 정보를 바로 추출할 수 있습니다.
```
print(d1[0].year)
print(d1[0].month)
print(d1[0].day)
```
#### dt 접근자 사용하기
문자열을 처리하려면 str 접근자를 사용한 다음 문자열 속성이나 메서드를 사용해야 했습니다. datetime 오브젝트도 마찬가지로 dt 접근자를 사용하면 datetime 속성이나 메서드를 사용하여 시계열 데이터를 처리할 수 있습니다.
#### dt 접근자로 시계열 데이터 정리하기
#### 1.
먼저 ebola 데이터 집합을 불러온 다음 Date 열을 datetime 오브젝트로 변환하여 새로운 열 (date_dt)로 추가합니다.
```
ebola = pd.read_csv('./data/country_timeseries.csv')
ebola['date_dt'] = pd.to_datetime(ebola['Date'])
```
#### 2.
다음은 dt 접근자를 사용하지 않고 인덱스가 3인 데이터의 년,월,일 데이터를 추출한 것입니다.
```
print(ebola[['Date', 'date_dt']].head())
print(ebola['date_dt'][3].year)
print(ebola['date_dt'][3].month)
print(ebola['date_dt'][3].day)
```
#### 3.
과정 2와 같은 방법은 date_dt 열의 특정 데이터를 인덱스로 접근해야 하기 때문에 불편합니다. 다음은 dt 접근자로 date_dt 열에 한번에 접근한 다음 year 속성을 이용하여 연도값을 추출한 것입니다. 추출한 연도값은 ebola 데이터프레임의 새로운 열 (year)로 추가 했습니다.
```
ebola['year'] = ebola['date_dt'].dt.year
print(ebola[['Date', 'date_dt', 'year']].head())
```
#### 4.
다음은 과정 3을 응용하여 월,일 데이터를 한 번에 추출해서 새로운 열(month, day)로 추가한 것입니다.
```
ebola['month'], ebola['day'] = (ebola['date_dt'].dt.month, ebola['date_dt'].dt.day)
print(ebola[['Date', 'date_dt', 'year', 'month', 'day']].head())
```
#### 5.
ebola 데이터프레임에 새로 추가한 date_dt, year, month, day 열의 자료형을 출력한 것입니다. date_dt 열은 datetime 오브젝트이고 나머지는 정수형이라는 것을 알 수 있습니다.
```
print(ebola.info())
```
# 12-2 사례별 시계열 데이터 계산하기
#### 에볼라 최초 발병일 계산하기
#### 1.
ebola 데이터프레임의 마지막 행과 열을 5개씩만 살펴보겠습니다. ebola 데이터프레임은 데이터가 시간 역순으로 정렬되어 있습니다. 즉, 시간 순으로 데이터를 살펴보려면 데이터프레임의 마지막부터 살펴봐야 합니다.
```
print(ebola.iloc[-5:,:5])
```
#### 2.
121행에서 볼 수 있듯이 에볼라가 발행하기 시작한 날은 2014년 3월 22일 입니다. 다으은 min 메서드를 사용하여 에볼라의 최초 발병일을 찾은 것입니다.
```
print(ebola['date_dt'].min())
print(type(ebola['date_dt'].min()))
```
#### 3.
에볼라의 최초 발병일을 알아냈으니 Date 열에서 에볼라의 최초 발병일을 빼면 에볼라의 진행 정도를 알 수 있습니다.
```
ebola['outbreak_d'] = ebola['date_dt'] - ebola['date_dt'].min()
print(ebola[['Date', 'Day', 'outbreak_d']].head())
```
#### 파산한 은행의 개수 계산하기
#### 1.
다음은 파산한 은행 데이터 집합을 불러온 것입니다. banks 데이터프레임의 앞부분울 살펴보면 Closing Date, Updated Date 열의 데이터 자료형이 시계열 데이터라는 것을 알 수 있습니다.
```
banks = pd.read_csv('./data/banklist.csv')
print(banks.head())
```
#### 2.
Closing Date, Updated Date 열의 데이터 자료형은 문자열입니다. 다음은 read_csv 메서드의 parse_dates 속성을 이용하여 문자열로 저장된 두 열을 datetime 오브젝트로 변환하여 불러온 것입니다.
```
banks_no_dates = pd.read_csv('./data/banklist.csv')
print(banks_no_dates.info())
banks = pd.read_csv('./data/banklist.csv', parse_dates=[5,6])
print(banks.info())
```
#### 3.
dt접근자와 quarter 속성을 이용하면 은행이 파산한 분기를 알 수 있습니다. 다음은 dt접근자와 year,quarter 속성을 이용하여 은행이 파산한 연도, 분기를 새로운 열로 추가한 것입니다.
```
banks['closing_quarter'], banks['closing_year'] = (banks['Closing Date'].dt.quarter, banks['Closing Date'].dt.year)
print(banks.head())
```
#### 4.
이제 연도별로 파산한 은행이 얼마나 되는지 알아볼까요? grouby 메서드를 사용하면 연도별로 파산한 은행의 개수를 구할 수 있습니다.
```
closing_year = banks.groupby(['closing_year']).size()
print(closing_year)
```
#### 5.
각 연도별, 분기별로 파산한 은행의 개수도 알아보겠습니다. 다음은 banks 데이터프레임을 연도별로 그룹화한 다음 다시 분기별로 그룹화하여 출력한 것입니다.
```
closing_year_q = banks.groupby(['closing_year', 'closing_quarter']).size()
print(closing_year_q)
```
#### 6.
다음은 과정5에서 얻은 값으로 그래프를 그린 것입니다.
```
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax = closing_year.plot()
plt.show()
fig, ax = plt.subplots()
ax = closing_year_q.plot()
plt.show()
```
#### 테슬라 주식 데이터로 시간 계산하기
이번에는 pandas-datareader 라이브러리를 이용하여 주식 데이터를 불러오겠습니다. 이 라이브러리는 지금까지 설치한 적이 없는 라이브러리입니다. 다음을 아나콘다 프롬프트에 입력하여 pandas-datareader 라이브러리를 설치하세요.
```
!pip install pandas-datareader
```
#### 1.
다음은 get_data_quanal 메서드에 TSLA라는 문자열을 전달하여 테슬라의 주식 데이터를 내려받은 다음 to_csv 메서드를 사용하여 data 폴더 안에 'tesla_stock_quandl.csv'라는 이름으로 저장한 것입니다.
```
pd.core.common.is_list_like = pd.api.types.is_list_like
import pandas_datareader as pdr
tesla = pdr.get_data_quandl('TSLA', api_key = 'srXDVTSXUEfYySwasC3N')
tesla.to_csv('./data/tesla_stock_quandl.csv')
```
#### 2.
tesla 데이터프레임의 Date 열은 문자열로 저장되어 있습니다. 즉, datetime 오브젝트로 자료형을 변환해야 시간 계산을 할 수 있습니다.
```
print(tesla.head())
```
#### 3.
Date 열을 Datetime 형으로 변환하려면 read_csv 메서드로 데이터 집합(tesla_stock_quandl.csv)을 불러올 때 parse_dates 인자에 Date 열을 전달하면 됩니다.
```
tesla = pd.read_csv('./data/tesla_stock_quandl.csv', parse_dates=[0])
print(tesla.info())
```
#### 4.
Date 열의 자료형이 datetime 오브젝트로 변환되었습니다. 이제 dt 접근자를 사용할 수 있습니다. 다음은 불린 추출로 2010년 6월의 데이터만 추출한 것입니다.
```
print(tesla.loc[(tesla.Date.dt.year == 2010) & (tesla.Date.dt.month == 6)])
```
#### datetime 오브젝트와 인덱스 - datetimelndex
datetime 오브젝트를 데이터프레임의 인덱스로 설정하면 원하는 시간의 데이터를 바로 추출할 수 있어 편리합니다. 이번에는 datetime 오브젝트를 인덱스로 지정하는 방법에 대해 알아보겠습니다.
#### datetime 오브젝트를 인덱스로 설정해 데이터 추출하기
#### 1.
계속해서 테슬라 주식 데이터를 사용하여 실습을 진행하겠습니다. 다음은 Date 열을 tesla 데이터프레임의 인덱스로 지정한 것입니다.
```
tesla.index = tesla['Date']
print(tesla.index)
```
#### 2.
datetime 오브젝트를 인덱스로 지정하면 다음과 같은 방법으로 원하는 시간의 데이터를 바로 추출할 수 있습니다. 다음은 2015년의 데이터를 추출한 것입니다.
```
print(tesla['2015'].iloc[:5, :5])
```
#### 3.
다음은 2010년 6월의 데이터를 추출한 것입니다.
```
print(tesla['2010-06'].iloc[:, :5])
```
#### 시간 간격과 인덱스 - Timedeltalndex
예를 들어 주식 데이터에서 최초 5일간 수집된 데이터만 살펴보고 싶다면 어떻게 해야 할까요? 이런 경우에는 시간 간격을 인덱스로 지정하여 데이터를 추출하면 됩니다. 이번에는 datetime 오브젝트를 인덱스로 지정하는 것이 아니라 시간 간격을 인덱스로 지정하여 진행하겠습니다.
#### 시간 간격을 인덱스로 지정해 데이터 추출하기
#### 1.
Date 열에서 Date 열의 최솟값(2010-06-29)을 빼면 데이터를 수집한 이후에 시간이 얼마나 흘렀는지 알 수 있습니다. 다음은 Date 열에서 Date 열의 최솟값을 뺀 다음 ref_date열로 추하한 것입니다.
```
tesla['ref_date'] = tesla['Date'] - tesla['Date'].min()
print(tesla.head())
```
#### 2.
다음과 같이 ref_date 열을 인덱스로 지정했습니다. 이제 시간 간격(ref_date)을 이용하여 데이터를 추출할 수 있습니다.
```
tesla.index = tesla['ref_date']
print(tesla.iloc[:5, :5])
```
#### 3.
다음은 데이터를 수집한 이후 최초 5일의 데이터를 추출한 것입니다.
```
print(tesla['5day':].iloc[:5, :5])
```
#### 시간 범위와 인덱스
앞에서 사용한 주식 데이터는 특정 일에 누락된 데이터가 없었습니다. 하지만 가끔은 데이터를 수집하지 못한 날도 있을 수 있겠죠. 만약 특정 일에 누락된 데이터도 포함시켜 데이터를 살펴보려면 어떻게 해야 할까요? 이런 경우에는 임의로 시간 범위를 생성하여 인덱스로 지정해야 합니다.
#### 시간 범위 생성해 인덱스로 지정하기
#### 1.
테슬라 주식 데이터는 특정 일에 누락된 데이터가 없습니다. 그래서 이번에는 에볼라 데이터 집합을 사용하겠습니다. 가장 앞쪽의 데이터를 살펴보면 2015년 01월 01일의 데이터가 누락된 것을 알 수 있습니다.
```
ebola = pd.read_csv('./data/country_timeseries.csv', parse_dates=[0])
print(ebola.iloc[:5, :5])
```
#### 2.
뒤쪽의 데이터도 마찬가지입니다. 2014년 03월 23일의 데이터가 누락되었습니다.
```
print(ebola.iloc[-5:, :5])
```
#### 3.
다음은 date_range 메서드를 사용하여 2014년 12월 31일부터 2015년 01월 05일 사이의 시간 인덱스(DatetimeIndex)를 생성한 것입니다.
```
head_range = pd.date_range(start='2014-12-31', end='2015-01-05')
print(head_range)
```
#### 4.
다음은 원본 데이터를 손상시키는 것을 방지하기 위해 ebola 데이터프레임의 앞쪽 5개의 데이터를 추출하여 새로운 데이터프레임을 만든 것입니다. 이때 Date 열을 인덱스로 먼저 지정하지 않으면 오류가 발생합니다. 반드시 Date 열을 인덱스로 지정한 다음 과정3에서 생성한 시간 범위를 인덱스로 지정해야 합니다.
```
ebola_5 = ebola.head()
ebola_5.index = ebola_5['Date']
ebola_5.reindex(head_range)
print(ebola_5.iloc[:5, :5])
```
#### 시간 범위의 주기 설정하기
시간 범위를 인덱스로 지정하면 DatetimeIndex 자료형이 만들어집니다. 그리고 DatetimeIndex에는 freq 속성이 포함되어 있죠. freq 속상값을 지정하면 시간 간격을 조절하여 DatetimeIndex를 만들 수 있습니다. 아래에 freq 속성값으로 사용할 수 있는 시간 주기를 표로 정리했습니다.
#### freq 속성값으로 사용할 수 있는 시간 주기
- B : 평일만 포함
- C : 사용자가 정의한 평일만 포함
- D : 달력 일자 단위
- W : 주간 단위
- M : 월 마지막 날만 포함
- SM : 15일과 월 마지막 날만 포함
- BM : M주기의 값이 휴일이면 제외하고 평일만 포함
- CBM : BM에 사용자 정의 평일을 적용
- MS : 월 시작일만 포함
- SMS : 월 시작일과 15일만 포함
- BMS : MS 주기의 값이 휴일이면 제외하고 평일만 포함
- CBMS : BMS에 사용자 정의 평일을 적용
- Q : 3,6,9,12월 마지막 날만 포함
- BQ : 3,6,9,12월 분기 마지막 나이 휴일이면 제외하고 평일만 포함
- BQS : 3,6,9,12월 분기 시작일이 휴일이면 제외하고 평일만 포함
- A : 년의 마지막 날만 포함
- BA : 년의 마지막 날이 휴일이면 제외하고 평일만 포함
- AS : 년의 시작일만 포함
- BAS : 년의 시작일이 휴일이면 제외하고 평일만 포함
- BH : 평일을 시간 단위로 포함 (09:00 ~ 16:00)
- H : 시간 단위로 포함 (00:00~00:00)
- T : 분 단위 포함
- S : 초 단위 포함
- L : 밀리초 단위 포함
- U : 마이크로초 단위 포함
- N : 나노초 단위 포함
다음은 date_range 메서드의 greq 인잣값을 B로 설정하여 평일만 포함시킨 DatetimeIndex를 만든 것입니다.
```
print(pd.date_range('2017-01-01', '2017-01-07', freq='B'))
```
#### 시간 범위 수정하고 데이터 밀어내기 - shift 메서드
만약 나라별로 에볼라의 확산 속도를 비교하려면 발생하기 시작한 날짜를 옮기는 것이 좋습니다. 왜 그럴까요? 일단 ebola 데이터프레임으로 그래프를 그려보고 에볼라의 확산 속도를 비교하는 데 어떤 문제가 있는지 그리고 해결 방법응 무엇인지 알아보겠습니다.
#### 에볼라의 확산 속도 비교하기
#### 1.
다음은 ebola 데이터프레임의 Date 열을 인덱스로 지정한 다음 x축을 Date 열로, y축을 사망자 수로 지정하여 그린 그래프입니다.
```
import matplotlib.pyplot as plt
ebola.index = ebola['Date']
fig, ax = plt.subplots( )
ax = ebola.iloc[0:, 1:].plot(ax=ax)
ax.legend(fontsize=7, loc=2, borderaxespad=0.)
plt.show()
```
#### 2.
그런데 과정 1의 그래프는 각 나라의 에볼라 발병일이 달라 그래프가 그려지기 시작한 지점도 다릅니다. 달리기 속도를 비교하려면 같은 출발선에서 출발하여 시간을 측정해야겠죠? 에볼라의 확산 속도도 같은 방법으로 측정해야 합니다. 즉, 각 나라의 발병일을 가장 처음 에볼라가 발병한 Guinea와 동일한 위치로 옮겨야 나라별 에볼라의 확산 속도를 제대로 비교할 수 있습니다.
```
ebola_sub = ebola[['Day', 'Cases_Guinea', 'Cases_Liberia']]
print(ebola_sub.tail(10))
```
#### . 그래프를 그리기 위한 데이터프레임 준비하기
다음은 Date 열의 자료형을 datetime 오브젝트로 변환하여 ebola 데이터프레임을 다시 생성한 것입니다. 그런데 중간에 아예 날짜가 없는 데이터(2015년 01월 01일)도 있습니다. 이 데이터도 포함시켜야 확산 속도를 제대로 비교할 수 있습니다.
```
ebola = pd.read_csv('./data/country_timeseries.csv', parse_dates= ['Date'])
print(ebola.head().iloc[:, :5])
print(ebola.tail().iloc[:, :5])
```
#### 4.
다음은 Date 열을 인덱스로 지정한 다음 ebola 데이터프레임의 Date 열의 최댓값과 최솟값으로 시간 범위를 생성하여 new_idx에 저장한 것입니다.
이렇게 하면 날자가 아예 없었던 데이터의 인덱스를 생성할 수 있습니다.
```
ebola.index = ebola['Date']
new_idx = pd.date_range(ebola.index.min(), ebola.index.max())
```
#### 5.
그런데 new_idx를 살펴보면 ebola 데이터 집합에 있는 시간순서와 반대로 생성되어 있습니다. 다음은 시간 순서를 맞추기 위해 reversed 메서드를 사용하여 인덱스를 반대로 뒤집은 것입니다.
```
print(new_idx)
new_idx = reversed(new_idx)
```
#### 6.
다음은 reindex 메서드를 사용하여 새로 생성한 인덱스(new_idx)를 새로운 인덱스로 지정한 것입니다. 그러면 2015년 01월 01일 데이터와 같은 ebola 데이터프레임에 아예 없었던 날짜가 추가됩니다. 이제 그래프를 그리기 위한 데이터프레임이 준비되었습니다.
```
ebola = ebola.reindex(new_idx)
print(ebola.head().iloc[:, :5])
print(ebola.tail().iloc[:, :5])
```
#### 7. 각 나라의 에볼라 발병일 옮기기
다음은 last_valid_index, first_valid_index 메서드를 사용하여 각 나라의 에볼라 발병일을 구한 것입니다. 각각의 메서드는 유효한 값이 있는 첫 번째와 마지막 인덱스를 반환합니다. 다음을 입력하고 결과를 확인해 보세요.
```
last_valid = ebola.apply(pd.Series.last_valid_index)
print(last_valid)
first_valid = ebola.apply (pd.Series.first_valid_index)
print(first_valid)
```
#### 8.
각 나라의 에볼라 발병일을 동일한 출발선으로 옮기려면 에볼라가 가장 처음 발병한 날(earliest_date)에서 각 나라의 에볼라 발병일을 뺀 만큼(shift_values)만 옮기면 됩니다.
```
earliest_date = ebola.index.min()
print(earliest_date)
shift_values = last_valid - earliest_date
print(shift_values)
```
#### 9.
이제 각 나라의 에볼라 발병일을 옮기면 됩니다. 다음은 shift 메서드를 사용하여 모든 열의 값을 shift_values 값만큼 옮긴 것입니다. shift 메서드는 인잣값만큼 데이터를 밀어내는 메서드입니다.
```
ebola_dict = {}
for idx, col in enumerate(ebola):
d = shift_values[idx].days
shifted = ebola[col].shift(d)
ebola_dict[col] =shifted
```
#### 10.
ebola_dict에는 시간을 다시 설정한 데이터가 딕셔너리 형태로 저장되어 있습니다 다음은 DataFrame 메서드를 사용하여 ebola_dict의 값을 데이터프레임으로 변환한 것입니다.
```
ebola_shift = pd.DataFrame(ebola_dict)
```
#### 11.
이제 에볼라의 최초 발병일(2014-03-22)을 기준으로 모든 열의 데이터가 옮겨졌습니다.
```
print(ebola_shift.tail())
```
#### 12.
마지막으로 인덱스를 Day 열로 지정하고 그래프에 필요 없는 Date, Day열은 삭제하면 그래프를 그리기 위한 데이터프레임이 완성됩니다.
```
ebola_shift.index = ebola_shift['Day']
ebola_shift = ebola_shift.drop(['Date', 'Day'], axis = 1)
print(ebola_shift.tail())
```
#### 13.
다음은 지금까지 만든 데이터프레임으로 다시 그린 그래프입니다.
```
fig, ax = plt.subplots()
ax = ebola_shift.iloc[:, :].plot(ax=ax)
ax.legend(fontsize=7, loc=2, borderaxespad=0.)
plt.show()
```
#### 마무리하며
판다스 라이브러리는 시간을 다룰 수 있는 다양한 기능을 제공합니다. 이 장에서는 시계열 데이터와 깊은 연관성이 있는 에볼라 데이터 및 주식 데이터를 주로 다루었습니다. 우리 주변의 상당수의 데이터는 시간과 깊은 연관성이 있는 경우가 많습니다. 시계열 데이터를 능숙하게 다루는 것은 데이터 분석가의 기본 소양이므로 이 장의 내용은 반드시 익혀두기 바랍니다.
#### 출처 : Doit 데이터 분석을 위한 판다스 입문
|
github_jupyter
|
from datetime import datetime
now1 = datetime.now()
print(now1)
now2 = datetime.today()
print(now2)
t1 = datetime.now()
t2 = datetime(1970, 1, 1)
t3 = datetime(1970, 12, 12, 13, 24, 34)
print(t1)
print(t2)
print(t3)
diff1 = t1 - t2
print(diff1)
print(type(diff1))
diff2 = t2 - t1
print(diff2)
print(type(diff2))
import pandas as pd
import os
ebola = pd.read_csv('./data/country_timeseries.csv')
print(ebola.info())
ebola['date_dt'] = pd.to_datetime(ebola['Date'])
print(ebola.info())
test_df1 = pd.DataFrame({'order_day':['01/01/15', '02/01/15', '03/01/15']})
test_df1['date_dt1'] = pd.to_datetime(test_df1['order_day'], format = '%d/%m/%y')
test_df1['date_dt2'] = pd.to_datetime(test_df1['order_day'], format = '%m/%d/%y')
test_df1['date_dt3'] = pd.to_datetime(test_df1['order_day'], format = '%y/%m/%d')
print(test_df1)
test_df2 = pd.DataFrame({'order_day':['01-01-15', '02-01-15', '03-01-15']})
test_df2['date_dt'] = pd.to_datetime(test_df2['order_day'], format='%d-%m-%y')
print(test_df2)
ebola1 = pd.read_csv('./data/country_timeseries.csv', parse_dates = ['Date'])
print(ebola1.info())
date_series = pd.Series(['2018-05-16', '2018-05-17', '2018-05-18'])
d1 = pd.to_datetime(date_series)
print(d1)
print(d1[0].year)
print(d1[0].month)
print(d1[0].day)
ebola = pd.read_csv('./data/country_timeseries.csv')
ebola['date_dt'] = pd.to_datetime(ebola['Date'])
print(ebola[['Date', 'date_dt']].head())
print(ebola['date_dt'][3].year)
print(ebola['date_dt'][3].month)
print(ebola['date_dt'][3].day)
ebola['year'] = ebola['date_dt'].dt.year
print(ebola[['Date', 'date_dt', 'year']].head())
ebola['month'], ebola['day'] = (ebola['date_dt'].dt.month, ebola['date_dt'].dt.day)
print(ebola[['Date', 'date_dt', 'year', 'month', 'day']].head())
print(ebola.info())
print(ebola.iloc[-5:,:5])
print(ebola['date_dt'].min())
print(type(ebola['date_dt'].min()))
ebola['outbreak_d'] = ebola['date_dt'] - ebola['date_dt'].min()
print(ebola[['Date', 'Day', 'outbreak_d']].head())
banks = pd.read_csv('./data/banklist.csv')
print(banks.head())
banks_no_dates = pd.read_csv('./data/banklist.csv')
print(banks_no_dates.info())
banks = pd.read_csv('./data/banklist.csv', parse_dates=[5,6])
print(banks.info())
banks['closing_quarter'], banks['closing_year'] = (banks['Closing Date'].dt.quarter, banks['Closing Date'].dt.year)
print(banks.head())
closing_year = banks.groupby(['closing_year']).size()
print(closing_year)
closing_year_q = banks.groupby(['closing_year', 'closing_quarter']).size()
print(closing_year_q)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax = closing_year.plot()
plt.show()
fig, ax = plt.subplots()
ax = closing_year_q.plot()
plt.show()
!pip install pandas-datareader
pd.core.common.is_list_like = pd.api.types.is_list_like
import pandas_datareader as pdr
tesla = pdr.get_data_quandl('TSLA', api_key = 'srXDVTSXUEfYySwasC3N')
tesla.to_csv('./data/tesla_stock_quandl.csv')
print(tesla.head())
tesla = pd.read_csv('./data/tesla_stock_quandl.csv', parse_dates=[0])
print(tesla.info())
print(tesla.loc[(tesla.Date.dt.year == 2010) & (tesla.Date.dt.month == 6)])
tesla.index = tesla['Date']
print(tesla.index)
print(tesla['2015'].iloc[:5, :5])
print(tesla['2010-06'].iloc[:, :5])
tesla['ref_date'] = tesla['Date'] - tesla['Date'].min()
print(tesla.head())
tesla.index = tesla['ref_date']
print(tesla.iloc[:5, :5])
print(tesla['5day':].iloc[:5, :5])
ebola = pd.read_csv('./data/country_timeseries.csv', parse_dates=[0])
print(ebola.iloc[:5, :5])
print(ebola.iloc[-5:, :5])
head_range = pd.date_range(start='2014-12-31', end='2015-01-05')
print(head_range)
ebola_5 = ebola.head()
ebola_5.index = ebola_5['Date']
ebola_5.reindex(head_range)
print(ebola_5.iloc[:5, :5])
print(pd.date_range('2017-01-01', '2017-01-07', freq='B'))
import matplotlib.pyplot as plt
ebola.index = ebola['Date']
fig, ax = plt.subplots( )
ax = ebola.iloc[0:, 1:].plot(ax=ax)
ax.legend(fontsize=7, loc=2, borderaxespad=0.)
plt.show()
ebola_sub = ebola[['Day', 'Cases_Guinea', 'Cases_Liberia']]
print(ebola_sub.tail(10))
ebola = pd.read_csv('./data/country_timeseries.csv', parse_dates= ['Date'])
print(ebola.head().iloc[:, :5])
print(ebola.tail().iloc[:, :5])
ebola.index = ebola['Date']
new_idx = pd.date_range(ebola.index.min(), ebola.index.max())
print(new_idx)
new_idx = reversed(new_idx)
ebola = ebola.reindex(new_idx)
print(ebola.head().iloc[:, :5])
print(ebola.tail().iloc[:, :5])
last_valid = ebola.apply(pd.Series.last_valid_index)
print(last_valid)
first_valid = ebola.apply (pd.Series.first_valid_index)
print(first_valid)
earliest_date = ebola.index.min()
print(earliest_date)
shift_values = last_valid - earliest_date
print(shift_values)
ebola_dict = {}
for idx, col in enumerate(ebola):
d = shift_values[idx].days
shifted = ebola[col].shift(d)
ebola_dict[col] =shifted
ebola_shift = pd.DataFrame(ebola_dict)
print(ebola_shift.tail())
ebola_shift.index = ebola_shift['Day']
ebola_shift = ebola_shift.drop(['Date', 'Day'], axis = 1)
print(ebola_shift.tail())
fig, ax = plt.subplots()
ax = ebola_shift.iloc[:, :].plot(ax=ax)
ax.legend(fontsize=7, loc=2, borderaxespad=0.)
plt.show()
| 0.182936 | 0.982271 |
```
import pandas as pd
import numpy as np
import networkx as x
```
# WORK IN PROGRESS
## Dynamics
We assume t-cell dynamics as below as from [Almocera et al](https://www.biorxiv.org/content/biorxiv/early/2017/08/11/174961.full.pdf), but with lysis (from NK cells) and delayed replication start as a separate state
dI/dt = p V (1 - V/Kv) - I/t
dV/dt = I/t - (cE + l)V
dE/dt = (E0 - E)δe + G(V)E
p = Ro * (1 - (c E + l) + l m) #
G(I) = rV/(V + Ke)
R0 = pδe/(cv Ne)
TODO: Model the regulation of NK cells (for lysis / apoptosis), instead of assuming they kill only through lysis a fixed rate
The slow virus takes sixty times as long to start producing copies
```
r_slow = 1e-2
r_fast = r_slow
carrying_v = 6e5
carrying_e = 3e3
delta_e = 3e-2
e_0 = 1e6
r0_fast = .5
t_fast = 1
c_v = 1e-6
t_slow = t_fast * 10
lysis_multiplier = 2
lysis_rate = 1e-2
r0_slow = r0_fast
def compute(I, V, E, r, carrying_v, carrying_e, delta_e, e_0, c_v, r0, t, initial, lysis_multiplier, lysis_rate):
for period in range(len(V) - 1):
I_old = I[period]
V_old = V[period]
E_old = E[period]
p = r0 * (max(0, (1 - c_v * E_old - lysis_rate)) + lysis_rate * lysis_multiplier)
flux_I_infection = max(0, p * V_old * (1 - (V_old + I_old)/carrying_v))
flux_I_lysis = lysis_rate * I_old
flux_V_ready = I_old/t
flux_V_lysis = lysis_rate * V_old
flux_V_cleanup = c_v * V_old
flux_E = (e_0 - E_old) * delta_e + r * V_old / (V_old + carrying_e) * E_old
I.loc[period + 1] = int(max(0, I_old + flux_I_infection - flux_V_ready - flux_I_lysis))
V.loc[period + 1] = int(max(0, V_old - flux_V_cleanup + flux_V_ready - flux_V_lysis))
E.loc[period + 1] = int(max(0, E_old + flux_E))
initial_infections = [1e2] #np.linspace(1e1, 1e3, 5)
# initial = 1e6
allele_multipliers = np.arange(.2, 2, .2)
results_I = []
results_V = []
results_E = []
results_fast_I = []
results_fast_V = []
results_fast_E = []
for initial in initial_infections:
for a in allele_multipliers:
slow = pd.DataFrame(np.zeros((1000, 3)), index=range(1000), columns=['I', 'V', 'E'])
fast = pd.DataFrame(np.zeros((1000, 3)), index=range(1000), columns=['I', 'V', 'E'])
slow.loc[0, :] = (initial, 0, e_0)
fast.loc[0, :] = (initial, 0, e_0)
compute(slow['I'], slow['V'], slow['E'], r_slow, carrying_v, carrying_e, delta_e, e_0, c_v * a, r0_slow, t_slow, initial, lysis_multiplier, lysis_rate)
compute(fast['I'], fast['V'], fast['E'], r_fast, carrying_v, carrying_e, delta_e, e_0, c_v * a, r0_fast, t_fast, initial, lysis_multiplier, lysis_rate)
results_I.append(slow['I'])
results_V.append(slow['V'])
results_E.append(slow['E'])
results_fast_I.append(fast['I'])
results_fast_V.append(fast['V'])
results_fast_E.append(fast['E'])
trajectories = pd.concat(results_V, axis=1)
trajectories_fast = pd.concat(results_fast_V, axis=1)
trajectories.T.reset_index(drop=True).T.plot(figsize=(30, 30))
trajectories_fast.T.reset_index(drop=True).T.plot(figsize=(30, 30))
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import networkx as x
r_slow = 1e-2
r_fast = r_slow
carrying_v = 6e5
carrying_e = 3e3
delta_e = 3e-2
e_0 = 1e6
r0_fast = .5
t_fast = 1
c_v = 1e-6
t_slow = t_fast * 10
lysis_multiplier = 2
lysis_rate = 1e-2
r0_slow = r0_fast
def compute(I, V, E, r, carrying_v, carrying_e, delta_e, e_0, c_v, r0, t, initial, lysis_multiplier, lysis_rate):
for period in range(len(V) - 1):
I_old = I[period]
V_old = V[period]
E_old = E[period]
p = r0 * (max(0, (1 - c_v * E_old - lysis_rate)) + lysis_rate * lysis_multiplier)
flux_I_infection = max(0, p * V_old * (1 - (V_old + I_old)/carrying_v))
flux_I_lysis = lysis_rate * I_old
flux_V_ready = I_old/t
flux_V_lysis = lysis_rate * V_old
flux_V_cleanup = c_v * V_old
flux_E = (e_0 - E_old) * delta_e + r * V_old / (V_old + carrying_e) * E_old
I.loc[period + 1] = int(max(0, I_old + flux_I_infection - flux_V_ready - flux_I_lysis))
V.loc[period + 1] = int(max(0, V_old - flux_V_cleanup + flux_V_ready - flux_V_lysis))
E.loc[period + 1] = int(max(0, E_old + flux_E))
initial_infections = [1e2] #np.linspace(1e1, 1e3, 5)
# initial = 1e6
allele_multipliers = np.arange(.2, 2, .2)
results_I = []
results_V = []
results_E = []
results_fast_I = []
results_fast_V = []
results_fast_E = []
for initial in initial_infections:
for a in allele_multipliers:
slow = pd.DataFrame(np.zeros((1000, 3)), index=range(1000), columns=['I', 'V', 'E'])
fast = pd.DataFrame(np.zeros((1000, 3)), index=range(1000), columns=['I', 'V', 'E'])
slow.loc[0, :] = (initial, 0, e_0)
fast.loc[0, :] = (initial, 0, e_0)
compute(slow['I'], slow['V'], slow['E'], r_slow, carrying_v, carrying_e, delta_e, e_0, c_v * a, r0_slow, t_slow, initial, lysis_multiplier, lysis_rate)
compute(fast['I'], fast['V'], fast['E'], r_fast, carrying_v, carrying_e, delta_e, e_0, c_v * a, r0_fast, t_fast, initial, lysis_multiplier, lysis_rate)
results_I.append(slow['I'])
results_V.append(slow['V'])
results_E.append(slow['E'])
results_fast_I.append(fast['I'])
results_fast_V.append(fast['V'])
results_fast_E.append(fast['E'])
trajectories = pd.concat(results_V, axis=1)
trajectories_fast = pd.concat(results_fast_V, axis=1)
trajectories.T.reset_index(drop=True).T.plot(figsize=(30, 30))
trajectories_fast.T.reset_index(drop=True).T.plot(figsize=(30, 30))
| 0.393269 | 0.78016 |
# ARMA Models
> Dive straight in and learn about the most important properties of time series. You'll learn about stationarity and how this is important for ARMA models. You'll learn how to test for stationarity by eye and with a standard statistical test. Finally, you'll learn the basic structure of ARMA models and use this to generate some ARMA data and fit an ARMA model. This is the Summary of lecture "ARIMA Models in Python", via datacamp.
- toc: true
- badges: true
- comments: true
- author: Chanseok Kang
- categories: [Python, Datacamp, Time_Series_Analysis]
- image: images/train_test.png
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['figure.figsize'] = (10, 5)
plt.style.use('fivethirtyeight')
```
## Intro to time series and stationarity
### Exploration
In this exercise you will kick off your journey to become an ARIMA master by loading and plotting a time series. You probably do this all the time, but this is just a refresher.
You will be exploring a dataset of monthly US candy production between 1972 and 2018.
Specifically, you are plotting the industrial production index IPG3113N. This is total amount of sugar and confectionery products produced in the USA per month, as a percentage of the January 2012 production. So 120 would be 120% of the January 2012 industrial production.
Check out how this quantity has changed over time and how it changes throughout the year.
```
# Load in the time series
candy = pd.read_csv('./dataset/candy_production.csv', index_col='date', parse_dates=True)
# Plot ant show the time series on axis ax
fig, ax = plt.subplots();
candy.plot(ax=ax);
```
### Train-test splits
In this exercise you are going to take the candy production dataset and split it into a train and a test set. Like you understood in the video exercise, the reason to do this is so that you can test the quality of your model fit when you are done.
```
# Split the data into a train and test set
candy_train = candy.loc[:'2006']
candy_test = candy.loc['2007':]
# Create an axis
fig, ax = plt.subplots();
# Plot the train and test sets on the axis ax
candy_train.plot(ax=ax);
candy_test.plot(ax=ax);
plt.savefig('../images/train_test.png')
```
### Is it stationary
Identifying whether a time series is stationary or non-stationary is very important. If it is stationary you can use ARMA models to predict the next values of the time series. If it is non-stationary then you cannot use ARMA models, however, as you will see in the next lesson, you can often transform non-stationary time series to stationary ones.
## Making time series stationary
- The augmented Dicky-Fuller test
- Tests for non-stationary
- Null hypothesis is time series is non-stationary
### Augmented Dicky-Fuller
In this exercise you will run the augmented Dicky-Fuller test on the earthquakes time series to test for stationarity. You plotted this time series in the last exercise. It looked like it could be stationary, but earthquakes are very damaging. If you want to make predictions about them you better be sure.
Remember that if it were not stationary this would mean that the number of earthquakes per year has a trend and is changing. This would be terrible news if it is trending upwards, as it means more damage. It would also be terrible news if it were trending downwards, it might suggest the core of our planet is changing and this could have lots of knock on effects for us!
```
earthquake = pd.read_csv('./dataset/earthquakes.csv', index_col='date', parse_dates=True)
earthquake.drop(['Year'], axis=1, inplace=True)
earthquake
from statsmodels.tsa.stattools import adfuller
# Run test
result = adfuller(earthquake['earthquakes_per_year'])
# Print test statistic
print(result[0])
# Print p-value
print(result[1])
# Print critical values
print(result[4])
```
### Taking the difference
In this exercise, you will to prepare a time series of the population of a city for modeling. If you could predict the growth rate of a city then it would be possible to plan and build the infrastructure that the city will need later, thus future-proofing public spending. In this case the time series is fictitious but its perfect to practice on.
You will test for stationarity by eye and use the Augmented Dicky-Fuller test, and take the difference to make the dataset stationary.
```
city = pd.read_csv('./dataset/city.csv', parse_dates=True, index_col='date')
# Run the ADF test on the time series
result = adfuller(city['city_population'])
# Plot the time series
fig, ax = plt.subplots();
city.plot(ax=ax);
# Print the test statistic and the p-value
print('ADF Statistic:', result[0])
print('p-value:', result[1])
# Calculate the first difference of the time series
city_stationary = city.diff().dropna()
# Run ADF test on the differenced time series
result = adfuller(city_stationary['city_population'])
# Plot the differenced time series
fig, ax = plt.subplots();
city_stationary.plot(ax=ax);
# Print the test statistic and the p-value
print('ADF Statistic:', result[0])
print('p-value:', result[1])
# Calculate the second difference of the time series
city_stationary = city.diff().diff().dropna()
# Run ADF test on the differenced time series
result = adfuller(city_stationary['city_population'])
# Plot the differenced time series
fig, ax = plt.subplots();
city_stationary.plot(ax=ax);
# Print the test statistic and the p-value
print('ADF Statistic:', result[0])
print('p-value:', result[1])
```
### Other tranforms
Differencing should be the first transform you try to make a time series stationary. But sometimes it isn't the best option.
A classic way of transforming stock time series is the log-return of the series. This is calculated as follows:
$$ \log\text{_return} (y_t) = \log \big(\frac{y_t}{y_{t-1}}\big)$$
You can calculate the log-return of this DataFrame by substituting:
$y_t$ → amazon
$y_{t-1}$ → amazon.shift(1)
$\log()$ → ```np.log()```
In this exercise you will compare the log-return transform and the first order difference of the Amazon stock time series to find which is better for making the time series stationary.
```
amazon = pd.read_csv('./dataset/amazon_close.csv', index_col='date', parse_dates=True)
amazon.head()
# Calculate the first difference and drop the nans
amazon_diff = amazon.diff()
amazon_diff = amazon_diff.dropna()
# Run test and print
result_diff = adfuller(amazon_diff['close'])
print(result_diff)
# Calculate the log-return and drop nans
amazon_log = np.log(amazon.div(amazon.shift(1)))
amazon_log = amazon_log.dropna()
# Run test and print
result_log = adfuller(amazon_log['close'])
print(result_log)
```
## Intro to AR, MA and ARMA models
- AR models
- Autoregressive (AR) model
- AR(1) model:
$$ y_t = a_1 y_{t-1} + \epsilon_t $$
- AR(2) model:
$$ y_t = a_1 y_{t-1} + a_2 y_{t-2} + \epsilon_t $$
- AR(p) model:
$$ y_t = a_1 y_{t-1} + a_2 y_{t-2} + \cdots + a_p y_{t-p} + \epsilon_t $$
- MA models
- Moving Average (MA) model
- MA(1) model:
$$ y_t = m_1 \epsilon_{t-1} + \epsilon_t $$
- MA(2) model:
$$ y_t = m_1 \epsilon_{t-1} + m_2 \epsilon_{t-2} + \epsilon_t $$
- MA(q) model:
$$ y_t = m_1 \epsilon_{t-1} + m_2 \epsilon_{t-2} + \cdots + m_q \epsilon_{t-q} + \epsilon_t $$
- ARMA models
- Autoregressive moving-average (ARMA) model
- ARMA = AR + MA
- ARMA(1, 1) model:
$$ y_t = a_1 y_{t-1} + m_1 \epsilon_{t-1} + \epsilon_t $$
- ARMA(p, q) model:
- p is order of AR part
- q is order of MA part
### Model order
When fitting and working with AR, MA and ARMA models it is very important to understand the model order. You will need to pick the model order when fitting. Picking this correctly will give you a better fitting model which makes better predictions. So in this section you will practice working with model order.
```
ar_coefs = [1, 0.4, -0.1]
ma_coefs = [1, 0.2]
from statsmodels.tsa.arima_process import arma_generate_sample
y = arma_generate_sample(ar_coefs, ma_coefs, nsample=100, scale=0.5)
plt.plot(y);
```
### Generating ARMA data
In this exercise you will generate 100 days worth of AR/MA/ARMA data. Remember that in the real world applications, this data could be changes in Google stock prices, the energy requirements of New York City, or the number of cases of flu.
You can use the ```arma_generate_sample()``` function available in your workspace to generate time series using different AR and MA coefficients.
Remember for any model ARMA(p,q):
- The list ar_coefs has the form $[1, -a_1, -a_2, ..., -a_p]$.
- The list ma_coefs has the form $[1, m_1, m_2, ..., m_q]$,
where $a_i$ are the lag-i AR coefficients and $m_j$ are the lag-j MA coefficients.
```
np.random.seed(1)
```
#### MA(1) model with MA lag coefficient of -0.7
```
# Set coefficients
ar_coefs = [1]
ma_coefs = [1, -0.7]
# Generate data
y = arma_generate_sample(ar_coefs, ma_coefs, nsample=100, scale=0.5)
plt.plot(y);
plt.ylabel(r'$y_t$');
plt.xlabel(r'$t$');
```
#### AR(2) model with AR lag-1 and lag-2 coefficients of 0.3 and 0.2
```
np.random.seed(2)
# Set coefficients
ar_coefs = [1, -0.3, -0.2]
ma_coefs = [1]
# Generate data
y = arma_generate_sample(ar_coefs, ma_coefs, nsample=100, scale=0.5)
plt.plot(y);
plt.ylabel(r'$y_t$');
plt.xlabel(r'$t$');
```
#### ARMA model with $y_t = -0.2 y_{t-1} + 0.3 \epsilon_{t-1} + 0.4 \epsilon_{t-2} + \epsilon_t$
```
np.random.seed(3)
# Set coefficients
ar_coefs = [1, 0.2]
ma_coefs = [1, 0.3, 0.4]
# Generate data
y = arma_generate_sample(ar_coefs, ma_coefs, nsample=100, scale=0.5)
plt.plot(y);
plt.ylabel(r'$y_t$');
plt.xlabel(r'$t$');
```
### Fitting Prelude
Great, you understand model order! Understanding the order is important when it comes to fitting models. You will always need to select the order of model you fit to your data, no matter what that data is.
In this exercise you will do some basic fitting. Fitting models is the next key step towards making predictions. We'll go into this more in the next chapter but let's get a head start.
Some example ARMA(1,1) data have been created and are available in your environment as y. This data could represent the amount of traffic congestion. You could use forecasts of this to suggest the efficient routes for drivers.
```
from statsmodels.tsa.arima_model import ARMA
# Instantiate the model
model = ARMA(y, order=(1, 1))
# Fit the model
results = model.fit()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['figure.figsize'] = (10, 5)
plt.style.use('fivethirtyeight')
# Load in the time series
candy = pd.read_csv('./dataset/candy_production.csv', index_col='date', parse_dates=True)
# Plot ant show the time series on axis ax
fig, ax = plt.subplots();
candy.plot(ax=ax);
# Split the data into a train and test set
candy_train = candy.loc[:'2006']
candy_test = candy.loc['2007':]
# Create an axis
fig, ax = plt.subplots();
# Plot the train and test sets on the axis ax
candy_train.plot(ax=ax);
candy_test.plot(ax=ax);
plt.savefig('../images/train_test.png')
earthquake = pd.read_csv('./dataset/earthquakes.csv', index_col='date', parse_dates=True)
earthquake.drop(['Year'], axis=1, inplace=True)
earthquake
from statsmodels.tsa.stattools import adfuller
# Run test
result = adfuller(earthquake['earthquakes_per_year'])
# Print test statistic
print(result[0])
# Print p-value
print(result[1])
# Print critical values
print(result[4])
city = pd.read_csv('./dataset/city.csv', parse_dates=True, index_col='date')
# Run the ADF test on the time series
result = adfuller(city['city_population'])
# Plot the time series
fig, ax = plt.subplots();
city.plot(ax=ax);
# Print the test statistic and the p-value
print('ADF Statistic:', result[0])
print('p-value:', result[1])
# Calculate the first difference of the time series
city_stationary = city.diff().dropna()
# Run ADF test on the differenced time series
result = adfuller(city_stationary['city_population'])
# Plot the differenced time series
fig, ax = plt.subplots();
city_stationary.plot(ax=ax);
# Print the test statistic and the p-value
print('ADF Statistic:', result[0])
print('p-value:', result[1])
# Calculate the second difference of the time series
city_stationary = city.diff().diff().dropna()
# Run ADF test on the differenced time series
result = adfuller(city_stationary['city_population'])
# Plot the differenced time series
fig, ax = plt.subplots();
city_stationary.plot(ax=ax);
# Print the test statistic and the p-value
print('ADF Statistic:', result[0])
print('p-value:', result[1])
In this exercise you will compare the log-return transform and the first order difference of the Amazon stock time series to find which is better for making the time series stationary.
## Intro to AR, MA and ARMA models
- AR models
- Autoregressive (AR) model
- AR(1) model:
$$ y_t = a_1 y_{t-1} + \epsilon_t $$
- AR(2) model:
$$ y_t = a_1 y_{t-1} + a_2 y_{t-2} + \epsilon_t $$
- AR(p) model:
$$ y_t = a_1 y_{t-1} + a_2 y_{t-2} + \cdots + a_p y_{t-p} + \epsilon_t $$
- MA models
- Moving Average (MA) model
- MA(1) model:
$$ y_t = m_1 \epsilon_{t-1} + \epsilon_t $$
- MA(2) model:
$$ y_t = m_1 \epsilon_{t-1} + m_2 \epsilon_{t-2} + \epsilon_t $$
- MA(q) model:
$$ y_t = m_1 \epsilon_{t-1} + m_2 \epsilon_{t-2} + \cdots + m_q \epsilon_{t-q} + \epsilon_t $$
- ARMA models
- Autoregressive moving-average (ARMA) model
- ARMA = AR + MA
- ARMA(1, 1) model:
$$ y_t = a_1 y_{t-1} + m_1 \epsilon_{t-1} + \epsilon_t $$
- ARMA(p, q) model:
- p is order of AR part
- q is order of MA part
### Model order
When fitting and working with AR, MA and ARMA models it is very important to understand the model order. You will need to pick the model order when fitting. Picking this correctly will give you a better fitting model which makes better predictions. So in this section you will practice working with model order.
### Generating ARMA data
In this exercise you will generate 100 days worth of AR/MA/ARMA data. Remember that in the real world applications, this data could be changes in Google stock prices, the energy requirements of New York City, or the number of cases of flu.
You can use the ```arma_generate_sample()``` function available in your workspace to generate time series using different AR and MA coefficients.
Remember for any model ARMA(p,q):
- The list ar_coefs has the form $[1, -a_1, -a_2, ..., -a_p]$.
- The list ma_coefs has the form $[1, m_1, m_2, ..., m_q]$,
where $a_i$ are the lag-i AR coefficients and $m_j$ are the lag-j MA coefficients.
#### MA(1) model with MA lag coefficient of -0.7
#### AR(2) model with AR lag-1 and lag-2 coefficients of 0.3 and 0.2
#### ARMA model with $y_t = -0.2 y_{t-1} + 0.3 \epsilon_{t-1} + 0.4 \epsilon_{t-2} + \epsilon_t$
### Fitting Prelude
Great, you understand model order! Understanding the order is important when it comes to fitting models. You will always need to select the order of model you fit to your data, no matter what that data is.
In this exercise you will do some basic fitting. Fitting models is the next key step towards making predictions. We'll go into this more in the next chapter but let's get a head start.
Some example ARMA(1,1) data have been created and are available in your environment as y. This data could represent the amount of traffic congestion. You could use forecasts of this to suggest the efficient routes for drivers.
| 0.738009 | 0.98752 |
# Setting of stack phase
At this phase we are going to set the stacked-phase dataset. This method is based just in apply method. It implies less memory.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from utils.trainFold import getVector
import sys
sys.path.append('../dsbase/src/main')
from AdaBoostClassificationDSBase import AdaBoostClassificationDSBaseModel
```
## Loading the original stacked dataset and shuffle it
```
#df = pd.read_csv('datasets/train_stack.csv')
#df_frac = df.sample(frac=1)
#df_frac.to_csv('datasets/train_stack_shuffled.csv')
# cat datasets/train_stack_shuffled.csv | head -n +4500001 > datasets/train_stack_shuffled_reduced.csv
df = pd.read_csv('datasets/train_stack_shuffled_reduced.csv.1')
df.shape
```
## Defining the Fold X processing
### Defining helping functions
```
def loadColumnCategoricalOrder(df, columns_categorical):
columns_categorical_order_dict = {}
for x in columns_categorical:
columns_categorical_order_dict[x] = np.where(df.columns == x)[0][0]
return columns_categorical_order_dict
def loadColumnCategoricalVectors(fold_id, columns_categorical):
columns_categorical_vectors_dict = {}
out_path = 'models/fold' + str(fold_id)
for c in columns_categorical:
vec = np.load('models/fold' + str(fold_id) + "/" + c + ".sav.npy")
columns_categorical_vectors_dict[c] = vec
return columns_categorical_vectors_dict
def loadModel(fold_id):
# --------------------------------------
# Load the i-th model and process
print(' loading model ...')
model = AdaBoostClassificationDSBaseModel('AB2',None,None,None,None,None,None)
model.load('models/fold' + str(fold_id))
return model
def calculate(x, cc, cc_o, cc_v, model):
xnp = x.values
acc=0
for c in cc:
index = cc_o[c] + acc
vec = cc_v[c]
new = getVector(xnp[index], vec)
xnp = np.delete(xnp, index)
xnp = np.insert(xnp, index, new)
acc += (new.size - 1)
pre_result = model.scalerX.transform(xnp.reshape(1,-1))
result = model.model.predict_proba(pre_result)
return result[0,1]
```
### calculating support variables
```
df_w = df.drop(['Unnamed: 0','MachineIdentifier','HasDetections','fold'], axis=1)
columns_categorical = df_w.select_dtypes(include=['object']).columns
cc_order = loadColumnCategoricalOrder(df_w,columns_categorical)
N = 9
for i in range(1,N+1):
print('-------- Process Fold ',i,' -------------------')
print('loading vectors ...')
cc_values_f = loadColumnCategoricalVectors(i,columns_categorical)
print('loading model ...')
model_f = loadModel(i)
print('applying folding prediction ...')
df['f' + str(i)] = df_w.apply(func=calculate, axis=1, args=(columns_categorical, cc_order, cc_values_f, model_f))
# save security DatFrame
df['f' + str(i)].to_csv('datasets/f_stack.csv.' + str(i))
```
## Lets obtain the final stacked dataset
```
df[['HasDetections','fold','f1','f2','f3','f4','f5','f6','f7','f8','f9']].describe()
df.to_csv('datasets/train_stack_set.csv')
```
# End of stack train setting!!
Local Environment: stimated time -> 322 sec / 1000 elements
AWS EC2: stimated time -> 322 sec / ???elements
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from utils.trainFold import getVector
import sys
sys.path.append('../dsbase/src/main')
from AdaBoostClassificationDSBase import AdaBoostClassificationDSBaseModel
#df = pd.read_csv('datasets/train_stack.csv')
#df_frac = df.sample(frac=1)
#df_frac.to_csv('datasets/train_stack_shuffled.csv')
# cat datasets/train_stack_shuffled.csv | head -n +4500001 > datasets/train_stack_shuffled_reduced.csv
df = pd.read_csv('datasets/train_stack_shuffled_reduced.csv.1')
df.shape
def loadColumnCategoricalOrder(df, columns_categorical):
columns_categorical_order_dict = {}
for x in columns_categorical:
columns_categorical_order_dict[x] = np.where(df.columns == x)[0][0]
return columns_categorical_order_dict
def loadColumnCategoricalVectors(fold_id, columns_categorical):
columns_categorical_vectors_dict = {}
out_path = 'models/fold' + str(fold_id)
for c in columns_categorical:
vec = np.load('models/fold' + str(fold_id) + "/" + c + ".sav.npy")
columns_categorical_vectors_dict[c] = vec
return columns_categorical_vectors_dict
def loadModel(fold_id):
# --------------------------------------
# Load the i-th model and process
print(' loading model ...')
model = AdaBoostClassificationDSBaseModel('AB2',None,None,None,None,None,None)
model.load('models/fold' + str(fold_id))
return model
def calculate(x, cc, cc_o, cc_v, model):
xnp = x.values
acc=0
for c in cc:
index = cc_o[c] + acc
vec = cc_v[c]
new = getVector(xnp[index], vec)
xnp = np.delete(xnp, index)
xnp = np.insert(xnp, index, new)
acc += (new.size - 1)
pre_result = model.scalerX.transform(xnp.reshape(1,-1))
result = model.model.predict_proba(pre_result)
return result[0,1]
df_w = df.drop(['Unnamed: 0','MachineIdentifier','HasDetections','fold'], axis=1)
columns_categorical = df_w.select_dtypes(include=['object']).columns
cc_order = loadColumnCategoricalOrder(df_w,columns_categorical)
N = 9
for i in range(1,N+1):
print('-------- Process Fold ',i,' -------------------')
print('loading vectors ...')
cc_values_f = loadColumnCategoricalVectors(i,columns_categorical)
print('loading model ...')
model_f = loadModel(i)
print('applying folding prediction ...')
df['f' + str(i)] = df_w.apply(func=calculate, axis=1, args=(columns_categorical, cc_order, cc_values_f, model_f))
# save security DatFrame
df['f' + str(i)].to_csv('datasets/f_stack.csv.' + str(i))
df[['HasDetections','fold','f1','f2','f3','f4','f5','f6','f7','f8','f9']].describe()
df.to_csv('datasets/train_stack_set.csv')
| 0.438304 | 0.847274 |
# <font color=green> PYTHON PARA DATA SCIENCE - NUMPY
---
# <font color=green> 1. INTRODUÇÃO AO PYTHON
---
# 1.1 Introdução
> Python é uma linguagem de programação de alto nível com suporte a múltiplos paradigmas de programação. É um projeto *open source* e desde seu surgimento, em 1991, vem se tornando uma das linguagens de programação interpretadas mais populares.
>
> Nos últimos anos Python desenvolveu uma comunidade ativa de processamento científico e análise de dados e vem se destacando como uma das linguagens mais relevantes quando o assunto é ciência de dados e machine learning, tanto no ambiente acadêmico como também no mercado.
# 1.2 Instalação e ambiente de desenvolvimento
### Instalação Local
### https://www.python.org/downloads/
### ou
### https://www.anaconda.com/distribution/
### Google Colaboratory
### https://colab.research.google.com
### Verificando versão
```
!python -V
```
# 1.3 Trabalhando com arrays Numpy
```
import numpy as np
km = np.loadtxt('carros-km.txt')
km
anos = np.loadtxt('carros-anos.txt', dtype = int)
anos
```
### Obtendo a quilometragem média por ano
```
km_media = km / (2019 - anos)
km_media
type(km_media)
```
# <font color=green> 2. CARACTERÍSTICAS BÁSICAS DA LINGUAGEM
---
# 2.1 Operações matemáticas
### Operadores aritméticos: $+$, $-$, $*$, $/$, $**$, $\%$, $//$
### Adição ($+$)
```
2 + 2
```
### Subtração ($-$)
```
2 - 2
```
### Multiplicação ($*$)
```
2 * 3
```
### Divisão ($/$) e ($//$)
A operação divisão sempre retorna um número de ponto flutuante
```
10 / 3
10 // 3
```
### Exponenciação ($**$)
```
2 ** 3
```
### Resto da divisão ($\%$)
```
10 % 3
10 % 2
```
### Expressões matemáticas
```
5 * 2 + 3 * 2
(5 * 2) + (3 * 2)
5 * (2 + 3) * 2
```
### A variável _
No modo interativo, o último resultado impresso é atribuído à variável _
```
5 * 2
_ + 3 * 2
_ / 2
```
# 2.2 Variáveis
### Nomes de variáveis
- Nomes de variáveis pode começar com letras (a - z, A - Z) ou o caractere *underscore* (_):
> Altura
>
> _peso
- O restante do nome pode conter letras, números e o caractere "_":
> nome_da_variavel
>
> _valor
>
> dia_28_11_
- O nomes são *case sensitive*:
> Nome_Da_Variável $\ne$ nome_da_variavel $\ne$ NOME_DA_VARIAVEL
### <font color=red>Observações:
- Existem algumas palavras reservadas da linguagem que não podem ser utilizadas como nomes de variável:
| |Lista de palavras <br>reservadas em Python| |
|:-------------:|:------------:|:-------------:|
| and | as | not |
| assert | finally | or |
| break | for | pass |
| class | from | nonlocal |
| continue | global | raise |
| def | if | return |
| del | import | try |
| elif | in | while |
| else | is | with |
| except | lambda | yield |
| False | True | None |
### Declaração de variáveis
### Operadores de atribuição: $=$, $+=$, $-=$, $*=$, $/=$, $**=$, $\%=$, $//=$
```
ano_atual = 2019
ano_fabricacao = 2003
km_total = 44410.0
ano_atual
ano_fabricacao
km_total
```
# $$km_{média} = \frac {km_{total}}{(Ano_{atual} - Ano_{fabricação})}$$
### Operações com variáveis
```
km_media = km_total / (ano_atual - ano_fabricacao)
km_media
ano_atual = 2019
ano_fabricacao = 2003
km_total = 44410.0
km_media = km_total / (ano_atual - ano_fabricacao)
km_media
ano_atual = 2019
ano_fabricacao = 2003
km_total = 44410.0
km_media = km_total / (ano_atual - ano_fabricacao)
km_total = km_total + km_media
km_total
ano_atual = 2019
ano_fabricacao = 2003
km_total = 44410.0
km_media = km_total / (ano_atual - ano_fabricacao)
km_total += km_media
km_total
```
### Conclusão:
```
"valor = valor + 1" é equivalente a "valor += 1"
```
### Declaração múltipla
```
ano_atual, ano_fabricacao, km_total = 2019, 2003, 44410.0
ano_atual
ano_fabricacao
km_total
ano_atual, ano_fabricacao, km_total = 2019, 2003, 44410.0
km_media = km_total / (ano_atual - ano_fabricacao)
km_media
```
# 2.3 Tipos de dados
Os tipos de dados especificam como números e caracteres serão armazenados e manipulados dentro de um programa. Os tipos de dados básicos do Python são:
1. **Números**
1. ***int*** - Inteiros
- ***float*** - Ponto flutuante
- **Booleanos** - Assume os valores True ou False. Essencial quando começarmos a trabalhar com declarações condicionais
- ***Strings*** - Sequência de um ou mais caracteres que pode incluir letras, números e outros tipos de caracteres. Representa um texto.
- **None** - Representa a ausência de valor
### Números
```
ano_atual = 2019
type(ano_atual)
km_total = 44410.0
type(km_total)
```
### Booleanos
```
zero_km = True
type(zero_km)
zero_km = False
type(zero_km)
```
### Strings
```
nome = 'Jetta Variant'
nome
nome = "Jetta Variant"
nome
nome = 'Jetta "Variant"'
nome
nome = "Jetta 'Variant'"
nome
carro = '''
Nome
Idade
Nota
'''
type(carro)
```
### None
```
quilometragem = None
quilometragem
type(quilometragem)
```
# 2.4 Conversão de tipos
```
a = 10
b = 20
c = 'Python é '
d = 'legal'
type(a)
type(b)
type(c)
type(d)
a + b
c + d
# c + a
```
### Conversões de tipo
Funções int(), float(), str()
```
str(a)
type(str(a))
c + str(a)
float(a)
var = 3.141592
int(var)
var = 3.99
int(var)
```
# 2.5 Indentação, comentários e formatação de *strings*
### Indentação
Na linguagem Python os programas são estruturados por meio de indentação. Em qualquer linguagem de programação a prática da indentação é bastante útil, facilitando a leitura e também a manutenção do código. Em Python a indentação não é somente uma questão de organização e estilo, mas sim um requisito da linguagem.
```
ano_atual = 2019
ano_fabricacao = 2019
if (ano_atual == ano_fabricacao):
print('Verdadeiro')
else:
print('Falso')
```
### Comentários
Comentários são extremamente importantes em um programa. Consiste em um texto que descreve o que o programa ou uma parte específica do programa está fazendo. Os comentários são ignorados pelo interpretador Python.
Podemos ter comentários de uma única linha ou de múltiplas linhas.
```
# Isto é um comentário
ano_atual = 2019
ano_atual
# Isto
# é um
# comentário
ano_atual = 2019
ano_atual
'''Isto é um
comentário'''
ano_atual = 2019
ano_atual
# Definindo variáveis
ano_atual = 2019
ano_fabricacao = 2019
'''
Estrutura condicional que vamos
aprender na próxima aula
'''
if (ano_atual == ano_fabricacao): # Testando se condição é verdadeira
print('Verdadeiro')
else: # Testando se condição é falsa
print('Falso')
```
### Formatação de *strings*
## *str.format()*
https://docs.python.org/3.6/library/stdtypes.html#str.format
```
print('Olá, {}!'.format('Rodrigo'))
print('Olá, {}! Este é seu acesso de número {}'.format('Rodrigo', 32))
print('Olá, {nome}! Este é seu acesso de número {acessos}'.format(nome = 'Rodrigo', acessos = 32))
```
## *f-Strings*
https://docs.python.org/3.6/reference/lexical_analysis.html#f-strings
```
nome = 'Rodrigo'
acessos = 32
print(f'Olá, {nome}! Este é seu acesso de número {acessos}')
```
# <font color=green> 3. TRABALHANDO COM LISTAS
---
# 3.1 Criando listas
Listas são sequências **mutáveis** que são utilizadas para armazenar coleções de itens, geralmente homogêneos. Podem ser construídas de várias formas:
```
- Utilizando um par de colchetes: [ ], [ 1 ]
- Utilizando um par de colchetes com itens separados por vírgulas: [ 1, 2, 3 ]
```
```
Acessorios = ['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva']
Acessorios
type(Acessorios)
```
### Lista com tipos de dados variados
```
Carro_1 = ['Jetta Variant', 'Motor 4.0 Turbo', 2003, 44410.0, False, ['Rodas de liga', 'Travas elétricas', 'Piloto automático'], 88078.64]
Carro_2 = ['Passat', 'Motor Diesel', 1991, 5712.0, False, ['Central multimídia', 'Teto panorâmico', 'Freios ABS'], 106161.94]
Carro_1
Carro_2
Carros = [Carro_1, Carro_2]
Carros
```
# 3.2 Operações com listas
https://docs.python.org/3.6/library/stdtypes.html#common-sequence-operations
## *x in A*
Retorna **True** se um elemento da lista *A* for igual a *x*.
```
Acessorios
'Rodas de liga' in Acessorios
'4 X 4' in Acessorios
'Rodas de liga' not in Acessorios
'4 X 4' not in Acessorios
```
## *A + B*
Concatena as listas *A* e *B*.
```
A = ['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro']
B = ['Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva']
A
B
A + B
```
## *len(A)*
Tamanho da lista A.
```
len(Acessorios)
```
# 3.3 Seleções em listas
## *A[ i ]*
Retorna o i-ésimo item da lista *A*.
<font color=red>**Observação:**</font> Listas têm indexação com origem no zero.
```
Acessorios
Acessorios[0]
Acessorios[1]
Acessorios[-1]
Carros
Carros[0]
Carros[0][0]
Carros[0][-2]
Carros[0][-2][1]
```
## *A[ i : j ]*
Recorta a lista *A* do índice i até o j. Neste fatiamento o elemento com índice i é **incluído** e o elemento com índice j **não é incluído** no resultado.
```
Acessorios
Acessorios[2:5]
Acessorios[2:]
Acessorios[:5]
```
# 3.4 Métodos de listas
https://docs.python.org/3.6/library/stdtypes.html#mutable-sequence-types
```
Acessorios = ['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva']
```
## *A.sort()*
Ordena a lista *A*.
```
Acessorios
Acessorios.sort()
Acessorios
```
## *A.append(x)*
Adiciona o elemento *x* no final da lista *A*.
```
Acessorios.append('4 X 4')
Acessorios
```
## *A.pop(i)*
Remove e retorna o elemento de índice i da lista *A*.
<font color=red>**Observação:**</font> Por *default* o método *pop()* remove e retorna o último elemento de uma lista.
```
Acessorios.pop()
Acessorios
Acessorios.pop(3)
Acessorios
```
## *A.copy()*
Cria uma cópia da lista *A*.
<font color=red>**Observação:**</font> O mesmo resultado pode ser obtido com o seguinte código:
```
A[:]
```
```
Acessorios_2 = Acessorios
Acessorios_2
Acessorios_2.append('4 X 4')
Acessorios_2
Acessorios
Acessorios.pop()
Acessorios
Acessorios_2
Acessorios_2 = Acessorios.copy()
Acessorios_2
Acessorios_2.append('4 X 4')
Acessorios_2
Acessorios
Acessorios_2 = Acessorios[:]
Acessorios_2
```
# <font color=green> 4. ESTRUTURAS DE REPETIÇÃO E CONDICIONAIS
---
# 4.1 Instrução *for*
#### Formato padrão
```
for <variável> in <coleção>:
<instruções>
```
### Loops com listas
```
Acessorios = ['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva']
Acessorios
for item in Acessorios:
print(item)
```
### List comprehensions
https://docs.python.org/3.6/tutorial/datastructures.html#list-comprehensions
*range()* -> https://docs.python.org/3.6/library/functions.html#func-range
```
range(10)
list(range(10))
for i in range(10):
print(i ** 2)
quadrado = []
for i in range(10):
quadrado.append(i ** 2)
quadrado
[i ** 2 for i in range(10)]
```
# 4.2 Loops aninhados
```
dados = [
['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva'],
['Central multimídia', 'Teto panorâmico', 'Freios ABS', '4 X 4', 'Painel digital', 'Piloto automático', 'Bancos de couro', 'Câmera de estacionamento'],
['Piloto automático', 'Controle de estabilidade', 'Sensor crepuscular', 'Freios ABS', 'Câmbio automático', 'Bancos de couro', 'Central multimídia', 'Vidros elétricos']
]
dados
for lista in dados:
print(lista)
for lista in dados:
for item in lista:
print(item)
Acessorios = []
for lista in dados:
for item in lista:
Acessorios.append(item)
Acessorios
```
## *set()*
https://docs.python.org/3.6/library/stdtypes.html#types-set
```
list(set(Acessorios))
```
### List comprehensions
```
[item for lista in dados for item in lista]
list(set([item for lista in dados for item in lista]))
```
# 4.3 Instrução *if*
#### Formato padrão
```
if <condição>:
<instruções caso a condição seja verdadeira>
```
### Operadores de comparação: $==$, $!=$, $>$, $<$, $>=$, $<=$
### e
### Operadores lógicos: $and$, $or$, $not$
```
# 1º item da lista - Nome do veículo
# 2º item da lista - Ano de fabricação
# 3º item da lista - Veículo é zero km?
dados = [
['Jetta Variant', 2003, False],
['Passat', 1991, False],
['Crossfox', 1990, False],
['DS5', 2019, True],
['Aston Martin DB4', 2006, False],
['Palio Weekend', 2012, False],
['A5', 2019, True],
['Série 3 Cabrio', 2009, False],
['Dodge Jorney', 2019, False],
['Carens', 2011, False]
]
dados
zero_km_Y = []
for lista in dados:
if(lista[2] == True):
zero_km_Y.append(lista)
zero_km_Y
zero_km_N = []
for lista in dados:
if(lista[2] == False):
zero_km_N.append(lista)
zero_km_N
```
### List comprehensions
```
[lista for lista in dados if lista[2] == True]
```
# 4.4 Instruções *if-else* e *if-elif-else*
#### Formato padrão
```
if <condição>:
<instruções caso a condição seja verdadeira>
else:
<instruções caso a condição não seja verdadeira>
```
```
zero_km_Y, zero_km_N = [], []
for lista in dados:
if(lista[2] == True):
zero_km_Y.append(lista)
else:
zero_km_N.append(lista)
zero_km_Y
zero_km_N
```
#### Formato padrão
```
if <condição 1>:
<instruções caso a condição 1 seja verdadeira>
elif <condição 2>:
<instruções caso a condição 2 seja verdadeira>
elif <condição 3>:
<instruções caso a condição 3 seja verdadeira>
.
.
.
else:
<instruções caso as condições anteriores não sejam verdadeiras>
```
```
dados
print('AND')
print(f'(True and True) o resultado é: {True and True}')
print(f'(True and False) o resultado é: {True and False}')
print(f'(False and True) o resultado é: {False and True}')
print(f'(False and False) o resultado é: {False and False}')
print('OR')
print(f'(True or True) o resultado é: {True or True}')
print(f'(True or False) o resultado é: {True or False}')
print(f'(False or True) o resultado é: {False or True}')
print(f'(False or False) o resultado é: {False or False}')
A, B, C = [], [], []
for lista in dados:
if(lista[1] <=2000):
A.append(lista)
elif(lista[1] > 2000 and lista[1] <= 2010):
B.append(lista)
else:
C.append(lista)
A
B
C
A, B, C = [], [], []
for lista in dados:
if(lista[1] <=2000):
A.append(lista)
elif(2000 < lista[1] <= 2010):
B.append(lista)
else:
C.append(lista)
```
# <font color=green> 5. NUMPY BÁSICO
---
Numpy é a abreviação de Numerical Python e é um dos pacotes mais importantes para processamento numérico em Python. Numpy oferece a base para a maioria dos pacotes de aplicações científicas que utilizem dados numéricos em Python (estruturas de dados e algoritmos). Pode-se destacar os seguintes recursos que o pacote Numpy contém:
- Um poderoso objeto array multidimensional;
- Funções matemáticas sofisticadas para operações com arrays sem a necessidade de utilização de laços *for*;
- Recursos de algebra linear e geração de números aleatórios
Além de seus óbvios usos científicos, o pacote NumPy também é muito utilizado em análise de dados como um eficiente contêiner multidimensional de dados genéricos para transporte entre diversos algoritmos e bibliotecas em Python.
**Versão:** 1.16.5
**Instalação:** https://scipy.org/install.html
**Documentação:** https://numpy.org/doc/1.16/
### Pacotes
Existem diversos pacotes Python disponíveis para download na internet. Cada pacote tem como objetivo a solução de determinado tipo de problema e para isso são desenvolvidos novos tipos, funções e métodos.
Alguns pacotes são bastante utilizados em um contexto de ciência de dados como por exemplo:
- Numpy
- Pandas
- Scikit-learn
- Matplotlib
Alguns pacotes não são distribuídos com a instalação default do Python. Neste caso devemos instalar os pacotes que necessitamos em nosso sistema para podermos utilizar suas funcionalidades.
### Importando todo o pacote
```
import numpy
```
https://numpy.org/doc/1.16/reference/generated/numpy.arange.html
```
numpy.arange(10)
```
### Importando todo o pacote e atribuindo um novo nome
```
import numpy as np
np.arange(10)
```
### Importando parte do pacote
```
from numpy import arange
arange(10)
```
# 5.1 Criando arrays Numpy
```
import numpy as np
```
### A partir de listas
https://numpy.org/doc/1.16/user/basics.creation.html
```
km = np.array([1000, 2300, 4987, 1500])
km
type(km)
```
https://numpy.org/doc/1.16/user/basics.types.html
```
km.dtype
```
### A partir de dados externos
https://numpy.org/doc/1.16/reference/generated/numpy.loadtxt.html
```
km = np.loadtxt(fname = 'carros-km.txt', dtype = int)
km
km.dtype
```
### Arrays com duas dimensões
```
dados = [
['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva'],
['Central multimídia', 'Teto panorâmico', 'Freios ABS', '4 X 4', 'Painel digital', 'Piloto automático', 'Bancos de couro', 'Câmera de estacionamento'],
['Piloto automático', 'Controle de estabilidade', 'Sensor crepuscular', 'Freios ABS', 'Câmbio automático', 'Bancos de couro', 'Central multimídia', 'Vidros elétricos']
]
dados
Acessorios = np.array(dados)
Acessorios
km.shape
Acessorios.shape
```
### Comparando desempenho com listas
```
np_array = np.arange(1000000)
py_list = list(range(1000000))
%time for _ in range(100): np_array *= 2
%time for _ in range(100): py_list = [x * 2 for x in py_list]
```
# 5.2 Operações aritméticas com arrays Numpy
### Operações entre arrays e constantes
```
km = [44410., 5712., 37123., 0., 25757.]
anos = [2003, 1991, 1990, 2019, 2006]
# idade = 2019 - anos
km = np.array([44410., 5712., 37123., 0., 25757.])
anos = np.array([2003, 1991, 1990, 2019, 2006])
idade = 2019 - anos
idade
```
### Operações entre arrays
```
km_media = km / idade
km_media
44410 / (2019 - 2003)
5712 / (2019 - 1991)
```
### Operações com arrays de duas dimensões
```
dados = np.array([km, anos])
dados
dados.shape
```
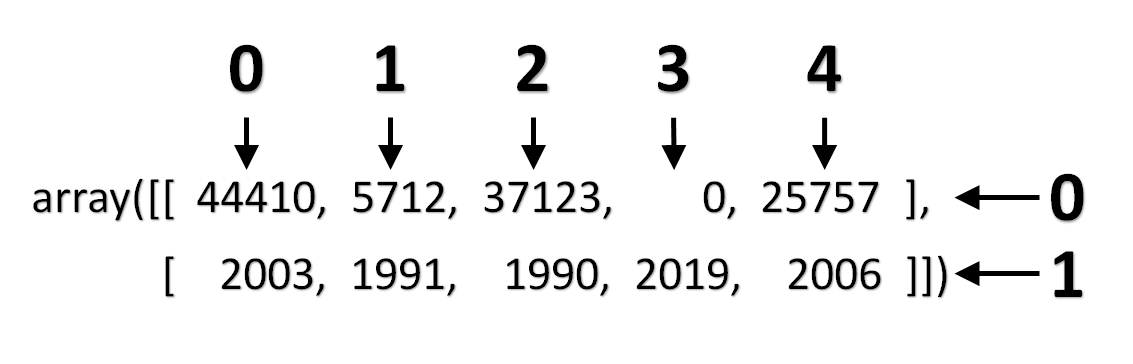
```
dados[0]
dados[1]
km_media = dados[0] / (2019 - dados[1])
km_media
```
# 5.3 Seleções com arrays Numpy

```
dados
```
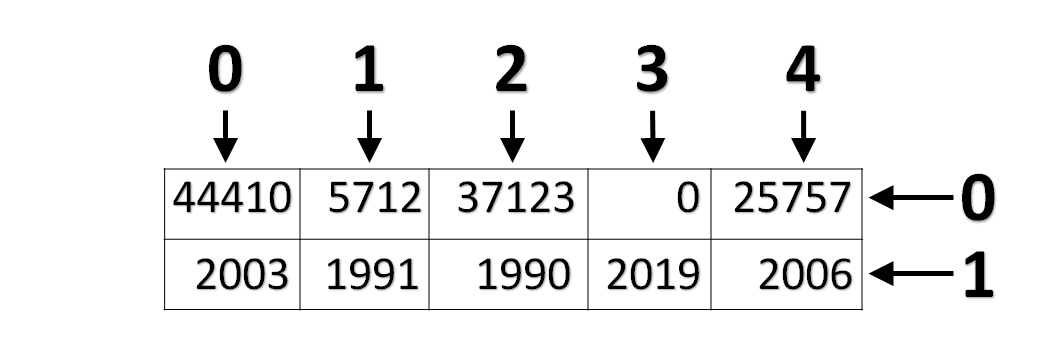
### Indexação
<font color=red>**Observação:**</font> A indexação tem origem no zero.
```
contador = np.arange(10)
contador
contador[0]
item = 6
index = item - 1
contador[index]
contador[-1]
dados[0]
dados[1]
```
## <font color=green>**Dica:**</font>
### *ndarray[ linha ][ coluna ]* ou *ndarray[ linha, coluna ]*
```
dados[1][2]
dados[1, 2]
```
### Fatiamentos
A sintaxe para realizar fatiamento em um array Numpy é $i : j : k$ onde $i$ é o índice inicial, $j$ é o índice de parada, e $k$ é o indicador de passo ($k\neq0$)
<font color=red>**Observação:**</font> Nos fatiamentos (*slices*) o item com índice i é **incluído** e o item com índice j **não é incluído** no resultado.

```
contador = np.arange(10)
contador
contador[1:4]
contador[1:8:2]
contador[::2]
contador[1::2]
dados
dados[:, 1:3]
dados[:, 1:3][0] / (2019 - dados[:, 1:3][1])
dados[0] / (2019 - dados[1])
```
### Indexação com array booleano
<font color=red>**Observação:**</font> Seleciona um grupo de linhas e colunas segundo os rótulos ou um array booleano.
```
contador = np.arange(10)
contador
contador > 5
contador[contador > 5]
contador[[False, False, False, False, False, False, True, True, True, True]]
dados
dados[1] > 2000
dados[:, dados[1] > 2000]
```
# 5.4 Atributos e métodos de arrays Numpy
```
dados = np.array([[44410., 5712., 37123., 0., 25757.],
[2003, 1991, 1990, 2019, 2006]])
dados
```
### Atributos
https://numpy.org/doc/1.16/reference/arrays.ndarray.html#array-attributes
## *ndarray.shape*
Retorna uma tupla com as dimensões do array.
```
dados.shape
```
## *ndarray.ndim*
Retorna o número de dimensões do array.
```
dados.ndim
```
## *ndarray.size*
Retorna o número de elementos do array.
```
dados.size
```
## *ndarray.dtype*
Retorna o tipo de dados dos elementos do array.
```
dados.dtype
```
## *ndarray.T*
Retorna o array transposto, isto é, converte linhas em colunas e vice versa.
```
dados.T
dados.transpose()
```
### Métodos
https://numpy.org/doc/1.16/reference/arrays.ndarray.html#array-methods
## *ndarray.tolist()*
Retorna o array como uma lista Python.
```
dados.tolist()
```
## *ndarray.reshape(shape[, order])*
Retorna um array que contém os mesmos dados com uma nova forma.
```
contador = np.arange(10)
contador
contador.reshape((5, 2))
contador.reshape((5, 2), order='C')
contador.reshape((5, 2), order='F')
km = [44410, 5712, 37123, 0, 25757]
anos = [2003, 1991, 1990, 2019, 2006]
info_carros = km + anos
info_carros
np.array(info_carros).reshape((2, 5))
np.array(info_carros).reshape((5, 2), order='F')
```
## *ndarray.resize(new_shape[, refcheck])*
Altera a forma e o tamanho do array.
```
dados_new = dados.copy()
dados_new
dados_new.resize((3, 5), refcheck=False)
dados_new
dados_new[2] = dados_new[0] / (2019 - dados_new[1])
dados_new
```
# 5.5 Estatísticas com arrays Numpy
https://numpy.org/doc/1.16/reference/arrays.ndarray.html#calculation
e
https://numpy.org/doc/1.16/reference/routines.statistics.html
e
https://numpy.org/doc/1.16/reference/routines.math.html
```
anos = np.loadtxt(fname = "carros-anos.txt", dtype = int)
km = np.loadtxt(fname = "carros-km.txt")
valor = np.loadtxt(fname = "carros-valor.txt")
anos.shape
```
https://numpy.org/doc/1.16/reference/generated/numpy.column_stack.html
```
dataset = np.column_stack((anos, km, valor))
dataset
dataset.shape
```
## *np.mean()*
Retorna a média dos elementos do array ao longo do eixo especificado.
```
np.mean(dataset, axis = 0)
np.mean(dataset, axis = 1)
np.mean(dataset[:, 1])
np.mean(dataset[:, 2])
```
## *np.std()*
Retorna o desvio padrão dos elementos do array ao longo do eixo especificado.
```
np.std(dataset[:, 2])
```
## *ndarray.sum()*
Retorna a soma dos elementos do array ao longo do eixo especificado.
```
dataset.sum(axis = 0)
dataset[:, 1].sum()
```
## *np.sum()*
Retorna a soma dos elementos do array ao longo do eixo especificado.
```
np.sum(dataset, axis = 0)
np.sum(dataset[:, 2])
```
|
github_jupyter
|
!python -V
import numpy as np
km = np.loadtxt('carros-km.txt')
km
anos = np.loadtxt('carros-anos.txt', dtype = int)
anos
km_media = km / (2019 - anos)
km_media
type(km_media)
2 + 2
2 - 2
2 * 3
10 / 3
10 // 3
2 ** 3
10 % 3
10 % 2
5 * 2 + 3 * 2
(5 * 2) + (3 * 2)
5 * (2 + 3) * 2
5 * 2
_ + 3 * 2
_ / 2
ano_atual = 2019
ano_fabricacao = 2003
km_total = 44410.0
ano_atual
ano_fabricacao
km_total
km_media = km_total / (ano_atual - ano_fabricacao)
km_media
ano_atual = 2019
ano_fabricacao = 2003
km_total = 44410.0
km_media = km_total / (ano_atual - ano_fabricacao)
km_media
ano_atual = 2019
ano_fabricacao = 2003
km_total = 44410.0
km_media = km_total / (ano_atual - ano_fabricacao)
km_total = km_total + km_media
km_total
ano_atual = 2019
ano_fabricacao = 2003
km_total = 44410.0
km_media = km_total / (ano_atual - ano_fabricacao)
km_total += km_media
km_total
"valor = valor + 1" é equivalente a "valor += 1"
ano_atual, ano_fabricacao, km_total = 2019, 2003, 44410.0
ano_atual
ano_fabricacao
km_total
ano_atual, ano_fabricacao, km_total = 2019, 2003, 44410.0
km_media = km_total / (ano_atual - ano_fabricacao)
km_media
ano_atual = 2019
type(ano_atual)
km_total = 44410.0
type(km_total)
zero_km = True
type(zero_km)
zero_km = False
type(zero_km)
nome = 'Jetta Variant'
nome
nome = "Jetta Variant"
nome
nome = 'Jetta "Variant"'
nome
nome = "Jetta 'Variant'"
nome
carro = '''
Nome
Idade
Nota
'''
type(carro)
quilometragem = None
quilometragem
type(quilometragem)
a = 10
b = 20
c = 'Python é '
d = 'legal'
type(a)
type(b)
type(c)
type(d)
a + b
c + d
# c + a
str(a)
type(str(a))
c + str(a)
float(a)
var = 3.141592
int(var)
var = 3.99
int(var)
ano_atual = 2019
ano_fabricacao = 2019
if (ano_atual == ano_fabricacao):
print('Verdadeiro')
else:
print('Falso')
# Isto é um comentário
ano_atual = 2019
ano_atual
# Isto
# é um
# comentário
ano_atual = 2019
ano_atual
'''Isto é um
comentário'''
ano_atual = 2019
ano_atual
# Definindo variáveis
ano_atual = 2019
ano_fabricacao = 2019
'''
Estrutura condicional que vamos
aprender na próxima aula
'''
if (ano_atual == ano_fabricacao): # Testando se condição é verdadeira
print('Verdadeiro')
else: # Testando se condição é falsa
print('Falso')
print('Olá, {}!'.format('Rodrigo'))
print('Olá, {}! Este é seu acesso de número {}'.format('Rodrigo', 32))
print('Olá, {nome}! Este é seu acesso de número {acessos}'.format(nome = 'Rodrigo', acessos = 32))
nome = 'Rodrigo'
acessos = 32
print(f'Olá, {nome}! Este é seu acesso de número {acessos}')
- Utilizando um par de colchetes: [ ], [ 1 ]
- Utilizando um par de colchetes com itens separados por vírgulas: [ 1, 2, 3 ]
Acessorios = ['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva']
Acessorios
type(Acessorios)
Carro_1 = ['Jetta Variant', 'Motor 4.0 Turbo', 2003, 44410.0, False, ['Rodas de liga', 'Travas elétricas', 'Piloto automático'], 88078.64]
Carro_2 = ['Passat', 'Motor Diesel', 1991, 5712.0, False, ['Central multimídia', 'Teto panorâmico', 'Freios ABS'], 106161.94]
Carro_1
Carro_2
Carros = [Carro_1, Carro_2]
Carros
Acessorios
'Rodas de liga' in Acessorios
'4 X 4' in Acessorios
'Rodas de liga' not in Acessorios
'4 X 4' not in Acessorios
A = ['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro']
B = ['Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva']
A
B
A + B
len(Acessorios)
Acessorios
Acessorios[0]
Acessorios[1]
Acessorios[-1]
Carros
Carros[0]
Carros[0][0]
Carros[0][-2]
Carros[0][-2][1]
Acessorios
Acessorios[2:5]
Acessorios[2:]
Acessorios[:5]
Acessorios = ['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva']
Acessorios
Acessorios.sort()
Acessorios
Acessorios.append('4 X 4')
Acessorios
Acessorios.pop()
Acessorios
Acessorios.pop(3)
Acessorios
A[:]
Acessorios_2 = Acessorios
Acessorios_2
Acessorios_2.append('4 X 4')
Acessorios_2
Acessorios
Acessorios.pop()
Acessorios
Acessorios_2
Acessorios_2 = Acessorios.copy()
Acessorios_2
Acessorios_2.append('4 X 4')
Acessorios_2
Acessorios
Acessorios_2 = Acessorios[:]
Acessorios_2
for <variável> in <coleção>:
<instruções>
Acessorios = ['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva']
Acessorios
for item in Acessorios:
print(item)
range(10)
list(range(10))
for i in range(10):
print(i ** 2)
quadrado = []
for i in range(10):
quadrado.append(i ** 2)
quadrado
[i ** 2 for i in range(10)]
dados = [
['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva'],
['Central multimídia', 'Teto panorâmico', 'Freios ABS', '4 X 4', 'Painel digital', 'Piloto automático', 'Bancos de couro', 'Câmera de estacionamento'],
['Piloto automático', 'Controle de estabilidade', 'Sensor crepuscular', 'Freios ABS', 'Câmbio automático', 'Bancos de couro', 'Central multimídia', 'Vidros elétricos']
]
dados
for lista in dados:
print(lista)
for lista in dados:
for item in lista:
print(item)
Acessorios = []
for lista in dados:
for item in lista:
Acessorios.append(item)
Acessorios
list(set(Acessorios))
[item for lista in dados for item in lista]
list(set([item for lista in dados for item in lista]))
if <condição>:
<instruções caso a condição seja verdadeira>
# 1º item da lista - Nome do veículo
# 2º item da lista - Ano de fabricação
# 3º item da lista - Veículo é zero km?
dados = [
['Jetta Variant', 2003, False],
['Passat', 1991, False],
['Crossfox', 1990, False],
['DS5', 2019, True],
['Aston Martin DB4', 2006, False],
['Palio Weekend', 2012, False],
['A5', 2019, True],
['Série 3 Cabrio', 2009, False],
['Dodge Jorney', 2019, False],
['Carens', 2011, False]
]
dados
zero_km_Y = []
for lista in dados:
if(lista[2] == True):
zero_km_Y.append(lista)
zero_km_Y
zero_km_N = []
for lista in dados:
if(lista[2] == False):
zero_km_N.append(lista)
zero_km_N
[lista for lista in dados if lista[2] == True]
if <condição>:
<instruções caso a condição seja verdadeira>
else:
<instruções caso a condição não seja verdadeira>
zero_km_Y, zero_km_N = [], []
for lista in dados:
if(lista[2] == True):
zero_km_Y.append(lista)
else:
zero_km_N.append(lista)
zero_km_Y
zero_km_N
if <condição 1>:
<instruções caso a condição 1 seja verdadeira>
elif <condição 2>:
<instruções caso a condição 2 seja verdadeira>
elif <condição 3>:
<instruções caso a condição 3 seja verdadeira>
.
.
.
else:
<instruções caso as condições anteriores não sejam verdadeiras>
dados
print('AND')
print(f'(True and True) o resultado é: {True and True}')
print(f'(True and False) o resultado é: {True and False}')
print(f'(False and True) o resultado é: {False and True}')
print(f'(False and False) o resultado é: {False and False}')
print('OR')
print(f'(True or True) o resultado é: {True or True}')
print(f'(True or False) o resultado é: {True or False}')
print(f'(False or True) o resultado é: {False or True}')
print(f'(False or False) o resultado é: {False or False}')
A, B, C = [], [], []
for lista in dados:
if(lista[1] <=2000):
A.append(lista)
elif(lista[1] > 2000 and lista[1] <= 2010):
B.append(lista)
else:
C.append(lista)
A
B
C
A, B, C = [], [], []
for lista in dados:
if(lista[1] <=2000):
A.append(lista)
elif(2000 < lista[1] <= 2010):
B.append(lista)
else:
C.append(lista)
import numpy
numpy.arange(10)
import numpy as np
np.arange(10)
from numpy import arange
arange(10)
import numpy as np
km = np.array([1000, 2300, 4987, 1500])
km
type(km)
km.dtype
km = np.loadtxt(fname = 'carros-km.txt', dtype = int)
km
km.dtype
dados = [
['Rodas de liga', 'Travas elétricas', 'Piloto automático', 'Bancos de couro', 'Ar condicionado', 'Sensor de estacionamento', 'Sensor crepuscular', 'Sensor de chuva'],
['Central multimídia', 'Teto panorâmico', 'Freios ABS', '4 X 4', 'Painel digital', 'Piloto automático', 'Bancos de couro', 'Câmera de estacionamento'],
['Piloto automático', 'Controle de estabilidade', 'Sensor crepuscular', 'Freios ABS', 'Câmbio automático', 'Bancos de couro', 'Central multimídia', 'Vidros elétricos']
]
dados
Acessorios = np.array(dados)
Acessorios
km.shape
Acessorios.shape
np_array = np.arange(1000000)
py_list = list(range(1000000))
%time for _ in range(100): np_array *= 2
%time for _ in range(100): py_list = [x * 2 for x in py_list]
km = [44410., 5712., 37123., 0., 25757.]
anos = [2003, 1991, 1990, 2019, 2006]
# idade = 2019 - anos
km = np.array([44410., 5712., 37123., 0., 25757.])
anos = np.array([2003, 1991, 1990, 2019, 2006])
idade = 2019 - anos
idade
km_media = km / idade
km_media
44410 / (2019 - 2003)
5712 / (2019 - 1991)
dados = np.array([km, anos])
dados
dados.shape
dados[0]
dados[1]
km_media = dados[0] / (2019 - dados[1])
km_media
dados
contador = np.arange(10)
contador
contador[0]
item = 6
index = item - 1
contador[index]
contador[-1]
dados[0]
dados[1]
dados[1][2]
dados[1, 2]
contador = np.arange(10)
contador
contador[1:4]
contador[1:8:2]
contador[::2]
contador[1::2]
dados
dados[:, 1:3]
dados[:, 1:3][0] / (2019 - dados[:, 1:3][1])
dados[0] / (2019 - dados[1])
contador = np.arange(10)
contador
contador > 5
contador[contador > 5]
contador[[False, False, False, False, False, False, True, True, True, True]]
dados
dados[1] > 2000
dados[:, dados[1] > 2000]
dados = np.array([[44410., 5712., 37123., 0., 25757.],
[2003, 1991, 1990, 2019, 2006]])
dados
dados.shape
dados.ndim
dados.size
dados.dtype
dados.T
dados.transpose()
dados.tolist()
contador = np.arange(10)
contador
contador.reshape((5, 2))
contador.reshape((5, 2), order='C')
contador.reshape((5, 2), order='F')
km = [44410, 5712, 37123, 0, 25757]
anos = [2003, 1991, 1990, 2019, 2006]
info_carros = km + anos
info_carros
np.array(info_carros).reshape((2, 5))
np.array(info_carros).reshape((5, 2), order='F')
dados_new = dados.copy()
dados_new
dados_new.resize((3, 5), refcheck=False)
dados_new
dados_new[2] = dados_new[0] / (2019 - dados_new[1])
dados_new
anos = np.loadtxt(fname = "carros-anos.txt", dtype = int)
km = np.loadtxt(fname = "carros-km.txt")
valor = np.loadtxt(fname = "carros-valor.txt")
anos.shape
dataset = np.column_stack((anos, km, valor))
dataset
dataset.shape
np.mean(dataset, axis = 0)
np.mean(dataset, axis = 1)
np.mean(dataset[:, 1])
np.mean(dataset[:, 2])
np.std(dataset[:, 2])
dataset.sum(axis = 0)
dataset[:, 1].sum()
np.sum(dataset, axis = 0)
np.sum(dataset[:, 2])
| 0.233008 | 0.827201 |
# Statis
## Carregar os corpora
```
import os
import copy
import numpy
from utils import lexical, tui
from nltk.corpus import stopwords
from string import punctuation
from prettytable import PrettyTable
stop_words = set(stopwords.words('portuguese') + list(punctuation) + [ '”', '“', '–'])
```
## Carregar corpora
```
BASE_DIR = '../data/corpora'
corpus_ocultismo = []
for dir in os.listdir('{}/ocultismo'.format(BASE_DIR)):
with open('{}/ocultismo/{}'.format(BASE_DIR, dir), 'r') as fl:
corpus_ocultismo.append(fl.readlines())
corpus_tecnologia = []
for dir in os.listdir('{}/tecnologia'.format(BASE_DIR)):
with open('{}/tecnologia/{}'.format(BASE_DIR, dir), 'r') as fl:
corpus_tecnologia.append(fl.readlines())
print('size ocultismo:', len(corpus_ocultismo))
print('size tecnologia:', len(corpus_tecnologia))
```
## Frequência de palavras
## Corpus Ocultismo
```
PP = lexical.Preprocessing()
P = tui.Progress(len(corpus_ocultismo), 'ocultismo')
freq_words = {}
sent_sizes = []
paragraphs_sizes = []
docs_size = []
for doc in corpus_ocultismo:
docs_size.append(len(doc))
for p in doc:
sentences = PP.tokenize_sentences(p)
paragraphs_sizes.append(len(sentences))
for sent in sentences:
sent_size = 0
s = PP.remove_punctuation(sent)
for word in PP.tokenize_words(s):
sent_size += 1
w = PP.lowercase(word)
try:
freq_words[w] += 1
except KeyError:
freq_words[w] = 1
sent_sizes.append(sent_size)
P.progressStep()
```
### 20 palavras mais usadas
```
fql = [ x for x in list(freq_words.items()) if x not in stop_words ]
fql.sort(key=lambda x: x[1], reverse=True)
pt = PrettyTable()
pt.field_names = [ 'Posição', 'Palavra', 'Quantidade' ]
for i in range(20):
pt.add_row((i+1, fql[i][0], fql[i][1]))
print(pt)
```
### 20 palavras menos usadas
```
pt = PrettyTable()
pt.field_names = [ 'Posição', 'Palavra', 'Quantidade' ]
for i in range(len(fql)-1, len(fql)-21, -1):
pt.add_row((i+1, fql[i][0], fql[i][1]))
print(pt)
```
### Tamanhos médios
```
print('Tamanho médio das sentenças: {:.02f}'.format(numpy.average(sent_sizes)))
word_sizes = [ len(x[0]) for x in fql ]
numpy.mean(word_sizes)
print('Tamanho médio das palavras: {:.02f}'.format(numpy.average(word_sizes)))
print('Tamanho médio dos pagrafos em sentenças: {:.02f}'.format(numpy.average(paragraphs_sizes)))
print('Tamanho médio dos documentos em pagrafos: {:.02f}'.format(numpy.average(docs_size)))
```
## Corpus Tecnologia
```
PP = lexical.Preprocessing()
P = tui.Progress(len(corpus_ocultismo), 'tecnologia')
freq_words = {}
sent_sizes = []
paragraphs_sizes = []
docs_size = []
for doc in corpus_tecnologia:
docs_size.append(len(doc))
for p in doc:
sentences = PP.tokenize_sentences(p)
paragraphs_sizes.append(len(sentences))
for sent in sentences:
sent_size = 0
s = PP.remove_punctuation(sent)
for word in PP.tokenize_words(s):
sent_size += 1
w = PP.lowercase(word)
try:
freq_words[w] += 1
except KeyError:
freq_words[w] = 1
sent_sizes.append(sent_size)
P.progressStep()
```
### 20 Palavras mais usadas
```
fql = [ x for x in list(freq_words.items()) if x not in stop_words ]
fql.sort(key=lambda x: x[1], reverse=True)
pt = PrettyTable()
pt.field_names = [ 'Posição', 'Palavra', 'Quantidade' ]
for i in range(20):
pt.add_row((i+1, fql[i][0], fql[i][1]))
print(pt)
```
### 20 Palavras menos usadas
```
pt = PrettyTable()
pt.field_names = [ 'Posição', 'Palavra', 'Quantidade' ]
for i in range(len(fql)-1, len(fql)-21, -1):
pt.add_row((i+1, fql[i][0], fql[i][1]))
print(pt)
```
### Tamanhos médios
```
print('Tamanho médio das sentenças: {:.02f}'.format(numpy.average(sent_sizes)))
word_sizes = [ len(x[0]) for x in fql ]
numpy.mean(word_sizes)
print('Tamanho médio das palavras: {:.02f}'.format(numpy.average(word_sizes)))
print('Tamanho médio dos pagrafos em sentenças: {:.02f}'.format(numpy.average(paragraphs_sizes)))
print('Tamanho médio dos documentos em pagrafos: {:.02f}'.format(numpy.average(docs_size)))
```
|
github_jupyter
|
import os
import copy
import numpy
from utils import lexical, tui
from nltk.corpus import stopwords
from string import punctuation
from prettytable import PrettyTable
stop_words = set(stopwords.words('portuguese') + list(punctuation) + [ '”', '“', '–'])
BASE_DIR = '../data/corpora'
corpus_ocultismo = []
for dir in os.listdir('{}/ocultismo'.format(BASE_DIR)):
with open('{}/ocultismo/{}'.format(BASE_DIR, dir), 'r') as fl:
corpus_ocultismo.append(fl.readlines())
corpus_tecnologia = []
for dir in os.listdir('{}/tecnologia'.format(BASE_DIR)):
with open('{}/tecnologia/{}'.format(BASE_DIR, dir), 'r') as fl:
corpus_tecnologia.append(fl.readlines())
print('size ocultismo:', len(corpus_ocultismo))
print('size tecnologia:', len(corpus_tecnologia))
PP = lexical.Preprocessing()
P = tui.Progress(len(corpus_ocultismo), 'ocultismo')
freq_words = {}
sent_sizes = []
paragraphs_sizes = []
docs_size = []
for doc in corpus_ocultismo:
docs_size.append(len(doc))
for p in doc:
sentences = PP.tokenize_sentences(p)
paragraphs_sizes.append(len(sentences))
for sent in sentences:
sent_size = 0
s = PP.remove_punctuation(sent)
for word in PP.tokenize_words(s):
sent_size += 1
w = PP.lowercase(word)
try:
freq_words[w] += 1
except KeyError:
freq_words[w] = 1
sent_sizes.append(sent_size)
P.progressStep()
fql = [ x for x in list(freq_words.items()) if x not in stop_words ]
fql.sort(key=lambda x: x[1], reverse=True)
pt = PrettyTable()
pt.field_names = [ 'Posição', 'Palavra', 'Quantidade' ]
for i in range(20):
pt.add_row((i+1, fql[i][0], fql[i][1]))
print(pt)
pt = PrettyTable()
pt.field_names = [ 'Posição', 'Palavra', 'Quantidade' ]
for i in range(len(fql)-1, len(fql)-21, -1):
pt.add_row((i+1, fql[i][0], fql[i][1]))
print(pt)
print('Tamanho médio das sentenças: {:.02f}'.format(numpy.average(sent_sizes)))
word_sizes = [ len(x[0]) for x in fql ]
numpy.mean(word_sizes)
print('Tamanho médio das palavras: {:.02f}'.format(numpy.average(word_sizes)))
print('Tamanho médio dos pagrafos em sentenças: {:.02f}'.format(numpy.average(paragraphs_sizes)))
print('Tamanho médio dos documentos em pagrafos: {:.02f}'.format(numpy.average(docs_size)))
PP = lexical.Preprocessing()
P = tui.Progress(len(corpus_ocultismo), 'tecnologia')
freq_words = {}
sent_sizes = []
paragraphs_sizes = []
docs_size = []
for doc in corpus_tecnologia:
docs_size.append(len(doc))
for p in doc:
sentences = PP.tokenize_sentences(p)
paragraphs_sizes.append(len(sentences))
for sent in sentences:
sent_size = 0
s = PP.remove_punctuation(sent)
for word in PP.tokenize_words(s):
sent_size += 1
w = PP.lowercase(word)
try:
freq_words[w] += 1
except KeyError:
freq_words[w] = 1
sent_sizes.append(sent_size)
P.progressStep()
fql = [ x for x in list(freq_words.items()) if x not in stop_words ]
fql.sort(key=lambda x: x[1], reverse=True)
pt = PrettyTable()
pt.field_names = [ 'Posição', 'Palavra', 'Quantidade' ]
for i in range(20):
pt.add_row((i+1, fql[i][0], fql[i][1]))
print(pt)
pt = PrettyTable()
pt.field_names = [ 'Posição', 'Palavra', 'Quantidade' ]
for i in range(len(fql)-1, len(fql)-21, -1):
pt.add_row((i+1, fql[i][0], fql[i][1]))
print(pt)
print('Tamanho médio das sentenças: {:.02f}'.format(numpy.average(sent_sizes)))
word_sizes = [ len(x[0]) for x in fql ]
numpy.mean(word_sizes)
print('Tamanho médio das palavras: {:.02f}'.format(numpy.average(word_sizes)))
print('Tamanho médio dos pagrafos em sentenças: {:.02f}'.format(numpy.average(paragraphs_sizes)))
print('Tamanho médio dos documentos em pagrafos: {:.02f}'.format(numpy.average(docs_size)))
| 0.132795 | 0.663785 |
# CenterNet
(The image above is taken from [author's github repository](https://github.com/xingyizhou/CenterNet))
This example interactively demonstrates [CenterNet](https://arxiv.org/pdf/1904.07850.pdf), a model for object detection.
# Preparation
Let's start by installing nnabla and accessing [nnabla-examples repository](https://github.com/sony/nnabla-examples). If you're running on Colab, make sure that your Runtime setting is set as GPU, which can be set up from the top menu (Runtime → change runtime type), and make sure to click **Connect** on the top right-hand side of the screen before you start.
```
!pip install nnabla-ext-cuda100
!git clone https://github.com/sony/nnabla-examples.git
%cd nnabla-examples/object-detection/centernet
```
Then you need to choose backbone network architecture and dataset the pretrained model has been trained on.
Just click the dropdown list and select one for each. After you choose, execute the cell.
```
#@title Choose backbone architecture and dataset which the model is trained on.
architecture = 'dlav0' #@param ['resnet', 'dlav0']
#@title Choose dataset
dataset = 'pascal' #@param ['coco', 'pascal']
if architecture == "resnet":
num_layer = 18
else:
num_layer = 34
param_url = f"https://nnabla.org/pretrained-models/nnabla-examples/object-detection/ceneternet/ctdet/{architecture}_{num_layer}_{dataset}_fp.h5"
param_path = param_url.split("/")[-1]
```
We will now download the pre-trained weight parameters for the selected neural network.
```
!wget $param_url
```
# Upload Image
Run the following cell to upload your own image. Note that too small images might cause poor result.
```
from google.colab import files
img = files.upload()
```
Let's rename the image for convenience.
```
import os
ext = os.path.splitext(list(img.keys())[-1])[-1]
os.rename(list(img.keys())[-1], "input_image{}".format(ext))
input_img = "input_image" + ext
```
# Object Detection
Now let's run CenterNet on your image and see how it performs object detection!
```
!python src/demo.py ctdet --dataset $dataset --arch $architecture --num_layers $num_layer --checkpoint $param_path --demo $input_img --gpus 0 --debug 1 --save_dir .
```
The following cell will show the detection result.
Play around with different types of images and different backbone architecture!
```
from IPython.display import Image,display
print('Output:')
display(Image("ctdet.jpg"))
```
|
github_jupyter
|
!pip install nnabla-ext-cuda100
!git clone https://github.com/sony/nnabla-examples.git
%cd nnabla-examples/object-detection/centernet
#@title Choose backbone architecture and dataset which the model is trained on.
architecture = 'dlav0' #@param ['resnet', 'dlav0']
#@title Choose dataset
dataset = 'pascal' #@param ['coco', 'pascal']
if architecture == "resnet":
num_layer = 18
else:
num_layer = 34
param_url = f"https://nnabla.org/pretrained-models/nnabla-examples/object-detection/ceneternet/ctdet/{architecture}_{num_layer}_{dataset}_fp.h5"
param_path = param_url.split("/")[-1]
!wget $param_url
from google.colab import files
img = files.upload()
import os
ext = os.path.splitext(list(img.keys())[-1])[-1]
os.rename(list(img.keys())[-1], "input_image{}".format(ext))
input_img = "input_image" + ext
!python src/demo.py ctdet --dataset $dataset --arch $architecture --num_layers $num_layer --checkpoint $param_path --demo $input_img --gpus 0 --debug 1 --save_dir .
from IPython.display import Image,display
print('Output:')
display(Image("ctdet.jpg"))
| 0.594198 | 0.917006 |
# Reference data accuracy assessment by Radiant Earth
Radiant Earth is conducting an accuracy assessment of DE Africa cropmask reference data using the airbus high-res satellite archive. This notebook produces a confusion matrix between DE AFrica's labels and Radiant Earth's labels.
Inputs will be:
1. `<AEZ-region_RE_sample_validation.geojson>` : The results from collecting training data in the CEO tool
Output will be:
1. A `confusion error matrix` containing Overall, Producer's, and User's accuracy, along with the F1 score.
***
```
import pandas as pd
import numpy as np
import seaborn as sn
import geopandas as gpd
import matplotlib.pyplot as plt
from sklearn.metrics import f1_score
```
## Analysis Parameters
```
folder = 'data/training_validation/collect_earth/southern/'
gjson = 'data/training_validation/collect_earth/southern/Southern_region_RE_sample_validated.geojson'
```
## Run this if doing validation results for the entire continent
```
so='data/training_validation/collect_earth/southern/Southern_region_RE_sample_validated.geojson'
sa='data/training_validation/collect_earth/sahel/Sahel_region_RE_sample_validated.geojson'
w='data/training_validation/collect_earth/western/Western_region_RE_sample_validated.geojson'
e='data/training_validation/collect_earth/eastern/Eastern_region_RE_sample_validated.geojson'
n='data/training_validation/collect_earth/northern/Northern_region_RE_sample_validated.geojson'
io='data/training_validation/collect_earth/indian_ocean/Indian_ocean_region_RE_sample_validated.geojson'
c='data/training_validation/collect_earth/central/Central_region_RE_sample_validated.geojson'
so=gpd.read_file(so)
sa=gpd.read_file(sa)
w=gpd.read_file(w)
e=gpd.read_file(e)
n=gpd.read_file(n)
io=gpd.read_file(io)
c=gpd.read_file(c)
df = pd.concat([so,sa,w,e,n,io,c]).drop(columns=['smpl_class', 'SMPL_SAMPLEID', 'smpl_gfsad_samp','smpl_sampleid']).reset_index(drop=True)
df.head()
```
## Otherwise, run this cell
```
#ground truth shapefile
df = gpd.read_file(gjson)
df.head()
```
### Clean up dataframe
```
#rename columns
df = df.rename(columns={'Class':'Prediction',
'Validation_Class':'Actual'})
df.head()
```
***
### Reclassify prediction & actual columns
1 = crop,
0 = non-crop
```
df['Prediction'] = np.where(df['Prediction']=='non-crop', 0, df['Prediction'])
df['Prediction'] = np.where(df['Prediction']=='crop', 1, df['Prediction'])
df['Actual'] = np.where(df['Actual']=='non-crop', 0, df['Actual'])
df['Actual'] = np.where(df['Actual']=='crop', 1, df['Actual'])
df.head()
```
### Generate a confusion matrix with all classes
```
confusion_matrix = pd.crosstab(df['Actual'],
df['Prediction'],
rownames=['Actual'],
colnames=['Prediction'],
margins=True)
confusion_matrix
```
### Reclassify into a binary assessment
```
counts = df.groupby('Actual').count()
print("Total number of samples: " + str(len(df)))
print("Number of 'mixed' samples: "+ str(counts[counts.index=='mixed']['Prediction'].values[0]))
print("Number of 'N/A' samples: "+ str(counts[counts.index=='N/A']['Prediction'].values[0]))
print("Dropping 'mixed' and 'N/A' samples")
df = df.drop(df[df['Actual']=='mixed'].index)
df = df.drop(df[df['Actual']=='N/A'].index)
```
---
### Recreate confusion matrix
```
confusion_matrix = pd.crosstab(df['Actual'],
df['Prediction'],
rownames=['Actual'],
colnames=['Prediction'],
margins=True)
confusion_matrix
# confusion_matrix.to_csv('radiant_earth_reference_data_accuracy_continental_results.csv')
```
### Calculate User's and Producer's Accuracy
`Producer's Accuracy`
```
confusion_matrix["Producer's"] = [confusion_matrix.loc[0, 0] / confusion_matrix.loc[0, 'All'] * 100,
confusion_matrix.loc[1, 1] / confusion_matrix.loc[1, 'All'] * 100,
np.nan]
```
`User's Accuracy`
```
users_accuracy = pd.Series([confusion_matrix[0][0] / confusion_matrix[0]['All'] * 100,
confusion_matrix[1][1] / confusion_matrix[1]['All'] * 100]
).rename("User's")
confusion_matrix = confusion_matrix.append(users_accuracy)
```
`Overall Accuracy`
```
confusion_matrix.loc["User's","Producer's"] = (confusion_matrix.loc[0, 0] +
confusion_matrix.loc[1, 1]) / confusion_matrix.loc['All', 'All'] * 100
```
`F1 Score`
The F1 score is the harmonic mean of the precision and recall, where an F1 score reaches its best value at 1 (perfect precision and recall), and is calculated as:
$$
\begin{aligned}
\text{Fscore} = 2 \times \frac{\text{UA} \times \text{PA}}{\text{UA} + \text{PA}}.
\end{aligned}
$$
Where UA = Users Accuracy, and PA = Producer's Accuracy
```
fscore = pd.Series([(2*(confusion_matrix.loc["User's", 0]*confusion_matrix.loc[0, "Producer's"]) / (confusion_matrix.loc["User's", 0]+confusion_matrix.loc[0, "Producer's"])) / 100,
f1_score(df['Actual'].astype(np.int8), df['Prediction'].astype(np.int8), average='binary')]
).rename("F-score")
confusion_matrix = confusion_matrix.append(fscore)
```
### Tidy Confusion Matrix
* Limit decimal places,
* Add readable class names
* Remove non-sensical values
```
# round numbers
confusion_matrix = confusion_matrix.round(decimals=2)
# rename booleans to class names
confusion_matrix = confusion_matrix.rename(columns={0:'Non-crop', 1:'Crop', 'All':'Total'},
index={0:'Non-crop', 1:'Crop', 'All':'Total'})
#remove the nonsensical values in the table
confusion_matrix.loc["User's", 'Total'] = '--'
confusion_matrix.loc['Total', "Producer's"] = '--'
confusion_matrix.loc["F-score", 'Total'] = '--'
confusion_matrix.loc["F-score", "Producer's"] = '--'
confusion_matrix
```
### Export csv
```
confusion_matrix.to_csv(folder+ 'radiant_earth_reference_data_accuracy_results.csv')
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sn
import geopandas as gpd
import matplotlib.pyplot as plt
from sklearn.metrics import f1_score
folder = 'data/training_validation/collect_earth/southern/'
gjson = 'data/training_validation/collect_earth/southern/Southern_region_RE_sample_validated.geojson'
so='data/training_validation/collect_earth/southern/Southern_region_RE_sample_validated.geojson'
sa='data/training_validation/collect_earth/sahel/Sahel_region_RE_sample_validated.geojson'
w='data/training_validation/collect_earth/western/Western_region_RE_sample_validated.geojson'
e='data/training_validation/collect_earth/eastern/Eastern_region_RE_sample_validated.geojson'
n='data/training_validation/collect_earth/northern/Northern_region_RE_sample_validated.geojson'
io='data/training_validation/collect_earth/indian_ocean/Indian_ocean_region_RE_sample_validated.geojson'
c='data/training_validation/collect_earth/central/Central_region_RE_sample_validated.geojson'
so=gpd.read_file(so)
sa=gpd.read_file(sa)
w=gpd.read_file(w)
e=gpd.read_file(e)
n=gpd.read_file(n)
io=gpd.read_file(io)
c=gpd.read_file(c)
df = pd.concat([so,sa,w,e,n,io,c]).drop(columns=['smpl_class', 'SMPL_SAMPLEID', 'smpl_gfsad_samp','smpl_sampleid']).reset_index(drop=True)
df.head()
#ground truth shapefile
df = gpd.read_file(gjson)
df.head()
#rename columns
df = df.rename(columns={'Class':'Prediction',
'Validation_Class':'Actual'})
df.head()
df['Prediction'] = np.where(df['Prediction']=='non-crop', 0, df['Prediction'])
df['Prediction'] = np.where(df['Prediction']=='crop', 1, df['Prediction'])
df['Actual'] = np.where(df['Actual']=='non-crop', 0, df['Actual'])
df['Actual'] = np.where(df['Actual']=='crop', 1, df['Actual'])
df.head()
confusion_matrix = pd.crosstab(df['Actual'],
df['Prediction'],
rownames=['Actual'],
colnames=['Prediction'],
margins=True)
confusion_matrix
counts = df.groupby('Actual').count()
print("Total number of samples: " + str(len(df)))
print("Number of 'mixed' samples: "+ str(counts[counts.index=='mixed']['Prediction'].values[0]))
print("Number of 'N/A' samples: "+ str(counts[counts.index=='N/A']['Prediction'].values[0]))
print("Dropping 'mixed' and 'N/A' samples")
df = df.drop(df[df['Actual']=='mixed'].index)
df = df.drop(df[df['Actual']=='N/A'].index)
confusion_matrix = pd.crosstab(df['Actual'],
df['Prediction'],
rownames=['Actual'],
colnames=['Prediction'],
margins=True)
confusion_matrix
# confusion_matrix.to_csv('radiant_earth_reference_data_accuracy_continental_results.csv')
confusion_matrix["Producer's"] = [confusion_matrix.loc[0, 0] / confusion_matrix.loc[0, 'All'] * 100,
confusion_matrix.loc[1, 1] / confusion_matrix.loc[1, 'All'] * 100,
np.nan]
users_accuracy = pd.Series([confusion_matrix[0][0] / confusion_matrix[0]['All'] * 100,
confusion_matrix[1][1] / confusion_matrix[1]['All'] * 100]
).rename("User's")
confusion_matrix = confusion_matrix.append(users_accuracy)
confusion_matrix.loc["User's","Producer's"] = (confusion_matrix.loc[0, 0] +
confusion_matrix.loc[1, 1]) / confusion_matrix.loc['All', 'All'] * 100
fscore = pd.Series([(2*(confusion_matrix.loc["User's", 0]*confusion_matrix.loc[0, "Producer's"]) / (confusion_matrix.loc["User's", 0]+confusion_matrix.loc[0, "Producer's"])) / 100,
f1_score(df['Actual'].astype(np.int8), df['Prediction'].astype(np.int8), average='binary')]
).rename("F-score")
confusion_matrix = confusion_matrix.append(fscore)
# round numbers
confusion_matrix = confusion_matrix.round(decimals=2)
# rename booleans to class names
confusion_matrix = confusion_matrix.rename(columns={0:'Non-crop', 1:'Crop', 'All':'Total'},
index={0:'Non-crop', 1:'Crop', 'All':'Total'})
#remove the nonsensical values in the table
confusion_matrix.loc["User's", 'Total'] = '--'
confusion_matrix.loc['Total', "Producer's"] = '--'
confusion_matrix.loc["F-score", 'Total'] = '--'
confusion_matrix.loc["F-score", "Producer's"] = '--'
confusion_matrix
confusion_matrix.to_csv(folder+ 'radiant_earth_reference_data_accuracy_results.csv')
| 0.273477 | 0.895477 |
# Copy an analysis job from a Flywheel Instance
Given the ID of a Flywheel job, this will create a python script to re-run it. You can then edit and run that script.
The cell below will get a Flywheel client if you are logged in to a Flywheel instance. It prints out the URL of the instance so you know where you are logged in.
```
import argparse
import os
import pprint
import stat
import flywheel
fw = flywheel.Client("")
print("Flywheel Instance", fw.get_config().site.api_url)
```
Get the job ID from the URL when you select the job of interest in the "Jobs Log" in the Flywheel UI.
Create a python script to re-run a job given the job ID for a gear that was run on Flywheel.
```
def write_script_to_run_job(job_id=None, analysis_id=None):
analysis = None
if analysis_id:
analysis = fw.get_analysis(analysis_id)
print(f"Getting job_id from analysis '{analysis.label}'")
job_id = analysis.job.id
elif job_id == None:
print(f"Must provide either job_id or analysis_id.")
os.sys.exit(1)
print("Job ID", job_id)
job = fw.get_job(job_id)
gear = fw.get_gear(job.gear_id)
print(f"gear.gear.name is {gear.gear.name}")
destination_id = job.destination.id
destination_type = job.destination.type
print(f"job's destination_id is {destination_id} type {destination_type}")
if job.destination.type == "analysis":
analysis = fw.get_analysis(destination_id)
destination_id = analysis.parent.id
destination_type = analysis.parent.type
print(f"job's analysis's parent id is {destination_id} type {destination_type}")
destination = fw.get(destination_id)
destination_label = destination.label
print(f"new job's destination is {destination_label} type {destination_type}")
group_id = destination.parents.group
print(f"Group id: {group_id}")
if destination_type == "project":
project = destination
else:
project = fw.get_project(destination.parents.project)
project_label = project.label
print(f"Project label: {project.label}")
script_name = f"{project_label}_{destination_type}_{destination.label}.py"
script_name = script_name.replace(" ", "_")
container_path = "Invalid"
if destination_type == "project":
container_path = f"{group_id}/{project_label}"
elif destination_type == "subject":
container_path = f"{group_id}/{project_label}/{destination.label}"
elif destination_type == "session":
container_path = (
f"{group_id}/{project_label}/{destination.subject.label}/"
+ f"{destination.label}"
)
elif destination_type == "acquisition":
subject = fw.get_subject(destination.parents.subject)
session = fw.get_session(destination.parents.session)
container_path = (
f"{group_id}/{project_label}/{subject.label}/{session.label}/"
+ f"{destination.label}"
)
else:
print(f"Error: unknown destination type {destination_type}")
print(f"container_path: {container_path}")
print(f"Creating script: {script_name} ...\n")
input_files = dict()
for key, val in job.config.get("inputs").items():
if "hierarchy" in val:
input_files[key] = {
"hierarchy_id": val["hierarchy"]["id"],
"location_name": val["location"]["name"],
}
lines = f"""#! /usr/bin/env python3
'''Run {gear.gear.name} on {destination_type} "{destination.label}"
This script was created to run Job ID {job_id}
In project "{group_id}/{project_label}"
On Flywheel Instance {fw.get_config().site.api_url}
'''
import os
import argparse
from datetime import datetime
import flywheel
input_files = {pprint.pformat(input_files)}
def main(fw):
gear = fw.lookup("gears/{gear.gear.name}")
print("gear.gear.version for job was = {gear.gear.version}")"""
sfp = open(script_name, "w")
for line in lines.split("\n"):
sfp.write(line + "\n")
sfp.write(' print(f"gear.gear.version now = {gear.gear.version}")\n')
sfp.write(f' print("destination_id = {destination_id}")\n')
sfp.write(f' print("destination type is: {destination_type}")\n')
sfp.write(f' destination = fw.lookup("{container_path}")\n')
sfp.write("\n")
sfp.write(" inputs = dict()\n")
sfp.write(" for key, val in input_files.items():\n")
sfp.write(" container = fw.get(val['hierarchy_id'])\n")
sfp.write(" inputs[key] = container.get_file(val['location_name'])\n")
sfp.write("\n")
sfp.write(f" config = {pprint.pformat(job['config']['config'], indent=4)}\n")
sfp.write("\n")
if job.destination.type == "analysis":
sfp.write(" now = datetime.now()\n")
sfp.write(" analysis_label = (\n")
sfp.write(
" f'{gear.gear.name} {now.strftime(\"%m-%d-%Y %H:%M:%S\")} SDK launched'\n"
)
sfp.write(" )\n")
sfp.write(" print(f'analysis_label = {analysis_label}')\n")
lines = f"""
analysis_id = gear.run(
analysis_label=analysis_label,
config=config,
inputs=inputs,
destination=destination,
)"""
for line in lines.split("\n"):
sfp.write(line + "\n")
sfp.write(" print(f'analysis_id = {analysis_id}')\n")
sfp.write(" return analysis_id\n")
else:
lines = f"""
job_id = gear.run(
config=config,
inputs=inputs,
destination=destination
)"""
for line in lines.split("\n"):
sfp.write(line + "\n")
sfp.write(" print(f'job_id = {job_id}')\n")
sfp.write(" return job_id\n")
lines = f"""
if __name__ == '__main__':
parser = argparse.ArgumentParser(description=__doc__)
args = parser.parse_args()
fw = flywheel.Client('')
print(fw.get_config().site.api_url)
analysis_id = main(fw)"""
for line in lines.split("\n"):
sfp.write(line + "\n")
sfp.write("\n")
sfp.write(" os.sys.exit(0)\n")
sfp.close()
os.system(f"black {script_name}")
st = os.stat(script_name)
os.chmod(script_name, st.st_mode | stat.S_IEXEC)
```
## Utility Job, destination type is: acquisition
```
write_script_to_run_job(job_id="60817598fb84816baf6f3572")
```
## Utility Job, destination type is: session
```
write_script_to_run_job(job_id="60817898f4a3a2bb836f35ca")
gear.run?
```
## Analysis Job, destination type is: project
```
write_script_to_run_job(job_id="603fb4ab146a36499c6e8aca")
```
## Analysis Job, destination type is: session
```
write_script_to_run_job(job_id="603fb0c775f2cd6a236e8ab5")
```
## Analysis Job, destination type is: subject
```
write_script_to_run_job(job_id="603fb4f225960896416e8ab6")
```
|
github_jupyter
|
import argparse
import os
import pprint
import stat
import flywheel
fw = flywheel.Client("")
print("Flywheel Instance", fw.get_config().site.api_url)
def write_script_to_run_job(job_id=None, analysis_id=None):
analysis = None
if analysis_id:
analysis = fw.get_analysis(analysis_id)
print(f"Getting job_id from analysis '{analysis.label}'")
job_id = analysis.job.id
elif job_id == None:
print(f"Must provide either job_id or analysis_id.")
os.sys.exit(1)
print("Job ID", job_id)
job = fw.get_job(job_id)
gear = fw.get_gear(job.gear_id)
print(f"gear.gear.name is {gear.gear.name}")
destination_id = job.destination.id
destination_type = job.destination.type
print(f"job's destination_id is {destination_id} type {destination_type}")
if job.destination.type == "analysis":
analysis = fw.get_analysis(destination_id)
destination_id = analysis.parent.id
destination_type = analysis.parent.type
print(f"job's analysis's parent id is {destination_id} type {destination_type}")
destination = fw.get(destination_id)
destination_label = destination.label
print(f"new job's destination is {destination_label} type {destination_type}")
group_id = destination.parents.group
print(f"Group id: {group_id}")
if destination_type == "project":
project = destination
else:
project = fw.get_project(destination.parents.project)
project_label = project.label
print(f"Project label: {project.label}")
script_name = f"{project_label}_{destination_type}_{destination.label}.py"
script_name = script_name.replace(" ", "_")
container_path = "Invalid"
if destination_type == "project":
container_path = f"{group_id}/{project_label}"
elif destination_type == "subject":
container_path = f"{group_id}/{project_label}/{destination.label}"
elif destination_type == "session":
container_path = (
f"{group_id}/{project_label}/{destination.subject.label}/"
+ f"{destination.label}"
)
elif destination_type == "acquisition":
subject = fw.get_subject(destination.parents.subject)
session = fw.get_session(destination.parents.session)
container_path = (
f"{group_id}/{project_label}/{subject.label}/{session.label}/"
+ f"{destination.label}"
)
else:
print(f"Error: unknown destination type {destination_type}")
print(f"container_path: {container_path}")
print(f"Creating script: {script_name} ...\n")
input_files = dict()
for key, val in job.config.get("inputs").items():
if "hierarchy" in val:
input_files[key] = {
"hierarchy_id": val["hierarchy"]["id"],
"location_name": val["location"]["name"],
}
lines = f"""#! /usr/bin/env python3
'''Run {gear.gear.name} on {destination_type} "{destination.label}"
This script was created to run Job ID {job_id}
In project "{group_id}/{project_label}"
On Flywheel Instance {fw.get_config().site.api_url}
'''
import os
import argparse
from datetime import datetime
import flywheel
input_files = {pprint.pformat(input_files)}
def main(fw):
gear = fw.lookup("gears/{gear.gear.name}")
print("gear.gear.version for job was = {gear.gear.version}")"""
sfp = open(script_name, "w")
for line in lines.split("\n"):
sfp.write(line + "\n")
sfp.write(' print(f"gear.gear.version now = {gear.gear.version}")\n')
sfp.write(f' print("destination_id = {destination_id}")\n')
sfp.write(f' print("destination type is: {destination_type}")\n')
sfp.write(f' destination = fw.lookup("{container_path}")\n')
sfp.write("\n")
sfp.write(" inputs = dict()\n")
sfp.write(" for key, val in input_files.items():\n")
sfp.write(" container = fw.get(val['hierarchy_id'])\n")
sfp.write(" inputs[key] = container.get_file(val['location_name'])\n")
sfp.write("\n")
sfp.write(f" config = {pprint.pformat(job['config']['config'], indent=4)}\n")
sfp.write("\n")
if job.destination.type == "analysis":
sfp.write(" now = datetime.now()\n")
sfp.write(" analysis_label = (\n")
sfp.write(
" f'{gear.gear.name} {now.strftime(\"%m-%d-%Y %H:%M:%S\")} SDK launched'\n"
)
sfp.write(" )\n")
sfp.write(" print(f'analysis_label = {analysis_label}')\n")
lines = f"""
analysis_id = gear.run(
analysis_label=analysis_label,
config=config,
inputs=inputs,
destination=destination,
)"""
for line in lines.split("\n"):
sfp.write(line + "\n")
sfp.write(" print(f'analysis_id = {analysis_id}')\n")
sfp.write(" return analysis_id\n")
else:
lines = f"""
job_id = gear.run(
config=config,
inputs=inputs,
destination=destination
)"""
for line in lines.split("\n"):
sfp.write(line + "\n")
sfp.write(" print(f'job_id = {job_id}')\n")
sfp.write(" return job_id\n")
lines = f"""
if __name__ == '__main__':
parser = argparse.ArgumentParser(description=__doc__)
args = parser.parse_args()
fw = flywheel.Client('')
print(fw.get_config().site.api_url)
analysis_id = main(fw)"""
for line in lines.split("\n"):
sfp.write(line + "\n")
sfp.write("\n")
sfp.write(" os.sys.exit(0)\n")
sfp.close()
os.system(f"black {script_name}")
st = os.stat(script_name)
os.chmod(script_name, st.st_mode | stat.S_IEXEC)
write_script_to_run_job(job_id="60817598fb84816baf6f3572")
write_script_to_run_job(job_id="60817898f4a3a2bb836f35ca")
gear.run?
write_script_to_run_job(job_id="603fb4ab146a36499c6e8aca")
write_script_to_run_job(job_id="603fb0c775f2cd6a236e8ab5")
write_script_to_run_job(job_id="603fb4f225960896416e8ab6")
| 0.261048 | 0.613352 |
<a href="https://colab.research.google.com/github/fonslucens/test_deeplearning/blob/master/Imdb_LSTM.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import tensorflow as tf
(x_train, y_train),(x_test, y_test) = tf.keras.datasets.imdb.load_data(num_words=10000)
x_train.shape, y_train.shape,x_test.shape, y_test.shape
print(type(x_train))
print(type(x_train[0]), x_train[0])
len(x_train[0])
(x_train_100, y_train_100),(x_test_100, y_test_100) = tf.keras.datasets.imdb.load_data(num_words=100)
x_train_100.shape, y_train_100.shape,x_test_100.shape, y_test_100.shape
print(type(x_train_100[0]), x_train_100[0])
print(type(y_train))
print(type(y_train[0]), y_train[0:5])
import numpy as np
np.unique(y_train)
word_index = tf.keras.datasets.imdb.get_word_index()
# print(type(word_index), word_index)
# word_index.items()
invert_word_index = dict()
for (key, value) in word_index.items():
invert_word_index[value] = key
# print(invert_word_index)
decode_str = str()
for num in x_train[0]:
# print(num, invert_word_index[num])
decode_str = decode_str + invert_word_index[num]+' '
decode_str
decode_str = str()
for num in x_train[20]:
# print(num, invert_word_index[num])
decode_str = decode_str + invert_word_index[num]+' '
decode_str
def f_decode_str(x_data):
decode_str = str()
for num in x_data:
# print(num, invert_word_index[num])
decode_str = decode_str + invert_word_index[num]+' '
return decode_str
f_decode_str(x_train[20])
f_decode_str(x_train_100[20])
```
# 데이터 전처리 작업
```
len(x_train[0]), len(x_train[50]) , len(x_train[500]), len(x_train[1000])
pad_x_train = tf.keras.preprocessing.sequence.pad_sequences(x_train, maxlen=500)
len(pad_x_train[500]), pad_x_train[500]
np.unique(y_train) #Dense :1, activation:sigmoid, loss : binary_crossentropy
```
# make model
```
model = tf.keras.Sequential()
model.add(tf.keras.layers.Embedding(input_dim = 10000 , output_dim = 24, input_length=500))
model.add(tf.keras.layers.LSTM(24, return_sequences=True, activation='tanh'))
model.add(tf.keras.layers.LSTM(12, activation='tanh'))
model.add(tf.keras.layers.Dense(1, activation= 'sigmoid'))
model.compile(optimizer = 'adam',loss = 'binary_crossentropy' , metrics=['acc'])
model.summary()
```
# training
```
his = model.fit(pad_x_train, y_train , epochs=100, validation_split=0.3, batch_size=256)
```
# evaluation
```
model.evaluate(pad_x_train, y_train)
# len(x_test[20])
pad_x_test = tf.keras.preprocessing.sequence.pad_sequences(x_test, maxlen=500)
len(pad_x_test[20])
model.evaluate(pad_x_test)
import matplotlib.pyplot as plt
plt.plot(his.history['loss'])
plt.plot(his.history['val_loss'])
plt.show()
```
|
github_jupyter
|
import tensorflow as tf
(x_train, y_train),(x_test, y_test) = tf.keras.datasets.imdb.load_data(num_words=10000)
x_train.shape, y_train.shape,x_test.shape, y_test.shape
print(type(x_train))
print(type(x_train[0]), x_train[0])
len(x_train[0])
(x_train_100, y_train_100),(x_test_100, y_test_100) = tf.keras.datasets.imdb.load_data(num_words=100)
x_train_100.shape, y_train_100.shape,x_test_100.shape, y_test_100.shape
print(type(x_train_100[0]), x_train_100[0])
print(type(y_train))
print(type(y_train[0]), y_train[0:5])
import numpy as np
np.unique(y_train)
word_index = tf.keras.datasets.imdb.get_word_index()
# print(type(word_index), word_index)
# word_index.items()
invert_word_index = dict()
for (key, value) in word_index.items():
invert_word_index[value] = key
# print(invert_word_index)
decode_str = str()
for num in x_train[0]:
# print(num, invert_word_index[num])
decode_str = decode_str + invert_word_index[num]+' '
decode_str
decode_str = str()
for num in x_train[20]:
# print(num, invert_word_index[num])
decode_str = decode_str + invert_word_index[num]+' '
decode_str
def f_decode_str(x_data):
decode_str = str()
for num in x_data:
# print(num, invert_word_index[num])
decode_str = decode_str + invert_word_index[num]+' '
return decode_str
f_decode_str(x_train[20])
f_decode_str(x_train_100[20])
len(x_train[0]), len(x_train[50]) , len(x_train[500]), len(x_train[1000])
pad_x_train = tf.keras.preprocessing.sequence.pad_sequences(x_train, maxlen=500)
len(pad_x_train[500]), pad_x_train[500]
np.unique(y_train) #Dense :1, activation:sigmoid, loss : binary_crossentropy
model = tf.keras.Sequential()
model.add(tf.keras.layers.Embedding(input_dim = 10000 , output_dim = 24, input_length=500))
model.add(tf.keras.layers.LSTM(24, return_sequences=True, activation='tanh'))
model.add(tf.keras.layers.LSTM(12, activation='tanh'))
model.add(tf.keras.layers.Dense(1, activation= 'sigmoid'))
model.compile(optimizer = 'adam',loss = 'binary_crossentropy' , metrics=['acc'])
model.summary()
his = model.fit(pad_x_train, y_train , epochs=100, validation_split=0.3, batch_size=256)
model.evaluate(pad_x_train, y_train)
# len(x_test[20])
pad_x_test = tf.keras.preprocessing.sequence.pad_sequences(x_test, maxlen=500)
len(pad_x_test[20])
model.evaluate(pad_x_test)
import matplotlib.pyplot as plt
plt.plot(his.history['loss'])
plt.plot(his.history['val_loss'])
plt.show()
| 0.493409 | 0.967225 |
```
# https://ipython.readthedocs.io/en/stable/config/extensions/autoreload.html
%load_ext autoreload
# Reload all modules (except those excluded by %aimport) every time before executing the Python code typed:
%autoreload 2
# General imports
from pathlib import Path
import numpy as np
import xarray as xr
import pandas as pd
# Plotting
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (20, 10)
plt.rcParams["figure.facecolor"] = "white"
# power_perceiver imports
from power_perceiver.load_prepared_batches.data_loader import HRVSatellite, GSP, PV, Sun
from power_perceiver.load_prepared_batches.prepared_dataset import PreparedDataset
from power_perceiver.transforms.pv import PVPowerRollingWindow
from power_perceiver.transforms.satellite import PatchSatellite
from power_perceiver.xr_batch_processor import ReduceNumPVSystems, SelectPVSystemsNearCenterOfImage, AlignGSPTo5Min
from power_perceiver.np_batch_processor import EncodeSpaceTime, Topography
from power_perceiver.consts import BatchKey
DATA_PATH = Path("~/dev/ocf/power_perceiver/data_for_testing/").expanduser()
assert DATA_PATH.exists()
BATCH_IDX = 0
gsp = GSP(data_path=DATA_PATH)[BATCH_IDX]
hrv = HRVSatellite(data_path=DATA_PATH)[BATCH_IDX]
pv = PV(data_path=DATA_PATH)[BATCH_IDX]
gsp
hrv
pv
31-24
# Find the corresponding GSP 30 minute timestep for each 5 minute satellite timestep.
# We do this by taking the `ceil("30T")` of each 5 minute satellite timestep.
# Most of the code below is just converting from xarray to Pandas and back
# so we can use `pd.DatetimeIndex.ceil` on each datetime:
time_5_min_series = hrv.time_utc.to_series()
time_5_min_dt_index = pd.DatetimeIndex(time_5_min_series)
time_30_min_dt_index = time_5_min_dt_index.ceil("30T")
time_30_min_series = pd.Series(
time_30_min_dt_index,
index=time_5_min_series.index
)
time_30_min_da = time_30_min_series.to_xarray()
# Loop through each example and find the index into the GSP time dimension
# of the GSP timestep corresponding to each 5 minute satellite timestep:
gsp_5_min_for_all_examples = []
max_time_idx = len(gsp.time) - 1
for example_i in gsp.example:
idx_into_gsp = np.searchsorted(
gsp.sel(example=example_i).time_utc.values,
time_30_min_da.sel(example=example_i).values,
)
gsp_5_min = gsp.isel(example=example_i, time=idx_into_gsp.clip(max=max_time_idx))
# Now, for any timestep where we don't have GSP data, set to NaN:
mask = idx_into_gsp <= max_time_idx
gsp_5_min = gsp_5_min.where(mask)
gsp_5_min["time_utc"] = gsp_5_min.time_utc.where(mask)
gsp_5_min_for_all_examples.append(gsp_5_min)
gsp_5_min_for_all_examples = xr.concat(gsp_5_min_for_all_examples, dim="example")
gsp_5_min_for_all_examples
time_30_min_da.sel(example=example_i)
hrv.time_utc.sel(example=example_i)
dataset = PreparedDataset(
data_path=DATA_PATH,
data_loaders=[
HRVSatellite(
transforms=[
PatchSatellite(),
]
),
PV(transforms=[PVPowerRollingWindow()]),
GSP(),
],
xr_batch_processors=[
SelectPVSystemsNearCenterOfImage(),
ReduceNumPVSystems(requested_num_pv_systems=8),
AlignGSPTo5Min(),
],
np_batch_processors=[
EncodeSpaceTime(),
Topography("/home/jack/europe_dem_2km_osgb.tif"),
],
)
%%time
np_batch = dataset[0]
np_batch.keys()
np_batch[BatchKey.gsp].shape
np_batch[BatchKey.gsp_x_osgb_fourier].shape
np_batch[BatchKey.gsp_5_min].shape
np_batch[BatchKey.gsp_5_min_time_utc]
np_batch[BatchKey.gsp_5_min_time_utc_fourier][:, :, 0]
np_batch[BatchKey.gsp_5_min][0]
```
|
github_jupyter
|
# https://ipython.readthedocs.io/en/stable/config/extensions/autoreload.html
%load_ext autoreload
# Reload all modules (except those excluded by %aimport) every time before executing the Python code typed:
%autoreload 2
# General imports
from pathlib import Path
import numpy as np
import xarray as xr
import pandas as pd
# Plotting
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (20, 10)
plt.rcParams["figure.facecolor"] = "white"
# power_perceiver imports
from power_perceiver.load_prepared_batches.data_loader import HRVSatellite, GSP, PV, Sun
from power_perceiver.load_prepared_batches.prepared_dataset import PreparedDataset
from power_perceiver.transforms.pv import PVPowerRollingWindow
from power_perceiver.transforms.satellite import PatchSatellite
from power_perceiver.xr_batch_processor import ReduceNumPVSystems, SelectPVSystemsNearCenterOfImage, AlignGSPTo5Min
from power_perceiver.np_batch_processor import EncodeSpaceTime, Topography
from power_perceiver.consts import BatchKey
DATA_PATH = Path("~/dev/ocf/power_perceiver/data_for_testing/").expanduser()
assert DATA_PATH.exists()
BATCH_IDX = 0
gsp = GSP(data_path=DATA_PATH)[BATCH_IDX]
hrv = HRVSatellite(data_path=DATA_PATH)[BATCH_IDX]
pv = PV(data_path=DATA_PATH)[BATCH_IDX]
gsp
hrv
pv
31-24
# Find the corresponding GSP 30 minute timestep for each 5 minute satellite timestep.
# We do this by taking the `ceil("30T")` of each 5 minute satellite timestep.
# Most of the code below is just converting from xarray to Pandas and back
# so we can use `pd.DatetimeIndex.ceil` on each datetime:
time_5_min_series = hrv.time_utc.to_series()
time_5_min_dt_index = pd.DatetimeIndex(time_5_min_series)
time_30_min_dt_index = time_5_min_dt_index.ceil("30T")
time_30_min_series = pd.Series(
time_30_min_dt_index,
index=time_5_min_series.index
)
time_30_min_da = time_30_min_series.to_xarray()
# Loop through each example and find the index into the GSP time dimension
# of the GSP timestep corresponding to each 5 minute satellite timestep:
gsp_5_min_for_all_examples = []
max_time_idx = len(gsp.time) - 1
for example_i in gsp.example:
idx_into_gsp = np.searchsorted(
gsp.sel(example=example_i).time_utc.values,
time_30_min_da.sel(example=example_i).values,
)
gsp_5_min = gsp.isel(example=example_i, time=idx_into_gsp.clip(max=max_time_idx))
# Now, for any timestep where we don't have GSP data, set to NaN:
mask = idx_into_gsp <= max_time_idx
gsp_5_min = gsp_5_min.where(mask)
gsp_5_min["time_utc"] = gsp_5_min.time_utc.where(mask)
gsp_5_min_for_all_examples.append(gsp_5_min)
gsp_5_min_for_all_examples = xr.concat(gsp_5_min_for_all_examples, dim="example")
gsp_5_min_for_all_examples
time_30_min_da.sel(example=example_i)
hrv.time_utc.sel(example=example_i)
dataset = PreparedDataset(
data_path=DATA_PATH,
data_loaders=[
HRVSatellite(
transforms=[
PatchSatellite(),
]
),
PV(transforms=[PVPowerRollingWindow()]),
GSP(),
],
xr_batch_processors=[
SelectPVSystemsNearCenterOfImage(),
ReduceNumPVSystems(requested_num_pv_systems=8),
AlignGSPTo5Min(),
],
np_batch_processors=[
EncodeSpaceTime(),
Topography("/home/jack/europe_dem_2km_osgb.tif"),
],
)
%%time
np_batch = dataset[0]
np_batch.keys()
np_batch[BatchKey.gsp].shape
np_batch[BatchKey.gsp_x_osgb_fourier].shape
np_batch[BatchKey.gsp_5_min].shape
np_batch[BatchKey.gsp_5_min_time_utc]
np_batch[BatchKey.gsp_5_min_time_utc_fourier][:, :, 0]
np_batch[BatchKey.gsp_5_min][0]
| 0.819135 | 0.673281 |
# Using ezancestry as a Python library
```
from pathlib import Path
from sklearn.model_selection import train_test_split
# load config variables
from ezancestry.config import aisnps_directory as _aisnps_directory
from ezancestry.config import aisnps_set as _aisnps_set
from ezancestry.config import algorithm as _algorithm
from ezancestry.config import k as _k
from ezancestry.config import models_directory as _models_directory
from ezancestry.config import n_components as _n_components
from ezancestry.config import population_level as _population_level
from ezancestry.config import samples_directory as _samples_directory
from ezancestry.config import thousand_genomes_directory as _thousand_genomes_directory
# load functions
from ezancestry.aisnps import extract_aisnps
from ezancestry.dimred import dimensionality_reduction
from ezancestry.evaluate import export_performance
from ezancestry.fetch import download_thousand_genomes
from ezancestry.model import predict_ancestry, train
from ezancestry.process import (encode_genotypes, get_1kg_labels,
process_user_input, vcf2df)
```
### pull aisnps from 1kG
```
# kidd
aisnps_file = Path(_aisnps_directory).joinpath("kidd.aisnp.txt")
extract_aisnps(_thousand_genomes_directory, aisnps_file, aisnps_set="kidd")
# Seldin
aisnps_file = Path(_aisnps_directory).joinpath("Seldin.aisnp.txt")
extract_aisnps(_thousand_genomes_directory, aisnps_file, aisnps_set="Seldin")
# pull the 1000 Genomes Project samples
dfsamples = get_1kg_labels(_samples_directory)
dfsamples.head(3)
vcf_fname = Path(_aisnps_directory).joinpath("kidd.aisnp.1kG.vcf")
df_kidd = vcf2df(vcf_fname, dfsamples)
vcf_fname = Path(_aisnps_directory).joinpath("Seldin.aisnp.1kG.vcf")
df_seldin = vcf2df(vcf_fname, dfsamples)
```
### could start here
```
train_kidd, test_kidd, y_train_kidd, y_test_kidd = train_test_split(
df_kidd,
df_kidd["superpopulation"],
test_size=0.2,
stratify=df_kidd["superpopulation"],
random_state=42,
)
```
### one-hot encode snps
```
# The user could have missing snps
df_user = df_kidd[df_kidd.columns[0:43]].copy()
# The user could have extra snps
df_user["extra_snp"] = "TT"
# The user could have genotypes that weren't in the original encoder
df_user.loc["HG00096", "rs3737576"] = "blah"
ohe_user = encode_genotypes(df_user, aisnps_set="kidd", overwrite_encoder=False)
# make sure "blah" genotype didn't get encoded
ohe_user.loc["HG00096", ["rs3737576_CC", "rs3737576_CT", "rs3737576_TT"]]
# change to True to write new encoders
OVERWRITE_ENCODER = False
# get an encoder for each snp set
df_kidd_encoded = encode_genotypes(df_kidd, aisnps_set="kidd", overwrite_encoder=OVERWRITE_ENCODER)
df_seldin_encoded = encode_genotypes(df_seldin, aisnps_set="Seldin", overwrite_encoder=OVERWRITE_ENCODER)
```
### dimensionality reduction & training
```
OVERWRITE_MODEL = False
# write all the super population dimred models for kidd and Seldin
for aisnps_set, df, df_labels in zip(
["kidd", "Seldin"],
[df_kidd_encoded, df_seldin_encoded],
[df_kidd["superpopulation"], df_seldin["superpopulation"]]
):
for algorithm, labels in zip(["pca", "umap", "nca"], [None, None, None, df_labels]):
df_reduced = dimensionality_reduction(df, algorithm=algorithm, aisnps_set=aisnps_set, overwrite_model=OVERWRITE_MODEL, labels=labels, population_level="super population")
knn_model = train(df_reduced, df_labels, algorithm=algorithm, aisnps_set=aisnps_set, k=9, population_level="superpopulation", overwrite_model=OVERWRITE_MODEL)
# write all the population dimred models for kidd and Seldin
for aisnps_set, df, df_labels in zip(
["kidd", "Seldin"],
[df_kidd_encoded, df_seldin_encoded],
[df_kidd["population"], df_seldin["population"]]
):
for algorithm, labels in zip(["nca"], [df_labels]):
df_reduced = dimensionality_reduction(df, algorithm=algorithm, aisnps_set=aisnps_set, overwrite_model=OVERWRITE_MODEL, labels=labels, population_level="population")
knn_model = train(df_reduced, labels, algorithm=algorithm, aisnps_set=aisnps_set, k=9, population_level="population", overwrite_model=OVERWRITE_MODEL)
```
# Predict
```
from ezancestry.commands import predict
from snps import SNPs
mygenomefile = "/Users/kevin/mygenome/genome2.txt"
```
## load from DataFrame
```
# the snps Python package will read the genome file properly
mygenome = SNPs(mygenomefile)
mygenomedf = mygenome.snps
mygenomedf.head(2)
# predict on the
predictions = predict(mygenomedf,
aisnps_set="kidd",
k=None,
n_components=None,
algorithm=None,
write_predictions=False,
models_directory=None,
output_directory=None,
aisnps_directory=None,
thousand_genomes_directory=None,
samples_directory=None
)
predictions
```
## or load directly from a file
```
predictions = predict(mygenomefile,
aisnps_set="kidd",
k=None,
n_components=None,
algorithm=None,
write_predictions=False,
models_directory=None,
output_directory=None,
aisnps_directory=None,
thousand_genomes_directory=None,
samples_directory=None
)
predictions
```
|
github_jupyter
|
from pathlib import Path
from sklearn.model_selection import train_test_split
# load config variables
from ezancestry.config import aisnps_directory as _aisnps_directory
from ezancestry.config import aisnps_set as _aisnps_set
from ezancestry.config import algorithm as _algorithm
from ezancestry.config import k as _k
from ezancestry.config import models_directory as _models_directory
from ezancestry.config import n_components as _n_components
from ezancestry.config import population_level as _population_level
from ezancestry.config import samples_directory as _samples_directory
from ezancestry.config import thousand_genomes_directory as _thousand_genomes_directory
# load functions
from ezancestry.aisnps import extract_aisnps
from ezancestry.dimred import dimensionality_reduction
from ezancestry.evaluate import export_performance
from ezancestry.fetch import download_thousand_genomes
from ezancestry.model import predict_ancestry, train
from ezancestry.process import (encode_genotypes, get_1kg_labels,
process_user_input, vcf2df)
# kidd
aisnps_file = Path(_aisnps_directory).joinpath("kidd.aisnp.txt")
extract_aisnps(_thousand_genomes_directory, aisnps_file, aisnps_set="kidd")
# Seldin
aisnps_file = Path(_aisnps_directory).joinpath("Seldin.aisnp.txt")
extract_aisnps(_thousand_genomes_directory, aisnps_file, aisnps_set="Seldin")
# pull the 1000 Genomes Project samples
dfsamples = get_1kg_labels(_samples_directory)
dfsamples.head(3)
vcf_fname = Path(_aisnps_directory).joinpath("kidd.aisnp.1kG.vcf")
df_kidd = vcf2df(vcf_fname, dfsamples)
vcf_fname = Path(_aisnps_directory).joinpath("Seldin.aisnp.1kG.vcf")
df_seldin = vcf2df(vcf_fname, dfsamples)
train_kidd, test_kidd, y_train_kidd, y_test_kidd = train_test_split(
df_kidd,
df_kidd["superpopulation"],
test_size=0.2,
stratify=df_kidd["superpopulation"],
random_state=42,
)
# The user could have missing snps
df_user = df_kidd[df_kidd.columns[0:43]].copy()
# The user could have extra snps
df_user["extra_snp"] = "TT"
# The user could have genotypes that weren't in the original encoder
df_user.loc["HG00096", "rs3737576"] = "blah"
ohe_user = encode_genotypes(df_user, aisnps_set="kidd", overwrite_encoder=False)
# make sure "blah" genotype didn't get encoded
ohe_user.loc["HG00096", ["rs3737576_CC", "rs3737576_CT", "rs3737576_TT"]]
# change to True to write new encoders
OVERWRITE_ENCODER = False
# get an encoder for each snp set
df_kidd_encoded = encode_genotypes(df_kidd, aisnps_set="kidd", overwrite_encoder=OVERWRITE_ENCODER)
df_seldin_encoded = encode_genotypes(df_seldin, aisnps_set="Seldin", overwrite_encoder=OVERWRITE_ENCODER)
OVERWRITE_MODEL = False
# write all the super population dimred models for kidd and Seldin
for aisnps_set, df, df_labels in zip(
["kidd", "Seldin"],
[df_kidd_encoded, df_seldin_encoded],
[df_kidd["superpopulation"], df_seldin["superpopulation"]]
):
for algorithm, labels in zip(["pca", "umap", "nca"], [None, None, None, df_labels]):
df_reduced = dimensionality_reduction(df, algorithm=algorithm, aisnps_set=aisnps_set, overwrite_model=OVERWRITE_MODEL, labels=labels, population_level="super population")
knn_model = train(df_reduced, df_labels, algorithm=algorithm, aisnps_set=aisnps_set, k=9, population_level="superpopulation", overwrite_model=OVERWRITE_MODEL)
# write all the population dimred models for kidd and Seldin
for aisnps_set, df, df_labels in zip(
["kidd", "Seldin"],
[df_kidd_encoded, df_seldin_encoded],
[df_kidd["population"], df_seldin["population"]]
):
for algorithm, labels in zip(["nca"], [df_labels]):
df_reduced = dimensionality_reduction(df, algorithm=algorithm, aisnps_set=aisnps_set, overwrite_model=OVERWRITE_MODEL, labels=labels, population_level="population")
knn_model = train(df_reduced, labels, algorithm=algorithm, aisnps_set=aisnps_set, k=9, population_level="population", overwrite_model=OVERWRITE_MODEL)
from ezancestry.commands import predict
from snps import SNPs
mygenomefile = "/Users/kevin/mygenome/genome2.txt"
# the snps Python package will read the genome file properly
mygenome = SNPs(mygenomefile)
mygenomedf = mygenome.snps
mygenomedf.head(2)
# predict on the
predictions = predict(mygenomedf,
aisnps_set="kidd",
k=None,
n_components=None,
algorithm=None,
write_predictions=False,
models_directory=None,
output_directory=None,
aisnps_directory=None,
thousand_genomes_directory=None,
samples_directory=None
)
predictions
predictions = predict(mygenomefile,
aisnps_set="kidd",
k=None,
n_components=None,
algorithm=None,
write_predictions=False,
models_directory=None,
output_directory=None,
aisnps_directory=None,
thousand_genomes_directory=None,
samples_directory=None
)
predictions
| 0.620737 | 0.554109 |
```
%matplotlib inline
from cosmodc2.sdss_colors import load_umachine_processed_sdss_catalog
sdss = load_umachine_processed_sdss_catalog()
print(sdss.keys())
def red_sequence_width(magr,
x=[-22.5, -21, -20, -18, -15],
y=[0.05, 0.06, 0.065, 0.06, 0.06]):
c2, c1, c0 = np.polyfit(x, y, deg=2)
return c0 + c1*magr + c2*magr**2
def main_sequence_width(magr,
x=[-22.5, -21, -20, -18, -15],
y=[0.1, 0.1, 0.1, 0.1, 0.1]):
c2, c1, c0 = np.polyfit(x, y, deg=2)
return c0 + c1*magr + c2*magr**2
def red_sequence_peak(magr,
x=[-22.5, -21, -20, -19, -18, -15],
y=[0.95, 0.95, 0.8, 0.7, 0.7, 0.7]):
c2, c1, c0 = np.polyfit(x, np.log(y), deg=2)
return np.exp(c0 + c1*magr + c2*magr**2)
def main_sequence_peak(magr,
x=[-22.5, -21, -20, -19, -18, -15],
y=[0.65, 0.65, 0.6, 0.4, 0.4, 0.35]):
c2, c1, c0 = np.polyfit(x, np.log(y), deg=2)
return np.exp(c0 + c1*magr + c2*magr**2)
def quiescent_fraction(magr,
x=[-22.5, -21, -20, -19.5, -19, -18, -15],
y=[0.85, 0.65, 0.6, 0.50, 0.50, 0.2, 0.1]):
c2, c1, c0 = np.polyfit(x, np.log(y), deg=2)
return np.exp(c0 + c1*magr + c2*magr**2)
from astropy.utils.misc import NumpyRNGContext
def g_minus_r(magr, seed=None):
magr = np.atleast_1d(magr)
ngals = len(magr)
with NumpyRNGContext(seed):
is_quiescent = np.random.rand(ngals) < quiescent_fraction(magr)
red_sequence = np.random.normal(
loc=red_sequence_peak(magr[is_quiescent]),
scale=red_sequence_width(magr[is_quiescent]))
star_forming_sequence = np.random.normal(
loc=main_sequence_peak(magr[~is_quiescent]),
scale=main_sequence_width(magr[~is_quiescent]))
result = np.zeros(ngals).astype('f4')
result[is_quiescent] = red_sequence
result[~is_quiescent] = star_forming_sequence
return result
npts = int(1e6)
from cosmodc2.sdss_colors.sdss_completeness_model import retrieve_sdss_sample_mask
magr_max = -18.
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(sdss['z'], sdss['restframe_extincted_sdss_abs_magr'],
magr_min, magr_max)
sdss_sample_gr = sdss['restframe_extincted_sdss_gr'][mask]
r = np.zeros(npts) + magr_max
gr = g_minus_r(r)
fig, ax = plt.subplots(1, 1)
nbins = 40
__=ax.hist(sdss_sample_gr, bins=nbins, alpha=0.8, normed=True)
__=ax.hist(gr, bins=nbins, alpha=0.8, normed=True, color='red')
# ylim = ax.set_ylim(0, 5)
xlim = ax.set_xlim(0, 1.2)
npts = int(1e6)
from cosmodc2.sdss_colors.sdss_completeness_model import retrieve_sdss_sample_mask
magr_max = -18.
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(
sdss['z'], sdss['restframe_extincted_sdss_abs_magr'], magr_min, magr_max)
sdss_sample_gr18 = sdss['restframe_extincted_sdss_gr'][mask]
gr18 = g_minus_r(np.zeros(npts) + magr_max)
magr_max = -19.5
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(
sdss['z'], sdss['restframe_extincted_sdss_abs_magr'], magr_min, magr_max)
sdss_sample_gr19p5 = sdss['restframe_extincted_sdss_gr'][mask]
gr19p5 = g_minus_r(np.zeros(npts) + magr_max)
magr_max = -21.
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(
sdss['z'], sdss['restframe_extincted_sdss_abs_magr'], magr_min, magr_max)
sdss_sample_gr21 = sdss['restframe_extincted_sdss_gr'][mask]
gr21 = g_minus_r(np.zeros(npts) + magr_max)
magr_max = -22.5
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(
sdss['z'], sdss['restframe_extincted_sdss_abs_magr'], magr_min, magr_max)
sdss_sample_gr22p5 = sdss['restframe_extincted_sdss_gr'][mask]
gr22p5 = g_minus_r(np.zeros(npts) + magr_max)
fig, _axes = plt.subplots(2, 2, figsize=(10, 8))
((ax1, ax2), (ax3, ax4)) = _axes
axes = ax1, ax2, ax3, ax4
nbins = 40
__=ax1.hist(sdss_sample_gr18, bins=nbins, alpha=0.8, normed=True, label=r'${\rm SDSS}$')
__=ax1.hist(gr18, bins=nbins, alpha=0.8, normed=True,
color='red', label=r'${\rm protoDC2\ v4}$')
__=ax2.hist(sdss_sample_gr19p5, bins=nbins, alpha=0.8, normed=True, label=r'${\rm SDSS}$')
__=ax2.hist(gr19p5, bins=nbins, alpha=0.8, normed=True,
color='red', label=r'${\rm protoDC2\ v4}$')
__=ax3.hist(sdss_sample_gr21, bins=nbins, alpha=0.8, normed=True, label=r'${\rm SDSS}$')
__=ax3.hist(gr21, bins=nbins, alpha=0.8, normed=True,
color='red', label=r'${\rm protoDC2\ v4}$')
__=ax4.hist(sdss_sample_gr22p5, bins=nbins, alpha=0.8, normed=True, label=r'${\rm SDSS}$')
__=ax4.hist(gr22p5, bins=nbins, alpha=0.8, normed=True,
color='red', label=r'${\rm protoDC2\ v4}$')
for ax in axes:
xlim = ax.set_xlim(0, 1.25)
leg = ax.legend()
ax1.set_xticklabels([''])
ax2.set_xticklabels([''])
title1 = ax1.set_title(r'$M_{\rm r} \approx -18$')
title2 = ax2.set_title(r'$M_{\rm r} \approx -19.5$')
title3 = ax3.set_title(r'$M_{\rm r} \approx -21$')
title4 = ax4.set_title(r'$M_{\rm r} \approx -22.5$')
xlabel3 = ax3.set_xlabel(r'${\rm g-r}$')
xlabel4 = ax4.set_xlabel(r'${\rm g-r}$')
figname = 'sdss_gr_distribution_vs_pdc2v4.pdf'
fig.savefig(figname, bbox_extra_artists=[xlabel3], bbox_inches='tight')
npts = int(1e6)
fig, ax = plt.subplots(1, 1)
nbins = 100
__=ax.hist(g_minus_r(np.zeros(npts) + -14), bins=nbins, normed=True,
alpha=0.8, color='purple', label=r'${M_{\rm r} = -14}$')
__=ax.hist(g_minus_r(np.zeros(npts) + -18), bins=nbins, normed=True,
alpha=0.8, color='blue', label=r'${M_{\rm r} = -18}$')
__=ax.hist(g_minus_r(np.zeros(npts) + -20), bins=nbins, normed=True,
alpha=0.8, color='green', label=r'${M_{\rm r} = -20}$')
__=ax.hist(g_minus_r(np.zeros(npts) + -21.5), bins=nbins, normed=True,
alpha=0.8, color='orange', label=r'${M_{\rm r} = -21.5}$')
__=ax.hist(g_minus_r(np.zeros(npts) + -23), bins=nbins, normed=True,
alpha=0.8, color='red', label=r'${M_{\rm r} = -23}$')
xlim = ax.set_xlim(0, 1.2)
legend = ax.legend()
xlabel = ax.set_xlabel(r'${\rm g-r}$')
ylabel = ax.set_ylabel(r'${\rm PDF}$')
title = ax.set_title(r'${\rm protoDC2\ v4:\ z=0}$')
figname = 'analytical_gr_distribution_pdc2v4.pdf'
fig.savefig(figname, bbox_extra_artists=[xlabel, ylabel], bbox_inches='tight')
magr_test = np.linspace(-25, -10, 100)
fig, ax = plt.subplots(1, 1)
__=ax.plot(magr_test, red_sequence_width(magr_test), color='red')
__=ax.plot(magr_test, main_sequence_width(magr_test), color='blue')
title = ax.set_title(r'${\rm width\ of\ sequences}$')
ylim = ax.set_ylim(0, 0.2)
xlim = ax.set_xlim(-10, -25)
xmin, xmax = -25, -10
magr_test = np.linspace(xmin, xmax, 100)
fig, ax = plt.subplots(1, 1)
__=ax.plot(magr_test, red_sequence_peak(magr_test), color='red')
__=ax.plot(magr_test, main_sequence_peak(magr_test), color='blue')
title = ax.set_title(r'${\rm location\ of\ sequences}$')
xlim = ax.set_xlim(xmin-1, xmax+1)
# ylim = ax.set_ylim(0, 1.5)
```
|
github_jupyter
|
%matplotlib inline
from cosmodc2.sdss_colors import load_umachine_processed_sdss_catalog
sdss = load_umachine_processed_sdss_catalog()
print(sdss.keys())
def red_sequence_width(magr,
x=[-22.5, -21, -20, -18, -15],
y=[0.05, 0.06, 0.065, 0.06, 0.06]):
c2, c1, c0 = np.polyfit(x, y, deg=2)
return c0 + c1*magr + c2*magr**2
def main_sequence_width(magr,
x=[-22.5, -21, -20, -18, -15],
y=[0.1, 0.1, 0.1, 0.1, 0.1]):
c2, c1, c0 = np.polyfit(x, y, deg=2)
return c0 + c1*magr + c2*magr**2
def red_sequence_peak(magr,
x=[-22.5, -21, -20, -19, -18, -15],
y=[0.95, 0.95, 0.8, 0.7, 0.7, 0.7]):
c2, c1, c0 = np.polyfit(x, np.log(y), deg=2)
return np.exp(c0 + c1*magr + c2*magr**2)
def main_sequence_peak(magr,
x=[-22.5, -21, -20, -19, -18, -15],
y=[0.65, 0.65, 0.6, 0.4, 0.4, 0.35]):
c2, c1, c0 = np.polyfit(x, np.log(y), deg=2)
return np.exp(c0 + c1*magr + c2*magr**2)
def quiescent_fraction(magr,
x=[-22.5, -21, -20, -19.5, -19, -18, -15],
y=[0.85, 0.65, 0.6, 0.50, 0.50, 0.2, 0.1]):
c2, c1, c0 = np.polyfit(x, np.log(y), deg=2)
return np.exp(c0 + c1*magr + c2*magr**2)
from astropy.utils.misc import NumpyRNGContext
def g_minus_r(magr, seed=None):
magr = np.atleast_1d(magr)
ngals = len(magr)
with NumpyRNGContext(seed):
is_quiescent = np.random.rand(ngals) < quiescent_fraction(magr)
red_sequence = np.random.normal(
loc=red_sequence_peak(magr[is_quiescent]),
scale=red_sequence_width(magr[is_quiescent]))
star_forming_sequence = np.random.normal(
loc=main_sequence_peak(magr[~is_quiescent]),
scale=main_sequence_width(magr[~is_quiescent]))
result = np.zeros(ngals).astype('f4')
result[is_quiescent] = red_sequence
result[~is_quiescent] = star_forming_sequence
return result
npts = int(1e6)
from cosmodc2.sdss_colors.sdss_completeness_model import retrieve_sdss_sample_mask
magr_max = -18.
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(sdss['z'], sdss['restframe_extincted_sdss_abs_magr'],
magr_min, magr_max)
sdss_sample_gr = sdss['restframe_extincted_sdss_gr'][mask]
r = np.zeros(npts) + magr_max
gr = g_minus_r(r)
fig, ax = plt.subplots(1, 1)
nbins = 40
__=ax.hist(sdss_sample_gr, bins=nbins, alpha=0.8, normed=True)
__=ax.hist(gr, bins=nbins, alpha=0.8, normed=True, color='red')
# ylim = ax.set_ylim(0, 5)
xlim = ax.set_xlim(0, 1.2)
npts = int(1e6)
from cosmodc2.sdss_colors.sdss_completeness_model import retrieve_sdss_sample_mask
magr_max = -18.
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(
sdss['z'], sdss['restframe_extincted_sdss_abs_magr'], magr_min, magr_max)
sdss_sample_gr18 = sdss['restframe_extincted_sdss_gr'][mask]
gr18 = g_minus_r(np.zeros(npts) + magr_max)
magr_max = -19.5
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(
sdss['z'], sdss['restframe_extincted_sdss_abs_magr'], magr_min, magr_max)
sdss_sample_gr19p5 = sdss['restframe_extincted_sdss_gr'][mask]
gr19p5 = g_minus_r(np.zeros(npts) + magr_max)
magr_max = -21.
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(
sdss['z'], sdss['restframe_extincted_sdss_abs_magr'], magr_min, magr_max)
sdss_sample_gr21 = sdss['restframe_extincted_sdss_gr'][mask]
gr21 = g_minus_r(np.zeros(npts) + magr_max)
magr_max = -22.5
magr_min = magr_max - 0.3
mask = retrieve_sdss_sample_mask(
sdss['z'], sdss['restframe_extincted_sdss_abs_magr'], magr_min, magr_max)
sdss_sample_gr22p5 = sdss['restframe_extincted_sdss_gr'][mask]
gr22p5 = g_minus_r(np.zeros(npts) + magr_max)
fig, _axes = plt.subplots(2, 2, figsize=(10, 8))
((ax1, ax2), (ax3, ax4)) = _axes
axes = ax1, ax2, ax3, ax4
nbins = 40
__=ax1.hist(sdss_sample_gr18, bins=nbins, alpha=0.8, normed=True, label=r'${\rm SDSS}$')
__=ax1.hist(gr18, bins=nbins, alpha=0.8, normed=True,
color='red', label=r'${\rm protoDC2\ v4}$')
__=ax2.hist(sdss_sample_gr19p5, bins=nbins, alpha=0.8, normed=True, label=r'${\rm SDSS}$')
__=ax2.hist(gr19p5, bins=nbins, alpha=0.8, normed=True,
color='red', label=r'${\rm protoDC2\ v4}$')
__=ax3.hist(sdss_sample_gr21, bins=nbins, alpha=0.8, normed=True, label=r'${\rm SDSS}$')
__=ax3.hist(gr21, bins=nbins, alpha=0.8, normed=True,
color='red', label=r'${\rm protoDC2\ v4}$')
__=ax4.hist(sdss_sample_gr22p5, bins=nbins, alpha=0.8, normed=True, label=r'${\rm SDSS}$')
__=ax4.hist(gr22p5, bins=nbins, alpha=0.8, normed=True,
color='red', label=r'${\rm protoDC2\ v4}$')
for ax in axes:
xlim = ax.set_xlim(0, 1.25)
leg = ax.legend()
ax1.set_xticklabels([''])
ax2.set_xticklabels([''])
title1 = ax1.set_title(r'$M_{\rm r} \approx -18$')
title2 = ax2.set_title(r'$M_{\rm r} \approx -19.5$')
title3 = ax3.set_title(r'$M_{\rm r} \approx -21$')
title4 = ax4.set_title(r'$M_{\rm r} \approx -22.5$')
xlabel3 = ax3.set_xlabel(r'${\rm g-r}$')
xlabel4 = ax4.set_xlabel(r'${\rm g-r}$')
figname = 'sdss_gr_distribution_vs_pdc2v4.pdf'
fig.savefig(figname, bbox_extra_artists=[xlabel3], bbox_inches='tight')
npts = int(1e6)
fig, ax = plt.subplots(1, 1)
nbins = 100
__=ax.hist(g_minus_r(np.zeros(npts) + -14), bins=nbins, normed=True,
alpha=0.8, color='purple', label=r'${M_{\rm r} = -14}$')
__=ax.hist(g_minus_r(np.zeros(npts) + -18), bins=nbins, normed=True,
alpha=0.8, color='blue', label=r'${M_{\rm r} = -18}$')
__=ax.hist(g_minus_r(np.zeros(npts) + -20), bins=nbins, normed=True,
alpha=0.8, color='green', label=r'${M_{\rm r} = -20}$')
__=ax.hist(g_minus_r(np.zeros(npts) + -21.5), bins=nbins, normed=True,
alpha=0.8, color='orange', label=r'${M_{\rm r} = -21.5}$')
__=ax.hist(g_minus_r(np.zeros(npts) + -23), bins=nbins, normed=True,
alpha=0.8, color='red', label=r'${M_{\rm r} = -23}$')
xlim = ax.set_xlim(0, 1.2)
legend = ax.legend()
xlabel = ax.set_xlabel(r'${\rm g-r}$')
ylabel = ax.set_ylabel(r'${\rm PDF}$')
title = ax.set_title(r'${\rm protoDC2\ v4:\ z=0}$')
figname = 'analytical_gr_distribution_pdc2v4.pdf'
fig.savefig(figname, bbox_extra_artists=[xlabel, ylabel], bbox_inches='tight')
magr_test = np.linspace(-25, -10, 100)
fig, ax = plt.subplots(1, 1)
__=ax.plot(magr_test, red_sequence_width(magr_test), color='red')
__=ax.plot(magr_test, main_sequence_width(magr_test), color='blue')
title = ax.set_title(r'${\rm width\ of\ sequences}$')
ylim = ax.set_ylim(0, 0.2)
xlim = ax.set_xlim(-10, -25)
xmin, xmax = -25, -10
magr_test = np.linspace(xmin, xmax, 100)
fig, ax = plt.subplots(1, 1)
__=ax.plot(magr_test, red_sequence_peak(magr_test), color='red')
__=ax.plot(magr_test, main_sequence_peak(magr_test), color='blue')
title = ax.set_title(r'${\rm location\ of\ sequences}$')
xlim = ax.set_xlim(xmin-1, xmax+1)
# ylim = ax.set_ylim(0, 1.5)
| 0.546496 | 0.615088 |
# What's in this notebook?
In this notebook, I've included everything that the code in the blog post will require to run successfully. I did so in an effort to reduce the amount of code in the final blog post. This notebook pulls from the analysis1.ipynb and the analysis2.ipynb notesbooks, which were too large in size to run efficiently in the final blog post.
## Set-up
```
%run functions.ipynb
%matplotlib inline
import tweepy
import configparser
import os
import json
import GetOldTweets3 as got
import datetime
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime
import nltk
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
import string
import random
from nltk.sentiment.vader import SentimentIntensityAnalyzer
import re
import csv
import math
from collections import Counter
jan_tweets = load_tweets('data/1/tweets_2020-01-01_to_2020-02-01.json')
feb_tweets = load_tweets('data/2/tweets_2020-02-01_to_2020-03-01.json')
mar_tweets = load_tweets('data/3/tweets_2020-03-01_to_2020-04-01.json')
apr_tweets = load_tweets('data/4/tweets_2020-04-01_to_2020-05-01.json')
all_time = load_tweets('data/all_time/tweets_2020-01-01_to_2020-05-01.json')
trump_tweets = load_tweets('data/all_time/realdonaldtrump_2020-01-01_to_2020-05-01.json')
pompeo_tweets = load_tweets('data/all_time/secpompeo_2020-01-01_to_2020-05-01.json')
racist_tweets = load_tweets('data/all_time/racist_tweets_2020-01-01_to_2020-05-01.json')
corpus1 = json.load(open('data/corpus_index1.json'))
corpus2 = json.load(open('data/corpus_index2.json'))
corpus3 = json.load(open('data/corpus_index3.json'))
corpus4 = json.load(open('data/corpus_index4.json'))
corp_all = json.load(open('data/corpus_index_all.json'))
```
## Tweet Cleaning
```
all_t_word_dist=Counter()
all_t_bigram_dist=Counter()
all_t_trigram_dist=Counter()
all_t_tokens = []
for tweet in all_time:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
all_t_tokens.extend(toks)
all_t_bigrams=get_ngram_tokens(all_t_tokens,2)
all_t_trigrams=get_ngram_tokens(all_t_tokens,3)
all_t_word_dist.update(all_t_tokens)
all_t_bigram_dist.update(all_t_bigrams)
all_t_trigram_dist.update(all_t_trigrams)
queries = ['asianamerican', 'asian', 'american', \
'racism', 'racist', 'xenophobia', 'racism', 'racist', 'xenophobia', \
'coronavirus', 'corona virus', 'covid19', 'covid 19', 'pandemic', 'virus', "chinese virus", "china virus", \
'coronavirus', 'covid19', 'pandemic', 'chinavirus', 'chinesevirus']
stripped_tweets_tokens = all_t_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_tweets_tokens):
if tweet in words_to_remove:
stripped_tweets_tokens.remove(tweet)
stripped_tweets_tokens = [x for x in stripped_tweets_tokens if not x.startswith('https')]
stripped_tweets_wfreq = Counter(stripped_tweets_tokens)
```
## Tweet Bi/Trigrams
**January**
```
jan_t_word_dist=Counter()
jan_t_bigram_dist=Counter()
jan_t_trigram_dist=Counter()
jan_t_tokens = []
for tweet in jan_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
jan_t_tokens.extend(toks)
jan_t_bigrams=get_ngram_tokens(jan_t_tokens,2)
jan_t_trigrams=get_ngram_tokens(jan_t_tokens,3)
jan_t_word_dist.update(jan_t_tokens)
jan_t_bigram_dist.update(jan_t_bigrams)
jan_t_trigram_dist.update(jan_t_trigrams)
```
**February**
```
feb_t_word_dist=Counter()
feb_t_bigram_dist=Counter()
feb_t_trigram_dist=Counter()
feb_t_tokens = []
for tweet in feb_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
feb_t_tokens.extend(toks)
feb_t_bigrams=get_ngram_tokens(feb_t_tokens,2)
feb_t_trigrams=get_ngram_tokens(feb_t_tokens,3)
feb_t_word_dist.update(feb_t_tokens)
feb_t_bigram_dist.update(feb_t_bigrams)
feb_t_trigram_dist.update(feb_t_trigrams)
feb_top_20_bigrams = feb_t_bigram_dist.most_common(20)
feb_top_20_trigrams = feb_t_trigram_dist.most_common(20)
feb_bigram_df = pd.DataFrame(feb_top_20_bigrams, columns = ['Bigram','Freq'])
feb_bigram_list = list(feb_bigram_df['Bigram'])
feb_trigram_df = pd.DataFrame(feb_top_20_trigrams, columns = ['Trigram','Freq'])
feb_trigram_list = list(feb_trigram_df['Trigram'])
rank = list(range(1, 21))
feb_bitrigram = pd.DataFrame(rank, columns = ['Rank'])
feb_bitrigram['Bigram']=feb_bigram_list
feb_bitrigram['Trigram']=feb_trigram_list
feb_bitrigram.set_index('Rank', inplace=True)
```
#### March
```
mar_t_word_dist=Counter()
mar_t_bigram_dist=Counter()
mar_t_trigram_dist=Counter()
mar_t_tokens = []
for tweet in mar_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
mar_t_tokens.extend(toks)
mar_t_bigrams=get_ngram_tokens(mar_t_tokens,2)
mar_t_trigrams=get_ngram_tokens(mar_t_tokens,3)
mar_t_word_dist.update(mar_t_tokens)
mar_t_bigram_dist.update(mar_t_bigrams)
mar_t_trigram_dist.update(mar_t_trigrams)
mar_top_20_bigrams = mar_t_bigram_dist.most_common(20)
mar_top_20_trigrams = mar_t_trigram_dist.most_common(20)
mar_bigram_df = pd.DataFrame(mar_top_20_bigrams, columns = ['Bigram','Freq'])
mar_bigram_list = list(mar_bigram_df['Bigram'])
mar_trigram_df = pd.DataFrame(mar_top_20_trigrams, columns = ['Trigram','Freq'])
mar_trigram_list = list(mar_trigram_df['Trigram'])
rank = list(range(1, 21))
mar_bitrigram = pd.DataFrame(rank, columns = ['Rank'])
mar_bitrigram['Bigram']=mar_bigram_list
mar_bitrigram['Trigram']=mar_trigram_list
mar_bitrigram.set_index('Rank', inplace=True)
```
#### April
```
apr_t_word_dist=Counter()
apr_t_bigram_dist=Counter()
apr_t_trigram_dist=Counter()
apr_t_tokens = []
for tweet in apr_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
apr_t_tokens.extend(toks)
apr_t_bigrams=get_ngram_tokens(apr_t_tokens,2)
apr_t_trigrams=get_ngram_tokens(apr_t_tokens,3)
apr_t_word_dist.update(apr_t_tokens)
apr_t_bigram_dist.update(apr_t_bigrams)
apr_t_trigram_dist.update(apr_t_trigrams)
apr_top_20_bigrams = apr_t_bigram_dist.most_common(20)
apr_top_20_trigrams = apr_t_trigram_dist.most_common(20)
apr_bigram_df = pd.DataFrame(apr_top_20_bigrams, columns = ['Bigram','Freq'])
apr_bigram_list = list(apr_bigram_df['Bigram'])
apr_trigram_df = pd.DataFrame(apr_top_20_trigrams, columns = ['Trigram','Freq'])
apr_trigram_list = list(apr_trigram_df['Trigram'])
rank = list(range(1, 21))
apr_bitrigram = pd.DataFrame(rank, columns = ['Rank'])
apr_bitrigram['Bigram']=apr_bigram_list
apr_bitrigram['Trigram']=apr_trigram_list
apr_bitrigram.set_index('Rank', inplace=True)
```
## Article distribution over time
```
jan_word_dist=Counter()
jan_bigram_dist=Counter()
jan_trigram_dist=Counter()
for article in corpus1:
filename = article['Filename']
text = open('data/text1/{}'.format(filename)).read()
article['text'] = text
jan_tokens = tokenize(article['text'], lowercase=True, strip_chars=string.punctuation)
article['tokens'] = jan_tokens
article['token_cnt'] = len(jan_tokens)
article['type_cnt'] = len(set(jan_tokens))
jan_tokens = article['tokens']
jan_bigrams=get_ngram_tokens(jan_tokens,2)
jan_trigrams=get_ngram_tokens(jan_tokens,3)
jan_word_dist.update(jan_tokens)
jan_bigram_dist.update(jan_bigrams)
jan_trigram_dist.update(jan_trigrams)
feb_word_dist=Counter()
feb_bigram_dist=Counter()
feb_trigram_dist=Counter()
feb_all_tokens = []
for article in corpus2:
filename = article['Filename']
text = open('data/text2/{}'.format(filename)).read()
article['text'] = text
feb_tokens = tokenize(article['text'], lowercase=True, strip_chars=string.punctuation)
feb_all_tokens.extend(feb_tokens)
article['tokens'] = feb_tokens
article['token_cnt'] = len(feb_tokens)
article['type_cnt'] = len(set(feb_tokens))
feb_tokens = article['tokens']
feb_bigrams=get_ngram_tokens(feb_tokens,2)
feb_trigrams=get_ngram_tokens(feb_tokens,3)
feb_word_dist.update(feb_tokens)
feb_bigram_dist.update(feb_bigrams)
feb_trigram_dist.update(feb_trigrams)
mar_word_dist=Counter()
mar_bigram_dist=Counter()
mar_trigram_dist=Counter()
for article in corpus3:
filename = article['Filename']
text = open('data/text3/{}'.format(filename)).read()
article['text'] = text
mar_tokens = tokenize(article['text'], lowercase=True, strip_chars=string.punctuation)
article['tokens'] = mar_tokens
article['token_cnt'] = len(mar_tokens)
article['type_cnt'] = len(set(mar_tokens))
mar_tokens = article['tokens']
mar_bigrams=get_ngram_tokens(mar_tokens,2)
mar_trigrams=get_ngram_tokens(mar_tokens,3)
mar_word_dist.update(mar_tokens)
mar_bigram_dist.update(mar_bigrams)
mar_trigram_dist.update(mar_trigrams)
apr_word_dist=Counter()
apr_bigram_dist=Counter()
apr_trigram_dist=Counter()
for article in corpus4:
filename = article['Filename']
text = open('data/text4/{}'.format(filename)).read()
article['text'] = text
apr_tokens = tokenize(article['text'], lowercase=True, strip_chars=string.punctuation)
article['tokens'] = apr_tokens
article['token_cnt'] = len(apr_tokens)
article['type_cnt'] = len(set(apr_tokens))
apr_tokens = article['tokens']
apr_bigrams=get_ngram_tokens(apr_tokens,2)
apr_trigrams=get_ngram_tokens(apr_tokens,3)
apr_word_dist.update(apr_tokens)
apr_bigram_dist.update(apr_bigrams)
apr_trigram_dist.update(apr_trigrams)
```
## Recent tweets
```
recent_tweets = DictListUpdate(mar_tweets,apr_tweets)
recent_tweets_tokens = []
for tweet in recent_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
recent_tweets_tokens.extend(toks)
stripped_recenttweets_tokens = recent_tweets_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_recenttweets_tokens):
if tweet in words_to_remove:
stripped_recenttweets_tokens.remove(tweet)
stripped_recenttweets_tokens = [x for x in stripped_recenttweets_tokens if not x.startswith('https')]
stripped_recenttweets_wfreq = Counter(stripped_recenttweets_tokens)
```
## Old tweets
```
old_tweets = DictListUpdate(jan_tweets,feb_tweets)
old_tweets_tokens = []
for tweet in old_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
old_tweets_tokens.extend(toks)
stripped_oldtweets_tokens = old_tweets_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_oldtweets_tokens):
if tweet in words_to_remove:
stripped_oldtweets_tokens.remove(tweet)
stripped_oldtweets_tokens = [x for x in stripped_oldtweets_tokens if not x.startswith('https')]
stripped_oldtweets_wfreq = Counter(stripped_oldtweets_tokens)
```
## Keyness Analysis
```
old_size = len(stripped_oldtweets_tokens)
recent_size = len(stripped_recenttweets_tokens)
top_old = stripped_oldtweets_wfreq.most_common(30)
top_recent = stripped_recenttweets_wfreq.most_common(30)
```
## Trump and Pompeo's Tweets Visualization
```
d = Counter(tweet['date'][:10] for tweet in all_time)
dftweets_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dftweets_cleaned = dftweets_raw.rename(columns = {"index": "date", 0: "count"})
dftweets = dftweets_cleaned.sort_values(by='date')
d = Counter(article['Date'] for article in corp_all)
dflexis_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dflexis_cleaned = dflexis_raw.rename(columns = {"index": "date", 0: "count"})
dflexis = dflexis_cleaned.sort_values(by='date')
d = Counter(tweet['date'][:10] for tweet in trump_tweets)
dftrump_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dftrump_cleaned = dftrump_raw.rename(columns = {"index": "date", 0: "count"})
dftrump = dftrump_cleaned.sort_values(by='date')
d = Counter(tweet['date'][:10] for tweet in pompeo_tweets)
dfpompeo_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dfpompeo_cleaned = dfpompeo_raw.rename(columns = {"index": "date", 0: "count"})
dfpompeo = dfpompeo_cleaned.sort_values(by='date')
d = Counter(tweet['date'][:10] for tweet in racist_tweets)
dfracist_tweets_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dfracist_tweets_cleaned = dfracist_tweets_raw.rename(columns = {"index": "date", 0: "count"})
dfracist_tweets = dfracist_tweets_cleaned.sort_values(by='date')
```
## Silent Tweets vs. Discussion Creators
```
silent_tweets = []
for tweet in all_time:
if tweet['replies']==0:
silent_tweets.append(tweet)
raw_silent_tokens = []
for tweet in silent_tweets:
text = tweet['text']
toks = tokenize(text, lowercase=True, strip_chars='')
raw_silent_tokens.extend(toks)
silent_tokens = []
for tweet in silent_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
silent_tokens.extend(toks)
stripped_silent_tokens = silent_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_silent_tokens):
if tweet in words_to_remove:
stripped_silent_tokens.remove(tweet)
stripped_silent_tokens = [x for x in stripped_silent_tokens if not x.startswith('https')]
stripped_silent_wfreq = Counter(stripped_silent_tokens)
discussion_creators = []
for tweet in all_time:
if tweet['replies']>0:
discussion_creators.append(tweet)
raw_discussion_tokens = []
for tweet in discussion_creators:
text = tweet['text']
toks = tokenize(text, lowercase=True, strip_chars='')
raw_discussion_tokens.extend(toks)
discussion_tokens = []
for tweet in discussion_creators:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
discussion_tokens.extend(toks)
stripped_discussion_tokens = discussion_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_discussion_tokens):
if tweet in words_to_remove:
stripped_discussion_tokens.remove(tweet)
stripped_discussion_tokens = [x for x in stripped_discussion_tokens if not x.startswith('https')]
stripped_discussion_wfreq = Counter(stripped_discussion_tokens)
```
## Shared vocab and word freq. visualization
```
all_word_dist=Counter()
all_bigram_dist=Counter()
all_trigram_dist=Counter()
all_tokens = []
for article in corp_all:
filename = article['Filename']
text = open('data/text_all/{}'.format(filename)).read()
tokens = tokenize(text, lowercase=True, strip_chars=string.punctuation)
all_tokens.extend(tokens)
article['token_cnt'] = len(tokens)
article['type_cnt'] = len(set(tokens))
bigrams=get_ngram_tokens(tokens,2)
trigrams=get_ngram_tokens(tokens,3)
all_word_dist.update(tokens)
all_bigram_dist.update(bigrams)
all_trigram_dist.update(trigrams)
s_all_tokens1 = all_tokens[:145449]
s_all_tokens2 = all_tokens[145449:290898]
s_all_tokens3 = all_tokens[290898:436347]
s_all_tokens4 = all_tokens[436347:581796]
s_all_tokens5 = all_tokens[581796:727245]
s_all_tokens6 = all_tokens[727245:872694]
s_all_tokens7 = all_tokens[872694:1018143]
s_all_tokens8 = all_tokens[1018143:1163592]
s_all_tokens9 = all_tokens[1163592:1309041]
s_all_tokens10 = all_tokens[1309041:]
queries = ['asianamerican', 'asian', 'american', \
'racism', 'racist', 'xenophobia', 'racism', 'racist', 'xenophobia', \
'coronavirus', 'corona virus', 'covid19', 'covid 19', 'pandemic', 'virus', "chinese virus", "china virus", \
'coronavirus', 'covid19', 'pandemic', 'chinavirus', 'chinesevirus']
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens1:
if article_word in words_to_remove:
s_all_tokens1.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens2:
if article_word in words_to_remove:
s_all_tokens2.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens3:
if article_word in words_to_remove:
s_all_tokens3.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens4:
if article_word in words_to_remove:
s_all_tokens4.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens5:
if article_word in words_to_remove:
s_all_tokens5.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens6:
if article_word in words_to_remove:
s_all_tokens6.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens7:
if article_word in words_to_remove:
s_all_tokens7.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens8:
if article_word in words_to_remove:
s_all_tokens8.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens9:
if article_word in words_to_remove:
s_all_tokens9.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens10:
if article_word in words_to_remove:
s_all_tokens10.remove(article_word)
s_all_tokens = s_all_tokens1+s_all_tokens2+s_all_tokens3+s_all_tokens4+s_all_tokens5+s_all_tokens6+s_all_tokens7+s_all_tokens8+s_all_tokens9+s_all_tokens10
s_all_tokens_dist = Counter(s_all_tokens)
all_shared_items = [(item, value, s_all_tokens_dist.get(item))
for item,value in stripped_tweets_wfreq.items() if s_all_tokens_dist.get(item)]
all_tweet_num_tokens = sum(stripped_tweets_wfreq.values())
all_article_num_tokens = sum(s_all_tokens_dist.values())
all_shared_items.sort(key=lambda i: i[1]+i[2], reverse=True)
cdf=pd.DataFrame(all_shared_items, columns=['word','Number of occurrences in Tweets','Number of occurrences in articles'])
cdf['Tweets_percent']=cdf['Number of occurrences in Tweets'] / all_tweet_num_tokens * 100
cdf['Articles_percent']=cdf['Number of occurrences in articles'] / all_article_num_tokens * 100
```
## "Community" and "Health" Collocation
```
article_community_colls = Counter()
article_community_colls.update(collocates(all_tokens, 'community',win=[5,5]))
tweet_community_colls = Counter()
tweet_community_colls.update(collocates(stripped_tweets_tokens, 'community',win=[5,5]))
article_health_colls = Counter()
article_health_colls.update(collocates(all_tokens, 'health',win=[5,5]))
tweet_health_colls = Counter()
tweet_health_colls.update(collocates(stripped_tweets_tokens, 'health',win=[5,5]))
```
## Sentiment Analyses
```
sid = SentimentIntensityAnalyzer()
```
**Tweets**
```
tweet_sid_scores=[]
for tweet in all_time:
scores = sid.polarity_scores(tweet['text'])
scores['text']=tweet['text']
scores['date']=tweet['date']
tweet_sid_scores.append(scores)
by_monthdate = {}
for tweet in tweet_sid_scores:
ymd = tweet['date'][:10]
try:
by_monthdate[ymd].append(tweet['compound'])
except:
by_monthdate[ymd] = [tweet['compound']]
data_tweets = [{ 'date': y, 'avg_sent': sum(d)/len(d)}
for y, d in by_monthdate.items() ]
```
**Articles**
```
article_sid_scores=[]
for article in corp_all:
filename = article['Filename']
text = open('data/text_all/{}'.format(filename)).read()
article['text']=text
scores = sid.polarity_scores(article['text'])
scores['text']=article['text']
scores['date']=article['Date']
article_sid_scores.append(scores)
a_by_monthdate = {}
for article in article_sid_scores:
ymd = article['date']
try:
a_by_monthdate[ymd].append(article['compound'])
except:
a_by_monthdate[ymd] = [article['compound']]
data_articles = [{ 'date': y, 'avg_sent': sum(d)/len(d)}
for y, d in a_by_monthdate.items() ]
t = pd.DataFrame(data_tweets)
a = pd.DataFrame(data_articles)
```
## Racist Tweets
```
raw_racist_tokens = []
for tweet in racist_tweets:
text = tweet['text']
toks = tokenize(text, lowercase=False, strip_chars='')
raw_racist_tokens.extend(toks)
racist_word_dist=Counter()
racist_bigram_dist=Counter()
racist_trigram_dist=Counter()
racist_tokens = []
for tweet in racist_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
racist_tokens.extend(toks)
racist_bigrams=get_ngram_tokens(racist_tokens,2)
racist_trigrams=get_ngram_tokens(racist_tokens,3)
racist_word_dist.update(racist_tokens)
racist_bigram_dist.update(racist_bigrams)
racist_trigram_dist.update(racist_trigrams)
racist_queries = ["ching chong",'ching','chong', 'chink', 'chingchong', "kung flu",'kung','fu', "kung fu flu", "ching chong virus",'coronavirus', 'corona virus', 'covid19', 'covid 19']
s_racist_tweets_tokens = racist_tokens
words_to_remove= stopwords.words('english')+racist_queries
for tweet in list(s_racist_tweets_tokens):
if tweet in words_to_remove:
s_racist_tweets_tokens.remove(tweet)
s_racist_tweets_tokens = [x for x in s_racist_tweets_tokens if not x.startswith('https')]
racist_tweets_wfreq = Counter(s_racist_tweets_tokens)
s_racist_bigrams = get_ngram_tokens(s_racist_tweets_tokens,2)
s_racist_bigrams_dist = Counter(s_racist_bigrams)
s_racist_trigrams = get_ngram_tokens(s_racist_tweets_tokens,3)
s_racist_trigrams_dist = Counter(s_racist_trigrams)
tweet_funny_colls = Counter()
tweet_funny_colls.update(collocates(racist_tokens, 'funny',win=[5,5]))
```
|
github_jupyter
|
%run functions.ipynb
%matplotlib inline
import tweepy
import configparser
import os
import json
import GetOldTweets3 as got
import datetime
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime
import nltk
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
import string
import random
from nltk.sentiment.vader import SentimentIntensityAnalyzer
import re
import csv
import math
from collections import Counter
jan_tweets = load_tweets('data/1/tweets_2020-01-01_to_2020-02-01.json')
feb_tweets = load_tweets('data/2/tweets_2020-02-01_to_2020-03-01.json')
mar_tweets = load_tweets('data/3/tweets_2020-03-01_to_2020-04-01.json')
apr_tweets = load_tweets('data/4/tweets_2020-04-01_to_2020-05-01.json')
all_time = load_tweets('data/all_time/tweets_2020-01-01_to_2020-05-01.json')
trump_tweets = load_tweets('data/all_time/realdonaldtrump_2020-01-01_to_2020-05-01.json')
pompeo_tweets = load_tweets('data/all_time/secpompeo_2020-01-01_to_2020-05-01.json')
racist_tweets = load_tweets('data/all_time/racist_tweets_2020-01-01_to_2020-05-01.json')
corpus1 = json.load(open('data/corpus_index1.json'))
corpus2 = json.load(open('data/corpus_index2.json'))
corpus3 = json.load(open('data/corpus_index3.json'))
corpus4 = json.load(open('data/corpus_index4.json'))
corp_all = json.load(open('data/corpus_index_all.json'))
all_t_word_dist=Counter()
all_t_bigram_dist=Counter()
all_t_trigram_dist=Counter()
all_t_tokens = []
for tweet in all_time:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
all_t_tokens.extend(toks)
all_t_bigrams=get_ngram_tokens(all_t_tokens,2)
all_t_trigrams=get_ngram_tokens(all_t_tokens,3)
all_t_word_dist.update(all_t_tokens)
all_t_bigram_dist.update(all_t_bigrams)
all_t_trigram_dist.update(all_t_trigrams)
queries = ['asianamerican', 'asian', 'american', \
'racism', 'racist', 'xenophobia', 'racism', 'racist', 'xenophobia', \
'coronavirus', 'corona virus', 'covid19', 'covid 19', 'pandemic', 'virus', "chinese virus", "china virus", \
'coronavirus', 'covid19', 'pandemic', 'chinavirus', 'chinesevirus']
stripped_tweets_tokens = all_t_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_tweets_tokens):
if tweet in words_to_remove:
stripped_tweets_tokens.remove(tweet)
stripped_tweets_tokens = [x for x in stripped_tweets_tokens if not x.startswith('https')]
stripped_tweets_wfreq = Counter(stripped_tweets_tokens)
jan_t_word_dist=Counter()
jan_t_bigram_dist=Counter()
jan_t_trigram_dist=Counter()
jan_t_tokens = []
for tweet in jan_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
jan_t_tokens.extend(toks)
jan_t_bigrams=get_ngram_tokens(jan_t_tokens,2)
jan_t_trigrams=get_ngram_tokens(jan_t_tokens,3)
jan_t_word_dist.update(jan_t_tokens)
jan_t_bigram_dist.update(jan_t_bigrams)
jan_t_trigram_dist.update(jan_t_trigrams)
feb_t_word_dist=Counter()
feb_t_bigram_dist=Counter()
feb_t_trigram_dist=Counter()
feb_t_tokens = []
for tweet in feb_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
feb_t_tokens.extend(toks)
feb_t_bigrams=get_ngram_tokens(feb_t_tokens,2)
feb_t_trigrams=get_ngram_tokens(feb_t_tokens,3)
feb_t_word_dist.update(feb_t_tokens)
feb_t_bigram_dist.update(feb_t_bigrams)
feb_t_trigram_dist.update(feb_t_trigrams)
feb_top_20_bigrams = feb_t_bigram_dist.most_common(20)
feb_top_20_trigrams = feb_t_trigram_dist.most_common(20)
feb_bigram_df = pd.DataFrame(feb_top_20_bigrams, columns = ['Bigram','Freq'])
feb_bigram_list = list(feb_bigram_df['Bigram'])
feb_trigram_df = pd.DataFrame(feb_top_20_trigrams, columns = ['Trigram','Freq'])
feb_trigram_list = list(feb_trigram_df['Trigram'])
rank = list(range(1, 21))
feb_bitrigram = pd.DataFrame(rank, columns = ['Rank'])
feb_bitrigram['Bigram']=feb_bigram_list
feb_bitrigram['Trigram']=feb_trigram_list
feb_bitrigram.set_index('Rank', inplace=True)
mar_t_word_dist=Counter()
mar_t_bigram_dist=Counter()
mar_t_trigram_dist=Counter()
mar_t_tokens = []
for tweet in mar_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
mar_t_tokens.extend(toks)
mar_t_bigrams=get_ngram_tokens(mar_t_tokens,2)
mar_t_trigrams=get_ngram_tokens(mar_t_tokens,3)
mar_t_word_dist.update(mar_t_tokens)
mar_t_bigram_dist.update(mar_t_bigrams)
mar_t_trigram_dist.update(mar_t_trigrams)
mar_top_20_bigrams = mar_t_bigram_dist.most_common(20)
mar_top_20_trigrams = mar_t_trigram_dist.most_common(20)
mar_bigram_df = pd.DataFrame(mar_top_20_bigrams, columns = ['Bigram','Freq'])
mar_bigram_list = list(mar_bigram_df['Bigram'])
mar_trigram_df = pd.DataFrame(mar_top_20_trigrams, columns = ['Trigram','Freq'])
mar_trigram_list = list(mar_trigram_df['Trigram'])
rank = list(range(1, 21))
mar_bitrigram = pd.DataFrame(rank, columns = ['Rank'])
mar_bitrigram['Bigram']=mar_bigram_list
mar_bitrigram['Trigram']=mar_trigram_list
mar_bitrigram.set_index('Rank', inplace=True)
apr_t_word_dist=Counter()
apr_t_bigram_dist=Counter()
apr_t_trigram_dist=Counter()
apr_t_tokens = []
for tweet in apr_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
apr_t_tokens.extend(toks)
apr_t_bigrams=get_ngram_tokens(apr_t_tokens,2)
apr_t_trigrams=get_ngram_tokens(apr_t_tokens,3)
apr_t_word_dist.update(apr_t_tokens)
apr_t_bigram_dist.update(apr_t_bigrams)
apr_t_trigram_dist.update(apr_t_trigrams)
apr_top_20_bigrams = apr_t_bigram_dist.most_common(20)
apr_top_20_trigrams = apr_t_trigram_dist.most_common(20)
apr_bigram_df = pd.DataFrame(apr_top_20_bigrams, columns = ['Bigram','Freq'])
apr_bigram_list = list(apr_bigram_df['Bigram'])
apr_trigram_df = pd.DataFrame(apr_top_20_trigrams, columns = ['Trigram','Freq'])
apr_trigram_list = list(apr_trigram_df['Trigram'])
rank = list(range(1, 21))
apr_bitrigram = pd.DataFrame(rank, columns = ['Rank'])
apr_bitrigram['Bigram']=apr_bigram_list
apr_bitrigram['Trigram']=apr_trigram_list
apr_bitrigram.set_index('Rank', inplace=True)
jan_word_dist=Counter()
jan_bigram_dist=Counter()
jan_trigram_dist=Counter()
for article in corpus1:
filename = article['Filename']
text = open('data/text1/{}'.format(filename)).read()
article['text'] = text
jan_tokens = tokenize(article['text'], lowercase=True, strip_chars=string.punctuation)
article['tokens'] = jan_tokens
article['token_cnt'] = len(jan_tokens)
article['type_cnt'] = len(set(jan_tokens))
jan_tokens = article['tokens']
jan_bigrams=get_ngram_tokens(jan_tokens,2)
jan_trigrams=get_ngram_tokens(jan_tokens,3)
jan_word_dist.update(jan_tokens)
jan_bigram_dist.update(jan_bigrams)
jan_trigram_dist.update(jan_trigrams)
feb_word_dist=Counter()
feb_bigram_dist=Counter()
feb_trigram_dist=Counter()
feb_all_tokens = []
for article in corpus2:
filename = article['Filename']
text = open('data/text2/{}'.format(filename)).read()
article['text'] = text
feb_tokens = tokenize(article['text'], lowercase=True, strip_chars=string.punctuation)
feb_all_tokens.extend(feb_tokens)
article['tokens'] = feb_tokens
article['token_cnt'] = len(feb_tokens)
article['type_cnt'] = len(set(feb_tokens))
feb_tokens = article['tokens']
feb_bigrams=get_ngram_tokens(feb_tokens,2)
feb_trigrams=get_ngram_tokens(feb_tokens,3)
feb_word_dist.update(feb_tokens)
feb_bigram_dist.update(feb_bigrams)
feb_trigram_dist.update(feb_trigrams)
mar_word_dist=Counter()
mar_bigram_dist=Counter()
mar_trigram_dist=Counter()
for article in corpus3:
filename = article['Filename']
text = open('data/text3/{}'.format(filename)).read()
article['text'] = text
mar_tokens = tokenize(article['text'], lowercase=True, strip_chars=string.punctuation)
article['tokens'] = mar_tokens
article['token_cnt'] = len(mar_tokens)
article['type_cnt'] = len(set(mar_tokens))
mar_tokens = article['tokens']
mar_bigrams=get_ngram_tokens(mar_tokens,2)
mar_trigrams=get_ngram_tokens(mar_tokens,3)
mar_word_dist.update(mar_tokens)
mar_bigram_dist.update(mar_bigrams)
mar_trigram_dist.update(mar_trigrams)
apr_word_dist=Counter()
apr_bigram_dist=Counter()
apr_trigram_dist=Counter()
for article in corpus4:
filename = article['Filename']
text = open('data/text4/{}'.format(filename)).read()
article['text'] = text
apr_tokens = tokenize(article['text'], lowercase=True, strip_chars=string.punctuation)
article['tokens'] = apr_tokens
article['token_cnt'] = len(apr_tokens)
article['type_cnt'] = len(set(apr_tokens))
apr_tokens = article['tokens']
apr_bigrams=get_ngram_tokens(apr_tokens,2)
apr_trigrams=get_ngram_tokens(apr_tokens,3)
apr_word_dist.update(apr_tokens)
apr_bigram_dist.update(apr_bigrams)
apr_trigram_dist.update(apr_trigrams)
recent_tweets = DictListUpdate(mar_tweets,apr_tweets)
recent_tweets_tokens = []
for tweet in recent_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
recent_tweets_tokens.extend(toks)
stripped_recenttweets_tokens = recent_tweets_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_recenttweets_tokens):
if tweet in words_to_remove:
stripped_recenttweets_tokens.remove(tweet)
stripped_recenttweets_tokens = [x for x in stripped_recenttweets_tokens if not x.startswith('https')]
stripped_recenttweets_wfreq = Counter(stripped_recenttweets_tokens)
old_tweets = DictListUpdate(jan_tweets,feb_tweets)
old_tweets_tokens = []
for tweet in old_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
old_tweets_tokens.extend(toks)
stripped_oldtweets_tokens = old_tweets_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_oldtweets_tokens):
if tweet in words_to_remove:
stripped_oldtweets_tokens.remove(tweet)
stripped_oldtweets_tokens = [x for x in stripped_oldtweets_tokens if not x.startswith('https')]
stripped_oldtweets_wfreq = Counter(stripped_oldtweets_tokens)
old_size = len(stripped_oldtweets_tokens)
recent_size = len(stripped_recenttweets_tokens)
top_old = stripped_oldtweets_wfreq.most_common(30)
top_recent = stripped_recenttweets_wfreq.most_common(30)
d = Counter(tweet['date'][:10] for tweet in all_time)
dftweets_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dftweets_cleaned = dftweets_raw.rename(columns = {"index": "date", 0: "count"})
dftweets = dftweets_cleaned.sort_values(by='date')
d = Counter(article['Date'] for article in corp_all)
dflexis_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dflexis_cleaned = dflexis_raw.rename(columns = {"index": "date", 0: "count"})
dflexis = dflexis_cleaned.sort_values(by='date')
d = Counter(tweet['date'][:10] for tweet in trump_tweets)
dftrump_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dftrump_cleaned = dftrump_raw.rename(columns = {"index": "date", 0: "count"})
dftrump = dftrump_cleaned.sort_values(by='date')
d = Counter(tweet['date'][:10] for tweet in pompeo_tweets)
dfpompeo_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dfpompeo_cleaned = dfpompeo_raw.rename(columns = {"index": "date", 0: "count"})
dfpompeo = dfpompeo_cleaned.sort_values(by='date')
d = Counter(tweet['date'][:10] for tweet in racist_tweets)
dfracist_tweets_raw = pd.DataFrame.from_dict(d, orient='index').reset_index()
dfracist_tweets_cleaned = dfracist_tweets_raw.rename(columns = {"index": "date", 0: "count"})
dfracist_tweets = dfracist_tweets_cleaned.sort_values(by='date')
silent_tweets = []
for tweet in all_time:
if tweet['replies']==0:
silent_tweets.append(tweet)
raw_silent_tokens = []
for tweet in silent_tweets:
text = tweet['text']
toks = tokenize(text, lowercase=True, strip_chars='')
raw_silent_tokens.extend(toks)
silent_tokens = []
for tweet in silent_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
silent_tokens.extend(toks)
stripped_silent_tokens = silent_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_silent_tokens):
if tweet in words_to_remove:
stripped_silent_tokens.remove(tweet)
stripped_silent_tokens = [x for x in stripped_silent_tokens if not x.startswith('https')]
stripped_silent_wfreq = Counter(stripped_silent_tokens)
discussion_creators = []
for tweet in all_time:
if tweet['replies']>0:
discussion_creators.append(tweet)
raw_discussion_tokens = []
for tweet in discussion_creators:
text = tweet['text']
toks = tokenize(text, lowercase=True, strip_chars='')
raw_discussion_tokens.extend(toks)
discussion_tokens = []
for tweet in discussion_creators:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
discussion_tokens.extend(toks)
stripped_discussion_tokens = discussion_tokens
words_to_remove= stopwords.words('english')+queries
for tweet in list(stripped_discussion_tokens):
if tweet in words_to_remove:
stripped_discussion_tokens.remove(tweet)
stripped_discussion_tokens = [x for x in stripped_discussion_tokens if not x.startswith('https')]
stripped_discussion_wfreq = Counter(stripped_discussion_tokens)
all_word_dist=Counter()
all_bigram_dist=Counter()
all_trigram_dist=Counter()
all_tokens = []
for article in corp_all:
filename = article['Filename']
text = open('data/text_all/{}'.format(filename)).read()
tokens = tokenize(text, lowercase=True, strip_chars=string.punctuation)
all_tokens.extend(tokens)
article['token_cnt'] = len(tokens)
article['type_cnt'] = len(set(tokens))
bigrams=get_ngram_tokens(tokens,2)
trigrams=get_ngram_tokens(tokens,3)
all_word_dist.update(tokens)
all_bigram_dist.update(bigrams)
all_trigram_dist.update(trigrams)
s_all_tokens1 = all_tokens[:145449]
s_all_tokens2 = all_tokens[145449:290898]
s_all_tokens3 = all_tokens[290898:436347]
s_all_tokens4 = all_tokens[436347:581796]
s_all_tokens5 = all_tokens[581796:727245]
s_all_tokens6 = all_tokens[727245:872694]
s_all_tokens7 = all_tokens[872694:1018143]
s_all_tokens8 = all_tokens[1018143:1163592]
s_all_tokens9 = all_tokens[1163592:1309041]
s_all_tokens10 = all_tokens[1309041:]
queries = ['asianamerican', 'asian', 'american', \
'racism', 'racist', 'xenophobia', 'racism', 'racist', 'xenophobia', \
'coronavirus', 'corona virus', 'covid19', 'covid 19', 'pandemic', 'virus', "chinese virus", "china virus", \
'coronavirus', 'covid19', 'pandemic', 'chinavirus', 'chinesevirus']
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens1:
if article_word in words_to_remove:
s_all_tokens1.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens2:
if article_word in words_to_remove:
s_all_tokens2.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens3:
if article_word in words_to_remove:
s_all_tokens3.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens4:
if article_word in words_to_remove:
s_all_tokens4.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens5:
if article_word in words_to_remove:
s_all_tokens5.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens6:
if article_word in words_to_remove:
s_all_tokens6.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens7:
if article_word in words_to_remove:
s_all_tokens7.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens8:
if article_word in words_to_remove:
s_all_tokens8.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens9:
if article_word in words_to_remove:
s_all_tokens9.remove(article_word)
words_to_remove= stopwords.words('english')+queries
for article_word in s_all_tokens10:
if article_word in words_to_remove:
s_all_tokens10.remove(article_word)
s_all_tokens = s_all_tokens1+s_all_tokens2+s_all_tokens3+s_all_tokens4+s_all_tokens5+s_all_tokens6+s_all_tokens7+s_all_tokens8+s_all_tokens9+s_all_tokens10
s_all_tokens_dist = Counter(s_all_tokens)
all_shared_items = [(item, value, s_all_tokens_dist.get(item))
for item,value in stripped_tweets_wfreq.items() if s_all_tokens_dist.get(item)]
all_tweet_num_tokens = sum(stripped_tweets_wfreq.values())
all_article_num_tokens = sum(s_all_tokens_dist.values())
all_shared_items.sort(key=lambda i: i[1]+i[2], reverse=True)
cdf=pd.DataFrame(all_shared_items, columns=['word','Number of occurrences in Tweets','Number of occurrences in articles'])
cdf['Tweets_percent']=cdf['Number of occurrences in Tweets'] / all_tweet_num_tokens * 100
cdf['Articles_percent']=cdf['Number of occurrences in articles'] / all_article_num_tokens * 100
article_community_colls = Counter()
article_community_colls.update(collocates(all_tokens, 'community',win=[5,5]))
tweet_community_colls = Counter()
tweet_community_colls.update(collocates(stripped_tweets_tokens, 'community',win=[5,5]))
article_health_colls = Counter()
article_health_colls.update(collocates(all_tokens, 'health',win=[5,5]))
tweet_health_colls = Counter()
tweet_health_colls.update(collocates(stripped_tweets_tokens, 'health',win=[5,5]))
sid = SentimentIntensityAnalyzer()
tweet_sid_scores=[]
for tweet in all_time:
scores = sid.polarity_scores(tweet['text'])
scores['text']=tweet['text']
scores['date']=tweet['date']
tweet_sid_scores.append(scores)
by_monthdate = {}
for tweet in tweet_sid_scores:
ymd = tweet['date'][:10]
try:
by_monthdate[ymd].append(tweet['compound'])
except:
by_monthdate[ymd] = [tweet['compound']]
data_tweets = [{ 'date': y, 'avg_sent': sum(d)/len(d)}
for y, d in by_monthdate.items() ]
article_sid_scores=[]
for article in corp_all:
filename = article['Filename']
text = open('data/text_all/{}'.format(filename)).read()
article['text']=text
scores = sid.polarity_scores(article['text'])
scores['text']=article['text']
scores['date']=article['Date']
article_sid_scores.append(scores)
a_by_monthdate = {}
for article in article_sid_scores:
ymd = article['date']
try:
a_by_monthdate[ymd].append(article['compound'])
except:
a_by_monthdate[ymd] = [article['compound']]
data_articles = [{ 'date': y, 'avg_sent': sum(d)/len(d)}
for y, d in a_by_monthdate.items() ]
t = pd.DataFrame(data_tweets)
a = pd.DataFrame(data_articles)
raw_racist_tokens = []
for tweet in racist_tweets:
text = tweet['text']
toks = tokenize(text, lowercase=False, strip_chars='')
raw_racist_tokens.extend(toks)
racist_word_dist=Counter()
racist_bigram_dist=Counter()
racist_trigram_dist=Counter()
racist_tokens = []
for tweet in racist_tweets:
text = tweet['text'].replace('&', '&').replace('”', '').replace('\'', '').replace('’', '').replace('“', '')
toks = tokenize(text, lowercase=True, strip_chars=string.punctuation)
racist_tokens.extend(toks)
racist_bigrams=get_ngram_tokens(racist_tokens,2)
racist_trigrams=get_ngram_tokens(racist_tokens,3)
racist_word_dist.update(racist_tokens)
racist_bigram_dist.update(racist_bigrams)
racist_trigram_dist.update(racist_trigrams)
racist_queries = ["ching chong",'ching','chong', 'chink', 'chingchong', "kung flu",'kung','fu', "kung fu flu", "ching chong virus",'coronavirus', 'corona virus', 'covid19', 'covid 19']
s_racist_tweets_tokens = racist_tokens
words_to_remove= stopwords.words('english')+racist_queries
for tweet in list(s_racist_tweets_tokens):
if tweet in words_to_remove:
s_racist_tweets_tokens.remove(tweet)
s_racist_tweets_tokens = [x for x in s_racist_tweets_tokens if not x.startswith('https')]
racist_tweets_wfreq = Counter(s_racist_tweets_tokens)
s_racist_bigrams = get_ngram_tokens(s_racist_tweets_tokens,2)
s_racist_bigrams_dist = Counter(s_racist_bigrams)
s_racist_trigrams = get_ngram_tokens(s_racist_tweets_tokens,3)
s_racist_trigrams_dist = Counter(s_racist_trigrams)
tweet_funny_colls = Counter()
tweet_funny_colls.update(collocates(racist_tokens, 'funny',win=[5,5]))
| 0.207054 | 0.776453 |
# 01. Basic Tutorial
In this tutorial, you can learn how to:
* Define Search Space
* Optimize Objective Function
This tutorial describes how to optimize Hyperparameters using HyperOpt without having a mathematical understanding of any algorithm implemented in HyperOpt.
```
# Import HyperOpt Library
from hyperopt import tpe, hp, fmin
```
Declares a purpose function to optimize. In this tutorial, we will optimize a simple function called `objective`, which is a simple quadratic function.
$$ y = (x-3)^2 + 2 $$
```
objective = lambda x: (x-3)**2 + 2
```
Now, let's visualize this objective function.
```
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-10, 10, 100)
y = objective(x)
fig = plt.figure()
plt.plot(x, y)
plt.show()
```
We are trying to optimize the objective function by changing the HyperParameter $x$. That's why we will declare a search space for $x$. The functions related to the search space are implemented in `hyperopt.hp`. The list is as follows.
* `hp.randint(label, upper)` or `hp.randint(label, low, high)`
* `hp.uniform(label, low, high)`
* `hp.loguniform(label, low, high)`
* `hp.normal(label, mu, sigma)`
* `hp.lognormal(label, mu, sigma)`
* `hp.quniform(label, low, high, q)`
* `hp.qloguniform(label, low, high, q)`
* `hp.qnormal(label, mu, sigma, q)`
* `hp.qlognormal(label, mu, sigma, q)`
* `hp.choice(label, list)`
We will use the most basic `hp.uniform` in this tutorial.
```
# Define the search space of x between -10 and 10.
space = hp.uniform('x', -10, 10)
```
Now, there's only one last step left. So far, we have defined a function of purpose, and we have defined a search space for $x$. Now we can search through the search space $x$ and find the value of $x$ that can optimize the objective function. HyperOpt performs it using `fmin`.
```
best = fmin(
fn=objective, # Objective Function to optimize
space=space, # Hyperparameter's Search Space
algo=tpe.suggest, # Optimization algorithm
max_evals=1000 # Number of optimization attempts
)
print(best)
```
The optimal $x$ value found by HyperOpt is approximately 3.0. This is very close to a solution of $y=(x-3)^2+2$.
```
fig = plt.figure()
plt.plot(x, y)
plt.scatter(best['x'], objective(best['x']), color='red')
plt.show()
```
## Using `space="annotated"`
Starting on release 0.2.6, it is allowed to declare the space within the function using type annotations. This saves one step and makes prototyping and space tuning faster.
```
def objective(
x: hp.uniform('x', -10, 10) # Declare space as typed
):
return (x-3)**2 + 2
best = fmin(
fn=objective, # Objective Function to optimize
space="annotated", # Hyperparameter's Search Space now is declared on objective
algo=tpe.suggest, # Optimization algorithm
max_evals=1000 # Number of optimization attempts
)
print(best)
fig = plt.figure()
plt.plot(x, y)
plt.scatter(best['x'], objective(best['x']), color='red')
plt.show()
```
|
github_jupyter
|
# Import HyperOpt Library
from hyperopt import tpe, hp, fmin
objective = lambda x: (x-3)**2 + 2
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-10, 10, 100)
y = objective(x)
fig = plt.figure()
plt.plot(x, y)
plt.show()
# Define the search space of x between -10 and 10.
space = hp.uniform('x', -10, 10)
best = fmin(
fn=objective, # Objective Function to optimize
space=space, # Hyperparameter's Search Space
algo=tpe.suggest, # Optimization algorithm
max_evals=1000 # Number of optimization attempts
)
print(best)
fig = plt.figure()
plt.plot(x, y)
plt.scatter(best['x'], objective(best['x']), color='red')
plt.show()
def objective(
x: hp.uniform('x', -10, 10) # Declare space as typed
):
return (x-3)**2 + 2
best = fmin(
fn=objective, # Objective Function to optimize
space="annotated", # Hyperparameter's Search Space now is declared on objective
algo=tpe.suggest, # Optimization algorithm
max_evals=1000 # Number of optimization attempts
)
print(best)
fig = plt.figure()
plt.plot(x, y)
plt.scatter(best['x'], objective(best['x']), color='red')
plt.show()
| 0.606732 | 0.993967 |
# Dependencies
```
import os
import random
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.utils import class_weight
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, cohen_kappa_score
from keras import backend as K
from keras.models import Model
from keras import optimizers, applications
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import EarlyStopping, ReduceLROnPlateau, Callback, LearningRateScheduler
from keras.layers import Dense, Dropout, GlobalAveragePooling2D, Input
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
def seed_everything(seed=0):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
set_random_seed(0)
seed = 0
seed_everything(seed)
%matplotlib inline
sns.set(style="whitegrid")
warnings.filterwarnings("ignore")
```
# Load data
```
hold_out_set = pd.read_csv('../input/aptos-data-split/hold-out.csv')
hold_out_set.head()
hold_out_set = pd.read_csv('../input/aptos-data-split/hold-out.csv')
X_train = hold_out_set[hold_out_set['set'] == 'train']
X_val = hold_out_set[hold_out_set['set'] == 'validation']
test = pd.read_csv('../input/aptos2019-blindness-detection/test.csv')
print('Number of train samples: ', X_train.shape[0])
print('Number of validation samples: ', X_val.shape[0])
print('Number of test samples: ', test.shape[0])
# Preprocecss data
X_train["id_code"] = X_train["id_code"].apply(lambda x: x + ".png")
X_val["id_code"] = X_val["id_code"].apply(lambda x: x + ".png")
test["id_code"] = test["id_code"].apply(lambda x: x + ".png")
X_train['diagnosis'] = X_train['diagnosis'].astype('str')
X_val['diagnosis'] = X_val['diagnosis'].astype('str')
display(X_train.head())
```
# Model parameters
```
# Model parameters
BATCH_SIZE = 32
EPOCHS = 40
WARMUP_EPOCHS = 3
LEARNING_RATE = 1e-4
WARMUP_LEARNING_RATE = 1e-3
HEIGHT = 320
WIDTH = 320
CANAL = 3
N_CLASSES = X_train['diagnosis'].nunique()
ES_PATIENCE = 5
RLROP_PATIENCE = 3
DECAY_DROP = 0.5
def kappa(y_true, y_pred, n_classes=5):
y_trues = K.cast(K.argmax(y_true), K.floatx())
y_preds = K.cast(K.argmax(y_pred), K.floatx())
n_samples = K.cast(K.shape(y_true)[0], K.floatx())
distance = K.sum(K.abs(y_trues - y_preds))
max_distance = n_classes - 1
kappa_score = 1 - ((distance**2) / (n_samples * (max_distance**2)))
return kappa_score
def step_decay(epoch):
lrate = 30e-5
if epoch > 3:
lrate = 15e-5
if epoch > 7:
lrate = 7.5e-5
if epoch > 11:
lrate = 3e-5
if epoch > 15:
lrate = 1e-5
return lrate
def focal_loss(y_true, y_pred):
gamma = 2.0
epsilon = K.epsilon()
pt = y_pred * y_true + (1-y_pred) * (1-y_true)
pt = K.clip(pt, epsilon, 1-epsilon)
CE = -K.log(pt)
FL = K.pow(1-pt, gamma) * CE
loss = K.sum(FL, axis=1)
return loss
def get_1cycle_schedule(lr_max=1e-3, n_data_points=8000, epochs=200, batch_size=40, verbose=0):
"""
Creates a look-up table of learning rates for 1cycle schedule with cosine annealing
See @sgugger's & @jeremyhoward's code in fastai library: https://github.com/fastai/fastai/blob/master/fastai/train.py
Wrote this to use with my Keras and (non-fastai-)PyTorch codes.
Note that in Keras, the LearningRateScheduler callback (https://keras.io/callbacks/#learningratescheduler) only operates once per epoch, not per batch
So see below for Keras callback
Keyword arguments:
lr_max chosen by user after lr_finder
n_data_points data points per epoch (e.g. size of training set)
epochs number of epochs
batch_size batch size
Output:
lrs look-up table of LR's, with length equal to total # of iterations
Then you can use this in your PyTorch code by counting iteration number and setting
optimizer.param_groups[0]['lr'] = lrs[iter_count]
"""
if verbose > 0:
print("Setting up 1Cycle LR schedule...")
pct_start, div_factor = 0.3, 25. # @sgugger's parameters in fastai code
lr_start = lr_max/div_factor
lr_end = lr_start/1e4
n_iter = (n_data_points * epochs // batch_size) + 1 # number of iterations
a1 = int(n_iter * pct_start)
a2 = n_iter - a1
# make look-up table
lrs_first = np.linspace(lr_start, lr_max, a1) # linear growth
lrs_second = (lr_max-lr_end)*(1+np.cos(np.linspace(0,np.pi,a2)))/2 + lr_end # cosine annealing
lrs = np.concatenate((lrs_first, lrs_second))
return lrs
class OneCycleScheduler(Callback):
"""My modification of Keras' Learning rate scheduler to do 1Cycle learning
which increments per BATCH, not per epoch
Keyword arguments
**kwargs: keyword arguments to pass to get_1cycle_schedule()
Also, verbose: int. 0: quiet, 1: update messages.
Sample usage (from my train.py):
lrsched = OneCycleScheduler(lr_max=1e-4, n_data_points=X_train.shape[0],
epochs=epochs, batch_size=batch_size, verbose=1)
"""
def __init__(self, **kwargs):
super(OneCycleScheduler, self).__init__()
self.verbose = kwargs.get('verbose', 0)
self.lrs = get_1cycle_schedule(**kwargs)
self.iteration = 0
def on_batch_begin(self, batch, logs=None):
lr = self.lrs[self.iteration]
K.set_value(self.model.optimizer.lr, lr) # here's where the assignment takes place
if self.verbose > 0:
print('\nIteration %06d: OneCycleScheduler setting learning '
'rate to %s.' % (self.iteration, lr))
self.iteration += 1
def on_epoch_end(self, epoch, logs=None): # this is unchanged from Keras LearningRateScheduler
logs = logs or {}
logs['lr'] = K.get_value(self.model.optimizer.lr)
self.iteration = 0
```
# Data generator
```
train_datagen=ImageDataGenerator(rescale=1./255,
rotation_range=360,
brightness_range=[0.5, 1.5],
zoom_range=[1, 1.2],
zca_whitening=True,
horizontal_flip=True,
vertical_flip=True,
fill_mode='reflect',
cval=0.)
test_datagen = ImageDataGenerator(rescale=1./255)
validation_datagen = ImageDataGenerator(rescale=1./255)
train_generator=train_datagen.flow_from_dataframe(
dataframe=X_train,
directory="../input/aptos2019-blindness-detection/train_images/",
x_col="id_code",
y_col="diagnosis",
class_mode="categorical",
batch_size=BATCH_SIZE,
target_size=(HEIGHT, WIDTH),
seed=seed)
valid_generator=validation_datagen.flow_from_dataframe(
dataframe=X_val,
directory="../input/aptos2019-blindness-detection/train_images/",
x_col="id_code",
y_col="diagnosis",
class_mode="categorical",
batch_size=BATCH_SIZE,
target_size=(HEIGHT, WIDTH),
seed=seed)
test_generator = test_datagen.flow_from_dataframe(
dataframe=test,
directory = "../input/aptos2019-blindness-detection/test_images/",
x_col="id_code",
batch_size=1,
class_mode=None,
shuffle=False,
target_size=(HEIGHT, WIDTH),
seed=seed)
```
# Model
```
def create_model(input_shape, n_out):
input_tensor = Input(shape=input_shape)
base_model = applications.ResNet50(weights=None,
include_top=False,
input_tensor=input_tensor)
base_model.load_weights('../input/resnet50/resnet50_weights_tf_dim_ordering_tf_kernels_notop.h5')
x = GlobalAveragePooling2D()(base_model.output)
x = Dropout(0.5)(x)
x = Dense(2048, activation='relu')(x)
x = Dropout(0.5)(x)
final_output = Dense(n_out, activation='softmax', name='final_output')(x)
model = Model(input_tensor, final_output)
return model
```
# Train top layers
```
model = create_model(input_shape=(HEIGHT, WIDTH, CANAL), n_out=N_CLASSES)
for layer in model.layers:
layer.trainable = False
for i in range(-5, 0):
model.layers[i].trainable = True
class_weights = class_weight.compute_class_weight('balanced', np.unique(X_train['diagnosis'].astype('int').values), X_train['diagnosis'].astype('int').values)
metric_list = ["accuracy", kappa]
optimizer = optimizers.Adam(lr=WARMUP_LEARNING_RATE)
model.compile(optimizer=optimizer, loss=focal_loss, metrics=metric_list)
model.summary()
STEP_SIZE_TRAIN = train_generator.n//train_generator.batch_size
STEP_SIZE_VALID = valid_generator.n//valid_generator.batch_size
history_warmup = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=WARMUP_EPOCHS,
class_weight=class_weights,
verbose=1).history
```
# Fine-tune the complete model (1st step)
```
for layer in model.layers:
layer.trainable = True
# lrstep = LearningRateScheduler(step_decay)
# lrcycle = OneCycleScheduler(lr_max=LEARNING_RATE, n_data_points=(train_generator.n + valid_generator.n), epochs=EPOCHS, batch_size=BATCH_SIZE, verbose=1)
es = EarlyStopping(monitor='val_loss', mode='min', patience=ES_PATIENCE, restore_best_weights=True, verbose=1)
rlrop = ReduceLROnPlateau(monitor='val_loss', mode='min', patience=RLROP_PATIENCE, factor=DECAY_DROP, min_lr=1e-6, verbose=1)
callback_list = [es, rlrop]
optimizer = optimizers.Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer, loss=focal_loss, metrics=metric_list)
model.summary()
history_finetunning = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=int(EPOCHS*0.8),
callbacks=callback_list,
class_weight=class_weights,
verbose=1).history
```
# Fine-tune the complete model (2nd step)
```
optimizer = optimizers.SGD(lr=LEARNING_RATE, momentum=0.9, nesterov=True)
model.compile(optimizer=optimizer, loss=focal_loss, metrics=metric_list)
history_finetunning_2 = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=int(EPOCHS*0.2),
callbacks=callback_list,
class_weight=class_weights,
verbose=1).history
```
# Model loss graph
```
history = {'loss': history_warmup['loss'] + history_finetunning['loss'] + history_finetunning_2['loss'],
'val_loss': history_warmup['val_loss'] + history_finetunning['val_loss'] + history_finetunning_2['val_loss'],
'acc': history_warmup['acc'] + history_finetunning['acc'] + history_finetunning_2['acc'],
'val_acc': history_warmup['val_acc'] + history_finetunning['val_acc'] + history_finetunning_2['val_acc'],
'kappa': history_warmup['kappa'] + history_finetunning['kappa'] + history_finetunning_2['kappa'],
'val_kappa': history_warmup['val_kappa'] + history_finetunning['val_kappa'] + history_finetunning_2['val_kappa']}
sns.set_style("whitegrid")
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, sharex='col', figsize=(20, 18))
ax1.plot(history['loss'], label='Train loss')
ax1.plot(history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('Loss')
ax2.plot(history['acc'], label='Train accuracy')
ax2.plot(history['val_acc'], label='Validation accuracy')
ax2.legend(loc='best')
ax2.set_title('Accuracy')
ax3.plot(history['kappa'], label='Train kappa')
ax3.plot(history['val_kappa'], label='Validation kappa')
ax3.legend(loc='best')
ax3.set_title('Kappa')
plt.xlabel('Epochs')
sns.despine()
plt.show()
# Create empty arays to keep the predictions and labels
lastFullTrainPred = np.empty((0, N_CLASSES))
lastFullTrainLabels = np.empty((0, N_CLASSES))
lastFullValPred = np.empty((0, N_CLASSES))
lastFullValLabels = np.empty((0, N_CLASSES))
# Add train predictions and labels
for i in range(STEP_SIZE_TRAIN+1):
im, lbl = next(train_generator)
scores = model.predict(im, batch_size=train_generator.batch_size)
lastFullTrainPred = np.append(lastFullTrainPred, scores, axis=0)
lastFullTrainLabels = np.append(lastFullTrainLabels, lbl, axis=0)
# Add validation predictions and labels
for i in range(STEP_SIZE_VALID+1):
im, lbl = next(valid_generator)
scores = model.predict(im, batch_size=valid_generator.batch_size)
lastFullValPred = np.append(lastFullValPred, scores, axis=0)
lastFullValLabels = np.append(lastFullValLabels, lbl, axis=0)
lastFullComPred = np.concatenate((lastFullTrainPred, lastFullValPred))
lastFullComLabels = np.concatenate((lastFullTrainLabels, lastFullValLabels))
train_preds = [np.argmax(pred) for pred in lastFullTrainPred]
train_labels = [np.argmax(label) for label in lastFullTrainLabels]
validation_preds = [np.argmax(pred) for pred in lastFullValPred]
validation_labels = [np.argmax(label) for label in lastFullValLabels]
complete_labels = [np.argmax(label) for label in lastFullComLabels]
```
# Threshold optimization
```
def find_best_fixed_threshold(preds, targs, do_plot=True):
best_thr_list = [0 for i in range(preds.shape[1])]
for index in range(1, preds.shape[1]):
score = []
thrs = np.arange(0, 1, 0.01)
for thr in thrs:
preds_thr = [index if x[index] > thr else np.argmax(x) for x in preds]
score.append(cohen_kappa_score(targs, preds_thr))
score = np.array(score)
pm = score.argmax()
best_thr, best_score = thrs[pm], score[pm].item()
best_thr_list[index] = best_thr
print('Label %s: thr=%.3f, Kappa=%.3f' % (index, best_thr, best_score))
if do_plot:
plt.plot(thrs, score)
plt.vlines(x=best_thr, ymin=score.min(), ymax=score.max())
plt.text(best_thr+0.03, best_score-0.01, ('Kappa[%s]=%.3f' % (index, best_score)), fontsize=14);
plt.show()
return best_thr_list
threshold_list = find_best_fixed_threshold(lastFullValPred, validation_labels, do_plot=True)
threshold_list[0] = 0 # In last instance assign label 0
# Apply optimized thresholds to the train predictions
train_preds_opt = [0 for i in range(lastFullTrainPred.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(lastFullTrainPred):
if pred[idx] > thr:
train_preds_opt[idx2] = idx
# Apply optimized thresholds to the validation predictions
validation_preds_opt = [0 for i in range(lastFullValPred.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(lastFullValPred):
if pred[idx] > thr:
validation_preds_opt[idx2] = idx
index_order = [0, 2, 1, 4, 3]
# Apply optimized thresholds to the train predictions by class distribution
train_preds_opt2 = [0 for i in range(lastFullTrainPred.shape[0])]
for idx in index_order:
thr = threshold_list[idx]
for idx2, pred in enumerate(lastFullTrainPred):
if pred[idx] > thr:
train_preds_opt2[idx2] = idx
# Apply optimized thresholds to the validation predictions by class distribution
validation_preds_opt2 = [0 for i in range(lastFullValPred.shape[0])]
for idx in index_order:
thr = threshold_list[idx]
for idx2, pred in enumerate(lastFullValPred):
if pred[idx] > thr:
validation_preds_opt2[idx2] = idx
```
# Model Evaluation
## Confusion Matrix
```
# Original thresholds
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
labels = ['0 - No DR', '1 - Mild', '2 - Moderate', '3 - Severe', '4 - Proliferative DR']
train_cnf_matrix = confusion_matrix(train_labels, train_preds)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation')
plt.show()
# Optimized thresholds
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
train_cnf_matrix = confusion_matrix(train_labels, train_preds_opt)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds_opt)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train optimized')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation optimized')
plt.show()
# Optimized thresholds by class
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
train_cnf_matrix = confusion_matrix(train_labels, train_preds_opt2)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds_opt2)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train optimized by class')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation optimized by class')
plt.show()
```
## Quadratic Weighted Kappa
```
print(" --- Original thresholds --- ")
print("Train Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds, train_labels, weights='quadratic'))
print("Validation Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds, validation_labels, weights='quadratic'))
print("Complete set Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds+validation_preds, train_labels+validation_labels, weights='quadratic'))
print(" --- Optimized thresholds --- ")
print("Train Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt, train_labels, weights='quadratic'))
print("Validation Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds_opt, validation_labels, weights='quadratic'))
print("Complete set Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt+validation_preds_opt, train_labels+validation_labels, weights='quadratic'))
print(" --- Optimized thresholds by class distribution --- ")
print("Train Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt2, train_labels, weights='quadratic'))
print("Validation Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds_opt2, validation_labels, weights='quadratic'))
print("Complete set Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt2+validation_preds_opt2, train_labels+validation_labels, weights='quadratic'))
```
## Apply model to test set and output predictions
```
test_generator.reset()
STEP_SIZE_TEST = test_generator.n//test_generator.batch_size
preds = model.predict_generator(test_generator, steps=STEP_SIZE_TEST)
predictions = [np.argmax(pred) for pred in preds]
predictions_opt = [0 for i in range(preds.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(preds):
if pred[idx] > thr:
predictions_opt[idx2] = idx
predictions_opt2 = [0 for i in range(preds.shape[0])]
for idx in index_order:
thr = threshold_list[idx]
for idx2, pred in enumerate(preds):
if pred[idx] > thr:
predictions_opt2[idx2] = idx
filenames = test_generator.filenames
results = pd.DataFrame({'id_code':filenames, 'diagnosis':predictions})
results['id_code'] = results['id_code'].map(lambda x: str(x)[:-4])
results_opt = pd.DataFrame({'id_code':filenames, 'diagnosis':predictions_opt})
results_opt['id_code'] = results_opt['id_code'].map(lambda x: str(x)[:-4])
results_opt2 = pd.DataFrame({'id_code':filenames, 'diagnosis':predictions_opt2})
results_opt2['id_code'] = results_opt2['id_code'].map(lambda x: str(x)[:-4])
```
# Predictions class distribution
```
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, sharex='col', figsize=(24, 8.7))
sns.countplot(x="diagnosis", data=results, palette="GnBu_d", ax=ax1).set_title('Test')
sns.countplot(x="diagnosis", data=results_opt, palette="GnBu_d", ax=ax2).set_title('Test optimized')
sns.countplot(x="diagnosis", data=results_opt2, palette="GnBu_d", ax=ax3).set_title('Test optimized by class')
sns.despine()
plt.show()
val_kappa = cohen_kappa_score(validation_preds, validation_labels, weights='quadratic')
val_opt_kappa = cohen_kappa_score(validation_preds_opt, validation_labels, weights='quadratic')
val_opt_kappa2 = cohen_kappa_score(validation_preds_opt2, validation_labels, weights='quadratic')
if (val_kappa > val_opt_kappa) and (val_kappa > val_opt_kappa2):
results_name = 'submission.csv'
results_opt_name = 'submission_opt.csv'
results_opt2_name = 'submission_opt2.csv'
elif (val_opt_kappa > val_kappa) and (val_opt_kappa > val_opt_kappa2):
results_name = 'submission_norm.csv'
results_opt_name = 'submission.csv'
results_opt2_name = 'submission_opt2.csv'
else:
results_name = 'submission_norm.csv'
results_opt_name = 'submission_opt.csv'
results_opt2_name = 'submission.csv'
results.to_csv(results_name, index=False)
results.head(10)
results_opt.to_csv(results_opt_name, index=False)
results_opt.head(10)
results_opt2.to_csv(results_opt2_name, index=False)
results_opt2.head(10)
```
|
github_jupyter
|
import os
import random
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.utils import class_weight
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, cohen_kappa_score
from keras import backend as K
from keras.models import Model
from keras import optimizers, applications
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import EarlyStopping, ReduceLROnPlateau, Callback, LearningRateScheduler
from keras.layers import Dense, Dropout, GlobalAveragePooling2D, Input
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
def seed_everything(seed=0):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
set_random_seed(0)
seed = 0
seed_everything(seed)
%matplotlib inline
sns.set(style="whitegrid")
warnings.filterwarnings("ignore")
hold_out_set = pd.read_csv('../input/aptos-data-split/hold-out.csv')
hold_out_set.head()
hold_out_set = pd.read_csv('../input/aptos-data-split/hold-out.csv')
X_train = hold_out_set[hold_out_set['set'] == 'train']
X_val = hold_out_set[hold_out_set['set'] == 'validation']
test = pd.read_csv('../input/aptos2019-blindness-detection/test.csv')
print('Number of train samples: ', X_train.shape[0])
print('Number of validation samples: ', X_val.shape[0])
print('Number of test samples: ', test.shape[0])
# Preprocecss data
X_train["id_code"] = X_train["id_code"].apply(lambda x: x + ".png")
X_val["id_code"] = X_val["id_code"].apply(lambda x: x + ".png")
test["id_code"] = test["id_code"].apply(lambda x: x + ".png")
X_train['diagnosis'] = X_train['diagnosis'].astype('str')
X_val['diagnosis'] = X_val['diagnosis'].astype('str')
display(X_train.head())
# Model parameters
BATCH_SIZE = 32
EPOCHS = 40
WARMUP_EPOCHS = 3
LEARNING_RATE = 1e-4
WARMUP_LEARNING_RATE = 1e-3
HEIGHT = 320
WIDTH = 320
CANAL = 3
N_CLASSES = X_train['diagnosis'].nunique()
ES_PATIENCE = 5
RLROP_PATIENCE = 3
DECAY_DROP = 0.5
def kappa(y_true, y_pred, n_classes=5):
y_trues = K.cast(K.argmax(y_true), K.floatx())
y_preds = K.cast(K.argmax(y_pred), K.floatx())
n_samples = K.cast(K.shape(y_true)[0], K.floatx())
distance = K.sum(K.abs(y_trues - y_preds))
max_distance = n_classes - 1
kappa_score = 1 - ((distance**2) / (n_samples * (max_distance**2)))
return kappa_score
def step_decay(epoch):
lrate = 30e-5
if epoch > 3:
lrate = 15e-5
if epoch > 7:
lrate = 7.5e-5
if epoch > 11:
lrate = 3e-5
if epoch > 15:
lrate = 1e-5
return lrate
def focal_loss(y_true, y_pred):
gamma = 2.0
epsilon = K.epsilon()
pt = y_pred * y_true + (1-y_pred) * (1-y_true)
pt = K.clip(pt, epsilon, 1-epsilon)
CE = -K.log(pt)
FL = K.pow(1-pt, gamma) * CE
loss = K.sum(FL, axis=1)
return loss
def get_1cycle_schedule(lr_max=1e-3, n_data_points=8000, epochs=200, batch_size=40, verbose=0):
"""
Creates a look-up table of learning rates for 1cycle schedule with cosine annealing
See @sgugger's & @jeremyhoward's code in fastai library: https://github.com/fastai/fastai/blob/master/fastai/train.py
Wrote this to use with my Keras and (non-fastai-)PyTorch codes.
Note that in Keras, the LearningRateScheduler callback (https://keras.io/callbacks/#learningratescheduler) only operates once per epoch, not per batch
So see below for Keras callback
Keyword arguments:
lr_max chosen by user after lr_finder
n_data_points data points per epoch (e.g. size of training set)
epochs number of epochs
batch_size batch size
Output:
lrs look-up table of LR's, with length equal to total # of iterations
Then you can use this in your PyTorch code by counting iteration number and setting
optimizer.param_groups[0]['lr'] = lrs[iter_count]
"""
if verbose > 0:
print("Setting up 1Cycle LR schedule...")
pct_start, div_factor = 0.3, 25. # @sgugger's parameters in fastai code
lr_start = lr_max/div_factor
lr_end = lr_start/1e4
n_iter = (n_data_points * epochs // batch_size) + 1 # number of iterations
a1 = int(n_iter * pct_start)
a2 = n_iter - a1
# make look-up table
lrs_first = np.linspace(lr_start, lr_max, a1) # linear growth
lrs_second = (lr_max-lr_end)*(1+np.cos(np.linspace(0,np.pi,a2)))/2 + lr_end # cosine annealing
lrs = np.concatenate((lrs_first, lrs_second))
return lrs
class OneCycleScheduler(Callback):
"""My modification of Keras' Learning rate scheduler to do 1Cycle learning
which increments per BATCH, not per epoch
Keyword arguments
**kwargs: keyword arguments to pass to get_1cycle_schedule()
Also, verbose: int. 0: quiet, 1: update messages.
Sample usage (from my train.py):
lrsched = OneCycleScheduler(lr_max=1e-4, n_data_points=X_train.shape[0],
epochs=epochs, batch_size=batch_size, verbose=1)
"""
def __init__(self, **kwargs):
super(OneCycleScheduler, self).__init__()
self.verbose = kwargs.get('verbose', 0)
self.lrs = get_1cycle_schedule(**kwargs)
self.iteration = 0
def on_batch_begin(self, batch, logs=None):
lr = self.lrs[self.iteration]
K.set_value(self.model.optimizer.lr, lr) # here's where the assignment takes place
if self.verbose > 0:
print('\nIteration %06d: OneCycleScheduler setting learning '
'rate to %s.' % (self.iteration, lr))
self.iteration += 1
def on_epoch_end(self, epoch, logs=None): # this is unchanged from Keras LearningRateScheduler
logs = logs or {}
logs['lr'] = K.get_value(self.model.optimizer.lr)
self.iteration = 0
train_datagen=ImageDataGenerator(rescale=1./255,
rotation_range=360,
brightness_range=[0.5, 1.5],
zoom_range=[1, 1.2],
zca_whitening=True,
horizontal_flip=True,
vertical_flip=True,
fill_mode='reflect',
cval=0.)
test_datagen = ImageDataGenerator(rescale=1./255)
validation_datagen = ImageDataGenerator(rescale=1./255)
train_generator=train_datagen.flow_from_dataframe(
dataframe=X_train,
directory="../input/aptos2019-blindness-detection/train_images/",
x_col="id_code",
y_col="diagnosis",
class_mode="categorical",
batch_size=BATCH_SIZE,
target_size=(HEIGHT, WIDTH),
seed=seed)
valid_generator=validation_datagen.flow_from_dataframe(
dataframe=X_val,
directory="../input/aptos2019-blindness-detection/train_images/",
x_col="id_code",
y_col="diagnosis",
class_mode="categorical",
batch_size=BATCH_SIZE,
target_size=(HEIGHT, WIDTH),
seed=seed)
test_generator = test_datagen.flow_from_dataframe(
dataframe=test,
directory = "../input/aptos2019-blindness-detection/test_images/",
x_col="id_code",
batch_size=1,
class_mode=None,
shuffle=False,
target_size=(HEIGHT, WIDTH),
seed=seed)
def create_model(input_shape, n_out):
input_tensor = Input(shape=input_shape)
base_model = applications.ResNet50(weights=None,
include_top=False,
input_tensor=input_tensor)
base_model.load_weights('../input/resnet50/resnet50_weights_tf_dim_ordering_tf_kernels_notop.h5')
x = GlobalAveragePooling2D()(base_model.output)
x = Dropout(0.5)(x)
x = Dense(2048, activation='relu')(x)
x = Dropout(0.5)(x)
final_output = Dense(n_out, activation='softmax', name='final_output')(x)
model = Model(input_tensor, final_output)
return model
model = create_model(input_shape=(HEIGHT, WIDTH, CANAL), n_out=N_CLASSES)
for layer in model.layers:
layer.trainable = False
for i in range(-5, 0):
model.layers[i].trainable = True
class_weights = class_weight.compute_class_weight('balanced', np.unique(X_train['diagnosis'].astype('int').values), X_train['diagnosis'].astype('int').values)
metric_list = ["accuracy", kappa]
optimizer = optimizers.Adam(lr=WARMUP_LEARNING_RATE)
model.compile(optimizer=optimizer, loss=focal_loss, metrics=metric_list)
model.summary()
STEP_SIZE_TRAIN = train_generator.n//train_generator.batch_size
STEP_SIZE_VALID = valid_generator.n//valid_generator.batch_size
history_warmup = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=WARMUP_EPOCHS,
class_weight=class_weights,
verbose=1).history
for layer in model.layers:
layer.trainable = True
# lrstep = LearningRateScheduler(step_decay)
# lrcycle = OneCycleScheduler(lr_max=LEARNING_RATE, n_data_points=(train_generator.n + valid_generator.n), epochs=EPOCHS, batch_size=BATCH_SIZE, verbose=1)
es = EarlyStopping(monitor='val_loss', mode='min', patience=ES_PATIENCE, restore_best_weights=True, verbose=1)
rlrop = ReduceLROnPlateau(monitor='val_loss', mode='min', patience=RLROP_PATIENCE, factor=DECAY_DROP, min_lr=1e-6, verbose=1)
callback_list = [es, rlrop]
optimizer = optimizers.Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer, loss=focal_loss, metrics=metric_list)
model.summary()
history_finetunning = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=int(EPOCHS*0.8),
callbacks=callback_list,
class_weight=class_weights,
verbose=1).history
optimizer = optimizers.SGD(lr=LEARNING_RATE, momentum=0.9, nesterov=True)
model.compile(optimizer=optimizer, loss=focal_loss, metrics=metric_list)
history_finetunning_2 = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=int(EPOCHS*0.2),
callbacks=callback_list,
class_weight=class_weights,
verbose=1).history
history = {'loss': history_warmup['loss'] + history_finetunning['loss'] + history_finetunning_2['loss'],
'val_loss': history_warmup['val_loss'] + history_finetunning['val_loss'] + history_finetunning_2['val_loss'],
'acc': history_warmup['acc'] + history_finetunning['acc'] + history_finetunning_2['acc'],
'val_acc': history_warmup['val_acc'] + history_finetunning['val_acc'] + history_finetunning_2['val_acc'],
'kappa': history_warmup['kappa'] + history_finetunning['kappa'] + history_finetunning_2['kappa'],
'val_kappa': history_warmup['val_kappa'] + history_finetunning['val_kappa'] + history_finetunning_2['val_kappa']}
sns.set_style("whitegrid")
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, sharex='col', figsize=(20, 18))
ax1.plot(history['loss'], label='Train loss')
ax1.plot(history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('Loss')
ax2.plot(history['acc'], label='Train accuracy')
ax2.plot(history['val_acc'], label='Validation accuracy')
ax2.legend(loc='best')
ax2.set_title('Accuracy')
ax3.plot(history['kappa'], label='Train kappa')
ax3.plot(history['val_kappa'], label='Validation kappa')
ax3.legend(loc='best')
ax3.set_title('Kappa')
plt.xlabel('Epochs')
sns.despine()
plt.show()
# Create empty arays to keep the predictions and labels
lastFullTrainPred = np.empty((0, N_CLASSES))
lastFullTrainLabels = np.empty((0, N_CLASSES))
lastFullValPred = np.empty((0, N_CLASSES))
lastFullValLabels = np.empty((0, N_CLASSES))
# Add train predictions and labels
for i in range(STEP_SIZE_TRAIN+1):
im, lbl = next(train_generator)
scores = model.predict(im, batch_size=train_generator.batch_size)
lastFullTrainPred = np.append(lastFullTrainPred, scores, axis=0)
lastFullTrainLabels = np.append(lastFullTrainLabels, lbl, axis=0)
# Add validation predictions and labels
for i in range(STEP_SIZE_VALID+1):
im, lbl = next(valid_generator)
scores = model.predict(im, batch_size=valid_generator.batch_size)
lastFullValPred = np.append(lastFullValPred, scores, axis=0)
lastFullValLabels = np.append(lastFullValLabels, lbl, axis=0)
lastFullComPred = np.concatenate((lastFullTrainPred, lastFullValPred))
lastFullComLabels = np.concatenate((lastFullTrainLabels, lastFullValLabels))
train_preds = [np.argmax(pred) for pred in lastFullTrainPred]
train_labels = [np.argmax(label) for label in lastFullTrainLabels]
validation_preds = [np.argmax(pred) for pred in lastFullValPred]
validation_labels = [np.argmax(label) for label in lastFullValLabels]
complete_labels = [np.argmax(label) for label in lastFullComLabels]
def find_best_fixed_threshold(preds, targs, do_plot=True):
best_thr_list = [0 for i in range(preds.shape[1])]
for index in range(1, preds.shape[1]):
score = []
thrs = np.arange(0, 1, 0.01)
for thr in thrs:
preds_thr = [index if x[index] > thr else np.argmax(x) for x in preds]
score.append(cohen_kappa_score(targs, preds_thr))
score = np.array(score)
pm = score.argmax()
best_thr, best_score = thrs[pm], score[pm].item()
best_thr_list[index] = best_thr
print('Label %s: thr=%.3f, Kappa=%.3f' % (index, best_thr, best_score))
if do_plot:
plt.plot(thrs, score)
plt.vlines(x=best_thr, ymin=score.min(), ymax=score.max())
plt.text(best_thr+0.03, best_score-0.01, ('Kappa[%s]=%.3f' % (index, best_score)), fontsize=14);
plt.show()
return best_thr_list
threshold_list = find_best_fixed_threshold(lastFullValPred, validation_labels, do_plot=True)
threshold_list[0] = 0 # In last instance assign label 0
# Apply optimized thresholds to the train predictions
train_preds_opt = [0 for i in range(lastFullTrainPred.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(lastFullTrainPred):
if pred[idx] > thr:
train_preds_opt[idx2] = idx
# Apply optimized thresholds to the validation predictions
validation_preds_opt = [0 for i in range(lastFullValPred.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(lastFullValPred):
if pred[idx] > thr:
validation_preds_opt[idx2] = idx
index_order = [0, 2, 1, 4, 3]
# Apply optimized thresholds to the train predictions by class distribution
train_preds_opt2 = [0 for i in range(lastFullTrainPred.shape[0])]
for idx in index_order:
thr = threshold_list[idx]
for idx2, pred in enumerate(lastFullTrainPred):
if pred[idx] > thr:
train_preds_opt2[idx2] = idx
# Apply optimized thresholds to the validation predictions by class distribution
validation_preds_opt2 = [0 for i in range(lastFullValPred.shape[0])]
for idx in index_order:
thr = threshold_list[idx]
for idx2, pred in enumerate(lastFullValPred):
if pred[idx] > thr:
validation_preds_opt2[idx2] = idx
# Original thresholds
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
labels = ['0 - No DR', '1 - Mild', '2 - Moderate', '3 - Severe', '4 - Proliferative DR']
train_cnf_matrix = confusion_matrix(train_labels, train_preds)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation')
plt.show()
# Optimized thresholds
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
train_cnf_matrix = confusion_matrix(train_labels, train_preds_opt)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds_opt)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train optimized')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation optimized')
plt.show()
# Optimized thresholds by class
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
train_cnf_matrix = confusion_matrix(train_labels, train_preds_opt2)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds_opt2)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train optimized by class')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation optimized by class')
plt.show()
print(" --- Original thresholds --- ")
print("Train Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds, train_labels, weights='quadratic'))
print("Validation Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds, validation_labels, weights='quadratic'))
print("Complete set Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds+validation_preds, train_labels+validation_labels, weights='quadratic'))
print(" --- Optimized thresholds --- ")
print("Train Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt, train_labels, weights='quadratic'))
print("Validation Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds_opt, validation_labels, weights='quadratic'))
print("Complete set Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt+validation_preds_opt, train_labels+validation_labels, weights='quadratic'))
print(" --- Optimized thresholds by class distribution --- ")
print("Train Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt2, train_labels, weights='quadratic'))
print("Validation Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds_opt2, validation_labels, weights='quadratic'))
print("Complete set Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt2+validation_preds_opt2, train_labels+validation_labels, weights='quadratic'))
test_generator.reset()
STEP_SIZE_TEST = test_generator.n//test_generator.batch_size
preds = model.predict_generator(test_generator, steps=STEP_SIZE_TEST)
predictions = [np.argmax(pred) for pred in preds]
predictions_opt = [0 for i in range(preds.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(preds):
if pred[idx] > thr:
predictions_opt[idx2] = idx
predictions_opt2 = [0 for i in range(preds.shape[0])]
for idx in index_order:
thr = threshold_list[idx]
for idx2, pred in enumerate(preds):
if pred[idx] > thr:
predictions_opt2[idx2] = idx
filenames = test_generator.filenames
results = pd.DataFrame({'id_code':filenames, 'diagnosis':predictions})
results['id_code'] = results['id_code'].map(lambda x: str(x)[:-4])
results_opt = pd.DataFrame({'id_code':filenames, 'diagnosis':predictions_opt})
results_opt['id_code'] = results_opt['id_code'].map(lambda x: str(x)[:-4])
results_opt2 = pd.DataFrame({'id_code':filenames, 'diagnosis':predictions_opt2})
results_opt2['id_code'] = results_opt2['id_code'].map(lambda x: str(x)[:-4])
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, sharex='col', figsize=(24, 8.7))
sns.countplot(x="diagnosis", data=results, palette="GnBu_d", ax=ax1).set_title('Test')
sns.countplot(x="diagnosis", data=results_opt, palette="GnBu_d", ax=ax2).set_title('Test optimized')
sns.countplot(x="diagnosis", data=results_opt2, palette="GnBu_d", ax=ax3).set_title('Test optimized by class')
sns.despine()
plt.show()
val_kappa = cohen_kappa_score(validation_preds, validation_labels, weights='quadratic')
val_opt_kappa = cohen_kappa_score(validation_preds_opt, validation_labels, weights='quadratic')
val_opt_kappa2 = cohen_kappa_score(validation_preds_opt2, validation_labels, weights='quadratic')
if (val_kappa > val_opt_kappa) and (val_kappa > val_opt_kappa2):
results_name = 'submission.csv'
results_opt_name = 'submission_opt.csv'
results_opt2_name = 'submission_opt2.csv'
elif (val_opt_kappa > val_kappa) and (val_opt_kappa > val_opt_kappa2):
results_name = 'submission_norm.csv'
results_opt_name = 'submission.csv'
results_opt2_name = 'submission_opt2.csv'
else:
results_name = 'submission_norm.csv'
results_opt_name = 'submission_opt.csv'
results_opt2_name = 'submission.csv'
results.to_csv(results_name, index=False)
results.head(10)
results_opt.to_csv(results_opt_name, index=False)
results_opt.head(10)
results_opt2.to_csv(results_opt2_name, index=False)
results_opt2.head(10)
| 0.715821 | 0.497803 |
# Physics 420/580 Final Exam
## December 19, 2019 2pm-5pm L1-150
Do three of the four following problems. If you attempt all four, your best three will be used for your mark. Use the Jupyter notebook, inserting your code and any textual answers/explanations in cells between the questions. (Feel free to add additional cells!) Marks will be given based on how clearly you demonstrate your understanding.
There are no restrictions on downloading from the internet, eclass, or the use of books, notes, or any other widely available computing resources. However, **you are not allowed** to communicate with each other or collaborate in any way and uploading to the internet or sending or receiving direct communications is not appropriate. You are required to sit the exam in L1-150, and to upload it before you leave.
When you are finished, upload the jupyter notebook to eclass.
Also be careful to save the notebook periodically and double check **that you upload the file that has your answers in it!**
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import scipy
from scipy.integrate import odeint
from scipy.integrate import quad
from scipy.optimize import minimize
from scipy.optimize import fsolve
from scipy.optimize import least_squares
from scipy.interpolate import interp1d
mpl.rc('figure',dpi=250)
mpl.rc('text',usetex=True)
def add_labels(xlabel, ylabel, title):
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.title(title)
plt.legend()
```
# The Normal Distribution
Write a simple program that:
a. Calculates and plots the function
$$G(x;\mu,\sigma)=1000e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$ with an average value $\mu=10$, width $\sigma=2$. This is proportional to the normal distribution.
```
"""
Plan:
-Here we just graph G, and plot it
"""
mu = 10
sigma = 2
def G(x, mu, sigma, A):
return A*np.exp(-(x - mu)**2/(2*sigma**2))
x = np.linspace(-25, 25)
plt.plot(x, G(x, mu, sigma, 1000), label=f"mu = {mu}, sigma = {sigma}, A = {1000}")
add_labels('x', 'G(x)', 'G(x)')
```
The three dimensional normal distribution is the product of normal distributions in the three coordinates:
\begin{equation} G(\vec{x}; \vec{x_0},\sigma, A)=Ae^{-\frac{(\vec{x}-\vec{x_0})^2}{2\sigma^2}}\end{equation}
Set $\vec{x_0}=(6,8,0)$ and throw 100000 random points by throwing the three coordinates independently with $\sigma=2$ for each coordinate.
Histogram and plot the distributions for each coordinate. Comment on how you pick the right number of bins for your histogram.
```
"""
Plan:
We could use our normal function G, and sample from it: just plug it into generate samples. However, but we realize that in numpy this is already done for us:
Numpy.random.normal. It's the same thing, just that np.random.normal just much more efficient and I trust it more than myself. It runs faster too.
"""
```
```
def generate_samples(func, bounds, N):
"""
Assignment 5: function for sampling from a custom 1d distribution.
Input: func - any function
bounds - tuple (a, b)
Output: 1d samples of size N
"""
a, b = bounds
x = np.linspace(a, b)
f_max = max(func(x))
x_rand = np.random.uniform(a, b, size=N)
y_rand = np.random.uniform(0, f_max, size=N)
samples = x_rand[y_rand < func(x_rand)]
return samples
```
```
x0 = np.array([6, 8, 0])
N = 100000
sigma = 2
throws = np.zeros((N, 3))
for i in range(N):
throws[i, 0] = np.random.normal(x0[0], sigma)
throws[i, 1] = np.random.normal(x0[1], sigma)
throws[i, 2] = np.random.normal(x0[2], sigma)
throws.shape
# I picked the bins based on the domain and through just visual comparison. The bins are 100 linearly spaced along the domain.
plt.figure()
plt.hist(throws[:, 0], bins=100, label=f'mu = {x0[0]}, sigma = 2')
add_labels('x', 'counts', 'distribution of x coordinate')
plt.figure()
plt.hist(throws[:, 1], bins=100, label=f'mu = {x0[1]}, sigma = 2')
add_labels('y', 'counts', 'distribution of y coordinate')
plt.figure()
plt.hist(throws[:, 2], bins=100, label=f'mu = {x0[2]}, sigma = 2')
add_labels('z', 'counts', 'distribution of z coordinate')
```
Now histogram and plot the distribution of $r=|\vec{x}-\vec{x_0}|$.
```
radial = np.linalg.norm(throws - x0, axis = 1)
plt.hist(radial, bins=100)
add_labels('r', 'counts', 'distribution of radial coordinate with respect to mean')
```
This should look like the analytic 3d normal distribution in spherical coordinates:
\begin{equation}G(r;\sigma,A)=4\pi A r^2 e^{-\frac{r^2}{2\sigma^2}}.\end{equation} We derived this equation by converting $G(\vec{x}; \vec{x_0},\sigma, A)$ into spherical coordinates and integrating over $\theta$ and $\phi.$
Determine A for 100000 points by numerically integrating:
\begin{equation}100000=\int_0^{20} G(r;\sigma,A)dr =A\int_0^{20} G(r;\sigma,1)dr\end{equation}
With a known A, you can now replot your histogram and overlay the calculation of $G(r;\sigma,A)$. To have $G(r;\sigma,A)$ overlay properly you will need to include the bin widths, which you can do either by the exact integral or the approximation: $\int_{r_i}^{r_{i+1}}G(r;\sigma,A)dr \approx G(r;\sigma,A)\Delta r$, where $r_i$ is the start of the i-th bin and $r_{i+1}$ is the start of the next bin, and $\Delta r=r_{i+1}-r_i$.
```
def radial_Gaussian(r, sigma):
return 4*np.pi*r**2*np.exp(-r**2/(2*sigma**2))
sigma = 2
integral = quad(radial_Gaussian, 0, 20, args=sigma)
A = 100000/integral[0]
print(f'A = {A} is the normalization factor')
r = np.linspace(0, 10)
plt.plot(r, A*radial_Gaussian(r, sigma))
plt.hist(radial, bins=100)
add_labels('r', 'counts', 'distribution of radial coordinate with respect to mean')
plt.plot(r, A*radial_Gaussian(r, sigma))
"""I have to normalize it now, and I have to fudge with some bins but if I have time after the exam I will do that. Right now, I need to solve the other 3 questions"""
```
# Monte Carlo
A radioactive source is placed into a large water Cerenkov detector (which is able to detect high energy electrons/gammas in pure water by looking at visible photons from the Cerenkov process.) Before the source is deployed, the detector measures background radiation at a rate of 200 events/second. The source produces two types of events:
1. single gamma rays with a rate of 100 events/second
2. events that produce both a gamma ray and a neutron at a rate of 100 events/second. The gamma ray is detected immediately after creation with an efficiency of 50% (for both gamma rays from the source- the singles and the gamma/neutron coincidences). The neutron is detected after a capture time, which is quantified with a mean of 250 microseconds. In math, this says that the time distribution of neutron captures is $$P(t)=250\times 10^{-6} e^{-t/(250\times 10^{-6})},$$ where t is the time difference (in seconds) between gamma/neutron creation and neutron capture. The neutron detection efficiency is. 40%. The time distribution of neutron captures is $$P(t)=250\times 10^{-6} e^{-t/(250\times 10^{-6})},$$ where t is the time difference (in seconds) between gamma/neutron creation and neutron capture.
Write a simple MC to model 1000 seconds of running time. Generate the times for background events, the single gamma rays from the source and the gamma/neutron coincidences. Then generate the neutron capture times and finally apply the detection efficiencies for each type of event.
Histogram and plot:
1. The times of each type of event (on an x-axis with a scale of 0-1000 seconds)
2. The intervals between a detected event and the next detected event (from 0-10 ms). To do this you might need to make an array with the times of all detections, sort it and then calculate the time from one event to the next.
3. Repeat plots 1 and 2 for the case where the background rate is 1000 events/second.
```
"""
Plan:
We need the times of each type of event.
Let's say the source produces events perfectly.
Sample from the uniform distribution then find the interavls
"""
N = 100000
efficiency_test = np.random.rand(N)
times = np.random.uniform(0, 1000, size=N)
plt.hist(times, bins=50, label='source/detector events')
add_labels('time of event', 'counts', 'times for event 1 (gamma)')
intervals = []
times = np.sort(times)
for i in range(len(times) - 1):
intervals.append(times[i+1] - times[i])
plt.hist(intervals, bins=50)
add_labels('interval between events', 'counts', 'time interval for event 1 (gamma)')
N = 100000
efficiency_test = np.random.rand(N)
efficiency_test_2 = np.random.rand(N)
times = np.random.uniform(0, 1000, size=N) #times for event 2.
mask = efficiency_test > 0.5
mask2 = efficiency_test_2 > 0.4
plt.hist(times, bins=50, label='source events',alpha=0.3)
plt.hist(times[mask], bins=50, label='gamma detector events', alpha=0.7)
plt.hist(times[mask2], bins=50, label='neutron detector events', alpha=0.7)
add_labels('time of event', 'counts', 'times for event 2 (gamma+neutron)')
meanTime = 250*10**-6
times = np.random.uniform(0, 1000, size=N) #times for event 2.
mask = efficiency_test > 0.5
mask2 = efficiency_test_2 > 0.4
gamma_events = np.sort(times[mask])
neutron_events = np.sort(times[mask2])
detector_events = neutron_events + np.random.exponential(meanTime, size = len(neutron_events))
intervals_gamma = []
intervals_neutron = []
detector_events = np.sort(detector_events)
for i in range(len(detector_events) - 1):
intervals_neutron.append(detector_events[i+1] - detector_events[i])
for i in range(len(gamma_events) - 1):
intervals_gamma.append(gamma_events[i+1] - gamma_events[i])
plt.hist(intervals_neutron, bins=50, label='neutron detector events', alpha = 0.7)
plt.hist(intervals_gamma, bins=50, label='gamma detector events', alpha=0.7)
add_labels('interval between events', 'counts', 'intervals between times for event 2 (gamma+neutron)')
"""Will repeat for the background rate later. Gotta do the last two questions"""
```
# Solving and Fitting
An object is viewed by 6 theodolites (telescopes that allow you to measure angles with respect to the vertical($\theta$) and with respect to a horizontal($\phi$). The locations of the telescopes and the measured angles are given in the code cell below (all with respect to a single coordinate system,) which you can run in order to avoid cutting and pasting.
Since each theodolite gives you two quantities we have 12 measurements. There are three unknowns- the x, y, and z coordinates of a point on an object. Consequently the system of equations is overdetermined, and we would typically be unable to solve.
In a case like this, we "solve" the system of equations by fitting.
Write a function that calculates the theta and phi angles (spherical coordinates) given an arbitrary point position and an theodolite position.
Using this function, write a second function that calculates the residuals of the calculation with respect to the data. Then find the position of the target by fitting the calculations to the data.
Extract the uncertainties on the position. In order to do this, you will need to estimate the size of the uncertainty in the angles to incorporate into the residual calculation. One way to do this is by histogramming the residuals ((data-calculation)/uncertainty) and getting a sense of how big they are- if the uncertainties are correct the RMS/width of the residuals distribution should be about 1.
```
import numpy as np
positions = np.array([[-0.0114519 , 9.99999344, 6.69130799],
[ 6.33116335, -7.74056655, 3.59009715],
[-9.85887257, -1.67410623, 4.56138703],
[ 4.09466118, 9.12325325, 7.32437587],
[-3.37815507, -9.41212348, 3.67927878],
[-5.4274145 , -8.39899827, 6.8865273 ]])
thetaMeasures = np.array( [2.3164460126412245, 1.6313464103926718, 1.6970719353033004, 2.533624050255211, 1.6289243873579955, 1.8159707640506253] )
phiMeasures = np.array( [-0.9844385514247201, 1.8432675248986576, 0.5831709514637226, -2.132723211863188, 1.2215622389804748, 1.0853416750730511] )
print('Theodolite x \t Theodolite y \t Theodolite z \t Meas.theta \t Meas. phi')
for i in range(0,6):
print('%f \t %f \t %f \t %f \t %f '%(positions[i,0],positions[i,1],positions[i,2],thetaMeasures[i],phiMeasures[i]))
def xyz_to_spherical(vector):
r = np.linalg.norm(vector)
theta = np.arccos(vector[2]/r)
phi = np.arctan2(vector[1], vector[0])
return np.array([r, theta , phi])
def find_theta_phi(point, telescope):
difference = point - telescope
return xyz_to_spherical(difference)
def find_residuals(point):
theta_res = np.zeros((6))
phi_res = np.zeros((6))
for i in range(6):
angles = find_theta_phi(point, positions[i, :3])
theta_res[i] = thetaMeasures[i] - angles[1]
phi_res[i] = phiMeasures[i] - angles[2]
return np.concatenate([theta_res, phi_res], axis=0)
from scipy.optimize import least_squares
params0 = np.array([1, 1, 1])
popt_minimization = least_squares(find_residuals, params0)
popt_minimization
uncertainty = 5e-10
plt.hist(find_residuals(popt_minimization.x)/uncertainty)
print(f'the uncertainty is about {uncertainty}')
```
# Ordinary Differential Equations
Consider the mechanics problem shown in the diagram below. We have a rigid bar $l=4$ meters long, with mass $m=20$ kg, at an angle $\theta$ to the floor and leaning against a wall. The center of mass of the bar is at coordinates (x,y). The normal force against the wall we designate as $N_1,$ while the normal force to the floor is $N_2.$ The coefficient of (sliding) friction with the floor is $\mu_2=0.2$, while the coefficient of friction with the wall is $\mu_1=0.4.$

Calculate how long it takes for the bar to fall to the floor. The acceleration due to gravity is $g.$ Start with an initial condition of $\theta_0= 1.15$ radians, and $\omega_0=\dot{\theta}(0)=0.$
From the mechanics perspective, this involves setting up Newton's second law for the acceleration of the center of mass, and using the torque equation for the rotation of the bar around the center of mass:
\begin{align}\\
-mg+N_2+\mu_1 N_1&=m\ddot{y}\\
N_1-\mu_2 N_2=m\ddot{x}\\
(N_1+\mu_2 N_2)\frac{l}{2} \sin\theta - (N_2-\mu_1 N_1) \frac{l}{2}\cos\theta &=I\ddot{\theta}\\
\end{align}
For a bar, the moment of inertia $I=\frac{1}{12}ml^2.$
The geometry of the situation means that we can't simply plug the equation above into an ODE integrator. Instead, we need to relate $x$ and $y$ to the angle $\theta:$
\begin{align}\\
x&=\frac{l}{2}\cos\theta\\
\dot{x}&=-\frac{l}{2}\sin\theta \dot{\theta}\\
\ddot{x}&=-\frac{l}{2}\sin\theta \ddot{\theta}-\frac{l}{2}\cos\theta \dot{\theta}^2\\
y&=\frac{l}{2}\sin\theta\\
\dot{y}&=\frac{l}{2}\cos\theta \dot{\theta}\\
\ddot{y}&=\frac{l}{2}\cos\theta \ddot{\theta}-\frac{l}{2}\sin\theta \dot{\theta}^2\\
\end{align}
Now substitute these equations for $\ddot{x}$ and $\ddot{y}$ into the original equation for Newton's laws.
Solve the ODE numerically. For each step, you will need to solve the set of simultaneous equations for $\ddot{\theta}$, $N_1,$ and $N_2$.
Plot $\theta$ as a function of time $t$. Graphically find the time the bar hits the floor ($\theta=0.$)
Plot $N_1$ and $N_2$ as a function of time $t$. Discuss any mathematical assumptions in our model that might not reflect reality and how the model would need to change to accommodate them.
```
m = 20
l = 4
mu2 = 0.2
mu1 = 0.4
I = (1/12)*m*l**2
g=9.81
global N1
global N2
global ddtheta
#x = l/2*np.cos(theta)
#y = l/2*np.sin(theta)
"""This is a coupled system.
Hence we need to update both the linear newtons law
and the angular newtons law. we know the linear newtons law is 0, -mg.
I can't seem to get the height of the ground
"""
N1 = []
N2 = []
def main(y, t):
"Main thing to integrate"
"""
y[0] - theta
y[1] - omega
y[2:4] - x,y
y[4:6] - dx, dy
"""
theta = y[0:2]
positions = y[2:4]
velocities = y[4:6]
ddx = 0
ddy = -m*g
#Solving for N. Need ddx, ddy
A = np.array([[mu1, -m*g],[1, -mu2]])
b = np.array([m*ddy, m*ddx])
N = np.linalg.solve(A, b)
N1.append(N[0])
N2.append(N[1])
dydt = np.empty(6)
dx = -l/2*np.sin(y[0])*y[1]
dy = l/2*np.sin(y[0])*y[1]
dydt[0] = y[1] #omega
dydt[1] = (1/I)*((N[0] + mu2*N[1])*(l/2)*np.sin(y[0]) - (N[1] - mu1*N[0])*(l/2)*np.cos(y[0]))
dydt[2:4] = np.array([dx, dy])
dydt[4:6] = np.array([ddx, ddy])
return dydt
t = np.linspace(0, 10, 10000)
y0 = np.array([1.15, 0, l/2*np.cos(1.15), l/2*np.sin(1.15), 0, 0], dtype='float64')
y = odeint(main, y0, t)
"""Grab all physical numbers: the bar cannot fall into the floor"""
mask = (y[:, 3] > 0) & (y[:, 0] > 0)
t = t[mask]
y = y[mask]
```
When you are finished, upload your completed exam onto eClass. Double check that the uploaded exam contains your latest work!
```
plt.plot(t, y[:, 0]/np.pi*180)
add_labels('t','$\\theta$ (degrees)','angle of bar')
t = np.linspace(0, 10, len(N1))
plt.plot(t, N1, label="N1")
plt.plot(t, N2, label="N2")
add_labels('time', 'N1 N2', 'N1, N2 as a function of time')
```
## Problems with the Model
N1, N2 are roughly constant which I think is not really correct, to get N1, N2 I had to let ddy = -mg which is gravity on the CoM. Otherwise there is no way to solve the problem due to recursion. We don't have enough variables.
I think that an good simulation should have friction be proportional to the velocity
If we plot the height of the bar, this is also not really correct as well. I think what's causing the problem is probably this assumption that friction is constant, when in reality, it's far from constant. So we know this model is wrong but I think I did the integration correctly.
```
t = np.linspace(0, 10, 10000)
y0 = np.array([1.15, 0, l/2*np.cos(1.15), l/2*np.sin(1.15), 0, 0], dtype='float64')
y = odeint(main, y0, t)
"""Grab all physical numbers: the bar cannot fall into the floor"""
mask = (y[:, 3] > 0) & (y[:, 0] > 0)
t = t[mask]
y = y[mask]
plt.plot(t, y[:, 3]/np.pi*180)
add_labels('t','y','height of bar')
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import scipy
from scipy.integrate import odeint
from scipy.integrate import quad
from scipy.optimize import minimize
from scipy.optimize import fsolve
from scipy.optimize import least_squares
from scipy.interpolate import interp1d
mpl.rc('figure',dpi=250)
mpl.rc('text',usetex=True)
def add_labels(xlabel, ylabel, title):
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.title(title)
plt.legend()
"""
Plan:
-Here we just graph G, and plot it
"""
mu = 10
sigma = 2
def G(x, mu, sigma, A):
return A*np.exp(-(x - mu)**2/(2*sigma**2))
x = np.linspace(-25, 25)
plt.plot(x, G(x, mu, sigma, 1000), label=f"mu = {mu}, sigma = {sigma}, A = {1000}")
add_labels('x', 'G(x)', 'G(x)')
"""
Plan:
We could use our normal function G, and sample from it: just plug it into generate samples. However, but we realize that in numpy this is already done for us:
Numpy.random.normal. It's the same thing, just that np.random.normal just much more efficient and I trust it more than myself. It runs faster too.
"""
def generate_samples(func, bounds, N):
"""
Assignment 5: function for sampling from a custom 1d distribution.
Input: func - any function
bounds - tuple (a, b)
Output: 1d samples of size N
"""
a, b = bounds
x = np.linspace(a, b)
f_max = max(func(x))
x_rand = np.random.uniform(a, b, size=N)
y_rand = np.random.uniform(0, f_max, size=N)
samples = x_rand[y_rand < func(x_rand)]
return samples
x0 = np.array([6, 8, 0])
N = 100000
sigma = 2
throws = np.zeros((N, 3))
for i in range(N):
throws[i, 0] = np.random.normal(x0[0], sigma)
throws[i, 1] = np.random.normal(x0[1], sigma)
throws[i, 2] = np.random.normal(x0[2], sigma)
throws.shape
# I picked the bins based on the domain and through just visual comparison. The bins are 100 linearly spaced along the domain.
plt.figure()
plt.hist(throws[:, 0], bins=100, label=f'mu = {x0[0]}, sigma = 2')
add_labels('x', 'counts', 'distribution of x coordinate')
plt.figure()
plt.hist(throws[:, 1], bins=100, label=f'mu = {x0[1]}, sigma = 2')
add_labels('y', 'counts', 'distribution of y coordinate')
plt.figure()
plt.hist(throws[:, 2], bins=100, label=f'mu = {x0[2]}, sigma = 2')
add_labels('z', 'counts', 'distribution of z coordinate')
radial = np.linalg.norm(throws - x0, axis = 1)
plt.hist(radial, bins=100)
add_labels('r', 'counts', 'distribution of radial coordinate with respect to mean')
def radial_Gaussian(r, sigma):
return 4*np.pi*r**2*np.exp(-r**2/(2*sigma**2))
sigma = 2
integral = quad(radial_Gaussian, 0, 20, args=sigma)
A = 100000/integral[0]
print(f'A = {A} is the normalization factor')
r = np.linspace(0, 10)
plt.plot(r, A*radial_Gaussian(r, sigma))
plt.hist(radial, bins=100)
add_labels('r', 'counts', 'distribution of radial coordinate with respect to mean')
plt.plot(r, A*radial_Gaussian(r, sigma))
"""I have to normalize it now, and I have to fudge with some bins but if I have time after the exam I will do that. Right now, I need to solve the other 3 questions"""
"""
Plan:
We need the times of each type of event.
Let's say the source produces events perfectly.
Sample from the uniform distribution then find the interavls
"""
N = 100000
efficiency_test = np.random.rand(N)
times = np.random.uniform(0, 1000, size=N)
plt.hist(times, bins=50, label='source/detector events')
add_labels('time of event', 'counts', 'times for event 1 (gamma)')
intervals = []
times = np.sort(times)
for i in range(len(times) - 1):
intervals.append(times[i+1] - times[i])
plt.hist(intervals, bins=50)
add_labels('interval between events', 'counts', 'time interval for event 1 (gamma)')
N = 100000
efficiency_test = np.random.rand(N)
efficiency_test_2 = np.random.rand(N)
times = np.random.uniform(0, 1000, size=N) #times for event 2.
mask = efficiency_test > 0.5
mask2 = efficiency_test_2 > 0.4
plt.hist(times, bins=50, label='source events',alpha=0.3)
plt.hist(times[mask], bins=50, label='gamma detector events', alpha=0.7)
plt.hist(times[mask2], bins=50, label='neutron detector events', alpha=0.7)
add_labels('time of event', 'counts', 'times for event 2 (gamma+neutron)')
meanTime = 250*10**-6
times = np.random.uniform(0, 1000, size=N) #times for event 2.
mask = efficiency_test > 0.5
mask2 = efficiency_test_2 > 0.4
gamma_events = np.sort(times[mask])
neutron_events = np.sort(times[mask2])
detector_events = neutron_events + np.random.exponential(meanTime, size = len(neutron_events))
intervals_gamma = []
intervals_neutron = []
detector_events = np.sort(detector_events)
for i in range(len(detector_events) - 1):
intervals_neutron.append(detector_events[i+1] - detector_events[i])
for i in range(len(gamma_events) - 1):
intervals_gamma.append(gamma_events[i+1] - gamma_events[i])
plt.hist(intervals_neutron, bins=50, label='neutron detector events', alpha = 0.7)
plt.hist(intervals_gamma, bins=50, label='gamma detector events', alpha=0.7)
add_labels('interval between events', 'counts', 'intervals between times for event 2 (gamma+neutron)')
"""Will repeat for the background rate later. Gotta do the last two questions"""
import numpy as np
positions = np.array([[-0.0114519 , 9.99999344, 6.69130799],
[ 6.33116335, -7.74056655, 3.59009715],
[-9.85887257, -1.67410623, 4.56138703],
[ 4.09466118, 9.12325325, 7.32437587],
[-3.37815507, -9.41212348, 3.67927878],
[-5.4274145 , -8.39899827, 6.8865273 ]])
thetaMeasures = np.array( [2.3164460126412245, 1.6313464103926718, 1.6970719353033004, 2.533624050255211, 1.6289243873579955, 1.8159707640506253] )
phiMeasures = np.array( [-0.9844385514247201, 1.8432675248986576, 0.5831709514637226, -2.132723211863188, 1.2215622389804748, 1.0853416750730511] )
print('Theodolite x \t Theodolite y \t Theodolite z \t Meas.theta \t Meas. phi')
for i in range(0,6):
print('%f \t %f \t %f \t %f \t %f '%(positions[i,0],positions[i,1],positions[i,2],thetaMeasures[i],phiMeasures[i]))
def xyz_to_spherical(vector):
r = np.linalg.norm(vector)
theta = np.arccos(vector[2]/r)
phi = np.arctan2(vector[1], vector[0])
return np.array([r, theta , phi])
def find_theta_phi(point, telescope):
difference = point - telescope
return xyz_to_spherical(difference)
def find_residuals(point):
theta_res = np.zeros((6))
phi_res = np.zeros((6))
for i in range(6):
angles = find_theta_phi(point, positions[i, :3])
theta_res[i] = thetaMeasures[i] - angles[1]
phi_res[i] = phiMeasures[i] - angles[2]
return np.concatenate([theta_res, phi_res], axis=0)
from scipy.optimize import least_squares
params0 = np.array([1, 1, 1])
popt_minimization = least_squares(find_residuals, params0)
popt_minimization
uncertainty = 5e-10
plt.hist(find_residuals(popt_minimization.x)/uncertainty)
print(f'the uncertainty is about {uncertainty}')
m = 20
l = 4
mu2 = 0.2
mu1 = 0.4
I = (1/12)*m*l**2
g=9.81
global N1
global N2
global ddtheta
#x = l/2*np.cos(theta)
#y = l/2*np.sin(theta)
"""This is a coupled system.
Hence we need to update both the linear newtons law
and the angular newtons law. we know the linear newtons law is 0, -mg.
I can't seem to get the height of the ground
"""
N1 = []
N2 = []
def main(y, t):
"Main thing to integrate"
"""
y[0] - theta
y[1] - omega
y[2:4] - x,y
y[4:6] - dx, dy
"""
theta = y[0:2]
positions = y[2:4]
velocities = y[4:6]
ddx = 0
ddy = -m*g
#Solving for N. Need ddx, ddy
A = np.array([[mu1, -m*g],[1, -mu2]])
b = np.array([m*ddy, m*ddx])
N = np.linalg.solve(A, b)
N1.append(N[0])
N2.append(N[1])
dydt = np.empty(6)
dx = -l/2*np.sin(y[0])*y[1]
dy = l/2*np.sin(y[0])*y[1]
dydt[0] = y[1] #omega
dydt[1] = (1/I)*((N[0] + mu2*N[1])*(l/2)*np.sin(y[0]) - (N[1] - mu1*N[0])*(l/2)*np.cos(y[0]))
dydt[2:4] = np.array([dx, dy])
dydt[4:6] = np.array([ddx, ddy])
return dydt
t = np.linspace(0, 10, 10000)
y0 = np.array([1.15, 0, l/2*np.cos(1.15), l/2*np.sin(1.15), 0, 0], dtype='float64')
y = odeint(main, y0, t)
"""Grab all physical numbers: the bar cannot fall into the floor"""
mask = (y[:, 3] > 0) & (y[:, 0] > 0)
t = t[mask]
y = y[mask]
plt.plot(t, y[:, 0]/np.pi*180)
add_labels('t','$\\theta$ (degrees)','angle of bar')
t = np.linspace(0, 10, len(N1))
plt.plot(t, N1, label="N1")
plt.plot(t, N2, label="N2")
add_labels('time', 'N1 N2', 'N1, N2 as a function of time')
t = np.linspace(0, 10, 10000)
y0 = np.array([1.15, 0, l/2*np.cos(1.15), l/2*np.sin(1.15), 0, 0], dtype='float64')
y = odeint(main, y0, t)
"""Grab all physical numbers: the bar cannot fall into the floor"""
mask = (y[:, 3] > 0) & (y[:, 0] > 0)
t = t[mask]
y = y[mask]
plt.plot(t, y[:, 3]/np.pi*180)
add_labels('t','y','height of bar')
| 0.709221 | 0.924891 |
<a href="https://colab.research.google.com/github/jamesfloe/cap-comp215/blob/main/Labs_lab5.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Cellular automata
Code examples from [Think Complexity, 2nd edition](https://thinkcomplex.com).
Copyright 2016 Allen Downey, [MIT License](http://opensource.org/licenses/MIT)
```
import os
if not os.path.exists('utils.py'):
!wget https://raw.githubusercontent.com/AllenDowney/ThinkComplexity2/master/notebooks/utils.py
%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import seaborn as sns
from utils import decorate
```
## Zero-dimensional CA
Here's a simple implementation of the 0-D CA I mentioned in the book, with one cell.
```
n = 10
x = np.zeros(n)
print(x)
```
To get the state of the cell in the next time step, we increment the current state mod 2.
```
x[1] = (x[0] + 1) % 2
x[1]
```
Filling in the rest of the array.
```
for i in range(2, n):
x[i] = (x[i-1] + 1) % 2
print(x)
```
So the behavior of this CA is simple: it blinks.
## One-dimensional CA
Just as we used a 1-D array to show the state of a single cell over time, we'll use a 2-D array to show the state of a 1-D CA over time, with one column per cell and one row per timestep.
```
rows = 5
cols = 11
array = np.zeros((rows, cols), dtype=np.uint8)
array[0, 5] = 1
print(array)
```
To plot the array I use `plt.imshow`
```
def plot_ca(array):
plt.imshow(array, cmap='Blues', interpolation='none')
```
Here's what it looks like after we initialize the first row.
```
plot_ca(array)
```
And here's the function that fills in the next row. The rule for this CA is to take the sum of a cell and its two neighbors mod 2.
```
def step(array, i):
"""Compute row i of a CA.
"""
rows, cols = array.shape
row = array[i-1]
for j in range(1, cols):
elts = row[j-1:j+2]
array[i, j] = sum(elts) % 2
```
Here's the second row.
```
step(array, 1)
plot_ca(array)
```
And here's what it looks like with the rest of the cells filled in.
```
for i in range(1, rows):
step(array, i)
plot_ca(array)
```
For a simple set of rules, the behavior is more interesting than you might expect.
**Exercise:** Modify this code to increase the number of rows and columns and see what this CA does after more time steps.
## Cross correlation
We can update the CA more quickly using "cross correlation". The cross correlation of an array, `a`, with a window, `w`, is a new array, `c`, where element `k` is:
$ c_k = \sum_{n=0}^{N-1} a_{n+k} \cdot w_n $
In Python, we can compute element `k` like this:
```
def c_k(a, w, k):
"""Compute element k of the cross correlation of a and w.
"""
N = len(w)
return sum(a[k:k+N] * w)
```
To see how this works, I'll create an array:
```
N = 10
row = np.arange(N, dtype=np.uint8)
print(row)
```
And a window:
```
window = [1, 1, 1]
print(window)
```
With this window, each element of `c` is the sum of three neighbors in the array:
```
c_k(row, window, 0)
c_k(row, window, 1)
```
The following function computes the elements of `c` for all values of `k` where the window can overlap with the array:
```
def correlate(row, window):
"""Compute the cross correlation of a and w.
"""
cols = len(row)
N = len(window)
c = [c_k(row, window, k) for k in range(cols-N+1)]
return np.array(c)
c = correlate(row, window)
print(c)
```
This operation is useful in many domains, so libraries like NumPy usually provide an implementation. Here's the version from NumPy.
```
c = np.correlate(row, window, mode='valid')
print(c)
```
With `mode='valid'`, the NumPy version does the same thing as mine: it only computes the elements of `c` where the window overlaps with the array. A drawback of this mode is that the result is smaller than `array`.
And alternative is `mode='same'`, which makes the result the same size as `array` by extending array with zeros on both sides. Here's the result:
```
c = np.correlate(row, window, mode='same')
print(c)
```
**Exercise:** Write a version of `correlate` that returns the same result as `np.correlate` with `mode='same'.`
```
# Hint: use np.pad to add zeros at the beginning and end of `row`
# Solution goes here
def myCorrelate(row, window):
"""Compute the cross correlation of a and w.
"""
N = len(window)
padded_c = np.pad(row, (1,), 'constant', constant_values=(0,0))
cols = len(padded_c)
print(padded_c)
c = [c_k(padded_c, window, k) for k in range(cols-N+1)]
return np.array(c)
c = myCorrelate(row, window)
print(c)
#Excercise 1 (b,c)
#1,
def myExperimentalCorrelate(row, window):
"""Compute the cross correlation of a and w.
"""
N = len(window)
padded_c = np.pad(row, (1,), mode='wrap')
cols = len(padded_c)
print(padded_c)
c = [c_k(padded_c, window, k) for k in range(cols-N+1)]
return np.array(c)
c = myExperimentalCorrelate(row, window)
print(c)
#1c
#Results are similar to my correlate function, except for the beginning.
```
## Update with correlate
Now we can use `np.correlate` to update the array. I'll start again with an array that contains one column for each cell and one row for each time step, and I'll initialize the first row with a single "on" cell in the middle:
```
rows = 5
cols = 11
array = np.zeros((rows, cols), dtype=np.uint8)
array[0, 5] = 1
print(array)
```
Now here's a version of `step` that uses `np.correlate`
```
def step2(array, i, window=[1,1,1]):
"""Compute row i of a CA.
"""
row = array[i-1]
c = np.correlate(row, window, mode='same')
array[i] = c % 2
```
And the result is the same.
```
for i in range(1, rows):
step2(array, i)
plot_ca(array)
```
## CA Tables
What we have so far is good enough for a CA that only depends on the total number of "on" cells, but for more general CAs, we need a table that maps from the configuration of the neighborhood to the future state of the center cell.
The following function makes the table by interpreting the Rule number in binary.
```
def make_table(rule):
"""Make the table for a given CA rule.
rule: int 0-255
returns: array of 8 0s and 1s
"""
rule = np.array([rule], dtype=np.uint8)
table = np.unpackbits(rule)[::-1]
return table
```
Here's what it looks like as an array:
```
table = make_table(150)
print(table)
```
If we correlate the row with the window `[4, 2, 1]`, it treats each neighborhood as a binary number between 000 and 111.
```
window = [4, 2, 1]
c = np.correlate(array[0], window, mode='same')
print(array[0])
print(c)
```
Now we can use the result from `np.correlate` as an index into the table; the result is the next row of the array.
```
array[1] = table[c]
print(array[1])
```
We can wrap up that code in a function:
```
def step3(array, i, window=[4,2,1]):
"""Compute row i of a CA.
"""
row = array[i-1]
c = np.correlate(row, window, mode='same')
array[i] = table[c]
```
And test it again.
```
for i in range(1, rows):
step3(array, i)
plot_ca(array)
```
How did I know that Rule 150 is the same as the previous CA? I wrote out the table and converted it to binary.
## The Cell1D object
`Cell1D` encapsulates the code from the previous section.
```
class Cell1D:
"""Represents a 1-D a cellular automaton"""
def __init__(self, rule, n, m=None):
"""Initializes the CA.
rule: integer
n: number of rows
m: number of columns
Attributes:
table: rule dictionary that maps from triple to next state.
array: the numpy array that contains the data.
next: the index of the next empty row.
"""
self.table = make_table(rule)
self.n = n
self.m = 2*n + 1 if m is None else m
self.array = np.zeros((n, self.m), dtype=np.int8)
self.next = 0
def start_single(self):
"""Starts with one cell in the middle of the top row."""
self.array[0, self.m//2] = 1
self.next += 1
def start_random(self, prop):
"""Start with random values in the top row."""
randoms = [0,1]
self.array[0] = np.array([int(np.random.choice(randoms, 1, p=[prop, 1-prop])) for item in range(self.m)])
self.next += 1
print(self.array)
def start_string(self, s):
"""Start with values from a string of 1s and 0s."""
# TODO: Check string length
self.array[0] = np.array([int(x) for x in s])
self.next += 1
def loop(self, steps=1):
"""Executes the given number of time steps."""
for i in range(steps):
self.step()
def step(self):
"""Executes one time step by computing the next row of the array."""
a = self.array
i = self.next
window = [4, 2, 1]
c = np.correlate(a[i-1], window, mode='same')
a[i] = self.table[c]
self.next += 1
def draw(self, start=0, end=None):
"""Draws the CA using pyplot.imshow.
start: index of the first column to be shown
end: index of the last column to be shown
"""
a = self.array[:, start:end]
plt.imshow(a, cmap='Blues', alpha=0.7)
# turn off axis tick marks
plt.xticks([])
plt.yticks([])
```
The following function makes and draws a CA.
```
def draw_ca(rule, n=32):
"""Makes and draw a 1D CA with a given rule.
rule: int rule number
n: number of rows
"""
ca = Cell1D(rule, n)
ca.start_single()
ca.loop(n-1)
ca.draw()
```
Here's an example that runs a Rule 50 CA for 10 steps.
```
draw_ca(rule=50, n=10)
plt.show('figs/chap05-1')
```
Another example:
```
draw_ca(rule=150, n=5)
plt.show('figs/chap05-2')
```
And one more example showing recursive structure.
```
draw_ca(rule=18, n=64)
plt.show('figs/chap05-3')
```
Rule 30 generates a sequence of bits that is indistinguishable from random:
```
draw_ca(rule=30, n=100)
plt.show('figs/chap05-4')
```
And Rule 110 is Turing complete!
```
draw_ca(rule=110, n=100)
plt.show('figs/chap05-5')
```
Here's a longer run that has some spaceships.
```
np.random.seed(21)
ca = Cell1D(rule=110, n=600)
ca.start_random(prop=0.5)
ca.loop(n-1)
ca.draw()
plt.show('figs/chap05-6')
```
## Exercises
**Exercise:** This exercise asks you to experiment with Rule 110 and see how
many spaceships you can find.
1. Read the Wikipedia page about Rule 110, which describes its background pattern and spaceships.
2. Create a Rule 110 CA with an initial condition that yields the
stable background pattern. Note that the CA class provides
`start_string`, which allow you to initialize the state of
the array using a string of `1`s and `0`s.
3. Modify the initial condition by adding different patterns in the
center of the row and see which ones yield spaceships. You might
want to enumerate all possible patterns of $n$ bits, for some
reasonable value of $n$. For each spaceship, can you find the
period and rate of translation? What is the biggest spaceship you
can find?
4. What happens when spaceships collide?
```
# Excercise 2 make_table
def myMake_Table(rule):
binString = ''
zero = 0
while rule >= 1:
binString = binString + str(rule%2)
rule = rule // 2
c = [int(item) for item in binString]
for i in range((abs(len(c) - 8))):
c.append(zero)
d = np.array(c)
return d
z = myMake_Table(50)
print(z)
# Exercise 3 start_random
def mydraw_ca(rule, n, p):
"""Makes and draw a 1D CA with a given rule.
rule: int rule number
n: number of rows
"""
ca = Cell1D(rule, n)
if p == 'none':
ca.start_single()
else:
ca.start_random(p)
ca.loop(n-1)
ca.draw()
mydraw_ca(30, 100, 0.3)
#Experiment 4 CA Experiment
# 1. Rule 0 will rapidly converge to a uniform state.
# 2. Rule 18 will converge to a repititive state.
# 3. Rule 30 is a class 3 rule, generating non-repeating random states.
# 4. Rule 110 is a class 4 rule, generating stable and non-stable areas, with areas that appear like spaceships, interacting in complex ways along each time-step.
plt.subplot(2, 2, 1)
draw_ca(rule=0, n = 100)
plt.subplot(2,2,2)
draw_ca(rule=18, n = 100)
plt.subplot(2,2,3)
draw_ca(rule=30, n = 100)
plt.subplot(2,2,4)
draw_ca(rule=110, n = 200)
#This system producing these wide range of behaviours, signifies that even a simple algorithm
#can produce complex results over time.
#We can see in the real world how simple living things, such as viruses, or monocellular organisms can
#be produced from a very simple pattern or 'seed.'
# Solution goes here
# Solution goes here
# Solution goes here
# Solution goes here
```
**Exercise:** The goal of this exercise is to implement a Turing machine.
1. Read about Turing machines.
2. Write a class called `Turing` that implements a Turing machine. For the action table, use the rules for a 3-state busy beaver.
3. Write a `draw` method that plots the state of the tape and the position and state of the head. For one example of what that might look like, see http://mathworld.wolfram.com/TuringMachine.html.
```
# Solution goes here
# Solution goes here
# Solution goes here
# Solution goes here
```
|
github_jupyter
|
import os
if not os.path.exists('utils.py'):
!wget https://raw.githubusercontent.com/AllenDowney/ThinkComplexity2/master/notebooks/utils.py
%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import seaborn as sns
from utils import decorate
n = 10
x = np.zeros(n)
print(x)
x[1] = (x[0] + 1) % 2
x[1]
for i in range(2, n):
x[i] = (x[i-1] + 1) % 2
print(x)
rows = 5
cols = 11
array = np.zeros((rows, cols), dtype=np.uint8)
array[0, 5] = 1
print(array)
def plot_ca(array):
plt.imshow(array, cmap='Blues', interpolation='none')
plot_ca(array)
def step(array, i):
"""Compute row i of a CA.
"""
rows, cols = array.shape
row = array[i-1]
for j in range(1, cols):
elts = row[j-1:j+2]
array[i, j] = sum(elts) % 2
step(array, 1)
plot_ca(array)
for i in range(1, rows):
step(array, i)
plot_ca(array)
def c_k(a, w, k):
"""Compute element k of the cross correlation of a and w.
"""
N = len(w)
return sum(a[k:k+N] * w)
N = 10
row = np.arange(N, dtype=np.uint8)
print(row)
window = [1, 1, 1]
print(window)
c_k(row, window, 0)
c_k(row, window, 1)
def correlate(row, window):
"""Compute the cross correlation of a and w.
"""
cols = len(row)
N = len(window)
c = [c_k(row, window, k) for k in range(cols-N+1)]
return np.array(c)
c = correlate(row, window)
print(c)
c = np.correlate(row, window, mode='valid')
print(c)
c = np.correlate(row, window, mode='same')
print(c)
# Hint: use np.pad to add zeros at the beginning and end of `row`
# Solution goes here
def myCorrelate(row, window):
"""Compute the cross correlation of a and w.
"""
N = len(window)
padded_c = np.pad(row, (1,), 'constant', constant_values=(0,0))
cols = len(padded_c)
print(padded_c)
c = [c_k(padded_c, window, k) for k in range(cols-N+1)]
return np.array(c)
c = myCorrelate(row, window)
print(c)
#Excercise 1 (b,c)
#1,
def myExperimentalCorrelate(row, window):
"""Compute the cross correlation of a and w.
"""
N = len(window)
padded_c = np.pad(row, (1,), mode='wrap')
cols = len(padded_c)
print(padded_c)
c = [c_k(padded_c, window, k) for k in range(cols-N+1)]
return np.array(c)
c = myExperimentalCorrelate(row, window)
print(c)
#1c
#Results are similar to my correlate function, except for the beginning.
rows = 5
cols = 11
array = np.zeros((rows, cols), dtype=np.uint8)
array[0, 5] = 1
print(array)
def step2(array, i, window=[1,1,1]):
"""Compute row i of a CA.
"""
row = array[i-1]
c = np.correlate(row, window, mode='same')
array[i] = c % 2
for i in range(1, rows):
step2(array, i)
plot_ca(array)
def make_table(rule):
"""Make the table for a given CA rule.
rule: int 0-255
returns: array of 8 0s and 1s
"""
rule = np.array([rule], dtype=np.uint8)
table = np.unpackbits(rule)[::-1]
return table
table = make_table(150)
print(table)
window = [4, 2, 1]
c = np.correlate(array[0], window, mode='same')
print(array[0])
print(c)
array[1] = table[c]
print(array[1])
def step3(array, i, window=[4,2,1]):
"""Compute row i of a CA.
"""
row = array[i-1]
c = np.correlate(row, window, mode='same')
array[i] = table[c]
for i in range(1, rows):
step3(array, i)
plot_ca(array)
class Cell1D:
"""Represents a 1-D a cellular automaton"""
def __init__(self, rule, n, m=None):
"""Initializes the CA.
rule: integer
n: number of rows
m: number of columns
Attributes:
table: rule dictionary that maps from triple to next state.
array: the numpy array that contains the data.
next: the index of the next empty row.
"""
self.table = make_table(rule)
self.n = n
self.m = 2*n + 1 if m is None else m
self.array = np.zeros((n, self.m), dtype=np.int8)
self.next = 0
def start_single(self):
"""Starts with one cell in the middle of the top row."""
self.array[0, self.m//2] = 1
self.next += 1
def start_random(self, prop):
"""Start with random values in the top row."""
randoms = [0,1]
self.array[0] = np.array([int(np.random.choice(randoms, 1, p=[prop, 1-prop])) for item in range(self.m)])
self.next += 1
print(self.array)
def start_string(self, s):
"""Start with values from a string of 1s and 0s."""
# TODO: Check string length
self.array[0] = np.array([int(x) for x in s])
self.next += 1
def loop(self, steps=1):
"""Executes the given number of time steps."""
for i in range(steps):
self.step()
def step(self):
"""Executes one time step by computing the next row of the array."""
a = self.array
i = self.next
window = [4, 2, 1]
c = np.correlate(a[i-1], window, mode='same')
a[i] = self.table[c]
self.next += 1
def draw(self, start=0, end=None):
"""Draws the CA using pyplot.imshow.
start: index of the first column to be shown
end: index of the last column to be shown
"""
a = self.array[:, start:end]
plt.imshow(a, cmap='Blues', alpha=0.7)
# turn off axis tick marks
plt.xticks([])
plt.yticks([])
def draw_ca(rule, n=32):
"""Makes and draw a 1D CA with a given rule.
rule: int rule number
n: number of rows
"""
ca = Cell1D(rule, n)
ca.start_single()
ca.loop(n-1)
ca.draw()
draw_ca(rule=50, n=10)
plt.show('figs/chap05-1')
draw_ca(rule=150, n=5)
plt.show('figs/chap05-2')
draw_ca(rule=18, n=64)
plt.show('figs/chap05-3')
draw_ca(rule=30, n=100)
plt.show('figs/chap05-4')
draw_ca(rule=110, n=100)
plt.show('figs/chap05-5')
np.random.seed(21)
ca = Cell1D(rule=110, n=600)
ca.start_random(prop=0.5)
ca.loop(n-1)
ca.draw()
plt.show('figs/chap05-6')
# Excercise 2 make_table
def myMake_Table(rule):
binString = ''
zero = 0
while rule >= 1:
binString = binString + str(rule%2)
rule = rule // 2
c = [int(item) for item in binString]
for i in range((abs(len(c) - 8))):
c.append(zero)
d = np.array(c)
return d
z = myMake_Table(50)
print(z)
# Exercise 3 start_random
def mydraw_ca(rule, n, p):
"""Makes and draw a 1D CA with a given rule.
rule: int rule number
n: number of rows
"""
ca = Cell1D(rule, n)
if p == 'none':
ca.start_single()
else:
ca.start_random(p)
ca.loop(n-1)
ca.draw()
mydraw_ca(30, 100, 0.3)
#Experiment 4 CA Experiment
# 1. Rule 0 will rapidly converge to a uniform state.
# 2. Rule 18 will converge to a repititive state.
# 3. Rule 30 is a class 3 rule, generating non-repeating random states.
# 4. Rule 110 is a class 4 rule, generating stable and non-stable areas, with areas that appear like spaceships, interacting in complex ways along each time-step.
plt.subplot(2, 2, 1)
draw_ca(rule=0, n = 100)
plt.subplot(2,2,2)
draw_ca(rule=18, n = 100)
plt.subplot(2,2,3)
draw_ca(rule=30, n = 100)
plt.subplot(2,2,4)
draw_ca(rule=110, n = 200)
#This system producing these wide range of behaviours, signifies that even a simple algorithm
#can produce complex results over time.
#We can see in the real world how simple living things, such as viruses, or monocellular organisms can
#be produced from a very simple pattern or 'seed.'
# Solution goes here
# Solution goes here
# Solution goes here
# Solution goes here
# Solution goes here
# Solution goes here
# Solution goes here
# Solution goes here
| 0.613815 | 0.987265 |
```
import pandas as pd
df_data = pd.read_csv('./data.csv')
df_data.head(4)
df_data.info()
# 데이터 길이가 같아 불용어처리 이외의 전처리는 하지 않아도 됨
df_data['Desc']
from nltk.tokenize import RegexpTokenizer
```
- RegexpTokenizer : https://regexr.com/
- Regular Expression Tokenizer : 내가 지정한 글자나 문자대로 자를 수 있음. 단어의 인접행렬을 알아내기 위해 하는 작업.
- apply : map 같은 기능
```
def remove_punctuation(text):
tokenizer = RegexpTokenizer('[a-zA-Z]+') # '따옴표'안에 있는 구문만 가져오기
text_list = tokenizer.tokenize(text)
print(type(text_list), text_list)
result = ' '.join(text_list)
print( type(result), result)
return result
text01 = 'We know that power is shifting: From West to E'
remove_punctuation(text01)
df_data['cleaned'] = df_data['Desc'].apply(remove_punctuation)
df_data.columns
# cleaned 가 추가되어있음
df_data['cleaned'].head(5)
df_data.info()
```
## Pre-Trained
문장을 입력할 때 마다 word2vec을 돌릴 수 없음 -> **Pre-trained** : 누군가가 엄청 많은 데이터를 Word2Vec으로 만들어 놓은 것을 가져와 쓰기
```
# 구글뉴스 위키피디아 - > Word2Vec 으로 만들어둔 자료
!curl -O https://s3.amazonaws.com/dl4j-distribution/GoogleNews-vectors-negative300.bin.gz
from gensim.models import Word2Vec
corpus = []
for words in df_data['cleaned']:
corpus.append(words.split())
print(type(corpus), corpus[4:8])
word2vec_model = Word2Vec(min_count=2, workers=-1, size=300)
# 300차원 word2vec
word2vec_model.build_vocab(corpus)
word2vec_model.intersect_word2vec_format('GoogleNews-vectors-negative300.bin.gz', lockf=1.0, binary=True)
word2vec_model.train(df_data['cleaned'], total_examples=word2vec_model.corpus_count, epochs=5 )
word2vec_model.wv.vocab
# 각 단어마다 gensim으로 한 Keyedvectors 가 들어감
# 단어를 word2vec에 저장되있는 숫자로 바꾸기
# 수치화된 것을 합산(사이즈 같을 경우)후 평균 구함
doc_embedding_list = list()
for line in df_data['cleaned']:
doc2vec = None
for word in line.split():
if word in word2vec_model.wv.vocab:
if doc2vec is None:
doc2vec = word2vec_model[word]
else :
doc2vec = doc2vec + word2vec_model[word] # 합산
if doc2vec is not None:
doc2vec = doc2vec / len(doc2vec) # 평균
doc_embedding_list.append(doc2vec)
print(doc_embedding_list)
type(doc_embedding_list), doc_embedding_list[3]
```
## Cosine Metrix 인접행렬
```
from sklearn.metrics.pairwise import cosine_similarity
cosine_sim = cosine_similarity(doc_embedding_list, doc_embedding_list) # 인접행렬 만들기
type(cosine_sim), cosine_sim.shape
# cosine_sim[3]
```
## Predict
```
# title = 'The Da Vinci Code'
title = 'The Four Pillars of Investing' # 3
idx = 3
sim_scores = list( enumerate(cosine_sim[3]) )
print(sim_scores)
# df_data의 값들과 title간에 관계성이 얼마나 있는지 나타냄
sim_scores_list = sorted(sim_scores, key=lambda x:x[1], reverse=True)
# title과 유사도를 나타낸 근사값들이 리스트로 나오게됨
sim_scores_list[1:6] # 자기자신은 제외
df_data.head(6)
```
|
github_jupyter
|
import pandas as pd
df_data = pd.read_csv('./data.csv')
df_data.head(4)
df_data.info()
# 데이터 길이가 같아 불용어처리 이외의 전처리는 하지 않아도 됨
df_data['Desc']
from nltk.tokenize import RegexpTokenizer
def remove_punctuation(text):
tokenizer = RegexpTokenizer('[a-zA-Z]+') # '따옴표'안에 있는 구문만 가져오기
text_list = tokenizer.tokenize(text)
print(type(text_list), text_list)
result = ' '.join(text_list)
print( type(result), result)
return result
text01 = 'We know that power is shifting: From West to E'
remove_punctuation(text01)
df_data['cleaned'] = df_data['Desc'].apply(remove_punctuation)
df_data.columns
# cleaned 가 추가되어있음
df_data['cleaned'].head(5)
df_data.info()
# 구글뉴스 위키피디아 - > Word2Vec 으로 만들어둔 자료
!curl -O https://s3.amazonaws.com/dl4j-distribution/GoogleNews-vectors-negative300.bin.gz
from gensim.models import Word2Vec
corpus = []
for words in df_data['cleaned']:
corpus.append(words.split())
print(type(corpus), corpus[4:8])
word2vec_model = Word2Vec(min_count=2, workers=-1, size=300)
# 300차원 word2vec
word2vec_model.build_vocab(corpus)
word2vec_model.intersect_word2vec_format('GoogleNews-vectors-negative300.bin.gz', lockf=1.0, binary=True)
word2vec_model.train(df_data['cleaned'], total_examples=word2vec_model.corpus_count, epochs=5 )
word2vec_model.wv.vocab
# 각 단어마다 gensim으로 한 Keyedvectors 가 들어감
# 단어를 word2vec에 저장되있는 숫자로 바꾸기
# 수치화된 것을 합산(사이즈 같을 경우)후 평균 구함
doc_embedding_list = list()
for line in df_data['cleaned']:
doc2vec = None
for word in line.split():
if word in word2vec_model.wv.vocab:
if doc2vec is None:
doc2vec = word2vec_model[word]
else :
doc2vec = doc2vec + word2vec_model[word] # 합산
if doc2vec is not None:
doc2vec = doc2vec / len(doc2vec) # 평균
doc_embedding_list.append(doc2vec)
print(doc_embedding_list)
type(doc_embedding_list), doc_embedding_list[3]
from sklearn.metrics.pairwise import cosine_similarity
cosine_sim = cosine_similarity(doc_embedding_list, doc_embedding_list) # 인접행렬 만들기
type(cosine_sim), cosine_sim.shape
# cosine_sim[3]
# title = 'The Da Vinci Code'
title = 'The Four Pillars of Investing' # 3
idx = 3
sim_scores = list( enumerate(cosine_sim[3]) )
print(sim_scores)
# df_data의 값들과 title간에 관계성이 얼마나 있는지 나타냄
sim_scores_list = sorted(sim_scores, key=lambda x:x[1], reverse=True)
# title과 유사도를 나타낸 근사값들이 리스트로 나오게됨
sim_scores_list[1:6] # 자기자신은 제외
df_data.head(6)
| 0.296654 | 0.768255 |
```
#usage:
#Line-155------>Test image path , image size expected 128x128x3
#Line 157------>Model path
import os
import sys
import random
import warnings
import numpy as np
import pandas as pd
import matplotlib
matplotlib.use('agg')
import matplotlib.pyplot as plt
from tqdm import tqdm
from itertools import chain
from skimage.io import imread, imshow, imread_collection, concatenate_images
from skimage.transform import resize
from skimage.morphology import label
from keras.models import Model, load_model
from keras.layers import Input
from keras.layers.core import Dropout, Lambda
from keras.layers.convolutional import Conv2D, Conv2DTranspose
from keras.layers.pooling import MaxPooling2D
from keras.layers.merge import concatenate
from keras.callbacks import EarlyStopping, ModelCheckpoint
from keras import backend as K
import tensorflow as tf
import cv2
class automaticmaplabelling():
def __init__(self,modelPath,full_chq,imagePath,width,height,channels):
print (modelPath)
print(imagePath)
print(width)
print(height)
print(channels)
self.modelPath=modelPath
self.full_chq=full_chq
self.imagePath=imagePath
self.IMG_WIDTH=width
self.IMG_HEIGHT=height
self.IMG_CHANNELS=channels
self.model = self.U_net()
def mean_iou(self,y_true, y_pred):
prec = []
for t in np.arange(0.5, 1.0, 0.05):
y_pred_ = tf.to_int32(y_pred > t)
score, up_opt = tf.metrics.mean_iou(y_true, y_pred_, 2)
K.get_session().run(tf.local_variables_initializer())
with tf.control_dependencies([up_opt]):
score = tf.identity(score)
prec.append(score)
return K.mean(K.stack(prec), axis=0)
def U_net(self):
# Build U-Net model
inputs = Input((self.IMG_HEIGHT, self.IMG_WIDTH, self.IMG_CHANNELS))
s = Lambda(lambda x: x / 255) (inputs)
c1 = Conv2D(16, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (s)
c1 = Dropout(0.1) (c1)
c1 = Conv2D(16, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c1)
p1 = MaxPooling2D((2, 2)) (c1)
c2 = Conv2D(32, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (p1)
c2 = Dropout(0.1) (c2)
c2 = Conv2D(32, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c2)
p2 = MaxPooling2D((2, 2)) (c2)
c3 = Conv2D(64, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (p2)
c3 = Dropout(0.2) (c3)
c3 = Conv2D(64, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c3)
p3 = MaxPooling2D((2, 2)) (c3)
c4 = Conv2D(128, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (p3)
c4 = Dropout(0.2) (c4)
c4 = Conv2D(128, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c4)
p4 = MaxPooling2D(pool_size=(2, 2)) (c4)
c5 = Conv2D(256, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (p4)
c5 = Dropout(0.3) (c5)
c5 = Conv2D(256, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c5)
u6 = Conv2DTranspose(128, (2, 2), strides=(2, 2), padding='same') (c5)
u6 = concatenate([u6, c4])
c6 = Conv2D(128, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (u6)
c6 = Dropout(0.2) (c6)
c6 = Conv2D(128, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c6)
u7 = Conv2DTranspose(64, (2, 2), strides=(2, 2), padding='same') (c6)
u7 = concatenate([u7, c3])
c7 = Conv2D(64, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (u7)
c7 = Dropout(0.2) (c7)
c7 = Conv2D(64, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c7)
u8 = Conv2DTranspose(32, (2, 2), strides=(2, 2), padding='same') (c7)
u8 = concatenate([u8, c2])
c8 = Conv2D(32, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (u8)
c8 = Dropout(0.1) (c8)
c8 = Conv2D(32, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c8)
u9 = Conv2DTranspose(16, (2, 2), strides=(2, 2), padding='same') (c8)
u9 = concatenate([u9, c1], axis=3)
c9 = Conv2D(16, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (u9)
c9 = Dropout(0.1) (c9)
c9 = Conv2D(16, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c9)
outputs = Conv2D(1, (1, 1), activation='sigmoid') (c9)
model = Model(inputs=[inputs], outputs=[outputs])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=[self.mean_iou])
model.load_weights(self.modelPath)
model.summary()
return model
def prediction(self):
img=cv2.imread(self.imagePath,0)
img=np.expand_dims(img,axis=-1)
x_test= np.zeros((1, self.IMG_HEIGHT, self.IMG_WIDTH, self.IMG_CHANNELS), dtype=np.uint8)
#testimg=resize(img,(self.IMG_HEIGHT,self.IMG_WIDTH),mode='constant',preserve_range=True)
x_test[0]=img
preds_test= self.model.predict(x_test, verbose=1)
preds_test = (preds_test > 0.5).astype(np.uint8)
mask=preds_test[0]
for i in range(mask.shape[0]):
for j in range(mask.shape[1]):
if mask[i][j] == 1:
mask[i][j] = 255
else:
mask[i][j] = 0
merged_image = cv2.merge((mask,mask,mask))
contours, hierarchy = cv2.findContours(mask,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
for each_contour in contours:
x,y,w,h = cv2.boundingRect(each_contour)
cv2.rectangle(merged_image,(x,y),(x+w,y+h),(0,0,255),4)
print (x,y,w,h)
cv2.imshow("merged_image",merged_image)
cv2.waitKey(0)
cv2.imwrite("mask.png",mask)
return x_test[0],mask
def main():
#Test image path , image size expected 128x128x3
test_image_name = r"C:\Users\dextr\OneDrive\Desktop\software_final\U-Net\code\test\test_128\1.png"
#Model path
model_path = r"C:\Users\dextr\OneDrive\Desktop\software_final\U-Net\code\test\model\model-dsbowl2018-1.h5"
automaticmaplabellingobj= automaticmaplabelling(model_path,True,test_image_name,128,128,3)
testimg,mask = automaticmaplabellingobj.prediction()
print('Showing images..')
cv2.imshow('img',testimg)
dim = (1280, 1280)
resized = cv2.resize(mask, dim, interpolation = cv2.INTER_AREA)
cv2.imshow('mask',mask)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite("resized_mask.png",resized)
if __name__ == "__main__":
main()
```
|
github_jupyter
|
#usage:
#Line-155------>Test image path , image size expected 128x128x3
#Line 157------>Model path
import os
import sys
import random
import warnings
import numpy as np
import pandas as pd
import matplotlib
matplotlib.use('agg')
import matplotlib.pyplot as plt
from tqdm import tqdm
from itertools import chain
from skimage.io import imread, imshow, imread_collection, concatenate_images
from skimage.transform import resize
from skimage.morphology import label
from keras.models import Model, load_model
from keras.layers import Input
from keras.layers.core import Dropout, Lambda
from keras.layers.convolutional import Conv2D, Conv2DTranspose
from keras.layers.pooling import MaxPooling2D
from keras.layers.merge import concatenate
from keras.callbacks import EarlyStopping, ModelCheckpoint
from keras import backend as K
import tensorflow as tf
import cv2
class automaticmaplabelling():
def __init__(self,modelPath,full_chq,imagePath,width,height,channels):
print (modelPath)
print(imagePath)
print(width)
print(height)
print(channels)
self.modelPath=modelPath
self.full_chq=full_chq
self.imagePath=imagePath
self.IMG_WIDTH=width
self.IMG_HEIGHT=height
self.IMG_CHANNELS=channels
self.model = self.U_net()
def mean_iou(self,y_true, y_pred):
prec = []
for t in np.arange(0.5, 1.0, 0.05):
y_pred_ = tf.to_int32(y_pred > t)
score, up_opt = tf.metrics.mean_iou(y_true, y_pred_, 2)
K.get_session().run(tf.local_variables_initializer())
with tf.control_dependencies([up_opt]):
score = tf.identity(score)
prec.append(score)
return K.mean(K.stack(prec), axis=0)
def U_net(self):
# Build U-Net model
inputs = Input((self.IMG_HEIGHT, self.IMG_WIDTH, self.IMG_CHANNELS))
s = Lambda(lambda x: x / 255) (inputs)
c1 = Conv2D(16, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (s)
c1 = Dropout(0.1) (c1)
c1 = Conv2D(16, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c1)
p1 = MaxPooling2D((2, 2)) (c1)
c2 = Conv2D(32, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (p1)
c2 = Dropout(0.1) (c2)
c2 = Conv2D(32, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c2)
p2 = MaxPooling2D((2, 2)) (c2)
c3 = Conv2D(64, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (p2)
c3 = Dropout(0.2) (c3)
c3 = Conv2D(64, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c3)
p3 = MaxPooling2D((2, 2)) (c3)
c4 = Conv2D(128, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (p3)
c4 = Dropout(0.2) (c4)
c4 = Conv2D(128, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c4)
p4 = MaxPooling2D(pool_size=(2, 2)) (c4)
c5 = Conv2D(256, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (p4)
c5 = Dropout(0.3) (c5)
c5 = Conv2D(256, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c5)
u6 = Conv2DTranspose(128, (2, 2), strides=(2, 2), padding='same') (c5)
u6 = concatenate([u6, c4])
c6 = Conv2D(128, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (u6)
c6 = Dropout(0.2) (c6)
c6 = Conv2D(128, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c6)
u7 = Conv2DTranspose(64, (2, 2), strides=(2, 2), padding='same') (c6)
u7 = concatenate([u7, c3])
c7 = Conv2D(64, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (u7)
c7 = Dropout(0.2) (c7)
c7 = Conv2D(64, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c7)
u8 = Conv2DTranspose(32, (2, 2), strides=(2, 2), padding='same') (c7)
u8 = concatenate([u8, c2])
c8 = Conv2D(32, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (u8)
c8 = Dropout(0.1) (c8)
c8 = Conv2D(32, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c8)
u9 = Conv2DTranspose(16, (2, 2), strides=(2, 2), padding='same') (c8)
u9 = concatenate([u9, c1], axis=3)
c9 = Conv2D(16, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (u9)
c9 = Dropout(0.1) (c9)
c9 = Conv2D(16, (3, 3), activation='elu', kernel_initializer='he_normal', padding='same') (c9)
outputs = Conv2D(1, (1, 1), activation='sigmoid') (c9)
model = Model(inputs=[inputs], outputs=[outputs])
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=[self.mean_iou])
model.load_weights(self.modelPath)
model.summary()
return model
def prediction(self):
img=cv2.imread(self.imagePath,0)
img=np.expand_dims(img,axis=-1)
x_test= np.zeros((1, self.IMG_HEIGHT, self.IMG_WIDTH, self.IMG_CHANNELS), dtype=np.uint8)
#testimg=resize(img,(self.IMG_HEIGHT,self.IMG_WIDTH),mode='constant',preserve_range=True)
x_test[0]=img
preds_test= self.model.predict(x_test, verbose=1)
preds_test = (preds_test > 0.5).astype(np.uint8)
mask=preds_test[0]
for i in range(mask.shape[0]):
for j in range(mask.shape[1]):
if mask[i][j] == 1:
mask[i][j] = 255
else:
mask[i][j] = 0
merged_image = cv2.merge((mask,mask,mask))
contours, hierarchy = cv2.findContours(mask,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
for each_contour in contours:
x,y,w,h = cv2.boundingRect(each_contour)
cv2.rectangle(merged_image,(x,y),(x+w,y+h),(0,0,255),4)
print (x,y,w,h)
cv2.imshow("merged_image",merged_image)
cv2.waitKey(0)
cv2.imwrite("mask.png",mask)
return x_test[0],mask
def main():
#Test image path , image size expected 128x128x3
test_image_name = r"C:\Users\dextr\OneDrive\Desktop\software_final\U-Net\code\test\test_128\1.png"
#Model path
model_path = r"C:\Users\dextr\OneDrive\Desktop\software_final\U-Net\code\test\model\model-dsbowl2018-1.h5"
automaticmaplabellingobj= automaticmaplabelling(model_path,True,test_image_name,128,128,3)
testimg,mask = automaticmaplabellingobj.prediction()
print('Showing images..')
cv2.imshow('img',testimg)
dim = (1280, 1280)
resized = cv2.resize(mask, dim, interpolation = cv2.INTER_AREA)
cv2.imshow('mask',mask)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.imwrite("resized_mask.png",resized)
if __name__ == "__main__":
main()
| 0.643889 | 0.477006 |
# 1. Business Problem
## 1.1 Introdução ao Problema
Você foi contratado(a) para fazer uma análise apurada do número de internações no
sistema de saúde brasileiro. Esta análise é de extrema importância para tomada de
decisões que deverão contribuir para melhorias no sistema e planejamento estratégico.
Para a análise foram fornecidos os dados referentes às internações que ocorreram no país durante o período de dez/17 a jul/19, separados por região e unidade de federação.
Nosso objetivo é, através do dados, montar um planejamento estratégico para diminuir o número de internações em hospitais do SUS.
# 2. Data cleaning
## 2.1 Library imports and settings
```
# imports que suportam o notebook
import pandas as pd
import numpy as np
import re
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from datetime import datetime
from unidecode import unidecode
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.ar_model import AutoReg
import warnings
warnings.filterwarnings('ignore', 'statsmodels.tsa.ar_model.AR', FutureWarning)
pd.set_option('display.float_format', lambda x: '%.3f' % x)
```
## 2.2 Data Import
```
# importando os dados do excel disponível
dfname=pd.ExcelFile('case_internacao_SUS.xls')
sheets = dfname.sheet_names
df=pd.DataFrame()
for sheet in sheets:
xls = pd.ExcelFile('case_internacao_SUS.xls')
data = pd.read_excel(xls, sheet)
df = pd.concat([df, data], axis = 0)
df.reset_index(drop = True, inplace = True)
# olhando pela primeira vez nossos dados para entendermos o que faremos primeiro
df
```
A princípio, vemos dados faltantes e a coluna de Região/Unidade da Federação precisando de formatação. Vamos explorar também os tipos atriuídos às variáveis e analisar as outras colunas para identificarmos necessidade de tratamento de dados faltantes.
## 2.3 Data processing
Nessa etapa vamos fazer a limpeza e formatação dos dados.
**Nomes das colunas**
A primeira coisa que vamos fazer é trocar o nome das colunas para que seja mais fácil trabalhar com elas, para isso foram usadas siglas, explicadas abaixo:
* AIH: Autorização de Internação Hospitalar
* VSH: Valor dos Serviços Hospitalares
* VSP: Valor dos Serviços Profissionais
```
df = df.rename(columns = {
'Valor_serviços_hospitalares': 'vsh',
'Val_serv_hosp_-_compl_federal': 'vsh_comp_fed',
'Val_serv_hosp_-_compl_gestor': 'vsh_comp_gest',
'Valor_serviços_profissionais': 'vsp',
'Val_serv_prof_-_compl_federal': 'vsp_comp_fed',
'Val_serv_prof_-_compl_gestor': 'vsp_comp_gest',
'Região/Unidade da Federação': 'estado',
'AIH_aprovadas': 'aih_aprvd',
'Valor_total': 'valor_total',
'Valor_médio_AIH': 'valor_medio_aih',
'Valor_médio_intern': 'valor_medio_intern',
'Dias_permanência': 'dias_permanencia',
'Média_permanência': 'media_permanencia',
'Óbitos': 'obitos',
'Taxa_mortalidade': 'taxa_mortalidade',
'Internações': 'internacoes'
})
```
**Tipos das colunas**
```
df.dtypes
```
Aparentemente os tipos das variáveis Val_serv_hosp_-_compl_federal, Val_serv_hosp_-_compl_gestor, Val_serv_prof_-_compl_federal e Val_serv_prof_-_compl_gestor_ estão incorretos, dado que são valores numéricos.
Para isso, vamos ter que substituir os valores de '-' por 0 e posteriormente transformar o tipo das colunas, como demonstrado abaixo:
```
# , Val_serv_hosp_-_compl_gestor, Val_serv_prof_-_compl_federal e Val_serv_prof_-_compl_gestor_
df['vsh_comp_fed'] = df['vsh_comp_fed'].apply(lambda x: str(x).replace('-', '0'))
df['vsh_comp_fed'] = df['vsh_comp_fed'].astype('float')
df['vsh_comp_gest'] = df['vsh_comp_gest'].apply(lambda x: str(x).replace('-', '0'))
df['vsh_comp_gest'] = df['vsh_comp_gest'].astype('float')
df['vsp_comp_fed'] = df['vsp_comp_fed'].apply(lambda x: str(x).replace('-', '0'))
df['vsp_comp_fed'] = df['vsp_comp_fed'].astype('float')
df['vsp_comp_gest'] = df['vsp_comp_gest'].apply(lambda x: str(x).replace('-', '0'))
df['vsp_comp_gest'] = df['vsp_comp_gest'].astype('float')
```
**Coluna 'estado' - primeira limpeza**
Vamos fazer duas etapas de limpeza na coluna 'estado':
1- Primeiramente vamos retirar quaisquer valores nulos e as sujeiras nos nomes dos estados;
2- Depois vamos deixar a coluna somente com os nomes dos estados, retirando "Totais" e as regiões;
Essa segragação foi feita pois vamos usar a coluna de "Totais" como referência para acrescentarmos a coluna de as datas das observações e, posteriormente, criar uma coluna com as regiões.
```
# vendo os valores únicos na coluna de estado
df['estado'].unique()
# além dos estados que queremos manter, temos sujeiras como "Total", valores nulos e " "
# observamos que as linhas cujo valor do estado era nulo ou vazio estavam completamente vazias, portanto serão deletadas
vazio = df[(df['estado'] == 'nan') | (df['estado'] == ' ')].index.to_list()
df.drop(labels = vazio, axis = 0, inplace = True)
df.reset_index(drop = True, inplace = True)
# como já fo comentado, vamos manter o "Total" para utilizarmos depois
# deletando os .. no nome dos estados
df['estado'] = df['estado'].apply(lambda x: str(x).replace('.. ', ''))
```
**Acrescentar e tratar coluna de datas**
Do arquivo em excel que importamos os dados, cada aba representada um mês de observação. Para acrescentarmos essa dimensão aos nossos dados vamos utilizar a linha de 'Total', que representa o fim dos dados de cada uma das abas.
```
# primeiro criamos um dataframe só com as linhas de "Total" e seus índices
totais = df[df['estado'] == 'Total']
totais['month_year'] = sheets
totais = totais.reset_index()
# traduzindo os meses para inglês
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('fev','feb'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('abr','apr'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('mai','may'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('ago','aug'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('set','sep'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('out','oct'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('dez','dec'))
# mudando o tipo de data
totais['month_year'] = totais['month_year'].apply(lambda x: datetime.strptime(x,'%b%y'))
totais.rename(columns={'month_year': 'date'}, inplace = True)
# vamos criar um novo dataframe, baseado no primeiro, mas com o index como coluna para unirmos ao total
df2 = df.reset_index()
df2 = pd.merge(df2, totais, how = 'left', on='index')
# agora vamos ajustar o df2
# dropamos colunas repetidas
dropped = ['estado_y', 'internacoes_y', 'aih_aprvd_y',
'valor_total_y', 'vsh_y', 'vsh_comp_fed_y', 'vsh_comp_gest_y', 'vsp_y',
'vsp_comp_fed_y', 'vsp_comp_gest_y', 'valor_medio_aih_y',
'valor_medio_intern_y', 'dias_permanencia_y', 'media_permanencia_y',
'obitos_y', 'taxa_mortalidade_y','index']
df2.drop(dropped, axis = 1, inplace = True)
## renomeando colunas
colunas = df.columns.to_list()
colunas.append('month_year')
df2.set_axis(colunas, axis = 1, inplace = True)
# preenchendo mês e ano para todas as ocorrências
df2['month_year'].bfill(inplace=True)
```
**Coluna 'estado' - segunda limpeza****
Agora que temos nossa coluna de datas preenchida no formato correto, podemos nos livrar das linhas de 'Totais' e segregar as regiões em uma nova coluna.
```
# dropando linhas de totais
list1 = df2[df2['estado'] == 'Total'].index
df2.drop(list1, axis = 0, inplace=True)
# criando a nova coluna de região e preenchendo ela
df2['regiao'] = df2['estado'].apply(lambda x: re.search('Região.+', x))
df2['regiao'] = df2['regiao'].apply(lambda x: x.group(0) if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Norte', 'norte') if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Nordeste', 'nordeste') if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Sudeste', 'sudeste') if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Sul', 'sul') if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Centro-Oeste', 'centro_oeste') if pd.notnull(x) else x)
df2['regiao'].ffill(inplace=True)
# dropando as linhas de região dentro da coluna de estado
list1 = df2[(df2['estado'] == 'Região Norte') | (df2['estado'] == 'Região Nordeste') | (df2['estado'] == 'Região Sudeste') | (df2['estado'] == 'Região Sul') | (df2['estado'] == 'Região Centro-Oeste')].index.to_list()
df2.drop(list1, axis = 0, inplace = True)
# ajustando o nome dos estados como snake_case
df2['estado'] = df2['estado'].apply(lambda x: x.lower())
df2['estado'] = df2['estado'].apply(lambda x: x.replace(' ', '_'))
df2['estado'] = df2['estado'].apply(lambda x: unidecode(x))
# rearrumando a ordem das colunas
df2 = df2[
['regiao',
'estado',
'internacoes',
'aih_aprvd',
'valor_total',
'vsh',
'vsh_comp_fed',
'vsh_comp_gest',
'vsp',
'vsp_comp_fed',
'vsp_comp_gest',
'valor_medio_aih',
'valor_medio_intern',
'dias_permanencia',
'media_permanencia',
'obitos',
'taxa_mortalidade',
'month_year']
]
# agora faremos o check final para averiguarmos a necessidade de tratamento adicional
df2.isnull().sum() / df2.shape[0]
# ainda temos 5 valores vazios em algumas colunas, que representam 1.3% dos nossos dados.
# como os valores representam uma parcela muito pequena dos nossos dados, vamos deletar.
df2.dropna(axis = 0, inplace = True)
# agora não temos valores nulos
df2.isnull().sum() / df2.shape[0]
# vamos observar como ficaram nossos dados depois da limpeza
df2.head(10)
```
## 2.4 Features
Antes de começarmos a análise exploratória dos dados, vamos criar novas variáveis para podermos acrescentar elas na dimensão das nossas análises.
```
df2.columns
df2['year'] = df2['month_year'].dt.year
df2['month'] = df2['month_year'].dt.month
df2['month_year'] = df2['month_year'].dt.strftime('%Y-%m')
```
# 3. EDA
Antes de começarmos a análise exploratória dos dados, temos que saber precisamente o que cada variável significa para termos o contexto dos valores apresentados. Abaixo a descrição das variáveis:
* regiao -> região onde a unidade hospitalar está estabelecida.
* estado -> estado onde a unidade hospitalar está estabelecida.
* internacoes -> quantidade de AIH aprovadas no período não considerando as de prorrogação; trata-se de um valor aproximado pois as transferências e reinternações também foram computadas.
* aih_aprovd -> AIH aprovadas no período, tanto de novas internações quanto de prorrogação.
* valor_total -> valor referente às AIH aprovadas no período, o que não necessariamente é o valor repassado ao estabelecimento; deve ser considerado como o valor aprovado da produção.
* vsh -> valor dos serviços hospitalares referente às AIH aprovadas no período; aplicam-se as mesmas observações referentes ao valor total.
* vsh_comp_fed -> complemento federal do valor dos serviços hospitalares; aplicam-se as mesmas observações referentes ao valor total.
* vsh_comp_gest -> complemento do gestor estadual ou municipal do valor dos serviços hospitalares; aplicam-se as mesmas observações referentes ao valor total.
* vsp -> valor dos serivços prestados referente às AIH aprovadas no período; aplicam-se as mesmas observações referentes ao valor total.
* vsp_comp_fed -> complemento federal do valor dos serviços profissionais; aplicam-se as mesmas observações referentes ao valor total.
* vsp_comp_gest -> complemento do gestor estadual ou municipal do valor dos serviços profissionais; aplicam-se as mesmas observações referentes ao valor total.
* valor_medio_aih -> valor médio das AIH aprovadas no período.
* valor_medio_intern -> valor médio das AIH aprovadas computadas como internações no período.
* dias_permanencia -> total de dias de internação referente às AIH aprovadas no período, são contados os dias entre a baixa e a alta; esse valor não pode ser utilizado para calcular a ocupação da unidade hospitalar, pois inclui períodos fora do mês e períodos em que o paciente utilizou UTI.
* media_permanencia -> média de permanência das internações referentes às AIH aprovadas, computadas como internações, no período.
* óbitos -> quantidade de internações que tiveram alta por óbito nas AIH aprovadas no período;
* taxa de mortalidade -> razão entre a quantidade de óbitos e o número de AIH aprovadas multiplicada por 100;
As demais variáveis são referentes ao período observado.
```
# criando um novo df baseado no df2 limpo
df3 = df2.copy()
```
## 3.1 Análise Univariada
Vamos observar as distribuições das variáveis numéricas. A princípio, focaremos a análise em (i) internações, (ii) valor total, (iii) óbitos e (iv) valor médio de AIH.
```
df3.hist(bins = 30, figsize = (15,12));
```
A princípio podemos perceber que a distribuição das internações e aih aprovadas são bem similares, assim como do valor total e do valor do serviço hospitalar (vsh).
Dadas as descrições da variáveis isso é bastante razoável, já que a diferença entre internações e aih aprovadas são a não contabilização de prorrogação nas internações. Além disso, é razoável pensar que a maior parte dos gastos com internações seja por parte do hospital e não de pessoal.
Ambas as distribuições de valor do serviço hospitalar (vsh) complementar federal e gestor são concentradas à esquerda, porém a de gestor parece ser mais concentrada, o que pode dar a entender que o estado e município pagariam valores menores em comparação à federação.
Entretanto, quando observamos o valor do serviço profissional (vsp) complementar, a distribuição correspondente ao estado e município possui alguns valores maiores do que o vsp federal.
Óbitos e taxa de mortalidade possuem uma distribuição similar, o que era esperado, já que a taxa de mortalidade leva em consideração o número de óbitos.
## 3.2 Análise Bivariada
Nessa análise, vamos comparar os valores das nossas variáveis *target* levando em consideração a análise simultânea de outras dimensões. Para isso, vamos criar alguas hipóteses sobre essas variáveis e, utilizando os dados, vamos explorar se elas são verdadeiras ou não.
**Hipóteses a serem validadas**
* Hipóteses de Internações
* 1- Existe um maior número de internações na região sudeste;
* 2- As internações ocorrem mais durante o inverno (junho-agosto);
* 3- O número total de internações está reduzindo ao longo dos anos;
* Hipóteses de Valor total e médio da AIH
* 1- A região com maior valor total das internações é a sudeste;
* 2- Em média, a maior parte do valor total da AIH é relativo aos serviços hospitalares;
* 3- Não existe sazonalidade no valor médio da AIH;
* 4- A região com o maior valor médio de internação é a sudeste;
* 5- A região com o maior valor médio de permanência é a sudeste;
* Óbitos e taxa de mortalidade
* 1- A região com maior número de óbitos é a sudeste;
* 2- Não existe sazonalidade na taxa de mortalidade;
* 3- A quantidade total de óbitos e a taxa de mortalidade estão reduzindo ao longo dos anos;
* 4- Os óbitos e a taxa de mortalidade médios anuais estão diminuindo;
### 3.2.1 Hipóteses de Internações (HI)
1- Existe um maior número de internações na região sudeste;
**VERDADEIRA**. A região sudeste é a que possui maior número de internações, o que faz sentido, dado que é a região com maior população no país.
```
hi = df3[['regiao', 'internacoes']].groupby('regiao').sum().reset_index()
sns.barplot(x='regiao', y='internacoes', data= hi).set_title('Nº de Internações por região');
```
2- As internações ocorrem mais durante o inverno (junho-agosto);
Apesar de pelo gráfico parecer falsa, temos que lembrar que o conjuntos de dados não está completo em todos os meses. Quando observamos a contagem dos meses, os que mais aparecem são os que possuem um número maior de internações, logo não conseguimos extrair nenhuma informação relevante nesse momento.
```
hi = df3[['month', 'internacoes']].groupby('month').sum().reset_index()
sns.barplot(x='month', y='internacoes', data = hi);
# observando as divergências de ocorrências entre os meses abordados
df3['month'].value_counts()
```
3- O número total de internações está reduzindo ao longo dos anos
Da mesma maneira que nossa última hipótese, a falta de dados históricos está prejudicando nossa análise. Portanto, não vamos concluir nada a princípio.
```
hi = df3[['year', 'internacoes']].groupby('year').sum().reset_index()
sns.barplot(x='year', y='internacoes', data = hi);
# observando as divergências de ocorrências entre os anos abordados
df3['year'].value_counts()
```
### 3.2.2 Hipóteses de Valor Total e Médio (HVTM)
1- A região com maior valor total das internações é a sudeste.
**VERDADEIRO**. A região com o maior valor total de internações é a sudeste, o que faz sentido dado que é também a região com o maior número de internações.
```
hvtm = df3[['regiao', 'valor_total']].groupby('regiao').sum().reset_index()
sns.barplot(x='regiao', y='valor_total', data=hvtm)
```
2- Em média, a maior parte do valor total da AIH é relativo aos serviços hospitalares
**VERDADEIRO**. Os valores de serviços hospitalares correspondem a 79.5% do valor total de internação, enquanto o valor dos serviços profissionais é 19.8%.
```
vsh_prop = df3['vsh'].sum()/df3['valor_total'].sum() *100
vsp_prop = df3['vsp'].sum()/df3['valor_total'].sum() *100
print("O valor hospitalar corresponde a {:.3}% do valor total enquanto o valor dos serviços corresponde a {:.3}%.".format(vsh_prop,vsp_prop))
```
3- Não existe sazonalidade no valor médio da AIH
**VERDADEIRO**. Ao longo dos meses registrados, não há uma variação grande do valor médio de AIH.
```
hvtm = df3[['month', 'valor_medio_aih']].groupby('month').mean().reset_index()
sns.barplot(x='month', y='valor_medio_aih', data = hvtm)
```
4- A região com o maior valor médio de internação é a sudeste.
**FALSO**. A região com o maior valor médio de internações é a sul.
```
hvtm = df3[['regiao', 'valor_medio_aih']].groupby('regiao').mean().reset_index()
sns.barplot(x='regiao', y='valor_medio_aih', data=hvtm)
```
5- A região com o maior valor médio de permanência é a sudeste.
**FALSO**. A região com maior valor médio por dias de permanência é a região sul.
```
hvtm = df3[['regiao', 'valor_medio_aih', 'media_permanencia']].groupby('regiao').mean().reset_index()
hvtm['media_valor_permanencia'] = hvtm['valor_medio_aih'] / hvtm['media_permanencia']
sns.barplot(x='regiao', y='media_valor_permanencia', data = hvtm)
```
### 3.2.3. Hipóteses de Óbitos e Taxa de Mortalidade
1- A região com maior número de óbitos é a sudeste.
**VERDADEIRO**. A região sudeste possui o maior número de óbitos nas nossas observações.
```
hotm = df3[['regiao', 'obitos']].groupby('regiao').sum().reset_index()
sns.barplot(data=hotm, x='regiao', y='obitos')
```
2- Não existe sazonalidade na taxa de mortalidade.
Parece haver uma sazonalidade, mas com os dados incompletos não conseguimos ter certeza dos movimentos.
```
hotm = df3[['month_year', 'obitos']].groupby('month_year').sum().reset_index()
sns.barplot(x='month_year', y='obitos', data = hotm)
hotm = df3[['month', 'obitos']].groupby('month').sum().reset_index()
sns.barplot(x='month', y='obitos', data = hotm)
```
3- A quantidade total de óbitos e a taxa de mortalidade estão reduzindo ao longo dos anos;
A falta de amostras iguais para os anos não nos permite concluir essa hipótese.
```
hotm = df3[['year', 'obitos']].groupby('year').sum().reset_index()
sns.barplot(x='year', y='obitos', data = hotm)
hotm = df3[['year', 'taxa_mortalidade']].groupby('year').sum().reset_index()
sns.barplot(x='year', y='taxa_mortalidade', data = hotm)
```
4- Os óbitos e a taxa de mortalidade médios anuais estão diminuindo;
**FALSO**. A média de óbitos e da taxa de mortalidade anuais estão aumentando.
```
hotm = df3[['year', 'obitos']].groupby('year').mean().reset_index()
sns.barplot(x='year', y='obitos', data = hotm)
hotm = df3[['year', 'taxa_mortalidade']].groupby('year').mean().reset_index()
sns.barplot(x='year', y='taxa_mortalidade', data = hotm)
```
## 3.3 Análise Multivariada
Agora, vamos avaliar a correlação entre todas as variáveis de maneira simultânea.
```
sns.set(rc={'figure.figsize':(11.7,8.27)})
sns.heatmap(df3.select_dtypes(include='float64').corr(method='pearson'), annot = True);
```
Vamos analisar as variáveis de interesse:
* Internações: Como já vimos nas distribuições, existe uma correlação forte entre o nº de internações e aih aprovadas, o que faz sentido. Além disso, as internações também possui uma alta correlação com o valor total, já que quanto maior o número de internações, maior será o dispêndio nisso.
* Óbitos: O número de óbitos é obviamente proporcional ao número de internações, já que com o maior número de internações consequentemente serão computadas mais mortes. E, como é proporcional ao número de internações, acaba sendo altamente correlacionado com as outras variáveis relacionadas a ela.
* Valor total: o custo total com internações é obviamente altamente correlacionado com o número total de internações.
Todas as variáveis de quantidade de internações e custo totais dessas internações (exceto pelo vsp complementar e vsh complementar do gestor) são altamente correlacionadas entre si e com as variáveis de óbitos totais e dias totais de permanência.
Nenhuma dessas correlações é realmente uma surpresa, apenas confirma o que seria lógico.
# 4. Data Preparation
## 4.1. Estimando datas faltantes
A falta de dados históricos completos foi um empecilho considerável na nossa análise exploratória, portanto nosso próximo passo será tratar esses dados. As observações na nossa base de dados começam em dezembro de 2017 e vão até julho de 2019, nesse período temos seis meses faltando: 2018-01, 2018-02, 2018-06, 2018-10, 2019-03, 2019-05.
Podemos estimar os valores de internações e valor total nos meses faltantes com algumas metodologias, entre elas:
* Mediana da variável, bom porque mantém a distribuição;
* Valor imediatamente anterior da variável, bom porque leva em consideração a tendência histórica;
* Média entre os valores anteriores e seguintes, bom porque mantém a tendência e é uma estimativa linear entre os valores anteriores e próximos.
No nosso caso, vamos utilizar a média entre os valores anteriores e próximos para estimar as variáveis.
```
# criando as datas de referência futura
date = pd.date_range(df3['month_year'].min(), df3['month_year'].max(), freq='M' ).to_list()
df4 = pd.DataFrame()
df4['month_year'] = date
df4['month_year'] = df4['month_year'].apply(lambda x: datetime.strftime(x, '%Y-%m'))
# internações mensais
aux1 = df3[['month_year', 'internacoes']].groupby('month_year').sum().reset_index()
df4.loc[len(df4)] = aux1['month_year'].iloc[-1]
df4 = pd.merge(aux1, df4, how = 'right', on = 'month_year')
# valor_total por month_year
aux1 = df3[['month_year', 'valor_total']].groupby('month_year').sum().reset_index()
df4 = pd.merge(aux1, df4, how = 'right', on = 'month_year')
# criando coluna auxiliar para preencher dados nulos
df4['internacoes_ffill'] = df4['internacoes'].fillna(method = 'ffill')
df4['internacoes_bfill'] = df4['internacoes'].fillna(method = 'bfill')
df4['valor_ffill'] = df4['valor_total'].fillna(method = 'ffill')
df4['valor_bfill'] = df4['valor_total'].fillna(method = 'bfill')
# preenchendo valores
df4['valor_total'] = (df4['valor_ffill'] + df4['valor_bfill'])/2
df4['internacoes'] = (df4['internacoes_ffill'] + df4['internacoes_bfill'])/2
# montando nossa df final com os períodos que faltavam preenchidos pela média entre períodos
df4 = df4[['month_year', 'valor_total', 'internacoes']]
df4['month_year'] = pd.to_datetime(df4['month_year'])
df4['month'] = df4['month_year'].dt.month
df4['year'] = df4['month_year'].dt.year
df4['month_year'] = df4['month_year'].apply(lambda x: datetime.strftime(x, '%Y-%m'))
df4
```
## 4.2 DF Internações
Como temos o objetivo de fazer a previsão de 6 meses após o fim dos nossos dados das internações, óbitos e valor médio aih, vamos preparar dataframes estratégicos para esse objetivo.
```
df_internacoes = df4[['month_year', 'internacoes']]
df_internacoes.head()
```
## 4.3 DF Óbitos
```
aux1 = df3[['month_year', 'obitos']].groupby('month_year').sum().reset_index()
df4 = pd.merge(aux1, df4, how = 'right', on = 'month_year')
df4['obitos_ffill'] = df4['obitos'].fillna(method = 'ffill')
df4['obitos_bfill'] = df4['obitos'].fillna(method = 'bfill')
df4['obitos'] = (df4['obitos_ffill'] + df4['obitos_bfill'])/2
df_obitos = df4[['month_year', 'internacoes','obitos']]
df_obitos.head()
```
## 4.2 DF Valor Médio AIH
```
aux1 = df3[['month_year', 'valor_medio_aih']].groupby('month_year').mean().reset_index()
df4 = pd.merge(aux1, df4, how = 'right', on = 'month_year')
df4['vmaih_ffill'] = df4['valor_medio_aih'].fillna(method = 'ffill')
df4['vmaih_bfill'] = df4['valor_medio_aih'].fillna(method = 'bfill')
df4['valor_medio_aih'] = (df4['vmaih_ffill'] + df4['vmaih_bfill'])/2
df_vmaih = df4[['month_year', 'internacoes', 'valor_total', 'valor_medio_aih']]
df_vmaih.head()
```
# 5. Modelo
Para criarmos modelos capazes de prever os valores de internações, número de óbitos e valor médio de AIH pelos próximos 6 meses temos que analisar nossas variáveis resposta.
* **Internações**
Dentro da nossa base de dados, temos variáveis altamente correlacionadas com as internações, como aih autorizadas, valor total, vsh, etc. Porém, quando paramos para pensar em modelos preditivos entendemos que essas variáveis, apesar de serem altamente correlacionadas, não serão úteis para a criação do modelo.
Isso ocorre porque elas são dependentes dos números de internações, não causadoras. Para prever o número de internações pelos próximos 6 meses precisamos de variáveis que causam o número de internações e estejam disponíveis antes do período que queremos prever.
Como não possuímos variáveis explicadoras, trataremos o modelo como uma série temporal auto regressiva.
* **Óbitos**
Também possuímos variáveis altamente correlacionadas com o número de óbitos, como internações. Entretanto, apesar de serem causadoras do número de óbitos, no sentido de que é preciso ter a internação para podermos contabilizar o óbito, não possuímos a informação de internação previamente. Enquanto a computação de internações está sendo feita, temos também a contabilização dos óbitos no mesmo período.
Portanto, o que usaremos são as internações do período anterior para estimar os óbitos do período atual.
* **Valor médio de AIH**
O valor de internações segue o mesmo racional dos óbitos, apesar de altamente correlacionado com as internações, elas são computadas e ocorrem simultaneamente. Por conta disso, utilizaremos a informação histórica de internações e valor total de internação para estimarmos o valor médio da AIH atual.
```
df5 = df4.copy()
```
## 5.1 Internações
### 5.1.1 Modelo Naive
O modelo naive é um modelo básico de séries temporais cuja premissa é que o valor de t será igual ao valor t-1. Esse modelo dificilmente apresenta um bom resultado e será usado como baseline, apenas para termos uma estimativa base para comparar o outro modelo.
```
df_internacoes = df_internacoes[['month_year', 'internacoes']]
df_internacoes['month_year'] = pd.to_datetime(df_internacoes['month_year'])
df_internacoes.set_index('month_year', inplace=True)
df_internacoes['naive'] = df_internacoes['internacoes'].shift(1)
df_internacoes.plot(figsize=(8,5));
```
Como métrica de avaliação do modelo, vamos usar a média de erro absoluta (MAE) e média de erro quadrático (MSE). A MAE mostra, em média, quanto erramos na previsão de cada um dos meses enquando a MSE mostra a média dos erros ao quadrado.
Por mais que seja mais fácil de interpretar a MAE a importância da MSE é nos mostrar se estamos errando os valores por grande diferença ou pequena. A MAE pode acabar apresentando um valor pequeno caso nossa grandeza de erros para mais e menos seja similar, e.g., se eu errar a previsão por -100.000 em um mês e + 100.000 em outro mês a média será zero, o uqe pode dar a impressão de não haver erro.
A MSE mostra a grandeza do nosso erro de maneira absoluta, já que eleva ao quadrado os valores, tornando os valores negativos em positivos.
```
mae = mean_absolute_error(df_internacoes['internacoes'].iloc[2:], df_internacoes['naive'].iloc[2:])
mse = mean_squared_error(df_internacoes['internacoes'].iloc[2:], df_internacoes['naive'].iloc[2:])
print("O erro absoluto médio mensal é de {:,.6} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
```
### 5.1.2 Modelo AutoRegressivo
#### 5.1.2.1 Um lag
```
df_internacoes['lag1'] = df_internacoes['internacoes'].shift(1)
df_internacoes.dropna(axis = 0, inplace = True)
ar1 = AutoReg(df_internacoes['internacoes'], lags = 1).fit()
mae = ar1.resid.mean()
mse = (ar1.resid ** 2).mean()
print("O erro absoluto médio mensal é de {:,.5} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
df_internacoes['ar1'] = ar1.predict()
df_internacoes[['internacoes', 'ar1']].plot();
```
#### 5.1.2.2 Dois lags
```
df_internacoes['lag1'] = df_internacoes['internacoes'].shift(1)
df_internacoes['lag2'] = df_internacoes['internacoes'].shift(2)
df_internacoes.dropna(axis = 0, inplace = True)
ar2 = AutoReg(df_internacoes['internacoes'], lags = 2).fit()
mae = ar2.resid.mean()
mse = (ar2.resid ** 2).mean()
print("O erro absoluto médio mensal é de {:,.5} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
df_internacoes['ar2'] = ar1.predict()
df_internacoes[['internacoes', 'ar2']].plot();
```
Testamos o modelo de 1 e 2 lags para a previsão do valor futuro das internações, ambos com resultado melhor que o Naive. Entretando o modelo de 1 lag possui um erro menor, então será utilizado para prever os próximos 6 meses.
Isso ocorre provavelmente porque, com o maior número de lags criados, temos que nos livrar das linhas que ficam com valores nulos e como nossa amostra é pequena essa perda de informação afeta negativamente o modelo.
### 5.1.3 Previsão
```
prev = pd.DataFrame(data = ar1.predict('2019-08-01', '2020-01-01'));
prev.rename(columns ={0: 'internacoes'})
prev.plot(figsize = (8,5));
```
Apesar de estarmos prevendo os valores dos próximos 6 meses, o ideal era que o modelo fosse utilizado somente para prever o valor imediatamente posterior ao último dado que efetivamente ocorreu. Logo, a previsão seria feita somente de Agosto/2019.
Isso ocorre porque, prevendo mais de um período, estamos utilizando as próprias previsões que fizemos como input do modelo, não dados reais, e isso acaba 'contaminando' o modelo.
## 5.2 Óbitos
```
df_obitos.head()
```
### 5.2.1 Modelo Naive
Nosso modelo base para a previsão de óbitos:
```
df_obitos['month_year'] = pd.to_datetime(df_obitos['month_year'])
df_obitos.set_index('month_year', inplace=True)
df_obitos['naive'] = df_obitos['obitos'].shift(1)
df_obitos[['naive', 'obitos']].plot(figsize=(8,5));
mae = mean_absolute_error(df_obitos['obitos'].iloc[2:], df_obitos['naive'].iloc[2:])
mse = mean_squared_error(df_obitos['obitos'].iloc[2:], df_obitos['naive'].iloc[2:])
print("O erro absoluto médio mensal é de {:,.6} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
```
### 5.2.2 Regressão Linear
Para as internações, usamos um modelo autoregressivo, que utiliza os lags da própria variável target para prever os valores futuros. No caso dos óbitos, vamos usar o lag da variável, mas também usaremos o lag das internações, já que a quantidade de óbitos é altamente correlacionada com ela.
```
df_obitos.rename(columns={'naive': 'lag1'}, inplace = True)
df_obitos['internacoes_lag'] = df_obitos['internacoes'].shift(1)
df_obitos.dropna(axis = 0, inplace = True)
# definindo x e y
X = df_obitos.drop(['obitos','internacoes'], axis = 1)
y = df_obitos['obitos']
# definindo dados de treino e teste
train_size = 0.75
X_train = X.iloc[:int(len(df_obitos)*train_size)]
X_test = X.iloc[int(len(df_obitos)*train_size):]
y_train = y.iloc[:int(len(df_obitos)*train_size)]
y_test = y.iloc[int(len(df_obitos)*train_size):]
# configurando modelo
reg = LinearRegression()
# treinando modelo
reg.fit(X_train, y_train)
# predizendo valores
y_pred = reg.predict(X_test)
# avaliação do modelo
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print("O erro absoluto médio é de {:,.5} e o erro quadrático é de {:,.10}.".format(mae,mse))
```
Nosso modelo de regressão tem resultado superior ao nosso baseline, então usaremos ele para a previsão de 6 meses.
### 5.2.1 Previsão
```
# usando os últimos dados reais que possuimos para prever o período imediatamente seguinte
# precisamos trocar o nome das colunas para o mesmo que treinamos o modelo
X_total = df_obitos[['obitos', 'internacoes']]
X_total.rename(columns={'internacoes':'internacoes_lag', 'obitos': 'lag1'}, inplace = True)
previ = reg.predict(X_total)
# acrescentando a previsão de óbitos no nosso df prev
prev = pd.concat([prev, pd.DataFrame(columns = ['previsao_obitos'])])
prev['previsao_obitos'].iloc[0] = previ[len(previ)-1]
prev.rename(columns = {0: 'previsao_internacoes'}, inplace = True)
# previsão do segundo período
X_total = pd.DataFrame(prev.iloc[0]).T
y = reg.predict(X_total)
y=y[0]
prev['previsao_obitos'].iloc[1] = y
# prevendo o segundo é possível perceber um padrão para fazer a previsão dos próximos períodos,
# com isso conseguimos automatizar essa parte:
for i in range(2, len(prev)):
X_total = pd.DataFrame(prev.iloc[i-1]).T
y=reg.predict(X_total)
y = y[0]
prev['previsao_obitos'].iloc[i] = y
prev
```
Agora temos também os resultados das previsões de óbitos. Lembrando que a mesma ressalva que foi feita no caso das previsões de internaçõe segue aqui: estamos usando dados que prevemos para fazer previsões de prazos posteriores, o que não é recomendado.
```
prev['previsao_obitos'].plot();
```
## 5.3 Valor Médio de AIH
Para o valor médio de AIH, vamos usar a mesma lógica que usamos para óbitos. Vamos usar as informações de internacoes e valor total disponíveis no período anterior para estimarmos o valor médio de aih do período atual.
Como queremos uma projeção de 6 meses, isso quer dizer que vamos ter que fazer o mesmo exercício de previsão para o valor total antes de prevermos o valor médio de AIH.
```
df_vt = df_vmaih.drop('valor_medio_aih', axis = 1).copy()
```
### 5.3.1 Previsão Valor Total de AIH
#### 5.3.1.1 Naive
```
df_vt['month_year'] = pd.to_datetime(df_vt['month_year'])
df_vt.set_index('month_year', inplace=True)
df_vt['naive'] = df_vt['valor_total'].shift(1)
df_vt[['naive', 'valor_total']].plot(figsize=(8,5));
mae = mean_absolute_error(df_vt['valor_total'].iloc[2:], df_vt['naive'].iloc[2:])
mse = mean_squared_error(df_vt['valor_total'].iloc[2:], df_vt['naive'].iloc[2:])
print("O erro absoluto médio mensal é de {:,.6} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
```
#### 5.3.1.2 Regressão Linear
```
df_vt['internacoes_lag'] = df_vt['internacoes'].shift(1)
df_vt['valor_total_lag'] = df_vt['valor_total'].shift(1)
df_vt.dropna(axis = 0, inplace = True)
# set X and y
X = df_vt[['internacoes_lag', 'valor_total_lag']]
y = df_vt['valor_total']
# define train and test set
train_size = 0.75
X_train = X.iloc[:int(len(df_vt)*train_size)]
X_test = X.iloc[int(len(df_vt)*train_size):]
y_train = y.iloc[:int(len(df_vt)*train_size)]
y_test = y.iloc[int(len(df_vt)*train_size):]
# set model
reg = LinearRegression()
# training model
reg.fit(X_train, y_train)
# predicting values
y_pred = reg.predict(X_test)
# evaluating model
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print("O erro absoluto médio é de {:,.5} e o erro quadrático é de {:,.10}.".format(mae,mse))
```
Nosso modelo de regressão teve performance inferior ao modelo naive, por isso usaremos o modelo mais simples para prever nosso valor total. Porém, isso vai fazer com que o nosso valor fique constante a partir do segundo mês previsto, já que não temos as ocorrências reais para balizar.
### 5.3.2 Previsão Valor Total
```
# joining the obitos prevision with the internacoes
prev = pd.concat([prev, pd.DataFrame(columns = ['previsao_vt'])])
prev['previsao_vt'].iloc[0] = df_vt['valor_total'].iloc[len(df_vt)-1]
prev['previsao_vt'].ffill(axis = 0, inplace = True)
prev
```
### 5.3.3. Modelo Valor Médio AIH
```
df_vmaih
```
#### 5.3.3.1 Naive
```
df_vmaih['month_year'] = pd.to_datetime(df_vmaih['month_year'])
df_vmaih.set_index('month_year', inplace=True)
df_vmaih['naive'] = df_vmaih['valor_medio_aih'].shift(1)
df_vmaih[['naive', 'valor_medio_aih']].plot(figsize=(8,5));
mae = mean_absolute_error(df_vmaih['valor_medio_aih'].iloc[2:], df_vmaih['naive'].iloc[2:])
mse = mean_squared_error(df_vmaih['valor_medio_aih'].iloc[2:], df_vmaih['naive'].iloc[2:])
print("O erro absoluto médio mensal é de {:,.6} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
```
#### 5.3.3.2 Regressão
```
df_vmaih['internacoes_lag'] = df_vmaih['internacoes'].shift(1)
df_vmaih['valor_total_lag'] = df_vmaih['valor_total'].shift(1)
df_vmaih['vmaih_lag'] = df_vmaih['valor_medio_aih'].shift(1)
df_vmaih.dropna(axis = 0, inplace = True)
# set X and y
X = df_vmaih[['internacoes_lag', 'valor_total_lag', 'vmaih_lag']]
y = df_vmaih['valor_medio_aih']
# define train and test set
train_size = 0.75
X_train = X.iloc[:int(len(df_vmaih)*train_size)]
X_test = X.iloc[int(len(df_vmaih)*train_size):]
y_train = y.iloc[:int(len(df_vmaih)*train_size)]
y_test = y.iloc[int(len(df_vmaih)*train_size):]
# set model
reg = LinearRegression()
# training model
reg.fit(X_train, y_train)
# predicting values
y_pred = reg.predict(X_test)
# evaluating model
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print("O erro absoluto médio é de {:,.5} e o erro quadrático é de {:,.10}.".format(mae,mse))
```
Assim como na previsão de valor total, o valor médio também é melhor previsto simplesmente pelo seu valor anterior, através do modelo Naive, então utilizaremos ele para fazer a previsão.
### 5.3.1 Previsão
```
# acrescentando a previsão de valor médio ao nosso df de previsões
prev = pd.concat([prev, pd.DataFrame(columns = ['previsao_media_aih'])])
prev['previsao_media_aih'].iloc[0] = df_vmaih['valor_medio_aih'].iloc[len(df_vmaih)-1]
prev['previsao_media_aih'].ffill(inplace=True)
prev
```
# 6. Planejamento estratégico
Para realizar um planejamento visando reduzir o número de informações, deveriamos lidar com variáveis causadoras das internações, dados que não tivemos acesso na nossa base original.
A relação deveria ser estudada, mas possíveis explicações para o número de internações poderia ser a população do local, o número de acidentes, o clima, campanhas de vacinação na região e sua adesão, índices de criminalidade, saneamento feito na região, etc. Poderíamos ter uma noção melhor se tivéssemos uma base de dados com todas as internações e a causa delas, assim poderíamos estudar as principais doenças ou acidentes que causam internações e estudar as principais causas de cada uma das doenças.
Dessa forma, para reduzir o número de internações deveria ser feito um estudo das principais causas de internações e procurar atuar para reduzir essas causas.
Essa visão geral de pesquisa e entendimento de situação funcionaria para qualquer cidade ou UF estudada.
Com essa base de dados o máximo que conseguimos é inferir o número de internações, óbitos e valores levando em consideração os valores anteriores das variáveis, preferencialmente somente para o período imediatamente seguinte.
|
github_jupyter
|
# imports que suportam o notebook
import pandas as pd
import numpy as np
import re
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from datetime import datetime
from unidecode import unidecode
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.ar_model import AutoReg
import warnings
warnings.filterwarnings('ignore', 'statsmodels.tsa.ar_model.AR', FutureWarning)
pd.set_option('display.float_format', lambda x: '%.3f' % x)
# importando os dados do excel disponível
dfname=pd.ExcelFile('case_internacao_SUS.xls')
sheets = dfname.sheet_names
df=pd.DataFrame()
for sheet in sheets:
xls = pd.ExcelFile('case_internacao_SUS.xls')
data = pd.read_excel(xls, sheet)
df = pd.concat([df, data], axis = 0)
df.reset_index(drop = True, inplace = True)
# olhando pela primeira vez nossos dados para entendermos o que faremos primeiro
df
df = df.rename(columns = {
'Valor_serviços_hospitalares': 'vsh',
'Val_serv_hosp_-_compl_federal': 'vsh_comp_fed',
'Val_serv_hosp_-_compl_gestor': 'vsh_comp_gest',
'Valor_serviços_profissionais': 'vsp',
'Val_serv_prof_-_compl_federal': 'vsp_comp_fed',
'Val_serv_prof_-_compl_gestor': 'vsp_comp_gest',
'Região/Unidade da Federação': 'estado',
'AIH_aprovadas': 'aih_aprvd',
'Valor_total': 'valor_total',
'Valor_médio_AIH': 'valor_medio_aih',
'Valor_médio_intern': 'valor_medio_intern',
'Dias_permanência': 'dias_permanencia',
'Média_permanência': 'media_permanencia',
'Óbitos': 'obitos',
'Taxa_mortalidade': 'taxa_mortalidade',
'Internações': 'internacoes'
})
df.dtypes
# , Val_serv_hosp_-_compl_gestor, Val_serv_prof_-_compl_federal e Val_serv_prof_-_compl_gestor_
df['vsh_comp_fed'] = df['vsh_comp_fed'].apply(lambda x: str(x).replace('-', '0'))
df['vsh_comp_fed'] = df['vsh_comp_fed'].astype('float')
df['vsh_comp_gest'] = df['vsh_comp_gest'].apply(lambda x: str(x).replace('-', '0'))
df['vsh_comp_gest'] = df['vsh_comp_gest'].astype('float')
df['vsp_comp_fed'] = df['vsp_comp_fed'].apply(lambda x: str(x).replace('-', '0'))
df['vsp_comp_fed'] = df['vsp_comp_fed'].astype('float')
df['vsp_comp_gest'] = df['vsp_comp_gest'].apply(lambda x: str(x).replace('-', '0'))
df['vsp_comp_gest'] = df['vsp_comp_gest'].astype('float')
# vendo os valores únicos na coluna de estado
df['estado'].unique()
# além dos estados que queremos manter, temos sujeiras como "Total", valores nulos e " "
# observamos que as linhas cujo valor do estado era nulo ou vazio estavam completamente vazias, portanto serão deletadas
vazio = df[(df['estado'] == 'nan') | (df['estado'] == ' ')].index.to_list()
df.drop(labels = vazio, axis = 0, inplace = True)
df.reset_index(drop = True, inplace = True)
# como já fo comentado, vamos manter o "Total" para utilizarmos depois
# deletando os .. no nome dos estados
df['estado'] = df['estado'].apply(lambda x: str(x).replace('.. ', ''))
# primeiro criamos um dataframe só com as linhas de "Total" e seus índices
totais = df[df['estado'] == 'Total']
totais['month_year'] = sheets
totais = totais.reset_index()
# traduzindo os meses para inglês
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('fev','feb'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('abr','apr'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('mai','may'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('ago','aug'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('set','sep'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('out','oct'))
totais['month_year'] = totais['month_year'].apply(lambda x: x.replace('dez','dec'))
# mudando o tipo de data
totais['month_year'] = totais['month_year'].apply(lambda x: datetime.strptime(x,'%b%y'))
totais.rename(columns={'month_year': 'date'}, inplace = True)
# vamos criar um novo dataframe, baseado no primeiro, mas com o index como coluna para unirmos ao total
df2 = df.reset_index()
df2 = pd.merge(df2, totais, how = 'left', on='index')
# agora vamos ajustar o df2
# dropamos colunas repetidas
dropped = ['estado_y', 'internacoes_y', 'aih_aprvd_y',
'valor_total_y', 'vsh_y', 'vsh_comp_fed_y', 'vsh_comp_gest_y', 'vsp_y',
'vsp_comp_fed_y', 'vsp_comp_gest_y', 'valor_medio_aih_y',
'valor_medio_intern_y', 'dias_permanencia_y', 'media_permanencia_y',
'obitos_y', 'taxa_mortalidade_y','index']
df2.drop(dropped, axis = 1, inplace = True)
## renomeando colunas
colunas = df.columns.to_list()
colunas.append('month_year')
df2.set_axis(colunas, axis = 1, inplace = True)
# preenchendo mês e ano para todas as ocorrências
df2['month_year'].bfill(inplace=True)
# dropando linhas de totais
list1 = df2[df2['estado'] == 'Total'].index
df2.drop(list1, axis = 0, inplace=True)
# criando a nova coluna de região e preenchendo ela
df2['regiao'] = df2['estado'].apply(lambda x: re.search('Região.+', x))
df2['regiao'] = df2['regiao'].apply(lambda x: x.group(0) if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Norte', 'norte') if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Nordeste', 'nordeste') if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Sudeste', 'sudeste') if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Sul', 'sul') if pd.notnull(x) else x)
df2['regiao'] = df2['regiao'].apply(lambda x: x.replace('Região Centro-Oeste', 'centro_oeste') if pd.notnull(x) else x)
df2['regiao'].ffill(inplace=True)
# dropando as linhas de região dentro da coluna de estado
list1 = df2[(df2['estado'] == 'Região Norte') | (df2['estado'] == 'Região Nordeste') | (df2['estado'] == 'Região Sudeste') | (df2['estado'] == 'Região Sul') | (df2['estado'] == 'Região Centro-Oeste')].index.to_list()
df2.drop(list1, axis = 0, inplace = True)
# ajustando o nome dos estados como snake_case
df2['estado'] = df2['estado'].apply(lambda x: x.lower())
df2['estado'] = df2['estado'].apply(lambda x: x.replace(' ', '_'))
df2['estado'] = df2['estado'].apply(lambda x: unidecode(x))
# rearrumando a ordem das colunas
df2 = df2[
['regiao',
'estado',
'internacoes',
'aih_aprvd',
'valor_total',
'vsh',
'vsh_comp_fed',
'vsh_comp_gest',
'vsp',
'vsp_comp_fed',
'vsp_comp_gest',
'valor_medio_aih',
'valor_medio_intern',
'dias_permanencia',
'media_permanencia',
'obitos',
'taxa_mortalidade',
'month_year']
]
# agora faremos o check final para averiguarmos a necessidade de tratamento adicional
df2.isnull().sum() / df2.shape[0]
# ainda temos 5 valores vazios em algumas colunas, que representam 1.3% dos nossos dados.
# como os valores representam uma parcela muito pequena dos nossos dados, vamos deletar.
df2.dropna(axis = 0, inplace = True)
# agora não temos valores nulos
df2.isnull().sum() / df2.shape[0]
# vamos observar como ficaram nossos dados depois da limpeza
df2.head(10)
df2.columns
df2['year'] = df2['month_year'].dt.year
df2['month'] = df2['month_year'].dt.month
df2['month_year'] = df2['month_year'].dt.strftime('%Y-%m')
# criando um novo df baseado no df2 limpo
df3 = df2.copy()
df3.hist(bins = 30, figsize = (15,12));
hi = df3[['regiao', 'internacoes']].groupby('regiao').sum().reset_index()
sns.barplot(x='regiao', y='internacoes', data= hi).set_title('Nº de Internações por região');
hi = df3[['month', 'internacoes']].groupby('month').sum().reset_index()
sns.barplot(x='month', y='internacoes', data = hi);
# observando as divergências de ocorrências entre os meses abordados
df3['month'].value_counts()
hi = df3[['year', 'internacoes']].groupby('year').sum().reset_index()
sns.barplot(x='year', y='internacoes', data = hi);
# observando as divergências de ocorrências entre os anos abordados
df3['year'].value_counts()
hvtm = df3[['regiao', 'valor_total']].groupby('regiao').sum().reset_index()
sns.barplot(x='regiao', y='valor_total', data=hvtm)
vsh_prop = df3['vsh'].sum()/df3['valor_total'].sum() *100
vsp_prop = df3['vsp'].sum()/df3['valor_total'].sum() *100
print("O valor hospitalar corresponde a {:.3}% do valor total enquanto o valor dos serviços corresponde a {:.3}%.".format(vsh_prop,vsp_prop))
hvtm = df3[['month', 'valor_medio_aih']].groupby('month').mean().reset_index()
sns.barplot(x='month', y='valor_medio_aih', data = hvtm)
hvtm = df3[['regiao', 'valor_medio_aih']].groupby('regiao').mean().reset_index()
sns.barplot(x='regiao', y='valor_medio_aih', data=hvtm)
hvtm = df3[['regiao', 'valor_medio_aih', 'media_permanencia']].groupby('regiao').mean().reset_index()
hvtm['media_valor_permanencia'] = hvtm['valor_medio_aih'] / hvtm['media_permanencia']
sns.barplot(x='regiao', y='media_valor_permanencia', data = hvtm)
hotm = df3[['regiao', 'obitos']].groupby('regiao').sum().reset_index()
sns.barplot(data=hotm, x='regiao', y='obitos')
hotm = df3[['month_year', 'obitos']].groupby('month_year').sum().reset_index()
sns.barplot(x='month_year', y='obitos', data = hotm)
hotm = df3[['month', 'obitos']].groupby('month').sum().reset_index()
sns.barplot(x='month', y='obitos', data = hotm)
hotm = df3[['year', 'obitos']].groupby('year').sum().reset_index()
sns.barplot(x='year', y='obitos', data = hotm)
hotm = df3[['year', 'taxa_mortalidade']].groupby('year').sum().reset_index()
sns.barplot(x='year', y='taxa_mortalidade', data = hotm)
hotm = df3[['year', 'obitos']].groupby('year').mean().reset_index()
sns.barplot(x='year', y='obitos', data = hotm)
hotm = df3[['year', 'taxa_mortalidade']].groupby('year').mean().reset_index()
sns.barplot(x='year', y='taxa_mortalidade', data = hotm)
sns.set(rc={'figure.figsize':(11.7,8.27)})
sns.heatmap(df3.select_dtypes(include='float64').corr(method='pearson'), annot = True);
# criando as datas de referência futura
date = pd.date_range(df3['month_year'].min(), df3['month_year'].max(), freq='M' ).to_list()
df4 = pd.DataFrame()
df4['month_year'] = date
df4['month_year'] = df4['month_year'].apply(lambda x: datetime.strftime(x, '%Y-%m'))
# internações mensais
aux1 = df3[['month_year', 'internacoes']].groupby('month_year').sum().reset_index()
df4.loc[len(df4)] = aux1['month_year'].iloc[-1]
df4 = pd.merge(aux1, df4, how = 'right', on = 'month_year')
# valor_total por month_year
aux1 = df3[['month_year', 'valor_total']].groupby('month_year').sum().reset_index()
df4 = pd.merge(aux1, df4, how = 'right', on = 'month_year')
# criando coluna auxiliar para preencher dados nulos
df4['internacoes_ffill'] = df4['internacoes'].fillna(method = 'ffill')
df4['internacoes_bfill'] = df4['internacoes'].fillna(method = 'bfill')
df4['valor_ffill'] = df4['valor_total'].fillna(method = 'ffill')
df4['valor_bfill'] = df4['valor_total'].fillna(method = 'bfill')
# preenchendo valores
df4['valor_total'] = (df4['valor_ffill'] + df4['valor_bfill'])/2
df4['internacoes'] = (df4['internacoes_ffill'] + df4['internacoes_bfill'])/2
# montando nossa df final com os períodos que faltavam preenchidos pela média entre períodos
df4 = df4[['month_year', 'valor_total', 'internacoes']]
df4['month_year'] = pd.to_datetime(df4['month_year'])
df4['month'] = df4['month_year'].dt.month
df4['year'] = df4['month_year'].dt.year
df4['month_year'] = df4['month_year'].apply(lambda x: datetime.strftime(x, '%Y-%m'))
df4
df_internacoes = df4[['month_year', 'internacoes']]
df_internacoes.head()
aux1 = df3[['month_year', 'obitos']].groupby('month_year').sum().reset_index()
df4 = pd.merge(aux1, df4, how = 'right', on = 'month_year')
df4['obitos_ffill'] = df4['obitos'].fillna(method = 'ffill')
df4['obitos_bfill'] = df4['obitos'].fillna(method = 'bfill')
df4['obitos'] = (df4['obitos_ffill'] + df4['obitos_bfill'])/2
df_obitos = df4[['month_year', 'internacoes','obitos']]
df_obitos.head()
aux1 = df3[['month_year', 'valor_medio_aih']].groupby('month_year').mean().reset_index()
df4 = pd.merge(aux1, df4, how = 'right', on = 'month_year')
df4['vmaih_ffill'] = df4['valor_medio_aih'].fillna(method = 'ffill')
df4['vmaih_bfill'] = df4['valor_medio_aih'].fillna(method = 'bfill')
df4['valor_medio_aih'] = (df4['vmaih_ffill'] + df4['vmaih_bfill'])/2
df_vmaih = df4[['month_year', 'internacoes', 'valor_total', 'valor_medio_aih']]
df_vmaih.head()
df5 = df4.copy()
df_internacoes = df_internacoes[['month_year', 'internacoes']]
df_internacoes['month_year'] = pd.to_datetime(df_internacoes['month_year'])
df_internacoes.set_index('month_year', inplace=True)
df_internacoes['naive'] = df_internacoes['internacoes'].shift(1)
df_internacoes.plot(figsize=(8,5));
mae = mean_absolute_error(df_internacoes['internacoes'].iloc[2:], df_internacoes['naive'].iloc[2:])
mse = mean_squared_error(df_internacoes['internacoes'].iloc[2:], df_internacoes['naive'].iloc[2:])
print("O erro absoluto médio mensal é de {:,.6} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
df_internacoes['lag1'] = df_internacoes['internacoes'].shift(1)
df_internacoes.dropna(axis = 0, inplace = True)
ar1 = AutoReg(df_internacoes['internacoes'], lags = 1).fit()
mae = ar1.resid.mean()
mse = (ar1.resid ** 2).mean()
print("O erro absoluto médio mensal é de {:,.5} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
df_internacoes['ar1'] = ar1.predict()
df_internacoes[['internacoes', 'ar1']].plot();
df_internacoes['lag1'] = df_internacoes['internacoes'].shift(1)
df_internacoes['lag2'] = df_internacoes['internacoes'].shift(2)
df_internacoes.dropna(axis = 0, inplace = True)
ar2 = AutoReg(df_internacoes['internacoes'], lags = 2).fit()
mae = ar2.resid.mean()
mse = (ar2.resid ** 2).mean()
print("O erro absoluto médio mensal é de {:,.5} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
df_internacoes['ar2'] = ar1.predict()
df_internacoes[['internacoes', 'ar2']].plot();
prev = pd.DataFrame(data = ar1.predict('2019-08-01', '2020-01-01'));
prev.rename(columns ={0: 'internacoes'})
prev.plot(figsize = (8,5));
df_obitos.head()
df_obitos['month_year'] = pd.to_datetime(df_obitos['month_year'])
df_obitos.set_index('month_year', inplace=True)
df_obitos['naive'] = df_obitos['obitos'].shift(1)
df_obitos[['naive', 'obitos']].plot(figsize=(8,5));
mae = mean_absolute_error(df_obitos['obitos'].iloc[2:], df_obitos['naive'].iloc[2:])
mse = mean_squared_error(df_obitos['obitos'].iloc[2:], df_obitos['naive'].iloc[2:])
print("O erro absoluto médio mensal é de {:,.6} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
df_obitos.rename(columns={'naive': 'lag1'}, inplace = True)
df_obitos['internacoes_lag'] = df_obitos['internacoes'].shift(1)
df_obitos.dropna(axis = 0, inplace = True)
# definindo x e y
X = df_obitos.drop(['obitos','internacoes'], axis = 1)
y = df_obitos['obitos']
# definindo dados de treino e teste
train_size = 0.75
X_train = X.iloc[:int(len(df_obitos)*train_size)]
X_test = X.iloc[int(len(df_obitos)*train_size):]
y_train = y.iloc[:int(len(df_obitos)*train_size)]
y_test = y.iloc[int(len(df_obitos)*train_size):]
# configurando modelo
reg = LinearRegression()
# treinando modelo
reg.fit(X_train, y_train)
# predizendo valores
y_pred = reg.predict(X_test)
# avaliação do modelo
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print("O erro absoluto médio é de {:,.5} e o erro quadrático é de {:,.10}.".format(mae,mse))
# usando os últimos dados reais que possuimos para prever o período imediatamente seguinte
# precisamos trocar o nome das colunas para o mesmo que treinamos o modelo
X_total = df_obitos[['obitos', 'internacoes']]
X_total.rename(columns={'internacoes':'internacoes_lag', 'obitos': 'lag1'}, inplace = True)
previ = reg.predict(X_total)
# acrescentando a previsão de óbitos no nosso df prev
prev = pd.concat([prev, pd.DataFrame(columns = ['previsao_obitos'])])
prev['previsao_obitos'].iloc[0] = previ[len(previ)-1]
prev.rename(columns = {0: 'previsao_internacoes'}, inplace = True)
# previsão do segundo período
X_total = pd.DataFrame(prev.iloc[0]).T
y = reg.predict(X_total)
y=y[0]
prev['previsao_obitos'].iloc[1] = y
# prevendo o segundo é possível perceber um padrão para fazer a previsão dos próximos períodos,
# com isso conseguimos automatizar essa parte:
for i in range(2, len(prev)):
X_total = pd.DataFrame(prev.iloc[i-1]).T
y=reg.predict(X_total)
y = y[0]
prev['previsao_obitos'].iloc[i] = y
prev
prev['previsao_obitos'].plot();
df_vt = df_vmaih.drop('valor_medio_aih', axis = 1).copy()
df_vt['month_year'] = pd.to_datetime(df_vt['month_year'])
df_vt.set_index('month_year', inplace=True)
df_vt['naive'] = df_vt['valor_total'].shift(1)
df_vt[['naive', 'valor_total']].plot(figsize=(8,5));
mae = mean_absolute_error(df_vt['valor_total'].iloc[2:], df_vt['naive'].iloc[2:])
mse = mean_squared_error(df_vt['valor_total'].iloc[2:], df_vt['naive'].iloc[2:])
print("O erro absoluto médio mensal é de {:,.6} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
df_vt['internacoes_lag'] = df_vt['internacoes'].shift(1)
df_vt['valor_total_lag'] = df_vt['valor_total'].shift(1)
df_vt.dropna(axis = 0, inplace = True)
# set X and y
X = df_vt[['internacoes_lag', 'valor_total_lag']]
y = df_vt['valor_total']
# define train and test set
train_size = 0.75
X_train = X.iloc[:int(len(df_vt)*train_size)]
X_test = X.iloc[int(len(df_vt)*train_size):]
y_train = y.iloc[:int(len(df_vt)*train_size)]
y_test = y.iloc[int(len(df_vt)*train_size):]
# set model
reg = LinearRegression()
# training model
reg.fit(X_train, y_train)
# predicting values
y_pred = reg.predict(X_test)
# evaluating model
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print("O erro absoluto médio é de {:,.5} e o erro quadrático é de {:,.10}.".format(mae,mse))
# joining the obitos prevision with the internacoes
prev = pd.concat([prev, pd.DataFrame(columns = ['previsao_vt'])])
prev['previsao_vt'].iloc[0] = df_vt['valor_total'].iloc[len(df_vt)-1]
prev['previsao_vt'].ffill(axis = 0, inplace = True)
prev
df_vmaih
df_vmaih['month_year'] = pd.to_datetime(df_vmaih['month_year'])
df_vmaih.set_index('month_year', inplace=True)
df_vmaih['naive'] = df_vmaih['valor_medio_aih'].shift(1)
df_vmaih[['naive', 'valor_medio_aih']].plot(figsize=(8,5));
mae = mean_absolute_error(df_vmaih['valor_medio_aih'].iloc[2:], df_vmaih['naive'].iloc[2:])
mse = mean_squared_error(df_vmaih['valor_medio_aih'].iloc[2:], df_vmaih['naive'].iloc[2:])
print("O erro absoluto médio mensal é de {:,.6} enquanto o erro quadrático médio mensal é de {:,.10}.".format(mae, mse))
df_vmaih['internacoes_lag'] = df_vmaih['internacoes'].shift(1)
df_vmaih['valor_total_lag'] = df_vmaih['valor_total'].shift(1)
df_vmaih['vmaih_lag'] = df_vmaih['valor_medio_aih'].shift(1)
df_vmaih.dropna(axis = 0, inplace = True)
# set X and y
X = df_vmaih[['internacoes_lag', 'valor_total_lag', 'vmaih_lag']]
y = df_vmaih['valor_medio_aih']
# define train and test set
train_size = 0.75
X_train = X.iloc[:int(len(df_vmaih)*train_size)]
X_test = X.iloc[int(len(df_vmaih)*train_size):]
y_train = y.iloc[:int(len(df_vmaih)*train_size)]
y_test = y.iloc[int(len(df_vmaih)*train_size):]
# set model
reg = LinearRegression()
# training model
reg.fit(X_train, y_train)
# predicting values
y_pred = reg.predict(X_test)
# evaluating model
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print("O erro absoluto médio é de {:,.5} e o erro quadrático é de {:,.10}.".format(mae,mse))
# acrescentando a previsão de valor médio ao nosso df de previsões
prev = pd.concat([prev, pd.DataFrame(columns = ['previsao_media_aih'])])
prev['previsao_media_aih'].iloc[0] = df_vmaih['valor_medio_aih'].iloc[len(df_vmaih)-1]
prev['previsao_media_aih'].ffill(inplace=True)
prev
| 0.282988 | 0.898633 |
### SOGComp is SOG run for comparison with SS2DSOG5x5
- compare starting values to check initialization of IC's
```
import numpy as np
import pandas as pd
import datetime as dtm
import matplotlib.pyplot as plt
import matplotlib.dates as dts
import netCDF4 as nc
import os
import re
import pytz
%matplotlib inline
```
# read in SOG data:
```
filename='/data/eolson/SOG/SOG-runs/SOGCompMZEff/profiles/hoff-SOG.dat'
file_obj = open(filename, 'rt')
for index, line in enumerate(file_obj):
line = line.strip()
if line.startswith('*FieldNames:'):
field_names = line.split(': ', 1)[1].split(', ')
elif line.startswith('*FieldUnits:'):
field_units = line.split(': ', 1)[1].split(', ')
elif line.startswith('*HoffmuellerStartYr:'):
year_start = line.split(': ', 1)[1]
elif line.startswith('*HoffmuellerStartDay:'):
day_start = line.split(': ', 1)[1]
elif line.startswith('*HoffmuellerStartSec:'):
sec_start = line.split(': ', 1)[1]
elif line.startswith('*HoffmuellerInterval:'):
interval = line.split(': ', 1)[1]
elif line.startswith('*EndOfHeader'):
break
data = pd.read_csv(filename, delim_whitespace=True, header=0, names=field_names, skiprows=index, chunksize=102)
# Timestamp in matplotlib time
dt_num = dts.date2num(dtm.datetime.strptime(year_start + ' ' + day_start, '%Y %j')) + float(sec_start)/86400
interval=float(interval)
# Extract dataframe chunks into dictionary
for index, chunk in enumerate(data):
if index==0:
da=chunk
else:
da=np.dstack((da,chunk))
z=da[:,0,0]
t=np.arange(da.shape[2])
t=(t+1.0)*3600
tt,zz=np.meshgrid(t,-z)
print(field_names)
#print t
#print day_start
#print dts.num2date(dt_num)
#print z
```
Load SS2DSOG nuts & bio data:
```
resultsDir='/data/eolson/MEOPAR/SS2DSOGruns/runSOG_01/'
fname='SalishSea_1h_20041019_20041019_ptrc_T.nc'
f=nc.Dataset(os.path.join(resultsDir,fname))
fkeys=f.variables.keys()
lons=f.variables['nav_lon'][1,:]
lats=f.variables['nav_lat'][:,1]
for ik in fkeys:
match = re.search(r'depth.',ik)
if match:
zkey=match.group(0)
zSS=f.variables[zkey][:]
xxSS,zzSS=np.meshgrid(lons,-z[:])
xtSS,ytSS=np.meshgrid(lons,lats)
print( fkeys)
f2name='/data/eolson/MEOPAR/SS2DSOGruns/nuts_SOG5x5_S3-2014-10-19-WithMRubraMicroZooRemin.nc'
f2=nc.Dataset(f2name)
print(f.variables['time_counter_bnds'][1]/3600)
```
REPEAT WITH LATER TIME FOR NEMO:
```
fig, axs = plt.subplots(2,2,figsize=(12,8))
ti=20 # hrs since start
nN=1
# Phyto
iii=4
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='r')
iii=5
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='g')
iii=6
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='b')
iii=7
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='k')
#pl0=axs[0,0].plot(f2.variables['PHY'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,0].set_ylabel('z (m)')
axs[1,0].set_xlabel('Phyto')
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar1=f.variables['PHY2'][:,:,:,:] # diatoms
pl3=axs[1,0].plot(ivar1[nN*ti,0:101,2,2],-zSS[0:101],'.',color='m')
pl3=axs[0,0].plot(ivar1[nN*ti,0:101,2,2],-zSS[0:101],'.',color='m')
ivar2=f.variables['PHY'][:,:,:,:]
pl3=axs[1,0].plot(ivar2[nN*ti,0:101,2,2],-zSS[0:101],'.',color='c')
pl3=axs[0,0].plot(ivar2[nN*ti,0:101,2,2],-zSS[0:101],'.',color='c')
ivar3=f.variables['ZOO2'][:,:,:,:]
pl3=axs[1,0].plot(ivar3[nN*ti,0:101,2,2],-zSS[0:101],'.',color='y')
pl3=axs[0,0].plot(ivar3[nN*ti,0:101,2,2],-zSS[0:101],'.',color='y')
ivar4=f.variables['ZOO'][:,:,:,:]
pl4=axs[1,0].plot(ivar4[nN*ti,0:101,2,2],-zSS[0:101],'.',color='k')
pl4=axs[0,0].plot(ivar4[nN*ti,0:101,2,2],-zSS[0:101],'.',color='k')
axs[0,0].set_ylim([-60,0])
# NO
iii=8
pl0=axs[0,1].plot(da[:,iii,ti],-z,'-',color='r')
#pl0=axs[0,1].plot(f2.variables['NO3'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,1].set_ylabel('z (m)')
axs[0,1].set_ylim([-20,0])
axs[1,1].set_xlabel(field_names[iii])
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar=f.variables['NO3'][:,:,:,:]
pl3=axs[1,1].plot(ivar[nN*ti-1,0:100,2,2],-zSS[0:100],'.',color='k')
pl3=axs[0,1].plot(ivar[nN*ti-1,0:100,2,2],-zSS[0:100],'.',color='k')
#print ivar[0,0:100,2,2]
fig, axs = plt.subplots(2,2,figsize=(12,8))
# Phyto
iii=16
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='r')
iii=17
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='b')
iii=19
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='g')
#pl0=axs[0,0].plot(f2.variables['PHY'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,0].set_ylabel('z (m)')
axs[1,0].set_xlabel('DON/PON/bSi')
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar1=f.variables['DOC'][:,:,:,:]/7.6
pl3=axs[1,0].plot(ivar1[nN*ti,0:101,2,2],-zSS[0:101],'.',color='m')
pl3=axs[0,0].plot(ivar1[nN*ti,0:101,2,2],-zSS[0:101],'.',color='m')
ivar2=f.variables['POC'][:,:,:,:]/7.6
pl3=axs[1,0].plot(ivar2[nN*ti,0:101,2,2],-zSS[0:101],'.',color='c')
pl3=axs[0,0].plot(ivar2[nN*ti,0:101,2,2],-zSS[0:101],'.',color='c')
ivar3=f.variables['DSi'][:,:,:,:]
pl3=axs[1,0].plot(ivar3[nN*ti,0:101,2,2],-zSS[0:101],'.',color='y')
pl3=axs[0,0].plot(ivar3[nN*ti,0:101,2,2],-zSS[0:101],'.',color='y')
axs[0,0].set_ylim([-50,0])
# NO
iii=8
pl0=axs[0,1].plot(da[:,iii,ti],-z,'-',color='r')
#pl0=axs[0,1].plot(f2.variables['NO3'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,1].set_ylabel('z (m)')
axs[0,1].set_ylim([-20,0])
axs[1,1].set_xlabel(field_names[iii])
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar=f.variables['NO3'][:,:,:,:]
pl3=axs[1,1].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='k')
pl3=axs[0,1].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='k')
#print ivar[0,0:100,2,2]
fig, axs = plt.subplots(2,2,figsize=(12,8))
# Si
iii=10
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='r')
axs[0,0].set_ylabel('z (m)')
axs[0,0].set_xlabel('Si')
axs[0,0].set_ylim([-20,0])
#pl0=axs[0,0].plot(f2.variables['Si'][0,0:101,2,2],-zSS[0:101],'-',color='k')
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar=f.variables['Si'][:,:,:,:]
pl3=axs[1,0].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='g')
pl4=axs[0,0].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='g')
# NH4
iii=9
pl0=axs[0,1].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'.',color='b')
#pl0=axs[0,1].plot(f2.variables['NH4'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,1].set_ylabel('z (m)')
axs[0,1].set_xlabel(field_names[iii])
axs[0,1].set_ylim([-20,0])
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar=f.variables['NH4'][:,:,:,:]
pl3=axs[1,1].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='g')
pl4=axs[0,1].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='g')
#axs[0,1].set_xlim([.8,1.2])
f.close()
f2.close()
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import datetime as dtm
import matplotlib.pyplot as plt
import matplotlib.dates as dts
import netCDF4 as nc
import os
import re
import pytz
%matplotlib inline
filename='/data/eolson/SOG/SOG-runs/SOGCompMZEff/profiles/hoff-SOG.dat'
file_obj = open(filename, 'rt')
for index, line in enumerate(file_obj):
line = line.strip()
if line.startswith('*FieldNames:'):
field_names = line.split(': ', 1)[1].split(', ')
elif line.startswith('*FieldUnits:'):
field_units = line.split(': ', 1)[1].split(', ')
elif line.startswith('*HoffmuellerStartYr:'):
year_start = line.split(': ', 1)[1]
elif line.startswith('*HoffmuellerStartDay:'):
day_start = line.split(': ', 1)[1]
elif line.startswith('*HoffmuellerStartSec:'):
sec_start = line.split(': ', 1)[1]
elif line.startswith('*HoffmuellerInterval:'):
interval = line.split(': ', 1)[1]
elif line.startswith('*EndOfHeader'):
break
data = pd.read_csv(filename, delim_whitespace=True, header=0, names=field_names, skiprows=index, chunksize=102)
# Timestamp in matplotlib time
dt_num = dts.date2num(dtm.datetime.strptime(year_start + ' ' + day_start, '%Y %j')) + float(sec_start)/86400
interval=float(interval)
# Extract dataframe chunks into dictionary
for index, chunk in enumerate(data):
if index==0:
da=chunk
else:
da=np.dstack((da,chunk))
z=da[:,0,0]
t=np.arange(da.shape[2])
t=(t+1.0)*3600
tt,zz=np.meshgrid(t,-z)
print(field_names)
#print t
#print day_start
#print dts.num2date(dt_num)
#print z
resultsDir='/data/eolson/MEOPAR/SS2DSOGruns/runSOG_01/'
fname='SalishSea_1h_20041019_20041019_ptrc_T.nc'
f=nc.Dataset(os.path.join(resultsDir,fname))
fkeys=f.variables.keys()
lons=f.variables['nav_lon'][1,:]
lats=f.variables['nav_lat'][:,1]
for ik in fkeys:
match = re.search(r'depth.',ik)
if match:
zkey=match.group(0)
zSS=f.variables[zkey][:]
xxSS,zzSS=np.meshgrid(lons,-z[:])
xtSS,ytSS=np.meshgrid(lons,lats)
print( fkeys)
f2name='/data/eolson/MEOPAR/SS2DSOGruns/nuts_SOG5x5_S3-2014-10-19-WithMRubraMicroZooRemin.nc'
f2=nc.Dataset(f2name)
print(f.variables['time_counter_bnds'][1]/3600)
fig, axs = plt.subplots(2,2,figsize=(12,8))
ti=20 # hrs since start
nN=1
# Phyto
iii=4
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='r')
iii=5
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='g')
iii=6
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='b')
iii=7
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='k')
#pl0=axs[0,0].plot(f2.variables['PHY'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,0].set_ylabel('z (m)')
axs[1,0].set_xlabel('Phyto')
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar1=f.variables['PHY2'][:,:,:,:] # diatoms
pl3=axs[1,0].plot(ivar1[nN*ti,0:101,2,2],-zSS[0:101],'.',color='m')
pl3=axs[0,0].plot(ivar1[nN*ti,0:101,2,2],-zSS[0:101],'.',color='m')
ivar2=f.variables['PHY'][:,:,:,:]
pl3=axs[1,0].plot(ivar2[nN*ti,0:101,2,2],-zSS[0:101],'.',color='c')
pl3=axs[0,0].plot(ivar2[nN*ti,0:101,2,2],-zSS[0:101],'.',color='c')
ivar3=f.variables['ZOO2'][:,:,:,:]
pl3=axs[1,0].plot(ivar3[nN*ti,0:101,2,2],-zSS[0:101],'.',color='y')
pl3=axs[0,0].plot(ivar3[nN*ti,0:101,2,2],-zSS[0:101],'.',color='y')
ivar4=f.variables['ZOO'][:,:,:,:]
pl4=axs[1,0].plot(ivar4[nN*ti,0:101,2,2],-zSS[0:101],'.',color='k')
pl4=axs[0,0].plot(ivar4[nN*ti,0:101,2,2],-zSS[0:101],'.',color='k')
axs[0,0].set_ylim([-60,0])
# NO
iii=8
pl0=axs[0,1].plot(da[:,iii,ti],-z,'-',color='r')
#pl0=axs[0,1].plot(f2.variables['NO3'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,1].set_ylabel('z (m)')
axs[0,1].set_ylim([-20,0])
axs[1,1].set_xlabel(field_names[iii])
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar=f.variables['NO3'][:,:,:,:]
pl3=axs[1,1].plot(ivar[nN*ti-1,0:100,2,2],-zSS[0:100],'.',color='k')
pl3=axs[0,1].plot(ivar[nN*ti-1,0:100,2,2],-zSS[0:100],'.',color='k')
#print ivar[0,0:100,2,2]
fig, axs = plt.subplots(2,2,figsize=(12,8))
# Phyto
iii=16
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='r')
iii=17
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='b')
iii=19
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='g')
#pl0=axs[0,0].plot(f2.variables['PHY'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,0].set_ylabel('z (m)')
axs[1,0].set_xlabel('DON/PON/bSi')
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar1=f.variables['DOC'][:,:,:,:]/7.6
pl3=axs[1,0].plot(ivar1[nN*ti,0:101,2,2],-zSS[0:101],'.',color='m')
pl3=axs[0,0].plot(ivar1[nN*ti,0:101,2,2],-zSS[0:101],'.',color='m')
ivar2=f.variables['POC'][:,:,:,:]/7.6
pl3=axs[1,0].plot(ivar2[nN*ti,0:101,2,2],-zSS[0:101],'.',color='c')
pl3=axs[0,0].plot(ivar2[nN*ti,0:101,2,2],-zSS[0:101],'.',color='c')
ivar3=f.variables['DSi'][:,:,:,:]
pl3=axs[1,0].plot(ivar3[nN*ti,0:101,2,2],-zSS[0:101],'.',color='y')
pl3=axs[0,0].plot(ivar3[nN*ti,0:101,2,2],-zSS[0:101],'.',color='y')
axs[0,0].set_ylim([-50,0])
# NO
iii=8
pl0=axs[0,1].plot(da[:,iii,ti],-z,'-',color='r')
#pl0=axs[0,1].plot(f2.variables['NO3'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,1].set_ylabel('z (m)')
axs[0,1].set_ylim([-20,0])
axs[1,1].set_xlabel(field_names[iii])
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar=f.variables['NO3'][:,:,:,:]
pl3=axs[1,1].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='k')
pl3=axs[0,1].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='k')
#print ivar[0,0:100,2,2]
fig, axs = plt.subplots(2,2,figsize=(12,8))
# Si
iii=10
pl0=axs[0,0].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'-',color='r')
axs[0,0].set_ylabel('z (m)')
axs[0,0].set_xlabel('Si')
axs[0,0].set_ylim([-20,0])
#pl0=axs[0,0].plot(f2.variables['Si'][0,0:101,2,2],-zSS[0:101],'-',color='k')
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar=f.variables['Si'][:,:,:,:]
pl3=axs[1,0].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='g')
pl4=axs[0,0].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='g')
# NH4
iii=9
pl0=axs[0,1].plot((da[:,iii,ti]+da[:,iii,ti+1])/2,-z,'.',color='b')
#pl0=axs[0,1].plot(f2.variables['NH4'][0,0:101,2,2],-zSS[0:101],'-',color='k')
axs[0,1].set_ylabel('z (m)')
axs[0,1].set_xlabel(field_names[iii])
axs[0,1].set_ylim([-20,0])
#pl1=axs[0].plot(da[:,iii,da.shape[2]-1],-z)
ivar=f.variables['NH4'][:,:,:,:]
pl3=axs[1,1].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='g')
pl4=axs[0,1].plot(ivar[nN*ti,0:100,2,2],-zSS[0:100],'.',color='g')
#axs[0,1].set_xlim([.8,1.2])
f.close()
f2.close()
| 0.05087 | 0.705329 |
# PrefixLSH tests with domains data
```
import sys
sys.path.append('..')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import floc
from utils.data import read_weeks_machines_domains
import prefixLSH
```
read in some pre-processed sessions data
- starting domains list: take a list of domains with at least 20 domains (n_domains)
- sampling domains list: take another 20 different domains to sample from.
create 20 lists of domains, where each list i in 1,...20 duplicates list (i-1) and then modifies the list by replacing item i with a new domain from the sampling domains list
domains list 1 is the starting domains list
```
# read in the pre-processed sessions data
# this maps week,machine_id -> domains set
weeks_machines_domains_fpath = '../output/weeks_machines_domains.csv'
weeks_machines_domains_df = read_weeks_machines_domains(weeks_machines_domains_fpath, nrows=100)
weeks_machines_domains_df.drop(['machine_id', 'domains'], axis=1).head()
n_domains = 20
starting_domains_list = weeks_machines_domains_df[
(weeks_machines_domains_df.n_domains == n_domains)
].domains.values[2]
starting_domains_list = list(starting_domains_list)
starting_domains_list
# use most frequent domains from sampled rows as other domain samples
other_domains = weeks_machines_domains_df.domains.values
other_domains = [d for domains in other_domains for d in domains if d not in starting_domains_list]
other_domains = pd.Series(other_domains).value_counts().head(20).index
other_domains
```
make a dataframe with columns
```
m, domains, simhash, ot_cohort, cohort_k2, cohort_k4, cohort_k8,
```
where
- each m differs from previous m by one domain
- ot_cohort generated via OT floc
- cohort_k* generated using our prefixLSH with given k
here the domains gradually transition from some unique user's domains to the most popular
We then expect similar cohort IDs to be clustered near each other in the list.
```
m = list(range(20))
m
domains = [starting_domains_list]
for i in range(19):
i1_domains = domains[i][:] # copy domains list from i
i1_domains[i] = other_domains[i] # alter domains by one entry
domains += [i1_domains]
test_df = pd.DataFrame({'m':m, 'domains':domains})
test_df['simhash'] = test_df.domains.apply(floc.hashes.sim_hash_string)
test_df['ot_cohort'] = test_df.domains.apply(floc.simulate)
for k in [2, 4, 8]:
cohort_k = 'cohort_k%s'%k
cohorts_dict = prefixLSH.get_cohorts_dict(test_df.simhash.astype(int), min_k=k)
test_df[cohort_k] = test_df.simhash.map(cohorts_dict)
test_df
```
|
github_jupyter
|
import sys
sys.path.append('..')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import floc
from utils.data import read_weeks_machines_domains
import prefixLSH
# read in the pre-processed sessions data
# this maps week,machine_id -> domains set
weeks_machines_domains_fpath = '../output/weeks_machines_domains.csv'
weeks_machines_domains_df = read_weeks_machines_domains(weeks_machines_domains_fpath, nrows=100)
weeks_machines_domains_df.drop(['machine_id', 'domains'], axis=1).head()
n_domains = 20
starting_domains_list = weeks_machines_domains_df[
(weeks_machines_domains_df.n_domains == n_domains)
].domains.values[2]
starting_domains_list = list(starting_domains_list)
starting_domains_list
# use most frequent domains from sampled rows as other domain samples
other_domains = weeks_machines_domains_df.domains.values
other_domains = [d for domains in other_domains for d in domains if d not in starting_domains_list]
other_domains = pd.Series(other_domains).value_counts().head(20).index
other_domains
m, domains, simhash, ot_cohort, cohort_k2, cohort_k4, cohort_k8,
m = list(range(20))
m
domains = [starting_domains_list]
for i in range(19):
i1_domains = domains[i][:] # copy domains list from i
i1_domains[i] = other_domains[i] # alter domains by one entry
domains += [i1_domains]
test_df = pd.DataFrame({'m':m, 'domains':domains})
test_df['simhash'] = test_df.domains.apply(floc.hashes.sim_hash_string)
test_df['ot_cohort'] = test_df.domains.apply(floc.simulate)
for k in [2, 4, 8]:
cohort_k = 'cohort_k%s'%k
cohorts_dict = prefixLSH.get_cohorts_dict(test_df.simhash.astype(int), min_k=k)
test_df[cohort_k] = test_df.simhash.map(cohorts_dict)
test_df
| 0.128307 | 0.761161 |
```
import numpy as np
def diag_2d(Y_prim_list):
N_cols = 0
for Y_prim in Y_prim_list:
N_cols += Y_prim.shape[1]
Y_prims = np.zeros((N_cols,N_cols))+0j
it = 0
for Y_prim in Y_prim_list:
N = Y_prim.shape[0]
Y_prims[it:(it+N),it:(it+N)] = Y_prim
it += N
return Y_prims
def trafo_yprim(S_n,U_1n,U_2n,Z_cc,connection='Dyg11'):
'''
Trafo primitive as developed in: (in the paper Ynd11)
R. C. Dugan and S. Santoso, “An example of 3-phase transformer modeling for distribution system analysis,”
2003 IEEE PES Transm. Distrib. Conf. Expo. (IEEE Cat. No.03CH37495), vol. 3, pp. 1028–1032, 2003.
'''
if connection=='Dyn11':
z_a = Z_cc*1.0**2/S_n*3
z_b = Z_cc*1.0**2/S_n*3
z_c = Z_cc*1.0**2/S_n*3
U_1 = U_1n
U_2 = U_2n/np.sqrt(3)
Z_B = np.array([[z_a, 0.0, 0.0],
[0.0, z_b, 0.0],
[0.0, 0.0, z_c],])
N_a = np.array([[ 1/U_1, 0],
[-1/U_1, 0],
[ 0, 1/U_2],
[ 0,-1/U_2]])
N_row_a = np.hstack((N_a,np.zeros((4,4))))
N_row_b = np.hstack((np.zeros((4,2)),N_a,np.zeros((4,2))))
N_row_c = np.hstack((np.zeros((4,4)),N_a))
N = np.vstack((N_row_a,N_row_b,N_row_c))
B = np.array([[ 1, 0, 0],
[-1, 0, 0],
[ 0, 1, 0],
[ 0,-1, 0],
[ 0, 0, 1],
[ 0, 0,-1]])
Y_1 = B @ np.linalg.inv(Z_B) @ B.T
Y_w = N @ Y_1 @ N.T
A_trafo = np.zeros((7,12))
A_trafo[0,0] = 1.0
A_trafo[0,9] = 1.0
A_trafo[1,1] = 1.0
A_trafo[1,4] = 1.0
A_trafo[2,5] = 1.0
A_trafo[2,8] = 1.0
A_trafo[3,2] = 1.0
A_trafo[4,6] = 1.0
A_trafo[5,10] = 1.0
A_trafo[6,3] = 1.0
A_trafo[6,7] = 1.0
A_trafo[6,11] = 1.0
Y_prim = A_trafo @ Y_w @ A_trafo.T
if connection=='Ynd11':
z_a = Z_cc*1.0**2/S_n*3
z_b = Z_cc*1.0**2/S_n*3
z_c = Z_cc*1.0**2/S_n*3
U_1 = U_1n/np.sqrt(3)
U_2 = U_2n
Z_B = np.array([[z_a, 0.0, 0.0],
[0.0, z_b, 0.0],
[0.0, 0.0, z_c],])
B = np.array([[ 1, 0, 0],
[-1, 0, 0],
[ 0, 1, 0],
[ 0,-1, 0],
[ 0, 0, 1],
[ 0, 0,-1]])
N_a = np.array([[ 1/U_1, 0],
[-1/U_1, 0],
[ 0, 1/U_2],
[ 0,-1/U_2]])
N_row_a = np.hstack((N_a,np.zeros((4,4))))
N_row_b = np.hstack((np.zeros((4,2)),N_a,np.zeros((4,2))))
N_row_c = np.hstack((np.zeros((4,4)),N_a))
N = np.vstack((N_row_a,N_row_b,N_row_c))
Y_1 = B @ np.linalg.inv(Z_B) @ B.T
Y_w = N @ Y_1 @ N.T
A_trafo = np.zeros((7,12))
A_trafo[0,0] = 1.0
A_trafo[1,4] = 1.0
A_trafo[2,8] = 1.0
A_trafo[3,1] = 1.0
A_trafo[3,5] = 1.0
A_trafo[3,9] = 1.0
A_trafo[4,2] = 1.0
A_trafo[4,11] = 1.0
A_trafo[5,3] = 1.0
A_trafo[5,6] = 1.0
A_trafo[6,7] = 1.0
A_trafo[6,10] = 1.0
Y_prim = A_trafo @ Y_w @ A_trafo.T
return Y_prim
Z_cc = (0.01+0.04j)
U_1n = 20e3
U_2n = 400.0
S_n = 500.0e3
Y_trafo_prim = trafo_yprim(S_n,U_1n,U_2n,Z_cc,connection='Dyn11')
Y_load_prim = np.eye(3)*1./10.0
Y_load_prim[0,0] = 1./10.0
Y_dummy_prim = np.eye(3)*1.0e-12
Y_th_prim = np.eye(3)*1e12
#Y_load_prim[0,0] = 10.0
#Y_load_prim[1,1] = 10.0
Y_prim = diag_2d([Y_th_prim,Y_dummy_prim,Y_trafo_prim,Y_load_prim])
```
### Incidence Matrix
```
id_nodes = np.array(['th_a','th_b','th_c','a_1','b_1','c_1','a_2','b_2','c_2','n_2'])
id_v = np.array(['th_a','th_b','th_c'])
id_i = np.array(['a_1','b_1','c_1','a_2','b_2','c_2','n_2'])
A = np.array([
[ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], # th_a 0
[ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], # th_b 1
[ 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], # th_c 2
[-1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], # a_1 3
[ 0, -1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], # b_1 4
[ 0, 0, -1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], # c_1 5
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0], # a_2 7
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0], # b_2 8
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1], # c_2 9
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, -1, -1, -1], # n_2 10
])
# th dummy trafo load 2
A_v = A[0:3,:]
A_i = A[3:11,:]
Y_ii = A_i @ Y_prim @ A_i.T
Y_iv = A_i @ Y_prim @ A_v.T
Y_vv = A_v @ Y_prim @ A_v.T
Y_vi = A_v @ Y_prim @ A_i.T
inv_Y_ii = np.linalg.inv(Y_ii+1.0e-6)
V_known = np.zeros((3,1))+0j
V_known[id_v=='th_a'] = U_2/np.sqrt(3.0)*np.exp(0.0j)
V_known[id_v=='th_b'] = U_2/np.sqrt(3.0)*np.exp(2.0/3*np.pi*1j)
V_known[id_v=='th_c'] = U_2/np.sqrt(3.0)*np.exp(4.0/3*np.pi*1j)
I_known = np.zeros((7,1))+0j
I = 0.0
phi =np.deg2rad(0.0)
I_known[id_i=='a_1'] = I*np.exp((0.0-phi)*1j)
I_known[id_i=='b_1'] = I*np.exp((2.0/3.0*np.pi-phi)*1j)
I_known[id_i=='c_1'] = I*np.exp((4.0/3.0*np.pi-phi)*1j)
I_known[id_i=='n_1'] = 0.0
#I_known =0*np.array([1.0*np.exp(0.0j),
# 1.0*np.exp(2.0/3*np.pi*1j),
# 1.0*np.exp(4.0/3*np.pi*1j)]).reshape((9,1))
V_unknown = inv_Y_ii @ ( I_known - Y_iv @ V_known)
I_unknown =Y_vv @ V_known + Y_vi @ V_unknown
V_known
for item in id_i:
V = V_unknown[id_i==item,0] - V_unknown[id_i=='n_2',0]
print(item,': V = {:2.4f}|{:2.1f}º V'.format(float(np.abs(V)), float(np.angle(V,deg=True))))
for item in id_v:
I = I_unknown[id_v==item,0]
print(item,': I = {:2.4f}|{:2.1f}'.format(float(np.abs(I)), float(np.angle(I,deg=True))))
for item in id_i:
I = (V_unknown[id_i==item,0] - V_unknown[id_i=='n_1',0])/10.0
print(item,': I = {:2.4f}|{:2.1f}º V'.format(float(np.abs(I)), float(np.angle(I,deg=True))))
np.abs(I_unknown.T @ A_v)
a_1 : V = 143.1010|-69.0º V
b_1 : V = 230.8814|89.9º V
c_1 : V = 230.8814|-150.1º V
n_1 : V = 0.0000|0.0º V
a_2 : V = 11509.8621|-0.0º V
b_2 : V = 11561.7395|120.2º V
c_2 : V = 11569.5053|-120.1º V
a_1 : V = 143.1010|-69.0º V
b_1 : V = 230.8814|89.9º V
c_1 : V = 230.8814|-150.1º V
n_1 : V = 0.0000|0.0º V
a_2 : V = 11509.8621|-0.0º V
b_2 : V = 11561.7395|120.2º V
c_2 : V = 11569.5053|-120.1º V
th_a : I = 165.0642|-68.9
th_b : I = 165.2755|111.3
th_c : I = 0.0000|0.0
a_1 : I = 14.3101|-69.0º V
b_1 : I = 23.0881|89.9º V
c_1 : I = 23.0881|-150.1º V
n_1 : I = 0.0000|0.0º V
a_2 : I = 1150.9862|-0.0º V
b_2 : I = 1156.1740|120.2º V
c_2 : I = 1156.9505|-120.1º V
20e3**2/630.0e3
0.04*635
20000/1.73/25.4
1/60
0.92-0.88
import numba
@numba.jit(nopython=True)
def hola_strings(s_list):
return s_list
s_list = np.array(['a_1','b_1','c_1','n_1','a_2','b_2','c_2','th_a','th_b','th_c'])
hola_strings('a_1')
c=1200/3.6
c/200
333/0.8
np.linalg.inv(Y_trafo_prim)
```
|
github_jupyter
|
import numpy as np
def diag_2d(Y_prim_list):
N_cols = 0
for Y_prim in Y_prim_list:
N_cols += Y_prim.shape[1]
Y_prims = np.zeros((N_cols,N_cols))+0j
it = 0
for Y_prim in Y_prim_list:
N = Y_prim.shape[0]
Y_prims[it:(it+N),it:(it+N)] = Y_prim
it += N
return Y_prims
def trafo_yprim(S_n,U_1n,U_2n,Z_cc,connection='Dyg11'):
'''
Trafo primitive as developed in: (in the paper Ynd11)
R. C. Dugan and S. Santoso, “An example of 3-phase transformer modeling for distribution system analysis,”
2003 IEEE PES Transm. Distrib. Conf. Expo. (IEEE Cat. No.03CH37495), vol. 3, pp. 1028–1032, 2003.
'''
if connection=='Dyn11':
z_a = Z_cc*1.0**2/S_n*3
z_b = Z_cc*1.0**2/S_n*3
z_c = Z_cc*1.0**2/S_n*3
U_1 = U_1n
U_2 = U_2n/np.sqrt(3)
Z_B = np.array([[z_a, 0.0, 0.0],
[0.0, z_b, 0.0],
[0.0, 0.0, z_c],])
N_a = np.array([[ 1/U_1, 0],
[-1/U_1, 0],
[ 0, 1/U_2],
[ 0,-1/U_2]])
N_row_a = np.hstack((N_a,np.zeros((4,4))))
N_row_b = np.hstack((np.zeros((4,2)),N_a,np.zeros((4,2))))
N_row_c = np.hstack((np.zeros((4,4)),N_a))
N = np.vstack((N_row_a,N_row_b,N_row_c))
B = np.array([[ 1, 0, 0],
[-1, 0, 0],
[ 0, 1, 0],
[ 0,-1, 0],
[ 0, 0, 1],
[ 0, 0,-1]])
Y_1 = B @ np.linalg.inv(Z_B) @ B.T
Y_w = N @ Y_1 @ N.T
A_trafo = np.zeros((7,12))
A_trafo[0,0] = 1.0
A_trafo[0,9] = 1.0
A_trafo[1,1] = 1.0
A_trafo[1,4] = 1.0
A_trafo[2,5] = 1.0
A_trafo[2,8] = 1.0
A_trafo[3,2] = 1.0
A_trafo[4,6] = 1.0
A_trafo[5,10] = 1.0
A_trafo[6,3] = 1.0
A_trafo[6,7] = 1.0
A_trafo[6,11] = 1.0
Y_prim = A_trafo @ Y_w @ A_trafo.T
if connection=='Ynd11':
z_a = Z_cc*1.0**2/S_n*3
z_b = Z_cc*1.0**2/S_n*3
z_c = Z_cc*1.0**2/S_n*3
U_1 = U_1n/np.sqrt(3)
U_2 = U_2n
Z_B = np.array([[z_a, 0.0, 0.0],
[0.0, z_b, 0.0],
[0.0, 0.0, z_c],])
B = np.array([[ 1, 0, 0],
[-1, 0, 0],
[ 0, 1, 0],
[ 0,-1, 0],
[ 0, 0, 1],
[ 0, 0,-1]])
N_a = np.array([[ 1/U_1, 0],
[-1/U_1, 0],
[ 0, 1/U_2],
[ 0,-1/U_2]])
N_row_a = np.hstack((N_a,np.zeros((4,4))))
N_row_b = np.hstack((np.zeros((4,2)),N_a,np.zeros((4,2))))
N_row_c = np.hstack((np.zeros((4,4)),N_a))
N = np.vstack((N_row_a,N_row_b,N_row_c))
Y_1 = B @ np.linalg.inv(Z_B) @ B.T
Y_w = N @ Y_1 @ N.T
A_trafo = np.zeros((7,12))
A_trafo[0,0] = 1.0
A_trafo[1,4] = 1.0
A_trafo[2,8] = 1.0
A_trafo[3,1] = 1.0
A_trafo[3,5] = 1.0
A_trafo[3,9] = 1.0
A_trafo[4,2] = 1.0
A_trafo[4,11] = 1.0
A_trafo[5,3] = 1.0
A_trafo[5,6] = 1.0
A_trafo[6,7] = 1.0
A_trafo[6,10] = 1.0
Y_prim = A_trafo @ Y_w @ A_trafo.T
return Y_prim
Z_cc = (0.01+0.04j)
U_1n = 20e3
U_2n = 400.0
S_n = 500.0e3
Y_trafo_prim = trafo_yprim(S_n,U_1n,U_2n,Z_cc,connection='Dyn11')
Y_load_prim = np.eye(3)*1./10.0
Y_load_prim[0,0] = 1./10.0
Y_dummy_prim = np.eye(3)*1.0e-12
Y_th_prim = np.eye(3)*1e12
#Y_load_prim[0,0] = 10.0
#Y_load_prim[1,1] = 10.0
Y_prim = diag_2d([Y_th_prim,Y_dummy_prim,Y_trafo_prim,Y_load_prim])
id_nodes = np.array(['th_a','th_b','th_c','a_1','b_1','c_1','a_2','b_2','c_2','n_2'])
id_v = np.array(['th_a','th_b','th_c'])
id_i = np.array(['a_1','b_1','c_1','a_2','b_2','c_2','n_2'])
A = np.array([
[ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], # th_a 0
[ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], # th_b 1
[ 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], # th_c 2
[-1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], # a_1 3
[ 0, -1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], # b_1 4
[ 0, 0, -1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], # c_1 5
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0], # a_2 7
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0], # b_2 8
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1], # c_2 9
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, -1, -1, -1], # n_2 10
])
# th dummy trafo load 2
A_v = A[0:3,:]
A_i = A[3:11,:]
Y_ii = A_i @ Y_prim @ A_i.T
Y_iv = A_i @ Y_prim @ A_v.T
Y_vv = A_v @ Y_prim @ A_v.T
Y_vi = A_v @ Y_prim @ A_i.T
inv_Y_ii = np.linalg.inv(Y_ii+1.0e-6)
V_known = np.zeros((3,1))+0j
V_known[id_v=='th_a'] = U_2/np.sqrt(3.0)*np.exp(0.0j)
V_known[id_v=='th_b'] = U_2/np.sqrt(3.0)*np.exp(2.0/3*np.pi*1j)
V_known[id_v=='th_c'] = U_2/np.sqrt(3.0)*np.exp(4.0/3*np.pi*1j)
I_known = np.zeros((7,1))+0j
I = 0.0
phi =np.deg2rad(0.0)
I_known[id_i=='a_1'] = I*np.exp((0.0-phi)*1j)
I_known[id_i=='b_1'] = I*np.exp((2.0/3.0*np.pi-phi)*1j)
I_known[id_i=='c_1'] = I*np.exp((4.0/3.0*np.pi-phi)*1j)
I_known[id_i=='n_1'] = 0.0
#I_known =0*np.array([1.0*np.exp(0.0j),
# 1.0*np.exp(2.0/3*np.pi*1j),
# 1.0*np.exp(4.0/3*np.pi*1j)]).reshape((9,1))
V_unknown = inv_Y_ii @ ( I_known - Y_iv @ V_known)
I_unknown =Y_vv @ V_known + Y_vi @ V_unknown
V_known
for item in id_i:
V = V_unknown[id_i==item,0] - V_unknown[id_i=='n_2',0]
print(item,': V = {:2.4f}|{:2.1f}º V'.format(float(np.abs(V)), float(np.angle(V,deg=True))))
for item in id_v:
I = I_unknown[id_v==item,0]
print(item,': I = {:2.4f}|{:2.1f}'.format(float(np.abs(I)), float(np.angle(I,deg=True))))
for item in id_i:
I = (V_unknown[id_i==item,0] - V_unknown[id_i=='n_1',0])/10.0
print(item,': I = {:2.4f}|{:2.1f}º V'.format(float(np.abs(I)), float(np.angle(I,deg=True))))
np.abs(I_unknown.T @ A_v)
a_1 : V = 143.1010|-69.0º V
b_1 : V = 230.8814|89.9º V
c_1 : V = 230.8814|-150.1º V
n_1 : V = 0.0000|0.0º V
a_2 : V = 11509.8621|-0.0º V
b_2 : V = 11561.7395|120.2º V
c_2 : V = 11569.5053|-120.1º V
a_1 : V = 143.1010|-69.0º V
b_1 : V = 230.8814|89.9º V
c_1 : V = 230.8814|-150.1º V
n_1 : V = 0.0000|0.0º V
a_2 : V = 11509.8621|-0.0º V
b_2 : V = 11561.7395|120.2º V
c_2 : V = 11569.5053|-120.1º V
th_a : I = 165.0642|-68.9
th_b : I = 165.2755|111.3
th_c : I = 0.0000|0.0
a_1 : I = 14.3101|-69.0º V
b_1 : I = 23.0881|89.9º V
c_1 : I = 23.0881|-150.1º V
n_1 : I = 0.0000|0.0º V
a_2 : I = 1150.9862|-0.0º V
b_2 : I = 1156.1740|120.2º V
c_2 : I = 1156.9505|-120.1º V
20e3**2/630.0e3
0.04*635
20000/1.73/25.4
1/60
0.92-0.88
import numba
@numba.jit(nopython=True)
def hola_strings(s_list):
return s_list
s_list = np.array(['a_1','b_1','c_1','n_1','a_2','b_2','c_2','th_a','th_b','th_c'])
hola_strings('a_1')
c=1200/3.6
c/200
333/0.8
np.linalg.inv(Y_trafo_prim)
| 0.263505 | 0.726329 |
# Ejercicios Weak Ties & Random Networks
Ejercicios básicos de redes
## Ejercicio Clustering Coeficient
Calcule el coeficiente de clustering para cada nodo y en la red (sin dirección)
```
edges = set([(1,2), (2,3), (2,4), (2,5), (4,5), (4,6), (5,6), (4,7)])
def get_vecinos(nodo):
vecinos = set() #Se crea un conjunto vacio para vecinos
for f,t in edges:
if f == nodo:
vecinos.add(t)
if t == nodo:
vecinos.add(f)
return vecinos
vecinos = get_vecinos(2)
N = len(vecinos)
posibles_links_entre_vecinos = N*(N-1)/2
posibles_links_entre_vecinos
nodos = set()
for f,t in edges:
nodos.add(f)
nodos.add(t)
nodos
vecinos
(1,2) in edges
#Numero de enlaces reales entre los vecinos
def get_links_vecinos(vecinos):
enlaces_vecinos = 0
for v in vecinos:
for i in vecinos:
if (v,i) in edges:
enlaces_vecinos = enlaces_vecinos+1
return enlaces_vecinos
# obtener coeficiente de clustering
def get_clustering_coeficient(nodo):
numero_vecinos = get_vecinos(nodo)
enlaces_entre_vecinos = get_links_vecinos(numero_vecinos)
if len(numero_vecinos) == 1:
ci = 0
else:
ci = (2*enlaces_entre_vecinos)/(len(numero_vecinos)*(len(numero_vecinos)-1))
return ci
get_clustering_coeficient(2)
# Obtener coeficiente de clustering para todos los nodos
for j in nodos:
coeficiente = get_clustering_coeficient(j)
print("para el nodo: "+ str(j) + " El coeficiente de clustering es: " + str(coeficiente))
```
## Ejercicio Weigthed Netwroks
Cree una red no direccionada con los siguientes pesos.
(a, b) = 0.3
(a, c) = 1.0
(a, d) = 0.9
(a, e) = 1.0
(a, f) = 0.4
(c, f) = 0.2
(b, h) = 0.2
(f, j) = 0.8
(f, g) = 0.9
(j, g) = 0.6
(g, k) = 0.4
(g, h) = 0.2
(k, h) = 1.0
```
import matplotlib
%matplotlib inline
import networkx as nx
#edges = set([('a','b'), ('a','c'), ('a','d'), ('a','e'), ('a','f'), ('c','f'), ('b','h'), ('f','j'), ('f','g'), ('j','g'), ('g','k'), ('g','h'), ('k','h')])
G = nx.Graph()
G.add_weighted_edges_from([('a','b',0.3),('a','c',1),('a','d',0.9),('a','e',1),('a','f',0.4),('c','f',0.2),('c','f',0.2),('b','h',0.2),('f','j',0.8),('f','g',0.9),('j','g',0.6),('g','k',0.4),('g','h',0.2),('k','h',1)])
nx.draw_networkx(G)
G.size(weight='weight')
```
Imprima la matriz de adyasencia
```
A = nx.adjacency_matrix(G)
print(A.todense())
```
## Ejercicio Weak & Strong ties
Con la misma red anterior asuma que un link debil es inferior a 0.5, cree un código que calcule si se cumple la propiedad "strong triadic closure"
Cambie un peso de los links anteriores para que se deje de cumplir la propiedad y calcule si es cierto. Explique.
Escriba un código que detecte puntes locales y que calcule el span de cada puente local
## Ejercicio Random Networks
genere 1000 redes aleatorias N = 12, p = 1/6 y grafique la distribución del número de enlaces
Grafique la distribución del promedio de grados en cada una de las redes generadas del ejercicio anterior
Haga lo mismo para redes con 100 nodos
## Ejercicio Random Networks - Componente Gigante
Grafique como crece el tamaño del componente más grande de una red aleatoria con N=100 nodos y diferentes valores de ___p___
(_grafique con promedio de grado entre 0 y 4 cada 0.05_)
Grafique cuál es el porcentaje de nodos del componente más grande para diferentes valores de ___p___
Identifique para que valores de ___p___ el componente mas grande esta totalmente interconectado
|
github_jupyter
|
edges = set([(1,2), (2,3), (2,4), (2,5), (4,5), (4,6), (5,6), (4,7)])
def get_vecinos(nodo):
vecinos = set() #Se crea un conjunto vacio para vecinos
for f,t in edges:
if f == nodo:
vecinos.add(t)
if t == nodo:
vecinos.add(f)
return vecinos
vecinos = get_vecinos(2)
N = len(vecinos)
posibles_links_entre_vecinos = N*(N-1)/2
posibles_links_entre_vecinos
nodos = set()
for f,t in edges:
nodos.add(f)
nodos.add(t)
nodos
vecinos
(1,2) in edges
#Numero de enlaces reales entre los vecinos
def get_links_vecinos(vecinos):
enlaces_vecinos = 0
for v in vecinos:
for i in vecinos:
if (v,i) in edges:
enlaces_vecinos = enlaces_vecinos+1
return enlaces_vecinos
# obtener coeficiente de clustering
def get_clustering_coeficient(nodo):
numero_vecinos = get_vecinos(nodo)
enlaces_entre_vecinos = get_links_vecinos(numero_vecinos)
if len(numero_vecinos) == 1:
ci = 0
else:
ci = (2*enlaces_entre_vecinos)/(len(numero_vecinos)*(len(numero_vecinos)-1))
return ci
get_clustering_coeficient(2)
# Obtener coeficiente de clustering para todos los nodos
for j in nodos:
coeficiente = get_clustering_coeficient(j)
print("para el nodo: "+ str(j) + " El coeficiente de clustering es: " + str(coeficiente))
import matplotlib
%matplotlib inline
import networkx as nx
#edges = set([('a','b'), ('a','c'), ('a','d'), ('a','e'), ('a','f'), ('c','f'), ('b','h'), ('f','j'), ('f','g'), ('j','g'), ('g','k'), ('g','h'), ('k','h')])
G = nx.Graph()
G.add_weighted_edges_from([('a','b',0.3),('a','c',1),('a','d',0.9),('a','e',1),('a','f',0.4),('c','f',0.2),('c','f',0.2),('b','h',0.2),('f','j',0.8),('f','g',0.9),('j','g',0.6),('g','k',0.4),('g','h',0.2),('k','h',1)])
nx.draw_networkx(G)
G.size(weight='weight')
A = nx.adjacency_matrix(G)
print(A.todense())
| 0.345436 | 0.862641 |
## Mixed variables
Mixed variables are those which values contain both numbers and labels.
Variables can be mixed for a variety of reasons. For example, when credit agencies gather and store financial information of users, usually, the values of the variables they store are numbers. However, in some cases the credit agencies cannot retrieve information for a certain user for different reasons. What Credit Agencies do in these situations is to code each different reason due to which they failed to retrieve information with a different code or 'label'. Like this, they generate mixed type variables. These variables contain numbers when the value could be retrieved, or labels otherwise.
As an example, think of the variable 'number_of_open_accounts'. It can take any number, representing the number of different financial accounts of the borrower. Sometimes, information may not be available for a certain borrower, for a variety of reasons. Each reason will be coded by a different letter, for example: 'A': couldn't identify the person, 'B': no relevant data, 'C': person seems not to have any open account.
Another example of mixed type variables, is for example the variable missed_payment_status. This variable indicates, whether a borrower has missed a (any) payment in their financial item. For example, if the borrower has a credit card, this variable indicates whether they missed a monthly payment on it. Therefore, this variable can take values of 0, 1, 2, 3 meaning that the customer has missed 0-3 payments in their account. And it can also take the value D, if the customer defaulted on that account.
Typically, once the customer has missed 3 payments, the lender declares the item defaulted (D), that is why this variable takes numerical values 0-3 and then D.
For this lecture, you will need to download a toy csv file that I created and uploaded at the end of the lecture in Udemy. It is called sample_s2.csv.
```
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# open_il_24m indicates:
# "Number of installment accounts opened in past 24 months".
# Installment accounts are those that, at the moment of acquiring them,
# there is a set period and amount of repayments agreed between the
# lender and borrower. An example of this is a car loan, or a student loan.
# the borrowers know that they are going to pay a certain,
# fixed amount over, for example 36 months.
data = pd.read_csv('sample_s2.csv')
data.head()
data.shape
# 'A': couldn't identify the person
# 'B': no relevant data
# 'C': person seems not to have any account open
data.open_il_24m.unique()
# Now, let's make a bar plot showing the different number of
# borrowers for each of the values of the mixed variable
fig = data.open_il_24m.value_counts().plot.bar()
fig.set_title('Number of installment accounts open')
fig.set_ylabel('Number of borrowers')
```
This is how a mixed variable looks like!
**That is all for this demonstration. I hope you enjoyed the notebook, and see you in the next one.**
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# open_il_24m indicates:
# "Number of installment accounts opened in past 24 months".
# Installment accounts are those that, at the moment of acquiring them,
# there is a set period and amount of repayments agreed between the
# lender and borrower. An example of this is a car loan, or a student loan.
# the borrowers know that they are going to pay a certain,
# fixed amount over, for example 36 months.
data = pd.read_csv('sample_s2.csv')
data.head()
data.shape
# 'A': couldn't identify the person
# 'B': no relevant data
# 'C': person seems not to have any account open
data.open_il_24m.unique()
# Now, let's make a bar plot showing the different number of
# borrowers for each of the values of the mixed variable
fig = data.open_il_24m.value_counts().plot.bar()
fig.set_title('Number of installment accounts open')
fig.set_ylabel('Number of borrowers')
| 0.394551 | 0.961606 |
# QAOA - Quantum Approximate Optimization Algorithm
In this notebook I would like to show you one of the most prominent algorithms in the quantum computing in the last few years.
In this tutorial you will learn the following:
- How to use pyQuil - python platform for quantum computing.
- How to solve MaxCut problem using QAOA implementation in pyQuil.
- What does it mean in practice that quantum computing is probabilistic.
- Basic information about how QAOA works.
This is probably the most theoretical notebook in this series, especially the second part. If you get discouraged by this and don't get everything, don't worry. Take your time, try reading different resources or just go to the next part and come back later. These ideas are that difficult, but are pretty complicated at times and they may just need some time to sink in :)
## Prerequisites
Before we can go into QAOA itself, you should prepare a couple of things:
1. Configure your Forest API Key - go to http://forest.rigetti.com, find section "Get API Key" and follow the instructions
2. Install [pyQuil](https://github.com/rigetticomputing/pyquil) and [Grove](https://github.com/rigetticomputing/grove)
3. Learn the basics of quantum computing by yourself - there are plenty of great resources about the basics in the web and I decided I don't want to reinvent the wheel in this tutorial. I recommend going to [pyQuil documentation](http://pyquil.readthedocs.io/en/stable/).
4. You can also check out [this tutorial](https://github.com/markf94/rigetti_training_material) by guys from [ProteinQure](https://proteinqure.com). It was designed for the workshops, not self-learning, but there are many hands-on exercises and it will be a good test of your pyQuil skills :)
Even though I tried to make this tutorial as accessible to the not-quantum-computing people as possible, you probably need some level of familiarity with the following concepts:
- qubits
- quantum gates
- superposition
- entanglement
You don't need to go very in-depth - I think spending about 30 minutes with the pyQuil docs should be enough for the beginning. And if something is still confusing later on you can always come back to the documentation when you need it :)
### Terminology
We need this line to have a proper [bra-ket](https://en.wikipedia.org/wiki/Bra–ket_notation) formatting in markdown.
$$
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bra}[1]{\left\langle #1 \right|}
$$
I try to use as easy language as possible and by easy I mean not very specific neither for physicists, programmers nor quantum computing people. But sometimes it's just not possible, so here I will try to explain you some important concepts in layman terms. These explanation won't give you deep understanding, rather a general overview.
`Operator` - well... if you are not very mathematically accurate, you can treat "operator" as a fancy name for a matrix. If you are - I'm not the best person to explain it to you ;) But in essence, operators represents some kind of action on a quantum state and there is a matrix associated with every operator, so these terms are sometimes used interchangeably.
`Hamiltonian` is an operator describing the quantum system. It's eigenvalues represent the energy values that the system can have.
`Pauli matrix` is one of the three 2x2 matrices commonly used in quantum computing. They have very interesting properties ([wiki](https://en.wikipedia.org/wiki/Pauli_matrices)) and they correspond to some very basic operations on qubits. You will see a lot of them while doing quantum computing.
- $\sigma_x$ -> X gate. It flips $\ket 0$ and $\ket 1$, so it's equivalent to logical NOT gate.
- $\sigma_y$ -> Y gate. It maps $\ket 0$ into $i \ket 1$ and $\ket 1$ into $-i \ket 0$
- $\sigma_z$ -> Z gate. It doesn't affect $\ket 0$ state, but changes $\ket 1$ -> - $\ket 1$
## QAOA - intro
QAOA is an algorithm for solving a broad range of optimization problems using NISQ (Noisy Intermediate-Scale Quantum) devices.
Let's start easy and instead of going straight to the TSP we will solve MaxCut problem. This part is based on the [Rigetti's tutorial on QAOA](https://grove-docs.readthedocs.io/en/latest/qaoa.html).
### MaxCut - explanation
In the MaxCut problem we start with a graph and we want to divide it into two subgraphs in such way, that the edges between them would have the highest possible sum.
Let's take look on an example. We will color the nodes with blue and red to distinguish into which group they fall - let's say blue represents 0 and red represents 1.
We start easy with a graph with two nodes and one connection:

We can color it in the following ways:

Now, a little more advanced example:

To understand it better I recommend drawing a 4-node graph on a paper and try to solve it by hand.
If you still don't get it, check out [this section of the Rigetti's tutorial](https://grove-docs.readthedocs.io/en/latest/qaoa.html#our-first-np-hard-problem).
### QAOA solves MaxCut - quick take
Let's take a graph with four nodes.
We encode it as a list of tuples, where each tuple represents an edge between given nodes.
```
first_graph = [(0, 1), (0, 2), (0, 3)]
```

The optimal solution for this graph is either 1000 or 0111:
Now let's try to solve MaxCut problem for this graph using maxcut_solver from the grove library.
Keep in mind that runtime of this algorithm are non-deterministic - it should finish running under a minute, but sometimes it takes longer.
```
import numpy as np
from grove.pyqaoa.maxcut_qaoa import maxcut_qaoa
import pyquil.api as api
qvm_connection = api.QVMConnection()
%%capture
#%%capture supresses printing.
#get_angles() prints out a lot of stuff that we don't care about right now.
maxcut_solver = maxcut_qaoa(graph=first_graph)
betas, gammas = maxcut_solver.get_angles()
```
Now that we have the values of betas and gammas we can run the actual program.
Don't worry about understanding what betas and gammas are for now. We will get back to it later.
```
angles = np.hstack((betas, gammas))
param_prog = maxcut_solver.get_parameterized_program()
prog = param_prog(angles)
qubits = [0, 1, 2, 3]
measurements = qvm_connection.run_and_measure(prog, qubits, trials=1000)
```
And see what are the results:
```
from collections import Counter
measurements = [tuple(measurement) for measurement in measurements]
measurements_counter = Counter(measurements)
measurements_counter.most_common()
```
So as we can see, the correct results are at the top of our lists - so everything seems good.
But why?
We will go through the code step by step in the next section
### QAOA solves MaxCut - details
#### Finding the right angles
```
# We initialize the maxcut_qaoa object with our graph
maxcut_solver = maxcut_qaoa(graph=first_graph)
# The QAOA algorithm tries to find the optimal values of betas and gammas.
# This line is where all the optimization takes place.
betas, gammas = maxcut_solver.get_angles()
print("Values of betas:", betas)
print("Values of gammas:", gammas)
```
This time we have not supressed the output and with every iteration of the algorithm you can see two lines being printed.
<br>
The first one is parameters - these are values of betas and gammas.
<br>
The second one is the cost value - it's what we try to minize. As you can probably see, the minimization process isn't ideally smooth. Value is generally getting smaller and smaller, but not necessarily every step yields an improvement.
<br>
We will deal with what exactly this energy means later on.
#### Creating a circuit
```
# We create an array of angles with correct format
angles = np.hstack((betas, gammas))
print(angles)
# We take a template for quil program from the maxcut_solver.
param_prog = maxcut_solver.get_parameterized_program()
# We initialize this program with the angles we have found
prog = param_prog(angles)
# Now we can print the program.
# Some of the values you see here are the angles we calculated earlier.
print(prog)
print("Number of gates:", len(prog))
```
#### Running the quantum program
```
# These are just the ids of qubits we want to use.
# It's not very important if you don't use the real QPU.
qubits = [0, 1, 2, 3]
# Here we connect to the Forest API and run our program there.
# We do that 1000 times and after each one we measure the output.
measurements = qvm_connection.run_and_measure(prog, qubits, trials=1000)
```
#### Analyzing the results
```
# Since list of 1000 elements is hard to analyze, we use Counter
from collections import Counter
# This is just a hack - we can't use Counter on a list of lists but we can on a list of tuples.
measurements = [tuple(measurement) for measurement in measurements]
measurements_counter = Counter(measurements)
# This line gives us the results in the diminishing order
measurements_counter.most_common()
```
#### Probabilistic nature of quantum computing
One of the most basic rules of the quantum mechanics is that the act of observation changes the state of the system that we observe.
<br>
Even though our algorithm produces some state which is a combination of all the states you see above, we can't measure it directly. What we can do (and we did) is to measure it repeatedly and get some distribution of the results.
<br>
Fortunately, we use a simulator and we can look how the state we produced looks exactly:
```
wf = qvm_connection.wavefunction(prog)
print(wf)
```
This is hard to read and interpret, so let's print it in a different form.
```
print("Probability amplitudes for all the possible states:")
for state_index in range(maxcut_solver.nstates):
print(maxcut_solver.states[state_index], wf[state_index])
```
These numbers are still not very easy to interpret, but we can calculate the actual probabilities based on this:
```
print("Probabilities of measuring given states:")
states_with_probs = []
for state_index in range(maxcut_solver.nstates):
states_with_probs.append([maxcut_solver.states[state_index], np.real(np.conj(wf[state_index])*wf[state_index])])
print(states_with_probs[-1][0], states_with_probs[-1][1])
```
These results correspond nicely with the values we got from the measurement. Not ideally, but you can increase the `trial` parameter to get closer.
```
%matplotlib inline
import matplotlib.pyplot as plt
def plot_state_histogram(states_with_probs):
states = np.array(states_with_probs)[:,0]
probs = np.array(states_with_probs)[:,1].astype(float)
n = len(states_with_probs)
plt.barh(range(n), probs, tick_label=states)
plt.show()
plot_state_histogram(states_with_probs)
```
#### Exercises
It's a good time to experiment a little bit by yourself. Here are some ideas:
- Run this code on different graphs.
- Print out what's the distribution of the results. How "convinced" the algorithm is that given solution is correct?
- Try running it several times on one graph. Do you get similar distributions every time?
- How big graphs you can solve with reasonable calculation times?
## QAOA - how does it work?
### Black box approach
The easiest way to look at QAOA is to think only about its inputs and outputs.
<br>
To solve the MaxCut problem the only thing we needed was the graph, which we passed to the instance of `maxcut_qaoa` class. But if you look into [its body](https://github.com/rigetticomputing/grove/blob/master/grove/pyqaoa/maxcut_qaoa.py), you will see that inside we use `qaoa` class with a little bit more advanced version of the following line:
```
QAOA_inst = QAOA(connection, qubits, steps=steps, cost_ham=cost_operators,
ref_ham=driver_operators,
init_betas=initial_beta,
init_gammas=initial_gamma,
minimizer_kwargs=minimizer_kwargs)
```
`connection` is just a regular `api.QVMConnection()` - so we tell QAOA how it should talk to the Forest cloud.
`qubits` are the same qubits that we used earlier.
`steps` is an integer, which specifies how long our quantum program will be. By default it's equal to 1 and that's the value we used in our MaxCut example. We will return to this later.
`cost_ham` (`cost_operators`) is how we encode our problem. This is where all the information about our graph sits and it's encoded as a combination of Pauli operators.
`ref_ham` (`driver_operators`) is how we encode what changes are possible in the realm of our problem. In `maxcut_qaoa` we say that we can flip every qubit from 0 to 1. Again - we use only Pauli operators to create it.
`init_gammas` and `init_betas` are just the initial values for the $\gamma$ and $\beta$ angles.
`minimizer_kwargs` is a dictionary with the minimizer arguments. As you can see in an example below, we specify the minimization method and its options.
```
minimizer_kwargs = {'method': 'Nelder-Mead',
'options': {'ftol': 1.0e-2, 'xtol': 1.0e-2,
'disp': False}}
```
You may wonder why it's a `minimizer` since we want to find a maximum cut. This is due to a nice property of optimization problems, that maximization is just a minimization with of the same problem but with a minus in the cost function. Since most optimization algorithms are stated in terms of minimization, we stick to this convention.
After we have all that we need to run the actual algorithm and find the right angles. Then we create a quantum program which gives us solution to the problem we specified with the `cost_operators`:
```
betas, gammas = QAOA_inst.get_angles()
QAOA_inst.get_parametrized_program()
```
Or actually, we can go straight for the answer with:
```
QAOA_inst.get_string(betas, gammas)
```
This is probably not the simplest black box interface, but honestly, it's not extremely complicated either. The only non-obvious part is what should the cost and driver operators be. Let's see in the next section!
### How to encode our problem
Since in MaxCut we want to create to subsets of nodes, given node is either in set $A$ or $B$.
<br>
The total cost of our solution is:
<br>
<br>
$C_{total} = \sum C_{ij} = \sum \frac{1}{2} w_{ij} (1 - z_i z_j) $,
<br>
<br>
where the sum goes through all the pairs of nodes and values $z_i$ are equal to 1 if given node is in the set $A$ and -1 if it's in the $B$. $w_{ij}$ is the weight of given edge, which in our current example is equal to 1.
<br>
It turns out that we can construct a matrix (Hamiltonian), which correspons to this cost function using only Pauli operators:
<br>
<br>
$H_{cost} = \sum \frac{1}{2} w_{ij} (\mathbb{1} - \sigma^z_i \sigma^z_j$)
<br>
If you wonder what $\mathbb{1}$ is, it's an identity matrix, which can also be considered as special a Pauli matrix.
How does it look like in the code?
```
from pyquil.paulis import PauliTerm, PauliSum
import networkx as nx
maxcut_graph = nx.Graph()
for edge in first_graph:
maxcut_graph.add_edge(*edge)
graph = maxcut_graph.copy()
cost_operators = []
for i, j in graph.edges():
cost_operators.append(PauliTerm("Z", i, 0.5)*PauliTerm("Z", j) + PauliTerm("I", 0, -0.5))
```
The code above is copied from the `maxcut_qaoa` class. Let's see how some of these operators look:
```
print(cost_operators[0])
print(cost_operators[1])
```
This is how we encode our `cost_operators`, so now let's go to the `driver_operators`.
They specify how our state can change. In this basic case, let's say that we allow every qubit to just change from 0 to 1 or otherwise. This means that we need a bunch of X gates (which correspond to $\sigma_x$ Pauli matrices):
```
driver_operators = []
for i in graph.nodes():
driver_operators.append(PauliSum([PauliTerm("X", i, -1.0)]))
```
You don't need to bother with the `PauliSum` function, it's here just so that the input type is correct, but it doesn't play any other role.
```
print(driver_operators[0])
```
And that's it!
<br>
Now let's try to actually run the QAOA by ourselves:
```
from grove.pyqaoa.qaoa import QAOA
initial_beta = 0
initial_gamma = 0
minimizer_kwargs = {'method': 'Nelder-Mead',
'options': {'ftol': 1.0e-2, 'xtol': 1.0e-2,
'disp': False}}
QAOA_inst = QAOA(qvm_connection, qubits, steps=1,
cost_ham=cost_operators,
ref_ham=driver_operators,
init_betas=initial_beta,
init_gammas=initial_gamma,
minimizer_kwargs=minimizer_kwargs)
betas, gammas = QAOA_inst.get_angles()
print("Values of betas:", betas)
print("Values of gammas:", gammas)
print("And the most common measurement is... ")
most_common_result, _ = QAOA_inst.get_string(betas, gammas)
print(most_common_result)
```
Awesome! Now you have all the tools to use QAOA, except the most important one...
Knowing how it actually works ;)
### What are betas and gammas?
Imagine you're in the mountains and you want to find the lowest valley. In this analogy if we used the classical gradient descent method, you will start from some point and climb downwards until we can't find anything better. Most of the classical algorithms work this way - you are a moving around the mountain range to find this valley.
<br>
Here it's a little bit different. You start with some simple landscape and standing in the lowest point. Then, very, very slowly, the mountains start erecting from the ground. If this means that the minimum shifts, you do a little step. In the end, the mountains are the same as they were in the previous example and you are standing in the lowest valley.
<br>
What's happening here is the adiabatic transformation from some initial hamiltonian to the hamiltonian representing our problem. It is proven that if it's done slowly enough, the ground state (state of the minimal energy) of the initial hamiltonian will transform smoothly into the ground state of the final hamiltonian. It is also how the quantum annealers work (e.g. D-Wave).
<br>
One of the problems is that using Rigetti's quantum computer (or any other gate based machine) we cannot do this transformation in infinite number of infinitely small steps. We need to set how many steps we want and this is what `steps` parameter does. The more steps we have, the higher chance we will get the good result, but we also need more gates and running the algorithm gets longer and longer. Also, it means we have more betas and gammas to optimize. In this metaphore, betas and gammas tell you how exactly should you add new mountains in each step.
For those of you, who prefer equations over methaphores - below is the short version of how it works. We start with some definitions and then go to the explanations:
${\displaystyle U(C,\gamma) = e^{-i \gamma C} = \prod_{\alpha} e^{-i \gamma C_{\alpha}} }$, where $C_{\alpha}$ are the cost operators we defined earlier.
<br>
${\displaystyle U(B,\beta) = e^{-i \beta B} = \prod_{j} e^{-i \beta B_{j}} }$, where $B_{j}$ are the driver operators we defined earlier.
<br>
$\ket{s}$ is the initial state.
<br>
And finally: $\ket{\beta, \gamma} = U(B, \beta) U(C, \gamma) \ket{s}$
<br>
This is for the case where `steps=2`, but it generalizes nicely to higher number of steps, e.g.:
<br>
$\ket{\beta, \gamma} = U(B, \beta_1) U(B, \beta_0) U(C, \gamma_1) U(C, \gamma_0)\ket{s}$
If you are not familiar with this notation here is a step-by-step description of what does it mean in practice:
- Let's take some initial state $\ket{s}$
- Evolve this state using the operator $U(C, \gamma_0)$
- Evolve this state further using the rest of operators, from right to left.
"Evolving" is just a fancy name for "changing" that we use when talking about the states in quantum computing.
And now, if the values of angles $\beta$ and $\gamma$ are the right ones, we get a state which is a ground state of the Hamiltonian defining our problem, which should correspond to our solution.
If you wonder why we call $\gamma$ and $\beta$ angles, that's because $U(C, \gamma)$ and $U(B, \beta)$ correspond to rotations by angles $\gamma$ and $\beta$ in some high dimensional space.
### How to find the right angles? The hybrid part
QAOA is an iterative algorithm, which in every iteration uses a quantum and a classical part.
**Quantum**
1. Prepare a quantum state based on the current values of $\gamma$ and $\beta$.
2. Measure the state.
3. Repeat many times to get some statistics.
**Classical**
Here we use some classical optimization method, e.g. Nelder-Mead algorithm, and in each iteration of this algorithm we perform the quantum operations to evaluate how good our current angles are.
<br>
The algorithm ends when we can't further improve the angles.
## Summary and next steps
What we learned?
- how to solve MaxCut problem using QAOA
- how to use QAOA class from grove
- how to encode an optimization problem for QAOA
- what the QAOA is and how it works
What's next?
- Solving TSP using QAOA
## Additional resources
- [Pauli matrices](https://en.wikipedia.org/wiki/Pauli_matrices)
- [Original QAOA paper](https://arxiv.org/abs/1411.4028)
- [QAOA Grove docs](https://grove-docs.readthedocs.io/en/latest/qaoa.html)
- [Source code of MaxCut QAOA in Grove](https://github.com/rigetticomputing/grove/blob/master/grove/pyqaoa/maxcut_qaoa.py)
- [Presentation from one of the creators of QAOA](https://youtu.be/J8y0VhnISi8)
|
github_jupyter
|
first_graph = [(0, 1), (0, 2), (0, 3)]
import numpy as np
from grove.pyqaoa.maxcut_qaoa import maxcut_qaoa
import pyquil.api as api
qvm_connection = api.QVMConnection()
%%capture
#%%capture supresses printing.
#get_angles() prints out a lot of stuff that we don't care about right now.
maxcut_solver = maxcut_qaoa(graph=first_graph)
betas, gammas = maxcut_solver.get_angles()
angles = np.hstack((betas, gammas))
param_prog = maxcut_solver.get_parameterized_program()
prog = param_prog(angles)
qubits = [0, 1, 2, 3]
measurements = qvm_connection.run_and_measure(prog, qubits, trials=1000)
from collections import Counter
measurements = [tuple(measurement) for measurement in measurements]
measurements_counter = Counter(measurements)
measurements_counter.most_common()
# We initialize the maxcut_qaoa object with our graph
maxcut_solver = maxcut_qaoa(graph=first_graph)
# The QAOA algorithm tries to find the optimal values of betas and gammas.
# This line is where all the optimization takes place.
betas, gammas = maxcut_solver.get_angles()
print("Values of betas:", betas)
print("Values of gammas:", gammas)
# We create an array of angles with correct format
angles = np.hstack((betas, gammas))
print(angles)
# We take a template for quil program from the maxcut_solver.
param_prog = maxcut_solver.get_parameterized_program()
# We initialize this program with the angles we have found
prog = param_prog(angles)
# Now we can print the program.
# Some of the values you see here are the angles we calculated earlier.
print(prog)
print("Number of gates:", len(prog))
# These are just the ids of qubits we want to use.
# It's not very important if you don't use the real QPU.
qubits = [0, 1, 2, 3]
# Here we connect to the Forest API and run our program there.
# We do that 1000 times and after each one we measure the output.
measurements = qvm_connection.run_and_measure(prog, qubits, trials=1000)
# Since list of 1000 elements is hard to analyze, we use Counter
from collections import Counter
# This is just a hack - we can't use Counter on a list of lists but we can on a list of tuples.
measurements = [tuple(measurement) for measurement in measurements]
measurements_counter = Counter(measurements)
# This line gives us the results in the diminishing order
measurements_counter.most_common()
wf = qvm_connection.wavefunction(prog)
print(wf)
print("Probability amplitudes for all the possible states:")
for state_index in range(maxcut_solver.nstates):
print(maxcut_solver.states[state_index], wf[state_index])
print("Probabilities of measuring given states:")
states_with_probs = []
for state_index in range(maxcut_solver.nstates):
states_with_probs.append([maxcut_solver.states[state_index], np.real(np.conj(wf[state_index])*wf[state_index])])
print(states_with_probs[-1][0], states_with_probs[-1][1])
%matplotlib inline
import matplotlib.pyplot as plt
def plot_state_histogram(states_with_probs):
states = np.array(states_with_probs)[:,0]
probs = np.array(states_with_probs)[:,1].astype(float)
n = len(states_with_probs)
plt.barh(range(n), probs, tick_label=states)
plt.show()
plot_state_histogram(states_with_probs)
QAOA_inst = QAOA(connection, qubits, steps=steps, cost_ham=cost_operators,
ref_ham=driver_operators,
init_betas=initial_beta,
init_gammas=initial_gamma,
minimizer_kwargs=minimizer_kwargs)
minimizer_kwargs = {'method': 'Nelder-Mead',
'options': {'ftol': 1.0e-2, 'xtol': 1.0e-2,
'disp': False}}
betas, gammas = QAOA_inst.get_angles()
QAOA_inst.get_parametrized_program()
QAOA_inst.get_string(betas, gammas)
from pyquil.paulis import PauliTerm, PauliSum
import networkx as nx
maxcut_graph = nx.Graph()
for edge in first_graph:
maxcut_graph.add_edge(*edge)
graph = maxcut_graph.copy()
cost_operators = []
for i, j in graph.edges():
cost_operators.append(PauliTerm("Z", i, 0.5)*PauliTerm("Z", j) + PauliTerm("I", 0, -0.5))
print(cost_operators[0])
print(cost_operators[1])
driver_operators = []
for i in graph.nodes():
driver_operators.append(PauliSum([PauliTerm("X", i, -1.0)]))
print(driver_operators[0])
from grove.pyqaoa.qaoa import QAOA
initial_beta = 0
initial_gamma = 0
minimizer_kwargs = {'method': 'Nelder-Mead',
'options': {'ftol': 1.0e-2, 'xtol': 1.0e-2,
'disp': False}}
QAOA_inst = QAOA(qvm_connection, qubits, steps=1,
cost_ham=cost_operators,
ref_ham=driver_operators,
init_betas=initial_beta,
init_gammas=initial_gamma,
minimizer_kwargs=minimizer_kwargs)
betas, gammas = QAOA_inst.get_angles()
print("Values of betas:", betas)
print("Values of gammas:", gammas)
print("And the most common measurement is... ")
most_common_result, _ = QAOA_inst.get_string(betas, gammas)
print(most_common_result)
| 0.60054 | 0.990874 |
```
! pip install -q tensorflow==2.0.0.alpha0
import tensorflow as tf
print(tf.__version__)
import numpy as np
num_exp, training_steps, learning_rate, disp = 1000, 1000, 0.001, 100
m, c = 6, -5
# This is the initialization of the variables
def train_data(n, m, c):
x = tf.random.normal([n])
noise = tf.random.normal([n])
y = m*x + c + noise
return x, y
# Forward propagation result
def prediction(x, weight, bias):
return weight*x + bias
# Loss function
def loss(x, weight, bias, y):
error = prediction(x, weight, bias) - y
sq_error = tf.square(error)
return tf.reduce_mean(input_tensor=sq_error)
# Calculates and returns the gradient using tf.GradientTape()
def grad(x, weight, bias, y):
with tf.GradientTape() as tape:
loss_ = loss(x, weight, bias, y)
return tape.gradient(loss_, [weight, bias])
# Visualize the initial results
import matplotlib.pyplot as plt
x, y = train_data(num_exp, m, c)
plt.scatter(x, y)
plt.xlabel('X values')
plt.ylabel('Y values')
plt.title('Initialization')
W = tf.Variable(np.random.randn())
B = tf.Variable(np.random.randn())
print(f'Initial loss is {loss(x, W, B, y)}')
# Gradient descent
for i in range(training_steps):
d_weight, d_bias = grad(x, W, B, y)
dW = d_weight * learning_rate
dB = d_bias * learning_rate
W.assign_sub(dW)
B.assign_sub(dB)
if i == 0 or i % disp == 0:
print(f'Loss after iteration {i}: {loss(x, W, B, y)}')
print(f'W: {W.numpy()} and B: {B.numpy()}')
x1 = np.linspace(-3, 4, 50)
y1 = W.numpy()*x1 + B.numpy()
plt.scatter(x1, y1)
plt.xlabel('X value')
plt.ylabel('Y value')
plt.title('Final result')
```
## Boston Housing Prices Prediction
```
! pip install -q tensorflow-gpu==2.0.0.alpha0
import tensorflow as tf
print(tf.__version__)
from sklearn.preprocessing import scale
from sklearn.datasets import load_boston
train = 300
val = 100
features, prices = load_boston(True)
test = len(features) - train - val
train_features = tf.cast(scale(features[:train]), tf.float32)
train_prices = prices[:train]
val_features = tf.cast(scale(features[train:train+val]), tf.float32)
val_prices = prices[train:train+val]
test_features = tf.cast(scale(features[val+train:train+val+test]), tf.float32)
test_prices = prices[val+train:train+val+test]
def loss(x, y, weights, bias):
error = tf.subtract(prediction(x, weights, bias), y)
sq_error = tf.square(error)
return tf.sqrt(tf.reduce_mean(input_tensor=sq_error))
def prediction(x, weights, bias):
return tf.add(tf.multiply(tf.transpose(weights), x), bias)
def grad(x, y, W, B):
with tf.GradientTape() as tape:
loss_ = loss(x, y, W, B)
return tape.gradient(loss_, [W, B])
W = tf.Variable(tf.random.normal([13, 1], mean=0.0, stddev=1.0, dtype=tf.float32))
B = tf.Variable(tf.zeros(1), dtype=tf.float32)
learning_rate = 0.01
for i in range(5000):
d_weights , d_bias = grad(train_features, train_prices, W, B)
dW = learning_rate * d_weights
dB = learning_rate * d_bias
W.assign_sub(dW)
B.assign_sub(dB)
if i == 0 or i % 100 == 0:
print(f'Iteration {i}: Loss = {loss(train_features, train_prices, W, B)}')
example_house = 69
y = test_prices[example_house]
y_pred = prediction(test_features,W.numpy(),B.numpy())[example_house]
print("Actual median house value",y," in $10K")
print("Predicted median house value ",y_pred.numpy()," in $10K")
```
|
github_jupyter
|
! pip install -q tensorflow==2.0.0.alpha0
import tensorflow as tf
print(tf.__version__)
import numpy as np
num_exp, training_steps, learning_rate, disp = 1000, 1000, 0.001, 100
m, c = 6, -5
# This is the initialization of the variables
def train_data(n, m, c):
x = tf.random.normal([n])
noise = tf.random.normal([n])
y = m*x + c + noise
return x, y
# Forward propagation result
def prediction(x, weight, bias):
return weight*x + bias
# Loss function
def loss(x, weight, bias, y):
error = prediction(x, weight, bias) - y
sq_error = tf.square(error)
return tf.reduce_mean(input_tensor=sq_error)
# Calculates and returns the gradient using tf.GradientTape()
def grad(x, weight, bias, y):
with tf.GradientTape() as tape:
loss_ = loss(x, weight, bias, y)
return tape.gradient(loss_, [weight, bias])
# Visualize the initial results
import matplotlib.pyplot as plt
x, y = train_data(num_exp, m, c)
plt.scatter(x, y)
plt.xlabel('X values')
plt.ylabel('Y values')
plt.title('Initialization')
W = tf.Variable(np.random.randn())
B = tf.Variable(np.random.randn())
print(f'Initial loss is {loss(x, W, B, y)}')
# Gradient descent
for i in range(training_steps):
d_weight, d_bias = grad(x, W, B, y)
dW = d_weight * learning_rate
dB = d_bias * learning_rate
W.assign_sub(dW)
B.assign_sub(dB)
if i == 0 or i % disp == 0:
print(f'Loss after iteration {i}: {loss(x, W, B, y)}')
print(f'W: {W.numpy()} and B: {B.numpy()}')
x1 = np.linspace(-3, 4, 50)
y1 = W.numpy()*x1 + B.numpy()
plt.scatter(x1, y1)
plt.xlabel('X value')
plt.ylabel('Y value')
plt.title('Final result')
! pip install -q tensorflow-gpu==2.0.0.alpha0
import tensorflow as tf
print(tf.__version__)
from sklearn.preprocessing import scale
from sklearn.datasets import load_boston
train = 300
val = 100
features, prices = load_boston(True)
test = len(features) - train - val
train_features = tf.cast(scale(features[:train]), tf.float32)
train_prices = prices[:train]
val_features = tf.cast(scale(features[train:train+val]), tf.float32)
val_prices = prices[train:train+val]
test_features = tf.cast(scale(features[val+train:train+val+test]), tf.float32)
test_prices = prices[val+train:train+val+test]
def loss(x, y, weights, bias):
error = tf.subtract(prediction(x, weights, bias), y)
sq_error = tf.square(error)
return tf.sqrt(tf.reduce_mean(input_tensor=sq_error))
def prediction(x, weights, bias):
return tf.add(tf.multiply(tf.transpose(weights), x), bias)
def grad(x, y, W, B):
with tf.GradientTape() as tape:
loss_ = loss(x, y, W, B)
return tape.gradient(loss_, [W, B])
W = tf.Variable(tf.random.normal([13, 1], mean=0.0, stddev=1.0, dtype=tf.float32))
B = tf.Variable(tf.zeros(1), dtype=tf.float32)
learning_rate = 0.01
for i in range(5000):
d_weights , d_bias = grad(train_features, train_prices, W, B)
dW = learning_rate * d_weights
dB = learning_rate * d_bias
W.assign_sub(dW)
B.assign_sub(dB)
if i == 0 or i % 100 == 0:
print(f'Iteration {i}: Loss = {loss(train_features, train_prices, W, B)}')
example_house = 69
y = test_prices[example_house]
y_pred = prediction(test_features,W.numpy(),B.numpy())[example_house]
print("Actual median house value",y," in $10K")
print("Predicted median house value ",y_pred.numpy()," in $10K")
| 0.842734 | 0.888517 |
# Numpy (Часть 1)
> 🚀 В этой практике нам понадобятся: `numpy==1.21.2`
> 🚀 Установить вы их можете с помощью команды: `!pip install numpy==1.21.2`
## Содержание
* [Создание массивов](#Создание-массивов)
* [Хитрая индексация](#Хитрая-индексация)
* [Задание - подумаем](#Задание---подумаем)
* [Задание - учимся обращать](#Задание---учимся-обращать)
* [Задание - подмассив](#Задание---подмассив)
* [Хитрая индексация в матрицах](#Хитрая-индексация-в-матрицах)
* [Задание - еще больше срезаем](#Задание---еще-больше-срезаем)
* [Задание - кручу-верчу - запутать хочу](#Задание---кручу-верчу---запутать-хочу)
* [Типы данных в массивах](#Типы-данных-в-массивах)
Numpy - это библиотека для математических вычислений. Написана на языке С, поэтому считается наиболее предпочтительным вариантом при работе с многомерными массивами из-за производительности.
[Официальный сайт](https://numpy.org/doc/stable/) последней стабильной версии.
Начало работы с `numpy` заключается в подключении модуля. При этом в практике применения есть уже общепринятое сокращение для него под названием `np`:
```
import numpy as np
```
> Если вы ранее работали с MATLAB, обратите внимание, как некоторые подходы и функции схожи.
## Создание массивов
Для того, чтобы начать работать с `numpy`, мы должны научиться создавать объекты `ndarray`, которые по сути являются N-мерными массивами.
```
# Самый просто способ создать массив numpy - взять уже существующий list и передать в функцию np.array()
arr_1d = np.array([1, 2, 3])
# Теперь проверим
# - тип объекта c помощью функции type()
# - размерность с помощью аттрибута .shape
# - доступ по индексам, как у обычного list
# Для отладки можно выводить небольшие массивы прямо через print()
print(arr_1d)
print(type(arr_1d))
print(arr_1d.shape)
print(arr_1d[0])
print(arr_1d[2])
print(arr_1d[-1])
```
> Обратите внимание, индекс с отрицательным значением означает индексацию с конца. Это возможность языка Python. В данном случае индекс -1 ~ 2, так как 2 - последний индекс в массиве из трёх элементов. Аналогично, если хотите взять второй элемент с конца, то можете использовать индекс -2 и т.д.
Как видите, объект имеет тип `np.ndarray`, таким образом описываются все массивы при работе с numpy. Размерность представляет собой кортеж с одним элементом (создали 1D массив ~ массив первого ранга в терминах numpy).
```
# Теперь создадим двумерный массив с помощью тех же list
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
# Проверим также тип, размерность и доступ по индексам
print(arr_2d)
print(type(arr_2d))
print(arr_2d.shape)
print(arr_2d[0, 0])
print(arr_2d[1, 2])
print(arr_2d[1, 0])
```
Теперь видно, что в кортеже размерности стало два элемента, при этом тип объекта никак не поменялся.
Индексация в 2D массиве делается уже посредством двух индексов:
- первый индекс - номер ряда (строки);
- второй индекс - номер колонки (столбца).
> В 1D массивах вообще никаких вопросов не возникает, в 2D (ряд, колонка), если разворачивать до 3D массивов, то можно интерпретировать как (ряд, колонка, глубина). Дальнейшие размерности уже сложнее в визуальной интерпретации, поэтому вместо названий для каждой размерности идет просто индексация.
Помимо способов создания массивов из уже существующих представлений в виде `list`, можно также создавать массивы по-другому. Рассмотрим некоторые из них:
```
# Создание массива фиксированного размера
np.ndarray((5, 3))
```
В представленном способе мы напрямую вызываем конструктор и передаем ему размерность. Какими числами будет заполнен массив - никто не знает. Вероятнее всего, это будут нули, но для уверенности лучше самостоятельно заполнить такой массив данными.
```
# Явное создание массива нулей
np.zeros((2, 3))
# Явное создание массива единиц
np.ones((3, 2))
# Создание массива, заполненного константным значением
np.full((3, 4), 5)
# 2D массив с единичной главной диагональю
# (*) В этой функции размерность задается не кортежем, а отдельными аргументами
np.eye(3, 2)
# Создание массива нулей с такой же размерностью, как уже существующий
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
np.zeros_like(arr_2d)
# Создание массива единиц с такой же размерностью, как уже существующий
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
np.ones_like(arr_2d)
# Создание массива со случайными значениями в интервале [0; 1.0)
np.random.random((2,2))
# Аналог функции range
np.arange(start=1, stop=10, step=1.5)
# Также создание диапазона значений, но уже с заданием количества элементов
# (*) stop уже входит в создаваемый диапазон
np.linspace(start=1, stop=2, num=10)
```
## Хитрая индексация
Индексация в Python не ограничивается заданием конкретных индексов для получения значений в контейнерах (стандартных или массивов `ndarray`). Существуют специальные символы и подходы для работы с диапазонами данных, которые не только упрощают и улучшают код, но и выполняются более быстро, нежели проходы по массивам циклом.
Начнём со знакомства с символом `:`, который позволяет задавать диапазон индексов для чтения/записи контейнеров.
```
# Для начала на простом списке (1D массива)
# Следующее создание массива можно заменить list(range(1, 11))
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# Простая индексация
print(arr[0])
print(arr[-2])
print(arr[5])
```
Для получения подмассива (части массива) или записи в подмассив используется нотация $$index_{start}:index_{end}:step$$
- $index_{start}$ - индекс начала подмассива
- $index_{end}$ - индекс конца подмассива
- $step$ - шаг подмассива
```
# Получение части массива c 3-го по 9-й элемент (не включительно)
# или со 2-го по 8-й (при индексации с нуля)
# с шагом 2
print(arr[2:8:2])
# Если шаг не задан, то он равен единице (при этом второй раз : не пишется)
print(arr[2:8])
# Шаг может быть и отрицательным (индексы меняются местами)
print(arr[8:2:-1])
# Если не задавать index_start или index_end,
# то они будут равны индексу начала и конца массива
print(arr[2:])
print(arr[:8])
# Можно комбинировать один из индексов и шаг
print(arr[2::2])
print(arr[:8:3])
# И не забываем, что все трюки работают и на запись
new_arr = list(range(1, 11))
new_arr[1:5] = arr[:4]
print(new_arr)
# Не самая полезная, но все же запись (получить весь диапазон)
print(arr[:])
```
### Задание - подумаем
Объясните результат операции:
```
print(arr[:5:-2])
```
### Задание - учимся обращать
Получите перевернутый список:
```
data = list(range(10))
print(data)
# TODO - [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
```
### Задание - подмассив
Получите массив без первого и двух последних элементов:
```
data = list(range(10))
print(data)
# TODO - [1, 2, 3, 4, 5, 6, 7]
```
## Хитрая индексация в матрицах
Работа с одномерными списками удобна даже через класс `list`, но 2D массивы уже удобнее использовать через библиотеку numpy. Использование numpy никак не ограничивает применение такой индексации, так что можно делать много классных штук:
```
arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(arr)
```
В индексации numpy есть очень полезное правило: если последующие индексы не заданы, то они принимаются как "весь диапазон". Например, в двумерном массиве мы индексируем по двум числам $[3, 2]$. Если в 2D массиве задать индекс $[3]$, то это эквивалентно индексации $[3, :]$, то есть третий ряд, все колонки.
В плане предшествующих индексов это не работает, поэтому, чтобы получить целую колонку, надо индексировать $[:, 2]$.
```
# Получим вторую строку массива
print(arr[2])
print(arr[2, :])
# Получим первую колонку массива
print(arr[:, 1])
# Получить первые два элемента (первые две колонки) первого ряда
print(arr[1, :2])
# Можно повторять целые части массива
# (но при этом должны соотноситься размерности)
# ndarray.copy() - функция копирования массива
# Копируем, чтобы не изменить оригинальный
new_arr = arr.copy()
print(arr)
new_arr[2, :] = arr[1, :]
print(new_arr)
# При этом, такая индексация - это новый массив со своей размерностью.
print(arr[:2, :2])
print(arr[:2, :2].shape)
# В качестве индексов можно также задавать другие массивы
# Получаем первую и последнюю колонки
print(arr[:, [0, -1]])
# И таким образом никто не заставляет писать в том же порядке индексы
# Перемешаем ряды
print(arr[[2, 0, 1], :])
# Также, можно комбинировать способы задания
print(arr[[2, 0], [1, 3]])
# То же самое, только первая запись дает массив
print(arr[2, 1], arr[0, 3])
# Создаем список возможных индексов для рядов массива
row_indices = list(range(arr.shape[0]))
print(row_indices)
# Переворачиваем его
row_indices = list(reversed(row_indices))
print(row_indices)
# Используем для индексации
print('----------------')
print(arr[row_indices])
```
### Задание - еще больше срезаем
Получите массив без крайних рядов и колонок (по одной с каждой стороны)
```
data = np.random.randint(low=0, high=10, size=(5, 6))
print(data)
# TODO - центральная часть массива размером (3, 4)
```
### Задание - кручу-верчу - запутать хочу
Произведите перемешивание колонок с помощью функции `numpy.random.permutation()`:
<details>
<summary>Подсказка</summary>
Перемешать колонки можно путем перемешивания списка возможных индексов колонок (`range(<col_count>)`) и затем индексацией этого списка по индексам колонок (`[:, cols]`).
</details>
```
data = np.random.randint(low=0, high=10, size=(3, 6))
print(data)
# TODO - такой же массив, но со случайной перестановкой колонок
```
## Типы данных в массивах
Массивы в numpy имеют не только размер, но и конкретный тип данных, которые хранятся внутри массива. При создании массива почти все функции создания имеют аргумент `dtype`, который означает, с каким типом создать данным массив. Также, класс `ndarray` имеет атрибут `dtype`, который означает тип хранимых данных.
Подробнее можно прочитать в [документации](https://numpy.org/doc/stable/reference/arrays.dtypes.html).
```
# Создадим массив без задания типа - тип будет определен автоматически
arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(arr.dtype)
# int, так как все элементы являются целочисленными
# Изменим один элемент на вещественный
arr = np.array([[1.5, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(arr.dtype)
# Один из элементов float, поэтому весь массив будет float
# Зададим явно тип массива
# Хоть массив и содержит вещественные числа
# мы создаем массив целочисленных, что приводит
# к округлению
arr = np.array([[1.1, 1.6, 2.4], [-1.7, 2.6, -1.2]], dtype=int)
print(arr)
print(arr.dtype)
# Создаем массив вещественных
arr = np.array([[1.1, 1.6, 2.4], [-1.7, 2.6, -1.2]])
print(arr)
print(arr.dtype)
print('----------')
# Но в какой-то момент нам нужно привести массив к целочисленным
# Воспользуемся методом ndarray.astype()
arr = arr.astype(int)
print(arr)
print(arr.dtype)
# При этом попытки записать в целочисленный массив
# вещественное число приводят к округлению
arr = np.array([[1.1, 1.6, 2.4], [-1.7, 2.6, -1.2]], dtype=int)
print(arr)
arr[0, 1] = 10.12
print(arr)
```
|
github_jupyter
|
import numpy as np
# Самый просто способ создать массив numpy - взять уже существующий list и передать в функцию np.array()
arr_1d = np.array([1, 2, 3])
# Теперь проверим
# - тип объекта c помощью функции type()
# - размерность с помощью аттрибута .shape
# - доступ по индексам, как у обычного list
# Для отладки можно выводить небольшие массивы прямо через print()
print(arr_1d)
print(type(arr_1d))
print(arr_1d.shape)
print(arr_1d[0])
print(arr_1d[2])
print(arr_1d[-1])
# Теперь создадим двумерный массив с помощью тех же list
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
# Проверим также тип, размерность и доступ по индексам
print(arr_2d)
print(type(arr_2d))
print(arr_2d.shape)
print(arr_2d[0, 0])
print(arr_2d[1, 2])
print(arr_2d[1, 0])
# Создание массива фиксированного размера
np.ndarray((5, 3))
# Явное создание массива нулей
np.zeros((2, 3))
# Явное создание массива единиц
np.ones((3, 2))
# Создание массива, заполненного константным значением
np.full((3, 4), 5)
# 2D массив с единичной главной диагональю
# (*) В этой функции размерность задается не кортежем, а отдельными аргументами
np.eye(3, 2)
# Создание массива нулей с такой же размерностью, как уже существующий
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
np.zeros_like(arr_2d)
# Создание массива единиц с такой же размерностью, как уже существующий
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
np.ones_like(arr_2d)
# Создание массива со случайными значениями в интервале [0; 1.0)
np.random.random((2,2))
# Аналог функции range
np.arange(start=1, stop=10, step=1.5)
# Также создание диапазона значений, но уже с заданием количества элементов
# (*) stop уже входит в создаваемый диапазон
np.linspace(start=1, stop=2, num=10)
# Для начала на простом списке (1D массива)
# Следующее создание массива можно заменить list(range(1, 11))
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# Простая индексация
print(arr[0])
print(arr[-2])
print(arr[5])
# Получение части массива c 3-го по 9-й элемент (не включительно)
# или со 2-го по 8-й (при индексации с нуля)
# с шагом 2
print(arr[2:8:2])
# Если шаг не задан, то он равен единице (при этом второй раз : не пишется)
print(arr[2:8])
# Шаг может быть и отрицательным (индексы меняются местами)
print(arr[8:2:-1])
# Если не задавать index_start или index_end,
# то они будут равны индексу начала и конца массива
print(arr[2:])
print(arr[:8])
# Можно комбинировать один из индексов и шаг
print(arr[2::2])
print(arr[:8:3])
# И не забываем, что все трюки работают и на запись
new_arr = list(range(1, 11))
new_arr[1:5] = arr[:4]
print(new_arr)
# Не самая полезная, но все же запись (получить весь диапазон)
print(arr[:])
print(arr[:5:-2])
data = list(range(10))
print(data)
# TODO - [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
data = list(range(10))
print(data)
# TODO - [1, 2, 3, 4, 5, 6, 7]
arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(arr)
# Получим вторую строку массива
print(arr[2])
print(arr[2, :])
# Получим первую колонку массива
print(arr[:, 1])
# Получить первые два элемента (первые две колонки) первого ряда
print(arr[1, :2])
# Можно повторять целые части массива
# (но при этом должны соотноситься размерности)
# ndarray.copy() - функция копирования массива
# Копируем, чтобы не изменить оригинальный
new_arr = arr.copy()
print(arr)
new_arr[2, :] = arr[1, :]
print(new_arr)
# При этом, такая индексация - это новый массив со своей размерностью.
print(arr[:2, :2])
print(arr[:2, :2].shape)
# В качестве индексов можно также задавать другие массивы
# Получаем первую и последнюю колонки
print(arr[:, [0, -1]])
# И таким образом никто не заставляет писать в том же порядке индексы
# Перемешаем ряды
print(arr[[2, 0, 1], :])
# Также, можно комбинировать способы задания
print(arr[[2, 0], [1, 3]])
# То же самое, только первая запись дает массив
print(arr[2, 1], arr[0, 3])
# Создаем список возможных индексов для рядов массива
row_indices = list(range(arr.shape[0]))
print(row_indices)
# Переворачиваем его
row_indices = list(reversed(row_indices))
print(row_indices)
# Используем для индексации
print('----------------')
print(arr[row_indices])
data = np.random.randint(low=0, high=10, size=(5, 6))
print(data)
# TODO - центральная часть массива размером (3, 4)
data = np.random.randint(low=0, high=10, size=(3, 6))
print(data)
# TODO - такой же массив, но со случайной перестановкой колонок
# Создадим массив без задания типа - тип будет определен автоматически
arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(arr.dtype)
# int, так как все элементы являются целочисленными
# Изменим один элемент на вещественный
arr = np.array([[1.5, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(arr.dtype)
# Один из элементов float, поэтому весь массив будет float
# Зададим явно тип массива
# Хоть массив и содержит вещественные числа
# мы создаем массив целочисленных, что приводит
# к округлению
arr = np.array([[1.1, 1.6, 2.4], [-1.7, 2.6, -1.2]], dtype=int)
print(arr)
print(arr.dtype)
# Создаем массив вещественных
arr = np.array([[1.1, 1.6, 2.4], [-1.7, 2.6, -1.2]])
print(arr)
print(arr.dtype)
print('----------')
# Но в какой-то момент нам нужно привести массив к целочисленным
# Воспользуемся методом ndarray.astype()
arr = arr.astype(int)
print(arr)
print(arr.dtype)
# При этом попытки записать в целочисленный массив
# вещественное число приводят к округлению
arr = np.array([[1.1, 1.6, 2.4], [-1.7, 2.6, -1.2]], dtype=int)
print(arr)
arr[0, 1] = 10.12
print(arr)
| 0.039232 | 0.964489 |
# VideoRcvKafka
The producer (VideoSendKafka.py) is sending video frames on the TOPIC,consume and render
the frames as they arrive. The frames are encoded and broken up into chunks.
Demotrate that we can send encoded images
```
import kafka
import os
import getpass
import sys
import json
import base64
import kafka
import ssl
import time
import datetime
import matplotlib.pyplot as plt
import io
from PIL import Image
import logging
import numpy as np
import cv2
import matplotlib.pyplot as plt
import ipywidgets as widgets
from ipywidgets import Button, HBox, VBox, Layout
from IPython.display import display, clear_output
if '../jupyter' not in sys.path:
sys.path.insert(0, '../jupyter')
import credential
## setup
TOPIC = 'VideoFrame'
def decode_img(bin64):
img = Image.open(io.BytesIO(base64.b64decode(bin64)))
return img
```
## Get the credentials.
```
creds = json.loads(credential.magsEventStream)
```
## Kafka arrive, decode and display
The producer (VideoSendKafka.py) is sending video frames on the TOPIC, here consume and write
the frames as they arrive.
```
img_obj = widgets.Output(layout={'border': '1px solid red','width':'50%','height':'300pt'})
dashboard_img = widgets.VBox([img_obj])
display(dashboard_img)
cons = kafka.KafkaConsumer(TOPIC,
bootstrap_servers=creds["kafka_brokers_sasl"],
security_protocol="SASL_SSL",
sasl_mechanism="PLAIN",
sasl_plain_username=creds["user"],
sasl_plain_password=creds["api_key"],
ssl_cafile=ssl.get_default_verify_paths().cafile, consumer_timeout_ms=30000)
start = time.time()
logging.getLogger("__name__").warning("start")
startup = True # get to begining of frame at startup.
for msg in cons:
chunk = json.loads(msg[6])
if startup:
if chunk['chunk_idx'] != 0:
continue
startup = False
if chunk['chunk_idx'] == 0:
# start of a new frame.
image_string = chunk['data']
continue
if chunk['chunk_idx'] == chunk['chunk_total']:
# frame complete - convert to image and display
image = decode_img(image_string)
with img_obj:
display(image)
clear_output(wait=True)
chunk_string = ""
continue
# building up frame
image_string = "".join([image_string, chunk['data']])
#print("message cnt:", len(chunks))
cons.close()
logging.getLogger("__name__").warning("done")
```
|
github_jupyter
|
import kafka
import os
import getpass
import sys
import json
import base64
import kafka
import ssl
import time
import datetime
import matplotlib.pyplot as plt
import io
from PIL import Image
import logging
import numpy as np
import cv2
import matplotlib.pyplot as plt
import ipywidgets as widgets
from ipywidgets import Button, HBox, VBox, Layout
from IPython.display import display, clear_output
if '../jupyter' not in sys.path:
sys.path.insert(0, '../jupyter')
import credential
## setup
TOPIC = 'VideoFrame'
def decode_img(bin64):
img = Image.open(io.BytesIO(base64.b64decode(bin64)))
return img
creds = json.loads(credential.magsEventStream)
img_obj = widgets.Output(layout={'border': '1px solid red','width':'50%','height':'300pt'})
dashboard_img = widgets.VBox([img_obj])
display(dashboard_img)
cons = kafka.KafkaConsumer(TOPIC,
bootstrap_servers=creds["kafka_brokers_sasl"],
security_protocol="SASL_SSL",
sasl_mechanism="PLAIN",
sasl_plain_username=creds["user"],
sasl_plain_password=creds["api_key"],
ssl_cafile=ssl.get_default_verify_paths().cafile, consumer_timeout_ms=30000)
start = time.time()
logging.getLogger("__name__").warning("start")
startup = True # get to begining of frame at startup.
for msg in cons:
chunk = json.loads(msg[6])
if startup:
if chunk['chunk_idx'] != 0:
continue
startup = False
if chunk['chunk_idx'] == 0:
# start of a new frame.
image_string = chunk['data']
continue
if chunk['chunk_idx'] == chunk['chunk_total']:
# frame complete - convert to image and display
image = decode_img(image_string)
with img_obj:
display(image)
clear_output(wait=True)
chunk_string = ""
continue
# building up frame
image_string = "".join([image_string, chunk['data']])
#print("message cnt:", len(chunks))
cons.close()
logging.getLogger("__name__").warning("done")
| 0.122379 | 0.500244 |
Kolekcia všetkých importov použitých v tomto projekte
```
import pandas as pd
import numpy as np
import math
```
Načítaj csv súbor, v ktorom už sú len riadky v danom rozsahu
```
data = pd.read_csv('/content/drive/MyDrive/Škola/WM/semestralny_projekt/wm2020.csv', ',')
data
```
###1. očistite dátový súbor od nepotrebných údajov *(RequestMethod/Version, StatusCode, URL)*
```
request = ['HEAD', 'POST']
suffix = ['.bmp','.jpg','.jpeg','.png','.gif','.JPG','.css','.flv','.ico','.swf','.rss','.xml','.cur','.js','.json','.svg','.svg','.woff','.eot']
```
Nechaj v dataframe len riadky, ktoré spĺňajú požiadavky
```
data = data[~data.url.str.contains('|'.join(suffix))]
data = data[~data.req_code.astype(str).str.match(r'1* | 4* | 5* ')]
data = data[~data.url.str.contains('|'.join(request))]
data = data[~data.url.str.contains('GET /navbar/')]
data = data[~data.url.str.contains('ctrl=cron')]
data
```
###2. očistite dátový súbor od prístupov robotov vyhľadávacích služieb
* identifikujte robotov na základe prístupu k súboru robots.txt (URL)
* identifikujte robotov na základe poľa User-Agent (Agent)
Získaj ip robotov do pola
```
ipArray = data[data.url.str.contains('robots.txt')]['clientIp'].unique()
print("Size: " + str(ipArray.size))
```
Odstráň ip robotov z csv súboru
```
data = data[~data.clientIp.str.contains('|'.join(ipArray))]
```
Odstráň robotov vďaka kľučovým slovám ako *(bot, crawl, spider)*
```
robotArray = ['bot', 'crawl', 'spider']
data = data[~data.useragent.str.contains('|'.join(robotArray), na=False)]
data
```
###3. Vyselektujte z dátového súboru len vaše skúmané obdobie a vytvorte premennú UnixTime
Vytvor nový stĺpec unix timestamp pomocou datetime
```
data['unixtime'] = pd.to_datetime(data['datetime'], format="%d/%b/%Y:%H:%M:%S %z")
data['unixtime'] = data['unixtime'].values.astype(np.int64) // 10 ** 9
data.head()
```
###4. Identifikujte používateľov na základe IP adresy a poľa User-Agent
Usporiadaj hodnoty pomocou *ip*, a potom *useragent* a *unixtime*
```
data = data.sort_values(by = ['clientIp', 'useragent', 'unixtime'])
```
Definuj stĺpec userid zo stĺpca clientIp a stĺpca useragent
```
previousIp = ""
previousUserAgent = ""
previousUserId = 0
for i, row in data.iterrows():
if (i == 0):
data.at[i,'userid'] = 0
previousIp = row['clientIp']
previousUserAgent = row['useragent']
else:
if ((row['clientIp'] == previousIp) & (row['useragent'] == previousUserAgent)):
data.at[i,'userid'] = previousUserId
else:
previousUserId += 1
previousIp = row['clientIp']
previousUserAgent = row['useragent']
data.at[i,'userid'] = previousUserId
data.head()
```
###5. Vytvorte premennú Length na základe User_ID a 60 min. STT.
```
data.reset_index(drop=True, inplace=True)
data['length'] = ''
for i, row in data.iterrows():
if (i < len(data) - 1):
if (data.at[i,'userid'] == data.at[i+1,'userid']):
if ((data.at[i+1,'unixtime'] - data.at[i,'unixtime']) < 3600):
data.at[i,'length'] = data.at[i+1,'unixtime'] - data.at[i,'unixtime']
data
```
###6. Identifikujte sedenia na základe metódy Reference Length (použite hodnotu pre podiel navigačných stránok: 40%)
```
data = data.replace('', np.nan)
data.head()
data['RLength'] = ''
count = 1
time = 0
l = 1 / data['length'].mean(skipna = True)
C = (-np.log(1-0.4)) / l
for i, row in data.iterrows():
if (i != 0):
if (data.at[i,'userid'] == data.at[i-1,'userid']):
if not (math.isnan(data.at[i-1, 'length'])):
time += data.at[i-1, 'length'].astype(int)
else:
count += 1
time = 0
if (time > C):
count += 1
time = 0
else:
count += 1
time = 0
data.at[i, 'RLength'] = count
data
```
###7. Doplňte chýbajúce požiadavky do identifikovaných sedení (dopĺňanie ciest)
```
data.info()
```
Nahraď 'GET / HTTP/1.1' s 'https://www.ukf.sk/'
```
for i, row in data.iterrows():
data.at[i,'url'] = ('https://www.ukf.sk/' + str(data.at[i,'url'])[5:-9])
data.head()
```
Vytvor triedu 'Stack'
```
class Stack:
def __init__(self):
self.stack = []
def add(self, dataval):
if dataval not in self.stack:
self.stack.append(dataval)
return True
else:
return False
def peek(self, i):
return self.stack[i]
def clear(self):
self.stack = []
def length(self):
return len(self.stack)
stack = Stack()
new_rows = []
stack2 = []
for i, row in data.iterrows():
if ((i < len(data) - 1) and (i > 0)):
if ((data.at[i, 'referer'].__contains__('https://www.ukf.sk/')) and (data.at[i+1, 'referer'].__contains__('https://www.ukf.sk/')) and (not ((data.at[i, 'url'].__contains__('image') ) == True) and (not ((data.at[i, 'url'].__contains__('iframe')== True )))) ):
if ((data.at[i,'RLength'] != data.at[i-1,'RLength']) and (data.at[i,'RLength'] == data.at[i+1,'RLength'])):
new_rows.append(row.values)
stack.add([data.at[i, 'url'], data.at[i+1, 'referer']])
elif (data.at[i,'RLength'] == data.at[i+1,'RLength']):
stack.add([data.at[i, 'url'], data.at[i+1, 'referer']])
if ((data.at[i, 'url']) == data.at[i+1, 'referer']):
new_rows.append(row.values)
else:
new_rows.append(row.values)
a = row.copy()
stack2 = []
stack2.append(stack.peek(-1))
a.url = stack2[0][1]
a.referrer = stack2[0][0]
a.length = 1
new_rows.append(a)
else:
new_rows.append(row.values)
else:
new_rows.append(row.values)
else:
new_rows.append(row.values)
df = pd.DataFrame(new_rows, columns = data.columns)
df
```
Vytvor finálne csv
```
df.to_csv('Laca_csv_final.csv', sep=';')
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import math
data = pd.read_csv('/content/drive/MyDrive/Škola/WM/semestralny_projekt/wm2020.csv', ',')
data
request = ['HEAD', 'POST']
suffix = ['.bmp','.jpg','.jpeg','.png','.gif','.JPG','.css','.flv','.ico','.swf','.rss','.xml','.cur','.js','.json','.svg','.svg','.woff','.eot']
data = data[~data.url.str.contains('|'.join(suffix))]
data = data[~data.req_code.astype(str).str.match(r'1* | 4* | 5* ')]
data = data[~data.url.str.contains('|'.join(request))]
data = data[~data.url.str.contains('GET /navbar/')]
data = data[~data.url.str.contains('ctrl=cron')]
data
ipArray = data[data.url.str.contains('robots.txt')]['clientIp'].unique()
print("Size: " + str(ipArray.size))
data = data[~data.clientIp.str.contains('|'.join(ipArray))]
robotArray = ['bot', 'crawl', 'spider']
data = data[~data.useragent.str.contains('|'.join(robotArray), na=False)]
data
data['unixtime'] = pd.to_datetime(data['datetime'], format="%d/%b/%Y:%H:%M:%S %z")
data['unixtime'] = data['unixtime'].values.astype(np.int64) // 10 ** 9
data.head()
data = data.sort_values(by = ['clientIp', 'useragent', 'unixtime'])
previousIp = ""
previousUserAgent = ""
previousUserId = 0
for i, row in data.iterrows():
if (i == 0):
data.at[i,'userid'] = 0
previousIp = row['clientIp']
previousUserAgent = row['useragent']
else:
if ((row['clientIp'] == previousIp) & (row['useragent'] == previousUserAgent)):
data.at[i,'userid'] = previousUserId
else:
previousUserId += 1
previousIp = row['clientIp']
previousUserAgent = row['useragent']
data.at[i,'userid'] = previousUserId
data.head()
data.reset_index(drop=True, inplace=True)
data['length'] = ''
for i, row in data.iterrows():
if (i < len(data) - 1):
if (data.at[i,'userid'] == data.at[i+1,'userid']):
if ((data.at[i+1,'unixtime'] - data.at[i,'unixtime']) < 3600):
data.at[i,'length'] = data.at[i+1,'unixtime'] - data.at[i,'unixtime']
data
data = data.replace('', np.nan)
data.head()
data['RLength'] = ''
count = 1
time = 0
l = 1 / data['length'].mean(skipna = True)
C = (-np.log(1-0.4)) / l
for i, row in data.iterrows():
if (i != 0):
if (data.at[i,'userid'] == data.at[i-1,'userid']):
if not (math.isnan(data.at[i-1, 'length'])):
time += data.at[i-1, 'length'].astype(int)
else:
count += 1
time = 0
if (time > C):
count += 1
time = 0
else:
count += 1
time = 0
data.at[i, 'RLength'] = count
data
data.info()
for i, row in data.iterrows():
data.at[i,'url'] = ('https://www.ukf.sk/' + str(data.at[i,'url'])[5:-9])
data.head()
class Stack:
def __init__(self):
self.stack = []
def add(self, dataval):
if dataval not in self.stack:
self.stack.append(dataval)
return True
else:
return False
def peek(self, i):
return self.stack[i]
def clear(self):
self.stack = []
def length(self):
return len(self.stack)
stack = Stack()
new_rows = []
stack2 = []
for i, row in data.iterrows():
if ((i < len(data) - 1) and (i > 0)):
if ((data.at[i, 'referer'].__contains__('https://www.ukf.sk/')) and (data.at[i+1, 'referer'].__contains__('https://www.ukf.sk/')) and (not ((data.at[i, 'url'].__contains__('image') ) == True) and (not ((data.at[i, 'url'].__contains__('iframe')== True )))) ):
if ((data.at[i,'RLength'] != data.at[i-1,'RLength']) and (data.at[i,'RLength'] == data.at[i+1,'RLength'])):
new_rows.append(row.values)
stack.add([data.at[i, 'url'], data.at[i+1, 'referer']])
elif (data.at[i,'RLength'] == data.at[i+1,'RLength']):
stack.add([data.at[i, 'url'], data.at[i+1, 'referer']])
if ((data.at[i, 'url']) == data.at[i+1, 'referer']):
new_rows.append(row.values)
else:
new_rows.append(row.values)
a = row.copy()
stack2 = []
stack2.append(stack.peek(-1))
a.url = stack2[0][1]
a.referrer = stack2[0][0]
a.length = 1
new_rows.append(a)
else:
new_rows.append(row.values)
else:
new_rows.append(row.values)
else:
new_rows.append(row.values)
df = pd.DataFrame(new_rows, columns = data.columns)
df
df.to_csv('Laca_csv_final.csv', sep=';')
| 0.067022 | 0.750781 |
```
import os
def fileWalker(path):
fileArray = []
for roots, dirs, files in os.walk(path):
for fn in files:
eachpath = str(roots + '/' + fn)
fileArray.append(eachpath)
# print(fileArray)
return fileArray
# fileWalker('/Users/zw/Desktop/Data Learning/Machine Learning Basics/Spam Filter')
def readText(path, encoding):
with open(path, 'r', encoding=encoding) as f:
lines = f.readlines()
# print(lines)
return lines
# readText('/Users/zw/Desktop/Data Learning/Machine Learning Basics/Spam Filter/ham/1.txt',
# encoding='utf-8')
def email_parser(email_path):
punctuations = """,.<>()*&^%$#@!'";~`[]{}|、\\/~+_-=?"""
content_list = readText(email_path, 'utf-8')
content = (' '.join(content_list)).replace('\r\n', ' ').replace('\t', ' ') # LF, CR, HT
clean_word = []
for punctuation in punctuations:
content = (' '.join(content.split(punctuation))).replace(' ', ' ')
clean_word = [word.lower for word in content.split(' ') if len(word) > 2]
# print(clean_word)
return clean_word
# email_parser('/Users/zw/Desktop/Data Learning/Machine Learning Basics/Spam Filter/ham/1.txt')
def get_word(email_dir):
word_list = []
word_set = []
email_paths = fileWalker(email_dir)
for each_email_path in email_paths:
clean_word = email_parser(each_email_path)
word_list.append(clean_word)
word_set.extend(clean_word)
# print(word_list)
# print(set(word_set))
# print(type(word_set))
return word_list, set(word_set)
# get_word('/Users/zw/Desktop/Data Learning/Machine Learning Basics/Spam Filter/ham/')
def count_word_prob(email_list, union_set):
word_prob = {}
for word in union_set:
counter = 0
for email in email_list:
if word in email:
counter += 1
else:
continue
# prob = 0.0
if counter != 0:
prob = counter/len(email_list)
else:
prob = 0.01
word_prob[word] = prob
return word_prob
def myfilter(ham_word_pro, spam_word_pro, test_file):
test_paths = fileWalker(test_file)
for test_path in test_paths:
# email_spam_prob = 0.0
spam_prob = 0.5
ham_prob = 0.5
file_name = test_path.split('/')[-1]
prob_dict = {}
words = set(email_parser(test_path))
for word in words:
# Psw = 0.0
if word not in spam_word_pro:
Psw = 0.4
else:
Pws = spam_word_pro[word]
Pwh = ham_word_pro[word]
Psw = spam_prob*(Pws/(Pwh*ham_prob+Pws*spam_prob))
prob_dict[word] = Psw
numerator = 1
denominator_h = 1
for k, v in prob_dict.items():
numerator *= v
denominator_h *= (1-v)
email_spam_prob = round(numerator/(numerator+denominator_h), 4)
if email_spam_prob > 0.5:
print(file_name, 'Spam', email_spam_prob)
else:
print(file_name, 'Ham', email_spam_prob)
def main():
ham_file = './ham'
spam_file = './spam'
test_file = './test'
ham_list, ham_set = get_word(ham_file)
spam_list, spam_set = get_word(spam_file)
union_set = ham_set | ham_set
ham_word_pro = count_word_prob(ham_list, union_set)
spam_word_pro = count_word_prob(spam_list, union_set)
myfilter(ham_word_pro, spam_word_pro, test_file)
main()
```
|
github_jupyter
|
import os
def fileWalker(path):
fileArray = []
for roots, dirs, files in os.walk(path):
for fn in files:
eachpath = str(roots + '/' + fn)
fileArray.append(eachpath)
# print(fileArray)
return fileArray
# fileWalker('/Users/zw/Desktop/Data Learning/Machine Learning Basics/Spam Filter')
def readText(path, encoding):
with open(path, 'r', encoding=encoding) as f:
lines = f.readlines()
# print(lines)
return lines
# readText('/Users/zw/Desktop/Data Learning/Machine Learning Basics/Spam Filter/ham/1.txt',
# encoding='utf-8')
def email_parser(email_path):
punctuations = """,.<>()*&^%$#@!'";~`[]{}|、\\/~+_-=?"""
content_list = readText(email_path, 'utf-8')
content = (' '.join(content_list)).replace('\r\n', ' ').replace('\t', ' ') # LF, CR, HT
clean_word = []
for punctuation in punctuations:
content = (' '.join(content.split(punctuation))).replace(' ', ' ')
clean_word = [word.lower for word in content.split(' ') if len(word) > 2]
# print(clean_word)
return clean_word
# email_parser('/Users/zw/Desktop/Data Learning/Machine Learning Basics/Spam Filter/ham/1.txt')
def get_word(email_dir):
word_list = []
word_set = []
email_paths = fileWalker(email_dir)
for each_email_path in email_paths:
clean_word = email_parser(each_email_path)
word_list.append(clean_word)
word_set.extend(clean_word)
# print(word_list)
# print(set(word_set))
# print(type(word_set))
return word_list, set(word_set)
# get_word('/Users/zw/Desktop/Data Learning/Machine Learning Basics/Spam Filter/ham/')
def count_word_prob(email_list, union_set):
word_prob = {}
for word in union_set:
counter = 0
for email in email_list:
if word in email:
counter += 1
else:
continue
# prob = 0.0
if counter != 0:
prob = counter/len(email_list)
else:
prob = 0.01
word_prob[word] = prob
return word_prob
def myfilter(ham_word_pro, spam_word_pro, test_file):
test_paths = fileWalker(test_file)
for test_path in test_paths:
# email_spam_prob = 0.0
spam_prob = 0.5
ham_prob = 0.5
file_name = test_path.split('/')[-1]
prob_dict = {}
words = set(email_parser(test_path))
for word in words:
# Psw = 0.0
if word not in spam_word_pro:
Psw = 0.4
else:
Pws = spam_word_pro[word]
Pwh = ham_word_pro[word]
Psw = spam_prob*(Pws/(Pwh*ham_prob+Pws*spam_prob))
prob_dict[word] = Psw
numerator = 1
denominator_h = 1
for k, v in prob_dict.items():
numerator *= v
denominator_h *= (1-v)
email_spam_prob = round(numerator/(numerator+denominator_h), 4)
if email_spam_prob > 0.5:
print(file_name, 'Spam', email_spam_prob)
else:
print(file_name, 'Ham', email_spam_prob)
def main():
ham_file = './ham'
spam_file = './spam'
test_file = './test'
ham_list, ham_set = get_word(ham_file)
spam_list, spam_set = get_word(spam_file)
union_set = ham_set | ham_set
ham_word_pro = count_word_prob(ham_list, union_set)
spam_word_pro = count_word_prob(spam_list, union_set)
myfilter(ham_word_pro, spam_word_pro, test_file)
main()
| 0.06869 | 0.177098 |
<a href="https://colab.research.google.com/github/RodriCalle/ComplejidadAlgoritmica/blob/main/3_MergeSort.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
def merge(a, ini, fin):
mid = (ini + fin) // 2
i = ini
j = mid + 1
n = fin - ini + 1
temp = [0]*n
for k in range(n):
if j > fin or (i <= mid and a[i] < a[j]):
temp[k] = a[i]
i += 1
else:
temp[k] = a[j]
j += 1
for k in range(n):
a[ini + k] = temp[k]
def mergeSort(a, ini, fin):
if ini < fin:
mid = (ini + fin) // 2
mergeSort(a, ini, mid)
mergeSort(a, mid + 1, fin)
merge(a, ini, fin)
import random
lst = [i+1 for i in range(20)]
print("Estado inicial: ", lst)
random.shuffle(lst)
print("Datos alterados: ", lst)
mergeSort(lst, 0, len(lst) - 1)
print("Datos ordenados:\n",lst)
```
##Merge Sort con un error
```
def merge2(a):
n = len(a)
mid = n // 2
i = 0
j = mid + 1
temp = [0]*n
k = 0
while i <= mid or j < n:
if j >= n or (i <= mid and a[i] < a[j]):
temp[k] = a[i]
i += 1
else:
temp[k] = a[j]
j += 1
k += 1
for k in range(n):
a[k] = temp[k]
def mergeSort2(a):
n = len(a)
if n > 1:
mid = n // 2
mergeSort2(a[:mid])
mergeSort2(a[mid:])
merge2(a)
random.shuffle(lst)
print(lst)
mergeSort2(lst)
print(lst)
```
Ojo: la segunda versión de mergesort (2) no funciona debido a que los slices de las listas son por valor, es decir son una copia de la porción de la lista original, como se demuestra en el siguiente ejemplo en el que el valor a[2] debería cambiar a 100 luego de la llamada a x()
```
a = [1, 2, 3, 4, 5]
def x(b):
print("List A: ", a)
print("List B: ", b)
b[1] = 100
print("List B, second element modified: ", b)
print("List A: ", a)
x(a[1: 4])
print("***********")
x(a)
```
##Analisis de complejidad
```
#Merge Sort
def mergeAnalysis(a, ini, fin): # T1(n)
mid = (ini + fin) // 2 # 1+1+1
i = ini # 1
j = mid + 1 # 1+1
n = fin - ini + 1 # 1+1+1
temp = [0]*n # 1 + n
for k in range(n): # n *
if j > fin or (i <= mid and a[i] < a[j]): # 7
temp[k] = a[i] # 1+1+1
i += 1 # 1+1
else:
temp[k] = a[j] # 1+1+1
j += 1 # 1+1
for k in range(n): # n *
a[ini + k] = temp[k] # 1+1+1+1
def mergeSortAnalysis(a, ini, fin): # T2(n)
if ini < fin: # 1 +
mid = (ini + fin) // 2 # 1+1+1
mergeSort(a, ini, mid) # T(n/2)
mergeSort(a, mid + 1, fin) # T(n/2)
merge(a, ini, fin) # O(n)
```
merge:
$
T1(n) = 3 + 1 + 2 + 3 + 1 + n + n * (7 + 3 + 2) + n * (4)
$
$
T1(n) = 10 + n + 12n + 4n
$
$
T1(n) = 10 + 17n
$
$
T1(n) => O(n)
$
mergeSort:
$
T(n) = 1 + (3 + T(n/2) + T(n/2) + O(n))
$
$
T(n) = 1 + (3 + 2T(n/2) + O(n))
$
$
T(n) = 4 + 2T(n/2) + O(n)
$
|
github_jupyter
|
def merge(a, ini, fin):
mid = (ini + fin) // 2
i = ini
j = mid + 1
n = fin - ini + 1
temp = [0]*n
for k in range(n):
if j > fin or (i <= mid and a[i] < a[j]):
temp[k] = a[i]
i += 1
else:
temp[k] = a[j]
j += 1
for k in range(n):
a[ini + k] = temp[k]
def mergeSort(a, ini, fin):
if ini < fin:
mid = (ini + fin) // 2
mergeSort(a, ini, mid)
mergeSort(a, mid + 1, fin)
merge(a, ini, fin)
import random
lst = [i+1 for i in range(20)]
print("Estado inicial: ", lst)
random.shuffle(lst)
print("Datos alterados: ", lst)
mergeSort(lst, 0, len(lst) - 1)
print("Datos ordenados:\n",lst)
def merge2(a):
n = len(a)
mid = n // 2
i = 0
j = mid + 1
temp = [0]*n
k = 0
while i <= mid or j < n:
if j >= n or (i <= mid and a[i] < a[j]):
temp[k] = a[i]
i += 1
else:
temp[k] = a[j]
j += 1
k += 1
for k in range(n):
a[k] = temp[k]
def mergeSort2(a):
n = len(a)
if n > 1:
mid = n // 2
mergeSort2(a[:mid])
mergeSort2(a[mid:])
merge2(a)
random.shuffle(lst)
print(lst)
mergeSort2(lst)
print(lst)
a = [1, 2, 3, 4, 5]
def x(b):
print("List A: ", a)
print("List B: ", b)
b[1] = 100
print("List B, second element modified: ", b)
print("List A: ", a)
x(a[1: 4])
print("***********")
x(a)
#Merge Sort
def mergeAnalysis(a, ini, fin): # T1(n)
mid = (ini + fin) // 2 # 1+1+1
i = ini # 1
j = mid + 1 # 1+1
n = fin - ini + 1 # 1+1+1
temp = [0]*n # 1 + n
for k in range(n): # n *
if j > fin or (i <= mid and a[i] < a[j]): # 7
temp[k] = a[i] # 1+1+1
i += 1 # 1+1
else:
temp[k] = a[j] # 1+1+1
j += 1 # 1+1
for k in range(n): # n *
a[ini + k] = temp[k] # 1+1+1+1
def mergeSortAnalysis(a, ini, fin): # T2(n)
if ini < fin: # 1 +
mid = (ini + fin) // 2 # 1+1+1
mergeSort(a, ini, mid) # T(n/2)
mergeSort(a, mid + 1, fin) # T(n/2)
merge(a, ini, fin) # O(n)
| 0.074563 | 0.92597 |
### Ejemplos tomados de un tutorial de sklearn
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.rcParams['figure.figsize'] = (20, 10)
pd.set_option('display.max_columns', None)
import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LogisticRegression
from imblearn.over_sampling import SMOTE
df = pd.read_csv("train.csv")
df.head()
df.info()
df.Cabin.value_counts()
df.Cabin.describe()
df["Survived"].value_counts(normalize=True)
import matplotlib.gridspec as gridspec
features=["Pclass","Age", "Fare", "Parch"]
nplots=np.size(features)
plt.figure(figsize=(15,4*nplots))
gs = gridspec.GridSpec(nplots,1)
for i, feat in enumerate(features):
ax = plt.subplot(gs[i])
sns.distplot(df[feat][df.Survived==0], bins=30)
sns.distplot(df[feat][df.Survived==1],bins=30)
ax.legend(['Survived 0', 'Survived 1'],loc='best')
ax.set_xlabel('')
ax.set_title('Distribución de: ' + feat)
X = df[["Pclass","Age", "Fare", "Parch"]]
y = df["Survived"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 1)
X_train = X_train.fillna(3)
X_test = X_test.fillna(30)
multi_log = linear_model.LogisticRegression(C=100.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=150,
multi_class='ovr', n_jobs=-1, penalty='l2',
random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
warm_start=False)
multi_log.fit(X_train, y_train)
y_pred = multi_log.predict(X_test)
y_pred_p = multi_log.predict_proba(X_test)
print("Y el accuracy es:",
metrics.accuracy_score(y_test, y_pred)*100)
import matplotlib.pyplot as plt
plt.hist(y_pred_p)
plt.show()
matriz_confusion = metrics.confusion_matrix(y_test, y_pred)
matriz_confusion
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
print("Precision:",metrics.precision_score(y_test, y_pred))
print("Recall:",metrics.recall_score(y_test, y_pred))
y_pred_proba = multi_log.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
```
## Ahora intentamos algo más...
```
corr_m = df[features+ ["Survived"]].corr()
corr_m["Survived"].sort_values(ascending=False)
sm = SMOTE(random_state = 2)
X_train_res, y_train_res = sm.fit_sample(X_train, y_train.ravel())
clf = LogisticRegression(random_state=20200611,max_iter=200)
model_res = clf.fit(X_train_res, y_train_res)
print(classification_report(model_res.predict(X_test), y_test))
probs = model_res.predict(X_test)
preds = probs#[:,1]
fpr, tpr, threshold = metrics.roc_curve(y_test, preds)
roc_auc = metrics.auc(fpr, tpr)
plt.figure()
plt.plot(fpr, tpr, label=' (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Curva ROC (Receiver operating characteristic) del modelo logístico')
plt.legend(loc="lower right")
plt.savefig('Log_ROC')
plt.show()
print(roc_auc)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.rcParams['figure.figsize'] = (20, 10)
pd.set_option('display.max_columns', None)
import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LogisticRegression
from imblearn.over_sampling import SMOTE
df = pd.read_csv("train.csv")
df.head()
df.info()
df.Cabin.value_counts()
df.Cabin.describe()
df["Survived"].value_counts(normalize=True)
import matplotlib.gridspec as gridspec
features=["Pclass","Age", "Fare", "Parch"]
nplots=np.size(features)
plt.figure(figsize=(15,4*nplots))
gs = gridspec.GridSpec(nplots,1)
for i, feat in enumerate(features):
ax = plt.subplot(gs[i])
sns.distplot(df[feat][df.Survived==0], bins=30)
sns.distplot(df[feat][df.Survived==1],bins=30)
ax.legend(['Survived 0', 'Survived 1'],loc='best')
ax.set_xlabel('')
ax.set_title('Distribución de: ' + feat)
X = df[["Pclass","Age", "Fare", "Parch"]]
y = df["Survived"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 1)
X_train = X_train.fillna(3)
X_test = X_test.fillna(30)
multi_log = linear_model.LogisticRegression(C=100.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=150,
multi_class='ovr', n_jobs=-1, penalty='l2',
random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
warm_start=False)
multi_log.fit(X_train, y_train)
y_pred = multi_log.predict(X_test)
y_pred_p = multi_log.predict_proba(X_test)
print("Y el accuracy es:",
metrics.accuracy_score(y_test, y_pred)*100)
import matplotlib.pyplot as plt
plt.hist(y_pred_p)
plt.show()
matriz_confusion = metrics.confusion_matrix(y_test, y_pred)
matriz_confusion
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
print("Precision:",metrics.precision_score(y_test, y_pred))
print("Recall:",metrics.recall_score(y_test, y_pred))
y_pred_proba = multi_log.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()
corr_m = df[features+ ["Survived"]].corr()
corr_m["Survived"].sort_values(ascending=False)
sm = SMOTE(random_state = 2)
X_train_res, y_train_res = sm.fit_sample(X_train, y_train.ravel())
clf = LogisticRegression(random_state=20200611,max_iter=200)
model_res = clf.fit(X_train_res, y_train_res)
print(classification_report(model_res.predict(X_test), y_test))
probs = model_res.predict(X_test)
preds = probs#[:,1]
fpr, tpr, threshold = metrics.roc_curve(y_test, preds)
roc_auc = metrics.auc(fpr, tpr)
plt.figure()
plt.plot(fpr, tpr, label=' (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Curva ROC (Receiver operating characteristic) del modelo logístico')
plt.legend(loc="lower right")
plt.savefig('Log_ROC')
plt.show()
print(roc_auc)
| 0.615203 | 0.847084 |
# Mother (father), Son (daughter) Programming:
## A guide to the basics of programming for people with techi kids
##### Written By: Martin Jay McKee
### Overview
It was 1983 and my parents had just bought their first computer. It was an original Tandy 1000 with dual 5 1/4" floppy drives -- and no hard drive. My current programmable, hand held, calculator (an HP 50) is dozens of times more powerful than this machine was, not to mention the cell phones that everyone carries with them these days (hundreds of times more powerful). But, this computer was my introduction to the world of computers. My mother was a scientific programmer, so what did she decide to do with her almost three-year-old son? What else? Teach him to program.
In those early years I wrote the beginning of a number of computer games with her -- all in the BASIC programming language. None of them were ever finished. That was never the point. Some were text based adventures, some had graphics and sound. All were terrible. What was important, however, was that I learned to understand computers as tools which were not mysterious and untouchable, but as imminently understandable and usable. I had a programmer for a mother so "of course" one might say, I would be able to learn how to program. The cool thing about programming, however, is that a little knowledge goes a long ways. No one needs to reach the "rock-star" level of programming to reap the benefits. Anyone can (and I belive should) take those first steps to pull the veil back... if only a little.
This tutorial has been written to help parents learn just enough about programming to be able to keep up with their children who wish to learn programming. At the end, you will not know enough to create anything from whole cloth; but following the tutorial should provide, at least, enough literacy in computer science and programming that it will allow one to be able to follow the general flow of most typical programming languages, understand when a program is described to you, and be able to make suggestions at a basic level.
This tutorial does not attempt to go into specific programming information. It is appropriate, however, as an introduction for most programming in the spaces of games and robotics logic, data manipulation and sorting, etc. Graphics, hardware interface, web programming and databases will all require external libraries. The good news is that once this tutorial is understood, it should be possible to understand the documentation for such libraries too!

This tutorial uses the Python programming language. Python is an interpreted scripting language that is widely used in a number of industries. Python's creator -- Guido Van Rossum -- started writing the first version of Python around Christmas 1989. He is now known as the BDFL (Benevolent Dictator For Life), and is a central member of Python development still. The name Python derives not from the snake (though it does have a snake mascot), but from the British comedy troupe Monty Python. It is typical for Python examples to depend upon (or be in the style of) Monty Python skits -- a convention which we shall follow here.
The tutorial is split into two parts. First it describes some basic computer science concepts which are crucial to understand if one is going to be doing any creative programming (it is certainly possible to just copy/paste without this understanding, but who wants to be limited to that?). The second part of the tutorial outlines the language syntax of Python.
#### *A final appendix, not really necessary to understand the remainder of the tutorial, compares the syntax of several widely used languages (C++, Java, JavaScript, Python, C#)
### Requirements
To work through this tutorial, it is necessary to install the Jupyter Notebook engine and a Python 3 interpreter. The simplest way to do this is to install the Anaconda scientific distribution. This can be found at, [Anaconda Distribution](https://www.anaconda.com/download/). Other information about installing the necessary software can be found at [Jupyter Installation Documentation](http://jupyter.readthedocs.io/en/latest/install.html). Once the software is correctly installed, continue on to the basics of Jupyter Notebook section before continuing to the primary tutorial.
### Intro to Jupyter
The Jupyter Notebook project provides a very nice way to produce books with executable code embedded in them. Notebooks are arranged as lists of _cells_. Each cell can be one of several types. This tutorial uses only two: Markdown and Code. Markdown cells contain all of the _text_ of the tutorial. They are informational. The Code cells are where executable Python code lives. To move between cells simply scroll until the cell you want is in view, and click on it. If you double click on a cell, it will enter edit mode. Code cells will look the same, if this happens. Markup cells will show the raw Markup with all the formatting information. To run a cell you can click the little run icon from the toolbar or press Shift-Enter. Running a code cell will print the results below the cell and running a Markup cell will format the text, and make it look nice again. As a test, double-click on this text here and then reformat it using Shift-Enter.
You now know all that is really needed in Jupyter for this tutorial. Jupyter is a really powerful project, however, so if you find this interesting, there's lots more to learn and maybe you'll find it useful for other reasons.
## Intro to CSci
### What is CSci?
Computer Science (*CSci*) is the study of how computers and computation work. Some programmers feel that *CSci* isn't an important part of being a programmer. But, being a programmer without having some basic knowledge of *CSci* is like being a writer without knowledge of Grammar. You can do it, but there are major tools missing from your tool box. And, if you don't know the rules, you can't tell when you are breaking them.
Computer Science is the glue that holds together all the programming disciplines. There are many topics that are important, however, we will talk only about computation, algorithms, language paradigms and program analysis.
### Computation
The theory of computation has supported dozens (possibly hundreds) of doctoral theses. Obviously we will only barely scratch the surface here. Computation Theory is a branch of mathematics (or, depending upon who you ask, *CSci*) that deals with the question of what sorts of problems are "computable". Some very interesting results in the early 20th century proved mathematically that there are problems that cannot be solved within the formal systems they are designed. One version of this was Godel's Incompleteness Theorm, another was Turning's proof of the unsolvability of the Halting problem. The first demonstrated that there is no single self-consistent system of mathematics that is based on a set of axioms (guesses) which can be proven by the same system. It showed that even math *must* be based on some guesses. And, actually, that there is no one "right" set of guesses. Different forms of math can be created using different axioms and they are all just as valid as any other. More importantly, they are homeomorphic to one another. There are ways to transform axioms into each other to show that all of these (different) systems are -- in some abstract manner -- identical.
The Halting problem came out of Alan Turing's search for the limits of "computable" functions. It may be phrased this way. Is there a process that can look at any finite program and decide that it will, absolutely, halt. That is, is there a single way to look at any program and to know, without a doubt, that that program will end at some point in the future. What Turing proved is that there *is no* procedure that can, in general, do this. The Halting problem is uncomputable.
By marking the limits of what isn't computable, however, early theorists were able to determine what computers *were* capable of, and it's quite a bit! Having knowledge of the existance of uncomputable problems is useful because it allows us to think, "if this isn't working, is that because what I want to do is simply impossible?" Usually the answer is no. But, as with all things in programming, it can be surprising the places that you run into such impossible problems.
Most computer languages are compiled. In a compiler, there are optimizers. Those optimizers typically run into a version of the Halting Problem. It is not much of an exaggeration to say that the majority of programs ever run has been limited in its performance because the Halting Problem made it impossible to solve the problem exactly and heuristic methods (again, guesses) had to be used instead.
There are a few requirements for a computer (or language) to be able to compute everything that is computable and we will look at all of those when we get to our Python introduction. Basically, a computational system must be able to store data (variables), to modify that data (arithmetic/assignment/and other operations), and to change the flow of the program based upon the data (conditionals/loops). A computational system which posesses all of these features is said to be Turing complete.
### Algorithms
Having examined what computation is and, therefore, what a computer is capable of doing. We will begin with the very core of any program -- algorithms. An algorithm (derived from the title of an Arabic mathematician, al-Kwarizimi), is a process by which something is achieved. In cooking, a recipie is an algorithm that converts ingredents into a final dish. In automotive tuning, algorithms are used to adjust spark plug and injector timing. And, in strength training, one may use an algorithm to determine the best number of reps for any particular exercise. Algorithms are everywhere.
In computer science, algorithms also form the basis of everything. There are sorting algorithms, search algorithms, comparison, and many others. Anywhere that a program needs to follow a certain process, it can be described as using an algorithm. And this is precisely why they are so important. By understanding a program as a combination of simpler algorithms, it becomes easier to understand how a program is working.
#### Bubble Sort
To see how this works, we'll look at a very basic sorting algorithm known as bubble sort. The idea of this algorithm is that you look at pairs of values in a list. If the second value is larger than the first, you swap them. You then advance one step to the left in the list. As you do this proceedure (algorithm) the larger values will "bubble" to the top. In fact, if you have a list of *N* items (the letter 'N' is often used to describe the length of a list, it stands for "*N*umber") then if you apply the check, swap, advance, proceedure to the list *N* times the list is guaranteed to be in ascending order.
In a very real way, however, what was just described can be broken into at least two nested algorithms. The operation, where we swap values is an algorithm in itself. While we haven't started looking at Python code, do your best to follow along (the comments on the right should help). A simple swap operation might look as follows. Be sure to run the the next cell (Shift-Enter) so that Jupyter knows the function is there later.
```
def swapIndex(data, first, second): # This line is defining (def) a function named swapIndex that has three parameters
temp = data[first] # Next we store one of the values in a temporary location, variable temp
data[first] = data[second] # After that, we store the second value into the location of the first
data[second] = temp # And, finally, store the first value (which was saved seperately) into the second
```
The first order of business is to describe how this simpler algorithm works. Perhaps an easy way to visualize this with two balls in two boxes. To begin with, ball A is in the first box and ball B is in the second box. We want ball B in the first box and ball A in the second box. There are rules though. To begin with, we can only lift one ball out of a box at a time. Additionally, each box can only ever hold a single ball. We seem to be stuck. But, the solution is simple. Introduce a third box -- the temporary box.
<img src="images/swap_example.png" alt="A graphic showing the process of a swap operation" style="width: 300px;"/>
At this point, the swap operation becomes simple. Ball A is moved to to the temporary box, Ball B (in the second box) is moved to the first box, and finally the ball in temporary (Ball A) is moved back to the second box. We've found an algorithm that follows all the rules. Before continuing, be sure that you really understand how this swap algorithm works (don't worry about the Python code, focus on the actual process). When you understand the process well, it beoomes possible to write your own code where other people might have to cut-and-paste a solution. It is also much more comfortable actually knowing _why_ a program works the way it does.
Having gotten some understanding of this simpler algorithm, let's take a look at the code for the full bubble sort. Again, do your best to follow the code, but understand that I'm throwing a lot at you. One of the most difficult things a programmer has to do is to look at a new codebase and figure out what the heck is going on. Sometimes just tracing the "flow" of a piece of code is a good starting point. Sometimes, trying to understand what the different variables and functions do is a good approach. If the programmer who wrote the code did a good job with names, that can be easy. If they chose names at random, it can lead you up the garden path.
A simple bubble sort might look like this (again, execute the code in the cell with Shift-Enter),
```
def bubbleSort(data): # Define the function bubbleSort, it has one parameter named data
N = len(data) - 1 # Get the one less than the length of the list, store it in variable N
for _ in range(N): # Just loop N times
for index in range(N-1): # Loop over all the list indicies from 0 to N-2 (skip the last one)
first = index # Get the index of the first element, it's just the current index
second = index + 1 # Get the index of the second element, it's just one past the current
if data[first] > data[second]: # Check if the first value is greater than the second value
swapIndex(data, first, second) # If it is, swap the first and second values
print(data) # Print out the list so that we can watch it being sorted
print('') # Print an empty line, so we can see the seperate loops
```
The code begins by defining a function that we will use shortly to sort lists. We name it bubbleSort. The function takes a single parameter, which is called _data_. The parameter, _data_, will be a Python list. We wish to loop over all the values except for the very last one, so we save the length of the list minus one into the variable _N_. That value is then used to define two loops. An outer loop, which simply goes over the inner loop _N_ times, and an inner loop which steps through the values in the list and does the actual bubble sort. The inner loop has a variable named _index_ which tells us where we are in the list. It'll have a value that starts at 0 (the first value in a Python list is called *0*) and it ends at N-2 (because the _range_ function gives values up to but not including the end value). Inside the loop we figure out what the indicies of the first and second values we wish to compare are, do the comparison (with the *if* statement) and swap the values (using the function we defined above) if the first is bigger than the second. We can test our algorithm by creating a list and passing it to the function. Run the following cell to see what the results are.
```
data = [1, 6, 2, 0]
bubbleSort(data)
```
As can be seen, the numbers begin out of order, but by the end they are increasing as they should be. The algorithm is working! Try modifying the list above and rerunning the code. It should work for any length of list, and with any numbers. What happens if the list has two elements? What about five? What about negative numbers? Just remember, a Python list starts with a left square brace '[', has a number of values seperated by commas, and ends with a right square brace ']'. If you get lots of funny colored warnings when you try to run the cell, check that the list syntax (we'll get to this word later!) is valid.
One advantage of the way that Python works is that it allows you to compare more than just numbers. The cheese shop owner has asked us to organize a list of cheese names alphabetically. Luckily, our bubbleSort() function will do that just fine!
```
data = ["parmesan", "mozzarella", "cheddar", "goda", "blue cheese"]
bubbleSort(data)
```
One thing that you may have noticed is that our bubble sort seems to be doing the same thing over and over. Obviously the algorithm is working, but could it be more efficient? Well, since I'm asking, the answer is obviously yes. But how? Well, one thing that we haven't talked about yet is that a bubble sort will always push the largest value remaining as far up as it goes. What's important about that is that every time we do our inner loop, we can actually look at a smaller part of the list.
The next function _bubbleSort2_ is slightly modified to do that. It looks almost the same, the changes are subtle.
```
def bubbleSort2(data): # Define the function bubbleSort2, it has one parameter named data
N = len(data) - 1 # Get the one less than the length of the list, store it in variable N
for end in reversed(range(N+1)): # Loop N times and change the length of the inner loop
for index in range(0, end): # Loop over all the list indicies from 0 to end (skip the last one)
first = index # Get the index of the first element, it's just the current index
second = index + 1 # Get the index of the second element, it's just one past the current
if data[first] > data[second]: # Check if the first value is greater than the second value
swapIndex(data, first, second) # If it is, swap the first and second values
print(data) # Print out the list so that we can watch it being sorted
print('') # Print an empty line, so we can see the seperate loops
```
Testing this new function on our cheese list, however, we get a totally different result.
```
data = ["parmesan", "mozzarella", "cheddar", "goda", "blue cheese"]
bubbleSort2(data)
```
Where before ever time we went throught the outer loop we executed the inner loop the same number of times, nowe the inner loop is being executed one time less each time. The result is that our initial function ran the inner loop 16 times and our modified algorithm ran the same inner loop 10 times. That's a savings of 37.5%! With a small modification to two lines, we have gained almost 40% speed. And this is why it's so important to understand algorithms. On the one hand, when we understand algorithms, we are able understand our program at a deeper level than if we treat algorithms as a mysterious black-box. Even more importantly, however, it is possible to make huge improvements in how fast a program is by making sure that it isn't doing things it doesn't need to do.
It is worth saying that our bubble sort could still be improved and, honestly, bubble sort is considered a poor sorting algorithm (though others are substantially more complicated, hence not using them here). If we needed to sort a list of every cheese in the world ([List of 1831 Cheeses](https://www.cheese.com/alphabetical/)), it would make sense to use a better algorithm. As it stands, we are getting results instantly, so who really cares? Fast enough is fast enough.
### Programming Paradigms
There are different ways that programming languages work. What we have seen thus far is a procedural style of programming, often called an imperative style. There are many others. We'll just look at some of the most popular.
#### Imperative
An imperative programming style is one in which program "state" is modified by commands. State may be something as simple as a number or as complicated as an entire database. Commands can range from assignment ( a=4 is a command that puts the value 4 in a box named _a_) to displaying a 3D model on the screen. What is important about an imperative style, however, is that the program functions at least in part as a result of its "side effects". When we say a=4, that might, also, change the color of a pixel on the screen. This is a very direct way to interact with the computer, but it can be dangerous. Many people feel that an imperative style is more prone to programming bugs than any other. At the same time, most languages (C/C++, C#, Java, JavaScript, Python, Perl, Ruby, Fortran, Cobol, Ada, etc.) are imperative in nature.
#### Functional
A pure functional language is one in which no program state is ever modified. If changes need to be made, completely new state is created. This has a number of advantages when it comes to program safety. On the one hand, it gets rid of side-effects as a way to make something happen. This makes it more clear what the program is doing, since everything is in the code, however, it often means that more code is needed to do the same thing. Another problem with the functional programming paradigm is that it hasn't been taught as often, so people are simply less familiar with it. Some functional languages are LISP, Scheme, Haskell and Clojure. More and more languages are getting some functional features, such as C++, Java, JavaScript, Ruby and Python.
#### Declarative
A declarative language describes what the desired result is rather than how to get there. Declarative languages can be extremely powerful and very easy to use, but they tend to be better as a DSL (Domain Specific Language). That is, a language that is targeted at doing one thing really well. An example of this might be a language that is used to configure another program. By making a language that can describe the color of buttons, text, etc. it becomes much simpler to change the look of a program. There are other domains that declarative languages excell in besides configuration. For instance, physical modeling (for bridges, for instance) can be easily described. It is also very good at solving logical equations (if 50% of politicians are murders and 50% of politicans are robbers, are all politicians crooks?). This is precisely what the declarative language Prolog was designed for.
While it is highly likely that you won't use a declarative language for the bulk of a program, any non-trivial project is likely to have a least one declarative language in it. Indeed, HTML (HyperText Markup Language) the language which describes almost every web site on the planet is declarative. So is CSS (Cascaded Style Sheets), which is used to configure colors, placement and so forth. JavaScript, however, is imperative, and all over the place. The web wouldn't be the same without it.
#### Object-Oriented
Object orientation is not, in itself, a paradigm. Any of the other paradigms can be made object oriented. In any case, it is such an important (and contriversal!) idea that it is worth mentioning. While there are probably dozens of definitions of object-oriented programming what we'll use here is that object-orientation combines state with operations within "objects". The idea is to combine everything into a single unit. For instance, a flashlight might have a switch, a bulb and a battery. Those are state. It has operations too: on and off.
Object-oriented programming is at the core of a number of very popular languages (C++, Java, Python, Ruby, Clojure, etc.) but it has lost popularity recently. Many projects have taken this paradigm to the extreme, building objects with hundreds of pieces of data and sometimes thousands of operations. At the same time, the data might be objects too, so that a programmer might have to look tens of layers down to figure out what is going on. There's a war going on about where and when object-orientation is good, and when it is taken too far. But, it's not going anywhere any time soon, because it alows for a much more logical organization of a program when it is done correctly.
#### Why Paradigm Matters
The above paradigms are not all of the paradigms that are to be found in programming right now. And this is already feeling complicated. So the real question is, why does this matter? Well, it's about making life easier for yourself (programmers are, as a whole, lazy). If a library uses a declarative style and you are thinking in an imperative style, it becomes much more difficult to write code and get it to work. Recognizing when to change approaches makes it possible to match thinking to how code works most effectively.
When schools teach an imperative language and send students out into the world saying, "you're a programmer now, go program!" They are doing a disservice. It is like that old idiom, "when all you have is a hammer, everything looks like a nail." If there is understanding that not everything in the world is imperative, people have more flexibility when something doesn't seem to work right off. And that's all that we really are looking for.
Honestly, programming is a very creative process. There are as many (good) solutions as there are programmers. It's when we get stuck in a rut, and cease being creative, that programming becomes hard.
### Program Analysis
Program analysis is just what it sounds. It is looking at a program and figuring out what it is intended to do, how it gets there, what the advantages and disadvantages of the approach are, and what improvements could be made. It is an important part of learning how to program. Indeed, as with teaching English, there is substantial evidence that people learn to program more effectively by reading programs than they do writing them.
The bulk of this tutorial will not have anything which is particularly conducive to analysis. The Python code snippets will be simple to the point of absurdity. At the end, however, there are a number of code examples that are ideal for analysis. They solve (fairly) easily understandable problems and the actual solutions are of fairly low complexity. The purpose of these examples are two fold. First, it is encouraged that the reader make an attempt to do an analysis on their own. Read through the code several times, use what you learned in the language introduction. Figure out how you might solve the problem on your own if you had to use a pen and paper. There are many ways to accomplish an analysis. In the process, and even if you do not reach a complete description of the program flow, you will be learning to decode the structure of a program. It takes practice. Secondly, however, each example is followed by a reasonably complete analysis (analyses can be painfully detailed, hopefully those included here are not!). The analyses included here are designed to show just one approach to analysis.
It should be noted, the code to solve these problems is not the "best" solution. I would hope that they can be considered good solutions, but they are nothing more than that. While it has been mentioned elsewhere, creativity is very important in programming. There are as many solutions to a problem as there are programmers. And, that is the main reason that having the skill of program analysis is so very important. The chances that someone else will approach a problem the same way that you would have is exceptionally small. We need to build the skill of viewing code in ways that are, perhaps, unnatural to us. It can be difficult, but it can also be very enlightening. Not many people sit down with code the same way they might with a good novel, but it can be just as satisfying to do so. Much can be learned in the process.
## Intro to Python
Now that we've introduced just a bit of computer science, let's take a look at a programming language that transfers well to other languages -- Python. Python is a multi-paradigm programming language. It can be used as an imperative language, object-oriented, functional and even declarative. Our introduction to Python, however, will be as an imperative language. This will hardly be a complete introduction to Python (however, an attempt will be made to identify where major ommissions occur). Nevertheless, it will cover the subset of the language that is most similar to other imperative languages which are widely used.
### A Note on Syntax
Unlike natural languages (i.e. English), programming languages are exceptionally strict when it comes to syntax. To make a program actually work, it is necessary to be careful with punctuation, careful with capitalization, careful with our words. In this tutorial, we will not be looking at precise syntax. When I later talk about code blocks, it can be useful to know that Python delineates them as sets of lines that are indented. We won't worry about exactly where and how we need to do this. There are places, also, that Python uses the colon (:). It introduces code blocks. While it is likely possible to determine the rules of usage from the examples that follow, that isn't the goal of this introduction.
Syntax is specific to the language (and language syntax is annyoingly similar, leading to confusion). The concepts of how programming languages work, however, are nearly universal. If exact syntax is specifically desired, there are plenty of places that the information can be found.
### Data Types
In any programming language, there are things called data "types". Ice cream is a _type_ of food. Breakfast cereal is another type of food. Sometimes there will be _subtypes_ (think, chocolate, rockyroad, strawberry, etc.) but we're not really going to worry about that now. The Python datatypes we will be examining are: integers, floats, strings and lists. Some other Python datatypes that we won't be looking at are: dictionaries, tuples and classes. In Python, we can request the type of a value with the _type_ function. We'll see how to use that below.
#### Integers
An integer is any number that does not have a fractional part. Integers can be positive or negitive. An integer in Python just consists of the number. For instance,
```
42
```
Is simply the integer with the value fourty-two. If we use the _type_ function we can see that this value is of type integer.
```
type(42)
```
That's really all there is to integers! They are the simplest data type.
#### Floats
Floats, or floating-point numbers, are the way that many languages deal with "real" numbers... that is, numbers that have numbers after the decimal point. While they are often refered to as real numbers, mathematically, they are not because floats have a limited range and not every number is representible. This is true also for the integers. There is a biggest and smallest float that the computer can represent. There are always two floats that are so close together that there is no representible number between them. Mathematically though, there should be an infinite list of numbers inbetween. Most of the time this doesn't matter. There are times, however, that it causes really annoying bugs.
```
print(3.1415926535)
print(type(3.1415926535))
```
Is the first 11 digits of pi. It's worth noting that this in the last cell there were two operations. We printed the value itself and we printed the type of the value. Having nested functions like this is actually indicative of a functional programming style. What do you know! These things show up everywhere. Floats seem to work nicely, but what happens if we subtract two numbers really close to one another?
```
3.1415926535 - 3.1415926534
```
Well, we get a kind of weird number. We expected 0.0000000001, but we don't get exactly that. Why? Well, that goes back to the fact that the computer doesn't store these "real" numbers perfectly. And this is why we have to be careful. Most the the time though, it really doesn't matter. Floats can be positive or negitive too. They can be entered either as numbers only or they can be be entered in scientific notation (using the letter 'e').
```
print(-42.0)
print(4.2e1)
print(1e-3)
```
#### Strings
Strings are the datatype that holds text -- words, letters, etc. In Python, strings can be wrapped in either single or double quotes. This lets you nest quotes inside a string, which is a nice feature many other languages don't have. Like other languages, however, there are some things that you may want in strings that must be inserted using "escaped characters". Once we've introduced strings, we'll look at escaped characters.
A very simple string might look like this,
```
"I am a string"
```
Or this,
```
'I am a string too!'
```
In both cases, the interpreter prints it out using a single quote. That's not really important, it's just the way the interpreter works. What's more important is the fact that when we have a string, we can look at parts of it. Python lets us use the subscript operator ([]) to do this. Before we get too deeply involved, lets create a variable to hold our string.
```
s = "The Pet Shop"
```
This code says, "Python, please take the string value I am creating and put it in the box named 's'". Once we've done that, we can refer to the value using the variable name. Let's look at a few different parts of the string.
```
print(s[-4:]) # Print the last four values in the string
print(s[0]) # Print the first value in the string -- remember, the first value is index 0!
print(s[4:8]) # Print the values in the string beginning at index 4 and up to but not including index 8
```
As mentioned above, there are also "escaped characters". These are used for things like new-line and tab. They are extremely useful for formatting text on the screen quickly. For instance,
```
print("This\nis\ta string")
```
So here, we used \n to go to a new line and then \t to insert a tab. The biggest problem with escaped characters is that it makes the strings in your code much more difficult to read. Sometimes it's worth it though.
Another important way to use strings is with their _format_ method. Strings, as it happens, are object. They have both data and operations. We've already seen one operation -- subscripting. Formatting allows us to insert values into strings. Let's see how this works using a loop.
```
for number in range(10):
print("The magic number is {}".format(number))
```
This short little piece of code is doing an awful lot! It is counting up and printing something that is different (though it follows a template, of course) each time. We don't need to worry about how the _for_ loop is working right now, what's more important is to see that we can access the _format_ method by putting a period and then the function name right after the string object. This is how all object operations are accessed except for a few things like subscripting which use square braces. The braces are used, however, because it is shorter and clearer. When a language does this, it is called syntactic sugar. There are ways in the language to do it normally, but sometimes it makes sense to make specific operations just a little clearer.
#### Lists
The last datatype that we will be looking at from Python is the list. A list is a mutable hetrogeneous sequence. Ok....? Let's break that down. A list is a sequence, which means it has an order. A string is a sequence too. And, just like the string, it is possible to access a list using subscripting. Another important thing to remember about a list is that it can hold any other Python datatype as an element, and the elements don't have to all be the same. For example, a list can hold ten integers; or, a list can hold five floats and a string. A list can even hold lists of lists, of lists, ad infinitum. This heterogenaity of lists is very useful and is a feature that many languages do not have. This is a result of Python being a dynamically typed list. But, I digress. The final thing that is important about a list is that it is mutable. The values in it can be changed without creating a new list. That is different from a string, which is immutable, and cannot be changed.
To create a list is more complicated than the other datatypes we have examined. A list begins and ends with a square brace, and the items are seperated by a comma. A simple list might look like this,
```
[1, 2, 3, 4, 5]
```
Of course, lists can get much more complicated,
```
[1.7, "Parrots", [[], "stuff", 1]]
```
Lists can also be empty, as shown in the last example. What's the point of a complicated list like the last one? Well, it's a really great way to transfer information that has a fixed structure. Python has other (arguably better) methods for achieving that, but lists are very fast, and if it doesn't get too large, it's easy enough to manage.
It is possible to create lists from other objects in Python too. For instance, let's create a list of the first ten natural numbers,
```
list(range(10))
```
We could replace that ten with any integer we want (or a variable that contains an integer!) and get a list up to the size of the largest integer that Python supports (which is often greater than 4 billion).
#### Other Data Types
As mentioned before, there are a number of other datatypes in Python. Tuples are similar to lists, but they're immutable. Dictionaries are much as they sound, data is tagged with a "key" that can be used to "look it up". And classes are the basis of Python's object oriented features. There are also the types boolean and none, as well as metaclasses, decimals, datetimes, etc. To really use Python in the real world it is good to understand more of these types. To get a basic overview of how programming works, however, we can profitably skip them here.
### Variables
The core of any imperative program is its state. And state is stored, primarily, in variables. Perhaps the easiest way to think about a variable is as a box with a name on it. Statically typed languages, such as C/C++ and Java, have boxes that are sized to only fit a single type of data. If the box is sized for an integer, only an integer can be put in the box. In a dynamically typed language, such as Python, the boxes will change size for whatever data you put in them. Either way works fine, it's just different approaches.
Every language has rules for the names of variables. In Python, the rules are pretty simple. First, a variable can begin with an underscore or a letter. After the first character, a variable name can have letters, numbers and underscores. There are several reserved names in the language that cannot be used as a variable name. And, the variable names are case sensitive. That is, the variable _a_ is different than the variable _A_. In Python, the rules for function names are the same as for variables. Which is nice.
In general, single character names are a bad idea. Writing programs in a way that they can be "read", kind of like English, is a very quick way to make a program more understandable -- both to other people, and to the programmer in two weeks!
Variables are assigned values using the equal sign. This is different than math. What '=' means in Python is, put the thing on the right *into* the box on the left. It isn't the two things are the same (Python uses two equal signs, '==', for that). It is also possible to reassign the value in a variable, even to a different type. For instance,
```
my_variable = 8
print(my_variable)
my_variable = "The bird is deceased!"
print(my_variable)
another_variable = my_variable
print(my_variable)
print(another_variable)
```
On the first line, we define a variable named <i>my_variable</i> and put the value 8 into it. When we print the variable, we get that value back. Next we reassign the variable to contain the value "The bird is deceased!". The original value, 8, is gone. We had to throw it out to put a new value in. In fact, when we print the variable, we get new value printed and the old one is nowhere to be found. Finally, we assign the original variable to a new variable. Now if we print both of them, they both contain the same value. The question is, are the two values the same, or different? This can be an important question, and is one of the reasons that programming can be difficult. Things don't always work the same way. Let's do some experiements. First, what happens if we use two integers?
```
x = 4 # Set up x and y to point to the same value
y = x
print("x = {}, y = {}".format(x, y)) # Check that they do
x = 5 # Set x to hold another value
print("x = {}, y = {}".format(x, y)) # What do we get?
```
So really, in this case, the code does what we would expect. When we simply assign to x, it changes only what is in that box, not the value in y as well. You can think of it as making a copy when we do the ```y = x```. So that each box holds a seperate 4. When we reassign the value of x, it is clear that we simply throw away the duplicated 4 and replace it with a 5. As it happens, the same thing will happen with floats, strings and lists too. But there's a way for us to change the behavior. What if we modify an element *in* a list?
```
x = [1, 2, 3] # Set up x and y to point to the same list of integers
y = x
print("x = {}, y = {}".format(x, y)) # Check that they do
x[1] = 5 # Set the second item in the list x to hold another value
print("x = {}, y = {}".format(x, y)) # What do we get?
```
Well that's odd. It appears that this time the list wasn't actually copied. The reason this happens is that we used the subscripting on the left side of the assignment. This actually always happens. We are just looking at a different variable than we initially thought. The list itself is a variable with a name that Python choses (it is a, so called, anonymous object). When we set the variable x to a new list, we simply replace the whole thing. What we are doing above, however, is to drill down into the value we stored in x (and in y, as it happens), and reassigning a part of it. Because the same object was assigned to two variables, the changes are represented in both variables.
If this doesn't make a lot of sense, join the club! It's kind of tricky. It could be thought of as boxes within boxes, with arrows pointing here there and everywhere -- no better! It is worth trying to tease out what is happening, however. This is probably a good time to just play with defining and printing some variables in the cell below. Use different datatypes, assign them to eachother, use subscripting. Data manipulation is at the heart of an imperative programming style. If it makes no sense, the rest of this tutorial is going to be rough going.
### Arithmetic
Potentially the most obvious operation that a computer can do is math. Heck, it's basically in the name. Computers compute. In many ways, arithmetic is one of the less interesting features of programming, but since it's at the core of almost everything a computer does, we need to at least look at it.
All of the basic operations that you learn in school are available in Python. Addition (+), subtraction (-), multiplication (*), division(/), exponentiation(**/pow()), modulus (%) and parenthesis (()) are core parts of the language. Using these, Python makes a really nifty calculator!
```
# Do some quick calculations to figure out the size of a bird cage
height = 24 # Here we define variables for height, width and depth
width = 18
depth = 15
area = width * depth # Calculate the area by just multiplying
volume = (height * area) / (12**3) # Calculate the volume in cu. in. then convert to cu. ft.
edge_perimeter = 4 * (width + height + depth) # There are four edges of each length, so, add then multiply
print("Base area = {} sq. in.".format(area))
print("Cage volume = {} cu. ft.".format(volume))
print("Length of cage edges = {} in.".format(edge_perimeter))
```
If trigonometric functions are required (sin, cos, tan, log, etc.) one can *import* the math library. This will be the first time that we look at something that isn't part of the Python language. We can use it just as if it _were_ part of the language though. That's what makes libraries so useful. A good library will basically extend the functionality of a language without adding any new syntax. That's very powerful.
The math library finds application in loads of game and robotics applications because it has the functions that are necessary to do coordinate transformations and the like. Still, very few programmers have to deal with it directly, because any game framework that one might choose will have another layer of library above the math library to do those sorts of things in the context of the game library. This is another place that programming can get difficult -- when there are many ways to do things. At a language level, Python tries to enforce only a single way of doing something. There are plenty of exceptions to that rule, but it is much more streamlined than many other languages.
One other thing to point out is that the math library routines use radians for angles, rather than degrees. While there are 360 degrees in a full circle, there are $2\pi$ (that is, two times pi) radians in a single revolution. Believe it or not, there are actually some very good reasons to work in radians rather than degrees. We won't get into that now. All that really matters is that we can convert from degrees to radians by dividing by 57.3, or go the other way by multiplying by the same number. In Python, that looks like this,
```
def toDegrees(rad): # Convert some number of radians to degrees
return 57.3 * rad
def toRadians(deg): # Convert some number of degrees to radians
return deg / 57.3
```
With these functions, we can use the math library with degrees,
```
from math import * # This will import everything (*) from the math library
print(sin(toRadians(0)))
print(sin(toRadians(45)))
print(sin(toRadians(90)))
```
Between the builtin arithmetic operations and the math library, there is not much that you can't do as far as math is concerned. It may not be fast, however. When it is important to do math fast, there are libraries that help with specific things. For Python there is the NumPy library, as well as SciPy. Other languages have their own "fast math" libraries. As always, if there is a need somewhere, there's probably a special-purpose library to fill it. That's not what this tutorial is about, however. Here we are mostly interested in the very basics of programming.
### Comparisons
Another very widely used operation in programming is value comparison. Checking if two values are the same, different, greater than or less than one another is a first step toward writing programs that are able to make decisions. And decisions are one of the steps toward Turing completeness. All six of the value comparisons are available in Python, they are listed below,
```
print(4 > 5) # Check strictly greater than
print(4 >= 5) # Check greater than or equal to
print(4 == 5) # Check strictly equal to
print(not 4 == 5) # Check strictly not equal to
print(4 <= 5) # Check less than or equal to
print(4 < 5) # Check strictly less than
```
It is possible to use these comparisons with any number type (integer, float, etc.) and it will also "work" with strings. Unfortunately, it may not work the way you *want* it to work with non-numeric values. For instance,
```
print('1' == 1)
print('1' > 1)
print('1' < 1)
```
The string representation of a number is not equal to its integer value. The magnitude comparisons (> and <) are also acting weirdly. To make this work, we can convert the string representation to an integer using the _int_ function. There are also _float_ and _str_ (string) functions available. So, doing the same as before, we are able to get the comparisions to work the way we would expect.
```
print(int('1') == 1)
print(int('1') > 1)
print(int('1') < 1)
```
Excellent! Comparisons return values of type *boolean*. We didn't look at them above because they are really very simple. A boolean holds one of two values: True or False. These values are of most use inside conditional statements so they weren't worth introducing earlier. We see them here though. And we can, as always, assign a variable to hold a boolean value. For instance,
```
bigger = 4 > 7
print("bigger = {}".format(bigger))
```
We can see that the variable _bigger_ holds the correct value as the number four is *not* greater than the number seven.
In addition to these comparison operators, Python (and most other languages) provide some boolean operators which are used to combine boolean values. Python has operators for _and_, _or_, and _not_. In fact, those are their names. We can see these working with a simple code fragment.
```
print(not True)
print(True and False)
print(True or False)
print(True and (not False))
```
Other combinations of boolean values, of course, will lead to different results. If this particular component of the language is of interest, a quick tutorial on boolean logic is in order. Certainly it is a very powerful facility when used properly. Many simple programs, however, may be able to get away without using boolean operators by simply splitting conditional statements into multiple steps.
### Conditional Statements
Now that we have introduced variables, arithmetic and conditions, it becomes much easier to discuss condition statements. Python has a number of conditional statements. Some languages, like C/C++ and Java, have even more. Conditional statements are a way to make a program do something different based upon the program's state.
#### _if_ Statement
Let's look at the following program which uses an _if_ statement. Before running it, try to figure out what it will print at the end. Read the conditional statement just as you would in English, saying _then_ for the colon (:). Make sure that the code starts by assigning x = 10.
```
x = 10 # To test other numbers, modify this line
if x > 10:
x = x / 2
print(x)
```
Having run this little program, did you get what you expected? If not, look back at it and see if you can figure out why you didn't. Conditional statements are really very simple. We, honestly, tend to make them more complicated than they need to be. This _if_ statement is going to do what is inside the "nested" block any time the condition is true. If x is assigned as 10, however, the condition will not be true and the block will be skipped. Thus, we end up printing the value ten at the end of the code. Run the code again, this time set x to something that will ensure that the condition is is true. Does it do what you expected?
It may not. In early versions of Python (2 and earlier) integer division would always return an integer value. This would mean that (3/2) == 1, and (1 / 2) = 0. Starting in Python 3, integer division will create a float if the computation would produce a fractional number. Another of those silly inconsistencies which makes programming interesting (difficult).
#### _else_ Statement
In addition to _if_, Python provides an _else_ statement. When the _if_ statement has a condition which is False, and if there are no other statements in the conditional block, the _else_ block will be run. Given that, what would we expect to be the result of the following code if x = 5? What about if x = 11?
```
x = 5 # To test other numbers, modify this line
if 0 <= x < 10: # This could also be written as (0 <= x) and (x < 10)
print("Option 1")
else:
print("Option 2")
```
The above code shows something that we didn't look at when we were finding out about condition expressions. Python has some nice syntactic sugar which allows you to chain comparisons if they will be combined using the boolean operator _and_. That is, conditions can be chained in this way if we want to know when the first condition *and* the second condition are True. In all other cases, we have to be explicit about combining them.
#### _elif_ Statement
The final form of conditional statement in Python is the _elif_ statement (short for else-if). This acts very much like an if statement. In fact, just like an _else_ statement, there must be an _if_ statement at the beginning for an _elif_ statement to be used. This allows for a single cascade of conditions to be used if a simple binary decision doesn't make sense.
```
x = 3 # To test other numbers, modify this line.
if x == 1:
print("We're number one!")
elif x == 2:
print("Silver, baby!")
elif x == 3:
print("Third is still placing.")
else:
print("Ughhh.....")
```
Think about what this code is doing. It's using all of our conditional statements. There are three conditions that are explicitly defined (for x = 1, x = 2 and x = 3). What happens if x = 4? What about if x = -1? Does that even make sense?
One has to be very careful to ensure that conditions are actually testing what you want to test. For instance, the last fragment will run just fine if x = -100, but what place is that? It doesn't make any sense. In a program, it would probably make sense to check that the value of x is in the correct range before continuing to print the correct value. One way we could do that is like this,
```
x = -100 # To test other numbers, modify this line.
number_of_places = 42
if x <= 0 or x > number_of_places:
print("ERROR: Invalid place")
elif x == 1:
print("We're number one!")
elif x == 2:
print("Silver, baby!")
elif x == 3:
print("Third is still placing.")
else:
print("Ughhh.....")
```
This modification checks two things. It rejects any place less than or equal to zero and it also rejects any place larger than the number of places that are possible. We don't want it to be possible to print something for place 50 out of 42. That doesn't make any sense. Using conditions like this is called defensive programming. It is a way to reduce the danger of the "garbage in, garbage out" problem.
It should be noted, this is not necessarily the *best* way to solve this problem in general, or even in Python. Consider what would happen if wanted to have a different comment for every place up to ten. This could get really messy. More than that, it would become "brittle". Brittle code is code that has a tendency to break even if it is handled carefully. The more paths there are in a conditional, the more difficult it is to make it work without bugs. As such, it makes sense to carefully check any conditions. The same is true of the next type of statement, loops.
#### Ternary Operator
Some languages, Python among them, have what is sometimes called a ternary operator. It is kind of like an _if_ statement and an _else_ statement crammed together; and, it makes some things much easier. The ternary operator is useful when you want one value under certain conditions and another value under all other conditions. For instance, maybe you want to print "Positive" or "Negative" based on whether a number is less than zero or not.
```
value = 7
print("Negative" if value < 0 else "Positive")
```
Mathematically, of course, this is incorrect. It is not deciding of the value is positive, but, rather, non-negative. Be that as it may, it demonstrates how the ternary operator can be useful in some cases. This doesn't add anything to the power of the other conditional statements, however. It is perfectly simple to do the same thing using just a variable assignment and an _if_ statement. It just isn't as compact.
```
value = 7
string = "Positive"
if value < 0:
string = "Negative"
print(string)
```
Choose your poision.
### Loops
There are not many different types of loops that are used in programming languages. They all have the same names _for_ loops, _while_ loops, and (sometimes) _do-while_ loops. These different loops can work in massively different ways in different languages, however. Despite the similarity in names. Python has particularly unusual _for_ loops when compared to the _for_ loops in traditional C/C++ and Java. It is worth noting that Java and C++ have both added "for-each" loops that are much more like the Python _for_ loop.
#### _for_ Loops
In Python, reducing the actual implementation to the point of absurdity, a for loop iterates over a list. That is, a for loop will remove each item of a list in turn and make it available for use inside the loop. This is much different than _for_ loops in earlier languages, and can be a major point of confusion when transitioning between languages. Let's look at an example,
```
adjectives = ['dead', 'pushing up daisies', 'deceased']
for adjective in adjectives:
print("The bird is {}.".format(adjective))
```
To begin, we create a list of adjectives (and adjectival phrases). The for loop steps through the list (which comes after the keyword, _in_) and assigns each of the items in the list to the local variable _adjective_ (coming after the keyword, _for_) in turn. The code inside the loop is then run, using this variable value. The result is a series of sentences. As it stands, there is really no complexity to this version of a for loop. But, what if you just want to do something _N_ times? How is that done?
Well, somehow, a list-like object needs to be created to step through. And, if we really don't care about a different value every time through the list, we can use a single underscore as the variable name. It tells Python, "I don't care about this value, so just throw it away." If we want to print something three times, we could do it like this.
```
print("Three cheers for King George!")
for _ in range(3):
print("Hip-Hip Hurray!")
```
The range function will create a list-like object that returns the values 0, 1 and 2. We really don't care what values it returns, however, so we tell Python that by using a single underscore as the variable name.
The same structure can be used if we simply want to do something with a list of numbers, say, from ten to twenty.
```
for value in range(10, 21):
print(value)
```
Now, why did I use the number twenty-one, when I wanted to go to the number twenty. That's just how the _range_ function works. It creates a list that starts with the first number (if only one number is given, the first number is zero) and it goes up to one less than the second value. As with all of this programming stuff, there's actually a good reason to do this. In such a simple program, however, it can seem really strange and it certainly leads to lots of bugs when you aren't prepared for it. In this case, the _range_ function is designed to be used to generate indicies for lists and, of course, Python lists are zero based. In a list with ten items, the first item is at position 0 and the last item is at position 9. This is messed up so much in programming and engineering that it even has a name, a fencepost error. If you have a yard 100' long and you want to divide it into segments 10' long, how many fenceposts do you need. The answer, of course, is eleven, which doesn't make immediate sense to most people. If it does to you, you may be blessed with never having problems with bounds errors on loops. Lucky you.
### _while_ Loops
Another type of loop in Python is the _while_ loop. This is a loop that continues to be executed "as long as" some condition is true. One of the things that means is that the condition needs to be changed somehow inside the loop or it will never end. That leads to programs that bog down a computer, sometimes crash it, and -- in all cases -- make it just a real pain. So, _while_ loops are often used only if you absolutely need their greater flexibility. Let's see how we could reimplement the last code using a while loop.
```
value = 10
while value < 21:
print(value)
value = value + 1
```
As you can see, the _while_ loop required more code than the _for_ loop version, twice as much, in fact. That is often the cost of greater flexibility. Any time you have more code, you also have more places to screw up. So, more code is just a bad thing. Which begs the question, when is it better to use a _while_ loop. The answer is annoyingly easy -- when you have to. Let's see what that means.
Let's implement a bit of code that will calculate the recursion used in the Collatz Conjecture. The math isn't really important, but there are two options, if the number is even then it is divided by two and if it is odd the number is multiplied by three and then one is added. The Collatz Conjecture says that all numbers will, eventually, end up being one. No one has managed to prove it; but, it has not been disproven either. Every number tested has (sometimes after a *very* long time) gone to one.
```
x = 14
while not x == 1:
print(x)
if (x % 2) == 0:
x = (x / 2)
else:
x = (3*x) + 1
print(x)
```
Before we look too closely at the loop, let's look at the line with the _if_ statement. That looks pretty knarly. This condition is checking if the variable _x_ is even. It does this using the modulus (%) operation which return the remainder of integer division. This remainder is then compared to the value zero. All even numbers will have a remainder of zero when divided by the number two, so the condition will be true. If a number is not even, it is odd, so the _else_ conditional statement will be executed only for odd numbers. That works.
The while loop will continue to be executed whenever the variable _x_ *is not* equal to one. Another way we could read this is to think, it will jump past the loop as soon as _x_ *is equal to* one. You can look at the condition whichever way makes the most sense to you, as they are both logically identical. In any case, this is a reasonable use of a _while_ loop and most other reasonable uses will look similar. What makes this different from a _for_ loop is that the list isn't known at the beginning. It's created as part of the loop.
### Functions
One of the major improvements in the quality of code comes from breaking the code up into sections that are understandible. In the computer science introduction, this was described as finding nested algorithms from which to construct a program. How are we able to seperate these algorithms though. As we saw in the bubble sort example, Python (as with all modern programming languages) provides the ability to create what are called functions. Functions are blocks of code with a name. Data can be passed *into* a function, as parameters, and returned *from* a function, as a return value. Functions are an important part of all programming paradigms. It's a way to create a block of code that we can check seperate from the rest of the program.
In a simple way, functions can be considered to be similar to functions in highschool math. If one were to say $y = x^{2}$, we can directly map that to the Python function,
```
def square(x):
return x**2
```
This function represents the right side of of our math function. In this case a function seems silly. Why, for instance, would we want to replace the simple math ```x**2``` with the equally long function name ```square()```? Well, obviously, this is only a short example. If our math function was much more complicated, it would make more sense. Additionally, however, Python actually allows passing around functions as values. This is a functional programming idea and it can be increadiby useful, even for very short functions. We won't look into this feature of the language any further here, as its usage is more advanced than need concern us. However, it is worth nothing that even very short functions have a purpose.
Getting back to our functions, let's examine the code. In Python, a function is defined by first using the keyword ```def``` (define). After that, we write the name of the function. Function names use exactly the same rules as variable names. Following the name, and inside parenthesis, are a list of parameters. These are, essentially, variables that are available inside the function. They are the way that data gets into the function (that's an oversimplification, of course, but it's good enough for now). In the code block that follows the declaration, we find the implementation of the function. The keyword ```return``` means "take the data that you are given and transfer it back to whoever called this function." Okay, what does that mean? Let's look at some simple code using this function.
```
y = square(3)
print(y)
```
If we pass the value three into the function, we get the value we would expect stored in the variable ```y```. The data passed in ends up in the variable ```x```. ```x``` is squared and the result is then returned to where the function was called from. In some ways, it can be viewed as the function call being replaced by the value it returns.
The thing is, we don't always know what a function is going to do. Being a language that allows side effects, Python doesn't make any attempt to limit things that functions do "invisibly." Take this function for instance,
```
def loudSquare(x):
print("Hello!!!")
return x**2
print(loudSquare(4))
```
Sometimes we want our functions to have additional side effects. In this case, we could use the ```print``` inside the function to help us debug. This is where functions deviate from the mathematical version, however. If we look at the inputs and outputs of a function, we may be able to learn what it does. Or, maybe not. With mathematical functions (and enough time) we could always work out what they do from just the inputs and outputs. Even worse, there are ways to create stateful functions, which is to say that the way a function works is based on how it was called in the past. These are complications that are difficult to avoid in an imperative style with side-effects and state mutation. And this is why we need good documentation... and _sometimes_ get it.
Bearing in mind all the complications of functions, it is possible to use them as if they are simple. It's never a bad idea to pull out code and make a function. Indeed, the idea of using functions to simplify code has been codified into the software engineering principle of *DRY* (*D*o not *R*epeat *Y*ourself). The code that we have seen thus far have been increadibly simple. There haven't been any places where we have needed the same functionality in multiple places. In real code, however, there are many times that the same functionality is needed all throughout the code. This is when functions come into their own. The function is written in only one place. It can be debugged just once and, in the case that it needs to be changed, the change is made only in a single place.
## Examples
At this point, we have examined all of the basic components of programming in an imperative style. All that's left is to put it together in some way. The easiest way to do this is to look at some examples. To use the examples, make a first effort to read the example and understand how it is working prior to reading the description below. Sometimes an example will have a fairly large setup before it (to make the context and purpose clear) and sometimes it will not. Either way, focus on the code components that you see. See if you can start blocking the code into small algorithms that do something specific. Build the whole code up from there.
### Guessing Random Number Game
This example is just a simple guessing game but it introduces a number of important concepts. You can change the difficulty of the game by changing the range of numbers it will choose from. After that, the game will ask you to make guesses until you either guess the correct number of you run out of guesses.
```
minimum_number = 0 # Change the smallest number to guess here
maximum_number = 100 # Change the largest number to guess here
# NOTHING BELOW HERE NEEDS T0 BE CHANGED
from random import randint # random is the random number library, import just the randint function
from math import log # math is the math library, import just the log function
real_value = randint(minimum_number, maximum_number + 1)
maximum_guesses = int(log(maximum_number - minimum_number) / log(2.0))
guess = 1
correct = False
while not correct and guess <= maximum_guesses:
remaining = maximum_guesses - guess + 1
print("You have {} {} left.".format(remaining, "guess" if remaining == 1 else "guesses"))
guessed_value = int(input("What number do you think it is? "))
if guessed_value == real_value:
correct = True
elif guessed_value > real_value:
print("Too high!")
else:
print("Too low!")
print('')
guess = guess + 1
if correct:
print("Great Job! The number was {}.".format(real_value))
else:
print("Too bad :( Number was {}.".format(real_value))
```
#### About the game code
This little game uses a little bit of everything -- variables, conditions and a loop. It also uses two libraries, the math library (which we saw in the section on arithmetic) and the random library which is used to get "random" numbers. It is worth mentioning that numbers in a computer are never really random. They are, at best, pseudorandom. It is good enough for our purposes here, however.
The program begins with a little bit of configuration. Two variables are set: one for the smallest number to guess and one for the largest. This is the part of the program that would need to be changed to make it act differently. It makes lots of sense to seperate this part out from the rest of the program whenever possible. It's much easier to modify just a few variable values at the beginning than it is to dig into a bunch of code deep in a program.
After the configuration, two functions are imported from the libraries. First, _randint_ is imported from the _random_ library. This function returns a random integer. It acts just like the _range_ function that we saw earlier. It will return numbers up to, but not including, the second number.
After the functions are imported, there are four variables set. The first one is a call to the _randint_ function. It will get a random number somewhere in the range that we specified and, of course, we add one to the maximum number, so that it is possible to get it. Next the maximum number of guesses is calculated. The reasoning behind this math is described below. Finally, the guess variable is initialized to one and the correct variable is initialized to False. These two variables are used to keep track of where the player is in the game.
Next we come to a while loop. We use a while loop because the user is going to make guesses inside the loop, there is no list to iterate over at the beginning. The loop will be executed if the last guess was *not* correct and the current guess is less than or equal to the maximum guess. If either of those is False (either the last guess *was* correct or too many guesses have been made) the loop will be skipped.
Inside the loop, the first operation is to calculate how many guesses are left. If the current guess is the same as the maximum guess, there is still one guess left, so we get the formula in the code. After calculating how many guesses remain, we print that so that the player knows. This is a complicated line of code and we should break it up. The outer function call is just a print function, so we know that it is going to display something for us. Next we see a string with a call to the _format_ method. There are two replacements we are going to be making (marked by curly braces) and, indeed, within the format function we pass two values. The first value is just the number of remaining guesses we just calculated. The second value is calculated using a ternary operator. Since we want to have proper grammar, we say "1 guess" or "x guesses". The condition in the ternary operator just looks for when the number of remaining guesses is exactly equal to one.
Next we read a new guessed value. The _input_ function is a Python built-in function and it does two things. First it will display a prompt, then it will read a string from the player and return it. Since we actually want an integer, rather than a string, we pass the return value of _input_ into the _int_ function. After all that, the _guessed_value_ variable will contain the value that the user entered. It is probably worth trying to enter things that aren't numbers, as it will break the program in strange ways. A more complete implementation of this game would check that the user is actually entering something that looks like a number before trying to use it.
Once the guessed value has been read in, the inner loop will compare the value to the _real_value_. If they match are equal then the _if_ statement will set the _correct_ variable to True which will, eventually, lead to the loop not being repeated. If the _guessed_value_ is not equal to _real_value_ then the _elif_ statement will be checked and either it or the _elese_ statement will be executed, telling the player if the guess was too high or too low.
The very end of the inner loop simply prints an empty line and increments (increses by one) the value of _guess_. These two actions prepare for the next attempt to guess the value. Depending upon the number of guesses completed and whether or not the last guess matched, the loop will either be executed again or skipped.
When the loop finally falls through, the remainder of the program consists of an _if-else_ statement which will select the final message to print based on the boolean value of _correct_. If the final guess *was* correct, the _if_ statement will be executed, printing "Good Job!" and also printing what the value was. If the _if_ statement is not executed, the _else_ statement will be executed, printing "Too bad :(" and informing the player what the correct value was.
#### About calculating the number of guesses
There's a really powerful algorithm in computer science called a binary search. It allows you to reduce the search space but one half each and every time you look, so it is a very fast algorithm. Indeed, in computation theory, it is considered O(log N), which is to say, big-Oh log of N. Algorithms that are order log N are some of the fastest algorithms available. In the case of guessing random numbers from a range like this, it is possible to use a binary search, so the program limits your number of guesses to a number which ensures that you never have extra guesses. And, that is where the ugly math used to calculate maximum_guesses comes from.
### Calculating first N prime numbers
Searching for prime numbers is big business. This program is just small fry. Still, it can be fun to print long lists of numbers... really, it can! This example will create a list of the first N prime numbers.
```
N = 250 # Set this to how many of the prime numbers should be found
from math import sqrt
def checkIsPrime(value, primes):
maximum_factor = sqrt(value)
for prime in primes:
if prime > maximum_factor:
return True
if (value % prime) == 0:
return False
return True
primes = [2]
value = 3
for _ in range(N-1):
found = False
while not found:
found = checkIsPrime(value, primes)
if found:
primes.append(value)
value = value + 1
print(primes)
```
#### About checking the primality of a number
A number is prime if it is only divisible by itself and the number one. That's the mathematical definition -- no problem. How do we check that a number *is* prime though? Let's take a look at the algorithm in the ```checkIsPrime``` function. Primality testing can be rephrased as being a check on a numbers factors. Factors are then numbers that are multiplied to get a number. Prime numbers have no factors. Compound numbers, however, have some factors. Thus, a way to check if a number is prime is to check if it has _any_ factors. If a number has a factor, then it isn't prime. This is the way that the primality check here works. The function assumes that there is a list of all the possible factors (as it happens, the prime numbers are the only possible factors). The function receives two parameters: a number to check and a list of factors. There is one other piece to the function, however. The largest factor that can be in a number is its square root. Any number larger than the square root can, therefore, be ignored. The primality checking function, therefore, takes advantage of what is called "early exit" when the factor to be checked is too large. This is an optimization which speeds up the code. It would work just as well without it.
The flow of the ```checkIsPrime``` function is fairly simple. On entry to the function, we calculate the square root of the number we are checking. Any factors must be less than or equal to this value. Next we enter a loop that iterates over the prime numbers that we already know. There if an ```if``` statement which checks if the current factor we are checking is larger than the largest factor. In that case, we know the number is prime because the only way to get there is to have checked all of the smaller (possible) factors. The second ```if``` statement in the checking loop tests if the value to test is evenly divisible by the current factor (```prime```). If any number evenly divides the number that we are checking then it is a compound number and, thus, is *not* prime. We, therefore, return ```False```. In general, we would expect the loop the function to be exited by one of the ```return``` statements within the loop. If, however, the function continues all the way to the end, we assume that the number is prime and return ```True```.
#### About the prime number main loop
This code uses nested loops -- both ```for``` and ```while``` loops. Nested loops are sometimes considered a code "smell". Code smell refers to the idea that some things in code just don't feel right. Nested loops can be complicated, they can be difficult. Sometimes they are necessary, but it's still reasonable to take pause if nested loops show up in a problem that does not seem to require them. Here, however, we have two things going on. We are looping over then number of prime numbers we want to store *and* looping over all the possible values we are testing. That's the source of our nested loops and we can't really reduce that much. It seems reasonable to use nested loops in this situation.
At the top of the code we define ```N``` as the number of primes we want to find. This code is actually pretty fast. Looking for the first 10000 primes is entirely possible -- it just takes a lot of space to print. We can play with how many primes we wish to view by simply changing the configuration here. Again, it is nice to have such configurations decoupled from the functional code.
Next we find the definition of the primality checking function. Since we have discussed how this function works already we will not do so again, however, in most languages (including Python) it is necessary that a function be defined before it is used. Therefore, we find that definition preceeding the bulk of the code.
The first thing the code does after having done what can be considered as setup is to create a variable ```primes``` which holds a list. To begin with, the list holds one number, the number two. There are many different ways that this code could have been written. The way it was done here, however, requires that the list of primes be "initialized" with something. In this case, the first prime number. One result of this is that the code will not work if asked to return zero prime numbers. Why would we do that? Who knows. People do strange things with software. As with our guessing game example, this is a place where we could validate program data to avoid the program doing the wrong things. The next action is to initialize the variable ```value``` to hold the number three, which is the first number that actual primality checking will happen on.
Having set up the main state of the program, there is a ```for``` loop that simply loops ```N-1``` times. The ```-1``` exists because the list of primes was initialized already with the first prime. The ```for``` loop is executed once for every prime which needs to be *added* to the list. The first step is to initialize the ```found``` variable to ```False``` to signify that new prime number has been found. This variable will be set to true as soon as a new prime number is found within the _while_ loop. The next step is, of course, the ```while``` loop that searches for a valid prime number. The ```found``` variable is assigned to the return value of the ```checkPrime``` function with the current value. Next an _if_ statement checks the value of the ```found``` variable. If the current value is prime, it will be added to the ```primes``` list using the ```append``` method. Regardless, the ```value``` variable is incremented (assigned to being one more than it initially was). This defines the end of the ```while``` loop, which will be repeated if the ```found``` variable remains ```False```. If, on the other hand, a prime number was found on the last iteration of the while loop the code will fall back to the outer for loop. The for loop, of course, will continue until it has iterated all ```N-1``` times.
At the very end, the code simply prints out the generated list of primes.
### Politicians are crooks!
There's an old logic puzzle. Assume that 50% of politicians are murders and 50% of politicians are robbers. Does that mean that all politicians are crooks? The answer (spoiler alert!) is no. There are lots of ways that we can show that using math and logic. A really fun way to demonstrate it, however, is to _simulate_ it. Simulation is where a program acts "like" something in reality. Simulation is one of the powerful problem-solving techniques in computer science. It is also a fun technique because we can test situations that are difficult (or impossible) to test in reality. This is a more advanced program, partly because it uses a number of Python features that we really haven't explored yet. As with the rest, work your way through the code slowly doing your best to identify the parts you know and get as much as you can from context. This also uses more in the way of math than anything else we have worked with. Don't let this frighten you. The math isn't difficult.
```
import random
N = 10000 # We'll just take a random sampling of politicians in the nation....
politicians = set(range(N))
def choosePoliticians(all_politicians, percentage):
number = int(len(all_politicians) * percentage / 100.0)
all_politicians = list(all_politicians)
random.shuffle(all_politicians)
return set(all_politicians[:number])
def simulateNefariousPublicServents(politicians, percent_of_burgulars=50, percent_of_murderers=50):
burgulars = choosePoliticians(politicians, percent_of_burgulars)
murderers = choosePoliticians(politicians, percent_of_murderers)
criminals = burgulars.union(murderers)
return (100.0 * len(criminals)) / len(politicians)
percent_crooks = simulateNefariousPublicServents(politicians)
print('{}% of politicians are crooks!'.format(percent_crooks))
```
#### About the problem
One especially interesting thing about this program is that it will not always give the same results. We can understand that, of course, because the code is using the ```random``` library which -- unsurprisingly -- deals with randomness. It begs the question though, if it doesn't always give the same answer, does that mean that it doesn't give the _correct_ answer? In fact, we would not _expect_ for the answer to be the same. Since this is a simulation, we are expecting for the code to represent different groups of random (potentially) nefarious politicians. The "correct" answer (in the terrifying limit of an infinite number of politicians) is 75.0%. Running the code several times, you should find that the numbers all fall around that.
We can understand why the answer is 75% rather than 100% in this way. If we are given one hundred empty cards and place a red dot on the top fifty, we have marked the 50% that are murders. We then shuffle the cards well. If the process is then repeated (placing a blue dot on the top fifty cards). There will be four kinds of card in the deck. Some will have a red dot, some a blue dot, some both, and some will not have any dots. The logical fallacy which often leads us to assume that there are no virtuous politicians is that we forget the subset who are _both_ murders and robbers. This process of "marking" cards is handled in the code by the ```choosePoliticians``` function which selects a small group out of a larger group. When this smaller group is choosen, that is similar to marking cards with colored dots. When these two groups are combined it gives a single group that consists of all politicians who are murders, robbers, or both.
#### About the code
At the top of the code, the ```random``` library is imported. Here we do not import a specific function from the library but, rather, import the whole _module_. By doing so, it becomes necessary to use the library name in the rest of code any time we wish to use a function in the module. In short programs like we have seen here it is rarely helpful to do this. However, as soon as programs begin to get larger and more complex, importing a module and accessing the functions through the module name becomes more useful as it reduces the possibility of so called namespace polution (which is a reasonable thing to look up, but won't be discussed further here). Next, we define a variable ```N``` that simply defines the number of politicians which will be used in the simulation. The larger N is, the more consistent the results of the simulation will be. It is worth reducing ```N``` to only 15 or 20, just to see what happens.
Following that, we create a set of politicians (called ```politicians```). A set is another Python datatype that we didn't introduce above. A "set" is a mathematic concept. It is a container that holds only one copy of anything. If we put the number 1 into the set and try to put the number 1 in again, there will only be a single copy of 1 in the set. Combining two sets (with the union operation) always leads to another set (that is, if two sets both contain the number 1 and they are combined, the resultant set will only contain one copy of the number 1). The code above creates the set by creating a _list-like_ object with the numbers from zero to ```N-1``` and passing that list into the ```set``` function.
We next find the first of two function definitions. In this case, the function, ```choosePoliticians``` will select a "subset" of a set passed into it. The function takes two arguments. The first argument, ```politicians``` is expected to be a set of politicians. At this point, it is worth noting that we have two variables named ```politicians``` in the code and not one. The first we created explicitly in the third line of code. This particular variable does not change through the course of the program. The second ```politicians``` variable is a parameter of the function. Inside the function, the value of the first variable is "shadowed", that is, it is hidden. There are specific rules in Python that determine when variables are seen or hidden. Sometimes these rules can be complicated. In this case, it is fairly easy to just remember that variables in a parameter list always hide variables outside a function.
|
github_jupyter
|
def swapIndex(data, first, second): # This line is defining (def) a function named swapIndex that has three parameters
temp = data[first] # Next we store one of the values in a temporary location, variable temp
data[first] = data[second] # After that, we store the second value into the location of the first
data[second] = temp # And, finally, store the first value (which was saved seperately) into the second
def bubbleSort(data): # Define the function bubbleSort, it has one parameter named data
N = len(data) - 1 # Get the one less than the length of the list, store it in variable N
for _ in range(N): # Just loop N times
for index in range(N-1): # Loop over all the list indicies from 0 to N-2 (skip the last one)
first = index # Get the index of the first element, it's just the current index
second = index + 1 # Get the index of the second element, it's just one past the current
if data[first] > data[second]: # Check if the first value is greater than the second value
swapIndex(data, first, second) # If it is, swap the first and second values
print(data) # Print out the list so that we can watch it being sorted
print('') # Print an empty line, so we can see the seperate loops
data = [1, 6, 2, 0]
bubbleSort(data)
data = ["parmesan", "mozzarella", "cheddar", "goda", "blue cheese"]
bubbleSort(data)
def bubbleSort2(data): # Define the function bubbleSort2, it has one parameter named data
N = len(data) - 1 # Get the one less than the length of the list, store it in variable N
for end in reversed(range(N+1)): # Loop N times and change the length of the inner loop
for index in range(0, end): # Loop over all the list indicies from 0 to end (skip the last one)
first = index # Get the index of the first element, it's just the current index
second = index + 1 # Get the index of the second element, it's just one past the current
if data[first] > data[second]: # Check if the first value is greater than the second value
swapIndex(data, first, second) # If it is, swap the first and second values
print(data) # Print out the list so that we can watch it being sorted
print('') # Print an empty line, so we can see the seperate loops
data = ["parmesan", "mozzarella", "cheddar", "goda", "blue cheese"]
bubbleSort2(data)
42
type(42)
print(3.1415926535)
print(type(3.1415926535))
3.1415926535 - 3.1415926534
print(-42.0)
print(4.2e1)
print(1e-3)
"I am a string"
'I am a string too!'
s = "The Pet Shop"
print(s[-4:]) # Print the last four values in the string
print(s[0]) # Print the first value in the string -- remember, the first value is index 0!
print(s[4:8]) # Print the values in the string beginning at index 4 and up to but not including index 8
print("This\nis\ta string")
for number in range(10):
print("The magic number is {}".format(number))
[1, 2, 3, 4, 5]
[1.7, "Parrots", [[], "stuff", 1]]
list(range(10))
my_variable = 8
print(my_variable)
my_variable = "The bird is deceased!"
print(my_variable)
another_variable = my_variable
print(my_variable)
print(another_variable)
x = 4 # Set up x and y to point to the same value
y = x
print("x = {}, y = {}".format(x, y)) # Check that they do
x = 5 # Set x to hold another value
print("x = {}, y = {}".format(x, y)) # What do we get?
x = [1, 2, 3] # Set up x and y to point to the same list of integers
y = x
print("x = {}, y = {}".format(x, y)) # Check that they do
x[1] = 5 # Set the second item in the list x to hold another value
print("x = {}, y = {}".format(x, y)) # What do we get?
# Do some quick calculations to figure out the size of a bird cage
height = 24 # Here we define variables for height, width and depth
width = 18
depth = 15
area = width * depth # Calculate the area by just multiplying
volume = (height * area) / (12**3) # Calculate the volume in cu. in. then convert to cu. ft.
edge_perimeter = 4 * (width + height + depth) # There are four edges of each length, so, add then multiply
print("Base area = {} sq. in.".format(area))
print("Cage volume = {} cu. ft.".format(volume))
print("Length of cage edges = {} in.".format(edge_perimeter))
def toDegrees(rad): # Convert some number of radians to degrees
return 57.3 * rad
def toRadians(deg): # Convert some number of degrees to radians
return deg / 57.3
from math import * # This will import everything (*) from the math library
print(sin(toRadians(0)))
print(sin(toRadians(45)))
print(sin(toRadians(90)))
print(4 > 5) # Check strictly greater than
print(4 >= 5) # Check greater than or equal to
print(4 == 5) # Check strictly equal to
print(not 4 == 5) # Check strictly not equal to
print(4 <= 5) # Check less than or equal to
print(4 < 5) # Check strictly less than
print('1' == 1)
print('1' > 1)
print('1' < 1)
print(int('1') == 1)
print(int('1') > 1)
print(int('1') < 1)
bigger = 4 > 7
print("bigger = {}".format(bigger))
print(not True)
print(True and False)
print(True or False)
print(True and (not False))
x = 10 # To test other numbers, modify this line
if x > 10:
x = x / 2
print(x)
x = 5 # To test other numbers, modify this line
if 0 <= x < 10: # This could also be written as (0 <= x) and (x < 10)
print("Option 1")
else:
print("Option 2")
x = 3 # To test other numbers, modify this line.
if x == 1:
print("We're number one!")
elif x == 2:
print("Silver, baby!")
elif x == 3:
print("Third is still placing.")
else:
print("Ughhh.....")
x = -100 # To test other numbers, modify this line.
number_of_places = 42
if x <= 0 or x > number_of_places:
print("ERROR: Invalid place")
elif x == 1:
print("We're number one!")
elif x == 2:
print("Silver, baby!")
elif x == 3:
print("Third is still placing.")
else:
print("Ughhh.....")
value = 7
print("Negative" if value < 0 else "Positive")
value = 7
string = "Positive"
if value < 0:
string = "Negative"
print(string)
adjectives = ['dead', 'pushing up daisies', 'deceased']
for adjective in adjectives:
print("The bird is {}.".format(adjective))
print("Three cheers for King George!")
for _ in range(3):
print("Hip-Hip Hurray!")
for value in range(10, 21):
print(value)
value = 10
while value < 21:
print(value)
value = value + 1
x = 14
while not x == 1:
print(x)
if (x % 2) == 0:
x = (x / 2)
else:
x = (3*x) + 1
print(x)
def square(x):
return x**2
y = square(3)
print(y)
def loudSquare(x):
print("Hello!!!")
return x**2
print(loudSquare(4))
minimum_number = 0 # Change the smallest number to guess here
maximum_number = 100 # Change the largest number to guess here
# NOTHING BELOW HERE NEEDS T0 BE CHANGED
from random import randint # random is the random number library, import just the randint function
from math import log # math is the math library, import just the log function
real_value = randint(minimum_number, maximum_number + 1)
maximum_guesses = int(log(maximum_number - minimum_number) / log(2.0))
guess = 1
correct = False
while not correct and guess <= maximum_guesses:
remaining = maximum_guesses - guess + 1
print("You have {} {} left.".format(remaining, "guess" if remaining == 1 else "guesses"))
guessed_value = int(input("What number do you think it is? "))
if guessed_value == real_value:
correct = True
elif guessed_value > real_value:
print("Too high!")
else:
print("Too low!")
print('')
guess = guess + 1
if correct:
print("Great Job! The number was {}.".format(real_value))
else:
print("Too bad :( Number was {}.".format(real_value))
N = 250 # Set this to how many of the prime numbers should be found
from math import sqrt
def checkIsPrime(value, primes):
maximum_factor = sqrt(value)
for prime in primes:
if prime > maximum_factor:
return True
if (value % prime) == 0:
return False
return True
primes = [2]
value = 3
for _ in range(N-1):
found = False
while not found:
found = checkIsPrime(value, primes)
if found:
primes.append(value)
value = value + 1
print(primes)
import random
N = 10000 # We'll just take a random sampling of politicians in the nation....
politicians = set(range(N))
def choosePoliticians(all_politicians, percentage):
number = int(len(all_politicians) * percentage / 100.0)
all_politicians = list(all_politicians)
random.shuffle(all_politicians)
return set(all_politicians[:number])
def simulateNefariousPublicServents(politicians, percent_of_burgulars=50, percent_of_murderers=50):
burgulars = choosePoliticians(politicians, percent_of_burgulars)
murderers = choosePoliticians(politicians, percent_of_murderers)
criminals = burgulars.union(murderers)
return (100.0 * len(criminals)) / len(politicians)
percent_crooks = simulateNefariousPublicServents(politicians)
print('{}% of politicians are crooks!'.format(percent_crooks))
| 0.453262 | 0.848972 |
```
import pandas as pd
import nltk
from nltk.corpus import brown
import jieba
import gensim
%matplotlib inline
from sklearn.decomposition import LatentDirichletAllocation
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
df = pd.read_csv(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\金庸-射雕英雄传txt精校版.txt", names=["txt"], sep='aaa', encoding="gbk")
# 构建新列
print(len(df))
print(df.shape)
def m_head(tmpstr):
return tmpstr[:1]
def m_mid(tmpstr):
return tmpstr.find("回 ")
df["head"] = df.txt.apply(m_mid)
df["mid"] = df.txt.apply(m_head)
df["len"] = df.txt.apply(len)
# 标明章序号
chapnum = 0
for i in range(len(df)):
if df["mid"][i] == "第" and df["head"][i] > 0 and df["len"][i] < 30:
chapnum += 1
if chapnum >= 40 and df.txt[i] == "附录一:成吉思汗家族":
chapnum = 00
df.loc[i, "chap"] = chapnum
dfgrp = df.groupby("chap")
chapter = dfgrp.apply(sum)
chapter = chapter[chapter.index != 0]
chapter.head()
def m_cut(intxt):
return [w for w in jieba.cut(intxt) if w not in stoplist and len(w) > 1]
stoplistdf = pd.read_csv(r'D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\停用词.txt', names=["w"], sep="aaa", encoding="utf-8")
stoplist = list(stoplistdf.w)
chaplist = [m_cut(w) for w in chapter.txt]
countvec = CountVectorizer(min_df=5)
wordmtx = countvec.fit_transform(chaplist[0])
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(wordmtx)
tfidf
import pyLDAvis
import pyLDAvis.sklearn
n_topics = 10
ldamodel = LatentDirichletAllocation(n_components=n_topics)
ldamodel.fit(wordmtx)
pyLDAvis.enable_notebook()
pyLDAvis.sklearn.prepare(ldamodel, tfidf, countvec)
```
# 文档相似度
```
chapter.head()
chapter["cut"] = chapter.txt.apply(m_cut)
chapter.head()
from gensim.models.word2vec import Word2Vec
n_dim = 300 # 向量维度
w2vmodel = Word2Vec(size=n_dim, min_count=10)
w2vmodel.build_vocab(chapter.cut) # 生成词
w2vmodel
%time w2vmodel.train(chapter.cut, total_examples=w2vmodel.corpus_count, epochs=10)
print(w2vmodel.wv["郭靖"].shape)
w2vmodel.wv["郭靖"]
w2vmodel.wv.most_similar("郭靖")
w2vmodel.wv.most_similar("黄蓉")
w2vmodel.wv.most_similar("黄蓉", topn=20)
w2vmodel.wv.most_similar("黄蓉道")
w2vmodel.wv.most_similar(["郭靖", "小红马"], ["黄药师"], topn=5)
w2vmodel.wv.most_similar(positive=['郭靖', '黄蓉'], negative=['杨康'], topn=10)
# 计算两个词的相似度/相关程度
print(w2vmodel.wv.similarity("郭靖", "黄蓉"))
print(w2vmodel.wv.similarity("郭靖", "杨康"))
print(w2vmodel.wv.similarity("郭靖", "杨铁心"))
w2vmodel.wv.doesnt_match("小红马 黄药师 鲁有脚".split())
w2vmodel.wv.doesnt_match("杨铁心 黄药师 黄蓉 洪七公".split())
```
## 文档相似度 基于词袋模型
```
cleanchap = [" ".join(m_cut(w)) for w in chapter.txt.iloc[:5]]
from sklearn.feature_extraction.text import CountVectorizer
countvec = CountVectorizer()
resmtx = countvec.fit_transform(cleanchap)
resmtx
from sklearn.metrics.pairwise import pairwise_distances
pairwise_distances(resmtx, metric ="cosine")
pairwise_distances(resmtx)
pairwise_distances(tfidf[:5], metric="cosine")
tfidf[:5]
```
## gensim 相似度实现
```
chaplist = [m_cut(w) for w in chapter.txt]
dictionary = gensim.corpora.Dictionary(chaplist)
corpus = [dictionary.doc2bow(text) for text in chaplist] # 仍为list in list
tfidf_model = gensim.models.TfidfModel(corpus) # 建立TF-IDF模型
corpus_tfidf = tfidf_model[corpus] # 对所需文档计算TF-IDF结果
corpus_tfidf
# 列出所消耗的时间备查
%time ldamodel = gensim.models.LdaModel(corpus, id2word = dictionary, num_topics = 10, passes = 2)
simmtx = gensim.similarities.MatrixSimilarity(corpus)
simmtx
simmtx.index[:2]
query = chapter.txt[1]
query_bow = dictionary.doc2bow(m_cut(query))
lda_vec = ldamodel[query_bow]
sims = simmtx[lda_vec]
sims = sorted(enumerate(sims), key=lambda item: -item[1])
sims
```
## 相似度 word2vec
```
def m_doc(doclist):
reslist = []
for i, doc in enumerate(doclist):
reslist.append(gensim.models.doc2vec.TaggedDocument(jieba.lcut(doc), [i]))
return reslist
corp = m_doc(chapter.txt)
corp[:2]
d2vmodel = gensim.models.Doc2Vec(vector_size=300, window=20, min_count=5)
%time d2vmodel.build_vocab(corp)
d2vmodel.wv.vocab
# 将新文本转换为相应维度空间下的向量
newvec = d2vmodel.infer_vector(jieba.lcut(chapter.txt[1]))
d2vmodel.docvecs.most_similar([newvec], topn = 10)
```
# 文档聚类
```
# 为章节增加名称标签
chapter.index = [df.txt[df.chap == i].iloc[0] for i in chapter.index]
chapter.head()
import jieba
cuttxt = lambda x: " ".join(m_cut(x))
cleanchap = chapter.txt.apply(cuttxt)
cleanchap[:2]
# 计算TF-IDF矩阵
from sklearn.feature_extraction.text import TfidfTransformer
vectorizer = CountVectorizer()
wordmtx = vectorizer.fit_transform(cleanchap) # 将文本中的词语转换为词频矩阵
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(wordmtx) #基于词频矩阵计算TF-IDF值
tfidf
# 进行聚类分析
from sklearn.cluster import KMeans
clf = KMeans(n_clusters = 5)
s = clf.fit(tfidf)
print(s)
clf.cluster_centers_
clf.cluster_centers_.shape
clf.labels_
chapter['clsres'] = clf.labels_
chapter.head()
chapter.sort_values('clsres').clsres
chapgrp = chapter.groupby('clsres')
chapcls = chapgrp.apply(sum) # 只有字符串列的情况下,sum函数自动转为合并字符串
cuttxt = lambda x: " ".join(m_cut(x))
chapclsres = chapcls.txt.apply(cuttxt)
chapclsres
# 列出关键词以刻画类别特征
import jieba.analyse as ana
ana.set_stop_words(r'D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\停用词.txt')
for item in chapclsres:
print(ana.extract_tags(item, topK = 10))
```
## 文本分类 朴素贝叶斯 sklearn
```
# 从原始语料df中提取出所需的前两章段落
raw12 = df[df.chap.isin([1,2])]
raw12ana = raw12.iloc[list(raw12.txt.apply(len) > 50), :] # 只使用超过50字的段落
raw12ana.reset_index(drop = True, inplace = True)
print(len(raw12ana))
raw12ana.head()
# 分词和预处理
import jieba
cuttxt = lambda x: " ".join(jieba.lcut(x)) # 这里不做任何清理工作,以保留情感词
raw12ana["cleantxt"] = raw12ana.txt.apply(cuttxt)
raw12ana.head()
from sklearn.feature_extraction.text import CountVectorizer
countvec = CountVectorizer()
wordmtx = countvec.fit_transform(raw12ana.cleantxt)
wordmtx
# 作用:将数据集划分为 训练集和测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(wordmtx, raw12ana.chap, test_size = 0.3, random_state = 111)
from sklearn import naive_bayes
NBmodel = naive_bayes.MultinomialNB()
# 拟合模型
NBmodel.fit(x_train, y_train)
x_test
NBmodel.predict(x_test)
# 预测准确率(给模型打分)
print('训练集:', NBmodel.score(x_train, y_train),
',验证集:', NBmodel.score(x_test, y_test))
from sklearn.metrics import classification_report
print(classification_report(y_test, NBmodel.predict(x_test)))
countvec.vocabulary_
string = "杨铁心和包惜弱收养穆念慈"
words = " ".join(jieba.lcut(string))
words_vecs = countvec.transform([words]) # 数据需要转换为可迭代的list格式
words_vecs
NBmodel.predict(words_vecs)
```
## NLTK 朴素贝叶斯
```
# 这里直接以章节为一个单元进行分析,以简化程序结构
import nltk
from nltk import FreqDist
# 生成完整的词条频数字典,这部分也可以用遍历方式实现
fdist1 = FreqDist(m_cut(chapter.txt[1]))
fdist2 = FreqDist(m_cut(chapter.txt[2]))
fdist3 = FreqDist(m_cut(chapter.txt[3]))
fdist1
from nltk.classify import NaiveBayesClassifier
training_data = [ [fdist1, 'chap1'], [fdist2, 'chap2'], [fdist3, 'chap3'] ]
# 训练分类模型
NLTKmodel = NaiveBayesClassifier.train(training_data)
print(NLTKmodel.classify(FreqDist(m_cut("杨铁心收养穆念慈"))))
print(NLTKmodel.classify(FreqDist(m_cut("钱塘江 日日夜夜 包惜弱 颜烈 使出杨家枪"))))
nltk.classify.accuracy(NLTKmodel, training_data) # 准确度评价
NLTKmodel.show_most_informative_features(5)#得到似然比,检测对于哪些特征有用
```
# 情感分析
```
# 读入原始数据集
import pandas as pd
dfpos = pd.read_excel(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\购物评论.xlsx", sheet_name = "正向", header=None)
dfpos['y'] = 1
dfneg = pd.read_excel(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\购物评论.xlsx", sheet_name = "负向", header=None)
dfneg['y'] = 0
df0 = dfpos.append(dfneg, ignore_index = True)
df0.head()
# 分词和预处理
import jieba
cuttxt = lambda x: " ".join(jieba.lcut(x)) # 这里不做任何清理工作,以保留情感词
df0["cleantxt"] = df0[0].apply(cuttxt)
df0.head()
from sklearn.feature_extraction.text import CountVectorizer
countvec = CountVectorizer(min_df = 5) # 出现5次以上的才纳入
wordmtx = countvec.fit_transform(df0.cleantxt)
wordmtx
# 按照7:3的比例生成训练集和测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(
wordmtx, df0.y, test_size=0.3) # 这里可以直接使用稀疏矩阵格式
x_train[0]
# 使用SVM进行建模
from sklearn.svm import SVC
clf=SVC(kernel = 'rbf', verbose = True)
clf.fit(x_train, y_train) # 内存占用可能较高
clf.score(x_train, y_train)
# 对模型效果进行评估
from sklearn.metrics import classification_report
print(classification_report(y_test, clf.predict(x_test)))
clf.predict(countvec.transform([df0.cleantxt[0]]))[0]
# 模型预测
import jieba
def m_pred(string, countvec, model) :
words = " ".join(jieba.lcut(string))
words_vecs = countvec.transform([words]) # 数据需要转换为可迭代格式
result = model.predict(words_vecs)
if int(result[0]) == 1:
print(string, ":正向")
else:
print(string, ":负向")
comment = "外观美观,速度也不错。上面一排触摸键挺实用。应该对得起这个价格。当然再降点大家肯定也不反对。风扇噪音也不大。"
m_pred(comment, countvec, clf)
```
# 基于分布式表达的情感分析
```
# 读入原始数据集
import pandas as pd
dfpos = pd.read_excel(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\购物评论.xlsx", sheet_name = "正向", header=None)
dfpos['y'] = 1
dfneg = pd.read_excel(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\购物评论.xlsx", sheet_name = "负向", header=None)
dfneg['y'] = 0
df0 = dfpos.append(dfneg, ignore_index = True)
df0.head()
# 分词和预处理,生成list of list格式
import jieba
df0['cut'] = df0[0].apply(jieba.lcut)
df0.head()
# 按照7:3的比例生成训练集和测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(
df0.cut, df0.y, test_size=0.3)
x_train[:2]
# 初始化word2vec模型和词表
from gensim.models.word2vec import Word2Vec
n_dim = 300 # 指定向量维度,大样本量时300~500较好
w2vmodel = Word2Vec(size = n_dim, min_count = 10)
w2vmodel.build_vocab(x_train) # 生成词表
# 在评论训练集上建模(大数据集时可能会花费几分钟)
# 本例消耗内存较少
%time w2vmodel.train(x_train, total_examples = w2vmodel.corpus_count, epochs = 10)
# 情感词向量间的相似度
w2vmodel.wv.most_similar("不错")
w2vmodel.wv.most_similar("失望")
# 生成整句所对应的所有词条的词向量矩阵
pd.DataFrame([w2vmodel.wv[w] for w in df0.cut[0] if w in w2vmodel.wv]).head()
# 用各个词向量直接平均的方式生成整句对应的向量
def m_avgvec(words, w2vmodel):
return pd.DataFrame([w2vmodel.wv[w] for w in words if w in w2vmodel.wv]).agg("mean")
# 生成建模用矩阵,耗时较长
%time train_vecs = pd.DataFrame([m_avgvec(s, w2vmodel) for s in x_train])
train_vecs.head()
# 用转换后的矩阵拟合SVM模型
from sklearn.svm import SVC
clf2 = SVC(kernel = 'rbf', verbose = True)
clf2.fit(train_vecs, y_train) # 占用内存小于1G
clf2.score(train_vecs, y_train)
from sklearn.metrics import classification_report
print(classification_report(y_train, clf2.predict(train_vecs))) # 此处未用验证集
# 模型预测
import jieba
def m_pred(string, model):
words = jieba.lcut(string)
words_vecs = pd.DataFrame(m_avgvec(words, w2vmodel)).T
result = model.predict(words_vecs)
if int(result[0]) == 1:
print(string, ":正向")
else:
print(string, ":负向")
comment = "作为女儿6.1的礼物。虽然晚到了几天。等拿到的时候,女儿爱不释手,上洗手间也看,告知不好。竟以学习毛主席来反驳我。我反对了几句,还说我对主席不敬。晕。上周末,告诉我她把火鞋和风鞋拿到学校,好多同学羡慕她。呵呵,我也看了其中的人鸦,只可惜没有看完就在老公的催促下睡了。说了这么多,归纳为一句:这套书买的值。"
m_pred(comment, clf2)
```
# 文档自动摘要
```
chapter.txt[1]
def cut_sentence(intxt):
delimiters = frozenset('。!?')
buf = []
for ch in intxt:
buf.append(ch)
if delimiters.__contains__(ch):
yield ''.join(buf)
buf = []
if buf:
yield ''.join(buf)
sentdf = pd.DataFrame(cut_sentence(chapter.txt[1]))
sentdf
# 去除过短的句子,避免摘要出现无意义的内容
sentdf['txtlen'] = sentdf[0].apply(len)
sentdf.head()
sentlist = sentdf[0][sentdf.txtlen > 20]
print(len(sentlist))
sentlist
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
txtlist = [ " ".join(jieba.lcut(w)) for w in sentlist]
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(txtlist) # 将文本中的词语转换为词频矩阵
tfidf_matrix = TfidfTransformer().fit_transform(X)
# 利用nx包实现pagerank算法
import networkx as nx
similarity = nx.from_scipy_sparse_matrix(tfidf_matrix * tfidf_matrix.T)
scores = nx.pagerank(similarity)
scores
tops = sorted(scores.items(), key = lambda x: x[1], reverse = True)
tops[:3]
print(sentlist.iloc[tops[0][0]])
print(sentlist.iloc[tops[1][0]])
print(sentlist.iloc[tops[2][0]])
topn = 5
topsent = sorted(tops[:topn])
abstract = ''
for item in topsent:
abstract = abstract + sentlist.iloc[item[0]] + "......"
abstract[:-6]
```
# 自动写作
|
github_jupyter
|
import pandas as pd
import nltk
from nltk.corpus import brown
import jieba
import gensim
%matplotlib inline
from sklearn.decomposition import LatentDirichletAllocation
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
df = pd.read_csv(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\金庸-射雕英雄传txt精校版.txt", names=["txt"], sep='aaa', encoding="gbk")
# 构建新列
print(len(df))
print(df.shape)
def m_head(tmpstr):
return tmpstr[:1]
def m_mid(tmpstr):
return tmpstr.find("回 ")
df["head"] = df.txt.apply(m_mid)
df["mid"] = df.txt.apply(m_head)
df["len"] = df.txt.apply(len)
# 标明章序号
chapnum = 0
for i in range(len(df)):
if df["mid"][i] == "第" and df["head"][i] > 0 and df["len"][i] < 30:
chapnum += 1
if chapnum >= 40 and df.txt[i] == "附录一:成吉思汗家族":
chapnum = 00
df.loc[i, "chap"] = chapnum
dfgrp = df.groupby("chap")
chapter = dfgrp.apply(sum)
chapter = chapter[chapter.index != 0]
chapter.head()
def m_cut(intxt):
return [w for w in jieba.cut(intxt) if w not in stoplist and len(w) > 1]
stoplistdf = pd.read_csv(r'D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\停用词.txt', names=["w"], sep="aaa", encoding="utf-8")
stoplist = list(stoplistdf.w)
chaplist = [m_cut(w) for w in chapter.txt]
countvec = CountVectorizer(min_df=5)
wordmtx = countvec.fit_transform(chaplist[0])
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(wordmtx)
tfidf
import pyLDAvis
import pyLDAvis.sklearn
n_topics = 10
ldamodel = LatentDirichletAllocation(n_components=n_topics)
ldamodel.fit(wordmtx)
pyLDAvis.enable_notebook()
pyLDAvis.sklearn.prepare(ldamodel, tfidf, countvec)
chapter.head()
chapter["cut"] = chapter.txt.apply(m_cut)
chapter.head()
from gensim.models.word2vec import Word2Vec
n_dim = 300 # 向量维度
w2vmodel = Word2Vec(size=n_dim, min_count=10)
w2vmodel.build_vocab(chapter.cut) # 生成词
w2vmodel
%time w2vmodel.train(chapter.cut, total_examples=w2vmodel.corpus_count, epochs=10)
print(w2vmodel.wv["郭靖"].shape)
w2vmodel.wv["郭靖"]
w2vmodel.wv.most_similar("郭靖")
w2vmodel.wv.most_similar("黄蓉")
w2vmodel.wv.most_similar("黄蓉", topn=20)
w2vmodel.wv.most_similar("黄蓉道")
w2vmodel.wv.most_similar(["郭靖", "小红马"], ["黄药师"], topn=5)
w2vmodel.wv.most_similar(positive=['郭靖', '黄蓉'], negative=['杨康'], topn=10)
# 计算两个词的相似度/相关程度
print(w2vmodel.wv.similarity("郭靖", "黄蓉"))
print(w2vmodel.wv.similarity("郭靖", "杨康"))
print(w2vmodel.wv.similarity("郭靖", "杨铁心"))
w2vmodel.wv.doesnt_match("小红马 黄药师 鲁有脚".split())
w2vmodel.wv.doesnt_match("杨铁心 黄药师 黄蓉 洪七公".split())
cleanchap = [" ".join(m_cut(w)) for w in chapter.txt.iloc[:5]]
from sklearn.feature_extraction.text import CountVectorizer
countvec = CountVectorizer()
resmtx = countvec.fit_transform(cleanchap)
resmtx
from sklearn.metrics.pairwise import pairwise_distances
pairwise_distances(resmtx, metric ="cosine")
pairwise_distances(resmtx)
pairwise_distances(tfidf[:5], metric="cosine")
tfidf[:5]
chaplist = [m_cut(w) for w in chapter.txt]
dictionary = gensim.corpora.Dictionary(chaplist)
corpus = [dictionary.doc2bow(text) for text in chaplist] # 仍为list in list
tfidf_model = gensim.models.TfidfModel(corpus) # 建立TF-IDF模型
corpus_tfidf = tfidf_model[corpus] # 对所需文档计算TF-IDF结果
corpus_tfidf
# 列出所消耗的时间备查
%time ldamodel = gensim.models.LdaModel(corpus, id2word = dictionary, num_topics = 10, passes = 2)
simmtx = gensim.similarities.MatrixSimilarity(corpus)
simmtx
simmtx.index[:2]
query = chapter.txt[1]
query_bow = dictionary.doc2bow(m_cut(query))
lda_vec = ldamodel[query_bow]
sims = simmtx[lda_vec]
sims = sorted(enumerate(sims), key=lambda item: -item[1])
sims
def m_doc(doclist):
reslist = []
for i, doc in enumerate(doclist):
reslist.append(gensim.models.doc2vec.TaggedDocument(jieba.lcut(doc), [i]))
return reslist
corp = m_doc(chapter.txt)
corp[:2]
d2vmodel = gensim.models.Doc2Vec(vector_size=300, window=20, min_count=5)
%time d2vmodel.build_vocab(corp)
d2vmodel.wv.vocab
# 将新文本转换为相应维度空间下的向量
newvec = d2vmodel.infer_vector(jieba.lcut(chapter.txt[1]))
d2vmodel.docvecs.most_similar([newvec], topn = 10)
# 为章节增加名称标签
chapter.index = [df.txt[df.chap == i].iloc[0] for i in chapter.index]
chapter.head()
import jieba
cuttxt = lambda x: " ".join(m_cut(x))
cleanchap = chapter.txt.apply(cuttxt)
cleanchap[:2]
# 计算TF-IDF矩阵
from sklearn.feature_extraction.text import TfidfTransformer
vectorizer = CountVectorizer()
wordmtx = vectorizer.fit_transform(cleanchap) # 将文本中的词语转换为词频矩阵
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(wordmtx) #基于词频矩阵计算TF-IDF值
tfidf
# 进行聚类分析
from sklearn.cluster import KMeans
clf = KMeans(n_clusters = 5)
s = clf.fit(tfidf)
print(s)
clf.cluster_centers_
clf.cluster_centers_.shape
clf.labels_
chapter['clsres'] = clf.labels_
chapter.head()
chapter.sort_values('clsres').clsres
chapgrp = chapter.groupby('clsres')
chapcls = chapgrp.apply(sum) # 只有字符串列的情况下,sum函数自动转为合并字符串
cuttxt = lambda x: " ".join(m_cut(x))
chapclsres = chapcls.txt.apply(cuttxt)
chapclsres
# 列出关键词以刻画类别特征
import jieba.analyse as ana
ana.set_stop_words(r'D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\停用词.txt')
for item in chapclsres:
print(ana.extract_tags(item, topK = 10))
# 从原始语料df中提取出所需的前两章段落
raw12 = df[df.chap.isin([1,2])]
raw12ana = raw12.iloc[list(raw12.txt.apply(len) > 50), :] # 只使用超过50字的段落
raw12ana.reset_index(drop = True, inplace = True)
print(len(raw12ana))
raw12ana.head()
# 分词和预处理
import jieba
cuttxt = lambda x: " ".join(jieba.lcut(x)) # 这里不做任何清理工作,以保留情感词
raw12ana["cleantxt"] = raw12ana.txt.apply(cuttxt)
raw12ana.head()
from sklearn.feature_extraction.text import CountVectorizer
countvec = CountVectorizer()
wordmtx = countvec.fit_transform(raw12ana.cleantxt)
wordmtx
# 作用:将数据集划分为 训练集和测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(wordmtx, raw12ana.chap, test_size = 0.3, random_state = 111)
from sklearn import naive_bayes
NBmodel = naive_bayes.MultinomialNB()
# 拟合模型
NBmodel.fit(x_train, y_train)
x_test
NBmodel.predict(x_test)
# 预测准确率(给模型打分)
print('训练集:', NBmodel.score(x_train, y_train),
',验证集:', NBmodel.score(x_test, y_test))
from sklearn.metrics import classification_report
print(classification_report(y_test, NBmodel.predict(x_test)))
countvec.vocabulary_
string = "杨铁心和包惜弱收养穆念慈"
words = " ".join(jieba.lcut(string))
words_vecs = countvec.transform([words]) # 数据需要转换为可迭代的list格式
words_vecs
NBmodel.predict(words_vecs)
# 这里直接以章节为一个单元进行分析,以简化程序结构
import nltk
from nltk import FreqDist
# 生成完整的词条频数字典,这部分也可以用遍历方式实现
fdist1 = FreqDist(m_cut(chapter.txt[1]))
fdist2 = FreqDist(m_cut(chapter.txt[2]))
fdist3 = FreqDist(m_cut(chapter.txt[3]))
fdist1
from nltk.classify import NaiveBayesClassifier
training_data = [ [fdist1, 'chap1'], [fdist2, 'chap2'], [fdist3, 'chap3'] ]
# 训练分类模型
NLTKmodel = NaiveBayesClassifier.train(training_data)
print(NLTKmodel.classify(FreqDist(m_cut("杨铁心收养穆念慈"))))
print(NLTKmodel.classify(FreqDist(m_cut("钱塘江 日日夜夜 包惜弱 颜烈 使出杨家枪"))))
nltk.classify.accuracy(NLTKmodel, training_data) # 准确度评价
NLTKmodel.show_most_informative_features(5)#得到似然比,检测对于哪些特征有用
# 读入原始数据集
import pandas as pd
dfpos = pd.read_excel(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\购物评论.xlsx", sheet_name = "正向", header=None)
dfpos['y'] = 1
dfneg = pd.read_excel(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\购物评论.xlsx", sheet_name = "负向", header=None)
dfneg['y'] = 0
df0 = dfpos.append(dfneg, ignore_index = True)
df0.head()
# 分词和预处理
import jieba
cuttxt = lambda x: " ".join(jieba.lcut(x)) # 这里不做任何清理工作,以保留情感词
df0["cleantxt"] = df0[0].apply(cuttxt)
df0.head()
from sklearn.feature_extraction.text import CountVectorizer
countvec = CountVectorizer(min_df = 5) # 出现5次以上的才纳入
wordmtx = countvec.fit_transform(df0.cleantxt)
wordmtx
# 按照7:3的比例生成训练集和测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(
wordmtx, df0.y, test_size=0.3) # 这里可以直接使用稀疏矩阵格式
x_train[0]
# 使用SVM进行建模
from sklearn.svm import SVC
clf=SVC(kernel = 'rbf', verbose = True)
clf.fit(x_train, y_train) # 内存占用可能较高
clf.score(x_train, y_train)
# 对模型效果进行评估
from sklearn.metrics import classification_report
print(classification_report(y_test, clf.predict(x_test)))
clf.predict(countvec.transform([df0.cleantxt[0]]))[0]
# 模型预测
import jieba
def m_pred(string, countvec, model) :
words = " ".join(jieba.lcut(string))
words_vecs = countvec.transform([words]) # 数据需要转换为可迭代格式
result = model.predict(words_vecs)
if int(result[0]) == 1:
print(string, ":正向")
else:
print(string, ":负向")
comment = "外观美观,速度也不错。上面一排触摸键挺实用。应该对得起这个价格。当然再降点大家肯定也不反对。风扇噪音也不大。"
m_pred(comment, countvec, clf)
# 读入原始数据集
import pandas as pd
dfpos = pd.read_excel(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\购物评论.xlsx", sheet_name = "正向", header=None)
dfpos['y'] = 1
dfneg = pd.read_excel(r"D:\资料\教程\NLP基础-网易云课堂\TMData190320\PythonData\购物评论.xlsx", sheet_name = "负向", header=None)
dfneg['y'] = 0
df0 = dfpos.append(dfneg, ignore_index = True)
df0.head()
# 分词和预处理,生成list of list格式
import jieba
df0['cut'] = df0[0].apply(jieba.lcut)
df0.head()
# 按照7:3的比例生成训练集和测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(
df0.cut, df0.y, test_size=0.3)
x_train[:2]
# 初始化word2vec模型和词表
from gensim.models.word2vec import Word2Vec
n_dim = 300 # 指定向量维度,大样本量时300~500较好
w2vmodel = Word2Vec(size = n_dim, min_count = 10)
w2vmodel.build_vocab(x_train) # 生成词表
# 在评论训练集上建模(大数据集时可能会花费几分钟)
# 本例消耗内存较少
%time w2vmodel.train(x_train, total_examples = w2vmodel.corpus_count, epochs = 10)
# 情感词向量间的相似度
w2vmodel.wv.most_similar("不错")
w2vmodel.wv.most_similar("失望")
# 生成整句所对应的所有词条的词向量矩阵
pd.DataFrame([w2vmodel.wv[w] for w in df0.cut[0] if w in w2vmodel.wv]).head()
# 用各个词向量直接平均的方式生成整句对应的向量
def m_avgvec(words, w2vmodel):
return pd.DataFrame([w2vmodel.wv[w] for w in words if w in w2vmodel.wv]).agg("mean")
# 生成建模用矩阵,耗时较长
%time train_vecs = pd.DataFrame([m_avgvec(s, w2vmodel) for s in x_train])
train_vecs.head()
# 用转换后的矩阵拟合SVM模型
from sklearn.svm import SVC
clf2 = SVC(kernel = 'rbf', verbose = True)
clf2.fit(train_vecs, y_train) # 占用内存小于1G
clf2.score(train_vecs, y_train)
from sklearn.metrics import classification_report
print(classification_report(y_train, clf2.predict(train_vecs))) # 此处未用验证集
# 模型预测
import jieba
def m_pred(string, model):
words = jieba.lcut(string)
words_vecs = pd.DataFrame(m_avgvec(words, w2vmodel)).T
result = model.predict(words_vecs)
if int(result[0]) == 1:
print(string, ":正向")
else:
print(string, ":负向")
comment = "作为女儿6.1的礼物。虽然晚到了几天。等拿到的时候,女儿爱不释手,上洗手间也看,告知不好。竟以学习毛主席来反驳我。我反对了几句,还说我对主席不敬。晕。上周末,告诉我她把火鞋和风鞋拿到学校,好多同学羡慕她。呵呵,我也看了其中的人鸦,只可惜没有看完就在老公的催促下睡了。说了这么多,归纳为一句:这套书买的值。"
m_pred(comment, clf2)
chapter.txt[1]
def cut_sentence(intxt):
delimiters = frozenset('。!?')
buf = []
for ch in intxt:
buf.append(ch)
if delimiters.__contains__(ch):
yield ''.join(buf)
buf = []
if buf:
yield ''.join(buf)
sentdf = pd.DataFrame(cut_sentence(chapter.txt[1]))
sentdf
# 去除过短的句子,避免摘要出现无意义的内容
sentdf['txtlen'] = sentdf[0].apply(len)
sentdf.head()
sentlist = sentdf[0][sentdf.txtlen > 20]
print(len(sentlist))
sentlist
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
txtlist = [ " ".join(jieba.lcut(w)) for w in sentlist]
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(txtlist) # 将文本中的词语转换为词频矩阵
tfidf_matrix = TfidfTransformer().fit_transform(X)
# 利用nx包实现pagerank算法
import networkx as nx
similarity = nx.from_scipy_sparse_matrix(tfidf_matrix * tfidf_matrix.T)
scores = nx.pagerank(similarity)
scores
tops = sorted(scores.items(), key = lambda x: x[1], reverse = True)
tops[:3]
print(sentlist.iloc[tops[0][0]])
print(sentlist.iloc[tops[1][0]])
print(sentlist.iloc[tops[2][0]])
topn = 5
topsent = sorted(tops[:topn])
abstract = ''
for item in topsent:
abstract = abstract + sentlist.iloc[item[0]] + "......"
abstract[:-6]
| 0.3492 | 0.364382 |
```
# default_exp models
```
# models
> The end models for regression and classification.
These are the models for specific tasks, like regression, multi-class classification and multi-label classification. In all these models we can choose to use single path MolMap architecture, which includes only one of descriptor map or fingerprint map, or double path MolMap, which combines the two.
These models are thin wrappers of MolMap nets, with different outcome activation functions.
```
#export
import torch
from torch import nn
import torch.nn.functional as F
from molmapnets.nets import SinglePathMolMapNet, DoublePathMolMapNet
```
## Regression
For regression the activation function is just another fully connected layer with output size 1.
```
#export
class MolMapRegression(nn.Module):
"Mol Map nets used for regression"
def __init__(self, conv_in1=13, conv_in2=None, conv_size=13):
super(MolMapRegression, self).__init__()
if conv_in2 is None:
self.net = SinglePathMolMapNet(conv_in=conv_in1, FC=[128, 32])
self.single = True
else:
self.net = DoublePathMolMapNet(conv_in1=conv_in1, conv_in2=conv_in2, FC=[256, 128, 32])
self.single = False
self.fc = nn.Linear(32, 1)
def forward(self, x):
"x: Tensor or tuple of Tensors"
if self.single:
x = self.net(x)
else:
x1, x2 = x
x = self.net(x1, x2)
return self.fc(x)
```
Single path, descriptor
```
descriptor = MolMapRegression()
i = torch.rand((10, 13, 37, 37))
o = descriptor(i)
o.shape
```
Single path, fingerprint
```
fingerprint = MolMapRegression(conv_in1=3)
i = torch.rand((10, 3, 37, 36))
o = fingerprint(i)
o.shape
```
If the network is double path then we pass in a tuple of inputs
```
double_path = MolMapRegression(conv_in1=13, conv_in2=3)
i1 = torch.rand((10, 13, 37, 37))
i2 = torch.rand((10, 3, 37, 36))
o = double_path((i1, i2))
o.shape
```
## Multi-class classification
For multi-class classification we use the softmax activation function. Softmax transforms a vector so that each value in the vector falls between 0 and 1 and the vector sums to one. It's the logistic transformation generalised to vectors. In practice we use [logsoftmax](https://pytorch.org/docs/stable/generated/torch.nn.LogSoftmax.html) because it's computationally more stable.
```
#export
class MolMapMultiClassClassification(nn.Module):
"MolMap nets used for multi-class classification"
def __init__(self, conv_in1=13, conv_in2=None, conv_size=13, n_class=10):
super(MolMapMultiClassClassification, self).__init__()
if conv_in2 is None:
self.net = SinglePathMolMapNet(conv_in=conv_in1, FC=[128, 32])
self.single = True
else:
self.net = DoublePathMolMapNet(conv_in1=conv_in1, conv_in2=conv_in2, FC=[256, 128, 32])
self.single = False
self.fc = nn.Linear(32, n_class)
def forward(self, x):
"x: Tensor or tuple of Tensors"
if self.single:
x = self.net(x)
else:
x1, x2 = x
x = self.net(x1, x2)
x = self.fc(x)
return F.log_softmax(x, dim=1)
```
Single path, descriptor
```
descriptor = MolMapMultiClassClassification()
i = torch.rand((10, 13, 37, 37))
o = descriptor(i)
o.shape
o.exp().sum(dim=1)
```
Single path, fingerprint
```
fingerprint = MolMapMultiClassClassification(conv_in1=3)
i = torch.rand((10, 3, 37, 36))
o = fingerprint(i)
o.shape
o.exp().sum(dim=1)
```
If the network is double path then we pass in a tuple of inputs
```
double_path = MolMapMultiClassClassification(conv_in1=13, conv_in2=3)
i1 = torch.rand((10, 13, 37, 37))
i2 = torch.rand((10, 3, 37, 36))
o = double_path((i1, i2))
o.shape
o.exp().sum(dim=1)
```
## Multi-label classification
For multi-label classification, each input can have multiple labels, and the belonging to one label is independent of belonging to the others, so we'll use the Sigmoid activation function.
Compared to the multi-class problem, we only have to switch the soft max activation to sigmoid.
```
#export
class MolMapMultiLabelClassification(nn.Module):
"MolMap nets used for multi-label classification"
def __init__(self, conv_in1=13, conv_in2=None, conv_size=13, n_label=5):
super(MolMapMultiLabelClassification, self).__init__()
if conv_in2 is None:
self.net = SinglePathMolMapNet(conv_in=conv_in1, FC=[128, 32])
self.single = True
else:
self.net = DoublePathMolMapNet(conv_in1=conv_in1, conv_in2=conv_in2, FC=[256, 128, 32])
self.single = False
self.fc = nn.Linear(32, n_label)
def forward(self, x):
"x: Tensor or tuple of Tensors"
if self.single:
x = self.net(x)
else:
x1, x2 = x
x = self.net(x1, x2)
x = self.fc(x)
return torch.sigmoid(x)
```
Single path, descriptor
```
descriptor = MolMapMultiLabelClassification()
i = torch.rand((10, 13, 37, 37))
o = descriptor(i)
o.shape
o
```
Single path, fingerprint
```
fingerprint = MolMapMultiLabelClassification(conv_in1=3)
i = torch.rand((10, 3, 37, 36))
o = fingerprint(i)
o.shape
o
```
If the network is double path then we pass in a tuple of inputs
```
double_path = MolMapMultiLabelClassification(conv_in1=13, conv_in2=3)
i1 = torch.rand((10, 13, 37, 37))
i2 = torch.rand((10, 3, 37, 36))
o = double_path((i1, i2))
o.shape
o
```
Switch the order of descriptor and fingerprint map
```
double_path = MolMapMultiLabelClassification(conv_in1=3, conv_in2=13)
i1 = torch.rand((10, 13, 37, 37))
i2 = torch.rand((10, 3, 37, 36))
o = double_path((i2, i1))
o.shape
o
```
|
github_jupyter
|
# default_exp models
#export
import torch
from torch import nn
import torch.nn.functional as F
from molmapnets.nets import SinglePathMolMapNet, DoublePathMolMapNet
#export
class MolMapRegression(nn.Module):
"Mol Map nets used for regression"
def __init__(self, conv_in1=13, conv_in2=None, conv_size=13):
super(MolMapRegression, self).__init__()
if conv_in2 is None:
self.net = SinglePathMolMapNet(conv_in=conv_in1, FC=[128, 32])
self.single = True
else:
self.net = DoublePathMolMapNet(conv_in1=conv_in1, conv_in2=conv_in2, FC=[256, 128, 32])
self.single = False
self.fc = nn.Linear(32, 1)
def forward(self, x):
"x: Tensor or tuple of Tensors"
if self.single:
x = self.net(x)
else:
x1, x2 = x
x = self.net(x1, x2)
return self.fc(x)
descriptor = MolMapRegression()
i = torch.rand((10, 13, 37, 37))
o = descriptor(i)
o.shape
fingerprint = MolMapRegression(conv_in1=3)
i = torch.rand((10, 3, 37, 36))
o = fingerprint(i)
o.shape
double_path = MolMapRegression(conv_in1=13, conv_in2=3)
i1 = torch.rand((10, 13, 37, 37))
i2 = torch.rand((10, 3, 37, 36))
o = double_path((i1, i2))
o.shape
#export
class MolMapMultiClassClassification(nn.Module):
"MolMap nets used for multi-class classification"
def __init__(self, conv_in1=13, conv_in2=None, conv_size=13, n_class=10):
super(MolMapMultiClassClassification, self).__init__()
if conv_in2 is None:
self.net = SinglePathMolMapNet(conv_in=conv_in1, FC=[128, 32])
self.single = True
else:
self.net = DoublePathMolMapNet(conv_in1=conv_in1, conv_in2=conv_in2, FC=[256, 128, 32])
self.single = False
self.fc = nn.Linear(32, n_class)
def forward(self, x):
"x: Tensor or tuple of Tensors"
if self.single:
x = self.net(x)
else:
x1, x2 = x
x = self.net(x1, x2)
x = self.fc(x)
return F.log_softmax(x, dim=1)
descriptor = MolMapMultiClassClassification()
i = torch.rand((10, 13, 37, 37))
o = descriptor(i)
o.shape
o.exp().sum(dim=1)
fingerprint = MolMapMultiClassClassification(conv_in1=3)
i = torch.rand((10, 3, 37, 36))
o = fingerprint(i)
o.shape
o.exp().sum(dim=1)
double_path = MolMapMultiClassClassification(conv_in1=13, conv_in2=3)
i1 = torch.rand((10, 13, 37, 37))
i2 = torch.rand((10, 3, 37, 36))
o = double_path((i1, i2))
o.shape
o.exp().sum(dim=1)
#export
class MolMapMultiLabelClassification(nn.Module):
"MolMap nets used for multi-label classification"
def __init__(self, conv_in1=13, conv_in2=None, conv_size=13, n_label=5):
super(MolMapMultiLabelClassification, self).__init__()
if conv_in2 is None:
self.net = SinglePathMolMapNet(conv_in=conv_in1, FC=[128, 32])
self.single = True
else:
self.net = DoublePathMolMapNet(conv_in1=conv_in1, conv_in2=conv_in2, FC=[256, 128, 32])
self.single = False
self.fc = nn.Linear(32, n_label)
def forward(self, x):
"x: Tensor or tuple of Tensors"
if self.single:
x = self.net(x)
else:
x1, x2 = x
x = self.net(x1, x2)
x = self.fc(x)
return torch.sigmoid(x)
descriptor = MolMapMultiLabelClassification()
i = torch.rand((10, 13, 37, 37))
o = descriptor(i)
o.shape
o
fingerprint = MolMapMultiLabelClassification(conv_in1=3)
i = torch.rand((10, 3, 37, 36))
o = fingerprint(i)
o.shape
o
double_path = MolMapMultiLabelClassification(conv_in1=13, conv_in2=3)
i1 = torch.rand((10, 13, 37, 37))
i2 = torch.rand((10, 3, 37, 36))
o = double_path((i1, i2))
o.shape
o
double_path = MolMapMultiLabelClassification(conv_in1=3, conv_in2=13)
i1 = torch.rand((10, 13, 37, 37))
i2 = torch.rand((10, 3, 37, 36))
o = double_path((i2, i1))
o.shape
o
| 0.84955 | 0.963334 |
# Welcome to Top Books Details Finder
# Library
```
import pandas as pd
from bs4 import BeautifulSoup
from urllib.request import urlopen, Request, urlretrieve
from IPython.display import IFrame, display
from PIL import Image
from selenium import webdriver
import os
```
# Input your favourate book
```
inp = input('Enter the topic to get top relevant books : ')
```
# Relevant Book Scraper
```
def relevant_book_scraper(inp):
url = 'https://www.google.com//search?tbm=bks&q='+ inp
driver = webdriver.Chrome(executable_path=r'C:\Users\jpravijo\Desktop\Anaconda\chromedriver_win32 (3)\chromedriver.exe')
driver.get(url)
html = driver.page_source
soup = BeautifulSoup(html,'lxml')
driver.close()
book_name_list, authors_list, relevant_no_list, links_list = [], [], [], []
k = 1
for i, content in enumerate(soup.find_all('div', class_='bHexk Tz5Hvf')):
if k>5:
break
# Book Names Scraping
try:
book_name = content.find('h3', class_='LC20lb DKV0Md').text
book_name = book_name.split('-')[0]
except:
book_name = 'Book Name not found'
# Authors Names Scraping
try:
authors = content.find('div', class_='N96wpd').text
authors = authors.split('·')[0]
except:
authors = ' Authors Name not found'
# Detailed Information links Scraping
try:
try:
links = content.find('a', class_='yKioRe VZ2GVc')['href']
except:
links = content.find('a')['href']
if 'edition' in links:
links = 'https://www.google.co.in' + links
except:
links = 'Links Not Found'
if book_name not in book_name_list:
book_name_list.append(book_name)
authors_list.append(authors)
relevant_no_list.append(k)
links_list.append(links)
k+=1
else:
continue
dic = {'Relevant_No': relevant_no_list, 'Books_Name' : book_name_list, 'Author_Names':authors_list, 'Links':links_list}
df = pd.DataFrame(dic)
df.set_index('Relevant_No', inplace=True)
return df
df = relevant_book_scraper(inp)
df.head()
```
# To Scrape the Detail of the Interested book
```
def book_details(df, index):
index-=1
url = df.iloc[index, 2]
book_name = df.iloc[index, 0]
driver = webdriver.Chrome(executable_path=r'C:\Users\jpravijo\Desktop\Anaconda\chromedriver_win32 (3)\chromedriver.exe')
driver.get(url)
html = driver.page_source
soup = BeautifulSoup(html,'lxml')
driver.close()
print(f'\n\033[1mTHE DETAILS ARE AS FOLLOWS \033[0m\n')
print(f'Book Name:\033[1m {book_name} \033[0m')
# Title page image scraping
filepath = r"C:\Users\jpravijo\Desktop\Anaconda\Book Images\\" + book_name + ".png"
try:
try:
name = soup.find('div', class_="WnWrFd").text
img = soup.find('img', alt=name)['src']
except:
img = soup.find('img', class_='rISBZc M4dUYb')['src']
urlretrieve(img, filepath)
image = Image.open(filepath)
except:
image='Not Found'
# To Scrape and Print the Details
for i, content in enumerate(soup.find_all('div', class_="Z1hOCe")):
print(content.text)
return image
index = int(input('enter the index of the favourate book from above for more details: '))
image = book_details(df, index)
print('\n \033[1mThe title page of the book you have searched \033[0m\n')
image
```
|
github_jupyter
|
import pandas as pd
from bs4 import BeautifulSoup
from urllib.request import urlopen, Request, urlretrieve
from IPython.display import IFrame, display
from PIL import Image
from selenium import webdriver
import os
inp = input('Enter the topic to get top relevant books : ')
def relevant_book_scraper(inp):
url = 'https://www.google.com//search?tbm=bks&q='+ inp
driver = webdriver.Chrome(executable_path=r'C:\Users\jpravijo\Desktop\Anaconda\chromedriver_win32 (3)\chromedriver.exe')
driver.get(url)
html = driver.page_source
soup = BeautifulSoup(html,'lxml')
driver.close()
book_name_list, authors_list, relevant_no_list, links_list = [], [], [], []
k = 1
for i, content in enumerate(soup.find_all('div', class_='bHexk Tz5Hvf')):
if k>5:
break
# Book Names Scraping
try:
book_name = content.find('h3', class_='LC20lb DKV0Md').text
book_name = book_name.split('-')[0]
except:
book_name = 'Book Name not found'
# Authors Names Scraping
try:
authors = content.find('div', class_='N96wpd').text
authors = authors.split('·')[0]
except:
authors = ' Authors Name not found'
# Detailed Information links Scraping
try:
try:
links = content.find('a', class_='yKioRe VZ2GVc')['href']
except:
links = content.find('a')['href']
if 'edition' in links:
links = 'https://www.google.co.in' + links
except:
links = 'Links Not Found'
if book_name not in book_name_list:
book_name_list.append(book_name)
authors_list.append(authors)
relevant_no_list.append(k)
links_list.append(links)
k+=1
else:
continue
dic = {'Relevant_No': relevant_no_list, 'Books_Name' : book_name_list, 'Author_Names':authors_list, 'Links':links_list}
df = pd.DataFrame(dic)
df.set_index('Relevant_No', inplace=True)
return df
df = relevant_book_scraper(inp)
df.head()
def book_details(df, index):
index-=1
url = df.iloc[index, 2]
book_name = df.iloc[index, 0]
driver = webdriver.Chrome(executable_path=r'C:\Users\jpravijo\Desktop\Anaconda\chromedriver_win32 (3)\chromedriver.exe')
driver.get(url)
html = driver.page_source
soup = BeautifulSoup(html,'lxml')
driver.close()
print(f'\n\033[1mTHE DETAILS ARE AS FOLLOWS \033[0m\n')
print(f'Book Name:\033[1m {book_name} \033[0m')
# Title page image scraping
filepath = r"C:\Users\jpravijo\Desktop\Anaconda\Book Images\\" + book_name + ".png"
try:
try:
name = soup.find('div', class_="WnWrFd").text
img = soup.find('img', alt=name)['src']
except:
img = soup.find('img', class_='rISBZc M4dUYb')['src']
urlretrieve(img, filepath)
image = Image.open(filepath)
except:
image='Not Found'
# To Scrape and Print the Details
for i, content in enumerate(soup.find_all('div', class_="Z1hOCe")):
print(content.text)
return image
index = int(input('enter the index of the favourate book from above for more details: '))
image = book_details(df, index)
print('\n \033[1mThe title page of the book you have searched \033[0m\n')
image
| 0.093901 | 0.510313 |
# SNGuess Training Data Set
In this notebook we describe de procedure we followed in order to generate the training set for SNGuess. The objective of SNGuess is to predict in the early stages of a lightcurve whether it will be of interest for future follow up observations. It may also have other secondary objectives, such as predicting if a certain lightcurve will, in the end, be classified as belonging to a certain source object type.
```
import pandas as pd
import numpy as np
import re
from astropy.time import Time
```
## Loading the input data files
First, we load the file `risedecline.csv`. This file contains a set of features, manually defined by a domain expert, and then calculated over a set of astronomical alerts, received and processed by the AMPEL broker system. Each row corresponds to features calculated from a single alert. A unique transient event (described by `snname`) thus frequently appear multiple times. `NaN` indicates a feature which could not be calculated based on the content of that specific alert. `RiseDecline` features calculated by the AMPEL T2 unit <https://github.com/AmpelProject/Ampel-contrib-HU/blob/master/ampel/contrib/hu/t2/T2RiseDeclineStat.py>.
```
features = pd.read_csv('risedecline.csv', index_col=0)
features
print("First detection:", Time(features.jd_last.min(), format='jd').iso)
print("Last detection:", Time(features.jd_last.max(), format='jd').iso)
print("Number of alerts:", len(features))
print("Number of candidates:", len(features.snname.unique()))
```
The alerts sometimes contain nonsensical values. We set these consisently to `None`.
```
features.loc[features['distnr_med']<0, 'distnr_med'] = None
features.loc[features['magnr_med']<0, 'magnr_med'] = None
features.loc[features['sgscore1_med']<0, 'sgscore1_med'] = None
features.loc[features['distpsnr1_med']<0, 'distpsnr1_med'] = None
features.loc[features['sgscore2_med']<0, 'sgscore2_med'] = None
features.loc[features['distpsnr2_med']<0, 'distpsnr2_med'] = None
features.loc[features['neargaia_med']<0, 'neargaia_med'] = None
features.loc[features['maggaia_med']<0, 'maggaia_med'] = None
```
Also, there are very rare cases with duplicated photopoints. Possibly alerts issued multiple times. These are very rare. They are labeled with a `cut_pp` value of `True`. We proceed to remove these.
```
iDup = np.where(features["cut_pp"]>0)[0]
dupTransients = features.iloc[iDup]['snname'].unique()
features = features[ ~features['snname'].isin(dupTransients) ].copy()
features.reset_index(inplace=True)
print("Number of alerts:", len(features))
print("Number of candidates: %s"%(len(features.snname.unique())))
```
Then, we load a file that contains a catalog of candidate lightcurves from RCF, complete with their spectroscopical classification information. Note that this information is only used to assign classification labels - the photometric observation data in this file is not used.
```
rcf_lc = pd.read_pickle('rcf_marshallc_sncosmo_200114.pkl')
print('Read %s RCF candidates.' % (len(rcf_lc)))
```
As the RCF scanning team consisently visually selects against likely CVs, we load a catalog of recent cataclysmic variable star lightcurves. Again, we will only make use of the IDs.
```
df_cv = pd.read_csv('CV_list_23Mar2020.txt', sep='\s+', skiprows=4, names=['name','ra','dec','l','b'])
rcf_cv = list(df_cv['name'])
print("Read %s CV candidates." % len(rcf_cv))
```
We also proceed to load a recently generated list of superluminous supernovae (SLSNe) that we can use to further update the classes of our dataset.
```
slsne = dict()
with open("list_of_superluminous_supernovae_slsne.txt") as fd:
for line in fd:
split_line = re.split(r'\s+', line)
ztfid = split_line[0]
subclass = split_line[9]
slsne[ztfid] = subclass
```
## Adding RCF information into features table
We then proceed, by using the common ZTF identification string, to cross-match the data from our rise-decline feature data set with the classes of the RCF and the CV list datasets. We do this in order to complete our lightcurve feature table with columns indicating the class of the source object.
```
rcf_class = dict()
for tid, tdata in rcf_lc.items():
rcf_class[tid] = tdata.meta['classification']
rcf_class = pd.Series(rcf_class, name='rcf_class')
features = features.merge(rcf_class, how='left', left_on='snname', right_index=True)
# Display ten most common type labels
features.rcf_class[features.rcf_class.notna()].value_counts()[:10]
print("Number of valid types:", len(features.rcf_class[features.rcf_class.notna()].unique()))
```
We add the result of the cross matching as boolean columns to the feature table (one column for every class we are interested in)...
```
# SN types
sn_mask = features.rcf_class.fillna('').str.match(r"(SL)?SN", case=False)
gap_mask = features.rcf_class.fillna('').str.match(r"Gap", case=False)
slsne_mask = features.snname.isin(list(slsne.keys()))
features['rcf_sn'] = False
features.loc[(sn_mask | gap_mask | slsne_mask), 'rcf_sn'] = True
# AGN types
agn_mask = features.rcf_class.fillna('').str.match(r"AGN", case=False)
qso_mask = features.rcf_class.fillna('').str.match(r"QSO", case=False)
features['rcf_agn'] = False
features.loc[(agn_mask | qso_mask), 'rcf_agn'] = True
# CV types
cv_mask = features.rcf_class.fillna('').str.match(r"cv", case=False)
cv_rcf_mask = features.snname.isin(rcf_cv)
features['rcf_cv'] = False
features.loc[(cv_mask | cv_rcf_mask), 'rcf_cv'] = True
print("rcf_sn candidates:", features[features.rcf_sn].snname.unique().shape[0])
print("rcf_agn candidates:", features[features.rcf_agn].snname.unique().shape[0])
print("rcf_cv candidates:", features[features.rcf_cv].snname.unique().shape[0])
```
Finally, using our catalog of RCF lightcurves, we add a field that indicates whether the alert's source has been targeted by BTS
```
targeted_by_bts = pd.DataFrame(True, index=rcf_lc.keys(), columns=['targeted_by_bts'])
features = pd.merge(features, targeted_by_bts, how='left', left_on='snname', right_index=True)
features['targeted_by_bts'] = features['targeted_by_bts'].fillna(False)
print("%d candidates targeted by BTS." % (features[features.targeted_by_bts].snname.unique().shape[0]))
features.targeted_by_bts.value_counts()
```
## Adding sub-class information into features table
We can also add a new column called `subclass` that holds more detailed and fine-grained class information to our lightcurve data when available. We'll do that by using our RCF, SLSNe and paper updated class data sources.
```
# Add subclass data from slsne list
for ztfid, subclass in slsne.items():
features.loc[features['snname'] == ztfid, 'subclass'] = subclass
```
We'll update some of the sub-classes of our samples with the corresponding reviewed information published in a 2018 paper by Fremling et al.
```
with open('rcf_2018paperchanges.txt') as f:
paper_changes = [re.findall(r'^(\w+) : (\S+) -> (\S+)',line)[0] for line in f]
# Add updated class data from paper
for ztfid, old_subclass, new_subclass in paper_changes:
features.loc[features['snname'] == ztfid, 'subclass'] = "SN " + str(new_subclass)
```
We organize sub-classes in a hierarchy.
```
subclass_tree = {}
# test - classes that we first keep as a test sample, for possible confirmation later
# based on the result of this we might update the classification and rerun
subclass_tree['remove'] = ['Duplicate', 'bogus', 'duplicate',]
subclass_tree['to_test'] = ['AGN?' ,'AGN? ','Bogus?','CV Candidate', 'CV?', None, 'None',
'QSO?', 'blazar?','nan','nova?','old','star?', 'stellar?',
'unclassified', 'unknown',]
subclass_tree['galaxy'] = ['AGN','CLAGN','LINER','LRN','NLS1','Q','QSO','Galaxy',
'blazar','galaxy']
subclass_tree['sn'] = ['SN', 'SNIIb?', 'SLSN-I?', 'SN Ia?', 'SN Ib/c?', 'SN Ib?', 'SN Ic?',
'SN?', 'SN? ', {} ]
subclass_tree['sn'][-1]['slsn'] = [ 'SLSN-I','SLSN-II', 'SLSN-R', 'SN SL-I']
subclass_tree['sn'][-1]['rare'] = ['Gap','Gap I', 'Gap I - Ca-rich','ILRT','LBV', 'TDE',]
subclass_tree['sn'][-1]['snii'] = ['SN II', 'SN IIL', 'SN IIP', 'SN IIb', 'SN IIn']
subclass_tree['sn'][-1]['snii_pec'] = ['SN II-87A', 'SN II-pec']
subclass_tree['sn'][-1]['snia'] = ['SNIa', 'SN Ia', 'SN Ia ', 'SN Ia 91T',
'SN Ia 91T-like', 'SN Ia-91T', 'SN Ia-norm']
subclass_tree['sn'][-1]['snia_pec'] = ['SN Ia 02cx-like', 'SN Ia 02ic-like', 'SN Ia 91bg-like',
'SN Ia-02cx', 'SN Ia-91bg', 'SN Ia-CSM', 'SN Ia-csm', 'SN Ia-pec','SN Iax']
subclass_tree['sn'][-1]['snibc'] = ['SN Ib','SN Ib/c','SN Ibn','SN Ic','SN Ic-BL',]
subclass_tree['stellar'] = ['CV','LRN','Nova', 'Var','star','varstar']
# Create a specific set of labels for easily distinguished sn subtypes:
# slsn, snii, snia, snibc
features.loc[:,'snclass'] = None
for subclass in ['slsn','snii','snia','snibc']:
subnames = subclass_tree['sn'][-1][subclass]
for subname in subnames:
features.loc[features['subclass']==subname,'snclass'] = subclass
```
## Saving the final set
```
features.drop(columns='index').to_csv('snguess_training.csv', index_label=False)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import re
from astropy.time import Time
features = pd.read_csv('risedecline.csv', index_col=0)
features
print("First detection:", Time(features.jd_last.min(), format='jd').iso)
print("Last detection:", Time(features.jd_last.max(), format='jd').iso)
print("Number of alerts:", len(features))
print("Number of candidates:", len(features.snname.unique()))
features.loc[features['distnr_med']<0, 'distnr_med'] = None
features.loc[features['magnr_med']<0, 'magnr_med'] = None
features.loc[features['sgscore1_med']<0, 'sgscore1_med'] = None
features.loc[features['distpsnr1_med']<0, 'distpsnr1_med'] = None
features.loc[features['sgscore2_med']<0, 'sgscore2_med'] = None
features.loc[features['distpsnr2_med']<0, 'distpsnr2_med'] = None
features.loc[features['neargaia_med']<0, 'neargaia_med'] = None
features.loc[features['maggaia_med']<0, 'maggaia_med'] = None
iDup = np.where(features["cut_pp"]>0)[0]
dupTransients = features.iloc[iDup]['snname'].unique()
features = features[ ~features['snname'].isin(dupTransients) ].copy()
features.reset_index(inplace=True)
print("Number of alerts:", len(features))
print("Number of candidates: %s"%(len(features.snname.unique())))
rcf_lc = pd.read_pickle('rcf_marshallc_sncosmo_200114.pkl')
print('Read %s RCF candidates.' % (len(rcf_lc)))
df_cv = pd.read_csv('CV_list_23Mar2020.txt', sep='\s+', skiprows=4, names=['name','ra','dec','l','b'])
rcf_cv = list(df_cv['name'])
print("Read %s CV candidates." % len(rcf_cv))
slsne = dict()
with open("list_of_superluminous_supernovae_slsne.txt") as fd:
for line in fd:
split_line = re.split(r'\s+', line)
ztfid = split_line[0]
subclass = split_line[9]
slsne[ztfid] = subclass
rcf_class = dict()
for tid, tdata in rcf_lc.items():
rcf_class[tid] = tdata.meta['classification']
rcf_class = pd.Series(rcf_class, name='rcf_class')
features = features.merge(rcf_class, how='left', left_on='snname', right_index=True)
# Display ten most common type labels
features.rcf_class[features.rcf_class.notna()].value_counts()[:10]
print("Number of valid types:", len(features.rcf_class[features.rcf_class.notna()].unique()))
# SN types
sn_mask = features.rcf_class.fillna('').str.match(r"(SL)?SN", case=False)
gap_mask = features.rcf_class.fillna('').str.match(r"Gap", case=False)
slsne_mask = features.snname.isin(list(slsne.keys()))
features['rcf_sn'] = False
features.loc[(sn_mask | gap_mask | slsne_mask), 'rcf_sn'] = True
# AGN types
agn_mask = features.rcf_class.fillna('').str.match(r"AGN", case=False)
qso_mask = features.rcf_class.fillna('').str.match(r"QSO", case=False)
features['rcf_agn'] = False
features.loc[(agn_mask | qso_mask), 'rcf_agn'] = True
# CV types
cv_mask = features.rcf_class.fillna('').str.match(r"cv", case=False)
cv_rcf_mask = features.snname.isin(rcf_cv)
features['rcf_cv'] = False
features.loc[(cv_mask | cv_rcf_mask), 'rcf_cv'] = True
print("rcf_sn candidates:", features[features.rcf_sn].snname.unique().shape[0])
print("rcf_agn candidates:", features[features.rcf_agn].snname.unique().shape[0])
print("rcf_cv candidates:", features[features.rcf_cv].snname.unique().shape[0])
targeted_by_bts = pd.DataFrame(True, index=rcf_lc.keys(), columns=['targeted_by_bts'])
features = pd.merge(features, targeted_by_bts, how='left', left_on='snname', right_index=True)
features['targeted_by_bts'] = features['targeted_by_bts'].fillna(False)
print("%d candidates targeted by BTS." % (features[features.targeted_by_bts].snname.unique().shape[0]))
features.targeted_by_bts.value_counts()
# Add subclass data from slsne list
for ztfid, subclass in slsne.items():
features.loc[features['snname'] == ztfid, 'subclass'] = subclass
with open('rcf_2018paperchanges.txt') as f:
paper_changes = [re.findall(r'^(\w+) : (\S+) -> (\S+)',line)[0] for line in f]
# Add updated class data from paper
for ztfid, old_subclass, new_subclass in paper_changes:
features.loc[features['snname'] == ztfid, 'subclass'] = "SN " + str(new_subclass)
subclass_tree = {}
# test - classes that we first keep as a test sample, for possible confirmation later
# based on the result of this we might update the classification and rerun
subclass_tree['remove'] = ['Duplicate', 'bogus', 'duplicate',]
subclass_tree['to_test'] = ['AGN?' ,'AGN? ','Bogus?','CV Candidate', 'CV?', None, 'None',
'QSO?', 'blazar?','nan','nova?','old','star?', 'stellar?',
'unclassified', 'unknown',]
subclass_tree['galaxy'] = ['AGN','CLAGN','LINER','LRN','NLS1','Q','QSO','Galaxy',
'blazar','galaxy']
subclass_tree['sn'] = ['SN', 'SNIIb?', 'SLSN-I?', 'SN Ia?', 'SN Ib/c?', 'SN Ib?', 'SN Ic?',
'SN?', 'SN? ', {} ]
subclass_tree['sn'][-1]['slsn'] = [ 'SLSN-I','SLSN-II', 'SLSN-R', 'SN SL-I']
subclass_tree['sn'][-1]['rare'] = ['Gap','Gap I', 'Gap I - Ca-rich','ILRT','LBV', 'TDE',]
subclass_tree['sn'][-1]['snii'] = ['SN II', 'SN IIL', 'SN IIP', 'SN IIb', 'SN IIn']
subclass_tree['sn'][-1]['snii_pec'] = ['SN II-87A', 'SN II-pec']
subclass_tree['sn'][-1]['snia'] = ['SNIa', 'SN Ia', 'SN Ia ', 'SN Ia 91T',
'SN Ia 91T-like', 'SN Ia-91T', 'SN Ia-norm']
subclass_tree['sn'][-1]['snia_pec'] = ['SN Ia 02cx-like', 'SN Ia 02ic-like', 'SN Ia 91bg-like',
'SN Ia-02cx', 'SN Ia-91bg', 'SN Ia-CSM', 'SN Ia-csm', 'SN Ia-pec','SN Iax']
subclass_tree['sn'][-1]['snibc'] = ['SN Ib','SN Ib/c','SN Ibn','SN Ic','SN Ic-BL',]
subclass_tree['stellar'] = ['CV','LRN','Nova', 'Var','star','varstar']
# Create a specific set of labels for easily distinguished sn subtypes:
# slsn, snii, snia, snibc
features.loc[:,'snclass'] = None
for subclass in ['slsn','snii','snia','snibc']:
subnames = subclass_tree['sn'][-1][subclass]
for subname in subnames:
features.loc[features['subclass']==subname,'snclass'] = subclass
features.drop(columns='index').to_csv('snguess_training.csv', index_label=False)
| 0.204898 | 0.974556 |
<table>
<tr><td><img style="height: 150px;" src="images/geo_hydro1.jpg"></td>
<td bgcolor="#FFFFFF">
<p style="font-size: xx-large; font-weight: 900; line-height: 100%">AG Dynamics of the Earth</p>
<p style="font-size: large; color: rgba(0,0,0,0.5);">Jupyter notebooks</p>
<p style="font-size: large; color: rgba(0,0,0,0.5);">Georg Kaufmann</p>
</td>
</tr>
</table>
# Dynamic systems: 3. Continuity
## Advection equation in 1D
----
*Georg Kaufmann,
Geophysics Section,
Institute of Geological Sciences,
Freie Universität Berlin,
Germany*
----
In this notebook, we solve a simple **transient advection equation** in one dimension,
using different numerical methods.
```
import numpy as np
import matplotlib.pyplot as plt
```
----
## Theoretical model
We start defining the transient advection equation. We describe a quantity $c(x,t)$ in an incompressible fluid,
which changes its position only through advection of the particle quantity:
$$
c(x,t+\Delta t) = c(x-v \Delta t,t)
$$
with
$x$ [m] the position,
$t$ [s] time,
$v$ [m/s] the velocity, and
$\Delta t$ [s] the time increment.
We expand both sides of the equation into a **Taylor series** til the first-order term:
$$
c(x,t) + \Delta t \frac{\partial c(x,t)}{\partial t}
\simeq
c(x,t) - v \Delta t \frac{\partial c(x,t)}{\partial x}
$$
which can be recasted into the `transient advection equation`:
$$
\fbox{$
\frac{\partial c(x,t)}{\partial t} + v \frac{\partial c(x,t)}{\partial x} = 0
$}
$$
The transient advection equation is a **hyperbolic partial differential equation**, which has a unique
solution for the **initial condition**:
$$
c(x,t=0) = c_0(x,0)
$$
----
## Gaussian function
We define the `Gaussian` function with mean $\mu$ and standard deviation $\sigma$:
$$
c(x,t) = e^{-\frac{(x-vt-\mu)^2}{\sigma^2}}
$$
which is a solution of the transient advection equation.
```
def gaussian(x,v=0.5,t=0.,mu=2.,sigma=1.):
f = np.exp(-(x-v*t-mu)**2/(sigma)**2)
return f
xstep = 101
x = np.linspace(0,10,xstep)
u0 = gaussian(x)
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0s')
#plt.plot(x,gaussian(x,t=4),label='t=4s')
#plt.plot(x,gaussian(x,t=8),label='t=8s')
#plt.plot(x,gaussian(x,t=10),label='t=10s')
plt.legend()
```
----
## Numerical solution methods
Next, we derive several numerical methods, which can be used to solve the transient advection equation.
We first need to assign the temporal and spatial time steps, $\Delta t$ [s] and $\Delta x$ [m],
and the velocity $c$ [m/s]:
```
dt = 0.05
dx = (x.max()-x.min()) / (xstep-1)
v = 0.5
```
Thus we have discretised both spatial and temporal variables:
$$
\begin{array}{rcl}
t_n &=& t_0 + n \Delta T, \quad n=0,N \\
x_i &=& x_0 + i \Delta x, \quad i=0,I
\end{array}
$$
The `Courant number`, defined as
$$
Co = \frac{c \Delta t}{\Delta x}
$$
defines the stability of the numerical solutions. Explicit solutions are stable
for $Co <1$.
```
Courant = v*dt/dx
print ('Courant number: ',Courant)
```
----
## FTCS scheme (forward time centered space)
Our first scheme is called `FTCS`, forward time, centered space, thus the derivatives in the
transient advection equations are replaced by **forward differences in time** and
**central differences is space**:
$$
\frac{c_{i}^{n+1}-c_{i}^{n}}{\Delta t}
=
-v \frac{c_{i+1}^{n}-c_{i-1}^{n}}{2 \Delta x}
$$
or solved for the next time step
$$
c_{i}^{n+1}
=
c_{i}^{n} -\frac{v \Delta t}{2 \Delta x} \left( c_{i+1}^{n}-c_{i-1}^{n} \right)
$$
<img src="images/PDE_FTCS.jpg" style="height:5cm;">
We implement the FTCS method:
```
# start time
t = 0
# initial values
u = gaussian(x)
# solution
for n in range(200):
t = t + dt
uold = u
for i in range(1,u.shape[0]-1):
u[i] = uold[i] - v*dt/2/dx*(uold[i+1]-uold[i-1])
if (np.abs(t-4) < dt/2):
u04 = np.copy(u)
elif (np.abs(t-8) < dt/2):
u08 = np.copy(u)
elif (np.abs(t-10) < dt/2):
u10 = np.copy(u)
print(x[np.where(u0 == np.amax(u0))],u0[np.where(u0 == np.amax(u0))])
print(x[np.where(u04 == np.amax(u04))],u04[np.where(u04 == np.amax(u04))])
print(x[np.where(u08 == np.amax(u08))],u08[np.where(u08 == np.amax(u08))])
print(x[np.where(u10 == np.amax(u10))],u10[np.where(u10 == np.amax(u10))])
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0')
plt.plot(x,u04,label='t=4s')
plt.plot(x,u08,label='t=8s')
plt.plot(x,u10,label='t=10s')
plt.title('FTCS method')
plt.legend()
```
----
## Upwind scheme
Our second scheme is from the group of `upwind scheme`, which promote a solution skewed in the direction
of the advective flow, thus on $c$. We keep the **forward operator in time**, and implement either
a **backward** or **forward operator in space**, depending of the sign of $c$:
$$
\begin{array}{rcl}
\frac{c_{i}^{n+1}-c_{i}^{n}}{\Delta t} &=& -v \frac{c_{i}^{n}-c_{i-1}^{n}}{\Delta x}, \quad c>0 \\
\frac{c_{i}^{n+1}-c_{i}^{n}}{\Delta t} &=& -v \frac{c_{i+1}^{n}-c_{i}^{n}}{\Delta x}, \quad c<0
\end{array}
$$
or solved for the next time step
$$
\begin{array}{rcl}
c_{i}^{n+1} &=& c_{i}^{n}-\frac{v \Delta t}{\Delta x} \left( c_{i}^{n}-c_{i-1}^{n} \right), \quad c>0 \\
c_{i}^{n+1} &=& c_{i}^{n}-\frac{v \Delta t}{\Delta x} \left( c_{i+1}^{n}-c_{i}^{n} \right), \quad c<0
\end{array}
$$
<img src="images/PDE_upwind.jpg" style="height:5cm;">
We implement the upwind method:
```
# start time
t = 0
# initial values
u = gaussian(x)
# solution
for n in range(200):
t = t + dt
uold = u
for i in range(1,u.shape[0]-1):
u[i] = uold[i] - v*dt/dx*(uold[i]-uold[i-1])
if (np.abs(t-4) < dt/2):
u04 = np.copy(u)
elif (np.abs(t-8) < dt/2):
u08 = np.copy(u)
elif (np.abs(t-10) < dt/2):
u10 = np.copy(u)
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0')
plt.plot(x,u04,label='t=4s')
plt.plot(x,u08,label='t=8s')
plt.plot(x,u10,label='t=10s')
plt.title('Upwind method')
plt.legend()
```
----
## Lax method
Our third scheme is called `Lax method`, it is derived from the FTCS method, but the term
$u_i^n$ is replaced by the average of its two neighbors:
$$
c_{i}^{n+1}
=
\frac{1}{2} \left( c_{i+1}^{n} + c_{i-1}^{n} \right)
-\frac{v \Delta t}{2 \Delta x} \left( c_{i+1}^{n}-c_{i-1}^{n} \right)
$$
<img src="images/PDE_FTCS.jpg" style="height:5cm;">
We implement the LAX method:
```
# start time
t = 0
# initial values
u = gaussian(x)
# solution
for n in range(200):
t = t + dt
uold = u
for i in range(1,u.shape[0]-1):
u[i] = (uold[i+1]+uold[i-1])/2. - v*dt/2/dx*(uold[i+1]-uold[i-1])
if (np.abs(t-4) < dt/2):
u04 = np.copy(u)
elif (np.abs(t-8) < dt/2):
u08 = np.copy(u)
elif (np.abs(t-10) < dt/2):
u10 = np.copy(u)
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0s')
plt.plot(x,u04,label='t=4s')
plt.plot(x,u08,label='t=8s')
plt.plot(x,u10,label='t=10s')
plt.title('Lax method')
plt.legend()
```
----
## Lax-Wendroff method
Our fourth scheme is called `Lax-Wendroff method`, it is a **two-step** procedure:
$$
\begin{array}{rcl}
c_{i-\frac{1}{2}}^{n+\frac{1}{2}} &=& \frac{1}{2} \left( c_{i-1}^{n} + c_{i}^{n} \right)
- \frac{v \Delta t}{2 \Delta x} \left( c_{i}^{n}-c_{i-1}^{n} \right) \\
c_{i+\frac{1}{2}}^{n+\frac{1}{2}} &=& \frac{1}{2} \left( c_{i}^{n} + c_{i+1}^{n} \right)
- \frac{v \Delta t}{2 \Delta x} \left( c_{i+1}^{n}-c_{i}^{n} \right) \\
c_{i}^{n+1} &=& u_{i}^{n} - \frac{v \Delta t}{\Delta x}
\left( c_{i+\frac{1}{2}}^{n+\frac{1}{2}} - c_{i-\frac{1}{2}}^{n+\frac{1}{2}}\right)
\end{array}
$$
<img src="images/PDE_LAX_WENDROFF.jpg" style="height:5cm;">
We implement the LAX-WENDROFF method:
```
# start time
t = 0
# initial values
u = gaussian(x)
# solution
for n in range(200):
t = t + dt
uold = u
for i in range(1,u.shape[0]-1):
uleft = (uold[i-1]+uold[i])/2. - v*dt/2/dx*(uold[i]-uold[i-1])
uright = (uold[i]+uold[i+1])/2. - v*dt/2/dx*(uold[i+1]-uold[i])
u[i] = uold[i] - v*dt/dx*(uright - uleft)
if (np.abs(t-4) < dt/2):
u04 = np.copy(u)
elif (np.abs(t-8) < dt/2):
u08 = np.copy(u)
elif (np.abs(t-10) < dt/2):
u10 = np.copy(u)
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0s')
plt.plot(x,u04,label='t=4s')
plt.plot(x,u08,label='t=8s')
plt.plot(x,u10,label='t=10s')
plt.title('Lax-Wendroff method')
plt.legend()
```
... done
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
def gaussian(x,v=0.5,t=0.,mu=2.,sigma=1.):
f = np.exp(-(x-v*t-mu)**2/(sigma)**2)
return f
xstep = 101
x = np.linspace(0,10,xstep)
u0 = gaussian(x)
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0s')
#plt.plot(x,gaussian(x,t=4),label='t=4s')
#plt.plot(x,gaussian(x,t=8),label='t=8s')
#plt.plot(x,gaussian(x,t=10),label='t=10s')
plt.legend()
dt = 0.05
dx = (x.max()-x.min()) / (xstep-1)
v = 0.5
Courant = v*dt/dx
print ('Courant number: ',Courant)
# start time
t = 0
# initial values
u = gaussian(x)
# solution
for n in range(200):
t = t + dt
uold = u
for i in range(1,u.shape[0]-1):
u[i] = uold[i] - v*dt/2/dx*(uold[i+1]-uold[i-1])
if (np.abs(t-4) < dt/2):
u04 = np.copy(u)
elif (np.abs(t-8) < dt/2):
u08 = np.copy(u)
elif (np.abs(t-10) < dt/2):
u10 = np.copy(u)
print(x[np.where(u0 == np.amax(u0))],u0[np.where(u0 == np.amax(u0))])
print(x[np.where(u04 == np.amax(u04))],u04[np.where(u04 == np.amax(u04))])
print(x[np.where(u08 == np.amax(u08))],u08[np.where(u08 == np.amax(u08))])
print(x[np.where(u10 == np.amax(u10))],u10[np.where(u10 == np.amax(u10))])
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0')
plt.plot(x,u04,label='t=4s')
plt.plot(x,u08,label='t=8s')
plt.plot(x,u10,label='t=10s')
plt.title('FTCS method')
plt.legend()
# start time
t = 0
# initial values
u = gaussian(x)
# solution
for n in range(200):
t = t + dt
uold = u
for i in range(1,u.shape[0]-1):
u[i] = uold[i] - v*dt/dx*(uold[i]-uold[i-1])
if (np.abs(t-4) < dt/2):
u04 = np.copy(u)
elif (np.abs(t-8) < dt/2):
u08 = np.copy(u)
elif (np.abs(t-10) < dt/2):
u10 = np.copy(u)
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0')
plt.plot(x,u04,label='t=4s')
plt.plot(x,u08,label='t=8s')
plt.plot(x,u10,label='t=10s')
plt.title('Upwind method')
plt.legend()
# start time
t = 0
# initial values
u = gaussian(x)
# solution
for n in range(200):
t = t + dt
uold = u
for i in range(1,u.shape[0]-1):
u[i] = (uold[i+1]+uold[i-1])/2. - v*dt/2/dx*(uold[i+1]-uold[i-1])
if (np.abs(t-4) < dt/2):
u04 = np.copy(u)
elif (np.abs(t-8) < dt/2):
u08 = np.copy(u)
elif (np.abs(t-10) < dt/2):
u10 = np.copy(u)
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0s')
plt.plot(x,u04,label='t=4s')
plt.plot(x,u08,label='t=8s')
plt.plot(x,u10,label='t=10s')
plt.title('Lax method')
plt.legend()
# start time
t = 0
# initial values
u = gaussian(x)
# solution
for n in range(200):
t = t + dt
uold = u
for i in range(1,u.shape[0]-1):
uleft = (uold[i-1]+uold[i])/2. - v*dt/2/dx*(uold[i]-uold[i-1])
uright = (uold[i]+uold[i+1])/2. - v*dt/2/dx*(uold[i+1]-uold[i])
u[i] = uold[i] - v*dt/dx*(uright - uleft)
if (np.abs(t-4) < dt/2):
u04 = np.copy(u)
elif (np.abs(t-8) < dt/2):
u08 = np.copy(u)
elif (np.abs(t-10) < dt/2):
u10 = np.copy(u)
plt.figure(figsize=(10,6))
plt.xlabel('x')
plt.ylabel('c')
plt.grid(alpha=0.3)
plt.plot(x,u0,label='t=0s')
plt.plot(x,u04,label='t=4s')
plt.plot(x,u08,label='t=8s')
plt.plot(x,u10,label='t=10s')
plt.title('Lax-Wendroff method')
plt.legend()
| 0.349977 | 0.97007 |
# 0. DEPENDENCIES
Fix for Jupyter Notebook imports:
```
import os
import sys
print(os.getcwd())
# sys.path.append("S:\Dropbox\\000 - CARND\CarND-T1-P5-Vehicle-Detection")
for path in sys.path: print(path)
```
Remove the additional entry if needed:
```
# sys.path = sys.path[:-1]
for path in sys.path: print(path)
```
Load all dependencies:
```
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import numpy as np
import cv2
import glob
import time
import pickle
from importlib import reload
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC, LinearSVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.pipeline import Pipeline
from sklearn.metrics import confusion_matrix
from sklearn.externals import joblib
import src.helpers.constants as C
import src.helpers.io as IO
import src.helpers.features as FT
import src.helpers.plot as PLT
# RELOAD:
reload(C)
reload(IO)
reload(FT)
reload(PLT)
```
# 1. LOAD DATA
First, load all images filenames on the datasets, split into cars and non-cars. Print the counts and percentages of each to verify that the dataset is balanced.
```
files_cars = glob.glob("../../input/images/dataset/vehicles/*/*.png")
files_no_cars = glob.glob("../../input/images/dataset/non-vehicles/*/*.png")
count_cars = len(files_cars)
count_no_cars = len(files_no_cars)
count_total = count_cars + count_no_cars
percent_cars = 100 * count_cars / count_total
percent_no_cars = 100 * count_no_cars / count_total
print(" CAR IMAGES {0:5d} = {1:6.2f} %".format(count_cars, percent_cars))
print("NON-CAR IMAGES {0:5d} = {1:6.2f} %".format(count_no_cars, percent_no_cars))
print("-------------------------------")
print(" TOTAL {0:5d} = 100.00 %".format(count_total))
```
The data looks quite balanced, so no need to do any augmentation.
Next, preload them and check their total size to see if it's feasible to preload them all in different color spaces.
```
# Load all images (RGB only):
imgs_cars = IO.load_images_rgb(files_cars)
imgs_no_cars = IO.load_images_rgb(files_no_cars)
# Calculate their size by dumping them:
size_cars_b = sys.getsizeof(pickle.dumps(imgs_cars))
size_no_cars_b = sys.getsizeof(pickle.dumps(imgs_no_cars))
size_total_b = size_cars_b + size_no_cars_b
```
Print results in multiple units and calculate total for all channels:
```
size_cars_mb = size_cars_b / 1048576
size_no_cars_mb = size_no_cars_b / 1048576
size_total_mb = size_total_b / 1048576
size_all_spaces_mb = size_total_mb * (1 + len(C.COLOR_SPACES)) # RGB not included in C.COLOR_SPACES
size_all_spaces_gb = size_all_spaces_mb / 1024
print(" CAR IMAGES SIZE = {0:12.2f} B = {1:6.2f} MB".format(size_cars_b, size_cars_mb))
print(" NON-CAR IMAGES SIZE = {0:12.2f} B = {1:6.2f} MB".format(size_no_cars_b, size_no_cars_mb))
print("---------------------------------------------------")
print(" TOTAL SIZE = {0:12.2f} B = {1:6.2f} MB".format(size_total_b, size_total_mb))
print("ESTIMATED ALL SPACES SIZE = {0:12.2f} MB = {1:6.2f} GB".format(size_all_spaces_mb, size_all_spaces_gb))
```
Free up space:
```
try: del imgs_cars
except NameError: pass # Was not defined
try: del imgs_no_cars
except NameError: pass # Was not defined
```
Load all images in all color spaces:
```
# CARS:
imgs_cars_rgb, \
imgs_cars_hsv, \
imgs_cars_luv, \
imgs_cars_hls, \
imgs_cars_yuv, \
imgs_cars_ycrcb, \
imgs_cars_gray = IO.load_images_all(files_cars)
# NON-CARS:
imgs_no_cars_rgb, \
imgs_no_cars_hsv, \
imgs_no_cars_luv, \
imgs_no_cars_hls, \
imgs_no_cars_yuv, \
imgs_no_cars_ycrcb, \
imgs_no_cars_gray = IO.load_images_all(files_no_cars)
```
Some basic checks:
```
# CARS:
assert len(imgs_cars_rgb) == count_cars
assert len(imgs_cars_hsv) == count_cars
assert len(imgs_cars_luv) == count_cars
assert len(imgs_cars_hls) == count_cars
assert len(imgs_cars_yuv) == count_cars
assert len(imgs_cars_ycrcb) == count_cars
assert len(imgs_cars_gray) == count_cars
# NON-CARS:
assert len(imgs_no_cars_rgb) == count_no_cars
assert len(imgs_no_cars_hsv) == count_no_cars
assert len(imgs_no_cars_luv) == count_no_cars
assert len(imgs_no_cars_hls) == count_no_cars
assert len(imgs_no_cars_yuv) == count_no_cars
assert len(imgs_no_cars_ycrcb) == count_no_cars
assert len(imgs_no_cars_gray) == count_no_cars
```
Let's see what the raw data of those images look like (helpful when using `matplotlib image`):
```
print(imgs_cars_rgb[0][0, 0], np.amin(imgs_cars_rgb[0]), np.amax(imgs_cars_rgb[0]))
print(imgs_cars_hsv[0][0, 0], np.amin(imgs_cars_hsv[0]), np.amax(imgs_cars_hsv[0]))
print(imgs_cars_luv[0][0, 0], np.amin(imgs_cars_luv[0]), np.amax(imgs_cars_luv[0]))
print(imgs_cars_hls[0][0, 0], np.amin(imgs_cars_hls[0]), np.amax(imgs_cars_hls[0]))
print(imgs_cars_yuv[0][0, 0], np.amin(imgs_cars_yuv[0]), np.amax(imgs_cars_yuv[0]))
print(imgs_cars_ycrcb[0][0, 0], np.amin(imgs_cars_ycrcb[0]), np.amax(imgs_cars_ycrcb[0]))
print(imgs_cars_gray[0][0, 0], np.amin(imgs_cars_gray[0]), np.amax(imgs_cars_gray[0]))
```
Let's see how the actual car images look like:
```
start = np.random.randint(0, count_cars)
PLT.showAll(imgs_cars_rgb[start:start+8], 8,)
```
And now the non-car ones:
```
start = np.random.randint(0, count_no_cars)
PLT.showAll(imgs_no_cars_rgb[start:start+8], 8,)
```
Free up space:
```
# CARS:
try: del imgs_cars_rgb
except NameError: pass # Was not defined
try: del imgs_cars_hsv
except NameError: pass # Was not defined
try: del imgs_cars_luv
except NameError: pass # Was not defined
try: del imgs_cars_hls
except NameError: pass # Was not defined
try: del imgs_cars_yuv
except NameError: pass # Was not defined
try: del imgs_cars_ycrcb
except NameError: pass # Was not defined
try: del imgs_cars_gray
except NameError: pass # Was not defined
# NON-CARS:
try: del imgs_no_cars_rgb
except NameError: pass # Was not defined
try: del imgs_no_cars_hsv
except NameError: pass # Was not defined
try: del imgs_no_cars_luv
except NameError: pass # Was not defined
try: del imgs_no_cars_hls
except NameError: pass # Was not defined
try: del imgs_no_cars_yuv
except NameError: pass # Was not defined
try: del imgs_no_cars_ycrcb
except NameError: pass # Was not defined
try: del imgs_no_cars_gray
except NameError: pass # Was not defined
```
## SECTION'S CONCERNS, IMPROVEMENTS, TODOS...
- Should images that belong to the same sequence be grouped together so that half of each of them can go to a different subset (training and test)?
- __Images visualizations in different color spaces.__
# 2. EXTRACT FEATURES
First, let's quickly check how HOG features look like for car and non-car HLS images:
```
# CAR:
car_image = imgs_cars_hls[start]
car_channels = [car_image[:,:,0], car_image[:,:,1], car_image[:,:,2]]
car_hogs = FT.features_hog(car_image, 9, 12, 2, visualise=True)[2]
PLT.showAll(car_channels + car_hogs, 6, "gray")
# NON-CAR:
non_car_image = imgs_no_cars_hls[start]
non_car_channels = [non_car_image[:,:,0], non_car_image[:,:,1], non_car_image[:,:,2]]
non_car_hogs = FT.features_hog(non_car_image, 9, 12, 2, visualise=True)[2]
PLT.showAll(non_car_channels + non_car_hogs, 6, "gray")
```
Ok, so now we are ready to extract all the features from all the images:
```
# Use a subset to train params!
# TODO: Add channel to all feature methods or check how I did it in project 4
# TOOO: Plot hog and histograms (cars VS non cars)
ft_car_binned = FT.extract_binned_color(imgs_cars_hls, size=(8, 8))
ft_no_car_binned = FT.extract_binned_color(imgs_no_cars_hls, size=(8, 8))
print("BINNED")
ft_car_hist = FT.extract_histogram_color(imgs_cars_hls, bins=32)
ft_no_car_hist = FT.extract_histogram_color(imgs_no_cars_hls, bins=32)
print("HIST")
ft_car_hog = FT.extract_hog(imgs_cars_hls, orients=9, ppc=12, cpb=2)
ft_no_car_hog = FT.extract_hog(imgs_no_cars_hls, orients=9, ppc=12, cpb=2)
print("HOG")
```
# 3. TRAIN CLASSIFIER (SVM)
First, generate the final features vectors:
```
features_car = FT.combine_features((ft_car_binned, ft_car_hist, ft_car_hog))
features_no_car = FT.combine_features((ft_no_car_binned, ft_no_car_hist, ft_no_car_hog))
print('Feature vector length:', len(features_car[0]))
```
Next, train a classifier with them and check some stats about its performance:
```
# Create an array stack of feature vectors and a vector of labels:
X = np.vstack((features_car, features_no_car)).astype(np.float64)
y = np.hstack((np.ones(count_cars), np.zeros(count_no_cars)))
# Split up data into randomized training and test sets
rand_state = np.random.randint(0, 1000)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=rand_state)
# Create a Pipeline to be able to save scaler and classifier together:
clf = Pipeline([
('SCALER', StandardScaler()),
('CLASSIFIER', LinearSVC(loss="hinge"))
# ('CLASSIFIER', SVC(kernel="linear"))
])
# Pipeline. See: http://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html
# SVC VS LinearSVC. See: https://stackoverflow.com/questions/35076586/linearsvc-vs-svckernel-linear-conflicting-arguments
# Train the model:
t0 = time.time()
clf.fit(X_train, y_train)
t = time.time() - t0
# Output model's stats:
print(" TRAINING TIME = {0:2.4f} SEC".format(t))
print("TRAINING ACCURACY = {0:2.4f} %".format(clf.score(X_train, y_train)))
print(" TEST ACCURACY = {0:2.4f} %".format(clf.score(X_test, y_test)))
print("\nCONFUSION MATRIX (TRAIN / TEST / ALL):")
t0 = time.time()
y_train_pred = clf.predict(X_train)
y_test_pred = clf.predict(X_test)
y_pred = clf.predict(X)
t = time.time() - t0
print(confusion_matrix(y_train, y_train_pred))
print(confusion_matrix(y_test, y_test_pred))
print(confusion_matrix(y, y_pred))
print("PREDICTION TIME = {0:2.4f} MS".format(t, 1000 * t / (2 * count_total)))
# TODO: Automatically adjust classifier's params!
# LinearSVC:
# 0.9859 with loss="hinge"
# 0.9840 with C=100, loss="hinge"
# 0.9825 with nothing
# 0.9825 with C=10, loss="hinge"
# 0.9823 with dual=False
# 0.9823 with C=10
# SVC kernel="linear": SLOW
# 0.9865 with nothing
# 0.9862 with C=10
# 0.9854 with C=100
# SVC kernel="rbf": SUPER SLOW
# 0.9913 with nothing
# 0.9620 with gamma=0.01
# SVC kernel="poly": SLOW
# 0.9524 with nothing
# DecisionTreeClassifier:
# 0.9657 with min_samples_split=10
# 0.9631 with max_depth=32
# 0.9628 with min_samples_split=32
# 0.9626 with min_samples_split=10, max_depth=16
# 0.9620 with max_depth=8
# 0.9614 with nothing
# 0.9614 with min_samples_split=10, max_depth=32
# 0.9592 with max_depth=16
# 0.9566 with min_samples_split=10, max_depth=8
# 0.9544 with criterion="entropy"
# GaussianNB:
# 0.8229 with nothing
# RandomForestClassifier:
# 0.9882 with n_estimators=20
# 0.9856 with n_estimators=24
# 0.9856 with n_estimators=32
# 0.9797 with nothing
# AdaBoostClassifier: SUPER SLOW
# 0.9891 with nothing
# 0.9885 with n_estimators=100
# ALL ABOVE WITH HSV IMAGES. BELOW, LinearSVC with loss="hinge" in other color spaces:
# RGB: 0.9820 - OK (very few false positives). Does not detect black car.
# HSV: 0.9859 - Lots of false positives (especially with bigger window). Does not detect black car.
# LUV: 0.9896 - Lots of false positives (especially with bigger window). Detects both cars.
# HSL: 0.9851 - OK (still problematic with bigger window). Detects both cars.
# YUV: 0.9893 - Lots of false positives (especially with bigger window). Detects both cars.
# YCRCB: 0.9842 - Lots of false positives (especially with bigger window). Detects both cars.
# RGB (binned + hist) + HSL (hog): 0.9814 - Lots of false positives. Does not detect black car.
# RGB (hog) + HSL (binned + hist): 0.9859 - Lots of false positives (especially with bigger window) quite ok.
```
# 4. ANALYZE ERRORS
Let's see which images are incorrectly classified:
```
# TODO
```
# 5. SAVE THE MODEL
```
# TODO: Save each model with the params used?
joblib.dump(clf, "../../output/models/classifier_augmented.pkl")
# See: http://scikit-learn.org/stable/modules/model_persistence.html
```
|
github_jupyter
|
import os
import sys
print(os.getcwd())
# sys.path.append("S:\Dropbox\\000 - CARND\CarND-T1-P5-Vehicle-Detection")
for path in sys.path: print(path)
# sys.path = sys.path[:-1]
for path in sys.path: print(path)
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import numpy as np
import cv2
import glob
import time
import pickle
from importlib import reload
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC, LinearSVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.pipeline import Pipeline
from sklearn.metrics import confusion_matrix
from sklearn.externals import joblib
import src.helpers.constants as C
import src.helpers.io as IO
import src.helpers.features as FT
import src.helpers.plot as PLT
# RELOAD:
reload(C)
reload(IO)
reload(FT)
reload(PLT)
files_cars = glob.glob("../../input/images/dataset/vehicles/*/*.png")
files_no_cars = glob.glob("../../input/images/dataset/non-vehicles/*/*.png")
count_cars = len(files_cars)
count_no_cars = len(files_no_cars)
count_total = count_cars + count_no_cars
percent_cars = 100 * count_cars / count_total
percent_no_cars = 100 * count_no_cars / count_total
print(" CAR IMAGES {0:5d} = {1:6.2f} %".format(count_cars, percent_cars))
print("NON-CAR IMAGES {0:5d} = {1:6.2f} %".format(count_no_cars, percent_no_cars))
print("-------------------------------")
print(" TOTAL {0:5d} = 100.00 %".format(count_total))
# Load all images (RGB only):
imgs_cars = IO.load_images_rgb(files_cars)
imgs_no_cars = IO.load_images_rgb(files_no_cars)
# Calculate their size by dumping them:
size_cars_b = sys.getsizeof(pickle.dumps(imgs_cars))
size_no_cars_b = sys.getsizeof(pickle.dumps(imgs_no_cars))
size_total_b = size_cars_b + size_no_cars_b
size_cars_mb = size_cars_b / 1048576
size_no_cars_mb = size_no_cars_b / 1048576
size_total_mb = size_total_b / 1048576
size_all_spaces_mb = size_total_mb * (1 + len(C.COLOR_SPACES)) # RGB not included in C.COLOR_SPACES
size_all_spaces_gb = size_all_spaces_mb / 1024
print(" CAR IMAGES SIZE = {0:12.2f} B = {1:6.2f} MB".format(size_cars_b, size_cars_mb))
print(" NON-CAR IMAGES SIZE = {0:12.2f} B = {1:6.2f} MB".format(size_no_cars_b, size_no_cars_mb))
print("---------------------------------------------------")
print(" TOTAL SIZE = {0:12.2f} B = {1:6.2f} MB".format(size_total_b, size_total_mb))
print("ESTIMATED ALL SPACES SIZE = {0:12.2f} MB = {1:6.2f} GB".format(size_all_spaces_mb, size_all_spaces_gb))
try: del imgs_cars
except NameError: pass # Was not defined
try: del imgs_no_cars
except NameError: pass # Was not defined
# CARS:
imgs_cars_rgb, \
imgs_cars_hsv, \
imgs_cars_luv, \
imgs_cars_hls, \
imgs_cars_yuv, \
imgs_cars_ycrcb, \
imgs_cars_gray = IO.load_images_all(files_cars)
# NON-CARS:
imgs_no_cars_rgb, \
imgs_no_cars_hsv, \
imgs_no_cars_luv, \
imgs_no_cars_hls, \
imgs_no_cars_yuv, \
imgs_no_cars_ycrcb, \
imgs_no_cars_gray = IO.load_images_all(files_no_cars)
# CARS:
assert len(imgs_cars_rgb) == count_cars
assert len(imgs_cars_hsv) == count_cars
assert len(imgs_cars_luv) == count_cars
assert len(imgs_cars_hls) == count_cars
assert len(imgs_cars_yuv) == count_cars
assert len(imgs_cars_ycrcb) == count_cars
assert len(imgs_cars_gray) == count_cars
# NON-CARS:
assert len(imgs_no_cars_rgb) == count_no_cars
assert len(imgs_no_cars_hsv) == count_no_cars
assert len(imgs_no_cars_luv) == count_no_cars
assert len(imgs_no_cars_hls) == count_no_cars
assert len(imgs_no_cars_yuv) == count_no_cars
assert len(imgs_no_cars_ycrcb) == count_no_cars
assert len(imgs_no_cars_gray) == count_no_cars
print(imgs_cars_rgb[0][0, 0], np.amin(imgs_cars_rgb[0]), np.amax(imgs_cars_rgb[0]))
print(imgs_cars_hsv[0][0, 0], np.amin(imgs_cars_hsv[0]), np.amax(imgs_cars_hsv[0]))
print(imgs_cars_luv[0][0, 0], np.amin(imgs_cars_luv[0]), np.amax(imgs_cars_luv[0]))
print(imgs_cars_hls[0][0, 0], np.amin(imgs_cars_hls[0]), np.amax(imgs_cars_hls[0]))
print(imgs_cars_yuv[0][0, 0], np.amin(imgs_cars_yuv[0]), np.amax(imgs_cars_yuv[0]))
print(imgs_cars_ycrcb[0][0, 0], np.amin(imgs_cars_ycrcb[0]), np.amax(imgs_cars_ycrcb[0]))
print(imgs_cars_gray[0][0, 0], np.amin(imgs_cars_gray[0]), np.amax(imgs_cars_gray[0]))
start = np.random.randint(0, count_cars)
PLT.showAll(imgs_cars_rgb[start:start+8], 8,)
start = np.random.randint(0, count_no_cars)
PLT.showAll(imgs_no_cars_rgb[start:start+8], 8,)
# CARS:
try: del imgs_cars_rgb
except NameError: pass # Was not defined
try: del imgs_cars_hsv
except NameError: pass # Was not defined
try: del imgs_cars_luv
except NameError: pass # Was not defined
try: del imgs_cars_hls
except NameError: pass # Was not defined
try: del imgs_cars_yuv
except NameError: pass # Was not defined
try: del imgs_cars_ycrcb
except NameError: pass # Was not defined
try: del imgs_cars_gray
except NameError: pass # Was not defined
# NON-CARS:
try: del imgs_no_cars_rgb
except NameError: pass # Was not defined
try: del imgs_no_cars_hsv
except NameError: pass # Was not defined
try: del imgs_no_cars_luv
except NameError: pass # Was not defined
try: del imgs_no_cars_hls
except NameError: pass # Was not defined
try: del imgs_no_cars_yuv
except NameError: pass # Was not defined
try: del imgs_no_cars_ycrcb
except NameError: pass # Was not defined
try: del imgs_no_cars_gray
except NameError: pass # Was not defined
# CAR:
car_image = imgs_cars_hls[start]
car_channels = [car_image[:,:,0], car_image[:,:,1], car_image[:,:,2]]
car_hogs = FT.features_hog(car_image, 9, 12, 2, visualise=True)[2]
PLT.showAll(car_channels + car_hogs, 6, "gray")
# NON-CAR:
non_car_image = imgs_no_cars_hls[start]
non_car_channels = [non_car_image[:,:,0], non_car_image[:,:,1], non_car_image[:,:,2]]
non_car_hogs = FT.features_hog(non_car_image, 9, 12, 2, visualise=True)[2]
PLT.showAll(non_car_channels + non_car_hogs, 6, "gray")
# Use a subset to train params!
# TODO: Add channel to all feature methods or check how I did it in project 4
# TOOO: Plot hog and histograms (cars VS non cars)
ft_car_binned = FT.extract_binned_color(imgs_cars_hls, size=(8, 8))
ft_no_car_binned = FT.extract_binned_color(imgs_no_cars_hls, size=(8, 8))
print("BINNED")
ft_car_hist = FT.extract_histogram_color(imgs_cars_hls, bins=32)
ft_no_car_hist = FT.extract_histogram_color(imgs_no_cars_hls, bins=32)
print("HIST")
ft_car_hog = FT.extract_hog(imgs_cars_hls, orients=9, ppc=12, cpb=2)
ft_no_car_hog = FT.extract_hog(imgs_no_cars_hls, orients=9, ppc=12, cpb=2)
print("HOG")
features_car = FT.combine_features((ft_car_binned, ft_car_hist, ft_car_hog))
features_no_car = FT.combine_features((ft_no_car_binned, ft_no_car_hist, ft_no_car_hog))
print('Feature vector length:', len(features_car[0]))
# Create an array stack of feature vectors and a vector of labels:
X = np.vstack((features_car, features_no_car)).astype(np.float64)
y = np.hstack((np.ones(count_cars), np.zeros(count_no_cars)))
# Split up data into randomized training and test sets
rand_state = np.random.randint(0, 1000)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=rand_state)
# Create a Pipeline to be able to save scaler and classifier together:
clf = Pipeline([
('SCALER', StandardScaler()),
('CLASSIFIER', LinearSVC(loss="hinge"))
# ('CLASSIFIER', SVC(kernel="linear"))
])
# Pipeline. See: http://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html
# SVC VS LinearSVC. See: https://stackoverflow.com/questions/35076586/linearsvc-vs-svckernel-linear-conflicting-arguments
# Train the model:
t0 = time.time()
clf.fit(X_train, y_train)
t = time.time() - t0
# Output model's stats:
print(" TRAINING TIME = {0:2.4f} SEC".format(t))
print("TRAINING ACCURACY = {0:2.4f} %".format(clf.score(X_train, y_train)))
print(" TEST ACCURACY = {0:2.4f} %".format(clf.score(X_test, y_test)))
print("\nCONFUSION MATRIX (TRAIN / TEST / ALL):")
t0 = time.time()
y_train_pred = clf.predict(X_train)
y_test_pred = clf.predict(X_test)
y_pred = clf.predict(X)
t = time.time() - t0
print(confusion_matrix(y_train, y_train_pred))
print(confusion_matrix(y_test, y_test_pred))
print(confusion_matrix(y, y_pred))
print("PREDICTION TIME = {0:2.4f} MS".format(t, 1000 * t / (2 * count_total)))
# TODO: Automatically adjust classifier's params!
# LinearSVC:
# 0.9859 with loss="hinge"
# 0.9840 with C=100, loss="hinge"
# 0.9825 with nothing
# 0.9825 with C=10, loss="hinge"
# 0.9823 with dual=False
# 0.9823 with C=10
# SVC kernel="linear": SLOW
# 0.9865 with nothing
# 0.9862 with C=10
# 0.9854 with C=100
# SVC kernel="rbf": SUPER SLOW
# 0.9913 with nothing
# 0.9620 with gamma=0.01
# SVC kernel="poly": SLOW
# 0.9524 with nothing
# DecisionTreeClassifier:
# 0.9657 with min_samples_split=10
# 0.9631 with max_depth=32
# 0.9628 with min_samples_split=32
# 0.9626 with min_samples_split=10, max_depth=16
# 0.9620 with max_depth=8
# 0.9614 with nothing
# 0.9614 with min_samples_split=10, max_depth=32
# 0.9592 with max_depth=16
# 0.9566 with min_samples_split=10, max_depth=8
# 0.9544 with criterion="entropy"
# GaussianNB:
# 0.8229 with nothing
# RandomForestClassifier:
# 0.9882 with n_estimators=20
# 0.9856 with n_estimators=24
# 0.9856 with n_estimators=32
# 0.9797 with nothing
# AdaBoostClassifier: SUPER SLOW
# 0.9891 with nothing
# 0.9885 with n_estimators=100
# ALL ABOVE WITH HSV IMAGES. BELOW, LinearSVC with loss="hinge" in other color spaces:
# RGB: 0.9820 - OK (very few false positives). Does not detect black car.
# HSV: 0.9859 - Lots of false positives (especially with bigger window). Does not detect black car.
# LUV: 0.9896 - Lots of false positives (especially with bigger window). Detects both cars.
# HSL: 0.9851 - OK (still problematic with bigger window). Detects both cars.
# YUV: 0.9893 - Lots of false positives (especially with bigger window). Detects both cars.
# YCRCB: 0.9842 - Lots of false positives (especially with bigger window). Detects both cars.
# RGB (binned + hist) + HSL (hog): 0.9814 - Lots of false positives. Does not detect black car.
# RGB (hog) + HSL (binned + hist): 0.9859 - Lots of false positives (especially with bigger window) quite ok.
# TODO
# TODO: Save each model with the params used?
joblib.dump(clf, "../../output/models/classifier_augmented.pkl")
# See: http://scikit-learn.org/stable/modules/model_persistence.html
| 0.339061 | 0.728145 |
# Import and extract gaze data
`3.gaze-data_import`
Import gaze data from the eye-tracking software, and incorporate trial outcomes into homogenized dataset
```
from _utils.transform import sum_oscillations,oscillation_rate
import os
derivs_dir = os.path.join('..','derivatives')
homog_dir = os.path.join(derivs_dir,'02.homogenized')
source_dir = os.path.join('..','sourcedata')
```
# Import dataframes
```
import pandas as pd
fpath = os.path.join(homog_dir,'econdec-full_task-main_beh.csv')
beh_frame = pd.read_csv(fpath)
fpath = os.path.join(source_dir,'raw-gaze-data.xlsx')
choice_gaze_frame = pd.read_excel(fpath, sheet_name=0)
outcome_gaze_frame = pd.read_excel(fpath, sheet_name=1)
```
# Extract only the gaze data for main task series
The dataframe contains gaze data for practice trials, where `practice == 1` or `practice == 2`.
It also contains gaze data for the Memory task trials, where `Phase == Fract` or `Phase == Face`.
We'll slice all these rows out, leaving only the relevant main task trials (1-72).
```
choice_gaze_frame = choice_gaze_frame[
choice_gaze_frame['practice']==3
][
choice_gaze_frame['Phase'] == 'Main Task'
]
outcome_gaze_frame = outcome_gaze_frame[
outcome_gaze_frame['practice'] == 3
][
outcome_gaze_frame['Phase'] == 'Main Task'
]
```
# Fix gaze trial numbers
They were offset by 4 by the practice trials (1-4) we removed. Re-setting to initialize at 1
```
choice_gaze_frame['TRIAL_LABEL'] = choice_gaze_frame['TRIAL_LABEL']-4
outcome_gaze_frame['TRIAL_LABEL'] = outcome_gaze_frame['TRIAL_LABEL']-4
```
# Drop irrelevant columns
There is a lot of data here, so we can implicitly select only the columns we need.
We'll rename them to be a little more clear next.
```
choice_gaze_frame = choice_gaze_frame[[
'RECORDING_SESSION_LABEL','TRIAL_LABEL',
'IA_LABEL','IA_ID',
'IA_FSA_COUNT_1','IA_FSA_COUNT_2',
'IA_FSA_COUNT_24','IA_FSA_COUNT_25',
'IA_FSA_COUNT_26','IA_FSA_COUNT_27',
]]
outcome_gaze_frame = outcome_gaze_frame[[
'RECORDING_SESSION_LABEL','TRIAL_LABEL',
'IA_ID','IA_LABEL',
'IA_DWELL_TIME'
]]
```
# Rename remaining columns
In the choice phase, we need to keep this entire matrix in order to calculate the oscillation rate. Each row represents an on-screen interest area for a given trial, denoted redundantly with `ia-id` and `ia-label`. There are six(6) relevant interest areas during the choice phase, so there are six(6) rows per trial.
The matrix tells us how many times a saccade started in one interest area and ended in another. Each of these is called a "fixation skip" (FSA), starting in that row's interest area, and ending in the interest area denoted by the `fsa-ia-` columns.
```
choice_gaze_frame = choice_gaze_frame.rename(columns={
'RECORDING_SESSION_LABEL':'subjnum',
'TRIAL_LABEL':'trial',
'IA_ID':'ia-id',
'IA_LABEL':'ia-label',
'IA_DWELL_TIME':'dwell-time',
'IA_FSA_COUNT_1':'fsa-ia-01',
'IA_FSA_COUNT_2':'fsa-ia-02',
'IA_FSA_COUNT_24':'fsa-ia-24',
'IA_FSA_COUNT_25':'fsa-ia-25',
'IA_FSA_COUNT_26':'fsa-ia-26',
'IA_FSA_COUNT_27':'fsa-ia-27'
})
outcome_dwell_time = outcome_gaze_frame.rename(columns={
'RECORDING_SESSION_LABEL':'subjnum',
'TRIAL_LABEL':'trial',
'IA_ID':'ia-id',
'IA_LABEL':'ia-label',
'IA_DWELL_TIME':'dwell-time'
})
```
# Transform matrix into oscillation sum
We'll first define a function `sum_oscillations` to use with `df.apply()` to sum up the number of oscillations from any a given row's interest area to any of the interest areas on the other side of the screen.
```
stock_ia_list = [1,24,26]
bond_ia_list = [2,25,27]
choice_gaze_frame['oscillations'] = choice_gaze_frame.apply(sum_oscillations,axis=1)
```
Next we use `df.groupby()` and `df.sum()` to collect and summate the oscillations into trialwise rows for merging into `beh_frame`
```
oscillations = choice_gaze_frame.groupby(['subjnum','trial'])
oscillations = oscillations.sum()['oscillations']
oscillations = oscillations.reset_index()
beh_frame = beh_frame.merge(oscillations,'left')
```
# Extract outcome "Bubble" dwell time
All we need here is the `dwell-time` for one interest area in particular (`ia-id == 5`)
```
outcome_dwell_time = outcome_dwell_time[outcome_dwell_time['ia-id']==5]
outcome_dwell_time = outcome_dwell_time[['subjnum','trial','dwell-time']]
beh_frame = beh_frame.merge(outcome_dwell_time,'left')
```
# Calculate oscillation rate
Divide the sum count of oscillations by the number of seconds spent on the choice phase
```
beh_frame['osc-rate'] = beh_frame.apply(oscillation_rate,axis=1)
```
# Output
```
gaze_dir = os.path.join(derivs_dir,'03.gaze-import')
try: os.mkdir(gaze_dir)
except OSError as e:
print(e)
fpath = os.path.join(gaze_dir,'econdec-full_task-all_eye.csv')
beh_frame.to_csv(fpath,index=False)
```
|
github_jupyter
|
from _utils.transform import sum_oscillations,oscillation_rate
import os
derivs_dir = os.path.join('..','derivatives')
homog_dir = os.path.join(derivs_dir,'02.homogenized')
source_dir = os.path.join('..','sourcedata')
import pandas as pd
fpath = os.path.join(homog_dir,'econdec-full_task-main_beh.csv')
beh_frame = pd.read_csv(fpath)
fpath = os.path.join(source_dir,'raw-gaze-data.xlsx')
choice_gaze_frame = pd.read_excel(fpath, sheet_name=0)
outcome_gaze_frame = pd.read_excel(fpath, sheet_name=1)
choice_gaze_frame = choice_gaze_frame[
choice_gaze_frame['practice']==3
][
choice_gaze_frame['Phase'] == 'Main Task'
]
outcome_gaze_frame = outcome_gaze_frame[
outcome_gaze_frame['practice'] == 3
][
outcome_gaze_frame['Phase'] == 'Main Task'
]
choice_gaze_frame['TRIAL_LABEL'] = choice_gaze_frame['TRIAL_LABEL']-4
outcome_gaze_frame['TRIAL_LABEL'] = outcome_gaze_frame['TRIAL_LABEL']-4
choice_gaze_frame = choice_gaze_frame[[
'RECORDING_SESSION_LABEL','TRIAL_LABEL',
'IA_LABEL','IA_ID',
'IA_FSA_COUNT_1','IA_FSA_COUNT_2',
'IA_FSA_COUNT_24','IA_FSA_COUNT_25',
'IA_FSA_COUNT_26','IA_FSA_COUNT_27',
]]
outcome_gaze_frame = outcome_gaze_frame[[
'RECORDING_SESSION_LABEL','TRIAL_LABEL',
'IA_ID','IA_LABEL',
'IA_DWELL_TIME'
]]
choice_gaze_frame = choice_gaze_frame.rename(columns={
'RECORDING_SESSION_LABEL':'subjnum',
'TRIAL_LABEL':'trial',
'IA_ID':'ia-id',
'IA_LABEL':'ia-label',
'IA_DWELL_TIME':'dwell-time',
'IA_FSA_COUNT_1':'fsa-ia-01',
'IA_FSA_COUNT_2':'fsa-ia-02',
'IA_FSA_COUNT_24':'fsa-ia-24',
'IA_FSA_COUNT_25':'fsa-ia-25',
'IA_FSA_COUNT_26':'fsa-ia-26',
'IA_FSA_COUNT_27':'fsa-ia-27'
})
outcome_dwell_time = outcome_gaze_frame.rename(columns={
'RECORDING_SESSION_LABEL':'subjnum',
'TRIAL_LABEL':'trial',
'IA_ID':'ia-id',
'IA_LABEL':'ia-label',
'IA_DWELL_TIME':'dwell-time'
})
stock_ia_list = [1,24,26]
bond_ia_list = [2,25,27]
choice_gaze_frame['oscillations'] = choice_gaze_frame.apply(sum_oscillations,axis=1)
oscillations = choice_gaze_frame.groupby(['subjnum','trial'])
oscillations = oscillations.sum()['oscillations']
oscillations = oscillations.reset_index()
beh_frame = beh_frame.merge(oscillations,'left')
outcome_dwell_time = outcome_dwell_time[outcome_dwell_time['ia-id']==5]
outcome_dwell_time = outcome_dwell_time[['subjnum','trial','dwell-time']]
beh_frame = beh_frame.merge(outcome_dwell_time,'left')
beh_frame['osc-rate'] = beh_frame.apply(oscillation_rate,axis=1)
gaze_dir = os.path.join(derivs_dir,'03.gaze-import')
try: os.mkdir(gaze_dir)
except OSError as e:
print(e)
fpath = os.path.join(gaze_dir,'econdec-full_task-all_eye.csv')
beh_frame.to_csv(fpath,index=False)
| 0.210198 | 0.873431 |
# Support Vector Machine
<!--<badge>--><a href="https://colab.research.google.com/github/TheAIDojo/Machine_Learning_Bootcamp/blob/main/Week%2003%20-%20Machine%20Learning%20Algorithms/SVM.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a><!--</badge>-->
This explaination is taken from [Datacamp.com](https://www.datacamp.com/community/tutorials/svm-classification-scikit-learn-python#how)
Generally, Support Vector Machines is considered to be a classification approach, it but can be employed in both types of classification and regression problems. It can easily handle multiple continuous and categorical variables. SVM constructs a hyperplane in multidimensional space to separate different classes. SVM generates optimal hyperplane in an iterative manner, which is used to minimize an error. The core idea of SVM is to find a maximum marginal hyperplane(MMH) that best divides the dataset into classes.

### Support Vectors
Support vectors are the data points, which are closest to the hyperplane. These points will define the separating line better by calculating margins. These points are more relevant to the construction of the classifier.
### Hyperplane
A hyperplane is a decision plane which separates between a set of objects having different class memberships.
### Margin
A margin is a gap between the two lines on the closest class points. This is calculated as the perpendicular distance from the line to support vectors or closest points. If the margin is larger in between the classes, then it is considered a good margin, a smaller margin is a bad margin.
### How does SVM work?
The main objective is to segregate the given dataset in the best possible way. The distance between the either nearest points is known as the margin. The objective is to select a hyperplane with the maximum possible margin between support vectors in the given dataset. SVM searches for the maximum marginal hyperplane in the following steps:
1.Generate hyperplanes which segregates the classes in the best way. Left-hand side figure showing three hyperplanes black, blue and orange. Here, the blue and orange have higher classification error, but the black is separating the two classes correctly.
2.Select the right hyperplane with the maximum segregation from the either nearest data points as shown in the right-hand side figure.

## SVM Kernels
The SVM algorithm is implemented in practice using a kernel. A kernel transforms an input data space into the required form. SVM uses a technique called the kernel trick. Here, the kernel takes a low-dimensional input space and transforms it into a higher dimensional space. In other words, you can say that it converts nonseparable problem to separable problems by adding more dimension to it. It is most useful in non-linear separation problem. Kernel trick helps you to build a more accurate classifier.
### Linear Kernel
A linear kernel can be used as normal dot product any two given observations. The product between two vectors is the sum of the multiplication of each pair of input values.
`K(x, xi) = sum(x * xi)`
### Polynomial Kernel
A polynomial kernel is a more generalized form of the linear kernel. The polynomial kernel can distinguish curved or nonlinear input space.
`K(x,xi) = 1 + sum(x * xi)^d`
Where d is the degree of the polynomial. d=1 is similar to the linear transformation. The degree needs to be manually specified in the learning algorithm.
### Radial Basis Function Kernel
The Radial basis function kernel is a popular kernel function commonly used in support vector machine classification. RBF can map an input space in infinite dimensional space.
`K(x,xi) = exp(-gamma * sum((x – xi^2))`
Here gamma is a parameter, which ranges from 0 to 1. A higher value of gamma will perfectly fit the training dataset, which causes over-fitting. Gamma=0.1 is considered to be a good default value. The value of gamma needs to be manually specified in the learning algorithm.
## Tuning Hyperparameters
**Kernel**: The main function of the kernel is to transform the given dataset input data into the required form. There are various types of functions such as linear, polynomial, and radial basis function (RBF). Polynomial and RBF are useful for non-linear hyperplane. Polynomial and RBF kernels compute the separation line in the higher dimension. In some of the applications, it is suggested to use a more complex kernel to separate the classes that are curved or nonlinear. This transformation can lead to more accurate classifiers.
**Regularization**: Regularization parameter in python's Scikit-learn C parameter used to maintain regularization. Here C is the penalty parameter, which represents misclassification or error term. The misclassification or error term tells the SVM optimization how much error is bearable. This is how you can control the trade-off between decision boundary and misclassification term. A smaller value of C creates a small-margin hyperplane and a larger value of C creates a larger-margin hyperplane.
**Gamma**: A lower value of Gamma will loosely fit the training dataset, whereas a higher value of gamma will exactly fit the training dataset, which causes over-fitting. In other words, you can say a low value of gamma considers only nearby points in calculating the separation line, while the a value of gamma considers all the data points in the calculation of the separation line.
We can summarize the effect of $C$ and $\gamma$ in the following table
| | Large Gamma | Small Gamma | Large C | Small C |
| ------------- |:-------------:| -----:| -----:| -----:|
| Variance | Low | High | High | Low |
| Bias | High | Low | Low | High |
As a reminder, this is what the bias and variance look like

## Scikit Learn Implementation
### SVM Classifier using SVC
Until now, you have learned about the theoretical background of SVM. Now you will learn about its implementation in Python using scikit-learn.
In the model the building part, you can use the cancer dataset, which is a very famous multi-class classification problem. This dataset is computed from a digitized image of a fine needle aspirate (FNA) of a breast mass. They describe characteristics of the cell nuclei present in the image.
The dataset comprises 30 features (mean radius, mean texture, mean perimeter, mean area, mean smoothness, mean compactness, mean concavity, mean concave points, mean symmetry, mean fractal dimension, radius error, texture error, perimeter error, area error, smoothness error, compactness error, concavity error, concave points error, symmetry error, fractal dimension error, worst radius, worst texture, worst perimeter, worst area, worst smoothness, worst compactness, worst concavity, worst concave points, worst symmetry, and worst fractal dimension) and a target (type of cancer).
This data has two types of cancer classes: malignant (harmful) and benign (not harmful). Here, you can build a model to classify the type of cancer. The dataset is available in the scikit-learn library or you can also download it from the UCI Machine Learning Library.
#### Import Libs
```
from sklearn import datasets, model_selection, svm, metrics
import pandas as pd
```
#### Loading Data
```
x, y = datasets.load_breast_cancer(return_X_y=True)
```
#### Splitting Data
```
X_train, X_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.2, random_state=42, stratify=y) # 80% training and 20% test
```
#### Creating Model
```
#Create a svm Classifier
clf = svm.SVC(kernel='linear') # Linear Kernel
#Train the model using the training sets
clf.fit(X_train, y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
```
#### Evaluating Model
```
metrics.f1_score(y_test, y_pred)
```
### SVM Regressor using SVR
#### Loading Data
```
x, y = datasets.fetch_california_housing(return_X_y=True) # this will download the dataset so it might take some time
x_mean=x.mean() # calculate the mean of x
x_std=x.std() # calculate the std of x
x_norm=(x-x_mean)/x_std # normalize the x
y_mean=y.mean() # calculate the mean of y
y_std=y.std() # calculate the std of y
y_norm=(y-y_mean)/y_std # normalize the y
```
#### Splitting Data
```
x_train, x_test, y_train, y_test = model_selection.train_test_split(x_norm, y_norm, test_size=0.2, random_state=42)
```
#### Creating Model
```
model = svm.SVR()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
```
#### Evaluating Model
```
metrics.mean_squared_error(y_test, y_pred)
```
|
github_jupyter
|
from sklearn import datasets, model_selection, svm, metrics
import pandas as pd
x, y = datasets.load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.2, random_state=42, stratify=y) # 80% training and 20% test
#Create a svm Classifier
clf = svm.SVC(kernel='linear') # Linear Kernel
#Train the model using the training sets
clf.fit(X_train, y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
metrics.f1_score(y_test, y_pred)
x, y = datasets.fetch_california_housing(return_X_y=True) # this will download the dataset so it might take some time
x_mean=x.mean() # calculate the mean of x
x_std=x.std() # calculate the std of x
x_norm=(x-x_mean)/x_std # normalize the x
y_mean=y.mean() # calculate the mean of y
y_std=y.std() # calculate the std of y
y_norm=(y-y_mean)/y_std # normalize the y
x_train, x_test, y_train, y_test = model_selection.train_test_split(x_norm, y_norm, test_size=0.2, random_state=42)
model = svm.SVR()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
metrics.mean_squared_error(y_test, y_pred)
| 0.752468 | 0.716367 |
# Hierarchical Clustering with PySpark
This notebook shows how to implement and measure a hierarchical (bisecting k-means) clustering model.
* Method: [Hierarchical clustering (bisecting k-means)](https://spark.apache.org/docs/2.2.0/ml-clustering.html#bisecting-k-means)
* Dataset: Spark KMeans Sample Data
```
from os import environ
# Set SPARK_HOME
environ["SPARK_HOME"] = "/home/students/spark-2.2.0"
import findspark
findspark.init()
import numpy as np
from pyspark import SparkContext
from pyspark.sql import SQLContext
from pyspark.ml.clustering import BisectingKMeans
import seaborn as sb
import matplotlib.pyplot as plt
from pylab import rcParams
%matplotlib inline
rcParams['figure.figsize'] = 10, 8
sb.set_style('whitegrid')
```
## Get Some Context
```
# Create a SparkContext and a SQLContext context to use
sc = SparkContext(appName="Hieararchical Clustering with Spark")
sqlContext = SQLContext(sc)
```
## Load and Prepare the Data
```
DATA_FILE = "/home/students/data/mllib/sample_kmeans_data.txt"
data = sqlContext.read.format("libsvm").load(DATA_FILE)
# View one of the records
data.take(3)
```
## Identify the Number of Clusters to Use
Arguments:
* k: number of clusters
* maxIter: max number of iterations
* initMode: initalization algoritm
* random: select random points as initial cluster centers
* k-means||: parallel variant of k-means++
* seed: random seed
```
# Define the cluster range
cluster_range = range(2, 10)
# Create a list of KMeans models with differing numbers of clusters
bkmeans_models = [BisectingKMeans(k=i, seed=42) for i in cluster_range]
# Let's take a look at one of the models
bkmeans_models[3]
# Fit each model and evaluate the clustering using Within Set Sum of Squared Errors
cluster_scores = list()
for i in range(len(bkmeans_models)):
bkmeans = bkmeans_models[i]
model = bkmeans.fit(data)
cluster_score = model.computeCost(data)
cluster_scores.append(cluster_score)
cluster_scores[2]
# Plot an elbow curve of the scores to find the optimal number of clusters
plt.plot(cluster_range, cluster_scores)
plt.xlabel('Number of Clusters')
plt.ylabel('Score')
plt.title('Elbow Curve')
plt.show()
```
**Interpretation**: it appears that 2 is the optimal number of clusters for this dataset. That's our first model.
## Fit a Hierarchical Clustering Model
```
# Get the index value of the max cluster score
max_score_index = cluster_scores.index(max(cluster_scores))
# Get the number of clusters used for the model with the max score
model_to_use = bkmeans_models[max_score_index]
best_number_of_clusters = model_to_use.getK()
print("Best number of clusters: {}".format(best_number_of_clusters))
# Fit the model with the best number of clusters
kmeans = BisectingKMeans(k=best_number_of_clusters, seed=42)
model = kmeans.fit(data)
model
```
## Model Evaluation
```
# Get the model summary
summary = model.summary
```
### Number of Observations in Each Cluster
```
summary.clusterSizes
```
### Within Set Sum of Squared Errors
A measure of the total variance in your dataset explained by the clustering. By assigning the samples to k clusters rather than n (number of samples) clusters achieved a reduction in sums of squares of X%. ([cite](https://discuss.analyticsvidhya.com/t/what-is-within-cluster-sum-of-squares-by-cluster-in-k-means/2706/2))
The higher this number the better.
```
wssse = model.computeCost(data)
print("Within Set Sum of Squared Errors: %0.2f" % wssse)
```
### Show the Cluster Centers
```
centers = model.clusterCenters()
for center in centers:
print(center)
```
### Model Predictions
```
# Show the predictions
summary.predictions.show()
```
## Clean Up
```
sc.stop()
```
|
github_jupyter
|
from os import environ
# Set SPARK_HOME
environ["SPARK_HOME"] = "/home/students/spark-2.2.0"
import findspark
findspark.init()
import numpy as np
from pyspark import SparkContext
from pyspark.sql import SQLContext
from pyspark.ml.clustering import BisectingKMeans
import seaborn as sb
import matplotlib.pyplot as plt
from pylab import rcParams
%matplotlib inline
rcParams['figure.figsize'] = 10, 8
sb.set_style('whitegrid')
# Create a SparkContext and a SQLContext context to use
sc = SparkContext(appName="Hieararchical Clustering with Spark")
sqlContext = SQLContext(sc)
DATA_FILE = "/home/students/data/mllib/sample_kmeans_data.txt"
data = sqlContext.read.format("libsvm").load(DATA_FILE)
# View one of the records
data.take(3)
# Define the cluster range
cluster_range = range(2, 10)
# Create a list of KMeans models with differing numbers of clusters
bkmeans_models = [BisectingKMeans(k=i, seed=42) for i in cluster_range]
# Let's take a look at one of the models
bkmeans_models[3]
# Fit each model and evaluate the clustering using Within Set Sum of Squared Errors
cluster_scores = list()
for i in range(len(bkmeans_models)):
bkmeans = bkmeans_models[i]
model = bkmeans.fit(data)
cluster_score = model.computeCost(data)
cluster_scores.append(cluster_score)
cluster_scores[2]
# Plot an elbow curve of the scores to find the optimal number of clusters
plt.plot(cluster_range, cluster_scores)
plt.xlabel('Number of Clusters')
plt.ylabel('Score')
plt.title('Elbow Curve')
plt.show()
# Get the index value of the max cluster score
max_score_index = cluster_scores.index(max(cluster_scores))
# Get the number of clusters used for the model with the max score
model_to_use = bkmeans_models[max_score_index]
best_number_of_clusters = model_to_use.getK()
print("Best number of clusters: {}".format(best_number_of_clusters))
# Fit the model with the best number of clusters
kmeans = BisectingKMeans(k=best_number_of_clusters, seed=42)
model = kmeans.fit(data)
model
# Get the model summary
summary = model.summary
summary.clusterSizes
wssse = model.computeCost(data)
print("Within Set Sum of Squared Errors: %0.2f" % wssse)
centers = model.clusterCenters()
for center in centers:
print(center)
# Show the predictions
summary.predictions.show()
sc.stop()
| 0.693992 | 0.989076 |
```
# HIDDEN
from datascience import *
from prob140 import *
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
import math
from scipy import stats
from sympy import *
init_printing()
```
## Beta Densities with Integer Parameters ##
In the previous section we learned how to work with joint densities, but many of the joint density functions seemed to appear out of nowhere. For example, we checked that the function
$$
f(x, y) = 120x(y-x)(1-y), ~~~~ 0 < x < y < 1
$$
is a joint density, but there was no clue where it came from. In this section we will find its origin and go on to develop an important family of densities on the unit interval.
### Order Statistics of IID Uniform $(0, 1)$ Variables ###
Let $U_1, U_2, \ldots, U_n$ be i.i.d. uniform on $(0, 1)$. Imagine each $U_i$ as the position of a dart thrown at the unit interval. The graph below shows the positions of five such darts, each shown as a star.
```
# NO CODE
np.random.seed(17) #make plot deterministic
plt.plot([0, 1], [0, 0], color='k', lw=2)
y = 1 - np.ones(5)
x = stats.uniform.rvs(size=5)
order_stats = np.sort(x)
plt.scatter(x, y, marker='*', color='r', s=100)
plt.text(0, -0.0007, r'0', size=16)
plt.text(0.98, -0.0007, r'1', size=16)
plt.xlim(0, 1)
plt.yticks([])
plt.xticks([])
plt.title('Five IID Uniform (0, 1) Variables');
```
Based on the graph above, can you tell which star corresponds to $U_1$? You can't, because $U_1$ could be any of the five stars. So also you can't identify any of the five variables $U_1, U_2, U_3, U_4, U_5$.
What you *can* see, however, is the list of $U_i$'s *sorted in increasing order*. You can see the value of the minimum, the second on the sorted list, the third, the fourth, and finally the fifth which is the maximum.
These are called the *order statistics* of $U_1, U_2, U_3, U_4, U_5$, and are denoted $U_{(1)}, U_{(2)}, U_{(3)}, U_{(4)}, U_{(5)}$.
Remember that because the $U_i$'s are independent random variables with densities, there can't be ties: the chance that two of them are equal is 0.
```
# NO CODE
plt.plot([0, 1], [0, 0], color='k', lw=2)
order_stats = np.sort(x)
plt.scatter(x, y, marker='*', color='r', s=100)
u_labels = make_array('$U_{(1)}$', '$U_{(2)}$', '$U_{(3)}$', '$U_{(4)}$', '$U_{(5)}$')
for i in range(5):
plt.text(order_stats[i], -0.0007, u_labels[i], size=16)
plt.text(0, -0.0007, r'0', size=16)
plt.text(0.98, -0.0007, r'1', size=16)
plt.xlim(0, 1)
plt.yticks([])
plt.xticks([])
plt.title('Order Statistics of the Five IID Uniform (0, 1) Variables');
```
In general for $1 \le k \le n$, the *$k$th order statistic* of $U_1, U_2, \ldots, U_n$ is the $k$th value when the $U_i$'s are sorted in increasing order. This can also be thought of as the $k$th *ranked* value when the minimum has rank 1. It is denoted $U_{(k)}$.
### Joint Density of Two Order Statistics ###
Let $n = 5$ as above and let's try to work out the joint density of $U_{(2)}$ and $U_{(4)}$. That's the joint density of the second and fourth values on the sorted list.
The graph below shows the event $\{U_{(2)} \in dx, U_{(4)} \in dy\}$ for values $x$ and $y$ such that $0 < x < y < 1$.
```
# NO CODE
plt.plot([0, 1], [0, 0], color='k', lw=2)
y = 1 - np.ones(5)
x = make_array(0.1, 0.3, 0.45, 0.7, 0.9)
plt.scatter(x, y, marker='*', color='r', s=100)
plt.plot([0.28, 0.32], [0, 0], color='gold', lw=2)
plt.text(0.28, -0.0007, r'$dx$', size=16)
plt.plot([0.68, 0.72], [0, 0], color='gold', lw=2)
plt.text(0.68, -0.0007, r'$dy$', size=16)
plt.text(0, -0.0007, r'0', size=16)
plt.text(0.98, -0.0007, r'1', size=16)
plt.xlim(0, 1)
plt.yticks([])
plt.xticks([])
plt.title('$n = 5$; $\{ U_{(2)} \in dx, U_{(4)} \in dy \}$');
```
To find $P(U_{(2)} \in dx, U_{(4)} \in dy)$, notice that for this event to occur:
- one of $U_1, U_2, U_3, U_4, U_5$ must be in $(0, x)$
- one must be in $dx$
- one must be in $(x, y)$
- one must be in $dy$
- one must be in $(y, 1)$
You can think of each of the five independent uniform $(0, 1)$ variables as a multinomial trial. It can land in any of the five intervals above, independently of the others and with the same chance as the others.
The chances are given by
$$
\begin{align*}
&P(U \in (0, x)) = x, ~~ P(U \in dx) \sim 1dx, ~~ P(U \in (x, y)) = (y-x)\\
&P(U \in dy) \sim 1dy, ~~ P(U \in (y, 1)) = 1-y
\end{align*}
$$
where $U$ is any uniform $(0, 1)$ random variable.
Apply the multinomial formula to get
$$
\begin{align*}
P(U_{(2)} \in dx, U_{(4)} \in dy) ~ &\sim ~
\frac{5!}{1!1!1!1!1!} x^1 (1dx)^1 (y-x)^1 (1dy)^1 (1-y)^1 \\
&\sim ~ 120x(y-x)(1-y)dxdy
\end{align*}
$$
and therefore the joint density of $U_{(2)}$ and $U_{(4)}$ is given by
$$
f(x, y) = 120x(y-x)(1-y), ~~~ 0 < x < y < 1
$$
This solves the mystery of how the formula arises.
But it also does much more. The *marginal* densities of the order statistics of i.i.d. uniform $(0, 1)$ variables form a family that is important in data science.
### The Density of $U_{(k)}$ ###
Let $U_{(k)}$ be the $k$th order statistic of $U_1, U_2, \ldots, U_n$. We will find the density of $U_{(k)}$ by following the same general process that we followed to find the joint density above.
The graph below displays the event $\{ U_{(k)} \in dx \}$. For the event to occur,
- One of the variables $U_1, U_2, \ldots, U_n$ has to be in $dx$.
- Of the remaining $n-1$ variables, $k-1$ must have values in $(0, x)$ and the rest in $(x, 1)$.
```
# NO CODE
plt.plot([0, 1], [0, 0], color='k', lw=2)
plt.scatter(0.4, 0, marker='*', color='r', s=100)
plt.plot([0.38, 0.42], [0, 0], color='gold', lw=2)
plt.text(0.38, -0.0007, r'$dx$', size=16)
plt.text(0.1, 0.001, '$k-1$ stars', size=16)
plt.text(0.1, 0.0005, 'in $(0, x)$', size=16)
plt.text(0.6, 0.001, '$n-k$ stars', size=16)
plt.text(0.6, 0.0005, 'in $(x, 1)$', size=16)
plt.text(0, -0.0007, r'0', size=16)
plt.text(0.98, -0.0007, r'1', size=16)
plt.xlim(0, 1)
plt.yticks([])
plt.xticks([])
plt.title('$\{ U_{(k)} \in dx \}$');
```
Apply the multinomial formula again.
$$
P(U_{(k)} \in dx) ~ \sim ~
\frac{n!}{(k-1)! 1! (n-k)!} x^{k-1} (1dx)^1 (1-x)^{n-k}
$$
Therefore the density of $U_{(k)}$ is given by
$$
f_{U_{(k)}} (x) = \frac{n!}{(k-1)!(n-k)!} x^{k-1}(1-x)^{n-k}, ~~~ 0 < x < 1
$$
For consistency, let's rewrite the exponents slightly so that each ends with $-1$:
$$
f_{U_{(k)}} (x) = \frac{n!}{(k-1)!((n-k+1)-1)!} x^{k-1}(1-x)^{(n-k+1)-1}, ~~~ 0 < x < 1
$$
Because $1 \le k \le n$, we know that $n-k+1$ is a positive integer. Since $n$ is an arbitrary positive integer, so is $n-k+1$.
### Beta Densities ###
We have shown that if $r$ and $s$ are any two positive integers, then the function
$$
f(x) ~ = ~ \frac{(r+s-1)!}{(r-1)!(s-1)!} x^{r-1}(1-x)^{s-1}, ~~~ 0 < x < 1
$$
is a probability density function. This is called the *beta density with parameters $r$ and $s$*.
By the derivation above, **the $k$th order statistic $U_{(k)}$ of $n$ i.i.d. uniform $(0, 1)$ random variables has the beta density with parameters $k$ and $n-k+1$.**
The shape of the density is determined by the two factors that involve $x$. All the factorials are just parts of the constant that make the density integrate to 1.
Notice that the uniform $(0, 1)$ density is the same as the beta density with parameters $r = 1$ and $s = 1$. The uniform $(0, 1)$ density is a member of the *beta family*.
The graph below shows some beta density curves. As you would expect, the beta $(3, 3)$ density is symmetric about 0.5.
```
x = np.arange(0, 1.01, 0.01)
for i in np.arange(1, 7, 1):
plt.plot(x, stats.beta.pdf(x, i, 6-i), lw=2)
plt.title('Beta $(i, 6-i)$ densities for $1 \leq i \leq 5$');
```
By choosing the parameters appropriately, you can create beta densities that put much of their mass near a prescribed value. That is one of the reasons beta densities are used to model *random proportions*. For example, if you think that the probability that an email is spam is most likely in the 60% to 90% range, but might be lower, you might model your belief by choosing the density that peaks at around 0.75 in the graph above.
The calculation below shows you how to get started on the process of picking parameters so that the beta density with those parameters has properties that reflect your beliefs.
### The Beta Integral ###
The beta density integrates to 1, and hence for all positive integers $r$ and $s$ we have
$$
\int_0^1 x^{r-1}(1-x)^{s-1}dx ~ = ~ \frac{(r-1)!(s-1)!}{(r+s-1)!}
$$
Thus probability theory makes short work of an otherwise laborious integral. Also, we can now find the expectation of a random variable with a beta density.
Let $X$ have the beta $(r, s)$ density for two positive integer parameters $r$ and $s$. Then
$$
\begin{align*}
E(X) &= \int_0^1 x \frac{(r+s-1)!}{(r-1)!(s-1)!} x^{r-1}(1-x)^{s-1}dx \\ \\
&= \frac{(r+s-1)!}{(r-1)!(s-1)!} \int_0^1 x^r(1-x)^{s-1}dx \\ \\
&= \frac{(r+s-1)!}{(r-1)!(s-1)!} \cdot \frac{r!(s-1)!}{(r+s)!} ~~~~~~~ \text{(beta integral for parameters } r+1 \text{and } s\text{)}\\ \\
&= \frac{r}{r+s}
\end{align*}
$$
You can follow the same method to find $E(X^2)$ and hence $Var(X)$.
The formula for the expectation allows you to pick parameters corresponding to your belief about the random proportion being modeled by $X$. For example, if you think the proportion is likely to be somewhere around 0.4, you might start by trying out a beta prior with $r = 2$ and $s = 3$.
You will have noticed that the form of the beta density looks rather like the binomial formula. Indeed, we used the binomial formula to derive the beta density. Later in the course you will see another close relation between the beta and the binomial. These properties make the beta family one of the most widely used families of densities in machine learning.
|
github_jupyter
|
# HIDDEN
from datascience import *
from prob140 import *
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
import math
from scipy import stats
from sympy import *
init_printing()
# NO CODE
np.random.seed(17) #make plot deterministic
plt.plot([0, 1], [0, 0], color='k', lw=2)
y = 1 - np.ones(5)
x = stats.uniform.rvs(size=5)
order_stats = np.sort(x)
plt.scatter(x, y, marker='*', color='r', s=100)
plt.text(0, -0.0007, r'0', size=16)
plt.text(0.98, -0.0007, r'1', size=16)
plt.xlim(0, 1)
plt.yticks([])
plt.xticks([])
plt.title('Five IID Uniform (0, 1) Variables');
# NO CODE
plt.plot([0, 1], [0, 0], color='k', lw=2)
order_stats = np.sort(x)
plt.scatter(x, y, marker='*', color='r', s=100)
u_labels = make_array('$U_{(1)}$', '$U_{(2)}$', '$U_{(3)}$', '$U_{(4)}$', '$U_{(5)}$')
for i in range(5):
plt.text(order_stats[i], -0.0007, u_labels[i], size=16)
plt.text(0, -0.0007, r'0', size=16)
plt.text(0.98, -0.0007, r'1', size=16)
plt.xlim(0, 1)
plt.yticks([])
plt.xticks([])
plt.title('Order Statistics of the Five IID Uniform (0, 1) Variables');
# NO CODE
plt.plot([0, 1], [0, 0], color='k', lw=2)
y = 1 - np.ones(5)
x = make_array(0.1, 0.3, 0.45, 0.7, 0.9)
plt.scatter(x, y, marker='*', color='r', s=100)
plt.plot([0.28, 0.32], [0, 0], color='gold', lw=2)
plt.text(0.28, -0.0007, r'$dx$', size=16)
plt.plot([0.68, 0.72], [0, 0], color='gold', lw=2)
plt.text(0.68, -0.0007, r'$dy$', size=16)
plt.text(0, -0.0007, r'0', size=16)
plt.text(0.98, -0.0007, r'1', size=16)
plt.xlim(0, 1)
plt.yticks([])
plt.xticks([])
plt.title('$n = 5$; $\{ U_{(2)} \in dx, U_{(4)} \in dy \}$');
# NO CODE
plt.plot([0, 1], [0, 0], color='k', lw=2)
plt.scatter(0.4, 0, marker='*', color='r', s=100)
plt.plot([0.38, 0.42], [0, 0], color='gold', lw=2)
plt.text(0.38, -0.0007, r'$dx$', size=16)
plt.text(0.1, 0.001, '$k-1$ stars', size=16)
plt.text(0.1, 0.0005, 'in $(0, x)$', size=16)
plt.text(0.6, 0.001, '$n-k$ stars', size=16)
plt.text(0.6, 0.0005, 'in $(x, 1)$', size=16)
plt.text(0, -0.0007, r'0', size=16)
plt.text(0.98, -0.0007, r'1', size=16)
plt.xlim(0, 1)
plt.yticks([])
plt.xticks([])
plt.title('$\{ U_{(k)} \in dx \}$');
x = np.arange(0, 1.01, 0.01)
for i in np.arange(1, 7, 1):
plt.plot(x, stats.beta.pdf(x, i, 6-i), lw=2)
plt.title('Beta $(i, 6-i)$ densities for $1 \leq i \leq 5$');
| 0.459561 | 0.942029 |
# 基于注意力的神经机器翻译
此笔记本训练一个将乌克兰语翻译为英语的序列到序列(sequence to sequence,简写为 seq2seq)模型。此例子难度较高,需要对序列到序列模型的知识有一定了解。
训练完此笔记本中的模型后,你将能够输入一个乌克兰语句子,例如 *"Мені дев'ятнадцять років."*,并返回其英语翻译 *"I'm 19."*
对于一个简单的例子来说,翻译质量令人满意。但是更有趣的可能是生成的注意力图:它显示在翻译过程中,输入句子的哪些部分受到了模型的注意。
<img src="https://tensorflow.google.cn/images/spanish-english.png" alt="spanish-english attention plot">
请注意:运行这个例子用一个 P100 GPU 需要花大约 10 分钟。
```
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.model_selection import train_test_split
import unicodedata
import re
import numpy as np
import os
import io
import time
```
## 下载和准备数据集
我们将使用 http://www.manythings.org/anki/ 提供的一个语言数据集。这个数据集包含如下格式的语言翻译对:
```
May I borrow this book? ¿Puedo tomar prestado este libro?
```
这个数据集中有很多种语言可供选择。我们将使用英语 - 乌克兰语数据集。为方便使用,我们在谷歌云上提供了此数据集的一份副本。但是你也可以自己下载副本。下载完数据集后,我们将采取下列步骤准备数据:
1. 给每个句子添加一个 *开始* 和一个 *结束* 标记(token)。
2. 删除特殊字符以清理句子。
3. 创建一个单词索引和一个反向单词索引(即一个从单词映射至 id 的词典和一个从 id 映射至单词的词典)。
4. 将每个句子填充(pad)到最大长度。
```
'''
# 下载文件
path_to_zip = tf.keras.utils.get_file(
'spa-eng.zip', origin='http://storage.googleapis.com/download.tensorflow.org/data/spa-eng.zip',
extract=True)
path_to_file = os.path.dirname(path_to_zip)+"/spa-eng/spa.txt"
'''
path_to_file = "./lan/ukr.txt"
# 将 unicode 文件转换为 ascii
def unicode_to_ascii(s):
return ''.join(c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn')
def preprocess_sentence(w):
w = unicode_to_ascii(w.lower().strip())
# 在单词与跟在其后的标点符号之间插入一个空格
# 例如: "he is a boy." => "he is a boy ."
# 参考:https://stackoverflow.com/questions/3645931/python-padding-punctuation-with-white-spaces-keeping-punctuation
w = re.sub(r"([?.!,¿])", r" \1 ", w)
w = re.sub(r'[" "]+', " ", w)
# 除了 (a-z, A-Z, ".", "?", "!", ","),将所有字符替换为空格
w = re.sub(r"[^a-zA-Z?.!,¿]+", " ", w)
w = w.rstrip().strip()
# 给句子加上开始和结束标记
# 以便模型知道何时开始和结束预测
w = '<start> ' + w + ' <end>'
return w
en_sentence = u"May I borrow this book?"
sp_sentence = u"¿Puedo tomar prestado este libro?"
print(preprocess_sentence(en_sentence))
print(preprocess_sentence(sp_sentence).encode('utf-8'))
# 1. 去除重音符号
# 2. 清理句子
# 3. 返回这样格式的单词对:[ENGLISH, SPANISH]
def create_dataset(path, num_examples):
lines = io.open(path, encoding='UTF-8').read().strip().split('\n')
word_pairs = [[preprocess_sentence(w) for w in l.split('\t')] for l in lines[:num_examples]]
return zip(*word_pairs)
en, sp = create_dataset(path_to_file, None)
print(en[-1])
print(sp[-1])
def max_length(tensor):
return max(len(t) for t in tensor)
def tokenize(lang):
lang_tokenizer = tf.keras.preprocessing.text.Tokenizer(
filters='')
lang_tokenizer.fit_on_texts(lang)
tensor = lang_tokenizer.texts_to_sequences(lang)
tensor = tf.keras.preprocessing.sequence.pad_sequences(tensor,
padding='post')
return tensor, lang_tokenizer
def load_dataset(path, num_examples=None):
# 创建清理过的输入输出对
targ_lang, inp_lang = create_dataset(path, num_examples)
input_tensor, inp_lang_tokenizer = tokenize(inp_lang)
target_tensor, targ_lang_tokenizer = tokenize(targ_lang)
return input_tensor, target_tensor, inp_lang_tokenizer, targ_lang_tokenizer
```
### 限制数据集的大小以加快实验速度(可选)
在超过 10 万个句子的完整数据集上训练需要很长时间。为了更快地训练,我们可以将数据集的大小限制为 3 万个句子(当然,翻译质量也会随着数据的减少而降低):
```
# 尝试实验不同大小的数据集
num_examples = 30000
input_tensor, target_tensor, inp_lang, targ_lang = load_dataset(path_to_file, num_examples)
# 计算目标张量的最大长度 (max_length)
max_length_targ, max_length_inp = max_length(target_tensor), max_length(input_tensor)
# 采用 80 - 20 的比例切分训练集和验证集
input_tensor_train, input_tensor_val, target_tensor_train, target_tensor_val = train_test_split(input_tensor, target_tensor, test_size=0.2)
# 显示长度
print(len(input_tensor_train), len(target_tensor_train), len(input_tensor_val), len(target_tensor_val))
def convert(lang, tensor):
for t in tensor:
if t!=0:
print ("%d ----> %s" % (t, lang.index_word[t]))
print ("Input Language; index to word mapping")
convert(inp_lang, input_tensor_train[0])
print ()
print ("Target Language; index to word mapping")
convert(targ_lang, target_tensor_train[0])
```
### 创建一个 tf.data 数据集
```
BUFFER_SIZE = len(input_tensor_train)
BATCH_SIZE = 64
steps_per_epoch = len(input_tensor_train)//BATCH_SIZE
embedding_dim = 256
units = 1024
vocab_inp_size = len(inp_lang.word_index)+1
vocab_tar_size = len(targ_lang.word_index)+1
dataset = tf.data.Dataset.from_tensor_slices((input_tensor_train, target_tensor_train)).shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE, drop_remainder=True)
example_input_batch, example_target_batch = next(iter(dataset))
example_input_batch.shape, example_target_batch.shape
```
## 编写编码器 (encoder) 和解码器 (decoder) 模型
实现一个基于注意力的编码器 - 解码器模型。关于这种模型,你可以阅读 TensorFlow 的 [神经机器翻译 (序列到序列) 教程](https://github.com/tensorflow/nmt)。本示例采用一组更新的 API。此笔记本实现了上述序列到序列教程中的 [注意力方程式](https://github.com/tensorflow/nmt#background-on-the-attention-mechanism)。下图显示了注意力机制为每个输入单词分配一个权重,然后解码器将这个权重用于预测句子中的下一个单词。下图和公式是 [Luong 的论文](https://arxiv.org/abs/1508.04025v5)中注意力机制的一个例子。
<img src="https://tensorflow.google.cn/images/seq2seq/attention_mechanism.jpg" width="500" alt="attention mechanism">
输入经过编码器模型,编码器模型为我们提供形状为 *(批大小,最大长度,隐藏层大小)* 的编码器输出和形状为 *(批大小,隐藏层大小)* 的编码器隐藏层状态。
下面是所实现的方程式:
<img src="https://tensorflow.google.cn/images/seq2seq/attention_equation_0.jpg" alt="attention equation 0" width="800">
<img src="https://tensorflow.google.cn/images/seq2seq/attention_equation_1.jpg" alt="attention equation 1" width="800">
本教程的编码器采用 [Bahdanau 注意力](https://arxiv.org/pdf/1409.0473.pdf)。在用简化形式编写之前,让我们先决定符号:
* FC = 完全连接(密集)层
* EO = 编码器输出
* H = 隐藏层状态
* X = 解码器输入
以及伪代码:
* `score = FC(tanh(FC(EO) + FC(H)))`
* `attention weights = softmax(score, axis = 1)`。 Softmax 默认被应用于最后一个轴,但是这里我们想将它应用于 *第一个轴*, 因为分数 (score) 的形状是 *(批大小,最大长度,隐藏层大小)*。最大长度 (`max_length`) 是我们的输入的长度。因为我们想为每个输入分配一个权重,所以 softmax 应该用在这个轴上。
* `context vector = sum(attention weights * EO, axis = 1)`。选择第一个轴的原因同上。
* `embedding output` = 解码器输入 X 通过一个嵌入层。
* `merged vector = concat(embedding output, context vector)`
* 此合并后的向量随后被传送到 GRU
每个步骤中所有向量的形状已在代码的注释中阐明:
```
class Encoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, enc_units, batch_sz):
super(Encoder, self).__init__()
self.batch_sz = batch_sz
self.enc_units = enc_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.enc_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
def call(self, x, hidden):
x = self.embedding(x)
output, state = self.gru(x, initial_state = hidden)
return output, state
def initialize_hidden_state(self):
return tf.zeros((self.batch_sz, self.enc_units))
encoder = Encoder(vocab_inp_size, embedding_dim, units, BATCH_SIZE)
# 样本输入
sample_hidden = encoder.initialize_hidden_state()
sample_output, sample_hidden = encoder(example_input_batch, sample_hidden)
print ('Encoder output shape: (batch size, sequence length, units) {}'.format(sample_output.shape))
print ('Encoder Hidden state shape: (batch size, units) {}'.format(sample_hidden.shape))
class BahdanauAttention(tf.keras.layers.Layer):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, query, values):
# 隐藏层的形状 == (批大小,隐藏层大小)
# hidden_with_time_axis 的形状 == (批大小,1,隐藏层大小)
# 这样做是为了执行加法以计算分数
hidden_with_time_axis = tf.expand_dims(query, 1)
# 分数的形状 == (批大小,最大长度,1)
# 我们在最后一个轴上得到 1, 因为我们把分数应用于 self.V
# 在应用 self.V 之前,张量的形状是(批大小,最大长度,单位)
score = self.V(tf.nn.tanh(
self.W1(values) + self.W2(hidden_with_time_axis)))
# 注意力权重 (attention_weights) 的形状 == (批大小,最大长度,1)
attention_weights = tf.nn.softmax(score, axis=1)
# 上下文向量 (context_vector) 求和之后的形状 == (批大小,隐藏层大小)
context_vector = attention_weights * values
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weights
attention_layer = BahdanauAttention(10)
attention_result, attention_weights = attention_layer(sample_hidden, sample_output)
print("Attention result shape: (batch size, units) {}".format(attention_result.shape))
print("Attention weights shape: (batch_size, sequence_length, 1) {}".format(attention_weights.shape))
class Decoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, dec_units, batch_sz):
super(Decoder, self).__init__()
self.batch_sz = batch_sz
self.dec_units = dec_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.dec_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc = tf.keras.layers.Dense(vocab_size)
# 用于注意力
self.attention = BahdanauAttention(self.dec_units)
def call(self, x, hidden, enc_output):
# 编码器输出 (enc_output) 的形状 == (批大小,最大长度,隐藏层大小)
context_vector, attention_weights = self.attention(hidden, enc_output)
# x 在通过嵌入层后的形状 == (批大小,1,嵌入维度)
x = self.embedding(x)
# x 在拼接 (concatenation) 后的形状 == (批大小,1,嵌入维度 + 隐藏层大小)
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# 将合并后的向量传送到 GRU
output, state = self.gru(x)
# 输出的形状 == (批大小 * 1,隐藏层大小)
output = tf.reshape(output, (-1, output.shape[2]))
# 输出的形状 == (批大小,vocab)
x = self.fc(output)
return x, state, attention_weights
decoder = Decoder(vocab_tar_size, embedding_dim, units, BATCH_SIZE)
sample_decoder_output, _, _ = decoder(tf.random.uniform((64, 1)),
sample_hidden, sample_output)
print ('Decoder output shape: (batch_size, vocab size) {}'.format(sample_decoder_output.shape))
```
## 定义优化器和损失函数
```
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')
def loss_function(real, pred):
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
```
## 检查点(基于对象保存)
```
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(optimizer=optimizer,
encoder=encoder,
decoder=decoder)
```
## 训练
1. 将 *输入* 传送至 *编码器*,编码器返回 *编码器输出* 和 *编码器隐藏层状态*。
2. 将编码器输出、编码器隐藏层状态和解码器输入(即 *开始标记*)传送至解码器。
3. 解码器返回 *预测* 和 *解码器隐藏层状态*。
4. 解码器隐藏层状态被传送回模型,预测被用于计算损失。
5. 使用 *教师强制 (teacher forcing)* 决定解码器的下一个输入。
6. *教师强制* 是将 *目标词* 作为 *下一个输入* 传送至解码器的技术。
7. 最后一步是计算梯度,并将其应用于优化器和反向传播。
```
@tf.function
def train_step(inp, targ, enc_hidden):
loss = 0
with tf.GradientTape() as tape:
enc_output, enc_hidden = encoder(inp, enc_hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']] * BATCH_SIZE, 1)
# 教师强制 - 将目标词作为下一个输入
for t in range(1, targ.shape[1]):
# 将编码器输出 (enc_output) 传送至解码器
predictions, dec_hidden, _ = decoder(dec_input, dec_hidden, enc_output)
loss += loss_function(targ[:, t], predictions)
# 使用教师强制
dec_input = tf.expand_dims(targ[:, t], 1)
batch_loss = (loss / int(targ.shape[1]))
variables = encoder.trainable_variables + decoder.trainable_variables
gradients = tape.gradient(loss, variables)
optimizer.apply_gradients(zip(gradients, variables))
return batch_loss
EPOCHS = 10
for epoch in range(EPOCHS):
start = time.time()
enc_hidden = encoder.initialize_hidden_state()
total_loss = 0
for (batch, (inp, targ)) in enumerate(dataset.take(steps_per_epoch)):
batch_loss = train_step(inp, targ, enc_hidden)
total_loss += batch_loss
if batch % 100 == 0:
print('Epoch {} Batch {} Loss {:.4f}'.format(epoch + 1,
batch,
batch_loss.numpy()))
# 每 2 个周期(epoch),保存(检查点)一次模型
if (epoch + 1) % 2 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print('Epoch {} Loss {:.4f}'.format(epoch + 1,
total_loss / steps_per_epoch))
print('Time taken for 1 epoch {} sec\n'.format(time.time() - start))
```
## 翻译
* 评估函数类似于训练循环,不同之处在于在这里我们不使用 *教师强制*。每个时间步的解码器输入是其先前的预测、隐藏层状态和编码器输出。
* 当模型预测 *结束标记* 时停止预测。
* 存储 *每个时间步的注意力权重*。
请注意:对于一个输入,编码器输出仅计算一次。
```
def evaluate(sentence):
attention_plot = np.zeros((max_length_targ, max_length_inp))
sentence = preprocess_sentence(sentence)
inputs = [inp_lang.word_index[i] for i in sentence.split(' ')]
inputs = tf.keras.preprocessing.sequence.pad_sequences([inputs],
maxlen=max_length_inp,
padding='post')
inputs = tf.convert_to_tensor(inputs)
result = ''
hidden = [tf.zeros((1, units))]
enc_out, enc_hidden = encoder(inputs, hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']], 0)
for t in range(max_length_targ):
predictions, dec_hidden, attention_weights = decoder(dec_input,
dec_hidden,
enc_out)
# 存储注意力权重以便后面制图
attention_weights = tf.reshape(attention_weights, (-1, ))
attention_plot[t] = attention_weights.numpy()
predicted_id = tf.argmax(predictions[0]).numpy()
result += targ_lang.index_word[predicted_id] + ' '
if targ_lang.index_word[predicted_id] == '<end>':
return result, sentence, attention_plot
# 预测的 ID 被输送回模型
dec_input = tf.expand_dims([predicted_id], 0)
return result, sentence, attention_plot
# 注意力权重制图函数
def plot_attention(attention, sentence, predicted_sentence):
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1)
ax.matshow(attention, cmap='viridis')
fontdict = {'fontsize': 14}
ax.set_xticklabels([''] + sentence, fontdict=fontdict, rotation=90)
ax.set_yticklabels([''] + predicted_sentence, fontdict=fontdict)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
plt.show()
def translate(sentence):
result, sentence, attention_plot = evaluate(sentence)
print('Input: %s' % (sentence))
print('Predicted translation: {}'.format(result))
attention_plot = attention_plot[:len(result.split(' ')), :len(sentence.split(' '))]
plot_attention(attention_plot, sentence.split(' '), result.split(' '))
```
## 恢复最新的检查点并验证
```
# 恢复检查点目录 (checkpoint_dir) 中最新的检查点
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
translate(u'hace mucho frio aqui.')
translate(u'esta es mi vida.')
translate(u'¿todavia estan en casa?')
# 错误的翻译
translate(u'trata de averiguarlo.')
```
|
github_jupyter
|
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.model_selection import train_test_split
import unicodedata
import re
import numpy as np
import os
import io
import time
May I borrow this book? ¿Puedo tomar prestado este libro?
'''
# 下载文件
path_to_zip = tf.keras.utils.get_file(
'spa-eng.zip', origin='http://storage.googleapis.com/download.tensorflow.org/data/spa-eng.zip',
extract=True)
path_to_file = os.path.dirname(path_to_zip)+"/spa-eng/spa.txt"
'''
path_to_file = "./lan/ukr.txt"
# 将 unicode 文件转换为 ascii
def unicode_to_ascii(s):
return ''.join(c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn')
def preprocess_sentence(w):
w = unicode_to_ascii(w.lower().strip())
# 在单词与跟在其后的标点符号之间插入一个空格
# 例如: "he is a boy." => "he is a boy ."
# 参考:https://stackoverflow.com/questions/3645931/python-padding-punctuation-with-white-spaces-keeping-punctuation
w = re.sub(r"([?.!,¿])", r" \1 ", w)
w = re.sub(r'[" "]+', " ", w)
# 除了 (a-z, A-Z, ".", "?", "!", ","),将所有字符替换为空格
w = re.sub(r"[^a-zA-Z?.!,¿]+", " ", w)
w = w.rstrip().strip()
# 给句子加上开始和结束标记
# 以便模型知道何时开始和结束预测
w = '<start> ' + w + ' <end>'
return w
en_sentence = u"May I borrow this book?"
sp_sentence = u"¿Puedo tomar prestado este libro?"
print(preprocess_sentence(en_sentence))
print(preprocess_sentence(sp_sentence).encode('utf-8'))
# 1. 去除重音符号
# 2. 清理句子
# 3. 返回这样格式的单词对:[ENGLISH, SPANISH]
def create_dataset(path, num_examples):
lines = io.open(path, encoding='UTF-8').read().strip().split('\n')
word_pairs = [[preprocess_sentence(w) for w in l.split('\t')] for l in lines[:num_examples]]
return zip(*word_pairs)
en, sp = create_dataset(path_to_file, None)
print(en[-1])
print(sp[-1])
def max_length(tensor):
return max(len(t) for t in tensor)
def tokenize(lang):
lang_tokenizer = tf.keras.preprocessing.text.Tokenizer(
filters='')
lang_tokenizer.fit_on_texts(lang)
tensor = lang_tokenizer.texts_to_sequences(lang)
tensor = tf.keras.preprocessing.sequence.pad_sequences(tensor,
padding='post')
return tensor, lang_tokenizer
def load_dataset(path, num_examples=None):
# 创建清理过的输入输出对
targ_lang, inp_lang = create_dataset(path, num_examples)
input_tensor, inp_lang_tokenizer = tokenize(inp_lang)
target_tensor, targ_lang_tokenizer = tokenize(targ_lang)
return input_tensor, target_tensor, inp_lang_tokenizer, targ_lang_tokenizer
# 尝试实验不同大小的数据集
num_examples = 30000
input_tensor, target_tensor, inp_lang, targ_lang = load_dataset(path_to_file, num_examples)
# 计算目标张量的最大长度 (max_length)
max_length_targ, max_length_inp = max_length(target_tensor), max_length(input_tensor)
# 采用 80 - 20 的比例切分训练集和验证集
input_tensor_train, input_tensor_val, target_tensor_train, target_tensor_val = train_test_split(input_tensor, target_tensor, test_size=0.2)
# 显示长度
print(len(input_tensor_train), len(target_tensor_train), len(input_tensor_val), len(target_tensor_val))
def convert(lang, tensor):
for t in tensor:
if t!=0:
print ("%d ----> %s" % (t, lang.index_word[t]))
print ("Input Language; index to word mapping")
convert(inp_lang, input_tensor_train[0])
print ()
print ("Target Language; index to word mapping")
convert(targ_lang, target_tensor_train[0])
BUFFER_SIZE = len(input_tensor_train)
BATCH_SIZE = 64
steps_per_epoch = len(input_tensor_train)//BATCH_SIZE
embedding_dim = 256
units = 1024
vocab_inp_size = len(inp_lang.word_index)+1
vocab_tar_size = len(targ_lang.word_index)+1
dataset = tf.data.Dataset.from_tensor_slices((input_tensor_train, target_tensor_train)).shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE, drop_remainder=True)
example_input_batch, example_target_batch = next(iter(dataset))
example_input_batch.shape, example_target_batch.shape
class Encoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, enc_units, batch_sz):
super(Encoder, self).__init__()
self.batch_sz = batch_sz
self.enc_units = enc_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.enc_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
def call(self, x, hidden):
x = self.embedding(x)
output, state = self.gru(x, initial_state = hidden)
return output, state
def initialize_hidden_state(self):
return tf.zeros((self.batch_sz, self.enc_units))
encoder = Encoder(vocab_inp_size, embedding_dim, units, BATCH_SIZE)
# 样本输入
sample_hidden = encoder.initialize_hidden_state()
sample_output, sample_hidden = encoder(example_input_batch, sample_hidden)
print ('Encoder output shape: (batch size, sequence length, units) {}'.format(sample_output.shape))
print ('Encoder Hidden state shape: (batch size, units) {}'.format(sample_hidden.shape))
class BahdanauAttention(tf.keras.layers.Layer):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, query, values):
# 隐藏层的形状 == (批大小,隐藏层大小)
# hidden_with_time_axis 的形状 == (批大小,1,隐藏层大小)
# 这样做是为了执行加法以计算分数
hidden_with_time_axis = tf.expand_dims(query, 1)
# 分数的形状 == (批大小,最大长度,1)
# 我们在最后一个轴上得到 1, 因为我们把分数应用于 self.V
# 在应用 self.V 之前,张量的形状是(批大小,最大长度,单位)
score = self.V(tf.nn.tanh(
self.W1(values) + self.W2(hidden_with_time_axis)))
# 注意力权重 (attention_weights) 的形状 == (批大小,最大长度,1)
attention_weights = tf.nn.softmax(score, axis=1)
# 上下文向量 (context_vector) 求和之后的形状 == (批大小,隐藏层大小)
context_vector = attention_weights * values
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weights
attention_layer = BahdanauAttention(10)
attention_result, attention_weights = attention_layer(sample_hidden, sample_output)
print("Attention result shape: (batch size, units) {}".format(attention_result.shape))
print("Attention weights shape: (batch_size, sequence_length, 1) {}".format(attention_weights.shape))
class Decoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, dec_units, batch_sz):
super(Decoder, self).__init__()
self.batch_sz = batch_sz
self.dec_units = dec_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.dec_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc = tf.keras.layers.Dense(vocab_size)
# 用于注意力
self.attention = BahdanauAttention(self.dec_units)
def call(self, x, hidden, enc_output):
# 编码器输出 (enc_output) 的形状 == (批大小,最大长度,隐藏层大小)
context_vector, attention_weights = self.attention(hidden, enc_output)
# x 在通过嵌入层后的形状 == (批大小,1,嵌入维度)
x = self.embedding(x)
# x 在拼接 (concatenation) 后的形状 == (批大小,1,嵌入维度 + 隐藏层大小)
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# 将合并后的向量传送到 GRU
output, state = self.gru(x)
# 输出的形状 == (批大小 * 1,隐藏层大小)
output = tf.reshape(output, (-1, output.shape[2]))
# 输出的形状 == (批大小,vocab)
x = self.fc(output)
return x, state, attention_weights
decoder = Decoder(vocab_tar_size, embedding_dim, units, BATCH_SIZE)
sample_decoder_output, _, _ = decoder(tf.random.uniform((64, 1)),
sample_hidden, sample_output)
print ('Decoder output shape: (batch_size, vocab size) {}'.format(sample_decoder_output.shape))
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')
def loss_function(real, pred):
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(optimizer=optimizer,
encoder=encoder,
decoder=decoder)
@tf.function
def train_step(inp, targ, enc_hidden):
loss = 0
with tf.GradientTape() as tape:
enc_output, enc_hidden = encoder(inp, enc_hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']] * BATCH_SIZE, 1)
# 教师强制 - 将目标词作为下一个输入
for t in range(1, targ.shape[1]):
# 将编码器输出 (enc_output) 传送至解码器
predictions, dec_hidden, _ = decoder(dec_input, dec_hidden, enc_output)
loss += loss_function(targ[:, t], predictions)
# 使用教师强制
dec_input = tf.expand_dims(targ[:, t], 1)
batch_loss = (loss / int(targ.shape[1]))
variables = encoder.trainable_variables + decoder.trainable_variables
gradients = tape.gradient(loss, variables)
optimizer.apply_gradients(zip(gradients, variables))
return batch_loss
EPOCHS = 10
for epoch in range(EPOCHS):
start = time.time()
enc_hidden = encoder.initialize_hidden_state()
total_loss = 0
for (batch, (inp, targ)) in enumerate(dataset.take(steps_per_epoch)):
batch_loss = train_step(inp, targ, enc_hidden)
total_loss += batch_loss
if batch % 100 == 0:
print('Epoch {} Batch {} Loss {:.4f}'.format(epoch + 1,
batch,
batch_loss.numpy()))
# 每 2 个周期(epoch),保存(检查点)一次模型
if (epoch + 1) % 2 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print('Epoch {} Loss {:.4f}'.format(epoch + 1,
total_loss / steps_per_epoch))
print('Time taken for 1 epoch {} sec\n'.format(time.time() - start))
def evaluate(sentence):
attention_plot = np.zeros((max_length_targ, max_length_inp))
sentence = preprocess_sentence(sentence)
inputs = [inp_lang.word_index[i] for i in sentence.split(' ')]
inputs = tf.keras.preprocessing.sequence.pad_sequences([inputs],
maxlen=max_length_inp,
padding='post')
inputs = tf.convert_to_tensor(inputs)
result = ''
hidden = [tf.zeros((1, units))]
enc_out, enc_hidden = encoder(inputs, hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']], 0)
for t in range(max_length_targ):
predictions, dec_hidden, attention_weights = decoder(dec_input,
dec_hidden,
enc_out)
# 存储注意力权重以便后面制图
attention_weights = tf.reshape(attention_weights, (-1, ))
attention_plot[t] = attention_weights.numpy()
predicted_id = tf.argmax(predictions[0]).numpy()
result += targ_lang.index_word[predicted_id] + ' '
if targ_lang.index_word[predicted_id] == '<end>':
return result, sentence, attention_plot
# 预测的 ID 被输送回模型
dec_input = tf.expand_dims([predicted_id], 0)
return result, sentence, attention_plot
# 注意力权重制图函数
def plot_attention(attention, sentence, predicted_sentence):
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1)
ax.matshow(attention, cmap='viridis')
fontdict = {'fontsize': 14}
ax.set_xticklabels([''] + sentence, fontdict=fontdict, rotation=90)
ax.set_yticklabels([''] + predicted_sentence, fontdict=fontdict)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
plt.show()
def translate(sentence):
result, sentence, attention_plot = evaluate(sentence)
print('Input: %s' % (sentence))
print('Predicted translation: {}'.format(result))
attention_plot = attention_plot[:len(result.split(' ')), :len(sentence.split(' '))]
plot_attention(attention_plot, sentence.split(' '), result.split(' '))
# 恢复检查点目录 (checkpoint_dir) 中最新的检查点
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
translate(u'hace mucho frio aqui.')
translate(u'esta es mi vida.')
translate(u'¿todavia estan en casa?')
# 错误的翻译
translate(u'trata de averiguarlo.')
| 0.518302 | 0.92462 |
# WeatherPy
----
#### Note
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
from scipy.stats import linregress
# Import API key
from api_keys import weather_api_key
# Incorporated citipy to determine city based on latitude and longitude
from citipy import citipy
# Output File (CSV)
output_data_file = "output_data/cities.csv"
# Range of latitudes and longitudes
lat_range = (-90, 90)
lng_range = (-180, 180)
```
## Generate Cities List
```
# List for holding lat_lngs and cities
lat_lngs = []
cities = []
# Create a set of random lat and lng combinations
lats = np.random.uniform(lat_range[0], lat_range[1], size=1500)
lngs = np.random.uniform(lng_range[0], lng_range[1], size=1500)
lat_lngs = zip(lats, lngs)
# Identify nearest city for each lat, lng combination
for lat_lng in lat_lngs:
city = citipy.nearest_city(lat_lng[0], lat_lng[1]).city_name
# If the city is unique, then add it to a our cities list
if city not in cities:
cities.append(city)
# Print the city count to confirm sufficient count
len(cities)
```
### Perform API Calls
* Perform a weather check on each city using a series of successive API calls.
* Include a print log of each city as it'sbeing processed (with the city number and city name).
```
print('''
================================
Beginning Weather Data Retrieval
================================
''')
weather_city_data=[]
for idx, city in enumerate(cities):
print(f"processing record {idx} | {city}")
base_url="http://api.openweathermap.org/data/2.5/weather"
params={
"q": city,
"units": "imperial",
"appid": weather_api_key
}
try:
response = requests.get(url=base_url, params=params)
except (ReadTimeoutError, TimeoutError, ReadTimeout):
print("Timed out. Skipping")
except:
print("Unknown error. Skipping to next record.")
if "404" in response.text:
print(f"{city} not found. Skipping.")
else:
weather_city = response.json()
weather_dict = {"City": city,
"Lat": weather_city["coord"]["lat"],
"Lng": weather_city["coord"]["lon"],
"Max Temp": weather_city["main"]["temp_max"],
"Humidity": weather_city["main"]["humidity"],
"Cloudiness": weather_city["clouds"]["all"],
"Wind Speed": weather_city["wind"]["speed"],
"Country": weather_city["sys"]["country"],
"Date": weather_city["dt"]
}
weather_city_data.append(weather_dict)
print('''
=============================
Ending Weather Data Retrieval
=============================
''')
len(weather_city_data)
```
### Convert Raw Data to DataFrame
* Export the city data into a .csv.
* Display the DataFrame
```
weather_city_df = pd.DataFrame(weather_city_data)
weather_city_df.to_csv(output_data_file)
weather_city_df.count()
weather_city_df.head()
```
## Inspect the data and remove the cities where the humidity > 100%.
----
Skip this step if there are no cities that have humidity > 100%.
```
assert len(weather_city_df.loc[weather_city_df["Humidity"] > 100]) == 0
```
Student Note: there are no cities with humidity over 100%. No further work needed.
```
# Extract relevant fields from the data frame
##### STUDENT NOTE: THERE ARE NO CITIES WITH HUMIDITY GREATER THAN 100%. NO WORK TO DO.
# Export the City_Data into a csv
weather_city_df.to_csv(output_data_file)
```
## Plotting the Data
* Use proper labeling of the plots using plot titles (including date of analysis) and axes labels.
* Save the plotted figures as .pngs.
```
from datetime import date
today = date.today()
analysis_date = today.strftime("%m/%d/%y")
```
## Latitude vs. Temperature Plot
```
xvalues=weather_city_df["Lat"]
yvalues=weather_city_df["Max Temp"]
plt.scatter(x=xvalues, y=yvalues, facecolors="orange", edgecolors="black")
plt.title(f"City Latitude vs Max Temperature {analysis_date}", color="green", fontsize=20)
plt.xlabel("Latitude")
plt.ylabel("Max Temperature (F)")
plt.grid()
plt.show()
```
Observations: The above chart demonstrates that the density of recorded temperatures increases as you move toward the equator (latitude = 0) from the poles (latitude=-90, latitude=90). In the month of July, the earth's tilt lends more exposure in the northern hemisphere (latitude > 0) to the sun which is why the recorded temperatures are highest in the (20 < latitude < 40) band than its counterpart in the southern hemisphere.
## Latitude vs. Humidity Plot
```
xvalues=weather_city_df["Lat"]
yvalues=weather_city_df["Humidity"]
plt.scatter(x=xvalues, y=yvalues, facecolors="red", edgecolors="black")
plt.title(f"City Latitude vs Humidity {analysis_date}", color="green", fontsize=20)
plt.xlabel("Latitude")
plt.ylabel("Humidity (%)")
plt.grid()
plt.show()
```
Observations: In this chart we can see that most cities at the equator or shortly north have humidity levels of at least 45% with the fewest outliers. As you proceed further north or south of the equator (< -20 or > +20 latitude) there are more uniform distributions of high and low humidity percentages. Proximity to the equator implies greater humidity percentages.
## Latitude vs. Cloudiness Plot
```
xvalues=weather_city_df["Lat"]
yvalues=weather_city_df["Cloudiness"]
plt.scatter(x=xvalues, y=yvalues, facecolors="purple", edgecolors="gold")
plt.title(f"City Latitude vs Cloudiness {analysis_date}", color="green", fontsize=20)
plt.xlabel("Latitude")
plt.ylabel("Cloudiness (%)")
plt.grid()
plt.show()
```
Observations: The cloudiness chart does not appear to show much correlation to the cities' distances from the equator. We might have cities reporting their cloudiness more frequently at 0% and 100% than an actual scientific percentage. We have comparable reports of 0% and 100% from cities at all latitudes between -55 and +65.
## Latitude vs. Wind Speed Plot
```
xvalues=weather_city_df["Lat"]
yvalues=weather_city_df["Wind Speed"]
plt.scatter(x=xvalues, y=yvalues, facecolors="pink", edgecolors="purple")
plt.title(f"City Latitude vs Wind Speed {analysis_date}", color="green", fontsize=20)
plt.xlabel("Latitude")
plt.ylabel("Wind Speed (mph)")
plt.grid()
plt.show()
```
Observations: During our snapshot on 7/31 the maximum wind speed is mostly in the 0- to 15 mph whether north or south of the equator. Fewer cities report wind speeds > 20 mph.
## Linear Regression
```
# OPTIONAL: Create a function to create Linear Regression plots
# Add the linear regression equation and line to plot
def plot_lr(x_values, y_values, y_label, title, x_anno, y_anno, figname):
(slope, intercept, rvalue, pvalue, stderr) = linregress(x_values, y_values) # Perform linear regression
regress_values = x_values * slope + intercept # Get x/y values for linear regression linear
line_eq = "y = " + str(round(slope,2)) + "x + " + str(round(intercept,2))
print(f"The r-squared is: {rvalue**2}")
plt.scatter(x_values,y_values)
plt.title(title, color="green", fontsize=15)
plt.plot(x_values,regress_values,"r-") # Add linear regression line to plot
plt.annotate(line_eq,(x_anno, y_anno),fontsize=15,color="red")
plt.xlabel("Latitude")
plt.ylabel(y_label)
plt.savefig(f"output_data/{figname}.png")
plt.show()
# Create Northern and Southern Hemisphere DataFrames
weather_city_N_df = weather_city_df.loc[weather_city_df["Lat"] >= 0]
weather_city_S_df = weather_city_df.loc[weather_city_df["Lat"] < 0]
weather_city_S_df.head()
```
#### Northern Hemisphere - Max Temp vs. Latitude Linear Regression
```
xvalues=weather_city_N_df["Lat"]
yvalues=weather_city_N_df["Max Temp"]
plot_lr(xvalues, yvalues, "Max Temp", "Northern Max Temp vs Latitude", 10, 45, "NMaxTemp")
```
#### Southern Hemisphere - Max Temp vs. Latitude Linear Regression
```
xvalues=weather_city_S_df["Lat"]
yvalues=weather_city_S_df["Max Temp"]
plot_lr(xvalues, yvalues, "Max Temp", "Southern Max Temp vs Latitude", -55, 85, "SMaxTemp")
```
Max Temp vs Latitude: In the northern hemisphere we see that there is a moderate negative correlation between max temperature and latitude while in the southern hemisphere we see a moderate positive correlation for predicting max temperature based on the latitude of the city and time of analysis.
#### Northern Hemisphere - Humidity (%) vs. Latitude Linear Regression
```
xvalues=weather_city_N_df["Lat"]
yvalues=weather_city_N_df["Humidity"]
plot_lr(xvalues, yvalues, "Humidity", "Northern Humidity(%) vs Latitude", 40, 15, "NHumidity")
```
#### Southern Hemisphere - Humidity (%) vs. Latitude Linear Regression
```
xvalues=weather_city_S_df["Lat"]
yvalues=weather_city_S_df["Humidity"]
plot_lr(xvalues, yvalues, "Humidity", "Southern Humidity(%) vs Latitude", -55, 35, "SHumidity")
```
%Humidity vs latitude: We have only slight correlations between humidity and latitude. Almost no correlation with very low r value.
#### Northern Hemisphere - Cloudiness (%) vs. Latitude Linear Regression
```
xvalues=weather_city_N_df["Lat"]
yvalues=weather_city_N_df["Cloudiness"]
plot_lr(xvalues, yvalues, "Cloudiness", "Northern Cloudiness(%) vs Latitude", 5, 47, "NCloudiness")
```
#### Southern Hemisphere - Cloudiness (%) vs. Latitude Linear Regression
```
xvalues=weather_city_S_df["Lat"]
yvalues=weather_city_S_df["Cloudiness"]
plot_lr(xvalues, yvalues, "Cloudiness", "Southern Cloudiness(%) vs Latitude", -55, 25, "SCloudiness")
```
Cloudiness vs latitude: We have no correlation between cloudiness and latitude. No correlation with very low r value.
#### Northern Hemisphere - Wind Speed (mph) vs. Latitude Linear Regression
```
xvalues=weather_city_N_df["Lat"]
yvalues=weather_city_N_df["Wind Speed"]
plot_lr(xvalues, yvalues, "Wind Speed (mph)", "Northern Wind Speed(mph) vs Latitude", 25, 23, "NWindSpeed")
```
#### Southern Hemisphere - Wind Speed (mph) vs. Latitude Linear Regression
```
xvalues=weather_city_S_df["Lat"]
yvalues=weather_city_S_df["Wind Speed"]
plot_lr(xvalues, yvalues, "Wind Speed (mph)", "Southern Wind Speed(mph) vs Latitude", -50, 22, "SWindSpeed")
```
Wind Speed vs latitude: We have no correlations between wind speed and latitude. No correlation with very low r value.
|
github_jupyter
|
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
from scipy.stats import linregress
# Import API key
from api_keys import weather_api_key
# Incorporated citipy to determine city based on latitude and longitude
from citipy import citipy
# Output File (CSV)
output_data_file = "output_data/cities.csv"
# Range of latitudes and longitudes
lat_range = (-90, 90)
lng_range = (-180, 180)
# List for holding lat_lngs and cities
lat_lngs = []
cities = []
# Create a set of random lat and lng combinations
lats = np.random.uniform(lat_range[0], lat_range[1], size=1500)
lngs = np.random.uniform(lng_range[0], lng_range[1], size=1500)
lat_lngs = zip(lats, lngs)
# Identify nearest city for each lat, lng combination
for lat_lng in lat_lngs:
city = citipy.nearest_city(lat_lng[0], lat_lng[1]).city_name
# If the city is unique, then add it to a our cities list
if city not in cities:
cities.append(city)
# Print the city count to confirm sufficient count
len(cities)
print('''
================================
Beginning Weather Data Retrieval
================================
''')
weather_city_data=[]
for idx, city in enumerate(cities):
print(f"processing record {idx} | {city}")
base_url="http://api.openweathermap.org/data/2.5/weather"
params={
"q": city,
"units": "imperial",
"appid": weather_api_key
}
try:
response = requests.get(url=base_url, params=params)
except (ReadTimeoutError, TimeoutError, ReadTimeout):
print("Timed out. Skipping")
except:
print("Unknown error. Skipping to next record.")
if "404" in response.text:
print(f"{city} not found. Skipping.")
else:
weather_city = response.json()
weather_dict = {"City": city,
"Lat": weather_city["coord"]["lat"],
"Lng": weather_city["coord"]["lon"],
"Max Temp": weather_city["main"]["temp_max"],
"Humidity": weather_city["main"]["humidity"],
"Cloudiness": weather_city["clouds"]["all"],
"Wind Speed": weather_city["wind"]["speed"],
"Country": weather_city["sys"]["country"],
"Date": weather_city["dt"]
}
weather_city_data.append(weather_dict)
print('''
=============================
Ending Weather Data Retrieval
=============================
''')
len(weather_city_data)
weather_city_df = pd.DataFrame(weather_city_data)
weather_city_df.to_csv(output_data_file)
weather_city_df.count()
weather_city_df.head()
assert len(weather_city_df.loc[weather_city_df["Humidity"] > 100]) == 0
# Extract relevant fields from the data frame
##### STUDENT NOTE: THERE ARE NO CITIES WITH HUMIDITY GREATER THAN 100%. NO WORK TO DO.
# Export the City_Data into a csv
weather_city_df.to_csv(output_data_file)
from datetime import date
today = date.today()
analysis_date = today.strftime("%m/%d/%y")
xvalues=weather_city_df["Lat"]
yvalues=weather_city_df["Max Temp"]
plt.scatter(x=xvalues, y=yvalues, facecolors="orange", edgecolors="black")
plt.title(f"City Latitude vs Max Temperature {analysis_date}", color="green", fontsize=20)
plt.xlabel("Latitude")
plt.ylabel("Max Temperature (F)")
plt.grid()
plt.show()
xvalues=weather_city_df["Lat"]
yvalues=weather_city_df["Humidity"]
plt.scatter(x=xvalues, y=yvalues, facecolors="red", edgecolors="black")
plt.title(f"City Latitude vs Humidity {analysis_date}", color="green", fontsize=20)
plt.xlabel("Latitude")
plt.ylabel("Humidity (%)")
plt.grid()
plt.show()
xvalues=weather_city_df["Lat"]
yvalues=weather_city_df["Cloudiness"]
plt.scatter(x=xvalues, y=yvalues, facecolors="purple", edgecolors="gold")
plt.title(f"City Latitude vs Cloudiness {analysis_date}", color="green", fontsize=20)
plt.xlabel("Latitude")
plt.ylabel("Cloudiness (%)")
plt.grid()
plt.show()
xvalues=weather_city_df["Lat"]
yvalues=weather_city_df["Wind Speed"]
plt.scatter(x=xvalues, y=yvalues, facecolors="pink", edgecolors="purple")
plt.title(f"City Latitude vs Wind Speed {analysis_date}", color="green", fontsize=20)
plt.xlabel("Latitude")
plt.ylabel("Wind Speed (mph)")
plt.grid()
plt.show()
# OPTIONAL: Create a function to create Linear Regression plots
# Add the linear regression equation and line to plot
def plot_lr(x_values, y_values, y_label, title, x_anno, y_anno, figname):
(slope, intercept, rvalue, pvalue, stderr) = linregress(x_values, y_values) # Perform linear regression
regress_values = x_values * slope + intercept # Get x/y values for linear regression linear
line_eq = "y = " + str(round(slope,2)) + "x + " + str(round(intercept,2))
print(f"The r-squared is: {rvalue**2}")
plt.scatter(x_values,y_values)
plt.title(title, color="green", fontsize=15)
plt.plot(x_values,regress_values,"r-") # Add linear regression line to plot
plt.annotate(line_eq,(x_anno, y_anno),fontsize=15,color="red")
plt.xlabel("Latitude")
plt.ylabel(y_label)
plt.savefig(f"output_data/{figname}.png")
plt.show()
# Create Northern and Southern Hemisphere DataFrames
weather_city_N_df = weather_city_df.loc[weather_city_df["Lat"] >= 0]
weather_city_S_df = weather_city_df.loc[weather_city_df["Lat"] < 0]
weather_city_S_df.head()
xvalues=weather_city_N_df["Lat"]
yvalues=weather_city_N_df["Max Temp"]
plot_lr(xvalues, yvalues, "Max Temp", "Northern Max Temp vs Latitude", 10, 45, "NMaxTemp")
xvalues=weather_city_S_df["Lat"]
yvalues=weather_city_S_df["Max Temp"]
plot_lr(xvalues, yvalues, "Max Temp", "Southern Max Temp vs Latitude", -55, 85, "SMaxTemp")
xvalues=weather_city_N_df["Lat"]
yvalues=weather_city_N_df["Humidity"]
plot_lr(xvalues, yvalues, "Humidity", "Northern Humidity(%) vs Latitude", 40, 15, "NHumidity")
xvalues=weather_city_S_df["Lat"]
yvalues=weather_city_S_df["Humidity"]
plot_lr(xvalues, yvalues, "Humidity", "Southern Humidity(%) vs Latitude", -55, 35, "SHumidity")
xvalues=weather_city_N_df["Lat"]
yvalues=weather_city_N_df["Cloudiness"]
plot_lr(xvalues, yvalues, "Cloudiness", "Northern Cloudiness(%) vs Latitude", 5, 47, "NCloudiness")
xvalues=weather_city_S_df["Lat"]
yvalues=weather_city_S_df["Cloudiness"]
plot_lr(xvalues, yvalues, "Cloudiness", "Southern Cloudiness(%) vs Latitude", -55, 25, "SCloudiness")
xvalues=weather_city_N_df["Lat"]
yvalues=weather_city_N_df["Wind Speed"]
plot_lr(xvalues, yvalues, "Wind Speed (mph)", "Northern Wind Speed(mph) vs Latitude", 25, 23, "NWindSpeed")
xvalues=weather_city_S_df["Lat"]
yvalues=weather_city_S_df["Wind Speed"]
plot_lr(xvalues, yvalues, "Wind Speed (mph)", "Southern Wind Speed(mph) vs Latitude", -50, 22, "SWindSpeed")
| 0.485844 | 0.814607 |
# Estatística Descritiva
Estatística é um domínio do conhecimento que se preocupar em compreender dados. Ela se ampara solidamente em métodos matemáticos e pode ser dividida em dois ramos: i) _estatística inferencial_, que se preocupa em tirar conclusões dos dados analisados, e ii) _estatística descritiva_, que procura apenas descrever dados quantitativamente valendo-se de conceitos como "amostra" e "população" e apresentado os dados de modo gerenciável.
## População e amostra
Uma _população_ é uma coleção de objetos, ou unidades, sobre a qual a informação é procurada. Uma _amostra_ é uma parte da população observada.
## Análise de dados exploratória
Dados extraídos a partir de medições realizadas em amostras representativas constituem o que chamamos de _observações_. Medições e categorias representam uma _distribuição amostral_ de uma certa variável, as quais podem ser usadas para representar aproximadamente a _distribuição populacional_ dessa variável. O papel da análise de dados exploratória é dar subsídios para visualizar e resumir distribuições amostrais de modo que possamos levantar hipóteses sobre a população envolvida.
## Descrição de dados
Neste capítulo, apresentaremos vários métodos desenvolvidos para *Series* e *DataFrames* relacionados à Estatística Descritiva. Começaremos importando as bibliotecas *pandas* e *numpy*.
```
import numpy as np
import pandas as pd
```
### Distribuição de frequência
Uma distribuição de frequência é uma tabela que contém um resumo das observações. A distribuição é organizada em uma tabela que contém _intervalos de classe (grupos)_ e _frequências_ correspondentes.
```{note}
Intervalos de classe são formados por um limite inferior L e um superior S. Eles costumam ser expressos por um "T" horizontal, em que $L \vdash S$ indica o intervalo $[L,S)$.
```
Abaixo vemos um exemplo simplificado de tabela de distribuição de frequência (número de alunos) e intervalos de classe de alturas para uma amostra de alunos.
| Altura (m) | No. de alunos |
| :-------------: |:-------------:|
|1,50 $\vdash$ 1,60 | 5 |
|1,60 $\vdash$ 1,70 | 15 |
|1,70 $\vdash$ 1,80 | 17 |
|1,80 $\vdash$ 1,90 | 3 |
|Total | 40 |
#### Construção de uma distribuição de frequência
Para ilustrar como se constrói uma distribuição de frequência, vamos considerar um exemplo específico. Suponha que uma pesquisa foi feita e o seguinte conjunto de dados foi obtido:
**Dados Brutos**: 24-23-22-28-35-21-23-33-34-24-21-25-36-26-22-30-32-25-26-33-34-21-31-25-31-26-25-35-33-31.
```
dados = [24,23,22,28,35,21,23,33,34,24,21,25,36,26,22,30,32,25,26,33,34,21,31,25,31,26,25,35,33,31]
```
#### Rol de dados
A primeira coisa a fazer é ordenar os dados do menor para o maior, formando o *rol de dados*:
**Rol de dados**: 21-21-21-22-22-23-23-24-25-25-25-25-26-26-26-28-30-31-31-31-32-33-33-33-34-34-34-35-35-36.
```
np.sort(dados)
```
#### Amplitude total
Em seguida, calculamos a *amplitude total* $R$ pela diferença entre o maior $M$ e menor $m$ valores obtidos na amostra.
$$R = M - m$$
Para o caso acima, $R = 36-21 = 15$.
```
R = np.max(dados) - np.min(dados); R
```
#### Tamanho Amostral
Vamos calcular agora o tamanho amostral, ou seja, o número de observações obtidas na amostra.
```
n = len(dados); n
```
Para *Series* e *DataFrames*, podemos usar o método `count()` para retornar o tamanho amostral.
```
n = pd.Series(dados).count(); n
```
#### Distribuições e histogramas
Para ter uma visão ampla sobre a distribuição de frequências para o nosso conjunto de dados, podemos plotar o histograma com `plot.hist` diretamente a partir da _Series_ de dados.
```
d = pd.Series(dados);
d.plot.hist(color='#1b3ac9',alpha=0.8);
```
#### Número de classes e _binning_
A divisão das amostras em intervalos de classe pode ser chamada de _binning_. _Bin_ é o termo utilizado para uma barra vertical no histograma. Por padrão, `plot.hist` usa 10 bins.
Há mais de uma forma de definir o *número de (intervalos) de classe* $K$. A seguir, temos duas regras práticas de decisão:
- Regra 1: $K=5$, para $n\leq 25$ e $K \approx \sqrt{n}$, para $n>25$.
- Regra 2 (Fórmula de Sturges): $K\approx 1 + 3,22\log n$.
Vamos aplicá-las aos nossos dados:
```
# binning usando np.ceil
def binning(d,rule='standard'):
if isinstance(d,list): d = np.array(d)
n = len(d)
if rule == 'standard':
if n <= 25: K = 5
else: K = int(np.ceil(np.sqrt(n)))
if rule == 'sturges':
K = int(np.ceil(1 + 3.22*np.log10(n)))
return K
K1,K2 = binning(dados,rule='standard'), binning(dados,rule='sturges');
K1,K2
```
Uma vez que ambos os valores são iguais, podemos tomar $K = K_1 = K_2 = 6$ e plotar o histograma especificando `bins`.
```
K = K1
d.plot.hist(bins=K,color='#1b3ac9',alpha=0.8,edgecolor='w');
```
#### Amplitude das classes
Para determinar o comprimento de cada intervalo, ou seja, a amplitude de cada classe $h$, podemos adotar uma divisão uniforme, de modo que:
$$h=\frac{R}{K}$$
```
h = np.ceil(R/K); h
```
#### Limites das classes
Os *limites das classes* são estabelecidos da seguinte forma. Começando a partir do menor valor obtido da amostra, ou equivalentemente, o primeiro valor do *rol de dados*, somamos a amplitude de maneira progressiva. Dessa maneira, as seguintes classes serão obtidas.
| Classes |
| :-------------:
| 21 $\vdash$ 24 |
| 24 $\vdash$ 27 |
| 27 $\vdash$ 30 |
| 30 $\vdash$ 33 |
| 33 $\vdash$ 36 |
| 36 $\vdash$ 39 |
```
bin_ = [np.min(dados) + i*h.astype('int') for i in range(K+1)];
bin_
```
#### Frequência dos dados
Ao calcular a frequência de cada intervalo, a chamada _frequência absoluta_, montamos a seguinte tabela de _distribuição de frequências_ será obtida.
| Classes | Frequência |
| :-------------:| :-------------:|
| 21 $\vdash$ 24 | 7 |
| 24 $\vdash$ 27 | 9 |
| 27 $\vdash$ 30 | 1 |
| 30 $\vdash$ 33 | 5 |
| 33 $\vdash$ 36 | 7 |
| 36 $\vdash$ 39 | 1 |
No *pandas*, a função `cut` cria classes a partir dos dados e o método `value_counts()` cria uma tabela de frequências.
```
T = pd.cut(dados, bins=bin_, right=False)
T
# labels
T.codes
# categorias
T.categories
# tabela de frequências
T.value_counts()
```
### Aplicações a testes aleatórios
```
# função genérica
def random_test(ns, dist='rand',binMethod='standard'):
if isinstance(ns,int): vals = '(' + str(ns) + ')'
elif isinstance(ns,tuple): vals = str(ns)
z = eval('np.random.' + dist + vals)
T = pd.cut(z,bins=binning(z,binMethod), right=False)
return pd.Series(z), T.value_counts()
```
- Números randômicos
```
z1,T1 = random_test(100, dist='rand',binMethod='standard')
z1.plot.hist(); T1
z2,T2 = random_test(100, dist='rand',binMethod='sturges')
z2.plot.hist(); T2
```
- Distribuição normal
```
z3,T3 = random_test((0,1,100), dist='normal',binMethod='standard')
z3.plot.hist(); T3
z4,T4 = random_test((0,1,100), dist='normal',binMethod='sturges')
z4.plot.hist(); T4
```
## Medidas de Tendência Central
As _medidas de tendência central_ (ou de centralidade) são as mais importantes de uma classe maior chamada de _medidas de posição_. Elas representam a tendência de concentração dos dados observados. A seguir, exploraremos algumas medidas de tendência central.
### Média
Quantidade que tem por característica dar um "resumo" para o conjunto de dados. A média $\overline{X}$ é obtida a partir de todos os elementos da distribuição e do tamanho da amostra.
Calculamos a média aritmética pela fórmula:
$$\overline{X}=\sum_{i=1}^{n}\frac{X_i}{n}.$$
Para *Series* e *DataFrames* o método `mean()` retorna a média dos valores.
```
pd.Series(dados).mean()
```
### Moda
Definimos a moda $Mo$ de um conjunto de dados como o valor mais frequente deste conjunto.
Exemplos:
* $\{1, 2, 4, 5, 8\}$. Não há moda (amodal).
* $\{2, 2, 3, 7, 8\}$. Para esta amostra, $Mo$ = 2 (unimodal).
* $\{1, 1, 10, 5, 5, 8, 7, 2\}$. Para esta amostra, $Mo$ = 1 e $Mo=$5 (bimodal).
Para _Series_ e _DataFrames_, o método `mode()` retorna a moda dos valores.
```
pd.Series(dados).mode()
pd.Series([1,2,2,2,3,4,4,4,5]).mode()
z4.mode()
```
### Mediana
A mediana $Md$ é o valor que divide o *rol de dados* em duas partes com a mesma quantidade de dados. O *elemento mediano*, $E_{Md}$, é a posição no *rol de dados* onde a mediana está localizada.
Se o tamanho amostral $n$ é ímpar, temos que $E_{Md} = \frac{(n+1)}{2}$; se par, dois valores são possíveis, $\frac{n}{2}$ e $\frac{n}{2}+1$. No último caso, a mediana será a média dos valores assumidos nestas posições.
Exemplos:
- $\{1, 2, 4, 5, 8\}$. Como $n$ é ímpar, $E_{Md} = 3$, e $Md = 4$.
- $\{2, 2, 4, 7, 8, 10\}$. Aqui, $n$ é par. Assim, $E_{Md,1} = \frac{6}{2} = 3$ e $E_{Md,2} = \frac{6}{2}+1 = 4$. Daí ${Md} = \frac{4+7}{2} = 5,5$.
* Para Series e DataFrames o método `median()` retorna a mediana dos valores.
```
pd.Series(dados).median()
z2.median()
```
## Quantis e percentis
Quantis e percentis são utilizados para compreender os dados sob a perspectiva de "partes". Por exemplo, dado o rol de dados $ d = \{x_i\}$ com $n$ valores, procuramos pelo valor $x_p$ que divide o rol em partes regulares. O valor $x_p$ é o $p$-ésimo _quantil_, ou o $100 \times p$-ésimo percentil. Em particular, $x_p = d[I_p]$, onde $I_p$ é o índice (número inteiro) para o quantil no rol de dados.
Os seguintes nomes são usados na prática:
- _Percentis_ variam no intervalo 0 a 100.
- _Quartis_ variam no intervalo 0 a 4.
- _Quantis_ variam de qualquer valor para outro.
Entretanto, outras definições existem: os 3-quantis são chamados de _tercis_, os 5-quantis são chamados de _quintis_, os 12-quantis são chamados de _duo-deciles_, e assim por diante.
Uma tabela de correspondência útil para compreensão é a seguinte:
- 0-percentil = 0-quartil = menor valor do rol de dados
- 25-percentil = 1-quartil
- 50-percentil = 2-quartil = mediana
- 75-percentil = 3-quartil
- 100-percentil = 4-quartil = máximo valor do rol de dados
Como se vê, a mediana é o 50-percentil. Isto significa que ela representa o valor que está abaixo de 50% dos valores no rol de dados. Quantis, por sua vez, são uma generalização da mediana.
O código abaixo retorna o $p$-percentil de um rol de dados.
```
# 0 < p < 1
def quantil(d,p):
I_p = int(p*len(d))
return sorted(d)[I_p]
```
Por exemplo, para o nosso conjunto:
```
print(sorted(d),sep=',')
quantil(d,0.0),quantil(d,0.25),quantil(d,0.5),quantil(d,0.75),quantil(d,0.9)
```
Comentário:
- A mediana é o valor $x_{1/2} = 26$. Ou seja, $p= 1/2 = 0.5$. Isto equivale a dizer que a mediana é o $1/2$-quantil ou $100 \times 1/2 = 50$-percentil.
- Para $p=1/4$, temos o $1/4$-quantil ou $100 \times 1/4 = 25$-percentil. Este valor equivale a $x_{1/4} = 24$.
- 24 é o primeiro quartil do rol, ou seja, 25% dos valores do rol são menores do que 24.
- 33 é o terceiro quartil do rol, ou seja, 75% dos valores do rol são menores do que 33.
```{note}
Para saber mais sobre a terminologia estatística "x-is", veja a tabela do Apêndice A deste artigo de [[Nicholas J. Cox]](https://www.doi.org/10.1177/1536867X1601600413).
```
O _pandas_ possui a função `quantile` para calcular os quantis que desejarmos.
```
z1.quantile(0.22)
# 1-, 2-, e 3-quartis
z4.quantile([0.25,0.5,0.75])
# 1-, 2- tercis
z2.quantile([0.33,0.66])
```
## Medidas de Dispersão
As medidas de dispersão medem o grau de variabilidade dos elementos de uma distribuição. O valor zero indica ausência de dispersão. As principais medidas de dispersão incluem: *amplitude*, *desvio médio*, *variância* e *desvio padrão*.
Como uma motivação para estudar as medidas de dispersão, consideremos a seguinte distribuição de notas é médias em uma classe.
|Discente||| Notas||| Média|
|:--:|:--:|:--:|:--:|:--:|:--:|:--:|
|Antônio|5|5|5|5|5|5|
|João |6|4|5|4|6|5|
|José |10|5|5|5|0|5|
|Pedro |10|10|5|0|0|5|
Observa-se que:
- as notas de Antônio não variaram;
- as notas de João variaram menos do que as notas de José;
- as notas de Pedro variaram mais do que as notas dos demais;
### Amplitude
A amplitude $R$ fornece a maior variação possível dos dados. Ela é dada pela fórmula:
$$R = X_{max} - X_{min},$$
onde $X_{max}$ é o valor máximo $X_{min}$ o mínimo entre os dados.
Para *Series* e *DataFrames* os métodos `max()` e `min()` retornam respectivamente o máximo e o mínimo.
```
R = pd.Series(dados).max()-pd.Series(dados).min(); R
```
### Desvio Médio
Para medir a dispersão dos dados em relação à média, é interessante analisar os desvios em torno da média, isto é, fazer a análise dos desvios:
$$d_i=(X_i-\overline{X}).$$
Porém, a soma de todos os desvios é igual a zero, como podemos verificar com
$$\sum_{i=1}^{n} d_i= \sum_{i=1}^{n} (X_i-\overline{X})= \sum_{i=1}^{n}X_i-\sum_{i=1}^{n}\overline{X}=\sum_{i=1}^{n}X_i-{n}\overline{X}=$$
$$=\sum_{i=1}^{n}X_i-n\frac{\sum_{i=1}^{n}X_i}{n}= \sum_{i=1}^{n}X_i-\sum_{i=1}^{n}X_i=0.$$
Logo, será preciso encontrar uma maneira de se trabalhar com os desvios sem que a soma dê zero. Dessa forma, define-se o *desvio médio* $DM$ pela fórmula:
$$DM=\sum_{i=1}^{n} \frac{|d_i|}{n}= \sum_{i=1}^{n} \frac{|X_i-\overline{X}|}{n}.$$
Para *Series* e *DataFrames* o método `mad()` retorna a *desvio médio* dos valores.
```
pd.Series(dados).mad()
pd.Series(z3).mad()
```
**Observações**:
* A *amplitude* não mede bem a dispersão dos dados porque usam-se apenas os valores extremos em vez de todos os elementos da distribuição.
* O *desvio médio* é mais vantajoso do que a *amplitude*, visto que leva em consideração todos os valores da distribuição e é menos sensível a *outliers*.
* No entanto, o *desvio médio* não é tão frequentemente empregado no ajuste de modelos, pois não apresenta propriedades matemáticas interessantes. Porém é bastante utilizado na validação e comparação de modelos.
```{note}
“Um _outlier_ é uma observação que se diferencia tanto das demais observações que levanta suspeitas de que aquela observação foi gerada por um mecanismo distinto” (Wikipedia, apud: Hawkins, 1980). Outlier é um dado que se distancia demasiadamente de todos os outros. Literalmente, o "ponto fora da curva".
```
### Variância
A *variância* $\sigma^2$ é a medida de dispersão mais utilizada. Ela é dada pelo quociente entre a soma dos quadrados dos desvios e o número de elementos, cuja fórmula é dada por:
$$\sigma^2=\sum_{i=1}^{N} \frac{d_i^2}{N}= \sum_{i=1}^{N} \frac{(X_i-\overline{X})^2}{N},$$
onde $\sigma^2$ indica a variância populacional (lê-se "sigma ao quadrado" ou "sigma dois"). Neste caso, $\overline{X}$ e $N$ na formúla representam a média populacional e o tamanho populacional, respectivamente.
### Variância Amostral
Temos a seguinte definição de *variância amostral*:
$$
S^2=\sum_{i=1}^{n} \frac{d_i^2}{n-1}= \sum_{i=1}^{n} \frac{(X_i-\overline{X})^2}{n-1}.
$$
Para *Series* e *DataFrames* o método `var()` retorna a *variância amostral* dos valores.
```
pd.Series(dados).var()
pd.Series(z3).var()
```
### Desvio Padrão
Temos também outra medida de dispersão, que é a raiz quadrada da variância, chamada de *desvio padrão*. Assim,
$$\sigma = \sqrt{\sigma^2}$$
é o desvio desvio padrão populacional, e
$$S = \sqrt{S^2}$$
é o desvio desvio padrão amostral.
Para o cálculo do *desvio padrão*, deve-se, primeiramente, determinar o valor da variância e, em seguida, extrair a raiz quadrada desse resultado.
Para *Series* e *DataFrames* o método `std()` retorna o *desvio padrão* dos valores.
```
pd.Series(dados).std()
np.sqrt(pd.Series(dados).var())
pd.Series(z3).std()
np.sqrt(pd.Series(z3).var())
```
## Resumo Estatístico de uma *Series* ou *DataFrame*
Para obtermos um resumo estatístico de uma *Series* ou *DataFrame* do *pandas*, utilizamos o método `describe`. O método `describe` exclui observações ausentes por padrão.
Exemplos:
```
pd.Series(dados).describe()
pd.DataFrame(z2).describe()
```
**Observações**
* Se as entradas da *Series* não forem numéricas, o método `describe` retornará uma tabela contendo as quantidades de valores únicos, o valor mais frequente e a quantidade de elementos do valor mais frequente.
* No caso de um *DataFrame* que contenha colunas numéricas e colunas não-numéricas, o método `describe` irá considerar apenas as colunas numéricas.
Exemplos:
```
serie_ex1 = pd.Series(['a','b','c','d','e','f','g','h','i','j'])
serie_ex2 = pd.Series(range(10))
serie_ex1.describe()
serie_ex2.describe()
```
Exemplo:
```
df_exemplo = pd.concat([serie_ex1, serie_ex2], axis=1)
df_exemplo
```
Exemplo:
```
df_exemplo.describe()
```
```{hint}
É possível controlar o que será considerado em `describe` utilizando os argumentos `include` ou `exclude`. No caso, devemos passar uma lista contendo os parâmetros a serem incluídos ou excluídos como argumento. Para uma lista dos parâmetros disponíveis, consulte a documentação da função `select_dtypes()`.
```
Exemplos:
```
df_exemplo.describe(exclude='number')
df_exemplo.describe(include='object')
```
Exemplo:
```
df_exemplo.describe(include='all')
```
|
github_jupyter
|
import numpy as np
import pandas as pd
Abaixo vemos um exemplo simplificado de tabela de distribuição de frequência (número de alunos) e intervalos de classe de alturas para uma amostra de alunos.
| Altura (m) | No. de alunos |
| :-------------: |:-------------:|
|1,50 $\vdash$ 1,60 | 5 |
|1,60 $\vdash$ 1,70 | 15 |
|1,70 $\vdash$ 1,80 | 17 |
|1,80 $\vdash$ 1,90 | 3 |
|Total | 40 |
#### Construção de uma distribuição de frequência
Para ilustrar como se constrói uma distribuição de frequência, vamos considerar um exemplo específico. Suponha que uma pesquisa foi feita e o seguinte conjunto de dados foi obtido:
**Dados Brutos**: 24-23-22-28-35-21-23-33-34-24-21-25-36-26-22-30-32-25-26-33-34-21-31-25-31-26-25-35-33-31.
#### Rol de dados
A primeira coisa a fazer é ordenar os dados do menor para o maior, formando o *rol de dados*:
**Rol de dados**: 21-21-21-22-22-23-23-24-25-25-25-25-26-26-26-28-30-31-31-31-32-33-33-33-34-34-34-35-35-36.
#### Amplitude total
Em seguida, calculamos a *amplitude total* $R$ pela diferença entre o maior $M$ e menor $m$ valores obtidos na amostra.
$$R = M - m$$
Para o caso acima, $R = 36-21 = 15$.
#### Tamanho Amostral
Vamos calcular agora o tamanho amostral, ou seja, o número de observações obtidas na amostra.
Para *Series* e *DataFrames*, podemos usar o método `count()` para retornar o tamanho amostral.
#### Distribuições e histogramas
Para ter uma visão ampla sobre a distribuição de frequências para o nosso conjunto de dados, podemos plotar o histograma com `plot.hist` diretamente a partir da _Series_ de dados.
#### Número de classes e _binning_
A divisão das amostras em intervalos de classe pode ser chamada de _binning_. _Bin_ é o termo utilizado para uma barra vertical no histograma. Por padrão, `plot.hist` usa 10 bins.
Há mais de uma forma de definir o *número de (intervalos) de classe* $K$. A seguir, temos duas regras práticas de decisão:
- Regra 1: $K=5$, para $n\leq 25$ e $K \approx \sqrt{n}$, para $n>25$.
- Regra 2 (Fórmula de Sturges): $K\approx 1 + 3,22\log n$.
Vamos aplicá-las aos nossos dados:
Uma vez que ambos os valores são iguais, podemos tomar $K = K_1 = K_2 = 6$ e plotar o histograma especificando `bins`.
#### Amplitude das classes
Para determinar o comprimento de cada intervalo, ou seja, a amplitude de cada classe $h$, podemos adotar uma divisão uniforme, de modo que:
$$h=\frac{R}{K}$$
#### Limites das classes
Os *limites das classes* são estabelecidos da seguinte forma. Começando a partir do menor valor obtido da amostra, ou equivalentemente, o primeiro valor do *rol de dados*, somamos a amplitude de maneira progressiva. Dessa maneira, as seguintes classes serão obtidas.
| Classes |
| :-------------:
| 21 $\vdash$ 24 |
| 24 $\vdash$ 27 |
| 27 $\vdash$ 30 |
| 30 $\vdash$ 33 |
| 33 $\vdash$ 36 |
| 36 $\vdash$ 39 |
#### Frequência dos dados
Ao calcular a frequência de cada intervalo, a chamada _frequência absoluta_, montamos a seguinte tabela de _distribuição de frequências_ será obtida.
| Classes | Frequência |
| :-------------:| :-------------:|
| 21 $\vdash$ 24 | 7 |
| 24 $\vdash$ 27 | 9 |
| 27 $\vdash$ 30 | 1 |
| 30 $\vdash$ 33 | 5 |
| 33 $\vdash$ 36 | 7 |
| 36 $\vdash$ 39 | 1 |
No *pandas*, a função `cut` cria classes a partir dos dados e o método `value_counts()` cria uma tabela de frequências.
### Aplicações a testes aleatórios
- Números randômicos
- Distribuição normal
## Medidas de Tendência Central
As _medidas de tendência central_ (ou de centralidade) são as mais importantes de uma classe maior chamada de _medidas de posição_. Elas representam a tendência de concentração dos dados observados. A seguir, exploraremos algumas medidas de tendência central.
### Média
Quantidade que tem por característica dar um "resumo" para o conjunto de dados. A média $\overline{X}$ é obtida a partir de todos os elementos da distribuição e do tamanho da amostra.
Calculamos a média aritmética pela fórmula:
$$\overline{X}=\sum_{i=1}^{n}\frac{X_i}{n}.$$
Para *Series* e *DataFrames* o método `mean()` retorna a média dos valores.
### Moda
Definimos a moda $Mo$ de um conjunto de dados como o valor mais frequente deste conjunto.
Exemplos:
* $\{1, 2, 4, 5, 8\}$. Não há moda (amodal).
* $\{2, 2, 3, 7, 8\}$. Para esta amostra, $Mo$ = 2 (unimodal).
* $\{1, 1, 10, 5, 5, 8, 7, 2\}$. Para esta amostra, $Mo$ = 1 e $Mo=$5 (bimodal).
Para _Series_ e _DataFrames_, o método `mode()` retorna a moda dos valores.
### Mediana
A mediana $Md$ é o valor que divide o *rol de dados* em duas partes com a mesma quantidade de dados. O *elemento mediano*, $E_{Md}$, é a posição no *rol de dados* onde a mediana está localizada.
Se o tamanho amostral $n$ é ímpar, temos que $E_{Md} = \frac{(n+1)}{2}$; se par, dois valores são possíveis, $\frac{n}{2}$ e $\frac{n}{2}+1$. No último caso, a mediana será a média dos valores assumidos nestas posições.
Exemplos:
- $\{1, 2, 4, 5, 8\}$. Como $n$ é ímpar, $E_{Md} = 3$, e $Md = 4$.
- $\{2, 2, 4, 7, 8, 10\}$. Aqui, $n$ é par. Assim, $E_{Md,1} = \frac{6}{2} = 3$ e $E_{Md,2} = \frac{6}{2}+1 = 4$. Daí ${Md} = \frac{4+7}{2} = 5,5$.
* Para Series e DataFrames o método `median()` retorna a mediana dos valores.
## Quantis e percentis
Quantis e percentis são utilizados para compreender os dados sob a perspectiva de "partes". Por exemplo, dado o rol de dados $ d = \{x_i\}$ com $n$ valores, procuramos pelo valor $x_p$ que divide o rol em partes regulares. O valor $x_p$ é o $p$-ésimo _quantil_, ou o $100 \times p$-ésimo percentil. Em particular, $x_p = d[I_p]$, onde $I_p$ é o índice (número inteiro) para o quantil no rol de dados.
Os seguintes nomes são usados na prática:
- _Percentis_ variam no intervalo 0 a 100.
- _Quartis_ variam no intervalo 0 a 4.
- _Quantis_ variam de qualquer valor para outro.
Entretanto, outras definições existem: os 3-quantis são chamados de _tercis_, os 5-quantis são chamados de _quintis_, os 12-quantis são chamados de _duo-deciles_, e assim por diante.
Uma tabela de correspondência útil para compreensão é a seguinte:
- 0-percentil = 0-quartil = menor valor do rol de dados
- 25-percentil = 1-quartil
- 50-percentil = 2-quartil = mediana
- 75-percentil = 3-quartil
- 100-percentil = 4-quartil = máximo valor do rol de dados
Como se vê, a mediana é o 50-percentil. Isto significa que ela representa o valor que está abaixo de 50% dos valores no rol de dados. Quantis, por sua vez, são uma generalização da mediana.
O código abaixo retorna o $p$-percentil de um rol de dados.
Por exemplo, para o nosso conjunto:
Comentário:
- A mediana é o valor $x_{1/2} = 26$. Ou seja, $p= 1/2 = 0.5$. Isto equivale a dizer que a mediana é o $1/2$-quantil ou $100 \times 1/2 = 50$-percentil.
- Para $p=1/4$, temos o $1/4$-quantil ou $100 \times 1/4 = 25$-percentil. Este valor equivale a $x_{1/4} = 24$.
- 24 é o primeiro quartil do rol, ou seja, 25% dos valores do rol são menores do que 24.
- 33 é o terceiro quartil do rol, ou seja, 75% dos valores do rol são menores do que 33.
O _pandas_ possui a função `quantile` para calcular os quantis que desejarmos.
## Medidas de Dispersão
As medidas de dispersão medem o grau de variabilidade dos elementos de uma distribuição. O valor zero indica ausência de dispersão. As principais medidas de dispersão incluem: *amplitude*, *desvio médio*, *variância* e *desvio padrão*.
Como uma motivação para estudar as medidas de dispersão, consideremos a seguinte distribuição de notas é médias em uma classe.
|Discente||| Notas||| Média|
|:--:|:--:|:--:|:--:|:--:|:--:|:--:|
|Antônio|5|5|5|5|5|5|
|João |6|4|5|4|6|5|
|José |10|5|5|5|0|5|
|Pedro |10|10|5|0|0|5|
Observa-se que:
- as notas de Antônio não variaram;
- as notas de João variaram menos do que as notas de José;
- as notas de Pedro variaram mais do que as notas dos demais;
### Amplitude
A amplitude $R$ fornece a maior variação possível dos dados. Ela é dada pela fórmula:
$$R = X_{max} - X_{min},$$
onde $X_{max}$ é o valor máximo $X_{min}$ o mínimo entre os dados.
Para *Series* e *DataFrames* os métodos `max()` e `min()` retornam respectivamente o máximo e o mínimo.
### Desvio Médio
Para medir a dispersão dos dados em relação à média, é interessante analisar os desvios em torno da média, isto é, fazer a análise dos desvios:
$$d_i=(X_i-\overline{X}).$$
Porém, a soma de todos os desvios é igual a zero, como podemos verificar com
$$\sum_{i=1}^{n} d_i= \sum_{i=1}^{n} (X_i-\overline{X})= \sum_{i=1}^{n}X_i-\sum_{i=1}^{n}\overline{X}=\sum_{i=1}^{n}X_i-{n}\overline{X}=$$
$$=\sum_{i=1}^{n}X_i-n\frac{\sum_{i=1}^{n}X_i}{n}= \sum_{i=1}^{n}X_i-\sum_{i=1}^{n}X_i=0.$$
Logo, será preciso encontrar uma maneira de se trabalhar com os desvios sem que a soma dê zero. Dessa forma, define-se o *desvio médio* $DM$ pela fórmula:
$$DM=\sum_{i=1}^{n} \frac{|d_i|}{n}= \sum_{i=1}^{n} \frac{|X_i-\overline{X}|}{n}.$$
Para *Series* e *DataFrames* o método `mad()` retorna a *desvio médio* dos valores.
**Observações**:
* A *amplitude* não mede bem a dispersão dos dados porque usam-se apenas os valores extremos em vez de todos os elementos da distribuição.
* O *desvio médio* é mais vantajoso do que a *amplitude*, visto que leva em consideração todos os valores da distribuição e é menos sensível a *outliers*.
* No entanto, o *desvio médio* não é tão frequentemente empregado no ajuste de modelos, pois não apresenta propriedades matemáticas interessantes. Porém é bastante utilizado na validação e comparação de modelos.
### Variância
A *variância* $\sigma^2$ é a medida de dispersão mais utilizada. Ela é dada pelo quociente entre a soma dos quadrados dos desvios e o número de elementos, cuja fórmula é dada por:
$$\sigma^2=\sum_{i=1}^{N} \frac{d_i^2}{N}= \sum_{i=1}^{N} \frac{(X_i-\overline{X})^2}{N},$$
onde $\sigma^2$ indica a variância populacional (lê-se "sigma ao quadrado" ou "sigma dois"). Neste caso, $\overline{X}$ e $N$ na formúla representam a média populacional e o tamanho populacional, respectivamente.
### Variância Amostral
Temos a seguinte definição de *variância amostral*:
$$
S^2=\sum_{i=1}^{n} \frac{d_i^2}{n-1}= \sum_{i=1}^{n} \frac{(X_i-\overline{X})^2}{n-1}.
$$
Para *Series* e *DataFrames* o método `var()` retorna a *variância amostral* dos valores.
### Desvio Padrão
Temos também outra medida de dispersão, que é a raiz quadrada da variância, chamada de *desvio padrão*. Assim,
$$\sigma = \sqrt{\sigma^2}$$
é o desvio desvio padrão populacional, e
$$S = \sqrt{S^2}$$
é o desvio desvio padrão amostral.
Para o cálculo do *desvio padrão*, deve-se, primeiramente, determinar o valor da variância e, em seguida, extrair a raiz quadrada desse resultado.
Para *Series* e *DataFrames* o método `std()` retorna o *desvio padrão* dos valores.
## Resumo Estatístico de uma *Series* ou *DataFrame*
Para obtermos um resumo estatístico de uma *Series* ou *DataFrame* do *pandas*, utilizamos o método `describe`. O método `describe` exclui observações ausentes por padrão.
Exemplos:
**Observações**
* Se as entradas da *Series* não forem numéricas, o método `describe` retornará uma tabela contendo as quantidades de valores únicos, o valor mais frequente e a quantidade de elementos do valor mais frequente.
* No caso de um *DataFrame* que contenha colunas numéricas e colunas não-numéricas, o método `describe` irá considerar apenas as colunas numéricas.
Exemplos:
Exemplo:
Exemplo:
Exemplos:
Exemplo:
| 0.634317 | 0.933127 |
<a href="https://colab.research.google.com/github/NinaMaz/mlss-tutorials/blob/master/solomon-embeddings-tutorial/riemannian_opt_for_ml_solution.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
This is a tutorial notebook on Riemannian optimization for machine learning, prepared for the Machine Learning Summer School 2019 (MLSS-2019, http://mlss2019.skoltech.ru) in Moscow, Russia, Skoltech (http://skoltech.ru).
Copyright 2019 by Alexey Artemov and ADASE 3DDL Team. Special thanks to Alexey Zaytsev for a valuable contribution.
## Riemannian optimization for machine learning
The purpose of this tutorial is to give a gentle introduction into the practice of Riemannian optimization. You will learn to:
1. Reformulate familiar optimization problems in terms of Riemannian optimization on manifolds.
2. Use a Riemannian optimization library `pymanopt`.
## Index
1. [Recap and the introduction: linear regression](#Recap-and-the-introduction:-linear-regression).
2. [Introduction into ManOpt and pymanopt](#Intoduction-into-ManOpt-package-for-Riemannian-optimization).
3. [Learning the shape space of facial landmarks](#Learning-the-shape-space-of-facial-landmarks):
- [Problem formulation and general reference](#Problem-formulation-and-general-reference).
- [Procrustes analysis for the alignment of facial landmarks](#Procrustes-analysis-for-the-alignment-of-facial-landmarks).
- [PCA for learning the shape space](#PCA-for-learning-the-shape-space).
4. [Analysing the shape space of facial landmarks via MDS](#Analysing-the-shape-space-of-facial-landmarks-via-MDS).
5. [Learning the Gaussian mixture models for word embeddings](#Learning-the-Gaussian-mixture-models-for-word-embeddings).
Install the necessary libraries
```
!pip install --upgrade git+https://github.com/mlss-skoltech/tutorials.git#subdirectory=geometric_techniques_in_ML
!pip install pymanopt autograd
!pip install scipy==1.2.1 -U
import pkg_resources
DATA_PATH = pkg_resources.resource_filename('riemannianoptimization', 'data/')
```
## Recap and the introduction: linear regression
_NB: This section of the notebook is for illustrative purposes only, no code input required_
#### Recall the maths behind it:
We're commonly working with a problem of finding the weights $w \in \mathbb{R}^n$ such that
$$
||\mathbf{y} - \mathbf{X} \mathbf{w}||^2_2 \to \min_{\mathbf{w}},
$$
with $\mathbf{x}_i \in \mathbb{R}^n$, i.e. features are vectors of numbers, and $y_i \in \mathbb{R}$.
$\mathbf{X} \in \mathbb{R}^{\ell \times n}$ is a matrix with $\ell$ objects and $n$ features.
A commonly computed least squares solution is of the form:
$$
\mathbf{w} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}.
$$
We could account for the non-zero mean case ($\mathrm{E} \mathbf{y} \neq 0$) by either adding and subtracting the mean, or by using an additional feature in $\mathbf{X}$ set to all ones.
The solution could simply be computed via:
```
def compute_weights_multivariate(X, y):
"""
Given feature array X [n_samples, 1], target vector y [n_samples],
compute the optimal least squares solution using the formulae above.
For brevity, no bias term!
"""
# Compute the "inverting operator"
R = np.dot(
np.linalg.inv(
np.dot(X.T, X)
), X.T
)
# Compute the actual solution
w = np.dot(R, y)
return w
```
#### Recall the gradient descent solution:
Let us view
$$
L(\mathbf{y}, \mathbf{X} \mathbf{w}) = \frac{1}{\ell} ||\mathbf{y} - \mathbf{X} \mathbf{w}||^2_2
\to \min_{\mathbf{w}},
$$
as pure unconstrained optimization problem of the type
$$
f(\mathbf{w}) \to \min\limits_{\mathbf{w} \in \mathbb{R}^n}
$$
with $f(\mathbf{w}) \equiv L(\mathbf{y}, \mathbf{X} \mathbf{w})$.
To use the gradient descent, we must
* initialize the weights $\mathbf{w}$ somehow,
* find a way of computing the __gradient__ of our quality measure $L(\mathbf{y}, \widehat{\mathbf{y}})$ w.r.t. $\mathbf{w}$,
* starting from the initialization, iteratively update weights using the gradient descent:
$$
\mathbf{w}^{(i+1)} \leftarrow \mathbf{w}^{(i)} - \gamma \nabla_{\mathbf{w}} L,
$$
where $\gamma$ is step size.
Since we choose $L(\mathbf{y}, \widehat{\mathbf{y}}) \equiv \frac 1 \ell ||\mathbf{y} - \mathbf{X} \mathbf{w} ||^2$, our gradient is $ \frac 2 \ell \mathbf{X}^T (\mathbf{y} - \mathbf{X} \mathbf{w}) $.
The solution is coded by:
```
from sklearn.metrics import mean_squared_error
def compute_gradient(X, y, w):
"""
Computes the gradient of MSE loss
for multivariate linear regression of X onto y
w.r.t. w, evaluated at the current w.
"""
prediction = np.dot(X, w) # [n_objects, n_features] * [n_features] -> [n_objects]
error = prediction - y # [n_objects]
return 2 * np.dot(error, X) / len(error) # [n_objects] * [n_objects, n_features] -> [n_features]
def gradient_descent(X, y, w_init, iterations=1, gamma=0.01):
"""
Performs the required number of iterations of gradient descent.
Parameters:
X [n_objects, n_features]: matrix of featues
y [n_objects]: responce (dependent) variable
w_init: the value of w used as an initializer
iterations: number of steps for gradient descent to compute
gamma: learning rate (gradient multiplier)
"""
costs, grads, ws = [], [], []
w = w_init
for i in range(iterations):
# Compute our cost in current point (before the gradient step)
costs.append(mean_squared_error(y, np.dot(X, w)) / len(y))
# Remember our weights w in current point
ws.append(w)
# Compute gradient for w
w_grad = compute_gradient(X, y, w)
grads.append(w_grad)
# Update the current weight w using the formula above (see comments)
w = w - gamma * w_grad
# record the last weight
ws.append(w)
return costs, grads, ws
```
## Intoduction into ManOpt package for Riemannian optimization
#### `ManOpt` and `pymanopt`
The Matlab library `ManOpt` (https://www.manopt.org) and its Python version `pymanopt` (http://pymanopt.github.io) are versatile toolboxes for optimization on manifolds.
The two libraries are built so that they separate the _manifolds_, the _solvers_ and the _problem descriptions_. For basic use, one only needs to:
* pick a manifold from the library,
* describe the cost function (and possible derivatives) on this manifold, and
* pass it on to a solver.
_NB: The purpose of the following is to get familiar with pymanopt and to serve as a reference point when coding your own optimization problems._
To start working with `pymanopt`, you'll need the following
1. Import the necessary backend for automatic differentiation
```python
import autograd.numpy as np```
but theano and TensorFlow backends are supported, too.
We will also require importing `pymanopt` itself, along with the necessary submodules:
```python
import pymanopt as opt
import pymanopt.solvers as solvers
import pymanopt.manifolds as manifolds```
2. Define (or rather, select) the manifold of interest. `pymanopt` provides a [large number](https://pymanopt.github.io/doc/#manifolds) of predefined manifold classes (however, a lot less than the [original ManOpt Matlab library](https://www.manopt.org/tutorial.html#manifolds)). E.g., to instantiate a manifold $V_{2}(\mathbb {R}^{5}) = \{X \in \mathbb{R}^{5 \times 2} : X^TX = I_2\}^k$ of orthogonal projection matrices from $\mathbb{R}^5$ to $\mathbb{R}^2$ you will write:
```python
manifold = manifolds.Stiefel(5, 2)```
Available manifolds include [Steifel](https://pymanopt.github.io/doc/#module-pymanopt.manifolds.stiefel) ([wiki](https://en.wikipedia.org/wiki/Stiefel_manifold)), Rotations or SO(n) ([wiki](https://en.wikipedia.org/wiki/Orthogonal_group)), [Euclidean](https://pymanopt.github.io/doc/#module-pymanopt.manifolds.euclidean), [Positive Definite](https://pymanopt.github.io/doc/#pymanopt.manifolds.psd.PositiveDefinite) ([wiki](https://en.wikipedia.org/wiki/Definiteness_of_a_matrix)), and [Product](https://pymanopt.github.io/doc/#pymanopt.manifolds.product.Product), along many others.
3. Define the **scalar** cost function (here using `autograd.numpy`) to be minimized by the
```python
def cost(X): return np.sum(X)```
Note that the scalar `cost` python function **will have access to objects defined elsewhere in code** (which allows accessing $X$ and $y$ for optimization).
4. Instantiate the `pymanopt` problem
```python
problem = opt.Problem(manifold=manifold, cost=cost, verbosity=2)```
The keyword `verbosity` controls hwo much output you get from the system (smaller values mean less output).
5. Instantiate a `pymanopt` solver, e.g.:
```python
solver = solvers.SteepestDescent()```
The library has a lot of solvers implemented, including SteepestDescent, TrustRegions, ConjugateGradient, and NelderMead objects.
6. Perform the optimization in a single blocking function call, obtaining the optimal value of the desired quantity:
```python
Xopt = solver.solve(problem)```
#### Linear regression using `pymanopt`
_The purpose of this section is to get the first hands-out experience using `pymanopt`. We compare its output with hand-coded gradient descent and the analytic solution._
```
import pymanopt as opt
import pymanopt.solvers as solvers
import pymanopt.manifolds as manifolds
# Import the differentiable numpy -- this is crucial,
# as `np` conventionally imported will not provide gradients.
# See more at https://github.com/HIPS/autograd
import autograd.numpy as np
# Generate random data
X = np.random.randn(200, 3)
y = np.random.randint(-5, 5, (200))
```
**Exercise:** program the linear regression using manifold optimization
**Hint:** create `Euclidean` manifold and the `SteepestDescent` solver.
**Hint:** write down the formula for the cost. Remember it has the access to `X` and `y` defined above.
**Solution:**
```
import autograd.numpy as np # import again to avoid errors
# Cost function is the squared error. Remember, cost is a scalar value!
def cost(w):
return np.sum(np.sum((y - np.dot(X, w))**2)) / len(y)
# A simplest possible solver (gradient descent)
solver = solvers.SteepestDescent()
# R^3
manifold = manifolds.Euclidean(3)
# Solve the problem with pymanopt
problem = opt.Problem(manifold=manifold, cost=cost)
wopt = solver.solve(problem)
print('The following regression weights were found to minimise the '
'squared error:')
print(wopt)
```
Compute the linear regression solution via numerical optimization using steepest descent over the Euclidean manifold $\mathbb{R}^3$, _only using our handcrafted gradient descent_.
```
gd_params = dict(w_init=np.random.rand(X.shape[1]),
iterations=20,
gamma=0.1)
costs, grads, ws = gradient_descent(X, y, **gd_params)
print(" iter\t\t cost val\t grad. norm")
for iteration, (cost, grad, w) in enumerate(zip(costs, grads, ws)):
gradnorm = np.linalg.norm(grad)
print("%5d\t%+.16e\t%.8e" % (iteration, cost, gradnorm))
print('\nThe following regression weights were found to minimise the '
'squared error:')
print(w)
```
Finally, use the analytic formula.
```
print('The closed form solution to this regression problem is:')
compute_weights_multivariate(X, y)
```
Recall that you can always look what's inside by either reading the [developer docs](https://pymanopt.github.io/doc/) or simply examining the code via typing:
```python
solvers.SteepestDescent??```
Compare the code there with our hand-crafted gradient descent.
## Learning the shape space of facial landmarks
#### Problem formulation and general reference
In this part, we will create the shape space of facial landmarks. Building such a shape space is of great interest in computer vision area, where numerous applications such as face detection, facial pose regression, and emotion recognition depend heavily on such models. Here are the basics of what one needs to know to proceed with this tutorial.
1. [Active Shape Models](https://en.wikipedia.org/wiki/Active_shape_model) are a class of statistical shape models that can iteratively deform to fit to an example of the object in a image. They are commonly build by analyzing variations in points distributions and _encode plausible variations, allowing one to discriminate them from unlikely ones_.
2. One great reference for all ASMs is Tim Cootes' paper: _Cootes, T., Baldock, E. R., & Graham, J. (2000)._ [An introduction to active shape models](https://person.hst.aau.dk/lasse/teaching/IACV/doc/asm_overview.pdf). _Image processing and analysis, 223-248._ It includes motivation, math, and algorithms behind the ASM.
3. Nice reference implementations of the Active Shape Model for faces include, e.g., [this Matlab code](https://github.com/johnwmillr/ActiveShapeModels) and [this one, featuring additionally dental image analysis](https://github.com/LennartCockx/Python-Active-shape-model-for-Incisor-Segmentation).
4. Production libraries such as [dlib](http://dlib.net) implement their own ASMs of facial landmarks.
 (image taken from [Neeraj Kumar's page on LPFW](https://neerajkumar.org/databases/lfpw/))
We will (1) [look at the data](#Obtain-and-view-the-dataset),
(2) [align shapes](#Procrustes-analysis-for-the-alignment-of-facial-landmarks),
and (3) [compute the shape space](#PCA-for-learning-the-shape-space).
### Obtain and view the dataset
_The goal of this section is to examine the dataset._
```
from riemannianoptimization.tutorial_helpers import load_data, plot_landmarks
landmarks = load_data(DATA_PATH)
```
View a random subset of the data. Run the cell below multiple times to view different subsets.
You can set `draw_landmark_id` and `draw_landmarks` to 0 to turn them off.
```
import matplotlib.pyplot as plt
idx = np.random.choice(len(landmarks), size=6) # sample random faces
fig, axs = plt.subplots(ncols=6, nrows=1, figsize=(18, 3))
for ax, image in zip(axs, landmarks[idx]):
plot_landmarks(image, ax=ax, draw_landmark_id=1, draw_landmarks=1)
```
### Procrustes analysis for the alignment of facial landmarks
_The purpose of this section is to learn how to use manifold optimization for shape alignment_.
One thing to note is that the landmarks are annotated in images with different resolution and are generally **misaligned**. One can easily understand this by observing landmark scatterplots. Subtracting the mean shape or standardizing the points doesn't help.
```
fig, (ax1, ax2, ax3) = plt.subplots(figsize=(15, 5), ncols=3)
ax1.scatter(landmarks[:, 0::2], -landmarks[:, 1::2], alpha=.01)
# compute the mean shape
mean_shape = np.mean(landmarks, axis=0)
landmarks_centered = landmarks - mean_shape
ax2.scatter(landmarks_centered[:, 0::2], -landmarks_centered[:, 1::2], alpha=.01)
# compute additionally the standard deviation in shape
std_shape = np.std(landmarks, axis=0)
landmarks_standardized = landmarks_centered / std_shape
ax3.scatter(landmarks_standardized[:, 0::2], -landmarks_standardized[:, 1::2], alpha=.01);
```
**Q:** Why such variation? Why we don't see separate clusters of "average keypoints", like average eye1, eye2, and etc."?
**A:** This alignment is due to variations in pose, gender, and emotion, as well as (an mostly due to) variation in viewing angles and occlusions found in real images.
We must _align_ shapes to a _canonical pose_ to proceed with building the ASM.
This will be done in a simple way via [Procrustes analysis](https://en.wikipedia.org/wiki/Procrustes_analysis). In its simplest form, Procrustes analysis aligns each shape so that the sum of distances of each shape to the mean $D = \sum\limits_i ||\mathbf{x}_i − \mathbf{\overline{x}}||^2_2)$ is minimised:
1. Translate each example so that its center of gravity is at the origin.
2. Choose one example as an initial estimate of the mean shape and scale.
3. Record the first estimate as $\overline{x}_0$ to define the default orientation.
4. Align all the shapes with the current estimate of the mean shape.
5. Re-estimate the mean from aligned shapes.
6. Apply constraints on scale and orientation to the current estimate of the mean by aligning it with x ̄0 and scaling so that $|\overline{x}| = 1$.
7. If not converged, return to 4.
(Convergence is declared if the estimate of the mean does not change
significantly after an iteration)

```
# A small helper function we will need
# to center the shape at the origin and scale it to a unit norm.
def standardize(shape):
# shape must have the shape [n_landmarks, 2], e.g. [35, 2]
shape -= np.mean(shape, 0)
shape_norm = np.linalg.norm(shape)
shape /= shape_norm
return shape
# A large helper function that we will employ to align
# the *entire collection* of shapes -- skip for now.
def align_landmarks(landmarks, mean_shape=None, aligner=None, n_iterations=1):
"""
Aligns landmarks to an estimated mean shape.
In this function, `landmarks` are always assumed to be array of shape [n, 35, 2].
aligner: a function getting two arguments (mean_shape and shape), returning
the transformation from shape to mean_shape
"""
# Translate each example so that its center of gravity is at the origin.
landmarks -= np.mean(landmarks, axis=1, keepdims=True)
# Choose one example as an initial estimate of the mean shape and scale
# so that |x ̄| = x ̄21 + y ̄12 + x ̄2 . . . = 1.
mean_shape = np.mean(landmarks, axis=0)
mean_shape = standardize(mean_shape)
# Record the first estimate as x0 to define the default orientation.
mean_shape_0 = mean_shape[:]
def align_to_mean(landmarks, mean_shape, aligner=None):
aligned_landmarks = []
for shape in landmarks:
shape = standardize(shape)
shape = aligner(mean_shape, shape)
aligned_landmarks.append(shape)
return np.array(aligned_landmarks)
print(" iter\t cost val.\t mean diff.")
for iteration in range(n_iterations):
# Align all the shapes with the current estimate of the mean shape.
aligned_landmarks = align_to_mean(landmarks, mean_shape, aligner=aligner)
mean_shape_prev = mean_shape
# Re-estimate the mean from aligned shapes.
mean_shape = np.mean(aligned_landmarks, axis=0)
# Apply constraints on scale and orientation to the current
# estimate of the mean by aligning it with x ̄0 and scaling so that |x ̄| = 1.
mean_shape = aligner(mean_shape_0, mean_shape)
mean_shape /= np.linalg.norm(mean_shape)
cost = np.sum(
np.linalg.norm(aligned_landmarks - mean_shape, axis=(1, 2))
)
mean_shape_diff = np.linalg.norm(mean_shape - mean_shape_prev)
print("%5d\t%+.8e\t%.8e" % (iteration, cost, mean_shape_diff))
# If not converged, return to 4.
# (Convergence is declared if the estimate of the mean does not change significantly after an iteration)
return np.array(aligned_landmarks), mean_shape
landmarks = landmarks.reshape(-1, 35, 2)
```
One may naturally resort to [scipy.spatial.procrustes](https://docs.scipy.org/doc/scipy-1.2.1/reference/generated/scipy.spatial.procrustes.html), which computes an optimal alignment using a scale vector $\mathbf{s}$ and a rotation matrix $\mathbf{R}$, solving [orthogonal Procrustes problem](https://en.wikipedia.org/wiki/Orthogonal_Procrustes_problem).
**Exercise:** Using `scipy.spatial.procrustes`, write a default aligner function for our `align_landmarks`. This function must accept two shapes and return the second one aligned to the first one.
**Solution:**
```
from scipy.spatial import procrustes
def default_procrustes(target_shape, source_shape):
"""Align the source shape to the target shape.
For standardized shapes, can skip translating/scaling
aligned source by target's parameters.
target_shape, source_shape: ndarrays of shape [35, 2]
return ndarray of shape [35, 2]
"""
target_shape_standardized, source_shape_standardized_aligned, _ = procrustes(target_shape, source_shape)
center = np.mean(target_shape, axis=0)
return source_shape_standardized_aligned * np.linalg.norm(target_shape - center) + center
# Try aligning a single shape
mean_shape = np.mean(landmarks, axis=0)
mean_shape = standardize(mean_shape)
shape_std = standardize(landmarks[400])
aligned_shape = default_procrustes(mean_shape, shape_std)
fig, (ax1, ax2, ax3) = plt.subplots(figsize=(15, 5), ncols=3)
plot_landmarks(mean_shape, ax=ax1)
ax1.set_title('Mean shape')
# compute the mean shape
plot_landmarks(mean_shape, ax=ax2, color_landmarks='grey', color_contour='grey', alpha=0.5)
plot_landmarks(shape_std, ax=ax2)
ax2.set_title('Another shape, distance = {0:.3f}'.format(np.linalg.norm(mean_shape - shape_std)))
# compute additionally the standard deviation in shape
plot_landmarks(mean_shape, ax=ax3, color_landmarks='grey', color_contour='grey', alpha=0.5)
plot_landmarks(aligned_shape, ax=ax3)
ax3.set_title('Aligned shapes, distance = {0:.3f}'.format(np.linalg.norm(mean_shape - aligned_shape)));
# Align the entire dataset to a mean shape
aligned_landmarks, mean_shape = align_landmarks(landmarks, aligner=default_procrustes, n_iterations=3)
fig, (ax1, ax2) = plt.subplots(figsize=(10, 5), ncols=2)
ax1.scatter(aligned_landmarks[:, :, 0], -aligned_landmarks[:, :, 1], alpha=.01)
ax1.set_title('Aligned landmarks cloud')
# compute the mean shape
plot_landmarks(mean_shape, ax=ax2)
ax2.set_title('Mean landmarks');
```
#### But let's do the same using Riemannian optimization!
**Q:** Why we need to optimize anything by hand, if we have the procrustes implemented in scipy?
**A:** To have more freedom in choosing the transforms!
```
import pymanopt as opt
import pymanopt.manifolds as manifolds
import pymanopt.solvers as solvers
```
Recall that the orthogonal Procrustus problem seeks for:
$$
R=\arg \min _{\Omega }\|\Omega A-B\|_{F}\quad \mathrm {subject\ to} \quad \Omega ^{T}\Omega =I,
$$
i.e. $R$ belongs to the Stiefel manifold. One can optimize that, however, it might be more reasonable to optimize using rotations + scaling.
In here, $A$ and $B$ are our shapes, and $\Omega$ is our seeked transform.
**Exercise:** program the variants of the Procrustes alignment using the following variants:
* $R \in \text{Stiefel}(2, 2)$, i.e. we seek a projection matrix using `Stiefel` object
* $R \in \text{SO}(2)$, i.e. we seek a rotation matrix using `Rotations` object
* $R \in \text{SO}(2)$ and $s \in R^2$, i.e. we seek a rotation + scaling transform using `Product` of `Rotations` and `Euclidean` manifolds, see example [here](https://github.com/pymanopt/pymanopt/blob/master/examples/regression_offset_autograd.py))
**Solution:**
```
import autograd.numpy as np # import here to avoid errors
def riemannian_procrustes_projection(mean_shape, shape):
"""Align the source shape to the target shape using projection.
target_shape, source_shape: ndarrays of shape [35, 2]
return ndarray of shape [35, 2]
"""
def cost(R):
return np.sum(
np.square(np.dot(shape, R.T) - mean_shape)
)
solver = solvers.SteepestDescent()
manifold = manifolds.Stiefel(2, 2)
problem = opt.Problem(manifold=manifold, cost=cost, verbosity=0)
R_opt = solver.solve(problem)
return np.dot(shape, R_opt.T)
def riemannian_procrustes_rotation(mean_shape, shape):
"""Align the source shape to the target shape using rotation.
target_shape, source_shape: ndarrays of shape [35, 2]
return ndarray of shape [35, 2]
"""
def cost(R):
return np.sum(
np.square(np.dot(shape, R.T) - mean_shape)
)
solver = solvers.SteepestDescent()
manifold = manifolds.Rotations(2)
problem = opt.Problem(manifold=manifold, cost=cost, verbosity=0)
R_opt = solver.solve(problem)
return np.dot(shape, R_opt.T)
def riemannian_procrustes_rotation_scaling(mean_shape, shape):
"""Align the source shape to the target shape using a combination rotation and scaling.
target_shape, source_shape: ndarrays of shape [35, 2]
return ndarray of shape [35, 2]
"""
def cost(Rs):
R, s = Rs
return np.sum(
np.square(np.dot(shape, R.T) * s - mean_shape)
)
solver = solvers.SteepestDescent()
manifold = manifolds.Product(
[manifolds.Rotations(2),
manifolds.Euclidean(2)]
)
problem = opt.Problem(manifold=manifold, cost=cost, verbosity=0)
Rs_opt = solver.solve(problem)
R_opt, s_opt = Rs_opt
return np.dot(shape, R_opt.T) * s_opt
# Stiefel
aligned_landmarks, mean_shape = align_landmarks(landmarks, aligner=riemannian_procrustes_projection, n_iterations=3)
fig, (ax1, ax2) = plt.subplots(figsize=(10, 5), ncols=2)
ax1.scatter(aligned_landmarks[:, :, 0], -aligned_landmarks[:, :, 1], alpha=.01)
ax1.set_title('Aligned landmarks cloud')
# compute the mean shape
plot_landmarks(mean_shape, ax=ax2)
ax2.set_title('Mean landmarks');
# Rotations
aligned_landmarks, mean_shape = align_landmarks(landmarks, aligner=riemannian_procrustes_rotation, n_iterations=3)
fig, (ax1, ax2) = plt.subplots(figsize=(10, 5), ncols=2)
ax1.scatter(aligned_landmarks[:, :, 0], -aligned_landmarks[:, :, 1], alpha=.01)
ax1.set_title('Aligned landmarks cloud')
# compute the mean shape
plot_landmarks(mean_shape, ax=ax2)
ax2.set_title('Mean landmarks');
# Rotations + scale
aligned_landmarks, mean_shape = align_landmarks(landmarks, aligner=riemannian_procrustes_rotation_scaling, n_iterations=3)
fig, (ax1, ax2) = plt.subplots(figsize=(10, 5), ncols=2)
ax1.scatter(aligned_landmarks[:, :, 0], -aligned_landmarks[:, :, 1], alpha=.01)
ax1.set_title('Aligned landmarks cloud')
# compute the mean shape
plot_landmarks(mean_shape, ax=ax2)
ax2.set_title('Mean landmarks');
```
### PCA for learning the shape space
_The goal of this section is to learn how to program the simple but powerful PCA linear dimensionality reduction technique using Riemannian optimization._
The typical way of learning the shape space is to find a low-dimensional manifold controlling most of the variability in shapes in a (hopefully) interpretable way. Such a manifold is commonly found using [PCA method](https://en.wikipedia.org/wiki/Principal_component_analysis).
We will apply PCA to a matrix $\mathbf{X} \in \mathbb{R}^{n \times 70}$ of aligned shapes.
A common way of learning PCA is using SVD implemented in the [`sklearn.decomposition.PCA` class](http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html).
```
aligned_landmarks = aligned_landmarks.reshape(-1, 70)
from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit(aligned_landmarks)
d0 = pca.inverse_transform(
pca.transform(aligned_landmarks)
)
data_scaled_vis = d0.reshape((-1, 35, 2))
plt.scatter(data_scaled_vis[:200, :, 0], -data_scaled_vis[:200, :, 1], alpha=.1)
```
#### Do the same using Riemannian optimization
Recall that PCA finds a low-dimensional linear subspace by searching for a corresponding orthogonal projection. Thus, PCA searches for an orthogonal projection $M$ such that:
$$
M = \arg \min _{\Omega }
\|X - \Omega \Omega^{\intercal} X\|^2_{F}
\quad
\mathrm {subject\ to} \quad \Omega ^{T}\Omega = I,
$$
i.e. $\Omega$ belongs to the Stiefel manifold $\mathcal{O}^{d \times r}$.
The value $\|X - M M^{\intercal} X\|^2_{F}$ is the reconstruction error from projecting $X$ to $r$-dimensional subspace and restoring back to $d$-dimensional (original) one.
**Exercise:** program the PCA by finding an orthogonal projection from 70-dimensional onto 2-dimensional subspace, using `pymanopt`.
**Hint:** use `Stiefel(70, 2)` manifold and the reconstruction error cost as described above.
**Solution:**
```
# Cost function is the reconstruction error
def cost(w):
return np.sum(np.sum(
(aligned_landmarks - np.dot(w, np.dot(w.T, aligned_landmarks.T)).T)**2
))
solver = solvers.TrustRegions()
manifold = manifolds.Stiefel(70, 2)
problem = opt.Problem(manifold=manifold, cost=cost)
wopt = solver.solve(problem)
print('The following projection matrix was found to minimise '
'the squared reconstruction error: ')
print(wopt)
```
Now construct a low-dimensional approximation of $X$, by projecting to $r$-dimensional parameter space and back.
```
aligned_landmarks_r = np.dot(wopt, np.dot(wopt.T, aligned_landmarks.T)).T
aligned_landmarks_r = aligned_landmarks_r.reshape((-1, 35, 2))
plt.scatter(aligned_landmarks_r[:200, :, 0], -aligned_landmarks_r[:200, :, 1], alpha=.1)
```
#### Exploring the lower-dimensional linear manifold parameterizing landmarks
_The purpose of this part is to understand how the coordinate values in the lower-dimensional space influences the landmark shape_.
Coordinates along principal components _parameterize_ the shape, i.e. smooth walk along these directions should result in interpolation between shapes.
**Exercise:** explore the lower-dimensional linear manifold parameterizing landmarks:
* Show samples _from the data_ with different coordinated along PC\#1 (hint: use `reconstructions_sorted_along_pc` below)
* Show _synthetic_ samples obtained by moving in the data manifold along PC\#1 (hint: modify `reconstructions_sorted_along_pc` below into `vary_on_manifold`)
```
def reconstructions_sorted_along_pc(landmarks, w, pc=1, n_shapes=6):
# project to r-dimensional manifold
projected_landmarks = np.dot(w.T, landmarks.T).T
# sort along dimension selected by pc
pc_idx = np.argsort(projected_landmarks[:, pc])
# reconstruct several shapes with varying degree
# of expressiveness in parameter pc
idx = np.linspace(0, len(landmarks), n_shapes).astype(int)
idx[-1] = idx[-1] - 1
shapes_to_reconstruct = projected_landmarks[pc_idx[idx]].T
reconstructions = np.dot(w, shapes_to_reconstruct).T
reconstructions = reconstructions.reshape((-1, 35, 2))
return reconstructions
def plot_variability_along_pc(landmarks, w, pc=1, n_shapes=6):
reconstructions = reconstructions_sorted_along_pc(landmarks, w, pc=pc, n_shapes=n_shapes)
fig, axs = plt.subplots(ncols=6, nrows=1, figsize=(18, 3))
for ax, image in zip(axs, reconstructions):
plot_landmarks(image, ax=ax)
plot_variability_along_pc(aligned_landmarks, wopt, pc=0)
```
**Q:** Would this variability necessary be exactly like the PCA?
**A:** It should, but the order of principal components is not guaranteed.
**Solution:**
```
# PC2
def vary_on_manifold(landmarks, id, w, pc=1, n_shapes=6):
projected_landmarks = np.dot(w.T, landmarks.T).T
min_pc_value = projected_landmarks[:, pc].min()
max_pc_value = projected_landmarks[:, pc].max()
pc_values = np.linspace(min_pc_value, max_pc_value, n_shapes)
the_one_projection = projected_landmarks[id][None]
shapes_to_reconstruct = np.tile(the_one_projection, (n_shapes, 1))
shapes_to_reconstruct[:, pc] = pc_values
reconstructions = np.dot(w, shapes_to_reconstruct.T).T
reconstructions = reconstructions.reshape((-1, 35, 2))
fig, axs = plt.subplots(ncols=n_shapes, nrows=1, figsize=(3 * n_shapes, 3))
for ax, image in zip(axs, reconstructions):
plot_landmarks(image, ax=ax)
vary_on_manifold(aligned_landmarks, 0, wopt, pc=1, n_shapes=30)
```
### Analysing the shape space of facial landmarks via MDS
#### Compute embedding of the shape space into 2D, preserving distances between shapes
Classic multidimensional scaling (MDS) aims to find an orthogonal mapping $M$ such that:
$$
M = \arg \min _{\Omega }
\sum_i \sum_j (d_X (\mathbf{x}_i, \mathbf{x}_j) -
d_Y (\Omega^{\intercal}\mathbf{x}_i, \Omega^{\intercal}\mathbf{x}_j))^2
\quad
\mathrm {subject\ to} \quad \Omega ^{T}\Omega = I,
$$
i.e. $\Omega$ belongs to the Stiefel manifold $\mathcal{O}^{d \times r}$ where $d$ is the dimensionality of the original space, and $r$ is the dimensionality of the compressed space.
In other words, consider distances $d_X (\mathbf{x}_i, \mathbf{x}_j)$ between ech pair $(i, j)$ of objects in the original space $X$. MDS aims at projecting $\mathbf{x}_i$'s to a linear subspace $Y$ such that each distance $d_Y (M^{\intercal}\mathbf{x}_i, M^{\intercal}\mathbf{x}_j)$ approximates $d_X (\mathbf{x}_i, \mathbf{x}_j)$ as closely as possible.
```
aligned_landmarks = aligned_landmarks.reshape((-1, 70))
# a slightly tricky way of computing pairwise distances for [n, d] matrixes of objects,
# see https://stackoverflow.com/questions/28687321/computing-euclidean-distance-for-numpy-in-python
def calculate_pairwise_distances(points):
return ((points[..., None] - points[..., None].T) ** 2).sum(1)
euclidean_distances = calculate_pairwise_distances(aligned_landmarks)
```
**Exercise:** program MDS dimensionality reduction method using `pymanopt`. Project from 70-dimensional to 2-dimensional space.
**Hint:** to compute distances, use `calculate_pairwise_distances` above.
**Hint:** use `Stiefel(70, 2)` manifold
**Solution:**
```
import autograd.numpy as np
def cost(w):
projected_shapes = np.dot(w.T, aligned_landmarks.T).T
projected_distances = \
((projected_shapes[:, :, None] - projected_shapes[:, :, None].T) ** 2).sum(1)
return np.sum(np.sum(
(euclidean_distances - projected_distances)**2
))
solver = solvers.TrustRegions()
manifold = manifolds.Stiefel(70, 2)
problem = opt.Problem(manifold=manifold, cost=cost)
wopt = solver.solve(problem)
print('The following projection matrix was found to minimise '
'the squared reconstruction error: ')
print(wopt)
projected_shapes = np.dot(wopt.T, aligned_landmarks.T).T
from riemannianoptimization.tutorial_helpers import prepare_html_for_visualization
from IPython.display import HTML
HTML(prepare_html_for_visualization(projected_shapes, aligned_landmarks, scatterplot_size=[700, 700],
annotation_size=[100, 100], floating_annotation=True))
```
## Learning the Gaussian mixture models for word embeddings
This part of the tutorial is in a separate notebook, `riemannian_opt_gmm_embeddings.ipynb`.
## Bibliography
This tutorial is in part inspired by the work _Cunningham, J. P., & Ghahramani, Z. (2015). [Linear dimensionality reduction: Survey, insights, and generalizations.](http://www.jmlr.org/papers/volume16/cunningham15a/cunningham15a.pdf) The Journal of Machine Learning Research, 16(1), 2859-2900._ Reading this work in full will help you greatly broaden your understanding of linear dimensionality reduction techniques, systematize your knowledge of optimization setups involved therein, and get an overview of this area.
_Townsend, J., Koep, N., & Weichwald, S. (2016). [Pymanopt: A python toolbox for optimization on manifolds using automatic differentiation](http://jmlr.org/papers/volume17/16-177/16-177.pdf). The Journal of Machine Learning Research, 17(1), 4755-4759._
_Boumal, N., Mishra, B., Absil, P. A., & Sepulchre, R. (2014). [Manopt, a Matlab toolbox for optimization on manifolds](http://www.jmlr.org/papers/volume15/boumal14a/boumal14a.pdf). The Journal of Machine Learning Research, 15(1), 1455-1459._
This tutorial uses data and annotations from the two works
_Belhumeur, P. N., Jacobs, D. W., Kriegman, D. J., & Kumar, N. (2013). [Localizing parts of faces using a consensus of exemplars](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.227.8441&rep=rep1&type=pdf). IEEE transactions on pattern analysis and machine intelligence, 35(12), 2930-2940._
and
_Huang, G. B., Mattar, M., Berg, T., & Learned-Miller, E. (2008, October)._ [Labeled faces in the wild: A database forstudying face recognition in unconstrained environments](https://hal.inria.fr/docs/00/32/19/23/PDF/Huang_long_eccv2008-lfw.pdf).
|
github_jupyter
|
!pip install --upgrade git+https://github.com/mlss-skoltech/tutorials.git#subdirectory=geometric_techniques_in_ML
!pip install pymanopt autograd
!pip install scipy==1.2.1 -U
import pkg_resources
DATA_PATH = pkg_resources.resource_filename('riemannianoptimization', 'data/')
def compute_weights_multivariate(X, y):
"""
Given feature array X [n_samples, 1], target vector y [n_samples],
compute the optimal least squares solution using the formulae above.
For brevity, no bias term!
"""
# Compute the "inverting operator"
R = np.dot(
np.linalg.inv(
np.dot(X.T, X)
), X.T
)
# Compute the actual solution
w = np.dot(R, y)
return w
from sklearn.metrics import mean_squared_error
def compute_gradient(X, y, w):
"""
Computes the gradient of MSE loss
for multivariate linear regression of X onto y
w.r.t. w, evaluated at the current w.
"""
prediction = np.dot(X, w) # [n_objects, n_features] * [n_features] -> [n_objects]
error = prediction - y # [n_objects]
return 2 * np.dot(error, X) / len(error) # [n_objects] * [n_objects, n_features] -> [n_features]
def gradient_descent(X, y, w_init, iterations=1, gamma=0.01):
"""
Performs the required number of iterations of gradient descent.
Parameters:
X [n_objects, n_features]: matrix of featues
y [n_objects]: responce (dependent) variable
w_init: the value of w used as an initializer
iterations: number of steps for gradient descent to compute
gamma: learning rate (gradient multiplier)
"""
costs, grads, ws = [], [], []
w = w_init
for i in range(iterations):
# Compute our cost in current point (before the gradient step)
costs.append(mean_squared_error(y, np.dot(X, w)) / len(y))
# Remember our weights w in current point
ws.append(w)
# Compute gradient for w
w_grad = compute_gradient(X, y, w)
grads.append(w_grad)
# Update the current weight w using the formula above (see comments)
w = w - gamma * w_grad
# record the last weight
ws.append(w)
return costs, grads, ws
import autograd.numpy as np```
but theano and TensorFlow backends are supported, too.
We will also require importing `pymanopt` itself, along with the necessary submodules:
2. Define (or rather, select) the manifold of interest. `pymanopt` provides a [large number](https://pymanopt.github.io/doc/#manifolds) of predefined manifold classes (however, a lot less than the [original ManOpt Matlab library](https://www.manopt.org/tutorial.html#manifolds)). E.g., to instantiate a manifold $V_{2}(\mathbb {R}^{5}) = \{X \in \mathbb{R}^{5 \times 2} : X^TX = I_2\}^k$ of orthogonal projection matrices from $\mathbb{R}^5$ to $\mathbb{R}^2$ you will write:
Available manifolds include [Steifel](https://pymanopt.github.io/doc/#module-pymanopt.manifolds.stiefel) ([wiki](https://en.wikipedia.org/wiki/Stiefel_manifold)), Rotations or SO(n) ([wiki](https://en.wikipedia.org/wiki/Orthogonal_group)), [Euclidean](https://pymanopt.github.io/doc/#module-pymanopt.manifolds.euclidean), [Positive Definite](https://pymanopt.github.io/doc/#pymanopt.manifolds.psd.PositiveDefinite) ([wiki](https://en.wikipedia.org/wiki/Definiteness_of_a_matrix)), and [Product](https://pymanopt.github.io/doc/#pymanopt.manifolds.product.Product), along many others.
3. Define the **scalar** cost function (here using `autograd.numpy`) to be minimized by the
Note that the scalar `cost` python function **will have access to objects defined elsewhere in code** (which allows accessing $X$ and $y$ for optimization).
4. Instantiate the `pymanopt` problem
The keyword `verbosity` controls hwo much output you get from the system (smaller values mean less output).
5. Instantiate a `pymanopt` solver, e.g.:
The library has a lot of solvers implemented, including SteepestDescent, TrustRegions, ConjugateGradient, and NelderMead objects.
6. Perform the optimization in a single blocking function call, obtaining the optimal value of the desired quantity:
#### Linear regression using `pymanopt`
_The purpose of this section is to get the first hands-out experience using `pymanopt`. We compare its output with hand-coded gradient descent and the analytic solution._
**Exercise:** program the linear regression using manifold optimization
**Hint:** create `Euclidean` manifold and the `SteepestDescent` solver.
**Hint:** write down the formula for the cost. Remember it has the access to `X` and `y` defined above.
**Solution:**
Compute the linear regression solution via numerical optimization using steepest descent over the Euclidean manifold $\mathbb{R}^3$, _only using our handcrafted gradient descent_.
Finally, use the analytic formula.
Recall that you can always look what's inside by either reading the [developer docs](https://pymanopt.github.io/doc/) or simply examining the code via typing:
Compare the code there with our hand-crafted gradient descent.
## Learning the shape space of facial landmarks
#### Problem formulation and general reference
In this part, we will create the shape space of facial landmarks. Building such a shape space is of great interest in computer vision area, where numerous applications such as face detection, facial pose regression, and emotion recognition depend heavily on such models. Here are the basics of what one needs to know to proceed with this tutorial.
1. [Active Shape Models](https://en.wikipedia.org/wiki/Active_shape_model) are a class of statistical shape models that can iteratively deform to fit to an example of the object in a image. They are commonly build by analyzing variations in points distributions and _encode plausible variations, allowing one to discriminate them from unlikely ones_.
2. One great reference for all ASMs is Tim Cootes' paper: _Cootes, T., Baldock, E. R., & Graham, J. (2000)._ [An introduction to active shape models](https://person.hst.aau.dk/lasse/teaching/IACV/doc/asm_overview.pdf). _Image processing and analysis, 223-248._ It includes motivation, math, and algorithms behind the ASM.
3. Nice reference implementations of the Active Shape Model for faces include, e.g., [this Matlab code](https://github.com/johnwmillr/ActiveShapeModels) and [this one, featuring additionally dental image analysis](https://github.com/LennartCockx/Python-Active-shape-model-for-Incisor-Segmentation).
4. Production libraries such as [dlib](http://dlib.net) implement their own ASMs of facial landmarks.
 (image taken from [Neeraj Kumar's page on LPFW](https://neerajkumar.org/databases/lfpw/))
We will (1) [look at the data](#Obtain-and-view-the-dataset),
(2) [align shapes](#Procrustes-analysis-for-the-alignment-of-facial-landmarks),
and (3) [compute the shape space](#PCA-for-learning-the-shape-space).
### Obtain and view the dataset
_The goal of this section is to examine the dataset._
View a random subset of the data. Run the cell below multiple times to view different subsets.
You can set `draw_landmark_id` and `draw_landmarks` to 0 to turn them off.
### Procrustes analysis for the alignment of facial landmarks
_The purpose of this section is to learn how to use manifold optimization for shape alignment_.
One thing to note is that the landmarks are annotated in images with different resolution and are generally **misaligned**. One can easily understand this by observing landmark scatterplots. Subtracting the mean shape or standardizing the points doesn't help.
**Q:** Why such variation? Why we don't see separate clusters of "average keypoints", like average eye1, eye2, and etc."?
**A:** This alignment is due to variations in pose, gender, and emotion, as well as (an mostly due to) variation in viewing angles and occlusions found in real images.
We must _align_ shapes to a _canonical pose_ to proceed with building the ASM.
This will be done in a simple way via [Procrustes analysis](https://en.wikipedia.org/wiki/Procrustes_analysis). In its simplest form, Procrustes analysis aligns each shape so that the sum of distances of each shape to the mean $D = \sum\limits_i ||\mathbf{x}_i − \mathbf{\overline{x}}||^2_2)$ is minimised:
1. Translate each example so that its center of gravity is at the origin.
2. Choose one example as an initial estimate of the mean shape and scale.
3. Record the first estimate as $\overline{x}_0$ to define the default orientation.
4. Align all the shapes with the current estimate of the mean shape.
5. Re-estimate the mean from aligned shapes.
6. Apply constraints on scale and orientation to the current estimate of the mean by aligning it with x ̄0 and scaling so that $|\overline{x}| = 1$.
7. If not converged, return to 4.
(Convergence is declared if the estimate of the mean does not change
significantly after an iteration)

One may naturally resort to [scipy.spatial.procrustes](https://docs.scipy.org/doc/scipy-1.2.1/reference/generated/scipy.spatial.procrustes.html), which computes an optimal alignment using a scale vector $\mathbf{s}$ and a rotation matrix $\mathbf{R}$, solving [orthogonal Procrustes problem](https://en.wikipedia.org/wiki/Orthogonal_Procrustes_problem).
**Exercise:** Using `scipy.spatial.procrustes`, write a default aligner function for our `align_landmarks`. This function must accept two shapes and return the second one aligned to the first one.
**Solution:**
#### But let's do the same using Riemannian optimization!
**Q:** Why we need to optimize anything by hand, if we have the procrustes implemented in scipy?
**A:** To have more freedom in choosing the transforms!
Recall that the orthogonal Procrustus problem seeks for:
$$
R=\arg \min _{\Omega }\|\Omega A-B\|_{F}\quad \mathrm {subject\ to} \quad \Omega ^{T}\Omega =I,
$$
i.e. $R$ belongs to the Stiefel manifold. One can optimize that, however, it might be more reasonable to optimize using rotations + scaling.
In here, $A$ and $B$ are our shapes, and $\Omega$ is our seeked transform.
**Exercise:** program the variants of the Procrustes alignment using the following variants:
* $R \in \text{Stiefel}(2, 2)$, i.e. we seek a projection matrix using `Stiefel` object
* $R \in \text{SO}(2)$, i.e. we seek a rotation matrix using `Rotations` object
* $R \in \text{SO}(2)$ and $s \in R^2$, i.e. we seek a rotation + scaling transform using `Product` of `Rotations` and `Euclidean` manifolds, see example [here](https://github.com/pymanopt/pymanopt/blob/master/examples/regression_offset_autograd.py))
**Solution:**
### PCA for learning the shape space
_The goal of this section is to learn how to program the simple but powerful PCA linear dimensionality reduction technique using Riemannian optimization._
The typical way of learning the shape space is to find a low-dimensional manifold controlling most of the variability in shapes in a (hopefully) interpretable way. Such a manifold is commonly found using [PCA method](https://en.wikipedia.org/wiki/Principal_component_analysis).
We will apply PCA to a matrix $\mathbf{X} \in \mathbb{R}^{n \times 70}$ of aligned shapes.
A common way of learning PCA is using SVD implemented in the [`sklearn.decomposition.PCA` class](http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html).
#### Do the same using Riemannian optimization
Recall that PCA finds a low-dimensional linear subspace by searching for a corresponding orthogonal projection. Thus, PCA searches for an orthogonal projection $M$ such that:
$$
M = \arg \min _{\Omega }
\|X - \Omega \Omega^{\intercal} X\|^2_{F}
\quad
\mathrm {subject\ to} \quad \Omega ^{T}\Omega = I,
$$
i.e. $\Omega$ belongs to the Stiefel manifold $\mathcal{O}^{d \times r}$.
The value $\|X - M M^{\intercal} X\|^2_{F}$ is the reconstruction error from projecting $X$ to $r$-dimensional subspace and restoring back to $d$-dimensional (original) one.
**Exercise:** program the PCA by finding an orthogonal projection from 70-dimensional onto 2-dimensional subspace, using `pymanopt`.
**Hint:** use `Stiefel(70, 2)` manifold and the reconstruction error cost as described above.
**Solution:**
Now construct a low-dimensional approximation of $X$, by projecting to $r$-dimensional parameter space and back.
#### Exploring the lower-dimensional linear manifold parameterizing landmarks
_The purpose of this part is to understand how the coordinate values in the lower-dimensional space influences the landmark shape_.
Coordinates along principal components _parameterize_ the shape, i.e. smooth walk along these directions should result in interpolation between shapes.
**Exercise:** explore the lower-dimensional linear manifold parameterizing landmarks:
* Show samples _from the data_ with different coordinated along PC\#1 (hint: use `reconstructions_sorted_along_pc` below)
* Show _synthetic_ samples obtained by moving in the data manifold along PC\#1 (hint: modify `reconstructions_sorted_along_pc` below into `vary_on_manifold`)
**Q:** Would this variability necessary be exactly like the PCA?
**A:** It should, but the order of principal components is not guaranteed.
**Solution:**
### Analysing the shape space of facial landmarks via MDS
#### Compute embedding of the shape space into 2D, preserving distances between shapes
Classic multidimensional scaling (MDS) aims to find an orthogonal mapping $M$ such that:
$$
M = \arg \min _{\Omega }
\sum_i \sum_j (d_X (\mathbf{x}_i, \mathbf{x}_j) -
d_Y (\Omega^{\intercal}\mathbf{x}_i, \Omega^{\intercal}\mathbf{x}_j))^2
\quad
\mathrm {subject\ to} \quad \Omega ^{T}\Omega = I,
$$
i.e. $\Omega$ belongs to the Stiefel manifold $\mathcal{O}^{d \times r}$ where $d$ is the dimensionality of the original space, and $r$ is the dimensionality of the compressed space.
In other words, consider distances $d_X (\mathbf{x}_i, \mathbf{x}_j)$ between ech pair $(i, j)$ of objects in the original space $X$. MDS aims at projecting $\mathbf{x}_i$'s to a linear subspace $Y$ such that each distance $d_Y (M^{\intercal}\mathbf{x}_i, M^{\intercal}\mathbf{x}_j)$ approximates $d_X (\mathbf{x}_i, \mathbf{x}_j)$ as closely as possible.
**Exercise:** program MDS dimensionality reduction method using `pymanopt`. Project from 70-dimensional to 2-dimensional space.
**Hint:** to compute distances, use `calculate_pairwise_distances` above.
**Hint:** use `Stiefel(70, 2)` manifold
**Solution:**
| 0.886899 | 0.991595 |
# Behavior Cloning Project
### Import Libraries
```
#keras
import keras
from keras.applications.resnet50 import ResNet50
from keras.layers import *
from keras.backend import clear_session
from keras.models import Model
import tensorflow as tf
# Helper libraries
import numpy as np
import pandas as pd
import math
import cv2
from PIL import Image
from sklearn.model_selection import train_test_split
import random
import csv
import matplotlib.pyplot as plt
from progressbar import *
import random
print('Keras Version: {}'.format(keras.__version__))
```
### Import Data
```
def process_sample(smpl, correction_factor):
prefix = ['dataK/','','data2/'][1]
cf = 0.075
cid = random.randrange(0,3)
smpl[1] = smpl[1].replace(' ', '')
smpl[2] = smpl[2].replace(' ', '')
if cid>=0:
crctn = cid*cf
else:
crctn = 0-cf
# crctn = 0
# return [cv2.imread(prefix + smpl[cid]), float(smpl[3])+crctn]
if random.random() >= 0.5:
return [cv2.flip(cv2.imread(prefix + smpl[cid]), 0),
(-1)*(float(smpl[3])+crctn)]
else:
return [cv2.imread(prefix + smpl[cid]),
float(smpl[3])+crctn]
reader = csv.reader(open('data/driving_log_rough.csv'))
lines = [line for line in reader][1:]
train_lines, valid_lines = train_test_split(lines, test_size=0.2)
images, measurements = zip(*[process_sample(smpl, 0.2) for smpl in progressbar(train_lines)])
X_train, y_train = [np.array(images), np.array(measurements)]
images, measurements = zip(*[process_sample(smpl, 0.2) for smpl in progressbar(valid_lines)])
X_valid, y_valid = [np.array(images), np.array(measurements)]
batch_size=32
count = 0
for x in X_train:
if x is None:
count+=1
print("{}% of X values empty".format(count/len(X_train)*100))
print("Average steering angle of {} angles in training set: {}".format(len(y_train), np.average(y_train)))
print("Average steering angle of {} angles validation set: {}".format(len(y_valid), np.average(y_valid)))
total = len(y_train) + len(y_valid)
print("Overall average steering angle: {}".format(np.average(y_train) * len(y_train) / total +
np.average(y_valid) * len(y_valid) / total))
```
### Define a Model
```
def create_model():
#Instantiate an empty model
model = keras.Sequential()
model.add(Lambda(lambda x: x / 255.0 - 0.5, input_shape=(160, 320, 3)))
model.add(Cropping2D(cropping=((70,25),(0,0))))
model.add(Conv2D(20, 6, 6, subsample=(2, 2), activation='relu'))
model.add(Conv2D(40, 5, 5, subsample=(2, 2), activation='relu'))
model.add(Conv2D(50, 5, 5, subsample=(2, 2), activation='relu'))
model.add(Conv2D(64, 3, 3, activation='relu'))
model.add(Conv2D(64, 3, 3, activation='relu'))
model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(1, activation='linear'))
# Compile the model
model.compile(loss='mse', optimizer='adam')
return model
```
### Save Model
```
clear_session()
model = create_model()
model.summary()
history = model.fit(x=X_train,
y=y_train,
batch_size=32,
epochs=10,
verbose=1,
validation_data=(X_valid, y_valid),
shuffle=True)
```
### Output Model
```
model.save('my_model.h5')
print(model.predict(X_valid[0:20]))
```
|
github_jupyter
|
#keras
import keras
from keras.applications.resnet50 import ResNet50
from keras.layers import *
from keras.backend import clear_session
from keras.models import Model
import tensorflow as tf
# Helper libraries
import numpy as np
import pandas as pd
import math
import cv2
from PIL import Image
from sklearn.model_selection import train_test_split
import random
import csv
import matplotlib.pyplot as plt
from progressbar import *
import random
print('Keras Version: {}'.format(keras.__version__))
def process_sample(smpl, correction_factor):
prefix = ['dataK/','','data2/'][1]
cf = 0.075
cid = random.randrange(0,3)
smpl[1] = smpl[1].replace(' ', '')
smpl[2] = smpl[2].replace(' ', '')
if cid>=0:
crctn = cid*cf
else:
crctn = 0-cf
# crctn = 0
# return [cv2.imread(prefix + smpl[cid]), float(smpl[3])+crctn]
if random.random() >= 0.5:
return [cv2.flip(cv2.imread(prefix + smpl[cid]), 0),
(-1)*(float(smpl[3])+crctn)]
else:
return [cv2.imread(prefix + smpl[cid]),
float(smpl[3])+crctn]
reader = csv.reader(open('data/driving_log_rough.csv'))
lines = [line for line in reader][1:]
train_lines, valid_lines = train_test_split(lines, test_size=0.2)
images, measurements = zip(*[process_sample(smpl, 0.2) for smpl in progressbar(train_lines)])
X_train, y_train = [np.array(images), np.array(measurements)]
images, measurements = zip(*[process_sample(smpl, 0.2) for smpl in progressbar(valid_lines)])
X_valid, y_valid = [np.array(images), np.array(measurements)]
batch_size=32
count = 0
for x in X_train:
if x is None:
count+=1
print("{}% of X values empty".format(count/len(X_train)*100))
print("Average steering angle of {} angles in training set: {}".format(len(y_train), np.average(y_train)))
print("Average steering angle of {} angles validation set: {}".format(len(y_valid), np.average(y_valid)))
total = len(y_train) + len(y_valid)
print("Overall average steering angle: {}".format(np.average(y_train) * len(y_train) / total +
np.average(y_valid) * len(y_valid) / total))
def create_model():
#Instantiate an empty model
model = keras.Sequential()
model.add(Lambda(lambda x: x / 255.0 - 0.5, input_shape=(160, 320, 3)))
model.add(Cropping2D(cropping=((70,25),(0,0))))
model.add(Conv2D(20, 6, 6, subsample=(2, 2), activation='relu'))
model.add(Conv2D(40, 5, 5, subsample=(2, 2), activation='relu'))
model.add(Conv2D(50, 5, 5, subsample=(2, 2), activation='relu'))
model.add(Conv2D(64, 3, 3, activation='relu'))
model.add(Conv2D(64, 3, 3, activation='relu'))
model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(1, activation='linear'))
# Compile the model
model.compile(loss='mse', optimizer='adam')
return model
clear_session()
model = create_model()
model.summary()
history = model.fit(x=X_train,
y=y_train,
batch_size=32,
epochs=10,
verbose=1,
validation_data=(X_valid, y_valid),
shuffle=True)
model.save('my_model.h5')
print(model.predict(X_valid[0:20]))
| 0.63341 | 0.743773 |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
df['t'] = pd.to_datetime(df['t'], unit='s')
df = df.rename(columns={'c': 'Close', 'h': 'High', 'l':'Low', 'o': 'Open', 's': 'Status', 't': 'Date', 'v': 'Volume'})
df.head()
```
# Linear Regression
```
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
df['t'] = pd.to_datetime(df['t'], unit='s')
X = df[['t']]
y = df['c'].values.reshape(-1, 1)
print(X.shape, y.shape)
data = X.copy()
data_binary_encoded = pd.get_dummies(data)
data_binary_encoded.head()
from sklearn.model_selection import train_test_split
X = pd.get_dummies(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
X_train.head()
from sklearn.preprocessing import StandardScaler
X_scaler = StandardScaler().fit(X_train)
y_scaler = StandardScaler().fit(y_train)
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
y_train_scaled = y_scaler.transform(y_train)
y_test_scaled = y_scaler.transform(y_test)
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train_scaled, y_train_scaled)
plt.scatter(model.predict(X_train_scaled), model.predict(X_train_scaled) - y_train_scaled, c="blue", label="Training Data")
plt.scatter(model.predict(X_test_scaled), model.predict(X_test_scaled) - y_test_scaled, c="orange", label="Testing Data")
plt.legend()
plt.hlines(y=0, xmin=y_test_scaled.min(), xmax=y_test_scaled.max())
plt.title("Residual Plot")
plt.show()
predictions = model.predict(X_test_scaled)
predictions
new_data['mon_fri'] = 0
for i in range(0,len(new_data)):
if (new_data['Dayofweek'][i] == 0 or new_data['Dayofweek'][i] == 4):
new_data['mon_fri'][i] = 1
else:
new_data['mon_fri'][i] = 0
#split into train and validation
train = new_data[:987]
valid = new_data[987:]
x_train = train.drop('Close', axis=1)
y_train = train['Close']
x_valid = valid.drop('Close', axis=1)
y_valid = valid['Close']
#implement linear regression
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x_train,y_train)
#make predictions and find the rmse
preds = model.predict(X_test_scaled)
rms=np.sqrt(np.mean(np.power((np.array(y_test_scaled)-np.array(preds)),2)))
rms
from sklearn.metrics import mean_squared_error
predictions = model.predict(X_test_scaled)
MSE = mean_squared_error(y_test_scaled, predictions)
r2 = model.score(X_test_scaled, y_test_scaled)
print(f"MSE: {MSE}, R2: {r2}")
#plot
valid['Predictions'] = 0
valid['Predictions'] = preds
valid.index = new_data[987:].index
train.index = new_data[:987].index
plt.plot(train['Close'])
plt.plot(valid[['Close', 'Predictions']])
```
# K-Nearest Neighbours
```
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
df['t'] = pd.to_datetime(df['t'], unit='s')
df = df.rename(columns={'c': 'Close', 'h': 'High', 'l':'Low', 'o': 'Open', 's': 'Status', 't': 'Date', 'v': 'Volume'})
df.head()
# Predictor variables
df['Open-Close']= df.Open -df.Close
df['High-Low'] = df.High - df.Low
df =df.dropna()
X= df[['Open-Close', 'High-Low']]
X.head()
# Target variable
Y= np.where(df['Close'].shift(-1)>df['Close'],1,-1)
# Splitting the dataset
split_percentage = 0.7
split = int(split_percentage*len(df))
X_train = X[:split]
Y_train = Y[:split]
X_test = X[split:]
Y_test = Y[split:]
train_scores = []
test_scores = []
for k in range(1, 50, 2):
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, Y_train)
train_score = knn.score(X_train, Y_train)
test_score = knn.score(X_test, Y_test)
train_scores.append(train_score)
test_scores.append(test_score)
print(f"k: {k}, Train/Test Score: {train_score:.3f}/{test_score:.3f}")
plt.plot(range(1, 50, 2), train_scores, marker='o')
plt.plot(range(1, 50, 2), test_scores, marker="x")
plt.xlabel("k neighbors")
plt.ylabel("Testing accuracy Score")
plt.show()
# Instantiate KNN learning model(k=15)
knn = KNeighborsClassifier(n_neighbors=15)
# fit the model
knn.fit(X_train, Y_train)
# Accuracy Score
accuracy_train = accuracy_score(Y_train, knn.predict(X_train))
accuracy_test = accuracy_score(Y_test, knn.predict(X_test))
print ('Train_data Accuracy: %.2f' %accuracy_train)
print ('Test_data Accuracy: %.2f' %accuracy_test)
len(Y_train)
pred = knn.predict(X_test)
pred
pd.DataFrame({"Prediction": pred, 'Actual': Y_test})
# Predicted Signal
df['Predicted_Signal'] = knn.predict(X)
# SPY Cumulative Returns
df['SPY_returns'] = np.log(df['Close']/df['Close'].shift(1))
Cumulative_SPY_returns = df[split:]['SPY_returns'].cumsum()*100
# Cumulative Strategy Returns
df['Startegy_returns'] = df['SPY_returns']* df['Predicted_Signal'].shift(1)
Cumulative_Strategy_returns = df[split:]['Startegy_returns'].cumsum()*100
# Plot the results to visualize the performance
plt.figure(figsize=(10,5))
plt.plot(Cumulative_SPY_returns, color='r',label = 'SPY Returns')
plt.plot(Cumulative_Strategy_returns, color='g', label = 'Strategy Returns')
plt.legend()
plt.show()
df
```
What is Sharpe Ratio?
Sharpe ratio is a measure for calculating risk-adjusted return. It is the ratio of the excess expected return of investment (over risk-free rate) per unit of volatility or standard deviation.
Let us see the formula for Sharpe ratio which will make things much clearer. The sharpe ratio calculation is done in the following manner
Sharpe Ratio = (Rx – Rf) / StdDev(x)
Where,
x is the investment
Rx is the average rate of return of x
Rf is the risk-free rate of return
StdDev(x) is the standard deviation of Rx
Once you see the formula, you will understand that we deduct the risk-free rate of return as this helps us in figuring out if the strategy makes sense or not. If the Numerator turned out negative, wouldn’t it be better to invest in a government bond which guarantees you a risk-free rate of return? Some of you would recognise this as the risk-adjusted return.
In the denominator, we have the standard deviation of the average return of the investment. It helps us in identifying the volatility as well as the risk associated with the investment.
Thus, the Sharpe ratio helps us in identifying which strategy gives better returns in comparison to the volatility. There, that is all when it comes to sharpe ratio calculation.
Let’s take an example now to see how the Sharpe ratio calculation helps us.
You have devised a strategy and created a portfolio of different stocks. After backtesting, you observe that this portfolio, let’s call it Portfolio A, will give a return of 11%. However, you are concerned with the volatility at 8%.
Now, you change certain parameters and pick different financial instruments to create another portfolio, Portfolio B. This portfolio gives an expected return of 8%, but the volatility now drops to 4%.
```
# Calculate Sharpe reatio
Std = Cumulative_Strategy_returns.std()
Sharpe = (Cumulative_Strategy_returns-Cumulative_SPY_returns)/Std
Sharpe = Sharpe.mean()
print ('Sharpe ratio: %.2f'%Sharpe )
```
Tested many neighbours and the lowest sharpe ratio was for 15.
# Auto ARIMA
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pandas.plotting import lag_plot
from pandas import datetime
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
plt.figure(figsize=(10,10))
lag_plot(df['c'], lag=5)
plt.title('Microsoft Autocorrelation plot')
size = len(df)
train_data, test_data = df[0:int(len(df)*0.8)], df[int(len(df)*0.8):]
plt.figure(figsize=(12,7))
plt.title('Microsoft Prices')
plt.xlabel('Dates')
plt.ylabel('Prices')
plt.plot(df['c'], 'blue', label='Training Data')
plt.plot(test_data['c'], 'green', label='Testing Data')
plt.xticks(np.arange(0,size, 300), df['t'][0:size:300])
plt.legend()
def smape_kun(y_true, y_pred):
return np.mean((np.abs(y_pred - y_true) * 200/ (np.abs(y_pred) + np.abs(y_true))))
train_ar = train_data['c'].values
test_ar = test_data['c'].values
history = [x for x in train_ar]
print(type(history))
predictions = list()
for t in range(len(test_ar)):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test_ar[t]
history.append(obs)
error = mean_squared_error(test_ar, predictions)
print('Testing Mean Squared Error: %.3f' % error)
error2 = smape_kun(test_ar, predictions)
print('Symmetric mean absolute percentage error: %.3f' % error2)
pd.DataFrame({"Prediction": predictions, 'Actual': test_ar})
plt.figure(figsize=(12,7))
plt.plot(df['c'], 'green', color='blue', label='Training Data')
plt.plot(test_data.index, predictions, color='green', marker='o', linestyle='dashed',
label='Predicted Price')
plt.plot(test_data.index, test_data['c'], color='red', label='Actual Price')
plt.title('Microsoft Prices Prediction')
plt.xlabel('Dates')
plt.ylabel('Prices')
plt.xticks(np.arange(0,size, 1300), df['t'][0:size:1300])
plt.legend()
```
# Prophet
```
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
df['t'] = pd.to_datetime(df['t'], unit='s')
df = df.rename(columns={'c': 'Close', 'h': 'High', 'l':'Low', 'o': 'Open', 's': 'Status', 't': 'Date', 'v': 'Volume'})
df.head()
size = len(df)
tsize = int(size/2)
#importing prophet
from fbprophet import Prophet
#creating dataframe
new_data = pd.DataFrame(index=range(0,len(df)),columns=['Date', 'Close'])
for i in range(0,len(df)):
new_data['Date'][i] = df['Date'][i]
new_data['Close'][i] = df['Close'][i]
new_data['Date'] = pd.to_datetime(new_data.Date,format='%Y-%m-%d')
new_data.index = new_data['Date']
#preparing data
new_data.rename(columns={'Close': 'y', 'Date': 'ds'}, inplace=True)
new_data[:size]
#train and validation
train = new_data[:tsize]
valid = new_data[tsize:]
len(valid)
#fit the model
model = Prophet()
model.fit(train)
#predictions
close_prices = model.make_future_dataframe(periods=len(valid))
forecast = model.predict(close_prices)
close_prices.tail(2)
#rmse
forecast_valid = forecast['yhat'][tsize:]
print(forecast_valid.shape, valid['y'].shape)
rms=np.sqrt(np.mean(np.power((np.array(valid['y'])-np.array(forecast_valid)),2)))
rms
valid['yhat'] = forecast['yhat']
#plot
valid['Predictions'] = 0
valid['Predictions'] = forecast_valid.values
plt.plot(train['y'])
plt.plot(valid[['y', 'Predictions']])
valid['Predictions']
pd.DataFrame({"Prediction": valid['Predictions'], "Actual": valid['y']})
fig1 =model.plot(forecast)
# to view the forecast components
fig1 = model.plot_components(forecast)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
df['t'] = pd.to_datetime(df['t'], unit='s')
df = df.rename(columns={'c': 'Close', 'h': 'High', 'l':'Low', 'o': 'Open', 's': 'Status', 't': 'Date', 'v': 'Volume'})
df.head()
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
df['t'] = pd.to_datetime(df['t'], unit='s')
X = df[['t']]
y = df['c'].values.reshape(-1, 1)
print(X.shape, y.shape)
data = X.copy()
data_binary_encoded = pd.get_dummies(data)
data_binary_encoded.head()
from sklearn.model_selection import train_test_split
X = pd.get_dummies(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
X_train.head()
from sklearn.preprocessing import StandardScaler
X_scaler = StandardScaler().fit(X_train)
y_scaler = StandardScaler().fit(y_train)
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
y_train_scaled = y_scaler.transform(y_train)
y_test_scaled = y_scaler.transform(y_test)
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train_scaled, y_train_scaled)
plt.scatter(model.predict(X_train_scaled), model.predict(X_train_scaled) - y_train_scaled, c="blue", label="Training Data")
plt.scatter(model.predict(X_test_scaled), model.predict(X_test_scaled) - y_test_scaled, c="orange", label="Testing Data")
plt.legend()
plt.hlines(y=0, xmin=y_test_scaled.min(), xmax=y_test_scaled.max())
plt.title("Residual Plot")
plt.show()
predictions = model.predict(X_test_scaled)
predictions
new_data['mon_fri'] = 0
for i in range(0,len(new_data)):
if (new_data['Dayofweek'][i] == 0 or new_data['Dayofweek'][i] == 4):
new_data['mon_fri'][i] = 1
else:
new_data['mon_fri'][i] = 0
#split into train and validation
train = new_data[:987]
valid = new_data[987:]
x_train = train.drop('Close', axis=1)
y_train = train['Close']
x_valid = valid.drop('Close', axis=1)
y_valid = valid['Close']
#implement linear regression
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x_train,y_train)
#make predictions and find the rmse
preds = model.predict(X_test_scaled)
rms=np.sqrt(np.mean(np.power((np.array(y_test_scaled)-np.array(preds)),2)))
rms
from sklearn.metrics import mean_squared_error
predictions = model.predict(X_test_scaled)
MSE = mean_squared_error(y_test_scaled, predictions)
r2 = model.score(X_test_scaled, y_test_scaled)
print(f"MSE: {MSE}, R2: {r2}")
#plot
valid['Predictions'] = 0
valid['Predictions'] = preds
valid.index = new_data[987:].index
train.index = new_data[:987].index
plt.plot(train['Close'])
plt.plot(valid[['Close', 'Predictions']])
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
df['t'] = pd.to_datetime(df['t'], unit='s')
df = df.rename(columns={'c': 'Close', 'h': 'High', 'l':'Low', 'o': 'Open', 's': 'Status', 't': 'Date', 'v': 'Volume'})
df.head()
# Predictor variables
df['Open-Close']= df.Open -df.Close
df['High-Low'] = df.High - df.Low
df =df.dropna()
X= df[['Open-Close', 'High-Low']]
X.head()
# Target variable
Y= np.where(df['Close'].shift(-1)>df['Close'],1,-1)
# Splitting the dataset
split_percentage = 0.7
split = int(split_percentage*len(df))
X_train = X[:split]
Y_train = Y[:split]
X_test = X[split:]
Y_test = Y[split:]
train_scores = []
test_scores = []
for k in range(1, 50, 2):
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, Y_train)
train_score = knn.score(X_train, Y_train)
test_score = knn.score(X_test, Y_test)
train_scores.append(train_score)
test_scores.append(test_score)
print(f"k: {k}, Train/Test Score: {train_score:.3f}/{test_score:.3f}")
plt.plot(range(1, 50, 2), train_scores, marker='o')
plt.plot(range(1, 50, 2), test_scores, marker="x")
plt.xlabel("k neighbors")
plt.ylabel("Testing accuracy Score")
plt.show()
# Instantiate KNN learning model(k=15)
knn = KNeighborsClassifier(n_neighbors=15)
# fit the model
knn.fit(X_train, Y_train)
# Accuracy Score
accuracy_train = accuracy_score(Y_train, knn.predict(X_train))
accuracy_test = accuracy_score(Y_test, knn.predict(X_test))
print ('Train_data Accuracy: %.2f' %accuracy_train)
print ('Test_data Accuracy: %.2f' %accuracy_test)
len(Y_train)
pred = knn.predict(X_test)
pred
pd.DataFrame({"Prediction": pred, 'Actual': Y_test})
# Predicted Signal
df['Predicted_Signal'] = knn.predict(X)
# SPY Cumulative Returns
df['SPY_returns'] = np.log(df['Close']/df['Close'].shift(1))
Cumulative_SPY_returns = df[split:]['SPY_returns'].cumsum()*100
# Cumulative Strategy Returns
df['Startegy_returns'] = df['SPY_returns']* df['Predicted_Signal'].shift(1)
Cumulative_Strategy_returns = df[split:]['Startegy_returns'].cumsum()*100
# Plot the results to visualize the performance
plt.figure(figsize=(10,5))
plt.plot(Cumulative_SPY_returns, color='r',label = 'SPY Returns')
plt.plot(Cumulative_Strategy_returns, color='g', label = 'Strategy Returns')
plt.legend()
plt.show()
df
# Calculate Sharpe reatio
Std = Cumulative_Strategy_returns.std()
Sharpe = (Cumulative_Strategy_returns-Cumulative_SPY_returns)/Std
Sharpe = Sharpe.mean()
print ('Sharpe ratio: %.2f'%Sharpe )
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pandas.plotting import lag_plot
from pandas import datetime
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
plt.figure(figsize=(10,10))
lag_plot(df['c'], lag=5)
plt.title('Microsoft Autocorrelation plot')
size = len(df)
train_data, test_data = df[0:int(len(df)*0.8)], df[int(len(df)*0.8):]
plt.figure(figsize=(12,7))
plt.title('Microsoft Prices')
plt.xlabel('Dates')
plt.ylabel('Prices')
plt.plot(df['c'], 'blue', label='Training Data')
plt.plot(test_data['c'], 'green', label='Testing Data')
plt.xticks(np.arange(0,size, 300), df['t'][0:size:300])
plt.legend()
def smape_kun(y_true, y_pred):
return np.mean((np.abs(y_pred - y_true) * 200/ (np.abs(y_pred) + np.abs(y_true))))
train_ar = train_data['c'].values
test_ar = test_data['c'].values
history = [x for x in train_ar]
print(type(history))
predictions = list()
for t in range(len(test_ar)):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test_ar[t]
history.append(obs)
error = mean_squared_error(test_ar, predictions)
print('Testing Mean Squared Error: %.3f' % error)
error2 = smape_kun(test_ar, predictions)
print('Symmetric mean absolute percentage error: %.3f' % error2)
pd.DataFrame({"Prediction": predictions, 'Actual': test_ar})
plt.figure(figsize=(12,7))
plt.plot(df['c'], 'green', color='blue', label='Training Data')
plt.plot(test_data.index, predictions, color='green', marker='o', linestyle='dashed',
label='Predicted Price')
plt.plot(test_data.index, test_data['c'], color='red', label='Actual Price')
plt.title('Microsoft Prices Prediction')
plt.xlabel('Dates')
plt.ylabel('Prices')
plt.xticks(np.arange(0,size, 1300), df['t'][0:size:1300])
plt.legend()
#read the file
df = pd.read_json (r'VZ.json')
#print the head
df
df['t'] = pd.to_datetime(df['t'], unit='s')
df = df.rename(columns={'c': 'Close', 'h': 'High', 'l':'Low', 'o': 'Open', 's': 'Status', 't': 'Date', 'v': 'Volume'})
df.head()
size = len(df)
tsize = int(size/2)
#importing prophet
from fbprophet import Prophet
#creating dataframe
new_data = pd.DataFrame(index=range(0,len(df)),columns=['Date', 'Close'])
for i in range(0,len(df)):
new_data['Date'][i] = df['Date'][i]
new_data['Close'][i] = df['Close'][i]
new_data['Date'] = pd.to_datetime(new_data.Date,format='%Y-%m-%d')
new_data.index = new_data['Date']
#preparing data
new_data.rename(columns={'Close': 'y', 'Date': 'ds'}, inplace=True)
new_data[:size]
#train and validation
train = new_data[:tsize]
valid = new_data[tsize:]
len(valid)
#fit the model
model = Prophet()
model.fit(train)
#predictions
close_prices = model.make_future_dataframe(periods=len(valid))
forecast = model.predict(close_prices)
close_prices.tail(2)
#rmse
forecast_valid = forecast['yhat'][tsize:]
print(forecast_valid.shape, valid['y'].shape)
rms=np.sqrt(np.mean(np.power((np.array(valid['y'])-np.array(forecast_valid)),2)))
rms
valid['yhat'] = forecast['yhat']
#plot
valid['Predictions'] = 0
valid['Predictions'] = forecast_valid.values
plt.plot(train['y'])
plt.plot(valid[['y', 'Predictions']])
valid['Predictions']
pd.DataFrame({"Prediction": valid['Predictions'], "Actual": valid['y']})
fig1 =model.plot(forecast)
# to view the forecast components
fig1 = model.plot_components(forecast)
| 0.417509 | 0.773281 |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Gena/landsat_median.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Gena/landsat_median.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Gena/landsat_median.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://geemap.org). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
import ee
import geemap
```
## Create an interactive map
The default basemap is `Google Maps`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/basemaps.py) can be added using the `Map.add_basemap()` function.
```
Map = geemap.Map(center=[40,-100], zoom=4)
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
collection = ee.ImageCollection('LANDSAT/LC08/C01/T1_TOA')\
.filter(ee.Filter.eq('WRS_PATH', 44))\
.filter(ee.Filter.eq('WRS_ROW', 34))\
.filterDate('2014-01-01', '2015-01-01')
median = collection.median()
Map.setCenter(-122.3578, 37.7726, 12)
Map.addLayer(median, {"bands": ['B4', 'B3', 'B2'], "max": 0.3}, 'median')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
|
github_jupyter
|
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
import ee
import geemap
Map = geemap.Map(center=[40,-100], zoom=4)
Map
# Add Earth Engine dataset
collection = ee.ImageCollection('LANDSAT/LC08/C01/T1_TOA')\
.filter(ee.Filter.eq('WRS_PATH', 44))\
.filter(ee.Filter.eq('WRS_ROW', 34))\
.filterDate('2014-01-01', '2015-01-01')
median = collection.median()
Map.setCenter(-122.3578, 37.7726, 12)
Map.addLayer(median, {"bands": ['B4', 'B3', 'B2'], "max": 0.3}, 'median')
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 0.448909 | 0.958226 |
### Linear Regression
**Author:** René Kopeinig<br>
**Description:** Time Series Prediction using Proba-V NDVI (Normalized Difference Vegetation Index), Landsat 8 NDVI and CHIRPS precipitation Time-Series.
```
%matplotlib inline
# Import Dependencies
import ee, datetime
import pandas as pd
import seaborn as sns
import matplotlib.dates as mdates
import statsmodels.formula.api as smf
from IPython.display import Image
from matplotlib import dates
from pylab import *
from numpy import fft
from statsmodels.tsa.stattools import adfuller
from pandas.tseries.offsets import MonthEnd
from sklearn.linear_model import LinearRegression
import matplotlib.pylab as plt
ee.Initialize()
def normalize(x):
normalized = (x - x.min(axis=0)) / (x.max(axis=0) - x.min(axis=0))
return normalized
```
### Load Proba-V, Landsat 8 TOA and CHIRPS image collection and point geometry
Selected Location of point is from the Proba-V Footprint X18Y02 in Luxembourg, Europe.
```
# Set start and end date
startTime = datetime.datetime(2013, 2, 3)
endTime = datetime.datetime(2018, 4, 15)
# Create image collection
l8 = ee.ImageCollection('LANDSAT/LC8_L1T_TOA').filterDate(startTime, endTime)
precipitation = ee.ImageCollection('UCSB-CHG/CHIRPS/PENTAD').filterDate(startTime, endTime)
probav = ee.ImageCollection('VITO/PROBAV/C1/S1_TOC_100M').filterDate(startTime, endTime)
# Create point in Luxembourg (Proba-V Footprint: X18Y02)
point = {'type':'Point', 'coordinates':[-99.545934,20.572173]};
```
### Retrieve information, reshape & calculate NDVI and extract precipitation information
Retrieving information from point geometry with a buffer of 500m over image collection. Reshaping data and calculating NDVI from **RED** and **NIR** band.
```
info_l8 = l8.getRegion(point,500).getInfo()
info_chirps = precipitation.getRegion(point, 500).getInfo()
info_probav = probav.getRegion(point, 500).getInfo()
# Reshape Landsat 8
header = info_l8[0]
data = array(info_l8[1:])
iTime = header.index('time')
time = [datetime.datetime.fromtimestamp(i/1000) for i in (data[0:,iTime].astype(int))]
# List of used image bands
band_list = ['B5',u'B4']
iBands = [header.index(b) for b in band_list]
yData = data[0:,iBands].astype(np.float)
# Calculate NDVI
red = yData[:,0]
nir = yData[:,1]
ndvi = (nir - red) / (nir + red)
# Reshape NDVI array into Pandas Dataframe
df = pd.DataFrame(data=ndvi*-1, index=time, columns=['ndvi'])
l8_time_series = df.dropna()
# Resampling
monthly_landsat = l8_time_series.resample('M', how='mean')
# Reshape Chirps precipitation data
header = info_chirps[0]
data = array(info_chirps[1:])
iTime = header.index('time')
time = [datetime.datetime.fromtimestamp(i/1000) for i in (data[0:,iTime].astype(int))]
band_list=['precipitation']
iBands = [header.index(b) for b in band_list]
chirps = data[0:,iBands].astype(np.float)
df = pd.DataFrame(data=chirps, index=time, columns=['precipitation'])
chirps_time_series = df.dropna()
# Resampling
monthly_chirps = chirps_time_series.resample('M', how='mean')
# Reshape Proba-V image collection
header = info_probav[0]
data = array(info_probav[1:])
iTime = header.index('time')
time = [datetime.datetime.fromtimestamp(i/1000) for i in (data[0:,iTime].astype(int))]
band_list=['NDVI']
iBands = [header.index(b) for b in band_list]
ndvi = data[0:,iBands].astype(np.float)
df = pd.DataFrame(data=ndvi, index=time, columns=['ndvi'])
probav_time_series = df.dropna()
# Resampling
monthly_probav = probav_time_series.resample('M', how='mean')
```
### Plot Landsat 8 NDVI Time Series
```
sns.set(rc={'figure.figsize':(15, 6)})
l8_time_series['ndvi'].plot(linewidth=1.2)
```
### Plot Proba-V NDVI Time Series
```
probav_time_series.plot(linewidth=1.2)
```
### Plot CHIRPS Precipitation Time Series
```
chirps_time_series.plot(linewidth=1.2)
```
### Reshape Data and plot
Let's bring all Time Series on an equal base, reshape and join them in one data frame. Creating Pair Plots in order to take a closer look into the data.
```
monthly_chirps = monthly_chirps['2014-04':'2017-04']
monthly_landsat = monthly_landsat['2014-04':'2017-04']
monthly_probav = monthly_probav['2014-04':'2017-04']
monthly = pd.DataFrame({'landsat': monthly_landsat['ndvi'],
'chirps': monthly_chirps['precipitation'],
'probav':monthly_probav['ndvi']},index = monthly_chirps.index)
sns.pairplot(monthly, x_vars=['landsat', 'probav'], y_vars=['chirps'], size=7, aspect=0.7)
```
### Linear Regression comparing Sklearn and Statsmodels
```
# Statsmodels
lm_1 = smf.ols(formula='chirps ~ landsat', data=monthly).fit()
# Print the coefficients
print(lm_1.params)
# Sklearn
cols = ['landsat']
X = monthly[cols]
y = monthly.chirps
# instantiate and fit
lm_2 = LinearRegression()
lm_2.fit(X, y)
# print the coefficients
print('Intercept: ', lm_2.intercept_)
print('landsat: ', lm_2.coef_[0])
```
### Plot Least Square Line
```
sns.jointplot("probav", "chirps", data=monthly, size=7, kind='reg')
sns.jointplot("landsat", "chirps", data=monthly, size=7, kind='reg')
```
### Linear Regression Prediction
```
lm = smf.ols(formula='chirps ~ landsat*probav', data=monthly).fit()
lm.summary()
model_linear_pred = lm.predict()
monthly['pred']=model_linear_pred
normalize(monthly).plot(linewidth=1.2)
```
|
github_jupyter
|
%matplotlib inline
# Import Dependencies
import ee, datetime
import pandas as pd
import seaborn as sns
import matplotlib.dates as mdates
import statsmodels.formula.api as smf
from IPython.display import Image
from matplotlib import dates
from pylab import *
from numpy import fft
from statsmodels.tsa.stattools import adfuller
from pandas.tseries.offsets import MonthEnd
from sklearn.linear_model import LinearRegression
import matplotlib.pylab as plt
ee.Initialize()
def normalize(x):
normalized = (x - x.min(axis=0)) / (x.max(axis=0) - x.min(axis=0))
return normalized
# Set start and end date
startTime = datetime.datetime(2013, 2, 3)
endTime = datetime.datetime(2018, 4, 15)
# Create image collection
l8 = ee.ImageCollection('LANDSAT/LC8_L1T_TOA').filterDate(startTime, endTime)
precipitation = ee.ImageCollection('UCSB-CHG/CHIRPS/PENTAD').filterDate(startTime, endTime)
probav = ee.ImageCollection('VITO/PROBAV/C1/S1_TOC_100M').filterDate(startTime, endTime)
# Create point in Luxembourg (Proba-V Footprint: X18Y02)
point = {'type':'Point', 'coordinates':[-99.545934,20.572173]};
info_l8 = l8.getRegion(point,500).getInfo()
info_chirps = precipitation.getRegion(point, 500).getInfo()
info_probav = probav.getRegion(point, 500).getInfo()
# Reshape Landsat 8
header = info_l8[0]
data = array(info_l8[1:])
iTime = header.index('time')
time = [datetime.datetime.fromtimestamp(i/1000) for i in (data[0:,iTime].astype(int))]
# List of used image bands
band_list = ['B5',u'B4']
iBands = [header.index(b) for b in band_list]
yData = data[0:,iBands].astype(np.float)
# Calculate NDVI
red = yData[:,0]
nir = yData[:,1]
ndvi = (nir - red) / (nir + red)
# Reshape NDVI array into Pandas Dataframe
df = pd.DataFrame(data=ndvi*-1, index=time, columns=['ndvi'])
l8_time_series = df.dropna()
# Resampling
monthly_landsat = l8_time_series.resample('M', how='mean')
# Reshape Chirps precipitation data
header = info_chirps[0]
data = array(info_chirps[1:])
iTime = header.index('time')
time = [datetime.datetime.fromtimestamp(i/1000) for i in (data[0:,iTime].astype(int))]
band_list=['precipitation']
iBands = [header.index(b) for b in band_list]
chirps = data[0:,iBands].astype(np.float)
df = pd.DataFrame(data=chirps, index=time, columns=['precipitation'])
chirps_time_series = df.dropna()
# Resampling
monthly_chirps = chirps_time_series.resample('M', how='mean')
# Reshape Proba-V image collection
header = info_probav[0]
data = array(info_probav[1:])
iTime = header.index('time')
time = [datetime.datetime.fromtimestamp(i/1000) for i in (data[0:,iTime].astype(int))]
band_list=['NDVI']
iBands = [header.index(b) for b in band_list]
ndvi = data[0:,iBands].astype(np.float)
df = pd.DataFrame(data=ndvi, index=time, columns=['ndvi'])
probav_time_series = df.dropna()
# Resampling
monthly_probav = probav_time_series.resample('M', how='mean')
sns.set(rc={'figure.figsize':(15, 6)})
l8_time_series['ndvi'].plot(linewidth=1.2)
probav_time_series.plot(linewidth=1.2)
chirps_time_series.plot(linewidth=1.2)
monthly_chirps = monthly_chirps['2014-04':'2017-04']
monthly_landsat = monthly_landsat['2014-04':'2017-04']
monthly_probav = monthly_probav['2014-04':'2017-04']
monthly = pd.DataFrame({'landsat': monthly_landsat['ndvi'],
'chirps': monthly_chirps['precipitation'],
'probav':monthly_probav['ndvi']},index = monthly_chirps.index)
sns.pairplot(monthly, x_vars=['landsat', 'probav'], y_vars=['chirps'], size=7, aspect=0.7)
# Statsmodels
lm_1 = smf.ols(formula='chirps ~ landsat', data=monthly).fit()
# Print the coefficients
print(lm_1.params)
# Sklearn
cols = ['landsat']
X = monthly[cols]
y = monthly.chirps
# instantiate and fit
lm_2 = LinearRegression()
lm_2.fit(X, y)
# print the coefficients
print('Intercept: ', lm_2.intercept_)
print('landsat: ', lm_2.coef_[0])
sns.jointplot("probav", "chirps", data=monthly, size=7, kind='reg')
sns.jointplot("landsat", "chirps", data=monthly, size=7, kind='reg')
lm = smf.ols(formula='chirps ~ landsat*probav', data=monthly).fit()
lm.summary()
model_linear_pred = lm.predict()
monthly['pred']=model_linear_pred
normalize(monthly).plot(linewidth=1.2)
| 0.528047 | 0.912045 |
<a href="https://colab.research.google.com/github/rockerritesh/easyOCR_Nepali/blob/main/Nepali_OCR.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Nepali OCR detector.
```
```
## importing Module
```
!pip install easyocr
import matplotlib.pyplot as plt
import cv2
import easyocr
import numpy as np
from pylab import rcParams
from IPython.display import Image
rcParams['figure.figsize'] = 8, 16
```
## Loading pre trained model.
'ne' for Nepali and 'en' for english and simillary for other
```
reader = easyocr.Reader(['ne']) #'ne' for Nepali and 'en' for english and simillary for other
```
## Normal image to Scaned image
```
def map(x, in_min, in_max, out_min, out_max):
return (x - in_min) * (out_max - out_min) / (in_max - in_min) + out_min
def highPassFilter(img,kSize):
if not kSize%2:
kSize +=1
kernel = np.ones((kSize,kSize),np.float32)/(kSize*kSize)
filtered = cv2.filter2D(img,-1,kernel)
filtered = img.astype('float32') - filtered.astype('float32')
filtered = filtered + 127*np.ones(img.shape, np.uint8)
filtered = filtered.astype('uint8')
return filtered
def blackPointSelect(img, blackPoint):
img = img.astype('int32')
img = map(img, blackPoint, 255, 0, 255)
_, img = cv2.threshold(img, 0, 255, cv2.THRESH_TOZERO)
img = img.astype('uint8')
return img
def whitePointSelect(img,whitePoint):
_,img = cv2.threshold(img, whitePoint, 255, cv2.THRESH_TRUNC)
img = img.astype('int32')
img = map(img, 0, whitePoint, 0, 255)
img = img.astype('uint8')
return img
def blackAndWhite(img):
lab = cv2.cvtColor(img, cv2.COLOR_BGR2LAB)
(l,a,b) = cv2.split(lab)
img = cv2.add( cv2.subtract(l,b), cv2.subtract(l,a) )
return img
def scan_effect(img):
blackPoint = 66
whitePoint = 130
image = highPassFilter(img,kSize = 51)
image_white = whitePointSelect(image, whitePoint)
img_black = blackPointSelect(image_white, blackPoint)
image=blackPointSelect(img,blackPoint)
white = whitePointSelect(image,whitePoint)
img_black = blackAndWhite(white)
return img_black
```
> Enter the location of image file
```
loc="2.jpg"
Image(loc)
img = cv2.imread(loc)
image = scan_effect(img)
#from google.colab.patches import cv2_imshow
#cv2_imshow(image)
filename = 'scanned.jpg'
cv2.imwrite(filename, image)
```
## Loading Image
```
path=filename
Image(path)
```
## Detecting character from image
```
output = reader.readtext(path)
```
## Output
```
output
```
## Total detection
```
print(f'Total number of detection',len(output))
```
## Previewing Output
```
image = cv2.imread(path)
for i in range(len(output)):
cord = output[i][0]
x_min, y_min = [int(min(idx)) for idx in zip(*cord)]
x_max, y_max = [int(max(idx)) for idx in zip(*cord)]
cv2.rectangle(image,(x_min,y_min),(x_max,y_max),(0,0,255),2)
print(output[i][1])
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
```
|
github_jupyter
|
```
## importing Module
## Loading pre trained model.
'ne' for Nepali and 'en' for english and simillary for other
## Normal image to Scaned image
> Enter the location of image file
## Loading Image
## Detecting character from image
## Output
## Total detection
## Previewing Output
| 0.47317 | 0.935524 |
# Medical Image Classification Tutorial with the MedNIST Dataset
In this tutorial, we introduce an end-to-end training and evaluation example based on the MedNIST dataset.
We'll go through the following steps:
* Create a dataset for training and testing
* Use MONAI transforms to pre-process data
* Use the DenseNet from MONAI for classification
* Train the model with a PyTorch program
* Evaluate on test dataset
[](https://colab.research.google.com/github/Project-MONAI/Tutorials/blob/master/mednist_tutorial.ipynb)
## Setup environment
```
%pip install -qU "monai[pillow]"
%pip install -qU matplotlib
%matplotlib inline
```
## Setup imports
```
# Copyright 2020 MONAI Consortium
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import os
import shutil
import tempfile
import matplotlib.pyplot as plt
import numpy as np
import PIL
import torch
from monai.apps import download_and_extract
from monai.config import print_config
from monai.metrics import compute_roc_auc
from monai.networks.nets import densenet121
from monai.transforms import (
AddChannel,
Compose,
LoadPNG,
RandFlip,
RandRotate,
RandZoom,
ScaleIntensity,
ToTensor,
)
from monai.utils import set_determinism
print_config()
```
## Setup data directory
You can specify a directory with the `MONAI_DATA_DIRECTORY` environment variable.
This allows you to save results and reuse downloads.
If not specified a temporary directory will be used.
```
directory = os.environ.get("MONAI_DATA_DIRECTORY")
root_dir = tempfile.mkdtemp() if directory is None else directory
print(root_dir)
```
## Download dataset
The MedNIST dataset was gathered from several sets from [TCIA](https://wiki.cancerimagingarchive.net/display/Public/Data+Usage+Policies+and+Restrictions),
[the RSNA Bone Age Challenge](http://rsnachallenges.cloudapp.net/competitions/4),
and [the NIH Chest X-ray dataset](https://cloud.google.com/healthcare/docs/resources/public-datasets/nih-chest).
The dataset is kindly made available by [Dr. Bradley J. Erickson M.D., Ph.D.](https://www.mayo.edu/research/labs/radiology-informatics/overview) (Department of Radiology, Mayo Clinic)
under the Creative Commons [CC BY-SA 4.0 license](https://creativecommons.org/licenses/by-sa/4.0/).
If you use the MedNIST dataset, please acknowledge the source.
```
resource = "https://www.dropbox.com/s/5wwskxctvcxiuea/MedNIST.tar.gz?dl=1"
md5 = "0bc7306e7427e00ad1c5526a6677552d"
compressed_file = os.path.join(root_dir, "MedNIST.tar.gz")
data_dir = os.path.join(root_dir, "MedNIST")
if not os.path.exists(data_dir):
download_and_extract(resource, compressed_file, root_dir, md5)
```
## Set deterministic training for reproducibility
```
set_determinism(seed=0)
```
## Read image filenames from the dataset folders
First of all, check the dataset files and show some statistics.
There are 6 folders in the dataset: Hand, AbdomenCT, CXR, ChestCT, BreastMRI, HeadCT,
which should be used as the labels to train our classification model.
```
class_names = sorted(x for x in os.listdir(data_dir) if os.path.isdir(os.path.join(data_dir, x)))
num_class = len(class_names)
image_files = [
[
os.path.join(data_dir, class_names[i], x)
for x in os.listdir(os.path.join(data_dir, class_names[i]))
]
for i in range(num_class)
]
num_each = [len(image_files[i]) for i in range(num_class)]
image_files_list = []
image_class = []
for i in range(num_class):
image_files_list.extend(image_files[i])
image_class.extend([i] * num_each[i])
num_total = len(image_class)
image_width, image_height = PIL.Image.open(image_files_list[0]).size
print(f"Total image count: {num_total}")
print(f"Image dimensions: {image_width} x {image_height}")
print(f"Label names: {class_names}")
print(f"Label counts: {num_each}")
```
## Randomly pick images from the dataset to visualize and check
```
plt.subplots(3, 3, figsize=(8, 8))
for i, k in enumerate(np.random.randint(num_total, size=9)):
im = PIL.Image.open(image_files_list[k])
arr = np.array(im)
plt.subplot(3, 3, i + 1)
plt.xlabel(class_names[image_class[k]])
plt.imshow(arr, cmap="gray", vmin=0, vmax=255)
plt.tight_layout()
plt.show()
```
## Prepare training, validation and test data lists
Randomly select 10% of the dataset as validation and 10% as test.
```
val_frac = 0.1
test_frac = 0.1
train_x = list()
train_y = list()
val_x = list()
val_y = list()
test_x = list()
test_y = list()
for i in range(num_total):
rann = np.random.random()
if rann < val_frac:
val_x.append(image_files_list[i])
val_y.append(image_class[i])
elif rann < test_frac + val_frac:
test_x.append(image_files_list[i])
test_y.append(image_class[i])
else:
train_x.append(image_files_list[i])
train_y.append(image_class[i])
print(f"Training count: {len(train_x)}, Validation count: {len(val_x)}, Test count: {len(test_x)}")
```
## Define MONAI transforms, Dataset and Dataloader to pre-process data
```
train_transforms = Compose(
[
LoadPNG(image_only=True),
AddChannel(),
ScaleIntensity(),
RandRotate(range_x=15, prob=0.5, keep_size=True),
RandFlip(spatial_axis=0, prob=0.5),
RandZoom(min_zoom=0.9, max_zoom=1.1, prob=0.5),
ToTensor(),
]
)
val_transforms = Compose([LoadPNG(image_only=True), AddChannel(), ScaleIntensity(), ToTensor()])
class MedNISTDataset(torch.utils.data.Dataset):
def __init__(self, image_files, labels, transforms):
self.image_files = image_files
self.labels = labels
self.transforms = transforms
def __len__(self):
return len(self.image_files)
def __getitem__(self, index):
return self.transforms(self.image_files[index]), self.labels[index]
train_ds = MedNISTDataset(train_x, train_y, train_transforms)
train_loader = torch.utils.data.DataLoader(train_ds, batch_size=300, shuffle=True, num_workers=10)
val_ds = MedNISTDataset(val_x, val_y, val_transforms)
val_loader = torch.utils.data.DataLoader(val_ds, batch_size=300, num_workers=10)
test_ds = MedNISTDataset(test_x, test_y, val_transforms)
test_loader = torch.utils.data.DataLoader(test_ds, batch_size=300, num_workers=10)
```
## Define network and optimizer
1. Set learning rate for how much the model is updated per batch.
1. Set total epoch number, as we have shuffle and random transforms, so the training data of every epoch is different.
And as this is just a get start tutorial, let's just train 4 epochs.
If train 10 epochs, the model can achieve 100% accuracy on test dataset.
1. Use DenseNet from MONAI and move to GPU devide, this DenseNet can support both 2D and 3D classification tasks.
1. Use Adam optimizer.
```
device = torch.device("cuda:0")
model = densenet121(spatial_dims=2, in_channels=1, out_channels=num_class).to(device)
loss_function = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), 1e-5)
epoch_num = 4
val_interval = 1
```
## Model training
Execute a typical PyTorch training that run epoch loop and step loop, and do validation after every epoch.
Will save the model weights to file if got best validation accuracy.
```
best_metric = -1
best_metric_epoch = -1
epoch_loss_values = list()
metric_values = list()
for epoch in range(epoch_num):
print("-" * 10)
print(f"epoch {epoch + 1}/{epoch_num}")
model.train()
epoch_loss = 0
step = 0
for batch_data in train_loader:
step += 1
inputs, labels = batch_data[0].to(device), batch_data[1].to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = loss_function(outputs, labels)
loss.backward()
optimizer.step()
epoch_loss += loss.item()
print(f"{step}/{len(train_ds) // train_loader.batch_size}, train_loss: {loss.item():.4f}")
epoch_len = len(train_ds) // train_loader.batch_size
epoch_loss /= step
epoch_loss_values.append(epoch_loss)
print(f"epoch {epoch + 1} average loss: {epoch_loss:.4f}")
if (epoch + 1) % val_interval == 0:
model.eval()
with torch.no_grad():
y_pred = torch.tensor([], dtype=torch.float32, device=device)
y = torch.tensor([], dtype=torch.long, device=device)
for val_data in val_loader:
val_images, val_labels = (
val_data[0].to(device),
val_data[1].to(device),
)
y_pred = torch.cat([y_pred, model(val_images)], dim=0)
y = torch.cat([y, val_labels], dim=0)
auc_metric = compute_roc_auc(y_pred, y, to_onehot_y=True, softmax=True)
metric_values.append(auc_metric)
acc_value = torch.eq(y_pred.argmax(dim=1), y)
acc_metric = acc_value.sum().item() / len(acc_value)
if auc_metric > best_metric:
best_metric = auc_metric
best_metric_epoch = epoch + 1
torch.save(model.state_dict(), os.path.join(root_dir, "best_metric_model.pth"))
print("saved new best metric model")
print(
f"current epoch: {epoch + 1} current AUC: {auc_metric:.4f}"
f" current accuracy: {acc_metric:.4f} best AUC: {best_metric:.4f}"
f" at epoch: {best_metric_epoch}"
)
print(f"train completed, best_metric: {best_metric:.4f} at epoch: {best_metric_epoch}")
```
## Plot the loss and metric
```
plt.figure("train", (12, 6))
plt.subplot(1, 2, 1)
plt.title("Epoch Average Loss")
x = [i + 1 for i in range(len(epoch_loss_values))]
y = epoch_loss_values
plt.xlabel("epoch")
plt.plot(x, y)
plt.subplot(1, 2, 2)
plt.title("Val AUC")
x = [val_interval * (i + 1) for i in range(len(metric_values))]
y = metric_values
plt.xlabel("epoch")
plt.plot(x, y)
plt.show()
```
## Evaluate the model on test dataset
After training and validation, we already got the best model on validation test.
We need to evaluate the model on test dataset to check whether it's robust and not over-fitting.
We'll use these predictions to generate a classification report.
```
model.load_state_dict(torch.load(os.path.join(root_dir, "best_metric_model.pth")))
model.eval()
y_true = list()
y_pred = list()
with torch.no_grad():
for test_data in test_loader:
test_images, test_labels = (
test_data[0].to(device),
test_data[1].to(device),
)
pred = model(test_images).argmax(dim=1)
for i in range(len(pred)):
y_true.append(test_labels[i].item())
y_pred.append(pred[i].item())
%pip install -qU sklearn
from sklearn.metrics import classification_report
print(classification_report(y_true, y_pred, target_names=class_names, digits=4))
```
## Cleanup data directory
Remove directory if a temporary was used.
```
if directory is None:
shutil.rmtree(root_dir)
```
|
github_jupyter
|
%pip install -qU "monai[pillow]"
%pip install -qU matplotlib
%matplotlib inline
# Copyright 2020 MONAI Consortium
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import os
import shutil
import tempfile
import matplotlib.pyplot as plt
import numpy as np
import PIL
import torch
from monai.apps import download_and_extract
from monai.config import print_config
from monai.metrics import compute_roc_auc
from monai.networks.nets import densenet121
from monai.transforms import (
AddChannel,
Compose,
LoadPNG,
RandFlip,
RandRotate,
RandZoom,
ScaleIntensity,
ToTensor,
)
from monai.utils import set_determinism
print_config()
directory = os.environ.get("MONAI_DATA_DIRECTORY")
root_dir = tempfile.mkdtemp() if directory is None else directory
print(root_dir)
resource = "https://www.dropbox.com/s/5wwskxctvcxiuea/MedNIST.tar.gz?dl=1"
md5 = "0bc7306e7427e00ad1c5526a6677552d"
compressed_file = os.path.join(root_dir, "MedNIST.tar.gz")
data_dir = os.path.join(root_dir, "MedNIST")
if not os.path.exists(data_dir):
download_and_extract(resource, compressed_file, root_dir, md5)
set_determinism(seed=0)
class_names = sorted(x for x in os.listdir(data_dir) if os.path.isdir(os.path.join(data_dir, x)))
num_class = len(class_names)
image_files = [
[
os.path.join(data_dir, class_names[i], x)
for x in os.listdir(os.path.join(data_dir, class_names[i]))
]
for i in range(num_class)
]
num_each = [len(image_files[i]) for i in range(num_class)]
image_files_list = []
image_class = []
for i in range(num_class):
image_files_list.extend(image_files[i])
image_class.extend([i] * num_each[i])
num_total = len(image_class)
image_width, image_height = PIL.Image.open(image_files_list[0]).size
print(f"Total image count: {num_total}")
print(f"Image dimensions: {image_width} x {image_height}")
print(f"Label names: {class_names}")
print(f"Label counts: {num_each}")
plt.subplots(3, 3, figsize=(8, 8))
for i, k in enumerate(np.random.randint(num_total, size=9)):
im = PIL.Image.open(image_files_list[k])
arr = np.array(im)
plt.subplot(3, 3, i + 1)
plt.xlabel(class_names[image_class[k]])
plt.imshow(arr, cmap="gray", vmin=0, vmax=255)
plt.tight_layout()
plt.show()
val_frac = 0.1
test_frac = 0.1
train_x = list()
train_y = list()
val_x = list()
val_y = list()
test_x = list()
test_y = list()
for i in range(num_total):
rann = np.random.random()
if rann < val_frac:
val_x.append(image_files_list[i])
val_y.append(image_class[i])
elif rann < test_frac + val_frac:
test_x.append(image_files_list[i])
test_y.append(image_class[i])
else:
train_x.append(image_files_list[i])
train_y.append(image_class[i])
print(f"Training count: {len(train_x)}, Validation count: {len(val_x)}, Test count: {len(test_x)}")
train_transforms = Compose(
[
LoadPNG(image_only=True),
AddChannel(),
ScaleIntensity(),
RandRotate(range_x=15, prob=0.5, keep_size=True),
RandFlip(spatial_axis=0, prob=0.5),
RandZoom(min_zoom=0.9, max_zoom=1.1, prob=0.5),
ToTensor(),
]
)
val_transforms = Compose([LoadPNG(image_only=True), AddChannel(), ScaleIntensity(), ToTensor()])
class MedNISTDataset(torch.utils.data.Dataset):
def __init__(self, image_files, labels, transforms):
self.image_files = image_files
self.labels = labels
self.transforms = transforms
def __len__(self):
return len(self.image_files)
def __getitem__(self, index):
return self.transforms(self.image_files[index]), self.labels[index]
train_ds = MedNISTDataset(train_x, train_y, train_transforms)
train_loader = torch.utils.data.DataLoader(train_ds, batch_size=300, shuffle=True, num_workers=10)
val_ds = MedNISTDataset(val_x, val_y, val_transforms)
val_loader = torch.utils.data.DataLoader(val_ds, batch_size=300, num_workers=10)
test_ds = MedNISTDataset(test_x, test_y, val_transforms)
test_loader = torch.utils.data.DataLoader(test_ds, batch_size=300, num_workers=10)
device = torch.device("cuda:0")
model = densenet121(spatial_dims=2, in_channels=1, out_channels=num_class).to(device)
loss_function = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), 1e-5)
epoch_num = 4
val_interval = 1
best_metric = -1
best_metric_epoch = -1
epoch_loss_values = list()
metric_values = list()
for epoch in range(epoch_num):
print("-" * 10)
print(f"epoch {epoch + 1}/{epoch_num}")
model.train()
epoch_loss = 0
step = 0
for batch_data in train_loader:
step += 1
inputs, labels = batch_data[0].to(device), batch_data[1].to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = loss_function(outputs, labels)
loss.backward()
optimizer.step()
epoch_loss += loss.item()
print(f"{step}/{len(train_ds) // train_loader.batch_size}, train_loss: {loss.item():.4f}")
epoch_len = len(train_ds) // train_loader.batch_size
epoch_loss /= step
epoch_loss_values.append(epoch_loss)
print(f"epoch {epoch + 1} average loss: {epoch_loss:.4f}")
if (epoch + 1) % val_interval == 0:
model.eval()
with torch.no_grad():
y_pred = torch.tensor([], dtype=torch.float32, device=device)
y = torch.tensor([], dtype=torch.long, device=device)
for val_data in val_loader:
val_images, val_labels = (
val_data[0].to(device),
val_data[1].to(device),
)
y_pred = torch.cat([y_pred, model(val_images)], dim=0)
y = torch.cat([y, val_labels], dim=0)
auc_metric = compute_roc_auc(y_pred, y, to_onehot_y=True, softmax=True)
metric_values.append(auc_metric)
acc_value = torch.eq(y_pred.argmax(dim=1), y)
acc_metric = acc_value.sum().item() / len(acc_value)
if auc_metric > best_metric:
best_metric = auc_metric
best_metric_epoch = epoch + 1
torch.save(model.state_dict(), os.path.join(root_dir, "best_metric_model.pth"))
print("saved new best metric model")
print(
f"current epoch: {epoch + 1} current AUC: {auc_metric:.4f}"
f" current accuracy: {acc_metric:.4f} best AUC: {best_metric:.4f}"
f" at epoch: {best_metric_epoch}"
)
print(f"train completed, best_metric: {best_metric:.4f} at epoch: {best_metric_epoch}")
plt.figure("train", (12, 6))
plt.subplot(1, 2, 1)
plt.title("Epoch Average Loss")
x = [i + 1 for i in range(len(epoch_loss_values))]
y = epoch_loss_values
plt.xlabel("epoch")
plt.plot(x, y)
plt.subplot(1, 2, 2)
plt.title("Val AUC")
x = [val_interval * (i + 1) for i in range(len(metric_values))]
y = metric_values
plt.xlabel("epoch")
plt.plot(x, y)
plt.show()
model.load_state_dict(torch.load(os.path.join(root_dir, "best_metric_model.pth")))
model.eval()
y_true = list()
y_pred = list()
with torch.no_grad():
for test_data in test_loader:
test_images, test_labels = (
test_data[0].to(device),
test_data[1].to(device),
)
pred = model(test_images).argmax(dim=1)
for i in range(len(pred)):
y_true.append(test_labels[i].item())
y_pred.append(pred[i].item())
%pip install -qU sklearn
from sklearn.metrics import classification_report
print(classification_report(y_true, y_pred, target_names=class_names, digits=4))
if directory is None:
shutil.rmtree(root_dir)
| 0.74158 | 0.974435 |
```
import pandas as pd
from sklearn.model_selection import train_test_split
import os
raw_data_path = 'data/news.csv'
destination_folder = 'lstm'
os.makedirs(destination_folder, exist_ok=True)
train_test_ratio = 0.10
train_valid_ratio = 0.80
first_n_words = 200
def trim_string(x):
x = x.split(maxsplit=first_n_words)
x = ' '.join(x[:first_n_words])
return x
# Read raw data
df_raw = pd.read_csv(raw_data_path)
# Prepare columns
df_raw['label'] = (df_raw['label'] == 'FAKE').astype('int')
df_raw['titletext'] = df_raw['title'] + ". " + df_raw['text']
df_raw = df_raw.reindex(columns=['label', 'title', 'text', 'titletext'])
# Drop rows with empty text
df_raw.drop( df_raw[df_raw.text.str.len() < 5].index, inplace=True)
# Trim text and titletext to first_n_words
df_raw['text'] = df_raw['text'].apply(trim_string)
df_raw['titletext'] = df_raw['titletext'].apply(trim_string)
# Split according to label
df_real = df_raw[df_raw['label'] == 0]
df_fake = df_raw[df_raw['label'] == 1]
# Train-test split
df_real_full_train, df_real_test = train_test_split(df_real, train_size = train_test_ratio, random_state = 1)
df_fake_full_train, df_fake_test = train_test_split(df_fake, train_size = train_test_ratio, random_state = 1)
# Train-valid split
df_real_train, df_real_valid = train_test_split(df_real_full_train, train_size = train_valid_ratio, random_state = 1)
df_fake_train, df_fake_valid = train_test_split(df_fake_full_train, train_size = train_valid_ratio, random_state = 1)
# Concatenate splits of different labels
df_train = pd.concat([df_real_train, df_fake_train], ignore_index=True, sort=False)
df_valid = pd.concat([df_real_valid, df_fake_valid], ignore_index=True, sort=False)
df_test = pd.concat([df_real_test, df_fake_test], ignore_index=True, sort=False)
# Write preprocessed data
df_train.to_csv(destination_folder + '/train.csv', index=False)
df_valid.to_csv(destination_folder + '/valid.csv', index=False)
df_test.to_csv(destination_folder + '/test.csv', index=False)
import matplotlib.pyplot as plt
import pandas as pd
import torch
# Preliminaries
from torchtext.legacy.data import Field, TabularDataset, BucketIterator
# Models
import torch.nn as nn
from torch.nn.utils.rnn import pack_padded_sequence, pad_packed_sequence
# Training
import torch.optim as optim
# Evaluation
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import seaborn as sns
if torch.cuda.is_available():
device = torch.device('cuda')
else:
device = torch.device('cpu')
# Fields
label_field = Field(sequential=False, use_vocab=False, batch_first=True, dtype=torch.float)
text_field = Field(tokenize='spacy', lower=True, include_lengths=True, batch_first=True)
fields = [('label', label_field), ('title', text_field), ('text', text_field), ('titletext', text_field)]
# TabularDataset
train, valid, test = TabularDataset.splits(path=destination_folder, train='train.csv', validation='valid.csv', test='test.csv',
format='CSV', fields=fields, skip_header=True)
# Iterators
train_iter = BucketIterator(train, batch_size=32, sort_key=lambda x: len(x.text),
device=device, sort=True, sort_within_batch=True)
valid_iter = BucketIterator(valid, batch_size=32, sort_key=lambda x: len(x.text),
device=device, sort=True, sort_within_batch=True)
test_iter = BucketIterator(test, batch_size=32, sort_key=lambda x: len(x.text),
device=device, sort=True, sort_within_batch=True)
# Vocabulary
text_field.build_vocab(train, min_freq=3)
class LSTM(nn.Module):
def __init__(self, dimension=128):
super(LSTM, self).__init__()
self.embedding = nn.Embedding(len(text_field.vocab), 300)
self.dimension = dimension
self.lstm = nn.LSTM(input_size=300,
hidden_size=dimension,
num_layers=1,
batch_first=True,
bidirectional=True)
self.drop = nn.Dropout(p=0.5)
self.fc = nn.Linear(2*dimension, 1)
def forward(self, text, text_len):
text_emb = self.embedding(text)
packed_input = pack_padded_sequence(text_emb, text_len, batch_first=True, enforce_sorted=False)
packed_output, _ = self.lstm(packed_input)
output, _ = pad_packed_sequence(packed_output, batch_first=True)
out_forward = output[range(len(output)), text_len - 1, :self.dimension]
out_reverse = output[:, 0, self.dimension:]
out_reduced = torch.cat((out_forward, out_reverse), 1)
text_fea = self.drop(out_reduced)
text_fea = self.fc(text_fea)
text_fea = torch.squeeze(text_fea, 1)
text_out = torch.sigmoid(text_fea)
return text_out
# Save and Load Functions
def save_checkpoint(save_path, model, optimizer, valid_loss):
if save_path == None:
return
state_dict = {'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'valid_loss': valid_loss}
torch.save(state_dict, save_path)
print(f'Model saved to ==> {save_path}')
def load_checkpoint(load_path, model, optimizer):
if load_path==None:
return
state_dict = torch.load(load_path, map_location=device)
print(f'Model loaded from <== {load_path}')
model.load_state_dict(state_dict['model_state_dict'])
optimizer.load_state_dict(state_dict['optimizer_state_dict'])
return state_dict['valid_loss']
def save_metrics(save_path, train_loss_list, valid_loss_list, global_steps_list):
if save_path == None:
return
state_dict = {'train_loss_list': train_loss_list,
'valid_loss_list': valid_loss_list,
'global_steps_list': global_steps_list}
torch.save(state_dict, save_path)
print(f'Model saved to ==> {save_path}')
def load_metrics(load_path):
if load_path==None:
return
state_dict = torch.load(load_path, map_location=device)
print(f'Model loaded from <== {load_path}')
return state_dict['train_loss_list'], state_dict['valid_loss_list'], state_dict['global_steps_list']
def train(model,
optimizer,
criterion = nn.BCELoss(),
train_loader = train_iter,
valid_loader = valid_iter,
num_epochs = 5,
eval_every = len(train_iter) // 2,
file_path = destination_folder,
best_valid_loss = float("Inf")):
# initialize running values
running_loss = 0.0
valid_running_loss = 0.0
global_step = 0
train_loss_list = []
valid_loss_list = []
global_steps_list = []
# training loop
model.train()
for epoch in range(num_epochs):
for (labels, (title, title_len), (text, text_len), (titletext, titletext_len)), _ in train_loader:
labels = labels.to(device)
titletext = titletext.to(device)
titletext_len = titletext_len.to(device)
output = model(titletext, titletext_len)
loss = criterion(output, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# update running values
running_loss += loss.item()
global_step += 1
# evaluation step
if global_step % eval_every == 0:
model.eval()
with torch.no_grad():
# validation loop
for (labels, (title, title_len), (text, text_len), (titletext, titletext_len)), _ in valid_loader:
labels = labels.to(device)
titletext = titletext.to(device)
titletext_len = titletext_len.to(device)
output = model(titletext, titletext_len)
loss = criterion(output, labels)
valid_running_loss += loss.item()
# evaluation
average_train_loss = running_loss / eval_every
average_valid_loss = valid_running_loss / len(valid_loader)
train_loss_list.append(average_train_loss)
valid_loss_list.append(average_valid_loss)
global_steps_list.append(global_step)
# resetting running values
running_loss = 0.0
valid_running_loss = 0.0
model.train()
# print progress
print('Epoch [{}/{}], Step [{}/{}], Train Loss: {:.4f}, Valid Loss: {:.4f}'
.format(epoch+1, num_epochs, global_step, num_epochs*len(train_loader),
average_train_loss, average_valid_loss))
# checkpoint
if best_valid_loss > average_valid_loss:
best_valid_loss = average_valid_loss
save_checkpoint(file_path + '/model.pt', model, optimizer, best_valid_loss)
save_metrics(file_path + '/metrics.pt', train_loss_list, valid_loss_list, global_steps_list)
save_metrics(file_path + '/metrics.pt', train_loss_list, valid_loss_list, global_steps_list)
print('Finished Training!')
model = LSTM().to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)
train(model=model, optimizer=optimizer, num_epochs=10)
```
|
github_jupyter
|
import pandas as pd
from sklearn.model_selection import train_test_split
import os
raw_data_path = 'data/news.csv'
destination_folder = 'lstm'
os.makedirs(destination_folder, exist_ok=True)
train_test_ratio = 0.10
train_valid_ratio = 0.80
first_n_words = 200
def trim_string(x):
x = x.split(maxsplit=first_n_words)
x = ' '.join(x[:first_n_words])
return x
# Read raw data
df_raw = pd.read_csv(raw_data_path)
# Prepare columns
df_raw['label'] = (df_raw['label'] == 'FAKE').astype('int')
df_raw['titletext'] = df_raw['title'] + ". " + df_raw['text']
df_raw = df_raw.reindex(columns=['label', 'title', 'text', 'titletext'])
# Drop rows with empty text
df_raw.drop( df_raw[df_raw.text.str.len() < 5].index, inplace=True)
# Trim text and titletext to first_n_words
df_raw['text'] = df_raw['text'].apply(trim_string)
df_raw['titletext'] = df_raw['titletext'].apply(trim_string)
# Split according to label
df_real = df_raw[df_raw['label'] == 0]
df_fake = df_raw[df_raw['label'] == 1]
# Train-test split
df_real_full_train, df_real_test = train_test_split(df_real, train_size = train_test_ratio, random_state = 1)
df_fake_full_train, df_fake_test = train_test_split(df_fake, train_size = train_test_ratio, random_state = 1)
# Train-valid split
df_real_train, df_real_valid = train_test_split(df_real_full_train, train_size = train_valid_ratio, random_state = 1)
df_fake_train, df_fake_valid = train_test_split(df_fake_full_train, train_size = train_valid_ratio, random_state = 1)
# Concatenate splits of different labels
df_train = pd.concat([df_real_train, df_fake_train], ignore_index=True, sort=False)
df_valid = pd.concat([df_real_valid, df_fake_valid], ignore_index=True, sort=False)
df_test = pd.concat([df_real_test, df_fake_test], ignore_index=True, sort=False)
# Write preprocessed data
df_train.to_csv(destination_folder + '/train.csv', index=False)
df_valid.to_csv(destination_folder + '/valid.csv', index=False)
df_test.to_csv(destination_folder + '/test.csv', index=False)
import matplotlib.pyplot as plt
import pandas as pd
import torch
# Preliminaries
from torchtext.legacy.data import Field, TabularDataset, BucketIterator
# Models
import torch.nn as nn
from torch.nn.utils.rnn import pack_padded_sequence, pad_packed_sequence
# Training
import torch.optim as optim
# Evaluation
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import seaborn as sns
if torch.cuda.is_available():
device = torch.device('cuda')
else:
device = torch.device('cpu')
# Fields
label_field = Field(sequential=False, use_vocab=False, batch_first=True, dtype=torch.float)
text_field = Field(tokenize='spacy', lower=True, include_lengths=True, batch_first=True)
fields = [('label', label_field), ('title', text_field), ('text', text_field), ('titletext', text_field)]
# TabularDataset
train, valid, test = TabularDataset.splits(path=destination_folder, train='train.csv', validation='valid.csv', test='test.csv',
format='CSV', fields=fields, skip_header=True)
# Iterators
train_iter = BucketIterator(train, batch_size=32, sort_key=lambda x: len(x.text),
device=device, sort=True, sort_within_batch=True)
valid_iter = BucketIterator(valid, batch_size=32, sort_key=lambda x: len(x.text),
device=device, sort=True, sort_within_batch=True)
test_iter = BucketIterator(test, batch_size=32, sort_key=lambda x: len(x.text),
device=device, sort=True, sort_within_batch=True)
# Vocabulary
text_field.build_vocab(train, min_freq=3)
class LSTM(nn.Module):
def __init__(self, dimension=128):
super(LSTM, self).__init__()
self.embedding = nn.Embedding(len(text_field.vocab), 300)
self.dimension = dimension
self.lstm = nn.LSTM(input_size=300,
hidden_size=dimension,
num_layers=1,
batch_first=True,
bidirectional=True)
self.drop = nn.Dropout(p=0.5)
self.fc = nn.Linear(2*dimension, 1)
def forward(self, text, text_len):
text_emb = self.embedding(text)
packed_input = pack_padded_sequence(text_emb, text_len, batch_first=True, enforce_sorted=False)
packed_output, _ = self.lstm(packed_input)
output, _ = pad_packed_sequence(packed_output, batch_first=True)
out_forward = output[range(len(output)), text_len - 1, :self.dimension]
out_reverse = output[:, 0, self.dimension:]
out_reduced = torch.cat((out_forward, out_reverse), 1)
text_fea = self.drop(out_reduced)
text_fea = self.fc(text_fea)
text_fea = torch.squeeze(text_fea, 1)
text_out = torch.sigmoid(text_fea)
return text_out
# Save and Load Functions
def save_checkpoint(save_path, model, optimizer, valid_loss):
if save_path == None:
return
state_dict = {'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'valid_loss': valid_loss}
torch.save(state_dict, save_path)
print(f'Model saved to ==> {save_path}')
def load_checkpoint(load_path, model, optimizer):
if load_path==None:
return
state_dict = torch.load(load_path, map_location=device)
print(f'Model loaded from <== {load_path}')
model.load_state_dict(state_dict['model_state_dict'])
optimizer.load_state_dict(state_dict['optimizer_state_dict'])
return state_dict['valid_loss']
def save_metrics(save_path, train_loss_list, valid_loss_list, global_steps_list):
if save_path == None:
return
state_dict = {'train_loss_list': train_loss_list,
'valid_loss_list': valid_loss_list,
'global_steps_list': global_steps_list}
torch.save(state_dict, save_path)
print(f'Model saved to ==> {save_path}')
def load_metrics(load_path):
if load_path==None:
return
state_dict = torch.load(load_path, map_location=device)
print(f'Model loaded from <== {load_path}')
return state_dict['train_loss_list'], state_dict['valid_loss_list'], state_dict['global_steps_list']
def train(model,
optimizer,
criterion = nn.BCELoss(),
train_loader = train_iter,
valid_loader = valid_iter,
num_epochs = 5,
eval_every = len(train_iter) // 2,
file_path = destination_folder,
best_valid_loss = float("Inf")):
# initialize running values
running_loss = 0.0
valid_running_loss = 0.0
global_step = 0
train_loss_list = []
valid_loss_list = []
global_steps_list = []
# training loop
model.train()
for epoch in range(num_epochs):
for (labels, (title, title_len), (text, text_len), (titletext, titletext_len)), _ in train_loader:
labels = labels.to(device)
titletext = titletext.to(device)
titletext_len = titletext_len.to(device)
output = model(titletext, titletext_len)
loss = criterion(output, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# update running values
running_loss += loss.item()
global_step += 1
# evaluation step
if global_step % eval_every == 0:
model.eval()
with torch.no_grad():
# validation loop
for (labels, (title, title_len), (text, text_len), (titletext, titletext_len)), _ in valid_loader:
labels = labels.to(device)
titletext = titletext.to(device)
titletext_len = titletext_len.to(device)
output = model(titletext, titletext_len)
loss = criterion(output, labels)
valid_running_loss += loss.item()
# evaluation
average_train_loss = running_loss / eval_every
average_valid_loss = valid_running_loss / len(valid_loader)
train_loss_list.append(average_train_loss)
valid_loss_list.append(average_valid_loss)
global_steps_list.append(global_step)
# resetting running values
running_loss = 0.0
valid_running_loss = 0.0
model.train()
# print progress
print('Epoch [{}/{}], Step [{}/{}], Train Loss: {:.4f}, Valid Loss: {:.4f}'
.format(epoch+1, num_epochs, global_step, num_epochs*len(train_loader),
average_train_loss, average_valid_loss))
# checkpoint
if best_valid_loss > average_valid_loss:
best_valid_loss = average_valid_loss
save_checkpoint(file_path + '/model.pt', model, optimizer, best_valid_loss)
save_metrics(file_path + '/metrics.pt', train_loss_list, valid_loss_list, global_steps_list)
save_metrics(file_path + '/metrics.pt', train_loss_list, valid_loss_list, global_steps_list)
print('Finished Training!')
model = LSTM().to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)
train(model=model, optimizer=optimizer, num_epochs=10)
| 0.822439 | 0.311047 |
## Mean encoding
In the previous lectures in this section on how to engineer the labels of categorical variables, we learnt how to convert a label into a number, by using one hot encoding or replacing by frequency or counts. These methods are simple, make no assumptions and work generally well in different scenarios.
There are however methods that allow us to capture information while pre-processing the labels of categorical variables. These methods include:
- Ordering the labels according to the target
- Replacing labels by the risk (of the target)
- Replacing the labels by the joint probability of the target being 1 or 0
- Weight of evidence.
### Monotonicity
All these methods create a monotonic relationship between the categorical variable and the target. A monotonic relationship is a relationship that does one of the following: (1) as the value of one variable increases, so does the value of the other variable; or (2) as the value of one variable increases, the other variable value decreases. In this case, as the value of the independent variable (predictor) increases, so does the target, or conversely, as the value of the variable increases, the target decreases.
In general:
### Advantages
- Capture information within the label, therefore rendering more predictive features
- Creates a monotonic relationship between the variable and the target
- Does not expand the feature space
### Disadvantage
- Prone to cause over-fitting
### Note
The methods discussed in this and the coming 3 lectures can be also used on numerical variables, after discretisation. This creates a monotonic relationship between the numerical variable and the target, and therefore improves the performance of linear models. I will discuss this in more detail in the section "Discretisation".
### Replace labels by the Risk Factor
Replacing labels by the risk factor means essentially replacing the label by the mean of the target for that label.
I have only seen this procedure applied in classifications scenarios, where the target can take just the values of 1 or 0. However, in principle, I don't see why this shouldn't be possible as well when the target is continuous. Just be mindful of over-fitting.
```
import pandas as pd
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline
# let's load again the titanic dataset
data = pd.read_csv('titanic.csv', usecols=['Cabin', 'Survived'])
data.head()
# let's first fill NA values with an additional label
data.Cabin.fillna('Missing', inplace=True)
data.head()
# Cabin has indeed a lot of labels, here for simplicity, I will capture the first letter of the cabin,
# but the procedure could be done as well without any prior variable manipulation
len(data.Cabin.unique()) # check number of different labels in Cabin
# Now we extract the first letter of the cabin
data['Cabin'] = data['Cabin'].astype(str).str[0]
data.head()
# check the labels
data.Cabin.unique()
```
### Important
The risk factor should be calculated per label considering ONLY on the training set, and then expanded it to the test set.
See below.
```
# Let's separate into training and testing set
X_train, X_test, y_train, y_test = train_test_split(data[['Cabin', 'Survived']], data.Survived, test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
# let's calculate the target frequency for each label
X_train.groupby(['Cabin'])['Survived'].mean()
# and now let's do the same but capturing the result in a dictionary
ordered_labels = X_train.groupby(['Cabin'])['Survived'].mean().to_dict()
ordered_labels
# replace the labels with the 'risk' (target frequency)
# note that we calculated the frequencies based on the training set only
X_train['Cabin_ordered'] = X_train.Cabin.map(ordered_labels)
X_test['Cabin_ordered'] = X_test.Cabin.map(ordered_labels)
# check the results
X_train.head()
# plot the original variable
fig = plt.figure()
fig = X_train.groupby(['Cabin'])['Survived'].mean().plot()
fig.set_title('Normal relationship between variable and target')
fig.set_ylabel('Survived')
# plot the transformed result: the monotonic variable
fig = plt.figure()
fig = X_train.groupby(['Cabin_ordered'])['Survived'].mean().plot()
fig.set_title('Monotonic relationship between variable and target')
fig.set_ylabel('Survived')
```
Here the relationship lies perfectly on a diagonal line, because this is how we replaced the categories.
|
github_jupyter
|
import pandas as pd
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline
# let's load again the titanic dataset
data = pd.read_csv('titanic.csv', usecols=['Cabin', 'Survived'])
data.head()
# let's first fill NA values with an additional label
data.Cabin.fillna('Missing', inplace=True)
data.head()
# Cabin has indeed a lot of labels, here for simplicity, I will capture the first letter of the cabin,
# but the procedure could be done as well without any prior variable manipulation
len(data.Cabin.unique()) # check number of different labels in Cabin
# Now we extract the first letter of the cabin
data['Cabin'] = data['Cabin'].astype(str).str[0]
data.head()
# check the labels
data.Cabin.unique()
# Let's separate into training and testing set
X_train, X_test, y_train, y_test = train_test_split(data[['Cabin', 'Survived']], data.Survived, test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
# let's calculate the target frequency for each label
X_train.groupby(['Cabin'])['Survived'].mean()
# and now let's do the same but capturing the result in a dictionary
ordered_labels = X_train.groupby(['Cabin'])['Survived'].mean().to_dict()
ordered_labels
# replace the labels with the 'risk' (target frequency)
# note that we calculated the frequencies based on the training set only
X_train['Cabin_ordered'] = X_train.Cabin.map(ordered_labels)
X_test['Cabin_ordered'] = X_test.Cabin.map(ordered_labels)
# check the results
X_train.head()
# plot the original variable
fig = plt.figure()
fig = X_train.groupby(['Cabin'])['Survived'].mean().plot()
fig.set_title('Normal relationship between variable and target')
fig.set_ylabel('Survived')
# plot the transformed result: the monotonic variable
fig = plt.figure()
fig = X_train.groupby(['Cabin_ordered'])['Survived'].mean().plot()
fig.set_title('Monotonic relationship between variable and target')
fig.set_ylabel('Survived')
| 0.607663 | 0.992975 |
.. _nb_results:
## Result
After an algorithm has been executed a result object is returned. In the following, single- and multi-objective runs with and without constraints are shown and the corresponding `Result` object is explained:
```
from pymoo.algorithms.so_genetic_algorithm import GA
from pymoo.factory import get_problem
from pymoo.optimize import minimize
problem = get_problem("sphere")
algorithm = GA(pop_size=5)
res = minimize(problem,
algorithm,
('n_gen', 30),
seed=1)
```
After an algorithm has been executed, a result object is returned. In the following, single- and multi-objective runs with and without constraints are shown, and the corresponding `Result` object is explained:
In this single-objective optimization problem, there exists a single best solution that was found.
The result directly contains the best-found values in the corresponding spaces.
- `res.X` design space values are
- `res.F` objective spaces values
- `res.G` constraint values
- `res.CV` aggregated constraint violation
- `res.algorithm` algorithm object
- `res.pop` final population object
- `res.history` history of algorithm object. (only if `save_history` has been enabled during the algorithm initialization)
- `res.time` the time required to run the algorithm
Note that when the `minimize` function is called, a deep copy of the algorithm object is created.
This ensures that two independent runs with the same algorithm and same random seed have the same results without any side effects.
```
res.X, res.F, res.G, res.CV
res.algorithm, res.pop
```
The values from the final population can be extracted by using the `get` method. The population object is used internally and store information for each individual. The `get` method allows returning vectors or matrices based on the provided properties.
```
res.pop.get("X"), res.pop.get("F")
```
In this run, the problem did not have any constraints, and `res.G` evaluated to `None`.
Also, note that `res.CV` will always be set to `0`, no matter if the problem has constraints or not.
Let us consider a problem that has, in fact, constraints:
```
problem = get_problem("g01")
algorithm = GA(pop_size=5)
res = minimize(problem,
algorithm,
('n_gen', 5),
verbose=True,
seed=1)
res.X, res.F, res.G, res.CV
```
Here, the algorithm was not able to find any feasible solution in 5 generations. Therefore, all values contained in the results are equals to `None`. If the least feasible solution should be returned when no feasible solution was found, the flag `return_least_infeasible` can be enabled:
```
problem = get_problem("g01")
algorithm = GA(pop_size=5)
res = minimize(problem,
algorithm,
('n_gen', 5),
verbose=True,
return_least_infeasible=True,
seed=1)
res.X, res.F, res.G, res.CV
```
We have made this design decision, because an infeasible solution can often not be considered as a solution
of the optimization problem. Therefore, having a solution equals to `None` indicates the fact no feasible solution has been found.
If the problem has multiple objectives, the result object has the same structure but `res.X`, `res.F`, `res .G`, `res.CV` is a set
of non-dominated solutions instead of a single one.
```
from pymoo.algorithms.nsga2 import NSGA2
problem = get_problem("zdt2")
algorithm = NSGA2()
res = minimize(problem,
algorithm,
('n_gen', 10),
seed=1)
res.F
```
|
github_jupyter
|
from pymoo.algorithms.so_genetic_algorithm import GA
from pymoo.factory import get_problem
from pymoo.optimize import minimize
problem = get_problem("sphere")
algorithm = GA(pop_size=5)
res = minimize(problem,
algorithm,
('n_gen', 30),
seed=1)
res.X, res.F, res.G, res.CV
res.algorithm, res.pop
res.pop.get("X"), res.pop.get("F")
problem = get_problem("g01")
algorithm = GA(pop_size=5)
res = minimize(problem,
algorithm,
('n_gen', 5),
verbose=True,
seed=1)
res.X, res.F, res.G, res.CV
problem = get_problem("g01")
algorithm = GA(pop_size=5)
res = minimize(problem,
algorithm,
('n_gen', 5),
verbose=True,
return_least_infeasible=True,
seed=1)
res.X, res.F, res.G, res.CV
from pymoo.algorithms.nsga2 import NSGA2
problem = get_problem("zdt2")
algorithm = NSGA2()
res = minimize(problem,
algorithm,
('n_gen', 10),
seed=1)
res.F
| 0.710327 | 0.979255 |
---------------------------------------
# $SPA$tial $G$rap$H$s: n$ET$works, $T$opology, & $I$nference
## Tutorial for `pysal.spaghetti`: Working with point patterns: empirical observations
#### James D. Gaboardi [<jgaboardi@fsu.edu>]
1. Instantiating a `pysal.spaghetti.Network`
2. Allocating observations to a network
* snapping
3. Visualizing original and snapped locations
* visualization with `geopandas` and `matplotlib`
```
import os
last_modified = None
if os.name == "posix":
last_modified = !stat -f\
"# This notebook was last updated: %Sm"\
Spaghetti_Pointpatterns_Empirical.ipynb
elif os.name == "nt":
last_modified = !for %a in (Spaghetti_Pointpatterns_Empirical.ipynb)\
do echo # This notebook was last updated: %~ta
if last_modified:
get_ipython().set_next_input(last_modified[-1])
# This notebook was last updated: Dec 9 14:23:58 2018
```
-----------------
```
from pysal.explore import spaghetti as spgh
from pysal.lib import examples
import geopandas as gpd
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
from shapely.geometry import Point, LineString
%matplotlib inline
__author__ = "James Gaboardi <jgaboardi@gmail.com>"
```
# 1. Instantiating a `pysal.spaghetti.Network`
### Instantiate the network from `.shp` file
```
ntw = spgh.Network(in_data=examples.get_path('streets.shp'))
```
# 2. Allocating observations to a network
### Snap point patterns to the network
```
# Crimes with attributes
ntw.snapobservations(examples.get_path('crimes.shp'),
'crimes',
attribute=True)
# Schools without attributes
ntw.snapobservations(examples.get_path('schools.shp'),
'schools',
attribute=False)
```
# 3. Visualizing original and snapped locations
## True and snapped school locations
```
schools_df = spgh.element_as_gdf(ntw,
pp_name='schools',
snapped=False)
snapped_schools_df = spgh.element_as_gdf(ntw,
pp_name='schools',
snapped=True)
```
## True and snapped crime locations
```
crimes_df = spgh.element_as_gdf(ntw,
pp_name='crimes',
snapped=False)
snapped_crimes_df = spgh.element_as_gdf(ntw,
pp_name='crimes',
snapped=True)
```
## Create `geopandas.GeoDataFrame` objects of the vertices and arcs
```
# network nodes and edges
vertices_df, arcs_df = spgh.element_as_gdf(ntw,
vertices=True,
arcs=True)
```
## Plotting `geopandas.GeoDataFrame` objects
```
# legend patches
arcs = mlines.Line2D([], [], color='k', label='Network Arcs', alpha=.5)
vtxs = mlines.Line2D([], [], color='k', linewidth=0, markersize=2.5,
marker='o', label='Network Vertices', alpha=1)
schl = mlines.Line2D([], [], color='k', linewidth=0, markersize=25,
marker='X', label='School Locations', alpha=1)
snp_schl = mlines.Line2D([], [], color='k', linewidth=0, markersize=12,
marker='o', label='Snapped Schools', alpha=1)
crme = mlines.Line2D([], [], color='r', linewidth=0, markersize=7,
marker='x', label='Crime Locations', alpha=.75)
snp_crme = mlines.Line2D([], [], color='r', linewidth=0, markersize=3,
marker='o', label='Snapped Crimes', alpha=.75)
patches = [arcs, vtxs, schl, snp_schl, crme, snp_crme]
# plot figure
base = arcs_df.plot(color='k', alpha=.25, figsize=(12,12), zorder=0)
vertices_df.plot(ax=base, color='k', markersize=5, alpha=1)
crimes_df.plot(ax=base, color='r', marker='x',
markersize=50, alpha=.5, zorder=1)
snapped_crimes_df.plot(ax=base, color='r',
markersize=20, alpha=.5, zorder=1)
schools_df.plot(ax=base, cmap='tab20', column='id', marker='X',
markersize=500, alpha=.5, zorder=2)
snapped_schools_df.plot(ax=base,cmap='tab20', column='id',
markersize=200, alpha=.5, zorder=2)
# add legend
plt.legend(handles=patches, fancybox=True, framealpha=0.8,
scatterpoints=1, fontsize="xx-large", bbox_to_anchor=(1.04, .6))
```
-----------
|
github_jupyter
|
import os
last_modified = None
if os.name == "posix":
last_modified = !stat -f\
"# This notebook was last updated: %Sm"\
Spaghetti_Pointpatterns_Empirical.ipynb
elif os.name == "nt":
last_modified = !for %a in (Spaghetti_Pointpatterns_Empirical.ipynb)\
do echo # This notebook was last updated: %~ta
if last_modified:
get_ipython().set_next_input(last_modified[-1])
# This notebook was last updated: Dec 9 14:23:58 2018
from pysal.explore import spaghetti as spgh
from pysal.lib import examples
import geopandas as gpd
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
from shapely.geometry import Point, LineString
%matplotlib inline
__author__ = "James Gaboardi <jgaboardi@gmail.com>"
ntw = spgh.Network(in_data=examples.get_path('streets.shp'))
# Crimes with attributes
ntw.snapobservations(examples.get_path('crimes.shp'),
'crimes',
attribute=True)
# Schools without attributes
ntw.snapobservations(examples.get_path('schools.shp'),
'schools',
attribute=False)
schools_df = spgh.element_as_gdf(ntw,
pp_name='schools',
snapped=False)
snapped_schools_df = spgh.element_as_gdf(ntw,
pp_name='schools',
snapped=True)
crimes_df = spgh.element_as_gdf(ntw,
pp_name='crimes',
snapped=False)
snapped_crimes_df = spgh.element_as_gdf(ntw,
pp_name='crimes',
snapped=True)
# network nodes and edges
vertices_df, arcs_df = spgh.element_as_gdf(ntw,
vertices=True,
arcs=True)
# legend patches
arcs = mlines.Line2D([], [], color='k', label='Network Arcs', alpha=.5)
vtxs = mlines.Line2D([], [], color='k', linewidth=0, markersize=2.5,
marker='o', label='Network Vertices', alpha=1)
schl = mlines.Line2D([], [], color='k', linewidth=0, markersize=25,
marker='X', label='School Locations', alpha=1)
snp_schl = mlines.Line2D([], [], color='k', linewidth=0, markersize=12,
marker='o', label='Snapped Schools', alpha=1)
crme = mlines.Line2D([], [], color='r', linewidth=0, markersize=7,
marker='x', label='Crime Locations', alpha=.75)
snp_crme = mlines.Line2D([], [], color='r', linewidth=0, markersize=3,
marker='o', label='Snapped Crimes', alpha=.75)
patches = [arcs, vtxs, schl, snp_schl, crme, snp_crme]
# plot figure
base = arcs_df.plot(color='k', alpha=.25, figsize=(12,12), zorder=0)
vertices_df.plot(ax=base, color='k', markersize=5, alpha=1)
crimes_df.plot(ax=base, color='r', marker='x',
markersize=50, alpha=.5, zorder=1)
snapped_crimes_df.plot(ax=base, color='r',
markersize=20, alpha=.5, zorder=1)
schools_df.plot(ax=base, cmap='tab20', column='id', marker='X',
markersize=500, alpha=.5, zorder=2)
snapped_schools_df.plot(ax=base,cmap='tab20', column='id',
markersize=200, alpha=.5, zorder=2)
# add legend
plt.legend(handles=patches, fancybox=True, framealpha=0.8,
scatterpoints=1, fontsize="xx-large", bbox_to_anchor=(1.04, .6))
| 0.513912 | 0.911653 |
# IMPORTING THE LIBRARIES
```
import os
import pandas as pd
import pickle
import numpy as np
import seaborn as sns
from sklearn.datasets import load_files
from keras.utils import np_utils
import matplotlib.pyplot as plt
from keras.layers import Conv2D, MaxPooling2D, GlobalAveragePooling2D
from keras.layers import Dropout, Flatten, Dense
from keras.models import Sequential
from keras.utils.vis_utils import plot_model
from keras.callbacks import ModelCheckpoint
from keras.utils import to_categorical
from sklearn.metrics import confusion_matrix
from keras.preprocessing import image
from tqdm import tqdm
import seaborn as sns
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score
# Pretty display for notebooks
%matplotlib inline
!ls
```
# Defining the train,test and model directories
We will create the directories for train,test and model training paths if not present
```
TEST_DIR = os.path.join(os.getcwd(),"imgs","test")
TRAIN_DIR = os.path.join(os.getcwd(),"imgs","train")
MODEL_PATH = os.path.join(os.getcwd(),"model","self_trained")
PICKLE_DIR = os.path.join(os.getcwd(),"pickle_files")
CSV_DIR = os.path.join(os.getcwd(),"csv_files")
if not os.path.exists(TEST_DIR):
print("Testing data does not exists")
if not os.path.exists(TRAIN_DIR):
print("Training data does not exists")
if not os.path.exists(MODEL_PATH):
print("Model path does not exists")
os.makedirs(MODEL_PATH)
print("Model path created")
if not os.path.exists(PICKLE_DIR):
os.makedirs(PICKLE_DIR)
if not os.path.exists(CSV_DIR):
os.makedirs(CSV_DIR)
```
# Data Preparation
We will create a csv file having the location of the files present for training and test images and their associated class if present so that it is easily traceable.
```
def create_csv(DATA_DIR,filename):
class_names = os.listdir(DATA_DIR)
data = list()
if(os.path.isdir(os.path.join(DATA_DIR,class_names[0]))):
for class_name in class_names:
file_names = os.listdir(os.path.join(DATA_DIR,class_name))
for file in file_names:
data.append({
"Filename":os.path.join(DATA_DIR,class_name,file),
"ClassName":class_name
})
else:
class_name = "test"
file_names = os.listdir(DATA_DIR)
for file in file_names:
data.append(({
"FileName":os.path.join(DATA_DIR,file),
"ClassName":class_name
}))
data = pd.DataFrame(data)
data.to_csv(os.path.join(os.getcwd(),"csv_files",filename),index=False)
create_csv(TRAIN_DIR,"train.csv")
create_csv(TEST_DIR,"test.csv")
data_train = pd.read_csv(os.path.join(os.getcwd(),"csv_files","train.csv"))
data_test = pd.read_csv(os.path.join(os.getcwd(),"csv_files","test.csv"))
data_train.info()
data_train['ClassName'].value_counts()
data_train.describe()
nf = data_train['ClassName'].value_counts(sort=False)
labels = data_train['ClassName'].value_counts(sort=False).index.tolist()
y = np.array(nf)
width = 1/1.5
N = len(y)
x = range(N)
fig = plt.figure(figsize=(20,15))
ay = fig.add_subplot(211)
plt.xticks(x, labels, size=15)
plt.yticks(size=15)
ay.bar(x, y, width, color="blue")
plt.title('Bar Chart',size=25)
plt.xlabel('classname',size=15)
plt.ylabel('Count',size=15)
plt.show()
data_test.head()
data_test.shape
```
## Observation:
1. There are total 22424 training samples
2. There are total 79726 training samples
3. The training dataset is equally balanced to a great extent and hence we need not do any downsampling of the data
## Converting into numerical values
```
labels_list = list(set(data_train['ClassName'].values.tolist()))
labels_id = {label_name:id for id,label_name in enumerate(labels_list)}
print(labels_id)
data_train['ClassName'].replace(labels_id,inplace=True)
with open(os.path.join(os.getcwd(),"pickle_files","labels_list.pkl"),"wb") as handle:
pickle.dump(labels_id,handle)
labels = to_categorical(data_train['ClassName'])
print(labels.shape)
```
## Splitting into Train and Test sets
```
from sklearn.model_selection import train_test_split
xtrain,xtest,ytrain,ytest = train_test_split(data_train.iloc[:,0],labels,test_size = 0.2,random_state=42)
```
### Converting into 64*64 images
You can substitute 64,64 to 224,224 for better results only if ram is >32gb
```
def path_to_tensor(img_path):
# loads RGB image as PIL.Image.Image type
img = image.load_img(img_path, target_size=(128, 128))
# convert PIL.Image.Image type to 3D tensor with shape (224, 224, 3)
x = image.img_to_array(img)
# convert 3D tensor to 4D tensor with shape (1, 224, 224, 3) and return 4D tensor
return np.expand_dims(x, axis=0)
def paths_to_tensor(img_paths):
list_of_tensors = [path_to_tensor(img_path) for img_path in tqdm(img_paths)]
return np.vstack(list_of_tensors)
from PIL import ImageFile
ImageFile.LOAD_TRUNCATED_IMAGES = True
# pre-process the data for Keras
train_tensors = paths_to_tensor(xtrain).astype('float32')/255 - 0.5
valid_tensors = paths_to_tensor(xtest).astype('float32')/255 - 0.5
##takes too much ram
## run this if your ram is greater than 16gb
# test_tensors = paths_to_tensor(data_test.iloc[:,0]).astype('float32')/255 - 0.5
```
# Defining the Model
```
model = Sequential()
model.add(Conv2D(filters=64, kernel_size=2, padding='same', activation='relu', input_shape=(128,128,3), kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=128, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=256, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=512, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax', kernel_initializer='glorot_normal'))
model.summary()
plot_model(model,to_file=os.path.join(MODEL_PATH,"model_distracted_driver.png"),show_shapes=True,show_layer_names=True)
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
filepath = os.path.join(MODEL_PATH,"distracted-{epoch:02d}-{val_accuracy:.2f}.hdf5")
checkpoint = ModelCheckpoint(filepath, monitor='val_accuracy', verbose=1, save_best_only=True, mode='max',period=1)
callbacks_list = [checkpoint]
model_history = model.fit(train_tensors,ytrain,validation_data = (valid_tensors, ytest),epochs=25, batch_size=40, shuffle=True,callbacks=callbacks_list)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 12))
ax1.plot(model_history.history['loss'], color='b', label="Training loss")
ax1.plot(model_history.history['val_loss'], color='r', label="validation loss")
ax1.set_xticks(np.arange(1, 25, 1))
ax1.set_yticks(np.arange(0, 1, 0.1))
ax2.plot(model_history.history['accuracy'], color='b', label="Training accuracy")
ax2.plot(model_history.history['val_accuracy'], color='r',label="Validation accuracy")
ax2.set_xticks(np.arange(1, 25, 1))
legend = plt.legend(loc='best', shadow=True)
plt.tight_layout()
plt.show()
```
# Model Analysis
Finding the Confusion matrix,Precision,Recall and F1 score to analyse the model thus created
```
def print_confusion_matrix(confusion_matrix, class_names, figsize = (10,7), fontsize=14):
df_cm = pd.DataFrame(
confusion_matrix, index=class_names, columns=class_names,
)
fig = plt.figure(figsize=figsize)
try:
heatmap = sns.heatmap(df_cm, annot=True, fmt="d")
except ValueError:
raise ValueError("Confusion matrix values must be integers.")
heatmap.yaxis.set_ticklabels(heatmap.yaxis.get_ticklabels(), rotation=0, ha='right', fontsize=fontsize)
heatmap.xaxis.set_ticklabels(heatmap.xaxis.get_ticklabels(), rotation=45, ha='right', fontsize=fontsize)
plt.ylabel('True label')
plt.xlabel('Predicted label')
fig.savefig(os.path.join(MODEL_PATH,"confusion_matrix.png"))
return fig
def print_heatmap(n_labels, n_predictions, class_names):
labels = n_labels #sess.run(tf.argmax(n_labels, 1))
predictions = n_predictions #sess.run(tf.argmax(n_predictions, 1))
# confusion_matrix = sess.run(tf.contrib.metrics.confusion_matrix(labels, predictions))
matrix = confusion_matrix(labels.argmax(axis=1),predictions.argmax(axis=1))
row_sum = np.sum(matrix, axis = 1)
w, h = matrix.shape
c_m = np.zeros((w, h))
for i in range(h):
c_m[i] = matrix[i] * 100 / row_sum[i]
c = c_m.astype(dtype = np.uint8)
heatmap = print_confusion_matrix(c, class_names, figsize=(18,10), fontsize=20)
class_names = list()
for name,idx in labels_id.items():
class_names.append(name)
# print(class_names)
ypred = model.predict(valid_tensors)
print_heatmap(ytest,ypred,class_names)
```
## Precision Recall F1 Score
```
ypred_class = np.argmax(ypred,axis=1)
# print(ypred_class[:10])
ytest = np.argmax(ytest,axis=1)
accuracy = accuracy_score(ytest,ypred_class)
print('Accuracy: %f' % accuracy)
# precision tp / (tp + fp)
precision = precision_score(ytest, ypred_class,average='weighted')
print('Precision: %f' % precision)
# recall: tp / (tp + fn)
recall = recall_score(ytest,ypred_class,average='weighted')
print('Recall: %f' % recall)
# f1: 2 tp / (2 tp + fp + fn)
f1 = f1_score(ytest,ypred_class,average='weighted')
print('F1 score: %f' % f1)
```
|
github_jupyter
|
import os
import pandas as pd
import pickle
import numpy as np
import seaborn as sns
from sklearn.datasets import load_files
from keras.utils import np_utils
import matplotlib.pyplot as plt
from keras.layers import Conv2D, MaxPooling2D, GlobalAveragePooling2D
from keras.layers import Dropout, Flatten, Dense
from keras.models import Sequential
from keras.utils.vis_utils import plot_model
from keras.callbacks import ModelCheckpoint
from keras.utils import to_categorical
from sklearn.metrics import confusion_matrix
from keras.preprocessing import image
from tqdm import tqdm
import seaborn as sns
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score
# Pretty display for notebooks
%matplotlib inline
!ls
TEST_DIR = os.path.join(os.getcwd(),"imgs","test")
TRAIN_DIR = os.path.join(os.getcwd(),"imgs","train")
MODEL_PATH = os.path.join(os.getcwd(),"model","self_trained")
PICKLE_DIR = os.path.join(os.getcwd(),"pickle_files")
CSV_DIR = os.path.join(os.getcwd(),"csv_files")
if not os.path.exists(TEST_DIR):
print("Testing data does not exists")
if not os.path.exists(TRAIN_DIR):
print("Training data does not exists")
if not os.path.exists(MODEL_PATH):
print("Model path does not exists")
os.makedirs(MODEL_PATH)
print("Model path created")
if not os.path.exists(PICKLE_DIR):
os.makedirs(PICKLE_DIR)
if not os.path.exists(CSV_DIR):
os.makedirs(CSV_DIR)
def create_csv(DATA_DIR,filename):
class_names = os.listdir(DATA_DIR)
data = list()
if(os.path.isdir(os.path.join(DATA_DIR,class_names[0]))):
for class_name in class_names:
file_names = os.listdir(os.path.join(DATA_DIR,class_name))
for file in file_names:
data.append({
"Filename":os.path.join(DATA_DIR,class_name,file),
"ClassName":class_name
})
else:
class_name = "test"
file_names = os.listdir(DATA_DIR)
for file in file_names:
data.append(({
"FileName":os.path.join(DATA_DIR,file),
"ClassName":class_name
}))
data = pd.DataFrame(data)
data.to_csv(os.path.join(os.getcwd(),"csv_files",filename),index=False)
create_csv(TRAIN_DIR,"train.csv")
create_csv(TEST_DIR,"test.csv")
data_train = pd.read_csv(os.path.join(os.getcwd(),"csv_files","train.csv"))
data_test = pd.read_csv(os.path.join(os.getcwd(),"csv_files","test.csv"))
data_train.info()
data_train['ClassName'].value_counts()
data_train.describe()
nf = data_train['ClassName'].value_counts(sort=False)
labels = data_train['ClassName'].value_counts(sort=False).index.tolist()
y = np.array(nf)
width = 1/1.5
N = len(y)
x = range(N)
fig = plt.figure(figsize=(20,15))
ay = fig.add_subplot(211)
plt.xticks(x, labels, size=15)
plt.yticks(size=15)
ay.bar(x, y, width, color="blue")
plt.title('Bar Chart',size=25)
plt.xlabel('classname',size=15)
plt.ylabel('Count',size=15)
plt.show()
data_test.head()
data_test.shape
labels_list = list(set(data_train['ClassName'].values.tolist()))
labels_id = {label_name:id for id,label_name in enumerate(labels_list)}
print(labels_id)
data_train['ClassName'].replace(labels_id,inplace=True)
with open(os.path.join(os.getcwd(),"pickle_files","labels_list.pkl"),"wb") as handle:
pickle.dump(labels_id,handle)
labels = to_categorical(data_train['ClassName'])
print(labels.shape)
from sklearn.model_selection import train_test_split
xtrain,xtest,ytrain,ytest = train_test_split(data_train.iloc[:,0],labels,test_size = 0.2,random_state=42)
def path_to_tensor(img_path):
# loads RGB image as PIL.Image.Image type
img = image.load_img(img_path, target_size=(128, 128))
# convert PIL.Image.Image type to 3D tensor with shape (224, 224, 3)
x = image.img_to_array(img)
# convert 3D tensor to 4D tensor with shape (1, 224, 224, 3) and return 4D tensor
return np.expand_dims(x, axis=0)
def paths_to_tensor(img_paths):
list_of_tensors = [path_to_tensor(img_path) for img_path in tqdm(img_paths)]
return np.vstack(list_of_tensors)
from PIL import ImageFile
ImageFile.LOAD_TRUNCATED_IMAGES = True
# pre-process the data for Keras
train_tensors = paths_to_tensor(xtrain).astype('float32')/255 - 0.5
valid_tensors = paths_to_tensor(xtest).astype('float32')/255 - 0.5
##takes too much ram
## run this if your ram is greater than 16gb
# test_tensors = paths_to_tensor(data_test.iloc[:,0]).astype('float32')/255 - 0.5
model = Sequential()
model.add(Conv2D(filters=64, kernel_size=2, padding='same', activation='relu', input_shape=(128,128,3), kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=128, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=256, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=512, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax', kernel_initializer='glorot_normal'))
model.summary()
plot_model(model,to_file=os.path.join(MODEL_PATH,"model_distracted_driver.png"),show_shapes=True,show_layer_names=True)
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
filepath = os.path.join(MODEL_PATH,"distracted-{epoch:02d}-{val_accuracy:.2f}.hdf5")
checkpoint = ModelCheckpoint(filepath, monitor='val_accuracy', verbose=1, save_best_only=True, mode='max',period=1)
callbacks_list = [checkpoint]
model_history = model.fit(train_tensors,ytrain,validation_data = (valid_tensors, ytest),epochs=25, batch_size=40, shuffle=True,callbacks=callbacks_list)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 12))
ax1.plot(model_history.history['loss'], color='b', label="Training loss")
ax1.plot(model_history.history['val_loss'], color='r', label="validation loss")
ax1.set_xticks(np.arange(1, 25, 1))
ax1.set_yticks(np.arange(0, 1, 0.1))
ax2.plot(model_history.history['accuracy'], color='b', label="Training accuracy")
ax2.plot(model_history.history['val_accuracy'], color='r',label="Validation accuracy")
ax2.set_xticks(np.arange(1, 25, 1))
legend = plt.legend(loc='best', shadow=True)
plt.tight_layout()
plt.show()
def print_confusion_matrix(confusion_matrix, class_names, figsize = (10,7), fontsize=14):
df_cm = pd.DataFrame(
confusion_matrix, index=class_names, columns=class_names,
)
fig = plt.figure(figsize=figsize)
try:
heatmap = sns.heatmap(df_cm, annot=True, fmt="d")
except ValueError:
raise ValueError("Confusion matrix values must be integers.")
heatmap.yaxis.set_ticklabels(heatmap.yaxis.get_ticklabels(), rotation=0, ha='right', fontsize=fontsize)
heatmap.xaxis.set_ticklabels(heatmap.xaxis.get_ticklabels(), rotation=45, ha='right', fontsize=fontsize)
plt.ylabel('True label')
plt.xlabel('Predicted label')
fig.savefig(os.path.join(MODEL_PATH,"confusion_matrix.png"))
return fig
def print_heatmap(n_labels, n_predictions, class_names):
labels = n_labels #sess.run(tf.argmax(n_labels, 1))
predictions = n_predictions #sess.run(tf.argmax(n_predictions, 1))
# confusion_matrix = sess.run(tf.contrib.metrics.confusion_matrix(labels, predictions))
matrix = confusion_matrix(labels.argmax(axis=1),predictions.argmax(axis=1))
row_sum = np.sum(matrix, axis = 1)
w, h = matrix.shape
c_m = np.zeros((w, h))
for i in range(h):
c_m[i] = matrix[i] * 100 / row_sum[i]
c = c_m.astype(dtype = np.uint8)
heatmap = print_confusion_matrix(c, class_names, figsize=(18,10), fontsize=20)
class_names = list()
for name,idx in labels_id.items():
class_names.append(name)
# print(class_names)
ypred = model.predict(valid_tensors)
print_heatmap(ytest,ypred,class_names)
ypred_class = np.argmax(ypred,axis=1)
# print(ypred_class[:10])
ytest = np.argmax(ytest,axis=1)
accuracy = accuracy_score(ytest,ypred_class)
print('Accuracy: %f' % accuracy)
# precision tp / (tp + fp)
precision = precision_score(ytest, ypred_class,average='weighted')
print('Precision: %f' % precision)
# recall: tp / (tp + fn)
recall = recall_score(ytest,ypred_class,average='weighted')
print('Recall: %f' % recall)
# f1: 2 tp / (2 tp + fp + fn)
f1 = f1_score(ytest,ypred_class,average='weighted')
print('F1 score: %f' % f1)
| 0.597608 | 0.623406 |
```
import textract
import numpy as np
import scipy
import gensim
import os
import pandas as pd
import re
import math
from collections import Counter
from matplotlib import pyplot as plt
from gensim import corpora, models
%matplotlib inline
!pip install bertopic
class FocusGroup:
def __init__(self, filename):
self.raw_text=str(textract.process('FocusGroups/' + filename + ".docx")).replace('b\'', '').replace('\'', '')
self.parent_moderator_discussion=self.raw_text.split('\\n\\n\\n')[0].split('\\n\\n')
self.within_moderator_discussion=self.raw_text.split('\\n\\n\\n')[1].split('\\n\\n')
self.talkers_including_parents=np.array([self.parent_moderator_discussion[i].replace(':', '')
for i in range(0, len(self.parent_moderator_discussion), 2)])
self.text_including_parents=np.array([self.parent_moderator_discussion[i].replace(':', '')
for i in range(1, len(self.parent_moderator_discussion), 2)])
self.talkers_only_moderators=np.array([self.within_moderator_discussion[i].replace(':', '')
for i in range(0, len(self.within_moderator_discussion), 2)])
self.text_only_moderators=np.array([self.within_moderator_discussion[i].replace(':', '')
for i in range(1, len(self.within_moderator_discussion), 2)])
self.parent_list=[participant for participant in set(self.talkers_including_parents) if 'Parent' in participant]
self.moderator_list=[participant for participant in set(self.talkers_including_parents) if 'Moderator' in participant]
def get_participant_text(self, participant):
if 'Parent' in participant:
mask=[member==participant for member in self.talkers_including_parents]
return list(self.text_including_parents[mask])
elif 'Moderator' in participant:
mask=[member==participant for member in self.talkers_including_parents]
text_from_parent_discussion=self.text_including_parents[mask]
mask=[member==participant for member in self.talkers_only_moderators]
text_from_moderator_discussion=self.text_only_moderators[mask]
return list(text_from_parent_discussion) + list(text_from_moderator_discussion)
focus_group=FocusGroup('Gaming_Group1')
participant='Parent 1'
focus_group.get_participant_text('Moderator 1')
```
|
github_jupyter
|
import textract
import numpy as np
import scipy
import gensim
import os
import pandas as pd
import re
import math
from collections import Counter
from matplotlib import pyplot as plt
from gensim import corpora, models
%matplotlib inline
!pip install bertopic
class FocusGroup:
def __init__(self, filename):
self.raw_text=str(textract.process('FocusGroups/' + filename + ".docx")).replace('b\'', '').replace('\'', '')
self.parent_moderator_discussion=self.raw_text.split('\\n\\n\\n')[0].split('\\n\\n')
self.within_moderator_discussion=self.raw_text.split('\\n\\n\\n')[1].split('\\n\\n')
self.talkers_including_parents=np.array([self.parent_moderator_discussion[i].replace(':', '')
for i in range(0, len(self.parent_moderator_discussion), 2)])
self.text_including_parents=np.array([self.parent_moderator_discussion[i].replace(':', '')
for i in range(1, len(self.parent_moderator_discussion), 2)])
self.talkers_only_moderators=np.array([self.within_moderator_discussion[i].replace(':', '')
for i in range(0, len(self.within_moderator_discussion), 2)])
self.text_only_moderators=np.array([self.within_moderator_discussion[i].replace(':', '')
for i in range(1, len(self.within_moderator_discussion), 2)])
self.parent_list=[participant for participant in set(self.talkers_including_parents) if 'Parent' in participant]
self.moderator_list=[participant for participant in set(self.talkers_including_parents) if 'Moderator' in participant]
def get_participant_text(self, participant):
if 'Parent' in participant:
mask=[member==participant for member in self.talkers_including_parents]
return list(self.text_including_parents[mask])
elif 'Moderator' in participant:
mask=[member==participant for member in self.talkers_including_parents]
text_from_parent_discussion=self.text_including_parents[mask]
mask=[member==participant for member in self.talkers_only_moderators]
text_from_moderator_discussion=self.text_only_moderators[mask]
return list(text_from_parent_discussion) + list(text_from_moderator_discussion)
focus_group=FocusGroup('Gaming_Group1')
participant='Parent 1'
focus_group.get_participant_text('Moderator 1')
| 0.220678 | 0.101991 |
# Better Retrieval via "Dense Passage Retrieval"
[](https://colab.research.google.com/github/deepset-ai/haystack/blob/master/tutorials/Tutorial6_Better_Retrieval_via_DPR.ipynb)
### Importance of Retrievers
The Retriever has a huge impact on the performance of our overall search pipeline.
### Different types of Retrievers
#### Sparse
Family of algorithms based on counting the occurrences of words (bag-of-words) resulting in very sparse vectors with length = vocab size.
**Examples**: BM25, TF-IDF
**Pros**: Simple, fast, well explainable
**Cons**: Relies on exact keyword matches between query and text
#### Dense
These retrievers use neural network models to create "dense" embedding vectors. Within this family there are two different approaches:
a) Single encoder: Use a **single model** to embed both query and passage.
b) Dual-encoder: Use **two models**, one to embed the query and one to embed the passage
Recent work suggests that dual encoders work better, likely because they can deal better with the different nature of query and passage (length, style, syntax ...).
**Examples**: REALM, DPR, Sentence-Transformers
**Pros**: Captures semantinc similarity instead of "word matches" (e.g. synonyms, related topics ...)
**Cons**: Computationally more heavy, initial training of model
### "Dense Passage Retrieval"
In this Tutorial, we want to highlight one "Dense Dual-Encoder" called Dense Passage Retriever.
It was introdoced by Karpukhin et al. (2020, https://arxiv.org/abs/2004.04906.
Original Abstract:
_"Open-domain question answering relies on efficient passage retrieval to select candidate contexts, where traditional sparse vector space models, such as TF-IDF or BM25, are the de facto method. In this work, we show that retrieval can be practically implemented using dense representations alone, where embeddings are learned from a small number of questions and passages by a simple dual-encoder framework. When evaluated on a wide range of open-domain QA datasets, our dense retriever outperforms a strong Lucene-BM25 system largely by 9%-19% absolute in terms of top-20 passage retrieval accuracy, and helps our end-to-end QA system establish new state-of-the-art on multiple open-domain QA benchmarks."_
Paper: https://arxiv.org/abs/2004.04906
Original Code: https://fburl.com/qa-dpr
*Use this* [link](https://colab.research.google.com/github/deepset-ai/haystack/blob/master/tutorials/Tutorial6_Better_Retrieval_via_DPR.ipynb) *to open the notebook in Google Colab.*
### Prepare environment
#### Colab: Enable the GPU runtime
Make sure you enable the GPU runtime to experience decent speed in this tutorial.
**Runtime -> Change Runtime type -> Hardware accelerator -> GPU**
<img src="https://raw.githubusercontent.com/deepset-ai/haystack/master/docs/_src/img/colab_gpu_runtime.jpg">
```
# Make sure you have a GPU running
!nvidia-smi
# Install the latest release of Haystack in your own environment
#! pip install farm-haystack
# Install the latest master of Haystack
!pip install grpcio-tools==1.34.1
!pip install git+https://github.com/deepset-ai/haystack.git
from haystack.preprocessor.cleaning import clean_wiki_text
from haystack.preprocessor.utils import convert_files_to_dicts, fetch_archive_from_http
from haystack.reader.farm import FARMReader
from haystack.reader.transformers import TransformersReader
from haystack.utils import print_answers
```
### Document Store
#### Option 1: FAISS
FAISS is a library for efficient similarity search on a cluster of dense vectors.
The `FAISSDocumentStore` uses a SQL(SQLite in-memory be default) database under-the-hood
to store the document text and other meta data. The vector embeddings of the text are
indexed on a FAISS Index that later is queried for searching answers.
The default flavour of FAISSDocumentStore is "Flat" but can also be set to "HNSW" for
faster search at the expense of some accuracy. Just set the faiss_index_factor_str argument in the constructor.
For more info on which suits your use case: https://github.com/facebookresearch/faiss/wiki/Guidelines-to-choose-an-index
```
from haystack.document_store import FAISSDocumentStore
document_store = FAISSDocumentStore(faiss_index_factory_str="Flat")
```
#### Option 2: Milvus
Milvus is an open source database library that is also optimized for vector similarity searches like FAISS.
Like FAISS it has both a "Flat" and "HNSW" mode but it outperforms FAISS when it comes to dynamic data management.
It does require a little more setup, however, as it is run through Docker and requires the setup of some config files.
See [their docs](https://milvus.io/docs/v1.0.0/milvus_docker-cpu.md) for more details.
```
from haystack.utils import launch_milvus
from haystack.document_store import MilvusDocumentStore
launch_milvus()
document_store = MilvusDocumentStore()
```
### Cleaning & indexing documents
Similarly to the previous tutorials, we download, convert and index some Game of Thrones articles to our DocumentStore
```
# Let's first get some files that we want to use
doc_dir = "data/article_txt_got"
s3_url = "https://s3.eu-central-1.amazonaws.com/deepset.ai-farm-qa/datasets/documents/wiki_gameofthrones_txt.zip"
fetch_archive_from_http(url=s3_url, output_dir=doc_dir)
# Convert files to dicts
dicts = convert_files_to_dicts(dir_path=doc_dir, clean_func=clean_wiki_text, split_paragraphs=True)
# Now, let's write the dicts containing documents to our DB.
document_store.write_documents(dicts)
```
### Initalize Retriever, Reader & Pipeline
#### Retriever
**Here:** We use a `DensePassageRetriever`
**Alternatives:**
- The `ElasticsearchRetriever`with custom queries (e.g. boosting) and filters
- Use `EmbeddingRetriever` to find candidate documents based on the similarity of embeddings (e.g. created via Sentence-BERT)
- Use `TfidfRetriever` in combination with a SQL or InMemory Document store for simple prototyping and debugging
```
from haystack.retriever.dense import DensePassageRetriever
retriever = DensePassageRetriever(document_store=document_store,
query_embedding_model="facebook/dpr-question_encoder-single-nq-base",
passage_embedding_model="facebook/dpr-ctx_encoder-single-nq-base",
max_seq_len_query=64,
max_seq_len_passage=256,
batch_size=16,
use_gpu=True,
embed_title=True,
use_fast_tokenizers=True)
# Important:
# Now that after we have the DPR initialized, we need to call update_embeddings() to iterate over all
# previously indexed documents and update their embedding representation.
# While this can be a time consuming operation (depending on corpus size), it only needs to be done once.
# At query time, we only need to embed the query and compare it the existing doc embeddings which is very fast.
document_store.update_embeddings(retriever)
```
#### Reader
Similar to previous Tutorials we now initalize our reader.
Here we use a FARMReader with the *deepset/roberta-base-squad2* model (see: https://huggingface.co/deepset/roberta-base-squad2)
##### FARMReader
```
# Load a local model or any of the QA models on
# Hugging Face's model hub (https://huggingface.co/models)
reader = FARMReader(model_name_or_path="deepset/roberta-base-squad2", use_gpu=True)
```
### Pipeline
With a Haystack `Pipeline` you can stick together your building blocks to a search pipeline.
Under the hood, `Pipelines` are Directed Acyclic Graphs (DAGs) that you can easily customize for your own use cases.
To speed things up, Haystack also comes with a few predefined Pipelines. One of them is the `ExtractiveQAPipeline` that combines a retriever and a reader to answer our questions.
You can learn more about `Pipelines` in the [docs](https://haystack.deepset.ai/docs/latest/pipelinesmd).
```
from haystack.pipeline import ExtractiveQAPipeline
pipe = ExtractiveQAPipeline(reader, retriever)
```
## Voilà! Ask a question!
```
# You can configure how many candidates the reader and retriever shall return
# The higher top_k for retriever, the better (but also the slower) your answers.
prediction = pipe.run(
query="Who created the Dothraki vocabulary?", params={"Retriever": {"top_k": 10}, "Reader": {"top_k": 5}}
)
print_answers(prediction, details="minimal")
```
## About us
This [Haystack](https://github.com/deepset-ai/haystack/) notebook was made with love by [deepset](https://deepset.ai/) in Berlin, Germany
We bring NLP to the industry via open source!
Our focus: Industry specific language models & large scale QA systems.
Some of our other work:
- [German BERT](https://deepset.ai/german-bert)
- [GermanQuAD and GermanDPR](https://deepset.ai/germanquad)
- [FARM](https://github.com/deepset-ai/FARM)
Get in touch:
[Twitter](https://twitter.com/deepset_ai) | [LinkedIn](https://www.linkedin.com/company/deepset-ai/) | [Slack](https://haystack.deepset.ai/community/join) | [GitHub Discussions](https://github.com/deepset-ai/haystack/discussions) | [Website](https://deepset.ai)
By the way: [we're hiring!](https://apply.workable.com/deepset/)
|
github_jupyter
|
# Make sure you have a GPU running
!nvidia-smi
# Install the latest release of Haystack in your own environment
#! pip install farm-haystack
# Install the latest master of Haystack
!pip install grpcio-tools==1.34.1
!pip install git+https://github.com/deepset-ai/haystack.git
from haystack.preprocessor.cleaning import clean_wiki_text
from haystack.preprocessor.utils import convert_files_to_dicts, fetch_archive_from_http
from haystack.reader.farm import FARMReader
from haystack.reader.transformers import TransformersReader
from haystack.utils import print_answers
from haystack.document_store import FAISSDocumentStore
document_store = FAISSDocumentStore(faiss_index_factory_str="Flat")
from haystack.utils import launch_milvus
from haystack.document_store import MilvusDocumentStore
launch_milvus()
document_store = MilvusDocumentStore()
# Let's first get some files that we want to use
doc_dir = "data/article_txt_got"
s3_url = "https://s3.eu-central-1.amazonaws.com/deepset.ai-farm-qa/datasets/documents/wiki_gameofthrones_txt.zip"
fetch_archive_from_http(url=s3_url, output_dir=doc_dir)
# Convert files to dicts
dicts = convert_files_to_dicts(dir_path=doc_dir, clean_func=clean_wiki_text, split_paragraphs=True)
# Now, let's write the dicts containing documents to our DB.
document_store.write_documents(dicts)
from haystack.retriever.dense import DensePassageRetriever
retriever = DensePassageRetriever(document_store=document_store,
query_embedding_model="facebook/dpr-question_encoder-single-nq-base",
passage_embedding_model="facebook/dpr-ctx_encoder-single-nq-base",
max_seq_len_query=64,
max_seq_len_passage=256,
batch_size=16,
use_gpu=True,
embed_title=True,
use_fast_tokenizers=True)
# Important:
# Now that after we have the DPR initialized, we need to call update_embeddings() to iterate over all
# previously indexed documents and update their embedding representation.
# While this can be a time consuming operation (depending on corpus size), it only needs to be done once.
# At query time, we only need to embed the query and compare it the existing doc embeddings which is very fast.
document_store.update_embeddings(retriever)
# Load a local model or any of the QA models on
# Hugging Face's model hub (https://huggingface.co/models)
reader = FARMReader(model_name_or_path="deepset/roberta-base-squad2", use_gpu=True)
from haystack.pipeline import ExtractiveQAPipeline
pipe = ExtractiveQAPipeline(reader, retriever)
# You can configure how many candidates the reader and retriever shall return
# The higher top_k for retriever, the better (but also the slower) your answers.
prediction = pipe.run(
query="Who created the Dothraki vocabulary?", params={"Retriever": {"top_k": 10}, "Reader": {"top_k": 5}}
)
print_answers(prediction, details="minimal")
| 0.717111 | 0.987664 |
```
import pandas as pd
import numpy as np
import scanpy as sc
import os
from sklearn.cluster import KMeans
from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics.cluster import adjusted_rand_score
from sklearn.metrics.cluster import adjusted_mutual_info_score
from sklearn.metrics.cluster import homogeneity_score
import rpy2.robjects as robjects
from rpy2.robjects import pandas2ri
df_metrics = pd.DataFrame(columns=['ARI_Louvain','ARI_kmeans','ARI_HC',
'AMI_Louvain','AMI_kmeans','AMI_HC',
'Homogeneity_Louvain','Homogeneity_kmeans','Homogeneity_HC'])
workdir = './output_new/'
path_fm = os.path.join(workdir,'feature_matrices/')
path_clusters = os.path.join(workdir,'clusters/')
path_metrics = os.path.join(workdir,'metrics/')
os.system('mkdir -p '+path_clusters)
os.system('mkdir -p '+path_metrics)
metadata = pd.read_csv('../input/metadata.tsv',sep='\t',index_col=0)
num_clusters = len(np.unique(metadata['label']))
print(num_clusters)
files = [x for x in os.listdir(path_fm) if x.startswith('fm')]
len(files)
files
def getNClusters(adata,n_cluster,range_min=0,range_max=3,max_steps=20):
this_step = 0
this_min = float(range_min)
this_max = float(range_max)
while this_step < max_steps:
print('step ' + str(this_step))
this_resolution = this_min + ((this_max-this_min)/2)
sc.tl.louvain(adata,resolution=this_resolution)
this_clusters = adata.obs['louvain'].nunique()
print('got ' + str(this_clusters) + ' at resolution ' + str(this_resolution))
if this_clusters > n_cluster:
this_max = this_resolution
elif this_clusters < n_cluster:
this_min = this_resolution
else:
return(this_resolution, adata)
this_step += 1
print('Cannot find the number of clusters')
print('Clustering solution from last iteration is used:' + str(this_clusters) + ' at resolution ' + str(this_resolution))
for file in files:
file_split = file[:-4].split('_')
method = file_split[1]
if(len(file_split)>2):
method = method + '_'+''.join(file_split[2:]).replace('2','_pca')
print(method)
pandas2ri.activate()
readRDS = robjects.r['readRDS']
df_rds = readRDS(os.path.join(path_fm,file))
fm_mat = pandas2ri.ri2py(robjects.r['data.frame'](robjects.r['as.matrix'](df_rds)))
fm_mat.fillna(0,inplace=True)
fm_mat.columns = metadata.index
adata = sc.AnnData(fm_mat.T)
adata.var_names_make_unique()
adata.obs = metadata.loc[adata.obs.index,]
df_metrics.loc[method,] = ""
#Louvain
sc.pp.neighbors(adata, n_neighbors=15,use_rep='X')
# sc.tl.louvain(adata)
getNClusters(adata,n_cluster=num_clusters)
#kmeans
kmeans = KMeans(n_clusters=num_clusters, random_state=2019).fit(adata.X)
adata.obs['kmeans'] = pd.Series(kmeans.labels_,index=adata.obs.index).astype('category')
#hierachical clustering
hc = AgglomerativeClustering(n_clusters=num_clusters).fit(adata.X)
adata.obs['hc'] = pd.Series(hc.labels_,index=adata.obs.index).astype('category')
#clustering metrics
#adjusted rank index
ari_louvain = adjusted_rand_score(adata.obs['label'], adata.obs['louvain'])
ari_kmeans = adjusted_rand_score(adata.obs['label'], adata.obs['kmeans'])
ari_hc = adjusted_rand_score(adata.obs['label'], adata.obs['hc'])
#adjusted mutual information
ami_louvain = adjusted_mutual_info_score(adata.obs['label'], adata.obs['louvain'],average_method='arithmetic')
ami_kmeans = adjusted_mutual_info_score(adata.obs['label'], adata.obs['kmeans'],average_method='arithmetic')
ami_hc = adjusted_mutual_info_score(adata.obs['label'], adata.obs['hc'],average_method='arithmetic')
#homogeneity
homo_louvain = homogeneity_score(adata.obs['label'], adata.obs['louvain'])
homo_kmeans = homogeneity_score(adata.obs['label'], adata.obs['kmeans'])
homo_hc = homogeneity_score(adata.obs['label'], adata.obs['hc'])
df_metrics.loc[method,['ARI_Louvain','ARI_kmeans','ARI_HC']] = [ari_louvain,ari_kmeans,ari_hc]
df_metrics.loc[method,['AMI_Louvain','AMI_kmeans','AMI_HC']] = [ami_louvain,ami_kmeans,ami_hc]
df_metrics.loc[method,['Homogeneity_Louvain','Homogeneity_kmeans','Homogeneity_HC']] = [homo_louvain,homo_kmeans,homo_hc]
adata.obs[['louvain','kmeans','hc']].to_csv(os.path.join(path_clusters ,method + '_clusters.tsv'),sep='\t')
df_metrics.to_csv(path_metrics+'clustering_scores.csv')
df_metrics
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import scanpy as sc
import os
from sklearn.cluster import KMeans
from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics.cluster import adjusted_rand_score
from sklearn.metrics.cluster import adjusted_mutual_info_score
from sklearn.metrics.cluster import homogeneity_score
import rpy2.robjects as robjects
from rpy2.robjects import pandas2ri
df_metrics = pd.DataFrame(columns=['ARI_Louvain','ARI_kmeans','ARI_HC',
'AMI_Louvain','AMI_kmeans','AMI_HC',
'Homogeneity_Louvain','Homogeneity_kmeans','Homogeneity_HC'])
workdir = './output_new/'
path_fm = os.path.join(workdir,'feature_matrices/')
path_clusters = os.path.join(workdir,'clusters/')
path_metrics = os.path.join(workdir,'metrics/')
os.system('mkdir -p '+path_clusters)
os.system('mkdir -p '+path_metrics)
metadata = pd.read_csv('../input/metadata.tsv',sep='\t',index_col=0)
num_clusters = len(np.unique(metadata['label']))
print(num_clusters)
files = [x for x in os.listdir(path_fm) if x.startswith('fm')]
len(files)
files
def getNClusters(adata,n_cluster,range_min=0,range_max=3,max_steps=20):
this_step = 0
this_min = float(range_min)
this_max = float(range_max)
while this_step < max_steps:
print('step ' + str(this_step))
this_resolution = this_min + ((this_max-this_min)/2)
sc.tl.louvain(adata,resolution=this_resolution)
this_clusters = adata.obs['louvain'].nunique()
print('got ' + str(this_clusters) + ' at resolution ' + str(this_resolution))
if this_clusters > n_cluster:
this_max = this_resolution
elif this_clusters < n_cluster:
this_min = this_resolution
else:
return(this_resolution, adata)
this_step += 1
print('Cannot find the number of clusters')
print('Clustering solution from last iteration is used:' + str(this_clusters) + ' at resolution ' + str(this_resolution))
for file in files:
file_split = file[:-4].split('_')
method = file_split[1]
if(len(file_split)>2):
method = method + '_'+''.join(file_split[2:]).replace('2','_pca')
print(method)
pandas2ri.activate()
readRDS = robjects.r['readRDS']
df_rds = readRDS(os.path.join(path_fm,file))
fm_mat = pandas2ri.ri2py(robjects.r['data.frame'](robjects.r['as.matrix'](df_rds)))
fm_mat.fillna(0,inplace=True)
fm_mat.columns = metadata.index
adata = sc.AnnData(fm_mat.T)
adata.var_names_make_unique()
adata.obs = metadata.loc[adata.obs.index,]
df_metrics.loc[method,] = ""
#Louvain
sc.pp.neighbors(adata, n_neighbors=15,use_rep='X')
# sc.tl.louvain(adata)
getNClusters(adata,n_cluster=num_clusters)
#kmeans
kmeans = KMeans(n_clusters=num_clusters, random_state=2019).fit(adata.X)
adata.obs['kmeans'] = pd.Series(kmeans.labels_,index=adata.obs.index).astype('category')
#hierachical clustering
hc = AgglomerativeClustering(n_clusters=num_clusters).fit(adata.X)
adata.obs['hc'] = pd.Series(hc.labels_,index=adata.obs.index).astype('category')
#clustering metrics
#adjusted rank index
ari_louvain = adjusted_rand_score(adata.obs['label'], adata.obs['louvain'])
ari_kmeans = adjusted_rand_score(adata.obs['label'], adata.obs['kmeans'])
ari_hc = adjusted_rand_score(adata.obs['label'], adata.obs['hc'])
#adjusted mutual information
ami_louvain = adjusted_mutual_info_score(adata.obs['label'], adata.obs['louvain'],average_method='arithmetic')
ami_kmeans = adjusted_mutual_info_score(adata.obs['label'], adata.obs['kmeans'],average_method='arithmetic')
ami_hc = adjusted_mutual_info_score(adata.obs['label'], adata.obs['hc'],average_method='arithmetic')
#homogeneity
homo_louvain = homogeneity_score(adata.obs['label'], adata.obs['louvain'])
homo_kmeans = homogeneity_score(adata.obs['label'], adata.obs['kmeans'])
homo_hc = homogeneity_score(adata.obs['label'], adata.obs['hc'])
df_metrics.loc[method,['ARI_Louvain','ARI_kmeans','ARI_HC']] = [ari_louvain,ari_kmeans,ari_hc]
df_metrics.loc[method,['AMI_Louvain','AMI_kmeans','AMI_HC']] = [ami_louvain,ami_kmeans,ami_hc]
df_metrics.loc[method,['Homogeneity_Louvain','Homogeneity_kmeans','Homogeneity_HC']] = [homo_louvain,homo_kmeans,homo_hc]
adata.obs[['louvain','kmeans','hc']].to_csv(os.path.join(path_clusters ,method + '_clusters.tsv'),sep='\t')
df_metrics.to_csv(path_metrics+'clustering_scores.csv')
df_metrics
| 0.310799 | 0.29445 |
# Loops
We previously discussed conditionals as a way to control the flow of your code. Here, we introduce the concept of loops. We'll discuss `while` loops and `for` loops and introduce how to incorporate these into your code.
Specifically, **loops** are a procedure utilized in code to repeat a piece of code more than once.
<div class="alert alert-success">
A <b>loop</b> is a procedure to repeat a piece of code.
</div>
More specifically, loops help you to avoid copy and pasting similar pieces of your code over and over again throughout your code. It's best to avoid copying and pasting code to (1) make your code more readable to yourself and others and (2) to avoid errors when debugging. By avoiding copying and pasting, when you make a change to improve your code, you only have to make that edit in one single location rather than in every place where the code has been copy and pasted.
This means that when it comes to repetitive actions in code, if you find yourself copying + pasting, rethink your strategy. Loops are one way to avoid this. We'll discuss other approaches later on.
## Why loops?
Imagine you wanted to send an email to all the email addresses in your list.
Well, if you only had two emails in your list, you could specify who the email is being sent to using something like what we see here:
```
email_list = ['friend@yahoo.com', 'them@bing.com']
email = email_list[0]
# send email
email = email_list[1]
# send email
```
But, what if you had 100 emails or 1000 emails? Going through and changing the index to refer to the individual in your list of emails would take a long time and would be prone to error.
This is when you want to turn to loops!
## `while` Loops
A `while` loop is a procedure to use that will repeat the code within the loop for as long as a condition is met. The loop will terminate (stop running the code) once the condition is no longer met.
<div class="alert alert-success">
A <b>while loop</b> is a procedure to repeat a piece of code while some condition is still met.
</div>
While loops always have the structure:
```python
while condition:
# Loop contents
```
`while` is followed by a condition. The condition is then followed by a colon (`:`). The contents within the loop - the code that you want to execute as long as the condition is met are on the subsequent lines and are all indented, visibly indicating that those lines of code are part of the while loop.
Note that `condition` can change - this is what determines whether your `while` loop continues to run. While `condition is `True`, the code contents will execute. The code within the loop will repeat until condition is no longer `True`.
Here, we have an example of a while loop, where `number` initially stores the value '-5'.
Then we have a `while` loop where the condition looks to see if `number` is less than (`<`) the number 0. This means that as long as `number` is negative, the contents within the `while` loop will execute.
Within the `while` loop, the current value stored in `number` will `print()` *and* the value stored in `number` will increase by 1.
Thus, the first time through the loop `number` will store -5. The second time through, it will increase by one to store the value -4. This will continue and the loop will continue to run, printing the current value stored in `number` each time through the loop.
However, once `number` stores the value 0, the condition `number < 0` will no longer be met. At this point, the `while` loop will stop executing, terminating the loop.
```
number = -5
while number < 0:
print(number)
number = number + 1
```
Note that `while` loops can be combined with the other code constructs you've previously learned - such as conditionals.
Here we see a `while` loop with a nested `if` statement.
```
keep_looping = True
counter = 0
while keep_looping:
counter = counter + 1
if counter > 2:
keep_looping = False
print(counter)
```
In this code, two variables are created: `keep_looping` which stores the boolean `True` and `counter`, which stores the value '0' to start.
From there, the `while` loop will execute, as `keep_looping` is `True`.
Within the `while` loop, `counter` will increment by 1. The first time through the loop, `counter` will update to store '1'.
Then, the conditional `if` statement is encountered. At this point, `counter` stores the value 1, which is *not* greater than (`>`) 2, so the code within the conditional will *not* execute.
The `while` loop will then enter its second iteration. `counter` will increase by 1 to store the value '2'. The conditional is still `False`, so the `while` loop will execute once again.
During its third iteration, `counter` will increase to store the value '3'. Now, the conditional statement evaluates as `True`, as the value 3 (stored in `counter`) *is* greater than 2.
`keep_looping` now stores the value `False`. The `while` condition is no longer `True`, and the loop terminates.
Note that the final line of code here (the `print()` statement) is *not* indented. This indicates that it is *not* part of the `while` loop. This line only executes, printing the last value stored in `counter` (3) once the `while` loop terminates.
## `for` Loops
The second type of loop we'll discuss for controlling the flow of your code is a `for` loop. This procedure repeats code for every element in a collection.
So if you have a list and want the same code to operate on every element in the list, you'll want to use a `for` loop.
<div class="alert alert-success">
A <b>for loop</b> is a procedure a to repeat code for every element in a sequence.
</div>
For example, here we create a list with three items. If we want to carry out some operation on each element in this list, we'll use a `for` loop.
The operation we'll carry out in this first example is simply to print each element of the list as it loops through the list.
What's most important in the code below is the use of the variable `my_item`. Note that this variable has *not* been previously defined. This variable is used to refer to each element in the list as the loop progresses.
```
# Define a list of items
list_of_items = ['A', True, 12]
# Loop across each element
for my_item in list_of_items:
print(my_item)
```
More specifically, the first time through the `for` loop, `my_item` will refer to the first element in `list_of_items` - the string `'A'`.
The code within the `for` loop specifies to `print(my_item)`. Thus, the information stored in `my_item` - the string `'A'` is printed.
With the first iteration of the loop, the `for` loop continues on, repeating the code within the `for` loop on the second element in the list - `True`. Now, `my_item` refers to the second element in the list - `True`. So when `print(my_item)` is encountered, the value `True` is printed.
The third time through the loop, `my_item` refers to the third element in the list - the value '12'. Thus, that is printed when `print(my_item)` is encountered.
After this third iteration, the `for` loop has reached the end of the list. Once the end of the collection the `for` loop is iterating through is reached, the execution of the loop will terminate.
After this loop executes, the value stored in `my_item` will be the last value stored in `my_item` in the loop - the last element of the list.
We can use `print(my_item)` to verify the contents stored in this variable:
```
# my_item exists outside the loop
print(my_item)
```
Above, we see that even though `my_item` was created and utilized within the `for` loop, it exists after the loop executes, storing whatever the last value stored during the `for` loops execution was.
### Looping through strings
Note that loops are not used exclusively with strings. You can loop through all of the collections we've discussed previously - strings, tuples, and dictionaries.
When we loop through strings, each character in the string is iterated through until the end of the string is encountered:
```
# Loop across items in a string
for char in 'python':
print(char)
```
### Looping through dictionaries
Further, when we loop through dictionaries, we iterate across the keys. To see what we mean, let's re-create a dictionary we've seen previously for use in this example:
```
student_emails = {
'Betty Jennings' : 'bjennings@eniac.org',
'Ada Lovelace' : 'ada@analyticengine.com',
'Alan Turing' : 'aturing@thebomb.gov',
'Grace Hopper' : 'ghopper@navy.usa'
}
```
In the example below, `person` refers to the keys in the dictionary. So, the first time through the loop, `person` will refer to the first person in the `student_emails` dictionary - 'Betty Jennings'. The second time through, the second key, and so on and so forth:
```
# Loop over a dictionary loops across the keys
for person in student_emails:
print(person)
```
This can be combined with indexing, if you want to see the values stored in the keys. Here, instead of printing the key, using `person`, we can **index** from the `student_emails` dictionary, which returns the values stored in the keys.
```
# Loop over a dictionary loops across the keys
# Inside the loop, you can use the key to access the associated value
for person in student_emails:
print(student_emails[person])
```
In each of these scenarios, as we loop through a dictionary, we are using `person` to refer to the keys in the `student_emails` dictionary. Within the `for` loop, we can *refer* to `person` to specify the *key* in the dictionary.
## `range`
As you begin to write loops, you'll become familiar with the `range` operator, which creates a range of numbers. This operator is frequently used with loops.
<div class="alert alert-success">
<code>range</code> is an operator to create a range of numbers, that is often used with loops.
</div>
To demonstrate why `range` is helpful, consider looping over a list of integers from 0 to 4, inclusive. To do this using the tools we've discussed so far, you would use the following:
```
for ind in [0, 1, 2, 3, 4]:
print(ind)
```
However, often we want to iterate across lists containing *many* more numbers. Typing each individual number out would become onerous and we'd likely make a typo.
Alternatively, we could use `range()`. `range` uses the same (`start`, `stop`, `step`) concept we used for indexing; however, the values are separated by commas when using range, rather than by colons (as we used for indexing).
The code below accomplishes the same procedure we saw above; however, instead of specifying each number in the list, we can use `range()` and specify the `start` and `stop` values. Recall that the `stop` value (here, 5) is *not* included in the range, just as the `stop` value specified in a slice was not included.
```
# Loop across a sequence of numbers, using range
for ind in range(0, 5):
print(ind)
```
By including a `step` value, `range` further allows us to skip over values in the range, to, for example, only include even values, as we see here:
```
# Range, like indexing, is defined by 'start', 'stop', 'step'
for ind in range(2, 6, 2):
print(ind)
```
## `continue`
Another helpful operator is `continue`. When encountered ina loop, `continue` specifies to jump ahead to the next iteration of a loop, regardless of the code below in the loop.
<div class="alert alert-success">
<code>continue</code> is a special operator to jump ahead to the next iteration of a loop.
</div>
For example, in this loop, when `item == 2`, `continue` is encountered, so the code skips to the top of the for loop, ignoring the `print(item)` statement below. However, for all other values in the range (when `item` is anything *other* than '2', `item` gets printed.
```
for item in range(0, 4):
if item == 2:
continue
print(item)
```
This concept applies across the varies types of collections we've talked about previously. For example, here we are looping through a string, and `continue`-ing on when `char` stores the letter 'p' or 'y'.
```
for char in 'love python':
if char == 'p' or char == 'y':
continue
print(char)
```
## `break`
Finally, `break` is a special operator that, when encountered will terminate the loop. Unlike `continue` which carries on immediately to the next iteration of the loop, `break`, when `break` is encountered, the whole loop terminates (stops executing)
<div class="alert alert-success">
<code>break</code> is a special operator to break out of a loop.
</div>
Using the example we saw above with `continue` but replacing `continue` with `break`, we see that once `item == 2` is `True`, `break` is encountered and the loop terminates. `item` never reaches the end of the list (the value 3) and thus that value never gets printed.
```
for item in range(0, 4):
if item == 2:
break
print(item)
```
The same concept applies for iterating through a string. Once `break` is encountered, the loop terminates immediately:
```
string = "love python"
for char in string:
if char == "p" or char == "y":
break
print(char)
```
## Exercises
Q1. **How many values will be output from this `while` loop before "The tea is cool enough." is printed?**
```python
temperature = 115
while temperature > 112:
print(temperature)
temperature = temperature - 1
print('The tea is cool enough.')
```
Q2. **What will be the value of `counter` after this loop executes?**
```python
keep_looping = True
counter = 0
while keep_looping:
counter = counter + 1
if counter > 3:
keep_looping = False
print(counter)
```
Q3. **What will the following loop print out?**
```python
my_lst = range(0, 5)
for item in my_lst[0:-1]:
print(item + 1)
```
Q4. **How many values will be output from this `for` loop before it *first* prints "The tea is too hot!"?
```python
temperatures = [114, 115, 116, 117, 118]
for temp in temperatures:
print(temp)
if(temp > 115):
print('The tea is too hot!')
```
Q5. **How many values would this loop print and what would be the last value printed?**
```python
for ind in range(1, 10, 3):
print(ind)
```
A) values printed: 3; last value: 7
B) values printed: 3; last value: 9
C) values printed: 4; last value: 9
D) values printed: 7; last value: 7
E) values printed: 7; last value: 9
Q6. **What will be the value of `counter` after this code has executed?**
```python
counter = 0
my_lst = [False, True, False, True]
for item in my_lst:
if item in my_lst:
continue
else:
counter = counter + 1
```
Q7. **What will the following code print out**?
```python
number = 1
while True:
if number % 3 == 0:
break
print(number)
number = number + 1
```
A) 1
B) 1 2
C) 1 2 3
D) Something else
E) This code prints forever
Q8. **For how many `temp` will output be printed from this for loop? (In other words, how many times in this for loop will something be printed out?)**
```python
for temp in range(114, 119):
if(temp < 116):
continue
elif(temp == 116):
print('The tea is too hot!')
else:
break
```
Q9. **Store your name as a string in a variable called `my_name`. Write a loop that will loop through all the letters in `my_name` and count all the vowels in your name.**
Q10. **Write a loop that adds all the *odd* numbers between 1 and 1000 together.**
|
github_jupyter
|
email_list = ['friend@yahoo.com', 'them@bing.com']
email = email_list[0]
# send email
email = email_list[1]
# send email
while condition:
# Loop contents
number = -5
while number < 0:
print(number)
number = number + 1
keep_looping = True
counter = 0
while keep_looping:
counter = counter + 1
if counter > 2:
keep_looping = False
print(counter)
# Define a list of items
list_of_items = ['A', True, 12]
# Loop across each element
for my_item in list_of_items:
print(my_item)
# my_item exists outside the loop
print(my_item)
# Loop across items in a string
for char in 'python':
print(char)
student_emails = {
'Betty Jennings' : 'bjennings@eniac.org',
'Ada Lovelace' : 'ada@analyticengine.com',
'Alan Turing' : 'aturing@thebomb.gov',
'Grace Hopper' : 'ghopper@navy.usa'
}
# Loop over a dictionary loops across the keys
for person in student_emails:
print(person)
# Loop over a dictionary loops across the keys
# Inside the loop, you can use the key to access the associated value
for person in student_emails:
print(student_emails[person])
for ind in [0, 1, 2, 3, 4]:
print(ind)
# Loop across a sequence of numbers, using range
for ind in range(0, 5):
print(ind)
# Range, like indexing, is defined by 'start', 'stop', 'step'
for ind in range(2, 6, 2):
print(ind)
for item in range(0, 4):
if item == 2:
continue
print(item)
for char in 'love python':
if char == 'p' or char == 'y':
continue
print(char)
for item in range(0, 4):
if item == 2:
break
print(item)
string = "love python"
for char in string:
if char == "p" or char == "y":
break
print(char)
temperature = 115
while temperature > 112:
print(temperature)
temperature = temperature - 1
print('The tea is cool enough.')
keep_looping = True
counter = 0
while keep_looping:
counter = counter + 1
if counter > 3:
keep_looping = False
print(counter)
my_lst = range(0, 5)
for item in my_lst[0:-1]:
print(item + 1)
temperatures = [114, 115, 116, 117, 118]
for temp in temperatures:
print(temp)
if(temp > 115):
print('The tea is too hot!')
for ind in range(1, 10, 3):
print(ind)
counter = 0
my_lst = [False, True, False, True]
for item in my_lst:
if item in my_lst:
continue
else:
counter = counter + 1
number = 1
while True:
if number % 3 == 0:
break
print(number)
number = number + 1
for temp in range(114, 119):
if(temp < 116):
continue
elif(temp == 116):
print('The tea is too hot!')
else:
break
| 0.213705 | 0.989034 |
CWPK \#21: Some Accumulated Tips
======================
Let's Recap Some Useful Python Guidance
--------------------------
<div style="float: left; width: 305px; margin-right: 10px;">
<img src="http://kbpedia.org/cwpk-files/cooking-with-kbpedia-305.png" title="Cooking with KBpedia" width="305" />
</div>
All installments in this [*Cooking with Python and KBpedia*](https://www.mkbergman.com/cooking-with-python-and-kbpedia/) series have been prepared and written in order, except for this one. I began collecting tips about how best to use the *cowpoke* package and Python about the time this installment occurred in sequence in the series. I have accumulated use tips up through **CWPK #60**, and now am reaching back to complete this narrative.
Since we are principally working through the interactive medium of Jupyter Notebook for the rest of this **CWPK** series, I begin by addressing some Notebook use tips. Most of the suggestions, however, deal with using the Python language directly. I have split that section up into numerous sub-topics.
An interesting aspect of using [owlready2](https://owlready2.readthedocs.io/en/latest/intro.html) as our API to OWL is its design decision to align classes within RDF and OWL to the class concept in Python. My intuition (and the results as we proceed) tells me that was the correct design decision, since it affords using Python directly against the API. However, it does impose the price of needing to have data types expressed in the right form at the right time. That means one of our Python tips is how to move owlready2 class objects into strings for manipulation and then the reverse. It is these kinds of lessons that we have assembled in this installment.
### General Tips
I began these **CWPK** efforts with a local system and my local file directories. However, as I began to release code and reference ontologies, my efforts inexorably shifted to the [GitHub](https://github.com/Cognonto/CWPK) environment. (One can also use [Bitbucket](https://bitbucket.org/product) if the need is to keep information proprietary.) This focus was further reinforced as we moved our code into the cloud, as discussed in the latter installments. Were I to start a new initiative from scratch, I would recommend starting with a GitHub-like focus first, and use Git to move code and data from there to all local and other remote or cloud environments.
### Notebook Tips
In just a short period of time, I have become an enthusiast about the Notebook environment. I like the idea of easily opening a new 'cell' and being able to insert code that executes or to provide nicely formatted narrative the explains what we are doing. I have also come to like the [Markdown](https://en.wikipedia.org/wiki/Markdown) markup language. I have been writing markup languages going back to SGML, XML, and now HTML and wikitext. I have found Markdown the most intuitive and fastest to use. So, I encourage you to enjoy your Notebook!
Here are some other tips I can offer about using Notebooks:
- Keep narrative (Markdown) cells relatively short, since when you run the cell the cursor places at bottom of cell and long narrative cells require too much scrolling
- Do not need to keep importing modules at the top of a cell if they have been imported before. However, you can lose notebook state. In which case, you need to Run all of the cells and in order to get back to the current state
- When working through the development of new routines, remember to run Kernel → Restart & Clear Output. You will again need to progress through the cells to return to the proper state, but without clearing after an error you can get a run failure just because of residue interim states. To get to any meaningful state with KBpedia, one needs at least to invoke these resources:
<div style="background-color:#eee; border:1px dotted #aaa; vertical-align:middle; margin:15px 60px; padding:8px;"><strong>Which environment?</strong> The specific load routine you should choose below depends on whether you are using the online MyBinder service (the 'raw' version) or local files. The one below is based on the local file approach. See <a href="https://www.mkbergman.com/2347/cwpk-17-choosing-and-installing-an-owl-api/"><strong>CWPK #17</strong></a> for further details.</div>
```
main = 'C:/1-PythonProjects/owlready2/kg/kbpedia_reference_concepts.owl'
skos_file = 'http://www.w3.org/2004/02/skos/core'
kko_file = 'C:/1-PythonProjects/owlready2/kg/kko.owl'
from owlready2 import *
world = World()
kb = world.get_ontology(main).load()
rc = kb.get_namespace('http://kbpedia.org/kko/rc/')
skos = world.get_ontology(skos_file).load()
kb.imported_ontologies.append(skos)
kko = world.get_ontology(kko_file).load()
kb.imported_ontologies.append(kko)
```
- When using a cell in Markdown mode for narratives, it is sometimes useful to be able to add HTML code directly. A nice Jupyter Notebook WYSIWYG assistant is:
- https://github.com/genepattern/jupyter-wysiwyg; install via:
<pre>
conda install -c genepattern jupyter-wysiwyg
</pre>
However, after a period of time I reversed that position, since I found using the assistant caused all of the cell code to be converted to HTML vs Markdown. It is actually easier to use Markdown for simple HTML formatting
- I tend to keep only one or two Notebook pages active at a time (closing out by first File → Save and Checkpoint, and then File → Close and Halt), because not properly closing a Notebook page means it is shown as open next you open the Notebook
- When working with notebook files, running certain cells that cause long lists to be generated or large data arrays to be analyzed can cause the notebook file when saved to grow into a very large size. To keep notebook file sizes manageable, invoke Cell → Current Output → Clear on the offending cells
- When starting a new installment, I tend to first set up the environment by loading all of the proper knowledge bases in the environment, then I am able to start working on new routines.
### Python Tips
We have some clusters of discussion areas below, but first, here are some general and largely unconnected observations of working with Python:
- A file name like <code>exercise_1.py</code> is better than the name <code>exercise-1.py</code>, since hyphens are disfavored in Python
- When in trouble, be aggressive using Web search. There is tremendous online Python assistance
- When routines do not work, make aggressive us of <code>print</code> statements, including a label or recall of a variable to place the error in context (also <code>logging</code>, but that is addressed much later in the series)
- Also use counters to make sure items are progressing properly through loops, which is more important when loops are nested
- Take advantage of the Notebook interactive environment by first entering and getting code snippets to work, then build up to more formal function definitions
- When debugging or trying to isolate issues, comment out working code blocks to speed execution and narrow the range of inspection
- Watch out for proper indenting on loops
- Stay with the most recent/used versions of Python. It is not a student's job to account for the legacy of a language. If earlier version compatibilty is needed, there are experienced programmers from that era and you will be better able to recognize the nuances in your modern implementation
- I think I like the dictionary ('<code>dict</code>') data structure within Python the best of all. Reportedly Python itself depends heavily on this construct, but I have found <code>dict</code> to be useful (though have not tested the accompanying performance betterment claims)
- Try to always begin your routines with the 'preliminaries' of first defining variables, setting counters or lists to empty, etc.
#### Anatomy of a Statement
A general Python statement tends to have a form similar to:
<pre>
world.search(iri = "*luggage*", _case_sensitive = False)
</pre>
The so-called 'dot' notation shows the hierarchy of namespaces and attributes. In this instance, 'world' is a namespace, and 'search' is a function. In other instances it might be 'class' 'property' or other hierarchical relationships.
An item that remains confusing to me is when to use namespace prefixes, and when not. I think as I state a couple of times throughout this **CWPK** series, how 'namespace' is implemented in Python is not intuitive to me, and has likely not yet been explained to me properly.
The arguments for the function appear within the parentheses. When first set up, many functions have 'default' arguments, and will be assigned if not specifically stated otherwise. There are some set formats for referring to these parameters; one [Web resource](https://medium.com/better-programming/what-are-args-and-kwargs-in-python-6aaf9e3cad73 ) is particularly helpful in deciphering them. You may also want to learn about the [drawbacks of defaults](https://florimond.dev/blog/articles/2018/08/python-mutable-defaults-are-the-source-of-all-evil/). Generally, as a first choice, you can test a function with empty parentheses and then decompose from there when it does not work or work as you think it should.
The <code>dir</code> and <code>type</code> statements can help elucidate what these internal parameters are:
```
dir(world.search)
```
or <code>type</code>:
```
type(world.search)
```
#### Directories and files
Any legal directory or file name is accepted by Python. For Windows, there is often automatic conversion of URI slashes. But non-Linux systems should investigate the specific compatibilities their operating systems have for Python. The differences and nuances are small, but can be a source of frustration if overlooked.
Here are some tips about directories and files:
- Don't put a <code>"""comment"""</code> in the middle of a dictionary listing
- A <code>"""comment"""</code> header is best practice for a function likely to be used multiple times
- When reading code, the real action tends to occur at the end of a listing, meaning that understanding the code is often easier working bottom up, as references higher up in the code are more often preliminary or condition setting
- Similarly, many routines tend to build from the inside out. At the core are the key processing and conversion steps. Prior to that is set-up, after that is staging output
- Follow best practices for directory set ups in Python packages (see **CWPK #37**).
#### Modules and libraries
A module name must be a valid Python name, limited to letters, digits and '_'s.
Modules are the largest construct in Python programs. Python programs consist of multiple module files, either included in the base package, or imported into the current program. Each module has its own container of variables. Variable names may be duplicated across modules, but are distinguished and prevented from name clashes by invoking them with the object (see earlier discussion about the 'dot notation'). You can also assign imported variables to local ones to keep the dot notation to a minimum and to promote easier to read code.
#### Namespaces
Python is an object-oriented language, wherein each object in the system has a name identifier. To prevent name conflicts, Python has a namespace construct wherein any grouping of existing object names may be linked to a namespace. The only constraint, within Python's naming conventions, is that two objects may not share the same name within a given namespace. They may share names between namespaces, but not within.
The namespace construct is both assigned automatically based on certain Python activities, and may also be directly set by assignment. Import events or import artifacts, like knowledge graphs or portions thereto, are natural targets for this convenient namespace convention.
When items are declared and how they are declared informs the basis of a namespace for a given item. If it is only a variable declared in a local context, it has that limited scope. But the variable may be declared in different ways or with different specified scope, in a progression that goes from local to enclosed to global and then built-in. This progression is known as the LEGB scope (see next).
All of this is logical and seemingly straightforward, but what is required by Python in a given context is dependent on just that: context. Sometimes it is difficult to know within a Python program or routine exactly where one is with regard to the LEGB scope. In some cases, prefixes are necessary to cross scope boundaries; in other cases, they are not. About the best rule of thumb I have been able to derive for my own experience is to be aware the the 'dot notation' hierarchies in my program objects, and if I have difficulties getting a specific value, to add or reduce more scope definitions in the 'dot notation'.
To gain a feel for namespace scope, I encourage you to test and run these examples: https://www.programiz.com/python-programming/namespace.
Namespaces may relate to Python concepts like classes, functions, inner functions, variables, exceptions, comprehensions, built-in functions, standard data structures, knowledge bases, and knowledge graphs.
To understand the Python objects within your knowledge graph namespace, you can Run the following cell, which will bring up a listing of objects in each of the imported files via its associated namespace:
```
main = 'C:/1-PythonProjects/owlready2/kg/kbpedia_reference_concepts.owl'
skos_file = 'http://www.w3.org/2004/02/skos/core'
kko_file = 'C:/1-PythonProjects/owlready2/kg/kko.owl'
print('startup()-> ', dir())
from owlready2 import *
print('owlready()-> ', dir(), '\n')
world = World()
kb = world.get_ontology(main).load()
rc = kb.get_namespace('http://kbpedia.org/kko/rc/')
print('main_import()-> ', dir(), '\n')
skos = world.get_ontology(skos_file).load()
kb.imported_ontologies.append(skos)
print('skos_import()-> ', dir(), '\n')
kko = world.get_ontology(kko_file).load()
kb.imported_ontologies.append(kko)
print('kko_import()-> ', dir(), '\n')
```
You'll see that each of the major namespaces (sometimes ontologies) list out their internal objects as imported. You may pick any of these objects, and then inspect *its* attributes:
```
dir(DataProperty)
```
You can always return to this page to get a global sense of what is in the knowledge graph. Similarly, you may import the *cowpoke* package (to be defined soon!) or any other Python package and inspect *its* code contents in the same manner. So, depending on how you lay out your namespaces, you may readily segregate code from knowledge graph from knowledge base, or whatever distinctions make sense for your circumstance.
#### LEGB Rule
The scope of a name or variable depends on the place in your code where you create that variable. The Python scope concept is generally presented using a rule known as the LEGB rule. The letters in the acronym LEGB stand for Local, Enclosing, Global, and Built-in scopes. A variable is evaluated in sequence in order across LEGB, and its scope depends on the context in which it was initially declared. A variable does not apply beyond the scope in which it was defined. One typical mistake, for example, is to declare a local variable and then assume it applies outside of its local scope. Another typical mistake is to declare a local variable that has the same name as one in a broader context, and then to wonder why it does not operate as declared when in a broader scope.
Probably the safest approach to the LEGB scope is to be aware of variables used in the core Python functions ('built-ins') or those in imported modules (the 'global' ones) and to avoid them in new declarations. Then, be cognizant that what you declare in local routines only apply there, unless you take explicit steps (through [declaration mechanisms](https://realpython.com/python-scope-legb-rule/#modifying-the-behavior-of-a-python-scope)) or the use of namespace and dot notation to make your intentions clear.
#### Setting Proper Data Type
Within owlready2, classes and properties are defined and treated as Python classes. Thus, when you retrieve an item or want to manipulate an item, the item needs to be specified as a proper Python class to the system. However, in moving from format to format or doing various conformance checks, the representation may come into the system as a string or list object. Knowing what representation the inputs are compared with the desired outputs is critical for certain activities in *cowpoke*. So, let's look at the canoncial means of shifting data types when dealing with listings of KBpedia classes.
##### From Python Class to String
Much of the staging of extractions is manipulating labels as strings after retrieving the objects as classes from the system. There is a simple iterator that allows us to obtain sets of classes, loop over them, and convert each item to a string in the process:
<pre>
new_str_items = []
for item in loop:
a_item = item.curResource # Retrieves curResource property for item
a_item = str(a_item) # Converts item to string
new_str_items.append(a_item) # Adds to new string list
</pre>
If you have nested items within loops, you can pick them up using the <code>enumerate</code> in the loop specification.
##### From Sting to Python Class
The reverse form has us specifying a string and a namespace, from which we obtain the class data type:
<pre>
for item in loop:
var1 = getattr(rc, str_item) # Need to remove prefix and get from proper namespace (RC)
var2 = getattr(rc, str_parent) # May need to do so for parent or item for property
var1.is_a.append(var2)
</pre>
The general challenge in this form is to make sure that items and parents are in the form of strings without namespaces, and that the proper namespace is referenced when retrieving the actual attribute value. Many code examples throughout show examples of how to test for trap multiple namespaces.
### Additional Documentation
I have not been comprehensive nor have found a 'great" Python book in relation to my needs and skills. I will likely acquire more, but here are three more-or-less general purpose Python introductions that have not met my needs:
- [Python Crash Course](https://www.amazon.com/dp/1593279280/ref=sspa_dk_detail_4?psc=1&spLa=ZW5jcnlwdGVkUXVhbGlmaWVyPUExODNaNjFaRDhZRkpLJmVuY3J5cHRlZElkPUEwMzYzODQ0MklLVjRXSU9IMTUyVCZlbmNyeXB0ZWRBZElkPUEwOTg4NzY4MzNaNTBHTldXVzEyNCZ3aWRnZXROYW1lPXNwX2RldGFpbCZhY3Rpb249Y2xpY2tSZWRpcmVjdCZkb05vdExvZ0NsaWNrPXRydWU=) - the index is lightweight and not generally useful; too much space devoted to their games examples; seems to lack basic program techniques
- [Python Cookbook](https://www.amazon.com/Python-Cookbook-Third-David-Beazley/dp/1449340377/ref=pd_bxgy_img_3/145-9690592-7275929?_encoding=UTF8&pd_rd_i=1449340377&pd_rd_r=ecdf1dd9-fac4-47c6-ae90-b0ccfdd33759&pd_rd_w=TRM4e&pd_rd_wg=MvG8h&pf_rd_p=4e3f7fc3-00c8-46a6-a4db-8457e6319578&pf_rd_r=5HWMJBEKWC0NQB3H3VP2&psc=1&refRID=5HWMJBEKWC0NQB3H3VP2) - wow, I hardly found anything of direct relevance or assistance
- [Learning Python](https://www.amazon.com/Learning-Python-5th-Mark-Lutz/dp/1449355730/ref=redir_mobile_desktop?ie=UTF8&aaxitk=pyyDguL4rBcaSnsVbpO9eA&hsa_cr_id=4158170100401&ref_=sbx_be_s_sparkle_mcd_asin_1) - perhaps the best of the three, but my verson is for Python 2 (2.6) and also lacks the intermediate, practical hands on I want (did not upgrade to later version because of the scope issues).
It actually seems like online resources, plus directed Web searches when key questions arise, can overcome this lack of a general intro resource per the above.
Another useful source are the [RealPython](https://realpython.com/) video tutorials, with generally the first introductory one in each area being free, has notable ones on:
- [classes](https://realpython.com/lessons/classes-python/)
- [variables](https://realpython.com/courses/variables-python/)
- [lists and tuples](https://realpython.com/courses/lists-tuples-python/)
- [dictionaries](https://realpython.com/courses/dictionaries-python/)
- [functions](https://realpython.com/defining-your-own-python-function/)
- [inner functions](https://realpython.com/inner-functions-what-are-they-good-for/#closures-and-factory-functions) (some nice code examples)
- [built-in functions](https://realpython.com/lessons/operators-and-built-functions/)
- [exceptions](https://realpython.com/courses/introduction-python-exceptions/)
- [comprehensions](https://realpython.com/courses/using-list-comprehensions-effectively/)
- [modules and packages](https://realpython.com/courses/python-modules-packages/)
- [LEGB scope](https://realpython.com/python-scope-legb-rule/) (see this for namespace exploration examples)
- [data types](https://realpython.com/courses/python-data-types/)
- [reading and writing files](https://realpython.com/courses/reading-and-writing-files-python/), including [CSV](https://realpython.com/courses/reading-and-writing-csv-files/).
<div style="background-color:#efefff; border:1px dotted #ceceff; vertical-align:middle; margin:15px 60px; padding:8px;">
<span style="font-weight: bold;">NOTE:</span> This article is part of the <a href="https://www.mkbergman.com/cooking-with-python-and-kbpedia/" style="font-style: italic;">Cooking with Python and KBpedia</a> series. See the <a href="https://www.mkbergman.com/cooking-with-python-and-kbpedia/"><strong>CWPK</strong> listing</a> for other articles in the series. <a href="http://kbpedia.org/">KBpedia</a> has its own Web site.
</div>
<div style="background-color:#ebf8e2; border:1px dotted #71c837; vertical-align:middle; margin:15px 60px; padding:8px;">
<span style="font-weight: bold;">NOTE:</span> This <strong>CWPK
installment</strong> is available both as an online interactive
file <a href="https://mybinder.org/v2/gh/Cognonto/CWPK/master" ><img src="https://mybinder.org/badge_logo.svg" style="display:inline-block; vertical-align: middle;" /></a> or as a <a href="https://github.com/Cognonto/CWPK" title="CWPK notebook" alt="CWPK notebook">direct download</a> to use locally. Make sure and pick the correct installment number. For the online interactive option, pick the <code>*.ipynb</code> file. It may take a bit of time for the interactive option to load.</div>
<div style="background-color:#feeedc; border:1px dotted #f7941d; vertical-align:middle; margin:15px 60px; padding:8px;">
<div style="float: left; margin-right: 5px;"><img src="http://kbpedia.org/cwpk-files/warning.png" title="Caution!" width="32" /></div>I am at best an amateur with Python. There are likely more efficient methods for coding these steps than what I provide. I encourage you to experiment -- which is part of the fun of Python -- and to <a href="mailto:mike@mkbergman.com">notify me</a> should you make improvements.
</div>
|
github_jupyter
|
main = 'C:/1-PythonProjects/owlready2/kg/kbpedia_reference_concepts.owl'
skos_file = 'http://www.w3.org/2004/02/skos/core'
kko_file = 'C:/1-PythonProjects/owlready2/kg/kko.owl'
from owlready2 import *
world = World()
kb = world.get_ontology(main).load()
rc = kb.get_namespace('http://kbpedia.org/kko/rc/')
skos = world.get_ontology(skos_file).load()
kb.imported_ontologies.append(skos)
kko = world.get_ontology(kko_file).load()
kb.imported_ontologies.append(kko)
dir(world.search)
type(world.search)
main = 'C:/1-PythonProjects/owlready2/kg/kbpedia_reference_concepts.owl'
skos_file = 'http://www.w3.org/2004/02/skos/core'
kko_file = 'C:/1-PythonProjects/owlready2/kg/kko.owl'
print('startup()-> ', dir())
from owlready2 import *
print('owlready()-> ', dir(), '\n')
world = World()
kb = world.get_ontology(main).load()
rc = kb.get_namespace('http://kbpedia.org/kko/rc/')
print('main_import()-> ', dir(), '\n')
skos = world.get_ontology(skos_file).load()
kb.imported_ontologies.append(skos)
print('skos_import()-> ', dir(), '\n')
kko = world.get_ontology(kko_file).load()
kb.imported_ontologies.append(kko)
print('kko_import()-> ', dir(), '\n')
dir(DataProperty)
| 0.134293 | 0.917635 |
# Meshed AC-DC example
This example has a 3-node AC network coupled via AC-DC converters to a 3-node DC network. There is also a single point-to-point DC using the Link component.
The data files for this example are in the examples folder of the github repository: <https://github.com/PyPSA/PyPSA>.
```
import pypsa
import numpy as np
import pandas as pd
import os
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
%matplotlib inline
plt.rc("figure", figsize=(8, 8))
network = pypsa.examples.ac_dc_meshed(from_master=True)
# get current type (AC or DC) of the lines from the buses
lines_current_type = network.lines.bus0.map(network.buses.carrier)
lines_current_type
network.plot(
line_colors=lines_current_type.map(lambda ct: "r" if ct == "DC" else "b"),
title="Mixed AC (blue) - DC (red) network - DC (cyan)",
color_geomap=True,
jitter=0.3,
)
plt.tight_layout()
network.links.loc["Norwich Converter", "p_nom_extendable"] = False
```
We inspect the topology of the network. Therefore use the function `determine_network_topology` and inspect the subnetworks in `network.sub_networks`.
```
network.determine_network_topology()
network.sub_networks["n_branches"] = [
len(sn.branches()) for sn in network.sub_networks.obj
]
network.sub_networks["n_buses"] = [len(sn.buses()) for sn in network.sub_networks.obj]
network.sub_networks
```
The network covers 10 time steps. These are given by the `snapshots` attribute.
```
network.snapshots
```
There are 6 generators in the network, 3 wind and 3 gas. All are attached to buses:
```
network.generators
```
We see that the generators have different capital and marginal costs. All of them have a `p_nom_extendable` set to `True`, meaning that capacities can be extended in the optimization.
The wind generators have a per unit limit for each time step, given by the weather potentials at the site.
```
network.generators_t.p_max_pu.plot.area(subplots=True)
plt.tight_layout()
```
Alright now we know how the network looks like, where the generators and lines are. Now, let's perform a optimization of the operation and capacities.
```
network.lopf();
```
The objective is given by:
```
network.objective
```
Why is this number negative? It considers the starting point of the optimization, thus the existent capacities given by `network.generators.p_nom` are taken into account.
The real system cost are given by
```
network.objective + network.objective_constant
```
The optimal capacities are given by `p_nom_opt` for generators, links and storages and `s_nom_opt` for lines.
Let's look how the optimal capacities for the generators look like.
```
network.generators.p_nom_opt.div(1e3).plot.bar(ylabel="GW", figsize=(8, 3))
plt.tight_layout()
```
Their production is again given as a time-series in `network.generators_t`.
```
network.generators_t.p.div(1e3).plot.area(subplots=True, ylabel="GW")
plt.tight_layout()
```
What are the Locational Marginal Prices in the network. From the optimization these are given for each bus and snapshot.
```
network.buses_t.marginal_price.mean(1).plot.area(figsize=(8, 3), ylabel="Euro per MWh")
plt.tight_layout()
```
We can inspect futher quantities as the active power of AC-DC converters and HVDC link.
```
network.links_t.p0
network.lines_t.p0
```
...or the active power injection per bus.
```
network.buses_t.p
```
|
github_jupyter
|
import pypsa
import numpy as np
import pandas as pd
import os
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
%matplotlib inline
plt.rc("figure", figsize=(8, 8))
network = pypsa.examples.ac_dc_meshed(from_master=True)
# get current type (AC or DC) of the lines from the buses
lines_current_type = network.lines.bus0.map(network.buses.carrier)
lines_current_type
network.plot(
line_colors=lines_current_type.map(lambda ct: "r" if ct == "DC" else "b"),
title="Mixed AC (blue) - DC (red) network - DC (cyan)",
color_geomap=True,
jitter=0.3,
)
plt.tight_layout()
network.links.loc["Norwich Converter", "p_nom_extendable"] = False
network.determine_network_topology()
network.sub_networks["n_branches"] = [
len(sn.branches()) for sn in network.sub_networks.obj
]
network.sub_networks["n_buses"] = [len(sn.buses()) for sn in network.sub_networks.obj]
network.sub_networks
network.snapshots
network.generators
network.generators_t.p_max_pu.plot.area(subplots=True)
plt.tight_layout()
network.lopf();
network.objective
network.objective + network.objective_constant
network.generators.p_nom_opt.div(1e3).plot.bar(ylabel="GW", figsize=(8, 3))
plt.tight_layout()
network.generators_t.p.div(1e3).plot.area(subplots=True, ylabel="GW")
plt.tight_layout()
network.buses_t.marginal_price.mean(1).plot.area(figsize=(8, 3), ylabel="Euro per MWh")
plt.tight_layout()
network.links_t.p0
network.lines_t.p0
network.buses_t.p
| 0.407098 | 0.985963 |
# Introduction to Predictive Maintenance
#### Author Nagdev Amruthnath
Date: 1/9/2019
##### Citation Info
If you are using this for your research, please use the following for citation.
Amruthnath, Nagdev, and Tarun Gupta. "A research study on unsupervised machine learning algorithms for early fault detection in predictive maintenance." In 2018 5th International Conference on Industrial Engineering and Applications (ICIEA), pp. 355-361. IEEE, 2018.
##### Disclaimer
This is a tutorial for performing fault detection using machine learning. You this code at your own risk. I do not gurantee that this would work as shown below. If you have any suggestions please branch this project.
## Introduction
This is the first of four part demostration series of using machine learning for predictive maintenance.
The area of predictive maintenance has taken a lot of prominence in the last couple of years due to various reasons. With new algorithms and methodologies growing across different learning methods, it has remained a challenge for industries to adopt which method is fit, robust and provide most accurate detection. Fault detection is one of the critical components of predictive maintenance; it is very much needed for industries to detect faults early and accurately. In a production environment, to minimize the cost of maintenance, sometimes it is required to build a model with minimal or no historical data. In such cases, unsupervised learning would be a better option model building. In this paper, we have chosen a simple vibration data collected from an exhaust fan, and have fit different unsupervised learning algorithms such as PCA T2 statistic, Hierarchical clustering, K-Means, Fuzzy C-Means clustering and model-based clustering to test its accuracy, performance, and robustness. In the end, we have proposed a methodology to benchmark different algorithms and choosing the final model
## Load libraries
```
options(warn=-1)
# load libraries
library(mdatools) #mdatools version 0.9.1
library(caret)
library(foreach)
library(dplyr)
library(mclust)
```
## Load data
Here we are using data from a bench press. There are total of four different states in this machine and they are split into four different csv files. We need to load the data first. In the data time represents the time between samples, ax is the acceleration on x axis, ay is the acceleration on y axis, az is the acceleration on z axis and at is the G's. The data was collected at sample rate of 100hz.
Four different states of the machine were collected
1. Nothing attached to drill press
2. Wooden base attached to drill press
3. Imbalance created by adding weight to one end of wooden base
4. Imbalacne created by adding weight to two ends of wooden base.
```
#setwd("/Experiment")
#read csv files
file1 = read.csv("dry run.csv", sep=",", header =T)
file2 = read.csv("base.csv", sep=",", header =T)
file3 = read.csv("imbalance 1.csv", sep=",", header =T)
file4 = read.csv("imbalance 2.csv", sep=",", header =T)
head(file1)
```
We can look at the summary of each file using summary function in R. Below, we can observe that 66 seconds long data is available. We also have min, max and mean for each of the variables.
```
# summary of each file
summary(file1)
```
## Data Aggregration and feature extraction
Here, the data is aggregated by 1 minute and features are extracted. Features are extracted to reduce the dimension of the data and only storing the representation of the data.
```
file1$group = as.factor(round(file1$time))
file2$group = as.factor(round(file2$time))
file3$group = as.factor(round(file3$time))
file4$group = as.factor(round(file4$time))
#(file1,20)
#list of all files
files = list(file1, file2, file3, file4)
#loop through all files and combine
features = NULL
for (i in 1:4){
res = files[[i]] %>%
group_by(group) %>%
summarize(ax_mean = mean(ax),
ax_sd = sd(ax),
ax_min = min(ax),
ax_max = max(ax),
ax_median = median(ax),
ay_mean = mean(ay),
ay_sd = sd(ay),
ay_min = min(ay),
ay_may = max(ay),
ay_median = median(ay),
az_mean = mean(az),
az_sd = sd(az),
az_min = min(az),
az_maz = max(az),
az_median = median(az),
aT_mean = mean(aT),
aT_sd = sd(aT),
aT_min = min(aT),
aT_maT = max(aT),
aT_median = median(aT)
)
features = rbind(features, res)
}
#view all features
head(features)
```
## Analyzing the data through plots
Plot all mean values to analyze the change in vibrations. From the first 3 plots we can observe that its very hard to analyze any significant change in vibration for all 4 states of the machines. On the other hand for the fourth plot we can identify 2 states of the machine.
```
#plot data
par(mfrow=c(4,1))
plot(features$ax_mean, main="X-Axis mean", xlab="Observations", ylab="G's", type="l", col="blue")
plot(features$ay_mean, main="Y-Axis mean", xlab="Observations", ylab="G's", type="l", col="blue")
plot(features$az_mean, main="Z-Axis mean", xlab="Observations", ylab="G's", type="l", col="blue")
plot(features$aT_mean, main="T mean", xlab="Observations", ylab="G's", type="l", col="blue")
```
## Fault Detection using PCA-T2 and SPE
Principal component analysis (PCA) is a mathematical algorithm that reduces the dimensionality of the data while retaining most of the variation (information) in the data set. T2 Statistic is a multivariate statistical analysis. SPE also referred to a Q-statistic is the square prediction error.
```
pca = function(train,test,variance, alpha,gamma) {
#remove columns with zero variance
train = train[sapply(train, function(x) length(levels(factor(x)))>1)]
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale"))
# transform the dataset using the parameters
traintransformed = predict(preprocessParams, train)
testtransformed = predict(preprocessParams, test[,colnames(train)])
#calibrate data for
pca.model = mdatools::pca(x = traintransformed,
x.test = testtransformed,
alpha = alpha,
gamma = gamma,
ncomp = ncol(train))
for(i in 1:ncol(train)){
if(pca.model$calres$cumexpvar[i] >= variance) { break }
}
trainRes = data.frame(train,
T2stats = pca.model$calres$T2[,i],
T2critical = pca.model$calres$T2lim[1,i],
T2outlier = pca.model$calres$T2lim[2,i],
SPEstats = pca.model$calres$Q[,i],
SPEcritical = pca.model$calres$Qlim[1,i],
SPEoutlier = pca.model$calres$Qlim[2,i]
)
testRes = data.frame(test[,colnames(train)],
T2stats = pca.model$testres$T2[,i],
T2critical = pca.model$testres$T2lim[1,i],
T2outlier = pca.model$testres$T2lim[2,i],
SPEstats = pca.model$testres$Q[,i],
SPEcritical = pca.model$testres$Qlim[1,i],
SPEoutlier = pca.model$testres$Qlim[2,i]
)
return(rbind(trainRes,testRes))
}
```
The above function is the generalized function for using PCA analysis for performing anomaly detection. The input variables are the train data, test data, alpha value, gamma value and variance among principal components.
```
train = features[1:67,2:ncol(features)]
test = features[68:nrow(features),2:ncol(features)]
alpha = 0.05
gamma = 0.01
variance = 0.95
#call pca function
pca_result = pca(train,test,variance, alpha,gamma)
```
The below are the graphial results for PCA analysis. From the PCA-T2 results, we can observe that the annomaly model was capable of detecting the annomalies. Likewise PCA-SPE model was capable of detecting the anomalies as well.
```
#plot results
par(mfrow=c(2,1))
plot(pca_result$T2stats, main="PCA T2 Result", ylab="stats", xlab="observations", col="blue", type="o")
abline(h=pca_result$T2critical, col="black")
abline(h=pca_result$T2outlier, col="red")
plot(pca_result$SPEstats, main="PCA SPE Result", ylab="stats", xlab="observations", col="blue", type="o")
abline(h=pca_result$SPEcritical, col="black")
abline(h=pca_result$SPEoutlier, col="red")
```
## Fault detection using K-means
K-means is one of the most common unsupervised learning clustering algorithms. This most straightforward algorithm’s goal is to divide the data set into pre-determined clusters based on distance. Here, we have used Euclidian distance.
```
kmeans = function(train, usePCA, variance) {
#remove columns with zero variance
train = train[sapply(train, function(x) length(levels(factor(x)))>1)]
if(usePCA == TRUE){
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale", "pca"),
thresh = variance,
na.remove = T,
freqCut = 95/5,
uniqueCut = 10
)
# transform the dataset using the parameters
transformed = predict(preprocessParams, train)
kmRes = stats::kmeans(as.matrix(transformed),2)
return(data.frame(train,cluster=kmRes$cluster))
}
if(usePCA == FALSE){
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale"),
na.remove = T
)
# transform the dataset using the parameters
transformed = predict(preprocessParams, train)
kmRes = stats::kmeans(transformed,2)
return(data.frame(train,cluster=kmRes$cluster))
}
}
#Anomaly detection without PCA
train = features[,2:ncol(features)]
usePCA = FALSE
Variance = 0.95
kmeans_res = kmeans(train, usePCA, variance)
#Anomaly detection with PCA
usePCA = TRUE
kmeans_pca_res = kmeans(train, usePCA, variance)
```
Using the genralized function developed above, kmeans is used in two ways with and without PCA. In both the cases from the graphical results, we can observe that kmeans was capable of detecting the anomalies. Also, it is interesting to not that, kmeans grouped data in file 1 and file 2 and one state and file 3 and file 4 as other state.
```
#plot results
par(mfrow=c(2,1))
pca.model = prcomp(train, scale=T)
plot(features$az_mean, features$aT_mean , main="Kmeans Result", ylab="az_mean", xlab="aT_mean", col=kmeans_res$cluster ,yaxt = 'n')
plot(pca.model$x, main="Kmeans PCA Result", ylab="PC 2", xlab="PC 1", col=kmeans_pca_res$cluster, yaxt = 'n')
```
# Fault Detection using Model Based clustering
A Gaussian mixture model (GMM) is used for modeling data that comes from one of the several groups: the groups might be different from each other, but data points within the same group can be well-modeled by a Gaussian distribution . Gaussian finite mixture model fitted by EM algorithm is an iterative algorithm where some initial random estimate starts and updates every iterate until convergence is detected . Initialization can be started based on a set of initial parameters and start E-step or set of initial weights and proceed to M-step. This step can be either set randomly or could be chosen based on some method.
```
gmm = function(train, usePCA, variance, n) {
#remove columns with zero variance
train = train[sapply(train, function(x) length(levels(factor(x)))>1)]
M = nrow(train)/4
if(usePCA == TRUE){
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale", "pca"),
thresh = variance,
na.remove = T,
freqCut = 95/5,
uniqueCut = 10
)
# transform the dataset using the parameters
traintransformed = predict(preprocessParams, train)
m = densityMclust(traintransformed,
G = n,
initialization = list(subset = sample(1:nrow(traintransformed),
size = M),
set.seed(11)))
traintransformed$y = m$classification
return(data.frame(traintransformed, m$z))
}
if(usePCA == FALSE){
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale"),
na.remove = T
)
# transform the dataset using the parameters
traintransformed = predict(preprocessParams, train)
m = densityMclust(traintransformed,
G = n,
initialization = list(subset = sample(1:nrow(traintransformed),
size = M),
set.seed(11)))
traintransformed$y = m$classification
return(data.frame(traintransformed, m$z))
}
}
#Anomaly detection without PCA
train = features[,2:ncol(features)]
usePCA = FALSE
variance = 0.95
n = 2
gmm_res = gmm(train, usePCA, variance, n)
#Anomaly detection with PCA
usePCA = TRUE
gmm_pca_res = gmm(train, usePCA, variance, n)
```
Using the genralized function developed above, GMM is used in two ways with and without PCA. In both the cases from the graphical results, we can observe that GMM was capable of detecting the anomalies. Also, it is interesting to not that, GMM grouped data in file 1 and file 2 and one state and file 3 and file 4 as other state.
```
#plot results
par(mfrow=c(2,1))
pca.model = prcomp(train, scale=T)
plot(features$az_mean, features$aT_mean , main="GMM Result", ylab="az_mean", xlab="aT_mean", col=gmm_res$y ,yaxt = 'n')
plot(pca.model$x, main="GMM PCA Result", ylab="PC 2", xlab="PC 1", col=gmm_pca_res$y, yaxt = 'n')
```
#### References
[1] Amruthnath, Nagdev, and Tarun Gupta. "A research study on unsupervised machine learning algorithms for early fault detection in predictive maintenance." In 2018 5th International Conference on Industrial Engineering and Applications (ICIEA), pp. 355-361. IEEE, 2018.
[2] Amruthnath, Nagdev, and Tarun Gupta. "Fault class prediction in unsupervised learning using model-based clustering approach." In Information and Computer Technologies (ICICT), 2018 International Conference on, pp. 5-12. IEEE, 2018.
|
github_jupyter
|
options(warn=-1)
# load libraries
library(mdatools) #mdatools version 0.9.1
library(caret)
library(foreach)
library(dplyr)
library(mclust)
#setwd("/Experiment")
#read csv files
file1 = read.csv("dry run.csv", sep=",", header =T)
file2 = read.csv("base.csv", sep=",", header =T)
file3 = read.csv("imbalance 1.csv", sep=",", header =T)
file4 = read.csv("imbalance 2.csv", sep=",", header =T)
head(file1)
# summary of each file
summary(file1)
file1$group = as.factor(round(file1$time))
file2$group = as.factor(round(file2$time))
file3$group = as.factor(round(file3$time))
file4$group = as.factor(round(file4$time))
#(file1,20)
#list of all files
files = list(file1, file2, file3, file4)
#loop through all files and combine
features = NULL
for (i in 1:4){
res = files[[i]] %>%
group_by(group) %>%
summarize(ax_mean = mean(ax),
ax_sd = sd(ax),
ax_min = min(ax),
ax_max = max(ax),
ax_median = median(ax),
ay_mean = mean(ay),
ay_sd = sd(ay),
ay_min = min(ay),
ay_may = max(ay),
ay_median = median(ay),
az_mean = mean(az),
az_sd = sd(az),
az_min = min(az),
az_maz = max(az),
az_median = median(az),
aT_mean = mean(aT),
aT_sd = sd(aT),
aT_min = min(aT),
aT_maT = max(aT),
aT_median = median(aT)
)
features = rbind(features, res)
}
#view all features
head(features)
#plot data
par(mfrow=c(4,1))
plot(features$ax_mean, main="X-Axis mean", xlab="Observations", ylab="G's", type="l", col="blue")
plot(features$ay_mean, main="Y-Axis mean", xlab="Observations", ylab="G's", type="l", col="blue")
plot(features$az_mean, main="Z-Axis mean", xlab="Observations", ylab="G's", type="l", col="blue")
plot(features$aT_mean, main="T mean", xlab="Observations", ylab="G's", type="l", col="blue")
pca = function(train,test,variance, alpha,gamma) {
#remove columns with zero variance
train = train[sapply(train, function(x) length(levels(factor(x)))>1)]
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale"))
# transform the dataset using the parameters
traintransformed = predict(preprocessParams, train)
testtransformed = predict(preprocessParams, test[,colnames(train)])
#calibrate data for
pca.model = mdatools::pca(x = traintransformed,
x.test = testtransformed,
alpha = alpha,
gamma = gamma,
ncomp = ncol(train))
for(i in 1:ncol(train)){
if(pca.model$calres$cumexpvar[i] >= variance) { break }
}
trainRes = data.frame(train,
T2stats = pca.model$calres$T2[,i],
T2critical = pca.model$calres$T2lim[1,i],
T2outlier = pca.model$calres$T2lim[2,i],
SPEstats = pca.model$calres$Q[,i],
SPEcritical = pca.model$calres$Qlim[1,i],
SPEoutlier = pca.model$calres$Qlim[2,i]
)
testRes = data.frame(test[,colnames(train)],
T2stats = pca.model$testres$T2[,i],
T2critical = pca.model$testres$T2lim[1,i],
T2outlier = pca.model$testres$T2lim[2,i],
SPEstats = pca.model$testres$Q[,i],
SPEcritical = pca.model$testres$Qlim[1,i],
SPEoutlier = pca.model$testres$Qlim[2,i]
)
return(rbind(trainRes,testRes))
}
train = features[1:67,2:ncol(features)]
test = features[68:nrow(features),2:ncol(features)]
alpha = 0.05
gamma = 0.01
variance = 0.95
#call pca function
pca_result = pca(train,test,variance, alpha,gamma)
#plot results
par(mfrow=c(2,1))
plot(pca_result$T2stats, main="PCA T2 Result", ylab="stats", xlab="observations", col="blue", type="o")
abline(h=pca_result$T2critical, col="black")
abline(h=pca_result$T2outlier, col="red")
plot(pca_result$SPEstats, main="PCA SPE Result", ylab="stats", xlab="observations", col="blue", type="o")
abline(h=pca_result$SPEcritical, col="black")
abline(h=pca_result$SPEoutlier, col="red")
kmeans = function(train, usePCA, variance) {
#remove columns with zero variance
train = train[sapply(train, function(x) length(levels(factor(x)))>1)]
if(usePCA == TRUE){
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale", "pca"),
thresh = variance,
na.remove = T,
freqCut = 95/5,
uniqueCut = 10
)
# transform the dataset using the parameters
transformed = predict(preprocessParams, train)
kmRes = stats::kmeans(as.matrix(transformed),2)
return(data.frame(train,cluster=kmRes$cluster))
}
if(usePCA == FALSE){
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale"),
na.remove = T
)
# transform the dataset using the parameters
transformed = predict(preprocessParams, train)
kmRes = stats::kmeans(transformed,2)
return(data.frame(train,cluster=kmRes$cluster))
}
}
#Anomaly detection without PCA
train = features[,2:ncol(features)]
usePCA = FALSE
Variance = 0.95
kmeans_res = kmeans(train, usePCA, variance)
#Anomaly detection with PCA
usePCA = TRUE
kmeans_pca_res = kmeans(train, usePCA, variance)
#plot results
par(mfrow=c(2,1))
pca.model = prcomp(train, scale=T)
plot(features$az_mean, features$aT_mean , main="Kmeans Result", ylab="az_mean", xlab="aT_mean", col=kmeans_res$cluster ,yaxt = 'n')
plot(pca.model$x, main="Kmeans PCA Result", ylab="PC 2", xlab="PC 1", col=kmeans_pca_res$cluster, yaxt = 'n')
gmm = function(train, usePCA, variance, n) {
#remove columns with zero variance
train = train[sapply(train, function(x) length(levels(factor(x)))>1)]
M = nrow(train)/4
if(usePCA == TRUE){
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale", "pca"),
thresh = variance,
na.remove = T,
freqCut = 95/5,
uniqueCut = 10
)
# transform the dataset using the parameters
traintransformed = predict(preprocessParams, train)
m = densityMclust(traintransformed,
G = n,
initialization = list(subset = sample(1:nrow(traintransformed),
size = M),
set.seed(11)))
traintransformed$y = m$classification
return(data.frame(traintransformed, m$z))
}
if(usePCA == FALSE){
# calculate the pre-process parameters from the dataset
preprocessParams = preProcess(train,
method=c("center", "scale"),
na.remove = T
)
# transform the dataset using the parameters
traintransformed = predict(preprocessParams, train)
m = densityMclust(traintransformed,
G = n,
initialization = list(subset = sample(1:nrow(traintransformed),
size = M),
set.seed(11)))
traintransformed$y = m$classification
return(data.frame(traintransformed, m$z))
}
}
#Anomaly detection without PCA
train = features[,2:ncol(features)]
usePCA = FALSE
variance = 0.95
n = 2
gmm_res = gmm(train, usePCA, variance, n)
#Anomaly detection with PCA
usePCA = TRUE
gmm_pca_res = gmm(train, usePCA, variance, n)
#plot results
par(mfrow=c(2,1))
pca.model = prcomp(train, scale=T)
plot(features$az_mean, features$aT_mean , main="GMM Result", ylab="az_mean", xlab="aT_mean", col=gmm_res$y ,yaxt = 'n')
plot(pca.model$x, main="GMM PCA Result", ylab="PC 2", xlab="PC 1", col=gmm_pca_res$y, yaxt = 'n')
| 0.460774 | 0.986218 |
<a href="https://colab.research.google.com/github/Smash08/PaginadeCaptura/blob/main/Projeto_AIRBNB.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Análise dos Dados do Airbnb - Rio de Janeiro
O [Airbnb](https://www.airbnb.com.br/) já é considerado como sendo a **maior empresa hoteleira da atualidade**. Ah, o detalhe é que ele **não possui nenhum hotel**!
Conectando pessoas que querem viajar (e se hospedar) com anfitriões que querem alugar seus imóveis de maneira prática, o Airbnb fornece uma plataforma inovadora para tornar essa hospedagem alternativa.
Em 2018, a Startup já havia **hospedado mais de 300 milhões** de pessoas ao redor de todo o mundo, desafiando as redes hoteleiras tradicionais.
Os dados foram adquiridos no próprio site Airbnb, por meio do portal [Inside Airbnb](http://insideairbnb.com/get-the-data.html).
**Neste *notebook*, iremos analisar os dados referentes à cidade do Rio de Janeiro, e ver quais insights podem ser extraídos a partir de dados brutos.**
```
# importar os pacotes necessarios
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
%matplotlib inline
# importar o arquivo listings.csv para um DataFrame
df = pd.read_csv("http://data.insideairbnb.com/brazil/rj/rio-de-janeiro/2021-07-17/data/listings.csv.gz")
```
#ANÁLISE DE DADOS
```
df.head()
# identificar o volume de dados do DataFrame
print(f'Entradas: {df.shape[0]}\nVariáveis:{df.shape[1]}')
# verificar as 5 primeiras entradas do dataset
display(df.dtypes)
# Verificar valores ausentes e a porcentagem de quais
# colunas possuem mais dados faltantes
valorAusente = df.isna().mean().sort_values(ascending=False)
valorAusente[0:30]
```
#DISTRIBUIÇÃO DE VARIAVEIS
```
df.hist(bins=15, figsize=(30,20));
sns.set()
```
Observe que os dados não estão bem distribuídos, bem como há faz-se necessário as exclusão de colunas faltantes pois prejudicam a visualização dos histogramas.
#INFORMAÇÕES ESTATISTICA
```
#função para limpeza de caracter na coluna, retirando o $
def removeSymbol(value):
value = value.replace('$', ' ').strip()
value = value.replace(',', '')
return value
#aplicando a função
df['price']= df['price'].apply(removeSymbol)
#mudando a entrada do dado para tipo float
df['price'] = df['price'].astype('float')
```
#Outliers
```
df[["price", "minimum_nights", "number_of_reviews", 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']].describe()
```
Observe a cima que há erros no dataset, o máximo de noites mínimas (1.100)(minimum_nights) ultrapassa o valor total de dias, sendo necessário realizar a limpeza dos dados quanto a isso.
```
df['price'].mean()
df.minimum_nights.plot(kind='box', vert=False, figsize=(15,3))
plt.show();
# ver quantidade de valores acima de 30 dias para minimum_nights
print("minimum_nights: valores acima de 30:")
print(f'Entradas: {len(df[df.minimum_nights > 30])}')
print(f'{(len(df[df.minimum_nights > 30 ])/df.shape[0])*100:.4f}%')
# remover os *outliers* em um novo DataFrame
df_clean = df.copy()
df_clean.drop(df_clean[df_clean.price > 5000].index, axis=0, inplace=True)
df_clean.drop(df_clean[df_clean.minimum_nights > 30].index, axis=0, inplace=True)
# remover variaveis vazias
df_clean.drop('license', axis=1, inplace=True)
df_clean.drop('scrape_id', axis=1, inplace=True)
df_clean.drop('bathrooms', axis=1, inplace=True)
df_clean.drop('calendar_updated', axis=1, inplace=True)
df_clean.drop('neighbourhood_group_cleansed', axis=1, inplace=True)
#plotar novamente o histograma
df_clean.hist(bins=15, figsize=(40,30))
sns.set()
# plot da matriz de correlação
correlation = df_clean[["price", "minimum_nights", "number_of_reviews", 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']].corr()
display(correlation)
sns.heatmap(correlation, cmap='RdBu', fmt='.2f', square=True, linecolor='white', annot=True);
```
#IMÓVEIS
Agora iremos analisar qual o tipo de imovel mais alugado
```
#conta variaveis categoricas
df_clean.room_type.value_counts()
#porcentagem
df_clean.room_type.value_counts()/df_clean.shape[0]
```
Região mais cara:
```
df_clean.groupby(['neighbourhood']).price.mean().sort_values(ascending=False)[:10]
df_clean.plot(kind="scatter", x='longitude', y='latitude', alpha=0.4, c=df_clean['price'], s=8,
cmap=plt.get_cmap('jet'), figsize=(12,8));
```
#CONCLUSÃO
Em análise aos dados disponibilizados no site do AIRBNB, foi possível observar os outliers e colunas vazias, o que acarretou em uma necessidade de tratamento dos dados.
Os imóveis que mais tendem a ser alugados no AirBnb são apartamentos, correspondendo a 72% dos dados, um número bastante expressivo, o que seria mais vantajoso para um negócio disponibilizar apartamentos na plataforma.
O Bairro mais caro para se alugar é Copacabana, tendo uma média de aluguel de R$ 2.400,00.
```
```
|
github_jupyter
|
# importar os pacotes necessarios
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
%matplotlib inline
# importar o arquivo listings.csv para um DataFrame
df = pd.read_csv("http://data.insideairbnb.com/brazil/rj/rio-de-janeiro/2021-07-17/data/listings.csv.gz")
df.head()
# identificar o volume de dados do DataFrame
print(f'Entradas: {df.shape[0]}\nVariáveis:{df.shape[1]}')
# verificar as 5 primeiras entradas do dataset
display(df.dtypes)
# Verificar valores ausentes e a porcentagem de quais
# colunas possuem mais dados faltantes
valorAusente = df.isna().mean().sort_values(ascending=False)
valorAusente[0:30]
df.hist(bins=15, figsize=(30,20));
sns.set()
#função para limpeza de caracter na coluna, retirando o $
def removeSymbol(value):
value = value.replace('$', ' ').strip()
value = value.replace(',', '')
return value
#aplicando a função
df['price']= df['price'].apply(removeSymbol)
#mudando a entrada do dado para tipo float
df['price'] = df['price'].astype('float')
df[["price", "minimum_nights", "number_of_reviews", 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']].describe()
df['price'].mean()
df.minimum_nights.plot(kind='box', vert=False, figsize=(15,3))
plt.show();
# ver quantidade de valores acima de 30 dias para minimum_nights
print("minimum_nights: valores acima de 30:")
print(f'Entradas: {len(df[df.minimum_nights > 30])}')
print(f'{(len(df[df.minimum_nights > 30 ])/df.shape[0])*100:.4f}%')
# remover os *outliers* em um novo DataFrame
df_clean = df.copy()
df_clean.drop(df_clean[df_clean.price > 5000].index, axis=0, inplace=True)
df_clean.drop(df_clean[df_clean.minimum_nights > 30].index, axis=0, inplace=True)
# remover variaveis vazias
df_clean.drop('license', axis=1, inplace=True)
df_clean.drop('scrape_id', axis=1, inplace=True)
df_clean.drop('bathrooms', axis=1, inplace=True)
df_clean.drop('calendar_updated', axis=1, inplace=True)
df_clean.drop('neighbourhood_group_cleansed', axis=1, inplace=True)
#plotar novamente o histograma
df_clean.hist(bins=15, figsize=(40,30))
sns.set()
# plot da matriz de correlação
correlation = df_clean[["price", "minimum_nights", "number_of_reviews", 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']].corr()
display(correlation)
sns.heatmap(correlation, cmap='RdBu', fmt='.2f', square=True, linecolor='white', annot=True);
#conta variaveis categoricas
df_clean.room_type.value_counts()
#porcentagem
df_clean.room_type.value_counts()/df_clean.shape[0]
df_clean.groupby(['neighbourhood']).price.mean().sort_values(ascending=False)[:10]
df_clean.plot(kind="scatter", x='longitude', y='latitude', alpha=0.4, c=df_clean['price'], s=8,
cmap=plt.get_cmap('jet'), figsize=(12,8));
| 0.249905 | 0.95222 |
# Project: Medical No Show Appointments Data Analysis
## Table of Contents
<ul>
<li><a href="#intro">Introduction</a></li>
<li><a href="#wrangling">Data Wrangling</a></li>
<li><a href="#eda">Exploratory Data Analysis</a>
<ul>
<li><a href="#dataOverview">Data Overview</a></li>
<li><a href="#researchQuestion1">Research Question 1: Does the number of SMS received by the patient affects the show-up probability?</a></li>
<li><a href="#researchQuestion2">Research Question 2: Does the day of week affect patient no-show rate?</a></li>
<li><a href="#researchQuestion3">Research Question 3: Does the gap between scheduled date and appointment date affect patient no-show rate?</a></li>
</ul>
</li>
<li><a href="#conclusions">Conclusions</a></li>
</ul>
```
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import re
%matplotlib inline
```
<a id='intro'></a>
## Introduction
In this dataset, I will analyze the Medical Appointment No Show dataset from Kaggle ([link to dataset](https://www.kaggle.com/joniarroba/noshowappointments)).
My analysis will answer the following questions:
- Does the number of SMS received by the patient affects the show-up probability?
- Does the day of week affect patient no-show rate?
- Does the gap between scheduled date and appointment date affect patient no-show rate?
<a id='wrangling'></a>
## Data Wrangling
### Loading Data
Below I will load the data and show the first rows of the data and the information about each columns of the data.
```
filename = 'data/noshowappointments-kagglev2-may-2016.csv'
df = pd.read_csv(filename)
```
### Fixing Column Names
First let's see the column names:
```
df.columns
```
Firstly we can look at the column names. As you can see, they are in camel case, and one of the column has "-" instead of "\_". So first I'll fix the column names to be python friendly by:
- converting "-" to be "_"
- converting the column names to snake case and lower case using regex
```
# correct the column names to be snake case
df.rename(columns=lambda x: x.replace('-', '_'), inplace=True)
df.rename(columns=lambda x: re.sub(r'(?<!^)(?=[A-Z])', '_', x).lower(), inplace=True)
```
Now let's see the column names:
```
df.columns
```
As you can see above, some camel case column names are converted wrongly like the "ID" becomes "i_d" and "SMS" becomes "s_m_s". So I'll fix them to be "id" and "sms" below.
```
df.rename(columns=lambda x: x.replace('s_m_s', 'sms'), inplace=True)
df.rename(columns=lambda x: x.replace('i_d', 'id'), inplace=True)
```
Now the column names have been fixed to be:
```
df.columns
```
Lastly if you notice, one of the column names is `handcap`, which I believe is a typo. I'll correct the name to be `handicap`.
```
df.rename(columns={'handcap': 'handicap'}, inplace=True)
df.columns
```
### Fixing Column Data Types
Now we'll move on to fixing the column types of the data. Below I'll show the data types of each column.
```
df.head()
df.info()
```
As you can see in the info above, there are some interesting aspects to be fixed, summarized in below points:
- `patient_id` and `appointment_id` are both of float and integer types. However, they are actually just for identification, and the quantity of the numbers have no actual significance (one ID is not "higher" than the other ID). So in this case I'll convert those columns to be string instead.
- `scheduled_day` and `appointment_day` are all in string type, while actually they are datetime. So I'll convert those columns into datetime.
- For `scholarship`, `hipertension`, `diabetes`, and `alcoholism`, the description of the dataset ([link to dataset](https://www.kaggle.com/joniarroba/noshowappointments)) explains that those columns are of boolean type. So I'll convert them to be boolean.
- As for `handicap` and `sms_received`, they're rather special and will be processed in the next cells. In summary, I'll swap both values of the columns and convert the column `handicap` to be boolean, while the column `sms_received` stays as integer.
- `no_show` column will be converted into boolean as well, and will be converted into `show_up` column (where the original values will be converted), as this new column will be more intuitive.
#### Converting `patient_id` and `appointment_id`
First to be safe, let's check for duplicate values of these columns
```
print(f' Number of duplicated patient_id: {sum(df.patient_id.duplicated())}')
print(f' Number of duplicated appointment_id: {sum(df.appointment_id.duplicated())}')
```
Duplicated `patient_id` is expected because one patient can have multiple appointments.
There is no duplicated `appointment_id`, which is good and as expected, because each appointment must have unique ID.
Now we'll move on to convert those columns to be string:
```
# casting to int64 is needed so that the resulting string does not contain the decimal points
df.patient_id = df.patient_id.astype('int64').astype(str)
df.appointment_id = df.appointment_id.astype(str)
df.head()[['patient_id', 'appointment_id']]
df[['patient_id', 'appointment_id']].info()
```
The info above now confirms that the `patient_id` and `appointment_id` are now of string type.
#### Converting `scheduled_day` and `appointment_day`
First let's check whether their values are of correct datetime format.
```
df[['scheduled_day', 'appointment_day']].head()
```
The format looks good. I'll then proceed to convert them into datetime:
```
df.scheduled_day = pd.to_datetime(df.scheduled_day, infer_datetime_format=True)
df.appointment_day = pd.to_datetime(df.appointment_day, infer_datetime_format=True)
df[['scheduled_day', 'appointment_day']].head()
df[['scheduled_day', 'appointment_day']].info()
```
An interesting finding from the conversion result is on `appointment_day`. It seems that the values of the column are all having time 00:00:00. This makes sense, because the column's purpose is to show the day of the appointment, and not the time. Nonetheless, the info above confirms that now the columns are of datetime type.
#### Converting `scholarship`, `hipertension`, `diabetes`, and `alcoholism`
To be safe, first I'll check the columns' unique values.
```
print(f'"scholarship" unique values: {df.scholarship.unique()}')
print(f'"hipertension" unique values: {df.hipertension.unique()}')
print(f'"diabetes" unique values: {df.diabetes.unique()}')
print(f'"alcoholism" unique values: {df.alcoholism.unique()}')
```
As you can see above, all of them are only of values 1's and 0's, so they are safe to be converted into boolean. What I mean by safe is: safe to be converted into boolean without altering the meaning of the columns. This point is crucial when we're dealing with the `handicap` and `sms_received` columns in the next section. I'll then convert them into boolean below.
```
df.scholarship = df.scholarship.astype(bool)
df.hipertension = df.hipertension.astype(bool)
df.diabetes = df.diabetes.astype(bool)
df.alcoholism = df.alcoholism.astype(bool)
df[['scholarship', 'hipertension', 'diabetes', 'alcoholism']].head()
df[['scholarship', 'hipertension', 'diabetes', 'alcoholism']].info()
```
The info above confirms that those columns are now of type boolean.
#### Processing `handicap` and `sms_received`
I assumed that `handicap` and `sms_received` columns were swapped by each other. Below I'll show you the reason why. First let's see the unique values of both columns.
```
print(f'"handicap" unique values: {df.handicap.unique()}')
print(f'"sms_received" unique values: {df.sms_received.unique()}')
```
As you can see above, `handicap` values consists of integers from 0 to 4, whereas values of `sms_received` is only 1 or 0. However, in the dataset description, it says that `handicap` is boolean value of whether the patient is handicapped or not, whereas `sms_received` is the number of messages received by the patient. The actual values, however, shows that the nature of `handicap` suits better for integer, whereas `sms_received` suits better for boolean, which is not what is expected from the dataset description. In this case, since those columns are next to each other, I believe that they're swapped by the creator of the dataset.
Based on the observation above, I'll then swap their values by simply renaming the columns.
```
df.rename(columns={'handicap': 'sms_received', 'sms_received': 'handicap'}, inplace=True)
print(f'"handicap" unique values: {df.handicap.unique()}')
print(f'"sms_received" unique values: {df.sms_received.unique()}')
```
The above print shows that now they are properly swapped. I'll then convert the `handicap` column to be boolean.
```
df.handicap = df.handicap.astype(bool)
df[['handicap', 'sms_received']].info()
```
The info above now shows that `handicap` is correctly typed as boolean, and `sms_received` stays as integer.
#### Converting `no_show` into `show_up`
Firstly I'll convert the `no_show` column into boolean, then I'll convert the column to be a `show_up` column (with all the original boolean values inverted) to have a column that says whether the patient shows up for the appointment or not. I believe this new `show_up` column is more intuitive.
To be safe, I'll first ensure that the unique values of `no_show` is safe to be converted into boolean.
```
print(f'"no_show" unique values: {df.no_show.unique()}')
```
Now we can see that `no_show` only consists of values 'Yes' or 'No', so it is safe to convert the column into boolean.
```
df.no_show = df.no_show.apply(lambda x: x == 'Yes')
print(f'"no_show" unique values: {df.no_show.unique()}')
df.no_show.dtype
```
The above prints show that now the `no_show` column are correctly of type boolean. I'll then now proceed to convert this column into `show_up` column, where I'll invert the original boolean values.
```
df['show_up'] = ~df.no_show
df[['no_show', 'show_up']].head()
```
As you can see above, the value of the `show_up` is correctly calculated from the `no_show` column. I'll now drop the `no_show` column as it is no longer useful.
```
df.drop(columns='no_show', inplace=True)
df.columns
```
The above print confirms that the column `no_show` has been removed.
#### Remaining columns...
For the remaining columns which are `gender`, `age`, and `neighbourhood`, their data types already matches their purpose, so they're good to go.
#### Column Data Types Conclusion
This concludes the column data types processing. Below I'll show the final state of the column data types, and their values.
```
df.head()
df.info()
```
### Fixing Column Values
In this section, I'll explore and fix the values of the columns.
#### Fixing `age` values
Firstly let's analyze the numeric columns.
```
df.describe()
```
`sms_received` seems to be good, but `age` column seems to be problematic. The column seems to have minimum value of -1, which does not makes sense. Now let's see the distribution of the value of `age` below.
```
df.age.hist(bins=50)
plt.title('Histogram of Age')
plt.xlabel('Age')
plt.ylabel('Count');
```
There seems to be smooth distribution of the values near 0, so kind of makes sense to have very low values for `age` (for babies for example). This opens the possibility that the -1 age might be fixed to become age of 0. So now let's count how many data there is that have age lower than 0.
```
print(f'Number of rows with negative valued age: {sum(df.age < 0)}')
```
There is only one row that has negative `age`, which means this is indeed a noise. To be safe and to avoid any wrong assumption, I'll just drop this single row with negative age.
```
df.drop(df[df.age < 0].index, inplace=True)
```
Now let's see the new distribution of `age`:
```
df.age.describe()
```
The print shows that we're good to go for `age`. As for the max value of 115, it is indeed possible for a human to be aged 115 years, because the oldest human in the world now is 122 years!
#### Confirming validity of `gender`
Firstly, let's check the `gender` unique values.
```
print(f'"gender" unique values: {df.gender.unique()}')
```
The `gender` column has only the unique values shown above, which is valid and has no surprises.
#### Confirming validity of `neighbourhood`
As for `neighbourhood`, let's see the unique values as well. Also, we'll sort the values to check for possible typo (any typo will have more or less similar value, so sorting might help).
```
neighbourhood_values = df.neighbourhood.unique()
neighbourhood_values.sort()
print('\n'.join(neighbourhood_values))
```
There seems to be no obvious typo from the values of the `neighbourhood`. One last check is to see the value with the minimum count, which might show typo as well.
```
df.neighbourhood.value_counts().idxmin()
```
As you can see, the value with minimum count seems to be a valid value, showing that no typo occurs in this column. Hence, this column is good to go.
#### `patient_id` and `appointment_id`
A simple duplicated value check will be done for these columns.
```
print(f'Number of duplicated patient_id: {sum(df.patient_id.duplicated())}')
print(f'Number of duplicated appointment_id: {sum(df.appointment_id.duplicated())}')
```
There is no duplicate values for `appointment_id` which is good and expected. Duplicated values for `patient_id` is expected because one patient can have many appointments.
#### `scheduled_day` and `appointment_day`
It'll be interesting to see any data that has `scheduled_day` being later than the `appointment_day`, which will be invalid. But note that we'll check only for the date, and will not care about the time, because the `appointment_day` does not have time information.
```
scheduled_later = df.scheduled_day.dt.date > df.appointment_day.dt.date
print(f'Number of rows that has scheduled_day date > appointment_day: {sum(scheduled_later)}')
df[scheduled_later]
```
Since they're not a lot (only 5 rows), to avoid any wrong assumption, we'll just drop the rows with this invalid `scheduled_day` and `appointment_day` pairs.
```
df.drop(df[scheduled_later].index, inplace=True)
scheduled_later = df.scheduled_day.dt.date > df.appointment_day
print(f'Number of rows that has scheduled_day date > appointment_day: {sum(scheduled_later)}')
```
Now let's see the min and max values of these columns.
```
print(f'Min value for "scheduled_day": {df.scheduled_day.min()}')
print(f'Max value for "scheduled_day": {df.scheduled_day.max()}')
print(f'Min value for "appointment_day": {df.appointment_day.min()}')
print(f'Max value for "appointment_day": {df.appointment_day.max()}')
```
It is indeed weird for the `scheduled_day` to have minimum value much earlier than the minimum value of `appointment_day`. Let's see the rows having `scheduled_day` earlier than the year 2016.
```
earlier_than_2016 = df.scheduled_day.dt.year < 2016
print(f'Number of rows earlier than 2016: {sum(earlier_than_2016)}')
df[earlier_than_2016].head()
```
There's a lot of rows whose `scheduled_day` is before 2016, so they are not noise. Also looking at the data, there seems to be nothing wrong with them, so we'll keep those rows.
#### Checking for null values
```
df.isna().sum()
```
It is confirmed that the column has no null values.
### Data Wrangling Checkpoint
For now we'll save the cleaned data.
```
df.to_csv('data/medical_appointment_no_show_cleaned.csv', index=False)
```
<a id='eda'></a>
## Exploratory Data Analysis
<a id='dataOverview'></a>
### Data Overview
Firstly we'll load the checkpoint data, and reprint the data here so that we can see the data easily without scrolling up.
```
df = pd.read_csv('data/medical_appointment_no_show_cleaned.csv',
dtype={'patient_id': 'str', 'appointment_id': 'str'},
parse_dates=['scheduled_day', 'appointment_day'],
infer_datetime_format=True)
df.info()
df
```
<a id='researchQuestion1'></a>
### Research Question 1: Does the number of SMS received by the patient affects the show-up probability?
Firstly we'll plot the bar chart to show the proportion of patients that show up for the appointment given the number of SMS received by the patient.
```
count = df.groupby('sms_received').show_up.value_counts()
total = df.groupby('sms_received').show_up.count()
proportion = count / total
proportion[:, True].plot(kind='bar', ylabel='Proportion of Show-Up',
xlabel='Number of SMS Received',
title='Proportion of Show-Up by Number of SMS Received',
ylim=(0.6, 0.835));
plt.xticks(rotation=0);
```
Looking at the above graph, we are tempted to say that increasing the number of SMS will reduce the likelihood of a patient showing up for the appointment. However, let's see the number of data points for each number of SMS received below.
```
count.sum(level='sms_received')
```
As you can see above, there are only 13 data points for 3 SMS received, and only 3 data points for 4 SMS received. This means that their proportion count may not be accurate enough, we cannot say any conclusion about them with high confidence. Thus, for this analysis, we'll only see that data whose number of data points is greater than 100, which in this case will be the data for SMS received being 0 to 2. Below we'll replot the bar chart.
```
proportion.loc[0:2, True].plot(kind='bar', ylabel='Proportion of Show-Up',
xlabel='Number of SMS Received',
title='Proportion of Show-Up by Number of SMS Received',
ylim=(0.75, 0.835),
xticks=[0, 1, 2]);
plt.xticks(rotation=0);
```
Below is to show the exact proportions for the analysis in the next paragraph.
```
proportion.loc[0:2, True]
```
As you can see in the graph above, we can see that the SMS sent to patient can increase the likelihood of the patient to show up for the appointment only up to 1 SMS. More than that, the effectivity of the SMS reduces. 1 SMS increases the likelihood of patient showing up by 2% (from 79.8% with 0 SMS to 82.2% with 1 SMS). However, when the SMS sent is 2, it doesn't increase the likelihood of the patient showing up (from 79.8% with 0 SMS to 79.8% with 2 SMS).
A possible explanation of this can be that 1 SMS can manage to remind any patient that forgot about their appointment. However, more than 1 SMS, for example 2 SMS in our analysis above, will no longer server to remind patients that forgot about their appointment. 1 SMS is already enough to remind them, and the second SMS is no longer useful. If after 1 SMS the patient still did not show up for the appointment, this means that they actually still remember about the appointment (maybe reminded after the first SMS), but they have decided to not go for the appointment. That is why increasing the number of SMS to the patient does not increase likelihood of the patient to show up for the appointment, because they no longer forget about it, but rather they have decided to not go for the appointment, which in this case more SMS will no longer serve its purpose to remind the patient about the appointment.
From another perspective, if the patient was sent more than 1 SMS, this means the patient did not respond to the first SMS, which either is because: the patient no longer interested in the appointment, or the patient is unable to receive the SMS at all. For both of the reasons mentioned, any more SMS will not be effective anymore in making the patient to show up for the appointment.
<a id='researchQuestion2'></a>
### Research Question 2: Does the day of week affect patient no-show rate?
Below we'll add a new column `weekday` to show the week day name of the appointment date.
```
df['appointment_weekday'] = df.appointment_day.dt.weekday
df[['appointment_day', 'appointment_weekday']].head()
```
Below we'll calculate the proportion of "no-show" for each weekday, e.g. no-show proportion on Mondays, Tuesdays, etc.
```
show_up_appt_day = df.groupby('appointment_weekday').show_up.value_counts()
show_up_appt_day_total = df.groupby('appointment_weekday').show_up.count()
show_up_appt_day_prop = show_up_appt_day / show_up_appt_day_total
show_up_appt_day_prop.loc[:, False].plot(kind='bar', title='No-Show Rate by Day')
labels = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat']
plt.xticks(ticks=range(6), labels=labels, rotation=0);
plt.ylim(0.15, 0.24);
plt.ylabel('Proportion of No Show-Up');
plt.xlabel('Day');
```
It can be seen above that Saturday has the highest proportion of having no-show, whereas Friday comes as the second highest. We can also see the trend where, in general, the no-show rate decreases from Monday to Thursday, then starts increasing again from Friday to Saturday. There is no record on Sunday, probably due to the hospital having holiday every Sunday.
This phenomenon is not that surprising, as on Mondays people are usually busier to catch up on their work. As they go into the midweek, they'd have settled their business and thus are more free to show up for the hospital appointments. Then there is an increase of no-show on Friday and Saturday, probably due to last minute weekend plans.
<a id='researchQuestion3'></a>
### Research Question 3: Does the gap between scheduled date and appointment date affect patient no-show rate?
Below we'll create a new column `schedule_gap_days` which will have the number of days gap between the scheduled day and the appointment day. If the appointment is on the same day as the scheduled day, then the gap will be 0. The column will be of integer values for the count of days.
```
df['schedule_gap_days'] = (df.appointment_day.dt.date - df.scheduled_day.dt.date).dt.days
df[['scheduled_day', 'appointment_day', 'schedule_gap_days']].tail()
```
To be able to analyze the proportions of no-show based on the schedule gap, we'll first categorize the schedule gap based on the 5-number summary statistics of the schedule gap days. Below we'll print the statistics of `schedule_gap_days`.
```
df.schedule_gap_days.describe()
```
Since the `min` and the `25%` quantile are both zero, we'll then make our lowest category to be `no_gap`. For the rest, we'll categorize the schedule gap as either `short`, `medium`, or `long` gap. The categorizations will then be as follows:
- `no_gap`: 0 days gap
- `short`: 1 to 4 days gap
- `medium`: 5 to 15 days gap
- `long` : 16 to 179 days gap
Below code will then do the categorization of `schedule_gap_days` and then put the values in the new column `schedule_gap_category`.
```
bins = df.schedule_gap_days.describe()[['min', '25%', '50%', '75%', 'max']].values
bins[1] = 0.1 # because the 25% quantile is also 0.0 days, so need to set to small number so that the cut can work
df['schedule_gap_category'] = pd.cut(df.schedule_gap_days, bins=bins, labels=['no_gap', 'short', 'medium', 'long'], right=False)
```
Below we'll calculate and plot the no-show proportion for each schedule gap category.
```
count = df.groupby('schedule_gap_category').show_up.value_counts()
total = df.groupby('schedule_gap_category').show_up.count()
schedule_gap_showup_prop = count / total
schedule_gap_showup_prop[:, False].plot(kind='bar')
plt.title('No-Show Proportion against Schedule-Appointment Gap')
plt.xlabel('Schedule-Appointment Gap')
plt.ylabel('No-Show Proportion')
plt.xticks(rotation=0);
```
As you can see above, the longer the gap between the day the appointment is made (`scheduled_day`) and the actual appointment day (`appointment_day`), the no-show proportion is higher. Even a short gap increases the no-show rate pretty significantly compared to the no-show rate for zero days gap. This probably is due to, after some period of time from the scheduled day, the patient might have changed their mind and decided that the appointment is no longer needed. If the appointment is made for the next day, it might be for something urgent, and hence it is very unlikely that the patient will not show up for the appointment.
<a id='conclusions'></a>
## Conclusions
In summary, here are the findings of this data analysis:
- SMS reminders seem to be only effective at reducing the rate of patient no-show up to 1 SMS. More than 1 SMS, the effect of it on the patient no-show starts to diminish.
- Against day of week, patient no-show rate seems to be decreasing from Monday to Thursday, then starts increasing again from Friday to Saturday, with the highest on Saturday.
- Comparing against the gap between the date when the appointment is made and the actual appointment date, it is found that the longer the gap, the more patient no-show occurs. Even a short gap increases the rate of patient no-show significantly compared to zero days gap.
Do note that this data analysis has limitation where there is no statistical test done, and this is purely just data analysis.
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import re
%matplotlib inline
filename = 'data/noshowappointments-kagglev2-may-2016.csv'
df = pd.read_csv(filename)
df.columns
# correct the column names to be snake case
df.rename(columns=lambda x: x.replace('-', '_'), inplace=True)
df.rename(columns=lambda x: re.sub(r'(?<!^)(?=[A-Z])', '_', x).lower(), inplace=True)
df.columns
df.rename(columns=lambda x: x.replace('s_m_s', 'sms'), inplace=True)
df.rename(columns=lambda x: x.replace('i_d', 'id'), inplace=True)
df.columns
df.rename(columns={'handcap': 'handicap'}, inplace=True)
df.columns
df.head()
df.info()
print(f' Number of duplicated patient_id: {sum(df.patient_id.duplicated())}')
print(f' Number of duplicated appointment_id: {sum(df.appointment_id.duplicated())}')
# casting to int64 is needed so that the resulting string does not contain the decimal points
df.patient_id = df.patient_id.astype('int64').astype(str)
df.appointment_id = df.appointment_id.astype(str)
df.head()[['patient_id', 'appointment_id']]
df[['patient_id', 'appointment_id']].info()
df[['scheduled_day', 'appointment_day']].head()
df.scheduled_day = pd.to_datetime(df.scheduled_day, infer_datetime_format=True)
df.appointment_day = pd.to_datetime(df.appointment_day, infer_datetime_format=True)
df[['scheduled_day', 'appointment_day']].head()
df[['scheduled_day', 'appointment_day']].info()
print(f'"scholarship" unique values: {df.scholarship.unique()}')
print(f'"hipertension" unique values: {df.hipertension.unique()}')
print(f'"diabetes" unique values: {df.diabetes.unique()}')
print(f'"alcoholism" unique values: {df.alcoholism.unique()}')
df.scholarship = df.scholarship.astype(bool)
df.hipertension = df.hipertension.astype(bool)
df.diabetes = df.diabetes.astype(bool)
df.alcoholism = df.alcoholism.astype(bool)
df[['scholarship', 'hipertension', 'diabetes', 'alcoholism']].head()
df[['scholarship', 'hipertension', 'diabetes', 'alcoholism']].info()
print(f'"handicap" unique values: {df.handicap.unique()}')
print(f'"sms_received" unique values: {df.sms_received.unique()}')
df.rename(columns={'handicap': 'sms_received', 'sms_received': 'handicap'}, inplace=True)
print(f'"handicap" unique values: {df.handicap.unique()}')
print(f'"sms_received" unique values: {df.sms_received.unique()}')
df.handicap = df.handicap.astype(bool)
df[['handicap', 'sms_received']].info()
print(f'"no_show" unique values: {df.no_show.unique()}')
df.no_show = df.no_show.apply(lambda x: x == 'Yes')
print(f'"no_show" unique values: {df.no_show.unique()}')
df.no_show.dtype
df['show_up'] = ~df.no_show
df[['no_show', 'show_up']].head()
df.drop(columns='no_show', inplace=True)
df.columns
df.head()
df.info()
df.describe()
df.age.hist(bins=50)
plt.title('Histogram of Age')
plt.xlabel('Age')
plt.ylabel('Count');
print(f'Number of rows with negative valued age: {sum(df.age < 0)}')
df.drop(df[df.age < 0].index, inplace=True)
df.age.describe()
print(f'"gender" unique values: {df.gender.unique()}')
neighbourhood_values = df.neighbourhood.unique()
neighbourhood_values.sort()
print('\n'.join(neighbourhood_values))
df.neighbourhood.value_counts().idxmin()
print(f'Number of duplicated patient_id: {sum(df.patient_id.duplicated())}')
print(f'Number of duplicated appointment_id: {sum(df.appointment_id.duplicated())}')
scheduled_later = df.scheduled_day.dt.date > df.appointment_day.dt.date
print(f'Number of rows that has scheduled_day date > appointment_day: {sum(scheduled_later)}')
df[scheduled_later]
df.drop(df[scheduled_later].index, inplace=True)
scheduled_later = df.scheduled_day.dt.date > df.appointment_day
print(f'Number of rows that has scheduled_day date > appointment_day: {sum(scheduled_later)}')
print(f'Min value for "scheduled_day": {df.scheduled_day.min()}')
print(f'Max value for "scheduled_day": {df.scheduled_day.max()}')
print(f'Min value for "appointment_day": {df.appointment_day.min()}')
print(f'Max value for "appointment_day": {df.appointment_day.max()}')
earlier_than_2016 = df.scheduled_day.dt.year < 2016
print(f'Number of rows earlier than 2016: {sum(earlier_than_2016)}')
df[earlier_than_2016].head()
df.isna().sum()
df.to_csv('data/medical_appointment_no_show_cleaned.csv', index=False)
df = pd.read_csv('data/medical_appointment_no_show_cleaned.csv',
dtype={'patient_id': 'str', 'appointment_id': 'str'},
parse_dates=['scheduled_day', 'appointment_day'],
infer_datetime_format=True)
df.info()
df
count = df.groupby('sms_received').show_up.value_counts()
total = df.groupby('sms_received').show_up.count()
proportion = count / total
proportion[:, True].plot(kind='bar', ylabel='Proportion of Show-Up',
xlabel='Number of SMS Received',
title='Proportion of Show-Up by Number of SMS Received',
ylim=(0.6, 0.835));
plt.xticks(rotation=0);
count.sum(level='sms_received')
proportion.loc[0:2, True].plot(kind='bar', ylabel='Proportion of Show-Up',
xlabel='Number of SMS Received',
title='Proportion of Show-Up by Number of SMS Received',
ylim=(0.75, 0.835),
xticks=[0, 1, 2]);
plt.xticks(rotation=0);
proportion.loc[0:2, True]
df['appointment_weekday'] = df.appointment_day.dt.weekday
df[['appointment_day', 'appointment_weekday']].head()
show_up_appt_day = df.groupby('appointment_weekday').show_up.value_counts()
show_up_appt_day_total = df.groupby('appointment_weekday').show_up.count()
show_up_appt_day_prop = show_up_appt_day / show_up_appt_day_total
show_up_appt_day_prop.loc[:, False].plot(kind='bar', title='No-Show Rate by Day')
labels = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat']
plt.xticks(ticks=range(6), labels=labels, rotation=0);
plt.ylim(0.15, 0.24);
plt.ylabel('Proportion of No Show-Up');
plt.xlabel('Day');
df['schedule_gap_days'] = (df.appointment_day.dt.date - df.scheduled_day.dt.date).dt.days
df[['scheduled_day', 'appointment_day', 'schedule_gap_days']].tail()
df.schedule_gap_days.describe()
bins = df.schedule_gap_days.describe()[['min', '25%', '50%', '75%', 'max']].values
bins[1] = 0.1 # because the 25% quantile is also 0.0 days, so need to set to small number so that the cut can work
df['schedule_gap_category'] = pd.cut(df.schedule_gap_days, bins=bins, labels=['no_gap', 'short', 'medium', 'long'], right=False)
count = df.groupby('schedule_gap_category').show_up.value_counts()
total = df.groupby('schedule_gap_category').show_up.count()
schedule_gap_showup_prop = count / total
schedule_gap_showup_prop[:, False].plot(kind='bar')
plt.title('No-Show Proportion against Schedule-Appointment Gap')
plt.xlabel('Schedule-Appointment Gap')
plt.ylabel('No-Show Proportion')
plt.xticks(rotation=0);
| 0.400515 | 0.980337 |
```
# 必要なパッケージのインストール
!pip install torch torchvision
!pip install tqdm
# Google Driveとのデータのやり取り
from google.colab import drive
drive_dir = '/content/drive'
drive.mount(drive_dir)
from google.colab import drive
drive.mount('/content/drive')
# パッケージのインストール
import os
import sys
import time
import datetime
import struct
import cv2
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data
import torchvision
from torch.utils.tensorboard import SummaryWriter
# よく使うファイル・ディレクトリ
colab_dir = os.path.join(drive_dir, 'My Drive', 'Colab Notebooks')
model_path = 'DCGAN_flower.pth'
# データセットの読み取り
class OxfordFlowerDataset(torch.utils.data.Dataset):
def __init__(self, root_dir, resize=128):
super(OxfordFlowerDataset, self).__init__()
self.root_dir = root_dir
self.resize = resize
self.image_list = [f for f in os.listdir(self.root_dir) if not f.startswith('.jpg')]
self.image_list = [os.path.join(self.root_dir, f) for f in self.image_list]
def __len__(self):
return len(self.image_list)
def __getitem__(self, idx):
# 画像の読み込み
image_file = self.image_list[idx]
image = cv2.imread(image_file, cv2.IMREAD_COLOR)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
# 画像のクロップ
h, w, _ = image.shape
size = min(h, w)
cx, cy = w // 2, h // 2
sx = max(0, cx - size // 2)
sy = max(0, cy - size // 2)
image = image[sy:sy+size, sx:sx+size, :]
image = cv2.resize(image, (self.resize, self.resize))
image = (image / 255.0).astype('float32')
image = np.transpose(image, axes=(2, 0, 1))
return {
'images': image
}
# 基本処理
class BlockG(nn.Module):
""" Basic convolution block for generator (Conv, BN, ReLU) """
def __init__(self, in_channels, out_channels):
super(BlockG, self).__init__()
self.net = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=1, padding=1),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=False)
)
def forward(self, x):
return self.net(x)
class BlockD(nn.Module):
""" Basic convolution block for discriminator (Conv, LeakyReLU) """
def __init__(self, in_channels, out_channels):
super(BlockD, self).__init__()
self.net = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=1, padding=1),
nn.LeakyReLU(0.1)
)
def forward(self, x):
return self.net(x)
class Up(nn.Module):
""" Up-sampling """
def __init__(self, in_channels, out_channels):
super(Up, self).__init__()
self.net = nn.Sequential(
nn.ConvTranspose2d(in_channels, out_channels, kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=False)
)
def forward(self, x):
return self.net(x)
class Down(nn.Module):
""" Down-sampling """
def __init__(self, in_channels, out_channels):
super(Down, self).__init__()
self.net = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=4, stride=2, padding=1),
nn.LeakyReLU(0.1)
)
def forward(self, x):
return self.net(x)
# Generatorの定義
class NetG(nn.Module):
def __init__(self, in_features=128, out_channels=3, base_filters=8):
super(NetG, self).__init__()
self.in_features = in_features
self.out_channels = out_channels
self.base_filters = base_filters
self.net = nn.Sequential(
nn.ConvTranspose2d(self.in_features, self.base_filters * 16,
kernel_size=4, stride=1, padding=0),
nn.BatchNorm2d(self.base_filters * 16),
nn.ReLU(inplace=True),
Up(self.base_filters * 16, self.base_filters * 16),
Up(self.base_filters * 16, self.base_filters * 8),
Up(self.base_filters * 8, self.base_filters * 4),
Up(self.base_filters * 4, self.base_filters * 2),
Up(self.base_filters * 2, self.base_filters * 1),
nn.Conv2d(base_filters * 1, self.out_channels,
kernel_size=3, stride=1, padding=1)
)
def forward(self, x):
n_batches, n_dims = x.size()
x = x.view(n_batches, n_dims, 1, 1)
x = self.net(x)
return torch.tanh(x)
# Discriminatorの定義
class NetD(nn.Module):
def __init__(self, in_channels=3, base_filters=8):
super(NetD, self).__init__()
self.in_channels = in_channels
self.base_filters = base_filters
self.net = nn.Sequential(
BlockD(self.in_channels, self.base_filters),
Down(self.base_filters, self.base_filters * 2),
Down(self.base_filters * 2, self.base_filters * 4),
Down(self.base_filters * 4, self.base_filters * 8),
Down(self.base_filters * 8, self.base_filters * 16),
Down(self.base_filters * 16, self.base_filters * 16),
nn.Conv2d(self.base_filters * 16, 1, kernel_size=4, stride=1, padding=0)
)
def forward(self, x):
x = self.net(x)
return x.squeeze() # BCELossWithLogitsを使うのでsigmoidに入れない
# 使用するデバイスの設定
if torch.cuda.is_available():
device = torch.device('cuda', 0)
else:
device = torch.device('cpu')
print('Device: {}'.format(device))
# 各種パラメータ
sample_dims = 32 # zの次元
base_lr = 2.0e-4 # 学習率
beta1 = 0.5 # Adamのbeta1
base_filters = 32 # CNNの基本チャンネル数
data_root = 'OxfordFlower' # データセットのディレクトリ
total_epochs = 20 # 総学習エポック数 (適宜増やす)
# ネットワークとoptimizerの定義
netD = NetD(in_channels=3, base_filters=base_filters)
netG = NetG(in_features=sample_dims, base_filters=base_filters)
netD.to(device)
netG.to(device)
optimD = torch.optim.Adam(netD.parameters(), lr=base_lr, betas=(beta1, 0.999))
optimG = torch.optim.Adam(netG.parameters(), lr=base_lr, betas=(beta1, 0.999))
criterion = nn.BCEWithLogitsLoss()
# モデルファイルの読み込み (続きから学習するときはresumeにフォルダ名を入れる)
resume = ''
start_epoch = 0
start_steps = 0
if resume != '':
# 保存済みモデルから読み込み
log_dir = os.path.join(colab_dir, 'runs', resume)
ckpt = torch.load(os.path.join(log_dir, model_path))
optimG.load_state_dict(ckpt['optimG'])
optimD.load_state_dict(ckpt['optimD'])
netG.load_state_dict(ckpt['netG'])
netD.load_state_dict(ckpt['netD'])
start_epoch = ckpt['epoch'] + 1
start_steps = ckpt['steps']
else:
# 学習の途中経過を保存するフォルダの作成
now = datetime.datetime.now()
time_stamp = now.strftime('%Y%m%d-%H%M%S')
runs_dir = os.path.join(colab_dir, 'runs')
log_dir = os.path.join(runs_dir, time_stamp)
os.makedirs(log_dir, exist_ok=True)
# データセットローダの準備
dataset = OxfordFlowerDataset(os.path.join(colab_dir, data_root), resize=128)
data_loader = torch.utils.data.DataLoader(dataset, batch_size=25, num_workers=4, shuffle=True, drop_last=True)
# 学習ループ
steps = start_steps
for epoch in range(start_epoch, 100):
tqdm_iter = tqdm(data_loader, file=sys.stdout)
for data in tqdm_iter:
x_real = data['images'].to(device)
x_real = 2.0 * x_real - 1.0
n_batches, _, _, _ = x_real.size()
netD.train()
netG.train()
# Discriminatorの学習
optimD.zero_grad()
z = torch.randn([n_batches, sample_dims], dtype=torch.float32, device=device)
x_fake = netG(z)
x_fake = x_fake.detach()
y_fake = netD(x_fake)
y_real = netD(x_real)
lossD = criterion(y_fake, torch.zeros_like(y_fake)) +\
criterion(y_real, torch.ones_like(y_real))
lossD.backward()
optimD.step()
# Generatorの学習
optimG.zero_grad()
z = torch.randn([n_batches, sample_dims], dtype=torch.float32, device=device)
x_fake = netG(z)
y_fake = netD(x_fake)
lossG = criterion(y_fake, torch.ones_like(y_fake))
lossG.backward()
optimG.step()
# ロスを標準出力する
tqdm_iter.set_description("epoch #{:d}, {:d} steps, lossD={:.4f}, lossG={:.4f}".format(epoch, steps, lossD.item(), lossG.item()))
# 途中経過の保存
if steps % 50 == 0:
outfile = os.path.join(log_dir, 'x_real_{:03d}.jpg'.format(epoch))
torchvision.utils.save_image(x_real * 0.5 + 0.5, outfile, nrow=5, padding=10)
outfile = os.path.join(log_dir, 'x_fake_{:03d}.jpg'.format(epoch))
torchvision.utils.save_image(x_fake * 0.5 + 0.5, outfile, nrow=5, padding=10)
steps += 1
# 学習途中のモデルを保存
ckpt = {
'optimG': optimG.state_dict(),
'optimD': optimD.state_dict(),
'netG': netG.state_dict(),
'netD': netD.state_dict(),
'epoch': epoch,
'steps': steps
}
torch.save(ckpt, os.path.join(log_dir, model_path))
# 10x10の画像を作る
rows = 10
cols = 10
netG.eval()
z = torch.randn([rows * cols, sample_dims], dtype=torch.float32, device=device)
x_fake = netG(z)
image_grid = torchvision.utils.make_grid(x_fake * 0.5 + 0.5, nrow=rows, padding=10)
image_grid = image_grid.detach().cpu().numpy()
image_grid = np.transpose(image_grid, axes=[1, 2, 0])
plt.figure(figsize=(15, 15))
plt.imshow(image_grid)
plt.show()
# 保存するときは以下をコメントアウト(適宜保存する名前は変更すること)
# cv2.imwrite('image_grid_10x10.png', image_grid)
```
|
github_jupyter
|
# 必要なパッケージのインストール
!pip install torch torchvision
!pip install tqdm
# Google Driveとのデータのやり取り
from google.colab import drive
drive_dir = '/content/drive'
drive.mount(drive_dir)
from google.colab import drive
drive.mount('/content/drive')
# パッケージのインストール
import os
import sys
import time
import datetime
import struct
import cv2
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data
import torchvision
from torch.utils.tensorboard import SummaryWriter
# よく使うファイル・ディレクトリ
colab_dir = os.path.join(drive_dir, 'My Drive', 'Colab Notebooks')
model_path = 'DCGAN_flower.pth'
# データセットの読み取り
class OxfordFlowerDataset(torch.utils.data.Dataset):
def __init__(self, root_dir, resize=128):
super(OxfordFlowerDataset, self).__init__()
self.root_dir = root_dir
self.resize = resize
self.image_list = [f for f in os.listdir(self.root_dir) if not f.startswith('.jpg')]
self.image_list = [os.path.join(self.root_dir, f) for f in self.image_list]
def __len__(self):
return len(self.image_list)
def __getitem__(self, idx):
# 画像の読み込み
image_file = self.image_list[idx]
image = cv2.imread(image_file, cv2.IMREAD_COLOR)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
# 画像のクロップ
h, w, _ = image.shape
size = min(h, w)
cx, cy = w // 2, h // 2
sx = max(0, cx - size // 2)
sy = max(0, cy - size // 2)
image = image[sy:sy+size, sx:sx+size, :]
image = cv2.resize(image, (self.resize, self.resize))
image = (image / 255.0).astype('float32')
image = np.transpose(image, axes=(2, 0, 1))
return {
'images': image
}
# 基本処理
class BlockG(nn.Module):
""" Basic convolution block for generator (Conv, BN, ReLU) """
def __init__(self, in_channels, out_channels):
super(BlockG, self).__init__()
self.net = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=1, padding=1),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=False)
)
def forward(self, x):
return self.net(x)
class BlockD(nn.Module):
""" Basic convolution block for discriminator (Conv, LeakyReLU) """
def __init__(self, in_channels, out_channels):
super(BlockD, self).__init__()
self.net = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=1, padding=1),
nn.LeakyReLU(0.1)
)
def forward(self, x):
return self.net(x)
class Up(nn.Module):
""" Up-sampling """
def __init__(self, in_channels, out_channels):
super(Up, self).__init__()
self.net = nn.Sequential(
nn.ConvTranspose2d(in_channels, out_channels, kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=False)
)
def forward(self, x):
return self.net(x)
class Down(nn.Module):
""" Down-sampling """
def __init__(self, in_channels, out_channels):
super(Down, self).__init__()
self.net = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=4, stride=2, padding=1),
nn.LeakyReLU(0.1)
)
def forward(self, x):
return self.net(x)
# Generatorの定義
class NetG(nn.Module):
def __init__(self, in_features=128, out_channels=3, base_filters=8):
super(NetG, self).__init__()
self.in_features = in_features
self.out_channels = out_channels
self.base_filters = base_filters
self.net = nn.Sequential(
nn.ConvTranspose2d(self.in_features, self.base_filters * 16,
kernel_size=4, stride=1, padding=0),
nn.BatchNorm2d(self.base_filters * 16),
nn.ReLU(inplace=True),
Up(self.base_filters * 16, self.base_filters * 16),
Up(self.base_filters * 16, self.base_filters * 8),
Up(self.base_filters * 8, self.base_filters * 4),
Up(self.base_filters * 4, self.base_filters * 2),
Up(self.base_filters * 2, self.base_filters * 1),
nn.Conv2d(base_filters * 1, self.out_channels,
kernel_size=3, stride=1, padding=1)
)
def forward(self, x):
n_batches, n_dims = x.size()
x = x.view(n_batches, n_dims, 1, 1)
x = self.net(x)
return torch.tanh(x)
# Discriminatorの定義
class NetD(nn.Module):
def __init__(self, in_channels=3, base_filters=8):
super(NetD, self).__init__()
self.in_channels = in_channels
self.base_filters = base_filters
self.net = nn.Sequential(
BlockD(self.in_channels, self.base_filters),
Down(self.base_filters, self.base_filters * 2),
Down(self.base_filters * 2, self.base_filters * 4),
Down(self.base_filters * 4, self.base_filters * 8),
Down(self.base_filters * 8, self.base_filters * 16),
Down(self.base_filters * 16, self.base_filters * 16),
nn.Conv2d(self.base_filters * 16, 1, kernel_size=4, stride=1, padding=0)
)
def forward(self, x):
x = self.net(x)
return x.squeeze() # BCELossWithLogitsを使うのでsigmoidに入れない
# 使用するデバイスの設定
if torch.cuda.is_available():
device = torch.device('cuda', 0)
else:
device = torch.device('cpu')
print('Device: {}'.format(device))
# 各種パラメータ
sample_dims = 32 # zの次元
base_lr = 2.0e-4 # 学習率
beta1 = 0.5 # Adamのbeta1
base_filters = 32 # CNNの基本チャンネル数
data_root = 'OxfordFlower' # データセットのディレクトリ
total_epochs = 20 # 総学習エポック数 (適宜増やす)
# ネットワークとoptimizerの定義
netD = NetD(in_channels=3, base_filters=base_filters)
netG = NetG(in_features=sample_dims, base_filters=base_filters)
netD.to(device)
netG.to(device)
optimD = torch.optim.Adam(netD.parameters(), lr=base_lr, betas=(beta1, 0.999))
optimG = torch.optim.Adam(netG.parameters(), lr=base_lr, betas=(beta1, 0.999))
criterion = nn.BCEWithLogitsLoss()
# モデルファイルの読み込み (続きから学習するときはresumeにフォルダ名を入れる)
resume = ''
start_epoch = 0
start_steps = 0
if resume != '':
# 保存済みモデルから読み込み
log_dir = os.path.join(colab_dir, 'runs', resume)
ckpt = torch.load(os.path.join(log_dir, model_path))
optimG.load_state_dict(ckpt['optimG'])
optimD.load_state_dict(ckpt['optimD'])
netG.load_state_dict(ckpt['netG'])
netD.load_state_dict(ckpt['netD'])
start_epoch = ckpt['epoch'] + 1
start_steps = ckpt['steps']
else:
# 学習の途中経過を保存するフォルダの作成
now = datetime.datetime.now()
time_stamp = now.strftime('%Y%m%d-%H%M%S')
runs_dir = os.path.join(colab_dir, 'runs')
log_dir = os.path.join(runs_dir, time_stamp)
os.makedirs(log_dir, exist_ok=True)
# データセットローダの準備
dataset = OxfordFlowerDataset(os.path.join(colab_dir, data_root), resize=128)
data_loader = torch.utils.data.DataLoader(dataset, batch_size=25, num_workers=4, shuffle=True, drop_last=True)
# 学習ループ
steps = start_steps
for epoch in range(start_epoch, 100):
tqdm_iter = tqdm(data_loader, file=sys.stdout)
for data in tqdm_iter:
x_real = data['images'].to(device)
x_real = 2.0 * x_real - 1.0
n_batches, _, _, _ = x_real.size()
netD.train()
netG.train()
# Discriminatorの学習
optimD.zero_grad()
z = torch.randn([n_batches, sample_dims], dtype=torch.float32, device=device)
x_fake = netG(z)
x_fake = x_fake.detach()
y_fake = netD(x_fake)
y_real = netD(x_real)
lossD = criterion(y_fake, torch.zeros_like(y_fake)) +\
criterion(y_real, torch.ones_like(y_real))
lossD.backward()
optimD.step()
# Generatorの学習
optimG.zero_grad()
z = torch.randn([n_batches, sample_dims], dtype=torch.float32, device=device)
x_fake = netG(z)
y_fake = netD(x_fake)
lossG = criterion(y_fake, torch.ones_like(y_fake))
lossG.backward()
optimG.step()
# ロスを標準出力する
tqdm_iter.set_description("epoch #{:d}, {:d} steps, lossD={:.4f}, lossG={:.4f}".format(epoch, steps, lossD.item(), lossG.item()))
# 途中経過の保存
if steps % 50 == 0:
outfile = os.path.join(log_dir, 'x_real_{:03d}.jpg'.format(epoch))
torchvision.utils.save_image(x_real * 0.5 + 0.5, outfile, nrow=5, padding=10)
outfile = os.path.join(log_dir, 'x_fake_{:03d}.jpg'.format(epoch))
torchvision.utils.save_image(x_fake * 0.5 + 0.5, outfile, nrow=5, padding=10)
steps += 1
# 学習途中のモデルを保存
ckpt = {
'optimG': optimG.state_dict(),
'optimD': optimD.state_dict(),
'netG': netG.state_dict(),
'netD': netD.state_dict(),
'epoch': epoch,
'steps': steps
}
torch.save(ckpt, os.path.join(log_dir, model_path))
# 10x10の画像を作る
rows = 10
cols = 10
netG.eval()
z = torch.randn([rows * cols, sample_dims], dtype=torch.float32, device=device)
x_fake = netG(z)
image_grid = torchvision.utils.make_grid(x_fake * 0.5 + 0.5, nrow=rows, padding=10)
image_grid = image_grid.detach().cpu().numpy()
image_grid = np.transpose(image_grid, axes=[1, 2, 0])
plt.figure(figsize=(15, 15))
plt.imshow(image_grid)
plt.show()
# 保存するときは以下をコメントアウト(適宜保存する名前は変更すること)
# cv2.imwrite('image_grid_10x10.png', image_grid)
| 0.722527 | 0.339691 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.