code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
```
from __future__ import print_function
import os
import sys
import gzip
import numpy as np
import pandas as pd
import datetime
from keras import backend as K
from keras.layers import Input, Dense, Dropout, Activation, Conv1D, MaxPooling1D, Flatten
from keras import optimizers
from keras.optimizers import SGD, Adam, RMSprop
from keras.models import Sequential, Model, model_from_json, model_from_yaml
from keras.utils import np_utils
from keras.callbacks import ModelCheckpoint, CSVLogger, ReduceLROnPlateau
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler, MinMaxScaler, MaxAbsScaler
```
### Now you define a few variables that could change as you attempt to optimize your model.
### Often, these are just hard coded, or else provided as command line parameters once you know what variables you might be interested in varying.
### Instead, we use a method to initialize these variables from either a config file or from command line parameters. This method is called by CANDLE.
```
import param_utils as p_utils
def initialize_parameters():
# Get command-line parameters
parser = p_utils.get_nt3_parser()
args = parser.parse_args()
# Get parameters from configuration file
fileParameters = p_utils.read_config_file(args.config_file)
# Consolidate parameter set. Command-line parameters overwrite file configuration
gParameters = p_utils.args_overwrite_config(args, fileParameters)
return gParameters
# HACK needed to parse command line params in notebook
import sys; sys.argv=['']; del sys
gParameters = initialize_parameters()
print(gParameters)
# Define the data
url_nt3 = gParameters['data_url']
FILE_TRAIN = url_nt3 + gParameters['train_data']
FILE_TEST = url_nt3 + gParameters['test_data']
# Define the reference model
CLASSES = gParameters['classes']
DROPOUT_RATE = gParameters['drop']
# Define optimizer
OPTIMIZER=gParameters['optimizer']
LEARNING_RATE = gParameters['learning_rate']
DECAY_RATE = gParameters['decay_rate']
# Compile the model
METRICS=gParameters['metrics']
LOSS='categorical_crossentropy'
# Train the model (the optimized model has a default of 400 epochs)
EPOCHS = gParameters['epochs']
BATCH_SIZE = gParameters['batch_size']
# Set up some variables for output files
MODEL_NAME = gParameters['model_name']
OUTPUT_DIR = gParameters['save']
```
### Now that you've set up your initial variables, it's time to load the data.
```
def load_data(train_path, test_path):
import threading
import queue
import sys
def load_train(train_path, queue):
sys.stdout.write('looking for '+ train_path + '\n')
sys.stdout.flush()
df_train = (pd.read_csv(train_path,header=None).values).astype('float32')
sys.stdout.write('done loading training data\n')
sys.stdout.flush()
queue.put(df_train)
def load_test(test_path, queue):
sys.stdout.write('looking for ' + test_path + '\n')
sys.stdout.flush()
df_test = (pd.read_csv(test_path,header=None).values).astype('float32')
sys.stdout.write('done loading test data\n')
sys.stdout.flush()
queue.put(df_test)
q1 = queue.Queue()
q2 = queue.Queue()
thread1 = threading.Thread(name='load_train', target=load_train, args=(train_path, q1,))
thread2 = threading.Thread(name='load_test' , target=load_test, args=(test_path, q2,))
thread1.start()
thread2.start()
thread1.join()
thread2.join()
df_train = q1.get()
df_test = q2.get()
print('df_train shape:', df_train.shape)
print('df_test shape:', df_test.shape)
seqlen = df_train.shape[1]
df_y_train = df_train[:,0].astype('int')
df_y_test = df_test[:,0].astype('int')
# Convert a class vector (integers) to binary class matrix.
Y_train = np_utils.to_categorical(df_y_train,CLASSES)
Y_test = np_utils.to_categorical(df_y_test,CLASSES)
df_x_train = df_train[:, 1:seqlen].astype(np.float32)
df_x_test = df_test[:, 1:seqlen].astype(np.float32)
X_train = df_x_train
X_test = df_x_test
scaler = MaxAbsScaler()
mat = np.concatenate((X_train, X_test), axis=0)
mat = scaler.fit_transform(mat)
X_train = mat[:X_train.shape[0], :]
X_test = mat[X_train.shape[0]:, :]
return X_train, Y_train, X_test, Y_test
```
### This alows the code to executed through the run method as an imported package.
### In the final version of nt3, the model is constructed dynamically from the config information in the nt3_default_model.txt file. You can see the final version at:
https://github.com/ECP-CANDLE/Benchmarks/blob/frameworks/Pilot1/NT3/nt3_baseline_keras2.py
```
def run(gParameters):
X_train, Y_train, X_test, Y_test = load_data(FILE_TRAIN, FILE_TEST)
# this reshaping is critical for the Conv1D to work
X_train = np.expand_dims(X_train, axis=2)
X_test = np.expand_dims(X_test, axis=2)
num_params = X_train.shape[1]
print('X_train shape:', X_train.shape)
print('X_test shape:', X_test.shape)
print('Number of parameters: ', num_params)
# Define the reference model
model = Sequential()
model.add(Conv1D(filters=128, kernel_size=20, strides=1, padding='valid', input_shape=(num_params, 1)))
model.add(Activation('relu'))
model.add(MaxPooling1D(pool_size=1))
model.add(Conv1D(filters=128, kernel_size=10, strides=1, padding='valid'))
model.add(Activation('relu'))
model.add(MaxPooling1D(pool_size=10))
model.add(Flatten())
model.add(Dense(200))
model.add(Activation('relu'))
model.add(Dropout(DROPOUT_RATE))
model.add(Dense(20))
model.add(Activation('relu'))
model.add(Dropout(DROPOUT_RATE))
model.add(Dense(CLASSES))
model.add(Activation('softmax'))
# Define the optimizer
optimizer = optimizers.SGD(lr=LEARNING_RATE, decay=DECAY_RATE)
# Compile the model
model.summary()
model.compile(loss=LOSS,
optimizer=optimizer,
metrics=[METRICS])
if not os.path.exists(OUTPUT_DIR):
os.makedirs(OUTPUT_DIR)
csv_logger = CSVLogger('{}/training.log'.format(OUTPUT_DIR))
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=10, verbose=1, mode='auto', epsilon=0.0001, cooldown=0, min_lr=0)
print (datetime.datetime.now())
history = model.fit(X_train, Y_train,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
verbose=1,
validation_data=(X_test, Y_test),
callbacks = [csv_logger, reduce_lr
])
score = model.evaluate(X_test, Y_test, verbose=0)
print (datetime.datetime.now())
# serialize model to JSON
model_json = model.to_json()
with open("{}/{}.model.json".format(OUTPUT_DIR, MODEL_NAME), "w") as json_file:
json_file.write(model_json)
print('Saved model to disk')
# serialize weights to HDF5
model.save_weights("{}/{}.model.h5".format(OUTPUT_DIR, MODEL_NAME))
print('Saved weights to disk')
```
### This allows the code to be executed at the command line.
```
def main():
gParameters = initialize_parameters()
run(gParameters)
if __name__ == '__main__':
main()
try:
K.clear_session()
except AttributeError: # theano does not have this function
pass
```
|
github_jupyter
|
from __future__ import print_function
import os
import sys
import gzip
import numpy as np
import pandas as pd
import datetime
from keras import backend as K
from keras.layers import Input, Dense, Dropout, Activation, Conv1D, MaxPooling1D, Flatten
from keras import optimizers
from keras.optimizers import SGD, Adam, RMSprop
from keras.models import Sequential, Model, model_from_json, model_from_yaml
from keras.utils import np_utils
from keras.callbacks import ModelCheckpoint, CSVLogger, ReduceLROnPlateau
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler, MinMaxScaler, MaxAbsScaler
import param_utils as p_utils
def initialize_parameters():
# Get command-line parameters
parser = p_utils.get_nt3_parser()
args = parser.parse_args()
# Get parameters from configuration file
fileParameters = p_utils.read_config_file(args.config_file)
# Consolidate parameter set. Command-line parameters overwrite file configuration
gParameters = p_utils.args_overwrite_config(args, fileParameters)
return gParameters
# HACK needed to parse command line params in notebook
import sys; sys.argv=['']; del sys
gParameters = initialize_parameters()
print(gParameters)
# Define the data
url_nt3 = gParameters['data_url']
FILE_TRAIN = url_nt3 + gParameters['train_data']
FILE_TEST = url_nt3 + gParameters['test_data']
# Define the reference model
CLASSES = gParameters['classes']
DROPOUT_RATE = gParameters['drop']
# Define optimizer
OPTIMIZER=gParameters['optimizer']
LEARNING_RATE = gParameters['learning_rate']
DECAY_RATE = gParameters['decay_rate']
# Compile the model
METRICS=gParameters['metrics']
LOSS='categorical_crossentropy'
# Train the model (the optimized model has a default of 400 epochs)
EPOCHS = gParameters['epochs']
BATCH_SIZE = gParameters['batch_size']
# Set up some variables for output files
MODEL_NAME = gParameters['model_name']
OUTPUT_DIR = gParameters['save']
def load_data(train_path, test_path):
import threading
import queue
import sys
def load_train(train_path, queue):
sys.stdout.write('looking for '+ train_path + '\n')
sys.stdout.flush()
df_train = (pd.read_csv(train_path,header=None).values).astype('float32')
sys.stdout.write('done loading training data\n')
sys.stdout.flush()
queue.put(df_train)
def load_test(test_path, queue):
sys.stdout.write('looking for ' + test_path + '\n')
sys.stdout.flush()
df_test = (pd.read_csv(test_path,header=None).values).astype('float32')
sys.stdout.write('done loading test data\n')
sys.stdout.flush()
queue.put(df_test)
q1 = queue.Queue()
q2 = queue.Queue()
thread1 = threading.Thread(name='load_train', target=load_train, args=(train_path, q1,))
thread2 = threading.Thread(name='load_test' , target=load_test, args=(test_path, q2,))
thread1.start()
thread2.start()
thread1.join()
thread2.join()
df_train = q1.get()
df_test = q2.get()
print('df_train shape:', df_train.shape)
print('df_test shape:', df_test.shape)
seqlen = df_train.shape[1]
df_y_train = df_train[:,0].astype('int')
df_y_test = df_test[:,0].astype('int')
# Convert a class vector (integers) to binary class matrix.
Y_train = np_utils.to_categorical(df_y_train,CLASSES)
Y_test = np_utils.to_categorical(df_y_test,CLASSES)
df_x_train = df_train[:, 1:seqlen].astype(np.float32)
df_x_test = df_test[:, 1:seqlen].astype(np.float32)
X_train = df_x_train
X_test = df_x_test
scaler = MaxAbsScaler()
mat = np.concatenate((X_train, X_test), axis=0)
mat = scaler.fit_transform(mat)
X_train = mat[:X_train.shape[0], :]
X_test = mat[X_train.shape[0]:, :]
return X_train, Y_train, X_test, Y_test
def run(gParameters):
X_train, Y_train, X_test, Y_test = load_data(FILE_TRAIN, FILE_TEST)
# this reshaping is critical for the Conv1D to work
X_train = np.expand_dims(X_train, axis=2)
X_test = np.expand_dims(X_test, axis=2)
num_params = X_train.shape[1]
print('X_train shape:', X_train.shape)
print('X_test shape:', X_test.shape)
print('Number of parameters: ', num_params)
# Define the reference model
model = Sequential()
model.add(Conv1D(filters=128, kernel_size=20, strides=1, padding='valid', input_shape=(num_params, 1)))
model.add(Activation('relu'))
model.add(MaxPooling1D(pool_size=1))
model.add(Conv1D(filters=128, kernel_size=10, strides=1, padding='valid'))
model.add(Activation('relu'))
model.add(MaxPooling1D(pool_size=10))
model.add(Flatten())
model.add(Dense(200))
model.add(Activation('relu'))
model.add(Dropout(DROPOUT_RATE))
model.add(Dense(20))
model.add(Activation('relu'))
model.add(Dropout(DROPOUT_RATE))
model.add(Dense(CLASSES))
model.add(Activation('softmax'))
# Define the optimizer
optimizer = optimizers.SGD(lr=LEARNING_RATE, decay=DECAY_RATE)
# Compile the model
model.summary()
model.compile(loss=LOSS,
optimizer=optimizer,
metrics=[METRICS])
if not os.path.exists(OUTPUT_DIR):
os.makedirs(OUTPUT_DIR)
csv_logger = CSVLogger('{}/training.log'.format(OUTPUT_DIR))
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=10, verbose=1, mode='auto', epsilon=0.0001, cooldown=0, min_lr=0)
print (datetime.datetime.now())
history = model.fit(X_train, Y_train,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
verbose=1,
validation_data=(X_test, Y_test),
callbacks = [csv_logger, reduce_lr
])
score = model.evaluate(X_test, Y_test, verbose=0)
print (datetime.datetime.now())
# serialize model to JSON
model_json = model.to_json()
with open("{}/{}.model.json".format(OUTPUT_DIR, MODEL_NAME), "w") as json_file:
json_file.write(model_json)
print('Saved model to disk')
# serialize weights to HDF5
model.save_weights("{}/{}.model.h5".format(OUTPUT_DIR, MODEL_NAME))
print('Saved weights to disk')
def main():
gParameters = initialize_parameters()
run(gParameters)
if __name__ == '__main__':
main()
try:
K.clear_session()
except AttributeError: # theano does not have this function
pass
| 0.623148 | 0.589244 |
<img align="left" src="https://lever-client-logos.s3.amazonaws.com/864372b1-534c-480e-acd5-9711f850815c-1524247202159.png" width=200>
<br></br>
<br></br>
## *Data Science Unit 4 Sprint 3 Assignment 1*
# Recurrent Neural Networks and Long Short Term Memory (LSTM)

It is said that [infinite monkeys typing for an infinite amount of time](https://en.wikipedia.org/wiki/Infinite_monkey_theorem) will eventually type, among other things, the complete works of Wiliam Shakespeare. Let's see if we can get there a bit faster, with the power of Recurrent Neural Networks and LSTM.
This text file contains the complete works of Shakespeare: https://www.gutenberg.org/files/100/100-0.txt
Use it as training data for an RNN - you can keep it simple and train character level, and that is suggested as an initial approach.
Then, use that trained RNN to generate Shakespearean-ish text. Your goal - a function that can take, as an argument, the size of text (e.g. number of characters or lines) to generate, and returns generated text of that size.
Note - Shakespeare wrote an awful lot. It's OK, especially initially, to sample/use smaller data and parameters, so you can have a tighter feedback loop when you're trying to get things running. Then, once you've got a proof of concept - start pushing it more!
```
import requests
import pandas as pd
url = "https://www.gutenberg.org/files/100/100-0.txt"
r = requests.get(url)
r.encoding = r.apparent_encoding
data = r.text
data = data.split('\r\n')
toc = [l.strip() for l in data[44:130:2]]
# Skip the Table of Contents
data = data[135:]
# Fixing Titles
toc[9] = 'THE LIFE OF KING HENRY V'
toc[18] = 'MACBETH'
toc[24] = 'OTHELLO, THE MOOR OF VENICE'
toc[34] = 'TWELFTH NIGHT: OR, WHAT YOU WILL'
locations = {id_:{'title':title, 'start':-99} for id_,title in enumerate(toc)}
# Start
for e,i in enumerate(data):
for t,title in enumerate(toc):
if title in i:
locations[t].update({'start':e})
df_toc = pd.DataFrame.from_dict(locations, orient='index')
df_toc['end'] = df_toc['start'].shift(-1).apply(lambda x: x-1)
df_toc.loc[42, 'end'] = len(data)
df_toc['end'] = df_toc['end'].astype('int')
df_toc['text'] = df_toc.apply(lambda x: '\r\n'.join(data[ x['start'] : int(x['end']) ]), axis=1)
#Shakespeare Data Parsed by Play
df_toc.head(3)
len(data)
data[0]
def long_lines(lst_ln):
clean = []
for ln in lst_ln:
if len(ln) == 0:
pass
else:
pct = len(ln.strip(' ')) / len(ln)
if pct >= .5:
clean.append(ln.lstrip())
return clean
sonets = long_lines(sonets)
plays = long_lines(plays)
text = '\r\n'.join(sonets)
chars = list(set(text))
char_int = {c:i for i,c in enumerate(chars)}
int_char = {i:c for i,c in enumerate(chars)}
print(f"Our corpus contains {len(chars)} unique characters.")
maxlen = 40
step = 5
encoded = [char_int[c] for c in text]
sequences = [] # Each element is 40 chars long
next_char = [] # One element for each sequence
for i in range(0, len(encoded) - maxlen, step):
sequences.append(encoded[i : i + maxlen])
next_char.append(encoded[i + maxlen])
print('sequences: ', len(sequences))
sequences[0]
next_char[0], int_char[next_char[0]]
x = np.zeros((len(sequences), maxlen, len(chars)), dtype=np.bool)
y = np.zeros((len(sequences),len(chars)), dtype=np.bool)
for i, sequence in enumerate(sequences):
for t, char in enumerate(sequence):
x[i,t,char] = 1
y[i, next_char[i]] = 1
x.shape
chars
(maxlen, len(chars))
model = Sequential()
model.add(LSTM(128, input_shape=(maxlen, len(chars))))
model.add(Dense(len(chars), activation='adam'))
model.compile(loss='categorical_crossentropy', optimizer='adam')
def sample(preds):
# helper function to sample an index from a probability array
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / 1
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, preds, 1)
return np.argmax(probas)
def on_epoch_end(epoch, _):
# Function invoked at end of each epoch. Prints generated text.
print()
print('----- Generating text after Epoch: %d' % epoch)
start_index = random.randint(0, len(text) - maxlen - 1)
generated = ''
sentence = text[start_index: start_index + maxlen]
generated += sentence
print('----- Generating with seed: "' + sentence + '"')
sys.stdout.write(generated)
for i in range(400):
x_pred = np.zeros((1, maxlen, len(chars)))
for t, char in enumerate(sentence):
x_pred[0, t, char_int[char]] = 1
preds = model.predict(x_pred, verbose=0)[0]
next_index = sample(preds)
next_char = int_char[next_index]
sentence = sentence[1:] + next_char
sys.stdout.write(next_char)
sys.stdout.flush()
print()
print_callback = LambdaCallback(on_epoch_end=on_epoch_end)
model.fit(x, y,
batch_size=128,
epochs=50,
callbacks=[print_callback],
)
```
# Resources and Stretch Goals
## Stretch goals:
- Refine the training and generation of text to be able to ask for different genres/styles of Shakespearean text (e.g. plays versus sonnets)
- Train a classification model that takes text and returns which work of Shakespeare it is most likely to be from
- Make it more performant! Many possible routes here - lean on Keras, optimize the code, and/or use more resources (AWS, etc.)
- Revisit the news example from class, and improve it - use categories or tags to refine the model/generation, or train a news classifier
- Run on bigger, better data
## Resources:
- [The Unreasonable Effectiveness of Recurrent Neural Networks](https://karpathy.github.io/2015/05/21/rnn-effectiveness/) - a seminal writeup demonstrating a simple but effective character-level NLP RNN
- [Simple NumPy implementation of RNN](https://github.com/JY-Yoon/RNN-Implementation-using-NumPy/blob/master/RNN%20Implementation%20using%20NumPy.ipynb) - Python 3 version of the code from "Unreasonable Effectiveness"
- [TensorFlow RNN Tutorial](https://github.com/tensorflow/models/tree/master/tutorials/rnn) - code for training a RNN on the Penn Tree Bank language dataset
- [4 part tutorial on RNN](http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/) - relates RNN to the vanishing gradient problem, and provides example implementation
- [RNN training tips and tricks](https://github.com/karpathy/char-rnn#tips-and-tricks) - some rules of thumb for parameterizing and training your RNN
|
github_jupyter
|
import requests
import pandas as pd
url = "https://www.gutenberg.org/files/100/100-0.txt"
r = requests.get(url)
r.encoding = r.apparent_encoding
data = r.text
data = data.split('\r\n')
toc = [l.strip() for l in data[44:130:2]]
# Skip the Table of Contents
data = data[135:]
# Fixing Titles
toc[9] = 'THE LIFE OF KING HENRY V'
toc[18] = 'MACBETH'
toc[24] = 'OTHELLO, THE MOOR OF VENICE'
toc[34] = 'TWELFTH NIGHT: OR, WHAT YOU WILL'
locations = {id_:{'title':title, 'start':-99} for id_,title in enumerate(toc)}
# Start
for e,i in enumerate(data):
for t,title in enumerate(toc):
if title in i:
locations[t].update({'start':e})
df_toc = pd.DataFrame.from_dict(locations, orient='index')
df_toc['end'] = df_toc['start'].shift(-1).apply(lambda x: x-1)
df_toc.loc[42, 'end'] = len(data)
df_toc['end'] = df_toc['end'].astype('int')
df_toc['text'] = df_toc.apply(lambda x: '\r\n'.join(data[ x['start'] : int(x['end']) ]), axis=1)
#Shakespeare Data Parsed by Play
df_toc.head(3)
len(data)
data[0]
def long_lines(lst_ln):
clean = []
for ln in lst_ln:
if len(ln) == 0:
pass
else:
pct = len(ln.strip(' ')) / len(ln)
if pct >= .5:
clean.append(ln.lstrip())
return clean
sonets = long_lines(sonets)
plays = long_lines(plays)
text = '\r\n'.join(sonets)
chars = list(set(text))
char_int = {c:i for i,c in enumerate(chars)}
int_char = {i:c for i,c in enumerate(chars)}
print(f"Our corpus contains {len(chars)} unique characters.")
maxlen = 40
step = 5
encoded = [char_int[c] for c in text]
sequences = [] # Each element is 40 chars long
next_char = [] # One element for each sequence
for i in range(0, len(encoded) - maxlen, step):
sequences.append(encoded[i : i + maxlen])
next_char.append(encoded[i + maxlen])
print('sequences: ', len(sequences))
sequences[0]
next_char[0], int_char[next_char[0]]
x = np.zeros((len(sequences), maxlen, len(chars)), dtype=np.bool)
y = np.zeros((len(sequences),len(chars)), dtype=np.bool)
for i, sequence in enumerate(sequences):
for t, char in enumerate(sequence):
x[i,t,char] = 1
y[i, next_char[i]] = 1
x.shape
chars
(maxlen, len(chars))
model = Sequential()
model.add(LSTM(128, input_shape=(maxlen, len(chars))))
model.add(Dense(len(chars), activation='adam'))
model.compile(loss='categorical_crossentropy', optimizer='adam')
def sample(preds):
# helper function to sample an index from a probability array
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / 1
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, preds, 1)
return np.argmax(probas)
def on_epoch_end(epoch, _):
# Function invoked at end of each epoch. Prints generated text.
print()
print('----- Generating text after Epoch: %d' % epoch)
start_index = random.randint(0, len(text) - maxlen - 1)
generated = ''
sentence = text[start_index: start_index + maxlen]
generated += sentence
print('----- Generating with seed: "' + sentence + '"')
sys.stdout.write(generated)
for i in range(400):
x_pred = np.zeros((1, maxlen, len(chars)))
for t, char in enumerate(sentence):
x_pred[0, t, char_int[char]] = 1
preds = model.predict(x_pred, verbose=0)[0]
next_index = sample(preds)
next_char = int_char[next_index]
sentence = sentence[1:] + next_char
sys.stdout.write(next_char)
sys.stdout.flush()
print()
print_callback = LambdaCallback(on_epoch_end=on_epoch_end)
model.fit(x, y,
batch_size=128,
epochs=50,
callbacks=[print_callback],
)
| 0.38549 | 0.852997 |
## TSA Evaluation Metrics
### Most common Evaluation Metrics for TSA/Regression Analysis:
@joydeepubuntu's [Blog](https://medium.com/@joydeepubuntu/common-metrics-for-time-series-analysis-f3ca4b29fe42) <br>
Rob Hyndmans's [Suggestions](https://www.sciencedirect.com/science/article/abs/pii/S0169207006000239) <br>
- $y_{i}$ : **real value** of the test data
- $\hat y_{i}$: **Predicted value** from our forecast
<br>`And Residual is how far the actual value is from the predicted value`, i.e. error in a prediciton
> here, $y_{i}-\hat y_{i}$ is the ***residual component***
<br>`-ve residual value = predicted value fall below the actual value`
<br>`+ve residual value = predicted value falls above the actual value`
1) <b> Mean Squared Error </b>: MAE misses on some large errors due to MEAN of rest of the values, thus MSE is more popular =>
$ \frac{1}{n} \sum_{i=1}^n (y_{i} - \hat y_{i})^2 $
```python
>>> from sklearn.metrics import mean_squared_error
>>> print(mean_squared_error(y_pred, y_true))
0.375
```
<br>
2) <b> Root Mean Squared Error </b>: Due to the square of residual values in MSE, units are also squared, i.e. $ Dollar^2, count of people^2,etc.$, thus
<br>
$\sqrt{\frac{1}{n} \sum_{i=1}^n (y_{i} - \hat y_{i})^2}$
```python
>>> from sklearn.metrics import mean_squared_error
>>> mse=mean_squared_error(y_pred, y_true)
>>> print(np.sqrt(rmse))
0.06
```
<br>
3) <b>Mean Absolute Error</b>: Mean of the absolute value of errors =>
$ \frac{1}{n} \sum_{i=1}^n | y_{i} - \hat y_{i} | $
```python
>>> from sklearn.metrics import mean_absolute_error
>>> print(mean_absolute_error(y_true, y_pred))
0.5
>>> from sklearn.metrics import median_absolute_error
>>> print(median_absolute_error(y_true, y_pred))
0.5
```
<br>
4) <b> Mean Absolute Percentage Error </b>:
$ \frac{1}{n} \sum_{i=1}^n \left\lvert{\frac{y_{i}-\hat y}{y_{i}}}\right\rvert $ or
$ \frac{1}{n} \sum_{i=1}^n \left\lvert{\frac{Act_{i}- F_{i}}{Act_{i}}}\right\rvert $
<br>
MAPE doesn't has nay implementation in sci-kit learn, thus <br>
```python
def mean_absolute_percentage_error(y_true, y_pred):
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
```
<br>
5) <b> Symmetric Mean Absolute Percentage Error </b>:
SMAPE = $\frac{100\%}{n} \sum_{t=1}^n \frac{|F_{t}-A_{t}|}{(|A_{t}|+|F_{t}|)/2}$
<br>
SMAPE doesn't has nay implementation in sci-kit learn, thus <br>
```python
def smape(Act, Fcst):
smape_val = round(100/len(Act) * np.sum(2 * np.abs(Fcst - Act) / (np.abs(Act) + np.abs(Fcst))),2)
return smape_val
```
<b><i> Reason for divison by 2 in sMAPE is justified by [Spyros Makridakis]("https://sci-hub.tw/10.1016/0169-2070(93)90079-3")</i></b> <br>
MAPE as an accuracy measure can be influenced by some problems:
- Equal errors above the actual value result in a greater APE (Absolute Percentage Error) than those below the actual value. For instance, when the actual value is 150 and the forecast is 100 (an error of 50) the APE(|(Act-Fcst/Act)|) is: 33%
- However, when the actual is 100 and the forecast 150 the APE is 50%
- This problem can be easily corrected by dividing the error (Act - Fcst) by the average of both Act and Fcst i.e. (Act + Fcst)/2
- The above formula will provide the APE of 40% in both cases
<br>
6) <b> $R^2$ </b>: Is a measure of how close each datapoint fits the regression line, So it tells us, how well the regression line predicts the actual value
```python
>>> from sklearn.metrics import r2_score
>>> r2_score(y_true, y_pred)
0.9486081370449679
```
@joydeepubuntu's [Blog](https://medium.com/@joydeepubuntu/common-metrics-for-time-series-analysis-f3ca4b29fe42) <br>
Rob Hyndmans's [Suggestions](https://www.sciencedirect.com/science/article/abs/pii/S0169207006000239) <br>
```
import datetime
import time
print("logs_fit_" + datetime.datetime.now().strftime("%Y_%m_%d_%H_%M_%S"))
```
|
github_jupyter
|
>>> from sklearn.metrics import mean_squared_error
>>> print(mean_squared_error(y_pred, y_true))
0.375
>>> from sklearn.metrics import mean_squared_error
>>> mse=mean_squared_error(y_pred, y_true)
>>> print(np.sqrt(rmse))
0.06
>>> from sklearn.metrics import mean_absolute_error
>>> print(mean_absolute_error(y_true, y_pred))
0.5
>>> from sklearn.metrics import median_absolute_error
>>> print(median_absolute_error(y_true, y_pred))
0.5
def mean_absolute_percentage_error(y_true, y_pred):
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
def smape(Act, Fcst):
smape_val = round(100/len(Act) * np.sum(2 * np.abs(Fcst - Act) / (np.abs(Act) + np.abs(Fcst))),2)
return smape_val
>>> from sklearn.metrics import r2_score
>>> r2_score(y_true, y_pred)
0.9486081370449679
import datetime
import time
print("logs_fit_" + datetime.datetime.now().strftime("%Y_%m_%d_%H_%M_%S"))
| 0.774498 | 0.949902 |
```
import requests
import time
import json
import os
import tempfile
from pprint import pprint
import SimpleITK as sitk
base_url = 'http://127.0.0.1:8001'
api_key = ''
algorithm_name = "
"
api_dicom_location = '{0}/api/dicomlocation'.format(base_url)
api_dataset = '{0}/api/dataset'.format(base_url)
api_dataset_ready = '{0}/api/dataset/ready'.format(base_url)
api_data_object = '{0}/api/dataobject'.format(base_url)
api_trigger = '{0}/api/trigger'.format(base_url)
api_algorithm = '{0}/api/algorithm'.format(base_url)
api_download = '{0}/api/dataobject/download'.format(base_url)
# Get the algorithm and the default settings
algorithm = None
r = requests.get(api_algorithm, headers={'API_KEY': api_key})
if r.status_code == 200:
for a in r.json():
pprint(a)
if a['name'] == algorithm_name:
algorithm = a
print("")
print("Look's Good!")
else:
print("Oops, something went wrong. Ensure the service is running at the base_url configured and that the API Key has been generated and set in api_key.")
# Create a new Dataset
dataset = None
data = {}
r = requests.post(api_dataset, headers={'API_KEY': api_key}, data=data)
if r.status_code >= 200:
dataset = r.json()
pprint(dataset)
# Use the phantom dicom data, both as primary and secondary
path_to_dicom = f"../../dicom/data/phantom/CT"
load_path = sitk.ImageSeriesReader().GetGDCMSeriesFileNames(path_to_dicom)
image = sitk.ReadImage(load_path)
tmp_dir = tempfile.mkdtemp()
tmp_file = os.path.join(tmp_dir, "img.nii.gz")
sitk.WriteImage(image, tmp_file)
data_object = None
# Add the primary image
with open(tmp_file,'rb') as file:
data = {'dataset': dataset['id'],
'type': 'FILE',
'meta_data': json.dumps({"type": "primary",}),
'file_name': 'primary.nii.gz'}
r = requests.post(api_data_object, headers={'API_KEY': api_key}, data=data, files={'file_data':file})
if r.status_code >= 200:
primary_data_object = r.json()
# Add a child struct in which to find points for primary
path_to_struct = f"../../dicom/data/phantom/masks/Test_MANDIBLE_PRI.nii.gz"
with open(path_to_struct,'rb') as file:
data = {'dataset': dataset['id'],
'type': 'FILE',
"parent": primary_data_object['id'],
'meta_data': json.dumps({"type": "contour","name": "Struct_1"}),
'file_name': 'struct.nii.gz'}
r = requests.post(api_data_object, headers={'API_KEY': api_key}, data=data, files={'file_data':file})
if r.status_code >= 200:
secondary_contour_data_object = r.json()
# Add the secondary Image
with open(tmp_file,'rb') as file:
data = {'dataset': dataset['id'],
'type': 'FILE',
'meta_data': json.dumps({"type": "secondary",}),
'file_name': 'secondary.nii.gz'}
r = requests.post(api_data_object, headers={'API_KEY': api_key}, data=data, files={'file_data':file})
if r.status_code >= 200:
secondary_data_object = r.json()
# Add a child struct in which to find points for primary
path_to_struct = f"../../dicom/data/phantom/masks/Test_MANDIBLE_PRI.nii.gz"
with open(path_to_struct,'rb') as file:
data = {'dataset': dataset['id'],
'type': 'FILE',
"parent": secondary_data_object['id'],
'meta_data': json.dumps({"type": "contour","name": "Struct_1"}),
'file_name': 'struct.nii.gz'}
r = requests.post(api_data_object, headers={'API_KEY': api_key}, data=data, files={'file_data':file})
if r.status_code >= 200:
primary_contour_data_object = r.json()
# Take a look at the dataset objects output
r = requests.get('{0}/{1}'.format(api_dataset, dataset['id']), headers={'API_KEY': api_key})
if r.status_code == 200:
dataset = r.json()
pprint(dataset)
# Get the algorithm and the default settings
algorithm = None
r = requests.get(api_algorithm, headers={'API_KEY': api_key})
if r.status_code == 200:
for a in r.json():
if algorithm_name in a['name']:
algorithm = a
print(a)
settings = algorithm['default_settings']
settings['includePointsMode'] = "BOUNDINGBOX"
settings['intensityRange'] = [-200, 200]
settings
# Trigger the algorithm with our dataset containing the data object
data={'dataset': dataset['id'],
'algorithm': algorithm['name'],
'config': json.dumps(settings)}
r = requests.post(api_trigger, headers={'API_KEY': api_key}, data=data)
if r.status_code == 200:
# Poll the URL given to determine the progress of the task
poll_url = '{0}{1}'.format(base_url, r.json()['poll'])
while(1):
r = requests.get(poll_url, headers={'API_KEY': api_key})
status = r.json()
print(status)
if status['state'] == 'SUCCESS' or status['state'] == 'FAILURE':
break
time.sleep(1)
else:
print(r.json())
print('Algorithm Processing Complete')
# Take a look at the dataset objects output
r = requests.get('{0}/{1}'.format(api_dataset, dataset['id']), headers={'API_KEY': api_key})
if r.status_code == 200:
dataset = r.json()
pprint(dataset)
for d in dataset['output_data_objects']:
r = requests.get('{0}/{1}'.format(api_download, d['id']), headers={'API_KEY': api_key})
filename = r.headers['Content-Disposition'].split('filename=')[1]
print('Downloading to: {0}'.format(filename))
open(filename, 'wb').write(r.content)
import pandas as pd
ds = pd.read_csv("primary_Struct_1_match.csv", header=None)
ds
```
|
github_jupyter
|
import requests
import time
import json
import os
import tempfile
from pprint import pprint
import SimpleITK as sitk
base_url = 'http://127.0.0.1:8001'
api_key = ''
algorithm_name = "
"
api_dicom_location = '{0}/api/dicomlocation'.format(base_url)
api_dataset = '{0}/api/dataset'.format(base_url)
api_dataset_ready = '{0}/api/dataset/ready'.format(base_url)
api_data_object = '{0}/api/dataobject'.format(base_url)
api_trigger = '{0}/api/trigger'.format(base_url)
api_algorithm = '{0}/api/algorithm'.format(base_url)
api_download = '{0}/api/dataobject/download'.format(base_url)
# Get the algorithm and the default settings
algorithm = None
r = requests.get(api_algorithm, headers={'API_KEY': api_key})
if r.status_code == 200:
for a in r.json():
pprint(a)
if a['name'] == algorithm_name:
algorithm = a
print("")
print("Look's Good!")
else:
print("Oops, something went wrong. Ensure the service is running at the base_url configured and that the API Key has been generated and set in api_key.")
# Create a new Dataset
dataset = None
data = {}
r = requests.post(api_dataset, headers={'API_KEY': api_key}, data=data)
if r.status_code >= 200:
dataset = r.json()
pprint(dataset)
# Use the phantom dicom data, both as primary and secondary
path_to_dicom = f"../../dicom/data/phantom/CT"
load_path = sitk.ImageSeriesReader().GetGDCMSeriesFileNames(path_to_dicom)
image = sitk.ReadImage(load_path)
tmp_dir = tempfile.mkdtemp()
tmp_file = os.path.join(tmp_dir, "img.nii.gz")
sitk.WriteImage(image, tmp_file)
data_object = None
# Add the primary image
with open(tmp_file,'rb') as file:
data = {'dataset': dataset['id'],
'type': 'FILE',
'meta_data': json.dumps({"type": "primary",}),
'file_name': 'primary.nii.gz'}
r = requests.post(api_data_object, headers={'API_KEY': api_key}, data=data, files={'file_data':file})
if r.status_code >= 200:
primary_data_object = r.json()
# Add a child struct in which to find points for primary
path_to_struct = f"../../dicom/data/phantom/masks/Test_MANDIBLE_PRI.nii.gz"
with open(path_to_struct,'rb') as file:
data = {'dataset': dataset['id'],
'type': 'FILE',
"parent": primary_data_object['id'],
'meta_data': json.dumps({"type": "contour","name": "Struct_1"}),
'file_name': 'struct.nii.gz'}
r = requests.post(api_data_object, headers={'API_KEY': api_key}, data=data, files={'file_data':file})
if r.status_code >= 200:
secondary_contour_data_object = r.json()
# Add the secondary Image
with open(tmp_file,'rb') as file:
data = {'dataset': dataset['id'],
'type': 'FILE',
'meta_data': json.dumps({"type": "secondary",}),
'file_name': 'secondary.nii.gz'}
r = requests.post(api_data_object, headers={'API_KEY': api_key}, data=data, files={'file_data':file})
if r.status_code >= 200:
secondary_data_object = r.json()
# Add a child struct in which to find points for primary
path_to_struct = f"../../dicom/data/phantom/masks/Test_MANDIBLE_PRI.nii.gz"
with open(path_to_struct,'rb') as file:
data = {'dataset': dataset['id'],
'type': 'FILE',
"parent": secondary_data_object['id'],
'meta_data': json.dumps({"type": "contour","name": "Struct_1"}),
'file_name': 'struct.nii.gz'}
r = requests.post(api_data_object, headers={'API_KEY': api_key}, data=data, files={'file_data':file})
if r.status_code >= 200:
primary_contour_data_object = r.json()
# Take a look at the dataset objects output
r = requests.get('{0}/{1}'.format(api_dataset, dataset['id']), headers={'API_KEY': api_key})
if r.status_code == 200:
dataset = r.json()
pprint(dataset)
# Get the algorithm and the default settings
algorithm = None
r = requests.get(api_algorithm, headers={'API_KEY': api_key})
if r.status_code == 200:
for a in r.json():
if algorithm_name in a['name']:
algorithm = a
print(a)
settings = algorithm['default_settings']
settings['includePointsMode'] = "BOUNDINGBOX"
settings['intensityRange'] = [-200, 200]
settings
# Trigger the algorithm with our dataset containing the data object
data={'dataset': dataset['id'],
'algorithm': algorithm['name'],
'config': json.dumps(settings)}
r = requests.post(api_trigger, headers={'API_KEY': api_key}, data=data)
if r.status_code == 200:
# Poll the URL given to determine the progress of the task
poll_url = '{0}{1}'.format(base_url, r.json()['poll'])
while(1):
r = requests.get(poll_url, headers={'API_KEY': api_key})
status = r.json()
print(status)
if status['state'] == 'SUCCESS' or status['state'] == 'FAILURE':
break
time.sleep(1)
else:
print(r.json())
print('Algorithm Processing Complete')
# Take a look at the dataset objects output
r = requests.get('{0}/{1}'.format(api_dataset, dataset['id']), headers={'API_KEY': api_key})
if r.status_code == 200:
dataset = r.json()
pprint(dataset)
for d in dataset['output_data_objects']:
r = requests.get('{0}/{1}'.format(api_download, d['id']), headers={'API_KEY': api_key})
filename = r.headers['Content-Disposition'].split('filename=')[1]
print('Downloading to: {0}'.format(filename))
open(filename, 'wb').write(r.content)
import pandas as pd
ds = pd.read_csv("primary_Struct_1_match.csv", header=None)
ds
| 0.188287 | 0.125574 |
# **Behavioral Cloning**
## Writeup Report
---
**Behavioral Cloning Project**
The goals / steps of this project are the following:
* Use the simulator to collect data of good driving behavior
* Build, a convolution neural network in Keras that predicts steering angles from images
* Train and validate the model with a training and validation set
* Test that the model successfully drives around track one without leaving the road
* Summarize the results with a written report
[//]: # (Image References)
[image1]: ./examples/placeholder.png "Model Visualization"
[image2]: ./examples/centerlane.png "Centerlane image"
[image3]: ./examples/original.png "Normal Image"
[image4]: ./examples/flipped.png "Flipped Image"
[image5]: ./examples/Learning1.jpg "Learning curve first 20 epochs"
[image6]: ./examples/Learning.jpg "Learning curve after another 20 epochs"
## Rubric Points
### Here I will consider the [rubric points](https://review.udacity.com/#!/rubrics/432/view) individually and describe how I addressed each point in my implementation.
---
### Files Submitted & Code Quality
#### 1. Submission includes all required files and can be used to run the simulator in autonomous mode
My project includes the following files:
* model.py containing the script to create and train the model
* drive.py for driving the car in autonomous mode
* model.h5 containing a trained convolution neural network
* writeup_report.md and writeup_report.pdf summarizing the results
* weights.h5 from previous training
* run1.mp4 containing the video of Autonomous driving using my model.
#### 2. Submission includes functional code
Using the Udacity provided simulator and my drive.py file, the car can be driven autonomously around the track by executing
```sh
python drive.py model.h5
```
#### 3. Submission code is usable and readable
The model.py file contains the code for training and saving the convolution neural network. The file shows the pipeline I used for training and validating the model, and it contains comments to explain how the code works.
### Model Architecture and Training Strategy
#### 1. An appropriate model architecture has been employed
The top layer is a Cropping2D layer which crops top and bottom parts of the input image.
My model consists of 5 Convolutional layers followed by one Maxpooling and 4 Fully Connected(Dense) layers.
The convolutional layers are designed for feature extraction. First 3 convolutional layers are designed with a 5x5 kernel and 2x2 strides and depths 24,36,48 respectively.(code line 59-61). The other 2 convolutional layers are non-strided with a 3x3 kernel and with a depth of 64(code line 63-64).
Then I have used a MaxPooling layers with a pool size of (2,2)(Code line 65). I flattened the network using keras Flatten() function(Code line 66).
These layers are followed by 4 Dense layers with sizes 100,50,10 and 1 (code line 68-74).
In the model I have used RELU activations to introduce nonlinearity, and the data is normalized in the model using a Keras lambda layer (code line 57).
#### 2. Attempts to reduce overfitting in the model
The model contains dropout layers in order to reduce overfitting (model.py lines 71 & 73).
The model was trained and validated on different data sets to ensure that the model was not overfitting. The model was tested by running it through the simulator and ensuring that the vehicle could stay on the track.
#### 3. Model parameter tuning
The model used an adam optimizer with a decaying learning rate from keras model callbacks. (model.py line 76).
#### 4. Appropriate training data
Training data was chosen to keep the vehicle driving on the road. I used a combination of center lane driving, recovering from the left and right sides of the road. I have collected the data by driving two laps on track 1 and two laps on track 2.
For details about how I created the training data, see the next section.
### Model Architecture and Training Strategy
#### 1. Solution Design Approach
My first step was to use a convolution neural network model similar to the NVIDIA autonomous car architecture. I thought this model might be appropriate because it has 5 convolutional layers for feature extraction followed by fully connected layers to estimate the steering angle.
In order to gauge how well the model was working, I split my image and steering angle data into a training and validation set. I found that my first model had a low mean squared error on the training set but a high mean squared error on the validation set. This implied that the model was overfitting.
To combat the overfitting, I have added MaxPooling layer before Flatenning the data and added dropout layers with probability 0.5. It reduced the validation loss from 0.1496 to 0.0547.
Then I ran the model for 5 epochs and save the weights from it to use in next training. Next I loaded the weights and trained the model for another 10 epochs it drastically reduced the training loss and validation loss.
The final step was to run the simulator to see how well the car was driving around track one. There were a few spots where the vehicle fell off the track. To improve the driving behavior in these cases, I have added more data from left and right cameras with a corection of 0.15. I have also added more data by flipping the images horizontally to generalize the model better.
At the end of the process, the vehicle is able to drive autonomously around the track without leaving the road.
#### 2. Final Model Architecture
The final model architecture (model.py lines 55-74) consisted of a convolution neural network with the following layers and layer sizes.
| Layer | Description |
|:---------------------:|:-----------------------------------------------------:|
| Input | 160x320x3 RGB image |
| Cropping2D | cropping=((50,20), (0,0)) |
| Lambda | Normalization (X/255-0.5) |
| Convolution 1 | 5x5 kernel,24 Filters, 2x2 stride, relu activation |
| Convolution 2 | 5x5 kernel,36 Filters, 2x2 stride, relu activation |
| Convolution 3 | 5x5 kernel,48 Filters, 2x2 stride, relu activation |
| Convolution 4 | 3x3 kernel,64 Filters, relu activation |
| Convolution 5 | 3x3 kernel,64 Filters, relu activation |
| Max pooling | 2x2 stride |
| Flatten | |
| Dense 1 | Outputs 100, relu activation |
| dropout | prob=0.5 |
| Dense 2 | Outputs 50, relu activation |
| dropout | prob=0.5 |
| Dense 3 | Outputs 10, relu activation |
| dropout | prob=0.5 |
| Dense 4 | Outputs 1, relu activation |
#### 3. Creation of the Training Set & Training Process
To capture good driving behavior, I first recorded two laps on track one using center lane driving. Here is an example image of center lane driving:
![alt text][image2]
I then recorded the vehicle recovering from the left side and right sides of the road back to center so that the vehicle would learn to go back to center if it is going out of the track.
Then I repeated this process on track two in order to get more data points.
To augment the data set, I also flipped images horizontally(code lines 41-47) and angles thinking that this would help the model generalize better while taking turns. For example, here is an image that has then been flipped:
![alt text][image3]
![alt text][image4]
Also, while reading the images I have converted them to RGB space since cv2.imread() reads images in BGR space and drive.py uses RGB images.
After the collection process, I had 42000 number of data points. I then preprocessed this data by cropping(code line 56) 50 pixels on the top, 20 pixels on the bottom and 10 pixels on the right in order to remove unwanted data from the images. I have used keras Cropping2D function to crop the images while training.
Then, I normalized the data using keras Lambda function(Code line 57).
I finally randomly shuffled the data set and put 20% of the data into a validation set.
I used this training data for training the model. The validation set helped determine if the model was over or under fitting. First I have trained the model for 5 epochs and saw that loss is still decreasing so I saved the weights and used them again while re traing the model and now I have used 20 epochs and observed that training loss and validation loss settled. I used an adam optimizer and used a keras callback fucntion LearningRateScheduler to use decaying leraning rate while training(code line 10 & 77) .
Below I have provided the Learning curves of my model.
![alt text][image5]
![alt text][image6]
|
github_jupyter
|
python drive.py model.h5
| 0.466603 | 0.991472 |
# Atividade 2: kNN Experiments
1. Volte ao notebook da prática anterior e divida a base em treinamento e testes
2. Crie um classificador kNN escolhendo um k que você deseje
3. Treine com todas as características numéricas 'escalonadas'
4. Faça a predição na base de testes
5. Avalie a qualidade do seu modelo de acordo com a quantidade de acertos e erros da predição quando comparada ao valor real - dê este valor como um percentual
6. Descubra o melhor valor de 'k' executando várias vezes os passos 3 a 6 com diferentes valores possíveis de 'k' e optando pela melhor avaliação.
### 1. Volte ao notebook da prática anterior e divida a base em treinamento e testes
**Carregue a base de dados Titanic do Kaggle (train) no Jupyter em um DataFrame**
```
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
df = pd.read_csv('../data/titanic/train.csv')
```
**Carregue, explore e visualize os dados através de gráficos**
```
df.info()
df.head()
df.describe()
# Visualize null fields
sns.heatmap(df.isnull(),
yticklabels=False,
cbar=False,
cmap='viridis')
# Explore correlation Sex Pclass and Survived
sns.countplot(x='Survived',
hue='Sex',
data=df,
palette='RdBu_r')
# Explore correlation between Pclass and Survived
sns.countplot(x='Pclass',
hue='Survived',
data=df,
palette='RdBu_r')
# Explore correlation between Parch and Survived
sns.countplot(x='Parch',
hue='Survived',
data=df,
palette='RdBu_r')
# Explore correlation between SibSp and Survived
sns.countplot(x='SibSp',
hue='Survived',
data=df,
palette='RdBu_r')
sns.boxplot(x='Pclass',
y='Age',
data=df,
palette='winter')
```
**Remova as colunas que não agregam valor e justifique**
- **Name**: valor agregado de 'Name' pode ser alcançado com 'Pclass', 'Fare', entre outros.
- **Cabin'**: muitos valores nulos e valor agregado de 'Cabin' pode ser alcançado com 'Pclass', 'Fare', entre outros.
- **PassengerId** e **Ticket**: identificadores únicos
```
cols = ['Name','Ticket','Cabin', 'PassengerId']
df = df.drop(cols, axis=1)
df.head()
```
**Trate valores nulos por coluna ou remova as linhas com dados nulos**
**Pegar valores únicos de cada coluna p/ usar no tratamento dos dados.**
```
pclass_vals = df.Pclass.unique().tolist()
sex_vals = df.Sex.unique().tolist()
```
**`Age`: preencher valores nulos baseado em `Pclass` e `Sex`.**
```
for sex in sex_vals:
for pclass in pclass_vals:
median_age = df.loc[(df.Sex == sex) & (df.Pclass == pclass) & (~df.Age.isnull())].Age.median()
df.loc[(df.Sex == sex) & (df.Pclass == pclass) & (df.Age.isnull()), ['Age']] = median_age
```
**`Embarked`: preencher valores nulos baseado na `moda`.**
```
embarked_mode = df.Embarked.dropna().mode()[0]
df.Embarked = df.Embarked.fillna(embarked_mode)
```
**Substitua colunas literais por valores numéricos**
**Transformar os valores de `Pclass`, `Sex` e `Embarked` em numéricos.**
```
dummies = []
literal_cols = ['Pclass','Sex','Embarked']
for col in literal_cols:
dummies.append(pd.get_dummies(df[col], drop_first=True))
titanic_dummies = pd.concat(dummies, axis=1)
titanic_dummies.head()
df = pd.concat((df, titanic_dummies), axis=1)
df.head()
```
**Normalize os valores numéricos que não são binários**
```
from sklearn.preprocessing import StandardScaler
def normalizer(column_list):
scaler = StandardScaler()
for column in column_list:
df[f'{column}_Scaled'] = StandardScaler().fit_transform(df[[column]])
normalizer(['Age', 'Fare'])
df
```
**Remova as colunas literais restantes**
```
drop_cols = ['Pclass','Sex','Embarked', 'Age', 'Fare']
df = df.drop(drop_cols, axis=1)
df
```
**Divida a base em treinamento e testes**
```
from sklearn.model_selection import train_test_split
y = df['Survived']
X = df.drop(['Survived'], axis=1)
# split train and test datasets into 20% and 80%, respectively
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=0.2,
random_state=42)
```
### 2. Crie um classificador kNN escolhendo um k que você deseje
```
from sklearn.neighbors import KNeighborsClassifier
knn_classifier = KNeighborsClassifier(n_neighbors=10)
```
### 3. Treine com todas as características numéricas 'escalonadas'
```
knn_classifier.fit(X_train, y_train)
```
### 4. Faça a predição na base de testes
```
y_pred = knn_classifier.predict(X_test)
y_pred
```
### 5. Avalie a qualidade do seu modelo de acordo com a quantidade de acertos e erros da predição quando comparada ao valor real - dê este valor como um percentual
```
from sklearn.metrics import confusion_matrix, classification_report
import numpy as np
accuracy = np.sum((y_pred == y_test) / len(y_pred))
print("\nAccuracy: ", accuracy * 100, "%")
print("\nConfusion Matrix:")
print(confusion_matrix(y_test, y_pred))
print("\nClassification Report:")
print(classification_report(y_test, y_pred))
```
### 6. Descubra o melhor valor de `k` executando várias vezes os passos 3 a 6 com diferentes valores possíveis de 'k' e optando pela melhor avaliação.
```
results = {}
for n in range(1,300):
model = KNeighborsClassifier(n_neighbors=n)
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
result = np.sum((y_pred == y_train) / len(y_pred))
results[n] = result
best_k = max(results, key=results.get)
print("Best 'accuracy' was achieved with 'n_neighbors=", best_k,"': ", results[best_k])
```
**Predição na base de testes**
```
from sklearn.neighbors import KNeighborsClassifier
knn_classifier_best_k = KNeighborsClassifier(n_neighbors=best_k)
knn_classifier_best_k.fit(X_train, y_train)
y_pred_best_k = knn_classifier_best_k.predict(X_test)
y_pred_best_k
```
**Avaliação da qualidade do seu modelo de acordo com a quantidade de acertos e erros da predição quando comparada ao valor real - dê este valor como um percentual**
```
from sklearn.metrics import confusion_matrix, classification_report
import numpy as np
accuracy = np.sum((y_pred_best_k == y_test) / len(y_pred_best_k))
print("\nAccuracy: ", accuracy * 100, "%")
print("\nConfusion Matrix:")
print(confusion_matrix(y_test, y_pred_best_k))
print("\nClassification Report:")
print(classification_report(y_test, y_pred_best_k))
```
|
github_jupyter
|
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
df = pd.read_csv('../data/titanic/train.csv')
df.info()
df.head()
df.describe()
# Visualize null fields
sns.heatmap(df.isnull(),
yticklabels=False,
cbar=False,
cmap='viridis')
# Explore correlation Sex Pclass and Survived
sns.countplot(x='Survived',
hue='Sex',
data=df,
palette='RdBu_r')
# Explore correlation between Pclass and Survived
sns.countplot(x='Pclass',
hue='Survived',
data=df,
palette='RdBu_r')
# Explore correlation between Parch and Survived
sns.countplot(x='Parch',
hue='Survived',
data=df,
palette='RdBu_r')
# Explore correlation between SibSp and Survived
sns.countplot(x='SibSp',
hue='Survived',
data=df,
palette='RdBu_r')
sns.boxplot(x='Pclass',
y='Age',
data=df,
palette='winter')
cols = ['Name','Ticket','Cabin', 'PassengerId']
df = df.drop(cols, axis=1)
df.head()
pclass_vals = df.Pclass.unique().tolist()
sex_vals = df.Sex.unique().tolist()
for sex in sex_vals:
for pclass in pclass_vals:
median_age = df.loc[(df.Sex == sex) & (df.Pclass == pclass) & (~df.Age.isnull())].Age.median()
df.loc[(df.Sex == sex) & (df.Pclass == pclass) & (df.Age.isnull()), ['Age']] = median_age
embarked_mode = df.Embarked.dropna().mode()[0]
df.Embarked = df.Embarked.fillna(embarked_mode)
dummies = []
literal_cols = ['Pclass','Sex','Embarked']
for col in literal_cols:
dummies.append(pd.get_dummies(df[col], drop_first=True))
titanic_dummies = pd.concat(dummies, axis=1)
titanic_dummies.head()
df = pd.concat((df, titanic_dummies), axis=1)
df.head()
from sklearn.preprocessing import StandardScaler
def normalizer(column_list):
scaler = StandardScaler()
for column in column_list:
df[f'{column}_Scaled'] = StandardScaler().fit_transform(df[[column]])
normalizer(['Age', 'Fare'])
df
drop_cols = ['Pclass','Sex','Embarked', 'Age', 'Fare']
df = df.drop(drop_cols, axis=1)
df
from sklearn.model_selection import train_test_split
y = df['Survived']
X = df.drop(['Survived'], axis=1)
# split train and test datasets into 20% and 80%, respectively
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=0.2,
random_state=42)
from sklearn.neighbors import KNeighborsClassifier
knn_classifier = KNeighborsClassifier(n_neighbors=10)
knn_classifier.fit(X_train, y_train)
y_pred = knn_classifier.predict(X_test)
y_pred
from sklearn.metrics import confusion_matrix, classification_report
import numpy as np
accuracy = np.sum((y_pred == y_test) / len(y_pred))
print("\nAccuracy: ", accuracy * 100, "%")
print("\nConfusion Matrix:")
print(confusion_matrix(y_test, y_pred))
print("\nClassification Report:")
print(classification_report(y_test, y_pred))
results = {}
for n in range(1,300):
model = KNeighborsClassifier(n_neighbors=n)
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
result = np.sum((y_pred == y_train) / len(y_pred))
results[n] = result
best_k = max(results, key=results.get)
print("Best 'accuracy' was achieved with 'n_neighbors=", best_k,"': ", results[best_k])
from sklearn.neighbors import KNeighborsClassifier
knn_classifier_best_k = KNeighborsClassifier(n_neighbors=best_k)
knn_classifier_best_k.fit(X_train, y_train)
y_pred_best_k = knn_classifier_best_k.predict(X_test)
y_pred_best_k
from sklearn.metrics import confusion_matrix, classification_report
import numpy as np
accuracy = np.sum((y_pred_best_k == y_test) / len(y_pred_best_k))
print("\nAccuracy: ", accuracy * 100, "%")
print("\nConfusion Matrix:")
print(confusion_matrix(y_test, y_pred_best_k))
print("\nClassification Report:")
print(classification_report(y_test, y_pred_best_k))
| 0.398875 | 0.946597 |
#Semantic Search
## Case Study: Transform idle FAQ to Question Answering Model
```
!pip install sentence-transformers
import pandas as pd
import sklearn
import numpy as np
```
https://www.wwf.org.uk/
World Wide Fund for Nature
Non-governmental organization
```
wwf_faq=["I haven’t received my adoption pack. What should I do?",
"How quickly will I receive my adoption pack?",
"How can I renew my adoption?",
"How do I change my address or other contact details?",
"Can I adopt an animal if I don’t live in the UK?",
"If I adopt an animal, will I be the only person who adopts that animal?",
"My pack doesn't contain a certicate",
"My adoption is a gift but won’t arrive on time. What can I do?",
"Can I pay for an adoption with a one-off payment?",
"Can I change the delivery address for my adoption pack after I’ve placed my order?",
"How long will my adoption last for?",
"How often will I receive updates about my adopted animal?",
"What animals do you have for adoption?",
"How can I nd out more information about my adopted animal?",
"How is my adoption money spent?",
"What is your refund policy?",
"An error has been made with my Direct Debit payment, can I receive a refund?",
"How do I change how you contact me?"]
from sentence_transformers import SentenceTransformer
model = SentenceTransformer("quora-distilbert-base")
faq_embeddings = model.encode(wwf_faq)
test_questions=["What should be done, if the adoption pack did not reach to me?",
" How fast is my adoption pack delivered to me?",
"What should I do to renew my adoption?",
"What should be done to change adress and contact details ?",
"I live outside of the UK, Can I still adopt an animal?"]
test_q_emb= model.encode(test_questions)
from scipy.spatial.distance import cdist
for q, qe in zip(test_questions, test_q_emb):
distances = cdist([qe], faq_embeddings, "cosine")[0]
ind = np.argsort(distances, axis=0)[:3]
print("\n Test Question: \n "+q)
for i,(dis,text) in enumerate(zip(distances[ind], [wwf_faq[i] for i in ind])):
print(dis,ind[i],text, sep="\t")
def get_best(query, K=3):
query_embedding = model.encode([query])
distances = cdist(query_embedding, faq_embeddings, "cosine")[0]
ind = np.argsort(distances, axis=0)
print("\n"+query)
for c,i in list(zip(distances[ind], ind))[:K]:
print(c,wwf_faq[i], sep="\t")
get_best("How do I change my contact info?",3)
get_best("How do I get my plane ticket if I bought it online?")
```
|
github_jupyter
|
!pip install sentence-transformers
import pandas as pd
import sklearn
import numpy as np
wwf_faq=["I haven’t received my adoption pack. What should I do?",
"How quickly will I receive my adoption pack?",
"How can I renew my adoption?",
"How do I change my address or other contact details?",
"Can I adopt an animal if I don’t live in the UK?",
"If I adopt an animal, will I be the only person who adopts that animal?",
"My pack doesn't contain a certicate",
"My adoption is a gift but won’t arrive on time. What can I do?",
"Can I pay for an adoption with a one-off payment?",
"Can I change the delivery address for my adoption pack after I’ve placed my order?",
"How long will my adoption last for?",
"How often will I receive updates about my adopted animal?",
"What animals do you have for adoption?",
"How can I nd out more information about my adopted animal?",
"How is my adoption money spent?",
"What is your refund policy?",
"An error has been made with my Direct Debit payment, can I receive a refund?",
"How do I change how you contact me?"]
from sentence_transformers import SentenceTransformer
model = SentenceTransformer("quora-distilbert-base")
faq_embeddings = model.encode(wwf_faq)
test_questions=["What should be done, if the adoption pack did not reach to me?",
" How fast is my adoption pack delivered to me?",
"What should I do to renew my adoption?",
"What should be done to change adress and contact details ?",
"I live outside of the UK, Can I still adopt an animal?"]
test_q_emb= model.encode(test_questions)
from scipy.spatial.distance import cdist
for q, qe in zip(test_questions, test_q_emb):
distances = cdist([qe], faq_embeddings, "cosine")[0]
ind = np.argsort(distances, axis=0)[:3]
print("\n Test Question: \n "+q)
for i,(dis,text) in enumerate(zip(distances[ind], [wwf_faq[i] for i in ind])):
print(dis,ind[i],text, sep="\t")
def get_best(query, K=3):
query_embedding = model.encode([query])
distances = cdist(query_embedding, faq_embeddings, "cosine")[0]
ind = np.argsort(distances, axis=0)
print("\n"+query)
for c,i in list(zip(distances[ind], ind))[:K]:
print(c,wwf_faq[i], sep="\t")
get_best("How do I change my contact info?",3)
get_best("How do I get my plane ticket if I bought it online?")
| 0.235021 | 0.747086 |
```
import importlib
from matplotlib import pyplot as plt
plt.plot([1,2,3])
from IPython.display import clear_output
import matplotlib
import numpy as np
import pandas as pd
import pdb
import time
from collections import deque, namedtuple
import torch
import cv2
from Environment.Env_new import RealExpEnv
from RL.sac import sac_agent, ReplayMemory, HerReplayMemory
from Environment.data_visualization import plot_graph, show_reset, show_done, show_step
from Environment.episode_memory import Episode_Memory
from Environment.get_atom_coordinate import atom_detection, blob_detection, get_atom_coordinate_nm
from skimage import morphology, measure
from Environment.createc_control import Createc_Controller
import glob
from collections import deque
matplotlib.rcParams['image.cmap'] = 'gray'
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print(device)
import Environment.data_visualization
importlib.reload(Environment.data_visualization)
from Environment.data_visualization import plot_graph, show_reset, show_done, show_step
import Environment.Env_new
importlib.reload(Environment.Env_new)
from Environment.Env_new import RealExpEnv
import RL.sac
importlib.reload(RL.sac)
from RL.sac import sac_agent, ReplayMemory, HerReplayMemory
# run this if want to reset env but keep the memory
import copy
amd_accuracy = copy.copy(env.accuracy)
print(amd_accuracy)
amd_true_positive = copy.copy(env.true_positive)
print(amd_true_positive)
amd_true_negative = copy.copy(env.true_negative)
print(amd_true_negative)
amd = copy.copy(env.atom_move_detector)
createc_controller = Createc_Controller(None, None, None, None)
img_forward = np.array(createc_controller.stm.scandata(1,4))
print(img_forward.shape)
top_left, w, h = (5,3), 3, 3
template = img_forward[top_left[1]:top_left[1]+h, top_left[0]:top_left[0]+w]
plt.imshow(template)
step_nm = 0.4
max_mvolt = 15 #min_mvolt = 0.5*max_mvolt
max_pcurrent_to_mvolt_ratio = 6E3 # min = 0.5*max
goal_nm = 2
current_jump = 4
pixel = 128
im_size_nm = 6
x_nm, y_nm = createc_controller.get_offset_nm()
offset_nm = np.array([x_nm, y_nm])
manip_limit_nm = np.array([x_nm - 0.5*im_size_nm+0.5, x_nm + 0.5*im_size_nm-0.5, y_nm+0.5, y_nm+im_size_nm-0.5]) #[left, right, up, down]
template_max_y = 3
scan_mV = 1000
max_len = 5
pull_back_mV = 10
pull_back_pA = 57000
env = RealExpEnv(step_nm, max_mvolt, max_pcurrent_to_mvolt_ratio, goal_nm,
template, current_jump, im_size_nm, offset_nm, manip_limit_nm, pixel,
template_max_y, scan_mV, max_len,
'C:/LocalUserData/User-data/phys-asp-lab/auto_manipulation/training_Ag/_atom_move_detector_conv.pth',
bottom=False, random_scan_rate = 0.9, pull_back_mV = pull_back_mV,
pull_back_pA = pull_back_pA)
# run this if want to reset env but keep the memory
env.accuracy = amd_accuracy
env.true_positive = amd_true_positive
env.true_negative = amd_true_negative
env.atom_move_detector = amd
print(len(memory))
memory = HerReplayMemory(replay_size, env, strategy = 'future')
a_4, a_5 = [], []
for i, np_name in enumerate(glob.glob(folder_name+'/*.npy')):
data = np.load(np_name,allow_pickle=True).item()
transitions = data['transitions']
for s, a, r, n, d, info in zip(transitions['state'], transitions['action'], transitions['reward'],
transitions['next_state'], transitions['done'], transitions['info']):
a_4.append(a[4])
a_5.append(a[5])
mask = float(not d)
memory.push(s, a, r, n, mask)
print(len(memory))
plt.hist(a_5)
plt.hist(a_4)
# run this if want to reset env but keep the memory
buffer = memory.buffer
memory = HerReplayMemory(replay_size, env)
memory.buffer = buffer
print(len(memory))
# ONLY RE-RUN if WANT TO RESET the AGENT
batch_size= 64
LEARNING_RATE = 0.0003
replay_size=1000000
i_episode = 1320
ACTION_SPACE = namedtuple('ACTION_SPACE', ['high', 'low'])
action_space = ACTION_SPACE(high = torch.tensor([1,1,1,1,1,1]), low = torch.tensor([-1,-1,-1,-1,1/3,1/2]))
alpha = torch.load('{}/_alpha_{}.pth'.format(folder_name,i_episode)).item()
print(alpha)
agent = sac_agent(num_inputs = 4, num_actions = 6, action_space = action_space, device=device, hidden_size=256, lr=LEARNING_RATE,
gamma=0.9, tau=0.005, alpha=alpha)
agent.critic.load_state_dict(torch.load('{}/_critic_{}.pth'.format(folder_name,i_episode)))
agent.policy.load_state_dict(torch.load('{}/_policy_{}.pth'.format(folder_name,i_episode)))
memory = HerReplayMemory(replay_size, env, strategy = 'future')
print(agent.alpha)
episode_memory = Episode_Memory()
folder_name = 'C:/LocalUserData/User-data/phys-asp-lab/auto_manipulation/training_Ag'
episode_rewards, alphas, precisions, episode_lengths = [], [], [], []
avg_episode_rewards, avg_alphas, avg_precisions, avg_episode_lengths = [], [], [], []
c_k_min = 2500
eta_0 = 0.996
eta_T = 1.0
n_interactions = 500
max_ep_len = max_len
eta = 0.997
def sac_train(max_steps, num_episodes = 50, episode_start = 0):
for i_episode in range(episode_start,episode_start+num_episodes):
print('Episode:', i_episode)
eta_t = np.minimum(eta_0 + (eta_T - eta_0)*(i_episode/n_interactions), eta_T)
episode_reward, episode_steps = 0, 0
done = False
state, info = env.reset(update_conv_net=True)
show_reset(env.img_info, env.atom_start_absolute_nm, env.destination_absolute_nm,
env.template_nm, env.template_wh)
episode_memory.update_memory_reset(env.img_info, i_episode, info)
for step in range(max_steps):
print('step:', step)
action = agent.select_action(state)
old_atom_nm = env.atom_absolute_nm
next_state, reward, done, info = env.step(action)
print('reward', reward)
episode_steps+=1
episode_reward+=reward
mask = float(not done)
memory.push(state,action,reward,next_state,mask)
episode_memory.update_memory_step(state, action, next_state, reward, done, info)
show_step(env.img_info, info['start_nm']+old_atom_nm, info['end_nm']+old_atom_nm,
env.atom_absolute_nm, env.atom_start_absolute_nm,
env.destination_absolute_nm, action[4]*env.max_mvolt,
action[5]*env.max_pcurrent_to_mvolt_ratio*action[4]*env.max_mvolt,
env.template_nm, env.template_wh)
_, size= blob_detection(env.img_info['img_forward'])
print('atom size:', size)
print('Precision:', env.dist_destination)
if done:
episode_memory.update_memory_done(env.img_info, env.atom_absolute_nm, env.atom_relative_nm)
episode_memory.save_memory(folder_name)
atom_to_start = env.atom_relative_nm - env.atom_start_relative_nm
print('Episode reward:', episode_reward)
'''show_done(env.img_info, env.atom_absolute_nm, env.atom_start_absolute_nm,
env.destination_absolute_nm, reward, env.template_nm, env.template_wh)'''
break
else:
state=next_state
if (len(memory)>batch_size):
episode_K = int(episode_steps)
for k in range(episode_K):
#c_k = max(int(memory.__len__()*eta_t**(k*(max_ep_len/episode_K))), c_k_min)
c_k = memory.__len__()
#print('TRAINING!')
#c_k = max(int(memory.__len__()*eta**(k*(1000/episode_K))), 500)
print(c_k)
agent.update_parameters(memory, batch_size, c_k)
episode_rewards.append(episode_reward)
alphas.append(agent.alpha.item())
precisions.append(env.dist_destination)
episode_lengths.append(episode_steps)
avg_episode_rewards.append(np.mean(episode_rewards[-min(100,len(episode_rewards)):]))
avg_alphas.append(np.mean(alphas[-min(100, len(alphas)):]))
avg_precisions.append(np.mean(precisions[-min(100, len(precisions)):]))
avg_episode_lengths.append(np.mean(episode_lengths[-min(100, len(episode_lengths)):]))
print('Average precision:',avg_precisions[-1])
if avg_precisions[-1]<0.144:
env.createc_controller.pixel = 256
if (i_episode+1)%2==0:
plot_graph(episode_rewards, precisions, alphas, episode_lengths,
avg_episode_rewards, avg_alphas, avg_precisions, avg_episode_lengths)
if (i_episode)%20 == 0:
torch.save(agent.critic.state_dict(), '{}/_critic_{}.pth'.format(folder_name,i_episode))
torch.save(agent.policy.state_dict(), '{}/_policy_{}.pth'.format(folder_name,i_episode))
torch.save(agent.alpha, '{}/_alpha_{}.pth'.format(folder_name,i_episode))
sac_train(max_steps=max_len, episode_start = 1751,num_episodes = 1000)
```
episode 460: experiment stops for work on the setup, tip could change
episode 602: experiment stops for building, tip could change
episode 620: cluster, tip could change
episode 640: tip forming
episode 1338: likely drastic tip change
episode 1420: likely drastic tip change
episode 1463: likely drastic tip change
```
torch.save(env.atom_move_detector.conv.state_dict(), '{}/_atom_move_detector_conv.pth'.format(folder_name))
env.atom_absolute_nm = None
```
|
github_jupyter
|
import importlib
from matplotlib import pyplot as plt
plt.plot([1,2,3])
from IPython.display import clear_output
import matplotlib
import numpy as np
import pandas as pd
import pdb
import time
from collections import deque, namedtuple
import torch
import cv2
from Environment.Env_new import RealExpEnv
from RL.sac import sac_agent, ReplayMemory, HerReplayMemory
from Environment.data_visualization import plot_graph, show_reset, show_done, show_step
from Environment.episode_memory import Episode_Memory
from Environment.get_atom_coordinate import atom_detection, blob_detection, get_atom_coordinate_nm
from skimage import morphology, measure
from Environment.createc_control import Createc_Controller
import glob
from collections import deque
matplotlib.rcParams['image.cmap'] = 'gray'
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print(device)
import Environment.data_visualization
importlib.reload(Environment.data_visualization)
from Environment.data_visualization import plot_graph, show_reset, show_done, show_step
import Environment.Env_new
importlib.reload(Environment.Env_new)
from Environment.Env_new import RealExpEnv
import RL.sac
importlib.reload(RL.sac)
from RL.sac import sac_agent, ReplayMemory, HerReplayMemory
# run this if want to reset env but keep the memory
import copy
amd_accuracy = copy.copy(env.accuracy)
print(amd_accuracy)
amd_true_positive = copy.copy(env.true_positive)
print(amd_true_positive)
amd_true_negative = copy.copy(env.true_negative)
print(amd_true_negative)
amd = copy.copy(env.atom_move_detector)
createc_controller = Createc_Controller(None, None, None, None)
img_forward = np.array(createc_controller.stm.scandata(1,4))
print(img_forward.shape)
top_left, w, h = (5,3), 3, 3
template = img_forward[top_left[1]:top_left[1]+h, top_left[0]:top_left[0]+w]
plt.imshow(template)
step_nm = 0.4
max_mvolt = 15 #min_mvolt = 0.5*max_mvolt
max_pcurrent_to_mvolt_ratio = 6E3 # min = 0.5*max
goal_nm = 2
current_jump = 4
pixel = 128
im_size_nm = 6
x_nm, y_nm = createc_controller.get_offset_nm()
offset_nm = np.array([x_nm, y_nm])
manip_limit_nm = np.array([x_nm - 0.5*im_size_nm+0.5, x_nm + 0.5*im_size_nm-0.5, y_nm+0.5, y_nm+im_size_nm-0.5]) #[left, right, up, down]
template_max_y = 3
scan_mV = 1000
max_len = 5
pull_back_mV = 10
pull_back_pA = 57000
env = RealExpEnv(step_nm, max_mvolt, max_pcurrent_to_mvolt_ratio, goal_nm,
template, current_jump, im_size_nm, offset_nm, manip_limit_nm, pixel,
template_max_y, scan_mV, max_len,
'C:/LocalUserData/User-data/phys-asp-lab/auto_manipulation/training_Ag/_atom_move_detector_conv.pth',
bottom=False, random_scan_rate = 0.9, pull_back_mV = pull_back_mV,
pull_back_pA = pull_back_pA)
# run this if want to reset env but keep the memory
env.accuracy = amd_accuracy
env.true_positive = amd_true_positive
env.true_negative = amd_true_negative
env.atom_move_detector = amd
print(len(memory))
memory = HerReplayMemory(replay_size, env, strategy = 'future')
a_4, a_5 = [], []
for i, np_name in enumerate(glob.glob(folder_name+'/*.npy')):
data = np.load(np_name,allow_pickle=True).item()
transitions = data['transitions']
for s, a, r, n, d, info in zip(transitions['state'], transitions['action'], transitions['reward'],
transitions['next_state'], transitions['done'], transitions['info']):
a_4.append(a[4])
a_5.append(a[5])
mask = float(not d)
memory.push(s, a, r, n, mask)
print(len(memory))
plt.hist(a_5)
plt.hist(a_4)
# run this if want to reset env but keep the memory
buffer = memory.buffer
memory = HerReplayMemory(replay_size, env)
memory.buffer = buffer
print(len(memory))
# ONLY RE-RUN if WANT TO RESET the AGENT
batch_size= 64
LEARNING_RATE = 0.0003
replay_size=1000000
i_episode = 1320
ACTION_SPACE = namedtuple('ACTION_SPACE', ['high', 'low'])
action_space = ACTION_SPACE(high = torch.tensor([1,1,1,1,1,1]), low = torch.tensor([-1,-1,-1,-1,1/3,1/2]))
alpha = torch.load('{}/_alpha_{}.pth'.format(folder_name,i_episode)).item()
print(alpha)
agent = sac_agent(num_inputs = 4, num_actions = 6, action_space = action_space, device=device, hidden_size=256, lr=LEARNING_RATE,
gamma=0.9, tau=0.005, alpha=alpha)
agent.critic.load_state_dict(torch.load('{}/_critic_{}.pth'.format(folder_name,i_episode)))
agent.policy.load_state_dict(torch.load('{}/_policy_{}.pth'.format(folder_name,i_episode)))
memory = HerReplayMemory(replay_size, env, strategy = 'future')
print(agent.alpha)
episode_memory = Episode_Memory()
folder_name = 'C:/LocalUserData/User-data/phys-asp-lab/auto_manipulation/training_Ag'
episode_rewards, alphas, precisions, episode_lengths = [], [], [], []
avg_episode_rewards, avg_alphas, avg_precisions, avg_episode_lengths = [], [], [], []
c_k_min = 2500
eta_0 = 0.996
eta_T = 1.0
n_interactions = 500
max_ep_len = max_len
eta = 0.997
def sac_train(max_steps, num_episodes = 50, episode_start = 0):
for i_episode in range(episode_start,episode_start+num_episodes):
print('Episode:', i_episode)
eta_t = np.minimum(eta_0 + (eta_T - eta_0)*(i_episode/n_interactions), eta_T)
episode_reward, episode_steps = 0, 0
done = False
state, info = env.reset(update_conv_net=True)
show_reset(env.img_info, env.atom_start_absolute_nm, env.destination_absolute_nm,
env.template_nm, env.template_wh)
episode_memory.update_memory_reset(env.img_info, i_episode, info)
for step in range(max_steps):
print('step:', step)
action = agent.select_action(state)
old_atom_nm = env.atom_absolute_nm
next_state, reward, done, info = env.step(action)
print('reward', reward)
episode_steps+=1
episode_reward+=reward
mask = float(not done)
memory.push(state,action,reward,next_state,mask)
episode_memory.update_memory_step(state, action, next_state, reward, done, info)
show_step(env.img_info, info['start_nm']+old_atom_nm, info['end_nm']+old_atom_nm,
env.atom_absolute_nm, env.atom_start_absolute_nm,
env.destination_absolute_nm, action[4]*env.max_mvolt,
action[5]*env.max_pcurrent_to_mvolt_ratio*action[4]*env.max_mvolt,
env.template_nm, env.template_wh)
_, size= blob_detection(env.img_info['img_forward'])
print('atom size:', size)
print('Precision:', env.dist_destination)
if done:
episode_memory.update_memory_done(env.img_info, env.atom_absolute_nm, env.atom_relative_nm)
episode_memory.save_memory(folder_name)
atom_to_start = env.atom_relative_nm - env.atom_start_relative_nm
print('Episode reward:', episode_reward)
'''show_done(env.img_info, env.atom_absolute_nm, env.atom_start_absolute_nm,
env.destination_absolute_nm, reward, env.template_nm, env.template_wh)'''
break
else:
state=next_state
if (len(memory)>batch_size):
episode_K = int(episode_steps)
for k in range(episode_K):
#c_k = max(int(memory.__len__()*eta_t**(k*(max_ep_len/episode_K))), c_k_min)
c_k = memory.__len__()
#print('TRAINING!')
#c_k = max(int(memory.__len__()*eta**(k*(1000/episode_K))), 500)
print(c_k)
agent.update_parameters(memory, batch_size, c_k)
episode_rewards.append(episode_reward)
alphas.append(agent.alpha.item())
precisions.append(env.dist_destination)
episode_lengths.append(episode_steps)
avg_episode_rewards.append(np.mean(episode_rewards[-min(100,len(episode_rewards)):]))
avg_alphas.append(np.mean(alphas[-min(100, len(alphas)):]))
avg_precisions.append(np.mean(precisions[-min(100, len(precisions)):]))
avg_episode_lengths.append(np.mean(episode_lengths[-min(100, len(episode_lengths)):]))
print('Average precision:',avg_precisions[-1])
if avg_precisions[-1]<0.144:
env.createc_controller.pixel = 256
if (i_episode+1)%2==0:
plot_graph(episode_rewards, precisions, alphas, episode_lengths,
avg_episode_rewards, avg_alphas, avg_precisions, avg_episode_lengths)
if (i_episode)%20 == 0:
torch.save(agent.critic.state_dict(), '{}/_critic_{}.pth'.format(folder_name,i_episode))
torch.save(agent.policy.state_dict(), '{}/_policy_{}.pth'.format(folder_name,i_episode))
torch.save(agent.alpha, '{}/_alpha_{}.pth'.format(folder_name,i_episode))
sac_train(max_steps=max_len, episode_start = 1751,num_episodes = 1000)
torch.save(env.atom_move_detector.conv.state_dict(), '{}/_atom_move_detector_conv.pth'.format(folder_name))
env.atom_absolute_nm = None
| 0.36557 | 0.328341 |
# Proyecto Final Ciencia de Datos e Inteligencia de Negocios

### Integrantes
- Flavio Cesar Palacios Salas
- Andres Gonzales Luna Diaz del Castillo
- Maximiliano Garcia Mora
### Introducción
Actualmente, con los avances en las tecnologías de la información, la
generación de datos de diversos tipos en un solo día tiene volúmenes muy
altos y con tendencia creciente. Con el fin del aprovechamiento de la
información valiosa que pueda estar oculta en los datos que se generan, se
requieren de tener conocimientos básicos de manejo de información y de
análisis exploratorio de datos.
De forma general, a menos que la persona sea una experta en el fenómeno en
el cual se están generando los datos, el ingeniero que se disponga al análisis
de los datos generados debe de realizar un análisis exploratorio para rescatar
las características básicas que poseen los datos. Además de realizar un
agrupamiento de los mismos datos en base a una característica de interés.
### Objetivo:
El objetivo de este proyecto de aplicación se puede separar en tres
fases:
1.- La limpieza y extracción de la información estadística básica que
tienen los datos que se están analizando.
2.- Realización de un agrupamiento (“Clustering”) de los datos en
base a una característica de interés.
3.- La obtención o formulación de conclusiones sobre el fenómeno del
cual provienen los datos en base a los resultados de los análisis
anteriores
### Actividades
>**1** Obtención de una base de datos que fuera generada por un
fenómeno de interés (La orientación o tema de los datos será
especificada para cada equipo por el profesor).
**2** Aplicar el estudio de calidad de los datos para determinar el tipo
de datos, categorías e información estadística básica.
**3** Realizar una limpieza de datos y obtener un análisis exploratorio
de datos (EDA) donde se muestren gráficas y conclusiones acerca del
análisis. Al menos obtener 5 insights.
**4** En base al estudio anterior, realizar un análisis de similitud entre
variables y entre muestras disponibles en su base de datos.
**5** Crear agrupamientos o “clusters” basados en el algoritmo
“hierarchical clustering” ó “Kmeans”, y presentar sus resultados (si
los datos lo permiten).
**6** Basados en los análisis anteriores, formular conclusiones sobre la
información importante que se haya logrado encontrar de los datos
analizados.
### Importación de librerías
```
import numpy as np
import pandas as pd
from CDIN import CDIN as cd
```
### Bases de datos
```
data2017 = pd.read_csv('../Data/incidentes-viales-c5-2017.csv')
data2018 = pd.read_csv('../Data/incidentes-viales-c5-2018.csv')
data2019 = pd.read_csv('../Data/incidentes-viales-c5-2019.csv')
```
### Data Quality Report
```
dqr2017 = cd.dqr(data2017)
dqr2017
dqr2018 = cd.dqr(data2018)
dqr2018
dqr2019 = cd.dqr(data2019)
dqr2019
dqr2017.index.to_list() == dqr2018.index.to_list() == dqr2019.index.to_list()
dqr2017['Present_values'][0]+dqr2018['Present_values'][0]+dqr2019['Present_values'][0]
```
Se puede comprobar que los datos de todos los años contienen las mismas columnas y que se pueden usar indistintamente
los datos o inclusive se pueden combinar las tablas, una de las ventajas de los datos es que en la mayoría de estos hay apenas una pequeña cantidad de datos perdidos, alrededor de 500 lo que facilitará el analisis además de que se cuentan con aproximadamente 680,000 datos
### EDA Exploratory Data Analysis
```
# unir data sets
data = pd.concat([data2017,data2018, data2019])
#quitar datos faltantes (los datos faltantes eran muy pocos comparados con el tamaño del data frame, por lo que los eliminé)
data = data.dropna()
#1.- Numero de accdientes por dia de la semana (dia_semana)
insight1 = (data['dia_semana'].value_counts())
insight1.plot(kind='bar')
plt.xlabel("Día de la semana", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por día de la semana", y=1.02)
```
Aqui se puede observar, como los días de la semana que más accidentes tiene son el Viernes y el Sábado. Se puede observar como a medida que la semana avanza (comienza en Domingo), la cantidad de accidentes aumenta.
```
#2. - numero de accidentes por tipo de accidente (incidente_c4)
insight5 = (data['incidente_c4'].value_counts())
insight5.plot(kind='bar')
plt.xlabel("Tipo de incidente", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por tipo de accidente", y=1.02)
```
Se puede observar que la gran mayoría de los accidentes son choques sin lesionados. Después sigue accidentes con choque con lesionados, pero la diferencia es bastante grande. Esto significa que la gran mayoría de los choque son choques leves. También hubo bastante atropellados.
```
#3.- numero de accidentes por delegacion (delegacion_inicio)
insight2 = (data['delegacion_inicio'].value_counts())
insight2.plot(kind='bar')
plt.xlabel("Delegación", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por delegación", y=1.02)
```
Aqui podemos observar cuales son las delegaciones con más accidentes. Iztapalapa es el lugar con más accidentes y por mucho.
```
#4.- numero de accidentes por tipo de entrada (tipo_entrada)
insight3 = (data['tipo_entrada'].value_counts())
insight3.plot(kind='bar')
plt.xlabel("Tipo de entrada", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por tipo de entrada", y=1.02)
```
El tipo de entrada que se uso para reportar el accidente fue una llamada al 911 por mucho.
```
#5.- numero de accidentes por mes (mes_cierre)
insight4 = (data['mes_cierre'].value_counts())
insight4.plot(kind='bar')
plt.xlabel("Mes", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por mes", y=1.02)
```
El mes en el que más accidentes bubo fue el de Octubre. Sorprendentemente Diciembre fue el mes con menos accidentes. Yo me hubiera imaginado qeu con las posadas y las fiestas, más gente chocaría porque iría tomada.
```
#6.- numero de accidentes por hora (hora_creacion)
data['Hora'] = data['hora_creacion'].str[:2]
i6 = (data['Hora'].value_counts())
i6 = i6.to_frame()
i6 = i6.sort_index()
i6 = i6.replace(to_replace =[17945],
value = 17945+3755)
i6 = i6.replace(to_replace =[13274],
value = 13274+2668)
i6 = i6.replace(to_replace =[9710],
value = 9710+2009)
i6 = i6.replace(to_replace =[8000],
value = 8000+1622)
i6 = i6.replace(to_replace =[7277],
value = 7277+1478)
i6 = i6.replace(to_replace =[8069],
value = 8069+1661)
i6 = i6.replace(to_replace =[12137],
value = 12137+2302)
i6 = i6.replace(to_replace =[17567],
value = 17567+3164)
i6 = i6.replace(to_replace =[21826],
value = 21826+4044)
i6 = i6.replace(to_replace =[22572],
value = 22572+4067)
i6 = i6.drop(["0:","1:",'2:','3:','4:','5:','6:','7:','8:','9:'])
i6 = df.squeeze()
i6.plot(kind='bar')
plt.xlabel("Hora", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por hora", y=1.02)
```
Podemos observar como la mayoría de los accidentes ocurrieron a las 19, 20, 21, 18 y 16 horas. Esto me sorprendío ya que yo esperaba que la mayoría de los accidentes ocurrieran en la madrugada cuando la gente va tomada. Pero no, ocurrieron a las horas en las que la gente va slaiendo del trabajo y hay bastante tráfico.
### Similitud entre los datos
### Clustering
### Conclusiones
|
github_jupyter
|
import numpy as np
import pandas as pd
from CDIN import CDIN as cd
data2017 = pd.read_csv('../Data/incidentes-viales-c5-2017.csv')
data2018 = pd.read_csv('../Data/incidentes-viales-c5-2018.csv')
data2019 = pd.read_csv('../Data/incidentes-viales-c5-2019.csv')
dqr2017 = cd.dqr(data2017)
dqr2017
dqr2018 = cd.dqr(data2018)
dqr2018
dqr2019 = cd.dqr(data2019)
dqr2019
dqr2017.index.to_list() == dqr2018.index.to_list() == dqr2019.index.to_list()
dqr2017['Present_values'][0]+dqr2018['Present_values'][0]+dqr2019['Present_values'][0]
# unir data sets
data = pd.concat([data2017,data2018, data2019])
#quitar datos faltantes (los datos faltantes eran muy pocos comparados con el tamaño del data frame, por lo que los eliminé)
data = data.dropna()
#1.- Numero de accdientes por dia de la semana (dia_semana)
insight1 = (data['dia_semana'].value_counts())
insight1.plot(kind='bar')
plt.xlabel("Día de la semana", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por día de la semana", y=1.02)
#2. - numero de accidentes por tipo de accidente (incidente_c4)
insight5 = (data['incidente_c4'].value_counts())
insight5.plot(kind='bar')
plt.xlabel("Tipo de incidente", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por tipo de accidente", y=1.02)
#3.- numero de accidentes por delegacion (delegacion_inicio)
insight2 = (data['delegacion_inicio'].value_counts())
insight2.plot(kind='bar')
plt.xlabel("Delegación", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por delegación", y=1.02)
#4.- numero de accidentes por tipo de entrada (tipo_entrada)
insight3 = (data['tipo_entrada'].value_counts())
insight3.plot(kind='bar')
plt.xlabel("Tipo de entrada", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por tipo de entrada", y=1.02)
#5.- numero de accidentes por mes (mes_cierre)
insight4 = (data['mes_cierre'].value_counts())
insight4.plot(kind='bar')
plt.xlabel("Mes", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por mes", y=1.02)
#6.- numero de accidentes por hora (hora_creacion)
data['Hora'] = data['hora_creacion'].str[:2]
i6 = (data['Hora'].value_counts())
i6 = i6.to_frame()
i6 = i6.sort_index()
i6 = i6.replace(to_replace =[17945],
value = 17945+3755)
i6 = i6.replace(to_replace =[13274],
value = 13274+2668)
i6 = i6.replace(to_replace =[9710],
value = 9710+2009)
i6 = i6.replace(to_replace =[8000],
value = 8000+1622)
i6 = i6.replace(to_replace =[7277],
value = 7277+1478)
i6 = i6.replace(to_replace =[8069],
value = 8069+1661)
i6 = i6.replace(to_replace =[12137],
value = 12137+2302)
i6 = i6.replace(to_replace =[17567],
value = 17567+3164)
i6 = i6.replace(to_replace =[21826],
value = 21826+4044)
i6 = i6.replace(to_replace =[22572],
value = 22572+4067)
i6 = i6.drop(["0:","1:",'2:','3:','4:','5:','6:','7:','8:','9:'])
i6 = df.squeeze()
i6.plot(kind='bar')
plt.xlabel("Hora", labelpad=14)
plt.ylabel("Cantidad de accidentes", labelpad=14)
plt.title("Cantidad de accidentes por hora", y=1.02)
| 0.136839 | 0.928668 |
## manual data augmentation
Data can be loaded downloaded [here](https://drive.google.com/drive/folders/1yZI5v3ws3b8GZMl_ACe4TO_qebdS2fUz?usp=sharing). The data is contained in the `srp_raw01.zip` and has to be moved to `/data/raw`.
The resulting folder structure looks like this:
`/data/raw/n`, `/data/raw/o` and `/data/raw/x`.
In this notebook the code written to augmentate data is consolidated into a few lines of code.
`src.utils` should not need any further explanation.
The code is basically emulation the behavior of the keras image generator, but also accepts another parameter `repetitions`.
The data is processed into the interim folder applying the modifications before training.
Therefore the manipulations do not take place during training, but a time independent preprocessing phase.
The images are copied to the `interim` directory first.
After the data is fully distributed into `interim`, the data gets augmented "inplace", meaning we only work with the `interim` data and the result is a `interim` directory with all the augmented data (in this case 32000 images per class).
`inline_augment_images` returns a list with dictionaries.
These dictionaries contain all necessary information to create records in the upcoming cell.
The parameters should be self explanatory.
```
import json
import shutil
import os
from os import path
import cv2
import numpy as np
from tqdm import tqdm
def augment_images_by_label(src_dir, target_dir, label_idx, target_size=(None, None),
repetitions=1, h_flip=False, v_flip=False, rotation_range=0, quantity=None):
"""Augments the images labelwise
Arguments:
src_dir: Where the (raw) images are taken from.
target_dir: Where the augmented images are going to be safed.
label: Label to add to the feature_description.
target_size: Size of the output image.
If at least one entry is None, the original size is used.
repetitions: How often should this run over the original dataset?
h_flip: Is it okay if the images are flipped horizontally?
v_flip: Is it okay if the images are flipped vertically?
rotation_range: In what range can the images be rotated (in degrees)?
quantity: How many images should be taken from the original dataset?
None means => all.
"""
data_list = []
filenames = list(filter(lambda x: x[-5:] == '.jpeg', os.listdir(src_dir)))
for filename in filenames[:quantity]:
image_path = path.join(src_dir, filename)
image = cv2.imread(image_path)
if h_flip:
image = cv2.flip(image, 0)
if v_flip:
image = cv2.flip(image, 1)
if None not in target_size:
image = cv2.resize(image, target_size)
angle = np.random.uniform(0.0, rotation_range)
rotmat = cv2.getRotationMatrix2D(tuple(np.divide(image.shape[:2], 2)), angle, 1.0)
image = cv2.warpAffine(image, rotmat, image.shape[:2])
os.makedirs(target_dir, exist_ok=True)
name = str(len(os.listdir(target_dir)))
# the angle should be labeled between [0, 180)
angle = int(abs(h_flip*360-abs(v_flip*180-angle))) % 180
data_list.append({
'image_path': path.join(target_dir, name + '.jpeg'),
'label': [label_idx, angle],
})
cv2.imwrite(data_list[-1]['image_path'], image)
return data_list
def augment_images(src_dir, target_dir, repetitions=1, *args, **kwargs):
"""Augments images in src_dir and saves them to target_dir.
Arguments:
src_dir: Where the (raw) images are taken from.
target_dir: Where the augmented images are going to be safed.
repetitions: How often should this run over the original dataset?
"""
os.makedirs(target_dir, exist_ok=True)
data_list = []
for label_idx, label in enumerate(os.listdir(src_dir)):
actual_src_dir = path.join(src_dir, label)
actual_target_dir = path.join(target_dir, label)
for i in tqdm(range(repetitions)):
data_list += augment_images_by_label(
actual_src_dir, actual_target_dir, label_idx, *args, **kwargs)
np.random.shuffle(data_list)
with open(path.join(target_dir, 'config.json'), 'w') as config:
json.dump(data_list, config)
return data_list
def inline_augment_images(directory, *args, **kwargs):
"""Augments images inplace (source and target directory are the same).
Arguments:
directory: source and target directory.
An intermediate 'directory_tmp' is created.
It is removed after the operation has finished.
"""
tmp = directory + '_tmp'
os.rename(directory, tmp)
data_list = augment_images(tmp, directory, *args, **kwargs)
try:
shutil.rmtree(tmp, ignore_errors=True)
except OSError as e:
print ("Error: %s - %s." % (e.filename, e.strerror))
return data_list
from src.utils import reset_and_distribute_data, encode_image_data_as_record
raw = path.join('data', 'raw')
interim = path.join('data', 'interim')
processed = path.join('data', 'processed')
reset_and_distribute_data(raw, interim, [1000, 100, 100])
shutil.rmtree(processed, ignore_errors=True)
target_size=(32, 32)
train_data_list = inline_augment_images(path.join(interim, 'train'),
repetitions=32, h_flip=True, v_flip=True, rotation_range=360, target_size=target_size)
validate_data_list = inline_augment_images(path.join(interim, 'validate'), target_size=target_size)
test_data_list = inline_augment_images(path.join(interim, 'test'), target_size=target_size)
```
`encode_record` takes the previously described list, which is hardcoded in this instance as:
```python
feature = {
'image': # /path/to/image
'label': # [label_idx, angle]
}
```
These features are then used to create protobufs.
protobufs can be read by Tensorflow very efficient and with no overhead of decoding the data (the decoding takes place during the preprocessing here).
This procedure also gives way more control over how the data is stored. For example the angle in this instance is saved, because maybe in the future it may be interesting to determine the angle of a linear node, where the data is way easier to generate by using only vertical lines (and the randomization is done by the augmentation).
```
labels = os.listdir(raw)
train_record = path.join(processed, 'train.tfrecord')
validate_record = path.join(processed, 'validate.tfrecord')
test_record = path.join(processed, 'test.tfrecord')
encode_image_data_as_record(train_data_list, train_record)
encode_image_data_as_record(validate_data_list, validate_record)
encode_image_data_as_record(test_data_list, test_record)
```
The next step is to create data generators or iterators for the model which can read these tensorflow records.
|
github_jupyter
|
import json
import shutil
import os
from os import path
import cv2
import numpy as np
from tqdm import tqdm
def augment_images_by_label(src_dir, target_dir, label_idx, target_size=(None, None),
repetitions=1, h_flip=False, v_flip=False, rotation_range=0, quantity=None):
"""Augments the images labelwise
Arguments:
src_dir: Where the (raw) images are taken from.
target_dir: Where the augmented images are going to be safed.
label: Label to add to the feature_description.
target_size: Size of the output image.
If at least one entry is None, the original size is used.
repetitions: How often should this run over the original dataset?
h_flip: Is it okay if the images are flipped horizontally?
v_flip: Is it okay if the images are flipped vertically?
rotation_range: In what range can the images be rotated (in degrees)?
quantity: How many images should be taken from the original dataset?
None means => all.
"""
data_list = []
filenames = list(filter(lambda x: x[-5:] == '.jpeg', os.listdir(src_dir)))
for filename in filenames[:quantity]:
image_path = path.join(src_dir, filename)
image = cv2.imread(image_path)
if h_flip:
image = cv2.flip(image, 0)
if v_flip:
image = cv2.flip(image, 1)
if None not in target_size:
image = cv2.resize(image, target_size)
angle = np.random.uniform(0.0, rotation_range)
rotmat = cv2.getRotationMatrix2D(tuple(np.divide(image.shape[:2], 2)), angle, 1.0)
image = cv2.warpAffine(image, rotmat, image.shape[:2])
os.makedirs(target_dir, exist_ok=True)
name = str(len(os.listdir(target_dir)))
# the angle should be labeled between [0, 180)
angle = int(abs(h_flip*360-abs(v_flip*180-angle))) % 180
data_list.append({
'image_path': path.join(target_dir, name + '.jpeg'),
'label': [label_idx, angle],
})
cv2.imwrite(data_list[-1]['image_path'], image)
return data_list
def augment_images(src_dir, target_dir, repetitions=1, *args, **kwargs):
"""Augments images in src_dir and saves them to target_dir.
Arguments:
src_dir: Where the (raw) images are taken from.
target_dir: Where the augmented images are going to be safed.
repetitions: How often should this run over the original dataset?
"""
os.makedirs(target_dir, exist_ok=True)
data_list = []
for label_idx, label in enumerate(os.listdir(src_dir)):
actual_src_dir = path.join(src_dir, label)
actual_target_dir = path.join(target_dir, label)
for i in tqdm(range(repetitions)):
data_list += augment_images_by_label(
actual_src_dir, actual_target_dir, label_idx, *args, **kwargs)
np.random.shuffle(data_list)
with open(path.join(target_dir, 'config.json'), 'w') as config:
json.dump(data_list, config)
return data_list
def inline_augment_images(directory, *args, **kwargs):
"""Augments images inplace (source and target directory are the same).
Arguments:
directory: source and target directory.
An intermediate 'directory_tmp' is created.
It is removed after the operation has finished.
"""
tmp = directory + '_tmp'
os.rename(directory, tmp)
data_list = augment_images(tmp, directory, *args, **kwargs)
try:
shutil.rmtree(tmp, ignore_errors=True)
except OSError as e:
print ("Error: %s - %s." % (e.filename, e.strerror))
return data_list
from src.utils import reset_and_distribute_data, encode_image_data_as_record
raw = path.join('data', 'raw')
interim = path.join('data', 'interim')
processed = path.join('data', 'processed')
reset_and_distribute_data(raw, interim, [1000, 100, 100])
shutil.rmtree(processed, ignore_errors=True)
target_size=(32, 32)
train_data_list = inline_augment_images(path.join(interim, 'train'),
repetitions=32, h_flip=True, v_flip=True, rotation_range=360, target_size=target_size)
validate_data_list = inline_augment_images(path.join(interim, 'validate'), target_size=target_size)
test_data_list = inline_augment_images(path.join(interim, 'test'), target_size=target_size)
feature = {
'image': # /path/to/image
'label': # [label_idx, angle]
}
labels = os.listdir(raw)
train_record = path.join(processed, 'train.tfrecord')
validate_record = path.join(processed, 'validate.tfrecord')
test_record = path.join(processed, 'test.tfrecord')
encode_image_data_as_record(train_data_list, train_record)
encode_image_data_as_record(validate_data_list, validate_record)
encode_image_data_as_record(test_data_list, test_record)
| 0.535098 | 0.927429 |
# Name
Data preparation using SparkSQL on YARN with Cloud Dataproc
# Label
Cloud Dataproc, GCP, Cloud Storage, YARN, SparkSQL, Kubeflow, pipelines, components
# Summary
A Kubeflow Pipeline component to prepare data by submitting a SparkSql job on YARN to Cloud Dataproc.
# Details
## Intended use
Use the component to run an Apache SparkSql job as one preprocessing step in a Kubeflow Pipeline.
## Runtime arguments
Argument| Description | Optional | Data type| Accepted values| Default |
:--- | :---------- | :--- | :------- | :------ | :------
project_id | The ID of the Google Cloud Platform (GCP) project that the cluster belongs to. | No| GCPProjectID | | |
region | The Cloud Dataproc region to handle the request. | No | GCPRegion|
cluster_name | The name of the cluster to run the job. | No | String| | |
queries | The queries to execute the SparkSQL job. Specify multiple queries in one string by separating them with semicolons. You do not need to terminate queries with semicolons. | Yes | List | | None |
query_file_uri | The HCFS URI of the script that contains the SparkSQL queries.| Yes | GCSPath | | None |
script_variables | Mapping of the query’s variable names to their values (equivalent to the SparkSQL command: SET name="value";).| Yes| Dict | | None |
sparksql_job | The payload of a [SparkSqlJob](https://cloud.google.com/dataproc/docs/reference/rest/v1/SparkSqlJob). | Yes | Dict | | None |
job | The payload of a [Dataproc job](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs). | Yes | Dict | | None |
wait_interval | The number of seconds to pause between polling the operation. | Yes |Integer | | 30 |
## Output
Name | Description | Type
:--- | :---------- | :---
job_id | The ID of the created job. | String
## Cautions & requirements
To use the component, you must:
* Set up a GCP project by following this [guide](https://cloud.google.com/dataproc/docs/guides/setup-project).
* [Create a new cluster](https://cloud.google.com/dataproc/docs/guides/create-cluster).
* The component can authenticate to GCP. Refer to [Authenticating Pipelines to GCP](https://www.kubeflow.org/docs/gke/authentication-pipelines/) for details.
* Grant the Kubeflow user service account the role `roles/dataproc.editor` on the project.
## Detailed Description
This component creates a Pig job from [Dataproc submit job REST API](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs/submit).
Follow these steps to use the component in a pipeline:
1. Install the Kubeflow Pipeline SDK:
```
%%capture --no-stderr
KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.14/kfp.tar.gz'
!pip3 install $KFP_PACKAGE --upgrade
```
2. Load the component using KFP SDK
```
import kfp.components as comp
dataproc_submit_sparksql_job_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/ff116b6f1a0f0cdaafb64fcd04214c169045e6fc/components/gcp/dataproc/submit_sparksql_job/component.yaml')
help(dataproc_submit_sparksql_job_op)
```
### Sample
Note: The following sample code works in an IPython notebook or directly in Python code. See the sample code below to learn how to execute the template.
#### Setup a Dataproc cluster
[Create a new Dataproc cluster](https://cloud.google.com/dataproc/docs/guides/create-cluster) (or reuse an existing one) before running the sample code.
#### Prepare a SparkSQL job
Either put your SparkSQL queries in the `queires` list, or upload your SparkSQL queries into a file to a Cloud Storage bucket and then enter the Cloud Storage bucket’s path in `query_file_uri`. In this sample, we will use a hard coded query in the `queries` list to select data from a public CSV file from Cloud Storage.
For more details about Spark SQL, see [Spark SQL, DataFrames and Datasets Guide](https://spark.apache.org/docs/latest/sql-programming-guide.html)
#### Set sample parameters
```
PROJECT_ID = '<Please put your project ID here>'
CLUSTER_NAME = '<Please put your existing cluster name here>'
REGION = 'us-central1'
QUERY = '''
DROP TABLE IF EXISTS natality_csv;
CREATE EXTERNAL TABLE natality_csv (
source_year BIGINT, year BIGINT, month BIGINT, day BIGINT, wday BIGINT,
state STRING, is_male BOOLEAN, child_race BIGINT, weight_pounds FLOAT,
plurality BIGINT, apgar_1min BIGINT, apgar_5min BIGINT,
mother_residence_state STRING, mother_race BIGINT, mother_age BIGINT,
gestation_weeks BIGINT, lmp STRING, mother_married BOOLEAN,
mother_birth_state STRING, cigarette_use BOOLEAN, cigarettes_per_day BIGINT,
alcohol_use BOOLEAN, drinks_per_week BIGINT, weight_gain_pounds BIGINT,
born_alive_alive BIGINT, born_alive_dead BIGINT, born_dead BIGINT,
ever_born BIGINT, father_race BIGINT, father_age BIGINT,
record_weight BIGINT
)
ROW FORMAT DELIMITED FIELDS TERMINATED BY ','
LOCATION 'gs://public-datasets/natality/csv';
SELECT * FROM natality_csv LIMIT 10;'''
EXPERIMENT_NAME = 'Dataproc - Submit SparkSQL Job'
```
#### Example pipeline that uses the component
```
import kfp.dsl as dsl
import json
@dsl.pipeline(
name='Dataproc submit SparkSQL job pipeline',
description='Dataproc submit SparkSQL job pipeline'
)
def dataproc_submit_sparksql_job_pipeline(
project_id = PROJECT_ID,
region = REGION,
cluster_name = CLUSTER_NAME,
queries = json.dumps([QUERY]),
query_file_uri = '',
script_variables = '',
sparksql_job='',
job='',
wait_interval='30'
):
dataproc_submit_sparksql_job_op(
project_id=project_id,
region=region,
cluster_name=cluster_name,
queries=queries,
query_file_uri=query_file_uri,
script_variables=script_variables,
sparksql_job=sparksql_job,
job=job,
wait_interval=wait_interval)
```
#### Compile the pipeline
```
pipeline_func = dataproc_submit_sparksql_job_pipeline
pipeline_filename = pipeline_func.__name__ + '.zip'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
```
#### Submit the pipeline for execution
```
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
```
## References
* [Spark SQL, DataFrames and Datasets Guide](https://spark.apache.org/docs/latest/sql-programming-guide.html)
* [SparkSqlJob](https://cloud.google.com/dataproc/docs/reference/rest/v1/SparkSqlJob)
* [Cloud Dataproc job](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs)
## License
By deploying or using this software you agree to comply with the [AI Hub Terms of Service](https://aihub.cloud.google.com/u/0/aihub-tos) and the [Google APIs Terms of Service](https://developers.google.com/terms/). To the extent of a direct conflict of terms, the AI Hub Terms of Service will control.
|
github_jupyter
|
%%capture --no-stderr
KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.14/kfp.tar.gz'
!pip3 install $KFP_PACKAGE --upgrade
import kfp.components as comp
dataproc_submit_sparksql_job_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/ff116b6f1a0f0cdaafb64fcd04214c169045e6fc/components/gcp/dataproc/submit_sparksql_job/component.yaml')
help(dataproc_submit_sparksql_job_op)
PROJECT_ID = '<Please put your project ID here>'
CLUSTER_NAME = '<Please put your existing cluster name here>'
REGION = 'us-central1'
QUERY = '''
DROP TABLE IF EXISTS natality_csv;
CREATE EXTERNAL TABLE natality_csv (
source_year BIGINT, year BIGINT, month BIGINT, day BIGINT, wday BIGINT,
state STRING, is_male BOOLEAN, child_race BIGINT, weight_pounds FLOAT,
plurality BIGINT, apgar_1min BIGINT, apgar_5min BIGINT,
mother_residence_state STRING, mother_race BIGINT, mother_age BIGINT,
gestation_weeks BIGINT, lmp STRING, mother_married BOOLEAN,
mother_birth_state STRING, cigarette_use BOOLEAN, cigarettes_per_day BIGINT,
alcohol_use BOOLEAN, drinks_per_week BIGINT, weight_gain_pounds BIGINT,
born_alive_alive BIGINT, born_alive_dead BIGINT, born_dead BIGINT,
ever_born BIGINT, father_race BIGINT, father_age BIGINT,
record_weight BIGINT
)
ROW FORMAT DELIMITED FIELDS TERMINATED BY ','
LOCATION 'gs://public-datasets/natality/csv';
SELECT * FROM natality_csv LIMIT 10;'''
EXPERIMENT_NAME = 'Dataproc - Submit SparkSQL Job'
import kfp.dsl as dsl
import json
@dsl.pipeline(
name='Dataproc submit SparkSQL job pipeline',
description='Dataproc submit SparkSQL job pipeline'
)
def dataproc_submit_sparksql_job_pipeline(
project_id = PROJECT_ID,
region = REGION,
cluster_name = CLUSTER_NAME,
queries = json.dumps([QUERY]),
query_file_uri = '',
script_variables = '',
sparksql_job='',
job='',
wait_interval='30'
):
dataproc_submit_sparksql_job_op(
project_id=project_id,
region=region,
cluster_name=cluster_name,
queries=queries,
query_file_uri=query_file_uri,
script_variables=script_variables,
sparksql_job=sparksql_job,
job=job,
wait_interval=wait_interval)
pipeline_func = dataproc_submit_sparksql_job_pipeline
pipeline_filename = pipeline_func.__name__ + '.zip'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
| 0.354433 | 0.959116 |
# Lab 2
#### Joseph Livesey
```
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats, signal
import warnings
warnings.filterwarnings('ignore')
```
## Problem 1
In this lab, we are exploring how summing and averaging background distributions over multiple trials affects physical investigations. Let's say we are searching for gamma ray sources, and must account for background noise derived from cosmic rays. Let the average cosmic-ray background in 1 day be $X = 7.5$ and the average number of gamma rays emitted by the source in question is $Y = 50$. We can see how this background changes when we sum over multiple days and average the resulting distributions. The background is Poissonian, $\sim \text{Pois}(7.5)$.
```
background_1 = [stats.poisson(7.5).pmf(k) for k in np.arange(0, 100)]
background_2 = signal.convolve(background_1, background_1)
background_3 = signal.convolve(background_2, background_1)
background_4 = signal.convolve(background_3, background_1)
background_5 = signal.convolve(background_4, background_1)
background_6 = signal.convolve(background_5, background_1)
background_7 = signal.convolve(background_6, background_1)
background_8 = signal.convolve(background_7, background_1)
background_9 = signal.convolve(background_8, background_1)
background_10 = signal.convolve(background_9, background_1)
k = np.arange(0, 80)
fig, ax = plt.subplots(2, 3, figsize=(16, 10))
ax[0, 0].bar(range(len(background_1)), background_1)
ax[0, 1].bar(range(len(background_2)), background_2)
ax[0, 2].bar(range(len(background_3)), background_3)
ax[1, 0].bar(range(len(background_4)), background_4)
ax[1, 1].bar(range(len(background_5)), background_5)
ax[1, 1].plot(k, stats.poisson(38).pmf(k), color='orange', lw=3)
ax[1, 2].bar(range(len(background_6)), background_6)
n = 1
for i in range(2):
for j in range(3):
ax[i, j].set_title('Total cosmic ray background: ' + str(n) + ' days')
n += 1
ax[i, j].set_xlabel('counts')
ax[i ,j].set_ylabel('probability')
ax[i, j].set_xlim(-1, 80)
ax[i, j].set_ylim(0, 0.15);
```
The background after 5 days has an average of 38 cosmic ray counts. Overplotting a Poisson pdf with parameter 38 reveals that this distribution remains Poissonian. The pmf of a Poisson-distributed (with parameter $\lambda$) random variable is
$$ f(k) = \frac{\lambda^k}{k!} e^{-\lambda}. $$
So, the convolution of a Poisson distribution with itself is
$$
(f * f)(k) = \sum_{t=0}^k \frac{\lambda^t e^{-\lambda}}{t!} \frac{\lambda^{k-t} e^{-\lambda}}{(k - t)!} = \lambda^k e^{-2\lambda} \sum_{t=0}^k \frac{1}{t!(k - t)!} = \frac{\lambda^k e^{-2\lambda}}{k!} \sum_{t=0}^k \frac{k!}{t!(k - t)!} = \frac{\lambda^k e^{-2\lambda}}{k!} \sum_{t=0}^k \binom{k}{t} = \frac{(2\lambda)^k e^{-2\lambda}}{k!},
$$
the pmf of a Poisson distribution with parameter $2\lambda$ (average twice as great). Mathematically, it makes sense that convolution of two Poisson distributions is always Poissonian. Conceptually, the Poisson distribution counts the number of independent events (like cosmic ray counts) over a certain interval of time or space. So, it makes sense that the background is always Poissonian.
Now, let's *average* the background over several observing days.
```
fig, ax = plt.subplots(2, 3, figsize=(16, 10))
ax[0, 0].bar(range(len(background_1)), background_1)
ax[0, 1].bar([k/2 for k in range(len(background_2))], background_2)
ax[0, 2].bar([k/3 for k in range(len(background_3))], background_3)
ax[1, 0].bar([k/4 for k in range(len(background_4))], background_4)
ax[1, 1].bar([k/5 for k in range(len(background_5))], background_5)
ax[1, 2].bar([k/6 for k in range(len(background_6))], background_6)
ax[1, 2].plot([k/6 for k in range(len(background_6))], stats.norm.pdf([k/6 for k in range(len(background_6))], loc=7.5, scale=1.2) / 6, color='orange', lw=3)
n = 1
for i in range(2):
for j in range(3):
ax[i, j].set_title('Average cosmic ray background: ' + str(n) + ' days')
n += 1
ax[i, j].set_xlabel('counts')
ax[i, j].set_ylabel('probability')
ax[i, j].set_xlim(-1, 20)
ax[i, j].set_ylim(0, 0.4);
```
Clearly, it is advantageous to average over multiple days, as this reduces the probability of a false measurement close to the mean of the distribution. By overplotting a Gaussian curve on the plot for 6 days of observation, we see that the background is approaching a Gaussian distribution. This accords with the Central Limit Theorem, by which any distribution averaged over enough time (or space, etc.) will approach a Gaussian distribution. This does not violate the principle explored with the last set of plots, that the non-averaged background integrated over time remains Poissonian. Averaging has the effect of reducing the variance by a factor of the number of trials, which changes the shape of the distribution.
Let's assume that we took measurements over $N=10$ days. We then expect that we have observed $YN = 500$ gamma rays in this time. We want to determine the significance of this measurement against the background. Concisely stated: What is the probability that the background created a signal of this strength (or greater)? In math: Let $\text{pmf}(k)$ be the probability mass function. What is the probability $p(YN)$?
$$ p(YN) = \sum_{k=YN}^\infty \text{pmf}(k) $$
We can use our already-calculated Poisson distribution convolved 10 times.
```
total = sum(background_10)
tail = sum(background_10[499:])
probability = tail/total
probability
```
We can now use `scipy` to convert this to a sigma value.
```
sigma = stats.norm.ppf(probability)
sigma
```
This situation I made up would be incredible in real life, because it corresponds to a $32\sigma$ measurement.
## Problem 2
Now, we will look at how a skewed distribution changes when averaged over many trials. Let the background over some observing interval be given by a Rayleigh distribution, centered on $x = 1.0$ for simplicity's sake.
```
xx = np.linspace(0, 10, 1000)
background_1 = [stats.rayleigh.pdf(x) for x in xx]
def background(original, n):
background = original
for _ in range(n - 1):
background = signal.convolve(background, original)
return background
days = 50
fig, ax = plt.subplots(1, 2, figsize=(18, 8))
ax[0].plot(xx, background_1 / sum(background_1), label='1 day')
ax[1].plot(xx, np.log(background_1 / sum(background_1)))
for n in np.arange(1, days):
if n % 5 == 0:
background_n = background(background_1, n)
n_range = np.linspace(0, 10, len(background_n))
ax[0].plot(n_range, n * background_n / sum(background_n), label=str(n)+' days')
ax[1].plot(n_range, np.log(n * background_n / sum(background_n)))
ax[0].legend(loc=0)
ax[0].set_title('Background distribution')
ax[0].set_xlabel('counts')
ax[0].set_ylabel('probability')
ax[1].set_title('Background distribution')
ax[1].set_xlabel('counts')
ax[1].set_ylabel('log probability')
ax[1].set_xlim(0, 4)
ax[1].set_ylim(-30, 5);
```
As we average over many observing intervals, we see that the variance of the background decreases. This means that we can make significant detections closer to the mean of the background. We also see that our originally-Rayleigh background noise begins to approach a Gaussian distribution. We can tell this first because it becomes more symmetric as time goes on, and because on a semilog plot it approaches a parabola. From visual inspection of the latter plot, it seems that it takes $\sim 30-40$ intervals for the distribution to look sufficiently Gaussian in the neighborhood of the mean.
## Problem 3
### Version 1
Now we will explore what happens when we do and do not know where to look for a signal. Let's imagine that our background is distributed as a zero-mean Gaussian, with $\sigma=6.0$, $X \sim \mathcal{N}(0,36)$. Say we detect a signal of strength $Y = 22.3328$. We will go through our usual method of determining the significance of this detection.
```
xx = np.linspace(0, 50, 1000)
1 - stats.norm.cdf(22.3328, scale=6.0)
```
This is the probability that the background produced a signal of strength $\geq Y$. We must now convert this to a sigma value, i.e., the corresponding position on the standard normal distribution.
```
stats.norm.ppf(9.877332738639222e-05)
```
This is roughly a $3.7\sigma$ detection, not nearly enough to claim a discovery (as we would need ).
### Version 2
Now we need to search 10,000 pixels for the brightest signal and determine whether this represents a significant detection. The one we find is still of strength $Y$. When we want to find the significance of a signal given some background over $N$ trials, we are finding its significance when measured against this background amplified by a factor of $N$. Therefore, to find the significance of the signal of strength $Y$ with the trials factor, we must integrate the one-pixel background distribution over $[Y/N, \infty)$.
```
1 - stats.norm.cdf(22.3328/10000, scale=6.0)
stats.norm.ppf(0.499851508367433)
```
We find a very low significance now, much less than when we were examining a signal in one pixel.
## Problem 4
We want to determine the "sensitivity penalty" introduced by the trials factor, *i.e.*, how much more the signal must deviate from the mean of the background in order to be considered significant when looking at all 10,000 pixels. To find the probability distribution of the background for 10,000 pixels, we took the original background for one pixel and scaled it by the number of "trials", 10,000. We want to calculate the detection threshold for the 1-pixel and 10k-pixel cases.
```
prob_5sigma = 1 - stats.norm.cdf(5.0)
stats.norm.ppf(1 - prob_5sigma, scale=6.0)
prob_5sigma = 1 - stats.norm.cdf(5.0)
stats.norm.ppf(1 - prob_5sigma/10000, scale=6.0)
```
This calculation indicates that the singal strengths necessary are of the same order of magnitude. The sensitivity penalty due to a trials factor is lower than one might initially expect, because when we look at "significant" detections, we are examining events on the tails of the Gaussian background distribution. In the tail, the cumulative distribution function is very close to unity. Thus, the measurement corresponding to $1 - \frac{\text{probability}}{10,000}$ is not much farther from the mean than that corresponding to $1 - \text{probability}$.
Finally, let's look at what happens when we try a larger trials factor, say 1 million.
```
prob_5sigma = 1 - stats.norm.cdf(5.0)
stats.norm.ppf(1 - prob_5sigma/1e6, scale=6.0)
```
The penalty is not that much higher than for a trials factor of 10 thousand.
I suspect that if we were to have a different distribution (non-Gaussian), then the sensitivity penalty of many trials would change. For instance, if we were to take a Rayleigh distribution, which has a thicker "tail" than a Gaussian, a change in the CDF would correspond to a larger change in the measured quantity that it would for a Gaussian distribution.
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats, signal
import warnings
warnings.filterwarnings('ignore')
background_1 = [stats.poisson(7.5).pmf(k) for k in np.arange(0, 100)]
background_2 = signal.convolve(background_1, background_1)
background_3 = signal.convolve(background_2, background_1)
background_4 = signal.convolve(background_3, background_1)
background_5 = signal.convolve(background_4, background_1)
background_6 = signal.convolve(background_5, background_1)
background_7 = signal.convolve(background_6, background_1)
background_8 = signal.convolve(background_7, background_1)
background_9 = signal.convolve(background_8, background_1)
background_10 = signal.convolve(background_9, background_1)
k = np.arange(0, 80)
fig, ax = plt.subplots(2, 3, figsize=(16, 10))
ax[0, 0].bar(range(len(background_1)), background_1)
ax[0, 1].bar(range(len(background_2)), background_2)
ax[0, 2].bar(range(len(background_3)), background_3)
ax[1, 0].bar(range(len(background_4)), background_4)
ax[1, 1].bar(range(len(background_5)), background_5)
ax[1, 1].plot(k, stats.poisson(38).pmf(k), color='orange', lw=3)
ax[1, 2].bar(range(len(background_6)), background_6)
n = 1
for i in range(2):
for j in range(3):
ax[i, j].set_title('Total cosmic ray background: ' + str(n) + ' days')
n += 1
ax[i, j].set_xlabel('counts')
ax[i ,j].set_ylabel('probability')
ax[i, j].set_xlim(-1, 80)
ax[i, j].set_ylim(0, 0.15);
fig, ax = plt.subplots(2, 3, figsize=(16, 10))
ax[0, 0].bar(range(len(background_1)), background_1)
ax[0, 1].bar([k/2 for k in range(len(background_2))], background_2)
ax[0, 2].bar([k/3 for k in range(len(background_3))], background_3)
ax[1, 0].bar([k/4 for k in range(len(background_4))], background_4)
ax[1, 1].bar([k/5 for k in range(len(background_5))], background_5)
ax[1, 2].bar([k/6 for k in range(len(background_6))], background_6)
ax[1, 2].plot([k/6 for k in range(len(background_6))], stats.norm.pdf([k/6 for k in range(len(background_6))], loc=7.5, scale=1.2) / 6, color='orange', lw=3)
n = 1
for i in range(2):
for j in range(3):
ax[i, j].set_title('Average cosmic ray background: ' + str(n) + ' days')
n += 1
ax[i, j].set_xlabel('counts')
ax[i, j].set_ylabel('probability')
ax[i, j].set_xlim(-1, 20)
ax[i, j].set_ylim(0, 0.4);
total = sum(background_10)
tail = sum(background_10[499:])
probability = tail/total
probability
sigma = stats.norm.ppf(probability)
sigma
xx = np.linspace(0, 10, 1000)
background_1 = [stats.rayleigh.pdf(x) for x in xx]
def background(original, n):
background = original
for _ in range(n - 1):
background = signal.convolve(background, original)
return background
days = 50
fig, ax = plt.subplots(1, 2, figsize=(18, 8))
ax[0].plot(xx, background_1 / sum(background_1), label='1 day')
ax[1].plot(xx, np.log(background_1 / sum(background_1)))
for n in np.arange(1, days):
if n % 5 == 0:
background_n = background(background_1, n)
n_range = np.linspace(0, 10, len(background_n))
ax[0].plot(n_range, n * background_n / sum(background_n), label=str(n)+' days')
ax[1].plot(n_range, np.log(n * background_n / sum(background_n)))
ax[0].legend(loc=0)
ax[0].set_title('Background distribution')
ax[0].set_xlabel('counts')
ax[0].set_ylabel('probability')
ax[1].set_title('Background distribution')
ax[1].set_xlabel('counts')
ax[1].set_ylabel('log probability')
ax[1].set_xlim(0, 4)
ax[1].set_ylim(-30, 5);
xx = np.linspace(0, 50, 1000)
1 - stats.norm.cdf(22.3328, scale=6.0)
stats.norm.ppf(9.877332738639222e-05)
1 - stats.norm.cdf(22.3328/10000, scale=6.0)
stats.norm.ppf(0.499851508367433)
prob_5sigma = 1 - stats.norm.cdf(5.0)
stats.norm.ppf(1 - prob_5sigma, scale=6.0)
prob_5sigma = 1 - stats.norm.cdf(5.0)
stats.norm.ppf(1 - prob_5sigma/10000, scale=6.0)
prob_5sigma = 1 - stats.norm.cdf(5.0)
stats.norm.ppf(1 - prob_5sigma/1e6, scale=6.0)
| 0.4856 | 0.980618 |
```
from CasingSimulations import *
%matplotlib inline
```
## Compare against an electric dipole in a wholespace
```
from SimPEG.EM import Analytics
csx, ncx, npadx = 0.4, 20, 42
csz, ncz, npadz = 0.4, 6, 40
hx = Utils.meshTensor([(csx, ncx), (csx, npadx, 1.2)])
hz = Utils.meshTensor([(csz, npadz, -1.2), (csz, ncz), (csz, npadz, 1.2)])
mesh = Mesh.CylMesh([hx, 1., hz], x0='00C')
mesh.plotGrid()
src_ind = (
(mesh.gridFz[:,0] < csx) &
(mesh.gridFz[:,2] <= csz*3) &
(mesh.gridFz[:,2] >= -csz*3)
)
src_vecz = np.zeros(mesh.vnF[2], dtype=complex)
src_vecz[src_ind] = 1.
src_vec = np.hstack([
np.zeros(mesh.vnF[0], dtype=complex),
np.zeros(mesh.vnF[1], dtype=complex),
src_vecz
])
fig, ax = plt.subplots(1,1)
mesh.plotGrid(ax=ax)
ax.plot(mesh.gridFz[src_ind, 0], mesh.gridFz[src_ind, 2], 'rd')
ax.set_xlim([0., 5.])
ax.set_ylim([-20, 20.])
freq = 1.
# mesh.getFaceInnerProduct(invMat=True) * src_vec
# src_vec / mesh.area
# src = FDEM.Src.RawVec_e([], freq, mesh.getFaceInnerProduct(invMat=True) * src_vec)
src = FDEM.Src.RawVec_e([], freq, (src_vec / mesh.area))
prob = FDEM.Problem3D_h(mesh, sigmaMap=Maps.IdentityMap(mesh), mu=mu_0)
prob.solver = Solver
survey = FDEM.Survey([src])
prob.pair(survey)
sigma = 0.6
print('skin depth {}'.format(500/np.sqrt(sigma*freq)))
fields = prob.fields(sigma*np.ones(mesh.nC))
plotCurrentDensity(mesh, fields[src, 'j'], xmax = 15., zmin=10, zmax=-10, csz=0.5, csx=0.5)
# pick a line and compare to electric dipole analytic
jx = fields[src, 'j'][:mesh.nFx].reshape(mesh.vnFx[0], mesh.vnFx[2], order='F')
jz = fields[src, 'j'][mesh.nFx:].reshape(mesh.vnFz[0], mesh.vnFz[2], order='F')
length = mesh.gridFz[src_ind,2]
length = length.max() - length.min() + mesh.hz.min()
# Look at Jz
x_ind = 40
XYZ = Utils.ndgrid([np.r_[mesh.vectorCCx[x_ind]], np.r_[1], mesh.vectorNz])
print XYZ.shape
# solve the analytic
jana_x, jana_y, jana_z = Analytics.E_from_ElectricDipoleWholeSpace(XYZ, np.r_[0., 0., 0.], sig=sigma, f=np.r_[freq], current=1., length=length, orientation='Z')
jana_x, jana_y, jana_z = sigma*jana_x, sigma*jana_y, sigma*jana_z,
# plt.plot()
fig, ax = plt.subplots(3, 1, figsize=(10,8))
ax[0].plot(mesh.vectorNz, jana_z.real)
ax[0].plot(mesh.vectorNz, jz[x_ind, :].real)
ax[0].legend(['ana', 'numeric'])
ax[1].plot(mesh.vectorNz, jz[x_ind, :].real - jana_z.real)
ax[2].plot(mesh.vectorNz, jz[x_ind, :].real / jana_z.real)
ax[2].set_ylim([0, 2])
print(np.linalg.norm(jz[x_ind, :].real - jana_z.real)/np.linalg.norm(jana_z.real))
print(np.linalg.norm(jz[x_ind, :].real)/np.linalg.norm(jana_z.real))
fig, ax = plt.subplots(3, 1, figsize=(10,8))
ax[0].plot(mesh.vectorNz, jana_z.imag)
ax[0].plot(mesh.vectorNz, jz[x_ind, :].imag)
ax[0].legend(['ana', 'numeric'])
ax[1].plot(mesh.vectorNz, jz[x_ind, :].imag - jana_z.imag)
ax[2].plot(mesh.vectorNz, jz[x_ind, :].imag / jana_z.imag)
ax[2].set_ylim([0, 2])
print(np.linalg.norm(jz[x_ind, :].imag - jana_z.imag)/np.linalg.norm(jana_z.imag))
print(np.linalg.norm(jz[x_ind, :].imag)/np.linalg.norm(jana_z.imag))
# Look at Jx
z_ind = 15
print np.r_[mesh.vectorCCz[z_ind]]
XYZ = Utils.ndgrid([mesh.vectorNx, np.r_[1], np.r_[mesh.vectorCCz[z_ind]]])
print XYZ.shape
# solve the analytic
jana_x, jana_y, jana_z = Analytics.E_from_ElectricDipoleWholeSpace(
XYZ, np.r_[0., 0., 0.], sig=sigma, f=np.r_[freq], current=1., length=length, orientation='Z'
)
jana_x, jana_y, jana_z = sigma*jana_x, sigma*jana_y, sigma*jana_z,
# plt.plot()
fig, ax = plt.subplots(3, 1, figsize=(10,8))
ax[0].plot(mesh.vectorNx, jana_x.real)
ax[0].plot(mesh.vectorNx, jx[:, z_ind].real)
ax[0].legend('ana', 'numeric')
ax[1].plot(mesh.vectorNx, jx[:, z_ind].real - jana_x.real)
ax[2].plot(mesh.vectorNx, jx[:, z_ind].real / jana_x.real)
ax[2].set_ylim([0, 2])
print(np.linalg.norm(jx[:, z_ind].real - jana_x.real)/np.linalg.norm(jana_x.real))
print(np.linalg.norm(jx[:, z_ind].real)/np.linalg.norm(jana_x.real))
fig, ax = plt.subplots(3, 1, figsize=(10,8))
ax[0].plot(mesh.vectorNx, jana_x.imag)
ax[0].plot(mesh.vectorNx, jx[:, z_ind].imag)
ax[0].legend('ana', 'numeric')
ax[1].plot(mesh.vectorNx, jx[:, z_ind].imag - jana_x.imag)
ax[2].plot(mesh.vectorNx, jx[:, z_ind].imag / jana_x.imag)
ax[2].set_ylim([0, 2])
print(np.linalg.norm(jx[:, z_ind].imag - jana_x.imag)/np.linalg.norm(jana_x.imag))
print(np.linalg.norm(jx[:, z_ind].imag)/np.linalg.norm(jana_x.imag))
```
|
github_jupyter
|
from CasingSimulations import *
%matplotlib inline
from SimPEG.EM import Analytics
csx, ncx, npadx = 0.4, 20, 42
csz, ncz, npadz = 0.4, 6, 40
hx = Utils.meshTensor([(csx, ncx), (csx, npadx, 1.2)])
hz = Utils.meshTensor([(csz, npadz, -1.2), (csz, ncz), (csz, npadz, 1.2)])
mesh = Mesh.CylMesh([hx, 1., hz], x0='00C')
mesh.plotGrid()
src_ind = (
(mesh.gridFz[:,0] < csx) &
(mesh.gridFz[:,2] <= csz*3) &
(mesh.gridFz[:,2] >= -csz*3)
)
src_vecz = np.zeros(mesh.vnF[2], dtype=complex)
src_vecz[src_ind] = 1.
src_vec = np.hstack([
np.zeros(mesh.vnF[0], dtype=complex),
np.zeros(mesh.vnF[1], dtype=complex),
src_vecz
])
fig, ax = plt.subplots(1,1)
mesh.plotGrid(ax=ax)
ax.plot(mesh.gridFz[src_ind, 0], mesh.gridFz[src_ind, 2], 'rd')
ax.set_xlim([0., 5.])
ax.set_ylim([-20, 20.])
freq = 1.
# mesh.getFaceInnerProduct(invMat=True) * src_vec
# src_vec / mesh.area
# src = FDEM.Src.RawVec_e([], freq, mesh.getFaceInnerProduct(invMat=True) * src_vec)
src = FDEM.Src.RawVec_e([], freq, (src_vec / mesh.area))
prob = FDEM.Problem3D_h(mesh, sigmaMap=Maps.IdentityMap(mesh), mu=mu_0)
prob.solver = Solver
survey = FDEM.Survey([src])
prob.pair(survey)
sigma = 0.6
print('skin depth {}'.format(500/np.sqrt(sigma*freq)))
fields = prob.fields(sigma*np.ones(mesh.nC))
plotCurrentDensity(mesh, fields[src, 'j'], xmax = 15., zmin=10, zmax=-10, csz=0.5, csx=0.5)
# pick a line and compare to electric dipole analytic
jx = fields[src, 'j'][:mesh.nFx].reshape(mesh.vnFx[0], mesh.vnFx[2], order='F')
jz = fields[src, 'j'][mesh.nFx:].reshape(mesh.vnFz[0], mesh.vnFz[2], order='F')
length = mesh.gridFz[src_ind,2]
length = length.max() - length.min() + mesh.hz.min()
# Look at Jz
x_ind = 40
XYZ = Utils.ndgrid([np.r_[mesh.vectorCCx[x_ind]], np.r_[1], mesh.vectorNz])
print XYZ.shape
# solve the analytic
jana_x, jana_y, jana_z = Analytics.E_from_ElectricDipoleWholeSpace(XYZ, np.r_[0., 0., 0.], sig=sigma, f=np.r_[freq], current=1., length=length, orientation='Z')
jana_x, jana_y, jana_z = sigma*jana_x, sigma*jana_y, sigma*jana_z,
# plt.plot()
fig, ax = plt.subplots(3, 1, figsize=(10,8))
ax[0].plot(mesh.vectorNz, jana_z.real)
ax[0].plot(mesh.vectorNz, jz[x_ind, :].real)
ax[0].legend(['ana', 'numeric'])
ax[1].plot(mesh.vectorNz, jz[x_ind, :].real - jana_z.real)
ax[2].plot(mesh.vectorNz, jz[x_ind, :].real / jana_z.real)
ax[2].set_ylim([0, 2])
print(np.linalg.norm(jz[x_ind, :].real - jana_z.real)/np.linalg.norm(jana_z.real))
print(np.linalg.norm(jz[x_ind, :].real)/np.linalg.norm(jana_z.real))
fig, ax = plt.subplots(3, 1, figsize=(10,8))
ax[0].plot(mesh.vectorNz, jana_z.imag)
ax[0].plot(mesh.vectorNz, jz[x_ind, :].imag)
ax[0].legend(['ana', 'numeric'])
ax[1].plot(mesh.vectorNz, jz[x_ind, :].imag - jana_z.imag)
ax[2].plot(mesh.vectorNz, jz[x_ind, :].imag / jana_z.imag)
ax[2].set_ylim([0, 2])
print(np.linalg.norm(jz[x_ind, :].imag - jana_z.imag)/np.linalg.norm(jana_z.imag))
print(np.linalg.norm(jz[x_ind, :].imag)/np.linalg.norm(jana_z.imag))
# Look at Jx
z_ind = 15
print np.r_[mesh.vectorCCz[z_ind]]
XYZ = Utils.ndgrid([mesh.vectorNx, np.r_[1], np.r_[mesh.vectorCCz[z_ind]]])
print XYZ.shape
# solve the analytic
jana_x, jana_y, jana_z = Analytics.E_from_ElectricDipoleWholeSpace(
XYZ, np.r_[0., 0., 0.], sig=sigma, f=np.r_[freq], current=1., length=length, orientation='Z'
)
jana_x, jana_y, jana_z = sigma*jana_x, sigma*jana_y, sigma*jana_z,
# plt.plot()
fig, ax = plt.subplots(3, 1, figsize=(10,8))
ax[0].plot(mesh.vectorNx, jana_x.real)
ax[0].plot(mesh.vectorNx, jx[:, z_ind].real)
ax[0].legend('ana', 'numeric')
ax[1].plot(mesh.vectorNx, jx[:, z_ind].real - jana_x.real)
ax[2].plot(mesh.vectorNx, jx[:, z_ind].real / jana_x.real)
ax[2].set_ylim([0, 2])
print(np.linalg.norm(jx[:, z_ind].real - jana_x.real)/np.linalg.norm(jana_x.real))
print(np.linalg.norm(jx[:, z_ind].real)/np.linalg.norm(jana_x.real))
fig, ax = plt.subplots(3, 1, figsize=(10,8))
ax[0].plot(mesh.vectorNx, jana_x.imag)
ax[0].plot(mesh.vectorNx, jx[:, z_ind].imag)
ax[0].legend('ana', 'numeric')
ax[1].plot(mesh.vectorNx, jx[:, z_ind].imag - jana_x.imag)
ax[2].plot(mesh.vectorNx, jx[:, z_ind].imag / jana_x.imag)
ax[2].set_ylim([0, 2])
print(np.linalg.norm(jx[:, z_ind].imag - jana_x.imag)/np.linalg.norm(jana_x.imag))
print(np.linalg.norm(jx[:, z_ind].imag)/np.linalg.norm(jana_x.imag))
| 0.602179 | 0.789802 |
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
import tensorflow as tf
sess = tf.InteractiveSession()
x = tf.placeholder(tf.float32, shape=[None, 784])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
sess.run(tf.global_variables_initializer())
y = tf.matmul(x,W) + b
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
for _ in range(1000):
batch = mnist.train.next_batch(100)
train_step.run(feed_dict={x: batch[0], y_: batch[1]})
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1, 28, 28, 1])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(20000):
batch = mnist.train.next_batch(50)
if i % 100 == 0:
train_accuracy = accuracy.eval(feed_dict={
x: batch[0], y_: batch[1], keep_prob: 1.0})
print('step %d, training accuracy %g' % (i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print('test accuracy %g' % accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
```
|
github_jupyter
|
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
import tensorflow as tf
sess = tf.InteractiveSession()
x = tf.placeholder(tf.float32, shape=[None, 784])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
sess.run(tf.global_variables_initializer())
y = tf.matmul(x,W) + b
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
for _ in range(1000):
batch = mnist.train.next_batch(100)
train_step.run(feed_dict={x: batch[0], y_: batch[1]})
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1, 28, 28, 1])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(20000):
batch = mnist.train.next_batch(50)
if i % 100 == 0:
train_accuracy = accuracy.eval(feed_dict={
x: batch[0], y_: batch[1], keep_prob: 1.0})
print('step %d, training accuracy %g' % (i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print('test accuracy %g' % accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
| 0.889655 | 0.785144 |
```
%run notebook_setup
```
# Reproducing the black hole discovery in Thompson et al. 2019
In this science demo tutorial, we will reproduce the results in [Thompson et al. 2019](https://ui.adsabs.harvard.edu/abs/2019Sci...366..637T/abstract), who found and followed-up a candidate stellar-mass black hole companion to a giant star in the Milky Way. We will first use *The Joker* to constrain the orbit of the system using the TRES follow-up radial velocity data released in their paper and show that we get consistent period and companion mass constraints from modeling these data. We will then do a joint analysis of the TRES and APOGEE data for this source by simultaneously fitting for and marginalizing over an unknown constant velocity offset between the two surveys.
A bunch of imports we will need later:
```
from astropy.io import ascii
from astropy.time import Time
import astropy.units as u
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import pymc3 as pm
import pymc3_ext as pmx
import exoplanet.units as xu
import exoplanet as xo
import corner
import arviz as az
import thejoker as tj
from twobody.transforms import get_m2_min
# set up a random number generator to ensure reproducibility
seed = 42
rnd = np.random.default_rng(seed=seed)
```
## Load the data
We will start by loading data, copy-pasted from Table S2 in Thompson et al. 2019):
```
tres_tbl = ascii.read(
"""8006.97517 0.000 0.075
8023.98151 -43.313 0.075
8039.89955 -27.963 0.045
8051.98423 10.928 0.118
8070.99556 43.782 0.075
8099.80651 -30.033 0.054
8106.91698 -42.872 0.135
8112.81800 -44.863 0.088
8123.79627 -25.810 0.115
8136.59960 15.691 0.146
8143.78352 34.281 0.087""",
names=['HJD', 'rv', 'rv_err'])
tres_tbl['rv'].unit = u.km/u.s
tres_tbl['rv_err'].unit = u.km/u.s
apogee_tbl = ascii.read(
"""6204.95544 -37.417 0.011
6229.92499 34.846 0.010
6233.87715 42.567 0.010""",
names=['HJD', 'rv', 'rv_err'])
apogee_tbl['rv'].unit = u.km/u.s
apogee_tbl['rv_err'].unit = u.km/u.s
tres_data = tj.RVData(
t=Time(tres_tbl['HJD'] + 2450000, format='jd', scale='tcb'),
rv=u.Quantity(tres_tbl['rv']),
rv_err=u.Quantity(tres_tbl['rv_err']))
apogee_data = tj.RVData(
t=Time(apogee_tbl['HJD'] + 2450000, format='jd', scale='tcb'),
rv=u.Quantity(apogee_tbl['rv']),
rv_err=u.Quantity(apogee_tbl['rv_err']))
```
Let's now plot the data from these two instruments:
```
for d, name in zip([tres_data, apogee_data], ['TRES', 'APOGEE']):
d.plot(color=None, label=name)
plt.legend(fontsize=18)
```
---
## Run The Joker with just the TRES data
The two data sets are separated by a large gap in observations between the end of APOGEE and the start of the RV follow-up with TRES. Since there are more observations with TRES, we will start by running *The Joker* with just data from TRES before using all of the data. Let's plot the TRES data alone:
```
_ = tres_data.plot()
```
It is pretty clear that there is a periodic signal in the data, with a period between 10s to ~100 days (from eyeballing the plot above), so this limits the range of periods we need to sample over with *The Joker* below. The reported uncertainties on the individual RV measurements (plotted above, I swear) are all very small (typically smaller than the markers). So, we may want to allow for the fact that these could be under-estimated. With *The Joker*, we support this by accepting an additional nonlinear parameter, `s`, that specifies a global, extra uncertainty that is added in quadrature to the data uncertainties while running the sampler. That is, the uncertainties used for computing the likelihood in *The Joker* are computed as:
$$
\sigma_n = \sqrt{\sigma_{n,0}^2 + s^2}
$$
where $\sigma_{n,0}$ are the values reported for each $n$ data point in the tables above. We'll use a log-normal prior on this extra error term, but will otherwise use the default prior form for The Joker:
```
with pm.Model() as model:
# Allow extra error to account for under-estimated error bars
s = xu.with_unit(pm.Lognormal('s', -2, 1),
u.km/u.s)
prior = tj.JokerPrior.default(
P_min=16*u.day, P_max=128*u.day, # Range of periods to consider
sigma_K0=30*u.km/u.s, P0=1*u.year, # scale of the prior on semiamplitude, K
sigma_v=25*u.km/u.s, # std dev of the prior on the systemic velocity, v0
s=s
)
```
With the prior set up, we can now generate prior samples, and run the rejection sampling step of *The Joker*:
```
# Generate a large number of prior samples:
prior_samples = prior.sample(size=1_000_000,
random_state=rnd)
# Run rejection sampling with The Joker:
joker = tj.TheJoker(prior, random_state=rnd)
samples = joker.rejection_sample(tres_data, prior_samples,
max_posterior_samples=256)
samples
```
Only 1 sample is returned from the rejection sampling step - let's see how well it matches the data:
```
_ = tj.plot_rv_curves(samples, data=tres_data)
```
Let's look at the values of the sample that was returned, and compare that to the values reported in Thompson et al. 2019, included below for convenience:
$$
P = 83.205 \pm 0.064\\
e = 0.00476 \pm 0.00255\\
K = 44.615 \pm 0.123
$$
```
samples.tbl['P', 'e', 'K']
```
Already these look very consistent with the values inferred in the paper!
Let's now also plot the data phase-folded on the period returned in the one sample we got from *The Joker*:
```
_ = tres_data.plot(phase_fold=samples[0]['P'])
```
At this point, since the data are very constraining, we could use this one *Joker* sample to initialize standard MCMC to generate posterior samplings in the orbital parameters for this system. We will do that below, but first let's see how things look if we include both TRES *and* APOGEE data in our modeling.
## Run The Joker with TRES+APOGEE data
One of the challenges with incorporating data from the two surveys is that they were taken with two different spectrographs, and there could be instrumental offsets that manifest as shifts in the absolute radial velocities measured between the two instruments. *The Joker* now supports simultaneously sampling over additional parameters that represent instrumental or calibratrion offsets, so let's take a look at how to run *The Joker* in this mode.
To start, we can pack the two datasets into a single list that contains data from both surveys:
```
data = [apogee_data, tres_data]
```
Before we run anything, let's try phase-folding both datasets on the period value we got from running on the TRES data alone:
```
tres_data.plot(color=None, phase_fold=np.mean(samples['P']))
apogee_data.plot(color=None, phase_fold=np.mean(samples['P']))
```
That looks pretty good, but the period is clearly slightly off and there seems to be a constant velocity offset between the two surveys, given that the APOGEE RV points don't seem to lie in the RV curve. So, let's now try running *The Joker* on the joined dataset!
To allow for an unknown constant velocity offset between TRES and APOGEE, we have to define a new parameter for this offset and specify a prior. We'll put a Gaussian prior on this offset parameter (named `dv0_1` below), with a mean of 0 and a standard deviation of 10 km/s, because it doesn't look like the surveys have a huge offset.
```
with pm.Model() as model:
# The parameter that represents the constant velocity offset between
# APOGEE and TRES:
dv0_1 = xu.with_unit(pm.Normal('dv0_1', 0, 5.),
u.km/u.s)
# The same extra uncertainty parameter as previously defined
s = xu.with_unit(pm.Lognormal('s', -2, 1),
u.km/u.s)
# We can restrict the prior on prior now, using the above
prior_joint = tj.JokerPrior.default(
# P_min=16*u.day, P_max=128*u.day,
P_min=75*u.day, P_max=90*u.day,
sigma_K0=30*u.km/u.s, P0=1*u.year,
sigma_v=25*u.km/u.s,
v0_offsets=[dv0_1],
s=s
)
prior_samples_joint = prior_joint.sample(size=10_000_000,
random_state=rnd)
# Run rejection sampling with The Joker:
joker_joint = tj.TheJoker(prior_joint, random_state=rnd)
samples_joint = joker_joint.rejection_sample(data,
prior_samples_joint,
max_posterior_samples=256)
samples_joint
```
Here we again only get one sample back from *The Joker*, because these ata are so constraining:
```
_ = tj.plot_rv_curves(samples_joint, data=data)
```
Now, let's fire up standard MCMC, using the one *Joker* sample to initialize. We will use the NUTS sampler in `pymc3` to run here. When running MCMC to model radial velocities with Keplerian orbits, it is typically important to think about the parametrization. There are several angle parameters in the two-body problem (e.g., argument of pericenter, phase, inclination, etc.) that can be especially hard to sample over naïvely. Here, for running MCMC, we will instead sample over $M_0 - \omega, \omega$ instead of $M_0, \omega$, and we will define these angles as `pymc3_ext.distributions.Angle` distributions, which [internally transform and sample in](https://exoplanet.dfm.io/en/stable/user/api/#exoplanet.distributions.Angle) $\cos{x}, \sin{x}$ instead:
```
from pymc3_ext.distributions import Angle
with pm.Model():
# See note above: when running MCMC, we will sample in the parameters
# (M0 - omega, omega) instead of (M0, omega)
M0_m_omega = xu.with_unit(Angle('M0_m_omega'), u.radian)
omega = xu.with_unit(Angle('omega'), u.radian)
# M0 = xu.with_unit(Angle('M0'), u.radian)
M0 = xu.with_unit(pm.Deterministic('M0', M0_m_omega + omega),
u.radian)
# The same offset and extra uncertainty parameters as above:
dv0_1 = xu.with_unit(pm.Normal('dv0_1', 0, 5.), u.km/u.s)
s = xu.with_unit(pm.Lognormal('s', -2, 0.5),
u.km/u.s)
prior_mcmc = tj.JokerPrior.default(
P_min=16*u.day, P_max=128*u.day,
sigma_K0=30*u.km/u.s, P0=1*u.year,
sigma_v=25*u.km/u.s,
v0_offsets=[dv0_1],
s=s,
pars={'M0': M0, 'omega': omega}
)
joker_mcmc = tj.TheJoker(prior_mcmc, random_state=rnd)
mcmc_init = joker_mcmc.setup_mcmc(data, samples_joint)
trace = pmx.sample(
tune=500, draws=1000,
start=mcmc_init,
random_seed=seed,
cores=1, chains=2)
```
We can now use `pymc3` to look at some statistics of the MC chains to assess convergence:
```
az.summary(trace, var_names=prior_mcmc.par_names)
```
We can then transform the MCMC samples back into a `JokerSamples` instance so we can manipulate and visualize the samples:
```
mcmc_samples = joker_mcmc.trace_to_samples(trace, data=data)
mcmc_samples.wrap_K()
```
For example, we can make a [corner](https://corner.readthedocs.io/en/latest/) plot of the orbital parameters (note the strong degenceracy between `M0` and `omega`! But also note that we don't sample in these parameters explicitly, so this shouldn't affect convergence):
```
df = mcmc_samples.tbl.to_pandas()
_ = corner.corner(df)
```
We can also use the median MCMC sample to fold the data and plot residuals relative to our inferred RV model:
```
fig, axes = plt.subplots(2, 1, figsize=(6, 8), sharex=True)
_ = tj.plot_phase_fold(mcmc_samples.median(), data, ax=axes[0], add_labels=False)
_ = tj.plot_phase_fold(mcmc_samples.median(), data, ax=axes[1], residual=True)
for ax in axes:
ax.set_ylabel(f'RV [{apogee_data.rv.unit:latex_inline}]')
axes[1].axhline(0, zorder=-10, color='tab:green', alpha=0.5)
axes[1].set_ylim(-1, 1)
```
Finally, let's convert our orbit samples into binary mass function, $f(M)$, values to compare with one of the main conclusions of the Thompson et al. paper. We can do this by first converting the samples to `KeplerOrbit` objects, and then using the `.m_f` attribute to get the binary mass function values:
```
mfs = u.Quantity([mcmc_samples.get_orbit(i).m_f
for i in np.random.choice(len(mcmc_samples), 1024)])
plt.hist(mfs.to_value(u.Msun), bins=32);
plt.xlabel(rf'$f(M)$ [{u.Msun:latex_inline}]');
# Values from Thompson et al., showing 1-sigma region
plt.axvline(0.766, zorder=100, color='tab:orange')
plt.axvspan(0.766 - 0.00637,
0.766 + 0.00637,
zorder=10, color='tab:orange',
alpha=0.4, lw=0)
```
In the end, using both the APOGEE and TRES data, we confirm the results from the paper, and find that the binary mass function value suggests a large mass companion. A success for reproducible science!
|
github_jupyter
|
%run notebook_setup
from astropy.io import ascii
from astropy.time import Time
import astropy.units as u
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import pymc3 as pm
import pymc3_ext as pmx
import exoplanet.units as xu
import exoplanet as xo
import corner
import arviz as az
import thejoker as tj
from twobody.transforms import get_m2_min
# set up a random number generator to ensure reproducibility
seed = 42
rnd = np.random.default_rng(seed=seed)
tres_tbl = ascii.read(
"""8006.97517 0.000 0.075
8023.98151 -43.313 0.075
8039.89955 -27.963 0.045
8051.98423 10.928 0.118
8070.99556 43.782 0.075
8099.80651 -30.033 0.054
8106.91698 -42.872 0.135
8112.81800 -44.863 0.088
8123.79627 -25.810 0.115
8136.59960 15.691 0.146
8143.78352 34.281 0.087""",
names=['HJD', 'rv', 'rv_err'])
tres_tbl['rv'].unit = u.km/u.s
tres_tbl['rv_err'].unit = u.km/u.s
apogee_tbl = ascii.read(
"""6204.95544 -37.417 0.011
6229.92499 34.846 0.010
6233.87715 42.567 0.010""",
names=['HJD', 'rv', 'rv_err'])
apogee_tbl['rv'].unit = u.km/u.s
apogee_tbl['rv_err'].unit = u.km/u.s
tres_data = tj.RVData(
t=Time(tres_tbl['HJD'] + 2450000, format='jd', scale='tcb'),
rv=u.Quantity(tres_tbl['rv']),
rv_err=u.Quantity(tres_tbl['rv_err']))
apogee_data = tj.RVData(
t=Time(apogee_tbl['HJD'] + 2450000, format='jd', scale='tcb'),
rv=u.Quantity(apogee_tbl['rv']),
rv_err=u.Quantity(apogee_tbl['rv_err']))
for d, name in zip([tres_data, apogee_data], ['TRES', 'APOGEE']):
d.plot(color=None, label=name)
plt.legend(fontsize=18)
_ = tres_data.plot()
with pm.Model() as model:
# Allow extra error to account for under-estimated error bars
s = xu.with_unit(pm.Lognormal('s', -2, 1),
u.km/u.s)
prior = tj.JokerPrior.default(
P_min=16*u.day, P_max=128*u.day, # Range of periods to consider
sigma_K0=30*u.km/u.s, P0=1*u.year, # scale of the prior on semiamplitude, K
sigma_v=25*u.km/u.s, # std dev of the prior on the systemic velocity, v0
s=s
)
# Generate a large number of prior samples:
prior_samples = prior.sample(size=1_000_000,
random_state=rnd)
# Run rejection sampling with The Joker:
joker = tj.TheJoker(prior, random_state=rnd)
samples = joker.rejection_sample(tres_data, prior_samples,
max_posterior_samples=256)
samples
_ = tj.plot_rv_curves(samples, data=tres_data)
samples.tbl['P', 'e', 'K']
_ = tres_data.plot(phase_fold=samples[0]['P'])
data = [apogee_data, tres_data]
tres_data.plot(color=None, phase_fold=np.mean(samples['P']))
apogee_data.plot(color=None, phase_fold=np.mean(samples['P']))
with pm.Model() as model:
# The parameter that represents the constant velocity offset between
# APOGEE and TRES:
dv0_1 = xu.with_unit(pm.Normal('dv0_1', 0, 5.),
u.km/u.s)
# The same extra uncertainty parameter as previously defined
s = xu.with_unit(pm.Lognormal('s', -2, 1),
u.km/u.s)
# We can restrict the prior on prior now, using the above
prior_joint = tj.JokerPrior.default(
# P_min=16*u.day, P_max=128*u.day,
P_min=75*u.day, P_max=90*u.day,
sigma_K0=30*u.km/u.s, P0=1*u.year,
sigma_v=25*u.km/u.s,
v0_offsets=[dv0_1],
s=s
)
prior_samples_joint = prior_joint.sample(size=10_000_000,
random_state=rnd)
# Run rejection sampling with The Joker:
joker_joint = tj.TheJoker(prior_joint, random_state=rnd)
samples_joint = joker_joint.rejection_sample(data,
prior_samples_joint,
max_posterior_samples=256)
samples_joint
_ = tj.plot_rv_curves(samples_joint, data=data)
from pymc3_ext.distributions import Angle
with pm.Model():
# See note above: when running MCMC, we will sample in the parameters
# (M0 - omega, omega) instead of (M0, omega)
M0_m_omega = xu.with_unit(Angle('M0_m_omega'), u.radian)
omega = xu.with_unit(Angle('omega'), u.radian)
# M0 = xu.with_unit(Angle('M0'), u.radian)
M0 = xu.with_unit(pm.Deterministic('M0', M0_m_omega + omega),
u.radian)
# The same offset and extra uncertainty parameters as above:
dv0_1 = xu.with_unit(pm.Normal('dv0_1', 0, 5.), u.km/u.s)
s = xu.with_unit(pm.Lognormal('s', -2, 0.5),
u.km/u.s)
prior_mcmc = tj.JokerPrior.default(
P_min=16*u.day, P_max=128*u.day,
sigma_K0=30*u.km/u.s, P0=1*u.year,
sigma_v=25*u.km/u.s,
v0_offsets=[dv0_1],
s=s,
pars={'M0': M0, 'omega': omega}
)
joker_mcmc = tj.TheJoker(prior_mcmc, random_state=rnd)
mcmc_init = joker_mcmc.setup_mcmc(data, samples_joint)
trace = pmx.sample(
tune=500, draws=1000,
start=mcmc_init,
random_seed=seed,
cores=1, chains=2)
az.summary(trace, var_names=prior_mcmc.par_names)
mcmc_samples = joker_mcmc.trace_to_samples(trace, data=data)
mcmc_samples.wrap_K()
df = mcmc_samples.tbl.to_pandas()
_ = corner.corner(df)
fig, axes = plt.subplots(2, 1, figsize=(6, 8), sharex=True)
_ = tj.plot_phase_fold(mcmc_samples.median(), data, ax=axes[0], add_labels=False)
_ = tj.plot_phase_fold(mcmc_samples.median(), data, ax=axes[1], residual=True)
for ax in axes:
ax.set_ylabel(f'RV [{apogee_data.rv.unit:latex_inline}]')
axes[1].axhline(0, zorder=-10, color='tab:green', alpha=0.5)
axes[1].set_ylim(-1, 1)
mfs = u.Quantity([mcmc_samples.get_orbit(i).m_f
for i in np.random.choice(len(mcmc_samples), 1024)])
plt.hist(mfs.to_value(u.Msun), bins=32);
plt.xlabel(rf'$f(M)$ [{u.Msun:latex_inline}]');
# Values from Thompson et al., showing 1-sigma region
plt.axvline(0.766, zorder=100, color='tab:orange')
plt.axvspan(0.766 - 0.00637,
0.766 + 0.00637,
zorder=10, color='tab:orange',
alpha=0.4, lw=0)
| 0.64579 | 0.974362 |
# Ex1 - Filtering and Sorting Data
Check out [Chipotle Exercises Video Tutorial](https://youtu.be/ZZPiWZpdekA) to watch a data scientist go through the exercises
This time we are going to pull data directly from the internet.
Special thanks to: https://github.com/justmarkham for sharing the dataset and materials.
### Step 1. Import the necessary libraries
```
import pandas as pd
```
### Step 2. Import the dataset from this [address](https://raw.githubusercontent.com/justmarkham/DAT8/master/data/chipotle.tsv).
### Step 3. Assign it to a variable called chipo.
```
url = 'https://raw.githubusercontent.com/justmarkham/DAT8/master/data/chipotle.tsv'
chipo = pd.read_csv(url, sep = '\t')
```
### Step 4. How many products cost more than $10.00?
```
# clean the item_price column and transform it in a float
prices = [float(value[1 : -1]) for value in chipo.item_price]
# reassign the column with the cleaned prices
chipo.item_price = prices
# delete the duplicates in item_name and quantity
# chipo_filtered = chipo.drop_duplicates(['item_name','quantity','choice_description'])
# chipo_filtered
# select only the products with quantity equals to 1
chipo_one_prod = chipo_filtered[chipo_filtered.quantity == 1]
# chipo_one_prod
chipo_one_prod[chipo_one_prod['item_price']>10].item_name.nunique()
# chipo_one_prod[chipo_one_prod['item_price']>10]
# chipo.query('price_per_item > 10').item_name.nunique()
```
### Step 5. What is the price of each item?
###### print a data frame with only two columns item_name and item_price
```
# delete the duplicates in item_name and quantity
# chipo_filtered = chipo.drop_duplicates(['item_name','quantity'])
chipo[(chipo['item_name'] == 'Chicken Bowl') & (chipo['quantity'] == 1)]
# select only the products with quantity equals to 1
# chipo_one_prod = chipo_filtered[chipo_filtered.quantity == 1]
# select only the item_name and item_price columns
# price_per_item = chipo_one_prod[['item_name', 'item_price']]
# sort the values from the most to less expensive
# price_per_item.sort_values(by = "item_price", ascending = False).head(20)
```
### Step 6. Sort by the name of the item
```
chipo.item_name.sort_values()
# OR
chipo.sort_values(by = "item_name")
```
### Step 7. What was the quantity of the most expensive item ordered?
```
chipo.sort_values(by = "item_price", ascending = False).head(1)
```
### Step 8. How many times was a Veggie Salad Bowl ordered?
```
chipo_salad = chipo[chipo.item_name == "Veggie Salad Bowl"]
len(chipo_salad)
```
### Step 9. How many times did someone order more than one Canned Soda?
```
chipo_drink_steak_bowl = chipo[(chipo.item_name == "Canned Soda") & (chipo.quantity > 1)]
len(chipo_drink_steak_bowl)
```
|
github_jupyter
|
import pandas as pd
url = 'https://raw.githubusercontent.com/justmarkham/DAT8/master/data/chipotle.tsv'
chipo = pd.read_csv(url, sep = '\t')
# clean the item_price column and transform it in a float
prices = [float(value[1 : -1]) for value in chipo.item_price]
# reassign the column with the cleaned prices
chipo.item_price = prices
# delete the duplicates in item_name and quantity
# chipo_filtered = chipo.drop_duplicates(['item_name','quantity','choice_description'])
# chipo_filtered
# select only the products with quantity equals to 1
chipo_one_prod = chipo_filtered[chipo_filtered.quantity == 1]
# chipo_one_prod
chipo_one_prod[chipo_one_prod['item_price']>10].item_name.nunique()
# chipo_one_prod[chipo_one_prod['item_price']>10]
# chipo.query('price_per_item > 10').item_name.nunique()
# delete the duplicates in item_name and quantity
# chipo_filtered = chipo.drop_duplicates(['item_name','quantity'])
chipo[(chipo['item_name'] == 'Chicken Bowl') & (chipo['quantity'] == 1)]
# select only the products with quantity equals to 1
# chipo_one_prod = chipo_filtered[chipo_filtered.quantity == 1]
# select only the item_name and item_price columns
# price_per_item = chipo_one_prod[['item_name', 'item_price']]
# sort the values from the most to less expensive
# price_per_item.sort_values(by = "item_price", ascending = False).head(20)
chipo.item_name.sort_values()
# OR
chipo.sort_values(by = "item_name")
chipo.sort_values(by = "item_price", ascending = False).head(1)
chipo_salad = chipo[chipo.item_name == "Veggie Salad Bowl"]
len(chipo_salad)
chipo_drink_steak_bowl = chipo[(chipo.item_name == "Canned Soda") & (chipo.quantity > 1)]
len(chipo_drink_steak_bowl)
| 0.283484 | 0.981997 |
# Sentiment analysis with SVM(support vector machines)
In this notebook, we will revisit a learning task that we encountered earlier in the course: predicting the *sentiment* (positive or negative) of a single sentence taken from a review of a movie, restaurant, or product. The data set consists of 3000 labeled sentences, which we divide into a training set of size 2500 and a test set of size 500. Previously we found a logistic regression classifier. Today we will use a support vector machine.
Before starting on this notebook, make sure the folder `sentiment_labelled_sentences` (containing the data file `full_set.txt`) is in the same directory. Recall that the data can be downloaded from https://archive.ics.uci.edu/ml/datasets/Sentiment+Labelled+Sentences.
## 1. Loading and preprocessing the data
Here we follow exactly the same steps as we did earlier.
```
%matplotlib inline
import string
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
matplotlib.rc('xtick', labelsize=14)
matplotlib.rc('ytick', labelsize=14)
from sklearn.feature_extraction.text import CountVectorizer
from sklearn import svm
# Find file
filename = 'full_set.txt'
!find . | grep '$filename'
```
### Import data
```
## Read in the data set.
with open("../../data/sentiment_labelled_sentences/full_set.txt") as f:
content = f.readlines()
```
### Split data and label
```
## Remove leading and trailing white space
content = [x.strip() for x in content]
## Separate the sentences from the labels
sentences = [x.split("\t")[0] for x in content]
labels = [x.split("\t")[1] for x in content]
## Transform the labels from '0 v.s. 1' to '-1 v.s. 1'
y = np.array(labels, dtype='int8')
y = 2*y - 1
```
### Clean and preprocess data
```
## full_remove takes a string x and a list of characters removal_list
## returns x with all the characters in removal_list replaced by ' '
def full_remove(x, removal_list):
for w in removal_list:
x = x.replace(w, ' ')
return x
## Remove digits
digits = [str(x) for x in range(10)]
digit_less = [full_remove(x, digits) for x in sentences]
## Remove punctuation
punc_less = [full_remove(x, list(string.punctuation)) for x in digit_less]
## Make everything lower-case
sents_lower = [x.lower() for x in punc_less]
## Define our stop words
stop_set = set(['the', 'a', 'an', 'i', 'he', 'she', 'they', 'to', 'of', 'it', 'from'])
## Remove stop words
sents_split = [x.split() for x in sents_lower]
sents_processed = [" ".join(list(filter(lambda a: a not in stop_set, x))) for x in sents_split]
```
### CountVectorizer
```
## Transform to bag of words representation.
vectorizer = CountVectorizer(analyzer = "word", tokenizer=None, preprocessor=None, stop_words=None, max_features=4500)
data_features = vectorizer.fit_transform(sents_processed)
## Append '1' to the end of each vector.
data_mat = data_features.toarray()
# TODO
```
### Split train and test sets
```
## Split the data into testing and training sets
np.random.seed(0)
test_inds = np.append(np.random.choice((np.where(y==-1))[0], 250, replace=False), np.random.choice((np.where(y==1))[0], 250, replace=False))
train_inds = list(set(range(len(labels))) - set(test_inds))
train_data = data_mat[train_inds,]
train_labels = y[train_inds]
test_data = data_mat[test_inds,]
test_labels = y[test_inds]
print("train data: ", train_data.shape)
print("test data: ", test_data.shape)
```
## 2. Fitting SVM to the data
In support vector machines, we are given a set of examples $(x_1, y_1), \ldots, (x_n, y_n)$ and we want to find a weight vector $w \in \mathbb{R}^d$ that solves the following optimization problem:
$$ \min_{w \in \mathbb{R}^d} \| w \|^2 + C \sum_{i=1}^n \xi_i $$
$$ \text{subject to } y_i \langle w, x_i \rangle \geq 1 - \xi_i \text{ for all } i=1,\ldots, n$$
`scikit-learn` provides an SVM solver that we will use. The following routine takes as input the constant `C` (from the above optimization problem) and returns the training and test error of the resulting SVM model. It is invoked as follows:
* `training_error, test_error = fit_classifier(C)`
The default value for parameter `C` is 1.0.
```
def fit_classifier(C_value=1.0):
clf = svm.LinearSVC(C=C_value, loss='hinge').fit(train_data,train_labels)
## Get predictions on training data
train_preds = clf.predict(train_data)
train_error = float(np.sum((train_preds > 0.0) != (train_labels > 0.0)))/len(train_labels)
## Get predictions on test data
test_preds = clf.predict(test_data)
test_error = float(np.sum((test_preds > 0.0) != (test_labels > 0.0)))/len(test_labels)
return train_error, test_error
cvals = [0.01, 0.1, 1.0, 10.0, 100.0, 1000.0, 10000.0]
for c in cvals:
train_error, test_error = fit_classifier(c)
print("Error rate for C = %0.2f: train %0.3f test %0.3f" % (c, train_error, test_error))
```
## 3. Evaluating C by k-fold cross-validation
As we can see, the choice of `C` has a very significant effect on the performance of the SVM classifier. We were able to assess this because we have a separate test set. In general, however, this is a luxury we won't possess. How can we choose `C` based only on the training set?
A reasonable way to estimate the error associated with a specific value of `C` is by **`k-fold cross validation`**:
* Partition the training set `S` into `k` equal-sized sized subsets `S_1, S_2, ..., S_k`.
* For `i=1,2,...,k`, train a classifier with parameter `C` on `S - S_i` (all the training data except `S_i`) and test it on `S_i` to get error estimate `e_i`.
* Average the errors: `(e_1 + ... + e_k)/k`
The following procedure, **cross_validation_error**, does exactly this. It takes as input:
* the training set `x,y`
* the value of `C` to be evaluated
* the integer `k`
and it returns the estimated error of the classifier for that particular setting of `C`. <font color="magenta">Look over the code carefully to understand exactly what it is doing.</font>
```
def cross_validation_error(x, y, C_value, k):
n = len(y)
## Randomly shuffle indices
indices = np.random.permutation(n)
## Initialize error
err = 0.0
## Iterate over partitions
for i in range(k):
## Partition indices
test_indices = indices[int(i*(n/k)):int((i+1)*(n/k) - 1)]
train_indices = np.setdiff1d(indices, test_indices)
## Train classifier with parameter c
clf = svm.LinearSVC(C=C_value, loss='hinge')
clf.fit(x[train_indices], y[train_indices])
## Get predictions on test partition
preds = clf.predict(x[test_indices])
## Compute error
err += float(np.sum((preds > 0.0) != (y[test_indices] > 0.0)))/len(test_indices)
return err/k
```
## 4. Picking a value of C
The procedure **cross_validation_error** (above) evaluates a single candidate value of `C`. We need to use it repeatedly to identify a good `C`.
<font color="magenta">**For you to do:**</font> Write a function to choose `C`. It will be invoked as follows:
* `c, err = choose_parameter(x,y,k)`
where
* `x,y` is the training data
* `k` is the number of folds of cross-validation
* `c` is chosen value of the parameter `C`
* `err` is the cross-validation error estimate at `c`
<font color="magenta">Note:</font> This is a tricky business because a priori, even the order of magnitude of `C` is unknown. Should it be 0.0001 or 10000? You might want to think about trying multiple values that are arranged in a geometric progression (such as powers of ten). *In addition to returning a specific value of `C`, your function should **plot** the cross-validation errors for all the values of `C` it tried out (possibly using a log-scale for the `C`-axis).*
```
plot_data = []
def zoom_range(c, err, low, hi, x, y, k):
if hi - low < 0.05:
# print('found in: [{:.3f} < {:.3f} < {:.3f}]'.format(low, err, hi))
fig, ax = plt.figure(), plt.gca()
ax.scatter([x for x, y in plot_data], [y for x, y in plot_data], linewidth=2, color='green')
ax.set_xscale('log')
plt.xlabel('C')
plt.ylabel('Error')
plt.show()
return (c, err)
c_space = np.linspace(low, hi, 5)
err_space = np.zeros(5)
for i, c in enumerate(c_space):
err_space[i] = cross_validation_error(x, y, c, k)
plot_data.append([c, err_space[i]])
# print('index: {}, error: {:.3f}, C: {:.3f} [{:.3f} - {:.3f}]'.format(i, err_space[i], c, low, hi))
if np.argmin(err_space) == 0:
return zoom_range(c_space[0], err_space[0], c_space[0]/4, c_space[0]*2, x, y, k)
elif np.argmin(err_space) == 4:
return zoom_range(c_space[4], err_space[4], c_space[4]/2, c_space[4]*4, x, y, k)
else:
return zoom_range(c_space[np.argmin(err_space)], err_space[np.argmin(err_space)],
c_space[np.argmin(err_space)-1], c_space[np.argmin(err_space)+1], x, y, k)
def choose_parameter(x, y, k):
return zoom_range(0, 1, 0.1, 10, x, y, k)
```
Now let's try out your routine!
```
c, err = choose_parameter(train_data, train_labels, 10)
print("Choice of C: ", c)
print("Cross-validation error estimate: ", err)
## Train it and test it
clf = svm.LinearSVC(C=c, loss='hinge')
clf.fit(train_data, train_labels)
preds = clf.predict(test_data)
error = float(np.sum((preds > 0.0) != (test_labels > 0.0)))/len(test_labels)
print("Test error: ", error)
```
<font color="magenta">**For you to ponder:**</font> How does the plot of cross-validation errors for different `C` look? Is there clearly a trough in which the returned value of `C` falls? Does the plot provide some reassurance that the choice is reasonable?
|
github_jupyter
|
%matplotlib inline
import string
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
matplotlib.rc('xtick', labelsize=14)
matplotlib.rc('ytick', labelsize=14)
from sklearn.feature_extraction.text import CountVectorizer
from sklearn import svm
# Find file
filename = 'full_set.txt'
!find . | grep '$filename'
## Read in the data set.
with open("../../data/sentiment_labelled_sentences/full_set.txt") as f:
content = f.readlines()
## Remove leading and trailing white space
content = [x.strip() for x in content]
## Separate the sentences from the labels
sentences = [x.split("\t")[0] for x in content]
labels = [x.split("\t")[1] for x in content]
## Transform the labels from '0 v.s. 1' to '-1 v.s. 1'
y = np.array(labels, dtype='int8')
y = 2*y - 1
## full_remove takes a string x and a list of characters removal_list
## returns x with all the characters in removal_list replaced by ' '
def full_remove(x, removal_list):
for w in removal_list:
x = x.replace(w, ' ')
return x
## Remove digits
digits = [str(x) for x in range(10)]
digit_less = [full_remove(x, digits) for x in sentences]
## Remove punctuation
punc_less = [full_remove(x, list(string.punctuation)) for x in digit_less]
## Make everything lower-case
sents_lower = [x.lower() for x in punc_less]
## Define our stop words
stop_set = set(['the', 'a', 'an', 'i', 'he', 'she', 'they', 'to', 'of', 'it', 'from'])
## Remove stop words
sents_split = [x.split() for x in sents_lower]
sents_processed = [" ".join(list(filter(lambda a: a not in stop_set, x))) for x in sents_split]
## Transform to bag of words representation.
vectorizer = CountVectorizer(analyzer = "word", tokenizer=None, preprocessor=None, stop_words=None, max_features=4500)
data_features = vectorizer.fit_transform(sents_processed)
## Append '1' to the end of each vector.
data_mat = data_features.toarray()
# TODO
## Split the data into testing and training sets
np.random.seed(0)
test_inds = np.append(np.random.choice((np.where(y==-1))[0], 250, replace=False), np.random.choice((np.where(y==1))[0], 250, replace=False))
train_inds = list(set(range(len(labels))) - set(test_inds))
train_data = data_mat[train_inds,]
train_labels = y[train_inds]
test_data = data_mat[test_inds,]
test_labels = y[test_inds]
print("train data: ", train_data.shape)
print("test data: ", test_data.shape)
def fit_classifier(C_value=1.0):
clf = svm.LinearSVC(C=C_value, loss='hinge').fit(train_data,train_labels)
## Get predictions on training data
train_preds = clf.predict(train_data)
train_error = float(np.sum((train_preds > 0.0) != (train_labels > 0.0)))/len(train_labels)
## Get predictions on test data
test_preds = clf.predict(test_data)
test_error = float(np.sum((test_preds > 0.0) != (test_labels > 0.0)))/len(test_labels)
return train_error, test_error
cvals = [0.01, 0.1, 1.0, 10.0, 100.0, 1000.0, 10000.0]
for c in cvals:
train_error, test_error = fit_classifier(c)
print("Error rate for C = %0.2f: train %0.3f test %0.3f" % (c, train_error, test_error))
def cross_validation_error(x, y, C_value, k):
n = len(y)
## Randomly shuffle indices
indices = np.random.permutation(n)
## Initialize error
err = 0.0
## Iterate over partitions
for i in range(k):
## Partition indices
test_indices = indices[int(i*(n/k)):int((i+1)*(n/k) - 1)]
train_indices = np.setdiff1d(indices, test_indices)
## Train classifier with parameter c
clf = svm.LinearSVC(C=C_value, loss='hinge')
clf.fit(x[train_indices], y[train_indices])
## Get predictions on test partition
preds = clf.predict(x[test_indices])
## Compute error
err += float(np.sum((preds > 0.0) != (y[test_indices] > 0.0)))/len(test_indices)
return err/k
plot_data = []
def zoom_range(c, err, low, hi, x, y, k):
if hi - low < 0.05:
# print('found in: [{:.3f} < {:.3f} < {:.3f}]'.format(low, err, hi))
fig, ax = plt.figure(), plt.gca()
ax.scatter([x for x, y in plot_data], [y for x, y in plot_data], linewidth=2, color='green')
ax.set_xscale('log')
plt.xlabel('C')
plt.ylabel('Error')
plt.show()
return (c, err)
c_space = np.linspace(low, hi, 5)
err_space = np.zeros(5)
for i, c in enumerate(c_space):
err_space[i] = cross_validation_error(x, y, c, k)
plot_data.append([c, err_space[i]])
# print('index: {}, error: {:.3f}, C: {:.3f} [{:.3f} - {:.3f}]'.format(i, err_space[i], c, low, hi))
if np.argmin(err_space) == 0:
return zoom_range(c_space[0], err_space[0], c_space[0]/4, c_space[0]*2, x, y, k)
elif np.argmin(err_space) == 4:
return zoom_range(c_space[4], err_space[4], c_space[4]/2, c_space[4]*4, x, y, k)
else:
return zoom_range(c_space[np.argmin(err_space)], err_space[np.argmin(err_space)],
c_space[np.argmin(err_space)-1], c_space[np.argmin(err_space)+1], x, y, k)
def choose_parameter(x, y, k):
return zoom_range(0, 1, 0.1, 10, x, y, k)
c, err = choose_parameter(train_data, train_labels, 10)
print("Choice of C: ", c)
print("Cross-validation error estimate: ", err)
## Train it and test it
clf = svm.LinearSVC(C=c, loss='hinge')
clf.fit(train_data, train_labels)
preds = clf.predict(test_data)
error = float(np.sum((preds > 0.0) != (test_labels > 0.0)))/len(test_labels)
print("Test error: ", error)
| 0.309337 | 0.990606 |
# Maximum possible efficiency of a solar thermal energy system #
By Steven J. Byrnes ([https://sjbyrnes.com/](https://sjbyrnes.com/)). This document lives at [https://github.com/sbyrnes321/SolarCellEfficiencyLimits](https://github.com/sbyrnes321/SolarCellEfficiencyLimits). Please email me any feedback: steven.byrnes@gmail.com
Here is the system I'm modeling: There's a flat panel absorbing sunlight, and it might or might not be sitting under a lens that concentrates the sunlight. The panel gets hot (thanks to the sunlight), and dumps heat into an ideal heat engine (running at the Carnot efficiency). The heat engine's waste heat goes into a heat sink at ambient temperature. We are interested in how much useful energy the heat engine generates, as a fraction of sunlight energy it absorbs.
If the panel loses heat to the environment, that's a waste, and it lowers the system's efficiency. Since I am interested in the maximum possible efficiency, I'll assume that no heat is lost to convection, conduction, etc. Unfortunately, the panel must inevitably lose energy to thermal radiation, because if it didn't radiate at all then it would be a "whitebody", and if it was a whitebody then it would not absorb any sunlight (cf. [Kirchhoff's law of thermal radiation](http://en.wikipedia.org/wiki/Kirchhoff's_law_of_thermal_radiation)). In order to absorb as much sunlight as possible, while emitting as little radiation as possible, I'll assume that the panel is a "blackbody" at short wavelength (so it can absorb sunlight) and a "whitebody" at long wavelength (so that it emits very little thermal radiation). I assume for simplicity that there's a sharp switch between blackbody and whitebody, at a wavelength called the "absorption edge", which is not known in advance. I will treat the absorption edge and the panel temperature as adjustable parameters that I can choose to maximize the output power.
(Note: You could in principle get slightly higher efficiency by having an emissivity profile that is more complicated than the form I'm assuming, i.e. a sharp edge separating blackbody and whitebody. But I doubt it makes a huge difference.)
## Direct light vs diffuse light ##
A concentrated-light system (with lenses or mirrors to focus the light on the cell) can collect only the light coming directly from the sun. The "diffuse" light coming from the rest of the sky cannot be focused, so it is wasted in a concentrated system (but it *is* used in unconcentrated systems). That diffuse light is at least ~15% of the total, up to ~100% if a cloud is blocking the sun.
<p style="font-size:80%">[Note for pedants: <a href="https://en.wikipedia.org/wiki/Luminescent_solar_concentrator">Luminescent solar concentrators</a> can "concentrate" diffuse light in a manner of speaking. But they discard some of the photon energy in the process. I believe that they cannot increase the theoretical efficiency of a thermal system of the type considered here. They do, however, mitigate the *further* loss if you use single-junction photovoltaic cells (see <a href="http://sjbyrnes.com/sq.html">Shockley-Queisser limit</a>). For more details see the paper: <a href="http://optoelectronics.eecs.berkeley.edu/ey1990sem2123.pdf">The thermodynamic limits of light concentrators</a>.]</p>
Therefore, a concentrated-light solar power system can *never* be more than ~85% efficient. That ~15% diffuse-light waste occurs before the light even reaches to the solar power system, i.e. this loss is *on top* of the losses discussed below (like the Carnot limit). For the rest of this document, I'll neglect this loss, but you should always keep it in mind. In other words, I'm calculating the power generated as a fraction of successfully-concentrated light, not as a fraction of total incident light. Multiply the efficiency numbers below by 0.85 to get the maximum possible total system efficiency for a concentrated system.
<p style="font-size:80%">[Note for pedants: Well, in theory, you could have a high-concentration system *supplemented by* an unconcentrated system that only collects the diffuse light. That would claw back some small fraction of the diffuse-light loss.]</p>
I'm using NREL's data for the solar spectrum and intensity. To keep things simple, I will use the spectrum which is appropriate for unconcentrated light ("AM1.5G"). In reality, the spectrum changes a bit if you're concentrating the light; it's less blue because the sky is blue. This is a minor shift and does not drastically change the efficiency figures calculated below (well, I don't expect that it does, but I haven't checked).
## Relevance to photovoltaics ##
A photovoltaic cell *seems* very different than a solar thermal power generator, but actually the calculation here applies to both. So a photovoltaic cell -- even a multijunction tandem solar cell in the limit of infinitely many junctions -- cannot have a higher efficiency than the one calculated here.
## How to exceed the limit ##
One thing is, a solar power system with concentration factor N has the same fundamental efficiency limit as a solar cell with no concentration but which only accepts light approaching from an angle in a narrow acceptance window with solid angle 1/N of the hemisphere. I'm using the term "concentration" loosely to refer to either of these strategies. Very narrow acceptance windows are rarely helpful in practical systems -- in particular, the system has to track the sun using either strategy.
Besides that technicality, I only know of one proposed strategy that can beat this limit: [This paper](http://dx.doi.org/10.1021/nl3034784). I believe that it's only a slight improvement (a few percentage points).
## General program setup ##
This document is a mix of text and Python code, written using [Jupyter Notebook](http://jupyter.org/) (You can install Jupyter notebook through [Anaconda](https://www.anaconda.com/distribution/).)
Import various python packages
```
import numpy as np
import matplotlib.pyplot as plt
import scipy.interpolate, scipy.integrate, pandas, sys
from math import pi as π
assert sys.version_info >= (3,6), 'Requires Python 3.6+'
```
One more package: A units-and-constants package I wrote: http://pypi.python.org/pypi/numericalunits
Example usage #1: `x = 5 * cm` means "x equals 5 centimeters".
Example usage #2: `y = x / mm` means "y is the numerical value of x in millimeters'".
```
from numericalunits import K, nm, W, m, um, hPlanck, c0, kB, σSB
```
## Ambient temperature ##
Ambient temperature is 300 kelvin:
```
T_ambient = 300 * K
```
## Incident sunlight ##
The incident light intensity and spectrum is assumed to be the NREL AM1.5G spectrum, which approximates the light coming from the sun and sky at a typical latitude on a clear day. For more information go to https://www.nrel.gov/grid/solar-resource/spectra.html (As discussed above, to get slightly more accurate numbers for concentrated systems, you should switch to the sun-only spectrum, i.e. column 3 of the downloaded file.)
```
worksheet = pandas.read_excel('https://www.nrel.gov/grid/solar-resource/assets/data/astmg173.xls')
downloaded_array = np.array(worksheet)
# Wavelength is in column 0, AM1.5G data is column 2
AM15 = downloaded_array[1:, [0,2]]
# The first line should be 280.0 , 4.7309E-23
# The last line should be 4000.0, 7.1043E-03
print(AM15)
```
Tack on the appropriate units:
```
AM15[:,0] *= nm
AM15[:,1] *= W * m**-2 * nm**-1
```
The NREL data spans the following spectral range:
```
λ_min = 280 * nm
λ_max = 4000 * nm
```
Interpolate to get a continuous function which I will be able to do integrals on:
```
AM15interp = scipy.interpolate.interp1d(AM15[:,0], AM15[:,1])
```
Here’s the plot, it looks correct:
```
λs = np.linspace(λ_min, λ_max, num=500)
y_values = np.array([AM15interp(x) for x in λs])
plt.plot(λs / nm , y_values / (W / m**2 / nm))
plt.xlabel("Wavelength (nm)")
plt.ylabel("Spectral intensity (W/m²/nm)")
plt.title("Light from the sun");
```
The "Solar constant" is the sun's total irradiance. If I did this right, it should be 1000 watts/meter$^2$, because that's how NREL normalized their data.
```
# quad() is ordinary integration; full_output=1 is (surprisingly) how you hide
# the messages warning about poor accuracy in integrating.
solar_constant = scipy.integrate.quad(AM15interp, λ_min, λ_max, full_output=1)[0]
print(solar_constant / (W/m**2))
```
Close enough!
Absorbed power is how much power is absorbed by the panel under unconcentrated sunlight. Remember, it only absorbs wavelengths shorter than absorption_edge.
```
def absorbed_power(absorption_edge):
if absorption_edge > λ_max:
return solar_constant
return scipy.integrate.quad(AM15interp, λ_min, absorption_edge, full_output=1)[0]
```
Plot the absorbed power:
```
absorption_edge_list = np.linspace(λ_min, λ_max, num=50)
absorbed_power_list = np.array([absorbed_power(x) for x in absorption_edge_list])
plt.plot(absorption_edge_list / nm, absorbed_power_list / (W / m**2))
plt.xlabel('Absorption edge (nm)')
plt.ylabel('Absorbed sunlight power (W/m²)');
```
It looks like ~2000nm is about right for absorbing almost all the sunlight while radiating as little as possible. But I won't commit to a specific value, I'll leave it to be optimized.
## Planck's law ##
We're assuming that the hot reservoir is a flat panel with a mirror on the bottom, that radiates into the hemisphere from the horizon to the zenith. By Planck's law:
$$\text{radiation} = 2\pi hc^2 \int_{\lambda = 0}^{\text{absorption edge}} \frac{1}{\lambda^5} \frac{1}{\exp(hc/(\lambda k_B T)) - 1} d\lambda$$
(Without the factor of $\pi$ in front, this formula would describe radiation per steradian, not total radiation into the sky hemisphere. The factor is $\pi$ because $\pi = \int_{\theta=0}^{\pi/2} \int_{\phi=0}^{2\pi} (\cos \theta) (\sin \theta \, d\theta \, d\phi)$. The $(\cos \theta)$ is included because the panel has a smaller area when you view it from an angle.)
```
def emitted_radiation(temperature, absorption_edge):
def integrand(λ):
E_over_kT = hPlanck * c0 / (λ * kB * temperature)
# avoid overflow error
return λ**-5 / (np.exp(E_over_kT) - 1) if E_over_kT < 20 else 0
integral = scipy.integrate.quad(integrand, 50 * nm, absorption_edge, full_output=1)[0]
return 2 * π * hPlanck * c0**2 * integral
```
I'll double-check that by comparing to the Stefan-Boltzmann law:
```
print("This ratio should equal 1:", σSB * (345 * K)**4 / emitted_radiation(345 * K, 80 * um))
def power_generation(T_hot, absorption_edge, concentration=1):
if T_hot <= T_ambient:
return 0
hot_side_absorption = absorbed_power(absorption_edge) * concentration
hot_side_emission = emitted_radiation(T_hot, absorption_edge)
if hot_side_emission >= hot_side_absorption:
return 0
hot_side_net_absorption = hot_side_absorption - hot_side_emission
carnot_efficiency = 1 - T_ambient / T_hot
return hot_side_net_absorption * carnot_efficiency
concentration_list = [1, 10, 100, 1000, 10000, 50000]
highest_T_to_plot_list = [x * K for x in (1200, 1400, 1600, 2000, 3000, 4000)]
for i in range(6):
concentration = concentration_list[i]
T_list = np.linspace(300 * K, highest_T_to_plot_list[i], num=25)
edge_list = np.linspace(1 * um, 3 * um, num=15)
powers = [[power_generation(T, edge, concentration) for T in T_list] for edge in edge_list]
efficiencies = 100 * np.array(powers) / (concentration * solar_constant)
max_efficiency = efficiencies.max()
ax = plt.figure().add_subplot(111)
ax.imshow(efficiencies,
extent=[T_list[0] / K, T_list[-1] / K,
edge_list[0] / um, edge_list[-1] / um],
origin='lower',
vmin=0, vmax = efficiencies.max(),
alpha=0.5)
contour_levels = [10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85]
CS = ax.contour(T_list / K, edge_list / um,
efficiencies, colors='k', levels=contour_levels)
ax.clabel(CS, inline=True, fmt='%1.0f')
ax.set_xlabel('Hot panel temperature (K)')
ax.set_ylabel('Absorption cutoff wavelength (μm)')
if concentration == 1:
title_string = 'Maximum efficiency (%) for unconcentrated sunlight'
else:
title_string = 'Maximum efficiency (%) at concentration = ' + str(concentration)
ax.set_title(title_string + '\n' + 'Best: {:.2f}%'.format(max_efficiency))
ax.set_aspect('auto')
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import scipy.interpolate, scipy.integrate, pandas, sys
from math import pi as π
assert sys.version_info >= (3,6), 'Requires Python 3.6+'
from numericalunits import K, nm, W, m, um, hPlanck, c0, kB, σSB
T_ambient = 300 * K
worksheet = pandas.read_excel('https://www.nrel.gov/grid/solar-resource/assets/data/astmg173.xls')
downloaded_array = np.array(worksheet)
# Wavelength is in column 0, AM1.5G data is column 2
AM15 = downloaded_array[1:, [0,2]]
# The first line should be 280.0 , 4.7309E-23
# The last line should be 4000.0, 7.1043E-03
print(AM15)
AM15[:,0] *= nm
AM15[:,1] *= W * m**-2 * nm**-1
λ_min = 280 * nm
λ_max = 4000 * nm
AM15interp = scipy.interpolate.interp1d(AM15[:,0], AM15[:,1])
λs = np.linspace(λ_min, λ_max, num=500)
y_values = np.array([AM15interp(x) for x in λs])
plt.plot(λs / nm , y_values / (W / m**2 / nm))
plt.xlabel("Wavelength (nm)")
plt.ylabel("Spectral intensity (W/m²/nm)")
plt.title("Light from the sun");
# quad() is ordinary integration; full_output=1 is (surprisingly) how you hide
# the messages warning about poor accuracy in integrating.
solar_constant = scipy.integrate.quad(AM15interp, λ_min, λ_max, full_output=1)[0]
print(solar_constant / (W/m**2))
def absorbed_power(absorption_edge):
if absorption_edge > λ_max:
return solar_constant
return scipy.integrate.quad(AM15interp, λ_min, absorption_edge, full_output=1)[0]
absorption_edge_list = np.linspace(λ_min, λ_max, num=50)
absorbed_power_list = np.array([absorbed_power(x) for x in absorption_edge_list])
plt.plot(absorption_edge_list / nm, absorbed_power_list / (W / m**2))
plt.xlabel('Absorption edge (nm)')
plt.ylabel('Absorbed sunlight power (W/m²)');
def emitted_radiation(temperature, absorption_edge):
def integrand(λ):
E_over_kT = hPlanck * c0 / (λ * kB * temperature)
# avoid overflow error
return λ**-5 / (np.exp(E_over_kT) - 1) if E_over_kT < 20 else 0
integral = scipy.integrate.quad(integrand, 50 * nm, absorption_edge, full_output=1)[0]
return 2 * π * hPlanck * c0**2 * integral
print("This ratio should equal 1:", σSB * (345 * K)**4 / emitted_radiation(345 * K, 80 * um))
def power_generation(T_hot, absorption_edge, concentration=1):
if T_hot <= T_ambient:
return 0
hot_side_absorption = absorbed_power(absorption_edge) * concentration
hot_side_emission = emitted_radiation(T_hot, absorption_edge)
if hot_side_emission >= hot_side_absorption:
return 0
hot_side_net_absorption = hot_side_absorption - hot_side_emission
carnot_efficiency = 1 - T_ambient / T_hot
return hot_side_net_absorption * carnot_efficiency
concentration_list = [1, 10, 100, 1000, 10000, 50000]
highest_T_to_plot_list = [x * K for x in (1200, 1400, 1600, 2000, 3000, 4000)]
for i in range(6):
concentration = concentration_list[i]
T_list = np.linspace(300 * K, highest_T_to_plot_list[i], num=25)
edge_list = np.linspace(1 * um, 3 * um, num=15)
powers = [[power_generation(T, edge, concentration) for T in T_list] for edge in edge_list]
efficiencies = 100 * np.array(powers) / (concentration * solar_constant)
max_efficiency = efficiencies.max()
ax = plt.figure().add_subplot(111)
ax.imshow(efficiencies,
extent=[T_list[0] / K, T_list[-1] / K,
edge_list[0] / um, edge_list[-1] / um],
origin='lower',
vmin=0, vmax = efficiencies.max(),
alpha=0.5)
contour_levels = [10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85]
CS = ax.contour(T_list / K, edge_list / um,
efficiencies, colors='k', levels=contour_levels)
ax.clabel(CS, inline=True, fmt='%1.0f')
ax.set_xlabel('Hot panel temperature (K)')
ax.set_ylabel('Absorption cutoff wavelength (μm)')
if concentration == 1:
title_string = 'Maximum efficiency (%) for unconcentrated sunlight'
else:
title_string = 'Maximum efficiency (%) at concentration = ' + str(concentration)
ax.set_title(title_string + '\n' + 'Best: {:.2f}%'.format(max_efficiency))
ax.set_aspect('auto')
| 0.482429 | 0.985814 |
<a href="https://colab.research.google.com/github/RodriCalle/ComplejidadAlgoritmica/blob/main/12_Componentes_Fuertemente_Conexos.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import graphviz as gv
import numpy as np
import pandas as pd
def readAdjl(fn, haslabels=False, weighted=False, sep="|"):
with open(fn) as f:
labels = None
if haslabels:
labels = f.readline().strip().split()
L = []
for line in f:
if weighted:
L.append([tuple(map(int, p.split(sep))) for p in line.strip().split()])
# line => "1|3 2|5 4|4" ==> [(1, 3), (2, 5), (4, 4)]
else:
L.append(list(map(int, line.strip().split()))) # "1 3 5" => [1, 3, 5]
# L.append([int(x) for x in line.strip().split()])
return L, labels
def adjlShow(L, labels=None, directed=False, weighted=False, path=[], layout="sfdp"):
g = gv.Digraph("G") if directed else gv.Graph("G")
g.graph_attr["layout"] = layout
g.edge_attr["color"] = "gray"
g.node_attr["color"] = "orangered"
g.node_attr["width"] = "0.1"
g.node_attr["height"] = "0.1"
g.node_attr["fontsize"] = "8"
g.node_attr["fontcolor"] = "mediumslateblue"
g.node_attr["fontname"] = "monospace"
n = len(L)
for u in range(n):
g.node(str(u), labels[u] if labels else str(u))
added = set()
for v, u in enumerate(path):
if u != None:
g.edge(str(u), str(v), dir="forward", penwidth="2", color="orange")
added.add(f"{u},{v}")
added.add(f"{v},{u}")
if weighted:
for u in range(n):
for v, w in L[u]:
if not directed and not f"{u},{v}" in added:
added.add(f"{u},{v}")
added.add(f"{v},{u}")
g.edge(str(u), str(v), str(w))
elif directed:
g.edge(str(u), str(v), str(w))
else:
for u in range(n):
for v in L[u]:
if not directed and not f"{u},{v}" in added:
added.add(f"{u},{v}")
added.add(f"{v},{u}")
g.edge(str(u), str(v))
elif directed:
g.edge(str(u), str(v))
return g
%%file 1.in
4
8
6
7
2
9
1
5 6
3 7
G, _ = readAdjl('1.in')
adjlShow(G, directed=True)
```
#Kosaraju
```
def reverse(G):
n =len(G)
Grev = [[] for _ in range(n)]
for u in range(n):
for v in G[u]:
Grev[v].append(u)
return Grev
def kosaraju(G):
n = len(G)
visited = [False]*n
f = []
#Producir grafo reverso
Grev = reverse(G)
#Producir orden de finalizacion con dfs sobre grafo reverso
def dfs1(u):
visited[u] = True
for v in Grev[u]:
if not visited[v]:
dfs1(v)
f.append(u)
def dfs2(u, scc):
visited[u] = True
for v in G[u]:
if not visited[v]:
dfs2(v, scc)
scc.append(u)
for u in range(n):
if not visited[u]:
dfs1(u)
scc = []
visited = [False]*n
for u in reversed(f):
if not visited[u]:
scc.append([])
dfs2(u, scc[-1])
return scc
kosaraju(G)
```
#Algoritmo exhaustivo
```
#Para cada nodo x hacer
# CFC[x] = x // cada nodo esta en su propia CFC
# Para cada arista x→y hacer
# Si CFC[x] != CFC[y] entonces
# Para cada nodo z hacer
# Si CFC[z]==CFC[y] entonces CFC[z]=CFC[x]
def algExh(G):
n =len(G)
CFC = [i for i in range(n)]
for x in range(n):
for y in G[x]:
if (CFC[x] != CFC[y] and CFC[y] == y):
for z in range(n):
if (CFC[z] == CFC[y]):
CFC[z] = CFC[x]
return CFC
cfc = algExh(G)
print(cfc)
scc = dict()
for i, j in enumerate(cfc):
if j not in scc.keys():
scc[j] = [i]
else:
scc[j].append(i)
print(scc)
```
|
github_jupyter
|
import graphviz as gv
import numpy as np
import pandas as pd
def readAdjl(fn, haslabels=False, weighted=False, sep="|"):
with open(fn) as f:
labels = None
if haslabels:
labels = f.readline().strip().split()
L = []
for line in f:
if weighted:
L.append([tuple(map(int, p.split(sep))) for p in line.strip().split()])
# line => "1|3 2|5 4|4" ==> [(1, 3), (2, 5), (4, 4)]
else:
L.append(list(map(int, line.strip().split()))) # "1 3 5" => [1, 3, 5]
# L.append([int(x) for x in line.strip().split()])
return L, labels
def adjlShow(L, labels=None, directed=False, weighted=False, path=[], layout="sfdp"):
g = gv.Digraph("G") if directed else gv.Graph("G")
g.graph_attr["layout"] = layout
g.edge_attr["color"] = "gray"
g.node_attr["color"] = "orangered"
g.node_attr["width"] = "0.1"
g.node_attr["height"] = "0.1"
g.node_attr["fontsize"] = "8"
g.node_attr["fontcolor"] = "mediumslateblue"
g.node_attr["fontname"] = "monospace"
n = len(L)
for u in range(n):
g.node(str(u), labels[u] if labels else str(u))
added = set()
for v, u in enumerate(path):
if u != None:
g.edge(str(u), str(v), dir="forward", penwidth="2", color="orange")
added.add(f"{u},{v}")
added.add(f"{v},{u}")
if weighted:
for u in range(n):
for v, w in L[u]:
if not directed and not f"{u},{v}" in added:
added.add(f"{u},{v}")
added.add(f"{v},{u}")
g.edge(str(u), str(v), str(w))
elif directed:
g.edge(str(u), str(v), str(w))
else:
for u in range(n):
for v in L[u]:
if not directed and not f"{u},{v}" in added:
added.add(f"{u},{v}")
added.add(f"{v},{u}")
g.edge(str(u), str(v))
elif directed:
g.edge(str(u), str(v))
return g
%%file 1.in
4
8
6
7
2
9
1
5 6
3 7
G, _ = readAdjl('1.in')
adjlShow(G, directed=True)
def reverse(G):
n =len(G)
Grev = [[] for _ in range(n)]
for u in range(n):
for v in G[u]:
Grev[v].append(u)
return Grev
def kosaraju(G):
n = len(G)
visited = [False]*n
f = []
#Producir grafo reverso
Grev = reverse(G)
#Producir orden de finalizacion con dfs sobre grafo reverso
def dfs1(u):
visited[u] = True
for v in Grev[u]:
if not visited[v]:
dfs1(v)
f.append(u)
def dfs2(u, scc):
visited[u] = True
for v in G[u]:
if not visited[v]:
dfs2(v, scc)
scc.append(u)
for u in range(n):
if not visited[u]:
dfs1(u)
scc = []
visited = [False]*n
for u in reversed(f):
if not visited[u]:
scc.append([])
dfs2(u, scc[-1])
return scc
kosaraju(G)
#Para cada nodo x hacer
# CFC[x] = x // cada nodo esta en su propia CFC
# Para cada arista x→y hacer
# Si CFC[x] != CFC[y] entonces
# Para cada nodo z hacer
# Si CFC[z]==CFC[y] entonces CFC[z]=CFC[x]
def algExh(G):
n =len(G)
CFC = [i for i in range(n)]
for x in range(n):
for y in G[x]:
if (CFC[x] != CFC[y] and CFC[y] == y):
for z in range(n):
if (CFC[z] == CFC[y]):
CFC[z] = CFC[x]
return CFC
cfc = algExh(G)
print(cfc)
scc = dict()
for i, j in enumerate(cfc):
if j not in scc.keys():
scc[j] = [i]
else:
scc[j].append(i)
print(scc)
| 0.177954 | 0.81457 |
# EventKG+Click dataset
This is a step by step walkthrough to the creation of EventKG+Click dataset which aims to facilitate the creation and evaluation of multilingual user interaction models and reflects the language-specific relevance of events and their relations. Our dataset EventKG+Click is based on two data sources:
* The Wikipedia clickstream2 that refleects real-world user interactions withevents and their relations within language-specific Wikipedia editions; and
* The EventKG knowledge graph that contains semantic information regarding events and their relations that partially originates from Wikipedia. EventKG+Click is available online3 to enable further analyses and applications.
## Dataset preparation
Link to clickstream dataset:
https://dumps.wikimedia.org/other/clickstream/
As EventKG+Click and our analysis are based on Wikipedia click behaviour, we only consider those (source, target) click pairs in the clickstream where both the source and target are Wikipedia articles connected by a hyperlink. In our dataset, we adopter Wikipedia clickstream that covers the period from December 1, 2019, to December 31, 2019 and in three language versions, **English**, **German** and **Russian**.
The following example shows how we get information from english version:
```
import pandas as pd
import json
from SPARQLWrapper import SPARQLWrapper, JSON, POST
English = pd.read_csv("C:/Users/Admin/Downloads/clickstream-enwiki-2019-12.tsv", sep='\t',header=None, error_bad_lines=False)
English.columns = ['source','target','link_type','count']
English=English.loc[English['link_type'] == 'link'] ### we only choose those that are in the wikipedia
wds = "http://eventkginterface.l3s.uni-hannover.de/sparql"
entity_mapping_rq='''
SELECT substr(str(?entity), 45)
{{
?entity owl:sameAs {0}
}}
'''
comention_rq='''
SELECT sum(?a) as ?cnt WHERE
{{
?relation2 rdf:subject eventKG-r:{0} .
?relation2 rdf:object eventKG-r:{1} .
?relation2 eventKG-s:mentions ?a.
}}
'''
event_location_rq= '''
SELECT DISTINCT "{0}" AS ?event ?location
WHERE {{
eventKG-r:{0} sem:hasPlace ?locationEventKG.
?locationEventKG so:containedInPlace ?co .
?co rdfs:label ?location .
?co rdf:type dbo:Country .
FILTER (LANG(?location)="en")
}}
'''
event_time_rq ='''
SELECT distinct "{0}" as ?event ?start
WHERE
{{
eventKG-r:{0} sem:hasBeginTimeStamp ?start .
}}
'''
def sparql_request(service, query):
sparql = SPARQLWrapper(service)
sparql.setQuery(query)
sparql.setReturnFormat(JSON)
result = sparql.query()
processed_results = json.load(result.response)
cols = processed_results['head']['vars']
out = []
for row in processed_results['results']['bindings']:
item = []
for c in cols:
item.append(row.get(c, {}).get('value'))
out.append(item)
return pd.DataFrame(out, columns=cols)
```
### Entity_mapping function
In order to leverage the rich information provided in EventKG and find interlinked wikipedia pages in different languages, we need to map title of Wikipedia pages to EventKG.
*input: label of wikipedia pages*
*output: entity_id in EventKG*
```
def entity_mapping (label):
#options for language: {"en","de","ru"}
dbpedia_page="<http://dbpedia.org/resource/"+label+">"
temp=get_sparql_dataframe(wds, entity_mapping_rq.format(dbpedia_page))
return temp.iloc[0][0]
```
In order to show how we have collected data using functions, we work on a small dataset which contains all clicked wikipedia
pages after exploring **"World War II"**.
```
en_data=pd.read_csv("World_War_II_clickstream.txt", sep='\t',error_bad_lines=False)
en_entity=list(en_data["source"].unique())+list(en_data["target"].unique())
mapped_labels = pd.DataFrame(columns=('label','ekg_entity'))
for t in range(len(en_entity)):
try:
temp=entity_mapping(str(en_entity[t]),"")
mapped_labels=mapped_labels.append({'label' : en_entity[t] , 'ekg_entity':temp} , ignore_index=True)
except:
print("The corresponding entity doesn't exist on EventKG")
en_mapped=pd.merge(left=en_data, right=en_mapped, how="left", left_on="target", right_on="label")
en_mapped=en_mapped.rename(columns={"ekg_entity":"target_ekg"})
en_mapped=pd.merge(left=en_data, right=en_mapped, how="left", left_on="source", right_on="label")
en_mapped=en_mapped.rename(columns={"ekg_entity":"source_ekg"})
en_mapped=en_mapped[["source","target","source_ekg","target_ekg","count"]]
en_data=pd.read_csv("World_War_II_clickstream", sep='\t',error_bad_lines=False)
en_entity=list(en_data["source"].unique())+list(en_data["target"].unique())
mapped_labels = pd.DataFrame(columns=('label','ekg_entity'))
for t in range(len(en_entity)):
try:
temp=entity_mapping(str(en_entity[t]))
mapped_labels=mapped_labels.append({'label' : en_entity[t] , 'ekg_entity':temp} , ignore_index=True)
#print(i)
except:
continue
en_mapped=pd.merge(left=en_data, right=mapped_labels, how="left", left_on="target", right_on="label")
en_mapped=en_mapped.rename(columns={"ekg_entity":"target_ekg"})
en_mapped=pd.merge(left=en_mapped, right=mapped_labels, how="left", left_on="source", right_on="label")
en_mapped=en_mapped.rename(columns={"ekg_entity":"source_ekg"})
en_mapped=en_mapped[["source","target","source_ekg","target_ekg","count"]]
en_mapped=en_mapped.dropna() ### because we are intereseted only on mapped entities and labels
```
### Joining three dataframes
After creating **ge_mapped** and **ru_mapped** corresponding mapped wikipedia pages to the knowledge graph, we join three dataframe to get the intersection of events. We are interested to compare relevance of events and relations with respect to the three languages.
And since we are intereseted to analyse the events, we only keep targets which are events. to do so, we could easily use the prefixes of entities in Eventkg.
```
intersection_table=pd.merge(pd.merge(de_mapped,en_mapped,how="inner", on=['source_ekg', 'target_ekg']),ru_mapped,how="inner",on=['source_ekg', 'target_ekg'])
intersection_table=intersection_table.loc[en_mapped["target_ekg"].str.startswith("event"),]
```
## Balancing data
Wikipedia language versions are different in terms of their size, number of user and the amount of edited content. in order to balance the effects of size in each language versions, we normalize the number of clicks with respect to the total
number of clicks in the respective language, which leads to normalized scores in the range [0; 1]. In order to create balanced click counts, we then multiply the normalised score by the total number of clicks in the clickstreams.
$balanced\_clicks(e_s,e_t,l) = clicks(e_s,e_t,l) \cdot \frac{\sum_{l' \in L}\sum_{e_s' \in E}\sum_{e_t' \in E} clicks(e_s',e_t',l')}{\sum_{e_s' \in E}\sum_{e_t' \in E} clicks(e_s',e_t',l)} $
Using the above formula, normalized scores for each language are as follows which we use directly on the **en_data** dataframe.
* English normalized score: 1.6
* German normalized score: 4.1
* Russian normalized score: 6.2
```
intersection_table["balanced_en_count"]= 1.6 * intersection_table["en_count"]
intersection_table["balanced_de_count"]= 4.1 * intersection_table["de_count"]
intersection_table["balanced_ru_count"]= 6.2 * intersection_table["ru_count"]
```
## Language-specific Relation Relevance
This score assigns a relevance score to the relation between a source entity and a target event et in a given language.
$relation\_relevance(e_s,e_t,l) = \frac{balanced\_clicks(e_s,e_t,l)}{\sum_{l' \in L} balanced\_clicks(e_s,e_t,l')} \in [0,1]$
```
intersection_table['en_normalized'] = intersection_table["en_count"]/(intersection_table["ru_count"]+intersection_table["de_count"]+intersection_table["en_count"])
intersection_table['de_normalized'] = intersection_table["de_count"]/(intersection_table["ru_count"]+intersection_table["de_count"]+intersection_table["en_count"])
intersection_table['ru_normalized'] = intersection_table["ru_count"]/(intersection_table["ru_count"]+intersection_table["de_count"]+intersection_table["en_count"])
```
# Event Location Closeness
Using the following function, we aim to get a set of binary influence factors that indicate whether an event happened in a location where the respective language (*Enlish, German, Russian*) is an offcial language. To do so, we have created **country_language** dataframe that contains countries where English, German, Russian are official languages.
*input: a list of events*
*output: event and 3 binary columns for English, German and Russian*
```
#input: list of events
#output: a dataframe with 3 columns which shows whether the event has happend in a english, german and russian, speaking location
def get_location(events):
events_location=pd.DataFrame()
country_language=pd.read_pickle("country_language")
events=list(en_mapped["target_ekg"].unique())
for i in range (len(events)):
temp=get_sparql_dataframe(wds, event_location_rq.format(events[i]))
events_location=events_location.append(temp)
events_language=pd.merge(left=events_location,right=country_language,how="left", left_on="location", right_on="country")
events_language=events_language.loc[events_language["language"].notna(),]
events_language['english'] = [1 if x =='English' else 0 for x in events_language['language']]
events_language['german'] = [1 if x =='German' else 0 for x in events_language['language']]
events_language['russian'] = [1 if x =='Russian' else 0 for x in events_language['language']]
events_language=events_language[["event","english","german","russian"]]
events_language=events_language.drop_duplicates()
return events_language
```
# Event Recency
To observe the impact of recency on the language-specific user click behaviour and using **get_recency** function we compute a recency score which is the number of days between the event start date and the start date of the clickstream dataset which is (2019-12-01)
*input: events list*
*output: dataframe of two columns: events, receny*
```
def get_recency():
events_time=pd.DataFrame()
for i in range (len(events)):
temp=get_sparql_dataframe(wds, event_time_rq.format(events[i]))
events_time=events_time.append(temp)
events_time["max_start_time"]=events_time.groupby(["event"])['start'].transform('max')
events_time['max_start_time'] = pd.to_datetime(events_time['max_start_time'], errors='coerce')
events_time["recency"]=events_time.apply(lambda row: pd.to_datetime("2019-12-1")-row.max_start_time, axis=1)
events_time["recency"]=events_time["recency"].dt.days
events_time=events_time[["event","recency"]]
events_time=events_time.drop_duplicates()
### since there might be more than one time for an event, therefore we use the most recent one
```
# Language Community Relevance - number of links to a wikipedia page
We use a dump and count the number of incoming links to wikipedia pages
```
links=pd.read_csv("worldwar_links.txt", sep="\t", error_bad_lines=False)
events_link=pd.merge(left=en_mapped, right=links, how="left", left_on=["target"], right_on=["page"])
del events_link["page"]
events_link["links"]=events_link["links"].fillna(0)
```
# Language Community Relevance - number of comentions
*input: mappend_data dataframe which contains source and target entities*
*output: number of comentions in whole wikipedia*
```
########## mentions
#input: source and target entities
#output: number of their comentions in whole wikipedia
def get_comentions(df):
comention=pd.DataFrame(columns={"source_ekg","target_ekg","comentions"})
for i in range(df.shape[0]):
try:
temp=get_sparql_dataframe(wds, comention_rq.format(df.iloc[i]["source_ekg"], df.iloc[i]["target_ekg"]))
comention = comention.append({"source_ekg":df.iloc[i]["source_ekg"], "target_ekg":df.iloc[i]["target_ekg"], "comentions":temp.loc[0,"cnt"]}, ignore_index=True)
except:
continue
return (comention)
#we use EventKG for that
final table correlation
#en_mapped
#en_comention
#events_link
#events_time
#events_language
```
## Correlations with Influence Factors
Given EventKG+Click and the influence factors, we now investigate the correlations between such influence factors and the language-specific relevance scores.To this end, we compute the Pearson correlation coefficients
```
en_merge=pd.merge(pd.merge(pd.merge(pd.merge(left=en_mapped, right=en_comention, how="left", left_on=["source_ekg","target_ekg"], right_on=["source_ekg","target_ekg"]),events_link,how="left",on=['target_ekg']),events_time, how="left", left_on=["target_ekg"], right_on=["event"]), events_language, how="left", left_on=["target_ekg"], right_on=["event"])
en_merge=en_merge[["source_x","target_x","source_ekg_x","target_ekg","count_x","comentions","links","recency","english","german","russian"]]
en_merge=en_merge.rename(columns={"source_x":"en_source","target_x":"en_target","source_ekg_x":"source_ekg","count_x":"en_count"})
en_merge["english"]=en_merge["english"].fillna(0)
en_merge["german"]=en_merge["german"].fillna(0)
en_merge["russian"]=en_merge["russian"].fillna(0)
en_merge["comentions"]=en_merge["comentions"].fillna(0)
en_merge["links"]=en_merge["links"].fillna(0)
en_merge["recency"]=en_merge["recency"].fillna(-1)
en_merge.corr()
```
|
github_jupyter
|
import pandas as pd
import json
from SPARQLWrapper import SPARQLWrapper, JSON, POST
English = pd.read_csv("C:/Users/Admin/Downloads/clickstream-enwiki-2019-12.tsv", sep='\t',header=None, error_bad_lines=False)
English.columns = ['source','target','link_type','count']
English=English.loc[English['link_type'] == 'link'] ### we only choose those that are in the wikipedia
wds = "http://eventkginterface.l3s.uni-hannover.de/sparql"
entity_mapping_rq='''
SELECT substr(str(?entity), 45)
{{
?entity owl:sameAs {0}
}}
'''
comention_rq='''
SELECT sum(?a) as ?cnt WHERE
{{
?relation2 rdf:subject eventKG-r:{0} .
?relation2 rdf:object eventKG-r:{1} .
?relation2 eventKG-s:mentions ?a.
}}
'''
event_location_rq= '''
SELECT DISTINCT "{0}" AS ?event ?location
WHERE {{
eventKG-r:{0} sem:hasPlace ?locationEventKG.
?locationEventKG so:containedInPlace ?co .
?co rdfs:label ?location .
?co rdf:type dbo:Country .
FILTER (LANG(?location)="en")
}}
'''
event_time_rq ='''
SELECT distinct "{0}" as ?event ?start
WHERE
{{
eventKG-r:{0} sem:hasBeginTimeStamp ?start .
}}
'''
def sparql_request(service, query):
sparql = SPARQLWrapper(service)
sparql.setQuery(query)
sparql.setReturnFormat(JSON)
result = sparql.query()
processed_results = json.load(result.response)
cols = processed_results['head']['vars']
out = []
for row in processed_results['results']['bindings']:
item = []
for c in cols:
item.append(row.get(c, {}).get('value'))
out.append(item)
return pd.DataFrame(out, columns=cols)
def entity_mapping (label):
#options for language: {"en","de","ru"}
dbpedia_page="<http://dbpedia.org/resource/"+label+">"
temp=get_sparql_dataframe(wds, entity_mapping_rq.format(dbpedia_page))
return temp.iloc[0][0]
en_data=pd.read_csv("World_War_II_clickstream.txt", sep='\t',error_bad_lines=False)
en_entity=list(en_data["source"].unique())+list(en_data["target"].unique())
mapped_labels = pd.DataFrame(columns=('label','ekg_entity'))
for t in range(len(en_entity)):
try:
temp=entity_mapping(str(en_entity[t]),"")
mapped_labels=mapped_labels.append({'label' : en_entity[t] , 'ekg_entity':temp} , ignore_index=True)
except:
print("The corresponding entity doesn't exist on EventKG")
en_mapped=pd.merge(left=en_data, right=en_mapped, how="left", left_on="target", right_on="label")
en_mapped=en_mapped.rename(columns={"ekg_entity":"target_ekg"})
en_mapped=pd.merge(left=en_data, right=en_mapped, how="left", left_on="source", right_on="label")
en_mapped=en_mapped.rename(columns={"ekg_entity":"source_ekg"})
en_mapped=en_mapped[["source","target","source_ekg","target_ekg","count"]]
en_data=pd.read_csv("World_War_II_clickstream", sep='\t',error_bad_lines=False)
en_entity=list(en_data["source"].unique())+list(en_data["target"].unique())
mapped_labels = pd.DataFrame(columns=('label','ekg_entity'))
for t in range(len(en_entity)):
try:
temp=entity_mapping(str(en_entity[t]))
mapped_labels=mapped_labels.append({'label' : en_entity[t] , 'ekg_entity':temp} , ignore_index=True)
#print(i)
except:
continue
en_mapped=pd.merge(left=en_data, right=mapped_labels, how="left", left_on="target", right_on="label")
en_mapped=en_mapped.rename(columns={"ekg_entity":"target_ekg"})
en_mapped=pd.merge(left=en_mapped, right=mapped_labels, how="left", left_on="source", right_on="label")
en_mapped=en_mapped.rename(columns={"ekg_entity":"source_ekg"})
en_mapped=en_mapped[["source","target","source_ekg","target_ekg","count"]]
en_mapped=en_mapped.dropna() ### because we are intereseted only on mapped entities and labels
intersection_table=pd.merge(pd.merge(de_mapped,en_mapped,how="inner", on=['source_ekg', 'target_ekg']),ru_mapped,how="inner",on=['source_ekg', 'target_ekg'])
intersection_table=intersection_table.loc[en_mapped["target_ekg"].str.startswith("event"),]
intersection_table["balanced_en_count"]= 1.6 * intersection_table["en_count"]
intersection_table["balanced_de_count"]= 4.1 * intersection_table["de_count"]
intersection_table["balanced_ru_count"]= 6.2 * intersection_table["ru_count"]
intersection_table['en_normalized'] = intersection_table["en_count"]/(intersection_table["ru_count"]+intersection_table["de_count"]+intersection_table["en_count"])
intersection_table['de_normalized'] = intersection_table["de_count"]/(intersection_table["ru_count"]+intersection_table["de_count"]+intersection_table["en_count"])
intersection_table['ru_normalized'] = intersection_table["ru_count"]/(intersection_table["ru_count"]+intersection_table["de_count"]+intersection_table["en_count"])
#input: list of events
#output: a dataframe with 3 columns which shows whether the event has happend in a english, german and russian, speaking location
def get_location(events):
events_location=pd.DataFrame()
country_language=pd.read_pickle("country_language")
events=list(en_mapped["target_ekg"].unique())
for i in range (len(events)):
temp=get_sparql_dataframe(wds, event_location_rq.format(events[i]))
events_location=events_location.append(temp)
events_language=pd.merge(left=events_location,right=country_language,how="left", left_on="location", right_on="country")
events_language=events_language.loc[events_language["language"].notna(),]
events_language['english'] = [1 if x =='English' else 0 for x in events_language['language']]
events_language['german'] = [1 if x =='German' else 0 for x in events_language['language']]
events_language['russian'] = [1 if x =='Russian' else 0 for x in events_language['language']]
events_language=events_language[["event","english","german","russian"]]
events_language=events_language.drop_duplicates()
return events_language
def get_recency():
events_time=pd.DataFrame()
for i in range (len(events)):
temp=get_sparql_dataframe(wds, event_time_rq.format(events[i]))
events_time=events_time.append(temp)
events_time["max_start_time"]=events_time.groupby(["event"])['start'].transform('max')
events_time['max_start_time'] = pd.to_datetime(events_time['max_start_time'], errors='coerce')
events_time["recency"]=events_time.apply(lambda row: pd.to_datetime("2019-12-1")-row.max_start_time, axis=1)
events_time["recency"]=events_time["recency"].dt.days
events_time=events_time[["event","recency"]]
events_time=events_time.drop_duplicates()
### since there might be more than one time for an event, therefore we use the most recent one
links=pd.read_csv("worldwar_links.txt", sep="\t", error_bad_lines=False)
events_link=pd.merge(left=en_mapped, right=links, how="left", left_on=["target"], right_on=["page"])
del events_link["page"]
events_link["links"]=events_link["links"].fillna(0)
########## mentions
#input: source and target entities
#output: number of their comentions in whole wikipedia
def get_comentions(df):
comention=pd.DataFrame(columns={"source_ekg","target_ekg","comentions"})
for i in range(df.shape[0]):
try:
temp=get_sparql_dataframe(wds, comention_rq.format(df.iloc[i]["source_ekg"], df.iloc[i]["target_ekg"]))
comention = comention.append({"source_ekg":df.iloc[i]["source_ekg"], "target_ekg":df.iloc[i]["target_ekg"], "comentions":temp.loc[0,"cnt"]}, ignore_index=True)
except:
continue
return (comention)
#we use EventKG for that
final table correlation
#en_mapped
#en_comention
#events_link
#events_time
#events_language
en_merge=pd.merge(pd.merge(pd.merge(pd.merge(left=en_mapped, right=en_comention, how="left", left_on=["source_ekg","target_ekg"], right_on=["source_ekg","target_ekg"]),events_link,how="left",on=['target_ekg']),events_time, how="left", left_on=["target_ekg"], right_on=["event"]), events_language, how="left", left_on=["target_ekg"], right_on=["event"])
en_merge=en_merge[["source_x","target_x","source_ekg_x","target_ekg","count_x","comentions","links","recency","english","german","russian"]]
en_merge=en_merge.rename(columns={"source_x":"en_source","target_x":"en_target","source_ekg_x":"source_ekg","count_x":"en_count"})
en_merge["english"]=en_merge["english"].fillna(0)
en_merge["german"]=en_merge["german"].fillna(0)
en_merge["russian"]=en_merge["russian"].fillna(0)
en_merge["comentions"]=en_merge["comentions"].fillna(0)
en_merge["links"]=en_merge["links"].fillna(0)
en_merge["recency"]=en_merge["recency"].fillna(-1)
en_merge.corr()
| 0.232833 | 0.894927 |
```
import pandas as pd
import csv
import sys
import re
import scipy
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint as sp_randint
from time import time
csv.field_size_limit(sys.maxsize)
metrics = ['cbo','wmc','rfc','lcom','nom','nopm','nosm','nof','nopf','nosf','nosi','loc', "commits","linesAdded","linesDeleted","authors","minorAuthors","majorAuthors","authorOwnership"]
def get_metrics(row):
features = []
for metric in metrics:
features.append(float(row[metric]))
return features
df = pd.read_pickle('../data/instances.pkl')
labels = list(set(df['target'].values))
X = []
Y = []
print("Preparing lists...")
for index, row in df.iterrows():
X.append(get_metrics(row))
Y.append(row["target"])
X_train, X_test, y_train, y_test = train_test_split(X, Y, train_size = 0.75, random_state=42)
```
# Default parameters
```
rf_classifier = RandomForestClassifier(random_state=42, verbose=1, n_jobs=-1)
rf_classifier.fit(X_train, y_train)
print("============ EVALUATION on test set:")
print(accuracy_score(y_test, rf_classifier.predict(X_test)))
def report(results, n_top=3):
for i in range(1, n_top + 1):
candidates = np.flatnonzero(results['rank_test_score'] == i)
for candidate in candidates:
print("Model with rank: {0}".format(i))
print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
results['mean_test_score'][candidate],
results['std_test_score'][candidate]))
print("Parameters: {0}".format(results['params'][candidate]))
print("")
param_dist = {"max_depth": [3, None],
"max_features": sp_randint(1, 11),
"min_samples_split": sp_randint(2, 11),
"bootstrap": [True, False],
"criterion": ["gini", "entropy"]}
rf_classifier = RandomForestClassifier(random_state=42, verbose=1, n_jobs=-1)
n_iter_search = 20
random_search = RandomizedSearchCV(rf_classifier,
param_distributions=param_dist,
n_iter=n_iter_search,
cv=5,
n_jobs=-1)
start = time()
print("Hyperparameter tuning...")
random_search.fit(X_train, y_train)
print("RandomizedSearchCV took %.2f seconds for %d candidates"
" parameter settings." % ((time() - start), n_iter_search))
report(random_search.cv_results_)
print("============ EVALUATION on test set:")
print(accuracy_score(y_test, random_search.best_estimator_.predict(X_test)))
```
|
github_jupyter
|
import pandas as pd
import csv
import sys
import re
import scipy
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint as sp_randint
from time import time
csv.field_size_limit(sys.maxsize)
metrics = ['cbo','wmc','rfc','lcom','nom','nopm','nosm','nof','nopf','nosf','nosi','loc', "commits","linesAdded","linesDeleted","authors","minorAuthors","majorAuthors","authorOwnership"]
def get_metrics(row):
features = []
for metric in metrics:
features.append(float(row[metric]))
return features
df = pd.read_pickle('../data/instances.pkl')
labels = list(set(df['target'].values))
X = []
Y = []
print("Preparing lists...")
for index, row in df.iterrows():
X.append(get_metrics(row))
Y.append(row["target"])
X_train, X_test, y_train, y_test = train_test_split(X, Y, train_size = 0.75, random_state=42)
rf_classifier = RandomForestClassifier(random_state=42, verbose=1, n_jobs=-1)
rf_classifier.fit(X_train, y_train)
print("============ EVALUATION on test set:")
print(accuracy_score(y_test, rf_classifier.predict(X_test)))
def report(results, n_top=3):
for i in range(1, n_top + 1):
candidates = np.flatnonzero(results['rank_test_score'] == i)
for candidate in candidates:
print("Model with rank: {0}".format(i))
print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
results['mean_test_score'][candidate],
results['std_test_score'][candidate]))
print("Parameters: {0}".format(results['params'][candidate]))
print("")
param_dist = {"max_depth": [3, None],
"max_features": sp_randint(1, 11),
"min_samples_split": sp_randint(2, 11),
"bootstrap": [True, False],
"criterion": ["gini", "entropy"]}
rf_classifier = RandomForestClassifier(random_state=42, verbose=1, n_jobs=-1)
n_iter_search = 20
random_search = RandomizedSearchCV(rf_classifier,
param_distributions=param_dist,
n_iter=n_iter_search,
cv=5,
n_jobs=-1)
start = time()
print("Hyperparameter tuning...")
random_search.fit(X_train, y_train)
print("RandomizedSearchCV took %.2f seconds for %d candidates"
" parameter settings." % ((time() - start), n_iter_search))
report(random_search.cv_results_)
print("============ EVALUATION on test set:")
print(accuracy_score(y_test, random_search.best_estimator_.predict(X_test)))
| 0.373304 | 0.352035 |
```
import tensorflow as tf
import numpy as np
from keras.datasets import cifar10
import matplotlib.pyplot as plt
import random
from keras.utils import to_categorical
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train= x_train/255
x_test = x_test/255
# one_hot maker
def one_hot(vector):
one_hot_vec = np.zeros([len(vector), int(max(vector[0:len(vector)])+1)])
for i in range(len(one_hot_vec)):
one_hot_vec[i, vector[i, 0]] = 1
return one_hot_vec
# creating minibatches
def mini_batch(X, Y, size):
idx = np.random.randint(np.size(Y[:, 0]), size = (size,1))
x_bat = X[idx]
x_bat = x_bat.reshape(size, 32, 32, 3)
y_bat = Y[idx]
y_bat = y_bat.reshape(size, 10)
return x_bat, y_bat
tf.reset_default_graph()
# placeholders
x = tf.placeholder(tf.float32, [None,32,32,3])
y = tf.placeholder(tf.float32,[None, 10])
# weights
w1 = tf.get_variable('w1', [2,2,3,80], initializer=tf.contrib.layers.xavier_initializer())
b1 = tf.get_variable('b1', [80], initializer=tf.contrib.layers.xavier_initializer())
w2 = tf.get_variable('w2', [2,2,80,80], initializer=tf.contrib.layers.xavier_initializer())
b2 = tf.get_variable('b2', [80], initializer=tf.contrib.layers.xavier_initializer())
# CNN model
with tf.device("/gpu:0"):
conv1 = tf.nn.conv2d(x, w1, strides = [1,1,1,1], padding = 'SAME')
bias1 = tf.nn.bias_add(conv1, b1)
h1 = tf.nn.relu(bias1)
m1 = tf.nn.max_pool(h1, ksize = [1,2,2,1], strides = [1,2,2,1], padding = 'SAME')
drop_1 = tf.nn.dropout(m1, 0.8)
conv2 = tf.nn.conv2d(drop_1, w2, strides = [1,1,1,1], padding = 'SAME')
bias2 = tf.nn.bias_add(conv2, b2)
h2 = tf.nn.relu(bias2)
m2 = tf.nn.max_pool(h2, ksize = [1,2,2,1], strides = [1,2,2,1], padding = 'SAME')
drop_2 = tf.nn.dropout(m2, 0.8)
flat_0 = tf.contrib.layers.flatten(drop_2)
flat_1 = tf.layers.dense(flat_0, 256, activation='relu')
classifier = tf.layers.dense(flat_1, 10, activation=tf.nn.softmax)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=classifier, labels=y))
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(loss)
print('model summary')
print('x : ', x.shape)
print('conv1 : ', drop_1.shape)
print('conv2 : ', drop_2.shape)
print('flat_0 : ', flat_0.shape)
print('flat_1 : ', flat_1.shape)
print('final : ', classifier.shape)
sess = tf.Session(config=tf.ConfigProto(log_device_placement=True))
sess.run(tf.global_variables_initializer())
cost = []
# training
for epoch in range(999):
x_batch, y_batch = mini_batch(x_train, to_categorical(y_train, num_classes=10), 600)
training_step = sess.run(optimizer, {x: x_batch, y: y_batch})
if epoch%200==0:
print("Iteration: ", epoch)
cost.append(sess.run(loss, {x: x_batch, y: y_batch}))
plt.plot(range(0, epoch+1), cost[:])
plt.xlabel("ITERATION")
plt.ylabel("LOSS")
plt.show()
randomness = range(1, 6000)
# test set evaluation
test_loss = sess.run(loss, {x: x_test[randomness], y: one_hot(y_test[randomness])})
print("loss on training set : ", cost[-1])
print("loss on test set : ", test_loss)
# metrics
test_true= tf.equal(np.argmax(sess.run(classifier, {x: x_test[randomness]}), axis=1), np.argmax(y_test[randomness], axis=1))
test_accuracy = tf.reduce_mean(tf.cast(test_true, dtype="float"))
train_true = tf.equal(np.argmax(sess.run(classifier, {x: x_train[randomness]}), axis=1), np.argmax(y_train[randomness], axis=1))
train_accuracy = tf.reduce_mean(tf.cast(train_true, dtype="float"))
train_score = sess.run(train_accuracy)*100
test_score = sess.run(test_accuracy)*100
print("train accuracy : %.2f" %train_score, "%")
print("test accuracy : %.2f" %test_score, "%")
```
## Things I've tried
1. Residual network
2. lots of learning rates
3. cnn with 4 to 7 layers
4. Average pooling
5. A **LOT** of neural network models
## What Worked
1. Switching from Adam optimizer to Gradient Descent optimizer
2. Using a wider network instead of a deeper one, since, the images are of smaller resolution which causes vanishing gradient problem
3. For Mini Batch SGD, the batch size should be somewhat bigger
4. messing around with the learning rate a **lot**
## Lessons learned
1. Always start with very simple and shallow model
2. **Always gather lots of data with high resolution images**
3. Early Stopping helps
## Helpful article
https://towardsdatascience.com/7-practical-deep-learning-tips-97a9f514100e
|
github_jupyter
|
import tensorflow as tf
import numpy as np
from keras.datasets import cifar10
import matplotlib.pyplot as plt
import random
from keras.utils import to_categorical
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train= x_train/255
x_test = x_test/255
# one_hot maker
def one_hot(vector):
one_hot_vec = np.zeros([len(vector), int(max(vector[0:len(vector)])+1)])
for i in range(len(one_hot_vec)):
one_hot_vec[i, vector[i, 0]] = 1
return one_hot_vec
# creating minibatches
def mini_batch(X, Y, size):
idx = np.random.randint(np.size(Y[:, 0]), size = (size,1))
x_bat = X[idx]
x_bat = x_bat.reshape(size, 32, 32, 3)
y_bat = Y[idx]
y_bat = y_bat.reshape(size, 10)
return x_bat, y_bat
tf.reset_default_graph()
# placeholders
x = tf.placeholder(tf.float32, [None,32,32,3])
y = tf.placeholder(tf.float32,[None, 10])
# weights
w1 = tf.get_variable('w1', [2,2,3,80], initializer=tf.contrib.layers.xavier_initializer())
b1 = tf.get_variable('b1', [80], initializer=tf.contrib.layers.xavier_initializer())
w2 = tf.get_variable('w2', [2,2,80,80], initializer=tf.contrib.layers.xavier_initializer())
b2 = tf.get_variable('b2', [80], initializer=tf.contrib.layers.xavier_initializer())
# CNN model
with tf.device("/gpu:0"):
conv1 = tf.nn.conv2d(x, w1, strides = [1,1,1,1], padding = 'SAME')
bias1 = tf.nn.bias_add(conv1, b1)
h1 = tf.nn.relu(bias1)
m1 = tf.nn.max_pool(h1, ksize = [1,2,2,1], strides = [1,2,2,1], padding = 'SAME')
drop_1 = tf.nn.dropout(m1, 0.8)
conv2 = tf.nn.conv2d(drop_1, w2, strides = [1,1,1,1], padding = 'SAME')
bias2 = tf.nn.bias_add(conv2, b2)
h2 = tf.nn.relu(bias2)
m2 = tf.nn.max_pool(h2, ksize = [1,2,2,1], strides = [1,2,2,1], padding = 'SAME')
drop_2 = tf.nn.dropout(m2, 0.8)
flat_0 = tf.contrib.layers.flatten(drop_2)
flat_1 = tf.layers.dense(flat_0, 256, activation='relu')
classifier = tf.layers.dense(flat_1, 10, activation=tf.nn.softmax)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=classifier, labels=y))
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(loss)
print('model summary')
print('x : ', x.shape)
print('conv1 : ', drop_1.shape)
print('conv2 : ', drop_2.shape)
print('flat_0 : ', flat_0.shape)
print('flat_1 : ', flat_1.shape)
print('final : ', classifier.shape)
sess = tf.Session(config=tf.ConfigProto(log_device_placement=True))
sess.run(tf.global_variables_initializer())
cost = []
# training
for epoch in range(999):
x_batch, y_batch = mini_batch(x_train, to_categorical(y_train, num_classes=10), 600)
training_step = sess.run(optimizer, {x: x_batch, y: y_batch})
if epoch%200==0:
print("Iteration: ", epoch)
cost.append(sess.run(loss, {x: x_batch, y: y_batch}))
plt.plot(range(0, epoch+1), cost[:])
plt.xlabel("ITERATION")
plt.ylabel("LOSS")
plt.show()
randomness = range(1, 6000)
# test set evaluation
test_loss = sess.run(loss, {x: x_test[randomness], y: one_hot(y_test[randomness])})
print("loss on training set : ", cost[-1])
print("loss on test set : ", test_loss)
# metrics
test_true= tf.equal(np.argmax(sess.run(classifier, {x: x_test[randomness]}), axis=1), np.argmax(y_test[randomness], axis=1))
test_accuracy = tf.reduce_mean(tf.cast(test_true, dtype="float"))
train_true = tf.equal(np.argmax(sess.run(classifier, {x: x_train[randomness]}), axis=1), np.argmax(y_train[randomness], axis=1))
train_accuracy = tf.reduce_mean(tf.cast(train_true, dtype="float"))
train_score = sess.run(train_accuracy)*100
test_score = sess.run(test_accuracy)*100
print("train accuracy : %.2f" %train_score, "%")
print("test accuracy : %.2f" %test_score, "%")
| 0.681939 | 0.640355 |
# Introduction
The **N**euro**d**ata's **Reg**istration module or **ndreg** is a set of python functions which can be used to align pairs of images. The module depends on
* SimpleITK - A simplified version of the Insight ToolKit an image segmentation and registration library
* numpy - A python numerical module simmilar to MATLAB
* matplotlib - A plotting and visuiazation module for numpy
* ndio - NeuroData's Input/Output module for accessing images and annotations stored in the NeuroData infrastructure
## Installation
See [README](../README.md) for platform specific installation instructions
## Infranstructure
Image volumes from a modern microscope can be over a terabyte in size, far too large to be stored on a personal computer. Thus in our infrastructure are stored on server cluster known as [ndstore](http://docs.neurodata.io/ndstore/). Accessing image data of this size poses many challenges. Thus ndstore organizes images in spatial database in such a way to minimize read and write times during random access of image cutouts. In ndstore each image dataset is encapsulated in a *project* which can consist of one or more channels. Each project has a *token* which is used to access the image data. A more detailed handling of ndstore's data model can be found [here](http://docs.neurodata.io/ndstore/sphinx/datamodel.html). Given a project token and a channel, images can be downloaded directly from the web to a personal computer using ndstore's RESTful API. In python, the API can be called using the NeuroData's Input/Output, *ndio* module. *ndio* functions save image data in [numpy arrays](http://docs.scipy.org/doc/numpy/reference/generated/numpy.array.html) for easy manipulation.
Although *numpy* is a powerful numerics library it's image processing capibilites are limited. Thus ndreg depends on *SimpleITK* for image processing. A detailed tutorial on the installation and usage of SimpleITK can be found [here](http://insightsoftwareconsortium.github.io/SimpleITK-Notebooks/00_Setup.html). SimpleITK images can be converted to and from numpy arrays using the *SimpleITK.GetArrayFromImage* and *SimpleITK.GetImageFromArray*
## Namespace conventions
In the following tutorials we use the following naming conventions for modules
```
import numpy as np
import SimpleITK as sitk
import matplotlib.pyplot as plt
```
## Outline
1. [Basic Input/Output](io.ipynb)
1. [2D Registration](2D_Registration.ipynb)
1. [Volumetric Registration and Analysis](3D_CLARITY_RegistrationAndAnalysis.ipynb)
|
github_jupyter
|
import numpy as np
import SimpleITK as sitk
import matplotlib.pyplot as plt
| 0.205535 | 0.989378 |
```
import pandas as pd
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
import numpy as np
import matplotlib.pyplot as plt
import hypertools as hyp
import seaborn as sns
import plotly.graph_objs as go
%matplotlib inline
import plotly.plotly as py
plotly.tools.set_credentials_file(username='jjanelee97', api_key='BYKuJO5q20amqPwH5zHw')
plotly.tools.set_config_file(sharing='public')
plotly.tools.set_config_file(world_readable=True,
sharing='public')
fname3 = 'uber-trip-data/uber-raw-data-apr14.csv'
columns3 = ('Time', 'Lat', 'Lon', 'Base')
april_df = pd.read_csv(fname3, skiprows=[0], names=columns3)
fname3 = 'uber-trip-data/uber-raw-data-apr14.csv'
columns3 = ('Time', 'Lat', 'Lon', 'Driver')
april_df = pd.read_csv(fname3, skiprows=[0], names=columns3)
fname4 = 'uber-trip-data/uber-raw-data-may14.csv'
columns4 = ('Time', 'Lat', 'Lon', 'Driver')
may_df = pd.read_csv(fname4, skiprows=[0], names=columns4)
fname5 = 'uber-trip-data/uber-raw-data-jun14.csv'
columns5 = ('Time', 'Lat', 'Lon', 'Driver')
jun_df = pd.read_csv(fname5, skiprows=[0], names=columns5)
fname6 = 'uber-trip-data/uber-raw-data-jul14.csv'
columns6 = ('Time', 'Lat', 'Lon', 'Driver')
jul_df = pd.read_csv(fname6, skiprows=[0], names=columns6)
fname7 = 'uber-trip-data/uber-raw-data-aug14.csv'
columns7 = ('Time', 'Lat', 'Lon', 'Driver')
aug_df = pd.read_csv(fname7, skiprows=[0], names=columns7)
fname8 = 'uber-trip-data/uber-raw-data-sep14.csv'
columns8 = ('Time', 'Lat', 'Lon', 'Driver')
sep_df = pd.read_csv(fname8, skiprows=[0], names=columns8)
print (april_df)
timeblocks_april = {}
for i in range(0,len(april_df)):
time = april_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_april:
timeblocks_april[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_april[hour[0]]:
timeblocks_april[hour[0]][time[0]] = 1
else:
timeblocks_april[hour[0]][time[0]] += 1
april = []
for i in timeblocks_april:
total = 0
for j in timeblocks_april[i]:
total += timeblocks_april[i][j]
avg = round((total/len(timeblocks_april[i])), 2)
april.append(avg)
print (april)
timeblocks_may = {}
for i in range(0,len(may_df)):
time = may_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_may:
timeblocks_may[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_may[hour[0]]:
timeblocks_may[hour[0]][time[0]] = 1
else:
timeblocks_may[hour[0]][time[0]] += 1
may = []
for i in timeblocks_may:
total = 0
for j in timeblocks_may[i]:
total += timeblocks_may[i][j]
avg = round((total/len(timeblocks_may[i])), 2)
may.append(avg)
print (may)
timeblocks_june = {}
for i in range(0,len(jun_df)):
time = jun_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_june:
timeblocks_june[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_june[hour[0]]:
timeblocks_june[hour[0]][time[0]] = 1
else:
timeblocks_june[hour[0]][time[0]] += 1
june = []
for i in timeblocks_june:
total = 0
for j in timeblocks_june[i]:
total += timeblocks_june[i][j]
avg = round((total/len(timeblocks_june[i])), 2)
june.append(avg)
print (june)
timeblocks_july = {}
for i in range(0,len(jul_df)):
time = jul_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_july:
timeblocks_july[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_july[hour[0]]:
timeblocks_july[hour[0]][time[0]] = 1
else:
timeblocks_july[hour[0]][time[0]] += 1
july = []
for i in timeblocks_july:
total = 0
for j in timeblocks_july[i]:
total += timeblocks_july[i][j]
avg = round((total/len(timeblocks_july[i])), 2)
july.append(avg)
print (july)
timeblocks_aug = {}
for i in range(0,len(aug_df)):
time = aug_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_aug:
timeblocks_aug[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_aug[hour[0]]:
timeblocks_aug[hour[0]][time[0]] = 1
else:
timeblocks_aug[hour[0]][time[0]] += 1
august = []
for i in timeblocks_aug:
total = 0
for j in timeblocks_aug[i]:
total += timeblocks_aug[i][j]
avg = round((total/len(timeblocks_aug[i])), 2)
august.append(avg)
print (august)
timeblocks_sep = {}
for i in range(0,len(sep_df)):
time = sep_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_sep:
timeblocks_sep[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_sep[hour[0]]:
timeblocks_sep[hour[0]][time[0]] = 1
else:
timeblocks_sep[hour[0]][time[0]] += 1
september = []
for i in timeblocks_sep:
total = 0
for j in timeblocks_sep[i]:
total += timeblocks_sep[i][j]
avg = round((total/len(timeblocks_sep[i])), 2)
september.append(avg)
print (september)
# Add data
time_of_day = ['12 AM', '1 AM', ' 2AM', '3 AM', '4 AM', '5 AM', '6 AM',
'7 AM', '8 AM', '9 AM', '10 AM', '11 AM', '12 PM',
'1 PM', '2 PM', '3 PM', '4 PM', '5 PM', '6 PM', '7 PM',
'8 PM', '9 PM', '10 PM', '11 PM']
# Create and style traces
trace0 = go.Scatter(
x = time_of_day,
y = april,
name = 'april',
line = dict(
color = ('rgb(205, 12, 24)'),
width = 4)
)
trace1 = go.Scatter(
x = time_of_day,
y = may,
name = 'may',
line = dict(
color = ('rgb(200, 10, 167)'),
width = 4)
)
trace2 = go.Scatter(
x = time_of_day,
y = june,
name = 'june',
line = dict(
color = ('rgb(149, 120, 240)'),
width = 4)
)
trace3 = go.Scatter(
x = time_of_day,
y = july,
name = 'july',
line = dict(
color = ('rgb(22, 96, 167)'),
width = 4)
)
trace4 = go.Scatter(
x = time_of_day,
y = august,
name = 'august',
line = dict(
color = ('rgb(255, 120, 24)'),
width = 4)
)
trace5 = go.Scatter(
x = time_of_day,
y = september,
name = 'september',
line = dict(
color = ('rgb(22, 190, 16)'),
width = 4,
dash = 'dot')
)
data = [trace0, trace1, trace2, trace3, trace4, trace5]
# Edit the layout
layout = dict(title = 'Average Rides Per Timeblock on a given Month (Apr-Sept)',
xaxis = dict(title = 'Timeblock'),
yaxis = dict(title = 'Number of Rides (avg)'),
)
fig = dict(data=data, layout=layout)
py.iplot(fig, filename='styled-line')
# possible explanation:
# https://www.uber.com/blog/new-york-city/three-septembers-of-uberx-in-new-york-city/
```
|
github_jupyter
|
import pandas as pd
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
import numpy as np
import matplotlib.pyplot as plt
import hypertools as hyp
import seaborn as sns
import plotly.graph_objs as go
%matplotlib inline
import plotly.plotly as py
plotly.tools.set_credentials_file(username='jjanelee97', api_key='BYKuJO5q20amqPwH5zHw')
plotly.tools.set_config_file(sharing='public')
plotly.tools.set_config_file(world_readable=True,
sharing='public')
fname3 = 'uber-trip-data/uber-raw-data-apr14.csv'
columns3 = ('Time', 'Lat', 'Lon', 'Base')
april_df = pd.read_csv(fname3, skiprows=[0], names=columns3)
fname3 = 'uber-trip-data/uber-raw-data-apr14.csv'
columns3 = ('Time', 'Lat', 'Lon', 'Driver')
april_df = pd.read_csv(fname3, skiprows=[0], names=columns3)
fname4 = 'uber-trip-data/uber-raw-data-may14.csv'
columns4 = ('Time', 'Lat', 'Lon', 'Driver')
may_df = pd.read_csv(fname4, skiprows=[0], names=columns4)
fname5 = 'uber-trip-data/uber-raw-data-jun14.csv'
columns5 = ('Time', 'Lat', 'Lon', 'Driver')
jun_df = pd.read_csv(fname5, skiprows=[0], names=columns5)
fname6 = 'uber-trip-data/uber-raw-data-jul14.csv'
columns6 = ('Time', 'Lat', 'Lon', 'Driver')
jul_df = pd.read_csv(fname6, skiprows=[0], names=columns6)
fname7 = 'uber-trip-data/uber-raw-data-aug14.csv'
columns7 = ('Time', 'Lat', 'Lon', 'Driver')
aug_df = pd.read_csv(fname7, skiprows=[0], names=columns7)
fname8 = 'uber-trip-data/uber-raw-data-sep14.csv'
columns8 = ('Time', 'Lat', 'Lon', 'Driver')
sep_df = pd.read_csv(fname8, skiprows=[0], names=columns8)
print (april_df)
timeblocks_april = {}
for i in range(0,len(april_df)):
time = april_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_april:
timeblocks_april[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_april[hour[0]]:
timeblocks_april[hour[0]][time[0]] = 1
else:
timeblocks_april[hour[0]][time[0]] += 1
april = []
for i in timeblocks_april:
total = 0
for j in timeblocks_april[i]:
total += timeblocks_april[i][j]
avg = round((total/len(timeblocks_april[i])), 2)
april.append(avg)
print (april)
timeblocks_may = {}
for i in range(0,len(may_df)):
time = may_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_may:
timeblocks_may[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_may[hour[0]]:
timeblocks_may[hour[0]][time[0]] = 1
else:
timeblocks_may[hour[0]][time[0]] += 1
may = []
for i in timeblocks_may:
total = 0
for j in timeblocks_may[i]:
total += timeblocks_may[i][j]
avg = round((total/len(timeblocks_may[i])), 2)
may.append(avg)
print (may)
timeblocks_june = {}
for i in range(0,len(jun_df)):
time = jun_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_june:
timeblocks_june[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_june[hour[0]]:
timeblocks_june[hour[0]][time[0]] = 1
else:
timeblocks_june[hour[0]][time[0]] += 1
june = []
for i in timeblocks_june:
total = 0
for j in timeblocks_june[i]:
total += timeblocks_june[i][j]
avg = round((total/len(timeblocks_june[i])), 2)
june.append(avg)
print (june)
timeblocks_july = {}
for i in range(0,len(jul_df)):
time = jul_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_july:
timeblocks_july[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_july[hour[0]]:
timeblocks_july[hour[0]][time[0]] = 1
else:
timeblocks_july[hour[0]][time[0]] += 1
july = []
for i in timeblocks_july:
total = 0
for j in timeblocks_july[i]:
total += timeblocks_july[i][j]
avg = round((total/len(timeblocks_july[i])), 2)
july.append(avg)
print (july)
timeblocks_aug = {}
for i in range(0,len(aug_df)):
time = aug_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_aug:
timeblocks_aug[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_aug[hour[0]]:
timeblocks_aug[hour[0]][time[0]] = 1
else:
timeblocks_aug[hour[0]][time[0]] += 1
august = []
for i in timeblocks_aug:
total = 0
for j in timeblocks_aug[i]:
total += timeblocks_aug[i][j]
avg = round((total/len(timeblocks_aug[i])), 2)
august.append(avg)
print (august)
timeblocks_sep = {}
for i in range(0,len(sep_df)):
time = sep_df.Time[i].strip().split()
hour = time[1].strip().split(':')
if hour[0] not in timeblocks_sep:
timeblocks_sep[hour[0]] = {time[0]: 1}
else:
if time[0] not in timeblocks_sep[hour[0]]:
timeblocks_sep[hour[0]][time[0]] = 1
else:
timeblocks_sep[hour[0]][time[0]] += 1
september = []
for i in timeblocks_sep:
total = 0
for j in timeblocks_sep[i]:
total += timeblocks_sep[i][j]
avg = round((total/len(timeblocks_sep[i])), 2)
september.append(avg)
print (september)
# Add data
time_of_day = ['12 AM', '1 AM', ' 2AM', '3 AM', '4 AM', '5 AM', '6 AM',
'7 AM', '8 AM', '9 AM', '10 AM', '11 AM', '12 PM',
'1 PM', '2 PM', '3 PM', '4 PM', '5 PM', '6 PM', '7 PM',
'8 PM', '9 PM', '10 PM', '11 PM']
# Create and style traces
trace0 = go.Scatter(
x = time_of_day,
y = april,
name = 'april',
line = dict(
color = ('rgb(205, 12, 24)'),
width = 4)
)
trace1 = go.Scatter(
x = time_of_day,
y = may,
name = 'may',
line = dict(
color = ('rgb(200, 10, 167)'),
width = 4)
)
trace2 = go.Scatter(
x = time_of_day,
y = june,
name = 'june',
line = dict(
color = ('rgb(149, 120, 240)'),
width = 4)
)
trace3 = go.Scatter(
x = time_of_day,
y = july,
name = 'july',
line = dict(
color = ('rgb(22, 96, 167)'),
width = 4)
)
trace4 = go.Scatter(
x = time_of_day,
y = august,
name = 'august',
line = dict(
color = ('rgb(255, 120, 24)'),
width = 4)
)
trace5 = go.Scatter(
x = time_of_day,
y = september,
name = 'september',
line = dict(
color = ('rgb(22, 190, 16)'),
width = 4,
dash = 'dot')
)
data = [trace0, trace1, trace2, trace3, trace4, trace5]
# Edit the layout
layout = dict(title = 'Average Rides Per Timeblock on a given Month (Apr-Sept)',
xaxis = dict(title = 'Timeblock'),
yaxis = dict(title = 'Number of Rides (avg)'),
)
fig = dict(data=data, layout=layout)
py.iplot(fig, filename='styled-line')
# possible explanation:
# https://www.uber.com/blog/new-york-city/three-septembers-of-uberx-in-new-york-city/
| 0.091078 | 0.321766 |
<h1 align=center><font size=5>Word Embeddings in Python</font></h1>
### Table of contents
- [Objective](#objective)
- [One-hot encoding](#one_hot)
- [Encode each word with a unique number](#integer_enc)
- [Word embeddings](#word_embeddings)
- [References](#ref)
### Objective <a id="objective"></a>
In this notebook, we learn different ways for converting strings to numbers (or to vectorize the text) before feeding it to machine learning models.
### One-hot encoding <a id="one_hot"></a>
As a first idea, we might "one-hot" encode each word in our vocabulary. Consider the sentence "The cat sat on the mat". The vocabulary (or unique words) in this sentence is (cat, mat, on, sat, the). To represent each word, we will create a zero vector with length equal to the vocabulary, then place a one in the index that corresponds to the word.
```
from sklearn.preprocessing import LabelEncoder
from tensorflow.keras.utils import to_categorical
text = 'The cat sat on the mat.'
text = text.lower().split()
print(text)
label_encoder = LabelEncoder()
integer_encoded = label_encoder.fit_transform(text)
print(integer_encoded)
onehot_encoded = to_categorical(integer_encoded)
print(onehot_encoded)
```
✍ What are downsides to this approach?
> This approach is inefficient. A one-hot encoded vector is sparse (meaning, most indicices are zero). Imagine we have 10,000 words in the vocabulary. To one-hot encode each word, we would create a vector where 99.99% of the elements are zero.
### Encode each word with a unique number <a id="integer_enc"></a>
A second approach we might try is to encode each word using a unique number. Continuing the example above, we could assign 1 to "cat", 2 to "mat", and so on. We could then encode the sentence "The cat sat on the mat" as a dense vector like [5, 1, 4, 3, 5, 2].
✍ What are pros and cons of this approach?
> This appoach is efficient. Instead of a sparse vector, we now have a dense one (where all elements are full).
> There are two downsides to this approach, however:
- The integer-encoding is arbitrary (it does not capture any relationship between words).
- An integer-encoding can be challenging for a model to interpret. A linear classifier, for example, learns a single weight for each feature. Because there is no relationship between the similarity of any two words and the similarity of their encodings, this feature-weight combination is not meaningful.
Text tokenization utility class in Tensorflow allows us to vectorize a text corpus, by turning each text into either a sequence of integers (each integer being the index of a token in a dictionary) or into a vector where the coefficient for each token could be binary, based on word count, based on tf-idf...
Arguments:
- __num_words__: the maximum number of words to keep, based on word frequency. Only the most common `num_words-1` words will be kept.
- __filters__: a string where each element is a character that will be filtered from the texts. The default is all punctuation, plus tabs and line breaks, minus the `'` character.
- __lower__: boolean. Whether to convert the texts to lowercase.
- __split__: str. Separator for word splitting.
- __char_level__: if True, every character will be treated as a token.
- __oov_token__: if given, it will be added to word_index and used to replace out-of-vocabulary words during text_to_sequence calls
By default, all punctuation is removed, turning the texts into space-separated sequences of words (words maybe include the `'` character). These sequences are then split into lists of tokens. They will then be indexed or vectorized. Note that `0` is a reserved index that won't be assigned to any word.
#### Text Tokenization
Here, we learn how to tokenize a text, and then turn sentences into sequences using tensorflow.
```
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.preprocessing.text import Tokenizer
texts = ['The cat sat on the mat.',
'The dog sat on the log.',
'Dogs and cats living together.']
tokenizer = Tokenizer(num_words = 20)
tokenizer.fit_on_texts(texts)
word_index = tokenizer.word_index
print('Word index:\n', word_index)
sequences = tokenizer.texts_to_sequences(texts) # Transforms each text into a sequence of integers
print('Sequences:\n', sequences)
```
#### Test Sequence
```
X_train = ['The cat sat on the mat.']
tokenizer = Tokenizer(num_words = 20)
tokenizer.fit_on_texts(X_train)
word_index = tokenizer.word_index
print('Word index:\n', word_index)
X_train_seq = tokenizer.texts_to_sequences(X_train)
print('Sequences:\n', X_train_seq)
# --------------------------------------------------------
X_test = ['The dog sat on the log.']
X_test_seq = tokenizer.texts_to_sequences(X_test)
print('Test sequence:\n', X_test_seq)# here the unseen words has ignored
```
#### Out Of Vocabulary (OOV) words
```
X_train = ['The cat sat on the mat.']
tokenizer = Tokenizer(num_words = 20, oov_token = '<OOV>')
tokenizer.fit_on_texts(X_train)
word_index = tokenizer.word_index
print('Word index:\n', word_index)
X_train_seq = tokenizer.texts_to_sequences(X_train)
print('Sequences:\n', X_train_seq)
# --------------------------------------------------------
X_test = ['The dog sat on the log.']
X_test_seq = tokenizer.texts_to_sequences(X_test)
print('Test sequence:\n', X_test_seq)
```
#### Padding <br>
https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/sequence/pad_sequences
```
from tensorflow.keras.preprocessing.sequence import pad_sequences
sentences = ['I love my dog',
'You love my dog!',
'Do you think my dog is amazing?']
tokenizer = Tokenizer(num_words = 20, oov_token = '<OOV>')
tokenizer.fit_on_texts(sentences)
word_index = tokenizer.word_index
print('Word index:\n', word_index)
sequences = tokenizer.texts_to_sequences(sentences)
print('Sequences:\n', sequences)
padded = pad_sequences(sequences)
print('Padded sequences:\n', padded)
matrix2 = tokenizer.texts_to_matrix(['I love my dog'])
print(matrix2)
padded = pad_sequences(sequences, padding = 'post', maxlen = 5, truncating = 'post')
print('Padded sequences:\n', padded)
print('Padded shape:', padded.shape)
texts = ['The the the the the cat sat on the mat cat.']
tokenizer = Tokenizer(num_words = 10)
tokenizer.fit_on_texts(texts)
word_index = tokenizer.word_index
print('Word index:', word_index)
sequences = tokenizer.texts_to_sequences(texts)
print('Sequences:', sequences)
for mode in ['binary', 'count', 'freq', 'tfidf']:
matrix = tokenizer.texts_to_matrix(texts, mode) # Convert a list of texts to a Numpy matrix.
print('-'*20, mode, '-'*20)
print(matrix)
```
### Word embeddings <a id="word_embeddings"></a>
Word embeddings give us a way to use an efficient, dense representation in which similar words have a similar encoding. Importantly, we do not have to specify this encoding by hand. An embedding is a dense vector of floating point values (the length of the vector is a parameter you specify). Instead of specifying the values for the embedding manually, they are trainable parameters (weights learned by the model during training, in the same way a model learns weights for a dense layer). It is common to see word embeddings that are 8-dimensional (for small datasets), up to 1024-dimensions when working with large datasets. A higher dimensional embedding can capture fine-grained relationships between words, but takes more data to learn.
### References <a id="ref"></a>
- https://keras.io/preprocessing/text/
- https://www.tensorflow.org/tutorials/text/word_embeddings
|
github_jupyter
|
from sklearn.preprocessing import LabelEncoder
from tensorflow.keras.utils import to_categorical
text = 'The cat sat on the mat.'
text = text.lower().split()
print(text)
label_encoder = LabelEncoder()
integer_encoded = label_encoder.fit_transform(text)
print(integer_encoded)
onehot_encoded = to_categorical(integer_encoded)
print(onehot_encoded)
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.preprocessing.text import Tokenizer
texts = ['The cat sat on the mat.',
'The dog sat on the log.',
'Dogs and cats living together.']
tokenizer = Tokenizer(num_words = 20)
tokenizer.fit_on_texts(texts)
word_index = tokenizer.word_index
print('Word index:\n', word_index)
sequences = tokenizer.texts_to_sequences(texts) # Transforms each text into a sequence of integers
print('Sequences:\n', sequences)
X_train = ['The cat sat on the mat.']
tokenizer = Tokenizer(num_words = 20)
tokenizer.fit_on_texts(X_train)
word_index = tokenizer.word_index
print('Word index:\n', word_index)
X_train_seq = tokenizer.texts_to_sequences(X_train)
print('Sequences:\n', X_train_seq)
# --------------------------------------------------------
X_test = ['The dog sat on the log.']
X_test_seq = tokenizer.texts_to_sequences(X_test)
print('Test sequence:\n', X_test_seq)# here the unseen words has ignored
X_train = ['The cat sat on the mat.']
tokenizer = Tokenizer(num_words = 20, oov_token = '<OOV>')
tokenizer.fit_on_texts(X_train)
word_index = tokenizer.word_index
print('Word index:\n', word_index)
X_train_seq = tokenizer.texts_to_sequences(X_train)
print('Sequences:\n', X_train_seq)
# --------------------------------------------------------
X_test = ['The dog sat on the log.']
X_test_seq = tokenizer.texts_to_sequences(X_test)
print('Test sequence:\n', X_test_seq)
from tensorflow.keras.preprocessing.sequence import pad_sequences
sentences = ['I love my dog',
'You love my dog!',
'Do you think my dog is amazing?']
tokenizer = Tokenizer(num_words = 20, oov_token = '<OOV>')
tokenizer.fit_on_texts(sentences)
word_index = tokenizer.word_index
print('Word index:\n', word_index)
sequences = tokenizer.texts_to_sequences(sentences)
print('Sequences:\n', sequences)
padded = pad_sequences(sequences)
print('Padded sequences:\n', padded)
matrix2 = tokenizer.texts_to_matrix(['I love my dog'])
print(matrix2)
padded = pad_sequences(sequences, padding = 'post', maxlen = 5, truncating = 'post')
print('Padded sequences:\n', padded)
print('Padded shape:', padded.shape)
texts = ['The the the the the cat sat on the mat cat.']
tokenizer = Tokenizer(num_words = 10)
tokenizer.fit_on_texts(texts)
word_index = tokenizer.word_index
print('Word index:', word_index)
sequences = tokenizer.texts_to_sequences(texts)
print('Sequences:', sequences)
for mode in ['binary', 'count', 'freq', 'tfidf']:
matrix = tokenizer.texts_to_matrix(texts, mode) # Convert a list of texts to a Numpy matrix.
print('-'*20, mode, '-'*20)
print(matrix)
| 0.643329 | 0.941493 |
```
import sys
sys.path.append('../../')
import spartan as st
import numpy as np
import sparse
```
# CPU Dense
```
A = st.DTensor.from_numpy(np.random.rand(3, 4))
print(A)
```
## Get Attributes
```
print(A.shape)
print(A.dtype)
print(A.T)
```
## Index and Slice
```
print(len(A))
print(A[0])
print(A[:, 1])
print(A[:, 0:2])
```
## Reduction operations
```
print(A.sum())
print(A.sum(axis=0))
print(st.sum(A))
print(st.sum(A, axis=0))
```
## Binary operations
```
B = st.DTensor.from_numpy(np.random.rand(3, 4))
print(A+B)
print(st.add(A, B))
print(A.dot(B.T))
print(st.dot(A, B.T))
```
# CPU Sparse
```
A = np.random.rand(3, 4)
A[A<0.8] = 0
A = st.STensor.from_numpy(A)
print(A)
print(A.todense())
```
## Get Attributes
```
print(A.shape)
print(A.dtype)
print(A.T)
```
## Index and Slice
```
print(len(A))
print(A[0])
print(A[:, 1])
print(A[:, 0:2])
```
## Reduction operations
```
print(A.sum())
print(A.sum(axis=0).todense())
print(st.sum(A))
print(st.sum(A, axis=0).todense())
```
## Binary operations
```
B = np.random.rand(3, 4)
B[B<0.8] = 0
B = st.STensor.from_numpy(B)
print(A+B)
print((A+B).todense())
print(st.add(A, B))
print(st.add(A, B).todense())
print(A.dot(B.T))
print(A.dot(B.T).todense())
print(st.dot(A, B.T))
print(st.dot(A, B.T).todense())
```
# GPU Dense
```
import sys
sys.path.append('../../')
import spartan as st
st.load_backend('gpu')
import torch
A = st.DTensor(torch.rand(3, 4))
```
## Attributes
```
print(A.shape)
print(A.dtype)
print(A.T)
```
## Slice
```
print(len(A))
print(A[0])
print(A[:, 1])
print(A[:, 0:2])
```
## Reduction Operations
```
print(A.sum())
print(A.sum(axis=0))
print(st.sum(A))
print(st.sum(A, axis=0))
```
## Binary Operations
```
B = st.DTensor(torch.rand(3, 4))
print(A+B)
print(st.add(A, B))
print(A.dot(B.T))
print(st.dot(A, B.T))
```
## GPU Sparse
**Notice**: Some oeprations are not supported for GPU STensor yet!
```
import scipy.sparse as ssp
A = np.random.rand(3, 4)
A[A<0.8] = 0
A = np.random.rand(3, 4)
A[A<0.8] = 0
A = st.STensor.from_numpy(A)
print(A)
print(A.todense())
```
## Attributes
```
print(A.shape)
print(A.dtype)
# print(A.T)
```
## Index and Slice
**Notice**: Pytorch GPU sparse tensor doesn't support complex slice yet!
```
print(len(A))
print(A[0])
```
## Reduction operations
```
print(A.sum())
print(A.sum(axis=0).todense())
# print(st.sum(A))
# print(st.sum(A, axis=0).todense())
```
## Binary operations
```
B = np.random.rand(3, 4)
B[B<0.8] = 0
B = st.STensor.from_numpy(B)
print(A+B)
print((A+B).todense())
# print(st.add(A, B))
# print(st.add(A, B).todense())
```
|
github_jupyter
|
import sys
sys.path.append('../../')
import spartan as st
import numpy as np
import sparse
A = st.DTensor.from_numpy(np.random.rand(3, 4))
print(A)
print(A.shape)
print(A.dtype)
print(A.T)
print(len(A))
print(A[0])
print(A[:, 1])
print(A[:, 0:2])
print(A.sum())
print(A.sum(axis=0))
print(st.sum(A))
print(st.sum(A, axis=0))
B = st.DTensor.from_numpy(np.random.rand(3, 4))
print(A+B)
print(st.add(A, B))
print(A.dot(B.T))
print(st.dot(A, B.T))
A = np.random.rand(3, 4)
A[A<0.8] = 0
A = st.STensor.from_numpy(A)
print(A)
print(A.todense())
print(A.shape)
print(A.dtype)
print(A.T)
print(len(A))
print(A[0])
print(A[:, 1])
print(A[:, 0:2])
print(A.sum())
print(A.sum(axis=0).todense())
print(st.sum(A))
print(st.sum(A, axis=0).todense())
B = np.random.rand(3, 4)
B[B<0.8] = 0
B = st.STensor.from_numpy(B)
print(A+B)
print((A+B).todense())
print(st.add(A, B))
print(st.add(A, B).todense())
print(A.dot(B.T))
print(A.dot(B.T).todense())
print(st.dot(A, B.T))
print(st.dot(A, B.T).todense())
import sys
sys.path.append('../../')
import spartan as st
st.load_backend('gpu')
import torch
A = st.DTensor(torch.rand(3, 4))
print(A.shape)
print(A.dtype)
print(A.T)
print(len(A))
print(A[0])
print(A[:, 1])
print(A[:, 0:2])
print(A.sum())
print(A.sum(axis=0))
print(st.sum(A))
print(st.sum(A, axis=0))
B = st.DTensor(torch.rand(3, 4))
print(A+B)
print(st.add(A, B))
print(A.dot(B.T))
print(st.dot(A, B.T))
import scipy.sparse as ssp
A = np.random.rand(3, 4)
A[A<0.8] = 0
A = np.random.rand(3, 4)
A[A<0.8] = 0
A = st.STensor.from_numpy(A)
print(A)
print(A.todense())
print(A.shape)
print(A.dtype)
# print(A.T)
print(len(A))
print(A[0])
print(A.sum())
print(A.sum(axis=0).todense())
# print(st.sum(A))
# print(st.sum(A, axis=0).todense())
B = np.random.rand(3, 4)
B[B<0.8] = 0
B = st.STensor.from_numpy(B)
print(A+B)
print((A+B).todense())
# print(st.add(A, B))
# print(st.add(A, B).todense())
| 0.076354 | 0.920433 |
# Vežbe 8: Symbolizer
Symbolizer je deo kompajlera koji u AST ugrađuje [tabelu simbola](https://en.wikipedia.org/wiki/Symbol_table), tj. svakom identifikatoru dodaje tip podataka i okruženje u kome je vidljiv.
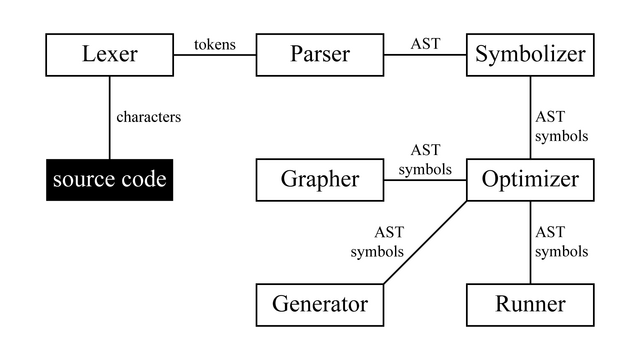
Autor: Lazar Jelić
Repozitorijum: https://github.com/jelic98/raf_pp_materials
Importovanje neophodnog modula za enumeraciju klasa tokena.
```
from enum import Enum, auto
```
Klasa **Class** definiše sve moguće klase leksema koje se mogu naći u izvornom kodu.
```
class Class(Enum):
PLUS = auto()
MINUS = auto()
STAR = auto()
FWDSLASH = auto()
PERCENT = auto()
OR = auto()
AND = auto()
NOT = auto()
EQ = auto()
NEQ = auto()
LT = auto()
GT = auto()
LTE = auto()
GTE = auto()
LPAREN = auto()
RPAREN = auto()
LBRACKET = auto()
RBRACKET = auto()
LBRACE = auto()
RBRACE = auto()
ASSIGN = auto()
SEMICOLON = auto()
COMMA = auto()
TYPE = auto()
INT = auto()
CHAR = auto()
STRING = auto()
IF = auto()
ELSE = auto()
WHILE = auto()
FOR = auto()
BREAK = auto()
CONTINUE = auto()
RETURN = auto()
ADDRESS = auto()
ID = auto()
EOF = auto()
```
Klasa **Token** predstavlja uređeni par (klasa, leksema).
Medota **str** vraća string reprezentaciju tokena koja se koristi u procesu pronalaženja grešaka.
```
class Token:
def __init__(self, class_, lexeme):
self.class_ = class_
self.lexeme = lexeme
def __str__(self):
return "<{} {}>".format(self.class_, self.lexeme)
```
Klasa **Lekser** sadrži metode za leksičku analizu izvornog koda.
Metoda **lex** formira niz tokena pozivajući metodu **next_token**.
Metoda **next_token** konstruiše token odgovarajuće klase pozivajući metodu **next_char**.
Metoda **next_char** pomera pokazivač na sledeći karakter.
Metoda **read_keyword** konstruiše token ključne reči pod uslovom da je trenutni karakter slovo.
Metoda **read_string** konstruiše token string literala pod uslovom da je trenutni karakter znak navodnika.
Metoda **read_char** konstruiše token literala karaktera pod uslovom da je trenutni karakter apostrof.
Metoda **read_int** konstruiše token literala celog broja pod uslovom da je trenutni karakter cifra.
Metoda **read_space** ne konstruiše token, ali pomera pokazivač na prvi sledeći karakter koji nije razmak.
Metoda **die** se koristi u slučaju da je lekser pročitao neočekivani karakter.
```
class Lexer:
def __init__(self, text):
self.text = text
self.len = len(text)
self.pos = -1
def read_space(self):
while self.pos + 1 < self.len and self.text[self.pos + 1].isspace():
self.next_char()
def read_int(self):
lexeme = self.text[self.pos]
while self.pos + 1 < self.len and self.text[self.pos + 1].isdigit():
lexeme += self.next_char()
return int(lexeme)
def read_char(self):
self.pos += 1
lexeme = self.text[self.pos]
self.pos += 1
return lexeme
def read_string(self):
lexeme = ''
while self.pos + 1 < self.len and self.text[self.pos + 1] != '"':
lexeme += self.next_char()
self.pos += 1
return lexeme
def read_keyword(self):
lexeme = self.text[self.pos]
while self.pos + 1 < self.len and self.text[self.pos + 1].isalnum():
lexeme += self.next_char()
if lexeme == 'if':
return Token(Class.IF, lexeme)
elif lexeme == 'else':
return Token(Class.ELSE, lexeme)
elif lexeme == 'while':
return Token(Class.WHILE, lexeme)
elif lexeme == 'for':
return Token(Class.FOR, lexeme)
elif lexeme == 'break':
return Token(Class.BREAK, lexeme)
elif lexeme == 'continue':
return Token(Class.CONTINUE, lexeme)
elif lexeme == 'return':
return Token(Class.RETURN, lexeme)
elif lexeme == 'int' or lexeme == 'char' or lexeme == 'void':
return Token(Class.TYPE, lexeme)
return Token(Class.ID, lexeme)
def next_char(self):
self.pos += 1
if self.pos >= self.len:
return None
return self.text[self.pos]
def next_token(self):
self.read_space()
curr = self.next_char()
if curr is None:
return Token(Class.EOF, curr)
token = None
if curr.isalpha():
token = self.read_keyword()
elif curr.isdigit():
token = Token(Class.INT, self.read_int())
elif curr == '\'':
token = Token(Class.CHAR, self.read_char())
elif curr == '"':
token = Token(Class.STRING, self.read_string())
elif curr == '+':
token = Token(Class.PLUS, curr)
elif curr == '-':
token = Token(Class.MINUS, curr)
elif curr == '*':
token = Token(Class.STAR, curr)
elif curr == '/':
token = Token(Class.FWDSLASH, curr)
elif curr == '%':
token = Token(Class.PERCENT, curr)
elif curr == '&':
curr = self.next_char()
if curr == '&':
token = Token(Class.AND, '&&')
else:
token = Token(Class.ADDRESS, '&')
self.pos -= 1
elif curr == '|':
curr = self.next_char()
if curr == '|':
token = Token(Class.OR, '||')
else:
self.die(curr)
elif curr == '!':
curr = self.next_char()
if curr == '=':
token = Token(Class.NEQ, '!=')
else:
token = Token(Class.NOT, '!')
self.pos -= 1
elif curr == '=':
curr = self.next_char()
if curr == '=':
token = Token(Class.EQ, '==')
else:
token = Token(Class.ASSIGN, '=')
self.pos -= 1
elif curr == '<':
curr = self.next_char()
if curr == '=':
token = Token(Class.LTE, '<=')
else:
token = Token(Class.LT, '<')
self.pos -= 1
elif curr == '>':
curr = self.next_char()
if curr == '=':
token = Token(Class.GTE, '>=')
else:
token = Token(Class.GT, '>')
self.pos -= 1
elif curr == '(':
token = Token(Class.LPAREN, curr)
elif curr == ')':
token = Token(Class.RPAREN, curr)
elif curr == '[':
token = Token(Class.LBRACKET, curr)
elif curr == ']':
token = Token(Class.RBRACKET, curr)
elif curr == '{':
token = Token(Class.LBRACE, curr)
elif curr == '}':
token = Token(Class.RBRACE, curr)
elif curr == ';':
token = Token(Class.SEMICOLON, curr)
elif curr == ',':
token = Token(Class.COMMA, curr)
else:
self.die(curr)
return token
def lex(self):
tokens = []
while True:
curr = self.next_token()
tokens.append(curr)
if curr.class_ == Class.EOF:
break
return tokens
def die(self, char):
raise SystemExit("Unexpected character: {}".format(char))
```
Klasa **Node** predstavlja baznu klasu za formiranje AST, a klase koje je nasleđuju odgovaraju svakoj ispravnoj semantičkoj strukturi.
```
class Node():
pass
class Program(Node):
def __init__(self, nodes):
self.nodes = nodes
class Decl(Node):
def __init__(self, type_, id_):
self.type_ = type_
self.id_ = id_
class ArrayDecl(Node):
def __init__(self, type_, id_, size, elems):
self.type_ = type_
self.id_ = id_
self.size = size
self.elems = elems
class ArrayElem(Node):
def __init__(self, id_, index):
self.id_ = id_
self.index = index
class Assign(Node):
def __init__(self, id_, expr):
self.id_ = id_
self.expr = expr
class If(Node):
def __init__(self, cond, true, false):
self.cond = cond
self.true = true
self.false = false
class While(Node):
def __init__(self, cond, block):
self.cond = cond
self.block = block
class For(Node):
def __init__(self, init, cond, step, block):
self.init = init
self.cond = cond
self.step = step
self.block = block
class FuncImpl(Node):
def __init__(self, type_, id_, params, block):
self.type_ = type_
self.id_ = id_
self.params = params
self.block = block
class FuncCall(Node):
def __init__(self, id_, args):
self.id_ = id_
self.args = args
class Block(Node):
def __init__(self, nodes):
self.nodes = nodes
class Params(Node):
def __init__(self, params):
self.params = params
class Args(Node):
def __init__(self, args):
self.args = args
class Elems(Node):
def __init__(self, elems):
self.elems = elems
class Break(Node):
pass
class Continue(Node):
pass
class Return(Node):
def __init__(self, expr):
self.expr = expr
class Type(Node):
def __init__(self, value):
self.value = value
class Int(Node):
def __init__(self, value):
self.value = value
class Char(Node):
def __init__(self, value):
self.value = value
class String(Node):
def __init__(self, value):
self.value = value
class Id(Node):
def __init__(self, value):
self.value = value
class BinOp(Node):
def __init__(self, symbol, first, second):
self.symbol = symbol
self.first = first
self.second = second
class UnOp(Node):
def __init__(self, symbol, first):
self.symbol = symbol
self.first = first
```
Klasa **Visitor** predstavlja baznu klasu za obilazak AST.
Metoda **visit** u trenutnom objektu traži metodu koja odgovara tipu prosleđenog čvora.
Metoda **die** se koristi u slučaju da tražena metoda ne postoji, tj. u slučaju kada je potrebno obići čvor čiji tip nije podržan.
```
class Visitor():
def visit(self, parent, node):
method = 'visit_' + type(node).__name__
visitor = getattr(self, method, self.die)
return visitor(parent, node)
def die(self, parent, node):
method = 'visit_' + type(node).__name__
raise SystemExit("Missing method: {}".format(method))
```
Importovanje neophodnih modula za čuvanje unutrašnjeg stanja objekta.
```
from functools import wraps
import pickle
```
Klasa **Parser** sadrži metode za semantičku analizu izvornog koda koje će iz prosleđenog [FIFO niza](https://en.wikipedia.org/wiki/FIFO_(computing_and_electronics)) tokena formirati AST čvor po čvor.
Metoda **parse** formira AST pomoću [Visitor dizajn šablona](https://sourcemaking.com/design_patterns/visitor) pozivom metode **program**.
Metoda **program** konstruiše AST čvor za deklaraciju globalnih promenljivih i implementaciju funkcija.
Metoda **id_** konstruiše AST čvor za identifikator.
Metoda **decl** konstruiše AST čvor za deklaraciju skalarne promenljive, niza ili funkcije.
Metoda **if_** konstruiše AST čvor za ispitivanje uslova, blok koji se izvršava u slučaju da je uslov tačan i opcioni blok koji se izvršava u slučaju da uslov nije tačan.
Metoda **while_** konstruiše AST čvor za ispitivanje uslova i blok koji se izvršava sve dok je uslov tačan.
Metoda **for_** konstruiše AST čvor za inicijalizaciju iteratora, ispitivanje uslova, inkrementiranje iteratora i blok koji se izvršava sve dok je uslov tačan.
Metoda **block** konstruiše AST čvor za blok instrukcija koje se izvršavaju u okviru neke semantičke celine.
Metoda **params** konstruiše AST čvor za deklarisane parametre funkcije. Svaki parametar ima naziv i tip.
Metoda **args** konstruiše AST čvor za prosleđene argumente pozivu funkcije. Svaki argument ima naziv i vrednost.
Metoda **elems** konstruiše AST čvor za definisane elemente pri inicijalizaciji niza.
Metoda **return_** konstruiše AST čvor za prekid funkcije uz opciono vraćanje vrednosti.
Metoda **break_** konstruiše AST čvor za prekid petlje.
Metoda **continue_** konstruiše AST čvor za skok na sledeću iteraciju petlje.
Metoda **type_** konstruiše AST čvor za tip podataka, tj. "int", "char" ili "void".
Metoda **factor** konstruiše AST čvor za matematičke operacije visokog prioriteta, tj. unarne operacije.
Metoda **term** konstruiše AST čvor za matematičke operacije srednjeg prioriteta, tj. multiplikativne operacije.
Metoda **expr** konstruiše AST čvor za matematičke operacije niskog prioriteta, tj. aditivne operacija.
Metoda **compare** konstruiše AST čvor za poređenje dva logička operanda.
Metoda **logic** konstruiše AST čvor za logičku konjunkciju i disjunkciju.
Metoda **eat** uzima token za početka niza i proverava da li njegova klasa odgovara prosleđenoj klasi.
Metoda **is_func_call** proverava da li trenutni identifikator odgovara pozivu ili implementaciji funkcije. Nakon provere vraća parser u originalno stanje.
Metoda **restorable** se dodaje kao anotacija drugoj metodi koja menja unutrašnje stanje objekta, a potrebno je da se objekat po završetku funkcije vrati u originalno stanje.
Metoda **die** se koristi u slučaju da se dogodi bilo koja greška.
Metoda **die_deriv** se koristi u slučaju da pročitani token ne odgovara sementičkoj strukturi koja se trenutno formira.
Metoda **die_type** se koristi u slučaju da klasa tokena sa početka niza ne odgovara klasi prosleđenoj pozivu metode **eat**.
```
class Parser:
def __init__(self, tokens):
self.tokens = tokens
self.curr = tokens.pop(0)
self.prev = None
def restorable(call):
@wraps(call)
def wrapper(self, *args, **kwargs):
state = pickle.dumps(self.__dict__)
result = call(self, *args, **kwargs)
self.__dict__ = pickle.loads(state)
return result
return wrapper
def eat(self, class_):
if self.curr.class_ == class_:
self.prev = self.curr
self.curr = self.tokens.pop(0)
else:
self.die_type(class_.name, self.curr.class_.name)
def program(self):
nodes = []
while self.curr.class_ != Class.EOF:
if self.curr.class_ == Class.TYPE:
nodes.append(self.decl())
else:
self.die_deriv(self.program.__name__)
return Program(nodes)
def id_(self):
is_array_elem = self.prev.class_ != Class.TYPE
id_ = Id(self.curr.lexeme)
self.eat(Class.ID)
if self.curr.class_ == Class.LPAREN and self.is_func_call():
self.eat(Class.LPAREN)
args = self.args()
self.eat(Class.RPAREN)
return FuncCall(id_, args)
elif self.curr.class_ == Class.LBRACKET and is_array_elem:
self.eat(Class.LBRACKET)
index = self.expr()
self.eat(Class.RBRACKET)
id_ = ArrayElem(id_, index)
if self.curr.class_ == Class.ASSIGN:
self.eat(Class.ASSIGN)
expr = self.expr()
return Assign(id_, expr)
else:
return id_
def decl(self):
type_ = self.type_()
id_ = self.id_()
if self.curr.class_ == Class.LBRACKET:
self.eat(Class.LBRACKET)
size = None
if self.curr.class_ != Class.RBRACKET:
size = self.expr()
self.eat(Class.RBRACKET)
elems = None
if self.curr.class_ == Class.ASSIGN:
self.eat(Class.ASSIGN)
self.eat(Class.LBRACE)
elems = self.elems()
self.eat(Class.RBRACE)
self.eat(Class.SEMICOLON)
return ArrayDecl(type_, id_, size, elems)
elif self.curr.class_ == Class.LPAREN:
self.eat(Class.LPAREN)
params = self.params()
self.eat(Class.RPAREN)
self.eat(Class.LBRACE)
block = self.block()
self.eat(Class.RBRACE)
return FuncImpl(type_, id_, params, block)
else:
self.eat(Class.SEMICOLON)
return Decl(type_, id_)
def if_(self):
self.eat(Class.IF)
self.eat(Class.LPAREN)
cond = self.logic()
self.eat(Class.RPAREN)
self.eat(Class.LBRACE)
true = self.block()
self.eat(Class.RBRACE)
false = None
if self.curr.class_ == Class.ELSE:
self.eat(Class.ELSE)
self.eat(Class.LBRACE)
false = self.block()
self.eat(Class.RBRACE)
return If(cond, true, false)
def while_(self):
self.eat(Class.WHILE)
self.eat(Class.LPAREN)
cond = self.logic()
self.eat(Class.RPAREN)
self.eat(Class.LBRACE)
block = self.block()
self.eat(Class.RBRACE)
return While(cond, block)
def for_(self):
self.eat(Class.FOR)
self.eat(Class.LPAREN)
init = self.id_()
self.eat(Class.SEMICOLON)
cond = self.logic()
self.eat(Class.SEMICOLON)
step = self.id_()
self.eat(Class.RPAREN)
self.eat(Class.LBRACE)
block = self.block()
self.eat(Class.RBRACE)
return For(init, cond, step, block)
def block(self):
nodes = []
while self.curr.class_ != Class.RBRACE:
if self.curr.class_ == Class.IF:
nodes.append(self.if_())
elif self.curr.class_ == Class.WHILE:
nodes.append(self.while_())
elif self.curr.class_ == Class.FOR:
nodes.append(self.for_())
elif self.curr.class_ == Class.BREAK:
nodes.append(self.break_())
elif self.curr.class_ == Class.CONTINUE:
nodes.append(self.continue_())
elif self.curr.class_ == Class.RETURN:
nodes.append(self.return_())
elif self.curr.class_ == Class.TYPE:
nodes.append(self.decl())
elif self.curr.class_ == Class.ID:
nodes.append(self.id_())
self.eat(Class.SEMICOLON)
else:
self.die_deriv(self.block.__name__)
return Block(nodes)
def params(self):
params = []
while self.curr.class_ != Class.RPAREN:
if len(params) > 0:
self.eat(Class.COMMA)
type_ = self.type_()
id_ = self.id_()
params.append(Decl(type_, id_))
return Params(params)
def args(self):
args = []
while self.curr.class_ != Class.RPAREN:
if len(args) > 0:
self.eat(Class.COMMA)
args.append(self.expr())
return Args(args)
def elems(self):
elems = []
while self.curr.class_ != Class.RBRACE:
if len(elems) > 0:
self.eat(Class.COMMA)
elems.append(self.expr())
return Elems(elems)
def return_(self):
self.eat(Class.RETURN)
expr = self.expr()
self.eat(Class.SEMICOLON)
return Return(expr)
def break_(self):
self.eat(Class.BREAK)
self.eat(Class.SEMICOLON)
return Break()
def continue_(self):
self.eat(Class.CONTINUE)
self.eat(Class.SEMICOLON)
return Continue()
def type_(self):
type_ = Type(self.curr.lexeme)
self.eat(Class.TYPE)
return type_
def factor(self):
if self.curr.class_ == Class.INT:
value = Int(self.curr.lexeme)
self.eat(Class.INT)
return value
elif self.curr.class_ == Class.CHAR:
value = Char(self.curr.lexeme)
self.eat(Class.CHAR)
return value
elif self.curr.class_ == Class.STRING:
value = String(self.curr.lexeme)
self.eat(Class.STRING)
return value
elif self.curr.class_ == Class.ID:
return self.id_()
elif self.curr.class_ in [Class.MINUS, Class.NOT, Class.ADDRESS]:
op = self.curr
self.eat(self.curr.class_)
first = None
if self.curr.class_ == Class.LPAREN:
self.eat(Class.LPAREN)
first = self.logic()
self.eat(Class.RPAREN)
else:
first = self.factor()
return UnOp(op.lexeme, first)
elif self.curr.class_ == Class.LPAREN:
self.eat(Class.LPAREN)
first = self.logic()
self.eat(Class.RPAREN)
return first
elif self.curr.class_ == Class.SEMICOLON:
return None
else:
self.die_deriv(self.factor.__name__)
def term(self):
first = self.factor()
while self.curr.class_ in [Class.STAR, Class.FWDSLASH, Class.PERCENT]:
if self.curr.class_ == Class.STAR:
op = self.curr.lexeme
self.eat(Class.STAR)
second = self.factor()
first = BinOp(op, first, second)
elif self.curr.class_ == Class.FWDSLASH:
op = self.curr.lexeme
self.eat(Class.FWDSLASH)
second = self.factor()
first = BinOp(op, first, second)
elif self.curr.class_ == Class.PERCENT:
op = self.curr.lexeme
self.eat(Class.PERCENT)
second = self.factor()
first = BinOp(op, first, second)
return first
def expr(self):
first = self.term()
while self.curr.class_ in [Class.PLUS, Class.MINUS]:
if self.curr.class_ == Class.PLUS:
op = self.curr.lexeme
self.eat(Class.PLUS)
second = self.term()
first = BinOp(op, first, second)
elif self.curr.class_ == Class.MINUS:
op = self.curr.lexeme
self.eat(Class.MINUS)
second = self.term()
first = BinOp(op, first, second)
return first
def compare(self):
first = self.expr()
if self.curr.class_ == Class.EQ:
op = self.curr.lexeme
self.eat(Class.EQ)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.NEQ:
op = self.curr.lexeme
self.eat(Class.NEQ)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.LT:
op = self.curr.lexeme
self.eat(Class.LT)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.GT:
op = self.curr.lexeme
self.eat(Class.GT)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.LTE:
op = self.curr.lexeme
self.eat(Class.LTE)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.GTE:
op = self.curr.lexeme
self.eat(Class.GTE)
second = self.expr()
return BinOp(op, first, second)
else:
return first
def logic_term(self):
first = self.compare()
while self.curr.class_ == Class.AND:
op = self.curr.lexeme
self.eat(Class.AND)
second = self.compare()
first = BinOp(op, first, second)
return first
def logic(self):
first = self.logic_term()
while self.curr.class_ == Class.OR:
op = self.curr.lexeme
self.eat(Class.OR)
second = self.logic_term()
first = BinOp(op, first, second)
return first
@restorable
def is_func_call(self):
try:
self.eat(Class.LPAREN)
self.args()
self.eat(Class.RPAREN)
return self.curr.class_ != Class.LBRACE
except:
return False
def parse(self):
return self.program()
def die(self, text):
raise SystemExit(text)
def die_deriv(self, fun):
self.die("Derivation error: {}".format(fun))
def die_type(self, expected, found):
self.die("Expected: {}, Found: {}".format(expected, found))
```
Klasa **Symbol** služi za konstrukciju objekata u tabeli simbola ugrađenoj u AST.
Metoda **copy** pravi kopiju trenutnog simbola i koristi se u fazi interpretiranja kako bi se podržala rekurzija.
```
class Symbol:
def __init__(self, id_, type_, scope):
self.id_ = id_
self.type_ = type_
self.scope = scope
def __str__(self):
return "<{} {} {}>".format(self.id_, self.type_, self.scope)
def copy(self):
return Symbol(self.id_, self.type_, self.scope)
```
Klasa **Symbols** predstavlja tabelu simbola i sadrži metode za modifikaciju njenog sadržaja. Konstruisani objekat će se ugraditi u odgovarajući čvor AST, tj. u čvor tipa **Block** u kome su simboli vidljivi.
Metoda **put** dodaje novi simbol u tabelu na osnovu prosleđenog identifikatora, tipa podataka i okruženja u kome je simbol vidljiv.
Metoda **get** vraća simbol iz tabele na osnovu prosleđenog identifikatora.
Metoda **contains** proverava da li tabela sadrži simbol na osnovu prosleđenog identifikatora.
Metoda **remove** uklanja simbol iz tabele na osnovu prosleđenog identifikatora.
```
class Symbols:
def __init__(self):
self.symbols = {}
def put(self, id_, type_, scope):
self.symbols[id_] = Symbol(id_, type_, scope)
def get(self, id_):
return self.symbols[id_]
def contains(self, id_):
return id_ in self.symbols
def remove(self, id_):
del self.symbols[id_]
def __len__(self):
return len(self.symbols)
def __str__(self):
out = ""
for _, value in self.symbols.items():
if len(out) > 0:
out += "\n"
out += str(value)
return out
def __iter__(self):
return iter(self.symbols.values())
def __next__(self):
return next(self.symbols.values())
```
Klasa **Symbolizer** sadrži metode za formiranje tabele simbola. Nije potrebno obići sve čvorove AST, već samo deklaracije simbola i blokove instrukcija u kojima se mogu naći te deklaracije.
Metoda **symbolize** formira tabelu simbola rekurzivim pozivom **visit** metode.
```
class Symbolizer(Visitor):
def __init__(self, ast):
self.ast = ast
def visit_Program(self, parent, node):
node.symbols = Symbols()
for n in node.nodes:
self.visit(node, n)
def visit_Decl(self, parent, node):
parent.symbols.put(node.id_.value, node.type_.value, id(parent))
def visit_ArrayDecl(self, parent, node):
node.symbols = Symbols()
parent.symbols.put(node.id_.value, node.type_.value, id(parent))
def visit_ArrayElem(self, parent, node):
pass
def visit_Assign(self, parent, node):
pass
def visit_If(self, parent, node):
self.visit(node, node.true)
if node.false is not None:
self.visit(node, node.false)
def visit_While(self, parent, node):
self.visit(node, node.block)
def visit_For(self, parent, node):
self.visit(node, node.block)
def visit_FuncImpl(self, parent, node):
parent.symbols.put(node.id_.value, node.type_.value, id(parent))
self.visit(node, node.block)
self.visit(node, node.params)
def visit_FuncCall(self, parent, node):
pass
def visit_Block(self, parent, node):
node.symbols = Symbols()
for n in node.nodes:
self.visit(node, n)
def visit_Params(self, parent, node):
node.symbols = Symbols()
for p in node.params:
self.visit(node, p)
self.visit(parent.block, p)
def visit_Args(self, parent, node):
pass
def visit_Elems(self, parent, node):
pass
def visit_Break(self, parent, node):
pass
def visit_Continue(self, parent, node):
pass
def visit_Return(self, parent, node):
pass
def visit_Type(self, parent, node):
pass
def visit_Int(self, parent, node):
pass
def visit_Char(self, parent, node):
pass
def visit_String(self, parent, node):
pass
def visit_Id(self, parent, node):
pass
def visit_BinOp(self, parent, node):
pass
def visit_UnOp(self, parent, node):
pass
def symbolize(self):
self.visit(None, self.ast)
```
Testiranje implementacije.
```
test_id = '01'
path = f'/content/drive/Shareddrives/Materijali 2020 2021/5. semestar/Programski prevodioci/Vezbe/data/test/{test_id}/src.c'
with open(path, 'r') as source:
text = source.read()
lexer = Lexer(text)
tokens = lexer.lex()
parser = Parser(tokens)
ast = parser.parse()
symbolizer = Symbolizer(ast)
symbolizer.symbolize()
print(ast)
```
|
github_jupyter
|
from enum import Enum, auto
class Class(Enum):
PLUS = auto()
MINUS = auto()
STAR = auto()
FWDSLASH = auto()
PERCENT = auto()
OR = auto()
AND = auto()
NOT = auto()
EQ = auto()
NEQ = auto()
LT = auto()
GT = auto()
LTE = auto()
GTE = auto()
LPAREN = auto()
RPAREN = auto()
LBRACKET = auto()
RBRACKET = auto()
LBRACE = auto()
RBRACE = auto()
ASSIGN = auto()
SEMICOLON = auto()
COMMA = auto()
TYPE = auto()
INT = auto()
CHAR = auto()
STRING = auto()
IF = auto()
ELSE = auto()
WHILE = auto()
FOR = auto()
BREAK = auto()
CONTINUE = auto()
RETURN = auto()
ADDRESS = auto()
ID = auto()
EOF = auto()
class Token:
def __init__(self, class_, lexeme):
self.class_ = class_
self.lexeme = lexeme
def __str__(self):
return "<{} {}>".format(self.class_, self.lexeme)
class Lexer:
def __init__(self, text):
self.text = text
self.len = len(text)
self.pos = -1
def read_space(self):
while self.pos + 1 < self.len and self.text[self.pos + 1].isspace():
self.next_char()
def read_int(self):
lexeme = self.text[self.pos]
while self.pos + 1 < self.len and self.text[self.pos + 1].isdigit():
lexeme += self.next_char()
return int(lexeme)
def read_char(self):
self.pos += 1
lexeme = self.text[self.pos]
self.pos += 1
return lexeme
def read_string(self):
lexeme = ''
while self.pos + 1 < self.len and self.text[self.pos + 1] != '"':
lexeme += self.next_char()
self.pos += 1
return lexeme
def read_keyword(self):
lexeme = self.text[self.pos]
while self.pos + 1 < self.len and self.text[self.pos + 1].isalnum():
lexeme += self.next_char()
if lexeme == 'if':
return Token(Class.IF, lexeme)
elif lexeme == 'else':
return Token(Class.ELSE, lexeme)
elif lexeme == 'while':
return Token(Class.WHILE, lexeme)
elif lexeme == 'for':
return Token(Class.FOR, lexeme)
elif lexeme == 'break':
return Token(Class.BREAK, lexeme)
elif lexeme == 'continue':
return Token(Class.CONTINUE, lexeme)
elif lexeme == 'return':
return Token(Class.RETURN, lexeme)
elif lexeme == 'int' or lexeme == 'char' or lexeme == 'void':
return Token(Class.TYPE, lexeme)
return Token(Class.ID, lexeme)
def next_char(self):
self.pos += 1
if self.pos >= self.len:
return None
return self.text[self.pos]
def next_token(self):
self.read_space()
curr = self.next_char()
if curr is None:
return Token(Class.EOF, curr)
token = None
if curr.isalpha():
token = self.read_keyword()
elif curr.isdigit():
token = Token(Class.INT, self.read_int())
elif curr == '\'':
token = Token(Class.CHAR, self.read_char())
elif curr == '"':
token = Token(Class.STRING, self.read_string())
elif curr == '+':
token = Token(Class.PLUS, curr)
elif curr == '-':
token = Token(Class.MINUS, curr)
elif curr == '*':
token = Token(Class.STAR, curr)
elif curr == '/':
token = Token(Class.FWDSLASH, curr)
elif curr == '%':
token = Token(Class.PERCENT, curr)
elif curr == '&':
curr = self.next_char()
if curr == '&':
token = Token(Class.AND, '&&')
else:
token = Token(Class.ADDRESS, '&')
self.pos -= 1
elif curr == '|':
curr = self.next_char()
if curr == '|':
token = Token(Class.OR, '||')
else:
self.die(curr)
elif curr == '!':
curr = self.next_char()
if curr == '=':
token = Token(Class.NEQ, '!=')
else:
token = Token(Class.NOT, '!')
self.pos -= 1
elif curr == '=':
curr = self.next_char()
if curr == '=':
token = Token(Class.EQ, '==')
else:
token = Token(Class.ASSIGN, '=')
self.pos -= 1
elif curr == '<':
curr = self.next_char()
if curr == '=':
token = Token(Class.LTE, '<=')
else:
token = Token(Class.LT, '<')
self.pos -= 1
elif curr == '>':
curr = self.next_char()
if curr == '=':
token = Token(Class.GTE, '>=')
else:
token = Token(Class.GT, '>')
self.pos -= 1
elif curr == '(':
token = Token(Class.LPAREN, curr)
elif curr == ')':
token = Token(Class.RPAREN, curr)
elif curr == '[':
token = Token(Class.LBRACKET, curr)
elif curr == ']':
token = Token(Class.RBRACKET, curr)
elif curr == '{':
token = Token(Class.LBRACE, curr)
elif curr == '}':
token = Token(Class.RBRACE, curr)
elif curr == ';':
token = Token(Class.SEMICOLON, curr)
elif curr == ',':
token = Token(Class.COMMA, curr)
else:
self.die(curr)
return token
def lex(self):
tokens = []
while True:
curr = self.next_token()
tokens.append(curr)
if curr.class_ == Class.EOF:
break
return tokens
def die(self, char):
raise SystemExit("Unexpected character: {}".format(char))
class Node():
pass
class Program(Node):
def __init__(self, nodes):
self.nodes = nodes
class Decl(Node):
def __init__(self, type_, id_):
self.type_ = type_
self.id_ = id_
class ArrayDecl(Node):
def __init__(self, type_, id_, size, elems):
self.type_ = type_
self.id_ = id_
self.size = size
self.elems = elems
class ArrayElem(Node):
def __init__(self, id_, index):
self.id_ = id_
self.index = index
class Assign(Node):
def __init__(self, id_, expr):
self.id_ = id_
self.expr = expr
class If(Node):
def __init__(self, cond, true, false):
self.cond = cond
self.true = true
self.false = false
class While(Node):
def __init__(self, cond, block):
self.cond = cond
self.block = block
class For(Node):
def __init__(self, init, cond, step, block):
self.init = init
self.cond = cond
self.step = step
self.block = block
class FuncImpl(Node):
def __init__(self, type_, id_, params, block):
self.type_ = type_
self.id_ = id_
self.params = params
self.block = block
class FuncCall(Node):
def __init__(self, id_, args):
self.id_ = id_
self.args = args
class Block(Node):
def __init__(self, nodes):
self.nodes = nodes
class Params(Node):
def __init__(self, params):
self.params = params
class Args(Node):
def __init__(self, args):
self.args = args
class Elems(Node):
def __init__(self, elems):
self.elems = elems
class Break(Node):
pass
class Continue(Node):
pass
class Return(Node):
def __init__(self, expr):
self.expr = expr
class Type(Node):
def __init__(self, value):
self.value = value
class Int(Node):
def __init__(self, value):
self.value = value
class Char(Node):
def __init__(self, value):
self.value = value
class String(Node):
def __init__(self, value):
self.value = value
class Id(Node):
def __init__(self, value):
self.value = value
class BinOp(Node):
def __init__(self, symbol, first, second):
self.symbol = symbol
self.first = first
self.second = second
class UnOp(Node):
def __init__(self, symbol, first):
self.symbol = symbol
self.first = first
class Visitor():
def visit(self, parent, node):
method = 'visit_' + type(node).__name__
visitor = getattr(self, method, self.die)
return visitor(parent, node)
def die(self, parent, node):
method = 'visit_' + type(node).__name__
raise SystemExit("Missing method: {}".format(method))
from functools import wraps
import pickle
class Parser:
def __init__(self, tokens):
self.tokens = tokens
self.curr = tokens.pop(0)
self.prev = None
def restorable(call):
@wraps(call)
def wrapper(self, *args, **kwargs):
state = pickle.dumps(self.__dict__)
result = call(self, *args, **kwargs)
self.__dict__ = pickle.loads(state)
return result
return wrapper
def eat(self, class_):
if self.curr.class_ == class_:
self.prev = self.curr
self.curr = self.tokens.pop(0)
else:
self.die_type(class_.name, self.curr.class_.name)
def program(self):
nodes = []
while self.curr.class_ != Class.EOF:
if self.curr.class_ == Class.TYPE:
nodes.append(self.decl())
else:
self.die_deriv(self.program.__name__)
return Program(nodes)
def id_(self):
is_array_elem = self.prev.class_ != Class.TYPE
id_ = Id(self.curr.lexeme)
self.eat(Class.ID)
if self.curr.class_ == Class.LPAREN and self.is_func_call():
self.eat(Class.LPAREN)
args = self.args()
self.eat(Class.RPAREN)
return FuncCall(id_, args)
elif self.curr.class_ == Class.LBRACKET and is_array_elem:
self.eat(Class.LBRACKET)
index = self.expr()
self.eat(Class.RBRACKET)
id_ = ArrayElem(id_, index)
if self.curr.class_ == Class.ASSIGN:
self.eat(Class.ASSIGN)
expr = self.expr()
return Assign(id_, expr)
else:
return id_
def decl(self):
type_ = self.type_()
id_ = self.id_()
if self.curr.class_ == Class.LBRACKET:
self.eat(Class.LBRACKET)
size = None
if self.curr.class_ != Class.RBRACKET:
size = self.expr()
self.eat(Class.RBRACKET)
elems = None
if self.curr.class_ == Class.ASSIGN:
self.eat(Class.ASSIGN)
self.eat(Class.LBRACE)
elems = self.elems()
self.eat(Class.RBRACE)
self.eat(Class.SEMICOLON)
return ArrayDecl(type_, id_, size, elems)
elif self.curr.class_ == Class.LPAREN:
self.eat(Class.LPAREN)
params = self.params()
self.eat(Class.RPAREN)
self.eat(Class.LBRACE)
block = self.block()
self.eat(Class.RBRACE)
return FuncImpl(type_, id_, params, block)
else:
self.eat(Class.SEMICOLON)
return Decl(type_, id_)
def if_(self):
self.eat(Class.IF)
self.eat(Class.LPAREN)
cond = self.logic()
self.eat(Class.RPAREN)
self.eat(Class.LBRACE)
true = self.block()
self.eat(Class.RBRACE)
false = None
if self.curr.class_ == Class.ELSE:
self.eat(Class.ELSE)
self.eat(Class.LBRACE)
false = self.block()
self.eat(Class.RBRACE)
return If(cond, true, false)
def while_(self):
self.eat(Class.WHILE)
self.eat(Class.LPAREN)
cond = self.logic()
self.eat(Class.RPAREN)
self.eat(Class.LBRACE)
block = self.block()
self.eat(Class.RBRACE)
return While(cond, block)
def for_(self):
self.eat(Class.FOR)
self.eat(Class.LPAREN)
init = self.id_()
self.eat(Class.SEMICOLON)
cond = self.logic()
self.eat(Class.SEMICOLON)
step = self.id_()
self.eat(Class.RPAREN)
self.eat(Class.LBRACE)
block = self.block()
self.eat(Class.RBRACE)
return For(init, cond, step, block)
def block(self):
nodes = []
while self.curr.class_ != Class.RBRACE:
if self.curr.class_ == Class.IF:
nodes.append(self.if_())
elif self.curr.class_ == Class.WHILE:
nodes.append(self.while_())
elif self.curr.class_ == Class.FOR:
nodes.append(self.for_())
elif self.curr.class_ == Class.BREAK:
nodes.append(self.break_())
elif self.curr.class_ == Class.CONTINUE:
nodes.append(self.continue_())
elif self.curr.class_ == Class.RETURN:
nodes.append(self.return_())
elif self.curr.class_ == Class.TYPE:
nodes.append(self.decl())
elif self.curr.class_ == Class.ID:
nodes.append(self.id_())
self.eat(Class.SEMICOLON)
else:
self.die_deriv(self.block.__name__)
return Block(nodes)
def params(self):
params = []
while self.curr.class_ != Class.RPAREN:
if len(params) > 0:
self.eat(Class.COMMA)
type_ = self.type_()
id_ = self.id_()
params.append(Decl(type_, id_))
return Params(params)
def args(self):
args = []
while self.curr.class_ != Class.RPAREN:
if len(args) > 0:
self.eat(Class.COMMA)
args.append(self.expr())
return Args(args)
def elems(self):
elems = []
while self.curr.class_ != Class.RBRACE:
if len(elems) > 0:
self.eat(Class.COMMA)
elems.append(self.expr())
return Elems(elems)
def return_(self):
self.eat(Class.RETURN)
expr = self.expr()
self.eat(Class.SEMICOLON)
return Return(expr)
def break_(self):
self.eat(Class.BREAK)
self.eat(Class.SEMICOLON)
return Break()
def continue_(self):
self.eat(Class.CONTINUE)
self.eat(Class.SEMICOLON)
return Continue()
def type_(self):
type_ = Type(self.curr.lexeme)
self.eat(Class.TYPE)
return type_
def factor(self):
if self.curr.class_ == Class.INT:
value = Int(self.curr.lexeme)
self.eat(Class.INT)
return value
elif self.curr.class_ == Class.CHAR:
value = Char(self.curr.lexeme)
self.eat(Class.CHAR)
return value
elif self.curr.class_ == Class.STRING:
value = String(self.curr.lexeme)
self.eat(Class.STRING)
return value
elif self.curr.class_ == Class.ID:
return self.id_()
elif self.curr.class_ in [Class.MINUS, Class.NOT, Class.ADDRESS]:
op = self.curr
self.eat(self.curr.class_)
first = None
if self.curr.class_ == Class.LPAREN:
self.eat(Class.LPAREN)
first = self.logic()
self.eat(Class.RPAREN)
else:
first = self.factor()
return UnOp(op.lexeme, first)
elif self.curr.class_ == Class.LPAREN:
self.eat(Class.LPAREN)
first = self.logic()
self.eat(Class.RPAREN)
return first
elif self.curr.class_ == Class.SEMICOLON:
return None
else:
self.die_deriv(self.factor.__name__)
def term(self):
first = self.factor()
while self.curr.class_ in [Class.STAR, Class.FWDSLASH, Class.PERCENT]:
if self.curr.class_ == Class.STAR:
op = self.curr.lexeme
self.eat(Class.STAR)
second = self.factor()
first = BinOp(op, first, second)
elif self.curr.class_ == Class.FWDSLASH:
op = self.curr.lexeme
self.eat(Class.FWDSLASH)
second = self.factor()
first = BinOp(op, first, second)
elif self.curr.class_ == Class.PERCENT:
op = self.curr.lexeme
self.eat(Class.PERCENT)
second = self.factor()
first = BinOp(op, first, second)
return first
def expr(self):
first = self.term()
while self.curr.class_ in [Class.PLUS, Class.MINUS]:
if self.curr.class_ == Class.PLUS:
op = self.curr.lexeme
self.eat(Class.PLUS)
second = self.term()
first = BinOp(op, first, second)
elif self.curr.class_ == Class.MINUS:
op = self.curr.lexeme
self.eat(Class.MINUS)
second = self.term()
first = BinOp(op, first, second)
return first
def compare(self):
first = self.expr()
if self.curr.class_ == Class.EQ:
op = self.curr.lexeme
self.eat(Class.EQ)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.NEQ:
op = self.curr.lexeme
self.eat(Class.NEQ)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.LT:
op = self.curr.lexeme
self.eat(Class.LT)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.GT:
op = self.curr.lexeme
self.eat(Class.GT)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.LTE:
op = self.curr.lexeme
self.eat(Class.LTE)
second = self.expr()
return BinOp(op, first, second)
elif self.curr.class_ == Class.GTE:
op = self.curr.lexeme
self.eat(Class.GTE)
second = self.expr()
return BinOp(op, first, second)
else:
return first
def logic_term(self):
first = self.compare()
while self.curr.class_ == Class.AND:
op = self.curr.lexeme
self.eat(Class.AND)
second = self.compare()
first = BinOp(op, first, second)
return first
def logic(self):
first = self.logic_term()
while self.curr.class_ == Class.OR:
op = self.curr.lexeme
self.eat(Class.OR)
second = self.logic_term()
first = BinOp(op, first, second)
return first
@restorable
def is_func_call(self):
try:
self.eat(Class.LPAREN)
self.args()
self.eat(Class.RPAREN)
return self.curr.class_ != Class.LBRACE
except:
return False
def parse(self):
return self.program()
def die(self, text):
raise SystemExit(text)
def die_deriv(self, fun):
self.die("Derivation error: {}".format(fun))
def die_type(self, expected, found):
self.die("Expected: {}, Found: {}".format(expected, found))
class Symbol:
def __init__(self, id_, type_, scope):
self.id_ = id_
self.type_ = type_
self.scope = scope
def __str__(self):
return "<{} {} {}>".format(self.id_, self.type_, self.scope)
def copy(self):
return Symbol(self.id_, self.type_, self.scope)
class Symbols:
def __init__(self):
self.symbols = {}
def put(self, id_, type_, scope):
self.symbols[id_] = Symbol(id_, type_, scope)
def get(self, id_):
return self.symbols[id_]
def contains(self, id_):
return id_ in self.symbols
def remove(self, id_):
del self.symbols[id_]
def __len__(self):
return len(self.symbols)
def __str__(self):
out = ""
for _, value in self.symbols.items():
if len(out) > 0:
out += "\n"
out += str(value)
return out
def __iter__(self):
return iter(self.symbols.values())
def __next__(self):
return next(self.symbols.values())
class Symbolizer(Visitor):
def __init__(self, ast):
self.ast = ast
def visit_Program(self, parent, node):
node.symbols = Symbols()
for n in node.nodes:
self.visit(node, n)
def visit_Decl(self, parent, node):
parent.symbols.put(node.id_.value, node.type_.value, id(parent))
def visit_ArrayDecl(self, parent, node):
node.symbols = Symbols()
parent.symbols.put(node.id_.value, node.type_.value, id(parent))
def visit_ArrayElem(self, parent, node):
pass
def visit_Assign(self, parent, node):
pass
def visit_If(self, parent, node):
self.visit(node, node.true)
if node.false is not None:
self.visit(node, node.false)
def visit_While(self, parent, node):
self.visit(node, node.block)
def visit_For(self, parent, node):
self.visit(node, node.block)
def visit_FuncImpl(self, parent, node):
parent.symbols.put(node.id_.value, node.type_.value, id(parent))
self.visit(node, node.block)
self.visit(node, node.params)
def visit_FuncCall(self, parent, node):
pass
def visit_Block(self, parent, node):
node.symbols = Symbols()
for n in node.nodes:
self.visit(node, n)
def visit_Params(self, parent, node):
node.symbols = Symbols()
for p in node.params:
self.visit(node, p)
self.visit(parent.block, p)
def visit_Args(self, parent, node):
pass
def visit_Elems(self, parent, node):
pass
def visit_Break(self, parent, node):
pass
def visit_Continue(self, parent, node):
pass
def visit_Return(self, parent, node):
pass
def visit_Type(self, parent, node):
pass
def visit_Int(self, parent, node):
pass
def visit_Char(self, parent, node):
pass
def visit_String(self, parent, node):
pass
def visit_Id(self, parent, node):
pass
def visit_BinOp(self, parent, node):
pass
def visit_UnOp(self, parent, node):
pass
def symbolize(self):
self.visit(None, self.ast)
test_id = '01'
path = f'/content/drive/Shareddrives/Materijali 2020 2021/5. semestar/Programski prevodioci/Vezbe/data/test/{test_id}/src.c'
with open(path, 'r') as source:
text = source.read()
lexer = Lexer(text)
tokens = lexer.lex()
parser = Parser(tokens)
ast = parser.parse()
symbolizer = Symbolizer(ast)
symbolizer.symbolize()
print(ast)
| 0.455199 | 0.84941 |
<a href="https://colab.research.google.com/github/agushery/TA/blob/main/PROGRAM_TUGAS_AKHIR.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Data Mining Untuk Peramalan Mobilitas Masyarakat Kota Denpasar Dengan Metode LSTM (Long Short-Term Memory)
```
from google.colab import drive
drive.mount('/content/drive')
```
## Persiapan Library
```
import pandas as pd
from pandas.tseries.offsets import DateOffset
import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Dropout
from tensorflow.keras.layers import LSTM
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.wrappers.scikit_learn import KerasRegressor
from tensorflow.keras import backend as K
import matplotlib.pyplot as plt
import seaborn as sns
```
## Insert Dataset
```
df = pd.read_csv("/content/drive/MyDrive/Dataset/TA/Data-Mobilitas.csv")
df.head()
```
## Preprocessing Data
```
df.shape
df.info()
df.drop('No', axis=1, inplace=True)
df.head()
df = df.melt(id_vars=['Tempat'], var_name='Tanggal', value_name='Jumlah')
df.head()
df.info()
df['Tanggal'] = pd.to_datetime(df['Tanggal'])
df.isnull().sum()
df = df.dropna()
df.shape
df_total = df.groupby('Tempat')['Jumlah'].sum()
df_total = df_total.to_frame().reset_index()
df_total.head()
df_total.shape
df_total.index = df_total['Tempat']
df_total = df_total.drop(['Tempat'], axis=1)
df_total.shape
def topcase(tipe, warna):
plt.axes(axisbelow=True)
plt.barh(
df_total.sort_values(tipe)[tipe].index[-10:],
df_total.sort_values(tipe)[tipe].values[-10:],
color=warna)
plt.tick_params(size=5,labelsize = 13)
plt.xlabel(tipe + " Mobilitas",fontsize=18)
plt.title("10 Tempat Dengan Mobilitas Tinggi",fontsize=20)
plt.grid()
plt.show()
topcase('Jumlah','darkcyan')
df_final = df.groupby('Tanggal')['Jumlah'].sum()
df_final = df_final.to_frame().reset_index()
df_final.head()
df_final.info()
df_final = df_final.set_index('Tanggal')
df_final['Jumlah'] = df_final['Jumlah'].astype(int)
df_final.info()
df_final
plt.figure(figsize=(10,5))
sns.lineplot(x='Tanggal', y='Jumlah', data=df_final)
plt.title('Mobilitas Masyarakat')
plt.grid()
plt.show()
print("MAX : ", max(df_final['Jumlah']))
print("MIN : ", min(df_final['Jumlah']))
df_final.head()
df_final.tail()
scaler = MinMaxScaler(feature_range=(0, 1))
df_final['scaled'] = scaler.fit_transform(df_final)
df_final
ratio = 0.9
n = int(ratio * len(df_final))
train = df_final[:n]
test = df_final[n:]
print(train.shape)
print(test.shape)
def sliding_window(data, time_steps):
sub_seq, next_values = [], []
for i in range(len(data)-time_steps):
sub_seq.append(data[i:i+time_steps])
next_values.append(data[i+time_steps])
X = np.stack(sub_seq)
y = np.array(next_values)
return X,y
time_steps = 5
X_train, y_train = sliding_window(train[['scaled']].values, time_steps)
X_test, y_test = sliding_window(df_final[len(df_final)-len(test)-time_steps:][['scaled']].values, time_steps)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
def root_mean_squared_error(y_true, y_pred):
return K.sqrt(K.mean(K.square(y_pred - y_true)))
# define the grid search parameters
LSTM_unit = [32,64,128,256,512]
dropout = [0.1,0.2,0.3]
optimizer= ['RMSProp', 'SGD', 'Adam']
def create_model(LSTM_unit=0, dropout=0, optimizer=''):
# create model
model = Sequential()
model.add(LSTM(units=LSTM_unit, return_sequences = True, input_shape=(time_steps, 1)))
model.add(Dropout(dropout))
model.add(LSTM(units=LSTM_unit, return_sequences = True))
model.add(Dropout(dropout))
model.add(LSTM(units=LSTM_unit))
model.add(Dropout(dropout))
model.add(Dense(1))
# Compile model
model.compile(loss = 'mse', optimizer = optimizer, metrics= root_mean_squared_error)
#model.summary()
return model
# Early Stopping
es = EarlyStopping(monitor = 'loss', mode = "min", patience = 20)
# Hypertunning
model = KerasRegressor(build_fn=create_model, epochs=500, batch_size=1, callbacks=[es])
param = dict(LSTM_unit=LSTM_unit, dropout=dropout, optimizer=optimizer)
grid = GridSearchCV(estimator=model, param_grid=param, n_jobs=-1, cv=2)
# training
grid_result = grid.fit(X_train, y_train)
# results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
# Mengambil model terbaik
best_model = grid_result.best_estimator_.model
best_model.summary()
history = best_model.history
# grafik loss function MSE
plt.figure(figsize=(15,8))
plt.plot(history.history['loss'], label='MSE')
plt.plot(history.history['root_mean_squared_error'], label='RMSE')
plt.title('Loss MSE & Metrics RMSE')
plt.ylabel('Value')
plt.xlabel('Epoch')
plt.legend()
plt.grid()
plt.show()
test['Prediksi'] = scaler.inverse_transform(best_model.predict(X_test))
test
rmse = np.sqrt(mean_squared_error(test['Jumlah'], test['Prediksi']))
print('Test RMSE: %.3f' % rmse)
plt.figure(figsize=(15,8))
plt.grid()
plt.title("Perbandingan Data Testing Dengan Prediksi")
plt.plot(train['Jumlah'], label="Data Training (Aktual)")
plt.plot(test['Jumlah'], label="Data Testing (Aktual)")
plt.plot(test['Prediksi'], label="Data Prediksi")
plt.legend(loc="upper left")
plt.show()
pred_list = []
batch = test[-time_steps:][['scaled']].values.reshape((1, time_steps, 1))
prediksi = 7
for i in range(prediksi):
pred_list.append(best_model.predict(batch)[0])
batch = np.append(batch[:,1:,:],[[pred_list[i]]],axis=1)
add_dates = [df_final.index[-1] + DateOffset(days=x) for x in range(0,prediksi+1) ]
df_prediksi = pd.DataFrame(scaler.inverse_transform(pred_list),
index=add_dates[1:],
columns=['Prediksi'])
df_prediksi
plt.figure(figsize=(15,8))
plt.grid()
plt.title("Hasil Peramalan Mobilitas Kota Denpasar 7 hari kedepan (LSTM Model)")
plt.plot(df_final['Jumlah'], label="Data Training Aktual")
plt.plot(test['Jumlah'], label="Data Testing Aktual")
plt.plot(test['Prediksi'], label="Data Prediksi Testing")
plt.plot(df_prediksi['Prediksi'], label="Data Peramalan")
plt.legend(loc="upper left")
best_model.save('best_model.h5')
std = pd.DataFrame(stds)
std.to_excel('std.xlsx')
means = pd.DataFrame(means)
means.to_excel('means.xlsx')
test.to_excel('test.xlsx')
train.to_excel('train.xlsx')
df_prediksi.to_excel('hasil-peramalan.xlsx')
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/drive')
import pandas as pd
from pandas.tseries.offsets import DateOffset
import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Dropout
from tensorflow.keras.layers import LSTM
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.wrappers.scikit_learn import KerasRegressor
from tensorflow.keras import backend as K
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv("/content/drive/MyDrive/Dataset/TA/Data-Mobilitas.csv")
df.head()
df.shape
df.info()
df.drop('No', axis=1, inplace=True)
df.head()
df = df.melt(id_vars=['Tempat'], var_name='Tanggal', value_name='Jumlah')
df.head()
df.info()
df['Tanggal'] = pd.to_datetime(df['Tanggal'])
df.isnull().sum()
df = df.dropna()
df.shape
df_total = df.groupby('Tempat')['Jumlah'].sum()
df_total = df_total.to_frame().reset_index()
df_total.head()
df_total.shape
df_total.index = df_total['Tempat']
df_total = df_total.drop(['Tempat'], axis=1)
df_total.shape
def topcase(tipe, warna):
plt.axes(axisbelow=True)
plt.barh(
df_total.sort_values(tipe)[tipe].index[-10:],
df_total.sort_values(tipe)[tipe].values[-10:],
color=warna)
plt.tick_params(size=5,labelsize = 13)
plt.xlabel(tipe + " Mobilitas",fontsize=18)
plt.title("10 Tempat Dengan Mobilitas Tinggi",fontsize=20)
plt.grid()
plt.show()
topcase('Jumlah','darkcyan')
df_final = df.groupby('Tanggal')['Jumlah'].sum()
df_final = df_final.to_frame().reset_index()
df_final.head()
df_final.info()
df_final = df_final.set_index('Tanggal')
df_final['Jumlah'] = df_final['Jumlah'].astype(int)
df_final.info()
df_final
plt.figure(figsize=(10,5))
sns.lineplot(x='Tanggal', y='Jumlah', data=df_final)
plt.title('Mobilitas Masyarakat')
plt.grid()
plt.show()
print("MAX : ", max(df_final['Jumlah']))
print("MIN : ", min(df_final['Jumlah']))
df_final.head()
df_final.tail()
scaler = MinMaxScaler(feature_range=(0, 1))
df_final['scaled'] = scaler.fit_transform(df_final)
df_final
ratio = 0.9
n = int(ratio * len(df_final))
train = df_final[:n]
test = df_final[n:]
print(train.shape)
print(test.shape)
def sliding_window(data, time_steps):
sub_seq, next_values = [], []
for i in range(len(data)-time_steps):
sub_seq.append(data[i:i+time_steps])
next_values.append(data[i+time_steps])
X = np.stack(sub_seq)
y = np.array(next_values)
return X,y
time_steps = 5
X_train, y_train = sliding_window(train[['scaled']].values, time_steps)
X_test, y_test = sliding_window(df_final[len(df_final)-len(test)-time_steps:][['scaled']].values, time_steps)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
def root_mean_squared_error(y_true, y_pred):
return K.sqrt(K.mean(K.square(y_pred - y_true)))
# define the grid search parameters
LSTM_unit = [32,64,128,256,512]
dropout = [0.1,0.2,0.3]
optimizer= ['RMSProp', 'SGD', 'Adam']
def create_model(LSTM_unit=0, dropout=0, optimizer=''):
# create model
model = Sequential()
model.add(LSTM(units=LSTM_unit, return_sequences = True, input_shape=(time_steps, 1)))
model.add(Dropout(dropout))
model.add(LSTM(units=LSTM_unit, return_sequences = True))
model.add(Dropout(dropout))
model.add(LSTM(units=LSTM_unit))
model.add(Dropout(dropout))
model.add(Dense(1))
# Compile model
model.compile(loss = 'mse', optimizer = optimizer, metrics= root_mean_squared_error)
#model.summary()
return model
# Early Stopping
es = EarlyStopping(monitor = 'loss', mode = "min", patience = 20)
# Hypertunning
model = KerasRegressor(build_fn=create_model, epochs=500, batch_size=1, callbacks=[es])
param = dict(LSTM_unit=LSTM_unit, dropout=dropout, optimizer=optimizer)
grid = GridSearchCV(estimator=model, param_grid=param, n_jobs=-1, cv=2)
# training
grid_result = grid.fit(X_train, y_train)
# results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
# Mengambil model terbaik
best_model = grid_result.best_estimator_.model
best_model.summary()
history = best_model.history
# grafik loss function MSE
plt.figure(figsize=(15,8))
plt.plot(history.history['loss'], label='MSE')
plt.plot(history.history['root_mean_squared_error'], label='RMSE')
plt.title('Loss MSE & Metrics RMSE')
plt.ylabel('Value')
plt.xlabel('Epoch')
plt.legend()
plt.grid()
plt.show()
test['Prediksi'] = scaler.inverse_transform(best_model.predict(X_test))
test
rmse = np.sqrt(mean_squared_error(test['Jumlah'], test['Prediksi']))
print('Test RMSE: %.3f' % rmse)
plt.figure(figsize=(15,8))
plt.grid()
plt.title("Perbandingan Data Testing Dengan Prediksi")
plt.plot(train['Jumlah'], label="Data Training (Aktual)")
plt.plot(test['Jumlah'], label="Data Testing (Aktual)")
plt.plot(test['Prediksi'], label="Data Prediksi")
plt.legend(loc="upper left")
plt.show()
pred_list = []
batch = test[-time_steps:][['scaled']].values.reshape((1, time_steps, 1))
prediksi = 7
for i in range(prediksi):
pred_list.append(best_model.predict(batch)[0])
batch = np.append(batch[:,1:,:],[[pred_list[i]]],axis=1)
add_dates = [df_final.index[-1] + DateOffset(days=x) for x in range(0,prediksi+1) ]
df_prediksi = pd.DataFrame(scaler.inverse_transform(pred_list),
index=add_dates[1:],
columns=['Prediksi'])
df_prediksi
plt.figure(figsize=(15,8))
plt.grid()
plt.title("Hasil Peramalan Mobilitas Kota Denpasar 7 hari kedepan (LSTM Model)")
plt.plot(df_final['Jumlah'], label="Data Training Aktual")
plt.plot(test['Jumlah'], label="Data Testing Aktual")
plt.plot(test['Prediksi'], label="Data Prediksi Testing")
plt.plot(df_prediksi['Prediksi'], label="Data Peramalan")
plt.legend(loc="upper left")
best_model.save('best_model.h5')
std = pd.DataFrame(stds)
std.to_excel('std.xlsx')
means = pd.DataFrame(means)
means.to_excel('means.xlsx')
test.to_excel('test.xlsx')
train.to_excel('train.xlsx')
df_prediksi.to_excel('hasil-peramalan.xlsx')
| 0.596081 | 0.859723 |
# Coreference Resolution
## Data preparation
#### Read training data set and split it into train and evaluate part.
```
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import pandas as pd
#label,distance,POS1,gramFct1,Case1,Gender1,Number1,POS2,gramFct2,Case2,Gender2,Number2,sameHead,samePOS,sameGramFct,matchOrNot,sameCase,sameGender,sameNumber
df = (pd.read_csv('df_gold_std_all_18_12_with_case_and_gender_number.csv',
header=0)
.replace({'?': 'unknown'})) # NaN are represented by '?'
#df=df.sample(frac=0.003)
#print(df)
X = df.drop(['no','label'], axis=1)#drop the 'label' and 'no' list.
y = df['label'].copy() # use the column 'label' as target y.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)#split the dataset to train and evaluate set with a ratio of 7:3
```
#### Read the extracted markable as test set
```
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import pandas as pd
#label,distance,POS1,gramFct1,Case1,Gender1,POS2,gramFct2,Case2,Gender2,sameHead,samePOS,sameGramFct,matchOrNot,sameCase,sameGender
df1 = (pd.read_csv('test_data_with_case_and_gender_number.csv',
header=0)
.replace({'?': 'unknown'})) # NaN are represented by '?'
#df1=df1.sample(frac=0.1) #shuffle the data and get a 1/10 subset
X_te = df1.drop(['no','label'], axis=1)
y_te = df1['label'].copy()
X_te,y_te
```
#### data details and distribution
```
df.info()
#df1.info()
df['label'].value_counts()#see the distrubution of y
import matplotlib.pyplot as plt
df=df.drop(columns=['no'])
df1=df1.drop(columns=['no'])
df.hist(bins=50,figsize=(20,15))# plot the distrabution of all the matching features in training dataset.
df1.hist(bins=50,figsize=(20,15))# plot the distrabution of all the matching features in testing dataset.
df.describe()
corr_matrix=df.corr()
corr_matrix["label"].sort_values(ascending=False) #find the correlate metrics of label in training set
corr_matrix1=df1.corr()
corr_matrix1["label"].sort_values(ascending=False)#find the correlate metrics of labels in testing set
```
# Data preprocessing
## Label encoding
### transfer the columns(features) into numeric metrics
```
class MultiColumnLabelEncoder:
def __init__(self, columns = None):
self.columns = columns # list of column to encode
def fit(self, X, y=None):
return self
def transform(self, X):
'''
Transforms columns of X specified in self.columns using
LabelEncoder(). If no columns specified, transforms all
columns in X.
'''
output = X.copy()
if self.columns is not None:
for col in self.columns:
output[col] = LabelEncoder().fit_transform(output[col])
else:
for colname, col in output.iteritems():
output[colname] = LabelEncoder().fit_transform(col)
return output
def fit_transform(self, X, y=None):
return self.fit(X, y).transform(X)
le = MultiColumnLabelEncoder(columns=['POS1','gramFct1','Case1','Gender1','Number1','POS2','gramFct2','gramFct2','Case2','Gender2','Number2'])
X_train_le = le.fit_transform(X_train)
X_train_le.head()
```
## one hot encoding of each features
### encode transfer the training set with one hot format
```
ohe = OneHotEncoder(sparse=True , handle_unknown='ignore')
X_train_ohe = ohe.fit_transform(X_train_le)
X_train_ohe
```
# Model training
## SGD
```
from sklearn.linear_model import SGDClassifier
sgd=SGDClassifier(random_state=42,max_iter=100)
sgd.fit(X_train_ohe,y_train)
```
### Evaluation with SGD
```
from sklearn.model_selection import cross_val_score
#transform the input(X) in evaluating and testing data to an approprate way for SGD
X_test_le = le.transform(X_test)
X_test_ohe = ohe.transform(X_test_le)
X_te_le = le.transform(X_te)
X_te_ohe = ohe.transform(X_te_le)
#calculate the accuracy of sgd classifier of both data set
scores1 = cross_val_score(sgd,X_test_ohe,y_test,scoring='accuracy',cv=5)
scores2=cross_val_score(sgd,X_te_ohe,y_te,scoring='accuracy',cv=5)
scores1,scores2
```
### Test on SGD
#### Test with precision, recall and f1 score
```
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
print("Evaluate results on training set")
y_eva=sgd.predict(X_test_ohe)
print(precision_score(y_test,y_eva), recall_score(y_test,y_eva), f1_score(y_test,y_eva))
print("Test results on generated markable")
y_te_predict=sgd.predict(X_te_ohe)
print(precision_score(y_te,y_te_predict), recall_score(y_te,y_te_predict), f1_score(y_te,y_te_predict))
```
## Decision Tree
```
from sklearn import tree
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(X_train_ohe,y_train)
y_test_predict=clf.predict(X_te_ohe)
print("Evaluation score:")
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
```
## Naive Bayes
```
from sklearn.naive_bayes import BernoulliNB
clf = BernoulliNB()
clf = clf.fit(X_train_ohe,y_train)
y_test_predict=clf.predict(X_te_ohe)
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
```
## Logistic Regression
```
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(C=1000.0, solver= 'liblinear', random_state=0)
clf.fit(X_train_ohe, y_train)
y_test_predict=clf.predict(X_te_ohe)
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
```
## Perceptron
```
from sklearn.linear_model import Perceptron
clf = Perceptron(tol=1e-5, random_state=0)
clf.fit(X_train_ohe, y_train)
y_test_predict=clf.predict(X_te_ohe)
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
```
## Multi-Layer-Perceptron
### parameter tuning: gridsearch
```
from sklearn import svm
from sklearn.model_selection import GridSearchCV
from sklearn.neural_network import MLPClassifier
from sklearn.pipeline import Pipeline
def svc_param_selection(X, y, nfolds):
Cs = [0.01, 0.1, 1, 10]
gammas = [0.01, 0.1, 1]
param_grid = {'C': Cs, 'gamma' : gammas}
grid_search = GridSearchCV(svm.SVC(kernel='rbf'), param_grid, cv=nfolds, n_jobs=-1)
grid_search.fit(X, y)
grid_search.best_params_
return grid_search.best_params_
def mlp_param_selection(X,y,nfolds):
mlp =MLPClassifier()
param_grid={
'hidden_layer_sizes':[(100, 100), (50,50), (100,)],
'activations':['logistic', 'tanh', 'relu'],
'solvers': ['adam'],
'alphas': [0.0001, 0.001],
'learning_rates':['constant', 'invscaling', 'adaptive'],
'max_iters':[100, 200, 300],
}
mlp_g = GridSearchCV(mlp, param_grid, cv=nfolds, n_jobs=-1, verbose=1)
mlp_g.fit(X, y)
grid_search.best_params_
return grid_search.best_params_
#p=svc_param_selection(X_train_ohe,y_train,2)
m=mlp_param_selection(X_train_ohe,y_train,5)
```
### MLP training and testing
```
from sklearn.metrics import f1_score
from sklearn.neural_network import MLPClassifier
mlp = MLPClassifier(solver='adam', alpha=1e-5, activation='relu',
hidden_layer_sizes=(200,200), random_state=1,max_iter=200, batch_size = 512, verbose=1)
mlp.fit(X_train_ohe,y_train)
y_test_predict=mlp.predict(X_te_ohe)
precision_score(y_te,y_test_predict,labels=np.unique(y_te_predict)), recall_score(y_te,y_test_predict,labels=np.unique(y_te_predict)), f1_score(y_te,y_test_predict,labels=np.unique(y_te_predict))
```
# KNN
```
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X_train_ohe,y_train)
y_test_predict=neigh.predict(X_te_ohe)
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
```
|
github_jupyter
|
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import pandas as pd
#label,distance,POS1,gramFct1,Case1,Gender1,Number1,POS2,gramFct2,Case2,Gender2,Number2,sameHead,samePOS,sameGramFct,matchOrNot,sameCase,sameGender,sameNumber
df = (pd.read_csv('df_gold_std_all_18_12_with_case_and_gender_number.csv',
header=0)
.replace({'?': 'unknown'})) # NaN are represented by '?'
#df=df.sample(frac=0.003)
#print(df)
X = df.drop(['no','label'], axis=1)#drop the 'label' and 'no' list.
y = df['label'].copy() # use the column 'label' as target y.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)#split the dataset to train and evaluate set with a ratio of 7:3
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import pandas as pd
#label,distance,POS1,gramFct1,Case1,Gender1,POS2,gramFct2,Case2,Gender2,sameHead,samePOS,sameGramFct,matchOrNot,sameCase,sameGender
df1 = (pd.read_csv('test_data_with_case_and_gender_number.csv',
header=0)
.replace({'?': 'unknown'})) # NaN are represented by '?'
#df1=df1.sample(frac=0.1) #shuffle the data and get a 1/10 subset
X_te = df1.drop(['no','label'], axis=1)
y_te = df1['label'].copy()
X_te,y_te
df.info()
#df1.info()
df['label'].value_counts()#see the distrubution of y
import matplotlib.pyplot as plt
df=df.drop(columns=['no'])
df1=df1.drop(columns=['no'])
df.hist(bins=50,figsize=(20,15))# plot the distrabution of all the matching features in training dataset.
df1.hist(bins=50,figsize=(20,15))# plot the distrabution of all the matching features in testing dataset.
df.describe()
corr_matrix=df.corr()
corr_matrix["label"].sort_values(ascending=False) #find the correlate metrics of label in training set
corr_matrix1=df1.corr()
corr_matrix1["label"].sort_values(ascending=False)#find the correlate metrics of labels in testing set
class MultiColumnLabelEncoder:
def __init__(self, columns = None):
self.columns = columns # list of column to encode
def fit(self, X, y=None):
return self
def transform(self, X):
'''
Transforms columns of X specified in self.columns using
LabelEncoder(). If no columns specified, transforms all
columns in X.
'''
output = X.copy()
if self.columns is not None:
for col in self.columns:
output[col] = LabelEncoder().fit_transform(output[col])
else:
for colname, col in output.iteritems():
output[colname] = LabelEncoder().fit_transform(col)
return output
def fit_transform(self, X, y=None):
return self.fit(X, y).transform(X)
le = MultiColumnLabelEncoder(columns=['POS1','gramFct1','Case1','Gender1','Number1','POS2','gramFct2','gramFct2','Case2','Gender2','Number2'])
X_train_le = le.fit_transform(X_train)
X_train_le.head()
ohe = OneHotEncoder(sparse=True , handle_unknown='ignore')
X_train_ohe = ohe.fit_transform(X_train_le)
X_train_ohe
from sklearn.linear_model import SGDClassifier
sgd=SGDClassifier(random_state=42,max_iter=100)
sgd.fit(X_train_ohe,y_train)
from sklearn.model_selection import cross_val_score
#transform the input(X) in evaluating and testing data to an approprate way for SGD
X_test_le = le.transform(X_test)
X_test_ohe = ohe.transform(X_test_le)
X_te_le = le.transform(X_te)
X_te_ohe = ohe.transform(X_te_le)
#calculate the accuracy of sgd classifier of both data set
scores1 = cross_val_score(sgd,X_test_ohe,y_test,scoring='accuracy',cv=5)
scores2=cross_val_score(sgd,X_te_ohe,y_te,scoring='accuracy',cv=5)
scores1,scores2
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
print("Evaluate results on training set")
y_eva=sgd.predict(X_test_ohe)
print(precision_score(y_test,y_eva), recall_score(y_test,y_eva), f1_score(y_test,y_eva))
print("Test results on generated markable")
y_te_predict=sgd.predict(X_te_ohe)
print(precision_score(y_te,y_te_predict), recall_score(y_te,y_te_predict), f1_score(y_te,y_te_predict))
from sklearn import tree
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(X_train_ohe,y_train)
y_test_predict=clf.predict(X_te_ohe)
print("Evaluation score:")
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
from sklearn.naive_bayes import BernoulliNB
clf = BernoulliNB()
clf = clf.fit(X_train_ohe,y_train)
y_test_predict=clf.predict(X_te_ohe)
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(C=1000.0, solver= 'liblinear', random_state=0)
clf.fit(X_train_ohe, y_train)
y_test_predict=clf.predict(X_te_ohe)
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
from sklearn.linear_model import Perceptron
clf = Perceptron(tol=1e-5, random_state=0)
clf.fit(X_train_ohe, y_train)
y_test_predict=clf.predict(X_te_ohe)
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
from sklearn import svm
from sklearn.model_selection import GridSearchCV
from sklearn.neural_network import MLPClassifier
from sklearn.pipeline import Pipeline
def svc_param_selection(X, y, nfolds):
Cs = [0.01, 0.1, 1, 10]
gammas = [0.01, 0.1, 1]
param_grid = {'C': Cs, 'gamma' : gammas}
grid_search = GridSearchCV(svm.SVC(kernel='rbf'), param_grid, cv=nfolds, n_jobs=-1)
grid_search.fit(X, y)
grid_search.best_params_
return grid_search.best_params_
def mlp_param_selection(X,y,nfolds):
mlp =MLPClassifier()
param_grid={
'hidden_layer_sizes':[(100, 100), (50,50), (100,)],
'activations':['logistic', 'tanh', 'relu'],
'solvers': ['adam'],
'alphas': [0.0001, 0.001],
'learning_rates':['constant', 'invscaling', 'adaptive'],
'max_iters':[100, 200, 300],
}
mlp_g = GridSearchCV(mlp, param_grid, cv=nfolds, n_jobs=-1, verbose=1)
mlp_g.fit(X, y)
grid_search.best_params_
return grid_search.best_params_
#p=svc_param_selection(X_train_ohe,y_train,2)
m=mlp_param_selection(X_train_ohe,y_train,5)
from sklearn.metrics import f1_score
from sklearn.neural_network import MLPClassifier
mlp = MLPClassifier(solver='adam', alpha=1e-5, activation='relu',
hidden_layer_sizes=(200,200), random_state=1,max_iter=200, batch_size = 512, verbose=1)
mlp.fit(X_train_ohe,y_train)
y_test_predict=mlp.predict(X_te_ohe)
precision_score(y_te,y_test_predict,labels=np.unique(y_te_predict)), recall_score(y_te,y_test_predict,labels=np.unique(y_te_predict)), f1_score(y_te,y_test_predict,labels=np.unique(y_te_predict))
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X_train_ohe,y_train)
y_test_predict=neigh.predict(X_te_ohe)
precision_score(y_te,y_test_predict), recall_score(y_te,y_test_predict), f1_score(y_te,y_test_predict)
| 0.70202 | 0.914176 |
<a href="https://colab.research.google.com/github/tallywiesenberg/DS-Unit-2-Kaggle-Challenge/blob/master/DS7_Sprint_Challenge_6.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
_Lambda School Data Science, Unit 2_
# Sprint Challenge: Predict Steph Curry's shots 🏀
For your Sprint Challenge, you'll use a dataset with all Steph Curry's NBA field goal attempts. (Regular season and playoff games, from October 28, 2009, through June 5, 2019.)
You'll predict whether each shot was made, using information about the shot and the game. This is hard to predict! Try to get above 60% accuracy. The dataset was collected with the [nba_api](https://github.com/swar/nba_api) Python library.
```
import sys
in_colab = 'google.colab' in sys.modules
if in_colab:
# Install packages in Colab
!pip install category_encoders==2.0.0
!pip install pandas-profiling==2.3.0
!pip install plotly==4.1.1
import pandas as pd
# Read data
url = 'https://drive.google.com/uc?export=download&id=1fL7KPyxgGYfQDsuJoBWHIWwCAf-HTFpX'
df = pd.read_csv(url)
# Check data shape
assert df.shape == (13958, 20)
```
To demonstrate mastery on your Sprint Challenge, do all the required, numbered instructions in this notebook.
To earn a score of "3", also do all the stretch goals.
You are permitted and encouraged to do as much data exploration as you want.
**1. Begin with baselines for classification.** Your target to predict is `shot_made_flag`. What is your baseline accuracy, if you guessed the majority class for every prediction?
**2. Hold out your test set.** Use the 2018-19 season to test. NBA seasons begin in October and end in June. You'll know you've split the data correctly when your test set has 1,709 observations.
**3. Engineer new feature.** Engineer at least **1** new feature, from this list, or your own idea.
- **Homecourt Advantage**: Is the home team (`htm`) the Golden State Warriors (`GSW`) ?
- **Opponent**: Who is the other team playing the Golden State Warriors?
- **Seconds remaining in the period**: Combine minutes remaining with seconds remaining, to get the total number of seconds remaining in the period.
- **Seconds remaining in the game**: Combine period, and seconds remaining in the period, to get the total number of seconds remaining in the game. A basketball game has 4 periods, each 12 minutes long.
- **Made previous shot**: Was Steph Curry's previous shot successful?
**4. Decide how to validate** your model. Choose one of the following options. Any of these options are good. You are not graded on which you choose.
- **Train/validate/test split: train on the 2009-10 season through 2016-17 season, validate with the 2017-18 season.** You'll know you've split the data correctly when your train set has 11,081 observations, and your validation set has 1,168 observations.
- **Train/validate/test split: random 80/20%** train/validate split.
- **Cross-validation** with independent test set. You may use any scikit-learn cross-validation method.
**5.** Use a scikit-learn **pipeline** to **encode categoricals** and fit a **Decision Tree** or **Random Forest** model.
**6.** Get your model's **validation accuracy.** (Multiple times if you try multiple iterations.)
**7.** Get your model's **test accuracy.** (One time, at the end.)
**8.** Given a **confusion matrix** for a hypothetical binary classification model, **calculate accuracy, precision, and recall.**
### Stretch Goals
- Engineer 4+ new features total, either from the list above, or your own ideas.
- Make 2+ visualizations to explore relationships between features and target.
- Optimize 3+ hyperparameters by trying 10+ "candidates" (possible combinations of hyperparameters). You can use `RandomizedSearchCV` or do it manually.
- Get and plot your model's feature importances.
```
df.head()
```
## 1. Begin with baselines for classification.
>Your target to predict is `shot_made_flag`. What would your baseline accuracy be, if you guessed the majority class for every prediction?
```
from sklearn.metrics import accuracy_score
df['shot_made_flag'].value_counts(normalize=True)
y_pred = [0] * df.shape[0] #predict no shots are made
print('Accuracy of baseline:', accuracy_score(df['shot_made_flag'], y_pred)) #every shot is bad shot is right 52 percent of the time
```
## 2. Hold out your test set.
>Use the 2018-19 season to test. NBA seasons begin in October and end in June. You'll know you've split the data correctly when your test set has 1,709 observations.
```
# df['game_date'] = pd.to_datetime(df['game_date'], infer_datetime_format = True)
```
## 3. Engineer new feature.
>Engineer at least **1** new feature, from this list, or your own idea.
>
>- **Homecourt Advantage**: Is the home team (`htm`) the Golden State Warriors (`GSW`) ?
>- **Opponent**: Who is the other team playing the Golden State Warriors?
>- **Seconds remaining in the period**: Combine minutes remaining with seconds remaining, to get the total number of seconds remaining in the period.
>- **Seconds remaining in the game**: Combine period, and seconds remaining in the period, to get the total number of seconds remaining in the game. A basketball game has 4 periods, each 12 minutes long.
>- **Made previous shot**: Was Steph Curry's previous shot successful?
```
df['homecourt_advantage'] = df['htm'] == 'GSW'
df['homecourt_advantage'].value_counts()
#Test mask
#train mask is everything else
mask = (df['game_date'] >= '2018-10-16') & (df['game_date'] <= '2019-06-13')
train = df[~mask]
test = df[mask]
train.shape, test.shape
```
## **4. Decide how to validate** your model.
>Choose one of the following options. Any of these options are good. You are not graded on which you choose.
>
>- **Train/validate/test split: train on the 2009-10 season through 2016-17 season, validate with the 2017-18 season.** You'll know you've split the data correctly when your train set has 11,081 observations, and your validation set has 1,168 observations.
>- **Train/validate/test split: random 80/20%** train/validate split.
>- **Cross-validation** with independent test set. You may use any scikit-learn cross-validation method.
```
from sklearn.model_selection import train_test_split
train, val = train_test_split(train,
train_size=0.8, test_size = 0.2,
shuffle = True,
stratify = train['shot_made_flag'],
random_state = 42)
train.shape, val.shape
```
## 5. Use a scikit-learn pipeline to encode categoricals and fit a Decision Tree or Random Forest model.
```
from sklearn.pipeline import make_pipeline
from category_encoders import OneHotEncoder
from category_encoders.ordinal import OrdinalEncoder
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
from sklearn.feature_selection import f_regression
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
from sklearn.linear_model import LogisticRegression
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier
features = df.columns[~(df.columns == 'shot_made_flag')] #every column but shot_made_flag is a feature
target = 'shot_made_flag' #shot made flag is the target
#splitting X and y sets
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
X_test = test[features]
y_test = test[target]
pipeline = make_pipeline(
OrdinalEncoder(),
StandardScaler(),
RandomForestClassifier()
)
pipeline.fit(X_train, y_train)
```
## 6.Get your model's validation accuracy
> (Multiple times if you try multiple iterations.)
```
print('Validation Score (Initial):', pipeline.score(X_val, y_val))
from sklearn.model_selection import RandomizedSearchCV
#pipeline
pipeline = make_pipeline(
OrdinalEncoder(),
StandardScaler(),
RandomForestClassifier(n_estimators = 200, n_jobs=-1, random_state=42)
)
#hyperparameters
param_distributions = {
'randomforestclassifier__max_depth': range(1, 100, 2),
'randomforestclassifier__min_samples_split': range(1, 500, 3),
'randomforestclassifier__min_samples_leaf': range(1, 500, 3),
}
search = RandomizedSearchCV(
pipeline,
param_distributions = param_distributions,
n_iter = 10,
cv = 10,
scoring = 'accuracy',
verbose = 10,
return_train_score = True,
n_jobs =-1
)
search.fit(X_train, y_train)
print('Best hyperparameters:', search.best_params_)
print('New benchmark score:', search.best_score_)
```
## 7. Get your model's test accuracy
> (One time, at the end.)
```
pipeline = make_pipeline(
OrdinalEncoder(),
StandardScaler(),
RandomForestClassifier(n_estimators = 200, n_jobs=-1, random_state=42,
min_samples_split = 181, min_samples_leaf = 25, max_depth = 17)
)
pipeline.fit(X_train, y_train)
print('Test score', pipeline.score(X_test, y_test))
```
## 8. Given a confusion matrix, calculate accuracy, precision, and recall.
Imagine this is the confusion matrix for a binary classification model. Use the confusion matrix to calculate the model's accuracy, precision, and recall.
<table>
<tr>
<td colspan="2" rowspan="2"></td>
<td colspan="2">Predicted</td>
</tr>
<tr>
<td>Negative</td>
<td>Positive</td>
</tr>
<tr>
<td rowspan="2">Actual</td>
<td>Negative</td>
<td style="border: solid">85</td>
<td style="border: solid">58</td>
</tr>
<tr>
<td>Positive</td>
<td style="border: solid">8</td>
<td style="border: solid"> 36</td>
</tr>
</table>
```
from sklearn.metrics import confusion_matrix
from sklearn.utils.multiclass import unique_labels
import seaborn as sns
y_pred = pipeline.predict(X_test)
def plot_confusion_matrix(y_true, y_pred):
labels = unique_labels(y_pred)
columns = [f'Predicted {label}' for label in labels]
index = [f'Actual {label}' for label in labels]
table = pd.DataFrame(confusion_matrix(y_true, y_pred), columns = columns, index = index)
sns.heatmap(table, annot=True, fmt = 'd')
return sns.heatmap(table, annot=True, fmt = 'd')
plot_confusion_matrix(y_test, y_pred)
```
### Calculate accuracy
```
accuracy = (634 + 429) / (634 + 278 + 368 + 429)
accuracy
```
### Calculate precision
```
precision = 634 / (634 + 278)
precision
```
### Calculate recall
```
recall = 634 / (634 + 368)
recall
```
|
github_jupyter
|
import sys
in_colab = 'google.colab' in sys.modules
if in_colab:
# Install packages in Colab
!pip install category_encoders==2.0.0
!pip install pandas-profiling==2.3.0
!pip install plotly==4.1.1
import pandas as pd
# Read data
url = 'https://drive.google.com/uc?export=download&id=1fL7KPyxgGYfQDsuJoBWHIWwCAf-HTFpX'
df = pd.read_csv(url)
# Check data shape
assert df.shape == (13958, 20)
df.head()
from sklearn.metrics import accuracy_score
df['shot_made_flag'].value_counts(normalize=True)
y_pred = [0] * df.shape[0] #predict no shots are made
print('Accuracy of baseline:', accuracy_score(df['shot_made_flag'], y_pred)) #every shot is bad shot is right 52 percent of the time
# df['game_date'] = pd.to_datetime(df['game_date'], infer_datetime_format = True)
df['homecourt_advantage'] = df['htm'] == 'GSW'
df['homecourt_advantage'].value_counts()
#Test mask
#train mask is everything else
mask = (df['game_date'] >= '2018-10-16') & (df['game_date'] <= '2019-06-13')
train = df[~mask]
test = df[mask]
train.shape, test.shape
from sklearn.model_selection import train_test_split
train, val = train_test_split(train,
train_size=0.8, test_size = 0.2,
shuffle = True,
stratify = train['shot_made_flag'],
random_state = 42)
train.shape, val.shape
from sklearn.pipeline import make_pipeline
from category_encoders import OneHotEncoder
from category_encoders.ordinal import OrdinalEncoder
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
from sklearn.feature_selection import f_regression
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
from sklearn.linear_model import LogisticRegression
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier
features = df.columns[~(df.columns == 'shot_made_flag')] #every column but shot_made_flag is a feature
target = 'shot_made_flag' #shot made flag is the target
#splitting X and y sets
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
X_test = test[features]
y_test = test[target]
pipeline = make_pipeline(
OrdinalEncoder(),
StandardScaler(),
RandomForestClassifier()
)
pipeline.fit(X_train, y_train)
print('Validation Score (Initial):', pipeline.score(X_val, y_val))
from sklearn.model_selection import RandomizedSearchCV
#pipeline
pipeline = make_pipeline(
OrdinalEncoder(),
StandardScaler(),
RandomForestClassifier(n_estimators = 200, n_jobs=-1, random_state=42)
)
#hyperparameters
param_distributions = {
'randomforestclassifier__max_depth': range(1, 100, 2),
'randomforestclassifier__min_samples_split': range(1, 500, 3),
'randomforestclassifier__min_samples_leaf': range(1, 500, 3),
}
search = RandomizedSearchCV(
pipeline,
param_distributions = param_distributions,
n_iter = 10,
cv = 10,
scoring = 'accuracy',
verbose = 10,
return_train_score = True,
n_jobs =-1
)
search.fit(X_train, y_train)
print('Best hyperparameters:', search.best_params_)
print('New benchmark score:', search.best_score_)
pipeline = make_pipeline(
OrdinalEncoder(),
StandardScaler(),
RandomForestClassifier(n_estimators = 200, n_jobs=-1, random_state=42,
min_samples_split = 181, min_samples_leaf = 25, max_depth = 17)
)
pipeline.fit(X_train, y_train)
print('Test score', pipeline.score(X_test, y_test))
from sklearn.metrics import confusion_matrix
from sklearn.utils.multiclass import unique_labels
import seaborn as sns
y_pred = pipeline.predict(X_test)
def plot_confusion_matrix(y_true, y_pred):
labels = unique_labels(y_pred)
columns = [f'Predicted {label}' for label in labels]
index = [f'Actual {label}' for label in labels]
table = pd.DataFrame(confusion_matrix(y_true, y_pred), columns = columns, index = index)
sns.heatmap(table, annot=True, fmt = 'd')
return sns.heatmap(table, annot=True, fmt = 'd')
plot_confusion_matrix(y_test, y_pred)
accuracy = (634 + 429) / (634 + 278 + 368 + 429)
accuracy
precision = 634 / (634 + 278)
precision
recall = 634 / (634 + 368)
recall
| 0.437103 | 0.983327 |
# Kolmogorov-Smirnov (KS) Test Statistic
### Description
This notebook demonstrates the [Kolmogorov-Smirnov (KS) test](https://en.wikipedia.org/wiki/Kolmogorov–Smirnov_test) $D$-statistic and [$p$-value](https://en.wikipedia.org/wiki/P-value) as a function of the number of points drawn from a given sample. The $D$-statistic represents the maximum distance between the CDFs of the sample distribution and the comparison distribution. A small $D$ statistic suggests that the samples are indeed drawn from the comparison distribution. I am unclear on how to interpret the $p$-value for this test, as described in further detail [below](#uncertainty).
First, we make the standard imports, and define a function to compare random samples drawn from our defined distribution with an underlying "truth" distribution. We vary the sample sizes from 1 to 10 million.
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from cycler import cycler
from scipy.stats import norm, uniform, kstest
np.random.seed(56) # ensure repeatability
def make_kstest_plots(dist, compare='norm'):
"""Plot KS test statistics and Gaussian KDE for test samples.
Parameters
----------
dist : rv_continuous
continuous distrubution object, i.e. scipy.stats.norm
compare : string, optional, default='norm'
scipy.stats continuous distribution object name
see <https://docs.scipy.org/doc/scipy/reference/stats.html#continuous-distributions>
Returns
-------
None
Only creates matplotlib plot objects for display
"""
fig = plt.figure(1)
plt.clf()
ax = plt.gca()
# log-space array from 1 to 10M
n = np.array([int(10**i) for i in range(7)])
n = np.hstack((n, 3*n))
n.sort()
D = np.zeros(n.size)
p = np.zeros(n.size)
rvs = []
for i in range(n.size):
# Kolmogorov-Smirnov test if RVs drawn from compare
rvs.append(dist.rvs(size=n[i]))
D[i], p[i] = kstest(rvs[i], compare)
ax.plot(n, D, c='C3', label='D statistic')
ax.plot(n, p, c='C0', label='p-value')
ax.set_title('KS Test Statistics')
ax.set_xlabel('Number of samples')
ax.set_ylabel('Statistic')
ax.set_xscale('log')
ax.set_ylim([0, 1])
ax.legend()
# Plot the Gaussian KDE of the samples
plt.figure(2, figsize=(11, 5))
plt.clf()
ax = plt.gca()
# Set the colors of the plot
ax.set_prop_cycle(cycler('color', [plt.cm.viridis(i) for i in np.linspace(0, 1, n.size)]))
for i in range(n.size):
sns.distplot(rvs[i], hist=False, ax=ax, label='n = {:2.2g}'.format(n[i]))
ax.set_title('Gaussian KDE')
ax.set_xlabel('$x$')
ax.set_ylabel('$f_x(x)$')
ax.legend()
plt.show(block=False)
```
## Comparing Uniform to Normal
In our next test, we compare samples drawn from a standard uniform distribution $X \sim U[0,1]$ to a standard normal distribution $\mathcal{N}(\mu, \sigma)$, where $\mu = 0$, $\sigma = 1$.
```
# Define uniform distribution
dist = uniform(loc=0, scale=1)
compare = 'norm' # compare to normal distribution
make_kstest_plots(dist, compare)
```
### Results
In this case, the $D$ statistic converges to $D = 0.5$ as $n \to \infty$. We expect this value given the definition of $D$ as the maximum distance between the sample CDF and the comparison distribution CDF. In this case, the $p$-value also decays to 0, meaning there is 0 probability that...?
## Comparing a uniform distribution to itself
Now, we run the test comparing a random variable $X$ drawn from a uniform distribution $X \sim U[0,1]$ to the underlying uniform distribution itself.
```
# Define uniform distribution
dist = uniform(loc=0, scale=1)
compare = 'uniform' # compare to itself
make_kstest_plots(dist, compare)
```
### Results
We see that, in the first plot, the $D$-statistic shrinks to 0 as $n \to \infty$, showing that our samples are indeed approaching a true uniform distribution. The second plot shows the Gaussian Kernel Density Estimate (KDE) of each of the sets of random samples, which also approach a true uniform distribution $X \sim U[0,1]$.
#### Uncertainty
<a id='uncertainty'></a>
The $p$-value of the test is quite noisy. I am not entirely sure how to interpret it. [Minitab docs](https://support.minitab.com/en-us/minitab/18/help-and-how-to/statistics/basic-statistics/how-to/normality-test/interpret-the-results/all-statistics-and-graphs/#ks) report:
> The $p$-value is the probability of obtaining a test statistic (such as the Kolmogorov-Smirnov statistic) that is at least as extreme as the value that is calculated from the sample, when the data are normal.
Does "extreme" mean "as small as"? Or "as large as"? Typically we'd like a small $p$-value so that we can reject the null hypothesis that our two samples are drawn from the same distribution, but in this case we are in fact trying to test that the samples are drawn from a know underlying distribution. The high noise suggests that the $p$-value loses its typical interpretation here.
We get a nearly identical result if we compare a standard normal distribution to itself [see below](#appendix).
## Appendix: Comparing Normal to Normal
<a id='appendix'></a>
Much like the test performed above, we compare random variables drawn from a standard normal distribution to the actual standard normal distribution from which they were drawn. We expect the $D$ statistic to approach 0 as $n \to \infty$.
```
# Define standard normal distribution
dist = norm(loc=0, scale=1)
compare = 'norm' # compare to normal distribution
make_kstest_plots(dist, compare)
```
|
github_jupyter
|
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from cycler import cycler
from scipy.stats import norm, uniform, kstest
np.random.seed(56) # ensure repeatability
def make_kstest_plots(dist, compare='norm'):
"""Plot KS test statistics and Gaussian KDE for test samples.
Parameters
----------
dist : rv_continuous
continuous distrubution object, i.e. scipy.stats.norm
compare : string, optional, default='norm'
scipy.stats continuous distribution object name
see <https://docs.scipy.org/doc/scipy/reference/stats.html#continuous-distributions>
Returns
-------
None
Only creates matplotlib plot objects for display
"""
fig = plt.figure(1)
plt.clf()
ax = plt.gca()
# log-space array from 1 to 10M
n = np.array([int(10**i) for i in range(7)])
n = np.hstack((n, 3*n))
n.sort()
D = np.zeros(n.size)
p = np.zeros(n.size)
rvs = []
for i in range(n.size):
# Kolmogorov-Smirnov test if RVs drawn from compare
rvs.append(dist.rvs(size=n[i]))
D[i], p[i] = kstest(rvs[i], compare)
ax.plot(n, D, c='C3', label='D statistic')
ax.plot(n, p, c='C0', label='p-value')
ax.set_title('KS Test Statistics')
ax.set_xlabel('Number of samples')
ax.set_ylabel('Statistic')
ax.set_xscale('log')
ax.set_ylim([0, 1])
ax.legend()
# Plot the Gaussian KDE of the samples
plt.figure(2, figsize=(11, 5))
plt.clf()
ax = plt.gca()
# Set the colors of the plot
ax.set_prop_cycle(cycler('color', [plt.cm.viridis(i) for i in np.linspace(0, 1, n.size)]))
for i in range(n.size):
sns.distplot(rvs[i], hist=False, ax=ax, label='n = {:2.2g}'.format(n[i]))
ax.set_title('Gaussian KDE')
ax.set_xlabel('$x$')
ax.set_ylabel('$f_x(x)$')
ax.legend()
plt.show(block=False)
# Define uniform distribution
dist = uniform(loc=0, scale=1)
compare = 'norm' # compare to normal distribution
make_kstest_plots(dist, compare)
# Define uniform distribution
dist = uniform(loc=0, scale=1)
compare = 'uniform' # compare to itself
make_kstest_plots(dist, compare)
# Define standard normal distribution
dist = norm(loc=0, scale=1)
compare = 'norm' # compare to normal distribution
make_kstest_plots(dist, compare)
| 0.867822 | 0.990015 |
<!-- dom:TITLE: From Variational Monte Carlo to Boltzmann Machines and Machine Learning -->
# From Variational Monte Carlo to Boltzmann Machines and Machine Learning
<!-- dom:AUTHOR: Morten Hjorth-Jensen Email hjensen@msu.edu Department of Physics and Astronomy and National Superconducting Cyclotron Laboratory, Michigan State University, East Lansing, 48824 MI, USA -->
<!-- Author: -->
**Morten Hjorth-Jensen Email hjensen@msu.edu Department of Physics and Astronomy and National Superconducting Cyclotron Laboratory, Michigan State University, East Lansing, 48824 MI, USA**
Date: **Notebook 1: Variational Monte Carlo**
## Introduction
### Structure and Aims
These notebooks serve the aim of linking traditional variational Monte
Carlo VMC calculations methods with recent progress on solving
many-particle problems using Machine Learning algorithms.
Furthermore, when linking with Machine Learning algorithms, in particular
so-called Boltzmann Machines, there are interesting connections between
these algorithms and so-called [Shadow Wave functions (SWFs)](https://journals.aps.org/pre/abstract/10.1103/PhysRevE.90.053304) (and references therein). The implications of the latter have been explored in various Monte Carlo calculations.
In total there are three notebooks:
1. the one you are reading now on Variational Monte Carlo methods,
2. notebook 2 on Machine Learning and quantum mechanical problems and in particular on Boltzmann Machines,
3. and finally notebook 3 on the link between Boltzmann machines and SWFs.
### This notebook
In this notebook the aim is to give you an introduction as well as an
understanding of the basic elements that are needed in order to
develop a professional variational Monte Carlo code. We will focus on
a simple system of two particles in an oscillator trap (or
alternatively two fermions moving in a Coulombic potential) which can
interact via repulsive or attrative force.
The advantage of these systems is that for two particles (boson or
fermions) we have analytical solutions for the eigenpairs for the
non-interacting case. Furthermore, for a two- or three-dimensional
system of two electrons moving in a harmonic oscillator trap, we have
[analytical solutions for the interacting case as well](https://iopscience.iop.org/article/10.1088/0305-4470/27/3/040/meta).
Having analytical eigenpairs is an invaluable feature that allow us
to assess the physical relevance of the trial wave functions, be
these either from a standard VMC procedure, from Boltzmann Machines or
from Shadow Wave functions.
In this notebook we start with the basics of a VMC calculation and
introduce concepts like Markow Chain Monte Carlo methods and the
Metropolis algorithm, importance sampling and Metropolis-Hastings
algorithm, resampling methods to obtain better estimates of the
statistical errors and minimization of the expectation values of the
energy and the variance. The latter is done in order to obtain the
best possible variational parameters. Furthermore it will define the
so-called **cost** function, a commonly encountered quantity in Machine
Learning algorithms. Minimizing the latter is the one which leads to
the determination of the optimal parameters in basically all Machine Learning algorithms.
For our purposes, it will serve as the first link between VMC methods and Machine Learning methods.
Topics like Markov Chain Monte Carlo and various resampling techniques
are also central to Machine Learning methods. Presenting them in the
context of VMC approaches leads hopefully to an easier starting point
for the understanding of these methods.
Finally, the reader may ask what do we actually want to achieve with
complicating life with Machine Learning methods when we can easily
study interacting systems with standard Monte Carlo approaches. Our
hope is that by adding additional degrees of freedom via Machine
Learning algorithms, we can let the algorithms we employ learn the
parameters of the model via a given optimization algorithm. In
standard Monte Carlo calculations the practitioners end fine tuning
the trial wave function using all possible insights about the system
understudy. This may not always lead to the best possible ansatz and
can in the long run be rather time-consuming. In fields like nuclear
many-body physics with complicated interaction terms, guessing an
analytical form for the trial wave fuction can be difficult. Letting
the machine learn the form of the trial function or find the optimal
parameters may lead to insights about the problem which cannot be
obtained by selecting various trial wave functions.
The emerging and rapidly expanding fields of Machine Learning and Quantum Computing hold also great promise in tackling the
dimensionality problems (the so-called dimensionality curse in many-body problems) we encounter when studying
complicated many-body problems.
The approach to Machine Learning we will focus on
is inspired by the idea of representing the wave function with
a restricted Boltzmann machine (RBM), presented recently by [G. Carleo and M. Troyer, Science **355**, Issue 6325, pp. 602-606 (2017)](http://science.sciencemag.org/content/355/6325/602). They
named such a wave function/network a *neural network quantum state* (NQS). In their article they apply it to the quantum mechanical
spin lattice systems of the Ising model and Heisenberg model, with
encouraging results.
Machine learning (ML) is an extremely rich field, in spite of its young age. The
increases we have seen during the last three decades in computational
capabilities have been followed by developments of methods and
techniques for analyzing and handling large date sets, relying heavily
on statistics, computer science and mathematics. The field is rather
new and developing rapidly.
Machine learning is the science of giving computers the ability to
learn without being explicitly programmed. The idea is that there
exist generic algorithms which can be used to find patterns in a broad
class of data sets without having to write code specifically for each
problem. The algorithm will build its own logic based on the data.
Machine learning is a subfield of computer science, and is closely
related to computational statistics. It evolved from the study of
pattern recognition in artificial intelligence (AI) research, and has
made contributions to AI tasks like computer vision, natural language
processing and speech recognition. It has also, especially in later
years, found applications in a wide variety of other areas, including
bioinformatics, economy, physics, finance and marketing.
An excellent reference we will come to back to is [Mehta *et al.*, arXiv:1803.08823](https://arxiv.org/abs/1803.08823).
Our focus will first be on the basics of VMC calculations.
## Basic Quantum Monte Carlo
We start with the variational principle.
Given a hamiltonian $H$ and a trial wave function $\Psi_T(\boldsymbol{R};\boldsymbol{\alpha})$, the variational principle states that the expectation value of $\langle H \rangle$, defined through
$$
E[H]= \langle H \rangle =
\frac{\int d\boldsymbol{R}\Psi^{\ast}_T(\boldsymbol{R};\boldsymbol{\alpha})H(\boldsymbol{R})\Psi_T(\boldsymbol{R};\boldsymbol{\alpha})}
{\int d\boldsymbol{R}\Psi^{\ast}_T(\boldsymbol{R};\boldsymbol{\alpha})\Psi_T(\boldsymbol{R};\boldsymbol{\alpha})},
$$
is an upper bound to the ground state energy $E_0$ of the hamiltonian $H$, that is
$$
E_0 \le \langle H \rangle .
$$
In general, the integrals involved in the calculation of various expectation values are multi-dimensional ones. Traditional integration methods such as the Gauss-Legendre will not be adequate for say the computation of the energy of a many-body system.
Here we have defined the vector $\boldsymbol{R} =[\boldsymbol{r}_1,\boldsymbol{r}_2,\dots,\boldsymbol{r}_n}]$ as an array that contains the positions of all particles $n$ while the vector $\boldsymbol{\alpha} = [\alpha_1,\alpha_2,\dots,\alpha_m]$ contains the variational parameters of the model, $m$ in total.
The trial wave function can be expanded in the eigenstates of the hamiltonian since they form a complete set, viz.,
$$
\Psi_T(\boldsymbol{R};\boldsymbol{\alpha})=\sum_i a_i\Psi_i(\boldsymbol{R}),
$$
and assuming the set of eigenfunctions to be normalized one obtains
$$
\frac{\sum_{nm}a^*_ma_n \int d\boldsymbol{R}\Psi^{\ast}_m(\boldsymbol{R})H(\boldsymbol{R})\Psi_n(\boldsymbol{R})}
{\sum_{nm}a^*_ma_n \int d\boldsymbol{R}\Psi^{\ast}_m(\boldsymbol{R})\Psi_n(\boldsymbol{R})} =\frac{\sum_{n}a^2_n E_n}
{\sum_{n}a^2_n} \ge E_0,
$$
where we used that $H(\boldsymbol{R})\Psi_n(\boldsymbol{R})=E_n\Psi_n(\boldsymbol{R})$.
In general, the integrals involved in the calculation of various expectation
values are multi-dimensional ones.
The variational principle yields the lowest state of a given symmetry.
In most cases, a wave function has only small values in large parts of
configuration space, and a straightforward procedure which uses
homogenously distributed random points in configuration space
will most likely lead to poor results. This may suggest that some kind
of importance sampling combined with e.g., the Metropolis algorithm
may be a more efficient way of obtaining the ground state energy.
The hope is then that those regions of configurations space where
the wave function assumes appreciable values are sampled more
efficiently.
The tedious part in a VMC calculation is the search for the variational
minimum. A good knowledge of the system is required in order to carry out
reasonable VMC calculations. This is not always the case,
and often VMC calculations
serve rather as the starting
point for so-called diffusion Monte Carlo calculations (DMC). DMC is a way of
solving exactly the many-body Schroedinger equation by means of
a stochastic procedure. A good guess on the binding energy
and its wave function is however necessary.
A carefully performed VMC calculation can aid in this context.
The basic procedure of a Variational Monte Carlo calculations consists thus of
1. Construct first a trial wave function $\psi_T(\boldsymbol{R};\boldsymbol{\alpha})$, for a many-body system consisting of $n$ particles located at positions $\boldsymbol{R}=(\boldsymbol{R}_1,\dots ,\boldsymbol{R}_n)$. The trial wave function depends on $\alpha$ variational parameters $\boldsymbol{\alpha}=(\alpha_1,\dots ,\alpha_M)$.
2. Then we evaluate the expectation value of the hamiltonian $H$
$$
\overline{E}[\boldsymbol{alpha}]=\frac{\int d\boldsymbol{R}\Psi^{\ast}_{T}(\boldsymbol{R},\boldsymbol{\alpha})H(\boldsymbol{R})\Psi_{T}(\boldsymbol{R},\boldsymbol{\alpha})}
{\int d\boldsymbol{R}\Psi^{\ast}_{T}(\boldsymbol{R},\boldsymbol{\alpha})\Psi_{T}(\boldsymbol{R},\boldsymbol{\alpha})}.
$$
1. Thereafter we vary $\boldsymbol{\alpha}$ according to some minimization algorithm and return eventually to the first step if we are not satisfied with the results.
Here we have used the notation $\overline{E}$ to label the expectation value of the energy.
### Linking with standard statistical expressions for expectation values
In order to bring in the Monte Carlo machinery, we define first a likelihood distribution, or probability density distribution (PDF). Using our ansatz for the trial wave function $\psi_T(\boldsymbol{R};\boldsymbol{\alpha})$.
$$
P(\boldsymbol{R})= \frac{\left|\psi_T(\boldsymbol{R};\boldsymbol{\alpha})\right|^2}{\int \left|\psi_T(\boldsymbol{R};\boldsymbol{\alpha})\right|^2d\boldsymbol{R}}.
$$
This is our new probability distribution function (PDF).
The approximation to the expectation value of the Hamiltonian is now
$$
\overline{E}[\boldsymbol{\alpha}] =
\frac{\int d\boldsymbol{R}\Psi^{\ast}_T(\boldsymbol{R};\boldsymbol{\alpha})H(\boldsymbol{R})\Psi_T(\boldsymbol{R};\boldsymbol{\alpha})}
{\int d\boldsymbol{R}\Psi^{\ast}_T(\boldsymbol{R};\boldsymbol{\alpha})\Psi_T(\boldsymbol{R};\boldsymbol{\alpha})}.
$$
Define a new quantity
<!-- Equation labels as ordinary links -->
<div id="eq:locale1"></div>
$$
E_L(\boldsymbol{R};\boldsymbol{\alpha})=\frac{1}{\psi_T(\boldsymbol{R};\boldsymbol{\alpha})}H\psi_T(\boldsymbol{R};\boldsymbol{\alpha}),
\label{eq:locale1} \tag{1}
$$
called the local energy, which, together with our trial PDF yields
<!-- Equation labels as ordinary links -->
<div id="eq:vmc1"></div>
$$
\overline{E}[\boldsymbol{\alpha}]=\int P(\boldsymbol{R})E_L(\boldsymbol{R};\boldsymbol{\alpha}) d\boldsymbol{R}\approx \frac{1}{N}\sum_{i=1}^NE_L(\boldsymbol{R_i};\boldsymbol{\alpha})
\label{eq:vmc1} \tag{2}
$$
with $N$ being the number of Monte Carlo samples.
The Algorithm for performing a variational Monte Carlo calculations runs thus as this
* Initialisation: Fix the number of Monte Carlo steps. Choose an initial $\boldsymbol{R}$ and variational parameters $\alpha$ and calculate $\left|\psi_T^{\alpha}(\boldsymbol{R})\right|^2$.
* Initialise the energy and the variance and start the Monte Carlo calculation.
* Calculate a trial position $\boldsymbol{R}_p=\boldsymbol{R}+r*step$ where $r$ is a random variable $r \in [0,1]$.
* Metropolis algorithm to accept or reject this move $w = P(\boldsymbol{R}_p)/P(\boldsymbol{R})$.
* If the step is accepted, then we set $\boldsymbol{R}=\boldsymbol{R}_p$.
* Update averages
* Finish and compute final averages.
Observe that the jumping in space is governed by the variable *step*. This is called brute-force sampling.
Need importance sampling to get more relevant sampling, see lectures below.
### Simple example, the hydrogen atom
The radial Schroedinger equation for the hydrogen atom can be
written as (when we have gotten rid of the first derivative term in the kinetic energy and used $rR(r)=u(r)$)
$$
-\frac{\hbar^2}{2m}\frac{\partial^2 u(r)}{\partial r^2}-
\left(\frac{ke^2}{r}-\frac{\hbar^2l(l+1)}{2mr^2}\right)u(r)=Eu(r).
$$
or with dimensionless variables
<!-- Equation labels as ordinary links -->
<div id="eq:hydrodimless1"></div>
$$
-\frac{1}{2}\frac{\partial^2 u(\rho)}{\partial \rho^2}-
\frac{u(\rho)}{\rho}+\frac{l(l+1)}{2\rho^2}u(\rho)-\lambda u(\rho)=0,
\label{eq:hydrodimless1} \tag{3}
$$
with the hamiltonian
$$
H=-\frac{1}{2}\frac{\partial^2 }{\partial \rho^2}-
\frac{1}{\rho}+\frac{l(l+1)}{2\rho^2}.
$$
Use variational parameter $\alpha$ in the trial
wave function
<!-- Equation labels as ordinary links -->
<div id="eq:trialhydrogen"></div>
$$
u_T^{\alpha}(\rho)=\alpha\rho e^{-\alpha\rho}.
\label{eq:trialhydrogen} \tag{4}
$$
Inserting this wave function into the expression for the
local energy $E_L$ gives
$$
E_L(\rho)=-\frac{1}{\rho}-
\frac{\alpha}{2}\left(\alpha-\frac{2}{\rho}\right).
$$
We note that at $\alpha=1$ we obtain the exact
result, and the variance is zero, as it should. The reason is that
we then have the exact wave function, and the action of the hamiltionan
on the wave function
$$
H\psi = \mathrm{constant}\times \psi,
$$
yields just a constant. The integral which defines various
expectation values involving moments of the hamiltonian becomes then
$$
\langle H^n \rangle =
\frac{\int d\boldsymbol{R}\Psi^{\ast}_T(\boldsymbol{R})H^n(\boldsymbol{R})\Psi_T(\boldsymbol{R})}
{\int d\boldsymbol{R}\Psi^{\ast}_T(\boldsymbol{R})\Psi_T(\boldsymbol{R})}=
\mathrm{constant}\times\frac{\int d\boldsymbol{R}\Psi^{\ast}_T(\boldsymbol{R})\Psi_T(\boldsymbol{R})}
{\int d\boldsymbol{R}\Psi^{\ast}_T(\boldsymbol{R})\Psi_T(\boldsymbol{R})}=\mathrm{constant}.
$$
**This gives an important information: the exact wave function leads to zero variance!**
Variation is then performed by minimizing both the energy and the variance.
## The Metropolis algorithm
The Metropolis algorithm , see [the original article](http://scitation.aip.org/content/aip/journal/jcp/21/6/10.1063/1.1699114) was invented by Metropolis et. al
and is often simply called the Metropolis algorithm.
It is a method to sample a normalized probability
distribution by a stochastic process. We define $\mathbf{P}_i^{(n)}$ to
be the probability for finding the system in the state $i$ at step $n$.
The algorithm is then
* Sample a possible new state $j$ with some probability $T_{i\rightarrow j}$.
* Accept the new state $j$ with probability $A_{i \rightarrow j}$ and use it as the next sample. With probability $1-A_{i\rightarrow j}$ the move is rejected and the original state $i$ is used again as a sample.
We wish to derive the required properties of $T$ and $A$ such that
$\mathbf{P}_i^{(n\rightarrow \infty)} \rightarrow p_i$ so that starting
from any distribution, the method converges to the correct distribution.
Note that the description here is for a discrete probability distribution.
Replacing probabilities $p_i$ with expressions like $p(x_i)dx_i$ will
take all of these over to the corresponding continuum expressions.
The dynamical equation for $\mathbf{P}_i^{(n)}$ can be written directly from
the description above. The probability of being in the state $i$ at step $n$
is given by the probability of being in any state $j$ at the previous step,
and making an accepted transition to $i$ added to the probability of
being in the state $i$, making a transition to any state $j$ and
rejecting the move:
$$
\mathbf{P}^{(n)}_i = \sum_j \left [
\mathbf{P}^{(n-1)}_jT_{j\rightarrow i} A_{j\rightarrow i}
+\mathbf{P}^{(n-1)}_iT_{i\rightarrow j}\left ( 1- A_{i\rightarrow j} \right)
\right ] \,.
$$
Since the probability of making some transition must be 1,
$\sum_j T_{i\rightarrow j} = 1$, and the above equation becomes
$$
\mathbf{P}^{(n)}_i = \mathbf{P}^{(n-1)}_i +
\sum_j \left [
\mathbf{P}^{(n-1)}_jT_{j\rightarrow i} A_{j\rightarrow i}
-\mathbf{P}^{(n-1)}_iT_{i\rightarrow j}A_{i\rightarrow j}
\right ] \,.
$$
For large $n$ we require that $\mathbf{P}^{(n\rightarrow \infty)}_i = p_i$,
the desired probability distribution. Taking this limit, gives the
balance requirement
$$
\sum_j \left [
p_jT_{j\rightarrow i} A_{j\rightarrow i}
-p_iT_{i\rightarrow j}A_{i\rightarrow j}
\right ] = 0 \,.
$$
The balance requirement is very weak. Typically the much stronger detailed
balance requirement is enforced, that is rather than the sum being
set to zero, we set each term separately to zero and use this
to determine the acceptance probabilities. Rearranging, the result is
$$
\frac{ A_{j\rightarrow i}}{A_{i\rightarrow j}}
= \frac{p_iT_{i\rightarrow j}}{ p_jT_{j\rightarrow i}} \,.
$$
The Metropolis choice is to maximize the $A$ values, that is
$$
A_{j \rightarrow i} = \min \left ( 1,
\frac{p_iT_{i\rightarrow j}}{ p_jT_{j\rightarrow i}}\right ).
$$
Other choices are possible, but they all correspond to multilplying
$A_{i\rightarrow j}$ and $A_{j\rightarrow i}$ by the same constant
smaller than unity.\footnote{The penalty function method uses just such
a factor to compensate for $p_i$ that are evaluated stochastically
and are therefore noisy.}
Having chosen the acceptance probabilities, we have guaranteed that
if the $\mathbf{P}_i^{(n)}$ has equilibrated, that is if it is equal to $p_i$,
it will remain equilibrated. Next we need to find the circumstances for
convergence to equilibrium.
The dynamical equation can be written as
$$
\mathbf{P}^{(n)}_i = \sum_j M_{ij}\mathbf{P}^{(n-1)}_j
$$
with the matrix $M$ given by
$$
M_{ij} = \delta_{ij}\left [ 1 -\sum_k T_{i\rightarrow k} A_{i \rightarrow k}
\right ] + T_{j\rightarrow i} A_{j\rightarrow i} \,.
$$
Summing over $i$ shows that $\sum_i M_{ij} = 1$, and since
$\sum_k T_{i\rightarrow k} = 1$, and $A_{i \rightarrow k} \leq 1$, the
elements of the matrix satisfy $M_{ij} \geq 0$. The matrix $M$ is therefore
a stochastic matrix.
The Metropolis method is simply the power method for computing the
right eigenvector of $M$ with the largest magnitude eigenvalue.
By construction, the correct probability distribution is a right eigenvector
with eigenvalue 1. Therefore, for the Metropolis method to converge
to this result, we must show that $M$ has only one eigenvalue with this
magnitude, and all other eigenvalues are smaller.
### The system: two electrons in a harmonic oscillator trap in two dimensions
The Hamiltonian of the quantum dot is given by
$$
\hat{H} = \hat{H}_0 + \hat{V},
$$
where $\hat{H}_0$ is the many-body HO Hamiltonian, and $\hat{V}$ is the
inter-electron Coulomb interactions. In dimensionless units,
$$
\hat{V}= \sum_{i < j}^N \frac{1}{r_{ij}},
$$
with $r_{ij}=\sqrt{\mathbf{r}_i^2 - \mathbf{r}_j^2}$.
This leads to the separable Hamiltonian, with the relative motion part given by ($r_{ij}=r$)
$$
\hat{H}_r=-\nabla^2_r + \frac{1}{4}\omega^2r^2+ \frac{1}{r},
$$
plus a standard Harmonic Oscillator problem for the center-of-mass motion.
This system has analytical solutions in two and three dimensions ([M. Taut 1993 and 1994](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.48.3561)).
We want to perform a Variational Monte Carlo calculation of the ground state of two electrons in a quantum dot well with different oscillator energies, assuming total spin $S=0$.
Our trial wave function has the following form
<!-- Equation labels as ordinary links -->
<div id="eq:trial"></div>
$$
\begin{equation}
\psi_{T}(\boldsymbol{r}_1,\boldsymbol{r}_2) =
C\exp{\left(-\alpha_1\omega(r_1^2+r_2^2)/2\right)}
\exp{\left(\frac{r_{12}}{(1+\alpha_2 r_{12})}\right)},
\label{eq:trial} \tag{5}
\end{equation}
$$
where the $\alpha$s represent our variational parameters, two in this case.
Why does the trial function look like this? How did we get there? **This will be our main motivation** for switching to
Machine Learning.
To find an ansatz for the correlated part of the wave function, it is useful to rewrite the two-particle
local energy in terms of the relative and center-of-mass motion.
Let us denote the distance between the two electrons as
$r_{12}$. We omit the center-of-mass motion since we are only interested in the case when
$r_{12} \rightarrow 0$. The contribution from the center-of-mass (CoM) variable $\boldsymbol{R}_{\mathrm{CoM}}$
gives only a finite contribution.
We focus only on the terms that are relevant for $r_{12}$ and for three dimensions. The relevant local energy becomes then
$$
\lim_{r_{12} \rightarrow 0}E_L(R)=
\frac{1}{{\cal R}_T(r_{12})}\left(2\frac{d^2}{dr_{ij}^2}+\frac{4}{r_{ij}}\frac{d}{dr_{ij}}+
\frac{2}{r_{ij}}-\frac{l(l+1)}{r_{ij}^2}+2E
\right){\cal R}_T(r_{12}) = 0.
$$
Set $l=0$ and we have the so-called **cusp** condition
$$
\frac{d {\cal R}_T(r_{12})}{dr_{12}} = -\frac{1}{2(l+1)}
{\cal R}_T(r_{12})\qquad r_{12}\to 0
$$
The above results in
$$
{\cal R}_T \propto \exp{(r_{ij}/2)},
$$
for anti-parallel spins and
$$
{\cal R}_T \propto \exp{(r_{ij}/4)},
$$
for anti-parallel spins.
This is the so-called cusp condition for the relative motion, resulting in a minimal requirement
for the correlation part of the wave fuction.
For general systems containing more than say two electrons, we have this
condition for each electron pair $ij$.
```
python code here
```
## Importance sampling
We need to replace the brute force
Metropolis algorithm with a walk in coordinate space biased by the trial wave function.
This approach is based on the Fokker-Planck equation and the Langevin equation for generating a trajectory in coordinate space. The link between the Fokker-Planck equation and the Langevin equations are explained, only partly, in the slides below.
An excellent reference on topics like Brownian motion, Markov chains, the Fokker-Planck equation and the Langevin equation is the text by [Van Kampen](http://www.elsevier.com/books/stochastic-processes-in-physics-and-chemistry/van-kampen/978-0-444-52965-7)
Here we will focus first on the implementation part first.
For a diffusion process characterized by a time-dependent probability density $P(x,t)$ in one dimension the Fokker-Planck
equation reads (for one particle /walker)
$$
\frac{\partial P}{\partial t} = D\frac{\partial }{\partial x}\left(\frac{\partial }{\partial x} -F\right)P(x,t),
$$
where $F$ is a drift term and $D$ is the diffusion coefficient.
The new positions in coordinate space are given as the solutions of the Langevin equation using Euler's method, namely,
we go from the Langevin equation
$$
\frac{\partial x(t)}{\partial t} = DF(x(t)) +\eta,
$$
with $\eta$ a random variable,
yielding a new position
$$
y = x+DF(x)\Delta t +\xi\sqrt{\Delta t},
$$
where $\xi$ is gaussian random variable and $\Delta t$ is a chosen time step.
The quantity $D$ is, in atomic units, equal to $1/2$ and comes from the factor $1/2$ in the kinetic energy operator. Note that $\Delta t$ is to be viewed as a parameter. Values of $\Delta t \in [0.001,0.01]$ yield in general rather stable values of the ground state energy.
The process of isotropic diffusion characterized by a time-dependent probability density $P(\mathbf{x},t)$ obeys (as an approximation) the so-called Fokker-Planck equation
$$
\frac{\partial P}{\partial t} = \sum_i D\frac{\partial }{\partial \mathbf{x_i}}\left(\frac{\partial }{\partial \mathbf{x_i}} -\mathbf{F_i}\right)P(\mathbf{x},t),
$$
where $\mathbf{F_i}$ is the $i^{th}$ component of the drift term (drift velocity) caused by an external potential, and $D$ is the diffusion coefficient. The convergence to a stationary probability density can be obtained by setting the left hand side to zero. The resulting equation will be satisfied if and only if all the terms of the sum are equal zero,
$$
\frac{\partial^2 P}{\partial {\mathbf{x_i}^2}} = P\frac{\partial}{\partial {\mathbf{x_i}}}\mathbf{F_i} + \mathbf{F_i}\frac{\partial}{\partial {\mathbf{x_i}}}P.
$$
The drift vector should be of the form $\mathbf{F} = g(\mathbf{x}) \frac{\partial P}{\partial \mathbf{x}}$. Then,
$$
\frac{\partial^2 P}{\partial {\mathbf{x_i}^2}} = P\frac{\partial g}{\partial P}\left( \frac{\partial P}{\partial {\mathbf{x}_i}} \right)^2 + P g \frac{\partial ^2 P}{\partial {\mathbf{x}_i^2}} + g \left( \frac{\partial P}{\partial {\mathbf{x}_i}} \right)^2.
$$
The condition of stationary density means that the left hand side equals zero. In other words, the terms containing first and second derivatives have to cancel each other. It is possible only if $g = \frac{1}{P}$, which yields
$$
\mathbf{F} = 2\frac{1}{\Psi_T}\nabla\Psi_T,
$$
which is known as the so-called *quantum force*. This term is responsible for pushing the walker towards regions of configuration space where the trial wave function is large, increasing the efficiency of the simulation in contrast to the Metropolis algorithm where the walker has the same probability of moving in every direction.
The Fokker-Planck equation yields a (the solution to the equation) transition probability given by the Green's function
$$
G(y,x,\Delta t) = \frac{1}{(4\pi D\Delta t)^{3N/2}} \exp{\left(-(y-x-D\Delta t F(x))^2/4D\Delta t\right)}
$$
which in turn means that our brute force Metropolis algorithm
$$
A(y,x) = \mathrm{min}(1,q(y,x))),
$$
with $q(y,x) = |\Psi_T(y)|^2/|\Psi_T(x)|^2$ is now replaced by the [Metropolis-Hastings algorithm](http://scitation.aip.org/content/aip/journal/jcp/21/6/10.1063/1.1699114) as well as [Hasting's article](http://biomet.oxfordjournals.org/content/57/1/97.abstract),
$$
q(y,x) = \frac{G(x,y,\Delta t)|\Psi_T(y)|^2}{G(y,x,\Delta t)|\Psi_T(x)|^2}
$$
```
add python code here
```
## Technical aspect, improvements and how to define the cost function
**The above procedure is not the smartest one**. Looping over all variational parameters becomes expensive.
Also, we don't use importance sampling and optimizations of the standard deviation (blocking, bootstrap, jackknife).
Such codes are included in the above Github address.
We can also be smarter and use minimization methods to find the **optimal** variational parameters with fewer Monte Carlo cycles and then
fire up our heavy artillery.
One way to achieve this is to minimize the energy as function of the variational parameters.
To find the derivatives of the local energy expectation value as function of the variational parameters, we can use the chain rule and the hermiticity of the Hamiltonian.
Let us define
$$
\bar{E}_{\alpha_i}=\frac{d\langle E_L\rangle}{d\alpha_i}.
$$
as the derivative of the energy with respect to the variational parameter $\alpha_i$
We define also the derivative of the trial function (skipping the subindex $T$) as
$$
\bar{\Psi}_{i}=\frac{d\Psi}{d\alpha_i}.
$$
The elements of the gradient of the local energy are then (using the chain rule and the hermiticity of the Hamiltonian)
$$
\bar{E}_{i}= 2\left( \langle \frac{\bar{\Psi}_{i}}{\Psi}E_L\rangle -\langle \frac{\bar{\Psi}_{i}}{\Psi}\rangle\langle E_L \rangle\right).
$$
From a computational point of view it means that you need to compute the expectation values of
$$
\langle \frac{\bar{\Psi}_{i}}{\Psi}E_L\rangle,
$$
and
$$
\langle \frac{\bar{\Psi}_{i}}{\Psi}\rangle\langle E_L\rangle
$$
These integrals are evaluted using MC intergration (with all its possible error sources).
We can then use methods like stochastic gradient or other minimization methods to find the optimal variational parameters (I don't discuss this topic here, but these methods are very important in ML).
We have a model, our likelihood function.
How should we define the cost function?
Suppose the trial function (our model) is the exact wave function. The action of the hamiltionan
on the wave function
$$
H\Psi = \mathrm{constant}\times \Psi,
$$
The integral which defines various
expectation values involving moments of the hamiltonian becomes then
$$
\langle E^n \rangle = \langle H^n \rangle =
\frac{\int d\boldsymbol{R}\Psi^{\ast}(\boldsymbol{R})H^n(\boldsymbol{R})\Psi(\boldsymbol{R})}
{\int d\boldsymbol{R}\Psi^{\ast}(\boldsymbol{R})\Psi(\boldsymbol{R})}=
\mathrm{constant}\times\frac{\int d\boldsymbol{R}\Psi^{\ast}(\boldsymbol{R})\Psi(\boldsymbol{R})}
{\int d\boldsymbol{R}\Psi^{\ast}(\boldsymbol{R})\Psi(\boldsymbol{R})}=\mathrm{constant}.
$$
**This gives an important information: If I want the variance, the exact wave function leads to zero variance!**
The variance is defined as
$$
\sigma_E = \langle E^2\rangle - \langle E\rangle^2.
$$
Variation is then performed by minimizing both the energy and the variance.
We can then take the derivatives of
$$
\sigma_E = \langle E^2\rangle - \langle E\rangle^2,
$$
with respect to the variational parameters. The derivatives of the variance can then be used to defined the
so-called Hessian matrix, which in turn allows us to use minimization methods like Newton's method or
standard gradient methods.
This leads to however a more complicated expression, with obvious errors when evaluating integrals by Monte Carlo integration. Less used, see however [Filippi and Umrigar](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.94.150201). The expression becomes complicated
$$
\bar{E}_{ij} = 2\left[ \langle (\frac{\bar{\Psi}_{ij}}{\Psi}+\frac{\bar{\Psi}_{j}}{\Psi}\frac{\bar{\Psi}_{i}}{\Psi})(E_L-\langle E\rangle)\rangle -\langle \frac{\bar{\Psi}_{i}}{\Psi}\rangle\bar{E}_j-\langle \frac{\bar{\Psi}_{j}}{\Psi}\rangle\bar{E}_i\right] +\langle \frac{\bar{\Psi}_{i}}{\Psi}E_L{_j}\rangle +\langle \frac{\bar{\Psi}_{j}}{\Psi}E_L{_i}\rangle -\langle \frac{\bar{\Psi}_{i}}{\Psi}\rangle\langle E_L{_j}\rangle \langle \frac{\bar{\Psi}_{j}}{\Psi}\rangle\langle E_L{_i}\rangle.
$$
Evaluating the cost function means having to evaluate the above second derivative of the energy.
|
github_jupyter
|
python code here
add python code here
| 0.264453 | 0.992297 |
# Introduction to Geopandas
In this lesson, we will cover basics steps needed for interacting with spatial data in Python using geopandas:
- Managing filepaths
- Reading spatial data from file
- Geometry calculations
- Writing spatial data to file
- Grouping and splitting spatial data into multiple layers
Geopandas (http://geopandas.org/) makes it possible to work with geospatial data in Python in a relatively easy way. Geopandas combines the capabilities of the data analysis library [pandas](https://pandas.pydata.org/pandas-docs/stable/) with other packages like [shapely](https://shapely.readthedocs.io/en/stable/manual.html) and [fiona](https://fiona.readthedocs.io/en/latest/manual.html) for managing spatial data.
The main data structures in geopandas are `GeoSeries` and `GeoDataFrame` which extend the capabilities of `Series` and `DataFrames` from pandas. This means that we can use all our pandas skills also when working with geopandas! If you need to refresh your memory about pandas, check out week 5 and 6 lesson materials from the [Geo-Python website](geo-python.github.io).
The main difference between geodataframes and pandas dataframes is that a [geodataframe](http://geopandas.org/data_structures.html#geodataframe) should contain one column for geometries. By default, the name of this column is `'geometry'`. The geometry column is a [geoseries](http://geopandas.org/data_structures.html#geoseries) which contains the geometries (points, lines, polygons, multipolygons etc.) as shapely objects.

As we learned in the Geo-Python course, it is conventional to import pandas as `pd`. Similarly,we will import geopandas as `gpd`:
```
import geopandas as gpd
```
## Input data: Finnish topographic database
In this lesson we will work with the [National Land Survey of Finland (NLS) topographic database (from 2018)](https://www.maanmittauslaitos.fi/en/maps-and-spatial-data/expert-users/product-descriptions/topographic-database).
- The data set is licensed under the NLS' [open data licence](https://www.maanmittauslaitos.fi/en/opendata-licence-cc40) (CC BY 4.0).
- Structure of the data is described in a separate Excel file ([download link](http://www.maanmittauslaitos.fi/sites/maanmittauslaitos.fi/files/attachments/2018/10/maastotietokanta_kohdemalli_eng.xlsx)).
- Further information about file naming is available at [fairdata.fi](https://etsin.fairdata.fi/dataset/5023ecc7-914a-4494-9e32-d0a39d3b56ae).
For this lesson, we have acquired a subset of the topographic database as shapefiles from the Helsinki Region in Finland via the [CSC open data portal](https://avaa.tdata.fi/web/paituli/latauspalvelu):

In this lesson, we will focus on **terrain objects** (Feature group: "Terrain/1" in the topographic database). The Terrain/1 feature group contains several feature classes. **Our aim in this lesson is to save all the Terrain/1 feature classes into separate files**.
*Terrain/1 features in the Topographic Database:*
| feature class | Name of feature | Feature group |
|----------------|------------------------------------------------------------|---------------|
| 32421 | Motor traffic area | Terrain/1 |
| 32200 | Cemetery | Terrain/1 |
| 34300 | Sand | Terrain/1 |
| 34100 | Rock - area | Terrain/1 |
| 34700 | Rocky area | Terrain/1 |
| 32500 | Quarry | Terrain/1 |
| 32112 | Mineral resources extraction area, fine-grained material | Terrain/1 |
| 32111 | Mineral resources extraction area, coarse-grained material | Terrain/1 |
| 32611 | Field | Terrain/1 |
| 32612 | Garden | Terrain/1 |
| 32800 | Meadow | Terrain/1 |
| 32900 | Park | Terrain/1 |
| 35300 | Paludified land | Terrain/1 |
| 35412 | Bog, easy to traverse forested | Terrain/1 |
| 35411 | Open bog, easy to traverse treeless | Terrain/1 |
| 35421 | Open fen, difficult to traverse treeless | Terrain/1 |
| 33000 | Earth fill | Terrain/1 |
| 33100 | Sports and recreation area | Terrain/1 |
| 36200 | Lake water | Terrain/1 |
| 36313 | Watercourse area | Terrain/1 |
According to the [naming convention](https://etsin.fairdata.fi/dataset/5023ecc7-914a-4494-9e32-d0a39d3b56ae), all files that start with a letter `m` and end with `p` contain the objects we are interested in (Terrain/1 polygons).
## Downloading data
You can use `wget` program (available in Binder and CSC Notebooks) to download the data from the command line from this download link: https://github.com/AutoGIS/data/raw/master/L2_data.zip. Let's download the data into the same folder with the lesson 2 notebooks (`.../notebooks/L2`):
1. Open up a new terminal window
2. Navigate to the correct folder in the terminal:
```
# Navigate to lesson 2 notebooks directory:
cd autogis/notebooks/L2
```
3. Use `wget` to dowload the data from the dowload link:
```
wget https://github.com/AutoGIS/data/raw/master/L2_data.zip
```
<div class="alert alert-info">
**Copy-paste**
You can paste copied text in JupyterLab Terminal by pressing `SHIFT` + `RIGHT-CLICK` on your mouse and choosing `Paste`.
</div>
Once you have downloaded the `L2_data.zip` file into your (cloud) computer, you can unzip the file using `unzip` command in the Terminal (or e.g. 7zip on Windows if working with own computer). Run the following commands in the `.../notebooks/L2` -directory:
```
$ unzip L2_data.zip
$ ls L2_data
```
You can also check the contents of the downloaded and unzipped file in the file browser window.
The L2_data folder contains several subfolders according to the file strucutre in the topographic database shapefile distribution. After unzipping the downloaded file, you can find the data for this tutorial under: `L2_data/NLS/2018/L4/L41/L4132R.shp`. Notice that Shapefile -fileformat contains many separate files such as `.dbf` that contains the attribute information, and `.prj` -file that contains information about coordinate reference system.
## Managing filepaths
Built-in module `os` provides many useful functions for interacting with the operating system. One of the most useful submodules in the os package is the [os.path-module](https://docs.python.org/2/library/os.path.html) for manipulating file paths. This week, we have data in different sub-folders and we can practice how to use `os` path tools when defining filepaths.
Let's import `os` and see how we can construct a filepath by joining a folder path and file name:
```
import os
# Define path to folder
input_folder = r"L2_data/NLS/2018/L4/L41/L4132R.shp"
# Join folder path and filename
fp = os.path.join(input_folder, "m_L4132R_p.shp")
# Print out the full file path
print(fp)
```
## Reading a Shapefile
Esri Shapefile is the default file format when reading in data usign geopandas, so we only need to pass the file path in order to read in our data:
```
import geopandas as gpd
# Read file using gpd.read_file()
data = gpd.read_file(fp)
```
Let's check the data type:
```
type(data)
```
Here we see that our `data` -variable is a `GeoDataFrame`. GeoDataFrame extends the functionalities of
`pandas.DataFrame` in a way that it is possible to handle spatial data using similar approaches and datastructures as in pandas (hence the name geopandas).
Let's check the first rows of data:
```
data.head()
```
- Check all column names:
```
data.columns.values
```
As you might guess, the column names are in Finnish.
Let's select only the useful columns and rename them into English:
```
data = data[['RYHMA', 'LUOKKA', 'geometry']]
```
Define new column names in a dictionary:
```
colnames = {'RYHMA':'GROUP', 'LUOKKA':'CLASS'}
```
Rename:
```
data.rename(columns=colnames, inplace=True)
```
Check the output:
```
data.head()
```
#### Check your understanding
<div class="alert alert-info">
Figure out the following information from our input data using your pandas skills:
- Number of rows?
- Number of classes?
- Number of groups?
</div>
```
print("Number of rows", len(data['CLASS']))
print("Number of classes", data['CLASS'].nunique())
print("Number of groups", data['GROUP'].nunique())
```
It is always a good idea to explore your data also on a map. Creating a simple map from a `GeoDataFrame` is really easy: you can use ``.plot()`` -function from geopandas that **creates a map based on the geometries of the data**. Geopandas actually uses matplotlib for plotting which we introduced in [Lesson 7 of the Geo-Python course](https://geo-python.github.io/site/notebooks/L7/matplotlib.html).
Let's try it out, and plot our GeoDataFrame:
```
data.plot()
```
Voilá! As we can see, it is really easy to produce a map out of your Shapefile with geopandas. Geopandas automatically positions your map in a way that it covers the whole extent of your data.
*If you are living in the Helsinki region, you might recognize the shapes plotted on the map!*
## Geometries in Geopandas
Geopandas takes advantage of Shapely's geometric objects. Geometries are stored in a column called *geometry* that is a default column name for
storing geometric information in geopandas.
Let's print the first 5 rows of the column 'geometry':
```
data['geometry'].head()
```
As we can see the `geometry` column contains familiar looking values, namely Shapely `Polygon` -objects. Since the spatial data is stored as Shapely objects, **it is possible to use Shapely methods** when dealing with geometries in geopandas.
Let's have a closer look at the polygons and try to apply some of the Shapely methods we are already familiar with.
Let's start by checking the area of the first polygon in the data:
```
# Access the geometry on the first row of data
data.at[0, "geometry"]
# Print information about the area
print("Area:", round(data.at[0, "geometry"].area, 0), "square meters")
```
Let's do the same for the first five rows in the data;
- Iterate over the GeoDataFrame rows using the `iterrows()` -function that we learned [during the Lesson 6 of the Geo-Python course](https://geo-python.github.io/site/notebooks/L6/pandas/advanced-data-processing-with-pandas.html#Iterating-rows-and-using-self-made-functions-in-Pandas).
- For each row, print the area of the polygon (here, we'll limit the for-loop to a selection of the first five rows):
```
# Iterate over rows and print the area of a Polygon
for index, row in data[0:5].iterrows():
# Get the area from the shapely-object stored in the geometry-column
poly_area = row['geometry'].area
# Print info
print("Polygon area at index {index} is: {area:.0f} square meters".format(index=index, area=poly_area))
```
As you see from here, all **pandas** methods, such as the `iterrows()` function, are directly available in Geopandas without the need to call pandas separately because Geopandas is an **extension** for pandas.
In practice, it is not necessary to use the iterrows()-approach to calculate the area for all features. Geodataframes and geoseries have an attribute `area` which we can use for accessing the area for each feature at once:
```
data.area
```
Let's next create a new column into our GeoDataFrame where we calculate and store the areas of individual polygons:
```
# Create a new column called 'area'
data['area'] = data.area
```
Check the output:
```
data['area']
```
These values correspond to the ones we saw in previous step when iterating rows.
Let's check what is the `min`, `max` and `mean` of those areas using familiar functions from our previous Pandas lessions.
```
# Maximum area
round(data['area'].max(), 2)
# Minimum area
round(data['area'].min(), 2)
# Average area
round(data['area'].mean(), 2)
```
## Writing data into a shapefile
It is possible to export GeoDataFrames into various data formats using the [to_file()](http://geopandas.org/io.html#writing-spatial-data) method. In our case, we want to export subsets of the data into Shapefiles (one file for each feature class).
Let's first select one class (class number `36200`, "Lake water") from the data as a new GeoDataFrame:
```
# Select a class
selection = data.loc[data["CLASS"]==36200]
```
Check the selection:
```
selection.plot()
```
- write this layer into a new Shapefile using the `gpd.to_file()` -function:
```
# Create a output path for the data
output_folder = r"L2_data/"
output_fp = os.path.join(output_folder, "Class_36200.shp")
# Write those rows into a new file (the default output file format is Shapefile)
selection.to_file(output_fp)
```
#### Check your understanding
<div class="alert alert-info">
Read the output Shapefile in a new geodataframe, and check that the data looks ok.
</div>
```
temp = gpd.read_file(output_fp)
# Check first rows
temp.head()
# You can also plot the data for a visual check
temp.plot()
```
## Grouping the Geodataframe
One really useful function that can be used in Pandas/Geopandas is [groupby()](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.groupby.html) which groups data based on values on selected column(s). We saw and used this function already in Lesson 6 of the Geo-Python course.
Next we will automate the file export task; we will group the data based on column `CLASS` and export a shapefile for each class.
Let's continue with the same input file we already read previously into the variable `data`. We also selected and renamed a subset of the columns.
Check again the first rows of our input data:
```
data.head()
```
The `CLASS` column in the data contains information about different land use types. With `.unique()` -function we can quickly see all different values in that column:
```
# Print all unique values in the column
data['CLASS'].unique()
```
- Now we can use that information to group our data and save all land use types into different layers:
```
# Group the data by class
grouped = data.groupby('CLASS')
# Let's see what we have
grouped
```
As we can see, `groupby` -function gives us an object called `DataFrameGroupBy` which is similar to list of keys and values (in a dictionary) that we can iterate over.
Check group keys:
```
grouped.groups.keys()
```
The group keys are unique values from the column by which we grouped the dataframe.
Check how many rows of data each group has:
```
# Iterate over the grouped object
for key, group in grouped:
# Let's check how many rows each group has:
print('Terrain class:', key)
print('Number of rows:', len(group), "\n")
```
There are, for example, 56 lake polygons in the input data.
We can also check how the _last_ group looks like (we have the variables in memory from the last iteration of the for-loop):
```
group.head()
```
Notice that the index numbers refer to the row numbers in the original data -GeoDataFrame.
Check also the data type of the group:
```
type(group)
```
As we can see, each set of data are now grouped into separate GeoDataFrames, and we can save them into separate files.
### Saving multiple output files
Let's **export each class into a separate Shapefile**. While doing this, we also want to **create unique filenames for each class**.
When looping over the grouped object, information about the class is stored in the variable `key`, and we can use this information for creating new variable names inside the for-loop. For example, we want to name the shapefile containing lake polygons as "terrain_36200.shp".
<div class="alert alert-info">
**String formatting**
There are different approaches for formatting strings in Python. Here are a couple of different ways for putting together file-path names using two variables:
```
basename = "terrain"
key = 36200
# OPTION 1. Concatenating using the `+` operator:
out_fp = basename + "_" + str(key) + ".shp"
# OPTION 2. Positional formatting using `%` operator
out_fp = "%s_%s.shp" %(basename, key)
# OPTION 3. Positional formatting using `.format()`
out_fp = "{}_{}.shp".format(basename, key)
```
Read more from here: https://pyformat.info/
</div>
Let's now export terrain classes into separate Shapefiles.
- First, create a new folder for the outputs:
```
# Determine output directory
output_folder = r"L2_data/"
# Create a new folder called 'Results'
result_folder = os.path.join(output_folder, 'Results')
# Check if the folder exists already
if not os.path.exists(result_folder):
print("Creating a folder for the results..")
# If it does not exist, create one
os.makedirs(result_folder)
else:
print("Results folder exists already.")
```
At this point, you can go to the file browser and check that the new folder was created successfully.
- Iterate over groups, create a file name, and save group to file:
```
# Iterate over the groups
for key, group in grouped:
# Format the filename
output_name = "terrain_{}.shp".format(key)
# Print information about the process
print("Saving file", os.path.basename(output_name))
# Create an output path
outpath = os.path.join(result_folder, output_name)
# Export the data
group.to_file(outpath)
```
Excellent! Now we have saved those individual classes into separate Shapefiles and named the file according to the class name. These kind of grouping operations can be really handy when dealing with layers of spatial data. Doing similar process manually would be really laborious and error-prone.
### Extra: save data to csv
We can also extract basic statistics from our geodataframe, and save this information as a text file.
Let's summarize the total area of each group:
```
area_info = grouped.area.sum().round()
area_info
```
- save area info to csv using pandas:
```
# Create an output path
area_info.to_csv(os.path.join(result_folder, "terrain_class_areas.csv"), header=True)
```
## Summary
In this tutorial we introduced the first steps of using geopandas. More specifically you should know how to:
1. Read data from Shapefile using geopandas
2. Access geometry information in a geodataframe
4. Write GeoDataFrame data from Shapefile using geopandas
5. Automate a task to save specific rows from data into Shapefile based on specific key using `groupby()` -function
6. Extra: saving attribute information to a csv file.
|
github_jupyter
|
import geopandas as gpd
# Navigate to lesson 2 notebooks directory:
cd autogis/notebooks/L2
wget https://github.com/AutoGIS/data/raw/master/L2_data.zip
You can also check the contents of the downloaded and unzipped file in the file browser window.
The L2_data folder contains several subfolders according to the file strucutre in the topographic database shapefile distribution. After unzipping the downloaded file, you can find the data for this tutorial under: `L2_data/NLS/2018/L4/L41/L4132R.shp`. Notice that Shapefile -fileformat contains many separate files such as `.dbf` that contains the attribute information, and `.prj` -file that contains information about coordinate reference system.
## Managing filepaths
Built-in module `os` provides many useful functions for interacting with the operating system. One of the most useful submodules in the os package is the [os.path-module](https://docs.python.org/2/library/os.path.html) for manipulating file paths. This week, we have data in different sub-folders and we can practice how to use `os` path tools when defining filepaths.
Let's import `os` and see how we can construct a filepath by joining a folder path and file name:
## Reading a Shapefile
Esri Shapefile is the default file format when reading in data usign geopandas, so we only need to pass the file path in order to read in our data:
Let's check the data type:
Here we see that our `data` -variable is a `GeoDataFrame`. GeoDataFrame extends the functionalities of
`pandas.DataFrame` in a way that it is possible to handle spatial data using similar approaches and datastructures as in pandas (hence the name geopandas).
Let's check the first rows of data:
- Check all column names:
As you might guess, the column names are in Finnish.
Let's select only the useful columns and rename them into English:
Define new column names in a dictionary:
Rename:
Check the output:
#### Check your understanding
<div class="alert alert-info">
Figure out the following information from our input data using your pandas skills:
- Number of rows?
- Number of classes?
- Number of groups?
</div>
It is always a good idea to explore your data also on a map. Creating a simple map from a `GeoDataFrame` is really easy: you can use ``.plot()`` -function from geopandas that **creates a map based on the geometries of the data**. Geopandas actually uses matplotlib for plotting which we introduced in [Lesson 7 of the Geo-Python course](https://geo-python.github.io/site/notebooks/L7/matplotlib.html).
Let's try it out, and plot our GeoDataFrame:
Voilá! As we can see, it is really easy to produce a map out of your Shapefile with geopandas. Geopandas automatically positions your map in a way that it covers the whole extent of your data.
*If you are living in the Helsinki region, you might recognize the shapes plotted on the map!*
## Geometries in Geopandas
Geopandas takes advantage of Shapely's geometric objects. Geometries are stored in a column called *geometry* that is a default column name for
storing geometric information in geopandas.
Let's print the first 5 rows of the column 'geometry':
As we can see the `geometry` column contains familiar looking values, namely Shapely `Polygon` -objects. Since the spatial data is stored as Shapely objects, **it is possible to use Shapely methods** when dealing with geometries in geopandas.
Let's have a closer look at the polygons and try to apply some of the Shapely methods we are already familiar with.
Let's start by checking the area of the first polygon in the data:
Let's do the same for the first five rows in the data;
- Iterate over the GeoDataFrame rows using the `iterrows()` -function that we learned [during the Lesson 6 of the Geo-Python course](https://geo-python.github.io/site/notebooks/L6/pandas/advanced-data-processing-with-pandas.html#Iterating-rows-and-using-self-made-functions-in-Pandas).
- For each row, print the area of the polygon (here, we'll limit the for-loop to a selection of the first five rows):
As you see from here, all **pandas** methods, such as the `iterrows()` function, are directly available in Geopandas without the need to call pandas separately because Geopandas is an **extension** for pandas.
In practice, it is not necessary to use the iterrows()-approach to calculate the area for all features. Geodataframes and geoseries have an attribute `area` which we can use for accessing the area for each feature at once:
Let's next create a new column into our GeoDataFrame where we calculate and store the areas of individual polygons:
Check the output:
These values correspond to the ones we saw in previous step when iterating rows.
Let's check what is the `min`, `max` and `mean` of those areas using familiar functions from our previous Pandas lessions.
## Writing data into a shapefile
It is possible to export GeoDataFrames into various data formats using the [to_file()](http://geopandas.org/io.html#writing-spatial-data) method. In our case, we want to export subsets of the data into Shapefiles (one file for each feature class).
Let's first select one class (class number `36200`, "Lake water") from the data as a new GeoDataFrame:
Check the selection:
- write this layer into a new Shapefile using the `gpd.to_file()` -function:
#### Check your understanding
<div class="alert alert-info">
Read the output Shapefile in a new geodataframe, and check that the data looks ok.
</div>
## Grouping the Geodataframe
One really useful function that can be used in Pandas/Geopandas is [groupby()](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.groupby.html) which groups data based on values on selected column(s). We saw and used this function already in Lesson 6 of the Geo-Python course.
Next we will automate the file export task; we will group the data based on column `CLASS` and export a shapefile for each class.
Let's continue with the same input file we already read previously into the variable `data`. We also selected and renamed a subset of the columns.
Check again the first rows of our input data:
The `CLASS` column in the data contains information about different land use types. With `.unique()` -function we can quickly see all different values in that column:
- Now we can use that information to group our data and save all land use types into different layers:
As we can see, `groupby` -function gives us an object called `DataFrameGroupBy` which is similar to list of keys and values (in a dictionary) that we can iterate over.
Check group keys:
The group keys are unique values from the column by which we grouped the dataframe.
Check how many rows of data each group has:
There are, for example, 56 lake polygons in the input data.
We can also check how the _last_ group looks like (we have the variables in memory from the last iteration of the for-loop):
Notice that the index numbers refer to the row numbers in the original data -GeoDataFrame.
Check also the data type of the group:
As we can see, each set of data are now grouped into separate GeoDataFrames, and we can save them into separate files.
### Saving multiple output files
Let's **export each class into a separate Shapefile**. While doing this, we also want to **create unique filenames for each class**.
When looping over the grouped object, information about the class is stored in the variable `key`, and we can use this information for creating new variable names inside the for-loop. For example, we want to name the shapefile containing lake polygons as "terrain_36200.shp".
<div class="alert alert-info">
**String formatting**
There are different approaches for formatting strings in Python. Here are a couple of different ways for putting together file-path names using two variables:
Read more from here: https://pyformat.info/
</div>
Let's now export terrain classes into separate Shapefiles.
- First, create a new folder for the outputs:
At this point, you can go to the file browser and check that the new folder was created successfully.
- Iterate over groups, create a file name, and save group to file:
Excellent! Now we have saved those individual classes into separate Shapefiles and named the file according to the class name. These kind of grouping operations can be really handy when dealing with layers of spatial data. Doing similar process manually would be really laborious and error-prone.
### Extra: save data to csv
We can also extract basic statistics from our geodataframe, and save this information as a text file.
Let's summarize the total area of each group:
- save area info to csv using pandas:
| 0.853073 | 0.987067 |
# Quantum Convolutional Neural Network with scikit-qulacs
[Quantum Convolutional Neural Networks](https://arxiv.org/abs/1810.03787)をTensorFlow Quantum(以降TFQ)で実装したチュートリアルの[Quantum Convolutional Neural Network](https://www.tensorflow.org/quantum/tutorials/qcnn?hl=en)(以降QCNN)のscikit-qulacs実装例です。
## インポート
`scikit-qulacs`の`QNNClassifier`と`create_qcnn_ansatz`をインポートします。`numpy`や`matplotlib.pyplot`等も併せてインポートします。
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import default_rng
from sklearn.metrics import f1_score
from skqulacs.qnn import QNNClassifier
from skqulacs.circuit.pre_defined import create_qcnn_ansatz
```
## テストデータの生成
TFQ版QCNNと同様に、テストデータを生成します。
TFQ版はデータの中に量子状態を表す回路を埋め込みテンソルに変換して持たせます。
`scikit-qulacs`の場合、入力データはInputParameterとして`create_qcnn_ansatz`の中でエンコードされます。
そのため、データとしては単純に回転角と正解ラベルを持たせます。
```
def generate_data(bits: int, random_seed: int = 0):
"""Generate training and testing data."""
rng = default_rng(random_seed)
n_rounds = 20
excitations = []
labels = []
for n in range(n_rounds):
for bit in range(bits):
r = rng.uniform(-np.pi, np.pi)
excitations.append(r)
labels.append(1 if (-np.pi / 2) <= r <= (np.pi / 2) else 0)
split_ind = int(len(excitations) * 0.7)
train_excitations = excitations[:split_ind]
test_excitations = excitations[split_ind:]
train_labels = labels[:split_ind]
test_labels = labels[split_ind:]
return train_excitations, np.array(train_labels), \
test_excitations, np.array(test_labels)
```
## QCNN回路の作成
`create_qcnn_ansatz()`を呼び出して回路を作成してください。
第一引数に量子ビットを指定します。現在は固定の8ビットに対応しています。
第二引数は乱数のシード値を指定してください。
```
nqubit = 8 # 量子ビット数。現在8固定
random_seed = 0 # 乱数のシード値
circuit = create_qcnn_ansatz(nqubit, random_seed)
```
## QNNClassifierクラスの作成
作成した回路を`QNNClassifierクラス`に指定してください。
第一引数に回路を指定します。第二引数に分類数を指定します。ここでは二値問題のため2を指定してください。
第三引数に探索アルゴリズムを指定します。`Adam`を指定してください。
```
num_class = 2 # 分類数(ここでは2つに分類)
solver="Adam" # 探索アルゴリズム。"Adam"を指定してください。
qcl = QNNClassifier(circuit, num_class, solver)
```
## 実行
`generate_data()`を呼び出してテストデータを生成し、`qcl.fit()`を実行し学習を行います。
`opt_params`に学習されたパラメータが入ります。
`qcl.predict()`で推論を行います。
`sklearn.metrics`の`f1_score`を使用して結果の精度を計算します。
```
maxiter = 20 # ループの最大。これが多いほど、正確になるが、時間がかかる。
x_train, y_train, x_test, y_test = generate_data(nqubit)
opt_loss, opt_params = qcl.fit(x_train, y_train, maxiter)
print("trained parameters: ", opt_params)
y_pred = qcl.predict(x_test)
print("f1_score: ", f1_score(y_test, y_pred, average="weighted"))
```
0.9以上の正解率となります。
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import default_rng
from sklearn.metrics import f1_score
from skqulacs.qnn import QNNClassifier
from skqulacs.circuit.pre_defined import create_qcnn_ansatz
def generate_data(bits: int, random_seed: int = 0):
"""Generate training and testing data."""
rng = default_rng(random_seed)
n_rounds = 20
excitations = []
labels = []
for n in range(n_rounds):
for bit in range(bits):
r = rng.uniform(-np.pi, np.pi)
excitations.append(r)
labels.append(1 if (-np.pi / 2) <= r <= (np.pi / 2) else 0)
split_ind = int(len(excitations) * 0.7)
train_excitations = excitations[:split_ind]
test_excitations = excitations[split_ind:]
train_labels = labels[:split_ind]
test_labels = labels[split_ind:]
return train_excitations, np.array(train_labels), \
test_excitations, np.array(test_labels)
nqubit = 8 # 量子ビット数。現在8固定
random_seed = 0 # 乱数のシード値
circuit = create_qcnn_ansatz(nqubit, random_seed)
num_class = 2 # 分類数(ここでは2つに分類)
solver="Adam" # 探索アルゴリズム。"Adam"を指定してください。
qcl = QNNClassifier(circuit, num_class, solver)
maxiter = 20 # ループの最大。これが多いほど、正確になるが、時間がかかる。
x_train, y_train, x_test, y_test = generate_data(nqubit)
opt_loss, opt_params = qcl.fit(x_train, y_train, maxiter)
print("trained parameters: ", opt_params)
y_pred = qcl.predict(x_test)
print("f1_score: ", f1_score(y_test, y_pred, average="weighted"))
| 0.507568 | 0.987055 |
```
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import seaborn as sns
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
# Import the 3 dimensionality reduction methods
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
df = pd.read_csv('insurance.csv')
df.head()
X = df.iloc[:,1:6]
target = df['charges']
regions = pd.get_dummies(X['region'], drop_first = True)
X = X.drop('region', axis = 1)
X = pd.concat([X, regions], axis = 1)
smokers = pd.get_dummies(X['smoker'], drop_first = True)
X = X.drop('smoker', axis = 1)
X = pd.concat([X, smokers], axis = 1)
s = pd.get_dummies(X['sex'], drop_first = True)
X = X.drop('sex', axis = 1)
X = pd.concat([X, s], axis = 1)
#After dummies the X
X.head()
# Standardize the data
from sklearn.preprocessing import StandardScaler
X = X.values
X_std = StandardScaler().fit_transform(X)
# Calculating Eigenvectors and eigenvalues of Cov matirx
mean_vec = np.mean(X_std, axis=0)
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
# Create a list of (eigenvalue, eigenvector) tuples
eig_pairs = [ (np.abs(eig_vals[i]),eig_vecs[:,i]) for i in range(len(eig_vals))]
# Sort the eigenvalue, eigenvector pair from high to low
eig_pairs.sort(key = lambda x: x[0], reverse= True)
# Calculation of Explained Variance from the eigenvalues
tot = sum(eig_vals)
var_exp = [(i/tot)*100 for i in sorted(eig_vals, reverse=True)] # Individual explained variance
cum_var_exp = np.cumsum(var_exp) # Cumulative explained variance
[ n for n,i in enumerate(cum_var_exp) if i>90 ][0]
# Find the eigenvector beyond which 90% of the data is explained
# Call the PCA method with 5 components.
pca = PCA(n_components= 5)
pca.fit(X_std)
X_5d = pca.transform(X_std)
print(X_5d.shape)
from sklearn import cross_validation
from sklearn.ensemble import RandomForestRegressor
n = len(X_5d)
kf_10 = cross_validation.KFold(n, n_folds=10, shuffle=True, random_state=2)
regr = RandomForestRegressor()
mse = []
score = -1*cross_validation.cross_val_score(regr, np.ones((n,1)), target.ravel(), cv=kf_10, scoring='mean_squared_error').mean()
mse.append(score)
for i in np.arange(1,6):
score = -1*cross_validation.cross_val_score(regr, X_5d[:,:i], target.ravel(), cv=kf_10, scoring='mean_squared_error').mean()
mse.append(score)
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(12,5))
ax1.plot(mse, '-v')
ax2.plot([1,2,3,4,5], mse[1:6], '-v')
ax2.set_title('Intercept excluded from plot')
for ax in fig.axes:
ax.set_xlabel('Number of principal components in regression')
ax.set_ylabel('MSE')
ax.set_xlim((-0.2,5.2))
X_new = pd.DataFrame(X_5d)
X_new.head()
# copy the data
target = target.copy()
# apply normalization techniques
for i in target:
target = target / target.abs().max()
target.head()
X_new = X_new.copy()
# apply normalization techniques
for column in X_new.columns:
X_new[column] = X_new[column] / X_new[column].abs().max()
X_new.head()
final_df = pd.concat([X_new, target], axis = 1)
final_df.head()
def clean_dataset(df):
assert isinstance(df, pd.DataFrame), "df needs to be a pd.DataFrame"
df.dropna(inplace=True)
indices_to_keep = ~df.isin([np.nan, np.inf, -np.inf]).any(1)
return df[indices_to_keep].astype(np.float64)
clean_dataset(final_df)
final_df.head()
X = X_new
Y = final_df['charges']
X.head()
X.shape
Y.shape
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.25, random_state =0)
regr.fit(X_train, Y_train)
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
# performance for training set:
y_train_predict = regr.predict(X_train)
rmse = (np.sqrt(mean_squared_error(Y_train, y_train_predict)))
r2 = r2_score(Y_train, y_train_predict)
print("The model performance for training set:")
print("\n")
print('RMSE is {}'.format(rmse))
print('R2 score is {}'.format(r2))
print("\n")
# model evaluation for testing set:
y_test_predict = regr.predict(X_test)
rmse = (np.sqrt(mean_squared_error(Y_test, y_test_predict)))
r2 = r2_score(Y_test, y_test_predict)
print("The model performance for testing set:")
print("\n")
print('RMSE is {}'.format(rmse))
print('R2 score is {}'.format(r2))
plt.scatter(Y_train,y_train_predict)
plt.show
plt.scatter(Y_test,y_test_predict)
plt.show
```
|
github_jupyter
|
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import seaborn as sns
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
# Import the 3 dimensionality reduction methods
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
df = pd.read_csv('insurance.csv')
df.head()
X = df.iloc[:,1:6]
target = df['charges']
regions = pd.get_dummies(X['region'], drop_first = True)
X = X.drop('region', axis = 1)
X = pd.concat([X, regions], axis = 1)
smokers = pd.get_dummies(X['smoker'], drop_first = True)
X = X.drop('smoker', axis = 1)
X = pd.concat([X, smokers], axis = 1)
s = pd.get_dummies(X['sex'], drop_first = True)
X = X.drop('sex', axis = 1)
X = pd.concat([X, s], axis = 1)
#After dummies the X
X.head()
# Standardize the data
from sklearn.preprocessing import StandardScaler
X = X.values
X_std = StandardScaler().fit_transform(X)
# Calculating Eigenvectors and eigenvalues of Cov matirx
mean_vec = np.mean(X_std, axis=0)
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
# Create a list of (eigenvalue, eigenvector) tuples
eig_pairs = [ (np.abs(eig_vals[i]),eig_vecs[:,i]) for i in range(len(eig_vals))]
# Sort the eigenvalue, eigenvector pair from high to low
eig_pairs.sort(key = lambda x: x[0], reverse= True)
# Calculation of Explained Variance from the eigenvalues
tot = sum(eig_vals)
var_exp = [(i/tot)*100 for i in sorted(eig_vals, reverse=True)] # Individual explained variance
cum_var_exp = np.cumsum(var_exp) # Cumulative explained variance
[ n for n,i in enumerate(cum_var_exp) if i>90 ][0]
# Find the eigenvector beyond which 90% of the data is explained
# Call the PCA method with 5 components.
pca = PCA(n_components= 5)
pca.fit(X_std)
X_5d = pca.transform(X_std)
print(X_5d.shape)
from sklearn import cross_validation
from sklearn.ensemble import RandomForestRegressor
n = len(X_5d)
kf_10 = cross_validation.KFold(n, n_folds=10, shuffle=True, random_state=2)
regr = RandomForestRegressor()
mse = []
score = -1*cross_validation.cross_val_score(regr, np.ones((n,1)), target.ravel(), cv=kf_10, scoring='mean_squared_error').mean()
mse.append(score)
for i in np.arange(1,6):
score = -1*cross_validation.cross_val_score(regr, X_5d[:,:i], target.ravel(), cv=kf_10, scoring='mean_squared_error').mean()
mse.append(score)
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(12,5))
ax1.plot(mse, '-v')
ax2.plot([1,2,3,4,5], mse[1:6], '-v')
ax2.set_title('Intercept excluded from plot')
for ax in fig.axes:
ax.set_xlabel('Number of principal components in regression')
ax.set_ylabel('MSE')
ax.set_xlim((-0.2,5.2))
X_new = pd.DataFrame(X_5d)
X_new.head()
# copy the data
target = target.copy()
# apply normalization techniques
for i in target:
target = target / target.abs().max()
target.head()
X_new = X_new.copy()
# apply normalization techniques
for column in X_new.columns:
X_new[column] = X_new[column] / X_new[column].abs().max()
X_new.head()
final_df = pd.concat([X_new, target], axis = 1)
final_df.head()
def clean_dataset(df):
assert isinstance(df, pd.DataFrame), "df needs to be a pd.DataFrame"
df.dropna(inplace=True)
indices_to_keep = ~df.isin([np.nan, np.inf, -np.inf]).any(1)
return df[indices_to_keep].astype(np.float64)
clean_dataset(final_df)
final_df.head()
X = X_new
Y = final_df['charges']
X.head()
X.shape
Y.shape
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.25, random_state =0)
regr.fit(X_train, Y_train)
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
# performance for training set:
y_train_predict = regr.predict(X_train)
rmse = (np.sqrt(mean_squared_error(Y_train, y_train_predict)))
r2 = r2_score(Y_train, y_train_predict)
print("The model performance for training set:")
print("\n")
print('RMSE is {}'.format(rmse))
print('R2 score is {}'.format(r2))
print("\n")
# model evaluation for testing set:
y_test_predict = regr.predict(X_test)
rmse = (np.sqrt(mean_squared_error(Y_test, y_test_predict)))
r2 = r2_score(Y_test, y_test_predict)
print("The model performance for testing set:")
print("\n")
print('RMSE is {}'.format(rmse))
print('R2 score is {}'.format(r2))
plt.scatter(Y_train,y_train_predict)
plt.show
plt.scatter(Y_test,y_test_predict)
plt.show
| 0.60778 | 0.589037 |
# Writing guides using EasyGuide
This tutorial describes the [pyro.contrib.easyguide](http://docs.pyro.ai/en/stable/contrib.easyguide.html) module. This tutorial assumes the reader is already familiar with [SVI](http://pyro.ai/examples/svi_part_ii.html) and [tensor shapes](http://pyro.ai/examples/tensor_shapes.html).
#### Summary
- For simple black-box guides, try using components in [pyro.infer.autoguide](http://docs.pyro.ai/en/stable/infer.autoguide.html).
- For more complex guides, try using components in [pyro.contrib.easyguide](http://docs.pyro.ai/en/stable/contrib.easyguide.html).
- Decorate with `@easy_guide(model)`.
- Select multiple model sites using `group = self.group(match="my_regex")`.
- Guide a group of sites by a single distribution using `group.sample(...)`.
- Inspect concatenated group shape using `group.batch_shape`, `group.event_shape`, etc.
- Use `self.plate(...)` instead of `pyro.plate(...)`.
- To be compatible with subsampling, pass the `event_dim` arg to `pyro.param(...)`.
- To MAP estimate model site "foo", use `foo = self.map_estimate("foo")`.
#### Table of contents
- [Modeling time series data](#Modeling-time-series-data)
- [Writing a guide without EasyGuide](#Writing-a-guide-without-EasyGuide)
- [Using EasyGuide](#Using-EasyGuide)
- [Amortized guides](#Amortized-guides)
```
import os
import torch
import pyro
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
from pyro.contrib.easyguide import easy_guide
from pyro.optim import Adam
from torch.distributions import constraints
pyro.enable_validation(True)
smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('0.5.1')
```
## Modeling time series data
Consider a time-series model with a slowly-varying continuous latent state and Bernoulli observations with a logistic link function.
```
def model(batch, subsample, full_size):
batch = list(batch)
num_time_steps = len(batch)
drift = pyro.sample("drift", dist.LogNormal(-1, 0.5))
with pyro.plate("data", full_size, subsample=subsample):
z = 0.
for t in range(num_time_steps):
z = pyro.sample("state_{}".format(t),
dist.Normal(z, drift))
batch[t] = pyro.sample("obs_{}".format(t),
dist.Bernoulli(logits=z),
obs=batch[t])
return torch.stack(batch)
```
Let's generate some data directly from the model.
```
full_size = 100
num_time_steps = 7
pyro.set_rng_seed(123456789)
data = model([None] * num_time_steps, torch.arange(full_size), full_size)
assert data.shape == (num_time_steps, full_size)
```
## Writing a guide without EasyGuide
Consider a possible guide for this model where we point-estimate the `drift` parameter using a `Delta` distribution, and then model local time series using shared uncertainty but local means, using a `LowRankMultivariateNormal` distribution. There is a single global sample site which we can model with a `param` and `sample` statement. Then we sample a global pair of uncertainty parameters `cov_diag` and `cov_factor`. Next we sample a local `loc` parameter using `pyro.param(..., event_dim=...)` and an auxiliary sample site. Finally we unpack that auxiliary site into one element per time series. The auxiliary-unpacked-to-`Delta`s pattern is quite common.
```
rank = 3
def guide(batch, subsample, full_size):
num_time_steps, batch_size = batch.shape
# MAP estimate the drift.
drift_loc = pyro.param("drift_loc", lambda: torch.tensor(0.1),
constraint=constraints.positive)
pyro.sample("drift", dist.Delta(drift_loc))
# Model local states using shared uncertainty + local mean.
cov_diag = pyro.param("state_cov_diag",
lambda: torch.full((num_time_steps,), 0.01),
constraint=constraints.positive)
cov_factor = pyro.param("state_cov_factor",
lambda: torch.randn(num_time_steps, rank) * 0.01)
with pyro.plate("data", full_size, subsample=subsample):
# Sample local mean.
loc = pyro.param("state_loc",
lambda: torch.full((full_size, num_time_steps), 0.5),
event_dim=1)
states = pyro.sample("states",
dist.LowRankMultivariateNormal(loc, cov_factor, cov_diag),
infer={"is_auxiliary": True})
# Unpack the joint states into one sample site per time step.
for t in range(num_time_steps):
pyro.sample("state_{}".format(t), dist.Delta(states[:, t]))
```
Let's train using [SVI](http://docs.pyro.ai/en/stable/inference_algos.html#module-pyro.infer.svi) and [Trace_ELBO](http://docs.pyro.ai/en/stable/inference_algos.html#pyro.infer.trace_elbo.Trace_ELBO), manually batching data into small minibatches.
```
def train(guide, num_epochs=1 if smoke_test else 101, batch_size=20):
full_size = data.size(-1)
pyro.get_param_store().clear()
pyro.set_rng_seed(123456789)
svi = SVI(model, guide, Adam({"lr": 0.02}), Trace_ELBO())
for epoch in range(num_epochs):
pos = 0
losses = []
while pos < full_size:
subsample = torch.arange(pos, pos + batch_size)
batch = data[:, pos:pos + batch_size]
pos += batch_size
losses.append(svi.step(batch, subsample, full_size=full_size))
epoch_loss = sum(losses) / len(losses)
if epoch % 10 == 0:
print("epoch {} loss = {}".format(epoch, epoch_loss / data.numel()))
train(guide)
```
## Using EasyGuide
Now let's simplify using the `@easy_guide` decorator. Our modifications are:
1. Decorate with `@easy_guide` and add `self` to args.
2. Replace the `Delta` guide for drift with a simple `map_estimate()`.
3. Select a `group` of model sites and read their concatenated `event_shape`.
4. Replace the auxiliary site and `Delta` slices with a single `group.sample()`.
```
@easy_guide(model)
def guide(self, batch, subsample, full_size):
# MAP estimate the drift.
self.map_estimate("drift")
# Model local states using shared uncertainty + local mean.
group = self.group(match="state_[0-9]*") # Selects all local variables.
cov_diag = pyro.param("state_cov_diag",
lambda: torch.full(group.event_shape, 0.01),
constraint=constraints.positive)
cov_factor = pyro.param("state_cov_factor",
lambda: torch.randn(group.event_shape + (rank,)) * 0.01)
with self.plate("data", full_size, subsample=subsample):
# Sample local mean.
loc = pyro.param("state_loc",
lambda: torch.full((full_size,) + group.event_shape, 0.5),
event_dim=1)
# Automatically sample the joint latent, then unpack and replay model sites.
group.sample("states", dist.LowRankMultivariateNormal(loc, cov_factor, cov_diag))
```
Note we've used `group.event_shape` to determine the total flattened concatenated shape of all matched sites in the group.
```
train(guide)
```
## Amortized guides
`EasyGuide` also makes it easy to write amortized guides (guides where we learn a function that predicts latent variables from data, rather than learning one parameter per datapoint). Let's modify the last guide to predict the latent `loc` as an affine function of observed data, rather than memorizing each data point's latent variable. This amortized guide is more useful in practice because it can handle new data.
```
@easy_guide(model)
def guide(self, batch, subsample, full_size):
num_time_steps, batch_size = batch.shape
self.map_estimate("drift")
group = self.group(match="state_[0-9]*")
cov_diag = pyro.param("state_cov_diag",
lambda: torch.full(group.event_shape, 0.01),
constraint=constraints.positive)
cov_factor = pyro.param("state_cov_factor",
lambda: torch.randn(group.event_shape + (rank,)) * 0.01)
# Predict latent propensity as an affine function of observed data.
if not hasattr(self, "nn"):
self.nn = torch.nn.Linear(group.event_shape.numel(), group.event_shape.numel())
self.nn.weight.data.fill_(1.0 / num_time_steps)
self.nn.bias.data.fill_(-0.5)
pyro.module("state_nn", self.nn)
with self.plate("data", full_size, subsample=subsample):
loc = self.nn(batch.t())
group.sample("states", dist.LowRankMultivariateNormal(loc, cov_factor, cov_diag))
train(guide)
```
|
github_jupyter
|
import os
import torch
import pyro
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
from pyro.contrib.easyguide import easy_guide
from pyro.optim import Adam
from torch.distributions import constraints
pyro.enable_validation(True)
smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('0.5.1')
def model(batch, subsample, full_size):
batch = list(batch)
num_time_steps = len(batch)
drift = pyro.sample("drift", dist.LogNormal(-1, 0.5))
with pyro.plate("data", full_size, subsample=subsample):
z = 0.
for t in range(num_time_steps):
z = pyro.sample("state_{}".format(t),
dist.Normal(z, drift))
batch[t] = pyro.sample("obs_{}".format(t),
dist.Bernoulli(logits=z),
obs=batch[t])
return torch.stack(batch)
full_size = 100
num_time_steps = 7
pyro.set_rng_seed(123456789)
data = model([None] * num_time_steps, torch.arange(full_size), full_size)
assert data.shape == (num_time_steps, full_size)
rank = 3
def guide(batch, subsample, full_size):
num_time_steps, batch_size = batch.shape
# MAP estimate the drift.
drift_loc = pyro.param("drift_loc", lambda: torch.tensor(0.1),
constraint=constraints.positive)
pyro.sample("drift", dist.Delta(drift_loc))
# Model local states using shared uncertainty + local mean.
cov_diag = pyro.param("state_cov_diag",
lambda: torch.full((num_time_steps,), 0.01),
constraint=constraints.positive)
cov_factor = pyro.param("state_cov_factor",
lambda: torch.randn(num_time_steps, rank) * 0.01)
with pyro.plate("data", full_size, subsample=subsample):
# Sample local mean.
loc = pyro.param("state_loc",
lambda: torch.full((full_size, num_time_steps), 0.5),
event_dim=1)
states = pyro.sample("states",
dist.LowRankMultivariateNormal(loc, cov_factor, cov_diag),
infer={"is_auxiliary": True})
# Unpack the joint states into one sample site per time step.
for t in range(num_time_steps):
pyro.sample("state_{}".format(t), dist.Delta(states[:, t]))
def train(guide, num_epochs=1 if smoke_test else 101, batch_size=20):
full_size = data.size(-1)
pyro.get_param_store().clear()
pyro.set_rng_seed(123456789)
svi = SVI(model, guide, Adam({"lr": 0.02}), Trace_ELBO())
for epoch in range(num_epochs):
pos = 0
losses = []
while pos < full_size:
subsample = torch.arange(pos, pos + batch_size)
batch = data[:, pos:pos + batch_size]
pos += batch_size
losses.append(svi.step(batch, subsample, full_size=full_size))
epoch_loss = sum(losses) / len(losses)
if epoch % 10 == 0:
print("epoch {} loss = {}".format(epoch, epoch_loss / data.numel()))
train(guide)
@easy_guide(model)
def guide(self, batch, subsample, full_size):
# MAP estimate the drift.
self.map_estimate("drift")
# Model local states using shared uncertainty + local mean.
group = self.group(match="state_[0-9]*") # Selects all local variables.
cov_diag = pyro.param("state_cov_diag",
lambda: torch.full(group.event_shape, 0.01),
constraint=constraints.positive)
cov_factor = pyro.param("state_cov_factor",
lambda: torch.randn(group.event_shape + (rank,)) * 0.01)
with self.plate("data", full_size, subsample=subsample):
# Sample local mean.
loc = pyro.param("state_loc",
lambda: torch.full((full_size,) + group.event_shape, 0.5),
event_dim=1)
# Automatically sample the joint latent, then unpack and replay model sites.
group.sample("states", dist.LowRankMultivariateNormal(loc, cov_factor, cov_diag))
train(guide)
@easy_guide(model)
def guide(self, batch, subsample, full_size):
num_time_steps, batch_size = batch.shape
self.map_estimate("drift")
group = self.group(match="state_[0-9]*")
cov_diag = pyro.param("state_cov_diag",
lambda: torch.full(group.event_shape, 0.01),
constraint=constraints.positive)
cov_factor = pyro.param("state_cov_factor",
lambda: torch.randn(group.event_shape + (rank,)) * 0.01)
# Predict latent propensity as an affine function of observed data.
if not hasattr(self, "nn"):
self.nn = torch.nn.Linear(group.event_shape.numel(), group.event_shape.numel())
self.nn.weight.data.fill_(1.0 / num_time_steps)
self.nn.bias.data.fill_(-0.5)
pyro.module("state_nn", self.nn)
with self.plate("data", full_size, subsample=subsample):
loc = self.nn(batch.t())
group.sample("states", dist.LowRankMultivariateNormal(loc, cov_factor, cov_diag))
train(guide)
| 0.851552 | 0.989254 |
# Image analysis in Python with SciPy, scikit-image, and napari
<div style="border: solid 1px; background: #abcfef; font-size: 150%; padding: 1em; margin: 1em; width: 75%;">
<p>To participate, please follow the preparation instructions at</p>
<p>https://github.com/jni/skimage-tutorials/blob/monash-df-2020-08/preparation.md</p>
</div>
<hr/>
TL;DR: Install Python 3.7+, scikit-image, napari, and the Jupyter notebook. Then clone this repo:
```python
git clone --depth 1 --single-branch --branch monash-df-2020-08 https://github.com/jni/skimage-tutorials
```
<hr/>
scikit-image is a collection of image processing algorithms for the
SciPy ecosystem. It aims to have a Pythonic API (read: does what you'd expect),
is well documented, and provides researchers and practitioners with well-tested,
fundamental building blocks for rapidly constructing sophisticated image
processing pipelines.
In this tutorial, we provide an interactive overview of the library,
where participants have the opportunity to try their hand at various
image processing challenges.
Attendees are expected to have a working knowledge of NumPy, SciPy, and Matplotlib, as well as use of Jupyter Notebooks.
Across domains, modalities, and scales of exploration, images form an integral subset of scientific measurements. Despite a deep appeal to human intuition, gaining understanding of image content remains challenging, and often relies on heuristics. Even so, the wealth of knowledge contained inside of images cannot be overstated, and <a href="http://scikit-image.org">scikit-image</a>, along with <a href="http://scipy.org">SciPy</a>, provides a strong foundation upon which to build algorithms and applications for exploring this domain.
# Prerequisites
Please see the [preparation instructions](https://github.com/jni/skimage-tutorials/blob/monash-df-2020-08/preparation.md).
# Schedule
- 1:00–1:50: Introduction & [images as NumPy arrays](/notebooks/lectures/00_images_are_arrays.ipynb)
- 2:00–2:50: [Filters](/notebooks/lectures/1_image_filters.ipynb)
- 3:10–3:50: [Segmentation](/notebooks/lectures/4_segmentation.ipynb)
- 4:00–5:00: [3D image analysis example](/notebooks/lectures/three_dimensional_image_processing.ipynb) and Q&A
# For later
- Check out the other [lectures](/notebooks/lectures)
- Some [real world use cases](http://bit.ly/skimage_real_world)
# After the workshop
We will upload our completed notebooks to the
`monash-df-2020-08-completed` branch. You can download it with git using:
```
git commit -a -m "Work completed in class"
git fetch origin monash-df-2020-08-completed
git switch monash-df-2020-08-completed
```
Or you can download them directly at:
https://github.com/jni/skimage-tutorials/archive/monash-df-2020-08-completed.zip
## Stay in touch!
- Follow the project's progress [on GitHub](https://github.com/scikit-image/scikit-image).
- Ask questions on [image.sc](https://forum.image.sc) (don't forget to tag with #skimage or #scikit-image!)
- Visit our [chat room](https://skimage.zulipchat.com)
- Ask the team questions on the [mailing list](https://mail.python.org/mailman/listinfo/scikit-image)
- [Contribute!](http://scikit-image.org/docs/dev/contribute.html)
- Read (and cite!) [our paper](https://peerj.com/articles/453/) (or [this other paper, for skimage in microtomography](https://ascimaging.springeropen.com/articles/10.1186/s40679-016-0031-0))
```
%run ../check_setup.py
```
|
github_jupyter
|
git clone --depth 1 --single-branch --branch monash-df-2020-08 https://github.com/jni/skimage-tutorials
git commit -a -m "Work completed in class"
git fetch origin monash-df-2020-08-completed
git switch monash-df-2020-08-completed
%run ../check_setup.py
| 0.525369 | 0.9821 |
```
import pandas as pd
import numpy as np
import glob
cols = ['Table Name',
'State Code',
'Distt. Code',
'Total/Rural/Urban',
'Area Name',
'Mode of travel',
'Persons Total',
'Male Total',
'Female Total',
'Persons No travel',
'Male No travel',
'Female No travel',
'Persons 0-1',
'Male 0-1',
'Female 0-1',
'Persons 2-5',
'Male 2-5',
'Female 2-5',
'Persons 6-10',
'Male 6-10',
'Female 6-10',
'Persons 11-20',
'Male 11-20',
'Female 11-20',
'Persons 21-30',
'Male 21-30',
'Female 21-30',
'Persons 31-50',
'Male 31-50',
'Female 31-50',
'Persons 51+',
'Male 51+',
'Female 51+',
'Persons Distance not stated',
'Male Distance not stated',
'Female Distance not stated']
df_data = pd.DataFrame(columns=cols)
# kar_data = pd.read_excel('DDW-2900B-28.xlsx',skiprows=38)
# kar_data.drop(kar_data.tail(3).index,inplace=True)
# kar_data.sample(5)
path = 'data'
all_files = glob.glob(path + "/*.xlsx")
for filename in all_files:
print(filename)
df = pd.read_excel(filename)
state = df.iloc[8,4]
df = df.iloc[38:]
df.drop(df.tail(3).index,inplace=True)
# print(df.dtypes)
# print(df.head())
df.columns = cols
df['Latitude'] = np.nan
df['Longitude'] = np.nan
df['State Code'] = state.strip()
df_data = df_data.append(df, ignore_index=True, sort=False)
df_data.sample(10)
df_data.shape
df_data['State Code'] = df_data['State Code'].str.strip()
df_data['Area Name'] = df_data['Area Name'].str.strip()
df_data['Total/Rural/Urban'] = df_data['Total/Rural/Urban'].str.strip()
df_data['Mode of travel'] = df_data['Mode of travel'].str.strip()
df_data.rename(columns={'State Code': 'State', 'Area Name' : 'City'}, inplace=True)
df_data.drop(columns={'Table Name', 'Distt. Code'}, inplace=True)
df_data.sample(10)
from urllib.request import urlopen
import json
def get_geo_code(area) :
url = 'https://maps.googleapis.com/maps/api/geocode/json?address=' + area + '&key=AIzaSyBfTMpfEQGsXfq1EolY4GKvJ3-uz0ge7Xo'
url = url.replace(' ','+')
print(url)
jsonurl = urlopen(url)
text = json.loads(jsonurl.read())
latitude = text['results'][0]['geometry']['location']['lat']
longitude = text['results'][0]['geometry']['location']['lng']
return latitude, longitude
df_data['temp_area'] = (df_data['City'] + ", " + df_data['State'] + ", India")
areas = df_data['temp_area'].unique()
areas = [x for x in areas if str(x) != 'nan']
areas = [x.strip() for x in areas]
#print(areas)
#areas = ['North+Delhi, NCT+OF+DELHI, India']
area_map = {}
for area in areas :
try :
area_map[area] = get_geo_code(area)
df_data.loc[df_data['temp_area'] == area,'Latitude'] = area_map[area][0]
df_data.loc[df_data['temp_area'] == area,'Longitude'] = area_map[area][1]
print("success")
except :
print("Error")
print(area_map)
len(areas)
df_data.to_csv('Indian_Work_Travel.csv',index=False)
df_data.isnull().sum()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import glob
cols = ['Table Name',
'State Code',
'Distt. Code',
'Total/Rural/Urban',
'Area Name',
'Mode of travel',
'Persons Total',
'Male Total',
'Female Total',
'Persons No travel',
'Male No travel',
'Female No travel',
'Persons 0-1',
'Male 0-1',
'Female 0-1',
'Persons 2-5',
'Male 2-5',
'Female 2-5',
'Persons 6-10',
'Male 6-10',
'Female 6-10',
'Persons 11-20',
'Male 11-20',
'Female 11-20',
'Persons 21-30',
'Male 21-30',
'Female 21-30',
'Persons 31-50',
'Male 31-50',
'Female 31-50',
'Persons 51+',
'Male 51+',
'Female 51+',
'Persons Distance not stated',
'Male Distance not stated',
'Female Distance not stated']
df_data = pd.DataFrame(columns=cols)
# kar_data = pd.read_excel('DDW-2900B-28.xlsx',skiprows=38)
# kar_data.drop(kar_data.tail(3).index,inplace=True)
# kar_data.sample(5)
path = 'data'
all_files = glob.glob(path + "/*.xlsx")
for filename in all_files:
print(filename)
df = pd.read_excel(filename)
state = df.iloc[8,4]
df = df.iloc[38:]
df.drop(df.tail(3).index,inplace=True)
# print(df.dtypes)
# print(df.head())
df.columns = cols
df['Latitude'] = np.nan
df['Longitude'] = np.nan
df['State Code'] = state.strip()
df_data = df_data.append(df, ignore_index=True, sort=False)
df_data.sample(10)
df_data.shape
df_data['State Code'] = df_data['State Code'].str.strip()
df_data['Area Name'] = df_data['Area Name'].str.strip()
df_data['Total/Rural/Urban'] = df_data['Total/Rural/Urban'].str.strip()
df_data['Mode of travel'] = df_data['Mode of travel'].str.strip()
df_data.rename(columns={'State Code': 'State', 'Area Name' : 'City'}, inplace=True)
df_data.drop(columns={'Table Name', 'Distt. Code'}, inplace=True)
df_data.sample(10)
from urllib.request import urlopen
import json
def get_geo_code(area) :
url = 'https://maps.googleapis.com/maps/api/geocode/json?address=' + area + '&key=AIzaSyBfTMpfEQGsXfq1EolY4GKvJ3-uz0ge7Xo'
url = url.replace(' ','+')
print(url)
jsonurl = urlopen(url)
text = json.loads(jsonurl.read())
latitude = text['results'][0]['geometry']['location']['lat']
longitude = text['results'][0]['geometry']['location']['lng']
return latitude, longitude
df_data['temp_area'] = (df_data['City'] + ", " + df_data['State'] + ", India")
areas = df_data['temp_area'].unique()
areas = [x for x in areas if str(x) != 'nan']
areas = [x.strip() for x in areas]
#print(areas)
#areas = ['North+Delhi, NCT+OF+DELHI, India']
area_map = {}
for area in areas :
try :
area_map[area] = get_geo_code(area)
df_data.loc[df_data['temp_area'] == area,'Latitude'] = area_map[area][0]
df_data.loc[df_data['temp_area'] == area,'Longitude'] = area_map[area][1]
print("success")
except :
print("Error")
print(area_map)
len(areas)
df_data.to_csv('Indian_Work_Travel.csv',index=False)
df_data.isnull().sum()
| 0.08152 | 0.438304 |
### Rendering map
For considering the map here we consider the following extensions
- [ipyleaflef](https://ipyleaflet.readthedocs.io/en/latest/installation.html)
- [gmplot](https://github.com/vgm64/gmplot)
```
import os
from scipy.io import loadmat
import pandas as pd
import numpy as np
import dask.array as da
import dask.dataframe as dd
from datetime import datetime, timedelta
import matplotlib.pyplot as plt
# Maps
from ipyleaflet import Marker, Map
from gmplot import gmplot
from matplotlib import rc
# Uncomment to export LaTeX
# rc('font',**{'family':'serif','serif':['Times']})
# rc('text', usetex=True)
```
Loading all data
```
data_dir_list = ('..','raw','20160316_061540_DE477VE_Description.mat')
kernel_path = os.getcwd()
data_dir_path = os.path.join(kernel_path,*data_dir_list)
dct_data = loadmat(data_dir_path, matlab_compatible= True, squeeze_me = True)
```
List of all posible variables
```
varname_lst = []
for fld in dct_data['DAY'].dtype.fields:
varname_lst.append(fld)
```
Extracting all position data
```
gps_var = ['DATE_HOUR_GPS', 'LATITUDE', 'LONGITUDE','ALTITUDE','SLOPE']
lst_gps = [data.transpose()[0].transpose() for var, data in zip(varname_lst, dct_data['DAY'][0][0]) if var in gps_var]
```
Cleaning the list of values. Droping out all `nan`
```
gps_flt = [row for row in zip(*lst_gps) if not np.isnan(row).any()]
```
Transform into data frame
```
gps_df = pd.DataFrame(gps_flt, columns = gps_var)
gps_df = gps_df.drop_duplicates()
```
Transform the date
```
def transform_date(matlab_datenum):
""" Convert a date to datetime """
python_datetime = datetime.fromordinal(int(matlab_datenum)) + timedelta(days=matlab_datenum%1) - timedelta(days = 366)
return python_datetime
gps_df['TIME'] = gps_df['DATE_HOUR_GPS'].apply(transform_date)
gps_df_flt = gps_df.set_index('TIME')
gps_df_flt.plot(x='LATITUDE',y='LONGITUDE')
ax = plt.gca()
ax.scatter(gps_df['LATITUDE'].mean(),gps_df['LONGITUDE'].mean());
```
Aggregation to reduce amount of data points
```
gps_df_agg = gps_df_flt.resample('5Min').mean()
gps_df_agg = gps_df_agg.dropna()
```
Put markers on top of a map
```
center = (gps_df['LATITUDE'].mean(),gps_df['LONGITUDE'].mean())
m = Map(center=center, zoom=8)
for key, val in gps_df_agg.iterrows():
center = (val['LATITUDE'],val['LONGITUDE'])
marker = Marker(location=center, draggable=False)
m.add_layer(marker);
m
# Place map
gmap = gmplot.GoogleMapPlotter(gps_df['LATITUDE'].mean(), gps_df['LONGITUDE'].mean(), zoom = 9)
# Polygon
gmap.plot(gps_df['LATITUDE'], gps_df['LONGITUDE'], 'cornflowerblue', edge_width=5)
# Draw
gmap.draw("../output/my_map.html")
```
Plot altitude
```
def transform_timestamp(matlab_datenum):
""" Convert a date to datetime string """
python_datetime = datetime.fromordinal(int(matlab_datenum)) + timedelta(days=matlab_datenum%1) - timedelta(days = 366)
return python_datetime.strftime('%H:%M:%S')
gps_df_agg.plot(y='ALTITUDE', grid = True, figsize = (10,10))
plt.xlabel(r'Time',fontsize=16);
plt.ylabel(r'Altitude [m]',fontsize=16);
# Recover locs
locs, labels = plt.xticks();
plt.xticks(locs,map(transform_timestamp,locs));
# plt.savefig('../output/height.pdf',format='pdf', bbox_inches='tight')
```
|
github_jupyter
|
import os
from scipy.io import loadmat
import pandas as pd
import numpy as np
import dask.array as da
import dask.dataframe as dd
from datetime import datetime, timedelta
import matplotlib.pyplot as plt
# Maps
from ipyleaflet import Marker, Map
from gmplot import gmplot
from matplotlib import rc
# Uncomment to export LaTeX
# rc('font',**{'family':'serif','serif':['Times']})
# rc('text', usetex=True)
data_dir_list = ('..','raw','20160316_061540_DE477VE_Description.mat')
kernel_path = os.getcwd()
data_dir_path = os.path.join(kernel_path,*data_dir_list)
dct_data = loadmat(data_dir_path, matlab_compatible= True, squeeze_me = True)
varname_lst = []
for fld in dct_data['DAY'].dtype.fields:
varname_lst.append(fld)
gps_var = ['DATE_HOUR_GPS', 'LATITUDE', 'LONGITUDE','ALTITUDE','SLOPE']
lst_gps = [data.transpose()[0].transpose() for var, data in zip(varname_lst, dct_data['DAY'][0][0]) if var in gps_var]
gps_flt = [row for row in zip(*lst_gps) if not np.isnan(row).any()]
gps_df = pd.DataFrame(gps_flt, columns = gps_var)
gps_df = gps_df.drop_duplicates()
def transform_date(matlab_datenum):
""" Convert a date to datetime """
python_datetime = datetime.fromordinal(int(matlab_datenum)) + timedelta(days=matlab_datenum%1) - timedelta(days = 366)
return python_datetime
gps_df['TIME'] = gps_df['DATE_HOUR_GPS'].apply(transform_date)
gps_df_flt = gps_df.set_index('TIME')
gps_df_flt.plot(x='LATITUDE',y='LONGITUDE')
ax = plt.gca()
ax.scatter(gps_df['LATITUDE'].mean(),gps_df['LONGITUDE'].mean());
gps_df_agg = gps_df_flt.resample('5Min').mean()
gps_df_agg = gps_df_agg.dropna()
center = (gps_df['LATITUDE'].mean(),gps_df['LONGITUDE'].mean())
m = Map(center=center, zoom=8)
for key, val in gps_df_agg.iterrows():
center = (val['LATITUDE'],val['LONGITUDE'])
marker = Marker(location=center, draggable=False)
m.add_layer(marker);
m
# Place map
gmap = gmplot.GoogleMapPlotter(gps_df['LATITUDE'].mean(), gps_df['LONGITUDE'].mean(), zoom = 9)
# Polygon
gmap.plot(gps_df['LATITUDE'], gps_df['LONGITUDE'], 'cornflowerblue', edge_width=5)
# Draw
gmap.draw("../output/my_map.html")
def transform_timestamp(matlab_datenum):
""" Convert a date to datetime string """
python_datetime = datetime.fromordinal(int(matlab_datenum)) + timedelta(days=matlab_datenum%1) - timedelta(days = 366)
return python_datetime.strftime('%H:%M:%S')
gps_df_agg.plot(y='ALTITUDE', grid = True, figsize = (10,10))
plt.xlabel(r'Time',fontsize=16);
plt.ylabel(r'Altitude [m]',fontsize=16);
# Recover locs
locs, labels = plt.xticks();
plt.xticks(locs,map(transform_timestamp,locs));
# plt.savefig('../output/height.pdf',format='pdf', bbox_inches='tight')
| 0.36727 | 0.852383 |
<a href="https://colab.research.google.com/github/Jun-629/20MA573/blob/master/src%5CHw5_Monte_Carlo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Example 1
- Using *Algo 1*, design estimator $\hat \pi(N)$ and compute $\hat \pi(10000)$
```
import numpy as np
def mcpi(N):
n = 0
for i in range(N):
x = np.random.uniform(-1,1)
y = np.random.uniform(-1,1)
if (x**2 + y**2 < 1):
n += 1
return 4*n/N
mcpi(10000)
```
# Example 3
Given i.i.d $\{\alpha_i : i \in 1, 2, ..., N\}$, we use
$$\bar \alpha_N = \frac{1}{N} \sum_{i=1}^N \alpha_i$$
as its estimator of the mean $\mathbb E[\alpha_1]$ and use
$$\beta_N = \frac{1}{N} \sum_{i=1}^N (\alpha_i - \bar \alpha_N)^2$$
as the estimator of $Var(\alpha_1)$. Suppose $\alpha_1 \in L^4$, then
- Prove $\beta_N$ is biased.
- Prove that $\beta_N$ is consistent in $L^2$.
- Can you propose an unbiased estimator?
__Proof:__
- To prove $\beta_N$ is biased, need to show that $\mathbb E[\beta_N] - Var(\alpha_1)$ does not equal to 0.
Because $\{\alpha_i\}_{i\in\mathbb{N}}$ is i.i.d., we can deduce that
\begin{equation}
\begin{aligned}
\mathbb E[\bar \alpha_N] &= \mathbb E[\frac{1}{N} \sum_{i=1}^N \alpha_i] \\
&= \frac{1}{N} \sum_{i=1}^N \mathbb E[\alpha_i] \\
&= \frac{1}{N} \cdot N \cdot \mathbb E[\alpha_1] \\
&= \mathbb E[\alpha_1], \\
Var(\bar \alpha_N) &= Var(\frac{1}{N} \sum_{i=1}^N \alpha_i) \\
&= \frac{1}{N^2} \sum_{i=1}^N Var(\alpha_i) \\
&= \frac{1}{N^2} \cdot N \cdot Var(\alpha_1) \\
&= \frac{1}{N} Var(\alpha_1)\\
\mathbb E[\bar \alpha_N^2] &= Var(\bar \alpha_N) + \mathbb E[\bar \alpha_N]^2 \\
&= \frac{1}{N} Var(\alpha_1) + \mathbb E[\alpha_1]^2 \\
\mathbb E[\alpha_1^2] &= \mathbb E[\alpha_1]^2 + Var(\alpha_1)
\end{aligned}
\end{equation}
Now observing $Bias(\beta_N)$, we have
\begin{equation}
\begin{aligned}
Bias(\beta_N) &= \mathbb E[\beta_N] - Var(\alpha_1) \\
&= \mathbb E[\frac{1}{N} \sum_{i=1}^N (\alpha_i - \bar \alpha_N)^2] - Var(\alpha_1) \\
&= \frac{1}{N} \mathbb E[\sum_{i=1}^N (\alpha_i^2- 2 \alpha_i \bar \alpha_N + \bar \alpha_N^2)] - Var(\alpha_1) \\
&= \frac{1}{N} \mathbb E[\sum_{i=1}^N \alpha_i^2 - 2N \cdot \bar \alpha_N^2 + N \cdot \bar \alpha_N^2] - Var(\alpha_1) \\
&= \frac{1}{N} \sum_{i=1}^N \mathbb E[\alpha_i^2] - \frac{1}{N}\mathbb E[N \cdot \bar \alpha_N^2] - Var(\alpha_1) \\
&= \mathbb E[\alpha_1^2] - \mathbb E[\bar \alpha_N^2]- Var(\alpha_1) \\
&= - \frac{1}{N} Var(\alpha_1) \neq 0.\\
\end{aligned}
\end{equation}
Therefore, $\beta_N$ is biased.
- To prove that $\beta_N$ is consistent in $L^2$, we need to show that $MSE(\beta_N) \to 0$, when $N \to 0$, which means that
$$\mathbb E[(\beta_N - Var(\alpha_1))^2] \to 0.$$
Now we observe $\mathbb E[(\beta_N - Var(\alpha_1))^2]$, we have:
\begin{equation}
\begin{split}
E[(\beta_N - Var(\alpha_1))^2] &= \mathbb E[\beta_N^2 - 2\beta_N Var(\alpha_1) + Var(\alpha_1)^2] \\
&= \mathbb E[\beta_N^2] + \frac{2-N}{N} Var(\alpha_1)^2 \\
&= Var(\beta_N) + \mathbb E[\beta_N]^2 + \frac{2-N}{N} Var(\alpha_1)^2 \\
&= Var(\beta_N) + \frac{1}{N^2} Var(\alpha_1)^2 \\
\end{split}
\end{equation}
Now, we will use $T := \frac{(n-1)S^2}{\sigma^2} \sim \chi (n-1)$, where $S = \frac{1}{N-1} \sum_{i=1}^N (\alpha_i - \bar \alpha_N)^2$ is the sample variance and $Var(\alpha_1) = \sigma^2$. Plus, we have $\mathbb E[T] = n-1, Var(T) = 2(n-1)$.
\begin{equation}
\begin{split}
Var(\beta_N) &= Var(\frac{N-1}{N} S) \\
&= \frac{(N-1)^2}{N^2} Var(S) \\
&= \frac{(N-1)^2}{N^2} \cdot \frac{2Var(\alpha_1)^2}{N-1} \\
&= \frac{2(N-1)}{N^2} Var(\alpha_1)^2 \\
E[(\beta_N - Var(\alpha_1))^2] &= \frac{2(N-1)}{N^2} Var(\alpha_1)^2 + \frac{1}{N^2} Var(\alpha_1)^2 \\
&= \frac{2N-1}{N^2} Var(\alpha_1)^2 \to 0, N \to \infty\\
\end{split}
\end{equation}
Therefore, $\beta_N$ is consitent in $L^2$.
- The unbiased estimator:
$$\hat \beta_N = \frac{1}{N-1} \sum_{i=1}^N (\alpha_i - \bar \alpha_N)^2$$
\begin{equation}
\begin{aligned}
Bias(\hat \beta_N) &= \mathbb E[\hat \beta_N] - Var(\alpha_1) \\
&= \frac{1}{N-1} \sum_{i=1}^N \mathbb E[\alpha_i^2] - \frac{1}{N-1}\mathbb E[N \cdot \bar \alpha_N^2] - Var(\alpha_1) \\
&= \frac{N}{N-1} \bigg (\mathbb E[\alpha_1^2] - \mathbb E[\bar \alpha_N^2] \bigg )- Var(\alpha_1) \\
&= Var(\alpha_1) - Var(\alpha_1) = 0.\\
\end{aligned}
\end{equation}
which shows that $\hat \beta_N$ is unbiased estimator.
__Q.E.D.__
```
def beta(N,M):
n = 0
m = 0
pi_list = []
for i in range(N):
pi_list.append(mcpi(M))
n += pi_list[i]
pi_bar = n/N
for i in range(N):
m += (pi_list[i] - pi_bar)**2
beta = m/N
return beta
beta(100,10000)
import matplotlib.pyplot as plt
y = []
for i in range (5,11):
y.append(beta(100,2**i))
x = [2**n for n in range(5,11)]
print(y)
plt.loglog(x,y)
def indi_func(a,sign1,b,sign2,x): # sign1 and sign 2 mean whether we can take the endpoint respectively
if (sign1 == 0): # 0 means that endpoint is not included
if (sign2 == 0):
if (a<x<b):
f = 1
else:
f = 0
elif (sign2 == 1): # 1 means that endpoint is included
if (a<x<=b):
f = 1
else:
f = 0
elif (sign1 == 1):
if (sign2 == 0):
if (a<=x<b):
f = 1
else:
f = 0
elif (sign2 == 1):
if (a<=x<=b):
f = 1
else:
f = 0
return f # Actually, there is no need to discuss whether endpoints are included or not
# Since P(ept) = 0, x is uniform distribution
def mcintegral(N):
s = 0
for i in range(N):
y = np.random.uniform(0,1)
h = 100 * indi_func(0,0,0.01,1,y) + indi_func(0.01,0,1,0,y)
s += h
return s/N
mcintegral(10000000)
def beta_prime(N,M):
n = 0
m = 0
pi_list = []
for i in range(N):
pi_list.append(mcintegral(M))
n += pi_list[i]
pi_bar = n/N
for i in range(N):
m += (pi_list[i] - pi_bar)**2
beta_prime = m/N
return beta_prime
y = []
for i in range (5,11):
y.append(beta_prime(100,2**i))
x = [2**n for n in range(5,11)]
plt.loglog(x,y)
```
|
github_jupyter
|
import numpy as np
def mcpi(N):
n = 0
for i in range(N):
x = np.random.uniform(-1,1)
y = np.random.uniform(-1,1)
if (x**2 + y**2 < 1):
n += 1
return 4*n/N
mcpi(10000)
def beta(N,M):
n = 0
m = 0
pi_list = []
for i in range(N):
pi_list.append(mcpi(M))
n += pi_list[i]
pi_bar = n/N
for i in range(N):
m += (pi_list[i] - pi_bar)**2
beta = m/N
return beta
beta(100,10000)
import matplotlib.pyplot as plt
y = []
for i in range (5,11):
y.append(beta(100,2**i))
x = [2**n for n in range(5,11)]
print(y)
plt.loglog(x,y)
def indi_func(a,sign1,b,sign2,x): # sign1 and sign 2 mean whether we can take the endpoint respectively
if (sign1 == 0): # 0 means that endpoint is not included
if (sign2 == 0):
if (a<x<b):
f = 1
else:
f = 0
elif (sign2 == 1): # 1 means that endpoint is included
if (a<x<=b):
f = 1
else:
f = 0
elif (sign1 == 1):
if (sign2 == 0):
if (a<=x<b):
f = 1
else:
f = 0
elif (sign2 == 1):
if (a<=x<=b):
f = 1
else:
f = 0
return f # Actually, there is no need to discuss whether endpoints are included or not
# Since P(ept) = 0, x is uniform distribution
def mcintegral(N):
s = 0
for i in range(N):
y = np.random.uniform(0,1)
h = 100 * indi_func(0,0,0.01,1,y) + indi_func(0.01,0,1,0,y)
s += h
return s/N
mcintegral(10000000)
def beta_prime(N,M):
n = 0
m = 0
pi_list = []
for i in range(N):
pi_list.append(mcintegral(M))
n += pi_list[i]
pi_bar = n/N
for i in range(N):
m += (pi_list[i] - pi_bar)**2
beta_prime = m/N
return beta_prime
y = []
for i in range (5,11):
y.append(beta_prime(100,2**i))
x = [2**n for n in range(5,11)]
plt.loglog(x,y)
| 0.256553 | 0.995032 |
# A thorough introduction to object-oriented Matplotlib - Part 1: Figures And Axes
There must be a million tutorials on matplotlib out there.
Most use Matplotlib's Pyplot interface, a stateful API, designed to look and feel like Matlab. It allows users to create simple graphs quickly and easily.
However, whenever the resulting figure needs to be manipulated and changed, users have to resort to Matplotlib's object-oriented user-interface which tends to be more verbose and low-level, but is also more explicit.
A result of these two APIs, lots of example code out there mixes the Pyplot- and the OOP-interface. This is even the case for Matplotlib's official tutorials on the Matplotlib website.
Because one API is stateful and the other isn't, and because it is often unclear why one or the other version is used, this can turn out to be very confusing.
For this reason, I decided to write this short into to Matplotlib's OOP-interface. I will try to stay as pure as possible.
## Matplotlib in general
Matplotlib is one of the oldest Python visualisation libraries. Its first version dates back to 2003. It pre-dates the evolution of the Grammar of Graphics, D3, interactive browser- and Javascript-based libraries and for that reason its default output can look a bit dated.
Matplotlib's APIs are often unpythonic, at times counterintuitive, and allow the user to do the same thing in many ways. Steps which are supposed to create similar outputs create slight differences from the way they are handled internally - and intransparently to the user. When this is the case, I will point it out.
Matplotlib is still worth learning. Matplotlib is well supported, it is ubiquitous in Python world and a little knowledge and insight will take you far.
This tutorial is here to help.
```
import matplotlib as mpl
```
Note that we are not importing pyplot at all.
There is no *import matplotlib.pyplot as plt* as in most tutorials.
```
%matplotlib inline
```
For this tutorial we inline all graphs in the notebook. For choice of backends and their differences see Part 3 - Backends.
## The most important illustration of the Matplotlib API
The best illustration of matplotlib's object hierarchy can be found in an old version of Matplotlib's documentation for version 1.5.
[Matplotlib 1.5](https://matplotlib.org/1.5.1/faq/usage_faq.html#parts-of-a-figure)

- Every Matplotlib plot is a *Figure*.
- Every Figure contains *one or more Axes*. Note the "e". *Axes* not *axis*.
- Every Axes contains *Axis*. Note the "i". Generally a *x-Axis* and *y-Axis*.
- On the x- and y-Axis we can plot different *Artists*, such a a 2d-lineplot and others, more on that later.
Let's create each elements of a *Figure* in turn using only the OOP-interface.
## Figure
Everything Matplotlib displays must be contained within a *Figure*. Creating a *Figure*-container is always the first step.
### Creating a Figure
```
import matplotlib.figure
```
Note that the submodule figure needs to be imported explicitely.
```
fig = matplotlib.figure.Figure()
```
*Figure* takes a number of arguments to set basic properties of the *Figure*-container at creation. However, these can also be set after the creation.
In order to see that parameters can be passed, who the full docstring for the figure using the ?-help function.
```
fig?
```
#### Figure parameters
So the parameters are
- figsize
- dpi
- facecolor
- edgecolor
- linewidth
- frameon
- subplotpars
- tight_layout
- constrinaed_layout
#### Configuring *Figure* at creation
When passing these parameters are creation, we can quickly set a basic configuration for the figure.
```
fig = matplotlib.figure.Figure(figsize=(5,5), facecolor='red', edgecolor='blue', linewidth=2)
```
#### Configuring *Figure* with setters and getters
Alternatively we can create *Figure* with default values, and set the values using the *Figure*'s setter methods.
```
fig.set_facecolor("red")
fig.set_edgecolor("blue")
fig.set_tight_layout(False)
```
Not all parameter attributes have a setter method. E.g. there is no `fig.set_linewidth`, but there are other setters for attributes which cannot be set at creation time.
#### Aside 1: Matplotlib's setters and getters
Unlike other OOP-languages, *pythonic* Python generally does not use getter- and setter- methods. Instead *properties* are widely used. A pythonic programmer would expect to be able to set the properties for a Figure like this:
`fig.facecolor = "red"` THIS DOES NOT WORK!
Unfortunately this is not how the Matplotlib OOP-interface works. It DOES use getters and setters as above for MOST properties, but then again - not all.
So remember, when using the OOP-interface, properties are set using setter functions, not assignments and assignments cause often weird error messages.
To make things even more confusing the Pyplot interface often DOES often ue function names which are similiar to the OOP-interface names, but leaves out the getter and setter prefix.
For example, to set the range of the x-axis in an Axes using the OOP-interface, you call:
`ax.set_xlim(0,10)`
whereas in the Pyplot interface you call:
`plt.xlim(0,10)`
### Constitutents of an object
A number of objects in matplotlib, have a generic method listing the objects consituents. This turns out to be rather useful, when exploring the state and makup of a figure. The method is called *get_children*.
```
fig.get_children()
```
The figure we created currently consists of only a *patch*-object
### Showing the Figure
Note that an empty figure - a figure which does not contain any *Axes* - cannot be displayed (in Jupyter).
```
fig
```
This simply returns a description of the *Figure*-object.
We see that this *Figure* references 0 *Axes*. The figure is empty.
We can verify this by calling the *Figure*'s get_axes method.
```
fig.get_axes()
```
This does not prevent us from configuring the *Figure* a bit more. We already set the facecolor and the edgecolor properties.
We can set a *Figure*-title.
Note that some properties are set by *setter*-methods as above, others are set by calling direct methods.
Generally the Matplotlib-API feels rather unpythonic in its use of getters and setters and using methods to set properties.
A more pythonic interface would be something like:
`fig.title = "My Figure Title"` THIS DOES NOT WORK!
But unfortunately, this is not how it works.
Instead we need to call the *suptitle*-method on the Figure-object. Note that is is not a *setter*-method like the ones above.
```
fig.suptitle("My Figure Title")
```
The Figure-title can be positioned, manipulated, the font can be changed, etc by providing parameters to this methods.
The tab-extension help is again of no uses, since it only references *kwargs, but again the ?-help is our friend for a view of the parameters.
```
fig.suptitle?
fig.get_children()
```
## Axes (not Axis!)
For a *Figure* to be displayed in a notebook, it needs to have at least one Axes.
Several *Axes* can be added to a *Figure*, which will be displayed as subplots to this figure.
### Adding Axes
An Axes can be added using the add_axes commend. The add_axes command takes as input a rectangle (a tuple of [left, bottom, width, height] ) which describes where exactly the new axes should be positioned within the *Figure*, expressed as a fraction of the *Figure* height and width.
This can turn out to be a very tricky and complex way to position an Axes within a *Figure*.
```
fig.add_axes([0.3, 0.3, 0.3, 0.3], label="Direct Position Axes")
```
### Displaying Figure and Axes
Since we added an Axes to the Figure, the Figure is no longer empty and can now be displayed on the backend.
All parameters set on the Figure-instance earlier are now visible, e.g. the blue edges, the red background and the Figure title.
```
fig
```
The Figure and Axes look funny and misplaced. This is because we have mispositioned the new Axes within the Figure when we were providing the parameters for the the rectangle-argument for add_axes.
It turns out positioneing the Axes via absoute positioning via the 'rectangle' methid above is too tricky.
### Adding A Subplot
A better method to add an Axes to a Figure is using the add_subplot method.
The difference between add_axes and add_subplot is that add_subplot takes care of the positioning of the axes in the Figure for us.
Instead of requiring a position as 'a fraction of the figure', add_subplot takes a generic position within the Figure, expressed as a row and column parameter.
We need to remove the funny axes from the figure:
```
def remove_all_axes(fig):
for ax in fig.get_axes():
ax.remove()
remove_all_axes(fig)
fig
```
The figure no longer has any Axes.
Let's add a subplot.
```
fig.get_axes()
```
An Axis is added with the add_sub_plot command.
```
fig.add_subplot()
```
The add_subplot command returns a reference to an Axes in the figure.
There are a few ways to get a reference to this Axes instance.
```
ax = fig.add_subplot(1,2,1)
ax
fig.get_axes()
```
We see that the Figure contains a collection of Axes.
add_subplot takes as positional parameters
- a row identifier
- a column identifier
- an index reference
This can be provided explicitly, or shortened as a 3-digit number.
When called without parameters, it *defaults to 111*.
```
ax = fig.get_axes()[0]
ax.numCols, ax.numRows
```
Let's start from scratch removing all axes and specifying the subplot explicitly by providing parameters.
```
remove_all_axes(fig)
fig.add_subplot(1, 1, 1)
# this can be shortened by matplotlib convention to fig.add_subplot(111)
```
It gives us a warning, explaining that an axes with this reference has already been added. This is because add_subplot() without parameters defaults to "111".
```
fig.add_subplot?
fig
```
Let's set some properties on the Axes object, to show how it differs from the Figure object.
```
# Get reference to the first axes in the axes colletion.
ax1 = fig.get_axes()[0]
ax1.set_facecolor('green')
ax1.set_title("First Axes")
ax1.grid(True)
fig
```
We add a second Axes to this Figure.
We want to show it underneath this Axes, so it will be in row 2, column 1, with the index 2.
```
ax2 = fig.add_subplot(2, 1, 2)
ax2
fig
```
And set some attributes on the second Axes.
```
ax2.set_facecolor('yellow')
ax2.set_title("Second Axes")
ax2.grid(True)
fig
```
There are some issues.
The Second Axes is now on top of the First Axes.
We remove them and try a differrent way.
```
remove_all_axes(fig)
fig
```
Using the subplots (note the s) method, we can add several Axes/subplots to the figure in one step.
An effect of this approach is that the subplots are more sensibly positioned in the *Figure*.
```
ax1, ax2 = fig.subplots(2,1)
fig
ax1.set_facecolor('green')
ax1.set_title("First Axes")
ax1.grid(True)
ax2.set_facecolor('yellow')
ax2.set_title("Second Axes")
ax2.grid(True)
fig
fig.tight_layout(pad=3)
fig
ax = fig.get_axes()[1]
fig.delaxes(ax)
fig
ax1
fig.get_axes()
```
## Working with an Axe
On the axe we can draw our graph. We can specify x-axis and y-axis, what we want to chart.
To illustrate we need some sample data.
```
x = list("abcdefghij")
x
y = list(range(10))
y
ax1.bar(x=x, height=y)
fig
ax1.bar(x=x, height=[n*2 for n in y])
fig
ax1.get_children()
ax1.set_alpha(1)
ax1.get_alpha()
fig
fig.get_children()
```
In this Part 1 of this Matplotlib OOP-introduction we focused on the top level Matplotlib object-hierarchy and the relationship between Figure and Axes.
In Part 2 we will look at Axes more closely, and start plotting several *Artists* on the same Axes and using different x-axis and y-axis on the same Axis or sharing x- and y-axis between Axes in the same Figure.
|
github_jupyter
|
import matplotlib as mpl
%matplotlib inline
import matplotlib.figure
fig = matplotlib.figure.Figure()
fig?
fig = matplotlib.figure.Figure(figsize=(5,5), facecolor='red', edgecolor='blue', linewidth=2)
fig.set_facecolor("red")
fig.set_edgecolor("blue")
fig.set_tight_layout(False)
fig.get_children()
fig
fig.get_axes()
fig.suptitle("My Figure Title")
fig.suptitle?
fig.get_children()
fig.add_axes([0.3, 0.3, 0.3, 0.3], label="Direct Position Axes")
fig
def remove_all_axes(fig):
for ax in fig.get_axes():
ax.remove()
remove_all_axes(fig)
fig
fig.get_axes()
fig.add_subplot()
ax = fig.add_subplot(1,2,1)
ax
fig.get_axes()
ax = fig.get_axes()[0]
ax.numCols, ax.numRows
remove_all_axes(fig)
fig.add_subplot(1, 1, 1)
# this can be shortened by matplotlib convention to fig.add_subplot(111)
fig.add_subplot?
fig
# Get reference to the first axes in the axes colletion.
ax1 = fig.get_axes()[0]
ax1.set_facecolor('green')
ax1.set_title("First Axes")
ax1.grid(True)
fig
ax2 = fig.add_subplot(2, 1, 2)
ax2
fig
ax2.set_facecolor('yellow')
ax2.set_title("Second Axes")
ax2.grid(True)
fig
remove_all_axes(fig)
fig
ax1, ax2 = fig.subplots(2,1)
fig
ax1.set_facecolor('green')
ax1.set_title("First Axes")
ax1.grid(True)
ax2.set_facecolor('yellow')
ax2.set_title("Second Axes")
ax2.grid(True)
fig
fig.tight_layout(pad=3)
fig
ax = fig.get_axes()[1]
fig.delaxes(ax)
fig
ax1
fig.get_axes()
x = list("abcdefghij")
x
y = list(range(10))
y
ax1.bar(x=x, height=y)
fig
ax1.bar(x=x, height=[n*2 for n in y])
fig
ax1.get_children()
ax1.set_alpha(1)
ax1.get_alpha()
fig
fig.get_children()
| 0.616705 | 0.987079 |
```
%matplotlib inline
import numpy as np
import math, random
import matplotlib.pyplot as plt
class Landmark:
def __init__(self,x,y):
self.position = np.array([x,y])
def __str__(self):
return "(%f,%f)" % (self.position[0],self.position[1])
def getX(self):
return self.position[0]
def getY(self):
return self.position[1]
actual_landmarks = (Landmark(-0.5,0),Landmark(0.5,0),Landmark(0,0.5))
xs = [e.getX() for e in actual_landmarks]
ys = [e.getY() for e in actual_landmarks]
plt.scatter(xs,ys,s=300,marker="*")
class Robot:
def __init__(self,x,y,rad):
self.actual_poses = [np.array([x,y,rad])]
self.guess_poses = [np.array([x,y,rad])]
random.seed()
def getX(self): return self.actual_poses[-1][0]
def getY(self): return self.actual_poses[-1][1]
def getTheta(self): return self.actual_poses[-1][2]
def getActualXs(self): return [e[0] for e in self.actual_poses]
def getActualYs(self): return [e[1] for e in self.actual_poses]
def getActualThetas(self): return [e[2] for e in self.actual_poses]
def getActualDXs(self): return [math.cos(e[2]) for e in self.actual_poses]
def getActualDYs(self): return [math.sin(e[2]) for e in self.actual_poses]
def getGuessXs(self): return [e[0] for e in self.guess_poses]
def getGuessYs(self): return [e[1] for e in self.guess_poses]
def getGuessThetas(self): return [e[2] for e in self.guess_poses]
def getGuessDXs(self): return [math.cos(e[2]) for e in self.guess_poses]
def getGuessDYs(self): return [math.sin(e[2]) for e in self.guess_poses]
def move(self,fw,rot):
actual_fw = random.gauss(fw,fw/10) #10% noise
actual_rot = random.gauss(rot,rot/10) #10% noise
p = self.actual_poses[-1]
px, py, pt = p[0],p[1],p[2]
x = px + actual_fw * math.cos(pt)
y = py + actual_fw * math.sin(pt)
t = pt + actual_rot
self.actual_poses.append(np.array([x,y,t]))
g = self.guess_poses[-1]
gx, gy, gt = g[0],g[1],g[2]
x = gx + fw * math.cos(gt)
y = gy + fw * math.sin(gt)
t = gt + rot
self.guess_poses.append(np.array([x,y,t]))
def observation(self,landmarks):
pass
robot = Robot(0,0,0)
for i in range(10):
robot.move(0.3,3.14/6)
plt.scatter(xs,ys,s=300,marker="*",label="landmarks",color="orange")
plt.quiver(robot.getActualXs(),robot.getActualYs(),robot.getActualDXs(),robot.getActualDYs(),
color="red",label="actual robot motion")
plt.quiver(robot.getGuessXs(),robot.getGuessYs(),robot.getGuessDXs(),robot.getGuessDYs(),
color="blue",label="robot guess")
plt.legend()
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import math, random
import matplotlib.pyplot as plt
class Landmark:
def __init__(self,x,y):
self.position = np.array([x,y])
def __str__(self):
return "(%f,%f)" % (self.position[0],self.position[1])
def getX(self):
return self.position[0]
def getY(self):
return self.position[1]
actual_landmarks = (Landmark(-0.5,0),Landmark(0.5,0),Landmark(0,0.5))
xs = [e.getX() for e in actual_landmarks]
ys = [e.getY() for e in actual_landmarks]
plt.scatter(xs,ys,s=300,marker="*")
class Robot:
def __init__(self,x,y,rad):
self.actual_poses = [np.array([x,y,rad])]
self.guess_poses = [np.array([x,y,rad])]
random.seed()
def getX(self): return self.actual_poses[-1][0]
def getY(self): return self.actual_poses[-1][1]
def getTheta(self): return self.actual_poses[-1][2]
def getActualXs(self): return [e[0] for e in self.actual_poses]
def getActualYs(self): return [e[1] for e in self.actual_poses]
def getActualThetas(self): return [e[2] for e in self.actual_poses]
def getActualDXs(self): return [math.cos(e[2]) for e in self.actual_poses]
def getActualDYs(self): return [math.sin(e[2]) for e in self.actual_poses]
def getGuessXs(self): return [e[0] for e in self.guess_poses]
def getGuessYs(self): return [e[1] for e in self.guess_poses]
def getGuessThetas(self): return [e[2] for e in self.guess_poses]
def getGuessDXs(self): return [math.cos(e[2]) for e in self.guess_poses]
def getGuessDYs(self): return [math.sin(e[2]) for e in self.guess_poses]
def move(self,fw,rot):
actual_fw = random.gauss(fw,fw/10) #10% noise
actual_rot = random.gauss(rot,rot/10) #10% noise
p = self.actual_poses[-1]
px, py, pt = p[0],p[1],p[2]
x = px + actual_fw * math.cos(pt)
y = py + actual_fw * math.sin(pt)
t = pt + actual_rot
self.actual_poses.append(np.array([x,y,t]))
g = self.guess_poses[-1]
gx, gy, gt = g[0],g[1],g[2]
x = gx + fw * math.cos(gt)
y = gy + fw * math.sin(gt)
t = gt + rot
self.guess_poses.append(np.array([x,y,t]))
def observation(self,landmarks):
pass
robot = Robot(0,0,0)
for i in range(10):
robot.move(0.3,3.14/6)
plt.scatter(xs,ys,s=300,marker="*",label="landmarks",color="orange")
plt.quiver(robot.getActualXs(),robot.getActualYs(),robot.getActualDXs(),robot.getActualDYs(),
color="red",label="actual robot motion")
plt.quiver(robot.getGuessXs(),robot.getGuessYs(),robot.getGuessDXs(),robot.getGuessDYs(),
color="blue",label="robot guess")
plt.legend()
| 0.484136 | 0.654522 |
# Introduction to Machine Learning : Python
## Table of contents
1. [Introduction](#Introduction)
2. [The problem domain](#The-problem-domain)
3. [Step 1: Answering the question](#Step-1:-Answering-the-question)
4. [Step 2: Checking the data](#Step-2:-Checking-the-data)
5. [Step 3: Tidying the data](#Step-3:-Tidying-the-data)
- [Bonus: Testing our data](#Bonus:-Testing-our-data)
6. [Step 4: Exploratory analysis](#Step-4:-Exploratory-analysis)
7. [Step 5: Classification](#Step-5:-Classification)
- [Cross-validation](#Cross-validation)
- [Parameter tuning](#Parameter-tuning)
8. [Step 6: Recap](#Step-6:-Recap)
9. [Further reading](#Further-reading)
## Introduction
[[ go back to the top ]](#Table-of-contents)
In the time it took you to read this sentence, terabytes of data have been collectively generated across the world — more data than any of us could ever hope to process, much less make sense of, on the machines we're using to read this notebook.
In response to this massive influx of data, the field of Data Science has come to the forefront in the past decade. Cobbled together by people from a diverse array of fields — statistics, physics, computer science, design, and many more — the field of Data Science represents our collective desire to understand and harness the abundance of data around us to build a better world.
Here, I'm going to go over a basic Python data analysis pipeline from start to finish to show you what a typical data science workflow looks like.
I will be following along with the data analysis checklist from [The Elements of Data Analytic Style](https://leanpub.com/datastyle), which I strongly recommend reading as a free and quick guidebook to performing outstanding data analysis.
## The problem domain
[[ go back to the top ]](#Table-of-contents)
For the purposes of this exercise, let's pretend we're working for a startup that just got funded to create a smartphone app that automatically identifies species of flowers from pictures taken on the smartphone. We're working with a moderately-sized team of data scientists and will be building part of the data analysis pipeline for this app.
We've been tasked by our head of data science to create a demo machine learning model that takes four measurements from the flowers (sepal length, sepal width, petal length, and petal width) and identifies the species based on those measurements alone.
<img src="images/petal_sepal.jpg" />
We've been given a [data set](https://github.com/rhiever/Data-Analysis-and-Machine-Learning-Projects/raw/master/example-data-science-notebook/iris-data.csv) from our field researchers to develop the demo, which only includes measurements for three types of *Iris* flowers:
### *Iris setosa*
<img src="images/iris_setosa.jpg" />
### *Iris versicolor*
<img src="images/iris_versicolor.jpg" />
### *Iris virginica*
<img src="images/iris_virginica.jpg" />
The four measurements we're using currently come from hand-measurements by the field researchers, but let's assume they will be automatically measured by an image processing model.
**Note:** The data set we're working with is the famous [*Iris* data set](https://archive.ics.uci.edu/ml/datasets/Iris) — included with this notebook — which I have modified slightly for demonstration purposes.
## Step 1: Answering the question
[[ go back to the top ]](#Table-of-contents)
The first step to any data analysis project is to define the question or problem we're looking to solve, and to define a measure (or set of measures) for our success at solving that task. The data analysis checklist has us answer a handful of questions to accomplish that, so let's work through those questions.
>Did you specify the type of data analytic question (e.g. exploration, association causality) before touching the data?
We're trying to classify the species (i.e., class) of the flower based on four measurements that we're provided: sepal length, sepal width, petal length, and petal width.
>Did you define the metric for success before beginning?
Let's do that now. Since we're performing classification, we can use [accuracy](https://en.wikipedia.org/wiki/Accuracy_and_precision) — the fraction of correctly classified flowers — to quantify how well our model is performing. Our head of data has told us that we should achieve at least 90% accuracy.
>Did you understand the context for the question and the scientific or business application?
We're building part of a data analysis pipeline for a smartphone app that will be able to classify the species of flowers from pictures taken on the smartphone. In the future, this pipeline will be connected to another pipeline that automatically measures from pictures the traits we're using to perform this classification.
>Did you record the experimental design?
Our head of data has told us that the field researchers are hand-measuring 50 randomly-sampled flowers of each species using a standardized methodology. The field researchers take pictures of each flower they sample from pre-defined angles so the measurements and species can be confirmed by the other field researchers at a later point. At the end of each day, the data is compiled and stored on a private company GitHub repository.
>Did you consider whether the question could be answered with the available data?
The data set we currently have is only for three types of *Iris* flowers. The model built off of this data set will only work for those *Iris* flowers, so we will need more data to create a general flower classifier.
<hr />
Notice that we've spent a fair amount of time working on the problem without writing a line of code or even looking at the data.
**Thinking about and documenting the problem we're working on is an important step to performing effective data analysis that often goes overlooked.** Don't skip it.
## Step 2: Checking the data
[[ go back to the top ]](#Table-of-contents)
The next step is to look at the data we're working with. Even curated data sets from the government can have errors in them, and it's vital that we spot these errors before investing too much time in our analysis.
Generally, we're looking to answer the following questions:
* Is there anything wrong with the data?
* Are there any quirks with the data?
* Do I need to fix or remove any of the data?
Let's start by reading the data into a pandas DataFrame.
```
import pandas as pd
iris_data = pd.read_csv('iris-data.csv')
iris_data.head()
```
We're in luck! The data seems to be in a usable format.
The first row in the data file defines the column headers, and the headers are descriptive enough for us to understand what each column represents. The headers even give us the units that the measurements were recorded in, just in case we needed to know at a later point in the project.
Each row following the first row represents an entry for a flower: four measurements and one class, which tells us the species of the flower.
**One of the first things we should look for is missing data.** Thankfully, the field researchers already told us that they put a 'NA' into the spreadsheet when they were missing a measurement.
We can tell pandas to automatically identify missing values if it knows our missing value marker.
```
iris_data = pd.read_csv('iris-data.csv', na_values=['NA'])
```
Voilà! Now pandas knows to treat rows with 'NA' as missing values.
Next, it's always a good idea to look at the distribution of our data — especially the outliers.
Let's start by printing out some summary statistics about the data set.
```
iris_data.describe()
```
We can see several useful values from this table. For example, we see that five `petal_width_cm` entries are missing.
If you ask me, though, tables like this are rarely useful unless we know that our data should fall in a particular range. It's usually better to visualize the data in some way. Visualization makes outliers and errors immediately stand out, whereas they might go unnoticed in a large table of numbers.
If you are using ipython, make sure you write the first line shown below.
```
# This line tells the notebook to show plots inside of the notebook
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sb
```
Next, let's create a **scatterplot matrix**. Scatterplot matrices plot the distribution of each column along the diagonal, and then plot a scatterplot matrix for the combination of each variable. They make for an efficient tool to look for errors in our data.
We can even have the plotting package color each entry by its class to look for trends within the classes.
```
# We have to temporarily drop the rows with 'NA' values
# because the Seaborn plotting function does not know
# what to do with them
sb.pairplot(iris_data.dropna(), hue='class')
```
From the scatterplot matrix, we can already see some issues with the data set:
1. There are five classes when there should only be three, meaning there were some coding errors.
2. There are some clear outliers in the measurements that may be erroneous: one `sepal_width_cm` entry for `Iris-setosa` falls well outside its normal range, and several `sepal_length_cm` entries for `Iris-versicolor` are near-zero for some reason.
3. We had to drop those rows with missing values.
In all of these cases, we need to figure out what to do with the erroneous data. Which takes us to the next step...
## Step 3: Tidying the data
[[ go back to the top ]](#Table-of-contents)
Now that we've identified several errors in the data set, we need to fix them before we proceed with the analysis.
Let's walk through the issues one-by-one.
>There are five classes when there should only be three, meaning there were some coding errors.
After talking with the field researchers, it sounds like one of them forgot to add `Iris-` before their `Iris-versicolor` entries. The other extraneous class, `Iris-setossa`, was simply a typo that they forgot to fix.
Let's use the DataFrame to fix these errors.
```
iris_data.loc[iris_data['class'] == 'versicolor', 'class'] = 'Iris-versicolor'
iris_data.loc[iris_data['class'] == 'Iris-setossa', 'class'] = 'Iris-setosa'
iris_data['class'].unique()
```
Much better! Now we only have three class types. Imagine how embarrassing it would've been to create a model that used the wrong classes.
>There are some clear outliers in the measurements that may be erroneous: one `sepal_width_cm` entry for `Iris-setosa` falls well outside its normal range, and several `sepal_length_cm` entries for `Iris-versicolor` are near-zero for some reason.
Fixing outliers can be tricky business. It's rarely clear whether the outlier was caused by measurement error, recording the data in improper units, or if the outlier is a real anomaly. For that reason, we should be judicious when working with outliers: if we decide to exclude any data, we need to make sure to document what data we excluded and provide solid reasoning for excluding that data. (i.e., "This data didn't fit my hypothesis" will not stand peer review.)
In the case of the one anomalous entry for `Iris-setosa`, let's say our field researchers know that it's impossible for `Iris-setosa` to have a sepal width below 2.5 cm. Clearly this entry was made in error, and we're better off just scrapping the entry than spending hours finding out what happened.
```
# This line drops any 'Iris-setosa' rows with a separal width less than 2.5 cm
iris_data = iris_data.loc[(iris_data['class'] != 'Iris-setosa') | (iris_data['sepal_width_cm'] >= 2.5)]
iris_data.loc[iris_data['class'] == 'Iris-setosa', 'sepal_width_cm'].hist()
```
Excellent! Now all of our `Iris-setosa` rows have a sepal width greater than 2.5.
The next data issue to address is the several near-zero sepal lengths for the `Iris-versicolor` rows. Let's take a look at those rows.
```
iris_data.loc[(iris_data['class'] == 'Iris-versicolor') &
(iris_data['sepal_length_cm'] < 1.0)]
```
How about that? All of these near-zero `sepal_length_cm` entries seem to be **off by two orders of magnitude**, as if they had been recorded in meters instead of centimeters.
After some brief correspondence with the field researchers, we find that one of them forgot to convert those measurements to centimeters. Let's do that for them.
```
iris_data.loc[(iris_data['class'] == 'Iris-versicolor') &
(iris_data['sepal_length_cm'] < 1.0),
'sepal_length_cm'] *= 100.0
iris_data.loc[iris_data['class'] == 'Iris-versicolor', 'sepal_length_cm'].hist()
```
Phew! Good thing we fixed those outliers. They could've really thrown our analysis off.
>We had to drop those rows with missing values.
Let's take a look at the rows with missing values:
```
iris_data.loc[(iris_data['sepal_length_cm'].isnull()) |
(iris_data['sepal_width_cm'].isnull()) |
(iris_data['petal_length_cm'].isnull()) |
(iris_data['petal_width_cm'].isnull())]
```
It's not ideal that we had to drop those rows, especially considering they're all `Iris-setosa` entries. Since it seems like the missing data is systematic — all of the missing values are in the same column for the same *Iris* type — this error could potentially bias our analysis.
One way to deal with missing data is **mean imputation**: If we know that the values for a measurement fall in a certain range, we can fill in empty values with the average of that measurement.
Let's see if we can do that here.
```
iris_data.loc[iris_data['class'] == 'Iris-setosa', 'petal_width_cm'].hist()
```
Most of the petal widths for `Iris-setosa` fall within the 0.2-0.3 range, so let's fill in these entries with the average measured petal width.
```
average_petal_width = iris_data.loc[iris_data['class'] == 'Iris-setosa', 'petal_width_cm'].mean()
iris_data.loc[(iris_data['class'] == 'Iris-setosa') &
(iris_data['petal_width_cm'].isnull()),
'petal_width_cm'] = average_petal_width
iris_data.loc[(iris_data['class'] == 'Iris-setosa') &
(iris_data['petal_width_cm'] == average_petal_width)]
iris_data.loc[(iris_data['sepal_length_cm'].isnull()) |
(iris_data['sepal_width_cm'].isnull()) |
(iris_data['petal_length_cm'].isnull()) |
(iris_data['petal_width_cm'].isnull())]
```
Great! Now we've recovered those rows and no longer have missing data in our data set.
**Note:** If you don't feel comfortable imputing your data, you can drop all rows with missing data with the `dropna()` call:
iris_data.dropna(inplace=True)
After all this hard work, we don't want to repeat this process every time we work with the data set. Let's save the tidied data file *as a separate file* and work directly with that data file from now on.
```
iris_data.to_csv('iris-data-clean.csv', index=False)
iris_data_clean = pd.read_csv('iris-data-clean.csv')
```
Now, let's take a look at the scatterplot matrix now that we've tidied the data.
```
sb.pairplot(iris_data_clean, hue='class')
```
Of course, I purposely inserted numerous errors into this data set to demonstrate some of the many possible scenarios you may face while tidying your data.
The general takeaways here should be:
* Make sure your data is encoded properly
* Make sure your data falls within the expected range, and use domain knowledge whenever possible to define that expected range
* Deal with missing data in one way or another: replace it if you can or drop it
* Never tidy your data manually because that is not easily reproducible
* Use code as a record of how you tidied your data
* Plot everything you can about the data at this stage of the analysis so you can *visually* confirm everything looks correct
## Bonus: Testing our data
[[ go back to the top ]](#Table-of-contents)
One thing I have learnt over the years is that, we should always test our data. Just how we use unit tests to verify our expectations from code, we can similarly set up unit tests to verify our expectations about a data set.
We can quickly test our data using `assert` statements: We assert that something must be true, and if it is, then nothing happens and we continue running. However, if our assertion is wrong, then it stops running and brings it to our attention. For example:
```
assert 1 == 2
```
Let's test a few things that we know about our data set now.
```
# We know that we should only have three classes
assert len(iris_data_clean['class'].unique()) == 3
# We know that sepal lengths for 'Iris-versicolor' should never be below 2.5 cm
assert iris_data_clean.loc[iris_data_clean['class'] == 'Iris-versicolor', 'sepal_length_cm'].min() >= 2.5
# We know that our data set should have no missing measurements
assert len(iris_data_clean.loc[(iris_data_clean['sepal_length_cm'].isnull()) |
(iris_data_clean['sepal_width_cm'].isnull()) |
(iris_data_clean['petal_length_cm'].isnull()) |
(iris_data_clean['petal_width_cm'].isnull())]) == 0
```
And so on. If any of these expectations are violated, then our analysis immediately stops and we have to return to the tidying stage.
## Step 4: Exploratory analysis
[[ go back to the top ]](#Table-of-contents)
Now after spending entirely too much time tidying our data, we can start analyzing it!
Exploratory analysis is the step where we start delving deeper into the data set beyond the outliers and errors. We'll be looking to answer questions such as:
* How is my data distributed?
* Are there any correlations in my data?
* Are there any confounding factors that explain these correlations?
This is the stage where we plot all the data in as many ways as possible. Create many charts, but don't bother making them pretty — these charts are for internal use.
Let's return to that scatterplot matrix that we used earlier.
```
sb.pairplot(iris_data_clean)
```
Our data is normally distributed for the most part, which is great news if we plan on using any modeling methods that assume the data is normally distributed.
There's something strange going with the petal measurements. Maybe it's something to do with the different `Iris` types. Let's color code the data by the class again to see if that clears things up.
```
sb.pairplot(iris_data_clean, hue='class')
```
Sure enough, the strange distribution of the petal measurements exist because of the different species. This is actually great news for our classification task since it means that the petal measurements will make it easy to distinguish between `Iris-setosa` and the other `Iris` types.
Distinguishing `Iris-versicolor` and `Iris-virginica` will prove more difficult given how much their measurements overlap.
There are also correlations between petal length and petal width, as well as sepal length and sepal width. The field biologists assure us that this is to be expected: Longer flower petals also tend to be wider, and the same applies for sepals.
We can also make **violin plots** of the data to compare the measurement distributions of the classes. Violin plots contain the same information as [box plots](https://en.wikipedia.org/wiki/Box_plot), but also scales the box according to the density of the data.
```
plt.figure(figsize=(10, 10))
for column_index, column in enumerate(iris_data_clean.columns):
if column == 'class':
continue
plt.subplot(2, 2, column_index + 1)
sb.violinplot(x='class', y=column, data=iris_data_clean)
```
Enough toying with the data. Let's get to modeling.
## Step 5: Classification
[[ go back to the top ]](#Table-of-contents)
Wow, all this work and we *still* haven't modeled the data!
As tiresome as it can be, tidying and exploring our data is a vital component to any data analysis. If we had jumped straight to the modeling step, we would have created a faulty classification model.
Remember: **Bad data leads to bad models.** Always check your data first.
<hr />
Assured that our data is now as clean as we can make it — and armed with some cursory knowledge of the distributions and relationships in our data set — it's time to make the next big step in our analysis: Splitting the data into training and testing sets.
A **training set** is a random subset of the data that we use to train our models.
A **testing set** is a random subset of the data (mutually exclusive from the training set) that we use to validate our models on unforseen data.
Especially in sparse data sets like ours, it's easy for models to **overfit** the data: The model will learn the training set so well that it won't be able to handle most of the cases it's never seen before. This is why it's important for us to build the model with the training set, but score it with the testing set.
Note that once we split the data into a training and testing set, we should treat the testing set like it no longer exists: We cannot use any information from the testing set to build our model or else we're cheating.
Let's set up our data first.
```
iris_data_clean = pd.read_csv('iris-data-clean.csv')
# We're using all four measurements as inputs
# Note that scikit-learn expects each entry to be a list of values, e.g.,
# [ [val1, val2, val3],
# [val1, val2, val3],
# ... ]
# such that our input data set is represented as a list of lists
# We can extract the data in this format from pandas like this:
all_inputs = iris_data_clean[['sepal_length_cm', 'sepal_width_cm',
'petal_length_cm', 'petal_width_cm']].values
# Similarly, we can extract the classes
all_classes = iris_data_clean['class'].values
# Make sure that you don't mix up the order of the entries
# all_inputs[5] inputs should correspond to the class in all_classes[5]
# Here's what a subset of our inputs looks like:
all_inputs[:5]
```
Now our data is ready to be split.
```
from sklearn.cross_validation import train_test_split
(training_inputs,
testing_inputs,
training_classes,
testing_classes) = train_test_split(all_inputs, all_classes, train_size=0.75, random_state=1)
```
With our data split, we can start fitting models to our data. Our head of data is all about decision tree classifiers, so let's start with one of those.
Decision tree classifiers are incredibly simple in theory. In their simplest form, decision tree classifiers ask a series of Yes/No questions about the data — each time getting closer to finding out the class of each entry — until they either classify the data set perfectly or simply can't differentiate a set of entries. Think of it like a game of [Twenty Questions](https://en.wikipedia.org/wiki/Twenty_Questions), except the computer is *much*, *much* better at it.
Here's an example decision tree classifier:
<img src="iris_dtc.png" />
Notice how the classifier asks Yes/No questions about the data — whether a certain feature is <= 1.75, for example — so it can differentiate the records. This is the essence of every decision tree.
The nice part about decision tree classifiers is that they are **scale-invariant**, i.e., the scale of the features does not affect their performance, unlike many Machine Learning models. In other words, it doesn't matter if our features range from 0 to 1 or 0 to 1,000; decision tree classifiers will work with them just the same.
There are several [parameters](http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html) that we can tune for decision tree classifiers, but for now let's use a basic decision tree classifier.
**Gini Coefficient** : The Gini coefficient measures the inequality among values of a frequency distribution (for example, sepal-width). A Gini coefficient of zero expresses perfect equality, where all values are the same (for example, where all flowers have same sepal-width). A Gini coefficient of 1 (or 100%) expresses maximal inequality among values (e.g., for a large number of flowers, where only one flower has very large sepal-width, and all others have almost no sepals, the Gini coefficient will be very nearly one)
```
from sklearn.tree import DecisionTreeClassifier
# Create the classifier
decision_tree_classifier = DecisionTreeClassifier()
# Train the classifier on the training set
decision_tree_classifier.fit(training_inputs, training_classes)
# Validate the classifier on the testing set using classification accuracy
decision_tree_classifier.score(testing_inputs, testing_classes)
```
Heck yeah! Our model achieves 97% classification accuracy without much effort.
However, there's a catch: Depending on how our training and testing set was sampled, our model can achieve anywhere from 80% to 100% accuracy:
```
model_accuracies = []
for repetition in range(1000):
(training_inputs,
testing_inputs,
training_classes,
testing_classes) = train_test_split(all_inputs, all_classes, train_size=0.75)
decision_tree_classifier = DecisionTreeClassifier()
decision_tree_classifier.fit(training_inputs, training_classes)
classifier_accuracy = decision_tree_classifier.score(testing_inputs, testing_classes)
model_accuracies.append(classifier_accuracy)
sb.distplot(model_accuracies)
```
It's obviously a problem that our model performs quite differently depending on the subset of the data it's trained on. This phenomenon is known as **overfitting**: The model is learning to classify the training set so well that it doesn't generalize and perform well on data it hasn't seen before.
### Cross-validation
[[ go back to the top ]](#Table-of-contents)
This problem is the main reason that most data scientists perform ***k*-fold cross-validation** on their models: Split the original data set into *k* subsets, use one of the subsets as the testing set, and the rest of the subsets are used as the training set. This process is then repeated *k* times such that each subset is used as the testing set exactly once.
10-fold cross-validation is the most common choice, so let's use that here. Performing 10-fold cross-validation on our data set looks something like this:
(each square is an entry in our data set)
```
import numpy as np
from sklearn.cross_validation import StratifiedKFold
def plot_cv(cv, n_samples):
masks = []
for train, test in cv:
mask = np.zeros(n_samples, dtype=bool)
mask[test] = 1
masks.append(mask)
plt.figure(figsize=(15, 15))
plt.imshow(masks, interpolation='none')
plt.ylabel('Fold')
plt.xlabel('Row #')
plot_cv(StratifiedKFold(all_classes, n_folds=10), len(all_classes))
```
You'll notice that we used **Stratified *k*-fold cross-validation** in the code above. Stratified *k*-fold keeps the class proportions the same across all of the folds, which is vital for maintaining a representative subset of our data set. (e.g., so we don't have 100% `Iris setosa` entries in one of the folds.)
We can perform 10-fold cross-validation on our model with the following code:
```
from sklearn.cross_validation import cross_val_score
decision_tree_classifier = DecisionTreeClassifier()
# cross_val_score returns a list of the scores, which we can visualize
# to get a reasonable estimate of our classifier's performance
cv_scores = cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10)
sb.distplot(cv_scores)
plt.title('Average score: {}'.format(np.mean(cv_scores)))
```
Now we have a much more consistent rating of our classifier's general classification accuracy.
### Parameter tuning
[[ go back to the top ]](#Table-of-contents)
Every Machine Learning model comes with a variety of parameters to tune, and these parameters can be vitally important to the performance of our classifier. For example, if we severely limit the depth of our decision tree classifier:
```
decision_tree_classifier = DecisionTreeClassifier(max_depth=1)
cv_scores = cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10)
sb.distplot(cv_scores, kde=False)
plt.title('Average score: {}'.format(np.mean(cv_scores)))
```
the classification accuracy falls tremendously.
Therefore, we need to find a systematic method to discover the best parameters for our model and data set.
The most common method for model parameter tuning is **Grid Search**. The idea behind Grid Search is simple: explore a range of parameters and find the best-performing parameter combination. Focus your search on the best range of parameters, then repeat this process several times until the best parameters are discovered.
Let's tune our decision tree classifier. We'll stick to only two parameters for now, but it's possible to simultaneously explore dozens of parameters if we want.
```
from sklearn.grid_search import GridSearchCV
decision_tree_classifier = DecisionTreeClassifier()
parameter_grid = {'max_depth': [1, 2, 3, 4, 5],
'max_features': [1, 2, 3, 4]}
cross_validation = StratifiedKFold(all_classes, n_folds=10)
grid_search = GridSearchCV(decision_tree_classifier,
param_grid=parameter_grid,
cv=cross_validation)
grid_search.fit(all_inputs, all_classes)
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))
```
Now let's visualize the grid search to see how the parameters interact.
```
grid_visualization = []
for grid_pair in grid_search.grid_scores_:
grid_visualization.append(grid_pair.mean_validation_score)
grid_visualization = np.array(grid_visualization)
grid_visualization.shape = (5, 4)
sb.heatmap(grid_visualization, cmap='Blues')
plt.xticks(np.arange(4) + 0.5, grid_search.param_grid['max_features'])
plt.yticks(np.arange(5) + 0.5, grid_search.param_grid['max_depth'][::-1])
plt.xlabel('max_features')
plt.ylabel('max_depth')
```
Now we have a better sense of the parameter space: We know that we need a `max_depth` of at least 2 to allow the decision tree to make more than a one-off decision.
`max_features` doesn't really seem to make a big difference here as long as we have 2 of them, which makes sense since our data set has only 4 features and is relatively easy to classify. (Remember, one of our data set's classes was easily separable from the rest based on a single feature.)
Let's go ahead and use a broad grid search to find the best settings for a handful of parameters.
```
decision_tree_classifier = DecisionTreeClassifier()
parameter_grid = {'criterion': ['gini', 'entropy'],
'splitter': ['best', 'random'],
'max_depth': [1, 2, 3, 4, 5],
'max_features': [1, 2, 3, 4]}
cross_validation = StratifiedKFold(all_classes, n_folds=10)
grid_search = GridSearchCV(decision_tree_classifier,
param_grid=parameter_grid,
cv=cross_validation)
grid_search.fit(all_inputs, all_classes)
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))
```
Now we can take the best classifier from the Grid Search and use that:
```
decision_tree_classifier = grid_search.best_estimator_
decision_tree_classifier
```
We can even visualize the decision tree with [GraphViz](http://www.graphviz.org/) to see how it's making the classifications:
```
import sklearn.tree as tree
from sklearn.externals.six import StringIO
with open('iris_dtc.dot', 'w') as out_file:
out_file = tree.export_graphviz(decision_tree_classifier, out_file=out_file)
```
<img src="iris_dtc.png" />
(This classifier may look familiar from earlier.)
Alright! We finally have our demo classifier. Let's create some visuals of its performance so we have something to show our head of data.
```
dt_scores = cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10)
sb.boxplot(dt_scores)
sb.stripplot(dt_scores, jitter=True, color='white')
```
Hmmm... that's a little boring by itself though. How about we compare another classifier to see how they perform?
We already know from previous projects that Random Forest classifiers usually work better than individual decision trees. A common problem that decision trees face is that they're prone to overfitting: They complexify to the point that they classify the training set near-perfectly, but fail to generalize to data they have not seen before.
**Random Forest classifiers** work around that limitation by creating a whole bunch of decision trees (hence "forest") — each trained on random subsets of training samples (drawn with replacement) and features (drawn without replacement) — and have the decision trees work together to make a more accurate classification.
Let that be a lesson for us: **Even in Machine Learning, we get better results when we work together!**
Let's see if a Random Forest classifier works better here.
The great part about scikit-learn is that the training, testing, parameter tuning, etc. process is the same for all models, so we only need to plug in the new classifier.
```
from sklearn.ensemble import RandomForestClassifier
random_forest_classifier = RandomForestClassifier()
parameter_grid = {'n_estimators': [5, 10, 25, 50],
'criterion': ['gini', 'entropy'],
'max_features': [1, 2, 3, 4],
'warm_start': [True, False]}
cross_validation = StratifiedKFold(all_classes, n_folds=10)
grid_search = GridSearchCV(random_forest_classifier,
param_grid=parameter_grid,
cv=cross_validation)
grid_search.fit(all_inputs, all_classes)
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))
grid_search.best_estimator_
```
Now we can compare their performance:
```
random_forest_classifier = grid_search.best_estimator_
rf_df = pd.DataFrame({'accuracy': cross_val_score(random_forest_classifier, all_inputs, all_classes, cv=10),
'classifier': ['Random Forest'] * 10})
dt_df = pd.DataFrame({'accuracy': cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10),
'classifier': ['Decision Tree'] * 10})
both_df = rf_df.append(dt_df)
sb.boxplot(x='classifier', y='accuracy', data=both_df)
sb.stripplot(x='classifier', y='accuracy', data=both_df, jitter=True, color='white')
```
How about that? They both seem to perform about the same on this data set. This is probably because of the limitations of our data set: We have only 4 features to make the classification, and Random Forest classifiers excel when there's hundreds of possible features to look at. In other words, there wasn't much room for improvement with this data set.
## Step 6: Recap
[[ go back to the top ]](#Table-of-contents)
Finally, let's extract the core of our work from Steps 1-5 and turn it into a single pipeline.
```
%matplotlib inline
import pandas as pd
import seaborn as sb
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import train_test_split
from sklearn.cross_validation import cross_val_score
# We can jump directly to working with the clean data because we saved our cleaned data set
iris_data_clean = pd.read_csv('iris-data-clean.csv')
# Testing our data: Our analysis will stop here if any of these assertions are wrong
# We know that we should only have three classes
assert len(iris_data_clean['class'].unique()) == 3
# We know that sepal lengths for 'Iris-versicolor' should never be below 2.5 cm
assert iris_data_clean.loc[iris_data_clean['class'] == 'Iris-versicolor', 'sepal_length_cm'].min() >= 2.5
# We know that our data set should have no missing measurements
assert len(iris_data_clean.loc[(iris_data_clean['sepal_length_cm'].isnull()) |
(iris_data_clean['sepal_width_cm'].isnull()) |
(iris_data_clean['petal_length_cm'].isnull()) |
(iris_data_clean['petal_width_cm'].isnull())]) == 0
all_inputs = iris_data_clean[['sepal_length_cm', 'sepal_width_cm',
'petal_length_cm', 'petal_width_cm']].values
all_classes = iris_data_clean['class'].values
# This is the classifier that came out of Grid Search
random_forest_classifier = RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features=3, max_leaf_nodes=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=5, n_jobs=1,
oob_score=False, random_state=None, verbose=0, warm_start=True)
# All that's left to do now is plot the cross-validation scores
rf_classifier_scores = cross_val_score(random_forest_classifier, all_inputs, all_classes, cv=10)
sb.boxplot(rf_classifier_scores)
sb.stripplot(rf_classifier_scores, jitter=True, color='white')
# ...and show some of the predictions from the classifier
(training_inputs,
testing_inputs,
training_classes,
testing_classes) = train_test_split(all_inputs, all_classes, train_size=0.75)
random_forest_classifier.fit(training_inputs, training_classes)
for input_features, prediction, actual in zip(testing_inputs[:10],
random_forest_classifier.predict(testing_inputs[:10]),
testing_classes[:10]):
print('{}\t-->\t{}\t(Actual: {})'.format(input_features, prediction, actual))
```
There we have it: We have a complete and reproducible Machine Learning pipeline to demo to our head of data. We've met the success criteria that we set from the beginning (>90% accuracy), and our pipeline is flexible enough to handle new inputs or flowers when that data set is ready. Not bad for our first week on the job!
## Further reading
[[ go back to the top ]](#Table-of-contents)
This covers a broad variety of topics but skips over many of the specifics. If you're looking to dive deeper into a particular topic, here's some recommended reading.
**Data Science**: William Chen compiled a [list of free books](http://www.wzchen.com/data-science-books/) for newcomers to Data Science, ranging from the basics of R & Python to Machine Learning to interviews and advice from prominent data scientists.
**Machine Learning**: /r/MachineLearning has a useful [Wiki page](https://www.reddit.com/r/MachineLearning/wiki/index) containing links to online courses, books, data sets, etc. for Machine Learning. There's also a [curated list](https://github.com/josephmisiti/awesome-machine-learning) of Machine Learning frameworks, libraries, and software sorted by language.
**Unit testing**: Dive Into Python 3 has a [great walkthrough](http://www.diveintopython3.net/unit-testing.html) of unit testing in Python, how it works, and how it should be used
**pandas** has [several tutorials](http://pandas.pydata.org/pandas-docs/stable/tutorials.html) covering its myriad features.
**scikit-learn** has a [bunch of tutorials](http://scikit-learn.org/stable/tutorial/index.html) for those looking to learn Machine Learning in Python. Andreas Mueller's [scikit-learn workshop materials](https://github.com/amueller/scipy_2015_sklearn_tutorial) are top-notch and freely available.
**matplotlib** has many [books, videos, and tutorials](http://matplotlib.org/resources/index.html) to teach plotting in Python.
**Seaborn** has a [basic tutorial](http://stanford.edu/~mwaskom/software/seaborn/tutorial.html) covering most of the statistical plotting features.
|
github_jupyter
|
import pandas as pd
iris_data = pd.read_csv('iris-data.csv')
iris_data.head()
iris_data = pd.read_csv('iris-data.csv', na_values=['NA'])
iris_data.describe()
# This line tells the notebook to show plots inside of the notebook
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sb
# We have to temporarily drop the rows with 'NA' values
# because the Seaborn plotting function does not know
# what to do with them
sb.pairplot(iris_data.dropna(), hue='class')
iris_data.loc[iris_data['class'] == 'versicolor', 'class'] = 'Iris-versicolor'
iris_data.loc[iris_data['class'] == 'Iris-setossa', 'class'] = 'Iris-setosa'
iris_data['class'].unique()
# This line drops any 'Iris-setosa' rows with a separal width less than 2.5 cm
iris_data = iris_data.loc[(iris_data['class'] != 'Iris-setosa') | (iris_data['sepal_width_cm'] >= 2.5)]
iris_data.loc[iris_data['class'] == 'Iris-setosa', 'sepal_width_cm'].hist()
iris_data.loc[(iris_data['class'] == 'Iris-versicolor') &
(iris_data['sepal_length_cm'] < 1.0)]
iris_data.loc[(iris_data['class'] == 'Iris-versicolor') &
(iris_data['sepal_length_cm'] < 1.0),
'sepal_length_cm'] *= 100.0
iris_data.loc[iris_data['class'] == 'Iris-versicolor', 'sepal_length_cm'].hist()
iris_data.loc[(iris_data['sepal_length_cm'].isnull()) |
(iris_data['sepal_width_cm'].isnull()) |
(iris_data['petal_length_cm'].isnull()) |
(iris_data['petal_width_cm'].isnull())]
iris_data.loc[iris_data['class'] == 'Iris-setosa', 'petal_width_cm'].hist()
average_petal_width = iris_data.loc[iris_data['class'] == 'Iris-setosa', 'petal_width_cm'].mean()
iris_data.loc[(iris_data['class'] == 'Iris-setosa') &
(iris_data['petal_width_cm'].isnull()),
'petal_width_cm'] = average_petal_width
iris_data.loc[(iris_data['class'] == 'Iris-setosa') &
(iris_data['petal_width_cm'] == average_petal_width)]
iris_data.loc[(iris_data['sepal_length_cm'].isnull()) |
(iris_data['sepal_width_cm'].isnull()) |
(iris_data['petal_length_cm'].isnull()) |
(iris_data['petal_width_cm'].isnull())]
iris_data.to_csv('iris-data-clean.csv', index=False)
iris_data_clean = pd.read_csv('iris-data-clean.csv')
sb.pairplot(iris_data_clean, hue='class')
assert 1 == 2
# We know that we should only have three classes
assert len(iris_data_clean['class'].unique()) == 3
# We know that sepal lengths for 'Iris-versicolor' should never be below 2.5 cm
assert iris_data_clean.loc[iris_data_clean['class'] == 'Iris-versicolor', 'sepal_length_cm'].min() >= 2.5
# We know that our data set should have no missing measurements
assert len(iris_data_clean.loc[(iris_data_clean['sepal_length_cm'].isnull()) |
(iris_data_clean['sepal_width_cm'].isnull()) |
(iris_data_clean['petal_length_cm'].isnull()) |
(iris_data_clean['petal_width_cm'].isnull())]) == 0
sb.pairplot(iris_data_clean)
sb.pairplot(iris_data_clean, hue='class')
plt.figure(figsize=(10, 10))
for column_index, column in enumerate(iris_data_clean.columns):
if column == 'class':
continue
plt.subplot(2, 2, column_index + 1)
sb.violinplot(x='class', y=column, data=iris_data_clean)
iris_data_clean = pd.read_csv('iris-data-clean.csv')
# We're using all four measurements as inputs
# Note that scikit-learn expects each entry to be a list of values, e.g.,
# [ [val1, val2, val3],
# [val1, val2, val3],
# ... ]
# such that our input data set is represented as a list of lists
# We can extract the data in this format from pandas like this:
all_inputs = iris_data_clean[['sepal_length_cm', 'sepal_width_cm',
'petal_length_cm', 'petal_width_cm']].values
# Similarly, we can extract the classes
all_classes = iris_data_clean['class'].values
# Make sure that you don't mix up the order of the entries
# all_inputs[5] inputs should correspond to the class in all_classes[5]
# Here's what a subset of our inputs looks like:
all_inputs[:5]
from sklearn.cross_validation import train_test_split
(training_inputs,
testing_inputs,
training_classes,
testing_classes) = train_test_split(all_inputs, all_classes, train_size=0.75, random_state=1)
from sklearn.tree import DecisionTreeClassifier
# Create the classifier
decision_tree_classifier = DecisionTreeClassifier()
# Train the classifier on the training set
decision_tree_classifier.fit(training_inputs, training_classes)
# Validate the classifier on the testing set using classification accuracy
decision_tree_classifier.score(testing_inputs, testing_classes)
model_accuracies = []
for repetition in range(1000):
(training_inputs,
testing_inputs,
training_classes,
testing_classes) = train_test_split(all_inputs, all_classes, train_size=0.75)
decision_tree_classifier = DecisionTreeClassifier()
decision_tree_classifier.fit(training_inputs, training_classes)
classifier_accuracy = decision_tree_classifier.score(testing_inputs, testing_classes)
model_accuracies.append(classifier_accuracy)
sb.distplot(model_accuracies)
import numpy as np
from sklearn.cross_validation import StratifiedKFold
def plot_cv(cv, n_samples):
masks = []
for train, test in cv:
mask = np.zeros(n_samples, dtype=bool)
mask[test] = 1
masks.append(mask)
plt.figure(figsize=(15, 15))
plt.imshow(masks, interpolation='none')
plt.ylabel('Fold')
plt.xlabel('Row #')
plot_cv(StratifiedKFold(all_classes, n_folds=10), len(all_classes))
from sklearn.cross_validation import cross_val_score
decision_tree_classifier = DecisionTreeClassifier()
# cross_val_score returns a list of the scores, which we can visualize
# to get a reasonable estimate of our classifier's performance
cv_scores = cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10)
sb.distplot(cv_scores)
plt.title('Average score: {}'.format(np.mean(cv_scores)))
decision_tree_classifier = DecisionTreeClassifier(max_depth=1)
cv_scores = cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10)
sb.distplot(cv_scores, kde=False)
plt.title('Average score: {}'.format(np.mean(cv_scores)))
from sklearn.grid_search import GridSearchCV
decision_tree_classifier = DecisionTreeClassifier()
parameter_grid = {'max_depth': [1, 2, 3, 4, 5],
'max_features': [1, 2, 3, 4]}
cross_validation = StratifiedKFold(all_classes, n_folds=10)
grid_search = GridSearchCV(decision_tree_classifier,
param_grid=parameter_grid,
cv=cross_validation)
grid_search.fit(all_inputs, all_classes)
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))
grid_visualization = []
for grid_pair in grid_search.grid_scores_:
grid_visualization.append(grid_pair.mean_validation_score)
grid_visualization = np.array(grid_visualization)
grid_visualization.shape = (5, 4)
sb.heatmap(grid_visualization, cmap='Blues')
plt.xticks(np.arange(4) + 0.5, grid_search.param_grid['max_features'])
plt.yticks(np.arange(5) + 0.5, grid_search.param_grid['max_depth'][::-1])
plt.xlabel('max_features')
plt.ylabel('max_depth')
decision_tree_classifier = DecisionTreeClassifier()
parameter_grid = {'criterion': ['gini', 'entropy'],
'splitter': ['best', 'random'],
'max_depth': [1, 2, 3, 4, 5],
'max_features': [1, 2, 3, 4]}
cross_validation = StratifiedKFold(all_classes, n_folds=10)
grid_search = GridSearchCV(decision_tree_classifier,
param_grid=parameter_grid,
cv=cross_validation)
grid_search.fit(all_inputs, all_classes)
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))
decision_tree_classifier = grid_search.best_estimator_
decision_tree_classifier
import sklearn.tree as tree
from sklearn.externals.six import StringIO
with open('iris_dtc.dot', 'w') as out_file:
out_file = tree.export_graphviz(decision_tree_classifier, out_file=out_file)
dt_scores = cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10)
sb.boxplot(dt_scores)
sb.stripplot(dt_scores, jitter=True, color='white')
from sklearn.ensemble import RandomForestClassifier
random_forest_classifier = RandomForestClassifier()
parameter_grid = {'n_estimators': [5, 10, 25, 50],
'criterion': ['gini', 'entropy'],
'max_features': [1, 2, 3, 4],
'warm_start': [True, False]}
cross_validation = StratifiedKFold(all_classes, n_folds=10)
grid_search = GridSearchCV(random_forest_classifier,
param_grid=parameter_grid,
cv=cross_validation)
grid_search.fit(all_inputs, all_classes)
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))
grid_search.best_estimator_
random_forest_classifier = grid_search.best_estimator_
rf_df = pd.DataFrame({'accuracy': cross_val_score(random_forest_classifier, all_inputs, all_classes, cv=10),
'classifier': ['Random Forest'] * 10})
dt_df = pd.DataFrame({'accuracy': cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10),
'classifier': ['Decision Tree'] * 10})
both_df = rf_df.append(dt_df)
sb.boxplot(x='classifier', y='accuracy', data=both_df)
sb.stripplot(x='classifier', y='accuracy', data=both_df, jitter=True, color='white')
%matplotlib inline
import pandas as pd
import seaborn as sb
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import train_test_split
from sklearn.cross_validation import cross_val_score
# We can jump directly to working with the clean data because we saved our cleaned data set
iris_data_clean = pd.read_csv('iris-data-clean.csv')
# Testing our data: Our analysis will stop here if any of these assertions are wrong
# We know that we should only have three classes
assert len(iris_data_clean['class'].unique()) == 3
# We know that sepal lengths for 'Iris-versicolor' should never be below 2.5 cm
assert iris_data_clean.loc[iris_data_clean['class'] == 'Iris-versicolor', 'sepal_length_cm'].min() >= 2.5
# We know that our data set should have no missing measurements
assert len(iris_data_clean.loc[(iris_data_clean['sepal_length_cm'].isnull()) |
(iris_data_clean['sepal_width_cm'].isnull()) |
(iris_data_clean['petal_length_cm'].isnull()) |
(iris_data_clean['petal_width_cm'].isnull())]) == 0
all_inputs = iris_data_clean[['sepal_length_cm', 'sepal_width_cm',
'petal_length_cm', 'petal_width_cm']].values
all_classes = iris_data_clean['class'].values
# This is the classifier that came out of Grid Search
random_forest_classifier = RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features=3, max_leaf_nodes=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=5, n_jobs=1,
oob_score=False, random_state=None, verbose=0, warm_start=True)
# All that's left to do now is plot the cross-validation scores
rf_classifier_scores = cross_val_score(random_forest_classifier, all_inputs, all_classes, cv=10)
sb.boxplot(rf_classifier_scores)
sb.stripplot(rf_classifier_scores, jitter=True, color='white')
# ...and show some of the predictions from the classifier
(training_inputs,
testing_inputs,
training_classes,
testing_classes) = train_test_split(all_inputs, all_classes, train_size=0.75)
random_forest_classifier.fit(training_inputs, training_classes)
for input_features, prediction, actual in zip(testing_inputs[:10],
random_forest_classifier.predict(testing_inputs[:10]),
testing_classes[:10]):
print('{}\t-->\t{}\t(Actual: {})'.format(input_features, prediction, actual))
| 0.6488 | 0.993063 |
```
import torch
import torchvision
from torchvision import transforms
from torch.utils.data.dataset import Dataset
import os, sys, random
import numpy as np
import PIL
from PIL import Image
from gen_utils import *
from ds import *
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
load_tfm = transforms.Compose([
transforms.ToTensor(),
lambda x : (x-x.min())/(x.max()-x.min())
])
train_set = XrayDset('../data/train/', load_tfm)
train_loader = torch.utils.data.DataLoader(dataset=train_set, batch_size=10, shuffle=True)
test_set = XrayDset('../data/test/', load_tfm)
test_loader = torch.utils.data.DataLoader(dataset=test_set, batch_size=10, shuffle=False)
class XrayResnet(torch.nn.Module):
def __init__(self):
super(XrayResnet, self).__init__()
self.C1 = torch.nn.Conv2d(in_channels=1, out_channels=3, kernel_size=3, padding=1, stride=1)
self.model_ft = torchvision.models.resnet18()
self.model_ft.avgpool = torch.nn.AvgPool2d(kernel_size=4, padding=0, stride=2)
self.model_ft.fc = torch.nn.Sequential(
torch.nn.Linear(512,256),
torch.nn.Linear(256,2)
)
def forward(self, x):
y = x
y = self.C1(y)
for lid, layer in enumerate(list(self.model_ft.children())[:9]):
y = layer(y)
y = y.squeeze(-1).squeeze(-1)
y = list(self.model_ft.children())[-1](y)
return y
```
# train and test loop
```
n_epochs = 50
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
M = XrayResnet()
M = M.to(device)
optimizer = torch.optim.Adam(M.parameters(), lr=6e-4, weight_decay=1e-2)
exp_lr_scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, n_epochs)
criterion = torch.nn.CrossEntropyLoss()
train_loss_track = []
test_loss_track = []
for eph in range(n_epochs):
print('epoch : {} ...'.format(eph))
n_correct = 0
avg_loss = 0
n_samples = 0
M.train()
exp_lr_scheduler.step()
for idx, xy in enumerate(train_loader):
x, y = xy
x, y = x.to(device), y.to(device)
outputs = M(x)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
n_correct += torch.sum(preds.data == y.data)
avg_loss += loss.item()
n_samples += x.size(0)
avg_loss = avg_loss/n_samples
train_loss_track.append(avg_loss)
print('train avg loss : ', avg_loss)
print('num of correct samples : {}/{}'.format(n_correct, n_samples))
n_correct = 0
avg_loss = 0
n_samples = 0
gt_labels = []
pred_labels = []
M.eval()
for idx, xy in enumerate(test_loader):
x, y = xy
x, y = x.cuda(), y.cuda()
outputs = M(x)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, y)
n_correct += torch.sum(preds.data == y.data)
gt_labels += list(y.data.cpu().numpy())
pred_labels += list(preds.data.cpu().numpy())
avg_loss += loss.item()
n_samples += x.size(0)
avg_loss = avg_loss/n_samples
test_loss_track.append(avg_loss)
print('test avg loss : ', avg_loss)
print('num of correct samples : {}/{}'.format(n_correct, n_samples))
plt.plot(train_loss_track, 'b')
plt.plot(test_loss_track, 'r')
plt.xlabel('epochs')
plt.ylabel('avg loss')
plt.show()
target_names = ['No TB', 'TB']
print(classification_report(gt_labels, pred_labels, target_names=target_names))
M
```
|
github_jupyter
|
import torch
import torchvision
from torchvision import transforms
from torch.utils.data.dataset import Dataset
import os, sys, random
import numpy as np
import PIL
from PIL import Image
from gen_utils import *
from ds import *
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
load_tfm = transforms.Compose([
transforms.ToTensor(),
lambda x : (x-x.min())/(x.max()-x.min())
])
train_set = XrayDset('../data/train/', load_tfm)
train_loader = torch.utils.data.DataLoader(dataset=train_set, batch_size=10, shuffle=True)
test_set = XrayDset('../data/test/', load_tfm)
test_loader = torch.utils.data.DataLoader(dataset=test_set, batch_size=10, shuffle=False)
class XrayResnet(torch.nn.Module):
def __init__(self):
super(XrayResnet, self).__init__()
self.C1 = torch.nn.Conv2d(in_channels=1, out_channels=3, kernel_size=3, padding=1, stride=1)
self.model_ft = torchvision.models.resnet18()
self.model_ft.avgpool = torch.nn.AvgPool2d(kernel_size=4, padding=0, stride=2)
self.model_ft.fc = torch.nn.Sequential(
torch.nn.Linear(512,256),
torch.nn.Linear(256,2)
)
def forward(self, x):
y = x
y = self.C1(y)
for lid, layer in enumerate(list(self.model_ft.children())[:9]):
y = layer(y)
y = y.squeeze(-1).squeeze(-1)
y = list(self.model_ft.children())[-1](y)
return y
n_epochs = 50
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
M = XrayResnet()
M = M.to(device)
optimizer = torch.optim.Adam(M.parameters(), lr=6e-4, weight_decay=1e-2)
exp_lr_scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, n_epochs)
criterion = torch.nn.CrossEntropyLoss()
train_loss_track = []
test_loss_track = []
for eph in range(n_epochs):
print('epoch : {} ...'.format(eph))
n_correct = 0
avg_loss = 0
n_samples = 0
M.train()
exp_lr_scheduler.step()
for idx, xy in enumerate(train_loader):
x, y = xy
x, y = x.to(device), y.to(device)
outputs = M(x)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
n_correct += torch.sum(preds.data == y.data)
avg_loss += loss.item()
n_samples += x.size(0)
avg_loss = avg_loss/n_samples
train_loss_track.append(avg_loss)
print('train avg loss : ', avg_loss)
print('num of correct samples : {}/{}'.format(n_correct, n_samples))
n_correct = 0
avg_loss = 0
n_samples = 0
gt_labels = []
pred_labels = []
M.eval()
for idx, xy in enumerate(test_loader):
x, y = xy
x, y = x.cuda(), y.cuda()
outputs = M(x)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, y)
n_correct += torch.sum(preds.data == y.data)
gt_labels += list(y.data.cpu().numpy())
pred_labels += list(preds.data.cpu().numpy())
avg_loss += loss.item()
n_samples += x.size(0)
avg_loss = avg_loss/n_samples
test_loss_track.append(avg_loss)
print('test avg loss : ', avg_loss)
print('num of correct samples : {}/{}'.format(n_correct, n_samples))
plt.plot(train_loss_track, 'b')
plt.plot(test_loss_track, 'r')
plt.xlabel('epochs')
plt.ylabel('avg loss')
plt.show()
target_names = ['No TB', 'TB']
print(classification_report(gt_labels, pred_labels, target_names=target_names))
M
| 0.790692 | 0.738763 |
## TOC
1. [Basic Statistics](#BasicStatistics)<br>
1.1 [Sideways Moves Allowed](#BasicStatisticsSidewaysAllowed)<br>
1.2 [Sideways Moves Not allowed](#BasicStatisticsSidewaysNotAllowed)<br>
1.3 [Sideways Moves Allowed (cached)](#BasicStatisticsSidewaysAllowedCached)<br>
1.4 [Sideways Moves Not Allowed (cached)](#BasicStatisticsSidewaysNotAllowedCached)<br>
2. [Run Time Diagrams](#RTD)<br>
2.1 [Sideways Moves Allowed](#RTDSidewaysAllowed)<br>
2.2 [Sideways Moves Not Allowed](#RTDSidewaysDisallowed)<br>
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
%matplotlib inline
plt.rcParams["figure.figsize"] = [15, 5]
```
### List of Files for each type of run (cached/uncached vs sideways-allowed/sideways-not-allowed)
```
no_sideways_no_cache = {
50: "no_sideways_no_cache_50.csv",
100: "no_sideways_no_cache_100.csv",
250: "no_sideways_no_cache_250.csv",
500: "no_sideways_no_cache_500.csv",
1000: "no_sideways_no_cache_1000.csv",
10000: "no_sideways_no_cache_10000.csv",
100000: "100_no_sideways_no_cache_early.csv",}
no_sideways_yes_cache = {
50: "no_sideways_cache_50.csv",
100: "no_sideways_cache_100.csv",
250: "no_sideways_cache_250.csv",
500: "no_sideways_cache_500.csv",
1000: "no_sideways_cache_1000.csv",
10000: "no_sideways_cache_10000.csv",
100000: "100_no_sideways_cache_early.csv",}
yes_sideways_no_cache = {
100000: "100_sideways_no_cache_100000.csv",
10000: "yes_sideways_no_cache_r10000.csv",
2500: "yes_sideways_no_cache_10000.csv",
1000: "yes_sideways_no_cache_1000.csv",
500: "yes_sideways_no_cache_500.csv",
250: "yes_sideways_no_cache_250.csv",
100: "yes_sideways_no_cache_100.csv",
50: "yes_sideways_no_cache_50.csv",
}
yes_sideways_yes_cache = {
100000: "100_sideways_cache_100000.csv",
10000: "yes_sideways_cache_r10000.csv",
2500: "yes_sideways_cache_10000.csv",
1000: "yes_sideways_cache_1000.csv",
500: "yes_sideways_cache_500.csv",
250: "yes_sideways_cache_250.csv",
100: "yes_sideways_cache_100.csv",
50: "yes_sideways_cache_50.csv"
}
```
<a id="section_ID"></a>
## Basic Statistics <a id="BasicStatistics"></a>
```
def fill_stats_helper(d:dict, val:float, name:str):
if name not in d.keys():
d[name] = []
d[name].append(val)
def fill_statistics(filename:str, column:str, out_dict:dict, iterations:int, multiplication_factor:int=1):
df = pd.read_csv(filename)
df = df[df['Cost'] == 0]
df = df[[column]]
data = df[column].to_numpy()
data = data * multiplication_factor
fill_stats_helper(out_dict, iterations, 'iterations')
fill_stats_helper(out_dict, np.min(data), 'min')
fill_stats_helper(out_dict, np.max(data), 'max')
fill_stats_helper(out_dict, np.mean(data), 'mean')
fill_stats_helper(out_dict, np.std(data), 'std')
fill_stats_helper(out_dict, np.std(data)/np.mean(data), 'cv')
fill_stats_helper(out_dict, np.median(data), 'median')
fill_stats_helper(out_dict, np.quantile(data, 0.25), 'q0.25')
fill_stats_helper(out_dict, np.quantile(data, 0.75), 'q0.75')
fill_stats_helper(out_dict, np.quantile(data, 0.1), 'q0.1')
fill_stats_helper(out_dict, np.quantile(data, 0.9), 'q0.9')
fill_stats_helper(out_dict, np.quantile(data, 0.75)/np.quantile(data, 0.25), 'q0.75/q0.25')
fill_stats_helper(out_dict, np.quantile(data, 0.9)/np.quantile(data, 0.1), 'q0.9/q0.1')
def get_stats(the_dict):
iters = sorted(list(the_dict.keys()))
time_dict = {}
operations_dict = {}
for i in iters:
fill_statistics(the_dict[i], 'Time', time_dict, i, 1)
fill_statistics(the_dict[i], 'HeuristicQueenCalls', operations_dict, i, 54)
return pd.DataFrame(time_dict), pd.DataFrame(operations_dict)
def read_file(filename):
return pd.read_csv(filename)
def print_success_rate(d):
iters = sorted(list(d.keys()))
print("%20s %20s %20s" % ("Iterations", "Success %", "mean restarts"))
for i in iters:
filename = d[i]
df = read_file(filename)
df2 = df[df['Cost'] == 0]
success = df2.shape[0]/df.shape[0]
restarts_required = np.mean(df['Restart'].to_numpy())
print("%20d %20.3f %20.3f" % (i, success, restarts_required))
```
### Basic Statistics Sideways Moves Allowed (No Cache)<a id="BasicStatisticsSidewaysAllowed"></a>
```
t, o = get_stats(yes_sideways_no_cache)
```
#### Run Time
```
t
```
#### Number of Operations
```
o
```
#### Success rate by iterations
```
print_success_rate(yes_sideways_no_cache)
```
### Basic Statistics Sideways Moves Not Allowed (No Cache)<a id='BasicStatisticsSidewaysNotAllowed'></a>
```
t, o = get_stats(no_sideways_no_cache)
```
#### Run time
```
t
```
#### Number of Operations
```
o
```
#### Success rate
```
print_success_rate(no_sideways_no_cache)
```
### Basic Statistics Sideways Moves Allowed (Cached)<a id="BasicStatisticsSidewaysAllowedCached"></a>
```
t, o = get_stats(yes_sideways_yes_cache)
```
#### Run Time
```
t
```
#### Number of Operations
```
o
```
### Basic Statistics Sideways Moves Not Allowed (cached)<a id="BasicStatisticsSidewaysNotAllowedCached"></a>
```
t, o = get_stats(no_sideways_yes_cache)
```
#### Run Time
```
t
```
#### Number of Operations
```
o
def get_plottable_columns(df:pd.DataFrame,\
x_column_name:str)->tuple:
"""
Returns k - the number of items
a pandas data frame with the X and y axis
"""
k = df.shape[0] # Number of experiments
df = df[df['Cost'] == 0]
df = df[[x_column_name]]
# drop all other columns except the column that we're interested in that
# measures the number of calls, or time
df = df.sort_values(by=[x_column_name])
df = df.reset_index()
# Now add the X axis which is i/k for all i in k_prime
k_prime = df.shape[0]
x = np.array([i/k for i in range(k_prime)])
x = pd.Series(x)
df['P_Solve'] = x
return k, df
def plot_one_file(filename:str,\
ax,\
x_column_name,
legend_text,
plot_failure_rate:bool=False,
multiplication_factor:int=1):
#print(f"Reading {filename}")
df = read_file(filename)
k, df = get_plottable_columns(df, x_column_name)
y = df['P_Solve'].to_numpy()
if plot_failure_rate:
y = 1 - y
x = df[x_column_name].to_numpy()
x = x * multiplication_factor
p = ax.plot(x, y, label=legend_text)
return None
def plot_entire_run(run_dict:dict,\
x_column_name:str,
plot_type:str='regular',
plot_failure_rate:bool=False,
title:str="",
multiplication_factor:int=1,
legend_position:str='figure'):
assert(plot_type == 'regular' or plot_type == 'loglog' or plot_type == 'semilog')
assert(legend_position == 'figure' or legend_position == 'ax')
fig, ax = plt.subplots(1)
iters_list = sorted(list(run_dict.keys()))
for i in iters_list:
plot_one_file(run_dict[i], ax, x_column_name, f"iters={i}",\
plot_failure_rate, multiplication_factor)
if legend_position == 'ax':
ax.legend()
else:
fig.legend()
ax.set_title(title)
xlabel = x_column_name
if plot_type == 'loglog' or plot_type == 'semilog':
xlabel = xlabel + " (log scale)"
ax.set_xscale('log')
ax.set_xlabel(xlabel)
ylabel = "P(Solve)"
if plot_failure_rate:
ylabel = "P(Fail)"
if plot_type == 'loglog':
ylabel = ylabel + " (log scale)"
ax.set_yscale('log')
ax.set_ylabel(ylabel)
return None
def plot_entire_run_all(run_dict:dict,
x_column_name:str,
plot_failure_rate:bool=False,
title:str="",
multiplication_factor:int=1,
legend_position:str='figure'):
assert(legend_position == 'figure' or legend_position == 'ax')
fig, ax = plt.subplots(1, 3)
iters_list = sorted(list(run_dict.keys()))
for i in iters_list:
for j in range(3):
if 'figure' == legend_position:
leg_str = f"{j}-iters={i}"
else:
leg_str = f"iters={i}"
plot_one_file(run_dict[i], ax[j], x_column_name, leg_str,\
plot_failure_rate, multiplication_factor)
if legend_position == 'ax':
for j in range(3):
ax[j].legend()
else:
fig.legend()
ylabel = "P(Solve)"
if plot_failure_rate:
ylabel = "P(Fail)"
ax[0].set_title('0')
ax[1].set_title('1')
ax[2].set_title('2')
ax[0].set_xlabel(x_column_name)
ax[1].set_xlabel(x_column_name + " (log scale)")
ax[2].set_xlabel(x_column_name + " (log scale)")
ax[0].set_ylabel(ylabel)
ax[1].set_ylabel(ylabel)
ax[2].set_ylabel(f'{ylabel} (log scale)')
ax[1].set_xscale('log')
ax[2].set_xscale('log')
ax[2].set_yscale('log')
fig.suptitle(title)
def plot_operations(run_dict:dict,\
plot_type:str='regular',
title:str="",
plot_failure_rate:bool=False,
legend_position:str='ax'):
return plot_entire_run(run_dict, 'HeuristicQueenCalls',\
plot_type=plot_type, plot_failure_rate=plot_failure_rate,\
title=title,multiplication_factor=54,\
legend_position=legend_position)
def plot_time(run_dict:dict,\
plot_type:str='regular',
title:str="",
plot_failure_rate:bool=False,
legend_position:str='ax'):
return plot_entire_run(run_dict, 'Time',\
plot_type=plot_type, plot_failure_rate=plot_failure_rate,\
title=title,multiplication_factor=1,\
legend_position=legend_position)
def plot_operations_all(run_dict:dict,
title:str="",
plot_failure_rate:bool=False,
legend_position:str='ax'):
plot_entire_run_all(run_dict, 'HeuristicQueenCalls',\
plot_failure_rate=plot_failure_rate, title=title,
multiplication_factor=54,
legend_position=legend_position)
def plot_time_all(run_dict:dict,
title:str="",
plot_failure_rate:bool=False,
legend_position:str='ax'):
plot_entire_run_all(run_dict, 'Time',\
plot_failure_rate=plot_failure_rate, title=title,
multiplication_factor=1,
legend_position=legend_position)
```
### Run Time Diagrams<a id="RTD"></a>
### Sideways Moves Allowed<a id='RTDSidewaysAllowed'></a>
#### Run Time Distribution - P(Solve)
```
plot_time_all(yes_sideways_no_cache, "Sideways (uncached)", plot_failure_rate=False, legend_position='ax')
```
#### Run Time Distribution (Failure Rate)
```
plot_time_all(yes_sideways_no_cache, "Sideways (uncached) Failure Rate", plot_failure_rate=True, legend_position='ax')
```
#### Run Length Distribution - P(Solve)
```
plot_operations_all(yes_sideways_no_cache, "Sideways (uncached)", plot_failure_rate=False, legend_position='ax')
```
#### Run Length Distribution - Failulre Rate
```
plot_operations_all(yes_sideways_no_cache, "Sideways (uncached) Failure Rate", plot_failure_rate=True, legend_position='ax')
```
### Sideways Not Allowed (uncached)<a id="RTDSidewaysDisallowed"></a>
#### Run Time Diagram P(Solve)
```
plot_time_all(no_sideways_no_cache, "No Sideways (uncached)", plot_failure_rate=False, legend_position='ax')
```
#### Run Time Diagram - Failure Rate
```
plot_time_all(no_sideways_no_cache, "No Sideways (uncached) Failure Rate", plot_failure_rate=True, legend_position='ax')
```
#### Run Length Diagram - P(Solve)
```
plot_operations_all(no_sideways_no_cache, "No Sideways (uncached)", plot_failure_rate=False, legend_position='ax')
```
Run Length Distribution (Failure Rate)
```
plot_operations_all(no_sideways_no_cache, "No Sideways (uncached) Failure Rate", plot_failure_rate=True, legend_position='ax')
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
%matplotlib inline
plt.rcParams["figure.figsize"] = [15, 5]
no_sideways_no_cache = {
50: "no_sideways_no_cache_50.csv",
100: "no_sideways_no_cache_100.csv",
250: "no_sideways_no_cache_250.csv",
500: "no_sideways_no_cache_500.csv",
1000: "no_sideways_no_cache_1000.csv",
10000: "no_sideways_no_cache_10000.csv",
100000: "100_no_sideways_no_cache_early.csv",}
no_sideways_yes_cache = {
50: "no_sideways_cache_50.csv",
100: "no_sideways_cache_100.csv",
250: "no_sideways_cache_250.csv",
500: "no_sideways_cache_500.csv",
1000: "no_sideways_cache_1000.csv",
10000: "no_sideways_cache_10000.csv",
100000: "100_no_sideways_cache_early.csv",}
yes_sideways_no_cache = {
100000: "100_sideways_no_cache_100000.csv",
10000: "yes_sideways_no_cache_r10000.csv",
2500: "yes_sideways_no_cache_10000.csv",
1000: "yes_sideways_no_cache_1000.csv",
500: "yes_sideways_no_cache_500.csv",
250: "yes_sideways_no_cache_250.csv",
100: "yes_sideways_no_cache_100.csv",
50: "yes_sideways_no_cache_50.csv",
}
yes_sideways_yes_cache = {
100000: "100_sideways_cache_100000.csv",
10000: "yes_sideways_cache_r10000.csv",
2500: "yes_sideways_cache_10000.csv",
1000: "yes_sideways_cache_1000.csv",
500: "yes_sideways_cache_500.csv",
250: "yes_sideways_cache_250.csv",
100: "yes_sideways_cache_100.csv",
50: "yes_sideways_cache_50.csv"
}
def fill_stats_helper(d:dict, val:float, name:str):
if name not in d.keys():
d[name] = []
d[name].append(val)
def fill_statistics(filename:str, column:str, out_dict:dict, iterations:int, multiplication_factor:int=1):
df = pd.read_csv(filename)
df = df[df['Cost'] == 0]
df = df[[column]]
data = df[column].to_numpy()
data = data * multiplication_factor
fill_stats_helper(out_dict, iterations, 'iterations')
fill_stats_helper(out_dict, np.min(data), 'min')
fill_stats_helper(out_dict, np.max(data), 'max')
fill_stats_helper(out_dict, np.mean(data), 'mean')
fill_stats_helper(out_dict, np.std(data), 'std')
fill_stats_helper(out_dict, np.std(data)/np.mean(data), 'cv')
fill_stats_helper(out_dict, np.median(data), 'median')
fill_stats_helper(out_dict, np.quantile(data, 0.25), 'q0.25')
fill_stats_helper(out_dict, np.quantile(data, 0.75), 'q0.75')
fill_stats_helper(out_dict, np.quantile(data, 0.1), 'q0.1')
fill_stats_helper(out_dict, np.quantile(data, 0.9), 'q0.9')
fill_stats_helper(out_dict, np.quantile(data, 0.75)/np.quantile(data, 0.25), 'q0.75/q0.25')
fill_stats_helper(out_dict, np.quantile(data, 0.9)/np.quantile(data, 0.1), 'q0.9/q0.1')
def get_stats(the_dict):
iters = sorted(list(the_dict.keys()))
time_dict = {}
operations_dict = {}
for i in iters:
fill_statistics(the_dict[i], 'Time', time_dict, i, 1)
fill_statistics(the_dict[i], 'HeuristicQueenCalls', operations_dict, i, 54)
return pd.DataFrame(time_dict), pd.DataFrame(operations_dict)
def read_file(filename):
return pd.read_csv(filename)
def print_success_rate(d):
iters = sorted(list(d.keys()))
print("%20s %20s %20s" % ("Iterations", "Success %", "mean restarts"))
for i in iters:
filename = d[i]
df = read_file(filename)
df2 = df[df['Cost'] == 0]
success = df2.shape[0]/df.shape[0]
restarts_required = np.mean(df['Restart'].to_numpy())
print("%20d %20.3f %20.3f" % (i, success, restarts_required))
t, o = get_stats(yes_sideways_no_cache)
t
o
print_success_rate(yes_sideways_no_cache)
t, o = get_stats(no_sideways_no_cache)
t
o
print_success_rate(no_sideways_no_cache)
t, o = get_stats(yes_sideways_yes_cache)
t
o
t, o = get_stats(no_sideways_yes_cache)
t
o
def get_plottable_columns(df:pd.DataFrame,\
x_column_name:str)->tuple:
"""
Returns k - the number of items
a pandas data frame with the X and y axis
"""
k = df.shape[0] # Number of experiments
df = df[df['Cost'] == 0]
df = df[[x_column_name]]
# drop all other columns except the column that we're interested in that
# measures the number of calls, or time
df = df.sort_values(by=[x_column_name])
df = df.reset_index()
# Now add the X axis which is i/k for all i in k_prime
k_prime = df.shape[0]
x = np.array([i/k for i in range(k_prime)])
x = pd.Series(x)
df['P_Solve'] = x
return k, df
def plot_one_file(filename:str,\
ax,\
x_column_name,
legend_text,
plot_failure_rate:bool=False,
multiplication_factor:int=1):
#print(f"Reading {filename}")
df = read_file(filename)
k, df = get_plottable_columns(df, x_column_name)
y = df['P_Solve'].to_numpy()
if plot_failure_rate:
y = 1 - y
x = df[x_column_name].to_numpy()
x = x * multiplication_factor
p = ax.plot(x, y, label=legend_text)
return None
def plot_entire_run(run_dict:dict,\
x_column_name:str,
plot_type:str='regular',
plot_failure_rate:bool=False,
title:str="",
multiplication_factor:int=1,
legend_position:str='figure'):
assert(plot_type == 'regular' or plot_type == 'loglog' or plot_type == 'semilog')
assert(legend_position == 'figure' or legend_position == 'ax')
fig, ax = plt.subplots(1)
iters_list = sorted(list(run_dict.keys()))
for i in iters_list:
plot_one_file(run_dict[i], ax, x_column_name, f"iters={i}",\
plot_failure_rate, multiplication_factor)
if legend_position == 'ax':
ax.legend()
else:
fig.legend()
ax.set_title(title)
xlabel = x_column_name
if plot_type == 'loglog' or plot_type == 'semilog':
xlabel = xlabel + " (log scale)"
ax.set_xscale('log')
ax.set_xlabel(xlabel)
ylabel = "P(Solve)"
if plot_failure_rate:
ylabel = "P(Fail)"
if plot_type == 'loglog':
ylabel = ylabel + " (log scale)"
ax.set_yscale('log')
ax.set_ylabel(ylabel)
return None
def plot_entire_run_all(run_dict:dict,
x_column_name:str,
plot_failure_rate:bool=False,
title:str="",
multiplication_factor:int=1,
legend_position:str='figure'):
assert(legend_position == 'figure' or legend_position == 'ax')
fig, ax = plt.subplots(1, 3)
iters_list = sorted(list(run_dict.keys()))
for i in iters_list:
for j in range(3):
if 'figure' == legend_position:
leg_str = f"{j}-iters={i}"
else:
leg_str = f"iters={i}"
plot_one_file(run_dict[i], ax[j], x_column_name, leg_str,\
plot_failure_rate, multiplication_factor)
if legend_position == 'ax':
for j in range(3):
ax[j].legend()
else:
fig.legend()
ylabel = "P(Solve)"
if plot_failure_rate:
ylabel = "P(Fail)"
ax[0].set_title('0')
ax[1].set_title('1')
ax[2].set_title('2')
ax[0].set_xlabel(x_column_name)
ax[1].set_xlabel(x_column_name + " (log scale)")
ax[2].set_xlabel(x_column_name + " (log scale)")
ax[0].set_ylabel(ylabel)
ax[1].set_ylabel(ylabel)
ax[2].set_ylabel(f'{ylabel} (log scale)')
ax[1].set_xscale('log')
ax[2].set_xscale('log')
ax[2].set_yscale('log')
fig.suptitle(title)
def plot_operations(run_dict:dict,\
plot_type:str='regular',
title:str="",
plot_failure_rate:bool=False,
legend_position:str='ax'):
return plot_entire_run(run_dict, 'HeuristicQueenCalls',\
plot_type=plot_type, plot_failure_rate=plot_failure_rate,\
title=title,multiplication_factor=54,\
legend_position=legend_position)
def plot_time(run_dict:dict,\
plot_type:str='regular',
title:str="",
plot_failure_rate:bool=False,
legend_position:str='ax'):
return plot_entire_run(run_dict, 'Time',\
plot_type=plot_type, plot_failure_rate=plot_failure_rate,\
title=title,multiplication_factor=1,\
legend_position=legend_position)
def plot_operations_all(run_dict:dict,
title:str="",
plot_failure_rate:bool=False,
legend_position:str='ax'):
plot_entire_run_all(run_dict, 'HeuristicQueenCalls',\
plot_failure_rate=plot_failure_rate, title=title,
multiplication_factor=54,
legend_position=legend_position)
def plot_time_all(run_dict:dict,
title:str="",
plot_failure_rate:bool=False,
legend_position:str='ax'):
plot_entire_run_all(run_dict, 'Time',\
plot_failure_rate=plot_failure_rate, title=title,
multiplication_factor=1,
legend_position=legend_position)
plot_time_all(yes_sideways_no_cache, "Sideways (uncached)", plot_failure_rate=False, legend_position='ax')
plot_time_all(yes_sideways_no_cache, "Sideways (uncached) Failure Rate", plot_failure_rate=True, legend_position='ax')
plot_operations_all(yes_sideways_no_cache, "Sideways (uncached)", plot_failure_rate=False, legend_position='ax')
plot_operations_all(yes_sideways_no_cache, "Sideways (uncached) Failure Rate", plot_failure_rate=True, legend_position='ax')
plot_time_all(no_sideways_no_cache, "No Sideways (uncached)", plot_failure_rate=False, legend_position='ax')
plot_time_all(no_sideways_no_cache, "No Sideways (uncached) Failure Rate", plot_failure_rate=True, legend_position='ax')
plot_operations_all(no_sideways_no_cache, "No Sideways (uncached)", plot_failure_rate=False, legend_position='ax')
plot_operations_all(no_sideways_no_cache, "No Sideways (uncached) Failure Rate", plot_failure_rate=True, legend_position='ax')
| 0.413714 | 0.697042 |
## L1 robustness simulations
Process for generating data from a log-linear (logistic regression) model:
* Sample features $x_{ij} \sim \mathcal{N}(0, 1)$
* Sample regression coefficients $\beta_k \sim \mathcal{N}(0, 1)$ for some $k \leq j$ (that is, features $k+1, \dots, j$ will not be correlated with the labels at all)
* Calculate Bernoulli parameters: $$\pi(x_i) = \frac{1}{1 + \exp(-(\beta_0 + \sum_j \beta_j x_{ij}))}$$
* Sample labels $y_i \sim \text{Bernoulli}(\pi(x_i))$
```
import sys; sys.path.append('..')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from utilities.classify_pytorch import TorchLR
from utilities.jaccard_utilities import compute_jaccard
# simulation parameters
import simulate_loglinear as ll
# seed for random numbers
seed = 42
np.random.seed(seed)
n, p = 100, 50
train_fraction = 0.8 # fraction of data used to fit the model
uncorrelated_fraction = 0.2 # fraction of features which will be uncorrelated with the outcome
X, y, pis, is_correlated = ll.simulate_ll(n, p, uncorrelated_fraction,
seed=seed, verbose=True)
train_ixs = ll.split_train_test(n, train_fraction, seed=seed, verbose=True)
X_train, X_test = X[train_ixs], X[~train_ixs]
y_train, y_test = y[train_ixs], y[~train_ixs]
# plot Bernoulli parameter distribution
sns.set_style('whitegrid')
sns.distplot(pis, hist_kws={'edgecolor': 'black'}, kde=False, bins=10)
plt.xlim(0.0, 1.0)
plt.xlabel('$\pi(x_i)$')
plt.ylabel('Count')
plt.title('Distribution of Bernoulli parameter $\pi(x_i)$')
plt.show()
# plot label distribution
sns.countplot(y)
plt.ylabel('Count')
plt.title('Label distribution')
plt.show()
```
Now, let's test how well logistic regression can predict the outcome.
```
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=seed, penalty='l1', solver='liblinear')
clf.fit(X_train, y_train)
print('Sklearn train accuracy: {:.3f}'.format(clf.score(X_train, y_train)))
print('Sklearn test accuracy: {:.3f}'.format(clf.score(X_test, y_test)))
params_map = {
'learning_rate': [1e-2],
'batch_size': [50],
'num_epochs': [200],
'l1_penalty': [0.01]
}
torch_model = TorchLR(params_map, seed=2)
losses, preds, preds_bn = torch_model.train_torch_model(X_train, X_test, y_train, y_test, save_weights=True)
y_pred_train, y_pred_test = preds_bn
print('Torch train accuracy: {:.3f}'.format(TorchLR.calculate_accuracy(y_train, y_pred_train.flatten())))
print('Torch test accuracy: {:.3f}'.format(TorchLR.calculate_accuracy(y_test, y_pred_test.flatten())))
```
As a measurement of "how accurate is our feature selection", here we use the Jaccard (binary) similarity of the known uncorrelated features with the features that our model sets to 0. If our feature selection algorithm is mostly zeroing features that are actually uninformative, it's doing well.
```
torch_coefs = torch_model.last_weights.flatten()
close_to_zero = (np.abs(torch_coefs) < (np.abs(torch_coefs).max() / 100))
torch_coefs[close_to_zero] = 0
sk_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(clf.coef_.flatten() == 0)[0])
torch_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(torch_coefs == 0)[0])
print('Scikit coefficient Jaccard similarity: {:.3f} ({}/{})'.format(*sk_jaccard))
print('Torch coefficient Jaccard similarity: {:.3f} ({}/{})'.format(*torch_jaccard))
print(clf.coef_.flatten())
print(torch_coefs)
print(is_correlated)
```
## Experiments
We want to look at:
* Accuracy: How well can we predict the outcome from the features?
* Feature selection: How well can we predict which features are uncorrelated with the outcome?
In these experiments, we record the above for varying dataset shapes (tall, square-ish, wide) and varying numbers of features that are uncorrelated with the outcome.
```
# one tall dataset (n > p), one square dataset (n = p), one wide dataset (n < p)
dataset_sizes = {
'tall': (1000, 20),
'square': (1000, 1000),
'wide': (1000, 10000)
}
uncorr_fracs = [0.0, 0.2, 0.5, 0.8]
# just keep this constant for now, 0.8/0.2 train/test split
train_frac = 0.8
results = []
for seed in range(5):
for ds, (n, p) in dataset_sizes.items():
for uncorr_frac in uncorr_fracs:
# generate data with given parameters
X, y, _, is_correlated = ll.simulate_ll(n, p, uncorr_frac, seed=seed)
train_ixs = ll.split_train_test(n, train_frac, seed=seed)
X_train, X_test = X[train_ixs], X[~train_ixs]
y_train, y_test = y[train_ixs], y[~train_ixs]
# fit sklearn classifier
clf = LogisticRegression(random_state=seed, penalty='l1', solver='liblinear')
clf.fit(X_train, y_train)
sk_train_acc = clf.score(X_train, y_train)
sk_test_acc = clf.score(X_test, y_test)
# fit torch classifier
torch_model = TorchLR(params_map, seed=seed)
_, __, preds_bn = torch_model.train_torch_model(X_train, X_test, y_train, y_test,
save_weights=True)
torch_train_acc = TorchLR.calculate_accuracy(y_train, preds_bn[0].flatten())
torch_test_acc = TorchLR.calculate_accuracy(y_test, preds_bn[1].flatten())
# random prediction baseline
random_preds_train = (np.random.uniform(size=len(y_train)) > 0.5).astype('int')
random_preds_test = (np.random.uniform(size=len(y_test)) > 0.5).astype('int')
random_train_acc = TorchLR.calculate_accuracy(y_train, random_preds_train)
random_test_acc = TorchLR.calculate_accuracy(y_test, random_preds_test)
# calculate coefficient overlap
torch_coefs = torch_model.last_weights.flatten()
close_to_zero = (np.abs(torch_coefs) < (np.abs(torch_coefs).max() / 1000))
torch_coefs[close_to_zero] = 0
# select random coefficients to zero out as a baseline
# just select the same number of zeros as the torch coefficients for now
random_coefs = np.ones(torch_coefs.shape)
random_coefs[:np.count_nonzero(torch_coefs == 0)] = 0
np.random.shuffle(random_coefs)
sk_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(clf.coef_.flatten() == 0)[0])
torch_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(torch_coefs == 0)[0])
random_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(random_coefs == 0)[0])
results.append([seed, ds, uncorr_frac, 'sklearn', sk_train_acc, sk_test_acc, sk_jaccard[0]])
results.append([seed, ds, uncorr_frac, 'torch', torch_train_acc, torch_test_acc, torch_jaccard[0]])
results.append([seed, ds, uncorr_frac, 'random', random_train_acc, random_test_acc, random_jaccard[0]])
results_df = pd.DataFrame(results, columns=['seed', 'dataset', 'uncorr_frac', 'imp', 'train_acc', 'test_acc', 'coef_sim'])
results_df.head()
tall_df = results_df[results_df['dataset'] == 'tall']
tall_df.head(n=20)
sns.set(style='whitegrid', rc={'figure.figsize': (15, 8)})
fig, axarr = plt.subplots(2, 3)
for ix, (dataset, (n, p)) in enumerate(dataset_sizes.items()):
ax1 = axarr[0, ix]
data_df = results_df[results_df['dataset'] == dataset]
sns.set_style('whitegrid')
sns.lineplot(data=data_df, x='uncorr_frac', y='train_acc', err_style='bars', style='imp', hue='imp', ax=ax1)
ax1.set_xlabel('Fraction of uncorrelated features')
ax1.set_ylim(0.45, 1.05)
if ix == 0:
ax1.set_ylabel('Predictive accuracy on training data')
else:
ax1.set_ylabel('')
ax1.set_title('{} dataset (dimensions: n={}, p={})'.format(dataset, n, p))
ax2 = axarr[1, ix]
data_df = results_df[results_df['dataset'] == dataset]
sns.set_style('whitegrid')
sns.lineplot(data=data_df, x='uncorr_frac', y='test_acc', err_style='bars', style='imp', hue='imp', ax=ax2)
ax2.set_xlabel('Fraction of uncorrelated features')
ax2.set_ylim(0.45, 1.05)
if ix == 0:
ax2.set_ylabel('Predictive accuracy on test data')
else:
ax2.set_ylabel('')
ax2.set_title('{} dataset (dimensions: n={}, p={})'.format(dataset, n, p))
plt.tight_layout()
fig.suptitle('Accuracy vs. number of uncorrelated features on log-linear simulated data')
fig.subplots_adjust(top=0.91)
plt.show()
sns.set(style='whitegrid', rc={'figure.figsize': (15, 4)})
fig, axarr = plt.subplots(1, 3)
for ix, (dataset, (n, p)) in enumerate(dataset_sizes.items()):
ax = axarr[ix]
data_df = results_df[results_df['dataset'] == dataset]
sns.set_style('whitegrid')
sns.lineplot(data=data_df, x='uncorr_frac', y='coef_sim', err_style='bars', style='imp', hue='imp', ax=ax)
ax.set_xlabel('Fraction of uncorrelated features')
if ix == 0:
ax.set_ylabel('Jaccard similarity of 0 coefficients')
else:
ax.set_ylabel('')
ax.set_title('{} dataset (dimensions: n={}, p={})'.format(dataset, n, p))
fig.suptitle('Coefficient similarity vs. number of uncorrelated features on log-linear simulated data')
plt.tight_layout()
fig.subplots_adjust(top=0.825)
plt.show()
```
We also want to test if adding collinearity makes it harder to find the features that are truly correlated with the outcome. It seems like this should be trivially true, since it should be impossible for the model to tell which features are just duplicates (or linear combinations) of the other features.
Here, we just duplicate a subset of the features - later we could test scaling them in different ways, etc.
```
# same parameters as earlier experiments, but also vary number of duplicated features
dataset_sizes = {
'tall': (1000, 20),
'square': (1000, 1000),
'wide': (1000, 10000)
}
uncorr_fracs = [0.0, 0.2, 0.5, 0.8]
train_frac = 0.8
results = []
duplicate_fracs = [0.0, 0.1, 0.2, 0.5, 1.0]
for seed in range(5):
for ds, (n, p) in dataset_sizes.items():
for dup_frac in duplicate_fracs:
num_duplicates = int(p * dup_frac)
for uncorr_frac in uncorr_fracs:
# generate data with given parameters
X, y, _, is_correlated = ll.simulate_ll(n, p, uncorr_frac,
duplicate_features=num_duplicates,
seed=seed)
train_ixs = ll.split_train_test(n, train_frac, seed=seed)
X_train, X_test = X[train_ixs], X[~train_ixs]
y_train, y_test = y[train_ixs], y[~train_ixs]
# fit sklearn classifier
clf = LogisticRegression(random_state=seed, penalty='l1', solver='liblinear')
clf.fit(X_train, y_train)
sk_train_acc = clf.score(X_train, y_train)
sk_test_acc = clf.score(X_test, y_test)
# fit torch classifier
torch_model = TorchLR(params_map, seed=seed)
_, __, preds_bn = torch_model.train_torch_model(X_train, X_test, y_train, y_test,
save_weights=True)
torch_train_acc = TorchLR.calculate_accuracy(y_train, preds_bn[0].flatten())
torch_test_acc = TorchLR.calculate_accuracy(y_test, preds_bn[1].flatten())
# random prediction baseline
random_preds_train = (np.random.uniform(size=len(y_train)) > 0.5).astype('int')
random_preds_test = (np.random.uniform(size=len(y_test)) > 0.5).astype('int')
random_train_acc = TorchLR.calculate_accuracy(y_train, random_preds_train)
random_test_acc = TorchLR.calculate_accuracy(y_test, random_preds_test)
# calculate coefficient overlap
torch_coefs = torch_model.last_weights.flatten()
close_to_zero = (np.abs(torch_coefs) < (np.abs(torch_coefs).max() / 1000))
torch_coefs[close_to_zero] = 0
# select random coefficients to zero out as a baseline
# just select the same number of zeros as the torch coefficients for now
random_coefs = np.ones(torch_coefs.shape)
random_coefs[:np.count_nonzero(torch_coefs == 0)] = 0
np.random.shuffle(random_coefs)
sk_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(clf.coef_.flatten() == 0)[0])
torch_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(torch_coefs == 0)[0])
random_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(random_coefs == 0)[0])
results.append([seed, ds, uncorr_frac, num_duplicates, 'sklearn', sk_train_acc, sk_test_acc, sk_jaccard[0]])
results.append([seed, ds, uncorr_frac, num_duplicates, 'torch', torch_train_acc, torch_test_acc, torch_jaccard[0]])
results.append([seed, ds, uncorr_frac, num_duplicates, 'random', random_train_acc, random_test_acc, random_jaccard[0]])
results_df = pd.DataFrame(results, columns=['seed', 'dataset', 'uncorr_frac', 'num_duplicates',
'imp', 'train_acc', 'test_acc', 'coef_sim'])
results_df.head()
sns.set(style='whitegrid', rc={'figure.figsize': (15, 20)})
fig, axarr = plt.subplots(5, 3)
duplicate_fracs = [0.0, 0.1, 0.2, 0.5, 1.0]
for ix1, dup_frac in enumerate(duplicate_fracs):
for ix2, (dataset, (n, p)) in enumerate(dataset_sizes.items()):
ax = axarr[ix1, ix2]
num_dups = int(p * dup_frac)
data_df = results_df[(results_df['num_duplicates'] == num_dups) &
(results_df['dataset'] == dataset)]
sns.set_style('whitegrid')
sns.lineplot(data=data_df, x='uncorr_frac', y='coef_sim', err_style='bars', style='imp', hue='imp', ax=ax)
ax.set_xlabel('Fraction of uncorrelated features')
if ix2 == 0:
ax.set_ylabel('Jaccard similarity of 0 coefficients')
else:
ax.set_ylabel('')
ax.set_ylim(-0.05, 1.05)
ax.set_title('{} (dimensions: n={}, p={}), {} duplicates'.format(dataset, n, p, num_dups))
fig.suptitle('Coefficient similarity vs. number of uncorrelated features on log-linear simulated data, '
'with added duplicate features')
plt.tight_layout()
fig.subplots_adjust(top=0.95)
plt.show()
```
The takeaway here is that adding more duplicate features to the model brings the Jaccard similarity of 0 coefficients closer to the random model (this is obvious in theory, but is a useful sanity check that our simulation code is doing what we want it to do).
|
github_jupyter
|
import sys; sys.path.append('..')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from utilities.classify_pytorch import TorchLR
from utilities.jaccard_utilities import compute_jaccard
# simulation parameters
import simulate_loglinear as ll
# seed for random numbers
seed = 42
np.random.seed(seed)
n, p = 100, 50
train_fraction = 0.8 # fraction of data used to fit the model
uncorrelated_fraction = 0.2 # fraction of features which will be uncorrelated with the outcome
X, y, pis, is_correlated = ll.simulate_ll(n, p, uncorrelated_fraction,
seed=seed, verbose=True)
train_ixs = ll.split_train_test(n, train_fraction, seed=seed, verbose=True)
X_train, X_test = X[train_ixs], X[~train_ixs]
y_train, y_test = y[train_ixs], y[~train_ixs]
# plot Bernoulli parameter distribution
sns.set_style('whitegrid')
sns.distplot(pis, hist_kws={'edgecolor': 'black'}, kde=False, bins=10)
plt.xlim(0.0, 1.0)
plt.xlabel('$\pi(x_i)$')
plt.ylabel('Count')
plt.title('Distribution of Bernoulli parameter $\pi(x_i)$')
plt.show()
# plot label distribution
sns.countplot(y)
plt.ylabel('Count')
plt.title('Label distribution')
plt.show()
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=seed, penalty='l1', solver='liblinear')
clf.fit(X_train, y_train)
print('Sklearn train accuracy: {:.3f}'.format(clf.score(X_train, y_train)))
print('Sklearn test accuracy: {:.3f}'.format(clf.score(X_test, y_test)))
params_map = {
'learning_rate': [1e-2],
'batch_size': [50],
'num_epochs': [200],
'l1_penalty': [0.01]
}
torch_model = TorchLR(params_map, seed=2)
losses, preds, preds_bn = torch_model.train_torch_model(X_train, X_test, y_train, y_test, save_weights=True)
y_pred_train, y_pred_test = preds_bn
print('Torch train accuracy: {:.3f}'.format(TorchLR.calculate_accuracy(y_train, y_pred_train.flatten())))
print('Torch test accuracy: {:.3f}'.format(TorchLR.calculate_accuracy(y_test, y_pred_test.flatten())))
torch_coefs = torch_model.last_weights.flatten()
close_to_zero = (np.abs(torch_coefs) < (np.abs(torch_coefs).max() / 100))
torch_coefs[close_to_zero] = 0
sk_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(clf.coef_.flatten() == 0)[0])
torch_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(torch_coefs == 0)[0])
print('Scikit coefficient Jaccard similarity: {:.3f} ({}/{})'.format(*sk_jaccard))
print('Torch coefficient Jaccard similarity: {:.3f} ({}/{})'.format(*torch_jaccard))
print(clf.coef_.flatten())
print(torch_coefs)
print(is_correlated)
# one tall dataset (n > p), one square dataset (n = p), one wide dataset (n < p)
dataset_sizes = {
'tall': (1000, 20),
'square': (1000, 1000),
'wide': (1000, 10000)
}
uncorr_fracs = [0.0, 0.2, 0.5, 0.8]
# just keep this constant for now, 0.8/0.2 train/test split
train_frac = 0.8
results = []
for seed in range(5):
for ds, (n, p) in dataset_sizes.items():
for uncorr_frac in uncorr_fracs:
# generate data with given parameters
X, y, _, is_correlated = ll.simulate_ll(n, p, uncorr_frac, seed=seed)
train_ixs = ll.split_train_test(n, train_frac, seed=seed)
X_train, X_test = X[train_ixs], X[~train_ixs]
y_train, y_test = y[train_ixs], y[~train_ixs]
# fit sklearn classifier
clf = LogisticRegression(random_state=seed, penalty='l1', solver='liblinear')
clf.fit(X_train, y_train)
sk_train_acc = clf.score(X_train, y_train)
sk_test_acc = clf.score(X_test, y_test)
# fit torch classifier
torch_model = TorchLR(params_map, seed=seed)
_, __, preds_bn = torch_model.train_torch_model(X_train, X_test, y_train, y_test,
save_weights=True)
torch_train_acc = TorchLR.calculate_accuracy(y_train, preds_bn[0].flatten())
torch_test_acc = TorchLR.calculate_accuracy(y_test, preds_bn[1].flatten())
# random prediction baseline
random_preds_train = (np.random.uniform(size=len(y_train)) > 0.5).astype('int')
random_preds_test = (np.random.uniform(size=len(y_test)) > 0.5).astype('int')
random_train_acc = TorchLR.calculate_accuracy(y_train, random_preds_train)
random_test_acc = TorchLR.calculate_accuracy(y_test, random_preds_test)
# calculate coefficient overlap
torch_coefs = torch_model.last_weights.flatten()
close_to_zero = (np.abs(torch_coefs) < (np.abs(torch_coefs).max() / 1000))
torch_coefs[close_to_zero] = 0
# select random coefficients to zero out as a baseline
# just select the same number of zeros as the torch coefficients for now
random_coefs = np.ones(torch_coefs.shape)
random_coefs[:np.count_nonzero(torch_coefs == 0)] = 0
np.random.shuffle(random_coefs)
sk_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(clf.coef_.flatten() == 0)[0])
torch_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(torch_coefs == 0)[0])
random_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(random_coefs == 0)[0])
results.append([seed, ds, uncorr_frac, 'sklearn', sk_train_acc, sk_test_acc, sk_jaccard[0]])
results.append([seed, ds, uncorr_frac, 'torch', torch_train_acc, torch_test_acc, torch_jaccard[0]])
results.append([seed, ds, uncorr_frac, 'random', random_train_acc, random_test_acc, random_jaccard[0]])
results_df = pd.DataFrame(results, columns=['seed', 'dataset', 'uncorr_frac', 'imp', 'train_acc', 'test_acc', 'coef_sim'])
results_df.head()
tall_df = results_df[results_df['dataset'] == 'tall']
tall_df.head(n=20)
sns.set(style='whitegrid', rc={'figure.figsize': (15, 8)})
fig, axarr = plt.subplots(2, 3)
for ix, (dataset, (n, p)) in enumerate(dataset_sizes.items()):
ax1 = axarr[0, ix]
data_df = results_df[results_df['dataset'] == dataset]
sns.set_style('whitegrid')
sns.lineplot(data=data_df, x='uncorr_frac', y='train_acc', err_style='bars', style='imp', hue='imp', ax=ax1)
ax1.set_xlabel('Fraction of uncorrelated features')
ax1.set_ylim(0.45, 1.05)
if ix == 0:
ax1.set_ylabel('Predictive accuracy on training data')
else:
ax1.set_ylabel('')
ax1.set_title('{} dataset (dimensions: n={}, p={})'.format(dataset, n, p))
ax2 = axarr[1, ix]
data_df = results_df[results_df['dataset'] == dataset]
sns.set_style('whitegrid')
sns.lineplot(data=data_df, x='uncorr_frac', y='test_acc', err_style='bars', style='imp', hue='imp', ax=ax2)
ax2.set_xlabel('Fraction of uncorrelated features')
ax2.set_ylim(0.45, 1.05)
if ix == 0:
ax2.set_ylabel('Predictive accuracy on test data')
else:
ax2.set_ylabel('')
ax2.set_title('{} dataset (dimensions: n={}, p={})'.format(dataset, n, p))
plt.tight_layout()
fig.suptitle('Accuracy vs. number of uncorrelated features on log-linear simulated data')
fig.subplots_adjust(top=0.91)
plt.show()
sns.set(style='whitegrid', rc={'figure.figsize': (15, 4)})
fig, axarr = plt.subplots(1, 3)
for ix, (dataset, (n, p)) in enumerate(dataset_sizes.items()):
ax = axarr[ix]
data_df = results_df[results_df['dataset'] == dataset]
sns.set_style('whitegrid')
sns.lineplot(data=data_df, x='uncorr_frac', y='coef_sim', err_style='bars', style='imp', hue='imp', ax=ax)
ax.set_xlabel('Fraction of uncorrelated features')
if ix == 0:
ax.set_ylabel('Jaccard similarity of 0 coefficients')
else:
ax.set_ylabel('')
ax.set_title('{} dataset (dimensions: n={}, p={})'.format(dataset, n, p))
fig.suptitle('Coefficient similarity vs. number of uncorrelated features on log-linear simulated data')
plt.tight_layout()
fig.subplots_adjust(top=0.825)
plt.show()
# same parameters as earlier experiments, but also vary number of duplicated features
dataset_sizes = {
'tall': (1000, 20),
'square': (1000, 1000),
'wide': (1000, 10000)
}
uncorr_fracs = [0.0, 0.2, 0.5, 0.8]
train_frac = 0.8
results = []
duplicate_fracs = [0.0, 0.1, 0.2, 0.5, 1.0]
for seed in range(5):
for ds, (n, p) in dataset_sizes.items():
for dup_frac in duplicate_fracs:
num_duplicates = int(p * dup_frac)
for uncorr_frac in uncorr_fracs:
# generate data with given parameters
X, y, _, is_correlated = ll.simulate_ll(n, p, uncorr_frac,
duplicate_features=num_duplicates,
seed=seed)
train_ixs = ll.split_train_test(n, train_frac, seed=seed)
X_train, X_test = X[train_ixs], X[~train_ixs]
y_train, y_test = y[train_ixs], y[~train_ixs]
# fit sklearn classifier
clf = LogisticRegression(random_state=seed, penalty='l1', solver='liblinear')
clf.fit(X_train, y_train)
sk_train_acc = clf.score(X_train, y_train)
sk_test_acc = clf.score(X_test, y_test)
# fit torch classifier
torch_model = TorchLR(params_map, seed=seed)
_, __, preds_bn = torch_model.train_torch_model(X_train, X_test, y_train, y_test,
save_weights=True)
torch_train_acc = TorchLR.calculate_accuracy(y_train, preds_bn[0].flatten())
torch_test_acc = TorchLR.calculate_accuracy(y_test, preds_bn[1].flatten())
# random prediction baseline
random_preds_train = (np.random.uniform(size=len(y_train)) > 0.5).astype('int')
random_preds_test = (np.random.uniform(size=len(y_test)) > 0.5).astype('int')
random_train_acc = TorchLR.calculate_accuracy(y_train, random_preds_train)
random_test_acc = TorchLR.calculate_accuracy(y_test, random_preds_test)
# calculate coefficient overlap
torch_coefs = torch_model.last_weights.flatten()
close_to_zero = (np.abs(torch_coefs) < (np.abs(torch_coefs).max() / 1000))
torch_coefs[close_to_zero] = 0
# select random coefficients to zero out as a baseline
# just select the same number of zeros as the torch coefficients for now
random_coefs = np.ones(torch_coefs.shape)
random_coefs[:np.count_nonzero(torch_coefs == 0)] = 0
np.random.shuffle(random_coefs)
sk_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(clf.coef_.flatten() == 0)[0])
torch_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(torch_coefs == 0)[0])
random_jaccard = compute_jaccard(np.where(~is_correlated)[0], np.where(random_coefs == 0)[0])
results.append([seed, ds, uncorr_frac, num_duplicates, 'sklearn', sk_train_acc, sk_test_acc, sk_jaccard[0]])
results.append([seed, ds, uncorr_frac, num_duplicates, 'torch', torch_train_acc, torch_test_acc, torch_jaccard[0]])
results.append([seed, ds, uncorr_frac, num_duplicates, 'random', random_train_acc, random_test_acc, random_jaccard[0]])
results_df = pd.DataFrame(results, columns=['seed', 'dataset', 'uncorr_frac', 'num_duplicates',
'imp', 'train_acc', 'test_acc', 'coef_sim'])
results_df.head()
sns.set(style='whitegrid', rc={'figure.figsize': (15, 20)})
fig, axarr = plt.subplots(5, 3)
duplicate_fracs = [0.0, 0.1, 0.2, 0.5, 1.0]
for ix1, dup_frac in enumerate(duplicate_fracs):
for ix2, (dataset, (n, p)) in enumerate(dataset_sizes.items()):
ax = axarr[ix1, ix2]
num_dups = int(p * dup_frac)
data_df = results_df[(results_df['num_duplicates'] == num_dups) &
(results_df['dataset'] == dataset)]
sns.set_style('whitegrid')
sns.lineplot(data=data_df, x='uncorr_frac', y='coef_sim', err_style='bars', style='imp', hue='imp', ax=ax)
ax.set_xlabel('Fraction of uncorrelated features')
if ix2 == 0:
ax.set_ylabel('Jaccard similarity of 0 coefficients')
else:
ax.set_ylabel('')
ax.set_ylim(-0.05, 1.05)
ax.set_title('{} (dimensions: n={}, p={}), {} duplicates'.format(dataset, n, p, num_dups))
fig.suptitle('Coefficient similarity vs. number of uncorrelated features on log-linear simulated data, '
'with added duplicate features')
plt.tight_layout()
fig.subplots_adjust(top=0.95)
plt.show()
| 0.521471 | 0.949106 |
# Scraping Job Postings from LinkedIn
```
#Import packages
import time, os
import pandas as pd
from selenium import webdriver
from selenium.webdriver.common.keys import Keys
from selenium.webdriver.support.ui import Select
from bs4 import BeautifulSoup as bs
import requests
import re
import pickle
#Hide Warnings
import warnings
warnings.filterwarnings('ignore')
chromedriver = "/Applications/chromedriver"
os.environ["webdriver.chrome.driver"] = chromedriver
driver = webdriver.Chrome(chromedriver)
source = 'https://www.linkedin.com/jobs'
driver.get(source)
# Get Location to Rancho Cordova
location_box_clear = driver.find_element_by_xpath('//*[@id="JOBS"]/section[2]/button')
location_box_clear.click()
location_box = driver.find_element_by_xpath('//*[@id="JOBS"]/section[2]/input')
location_box.click()
location_box.send_keys("Rancho Cordova, California, United States")
location_box.send_keys(Keys.RETURN)
# past two weeks
time_dropdown = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[1]/div/div/button')
time_dropdown.click()
past_month_button = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[1]/div/div/div/fieldset/div/div[3]/label')
past_month_button.click()
time_done_button = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[1]/div/div/div/button')
time_done_button.click()
# pause in action or linkedin will jump to sign in page
time.sleep(5)
# within 10 miles
distance_dropdown = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[2]/div/div/button')
distance_dropdown.click()
filter_10mi = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[2]/div/div/div/fieldset/div/div[1]/label')
filter_10mi.click()
distance_done_button = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[2]/div/div/div/button')
distance_done_button.click()
## Can specify these later, but for now we'll scrape the first 1000 jobs within 25 miles of RC
# Company
# Salary
# Location
# Job Type
# Experience Level
# On-site/Remote
#How many jobs are curently available within 10 miles of Rancho Cordova on LinkedIn
no_of_jobs = driver.find_element_by_css_selector('h1>span').get_attribute('innerText')
print('There are', no_of_jobs, 'jobs available within 10 miles of Rancho Cordova on LinkedIn over the past month.')
#Browse all jobs for the search.
# Set pause time
SCROLL_PAUSE_TIME = 10
last_height = driver.execute_script("return document.body.scrollHeight")
while True:
#Scroll until hit the see more jobs button.
driver.execute_script('window.scrollTo(0, document.body.scrollHeight);')
# Wait to load page
time.sleep(SCROLL_PAUSE_TIME)
try:
#Click the see more jobs button and then keep scrolling.
driver.find_element_by_xpath('//*[@id="main-content"]/section/button').click()
time.sleep(15)
print("clicked loading button")
except:
pass
time.sleep(15)
print("no loading button")
# Calculate new scroll height and compare with last scroll height
new_height = driver.execute_script("return document.body.scrollHeight")
# Wait to load page
time.sleep(SCROLL_PAUSE_TIME)
# Stop the scrolling and button clicking if the page isn't loading more jobs
if new_height == last_height:
break
last_height = new_height
# No more loading with clicking on the button on the webdriver
##### Create a list of all jobs in the search.
#Create a list of the jobs.
job_lists = driver.find_element_by_class_name('jobs-search__results-list')
jobs = job_lists.find_elements_by_tag_name('li')
#Test that it collected all jobs.
#If it significantly dropped, the sleep.time time may need to be increased to allow:
#More loading time or
#Not set off restrictions for the site.
print(len(jobs), 'were collected from the search')
# It seems like LinkedIn only lets you get to that amount of job listings (same number as previous cohort)
# Another option is adding more filter for the search
#Pull basic information from each job.
job_title = []
company_name = []
date = []
job_link = []
for job in jobs:
job_title0 = job.find_element_by_css_selector('h3').get_attribute('innerText')
job_title.append(job_title0)
company_name0 = job.find_element_by_css_selector('h4').get_attribute('innerText')
company_name.append(company_name0)
date0 = job.find_element_by_css_selector('div>div>time').get_attribute('datetime')
date.append(date0)
job_link0 = job.find_element_by_css_selector('a').get_attribute('href')
job_link.append(job_link0)
#See first 5 of each for verification.
print('Job Titles:',job_title[:5])
print(' ')
print('Company Names:',company_name[:5])
print(' ')
print('Date:', date[:5])
# Verify that all lists are the same length.
print(len(job_title))
print(len(company_name))
print(len(date))
print(len(job_link))
# print(len(cl))
# print(len(jd))
# Create and save a dataframe of the collected data.
job_post_data = pd.DataFrame({'Date': date,
'Company': company_name,
'Title': job_title,
'Job Link': job_link})
job_post_data.head()
len(job_post_data)
job_post_data.to_csv('LinkedIn_Job_Postings.csv', index = False)
```
|
github_jupyter
|
#Import packages
import time, os
import pandas as pd
from selenium import webdriver
from selenium.webdriver.common.keys import Keys
from selenium.webdriver.support.ui import Select
from bs4 import BeautifulSoup as bs
import requests
import re
import pickle
#Hide Warnings
import warnings
warnings.filterwarnings('ignore')
chromedriver = "/Applications/chromedriver"
os.environ["webdriver.chrome.driver"] = chromedriver
driver = webdriver.Chrome(chromedriver)
source = 'https://www.linkedin.com/jobs'
driver.get(source)
# Get Location to Rancho Cordova
location_box_clear = driver.find_element_by_xpath('//*[@id="JOBS"]/section[2]/button')
location_box_clear.click()
location_box = driver.find_element_by_xpath('//*[@id="JOBS"]/section[2]/input')
location_box.click()
location_box.send_keys("Rancho Cordova, California, United States")
location_box.send_keys(Keys.RETURN)
# past two weeks
time_dropdown = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[1]/div/div/button')
time_dropdown.click()
past_month_button = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[1]/div/div/div/fieldset/div/div[3]/label')
past_month_button.click()
time_done_button = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[1]/div/div/div/button')
time_done_button.click()
# pause in action or linkedin will jump to sign in page
time.sleep(5)
# within 10 miles
distance_dropdown = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[2]/div/div/button')
distance_dropdown.click()
filter_10mi = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[2]/div/div/div/fieldset/div/div[1]/label')
filter_10mi.click()
distance_done_button = driver.find_element_by_xpath('//*[@id="jserp-filters"]/ul/li[2]/div/div/div/button')
distance_done_button.click()
## Can specify these later, but for now we'll scrape the first 1000 jobs within 25 miles of RC
# Company
# Salary
# Location
# Job Type
# Experience Level
# On-site/Remote
#How many jobs are curently available within 10 miles of Rancho Cordova on LinkedIn
no_of_jobs = driver.find_element_by_css_selector('h1>span').get_attribute('innerText')
print('There are', no_of_jobs, 'jobs available within 10 miles of Rancho Cordova on LinkedIn over the past month.')
#Browse all jobs for the search.
# Set pause time
SCROLL_PAUSE_TIME = 10
last_height = driver.execute_script("return document.body.scrollHeight")
while True:
#Scroll until hit the see more jobs button.
driver.execute_script('window.scrollTo(0, document.body.scrollHeight);')
# Wait to load page
time.sleep(SCROLL_PAUSE_TIME)
try:
#Click the see more jobs button and then keep scrolling.
driver.find_element_by_xpath('//*[@id="main-content"]/section/button').click()
time.sleep(15)
print("clicked loading button")
except:
pass
time.sleep(15)
print("no loading button")
# Calculate new scroll height and compare with last scroll height
new_height = driver.execute_script("return document.body.scrollHeight")
# Wait to load page
time.sleep(SCROLL_PAUSE_TIME)
# Stop the scrolling and button clicking if the page isn't loading more jobs
if new_height == last_height:
break
last_height = new_height
# No more loading with clicking on the button on the webdriver
##### Create a list of all jobs in the search.
#Create a list of the jobs.
job_lists = driver.find_element_by_class_name('jobs-search__results-list')
jobs = job_lists.find_elements_by_tag_name('li')
#Test that it collected all jobs.
#If it significantly dropped, the sleep.time time may need to be increased to allow:
#More loading time or
#Not set off restrictions for the site.
print(len(jobs), 'were collected from the search')
# It seems like LinkedIn only lets you get to that amount of job listings (same number as previous cohort)
# Another option is adding more filter for the search
#Pull basic information from each job.
job_title = []
company_name = []
date = []
job_link = []
for job in jobs:
job_title0 = job.find_element_by_css_selector('h3').get_attribute('innerText')
job_title.append(job_title0)
company_name0 = job.find_element_by_css_selector('h4').get_attribute('innerText')
company_name.append(company_name0)
date0 = job.find_element_by_css_selector('div>div>time').get_attribute('datetime')
date.append(date0)
job_link0 = job.find_element_by_css_selector('a').get_attribute('href')
job_link.append(job_link0)
#See first 5 of each for verification.
print('Job Titles:',job_title[:5])
print(' ')
print('Company Names:',company_name[:5])
print(' ')
print('Date:', date[:5])
# Verify that all lists are the same length.
print(len(job_title))
print(len(company_name))
print(len(date))
print(len(job_link))
# print(len(cl))
# print(len(jd))
# Create and save a dataframe of the collected data.
job_post_data = pd.DataFrame({'Date': date,
'Company': company_name,
'Title': job_title,
'Job Link': job_link})
job_post_data.head()
len(job_post_data)
job_post_data.to_csv('LinkedIn_Job_Postings.csv', index = False)
| 0.167151 | 0.213951 |
# 2-4.2 Intro Python
## Working with Files
4.1 File import in Jupyter Notebooks
4.1 File **`open()`** and **`.read()`**
4.2 **File Read as a list with `.readlines()`**
4.2 **File Closing to free resources with `.close()`**
4.3 Remove characters using **`.strip()`**
4.3 File Read a line at a time with **`.readline()`**
4.4 File **`.write()`** with **`.seek()`**
4.4 File append mode
-----
><font size="5" color="#00A0B2" face="verdana"> <B>Student will be able to</B></font>
4.1 Import files in Jupyter Notebooks using the curl command
4.1 **`open()`** and **`.read()`** local files in memory
4.1 **`.read(`)** a specific number of characters
4.2 **Use `.readlines()` to read text from files as a list of lines**
4.2 **Use `.close` to free system resources**
4.3 Use **`.readline()`** to read data from file a line at a time
4.3 Use **`.strip()`** to remove new line characters
4.4 **`.write()`** data to a new local file
4.4 Use **`.seek()`** to set file read or write location
4.4 Use file append mode
#
<font size="6" color="#00A0B2" face="verdana"> <B>Concepts</B></font>
## `.readlines()`
[]( http://edxinteractivepage.blob.core.windows.net/edxpages/f7cff1a7-5601-48a1-95a6-fd1fdfabd20e.html?details=[{"src":"http://jupyternootbookwams.streaming.mediaservices.windows.net/0cd43d02-5eac-40b5-ba2d-97f078415ddd/Unit2_Section4.2a-Readlines-Open_Text_as_List.ism/manifest","type":"application/vnd.ms-sstr+xml"}],[{"src":"http://jupyternootbookwams.streaming.mediaservices.windows.net/0cd43d02-5eac-40b5-ba2d-97f078415ddd/Unit2_Section4.2a-Readlines-Open_Text_as_List.vtt","srclang":"en","kind":"subtitles","label":"english"}])
### File read as a list with .readlines()
converts the lines of a file into a **list** of strings
```python
poem_lines = poem1.readlines()
```
#
<font size="6" color="#00A0B2" face="verdana"> <B>Examples</B></font>
```
# [ ] Run to download file to notebook
!curl https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/poem1.txt -o poem1.txt
# [ ] review and run example
# open address to file
poem1 = open('poem1.txt', 'r')
# readlines and print as a list
poem_lines = poem1.readlines()
poem_lines
# [ ] review and run example
for line in poem_lines:
print(line)
```
#
<font size="6" color="#B24C00" face="verdana"> <B>Task 1</B></font>
## `.readlines()`
### open the cities file as a list
1. **Import a list of cities using curl**
a. git the list from https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/cities
b. name the list cities.txt
2. **Open cities.txt in read mode using a variable: cities_file**
3. **Read cities_file as a list variable: cities_lines using `.readlines()`**
4. **Print each line of cities_lines by iterating the list**
```
# [ ] import cities
!curl https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/cities -o cities.txt
# [ ] open cities.txt as cities_file and read the file as a list: cities_lines
cities_file = open('cities.txt', 'r')
cities_lines = cities_file.readlines()
cities_lines
# [ ] use list iteration to print each city in cities_lines list
for line in cities_lines:
print(line)
```
#
<font size="6" color="#00A0B2" face="verdana"> <B>Concepts</B></font>
## working with lists from .readlines()
[]( http://edxinteractivepage.blob.core.windows.net/edxpages/f7cff1a7-5601-48a1-95a6-fd1fdfabd20e.html?details=[{"src":"http://jupyternootbookwams.streaming.mediaservices.windows.net/ed9b1523-6d69-462c-b18c-01e5423c1e52/Unit2_Section4.2b-Readlines-Remove_Characters.ism/manifest","type":"application/vnd.ms-sstr+xml"}],[{"src":"http://jupyternootbookwams.streaming.mediaservices.windows.net/ed9b1523-6d69-462c-b18c-01e5423c1e52/Unit2_Section4.2b-Readlines-Remove_Characters.vtt","srclang":"en","kind":"subtitles","label":"english"}])
### remove newline characters from lists created using .readlines()
```python
for line in poem_lines:
poem_lines[count] = line[:-1]
count += 1
```
**`line[:-1]`** sets the end point at the last character of the string, the result is the **`'\n'`** (newline) character is omitted
| list item | list item contents |
|-----|-----|
| poem_lines[0] | 'Loops I repeat\n' |
| poem_lines[1] | 'loops\n' |
| poem_lines[2] | 'loops\n' |
| poem_lines[3] | 'I repeat\n' |
|... | ... |
###
<font size="6" color="#00A0B2" face="verdana"> <B>Examples</B></font>
This example assumes that poem1.txt has been imported in 1st example above
```
# [ ] review and run examples
# [ ] re-open file and read file as a list of strings
poem1 = open('poem1.txt', 'r')
poem_lines = poem1.readlines()
print(poem_lines)
# [ ] print each list item
for line in poem_lines:
print(line)
# [ ] remove the last character of each list item, which is "\n"
count = 0
for line in poem_lines:
poem_lines[count] = line[:-1]
count += 1
print(poem_lines)
# [ ] print each list item
for line in poem_lines:
print(line)
```
#
<font size="6" color="#B24C00" face="verdana"> <B>Task 2</B></font>
## remove newline characters from cities lists created using .readlines()
- This task assumes that cites.txt has been imported in Task 1 above
- In task 1, the cities were printed with a blank line between each city - this task removes the blank lines
```
# [ ] re-open file and read file as a list of strings
# [ ] open cities.txt as cities_file and read the file as a list: cities_lines
# [ ] open cities.txt as cities_file and read the file as a list: cities_lines
cities_file = open('cities.txt', 'r')
cities_lines = cities_file.readlines()
cities_lines
# [ ] remove the last character, "\n", of each cities_lines list item
# [ ] open cities.txt as cities_file and read the file as a list: cities_lines
cities_file = open('cities.txt', 'r')
cities_lines = cities_file.readlines()
cities_lines
count = 0
for line in cities_lines:
cities_lines[count] = line[:-1]
count += 1
print(cities_lines)
# [ ] print each list item in cities_lines
for line in cities_lines:
print(line)
```
#
<font size="6" color="#00A0B2" face="verdana"> <B>Concepts</B></font>
## `.close()`
[]( http://edxinteractivepage.blob.core.windows.net/edxpages/f7cff1a7-5601-48a1-95a6-fd1fdfabd20e.html?details=[{"src":"http://jupyternootbookwams.streaming.mediaservices.windows.net/50a925e8-25e2-4bfa-936b-e2d181af36f0/Unit2_Section4.2c-File_Close_Method.ism/manifest","type":"application/vnd.ms-sstr+xml"}],[{"src":"http://jupyternootbookwams.streaming.mediaservices.windows.net/50a925e8-25e2-4bfa-936b-e2d181af36f0/Unit2_Section4.2c-File_Close_Method.vtt","srclang":"en","kind":"subtitles","label":"english"}])
### File .close() method frees resources
flie.close() method removes the reference created from file open() function
```python
poem1.close()
```
#
<font size="6" color="#00A0B2" face="verdana"> <B>Examples</B></font>
This example assumes that poem1.txt has been imported in 1st example above
```
# [ ] review and run example: open and readlines of poem1.txt
poem1 = open('poem1.txt', 'r')
# [ ] review and run example: readlines breaks if file is no longer open
poem_lines = poem1.readlines()
print(poem_lines)
# [ ] review and run example: Close poem1
poem1.close()
```
#
<font size="6" color="#B24C00" face="verdana"> <B>Task 3</B></font>
## File .close()
write each item in it's own cell
- open cities.txt as cities_file
- read the lines as cities_lines
- print the cities that **start with the letter "D" or greater**
- close cities_file
- test that file is closed
```
# [ ] open cities.txt as cities_file
cities_file = open('cities.txt', 'r')
# [ ] read the lines as cities_lines
cities_lines = cities_file.readlines()
# [ ] print the cities that start with the letter "D" or greater
for line in cities_lines:
if line[0] >= "D":
print(line)
# [ ] test that file is closed
cities_file.closed
# [ ] close cities_file
cities_file.close()
```
#
<font size="6" color="#B24C00" face="verdana"> <B>Task 4</B></font>
## readlines() poem2
write each item in its own cell
- import https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/poem2.txt as poem2.txt
- open poem2.txt as poem2_file in read mode
- create a list of strings, called poem2_lines, from each line of poem2_text (use **.readlines()**)
- remove the newline character for each list item in poem2_lines
- print the poem2 lines in reverse order
```
# [ ] import https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/poem2.txt as poem2.txt
!curl https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/poem2.txt -o poem2.txt
# [ ] open poem2.txt as poem2_text in read mode
poem2_text = open('poem2.txt', 'r')
poem2_text
# [ ] create a list of strings, called poem2_lines, from each line of poem2_text
poem2_text = open('poem2.txt', 'r')
poem2_lines = poem2_text.readlines()
print(poem2_lines)
# [ ] remove the newline character for each list item in poem2_lines
count = 0
for line in poem2_lines:
poem2_lines[count] = line[:-1]
count += 1
print(poem2_lines)
# [ ] print the poem2 lines in reverse order
poem2_lines.reverse()
print(poem2_lines)
```
[Terms of use](http://go.microsoft.com/fwlink/?LinkID=206977) [Privacy & cookies](https://go.microsoft.com/fwlink/?LinkId=521839) © 2017 Microsoft
|
github_jupyter
|
poem_lines = poem1.readlines()
# [ ] Run to download file to notebook
!curl https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/poem1.txt -o poem1.txt
# [ ] review and run example
# open address to file
poem1 = open('poem1.txt', 'r')
# readlines and print as a list
poem_lines = poem1.readlines()
poem_lines
# [ ] review and run example
for line in poem_lines:
print(line)
# [ ] import cities
!curl https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/cities -o cities.txt
# [ ] open cities.txt as cities_file and read the file as a list: cities_lines
cities_file = open('cities.txt', 'r')
cities_lines = cities_file.readlines()
cities_lines
# [ ] use list iteration to print each city in cities_lines list
for line in cities_lines:
print(line)
for line in poem_lines:
poem_lines[count] = line[:-1]
count += 1
# [ ] review and run examples
# [ ] re-open file and read file as a list of strings
poem1 = open('poem1.txt', 'r')
poem_lines = poem1.readlines()
print(poem_lines)
# [ ] print each list item
for line in poem_lines:
print(line)
# [ ] remove the last character of each list item, which is "\n"
count = 0
for line in poem_lines:
poem_lines[count] = line[:-1]
count += 1
print(poem_lines)
# [ ] print each list item
for line in poem_lines:
print(line)
# [ ] re-open file and read file as a list of strings
# [ ] open cities.txt as cities_file and read the file as a list: cities_lines
# [ ] open cities.txt as cities_file and read the file as a list: cities_lines
cities_file = open('cities.txt', 'r')
cities_lines = cities_file.readlines()
cities_lines
# [ ] remove the last character, "\n", of each cities_lines list item
# [ ] open cities.txt as cities_file and read the file as a list: cities_lines
cities_file = open('cities.txt', 'r')
cities_lines = cities_file.readlines()
cities_lines
count = 0
for line in cities_lines:
cities_lines[count] = line[:-1]
count += 1
print(cities_lines)
# [ ] print each list item in cities_lines
for line in cities_lines:
print(line)
#
<font size="6" color="#00A0B2" face="verdana"> <B>Examples</B></font>
This example assumes that poem1.txt has been imported in 1st example above
#
<font size="6" color="#B24C00" face="verdana"> <B>Task 3</B></font>
## File .close()
write each item in it's own cell
- open cities.txt as cities_file
- read the lines as cities_lines
- print the cities that **start with the letter "D" or greater**
- close cities_file
- test that file is closed
#
<font size="6" color="#B24C00" face="verdana"> <B>Task 4</B></font>
## readlines() poem2
write each item in its own cell
- import https://raw.githubusercontent.com/MicrosoftLearning/intropython/master/poem2.txt as poem2.txt
- open poem2.txt as poem2_file in read mode
- create a list of strings, called poem2_lines, from each line of poem2_text (use **.readlines()**)
- remove the newline character for each list item in poem2_lines
- print the poem2 lines in reverse order
| 0.339937 | 0.904735 |
# <center><span style="color:red">**Cálculo Numérico - Avaliação 01**</span><br/></center>
# <center><font color='purple'>**Installing dependencies**</font></center>
## <font color='orange'>**To install dependencies, run this cell**</font>
```
!pip install -r requirements.txt
```
## <font color='orange'>**Importing dependencies**</font>
### <font color='#0f3f21'> **To import dependencies, run this cell** </font>
```
from fractions import Fraction
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
```
# <center><span style="color:green">**Exercício 00**</span><br/></center>
### <center><span style="color:blue">Calculando matriz de Hilbert de ordem 4</span><br/></center>
```
def Hilbert_matrix_string(a, b):
return [[str(Fraction(1 / (i + j + 1)).limit_denominator()) for j in range(b)] for i in range(a)]
Hilbert_order_4_matrix = Hilbert_matrix_string(4,4)
print("Matriz de Hilbert ordem 4:")
Hilbert_order_4_matrix
```
### <center><span style="color:blue">Calculando matriz inversa</span><br/></center>
```
def Hilbert_matrix_array(a, b):
return np.array([[Fraction(1 / (i + j + 1)).limit_denominator() for j in range(b)] for i in range(a)])
hilbert_matrix_array_order_4 = Hilbert_matrix_array(4,4).astype('float64')
Hilbert_inverse_matrix_array_order_4 = np.linalg.inv(hilbert_matrix_array_order_4)
print("\n\nMatriz inversa de Hilbert de ordem 4:")
Hilbert_inverse_matrix_array_order_4
```
### <center><span style="color:blue">Descrevendo vetor solução usando pinv (pseudo-inverse) function</span><br/></center>
```
pinv = np.linalg.pinv(hilbert_matrix_array_order_4)
b = [0 ,1, 10, 100]
solution_vector = pinv.dot(b)
print("O vetor solucao é dado por:")
solution_vector.tolist()
```
# <center><span style="color:green">**Exercício 01 parte a - Calculando xm para altura máxima**</span><br/></center>
```
x = symbols('x')
g, y0, v0, m, c = 9.81, 100, 55, 80, 15
y = y0 + (m / c) * (v0 + ((m * g) / c)) * (1 - exp(- (c / m) * x)) - ((m * g) / c) * x
print('Equacao:')
y
```
### <font color='orange'>Altura maxima de xm é dada para y'(x) = 0 </font>
```
y_diff = diff(y)
print("y(x)' = ", y_diff)
print("Calculando y(x)'= 0, resulta em xm, em metros, com o valor de")
solve(y_diff)[0]
```
# <center><span style="color:green">**Parte b - Calculando x para y(x) = 0**</span><br/></center>
```
print("Valor de y(x) = 0: ")
solve(y, rational = False)[0]
```
### <center><span style="color:blue">O processo deve ser iterativo, pois a equacao -52.32 * x + 672.373333333333 - 572.373333333333 * exp(-0.1875 * x) = 0 nao possui uma fórmula simples para resolucao da equacao.</span><br/></center>
```
def Jacobian(v_str, f_list):
vars = symbols(v_str)
f = sympify(f_list)
J = zeros(len(f),len(vars))
for i, fi in enumerate(f):
for j, s in enumerate(vars):
J[i,j] = diff(fi, s)
return J
```
# <center><span style="color:green">**Exercicio 02 parte a - Resolvendo o primeiro sistema de equacoes**</span><br/></center>
```
x, y = symbols('x y')
f1 = x**2 + y**2
f2 = -exp(x) + y
print("Usando como chute inicial o par (I,I), pois a equacao nao possui solucoes reais, por conta de x² + y² = 0 possuir solucoes complexas, a solucao é dada por:")
nsolve((f1, f2), (x, y), (I, I))
print("Matriz Jacobiana do sistema:")
Jacobian('x y',['x**2 + y**2', '-exp(x) + y'])
x = [1,2,3,4]
y = [1, -1.33,-2.77,-3.233]
plt.plot(x, y)
plt.xlabel('Iteracoes')
plt.ylabel('Valores da raíz')
plt.title('Gráfico relacionando vetor solucao x X i')
plt.show()
```
# <center><span style="color:green">**Parte b - Mostrando que o segundo sistema de equacoes possui infinitas solucoes**</span><br/></center>
```
print("Matriz Jacobiana do sistema:")
jacobian_matrix = Jacobian('x y', ['-exp(x) + y','-sin(x) + y'])
jacobian_matrix
delta = 0.025
x, y = np.meshgrid(np.arange(-50, 4, delta),np.arange(-1, 1, delta))
plt.contour(x, y,- np.sin(x) + y, [0]
)
plt.contour(x, y, -np.exp(x) + y, [0])
plt.show()
```
### <center><span style="color:blue">Como mostrado no gráfico, o sistema possui infinitas solucoes.</span><br/></center>
# <center><span style="color:green">**Exercicio 03 - descobrindo valor de d**</span><br/></center>
```
d = symbols('d')
k1, k2, m, g, h = 40000, 40, 95, 9.81, 0.43
f = -(k1 * d + k2 * d ** (3/2))
energy_conservation = (2 * k2 * d ** (5/2))/5 + (1/2) * k1 * d ** 2 - m *g * d - m * g *h
print("Equacao:")
energy_conservation
t = symbols('t')
f = (0.4 * t - t**3 + 0.141)
solved_equation = solve(f)
print("Os valores de t para que a matriz seja singular são:")
solved_equation
print("Com a aproximacao inicial de d = 0.4, o valor de d, em metros, é igual a:")
nsolve(energy_conservation,0.4)
```
|
github_jupyter
|
!pip install -r requirements.txt
from fractions import Fraction
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
def Hilbert_matrix_string(a, b):
return [[str(Fraction(1 / (i + j + 1)).limit_denominator()) for j in range(b)] for i in range(a)]
Hilbert_order_4_matrix = Hilbert_matrix_string(4,4)
print("Matriz de Hilbert ordem 4:")
Hilbert_order_4_matrix
def Hilbert_matrix_array(a, b):
return np.array([[Fraction(1 / (i + j + 1)).limit_denominator() for j in range(b)] for i in range(a)])
hilbert_matrix_array_order_4 = Hilbert_matrix_array(4,4).astype('float64')
Hilbert_inverse_matrix_array_order_4 = np.linalg.inv(hilbert_matrix_array_order_4)
print("\n\nMatriz inversa de Hilbert de ordem 4:")
Hilbert_inverse_matrix_array_order_4
pinv = np.linalg.pinv(hilbert_matrix_array_order_4)
b = [0 ,1, 10, 100]
solution_vector = pinv.dot(b)
print("O vetor solucao é dado por:")
solution_vector.tolist()
x = symbols('x')
g, y0, v0, m, c = 9.81, 100, 55, 80, 15
y = y0 + (m / c) * (v0 + ((m * g) / c)) * (1 - exp(- (c / m) * x)) - ((m * g) / c) * x
print('Equacao:')
y
y_diff = diff(y)
print("y(x)' = ", y_diff)
print("Calculando y(x)'= 0, resulta em xm, em metros, com o valor de")
solve(y_diff)[0]
print("Valor de y(x) = 0: ")
solve(y, rational = False)[0]
def Jacobian(v_str, f_list):
vars = symbols(v_str)
f = sympify(f_list)
J = zeros(len(f),len(vars))
for i, fi in enumerate(f):
for j, s in enumerate(vars):
J[i,j] = diff(fi, s)
return J
x, y = symbols('x y')
f1 = x**2 + y**2
f2 = -exp(x) + y
print("Usando como chute inicial o par (I,I), pois a equacao nao possui solucoes reais, por conta de x² + y² = 0 possuir solucoes complexas, a solucao é dada por:")
nsolve((f1, f2), (x, y), (I, I))
print("Matriz Jacobiana do sistema:")
Jacobian('x y',['x**2 + y**2', '-exp(x) + y'])
x = [1,2,3,4]
y = [1, -1.33,-2.77,-3.233]
plt.plot(x, y)
plt.xlabel('Iteracoes')
plt.ylabel('Valores da raíz')
plt.title('Gráfico relacionando vetor solucao x X i')
plt.show()
print("Matriz Jacobiana do sistema:")
jacobian_matrix = Jacobian('x y', ['-exp(x) + y','-sin(x) + y'])
jacobian_matrix
delta = 0.025
x, y = np.meshgrid(np.arange(-50, 4, delta),np.arange(-1, 1, delta))
plt.contour(x, y,- np.sin(x) + y, [0]
)
plt.contour(x, y, -np.exp(x) + y, [0])
plt.show()
d = symbols('d')
k1, k2, m, g, h = 40000, 40, 95, 9.81, 0.43
f = -(k1 * d + k2 * d ** (3/2))
energy_conservation = (2 * k2 * d ** (5/2))/5 + (1/2) * k1 * d ** 2 - m *g * d - m * g *h
print("Equacao:")
energy_conservation
t = symbols('t')
f = (0.4 * t - t**3 + 0.141)
solved_equation = solve(f)
print("Os valores de t para que a matriz seja singular são:")
solved_equation
print("Com a aproximacao inicial de d = 0.4, o valor de d, em metros, é igual a:")
nsolve(energy_conservation,0.4)
| 0.476336 | 0.928733 |
# Named entity recognition model built in keras, trained on putput utterances and tokens
This notebook demonstrates using putput to generate data and train a named entity recognition model. Specifically, the notebook considers the scenario in which customers place orders at a restaurant. Labels follow the <a href="https://en.wikipedia.org/wiki/Inside%E2%80%93outside%E2%80%93beginning_(tagging)">IOB2 format</a>.
For instance, given a customer's utterance:
* "can i have a chicken sandwich please and remove the coke"
the model should output the tokens
* "B-ADD_TO_ORDER I-ADD_TO_ORDER I-ADD_TO_ORDER B-QUANTITY B-ITEM I-ITEM O B-REMOVE B-QUANTITY B-ITEM".
and the groups
* "B-ADD_INTENT I-ADD_INTENT I-ADD_INTENT I-ADD_INTENT I-ADD_INTENT I-ADD_INTENT O B-REMOVE_INTENT I-REMOVE_INTENT I-REMOVE_INTENT".
where "B-" indicates the beginning of a chunk, "I-" indicates inside a chunk, and "O-" indicates outside a chunk. In this scenario "can i have" is an ADD_TO_ORDER chunk, "a" is a QUANTITY chunk, and "please" is not part of any chunk.
This notebook borrows heavily from [an awesome blog series on deep learning for named entity recognition](https://www.depends-on-the-definition.com/guide-sequence-tagging-neural-networks-python/).
**If you would like to run this notebook yourself, you will need a GPU for training the LSTM.**
```
import itertools
import os
import random
from pathlib import Path
import h5py
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import randomcolor
import spacy
from keras.layers import (LSTM, Bidirectional, Dense, Dropout, Embedding, TimeDistributed)
from keras.models import Input, Model, load_model
from keras.preprocessing.sequence import pad_sequences
from keras.utils import to_categorical
from keras_tqdm import TQDMNotebookCallback
from seqeval.metrics import classification_report
from sklearn.model_selection import train_test_split
from spacy import displacy
from putput import ComboOptions, Pipeline
```
# Define Environment variables
```
MAX_SAMPLE_SIZE = 3000
EPOCHS = 2
BATCH_SIZE = 64
random.seed(1)
# Ignore this, used for running continuous integration quickly
if os.environ.get('CI'):
CI_DATA_SIZE = 10
EPOCHS = 1
try:
pattern_def_path = Path(os.path.dirname(os.path.abspath(__file__))) / "patterns.yml"
putput_model_path = Path(os.path.dirname(os.path.abspath(__file__))) / 'multiple_output_lstm_custom_word_emb.h5'
except NameError:
pattern_def_path = Path(os.getcwd()) / "patterns.yml"
putput_model_path = Path(os.getcwd()) / 'multiple_output_lstm_custom_word_emb.h5'
def random_color_dict(tags, seed=0):
rand_color = randomcolor.RandomColor(seed=seed)
colors = rand_color.generate(count=len(tags), luminosity='light')
return dict(zip(tags, colors))
def clean_bio_tag(tag):
if tag.startswith('I-') or tag.startswith('B-'):
return tag[2:]
return tag
def to_visualizer(words, tags, title):
current_letter_index = 0
ents = []
for word, tag in zip(words, tags):
if tag[0] == 'I' and len(ents) > 0:
ents[-1]['end'] += len(word) + 1
else:
ent = {'start': current_letter_index,
'end': current_letter_index + len(word) + 1,
'label': tag.split('-')[-1]}
ents.append(ent)
current_letter_index += len(word) + 1
return {'text': ' '.join(words),
'ents': ents,
'title': title}
def display_sentence(utterance, tokens, groups, options, suffix=''):
sentence_visualizer = {'text': ' '.join(utterance), 'ents': [], 'title': 'SENTENCE' + suffix}
token_visualizer = to_visualizer(utterance, tokens, 'TOKENS')
group_visualizer = to_visualizer(utterance, groups, 'GROUPS')
displacy.render([sentence_visualizer, token_visualizer, group_visualizer], style='ent', manual=True, jupyter=True, options=options)
def display_sentences(utterances, utterance_tokens, utterance_groups, options, sample_size):
indicies = random.sample(range(0, len(utterances)), sample_size)
for sample_index in indicies:
display_sentence(utterances[sample_index],
utterance_tokens[sample_index],
utterance_groups[sample_index],
options,
suffix=' {}:'.format(sample_index))
print()
```
# How to use putput
### 1) Pattern definition file:
let's take a look at our pattern definition file
```
if not os.environ.get('CI'):
! cat "{str(pattern_def_path)}"
```
### 2) Define dynamic tokens:
In the real world the items would most likely be pulled in from some menu service and inserted here, but you get the idea.
```
dynamic_token_patterns_map = {
"ITEM": ("burger", "hamburger", "coke", "french fries", "chicken sandwich", "ten chicken strips"),
"QUANTITY": ("a", "no", "extra", "the", "one", "two", "three", "four", "five", "six", "seven", "eight", "nine", "ten"),
}
```
### 3) [Optional] Define combination options
```
# Define how we want to generate utterances and sample size. More info here:
# https://github.com/michaelperel/putput/blob/00877147373690f8cc6ad16f164c2a44ba728c62/putput/joiner.py#L17
combo_options_map = {
'DEFAULT': ComboOptions(max_sample_size=MAX_SAMPLE_SIZE, with_replacement=True)
}
```
### 4) [Optional] Define expansion hooks, combination hooks, or final hooks:
```
# This function buckets groups into either REMOVE, SUBSTITUTE, ADD, or None.
# We do this because a lot of the groups overlap so we want to put them into general groupings
def _generalize_groups(utterance, handled_tokens, handled_groups):
new_handled_groups = []
for groups in handled_groups:
new_groups = []
for group in groups.split():
prefix = ''
if '-' in group:
prefix = group[:2]
if 'REMOVE' in group:
new_groups.append(prefix + 'REMOVE')
elif 'SUBSTITUTE' in group:
new_groups.append(prefix +'SUBSTITUTE')
elif 'None' in group:
new_groups.append('None')
else:
new_groups.append(prefix + 'ADD')
new_handled_groups.append(' '.join(new_groups))
return utterance, handled_tokens, new_handled_groups
# This function converts the final output to lists of words, tokens, and groups.
def _output_to_lists(utterance, tokens, groups):
return utterance.replace(" '", "'").split(), ' '.join(tokens).split(), ' '.join(groups).split()
combo_hooks_map = {
'DEFAULT': (_generalize_groups,_output_to_lists)
}
```
### 5) Create and use putput pipeline to generate utterances, tokens, and groups:
```
def compute_utterances_and_tokens_and_groups(pattern_def_path):
# We choose the IOB preset for use in training a Named Entity Recognition model
iob_pipeline = Pipeline.from_preset('IOB2',
pattern_def_path,
dynamic_token_patterns_map=dynamic_token_patterns_map,
combo_options_map=combo_options_map,
combo_hooks_map=combo_hooks_map,
)
# putput outputs to a generator for efficient use of memory
iob_generator = iob_pipeline.flow(disable_progress_bar=True)
# Ignore this, used for running continuous integration
if os.environ.get('CI'):
iob_generator = itertools.islice(iob_generator, CI_DATA_SIZE)
# Unpack generator
utterances, utterance_tokens, utterance_groups = zip(*iob_generator)
return utterances, utterance_tokens, utterance_groups
utterances, utterance_tokens, utterance_groups = compute_utterances_and_tokens_and_groups(pattern_def_path)
print('Generated: {} utterances and {} tokens and {} groups'.format(len(utterances), len(utterance_tokens), len(utterance_groups)))
print(utterances[0])
print(utterance_tokens[0])
print(utterance_groups[0])
```
## [Optional] Displacy
```
# [OPTIONAL] This is just for making displacy pretty with a color map
# we generate a tag to color dictionary for displacy to use
unique_tokens = set([clean_bio_tag(token) for tokens in utterance_tokens for token in tokens])
unique_groups = set([clean_bio_tag(group) for groups in utterance_groups for group in groups])
unique_tags = list(unique_tokens | unique_groups)
color_dict = random_color_dict(unique_tags, seed=1)
displacy_options = {'ents': unique_tags, 'colors': color_dict}
display_sentences(utterances, utterance_tokens, utterance_groups, displacy_options, 5)
```
# Using putput for Named Entity Recognition (keras)
```
def compute_word2idx(utterances):
words = list(set(list(itertools.chain.from_iterable(utterances))))
words.append("ENDPAD")
words.append("UNKNOWN")
word2idx = {w: i for i, w in enumerate(words)}
return word2idx
def compute_tag2idx(tokens):
tags = list(set(list(itertools.chain.from_iterable(tokens))))
if 'O' not in tags:
tags.append('O')
tag2idx = {t: i for i, t in enumerate(tags)}
return tag2idx
def plot_histogram_length_of_utterances(utterances):
plt.hist([len(utterance) for utterance in utterances], bins=50)
plt.show()
def transform_utterances_for_keras(utterances, max_utterance_length, word2idx):
X = [[(word2idx.get(word) or word2idx.get("UNKNOWN")) for word in phrase] for phrase in utterances]
X = pad_sequences(maxlen=max_utterance_length, sequences=X, padding="post", value=word2idx['ENDPAD'])
return X
def transform_tokens_for_keras(tokens, max_utterance_length, tag2idx):
y = [[tag2idx[tag] for tag in token] for token in tokens]
y = pad_sequences(maxlen=max_utterance_length, sequences=y, padding="post", value=tag2idx["O"])
y = [to_categorical(i, num_classes=len(tag2idx)) for i in y]
return y
def train_test(utternaces, tokens, groups):
return train_test_split(utternaces, tokens, groups, test_size=0.1, random_state=1)
def define_and_compile_model(max_utterance_length, num_unique_words, num_unique_tags, num_unique_groups):
# bidirectional LSTM with custom word embeddings
input = Input(shape=(max_utterance_length,))
model = Embedding(input_dim=num_unique_words, output_dim=16, input_length=max_utterance_length)(input)
model = Dropout(0.1)(model)
model = Bidirectional(LSTM(units=16, return_sequences=True, recurrent_dropout=0.2))(model)
token_output = TimeDistributed(Dense(num_unique_tags, activation="softmax"), name='token_output')(model) # softmax output layer
group_output = TimeDistributed(Dense(num_unique_groups, activation="softmax"), name='group_output')(model)
model = Model(input, outputs=[token_output, group_output])
model.compile(optimizer="rmsprop", loss="categorical_crossentropy", metrics=["accuracy"])
return model
def train_model(X_tr, y_tr, z_tr):
history = model.fit(X_tr, [np.array(y_tr), np.array(z_tr)], batch_size=BATCH_SIZE,
epochs=EPOCHS, validation_split=0.1, verbose=0,
callbacks=[TQDMNotebookCallback()])
return history
def plot_model_training(history, suffix):
hist = pd.DataFrame(history.history)
plt.figure(figsize=(12,12))
plt.plot(hist["token_output_" + suffix])
plt.plot(hist["val_token_output_" + suffix])
plt.plot(hist["group_output_" + suffix])
plt.plot(hist["val_group_output_" + suffix])
plt.legend()
plt.ylabel('Accuracy/Loss')
plt.xlabel('Epoch')
plt.show()
def _convert_model_output_to_labels(pred, idx2tag):
out = []
for pred_i in pred:
out_i = []
for p in pred_i:
p_i = np.argmax(p)
out_i.append(idx2tag[p_i])
out.append(out_i)
return out
def evaluate_model_on_test_split(model, X_te, y_te, z_te, tag2idx, group2idx):
idx2tag = {i: w for w, i in tag2idx.items()}
idx2group = {i: w for w, i in group2idx.items()}
token_test_pred, group_test_pred = model.predict(X_te, verbose=0)
token_pred_labels = _convert_model_output_to_labels(token_test_pred, idx2tag)
if os.environ.get('CI'):
token_pred_labels = _convert_model_output_to_labels(y_te, idx2tag)
token_test_labels = _convert_model_output_to_labels(y_te, idx2tag)
group_pred_labels = _convert_model_output_to_labels(group_test_pred, idx2group)
if os.environ.get('CI'):
group_pred_labels = _convert_model_output_to_labels(z_te, idx2group)
group_test_labels = _convert_model_output_to_labels(z_te, idx2group)
return classification_report(token_pred_labels, token_test_labels), classification_report(group_pred_labels, group_test_labels)
def predict(model, pred_utterance, max_utterance_length, word2idx, tag2idx, groups2idx, options):
pred_utterances = [pred_utterance.split()]
X = transform_utterances_for_keras(pred_utterances, max_utterance_length, word2idx)
token_test_pred, group_test_pred = model.predict(np.array([X[0]]))
token_test_pred = np.argmax(token_test_pred, axis=-1)
group_test_pred = np.argmax(group_test_pred, axis=-1)
idx2word = {idx: word for word, idx in word2idx.items()}
idx2tag = {idx: word for word, idx in tag2idx.items()}
idx2group = {idx: word for word, idx in groups2idx.items()}
words = []
tokens = []
groups = []
for w, token_pred, group_pred in zip(X[0], token_test_pred[0], group_test_pred[0]):
if 'ENDPAD' not in idx2word[w]:
words.append(idx2word[w])
tokens.append(idx2tag[token_pred])
groups.append(idx2group[group_pred])
display_sentence(words, tokens, groups, options)
```
# Analyze the utterances and tokens to determine max utterance length
```
plot_histogram_length_of_utterances(utterances)
max_utterance_length = 40 # based on the histogram
```
Keras expects all utterances to be of the same length. Therefore we look at the distribution of lengths of utterances to determine what an appropriate maximum length should be.
# Create a train test split of the data, in a format amenable to keras
```
word2idx = compute_word2idx(utterances)
tag2idx = compute_tag2idx(utterance_tokens)
groups2idx = compute_tag2idx(utterance_groups)
X = transform_utterances_for_keras(utterances, max_utterance_length, word2idx)
y = transform_tokens_for_keras(utterance_tokens, max_utterance_length, tag2idx)
z = transform_tokens_for_keras(utterance_groups, max_utterance_length, groups2idx)
X_tr, X_te, y_tr, y_te, z_tr, z_te = train_test(X, y, z)
```
# Define and compile the model
```
model = define_and_compile_model(max_utterance_length, len(word2idx), len(tag2idx), len(groups2idx))
model.summary()
```
# Plot model training and analyze training
```
history = train_model(X_tr, y_tr, z_tr)
plot_model_training(history, 'acc')
plot_model_training(history, 'loss')
```
Note: Here we can see that the model overfits the data from putput very quickly. This is both good and bad. It is good because it demonstrates that if you already have an existing model with this architecture, and you want to train it with utterances from putput, it is likely that the model has the capacity to learn the patterns well. It is bad because if you only have data from putput, the model will not generalize.
# Save and load model
```
if not os.environ.get('CI') and not putput_model_path.is_file():
model.save('multiple_output_lstm_custom_word_emb.h5')
if not os.environ.get('CI') and putput_model_path.is_file():
model = load_model('multiple_output_lstm_custom_word_emb.h5')
```
# Evaluate on test data
```
token_eval, group_eval = evaluate_model_on_test_split(model, X_te, y_te, z_te, tag2idx, groups2idx)
print(token_eval)
print(group_eval)
```
# Make predictions
```
predict(model, 'three burger', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
predict(model, 'i want ten burger make that a chicken sandwich and remove one burger', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
predict(model, 'i want a chicken sandwich and remove one burger and she need to order french fries', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
predict(model, 'i want a chicken sandwich and ten ten chicken strips remove five french fries', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
predict(model, 'i want a chicken sandwich with coke actually make the chicken sandwich a hamburger and give me a burger', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
```
|
github_jupyter
|
import itertools
import os
import random
from pathlib import Path
import h5py
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import randomcolor
import spacy
from keras.layers import (LSTM, Bidirectional, Dense, Dropout, Embedding, TimeDistributed)
from keras.models import Input, Model, load_model
from keras.preprocessing.sequence import pad_sequences
from keras.utils import to_categorical
from keras_tqdm import TQDMNotebookCallback
from seqeval.metrics import classification_report
from sklearn.model_selection import train_test_split
from spacy import displacy
from putput import ComboOptions, Pipeline
MAX_SAMPLE_SIZE = 3000
EPOCHS = 2
BATCH_SIZE = 64
random.seed(1)
# Ignore this, used for running continuous integration quickly
if os.environ.get('CI'):
CI_DATA_SIZE = 10
EPOCHS = 1
try:
pattern_def_path = Path(os.path.dirname(os.path.abspath(__file__))) / "patterns.yml"
putput_model_path = Path(os.path.dirname(os.path.abspath(__file__))) / 'multiple_output_lstm_custom_word_emb.h5'
except NameError:
pattern_def_path = Path(os.getcwd()) / "patterns.yml"
putput_model_path = Path(os.getcwd()) / 'multiple_output_lstm_custom_word_emb.h5'
def random_color_dict(tags, seed=0):
rand_color = randomcolor.RandomColor(seed=seed)
colors = rand_color.generate(count=len(tags), luminosity='light')
return dict(zip(tags, colors))
def clean_bio_tag(tag):
if tag.startswith('I-') or tag.startswith('B-'):
return tag[2:]
return tag
def to_visualizer(words, tags, title):
current_letter_index = 0
ents = []
for word, tag in zip(words, tags):
if tag[0] == 'I' and len(ents) > 0:
ents[-1]['end'] += len(word) + 1
else:
ent = {'start': current_letter_index,
'end': current_letter_index + len(word) + 1,
'label': tag.split('-')[-1]}
ents.append(ent)
current_letter_index += len(word) + 1
return {'text': ' '.join(words),
'ents': ents,
'title': title}
def display_sentence(utterance, tokens, groups, options, suffix=''):
sentence_visualizer = {'text': ' '.join(utterance), 'ents': [], 'title': 'SENTENCE' + suffix}
token_visualizer = to_visualizer(utterance, tokens, 'TOKENS')
group_visualizer = to_visualizer(utterance, groups, 'GROUPS')
displacy.render([sentence_visualizer, token_visualizer, group_visualizer], style='ent', manual=True, jupyter=True, options=options)
def display_sentences(utterances, utterance_tokens, utterance_groups, options, sample_size):
indicies = random.sample(range(0, len(utterances)), sample_size)
for sample_index in indicies:
display_sentence(utterances[sample_index],
utterance_tokens[sample_index],
utterance_groups[sample_index],
options,
suffix=' {}:'.format(sample_index))
print()
if not os.environ.get('CI'):
! cat "{str(pattern_def_path)}"
dynamic_token_patterns_map = {
"ITEM": ("burger", "hamburger", "coke", "french fries", "chicken sandwich", "ten chicken strips"),
"QUANTITY": ("a", "no", "extra", "the", "one", "two", "three", "four", "five", "six", "seven", "eight", "nine", "ten"),
}
# Define how we want to generate utterances and sample size. More info here:
# https://github.com/michaelperel/putput/blob/00877147373690f8cc6ad16f164c2a44ba728c62/putput/joiner.py#L17
combo_options_map = {
'DEFAULT': ComboOptions(max_sample_size=MAX_SAMPLE_SIZE, with_replacement=True)
}
# This function buckets groups into either REMOVE, SUBSTITUTE, ADD, or None.
# We do this because a lot of the groups overlap so we want to put them into general groupings
def _generalize_groups(utterance, handled_tokens, handled_groups):
new_handled_groups = []
for groups in handled_groups:
new_groups = []
for group in groups.split():
prefix = ''
if '-' in group:
prefix = group[:2]
if 'REMOVE' in group:
new_groups.append(prefix + 'REMOVE')
elif 'SUBSTITUTE' in group:
new_groups.append(prefix +'SUBSTITUTE')
elif 'None' in group:
new_groups.append('None')
else:
new_groups.append(prefix + 'ADD')
new_handled_groups.append(' '.join(new_groups))
return utterance, handled_tokens, new_handled_groups
# This function converts the final output to lists of words, tokens, and groups.
def _output_to_lists(utterance, tokens, groups):
return utterance.replace(" '", "'").split(), ' '.join(tokens).split(), ' '.join(groups).split()
combo_hooks_map = {
'DEFAULT': (_generalize_groups,_output_to_lists)
}
def compute_utterances_and_tokens_and_groups(pattern_def_path):
# We choose the IOB preset for use in training a Named Entity Recognition model
iob_pipeline = Pipeline.from_preset('IOB2',
pattern_def_path,
dynamic_token_patterns_map=dynamic_token_patterns_map,
combo_options_map=combo_options_map,
combo_hooks_map=combo_hooks_map,
)
# putput outputs to a generator for efficient use of memory
iob_generator = iob_pipeline.flow(disable_progress_bar=True)
# Ignore this, used for running continuous integration
if os.environ.get('CI'):
iob_generator = itertools.islice(iob_generator, CI_DATA_SIZE)
# Unpack generator
utterances, utterance_tokens, utterance_groups = zip(*iob_generator)
return utterances, utterance_tokens, utterance_groups
utterances, utterance_tokens, utterance_groups = compute_utterances_and_tokens_and_groups(pattern_def_path)
print('Generated: {} utterances and {} tokens and {} groups'.format(len(utterances), len(utterance_tokens), len(utterance_groups)))
print(utterances[0])
print(utterance_tokens[0])
print(utterance_groups[0])
# [OPTIONAL] This is just for making displacy pretty with a color map
# we generate a tag to color dictionary for displacy to use
unique_tokens = set([clean_bio_tag(token) for tokens in utterance_tokens for token in tokens])
unique_groups = set([clean_bio_tag(group) for groups in utterance_groups for group in groups])
unique_tags = list(unique_tokens | unique_groups)
color_dict = random_color_dict(unique_tags, seed=1)
displacy_options = {'ents': unique_tags, 'colors': color_dict}
display_sentences(utterances, utterance_tokens, utterance_groups, displacy_options, 5)
def compute_word2idx(utterances):
words = list(set(list(itertools.chain.from_iterable(utterances))))
words.append("ENDPAD")
words.append("UNKNOWN")
word2idx = {w: i for i, w in enumerate(words)}
return word2idx
def compute_tag2idx(tokens):
tags = list(set(list(itertools.chain.from_iterable(tokens))))
if 'O' not in tags:
tags.append('O')
tag2idx = {t: i for i, t in enumerate(tags)}
return tag2idx
def plot_histogram_length_of_utterances(utterances):
plt.hist([len(utterance) for utterance in utterances], bins=50)
plt.show()
def transform_utterances_for_keras(utterances, max_utterance_length, word2idx):
X = [[(word2idx.get(word) or word2idx.get("UNKNOWN")) for word in phrase] for phrase in utterances]
X = pad_sequences(maxlen=max_utterance_length, sequences=X, padding="post", value=word2idx['ENDPAD'])
return X
def transform_tokens_for_keras(tokens, max_utterance_length, tag2idx):
y = [[tag2idx[tag] for tag in token] for token in tokens]
y = pad_sequences(maxlen=max_utterance_length, sequences=y, padding="post", value=tag2idx["O"])
y = [to_categorical(i, num_classes=len(tag2idx)) for i in y]
return y
def train_test(utternaces, tokens, groups):
return train_test_split(utternaces, tokens, groups, test_size=0.1, random_state=1)
def define_and_compile_model(max_utterance_length, num_unique_words, num_unique_tags, num_unique_groups):
# bidirectional LSTM with custom word embeddings
input = Input(shape=(max_utterance_length,))
model = Embedding(input_dim=num_unique_words, output_dim=16, input_length=max_utterance_length)(input)
model = Dropout(0.1)(model)
model = Bidirectional(LSTM(units=16, return_sequences=True, recurrent_dropout=0.2))(model)
token_output = TimeDistributed(Dense(num_unique_tags, activation="softmax"), name='token_output')(model) # softmax output layer
group_output = TimeDistributed(Dense(num_unique_groups, activation="softmax"), name='group_output')(model)
model = Model(input, outputs=[token_output, group_output])
model.compile(optimizer="rmsprop", loss="categorical_crossentropy", metrics=["accuracy"])
return model
def train_model(X_tr, y_tr, z_tr):
history = model.fit(X_tr, [np.array(y_tr), np.array(z_tr)], batch_size=BATCH_SIZE,
epochs=EPOCHS, validation_split=0.1, verbose=0,
callbacks=[TQDMNotebookCallback()])
return history
def plot_model_training(history, suffix):
hist = pd.DataFrame(history.history)
plt.figure(figsize=(12,12))
plt.plot(hist["token_output_" + suffix])
plt.plot(hist["val_token_output_" + suffix])
plt.plot(hist["group_output_" + suffix])
plt.plot(hist["val_group_output_" + suffix])
plt.legend()
plt.ylabel('Accuracy/Loss')
plt.xlabel('Epoch')
plt.show()
def _convert_model_output_to_labels(pred, idx2tag):
out = []
for pred_i in pred:
out_i = []
for p in pred_i:
p_i = np.argmax(p)
out_i.append(idx2tag[p_i])
out.append(out_i)
return out
def evaluate_model_on_test_split(model, X_te, y_te, z_te, tag2idx, group2idx):
idx2tag = {i: w for w, i in tag2idx.items()}
idx2group = {i: w for w, i in group2idx.items()}
token_test_pred, group_test_pred = model.predict(X_te, verbose=0)
token_pred_labels = _convert_model_output_to_labels(token_test_pred, idx2tag)
if os.environ.get('CI'):
token_pred_labels = _convert_model_output_to_labels(y_te, idx2tag)
token_test_labels = _convert_model_output_to_labels(y_te, idx2tag)
group_pred_labels = _convert_model_output_to_labels(group_test_pred, idx2group)
if os.environ.get('CI'):
group_pred_labels = _convert_model_output_to_labels(z_te, idx2group)
group_test_labels = _convert_model_output_to_labels(z_te, idx2group)
return classification_report(token_pred_labels, token_test_labels), classification_report(group_pred_labels, group_test_labels)
def predict(model, pred_utterance, max_utterance_length, word2idx, tag2idx, groups2idx, options):
pred_utterances = [pred_utterance.split()]
X = transform_utterances_for_keras(pred_utterances, max_utterance_length, word2idx)
token_test_pred, group_test_pred = model.predict(np.array([X[0]]))
token_test_pred = np.argmax(token_test_pred, axis=-1)
group_test_pred = np.argmax(group_test_pred, axis=-1)
idx2word = {idx: word for word, idx in word2idx.items()}
idx2tag = {idx: word for word, idx in tag2idx.items()}
idx2group = {idx: word for word, idx in groups2idx.items()}
words = []
tokens = []
groups = []
for w, token_pred, group_pred in zip(X[0], token_test_pred[0], group_test_pred[0]):
if 'ENDPAD' not in idx2word[w]:
words.append(idx2word[w])
tokens.append(idx2tag[token_pred])
groups.append(idx2group[group_pred])
display_sentence(words, tokens, groups, options)
plot_histogram_length_of_utterances(utterances)
max_utterance_length = 40 # based on the histogram
word2idx = compute_word2idx(utterances)
tag2idx = compute_tag2idx(utterance_tokens)
groups2idx = compute_tag2idx(utterance_groups)
X = transform_utterances_for_keras(utterances, max_utterance_length, word2idx)
y = transform_tokens_for_keras(utterance_tokens, max_utterance_length, tag2idx)
z = transform_tokens_for_keras(utterance_groups, max_utterance_length, groups2idx)
X_tr, X_te, y_tr, y_te, z_tr, z_te = train_test(X, y, z)
model = define_and_compile_model(max_utterance_length, len(word2idx), len(tag2idx), len(groups2idx))
model.summary()
history = train_model(X_tr, y_tr, z_tr)
plot_model_training(history, 'acc')
plot_model_training(history, 'loss')
if not os.environ.get('CI') and not putput_model_path.is_file():
model.save('multiple_output_lstm_custom_word_emb.h5')
if not os.environ.get('CI') and putput_model_path.is_file():
model = load_model('multiple_output_lstm_custom_word_emb.h5')
token_eval, group_eval = evaluate_model_on_test_split(model, X_te, y_te, z_te, tag2idx, groups2idx)
print(token_eval)
print(group_eval)
predict(model, 'three burger', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
predict(model, 'i want ten burger make that a chicken sandwich and remove one burger', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
predict(model, 'i want a chicken sandwich and remove one burger and she need to order french fries', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
predict(model, 'i want a chicken sandwich and ten ten chicken strips remove five french fries', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
predict(model, 'i want a chicken sandwich with coke actually make the chicken sandwich a hamburger and give me a burger', max_utterance_length, word2idx, tag2idx, groups2idx, displacy_options)
| 0.494385 | 0.835584 |
```
import numpy as np
import matplotlib.pyplot as plt
import cv2
from sklearn.decomposition import PCA
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
```
# Problem : Principal Component Analysis
**Principal component analysis** (PCA) is a technique of dimensionality reduction, which linearly maps data onto a lower-dimensional space, so that the variance of the projected data in the associated dimensions would be maximized. In this problem, you will perform PCA on a dataset of face images.
```
X_train, X_test = [], []
Y_train, Y_test = [], []
for i in range(1, 41):
for j in range(1, 10):
img = cv2.imread('data/{}_{}.png'.format(i, j), cv2.IMREAD_GRAYSCALE)
X_train.append(img)
Y_train.append(i)
img = cv2.imread('data/{}_10.png'.format(i), cv2.IMREAD_GRAYSCALE)
X_test.append(img)
Y_test.append(i)
X_train = np.array(X_train)
X_test = np.array(X_test)
Y_train = np.array(Y_train)
Y_test = np.array(Y_test)
print(X_train.shape, Y_train.shape)
print(X_test.shape, Y_test.shape)
```
## 1. mean face & first four eigenfaces
```
pca = PCA()
pca.fit(X_train.reshape(len(Y_train), -1))
plt.figure(figsize=(16, 12))
plt.subplot(1, 5, 1)
plt.axis('off')
plt.title('Mean face')
plt.imshow(pca.mean_.reshape(X_train[0].shape), cmap='gray')
for i in range(4):
plt.subplot(1, 5, i + 2)
plt.axis('off')
plt.title('Eigenface {}'.format(i + 1))
plt.imshow(pca.components_[i].reshape(X_train[0].shape), cmap='gray')
plt.show()
```
## 2. Reconstruct person2 image1 using the first n = 3, 50, 170, 240, 345 eigenfaces
## 3. compute the mean squared error
```
img = cv2.imread('data/2_1.png', cv2.IMREAD_GRAYSCALE).reshape(1, -1)
a = pca.transform(img)
plt.figure(figsize=(16, 12))
n_components = [3, 50, 170, 240, 345]
for i, n in enumerate(n_components):
face = np.zeros(img.shape)
for j in range(n):
face = face + a[0][j] * pca.components_[j]
face = face + pca.mean_
MSE = np.mean((face - img) ** 2)
plt.subplot(1, 5, i + 1)
plt.axis('off')
plt.title('n={}, MSE={:.2f}'.format(n, MSE))
plt.imshow(face.reshape(X_train[0].shape), cmap='gray')
```
## 4. cross-validation results
```
reduced_X_train = pca.transform(X_train.reshape(len(Y_train), -1))
K = [1, 3, 5]
N = [3, 50, 170]
random = np.random.permutation(len(Y_train))
reduced_X_train = reduced_X_train[random]
Y_train_random = Y_train[random]
for k in K:
print(f'k={k}')
knn = KNeighborsClassifier(n_neighbors=k)
for n in N:
print(' n={}, '.format(n), end='')
score = cross_val_score(knn, reduced_X_train[:, :n], Y_train_random, cv=3)
print('score={:.4f}'.format(score.mean()))
```
## 5. recognition rate of the testing set
```
k = 1
n = 50
reduced_X_test = pca.transform(X_test.reshape(len(Y_test), -1))
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(reduced_X_train[:, :n], Y_train_random)
print(f'accuracy = {knn.score(reduced_X_test[:, :n], Y_test)}')
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import cv2
from sklearn.decomposition import PCA
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
X_train, X_test = [], []
Y_train, Y_test = [], []
for i in range(1, 41):
for j in range(1, 10):
img = cv2.imread('data/{}_{}.png'.format(i, j), cv2.IMREAD_GRAYSCALE)
X_train.append(img)
Y_train.append(i)
img = cv2.imread('data/{}_10.png'.format(i), cv2.IMREAD_GRAYSCALE)
X_test.append(img)
Y_test.append(i)
X_train = np.array(X_train)
X_test = np.array(X_test)
Y_train = np.array(Y_train)
Y_test = np.array(Y_test)
print(X_train.shape, Y_train.shape)
print(X_test.shape, Y_test.shape)
pca = PCA()
pca.fit(X_train.reshape(len(Y_train), -1))
plt.figure(figsize=(16, 12))
plt.subplot(1, 5, 1)
plt.axis('off')
plt.title('Mean face')
plt.imshow(pca.mean_.reshape(X_train[0].shape), cmap='gray')
for i in range(4):
plt.subplot(1, 5, i + 2)
plt.axis('off')
plt.title('Eigenface {}'.format(i + 1))
plt.imshow(pca.components_[i].reshape(X_train[0].shape), cmap='gray')
plt.show()
img = cv2.imread('data/2_1.png', cv2.IMREAD_GRAYSCALE).reshape(1, -1)
a = pca.transform(img)
plt.figure(figsize=(16, 12))
n_components = [3, 50, 170, 240, 345]
for i, n in enumerate(n_components):
face = np.zeros(img.shape)
for j in range(n):
face = face + a[0][j] * pca.components_[j]
face = face + pca.mean_
MSE = np.mean((face - img) ** 2)
plt.subplot(1, 5, i + 1)
plt.axis('off')
plt.title('n={}, MSE={:.2f}'.format(n, MSE))
plt.imshow(face.reshape(X_train[0].shape), cmap='gray')
reduced_X_train = pca.transform(X_train.reshape(len(Y_train), -1))
K = [1, 3, 5]
N = [3, 50, 170]
random = np.random.permutation(len(Y_train))
reduced_X_train = reduced_X_train[random]
Y_train_random = Y_train[random]
for k in K:
print(f'k={k}')
knn = KNeighborsClassifier(n_neighbors=k)
for n in N:
print(' n={}, '.format(n), end='')
score = cross_val_score(knn, reduced_X_train[:, :n], Y_train_random, cv=3)
print('score={:.4f}'.format(score.mean()))
k = 1
n = 50
reduced_X_test = pca.transform(X_test.reshape(len(Y_test), -1))
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(reduced_X_train[:, :n], Y_train_random)
print(f'accuracy = {knn.score(reduced_X_test[:, :n], Y_test)}')
| 0.57523 | 0.944434 |
RMedian : Phase 2 / Probing Phase
```
import random
```
Testfälle:
```
# User input: Distance from n/2 for C, |C| = 2*r, Testcases: 0 ~ user input
n = 40
r = 5
test = 0
# ------------------------------------------------------------
# Automatic
X = [i for i in range(n)]
cnt = [0 for i in range(n)]
S = [i for i in range(0, n, 2)]
XS = [i + 1 for i in range(0, n, 2)]
C = []
for i in range(0, 2*r, 2):
C.append(int(n/2) - r + i - 1)
L = [[i] for i in reversed(range(0, int(n/2) - r - 1, 2))]
R = [[i] for i in range(int(n/2) + r - 1, n, 2)]
# ------------------------------------------------------------
# Testcase 1
if test == 1:
X = [i for i in range(38)]
S = [2*i for i in range(19)]
XS = [2*i + 1 for i in range(19)]
L = [[14, 12], [10, 8], [6, 4], [2, 0]]
C = [16, 18, 20]
R = [[22, 24], [26, 28], [30, 32], [34, 36]]
# ------------------------------------------------------------
# Testcase 2
elif test == 2:
X = [i for i in range(38)]
S = [2*i for i in range(19)]
XS = [2*i + 1 for i in range(19)]
L = [[14], [12], [10], [8], [6], [4], [2], [0]]
C = [16, 18, 20]
R = [[22], [24], [26], [28], [30], [32], [34], [36]]
# ------------------------------------------------------------
print('')
print('X :', X)
print('---')
print('S :', S)
print('XS :', XS)
print('---')
print('L :', L)
print('C :', C)
print('R :', R)
```
Algorithmus : Phase 2
```
def phase2(S, XS, L, C, R, cnt):
mark = [False for _ in range(len(XS)+len(S))]
b = len(L)
random.shuffle(XS)
for x_i in XS:
med = True
for j in reversed(range(0, b - 1)):
current = 2**50
random.shuffle(L[j])
for l in L[j]:
if cnt[l] < current:
x_A = l
if mark[x_A] == True:
c = 1
else:
c = 2
cnt[x_i] += 1
if x_i < x_A:
if j + c < b:
mark[x_i] = True
L[j + c].append(x_i)
med = False
break
current2 = 2**50
random.shuffle(R[j])
for r in R[j]:
if cnt[r] < current2:
x_B = r
if mark[x_B] == True:
c = 1
else:
c = 2
cnt[x_i] += 1
if x_i > x_B:
if j + c < b:
mark[x_i] = True
R[j + c].append(x_i)
med = False
break
if med:
C.append(x_i)
return S, XS, L, C, R, cnt
# Testfall
S, XS, L, C, R, cnt = phase2(S, XS, L, C, R, cnt)
```
Resultat :
```
def test(X, S, XS, L, C, R, cnt):
n, s, xs, l, c, r, sumL, sumR, mx = len(X), len(S), len(XS), len(L), len(C), len(R), 0, 0, max(cnt)
A = []
A += C
for i in range(len(L)):
sumL += len(L[i])
sumR += len(R[i])
A += L[i]
A += R[i]
disc = []
for i in range(n):
if not i in A:
disc.append(i)
print('')
print('Testfall:')
print('=======================================')
print('|X| / |S| / |XS| :', n, '/', s, '/', xs)
print('=======================================')
print('L :', L)
print('C :', C)
print('R :', R)
print('---------------------------------------')
print('|L| / |C| / |R| :', sumL, '/', c, '/', sumR)
print('|L + C + R| / |X| :', sumL + c + sumR, '/', n)
print('---------------------------------------')
print('Discarded :', disc)
print('=======================================')
print('cnt :', cnt)
print('---------------------------------------')
print('max(cnt) :', mx)
print('=======================================')
return
# Testfall
test(X, S, XS, L, C, R, cnt)
```
|
github_jupyter
|
import random
# User input: Distance from n/2 for C, |C| = 2*r, Testcases: 0 ~ user input
n = 40
r = 5
test = 0
# ------------------------------------------------------------
# Automatic
X = [i for i in range(n)]
cnt = [0 for i in range(n)]
S = [i for i in range(0, n, 2)]
XS = [i + 1 for i in range(0, n, 2)]
C = []
for i in range(0, 2*r, 2):
C.append(int(n/2) - r + i - 1)
L = [[i] for i in reversed(range(0, int(n/2) - r - 1, 2))]
R = [[i] for i in range(int(n/2) + r - 1, n, 2)]
# ------------------------------------------------------------
# Testcase 1
if test == 1:
X = [i for i in range(38)]
S = [2*i for i in range(19)]
XS = [2*i + 1 for i in range(19)]
L = [[14, 12], [10, 8], [6, 4], [2, 0]]
C = [16, 18, 20]
R = [[22, 24], [26, 28], [30, 32], [34, 36]]
# ------------------------------------------------------------
# Testcase 2
elif test == 2:
X = [i for i in range(38)]
S = [2*i for i in range(19)]
XS = [2*i + 1 for i in range(19)]
L = [[14], [12], [10], [8], [6], [4], [2], [0]]
C = [16, 18, 20]
R = [[22], [24], [26], [28], [30], [32], [34], [36]]
# ------------------------------------------------------------
print('')
print('X :', X)
print('---')
print('S :', S)
print('XS :', XS)
print('---')
print('L :', L)
print('C :', C)
print('R :', R)
def phase2(S, XS, L, C, R, cnt):
mark = [False for _ in range(len(XS)+len(S))]
b = len(L)
random.shuffle(XS)
for x_i in XS:
med = True
for j in reversed(range(0, b - 1)):
current = 2**50
random.shuffle(L[j])
for l in L[j]:
if cnt[l] < current:
x_A = l
if mark[x_A] == True:
c = 1
else:
c = 2
cnt[x_i] += 1
if x_i < x_A:
if j + c < b:
mark[x_i] = True
L[j + c].append(x_i)
med = False
break
current2 = 2**50
random.shuffle(R[j])
for r in R[j]:
if cnt[r] < current2:
x_B = r
if mark[x_B] == True:
c = 1
else:
c = 2
cnt[x_i] += 1
if x_i > x_B:
if j + c < b:
mark[x_i] = True
R[j + c].append(x_i)
med = False
break
if med:
C.append(x_i)
return S, XS, L, C, R, cnt
# Testfall
S, XS, L, C, R, cnt = phase2(S, XS, L, C, R, cnt)
def test(X, S, XS, L, C, R, cnt):
n, s, xs, l, c, r, sumL, sumR, mx = len(X), len(S), len(XS), len(L), len(C), len(R), 0, 0, max(cnt)
A = []
A += C
for i in range(len(L)):
sumL += len(L[i])
sumR += len(R[i])
A += L[i]
A += R[i]
disc = []
for i in range(n):
if not i in A:
disc.append(i)
print('')
print('Testfall:')
print('=======================================')
print('|X| / |S| / |XS| :', n, '/', s, '/', xs)
print('=======================================')
print('L :', L)
print('C :', C)
print('R :', R)
print('---------------------------------------')
print('|L| / |C| / |R| :', sumL, '/', c, '/', sumR)
print('|L + C + R| / |X| :', sumL + c + sumR, '/', n)
print('---------------------------------------')
print('Discarded :', disc)
print('=======================================')
print('cnt :', cnt)
print('---------------------------------------')
print('max(cnt) :', mx)
print('=======================================')
return
# Testfall
test(X, S, XS, L, C, R, cnt)
| 0.093461 | 0.843959 |
# Amazon SageMaker XGBoost Bring Your Own Model
_**Hosting a Pre-Trained scikit-learn Model in Amazon SageMaker XGBoost Algorithm Container**_
---
---
## Contents
1. [Background](#Background)
1. [Setup](#Setup)
1. [Optionally, train a scikit learn XGBoost model](#Optionally,-train-a-scikit-learn-XGBoost-model)
1. [Upload the pre-trained model to S3](#Upload-the-pre-trained-model-to-S3)
1. [Set up hosting for the model](#Set-up-hosting-for-the-model)
1. [Validate the model for use](#Validate-the-model-for-use)
---
## Background
Amazon SageMaker includes functionality to support a hosted notebook environment, distributed, serverless training, and real-time hosting. We think it works best when all three of these services are used together, but they can also be used independently. Some use cases may only require hosting. Maybe the model was trained prior to Amazon SageMaker existing, in a different service.
This notebook shows how to use a pre-existing scikit-learn trained XGBoost model with the Amazon SageMaker XGBoost Algorithm container to quickly create a hosted endpoint for that model. Please note that scikit-learn XGBoost model is compatible with SageMaker XGBoost container, whereas other gradient boosted tree models (such as one trained in SparkML) are not.
---
## Setup
Let's start by specifying:
* AWS region.
* The IAM role arn used to give learning and hosting access to your data. See the documentation for how to specify these.
* The S3 bucket that you want to use for training and model data.
```
%%time
import os
import boto3
import re
import json
from sagemaker import get_execution_role
region = boto3.Session().region_name
role = get_execution_role()
bucket='<s3 bucket>' # put your s3 bucket name here, and create s3 bucket
prefix = 'sagemaker/DEMO-xgboost-byo'
bucket_path = 'https://s3-{}.amazonaws.com/{}'.format(region,bucket)
# customize to your bucket where you have stored the data
```
## Optionally, train a scikit learn XGBoost model
These steps are optional and are needed to generate the scikit-learn model that will eventually be hosted using the SageMaker Algorithm contained.
### Install XGboost
Note that for conda based installation, you'll need to change the Notebook kernel to the environment with conda and Python3.
```
!conda install -y -c conda-forge xgboost
```
### Fetch the dataset
```
%%time
import pickle, gzip, numpy, urllib.request, json
# Load the dataset
urllib.request.urlretrieve("http://deeplearning.net/data/mnist/mnist.pkl.gz", "mnist.pkl.gz")
f = gzip.open('mnist.pkl.gz', 'rb')
train_set, valid_set, test_set = pickle.load(f, encoding='latin1')
f.close()
```
### Prepare the dataset for training
```
%%time
import struct
import io
import boto3
def get_dataset():
import pickle
import gzip
with gzip.open('mnist.pkl.gz', 'rb') as f:
u = pickle._Unpickler(f)
u.encoding = 'latin1'
return u.load()
train_set, valid_set, test_set = get_dataset()
train_X = train_set[0]
train_y = train_set[1]
valid_X = valid_set[0]
valid_y = valid_set[1]
test_X = test_set[0]
test_y = test_set[1]
```
### Train the XGBClassifier
```
import xgboost as xgb
import sklearn as sk
bt = xgb.XGBClassifier(max_depth=5,
learning_rate=0.2,
n_estimators=10,
objective='multi:softmax') # Setup xgboost model
bt.fit(train_X, train_y, # Train it to our data
eval_set=[(valid_X, valid_y)],
verbose=False)
```
### Save the trained model file
Note that the model file name must satisfy the regular expression pattern: `^[a-zA-Z0-9](-*[a-zA-Z0-9])*;`. The model file also need to tar-zipped.
```
model_file_name = "DEMO-local-xgboost-model"
bt._Booster.save_model(model_file_name)
!tar czvf model.tar.gz $model_file_name
```
## Upload the pre-trained model to S3
```
fObj = open("model.tar.gz", 'rb')
key= os.path.join(prefix, model_file_name, 'model.tar.gz')
boto3.Session().resource('s3').Bucket(bucket).Object(key).upload_fileobj(fObj)
```
## Set up hosting for the model
### Import model into hosting
This involves creating a SageMaker model from the model file previously uploaded to S3.
```
containers = {'us-west-2': '433757028032.dkr.ecr.us-west-2.amazonaws.com/xgboost:latest',
'us-east-1': '811284229777.dkr.ecr.us-east-1.amazonaws.com/xgboost:latest',
'us-east-2': '825641698319.dkr.ecr.us-east-2.amazonaws.com/xgboost:latest',
'eu-west-1': '685385470294.dkr.ecr.eu-west-1.amazonaws.com/xgboost:latest',
'ap-northeast-1': '501404015308.dkr.ecr.ap-northeast-1.amazonaws.com/xgboost:latest',
'ap-northeast-2': '306986355934.dkr.ecr.ap-northeast-2.amazonaws.com/xgboost:latest'}
container = containers[boto3.Session().region_name]
%%time
from time import gmtime, strftime
model_name = model_file_name + strftime("%Y-%m-%d-%H-%M-%S", gmtime())
model_url = 'https://s3-{}.amazonaws.com/{}/{}'.format(region,bucket,key)
sm_client = boto3.client('sagemaker')
print (model_url)
primary_container = {
'Image': container,
'ModelDataUrl': model_url,
}
create_model_response2 = sm_client.create_model(
ModelName = model_name,
ExecutionRoleArn = role,
PrimaryContainer = primary_container)
print(create_model_response2['ModelArn'])
```
### Create endpoint configuration
SageMaker supports configuring REST endpoints in hosting with multiple models, e.g. for A/B testing purposes. In order to support this, you can create an endpoint configuration, that describes the distribution of traffic across the models, whether split, shadowed, or sampled in some way. In addition, the endpoint configuration describes the instance type required for model deployment.
```
from time import gmtime, strftime
endpoint_config_name = 'DEMO-XGBoostEndpointConfig-' + strftime("%Y-%m-%d-%H-%M-%S", gmtime())
print(endpoint_config_name)
create_endpoint_config_response = sm_client.create_endpoint_config(
EndpointConfigName = endpoint_config_name,
ProductionVariants=[{
'InstanceType':'ml.m4.xlarge',
'InitialInstanceCount':1,
'InitialVariantWeight':1,
'ModelName':model_name,
'VariantName':'AllTraffic'}])
print("Endpoint Config Arn: " + create_endpoint_config_response['EndpointConfigArn'])
```
### Create endpoint
Lastly, you create the endpoint that serves up the model, through specifying the name and configuration defined above. The end result is an endpoint that can be validated and incorporated into production applications. This takes 9-11 minutes to complete.
```
%%time
import time
endpoint_name = 'DEMO-XGBoostEndpoint-' + strftime("%Y-%m-%d-%H-%M-%S", gmtime())
print(endpoint_name)
create_endpoint_response = sm_client.create_endpoint(
EndpointName=endpoint_name,
EndpointConfigName=endpoint_config_name)
print(create_endpoint_response['EndpointArn'])
resp = sm_client.describe_endpoint(EndpointName=endpoint_name)
status = resp['EndpointStatus']
print("Status: " + status)
while status=='Creating':
time.sleep(60)
resp = sm_client.describe_endpoint(EndpointName=endpoint_name)
status = resp['EndpointStatus']
print("Status: " + status)
print("Arn: " + resp['EndpointArn'])
print("Status: " + status)
```
## Validate the model for use
Now you can obtain the endpoint from the client library using the result from previous operations and generate classifications from the model using that endpoint.
```
runtime_client = boto3.client('runtime.sagemaker')
```
Lets generate the prediction for a single datapoint. We'll pick one from the test data generated earlier.
```
import numpy as np
point_X = test_X[0]
point_X = np.expand_dims(point_X, axis=0)
point_y = test_y[0]
np.savetxt("test_point.csv", point_X, delimiter=",")
%%time
import json
file_name = 'test_point.csv' #customize to your test file, will be 'mnist.single.test' if use data above
with open(file_name, 'r') as f:
payload = f.read().strip()
response = runtime_client.invoke_endpoint(EndpointName=endpoint_name,
ContentType='text/csv',
Body=payload)
result = response['Body'].read().decode('ascii')
print('Predicted Class Probabilities: {}.'.format(result))
```
### Post process the output
Since the result is a string, let's process it to determine the the output class label.
```
floatArr = np.array(json.loads(result))
predictedLabel = np.argmax(floatArr)
print('Predicted Class Label: {}.'.format(predictedLabel))
print('Actual Class Label: {}.'.format(point_y))
```
### (Optional) Delete the Endpoint
If you're ready to be done with this notebook, please run the delete_endpoint line in the cell below. This will remove the hosted endpoint you created and avoid any charges from a stray instance being left on.
```
sm_client.delete_endpoint(EndpointName=endpoint_name)
```
|
github_jupyter
|
%%time
import os
import boto3
import re
import json
from sagemaker import get_execution_role
region = boto3.Session().region_name
role = get_execution_role()
bucket='<s3 bucket>' # put your s3 bucket name here, and create s3 bucket
prefix = 'sagemaker/DEMO-xgboost-byo'
bucket_path = 'https://s3-{}.amazonaws.com/{}'.format(region,bucket)
# customize to your bucket where you have stored the data
!conda install -y -c conda-forge xgboost
%%time
import pickle, gzip, numpy, urllib.request, json
# Load the dataset
urllib.request.urlretrieve("http://deeplearning.net/data/mnist/mnist.pkl.gz", "mnist.pkl.gz")
f = gzip.open('mnist.pkl.gz', 'rb')
train_set, valid_set, test_set = pickle.load(f, encoding='latin1')
f.close()
%%time
import struct
import io
import boto3
def get_dataset():
import pickle
import gzip
with gzip.open('mnist.pkl.gz', 'rb') as f:
u = pickle._Unpickler(f)
u.encoding = 'latin1'
return u.load()
train_set, valid_set, test_set = get_dataset()
train_X = train_set[0]
train_y = train_set[1]
valid_X = valid_set[0]
valid_y = valid_set[1]
test_X = test_set[0]
test_y = test_set[1]
import xgboost as xgb
import sklearn as sk
bt = xgb.XGBClassifier(max_depth=5,
learning_rate=0.2,
n_estimators=10,
objective='multi:softmax') # Setup xgboost model
bt.fit(train_X, train_y, # Train it to our data
eval_set=[(valid_X, valid_y)],
verbose=False)
model_file_name = "DEMO-local-xgboost-model"
bt._Booster.save_model(model_file_name)
!tar czvf model.tar.gz $model_file_name
fObj = open("model.tar.gz", 'rb')
key= os.path.join(prefix, model_file_name, 'model.tar.gz')
boto3.Session().resource('s3').Bucket(bucket).Object(key).upload_fileobj(fObj)
containers = {'us-west-2': '433757028032.dkr.ecr.us-west-2.amazonaws.com/xgboost:latest',
'us-east-1': '811284229777.dkr.ecr.us-east-1.amazonaws.com/xgboost:latest',
'us-east-2': '825641698319.dkr.ecr.us-east-2.amazonaws.com/xgboost:latest',
'eu-west-1': '685385470294.dkr.ecr.eu-west-1.amazonaws.com/xgboost:latest',
'ap-northeast-1': '501404015308.dkr.ecr.ap-northeast-1.amazonaws.com/xgboost:latest',
'ap-northeast-2': '306986355934.dkr.ecr.ap-northeast-2.amazonaws.com/xgboost:latest'}
container = containers[boto3.Session().region_name]
%%time
from time import gmtime, strftime
model_name = model_file_name + strftime("%Y-%m-%d-%H-%M-%S", gmtime())
model_url = 'https://s3-{}.amazonaws.com/{}/{}'.format(region,bucket,key)
sm_client = boto3.client('sagemaker')
print (model_url)
primary_container = {
'Image': container,
'ModelDataUrl': model_url,
}
create_model_response2 = sm_client.create_model(
ModelName = model_name,
ExecutionRoleArn = role,
PrimaryContainer = primary_container)
print(create_model_response2['ModelArn'])
from time import gmtime, strftime
endpoint_config_name = 'DEMO-XGBoostEndpointConfig-' + strftime("%Y-%m-%d-%H-%M-%S", gmtime())
print(endpoint_config_name)
create_endpoint_config_response = sm_client.create_endpoint_config(
EndpointConfigName = endpoint_config_name,
ProductionVariants=[{
'InstanceType':'ml.m4.xlarge',
'InitialInstanceCount':1,
'InitialVariantWeight':1,
'ModelName':model_name,
'VariantName':'AllTraffic'}])
print("Endpoint Config Arn: " + create_endpoint_config_response['EndpointConfigArn'])
%%time
import time
endpoint_name = 'DEMO-XGBoostEndpoint-' + strftime("%Y-%m-%d-%H-%M-%S", gmtime())
print(endpoint_name)
create_endpoint_response = sm_client.create_endpoint(
EndpointName=endpoint_name,
EndpointConfigName=endpoint_config_name)
print(create_endpoint_response['EndpointArn'])
resp = sm_client.describe_endpoint(EndpointName=endpoint_name)
status = resp['EndpointStatus']
print("Status: " + status)
while status=='Creating':
time.sleep(60)
resp = sm_client.describe_endpoint(EndpointName=endpoint_name)
status = resp['EndpointStatus']
print("Status: " + status)
print("Arn: " + resp['EndpointArn'])
print("Status: " + status)
runtime_client = boto3.client('runtime.sagemaker')
import numpy as np
point_X = test_X[0]
point_X = np.expand_dims(point_X, axis=0)
point_y = test_y[0]
np.savetxt("test_point.csv", point_X, delimiter=",")
%%time
import json
file_name = 'test_point.csv' #customize to your test file, will be 'mnist.single.test' if use data above
with open(file_name, 'r') as f:
payload = f.read().strip()
response = runtime_client.invoke_endpoint(EndpointName=endpoint_name,
ContentType='text/csv',
Body=payload)
result = response['Body'].read().decode('ascii')
print('Predicted Class Probabilities: {}.'.format(result))
floatArr = np.array(json.loads(result))
predictedLabel = np.argmax(floatArr)
print('Predicted Class Label: {}.'.format(predictedLabel))
print('Actual Class Label: {}.'.format(point_y))
sm_client.delete_endpoint(EndpointName=endpoint_name)
| 0.285372 | 0.900617 |
```
import os
from os import path
import pandas as pd
import gensim
from gensim import corpora
import numpy as np
from numpy import percentile
from gensim import similarities
from gensim.similarities import Similarity
from gensim import models
from skimage import data, img_as_float
from skimage.measure import compare_ssim
from sklearn.metrics.pairwise import cosine_similarity
from scipy import ndimage
import random
tmp_dir = '/data/katya/tmp'
# Percentile: higher values lead to skipping more pixels (from 0 to 1 - quantile, from 0 to 100 percentile)
quan = 0.5
# use tfidf modeling
tfidf = True
# log of intensities
log = False
# square root of intensities
sqrt = False
# hotspot removal
hotspot = False
# median filter window size
med_win = 3
def compute_similarities(ds_path):
counter = 0
int_df = None
ion_corpus = []
first_run = True
ions = []
images = []
for ion_file_name in os.listdir(ds_path):
(sf, adduct) = ion_file_name.split('.')[0].split('_')
ions.append((sf, adduct))
f_path = path.join(ds_path, ion_file_name)
img = np.load(f_path)
if log: img = np.log(img)
if sqrt: img = np.sqrt(img)
# remove hot spots
if hotspot:
q = np.quantile(img, 0.99)
img[img>q] = q
# compute intensity threshold
if quan > 0:
q = np.quantile(img, quan)
img[img<q] = 0
# median filter
if med_win > 0:
img = ndimage.median_filter(img, med_win)
images.append(img)
x = img.flatten()
if first_run:
int_df = pd.DataFrame(columns = list(range(0, x.shape[0])))
first_run = False
int_df.loc[counter] = x
# build ion-pixel gensim corpus
non_zero_x = x.nonzero()[0]
ion_doc = list(zip(non_zero_x, x[non_zero_x]))
ion_corpus.append(ion_doc)
counter += 1
sim_index = gensim.similarities.docsim.Similarity(tmp_dir, ion_corpus, num_features = x.shape[0])
cosine = sim_index[ion_corpus]
if tfidf:
tfidf_model = gensim.models.TfidfModel(ion_corpus)
tfidf_corpus = tfidf_model[ion_corpus]
sim_index = gensim.similarities.docsim.Similarity(tmp_dir, ion_corpus, num_features = x.shape[0])
tfidf_cosine = sim_index[tfidf_corpus]
pearson = int_df.T.corr(method='pearson')
spearman = int_df.T.corr(method='spearman')
# compute ssim similarity
ssims = np.ones((len(images), len(images)))
for i in range(0, len(images)):
for j in range(i+1, len(images)):
ssim = compare_ssim(images[i], images[j], win_size=None, gradient=False, data_range=None, multichannel=False, gaussian_weights=True, full=False)
ssims[i][j] = ssim
ssims[j][i] = ssim
int_df = None
ion_corpus = None
tfidf_corpus = None
images = None
for f in os.listdir(tmp_dir): os.remove(path.join(tmp_dir, f))
return (ions, cosine, tfidf_cosine, pearson.values.tolist(), spearman.values.tolist(), ssims)
# choose random dataset and compute similarities between all ions
img_dir = '/data/katya/coloc/gs_imgs'
random_ds_name = random.choice(os.listdir(img_dir))
ds_path = path.join(img_dir, random_ds_name)
(ions, cosine, tfidf_cosine, pearson, spearman, ssims) = compute_similarities(ds_path)
# choose random ion from the dataset and show n most similar ions according to measure of choice
%matplotlib inline
import matplotlib.pyplot as plt
n = 10
i = random.choice(range(len(ions)))
random_ion = ions[i]
def show_ion_img(ion):
f_path = '%s/%s/%s_%s.npy' % (img_dir, random_ds_name, ion[0], ion[1])
img = np.load(f_path)
plt.pcolormesh(img,cmap='viridis')
#plt.axes().set_aspect('equal', 'datalim')
#plt.axes().axis('off')
plt.show()
print('RANDOM ION:', random_ion)
show_ion_img(random_ion)
sims = cosine[i]
most_sim_inds = sims.argsort()[-(n+1):][::-1]
for j in most_sim_inds:
if i == j: continue
print(ions[j], sims[j])
show_ion_img(ions[j])
# compute similarities for gold standard
gs_file = '/data/katya/coloc/coloc_gs.csv'
coloc_gs_df = pd.read_csv(gs_file)
coloc_gs_df['rev_rank'] = 10-coloc_gs_df['rank']
for datasetId, dsrows in coloc_gs_df.groupby('datasetId'):
print(datasetId)
ds_path = path.join(img_dir, datasetId)
(ions, cosine, tfidf_cosine, pearson, spearman, ssims) = compute_similarities(ds_path)
for i, row in dsrows.iterrows():
base_i = ions.index((row.baseSf, row.baseAdduct))
other_i = ions.index((row.otherSf, row.otherAdduct))
coloc_gs_df.at[i, 'cosine'] = cosine[base_i][other_i]
coloc_gs_df.at[i, 'tfidf_cosine'] = tfidf_cosine[base_i][other_i]
coloc_gs_df.at[i, 'pearson'] = pearson[base_i][other_i]
coloc_gs_df.at[i, 'spearman'] = spearman[base_i][other_i]
coloc_gs_df.at[i, 'ssim'] = ssims[base_i][other_i]
# evaluate gs measures
from scipy import stats
measures = ['cosine', 'tfidf_cosine', 'pearson', 'spearman', 'ssim']
set_results = pd.DataFrame(columns = ['measure', 'spearman', 'kendall'])
# calculate correlation coefficients for each set
counter = 0
for (d, s, a), rows in coloc_gs_df.groupby(['datasetId', 'baseSf', 'baseAdduct']):
for m in measures:
s = stats.spearmanr(rows.rev_rank.values, rows[m].values)
k = stats.kendalltau(rows.rev_rank.values, rows[m].values)
set_results.loc[counter] = [m, s[0], k[0]]
counter += 1
# report average over sets
for m, rows in set_results.groupby('measure'):
print('%s: spearman = %.3f, kendall = %.3f' % (m, rows['spearman'].mean(), rows['kendall'].mean()))
```
|
github_jupyter
|
import os
from os import path
import pandas as pd
import gensim
from gensim import corpora
import numpy as np
from numpy import percentile
from gensim import similarities
from gensim.similarities import Similarity
from gensim import models
from skimage import data, img_as_float
from skimage.measure import compare_ssim
from sklearn.metrics.pairwise import cosine_similarity
from scipy import ndimage
import random
tmp_dir = '/data/katya/tmp'
# Percentile: higher values lead to skipping more pixels (from 0 to 1 - quantile, from 0 to 100 percentile)
quan = 0.5
# use tfidf modeling
tfidf = True
# log of intensities
log = False
# square root of intensities
sqrt = False
# hotspot removal
hotspot = False
# median filter window size
med_win = 3
def compute_similarities(ds_path):
counter = 0
int_df = None
ion_corpus = []
first_run = True
ions = []
images = []
for ion_file_name in os.listdir(ds_path):
(sf, adduct) = ion_file_name.split('.')[0].split('_')
ions.append((sf, adduct))
f_path = path.join(ds_path, ion_file_name)
img = np.load(f_path)
if log: img = np.log(img)
if sqrt: img = np.sqrt(img)
# remove hot spots
if hotspot:
q = np.quantile(img, 0.99)
img[img>q] = q
# compute intensity threshold
if quan > 0:
q = np.quantile(img, quan)
img[img<q] = 0
# median filter
if med_win > 0:
img = ndimage.median_filter(img, med_win)
images.append(img)
x = img.flatten()
if first_run:
int_df = pd.DataFrame(columns = list(range(0, x.shape[0])))
first_run = False
int_df.loc[counter] = x
# build ion-pixel gensim corpus
non_zero_x = x.nonzero()[0]
ion_doc = list(zip(non_zero_x, x[non_zero_x]))
ion_corpus.append(ion_doc)
counter += 1
sim_index = gensim.similarities.docsim.Similarity(tmp_dir, ion_corpus, num_features = x.shape[0])
cosine = sim_index[ion_corpus]
if tfidf:
tfidf_model = gensim.models.TfidfModel(ion_corpus)
tfidf_corpus = tfidf_model[ion_corpus]
sim_index = gensim.similarities.docsim.Similarity(tmp_dir, ion_corpus, num_features = x.shape[0])
tfidf_cosine = sim_index[tfidf_corpus]
pearson = int_df.T.corr(method='pearson')
spearman = int_df.T.corr(method='spearman')
# compute ssim similarity
ssims = np.ones((len(images), len(images)))
for i in range(0, len(images)):
for j in range(i+1, len(images)):
ssim = compare_ssim(images[i], images[j], win_size=None, gradient=False, data_range=None, multichannel=False, gaussian_weights=True, full=False)
ssims[i][j] = ssim
ssims[j][i] = ssim
int_df = None
ion_corpus = None
tfidf_corpus = None
images = None
for f in os.listdir(tmp_dir): os.remove(path.join(tmp_dir, f))
return (ions, cosine, tfidf_cosine, pearson.values.tolist(), spearman.values.tolist(), ssims)
# choose random dataset and compute similarities between all ions
img_dir = '/data/katya/coloc/gs_imgs'
random_ds_name = random.choice(os.listdir(img_dir))
ds_path = path.join(img_dir, random_ds_name)
(ions, cosine, tfidf_cosine, pearson, spearman, ssims) = compute_similarities(ds_path)
# choose random ion from the dataset and show n most similar ions according to measure of choice
%matplotlib inline
import matplotlib.pyplot as plt
n = 10
i = random.choice(range(len(ions)))
random_ion = ions[i]
def show_ion_img(ion):
f_path = '%s/%s/%s_%s.npy' % (img_dir, random_ds_name, ion[0], ion[1])
img = np.load(f_path)
plt.pcolormesh(img,cmap='viridis')
#plt.axes().set_aspect('equal', 'datalim')
#plt.axes().axis('off')
plt.show()
print('RANDOM ION:', random_ion)
show_ion_img(random_ion)
sims = cosine[i]
most_sim_inds = sims.argsort()[-(n+1):][::-1]
for j in most_sim_inds:
if i == j: continue
print(ions[j], sims[j])
show_ion_img(ions[j])
# compute similarities for gold standard
gs_file = '/data/katya/coloc/coloc_gs.csv'
coloc_gs_df = pd.read_csv(gs_file)
coloc_gs_df['rev_rank'] = 10-coloc_gs_df['rank']
for datasetId, dsrows in coloc_gs_df.groupby('datasetId'):
print(datasetId)
ds_path = path.join(img_dir, datasetId)
(ions, cosine, tfidf_cosine, pearson, spearman, ssims) = compute_similarities(ds_path)
for i, row in dsrows.iterrows():
base_i = ions.index((row.baseSf, row.baseAdduct))
other_i = ions.index((row.otherSf, row.otherAdduct))
coloc_gs_df.at[i, 'cosine'] = cosine[base_i][other_i]
coloc_gs_df.at[i, 'tfidf_cosine'] = tfidf_cosine[base_i][other_i]
coloc_gs_df.at[i, 'pearson'] = pearson[base_i][other_i]
coloc_gs_df.at[i, 'spearman'] = spearman[base_i][other_i]
coloc_gs_df.at[i, 'ssim'] = ssims[base_i][other_i]
# evaluate gs measures
from scipy import stats
measures = ['cosine', 'tfidf_cosine', 'pearson', 'spearman', 'ssim']
set_results = pd.DataFrame(columns = ['measure', 'spearman', 'kendall'])
# calculate correlation coefficients for each set
counter = 0
for (d, s, a), rows in coloc_gs_df.groupby(['datasetId', 'baseSf', 'baseAdduct']):
for m in measures:
s = stats.spearmanr(rows.rev_rank.values, rows[m].values)
k = stats.kendalltau(rows.rev_rank.values, rows[m].values)
set_results.loc[counter] = [m, s[0], k[0]]
counter += 1
# report average over sets
for m, rows in set_results.groupby('measure'):
print('%s: spearman = %.3f, kendall = %.3f' % (m, rows['spearman'].mean(), rows['kendall'].mean()))
| 0.343672 | 0.335351 |
```
exec('from __future__ import unicode_literals')
import os
import sys
import random
import json
module_path = os.path.abspath(os.path.join('../'))
if module_path not in sys.path:
sys.path.append(module_path)
module_path = os.path.abspath(os.path.join('../onmt'))
if module_path not in sys.path:
sys.path.append(module_path)
from itertools import repeat
from onmt.utils.logging import init_logger
from onmt.utils.misc import split_corpus
import onmt.translate.translator as translator
import onmt.opts as opts
from onmt.utils.parse import ArgumentParser
from kp_gen_eval import _get_parser
from nltk.corpus import stopwords
stoplist = stopwords.words('english')
from string import punctuation
import onmt.keyphrase.pke as pke
from nltk.corpus import stopwords
import onmt.keyphrase.kp_inference as kp_inference
import importlib
importlib.reload(kp_inference)
importlib.reload(translator)
```
### Load a text (assume current directory is OpenNMT-kpg/notebook/)
```
data_root_path = '../data/keyphrase/json/duc/duc_test.json'
doc_dicts = []
with open(data_root_path, 'r') as data_file:
doc_dicts = [json.loads(l) for l in data_file]
print('Loaded #(docs)=%d' % (len(doc_dicts)))
```
##### Sample a paragraph
```
doc_id = random.randint(0, len(doc_dicts))
doc = doc_dicts[doc_id]
print(doc.keys())
text_to_extract = doc['abstract']
print(doc_id)
print(text_to_extract)
```
### Supervised Deep Keyphrase Model
```
parser = _get_parser()
config_path = '/zfs1/pbrusilovsky/rum20/kp/OpenNMT-kpg/config/translate/config-rnn-keyphrase.yml'
print(os.path.abspath('../config/translate/config-rnn-keyphrase.yml'))
print(os.path.exists(config_path))
# one2one_ckpt_path = 'models/keyphrase/keyphrase/meng17-one2seq/meng17-one2seq-kp20k/kp20k-meng17-one2one-rnn-BS128-LR0.05-Layer1-Dim150-Emb100-Dropout0.0-Copytrue-Covfalse-Contboth-IF1_step_30000.pt'
one2seq_ckpt_path = '/zfs1/pbrusilovsky/rum20/kp/OpenNMT-kpg/models/keyphrase/meng17-one2seq/meng17-one2seq-kp20k/kp20k-meng17-verbatim_append-rnn-BS64-LR0.05-Layer1-Dim150-Emb100-Dropout0.0-Copytrue-Reusetrue-Covtrue-PEfalse-Contboth-IF1_step_50000.pt'
opt = parser.parse_args('-config %s' % (config_path))
setattr(opt, 'models', [one2seq_ckpt_path])
translator = translator.build_translator(opt, report_score=False)
scores, predictions = translator.translate(
src=[text_to_extract],
tgt=None,
src_dir=opt.src_dir,
batch_size=opt.batch_size,
attn_debug=opt.attn_debug,
opt=opt
)
print('Paragraph:\n\t'+text_to_extract)
print('Top predictions:')
keyphrases = [kp.lower().strip() for kp in predictions[0] if (not kp.lower().strip() in stoplist) and (kp != '<unk>') and (len(kp.strip())) > 0]
for kp_id, kp in enumerate(keyphrases[: min(len(keyphrases), 20)]):
print('\t%d: %s' % (kp_id+1, kp))
```
### PKE models
#### TF-IDF
```
dataset_name = 'test'
dataset_path = '../data/%s/' % dataset_name
_ = kp_inference.extract_pke(text_to_extract, method='tfidf' , dataset_path=dataset_path,
df_path=os.path.abspath(dataset_path + '../%s.df.tsv.gz' % dataset_name), top_k=20)
```
#### YAKE
```
_ = kp_inference.extract_pke(text_to_extract, method='yake', top_k=20)
```
#### TextRank
```
# define the set of valid Part-of-Speeches
pos = {'NOUN', 'PROPN', 'ADJ'}
# 1. create a TextRank extractor.
extractor = pke.unsupervised.TextRank()
# 2. load the content of the document.
extractor.load_document(input=text_to_extract,
language='en_core_web_sm',
normalization=None)
# 3. build the graph representation of the document and rank the words.
# Keyphrase candidates are composed from the 33-percent
# highest-ranked words.
extractor.candidate_weighting(window=2,
pos=pos,
top_percent=0.33)
# 4. get the 10-highest scored candidates as keyphrases
keyphrases = extractor.get_n_best(n=10)
for kp_id, kp in enumerate(keyphrases):
print('\t%d: %s (%.4f)' % (kp_id+1, kp[0], kp[1]))
```
|
github_jupyter
|
exec('from __future__ import unicode_literals')
import os
import sys
import random
import json
module_path = os.path.abspath(os.path.join('../'))
if module_path not in sys.path:
sys.path.append(module_path)
module_path = os.path.abspath(os.path.join('../onmt'))
if module_path not in sys.path:
sys.path.append(module_path)
from itertools import repeat
from onmt.utils.logging import init_logger
from onmt.utils.misc import split_corpus
import onmt.translate.translator as translator
import onmt.opts as opts
from onmt.utils.parse import ArgumentParser
from kp_gen_eval import _get_parser
from nltk.corpus import stopwords
stoplist = stopwords.words('english')
from string import punctuation
import onmt.keyphrase.pke as pke
from nltk.corpus import stopwords
import onmt.keyphrase.kp_inference as kp_inference
import importlib
importlib.reload(kp_inference)
importlib.reload(translator)
data_root_path = '../data/keyphrase/json/duc/duc_test.json'
doc_dicts = []
with open(data_root_path, 'r') as data_file:
doc_dicts = [json.loads(l) for l in data_file]
print('Loaded #(docs)=%d' % (len(doc_dicts)))
doc_id = random.randint(0, len(doc_dicts))
doc = doc_dicts[doc_id]
print(doc.keys())
text_to_extract = doc['abstract']
print(doc_id)
print(text_to_extract)
parser = _get_parser()
config_path = '/zfs1/pbrusilovsky/rum20/kp/OpenNMT-kpg/config/translate/config-rnn-keyphrase.yml'
print(os.path.abspath('../config/translate/config-rnn-keyphrase.yml'))
print(os.path.exists(config_path))
# one2one_ckpt_path = 'models/keyphrase/keyphrase/meng17-one2seq/meng17-one2seq-kp20k/kp20k-meng17-one2one-rnn-BS128-LR0.05-Layer1-Dim150-Emb100-Dropout0.0-Copytrue-Covfalse-Contboth-IF1_step_30000.pt'
one2seq_ckpt_path = '/zfs1/pbrusilovsky/rum20/kp/OpenNMT-kpg/models/keyphrase/meng17-one2seq/meng17-one2seq-kp20k/kp20k-meng17-verbatim_append-rnn-BS64-LR0.05-Layer1-Dim150-Emb100-Dropout0.0-Copytrue-Reusetrue-Covtrue-PEfalse-Contboth-IF1_step_50000.pt'
opt = parser.parse_args('-config %s' % (config_path))
setattr(opt, 'models', [one2seq_ckpt_path])
translator = translator.build_translator(opt, report_score=False)
scores, predictions = translator.translate(
src=[text_to_extract],
tgt=None,
src_dir=opt.src_dir,
batch_size=opt.batch_size,
attn_debug=opt.attn_debug,
opt=opt
)
print('Paragraph:\n\t'+text_to_extract)
print('Top predictions:')
keyphrases = [kp.lower().strip() for kp in predictions[0] if (not kp.lower().strip() in stoplist) and (kp != '<unk>') and (len(kp.strip())) > 0]
for kp_id, kp in enumerate(keyphrases[: min(len(keyphrases), 20)]):
print('\t%d: %s' % (kp_id+1, kp))
dataset_name = 'test'
dataset_path = '../data/%s/' % dataset_name
_ = kp_inference.extract_pke(text_to_extract, method='tfidf' , dataset_path=dataset_path,
df_path=os.path.abspath(dataset_path + '../%s.df.tsv.gz' % dataset_name), top_k=20)
_ = kp_inference.extract_pke(text_to_extract, method='yake', top_k=20)
# define the set of valid Part-of-Speeches
pos = {'NOUN', 'PROPN', 'ADJ'}
# 1. create a TextRank extractor.
extractor = pke.unsupervised.TextRank()
# 2. load the content of the document.
extractor.load_document(input=text_to_extract,
language='en_core_web_sm',
normalization=None)
# 3. build the graph representation of the document and rank the words.
# Keyphrase candidates are composed from the 33-percent
# highest-ranked words.
extractor.candidate_weighting(window=2,
pos=pos,
top_percent=0.33)
# 4. get the 10-highest scored candidates as keyphrases
keyphrases = extractor.get_n_best(n=10)
for kp_id, kp in enumerate(keyphrases):
print('\t%d: %s (%.4f)' % (kp_id+1, kp[0], kp[1]))
| 0.300438 | 0.251636 |
```
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
from torchvision.datasets import FashionMNIST
import torch.nn as nn
import torch.nn.functional as F
import torch
latent_dims = 2
num_epochs = 100
batch_size = 128
capacity = 64
learning_rate = 1e-3
variational_beta = 1
use_gpu = True
img_transform = transforms.Compose([
transforms.ToTensor()
])
batch_size = 128
train_dataset = FashionMNIST(root='./data/FashionMNIST', download=True, train=True, transform=img_transform)
train_dataloader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_dataset = FashionMNIST(root='./data/FashionMNIST', download=True, train=False, transform=img_transform)
test_dataloader = DataLoader(test_dataset, batch_size=batch_size, shuffle=True)
class Encoder(nn.Module):
def __init__(self):
super(Encoder, self).__init__()
c = capacity
self.conv1 = nn.Conv2d(in_channels=1, out_channels=c, kernel_size=4, padding=1, stride=2)
self.conv2 = nn.Conv2d(in_channels=c, out_channels=c*2, kernel_size=4, stride=2, padding=1)
self.fc_mu = nn.Linear(in_features=c*2*7*7, out_features=latent_dims)
self.fc_logvar = nn.Linear(in_features=c*2*7*7, out_features=latent_dims)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
x = x.view(x.size(0), -1)
x_mu = self.fc_mu(x)
x_logvar = self.fc_logvar(x)
return x_mu, x_logvar
class Decoder(nn.Module):
def __init__(self):
super(Decoder, self).__init__()
c=capacity
self.fc = nn.Linear(in_features=latent_dims, out_features=c*2*7*7)
self.conv2 = nn.ConvTranspose2d(in_channels=c*2, out_channels=c, kernel_size=4, stride=2, padding=1)
self.conv1 = nn.ConvTranspose2d(in_channels=c, out_channels=1, kernel_size=4, stride=2, padding=1)
def forward(self, x):
x = self.fc(x)
x = x.view(x.size(0),capacity*2, 7, 7)
x = F.relu(self.conv2(x))
x = torch.sigmoid(self.conv1(x))
return x
class VariationalAutoencoder(nn.Module):
def __init__(self):
super(VariationalAutoencoder, self).__init__()
self.encoder= Encoder()
self.decoder = Decoder()
def forward(self,x):
latent_mu, latent_logvar = self.encoder(x)
latent = self.latent_sample(latent_mu, latent_logvar)
x_recon = self.decoder(latent)
return x_recon, latent_mu, latent_logvar
def latent_sample(self, mu, logvar):
if self.training:
std = logvar.mul(0.5).exp()
eps = torch.empty_like(std).normal_()
return eps.mul(std).add_(mu)
else:
return mu
def vae_loss(recon_x, x, mu, logvar):
recon_loss = F.binary_cross_entropy(recon_x.view(-1,784), x.view(-1, 784), reduction='sum')
kldivergence = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
return recon_loss + variational_beta * kldivergence
vae = VariationalAutoencoder()
device = torch.device("cuda:0" if use_gpu and torch.cuda.is_available() else "cpu")
vae = vae.to(device)
num_params = sum(p.numel() for p in vae.parameters() if p.requires_grad)
print('Number of parameters: %d' % num_params)
optimizer = torch.optim.Adam(params=vae.parameters(), lr=learning_rate, weight_decay=1e-5)
vae.train()
train_loss_avg = []
print('Training ...')
for epoch in range(num_epochs):
train_loss_avg.append(0)
num_batches = 0
for image_batch, _ in train_dataloader:
image_batch = image_batch.to(device)
# vae reconstruction
image_batch_recon, latent_mu, latent_logvar = vae(image_batch)
# reconstruction error
loss = vae_loss(image_batch_recon, image_batch, latent_mu, latent_logvar)
# backpropagation
optimizer.zero_grad()
loss.backward()
# one step of the optmizer (using the gradients from backpropagation)
optimizer.step()
train_loss_avg[-1] += loss.item()
num_batches += 1
train_loss_avg[-1] /= num_batches
print('Epoch [%d / %d] average reconstruction error: %f' % (epoch+1, num_epochs, train_loss_avg[-1]))
import matplotlib.pyplot as plt
plt.ion()
fig = plt.figure()
plt.plot(train_loss_avg)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()
vae.eval()
test_loss_avg, num_batches = 0, 0
for image_batch, _ in test_dataloader:
with torch.no_grad():
image_batch = image_batch.to(device)
# vae reconstruction
image_batch_recon, latent_mu, latent_logvar = vae(image_batch)
# reconstruction error
loss = vae_loss(image_batch_recon, image_batch, latent_mu, latent_logvar)
test_loss_avg += loss.item()
num_batches += 1
test_loss_avg /= num_batches
print('average reconstruction error: %f' % (test_loss_avg))
import numpy as np
import matplotlib.pyplot as plt
plt.ion()
import torchvision.utils
vae.eval()
# This function takes as an input the images to reconstruct
# and the name of the model with which the reconstructions
# are performed
def to_img(x):
x = x.clamp(0, 1)
return x
def show_image(img):
img = to_img(img)
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
def visualise_output(images, model):
with torch.no_grad():
images = images.to(device)
images, _, _ = model(images)
images = images.cpu()
images = to_img(images)
np_imagegrid = torchvision.utils.make_grid(images[1:50], 10, 5).numpy()
plt.imshow(np.transpose(np_imagegrid, (1, 2, 0)))
plt.show()
images, labels = iter(test_dataloader).next()
# First visualise the original images
print('Original images')
show_image(torchvision.utils.make_grid(images[1:50],10,5))
plt.show()
# Reconstruct and visualise the images using the vae
print('VAE reconstruction:')
visualise_output(images, vae)
```
|
github_jupyter
|
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
from torchvision.datasets import FashionMNIST
import torch.nn as nn
import torch.nn.functional as F
import torch
latent_dims = 2
num_epochs = 100
batch_size = 128
capacity = 64
learning_rate = 1e-3
variational_beta = 1
use_gpu = True
img_transform = transforms.Compose([
transforms.ToTensor()
])
batch_size = 128
train_dataset = FashionMNIST(root='./data/FashionMNIST', download=True, train=True, transform=img_transform)
train_dataloader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_dataset = FashionMNIST(root='./data/FashionMNIST', download=True, train=False, transform=img_transform)
test_dataloader = DataLoader(test_dataset, batch_size=batch_size, shuffle=True)
class Encoder(nn.Module):
def __init__(self):
super(Encoder, self).__init__()
c = capacity
self.conv1 = nn.Conv2d(in_channels=1, out_channels=c, kernel_size=4, padding=1, stride=2)
self.conv2 = nn.Conv2d(in_channels=c, out_channels=c*2, kernel_size=4, stride=2, padding=1)
self.fc_mu = nn.Linear(in_features=c*2*7*7, out_features=latent_dims)
self.fc_logvar = nn.Linear(in_features=c*2*7*7, out_features=latent_dims)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
x = x.view(x.size(0), -1)
x_mu = self.fc_mu(x)
x_logvar = self.fc_logvar(x)
return x_mu, x_logvar
class Decoder(nn.Module):
def __init__(self):
super(Decoder, self).__init__()
c=capacity
self.fc = nn.Linear(in_features=latent_dims, out_features=c*2*7*7)
self.conv2 = nn.ConvTranspose2d(in_channels=c*2, out_channels=c, kernel_size=4, stride=2, padding=1)
self.conv1 = nn.ConvTranspose2d(in_channels=c, out_channels=1, kernel_size=4, stride=2, padding=1)
def forward(self, x):
x = self.fc(x)
x = x.view(x.size(0),capacity*2, 7, 7)
x = F.relu(self.conv2(x))
x = torch.sigmoid(self.conv1(x))
return x
class VariationalAutoencoder(nn.Module):
def __init__(self):
super(VariationalAutoencoder, self).__init__()
self.encoder= Encoder()
self.decoder = Decoder()
def forward(self,x):
latent_mu, latent_logvar = self.encoder(x)
latent = self.latent_sample(latent_mu, latent_logvar)
x_recon = self.decoder(latent)
return x_recon, latent_mu, latent_logvar
def latent_sample(self, mu, logvar):
if self.training:
std = logvar.mul(0.5).exp()
eps = torch.empty_like(std).normal_()
return eps.mul(std).add_(mu)
else:
return mu
def vae_loss(recon_x, x, mu, logvar):
recon_loss = F.binary_cross_entropy(recon_x.view(-1,784), x.view(-1, 784), reduction='sum')
kldivergence = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
return recon_loss + variational_beta * kldivergence
vae = VariationalAutoencoder()
device = torch.device("cuda:0" if use_gpu and torch.cuda.is_available() else "cpu")
vae = vae.to(device)
num_params = sum(p.numel() for p in vae.parameters() if p.requires_grad)
print('Number of parameters: %d' % num_params)
optimizer = torch.optim.Adam(params=vae.parameters(), lr=learning_rate, weight_decay=1e-5)
vae.train()
train_loss_avg = []
print('Training ...')
for epoch in range(num_epochs):
train_loss_avg.append(0)
num_batches = 0
for image_batch, _ in train_dataloader:
image_batch = image_batch.to(device)
# vae reconstruction
image_batch_recon, latent_mu, latent_logvar = vae(image_batch)
# reconstruction error
loss = vae_loss(image_batch_recon, image_batch, latent_mu, latent_logvar)
# backpropagation
optimizer.zero_grad()
loss.backward()
# one step of the optmizer (using the gradients from backpropagation)
optimizer.step()
train_loss_avg[-1] += loss.item()
num_batches += 1
train_loss_avg[-1] /= num_batches
print('Epoch [%d / %d] average reconstruction error: %f' % (epoch+1, num_epochs, train_loss_avg[-1]))
import matplotlib.pyplot as plt
plt.ion()
fig = plt.figure()
plt.plot(train_loss_avg)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()
vae.eval()
test_loss_avg, num_batches = 0, 0
for image_batch, _ in test_dataloader:
with torch.no_grad():
image_batch = image_batch.to(device)
# vae reconstruction
image_batch_recon, latent_mu, latent_logvar = vae(image_batch)
# reconstruction error
loss = vae_loss(image_batch_recon, image_batch, latent_mu, latent_logvar)
test_loss_avg += loss.item()
num_batches += 1
test_loss_avg /= num_batches
print('average reconstruction error: %f' % (test_loss_avg))
import numpy as np
import matplotlib.pyplot as plt
plt.ion()
import torchvision.utils
vae.eval()
# This function takes as an input the images to reconstruct
# and the name of the model with which the reconstructions
# are performed
def to_img(x):
x = x.clamp(0, 1)
return x
def show_image(img):
img = to_img(img)
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
def visualise_output(images, model):
with torch.no_grad():
images = images.to(device)
images, _, _ = model(images)
images = images.cpu()
images = to_img(images)
np_imagegrid = torchvision.utils.make_grid(images[1:50], 10, 5).numpy()
plt.imshow(np.transpose(np_imagegrid, (1, 2, 0)))
plt.show()
images, labels = iter(test_dataloader).next()
# First visualise the original images
print('Original images')
show_image(torchvision.utils.make_grid(images[1:50],10,5))
plt.show()
# Reconstruct and visualise the images using the vae
print('VAE reconstruction:')
visualise_output(images, vae)
| 0.954764 | 0.732305 |
```
!pip install python-dotenv
from dotenv import load_dotenv, find_dotenv
dotenv_path = find_dotenv()
load_dotenv(dotenv_path)
import os
from requests import session
kaggle_username = os.environ.get("KAGGLE_USERNAME")
kaggle_password = os.environ.get("KAGGLE_PASSWORD")
payload = {
'action': 'login',
'username': kaggle_username,
'password': kaggle_password
}
print(payload)
# url = 'https://www.kaggle.com/c/titanic/download/GQf0y8ebHO0C4JXscPPp%2Fversions%2FXkNkvXwqPPVG0Qt3MtQT%2Ffiles%2Ftrain.csv'
url = 'https://www.kaggle.com/c/titanic/download/GQf0y8ebHO0C4JXscPPp%2Fversions%2FXkNkvXwqPPVG0Qt3MtQT%2Ffiles%2Ftrain.csv'
with session() as c:
c.post('https://www.kaggle.com/account/login', data=payload)
response = c.get(url)
print(response.text)
get_raw_data_script_file = os.path.join(os.path.pardir, 'src', 'data', 'get_raw_data.py')
%%writefile $get_raw_data_script_file
# --*-- coding: utf-8 -*-
import os
from dotenv import find_dotenv, load_dotenv
from requests import session
import logging
payload = {
'action': 'login',
'username': os.environ.get("KAGGLE_USERNAME"),
'password': os.environ.get("KAGGLE_PASSWORD")
}
def extract_data(url, file_path):
with session() as c:
c.post('https://www.kaggle.com/account/login', data=payload)
with open(file_path, 'w') as handle:
response = c.get(url, stream=True)
for block in response.iter_content(1024):
handle.write(str(block))
def main(project_dir):
logger = logging.getLogger(__name__)
logger.info('getting raw data')
train_url = 'https://www.kaggle.com/c/titanic/download/GQf0y8ebHO0C4JXscPPp%2Fversions%2FXkNkvXwqPPVG0Qt3MtQT%2Ffiles%2Ftrain.csv'
test_url = 'https://www.kaggle.com/c/titanic/download/GQf0y8ebHO0C4JXscPPp%2Fversions%2FXkNkvXwqPPVG0Qt3MtQT%2Ffiles%2Ftest.csv'
raw_data_path = os.path.join(project_dir, 'data', 'raw')
train_data_path = os.path.join(raw_data_path, 'train.csv')
test_data_path = os.path.join(raw_data_path, 'test.csv')
extract_data(train_url, train_data_path)
extract_data(test_url, test_data_path)
logger.info('downloaded raw training and test data')
if __name__ == '__main__':
project_dir = os.path.join(os.path.dirname(__file__), os.pardir, os.pardir)
log_fmt = '%(asctime)s - %(name)s - %(levelname)s - %(message)s'
logging.basicConfig(level=logging.INFO, format=log_fmt)
dotenv_path = find_dotenv()
load_dotenv(dotenv_path)
main(project_dir)
!python3 $get_raw_data_script_file
```
|
github_jupyter
|
!pip install python-dotenv
from dotenv import load_dotenv, find_dotenv
dotenv_path = find_dotenv()
load_dotenv(dotenv_path)
import os
from requests import session
kaggle_username = os.environ.get("KAGGLE_USERNAME")
kaggle_password = os.environ.get("KAGGLE_PASSWORD")
payload = {
'action': 'login',
'username': kaggle_username,
'password': kaggle_password
}
print(payload)
# url = 'https://www.kaggle.com/c/titanic/download/GQf0y8ebHO0C4JXscPPp%2Fversions%2FXkNkvXwqPPVG0Qt3MtQT%2Ffiles%2Ftrain.csv'
url = 'https://www.kaggle.com/c/titanic/download/GQf0y8ebHO0C4JXscPPp%2Fversions%2FXkNkvXwqPPVG0Qt3MtQT%2Ffiles%2Ftrain.csv'
with session() as c:
c.post('https://www.kaggle.com/account/login', data=payload)
response = c.get(url)
print(response.text)
get_raw_data_script_file = os.path.join(os.path.pardir, 'src', 'data', 'get_raw_data.py')
%%writefile $get_raw_data_script_file
# --*-- coding: utf-8 -*-
import os
from dotenv import find_dotenv, load_dotenv
from requests import session
import logging
payload = {
'action': 'login',
'username': os.environ.get("KAGGLE_USERNAME"),
'password': os.environ.get("KAGGLE_PASSWORD")
}
def extract_data(url, file_path):
with session() as c:
c.post('https://www.kaggle.com/account/login', data=payload)
with open(file_path, 'w') as handle:
response = c.get(url, stream=True)
for block in response.iter_content(1024):
handle.write(str(block))
def main(project_dir):
logger = logging.getLogger(__name__)
logger.info('getting raw data')
train_url = 'https://www.kaggle.com/c/titanic/download/GQf0y8ebHO0C4JXscPPp%2Fversions%2FXkNkvXwqPPVG0Qt3MtQT%2Ffiles%2Ftrain.csv'
test_url = 'https://www.kaggle.com/c/titanic/download/GQf0y8ebHO0C4JXscPPp%2Fversions%2FXkNkvXwqPPVG0Qt3MtQT%2Ffiles%2Ftest.csv'
raw_data_path = os.path.join(project_dir, 'data', 'raw')
train_data_path = os.path.join(raw_data_path, 'train.csv')
test_data_path = os.path.join(raw_data_path, 'test.csv')
extract_data(train_url, train_data_path)
extract_data(test_url, test_data_path)
logger.info('downloaded raw training and test data')
if __name__ == '__main__':
project_dir = os.path.join(os.path.dirname(__file__), os.pardir, os.pardir)
log_fmt = '%(asctime)s - %(name)s - %(levelname)s - %(message)s'
logging.basicConfig(level=logging.INFO, format=log_fmt)
dotenv_path = find_dotenv()
load_dotenv(dotenv_path)
main(project_dir)
!python3 $get_raw_data_script_file
| 0.215433 | 0.114666 |
## 토큰화 & 형태소 분석
토큰화 (Tokenizing) : 글, 문단, 문장 따위를 그 하위 요소(문단, 문장, 단어)로 분절하는 것
형태소 분석 (morpheme analysis) : 이러한 토큰화 중 문장을 의미가 있는 요소 별로 분절하여 이를 분석하는 것
### 문장의 토큰화와 형태소 분석을 위해 필요한 함수/라이브러리
* from konlpy.tag import Okt
: 한국어 자연어 처리를 위한 konlpy 라이브러리 Okt 모듈 <br>
Okt 모듈은 konlpy에 속한 여러 형태소 분석기 중 하나 <br><br>
* Okt.morphs(sentence)
: 한국어 문장인 sentence를 형태소에 따라 분할 <br><br>
* Okt.pos(sentence)
: 한국어 문장인 sentence를 형태소와 그에 따른 품사에 따라 분할 <br>
```
import numpy as np
from konlpy.tag import Okt
def load_data(path):
with open(path, 'r', encoding='UTF-8') as f:
data = f.read()
return data
```
### doc2para
'문서'를 '문단'의 리스트로 변환하는 함수
* 문장의 마침표(.) 뒤에 있는 개행 표시(\n)를 기준으로 문서 내 글들을 리스트 요소 즉, 문단으로 나눈다.
* 나누어진 글들 중 마지막 글자가 "."인 경우만 문단이 나누어진 것으로 보고 그 외의 문장들은 서로 병합한다.
```
def doc2para(writing):
paragraphs = []
# 개행문자를 구분해서 처리
splited = writing.split('\n')
# 리스트의 길이가 0보다 큰 값 (공백인 경우 제거)
splited = list(filter(lambda x: len(x) > 0 , splited))
para = ""
for sentence in splited:
if sentence[-1] != '.':
para += sentence
else:
paragraphs.append(para)
# 아래 코드를 추가하여 문단 내 마지막 문장을 읽어올 수 있습니다.
para += sentence
return paragraphs
```
### para2sen
'문단'을 '문장'의 리스트로 변환하는 함수
* 문단을 "."으로 나누어 리스트로 만들고, 변수 sentences에 저장
* sentences 내 문장들에 대해서 "?"로 재분할 한 후,<br> ndarray.flatten()을 활용하여 재분할된 문장이 합쳐질 수 있도록 리스트로 만든다. <br> ("!"에 대해서도 마찬가지로 적용)
```
def para2sen(paragraph):
sentences = []
# Step01.
sentences = paragraph.split('.')
# Step02.
sentences = [sentence.split('?') for sentence in sentences]
sentences = np.array(sentences).flatten()
sentences = [sentence.split('!') for sentence in sentences]
sentences = np.array(sentences).flatten()
sentences = [ sentence.replace('"','') for sentence in sentences]
return sentences
```
### sen2words_byspace
띄어쓰기로 문장을 구분하는 함수
```
def sen2words_byspace(sentence):
words = []
words = sentence.strip().split(" ")
return words
```
### sen2morph
'Okt()'로 선언된 Tokenizer인 'analyzer'를 이용해 형태소에 따라 분할된 문장의 리스트를 변수 'morphs'에 저장하는 sen2morph
함수
* Okt.morphs 메소드를 사용
```
def sen2morph(sentence):
morphs = []
analyzer = Okt()
morphs = analyzer.morphs(sentence)
return morphs
```
### analyzing_morphs
'Okt()'로 선언된 Tokenizer인 'analyzer'를 이용해 형태소와 그에 따른 품사를 분할하는 analyzing_morphs 함수
* Okt.pos 메소드를 사용
```
def analyzing_morphs(sentence):
analyzer = Okt()
return analyzer.pos(sentence)
def main():
DATA_PATH = "blood_rain.txt"
blood_rain = load_data(DATA_PATH)
paragraphs = doc2para(blood_rain)
sentences = para2sen(paragraphs[4])
words_byspace = sen2words_byspace(sentences[3])
words_bymorphs = sen2morph(sentences[3])
morphs_analyzed = analyzing_morphs(sentences[3])
# 출력을 통해 토큰화가 잘 되었는지 확인합니다.
print("문장으로 구분된 5번째 문단: ", sentences)
print("\n띄어쓰기로 구분된 문장 (5번째 문단의 4번째 문장): ", words_byspace)
print("\n형태소 별로 구분된 문장 (5번째 문단의 4번째 문장): ", words_bymorphs)
print("\n형태소와 그에 따른 품사로 분류된 문장 (5번째 문단의 4번째 문장): ", morphs_analyzed)
return words_byspace, words_bymorphs, morphs_analyzed
if __name__=='__main__':
main()
```
---
### 전체 코드
```
def doc2para(writing):
paragraphs = []
splited = writing.split('\n')
# 리스트의 길이가 0보다 큰 값 (공백인 경우 제거)
splited = list(filter(lambda x: len(x) > 0 , splited))
para = ""
for sentence in splited:
if sentence[-1] != '.':
para += sentence
else:
paragraphs.append(para)
# 아래 코드를 추가하여 문단 내 마지막 문장을 읽어올 수 있다.
para += sentence
return paragraphs
def para2sen(paragraph):
sentences = []
# 1.split
sentences = paragraph.split('.')
# 2.split, replace
sentences = [sentence.split('?') for sentence in sentences]
sentences = np.array(sentences).flatten()
sentences = [sentence.split('!') for sentence in sentences]
sentences = np.array(sentences).flatten()
sentences = [ sentence.replace('"','') for sentence in sentences]
return sentences
def sen2words_byspace(sentence):
words = []
words = sentence.strip().split(" ")
return words
def sen2morph(sentence):
morphs = []
analyzer = Okt()
morphs = analyzer.morphs(sentence)
return morphs
def analyzing_morphs(sentence):
analyzer = Okt()
return analyzer.pos(sentence)
# 위에서 정의한 함수들을 바탕으로 문서를 토큰화를 진행합니다.
def main():
DATA_PATH = "blood_rain.txt"
blood_rain = load_data(DATA_PATH)
paragraphs = doc2para(blood_rain)
sentences = para2sen(paragraphs[4])
words_byspace = sen2words_byspace(sentences[3])
words_bymorphs = sen2morph(sentences[3])
morphs_analyzed = analyzing_morphs(sentences[3])
# 출력을 통해 토큰화가 잘 되었는지 확인합니다.
print("문장으로 구분된 5번째 문단: ", sentences)
print("\n띄어쓰기로 구분된 문장 (5번째 문단의 4번째 문장): ", words_byspace)
print("\n형태소 별로 구분된 문장 (5번째 문단의 4번째 문장): ", words_bymorphs)
print("\n형태소와 그에 따른 품사로 분류된 문장 (5번째 문단의 4번째 문장): ", morphs_analyzed)
return words_byspace, words_bymorphs, morphs_analyzed
if __name__=='__main__':
main()
```
|
github_jupyter
|
import numpy as np
from konlpy.tag import Okt
def load_data(path):
with open(path, 'r', encoding='UTF-8') as f:
data = f.read()
return data
def doc2para(writing):
paragraphs = []
# 개행문자를 구분해서 처리
splited = writing.split('\n')
# 리스트의 길이가 0보다 큰 값 (공백인 경우 제거)
splited = list(filter(lambda x: len(x) > 0 , splited))
para = ""
for sentence in splited:
if sentence[-1] != '.':
para += sentence
else:
paragraphs.append(para)
# 아래 코드를 추가하여 문단 내 마지막 문장을 읽어올 수 있습니다.
para += sentence
return paragraphs
def para2sen(paragraph):
sentences = []
# Step01.
sentences = paragraph.split('.')
# Step02.
sentences = [sentence.split('?') for sentence in sentences]
sentences = np.array(sentences).flatten()
sentences = [sentence.split('!') for sentence in sentences]
sentences = np.array(sentences).flatten()
sentences = [ sentence.replace('"','') for sentence in sentences]
return sentences
def sen2words_byspace(sentence):
words = []
words = sentence.strip().split(" ")
return words
def sen2morph(sentence):
morphs = []
analyzer = Okt()
morphs = analyzer.morphs(sentence)
return morphs
def analyzing_morphs(sentence):
analyzer = Okt()
return analyzer.pos(sentence)
def main():
DATA_PATH = "blood_rain.txt"
blood_rain = load_data(DATA_PATH)
paragraphs = doc2para(blood_rain)
sentences = para2sen(paragraphs[4])
words_byspace = sen2words_byspace(sentences[3])
words_bymorphs = sen2morph(sentences[3])
morphs_analyzed = analyzing_morphs(sentences[3])
# 출력을 통해 토큰화가 잘 되었는지 확인합니다.
print("문장으로 구분된 5번째 문단: ", sentences)
print("\n띄어쓰기로 구분된 문장 (5번째 문단의 4번째 문장): ", words_byspace)
print("\n형태소 별로 구분된 문장 (5번째 문단의 4번째 문장): ", words_bymorphs)
print("\n형태소와 그에 따른 품사로 분류된 문장 (5번째 문단의 4번째 문장): ", morphs_analyzed)
return words_byspace, words_bymorphs, morphs_analyzed
if __name__=='__main__':
main()
def doc2para(writing):
paragraphs = []
splited = writing.split('\n')
# 리스트의 길이가 0보다 큰 값 (공백인 경우 제거)
splited = list(filter(lambda x: len(x) > 0 , splited))
para = ""
for sentence in splited:
if sentence[-1] != '.':
para += sentence
else:
paragraphs.append(para)
# 아래 코드를 추가하여 문단 내 마지막 문장을 읽어올 수 있다.
para += sentence
return paragraphs
def para2sen(paragraph):
sentences = []
# 1.split
sentences = paragraph.split('.')
# 2.split, replace
sentences = [sentence.split('?') for sentence in sentences]
sentences = np.array(sentences).flatten()
sentences = [sentence.split('!') for sentence in sentences]
sentences = np.array(sentences).flatten()
sentences = [ sentence.replace('"','') for sentence in sentences]
return sentences
def sen2words_byspace(sentence):
words = []
words = sentence.strip().split(" ")
return words
def sen2morph(sentence):
morphs = []
analyzer = Okt()
morphs = analyzer.morphs(sentence)
return morphs
def analyzing_morphs(sentence):
analyzer = Okt()
return analyzer.pos(sentence)
# 위에서 정의한 함수들을 바탕으로 문서를 토큰화를 진행합니다.
def main():
DATA_PATH = "blood_rain.txt"
blood_rain = load_data(DATA_PATH)
paragraphs = doc2para(blood_rain)
sentences = para2sen(paragraphs[4])
words_byspace = sen2words_byspace(sentences[3])
words_bymorphs = sen2morph(sentences[3])
morphs_analyzed = analyzing_morphs(sentences[3])
# 출력을 통해 토큰화가 잘 되었는지 확인합니다.
print("문장으로 구분된 5번째 문단: ", sentences)
print("\n띄어쓰기로 구분된 문장 (5번째 문단의 4번째 문장): ", words_byspace)
print("\n형태소 별로 구분된 문장 (5번째 문단의 4번째 문장): ", words_bymorphs)
print("\n형태소와 그에 따른 품사로 분류된 문장 (5번째 문단의 4번째 문장): ", morphs_analyzed)
return words_byspace, words_bymorphs, morphs_analyzed
if __name__=='__main__':
main()
| 0.216674 | 0.950915 |
# Cross-Entropy Method
---
In this notebook, we will train the Cross-Entropy Method with OpenAI Gym's MountainCarContinuous environment.
### 1. Import the Necessary Packages
```
import gym
import math
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
```
### 2. Instantiate the Environment and Agent
```
env = gym.make('MountainCarContinuous-v0')
env.seed(101)
np.random.seed(101)
print('observation space:', env.observation_space)
print('action space:', env.action_space)
print(' - low:', env.action_space.low)
print(' - high:', env.action_space.high)
class Linear(tf.keras.layers.Layer):
def __init__(self, units=32, input_dim=32):
super(Linear, self).__init__(autocast=False)
self.w = self.add_weight(shape=(input_dim, units),
initializer='random_normal',
dtype=tf.float64,
name='weight',
trainable=True)
self.b = self.add_weight(shape=(units,),
initializer='zeros',
dtype=tf.float64,
name='bias',
trainable=True)
def call(self, inputs):
return tf.matmul(inputs, self.w) + self.b
class Agent(tf.keras.Model):
def __init__(self, env, h_size=16):
super(Agent, self).__init__(name='cross-entropy-method')
self.env = env
# state, hidden layer, action sizes
self.s_size = env.observation_space.shape[0]
self.h_size = h_size
self.a_size = env.action_space.shape[0]
# define layers
self.fc1 = Linear(units=self.h_size, input_dim=self.s_size)
self.fc2 = Linear(units = self.a_size, input_dim=self.h_size)
def set_weights(self, weights):
s_size = self.s_size
h_size = self.h_size
a_size = self.a_size
# separate the weights for each layer
fc1_end = (s_size*h_size)+h_size
fc1_W = tf.convert_to_tensor(weights[:s_size*h_size].reshape(s_size, h_size))
fc1_b = tf.convert_to_tensor(weights[s_size*h_size:fc1_end])
fc2_W = tf.convert_to_tensor(weights[fc1_end:fc1_end+(h_size*a_size)].reshape(h_size, a_size))
fc2_b = tf.convert_to_tensor(weights[fc1_end+(h_size*a_size):])
# set the weights for each layer
self.fc1.w.assign(fc1_W)
self.fc1.b.assign(fc1_b)
self.fc2.w.assign(fc2_W)
self.fc2.b.assign(fc2_b)
def get_weights_dim(self):
return (self.s_size+1)*self.h_size + (self.h_size+1)*self.a_size
@tf.function
def call(self, x):
out = tf.nn.relu(self.fc1(x))
out = tf.nn.tanh(self.fc2(out))
return out
def evaluate(self, weights, gamma=1.0, max_t=5000):
self.set_weights(weights)
episode_return = 0.0
state = self.env.reset()
for t in range(max_t):
state = np.array(state)[None]
action = self.call(state)
state, reward, done, _ = self.env.step(action[0])
episode_return += reward * math.pow(gamma, t)
if done:
break
return episode_return
agent = Agent(env)
```
### 3. Train the Agent with the Cross-Entropy Method
Run the code cell below to train the agent from scratch. Alternatively, you can skip to the next code cell to load the pre-trained weights from file.
```
def cem(n_iterations=500, max_t=1000, gamma=1.0, print_every=10, pop_size=50, elite_frac=0.2, sigma=0.5):
"""Tensorflow implementation of the cross-entropy method.
Params
======
n_iterations (int): maximum number of training iterations
max_t (int): maximum number of timesteps per episode
gamma (float): discount rate
print_every (int): how often to print average score (over last 100 episodes)
pop_size (int): size of population at each iteration
elite_frac (float): percentage of top performers to use in update
sigma (float): standard deviation of additive noise
"""
ckpt = tf.train.Checkpoint(step=tf.Variable(0), model=agent)
ckpt_manager = tf.train.CheckpointManager(ckpt, 'model/', max_to_keep=3)
n_elite=int(pop_size*elite_frac)
scores_deque = deque(maxlen=100)
scores = []
best_weight = sigma*np.random.randn(agent.get_weights_dim())
for i_iteration in range(1, n_iterations+1):
weights_pop = [best_weight + (sigma*np.random.randn(agent.get_weights_dim())) for i in range(pop_size)]
rewards = np.array([agent.evaluate(weights, gamma, max_t) for weights in weights_pop])
elite_idxs = rewards.argsort()[-n_elite:]
elite_weights = [weights_pop[i] for i in elite_idxs]
best_weight = np.array(elite_weights).mean(axis=0)
reward = agent.evaluate(best_weight, gamma=1.0)
scores_deque.append(reward)
scores.append(reward)
ckpt.step.assign_add(1)
ckpt_manager.save()
if i_iteration % print_every == 0:
print('Episode {}\tAverage Score: {:.2f}'.format(i_iteration, np.mean(scores_deque)))
if np.mean(scores_deque)>=90.0:
print('\nEnvironment solved in {:d} iterations!\tAverage Score: {:.2f}'.format(i_iteration-100, np.mean(scores_deque)))
break
return scores
scores = cem()
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(1, len(scores)+1), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
```
### 4. Watch a Smart Agent!
In the next code cell, you will load the trained weights from file to watch a smart agent!
```
# load the weights from file
env = gym.wrappers.Monitor(env, 'videos/', force=True)
new_agent = Agent(env)
ckpt = tf.train.Checkpoint(model=new_agent)
latestSnapshot= tf.train.latest_checkpoint("model/")
if not latestSnapshot:
raise Exception('No saved model found in: ' + 'model/')
ckpt.restore(latestSnapshot)
print("Restored saved model from latest snapshot")
state = env.reset()
while True:
state = np.array(state)[None]
action = agent(state)
env.render()
next_state, reward, done, _ = env.step(action[0])
state = next_state
if done:
break
env.close()
```
|
github_jupyter
|
import gym
import math
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
env = gym.make('MountainCarContinuous-v0')
env.seed(101)
np.random.seed(101)
print('observation space:', env.observation_space)
print('action space:', env.action_space)
print(' - low:', env.action_space.low)
print(' - high:', env.action_space.high)
class Linear(tf.keras.layers.Layer):
def __init__(self, units=32, input_dim=32):
super(Linear, self).__init__(autocast=False)
self.w = self.add_weight(shape=(input_dim, units),
initializer='random_normal',
dtype=tf.float64,
name='weight',
trainable=True)
self.b = self.add_weight(shape=(units,),
initializer='zeros',
dtype=tf.float64,
name='bias',
trainable=True)
def call(self, inputs):
return tf.matmul(inputs, self.w) + self.b
class Agent(tf.keras.Model):
def __init__(self, env, h_size=16):
super(Agent, self).__init__(name='cross-entropy-method')
self.env = env
# state, hidden layer, action sizes
self.s_size = env.observation_space.shape[0]
self.h_size = h_size
self.a_size = env.action_space.shape[0]
# define layers
self.fc1 = Linear(units=self.h_size, input_dim=self.s_size)
self.fc2 = Linear(units = self.a_size, input_dim=self.h_size)
def set_weights(self, weights):
s_size = self.s_size
h_size = self.h_size
a_size = self.a_size
# separate the weights for each layer
fc1_end = (s_size*h_size)+h_size
fc1_W = tf.convert_to_tensor(weights[:s_size*h_size].reshape(s_size, h_size))
fc1_b = tf.convert_to_tensor(weights[s_size*h_size:fc1_end])
fc2_W = tf.convert_to_tensor(weights[fc1_end:fc1_end+(h_size*a_size)].reshape(h_size, a_size))
fc2_b = tf.convert_to_tensor(weights[fc1_end+(h_size*a_size):])
# set the weights for each layer
self.fc1.w.assign(fc1_W)
self.fc1.b.assign(fc1_b)
self.fc2.w.assign(fc2_W)
self.fc2.b.assign(fc2_b)
def get_weights_dim(self):
return (self.s_size+1)*self.h_size + (self.h_size+1)*self.a_size
@tf.function
def call(self, x):
out = tf.nn.relu(self.fc1(x))
out = tf.nn.tanh(self.fc2(out))
return out
def evaluate(self, weights, gamma=1.0, max_t=5000):
self.set_weights(weights)
episode_return = 0.0
state = self.env.reset()
for t in range(max_t):
state = np.array(state)[None]
action = self.call(state)
state, reward, done, _ = self.env.step(action[0])
episode_return += reward * math.pow(gamma, t)
if done:
break
return episode_return
agent = Agent(env)
def cem(n_iterations=500, max_t=1000, gamma=1.0, print_every=10, pop_size=50, elite_frac=0.2, sigma=0.5):
"""Tensorflow implementation of the cross-entropy method.
Params
======
n_iterations (int): maximum number of training iterations
max_t (int): maximum number of timesteps per episode
gamma (float): discount rate
print_every (int): how often to print average score (over last 100 episodes)
pop_size (int): size of population at each iteration
elite_frac (float): percentage of top performers to use in update
sigma (float): standard deviation of additive noise
"""
ckpt = tf.train.Checkpoint(step=tf.Variable(0), model=agent)
ckpt_manager = tf.train.CheckpointManager(ckpt, 'model/', max_to_keep=3)
n_elite=int(pop_size*elite_frac)
scores_deque = deque(maxlen=100)
scores = []
best_weight = sigma*np.random.randn(agent.get_weights_dim())
for i_iteration in range(1, n_iterations+1):
weights_pop = [best_weight + (sigma*np.random.randn(agent.get_weights_dim())) for i in range(pop_size)]
rewards = np.array([agent.evaluate(weights, gamma, max_t) for weights in weights_pop])
elite_idxs = rewards.argsort()[-n_elite:]
elite_weights = [weights_pop[i] for i in elite_idxs]
best_weight = np.array(elite_weights).mean(axis=0)
reward = agent.evaluate(best_weight, gamma=1.0)
scores_deque.append(reward)
scores.append(reward)
ckpt.step.assign_add(1)
ckpt_manager.save()
if i_iteration % print_every == 0:
print('Episode {}\tAverage Score: {:.2f}'.format(i_iteration, np.mean(scores_deque)))
if np.mean(scores_deque)>=90.0:
print('\nEnvironment solved in {:d} iterations!\tAverage Score: {:.2f}'.format(i_iteration-100, np.mean(scores_deque)))
break
return scores
scores = cem()
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(1, len(scores)+1), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
# load the weights from file
env = gym.wrappers.Monitor(env, 'videos/', force=True)
new_agent = Agent(env)
ckpt = tf.train.Checkpoint(model=new_agent)
latestSnapshot= tf.train.latest_checkpoint("model/")
if not latestSnapshot:
raise Exception('No saved model found in: ' + 'model/')
ckpt.restore(latestSnapshot)
print("Restored saved model from latest snapshot")
state = env.reset()
while True:
state = np.array(state)[None]
action = agent(state)
env.render()
next_state, reward, done, _ = env.step(action[0])
state = next_state
if done:
break
env.close()
| 0.759136 | 0.903805 |
```
import json
from datetime import datetime, timedelta, timezone, time, date
import pandas as pd
import numpy as np
def get_arrivals(filename = 'sample_routes_stops_15s.json'):
with open(filename, 'r') as f:
return json.load(f)
arrivals = pd.DataFrame.from_dict(get_arrivals())
arrivals.sample(10)
# find the smallest nonnegative waiting time
def absmin(series):
return series[series >= 0].min()
# # input: df with entries from one day
# # possible optimzation: sort df by timestamp, then pick first timestamp > minute for each minute (need to time to make sure but should be faster)
def minimum_waiting_times(df, start_time, end_time, group):
minute_range = [start_time + timedelta(minutes=i) for i in range(
(end_time - start_time).seconds//60)]
wait_times = pd.DataFrame(columns=[])
for minute in minute_range:
# TODO (jtanquil): we get this error, see if you can fix it
# A value is trying to be set on a copy of a slice from a DataFrame.
# Try using .loc[row_indexer,col_indexer] = value instead
# See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy
# df['WAIT'] = df['timestamp'].apply(lambda x: (x - minute).total_seconds())
df['WAIT'] = df['timestamp'].apply(lambda x: (x - minute).total_seconds())
pivot = df[group + ['WAIT']].pivot_table(values = ['WAIT'], index = group, aggfunc = absmin)
pivot['TIME'] = minute
pivot = pivot.reset_index()
wait_times = wait_times.append(pivot, sort = True)
return wait_times
def all_wait_times(df, timespan = ("00:00", "23:59"), group = []):
# parse timestamp
df[
dates = df['DATE'].unique()
avg_over_pd = pd.DataFrame(columns = group + ['DATE', 'TIME', 'WAIT'])
for date in dates:
#print(f"{datetime.now().strftime('%a %b %d %I:%M:%S %p')}: start processing {date}.")
start_time = datetime.strptime(f"{date.isoformat()} {timespan[0]} -0800", "%Y-%m-%d %H:%M %z")
end_time = datetime.strptime(f"{date.isoformat()} {timespan[1]} -0800", "%Y-%m-%d %H:%M %z")
daily_wait = minimum_waiting_times(df[df['DATE'] == date], start_time, end_time, group)
#print(f"{datetime.now().strftime('%a %b %d %I:%M:%S %p')}: found waits for {date}.")
#daily_wait = daily_wait.pivot_table(values = ['WAIT'], index = group).reset_index()
daily_wait['DATE'] = date
daily_wait['TIME'] = daily_wait['TIME'].apply(lambda x: x.time())
avg_over_pd = avg_over_pd.append(daily_wait, sort = True)
return avg_over_pd
def quantiles(series):
return [np.percentile(series, i) for i in [5, 25, 50, 75, 95]]
def get_summary_statistics(df, group):
waits = df.pivot_table(values = ['WAIT'], index = group, aggfunc = {'WAIT': [np.mean, np.std, quantiles]}).reset_index()
waits.columns = ['_'.join(col) if col[0] == 'WAIT' else ''.join(col) for col in waits.columns.values]
waits[[f"{i}th percentile" for i in [5, 25, 50, 75, 95]]] = waits['WAIT_quantiles'].apply(lambda x: pd.Series(x))
waits = waits.drop('WAIT_quantiles', axis = 1)
return waits
waits = all_wait_times(arrivals)
arrivals['TIME'].apply(lambda x: datetime.fromtimestamp(x))
datetime.fromtimestamp(1539623292000)
```
|
github_jupyter
|
import json
from datetime import datetime, timedelta, timezone, time, date
import pandas as pd
import numpy as np
def get_arrivals(filename = 'sample_routes_stops_15s.json'):
with open(filename, 'r') as f:
return json.load(f)
arrivals = pd.DataFrame.from_dict(get_arrivals())
arrivals.sample(10)
# find the smallest nonnegative waiting time
def absmin(series):
return series[series >= 0].min()
# # input: df with entries from one day
# # possible optimzation: sort df by timestamp, then pick first timestamp > minute for each minute (need to time to make sure but should be faster)
def minimum_waiting_times(df, start_time, end_time, group):
minute_range = [start_time + timedelta(minutes=i) for i in range(
(end_time - start_time).seconds//60)]
wait_times = pd.DataFrame(columns=[])
for minute in minute_range:
# TODO (jtanquil): we get this error, see if you can fix it
# A value is trying to be set on a copy of a slice from a DataFrame.
# Try using .loc[row_indexer,col_indexer] = value instead
# See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy
# df['WAIT'] = df['timestamp'].apply(lambda x: (x - minute).total_seconds())
df['WAIT'] = df['timestamp'].apply(lambda x: (x - minute).total_seconds())
pivot = df[group + ['WAIT']].pivot_table(values = ['WAIT'], index = group, aggfunc = absmin)
pivot['TIME'] = minute
pivot = pivot.reset_index()
wait_times = wait_times.append(pivot, sort = True)
return wait_times
def all_wait_times(df, timespan = ("00:00", "23:59"), group = []):
# parse timestamp
df[
dates = df['DATE'].unique()
avg_over_pd = pd.DataFrame(columns = group + ['DATE', 'TIME', 'WAIT'])
for date in dates:
#print(f"{datetime.now().strftime('%a %b %d %I:%M:%S %p')}: start processing {date}.")
start_time = datetime.strptime(f"{date.isoformat()} {timespan[0]} -0800", "%Y-%m-%d %H:%M %z")
end_time = datetime.strptime(f"{date.isoformat()} {timespan[1]} -0800", "%Y-%m-%d %H:%M %z")
daily_wait = minimum_waiting_times(df[df['DATE'] == date], start_time, end_time, group)
#print(f"{datetime.now().strftime('%a %b %d %I:%M:%S %p')}: found waits for {date}.")
#daily_wait = daily_wait.pivot_table(values = ['WAIT'], index = group).reset_index()
daily_wait['DATE'] = date
daily_wait['TIME'] = daily_wait['TIME'].apply(lambda x: x.time())
avg_over_pd = avg_over_pd.append(daily_wait, sort = True)
return avg_over_pd
def quantiles(series):
return [np.percentile(series, i) for i in [5, 25, 50, 75, 95]]
def get_summary_statistics(df, group):
waits = df.pivot_table(values = ['WAIT'], index = group, aggfunc = {'WAIT': [np.mean, np.std, quantiles]}).reset_index()
waits.columns = ['_'.join(col) if col[0] == 'WAIT' else ''.join(col) for col in waits.columns.values]
waits[[f"{i}th percentile" for i in [5, 25, 50, 75, 95]]] = waits['WAIT_quantiles'].apply(lambda x: pd.Series(x))
waits = waits.drop('WAIT_quantiles', axis = 1)
return waits
waits = all_wait_times(arrivals)
arrivals['TIME'].apply(lambda x: datetime.fromtimestamp(x))
datetime.fromtimestamp(1539623292000)
| 0.330255 | 0.419113 |
# Exp 105 analysis
See `./informercial/Makefile` for experimental
details.
```
import os
import numpy as np
from IPython.display import Image
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set_style('ticks')
matplotlib.rcParams.update({'font.size': 16})
matplotlib.rc('axes', titlesize=16)
from infomercial.exp import meta_bandit
from infomercial.exp import epsilon_bandit
from infomercial.exp import beta_bandit
from infomercial.exp import softbeta_bandit
from infomercial.local_gym import bandit
from infomercial.exp.meta_bandit import load_checkpoint
import gym
def plot_meta(env_name, result):
"""Plots!"""
# episodes, actions, scores_E, scores_R, values_E, values_R, ties, policies
episodes = result["episodes"]
actions =result["actions"]
bests =result["p_bests"]
scores_E = result["scores_E"]
scores_R = result["scores_R"]
values_R = result["values_R"]
values_E = result["values_E"]
ties = result["ties"]
policies = result["policies"]
# -
env = gym.make(env_name)
best = env.best
print(f"Best arm: {best}, last arm: {actions[-1]}")
# Plotz
fig = plt.figure(figsize=(6, 14))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0, 0])
plt.scatter(episodes, actions, color="black", alpha=.5, s=2, label="Bandit")
plt.plot(episodes, np.repeat(best, np.max(episodes)+1),
color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylim(-.1, np.max(actions)+1.1)
plt.ylabel("Arm choice")
plt.xlabel("Episode")
# Policy
policies = np.asarray(policies)
episodes = np.asarray(episodes)
plt.subplot(grid[1, 0])
m = policies == 0
plt.scatter(episodes[m], policies[m], alpha=.4, s=2, label="$\pi_E$", color="purple")
m = policies == 1
plt.scatter(episodes[m], policies[m], alpha=.4, s=2, label="$\pi_R$", color="grey")
plt.ylim(-.1, 1+.1)
plt.ylabel("Controlling\npolicy")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# score
plt.subplot(grid[2, 0])
plt.scatter(episodes, scores_E, color="purple", alpha=0.4, s=2, label="E")
plt.plot(episodes, scores_E, color="purple", alpha=0.4)
plt.scatter(episodes, scores_R, color="grey", alpha=0.4, s=2, label="R")
plt.plot(episodes, scores_R, color="grey", alpha=0.4)
plt.plot(episodes, np.repeat(tie_threshold, np.max(episodes)+1),
color="violet", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Score")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Q
plt.subplot(grid[3, 0])
plt.scatter(episodes, values_E, color="purple", alpha=0.4, s=2, label="$Q_E$")
plt.scatter(episodes, values_R, color="grey", alpha=0.4, s=2, label="$Q_R$")
plt.plot(episodes, np.repeat(tie_threshold, np.max(episodes)+1),
color="violet", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Value")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Ties
plt.subplot(grid[4, 0])
plt.scatter(episodes, bests, color="red", alpha=.5, s=2)
plt.ylabel("p(best)")
plt.xlabel("Episode")
plt.ylim(0, 1)
# Ties
plt.subplot(grid[5, 0])
plt.scatter(episodes, ties, color="black", alpha=.5, s=2, label="$\pi_{tie}$ : 1\n $\pi_\pi$ : 0")
plt.ylim(-.1, 1+.1)
plt.ylabel("Ties index")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
def plot_epsilon(env_name, result):
"""Plots!"""
# episodes, actions, scores_E, scores_R, values_E, values_R, ties, policies
episodes = result["episodes"]
actions =result["actions"]
bests =result["p_bests"]
scores_R = result["scores_R"]
values_R = result["values_R"]
epsilons = result["epsilons"]
# -
env = gym.make(env_name)
best = env.best
print(f"Best arm: {best}, last arm: {actions[-1]}")
# Plotz
fig = plt.figure(figsize=(6, 14))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0, 0])
plt.scatter(episodes, actions, color="black", alpha=.5, s=2, label="Bandit")
plt.plot(episodes, np.repeat(best, np.max(episodes)+1),
color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylim(-.1, np.max(actions)+1.1)
plt.ylabel("Arm choice")
plt.xlabel("Episode")
# score
plt.subplot(grid[1, 0])
plt.scatter(episodes, scores_R, color="grey", alpha=0.4, s=2, label="R")
plt.ylabel("Score")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Q
plt.subplot(grid[2, 0])
plt.scatter(episodes, values_R, color="grey", alpha=0.4, s=2, label="$Q_R$")
plt.ylabel("Value")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# best
plt.subplot(grid[3, 0])
plt.scatter(episodes, bests, color="red", alpha=.5, s=2)
plt.ylabel("p(best)")
plt.xlabel("Episode")
plt.ylim(0, 1)
# Decay
plt.subplot(grid[4, 0])
plt.scatter(episodes, epsilons, color="black", alpha=.5, s=2)
plt.ylabel("$\epsilon_R$")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
def plot_critic(critic_name, env_name, result):
# -
env = gym.make(env_name)
best = env.best
# Data
critic = result[critic_name]
arms = list(critic.keys())
values = list(critic.values())
# Plotz
fig = plt.figure(figsize=(8, 3))
grid = plt.GridSpec(1, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0])
plt.scatter(arms, values, color="black", alpha=.5, s=30)
plt.plot([best]*10, np.linspace(min(values), max(values), 10), color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Value")
plt.xlabel("Arm")
```
# Load and process data
```
data_path ="/Users/qualia/Code/infomercial/data/"
exp_name = "exp105"
sorted_params = load_checkpoint(os.path.join(data_path, f"{exp_name}_sorted.pkl"))
# print(sorted_params.keys())
best_params = sorted_params[0]
sorted_params
```
# Performance
of best parameters
```
env_name = 'BanditUniform121-v0'
num_episodes = 60500
# Run w/ best params
result = epsilon_bandit(
env_name=env_name,
num_episodes=num_episodes,
lr_R=best_params["lr_R"],
epsilon=best_params["epsilon"],
seed_value=2,
)
print(best_params)
plot_epsilon(env_name, result=result)
plot_critic('critic_R', env_name, result)
```
# Sensitivity
to parameter choices
```
total_Rs = []
eps = []
lrs_R = []
lrs_E = []
trials = list(sorted_params.keys())
for t in trials:
total_Rs.append(sorted_params[t]['total_R'])
lrs_R.append(sorted_params[t]['lr_R'])
eps.append(sorted_params[t]['epsilon'])
# Init plot
fig = plt.figure(figsize=(5, 18))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Do plots:
# Arm
plt.subplot(grid[0, 0])
plt.scatter(trials, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("Sorted params")
plt.ylabel("total R")
_ = sns.despine()
plt.subplot(grid[1, 0])
plt.scatter(trials, lrs_R, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("Sorted params")
plt.ylabel("lr_R")
_ = sns.despine()
plt.subplot(grid[2, 0])
plt.scatter(lrs_R, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("lrs_R")
plt.ylabel("total_Rs")
_ = sns.despine()
plt.subplot(grid[3, 0])
plt.scatter(eps, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("epsilon")
plt.ylabel("total_Rs")
_ = sns.despine()
```
# Parameter correlations
```
from scipy.stats import spearmanr
spearmanr(eps, lrs_R)
spearmanr(eps, total_Rs)
spearmanr(lrs_R, total_Rs)
```
# Distributions
of parameters
```
# Init plot
fig = plt.figure(figsize=(5, 6))
grid = plt.GridSpec(3, 1, wspace=0.3, hspace=0.8)
plt.subplot(grid[0, 0])
plt.hist(eps, color="black")
plt.xlabel("epsilon")
plt.ylabel("Count")
_ = sns.despine()
plt.subplot(grid[1, 0])
plt.hist(lrs_R, color="black")
plt.xlabel("lr_R")
plt.ylabel("Count")
_ = sns.despine()
```
of total reward
```
# Init plot
fig = plt.figure(figsize=(5, 2))
grid = plt.GridSpec(1, 1, wspace=0.3, hspace=0.8)
plt.subplot(grid[0, 0])
plt.hist(total_Rs, color="black", bins=50)
plt.xlabel("Total reward")
plt.ylabel("Count")
# plt.xlim(0, 10)
_ = sns.despine()
```
|
github_jupyter
|
import os
import numpy as np
from IPython.display import Image
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set_style('ticks')
matplotlib.rcParams.update({'font.size': 16})
matplotlib.rc('axes', titlesize=16)
from infomercial.exp import meta_bandit
from infomercial.exp import epsilon_bandit
from infomercial.exp import beta_bandit
from infomercial.exp import softbeta_bandit
from infomercial.local_gym import bandit
from infomercial.exp.meta_bandit import load_checkpoint
import gym
def plot_meta(env_name, result):
"""Plots!"""
# episodes, actions, scores_E, scores_R, values_E, values_R, ties, policies
episodes = result["episodes"]
actions =result["actions"]
bests =result["p_bests"]
scores_E = result["scores_E"]
scores_R = result["scores_R"]
values_R = result["values_R"]
values_E = result["values_E"]
ties = result["ties"]
policies = result["policies"]
# -
env = gym.make(env_name)
best = env.best
print(f"Best arm: {best}, last arm: {actions[-1]}")
# Plotz
fig = plt.figure(figsize=(6, 14))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0, 0])
plt.scatter(episodes, actions, color="black", alpha=.5, s=2, label="Bandit")
plt.plot(episodes, np.repeat(best, np.max(episodes)+1),
color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylim(-.1, np.max(actions)+1.1)
plt.ylabel("Arm choice")
plt.xlabel("Episode")
# Policy
policies = np.asarray(policies)
episodes = np.asarray(episodes)
plt.subplot(grid[1, 0])
m = policies == 0
plt.scatter(episodes[m], policies[m], alpha=.4, s=2, label="$\pi_E$", color="purple")
m = policies == 1
plt.scatter(episodes[m], policies[m], alpha=.4, s=2, label="$\pi_R$", color="grey")
plt.ylim(-.1, 1+.1)
plt.ylabel("Controlling\npolicy")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# score
plt.subplot(grid[2, 0])
plt.scatter(episodes, scores_E, color="purple", alpha=0.4, s=2, label="E")
plt.plot(episodes, scores_E, color="purple", alpha=0.4)
plt.scatter(episodes, scores_R, color="grey", alpha=0.4, s=2, label="R")
plt.plot(episodes, scores_R, color="grey", alpha=0.4)
plt.plot(episodes, np.repeat(tie_threshold, np.max(episodes)+1),
color="violet", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Score")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Q
plt.subplot(grid[3, 0])
plt.scatter(episodes, values_E, color="purple", alpha=0.4, s=2, label="$Q_E$")
plt.scatter(episodes, values_R, color="grey", alpha=0.4, s=2, label="$Q_R$")
plt.plot(episodes, np.repeat(tie_threshold, np.max(episodes)+1),
color="violet", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Value")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Ties
plt.subplot(grid[4, 0])
plt.scatter(episodes, bests, color="red", alpha=.5, s=2)
plt.ylabel("p(best)")
plt.xlabel("Episode")
plt.ylim(0, 1)
# Ties
plt.subplot(grid[5, 0])
plt.scatter(episodes, ties, color="black", alpha=.5, s=2, label="$\pi_{tie}$ : 1\n $\pi_\pi$ : 0")
plt.ylim(-.1, 1+.1)
plt.ylabel("Ties index")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
def plot_epsilon(env_name, result):
"""Plots!"""
# episodes, actions, scores_E, scores_R, values_E, values_R, ties, policies
episodes = result["episodes"]
actions =result["actions"]
bests =result["p_bests"]
scores_R = result["scores_R"]
values_R = result["values_R"]
epsilons = result["epsilons"]
# -
env = gym.make(env_name)
best = env.best
print(f"Best arm: {best}, last arm: {actions[-1]}")
# Plotz
fig = plt.figure(figsize=(6, 14))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0, 0])
plt.scatter(episodes, actions, color="black", alpha=.5, s=2, label="Bandit")
plt.plot(episodes, np.repeat(best, np.max(episodes)+1),
color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylim(-.1, np.max(actions)+1.1)
plt.ylabel("Arm choice")
plt.xlabel("Episode")
# score
plt.subplot(grid[1, 0])
plt.scatter(episodes, scores_R, color="grey", alpha=0.4, s=2, label="R")
plt.ylabel("Score")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Q
plt.subplot(grid[2, 0])
plt.scatter(episodes, values_R, color="grey", alpha=0.4, s=2, label="$Q_R$")
plt.ylabel("Value")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# best
plt.subplot(grid[3, 0])
plt.scatter(episodes, bests, color="red", alpha=.5, s=2)
plt.ylabel("p(best)")
plt.xlabel("Episode")
plt.ylim(0, 1)
# Decay
plt.subplot(grid[4, 0])
plt.scatter(episodes, epsilons, color="black", alpha=.5, s=2)
plt.ylabel("$\epsilon_R$")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
def plot_critic(critic_name, env_name, result):
# -
env = gym.make(env_name)
best = env.best
# Data
critic = result[critic_name]
arms = list(critic.keys())
values = list(critic.values())
# Plotz
fig = plt.figure(figsize=(8, 3))
grid = plt.GridSpec(1, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0])
plt.scatter(arms, values, color="black", alpha=.5, s=30)
plt.plot([best]*10, np.linspace(min(values), max(values), 10), color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Value")
plt.xlabel("Arm")
data_path ="/Users/qualia/Code/infomercial/data/"
exp_name = "exp105"
sorted_params = load_checkpoint(os.path.join(data_path, f"{exp_name}_sorted.pkl"))
# print(sorted_params.keys())
best_params = sorted_params[0]
sorted_params
env_name = 'BanditUniform121-v0'
num_episodes = 60500
# Run w/ best params
result = epsilon_bandit(
env_name=env_name,
num_episodes=num_episodes,
lr_R=best_params["lr_R"],
epsilon=best_params["epsilon"],
seed_value=2,
)
print(best_params)
plot_epsilon(env_name, result=result)
plot_critic('critic_R', env_name, result)
total_Rs = []
eps = []
lrs_R = []
lrs_E = []
trials = list(sorted_params.keys())
for t in trials:
total_Rs.append(sorted_params[t]['total_R'])
lrs_R.append(sorted_params[t]['lr_R'])
eps.append(sorted_params[t]['epsilon'])
# Init plot
fig = plt.figure(figsize=(5, 18))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Do plots:
# Arm
plt.subplot(grid[0, 0])
plt.scatter(trials, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("Sorted params")
plt.ylabel("total R")
_ = sns.despine()
plt.subplot(grid[1, 0])
plt.scatter(trials, lrs_R, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("Sorted params")
plt.ylabel("lr_R")
_ = sns.despine()
plt.subplot(grid[2, 0])
plt.scatter(lrs_R, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("lrs_R")
plt.ylabel("total_Rs")
_ = sns.despine()
plt.subplot(grid[3, 0])
plt.scatter(eps, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("epsilon")
plt.ylabel("total_Rs")
_ = sns.despine()
from scipy.stats import spearmanr
spearmanr(eps, lrs_R)
spearmanr(eps, total_Rs)
spearmanr(lrs_R, total_Rs)
# Init plot
fig = plt.figure(figsize=(5, 6))
grid = plt.GridSpec(3, 1, wspace=0.3, hspace=0.8)
plt.subplot(grid[0, 0])
plt.hist(eps, color="black")
plt.xlabel("epsilon")
plt.ylabel("Count")
_ = sns.despine()
plt.subplot(grid[1, 0])
plt.hist(lrs_R, color="black")
plt.xlabel("lr_R")
plt.ylabel("Count")
_ = sns.despine()
# Init plot
fig = plt.figure(figsize=(5, 2))
grid = plt.GridSpec(1, 1, wspace=0.3, hspace=0.8)
plt.subplot(grid[0, 0])
plt.hist(total_Rs, color="black", bins=50)
plt.xlabel("Total reward")
plt.ylabel("Count")
# plt.xlim(0, 10)
_ = sns.despine()
| 0.647241 | 0.838349 |
<img src="src/img/bg.jpg" align="center">
<h1>Venda de jogos de videogames na História</h1>
<br>
Este projeto foi criado por: <b>RodriguesFAS</b>. Aqui eu irei realizar algumas análises sobres os dados encontrados <a href="https://www.kaggle.com/gregorut/videogamesales" target="_blank"> neste dataset.</a>
# Tutorial
[Como criar seu portfólio de Data Scientist e divulgar seus trabalho](https://paulovasconcellos.com.br/como-criar-seu-portfolio-de-data-scientist-cc7e6b23b996)
[Como criar seu primeiro projeto de Data Science — Parte 1 de 2](https://paulovasconcellos.com.br/como-criar-seu-primeiro-projeto-de-data-science-parte-1-de-2-d846c4c8d314)
[Como criar seu primeiro projeto de Data Science — Parte 2 de 2](https://paulovasconcellos.com.br/como-criar-seu-primeiro-projeto-de-data-science-parte-2-de-2-cb9a2fe05eff)
```
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('ggplot')
#Leitura do arquivo "carrega dataset na memória por meio da ferramenta pandas"
videogames = pd.read_csv('src/dataset/vgsales.csv')
```
# A baixo você pode conferir as colunas encontradas no arquivo “vgsales.csv”
<b>Rank:</b> posição no ranking de vendas<br>
<b>Name:</b> nome do jogo<br>
<b>Platform:</b> plataforma em que o jogo foi liberado (PC, PS4, Xbox, etc.)<br>
<b>Year:</b> ano de lançamento do game<br>
<b>Genre:</b> gênero do jogo<br>
<b>Publisher:</b> empresa que publicou o jogo<br>
<b>NA_Sales:</b> vendas na América do Norte (em milhões de dólares)<br>
<b>EU_Sales:</b> vendas na Europa (em milhões de dólares)<br>
<b>JP_Sales:</b> vendas no Japão (em milhões de dólares)<br>
<b>Other_Sales:</b> vendas no restante do mundo (em milhões de dólares)<br>
<b>Global_Sales:</b> total de vendas no mundo inteiro<br>
```
#Exibindo as 10 primeira linhs do Dataframe
videogames.head(10)
#Resulmo de informações em todas as colunas
'''
A função describe() mostra um resumo das variáveis numéricas.
'''
videogames.describe()
#Tipos de dado em cada coluna
videogames.dtypes
'''
Quantidade de linhas e colunas do Dataframe.
A função shape mostra quantas linhas e colunas um Dataframe possui.
'''
videogames.shape
#Renomeando colunas
videogames.columns = ['Ranking', 'Nome', 'Plataforma', 'Ano', 'Gênero',
'Editora', 'Vendas América do Norte', 'Vendas EUA',
'Vendas Japão', 'Outras vendas', 'Vendas Global']
#Exibindo as 10 primeiras linhas do arquivo
videogames.head(10)
'''
Verificando linhas onde não há ano de lançamento definido
NaN seguinifica Not a Number
'''
videogames[videogames['Ano'].isnull()].head()
#Verificando quantos jogos foram lançado para cada plataforma.
videogames['Plataforma'].value_counts()
#Criando gricos com pandas
titulos_lancados = videogames['Plataforma'].value_counts()
titulos_lancados.plot()
videogames['Plataforma'].value_counts().plot()
#Crinado um gráfico utilizando apenas uma linha de código.
videogames['Plataforma'].value_counts().head(10).plot(kind='bar', figsize=(11,5), grid=False, rot=0, color='green')
#Alegorias do gráfico
plt.title('Os 10 videogames com mais títuos lançados')
plt.xlabel('Videogame')
plt.ylabel('Quantidade de jogos lançados')
plt.show()
top_10_vendidos = videogames[['Nome', 'Vendas Global']].head(10).set_index('Nome').sort_values('Vendas Global', ascending=True)
top_10_vendidos.plot(kind='barh', figsize=(11,7), grid=False, color='darkred', legend=False)
plt.title('Os 10 jogos mais vendidos no mundo')
plt.xlabel('Total de vendas em milhoes de doláres')
plt.show()
#informações cruzadas
crosstab_vg = pd.crosstab(videogames['Plataforma'], videogames['Gênero'])
crosstab_vg.head()
#Adiciona uma coluna Total
crosstab_vg['Total'] = crosstab_vg.sum(axis=1)
crosstab_vg.head()
# Mapa de calor
top10_platforms = crosstab_vg[crosstab_vg['Total'] > 1000].sort_values('Total', ascending = False)
top10_final = top10_platforms.append(pd.DataFrame(top10_platforms.sum(), columns=['total']).T, ignore_index=False)
sns.set(font_scale=1)
plt.figure(figsize=(18,9))
sns.heatmap(top10_final, annot=True, vmax=top10_final.loc[:'PS', :'Strategy'].values.max(), vmin=top10_final.loc[:, :'Strategy'].values.min(), fmt='d')
plt.xlabel('Gênero')
plt.ylabel('Console')
plt.title('Quantidade de Títulos Por Gênero e Console')
plt.show()
```
|
github_jupyter
|
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('ggplot')
#Leitura do arquivo "carrega dataset na memória por meio da ferramenta pandas"
videogames = pd.read_csv('src/dataset/vgsales.csv')
#Exibindo as 10 primeira linhs do Dataframe
videogames.head(10)
#Resulmo de informações em todas as colunas
'''
A função describe() mostra um resumo das variáveis numéricas.
'''
videogames.describe()
#Tipos de dado em cada coluna
videogames.dtypes
'''
Quantidade de linhas e colunas do Dataframe.
A função shape mostra quantas linhas e colunas um Dataframe possui.
'''
videogames.shape
#Renomeando colunas
videogames.columns = ['Ranking', 'Nome', 'Plataforma', 'Ano', 'Gênero',
'Editora', 'Vendas América do Norte', 'Vendas EUA',
'Vendas Japão', 'Outras vendas', 'Vendas Global']
#Exibindo as 10 primeiras linhas do arquivo
videogames.head(10)
'''
Verificando linhas onde não há ano de lançamento definido
NaN seguinifica Not a Number
'''
videogames[videogames['Ano'].isnull()].head()
#Verificando quantos jogos foram lançado para cada plataforma.
videogames['Plataforma'].value_counts()
#Criando gricos com pandas
titulos_lancados = videogames['Plataforma'].value_counts()
titulos_lancados.plot()
videogames['Plataforma'].value_counts().plot()
#Crinado um gráfico utilizando apenas uma linha de código.
videogames['Plataforma'].value_counts().head(10).plot(kind='bar', figsize=(11,5), grid=False, rot=0, color='green')
#Alegorias do gráfico
plt.title('Os 10 videogames com mais títuos lançados')
plt.xlabel('Videogame')
plt.ylabel('Quantidade de jogos lançados')
plt.show()
top_10_vendidos = videogames[['Nome', 'Vendas Global']].head(10).set_index('Nome').sort_values('Vendas Global', ascending=True)
top_10_vendidos.plot(kind='barh', figsize=(11,7), grid=False, color='darkred', legend=False)
plt.title('Os 10 jogos mais vendidos no mundo')
plt.xlabel('Total de vendas em milhoes de doláres')
plt.show()
#informações cruzadas
crosstab_vg = pd.crosstab(videogames['Plataforma'], videogames['Gênero'])
crosstab_vg.head()
#Adiciona uma coluna Total
crosstab_vg['Total'] = crosstab_vg.sum(axis=1)
crosstab_vg.head()
# Mapa de calor
top10_platforms = crosstab_vg[crosstab_vg['Total'] > 1000].sort_values('Total', ascending = False)
top10_final = top10_platforms.append(pd.DataFrame(top10_platforms.sum(), columns=['total']).T, ignore_index=False)
sns.set(font_scale=1)
plt.figure(figsize=(18,9))
sns.heatmap(top10_final, annot=True, vmax=top10_final.loc[:'PS', :'Strategy'].values.max(), vmin=top10_final.loc[:, :'Strategy'].values.min(), fmt='d')
plt.xlabel('Gênero')
plt.ylabel('Console')
plt.title('Quantidade de Títulos Por Gênero e Console')
plt.show()
| 0.322206 | 0.882529 |
```
from collections import OrderedDict
import re
import pandas as pd
import pickle
import torch
import tqdm
import transformers
print(torch.__version__)
print(transformers.__version__)
```
# Load tokenizer and fine-tuned model
```
TOKENIZER_PATH = "data/gpt2_runs/tokenizers/gpt2_large"
MODEL_PATH = "data/gpt2_runs/v2/step_290000/"
tokenizer = transformers.GPT2Tokenizer.from_pretrained(TOKENIZER_PATH)
model = transformers.AutoModelForCausalLM.from_pretrained(
MODEL_PATH,
pad_token_id=tokenizer.eos_token_id
)
model = model.to('cuda:1')
```
# Greedy Output
```
input_prompt = "<|startoftext|> [prompt] Walter Hansel Cuvee Alyce Chardonnay 2015 [response] "
input_ids = tokenizer.encode(input_prompt, return_tensors='pt').to('cuda:1')
print("Tokens: ", input_ids)
greedy_output = model.generate(input_ids, max_length=200)
print(tokenizer.decode(greedy_output[0]))
```
# Beam Output
```
input_prompt = "<|startoftext|> [prompt] Walter Hansel Cuvee Alyce Chardonnay 2015 [response] "
input_ids = tokenizer.encode(input_prompt, return_tensors='pt').to('cuda:1')
# activate beam search and early_stopping
beam_outputs = model.generate(
input_ids,
max_length=200,
num_beams=5,
no_repeat_ngram_size=2,
num_return_sequences=3,
early_stopping=True
)
print("Output:\n" + 80 * '-')
for i, beam_output in enumerate(beam_outputs):
print("="*20)
print("{}: {}".format(i, tokenizer.decode(beam_output, skip_special_tokens=True)))
print('\n')
```
# Random Sampling Output
```
input_prompt = "<|startoftext|> " + "[prompt] " + "Vendange Chardonnay " + "[response] "
input_ids = tokenizer.encode(input_prompt, return_tensors='pt')
print(input_ids)
# Send to GPU
model.to('cuda:1')
input_ids = input_ids.to('cuda:1')
sample_output = model.generate(
input_ids,
do_sample=True,
max_length=250,
top_p=0.8,
top_k=200,
temperature=0.9,
eos_token_id=tokenizer.eos_token_id,
bos_token_id=tokenizer.eos_token_id,
early_stopping=True
)
print("Output:\n" + 100 * '-')
print("="*20)
print(tokenizer.decode(sample_output[0], skip_special_tokens=True))
print('\n')
```
# Generate descriptions on fake wine names
```
names_path = 'data/fake/fake_names_12184_2020-11-19.pickle'
with open(names_path, 'rb',) as file:
fake_names = pickle.load(file)
fake_names.head(3)
# Send to GPU
model.to('cuda:1')
#input_ids = input_ids.to('cuda:1')
generated_descriptions = OrderedDict()
for fake_name in tqdm.tqdm(fake_names[:1000]):
#print(f"Name: {fake_name}")
# Create token from fake wine name
try:
input_ids = tokenizer.encode(
text=("<|startoftext|> [prompt] " + fake_name + " " + "[response] "),
return_tensors='pt'
).to('cuda:1')
# Generate a fake description based on the name
model_output = model.generate(
input_ids,
do_sample=True,
max_length=300,
min_length=80,
top_p=0.8,
top_k=200,
temperature=0.9,
eos_token_id=tokenizer.eos_token_id,
bos_token_id=tokenizer.bos_token_id,
early_stopping=True
)
generated_descriptions[fake_name] = tokenizer.decode(
token_ids=model_output[0],
skip_special_tokens=True
)
except:
continue
wine_df = pd.DataFrame.from_dict(generated_descriptions.items())
wine_df.columns = ['name', 'response']
print(wine_df.shape)
wine_df['category_1'] = wine_df['response'].str.split('\[category_1\]').str[1].str.split('\[category_2\]').str[0]
wine_df['category_2'] = wine_df['response'].str.split('\[category_2\]').str[1].str.split('\[origin\]').str[0]
wine_df['origin'] = wine_df['response'].str.split('\[origin\]').str[1].str.split('\[description\]').str[0]
wine_df['description'] = wine_df['response'].str.split('\[description\]').str[1]
#wine_df['description'] = wine_df['description'].str.strip()
#wine_df['description'] = wine_df['description'].str.strip('"')
#wine_df = wine_df[wine_df['description'].str.len() > 100]
wine_df = wine_df.applymap(str)\
.applymap(lambda x: x.replace('"', ''))\
.drop(['response'], axis=1)
print(wine_df.shape)
wine_df.head()
wine_df.to_csv("data/fake/descriptions/gpt2_desc_v2_20210127.csv")
```
|
github_jupyter
|
from collections import OrderedDict
import re
import pandas as pd
import pickle
import torch
import tqdm
import transformers
print(torch.__version__)
print(transformers.__version__)
TOKENIZER_PATH = "data/gpt2_runs/tokenizers/gpt2_large"
MODEL_PATH = "data/gpt2_runs/v2/step_290000/"
tokenizer = transformers.GPT2Tokenizer.from_pretrained(TOKENIZER_PATH)
model = transformers.AutoModelForCausalLM.from_pretrained(
MODEL_PATH,
pad_token_id=tokenizer.eos_token_id
)
model = model.to('cuda:1')
input_prompt = "<|startoftext|> [prompt] Walter Hansel Cuvee Alyce Chardonnay 2015 [response] "
input_ids = tokenizer.encode(input_prompt, return_tensors='pt').to('cuda:1')
print("Tokens: ", input_ids)
greedy_output = model.generate(input_ids, max_length=200)
print(tokenizer.decode(greedy_output[0]))
input_prompt = "<|startoftext|> [prompt] Walter Hansel Cuvee Alyce Chardonnay 2015 [response] "
input_ids = tokenizer.encode(input_prompt, return_tensors='pt').to('cuda:1')
# activate beam search and early_stopping
beam_outputs = model.generate(
input_ids,
max_length=200,
num_beams=5,
no_repeat_ngram_size=2,
num_return_sequences=3,
early_stopping=True
)
print("Output:\n" + 80 * '-')
for i, beam_output in enumerate(beam_outputs):
print("="*20)
print("{}: {}".format(i, tokenizer.decode(beam_output, skip_special_tokens=True)))
print('\n')
input_prompt = "<|startoftext|> " + "[prompt] " + "Vendange Chardonnay " + "[response] "
input_ids = tokenizer.encode(input_prompt, return_tensors='pt')
print(input_ids)
# Send to GPU
model.to('cuda:1')
input_ids = input_ids.to('cuda:1')
sample_output = model.generate(
input_ids,
do_sample=True,
max_length=250,
top_p=0.8,
top_k=200,
temperature=0.9,
eos_token_id=tokenizer.eos_token_id,
bos_token_id=tokenizer.eos_token_id,
early_stopping=True
)
print("Output:\n" + 100 * '-')
print("="*20)
print(tokenizer.decode(sample_output[0], skip_special_tokens=True))
print('\n')
names_path = 'data/fake/fake_names_12184_2020-11-19.pickle'
with open(names_path, 'rb',) as file:
fake_names = pickle.load(file)
fake_names.head(3)
# Send to GPU
model.to('cuda:1')
#input_ids = input_ids.to('cuda:1')
generated_descriptions = OrderedDict()
for fake_name in tqdm.tqdm(fake_names[:1000]):
#print(f"Name: {fake_name}")
# Create token from fake wine name
try:
input_ids = tokenizer.encode(
text=("<|startoftext|> [prompt] " + fake_name + " " + "[response] "),
return_tensors='pt'
).to('cuda:1')
# Generate a fake description based on the name
model_output = model.generate(
input_ids,
do_sample=True,
max_length=300,
min_length=80,
top_p=0.8,
top_k=200,
temperature=0.9,
eos_token_id=tokenizer.eos_token_id,
bos_token_id=tokenizer.bos_token_id,
early_stopping=True
)
generated_descriptions[fake_name] = tokenizer.decode(
token_ids=model_output[0],
skip_special_tokens=True
)
except:
continue
wine_df = pd.DataFrame.from_dict(generated_descriptions.items())
wine_df.columns = ['name', 'response']
print(wine_df.shape)
wine_df['category_1'] = wine_df['response'].str.split('\[category_1\]').str[1].str.split('\[category_2\]').str[0]
wine_df['category_2'] = wine_df['response'].str.split('\[category_2\]').str[1].str.split('\[origin\]').str[0]
wine_df['origin'] = wine_df['response'].str.split('\[origin\]').str[1].str.split('\[description\]').str[0]
wine_df['description'] = wine_df['response'].str.split('\[description\]').str[1]
#wine_df['description'] = wine_df['description'].str.strip()
#wine_df['description'] = wine_df['description'].str.strip('"')
#wine_df = wine_df[wine_df['description'].str.len() > 100]
wine_df = wine_df.applymap(str)\
.applymap(lambda x: x.replace('"', ''))\
.drop(['response'], axis=1)
print(wine_df.shape)
wine_df.head()
wine_df.to_csv("data/fake/descriptions/gpt2_desc_v2_20210127.csv")
| 0.385606 | 0.454048 |
# Vector Fitting
This is a brief introduction to Vector Fitting. The concept and its algorithm was proposed in 1999 by Bjørn Gustavsen and Adam Semlyen [[1](#link_ref1)]. See the Vector Fitting website for more information [[2](#link_ref2)].
The main application of Vector Fitting is to model the original sampled frequency responses of an active or passive device in a circuit simulator.
## Mathematical Description
The idea of Vector Fitting is to fit a set of rational model functions to a set of sampled frequency responses $\mathbf{\underline{H}}_\mathrm{sampled}$, for example from a [S](https://en.wikipedia.org/wiki/Scattering_parameters), [Y](https://en.wikipedia.org/wiki/Admittance_parameters) or [Z](https://en.wikipedia.org/wiki/Impedance_parameters) matrix. The model function $\mathbf{\underline{H}}(\mathrm{\underline{s}})$ is defined in the Laplace domain with $\mathrm{\underline{s}} = \sigma + \mathrm{j} \omega$:
\begin{equation}
\mathbf{\underline{H}}(\mathrm{\underline{s}}) = \mathbf{d} + \mathrm{\underline{s}} \mathbf{e} + \sum_{k=1}^K \frac{\underline{\mathbf{z}}_{k}}{\mathrm{\underline{s}}-\underline{p}_k}
\end{equation}
For the desired fit, that model function shall match the given frequency responses at their frequency samples $\omega_n$:
\begin{equation}
\mathbf{\underline{H}}(\mathrm{\underline{s}} = \mathrm{j} \omega_n) \overset{!}{=} \mathbf{\underline{H}}_\mathrm{sampled}(\omega_n)
\end{equation}
Generally, $\mathbf{\underline{H}}(\mathrm{\underline{s}})$ is a vector holding the individual complex frequency responses $\underline{H}_1(\mathrm{\underline{s}})$, $\underline{H}_2(\mathrm{\underline{s}})$, ..., $\underline{H}_M(\mathrm{\underline{s}})$ of the model. All elements in $\mathbf{\underline{H}}(\mathrm{\underline{s}})$ share a common set of complex poles $\underline{p}_k$, but have individual sets of complex zeros $\mathbf{\underline{z}}_k$, real constants $\mathbf{d}$ and real proportional coefficients $\mathbf{e}$, which are therefore vectors as well:
\begin{equation}
\mathbf{\underline{p}} = \begin{pmatrix} \underline{p}_1 & \underline{p}_2 & \underline{p}_3 & \cdots & \underline{p}_K \end{pmatrix}
\end{equation}
\begin{equation}
\mathbf{\underline{z}} = \begin{pmatrix}
\underline{z}_{1,1} & \underline{z}_{2,1} & \underline{z}_{3,1} & \cdots & \underline{z}_{K,1} \\
\underline{z}_{1,2} & \underline{z}_{2,2} & \underline{z}_{3,2} & \cdots & \underline{z}_{K,2} \\
\vdots\\
\underline{z}_{1,M} & \underline{z}_{2,M} & \underline{z}_{3,M} & \cdots & \underline{z}_{K,M} \\
\end{pmatrix}
\end{equation}
\begin{equation}
\mathbf{d} = \begin{pmatrix} d_1 \\ d_2 \\ \vdots \\ d_M \end{pmatrix}
\end{equation}
\begin{equation}
\mathbf{e} = \begin{pmatrix} e_1 \\ e_2 \\ \vdots \\ e_M \end{pmatrix}
\end{equation}
The number of poles, $K$, required for a good fit of $\mathbf{\underline{H}}(\mathrm{\underline{s}})$ to $\mathbf{\underline{H}}_\mathrm{sampled}$ depends on the shape of the responses.
As an example, the goal could be to fit the rational model function to the S matrix of a 2-port ($M = 4$) sampled at $N$ frequencies $\omega_n$:
\begin{equation}
\begin{pmatrix}
\underline{S}_{11}(\omega_n) \\
\underline{S}_{12}(\omega_n) \\
\underline{S}_{21}(\omega_n) \\
\underline{S}_{22}(\omega_n)
\end{pmatrix}
\overset{!}{=}
\begin{pmatrix}
d_{11} + \mathrm{j} \omega_n e_{11} + \sum_{k=1}^K \frac{\underline{z}_{k,11}}{\mathrm{j} \omega_n-\underline{p}_k}
\\
d_{12} + \mathrm{j} \omega_n e_{12} + \sum_{k=1}^K \frac{\underline{z}_{k,12}}{\mathrm{j} \omega_n-\underline{p}_k}
\\
d_{21} + \mathrm{j} \omega_n e_{21} + \sum_{k=1}^K \frac{\underline{z}_{k,21}}{\mathrm{j} \omega_n-\underline{p}_k}
\\
d_{22} + \mathrm{j} \omega_n e_{22} + \sum_{k=1}^K \frac{\underline{z}_{k,22}}{\mathrm{j} \omega_n-\underline{p}_k}
\end{pmatrix}
\end{equation}
During the Vector Fitting process, the model parameters $\mathbf{\underline{p}}$, $\mathbf{\underline{z}}$, $\mathbf{d}$ and $\mathbf{e}$ will be optimized in an iterative manner until a good fit is achieved.
## Equivalent Electrical Circuits
The benefit of Vector Fitting the sampled frequency responses is the easy representation of the rational basis function with equivalent electrical circuits. A detailed derivation can be found in [[3](#link_ref3)].
### Constant and Proportional Term
The constant and proportional terms $\mathbf{d} + \mathrm{\underline{s}} \mathbf{e}$ can be represented in an electrical circuit by equivalent impedances $\underline{Z}_\mathrm{RL}(\mathrm{\underline{s}})$ or equivalent admittances $\underline{Y}_\mathrm{RC}(\mathrm{\underline{s}})$ build out of a series RL or parallel RC circuits.
<img src='./figures/circuit_series_RL.svg' style='width:170px /'>
<img src='./figures/circuit_parallel_RC.svg' style='width:150px' />
Target response of the constant and proportional term:
\begin{equation}
\underline{H}_\mathrm{target}(\mathrm{\underline{s}}) = d_i + \mathrm{\underline{s}} e_i
\end{equation}
#### Impedance of a series RL circuit:
\begin{equation}
\underline{Z}_\mathrm{RL}(\mathrm{\underline{s}}) = R + \mathrm{\underline{s}} L
\end{equation}
This impedance matches the target response if $R = d_i$ and $L = e_i$.
#### Admittance of a parallel RC circuit:
\begin{equation}
\underline{Y}_\mathrm{RC}(\mathrm{\underline{s}}) = \frac{1}{R} + \mathrm{\underline{s}} C
\end{equation}
This admittance matches the target response if $R = \frac{1}{d_i}$ and $C = e_i$.
### Real Poles and Zeros
The individual terms $\frac{z_{k,i}}{\mathrm{\underline{s}} - p_{k,i}}$ of the fit with a real pole $p_{k,i}$ and a real zero $z_{k,i}$ can be represented in an electrical circuit by equivalent impedances $\underline{Z}_\mathrm{RC}(\mathrm{\underline{s}})$ or equivalent admittances $\underline{Y}_\mathrm{RL}(\mathrm{\underline{s}})$ build out of a parallel RC or series RL circuits.
Target response of the real pole/zero term:
\begin{equation}
\underline{H}_\mathrm{target}(\mathrm{\underline{s}}) = \frac{z_{k,i}}{\mathrm{\underline{s}} - p_{k,i}}
\end{equation}
#### Impedance of a parallel RC circuit:
The parallel RC circuit is the same as above for the constant and proportional term, but this time its impedance $\underline{Z}_\mathrm{RC}(\mathrm{\underline{s}})$ is used instead of its admittance:
\begin{equation}
\underline{Z}_\mathrm{RC}(\mathrm{\underline{s}}) = \frac{\frac{1}{C}}{\mathrm{\underline{s}} + \frac{1}{RC}}
\end{equation}
This impedance matches the target response if $C = \frac{1}{z_{k,i}}$ and $R = \frac{z_{k,i}}{-p_{k,i}}$.
#### Admittance of a series RL circuit:
The series RL circuit is the same as above for the constant and proportional term, but this time its admittance $\underline{Y}_\mathrm{RL}(\mathrm{\underline{s}})$ is used instead of its impedance:
\begin{equation}
\underline{Y}_\mathrm{RL}(\mathrm{\underline{s}}) = \frac{\frac{1}{L}}{\mathrm{\underline{s}} + \frac{R}{L}}
\end{equation}
This admittance matches the target response if $L = \frac{1}{z_{k,i}}$ and $R = \frac{-p_{k,i}}{z_{k,i}}$.
### Complex Conjugate Poles and Zeros
In Vector Fitting, complex poles $\underline{p}_k = p'_k + \mathrm{j} p''_k$ and zeros $\underline{z}_k = z'_k + \mathrm{j} z''_k$ always come in complex conjugate pairs $(\underline{p}_k, \underline{p}_k^*)$ and $(\underline{z}_k, \underline{z}_k^*)$. The target response for an equivalent electrical circuit of such a complex conjugate pair is therefore:
\begin{equation}
\underline{H}_\mathrm{target}(\mathrm{\underline{s}}) = \frac{\underline{z}_k}{\mathrm{\underline{s}} - \underline{p}_k} + \frac{\underline{z}^*_k}{\mathrm{\underline{s}} - \underline{p}^*_k} = \frac{2 z'_k \mathrm{\underline{s}} - 2 (z'_k p'_k + z''_k p''_k)}{\mathrm{\underline{s}}^2 - 2 p'_k \mathrm{\underline{s}} + |\underline{p}_k|^2}
\end{equation}
There are different ways to build an equivalent circuit out of passive or active components, which can be dimensioned to match this target frequency response. Four such circuits are presented and analyzed in [[3](#link_ref3)], for example a series RLC circuit combined with a parallel current source controlled by the voltage over the capacitor.
<img src='./figures/circuit_series_RCL_parallel_current.svg' style='width:200px'>
This circuit is providing an admittance $\underline{Y}_\mathrm{RCL,I}(\mathrm{\underline{s}})$ that can be matched to the target response:
\begin{equation}
\underline{Y}_\mathrm{RCL,I}(\mathrm{\underline{s}}) = \frac{1/L \mathrm{\underline{s}} + b}{\mathrm{\underline{s}}^2 + R/L \mathrm{\underline{s}} + 1 / (LC)}
\end{equation}
This admittance matches the target response if $L = \frac{1}{2 z'_k}$, $R = \frac{-p'_k}{ z'_k}$, $C = \frac{2 z'_k}{|\underline{p}_k|^2}$ and $b = -2 (z'_k p'_k + z''_k p''_k)$ with $g_\mathrm{m} = bLC = \frac{b}{|\underline{p}_k|^2}$.
## Equivalent Circuit of a Vector Fitted $N$-Port
### Case 1: Vector Fitted S Parameters
The equivalent circuit of a $N$-port with a Vector Fitted S matrix consists of an interface network and a transfer network for each port. The figure below shows the structure of the interface and transfer networks of one such port $i$ with the external port voltage $V_i$ and port current $I_i$. The individual frequency responses $\underline{S}_{i,j}$ of the Vector Fit are reproduced with the equivalent admittances $\underline{Y}_{\mathrm{S},i,j}$ based on the fitting parameters $\mathbf{\underline{p}}$, $\mathbf{\underline{z}}$, $\mathbf{d}$ and $\mathbf{e}$ as described above.
<img src='./figures/circuit_equivalent_Nport_S.svg' style='width:500px' />
### Case 2: Vector Fitted Y Parameters
Not implemented. See [Y Parameters](https://en.wikipedia.org/wiki/Admittance_parameters) for a general equivalent circuit.
### Case 3: Vector Fitted Z Parameters
Not implemented. See [Z Parameters](https://en.wikipedia.org/wiki/Impedance_parameters) for a general equivalent circuit.
## References
<a id='link_ref1'>[1]</a> B. Gustavsen and A. Semlyen, "Rational approximation of frequency domain responses by vector fitting," in IEEE Transactions on Power Delivery, vol. 14, no. 3, pp. 1052-1061, July 1999, DOI: [10.1109/61.772353](https://doi.org/10.1109/61.772353).
<a id='link_ref2'>[2]</a> https://www.sintef.no/projectweb/vectorfitting/
<a id='link_ref3'>[3]</a> G. Antonini, "SPICE equivalent circuits of frequency-domain responses," in IEEE Transactions on Electromagnetic Compatibility, vol. 45, no. 3, pp. 502-512, Aug. 2003, DOI: [10.1109/TEMC.2003.815528](https://doi.org/10.1109/TEMC.2003.815528).
|
github_jupyter
|
# Vector Fitting
This is a brief introduction to Vector Fitting. The concept and its algorithm was proposed in 1999 by Bjørn Gustavsen and Adam Semlyen [[1](#link_ref1)]. See the Vector Fitting website for more information [[2](#link_ref2)].
The main application of Vector Fitting is to model the original sampled frequency responses of an active or passive device in a circuit simulator.
## Mathematical Description
The idea of Vector Fitting is to fit a set of rational model functions to a set of sampled frequency responses $\mathbf{\underline{H}}_\mathrm{sampled}$, for example from a [S](https://en.wikipedia.org/wiki/Scattering_parameters), [Y](https://en.wikipedia.org/wiki/Admittance_parameters) or [Z](https://en.wikipedia.org/wiki/Impedance_parameters) matrix. The model function $\mathbf{\underline{H}}(\mathrm{\underline{s}})$ is defined in the Laplace domain with $\mathrm{\underline{s}} = \sigma + \mathrm{j} \omega$:
\begin{equation}
\mathbf{\underline{H}}(\mathrm{\underline{s}}) = \mathbf{d} + \mathrm{\underline{s}} \mathbf{e} + \sum_{k=1}^K \frac{\underline{\mathbf{z}}_{k}}{\mathrm{\underline{s}}-\underline{p}_k}
\end{equation}
For the desired fit, that model function shall match the given frequency responses at their frequency samples $\omega_n$:
\begin{equation}
\mathbf{\underline{H}}(\mathrm{\underline{s}} = \mathrm{j} \omega_n) \overset{!}{=} \mathbf{\underline{H}}_\mathrm{sampled}(\omega_n)
\end{equation}
Generally, $\mathbf{\underline{H}}(\mathrm{\underline{s}})$ is a vector holding the individual complex frequency responses $\underline{H}_1(\mathrm{\underline{s}})$, $\underline{H}_2(\mathrm{\underline{s}})$, ..., $\underline{H}_M(\mathrm{\underline{s}})$ of the model. All elements in $\mathbf{\underline{H}}(\mathrm{\underline{s}})$ share a common set of complex poles $\underline{p}_k$, but have individual sets of complex zeros $\mathbf{\underline{z}}_k$, real constants $\mathbf{d}$ and real proportional coefficients $\mathbf{e}$, which are therefore vectors as well:
\begin{equation}
\mathbf{\underline{p}} = \begin{pmatrix} \underline{p}_1 & \underline{p}_2 & \underline{p}_3 & \cdots & \underline{p}_K \end{pmatrix}
\end{equation}
\begin{equation}
\mathbf{\underline{z}} = \begin{pmatrix}
\underline{z}_{1,1} & \underline{z}_{2,1} & \underline{z}_{3,1} & \cdots & \underline{z}_{K,1} \\
\underline{z}_{1,2} & \underline{z}_{2,2} & \underline{z}_{3,2} & \cdots & \underline{z}_{K,2} \\
\vdots\\
\underline{z}_{1,M} & \underline{z}_{2,M} & \underline{z}_{3,M} & \cdots & \underline{z}_{K,M} \\
\end{pmatrix}
\end{equation}
\begin{equation}
\mathbf{d} = \begin{pmatrix} d_1 \\ d_2 \\ \vdots \\ d_M \end{pmatrix}
\end{equation}
\begin{equation}
\mathbf{e} = \begin{pmatrix} e_1 \\ e_2 \\ \vdots \\ e_M \end{pmatrix}
\end{equation}
The number of poles, $K$, required for a good fit of $\mathbf{\underline{H}}(\mathrm{\underline{s}})$ to $\mathbf{\underline{H}}_\mathrm{sampled}$ depends on the shape of the responses.
As an example, the goal could be to fit the rational model function to the S matrix of a 2-port ($M = 4$) sampled at $N$ frequencies $\omega_n$:
\begin{equation}
\begin{pmatrix}
\underline{S}_{11}(\omega_n) \\
\underline{S}_{12}(\omega_n) \\
\underline{S}_{21}(\omega_n) \\
\underline{S}_{22}(\omega_n)
\end{pmatrix}
\overset{!}{=}
\begin{pmatrix}
d_{11} + \mathrm{j} \omega_n e_{11} + \sum_{k=1}^K \frac{\underline{z}_{k,11}}{\mathrm{j} \omega_n-\underline{p}_k}
\\
d_{12} + \mathrm{j} \omega_n e_{12} + \sum_{k=1}^K \frac{\underline{z}_{k,12}}{\mathrm{j} \omega_n-\underline{p}_k}
\\
d_{21} + \mathrm{j} \omega_n e_{21} + \sum_{k=1}^K \frac{\underline{z}_{k,21}}{\mathrm{j} \omega_n-\underline{p}_k}
\\
d_{22} + \mathrm{j} \omega_n e_{22} + \sum_{k=1}^K \frac{\underline{z}_{k,22}}{\mathrm{j} \omega_n-\underline{p}_k}
\end{pmatrix}
\end{equation}
During the Vector Fitting process, the model parameters $\mathbf{\underline{p}}$, $\mathbf{\underline{z}}$, $\mathbf{d}$ and $\mathbf{e}$ will be optimized in an iterative manner until a good fit is achieved.
## Equivalent Electrical Circuits
The benefit of Vector Fitting the sampled frequency responses is the easy representation of the rational basis function with equivalent electrical circuits. A detailed derivation can be found in [[3](#link_ref3)].
### Constant and Proportional Term
The constant and proportional terms $\mathbf{d} + \mathrm{\underline{s}} \mathbf{e}$ can be represented in an electrical circuit by equivalent impedances $\underline{Z}_\mathrm{RL}(\mathrm{\underline{s}})$ or equivalent admittances $\underline{Y}_\mathrm{RC}(\mathrm{\underline{s}})$ build out of a series RL or parallel RC circuits.
<img src='./figures/circuit_series_RL.svg' style='width:170px /'>
<img src='./figures/circuit_parallel_RC.svg' style='width:150px' />
Target response of the constant and proportional term:
\begin{equation}
\underline{H}_\mathrm{target}(\mathrm{\underline{s}}) = d_i + \mathrm{\underline{s}} e_i
\end{equation}
#### Impedance of a series RL circuit:
\begin{equation}
\underline{Z}_\mathrm{RL}(\mathrm{\underline{s}}) = R + \mathrm{\underline{s}} L
\end{equation}
This impedance matches the target response if $R = d_i$ and $L = e_i$.
#### Admittance of a parallel RC circuit:
\begin{equation}
\underline{Y}_\mathrm{RC}(\mathrm{\underline{s}}) = \frac{1}{R} + \mathrm{\underline{s}} C
\end{equation}
This admittance matches the target response if $R = \frac{1}{d_i}$ and $C = e_i$.
### Real Poles and Zeros
The individual terms $\frac{z_{k,i}}{\mathrm{\underline{s}} - p_{k,i}}$ of the fit with a real pole $p_{k,i}$ and a real zero $z_{k,i}$ can be represented in an electrical circuit by equivalent impedances $\underline{Z}_\mathrm{RC}(\mathrm{\underline{s}})$ or equivalent admittances $\underline{Y}_\mathrm{RL}(\mathrm{\underline{s}})$ build out of a parallel RC or series RL circuits.
Target response of the real pole/zero term:
\begin{equation}
\underline{H}_\mathrm{target}(\mathrm{\underline{s}}) = \frac{z_{k,i}}{\mathrm{\underline{s}} - p_{k,i}}
\end{equation}
#### Impedance of a parallel RC circuit:
The parallel RC circuit is the same as above for the constant and proportional term, but this time its impedance $\underline{Z}_\mathrm{RC}(\mathrm{\underline{s}})$ is used instead of its admittance:
\begin{equation}
\underline{Z}_\mathrm{RC}(\mathrm{\underline{s}}) = \frac{\frac{1}{C}}{\mathrm{\underline{s}} + \frac{1}{RC}}
\end{equation}
This impedance matches the target response if $C = \frac{1}{z_{k,i}}$ and $R = \frac{z_{k,i}}{-p_{k,i}}$.
#### Admittance of a series RL circuit:
The series RL circuit is the same as above for the constant and proportional term, but this time its admittance $\underline{Y}_\mathrm{RL}(\mathrm{\underline{s}})$ is used instead of its impedance:
\begin{equation}
\underline{Y}_\mathrm{RL}(\mathrm{\underline{s}}) = \frac{\frac{1}{L}}{\mathrm{\underline{s}} + \frac{R}{L}}
\end{equation}
This admittance matches the target response if $L = \frac{1}{z_{k,i}}$ and $R = \frac{-p_{k,i}}{z_{k,i}}$.
### Complex Conjugate Poles and Zeros
In Vector Fitting, complex poles $\underline{p}_k = p'_k + \mathrm{j} p''_k$ and zeros $\underline{z}_k = z'_k + \mathrm{j} z''_k$ always come in complex conjugate pairs $(\underline{p}_k, \underline{p}_k^*)$ and $(\underline{z}_k, \underline{z}_k^*)$. The target response for an equivalent electrical circuit of such a complex conjugate pair is therefore:
\begin{equation}
\underline{H}_\mathrm{target}(\mathrm{\underline{s}}) = \frac{\underline{z}_k}{\mathrm{\underline{s}} - \underline{p}_k} + \frac{\underline{z}^*_k}{\mathrm{\underline{s}} - \underline{p}^*_k} = \frac{2 z'_k \mathrm{\underline{s}} - 2 (z'_k p'_k + z''_k p''_k)}{\mathrm{\underline{s}}^2 - 2 p'_k \mathrm{\underline{s}} + |\underline{p}_k|^2}
\end{equation}
There are different ways to build an equivalent circuit out of passive or active components, which can be dimensioned to match this target frequency response. Four such circuits are presented and analyzed in [[3](#link_ref3)], for example a series RLC circuit combined with a parallel current source controlled by the voltage over the capacitor.
<img src='./figures/circuit_series_RCL_parallel_current.svg' style='width:200px'>
This circuit is providing an admittance $\underline{Y}_\mathrm{RCL,I}(\mathrm{\underline{s}})$ that can be matched to the target response:
\begin{equation}
\underline{Y}_\mathrm{RCL,I}(\mathrm{\underline{s}}) = \frac{1/L \mathrm{\underline{s}} + b}{\mathrm{\underline{s}}^2 + R/L \mathrm{\underline{s}} + 1 / (LC)}
\end{equation}
This admittance matches the target response if $L = \frac{1}{2 z'_k}$, $R = \frac{-p'_k}{ z'_k}$, $C = \frac{2 z'_k}{|\underline{p}_k|^2}$ and $b = -2 (z'_k p'_k + z''_k p''_k)$ with $g_\mathrm{m} = bLC = \frac{b}{|\underline{p}_k|^2}$.
## Equivalent Circuit of a Vector Fitted $N$-Port
### Case 1: Vector Fitted S Parameters
The equivalent circuit of a $N$-port with a Vector Fitted S matrix consists of an interface network and a transfer network for each port. The figure below shows the structure of the interface and transfer networks of one such port $i$ with the external port voltage $V_i$ and port current $I_i$. The individual frequency responses $\underline{S}_{i,j}$ of the Vector Fit are reproduced with the equivalent admittances $\underline{Y}_{\mathrm{S},i,j}$ based on the fitting parameters $\mathbf{\underline{p}}$, $\mathbf{\underline{z}}$, $\mathbf{d}$ and $\mathbf{e}$ as described above.
<img src='./figures/circuit_equivalent_Nport_S.svg' style='width:500px' />
### Case 2: Vector Fitted Y Parameters
Not implemented. See [Y Parameters](https://en.wikipedia.org/wiki/Admittance_parameters) for a general equivalent circuit.
### Case 3: Vector Fitted Z Parameters
Not implemented. See [Z Parameters](https://en.wikipedia.org/wiki/Impedance_parameters) for a general equivalent circuit.
## References
<a id='link_ref1'>[1]</a> B. Gustavsen and A. Semlyen, "Rational approximation of frequency domain responses by vector fitting," in IEEE Transactions on Power Delivery, vol. 14, no. 3, pp. 1052-1061, July 1999, DOI: [10.1109/61.772353](https://doi.org/10.1109/61.772353).
<a id='link_ref2'>[2]</a> https://www.sintef.no/projectweb/vectorfitting/
<a id='link_ref3'>[3]</a> G. Antonini, "SPICE equivalent circuits of frequency-domain responses," in IEEE Transactions on Electromagnetic Compatibility, vol. 45, no. 3, pp. 502-512, Aug. 2003, DOI: [10.1109/TEMC.2003.815528](https://doi.org/10.1109/TEMC.2003.815528).
| 0.923208 | 0.995669 |
<a href="https://colab.research.google.com/github/erivetna87/DS-Unit-1-Sprint-3-Statistical-Tests-and-Experiments/blob/master/module1-statistics-probability-and-inference/Eric_Rivetna_LS_DS_131_Statistics_Probability_Assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<img align="left" src="https://lever-client-logos.s3.amazonaws.com/864372b1-534c-480e-acd5-9711f850815c-1524247202159.png" width=200>
<br></br>
<br></br>
## *Data Science Unit 1 Sprint 3 Assignment 1*
# Apply the t-test to real data
Your assignment is to determine which issues have "statistically significant" differences between political parties in this [1980s congressional voting data](https://archive.ics.uci.edu/ml/datasets/Congressional+Voting+Records). The data consists of 435 instances (one for each congressperson), a class (democrat or republican), and 16 binary attributes (yes or no for voting for or against certain issues). Be aware - there are missing values!
Your goals:
1. Load and clean the data (or determine the best method to drop observations when running tests)
2. Using hypothesis testing, find an issue that democrats support more than republicans with p < 0.01
3. Using hypothesis testing, find an issue that republicans support more than democrats with p < 0.01
4. Using hypothesis testing, find an issue where the difference between republicans and democrats has p > 0.1 (i.e. there may not be much of a difference)
Note that this data will involve *2 sample* t-tests, because you're comparing averages across two groups (republicans and democrats) rather than a single group against a null hypothesis.
Stretch goals:
1. Refactor your code into functions so it's easy to rerun with arbitrary variables
2. Apply hypothesis testing to your personal project data (for the purposes of this notebook you can type a summary of the hypothesis you formed and tested)
```
import pandas as pd
import pprint as pp
from pandas.util.testing import assert_frame_equal
from scipy.stats import ttest_1samp
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 1000)
plt.style.use('seaborn-white')
pd.set_option('precision', 0)
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/voting-records/house-votes-84.data'
df = pd.read_csv(url)
df.head(1)
cols = ['Class Name: 2 (democrat, republican)',
'handicapped-infants: 2 (y,n)',
'water-project-cost-sharing: 2 (y,n)',
'adoption-of-the-budget-resolution: 2 (y,n)',
'physician-fee-freeze: 2 (y,n)',
'el-salvador-aid: 2 (y,n)',
'religious-groups-in-schools: 2 (y,n)',
'anti-satellite-test-ban: 2 (y,n)',
'aid-to-nicaraguan-contras: 2 (y,n)',
'mx-missile: 2 (y,n)',
'immigration: 2 (y,n)',
'synfuels-corporation-cutback: 2 (y,n)',
'education-spending: 2 (y,n)',
'superfund-right-to-sue: 2 (y,n)',
'crime: 2 (y,n)',
'duty-free-exports: 2 (y,n)',
'export-administration-act-south-africa: 2 (y,n)']
df.columns = cols
df.rename(columns = lambda x: x.replace(': 2 (y,n)','')[0:],inplace = True)
df.rename(columns = lambda x: x.replace('Class Name: 2 (democrat, republican)',
'Political Party')[0:],inplace = True)
df.columns = map(str.title, df.columns)
#to call column list in future cells as needed.
cols = df.columns.get_values().tolist()
# df.head(1)
print('Head of 1980s congressional voting data:')
print('\n')
print(df.head(5))
print('\n')
print('\n')
print('Tail of 1980s congressional voting data:')
print('\n')
print(df.tail(5))
#Checking for null values
df.isnull().sum()
#Looking at all Unique Values in each df series
[df[str(i)].unique() for i in cols]
df.replace({'?':np.NaN,'y': 1,'n':0},inplace=True)
#Second check for null values - NaN will be dropped in statistical analysis
df.isnull().sum()
#Separating party lines in DataFrames
rep = df[df['Political Party'] == 'republican']
dem = df[df['Political Party'] == 'democrat']
df_assert = rep + dem
if df.shape == df_assert.shape:
print(df['Political Party'].value_counts())
print('Combined DataFrames are Equal to Original DataFrame')
else:
print('DataFrames not Equal')
```
# Political Party T-test
```
rep['Handicapped-Infants'].mean()
# Null Hypothesis: Republican support is evenly divided
# Alternative: Republican support is not evenly divided.
pp.pprint([str(i) + ' 1 samp t-test: ' + str(ttest_1samp(rep[str(i)], .5, nan_policy='omit')) for i in cols[1:]])
# Null Hypothesis: There is 0 support for bills among Republicans in the House
# Alternative: There is non-0 support (some support) for some bills
pp.pprint([str(i) + ' 1 samp t-test: ' + str(ttest_1samp(rep[str(i)], 0, nan_policy='omit')) for i in cols[1:]])
```
|
github_jupyter
|
import pandas as pd
import pprint as pp
from pandas.util.testing import assert_frame_equal
from scipy.stats import ttest_1samp
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 1000)
plt.style.use('seaborn-white')
pd.set_option('precision', 0)
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/voting-records/house-votes-84.data'
df = pd.read_csv(url)
df.head(1)
cols = ['Class Name: 2 (democrat, republican)',
'handicapped-infants: 2 (y,n)',
'water-project-cost-sharing: 2 (y,n)',
'adoption-of-the-budget-resolution: 2 (y,n)',
'physician-fee-freeze: 2 (y,n)',
'el-salvador-aid: 2 (y,n)',
'religious-groups-in-schools: 2 (y,n)',
'anti-satellite-test-ban: 2 (y,n)',
'aid-to-nicaraguan-contras: 2 (y,n)',
'mx-missile: 2 (y,n)',
'immigration: 2 (y,n)',
'synfuels-corporation-cutback: 2 (y,n)',
'education-spending: 2 (y,n)',
'superfund-right-to-sue: 2 (y,n)',
'crime: 2 (y,n)',
'duty-free-exports: 2 (y,n)',
'export-administration-act-south-africa: 2 (y,n)']
df.columns = cols
df.rename(columns = lambda x: x.replace(': 2 (y,n)','')[0:],inplace = True)
df.rename(columns = lambda x: x.replace('Class Name: 2 (democrat, republican)',
'Political Party')[0:],inplace = True)
df.columns = map(str.title, df.columns)
#to call column list in future cells as needed.
cols = df.columns.get_values().tolist()
# df.head(1)
print('Head of 1980s congressional voting data:')
print('\n')
print(df.head(5))
print('\n')
print('\n')
print('Tail of 1980s congressional voting data:')
print('\n')
print(df.tail(5))
#Checking for null values
df.isnull().sum()
#Looking at all Unique Values in each df series
[df[str(i)].unique() for i in cols]
df.replace({'?':np.NaN,'y': 1,'n':0},inplace=True)
#Second check for null values - NaN will be dropped in statistical analysis
df.isnull().sum()
#Separating party lines in DataFrames
rep = df[df['Political Party'] == 'republican']
dem = df[df['Political Party'] == 'democrat']
df_assert = rep + dem
if df.shape == df_assert.shape:
print(df['Political Party'].value_counts())
print('Combined DataFrames are Equal to Original DataFrame')
else:
print('DataFrames not Equal')
rep['Handicapped-Infants'].mean()
# Null Hypothesis: Republican support is evenly divided
# Alternative: Republican support is not evenly divided.
pp.pprint([str(i) + ' 1 samp t-test: ' + str(ttest_1samp(rep[str(i)], .5, nan_policy='omit')) for i in cols[1:]])
# Null Hypothesis: There is 0 support for bills among Republicans in the House
# Alternative: There is non-0 support (some support) for some bills
pp.pprint([str(i) + ' 1 samp t-test: ' + str(ttest_1samp(rep[str(i)], 0, nan_policy='omit')) for i in cols[1:]])
| 0.367497 | 0.906901 |
## 1. 데이터 로드!
```
import os
import json
import h5py
import pandas as pd
import numpy as np
```
### 우리가 분류해야되는 Class를 확인해보자
❕ 원래 대/중/소/세분류로 나누어져 있지만, 대분류만 Classify할 예정이다!
```
cate = json.loads(open('./data/cate1.json', 'rb').read().decode('utf-8'))
count_big = len(cate['b']);
print(f'대분류 갯수 : {count_big}')
str(cate['b'])[:500] # 대분류 조금만 살펴보기!
cate_dict = {v:k for k,v in cate['b'].items()} # key-value바꾼 딕셔너리 만들기!
cate_dict[27]
```
### 우리가 traing해야되는 data를 살펴보자
```
data = h5py.File('./data/train.chunk.01', 'r')
train = data['train']
train.keys() # 상품의 feature
```
bcateid | brand | dcateid | img_feat | maker | mcateid | model | pid | price | product | scateid | updttm
-------- | ------ | -------- | -------- | ------ | -------- | ------ | ------ | ---- | ------ | --------- | -------------
대분류ID | 브랜드 | 세분류ID | 이미지특징 | 제조사 | 중분류ID | 상품ID | 상품ID | 가격 | 상품명 | 소분류ID | 업데이트 시간
```
# 첫 데이터만 살펴보자!
for i in train.keys():
sample = train[i][0]
if i in ['brand', 'product', 'maker', 'model']:
sample = sample.decode('utf-8')
print(f'{i}: {sample}');
train["img_feat"]
```
~~오픈소스 플젝은 이미지 Classification을 해서 재밌게 해야지 라고 생각했는데 이미지가 픽셀 정보가 아니라 이미 처리가 되어있었다.. 이걸 원본 이미지로 돌릴 순 없겠죠..?😂 ~~
```
count_data = len(train["bcateid"])
print(f'데이터 갯수 : {count_data}')
```
## 2. Train Data를 Train / Validation / Test로 분리!
```
from keras.utils.np_utils import to_categorical
on_hot_label = to_categorical(train["bcateid"]) # 대분류를 one-hot 인코딩!
on_hot_label
# train : vlidation : test = 640000 : 160000 : 200000
X_train = train["img_feat"][:6400]
X_val = train["img_feat"][6400:6400+1600]
X_test = train["img_feat"][6400+1600:]
y_train = on_hot_label[:6400]
y_val = on_hot_label[6400:6400+1600]
y_test = on_hot_label[6400+1600:]
y_train
```
## 3. 모델 training
데이터 전처리를 해야되지만.. 앞에서 마주친 작지만 나를 힘들게한 오류들 때문에.. 시간이 부족하니 냅다 훈련부터 해본다..!
❕ 모델은 img_feat만 가지고 훈련해볼 것이다!
☑️ Hyperparameter
| Hyperparameter | My Model |
| :---------- | :---------------------------------------------- |
| # input neurons | 2048(img_feat의 colums) |
| # hidden layers | 1 |
| # neurons per hidden layer | 100 |
| # output neurons | 57(대분류 갯수) |
| output layer activation | Softmax(1개의 class에만 할당될 수 있어서!) |
| Loss function | Cross entropy(Classification 문제라서!) |
*왜인지 모르겠지만 output neurons을 53으로 바꾸라고 오류가 나서 57 -> 53으로 바꾸었다!!*
```
from keras.models import Sequential
from keras import layers
model = Sequential()
model.add(layers.Dense(2048, activation='relu'))# input layer
model.add(layers.Dense(100, activation='relu')) # hidden layer
model.add(layers.Dense(53, activation='softmax')) # output layer
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(X_train,
y_train,
epochs=20,
validation_data=(X_val, y_val))
```
### 결과를 한 번 그려봅시다!
```
import matplotlib.pyplot as plt
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and Validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and Validation loss')
plt.legend()
plt.show()
```
헿 오버피팅됐다..!! 😅
```
model.evaluate(X_test, y_test)
```
## 최종 정확도: 62% 👏👏
아주 만족스럽진 않지만, 끝까지 마무리한 나 자신이 너무 대견하다🥺 아쉬운 결과가 아른거린다면 이 모델을 좀 더 개선시키러 돌아와야지..!
|
github_jupyter
|
import os
import json
import h5py
import pandas as pd
import numpy as np
cate = json.loads(open('./data/cate1.json', 'rb').read().decode('utf-8'))
count_big = len(cate['b']);
print(f'대분류 갯수 : {count_big}')
str(cate['b'])[:500] # 대분류 조금만 살펴보기!
cate_dict = {v:k for k,v in cate['b'].items()} # key-value바꾼 딕셔너리 만들기!
cate_dict[27]
data = h5py.File('./data/train.chunk.01', 'r')
train = data['train']
train.keys() # 상품의 feature
# 첫 데이터만 살펴보자!
for i in train.keys():
sample = train[i][0]
if i in ['brand', 'product', 'maker', 'model']:
sample = sample.decode('utf-8')
print(f'{i}: {sample}');
train["img_feat"]
count_data = len(train["bcateid"])
print(f'데이터 갯수 : {count_data}')
from keras.utils.np_utils import to_categorical
on_hot_label = to_categorical(train["bcateid"]) # 대분류를 one-hot 인코딩!
on_hot_label
# train : vlidation : test = 640000 : 160000 : 200000
X_train = train["img_feat"][:6400]
X_val = train["img_feat"][6400:6400+1600]
X_test = train["img_feat"][6400+1600:]
y_train = on_hot_label[:6400]
y_val = on_hot_label[6400:6400+1600]
y_test = on_hot_label[6400+1600:]
y_train
from keras.models import Sequential
from keras import layers
model = Sequential()
model.add(layers.Dense(2048, activation='relu'))# input layer
model.add(layers.Dense(100, activation='relu')) # hidden layer
model.add(layers.Dense(53, activation='softmax')) # output layer
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(X_train,
y_train,
epochs=20,
validation_data=(X_val, y_val))
import matplotlib.pyplot as plt
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and Validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and Validation loss')
plt.legend()
plt.show()
model.evaluate(X_test, y_test)
| 0.55254 | 0.80784 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV
from simforest import SimilarityForestRegressor, SimilarityTreeRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from yellowbrick.regressor import ResidualsPlot, PredictionError
from yellowbrick.model_selection import ValidationCurve, LearningCurve
from simforest.utils import plot_model_selection
%matplotlib inline
pd.options.display.max_columns = 500
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
```
I will start with a mpg dataset, for which Similarity Forest performs better than Random Forest. The data have been taken from libsvm website, but it originaly comes from UCI Machine Learning Repository.
I am going to use some cross-validation, so I shuffled the data. What is also important is to scale the features.
```
X, y = load_boston(return_X_y=True)
y = y + np.abs(np.min(y))
random_state = np.random.RandomState(42)
shuffled_indices = random_state.permutation(len(y))
X, y = X[shuffled_indices], y[shuffled_indices]
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
```
Target distribution
```
sns.distplot(y);
```
# Residual Plot
Residual plot tells us how a model fits the data. It can help to identify in which regions of target distribution our model makes the biggest mistakes. Both Random Forest and Similarity Forest make more mistakes for data-points with larger target value - it's probably due to the fact, that target distribution is a little bit negatively skewed.
```
sf = SimilarityForestRegressor(n_estimators=100, random_state=42)
visualizer = ResidualsPlot(sf)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
rf = RandomForestRegressor(random_state=42)
visualizer = ResidualsPlot(rf)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
```
Residual plots for the trees:
```
st = SimilarityTreeRegressor(random_state=42)
visualizer = ResidualsPlot(st)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
dt = DecisionTreeRegressor(random_state=42)
visualizer = ResidualsPlot(dt)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
```
# Prediction error plot
It may also be useful to check how fitted model's prediction correlate with actual target values.
```
visualizer = PredictionError(sf)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
visualizer = PredictionError(rf)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
visualizer = PredictionError(st)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
visualizer = PredictionError(dt)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
```
# Model selection
Both Random Forest's and Similarity Forest's results stabilize for 100 trees.
```
visualizer = ValidationCurve(
SimilarityForestRegressor(), param_name='n_estimators',
param_range=[10, 20, 30, 50, 70, 100, 150, 200], cv=5, scoring='r2'
)
visualizer.fit(X_train, y_train)
visualizer.show();
visualizer = ValidationCurve(
RandomForestRegressor(), param_name='n_estimators',
param_range=[10, 20, 30, 50, 70, 100, 150, 200], cv=5, scoring='r2'
)
visualizer.fit(X_train, y_train)
visualizer.show();
```
We can also control depth of the trees.
```
visualizer = ValidationCurve(
SimilarityForestRegressor(n_estimators=100), param_name='max_depth',
param_range=[6, 8, 10, 12, 14], cv=5, scoring='r2'
)
visualizer.fit(X_train, y_train)
visualizer.show();
visualizer = ValidationCurve(
RandomForestRegressor(), param_name='max_depth',
param_range=[6, 8, 10, 12, 14], cv=5, scoring='r2'
)
visualizer.fit(X_train, y_train)
visualizer.show();
```
# Learning curve
```
visualizer = LearningCurve(SimilarityForestRegressor(n_estimators=100), scoring='r2')
visualizer.fit(X_train, y_train)
visualizer.show();
visualizer = LearningCurve(RandomForestRegressor(), scoring='r2')
visualizer.fit(X_train, y_train)
visualizer.show();
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV
from simforest import SimilarityForestRegressor, SimilarityTreeRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from yellowbrick.regressor import ResidualsPlot, PredictionError
from yellowbrick.model_selection import ValidationCurve, LearningCurve
from simforest.utils import plot_model_selection
%matplotlib inline
pd.options.display.max_columns = 500
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
X, y = load_boston(return_X_y=True)
y = y + np.abs(np.min(y))
random_state = np.random.RandomState(42)
shuffled_indices = random_state.permutation(len(y))
X, y = X[shuffled_indices], y[shuffled_indices]
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
sns.distplot(y);
sf = SimilarityForestRegressor(n_estimators=100, random_state=42)
visualizer = ResidualsPlot(sf)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
rf = RandomForestRegressor(random_state=42)
visualizer = ResidualsPlot(rf)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
st = SimilarityTreeRegressor(random_state=42)
visualizer = ResidualsPlot(st)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
dt = DecisionTreeRegressor(random_state=42)
visualizer = ResidualsPlot(dt)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
visualizer = PredictionError(sf)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
visualizer = PredictionError(rf)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
visualizer = PredictionError(st)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
visualizer = PredictionError(dt)
visualizer.fit(X_train, y_train)
visualizer.score(X_test, y_test)
visualizer.show();
visualizer = ValidationCurve(
SimilarityForestRegressor(), param_name='n_estimators',
param_range=[10, 20, 30, 50, 70, 100, 150, 200], cv=5, scoring='r2'
)
visualizer.fit(X_train, y_train)
visualizer.show();
visualizer = ValidationCurve(
RandomForestRegressor(), param_name='n_estimators',
param_range=[10, 20, 30, 50, 70, 100, 150, 200], cv=5, scoring='r2'
)
visualizer.fit(X_train, y_train)
visualizer.show();
visualizer = ValidationCurve(
SimilarityForestRegressor(n_estimators=100), param_name='max_depth',
param_range=[6, 8, 10, 12, 14], cv=5, scoring='r2'
)
visualizer.fit(X_train, y_train)
visualizer.show();
visualizer = ValidationCurve(
RandomForestRegressor(), param_name='max_depth',
param_range=[6, 8, 10, 12, 14], cv=5, scoring='r2'
)
visualizer.fit(X_train, y_train)
visualizer.show();
visualizer = LearningCurve(SimilarityForestRegressor(n_estimators=100), scoring='r2')
visualizer.fit(X_train, y_train)
visualizer.show();
visualizer = LearningCurve(RandomForestRegressor(), scoring='r2')
visualizer.fit(X_train, y_train)
visualizer.show();
| 0.768125 | 0.915205 |
```
import pyspeckit as psk
import pyspeckit.spectrum.models.ammonia_constants as nh3const
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 150
```
This builds up an equivalent-width formalism for treating the ammonia model in RADEX. RADEX (I think) assumes a Gaussian line width model. Using our formalism, we have that
$$ \alpha(\nu) = \frac{c^2}{4\pi} \frac{1}{\nu_0^2}\frac{g_u}{g_l} n_l A_{ul}\left[1-\exp\left(\frac{h\nu}{kT_{ex}}\right)\right] \phi(\nu) = C n_l \, \phi(\nu)$$
Integrating over line of sight depth gives the specific optical depth:
$$ \tau(\nu) = \int ds\,\frac{c^2}{4\pi} \frac{1}{\nu_0^2}\frac{g_u}{g_l} n_l A_{ul}\left[1-\exp\left(\frac{h\nu}{kT_{ex}}\right)\right] \phi(\nu) = C N_l\, \phi(\nu)$$
Thus, it suffices to compare the two different line shape functions. Internally, we use a multi-Gaussian model for the line profile
$$\phi_{\mathrm{hfs}}(\nu) = \sum_i \frac{w_i}{\sqrt{2\pi}\sigma_\nu} \exp\left[-\frac{(\nu - \nu_0 - \delta\nu_i)^2}{2\sigma_\nu^2}\right]$$
RADEX presumably uses a Gaussian model with
$$\phi_{\mathrm{g}}(\nu) = \frac{1}{\sqrt{2\pi}\sigma_{\nu,g}} \exp\left[-\frac{(\nu - \nu_0)^2}{2\sigma_{\nu,g}^2}\right]$$
Thus, we aim to mimic the distribution of values of $\phi_{\mathrm{hfs}}$ for a line width of $\sigma_\nu$ using using a Gaussian with a modified spectral width $\sigma_{\nu,g}$. For a simple Gaussian distribution, this isn't possible to do perfectly. Instead, we use a model where we broaden the Gaussian line width so that the maximum of the Gaussian line profile function with the modified line width is the same as for the ammonia distribution. The integral will still be set to 1. First, let's measure the ratio of areas between an ammonia profile and a Gaussian profile with the same width and peak amplitude as the ammonia profile.
$$\phi^*_{\mathrm{g}}(\nu) = \frac{\max[\phi_{\mathrm{hfs}}(\nu)]}{\sqrt{2\pi}\sigma_{\nu}} \exp\left[-\frac{(\nu - \nu_0)^2}{2\sigma_{\nu}^2}\right]$$
Then the line width we plug into RADEX should be:
$$\sigma_{v,g} = \sigma_{v,\mathrm{hfs}} \frac{\int \phi_{\mathrm{hfs}}(\nu) d\nu }{\int \phi^*_{\mathrm{g}}(\nu) d\nu}$$
```
lines = nh3const.line_names
# Search up to 10 km/s
sigmav = np.logspace(np.log10(0.05),1,51)
# equivalent width for spectral profiles at a given line width
EW_hf = np.zeros((len(lines), len(sigmav)))
EW_gauss = np.zeros((len(lines), len(sigmav)))
vax = np.linspace(-100,100,10001)
dv = vax[1]-vax[0]
for i, thisline in enumerate(lines):
voff = nh3const.voff_lines_dict[thisline]
wts = np.array(nh3const.tau_wts_dict[thisline])
wts = wts / wts.sum()
for j, sig in enumerate(sigmav):
spec = np.zeros_like(vax)
for w, v in zip(wts, voff):
spec += w * np.exp(-(vax - v)**2/(2 * sig**2)) / (np.sqrt(2*np.pi) * sig) * dv
gauss = spec.max() * np.exp(-vax**2/(2*sig**2))
EW_hf[i, j] = np.sum(spec)
EW_gauss[i, j] = np.sum(gauss)
```
Let's take a look at how far off our equivalent width distribution is for the $(1,1)$ line. The distributions don't match too well but the max opacity is correctly matched. The (1,1) line has more low opacity parts of the spectrum but the high opacity parts of the distribution match well.
```
wts = np.array(nh3const.tau_wts_dict['oneone'])
voff = nh3const.voff_lines_dict['oneone']
wts = wts / wts.sum()
sig = 0.7
spec = np.zeros_like(vax)
for w, v in zip(wts, voff):
spec += w * np.exp(-(vax - v)**2/(2 * sig**2)) / (np.sqrt(2*np.pi) * sig) * dv
gauss = spec.max() * np.exp(-vax**2/(2*sig**2))
fig, ax = plt.subplots(1,1)
ax.hist((spec[spec>0.001]), label='Hyperfine Model',log=True)
ax.hist((gauss[gauss>0.001]),alpha=0.5, label='Gaussian',log=True)
ax.legend()
ax.set_xlabel(r'$\tau$')
ax.set_ylabel('PDF')
fig.set_size_inches(4.5, 3.5)
```
Now that we've measured the ratio of the areas, we want to scale the width of the Gaussian up by this ratio to reduce the max amplitude of the Gaussian profile by the same ratio. We fit a power-law relationship between this scaling for each line:
$$ \log_{10} \sigma_{v,g} = c_1 \log_{10} \sigma_{v,\mathrm{hfs}} + c_0$$
where the velocities here are expressed in km/s.
```
fig, axlist = plt.subplots(3,3, constrained_layout=True)
fig.set_size_inches(9,9)
coeffarray = np.zeros((len(lines),2))
for i, ax in enumerate(axlist.flatten()):
ax.plot(np.log10(sigmav), np.log10(sigmav * np.squeeze(EW_hf[i]/EW_gauss[i])), label='Empirical')
coeffs = np.polyfit(np.log10(sigmav), np.log10(sigmav * np.squeeze(EW_hf[i]/EW_gauss[i])), 1)
coeffarray[i, :] = coeffs
ax.plot(np.log10(sigmav), np.polyval(coeffs, np.log10(sigmav)),linestyle='--', label='Fit')
ax.axhline(0, color='k')
ax.axvline(0, color='k')
ax.set_xlabel(r'$\log_{10}(\sigma_v/\mathrm{km\ s^{-1}})$')
ax.set_ylabel(r'$\log_{10}(\sigma_{v,g}/\mathrm{km\ s^{-1}})$')
ax.text(-1,1,lines[i])
# ax.legend()
```
Given these coefficients, we transform a given velocity dispersion to a line appropriate velocity dispersion for that line using $c_0, c_1$ as defined above.
We have one final issue though. The transfer of the different states has different corrections to the line width because the HF components have different spacings for different $J,K$ states. This means we do a different lookup for the different lines but this means that we're solving the radiative transfer problem inconsistently (i.e., a lower opacity $(1,1)$ line would affect the population in $(2,2)$.
|
github_jupyter
|
import pyspeckit as psk
import pyspeckit.spectrum.models.ammonia_constants as nh3const
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 150
lines = nh3const.line_names
# Search up to 10 km/s
sigmav = np.logspace(np.log10(0.05),1,51)
# equivalent width for spectral profiles at a given line width
EW_hf = np.zeros((len(lines), len(sigmav)))
EW_gauss = np.zeros((len(lines), len(sigmav)))
vax = np.linspace(-100,100,10001)
dv = vax[1]-vax[0]
for i, thisline in enumerate(lines):
voff = nh3const.voff_lines_dict[thisline]
wts = np.array(nh3const.tau_wts_dict[thisline])
wts = wts / wts.sum()
for j, sig in enumerate(sigmav):
spec = np.zeros_like(vax)
for w, v in zip(wts, voff):
spec += w * np.exp(-(vax - v)**2/(2 * sig**2)) / (np.sqrt(2*np.pi) * sig) * dv
gauss = spec.max() * np.exp(-vax**2/(2*sig**2))
EW_hf[i, j] = np.sum(spec)
EW_gauss[i, j] = np.sum(gauss)
wts = np.array(nh3const.tau_wts_dict['oneone'])
voff = nh3const.voff_lines_dict['oneone']
wts = wts / wts.sum()
sig = 0.7
spec = np.zeros_like(vax)
for w, v in zip(wts, voff):
spec += w * np.exp(-(vax - v)**2/(2 * sig**2)) / (np.sqrt(2*np.pi) * sig) * dv
gauss = spec.max() * np.exp(-vax**2/(2*sig**2))
fig, ax = plt.subplots(1,1)
ax.hist((spec[spec>0.001]), label='Hyperfine Model',log=True)
ax.hist((gauss[gauss>0.001]),alpha=0.5, label='Gaussian',log=True)
ax.legend()
ax.set_xlabel(r'$\tau$')
ax.set_ylabel('PDF')
fig.set_size_inches(4.5, 3.5)
fig, axlist = plt.subplots(3,3, constrained_layout=True)
fig.set_size_inches(9,9)
coeffarray = np.zeros((len(lines),2))
for i, ax in enumerate(axlist.flatten()):
ax.plot(np.log10(sigmav), np.log10(sigmav * np.squeeze(EW_hf[i]/EW_gauss[i])), label='Empirical')
coeffs = np.polyfit(np.log10(sigmav), np.log10(sigmav * np.squeeze(EW_hf[i]/EW_gauss[i])), 1)
coeffarray[i, :] = coeffs
ax.plot(np.log10(sigmav), np.polyval(coeffs, np.log10(sigmav)),linestyle='--', label='Fit')
ax.axhline(0, color='k')
ax.axvline(0, color='k')
ax.set_xlabel(r'$\log_{10}(\sigma_v/\mathrm{km\ s^{-1}})$')
ax.set_ylabel(r'$\log_{10}(\sigma_{v,g}/\mathrm{km\ s^{-1}})$')
ax.text(-1,1,lines[i])
# ax.legend()
| 0.501465 | 0.982031 |
# Navigation
---
In this notebook, we will learn how to use the Unity ML-Agents environment for the first project navigation.
### 1. Start the Environment
We begin by importing some necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
<img src="results/navigation.gif">
```
from unityagents import UnityEnvironment
import numpy as np
from IPython.core.debugger import set_trace
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Banana.app"`
- **Windows** (x86): `"path/to/Banana_Windows_x86/Banana.exe"`
- **Windows** (x86_64): `"path/to/Banana_Windows_x86_64/Banana.exe"`
- **Linux** (x86): `"path/to/Banana_Linux/Banana.x86"`
- **Linux** (x86_64): `"path/to/Banana_Linux/Banana.x86_64"`
- **Linux** (x86, headless): `"path/to/Banana_Linux_NoVis/Banana.x86"`
- **Linux** (x86_64, headless): `"path/to/Banana_Linux_NoVis/Banana.x86_64"`
For instance, if you are using a Mac, then you downloaded `Banana.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Banana.app")
```
```
env = UnityEnvironment(file_name="Banana_Linux/Banana.x86", no_graphics=True)
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
print('brain name: {}'.format(brain_name))
```
### 2. Examine the State and Action Spaces
The simulation contains a single agent that navigates a large environment. At each time step, it has four actions at its disposal:
- `0` - walk forward
- `1` - walk backward
- `2` - turn left
- `3` - turn right
The state space has `37` dimensions and contains the agent's velocity, along with ray-based perception of objects around agent's forward direction. A reward of `+1` is provided for collecting a yellow banana, and a reward of `-1` is provided for collecting a blue banana.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents in the environment
print('Number of agents:', len(env_info.agents))
# number of actions
action_size = brain.vector_action_space_size
print('Number of actions:', action_size)
# examine the state space
state = env_info.vector_observations[0]
print('States look like:', state)
state_size = len(state)
print('States have length:', state_size)
```
### 3. Take Random Actions in the Environment
In the next code cell, we will learn how to use the Python API to control the agent and receive feedback from the environment.
Once this cell is executed, we will watch the agent's performance, if it selects an action (uniformly) at random with each time step. A window should pop up that allows you to observe the agent, as it moves through the environment.
As part of the project, we'll change the code so that the agent is able to use its experience to gradually choose better actions when interacting with the environment!
```
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
state = env_info.vector_observations[0] # get the current state
score = 0 # initialize the score
while True:
action = np.random.randint(action_size) # select an action
env_info = env.step(action)[brain_name] # send the action to the environment
next_state = env_info.vector_observations[0] # get the next state
reward = env_info.rewards[0] # get the reward
done = env_info.local_done[0] # see if episode has finished
#print('action:{}, reward:{}, done:{}'.format(action, score, done))
score += reward # update the score
state = next_state # roll over the state to next time step
if done: # exit loop if episode finished
break
print("Score of agent using random policy: {}".format(score))
```
Closing the environment before starting in training mode.
```
env.close()
```
### 4. Train the Agent with DQN!
Refer to start.py to see training code. Our agent is defined in dqn_agent. It uses basic DQN implementation. When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
```python
env_info = env.reset(train_mode=True)[brain_name]
```
```
import start
scores = start.run()
```
### Training plot
We can see the agent actions are not very smooth. There is lot of jitter in the movements. Some of the hyper parameters and results as follows.
```
NN with [256, 128, 64, 32] hidden layers was used for training (model.py)
Batch size : 256
Discount rate : 0.98
TAU : 1e-3
LR : 1e-4
Experience lag: 4
1. eps_decay 0.997 - score 16 after 1080 episodes
2. eps_decay 0.996 - score 13.72 @ 690 / decay 0.060
3. eps_start 0.8 - score 13 @ 740 episodes
```
```
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
```
### Epsilon decay plot
Exploration vs exploitation
```
import matplotlib.pyplot as plt
import numpy as np
eps_array = []
eps = 1.0
eps_decay = 0.994
for i in range(1000):
eps = max(0.01, eps_decay*eps)
eps_array.append(eps)
plt.plot(np.arange(len(eps_array)), eps_array)
plt.show()
```
### Trained agent Behaviour
```
from dqn_agent import Agent
from unityagents import UnityEnvironment
import torch
env = UnityEnvironment(file_name="Banana_Linux/Banana.x86")
agent = Agent(state_size=37, action_size=4, seed=0)
agent.network_local.load_state_dict(torch.load('checkpoint.pth'))
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
state = env_info.vector_observations[0] # get the current state
score = 0 # initialize the score
while True:
action = agent.act(state, 0.2) # select an action with 20% exploration
env_info = env.step(action)[brain_name] # send the action to the environment
next_state = env_info.vector_observations[0] # get the next state
reward = env_info.rewards[0] # get the reward
done = env_info.local_done[0] # see if episode has finished
#print('action:{}, reward:{}, done:{}'.format(action, score, done))
score += reward # update the score
state = next_state # roll over the state to next time step
if done: # exit loop if episode finished
break
print("Score: {}".format(score))
```
### Trained agent in the environment.
<img src="results/navigation_unseen.gif">
```
env.close()
```
### Summary
The following observations were made in this exercise:
1. Eps decay and hence mse_error effects exploration duration.
2. Various architectures were tried (as defined in models.py). No significant differences were found in either training time or overall scores. Final model has 4 layers, they very well could have been just 2.
3. Agent's action are very jittery. Agent does not generalize well for state where lot of blue bananas are clustered.
4. Learning rate was kept constant but could have been modified with eps decay.
### Parting thoughts
Q: How to figure if your network is overfitting? Or are DRL networks are operating in an environment where all possible states cannot be fit unless a general policy is learnt?
|
github_jupyter
|
from unityagents import UnityEnvironment
import numpy as np
from IPython.core.debugger import set_trace
env = UnityEnvironment(file_name="Banana.app")
env = UnityEnvironment(file_name="Banana_Linux/Banana.x86", no_graphics=True)
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
print('brain name: {}'.format(brain_name))
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents in the environment
print('Number of agents:', len(env_info.agents))
# number of actions
action_size = brain.vector_action_space_size
print('Number of actions:', action_size)
# examine the state space
state = env_info.vector_observations[0]
print('States look like:', state)
state_size = len(state)
print('States have length:', state_size)
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
state = env_info.vector_observations[0] # get the current state
score = 0 # initialize the score
while True:
action = np.random.randint(action_size) # select an action
env_info = env.step(action)[brain_name] # send the action to the environment
next_state = env_info.vector_observations[0] # get the next state
reward = env_info.rewards[0] # get the reward
done = env_info.local_done[0] # see if episode has finished
#print('action:{}, reward:{}, done:{}'.format(action, score, done))
score += reward # update the score
state = next_state # roll over the state to next time step
if done: # exit loop if episode finished
break
print("Score of agent using random policy: {}".format(score))
env.close()
env_info = env.reset(train_mode=True)[brain_name]
import start
scores = start.run()
NN with [256, 128, 64, 32] hidden layers was used for training (model.py)
Batch size : 256
Discount rate : 0.98
TAU : 1e-3
LR : 1e-4
Experience lag: 4
1. eps_decay 0.997 - score 16 after 1080 episodes
2. eps_decay 0.996 - score 13.72 @ 690 / decay 0.060
3. eps_start 0.8 - score 13 @ 740 episodes
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
import matplotlib.pyplot as plt
import numpy as np
eps_array = []
eps = 1.0
eps_decay = 0.994
for i in range(1000):
eps = max(0.01, eps_decay*eps)
eps_array.append(eps)
plt.plot(np.arange(len(eps_array)), eps_array)
plt.show()
from dqn_agent import Agent
from unityagents import UnityEnvironment
import torch
env = UnityEnvironment(file_name="Banana_Linux/Banana.x86")
agent = Agent(state_size=37, action_size=4, seed=0)
agent.network_local.load_state_dict(torch.load('checkpoint.pth'))
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
state = env_info.vector_observations[0] # get the current state
score = 0 # initialize the score
while True:
action = agent.act(state, 0.2) # select an action with 20% exploration
env_info = env.step(action)[brain_name] # send the action to the environment
next_state = env_info.vector_observations[0] # get the next state
reward = env_info.rewards[0] # get the reward
done = env_info.local_done[0] # see if episode has finished
#print('action:{}, reward:{}, done:{}'.format(action, score, done))
score += reward # update the score
state = next_state # roll over the state to next time step
if done: # exit loop if episode finished
break
print("Score: {}".format(score))
env.close()
| 0.241937 | 0.987142 |
<a href="https://colab.research.google.com/github/hari0624/Tensorflow/blob/master/Text_Classification_Using_Keras.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
In this notebook, IMDB data set is used to perform sentiment analysis by using Natural Language Processing in Keras.
```
import tensorflow as tf
import numpy as np
```
Load Data
```
!curl -O https://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz
!tar -xf aclImdb_v1.tar.gz
!ls aclImdb
!ls aclImdb/test
!ls aclImdb/train
!cat aclImdb/train/pos/6248_7.txt
```
unsup does not require, hence it can be deleted
```
!rm -r aclImdb/train/unsup
!ls aclImdb/test
```
Data Preprocessing
Note:
You can use the utility tf.keras.preprocessing.text_dataset_from_directory to generate a labeled tf.data.Dataset object from a set of text files on disk filed into class-specific folders.
When using the validation_split & subset arguments, make sure to either specify a random seed, or to pass shuffle=False, so that the validation & training splits you get have no overlap.
```
batch_size=32
raw_train_ds = tf.keras.preprocessing.text_dataset_from_directory(
"aclImdb/train",
batch_size=batch_size,
validation_split=0.2,
subset="training",
seed=1337,
)
raw_val_ds = tf.keras.preprocessing.text_dataset_from_directory(
"aclImdb/train",
batch_size=batch_size,
validation_split=0.2,
subset="validation",
seed=1337
)
raw_test_ds = tf.keras.preprocessing.text_dataset_from_directory(
"aclImdb/test",
batch_size=batch_size
)
```
Printing the DS results
```
print("no of batches in raw_train_ds: %d" % tf.data.experimental.cardinality(raw_train_ds))
print("no of batches in raw_val_ds: %d" % tf.data.experimental.cardinality(raw_val_ds))
print("no of batches in raw_test_ds: %d" % tf.data.experimental.cardinality(raw_test_ds))
```
Data Preview:
```
# It's important to take a look at your raw data to ensure your normalization
# and tokenization will work as expected. We can do that by taking a few
# examples from the training set and looking at them.
# This is one of the places where eager execution shines:
# we can just evaluate these tensors using .numpy()
# instead of needing to evaluate them in a Session/Graph context.
for text, label in raw_train_ds.take(1):
for i in range(5):
print(text.numpy()[i])
print(label.numpy()[i])
```
Data Preprocessing
Note: in the baove sample data, remove <br, />
```
from tensorflow.keras.layers.experimental.preprocessing import TextVectorization
import string
import re
# Having looked at our data above, we see that the raw text contains HTML break
# tags of the form '<br />'. These tags will not be removed by the default
# standardizer (which doesn't strip HTML). Because of this, we will need to
# create a custom standardization function.
def custom_standardization(input_data):
lowercase = tf.strings.lower(input_data)
stripped_html = tf.strings.regex_replace(lowercase, "<br />", " ")
return tf.strings.regex_replace(
stripped_html, "[%s]" % re.escape(string.punctuation), ""
)
#model constants
max_features=20000
embedding_dim=128
sequence_length=500
# Now that we have our custom standardization, we can instantiate our text
# vectorization layer. We are using this layer to normalize, split, and map
# strings to integers, so we set our 'output_mode' to 'int'.
# Note that we're using the default split function,
# and the custom standardization defined above.
# We also set an explicit maximum sequence length, since the CNNs later in our
# model won't support ragged sequences.
vectorize_layer=TextVectorization(
standardize=custom_standardization,
max_tokens=max_features,
output_mode='int',
output_sequence_length=sequence_length,
)
# Now that the vocab layer has been created, call `adapt` on a text-only
# dataset to create the vocabulary. You don't have to batch, but for very large
# datasets this means you're not keeping spare copies of the dataset in memory.
# Let's make a text-only dataset (no labels):
text_ds = raw_train_ds.map(lambda x, y :x)
# Let's call `adapt`:
vectorize_layer.adapt(text_ds)
```
Two options to vectorize the data
There are 2 ways we can use our text vectorization layer:
Option 1: Make it part of the model, so as to obtain a model that processes raw strings, like this:
```
text_input = tf.keras.Input(shape=(1,), dtype=tf.string, name='text')
x = vectorize_layer(text_input)
x = layers.Embedding(max_features + 1, embedding_dim)(x)
...
```
Option 2: Apply it to the text dataset to obtain a dataset of word indices, then feed it into a model that expects integer sequences as inputs.
An important difference between the two is that option 2 enables you to do asynchronous CPU processing and buffering of your data when training on GPU. So if you're training the model on GPU, you probably want to go with this option to get the best performance. This is what we will do below.
If we were to export our model to production, we'd ship a model that accepts raw strings as input, like in the code snippet for option 1 above. This can be done after training. We do this in the last section.
```
def vectorize_text(text, label):
text = tf.expand_dims(text, -1)
return vectorize_layer(text), label
```
Now vectorize the data
```
train_ds = raw_train_ds.map(vectorize_text)
val_ds = raw_val_ds.map(vectorize_text)
test_ds = raw_test_ds.map(vectorize_text)
```
Do async prefetching / buffering of the data for best performance on GPU.
```
train_ds = train_ds.cache().prefetch(buffer_size=10)
val_ds = val_ds.cache().prefetch(buffer_size=10)
test_ds = test_ds.cache().prefetch(buffer_size=10)
```
Model Building
1D Convnet is used starting with an embedding layer
```
from tensorflow.keras import layers
#int input for vocab indicies
inputs = tf.keras.Input(shape=(None,), dtype="int64")
# adding a layer to map those vocab indices into a space of dimensionality 'embedding_dim'.
# this is the embedding layer
x = layers.Embedding(max_features, embedding_dim)(inputs)
x = layers.Dropout(0.5)(x)
# adding 2 conv1D layers and Globalmaxpooling layer
x = layers.Conv1D(128, 7, padding="valid", activation = "relu", strides=3)(x)
x = layers.Conv1D(128, 7, padding="valid", activation = "relu", strides=3)(x)
x = layers.GlobalMaxPooling1D()(x)
#adding a vanilla hidden layer
x = layers.Dense(128, activation = "relu")(x)
x = layers.Dropout(0.5)(x)
# Projecting to a single output layer with sigmoid function
predictions = layers.Dense(1, activation = "sigmoid", name = "predictions")(x)
model = tf.keras.Model(inputs, predictions)
# compling the model using binary cross entropy loss with Adam optimizer
model.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
```
Train the Model
```
epoch = 3
# fitting the model using train and test data sets
model.fit(train_ds, validation_data=val_ds, epochs=epoch)
```
Model evaluation on test data
```
model.evaluate(test_ds)
```
|
github_jupyter
|
import tensorflow as tf
import numpy as np
!curl -O https://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz
!tar -xf aclImdb_v1.tar.gz
!ls aclImdb
!ls aclImdb/test
!ls aclImdb/train
!cat aclImdb/train/pos/6248_7.txt
!rm -r aclImdb/train/unsup
!ls aclImdb/test
batch_size=32
raw_train_ds = tf.keras.preprocessing.text_dataset_from_directory(
"aclImdb/train",
batch_size=batch_size,
validation_split=0.2,
subset="training",
seed=1337,
)
raw_val_ds = tf.keras.preprocessing.text_dataset_from_directory(
"aclImdb/train",
batch_size=batch_size,
validation_split=0.2,
subset="validation",
seed=1337
)
raw_test_ds = tf.keras.preprocessing.text_dataset_from_directory(
"aclImdb/test",
batch_size=batch_size
)
print("no of batches in raw_train_ds: %d" % tf.data.experimental.cardinality(raw_train_ds))
print("no of batches in raw_val_ds: %d" % tf.data.experimental.cardinality(raw_val_ds))
print("no of batches in raw_test_ds: %d" % tf.data.experimental.cardinality(raw_test_ds))
# It's important to take a look at your raw data to ensure your normalization
# and tokenization will work as expected. We can do that by taking a few
# examples from the training set and looking at them.
# This is one of the places where eager execution shines:
# we can just evaluate these tensors using .numpy()
# instead of needing to evaluate them in a Session/Graph context.
for text, label in raw_train_ds.take(1):
for i in range(5):
print(text.numpy()[i])
print(label.numpy()[i])
from tensorflow.keras.layers.experimental.preprocessing import TextVectorization
import string
import re
# Having looked at our data above, we see that the raw text contains HTML break
# tags of the form '<br />'. These tags will not be removed by the default
# standardizer (which doesn't strip HTML). Because of this, we will need to
# create a custom standardization function.
def custom_standardization(input_data):
lowercase = tf.strings.lower(input_data)
stripped_html = tf.strings.regex_replace(lowercase, "<br />", " ")
return tf.strings.regex_replace(
stripped_html, "[%s]" % re.escape(string.punctuation), ""
)
#model constants
max_features=20000
embedding_dim=128
sequence_length=500
# Now that we have our custom standardization, we can instantiate our text
# vectorization layer. We are using this layer to normalize, split, and map
# strings to integers, so we set our 'output_mode' to 'int'.
# Note that we're using the default split function,
# and the custom standardization defined above.
# We also set an explicit maximum sequence length, since the CNNs later in our
# model won't support ragged sequences.
vectorize_layer=TextVectorization(
standardize=custom_standardization,
max_tokens=max_features,
output_mode='int',
output_sequence_length=sequence_length,
)
# Now that the vocab layer has been created, call `adapt` on a text-only
# dataset to create the vocabulary. You don't have to batch, but for very large
# datasets this means you're not keeping spare copies of the dataset in memory.
# Let's make a text-only dataset (no labels):
text_ds = raw_train_ds.map(lambda x, y :x)
# Let's call `adapt`:
vectorize_layer.adapt(text_ds)
text_input = tf.keras.Input(shape=(1,), dtype=tf.string, name='text')
x = vectorize_layer(text_input)
x = layers.Embedding(max_features + 1, embedding_dim)(x)
...
def vectorize_text(text, label):
text = tf.expand_dims(text, -1)
return vectorize_layer(text), label
train_ds = raw_train_ds.map(vectorize_text)
val_ds = raw_val_ds.map(vectorize_text)
test_ds = raw_test_ds.map(vectorize_text)
train_ds = train_ds.cache().prefetch(buffer_size=10)
val_ds = val_ds.cache().prefetch(buffer_size=10)
test_ds = test_ds.cache().prefetch(buffer_size=10)
from tensorflow.keras import layers
#int input for vocab indicies
inputs = tf.keras.Input(shape=(None,), dtype="int64")
# adding a layer to map those vocab indices into a space of dimensionality 'embedding_dim'.
# this is the embedding layer
x = layers.Embedding(max_features, embedding_dim)(inputs)
x = layers.Dropout(0.5)(x)
# adding 2 conv1D layers and Globalmaxpooling layer
x = layers.Conv1D(128, 7, padding="valid", activation = "relu", strides=3)(x)
x = layers.Conv1D(128, 7, padding="valid", activation = "relu", strides=3)(x)
x = layers.GlobalMaxPooling1D()(x)
#adding a vanilla hidden layer
x = layers.Dense(128, activation = "relu")(x)
x = layers.Dropout(0.5)(x)
# Projecting to a single output layer with sigmoid function
predictions = layers.Dense(1, activation = "sigmoid", name = "predictions")(x)
model = tf.keras.Model(inputs, predictions)
# compling the model using binary cross entropy loss with Adam optimizer
model.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
epoch = 3
# fitting the model using train and test data sets
model.fit(train_ds, validation_data=val_ds, epochs=epoch)
model.evaluate(test_ds)
| 0.887668 | 0.941975 |
# Image processing
1. Image are matricies, and all operations are matrix operations
## Color Transformations
### 1. Invert color: transform any color to its complimentary color
$$img(x,y) = 255- img(x,y)$$
```
import cv2
import sys
import os
import matplotlib.pyplot as plt
import numpy as np
def trans2show(img):
return cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
img = cv2.imread("lena.jpg")
def invert(img):
#map invert function to img
#convert map object to list then to np array
return np.array(list(map(lambda x: 255-x, img)))
print(img[:10,0,0])
print(invert(img[:10,0,0]))
plt.figure()
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
plt.imshow(trans2show(cv2.hconcat([img,invert(img)])))
plt.title('Invert BGR')
plt.figure()
plt.imshow(cv2.hconcat([trans2show(img),invert(trans2show(img))]))
plt.title('Invert RGB')
plt.figure()
plt.imshow(trans2show(cv2.hconcat([gray,invert(gray)])))
plt.title('Invert GRAY')
```
### 2. Gamma transformation
This is one simple function that applies curve (as in photoshop) on the image.
$$V_{\mathrm{out}}=C V_{\mathrm{in}}^{\gamma}$$
1. $\gamma<1$: brighten up dark regions
2. $\gamma>1$: darken bright regions
3. Need to normalize after the transformation for display, or else the image will clip
$$C = \dfrac{255}{max(img^\gamma)}$$
<img src="https://www.researchgate.net/profile/Qijie_Zhao/publication/271632132/figure/fig5/AS:703987527454724@1544855114909/Gamma-transformation-of-grey-level.png" alt="Gamma plot" width="500" height="500">
```
def gamma(img,gamma):
#convert to exactly the same type as img
img_g = np.array(list(map(lambda x: x**gamma, img)))
C = 255/np.max(img_g)
res = img_g*C
print(C)
return res.astype('uint8')
plt.figure(figsize=(10,20))
plt.imshow(trans2show(cv2.hconcat([img,gamma(img,0.3),gamma(img,1.2)])))
plt.title('gamma BGR')
plt.figure(figsize=(10,20))
plt.imshow(trans2show(cv2.hconcat([gray,gamma(gray,0.3),gamma(gray,1.2)])))
plt.title('gamma gray')
```
### 3. Histogram
A histogram of intensity value counted over all pixels.
1. Create histogram
2. Equilization
<img src="https://miro.medium.com/max/1280/1*Vd5OY8LRaybkFj2NjBbpbA.png" alt="Gamma plot" width="500" height="500">
```
# great histogram
def plot_histogram(img, channel=0):
if len(img.shape)==3:
img = img[:,:,channel]
unique, counts = np.unique(img, return_counts=True)
plt.plot(unique,counts)
return dict(zip(unique, counts))
plt.figure()
for i in range(3):
plot_histogram(img, i)
plt.xlabel('Intensity Value')
plt.ylabel('Count')
plt.figure()
plt.imshow(trans2show(gray))
plt.figure()
hist = plot_histogram(gray,0)
```
#### Equilization of Histogram
<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/c/ca/Histogrammeinebnung.png/600px-Histogrammeinebnung.png" alt="Equilization" width="500" height="500">
```
def equalization(img, hist, channel):
size = img.shape[0]*img.shape[1]
values = np.array(list(hist.values()))
for i in range(1,len(values)):
values[i] = values[i-1]+values[i]
hist = dict(zip(hist.keys(), values*255/size))
if len(img.shape)==3:
img = img[:,:,channel]
def helper(x):
return hist[x]
equalized = np.array([[helper(x) for x in row] for row in img])
return equalized.astype('uint8')
equalized = equalization(gray,hist,0)
plt.figure(figsize=(10,20))
plt.imshow(trans2show(cv2.hconcat([gray,equalization(gray,hist,0)])))
plt.title('equalized gray')
plt.figure()
_ =plot_histogram(equalized)
plt.figure()
_ =plot_histogram(gray)
```
## Major difference between image process and computer vision
Computer vision: requires decision
# Computer vision
__input__: image (matrix), video(sequence)
__output__:
1. classification: class id
2. detection: location
3. segmentation: detailed mask/ outline
4. description: texts
## Classification, process
0. preprocess: transformations
1. feature extraction (descriptor)
a. projection (vertical, horizontal)
b. symmetry
c. histogram
d. direct location of pixels
2. classification to class id: (decision function, use model parameters)
a. from direct equation between image feature and class feature, do not work for large number of images
b. calculate distance between image feature and class feature, if the distance < some number.
__types of decision(error) functions:__
1. distance(Euclidean/L2, L1)
2. min distance
3. inner product
__types of features__:
1. Hog (Histogram of oriented gradient): common for human detection
1. BGR2GRAY: gradient only for grey scale
1. can involve aforementioned transformations, such as gamma transformation.
2. calculate gradient for every pixel (magnitude and direction)
1. use gradient filters (kernel), eg. y gradient, use this kernel to convolute over whole image to get directional gradient for each pixel:
\begin{matrix}
-1 & -1 & -1\\
0 & 0 & 0\\
1 & 1 & 1\\
\end{matrix}
2. magnitude of gradient: $\sqrt{dx^2+dy^2}$
3. orientation: $\arctan{\dfrac{dy}{dx}}$
4. output: magnitude matrix, orientation matrix
3. divide image into small cells (eg 8*8)
4. obtain gradient histogram for each cell
1. ```plot(angle, count)```: angle in range, eg. [0,20], [20,40]....
2. output shape: (1, # ranges)
5. group every 3*3 cells into a block in a similar fasion to convolution (with block size and stride=1). Concatenate histogram descriptors of these cells: concat([...],[...],[...]) = [.........].
1. output: (1, 3*3* #ranges)
2. can add one more layer between cell and block (window)
6. concat descriptors of every block, normalize to give the final descriptor.
2. LBP (local binary pattern)
1. for a 3*3 cell, select center, for every pixel in the window, ```descriptor=1 if value >=center.value, else=0 ```
1. for pixels on edges, padding
2. achieve rotation invariant: let the window rotate, and use min value during the rotation
2. calculate histogram of each cell, normalize
3. concat histograms of cells
3. Haar-like: change of image gray scale
1. use a number of different filters:
1. vertical edge
\begin{matrix}
-1 & -1 & -1 &-1\\
-1 & -1 & -1&-1\\
1 & 1 & 1&1\\
1 & 1 & 1&1\\
\end{matrix}
2. horizontal edge
\begin{matrix}
1 & 1 & -1 &-1\\
1 & 1 & -1&-1\\
1 & 1 & -1&-1\\
1 & 1 & -1&-1\\
\end{matrix}
3. diagonal edge
4. Checkerboard filter
5. and more...
## Homework
1. classification of 10 images
1. create 10 images of 10 numbers: 0, 1,...9
2. extract feature
3. design decision function f(x) for classification
|
github_jupyter
|
import cv2
import sys
import os
import matplotlib.pyplot as plt
import numpy as np
def trans2show(img):
return cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
img = cv2.imread("lena.jpg")
def invert(img):
#map invert function to img
#convert map object to list then to np array
return np.array(list(map(lambda x: 255-x, img)))
print(img[:10,0,0])
print(invert(img[:10,0,0]))
plt.figure()
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
plt.imshow(trans2show(cv2.hconcat([img,invert(img)])))
plt.title('Invert BGR')
plt.figure()
plt.imshow(cv2.hconcat([trans2show(img),invert(trans2show(img))]))
plt.title('Invert RGB')
plt.figure()
plt.imshow(trans2show(cv2.hconcat([gray,invert(gray)])))
plt.title('Invert GRAY')
def gamma(img,gamma):
#convert to exactly the same type as img
img_g = np.array(list(map(lambda x: x**gamma, img)))
C = 255/np.max(img_g)
res = img_g*C
print(C)
return res.astype('uint8')
plt.figure(figsize=(10,20))
plt.imshow(trans2show(cv2.hconcat([img,gamma(img,0.3),gamma(img,1.2)])))
plt.title('gamma BGR')
plt.figure(figsize=(10,20))
plt.imshow(trans2show(cv2.hconcat([gray,gamma(gray,0.3),gamma(gray,1.2)])))
plt.title('gamma gray')
# great histogram
def plot_histogram(img, channel=0):
if len(img.shape)==3:
img = img[:,:,channel]
unique, counts = np.unique(img, return_counts=True)
plt.plot(unique,counts)
return dict(zip(unique, counts))
plt.figure()
for i in range(3):
plot_histogram(img, i)
plt.xlabel('Intensity Value')
plt.ylabel('Count')
plt.figure()
plt.imshow(trans2show(gray))
plt.figure()
hist = plot_histogram(gray,0)
def equalization(img, hist, channel):
size = img.shape[0]*img.shape[1]
values = np.array(list(hist.values()))
for i in range(1,len(values)):
values[i] = values[i-1]+values[i]
hist = dict(zip(hist.keys(), values*255/size))
if len(img.shape)==3:
img = img[:,:,channel]
def helper(x):
return hist[x]
equalized = np.array([[helper(x) for x in row] for row in img])
return equalized.astype('uint8')
equalized = equalization(gray,hist,0)
plt.figure(figsize=(10,20))
plt.imshow(trans2show(cv2.hconcat([gray,equalization(gray,hist,0)])))
plt.title('equalized gray')
plt.figure()
_ =plot_histogram(equalized)
plt.figure()
_ =plot_histogram(gray)
| 0.365117 | 0.947284 |
# Interactive fracture analysis
```
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from ipywidgets import interact
import ipywidgets as widgets
import mplstereonet as mpl
from mpl_toolkits.axes_grid1.inset_locator import inset_axes
```
## Import fracture data using Pandas
```
df = pd.read_csv('../data/image_data.csv', index_col='Unnamed: 0')
df.head()
df.shape
df.describe()
```
## Inspect fracture data with matplotlib/seaborn
```
df.columns
sns.pairplot(data=df,
vars=['DIP', 'AZIM'],
hue='DIPTYPE',
palette='colorblind',
markers=['x','o','v','^','s','p'],
height=3
)
plt.show()
```
## Inspect fracture data with interactive mplstereonet
```
@interact(diptype=['FRACTURE', 'HEALEDFRACTURE', 'DRILL.IND.FRAC.', 'BREAKOUT', 'BED', 'BED_LOW_CONF'],
alpha=widgets.FloatSlider(min=0, max=1, step=0.05, continuous_update=False),
poles=False,
show_mean=False,
density=False,
)
def plot_data(diptype, alpha, poles, show_mean, density):
"""
plot a stereonet of image data
args:
diptype, alpha, poles, show_mean, density
returns:
None
"""
# set up the plot
fig, ax = mpl.subplots(figsize=(6,6), ncols=1, nrows=1)
# get data
strike, dip = df.AZIM.loc[df['DIPTYPE'] == diptype], df.DIP.loc[df['DIPTYPE'] == diptype]
# great circles
ax.plane(strike, dip, 'g-', linewidth=1, alpha=alpha)
# plot decoration
ax.grid(color='k', alpha=0.2)
data_count = strike.count()
mean_azim = strike.mean()
mean_dip = dip.mean()
ax.text(0, 10, f'N points: {data_count}\nmean Azim: {mean_azim:.1f}\nmean Dip: {mean_dip:.1f}')
# options
if poles:
ax.pole(strike, dip, 'kx', markersize=3, alpha=1)
if show_mean:
ax.plane(mean_azim, mean_dip, 'r--', lw=3, alpha=0.7)
ax.pole(mean_azim, mean_dip, 'rs', markersize=5, alpha=0.7)
if density:
im = ax.density_contourf(strike, dip, measurement='poles', alpha=0.3)
axins = inset_axes(ax,
width="5%",
height="45%",
loc='lower left',
bbox_to_anchor=(1.05, 0., 1, 1),
bbox_transform=ax.transAxes,
borderpad=0,
)
cbar = fig.colorbar(im, cax=axins)
cbar.ax.get_yaxis().labelpad = 15
cbar.ax.set_ylabel('Orientation density distribution', rotation=90)
return None
```
|
github_jupyter
|
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from ipywidgets import interact
import ipywidgets as widgets
import mplstereonet as mpl
from mpl_toolkits.axes_grid1.inset_locator import inset_axes
df = pd.read_csv('../data/image_data.csv', index_col='Unnamed: 0')
df.head()
df.shape
df.describe()
df.columns
sns.pairplot(data=df,
vars=['DIP', 'AZIM'],
hue='DIPTYPE',
palette='colorblind',
markers=['x','o','v','^','s','p'],
height=3
)
plt.show()
@interact(diptype=['FRACTURE', 'HEALEDFRACTURE', 'DRILL.IND.FRAC.', 'BREAKOUT', 'BED', 'BED_LOW_CONF'],
alpha=widgets.FloatSlider(min=0, max=1, step=0.05, continuous_update=False),
poles=False,
show_mean=False,
density=False,
)
def plot_data(diptype, alpha, poles, show_mean, density):
"""
plot a stereonet of image data
args:
diptype, alpha, poles, show_mean, density
returns:
None
"""
# set up the plot
fig, ax = mpl.subplots(figsize=(6,6), ncols=1, nrows=1)
# get data
strike, dip = df.AZIM.loc[df['DIPTYPE'] == diptype], df.DIP.loc[df['DIPTYPE'] == diptype]
# great circles
ax.plane(strike, dip, 'g-', linewidth=1, alpha=alpha)
# plot decoration
ax.grid(color='k', alpha=0.2)
data_count = strike.count()
mean_azim = strike.mean()
mean_dip = dip.mean()
ax.text(0, 10, f'N points: {data_count}\nmean Azim: {mean_azim:.1f}\nmean Dip: {mean_dip:.1f}')
# options
if poles:
ax.pole(strike, dip, 'kx', markersize=3, alpha=1)
if show_mean:
ax.plane(mean_azim, mean_dip, 'r--', lw=3, alpha=0.7)
ax.pole(mean_azim, mean_dip, 'rs', markersize=5, alpha=0.7)
if density:
im = ax.density_contourf(strike, dip, measurement='poles', alpha=0.3)
axins = inset_axes(ax,
width="5%",
height="45%",
loc='lower left',
bbox_to_anchor=(1.05, 0., 1, 1),
bbox_transform=ax.transAxes,
borderpad=0,
)
cbar = fig.colorbar(im, cax=axins)
cbar.ax.get_yaxis().labelpad = 15
cbar.ax.set_ylabel('Orientation density distribution', rotation=90)
return None
| 0.61173 | 0.866246 |
**Download** (right-click, save target as ...) this page as a jupyterlab notebook from:
[Laboratory 0](https://atomickitty.ddns.net/engr-1330-webroot/8-Labs/Lab00/Lab00.ipynb)
___
## Submitting your laboratory.
Replace the missing items below
**LAST NAME, FIRST NAME**
**R00000000**
ENGR 1330 Laboratory 0
then
- run all cells (laboratory instructor will show how)
- export notebook as PDF (if nbconvert error, then export as html, use html2pdf online converter)
- upload your pdf to the Blackboard server to hand in your completed laboratory
# <font color=darkblue>Laboratory 0: Yes, That's how we count in python!</font>
Counting, is our most fundamental arithmetic construct. Where it start matters.
At Harvard they start at (0) zero [https://www.youtube.com/watch?v=jjqgP9dpD1k&t=12s](https://www.youtube.com/watch?v=jjqgP9dpD1k&t=12s), at MIT they start at (1) one [https://www.youtube.com/watch?v=3zTO3LEY-cM](https://www.youtube.com/watch?v=3zTO3LEY-cM), and the rest of us are a bit (pun intended) confused!
Well python developers decided to start at Zero, hence laboratory 0 - our beginning.
Our goal is to get a working JupyterLab/Notebook environment on your laptop.
## This "document" is a Jupyter Notebook; the medium that we will be using throughout the semester.
___
## How do you get here?
We suggest, recommend (demand?) you install Anaconda on your laptop. The remainder of this lab meeting is to get your Anaconda install started and maybe even completed. If you started before lab, you may be in good shape.
 <br>
There are online services that allow you create, modify, and export Jupyter notebooks. However, to have this on your local machines (computers), you can install [Anaconda](https://www.anaconda.com/products/individual). Anaconda is a package of different software suites/launchers including "Jupyter Notebook".
You can find videos on how to install Anaconda on your devices on BlackBoard:
- Go to [Anaconda.com](https://www.anaconda.com/products/individual)
- Scroll down to the bottom of the page or click on products > individual edition
- Download the correct version for your operating system: Windows, MacOS, and Linux; and possibly hardware - This may take a while depending on your connection speed
- Once the installer file is downloaded, run it and install Anaconda on your machine.
- Anaconda requires almost 3 GB of free space
- Install it in a separate folder- Preferably on a drive with lots of free memory!
- BE PATIENT!- It will take a while.
**MacOS and Windows are x86-64 architecture. Chromebooks, Apple M1/M2, Raspberry Pi are arm64 architecture**
___
**To Download A Visual Guide On Installing ANACONDA** ,right-click, and download (save) this file:
[ANACONDA Install Help](https://atomickitty.ddns.net/engr-1330-webroot/8-Labs/Lab00/Anaconda%20Install.pptx)
___
## Lab Exercise 1
The classic hello world script!
```
# print('hello YOUR NAME HERE') # activate and run this cell
```
## Lab Exercise 2
Identify the cell types below:
```
# I am what kind of cell?
```
# I am what kind of cell?
## Readings
Driscoll, M. (2021) *Jupyter Notebook: An Introduction*, [https://realpython.com/jupyter-notebook-introduction/](https://realpython.com/jupyter-notebook-introduction/)
|
github_jupyter
|
# print('hello YOUR NAME HERE') # activate and run this cell
# I am what kind of cell?
| 0.051594 | 0.718026 |
# Basic Python Semantics: Operators
## Arithmetic Operations
| Operator | Name | Description |
|--------------|----------------|--------------------------------------------------------|
| ``a + b`` | Addition | Sum of ``a`` and ``b`` |
| ``a - b`` | Subtraction | Difference of ``a`` and ``b`` |
| ``a * b`` | Multiplication | Product of ``a`` and ``b`` |
| ``a / b`` | True division | Quotient of ``a`` and ``b`` |
| ``a // b`` | Floor division | Quotient of ``a`` and ``b``, removing fractional parts |
| ``a % b`` | Modulus | Integer remainder after division of ``a`` by ``b`` |
| ``a ** b`` | Exponentiation | ``a`` raised to the power of ``b`` |
| ``-a`` | Negation | The negative of ``a`` |
| ``+a`` | Unary plus | ``a`` unchanged (rarely used) |
```
# addition, subtraction, multiplication
(4 + 8) * (6- 3)
# True division
print(11 / 2)
# Floor division
print(11 // 2)
```
The floor division operator was added in Python 3; you should be aware if working in Python 2 that the standard division operator (``/``) acts like floor division for integers and like true division for floating-point numbers.
An additional operator that was added in Python 3.5: the ``a @ b`` operator, which is meant to indicate the *matrix product* of ``a`` and ``b``.
## Assignment Operations
We've seen that variables can be assigned with the "``=``" operator, and the values stored for later use. For example:
```
a = 24
print(a)
```
We can use these variables in expressions with any of the operators mentioned earlier.
For example, to add 2 to ``a`` we write:
```
a + 2
```
* We might want to update the variable ``a`` with this new value, e.g. ``a = a + 2``.
* Python includes built-in update operators for all of the arithmetic operations:
```
a += 2 # equivalent to a = a + 2
print(a)
```
#### Augmented assignment operator
|||||
|-|-|
|``a += b``| ``a -= b``|``a *= b``| ``a /= b``|
|``a //= b``| ``a %= b``|``a **= b``|``a &= b``|
|<code>a |= b</code>| ``a ^= b``|``a <<= b``| ``a >>= b``|
For any operator "``■``", the expression ``a ■= b`` is equivalent to ``a = a ■ b``.
##### One catch:
For mutable objects like lists, arrays, or DataFrames, these augmented assignment operations are subtly different: they modify the contents of the original object rather than creating a new object to store the result.
## Comparison Operations
Another type of operation which can be very useful is comparison of different values.
For this, Python implements standard comparison operators, which return Boolean values ``True`` and ``False``.
| Operation | Description || Operation | Description |
|---------------|-----------------------------------||---------------|--------------------------------------|
| ``a == b`` | ``a`` equal to ``b`` || ``a != b`` | ``a`` not equal to ``b`` |
| ``a < b`` | ``a`` less than ``b`` || ``a > b`` | ``a`` greater than ``b`` |
| ``a <= b`` | ``a`` less than or equal to ``b`` || ``a >= b`` | ``a`` greater than or equal to ``b`` |
```
# 25 is odd
25 % 2 == 1
# 66 is odd
66 % 2 == 1
```
We can string-together multiple comparisons to check more complicated relationships:
```
# check if a is between 15 and 30
a = 25
15 < a < 30
```
## Boolean Operations
* Python provides operators to combine the values using the standard concepts of "and", "or", and "not".
* They are literally called "and", "or", and "not".
```
x = 4
(x < 6) and (x > 2)
(x > 10) or (x % 2 == 0)
not (x < 6)
```
We will come back to the Boolean operations in the *control flow statements* section.
### Boolean vs bitwise operators
#### When to use Boolean operators (``and``, ``or``, ``not``), and when to use bitwise operations (``&``, ``|``, ``~``)?
* Boolean operators: when you compute *Boolean values (i.e., truth or falsehood) of entire statements*.
* Bitwise operations: when you *operate on individual bits or components of the objects in question*.
## Identity and Membership Operators
Like ``and``, ``or``, and ``not``, Python also contains prose-like operators to check for identity and membership.
They are the following:
| Operator | Description |
|---------------|---------------------------------------------------|
| ``a is b`` | True if ``a`` and ``b`` are identical objects |
| ``a is not b``| True if ``a`` and ``b`` are not identical objects |
| ``a in b`` | True if ``a`` is a member of ``b`` |
| ``a not in b``| True if ``a`` is not a member of ``b`` |
### Identity Operators: "``is``" and "``is not``"
The identity operators, "``is``" and "``is not``" check for *object identity*.
Object identity is different than equality, as we can see here:
```
a = [1, 2, 3]
b = [1, 2, 3]
a == b
a is b
a is not b
```
What do identical objects look like? Here is an example:
```
a = [1, 2, 3]
b = a
a is b
```
* Frist case: ``a`` and ``b`` point to *different objects*
* Second case: they point to the *same object*.
As we saw in the previous section, Python variables are pointers. The "``is``" operator checks whether the two variables are pointing to the same container (object), rather than referring to what the container contains.
Often, you might be tempted to use "``is``" what they really mean is ``==``.
## Membership operators
Membership operators check for membership within compound objects.
So, for example, we can write:
```
1 in [1, 2, 3]
4 in [1, 2, 3]
2 not in [1, 2, 3]
4 not in [1, 2, 3]
```
* These membership operations are an example of what makes Python so easy to use compared to lower-level languages such as FORTRAN or C.
* In FORTRAN, membership would generally be determined by manually constructing a loop over the list and checking for equality of each value.
* In Python, you just type what you want to know
## References
*A Whirlwind Tour of Python* by Jake VanderPlas (O’Reilly). Copyright 2016 O’Reilly Media, Inc., 978-1-491-96465-1
|
github_jupyter
|
# addition, subtraction, multiplication
(4 + 8) * (6- 3)
# True division
print(11 / 2)
# Floor division
print(11 // 2)
a = 24
print(a)
a + 2
a += 2 # equivalent to a = a + 2
print(a)
# 25 is odd
25 % 2 == 1
# 66 is odd
66 % 2 == 1
# check if a is between 15 and 30
a = 25
15 < a < 30
x = 4
(x < 6) and (x > 2)
(x > 10) or (x % 2 == 0)
not (x < 6)
a = [1, 2, 3]
b = [1, 2, 3]
a == b
a is b
a is not b
a = [1, 2, 3]
b = a
a is b
1 in [1, 2, 3]
4 in [1, 2, 3]
2 not in [1, 2, 3]
4 not in [1, 2, 3]
| 0.422266 | 0.984048 |
## Dependencies
```
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint, LearningRateScheduler
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
```
# Load data
```
database_base_path = '/kaggle/input/tweet-dataset-split-roberta-base-96/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# Unzip files
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_1.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_2.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_3.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_4.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_5.tar.gz
```
# Model parameters
```
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
"MAX_LEN": 96,
"BATCH_SIZE": 32,
"EPOCHS": 5,
"LEARNING_RATE": 3e-5,
"ES_PATIENCE": 1,
"question_size": 4,
"N_FOLDS": 5,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
```
# Tokenizer
```
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
```
## Learning rate schedule
```
LR_MIN = 1e-6
LR_MAX = config['LEARNING_RATE']
LR_EXP_DECAY = .5
@tf.function
def lrfn(epoch):
lr = LR_MAX * LR_EXP_DECAY**epoch
if lr < LR_MIN:
lr = LR_MIN
return lr
rng = [i for i in range(config['EPOCHS'])]
y = [lrfn(x) for x in rng]
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
```
# Model
```
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
x = layers.Dropout(.1)(last_hidden_state)
x_start = layers.Dense(1)(x)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.Dense(1)(x)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
return model
```
# Train
```
AUTO = tf.data.experimental.AUTOTUNE
strategy = tf.distribute.get_strategy()
history_list = []
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
step_size = x_train.shape[1] // config['BATCH_SIZE']
valid_step_size = x_valid.shape[1] // config['BATCH_SIZE']
### Delete data dir
shutil.rmtree(base_data_path)
# Build TF datasets
train_dist_ds = strategy.experimental_distribute_dataset(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO, seed=SEED))
valid_dist_ds = strategy.experimental_distribute_dataset(get_validation_dataset(x_valid, y_valid, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED))
train_data_iter = iter(train_dist_ds)
valid_data_iter = iter(valid_dist_ds)
# Step functions
@tf.function
def train_step(data_iter):
def train_step_fn(x, y):
with tf.GradientTape() as tape:
probabilities = model(x, training=True)
loss_start = loss_fn_start(y['y_start'], probabilities[0], label_smoothing=0.2)
loss_end = loss_fn_end(y['y_end'], probabilities[1], label_smoothing=0.2)
loss = tf.math.add(loss_start, loss_end)
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# update metrics
train_acc_start.update_state(y['y_start'], probabilities)
train_acc_end.update_state(y['y_end'], probabilities)
train_loss.update_state(loss)
train_loss_start.update_state(loss_start)
train_loss_end.update_state(loss_end)
for _ in tf.range(step_size):
strategy.experimental_run_v2(train_step_fn, next(data_iter))
@tf.function
def valid_step(data_iter):
def valid_step_fn(x, y):
probabilities = model(x, training=False)
loss_start = loss_fn_start(y['y_start'], probabilities[0], label_smoothing=0.2)
loss_end = loss_fn_end(y['y_end'], probabilities[1], label_smoothing=0.2)
loss = tf.math.add(loss_start, loss_end)
# update metrics
valid_acc_start.update_state(y['y_start'], probabilities)
valid_acc_end.update_state(y['y_end'], probabilities)
valid_loss.update_state(loss)
valid_loss_start.update_state(loss_start)
valid_loss_end.update_state(loss_end)
for _ in tf.range(valid_step_size):
strategy.experimental_run_v2(valid_step_fn, next(data_iter))
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
optimizer = optimizers.Adam(learning_rate=lambda: lrfn(tf.cast(optimizer.iterations, tf.float32)//step_size))
loss_fn_start = losses.categorical_crossentropy
loss_fn_end = losses.categorical_crossentropy
train_acc_start = metrics.CategoricalAccuracy()
valid_acc_start = metrics.CategoricalAccuracy()
train_acc_end = metrics.CategoricalAccuracy()
valid_acc_end = metrics.CategoricalAccuracy()
train_loss = metrics.Sum()
valid_loss = metrics.Sum()
train_loss_start = metrics.Sum()
valid_loss_start = metrics.Sum()
train_loss_end = metrics.Sum()
valid_loss_end = metrics.Sum()
metrics_dict = {'loss': train_loss, 'loss_start': train_loss_start, 'loss_end': train_loss_end,
'acc_start': train_acc_start, 'acc_end': train_acc_end,
'val_loss': valid_loss, 'val_loss_start': valid_loss_start, 'val_loss_end': valid_loss_end,
'val_acc_start': valid_acc_start, 'val_acc_end': valid_acc_end}
history = custom_fit(model, metrics_dict, train_step, valid_step, train_data_iter, valid_data_iter,
step_size, valid_step_size, config['BATCH_SIZE'], config['EPOCHS'], config['ES_PATIENCE'], model_path)
history_list.append(history)
model.load_weights(model_path)
# Make predictions
train_preds = model.predict(list(x_train))
valid_preds = model.predict(list(x_valid))
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold['end_fold_%d' % (n_fold)] = k_fold['end_fold_%d' % (n_fold)].astype(int)
k_fold['start_fold_%d' % (n_fold)] = k_fold['start_fold_%d' % (n_fold)].astype(int)
k_fold['end_fold_%d' % (n_fold)].clip(0, k_fold['text_len'], inplace=True)
k_fold['start_fold_%d' % (n_fold)].clip(0, k_fold['end_fold_%d' % (n_fold)], inplace=True)
k_fold['prediction_fold_%d' % (n_fold)] = k_fold.apply(lambda x: decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], config['question_size'], tokenizer), axis=1)
k_fold['prediction_fold_%d' % (n_fold)].fillna(k_fold["text"], inplace=True)
k_fold['jaccard_fold_%d' % (n_fold)] = k_fold.apply(lambda x: jaccard(x['selected_text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
```
# Model loss graph
```
sns.set(style="whitegrid")
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
```
# Model evaluation
```
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Visualize predictions
```
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
```
|
github_jupyter
|
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint, LearningRateScheduler
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
database_base_path = '/kaggle/input/tweet-dataset-split-roberta-base-96/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# Unzip files
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_1.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_2.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_3.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_4.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_5.tar.gz
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
"MAX_LEN": 96,
"BATCH_SIZE": 32,
"EPOCHS": 5,
"LEARNING_RATE": 3e-5,
"ES_PATIENCE": 1,
"question_size": 4,
"N_FOLDS": 5,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
LR_MIN = 1e-6
LR_MAX = config['LEARNING_RATE']
LR_EXP_DECAY = .5
@tf.function
def lrfn(epoch):
lr = LR_MAX * LR_EXP_DECAY**epoch
if lr < LR_MIN:
lr = LR_MIN
return lr
rng = [i for i in range(config['EPOCHS'])]
y = [lrfn(x) for x in rng]
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
x = layers.Dropout(.1)(last_hidden_state)
x_start = layers.Dense(1)(x)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.Dense(1)(x)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
return model
AUTO = tf.data.experimental.AUTOTUNE
strategy = tf.distribute.get_strategy()
history_list = []
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
step_size = x_train.shape[1] // config['BATCH_SIZE']
valid_step_size = x_valid.shape[1] // config['BATCH_SIZE']
### Delete data dir
shutil.rmtree(base_data_path)
# Build TF datasets
train_dist_ds = strategy.experimental_distribute_dataset(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO, seed=SEED))
valid_dist_ds = strategy.experimental_distribute_dataset(get_validation_dataset(x_valid, y_valid, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED))
train_data_iter = iter(train_dist_ds)
valid_data_iter = iter(valid_dist_ds)
# Step functions
@tf.function
def train_step(data_iter):
def train_step_fn(x, y):
with tf.GradientTape() as tape:
probabilities = model(x, training=True)
loss_start = loss_fn_start(y['y_start'], probabilities[0], label_smoothing=0.2)
loss_end = loss_fn_end(y['y_end'], probabilities[1], label_smoothing=0.2)
loss = tf.math.add(loss_start, loss_end)
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# update metrics
train_acc_start.update_state(y['y_start'], probabilities)
train_acc_end.update_state(y['y_end'], probabilities)
train_loss.update_state(loss)
train_loss_start.update_state(loss_start)
train_loss_end.update_state(loss_end)
for _ in tf.range(step_size):
strategy.experimental_run_v2(train_step_fn, next(data_iter))
@tf.function
def valid_step(data_iter):
def valid_step_fn(x, y):
probabilities = model(x, training=False)
loss_start = loss_fn_start(y['y_start'], probabilities[0], label_smoothing=0.2)
loss_end = loss_fn_end(y['y_end'], probabilities[1], label_smoothing=0.2)
loss = tf.math.add(loss_start, loss_end)
# update metrics
valid_acc_start.update_state(y['y_start'], probabilities)
valid_acc_end.update_state(y['y_end'], probabilities)
valid_loss.update_state(loss)
valid_loss_start.update_state(loss_start)
valid_loss_end.update_state(loss_end)
for _ in tf.range(valid_step_size):
strategy.experimental_run_v2(valid_step_fn, next(data_iter))
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
optimizer = optimizers.Adam(learning_rate=lambda: lrfn(tf.cast(optimizer.iterations, tf.float32)//step_size))
loss_fn_start = losses.categorical_crossentropy
loss_fn_end = losses.categorical_crossentropy
train_acc_start = metrics.CategoricalAccuracy()
valid_acc_start = metrics.CategoricalAccuracy()
train_acc_end = metrics.CategoricalAccuracy()
valid_acc_end = metrics.CategoricalAccuracy()
train_loss = metrics.Sum()
valid_loss = metrics.Sum()
train_loss_start = metrics.Sum()
valid_loss_start = metrics.Sum()
train_loss_end = metrics.Sum()
valid_loss_end = metrics.Sum()
metrics_dict = {'loss': train_loss, 'loss_start': train_loss_start, 'loss_end': train_loss_end,
'acc_start': train_acc_start, 'acc_end': train_acc_end,
'val_loss': valid_loss, 'val_loss_start': valid_loss_start, 'val_loss_end': valid_loss_end,
'val_acc_start': valid_acc_start, 'val_acc_end': valid_acc_end}
history = custom_fit(model, metrics_dict, train_step, valid_step, train_data_iter, valid_data_iter,
step_size, valid_step_size, config['BATCH_SIZE'], config['EPOCHS'], config['ES_PATIENCE'], model_path)
history_list.append(history)
model.load_weights(model_path)
# Make predictions
train_preds = model.predict(list(x_train))
valid_preds = model.predict(list(x_valid))
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold['end_fold_%d' % (n_fold)] = k_fold['end_fold_%d' % (n_fold)].astype(int)
k_fold['start_fold_%d' % (n_fold)] = k_fold['start_fold_%d' % (n_fold)].astype(int)
k_fold['end_fold_%d' % (n_fold)].clip(0, k_fold['text_len'], inplace=True)
k_fold['start_fold_%d' % (n_fold)].clip(0, k_fold['end_fold_%d' % (n_fold)], inplace=True)
k_fold['prediction_fold_%d' % (n_fold)] = k_fold.apply(lambda x: decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], config['question_size'], tokenizer), axis=1)
k_fold['prediction_fold_%d' % (n_fold)].fillna(k_fold["text"], inplace=True)
k_fold['jaccard_fold_%d' % (n_fold)] = k_fold.apply(lambda x: jaccard(x['selected_text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
sns.set(style="whitegrid")
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
| 0.614972 | 0.277712 |
# Getting Started
## Platforms to Practice
Let us understand different platforms we can leverage to practice Apache Spark using Python.
* Local Setup
* Databricks Platform
* Setting up your own cluster
* Cloud based labs
## Setup Spark Locally - Ubuntu
Let us setup Spark Locally on Ubuntu.
* Install latest version of Anaconda
* Make sure Jupyter Notebook is setup and validated.
* Setup Spark and Validate.
* Setup Environment Variables to integrate Pyspark with Jupyter Notebook.
* Launch Jupyter Notebook using ` pyspark ` command.
* Setup PyCharm (IDE) for application development.
## Setup Spark Locally - Mac
### Let us setup Spark Locally on Ubuntu.
* Install latest version of Anaconda
* Make sure Jupyter Notebook is setup and validated.
* Setup Spark and Validate.
* Setup Environment Variables to integrate Pyspark with Jupyter Notebook.
* Launch Jupyter Notebook using ` pyspark ` command.
* Setup PyCharm (IDE) for application development.
## Signing up for ITVersity Labs
*
## Using ITVersity Labs
Let us understand how to submit the Spark Jobs in ITVersity Labs.
* As we are using Python we can also use the help command to get the documentation - for example ` help(spark.read.csv)`
## Interacting with File Systems
Let us understand how to interact with file system using %fs command from Databricks Notebook.
* We can access datasets using %fs magic command in Databricks notebook
* By default, we will see files under dbfs
* We can list the files using ls command - e. g.: ` (%fs ls)`
* Databricks provides lot of datasets for free under databricks-datasets
* If the cluster is integrated with AWS or Azure Blob we can access files by specifying the appropriate protocol (e.g.: s3:// for s3)
* List of commands available under %fs
* Copying files or directories `-cp`
* Moving files or directories `- mv `
* Creating directories ` - mkdirs `
* Deleting files and directories ` - rm `
* We can copy or delete directories recursively using ` -r` or `--recursive`
## Getting File Metadata
Let us review the source location to get number of files and the size of the data we are going to process.
* Location of airlines data dbfs:/databricks-datasets/airlines
* We can get first 1000 files using %fs ls dbfs:/databricks-datasets/airlines
* Location contain 1919 Files, however we will not be able to see all the details using %fs command.
* Databricks File System commands does not have capability to understand metadata of files such as size in details.
* When Spark Cluster is started, it will create 2 objects - spark and sc
* sc is of type SparkContext and spark is of type SparkSession
* Spark uses HDFS APIs to interact with the file system and we can access HDFS APIs using sc._jsc and sc._jvm to get file metadata.
Here are the steps to get the file metadata.
* Get Hadoop Configuration using ` sc._jsc.hadoopConfiguration()` - let"s say `conf`
* We can pass conf to ` sc._jvm.org.apache.hadoop.fs.FileSystem.` get to get FileSystem object - let"s say `fs`
* We can build ` path` object by passing the path as string to `sc._jvm.org.apache.hadoop.fs.Path`
* We can invoke `listStatus` on top of fs by passing path which will return an array of FileStatus objects - let"s say files.
* Each `FileStatus` object have all the metadata of each file.
* We can use `len` on files to get number of files.
* We can use `getLen` on each `FileStatus` object to get the size of each file.
* Cumulative size of all files can be achieved using `sum(map(lambda file: file.getLen(), files))`
* Let us first get list of files
```
%fs ls dbfs:/databricks-datasets/airlines
```
Here is the consolidated script to get number of files and cumulative size of all files in a given folder.
```
import org.apache.spark.sql.SparkSession
val spark = SparkSession.
builder.
appName("Getting Started").
master("yarn").
getOrCreate
val conf = spark.sparkContext.hadoopConfiguration
import org.apache.hadoop.fs.FileSystem
val fs = FileSystem.get(conf)
import org.apache.hadoop.fs.Path
val path = new Path("/public/airlines_all/airlines")
val files = fs.listStatus(path)
files.map(file => file.getLen).sum/1024/1024/1024
```
|
github_jupyter
|
%fs ls dbfs:/databricks-datasets/airlines
import org.apache.spark.sql.SparkSession
val spark = SparkSession.
builder.
appName("Getting Started").
master("yarn").
getOrCreate
val conf = spark.sparkContext.hadoopConfiguration
import org.apache.hadoop.fs.FileSystem
val fs = FileSystem.get(conf)
import org.apache.hadoop.fs.Path
val path = new Path("/public/airlines_all/airlines")
val files = fs.listStatus(path)
files.map(file => file.getLen).sum/1024/1024/1024
| 0.167253 | 0.940898 |
```
# Import Libaries and Packages
import numpy as np
import pandas as pd
import re
```
## Clean Articles Final
This noteboks performs the following procedures:
1. Reads in extracted and cleanded data from prior processes as a csv.
2. Performs addtional preprocessing.
3. Discards data that does not contain selected keywords.
```
articles_raw = pd.read_csv("use_rEx.csv") #Do not run more than once - hogs memory and takes some time
articles_raw.head()
articles_raw.tail()
articles_raw.describe()
```
__Preprocess and Clean Data__
```
#Reset index
articles_raw = articles_raw.reset_index()
articles_raw = articles_raw.drop('index', axis = 1)
articles_raw.head()
```
#### Methodology:
We have a list of keywords (defined below) that we deem relevant to Bitcoin trading and price. If an article does not mention one of these keywords in the first 300 characters (heuristic/empirical analysis of where the lede of an article ends) we deem it irrelevant.
```
#Sample of first 300 characters of the first 30 articles.
#As you can see, relevant articles will mention Bitcoin or a keyword in this selection.
for article in articles_raw['contents'][:30]:
print(article[:300])
print()
```
__Filtering Keyword List__
```
#Define list of keywords and new
keywords = [
"BTC", "btc", "BCH", "bch", "Bitcoin", "bitcoin", \
"Litecoin", "litecoin", "LTC", "ltc", \
"Ether", "ether", "Ethereum", "ethereum", \
"ETH", "eth", \
"hodl", "HODL", \
"crypto", "cryptocurrency", "cryptocurrencies", \
"Crypto", "Cryptocurrency", "Cryptocurrencies", \
"ICO", "ico", "GDAX", "gdax", \
"Blockchain", "blockchain", \
]
articles_final = articles_raw
articles_final.head()
#Traverse the articles array.
#If you find an article that does not contain a keyword in the first 300 characters, remove it.
n_removed = 0
indices_to_drop = []
for i in articles_final.index:
first300 = articles_final['contents'][i][:300] #Grab first 300 characters of article text
title = articles_final['title'][i]
n_keywords = 0
try:
assert type(first300) is str
assert type(title) is str
except:
print("Found error in article", i, "- Passing")
indices_to_drop.append(i)
continue
for keyword in keywords:
if keyword in first300 or keyword in title:
n_keywords += 1
break
else:
pass
if n_keywords == 0:
indices_to_drop.append(i)
if len(indices_to_drop) % 100 == 0:
print("Marked", len(indices_to_drop), "articles for removal")
if i % 10 == 0:
print("Article", i)
print("Total:", len(indices_to_drop), "articles marked for removal.")
articles_final = articles_final.drop(indices_to_drop)
articles_final = articles_final.reset_index()
articles_final = articles_final.drop('index', axis = 1)
articles_final.head()
articles_final.to_csv("final_articles.csv")
```
___
|
github_jupyter
|
# Import Libaries and Packages
import numpy as np
import pandas as pd
import re
articles_raw = pd.read_csv("use_rEx.csv") #Do not run more than once - hogs memory and takes some time
articles_raw.head()
articles_raw.tail()
articles_raw.describe()
#Reset index
articles_raw = articles_raw.reset_index()
articles_raw = articles_raw.drop('index', axis = 1)
articles_raw.head()
#Sample of first 300 characters of the first 30 articles.
#As you can see, relevant articles will mention Bitcoin or a keyword in this selection.
for article in articles_raw['contents'][:30]:
print(article[:300])
print()
#Define list of keywords and new
keywords = [
"BTC", "btc", "BCH", "bch", "Bitcoin", "bitcoin", \
"Litecoin", "litecoin", "LTC", "ltc", \
"Ether", "ether", "Ethereum", "ethereum", \
"ETH", "eth", \
"hodl", "HODL", \
"crypto", "cryptocurrency", "cryptocurrencies", \
"Crypto", "Cryptocurrency", "Cryptocurrencies", \
"ICO", "ico", "GDAX", "gdax", \
"Blockchain", "blockchain", \
]
articles_final = articles_raw
articles_final.head()
#Traverse the articles array.
#If you find an article that does not contain a keyword in the first 300 characters, remove it.
n_removed = 0
indices_to_drop = []
for i in articles_final.index:
first300 = articles_final['contents'][i][:300] #Grab first 300 characters of article text
title = articles_final['title'][i]
n_keywords = 0
try:
assert type(first300) is str
assert type(title) is str
except:
print("Found error in article", i, "- Passing")
indices_to_drop.append(i)
continue
for keyword in keywords:
if keyword in first300 or keyword in title:
n_keywords += 1
break
else:
pass
if n_keywords == 0:
indices_to_drop.append(i)
if len(indices_to_drop) % 100 == 0:
print("Marked", len(indices_to_drop), "articles for removal")
if i % 10 == 0:
print("Article", i)
print("Total:", len(indices_to_drop), "articles marked for removal.")
articles_final = articles_final.drop(indices_to_drop)
articles_final = articles_final.reset_index()
articles_final = articles_final.drop('index', axis = 1)
articles_final.head()
articles_final.to_csv("final_articles.csv")
| 0.246624 | 0.823683 |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/HowEarthEngineWorks/Projections.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/HowEarthEngineWorks/Projections.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/HowEarthEngineWorks/Projections.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
|
github_jupyter
|
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
# Add Earth Engine dataset
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 0.524882 | 0.964187 |
# mocksurvey.py
# Prerequisites
- Python >= 3.7
### for halotools:
- numpy (check with `pip show numpy`)
- g++ (check with `g++ --version`)
### for Corrfunc:
- gcc (check with `gcc --version`)
- gsl (check with `gsl-config --version`)
# Installation
```
git clone https://github.com/AlanPearl/mocksurvey
cd mocksurvey
python setup.py install
bash get_smdpl
```
Tutorial
======
```
import mocksurvey as ms
import numpy as np
import matplotlib.pyplot as plt
```
______________________
Classes:
==========
______________________
### Instantiate a SimBox (simulation box -- the source of all model data)
- Given simulation name/redshift, SimBox will grab the halo data
- Given HOD / Subhalo / CLF model name, SimBox can use that model to populate galaxies over the halos via `SimBox.populate_mock()`
```
simbox = ms.SimBox(populate_on_instantiation=False);
simbox.populate_mock()
```
### Instantiate a BoxField (view the galaxies populated by SimBox)
- By default, selects all galaxies in the SimBox data cube
- Given `center`$=(x_c, y_c, z_c)$, and `shape`$=(L_x, L_y, L_z)$, selects galaxies in that field
- Access data through `get_data()`, `get_rands()`, or `get_redshift()`
```
field = simbox.boxfield()
field.make_rands(density_factor=10)
ms.tp.plot_pos_scatter(field, s=.5)
plt.show()
```
### Instantiate a MockField (observation of SimBox populated galaxies)
- Given a SimBox coordinate `center`, field shape `scheme` (`"circ"`, `"sq"`, or `"hex"`), and field size `sqdeg`, selects galaxies in that field
- Access data through `get_data()`, `get_rands()`, or `get_redshift()`
```
field = simbox.field(scheme="hex", sqdeg=1.5)
field.make_rands(density_factor=100)
ms.tp.plot_pos_scatter(field, s=5)
plt.show()
```
### Instantiate a MockSurvey (set of MockField instances)
- Give the usual MockField arguments (`center`, `scheme`, `sqdeg` etc.), in addition to `rdz_centers`
- Each element of `rdz_centers` must be an array-like object, of shape (2,) or (3,) specifying the (ra,dec) or (ra,dec,z) of each field's center
- **If the z center of a field is given, it is ignored**
### Define some functions to calculate clustering statistics
- $\xi(r)$: `xi_r(data, rands, rbins, ...)`
- $\xi(r_{\rm p}, \pi)$: `xi_rp_pi(data, rands, rpbins, pibins, ...)`
- $w_{\rm p}(r_{\rm p})$: `wp_rp(data, rands, rpbins, ...)`
- $b_{\rm g}(r_{\rm p})$: `bias_rp(data, rands, rpbinses, ...)`
______________________
PFS Plots:
======
______________________
```
simbox = ms.SimBox(hodname="hearin15", threshold=10.5, redshift=1.35, Nbox=(1,1,3), rotation=0)
field = simbox.field(scheme="hex", sqdeg=1.5, collision_fraction=0.3, delta_z=.7, rand_density_factor=100)
fig,ax = plt.subplots()
ax.set_aspect('equal', 'box')
ms.tp.plot_sky_scatter(field, s=.9)
plt.savefig("pfs-celestial.png", bbox_inches="tight")
plt.show()
fig,ax = plt.subplots()
ax.set_aspect(5., 'box')
ms.tp.plot_pos_scatter(field, s=.9, axes=[2,1])
plt.savefig("pfs-cartesian.png", bbox_inches="tight")
plt.show()
```
______________________
Correlation Function Plotting:
======
______________________
```
fullbox = simbox.boxfield()
ms.tp.plot_xi_rp_pi(fullbox)
plt.show()
```
______________________
HOD Moments/Occupation Plots:
======
______________________
```
galbox = ms.GalBox(hodname="zheng07", threshold=-20)
ms.tp.plot_hod_occupation(galbox)
plt.show()
```
______________________
Halo Mass Function:
======
______________________
```
halobox = ms.HaloBox(simname="smdpl")
ms.tp.plot_halo_mass(halobox)
plt.show()
```
# Runtime testing
### List of expensive functions -- tested with SMDPL halos at z=1.35, Zheng07, threshold=-20?
- `ms.stats.cf.paircount_rp_pi()`/`cf.paircount_r()`
- Wrapper for the extremely well-optimized function `Corrfunc.theory.DD`.
- Runtime is usually quick, but can be still be VERY long for large/dense sets of galaxies.
- Can be sped up by passing the `precomputed=(DD,DR,RR)` argument.
- Alternatively, use `cf.wp_rp` with `rands=None` and specify the `boxsize` if the geometry is a perfect cube
- `ms.SimBox.populate_mock()`
- Runtime (~800 ms for Zheng07, ~4 s for Hearin15) depends on number of halos.
- Can be sped up via the `masking_function` agument (see `SimBox.get_halo_masking_function()`).
- Sped up times with precomputed selection over 15 sqdeg field (selection takes ~200 ms): ~350 ms for Zheng07, ~1 s for Hearin15.
- `ms.hf.ra_dec_z()`
- Runtime is generally around ~18 ms (zprec $\geq$ 1e-3) or ~61 ms (zprec = 1e-4), but takes slightly longer for higher redshift.
- `hf.distance2redshift()` -> `cosmo.comoving_distance()` is the culprit. If too slow, reduce `zprec` to lose redshift precision.
- This may also be sped up significantly from the previously mentioned `masking_function` argument because there will be fewer galaxies to select from.
______________________
TO DO:
======
______________________
### Test sources of error
- Poisson error of the...
- Data
- Randoms
- this test requires repopulating data ***or*** randoms over a ***single*** field of halos
- Sampling error (i.e. cosmic variance) of the...
- Field, either...
- universally: no overlapping fields so they are ~independent of halos
- ~~with respect to simbox: allowing overlapping fields~~
- this test inherently contains Poisson error terms, which must be subtracted out in quadrature
- ~~Simulation box (would be required if we allowed for overlapping fields, but we aren't)~~
### Calibrate bootstrap
According to Norberg et al. (2008), bootstraps overestimate the uncertainty by 40-50% on all scales. This is roughly consistent with what I have found.
Their suggestion is to select $3\times$ more data per random resampling. So instead of $N_{\rm r} = N_{\rm sub}$, use $N_{\rm r} = 3N_{\rm sub}$
|
github_jupyter
|
git clone https://github.com/AlanPearl/mocksurvey
cd mocksurvey
python setup.py install
bash get_smdpl
import mocksurvey as ms
import numpy as np
import matplotlib.pyplot as plt
simbox = ms.SimBox(populate_on_instantiation=False);
simbox.populate_mock()
field = simbox.boxfield()
field.make_rands(density_factor=10)
ms.tp.plot_pos_scatter(field, s=.5)
plt.show()
field = simbox.field(scheme="hex", sqdeg=1.5)
field.make_rands(density_factor=100)
ms.tp.plot_pos_scatter(field, s=5)
plt.show()
simbox = ms.SimBox(hodname="hearin15", threshold=10.5, redshift=1.35, Nbox=(1,1,3), rotation=0)
field = simbox.field(scheme="hex", sqdeg=1.5, collision_fraction=0.3, delta_z=.7, rand_density_factor=100)
fig,ax = plt.subplots()
ax.set_aspect('equal', 'box')
ms.tp.plot_sky_scatter(field, s=.9)
plt.savefig("pfs-celestial.png", bbox_inches="tight")
plt.show()
fig,ax = plt.subplots()
ax.set_aspect(5., 'box')
ms.tp.plot_pos_scatter(field, s=.9, axes=[2,1])
plt.savefig("pfs-cartesian.png", bbox_inches="tight")
plt.show()
fullbox = simbox.boxfield()
ms.tp.plot_xi_rp_pi(fullbox)
plt.show()
galbox = ms.GalBox(hodname="zheng07", threshold=-20)
ms.tp.plot_hod_occupation(galbox)
plt.show()
halobox = ms.HaloBox(simname="smdpl")
ms.tp.plot_halo_mass(halobox)
plt.show()
| 0.677687 | 0.923661 |
```
# -*- coding: utf-8 -*-
"""
@author: lrhao
@software: jupyter
@file: baseline.ipynb
@time: 2020-12-11
@description:
"""
import pandas as pd
import numpy as np
from tqdm import tqdm
import os
import matplotlib.pyplot as plt
import seaborn as sns
train = pd.read_csv('../公积金逾期预测-数据/train.csv')
test = pd.read_csv('../公积金逾期预测-数据/test.csv')
submit = pd.read_csv('../公积金逾期预测-数据/submit.csv')
train.shape, test.shape, submit.shape
train.head()
cate_2_cols = ['XINGBIE', 'ZHIWU', 'XUELI']
cate_cols = ['HYZK', 'ZHIYE', 'ZHICHEN', 'DWJJLX', 'DWSSHY', 'GRZHZT']
train[cate_cols]
num_cols = ['GRJCJS', 'GRZHYE', 'GRZHSNJZYE', 'GRZHDNGJYE', 'GRYJCE', 'DWYJCE','DKFFE', 'DKYE', 'DKLL']
train[num_cols]
```
特征工程
```
df = pd.concat([train, test], axis = 0).reset_index(drop = True)
df['missing_rate'] = (df.shape[1] - df.count(axis = 1)) / df.shape[1]
df['DKFFE_DKYE'] = df['DKFFE'] + df['DKYE']
df['DKFFE_DKY_multi_DKLL'] = (df['DKFFE'] + df['DKYE']) * df['DKLL']
df['DKFFE_multi_DKLL'] = df['DKFFE'] * df['DKLL']
df['DKYE_multi_DKLL'] = df['DKYE'] * df['DKLL']
df['GRYJCE_DWYJCE'] = df['GRYJCE'] + df['DWYJCE']
df['GRZHDNGJYE_GRZHSNJZYE'] = df['GRZHDNGJYE'] + df['GRZHSNJZYE']
df['DKFFE_multi_DKLL_ratio'] = df['DKFFE'] * df['DKLL'] / df['DKFFE_DKY_multi_DKLL']
df['DKYE_multi_DKLL_ratio'] = df['DKYE'] * df['DKLL'] / df['DKFFE_DKY_multi_DKLL']
df['DKYE_DKFFE_ratio'] = df['DKYE'] / df['DKFFE_DKYE']
df['DKFFE_DKYE_ratio'] = df['DKFFE'] / df['DKFFE_DKYE']
df['GRZHYE_diff_GRZHDNGJYE'] = df['GRZHYE'] - df['GRZHDNGJYE']
df['GRZHYE_diff_GRZHSNJZYE'] = df['GRZHYE'] - df['GRZHSNJZYE']
df['GRYJCE_DWYJCE_ratio'] = df['GRYJCE'] / df['GRYJCE_DWYJCE']
df['DWYJCE_GRYJCE_ratio'] = df['DWYJCE'] / df['GRYJCE_DWYJCE']
gen_feats = ['DKFFE_DKYE', 'DKFFE_DKY_multi_DKLL', 'DKFFE_multi_DKLL', 'DKYE_multi_DKLL', 'GRYJCE_DWYJCE',
'GRZHDNGJYE_GRZHSNJZYE', 'DKFFE_multi_DKLL_ratio', 'DKYE_multi_DKLL_ratio', 'GRZHYE_diff_GRZHDNGJYE',
'GRZHYE_diff_GRZHSNJZYE', 'GRYJCE_DWYJCE_ratio', 'DWYJCE_GRYJCE_ratio', 'DKYE_DKFFE_ratio', 'DKFFE_DKYE_ratio']
df.head()
def get_age(df,col = 'age'):
df[col+"_genFeat1"]=(df['age'] > 18).astype(int)
df[col+"_genFeat2"]=(df['age'] > 25).astype(int)
df[col+"_genFeat3"]=(df['age'] > 30).astype(int)
df[col+"_genFeat4"]=(df['age'] > 35).astype(int)
df[col+"_genFeat5"]=(df['age'] > 40).astype(int)
df[col+"_genFeat6"]=(df['age'] > 45).astype(int)
return df, [col + f'_genFeat{i}' for i in range(1, 7)]
df['age'] = ((1609430399 - df['CSNY']) / (365 * 24 * 3600)).astype(int)
df, genFeats1 = get_age(df, col = 'age')
sns.distplot(df['age'][df['age'] > 0])
def get_daikuanYE(df,col):
df[col + '_genFeat1'] = (df[col] > 100000).astype(int)
df[col + '_genFeat2'] = (df[col] > 120000).astype(int)
df[col + '_genFeat3'] = (df[col] > 140000).astype(int)
df[col + '_genFeat4'] = (df[col] > 180000).astype(int)
df[col + '_genFeat5'] = (df[col] > 220000).astype(int)
df[col + '_genFeat6'] = (df[col] > 260000).astype(int)
df[col + '_genFeat7'] = (df[col] > 300000).astype(int)
return df, [col + f'_genFeat{i}' for i in range(1, 8)]
df, genFeats2 = get_daikuanYE(df, col = 'DKYE')
df, genFeats3 = get_daikuanYE(df, col = 'DKFFE')
plt.figure(figsize = (8, 2))
plt.subplot(1,2,1)
sns.distplot(df['DKYE'][df['label'] == 1])
plt.subplot(1,2,2)
sns.distplot(df['DKFFE'][df['label'] == 1])
for f in tqdm(cate_cols):
df[f] = df[f].map(dict(zip(df[f].unique(), range(df[f].nunique()))))
df[f + '_count'] = df[f].map(df[f].value_counts())
df = pd.concat([df,pd.get_dummies(df[f],prefix=f"{f}")],axis=1)
cate_cols_combine = [[cate_cols[i], cate_cols[j]] for i in range(len(cate_cols)) \
for j in range(i + 1, len(cate_cols))]
for f1, f2 in tqdm(cate_cols_combine):
df['{}_{}_count'.format(f1, f2)] = df.groupby([f1, f2])['id'].transform('count')
df['{}_in_{}_prop'.format(f1, f2)] = df['{}_{}_count'.format(f1, f2)] / df[f2 + '_count']
df['{}_in_{}_prop'.format(f2, f1)] = df['{}_{}_count'.format(f1, f2)] / df[f1 + '_count']
for f1 in tqdm(cate_cols):
g = df.groupby(f1)
for f2 in num_cols + gen_feats:
for stat in ['sum', 'mean', 'std', 'max', 'min', 'std']:
df['{}_{}_{}'.format(f1, f2, stat)] = g[f2].transform(stat)
for f3 in genFeats2 + genFeats3:
for stat in ['sum', 'mean']:
df['{}_{}_{}'.format(f1, f2, stat)] = g[f2].transform(stat)
num_cols_gen_feats = num_cols + gen_feats
for f1 in tqdm(num_cols_gen_feats):
g = df.groupby(f1)
for f2 in num_cols_gen_feats:
if f1 != f2:
for stat in ['sum', 'mean', 'std', 'max', 'min', 'std']:
df['{}_{}_{}'.format(f1, f2, stat)] = g[f2].transform(stat)
for i in tqdm(range(len(num_cols_gen_feats))):
for j in range(i + 1, len(num_cols_gen_feats)):
df[f'numsOf_{num_cols_gen_feats[i]}_{num_cols_gen_feats[j]}_add'] = df[num_cols_gen_feats[i]] + df[num_cols_gen_feats[j]]
df[f'numsOf_{num_cols_gen_feats[i]}_{num_cols_gen_feats[j]}_diff'] = df[num_cols_gen_feats[i]] - df[num_cols_gen_feats[j]]
df[f'numsOf_{num_cols_gen_feats[i]}_{num_cols_gen_feats[j]}_multi'] = df[num_cols_gen_feats[i]] * df[num_cols_gen_feats[j]]
df[f'numsOf_{num_cols_gen_feats[i]}_{num_cols_gen_feats[j]}_div'] = df[num_cols_gen_feats[i]] / (df[num_cols_gen_feats[j]] + 0.0000000001)
```
训练集、测试集
```
train_df = df[df['label'].isna() == False].reset_index(drop=True)
test_df = df[df['label'].isna() == True].reset_index(drop=True)
display(train_df.shape, test_df.shape)
drop_feats = [f for f in train_df.columns if train_df[f].nunique() == 1 or train_df[f].nunique() == 0]
len(drop_feats), drop_feats
cols = [col for col in train_df.columns if col not in ['id', 'label'] + drop_feats]
from sklearn.model_selection import StratifiedKFold
from lightgbm.sklearn import LGBMClassifier
from sklearn.metrics import f1_score, roc_auc_score
from sklearn.ensemble import RandomForestClassifier,VotingClassifier
from xgboost import XGBClassifier
import time
oof = np.zeros(train_df.shape[0])
# feat_imp_df = pd.DataFrame({'feat': cols, 'imp': 0})
test_df['prob'] = 0
clf = LGBMClassifier(
learning_rate=0.05,
n_estimators=10230,
num_leaves=31,
subsample=0.8,
colsample_bytree=0.8,
random_state=1023,
metric=None
)
val_aucs = []
seeds = [1023, 2048, 2098]
for seed in seeds:
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=seed)
for i, (trn_idx, val_idx) in enumerate(skf.split(train_df, train_df['label'])):
print('--------------------- {} fold ---------------------'.format(i))
t = time.time()
trn_x, trn_y = train_df[cols].iloc[trn_idx].reset_index(drop=True), train_df['label'].values[trn_idx]
val_x, val_y = train_df[cols].iloc[val_idx].reset_index(drop=True), train_df['label'].values[val_idx]
clf.fit(
trn_x, trn_y,
eval_set=[(val_x, val_y)],
# categorical_feature=cate_cols,
eval_metric='auc',
early_stopping_rounds=200,
verbose=200
)
# feat_imp_df['imp'] += clf.feature_importances_ / skf.n_splits
oof[val_idx] = clf.predict_proba(val_x)[:, 1]
test_df['prob'] += clf.predict_proba(test_df[cols])[:, 1] / skf.n_splits / len(seeds)
cv_auc = roc_auc_score(train_df['label'], oof)
val_aucs.append(cv_auc)
print('\ncv_auc: ', cv_auc)
print(val_aucs, np.mean(val_aucs))
print(val_aucs, np.mean(val_aucs))
def tpr_weight_funtion(y_true,y_predict):
d = pd.DataFrame()
d['prob'] = list(y_predict)
d['y'] = list(y_true)
d = d.sort_values(['prob'], ascending=[0])
y = d.y
PosAll = pd.Series(y).value_counts()[1]
NegAll = pd.Series(y).value_counts()[0]
pCumsum = d['y'].cumsum()
nCumsum = np.arange(len(y)) - pCumsum + 1
pCumsumPer = pCumsum / PosAll
nCumsumPer = nCumsum / NegAll
TR1 = pCumsumPer[abs(nCumsumPer-0.001).idxmin()]
TR2 = pCumsumPer[abs(nCumsumPer-0.005).idxmin()]
TR3 = pCumsumPer[abs(nCumsumPer-0.01).idxmin()]
return 0.4 * TR1 + 0.3 * TR2 + 0.3 * TR3
tpr = round(tpr_weight_funtion(train_df['label'], oof), 6)
tpr, round(np.mean(val_aucs), 5)
submit.head()
submit['id'] = test_df['id']
submit['label'] = test_df['prob']
submit.to_csv('../sub/submission{}_{}.csv'.format(tpr, round(np.mean(val_aucs), 6)), index = False)
submit.head()
```
|
github_jupyter
|
# -*- coding: utf-8 -*-
"""
@author: lrhao
@software: jupyter
@file: baseline.ipynb
@time: 2020-12-11
@description:
"""
import pandas as pd
import numpy as np
from tqdm import tqdm
import os
import matplotlib.pyplot as plt
import seaborn as sns
train = pd.read_csv('../公积金逾期预测-数据/train.csv')
test = pd.read_csv('../公积金逾期预测-数据/test.csv')
submit = pd.read_csv('../公积金逾期预测-数据/submit.csv')
train.shape, test.shape, submit.shape
train.head()
cate_2_cols = ['XINGBIE', 'ZHIWU', 'XUELI']
cate_cols = ['HYZK', 'ZHIYE', 'ZHICHEN', 'DWJJLX', 'DWSSHY', 'GRZHZT']
train[cate_cols]
num_cols = ['GRJCJS', 'GRZHYE', 'GRZHSNJZYE', 'GRZHDNGJYE', 'GRYJCE', 'DWYJCE','DKFFE', 'DKYE', 'DKLL']
train[num_cols]
df = pd.concat([train, test], axis = 0).reset_index(drop = True)
df['missing_rate'] = (df.shape[1] - df.count(axis = 1)) / df.shape[1]
df['DKFFE_DKYE'] = df['DKFFE'] + df['DKYE']
df['DKFFE_DKY_multi_DKLL'] = (df['DKFFE'] + df['DKYE']) * df['DKLL']
df['DKFFE_multi_DKLL'] = df['DKFFE'] * df['DKLL']
df['DKYE_multi_DKLL'] = df['DKYE'] * df['DKLL']
df['GRYJCE_DWYJCE'] = df['GRYJCE'] + df['DWYJCE']
df['GRZHDNGJYE_GRZHSNJZYE'] = df['GRZHDNGJYE'] + df['GRZHSNJZYE']
df['DKFFE_multi_DKLL_ratio'] = df['DKFFE'] * df['DKLL'] / df['DKFFE_DKY_multi_DKLL']
df['DKYE_multi_DKLL_ratio'] = df['DKYE'] * df['DKLL'] / df['DKFFE_DKY_multi_DKLL']
df['DKYE_DKFFE_ratio'] = df['DKYE'] / df['DKFFE_DKYE']
df['DKFFE_DKYE_ratio'] = df['DKFFE'] / df['DKFFE_DKYE']
df['GRZHYE_diff_GRZHDNGJYE'] = df['GRZHYE'] - df['GRZHDNGJYE']
df['GRZHYE_diff_GRZHSNJZYE'] = df['GRZHYE'] - df['GRZHSNJZYE']
df['GRYJCE_DWYJCE_ratio'] = df['GRYJCE'] / df['GRYJCE_DWYJCE']
df['DWYJCE_GRYJCE_ratio'] = df['DWYJCE'] / df['GRYJCE_DWYJCE']
gen_feats = ['DKFFE_DKYE', 'DKFFE_DKY_multi_DKLL', 'DKFFE_multi_DKLL', 'DKYE_multi_DKLL', 'GRYJCE_DWYJCE',
'GRZHDNGJYE_GRZHSNJZYE', 'DKFFE_multi_DKLL_ratio', 'DKYE_multi_DKLL_ratio', 'GRZHYE_diff_GRZHDNGJYE',
'GRZHYE_diff_GRZHSNJZYE', 'GRYJCE_DWYJCE_ratio', 'DWYJCE_GRYJCE_ratio', 'DKYE_DKFFE_ratio', 'DKFFE_DKYE_ratio']
df.head()
def get_age(df,col = 'age'):
df[col+"_genFeat1"]=(df['age'] > 18).astype(int)
df[col+"_genFeat2"]=(df['age'] > 25).astype(int)
df[col+"_genFeat3"]=(df['age'] > 30).astype(int)
df[col+"_genFeat4"]=(df['age'] > 35).astype(int)
df[col+"_genFeat5"]=(df['age'] > 40).astype(int)
df[col+"_genFeat6"]=(df['age'] > 45).astype(int)
return df, [col + f'_genFeat{i}' for i in range(1, 7)]
df['age'] = ((1609430399 - df['CSNY']) / (365 * 24 * 3600)).astype(int)
df, genFeats1 = get_age(df, col = 'age')
sns.distplot(df['age'][df['age'] > 0])
def get_daikuanYE(df,col):
df[col + '_genFeat1'] = (df[col] > 100000).astype(int)
df[col + '_genFeat2'] = (df[col] > 120000).astype(int)
df[col + '_genFeat3'] = (df[col] > 140000).astype(int)
df[col + '_genFeat4'] = (df[col] > 180000).astype(int)
df[col + '_genFeat5'] = (df[col] > 220000).astype(int)
df[col + '_genFeat6'] = (df[col] > 260000).astype(int)
df[col + '_genFeat7'] = (df[col] > 300000).astype(int)
return df, [col + f'_genFeat{i}' for i in range(1, 8)]
df, genFeats2 = get_daikuanYE(df, col = 'DKYE')
df, genFeats3 = get_daikuanYE(df, col = 'DKFFE')
plt.figure(figsize = (8, 2))
plt.subplot(1,2,1)
sns.distplot(df['DKYE'][df['label'] == 1])
plt.subplot(1,2,2)
sns.distplot(df['DKFFE'][df['label'] == 1])
for f in tqdm(cate_cols):
df[f] = df[f].map(dict(zip(df[f].unique(), range(df[f].nunique()))))
df[f + '_count'] = df[f].map(df[f].value_counts())
df = pd.concat([df,pd.get_dummies(df[f],prefix=f"{f}")],axis=1)
cate_cols_combine = [[cate_cols[i], cate_cols[j]] for i in range(len(cate_cols)) \
for j in range(i + 1, len(cate_cols))]
for f1, f2 in tqdm(cate_cols_combine):
df['{}_{}_count'.format(f1, f2)] = df.groupby([f1, f2])['id'].transform('count')
df['{}_in_{}_prop'.format(f1, f2)] = df['{}_{}_count'.format(f1, f2)] / df[f2 + '_count']
df['{}_in_{}_prop'.format(f2, f1)] = df['{}_{}_count'.format(f1, f2)] / df[f1 + '_count']
for f1 in tqdm(cate_cols):
g = df.groupby(f1)
for f2 in num_cols + gen_feats:
for stat in ['sum', 'mean', 'std', 'max', 'min', 'std']:
df['{}_{}_{}'.format(f1, f2, stat)] = g[f2].transform(stat)
for f3 in genFeats2 + genFeats3:
for stat in ['sum', 'mean']:
df['{}_{}_{}'.format(f1, f2, stat)] = g[f2].transform(stat)
num_cols_gen_feats = num_cols + gen_feats
for f1 in tqdm(num_cols_gen_feats):
g = df.groupby(f1)
for f2 in num_cols_gen_feats:
if f1 != f2:
for stat in ['sum', 'mean', 'std', 'max', 'min', 'std']:
df['{}_{}_{}'.format(f1, f2, stat)] = g[f2].transform(stat)
for i in tqdm(range(len(num_cols_gen_feats))):
for j in range(i + 1, len(num_cols_gen_feats)):
df[f'numsOf_{num_cols_gen_feats[i]}_{num_cols_gen_feats[j]}_add'] = df[num_cols_gen_feats[i]] + df[num_cols_gen_feats[j]]
df[f'numsOf_{num_cols_gen_feats[i]}_{num_cols_gen_feats[j]}_diff'] = df[num_cols_gen_feats[i]] - df[num_cols_gen_feats[j]]
df[f'numsOf_{num_cols_gen_feats[i]}_{num_cols_gen_feats[j]}_multi'] = df[num_cols_gen_feats[i]] * df[num_cols_gen_feats[j]]
df[f'numsOf_{num_cols_gen_feats[i]}_{num_cols_gen_feats[j]}_div'] = df[num_cols_gen_feats[i]] / (df[num_cols_gen_feats[j]] + 0.0000000001)
train_df = df[df['label'].isna() == False].reset_index(drop=True)
test_df = df[df['label'].isna() == True].reset_index(drop=True)
display(train_df.shape, test_df.shape)
drop_feats = [f for f in train_df.columns if train_df[f].nunique() == 1 or train_df[f].nunique() == 0]
len(drop_feats), drop_feats
cols = [col for col in train_df.columns if col not in ['id', 'label'] + drop_feats]
from sklearn.model_selection import StratifiedKFold
from lightgbm.sklearn import LGBMClassifier
from sklearn.metrics import f1_score, roc_auc_score
from sklearn.ensemble import RandomForestClassifier,VotingClassifier
from xgboost import XGBClassifier
import time
oof = np.zeros(train_df.shape[0])
# feat_imp_df = pd.DataFrame({'feat': cols, 'imp': 0})
test_df['prob'] = 0
clf = LGBMClassifier(
learning_rate=0.05,
n_estimators=10230,
num_leaves=31,
subsample=0.8,
colsample_bytree=0.8,
random_state=1023,
metric=None
)
val_aucs = []
seeds = [1023, 2048, 2098]
for seed in seeds:
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=seed)
for i, (trn_idx, val_idx) in enumerate(skf.split(train_df, train_df['label'])):
print('--------------------- {} fold ---------------------'.format(i))
t = time.time()
trn_x, trn_y = train_df[cols].iloc[trn_idx].reset_index(drop=True), train_df['label'].values[trn_idx]
val_x, val_y = train_df[cols].iloc[val_idx].reset_index(drop=True), train_df['label'].values[val_idx]
clf.fit(
trn_x, trn_y,
eval_set=[(val_x, val_y)],
# categorical_feature=cate_cols,
eval_metric='auc',
early_stopping_rounds=200,
verbose=200
)
# feat_imp_df['imp'] += clf.feature_importances_ / skf.n_splits
oof[val_idx] = clf.predict_proba(val_x)[:, 1]
test_df['prob'] += clf.predict_proba(test_df[cols])[:, 1] / skf.n_splits / len(seeds)
cv_auc = roc_auc_score(train_df['label'], oof)
val_aucs.append(cv_auc)
print('\ncv_auc: ', cv_auc)
print(val_aucs, np.mean(val_aucs))
print(val_aucs, np.mean(val_aucs))
def tpr_weight_funtion(y_true,y_predict):
d = pd.DataFrame()
d['prob'] = list(y_predict)
d['y'] = list(y_true)
d = d.sort_values(['prob'], ascending=[0])
y = d.y
PosAll = pd.Series(y).value_counts()[1]
NegAll = pd.Series(y).value_counts()[0]
pCumsum = d['y'].cumsum()
nCumsum = np.arange(len(y)) - pCumsum + 1
pCumsumPer = pCumsum / PosAll
nCumsumPer = nCumsum / NegAll
TR1 = pCumsumPer[abs(nCumsumPer-0.001).idxmin()]
TR2 = pCumsumPer[abs(nCumsumPer-0.005).idxmin()]
TR3 = pCumsumPer[abs(nCumsumPer-0.01).idxmin()]
return 0.4 * TR1 + 0.3 * TR2 + 0.3 * TR3
tpr = round(tpr_weight_funtion(train_df['label'], oof), 6)
tpr, round(np.mean(val_aucs), 5)
submit.head()
submit['id'] = test_df['id']
submit['label'] = test_df['prob']
submit.to_csv('../sub/submission{}_{}.csv'.format(tpr, round(np.mean(val_aucs), 6)), index = False)
submit.head()
| 0.17621 | 0.353651 |
```
%load_ext autoreload
%autoreload 2
import os
import numpy as np
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchtext.data.utils import get_tokenizer
from genomic_benchmarks.dataset_getters.pytorch_datasets import DemoCodingVsIntergenomicSeqs
from genomic_benchmarks.dataset_getters.utils import coll_factory, LetterTokenizer, build_vocab, check_seq_lengths, check_config
from cnn_model import CNN
```
## Config
```
config = {
"use_padding": False,
"run_on_gpu": True,
"dataset": DemoCodingVsIntergenomicSeqs,
"number_of_classes": 2,
"dataset_version": 0,
"force_download": False,
"epochs": 15,
"embedding_dim": 100,
"batch_size": 32,
# vocabulary that is not present in the training set but is present in the test set
"vocab_to_add": ["N"],
}
check_config(config)
```
## Choose the dataset
```
get_dataset_fn = config["dataset"]
train_dset = get_dataset_fn('train', force_download=config["force_download"], version=config["dataset_version"])
```
## Tokenizer and vocab
```
tokenizer = get_tokenizer(LetterTokenizer())
vocabulary = build_vocab(train_dset, tokenizer, use_padding=config["use_padding"])
print("vocab len:" ,vocabulary.__len__())
print(vocabulary.get_stoi())
```
## Dataloader and batch preparation
```
# Run on GPU or CPU
device = 'cuda' if config["run_on_gpu"] and torch.cuda.is_available() else 'cpu'
print('Using {} device'.format(device))
max_seq_len, nn_input_len = check_seq_lengths(dataset=train_dset, config=config)
# Data Loader
if(config["use_padding"]):
collate = coll_factory(vocabulary, tokenizer, device, pad_to_length = nn_input_len)
else:
collate = coll_factory(vocabulary, tokenizer, device, pad_to_length = None)
train_loader = DataLoader(train_dset, batch_size=config["batch_size"], shuffle=True, collate_fn=collate)
```
## Model
```
model = CNN(
number_of_classes=config["number_of_classes"],
vocab_size=vocabulary.__len__(),
embedding_dim=config["embedding_dim"],
input_len=nn_input_len
).to(device)
```
## Training
```
model.train(train_loader, epochs=config["epochs"])
```
## Testing
```
test_dset = get_dataset_fn('test', force_download=config["force_download"], version=config["dataset_version"])
test_loader = DataLoader(test_dset, batch_size=config["batch_size"], shuffle=True, collate_fn=collate)
model.test(test_loader)
def export_evaluation(model, dataloader):
size = dataloader.dataset.__len__()
num_batches = len(dataloader)
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
pred = model(X)
test_loss += model.loss(pred, y).item()
correct += (torch.round(pred) == y).sum().item()
print('test_loss ', test_loss)
print('num_batches', num_batches)
print('correct', correct)
print('size', size)
test_loss /= num_batches
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
export_evaluation(model, test_loader)
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
import os
import numpy as np
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchtext.data.utils import get_tokenizer
from genomic_benchmarks.dataset_getters.pytorch_datasets import DemoCodingVsIntergenomicSeqs
from genomic_benchmarks.dataset_getters.utils import coll_factory, LetterTokenizer, build_vocab, check_seq_lengths, check_config
from cnn_model import CNN
config = {
"use_padding": False,
"run_on_gpu": True,
"dataset": DemoCodingVsIntergenomicSeqs,
"number_of_classes": 2,
"dataset_version": 0,
"force_download": False,
"epochs": 15,
"embedding_dim": 100,
"batch_size": 32,
# vocabulary that is not present in the training set but is present in the test set
"vocab_to_add": ["N"],
}
check_config(config)
get_dataset_fn = config["dataset"]
train_dset = get_dataset_fn('train', force_download=config["force_download"], version=config["dataset_version"])
tokenizer = get_tokenizer(LetterTokenizer())
vocabulary = build_vocab(train_dset, tokenizer, use_padding=config["use_padding"])
print("vocab len:" ,vocabulary.__len__())
print(vocabulary.get_stoi())
# Run on GPU or CPU
device = 'cuda' if config["run_on_gpu"] and torch.cuda.is_available() else 'cpu'
print('Using {} device'.format(device))
max_seq_len, nn_input_len = check_seq_lengths(dataset=train_dset, config=config)
# Data Loader
if(config["use_padding"]):
collate = coll_factory(vocabulary, tokenizer, device, pad_to_length = nn_input_len)
else:
collate = coll_factory(vocabulary, tokenizer, device, pad_to_length = None)
train_loader = DataLoader(train_dset, batch_size=config["batch_size"], shuffle=True, collate_fn=collate)
model = CNN(
number_of_classes=config["number_of_classes"],
vocab_size=vocabulary.__len__(),
embedding_dim=config["embedding_dim"],
input_len=nn_input_len
).to(device)
model.train(train_loader, epochs=config["epochs"])
test_dset = get_dataset_fn('test', force_download=config["force_download"], version=config["dataset_version"])
test_loader = DataLoader(test_dset, batch_size=config["batch_size"], shuffle=True, collate_fn=collate)
model.test(test_loader)
def export_evaluation(model, dataloader):
size = dataloader.dataset.__len__()
num_batches = len(dataloader)
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
pred = model(X)
test_loss += model.loss(pred, y).item()
correct += (torch.round(pred) == y).sum().item()
print('test_loss ', test_loss)
print('num_batches', num_batches)
print('correct', correct)
print('size', size)
test_loss /= num_batches
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
export_evaluation(model, test_loader)
| 0.756178 | 0.653763 |
___
<a href='http://www.pieriandata.com'> <img src='../../Pierian_Data_Logo.png' /></a>
___
# Ecommerce Purchases Exercise
In this Exercise you will be given some Fake Data about some purchases done through Amazon! Just go ahead and follow the directions and try your best to answer the questions and complete the tasks. Feel free to reference the solutions. Most of the tasks can be solved in different ways. For the most part, the questions get progressively harder.
Please excuse anything that doesn't make "Real-World" sense in the dataframe, all the data is fake and made-up.
Also note that all of these questions can be answered with one line of code.
____
** Import pandas and read in the Ecommerce Purchases csv file and set it to a DataFrame called ecom. **
```
import pandas as pd
ecom = pd.read_csv('Ecommerce Purchases')
```
**Check the head of the DataFrame.**
```
ecom.head(3)
```
** How many rows and columns are there? **
```
ecom.info()
```
** What is the average Purchase Price? **
```
ecom['Purchase Price'].mean()
```
** What were the highest and lowest purchase prices? **
```
ecom['Purchase Price'].max()
ecom['Purchase Price'].min()
```
** How many people have English 'en' as their Language of choice on the website? **
```
sum(ecom['Language'] == 'en')
ecom[ecom['Language'] == 'en']['Language'].count()
```
** How many people have the job title of "Lawyer" ? **
```
ecom[ecom['Job'] == 'Lawyer']['Job'].count()
```
** How many people made the purchase during the AM and how many people made the purchase during PM ? **
**(Hint: Check out [value_counts()](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.value_counts.html) ) **
```
ecom["AM or PM"].value_counts()
```
** What are the 5 most common Job Titles? **
```
ecom['Job'].value_counts().head(5)
```
** Someone made a purchase that came from Lot: "90 WT" , what was the Purchase Price for this transaction? **
```
ecom[ecom['Lot'] == '90 WT']['Purchase Price']
```
** What is the email of the person with the following Credit Card Number: 4926535242672853 **
```
ecom[ecom['Credit Card'] == 4926535242672853]['Email']
```
** How many people have American Express as their Credit Card Provider *and* made a purchase above $95 ?**
```
ecom[(ecom['CC Provider'] == 'American Express')&(ecom['Purchase Price'] > 95)].count()
```
** Hard: How many people have a credit card that expires in 2025? **
```
sum(ecom['CC Exp Date'].apply(lambda exp: exp[-2:] == '25'))
```
** Hard: What are the top 5 most popular email providers/hosts (e.g. gmail.com, yahoo.com, etc...) **
```
ecom['Email'].apply(lambda email: email.split('@')[1]).value_counts().head(5)
```
# Great Job!
|
github_jupyter
|
import pandas as pd
ecom = pd.read_csv('Ecommerce Purchases')
ecom.head(3)
ecom.info()
ecom['Purchase Price'].mean()
ecom['Purchase Price'].max()
ecom['Purchase Price'].min()
sum(ecom['Language'] == 'en')
ecom[ecom['Language'] == 'en']['Language'].count()
ecom[ecom['Job'] == 'Lawyer']['Job'].count()
ecom["AM or PM"].value_counts()
ecom['Job'].value_counts().head(5)
ecom[ecom['Lot'] == '90 WT']['Purchase Price']
ecom[ecom['Credit Card'] == 4926535242672853]['Email']
ecom[(ecom['CC Provider'] == 'American Express')&(ecom['Purchase Price'] > 95)].count()
sum(ecom['CC Exp Date'].apply(lambda exp: exp[-2:] == '25'))
ecom['Email'].apply(lambda email: email.split('@')[1]).value_counts().head(5)
| 0.134066 | 0.99045 |
```
%matplotlib inline
from pyqubo import Array, Placeholder, solve_qubo, Constraint, Sum
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
```
## Traveling Salesman Problem (TSP)
Find the shortest route that visits each city and returns to the origin city.
```
def plot_city(cities, sol = {}):
n_city = len(cities)
cities_dict = dict(cities)
G = nx.Graph()
for city in cities_dict:
G.add_node(city)
# draw path
if sol:
city_order = []
for i, v in sol.items():
for j, v2 in v.items():
if v2 == 1:
city_order.append(j)
for i in range(n_city):
city_index1 = city_order[i]
city_index2 = city_order[(i+1) % n_city]
G.add_edge(cities[city_index1][0], cities[city_index2][0])
plt.figure(figsize=(3,3))
pos = nx.spring_layout(G)
nx.draw_networkx(G, cities_dict)
plt.axis("off")
plt.show()
def dist(i, j, cities):
pos_i = cities[i][1]
pos_j = cities[j][1]
return np.sqrt((pos_i[0] - pos_j[0])**2 + (pos_i[1] - pos_j[1])**2)
# City names and coordinates list[("name", (x, y))]
cities = [
("a", (0, 0)),
("b", (1, 3)),
("c", (3, 2)),
("d", (2, 1)),
("e", (0, 1))
]
plot_city(cities)
```
Prepare binary vector with bit $(i, j)$ representing to visit $j$ city at time $i$
```
n_city = len(cities)
x = Array.create('c', (n_city, n_city), 'BINARY')
# Constraint not to visit more than two cities at the same time.
time_const = 0.0
for i in range(n_city):
# If you wrap the hamiltonian by Const(...), this part is recognized as constraint
time_const += Constraint((Sum(0, n_city, lambda j: x[i, j]) - 1)**2, label="time{}".format(i))
# Constraint not to visit the same city more than twice.
city_const = 0.0
for j in range(n_city):
city_const += Constraint((Sum(0, n_city, lambda i: x[i, j]) - 1)**2, label="city{}".format(i))
# distance of route
distance = 0.0
for i in range(n_city):
for j in range(n_city):
for k in range(n_city):
d_ij = dist(i, j, cities)
distance += d_ij * x[k, i] * x[(k+1)%n_city, j]
# Construct hamiltonian
A = Placeholder("A")
H = distance + A * (time_const + city_const)
# Compile model
model = H.compile()
# Generate QUBO
feed_dict = {'A': 4.0}
qubo, offset = model.to_qubo(feed_dict=feed_dict)
sol = solve_qubo(qubo)
solution, broken, energy = model.decode_solution(sol, vartype="BINARY", feed_dict=feed_dict)
print("number of broken constarint = {}".format(len(broken)))
if len(broken) == 0:
plot_city(cities, solution["c"])
```
|
github_jupyter
|
%matplotlib inline
from pyqubo import Array, Placeholder, solve_qubo, Constraint, Sum
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
def plot_city(cities, sol = {}):
n_city = len(cities)
cities_dict = dict(cities)
G = nx.Graph()
for city in cities_dict:
G.add_node(city)
# draw path
if sol:
city_order = []
for i, v in sol.items():
for j, v2 in v.items():
if v2 == 1:
city_order.append(j)
for i in range(n_city):
city_index1 = city_order[i]
city_index2 = city_order[(i+1) % n_city]
G.add_edge(cities[city_index1][0], cities[city_index2][0])
plt.figure(figsize=(3,3))
pos = nx.spring_layout(G)
nx.draw_networkx(G, cities_dict)
plt.axis("off")
plt.show()
def dist(i, j, cities):
pos_i = cities[i][1]
pos_j = cities[j][1]
return np.sqrt((pos_i[0] - pos_j[0])**2 + (pos_i[1] - pos_j[1])**2)
# City names and coordinates list[("name", (x, y))]
cities = [
("a", (0, 0)),
("b", (1, 3)),
("c", (3, 2)),
("d", (2, 1)),
("e", (0, 1))
]
plot_city(cities)
n_city = len(cities)
x = Array.create('c', (n_city, n_city), 'BINARY')
# Constraint not to visit more than two cities at the same time.
time_const = 0.0
for i in range(n_city):
# If you wrap the hamiltonian by Const(...), this part is recognized as constraint
time_const += Constraint((Sum(0, n_city, lambda j: x[i, j]) - 1)**2, label="time{}".format(i))
# Constraint not to visit the same city more than twice.
city_const = 0.0
for j in range(n_city):
city_const += Constraint((Sum(0, n_city, lambda i: x[i, j]) - 1)**2, label="city{}".format(i))
# distance of route
distance = 0.0
for i in range(n_city):
for j in range(n_city):
for k in range(n_city):
d_ij = dist(i, j, cities)
distance += d_ij * x[k, i] * x[(k+1)%n_city, j]
# Construct hamiltonian
A = Placeholder("A")
H = distance + A * (time_const + city_const)
# Compile model
model = H.compile()
# Generate QUBO
feed_dict = {'A': 4.0}
qubo, offset = model.to_qubo(feed_dict=feed_dict)
sol = solve_qubo(qubo)
solution, broken, energy = model.decode_solution(sol, vartype="BINARY", feed_dict=feed_dict)
print("number of broken constarint = {}".format(len(broken)))
if len(broken) == 0:
plot_city(cities, solution["c"])
| 0.428712 | 0.857052 |
# Object detection
The objective is to locate objects in the image. Our model will predict the coordinates of a box that encloses the object.
```
import mxnet as mx
import gluoncv as gcv
import matplotlib.pyplot as plt
mx.__version__
gcv.__version__
```
## Download de image
This will save the image in the local path of Jupyter installation:
```
image_url = 'https://raw.githubusercontent.com/zhreshold/mxnet-ssd/master/data/demo/dog.jpg'
image_file_path = 'dog.jpg'
gcv.utils.download(url=image_url, path=image_file_path)
```
## Load the image
```
image = mx.image.imread('dog.jpg')
print(f'image type: {type(image)}')
print(f'image shape: {image.shape}')
print(f'image data type: {image.dtype}')
print(f'image, minimum value: {image.min().asscalar()}')
print(f'image, maximum value: {image.max().asscalar()}')
```
In the **image type** shows that image is loaded as an MXNet ndarray.
In the **image shape** shows we have a data layout in HWC format, i.e. the image has a **H**eight of 576 pixels with a **W**idth of 768 pixels and it's a colored image with three **C**hannels.
```
plt.imshow(image.asnumpy())
```
## Transform image
We need to transform the image to send it to the network or apply the CV model on it. We need to add **N** as a fourth dimension to the HWC format to transform it to NCHW (**N**: batch **C**: channel **H**: hight **W**: width).
```
transformed_image, chw_image = gcv.data.transforms.presets.yolo.transform_test(
image, short=512)
print(f'image shape: {transformed_image.shape}')
print(f'image data type: {transformed_image.dtype}')
print(f'image, minimum value: {transformed_image.min().asscalar()}')
print(f'image, maximum value: {transformed_image.max().asscalar()}')
```
**transformed_image** variable is the image in the new format (NCHW) and the height will be resized to 512 pixels but maintaining the aspect ratio. Furthermore, it's a batch of one image. And it's an array of 32-bit floats instead of 8-bit integers.
**chw_image** variable is a resized version of the image (transformed_image).
## Download and load pre-trained model
We'll use the [**YOLOv3**](https://github.com/ultralytics/yolov3) (You Only Look Once) network, which is the most popular algorithm to object detection, with a [**darknet53**](https://github.com/pjreddie/darknet) backbone that has been trained on the Microsoft's [**COCO**](https://cocodataset.org/) image dataset. Our network parameters are 237 megabytes size and are stored in the mxnet cache, i.e. ~/.mxnet/models/ is the path where we can find the downloaded models.
```
network = gcv.model_zoo.get_model('yolo3_darknet53_coco', pretrained=True)
```
## Make a prediction
Run forward pass to obtain the predicted score for each class
```
prediction = network(transformed_image)
print(f'Type Prediction object: {type(prediction)}')
for index, array in enumerate(prediction):
print(f'#{index + 1} {array.shape}')
```
- The first array contains the object class indexes, i.e. with a shape of (1, 100, 1), we have 1 image, 100 potential objects (the model can predict up to 100 objects in a single image), and 1 class index per object.
- The second array contains the object class probabilities.
- The third array contains the object bounding box coordinates, i.e. with shape (1, 100, 4), we have 1 image, 100 potential objects, and 4 values for each object to define its bounding box (which delimited the object predicted).
## Remove additionalbatch dimension
Remove additional batch dimension for all of the arrays.
```
prediction = [array[0] for array in prediction]
class_indicies, probabilities, bounding_boxes = prediction
k = 10
print(class_indicies[:k])
```
The first detected object has a predicted class with number 16, and we see more objects with classes 1, 7, 2, 13 and 0. After this, we have a number of objects with a class index of -1. Where -1 is a special class index that is used to indicate there is no detected object. We have six detected objects in total, with the remaining 94 potential objects being padded with -1 values.
We can show what refers to class 16, for example:
```
class_index = 16
print(f'{network.classes[class_index]} => {class_index}')
```
And how many classes do we have in the network? We have 80 which are the image categories that can find in the [COCO dataset](https://cocodataset.org/#detection-eval).
```
len(network.classes)
```
## Object probabilities
Now, we have the associated object class probability. We can interpret this as our confidence that the class index (image category) is correct.
```
print(probabilities[:k])
```
If we use a confidence of 50%, then we can say that the first three objects were detected. The -1 values means that there is not confidence in that classes (image categories).
## Object boundings
Now, we have the coordinates of the bounding boxes for each object detected. They specify the coordinates for the top-left corner, and the bottom-right corner.
```
print(bounding_boxes[:k])
```
## Visualize prediction
Now, wen can graph the result using the resized image above.
```
gcv.utils.viz.plot_bbox(chw_image, bounding_boxes,
probabilities, class_indicies, class_names=network.classes)
```
We can see that our network has done a good job of detecting the objects. We have detected a dog, a bike and a truck. Our network missed the tree in the background. But that's because we're using a model that's been pretrained on COCO. And [COCO](https://cocodataset.org/#explore) doesn't have an object class for trees.
|
github_jupyter
|
import mxnet as mx
import gluoncv as gcv
import matplotlib.pyplot as plt
mx.__version__
gcv.__version__
image_url = 'https://raw.githubusercontent.com/zhreshold/mxnet-ssd/master/data/demo/dog.jpg'
image_file_path = 'dog.jpg'
gcv.utils.download(url=image_url, path=image_file_path)
image = mx.image.imread('dog.jpg')
print(f'image type: {type(image)}')
print(f'image shape: {image.shape}')
print(f'image data type: {image.dtype}')
print(f'image, minimum value: {image.min().asscalar()}')
print(f'image, maximum value: {image.max().asscalar()}')
plt.imshow(image.asnumpy())
transformed_image, chw_image = gcv.data.transforms.presets.yolo.transform_test(
image, short=512)
print(f'image shape: {transformed_image.shape}')
print(f'image data type: {transformed_image.dtype}')
print(f'image, minimum value: {transformed_image.min().asscalar()}')
print(f'image, maximum value: {transformed_image.max().asscalar()}')
network = gcv.model_zoo.get_model('yolo3_darknet53_coco', pretrained=True)
prediction = network(transformed_image)
print(f'Type Prediction object: {type(prediction)}')
for index, array in enumerate(prediction):
print(f'#{index + 1} {array.shape}')
prediction = [array[0] for array in prediction]
class_indicies, probabilities, bounding_boxes = prediction
k = 10
print(class_indicies[:k])
class_index = 16
print(f'{network.classes[class_index]} => {class_index}')
len(network.classes)
print(probabilities[:k])
print(bounding_boxes[:k])
gcv.utils.viz.plot_bbox(chw_image, bounding_boxes,
probabilities, class_indicies, class_names=network.classes)
| 0.356783 | 0.989521 |
<center><h1>Teoria Regulacji, Wtorek 17:05-18:45</h1></center>
<center><h2>Jan Bronicki 249011</h2></center>
### Zadanie 2 z Listy 2 ("mini-projekt")
Dla systemu o następującej transmitancji:
$$ K(s) = \frac{1}{(s+1)(s+2)} $$
Należy wyznaczyć pobudzienie na wejście:
$u(t) = 1(t)$
Z następującymi warunkami początkowymi:
$y(0)=1$
$y^{\prime}(0)=2$
System dodatkowo można przedstawić graficznie za pomocą schematu blokowego jako:

Na początku wiedząc, że $Y(s) = K(s) \cdot U(s)$ obliczamy $y_{1}(t)$:
Gdzie za $U(s)$ podstawiamy to, czemu równałoby się $u(t)$ po transformacie Laplace'a:
$$ Y(s) = \frac{1}{(s+1)(s+2)} \cdot \frac{1}{s} $$
$$ Y(s) = \frac{A}{s} + \frac{B}{s+1} + \frac{C}{s+2} $$
\begin{cases}
A=\frac{1}{2}
\\
B=-1
\\
C=\frac{1}{2}
\end{cases}
$$ Y(s) = \frac{\frac{1}{2}}{s} + \frac{-1}{s+1} + \frac{\frac{1}{2}}{s+2} $$
Następnie stosująć wzory na odwrotną transformatę Laplace'a, uzyskujemy wynik w dziedzinie czasu:
$$ \mathcal{L}^{-1}\left\{Y(s)\right\} = \mathcal{L}^{-1}\left\{\frac{\frac{1}{2}}{s} + \frac{-1}{s+1} + \frac{\frac{1}{2}}{s+2}\right\} $$
$$ y_{1}(t) = \frac{1}{2}e^{-2t} - e^{-t} + \frac{1}{2} $$
#### Możemy to osiągnąć również stosując bibliotekę taką jak SymPy umożliwiającą, nam używanie zapisów symbolicznych w Python'ie
```
# Biblioteka SymPy
import sympy as sp
# NumPy uzywanany do numerycznych operacji matematycznych
import numpy as np
# Matplotlib sluzacy do wizualizacji
import matplotlib.pyplot as plt
# Definiujemy obiekty biblioteki SymPy
t, y, s = sp.symbols('t y s')
# Tworzymy rownanie
Ys = 1/(s*(s+1)*(s+2))
Ys
```
Następnie dokonujemy rozbicia:
```
Ys = Ys.apart()
Ys
y1 = sp.expand(sp.inverse_laplace_transform(Ys.apart(), s, t))
y1
# theta(t) to 1(t) w bibliotece SymPy
```
Teraz możemy narysować rozwiązanie $y_{1}(t)$:
```
'''
"time" bedzie nasza osia czasu,
a y1_time odpowiedza jaka dostaniemy w konkretnym punkcie czasu
'''
time = np.arange(0, 10, 0.01)
y1_time = np.arange(0, 10, 0.01)
y1_lambda = sp.lambdify(t, y1, modules=['numpy', 'sympy'])
for each in range(0, len(time)):
y1_time[each] = y1_lambda(time[each])
```
Teraz możemy narysować wynik rozwiązania numerycznego poprzez, zamienienie równania symbolicznego biblioteki SymPy na funkcję (lambdę) w Pythonie z implementacją w NumPy'u dzięki funkcji:
```python
sympy.utilities.lambdify(symfunc, implementation)
```
```
plt.plot(time, y1_time, label=("$y_{1}(t)$"))
plt.grid(True)
plt.title("Odpowiedz "+"$"+"y_{1}(t) = "+sp.latex(y1)+"$")
plt.xlabel("Czas[s]")
plt.ylabel("Amplituda")
plt.legend()
plt.show()
```
#### Następnie na podstawie równania charakterystycznego $(s+1)(s+2)$ możemy dojść do oryginalnego równania różniczkowego:
$$Y(s) = \frac{1}{(s+1)(s+2)} \cdot \frac{1}{s}$$
$$ Y(s)\left[s^{2}+3s+2\right] = \frac{1}{s}$$
$$ y^{\prime\prime}+3y^{\prime}+2y=u(t) $$
$$ s^{2}Y(s)-sy(0)-y^{\prime}+3sY(s)-3y(0)+2Y(s) = 0 $$
<center>gdzie $y(0)=1$ oraz $y^{\prime}(0)=2 $</center>
$$ Y(s) = \frac{s+5}{s^{2}+3s+2} $$
$$ Y(s) = \frac{s+5}{(s+2)(s+1)} $$
$$ Y(s) = \frac{A}{s+1}+\frac{B}{s+2} $$
\begin{cases}
A=4
\\
B=-3
\end{cases}
$$ Y(s) = \frac{4}{s+1}+\frac{-3}{s+2} $$
Następnie stosujemy odwrotną transformatę Laplace'a:
$$ \mathcal{L}^{-1}\left\{Y(s)\right\} = \mathcal{L}^{-1}\left\{\frac{4}{s+1}+\frac{-3}{s+2}\right\} $$
$$ y_{2}(t) = 4e^{-t}-3e^{-2t} $$
#### Następnie tak samo możemy postąpić w tym przypadku, używając możliwości symbolicznych obliczeń jakie daje nam Python
```
Ys = (s+5)/((s**2)+3*s+2)
Ys
Ys = Ys.factor()
Ys
Ys = Ys.apart()
Ys
y2 = sp.expand(sp.inverse_laplace_transform(Ys.apart(), s, t))
y2
```
Teraz zamieniamy postać symboliczną na funkcję z, której uzyskamy wartości numeryczne:
```
'''
"time" bedzie nasza osia czasu,
a y2_time odpowiedza jaka dostaniemy w konkretnym punkcie czasu
'''
time = np.arange(0, 10, 0.01)
y2_time = np.arange(0, 10, 0.01)
y2_lambda = sp.lambdify(t, y2, modules=['numpy', 'sympy'])
'''
Z powodu implementacji Heaviside w SymPy'u obecna funkcja nie bedzie mogla zostac wyliczona,
dla 0, dlatego wpisujemy jej wartosc, dla 0 reczne
'''
y2_time[0] = 1.0
for each in range(1, len(time)):
y2_time[each] = y2_lambda(time[each])
plt.plot(time, y2_time, label=("$y_{2}(t)$"))
plt.grid(True)
plt.title("Odpowiedz "+"$"+"y_{2}(t) = "+sp.latex(y2)+"$")
plt.xlabel("Czas[s]")
plt.ylabel("Amplituda")
plt.legend()
plt.show()
```
#### Teraz możemy końcowo dodać nasze dwie otrzymane funkcje $y_{1}(t)$ oraz $y_{2}(t)$:
$$ y(t) = y_{1}(t) + y_{2}(t) = 3e^{-t} - \frac{5}{2}e^{-2t} + \frac{1}{2} $$
Następnie rysujemy otrzymane $y(t)$ wraz z $y_{1}(t) + y_{2}(t)$, dla porównania:
```
y = y1+y2
y
# y1(t)
plt.plot(time, y1_time, label=("$y_{1}(t)$"))
# y2(t)
plt.plot(time, y2_time, label=("$y_{2}(t)$"))
plt.plot(time, y1_time+y2_time, label=("$y(t)=y_{1}(t)+y_{2}(t)$"))
plt.grid(True)
plt.title("Odpowiedz "+"$"+"y_{1}(t), y_{2}(t), y(t)"+"$")
plt.xlabel("Czas[s]")
plt.ylabel("Amplituda")
plt.legend()
plt.show()
```
### Przykład zastosowania
Przykładem zjawiska fizycznego, które jest opisywane za pomocą równania różniczkoweo drugiego stopnia jest sprężyna, której drgania są tłumione przez otoczenie (np.: gęsty gaz, ciecz itp.). Taka sprężyna jest zwykle opisana w następujący sposób:
$$ mx^{\prime\prime}(t)+bx^{\prime}(t)+kx(t) = 0$$
Gdzie:
* m - masa
* b - stała np. współczcynnik tarcia, charakterystyczny, dla otoczenia
* k - stała np. współczynnik sprężystości, charakterystyczny, dla sprężyny
* $x(t)$ - jest wtedy pozycją na osi $x$
* $x^{\prime}(t)$ - jest wtedy prędkością na osi $x$
* $x^{\prime\prime}(t)$ - jest wtedy przyspieszeniem na osi $x$
Zajwiska opisywane tego stopnia równaniem są prawdopodobnie najczęściej spotykanymi.
### Wnioski
Matematyczny opis modeli fizycznych jest bardzo przydatny w inżynierii, pozwala nam opisać oraz przewidzieć zachowanie jakiegoś systemu. Zwłaszcza dzięki rozwiązaniom numerycznym, rysując odpowiedź jakiegoś modelu na jakieś wejście, dzieki takiej wizualizacji bardzo łatwo nam jest zrozumieć model.
Dodatkowo uważam, że forma zadania jest bardzo ciekawa, ale prosiłbym o więcej szczegółów apropos tego co Pan oczekuje/w jaki sposob Pan oczekuje, że wykonamy zadanie.
|
github_jupyter
|
# Biblioteka SymPy
import sympy as sp
# NumPy uzywanany do numerycznych operacji matematycznych
import numpy as np
# Matplotlib sluzacy do wizualizacji
import matplotlib.pyplot as plt
# Definiujemy obiekty biblioteki SymPy
t, y, s = sp.symbols('t y s')
# Tworzymy rownanie
Ys = 1/(s*(s+1)*(s+2))
Ys
Ys = Ys.apart()
Ys
y1 = sp.expand(sp.inverse_laplace_transform(Ys.apart(), s, t))
y1
# theta(t) to 1(t) w bibliotece SymPy
'''
"time" bedzie nasza osia czasu,
a y1_time odpowiedza jaka dostaniemy w konkretnym punkcie czasu
'''
time = np.arange(0, 10, 0.01)
y1_time = np.arange(0, 10, 0.01)
y1_lambda = sp.lambdify(t, y1, modules=['numpy', 'sympy'])
for each in range(0, len(time)):
y1_time[each] = y1_lambda(time[each])
sympy.utilities.lambdify(symfunc, implementation)
plt.plot(time, y1_time, label=("$y_{1}(t)$"))
plt.grid(True)
plt.title("Odpowiedz "+"$"+"y_{1}(t) = "+sp.latex(y1)+"$")
plt.xlabel("Czas[s]")
plt.ylabel("Amplituda")
plt.legend()
plt.show()
Ys = (s+5)/((s**2)+3*s+2)
Ys
Ys = Ys.factor()
Ys
Ys = Ys.apart()
Ys
y2 = sp.expand(sp.inverse_laplace_transform(Ys.apart(), s, t))
y2
'''
"time" bedzie nasza osia czasu,
a y2_time odpowiedza jaka dostaniemy w konkretnym punkcie czasu
'''
time = np.arange(0, 10, 0.01)
y2_time = np.arange(0, 10, 0.01)
y2_lambda = sp.lambdify(t, y2, modules=['numpy', 'sympy'])
'''
Z powodu implementacji Heaviside w SymPy'u obecna funkcja nie bedzie mogla zostac wyliczona,
dla 0, dlatego wpisujemy jej wartosc, dla 0 reczne
'''
y2_time[0] = 1.0
for each in range(1, len(time)):
y2_time[each] = y2_lambda(time[each])
plt.plot(time, y2_time, label=("$y_{2}(t)$"))
plt.grid(True)
plt.title("Odpowiedz "+"$"+"y_{2}(t) = "+sp.latex(y2)+"$")
plt.xlabel("Czas[s]")
plt.ylabel("Amplituda")
plt.legend()
plt.show()
y = y1+y2
y
# y1(t)
plt.plot(time, y1_time, label=("$y_{1}(t)$"))
# y2(t)
plt.plot(time, y2_time, label=("$y_{2}(t)$"))
plt.plot(time, y1_time+y2_time, label=("$y(t)=y_{1}(t)+y_{2}(t)$"))
plt.grid(True)
plt.title("Odpowiedz "+"$"+"y_{1}(t), y_{2}(t), y(t)"+"$")
plt.xlabel("Czas[s]")
plt.ylabel("Amplituda")
plt.legend()
plt.show()
| 0.176175 | 0.930015 |
# Формирование корпусов в csv-файлы
```
import pandas as pd
from os import listdir
import gzip
from csv import DictWriter
from tqdm.notebook import tqdm as tn
```
## Англо-русский набор
```
listdir('../../Desktop/eng-rus/')
path = '../../Desktop/eng-rus/'
inx_file = path + 'train.id.gz'
en_file = path + 'train.src.gz'
ru_file = path + 'train.trg.gz'
inx = gzip.open(inx_file, mode='r')
en = gzip.open(en_file, mode='r')
ru = gzip.open(ru_file, mode='r')
headers = ['INDEX','EN','RU']
with open(path + 'file.csv', 'w', encoding='utf-8') as f:
head = ",".join(headers)
f.write(f'{head}\n')
file = open(path + 'file.csv', 'a', newline='', encoding='utf-8')
s = 0
dictwriter_object = DictWriter(file, fieldnames=headers)
for i, e, r in tn(zip(inx, en, ru)):
i = i.decode('utf-8').strip().split()[0]
e = e.decode('utf-8').strip()
r = r.decode('utf-8').strip()
row = {'INDEX': i, 'EN': e,'RU': r}
dictwriter_object.writerow(row)
s += 1
if not s % 100000:
print('.', end='', sep='')
inx.close()
en.close()
ru.close()
file.close()
print(f'\nОбработано {s} предложений')
```
## Арабско-русский набор
```
path = '../../Desktop/ara-rus/'
inx_file = path + 'train.id.gz'
ar_file = path + 'train.src.gz'
ru_file = path + 'train.trg.gz'
inx = gzip.open(inx_file, mode='r')
ar = gzip.open(ar_file, mode='r')
ru = gzip.open(ru_file, mode='r')
headers = ['INDEX','AR','RU']
with open(path + 'file.csv', 'w', encoding='utf-8') as f:
head = ",".join(headers)
f.write(f'{head}\n')
file = open(path + 'file.csv', 'a', newline='', encoding='utf-8')
s = 0
dictwriter_object = DictWriter(file, fieldnames=headers)
for i, a, r in tn(zip(inx, en, ru)):
i = i.decode('utf-8').strip().split()[0]
a = a.decode('utf-8').strip()
r = r.decode('utf-8').strip()
row = {'INDEX': i, 'AR': a,'RU': r}
dictwriter_object.writerow(row)
s += 1
if not s % 100000:
print('.', end='', sep='')
inx.close()
ar.close()
ru.close()
file.close()
print(f'\nОбработано {s} предложений')
```
## Арабско-английский набор
```
path = '../../Desktop/ara-eng/'
inx_file = path + 'train.id.gz'
ar_file = path + 'train.src.gz'
en_file = path + 'train.trg.gz'
inx = gzip.open(inx_file, mode='r')
ar = gzip.open(ar_file, mode='r')
en = gzip.open(en_file, mode='r')
headers = ['INDEX','AR','EN']
with open(path + 'file.csv', 'w', encoding='utf-8') as f:
head = ",".join(headers)
f.write(f'{head}\n')
file = open(path + 'file.csv', 'a', newline='', encoding='utf-8')
s = 0
dictwriter_object = DictWriter(file, fieldnames=headers)
for i, a, e in tn(zip(inx, ar, en)):
i = i.decode('utf-8').strip().split()[0]
a = a.decode('utf-8').strip()
e = e.decode('utf-8').strip()
row = {'INDEX': i, 'AR': a,'EN': e}
dictwriter_object.writerow(row)
s += 1
if not s % 100000:
print('.', end='', sep='')
inx.close()
ar.close()
en.close()
file.close()
print(f'\nОбработано {s} предложений')
```
|
github_jupyter
|
import pandas as pd
from os import listdir
import gzip
from csv import DictWriter
from tqdm.notebook import tqdm as tn
listdir('../../Desktop/eng-rus/')
path = '../../Desktop/eng-rus/'
inx_file = path + 'train.id.gz'
en_file = path + 'train.src.gz'
ru_file = path + 'train.trg.gz'
inx = gzip.open(inx_file, mode='r')
en = gzip.open(en_file, mode='r')
ru = gzip.open(ru_file, mode='r')
headers = ['INDEX','EN','RU']
with open(path + 'file.csv', 'w', encoding='utf-8') as f:
head = ",".join(headers)
f.write(f'{head}\n')
file = open(path + 'file.csv', 'a', newline='', encoding='utf-8')
s = 0
dictwriter_object = DictWriter(file, fieldnames=headers)
for i, e, r in tn(zip(inx, en, ru)):
i = i.decode('utf-8').strip().split()[0]
e = e.decode('utf-8').strip()
r = r.decode('utf-8').strip()
row = {'INDEX': i, 'EN': e,'RU': r}
dictwriter_object.writerow(row)
s += 1
if not s % 100000:
print('.', end='', sep='')
inx.close()
en.close()
ru.close()
file.close()
print(f'\nОбработано {s} предложений')
path = '../../Desktop/ara-rus/'
inx_file = path + 'train.id.gz'
ar_file = path + 'train.src.gz'
ru_file = path + 'train.trg.gz'
inx = gzip.open(inx_file, mode='r')
ar = gzip.open(ar_file, mode='r')
ru = gzip.open(ru_file, mode='r')
headers = ['INDEX','AR','RU']
with open(path + 'file.csv', 'w', encoding='utf-8') as f:
head = ",".join(headers)
f.write(f'{head}\n')
file = open(path + 'file.csv', 'a', newline='', encoding='utf-8')
s = 0
dictwriter_object = DictWriter(file, fieldnames=headers)
for i, a, r in tn(zip(inx, en, ru)):
i = i.decode('utf-8').strip().split()[0]
a = a.decode('utf-8').strip()
r = r.decode('utf-8').strip()
row = {'INDEX': i, 'AR': a,'RU': r}
dictwriter_object.writerow(row)
s += 1
if not s % 100000:
print('.', end='', sep='')
inx.close()
ar.close()
ru.close()
file.close()
print(f'\nОбработано {s} предложений')
path = '../../Desktop/ara-eng/'
inx_file = path + 'train.id.gz'
ar_file = path + 'train.src.gz'
en_file = path + 'train.trg.gz'
inx = gzip.open(inx_file, mode='r')
ar = gzip.open(ar_file, mode='r')
en = gzip.open(en_file, mode='r')
headers = ['INDEX','AR','EN']
with open(path + 'file.csv', 'w', encoding='utf-8') as f:
head = ",".join(headers)
f.write(f'{head}\n')
file = open(path + 'file.csv', 'a', newline='', encoding='utf-8')
s = 0
dictwriter_object = DictWriter(file, fieldnames=headers)
for i, a, e in tn(zip(inx, ar, en)):
i = i.decode('utf-8').strip().split()[0]
a = a.decode('utf-8').strip()
e = e.decode('utf-8').strip()
row = {'INDEX': i, 'AR': a,'EN': e}
dictwriter_object.writerow(row)
s += 1
if not s % 100000:
print('.', end='', sep='')
inx.close()
ar.close()
en.close()
file.close()
print(f'\nОбработано {s} предложений')
| 0.046217 | 0.456289 |
# Reference
This example is taken from the book [DL with Python](https://www.manning.com/books/deep-learning-with-python) by F. Chollet.
All the notebooks from the book are available for free on [Github](https://github.com/fchollet/deep-learning-with-python-notebooks)
If you like to run the example locally follow the instructions provided on [Keras website](https://keras.io/#installation)
---
```
import keras
keras.__version__
```
# Understanding recurrent neural networks
This notebook contains the code samples found in Chapter 6, Section 2 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
---
[...]
## A first recurrent layer in Keras
The process we just naively implemented in Numpy corresponds to an actual Keras layer: the `SimpleRNN` layer:
```
from keras.layers import SimpleRNN
```
There is just one minor difference: `SimpleRNN` processes batches of sequences, like all other Keras layers, not just a single sequence like
in our Numpy example. This means that it takes inputs of shape `(batch_size, timesteps, input_features)`, rather than `(timesteps,
input_features)`.
Like all recurrent layers in Keras, `SimpleRNN` can be run in two different modes: it can return either the full sequences of successive
outputs for each timestep (a 3D tensor of shape `(batch_size, timesteps, output_features)`), or it can return only the last output for each
input sequence (a 2D tensor of shape `(batch_size, output_features)`). These two modes are controlled by the `return_sequences` constructor
argument. Let's take a look at an example:
```
from keras.models import Sequential
from keras.layers import Embedding, SimpleRNN
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32))
model.summary()
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.summary()
```
It is sometimes useful to stack several recurrent layers one after the other in order to increase the representational power of a network.
In such a setup, you have to get all intermediate layers to return full sequences:
```
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32)) # This last layer only returns the last outputs.
model.summary()
```
Now let's try to use such a model on the IMDB movie review classification problem. First, let's preprocess the data:
```
from keras.datasets import imdb
from keras.preprocessing import sequence
max_features = 10000 # number of words to consider as features
maxlen = 500 # cut texts after this number of words (among top max_features most common words)
batch_size = 32
print('Loading data...')
(input_train, y_train), (input_test, y_test) = imdb.load_data(num_words=max_features)
print(len(input_train), 'train sequences')
print(len(input_test), 'test sequences')
print('Pad sequences (samples x time)')
input_train = sequence.pad_sequences(input_train, maxlen=maxlen)
input_test = sequence.pad_sequences(input_test, maxlen=maxlen)
print('input_train shape:', input_train.shape)
print('input_test shape:', input_test.shape)
```
Let's train a simple recurrent network using an `Embedding` layer and a `SimpleRNN` layer:
```
from keras.layers import Dense
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
```
Let's display the training and validation loss and accuracy:
```
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
As a reminder, in chapter 3, our very first naive approach to this very dataset got us to 88% test accuracy. Unfortunately, our small
recurrent network doesn't perform very well at all compared to this baseline (only up to 85% validation accuracy). Part of the problem is
that our inputs only consider the first 500 words rather the full sequences --
hence our RNN has access to less information than our earlier baseline model. The remainder of the problem is simply that `SimpleRNN` isn't very good at processing long sequences, like text. Other types of recurrent layers perform much better. Let's take a look at some
more advanced layers.
[...]
## A concrete LSTM example in Keras
Now let's switch to more practical concerns: we will set up a model using a LSTM layer and train it on the IMDB data. Here's the network,
similar to the one with `SimpleRNN` that we just presented. We only specify the output dimensionality of the LSTM layer, and leave every
other argument (there are lots) to the Keras defaults. Keras has good defaults, and things will almost always "just work" without you
having to spend time tuning parameters by hand.
```
from keras.layers import LSTM
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(LSTM(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
|
github_jupyter
|
import keras
keras.__version__
from keras.layers import SimpleRNN
from keras.models import Sequential
from keras.layers import Embedding, SimpleRNN
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32))
model.summary()
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.summary()
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32)) # This last layer only returns the last outputs.
model.summary()
from keras.datasets import imdb
from keras.preprocessing import sequence
max_features = 10000 # number of words to consider as features
maxlen = 500 # cut texts after this number of words (among top max_features most common words)
batch_size = 32
print('Loading data...')
(input_train, y_train), (input_test, y_test) = imdb.load_data(num_words=max_features)
print(len(input_train), 'train sequences')
print(len(input_test), 'test sequences')
print('Pad sequences (samples x time)')
input_train = sequence.pad_sequences(input_train, maxlen=maxlen)
input_test = sequence.pad_sequences(input_test, maxlen=maxlen)
print('input_train shape:', input_train.shape)
print('input_test shape:', input_test.shape)
from keras.layers import Dense
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
from keras.layers import LSTM
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(LSTM(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
| 0.912853 | 0.981131 |
```
import pandas as pd
import pandas as pd
import re
import nltk
from nltk.tokenize.stanford_segmenter import StanfordSegmenter
import os
java_path = "C:\\Program Files\\Java\\jdk1.8.0_131\\bin\\java.exe"
slf4j_path ='C:\\stanford-segmenter\\slf4j-api.jar'
stanford_models_paths = 'C:\\stanford-segmenter\\data'
classpath = 'C:\\stanford-segmenter\\slf4j-api.jar;C:\\stanford-segmenter\\stanford-segmenter.jar'
nltk.internals.config_java(java_path)
os.environ['JAVAHOME'] = java_path
os.environ['SLF4J'] =slf4j_path
os.environ['STANFORD_MODELS'] =stanford_models_paths
os.environ['CLASSPATH'] = classpath
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def get_emojis(string):
pattern = re.compile(u'['
u'\U0001F300-\U0001F64F'
u'\U0001F680-\U0001F6FF'
u'\u2600-\u26FF\u2700-\u27BF]+', re.UNICODE)
iterator = re.findall(pattern, string)
emojis = []
for emoji in iterator:
for m in emoji:
emojis.append(m)
return emojis
def preprocessing(string):
string = re.sub(r'\s+', ' ', string)
string = re.sub(r'[A-Za-z]', ' ', string)
return re.sub(r"\s{2,}", " ", string).strip()
def get_num_numbers(string):
regex = re.compile(r"(\d|[\u0660\u0661\u0662\u0663\u0664\u0665\u0666\u0667\u0668\u0669])+")
return len(re.findall(regex, string))
def get_num_emojis(string):
return len(get_emojis(string))
def get_spaces_ratio(string):
regex =re.compile(r"\s")
num_epaces = len(re.findall(regex, string))
num_carracters= len(string)
return num_epaces/num_carracters
def get_numeric_ratio(string):
regex =re.compile(r"\d")
num_numeric = len(re.findall(regex, string))
num_carracters= len(string)
return num_numeric/num_carracters
def get_max_length(string):
lengths= [len(s) for s in string.split()]
return max(lengths)
def get_min_length(string):
lengths= [len(s) for s in string.split()]
return min(lengths)
def get_num_words(string):
return len(string.split())
def get_num_short_words(string):
short_words = [1 if len(s)<4 else 0 for s in string.split()]
return sum(short_words)
def get_num_unique_words(string):
return len(set(string.split()))
def get_num_stopwords(string):
stopwords = open('./data/stopwords.txt',encoding='utf8').read().split()
counter = [1 if word in stopwords else 0 for word in string.split()]
return sum(counter)
tokenizer = StanfordSegmenter()
tokenizer.default_config('ar')
```
def tokenize(string):
tokens = string.split()
sentence_tekonizeds = tokenizer.segment(tokens)
return re.sub(r'\s+', ' ', sentence_tekonizeds)
```
from sklearn.preprocessing import normalize
file_name ='./data/dataexcel.xlsx'
df = pd.read_excel(file_name)
df = df[['sexe','comment']].copy()
df['text'] =df.comment.apply(preprocessing)
df['text'].replace('', np.nan, inplace=True)
df.dropna(inplace=True)
df.reset_index()
print('done')
sentences = [string.split() for string in df.text.values]
sentences = tokenizer.segment_sents(sentences).split('\n')
sentencess = [string for string in sentences if len(string)>0 ]
s1 = pd.DataFrame(sentencess,columns=['text'])
df = df.assign(etext=s1.text.values)
df['etext'] =df.comment.apply(preprocessing)
df['sexe'].replace('f', 'F', inplace=True)
df['num_emojis'] =df.comment.apply(get_num_emojis)
df['spaces_ratio'] =df.comment.apply(get_spaces_ratio)
df['numeric_ratio'] =df.comment.apply(get_numeric_ratio)
df['max_length'] =df.comment.apply(get_max_length)
df['min_length'] =df.comment.apply(get_min_length)
df['num_words'] =df.comment.apply(get_num_words)
df['num_short_words'] =df.comment.apply(get_num_short_words)
df['num_unique_words'] =df.comment.apply(get_num_unique_words)
df['num_carracters'] = df.comment.apply(len)
df['num_stopwords'] =df.comment.apply(get_num_stopwords)
#df.columns=['sexe','comment','text','etext','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
#df_norm = df[['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']].copy()
#df.sexe.value_counts()
#df[['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']] = (df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']] - df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].mean()) / (df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].max() - df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].min())
df[['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']] = (df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']] - df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].mean()) / (df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].max() - df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].min())
df.columns
from nltk.tag import StanfordPOSTagger
java_path = "C:\\Program Files\\Java\\jdk1.8.0_131\\bin\\java.exe"
slf4j_path ='C:\\stanford-segmenter\\slf4j-api.jar'
stanford_models_paths = 'C:\\stanford-postagger\\models'
classpath = 'C:\\stanford-postagger\\stanford-postagger.jar'
nltk.internals.config_java(java_path)
os.environ['JAVAHOME'] = java_path
os.environ['SLF4J'] =slf4j_path
os.environ['STANFORD_MODELS'] =stanford_models_paths
os.environ['CLASSPATH'] = classpath
arabic_tager ='C:\stanford-postagger\\models\\arabic.tagger'
def get_num_of_pos(pos,string):
return len(re.findall(pos,string))
#list(set(re.findall(r'[A-Z]+',string)))
POSs=['VBN', 'DTJJ', 'WP', 'JJR', 'NNS', 'VBG', 'RB', 'DTNN', 'VN', 'PUNC', 'DTJJR', 'NNP', 'UH', 'NN', 'VBD', 'DTNNPS', 'CC', 'DT', 'IN', 'NOUN', 'VB', 'CD', 'DTNNS', 'RP', 'PRP', 'VBP', 'WRB', 'ADJ', 'DTNNP', 'JJ']
tagger = StanfordPOSTagger(arabic_tager)
def tag(string):
return ' '.join(reversed([w[1] for w in string]))
def tag_sents(sentences):
return [tag(sentence) for sentence in sentences]
sentences =[s.split() for s in df.etext.values]
sentences_tags = tagger.tag_sents(sentences)
sents = tag_sents(sentences_tags)
s1 = pd.DataFrame(sents,columns=['pos_text'])
df = df.assign(pos_text=s1.pos_text.values)
for pos in POSs:
df[pos]=0
for pos in POSs:
for index,row in df.iterrows():
df.loc[index,pos]= get_num_of_pos(pos,row.pos_text)
df.to_json('df.json',orient='records')
df.columns
df = pd.read_json('df.json',encoding='utf8')
df.columns
```
|
github_jupyter
|
import pandas as pd
import pandas as pd
import re
import nltk
from nltk.tokenize.stanford_segmenter import StanfordSegmenter
import os
java_path = "C:\\Program Files\\Java\\jdk1.8.0_131\\bin\\java.exe"
slf4j_path ='C:\\stanford-segmenter\\slf4j-api.jar'
stanford_models_paths = 'C:\\stanford-segmenter\\data'
classpath = 'C:\\stanford-segmenter\\slf4j-api.jar;C:\\stanford-segmenter\\stanford-segmenter.jar'
nltk.internals.config_java(java_path)
os.environ['JAVAHOME'] = java_path
os.environ['SLF4J'] =slf4j_path
os.environ['STANFORD_MODELS'] =stanford_models_paths
os.environ['CLASSPATH'] = classpath
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def get_emojis(string):
pattern = re.compile(u'['
u'\U0001F300-\U0001F64F'
u'\U0001F680-\U0001F6FF'
u'\u2600-\u26FF\u2700-\u27BF]+', re.UNICODE)
iterator = re.findall(pattern, string)
emojis = []
for emoji in iterator:
for m in emoji:
emojis.append(m)
return emojis
def preprocessing(string):
string = re.sub(r'\s+', ' ', string)
string = re.sub(r'[A-Za-z]', ' ', string)
return re.sub(r"\s{2,}", " ", string).strip()
def get_num_numbers(string):
regex = re.compile(r"(\d|[\u0660\u0661\u0662\u0663\u0664\u0665\u0666\u0667\u0668\u0669])+")
return len(re.findall(regex, string))
def get_num_emojis(string):
return len(get_emojis(string))
def get_spaces_ratio(string):
regex =re.compile(r"\s")
num_epaces = len(re.findall(regex, string))
num_carracters= len(string)
return num_epaces/num_carracters
def get_numeric_ratio(string):
regex =re.compile(r"\d")
num_numeric = len(re.findall(regex, string))
num_carracters= len(string)
return num_numeric/num_carracters
def get_max_length(string):
lengths= [len(s) for s in string.split()]
return max(lengths)
def get_min_length(string):
lengths= [len(s) for s in string.split()]
return min(lengths)
def get_num_words(string):
return len(string.split())
def get_num_short_words(string):
short_words = [1 if len(s)<4 else 0 for s in string.split()]
return sum(short_words)
def get_num_unique_words(string):
return len(set(string.split()))
def get_num_stopwords(string):
stopwords = open('./data/stopwords.txt',encoding='utf8').read().split()
counter = [1 if word in stopwords else 0 for word in string.split()]
return sum(counter)
tokenizer = StanfordSegmenter()
tokenizer.default_config('ar')
from sklearn.preprocessing import normalize
file_name ='./data/dataexcel.xlsx'
df = pd.read_excel(file_name)
df = df[['sexe','comment']].copy()
df['text'] =df.comment.apply(preprocessing)
df['text'].replace('', np.nan, inplace=True)
df.dropna(inplace=True)
df.reset_index()
print('done')
sentences = [string.split() for string in df.text.values]
sentences = tokenizer.segment_sents(sentences).split('\n')
sentencess = [string for string in sentences if len(string)>0 ]
s1 = pd.DataFrame(sentencess,columns=['text'])
df = df.assign(etext=s1.text.values)
df['etext'] =df.comment.apply(preprocessing)
df['sexe'].replace('f', 'F', inplace=True)
df['num_emojis'] =df.comment.apply(get_num_emojis)
df['spaces_ratio'] =df.comment.apply(get_spaces_ratio)
df['numeric_ratio'] =df.comment.apply(get_numeric_ratio)
df['max_length'] =df.comment.apply(get_max_length)
df['min_length'] =df.comment.apply(get_min_length)
df['num_words'] =df.comment.apply(get_num_words)
df['num_short_words'] =df.comment.apply(get_num_short_words)
df['num_unique_words'] =df.comment.apply(get_num_unique_words)
df['num_carracters'] = df.comment.apply(len)
df['num_stopwords'] =df.comment.apply(get_num_stopwords)
#df.columns=['sexe','comment','text','etext','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
#df_norm = df[['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']].copy()
#df.sexe.value_counts()
#df[['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']] = (df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']] - df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].mean()) / (df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].max() - df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].min())
df[['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']] = (df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']] - df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].mean()) / (df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].max() - df[['num_emojis','spaces_ratio','numeric_ratio','max_length','min_length','num_words','num_short_words','num_unique_words','num_carracters','num_stopwords']].min())
df.columns
from nltk.tag import StanfordPOSTagger
java_path = "C:\\Program Files\\Java\\jdk1.8.0_131\\bin\\java.exe"
slf4j_path ='C:\\stanford-segmenter\\slf4j-api.jar'
stanford_models_paths = 'C:\\stanford-postagger\\models'
classpath = 'C:\\stanford-postagger\\stanford-postagger.jar'
nltk.internals.config_java(java_path)
os.environ['JAVAHOME'] = java_path
os.environ['SLF4J'] =slf4j_path
os.environ['STANFORD_MODELS'] =stanford_models_paths
os.environ['CLASSPATH'] = classpath
arabic_tager ='C:\stanford-postagger\\models\\arabic.tagger'
def get_num_of_pos(pos,string):
return len(re.findall(pos,string))
#list(set(re.findall(r'[A-Z]+',string)))
POSs=['VBN', 'DTJJ', 'WP', 'JJR', 'NNS', 'VBG', 'RB', 'DTNN', 'VN', 'PUNC', 'DTJJR', 'NNP', 'UH', 'NN', 'VBD', 'DTNNPS', 'CC', 'DT', 'IN', 'NOUN', 'VB', 'CD', 'DTNNS', 'RP', 'PRP', 'VBP', 'WRB', 'ADJ', 'DTNNP', 'JJ']
tagger = StanfordPOSTagger(arabic_tager)
def tag(string):
return ' '.join(reversed([w[1] for w in string]))
def tag_sents(sentences):
return [tag(sentence) for sentence in sentences]
sentences =[s.split() for s in df.etext.values]
sentences_tags = tagger.tag_sents(sentences)
sents = tag_sents(sentences_tags)
s1 = pd.DataFrame(sents,columns=['pos_text'])
df = df.assign(pos_text=s1.pos_text.values)
for pos in POSs:
df[pos]=0
for pos in POSs:
for index,row in df.iterrows():
df.loc[index,pos]= get_num_of_pos(pos,row.pos_text)
df.to_json('df.json',orient='records')
df.columns
df = pd.read_json('df.json',encoding='utf8')
df.columns
| 0.309232 | 0.259386 |
```
import pandas as pd
import copy
from matplotlib import pyplot as plt
import numpy as np
# ***************************************** DEATHS *****************************************
total_deaths_number = pd.read_csv("../randvaccine/results/corona_n_dead{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
total_sus_number = pd.read_csv("../randvaccine/results/corona_n_susceptible{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
total_inf_number = pd.read_csv("../randvaccine/results/corona_n_infected{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
total_rec_number = pd.read_csv("../randvaccine/results/corona_n_recovered{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
total_vac_number = pd.read_csv("../randvaccine/results/corona_#V__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
mean_deaths_number = total_deaths_number["mean"]
mean_sus_number = total_sus_number["mean"]
mean_inf_number = total_inf_number["mean"]
mean_rec_number = total_rec_number["mean"]
mean_vac_number = total_vac_number["mean"]
mean_deaths = pd.concat([mean_sus_number, mean_inf_number, mean_rec_number, mean_deaths_number, mean_vac_number], axis=1)
f = plt.figure()
plt.plot(mean_deaths, label=["Susceptible", "Infected", "Recovered", "Dead", "Vaccinated"])
plt.legend()
f.savefig("../total_results/randvaccine_distribution.pdf")
total_deaths_number = pd.read_csv("../randvaccine/results/corona_n_dead{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
f = plt.figure()
plt.plot(total_deaths_number["mean"], label="Dead", color="red")
plt.yticks(range(0, 201, 20))
plt.legend()
print(total_deaths_number["mean"].values[-1])
print(total_deaths_number["std_dev"].values[-1])
# f.savefig("../total_results/randvaccine_deaths.pdf")
n_dead = copy.deepcopy(total_deaths_number)
dead_vals = n_dead["mean"].values
dead_inc = []
for i in range(1, len(dead_vals)):
#print(dead_vals[i])
dead_inc.append(abs(dead_vals[i] - dead_vals[i-1]))
mean_dead_inc = [dead_inc[i-7:i] for i in range(7, len(dead_inc))]
mean_dead_inc = list(map(lambda x: np.mean(x), mean_dead_inc))
index = 0
for i, d in enumerate(dead_inc):
if d < 0.05:
index = i
print(i)
break
f = plt.figure()
plt.hlines(mean_dead_inc[index], 0, 2190, linestyles="dashed", colors="green", label="threshold")
plt.vlines(index, 0, 0.6, linestyles="dotted", colors="black")
plt.plot(dead_inc, label="Deaths increment per t.u.")
plt.plot(mean_dead_inc, label="Mean Deaths increment per t.u.")
plt.legend()
# f.savefig("../total_results/randvaccine_deaths_increment.pdf")
# *************************************************** POSITIVES *************************************************
total_positives_number = pd.read_csv("../randvaccine/results/corona_n_infected{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
n_positives = copy.deepcopy(total_positives_number)
positives_vals = n_positives["mean"].values
positives_inc = []
for i in range(1, len(positives_vals)):
#print(positives_vals[i])
positives_inc.append(abs(positives_vals[i] - positives_vals[i-1]))
mean_positives_inc = [positives_inc[i-7:i] for i in range(7, len(positives_inc))]
mean_positives_inc = list(map(lambda x: np.mean(x), mean_positives_inc))
glob_mean_inc = np.average(positives_inc[:1000])
print(glob_mean_inc)
glob_pos_std_dev_inc = [glob_mean_inc + np.std(positives_inc[:1000])] * len(positives_inc)
glob_neg_std_dev_inc = [glob_mean_inc - np.std(positives_inc[:1000])] * len(positives_inc)
glob_mean_inc = [glob_mean_inc] * len(positives_inc)
f = plt.figure()
plt.plot(positives_inc, label="Infections increment per t.u.")
plt.plot(mean_positives_inc, label="Mean Infections increment per t.u.")
plt.plot(glob_mean_inc, label="Average increment per t.u.")
plt.plot(glob_pos_std_dev_inc, label="Positive standard deviation per t.u.")
plt.plot(glob_neg_std_dev_inc, label="Negative standard deviation per t.u.")
plt.legend()
f.savefig("../total_results/randvaccine_positives_increment.pdf")
index_max_positives_mean = np.argmax(total_positives_number["mean"])
max_positives_mean = total_positives_number["mean"][index_max_positives_mean]
max_positives_dev = total_positives_number["std_dev"][index_max_positives_mean]
print(index_max_positives_mean, max_positives_mean, max_positives_dev)
```
|
github_jupyter
|
import pandas as pd
import copy
from matplotlib import pyplot as plt
import numpy as np
# ***************************************** DEATHS *****************************************
total_deaths_number = pd.read_csv("../randvaccine/results/corona_n_dead{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
total_sus_number = pd.read_csv("../randvaccine/results/corona_n_susceptible{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
total_inf_number = pd.read_csv("../randvaccine/results/corona_n_infected{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
total_rec_number = pd.read_csv("../randvaccine/results/corona_n_recovered{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
total_vac_number = pd.read_csv("../randvaccine/results/corona_#V__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
mean_deaths_number = total_deaths_number["mean"]
mean_sus_number = total_sus_number["mean"]
mean_inf_number = total_inf_number["mean"]
mean_rec_number = total_rec_number["mean"]
mean_vac_number = total_vac_number["mean"]
mean_deaths = pd.concat([mean_sus_number, mean_inf_number, mean_rec_number, mean_deaths_number, mean_vac_number], axis=1)
f = plt.figure()
plt.plot(mean_deaths, label=["Susceptible", "Infected", "Recovered", "Dead", "Vaccinated"])
plt.legend()
f.savefig("../total_results/randvaccine_distribution.pdf")
total_deaths_number = pd.read_csv("../randvaccine/results/corona_n_dead{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
f = plt.figure()
plt.plot(total_deaths_number["mean"], label="Dead", color="red")
plt.yticks(range(0, 201, 20))
plt.legend()
print(total_deaths_number["mean"].values[-1])
print(total_deaths_number["std_dev"].values[-1])
# f.savefig("../total_results/randvaccine_deaths.pdf")
n_dead = copy.deepcopy(total_deaths_number)
dead_vals = n_dead["mean"].values
dead_inc = []
for i in range(1, len(dead_vals)):
#print(dead_vals[i])
dead_inc.append(abs(dead_vals[i] - dead_vals[i-1]))
mean_dead_inc = [dead_inc[i-7:i] for i in range(7, len(dead_inc))]
mean_dead_inc = list(map(lambda x: np.mean(x), mean_dead_inc))
index = 0
for i, d in enumerate(dead_inc):
if d < 0.05:
index = i
print(i)
break
f = plt.figure()
plt.hlines(mean_dead_inc[index], 0, 2190, linestyles="dashed", colors="green", label="threshold")
plt.vlines(index, 0, 0.6, linestyles="dotted", colors="black")
plt.plot(dead_inc, label="Deaths increment per t.u.")
plt.plot(mean_dead_inc, label="Mean Deaths increment per t.u.")
plt.legend()
# f.savefig("../total_results/randvaccine_deaths_increment.pdf")
# *************************************************** POSITIVES *************************************************
total_positives_number = pd.read_csv("../randvaccine/results/corona_n_infected{}__.csv", sep=";", names=['t.u.', 'mean', 'variance', 'std_dev'])
n_positives = copy.deepcopy(total_positives_number)
positives_vals = n_positives["mean"].values
positives_inc = []
for i in range(1, len(positives_vals)):
#print(positives_vals[i])
positives_inc.append(abs(positives_vals[i] - positives_vals[i-1]))
mean_positives_inc = [positives_inc[i-7:i] for i in range(7, len(positives_inc))]
mean_positives_inc = list(map(lambda x: np.mean(x), mean_positives_inc))
glob_mean_inc = np.average(positives_inc[:1000])
print(glob_mean_inc)
glob_pos_std_dev_inc = [glob_mean_inc + np.std(positives_inc[:1000])] * len(positives_inc)
glob_neg_std_dev_inc = [glob_mean_inc - np.std(positives_inc[:1000])] * len(positives_inc)
glob_mean_inc = [glob_mean_inc] * len(positives_inc)
f = plt.figure()
plt.plot(positives_inc, label="Infections increment per t.u.")
plt.plot(mean_positives_inc, label="Mean Infections increment per t.u.")
plt.plot(glob_mean_inc, label="Average increment per t.u.")
plt.plot(glob_pos_std_dev_inc, label="Positive standard deviation per t.u.")
plt.plot(glob_neg_std_dev_inc, label="Negative standard deviation per t.u.")
plt.legend()
f.savefig("../total_results/randvaccine_positives_increment.pdf")
index_max_positives_mean = np.argmax(total_positives_number["mean"])
max_positives_mean = total_positives_number["mean"][index_max_positives_mean]
max_positives_dev = total_positives_number["std_dev"][index_max_positives_mean]
print(index_max_positives_mean, max_positives_mean, max_positives_dev)
| 0.267408 | 0.244938 |
```
import this
```
### Arithmetic Operators
| Symbol | Task Performed |
|----|---|
| + | Addition |
| - | Subtraction |
| / | division |
| % | mod |
| * | multiplication |
| // | floor division |
| ** | to the power of |
```
x = 2
y = 4
print(x+y)
print(x-y)
print(x*y)
print(x/y)
print(x//y)
print(y%x)
x**y
```
### Relational Operators
| Symbol | Task Performed |
|----|---|
| = | Assignment|
| == | True, if it is equal |
| != | True, if not equal to |
| < | less than |
| > | greater than |
| <= | less than or equal to |
| >= | greater than or equal to |
```
print(x==y)
print(x==2)
print(x!=y)
print(x>y)
print(x>2)
print(x>=2)
x>1 and y<10
x>1 or y<1
1 < x < 3
```
# Types
```
type
print(type(False))
print(type(1))
print(type(1.5))
```
## Boolean
```
bool
```
## integer, float
```
int
float
x = 1.3
type(x)
int(1.9)
```
## String
```
str(1)
s1 = 'Hi, this is Python course.'
s2 = "It's good to see you here!"
print(s1)
print(s2)
'aaaaaa'.capitalize()
s1.count('i')
s1.endswith('.')
# startswith
s1.find('P')
s1.index('H')
'-'.join(['1','2','3','4'])
s1.lower()
# upper
s1.replace('H','M')
s1.split(',')
'100'.zfill(4)
s1 = 'aaa'
s2 = 'bbb'
s1*2
s1+s2
```
## List
```
list
print(type([]))
print(type([1]))
x = [1,2,3,4,5,6,7,8,9,10]
x
x[4]
x[-3]
x[3:6]
x[2:-1]
x[2:]
x[:-4]
# [<begin>:<end>:<step>]
x[1:7:2]
x[::-1]
x*2
x+[4]
[1,2,3,'Hi',[],[1,2,3]]
x = [1,2,3]
x.append(5)
x
x.insert(3,6)
x
x.clear()
x
x.remove(1)
x
x.pop(2)
x.reverse()
x
x = [1,2,3,'Hi',[],[1,2,3]]
x[3]
```
## Dictionary
```
x={"a":1,4:10,12:[]}
print(type(x))
print(x)
print(x['a'])
x.keys()
```
### Other types
```
tuple
set
```
# Loop
```
for i in [1,2,3]:
print(i)
print('Hi')
print('Bye!')
list(range(10))
for i in range(3,10):
print(i)
n = 0
while n<10:
print(n)
n += 1
x = 1
while x>1e-4:
print(x)
x = x/5
```
# Condition control
```
if 3<2:
print('Hello!')
for i in range(10):
print(i)
if i%2==0:
continue
print(i)
n = 0
while True:
if n>10:
break
print(n)
n += 1
for i in range(4):
for j in range(2):
print(i,j)
```
# Functions
```
def echo(i):
print(i)
x = echo('Salaam!')
print(x)
def mean3(x,y,z):
return (x+y+z)/3.
m = mean3(2,3.5,6)
print(m)
func1 = lambda a, b, c : a + b +c
func1(1,2,3)
```
# IO
```
x = float(input('Enter the first number:'))
y = float(input('Enter the second number:'))
print('The result is: ',x+y)
# Python 2:
# y=raw_input()
f = open("./files/demofile.txt", "r")
for x in f:
print(x)
f.close()
f = open("./files/demofile2.txt", "w")
f.write("Woops! I have deleted the content!")
f.close()
f = open("./files/demofile3.txt", "a")
f.write("Now the file has more content!")
f.close()
```
# Print format
You can find a good reference [HERE](https://pyformat.info/).
```
print('The first variable is {} and the second variable is {}'.format('one', 'two'))
print('{:10}'.format('Alireza'))
print('{:10}'.format('Mona'))
print('{:10}'.format('Mahsa'))
print('{:>10}'.format('test'))
print('{:>10}'.format('Alireza'))
print('{:>10}'.format('Mona'))
print('{:>10}'.format('Mahsa'))
print('{:_>10}'.format('test'))
print('{:d}'.format(42))
print('{:04d}'.format(42))
print('{:2.3f}'.format(42))
print('{:06.4f}'.format(3.141592653589793))
```
# Exceptions
```
1.2/0
x = 6
if x > 5:
raise Exception('x should not exceed 5. The value of x was: {}'.format(x))
import sys
assert ('Windows' in sys.platform), "This code runs on Windows only."
x = 0
try:
print(10/x)
except:
print('The number you have chosen is not acceptable!')
```
# Modules
```
import something
import something as st
from something import echo as ech
import numpy as np
np.sqrt(2.)
from numpy import sqrt
sqrt(2.)
```
How to install Python modules:
pip install numpy
## Sys module
```
import sys
print(sys.argv)
sys.path
sys.exit(0)
```
## Os Module
```
import os
os.getcwd
os.listdir
os.mkdir
os.chdir
os.rename
os.path.exists()
os.path.isdir
os.path.isfile
```
## Time module
```
import time
x = time.time()
time.sleep(2)
time.time()-x
time.time()
?time.time
```
# Object oriented programming
```
print(type(3))
from numpy import mean
class Classroom:
def __init__(self, name, teacher, number_of_students, makrs):
self.name = name
self.teacher = teacher
self.number_of_students = number_of_students
self.makrs = makrs
assert len(makrs)==number_of_students, 'NUmber of students does not match the marks list.'
def average(self):
print(mean(self.makrs))
classroom_1 = Classroom('A', 'Javad', 5, [20,19,17,19,16])
classroom_1.number_of_students
classroom_1.average()
classroom_2 = Classroom('B', 'Zahra', 7, [20,19,17,19,16, 10, 11])
classroom_2.average()
class Power:
def __init__(self,pow_):
self.pow = pow_
def __call__(self,x):
for i in x:
print(i**self.pow)
x = [1,2,3,4,5,6]
pow2 = Power(2)
pow3 = Power(3)
pow2(x)
pow3(x)
```
# Init VS ini problem
```
class Classroom_false:
def __ini__(self, name, teacher, number_of_students, makrs):
self.name = name
self.teacher = teacher
self.number_of_students = number_of_students
self.makrs = makrs
assert len(makrs)==number_of_students, 'NUmber of students does not match the marks list.'
def average(self):
print(mean(self.makrs))
c1 = Classroom_false()
c1.__ini__('A', 'Javad', 5, [20,19,17,19,16])
```
## Let's make our own variable class
```
class Knowledge:
def __init__(self,know):
self.know = know
def __add__(self, x):
print(set(self.know+x.know))
ali_k = Knowledge('AB')
hassan_k = Knowledge('BCS')
# hassan_k.know
ali_k+hassan_k
```
# Questions
```
for i in range(10):
print(i, end = '-')
ss = input('Please input yout values (separate them by hyphen):')
ss.split('-')
```
|
github_jupyter
|
import this
x = 2
y = 4
print(x+y)
print(x-y)
print(x*y)
print(x/y)
print(x//y)
print(y%x)
x**y
print(x==y)
print(x==2)
print(x!=y)
print(x>y)
print(x>2)
print(x>=2)
x>1 and y<10
x>1 or y<1
1 < x < 3
type
print(type(False))
print(type(1))
print(type(1.5))
bool
int
float
x = 1.3
type(x)
int(1.9)
str(1)
s1 = 'Hi, this is Python course.'
s2 = "It's good to see you here!"
print(s1)
print(s2)
'aaaaaa'.capitalize()
s1.count('i')
s1.endswith('.')
# startswith
s1.find('P')
s1.index('H')
'-'.join(['1','2','3','4'])
s1.lower()
# upper
s1.replace('H','M')
s1.split(',')
'100'.zfill(4)
s1 = 'aaa'
s2 = 'bbb'
s1*2
s1+s2
list
print(type([]))
print(type([1]))
x = [1,2,3,4,5,6,7,8,9,10]
x
x[4]
x[-3]
x[3:6]
x[2:-1]
x[2:]
x[:-4]
# [<begin>:<end>:<step>]
x[1:7:2]
x[::-1]
x*2
x+[4]
[1,2,3,'Hi',[],[1,2,3]]
x = [1,2,3]
x.append(5)
x
x.insert(3,6)
x
x.clear()
x
x.remove(1)
x
x.pop(2)
x.reverse()
x
x = [1,2,3,'Hi',[],[1,2,3]]
x[3]
x={"a":1,4:10,12:[]}
print(type(x))
print(x)
print(x['a'])
x.keys()
tuple
set
for i in [1,2,3]:
print(i)
print('Hi')
print('Bye!')
list(range(10))
for i in range(3,10):
print(i)
n = 0
while n<10:
print(n)
n += 1
x = 1
while x>1e-4:
print(x)
x = x/5
if 3<2:
print('Hello!')
for i in range(10):
print(i)
if i%2==0:
continue
print(i)
n = 0
while True:
if n>10:
break
print(n)
n += 1
for i in range(4):
for j in range(2):
print(i,j)
def echo(i):
print(i)
x = echo('Salaam!')
print(x)
def mean3(x,y,z):
return (x+y+z)/3.
m = mean3(2,3.5,6)
print(m)
func1 = lambda a, b, c : a + b +c
func1(1,2,3)
x = float(input('Enter the first number:'))
y = float(input('Enter the second number:'))
print('The result is: ',x+y)
# Python 2:
# y=raw_input()
f = open("./files/demofile.txt", "r")
for x in f:
print(x)
f.close()
f = open("./files/demofile2.txt", "w")
f.write("Woops! I have deleted the content!")
f.close()
f = open("./files/demofile3.txt", "a")
f.write("Now the file has more content!")
f.close()
print('The first variable is {} and the second variable is {}'.format('one', 'two'))
print('{:10}'.format('Alireza'))
print('{:10}'.format('Mona'))
print('{:10}'.format('Mahsa'))
print('{:>10}'.format('test'))
print('{:>10}'.format('Alireza'))
print('{:>10}'.format('Mona'))
print('{:>10}'.format('Mahsa'))
print('{:_>10}'.format('test'))
print('{:d}'.format(42))
print('{:04d}'.format(42))
print('{:2.3f}'.format(42))
print('{:06.4f}'.format(3.141592653589793))
1.2/0
x = 6
if x > 5:
raise Exception('x should not exceed 5. The value of x was: {}'.format(x))
import sys
assert ('Windows' in sys.platform), "This code runs on Windows only."
x = 0
try:
print(10/x)
except:
print('The number you have chosen is not acceptable!')
import something
import something as st
from something import echo as ech
import numpy as np
np.sqrt(2.)
from numpy import sqrt
sqrt(2.)
import sys
print(sys.argv)
sys.path
sys.exit(0)
import os
os.getcwd
os.listdir
os.mkdir
os.chdir
os.rename
os.path.exists()
os.path.isdir
os.path.isfile
import time
x = time.time()
time.sleep(2)
time.time()-x
time.time()
?time.time
print(type(3))
from numpy import mean
class Classroom:
def __init__(self, name, teacher, number_of_students, makrs):
self.name = name
self.teacher = teacher
self.number_of_students = number_of_students
self.makrs = makrs
assert len(makrs)==number_of_students, 'NUmber of students does not match the marks list.'
def average(self):
print(mean(self.makrs))
classroom_1 = Classroom('A', 'Javad', 5, [20,19,17,19,16])
classroom_1.number_of_students
classroom_1.average()
classroom_2 = Classroom('B', 'Zahra', 7, [20,19,17,19,16, 10, 11])
classroom_2.average()
class Power:
def __init__(self,pow_):
self.pow = pow_
def __call__(self,x):
for i in x:
print(i**self.pow)
x = [1,2,3,4,5,6]
pow2 = Power(2)
pow3 = Power(3)
pow2(x)
pow3(x)
class Classroom_false:
def __ini__(self, name, teacher, number_of_students, makrs):
self.name = name
self.teacher = teacher
self.number_of_students = number_of_students
self.makrs = makrs
assert len(makrs)==number_of_students, 'NUmber of students does not match the marks list.'
def average(self):
print(mean(self.makrs))
c1 = Classroom_false()
c1.__ini__('A', 'Javad', 5, [20,19,17,19,16])
class Knowledge:
def __init__(self,know):
self.know = know
def __add__(self, x):
print(set(self.know+x.know))
ali_k = Knowledge('AB')
hassan_k = Knowledge('BCS')
# hassan_k.know
ali_k+hassan_k
for i in range(10):
print(i, end = '-')
ss = input('Please input yout values (separate them by hyphen):')
ss.split('-')
| 0.113052 | 0.839603 |
# Assignment 4
Using data from this [FiveThirtyEight](http://fivethirtyeight.com/datalab/opinions-about-the-iran-deal-are-more-about-obama-than-iran/) post, write code to calculate the correlation of the responses from the poll. Respond to the story in your PR. Is this a good example of data journalism? Why or why not?
Extracted polling info on [pages 20/21](http://www.foxnews.com/politics/interactive/2015/06/24/0624152016iranweb/) using [Tabula](http://tabula.technology/). (Astoundingly good results, if you leave the headers out)
```
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
```
# First for the Obama Love and Iran Deal Approval
```
df_Obama = pd.read_csv("data/Fox_polls - Obama Job.csv")
df_Iran_Deal = pd.read_csv("data/Fox_polls - Iran Deal.csv")
df_Iran_Nego = pd.read_csv("data/Fox_polls - Iran Nego.csv")
df_Obama.head(3)
df_Iran_Deal.head(3)
df_Obama_Iran_Deal = df_Obama.merge(df_Iran_Deal, left_on = 'Unnamed: 0', right_on='Unnamed: 0')
del df_Obama_Iran_Deal['Disapprove']
del df_Obama_Iran_Deal["(Don't know)_x"]
del df_Obama_Iran_Deal["Oppose"]
del df_Obama_Iran_Deal["(Don't know)_y"]
df_Obama_Iran_Deal.head(3)
df_Obama_Iran_Deal.columns = ['Group', 'Obama', 'Iran_Deal']
fig, ax = plt.subplots(figsize =(7,5))
#Font
csfont = {'fontname':'DIN Condensed'}
lm = smf.ols(formula='Iran_Deal~Obama',data=df_Obama_Iran_Deal).fit()
lm.params
Intercept, Obama_love = lm.params
df_Obama_Iran_Deal.plot(kind='scatter', x='Obama', y='Iran_Deal', ax= ax, color='tomato')
ax.plot(df_Obama_Iran_Deal["Obama"],Obama_love*df_Obama_Iran_Deal["Obama"]+Intercept,"-",color="green")
ax.set_axis_bgcolor("WhiteSmoke")
ax.set_ylabel('')
ax.xaxis.grid(color='darkgrey', linestyle=':', linewidth=0.5)
ax.yaxis.grid(color='darkgrey', linestyle=':', linewidth=0.5)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)
plt.tick_params(
#axis='x',
top='off',
which='off',
left='off',
right='off',
bottom='off',
labeltop='off',
labelbottom='off')
#labelling, getting rid of boarders
ax.set_xlabel('Obama Love', **csfont, fontsize=12)
ax.set_title("Obama Love versus approval of Iran Deal", **csfont, fontsize=24)
ax.set_ylabel('Iran Deal Approval', **csfont, fontsize=12)
ax.set_axisbelow(True)
```
# Now for Obama Love and Confidence in Negotiations with Iran
```
df_Obama.head()
df_Iran_Nego.head()
df_Iran_Nego['Confident'] = df_Iran_Nego['Very confident'] + df_Iran_Nego['Somewhat confident']
df_Obama_Iran_Nego = df_Obama.merge(df_Iran_Nego, left_on = 'Unnamed: 0', right_on='Unnamed: 0')
del df_Obama_Iran_Nego['Disapprove']
del df_Obama_Iran_Nego["(Don't know)_x"]
del df_Obama_Iran_Nego["Very confident"]
del df_Obama_Iran_Nego["Somewhat confident"]
del df_Obama_Iran_Nego['Not very confident']
del df_Obama_Iran_Nego["Not at all confident"]
del df_Obama_Iran_Nego["(Don't know)_y"]
df_Obama_Iran_Nego.head()
df_Obama_Iran_Nego.columns = ['Group', 'ObamaApp', 'Confidence']
df_Obama_Iran_Nego.head()
fig, ax = plt.subplots(figsize =(7,5))
#Font
csfont = {'fontname':'DIN Condensed'}
lm = smf.ols(formula='Confidence~ObamaApp',data=df_Obama_Iran_Nego).fit()
lm.params
Intercept, Obama_love = lm.params
df_Obama_Iran_Nego.plot(kind='scatter', x='ObamaApp', y='ObamaApp', ax= ax, color='tomato')
ax.plot(df_Obama_Iran_Nego["ObamaApp"],Obama_love*df_Obama_Iran_Nego["ObamaApp"]+Intercept,"-",color="green")
ax.set_axis_bgcolor("WhiteSmoke")
ax.set_ylabel('')
ax.xaxis.grid(color='darkgrey', linestyle=':', linewidth=0.5)
ax.yaxis.grid(color='darkgrey', linestyle=':', linewidth=0.5)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)
plt.tick_params(
#axis='x',
top='off',
which='off',
left='off',
right='off',
bottom='off',
labeltop='off',
labelbottom='off')
#labelling, getting rid of boarders
ax.set_xlabel('Obama Love', **csfont, fontsize=12)
ax.set_title("Obama Love versus confidence in Admins Negotiations", **csfont, fontsize=24)
ax.set_ylabel('Confindence in Negotiations', **csfont, fontsize=12)
ax.set_axisbelow(True)
```
|
github_jupyter
|
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
df_Obama = pd.read_csv("data/Fox_polls - Obama Job.csv")
df_Iran_Deal = pd.read_csv("data/Fox_polls - Iran Deal.csv")
df_Iran_Nego = pd.read_csv("data/Fox_polls - Iran Nego.csv")
df_Obama.head(3)
df_Iran_Deal.head(3)
df_Obama_Iran_Deal = df_Obama.merge(df_Iran_Deal, left_on = 'Unnamed: 0', right_on='Unnamed: 0')
del df_Obama_Iran_Deal['Disapprove']
del df_Obama_Iran_Deal["(Don't know)_x"]
del df_Obama_Iran_Deal["Oppose"]
del df_Obama_Iran_Deal["(Don't know)_y"]
df_Obama_Iran_Deal.head(3)
df_Obama_Iran_Deal.columns = ['Group', 'Obama', 'Iran_Deal']
fig, ax = plt.subplots(figsize =(7,5))
#Font
csfont = {'fontname':'DIN Condensed'}
lm = smf.ols(formula='Iran_Deal~Obama',data=df_Obama_Iran_Deal).fit()
lm.params
Intercept, Obama_love = lm.params
df_Obama_Iran_Deal.plot(kind='scatter', x='Obama', y='Iran_Deal', ax= ax, color='tomato')
ax.plot(df_Obama_Iran_Deal["Obama"],Obama_love*df_Obama_Iran_Deal["Obama"]+Intercept,"-",color="green")
ax.set_axis_bgcolor("WhiteSmoke")
ax.set_ylabel('')
ax.xaxis.grid(color='darkgrey', linestyle=':', linewidth=0.5)
ax.yaxis.grid(color='darkgrey', linestyle=':', linewidth=0.5)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)
plt.tick_params(
#axis='x',
top='off',
which='off',
left='off',
right='off',
bottom='off',
labeltop='off',
labelbottom='off')
#labelling, getting rid of boarders
ax.set_xlabel('Obama Love', **csfont, fontsize=12)
ax.set_title("Obama Love versus approval of Iran Deal", **csfont, fontsize=24)
ax.set_ylabel('Iran Deal Approval', **csfont, fontsize=12)
ax.set_axisbelow(True)
df_Obama.head()
df_Iran_Nego.head()
df_Iran_Nego['Confident'] = df_Iran_Nego['Very confident'] + df_Iran_Nego['Somewhat confident']
df_Obama_Iran_Nego = df_Obama.merge(df_Iran_Nego, left_on = 'Unnamed: 0', right_on='Unnamed: 0')
del df_Obama_Iran_Nego['Disapprove']
del df_Obama_Iran_Nego["(Don't know)_x"]
del df_Obama_Iran_Nego["Very confident"]
del df_Obama_Iran_Nego["Somewhat confident"]
del df_Obama_Iran_Nego['Not very confident']
del df_Obama_Iran_Nego["Not at all confident"]
del df_Obama_Iran_Nego["(Don't know)_y"]
df_Obama_Iran_Nego.head()
df_Obama_Iran_Nego.columns = ['Group', 'ObamaApp', 'Confidence']
df_Obama_Iran_Nego.head()
fig, ax = plt.subplots(figsize =(7,5))
#Font
csfont = {'fontname':'DIN Condensed'}
lm = smf.ols(formula='Confidence~ObamaApp',data=df_Obama_Iran_Nego).fit()
lm.params
Intercept, Obama_love = lm.params
df_Obama_Iran_Nego.plot(kind='scatter', x='ObamaApp', y='ObamaApp', ax= ax, color='tomato')
ax.plot(df_Obama_Iran_Nego["ObamaApp"],Obama_love*df_Obama_Iran_Nego["ObamaApp"]+Intercept,"-",color="green")
ax.set_axis_bgcolor("WhiteSmoke")
ax.set_ylabel('')
ax.xaxis.grid(color='darkgrey', linestyle=':', linewidth=0.5)
ax.yaxis.grid(color='darkgrey', linestyle=':', linewidth=0.5)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)
plt.tick_params(
#axis='x',
top='off',
which='off',
left='off',
right='off',
bottom='off',
labeltop='off',
labelbottom='off')
#labelling, getting rid of boarders
ax.set_xlabel('Obama Love', **csfont, fontsize=12)
ax.set_title("Obama Love versus confidence in Admins Negotiations", **csfont, fontsize=24)
ax.set_ylabel('Confindence in Negotiations', **csfont, fontsize=12)
ax.set_axisbelow(True)
| 0.362405 | 0.869105 |
# Import Libraries
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
```
## Data Transformations
We first start with defining our data transformations. We need to think what our data is and how can we augment it to correct represent images which it might not see otherwise.
Here is the list of all the transformations which come pre-built with PyTorch
1. Compose
2. ToTensor
3. ToPILImage
4. Normalize
5. Resize
6. Scale
7. CenterCrop
8. Pad
9. Lambda
10. RandomApply
11. RandomChoice
12. RandomOrder
13. RandomCrop
14. RandomHorizontalFlip
15. RandomVerticalFlip
16. RandomResizedCrop
17. RandomSizedCrop
18. FiveCrop
19. TenCrop
20. LinearTransformation
21. ColorJitter
22. RandomRotation
23. RandomAffine
24. Grayscale
25. RandomGrayscale
26. RandomPerspective
27. RandomErasing
You can read more about them [here](https://pytorch.org/docs/stable/_modules/torchvision/transforms/transforms.html)
```
# Train Phase transformations
train_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
# Test Phase transformations
test_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
```
# Dataset and Creating Train/Test Split
```
train = datasets.MNIST('./data', train=True, download=True, transform=train_transforms)
test = datasets.MNIST('./data', train=False, download=True, transform=test_transforms)
```
# Dataloader Arguments & Test/Train Dataloaders
```
SEED = 1
# CUDA?
cuda = torch.cuda.is_available()
print("CUDA Available?", cuda)
# For reproducibility
torch.manual_seed(SEED)
if cuda:
torch.cuda.manual_seed(SEED)
# dataloader arguments - something you'll fetch these from cmdprmt
dataloader_args = dict(shuffle=True, batch_size=128, num_workers=4, pin_memory=True) if cuda else dict(shuffle=True, batch_size=64)
# train dataloader
train_loader = torch.utils.data.DataLoader(train, **dataloader_args)
# test dataloader
test_loader = torch.utils.data.DataLoader(test, **dataloader_args)
```
# Data Statistics
It is important to know your data very well. Let's check some of the statistics around our data and how it actually looks like
```
# We'd need to convert it into Numpy! Remember above we have converted it into tensors already
train_data = train.train_data
train_data = train.transform(train_data.numpy())
print('[Train]')
print(' - Numpy Shape:', train.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', train.train_data.size())
print(' - min:', torch.min(train_data))
print(' - max:', torch.max(train_data))
print(' - mean:', torch.mean(train_data))
print(' - std:', torch.std(train_data))
print(' - var:', torch.var(train_data))
dataiter = iter(train_loader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
# Let's visualize some of the images
%matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(images[0].numpy().squeeze(), cmap='gray_r')
```
## MORE
It is important that we view as many images as possible. This is required to get some idea on image augmentation later on
```
figure = plt.figure()
num_of_images = 60
for index in range(1, num_of_images + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(images[index].numpy().squeeze(), cmap='gray_r')
```
# How did we get those mean and std values which we used above?
Let's run a small experiment
```
# simple transform
simple_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
# transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
exp = datasets.MNIST('./data', train=True, download=True, transform=simple_transforms)
exp_data = exp.train_data
exp_data = exp.transform(exp_data.numpy())
print('[Train]')
print(' - Numpy Shape:', exp.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', exp.train_data.size())
print(' - min:', torch.min(exp_data))
print(' - max:', torch.max(exp_data))
print(' - mean:', torch.mean(exp_data))
print(' - std:', torch.std(exp_data))
print(' - var:', torch.var(exp_data))
```
# The model
Let's start with the model we first saw
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, padding=1) #input -? OUtput? RF
self.conv2 = nn.Conv2d(32, 64, 3, padding=1)
self.pool1 = nn.MaxPool2d(2, 2)
self.conv3 = nn.Conv2d(64, 128, 3, padding=1)
self.conv4 = nn.Conv2d(128, 256, 3, padding=1)
self.pool2 = nn.MaxPool2d(2, 2)
self.conv5 = nn.Conv2d(256, 512, 3)
self.conv6 = nn.Conv2d(512, 1024, 3)
self.conv7 = nn.Conv2d(1024, 10, 3)
def forward(self, x):
x = self.pool1(F.relu(self.conv2(F.relu(self.conv1(x)))))
x = self.pool2(F.relu(self.conv4(F.relu(self.conv3(x)))))
x = F.relu(self.conv6(F.relu(self.conv5(x))))
# x = F.relu(self.conv7(x))
x = self.conv7(x)
x = x.view(-1, 10)
return F.log_softmax(x, dim=-1)
```
# Model Params
Can't emphasize on how important viewing Model Summary is.
Unfortunately, there is no in-built model visualizer, so we have to take external help
```
!pip install torchsummary
from torchsummary import summary
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
print(device)
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
```
# Training and Testing
All right, so we have 6.3M params, and that's too many, we know that. But the purpose of this notebook is to set things right for our future experiments.
Looking at logs can be boring, so we'll introduce **tqdm** progressbar to get cooler logs.
Let's write train and test functions
```
from tqdm import tqdm
train_losses = []
test_losses = []
train_acc = []
test_acc = []
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
correct = 0
processed = 0
for batch_idx, (data, target) in enumerate(pbar):
# get samples
data, target = data.to(device), target.to(device)
# Init
optimizer.zero_grad()
# In PyTorch, we need to set the gradients to zero before starting to do backpropragation because PyTorch accumulates the gradients on subsequent backward passes.
# Because of this, when you start your training loop, ideally you should zero out the gradients so that you do the parameter update correctly.
# Predict
y_pred = model(data)
# Calculate loss
loss = F.nll_loss(y_pred, target)
train_losses.append(loss)
# Backpropagation
loss.backward()
optimizer.step()
# Update pbar-tqdm
pred = y_pred.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
processed += len(data)
pbar.set_description(desc= f'Loss={loss.item()} Batch_id={batch_idx} Accuracy={100*correct/processed:0.2f}')
train_acc.append(100*correct/processed)
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
test_acc.append(100. * correct / len(test_loader.dataset))
```
# Let's Train and test our model
```
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
EPOCHS = 20
for epoch in range(EPOCHS):
print("EPOCH:", epoch)
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
fig, axs = plt.subplots(2,2,figsize=(15,10))
axs[0, 0].plot(train_losses)
axs[0, 0].set_title("Training Loss")
axs[1, 0].plot(train_acc)
axs[1, 0].set_title("Training Accuracy")
axs[0, 1].plot(test_losses)
axs[0, 1].set_title("Test Loss")
axs[1, 1].plot(test_acc)
axs[1, 1].set_title("Test Accuracy")
```
|
github_jupyter
|
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
# Train Phase transformations
train_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
# Test Phase transformations
test_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
train = datasets.MNIST('./data', train=True, download=True, transform=train_transforms)
test = datasets.MNIST('./data', train=False, download=True, transform=test_transforms)
SEED = 1
# CUDA?
cuda = torch.cuda.is_available()
print("CUDA Available?", cuda)
# For reproducibility
torch.manual_seed(SEED)
if cuda:
torch.cuda.manual_seed(SEED)
# dataloader arguments - something you'll fetch these from cmdprmt
dataloader_args = dict(shuffle=True, batch_size=128, num_workers=4, pin_memory=True) if cuda else dict(shuffle=True, batch_size=64)
# train dataloader
train_loader = torch.utils.data.DataLoader(train, **dataloader_args)
# test dataloader
test_loader = torch.utils.data.DataLoader(test, **dataloader_args)
# We'd need to convert it into Numpy! Remember above we have converted it into tensors already
train_data = train.train_data
train_data = train.transform(train_data.numpy())
print('[Train]')
print(' - Numpy Shape:', train.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', train.train_data.size())
print(' - min:', torch.min(train_data))
print(' - max:', torch.max(train_data))
print(' - mean:', torch.mean(train_data))
print(' - std:', torch.std(train_data))
print(' - var:', torch.var(train_data))
dataiter = iter(train_loader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
# Let's visualize some of the images
%matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(images[0].numpy().squeeze(), cmap='gray_r')
figure = plt.figure()
num_of_images = 60
for index in range(1, num_of_images + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(images[index].numpy().squeeze(), cmap='gray_r')
# simple transform
simple_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
# transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
exp = datasets.MNIST('./data', train=True, download=True, transform=simple_transforms)
exp_data = exp.train_data
exp_data = exp.transform(exp_data.numpy())
print('[Train]')
print(' - Numpy Shape:', exp.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', exp.train_data.size())
print(' - min:', torch.min(exp_data))
print(' - max:', torch.max(exp_data))
print(' - mean:', torch.mean(exp_data))
print(' - std:', torch.std(exp_data))
print(' - var:', torch.var(exp_data))
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, padding=1) #input -? OUtput? RF
self.conv2 = nn.Conv2d(32, 64, 3, padding=1)
self.pool1 = nn.MaxPool2d(2, 2)
self.conv3 = nn.Conv2d(64, 128, 3, padding=1)
self.conv4 = nn.Conv2d(128, 256, 3, padding=1)
self.pool2 = nn.MaxPool2d(2, 2)
self.conv5 = nn.Conv2d(256, 512, 3)
self.conv6 = nn.Conv2d(512, 1024, 3)
self.conv7 = nn.Conv2d(1024, 10, 3)
def forward(self, x):
x = self.pool1(F.relu(self.conv2(F.relu(self.conv1(x)))))
x = self.pool2(F.relu(self.conv4(F.relu(self.conv3(x)))))
x = F.relu(self.conv6(F.relu(self.conv5(x))))
# x = F.relu(self.conv7(x))
x = self.conv7(x)
x = x.view(-1, 10)
return F.log_softmax(x, dim=-1)
!pip install torchsummary
from torchsummary import summary
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
print(device)
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
from tqdm import tqdm
train_losses = []
test_losses = []
train_acc = []
test_acc = []
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
correct = 0
processed = 0
for batch_idx, (data, target) in enumerate(pbar):
# get samples
data, target = data.to(device), target.to(device)
# Init
optimizer.zero_grad()
# In PyTorch, we need to set the gradients to zero before starting to do backpropragation because PyTorch accumulates the gradients on subsequent backward passes.
# Because of this, when you start your training loop, ideally you should zero out the gradients so that you do the parameter update correctly.
# Predict
y_pred = model(data)
# Calculate loss
loss = F.nll_loss(y_pred, target)
train_losses.append(loss)
# Backpropagation
loss.backward()
optimizer.step()
# Update pbar-tqdm
pred = y_pred.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
processed += len(data)
pbar.set_description(desc= f'Loss={loss.item()} Batch_id={batch_idx} Accuracy={100*correct/processed:0.2f}')
train_acc.append(100*correct/processed)
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
test_acc.append(100. * correct / len(test_loader.dataset))
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
EPOCHS = 20
for epoch in range(EPOCHS):
print("EPOCH:", epoch)
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
fig, axs = plt.subplots(2,2,figsize=(15,10))
axs[0, 0].plot(train_losses)
axs[0, 0].set_title("Training Loss")
axs[1, 0].plot(train_acc)
axs[1, 0].set_title("Training Accuracy")
axs[0, 1].plot(test_losses)
axs[0, 1].set_title("Test Loss")
axs[1, 1].plot(test_acc)
axs[1, 1].set_title("Test Accuracy")
| 0.93981 | 0.920504 |
```
%matplotlib inline
```
# Dimensionality Reduction with Neighborhood Components Analysis
Sample usage of Neighborhood Components Analysis for dimensionality reduction.
This example compares different (linear) dimensionality reduction methods
applied on the Digits data set. The data set contains images of digits from
0 to 9 with approximately 180 samples of each class. Each image is of
dimension 8x8 = 64, and is reduced to a two-dimensional data point.
Principal Component Analysis (PCA) applied to this data identifies the
combination of attributes (principal components, or directions in the
feature space) that account for the most variance in the data. Here we
plot the different samples on the 2 first principal components.
Linear Discriminant Analysis (LDA) tries to identify attributes that
account for the most variance *between classes*. In particular,
LDA, in contrast to PCA, is a supervised method, using known class labels.
Neighborhood Components Analysis (NCA) tries to find a feature space such
that a stochastic nearest neighbor algorithm will give the best accuracy.
Like LDA, it is a supervised method.
One can see that NCA enforces a clustering of the data that is visually
meaningful despite the large reduction in dimension.
```
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neighbors import (KNeighborsClassifier,
NeighborhoodComponentsAnalysis)
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
print(__doc__)
n_neighbors = 3
random_state = 0
# Load Digits dataset
X, y = datasets.load_digits(return_X_y=True)
# Split into train/test
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.5, stratify=y,
random_state=random_state)
dim = len(X[0])
n_classes = len(np.unique(y))
# Reduce dimension to 2 with PCA
pca = make_pipeline(StandardScaler(),
PCA(n_components=2, random_state=random_state))
# Reduce dimension to 2 with LinearDiscriminantAnalysis
lda = make_pipeline(StandardScaler(),
LinearDiscriminantAnalysis(n_components=2))
# Reduce dimension to 2 with NeighborhoodComponentAnalysis
nca = make_pipeline(StandardScaler(),
NeighborhoodComponentsAnalysis(n_components=2,
random_state=random_state))
# Use a nearest neighbor classifier to evaluate the methods
knn = KNeighborsClassifier(n_neighbors=n_neighbors)
# Make a list of the methods to be compared
dim_reduction_methods = [('PCA', pca), ('LDA', lda), ('NCA', nca)]
# plt.figure()
for i, (name, model) in enumerate(dim_reduction_methods):
plt.figure()
# plt.subplot(1, 3, i + 1, aspect=1)
# Fit the method's model
model.fit(X_train, y_train)
# Fit a nearest neighbor classifier on the embedded training set
knn.fit(model.transform(X_train), y_train)
# Compute the nearest neighbor accuracy on the embedded test set
acc_knn = knn.score(model.transform(X_test), y_test)
# Embed the data set in 2 dimensions using the fitted model
X_embedded = model.transform(X)
# Plot the projected points and show the evaluation score
plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, s=30, cmap='Set1')
plt.title("{}, KNN (k={})\nTest accuracy = {:.2f}".format(name,
n_neighbors,
acc_knn))
plt.show()
```
|
github_jupyter
|
%matplotlib inline
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neighbors import (KNeighborsClassifier,
NeighborhoodComponentsAnalysis)
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
print(__doc__)
n_neighbors = 3
random_state = 0
# Load Digits dataset
X, y = datasets.load_digits(return_X_y=True)
# Split into train/test
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.5, stratify=y,
random_state=random_state)
dim = len(X[0])
n_classes = len(np.unique(y))
# Reduce dimension to 2 with PCA
pca = make_pipeline(StandardScaler(),
PCA(n_components=2, random_state=random_state))
# Reduce dimension to 2 with LinearDiscriminantAnalysis
lda = make_pipeline(StandardScaler(),
LinearDiscriminantAnalysis(n_components=2))
# Reduce dimension to 2 with NeighborhoodComponentAnalysis
nca = make_pipeline(StandardScaler(),
NeighborhoodComponentsAnalysis(n_components=2,
random_state=random_state))
# Use a nearest neighbor classifier to evaluate the methods
knn = KNeighborsClassifier(n_neighbors=n_neighbors)
# Make a list of the methods to be compared
dim_reduction_methods = [('PCA', pca), ('LDA', lda), ('NCA', nca)]
# plt.figure()
for i, (name, model) in enumerate(dim_reduction_methods):
plt.figure()
# plt.subplot(1, 3, i + 1, aspect=1)
# Fit the method's model
model.fit(X_train, y_train)
# Fit a nearest neighbor classifier on the embedded training set
knn.fit(model.transform(X_train), y_train)
# Compute the nearest neighbor accuracy on the embedded test set
acc_knn = knn.score(model.transform(X_test), y_test)
# Embed the data set in 2 dimensions using the fitted model
X_embedded = model.transform(X)
# Plot the projected points and show the evaluation score
plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, s=30, cmap='Set1')
plt.title("{}, KNN (k={})\nTest accuracy = {:.2f}".format(name,
n_neighbors,
acc_knn))
plt.show()
| 0.895927 | 0.983738 |
https://www.kaggle.com/c/titanic/data
```
import pandas as pd
```
# Load Data
```
data = pd.read_csv('train.csv')
data.head()
data.describe()
```
# Data pre-processing
```
data_with_string_values = data.select_dtypes('object')# string
data_with_string_values.describe()
```
Sex, Cabin and Embarked columns seems to have less unique values so they can be of type catergory
```
for i in ['Sex', 'Cabin','Embarked']:
data[i]= data[i].astype('category')
data.dtypes
# Convert categorical variable to number
categorical_columns = data.select_dtypes('category').columns# string
for i in categorical_columns:
data[i] = data[i].cat.codes
data.head()
data = data.fillna(data.mean())
```
# Train/Test Split
```
from sklearn.model_selection import train_test_split
columns_for_training = data.select_dtypes(exclude='object')
columns_for_training = columns_for_training[[i for i in columns_for_training.columns.values if i not in ['PassengerId','Survived']]]
columns_for_training.head()
X = columns_for_training
y = data['Survived']
train_x, test_x, train_y, test_y = train_test_split(X,y, train_size=0.8)
train_y.head()
```
# Building Classifier
```
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier()
tree.fit(train_x,train_y)
# Visualization
from sklearn.tree import export_graphviz
import graphviz
dot_data = export_graphviz(tree, out_file=None, feature_names=X.columns.values,class_names=['Survived','Not'],filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
# run to print tree
graph
tree.predict(test_x)
from sklearn.model_selection import cross_val_score
cross_val_score(tree,test_x,test_y,cv=10)
```
# Preparing Output File
```
submission_data=pd.read_csv('test.csv')
for i in ['Sex', 'Cabin','Embarked']:
submission_data[i]= submission_data[i].astype('category')
categorical_columns = submission_data.select_dtypes('category').columns# string
for i in categorical_columns:
submission_data[i] = submission_data[i].cat.codes
passenger_ids = submission_data['PassengerId']
submission_data.fillna(submission_data.mean())
submission_data = submission_data[[i for i in columns_for_training.columns.values if i not in ['PassengerId','Survived']]]
submission_data = submission_data.fillna(submission_data.mean())
submission_data.head()
prediction = tree.predict(submission_data)
prediction
df = pd.DataFrame({'PassengerId':passenger_ids,'Survived':prediction})
df.head()
df.to_csv('sklearn_decision_tree_submission.csv', index=False)
```
|
github_jupyter
|
import pandas as pd
data = pd.read_csv('train.csv')
data.head()
data.describe()
data_with_string_values = data.select_dtypes('object')# string
data_with_string_values.describe()
for i in ['Sex', 'Cabin','Embarked']:
data[i]= data[i].astype('category')
data.dtypes
# Convert categorical variable to number
categorical_columns = data.select_dtypes('category').columns# string
for i in categorical_columns:
data[i] = data[i].cat.codes
data.head()
data = data.fillna(data.mean())
from sklearn.model_selection import train_test_split
columns_for_training = data.select_dtypes(exclude='object')
columns_for_training = columns_for_training[[i for i in columns_for_training.columns.values if i not in ['PassengerId','Survived']]]
columns_for_training.head()
X = columns_for_training
y = data['Survived']
train_x, test_x, train_y, test_y = train_test_split(X,y, train_size=0.8)
train_y.head()
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier()
tree.fit(train_x,train_y)
# Visualization
from sklearn.tree import export_graphviz
import graphviz
dot_data = export_graphviz(tree, out_file=None, feature_names=X.columns.values,class_names=['Survived','Not'],filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
# run to print tree
graph
tree.predict(test_x)
from sklearn.model_selection import cross_val_score
cross_val_score(tree,test_x,test_y,cv=10)
submission_data=pd.read_csv('test.csv')
for i in ['Sex', 'Cabin','Embarked']:
submission_data[i]= submission_data[i].astype('category')
categorical_columns = submission_data.select_dtypes('category').columns# string
for i in categorical_columns:
submission_data[i] = submission_data[i].cat.codes
passenger_ids = submission_data['PassengerId']
submission_data.fillna(submission_data.mean())
submission_data = submission_data[[i for i in columns_for_training.columns.values if i not in ['PassengerId','Survived']]]
submission_data = submission_data.fillna(submission_data.mean())
submission_data.head()
prediction = tree.predict(submission_data)
prediction
df = pd.DataFrame({'PassengerId':passenger_ids,'Survived':prediction})
df.head()
df.to_csv('sklearn_decision_tree_submission.csv', index=False)
| 0.325735 | 0.843573 |
```
import nltk
nltk.download_shell()
messages = [line.rstrip() for line in open('smsspamcollection copy/SMSSpamCollection')]
print(len(messages))
for mess_no,message in enumerate(messages[:10]):
print(mess_no,message)
print('\n')
import pandas as pd
messages = pd.read_csv('smsspamcollection copy/SMSSpamCollection',sep='\t',names=['label','message'])
messages.head()
messages.describe()
messages.groupby('label').describe()
messages['length'] = messages['message'].apply(len)
messages.head()
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
messages['length'].plot.hist(bins=150)
messages['length'].describe()
messages[messages['length'] == 910]
messages[messages['length']==910]['message'].iloc[0]
messages.hist(column='length',by='label',bins=60,figsize=(12,4))
import string
mess = 'Sample Message! Notice: it has punctuation.'
string.punctuation
nopunc = [c for c in mess if c not in string.punctuation]
nopunc
from nltk.corpus import stopwords
stopwords.words('english')
nopunc = ''.join(nopunc)
nopunc
x = ['a','b','c','d']
'+++'.join(x)
nopunc.split()
clean_mess = [word for word in nopunc.split() if word.lower() not in stopwords.words('english')]
clean_mess
def text_process(mess):
'''
1. remove punctuation
2. remove stopwords
3. return list of clean text words
'''
nopunc = [word for word in mess if word not in string.punctuation]
nopunc = ''.join(nopunc)
return [word for word in nopunc.split() if word.lower() not in stopwords.words('english')]
messages.head()
messages['message'].head(5).apply(text_process)
from sklearn.feature_extraction.text import CountVectorizer
bow_transformer = CountVectorizer(analyzer=text_process).fit(messages['message'])
print(len(bow_transformer.vocabulary_))
mess4 = messages['message'][3]
print(mess4)
bow4 = bow_transformer.transform([mess4])
print(bow4)
print(bow4.shape)
bow_transformer.get_feature_names()[9554]
messages_bow = bow_transformer.transform(messages['message'])
print('Shape of the Sparse Matric: ',messages_bow.shape)
messages_bow.nnz
sparsity = (100.0 * messages_bow.nnz / (messages_bow.shape[0] * messages_bow.shape[1]))
print('sparsity: {}'.format(round(sparsity)))
from sklearn.feature_extraction.text import TfidfTransformer
tfidf_transformer = TfidfTransformer().fit(messages_bow)
tfidf4 = tfidf_transformer.transform(bow4)
print(tfidf4)
tfidf_transformer.idf_[bow_transformer.vocabulary_['university']]
messages_tfidf = tfidf_transformer.transform(messages_bow)
from sklearn.naive_bayes import MultinomialNB
spam_detect_model = MultinomialNB().fit(messages_tfidf,messages['label'])
spam_detect_model.predict(tfidf4)[0]
messages['label'][3]
from sklearn.model_selection import train_test_split
msg_train,msg_test,label_train,label_test = train_test_split(messages['message'],messages['label'],test_size=0.3)
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
('bow',CountVectorizer(analyzer=text_process)),
('tfidf',TfidfTransformer()),
('classifier',MultinomialNB())
])
pipeline.fit(msg_train,label_train)
predictions = pipeline.predict(msg_test)
from sklearn.metrics import classification_report
print(classification_report(label_test,predictions))
print(classification_report(label_test,predictions))
```
|
github_jupyter
|
import nltk
nltk.download_shell()
messages = [line.rstrip() for line in open('smsspamcollection copy/SMSSpamCollection')]
print(len(messages))
for mess_no,message in enumerate(messages[:10]):
print(mess_no,message)
print('\n')
import pandas as pd
messages = pd.read_csv('smsspamcollection copy/SMSSpamCollection',sep='\t',names=['label','message'])
messages.head()
messages.describe()
messages.groupby('label').describe()
messages['length'] = messages['message'].apply(len)
messages.head()
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
messages['length'].plot.hist(bins=150)
messages['length'].describe()
messages[messages['length'] == 910]
messages[messages['length']==910]['message'].iloc[0]
messages.hist(column='length',by='label',bins=60,figsize=(12,4))
import string
mess = 'Sample Message! Notice: it has punctuation.'
string.punctuation
nopunc = [c for c in mess if c not in string.punctuation]
nopunc
from nltk.corpus import stopwords
stopwords.words('english')
nopunc = ''.join(nopunc)
nopunc
x = ['a','b','c','d']
'+++'.join(x)
nopunc.split()
clean_mess = [word for word in nopunc.split() if word.lower() not in stopwords.words('english')]
clean_mess
def text_process(mess):
'''
1. remove punctuation
2. remove stopwords
3. return list of clean text words
'''
nopunc = [word for word in mess if word not in string.punctuation]
nopunc = ''.join(nopunc)
return [word for word in nopunc.split() if word.lower() not in stopwords.words('english')]
messages.head()
messages['message'].head(5).apply(text_process)
from sklearn.feature_extraction.text import CountVectorizer
bow_transformer = CountVectorizer(analyzer=text_process).fit(messages['message'])
print(len(bow_transformer.vocabulary_))
mess4 = messages['message'][3]
print(mess4)
bow4 = bow_transformer.transform([mess4])
print(bow4)
print(bow4.shape)
bow_transformer.get_feature_names()[9554]
messages_bow = bow_transformer.transform(messages['message'])
print('Shape of the Sparse Matric: ',messages_bow.shape)
messages_bow.nnz
sparsity = (100.0 * messages_bow.nnz / (messages_bow.shape[0] * messages_bow.shape[1]))
print('sparsity: {}'.format(round(sparsity)))
from sklearn.feature_extraction.text import TfidfTransformer
tfidf_transformer = TfidfTransformer().fit(messages_bow)
tfidf4 = tfidf_transformer.transform(bow4)
print(tfidf4)
tfidf_transformer.idf_[bow_transformer.vocabulary_['university']]
messages_tfidf = tfidf_transformer.transform(messages_bow)
from sklearn.naive_bayes import MultinomialNB
spam_detect_model = MultinomialNB().fit(messages_tfidf,messages['label'])
spam_detect_model.predict(tfidf4)[0]
messages['label'][3]
from sklearn.model_selection import train_test_split
msg_train,msg_test,label_train,label_test = train_test_split(messages['message'],messages['label'],test_size=0.3)
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
('bow',CountVectorizer(analyzer=text_process)),
('tfidf',TfidfTransformer()),
('classifier',MultinomialNB())
])
pipeline.fit(msg_train,label_train)
predictions = pipeline.predict(msg_test)
from sklearn.metrics import classification_report
print(classification_report(label_test,predictions))
print(classification_report(label_test,predictions))
| 0.489015 | 0.179818 |
```
import json
import os.path as osp
import numpy as np
def _get_list(identities):
ret = []
for views in identities:
for v in views:
for file in v:
label = int(osp.basename(file)[:5])
ret.append((file, label))
return np.asarray(ret)
base_path = '../datasets/CUHK01_original'
with open(osp.join(base_path, 'split.json')) as f:
split = json.load(f)
# data = json.load(f)
# trainval = data['trainval']
# test_probe = data['test_probe']
# test_gallery = data['test_gallery']
# del data
with open(osp.join(base_path, 'meta.json')) as f:
data = json.load(f)
# for key, value in data.items():
# print(key)
shot = data['shot']
identities = np.asarray(data['identities'])
dabase_name = data['name']
num_cameras = data['num_cameras']
del data
# # extract features
# print(meta)
test_probe, test_gallery = [], []
for views in identities[split['test_probe']]:
test_probe.append(views[:len(views) // 2])
test_gallery.append(views[len(views) // 2:])
only_in_gallery = list(set(split['test_gallery']) - set(split['test_probe']))
test_gallery.extend(identities[only_in_gallery])
test_probe = _get_list(test_probe)
test_gallery = _get_list(test_gallery)
def _split(pairs):
path = [osp.join(base_path, pair[0]) for pair in pairs]
label = [int(pair[1]) for pair in pairs]
return path, label
PP, PY = _split(test_probe)
GP, GY = _split(test_gallery)
unique_labels = np.unique(np.r_[PY, GY])
labels_map = {l: i for i, l in enumerate(unique_labels)}
PY = np.asarray([labels_map[l] for l in PY])
GY = np.asarray([labels_map[l] for l in GY])
# extract features
def extract_features(model_path, image_paths):
import tensorflow as tf
import importlib
import facenet
import scipy.misc
with tf.Graph().as_default():
with tf.Session() as sess:
with tf.device("/cpu:0"):
# Load the model
print('Loading model "%s"' % model_path)
facenet.load_model(model_path)
# Get input and output tensors
images_placeholder = tf.get_default_graph().get_tensor_by_name("input:0")
phase_train_placeholder = tf.get_default_graph().get_tensor_by_name("phase_train:0")
embeddings = tf.get_default_graph().get_tensor_by_name("embeddings:0")
image_size = images_placeholder.get_shape()
n = len(image_paths)
features = np.zeros((n, 128))
images = np.zeros((n, image_size[1], image_size[2], image_size[3]))
for i, image_path in enumerate(image_paths):
image = scipy.misc.imread(image_path)
images[i, :, :, :] = scipy.misc.imresize(image, (160, 60))
feed_dict = { images_placeholder:images, phase_train_placeholder:True }
features = sess.run(embeddings, feed_dict=feed_dict)
return features
# pretrained_model_file = '../trained/nn4_small2_reid3/20161103-003809/model.ckpt-200000'
# pretrained_model_file = '../trained/nn4_small2_reid3/20161103-054027/model.ckpt-294800'
# pretrained_model_file = '../trained/nn4_small2_reid3/20161103-105422/model.ckpt-336200'
# pretrained_model_file = '../trained/nn4_small2_reid3/cuhk01/20161103-132622/model.ckpt-10000'
# pretrained_model_file = '../trained/nn4_small2_reid3/cuhk01/20161103-142316/model.ckpt-20000'
# pretrained_model_file = '../trained/nn4_small2_reid3/cuhk01/20161103-144912/model.ckpt-23200'
pretrained_model_file = '../trained/nn4_small2_reid3/cuhk01/20161103-151633/model.ckpt-30000'
# pretrained_model_file = '../trained/nn4_small2_reid3/cuhk03/20161102-191257/model.ckpt-10000'
PX = extract_features(pretrained_model_file, PP)
GX = extract_features(pretrained_model_file, GP)
from sklearn.metrics.pairwise import pairwise_distances
from utils import *
D = pairwise_distances(GX, PX, n_jobs=-2)
C = cmc(D, GY, PY)
%matplotlib inline
import matplotlib.pyplot as plt
N = 20
plt.plot(range(1, N+1), C[:N])
plt.title('Cumulative Match Characteristic(CMC) curve')
plt.xlabel('Rank')
plt.ylabel('Recognition rate')
plt.show()
```
|
github_jupyter
|
import json
import os.path as osp
import numpy as np
def _get_list(identities):
ret = []
for views in identities:
for v in views:
for file in v:
label = int(osp.basename(file)[:5])
ret.append((file, label))
return np.asarray(ret)
base_path = '../datasets/CUHK01_original'
with open(osp.join(base_path, 'split.json')) as f:
split = json.load(f)
# data = json.load(f)
# trainval = data['trainval']
# test_probe = data['test_probe']
# test_gallery = data['test_gallery']
# del data
with open(osp.join(base_path, 'meta.json')) as f:
data = json.load(f)
# for key, value in data.items():
# print(key)
shot = data['shot']
identities = np.asarray(data['identities'])
dabase_name = data['name']
num_cameras = data['num_cameras']
del data
# # extract features
# print(meta)
test_probe, test_gallery = [], []
for views in identities[split['test_probe']]:
test_probe.append(views[:len(views) // 2])
test_gallery.append(views[len(views) // 2:])
only_in_gallery = list(set(split['test_gallery']) - set(split['test_probe']))
test_gallery.extend(identities[only_in_gallery])
test_probe = _get_list(test_probe)
test_gallery = _get_list(test_gallery)
def _split(pairs):
path = [osp.join(base_path, pair[0]) for pair in pairs]
label = [int(pair[1]) for pair in pairs]
return path, label
PP, PY = _split(test_probe)
GP, GY = _split(test_gallery)
unique_labels = np.unique(np.r_[PY, GY])
labels_map = {l: i for i, l in enumerate(unique_labels)}
PY = np.asarray([labels_map[l] for l in PY])
GY = np.asarray([labels_map[l] for l in GY])
# extract features
def extract_features(model_path, image_paths):
import tensorflow as tf
import importlib
import facenet
import scipy.misc
with tf.Graph().as_default():
with tf.Session() as sess:
with tf.device("/cpu:0"):
# Load the model
print('Loading model "%s"' % model_path)
facenet.load_model(model_path)
# Get input and output tensors
images_placeholder = tf.get_default_graph().get_tensor_by_name("input:0")
phase_train_placeholder = tf.get_default_graph().get_tensor_by_name("phase_train:0")
embeddings = tf.get_default_graph().get_tensor_by_name("embeddings:0")
image_size = images_placeholder.get_shape()
n = len(image_paths)
features = np.zeros((n, 128))
images = np.zeros((n, image_size[1], image_size[2], image_size[3]))
for i, image_path in enumerate(image_paths):
image = scipy.misc.imread(image_path)
images[i, :, :, :] = scipy.misc.imresize(image, (160, 60))
feed_dict = { images_placeholder:images, phase_train_placeholder:True }
features = sess.run(embeddings, feed_dict=feed_dict)
return features
# pretrained_model_file = '../trained/nn4_small2_reid3/20161103-003809/model.ckpt-200000'
# pretrained_model_file = '../trained/nn4_small2_reid3/20161103-054027/model.ckpt-294800'
# pretrained_model_file = '../trained/nn4_small2_reid3/20161103-105422/model.ckpt-336200'
# pretrained_model_file = '../trained/nn4_small2_reid3/cuhk01/20161103-132622/model.ckpt-10000'
# pretrained_model_file = '../trained/nn4_small2_reid3/cuhk01/20161103-142316/model.ckpt-20000'
# pretrained_model_file = '../trained/nn4_small2_reid3/cuhk01/20161103-144912/model.ckpt-23200'
pretrained_model_file = '../trained/nn4_small2_reid3/cuhk01/20161103-151633/model.ckpt-30000'
# pretrained_model_file = '../trained/nn4_small2_reid3/cuhk03/20161102-191257/model.ckpt-10000'
PX = extract_features(pretrained_model_file, PP)
GX = extract_features(pretrained_model_file, GP)
from sklearn.metrics.pairwise import pairwise_distances
from utils import *
D = pairwise_distances(GX, PX, n_jobs=-2)
C = cmc(D, GY, PY)
%matplotlib inline
import matplotlib.pyplot as plt
N = 20
plt.plot(range(1, N+1), C[:N])
plt.title('Cumulative Match Characteristic(CMC) curve')
plt.xlabel('Rank')
plt.ylabel('Recognition rate')
plt.show()
| 0.506836 | 0.288322 |
# Glossary
> Ontology recapitulates philology
> –Willard Van Orman Quine (c.f. Ernst Haeckel)
## Accuracy
In a classification model, there are numerous *metrics* that might express the "goodness" of a model. Accuracy is often the default metric used, and is simply the number of right answers divided by the number of data points. For example, consider this hypothetical *confusion matrix*:
| Predict/Actual | Human | Octopus | Penguin |
|----------------|----------|----------|----------|
| Human | **5** | 0 | 2 |
| Octopus | 3 | **3** | 3 |
| Penguin | 0 | 1 | **11** |
There are 28 observations of organisms, and 19 were classified accurately, hence the accuracy is approximately 68%. Other commonly used metrics are precision, recall, and F1 score.
Related concepts: **F1 score**, **precision**, **recall**
## ActiveMQ
Apache ActiveMQ is an open source message broker. As with other message brokers, the aggregations of messages sent among systems is often a fruitful domain for data science analysis.
## BeautifulSoup
Beautiful Soup is a Python library for parsing and processing HTML and XML documents, and also for handling not-quite-grammatical HTML that often occurs on the World Wide Web. Beautiful Soup is often useful for acquiring data via web scraping.
## Berkeley DB
Berkeley DB is an open source library for providing key/value storage systems.
## Big Data
The concept of "big data" is one that shifts with time, as computing and storage capabilities increase. Generally, big data is simply data that is too large to handle using "traditional" and simple tools. What tools are traditional or simple, in turn, varies with organization, project, and over time. As s rough guideline, data that can fit inside the memory on a single available server or workstation is "small data," or at most "medium-sized data."
As of 2021, a reasonably powerful single system might have 256 GiB, so big data is at least tens or hundreds of gigabytes ($10^9$) in size. Within a few years of this writing, the threshhold for big data will be at least terabytes ($10^{12}$), and already today some data sets reach into exabytes ($10^{18}$).
## Big-endian (see Endianness)
Data arranged into "words" (typically 32-bits), or other units, where the largest magnitude component (typically a byte) is stored in the last position.
## BSON (Binary JSON)
BSON is a binary-encoded serialization of JSON-like documents.
## caret (Classification And REgression Training)
The R package caret is a rich collection of functions for data splitting, pre-processing, feature selection, resampling, and variable importance estimation.
## Cassandra
Apache Cassandra is an open source distributed database system that uses the Cassandra Query Language (CQL), rather than standard SQL for queries. CQL and SQL are largely similar, but vary in specific details.
## Categorical variable (see NOIR)
Related concepts: **continuous variable**, **interval variable**, **nominal variable**, **ordinal variable**, **ratio variable**
## chardet
The `chardet` module in Python, and analogous versions in other programming languages, applies a colleciton of heuristics to a sequence of bytes thought likely to encode text. If the protocol or format you encounter explicitly declares an encoding, try that first. As a fallback, `chardet` can often make reasonable guesses based on letter and n-gram frequencies that occur in a different language, and which byte values are permitted by a given encoding.
## Chimera
In Greek mythology, a chimera is an animal combining elements of several dramatically disparate animals; most commonly these include the head of a lion, the body of a goat, and the tail of a snake. In adapted uses as a generic but evocative adjective, anything that combines surprisingly juxtaposed elements together can be called *chimerical*; or metaphorically, the thing might be called a *chimera*.
## Column
A single kind of data item that may have, and usually has, many exemplars, one per *row* (a.k.a. sample, observation, record, etc.). A column consists of ordered data items of the same data type but varying values. A number of synonyms are used for "columns" with slightly varying focus. *Features* emphasize the way that columns are used by machine learning algorithms. *Field* focuses on the data format used to store the data items. *Measurement* is used most often when a column collects empirical observations, often using some particular instrument. *Variable* is used when thinking of equational relationships among different columns (e.g. independent versus dependent).
Overall, columns and rows form *columnar* or *tabular* data.
Synonyms: **feature**, **field**, **measurement**, **variable**
## Comma-separated values (CSV)
A representation of columnar data in which each line of text is separated by a newline character (or carriage return, or CR/LF). Within each line, data values are separated by commas. Values separated by other delimiters, such as tab or `|`, are also often informally called CSV (the acronym, not the full words).
Variations on the format use several quoting and escaping conventions. String data items containing commas internally need to be either quoted (usually with quote characters) or escaped (usually with backslash); but if so, those characters in turn need special behaviors.
## Continuous variable (see NOIR)
Related concepts: **categorical variable**, **interval variable**, **nominal variable**, **ordinal variable**, **ratio variable**
## Coreutils (GNU Core Utilities)
A collection of shell-oriented utilities for processing text and data. The subset of these tools that was formerly contained in the separate **textutils** package, in particular, are relevant to processing textual data sources. These tools include `cat`, `cut`, `fmt`, `fold`, `head`, `sort`, `tail`, `tee`, `tr`, `uniq`, `wc`. Other command-line tools like `grep`, `sed`, `shuf`, and `awk` are also widely used in interaction with these tools.
## Corpus (pl. corpora)
Corpus is a term from linguistics, but used also in related natural language processing (NLP). It simply refers to a large "body" (the Latin root) of text covering a similar domain, such as a common publisher, genre, or dialect. In general, some sort of modeling or statistical analysis may apply to a particular body of text, and by extension to texts of a similar domain.
## CouchDB
Apache CouchDB is an open-source document-oriented database. Internally, data in CouchDB is represented in JSON format.
## CrateDB
CrateDB is an open-source document-oriented database. CrateDB occupies an overlapping space with MongoDB or CouchDB, but emphasizes real-time performance.
## Curse of dimensionality
The phrase "curse of dimensionality" was coined by Richard E. Bellman in 1957. It applies to a number of different numeric or scientific fields. In relation to machine learning, in particular, the problem is that as the number of dimensions increases, the size of the parameter space they occupy increases even faster. Even very large data sets will occupy only a tiny portion of that parameter space defined by the dimensions. Models are fairly uniformly poor at predicting or characterizing regions of parameter space where they have few or no observations to train on.
A very rough rule of thumb is that you wish to have fewer than ⅒ as many dimensions/features as you do observations. However, even very large data sets perform best if feature engineering, dimensionality reduction, and/or feature selection can be used to reduce their parameter space to hundreds of dimensions (i.e. not thousands, often tens are better than hundreds).
However, as a flip side of the curse of dimensionality, we also sometimes see a "blessing of dimensionality." Linear models especially can perform very poorly with only a few dimensions to work with. The very same types of models can become very good if it is possible to obtain or construct additional (synthetic) features. Generally, this blessing occurs when models move from, e.g. 5 to 10 features, not when they move from 100 to 200 features.
As John von Neumann famously quipped: “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.”
## Data artifact
An unintended alteration of data, generally as a consequence of hardware of software bugs. Some artifact can be caused by flaws in data collection instruments; others result from errors in transcription, collation, or data transfer. Data artifacts are often only detectable as anomolies in a data set.
## Data frame
A data frame (sometimes "dataframe") is an abstraction of tabular data provided by a variety of programming languages and software library. At heart, a data frame bundles together multiple data-type homogeneous series or arrays (columns), enforcing a few regularities:
* All *columns* in a data frame have the same number of data items within them (some might be explicitly a "missing" sentinel).
* Each column has data items of the same data type.
* Data may be selected by indicating collections of rows and collections of columns.
* Predicates may be used to select row sets based on properties of data on a given row.
* Operations on columns are expressed in a *vectorized* way, operating conceptually on all elements of a column simultaneously.
* Both columns and rows may have names; in some libraries rows are only named by index position, but all name columns descriptively.
Popular data frames libraries include Python Pandas and Vaex, R data.table and tibble, Scala DataFrame, and Julia DataFrames.jl.
## data.frame
The data frame library that is included with a standard R distribution. The R standard data.frame is the oldest data frame object for R, and remains widely used. However, either the Tidyverse tibble or the data.table library are generally preferable for new development, having been refined based on experience with data.frame.
See also: **data frame**, **data.table**, **tibble**
## data.table
A popular data frame library for R. Philosophically, data.table tries to perform filtering, aggregation, and grouping all with standard arguments to its indexing operation. The data.table library has a somewhat different attitude than the Tidyverse, but is generally interoperable with it.
See also: **tibble**, **data.frame**
## Data set
A data set is simply a collection of related data. Often, if the data is tabular, it will consist of a table; but it may be a number of related tables. In related data that is arranged in hierarchical or other formats, one or more files (in varying formats) may constitute the data set. Often, but not always, a data set is distributed as a single archive file containing all relevant components of it.
## Denormalization
Denormalization is the duplication of data within a database system to allow for more "locality" of data to queries performed. This will result in larger storage size, but in many cases also in faster performance of read queries. Denormalization potentially introduces data integrity problems where data in different locations falls out of sync.
## DMwR (Data Mining with R)
The R package DMwR includes functions and data accompanying the book <u>Data Mining with R, learning with case studies</u> by Luis Torgo, CRC Press 2010. A wide variety of utilities are included, but from the perspective of this book, it is mentioned because of its inclusion of a SMOTE implementation.
## DOM (Document Object Model)
The Document Object Model (DOM) is a language-neutral application programming interface (API) for working with XML or HTML document. While the specification gives a collection of method names that might be implemented in any language, the inspiration and style is especially inspired by JavaScript.
## Domain-specific knowledge
Much of data science, including even that part of it concerning this book topic, cleaning data, can be driven by "the shape of the data itself." Certain data items may follow patterns or stand out as anamolous on a purely numeric or analytic basis. However, in many cases, accurate judgements about which data is important, or which is of greater importance, lies not in the data themselves but in knowledge we have about the domains the data describe.
Domain-specific knowledge—or just "domain knowledge"—is what informs us of those distinctions that the data alone cannot reveal. Not all domain knowledge is extremely technical, the term might refer to topics that are more "common sense" as well. For example, it is general knowledge that outdoor temperatures in the northern hemisphere are usually higher in July than in January. A data set that conflicted with this background knowledge would be suspicious even if the individual data values were all, in themselves, in a reasonable numeric range. Bringing that very common domain knowledge to a problem is important, where applicable.
Equally, some domain knowledge requires deep subject-area expertise. Data in a psychological survey might show particular population distributions of subscales from the Minnesota Multiphasic Personality Inventory (MMPI). Some distributions might be implausible and indicate likely data integrity or sample bias problems, but a specialized knowledge is needed to judge that. Or radio astronomy data might show particular emission frequency bands from distant objects. A specialized knowledge is needed to determine whether that is consistent with expectations of Hubble red-shift distances or might be data errors. Likewise in many domains.
## Eagerness
In computer programming and computer science, sometimes the words "lazy" and "eager" are used to distinguish approaches to solving a larger problem. Commonly, for example, an algorithm might transform a large data set. An eager program will process all the data at once. In contrast, a lazy program will only perform an individual transformation when that specific result is needed.
See also: **Laziness**
## Elasticsearch
Elasticsearch is a search engine based on the Lucene library. As a part of implementing a search engine, Elasticsearch contains a document-oriented database or data store.
## Endianness
Endianness in computer representations of numbers is typically either **big-endian** or **little-endian**. This refers to the scaled magnitude of composite values stored in a particular order. Most typically, the composite values are bytes, and they are arranged into "words" of 16-bits, 32-bits, 64-bits, or 128-bits (i.e. 2, 4, 8, or 16 bytes per word).
For example, suppose we wish to store an (unsigned) integer value in a contiguous 32-bit word. Computer systems and filesystems typically have an addressing resolution of one byte, not of individual bits directly, so this is 4 such slots in which scaled values may be stored. For example, we wish to store the number 1,908,477,236.
First, we can notice that since each byte stores values 0-255, this is a reasonable way to describe that number:
$$1,908,477,236 = (52 \times 2^0) + (13 \times 2^8) + (193 \times 2^{16}) + (113 \times 2^{24})$$
Storing values in each of the 4 bytes in the word could use either of these approaches:
Byte-order | Byte 1 | Byte 2 | Byte 3 | Byte 4
--------------|--------|--------|--------|--------
Little-endian | 52 | 13 | 193 | 113
Big-endian | 113 | 193 | 13 | 52
Historically, most CPUs used only one of big-endian and little-endian word representation, but most modern CPUs offer switchable *bi-endianess*. Likewise, many libraries such as *NumPy* allow flexibility in reading and writing data of different endianness in storage format.
Formats other than computer words used to store numeric values may also be endian. Notably, different date formats can be big-endian, little-endian, or indeed *middle-endian*. For example, ISO-8601 date format prescribes the big-endianness, e.g. `2020-10-31`. The year represents the largest magnitude, month next largest, and day number the smallest resolution of a date. The extension to time components is similar.
In contrast, a common United States date format can read, e.g. `October 31, 2020`. A spelled out month name indirectly represents a number here (numbers are also used with the same endianness and different delimiter, e.g. `10/31/2020`). From an endianness perspective, this is middle-endian. The largest magnitude (year) is placed at the end, the next largest magnitude (month) at the start, and the smallest magnitude (day) in the middle. Clearly, a *different* middle-endian format is also possible, but is not widely used (e.g. `2020 31 Oct`).
Much of the world outside of the United States uses a little-endian date representation, such as `31/10/2020`. While the specific values in the representation of October 31 would disambiguate the endianness used, for dates such as October 11 or November 10, this is not the case.
## F1 Score
In a classification model, there are numerous *metrics* that might express the "goodness" of a model. F1 score blends *recall* and *precision* avoiding the extremes that occur in certain models, and is often a balanced metric. F1 score is derived as:
$$\text{F1} = 2 \times \cfrac{precision \times recall}{precision + recall}$$
Related concepts: **accuracy**, **precision**, **recall**
## Feature (see Column)
Synonyms: *column*, *field*, *measurement*, *variable*
## Field (see Column)
Synonyms: *column*, *feature*, *measurement*, *variable*
## Fuzzy
Fuzzy is a Python library for analyzing phonetic similarity in English texts.
## GDBM (GNU dbm)
GDBM is an open source library for providing key/value storage systems.
## General Decimal Arithmetic Specification
The General Decimal Arithmetic Specification is a standard for implementation of arbitrary precision base-10 arithmetic and numeric representation. It incorporates configurable "contexts" such as rounding rules in effect. The Python standard library `decimal` module, in particular, is an implementation of this standard.
## Gensim
Gensim is an open-source Python library for natural language processing (NLP), specifically around unsupervised topic modeling. Gensim contains an implementation of the word2vec algorithm and a few closely related variants of it.
## Gibibyte (GiB)
Metric prefixes are standardized in the International System of Units (SI), by the International Bureau of Weights and Measures (BIPM). Orders of magnitude—powers of 10—are indicated by prefixes ranging from *yotta-* ($10^{24}$) down to *yocto-* ($10^{-24}$). In partcular, the multipliers of $10^3$ (*kilo-*), $10^6$ (*mega-*), and $10^9$ (*giga-*) are *almost* right for dealing with typical quantities seen in computer storage.
However, for both historical and practical reasons, bytes of memory or storage are typically expressed as multiples of $2^{10}$ (1024) rather than of $10^3$ (1000). These numbers are relatively close, but while it is common to misname $2^{10}$, $2^{20}$, and $2^{30}$ as *kilobyte*, *megabyte*, and *gigabyte*, these are wrong. Since 1998, the International Electrotechnical Commission (IEC) has standardized the use of *kibibyte* (GiB), *mebibyte* (MiB), *gibibyte* (GiB) for accurate description of these powers of 2. For larger sizes, we also have *tebibyte* (TiB), *pebibyte* (PiB), *exbibyte* (EiB), *zebibyte* (ZiB), and *yobibyte* (YiB).
## ggplot2
A popular book, <u>The Grammar of Graphics (Statistics and Computing)</u>, by Leland Wilkinson (ISBN: 978-0387245447), first published in 2000, introduced a way of thinking about graphs and data visualizations that breaks down a graph into components that can be expressed independently. Changing one such orthogonal component may change the entire appearance of a graph, but will still reflect the same underlying data in a different manner.
The R library `ggplot2` attempts to translate the concepts of that book into concrete APIs, and has been widely adopted by the R community. The Python libraries **ggplot**, to a strong degree, and **Bokeh** and **Altair**, to a somewhat lesser extent, also try to emulate Wilkinson's "grammar." Altair is in turn, built on top of **Vega-Lite** and **Vega** which have a similar goal as JavaScript libraries.
## Glob
A common and simple pattern-matching language that is most frequently used to identify collections of filenames. Both the Bash shell and libraries in many programming languages support this syntax.
## GQL (Graph Query Language)
Graph Query Language is a (pending) standard for querying graph databases, based on the Cypher language developed by Neo4j for their product.
## Gremlin
Gremlin is a graph query language, distinct from GQL. Queries in Gremlin emphasize a "fluent programming" and functional style of description of nodes and classes of interest.
## Halting problem
The halting problem is probably the most famous result in the theory of computation. Alan Turing proved in 1936 that there cannot exist any general purpose algorithm that answers the question "Will this program ever terminate?" For some programs it is provable, of course, but in the general case it is not. Even running a program for any finite amount of time, N steps, does not answer the question, since it might yet terminate at step N+1.
In slightly more informal parlance, saying that a given task is "equivalent to the halting problem" is an idiomatic way of saying that it cannot be solved. At times the phrase is used as a speculation about the difficulty of a problem, but at other times a mathematical proof is known that shows that solving the novel problem would imply a solution to the halting problem. Within this book, the phrase is used only in the strict sense, but with an affection for the jargon of computer science.
## h5py
H5py is a Python library for working with hierarchical data sets stored in the HDF5 format.
## HDF Compass
HDF Compass is an open source GUI tool for examing the content of HDF5 data files.
## Hierarchical data format (HDF5)
The Hierarchical Data Format (HDF5) is an open source file format that supports large, complex, heterogeneous data. HDF5 uses a hierarchical structure that allows you to organize data within a file in nested groups. The "leaf" of a hierarchy is a dataset. An HDF5 file may contain arbitrary and domain-specific metadata about each *dataset* or *group*. Since many HDF5 files contain (vastly) more data than will fit in computer memory, tools that work with HDF5 generally provide a means of *lazily reading* content so that most data remains solely on disk unless or until it is needed.
## Hyperparameter
In machine learning models, a general model type is often pre-configured before it is trained on actual data. Hyperparameters may comprise multipliers, numeric limits, recursion depths, algorithm variations, or other differences that still make up the same kind of model. Models can perform dramatically differently with different hyperparameters.
## Idempotent
*Idempotence* is a useful concept in mathematics, computer science, and generally in programming. It means that calling the same function again on its own output will continue to produce the same answer. This is related to the even fancier concept in mathematics of an *attractor*.
## Imager
Imager reads and writes many image formats and can perform a variety of analysis processing actions on such images programmatically within R. Images within the library are treated as 4-dimensional vectors with two spatial dimensions, one time dimension, and one color dimension. By including time as a dimension, imager can work with video as well.
## imbalanced-learn
Imbalanced-learn is an open source Python software library for sensitive oversampling data. It implements the SMOTE (Synthetic Minority Oversampling TEchnique), ADASYN (Adaptive Synthetic), variations of those algorithms, as well as undersampling techniques. In the main, imbalanced-learn emulates the APIs of scikit-learn.
## Imputation
The process of replacing missing data points with values that are *likely*, or at least *plausible* to allow machine learning or statistical tools to process all observations.
## Interval variable (see NOIR)
Related concepts: **categorical variable**, **continuous variable**, **nominal variable**, **ordinal variable**, **ratio variable**
## ISO-8601
ISO-8601 (Data elements and interchange formats – Information interchange – Representation of dates and times) is an international standard for the representation of dataes and times. For example, generating one while writing this entry, using Python:
```python
>>> from datetime import datetime
>>> datetime.now().isoformat()
'2020-11-23T14:43:09.083771'
```
## jq
jq is a flexible and powerful tool for command-line filtering, searching, and formatting JSON, including JSON Lines.
## JSON (Javascript Object Notation)
JSON is a language-independent and human readable format for representation of the data structures and scalar values typically encountered in programming languages. It is widely used both as a data storage format and as a message format to communicate among services.
## Jupyter
Project Jupyter is an open source library, written primarily in Python, but supporting numerous programming languages, to create, view, run, and edit "notebooks" for *literate programming*. This book was written using Jupyter Lab, and its notebooks can be obtained at the book's repository. In literate programming, code and documentation are freely interspersed while both rendering as formatted documents and running as executable code. Whereas **R Markdown** achieves similar goals using lightly annotated plain text, Jupyter uses JSON as the storage format for its notebooks.
Jupyter supports both the somewhat older "notebook" interface and the more recent "JupyterLab" interface. Both work with the same underlying notebook documents.
## Kafka
Apache Kafka is an open source stream processor. As with other stream processors, and related message brokers, the aggregations of messages sent among systems is often a fruitful domain for data science analysis.
## Kdb+
Kdb+ is a column-store database that was designed for rapid transactions. It is widely used within high-frequency trading.
## Laziness
In computer programming and computer science, sometimes the words "lazy" and "eager" are used to distinguish approaches to solving a larger problem. Commonly, for example, an algorithm might transform a large data set. An eager program will process all the data at once. In contrast, a lazy program will only perform an individual transformation when that specific result is needed.
See also: **Eagerness**
## LDBM (Lightning Memory-Mapped Database)
LDBM is an open source library for providing key/value storage systems.
## Lemmatization
Canonicalization of words to their grammatical roots for natural language processing purposes. In contrast to stemming, lemmatization will look at the context a word occurs in to try to derive both the simplified form and the part of speech.
For example, the English word "dog" is used both as a noun for the animal, and occasionally as a verb meaning "annoy." A lemmatization might produce:
> we[PRON] dog[VERB] the[DET] dog[NOUN]
Related concept: *stemming*
## Little-endian (see Endianness)
Data arranged into "words" (typically 32-bits), or other units, where the largest magnitude component (typically a byte) is stored in the earliest position.
## MariaDB
MariaDB is a popular open source relational database managment system (RDBMS). It uses standard SQL for queries and interaction, and implements a few custom features on top of those required by SQL standards. At a point when the GPL-licensed MySQL was purchased by Oracle, its creator Michael (Monty) Widenius forked the project to create MariaDB. Widenius' elder daughter is named 'My' and his younger daughter 'Maria'.
MariaDB is API and ABI compatible with MySQL, but it adds a few features such as additional storage engines.
See also: **MySQL**
## Matplotlib
Matplotlib is a powerful and versatile open soure plotting library for Python. For historical reasons, its API originally resembled MATLAB's, but a more object oriented approach is now encouraged. Numerous higher-level libraries and abstractions are built on top of Matplotlib, including Basemap, Cartopy, Geoplot, ggplot, holoviews, Seaborn, Pandas, and others.
## Measurement (see Column)
Synonyms: **column**, **feature**, **field**, **variable**
## Memcached
Software that keeps key/value associative arrays in memory for purposes of caching or proxying slower server responses. Although contents of a memcached server are transient, snapshotted contents may be useful to analyze for data science purposes.
## Metaphone
Metaphone is an algorithm for phonetic canonicalization of English word, published by Lawrence Philips in 1990. The same author later published Double Metaphone, then Metaphone 3, each of which successively better take advantage of known patterns in words derived from non-English languages. Metaphone, and its followups, are more precise than the early Soundex developed for the same purpose.
## Mojibake
Mojibake is the nonsensical text that generally results from trying to decode text using a character encoding different from that used to encode it. Often this will produce individual characters that belong to a given language or alphabet, but in combinations that make no sense (sometimes to humorous effect). The word comes from Japanese, meaning roughly "character transformation."
## MonetDB
MonetDB is an open source column-oriented database management system that supports SQL and several other query languages or extensions.
## MongoDB
MongoDB is a popular document-oriented database management system. It uses JSON-like storage of its underlying data, and both queries and responses use JSON documents. MongoDB uses a distinct query language that reflects its mostly hierarchical arrangement of data into linked documents.
## MySQL
MySQL is a widely popular open source relational database management system (RDBMS). It uses standard SQL for queries and interaction, and implements a few custom features on top of those required by SQL standards. At a point when the GPL-licensed MySQL was purchased by Oracle, its creator Michael (Monty) Widenius forked the project to create MariaDB. Widenius' elder daughter is named 'My' and his younger daughter 'Maria'.
See also: **MariaDB**
## Neo4j
Neo4j is an open source graph database and database management system.
## netcdf4-python
netcdf4-python is a Python interface to the netCDF C library.
## Network Common Data Form (NetCDF)
NetCDF (Network Common Data Form) is a set of software libraries and machine-independent data formats that support the creation, access, and sharing of array-oriented scientific data. It is built on top of HDF5.
## NLTK (Natural Language Toolkit)
NLTK is a suite of tools for natural language processing (NLP) in Python. It includes numerous corpora, tools for lexical analysis, for named entity recognition, a part of speech tagger, stemmers and lemmatizers, and a variety of other tools for NLP.
See also: **gensim**, **spaCy**
## Node.js
Node.js is an open source, standalone JavaScript interpreter that runs outside of embedded JavaScript in web browsers. It can be used at the command line in the manner of scripting languages, with an interactive shell, or as a means to run server processes. The Node.js environment comes with an excellent package manager called npm (Node Package Manager) that allows you to install additional libraries easily (much like pip or conda for Python, RubyGems for Ruby, Cabal for Haskell, Pkg.jl: for Julia, Maven for Java, and so on).
## Nominal variable (see NOIR)
Related concepts: **categorical variable**, **continuous variable**, **interval variable**, **ratio variable**
## NOIR (Nominal, Ordinal, Interval, Ratio)
The acronym NOIR is sometimes used as a mnemonic for different feature types. This is the French word for "black" but is especially associated, in English, with a style of "dark" literature or film. The acronym stands for Nominal / Ordinal / Interval / Ratio.
*Nominal* or *ordinal* variables simply record which of a finite number of possible labels a data item records. This is sometimes called the *classes* of the variable.
*Ordinal* variables express a scale from low to high in the data values, but the spacing in the data may have little to no relationship to the underlying phenomenon. For example, perhaps a foot race records the first place, second place, third place, etc. winners, but not the times taken by each. 1st place crossed the line before 2nd place; but we have no information on whether it was milliseconds sooner or hours sooner. Likewise between 2nd and 3rd position, which might differ significantly from the first gap.
The last variable types are *continuous* variables, but *interval* and *ratio* variables are importantly different. The difference is in whether there is a "natural zero" in the data. The domain zero need not always be numeric zero, but commonly it is. Acidity or alkalinity measured on pH scale has a natural zero of 7, and generally values between 0 and 14 (although those are not sharp physical limits). If we used pH measure as a feature, we might re-center to numeric zero to express actual ratios (albeit, log ratios for this measure). It is reasonable to treated pH as a ratio variable.
As an example of an interval that is not a ratio, a newspaper article claimed that the temperature on a certain winter day, in some city, was *twice* as hot as in average years based on an artifact of the Fahrenheit scale in which a difference was between 25℉ and 50℉. This is nonsense as a ratio. It is perfectly useful to talk about the *mean temperature* or the *standard deviation* in temperature, but the numeric ratio is meaningless (in Celsius or Fahrenheit; in Kelvin or Rankine its minimally meaningful, but rarely used to describe temperatures in the range that occur on the surface of the earth). In contrast, the *ratio variable* of rainfall has a natural zero which is also numeric zero. Zero inches (or centimeters) of rain means there was none. 2 inches of rain is twice as much water falling as 1 inch of rain is.
## NumPy
NumPy is an open source Python library for fast and vectorized computations on multi-dimensional arrays. Nearly all Python libraries that perform numeric or scientific computation rely on NumPy as an underlying support library. This includes tools in machine learning, modeling, statistics, visualization, and so on.
## Observation (see Row)
Synonyms: **record**, **row**, **sample**, **tuple**
## Ontology
Ontology in philosophy is the study of "what there is." In data science an ontology describes not only what class/subclass and class/instance relationship exist among entities, but also the kinds of features an entity has. Perhaps most importantly, an ontology can describe the kinds of relationships that can exist among various entities.
When different kinds of observations can be made, describing the particular collection of features that pertain to that observation, and the particular data types and ranges of permissible values each can take on, is an element of the ontology of the data. Different tables, or data subsets, may have different features sets and hence a different ontological role.
Ontology can be important for categorical data especially. Some labels may be instances of other labels, for example with varying degrees of specificity. If one categorical variable indicates the entity is "mammal", another that it is "feline", and another that it is "house cat" those are all possibly descriptions of the identical entity under different taxonomic levels, and hence part of the ontology of the domain.
The relationships among entities can sometimes be derived from the data themselves, but often requires domain knowledge. These relationships can often inform the kinds of models or statistical analysis that make sense. For example, if the *entity* underlying a collection of data is a medical patient, parts of the ontology of the domain might concern whether several different features observed were collected with the same instrument, or from the same blood sample, or whether the observations were made on the same day. Even though the features might measure very different quanties, the relationships "same-day" or "same-instrument" can inform analysis.
See also: **taxonomy**
## Ordinal variable (see NOIR)
Related concepts: **categorical variable**, **continuous variable**, **interval variable**, **ratio variable**
## OrientDB
OrientDB is an open source, multi-model database management system. It supports graph, document, key/value, and object models. Querying may use either Gremlin or SQL.
## Orthonormal basis
Within a highly dimensional space, specifically a parameter space, the location of an observation point is simply a parameterized sum of each of the dimensions. For example, if we measure 3 features in an observation as having values $a$, $b$, and $c$, we can express those measurements in 3-D **parameter space**, with orthogonal unit vectors $\vec{x}$, $\vec{y}$, and $\vec{z}$ as:
$$ observation = a\vec{x} + b\vec{y} + c\vec{z} $$
However, the choice to represent the observation using those particular unit vectors $\vec{x}$, $\vec{y}$, and $\vec{z}$ is somewhat arbitrary. As long as we choose any orthonormal basis—that is, N mutually perpendicular unit vectors—we can equally well represent all the relationships among observations. For example:
$$ a\vec{x} + b\vec{y} + c\vec{z} = a′\vec{x′} + b′\vec{y′} + c′\vec{z′} $$
Decompositions are a means of selecting an alternate orthonormal basis that distributes the data within the parameter space in a more useful way. Usually this means in a way concentrating variance within the initial *components* (lowest numbered axes).
## Pandas
Pandas is a widely popular, open source, Python library for working with data frames. The name derives from the econometrics term "panel data." Pandas is built on top of NumPy, but adds numerous additional capabilities. One of the great strengths of Pandas is working with time-series data. But as with the underlying NumPy array library and other data frame libraries, most operations on columns are fast and vectorized.
## Parameter space
The parameter space of a set of observations with N features is simply an N-dimensional space in which each observation occupies a single point. By default, the vector bases that define the location of a point correspond directly with the features themselves. For example, in analyzing weather data we might define "temperature" as the X-axis, "humidity" as the Y-axis, and "barametric pressure" as the Z-axis. Some portion of that 3-D space has points within it, and they form some pattern or shape that models might analyze and make predictions about.
Under decompositions of the features, we might choose a new **orthonormal basis** in which to represent the same data points in a rotated or mirrored N-dimensional space.
## Parquet
Apache Parquet is an open source, column-oriented data storage format that originated in the Hadoop ecosystem, but is widely supported in other programming languages as well.
## PDF (Portable Document Format)
Portable Document Format is a widely used format used to accurately represent the appearance of documents in a cross-platform, cross-device manner. For example, the same document will look nearly identical on a computer monitor, a personal printer, or from a professional press. Fonts, text, images, colors, and lines are some of the elements PDF renders to a page, whether displayed or printed. PDF was developed by Adobe, but is currently governed by the open and freely usable standard ISO 32000-2.
## Pillow (forked from PIL)
The Python Imaging Library reads and writes many image formats and can perform a variety of processing actions on such images programmatically within Python.
## Poppler
An open source viewing and processing library for Portable Document Format (PDF). In particular, Poppler contains numerous command-line tools for converting PDF files to other formats, including text. Poppler is a fork of **Xpdf** that aims to incorporate additional capabilities.
See also: **Xpdf**
## PostgreSQL
PostgreSQL is a widely popular open source relational database management system (RDBMS). It uses standard SQL for queries and interaction, and implements custom features and numerous custom data types on top of those required by SQL standards.
## Precision
In a classification model, there are numerous *metrics* that might express the "goodness" of a model. Precision is also called "positive predictive value" and is the fraction of relevant observations among the predicted observations. More informally, precision answers the question "given it was predicted, how likely is the prediction to be accurate?"
For example, consider this hypothetical *confusion matrix*:
| Predict/Actual | Human | Octopus | Penguin |
|----------------|----------|----------|----------|
| Human | **5** | 0 | 2 |
| Octopus | 3 | **3** | 3 |
| Penguin | 0 | 1 | **11** |
In a binary problem, this can be expressed as:
$$\text{Precision} = \frac{true\: positive}{true\: positive + false\: positive}$$
For a multiclass problem, as in the confusion matrix, each label has its own precision. Given the 8 true humans in the data set, 5 of them were correctly identified. However, 2 non-humans were also so identified. I.e.:
$$\text{Precision}_{human} = \frac{5}{5 + 2} \approx 71\%$$
An overall precision for a model is often given by averaging (weighted or unweighted) the precision for each label.
Related concepts: **accuracy**, **F1 score**, **recall**
## PyTables
PyTables is a Python library for working with hierarchical data sets stored in the HDF5 format.
## Query planner
When a query is formulated against a database, whether using SQL or another querying language, the database management system (DBMS) will internally create a set of planned steps involved in executing that query. Many DBMSs can expose these plans prior to executing them; users can use this information to judge the efficiency of database access (and possibly modify queries or refactor the databases themselves).
A query planner will make decisions about which indices to use, in what order, the style of search and comparisons across data that may live in many tables or documents, and other aspects of how a query may be executed efficiently. When accessing big data sets, the quality of a query planner can often differentiate different DBMSs.
## R Markdown
R Markdown is a format and technology for *literate programming*. In literate programming, code and documentation are freely interspersed while both rendering as formatted documents and running as executable code. Whereas **Jupyter** notebooks, which have many of the same qualities, are stored as JSON documents, R Markdown is purely an extension of the easily human readable and editable Markdown format which lightly annotates plain text with regular punctuation characters to describe specific visual and conceptual elements. With R Markdown, code segments are also included as plain text by indicating their sections with a textual annotation.
## RabbitMQ
RabbitMQ is an open source message broker. As with other message brokers, the aggregations of messages sent among systems is often a fruitful domain for data science analysis.
## Ratio variable (see NOIR)
Related concepts: **categorical variable**, **continuous variable**, **interval variable**, **nominal variable**, **ordinal variable**
## Recall
In a classification model, there are numerous *metrics* that might express the "goodness" of a model. Recall is also called "sensitivity." It is the fraction of true occurences that are identified by a model.
For example, consider this hypothetical *confusion matrix*:
| Predict/Actual | Human | Octopus | Penguin |
|----------------|----------|----------|----------|
| Human | **5** | 0 | 2 |
| Octopus | 3 | **3** | 3 |
| Penguin | 0 | 1 | **11** |
In a binary problem, this can be expressed as:
$$\text{Recall} = \frac{true\: positive}{true\: positive + false\: negative}$$
For a multiclass problem, as in the confusion matrix, each label has its own recall. There are 8 true humans in the data set, 5 of them were correctly identified. However, 3 humans failed to be identified (in the whimsical example, all were predicted to be octopi). I.e.:
$$\text{Recall}_{human} = \frac{5}{5 + 3} \approx 62\%$$
An overall recall for a model is often given by averaging (weighted or unweighted) the recall for each label.
Related concepts: **accuracy**, **F1 score**, **precision**
## Record (see Row)
Synonyms: **observation**, **row**, **sample**, **tuple**
## Redis (Remote Dictionary Server)
Redis is an open source, in-memory key/value database. Redis supports numerous data types and data structures, including strings, lists, maps, sets, sorted sets, HyperLogLogs, bitmaps, streams, and spatial indices.
## Relational database management system (RDBMS)
An RDBMS is a system to store data and implement the relational model developed by E. F. Codd in 1970. Under this relational model, data is stored in tables, with each row constituting a *tuple* of values, the keys to those values named by the columns of the table. The term "relational" in the name pertains to the fact that data in one table may be *related* to data in other tables by declaring *foreign key* relations and/or by performing *joins* in the query syntax.
For several decades, all RDBMSs have supported the SQL querying language, sometimes with optional extension syntax related to their additional features or data types. Often, but not quite always, RDBMSs are used on multi-user distributed servers, with *transactions* used to orchestrates write actions among those multiple users.
Popular RDBMSs include PostgreSQL, MySQL, SQLite, Oracle, Microsoft SQL Server, IBM DB2, and others.
## Requests
Requests is a full-featured, open source HTTP access library for Python. It is not included in the Python standard library, but is ubiquitious and generally preferred to tools included with minimal Python distributions.
## REST (Representational State Transfer)
REST is a software educational style that normatively describes patterns of interactions between HTTP servers and clients. The adjective *RESTful* is also frequently used. Under this style, the HTTP methods GET, POST, PUT, and DELETE are clearly separated by their intended functions. A main emphasis of the style is *statelessness*: each request must contain all information needed to elicit a response, and that response should not be dependent on the sequence of prior actions that client made.
## rhdf5
Rhdf5 is an R library for working with hierarchical data sets stored in the HDF5 format.
## rjson
Rjson is an R library for working with JavaScript Object Notation.
## ROSE (Random Over-Sampling Examples)
ROSE is an R package that creates synthetic samplings in the presence of class imbalance. It serves a similar purpose to SMOTE oversampling.
## Row
A collection of data consisting of multiple named data items pertaining to the same *entity*. Depending on the context, the entity can be defined in various ways. For an object in the physical world, for example, it is common in scientific, and other, procedures to take a number of different measurements of that same object, and a row will describe that object. In simulations or other mathematical modeling, a row may contain the results of synthetic *sampling* of possible values. Considered from the point of view of the actual storage of the data, a focus on the *tuple* or *record* structure of the row are more emphasized.
The named data items collected about a single row are generally indicated in the *columns* of the data. Each column may have a different data type within it, but each different row within that column will share the data type but not generally the data value.
Synonyms: **observation**, **record**, **sample**, **tuple**
## rvest
The rvest package for R is used to scrape and extract data from HTML web pages.
## Sample (see Row)
Synonyms: **observation**, **record**, **row**, **tuple**
## Scikit-learn
Scikit-learn is a wide-ranging open source Python library for many machine learning (ML) and data science tasks. It implements a large number of ML models (both supervised and unsupervised), metrics, sampling techniques, decompositions, clustering algorithms, and other tools useful for data science. Throughout its capabilities, scikit-learn maintains a common API; many additional libraries have chosen to implement identical or compatible APIs was well.
## Scipy.stats
Scipy.stats is a Python module in the NumPy ecosystem that implements many probability distributions and statistical functions.
## Scrapy
Scrapy is a Python library for spidering and analyzing collections of web pages, including a high-performance engine to coordinate retrievals of many pages.
## Seaborn
Seaborn is a Python data visualization library based on matplotlib. It provides a high-level interface for drawing attractive and informative statistical graphics.
## SeqKit
SeqKit is a toolkit for maninipulating files in the FASTA and FASTQ formats that are used for storing nucleotide and protein sequences.
## Signed integer
An integer represented in computer bits of some specific length. In signed integers, one bit is reserved to hold the sign (negative or positive) of an integer. The largest integer that can be represented, for N bits storing a number, is $2^{N-1}-1$. The smallest integer that can be represented is $-2^{N-1}$
Sizes of integers in many programming languages match sizes of memory units in modern CPUs, and can be 8-bit, 16-bit, 32-bit, 64-bit, or 128-bit. Other bit lengths are rarely defined. In data formats and databases, sizes might be defined by a number of decimal digits rather than binary bits. Some programming languages like Python, TCL, and Mathematica in their default integers, and numerous other programming languages using specific libraries, allow for arbitrary-precision integers that have no size bound. They do this by dynamically allocating more bits to store larger numbers as needed.
See also: **unsigned integer**
## Solr
Apache Solr is a search engine based on the Lucene library. As a part of implementing a search engine, Solr contains a document-oriented database or data store.
## spaCy
SpaCy is an open-source software library for advanced natural language processing. It is focused on production use and integrates with deep-learning frameworks.
## SPARQL Protocol and RDF Query Language
Had J. B. S. Haldane lived later, he might have commented that Free Software developers have "an inordinate fondness for recursive acronyms" (YAML, GNU, etc.). SPARQL is a query language for RDF (Resource Description Framework), or the "semantic web." It has been implemented for a variety of programming languages. SPARQL expresses queries in the form of "subject-predicate-object" triples. This has some similarity to key/value stores, but more to graph databases.
## Sphering (see whitening)
Normalization of data under a decomposition.
Synonym: **whitening**
## SQLAlchemy
SQLAlchemy is a Python library that provides an "object-relational mapping" between the tabular and relational structure of RDBMS tables and an object-oriented interface. SQLAlchemy can use drivers for all popular SQL databases, and exposes a variety of methods for manipulating their data within Python.
## SQLite
SQLite is a small, fast, self-contained, high-reliability, full-featured, SQL database engine that stores multiple data tables in single files. Binding to access SQLite (version 3) are available for all popular programming languages. The library also comes with a command line tool and shell for manipulation of data using only SQL.
## State machine
A "finite-state machine, "finite automaton", or simply "state machine," is a model of computation in which focus moves among a finite number of states or nodes based on a specific sequence of input.
## STDOUT / STDERR / STDIN
In Unix-like command shells there are three special files/streams called "standard output", "standard error" and "standard input." They are ubiquitously abbreviated as "STDOUT", "STDERR", and "STDIN" respectively. Composed command-line tools treat these streams in special ways, and they are utilized widely. In particular, STDOUT is usually "data" output while STDERR is usually "status" output, even though they may appear interspersed in terminal sessions.
## Stemming
Canonicalization of words to their grammatical roots for natural language processing purposes. In contrast to lemmatization, stemming only treats words individually without their context, and hence can be less accurate.
Related concept: **lemmatization**
## Structured data
While the term "unstructured data" is often used, it is somewhat of a misnomer. "Loosely structured" or "semi-structured" would be more accurate. For example, the paradigmatic example of textual data is at very least structured by the particular sequence in which words occur. Quite likely it is further organized by sequences belonging to chapters, separate messages, or other such units (themselves likely structured by sequence), and moreover usually a variety of metadata such as author identity, subject line, forum, thread, and so on, also pertain to the text itself.
## Tab-separated values (TSV; see Comma-separated values)
Delimted files where tabs are used as the line delimiter.
## Tabula
Tabula-java is the underlying engine for the GUI tool Tabula. Other bindings include *tabula-extractor* for Ruby, *tabula-py* for Python, *tabulizer* for R, and *tabula-js* for Node.js. The engine and the tools that utilize it provide interfaces to extract tabular data represented in PDF documents.
## Taxonomy
Taxonomy is, in some sense, a special aspect of ontology, it describes the hierarchical relationships among categories of entities. Some labels may be instances of other labels, for example with varying degrees of specificity. If one categorical variable indicates the entity is "mammal", another that it is "feline", and another that it is "house cat" those are all possibly descriptions of the identical entity under different taxonomic levels, and hence part of the ontology of the domain.
While taxonomy is largely narrower than ontology, taxonomy also tends to indicate a focus on the more global level of the domain, not a narrow region of that domain. When one speaks of a taxonomy, it generally indicates an interest in all the relationships among all the classes of entities, and an expectation that those relationships will be tree-like and hierarchical. One might describe *ontological* features of a single entity, or a small collection of entities, but a taxonomy will normally describe the entire domain of all possible entities.
See also: **ontology**
## tibble
The R library tibble is an implementation of the data frame abstraction, but one that tries to do *less* than other libraries. Quoting from the official documentation:
>Tibbles are data.frames that are lazy and surly: they do less (i.e. they don’t change variable names or types, and don’t do partial matching) and complain more (e.g. when a variable does not exist). This forces you to confront problems earlier, typically leading to cleaner, more expressive code.
See also: **data.frame**, **data.table**
## Tidyverse
The Tidyverse is a collection of R packages that share a common philosophy of API design and that are designed to work well together. Core libraries of the Tidyverse are ggplot2, dplyr, tidyr, readr, purrr, **tibble**, stringr, forcats. A variety of other optional packages are also designed to work well with the base collection.
At core, the Tidyverse has an attitude of making data into "tidy" forms, in the sense discussed at more length in chapter 1. As well, the tools within the Tidyverse lend themselves to composition by piping data between methods in a "fluent programming" style.
## Tuple (see Row)
Synonyms: **observation**, **record**, **row**, **sample**
## Unsigned integer
An integer represented in computer bits of some specific length. In unsigned integers, no bits are reserved to hold the sign (negative or positive) of an integer, and hence only number zero through a maximum size can be represented. For N bits storing a number, the largest number representable is $2^N-1$.
Sizes of integers in many programming languages match sizes of memory units in modern CPUs, and can be 8-bit, 16-bit, 32-bit, 64-bit, or 128-bit. Other bit lengths are rarely defined. In data formats and databases, sizes might be defined by a number of decimal digits rather than binary bits. Some programming languages like Python, TCL, and Mathematica in their default integers, and numerous other programming languages using specific libraries, allow for arbitrary-precision integers that have no size bound. They do this by dynamically allocating more bits to store larger numbers as needed.
See also: **signed integer**
## Variable (see Column)
Synonyms: **column**, **feature**, **field**, **measurement**
## Web 0.5
The term "Web 0.5" is a neologism and back-construction from the term "Web 2.0." The latter became popular as a term in the late 2000s. Whereas Web 2.0 was meant as an evolution of the World Wide Web into highly interactive, highly dynamic, visually rich content, Web 0.5 is meant to hearken back to the static, compact, and text-oriented web pages that were developed in the early 1990s. The writer Danny Yee publicized this term, to the minor extent it is used.
*Web 0.5* web pages are intended primarily for human readership, in contrast to RESTful web services that are primarily intended to communicate data among computer servers and applications. Their simplicity, however, also makes them easily accessible to web scraping techniques, where relevant.
## Whitening
Normalization of data under a decomposition. Transformations such as Principle Component Analysis (PCA) reduce the variance of each subsequent component successively. Whitening is simply rescaling the data within each component to a common scale and center.
Synonym: **sphering**
## XML (eXtensible Markup Language)
XML is a markup language that defines a grammar for representing documents and ancillary schema languages for defining dialects within that broad grammar. The content of XML is always text, and is in-principle human readable while also enforcing a strict structure for automated processing. In essence, XML defines a hierarchical format in which arbitrary elements may be arranged.
XML is used widely in domains such as internal formats for office applications, for representing geospatial data, for message passing among cooperating services, for scientific data, and for many other application uses.
## Xpdf
An open source viewing and processing library for Portable Document Format. In particular, Xpdf contains several command-line tools for converting PDF files to other formats, including text. The fork **Poppler** aims to incorporate additional capabilities that the Xpdf authors consider out of scope for that project.
See also: **Poppler**
## YAML
YAML is, light-heartedly, an acronym for either "YAML Ain't Markup Language" or "Yet Another Markup Language." It is intended as a highly human-readable and human-writable format that can represent most of the data structures and data types widely used in programming languages. Libraries supporting reading and writing YAML from or to native data structures are available for numerous programming languages.
|
github_jupyter
|
>>> from datetime import datetime
>>> datetime.now().isoformat()
'2020-11-23T14:43:09.083771'
| 0.50293 | 0.824956 |
# Chapter 2
# Python Data Structures and Control Flow
## List, Tuples, Set, Dictionary, Sequence
## List
Most of the time you will need to store a list of data and/or values
```
cubes = [1, 9, 27, 64, 125]
cubes
```
Length or size of the list is determined by function *len*
```
len(cubes)
```
Both ***Indexing*** and ***Slicing*** also works for list.
```
cubes[0]
cubes[1:3]
cubes = [1, 9, 27, 64, 125]
cubes[-1]
cubes[2:]
cubes[:2]
```
Changing the value of a list.
```
print(cubes[1])
cubes[1] = 2**3
cubes[1]
```
Lists are mutable type, i.e when a new value is assigned to their contented they are permanently changed. Unlist String type that are immutable. Notice that the cube of 2 was changes from 9 to 8 the correct value..
```
cubes[:]
```
Lists can be added (concatenate) and its slice can be assign. Both operation can increase the size of the list.
```
title = ['C','H','e','E']
code = [3,0,6]
title + code
title[1:3]=['F','K','K']
title
```
Clear the list by assigning all elements with an empty list.
```
title[:]=[]
title
```
### Multidimensional Lists can be created from nested lists.
```
title = ['C','H','e','E']
code = [3,0,6]
mult_list = [title,code]
mult_list
mult_list = [title,code]
print(mult_list)
mult_list[0]
mult_list[1]
mult_list[0][1]
```
Lets create list of squared numbers from 0-10.
```
num_list = [1,2,3,4,5,6,7,8,9]
squares = []
for n in num_list:
print(n)
squares.append(n**2)
squares
```
The above is a small program on getting the list of squares. More explanation as we proceed in the book.
> 1. *num_list = [1,2,3,4,5,6,7,8,9]* : creates a list of numbers from 1 - 9
> 1. *squares = []* : creates an empty list
> 2. *for n in num_list:* : for iterate over the values in num_list and put them in n.
> 3. *print(n)* : print n to screen.
> 4. *squares.append(n\*\*2)* : compute the square of n and append to the end of the squares list.
There are other functions for List such as extend, insert, pop, reverse, remove etc. Please check them out.
```
squares.pop()
print(squares)
squares.insert(0,81)
squares
squares.reverse()
squares
```
## Tuples and Sequences
***string***, ***list*** allow indexing and slicing, they are Sequence data types and so is ***tuple and range***
A tuple consists of values separated by commas:
```
t = 1357, 2468, 'python!'
t
t[1]
```
Nested tuple can be created. However tuples are immutable like string.
```
tt = t,(1,2,3,4)
tt
tt[0]
tt[0]=28,'kate'
```
### Packing and Unpacking
```
# packing
t = 1357, 2468, 'python!'
t
# unpacking
x,y,z = t
print('x: ', x)
print('y: ', y)
print('z: ', z)
```
## range() Function
The *range()* function returns a sequence of integer. It takes one to three (1-3) arguments. *range(start, end, step)* all are optional except end.
```
range(10)
```
The best way is to iterate over the sequence or convert to a list.
```
# get value from 0 to 5
for i in range(5):
print(i)
# get value from 3 to 8
list(range(3,9))
# get value from 0 to 9 at step of 3
list(range(0,10,3))
```
## Dictionaries
Dictionary (Dict) are key-value type. The indexing is the key and not number.
```
my_dict = {'a': 65, 'b': 66, 'c': 67, 'd':68}
my_dict
my_dict['b']
for (k,v) in my_dict.items():
print(k,v)
```
## Sets
Set is an unoredered collection and does not allow duplicate value.
```
my_set = {'mon', 'tue', 'wed', 'thu', 'fri', 'sat', 'sun', 'mon'}
my_set
'wed' in my_set
```
## Boolean
Boolean data type contains two values *True* or *False*.
```
2 < 0
2 > 0
b_cond = 5 > 10
b_cond
is_done = True
is_done
is_not_done = False
is_not_done
```
## Decision making and conditional statements
## *if* Statements
The if statement type is a conditional or decision statement. It operates on the principle that a thing is done base on the truthee state of a question.
```
yob = int(input("Please enter your year of birth: "))
current_year = 2020
if yob < 0:
print('Your year of birth is negative ???')
elif yob == 0:
print('Your year of birth is zero ??')
elif yob < 1900:
print('Your year of birth is less than 1900 ?')
elif yob > current_year:
print('Your year of birth greater than 2020 ?')
else:
age = current_year - yob
msg1 = 'You are {age} years old in {cy}'.format(age=age, cy=current_year)
msg2 = 'You are {0} years old in {1}'.format(age, current_year)
msg3 = 'You are {} years old in {}'.format(age, current_year)
print(msg1)
print(msg2)
print(msg3)
```
The code above receive input from keyboard using :
> *input("Please enter your year of birth: ")*
and convert or cast the value to integer using the expression.
> *int( )*
## *for* Statements
We have used the ***for** statement in earlier sections. The ***for*** statement iterate over a *list* items.
```
props = ['name','formulae','molar mass']
for p in props:
print(p, len(p))
```
To get the sum of odd numbers from 1-10.
```
start = 1
step = 2
N = 10
sum = 0
for n in range(start,N,step):
sum = sum + n
print('odd={0}: sum = {1}'.format(n,sum))
```
**Quiz**
Try the sum of even numbers.
## *while* Statements
**while** statements also iterates over a list. However, it only checks if a condition is *True* or *False* to continue to iterate.
```
n = 0
step = 1
end = 5
while n < end:
print(n)
n += step
n = 0
step = 2
end = 10
sum = 0
while n < end:
sum += n
print('even: {n} -> sum: {sum}'.format(n=n,sum=sum))
n += step
```
## *break and continue Statements, and else Clauses* on Loops
The ***break*** statement breaks out of a loop, the innermost enclosing loop in a ***for*** or ***while***.
Unlike any main programming language the ***Python*** has a cool feature in loop statements having an ***else*** clause. It is executed after ***for*** loop termination and ***while*** loop condition is false.
Example: Find the prime numbers from zero to a number.
```
start = 2
end = 10
primes = []
for n in range(start, end):
for x in primes:
if n % x == 0:
print(n, 'is a multiple of', x)
break
else:
# loop fell through without finding a factor
print(n, 'is a prime number')
primes.append(n)
primes
```
## *pass* Statements
The ***pass*** statement is a placeholder and does nothing. It is commonly used for creating minimal ***functions*** and ***classes***.
```
class MyEmptyClass:
pass
def my_empty_func(*args):
pass
```
|
github_jupyter
|
cubes = [1, 9, 27, 64, 125]
cubes
len(cubes)
cubes[0]
cubes[1:3]
cubes = [1, 9, 27, 64, 125]
cubes[-1]
cubes[2:]
cubes[:2]
print(cubes[1])
cubes[1] = 2**3
cubes[1]
cubes[:]
title = ['C','H','e','E']
code = [3,0,6]
title + code
title[1:3]=['F','K','K']
title
title[:]=[]
title
title = ['C','H','e','E']
code = [3,0,6]
mult_list = [title,code]
mult_list
mult_list = [title,code]
print(mult_list)
mult_list[0]
mult_list[1]
mult_list[0][1]
num_list = [1,2,3,4,5,6,7,8,9]
squares = []
for n in num_list:
print(n)
squares.append(n**2)
squares
squares.pop()
print(squares)
squares.insert(0,81)
squares
squares.reverse()
squares
t = 1357, 2468, 'python!'
t
t[1]
tt = t,(1,2,3,4)
tt
tt[0]
tt[0]=28,'kate'
# packing
t = 1357, 2468, 'python!'
t
# unpacking
x,y,z = t
print('x: ', x)
print('y: ', y)
print('z: ', z)
range(10)
# get value from 0 to 5
for i in range(5):
print(i)
# get value from 3 to 8
list(range(3,9))
# get value from 0 to 9 at step of 3
list(range(0,10,3))
my_dict = {'a': 65, 'b': 66, 'c': 67, 'd':68}
my_dict
my_dict['b']
for (k,v) in my_dict.items():
print(k,v)
my_set = {'mon', 'tue', 'wed', 'thu', 'fri', 'sat', 'sun', 'mon'}
my_set
'wed' in my_set
2 < 0
2 > 0
b_cond = 5 > 10
b_cond
is_done = True
is_done
is_not_done = False
is_not_done
yob = int(input("Please enter your year of birth: "))
current_year = 2020
if yob < 0:
print('Your year of birth is negative ???')
elif yob == 0:
print('Your year of birth is zero ??')
elif yob < 1900:
print('Your year of birth is less than 1900 ?')
elif yob > current_year:
print('Your year of birth greater than 2020 ?')
else:
age = current_year - yob
msg1 = 'You are {age} years old in {cy}'.format(age=age, cy=current_year)
msg2 = 'You are {0} years old in {1}'.format(age, current_year)
msg3 = 'You are {} years old in {}'.format(age, current_year)
print(msg1)
print(msg2)
print(msg3)
props = ['name','formulae','molar mass']
for p in props:
print(p, len(p))
start = 1
step = 2
N = 10
sum = 0
for n in range(start,N,step):
sum = sum + n
print('odd={0}: sum = {1}'.format(n,sum))
n = 0
step = 1
end = 5
while n < end:
print(n)
n += step
n = 0
step = 2
end = 10
sum = 0
while n < end:
sum += n
print('even: {n} -> sum: {sum}'.format(n=n,sum=sum))
n += step
start = 2
end = 10
primes = []
for n in range(start, end):
for x in primes:
if n % x == 0:
print(n, 'is a multiple of', x)
break
else:
# loop fell through without finding a factor
print(n, 'is a prime number')
primes.append(n)
primes
class MyEmptyClass:
pass
def my_empty_func(*args):
pass
| 0.07262 | 0.93646 |
```
%matplotlib inline
from ndreg import *
import matplotlib
import ndio.remote.neurodata as neurodata
import clarityviz as cl
import numpy as np
import nibabel as nib
reload(cl)
path = 's275_to_ara3_regis.nii'
im = nib.load(path)
im = im.get_data()
print(im.shape)
im_slice = im[:,:,660]
plt.imshow(im_slice, cmap='gray')
plt.show()
im_slice = im[600,201:300,201:400]
plt.imshow(im_slice, cmap='gray')
plt.show()
im_slice = im[600,201:300,201:400]
plt.imshow(im_slice, cmap='gray')
plt.show()
```
# Extracting the top 10% brightest points
```
points = extract(im_slice, b_percentile = 0.9)
print(im_slice.shape)
print(points)
hist,bins = np.histogram(im_slice.flatten())
print(max(bins))
bim = np.zeros(im_slice.shape)
for point in points:
bim[point[0], point[1]] = point[2]
plt.imshow(bim, cmap='gray')
plt.show()
plt.imshow(im_slice, cmap='gray')
plt.show()
def extract_bright_points(im, num_points=10000, b_percentile=0.75, optimize=True):
"""
Function to extract points data from a np array representing a brain (i.e. an object loaded
from a .nii file).
:param im: The image array.
:param num_points: The desired number of points to be downsampled to.
:param b_percentile: The brightness percentile.
:param optimize:
:return: The bright points in a np array.
"""
# obtaining threshold
(values, bins) = np.histogram(im, bins=1000)
cumValues = np.cumsum(values).astype(float)
cumValues = (cumValues - cumValues.min()) / cumValues.ptp()
maxIndex = np.argmax(cumValues > b_percentile) - 1
threshold = bins[maxIndex]
print(threshold)
total = im.shape[0] * im.shape[1] * im.shape[2]
# print("Coverting to points...\ntoken=%s\ntotal=%d\nmax=%f\nthreshold=%f\nnum_points=%d" \
# %(self._token,total,self._max,threshold,num_points))
print("(This will take couple minutes)")
# threshold
im_max = np.max(im)
filt = im > threshold
# a is just a container to hold another value for ValueError: too many values to unpack
# x, y, z, a = np.where(filt)
t = np.where(filt)
x = t[0]
y = t[1]
z = t[2]
v = im[filt]
# if optimize:
# self.discardImg()
# v = np.int16(255 * (np.float32(v) / np.float32(self._max)))
l = v.shape
print("Above threshold=%d" % (l))
# sample
total_points = l[0]
print('total points: %d' % total_points)
if not 0 <= num_points <= total_points:
raise ValueError("Number of points given should be at most equal to total points: %d" % total_points)
fraction = num_points / float(total_points)
if fraction < 1.0:
# np.random.random returns random floats in the half-open interval [0.0, 1.0)
filt = np.random.random(size=l) < fraction
print('v.shape:')
print(l)
# print('x.size before downsample: %d' % x.size)
# print('y.size before downsample: %d' % y.size)
# print('z.size before downsample: %d' % z.size)
print('v.size before downsample: %d' % v.size)
x = x[filt]
y = y[filt]
z = z[filt]
v = v[filt]
# print('x.size after downsample: %d' % x.size)
# print('y.size after downsample: %d' % y.size)
# print('z.size after downsample: %d' % z.size)
print('v.size after downsample: %d' % v.size)
points = np.vstack([x, y, z, v])
points = np.transpose(points)
print("Output num points: %d" % (points.shape[0]))
print("Finished")
return points
def extract(im, num_points=10000, b_percentile=0.75, optimize=True):
"""
Function to extract points data from a np array representing a brain (i.e. an object loaded
from a .nii file).
:param im: The image array.
:param num_points: The desired number of points to be downsampled to.
:param b_percentile: The brightness percentile.
:param optimize:
:return: The bright points in a np array.
"""
# obtaining threshold
(values, bins) = np.histogram(im, bins=1000)
cumValues = np.cumsum(values).astype(float)
cumValues = (cumValues - cumValues.min()) / cumValues.ptp()
maxIndex = np.argmax(cumValues > b_percentile) - 1
threshold = bins[maxIndex]
print(threshold)
# total = im.shape[0] * im.shape[1] * im.shape[2]
total = im.shape[0] * im.shape[1]
# print("Coverting to points...\ntoken=%s\ntotal=%d\nmax=%f\nthreshold=%f\nnum_points=%d" \
# %(self._token,total,self._max,threshold,num_points))
print("(This will take couple minutes)")
# threshold
im_max = np.max(im)
filt = im > threshold
# a is just a container to hold another value for ValueError: too many values to unpack
# x, y, z, a = np.where(filt)
t = np.where(filt)
x = t[0]
y = t[1]
# z = t[2]
v = im[filt]
# if optimize:
# self.discardImg()
# v = np.int16(255 * (np.float32(v) / np.float32(self._max)))
l = v.shape
print("Above threshold=%d" % (l))
# sample
total_points = l[0]
print('total points: %d' % total_points)
# if not 0 <= num_points <= total_points:
# raise ValueError("Number of points given should be at most equal to total points: %d" % total_points)
# fraction = num_points / float(total_points)
# if fraction < 1.0:
# # np.random.random returns random floats in the half-open interval [0.0, 1.0)
# filt = np.random.random(size=l) < fraction
# print('v.shape:')
# print(l)
# # print('x.size before downsample: %d' % x.size)
# # print('y.size before downsample: %d' % y.size)
# # print('z.size before downsample: %d' % z.size)
# print('v.size before downsample: %d' % v.size)
# x = x[filt]
# y = y[filt]
# z = z[filt]
# v = v[filt]
# # print('x.size after downsample: %d' % x.size)
# # print('y.size after downsample: %d' % y.size)
# # print('z.size after downsample: %d' % z.size)
# print('v.size after downsample: %d' % v.size)
points = np.vstack([x, y, v])
# points = np.vstack([x, y, z, v])
points = np.transpose(points)
print("Output num points: %d" % (points.shape[0]))
print("Finished")
return points
def plot_hist(im, title=''):
hist,bins = np.histogram(im.flatten(),256,[0,256])
cdf = hist.cumsum()
cdf_normalized = cdf * hist.max()/ cdf.max()
plt.plot(cdf_normalized, color = 'b')
plt.hist(im.flatten(),256,[0,256], color = 'r')
plt.title(title)
plt.xlim([0,256])
plt.legend(('cdf','histogram'), loc = 'upper left')
plt.show()
fig = plt.figure()
a=fig.add_subplot(1,2,1)
imgplot = plt.imshow(im[:,:,1000])
a.set_title('Before')
plt.colorbar(ticks=[0.1,0.3,0.5,0.7], orientation ='horizontal')
a=fig.add_subplot(1,2,2)
imgplot = plt.imshow(im[600,:,:])
imgplot.set_clim(0.0,0.7)
a.set_title('After')
plt.colorbar(ticks=[0.1,0.3,0.5,0.7], orientation='horizontal')
```
|
github_jupyter
|
%matplotlib inline
from ndreg import *
import matplotlib
import ndio.remote.neurodata as neurodata
import clarityviz as cl
import numpy as np
import nibabel as nib
reload(cl)
path = 's275_to_ara3_regis.nii'
im = nib.load(path)
im = im.get_data()
print(im.shape)
im_slice = im[:,:,660]
plt.imshow(im_slice, cmap='gray')
plt.show()
im_slice = im[600,201:300,201:400]
plt.imshow(im_slice, cmap='gray')
plt.show()
im_slice = im[600,201:300,201:400]
plt.imshow(im_slice, cmap='gray')
plt.show()
points = extract(im_slice, b_percentile = 0.9)
print(im_slice.shape)
print(points)
hist,bins = np.histogram(im_slice.flatten())
print(max(bins))
bim = np.zeros(im_slice.shape)
for point in points:
bim[point[0], point[1]] = point[2]
plt.imshow(bim, cmap='gray')
plt.show()
plt.imshow(im_slice, cmap='gray')
plt.show()
def extract_bright_points(im, num_points=10000, b_percentile=0.75, optimize=True):
"""
Function to extract points data from a np array representing a brain (i.e. an object loaded
from a .nii file).
:param im: The image array.
:param num_points: The desired number of points to be downsampled to.
:param b_percentile: The brightness percentile.
:param optimize:
:return: The bright points in a np array.
"""
# obtaining threshold
(values, bins) = np.histogram(im, bins=1000)
cumValues = np.cumsum(values).astype(float)
cumValues = (cumValues - cumValues.min()) / cumValues.ptp()
maxIndex = np.argmax(cumValues > b_percentile) - 1
threshold = bins[maxIndex]
print(threshold)
total = im.shape[0] * im.shape[1] * im.shape[2]
# print("Coverting to points...\ntoken=%s\ntotal=%d\nmax=%f\nthreshold=%f\nnum_points=%d" \
# %(self._token,total,self._max,threshold,num_points))
print("(This will take couple minutes)")
# threshold
im_max = np.max(im)
filt = im > threshold
# a is just a container to hold another value for ValueError: too many values to unpack
# x, y, z, a = np.where(filt)
t = np.where(filt)
x = t[0]
y = t[1]
z = t[2]
v = im[filt]
# if optimize:
# self.discardImg()
# v = np.int16(255 * (np.float32(v) / np.float32(self._max)))
l = v.shape
print("Above threshold=%d" % (l))
# sample
total_points = l[0]
print('total points: %d' % total_points)
if not 0 <= num_points <= total_points:
raise ValueError("Number of points given should be at most equal to total points: %d" % total_points)
fraction = num_points / float(total_points)
if fraction < 1.0:
# np.random.random returns random floats in the half-open interval [0.0, 1.0)
filt = np.random.random(size=l) < fraction
print('v.shape:')
print(l)
# print('x.size before downsample: %d' % x.size)
# print('y.size before downsample: %d' % y.size)
# print('z.size before downsample: %d' % z.size)
print('v.size before downsample: %d' % v.size)
x = x[filt]
y = y[filt]
z = z[filt]
v = v[filt]
# print('x.size after downsample: %d' % x.size)
# print('y.size after downsample: %d' % y.size)
# print('z.size after downsample: %d' % z.size)
print('v.size after downsample: %d' % v.size)
points = np.vstack([x, y, z, v])
points = np.transpose(points)
print("Output num points: %d" % (points.shape[0]))
print("Finished")
return points
def extract(im, num_points=10000, b_percentile=0.75, optimize=True):
"""
Function to extract points data from a np array representing a brain (i.e. an object loaded
from a .nii file).
:param im: The image array.
:param num_points: The desired number of points to be downsampled to.
:param b_percentile: The brightness percentile.
:param optimize:
:return: The bright points in a np array.
"""
# obtaining threshold
(values, bins) = np.histogram(im, bins=1000)
cumValues = np.cumsum(values).astype(float)
cumValues = (cumValues - cumValues.min()) / cumValues.ptp()
maxIndex = np.argmax(cumValues > b_percentile) - 1
threshold = bins[maxIndex]
print(threshold)
# total = im.shape[0] * im.shape[1] * im.shape[2]
total = im.shape[0] * im.shape[1]
# print("Coverting to points...\ntoken=%s\ntotal=%d\nmax=%f\nthreshold=%f\nnum_points=%d" \
# %(self._token,total,self._max,threshold,num_points))
print("(This will take couple minutes)")
# threshold
im_max = np.max(im)
filt = im > threshold
# a is just a container to hold another value for ValueError: too many values to unpack
# x, y, z, a = np.where(filt)
t = np.where(filt)
x = t[0]
y = t[1]
# z = t[2]
v = im[filt]
# if optimize:
# self.discardImg()
# v = np.int16(255 * (np.float32(v) / np.float32(self._max)))
l = v.shape
print("Above threshold=%d" % (l))
# sample
total_points = l[0]
print('total points: %d' % total_points)
# if not 0 <= num_points <= total_points:
# raise ValueError("Number of points given should be at most equal to total points: %d" % total_points)
# fraction = num_points / float(total_points)
# if fraction < 1.0:
# # np.random.random returns random floats in the half-open interval [0.0, 1.0)
# filt = np.random.random(size=l) < fraction
# print('v.shape:')
# print(l)
# # print('x.size before downsample: %d' % x.size)
# # print('y.size before downsample: %d' % y.size)
# # print('z.size before downsample: %d' % z.size)
# print('v.size before downsample: %d' % v.size)
# x = x[filt]
# y = y[filt]
# z = z[filt]
# v = v[filt]
# # print('x.size after downsample: %d' % x.size)
# # print('y.size after downsample: %d' % y.size)
# # print('z.size after downsample: %d' % z.size)
# print('v.size after downsample: %d' % v.size)
points = np.vstack([x, y, v])
# points = np.vstack([x, y, z, v])
points = np.transpose(points)
print("Output num points: %d" % (points.shape[0]))
print("Finished")
return points
def plot_hist(im, title=''):
hist,bins = np.histogram(im.flatten(),256,[0,256])
cdf = hist.cumsum()
cdf_normalized = cdf * hist.max()/ cdf.max()
plt.plot(cdf_normalized, color = 'b')
plt.hist(im.flatten(),256,[0,256], color = 'r')
plt.title(title)
plt.xlim([0,256])
plt.legend(('cdf','histogram'), loc = 'upper left')
plt.show()
fig = plt.figure()
a=fig.add_subplot(1,2,1)
imgplot = plt.imshow(im[:,:,1000])
a.set_title('Before')
plt.colorbar(ticks=[0.1,0.3,0.5,0.7], orientation ='horizontal')
a=fig.add_subplot(1,2,2)
imgplot = plt.imshow(im[600,:,:])
imgplot.set_clim(0.0,0.7)
a.set_title('After')
plt.colorbar(ticks=[0.1,0.3,0.5,0.7], orientation='horizontal')
| 0.475849 | 0.74361 |
<img src="https://raw.githubusercontent.com/Qiskit/qiskit-tutorials/master/images/qiskit-heading.png" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" width="500 px" align="left">
# _*Laurel or Yanny?*_
The latest version of this notebook is available on https://github.com/QISKit/qiskit-tutorial.
For more information about how to use the IBM Q Experience (QX), consult the [tutorials](https://quantumexperience.ng.bluemix.net/qstage/#/tutorial?sectionId=c59b3710b928891a1420190148a72cce&pageIndex=0), or check out the [community](https://quantumexperience.ng.bluemix.net/qstage/#/community).
***
### Contributors
Adam D. Perruzzi, IBM Q Consulting
#### Copyright Attribution
The audio files used in this notebook are equalized versions of the recording found at [https://www.vocabulary.com/dictionary/laurel](https://www.vocabulary.com/dictionary/laurel), used under Fair Use provisions and cited as follows: "Text from Vocabulary.com, Copyright ©1998-2018 Thinkmap, Inc. All rights reserved."
***
#### Prerequisite
To run this tutorial, you must have audio-related libraries installed.
In MacOS, they can be installed by:
```
pip install pydub
brew install portaudio
pip install pyaudio
```
***
This program is a 'Hello World' type introduction to the world of quantum computing. It introduces some of the basic concepts of quantum computing in a way that is informative, fun, and engaging.
One of the functions of quantum computers - more specifically of the qubits that comprise the quantum computer - is the ability to generate truly random numbers. Classical random number generators are often [pseudo-random](https://www.random.org/randomness), meaning that they are not truly random. Instead, these numbers are often generated using a seed, such as the curent timestamp.
One can obtain a random number from a quantum computer by polling a single qubit. In doing so, the qubit 'chooses' to be either a 0 or a 1 in a purely random way. Repeating this polling many times and averaging the results will tend towards an average value of 0.5. That is the method we'll use for this program.
And what can we use our random number for? Certainly a great number of important things, but also to try and settle one of the great debates of our time: Laurel or Yanny?
In May 2018, an audio clip was discovered on Vocabulary.com accompanying the word [laurel](https://www.vocabulary.com/dictionary/laurel). The clip went viral as part of a tweet, and listeners from around the world weighed in on what they thought they heard. Some heard the intended word 'laurel' while others heard 'yanny'. There are some interesting notes on why this is the case in [this Wired article](https://www.wired.com/story/yanny-and-laurel-true-history).
As the jury is still out on exactly what word people are hearing, let's ask a quantum computer what it thinks! The first step is to import the required libraries and initialize the quantum and classical registers that will be used for this program.
```
from qiskit import ClassicalRegister, QuantumRegister
from qiskit import QuantumCircuit, execute
from qiskit.tools.visualization import plot_histogram
from qiskit import IBMQ, available_backends, get_backend
from pydub import AudioSegment
from pydub.playback import play
#Set up the quantum and classical registers, and combine them into a circuit
qr = QuantumRegister(1)
cr = ClassicalRegister(1)
qc = QuantumCircuit(qr, cr)
qc.h(qr[0]) #Create a superposition on the single quantum bit
qc.measure(qr[0], cr[0]) #Measure the single bit, and store its value in the clasical bit
```
We also need to set up the credentials to access the IBM quantum computers. Make sure you've got an IBM Q Experience account set up, and you retrieve your API to paste below (or into the Qconfig.py file, if desired).
```
# Load saved IBMQ accounts
IBMQ.load_account()
```
We can now run the program on the quantum simulator. You can replace the selected simulation backend with the real quantum computer, if you don't mind a bit of a wait in the queue.
You can also change the number of 'shots' taken, or the number of times the program is run. The smaller this number is, the more likely the average will favor one outcome over the other. The larger this number is, the more likely the results will be split 50-50. You'll be able to see the effects of this difference in the eventual audio output.
```
backend = 'ibmq_qasm_simulator' #Replace 'ibmq_qasm_simulator' with 'ibmqx5' to run on the quantum computer
shots_sim = 100 #Adjust this number as desired, with effects as described above
job_sim = execute(qc, backend, shots=shots_sim) #Run job on chosen backend for chosen number of shots
stats_sim = job_sim.result().get_counts() #Retrieve results
#Select '0' to represent 'laurel'
if '0' not in stats_sim.keys():
stats_sim['laurel'] = 0
else:
stats_sim['laurel'] = stats_sim.pop('0')
#Which leaves '1' to represent 'yanny'
if '1' not in stats_sim.keys():
stats_sim['yanny'] = 0
else:
stats_sim['yanny'] = stats_sim.pop('1')
plot_histogram(stats_sim)
```
This graph shows how often the qubit was measured to be a 0, and how often it was measured to be a 1. We can use these results to help us find the answer to the laurel/yanny debate.
We can do this by starting with two separate audio tracks, one for laurel and one for yanny. These tracks have been equalized to highlight one name or the other. First we have to install the required libraries. If you're having trouble, follow the guide for pydub installation available [here](https://github.com/jiaaro/pydub#installation).
```
#Import two tracks
laurel = AudioSegment.from_wav('laurel_or_yanny_audio_files/laurel.wav')
yanny = AudioSegment.from_wav('laurel_or_yanny_audio_files/yanny.wav')
```
If you've never been able to hear one name or the other, take a listen to either or both of the two tracks below. I can't guarantee you'll hear both distinctly, but these tracks will get you as close as possible!
```
play(laurel) #Listen to the laurel-specific track
play(yanny) #Listen to the yanny-specific track
```
Now we can apply our results from the quantum computer to these audio tracks. We can do this by proportionally reducing the volume for the less common track, and increasing the volume for the more common track.
```
#Modify the volumes based on the results of the experiment
laurel = laurel + ((100*stats_sim['laurel']/shots_sim)-50) #Laurel
yanny = yanny + ((100*stats_sim['yanny']/shots_sim)-50) #Yanny
#Mix the two together and play the result
mixed = laurel.overlay(yanny)
play(mixed)
```
If you're having trouble getting the above clip to play in the notebook, you can run the code below to download the clip using your audio player of choice. The audio file will be placed in the same folder as the other audio files.
```
mixed.export('laurel_or_yanny_audio_files/quantumLaurelYanny.wav', format='wav')
```
If the results above are roughly 50-50, the combination will sound similar to the original track. If the experiment was conducted with fewer shots, the clip may lean more towards one sound or another. Go back earlier in the program to change the number of shots, re-run, and see if you can get one or the other to sound stronger or weaker.
You can also change the backend to run this on an actual quantum computer, instead of a simulation. It may take a while to run, as there may be a queue for the machine.
***
And there you have it! Clearly the quantum computer can't make up its mind what it hears either, so the question will just have to go unanswered for the time being :)
```
print("Installed packages are as the following")
!python --version
print()
!conda list 'qiskit|IBMQuantumExperience|numpy|scipy'
```
|
github_jupyter
|
pip install pydub
brew install portaudio
pip install pyaudio
from qiskit import ClassicalRegister, QuantumRegister
from qiskit import QuantumCircuit, execute
from qiskit.tools.visualization import plot_histogram
from qiskit import IBMQ, available_backends, get_backend
from pydub import AudioSegment
from pydub.playback import play
#Set up the quantum and classical registers, and combine them into a circuit
qr = QuantumRegister(1)
cr = ClassicalRegister(1)
qc = QuantumCircuit(qr, cr)
qc.h(qr[0]) #Create a superposition on the single quantum bit
qc.measure(qr[0], cr[0]) #Measure the single bit, and store its value in the clasical bit
# Load saved IBMQ accounts
IBMQ.load_account()
backend = 'ibmq_qasm_simulator' #Replace 'ibmq_qasm_simulator' with 'ibmqx5' to run on the quantum computer
shots_sim = 100 #Adjust this number as desired, with effects as described above
job_sim = execute(qc, backend, shots=shots_sim) #Run job on chosen backend for chosen number of shots
stats_sim = job_sim.result().get_counts() #Retrieve results
#Select '0' to represent 'laurel'
if '0' not in stats_sim.keys():
stats_sim['laurel'] = 0
else:
stats_sim['laurel'] = stats_sim.pop('0')
#Which leaves '1' to represent 'yanny'
if '1' not in stats_sim.keys():
stats_sim['yanny'] = 0
else:
stats_sim['yanny'] = stats_sim.pop('1')
plot_histogram(stats_sim)
#Import two tracks
laurel = AudioSegment.from_wav('laurel_or_yanny_audio_files/laurel.wav')
yanny = AudioSegment.from_wav('laurel_or_yanny_audio_files/yanny.wav')
play(laurel) #Listen to the laurel-specific track
play(yanny) #Listen to the yanny-specific track
#Modify the volumes based on the results of the experiment
laurel = laurel + ((100*stats_sim['laurel']/shots_sim)-50) #Laurel
yanny = yanny + ((100*stats_sim['yanny']/shots_sim)-50) #Yanny
#Mix the two together and play the result
mixed = laurel.overlay(yanny)
play(mixed)
mixed.export('laurel_or_yanny_audio_files/quantumLaurelYanny.wav', format='wav')
print("Installed packages are as the following")
!python --version
print()
!conda list 'qiskit|IBMQuantumExperience|numpy|scipy'
| 0.741955 | 0.981524 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.